PEFT documentation
Orthogonal Finetuning (OFT and BOFT)
Orthogonal Finetuning (OFT and BOFT)
This conceptual guide gives a brief overview of OFT and BOFT, a parameter-efficient fine-tuning technique that utilizes orthogonal matrix to multiplicatively transform the pretrained weight matrices.
To achieve efficient fine-tuning, OFT represents the weight updates with an orthogonal transformation. The orthogonal transformation is parameterized by an orthogonal matrix multiplied to the pretrained weight matrix. These new matrices can be trained to adapt to the new data while keeping the overall number of changes low. The original weight matrix remains frozen and doesn’t receive any further adjustments. To produce the final results, both the original and the adapted weights are multiplied togethor.
Orthogonal Butterfly (BOFT) generalizes OFT with Butterfly factorization and further improves its parameter efficiency and finetuning flexibility. In short, OFT can be viewed as a special case of BOFT. Different from LoRA that uses additive low-rank weight updates, BOFT uses multiplicative orthogonal weight updates. The comparison is shown below.
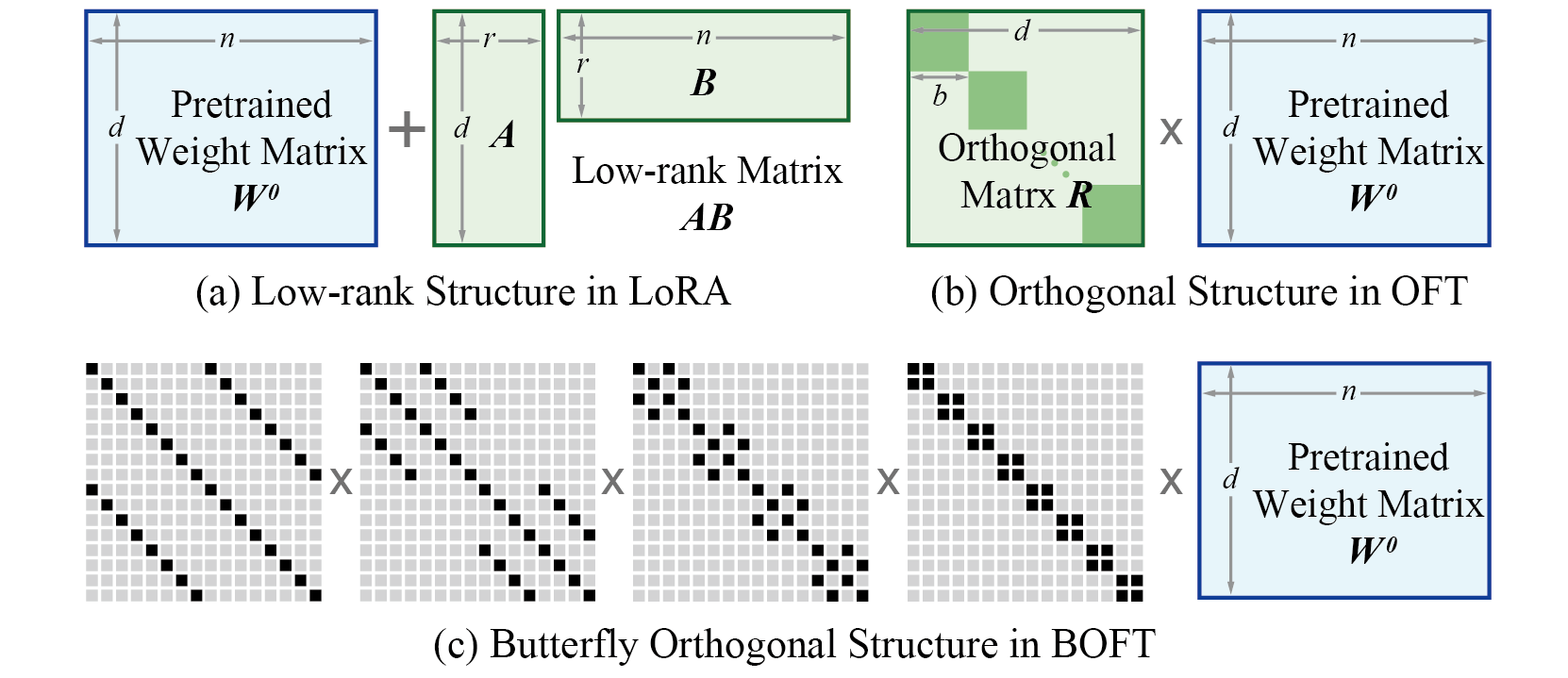
BOFT has some advantages compared to LoRA:
- BOFT proposes a simple yet generic way to finetune pretrained models to downstream tasks, yielding a better preservation of pretraining knowledge and a better parameter efficiency.
- Through the orthogonality, BOFT introduces a structural constraint, i.e., keeping the hyperspherical energy unchanged during finetuning. This can effectively reduce the forgetting of pretraining knowledge.
- BOFT uses the butterfly factorization to efficiently parameterize the orthogonal matrix, which yields a compact yet expressive learning space (i.e., hypothesis class).
- The sparse matrix decomposition in BOFT brings in additional inductive biases that are beneficial to generalization.
In principle, BOFT can be applied to any subset of weight matrices in a neural network to reduce the number of trainable parameters. Given the target layers for injecting BOFT parameters, the number of trainable parameters can be determined based on the size of the weight matrices.
Merge OFT/BOFT weights into the base model
Similar to LoRA, the weights learned by OFT/BOFT can be integrated into the pretrained weight matrices using the merge_and_unload() function. This function merges the adapter weights with the base model which allows you to effectively use the newly merged model as a standalone model.

This works because during training, the orthogonal weight matrix (R in the diagram above) and the pretrained weight matrices are separate. But once training is complete, these weights can actually be merged (multiplied) into a new weight matrix that is equivalent.
Utils for OFT / BOFT
Common OFT / BOFT parameters in PEFT
As with other methods supported by PEFT, to fine-tune a model using OFT or BOFT, you need to:
- Instantiate a base model.
- Create a configuration (
OFTConfigorBOFTConfig) where you define OFT/BOFT-specific parameters. - Wrap the base model with
get_peft_model()to get a trainablePeftModel. - Train the
PeftModelas you normally would train the base model.
BOFT-specific paramters
BOFTConfig allows you to control how OFT/BOFT is applied to the base model through the following parameters:
boft_block_size: the BOFT matrix block size across different layers, expressed inint. Smaller block size results in sparser update matrices with fewer trainable paramters. Note, please chooseboft_block_sizeto be divisible by most layer’s input dimension (in_features), e.g., 4, 8, 16. Also, please only specify eitherboft_block_sizeorboft_block_num, but not both simultaneously or leaving both to 0, becauseboft_block_sizexboft_block_nummust equal the layer’s input dimension.boft_block_num: the number of BOFT matrix blocks across different layers, expressed inint. Fewer blocks result in sparser update matrices with fewer trainable paramters. Note, please chooseboft_block_numto be divisible by most layer’s input dimension (in_features), e.g., 4, 8, 16. Also, please only specify eitherboft_block_sizeorboft_block_num, but not both simultaneously or leaving both to 0, becauseboft_block_sizexboft_block_nummust equal the layer’s input dimension.boft_n_butterfly_factor: the number of butterfly factors. Note, forboft_n_butterfly_factor=1, BOFT is the same as vanilla OFT, forboft_n_butterfly_factor=2, the effective block size of OFT becomes twice as big and the number of blocks become half.bias: specify if thebiasparameters should be trained. Can be"none","all"or"boft_only".boft_dropout: specify the probability of multiplicative dropout.target_modules: The modules (for example, attention blocks) to inject the OFT/BOFT matrices.modules_to_save: List of modules apart from OFT/BOFT matrices to be set as trainable and saved in the final checkpoint. These typically include model’s custom head that is randomly initialized for the fine-tuning task.
BOFT Example Usage
For an example of the BOFT method application to various downstream tasks, please refer to the following guides:
Take a look at the following step-by-step guides on how to finetune a model with BOFT:
For the task of image classification, one can initialize the BOFT config for a DinoV2 model as follows:
import transformers
from transformers import AutoModelForSeq2SeqLM, BOFTConfig
from peft import BOFTConfig, get_peft_model
config = BOFTConfig(
boft_block_size=4,
boft_n_butterfly_factor=2,
target_modules=["query", "value", "key", "output.dense", "mlp.fc1", "mlp.fc2"],
boft_dropout=0.1,
bias="boft_only",
modules_to_save=["classifier"],
)
model = transformers.Dinov2ForImageClassification.from_pretrained(
"facebook/dinov2-large",
num_labels=100,
)
boft_model = get_peft_model(model, config)