🌞🚀 SOLAR-math-10.7x2-v0.2_19B
Merge of two Solar-10.7B instruct finetunes.
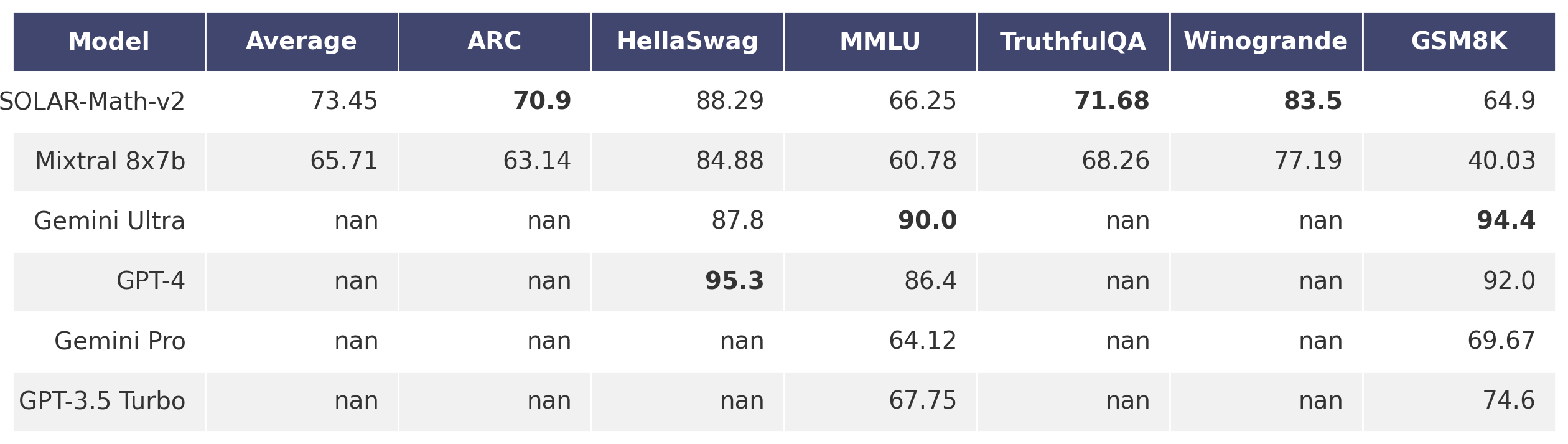
This model performs in line with GPT-3.5 and Gemini Pro. Exceeding all scores of Mixtral-8x7b
Here is a brief overview of the evaluation results. These are simply for the user to have the values available for comparison. This table does not represent a complete analysis.
🌅 Code Example
Example also available in colab
from transformers import AutoModelForCausalLM, AutoTokenizer
def generate_response(prompt):
"""
Generate a response from the model based on the input prompt.
Args:
prompt (str): Prompt for the model.
Returns:
str: The generated response from the model.
"""
# Tokenize the input prompt
inputs = tokenizer(prompt, return_tensors="pt")
# Generate output tokens
outputs = model.generate(**inputs, max_new_tokens=512, eos_token_id=tokenizer.eos_token_id, pad_token_id=tokenizer.pad_token_id)
# Decode the generated tokens to a string
response = tokenizer.decode(outputs[0], skip_special_tokens=True)
return response
# Load the model and tokenizer
model_id = "macadeliccc/SOLAR-math-2x10.7B-v0.2"
tokenizer = AutoTokenizer.from_pretrained(model_id)
model = AutoModelForCausalLM.from_pretrained(model_id, load_in_4bit=True)
prompt = "Explain the proof of Fermat's Last Theorem and its implications in number theory."
print("Response:")
print(generate_response(prompt), "\n")
Example output:
Explain the proof of Fermat's Last Theorem and its implications in number theory.
Fermat's Last Theorem, also known as FLT, is a famous mathematical conjecture that states "no three positive integers a, b, and c can satisfy the equation a^n + b^n = c^n for any integer value of n greater than 2." This theorem was first proposed by Pierre de Fermat in the 17th century, but its proof was only discovered in the late 20th century by Andrew Wiles.
The proof of Fermat's Last Theorem, published by Andrew Wiles in 1993 and 1994, is complex and involves several advanced mathematical concepts. The main idea behind the proof is the use of modular elliptic curves, which are algebraic curves defined by polynomial equations. Wiles introduced a new concept called the Taniyama-Shimura conjecture, which states that there is a one-to-one correspondence between certain elliptic curves over the rational numbers and certain cusp forms.
Wiles' proof of FLT is based on the assumption that the Taniyama-Shimura conjecture is true. He showed that if the Taniyama-Shimura conjecture is true, then Fermat's Last Theorem must also be true. This proof strategy is known as a "proof by contradiction." Wiles demonstrated that if FLT were false, then there would exist a counterexample to the Taniyama-Shimura conjecture. However, since the Taniyama-Shimura conjecture is believed to be true, this leads to a contradiction. Therefore, by the principle of contradiction, Fermat's Last Theorem must be true.
The implications of Fermat's Last Theorem in number theory are significant. FLT is a fundamental result in the study of integers, and its proof has led to a better understanding of various mathematical concepts. The proof of FLT has also contributed to the development of other areas of mathematics, such as algebraic geometry, representation theory, and number theory itself.
Moreover, the theorem has helped to strengthen the foundations of number theory by providing a resolution to a long-standing open problem. It has also encouraged mathematicians to explore new directions in research, as the proof of FLT has opened up new avenues for investigation in related fields.
🏆 Evaluations
ARC
| Task | Version | Metric | Value | Stderr | |
|---|---|---|---|---|---|
| arc_challenge | 1 | acc,none | 0.68 | ||
| acc_stderr,none | 0.01 | ||||
| acc_norm,none | 0.72 | ||||
| acc_norm_stderr,none | 0.01 | ||||
| alias | arc_challenge |
Average: 71.76%
HellaSwag
| Task | Version | Metric | Value | Stderr | |
|---|---|---|---|---|---|
| hellaswag | 1 | acc,none | 0.71 | ||
| acc_stderr,none | 0 | ||||
| acc_norm,none | 0.88 | ||||
| acc_norm_stderr,none | 0 | ||||
| alias | hellaswag |
Average: 88.01%
📚 Citations
@misc{kim2023solar,
title={SOLAR 10.7B: Scaling Large Language Models with Simple yet Effective Depth Up-Scaling},
author={Dahyun Kim and Chanjun Park and Sanghoon Kim and Wonsung Lee and Wonho Song and Yunsu Kim and Hyeonwoo Kim and Yungi Kim and Hyeonju Lee and Jihoo Kim and Changbae Ahn and Seonghoon Yang and Sukyung Lee and Hyunbyung Park and Gyoungjin Gim and Mikyoung Cha and Hwalsuk Lee and Sunghun Kim},
year={2023},
eprint={2312.15166},
archivePrefix={arXiv},
primaryClass={cs.CL}
}
Open LLM Leaderboard Evaluation Results
Detailed results can be found here
| Metric | Value |
|---|---|
| Avg. | 74.25 |
| AI2 Reasoning Challenge (25-Shot) | 70.90 |
| HellaSwag (10-Shot) | 88.29 |
| MMLU (5-Shot) | 66.25 |
| TruthfulQA (0-shot) | 71.68 |
| Winogrande (5-shot) | 83.50 |
| GSM8k (5-shot) | 64.90 |
- Downloads last month
- 1,163
Spaces using macadeliccc/SOLAR-math-2x10.7b-v0.2 14
Collection including macadeliccc/SOLAR-math-2x10.7b-v0.2
Evaluation results
- normalized accuracy on AI2 Reasoning Challenge (25-Shot)test set Open LLM Leaderboard70.900
- normalized accuracy on HellaSwag (10-Shot)validation set Open LLM Leaderboard88.290
- accuracy on MMLU (5-Shot)test set Open LLM Leaderboard66.250
- mc2 on TruthfulQA (0-shot)validation set Open LLM Leaderboard71.680
- accuracy on Winogrande (5-shot)validation set Open LLM Leaderboard83.500
- accuracy on GSM8k (5-shot)test set Open LLM Leaderboard64.900

