The Bellman Equation: simplify our value estimation

The Bellman equation simplifies our state value or state-action value calculation.

With what we have learned so far, we know that if we calculate$V(S_t)$ (the value of a state), we need to calculate the return starting at that state and then follow the policy forever after. (The policy we defined in the following example is a Greedy Policy; for simplification, we don’t discount the reward).

So to calculate$V(S_t)$, we need to calculate the sum of the expected rewards. Hence:

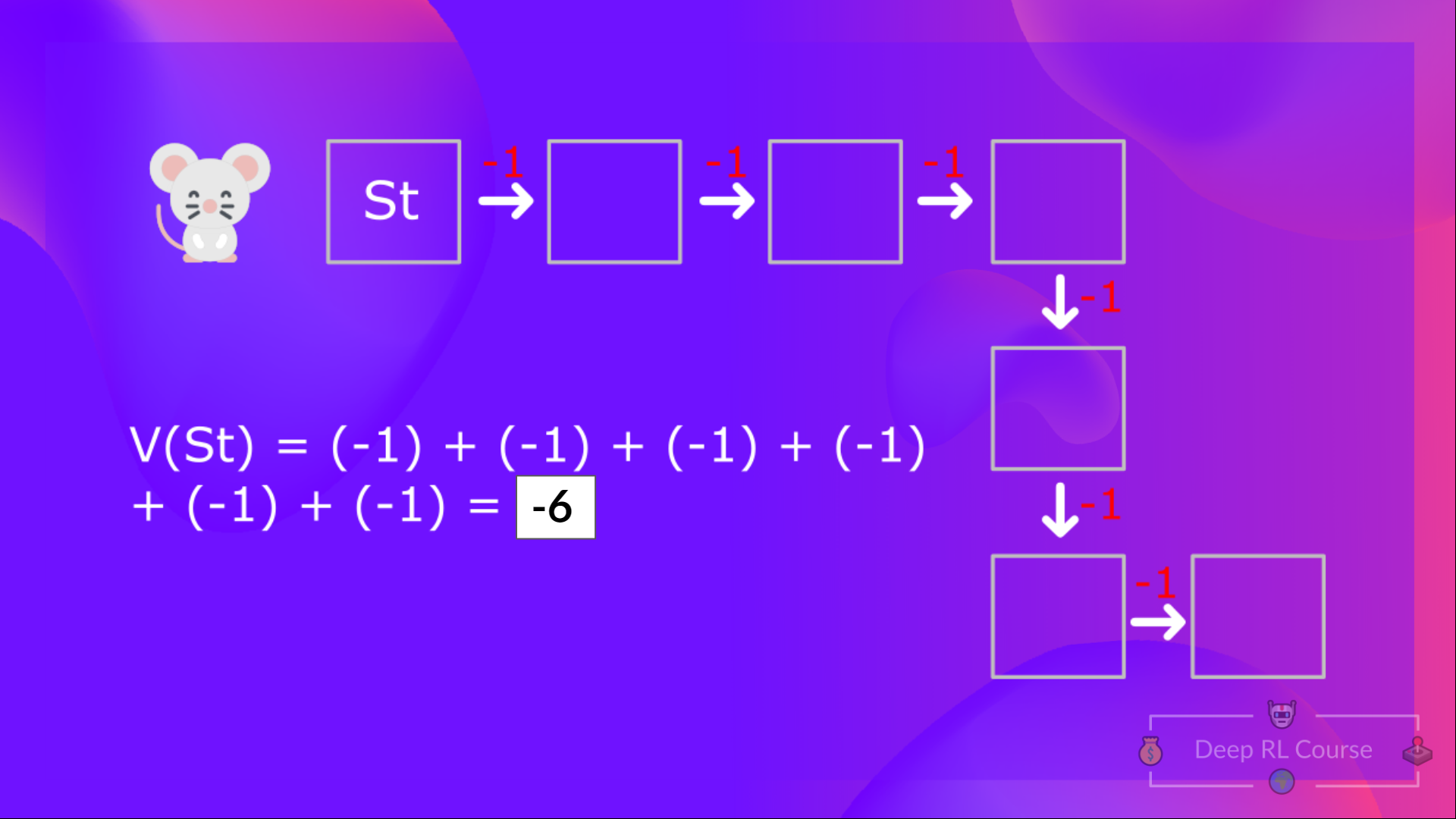
Then, to calculate the$V(S_{t+1})$, we need to calculate the return starting at that state$S_{t+1}$.

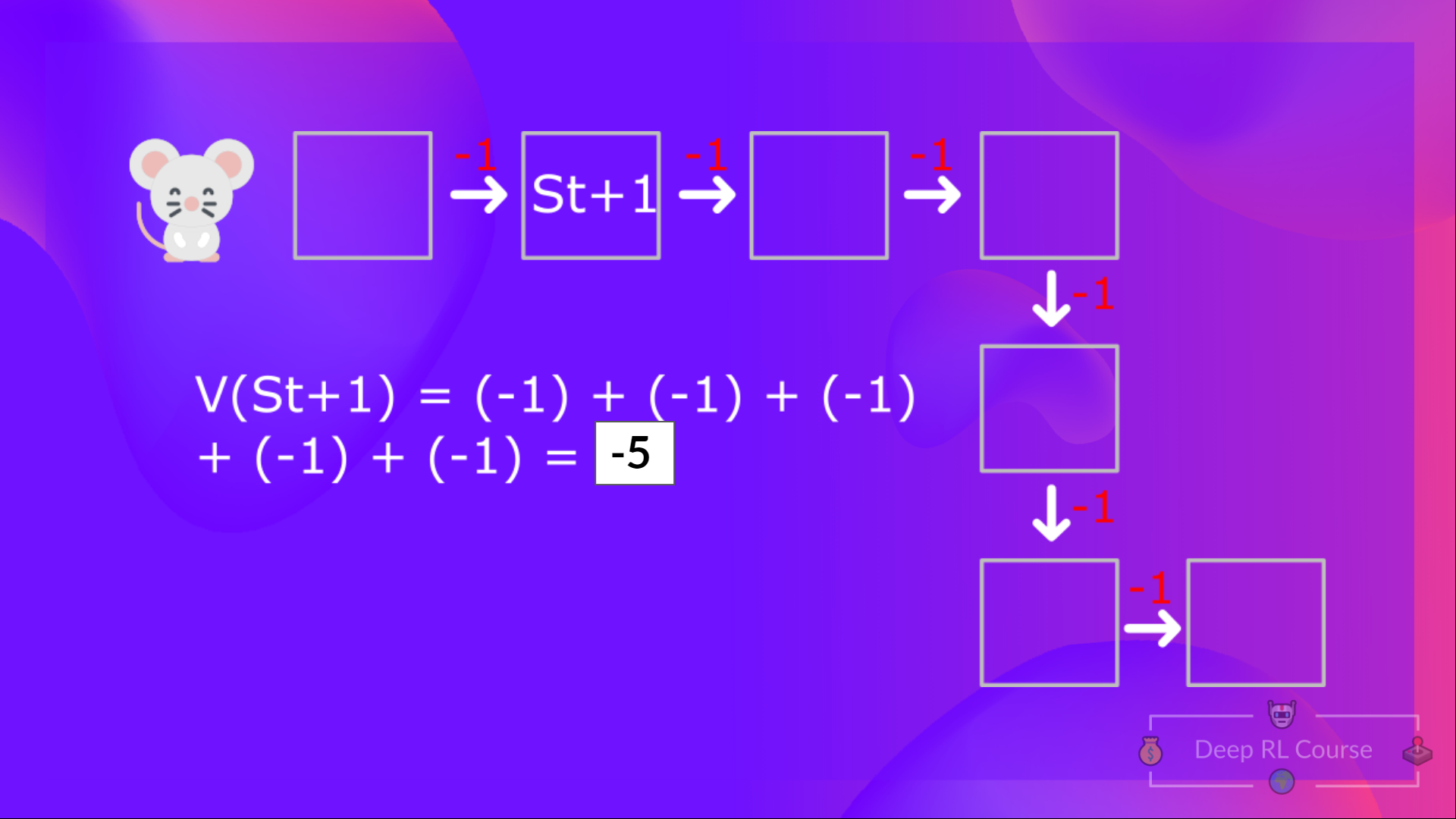
So you may have noticed, we’re repeating the computation of the value of different states, which can be tedious if you need to do it for each state value or state-action value.

Instead of calculating the expected return for each state or each state-action pair, we can use the Bellman equation. (hint: if you know what Dynamic Programming is, this is very similar! if you don’t know what it is, no worries!)

The Bellman equation is a recursive equation that works like this: instead of starting for each state from the beginning and calculating the return, we can consider the value of any state as:

The immediate reward $R_{t+1}$ + the discounted value of the state that follows ($\gamma * V(S_{t+1})$ ) .

If we go back to our example, we can say that the value of State 1 is equal to the expected cumulative return if we start at that state.

To calculate the value of State 1: the sum of rewards if the agent started in that state 1 and then followed the policy for all the time steps.

This is equivalent to $V(S_{t})$ = Immediate reward $R_{t+1}$ + Discounted value of the next state $\gamma * V(S_{t+1})$

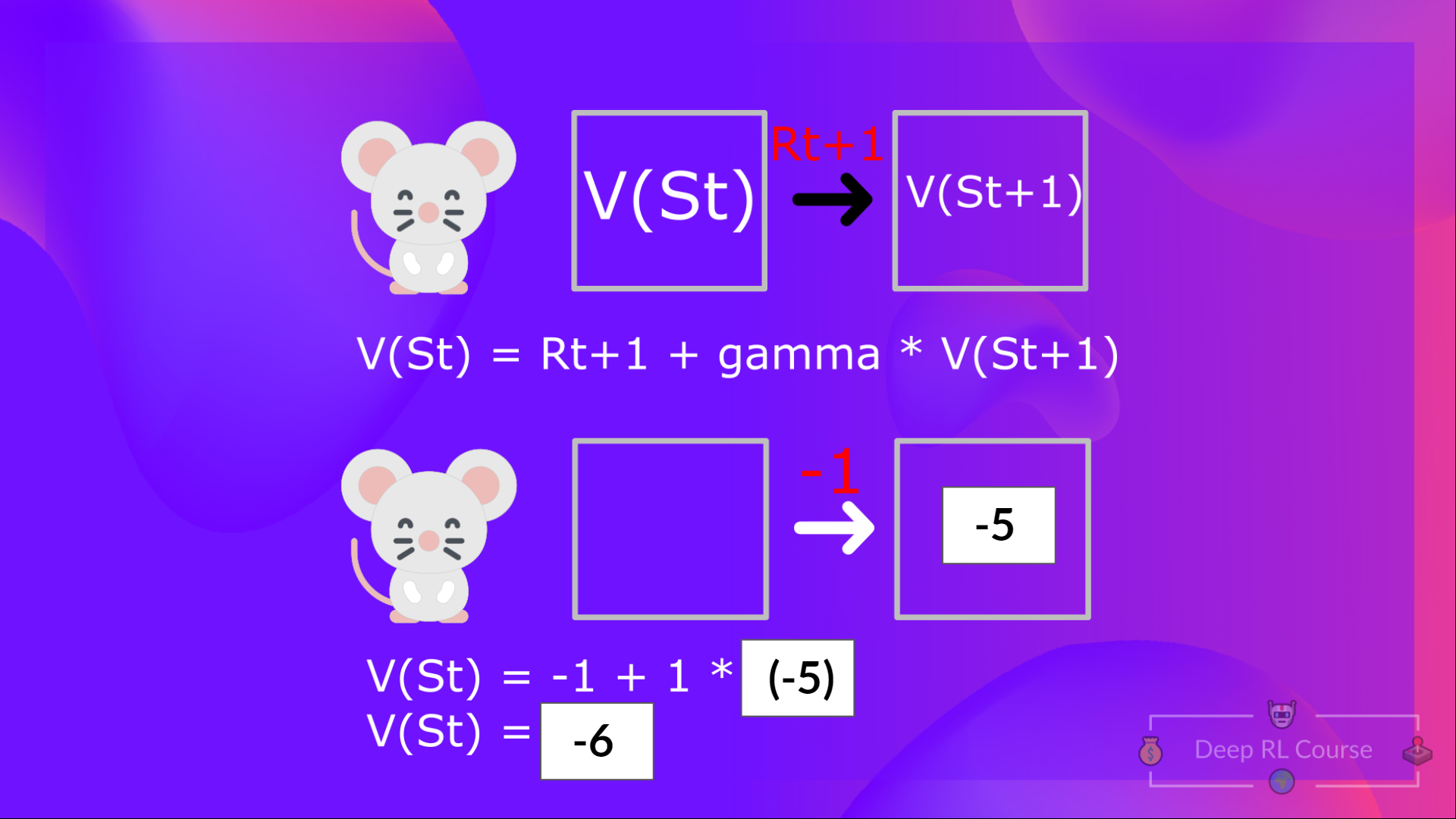
In the interest of simplicity, here we don’t discount, so gamma = 1. But you’ll study an example with gamma = 0.99 in the Q-Learning section of this unit.

• The value of $V(S_{t+1})$ = Immediate reward $R_{t+2}$ + Discounted value of the next state ($gamma * V(S_{t+2})$ ).
• And so on.

To recap, the idea of the Bellman equation is that instead of calculating each value as the sum of the expected return, which is a long process, we calculate the value as the sum of immediate reward + the discounted value of the state that follows.

Before going to the next section, think about the role of gamma in the Bellman equation. What happens if the value of gamma is very low (e.g. 0.1 or even 0)? What happens if the value is 1? What happens if the value is very high, such as a million?

< > Update on GitHub