Introducing Q-Learning
What is Q-Learning?
Q-Learning is an off-policy value-based method that uses a TD approach to train its action-value function:
- Off-policy: we’ll talk about that at the end of this unit.
- Value-based method: finds the optimal policy indirectly by training a value or action-value function that will tell us the value of each state or each state-action pair.
- TD approach: updates its action-value function at each step instead of at the end of the episode.
Q-Learning is the algorithm we use to train our Q-function, an action-value function that determines the value of being at a particular state and taking a specific action at that state.

The Q comes from “the Quality” (the value) of that action at that state.
Let’s recap the difference between value and reward:
- The value of a state, or a state-action pair is the expected cumulative reward our agent gets if it starts at this state (or state-action pair) and then acts accordingly to its policy.
- The reward is the feedback I get from the environment after performing an action at a state.
Internally, our Q-function is encoded by a Q-table, a table where each cell corresponds to a state-action pair value. Think of this Q-table as the memory or cheat sheet of our Q-function.
Let’s go through an example of a maze.

The Q-table is initialized. That’s why all values are = 0. This table contains, for each state and action, the corresponding state-action values. For this simple example, the state is only defined by the position of the mouse. Therefore, we have 2*3 rows in our Q-table, one row for each possible position of the mouse. In more complex scenarios, the state could contain more information than the position of the actor.

Here we see that the state-action value of the initial state and going up is 0:

So: the Q-function uses a Q-table that has the value of each state-action pair. Given a state and action, our Q-function will search inside its Q-table to output the value.

If we recap, Q-Learning is the RL algorithm that:
- Trains a Q-function (an action-value function), which internally is a Q-table that contains all the state-action pair values.
- Given a state and action, our Q-function will search its Q-table for the corresponding value.
- When the training is done, we have an optimal Q-function, which means we have optimal Q-table.
- And if we have an optimal Q-function, we have an optimal policy since we know the best action to take at each state.

In the beginning, our Q-table is useless since it gives arbitrary values for each state-action pair (most of the time, we initialize the Q-table to 0). As the agent explores the environment and we update the Q-table, it will give us a better and better approximation to the optimal policy.

Now that we understand what Q-Learning, Q-functions, and Q-tables are, let’s dive deeper into the Q-Learning algorithm.
The Q-Learning algorithm
This is the Q-Learning pseudocode; let’s study each part and see how it works with a simple example before implementing it. Don’t be intimidated by it, it’s simpler than it looks! We’ll go over each step.

Step 1: We initialize the Q-table

We need to initialize the Q-table for each state-action pair. Most of the time, we initialize with values of 0.
Step 2: Choose an action using the epsilon-greedy strategy
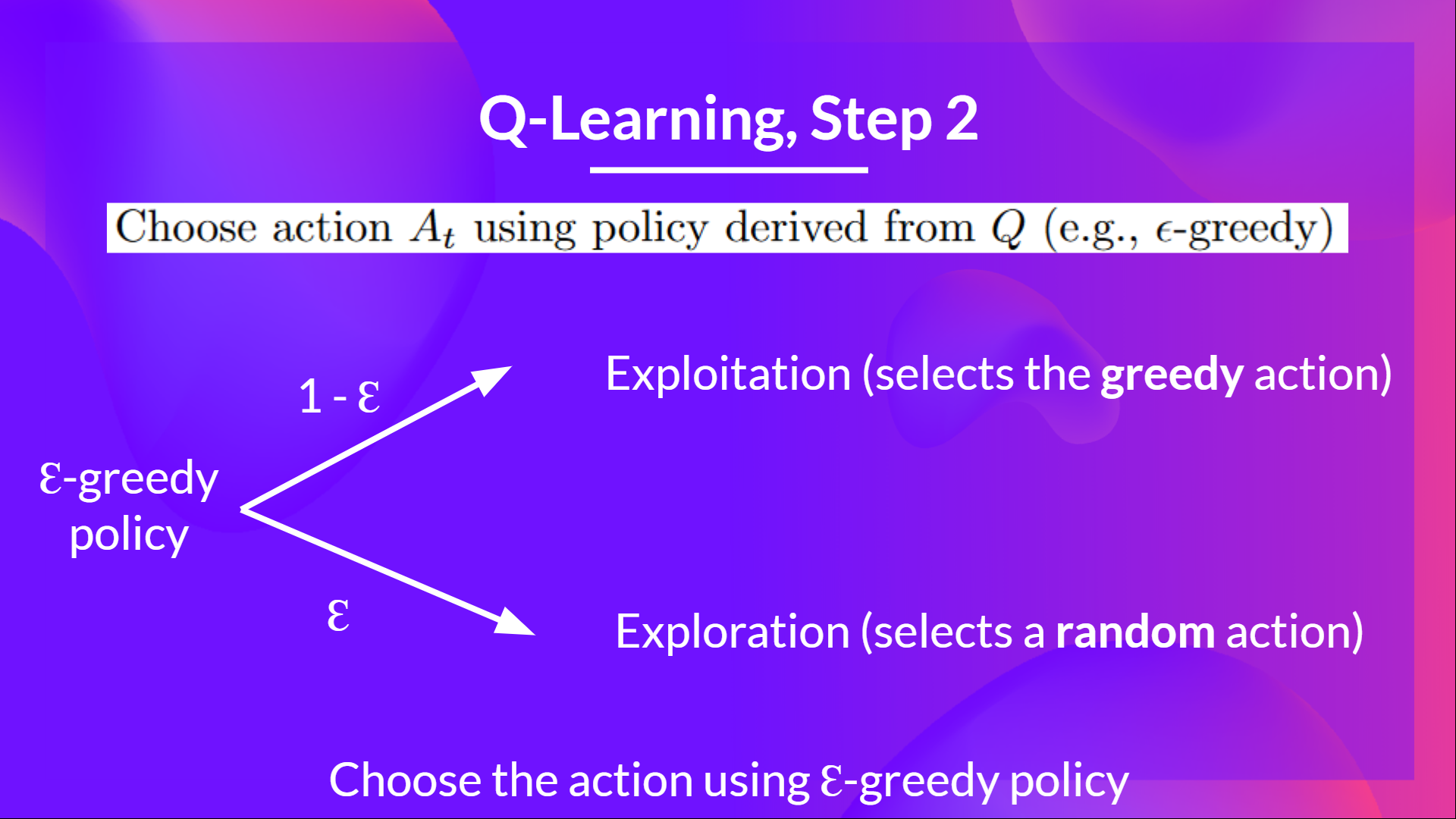
The epsilon-greedy strategy is a policy that handles the exploration/exploitation trade-off.
The idea is that, with an initial value of ɛ = 1.0:
- With probability 1 — ɛ : we do exploitation (aka our agent selects the action with the highest state-action pair value).
- With probability ɛ: we do exploration (trying random action).
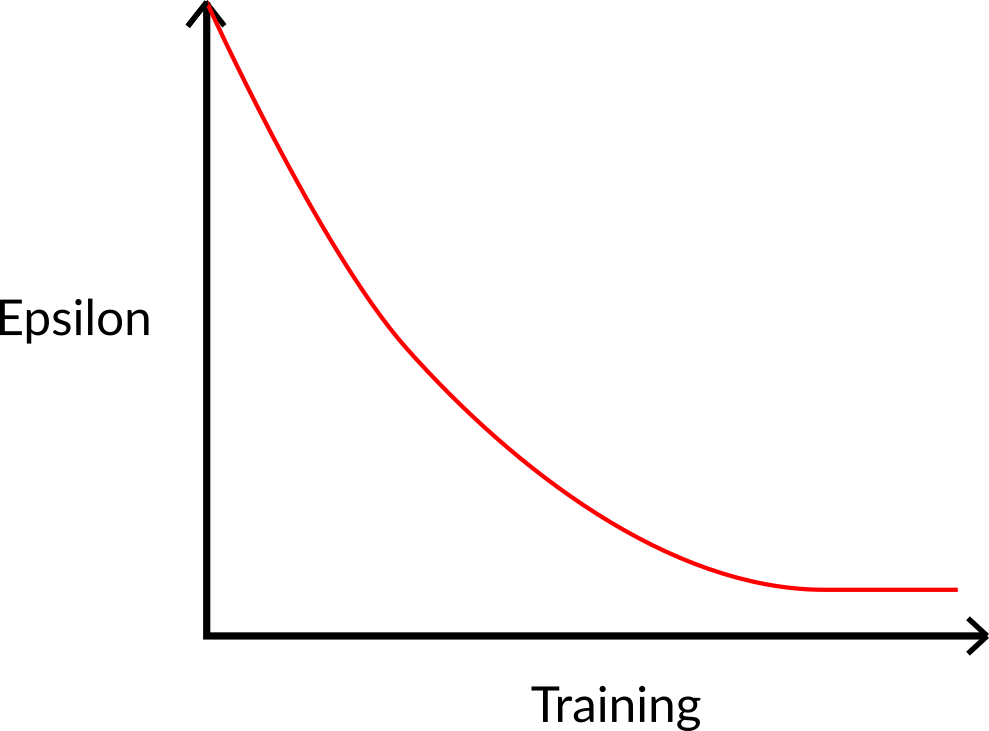
At the beginning of the training, the probability of doing exploration will be huge since ɛ is very high, so most of the time, we’ll explore. But as the training goes on, and consequently our Q-table gets better and better in its estimations, we progressively reduce the epsilon value since we will need less and less exploration and more exploitation.
Step 3: Perform action At, get reward Rt+1 and next state St+1

Step 4: Update Q(St, At)
Remember that in TD Learning, we update our policy or value function (depending on the RL method we choose) after one step of the interaction.
To produce our TD target, we used the immediate reward plus the discounted value of the next state, computed by finding the action that maximizes the current Q-function at the next state. (We call that bootstrap).
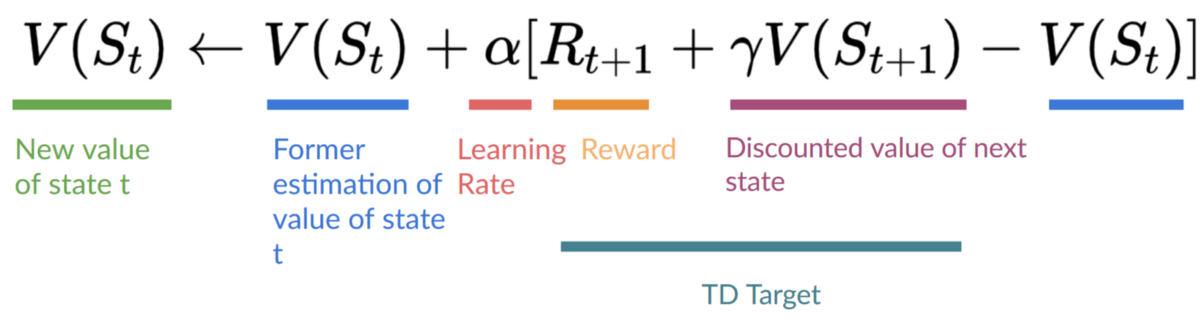
Therefore, our update formula goes like this:
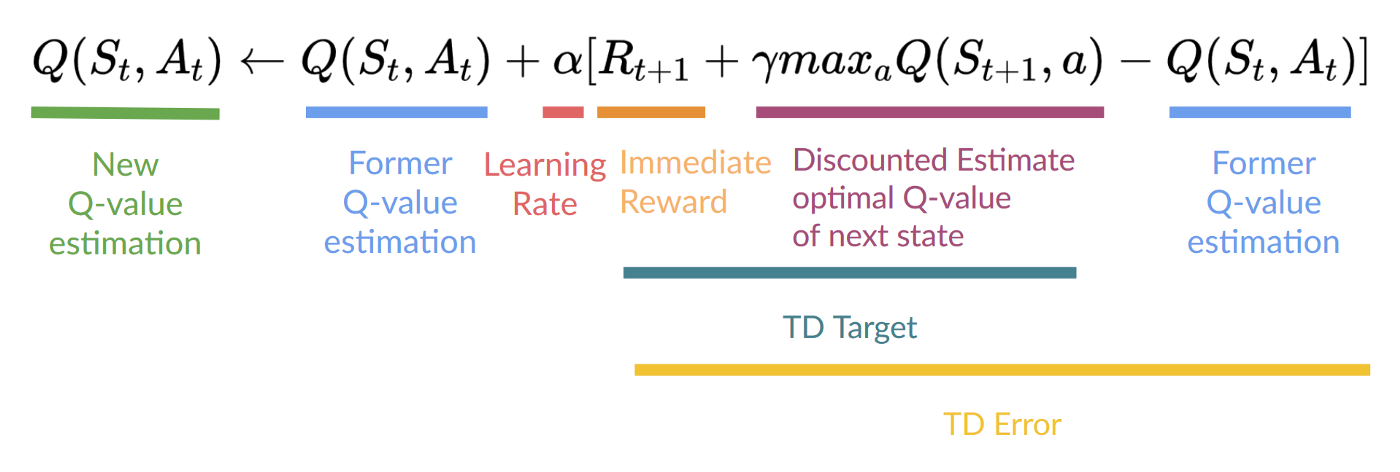
This means that to update our:
- We need.
- To update our Q-value at a given state-action pair, we use the TD target.
How do we form the TD target?
- We obtain the reward after taking the action.
- To get the best state-action pair value for the next state, we use a greedy policy to select the next best action. Note that this is not an epsilon-greedy policy, this will always take the action with the highest state-action value.
Then when the update of this Q-value is done, we start in a new state and select our action using a epsilon-greedy policy again.
This is why we say that Q Learning is an off-policy algorithm.
Off-policy vs On-policy
The difference is subtle:
- Off-policy: using a different policy for acting (inference) and updating (training).
For instance, with Q-Learning, the epsilon-greedy policy (acting policy), is different from the greedy policy that is used to select the best next-state action value to update our Q-value (updating policy).
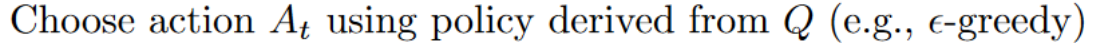
Is different from the policy we use during the training part:
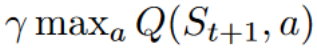
- On-policy: using the same policy for acting and updating.
For instance, with Sarsa, another value-based algorithm, the epsilon-greedy policy selects the next state-action pair, not a greedy policy.

