text
stringlengths 2.5k
6.39M
| kind
stringclasses 3
values |
|---|---|
```
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import rcParams
import seaborn as sns
%matplotlib inline
rcParams['figure.figsize'] = 10, 8
sns.set_style('whitegrid')
num = 50
xv = np.linspace(-500,400,num)
yv = np.linspace(-500,400,num)
X,Y = np.meshgrid(xv,yv)
# frist X,Y
a = 8.2
intervalo = 10
valor = 100
ke = 1/(4*np.pi*8.85418e-12)
V = np.zeros((num,num))
print(V)
# v = np.zeros((2,10))
kl = 1e-12
# x -> i
# y -> j
# x = a + intervalo/2
i = j = 0
for xi in xv:
for yj in yv:
x = a + intervalo/2
for k in range(100):
#print(k,x)
# calcula o valor da carga do intevalor de linha
Q = ( (kl*x) / ((x**2) + (a**2)) ) * intervalo # pL * dx
d = np.sqrt((x-xi)**2 + yj**2)
if d<0.01:
d == 0.01
V[j][i] += ke*(Q/d)
x = x + intervalo
# print(i,j)
j += 1
i += 1
j = 0
fig = plt.figure()
ax = plt.axes(projection='3d')
ax.plot_wireframe(X, Y, V, color='black')
plt.show()
print(V[0][0])
print(V[0][1])
num = 50
xv = np.linspace(-500,400,num)
yv = np.linspace(-500,400,num)
i = j = 0
for xi in xv:
i += 1
print(i)
print("50 ou", (900/50))
%% Descobrir o E1 - Campo eletrico dentro do cilindro
%tem que ser por gauss pq é um fio infinito
%% Variaveis Dadas
clc
clear all
close all
%% variaveis do problema
e0 = 8.854*10^-12;
kc = 8.8*10^-12;
a = 10;
const=1/(4*pi*e0); %Constante
%% Variaveis Criadas
passe = 1;
limites = 20;
%Onde o campo sera medido:
x= -limites:passe:limites; %vetor na coordenada x onde será calculado E
y= -limites:passe:limites; %vetor na coordenada z onde será calculado E
z= -limites:passe:limites; %vetor na coordenada z onde será calculado E
%Gerador do campo:
xl= a:passe:(5*limites); % variação da coordenada x onde está a carga
% yl= -passe:passe:passe; % variação da coordenada y onde está a carga
dL = passe; %tamanho de cada segmento
%inicializa o campo elétrico:
V(:,:,:) = zeros (length(x),length(y),length(z));
%% Desenvolvimento
for i = 1:length(x)% varre a coordenada x onde E será calculado
disp(i)
for j = 1: length(y) % varre a coordenada y onde E será calculado
for k = 1: length(z) % varre a coordenada z onde E será calculado
for m = 1:length(xl) % varre a coordenada x da carga
% #for n = 1:length(yl) % varre a coordenada y da carga
r = [x(i),y(j),z(k)]; %vetor posição apontando para onde estamos calculando E
rl= [xl(m),0,0];% vetor posição apontando para a carga
if ((r-rl)*(r-rl)'>0.00000001)
V(i,j,k) = V(i,j,k) + const*((((kc.*xl(m))/(xl(m).^2 + a^2)).*dL)/(sqrt((r-rl)*(r-rl)'))');
Q = ke/sqrt((x-xi)**2 + yj**2)*( (kl*x) / ((x**2) + (a**2)) ) * intervalo # pL * dx
end
% # end
end
end
end
end
%% Grafico
% xd = linspace(-limites,limites);
% yd = linspace(-limites,limites);
% zd = linspace(-limites,limites);
% [X,Y] = meshgrid(xd,yd);
%
% figure(1)
% surf(x,y,V(:,:,0));
% xlabel('x')
% ylabel('y')
% zlabel('z')
% axis([-5 20 -20 20 -inf inf])
% grid on
% colormap(jet(20))
% colorbar
%% prof
[X,Z] = meshgrid(x,z);
figure
[C,h] = contour(x,z,squeeze(V(:,3,:)),20);%faz o gráfico das curvas de nível para o potencial
set(h,'ShowText','on','TextStep',get(h,'LevelStep'))
xlabel('eixo x (m)')
ylabel('eixo z (m)')
%% Print resultado
max = int64(length(x));
V0 = V(max/2,max/2);
Vinf = 0;
disp(0-V0)
```
|
github_jupyter
|
```
from egocom import audio
from egocom.multi_array_alignment import gaussian_kernel
from egocom.transcription import async_srt_format_timestamp
from scipy.io import wavfile
import os
import numpy as np
import pandas as pd
from sklearn.metrics import accuracy_score
from egocom.transcription import write_subtitles
def gaussian_smoothing(arr, samplerate = 44100, window_size = 0.1):
'''Returns a locally-normalized array by dividing each point by a the
sum of the points around it, with greater emphasis on the points
nearest (using a Guassian convolution)
Parameters
----------
arr : np.array
samplerate : int
window_size : float (in seconds)
Returns
-------
A Guassian smoothing of the input arr'''
kern = gaussian_kernel(kernel_length=int(samplerate * window_size), nsigma=3)
return np.convolve(arr, kern, 'same')
# Tests for audio.avg_pool_1d
def test_exact_recoverability(
arr = range(10),
pool_size = 4,
weights = [0.2,0.3,0.3,0.2],
):
'''Verify that downsampled signal can be fully recovered exactly.'''
complete_result = audio.avg_pool_1d(range(10), pool_size, filler = True, weights = weights)
downsampled_result = audio.avg_pool_1d(range(10), pool_size, filler = False, weights = weights)
# Try to recover filled_pooled_mags using the downsampled pooled_mags
upsampled_result = audio.upsample_1d(downsampled_result, len(arr), pool_size)
assert(np.all(upsampled_result == complete_result))
def test_example(
arr = range(10),
pool_size = 4,
weights = [0.2,0.3,0.3,0.2],
):
'''Verify that avg_pool_1d produces the result we expect.'''
result = audio.avg_pool_1d(range(10), pool_size, weights = weights)
expected = np.array([1.5, 1.5, 1.5, 1.5, 5.5, 5.5, 5.5, 5.5, 8.5, 8.5])
assert(np.all(result - expected < 1e-6))
test_exact_recoverability()
test_example()
```
# Generate speaker labels from max raw audio magnitudes
```
data_dir = '/Users/cgn/Dropbox (Facebook)/EGOCOM/raw_audio/wav/'
fn_dict = {}
for fn in sorted(os.listdir(data_dir)):
key = fn[9:23] + fn[32:37] if 'part' in fn else fn[9:21]
fn_dict[key] = fn_dict[key] + [fn] if key in fn_dict else [fn]
samplerate = 44100
window = 1 # Averages signals with windows of N seconds.
window_length = int(samplerate * window)
labels = {}
for key in list(fn_dict.keys()):
print(key, end = " | ")
fns = fn_dict[key]
wavs = [wavfile.read(data_dir + fn)[1] for fn in fns]
duration = min(len(w) for w in wavs)
wavs = np.stack([w[:duration] for w in wavs])
# Only use the magnitudes of both left and right for each audio wav.
mags = abs(wavs).sum(axis = 2)
# DOWNSAMPLED (POOLED) Discretized/Fast (no overlap) gaussian smoothing with one-second time window.
kwargs = {
'pool_size': window_length,
'weights': gaussian_kernel(kernel_length=window_length),
'filler': False,
}
pooled_mags = np.apply_along_axis(audio.avg_pool_1d, 1, mags, **kwargs)
# Create noisy speaker labels
threshold = np.percentile(pooled_mags, 10, axis = 1)
no_one_speaking = (pooled_mags > np.expand_dims(threshold, axis = 1)).sum(axis = 0) == 0
speaker_labels = np.argmax(pooled_mags, axis = 0)
speaker_labels[no_one_speaking] = -1
# User 1-based indexing for speaker labels (ie increase by 1)
speaker_labels = [z if z < 0 else z + 1 for z in speaker_labels]
# Store results
labels[key] = speaker_labels
# Write result to file
loc = '/Users/cgn/Dropbox (Facebook)/EGOCOM/raw_audio_speaker_labels_{}.json'.format(str(window))
def default(o):
if isinstance(o, np.int64): return int(o)
raise TypeError
import json
with open(loc, 'w') as fp:
json.dump(labels, fp, default = default)
fp.close()
# Read result into a dict
import json
with open(loc, 'r') as fp:
labels = json.load(fp)
fp.close()
```
## Generate ground truth speaker labels
```
def create_gt_speaker_labels(
df_times_speaker,
duration_in_seconds,
time_window_seconds = 0.5,
):
stack = rev_times[::-1]
stack_time = stack.pop()
label_times = np.arange(0, duration_in_seconds, time_window_seconds)
result = [-1] * len(label_times)
for i, t in enumerate(label_times):
while stack_time['endTime'] > t and stack_time['endTime'] <= t + time_window_seconds:
result[i] = stack_time['speaker']
if len(stack) == 0:
break
stack_time = stack.pop()
return result
df = pd.read_csv("/Users/cgn/Dropbox (Facebook)/EGOCOM/ground_truth_transcriptions.csv")[
["key", "endTime", "speaker", ]
].dropna()
gt_speaker_labels = {}
for key, sdf in df.groupby('key'):
print(key, end = " | ")
wavs = [wavfile.read(data_dir + fn)[1] for fn in fn_dict[key]]
duration = min(len(w) for w in wavs)
DL = sdf[["endTime", "speaker"]].to_dict('list')
rev_times = [dict(zip(DL,t)) for t in zip(*DL.values())]
duration_in_seconds = np.ceil(duration / float(samplerate))
gt_speaker_labels[key] = create_gt_speaker_labels(rev_times, duration_in_seconds, window)
# Write result to file
loc = '/Users/cgn/Dropbox (Facebook)/EGOCOM/rev_ground_truth_speaker_labels_{}.json'.format(str(window))
with open(loc, 'w') as fp:
json.dump(gt_speaker_labels, fp, default = default)
fp.close()
# Read result into a dict
with open(loc, 'r') as fp:
gt_speaker_labels = json.load(fp)
fp.close()
scores = []
for key in labels.keys():
true = gt_speaker_labels[key]
pred = labels[key]
if len(true) > len(pred):
true = true[:-1]
# diff = round(accuracy_score(true[:-1], pred) - accuracy_score(true[1:], pred), 3)
# scores.append(diff)
# print(key, accuracy_score(true[1:], pred), accuracy_score(true[:-1], pred), diff)
score = accuracy_score(true, pred)
scores.append(score)
print(key, np.round(score, 3))
print('Average accuracy:', str(np.round(np.mean(scores), 3)* 100) + '%')
loc = '/Users/cgn/Dropbox (Facebook)/EGOCOM/subtitles/'
for key in labels.keys():
gt = gt_speaker_labels[key]
est = labels[key]
with open(loc + "speaker_" + key + '.srt', 'w') as f:
print(key, end = " | ")
for t, s_est in enumerate(est):
s_gt = gt[t]
print(t + 1, file = f)
print(async_srt_format_timestamp(t*window), end = "", file = f)
print(' --> ', end = '', file = f)
print(async_srt_format_timestamp(t*window+window), file = f)
print('Rev.com Speaker:', end = " ", file = f)
if s_gt == -1:
print('No one is speaking', file = f)
elif s_gt == 1:
print('Curtis', file = f)
else:
print('Speaker ' + str(s_gt), file = f)
print('MaxMag Speaker:', end = " ", file = f)
if s_est == -1:
print('No one is speaking', file = f)
elif s_est == 1:
print('Curtis', file = f)
else:
print('Speaker ' + str(s_est), file = f)
print(file = f)
```
## Generate subtitles
```
for key in labels.keys():
gt = labels[key]
with open("subtitles/est_" + key + '.srt', 'w') as f:
for t, s in enumerate(gt):
print(t + 1, file = f)
print(async_srt_format_timestamp(t*window), end = "", file = f)
print(' --> ', end = '', file = f)
print(async_srt_format_timestamp(t*window+window), file = f)
print('Max mag of wavs speaker id', file = f)
if s == -1:
print('No one is speaking', file = f)
elif s == 1:
print('Curtis', file = f)
else:
print('Speaker ' + str(s), file = f)
print(file = f)
```
|
github_jupyter
|
# Running and Plotting Coeval Cubes
The aim of this tutorial is to introduce you to how `21cmFAST` does the most basic operations: producing single coeval cubes, and visually verifying them. It is a great place to get started with `21cmFAST`.
```
%matplotlib inline
import matplotlib.pyplot as plt
import os
# We change the default level of the logger so that
# we can see what's happening with caching.
import logging, sys, os
logger = logging.getLogger('21cmFAST')
logger.setLevel(logging.INFO)
import py21cmfast as p21c
# For plotting the cubes, we use the plotting submodule:
from py21cmfast import plotting
# For interacting with the cache
from py21cmfast import cache_tools
print(f"Using 21cmFAST version {p21c.__version__}")
```
Clear the cache so that we get the same results for the notebook every time (don't worry about this for now). Also, set the default output directory to `_cache/`:
```
if not os.path.exists('_cache'):
os.mkdir('_cache')
p21c.config['direc'] = '_cache'
cache_tools.clear_cache(direc="_cache")
```
## Basic Usage
The simplest (and typically most efficient) way to produce a coeval cube is simply to use the `run_coeval` method. This consistently performs all steps of the calculation, re-using any data that it can without re-computation or increased memory overhead.
```
coeval8, coeval9, coeval10 = p21c.run_coeval(
redshift = [8.0, 9.0, 10.0],
user_params = {"HII_DIM": 100, "BOX_LEN": 100, "USE_INTERPOLATION_TABLES": True},
cosmo_params = p21c.CosmoParams(SIGMA_8=0.8),
astro_params = p21c.AstroParams({"HII_EFF_FACTOR":20.0}),
random_seed=12345
)
```
There are a number of possible inputs for `run_coeval`, which you can check out either in the [API reference](../reference/py21cmfast.html) or by calling `help(p21c.run_coeval)`. Notably, the `redshift` must be given: it can be a single number, or a list of numbers, defining the redshift at which the output coeval cubes will be defined.
Other params we've given here are `user_params`, `cosmo_params` and `astro_params`. These are all used for defining input parameters into the backend C code (there's also another possible input of this kind; `flag_options`). These can be given either as a dictionary (as `user_params` has been), or directly as a relevant object (like `cosmo_params` and `astro_params`). If creating the object directly, the parameters can be passed individually or via a single dictionary. So there's a lot of flexibility there! Nevertheless we *encourage* you to use the basic dictionary. The other ways of passing the information are there so we can use pre-defined objects later on. For more information about these "input structs", see the [API docs](../reference/_autosummary/py21cmfast.inputs.html).
We've also given a `direc` option: this is the directory in which to search for cached data (and also where cached data should be written). Throughout this notebook we're going to set this directly to the `_cache` folder, which allows us to manage it directly. By default, the cache location is set in the global configuration in `~/.21cmfast/config.yml`. You'll learn more about caching further on in this tutorial.
Finally, we've given a random seed. This sets all the random phases for the simulation, and ensures that we can exactly reproduce the same results on every run.
The output of `run_coeval` is a list of `Coeval` instances, one for each input redshift (it's just a single object if a single redshift was passed, not a list). They store *everything* related to that simulation, so that it can be completely compared to other simulations.
For example, the input parameters:
```
print("Random Seed: ", coeval8.random_seed)
print("Redshift: ", coeval8.redshift)
print(coeval8.user_params)
```
This is where the utility of being able to pass a *class instance* for the parameters arises: we could run another iteration of coeval cubes, with the same user parameters, simply by doing `p21c.run_coeval(user_params=coeval8.user_params, ...)`.
Also in the `Coeval` instance are the various outputs from the different steps of the computation. You'll see more about what these steps are further on in the tutorial. But for now, we show that various boxes are available:
```
print(coeval8.hires_density.shape)
print(coeval8.brightness_temp.shape)
```
Along with these, full instances of the output from each step are available as attributes that end with "struct". These instances themselves contain the `numpy` arrays of the data cubes, and some other attributes that make them easier to work with:
```
coeval8.brightness_temp_struct.global_Tb
```
By default, each of the components of the cube are cached to disk (in our `_cache/` folder) as we run it. However, the `Coeval` cube itself is _not_ written to disk by default. Writing it to disk incurs some redundancy, since that data probably already exists in the cache directory in seperate files.
Let's save to disk. The save method by default writes in the current directory (not the cache!):
```
filename = coeval8.save(direc='_cache')
```
The filename of the saved file is returned:
```
print(os.path.basename(filename))
```
Such files can be read in:
```
new_coeval8 = p21c.Coeval.read(filename, direc='.')
```
Some convenient plotting functions exist in the `plotting` module. These can work directly on `Coeval` objects, or any of the output structs (as we'll see further on in the tutorial). By default the `coeval_sliceplot` function will plot the `brightness_temp`, using the standard traditional colormap:
```
fig, ax = plt.subplots(1,3, figsize=(14,4))
for i, (coeval, redshift) in enumerate(zip([coeval8, coeval9, coeval10], [8,9,10])):
plotting.coeval_sliceplot(coeval, ax=ax[i], fig=fig);
plt.title("z = %s"%redshift)
plt.tight_layout()
```
Any 3D field can be plotted, by setting the `kind` argument. For example, we could alternatively have plotted the dark matter density cubes perturbed to each redshift:
```
fig, ax = plt.subplots(1,3, figsize=(14,4))
for i, (coeval, redshift) in enumerate(zip([coeval8, coeval9, coeval10], [8,9,10])):
plotting.coeval_sliceplot(coeval, kind='density', ax=ax[i], fig=fig);
plt.title("z = %s"%redshift)
plt.tight_layout()
```
To see more options for the plotting routines, see the [API Documentation](../reference/_autosummary/py21cmfast.plotting.html).
`Coeval` instances are not cached themselves -- they are containers for data that is itself cached (i.e. each of the `_struct` attributes of `Coeval`). See the [api docs](../reference/_autosummary/py21cmfast.outputs.html) for more detailed information on these.
You can see the filename of each of these structs (or the filename it would have if it were cached -- you can opt to *not* write out any given dataset):
```
coeval8.init_struct.filename
```
You can also write the struct anywhere you'd like on the filesystem. This will not be able to be automatically used as a cache, but it could be useful for sharing files with colleagues.
```
coeval8.init_struct.save(fname='my_init_struct.h5')
```
This brief example covers most of the basic usage of `21cmFAST` (at least with `Coeval` objects -- there are also `Lightcone` objects for which there is a separate tutorial).
For the rest of the tutorial, we'll cover a more advanced usage, in which each step of the calculation is done independently.
## Advanced Step-by-Step Usage
Most users most of the time will want to use the high-level `run_coeval` function from the previous section. However, there are several independent steps when computing the brightness temperature field, and these can be performed one-by-one, adding any other effects between them if desired. This means that the new `21cmFAST` is much more flexible. In this section, we'll go through in more detail how to use the lower-level methods.
Each step in the chain will receive a number of input-parameter classes which define how the calculation should run. These are the `user_params`, `cosmo_params`, `astro_params` and `flag_options` that we saw in the previous section.
Conversely, each step is performed by running a function which will return a single object. Every major function returns an object of the same fundamental class (an ``OutputStruct``) which has various methods for reading/writing the data, and ensuring that it's in the right state to receive/pass to and from C.
These are the objects stored as `init_box_struct` etc. in the `Coeval` class.
As we move through each step, we'll outline some extra details, hints and tips about using these inputs and outputs.
### Initial Conditions
The first step is to get the initial conditions, which defines the *cosmological* density field before any redshift evolution is applied.
```
initial_conditions = p21c.initial_conditions(
user_params = {"HII_DIM": 100, "BOX_LEN": 100},
cosmo_params = p21c.CosmoParams(SIGMA_8=0.8),
random_seed=54321
)
```
We've already come across all these parameters as inputs to the `run_coeval` function. Indeed, most of the steps have very similar interfaces, and are able to take a random seed and parameters for where to look for the cache. We use a different seed than in the previous section so that all our boxes are "fresh" (we'll show how the caching works in a later section).
These initial conditions have 100 cells per side, and a box length of 100 Mpc. Note again that they can either be passed as a dictionary containing the input parameters, or an actual instance of the class. While the former is the suggested way, one benefit of the latter is that it can be queried for the relevant parameters (by using ``help`` or a post-fixed ``?``), or even queried for defaults:
```
p21c.CosmoParams._defaults_
```
(these defaults correspond to the Planck15 cosmology contained in Astropy).
So what is in the ``initial_conditions`` object? It is what we call an ``OutputStruct``, and we have seen it before, as the `init_box_struct` attribute of `Coeval`. It contains a number of arrays specifying the density and velocity fields of our initial conditions, as well as the defining parameters. For example, we can easily show the cosmology parameters that are used (note the non-default $\sigma_8$ that we passed):
```
initial_conditions.cosmo_params
```
A handy tip is that the ``CosmoParams`` class also has a reference to a corresponding Astropy cosmology, which can be used more broadly:
```
initial_conditions.cosmo_params.cosmo
```
Merely printing the initial conditions object gives a useful representation of its dependent parameters:
```
print(initial_conditions)
```
(side-note: the string representation of the object is used to uniquely define it in order to save it to the cache... which we'll explore soon!).
To see which arrays are defined in the object, access the ``fieldnames`` (this is true for *all* `OutputStruct` objects):
```
initial_conditions.fieldnames
```
The `coeval_sliceplot` function also works on `OutputStruct` objects (as well as the `Coeval` object as we've already seen). It takes the object, and a specific field name. By default, the field it plots is the _first_ field in `fieldnames` (for any `OutputStruct`).
```
plotting.coeval_sliceplot(initial_conditions, "hires_density");
```
### Perturbed Field
After obtaining the initial conditions, we need to *perturb* the field to a given redshift (i.e. the redshift we care about). This step clearly requires the results of the previous step, which we can easily just pass in. Let's do that:
```
perturbed_field = p21c.perturb_field(
redshift = 8.0,
init_boxes = initial_conditions
)
```
Note that we didn't need to pass in any input parameters, because they are all contained in the `initial_conditions` object itself. The random seed is also taken from this object.
Again, the output is an `OutputStruct`, so we can view its fields:
```
perturbed_field.fieldnames
```
This time, it has only density and velocity (the velocity direction is chosen without loss of generality). Let's view the perturbed density field:
```
plotting.coeval_sliceplot(perturbed_field, "density");
```
It is clear here that the density used is the *low*-res density, but the overall structure of the field looks very similar.
### Ionization Field
Next, we need to ionize the box. This is where things get a little more tricky. In the simplest case (which, let's be clear, is what we're going to do here) the ionization occurs at the *saturated limit*, which means we can safely ignore the contribution of the spin temperature. This means we can directly calculate the ionization on the density/velocity fields that we already have. A few more parameters are needed here, and so two more "input parameter dictionaries" are available, ``astro_params`` and ``flag_options``. Again, a reminder that their parameters can be viewed by using eg. `help(p21c.AstroParams)`, or by looking at the [API docs](../reference/_autosummary/py21cmfast.inputs.html).
For now, let's leave everything as default. In that case, we can just do:
```
ionized_field = p21c.ionize_box(
perturbed_field = perturbed_field
)
```
That was easy! All the information required by ``ionize_box`` was given directly by the ``perturbed_field`` object. If we had _also_ passed a redshift explicitly, this redshift would be checked against that from the ``perturbed_field`` and an error raised if they were incompatible:
Let's see the fieldnames:
```
ionized_field.fieldnames
```
Here the ``first_box`` field is actually just a flag to tell the C code whether this has been *evolved* or not. Here, it hasn't been, it's the "first box" of an evolutionary chain. Let's plot the neutral fraction:
```
plotting.coeval_sliceplot(ionized_field, "xH_box");
```
### Brightness Temperature
Now we can use what we have to get the brightness temperature:
```
brightness_temp = p21c.brightness_temperature(ionized_box=ionized_field, perturbed_field=perturbed_field)
```
This has only a single field, ``brightness_temp``:
```
plotting.coeval_sliceplot(brightness_temp);
```
### The Problem
And there you have it -- you've computed each of the four steps (there's actually another, `spin_temperature`, that you require if you don't assume the saturated limit) individually.
However, some problems quickly arise. What if you want the `perturb_field`, but don't care about the initial conditions? We know how to get the full `Coeval` object in one go, but it would seem that the sub-boxes have to _each_ be computed as the input to the next.
A perhaps more interesting problem is that some quantities require *evolution*: i.e. a whole bunch of simulations at a string of redshifts must be performed in order to obtain the current redshift. This is true when not in the saturated limit, for example. That means you'd have to manually compute each redshift in turn, and pass it to the computation at the next redshift. While this is definitely possible, it becomes difficult to set up manually when all you care about is the box at the final redshift.
`py21cmfast` solves this by making each of the functions recursive: if `perturb_field` is not passed the `init_boxes` that it needs, it will go and compute them, based on the parameters that you've passed it. If the previous `spin_temp` box required for the current redshift is not passed -- it will be computed (and if it doesn't have a previous `spin_temp` *it* will be computed, and so on).
That's all good, but what if you now want to compute another `perturb_field`, with the same fundamental parameters (but at a different redshift)? Since you didn't ever see the `init_boxes`, they'll have to be computed all over again. That's where the automatic caching comes in, which is where we turn now...
## Using the Automatic Cache
To solve all this, ``21cmFAST`` uses an on-disk caching mechanism, where all boxes are saved in HDF5 format in a default location. The cache allows for reading in previously-calculated boxes automatically if they match the parameters that are input. The functions used at every step (in the previous section) will try to use a cached box instead of calculating a new one, unless its explicitly asked *not* to.
Thus, we could do this:
```
perturbed_field = p21c.perturb_field(
redshift = 8.0,
user_params = {"HII_DIM": 100, "BOX_LEN": 100},
cosmo_params = p21c.CosmoParams(SIGMA_8=0.8),
)
plotting.coeval_sliceplot(perturbed_field, "density");
```
Note that here we pass exactly the same parameters as were used in the previous section. It gives a message that the full box was found in the cache and immediately returns. However, if we change the redshift:
```
perturbed_field = p21c.perturb_field(
redshift = 7.0,
user_params = {"HII_DIM": 100, "BOX_LEN": 100},
cosmo_params = p21c.CosmoParams(SIGMA_8=0.8),
)
plotting.coeval_sliceplot(perturbed_field, "density");
```
Now it finds the initial conditions, but it must compute the perturbed field at the new redshift. If we had changed the initial parameters as well, it would have to calculate everything:
```
perturbed_field = p21c.perturb_field(
redshift = 8.0,
user_params = {"HII_DIM": 50, "BOX_LEN": 100},
cosmo_params = p21c.CosmoParams(SIGMA_8=0.8),
)
plotting.coeval_sliceplot(perturbed_field, "density");
```
This shows that we don't need to perform the *previous* step to do any of the steps, they will be calculated automatically.
Now, let's get an ionized box, but this time we won't assume the saturated limit, so we need to use the spin temperature. We can do this directly in the ``ionize_box`` function, but let's do it explicitly. We will use the auto-generation of the initial conditions and perturbed field. However, the spin temperature is an *evolved* field, i.e. to compute the field at $z$, we need to know the field at $z+\Delta z$. This continues up to some redshift, labelled ``z_heat_max``, above which the spin temperature can be defined directly from the perturbed field.
Thus, one option is to pass to the function a *previous* spin temperature box, to evolve to *this* redshift. However, we don't have a previous spin temperature box yet. Of course, the function itself will go and calculate that box if it's not given (or read it from cache if it's been calculated before!). When it tries to do that, it will go to the one before, and so on until it reaches ``z_heat_max``, at which point it will calculate it directly.
To facilitate this recursive progression up the redshift ladder, there is a parameter, ``z_step_factor``, which is a multiplicate factor that determines the previous redshift at each step.
We can also pass the dependent boxes explicitly, which provides the parameters necessary.
**WARNING: THIS IS THE MOST TIME-CONSUMING STEP OF THE CALCULATION!**
```
spin_temp = p21c.spin_temperature(
perturbed_field = perturbed_field,
zprime_step_factor=1.05,
)
plotting.coeval_sliceplot(spin_temp, "Ts_box");
```
Let's note here that each of the functions accepts a few of the same arguments that modifies how the boxes are cached. There is a ``write`` argument, which if set to ``False``, will disable writing that box to cache (and it is passed through the recursive heirarchy). There is also ``regenerate``, which if ``True``, forces this box and all its predecessors to be re-calculated even if they exist in the cache. Then there is ``direc``, which we have seen before.
Finally note that by default, ``random_seed`` is set to ``None``. If this is the case, then any cached dataset matching all other parameters will be read in, and the ``random_seed`` will be set based on the file read in. If it is set to an integer number, then the cached dataset must also match the seed. If it is ``None``, and no matching dataset is found, a random seed will be autogenerated.
Now if we calculate the ionized box, ensuring that it uses the spin temperature, then it will also need to be evolved. However, due to the fact that we cached each of the spin temperature steps, these should be read in accordingly:
```
ionized_box = p21c.ionize_box(
spin_temp = spin_temp,
zprime_step_factor=1.05,
)
plotting.coeval_sliceplot(ionized_box, "xH_box");
```
Great! So again, we can just get the brightness temp:
```
brightness_temp = p21c.brightness_temperature(
ionized_box = ionized_box,
perturbed_field = perturbed_field,
spin_temp = spin_temp
)
```
Now lets plot our brightness temperature, which has been evolved from high redshift with spin temperature fluctuations:
```
plotting.coeval_sliceplot(brightness_temp);
```
We can also check what the result would have been if we had limited the maximum redshift of heating. Note that this *recalculates* all previous spin temperature and ionized boxes, because they depend on both ``z_heat_max`` and ``zprime_step_factor``.
```
ionized_box = p21c.ionize_box(
spin_temp = spin_temp,
zprime_step_factor=1.05,
z_heat_max = 20.0
)
brightness_temp = p21c.brightness_temperature(
ionized_box = ionized_box,
perturbed_field = perturbed_field,
spin_temp = spin_temp
)
plotting.coeval_sliceplot(brightness_temp);
```
As we can see, it's very similar!
|
github_jupyter
|
# Determinant Quantum Monte Carlo
## 1 Hubbard model
The Hubbard model is defined as
\begin{align}
\label{eq:ham} \tag{1}
H &= -\sum_{ij\sigma} t_{ij} \left( \hat{c}_{i\sigma}^\dagger \hat{c}_{j\sigma} + hc \right)
+ \sum_{i\sigma} (\varepsilon_i - \mu) \hat{n}_{i\sigma}
+ U \sum_{i} \left( \hat{n}_{i\uparrow} - \tfrac{1}{2} \right) \left( \hat{n}_{i\downarrow} - \tfrac{1}{2} \right)
\end{align}
where $U$ is the interaction strength, $\varepsilon_i$ the on-site energy at site $i$ and $t_{ij}$ the hopping energy between the sites $i$ and $j$. The chemical potential is defined to be $\mu = 0$ for a half filled Hubabrd model since the total chemical potential is given as $\mu + \tfrac{U}{2}$:
\begin{equation}
H = -\sum_{ij\sigma} t_{ij} \left( \hat{c}_{i\sigma}^\dagger \hat{c}_{j\sigma} + hc \right)
+ \sum_{i\sigma} \left(\varepsilon_i - \mu - \tfrac{U}{2}\right) \hat{n}_{i\sigma}
+ U \sum_{i} \hat{n}_{i\uparrow} \hat{n}_{i\downarrow}.
\end{equation}
The non-interacting of the Hubbard Hamiltonian is quadratic in the creation and annihilation operators,
\begin{equation}
K = -\sum_{ij\sigma} t_{ij} \left( \hat{c}_{i\sigma}^\dagger \hat{c}_{j\sigma} + hc \right)
+ \sum_{i\sigma} (\varepsilon_i - \mu) \hat{n}_{i\sigma},
\label{eq:ham_kin} \tag{2}
\end{equation}
while the interaction part is quartic in the fermion operators:
\begin{equation}
V = U \sum_{i} \left( \hat{n}_{i\uparrow} - \tfrac{1}{2} \right) \left( \hat{n}_{i\downarrow} - \tfrac{1}{2} \right).
\label{eq:ham_inter} \tag{3}
\end{equation}
## 2 Distribution operator
The expectation value of a observable $O$ is given by
\begin{equation}
\langle O \rangle = \text{Tr}(O \mathcal{P}),
\end{equation}
where $\mathcal{P}$ is the distribution operator,
\begin{equation}
\mathcal{P} = \frac{1}{\mathcal{Z}} e^{-\beta H},
\label{eq:distop} \tag{4}
\end{equation}
$\mathcal{Z}$ is the partition function,
\begin{equation}
\mathcal{Z} = \text{Tr}(e^{-\beta H}),
\label{eq:partition}
\end{equation}
and $\beta = 1/k_B T$ is the inverse of the temperature. The trace is taken over the Hilbert space describing all occupied states of the system:
\begin{equation}
\text{Tr}(e^{-\beta H}) = \sum_i \langle \psi_i | e^{-\beta H} | \psi_i \rangle.
\end{equation}
In order to obtain a computable approximation of the distribution operator the partition function has to be approximated. Since the quadratic term $ K $ and quartic term $ V $ of the Hubbard Hamiltonian do not commute a Trotter-Suzuki decomposition has to be used to approximate $\mathcal{Z}$. By dividing the imaginary-time interval from $0$ to $\beta$ into $L$ intervals of size $\Delta \tau = \beta / L$, the partition function can be written as
\begin{equation}
\label{eq:partitionTrotterDecomp}
\mathcal{Z} = \text{Tr}(e^{-\beta H }) = \text{Tr}( \prod_{l=1}^{L} e^{-\Delta \tau H})
= \text{Tr}( \prod_{l=1}^{L} e^{-\Delta \tau K} e^{-\Delta \tau V}) + \mathcal{O}(\Delta \tau^2).
\end{equation}
The spin-up and spin-down operators of the quadratic kinetic energy term are independent and can be written as
\begin{equation}
e^{-\Delta \tau K} = e^{-\Delta \tau K_\uparrow} e^{-\Delta \tau K_\downarrow}.
\end{equation}
The particle number operators $\hat{n}_{i\sigma}$ in the interacting term of the Hubbard Hamiltonian are independent of the site index $i$:
\begin{equation}
e^{-\Delta \tau V} = e^{- U \Delta\tau \sum_{i=1}^N
\left( \hat{n}_{i\uparrow} - \tfrac{1}{2} \right) \left( \hat{n}_{i\downarrow} - \tfrac{1}{2} \right)}
= \prod_{i=1}^N e^{- U \Delta\tau \left( \hat{n}_{i\uparrow} - \tfrac{1}{2} \right) \left( \hat{n}_{i\downarrow} - \tfrac{1}{2} \right)}
\end{equation}
The quartic contributions of the interacting term need to be represented in a quadratic form. This can be achieved by using the discrete \emph{Hubbard-Stratonovich} transformation, which replaces the term $\left( \hat{n}_{i\uparrow} - \tfrac{1}{2} \right) \left( \hat{n}_{i\downarrow} - \tfrac{1}{2} \right)$ by a quadratic term of the form $\left( \hat{n}_{i\uparrow} - \hat{n}_{i\downarrow} \right)$. For $U>0$, this yields
\begin{equation}
\label{eq:hubbardStratanovichInteractionTerm}
e^{- U \Delta\tau \left( \hat{n}_{i\uparrow} - \tfrac{1}{2} \right) \left( \hat{n}_{i\downarrow} - \tfrac{1}{2} \right)} = C \sum_{h_i = \pm 1} e^{\nu h_i \left( \hat{n}_{i\uparrow} - \hat{n}_{i\downarrow} \right)},
\end{equation}
where $C=\frac{1}{2} e^{-\frac{U \Delta\tau}{4}}$ and the constant $\nu$ is defined by
\begin{equation}
\label{eq:lambda}
\cosh \nu = e^{-\frac{U \Delta\tau}{2}}.
\end{equation}
The set of auxiliary variables $\lbrace h_i \rbrace$ is called the *Hubbard-Stratonovich field* or *configuration*. The variables $h_i$ take the values $\pm 1$ for a up- or down-spin, respectively. Using the Hubbard-Stratanovich transformation the interaction term can be formulated as
\begin{equation}
\begin{split}
\label{eq:hubbardStratanovichInteractionFull}
e^{-\Delta\tau V} &= \prod_{i=1}^N \left(C \sum_{h_i = \pm 1} e^{\nu h_i \left( \hat{n}_{i\uparrow} - \hat{n}_{i\downarrow} \right)}\right) \\
&= C^N \sum_{h_i = \pm 1} e^{\sum_{i=1}^N \nu h_i \left( \hat{n}_{i\uparrow} - \hat{n}_{i\downarrow} \right)} \\
&= C^N \text{Tr}_h e^{\sum_{i=1}^N \nu h_i \left( \hat{n}_{i\uparrow} - \hat{n}_{i\downarrow} \right)} \\
&= C^N \text{Tr}_h e^{\sum_{i=1}^N \nu h_i \hat{n}_{i\uparrow}} e^{-\sum_{i=1}^N \nu h_i \hat{n}_{i\downarrow}} \\
&= C^N \text{Tr}_h e^{V_\uparrow} e^{V_\downarrow}
\end{split}
\end{equation}
where
\begin{equation}
V_\sigma = \sum_{i=1}^N \nu h_i \hat{n}_{i\sigma} = \sigma \nu \boldsymbol{\hat{c}}_\sigma^\dagger V(h) \boldsymbol{\hat{c}}_\sigma
\end{equation}
and $V(h)$ is a diagonal matrix of the configurations $V(h) = \text{diag}(h_1, h_2, \dots, h_N)$. Taking into account the $L$ imaginary time slices, the Hubbard-Stratonovich variables are expanded to have two indices $h_{i, l}$, where $i$ represents the site index and $l$ the imaginary time slice:
\begin{equation}
h_i \longrightarrow h_{il}, \quad V(h) \longrightarrow V_l(h_l), \quad V_\sigma \longrightarrow V_{l\sigma}.
\end{equation}
The Hubbard-Stratonovich field or configuration now is a $N \times L$ matrix for a system of $N$ sites with $L$ time steps.
Therefore, the partition function can be approximated by
\begin{equation}
\label{eq:partitionApproximation} \tag{5}
\mathcal{Z} = \eta_d \text{Tr}_h \text{Tr} \left( \prod_{l=1}^L e^{-\Delta\tau K_\uparrow} e^{V_{l\uparrow}} \right) \left( \prod_{l=1}^L e^{-\Delta\tau K_\downarrow} e^{V_{l\downarrow}} \right),
\end{equation}
where $\eta_d = C^{NL}$ is a normalization constant. At this point, all operators are quadratic in the fermion operators. For any quadratic operator
\begin{equation}
H_l = \sum_{ij} \hat{c}_i^\dagger (H_l)_{ij} \hat{c}_j
\end{equation}
the trace can be computed via the a determinant:
\begin{equation}
\text{Tr}(e^{-H_1}e^{-H_2} \dots e^{-H_L}) = \det(I + e^{-H_L} e^{-H_{L-1}} \dots e^{-H_1} )
\end{equation}
Using this identity, the trace in the expression of the partition function \eqref{eq:partitionApproximation} can be turned into a computable form:
\begin{equation}
\label{eq:partitionComputable} \tag{6}
\mathcal{Z}_h = \eta_d \text{Tr}_h \det[M_\uparrow(h)] \det[M_\downarrow(h)],
\end{equation}
where for $\sigma = \pm1$ and $h=(h_1, h_2, \dots, h_L)$ the matrix
\begin{equation}
\label{eq:mMatrix} \tag{7}
M_\sigma(h) = I + B_{L,\sigma}(h_L) B_{L-1,\sigma}(h_{L-1}) \dots B_{1,\sigma}(h_1)
\end{equation}
consist of the time step matrices $B_{l,\sigma}(h_l)$, which are associated with the operators $e^{-\Delta\tau K_\sigma} e^{V_{l\sigma}}$:
\begin{equation}
\label{eq:bMatrix}
B_{l,\sigma}(h_l) = e^{-\Delta\tau K_\sigma} e^{\sigma \nu V_l(h_l)}.
\end{equation}
With the approximation \eqref{eq:partitionComputable} the distribution operator $\mathcal{P}$, defined in \eqref{eq:distop}, can be expressed as the computable approximation
\begin{equation}
\label{eq:distopComputable} \tag{8}
\mathcal{P}(h) = \frac{\eta_d}{\mathcal{Z}_h} \det[M_\uparrow(h)] \det[M_\downarrow(h)].
\end{equation}
The Green's function $G$ associated with the configuration $h$ is defined as the inverse of the matrix $M_\sigma(h)$:
\begin{equation}
G_\sigma(h) = \left[M_\sigma(h)\right]^{-1}
\end{equation}
## 3 Determinant Quantum Monte Carlo algorithm
The simulation of the Hubbard model is a classical Monte Carlo problem. The Hubbard-Stratanovich variables or configurations $h$ are sampled such that the follow the probability distribution $\mathcal{P}(h)$. The determinant QMC (DQMC) algorithm can be summarized by the following steps:
First, the configuration $h$ is initialized with an array of randomly distributed values of $\pm 1$. Starting from the time slice $l=1$, a change in the Hubbard-Stratanovich field on the lattice site $i=1$ is proposed:
\begin{equation}
h^\prime_{1, 1} = -h_{1, 1}.
\end{equation}
With the new configuration $h^\prime$ the Metropolis ratio
\begin{equation}
d_{1, 1} = \frac{\det[M_\uparrow(h^\prime)] \det[M_\downarrow(h^\prime)]}{\det[M_\uparrow(h)] \det[M_\downarrow(h)]},
\end{equation}
can be computed. A random number generator is then used to sample a uniformly distributed random number $r$. If $r < d_{1, 1}$, the proposed update to the configuration is accepted:
\begin{equation}
h = h^\prime.
\end{equation}
After all lattice sites $i = 1, \dots, N$ of the imaginary time slice $l=1$ have been updated, the procedure is continued with the next time slice $l=2$ until all imaginary time slices $l=1, \dots, L$ are updated. This concludes one \emph{sweep} through the Hubbard-Stratanovich field. After a few hundred "warmup-sweeps" have been performed, measurements can be made after completing an entire set of updates to all space-time points of the system (see section \ref{sec:measurements}). The measurement results have to be normalized with the number of "measurement-sweeps". One iteration (sweep) of the DQMC algorithm can be summarized as
1. Set $l=1$ and $i=1$
2. Propose new coonfiguration $h^\prime$ by flipping spin:
\begin{equation}
h^\prime_{i, l} = -h_{i, l}.
\end{equation}
3. Compute Metropolis ratio:
\begin{equation}
d_{i, l} = \frac{\det[M_\uparrow(h^\prime)] \det[M_\downarrow(h^\prime)]}{\det[M_\uparrow(h)] \det[M_\downarrow(h)]},
\end{equation}
where
\begin{equation}
M_\sigma(h) = I + B_{l-1,\sigma} \dots B_{1, \sigma} B_{L,\sigma}B_{L-1,\sigma} \dots B_{l,\sigma}.
\end{equation}
4. Sample random number $r$
5. Accept new configuration, if $r < d_{i, l}$:
\begin{equation}
h_{i, l} = \begin{cases} h^\prime_{i, l} &\text{if } r < d_{i, l} \\
h_{i, l} &\text{else }
\end{cases}
\end{equation}
6. Increment site $i = i+1$ if $i < N$
7. Increment time slice $l = l+1$ if $i=N$
### 3.1 Rank-one update scheme
The one-site update of the inner DQMC loop leads to a simple rank-one update of the matrix $M_\sigma(h)$, which leads to an efficient method of computing the Metropolis ratio $d_{i,l}$ and Green's function $G_\sigma$.
The DQMC simulation requires the computation of $NL$ Metropolis ratios
\begin{equation}
d = \frac{\det[M_\uparrow(h^\prime)] \det[M_\downarrow(h^\prime)]}{\det[M_\uparrow(h)] \det[M_\downarrow(h)]}
\end{equation}
for the configurations $h = (h_1, h_2, \dots, h_l)$ and $h^\prime = (h^\prime_1, h^\prime_2, \dots, h^\prime_L)$ per sweep. The matrix $M_\sigma(h)$, defined in \eqref{eq:mMatrix}, is given by
\begin{equation}
M_\sigma = I + B_{L,\sigma} B_{L-1,\sigma} \dots B_{1,\sigma}.
\end{equation}
with the time step matrices
\begin{equation}
B_{l,\sigma} = e^{-\Delta\tau K_\sigma} e^{\sigma \nu V_l(h_l)}.
\end{equation}
The Green's function of the configuration $h$ is defined as
\begin{equation}
G_\sigma(h) = M_\sigma^{-1}.
\end{equation}
The elements of the configuration $h$ and $h^\prime$ differ only by one element at a specific time slice $l$ and spatial site $i$, which gets inverted by a proposed update:
\begin{equation}
h^\prime_{i,l} = - h_{i, l}.
\end{equation}
During one sweep of the QMC iteration the inner loops run over the $l=1, \dots, L$ imaginary time slices and $i=1, \dots, N$ lattice sites. Starting with the first time slice, $l=1$, the Metropolis ratio $d_{i, 1}$ for each lattice site $i$ is given by
\begin{equation}
d_{i, 1} = d_\uparrow d_\downarrow,
\end{equation}
where for $\sigma = \pm 1$
\begin{equation}
d_\sigma = 1 + \alpha_{i,\sigma} \left[ 1 - \boldsymbol{e}_i^T M_\sigma^{-1}(h) \boldsymbol{e}_i \right] = 1 + \alpha_{i, \sigma} \left[ 1 - G_{ii}^\sigma(h) \right]
\end{equation}
and
\begin{equation}
\alpha_{i,\sigma} = e^{-2\sigma \nu h_{i,1}} - 1.
\end{equation}
The Metropolis ration $d_{i, 1}$ can therefore be obtained by computing the inverse of the matrix $M_\sigma(h)$, which corresponds to the Green's function $G_\sigma(h)$. If $G_\sigma(h)$ has already been computed in a previous step, then it is essentially free to compute the Metropolis ratio.\\
If the proposed update $h^\prime$ to the configuration is accepted, the Green's function needs to be updated by a rank-1 matrix update:
\begin{equation}
G_\sigma(h^\prime) = G_\sigma(h) - \frac{\alpha_{i, \sigma}}{d_{i, 1}} \boldsymbol{u}_\sigma \boldsymbol{w}_\sigma^T,
\end{equation}
where
\begin{equation}
\boldsymbol{u}_\sigma = \left[I - G_\sigma(h)\right] \boldsymbol{e}_i, \qquad \boldsymbol{w}_\sigma = \left[G_\sigma(h)\right]^T \boldsymbol{e}_i.
\end{equation}
After all spatial sites $i=1, \dots, N$ have been updated, we can move to the next time slice $l=2$. The matrices $M_\sigma(h)$ and $M_\sigma(h^\prime)$ can be written as
\begin{equation}
\begin{split}
M_\sigma(h) &= B_{1, \sigma}^{-1}(h_1) \hat{M}_\sigma(h) B_{1, \sigma}(h_1)\\
M_\sigma(h^\prime) &= B_{1, \sigma}^{-1}(h_1^\prime) \hat{M}_\sigma(h^\prime) B_{1, \sigma}(h_1^\prime)
\end{split}
\end{equation}
where
\begin{equation}
\begin{split}
\hat{M}_\sigma(h) &= I + B_{1, \sigma}(h_1) B_{L, \sigma}(h_L) B_{L-1, \sigma}(h_{L-1}) \dots B_{2, \sigma}(h_2)\\
\hat{M}_\sigma(h^\prime) &= I + B_{1, \sigma}(h_1^\prime) B_{L, \sigma}(h_L^\prime) B_{L-1, \sigma}(h_{L-1}^\prime) \dots B_{2, \sigma}(h_2^\prime)
\end{split}
\end{equation}
are obtained by a cyclic permutation of the time step matrices $B_{l,\sigma}(h_l)$. The Metropolis ratios $d_{i, 2}$ corresponding to the time slice $l=2$ can therefore be written as
\begin{equation}
d_{i,2} = \frac{\det\big[M_\uparrow(h^\prime)\big] \det\big[M_\downarrow(h^\prime)\big]}{\det\big[M_\uparrow(h)\big] \det\big[M_\downarrow(h)\big]}
= \frac{\det\big[\hat{M}_\uparrow(h^\prime)\big] \det\big[\hat{M}_\downarrow(h^\prime)\big]}{\det\big[\hat{M}_\uparrow(h)\big] \det\big[\hat{M}_\downarrow(h)\big]}.
\end{equation}
The associated Green's functions are given by "wrapping":
\begin{equation}
\hat{G}_\sigma(h) = B^{-1}_{1,\sigma}(h_1) G_\sigma(h) B_{1,\sigma}(h_1).
\end{equation}
Wrapping the Green's function ensures that the configurations $h_2$ and $h_2^\prime$ associated with the time slice $l=2$ appear at the same location of the matrices $\hat{M}_\sigma(h)$ and $\hat{M}_\sigma(h^\prime)$ as the configurations $h_1$ and $h_1^\prime$ at the time slice $l=1$. Therefore the same formulation can be used for the time slice $l=2$ as for the time slice $l=1$ to compute the Metropolis ratio and update the Green's functions. This procedure can be repeated for all the remaining time slices $l=3, 4, \dots, L$.
|
github_jupyter
|
```
import os.path
from collections import Counter
from glob import glob
import inspect
import os
import pickle
import sys
from cltk.corpus.latin.phi5_index import PHI5_INDEX
from cltk.corpus.readers import get_corpus_reader
from cltk.stem.latin.j_v import JVReplacer
from cltk.stem.lemma import LemmaReplacer
from cltk.tokenize.latin.sentence import SentenceTokenizer
from cltk.tokenize.word import WordTokenizer
from random import sample
from tqdm import tqdm
from typing import List, Dict, Tuple
currentdir = os.path.dirname(os.path.abspath(inspect.getfile(inspect.currentframe())))
parentdir = os.path.dirname(currentdir)
sys.path.insert(0,parentdir)
from mlyoucanuse.aeoe_replacer import AEOEReplacer
from mlyoucanuse.text_cleaners import ( normalize_accents, disappear_angle_brackets,
drop_punct, disappear_round_brackets,
truecase, dehyphenate, accept_editorial,
swallow_braces, swallow_obelized_words,
swallow_square_brackets)
import cltk
cltk.__version__
```
## Text Cleaning
from http://udallasclassics.org/wp-content/uploads/maurer_files/APPARATUSABBREVIATIONS.pdf
[...] Square brackets, or in recent editions wavy brackets ʺ{...}ʺ, enclose words etc. that an editor thinks should be deleted (see ʺdel.ʺ) or marked as out of place (see ʺsecl.ʺ).
[...] Square brackets in a papyrus text, or in an inscription, enclose places where words have been lost through physical damage. If this happens in mid-line, editors use ʺ[...]ʺ. If only the end of the line is missing, they use a single bracket ʺ[...ʺ If the lineʹs beginning is missing, they use ʺ...]ʺ Within the brackets, often each dot represents one missing letter.
[[...]] Double brackets enclose letters or words deleted by the medieval copyist himself.
(...) Round brackets are used to supplement words abbreviated by the original copyist; e.g. in an inscription: ʺtrib(unus) mil(itum) leg(ionis) IIIʺ
<...> diamond ( = elbow = angular) brackets enclose words etc. that an editor has added (see ʺsuppl.ʺ)
† An obelus (pl. obeli) means that the word(s etc.) is very plainly corrupt, but the editor cannot see how to emend. If only one word is corrupt, there is only one obelus, which precedes the word; if two or more words are corrupt, two obeli enclose them. (Such at least is the rule--but that rule is often broken, especially in older editions, which sometimes dagger several words using only one obelus.) To dagger words in this way is to ʺobelizeʺ them.
## Load/Build Truecasing dictionary; count all cased tokens, use to normalize cases later
```
truecase_file = 'truecase_counter.latin.pkl'
if os.path.exists(truecase_file):
with open(truecase_file, 'rb') as fin:
case_counts = pickle.load(fin)
else:
tesserae = get_corpus_reader(corpus_name='latin_text_tesserae', language='latin')
case_counts = Counter()
jv_replacer = JVReplacer()
aeoe_replacer = AEOEReplacer()
toker = WordTokenizer('latin')
sent_toker = SentenceTokenizer()
lemmatizer = LemmaReplacer('latin')
for file in tqdm(tesserae.fileids(), total=len(tesserae.fileids())):
for sent in tesserae.sents(file):
sent = aeoe_replacer.replace(jv_replacer.replace(drop_punct(sent)))
sent = normalize_accents(sent)
sent = accept_editorial(sent)
for token in toker.tokenize(sent):
case_counts.update({token:1})
with open(truecase_file, 'wb') as fout:
pickle.dump(case_counts, fout)
len(case_counts)
# 344393, 322711
# 318451
# 316722
# 311399
# 310384
# 310567
# 309529
print(sample(list(case_counts.items()), 25))
def get_word_counts(files:List[str])->Tuple[Dict[str, int], Dict[str, int]]:
"""
Given a list of files,
clean & tokenize the documents
return Counters for:
lemmatized words in the documents
inflected words in the documents
"""
word_counter = Counter()
inflected_word_counter = Counter()
jv_replacer = JVReplacer()
aeoe_replacer = AEOEReplacer()
toker = WordTokenizer('latin')
sent_toker = SentenceTokenizer()
lemmatizer = LemmaReplacer('latin')
for file in tqdm(files , total=len(files), unit='files'):
with open(file, 'rt') as fin:
text = fin.read()
text = text.replace("-\n", "")
text = text.replace("\n", " ")
text = aeoe_replacer.replace(jv_replacer.replace( text))
for sent in sent_toker.tokenize(text):
sent = dehyphenate(sent) # because it's Phi5
sent = swallow_braces(sent)
sent = swallow_square_brackets(sent)
sent = disappear_round_brackets(sent)
sent = swallow_obelized_words(sent)
sent = disappear_angle_brackets(sent)
sent = drop_punct(sent)
sent = normalize_accents(sent)
# lemmatizer prefers lower
# sent = lemmatizer.lemmatize(sent.lower(), return_string=True)
for word in toker.tokenize(sent):
if word.isnumeric():
continue
inflected_word_counter.update({truecase(word, case_counts):1})
word = lemmatizer.lemmatize(word.lower(), return_string=True)
# normalize capitals
word_counter.update({truecase(word, case_counts) : 1})
return word_counter, inflected_word_counter
def word_stats(author:str, lemma_counter:Counter,
inflected_counter:Counter)->Tuple[float, float]:
"""
"""
nw = sum(lemma_counter.values())
print(f"Total count of all tokens in {author} corpus: {nw:,}")
print(f"Total number of distinct inflected words/tokens in {author} corpus: {len(inflected_counter):,}")
print(f"Total number of lemmatized words/tokens in {author} corpus {len(lemma_counter):,}")
ciw1 = sum([1 for key, val in inflected_counter.items() if val == 1])
print(f"Count of inflected tokens only occuring once {ciw1:,}")
cw1 = sum([1 for key, val in lemma_counter.items() if val == 1])
print(f"Count of lemmatized tokens only occuring once {cw1:,}")
Piu_one = ciw1 / nw
print(f"Probability of a single count unigram occuring in the {author} corpus: {Piu_one:.3f}")
Plu_one = cw1 / nw
print(f"Probability of a single count unigram in the lemmatized {author} corpus: {Plu_one:.3f}")
return (Piu_one, Plu_one)
# Cicero works
cicero_files = glob(f"{os.path.expanduser('~')}/cltk_data/latin/text/phi5/individual_works/LAT0474.TXT-0*.txt")
len (cicero_files)
cicero_lemmas, cicero_inflected_words = get_word_counts(cicero_files)
word_stats(author='Cicero',
lemma_counter=cicero_lemmas,
inflected_counter=cicero_inflected_words)
cicero_lemmas_counter_file = 'cicero_lemmas_counter.pkl'
cicero_inflected_counter_file = 'cicero_inflected_counter.pkl'
if not os.path.exists(cicero_lemmas_counter_file):
with open(cicero_lemmas_counter_file, 'wb') as fout:
pickle.dump(cicero_lemmas, fout)
if not os.path.exists(cicero_inflected_counter_file):
with open(cicero_inflected_counter_file, 'wb') as fout:
pickle.dump(cicero_inflected_words, fout)
author_index = {val:key for key,val in PHI5_INDEX.items()
if val != 'Marcus Tullius Cicero, Cicero, Tully'}
def get_phi5_author_files(author_name, author_index):
stub = author_index[author_name]
return glob(os.path.expanduser(f'~/cltk_data/latin/text/phi5/individual_works/{stub}*.txt'))
```
## Visualization of our corpus comparison:
If you took one page from one author and placed it into Cicero, how surprising would it be?
If the other author's vocabulary was substantially different, it would be noticeable. We can quantify this.
As a result, since we want to predict as close as possible to the author, we should only train a language model where the underlying corpus vocabularies are within a reasonable window of surprise.
```
results = []
for author in author_index:
files = get_phi5_author_files(author, author_index)
# cicero_lemmas, cicero_inflected_words = get_word_counts(cicero_files)
author_lemmas, author_inflected_words = get_word_counts(files)
author_words = set(author_lemmas.keys())
cicero_words = set(cicero_lemmas.keys())
common = author_words & cicero_words
author_uniq = author_words - common
P_one_x_lemma_unigram = len(author_uniq) / sum(author_lemmas.values())
author_words = set(author_inflected_words.keys())
cicero_words = set(cicero_inflected_words.keys())
common = author_words & cicero_words
author_uniq = author_words - common
P_one_x_inflected_unigram = len(author_uniq) / sum(author_inflected_words.values())
results.append((author, P_one_x_lemma_unigram, P_one_x_inflected_unigram ))
# sorted(results, key=lambda x:x[1])
results_map = {key: (val, val2) for key,val,val2 in results}
for author in author_index:
files = get_phi5_author_files(author, author_index)
if len(files) >= 3:
print(author, results_map[author])
# the values analogous to Cicero are: (0.02892407263780054, 0.008905886443261747)
# grab prose authors
# grab poets
# consider individual files
# Gaius Iulius Caesar, Caesar (0.016170899832329378, 0.0464137117307334)
# Apuleius Madaurensis (0.039956560814859196, 0.12101183343319354)
# Caelius Apicius (0.04383594547528974, 0.09950159130486999)
# Anonymi Comici et Tragici (0.05979473449352968, 0.10397144132083891)
# C. Iul. Caes. Augustus Octavianus (0.16793743890518084, 0.20527859237536658)
# Publius Papinius Statius (0.03662215849687846, 0.1022791767482152)
# Lucius Accius (0.0845518118245391, 0.16634880271243907)
# Gaius Caesius Bassus (0.040359504832965916, 0.07953196540613872)
# Publius Vergilius Maro, Virgil, Vergil (0.03315200072836527, 0.0929348568307006)
# Publius Ovidius Naso (0.023965644822556705, 0.06525858344775079)
# Gnaeus Naevius (0.11655300681959083, 0.20644761314321142)
# Fragmenta Bobiensia (0.07398076042143839, 0.1385707741639945)
# Scriptores Historiae Augustae (0.03177853760216489, 0.071072022819111)
# Publius Terentius Afer, Terence (0.028577576089507863, 0.058641733823644474)
# Aulus Cornelius Celsus (0.017332921313593843, 0.0558848592109822)
# Gaius Suetonius Tranquillus (0.033629947836759745, 0.0958944461491255)
# Marcus Terentius Varro, Varro (0.045866176600832524, 0.093891152245151)
# Appendix Vergiliana (0.0500247341083354, 0.1418501113034875)
# Annius Florus (0.038297569987210456, 0.09140969162995595)
# Pomponius Porphyrio (0.04030915576694411, 0.09312987184568636)
# Marcus Valerius Probus (0.03835521769177609, 0.08431237042156185)
# Quintus Ennius (0.05652467883705206, 0.12021636240703178)
# Didascaliae et Per. in Terentium (0.0782967032967033, 0.13598901098901098)
# Cornelius Tacitus (0.02469418086200983, 0.07631488690859423)
# Titus Livius, Livy (0.011407436246836674, 0.03913716547549524)
# Lucius Annaeus Seneca senior (0.01619733327917297, 0.052095498258405856)
# Quintus Horatius Flaccus, Horace (0.04486396446418656, 0.12253192670738479)
# Gaius Asinius Pollio (0.03592814371257485, 0.08982035928143713)
# Gaius Sallustius Crispus (0.020570966643975494, 0.059330326752893126)
# C. Plinius Caecilius Secundus, Pliny (0.01694301397770358, 0.06551977816761927)
# Marcus Fabius Quintilianus (0.009342494688624445, 0.0416682017463066)
# Hyginus Gromaticus (0.0285692634131555, 0.08320703243407093)
# Titus Lucretius Carus (0.022190184885737107, 0.06787585965048998)
# Claudius Caesar Germanicus (0.04035804020100502, 0.12861180904522612)
# Gaius, iur., Gaius (0.011268643689753487, 0.035144203727768185)
# Quintus Terentius Scaurus (0.04715169618092597, 0.09174311926605505)
# Lucius Livius Andronicus (0.14615384615384616, 0.25)
# Marcus Cornelius Fronto (0.03605195520469984, 0.08350927115843583)
# Didascaliae et Argum. in Plautum (0.07712590639419907, 0.14831905075807514)
# Argum. Aen. et Tetrast. (0.07066381156316917, 0.1441827266238401)
# Anonymi Epici et Lyrici (0.09684487291849254, 0.19237510955302367)
# Marcus Porcius Cato, Cato (0.061287538049157236, 0.13079823724501385)
# Sextus Iulius Frontinus (0.03041633518960488, 0.09337045876425351)
# Lucius Annaeus Seneca iunior (0.012655345175352984, 0.05447654369184723)
# Titus Maccius Plautus (0.02682148990105487, 0.062141513731995376)
# Maurus Servius Honoratus, Servius (0.025347881711764008, 0.05923711189138313)
# Quintus Asconius Pedianus (0.010382059800664452, 0.029663028001898434)
```
|
github_jupyter
|
```
from __future__ import print_function
import numpy as np
np.random.seed(1337) # for reproducibility
import keras
from keras.datasets import mnist
from keras.models import Sequential
from keras.layers import Dense, Dropout, Activation, Flatten
from keras.layers import Convolution2D, MaxPooling2D
from keras.utils import np_utils
from keras import backend as K
```
Preprocess data
```
nb_classes = 10
# input image dimensions
img_rows, img_cols = 28, 28
# number of convolutional filters to use
nb_filters = 32
# size of pooling area for max pooling
pool_size = (2, 2)
# convolution kernel size
kernel_size = (3, 3)
# the data, shuffled and split between train and test sets
(X_train, y_train), (X_test, y_test) = mnist.load_data()
if K.image_dim_ordering() == 'th':
X_train = X_train.reshape(X_train.shape[0], 1, img_rows, img_cols)
X_test = X_test.reshape(X_test.shape[0], 1, img_rows, img_cols)
input_shape = (1, img_rows, img_cols)
else:
X_train = X_train.reshape(X_train.shape[0], img_rows, img_cols, 1)
X_test = X_test.reshape(X_test.shape[0], img_rows, img_cols, 1)
input_shape = (img_rows, img_cols, 1)
X_train = X_train.astype('float32')
X_test = X_test.astype('float32')
X_train /= 255
X_test /= 255
print('X_train shape:', X_train.shape)
print(X_train.shape[0], 'train samples')
print(X_test.shape[0], 'test samples')
# convert class vectors to binary class matrices
Y_train = np_utils.to_categorical(y_train, nb_classes)
Y_test = np_utils.to_categorical(y_test, nb_classes)
```
Build a Keras model using the `Sequential API`
```
batch_size = 50
nb_epoch = 10
model = Sequential()
model.add(Convolution2D(nb_filters, kernel_size,
padding='valid',
input_shape=input_shape,
activation='relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Convolution2D(nb_filters, kernel_size,activation='relu'))
model.add(Dropout(rate=0.25))
model.add(Flatten())
model.add(Dense(64,activation='relu'))
model.add(Dropout(rate=5))
model.add(Dense(nb_classes,activation='softmax'))
model.compile(loss='categorical_crossentropy',
optimizer='adam',
metrics=['accuracy'])
model.summary()
```
Train and evaluate the model
```
model.fit(X_train[0:10000, ...], Y_train[0:10000, ...], batch_size=batch_size, epochs=nb_epoch,
verbose=1, validation_data=(X_test, Y_test))
score = model.evaluate(X_test, Y_test, verbose=0)
print('Test score:', score[0])
print('Test accuracy:', score[1])
```
Save the model
```
model.save('example_keras_mnist_model.h5')
```
|
github_jupyter
|
# Compute forcing for 1%CO2 data
```
import os
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
filedir1 = '/Users/hege-beatefredriksen/OneDrive - UiT Office 365/Data/CMIP5_globalaverages/Forcingpaperdata'
storedata = False # store anomalies in file?
storeforcingdata = False
createnewfile = False # if it is the first time this is run, new files should be created, that can later be loaded
exp = '1pctCO2'
filenameT = 'annualTanom_1pctCO2.txt'
filenameN = 'annualNanom_1pctCO2.txt'
filenameFF = 'forcing_F13method_1pctCO2.txt'
filenameNF = 'forcing_estimates_1pctCO2.txt'
# create file first time code is run:
if createnewfile == True:
cols = ['year','ACCESS1-0','ACCESS1-3','CanESM2','CCSM4','CNRM-CM5','CSIRO-Mk3-6-0','GFDL-CM3','GFDL-ESM2G','GFDL-ESM2M','GISS-E2-H','GISS-E2-R','HadGEM2-ES','inmcm4','IPSL-CM5A-LR','IPSL-CM5B-LR','MIROC-ESM','MIROC5','MPI-ESM-LR','MPI-ESM-MR','MRI-CGCM3','NorESM1-M']
dfT = pd.DataFrame(np.full((140, len(cols)),'-'), columns = cols); dfT['year'] = np.arange(1,140+1)
dfN = pd.DataFrame(np.full((140, len(cols)),'-'), columns = cols); dfN['year'] = np.arange(1,140+1)
dfT.to_csv(filenameT, sep='\t'); dfN.to_csv(filenameN, sep='\t');
dfFF = pd.DataFrame(np.full((140, len(cols)),'-'), columns = cols); dfFF['year'] = np.arange(1,140+1)
dfNF = pd.DataFrame(np.full((140, len(cols)),'-'), columns = cols); dfNF['year'] = np.arange(1,140+1)
dfFF.to_csv(filenameFF, sep='\t'); dfNF.to_csv(filenameNF, sep='\t');
#model = 'ACCESS1-0'
#model = 'ACCESS1-3'
#model = 'CanESM2'
#model = 'CCSM4'
#model = 'CNRM-CM5'
#model = 'CSIRO-Mk3-6-0'
#model = 'GFDL-CM3'
#model = 'GFDL-ESM2G' # 1pctco2 only for 70 years
#model = 'GFDL-ESM2M' # 1pctco2 only for 70 years
#model = 'GISS-E2-H'
#model = 'GISS-E2-R'
#model = 'HadGEM2-ES'
#model = 'inmcm4'
#model = 'IPSL-CM5A-LR'
#model = 'IPSL-CM5B-LR'
#model = 'MIROC-ESM'
#model = 'MIROC5'
#model = 'MPI-ESM-LR'
#model = 'MPI-ESM-MR'
#model = 'MRI-CGCM3'
model = 'NorESM1-M'
realm = 'Amon'
ensemble = 'r1i1p1'
## define time periods of data:
if model == 'ACCESS1-0':
controltimeperiod = '030001-079912'
exptimeperiod = '030001-043912'
control_branch_yr = 300
elif model == 'ACCESS1-3':
controltimeperiod = '025001-074912'
exptimeperiod = '025001-038912'
control_branch_yr = 250
elif model == 'CanESM2':
controltimeperiod = '201501-301012'
exptimeperiod = '185001-198912'
control_branch_yr = 2321
elif model == 'CCSM4':
controltimeperiod = '025001-130012'
exptimeperiod = '185001-200512'
control_branch_yr = 251
elif model == 'CNRM-CM5':
controltimeperiod = '185001-269912'
exptimeperiod = '185001-198912'
control_branch_yr = 1850
elif model == 'CSIRO-Mk3-6-0':
controltimeperiod = '000101-050012'
exptimeperiod = '000101-014012'
control_branch_yr = 104
elif model == 'GFDL-CM3':
controltimeperiod = '000101-050012'
exptimeperiod = '000101-014012'
control_branch_yr = 1
elif model == 'GFDL-ESM2G' or model == 'GFDL-ESM2M':
controltimeperiod = '000101-050012'
exptimeperiod = '000101-020012' # 1pctco2 only for 70 years.
control_branch_yr = 1
elif model == 'GISS-E2-H':
print(model + 'has control run for two different periods')
#controltimeperiod = '118001-141912'
controltimeperiod = '241001-294912'
exptimeperiod = '185001-200012'
control_branch_yr = 2410
elif model == 'GISS-E2-R':
#controltimeperiod = '333101-363012'
#controltimeperiod1 = '398101-453012'
controltimeperiod2 = '398101-920512'
exptimeperiod = '185001-200012'
control_branch_yr = 3981
# Note: The two blocks of years that are present (3331-3630 and 3981-4530) represent different control runs
elif model == 'HadGEM2-ES':
controltimeperiod = '186001-243511'
exptimeperiod = '186001-199912'
control_branch_yr = 1860 # or actually december 1859, but I ignore this first month is the annual average
elif model == 'inmcm4':
controltimeperiod = '185001-234912'
exptimeperiod = '209001-222912'
control_branch_yr = 2090
elif model == 'IPSL-CM5A-LR':
controltimeperiod = '180001-279912'
exptimeperiod = '185001-198912'
control_branch_yr = 1850
elif model == 'IPSL-CM5B-LR':
controltimeperiod = '183001-212912'
exptimeperiod = '185001-200012'
control_branch_yr = 1850
elif model == 'MIROC-ESM':
controltimeperiod = '180001-242912'
exptimeperiod = '000101-014012'
control_branch_yr = 1880
elif model == 'MIROC5':
controltimeperiod = '200001-286912'
exptimeperiod = '220001-233912'
control_branch_yr = 2200
elif model == 'MPI-ESM-LR':
controltimeperiod = '185001-284912'
exptimeperiod = '185001-199912'
control_branch_yr = 1880
elif model == 'MPI-ESM-MR':
controltimeperiod = '185001-284912'
exptimeperiod = '185001-199912'
control_branch_yr = 1850
elif model == 'MRI-CGCM3':
controltimeperiod = '185101-235012'
exptimeperiod = '185101-199012'
control_branch_yr = 1891
elif model == 'NorESM1-M':
controltimeperiod = '070001-120012'
exptimeperiod = '000101-014012'
control_branch_yr = 700
#### load 1pctCO2 data ####
var = 'tas' # temperatures
strings = [var, realm, model, exp, ensemble, exptimeperiod]
filename = 'glannual_' + "_".join(strings) + '.txt'
file = os.path.join(filedir1, model, exp, filename)
datatable = pd.read_table(file, header=None,sep=" ")
temp=datatable.iloc[0:len(datatable),0]
var = 'rlut' # rlut
strings = [var, realm, model, exp, ensemble, exptimeperiod]
filename = 'glannual_' + "_".join(strings) + '.txt'
file = os.path.join(filedir1, model, exp, filename)
datatable = pd.read_table(file, header=None,sep=" ")
rlut=datatable.iloc[0:len(datatable),0]
var = 'rsut' # rsut
strings = [var, realm, model, exp, ensemble, exptimeperiod]
filename = 'glannual_' + "_".join(strings) + '.txt'
file = os.path.join(filedir1, model, exp, filename)
datatable = pd.read_table(file, header=None,sep=" ")
rsut=datatable.iloc[0:len(datatable),0]
var = 'rsdt' # rsdt
strings = [var, realm, model, exp, ensemble, exptimeperiod]
filename = 'glannual_' + "_".join(strings) + '.txt'
file = os.path.join(filedir1, model, exp, filename)
datatable = pd.read_table(file, header=None,sep=" ")
rsdt=datatable.iloc[0:len(datatable),0]
# drop all data after 140 years
temp = temp[:140]; rlut = rlut[:140]; rsut = rsut[:140]; rsdt = rsdt[:140]
###### load control run data ######
exp = 'piControl'
var = 'tas' # temperatures
if model == 'GISS-E2-R':
controltimeperiod = controltimeperiod2
strings = [var, realm, model, exp, ensemble, controltimeperiod]
filename = 'glannual_' + "_".join(strings) + '.txt'
file = os.path.join(filedir1, model, exp, filename)
datatable = pd.read_table(file, header=None,sep=" ")
controltemp=datatable.iloc[:,0]
var = 'rlut' # rlut
strings = [var, realm, model, exp, ensemble, controltimeperiod]
filename = 'glannual_' + "_".join(strings) + '.txt'
file = os.path.join(filedir1, model, exp, filename)
datatable = pd.read_table(file, header=None,sep=" ")
controlrlut=datatable.iloc[0:len(controltemp),0]
var = 'rsut' # rsut
strings = [var, realm, model, exp, ensemble, controltimeperiod]
filename = 'glannual_' + "_".join(strings) + '.txt'
file = os.path.join(filedir1, model, exp, filename)
datatable = pd.read_table(file, header=None,sep=" ")
controlrsut=datatable.iloc[0:len(controltemp),0]
var = 'rsdt' # rsdt
strings = [var, realm, model, exp, ensemble, controltimeperiod]
filename = 'glannual_' + "_".join(strings) + '.txt'
file = os.path.join(filedir1, model, exp, filename)
datatable = pd.read_table(file, header=None,sep=" ")
controlrsdt=datatable.iloc[0:len(controltemp),0]
years = np.arange(1,len(temp)+1)
# create figure
fig, ax = plt.subplots(nrows=2,ncols=2,figsize = [16,10])
# plot temperature
var = temp[:]; label = 'tas'
ax[0,0].plot(years,var,linewidth=2,color = "black")
#ax[0,0].set_xlabel('t',fontsize = 18)
ax[0,0].set_ylabel(label + '(t)',fontsize = 18)
ax[0,0].set_title('1pctCO2 ' + label,fontsize = 18)
ax[0,0].grid()
ax[0,0].set_xlim(min(years),max(years))
ax[0,0].tick_params(axis='both',labelsize=18)
# plot rlut
var = rlut[:]; label = 'rlut'
ax[0,1].plot(years,var,linewidth=2,color = "black")
#ax[0,1].set_xlabel('t',fontsize = 18)
ax[0,1].set_ylabel(label + '(t)',fontsize = 18)
ax[0,1].set_title('1pctCO2 ' + label,fontsize = 18)
ax[0,1].grid()
ax[0,1].set_xlim(min(years),max(years))
ax[0,1].tick_params(axis='both',labelsize=18)
# plot rsdt
var = rsdt[:]; label = 'rsdt'
ax[1,0].plot(years,var,linewidth=2,color = "black")
ax[1,0].set_xlabel('t',fontsize = 18)
ax[1,0].set_ylabel(label + '(t)',fontsize = 18)
ax[1,0].set_title('1pctCO2 ' + label,fontsize = 18)
ax[1,0].grid()
ax[1,0].set_xlim(min(years),max(years))
ax[1,0].tick_params(axis='both',labelsize=18)
# plot rsut
var = rsut[:]; label = 'rsut'
ax[1,1].plot(years,var,linewidth=2,color = "black")
ax[1,1].set_xlabel('t',fontsize = 18)
ax[1,1].set_ylabel(label + '(t)',fontsize = 18)
ax[1,1].set_title('1pctCO2 ' + label,fontsize = 18)
ax[1,1].grid()
ax[1,1].set_xlim(min(years),max(years))
ax[1,1].tick_params(axis='both',labelsize=18)
# plot control run data and linear trends
controlyears = np.arange(0,len(controltemp))
branchindex = control_branch_yr - int(controltimeperiod[0:4])
print(branchindex)
# create figure
fig, ax = plt.subplots(nrows=2,ncols=2,figsize = [16,10])
# plot temperature
var = controltemp[:]; label = 'tas'
ax[0,0].plot(controlyears,var,linewidth=2,color = "black")
# find linear fits to control T and nettoarad in the same period as exp:
p1 = np.polyfit(controlyears[branchindex:(branchindex + len(temp))], controltemp[branchindex:(branchindex + len(temp))], deg = 1)
lintrendT = np.polyval(p1,controlyears[branchindex:(branchindex + len(temp))])
ax[0,0].plot(controlyears[branchindex:(branchindex + len(temp))], lintrendT, linewidth = 4)
ax[0,0].set_ylabel(label + '(t)',fontsize = 18)
ax[0,0].set_title('Control ' + label,fontsize = 18)
ax[0,0].grid()
ax[0,0].set_xlim(min(controlyears),max(controlyears))
ax[0,0].tick_params(axis='both',labelsize=18)
# plot rlut
var = controlrlut[:]; label = 'rlut'
ax[0,1].plot(controlyears,var,linewidth=2,color = "black")
p2 = np.polyfit(controlyears[branchindex:(branchindex + len(temp))], controlrlut[branchindex:(branchindex + len(temp))], deg = 1)
lintrend_rlut = np.polyval(p2,controlyears[branchindex:(branchindex + len(temp))])
ax[0,1].plot(controlyears[branchindex:(branchindex + len(temp))], lintrend_rlut, linewidth = 4)
ax[0,1].set_ylabel(label + '(t)',fontsize = 18)
ax[0,1].set_title('Control ' + label,fontsize = 18)
ax[0,1].grid()
ax[0,1].set_xlim(min(controlyears),max(controlyears))
ax[0,1].tick_params(axis='both',labelsize=18)
# plot rsdt
var = controlrsdt[:]; label = 'rsdt'
ax[1,0].plot(controlyears,var,linewidth=2,color = "black")
p3 = np.polyfit(controlyears[branchindex:(branchindex + len(temp))], controlrsdt[branchindex:(branchindex + len(temp))], deg = 1)
lintrend_rsdt = np.polyval(p3,controlyears[branchindex:(branchindex + len(temp))])
ax[1,0].plot(controlyears[branchindex:(branchindex + len(temp))], lintrend_rsdt, linewidth = 4)
ax[1,0].set_xlabel('t',fontsize = 18)
ax[1,0].set_ylabel(label + '(t)',fontsize = 18)
ax[1,0].set_title('Control ' + label,fontsize = 18)
ax[1,0].grid()
ax[1,0].set_xlim(min(controlyears),max(controlyears))
ax[1,0].set_ylim(var[0]-2,var[0]+2)
ax[1,0].tick_params(axis='both',labelsize=18)
# plot rsut
var = controlrsut[:]; label = 'rsut'
ax[1,1].plot(controlyears,var,linewidth=2,color = "black")
p4 = np.polyfit(controlyears[branchindex:(branchindex + len(temp))], controlrsut[branchindex:(branchindex + len(temp))], deg = 1)
lintrend_rsut = np.polyval(p4,controlyears[branchindex:(branchindex + len(temp))])
ax[1,1].plot(controlyears[branchindex:(branchindex + len(temp))], lintrend_rsut, linewidth = 4)
ax[1,1].set_xlabel('t',fontsize = 18)
ax[1,1].set_ylabel(label + '(t)',fontsize = 18)
ax[1,1].set_title('Control ' + label,fontsize = 18)
ax[1,1].grid()
ax[1,1].set_xlim(min(controlyears),max(controlyears))
ax[1,1].tick_params(axis='both',labelsize=18)
nettoarad = rsdt - rsut - rlut
controlnettoarad = controlrsdt - controlrsut - controlrlut
lintrendN = lintrend_rsdt - lintrend_rsut - lintrend_rlut
deltaN = nettoarad - lintrendN
deltaT = temp - lintrendT
# create figure
fig, ax = plt.subplots(nrows=1,ncols=2,figsize = [16,5])
# plot 1pctCO2 net TOA rad
var = nettoarad[:]; label = 'net TOA rad'
ax[0,].plot(years,var,linewidth=2,color = "black")
ax[0,].set_xlabel('t',fontsize = 18)
ax[0,].set_ylabel(label + '(t)',fontsize = 18)
ax[0,].set_title('1pctCO2 ' + label,fontsize = 18)
ax[0,].grid()
ax[0,].set_xlim(min(years),max(years))
ax[0,].tick_params(axis='both',labelsize=18)
# plot control net TOA rad
var = controlnettoarad[:]; label = 'net TOA rad'
ax[1,].plot(controlyears,var,linewidth=2,color = "black")
ax[1,].plot(controlyears[branchindex:(branchindex + len(temp))],lintrendN,linewidth=4)
ax[1,].set_xlabel('t',fontsize = 18)
ax[1,].set_ylabel(label + '(t)',fontsize = 18)
ax[1,].set_title('Control ' + label,fontsize = 18)
ax[1,].grid()
ax[1,].set_xlim(min(controlyears),max(controlyears))
ax[1,].tick_params(axis='both',labelsize=18)
########### plot also anomalies: ###########
# create figure
fig, ax = plt.subplots(nrows=1,ncols=1,figsize = [8,5])
var = deltaN; label = 'net TOA rad'
ax.plot(years,var,linewidth=2,color = "black")
ax.set_xlabel('t',fontsize = 18)
ax.set_ylabel(label + '(t)',fontsize = 18)
ax.set_title('1pctCO2 ' + label + ' anomaly',fontsize = 18)
ax.grid()
ax.set_xlim(min(years),max(years))
ax.tick_params(axis='both',labelsize=18)
# write time series to a dataframe?
if storedata == True:
dfT = pd.read_table(filenameT, index_col=0); dfN = pd.read_table(filenameN, index_col=0); # load files
dfT[model] = deltaT; dfN[model] = deltaN
dfT.to_csv(filenameT, sep='\t'); dfN.to_csv(filenameN, sep='\t') # save files again
```
## Load my estimated parameters
```
filename = 'best_estimated_parameters.txt'
parameter_table = pd.read_table(filename,index_col=0)
GregoryT2x = parameter_table.loc[model,'GregoryT2x']
GregoryF2x = parameter_table.loc[model,'GregoryF2x']
fbpar = GregoryF2x/GregoryT2x #feedback parameter from Gregory plot
print(fbpar)
F = deltaN + fbpar*deltaT
fig, ax = plt.subplots(figsize = [9,5])
plt.plot(years,F,linewidth=2,color = "black")
ax.set_xlabel('t (years)',fontsize = 18)
ax.set_ylabel('F(t) [$W/m^2$]',fontsize = 18)
ax.set_title('1pctCO2 forcing',fontsize = 18)
ax.grid()
ax.set_xlim(min(years),max(years))
ax.tick_params(axis='both',labelsize=22)
if storeforcingdata == True:
dfFF = pd.read_table(filenameFF, index_col=0); # load files
dfFF[model] = F;
dfFF.to_csv(filenameFF, sep='\t'); # save file again
# load remaining parameters:
taulist = np.array(parameter_table.loc[model,'tau1':'tau3'])
a_n = np.array(parameter_table.loc[model,'a_1':'a_4'])
b_n = np.array(parameter_table.loc[model,'b_1':'b_4'])
F2x = parameter_table.loc[model,'F2x']
T2x = parameter_table.loc[model,'T2x']
# compute other needed parameters from these:
dim = len(taulist)
if any(a_n == 0):
dim = np.count_nonzero(a_n[:dim])
zeroindex = np.where(a_n == 0)[0]
a_n = np.delete(a_n,zeroindex)
b_n = np.delete(b_n,zeroindex)
taulist = np.delete(taulist,zeroindex)
fbparlist = (b_n/a_n)[:dim]
print(fbparlist)
amplitudes = a_n[:dim]/(2*F2x*taulist)
print(np.sum(a_n)/2)
print(T2x)
# compute components T_n(t) = exp(-t/tau_n)*F(t) (Here * is a convolution)
dim = len(taulist)
lf = len(F)
predictors = np.full((lf,dim),np.nan)
# compute exact predictors by integrating greens function
for k in range(0,dim):
intgreensti = np.full((lf,lf),0.) # remember dot after 0 to create floating point number array instead of integer
for t in range(0,lf):
# compute one new contribution to the matrix:
intgreensti[t,0] = taulist[k]*(np.exp(-t/taulist[k]) - np.exp(-(t+1)/taulist[k]))
# take the rest from row above:
if t > 0:
intgreensti[t,1:(t+1)] = intgreensti[t-1,0:t]
# compute discretized convolution integral by this matrix product:
predictors[:,k] = intgreensti@np.array(F)
Tn = amplitudes*predictors
fig, ax = plt.subplots(figsize = [9,5])
plt.plot(years,Tn[:,0],linewidth=2,color = "black",label = 'Mode with time scale ' + str(np.round(taulist[0])) + ' years')
plt.plot(years,Tn[:,1],linewidth=2,color = "blue",label = 'Mode with time scale ' + str(np.round(taulist[1])) + ' years')
if dim>2:
plt.plot(years,Tn[:,2],linewidth=2,color = "red",label = 'Mode with time scale ' + str(np.round(taulist[2],1)) + ' years')
ax.set_xlabel('t',fontsize = 18)
ax.set_ylabel('T(t)',fontsize = 18)
ax.set_title('Temperature responses to forcing',fontsize = 18)
ax.grid()
ax.set_xlim(min(years),max(years))
ax.tick_params(axis='both',labelsize=22)
ax.legend(loc=2, prop={'size': 18});
fig, ax = plt.subplots(figsize = [9,5])
plt.plot(years,np.sum(Tn, axis=1),linewidth=2,color = "black",label = 'Mode with time scale ' + str(np.round(taulist[0])) + ' years')
ax.set_xlabel('t (years)',fontsize = 18)
ax.set_ylabel('T(t) [°C]',fontsize = 18)
ax.set_title('Linear response to forcing',fontsize = 18)
ax.grid()
ax.set_xlim(min(years),max(years))
ax.tick_params(axis='both',labelsize=22)
# Compute new estimate of adjusted forcing
it = 20 # number of iterations
Fiarray = np.full((lf,it),np.nan)
Fi = F
for i in range(0,it):
# iterate
predictors = np.full((lf,dim),np.nan)
# compute exact predictors by integrating greens function
for k in range(0,dim):
intgreensti = np.full((lf,lf),0.) # remember dot after 0 to create floating point number array instead of integer
for t in range(0,lf):
# compute one new contribution to the matrix:
intgreensti[t,0] = taulist[k]*(np.exp(-t/taulist[k]) - np.exp(-(t+1)/taulist[k]))
# take the rest from row above:
if t > 0:
intgreensti[t,1:(t+1)] = intgreensti[t-1,0:t]
# compute discretized convolution integral by this matrix product:
predictors[:,k] = intgreensti@np.array(Fi)
Tni = amplitudes*predictors
Fi = deltaN + Tni@fbparlist
Fiarray[:,i] = Fi
fig, ax = plt.subplots(nrows=1,ncols=2,figsize = [16,5])
ax[0,].plot(years,F,linewidth=2,color = "black",label = "Old forcing")
for i in range(0,it-1):
ax[0,].plot(years,Fiarray[:,i],linewidth=1,color = "gray")
ax[0,].plot(years,Fiarray[:,it-1],linewidth=1,color = "blue",label = "New forcing")
ax[0,].set_xlabel('t (years)',fontsize = 18)
ax[0,].set_ylabel('F(t) [$W/m^2$]',fontsize = 18)
ax[0,].grid()
ax[0,].set_xlim(min(years),max(years))
ax[0,].tick_params(axis='both',labelsize=18)
if model == 'GFDL-ESM2G' or model == 'GFDL-ESM2M': # linear fit for only 70 years
# linear fit to forster forcing:
linfitpar1 = np.polyfit(years[:70],F[:70],deg = 1)
linfit_forcing1 = np.polyval(linfitpar1,years[:70])
ax[0,].plot(years[:70],linfit_forcing1,'--',linewidth=1,color = "black")
# linear fit to new forcing:
linfitpar2 = np.polyfit(years[:70],Fiarray[:70,it-1],deg = 1)
linfit_forcing2 = np.polyval(linfitpar2,years[:70])
ax[0,].plot(years[:70],linfit_forcing2,'--',linewidth=1,color = "blue")
else: # linear fit for 140 years
# linear fit to forster forcing:
linfitpar1 = np.polyfit(years,F,deg = 1)
linfit_forcing1 = np.polyval(linfitpar1,years)
ax[0,].plot(years,linfit_forcing1,'--',linewidth=1,color = "black")
# linear fit to new forcing:
linfitpar2 = np.polyfit(years,Fiarray[:,it-1],deg = 1)
linfit_forcing2 = np.polyval(linfitpar2,years)
ax[0,].plot(years,linfit_forcing2,'--',linewidth=1,color = "blue")
# Estimate and print out 4xCO2 forcing from end values of linear fits:
print(linfit_forcing1[-1])
print(linfit_forcing2[-1])
# compare responses
label = 'temperature'
# plot temperature
ax[1,].plot(years,deltaT,linewidth=3,color = "black",label = model + " modelled response")
# plot response
ax[1,].plot(years,np.sum(Tn,axis=1),'--',linewidth=2,color = "black",label = "Linear response to old forcing")
ax[1,].plot(years,np.sum(Tni,axis=1),'--',linewidth=2,color = "blue",label = "Linear response to new forcing")
ax[1,].set_xlabel('t (years)',fontsize = 18)
ax[1,].set_ylabel('T(t) [°C]',fontsize = 18)
ax[1,].set_title('1% CO$_2$ ' + label,fontsize = 18)
ax[0,].set_title('1% CO$_2$ effective forcing',fontsize = 18)
ax[1,].grid()
ax[1,].set_xlim(min(years),max(years))
ax[1,].tick_params(axis='both',labelsize=18)
ax[0,].text(0,1.03,'a)',transform=ax[0,].transAxes, fontsize=20)
ax[1,].text(0,1.03,'b)',transform=ax[1,].transAxes, fontsize=20)
#plt.savefig('/Users/hege-beatefredriksen/OneDrive - UiT Office 365/Papers/Forcingpaper/Figures/' + model + '_1pctCO2_forcing_and_response.pdf', format='pdf', dpi=600, bbox_inches="tight")
if storeforcingdata == True:
dfNF = pd.read_table(filenameNF, index_col=0); dfNF = pd.read_table(filenameNF, index_col=0); # load file
dfNF[model] = Fiarray[:,it-1];
dfNF.to_csv(filenameNF, sep='\t'); # save file again
# put results in pandas dataframe:
columnnames = ['4xCO2forcingest_1pctCO2', '4xCO2forcingest_1pctCO2_F13method'];
# if file is not already created, create a new file to store the results in:
filename = 'estimated_4xCO2forcing_from1pctCO2.txt'
#dataframe = pd.DataFrame([np.concatenate((linfit_forcing2[-1], linfit_forcing1[-1]), axis=None)], index = [model], columns=columnnames)
#dataframe.to_csv(filename, sep='\t')
#dataframe
# load existing dataframe, and append present result:
loaded_dataframe = pd.read_table(filename,index_col=0)
pd.set_option('display.expand_frame_repr', False)
# fill numbers into table:
if model == 'GFDL-ESM2G' or model == 'GFDL-ESM2M':
loaded_dataframe.loc[model,columnnames] = [np.concatenate((2*linfit_forcing2[-1], 2*linfit_forcing1[-1]), axis=None)]
else:
loaded_dataframe.loc[model,columnnames] = [np.concatenate((linfit_forcing2[-1], linfit_forcing1[-1]), axis=None)]
# write them to a file:
loaded_dataframe.to_csv(filename, sep='\t')
loaded_dataframe
timedep_fbpar1 = Tni@fbparlist/np.sum(Tni,axis=1) # two alternative definitions
timedep_fbpar2 = Tni@fbparlist/deltaT
fig, ax = plt.subplots(figsize = [9,5])
label = 'Instantaneous feedback parameter'
# plot response
ax.plot(years,timedep_fbpar1,linewidth=3,color = "black")
ax.plot(years,timedep_fbpar2,linewidth=1,color = "gray")
ax.plot(years,np.full((len(years),1),fbpar),linewidth=2,color = "green")
ax.set_xlabel('t',fontsize = 18)
ax.set_ylabel('$\lambda$ (t)',fontsize = 18)
ax.set_title(label,fontsize = 18)
ax.grid()
ax.set_xlim(min(years),max(years))
ax.set_ylim(0,3)
ax.tick_params(axis='both',labelsize=18)
fig, ax = plt.subplots(figsize = [9,5])
label = 'Instantaneous climate sensitivity parameter'
# plot response
ax.plot(years,1/timedep_fbpar1,linewidth=3,color = "black")
ax.plot(years,1/timedep_fbpar2,linewidth=1,color = "gray")
ax.plot(years,np.full((len(years),1),1/fbpar),linewidth=2,color = "green")
ax.set_xlabel('t',fontsize = 18)
ax.set_ylabel('S(t)',fontsize = 18)
ax.set_title(label,fontsize = 18)
ax.grid()
ax.set_xlim(min(years),max(years))
ax.set_ylim(0,2)
ax.tick_params(axis='both',labelsize=18)
fig, ax = plt.subplots(figsize = [9,5])
label = 'Instantaneous climate sensitivity'
# plot response
ax.plot(years,F2x/timedep_fbpar1,linewidth=3,color = "black")
ax.plot(years,F2x/timedep_fbpar2,linewidth=1,color = "gray")
ax.plot(years,np.full((len(years),1),F2x/fbpar),linewidth=2,color = "green")
ax.set_xlabel('t',fontsize = 18)
ax.set_ylabel('ECS(t)',fontsize = 18)
ax.set_title(label,fontsize = 18)
ax.grid()
ax.set_xlim(min(years),max(years))
ax.set_ylim(0,6)
ax.tick_params(axis='both',labelsize=18)
```
|
github_jupyter
|
# Bayesian Parametric Regression
Notebook version: 1.5 (Sep 24, 2019)
Author: Jerónimo Arenas García (jarenas@tsc.uc3m.es)
Jesús Cid-Sueiro (jesus.cid@uc3m.es)
Changes: v.1.0 - First version
v.1.1 - ML Model selection included
v.1.2 - Some typos corrected
v.1.3 - Rewriting text, reorganizing content, some exercises.
v.1.4 - Revised introduction
v.1.5 - Revised notation. Solved exercise 5
Pending changes: * Include regression on the stock data
```
# Import some libraries that will be necessary for working with data and displaying plots
# To visualize plots in the notebook
%matplotlib inline
from IPython import display
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import scipy.io # To read matlab files
import pylab
import time
```
## A quick note on the mathematical notation
In this notebook we will make extensive use of probability distributions. In general, we will use capital letters
${\bf X}$, $S$, $E$ ..., to denote random variables, and lower-case letters ${\bf x}$, $s$, $\epsilon$ ..., to denote the values they can take.
In general, we will use letter $p$ for probability density functions (pdf). When necessary, we will use, capital subindices to make the random variable explicit. For instance, $p_{{\bf X}, S}({\bf x}, s)$ would be the joint pdf of random variables ${\bf X}$ and $S$ at values ${\bf x}$ and $s$, respectively.
However, to avoid a notation overload, we will omit subindices when they are clear from the context. For instance, we will use $p({\bf x}, s)$ instead of $p_{{\bf X}, S}({\bf x}, s)$.
## 1. Model-based parametric regression
### 1.1. The regression problem.
Given an observation vector ${\bf x}$, the goal of the regression problem is to find a function $f({\bf x})$ providing *good* predictions about some unknown variable $s$. To do so, we assume that a set of *labelled* training examples, $\{{\bf x}_k, s_k\}_{k=0}^{K-1}$ is available.
The predictor function should make good predictions for new observations ${\bf x}$ not used during training. In practice, this is tested using a second set (the *test set*) of labelled samples.
### 1.2. Model-based parametric regression
Model-based regression methods assume that all data in the training and test dataset have been generated by some stochastic process. In parametric regression, we assume that the probability distribution generating the data has a known parametric form, but the values of some parameters are unknown.
In particular, in this notebook we will assume the target variables in all pairs $({\bf x}_k, s_k)$ from the training and test sets have been generated independently from some posterior distribution $p(s| {\bf x}, {\bf w})$, were ${\bf w}$ is some unknown parameter. The training dataset is used to estimate ${\bf w}$.
<img src="figs/ParametricReg.png" width=300>
### 1.3. Model assumptions
In order to estimate ${\bf w}$ from the training data in a mathematicaly rigorous and compact form let us group the target variables into a vector
$$
{\bf s} = \left(s_0, \dots, s_{K-1}\right)^\top
$$
and the input vectors into a matrix
$$
{\bf X} = \left({\bf x}_0, \dots, {\bf x}_{K-1}\right)^\top
$$
We will make the following assumptions:
* A1. All samples in ${\cal D}$ have been generated by the same distribution, $p({\bf x}, s \mid {\bf w})$
* A2. Input variables ${\bf x}$ do not depend on ${\bf w}$. This implies that
$$
p({\bf X} \mid {\bf w}) = p({\bf X})
$$
* A3. Targets $s_0, \dots, s_{K-1}$ are statistically independent, given ${\bf w}$ and the inputs ${\bf x}_0,\ldots, {\bf x}_{K-1}$, that is:
$$
p({\bf s} \mid {\bf X}, {\bf w}) = \prod_{k=0}^{K-1} p(s_k \mid {\bf x}_k, {\bf w})
$$
## 2. Bayesian inference.
### 2.1. The Bayesian approach
The main idea of Bayesian inference is the following: assume we want to estimate some unknown variable $U$ given an observed variable $O$. If $U$ and $O$ are random variables, we can describe the relation between $U$ and $O$ through the following functions:
* **Prior distribution**: $p_U(u)$. It describes our uncertainty on the true value of $U$ before observing $O$.
* **Likelihood function**: $p_{O \mid U}(o \mid u)$. It describes how the value of the observation is generated for a given value of $U$.
* **Posterior distribution**: $p_{U|O}(u \mid o)$. It describes our uncertainty on the true value of $U$ once the true value of $O$ is observed.
The major component of the Bayesian inference is the posterior distribution. All Bayesian estimates are computed as some of its central statistics (e.g. the mean, the median or the mode), for instance
* **Maximum A Posteriori (MAP) estimate**: $\qquad{\widehat{u}}_{\text{MAP}} = \arg\max_u p_{U \mid O}(u \mid o)$
* **Minimum Mean Square Error (MSE) estimate**: $\qquad\widehat{u}_{\text{MSE}} = \mathbb{E}\{U \mid O=o\}$
The choice between the MAP or the MSE estimate may depend on practical or computational considerations. From a theoretical point of view, $\widehat{u}_{\text{MSE}}$ has some nice properties: it minimizes $\mathbb{E}\{(U-\widehat{u})^2\}$ among all possible estimates, $\widehat{u}$, so it is a natural choice. However, it involves the computation of an integral, which may not have a closed-form solution. In such cases, the MAP estimate can be a better choice.
The prior and the likelihood function are auxiliary distributions: if the posterior distribution is unknown, it can be computed from them using the Bayes rule:
\begin{equation}
p_{U|O}(u \mid o) = \frac{p_{O|U}(o \mid u) \cdot p_{U}(u)}{p_{O}(o)}
\end{equation}
In the next two sections we show that the Bayesian approach can be applied to both the prediction and the estimation problems.
### 2.2. Bayesian prediction under a known model
Assuming that the model parameters ${\bf w}$ are known, we can apply the Bayesian approach to predict ${\bf s}$ for an input ${\bf x}$. In that case, we can take
* Unknown variable: ${\bf s}$, and
* Observations: ${\bf x}$
the MAP and MSE predictions become
* Maximum A Posterior (MAP): $\qquad\widehat{s}_{\text{MAP}} = \arg\max_s p(s| {\bf x}, {\bf w})$
* Minimum Mean Square Error (MSE): $\qquad\widehat{s}_{\text{MSE}} = \mathbb{E}\{S |{\bf x}, {\bf w}\}$
#### Exercise 1:
Assuming
$$
p(s\mid x, w) = \frac{s}{w x^2} \exp\left({-\frac{s^2}{2 w x^2}}\right), \qquad s \geq 0,
$$
compute the MAP and MSE predictions of $s$ given $x$ and $w$.
#### Solution:
<SOL>
\begin{align}
\widehat{s}_\text{MAP}
&= \arg\max_s \left\{\frac{s}{w x^2} \exp\left({-\frac{s^2}{2 w x^2}}\right) \right\} \\
&= \arg\max_s \left\{\log(s) - \log(w x^2) -\frac{s^2}{2 w x^2} \right\} \\
&= \sqrt{w}x
\end{align}
where the last step results from maximizing by differentiation.
\begin{align}
\widehat{s}_\text{MSE}
&= \mathbb{E}\{s | x, w\} \\
&= \int_0^\infty \frac{s^2}{w x^2} \exp\left({-\frac{s^2}{2 w x^2}}\right) \\
&= \frac{1}{2} \int_{-\infty}^\infty \frac{s^2}{w x^2} \exp\left({-\frac{s^2}{2 w x^2}}\right) \\
&= \frac{\sqrt{2\pi}}{2\sqrt{w x^2}} \int_{-\infty}^\infty \frac{s^2}{\sqrt{2\pi w x^2}} \exp\left({-\frac{s^2}{2 w x^2}}\right)
\end{align}
Noting that the last integral corresponds to the variance of a zero-mean Gaussian distribution, we get
\begin{align}
\widehat{s}_\text{MSE}
&= \frac{\sqrt{2\pi}}{2\sqrt{w x^2}} w x^2 \\
&= \sqrt{\frac{\pi w}{2}}x
\end{align}
</SOL>
#### 2.2.1. The Gaussian case
A particularly interesting case arises when the data model is Gaussian:
$$p(s|{\bf x}, {\bf w}) =
\frac{1}{\sqrt{2\pi}\sigma_\varepsilon}
\exp\left(-\frac{(s-{\bf w}^\top{\bf z})^2}{2\sigma_\varepsilon^2}\right)
$$
where ${\bf z}=T({\bf x})$ is a vector with components which can be computed directly from the observed variables. For a Gaussian distribution (and for any unimodal symetric distributions) the mean and the mode are the same and, thus,
$$
\widehat{s}_\text{MAP} = \widehat{s}_\text{MSE} = {\bf w}^\top{\bf z}
$$
Such expression includes a linear regression model, where ${\bf z} = [1; {\bf x}]$, as well as any other non-linear model as long as it can be expressed as a <i>"linear in the parameters"</i> model.
### 2.3. Bayesian Inference for Parameter Estimation
In a similar way, we can apply Bayesian inference to estimate the model parameters ${\bf w}$ from a given dataset, $\cal{D}$. In that case
* the unknown variable is ${\bf w}$, and
* the observation is $\cal{D} \equiv \{{\bf X}, {\bf s}\}$
so that
* Maximum A Posterior (MAP): $\qquad\widehat{\bf w}_{\text{MAP}} = \arg\max_{\bf w} p({\bf w}| {\cal D})$
* Minimum Mean Square Error (MSE): $\qquad\widehat{\bf w}_{\text{MSE}} = \mathbb{E}\{{\bf W} | {\cal D}\}$
## 3. Bayesian parameter estimation
NOTE: Since the training data inputs are known, all probability density functions and expectations in the remainder of this notebook will be conditioned on the data matrix, ${\bf X}$. To simplify the mathematical notation, from now on we will remove ${\bf X}$ from all conditions. For instance, we will write $p({\bf s}|{\bf w})$ instead of $p({\bf s}|{\bf w}, {\bf X})$, etc. Keep in mind that, in any case, all probabilities and expectations may depend on ${\bf X}$ implicitely.
Summarizing, the steps to design a Bayesian parametric regresion algorithm are the following:
1. Assume a parametric data model $p(s| {\bf x},{\bf w})$ and a prior distribution $p({\bf w})$.
2. Using the data model and the i.i.d. assumption, compute $p({\bf s}|{\bf w})$.
3. Applying the bayes rule, compute the posterior distribution $p({\bf w}|{\bf s})$.
4. Compute the MAP or the MSE estimate of ${\bf w}$ given ${\bf x}$.
5. Compute predictions using the selected estimate.
### 3.1. Bayesian Inference and Maximum Likelihood.
Applying the Bayes rule the MAP estimate can be alternatively expressed as
\begin{align}
\qquad\widehat{\bf w}_{\text{MAP}}
&= \arg\max_{\bf w} \frac{p({\cal D}| {\bf w}) \cdot p({\bf w})}{p({\cal D})} \\
&= \arg\max_{\bf w} p({\cal D}| {\bf w}) \cdot p({\bf w})
\end{align}
By comparisons, the ML (Maximum Likelihood) estimate has the form:
$$
\widehat{\bf w}_{\text{ML}} = \arg \max_{\bf w} p(\mathcal{D}|{\bf w})
$$
This shows that the MAP estimate takes into account the prior distribution on the unknown parameter.
Another advantage of the Bayesian approach is that it provides not only a point estimate of the unknown parameter, but a whole funtion, the posterior distribution, which encompasses our belief on the unknown parameter given the data. For instance, we can take second order statistics like the variance of the posterior distributions to measure the uncertainty on the true value of the parameter around the mean.
### 3.2. The prior distribution
Since each value of ${\bf w}$ determines a regression function, by stating a prior distribution over the weights we state also a prior distribution over the space of regression functions.
For instance, assume that the data likelihood follows the Gaussian model in sec. 2.2.1, with $T(x) = (1, x, x^2, x^3)$, i.e. the regression functions have the form
$$
w_0 + w_1 x + w_2 x^2 + w_3 x^3
$$
Each value of ${\bf w}$ determines a specific polynomial of degree 3. Thus, the prior distribution over ${\bf w}$ describes which polynomials are more likely before observing the data.
For instance, assume a Gaussian prior with zero mean and variance ${\bf V}_p$, i.e.,
$$
p({\bf w}) = \frac{1}{(2\pi)^{D/2} |{\bf V}_p|^{1/2}}
\exp \left(-\frac{1}{2} {\bf w}^\intercal {\bf V}_{p}^{-1}{\bf w} \right)
$$
where $D$ is the dimension of ${\bf w}$. To abbreviate, we will also express this as
$${\bf w} \sim {\cal N}\left({\bf 0},{\bf V}_{p} \right)$$
The following code samples ${\bf w}$ according to this distribution for ${\bf V}_p = 0.002 \, {\bf I}$, and plots the resulting polynomial over the scatter plot of an arbitrary dataset.
You can check the effect of modifying the variance of the prior distribution.
```
n_grid = 200
degree = 3
nplots = 20
# Prior distribution parameters
mean_w = np.zeros((degree+1,))
v_p = 0.2 ### Try increasing this value
var_w = v_p * np.eye(degree+1)
xmin = -1
xmax = 1
X_grid = np.linspace(xmin, xmax, n_grid)
fig = plt.figure()
ax = fig.add_subplot(111)
for k in range(nplots):
#Draw weigths fromt the prior distribution
w_iter = np.random.multivariate_normal(mean_w, var_w)
S_grid_iter = np.polyval(w_iter, X_grid)
ax.plot(X_grid, S_grid_iter,'g-')
ax.set_xlim(xmin, xmax)
ax.set_ylim(-1, 1)
ax.set_xlabel('$x$')
ax.set_ylabel('$s$')
plt.show()
```
The data observation will modify our belief about the true data model according to the posterior distribution. In the following we will analyze this in a Gaussian case.
## 4. Bayesian regression for a Gaussian model.
We will apply the above steps to derive a Bayesian regression algorithm for a Gaussian model.
### 4.1. Step 1: The Gaussian model.
Let us assume that the likelihood function is given by the Gaussian model described in Sec. 1.3.2.
$$
s~|~{\bf w} \sim {\cal N}\left({\bf z}^\top{\bf w}, \sigma_\varepsilon^2 \right)
$$
that is
$$p(s|{\bf x}, {\bf w}) =
\frac{1}{\sqrt{2\pi}\sigma_\varepsilon}
\exp\left(-\frac{(s-{\bf w}^\top{\bf z})^2}{2\sigma_\varepsilon^2}\right)
$$
Assume, also, that the prior is Gaussian
$$
{\bf w} \sim {\cal N}\left({\bf 0},{\bf V}_{p} \right)
$$
### 4.2. Step 2: Complete data likelihood
Using the assumptions A1, A2 and A3, it can be shown that
$$
{\bf s}~|~{\bf w} \sim {\cal N}\left({\bf Z}{\bf w},\sigma_\varepsilon^2 {\bf I} \right)
$$
that is
$$
p({\bf s}| {\bf w})
= \frac{1}{\left(\sqrt{2\pi}\sigma_\varepsilon\right)^K}
\exp\left(-\frac{1}{2\sigma_\varepsilon^2}\|{\bf s}-{\bf Z}{\bf w}\|^2\right)
$$
### 4.3. Step 3: Posterior weight distribution
The posterior distribution of the weights can be computed using the Bayes rule
$$p({\bf w}|{\bf s}) = \frac{p({\bf s}|{\bf w})~p({\bf w})}{p({\bf s})}$$
Since both $p({\bf s}|{\bf w})$ and $p({\bf w})$ follow a Gaussian distribution, we know also that the joint distribution and the posterior distribution of ${\bf w}$ given ${\bf s}$ are also Gaussian. Therefore,
$${\bf w}~|~{\bf s} \sim {\cal N}\left({\bf w}_\text{MSE}, {\bf V}_{\bf w}\right)$$
After some algebra, it can be shown that mean and the covariance matrix of the distribution are:
$${\bf V}_{\bf w} = \left[\frac{1}{\sigma_\varepsilon^2} {\bf Z}^{\top}{\bf Z}
+ {\bf V}_p^{-1}\right]^{-1}$$
$${\bf w}_\text{MSE} = {\sigma_\varepsilon^{-2}} {\bf V}_{\bf w} {\bf Z}^\top {\bf s}$$
#### Exercise 2:
Consider the dataset with one-dimensional inputs given by
```
# True data parameters
w_true = 3
std_n = 0.4
# Generate the whole dataset
n_max = 64
X_tr = 3 * np.random.random((n_max,1)) - 0.5
S_tr = w_true * X_tr + std_n * np.random.randn(n_max,1)
# Plot data
plt.figure()
plt.plot(X_tr, S_tr, 'b.')
plt.xlabel('$x$')
plt.ylabel('$s$')
plt.show()
```
Fit a Bayesian linear regression model assuming $z= x$ and
```
# Model parameters
sigma_eps = 0.4
mean_w = np.zeros((1,))
sigma_p = 1e6
Var_p = sigma_p**2* np.eye(1)
```
To do so, compute the posterior weight distribution using the first $k$ samples in the complete dataset, for $k = 1,2,4,8,\ldots 128$. Draw all these posteriors along with the prior distribution in the same plot.
```
# No. of points to analyze
n_points = [1, 2, 4, 8, 16, 32, 64]
# Prepare plots
w_grid = np.linspace(2.7, 3.4, 5000) # Sample the w axis
plt.figure()
# Compute the prior distribution over the grid points in w_grid
# p = <FILL IN>
p = 1.0/(sigma_p*np.sqrt(2*np.pi)) * np.exp(-(w_grid**2)/(2*sigma_p**2))
plt.plot(w_grid, p,'g-')
for k in n_points:
# Select the first k samples
Zk = X_tr[0:k, :]
Sk = S_tr[0:k]
# Parameters of the posterior distribution
# 1. Compute the posterior variance.
# (Make sure that the resulting variable, Var_w, is a 1x1 numpy array.)
# Var_w = <FILL IN>
Var_w = np.linalg.inv(np.dot(Zk.T, Zk)/(sigma_eps**2) + np.linalg.inv(Var_p))
# 2. Compute the posterior mean.
# (Make sure that the resulting variable, w_MSE, is a scalar)
# w_MSE = <FILL IN>
w_MSE = (Var_w.dot(Zk.T).dot(Sk)/(sigma_eps**2)).flatten()
# Compute the posterior distribution over the grid points in w_grid
sigma_w = np.sqrt(Var_w.flatten()) # First we take a scalar standard deviation
# p = <FILL IN>
p = 1.0/(sigma_w*np.sqrt(2*np.pi)) * np.exp(-((w_grid-w_MSE)**2)/(2*sigma_w**2))
plt.plot(w_grid, p,'g-')
plt.fill_between(w_grid, 0, p, alpha=0.8, edgecolor='#1B2ACC', facecolor='#089FFF',
linewidth=1, antialiased=True)
plt.title('Posterior distribution after {} samples'.format(k))
plt.xlim(w_grid[0], w_grid[-1])
plt.ylim(0, np.max(p))
plt.xlabel('$w$')
plt.ylabel('$p(w|s)$')
display.clear_output(wait=True)
display.display(plt.gcf())
time.sleep(2.0)
# Remove the temporary plots and fix the last one
display.clear_output(wait=True)
plt.show()
```
#### Exercise 3:
Note that, in the example above, the model assumptions are correct: the target variables have been generated by a linear model with noise standard deviation `sigma_n` which is exactly equal to the value assumed by the model, stored in variable `sigma_eps`. Check what happens if we take `sigma_eps=4*sigma_n` or `sigma_eps=sigma_n/4`.
* Does the algorithm fail in that cases?
* What differences can you observe with respect to the ideal case `sigma_eps=sigma_n`?
### 4.4. Step 4: Weight estimation.
Since the posterior weight distribution is Gaussian, both the MAP and the MSE estimates are equal to the posterior mean, which has been already computed in step 3:
$$\widehat{\bf w}_\text{MAP} = \widehat{\bf w}_\text{MSE} = {\sigma_\varepsilon^{-2}} {\bf V}_{\bf w} {\bf Z}^\top {\bf s}$$
### 4.5. Step 5: Prediction
Using the MSE estimate, the final predictions are given by
$$
\widehat{s}_\text{MSE} = \widehat{\bf w}_\text{MSE}^\top{\bf z}
$$
#### Exercise 4:
Plot the minimum MSE predictions of $s$ for inputs $x$ in the interval [-1, 3].
```
# <SOL>
x = np.array([-1.0, 3.0])
s_pred = w_MSE * x
plt.figure()
plt.plot(X_tr, S_tr,'b.')
plt.plot(x, s_pred)
plt.show()
# </SOL>
```
## 5. Maximum likelihood vs Bayesian Inference.
### 5.1. The Maximum Likelihood Estimate.
For comparative purposes, it is interesting to see here that the likelihood function is enough to compute the Maximum Likelihood (ML) estimate
\begin{align}
{\bf w}_\text{ML} &= \arg \max_{\bf w} p(\mathcal{D}|{\bf w}) \\
&= \arg \min_{\bf w} \|{\bf s}-{\bf Z}{\bf w}\|^2
\end{align}
which leads to the Least Squares (LS) solution
$$
{\bf w}_\text{ML} = ({\bf Z}^\top{\bf Z})^{-1}{\bf Z}^\top{\bf s}
$$
ML estimation is prone to overfiting. In general, if the number of parameters (i.e. the dimension of ${\bf w}$) is large in relation to the size of the training data, the predictor based on the ML estimate may have a small square error over the training set but a large error over the test set. Therefore, in practice, some cross validation procedure is required to keep the complexity of the predictor function under control depending on the size of the training set.
By defining a prior distribution over the unknown parameters, and using the Bayesian inference methods, the overfitting problems can be alleviated
### 5.2 Making predictions
- Following an **ML approach**, we retain a single model, ${\bf w}_{ML} = \arg \max_{\bf w} p({\bf s}|{\bf w})$. Then, the predictive distribution of the target value for a new point would be obtained as:
$$p({s^*}|{\bf w}_{ML},{\bf x}^*) $$
For the generative model of Section 3.1.2 (additive i.i.d. Gaussian noise), this distribution is:
$$p({s^*}|{\bf w}_{ML},{\bf x}^*) = \frac{1}{\sqrt{2\pi\sigma_\varepsilon^2}} \exp \left(-\frac{\left(s^* - {\bf w}_{ML}^\top {\bf z}^*\right)^2}{2 \sigma_\varepsilon^2} \right)$$
* The mean of $s^*$ is just the same as the prediction of the LS model, and the same uncertainty is assumed independently of the observation vector (i.e., the variance of the noise of the model).
* If a single value is to be kept, we would probably keep the mean of the distribution, which is equivalent to the LS prediction.
- Using <b>Bayesian inference</b>, we retain all models. Then, the inference of the value $s^* = s({\bf x}^*)$ is carried out by mixing all models, according to the weights given by the posterior distribution.
\begin{align}
p({s^*}|{\bf x}^*,{\bf s})
& = \int p({s^*}~|~{\bf w},{\bf x}^*) p({\bf w}~|~{\bf s}) d{\bf w}
\end{align}
where:
* $p({s^*}|{\bf w},{\bf x}^*) = \dfrac{1}{\sqrt{2\pi\sigma_\varepsilon^2}} \exp \left(-\frac{\left(s^* - {\bf w}^\top {\bf z}^*\right)^2}{2 \sigma_\varepsilon^2} \right)$
* $p({\bf w} \mid {\bf s})$ is the posterior distribution of the weights, that can be computed using Bayes' Theorem.
In general the integral expression of the posterior distribution $p({s^*}|{\bf x}^*,{\bf s})$ cannot be computed analytically. Fortunately, for the Gaussian model, the computation of the posterior is simple, as we will show in the following section.
## 6. Posterior distribution of the target variable
In the same way that we have computed a distribution on ${\bf w}$, we can compute a distribution on the target variable for a given input ${\bf x}$ and given the whole dataset.
Since ${\bf w}$ is a random variable, the noise-free component of the target variable for an arbitrary input ${\bf x}$, that is, $f = f({\bf x}) = {\bf w}^\top{\bf z}$ is also a random variable, and we can compute its distribution from the posterior distribution of ${\bf w}$
Since ${\bf w}$ is Gaussian and $f$ is a linear transformation of ${\bf w}$, $f$ is also a Gaussian random variable, whose posterior mean and variance can be calculated as follows:
\begin{align}
\mathbb{E}\{f \mid {\bf s}, {\bf z}\}
&= \mathbb{E}\{{\bf w}^\top {\bf z}~|~{\bf s}, {\bf z}\}
= \mathbb{E}\{{\bf w} ~|~{\bf s}, {\bf z}\}^\top {\bf z} \\
&= \widehat{\bf w}_\text{MSE} ^\top {\bf z} \\
% &= {\sigma_\varepsilon^{-2}} {{\bf z}}^\top {\bf V}_{\bf w} {\bf Z}^\top {\bf s}
\end{align}
\begin{align}
\text{Cov}\left[{{\bf z}}^\top {\bf w}~|~{\bf s}, {\bf z}\right]
&= {\bf z}^\top \text{Cov}\left[{\bf w}~|~{\bf s}\right] {\bf z} \\
&= {\bf z}^\top {\bf V}_{\bf w} {{\bf z}}
\end{align}
Therefore,
$$
f^*~|~{\bf s}, {\bf x}
\sim {\cal N}\left(\widehat{\bf w}_\text{MSE} ^\top {\bf z}, ~~
{\bf z}^\top {\bf V}_{\bf w} {\bf z} \right)
$$
Finally, for $s = f + \varepsilon$, the posterior distribution is
$$
s ~|~{\bf s}, {\bf z}^*
\sim {\cal N}\left(\widehat{\bf w}_\text{MSE} ^\top {\bf z}, ~~
{\bf z}^\top {\bf V}_{\bf w} {\bf z} + \sigma_\varepsilon^2\right)
$$
#### Example:
The next figure shows a one-dimensional dataset with 15 points, which are noisy samples from a cosine signal (shown in the dotted curve)
```
n_points = 15
n_grid = 200
frec = 3
std_n = 0.2
# Data generation
X_tr = 3 * np.random.random((n_points,1)) - 0.5
S_tr = - np.cos(frec*X_tr) + std_n * np.random.randn(n_points,1)
# Signal
xmin = np.min(X_tr) - 0.1
xmax = np.max(X_tr) + 0.1
X_grid = np.linspace(xmin, xmax, n_grid)
S_grid = - np.cos(frec*X_grid) #Noise free for the true model
# Compute matrix with training input data for the polynomial model
Z = []
for x_val in X_tr.tolist():
Z.append([x_val[0]**k for k in range(degree+1)])
Z = np.asmatrix(Z)
# Plot data
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(X_tr,S_tr,'b.',markersize=10)
# Plot noise-free function
ax.plot(X_grid, S_grid, 'b:', label='Noise-free signal')
# Set axes
ax.set_xlim(xmin, xmax)
ax.set_ylim(S_tr[0] - 2, S_tr[-1] + 2)
ax.legend(loc='best')
plt.show()
```
Let us assume that the cosine form of the noise-free signal is unknown, and we assume a polynomial model with a high degree. The following code plots the LS estimate
```
degree = 12
# We plot also the least square solution
w_LS = np.polyfit(X_tr.flatten(), S_tr.flatten(), degree)
S_grid_LS = np.polyval(w_LS,X_grid)
# Plot data
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(X_tr,S_tr,'b.',markersize=10)
# Plot noise-free function
ax.plot(X_grid, S_grid, 'b:', label='Noise-free signal')
# Plot LS regression function
ax.plot(X_grid, S_grid_LS, 'm-', label='LS regression')
# Set axis
ax.set_xlim(xmin, xmax)
ax.set_ylim(S_tr[0] - 2, S_tr[-1] + 2)
ax.legend(loc='best')
plt.show()
```
The following fragment of code computes the posterior weight distribution, draws random vectors from $p({\bf w}|{\bf s})$, and plots the corresponding regression curves along with the training points. Compare these curves with those extracted from the prior distribution of ${\bf w}$ and with the LS solution.
```
nplots = 6
# Prior distribution parameters
sigma_eps = 0.2
mean_w = np.zeros((degree+1,))
sigma_p = .5
Var_p = sigma_p**2 * np.eye(degree+1)
# Compute matrix with training input data for the polynomial model
Z = []
for x_val in X_tr.tolist():
Z.append([x_val[0]**k for k in range(degree+1)])
Z = np.asmatrix(Z)
#Compute posterior distribution parameters
Var_w = np.linalg.inv(np.dot(Z.T,Z)/(sigma_eps**2) + np.linalg.inv(Var_p))
posterior_mean = Var_w.dot(Z.T).dot(S_tr)/(sigma_eps**2)
posterior_mean = np.array(posterior_mean).flatten()
# Plot data
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(X_tr,S_tr,'b.',markersize=10)
# Plot noise-free function
ax.plot(X_grid, S_grid, 'b:', label='Noise-free signal')
# Plot LS regression function
ax.plot(X_grid, S_grid_LS, 'm-', label='LS regression')
for k in range(nplots):
# Draw weights from the posterior distribution
w_iter = np.random.multivariate_normal(posterior_mean, Var_w)
# Note that polyval assumes the first element of weight vector is the coefficient of
# the highest degree term. Thus, we need to reverse w_iter
S_grid_iter = np.polyval(w_iter[::-1], X_grid)
ax.plot(X_grid,S_grid_iter,'g-')
# Set axis
ax.set_xlim(xmin, xmax)
ax.set_ylim(S_tr[0] - 2, S_tr[-1] + 2)
ax.legend(loc='best')
plt.show()
```
Not only do we obtain a better predictive model, but we also have confidence intervals (error bars) for the predictions.
```
# Compute standard deviation
std_x = []
for el in X_grid:
x_ast = np.array([el**k for k in range(degree+1)])
std_x.append(np.sqrt(x_ast.dot(Var_w).dot(x_ast)[0,0]))
std_x = np.array(std_x)
# Plot data
fig = plt.figure(figsize=(10,6))
ax = fig.add_subplot(111)
ax.plot(X_tr,S_tr,'b.',markersize=10)
# Plot the posterior mean
# Note that polyval assumes the first element of weight vector is the coefficient of
# the highest degree term. Thus, we need to reverse w_iter
S_grid_iter = np.polyval(posterior_mean[::-1],X_grid)
ax.plot(X_grid,S_grid_iter,'g-',label='Predictive mean, BI')
#Plot confidence intervals for the Bayesian Inference
plt.fill_between(X_grid, S_grid_iter-std_x, S_grid_iter+std_x,
alpha=0.4, edgecolor='#1B2ACC', facecolor='#089FFF',
linewidth=2, antialiased=True)
#We plot also the least square solution
w_LS = np.polyfit(X_tr.flatten(), S_tr.flatten(), degree)
S_grid_iter = np.polyval(w_LS,X_grid)
# Plot noise-free function
ax.plot(X_grid, S_grid, 'b:', label='Noise-free signal')
# Plot LS regression function
ax.plot(X_grid, S_grid_LS, 'm-', label='LS regression')
# Set axis
ax.set_xlim(xmin, xmax)
ax.set_ylim(S_tr[0]-2,S_tr[-1]+2)
ax.set_title('Predicting the target variable')
ax.set_xlabel('Input variable')
ax.set_ylabel('Target variable')
ax.legend(loc='best')
plt.show()
```
#### Exercise 5:
Assume the dataset ${\cal{D}} = \left\{ x_k, s_k \right\}_{k=0}^{K-1}$ containing $K$ i.i.d. samples from a distribution
$$p(s|x,w) = w x \exp(-w x s), \qquad s>0,\quad x> 0,\quad w> 0$$
We model also our uncertainty about the value of $w$ assuming a prior distribution for $w$ following a Gamma distribution with parameters $\alpha>0$ and $\beta>0$.
$$
w \sim \text{Gamma}\left(\alpha, \beta \right)
= \frac{\beta^\alpha}{\Gamma(\alpha)} w^{\alpha-1} \exp\left(-\beta w\right), \qquad w>0
$$
Note that the mean and the mode of a Gamma distribution can be calculated in closed-form as
$$
\mathbb{E}\left\{w\right\}=\frac{\alpha}{\beta}; \qquad
$$
$$
\text{mode}\{w\} = \arg\max_w p(w) = \frac{\alpha-1}{\beta}
$$
**1.** Determine an expression for the likelihood function.
#### Solution:
[comment]: # (<SOL>)
\begin{align}
p({\bf s}| w)
&= \prod_{k=0}^{K-1} p(s_k|w, x_k) = \prod_{k=0}^{K-1} \left(w x_k \exp(-w x_k s_k)\right) \nonumber\\
&= w^K \cdot \left(\prod_{k=0}^{K-1} x_k \right) \exp\left( -w \sum_{k=0}^{K-1} x_k s_k\right)
\end{align}
[comment]: # (</SOL>)
**2.** Determine the maximum likelihood coefficient, $\widehat{w}_{\text{ML}}$.
#### Solution:
[comment]: # (<SOL>)
\begin{align}
\widehat{w}_{\text{ML}}
&= \arg\max_w w^K \cdot \left(\prod_{k=0}^{K-1} x_k \right) \exp\left( -w \sum_{k=0}^{K-1} x_k s_k\right)
\\
&= \arg\max_w \left(w^K \cdot \exp\left( -w \sum_{k=0}^{K-1} x_k s_k\right)\right)
\\
&= \arg\max_w \left(K \log(w) - w \sum_{k=0}^{K-1} x_k s_k \right)
\\
&= \frac{K}{\sum_{k=0}^{K-1} x_k s_k}
\end{align}
[comment]: # (</SOL>)
**3.** Obtain the posterior distribution $p(w|{\bf s})$. Note that you do not need to calculate $p({\bf s})$ since the posterior distribution can be readily identified as another Gamma distribution.
#### Solution:
[comment]: # (<SOL>)
\begin{align}
p(w|{\bf s})
&= \frac{p({\bf s}|w) p(w)}{p(s)} \\
&= \frac{1}{p(s)}
\left(w^K \cdot \left(\prod_{k=0}^{K-1} x_k \right) \exp\left( -w \sum_{k=0}^{K-1} x_k s_k\right) \right)
\left(\frac{\beta^\alpha}{\Gamma(\alpha)} w^{\alpha-1} \exp\left(-\beta w\right)\right) \\
&= \frac{1}{p(s)} \frac{\beta^\alpha}{\Gamma(\alpha)} \left(\prod_{k=0}^{K-1} x_k \right)
\left(w^{K + \alpha - 1} \cdot
\exp\left( -w \left(\beta + \sum_{k=0}^{K-1} x_k s_k\right) \right) \right)
\end{align}
that is
$$
w \mid {\bf s} \sim Gamma\left(K+\alpha, \beta + \sum_{k=0}^{K-1} x_k s_k \right)
$$
[comment]: # (</SOL>)
**4.** Determine the MSE and MAP a posteriori estimators of $w$: $w_\text{MSE}=\mathbb{E}\left\{w|{\bf s}\right\}$ and $w_\text{MAP} = \max_w p(w|{\bf s})$.
#### Solution:
[comment]: # (<SOL>)
$$
w_{\text{MSE}} = \mathbb{E}\left\{w \mid {\bf s} \right\}
= \frac{K + \alpha}{\beta + \sum_{k=0}^{K-1} x_k s_k}
$$
$$
w_{\text{MAP}} = \text{mode}\{w\} = \arg\max_w p(w) = \frac{K + \alpha-1}{\beta + \sum_{k=0}^{K-1} x_k s_k}
$$
[comment]: # (</SOL>)
**5.** Compute the following estimators of $S$:
$\qquad\widehat{s}_1 = \mathbb{E}\{s|w_\text{ML},x\}$
$\qquad\widehat{s}_2 = \mathbb{E}\{s|w_\text{MSE},x\}$
$\qquad\widehat{s}_3 = \mathbb{E}\{s|w_\text{MAP},x\}$
#### Solution:
[comment]: # (<SOL>)
$$
\widehat{s}_1 = \mathbb{E}\{s|w_\text{ML},x\} = w_\text{ML} x
$$
$$
\widehat{s}_2 = \mathbb{E}\{s|w_\text{MSE},x\} = w_\text{MSE} x
$$
$$
\widehat{s}_3 = \mathbb{E}\{s|w_\text{MAP},x\} = w_\text{MAP} x
$$
[comment]: # (</SOL>)
## 7. Maximum evidence model selection
We have already addressed with Bayesian Inference the following two issues:
- For a given degree, how do we choose the weights?
- Should we focus on just one model, or can we use several models at once?
However, we still needed some assumptions: a parametric model (i.e., polynomial function and <i>a priori</i> degree selection) and several parameters needed to be adjusted.
Though we can recur to cross-validation, Bayesian inference opens the door to other strategies.
- We could argue that rather than keeping single selections of these parameters, we could use simultaneously several sets of parameters (and/or several parametric forms), and average them in a probabilistic way ... (like we did with the models)
- We will follow a simpler strategy, selecting just the most likely set of parameters according to an ML criterion
### 7.1 Model evidence
The evidence of a model is defined as
$$L = p({\bf s}~|~{\cal M})$$
where ${\cal M}$ denotes the model itself and any free parameters it may have. For instance, for the polynomial model we have assumed so far, ${\cal M}$ would represent the degree of the polynomia, the variance of the additive noise, and the <i>a priori</i> covariance matrix of the weights
Applying the Theorem of Total probability, we can compute the evidence of the model as
$$L = \int p({\bf s}~|~{\bf f},{\cal M}) p({\bf f}~|~{\cal M}) d{\bf f} $$
For the linear model $f({\bf x}) = {\bf w}^\top{\bf z}$, the evidence can be computed as
$$L = \int p({\bf s}~|~{\bf w},{\cal M}) p({\bf w}~|~{\cal M}) d{\bf w} $$
It is important to notice that these probability density functions are exactly the ones we computed on the previous section. We are just making explicit that they depend on a particular model and the selection of its parameters. Therefore:
- $p({\bf s}~|~{\bf w},{\cal M})$ is the likelihood of ${\bf w}$
- $p({\bf w}~|~{\cal M})$ is the <i>a priori</i> distribution of the weights
### 7.2 Model selection via evidence maximization
- As we have already mentioned, we could propose a prior distribution for the model parameters, $p({\cal M})$, and use it to infer the posterior. However, this can be very involved (usually no closed-form expressions can be derived)
- Alternatively, maximizing the evidence is normally good enough
$${\cal M}_\text{ML} = \arg\max_{\cal M} p(s~|~{\cal M})$$
Note that we are using the subscript 'ML' because the evidence can also be referred to as the likelihood of the model
### 7.3 Example: Selection of the degree of the polynomia
For the previous example we had (we consider a spherical Gaussian for the weights):
- ${\bf s}~|~{\bf w},{\cal M}~\sim~{\cal N}\left({\bf Z}{\bf w},~\sigma_\varepsilon^2 {\bf I} \right)$
- ${\bf w}~|~{\cal M}~\sim~{\cal N}\left({\bf 0},~\sigma_p^2 {\bf I} \right)$
In this case, $p({\bf s}~|~{\cal M})$ follows also a Gaussian distribution, and it can be shown that
- $L = p({\bf s}~|~{\cal M}) = {\cal N}\left({\bf 0},\sigma_p^2 {\bf Z} {\bf Z}^\top+\sigma_\varepsilon^2 {\bf I} \right)$
If we just pursue the maximization of $L$, this is equivalent to maximizing the log of the evidence
$$\log(L) = -\frac{M}{2} \log(2\pi) -{\frac{1}{2}}\log\mid\sigma_p^2 {\bf Z} {\bf Z}^\top+\sigma_\varepsilon^2 {\bf I}\mid - \frac{1}{2} {\bf s}^\top \left(\sigma_p^2 {\bf Z} {\bf Z}^\top+\sigma_\varepsilon^2 {\bf I}\right)^{-1} {\bf s}$$
where $M$ denotes the length of vector ${\bf z}$ (the degree of the polynomia minus 1).
The following fragment of code evaluates the evidence of the model as a function of the degree of the polynomia
```
from math import pi
n_points = 15
frec = 3
std_n = 0.2
max_degree = 12
#Prior distribution parameters
sigma_eps = 0.2
mean_w = np.zeros((degree+1,))
sigma_p = 0.5
X_tr = 3 * np.random.random((n_points,1)) - 0.5
S_tr = - np.cos(frec*X_tr) + std_n * np.random.randn(n_points,1)
#Compute matrix with training input data for the polynomial model
Z = []
for x_val in X_tr.tolist():
Z.append([x_val[0]**k for k in range(degree+1)])
Z=np.asmatrix(Z)
#Evaluate the posterior evidence
logE = []
for deg in range(max_degree):
Z_iter = Z[:,:deg+1]
logE_iter = -((deg+1)*np.log(2*pi)/2) \
-np.log(np.linalg.det((sigma_p**2)*Z_iter.dot(Z_iter.T) + (sigma_eps**2)*np.eye(n_points)))/2 \
-S_tr.T.dot(np.linalg.inv((sigma_p**2)*Z_iter.dot(Z_iter.T) + (sigma_eps**2)*np.eye(n_points))).dot(S_tr)/2
logE.append(logE_iter[0,0])
plt.plot(np.array(range(max_degree))+1,logE)
plt.xlabel('Polynomia degree')
plt.ylabel('log evidence')
plt.show()
```
The above curve may change the position of its maximum from run to run.
We conclude the notebook by plotting the result of the Bayesian inference for $M=6$
```
n_points = 15
n_grid = 200
frec = 3
std_n = 0.2
degree = 5 #M-1
nplots = 6
#Prior distribution parameters
sigma_eps = 0.1
mean_w = np.zeros((degree+1,))
sigma_p = .5 * np.eye(degree+1)
X_tr = 3 * np.random.random((n_points,1)) - 0.5
S_tr = - np.cos(frec*X_tr) + std_n * np.random.randn(n_points,1)
X_grid = np.linspace(-1,3,n_grid)
S_grid = - np.cos(frec*X_grid) #Noise free for the true model
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(X_tr,S_tr,'b.',markersize=10)
#Compute matrix with training input data for the polynomial model
Z = []
for x_val in X_tr.tolist():
Z.append([x_val[0]**k for k in range(degree+1)])
Z=np.asmatrix(Z)
#Compute posterior distribution parameters
Sigma_w = np.linalg.inv(np.dot(Z.T,Z)/(sigma_eps**2) + np.linalg.inv(sigma_p))
posterior_mean = Sigma_w.dot(Z.T).dot(S_tr)/(sigma_eps**2)
posterior_mean = np.array(posterior_mean).flatten()
#Plot the posterior mean
#Note that polyval assumes the first element of weight vector is the coefficient of
#the highest degree term. Thus, we need to reverse w_iter
S_grid_iter = np.polyval(posterior_mean[::-1],X_grid)
ax.plot(X_grid,S_grid_iter,'g-',label='Predictive mean, BI')
#Plot confidence intervals for the Bayesian Inference
std_x = []
for el in X_grid:
x_ast = np.array([el**k for k in range(degree+1)])
std_x.append(np.sqrt(x_ast.dot(Sigma_w).dot(x_ast)[0,0]))
std_x = np.array(std_x)
plt.fill_between(X_grid, S_grid_iter-std_x, S_grid_iter+std_x,
alpha=0.2, edgecolor='#1B2ACC', facecolor='#089FFF',
linewidth=4, linestyle='dashdot', antialiased=True)
#We plot also the least square solution
w_LS = np.polyfit(X_tr.flatten(), S_tr.flatten(), degree)
S_grid_iter = np.polyval(w_LS,X_grid)
ax.plot(X_grid,S_grid_iter,'m-',label='LS regression')
ax.set_xlim(-1,3)
ax.set_ylim(S_tr[0]-2,S_tr[-1]+2)
ax.legend(loc='best')
plt.show()
```
We can check, that now the model also seems quite appropriate for LS regression, but keep in mind that selection of such parameter was itself carried out using Bayesian inference.
|
github_jupyter
|
# Goals
### 1. Learn to implement Resnet V2 Block (Type - 1) using monk
- Monk's Keras
- Monk's Pytorch
- Monk's Mxnet
### 2. Use network Monk's debugger to create complex blocks
### 3. Understand how syntactically different it is to implement the same using
- Traditional Keras
- Traditional Pytorch
- Traditional Mxnet
# Resnet V2 Block - Type 1
- Note: The block structure can have variations too, this is just an example
```
from IPython.display import Image
Image(filename='imgs/resnet_v2_with_downsample.png')
```
# Table of contents
[1. Install Monk](#1)
[2. Block basic Information](#2)
- [2.1) Visual structure](#2-1)
- [2.2) Layers in Branches](#2-2)
[3) Creating Block using monk visual debugger](#3)
- [3.1) Create the first branch](#3-1)
- [3.2) Create the second branch](#3-2)
- [3.3) Merge the branches](#3-3)
- [3.4) Debug the merged network](#3-4)
- [3.5) Compile the network](#3-5)
- [3.6) Visualize the network](#3-6)
- [3.7) Run data through the network](#3-7)
[4) Creating Block Using MONK one line API call](#4)
- [Mxnet Backend](#4-1)
- [Pytorch Backend](#4-2)
- [Keras Backend](#4-3)
[5) Appendix](#5)
- [Study Material](#5-1)
- [Creating block using traditional Mxnet](#5-2)
- [Creating block using traditional Pytorch](#5-3)
- [Creating block using traditional Keras](#5-4)
<a id='1'></a>
# Install Monk
- git clone https://github.com/Tessellate-Imaging/monk_v1.git
- cd monk_v1/installation/Linux && pip install -r requirements_cu9.txt
- (Select the requirements file as per OS and CUDA version)
```
!git clone https://github.com/Tessellate-Imaging/monk_v1.git
```
# Imports
```
# Common
import numpy as np
import math
import netron
from collections import OrderedDict
from functools import partial
# Monk
import os
import sys
sys.path.append("monk_v1/monk/");
```
<a id='2'></a>
# Block Information
<a id='2_1'></a>
## Visual structure
```
from IPython.display import Image
Image(filename='imgs/resnet_v2_with_downsample.png')
```
<a id='2_2'></a>
## Layers in Branches
- Number of branches: 2
- Common element
- batchnorm -> relu
- Branch 1
- conv_1x1
- Branch 2
- conv_3x3 -> batchnorm -> relu -> conv_3x3
- Branches merged using
- Elementwise addition
(See Appendix to read blogs on resnets)
<a id='3'></a>
# Creating Block using monk debugger
```
# Imports and setup a project
# To use pytorch backend - replace gluon_prototype with pytorch_prototype
# To use keras backend - replace gluon_prototype with keras_prototype
from gluon_prototype import prototype
# Create a sample project
gtf = prototype(verbose=1);
gtf.Prototype("sample-project-1", "sample-experiment-1");
```
<a id='3-1'></a>
## Create the first branch
```
def first_branch(output_channels=128, stride=1):
network = [];
network.append(gtf.convolution(output_channels=output_channels, kernel_size=1, stride=stride));
return network;
# Debug the branch
branch_1 = first_branch(output_channels=128, stride=1)
network = [];
network.append(branch_1);
gtf.debug_custom_model_design(network);
```
<a id='3-2'></a>
## Create the second branch
```
def second_branch(output_channels=128, stride=1):
network = [];
network.append(gtf.convolution(output_channels=output_channels, kernel_size=3, stride=stride));
network.append(gtf.batch_normalization());
network.append(gtf.relu());
network.append(gtf.convolution(output_channels=output_channels, kernel_size=3, stride=1));
return network;
# Debug the branch
branch_2 = second_branch(output_channels=128, stride=1)
network = [];
network.append(branch_2);
gtf.debug_custom_model_design(network);
```
<a id='3-3'></a>
## Merge the branches
```
def final_block(output_channels=128, stride=1):
network = [];
# Common elements
network.append(gtf.batch_normalization());
network.append(gtf.relu());
#Create subnetwork and add branches
subnetwork = [];
branch_1 = first_branch(output_channels=output_channels, stride=stride)
branch_2 = second_branch(output_channels=output_channels, stride=stride)
subnetwork.append(branch_1);
subnetwork.append(branch_2);
# Add merging element
subnetwork.append(gtf.add());
# Add the subnetwork
network.append(subnetwork);
return network;
```
<a id='3-4'></a>
## Debug the merged network
```
final = final_block(output_channels=128, stride=1)
network = [];
network.append(final);
gtf.debug_custom_model_design(network);
```
<a id='3-5'></a>
## Compile the network
```
gtf.Compile_Network(network, data_shape=(3, 224, 224), use_gpu=False);
```
<a id='3-6'></a>
## Run data through the network
```
import mxnet as mx
x = np.zeros((1, 3, 224, 224));
x = mx.nd.array(x);
y = gtf.system_dict["local"]["model"].forward(x);
print(x.shape, y.shape)
```
<a id='3-7'></a>
## Visualize network using netron
```
gtf.Visualize_With_Netron(data_shape=(3, 224, 224))
```
<a id='4'></a>
# Creating Using MONK LOW code API
<a id='4-1'></a>
## Mxnet backend
```
from gluon_prototype import prototype
gtf = prototype(verbose=1);
gtf.Prototype("sample-project-1", "sample-experiment-1");
network = [];
# Single line addition of blocks
network.append(gtf.resnet_v2_block(output_channels=128));
gtf.Compile_Network(network, data_shape=(3, 224, 224), use_gpu=False);
```
<a id='4-2'></a>
## Pytorch backend
- Only the import changes
```
#Change gluon_prototype to pytorch_prototype
from pytorch_prototype import prototype
gtf = prototype(verbose=1);
gtf.Prototype("sample-project-1", "sample-experiment-1");
network = [];
# Single line addition of blocks
network.append(gtf.resnet_v2_block(output_channels=128));
gtf.Compile_Network(network, data_shape=(3, 224, 224), use_gpu=False);
```
<a id='4-3'></a>
## Keras backend
- Only the import changes
```
#Change gluon_prototype to keras_prototype
from keras_prototype import prototype
gtf = prototype(verbose=1);
gtf.Prototype("sample-project-1", "sample-experiment-1");
network = [];
# Single line addition of blocks
network.append(gtf.resnet_v1_block(output_channels=128));
gtf.Compile_Network(network, data_shape=(3, 224, 224), use_gpu=False);
```
<a id='5'></a>
# Appendix
<a id='5-1'></a>
## Study links
- https://towardsdatascience.com/residual-blocks-building-blocks-of-resnet-fd90ca15d6ec
- https://medium.com/@MaheshNKhatri/resnet-block-explanation-with-a-terminology-deep-dive-989e15e3d691
- https://medium.com/analytics-vidhya/understanding-and-implementation-of-residual-networks-resnets-b80f9a507b9c
- https://hackernoon.com/resnet-block-level-design-with-deep-learning-studio-part-1-727c6f4927ac
<a id='5-2'></a>
## Creating block using traditional Mxnet
- Code credits - https://mxnet.incubator.apache.org/
```
# Traditional-Mxnet-gluon
import mxnet as mx
from mxnet.gluon import nn
from mxnet.gluon.nn import HybridBlock, BatchNorm
from mxnet.gluon.contrib.nn import HybridConcurrent, Identity
from mxnet import gluon, init, nd
def _conv3x3(channels, stride, in_channels):
return nn.Conv2D(channels, kernel_size=3, strides=stride, padding=1,
use_bias=False, in_channels=in_channels)
class ResnetBlockV2(HybridBlock):
def __init__(self, channels, stride, in_channels=0,
last_gamma=False,
norm_layer=BatchNorm, norm_kwargs=None, **kwargs):
super(ResnetBlockV2, self).__init__(**kwargs)
#Branch - 1
self.downsample = nn.Conv2D(channels, 1, stride, use_bias=False,
in_channels=in_channels)
# Branch - 2
self.bn1 = norm_layer(**({} if norm_kwargs is None else norm_kwargs))
self.conv1 = _conv3x3(channels, stride, in_channels)
if not last_gamma:
self.bn2 = norm_layer(**({} if norm_kwargs is None else norm_kwargs))
else:
self.bn2 = norm_layer(gamma_initializer='zeros',
**({} if norm_kwargs is None else norm_kwargs))
self.conv2 = _conv3x3(channels, 1, channels)
def hybrid_forward(self, F, x):
residual = x
x = self.bn1(x)
x = F.Activation(x, act_type='relu')
residual = self.downsample(x)
x = self.conv1(x)
x = self.bn2(x)
x = F.Activation(x, act_type='relu')
x = self.conv2(x)
return x + residual
# Invoke the block
block = ResnetBlockV2(64, 1)
# Initialize network and load block on machine
ctx = [mx.cpu()];
block.initialize(init.Xavier(), ctx = ctx);
block.collect_params().reset_ctx(ctx)
block.hybridize()
# Run data through network
x = np.zeros((1, 3, 224, 224));
x = mx.nd.array(x);
y = block.forward(x);
print(x.shape, y.shape)
# Export Model to Load on Netron
block.export("final", epoch=0);
netron.start("final-symbol.json", port=8082)
```
<a id='5-3'></a>
## Creating block using traditional Pytorch
- Code credits - https://pytorch.org/
```
# Traiditional-Pytorch
import torch
from torch import nn
from torch.jit.annotations import List
import torch.nn.functional as F
def conv3x3(in_planes, out_planes, stride=1, groups=1, dilation=1):
"""3x3 convolution with padding"""
return nn.Conv2d(in_planes, out_planes, kernel_size=3, stride=stride,
padding=dilation, groups=groups, bias=False, dilation=dilation)
def conv1x1(in_planes, out_planes, stride=1):
"""1x1 convolution"""
return nn.Conv2d(in_planes, out_planes, kernel_size=1, stride=stride, bias=False)
class ResnetBlock(nn.Module):
expansion = 1
__constants__ = ['downsample']
def __init__(self, inplanes, planes, stride=1, groups=1,
base_width=64, dilation=1, norm_layer=None):
super(ResnetBlock, self).__init__()
norm_layer = nn.BatchNorm2d
# Common Element
self.bn0 = norm_layer(inplanes)
self.relu0 = nn.ReLU(inplace=True)
# Branch - 1
self.downsample = conv1x1(inplanes, planes, stride)
# Branch - 2
self.conv1 = conv3x3(inplanes, planes, stride)
self.bn1 = norm_layer(planes)
self.relu = nn.ReLU(inplace=True)
self.conv2 = conv3x3(planes, planes)
self.stride = stride
def forward(self, x):
x = self.bn0(x);
x = self.relu0(x);
identity = self.downsample(x)
out = self.conv1(x)
out = self.bn1(out)
out = self.relu(out)
out = self.conv2(out)
out += identity
out = self.relu(out)
return out
# Invoke the block
block = ResnetBlock(3, 64, stride=1);
# Initialize network and load block on machine
layers = []
layers.append(block);
net = nn.Sequential(*layers);
# Run data through network
x = torch.randn(1, 3, 224, 224)
y = net(x)
print(x.shape, y.shape);
# Export Model to Load on Netron
torch.onnx.export(net, # model being run
x, # model input (or a tuple for multiple inputs)
"model.onnx", # where to save the model (can be a file or file-like object)
export_params=True, # store the trained parameter weights inside the model file
opset_version=10, # the ONNX version to export the model to
do_constant_folding=True, # whether to execute constant folding for optimization
input_names = ['input'], # the model's input names
output_names = ['output'], # the model's output names
dynamic_axes={'input' : {0 : 'batch_size'}, # variable lenght axes
'output' : {0 : 'batch_size'}})
netron.start('model.onnx', port=9998);
```
<a id='5-4'></a>
## Creating block using traditional Keras
- Code credits: https://keras.io/
```
# Traditional-Keras
import keras
import keras.layers as kla
import keras.models as kmo
import tensorflow as tf
from keras.models import Model
backend = 'channels_last'
from keras import layers
def resnet_conv_block(input_tensor,
kernel_size,
filters,
stage,
block,
strides=(2, 2)):
filters1, filters2, filters3 = filters
bn_axis = 3
conv_name_base = 'res' + str(stage) + block + '_branch'
bn_name_base = 'bn' + str(stage) + block + '_branch'
# Common Element
start = layers.BatchNormalization(axis=bn_axis, name=bn_name_base + '0a')(input_tensor)
start = layers.Activation('relu')(start)
#Branch - 1
shortcut = layers.Conv2D(filters3, (1, 1), strides=strides,
kernel_initializer='he_normal',
name=conv_name_base + '1')(start)
#Branch - 2
x = layers.Conv2D(filters1, (1, 1), strides=strides,
kernel_initializer='he_normal',
name=conv_name_base + '2a')(start)
x = layers.BatchNormalization(axis=bn_axis, name=bn_name_base + '2a')(x)
x = layers.Activation('relu')(x)
x = layers.Conv2D(filters2, kernel_size, padding='same',
kernel_initializer='he_normal',
name=conv_name_base + '2b')(x)
x = layers.add([x, shortcut])
x = layers.Activation('relu')(x)
return x
def create_model(input_shape, kernel_size, filters, stage, block):
img_input = layers.Input(shape=input_shape);
x = resnet_conv_block(img_input, kernel_size, filters, stage, block)
return Model(img_input, x);
# Invoke the block
kernel_size=3;
filters=[64, 64, 64];
input_shape=(224, 224, 3);
model = create_model(input_shape, kernel_size, filters, 0, "0");
# Run data through network
x = tf.placeholder(tf.float32, shape=(1, 224, 224, 3))
y = model(x)
print(x.shape, y.shape)
# Export Model to Load on Netron
model.save("final.h5");
netron.start("final.h5", port=8082)
```
|
github_jupyter
|
```
from misc import HP
import argparse
import random
import time
import pickle
import copy
import SYCLOP_env as syc
from misc import *
import sys
import os
import cv2
import argparse
import tensorflow.keras as keras
from keras_networks import rnn_model_102, rnn_model_multicore_201, rnn_model_multicore_202
from curriculum_utils import create_mnist_dataset, bad_res102
def generate_trajectory(n_steps,max_q,acceleration_mode):
starting_point = np.array([max_q[0] // 2, max_q[1] // 2])
steps = []
qdot=0
for j in range(n_steps):
steps.append(starting_point * 1)
if acceleration_mode:
qdot += np.random.randint(-1, 2, 2)
starting_point += qdot
else:
starting_point += np.random.randint(-5, 6, 2)
return np.array(steps)
def split_dataset_xy(dataset):
dataset_x1 = [uu[0] for uu in dataset]
dataset_x2 = [uu[1] for uu in dataset]
dataset_y = [uu[-1] for uu in dataset]
return (np.array(dataset_x1)[...,np.newaxis],np.array(dataset_x2)[:,:n_timesteps,:]),np.array(dataset_y)
#parse hyperparameters
lsbjob = os.getenv('LSB_JOBID')
lsbjob = '' if lsbjob is None else lsbjob
hp = HP()
hp.save_path = 'saved_runs'
hp.description=''
parser = argparse.ArgumentParser()
parser.add_argument('--tau_int', default=4., type=float, help='Integration timescale for adaaptation')
parser.add_argument('--resize', default=1.0, type=float, help='resize of images')
parser.add_argument('--run_name_suffix', default='', type=str, help='suffix for runname')
parser.add_argument('--eval_dir', default=None, type=str, help='eval dir')
parser.add_argument('--dqn_initial_network', default=None, type=str, help='dqn_initial_network')
parser.add_argument('--decoder_initial_network', default=None, type=str, help='decoder_initial_network')
parser.add_argument('--decoder_arch', default='default', type=str, help='decoder_network architecture: default / multicore_201')
parser.add_argument('--decoder_n_cores', default=1, type=int, help='decoder number of cores')
parser.add_argument('--decoder_learning_rate', default=1e-3, type=float, help='decoder learning rate')
parser.add_argument('--decoder_dropout', default=0.0, type=float, help='decoder dropout')
parser.add_argument('--decoder_rnn_type', default='gru', type=str, help='gru or rnn')
parser.add_argument('--decoder_rnn_units', default=100, type=int, help='decoder rnn units')
parser.add_argument('--decoder_rnn_layers', default=1, type=int, help='decoder rnn units')
parser.add_argument('--decoder_ignore_position', dest='decoder_ignore_position', action='store_true')
parser.add_argument('--no-decoder_ignore_position', dest='decoder_ignore_position', action='store_false')
parser.add_argument('--syclop_learning_rate', default=2.5e-3, type=float, help='syclop (RL) learning rate')
parser.add_argument('--color', default='grayscale', type=str, help='grayscale/rgb')
parser.add_argument('--speed_reward', default=0.0, type=float, help='speed reward, typically negative')
parser.add_argument('--intensity_reward', default=0.0, type=float, help='speed penalty reward')
parser.add_argument('--loss_reward', default=-1.0, type=float, help='reward for loss, typically negative')
parser.add_argument('--resolution', default=28, type=int, help='resolution')
parser.add_argument('--max_eval_episodes', default=10000, type=int, help='episodes for evaluation mode')
parser.add_argument('--steps_per_episode', default=5, type=int, help='time steps in each episode in ')
parser.add_argument('--fit_verbose', default=1, type=int, help='verbose level for model.fit ')
parser.add_argument('--steps_between_learnings', default=100, type=int, help='steps_between_learnings')
parser.add_argument('--num_epochs', default=100, type=int, help='steps_between_learnings')
parser.add_argument('--alpha_increment', default=0.01, type=float, help='reward for loss, typically negative')
parser.add_argument('--beta_t1', default=400000, type=int, help='time rising bete')
parser.add_argument('--beta_t2', default=700000, type=int, help='end rising beta')
parser.add_argument('--beta_b1', default=0.1, type=float, help='beta initial value')
parser.add_argument('--beta_b2', default=1.0, type=float, help='beta final value')
parser.add_argument('--curriculum_enable', dest='curriculum_enable', action='store_true')
parser.add_argument('--no-curriculum_enable', dest='curriculum_enable', action='store_false')
parser.add_argument('--conv_fe', dest='conv_fe', action='store_true')
parser.add_argument('--no-conv_fe', dest='conv_fe', action='store_false')
parser.add_argument('--acceleration_mode', dest='acceleration_mode', action='store_true')
parser.add_argument('--no-acceleration_mode', dest='acceleration_mode', action='store_false')
parser.set_defaults(eval_mode=False, decode_from_dvs=False,test_mode=False,rising_beta_schedule=True,decoder_ignore_position=False, curriculum_enable=True, conv_fe=False,
acceleration_mode=True)
config = parser.parse_args('')
# config = parser.parse_args()
config = vars(config)
hp.upadte_from_dict(config)
hp.this_run_name = sys.argv[0] + '_noname_' + hp.run_name_suffix + '_' + lsbjob + '_' + str(int(time.time()))
#define model
n_timesteps = hp.steps_per_episode
##
# deploy_logs()
##
# if hp.decoder_arch == 'multicore_201':
# decoder = rnn_model_multicore_201(n_cores=hp.decoder_n_cores,lr=hp.decoder_learning_rate,ignore_input_B=hp.decoder_ignore_position,dropout=hp.decoder_dropout,rnn_type=hp.decoder_rnn_type,
# input_size=(hp.resolution,hp.resolution, 1),rnn_layers=hp.decoder_rnn_layers,conv_fe=hp.conv_fe, rnn_units=hp.decoder_rnn_units, n_timesteps=hp.steps_per_episode)
# if hp.decoder_arch == 'multicore_202':
# decoder = rnn_model_multicore_202(n_cores=hp.decoder_n_cores, lr=hp.decoder_learning_rate,
# ignore_input_B=hp.decoder_ignore_position, dropout=hp.decoder_dropout,
# rnn_type=hp.decoder_rnn_type,
# input_size=(hp.resolution, hp.resolution, 1),
# rnn_layers=hp.decoder_rnn_layers, conv_fe=hp.conv_fe,
# rnn_units=hp.decoder_rnn_units, n_timesteps=hp.steps_per_episode)
# elif hp.decoder_arch == 'default':
# decoder = rnn_model_102(lr=hp.decoder_learning_rate,ignore_input_B=hp.decoder_ignore_position,dropout=hp.decoder_dropout,rnn_type=hp.decoder_rnn_type,
# input_size=(hp.resolution,hp.resolution, 1),rnn_layers=hp.decoder_rnn_layers,conv_fe=hp.conv_fe,rnn_units=hp.decoder_rnn_units, n_timesteps=hp.steps_per_episode)
decoder_initial_network = 'saved_runs/trajectory_curriculum101.py_noname__613128_1624010531_1//final_decoder.nwk'
decoder = keras.models.load_model(decoder_initial_network)
#define dataset
(images, labels), (images_test, labels_test) = keras.datasets.mnist.load_data(path="mnist.npz")
#fit one epoch in a time
# scheduler = Scheduler(hp.lambda_schedule)
# for epoch in range(hp.num_epochs):
# lambda_epoch = scheduler.step(epoch)
hp.acceleration_mode
alpha=0
hp.num_trials = 30
trajectories = []
train_pred_pred = []
val_pred_pred = []
for trial in range(hp.num_trials):
this_trajectory=generate_trajectory(hp.steps_per_episode,[72,72],hp.acceleration_mode)
# this_trajectory=trajectories[trial]
train_dataset, test_dataset = create_mnist_dataset(images, labels, 6, sample=hp.steps_per_episode, bad_res_func=bad_res102,
return_datasets=True, q_0=this_trajectory, alpha=0.0,
random_trajectories=True,acceleration_mode=hp.acceleration_mode)
train_dataset_x, train_dataset_y = split_dataset_xy(train_dataset)
test_dataset_x, test_dataset_y = split_dataset_xy(test_dataset)
q_prime = train_dataset_x[1][0]
# print('epoch', epoch, ' CONTROL!!!',' first q --', q_prime.reshape([-1]))
print("evaluating trajectory ", trial)
train_preds = decoder.predict(
train_dataset_x,
batch_size=64,
verbose=hp.fit_verbose,
# We pass some validation for
# monitoring validation loss and metrics
# at the end of each epoch
)
val_preds = decoder.predict(
test_dataset_x,
batch_size=64,
verbose=hp.fit_verbose,
# We pass some validation for
# monitoring validation loss and metrics
# at the end of each epoch
)
accuracy = np.mean(np.argmax(val_preds, axis=1)==test_dataset_y)
print('accuracy:', accuracy)
trajectories.append(this_trajectory+0.)
train_pred_pred.append(train_preds+0.0)
val_pred_pred.append(val_preds+0.0)
accuracy = np.mean(np.argmax(val_preds, axis=1)==test_dataset_y)
accuracy
ent = np.zeros([np.shape(test_dataset_y)[0],hp.num_trials])
lablab = np.zeros([np.shape(test_dataset_y)[0],hp.num_trials])
for jj,preds in enumerate(val_pred_pred):
ent[:,jj]=np.sum(-preds*np.log(preds),axis=1)
lablab[:,jj]=np.argmax(preds, axis=1)
ii=np.argmin(ent,axis=1)
best_lbl=[]
for jj,uu in enumerate(ii):
best_lbl.append(lablab[jj,uu])
np.mean(best_lbl==test_dataset_y)
#random syclop,
np.mean(lablab==test_dataset_y.reshape([-1,1]))
accuracies=np.mean(lablab==test_dataset_y.reshape([-1,1]),axis=0)
best_ii=np.argmax(np.mean(lablab==test_dataset_y.reshape([-1,1]),axis=0))
np.mean(ii==best_ii)
np.mean(np.any(lablab==test_dataset_y.reshape([-1,1]),axis=1))
best_ent=np.min(ent,axis=1)
_=plt.hist(best_ent,bins=20)
_=plt.hist(best_ent[best_lbl!=test_dataset_y],bins=20)
_=plt.hist(best_ent[best_lbl==test_dataset_y],bins=20)
super_pred=np.sum(val_pred_pred,axis=0)
super_label=np.argmax(super_pred,axis=1)
np.mean(super_label==test_dataset_y)
super_label.shape
with open('committee103s5_traj_30.pkl','wb') as f:
pickle.dump(trajectories,f)
def super_pred_fun(pred,T=1):
logits = np.log(pred)
pred_T = np.exp(1./T*logits)
pred_T = pred_T/np.sum(pred_T,axis=-1)[...,np.newaxis]
super_pred=np.sum(pred_T,axis=0)
return super_pred
super_pred = super_pred_fun(train_pred_pred)
super_pred = super_pred_fun(val_pred_pred,T=1000)
super_label=np.argmax(super_pred,axis=1)
print(np.mean(super_label==test_dataset_y))
np.linspace(0.1,5.0,100)
super_pred = super_pred_fun(val_pred_pred[:15],T=1000)
super_label=np.argmax(super_pred,axis=1)
print(np.mean(super_label==test_dataset_y))
super_pred = super_pred_fun(val_pred_pred[:5],T=1000)
super_label=np.argmax(super_pred,axis=1)
print(np.mean(super_label==test_dataset_y))
super_pred = super_pred_fun(val_pred_pred[:2],T=1000)
super_label=np.argmax(super_pred,axis=1)
print(np.mean(super_label==test_dataset_y))
# x = np.linspace(0, 2*np.pi, 64)
# y = np.cos(x)
# pl.figure()
# pl.plot(x,y)
n = hp.num_trials
# colors = plt.cm.jet(accuracies)
colors = plt.cm.jet((accuracies-np.min(accuracies))/(np.max(accuracies)-np.min(accuracies)))
#
for trial in range(hp.num_trials):
plt.plot(trajectories[trial][:,0],trajectories[trial][:,1], color=colors[trial])
# plt.colorbar()
colors = plt.cm.jet((accuracies-np.min(accuracies))/(np.max(accuracies)-np.min(accuracies)))
n = hp.num_trials
# colors = plt.cm.jet(accuracies)
colors = plt.cm.RdYlGn((accuracies-np.min(accuracies))/(np.max(accuracies)-np.min(accuracies)))
#
for trial in range(hp.num_trials):
plt.plot(trajectories[trial][:,0],trajectories[trial][:,1], color=colors[trial],linewidth=3)
plt.cm.jet(1.0)
n_lines = hp.num_trials
x = np.arange(100)
yint = np.arange(0, n_lines*10, 10)
ys = np.array([x + b for b in yint])
xs = np.array([x for i in range(n_lines)]) # could also use np.tile
colors = np.arange(n_lines)
fig, ax = plt.subplots()
lc = multiline(xs, ys, yint, cmap='bwr', lw=2)
axcb = fig.colorbar(lc)
axcb.set_label('Y-intercept')
ax.set_title('Line Collection with mapped colors')
# Set the input shape
input_shape = (300,)
# print(f'Feature shape: {input_shape}')
# Create the model
model = keras.Sequential()
model.add(keras.layers.Dense(300, input_shape=input_shape, activation='relu'))
model.add(keras.layers.Dropout(0.4))
model.add(keras.layers.Dense(100, activation='relu'))
model.add(keras.layers.Dropout(0.4))
model.add(keras.layers.Dense(50, activation='relu'))
model.add(keras.layers.Dropout(0.2))
model.add(keras.layers.Dense(10, activation='softmax'))
# Configure the model and start training
model.compile(loss='sparse_categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
model.fit(np.transpose(train_pred_pred,[1,2,0]).reshape([-1,300]), train_dataset_y.astype(int), epochs=100, batch_size=250, verbose=1, validation_split=0.2)
plt.hist(accuracies,bins=30)
for pred in np.array(val_pred_pred)[:,7,:]:
plt.plot(pred)
plt.xlabel('label')
plt.ylabel('probability')
np.array(val_pred_pred[:,0,:])
```
|
github_jupyter
|
```
import numpy as np
import matplotlib.pyplot as plt
```
# 1.
## a)
```
def simetrica(A):
"Verifică dacă matricea A este simetrică"
return np.all(A == A.T)
def pozitiv_definita(A):
"Verifică dacă matricea A este pozitiv definită"
for i in range(1, len(A) + 1):
d_minor = np.linalg.det(A[:i, :i])
if d_minor < 0:
return False
return True
def fact_ll(A):
# Pasul 1
if not simetrica(A):
raise Exception("Nu este simetrica")
if not pozitiv_definita(A):
raise Exception("Nu este pozitiv definită")
N = A.shape[0]
# Pasul 2
S = A.copy()
L = np.zeros((N, N))
# Pasul 3
for i in range(N):
# Actualizez coloana i din matricea L
L[:, i] = S[:, i] / np.sqrt(S[i, i])
# Calculez noul complement Schur
S_21 = S[i + 1:, i]
S_nou = np.eye(N)
S_nou[i + 1:, i + 1:] = S[i + 1:, i + 1:] - np.outer(S_21, S_21.T) / S[i, i]
S = S_nou
# Returnez matricea calculată
return L
A = np.array([
[25, 15, -5],
[15, 18, 0],
[-5, 0, 11]
], dtype=np.float64)
L = fact_ll(A)
print("L este:")
print(L)
print("Verificare:")
print(L @ L.T)
```
## b)
```
b = np.array([1, 2, 3], dtype=np.float64)
y = np.zeros(3)
x = np.zeros(3)
# Substituție ascendentă
for i in range(0, 3):
coefs = L[i, :i + 1]
values = y[:i + 1]
y[i] = (b[i] - coefs @ values) / L[i, i]
L_t = L.T
# Substituție descendentă
for i in range(2, -1, -1):
coefs = L_t[i, i + 1:]
values = x[i + 1:]
x[i] = (y[i] - coefs @ values) / L_t[i, i]
print("x =", x)
print()
print("Verificare: A @ x =", A @ x)
```
## 2.
```
def step(x, f, df):
"Calculează un pas din metoda Newton-Rhapson."
return x - f(x) / df(x)
def newton_rhapson(f, df, x0, eps):
"Determină o soluție a f(x) = 0 plecând de la x_0"
# Primul punct este cel primit ca parametru
prev_x = x0
# Execut o iterație
x = step(x0, f, df)
N = 1
while True:
# Verific condiția de oprire
if abs(x - prev_x) / abs(prev_x) < eps:
break
# Execut încă un pas
prev_x = x
x = step(x, f, df)
# Contorizez numărul de iterații
N += 1
return x, N
```
Funcția dată este
$$
f(x) = x^3 + 3 x^2 - 18 x - 40
$$
iar derivatele ei sunt
$$
f'(x) = 3x^2 + 6 x - 18
$$
$$
f''(x) = 6x + 6
$$
```
f = lambda x: (x ** 3) + 3 * (x ** 2) - 18 * x - 40
df = lambda x: 3 * (x ** 2) + 6 * x - 18
ddf = lambda x: 6 * x + 6
left = -8
right = +8
x_grafic = np.linspace(left, right, 500)
def set_spines(ax):
# Mut axele de coordonate
ax.spines['bottom'].set_position('zero')
ax.spines['top'].set_color('none')
ax.spines['left'].set_position('zero')
ax.spines['right'].set_color('none')
fig, ax = plt.subplots(dpi=120)
set_spines(ax)
plt.plot(x_grafic, f(x_grafic), label='$f$')
plt.plot(x_grafic, df(x_grafic), label="$f'$")
plt.plot(x_grafic, ddf(x_grafic), label="$f''$")
plt.legend()
plt.show()
```
Alegem subintervale astfel încât $f(a) f(b) < 0$:
- $[-8, -4]$
- $[-4, 0]$
- $[2, 6]$
Pentru fiecare dintre acestea, căutăm un punct $x_0$ astfel încât $f(x_0) f''(x_0) > 0$:
- $-6$
- $-1$
- $5$
```
eps = 1e-3
x1, _ = newton_rhapson(f, df, -6, eps)
x2, _ = newton_rhapson(f, df, -1, eps)
x3, _ = newton_rhapson(f, df, 5, eps)
fig, ax = plt.subplots(dpi=120)
plt.suptitle('Soluțiile lui $f(x) = 0$')
set_spines(ax)
plt.plot(x_grafic, f(x_grafic))
plt.scatter(x1, 0)
plt.scatter(x2, 0)
plt.scatter(x3, 0)
plt.show()
```
|
github_jupyter
|
# Input data representation as 2D array of 3D blocks
> An easy way to represent input data to neural networks or any other machine learning algorithm in the form of 2D array of 3D-blocks
- toc: false
- branch: master
- badges: true
- comments: true
- categories: [machine learning, jupyter, graphviz]
- image: images/array_visualiser/thumbnail.png
- search_exclude: false
---
Often while working with machine learning algorithms the developer has a good picture of how the input data looks like apart from knowing what the input data is. Also, most of the times the input data is usually represented or decribed with array terminology. Hence, this particular post is one such attempt to create simple 2D representations of 3D-blocks symbolising the arrays used for input.
[Graphviz](https://graphviz.readthedocs.io/en/stable/) a highly versatile graphing library that creates graphs based on DOT language is used to create the 2D array representation of 3D blocks with annotation and color uniformity to create quick and concise graphs/pictures for good explanations of input data used in various machine learning/deep learning algorithms.
In what follows is a script to create the 2D array representation og 3D blocks mainly intented for time-series data. The script facilitates some features which include-
* Starting at time instant 0 or -1
* counting backwards i.e. t-4 -> t-3 -> t-2 -> t-1 -> t-0 or counting forwards t-0 -> t-1 -> t-2 -> t-3 -> t-4 -> t-5
### Imports and global constants
```
import graphviz as G # to create the required graphs
import random # to generate random hex codes for colors
FORWARDS = True # to visualise array from left to right
BACKWARDS = False # to visualise array from right to left
```
### Properties of 2D representation of 3D array blocks
Main features/properties of the array visualisation needed are defined gere before actually creating the graph/picture.
1) Number of Rows: similar to rows in a matrix where each each row corresponds to one particular data type with data across different time instants arranged in columns
2) Blocks: which corresponds to the number of time instants in each row (jagged arrays can also be graphed)
3) Prefix: the annotation used to annotate each 3D block in the 2D array representation
```
ROW_NUMS = [1, 2] # Layer numbers corresponding to the number of rows of array data (must be contiguous)
BLOCKS = [3, 3] # number of data fields in each row i.e., columns in each row
diff = [x - ROW_NUMS[i] for i, x in enumerate(ROW_NUMS[1:])]
assert diff == [1]*(len(ROW_NUMS) - 1), '"layer_num" should contain contiguous numbers only'
assert len(ROW_NUMS) == len(BLOCKS), "'cells' list and 'layer_num' list should contain same number of entries"
direction = BACKWARDS # control the direction of countdown of timesteps
INCLUDE_ZERO = True # for time series based data
START_AT = 0 if INCLUDE_ZERO else 1
# names = [['Softmax\nprobabilities', 'p1', 'p2', 'p3', 'p4', 'p5', 'p6', 'p7', 'p8', 'p9', 'p10'],['', ' +', ' +', ' +', ' +', ' +', ' +'],['GMM\nprobabilities', 'p1', 'p2', 'p3', 'p4', 'p5', 'p6']]
# the trick to adding symbols like the "partial(dou)" i.e. '∂' is to write these symbols in a markdown cell using the $\partial$ utilising the mathjax support and
# copying the content after being rendered and paste in the code as a string wherever needed
prefix = ['∂(i)-', '∂(v)-']
r = lambda: random.randint(0,255) # to generate random colors for each row
# intantiate a directed graph with intial properties
dot = G.Digraph(comment='Matrix',
graph_attr={'nodesep':'0.02', 'ranksep':'0.02', 'bgcolor':'transparent'},
node_attr={'shape':'box3d','fixedsize':'true', 'width':'1.1'})
for row_no in ROW_NUMS:
if row_no != 1:
dot.edge(str(row_no-1)+str(START_AT), str(row_no)+str(START_AT), style='invis') # invisible edges to contrain layout
with dot.subgraph() as sg:
sg.attr(rank='same')
color = '#{:02x}{:02x}{:02x}'.format(r(),r(),r())
for block_no in range(START_AT, BLOCKS[row_no-1]+START_AT):
if direction:
sg.node(str(row_no)+str(block_no), 't-'+str(block_no), style='filled', fillcolor=color)
else:
if START_AT == 0:
sg.node(str(row_no)+str(block_no), prefix[row_no-1]+str(BLOCKS[row_no-1]-block_no-1), style='filled', fillcolor=color)
else:
sg.node(str(row_no)+str(block_no), prefix[row_no-1]+str(BLOCKS[row_no-1]-block_no-1), style='filled', fillcolor=color)
```
### Render
```
dot
```
### Save/Export
```
# dot.format = 'jpeg' # or PDF, SVG, JPEG, PNG, etc.
# to save the file, pdf is default
dot.render('./lstm_input')
```
### Additional script to just show the breakdown of train-test data of the dataset being used
```
import random
r = lambda: random.randint(0,255) # to generate random colors for each row
folders = G.Digraph(node_attr={'style':'filled'}, graph_attr={'style':'invis', 'rankdir':'LR'},edge_attr={'color':'black', 'arrowsize':'.2'})
color = '#{:02x}{:02x}{:02x}'.format(r(),r(),r())
with folders.subgraph(name='cluster0') as f:
f.node('root', 'Dataset \n x2000', shape='folder', fillcolor=color)
color = '#{:02x}{:02x}{:02x}'.format(r(),r(),r())
with folders.subgraph(name='cluster1') as f:
f.node('train', 'Train \n 1800', shape='note', fillcolor=color)
f.node('test', 'Test \n x200', shape='note', fillcolor=color)
folders.edge('root', 'train')
folders.edge('root', 'test')
folders
folders.render('./dataset')
```
|
github_jupyter
|
# Visualize Counts for the three classes
The number of volume-wise predictions for each of the three classes can be visualized in a 2D-space (with two classes as the axes and the remained or class1-class2 as the value of the third class). Also, the percentage of volume-wise predictions can be shown in a modified pie-chart, i.e. a doughnut plot.
### import modules
```
import os
import pickle
import numpy as np
import pandas as pd
from sklearn import preprocessing
from sklearn import svm
import scipy.misc
from scipy import ndimage
from scipy.stats import beta
from PIL import Image
import matplotlib
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_context('poster')
sns.set_style('ticks')
# after converstion to .py, we can use __file__ to get the module folder
try:
thisDir = os.path.realpath(__file__)
# in notebook form, we take the current working directory (we need to be in 'notebooks/' for this!)
except:
thisDir = '.'
# convert relative path into absolute path, so this will work with notebooks and py modules
supDir = os.path.abspath(os.path.join(os.path.dirname(thisDir), '..'))
supDir
```
## Outline the WTA prediction model
### make all possible values
```
def make_all_dummy():
my_max = 100
d = {}
count = 0
for bi in np.arange(0,my_max+(10**-10),0.5):
left_and_right = my_max - bi
for left in np.arange(0,left_and_right+(10**-10),0.5):
right = left_and_right-left
d[count] = {'left':left,'bilateral':bi,'right':right}
count+=1
df = pd.DataFrame(d).T
assert np.unique(df.sum(axis=1))[-1] == my_max
df['pred'] = df.idxmax(axis=1)
return df
dummy_df = make_all_dummy()
dummy_df.tail()
```
### transform labels into numbers
```
my_labeler = preprocessing.LabelEncoder()
my_labeler.fit(['left','bilateral','right','inconclusive'])
my_labeler.classes_
```
### 2d space where highest number indiciates class membership (WTA)
```
def make_dummy_space(dummy_df):
space_df = dummy_df.copy()
space_df['pred'] = my_labeler.transform(dummy_df['pred'])
space_df.index = [space_df.left, space_df.right]
space_df = space_df[['pred']]
space_df = space_df.unstack(1)['pred']
return space_df
dummy_space_df = make_dummy_space(dummy_df)
dummy_space_df.tail()
```
### define color map
```
colors_file = os.path.join(supDir,'models','colors.p')
with open(colors_file, 'rb') as f:
color_dict = pickle.load(f)
my_cols = {}
for i, j in zip(['red','yellow','blue','trans'], ['left','bilateral','right','inconclusive']):
my_cols[j] = color_dict[i]
my_col_order = np.array([my_cols[g] for g in my_labeler.classes_])
cmap = matplotlib.colors.LinearSegmentedColormap.from_list("", my_col_order)
```
### plot WTA predictions
```
plt.figure(figsize=(6,6))
plt.imshow(dummy_space_df, origin='image',cmap=cmap,extent=(0,100,0,100),alpha=0.8)
plt.contour(dummy_space_df[::-1],colors='white',alpha=1,origin='image',extent=(0,100,0,100),antialiased=True)
plt.xlabel('right',fontsize=32)
plt.xticks(range(0,101,25),np.arange(0,1.01,.25),fontsize=28)
plt.yticks(range(0,101,25),np.arange(0,1.01,.25),fontsize=28)
plt.ylabel('left',fontsize=32)
sns.despine()
plt.show()
```
### load data
```
groupdata_filename = '../data/processed/csv/withinconclusive_prediction_df.csv'
prediction_df = pd.read_csv(groupdata_filename,index_col=[0,1],header=0)
```
#### toolbox use
```
#groupdata_filename = os.path.join(supDir,'models','withinconclusive_prediction_df.csv')
#prediction_df = pd.read_csv(groupdata_filename,index_col=[0,1],header=0)
prediction_df.tail()
```
### show data and WTA space
```
plt.figure(figsize=(6,6))
plt.imshow(dummy_space_df, origin='image',cmap=cmap,extent=(0,100,0,100),alpha=0.8)
plt.contour(dummy_space_df[::-1],colors='white',alpha=1,origin='image',extent=(0,100,0,100),antialiased=True)
for c in ['left','right','bilateral']:
a_df = prediction_df.loc[c,['left','right']] * 100
plt.scatter(a_df['right'],a_df['left'],c=[my_cols[c]],edgecolor='k',linewidth=2,s=200,alpha=0.6)
plt.xlabel('right',fontsize=32)
plt.xticks(range(0,101,25),np.arange(0,1.01,.25),fontsize=28)
plt.yticks(range(0,101,25),np.arange(0,1.01,.25),fontsize=28)
plt.ylabel('left',fontsize=32)
sns.despine()
plt.savefig('../reports/figures/14-prediction-space.png',dpi=300,bbox_inches='tight')
plt.show()
```
## show one patient's data
### doughnut plot
```
p_name = 'pat###'
p_count_df = pd.read_csv('../data/processed/csv/%s_counts_df.csv'%p_name,index_col=[0,1],header=0)
p_count_df
def make_donut(p_count_df, ax, my_cols=my_cols):
"""show proportion of the number of volumes correlating highest with one of the three groups"""
percentages = p_count_df/p_count_df.sum(axis=1).values[-1] * 100
## donut plot visualization adapted from https://gist.github.com/krishnakummar/ad00d05311977732764f#file-donut-example-py
ax.pie(
percentages.values[-1],
pctdistance=0.75,
colors=[my_cols[x] for x in percentages.columns],
autopct='%0.0f%%',
shadow=False,
textprops={'fontsize': 40})
centre_circle = plt.Circle((0, 0), 0.55, fc='white')
ax.add_artist(centre_circle)
ax.set_aspect('equal')
return ax
fig,ax = plt.subplots(1,1,figsize=(8,8))
ax = make_donut(p_count_df,ax)
plt.savefig('../examples/%s_donut.png'%p_name,dpi=300,bbox_inches='tight')
plt.show()
```
### prediction space
```
def make_pred_space(p_count_df, prediction_df, ax, dummy_space_df=dummy_space_df):
ax.imshow(dummy_space_df, origin='image',cmap=cmap,extent=(0,100,0,100),alpha=0.8)
ax.contour(dummy_space_df[::-1],colors='white',alpha=1,origin='image',extent=(0,100,0,100),antialiased=True)
for c in ['left','right','bilateral']:
a_df = prediction_df.loc[c,['left','right']] * 100
ax.scatter(a_df['right'],a_df['left'],c=[my_cols[c]],edgecolor='k',linewidth=2,s=200,alpha=0.6)
percentages = p_count_df/p_count_df.sum(axis=1).values[-1] * 100
y_pred = percentages.idxmax(axis=1).values[-1]
ax.scatter(percentages['right'],percentages['left'],c=[my_cols[y_pred]],edgecolor='white',linewidth=4,s=1500,alpha=1)
plt.xlabel('right',fontsize=32)
plt.xticks(range(0,101,25),np.arange(0,1.01,.25),fontsize=28)
plt.yticks(range(0,101,25),np.arange(0,1.01,.25),fontsize=28)
plt.ylabel('left',fontsize=32)
sns.despine()
return ax
fig,ax = plt.subplots(1,1,figsize=(8,8))
ax = make_pred_space(p_count_df,prediction_df,ax)
plt.savefig('../examples/%s_predSpace.png'%p_name,dpi=300,bbox_inches='tight')
plt.show()
```
#### toolbox use
```
#def make_p(pFolder,pName,prediction_df=prediction_df):
#
# count_filename = os.path.join(pFolder,''.join([pName,'_counts_df.csv']))
# p_count_df = pd.read_csv(count_filename,index_col=[0,1],header=0)
#
# fig = plt.figure(figsize=(8,8))
# ax = plt.subplot(111)
# ax = make_donut(p_count_df,ax)
# out_name_donut = os.path.join(pFolder,''.join([pName,'_donut.png']))
# plt.savefig(out_name_donut,dpi=300,bbox_inches='tight')
# plt.close()
#
# fig = plt.figure(figsize=(8,8))
# with sns.axes_style("ticks"):
# ax = plt.subplot(111)
# ax = make_pred_space(p_count_df,prediction_df,ax)
# out_name_space = os.path.join(pFolder,''.join([pName,'_predSpace.png']))
# plt.savefig(out_name_space,dpi=300,bbox_inches='tight')
# plt.close()
#
# return out_name_donut, out_name_space
```
### summary
The prediction space allows to see the results on the group level. If used in an application on the level of N=1, the value of the patient of interest in relation to the rest of the group can be seen. If one is interested in the precise numbers, scaled to sum up to 100%, the doughnut plot supplements the prediction space plot in this regard.
**************
< [Previous](13-mw-make-group-predictions.ipynb) | [Contents](00-mw-overview-notebook.ipynb) | [Next >](15-mw-visualize-logistic-regression.ipynb)
|
github_jupyter
|
# Soft Computing
## Vežba 1 - Digitalna slika, computer vision, OpenCV
### OpenCV
Open source biblioteka namenjena oblasti računarske vizije (eng. computer vision). Dokumentacija dostupna <a href="https://opencv.org/">ovde</a>.
### matplotlib
Plotting biblioteka za programski jezik Python i njegov numerički paket NumPy. Dokumentacija dostupna <a href="https://matplotlib.org/">ovde</a>.
### Učitavanje slike
OpenCV metoda za učitavanje slike sa diska je <b>imread(path_to_image)</b>, koja kao parametar prima putanju do slike na disku. Učitana slika <i>img</i> je zapravo NumPy matrica, čije dimenzije zavise od same prirode slike. Ako je slika u boji, onda je <i>img</i> trodimenzionalna matrica, čije su prve dve dimenzije visina i širina slike, a treća dimenzija je veličine 3, zato što ona predstavlja boju (RGB, po jedan segment za svaku osnonvu boju).
```
import numpy as np
import cv2 # OpenCV biblioteka
import matplotlib
import matplotlib.pyplot as plt
# iscrtavanje slika i grafika unutar samog browsera
%matplotlib inline
# prikaz vecih slika
matplotlib.rcParams['figure.figsize'] = 16,12
img = cv2.imread('images/girl.jpg') # ucitavanje slike sa diska
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB) # konvertovanje iz BGR u RGB model boja (OpenCV ucita sliku kao BGR)
plt.imshow(img) # prikazivanje slike
```
### Prikazivanje dimenzija slike
```
print(img.shape) # shape je property Numpy array-a za prikaz dimenzija
```
Obratiti pažnju da slika u boji ima 3 komponente za svaki piksel na slici - R (red), G (green) i B (blue).

```
img
```
Primetite da je svaki element matrice **uint8** (unsigned 8-bit integer), odnosno celobroja vrednost u interval [0, 255].
```
img.dtype
```
### Osnovne operacije pomoću NumPy
Predstavljanje slike kao NumPy array je vrlo korisna stvar, jer omogućava jednostavnu manipulaciju i izvršavanje osnovih operacija nad slikom.
#### Isecanje (crop)
```
img_crop = img[100:200, 300:600] # prva koordinata je po visini (formalno red), druga po širini (formalo kolona)
plt.imshow(img_crop)
```
#### Okretanje (flip)
```
img_flip_h = img[:, ::-1] # prva koordinata ostaje ista, a kolone se uzimaju unazad
plt.imshow(img_flip_h)
img_flip_v = img[::-1, :] # druga koordinata ostaje ista, a redovi se uzimaju unazad
plt.imshow(img_flip_v)
img_flip_c = img[:, :, ::-1] # možemo i izmeniti redosled boja (RGB->BGR), samo je pitanje koliko to ima smisla
plt.imshow(img_flip_c)
```
#### Invertovanje
```
img_inv = 255 - img # ako su pikeli u intervalu [0,255] ovo je ok, a ako su u intervalu [0.,1.] onda bi bilo 1. - img
plt.imshow(img_inv)
```
### Konvertovanje iz RGB u "grayscale"
Konvertovanjem iz RGB modela u nijanse sivih (grayscale) se gubi informacija o boji piksela na slici, ali sama slika postaje mnogo lakša za dalju obradu.
Ovo se može uraditi na više načina:
1. **Srednja vrednost** RGB komponenti - najjednostavnija varijanta $$ G = \frac{R+G+B}{3} $$
2. **Metod osvetljenosti** - srednja vrednost najjače i najslabije boje $$ G = \frac{max(R,G,B) + min(R,G,B)}{2} $$
3. **Metod perceptivne osvetljenosti** - težinska srednja vrednost koja uzima u obzir ljudsku percepciju (npr. najviše smo osetljivi na zelenu boju, pa to treba uzeti u obzir)$$ G = 0.21*R + 0.72*G + 0.07*B $$
```
# implementacija metode perceptivne osvetljenosti
def my_rgb2gray(img_rgb):
img_gray = np.ndarray((img_rgb.shape[0], img_rgb.shape[1])) # zauzimanje memorije za sliku (nema trece dimenzije)
img_gray = 0.21*img_rgb[:, :, 0] + 0.77*img_rgb[:, :, 1] + 0.07*img_rgb[:, :, 2]
img_gray = img_gray.astype('uint8') # u prethodnom koraku smo mnozili sa float, pa sada moramo da vratimo u [0,255] opseg
return img_gray
img_gray = my_rgb2gray(img)
plt.imshow(img_gray, 'gray') # kada se prikazuje slika koja nije RGB, obavezno je staviti 'gray' kao drugi parametar
```
Ipak je najbolje se držati implementacije u **OpenCV** biblioteci :).
```
img_gray = cv2.cvtColor(img, cv2.COLOR_RGB2GRAY)
img_gray.shape
plt.imshow(img_gray, 'gray')
img_gray
```
### Binarna slika
Slika čiji pikseli imaju samo dve moguće vrednosti: crno i belo. U zavisnosti da li interval realan (float32) ili celobrojan (uint8), ove vrednosti mogu biti {0,1} ili {0,255}.
U binarnoj slici često izdvajamo ono što nam je bitno (**foreground**), od ono što nam je nebitno (**background**). Formalnije, ovaj postupak izdvajanja bitnog od nebitnog na slici nazivamo **segmentacija**.
Najčešći način dobijanja binarne slike je korišćenje nekog praga (**threshold**), pa ako je vrednost piksela veća od zadatog praga taj piksel dobija vrednost 1, u suprotnom 0. Postoji više tipova threshold-ovanja:
1. Globalni threshold - isti prag se primenjuje na sve piksele
2. Lokalni threshold - različiti pragovi za različite delove slike
3. Adaptivni threshold - prag se ne određuje ručno (ne zadaje ga čovek), već kroz neki postupak. Može biti i globalni i lokalni.
#### Globalni threshold
Kako izdvojiti npr. samo lice?
```
img_tr = img_gray > 127 # svi piskeli koji su veci od 127 ce dobiti vrednost True, tj. 1, i obrnuto
plt.imshow(img_tr, 'gray')
```
OpenCV ima metodu <b>threshold</b> koja kao prvi parametar prima sliku koja se binarizuje, kao drugi parametar prima prag binarizacije, treći parametar je vrednost rezultujućeg piksela ako je veći od praga (255=belo), poslednji parametar je tip thresholda (u ovo slučaju je binarizacija).
```
ret, image_bin = cv2.threshold(img_gray, 100, 255, cv2.THRESH_BINARY) # ret je vrednost praga, image_bin je binarna slika
print(ret)
plt.imshow(image_bin, 'gray')
```
#### Otsu threshold
<a href="https://en.wikipedia.org/wiki/Otsu%27s_method">Otsu metoda</a> se koristi za automatsko pronalaženje praga za threshold na slici.
```
ret, image_bin = cv2.threshold(img_gray, 0, 255, cv2.THRESH_OTSU) # ret je izracunata vrednost praga, image_bin je binarna slika
print("Otsu's threshold: " + str(ret))
plt.imshow(image_bin, 'gray')
```
#### Adaptivni threshold
U nekim slučajevima primena globalnog praga za threshold ne daje dobre rezultate. Dobar primer su slike na kojima se menja osvetljenje, gde globalni threshold praktično uništi deo slike koji je previše osvetljen ili zatamnjen.
Adaptivni threshold je drugačiji pristup, gde se za svaki piksel na slici izračunava zaseban prag, na osnovu njemu okolnnih piksela. <a href="https://docs.opencv.org/master/d7/d4d/tutorial_py_thresholding.html#gsc.tab=0">Primer</a>
```
image_ada = cv2.imread('images/sonnet.png')
image_ada = cv2.cvtColor(image_ada, cv2.COLOR_BGR2GRAY)
plt.imshow(image_ada, 'gray')
ret, image_ada_bin = cv2.threshold(image_ada, 100, 255, cv2.THRESH_BINARY)
plt.imshow(image_ada_bin, 'gray')
```
Loši rezultati su dobijeni upotrebom globalnog thresholda.
Poboljšavamo rezultate korišćenjem adaptivnog thresholda. Pretposlednji parametar metode <b>adaptiveThreshold</b> je ključan, jer predstavlja veličinu bloka susednih piksela (npr. 15x15) na osnovnu kojih se računa lokalni prag.
```
# adaptivni threshold gde se prag racuna = srednja vrednost okolnih piksela
image_ada_bin = cv2.adaptiveThreshold(image_ada, 255, cv2.ADAPTIVE_THRESH_MEAN_C, cv2.THRESH_BINARY, 15, 5)
plt.figure() # ako je potrebno da se prikaze vise slika u jednoj celiji
plt.imshow(image_ada_bin, 'gray')
# adaptivni threshold gde se prag racuna = tezinska suma okolnih piksela, gde su tezine iz gausove raspodele
image_ada_bin = cv2.adaptiveThreshold(image_ada, 255, cv2.ADAPTIVE_THRESH_GAUSSIAN_C, cv2.THRESH_BINARY, 15, 5)
plt.figure()
plt.imshow(image_ada_bin, 'gray')
```
### Histogram
Možemo koristiti **histogram**, koji će nam dati informaciju o distribuciji osvetljenosti piksela.
Vrlo koristan kada je potrebno odrediti prag za globalni threshold.
Pseudo-kod histograma za grayscale sliku:
```code
inicijalizovati nula vektor od 256 elemenata
za svaki piksel na slici:
preuzeti inicijalni intezitet piksela
uvecati za 1 broj piksela tog inteziteta
plotovati histogram
```
```
def hist(image):
height, width = image.shape[0:2]
x = range(0, 256)
y = np.zeros(256)
for i in range(0, height):
for j in range(0, width):
pixel = image[i, j]
y[pixel] += 1
return (x, y)
x,y = hist(img_gray)
plt.plot(x, y, 'b')
plt.show()
```
Koristeći <b>matplotlib</b>:
```
plt.hist(img_gray.ravel(), 255, [0, 255])
plt.show()
```
Koristeći <b>OpenCV</b>:
```
hist_full = cv2.calcHist([img_gray], [0], None, [255], [0, 255])
plt.plot(hist_full)
plt.show()
```
Pretpostavimo da su vrednosti piksela lica između 100 i 200.
```
img_tr = (img_gray > 100) * (img_gray < 200)
plt.imshow(img_tr, 'gray')
```
### Konverovanje iz "grayscale" u RGB
Ovo je zapravo trivijalna operacija koja za svaki kanal boje (RGB) napravi kopiju od originalne grayscale slike. Ovo je zgodno kada nešto što je urađeno u grayscale modelu treba iskoristiti zajedno sa RGB slikom.
```
img_tr_rgb = cv2.cvtColor(img_tr.astype('uint8'), cv2.COLOR_GRAY2RGB)
plt.imshow(img*img_tr_rgb) # množenje originalne RGB slike i slike sa izdvojenim pikselima lica
```
### Morfološke operacije
Veliki skup operacija za obradu digitalne slike, gde su te operacije zasnovane na oblicima, odnosno **strukturnim elementima**. U morfološkim operacijama, vrednost svakog piksela rezultujuće slike se zasniva na poređenju odgovarajućeg piksela na originalnoj slici sa svojom okolinom. Veličina i oblik ove okoline predstavljaju strukturni element.
```
kernel = np.ones((3, 3)) # strukturni element 3x3 blok
print(kernel)
```
#### Erozija
Morfološka erozija postavlja vrednost piksela rez. slike na ```(i,j)``` koordinatama na **minimalnu** vrednost svih piksela u okolini ```(i,j)``` piksela na orig. slici.
U suštini erozija umanjuje regione belih piksela, a uvećava regione crnih piksela. Često se koristi za uklanjanje šuma (u vidu sitnih regiona belih piksela).

```
plt.imshow(cv2.erode(image_bin, kernel, iterations=1), 'gray')
```
#### Dilacija
Morfološka dilacija postavlja vrednost piksela rez. slike na ```(i,j)``` koordinatama na **maksimalnu** vrednost svih piksela u okolini ```(i,j)``` piksela na orig. slici.
U suštini dilacija uvećava regione belih piksela, a umanjuje regione crnih piksela. Zgodno za izražavanje regiona od interesa.

```
# drugaciji strukturni element
kernel = cv2.getStructuringElement(cv2.MORPH_CROSS, (5,5)) # MORPH_ELIPSE, MORPH_RECT...
print(kernel)
plt.imshow(cv2.dilate(image_bin, kernel, iterations=5), 'gray') # 5 iteracija
```
#### Otvaranje i zatvaranje
**```otvaranje = erozija + dilacija```**, uklanjanje šuma erozijom i vraćanje originalnog oblika dilacijom.
**```zatvaranje = dilacija + erozija```**, zatvaranje sitnih otvora među belim pikselima
```
kernel = cv2.getStructuringElement(cv2.MORPH_ELLIPSE, (5, 5))
print(kernel)
img_ero = cv2.erode(image_bin, kernel, iterations=1)
img_open = cv2.dilate(img_ero, kernel, iterations=1)
plt.imshow(img_open, 'gray')
img_dil = cv2.dilate(image_bin, kernel, iterations=1)
img_close = cv2.erode(img_dil, kernel, iterations=1)
plt.imshow(img_close, 'gray')
```
Primer detekcije ivica na binarnoj slici korišćenjem dilatacije i erozije:
```
kernel = cv2.getStructuringElement(cv2.MORPH_ELLIPSE, (3, 3))
image_edges = cv2.dilate(image_bin, kernel, iterations=1) - cv2.erode(image_bin, kernel, iterations=1)
plt.imshow(image_edges, 'gray')
```
### Zamućenje (blur)
Zamućenje slike se dobija tako što se za svaki piksel slike kao nova vrednost uzima srednja vrednost okolnih piksela, recimo u okolini 5 x 5. Kernel <b>k</b> predstavlja kernel za <i>uniformno zamućenje</i>. Ovo je jednostavnija verzija <a href="https://en.wikipedia.org/wiki/Gaussian_blur">Gausovskog zamućenja</a>.
<img src="https://render.githubusercontent.com/render/math?math=k%285x5%29%3D%0A%20%20%5Cbegin%7Bbmatrix%7D%0A%20%20%20%201%2F25%20%26amp%3B%201%2F25%20%26amp%3B%201%2F25%20%26amp%3B%201%2F25%20%26amp%3B%201%2F25%20%5C%5C%0A%20%20%20%201%2F25%20%26amp%3B%201%2F25%20%26amp%3B%201%2F25%20%26amp%3B%201%2F25%20%26amp%3B%201%2F25%20%5C%5C%0A%20%20%20%201%2F25%20%26amp%3B%201%2F25%20%26amp%3B%201%2F25%20%26amp%3B%201%2F25%20%26amp%3B%201%2F25%20%5C%5C%0A%20%20%20%201%2F25%20%26amp%3B%201%2F25%20%26amp%3B%201%2F25%20%26amp%3B%201%2F25%20%26amp%3B%201%2F25%20%5C%5C%0A%20%20%20%201%2F25%20%26amp%3B%201%2F25%20%26amp%3B%201%2F25%20%26amp%3B%201%2F25%20%26amp%3B%201%2F25%0A%20%20%5Cend%7Bbmatrix%7D&mode=display">
```
from scipy import signal
k_size = 5
k = (1./k_size*k_size) * np.ones((k_size, k_size))
image_blur = signal.convolve2d(img_gray, k)
plt.imshow(image_blur, 'gray')
```
### Regioni i izdvajanje regiona
Najjednostavnije rečeno, region je skup međusobno povezanih belih piksela. Kada se kaže povezanih, misli se na to da se nalaze u neposrednoj okolini. Razlikuju se dve vrste povezanosti: tzv. **4-connectivity** i **8-connectivity**:

Postupak kojim se izdvajanju/obeležavaju regioni se naziva **connected components labelling**. Ovo ćemo primeniti na problemu izdvajanja barkoda.
```
# ucitavanje slike i convert u RGB
img_barcode = cv2.cvtColor(cv2.imread('images/barcode.jpg'), cv2.COLOR_BGR2RGB)
plt.imshow(img_barcode)
```
Recimo da želimo da izdvojimo samo linije barkoda sa slike.
Za početak, uradimo neke standardne operacije, kao što je konvertovanje u grayscale i adaptivni threshold.
```
img_barcode_gs = cv2.cvtColor(img_barcode, cv2.COLOR_RGB2GRAY) # konvert u grayscale
plt.imshow(img_barcode_gs, 'gray')
#ret, image_barcode_bin = cv2.threshold(img_barcode_gs, 80, 255, cv2.THRESH_BINARY)
image_barcode_bin = cv2.adaptiveThreshold(img_barcode_gs, 255, cv2.ADAPTIVE_THRESH_MEAN_C, cv2.THRESH_BINARY, 35, 10)
plt.imshow(image_barcode_bin, 'gray')
```
### Pronalaženje kontura/regiona
Konture, odnosno regioni na slici su grubo rečeno grupe crnih piksela. OpenCV metoda <b>findContours</b> pronalazi sve ove grupe crnih piksela, tj. regione. Druga povratna vrednost metode, odnosno <i>contours</i> je lista pronađeih kontura na slici.
Ove konture je zaim moguće iscrtati metodom <b>drawContours</b>, gde je prvi parametar slika na kojoj se iscrtavaju pronađene konture, drugi parametar je lista kontura koje je potrebno iscrtati, treći parametar određuje koju konturu po redosledu iscrtati (-1 znači iscrtavanje svih kontura), četvrti parametar je boja kojom će se obeležiti kontura, a poslednji parametar je debljina linije.
```
contours, hierarchy = cv2.findContours(image_barcode_bin, cv2.RETR_LIST, cv2.CHAIN_APPROX_SIMPLE)
img = img_barcode.copy()
cv2.drawContours(img, contours, -1, (255, 0, 0), 1)
plt.imshow(img)
```
#### Osobine regiona
Svi pronađeni regioni imaju neke svoje karakteristične osobine: površina, obim, konveksni omotač, konveksnost, obuhvatajući pravougaonik, ugao... Ove osobine mogu biti izuzetno korisne kada je neophodno izdvojiti samo određene regione sa slike koji ispoljavaju neku osobinu. Za sve osobine pogledati <a href="https://opencv-python-tutroals.readthedocs.io/en/latest/py_tutorials/py_imgproc/py_contours/py_contour_features/py_contour_features.html">ovo</a> i <a href="https://opencv-python-tutroals.readthedocs.io/en/latest/py_tutorials/py_imgproc/py_contours/py_contour_properties/py_contour_properties.html">ovo</a>.
Izdvajamo samo bar-kod sa slike.
```
contours_barcode = [] #ovde ce biti samo konture koje pripadaju bar-kodu
for contour in contours: # za svaku konturu
center, size, angle = cv2.minAreaRect(contour) # pronadji pravougaonik minimalne povrsine koji ce obuhvatiti celu konturu
width, height = size
if width > 3 and width < 30 and height > 300 and height < 400: # uslov da kontura pripada bar-kodu
contours_barcode.append(contour) # ova kontura pripada bar-kodu
img = img_barcode.copy()
cv2.drawContours(img, contours_barcode, -1, (255, 0, 0), 1)
plt.imshow(img)
print('Ukupan broj regiona: %d' % len(contours_barcode))
```
Naravno, u ogromnom broj slučajeva odnos visine i širine neće biti dovoljan, već se moraju koristiti i ostale osobine.
## Zadaci
* Sa slike sa sijalicama (**images/bulbs.jpg**) prebrojati koliko ima sijalica.
* Sa slike barkoda (**images/barcode.jpg**) izdvojiti samo brojeve i slova, bez linija barkoda.
* Na slici sa snouborderima (**images/snowboarders.jpg**) prebrojati koliko ima snoubordera.
* Na slici sa fudbalerima (**images/football.jpg**) izdvojiti samo one fudbalere u belim dresovima.
* Na slici sa crvenim krvnim zrncima (**images/bloodcells.jpg**), prebrojati koliko ima crvenih krvnih zrnaca.
|
github_jupyter
|
## <center>Ensemble models from machine learning: an example of wave runup and coastal dune erosion</center>
### <center>Tomas Beuzen<sup>1</sup>, Evan B. Goldstein<sup>2</sup>, Kristen D. Splinter<sup>1</sup></center>
<center><sup>1</sup>Water Research Laboratory, School of Civil and Environmental Engineering, UNSW Sydney, NSW, Australia</center>
<center><sup>2</sup>Department of Geography, Environment, and Sustainability, University of North Carolina at Greensboro, Greensboro, NC, USA</center>
This notebook contains the code required to develop the Gaussian Process (GP) runup predictor developed in the manuscript "*Ensemble models from machine learning: an example of wave runup and coastal dune erosion*" by Beuzen et al.
**Citation:** Beuzen, T, Goldstein, E.B., Splinter, K.S. (In Review). Ensemble models from machine learning: an example of wave runup and coastal dune erosion, Natural Hazards and Earth Systems Science, SI Advances in computational modeling of geoprocesses and geohazards.
### Table of Contents:
1. [Imports](#bullet-0)
2. [Load and Visualize Data](#bullet-1)
3. [Develop GP Runup Predictor](#bullet-2)
4. [Test GP Runup Predictor](#bullet-3)
5. [Explore GP Prediction Uncertainty](#bullet-4)
## 1. Imports <a class="anchor" id="bullet-0"></a>
```
# Required imports
# Standard computing packages
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# Gaussian Process tools
from sklearn.metrics import mean_squared_error
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import RBF, WhiteKernel
# Notebook functionality
%matplotlib inline
```
## 2. Load and Visualize Data <a class="anchor" id="bullet-1"></a>
In this section, we will load and visualise the wave, beach slope, and runup data we will use to develop the Gaussian process (GP) runup predictor.
```
# Read in .csv data file as a pandas dataframe
df = pd.read_csv('../data_repo_temporary/lidar_runup_data_for_GP_training.csv',index_col=0)
# Print the size and head of the dataframe
print('Data size:', df.shape)
df.head()
# This cell plots histograms of the data
# Initialize the figure and axes
fig, axes = plt.subplots(2,2,figsize=(6,6))
plt.tight_layout(w_pad=0.1, h_pad=3)
# Subplot (0,0): Hs
ax = axes[0,0]
ax.hist(df.Hs,28,color=(0.6,0.6,0.6),edgecolor='k',lw=0.5) # Plot histogram
ax.set_xlabel('H$_s$ (m)') # Format plot
ax.set_ylabel('Frequency')
ax.set_xticks((0,1.5,3,4.5))
ax.set_xlim((0,4.5))
ax.set_ylim((0,50))
ax.grid(lw=0.5,alpha=0.7)
ax.text(-1.1, 52, 'A)', fontsize=12)
ax.tick_params(direction='in')
ax.set_axisbelow(True)
# Subplot (0,1): Tp
ax = axes[0,1]
ax.hist(df.Tp,20,color=(0.6,0.6,0.6),edgecolor='k',lw=0.5) # Plot histogram
ax.set_xlabel('T$_p$ (s)') # Format plot
ax.set_xticks((0,6,12,18))
ax.set_xlim((0,18))
ax.set_ylim((0,50))
ax.set_yticklabels([])
ax.grid(lw=0.5,alpha=0.7)
ax.text(-2.1, 52, 'B)', fontsize=12)
ax.tick_params(direction='in')
ax.set_axisbelow(True)
# Subplot (1,0): beta
ax = axes[1,0]
ax.hist(df.beach_slope,20,color=(0.6,0.6,0.6),edgecolor='k',lw=0.5) # Plot histogram
ax.set_xlabel(r'$\beta$') # Format plot
ax.set_ylabel('Frequency')
ax.set_xticks((0,0.1,0.2,0.3))
ax.set_xlim((0,0.3))
ax.set_ylim((0,50))
ax.grid(lw=0.5,alpha=0.7)
ax.text(-0.073, 52, 'C)', fontsize=12)
ax.tick_params(direction='in')
ax.set_axisbelow(True)
# Subplot (1,1): R2
ax = axes[1,1]
ax.hist(df.runup,24,color=(0.9,0.2,0.2),edgecolor='k',lw=0.5) # Plot histogram
ax.set_xlabel('R$_2$ (m)') # Format plot
ax.set_xticks((0,1,2,3))
ax.set_xlim((0,3))
ax.set_ylim((0,50))
ax.set_yticklabels([])
ax.grid(lw=0.5,alpha=0.7)
ax.text(-0.35, 52, 'D)', fontsize=12)
ax.tick_params(direction='in')
ax.set_axisbelow(True);
```
## 3. Develop GP Runup Predictor <a class="anchor" id="bullet-2"></a>
In this section we will develop the GP runup predictor.
We standardize the data for use in the GP by removing the mean and scaling to unit variance. This does not really affect GP performance but improves computational efficiency (see sklearn documentation for more information).
A kernel must be specified to develop the GP. Many kernels were trialled in initial GP development. The final kernel is a combination of the RBF and WhiteKernel. See **Section 2.1** and **Section 2.2** of the manuscript for further discussion.
```
# Define features and response data
X = df.drop(columns=df.columns[-1]) # Drop the last column to retain input features (Hs, Tp, slope)
y = df[[df.columns[-1]]] # The last column is the predictand (R2)
```
```
# Specify the kernel to use in the GP
kernel = RBF(0.1, (1e-2, 1e2)) + WhiteKernel(1,(1e-2,1e2))
# Train GP model on training dataset
gp = GaussianProcessRegressor(kernel=kernel,
n_restarts_optimizer=9,
normalize_y=True,
random_state=123)
gp.fit(X, y);
```
## 4. Test GP Runup Predictor <a class="anchor" id="bullet-3"></a>
This section now shows how the GP runup predictor can be used to test 50 test samples not previosuly used in training.
```
# Read in .csv test data file as a pandas dataframe
df_test = pd.read_csv('../data_repo_temporary/lidar_runup_data_for_GP_testing.csv',index_col=0)
# Print the size and head of the dataframe
print('Data size:', df_test.shape)
df_test.head()
# Predict the data
X_test = df_test.drop(columns=df.columns[-1]) # Drop the last column to retain input features (Hs, Tp, slope)
y_test = df_test[[df_test.columns[-1]]] # The last column is the predictand (R2)
y_test_predictions = gp.predict(X_test)
print('GP RMSE on test data =', format(np.sqrt(mean_squared_error(y_test,y_test_predictions)),'.2f'))
# This cell plots a figure comparing GP predictions to observations for the testing dataset
# Similar to Figure 4 in the manuscript
# Initialize the figure and axes
fig, axes = plt.subplots(figsize=(6,6))
plt.tight_layout(pad=2.2)
# Plot and format
axes.scatter(y_test,y_test_predictions,s=20,c='b',marker='.')
axes.plot([0,4],[0,4],'k--')
axes.set_ylabel('Predicted R$_2$ (m)')
axes.set_xlabel('Observed R$_2$ (m)')
axes.grid(lw=0.5,alpha=0.7)
axes.set_xlim(0,1.5)
axes.set_ylim(0,1.5)
# Print some statistics
print('GP RMSE on test data =', format(np.sqrt(mean_squared_error(y_test,y_test_predictions)),'.2f'))
print('GP bias on test data =', format(np.mean(y_test_predictions-y_test.values),'.2f'))
```
## 5. Explore GP Prediction Uncertainty <a class="anchor" id="bullet-3"></a>
This section explores how we can draw random samples from the GP to explain scatter in the runup predictions. We randomly draw 100 samples from the GP and calculate how much of the scatter in the runup predictions is captured by the ensemble envelope for different ensemble sizes. The process is repeated 100 times for robustness. See **Section 3.3** of the manuscript for further discussion.
We then plot the prediction with prediction uncertainty to help visualize.
```
# Draw 100 samples from the GP model using the testing dataset
GP_draws = gp.sample_y(X_test, n_samples=100, random_state=123).squeeze() # Draw 100 random samples from the GP
# Initialize result arrays
perc_ens = np.zeros((100,100)) # Initialize ensemble capture array
perc_err = np.zeros((100,)) # Initialise arbitray error array
# Loop to get results
for i in range(0,perc_ens.shape[0]):
# Caclulate capture % in envelope created by adding arbitrary, uniform error to mean GP prediction
lower = y_test_predictions*(1-i/100) # Lower bound
upper = y_test_predictions*(1+i/100) # Upper bound
perc_err[i] = sum((np.squeeze(y_test)>=np.squeeze(lower)) & (np.squeeze(y_test)<=np.squeeze(upper)))/y_test.shape[0] # Store percent capture
for j in range(0,perc_ens.shape[1]):
ind = np.random.randint(0,perc_ens.shape[0],i+1) # Determine i random integers
lower = np.min(GP_draws[:,ind],axis=1) # Lower bound of ensemble of i random members
upper = np.max(GP_draws[:,ind],axis=1) # Upper bound of ensemble of i random members
perc_ens[i,j] = sum((np.squeeze(y_test)>=lower) & (np.squeeze(y_test)<=upper))/y_test.shape[0] # Store percent capture
# This cell plots a figure showing how samples from the GP can help to capture uncertainty in predictions
# Similar to Figure 5 from the manuscript
# Initialize the figure and axes
fig, axes = plt.subplots(1,2,figsize=(9,4))
plt.tight_layout()
lim = 0.95 # Desired limit to test
# Plot ensemble results
ax = axes[0]
perc_ens_mean = np.mean(perc_ens,axis=1)
ax.plot(perc_ens_mean*100,'k-',lw=2)
ind = np.argmin(abs(perc_ens_mean-lim)) # Find where the capture rate > lim
ax.plot([ind,ind],[0,perc_ens_mean[ind]*100],'r--')
ax.plot([0,ind],[perc_ens_mean[ind]*100,perc_ens_mean[ind]*100],'r--')
ax.set_xlabel('# Draws from GP')
ax.set_ylabel('Observations captured \n within ensemble range (%)')
ax.grid(lw=0.5,alpha=0.7)
ax.minorticks_on()
ax.set_xlim(0,100);
ax.set_ylim(0,100);
ax.text(-11.5, 107, 'A)', fontweight='bold', fontsize=12)
print('# draws needed for ' + format(lim*100,'.0f') + '% capture = ' + str(ind))
print('Mean/Min/Max for ' + str(ind) + ' draws = '
+ format(np.mean(perc_ens[ind,:])*100,'.1f') + '%/'
+ format(np.min(perc_ens[ind,:])*100,'.1f') + '%/'
+ format(np.max(perc_ens[ind,:])*100,'.1f') + '%')
# Plot arbitrary error results
ax = axes[1]
ax.plot(perc_err*100,'k-',lw=2)
ind = np.argmin(abs(perc_err-lim)) # Find where the capture rate > lim
ax.plot([ind,ind],[0,perc_err[ind]*100],'r--')
ax.plot([0,ind],[perc_err[ind]*100,perc_err[ind]*100],'r--')
ax.set_xlabel('% Error added to mean GP estimate')
ax.grid(lw=0.5,alpha=0.7)
ax.minorticks_on()
ax.set_xlim(0,100);
ax.set_ylim(0,100);
ax.text(-11.5, 107, 'B)', fontweight='bold', fontsize=12)
print('% added error needed for ' + format(lim*100,'.0f') + '% capture = ' + str(ind) + '%')
# This cell plots predictions for all 50 test samples with prediction uncertainty from 12 ensemble members.
# In the cell above, 12 members was identified as optimal for capturing 95% of observations.
# Initialize the figure and axes
fig, axes = plt.subplots(1,1,figsize=(10,6))
# Make some data for plotting
x = np.arange(1, len(y_test)+1)
lower = np.min(GP_draws[:,:12],axis=1) # Lower bound of ensemble of 12 random members
upper = np.max(GP_draws[:,:12],axis=1) # Upper bound of ensemble of 12 random members
# Plot
axes.plot(x,y_test,'o',linestyle='-',color='C0',mfc='C0',mec='k',zorder=10,label='Observed')
axes.plot(x,y_test_predictions,'k',marker='o',color='C1',mec='k',label='GP Ensemble Mean')
axes.fill_between(x,
lower,
upper,
alpha=0.2,
facecolor='C1',
label='GP Ensemble Range')
# Formatting
axes.set_xlim(0,50)
axes.set_ylim(0,2.5)
axes.set_xlabel('Observation')
axes.set_ylabel('R2 (m)')
axes.grid()
axes.legend(framealpha=1)
```
|
github_jupyter
|
```
import os
os.environ['CUDA_VISIBLE_DEVICES'] = ''
# !git pull
import tensorflow as tf
import malaya_speech
import malaya_speech.train
from malaya_speech.train.model import fastspeech2
import numpy as np
_pad = 'pad'
_start = 'start'
_eos = 'eos'
_punctuation = "!'(),.:;? "
_special = '-'
_letters = 'ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz'
_rejected = '\'():;"'
MALAYA_SPEECH_SYMBOLS = (
[_pad, _start, _eos] + list(_special) + list(_punctuation) + list(_letters)
)
input_ids = tf.placeholder(tf.int32, [None, None])
lens = tf.placeholder(tf.int32, [None, None])
mel_outputs = tf.placeholder(tf.float32, [None, None, 80])
mel_lengths = tf.placeholder(tf.int32, [None])
energies = tf.placeholder(tf.float32, [None, None])
energies_lengths = tf.placeholder(tf.int32, [None])
f0s = tf.placeholder(tf.float32, [None, None])
f0s_lengths = tf.placeholder(tf.int32, [None])
config = malaya_speech.config.fastspeech2_config
config = fastspeech2.Config(
vocab_size = len(MALAYA_SPEECH_SYMBOLS), **config
)
model = fastspeech2.Model(config)
r_training = model(input_ids, lens, f0s, energies, training = False)
speed_ratios = tf.placeholder(tf.float32, [None], name = 'speed_ratios')
f0_ratios = tf.placeholder(tf.float32, [None], name = 'f0_ratios')
energy_ratios = tf.placeholder(tf.float32, [None], name = 'energy_ratios')
r = model.inference(input_ids, speed_ratios, f0_ratios, energy_ratios)
r
decoder_output = tf.identity(r[0], name = 'decoder_output')
post_mel_outputs = tf.identity(r[1], name = 'post_mel_outputs')
sess = tf.InteractiveSession()
sess.run(tf.global_variables_initializer())
path = 'fastspeech2-haqkiem'
ckpt_path = tf.train.latest_checkpoint(path)
ckpt_path
saver = tf.train.Saver()
saver.restore(sess, ckpt_path)
import re
from unidecode import unidecode
import malaya
normalizer = malaya.normalize.normalizer(date = False, time = False)
pad_to = 8
def tts_encode(string: str, add_eos: bool = True):
r = [MALAYA_SPEECH_SYMBOLS.index(c) for c in string if c in MALAYA_SPEECH_SYMBOLS]
if add_eos:
r = r + [MALAYA_SPEECH_SYMBOLS.index('eos')]
return r
def put_spacing_num(string):
string = re.sub('[A-Za-z]+', lambda ele: ' ' + ele[0] + ' ', string)
return re.sub(r'[ ]+', ' ', string).strip()
def convert_to_ascii(string):
return unidecode(string)
def collapse_whitespace(string):
return re.sub(_whitespace_re, ' ', string)
def cleaning(string, normalize = True, add_eos = False):
sequence = []
string = convert_to_ascii(string)
if string[-1] in '-,':
string = string[:-1]
if string[-1] not in '.,?!':
string = string + '.'
string = string.replace('&', ' dan ')
string = string.replace(':', ',').replace(';', ',')
if normalize:
t = normalizer._tokenizer(string)
for i in range(len(t)):
if t[i] == '-':
t[i] = ','
string = ' '.join(t)
string = normalizer.normalize(string,
check_english = False,
normalize_entity = False,
normalize_text = False,
normalize_url = True,
normalize_email = True,
normalize_year = True)
string = string['normalize']
else:
string = string
string = put_spacing_num(string)
string = ''.join([c for c in string if c in MALAYA_SPEECH_SYMBOLS and c not in _rejected])
string = re.sub(r'[ ]+', ' ', string).strip()
string = string.lower()
ids = tts_encode(string, add_eos = add_eos)
text_input = np.array(ids)
num_pad = pad_to - ((len(text_input) + 2) % pad_to)
text_input = np.pad(
text_input, ((1, 1)), 'constant', constant_values = ((1, 2))
)
text_input = np.pad(
text_input, ((0, num_pad)), 'constant', constant_values = 0
)
return string, text_input
import matplotlib.pyplot as plt
# https://umno-online.my/2020/12/28/isu-kartel-daging-haram-lagi-pihak-gesa-kerajaan-ambil-tindakan-tegas-drastik/
t, ids = cleaning('Haqkiem adalah pelajar tahun akhir yang mengambil Ijazah Sarjana Muda Sains Komputer Kecerdasan Buatan utama dari Universiti Teknikal Malaysia Melaka (UTeM) yang kini berusaha untuk latihan industri di mana dia secara praktikal dapat menerapkan pengetahuannya dalam Perisikan Perisian dan Pengaturcaraan ke arah organisasi atau industri yang berkaitan.')
t, ids
%%time
o = sess.run([decoder_output, post_mel_outputs], feed_dict = {input_ids: [ids],
speed_ratios: [1.0],
f0_ratios: [1.0],
energy_ratios: [1.0]})
o[1].shape
mel_outputs_ = np.reshape(o[1], [-1, 80])
fig = plt.figure(figsize=(10, 8))
ax1 = fig.add_subplot(311)
ax1.set_title(f'Predicted Mel-before-Spectrogram')
im = ax1.imshow(np.rot90(mel_outputs_), aspect='auto', interpolation='none')
fig.colorbar(mappable=im, shrink=0.65, orientation='horizontal', ax=ax1)
plt.show()
mel_outputs_ = np.reshape(o[0], [-1, 80])
fig = plt.figure(figsize=(10, 8))
ax1 = fig.add_subplot(311)
ax1.set_title(f'Predicted Mel-before-Spectrogram')
im = ax1.imshow(np.rot90(mel_outputs_), aspect='auto', interpolation='none')
fig.colorbar(mappable=im, shrink=0.65, orientation='horizontal', ax=ax1)
plt.show()
import pickle
with open('a.pkl', 'wb') as fopen:
pickle.dump([np.reshape(o[0], [-1, 80]), np.reshape(o[1], [-1, 80])], fopen)
saver = tf.train.Saver()
saver.save(sess, 'fastspeech2-haqkiem-output/model.ckpt')
strings = ','.join(
[
n.name
for n in tf.get_default_graph().as_graph_def().node
if ('Variable' in n.op
or 'gather' in n.op.lower()
or 'Placeholder' in n.name
or 'ratios' in n.name
or 'post_mel_outputs' in n.name
or 'decoder_output' in n.name
or 'alignment_histories' in n.name)
and 'adam' not in n.name
and 'global_step' not in n.name
and 'Assign' not in n.name
and 'ReadVariableOp' not in n.name
and 'Gather' not in n.name
and 'IsVariableInitialized' not in n.name
]
)
strings.split(',')
def freeze_graph(model_dir, output_node_names):
if not tf.gfile.Exists(model_dir):
raise AssertionError(
"Export directory doesn't exists. Please specify an export "
'directory: %s' % model_dir
)
checkpoint = tf.train.get_checkpoint_state(model_dir)
input_checkpoint = checkpoint.model_checkpoint_path
absolute_model_dir = '/'.join(input_checkpoint.split('/')[:-1])
output_graph = absolute_model_dir + '/frozen_model.pb'
clear_devices = True
with tf.Session(graph = tf.Graph()) as sess:
saver = tf.train.import_meta_graph(
input_checkpoint + '.meta', clear_devices = clear_devices
)
saver.restore(sess, input_checkpoint)
output_graph_def = tf.graph_util.convert_variables_to_constants(
sess,
tf.get_default_graph().as_graph_def(),
output_node_names.split(','),
)
with tf.gfile.GFile(output_graph, 'wb') as f:
f.write(output_graph_def.SerializeToString())
print('%d ops in the final graph.' % len(output_graph_def.node))
freeze_graph('fastspeech2-haqkiem-output', strings)
def load_graph(frozen_graph_filename):
with tf.gfile.GFile(frozen_graph_filename, 'rb') as f:
graph_def = tf.GraphDef()
graph_def.ParseFromString(f.read())
with tf.Graph().as_default() as graph:
tf.import_graph_def(graph_def)
return graph
g = load_graph('fastspeech2-haqkiem-output/frozen_model.pb')
test_sess = tf.InteractiveSession(graph = g)
X = g.get_tensor_by_name('import/Placeholder:0')
speed_ratios = g.get_tensor_by_name('import/speed_ratios:0')
f0_ratios = g.get_tensor_by_name('import/f0_ratios:0')
energy_ratios = g.get_tensor_by_name('import/energy_ratios:0')
output_nodes = ['decoder_output', 'post_mel_outputs']
outputs = {n: g.get_tensor_by_name(f'import/{n}:0') for n in output_nodes}
%%time
o = test_sess.run(outputs, feed_dict = {X: [ids],
speed_ratios: [1.0],
f0_ratios: [1.0],
energy_ratios: [1.0]})
mel_outputs_ = np.reshape(o['decoder_output'], [-1, 80])
fig = plt.figure(figsize=(10, 8))
ax1 = fig.add_subplot(311)
ax1.set_title(f'Predicted Mel-before-Spectrogram')
im = ax1.imshow(np.rot90(mel_outputs_), aspect='auto', interpolation='none')
fig.colorbar(mappable=im, shrink=0.65, orientation='horizontal', ax=ax1)
plt.show()
mel_outputs_ = np.reshape(o['post_mel_outputs'], [-1, 80])
fig = plt.figure(figsize=(10, 8))
ax1 = fig.add_subplot(311)
ax1.set_title(f'Predicted Mel-before-Spectrogram')
im = ax1.imshow(np.rot90(mel_outputs_), aspect='auto', interpolation='none')
fig.colorbar(mappable=im, shrink=0.65, orientation='horizontal', ax=ax1)
plt.show()
from tensorflow.tools.graph_transforms import TransformGraph
transforms = ['add_default_attributes',
'remove_nodes(op=Identity, op=CheckNumerics)',
'fold_batch_norms',
'fold_old_batch_norms',
'quantize_weights(fallback_min=-1024, fallback_max=1024)',
'strip_unused_nodes',
'sort_by_execution_order']
pb = 'fastspeech2-haqkiem-output/frozen_model.pb'
input_graph_def = tf.GraphDef()
with tf.gfile.FastGFile(pb, 'rb') as f:
input_graph_def.ParseFromString(f.read())
transformed_graph_def = TransformGraph(input_graph_def,
['Placeholder', 'speed_ratios', 'f0_ratios', 'energy_ratios'],
output_nodes, transforms)
with tf.gfile.GFile(f'{pb}.quantized', 'wb') as f:
f.write(transformed_graph_def.SerializeToString())
g = load_graph('fastspeech2-haqkiem-output/frozen_model.pb.quantized')
test_sess = tf.InteractiveSession(graph = g)
X = g.get_tensor_by_name(f'import/Placeholder:0')
speed_ratios = g.get_tensor_by_name('import/speed_ratios:0')
f0_ratios = g.get_tensor_by_name('import/f0_ratios:0')
energy_ratios = g.get_tensor_by_name('import/energy_ratios:0')
outputs = {n: g.get_tensor_by_name(f'import/{n}:0') for n in output_nodes}
%%time
o = test_sess.run(outputs, feed_dict = {X: [ids],
speed_ratios: [1.0],
f0_ratios: [1.0],
energy_ratios: [1.0]})
mel_outputs_ = np.reshape(o['decoder_output'], [-1, 80])
fig = plt.figure(figsize=(10, 8))
ax1 = fig.add_subplot(311)
ax1.set_title(f'Predicted Mel-before-Spectrogram')
im = ax1.imshow(np.rot90(mel_outputs_), aspect='auto', interpolation='none')
fig.colorbar(mappable=im, shrink=0.65, orientation='horizontal', ax=ax1)
plt.show()
mel_outputs_ = np.reshape(o['post_mel_outputs'], [-1, 80])
fig = plt.figure(figsize=(10, 8))
ax1 = fig.add_subplot(311)
ax1.set_title(f'Predicted Mel-before-Spectrogram')
im = ax1.imshow(np.rot90(mel_outputs_), aspect='auto', interpolation='none')
fig.colorbar(mappable=im, shrink=0.65, orientation='horizontal', ax=ax1)
plt.show()
```
|
github_jupyter
|
# Building and using data schemas for computer vision
This tutorial illustrates how to use raymon profiling to guard image quality in your production system. The image data is taken from [Kaggle](https://www.kaggle.com/ravirajsinh45/real-life-industrial-dataset-of-casting-product) and is courtesy of PILOT TECHNOCAST, Shapar, Rajkot. Commercial use of this data is not permitted, but we have received permission to use this data in our tutorials.
Note that some outputs may not work when viewing on Github since they are shown in iframes. We recommend to clone this repo and execute the notebooks locally.
```
%load_ext autoreload
%autoreload 2
from PIL import Image
from pathlib import Path
```
First, let's load some data. In this tutorial, we'll take the example of quality inspection in manufacturing. The puprose of our system may be to determine whether a manufactured part passes the required quality checks. These checks may measure the roudness of the part, the smoothness of the edges, the smoothness of the part overall, etc... let's assume you have automated those checks with an ML based system.
What we demonstrate here is how you can easily set up quality checks on the incoming data like whether the image is sharp enough and whether it is similar enough to the data the model was trained on. Doing checks like this may be important because people's actions, periodic maintenance and wear and tear may have an impact on what data exaclty is sent to your system. If your data changes, your system may keep running but will suffer from reduced performance, resulting in lower business value.
```
DATA_PATH = Path("../raymon/tests/sample_data/castinginspection/ok_front/")
LIM = 150
def load_data(dpath, lim):
files = dpath.glob("*.jpeg")
images = []
for n, fpath in enumerate(files):
if n == lim:
break
img = Image.open(fpath)
images.append(img)
return images
loaded_data = load_data(dpath=DATA_PATH, lim=LIM)
loaded_data[0]
```
## Constructing and building a profile
For this tutorial, we'll construct a profile that checks the image sharpness and will calculate an outlier score on the image. This way, we hope to get alerting when something seems off with the input data.
Just like in the case of structured data, we need to start by specifying a profile and its components.
```
from raymon import ModelProfile, InputComponent
from raymon.profiling.extractors.vision import Sharpness, DN2AnomalyScorer
profile = ModelProfile(
name="casting-inspection",
version="0.0.1",
components=[
InputComponent(name="sharpness", extractor=Sharpness()),
InputComponent(name="outlierscore", extractor=DN2AnomalyScorer(k=16))
],
)
profile.build(input=loaded_data)
## Inspect the schema
profile.view(poi=loaded_data[-1], mode="external")
```
## Use the profile to check new data
We can save the schema to JSON, load it again (in your production system), and use it to validate incoming data.
```
profile.save(".")
profile = ModelProfile.load("casting-inspection@0.0.1.json")
tags = profile.validate_input(loaded_data[-1])
tags
```
As you can see, all the extracted feature values are returned. This is useful for when you want to track feature distributions on your monitoring backend (which is what happens on the Raymon.ai platform). Also note that these features are not necessarily the ones going into your ML model.
## Corrupting inputs
Let's see what happens when we blur an image.
```
from PIL import ImageFilter
img_blur = loaded_data[-1].copy().filter(ImageFilter.GaussianBlur(radius=5))
img_blur
profile.validate_input(img_blur)
```
As can be seen, every feature extractor now gives rise to 2 tags: one being the feature and one being a schema error, indicating that the data has failed both sanity checks. Awesome.
We can visualize this datum while inspecting the profile.
```
profile.view(poi=img_blur, mode="external")
```
As we can see, the calculated feature values are way outside the range that were seen during training. Having alerting set up for this is crucial to deliver reliable systems.
|
github_jupyter
|
```
pip install pandas
pip install numpy
pip install sklearn
pip install matplotlib
from sklearn import cluster
from sklearn.cluster import KMeans
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
df = pd.read_csv("sample_stocks.csv")
df
df.describe()
df.head()
df.info()
# x = df['returns']
# idx = np.argsort(x)
# dividen = df['dividendyield']
# plt.figure(figsize = (20, 7))
# Plotar a dispersão de Returns vs dividendyield
plt.scatter(df["returns"], df["dividendyield"])
plt.show()
# Normalizar os dados
from sklearn.preprocessing import StandardScaler
normalize = StandardScaler()
x = pd.DataFrame(normalize.fit_transform(df))
# Plotar a dispersão novamente
plt.scatter(x[0], x[1])
plt.show()
# Crie e treine o Kmeans
from sklearn import cluster
kmeans = cluster.KMeans(n_clusters = 2)
kmeans = kmeans.fit(x)
# Plote a dispersão juntamente com o KMeans.cluster_centers_
# Na primeira linha foi usado "c", pois é: color, sequence, or sequence of colors
plt.scatter(x[0], x[1], c = kmeans.labels_, cmap = "viridis_r")
plt.scatter(kmeans.cluster_centers_, kmeans.cluster_centers_, color = "blue")
plt.show()
# Analisar K, usando o método Elbow
inertia = []
for i in range(1,15):
kmeans = KMeans(n_clusters = i)
kmeans = kmeans.fit(x)
inertia.append(kmeans.inertia_)
print(kmeans.inertia_)
plt.plot(range(1, 15), inertia, "bx-")
plt.plot(range(1, 15), inertia, "bx-")
plt.show()
```
# Clustering hierárquico
```
# imports necessários
from sklearn.cluster import AgglomerativeClustering
from scipy.cluster.hierarchy import dendrogram
# Implemente Clustering Hierárquico
modelo = AgglomerativeClustering(distance_threshold = 0, n_clusters = None, linkage = "single")
modelo.fit_predict(x)
# clusters.children_
# Plotando o dendograma
def plot_dendrogram(modelo, **kwargs):
counts = np.zeros(modelo.children_.shape[0])
n_samples = len(modelo.labels_)
for i, merge in enumerate(modelo.children_):
current_count = 0
for child_index in merge:
if child_index < n_samples:
current_count += 1
else:
current_count += counts[child_index - n_samples]
counts[i] = current_count
linkage_matrix = np.column_stack([modelo.children_, modelo.distances_, counts]).astype(float)
dendrogram(linkage_matrix, **kwargs)
plot_dendrogram(modelo, truncate_mode = 'level', p = 12)
plt.show()
# DBSCAN
# https://scikit-learn.org/stable/modules/generated/sklearn.cluster.dbscan.html?highlight=dbscan#sklearn.cluster.dbscan
from sklearn.cluster import DBSCAN
dbscan = DBSCAN(eps = .5, min_samples = 15).fit(x)
# Não consegui desenvolver essa forma de clustering
```
|
github_jupyter
|
```
import numpy as np
import sklearn
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
# Load the Boston Housing Dataset from sklearn
from sklearn.datasets import load_boston
boston_dataset = load_boston()
print(boston_dataset.keys())
print(boston_dataset.DESCR)
# Create the dataset
boston = pd.DataFrame(boston_dataset.data, columns=boston_dataset.feature_names)
boston['MEDV'] = boston_dataset.target
boston.head()
# Introductory Data Analysis
# First, let us make sure there are no missing values or NANs in the dataset
print(boston.isnull().sum())
# Next, let us plot the target vaqriable MEDV
sns.set(rc={'figure.figsize':(11.7,8.27)})
sns.distplot(boston['MEDV'], bins=30)
plt.show()
# Finally, let us get the correlation matrix
correlation_matrix = boston.corr().round(2)
# annot = True to print the values inside the square
sns.heatmap(data=correlation_matrix, annot=True)
# Let us take few of the features and see how they relate to the target in a 1D plot
plt.figure(figsize=(20, 5))
features = ['LSTAT', 'RM','CHAS','NOX','AGE','DIS']
target = boston['MEDV']
for i, col in enumerate(features):
plt.subplot(1, len(features) , i+1)
x = boston[col]
y = target
plt.scatter(x, y, marker='o')
plt.title(col)
plt.xlabel(col)
plt.ylabel('MEDV')
from sklearn.model_selection import train_test_split
X = boston.to_numpy()
X = np.delete(X, 13, 1)
y = boston['MEDV'].to_numpy()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state=5)
print(X_train.shape)
print(X_test.shape)
print(y_train.shape)
print(y_test.shape)
# Lets now train the model
from sklearn.linear_model import LinearRegression
lin_model = LinearRegression()
lin_model.fit(X_train, y_train)
# Model Evaluation
# Lets first evaluate on training set
from sklearn.metrics import r2_score
def rmse(predictions, targets):
return np.sqrt(((predictions - targets) ** 2).mean())
y_pred_train = lin_model.predict(X_train)
rmse_train = rmse(y_pred_train, y_train)
r2_train = r2_score(y_train, y_pred_train)
print("Training RMSE = " + str(rmse_train))
print("Training R2 = " + str(r2_train))
# Let us now evaluate on the test set
y_pred_test = lin_model.predict(X_test)
rmse_test = rmse(y_pred_test, y_test)
r2_test = r2_score(y_test, y_pred_test)
print("Test RMSE = " + str(rmse_test))
print("Test R2 = " + str(r2_test))
# Finally, let us see the learnt weights!
np.set_printoptions(precision=3)
print(lin_model.coef_)
# Now, what if we use lesser number of features?
# For example, suppose we choose two of the highly correlated features 'LSTAT' and 'RM'
X = pd.DataFrame(np.c_[boston['LSTAT'], boston['RM']], columns = ['LSTAT','RM'])
y = boston['MEDV']
X = np.array(X)
y = np.array(y)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state=5)
# Training Phase
lin_model = LinearRegression()
lin_model.fit(X_train, y_train)
# Evaluation Phase
y_pred_train = lin_model.predict(X_train)
rmse_train = rmse(y_pred_train, y_train)
r2_train = r2_score(y_train, y_pred_train)
print("Training RMSE = " + str(rmse_train))
print("Training R2 = " + str(r2_train))
# Let us now evaluate on the test set
y_pred_test = lin_model.predict(X_test)
rmse_test = rmse(y_pred_test, y_test)
r2_test = r2_score(y_test, y_pred_test)
print("Test RMSE = " + str(rmse_test))
print("Test R2 = " + str(r2_test))
```
|
github_jupyter
|
```
from IPython.core.display import display, HTML
import pandas as pd
import numpy as np
import copy
import os
%load_ext autoreload
%autoreload 2
import sys
sys.path.insert(0,"/local/rankability_toolbox")
PATH_TO_RANKLIB='/local/ranklib'
from numpy import ix_
import numpy as np
D = np.loadtxt(PATH_TO_RANKLIB+"/problem_instances/instances/graphs/NFL-2007-D_Matrix.txt",delimiter=",")
Dsmall = D[ix_(np.arange(8),np.arange(8))]
Dsmall
import pyrankability
(6*6-6)/2.-9
import itertools
import random
from collections import Counter
import math
D = np.zeros((6,6),dtype=int)
for i in range(D.shape[0]):
for j in range(i+1,D.shape[0]):
D[i,j] = 1
Dtest = np.zeros((6,6),dtype=int)
Dtest[0,5] = 1
Dtest[0,4] = 1
Dtest[0,1] = 1
Dtest[1,2] = 1
Dtest[1,3] = 1
Dtest[2,1] = 1
Dtest[3,0] = 1
Dtest[3,5] = 1
Dtest[5,1] = 1
Dtest[5,2] = 1
Dtest[5,4] = 1
D = Dtest
target_k = 9
target_p = 12
match_k = []
match_p = []
match_both = []
max_count = 100000
for num_ones in [1]:#[target_k]:
possible_inxs = list(set(list(range(D.shape[0]*D.shape[0]))) - set([0,6+1,6+6+2,6+6+6+3,6+6+6+6+4,6+6+6+6+6+5]))
n = len(possible_inxs)
r = num_ones
total = math.factorial(n) / math.factorial(r) / math.factorial(n-r)
print(total)
count = 0
for one_inxs in itertools.combinations(possible_inxs,num_ones):
count += 1
if count > max_count:
print("reached max")
break
if count % 100 == 0:
print(count/total)
remaining_inxs = list(set(possible_inxs) - set(one_inxs))
Dcopy = copy.copy(D)
for ix in one_inxs:
if Dcopy.flat[ix] == 1:
Dcopy.flat[ix] = 0
else:
Dcopy.flat[ix] = 1
k,P = pyrankability.exact.find_P_simple(Dcopy)
if len(P) != target_p:
continue
P = np.array(P)+1
d = dict(Counter(P[:,0]))
t1 = len(d.values())
vs = list(d.values())
vs.sort()
d2 = dict(Counter(P[:,1]))
t2 = len(d2.values())
vs2 = list(d2.values())
vs2.sort()
if tuple(vs) == (2,10) and tuple(vs2) == (2,2,2,6):
print(Dcopy)
match_p.append(Dcopy)
print('finished')
Dcopy
k,P = pyrankability.exact.find_P_simple(match_p[-1])
print(k)
np.array(P).transpose()
match_p
Dtest = np.zeros((6,6),dtype=int)
Dtest[0,5] = 1
Dtest[0,4] = 1
Dtest[0,1] = 1
Dtest[1,2] = 1
Dtest[1,3] = 1
Dtest[2,1] = 1
#Dtest[3,0] = 1
Dtest[3,5] = 1
Dtest[5,1] = 1
Dtest[5,2] = 1
Dtest[5,4] = 1
k,P = pyrankability.exact.find_P_simple(Dtest)
k,P
from collections import Counter
for Dcopy in [match_p[-1]]:
k,P = pyrankability.exact.find_P_simple(Dcopy)
P = np.array(P)+1
#t1 = len(dict(Counter(P[:,0])).values())
print("k",k)
print(P.transpose())
for i in range(6):
d = dict(Counter(P[:,i]))
t = list(d.values())
t.sort()
print(t)
perm = np.array([1,2,5,4,3,6])-1
Dnew = pyrankability.common.permute_D(match_p[-1],perm)
rows,cols = np.where(Dnew == 0)
inxs = []
for i in range(len(rows)):
if rows[i] == cols[i]:
continue
inxs.append((rows[i],cols[i]))
saved = []
for choice in itertools.combinations(inxs,2):
Dcopy = copy.copy(Dnew)
for item in choice:
Dcopy[item[0],item[1]] = 1
k,P = pyrankability.exact.find_P_simple(Dcopy)
P = np.array(P)+1
if len(P) == 2 and k == 7:
saved.append((Dcopy,choice))
from collections import Counter
i = 1
for Dcopy,choice in saved:
print("Option",i)
k,P = pyrankability.exact.find_P_simple(Dcopy)
P = np.array(P)+1
#t1 = len(dict(Counter(P[:,0])).values())
print(Dcopy)
print(np.array(choice)+1)
print("k",k)
print(P.transpose())
i+=1
P_target = [[5,4,1,6,3,2],
[5,4,1,6,2,3],
[4,5,1,6,2,3],
[4,5,1,6,3,2],
[4,1,6,3,5,2],
[4,1,6,3,2,5],
[4,1,6,2,5,3],
[4,1,6,2,3,5],
[4,1,6,5,2,3],
[4,1,6,5,3,2],
[4,6,5,1,3,2],
[4,6,5,1,2,3]
]
for i in range(len(P_target)):
P_target[i] = tuple(P_target[i])
for perm in P:
if tuple(perm) in P_target:
print('here')
else:
print('not')
P_target = [[5,4,1,6,3,2],
[5,4,1,6,2,3],
[4,5,1,6,2,3],
[4,5,1,6,3,2],
[4,1,6,3,5,2],
[4,1,6,3,2,5],
[4,1,6,2,5,3],
[4,1,6,2,3,5],
[4,1,6,5,2,3],
[4,1,6,5,3,2],
[4,6,5,1,3,2],
[4,6,5,1,2,3]
]
P_determined = [[4 1 6 2 3 5]
[4 1 6 2 5 3]
[4 1 6 3 2 5]
[4 1 6 3 5 2]
[4 1 6 5 2 3]
[4 1 6 5 3 2]
[4 5 1 6 2 3]
[4 5 1 6 3 2]
[4 6 5 1 2 3]
[4 6 5 1 3 2]
[5 4 1 6 2 3]
[5 4 1 6 3 2]]
P_target = np.array(P_target)
print(P_target.transpose())
for i in range(6):
d = dict(Counter(P_target[:,i]))
t = list(d.values())
t.sort()
print(t)
[2, 5]
[2, 5, 6]
[4, 5, 6]
[3, 4, 5, 7]
[3, 5, 7]
[3, 5, 7]
Dtilde, changes, output = pyrankability.improve.greedy(D,1,verbose=False)
Dchanges
if D.shape[0] <= 8: # Only solve small problems
search = pyrankability.exact.ExhaustiveSearch(Dsmall)
search.find_P()
print(pyrankability.common.as_json(search.k,search.P,{}))
p = len(search.P)
k = search.k
def greedy(D,l):
D = np.copy(D) # Leave the original untouched
for niter in range(l):
n=D.shape[0]
k,P,X,Y,k2 = pyrankability.lp.lp(D)
mult = 100
X = np.round(X*mult)/mult
Y = np.round(Y*mult)/mult
T0 = np.zeros((n,n))
T1 = np.zeros((n,n))
inxs = np.where(D + D.transpose() == 0)
T0[inxs] = 1
inxs = np.where(D + D.transpose() == 2)
T1[inxs] = 1
T0[np.arange(n),np.arange(n)]= 0
T1[np.arange(n),np.arange(n)] = 0
DOM = D + X - Y
Madd=T0*DOM # note: DOM = P_> in paper
M1 = Madd # Copy Madd into M, % Madd identifies values >0 in P_> that have 0-tied values in D
M1[Madd<=0] = np.nan # Set anything <= 0 to NaN
min_inx = np.nanargmin(M1) # Find min value and index
bestlinktoadd_i, bestlinktoadd_j = np.unravel_index(min_inx,M1.shape) # adding (i,j) link associated with
# smallest nonzero value in Madd is likely to produce greatest improvement in rankability
minMadd = M1[bestlinktoadd_i, bestlinktoadd_j]
Mdelete=T1*DOM # note: DOM = P_> in paper
Mdelete=Mdelete*(Mdelete<1) # Mdelete identifies values <1 in P_> that have 1-tied values in D
bestlinktodelete_i, bestlinktodelete_j=np.unravel_index(np.nanargmax(Mdelete), Mdelete.shape) # deleting (i,j) link associated with
# largest non-unit (less than 1) value in Mdelete is likely to produce greatest improvement in rankability
maxMdelete = Mdelete[bestlinktodelete_i, bestlinktodelete_j]
# This next section modifies D to create Dtilde
Dtilde = np.copy(D) # initialize Dtilde
# choose whether to add or remove a link depending on which will have the biggest
# impact on reducing the size of the set P
# PAUL: Or if we only want to do link addition, you don't need to form
# Mdelete and find the largest non-unit value in it. And vice versa, if
# only link removal is desired, don't form Madd.
if (1-minMadd)>maxMdelete and p>=2:
formatSpec = 'The best one-link way to improve rankability is by adding a link from %d to %d.\nThis one modification removes about %.10f percent of the rankings in P.'%(bestlinktoadd_i,bestlinktoadd_j,(1-minMadd)*100)
print(formatSpec)
Dtilde[bestlinktoadd_i,bestlinktoadd_j]=1 # adds this link, creating one-mod Dtilde
elif 1-minMadd<maxMdelete and p>=2:
formatSpec = 'The best one-link way to improve rankability is by deleting the link from %d to %d.\nThis one modification removes about %.10f percent of the rankings in P.' % (bestlinktodelete_i,bestlinktodelete_j,maxMdelete*100)
print(formatSpec)
Dtilde[bestlinktodelete_i,bestlinktodelete_j] = 0 # removes this link, creating one-mod Dtilde
D = Dtilde
Dtilde = greedy(D,1)
search = pyrankability.exact.ExhaustiveSearch(Dtilde)
search.find_P()
print(pyrankability.common.as_json(search.k,search.P,{}))
bestlinktoadd_i, bestlinktoadd_j
% Form modification matrices Madd (M_+) and Mdelete (M_-), which are used
% to determine which link modification most improves rankability
Mdelete=T1.*DOM; % note: DOM = P_> in paper
Mdelete=Mdelete.*(Mdelete<1); % Mdelete identifies values <1 in P_> that have 1-tied values in D
maxMdelete=max(max(Mdelete));
[bestlinktodelete_i bestlinktodelete_j]=find(Mdelete==maxMdelete); % deleting (i,j) link associated with
% largest non-unit (less than 1) value in Mdelete is likely to produce greatest improvement in rankability
% This next section modifies D to create Dtilde
Dtilde=D; % initialize Dtilde
% choose whether to add or remove a link depending on which will have the biggest
% impact on reducing the size of the set P
% PAUL: Or if we only want to do link addition, you don't need to form
% Mdelete and find the largest non-unit value in it. And vice versa, if
% only link removal is desired, don't form Madd.
if 1-minMadd>maxMdelete & p>=2
formatSpec = 'The best one-link way to improve rankability is by adding a link from %4.f to %4.f.\nThis one modification removes about %2.f percent of the rankings in P.';
fprintf(formatSpec,bestlinktoadd_i(1),bestlinktoadd_j(1),(1-minMadd)*100)
Dtilde(bestlinktoadd_i(1),bestlinktoadd_j(1))=1; % adds this link, creating one-mod Dtilde
elseif 1-minMadd<maxMdelete & p>=2
formatSpec = 'The best one-link way to improve rankability is by deleting the link from %4.f to %4.f.\nThis one modification removes about %2.f percent of the rankings in P.';
fprintf(formatSpec,bestlinktodelete_i(1),bestlinktodelete_j(1),maxMdelete*100)
Dtilde(bestlinktodelete_i(1),bestlinktodelete_j(1))=0; % removes this link, creating one-mod Dtilde
end
% set D=Dtilde and repeat until l link modifications have been made or
% p=1
D=Dtilde;
```
|
github_jupyter
|
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import RandomForestRegressor, RandomForestClassifier
from sklearn.metrics import mean_squared_error, accuracy_score, f1_score, r2_score, explained_variance_score, roc_auc_score
from sklearn.preprocessing import MinMaxScaler, OneHotEncoder, LabelBinarizer
from sklearn.neural_network import MLPClassifier, MLPRegressor
from sklearn.linear_model import Lasso
import torch
from torch import nn
import torch.nn.functional as F
from dp_wgan import Generator, Discriminator
from dp_autoencoder import Autoencoder
from evaluation import *
import dp_optimizer, sampling, analysis, evaluation
torch.manual_seed(0)
np.random.seed(0)
names = ['age', 'workclass', 'fnlwgt', 'education', 'education-num', 'marital-status', 'occupation', 'relationship', 'race', 'sex', 'capital-gain', 'capital-loss', 'hours-per-week', 'native-country', 'salary']
train = pd.read_csv('adult.data', names=names)
test = pd.read_csv('adult.test', names=names)
df = pd.concat([train, test])
df
class Processor:
def __init__(self, datatypes):
self.datatypes = datatypes
def fit(self, matrix):
preprocessors, cutoffs = [], []
for i, (column, datatype) in enumerate(self.datatypes):
preprocessed_col = matrix[:,i].reshape(-1, 1)
if 'categorical' in datatype:
preprocessor = LabelBinarizer()
else:
preprocessor = MinMaxScaler()
preprocessed_col = preprocessor.fit_transform(preprocessed_col)
cutoffs.append(preprocessed_col.shape[1])
preprocessors.append(preprocessor)
self.cutoffs = cutoffs
self.preprocessors = preprocessors
def transform(self, matrix):
preprocessed_cols = []
for i, (column, datatype) in enumerate(self.datatypes):
preprocessed_col = matrix[:,i].reshape(-1, 1)
preprocessed_col = self.preprocessors[i].transform(preprocessed_col)
preprocessed_cols.append(preprocessed_col)
return np.concatenate(preprocessed_cols, axis=1)
def fit_transform(self, matrix):
self.fit(matrix)
return self.transform(matrix)
def inverse_transform(self, matrix):
postprocessed_cols = []
j = 0
for i, (column, datatype) in enumerate(self.datatypes):
postprocessed_col = self.preprocessors[i].inverse_transform(matrix[:,j:j+self.cutoffs[i]])
if 'categorical' in datatype:
postprocessed_col = postprocessed_col.reshape(-1, 1)
else:
if 'positive' in datatype:
postprocessed_col = postprocessed_col.clip(min=0)
if 'int' in datatype:
postprocessed_col = postprocessed_col.round()
postprocessed_cols.append(postprocessed_col)
j += self.cutoffs[i]
return np.concatenate(postprocessed_cols, axis=1)
datatypes = [
('age', 'positive int'),
('workclass', 'categorical'),
('education-num', 'categorical'),
('marital-status', 'categorical'),
('occupation', 'categorical'),
('relationship', 'categorical'),
('race', 'categorical'),
('sex', 'categorical binary'),
('capital-gain', 'positive float'),
('capital-loss', 'positive float'),
('hours-per-week', 'positive int'),
('native-country', 'categorical'),
('salary', 'categorical binary'),
]
np.random.seed(0)
processor = Processor(datatypes)
relevant_df = df.drop(columns=['education', 'fnlwgt'])
for column, datatype in datatypes:
if 'categorical' in datatype:
relevant_df[column] = relevant_df[column].astype('category').cat.codes
train_df = relevant_df.head(32562)
X_real = torch.tensor(relevant_df.values.astype('float32'))
X_encoded = torch.tensor(processor.fit_transform(X_real).astype('float32'))
train_cutoff = 32562
X_train_real = X_real[:train_cutoff]
X_test_real = X_real[:train_cutoff]
X_train_encoded = X_encoded[:train_cutoff]
X_test_encoded = X_encoded[train_cutoff:]
X_encoded.shape
print(X_train_encoded)
print(X_test_encoded)
ae_params = {
'b1': 0.9,
'b2': 0.999,
'binary': False,
'compress_dim': 15,
'delta': 1e-5,
'device': 'cuda',
'iterations': 20000,
'lr': 0.005,
'l2_penalty': 0.,
'l2_norm_clip': 0.012,
'minibatch_size': 64,
'microbatch_size': 1,
'noise_multiplier': 2.5,
'nonprivate': True,
}
autoencoder = Autoencoder(
example_dim=len(X_train_encoded[0]),
compression_dim=ae_params['compress_dim'],
binary=ae_params['binary'],
device=ae_params['device'],
)
decoder_optimizer = dp_optimizer.DPAdam(
l2_norm_clip=ae_params['l2_norm_clip'],
noise_multiplier=ae_params['noise_multiplier'],
minibatch_size=ae_params['minibatch_size'],
microbatch_size=ae_params['microbatch_size'],
nonprivate=ae_params['nonprivate'],
params=autoencoder.get_decoder().parameters(),
lr=ae_params['lr'],
betas=(ae_params['b1'], ae_params['b2']),
weight_decay=ae_params['l2_penalty'],
)
encoder_optimizer = torch.optim.Adam(
params=autoencoder.get_encoder().parameters(),
lr=ae_params['lr'] * ae_params['microbatch_size'] / ae_params['minibatch_size'],
betas=(ae_params['b1'], ae_params['b2']),
weight_decay=ae_params['l2_penalty'],
)
weights, ds = [], []
for name, datatype in datatypes:
if 'categorical' in datatype:
num_values = len(np.unique(relevant_df[name]))
if num_values == 2:
weights.append(1.)
ds.append((datatype, 1))
else:
for i in range(num_values):
weights.append(1. / num_values)
ds.append((datatype, num_values))
else:
weights.append(1.)
ds.append((datatype, 1))
weights = torch.tensor(weights).to(ae_params['device'])
#autoencoder_loss = (lambda input, target: torch.mul(weights, torch.pow(input-target, 2)).sum(dim=1).mean(dim=0))
#autoencoder_loss = lambda input, target: torch.mul(weights, F.binary_cross_entropy(input, target, reduction='none')).sum(dim=1).mean(dim=0)
autoencoder_loss = nn.BCELoss()
#autoencoder_loss = nn.MSELoss()
print(autoencoder)
print('Achieves ({}, {})-DP'.format(
analysis.epsilon(
len(X_train_encoded),
ae_params['minibatch_size'],
ae_params['noise_multiplier'],
ae_params['iterations'],
ae_params['delta']
),
ae_params['delta'],
))
minibatch_loader, microbatch_loader = sampling.get_data_loaders(
minibatch_size=ae_params['minibatch_size'],
microbatch_size=ae_params['microbatch_size'],
iterations=ae_params['iterations'],
nonprivate=ae_params['nonprivate'],
)
train_losses, validation_losses = [], []
X_train_encoded = X_train_encoded.to(ae_params['device'])
X_test_encoded = X_test_encoded.to(ae_params['device'])
for iteration, X_minibatch in enumerate(minibatch_loader(X_train_encoded)):
encoder_optimizer.zero_grad()
decoder_optimizer.zero_grad()
for X_microbatch in microbatch_loader(X_minibatch):
decoder_optimizer.zero_microbatch_grad()
output = autoencoder(X_microbatch)
loss = autoencoder_loss(output, X_microbatch)
loss.backward()
decoder_optimizer.microbatch_step()
validation_loss = autoencoder_loss(autoencoder(X_test_encoded).detach(), X_test_encoded)
encoder_optimizer.step()
decoder_optimizer.step()
train_losses.append(loss.item())
validation_losses.append(validation_loss.item())
if iteration % 1000 == 0:
print ('[Iteration %d/%d] [Loss: %f] [Validation Loss: %f]' % (
iteration, ae_params['iterations'], loss.item(), validation_loss.item())
)
pd.DataFrame(data={'train': train_losses, 'validation': validation_losses}).plot()
with open('ae_eps_inf.dat', 'wb') as f:
torch.save(autoencoder, f)
gan_params = {
'alpha': 0.99,
'binary': False,
'clip_value': 0.01,
'd_updates': 15,
'delta': 1e-5,
'device': 'cuda',
'iterations': 15000,
'latent_dim': 64,
'lr': 0.005,
'l2_penalty': 0.,
'l2_norm_clip': 0.022,
'minibatch_size': 128,
'microbatch_size': 1,
'noise_multiplier': 3.5,
'nonprivate': False,
}
with open('ae_eps_inf.dat', 'rb') as f:
autoencoder = torch.load(f)
decoder = autoencoder.get_decoder()
generator = Generator(
input_dim=gan_params['latent_dim'],
output_dim=autoencoder.get_compression_dim(),
binary=gan_params['binary'],
device=gan_params['device'],
)
g_optimizer = torch.optim.RMSprop(
params=generator.parameters(),
lr=gan_params['lr'],
alpha=gan_params['alpha'],
weight_decay=gan_params['l2_penalty'],
)
discriminator = Discriminator(
input_dim=len(X_train_encoded[0]),
device=gan_params['device'],
)
d_optimizer = dp_optimizer.DPRMSprop(
l2_norm_clip=gan_params['l2_norm_clip'],
noise_multiplier=gan_params['noise_multiplier'],
minibatch_size=gan_params['minibatch_size'],
microbatch_size=gan_params['microbatch_size'],
nonprivate=gan_params['nonprivate'],
params=discriminator.parameters(),
lr=gan_params['lr'],
alpha=gan_params['alpha'],
weight_decay=gan_params['l2_penalty'],
)
print(generator)
print(discriminator)
print('Achieves ({}, {})-DP'.format(
analysis.epsilon(
len(X_train_encoded),
gan_params['minibatch_size'],
gan_params['noise_multiplier'],
gan_params['iterations'],
gan_params['delta']
),
gan_params['delta'],
))
minibatch_loader, microbatch_loader = sampling.get_data_loaders(
minibatch_size=gan_params['minibatch_size'],
microbatch_size=gan_params['microbatch_size'],
iterations=gan_params['iterations'],
nonprivate=gan_params['nonprivate'],
)
X_train_encoded = X_train_encoded.to(gan_params['device'])
X_test_encoded = X_test_encoded.to(ae_params['device'])
for iteration, X_minibatch in enumerate(minibatch_loader(X_train_encoded)):
d_optimizer.zero_grad()
for real in microbatch_loader(X_minibatch):
z = torch.randn(real.size(0), gan_params['latent_dim'], device=gan_params['device'])
fake = decoder(generator(z)).detach()
d_optimizer.zero_microbatch_grad()
d_loss = -torch.mean(discriminator(real)) + torch.mean(discriminator(fake))
d_loss.backward()
d_optimizer.microbatch_step()
d_optimizer.step()
for parameter in discriminator.parameters():
parameter.data.clamp_(-gan_params['clip_value'], gan_params['clip_value'])
if iteration % gan_params['d_updates'] == 0:
z = torch.randn(X_minibatch.size(0), gan_params['latent_dim'], device=gan_params['device'])
fake = decoder(generator(z))
g_optimizer.zero_grad()
g_loss = -torch.mean(discriminator(fake))
g_loss.backward()
g_optimizer.step()
if iteration % 1000 == 0:
print('[Iteration %d/%d] [D loss: %f] [G loss: %f]' % (
iteration, gan_params['iterations'], d_loss.item(), g_loss.item()
))
z = torch.randn(len(X_train_real), gan_params['latent_dim'], device=gan_params['device'])
X_synthetic_encoded = decoder(generator(z)).cpu().detach().numpy()
X_synthetic_real = processor.inverse_transform(X_synthetic_encoded)
X_synthetic_encoded = processor.transform(X_synthetic_real)
synthetic_data = pd.DataFrame(X_synthetic_real, columns=relevant_df.columns)
i = 0
columns = relevant_df.columns
relevant_df[columns[i]].hist()
synthetic_data[columns[i]].hist()
plt.show()
#pca_evaluation(pd.DataFrame(X_train_real), pd.DataFrame(X_synthetic_real))
#plt.show()
with open('gen_eps_inf.dat', 'wb') as f:
torch.save(generator, f)
X_train_encoded = X_train_encoded.cpu()
X_test_encoded = X_test_encoded.cpu()
clf = RandomForestClassifier(n_estimators=100)
clf.fit(X_train_encoded[:,:-1], X_train_encoded[:,-1])
prediction = clf.predict(X_test_encoded[:,:-1])
print(accuracy_score(X_test_encoded[:,-1], prediction))
print(f1_score(X_test_encoded[:,-1], prediction))
with open('gen_eps_inf.dat', 'rb') as f:
generator = torch.load(f)
with open('ae_eps_inf.dat', 'rb') as f:
autoencoder = torch.load(f)
decoder = autoencoder.get_decoder()
z = torch.randn(len(X_train_real), gan_params['latent_dim'], device=gan_params['device'])
X_synthetic_encoded = decoder(generator(z)).cpu().detach().numpy()
X_synthetic_real = processor.inverse_transform(X_synthetic_encoded)
X_synthetic_encoded = processor.transform(X_synthetic_real)
#pd.DataFrame(X_encoded.numpy()).to_csv('real.csv')
pd.DataFrame(X_synthetic_encoded).to_csv('synthetic.csv')
with open('gen_eps_inf.dat', 'rb') as f:
generator = torch.load(f)
with open('ae_eps_inf.dat', 'rb') as f:
autoencoder = torch.load(f)
decoder = autoencoder.get_decoder()
X_test_encoded = X_test_encoded.cpu()
z = torch.randn(len(X_train_real), gan_params['latent_dim'], device=gan_params['device'])
X_synthetic_encoded = decoder(generator(z)).cpu().detach().numpy()
X_synthetic_real = processor.inverse_transform(X_synthetic_encoded)
X_synthetic_encoded = processor.transform(X_synthetic_real)
clf = RandomForestClassifier(n_estimators=100)
clf.fit(X_synthetic_encoded[:,:-1], X_synthetic_encoded[:,-1])
prediction = clf.predict(X_test_encoded[:,:-1])
print(accuracy_score(X_test_encoded[:,-1], prediction))
print(f1_score(X_test_encoded[:,-1], prediction))
with open('gen_eps_inf.dat', 'rb') as f:
generator = torch.load(f)
with open('ae_eps_inf.dat', 'rb') as f:
autoencoder = torch.load(f)
decoder = autoencoder.get_decoder()
z = torch.randn(len(X_train_real), gan_params['latent_dim'], device=gan_params['device'])
X_synthetic_encoded = decoder(generator(z)).cpu().detach().numpy()
X_synthetic_real = processor.inverse_transform(X_synthetic_encoded)
synthetic_data = pd.DataFrame(X_synthetic_real, columns=relevant_df.columns)
column = 'age'
fig = plt.figure()
ax = fig.add_subplot()
ax.hist(train_df[column].values,)# bins=)
ax.hist(synthetic_data[column].values, color='red', alpha=0.35,)# bins10)
with open('gen_eps_inf.dat', 'rb') as f:
generator = torch.load(f)
with open('ae_eps_inf.dat', 'rb') as f:
autoencoder = torch.load(f)
decoder = autoencoder.get_decoder()
z = torch.randn(len(X_train_real), gan_params['latent_dim'], device=gan_params['device'])
X_synthetic_encoded = decoder(generator(z)).cpu().detach().numpy()
X_synthetic_real = processor.inverse_transform(X_synthetic_encoded)
synthetic_data = pd.DataFrame(X_synthetic_real, columns=relevant_df.columns)
regression_real = []
classification_real = []
regression_synthetic = []
classification_synthetic = []
target_real = []
target_synthetic = []
for column, datatype in datatypes:
p = Processor([datatype for datatype in datatypes if datatype[0] != column])
train_cutoff = 32562
p.fit(relevant_df.drop(columns=[column]).values)
X_enc = p.transform(relevant_df.drop(columns=[column]).values)
y_enc = relevant_df[column]
X_enc_train = X_enc[:train_cutoff]
X_enc_test = X_enc[train_cutoff:]
y_enc_train = y_enc[:train_cutoff]
y_enc_test = y_enc[train_cutoff:]
X_enc_syn = p.transform(synthetic_data.drop(columns=[column]).values)
y_enc_syn = synthetic_data[column]
if 'binary' in datatype:
model = lambda: RandomForestClassifier(n_estimators=10)
score = lambda true, pred: f1_score(true, pred)
elif 'categorical' in datatype:
model = lambda: RandomForestClassifier(n_estimators=10)
score = lambda true, pred: f1_score(true, pred, average='micro')
else:
model = lambda: Lasso()
explained_var = lambda true, pred: explained_variance_score(true, pred)
score = r2_score
real, synthetic = model(), model()
real.fit(X_enc_train, y_enc_train)
synthetic.fit(X_enc_syn, y_enc_syn)
real_preds = real.predict(X_enc_test)
synthetic_preds = synthetic.predict(X_enc_test)
print(column, datatype)
if column == 'salary':
target_real.append(score(y_enc_test, real_preds))
target_synthetic.append(score(y_enc_test, synthetic_preds))
elif 'categorical' in datatype:
classification_real.append(score(y_enc_test, real_preds))
classification_synthetic.append(score(y_enc_test, synthetic_preds))
else:
regression_real.append(score(y_enc_test, real_preds))
regression_synthetic.append(score(y_enc_test, synthetic_preds))
print(score.__name__)
print('Real: {}'.format(score(y_enc_test, real_preds)))
print('Synthetic: {}'.format(score(y_enc_test, synthetic_preds)))
print('')
plt.scatter(classification_real, classification_synthetic, c='blue')
plt.scatter(regression_real, regression_synthetic, c='red')
plt.scatter(target_real, target_synthetic, c='green')
plt.xlabel('Real Data')
plt.ylabel('Synthetic Data')
plt.axis((0., 1., 0., 1.))
plt.plot((0, 1), (0, 1))
plt.show()
```
|
github_jupyter
|
<a href="https://qworld.net" target="_blank" align="left"><img src="../qworld/images/header.jpg" align="left"></a>
$ \newcommand{\bra}[1]{\langle #1|} $
$ \newcommand{\ket}[1]{|#1\rangle} $
$ \newcommand{\braket}[2]{\langle #1|#2\rangle} $
$ \newcommand{\dot}[2]{ #1 \cdot #2} $
$ \newcommand{\biginner}[2]{\left\langle #1,#2\right\rangle} $
$ \newcommand{\mymatrix}[2]{\left( \begin{array}{#1} #2\end{array} \right)} $
$ \newcommand{\myvector}[1]{\mymatrix{c}{#1}} $
$ \newcommand{\myrvector}[1]{\mymatrix{r}{#1}} $
$ \newcommand{\mypar}[1]{\left( #1 \right)} $
$ \newcommand{\mybigpar}[1]{ \Big( #1 \Big)} $
$ \newcommand{\sqrttwo}{\frac{1}{\sqrt{2}}} $
$ \newcommand{\dsqrttwo}{\dfrac{1}{\sqrt{2}}} $
$ \newcommand{\onehalf}{\frac{1}{2}} $
$ \newcommand{\donehalf}{\dfrac{1}{2}} $
$ \newcommand{\hadamard}{ \mymatrix{rr}{ \sqrttwo & \sqrttwo \\ \sqrttwo & -\sqrttwo }} $
$ \newcommand{\vzero}{\myvector{1\\0}} $
$ \newcommand{\vone}{\myvector{0\\1}} $
$ \newcommand{\stateplus}{\myvector{ \sqrttwo \\ \sqrttwo } } $
$ \newcommand{\stateminus}{ \myrvector{ \sqrttwo \\ -\sqrttwo } } $
$ \newcommand{\myarray}[2]{ \begin{array}{#1}#2\end{array}} $
$ \newcommand{\X}{ \mymatrix{cc}{0 & 1 \\ 1 & 0} } $
$ \newcommand{\I}{ \mymatrix{rr}{1 & 0 \\ 0 & 1} } $
$ \newcommand{\Z}{ \mymatrix{rr}{1 & 0 \\ 0 & -1} } $
$ \newcommand{\Htwo}{ \mymatrix{rrrr}{ \frac{1}{2} & \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & -\frac{1}{2} & \frac{1}{2} & -\frac{1}{2} \\ \frac{1}{2} & \frac{1}{2} & -\frac{1}{2} & -\frac{1}{2} \\ \frac{1}{2} & -\frac{1}{2} & -\frac{1}{2} & \frac{1}{2} } } $
$ \newcommand{\CNOT}{ \mymatrix{cccc}{1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0} } $
$ \newcommand{\norm}[1]{ \left\lVert #1 \right\rVert } $
$ \newcommand{\pstate}[1]{ \lceil \mspace{-1mu} #1 \mspace{-1.5mu} \rfloor } $
$ \newcommand{\greenbit}[1] {\mathbf{{\color{green}#1}}} $
$ \newcommand{\bluebit}[1] {\mathbf{{\color{blue}#1}}} $
$ \newcommand{\redbit}[1] {\mathbf{{\color{red}#1}}} $
$ \newcommand{\brownbit}[1] {\mathbf{{\color{brown}#1}}} $
$ \newcommand{\blackbit}[1] {\mathbf{{\color{black}#1}}} $
<font style="font-size:28px;" align="left"><b> <font color="blue"> Solutions for </font> Matrices: Tensor Product</b></font>
<br>
_prepared by Abuzer Yakaryilmaz_
<br><br>
<a id="task1"></a>
<h3> Task 1 </h3>
Find $ u \otimes v $ and $ v \otimes u $ for the given vectors $ u = \myrvector{-2 \\ -1 \\ 0 \\ 1} $ and $ v = \myrvector{ 1 \\ 2 \\ 3 } $.
<h3>Solution</h3>
```
u = [-2,-1,0,1]
v = [1,2,3]
uv = []
vu = []
for i in range(len(u)): # one element of u is picked
for j in range(len(v)): # now we iteratively select every element of v
uv.append(u[i]*v[j]) # this one element of u is iteratively multiplied with every element of v
print("u-tensor-v is",uv)
for i in range(len(v)): # one element of v is picked
for j in range(len(u)): # now we iteratively select every element of u
vu.append(v[i]*u[j]) # this one element of v is iteratively multiplied with every element of u
print("v-tensor-u is",vu)
```
<a id="task2"></a>
<h3> Task 2 </h3>
Find $ A \otimes B $ for the given matrices
$
A = \mymatrix{rrr}{-1 & 0 & 1 \\ -2 & -1 & 2} ~~\mbox{and}~~
B = \mymatrix{rr}{0 & 2 \\ 3 & -1 \\ -1 & 1 }.
$
<h3>Solution</h3>
```
A = [
[-1,0,1],
[-2,-1,2]
]
B = [
[0,2],
[3,-1],
[-1,1]
]
print("A =")
for i in range(len(A)):
print(A[i])
print() # print a line
print("B =")
for i in range(len(B)):
print(B[i])
# let's define A-tensor-B as a (6x6)-dimensional zero matrix
AB = []
for i in range(6):
AB.append([])
for j in range(6):
AB[i].append(0)
# let's find A-tensor-B
for i in range(2):
for j in range(3):
# for each A(i,j) we execute the following codes
a = A[i][j]
# we access each element of B
for m in range(3):
for n in range(2):
b = B[m][n]
# now we put (a*b) in the appropriate index of AB
AB[3*i+m][2*j+n] = a * b
print() # print a line
print("A-tensor-B =")
print() # print a line
for i in range(6):
print(AB[i])
```
<a id="task3"></a>
<h3> Task 3 </h3>
Find $ B \otimes A $ for the given matrices
$
A = \mymatrix{rrr}{-1 & 0 & 1 \\ -2 & -1 & 2} ~~\mbox{and}~~
B = \mymatrix{rr}{0 & 2 \\ 3 & -1 \\ -1 & 1 }.
$
<h3>Solution</h3>
```
A = [
[-1,0,1],
[-2,-1,2]
]
B = [
[0,2],
[3,-1],
[-1,1]
]
print() # print a line
print("B =")
for i in range(len(B)):
print(B[i])
print("A =")
for i in range(len(A)):
print(A[i])
# let's define B-tensor-A as a (6x6)-dimensional zero matrix
BA = []
for i in range(6):
BA.append([])
for j in range(6):
BA[i].append(0)
# let's find B-tensor-A
for i in range(3):
for j in range(2):
# for each B(i,j) we execute the following codes
b = B[i][j]
# we access each element of A
for m in range(2):
for n in range(3):
a = A[m][n]
# now we put (a*b) in the appropriate index of AB
BA[2*i+m][3*j+n] = b * a
print() # print a line
print("B-tensor-A =")
print() # print a line
for i in range(6):
print(BA[i])
```
|
github_jupyter
|
# SQLAlchemy Homework - Surfs Up!
### Before You Begin
1. Create a new repository for this project called `sqlalchemy-challenge`. **Do not add this homework to an existing repository**.
2. Clone the new repository to your computer.
3. Add your Jupyter notebook and `app.py` to this folder. These will be the main scripts to run for analysis.
4. Push the above changes to GitHub or GitLab.

Congratulations! You've decided to treat yourself to a long holiday vacation in Honolulu, Hawaii! To help with your trip planning, you need to do some climate analysis on the area. The following outlines what you need to do.
## Step 1 - Climate Analysis and Exploration
To begin, use Python and SQLAlchemy to do basic climate analysis and data exploration of your climate database. All of the following analysis should be completed using SQLAlchemy ORM queries, Pandas, and Matplotlib.
* Use the provided [starter notebook](climate_starter.ipynb) and [hawaii.sqlite](Resources/hawaii.sqlite) files to complete your climate analysis and data exploration.
* Choose a start date and end date for your trip. Make sure that your vacation range is approximately 3-15 days total.
* Use SQLAlchemy `create_engine` to connect to your sqlite database.
* Use SQLAlchemy `automap_base()` to reflect your tables into classes and save a reference to those classes called `Station` and `Measurement`.
### Precipitation Analysis
* Design a query to retrieve the last 12 months of precipitation data.
* Select only the `date` and `prcp` values.
* Load the query results into a Pandas DataFrame and set the index to the date column.
* Sort the DataFrame values by `date`.
* Plot the results using the DataFrame `plot` method.

* Use Pandas to print the summary statistics for the precipitation data.
### Station Analysis
* Design a query to calculate the total number of stations.
* Design a query to find the most active stations.
* List the stations and observation counts in descending order.
* Which station has the highest number of observations?
* Hint: You will need to use a function such as `func.min`, `func.max`, `func.avg`, and `func.count` in your queries.
* Design a query to retrieve the last 12 months of temperature observation data (TOBS).
* Filter by the station with the highest number of observations.
* Plot the results as a histogram with `bins=12`.

- - -
## Step 2 - Climate App
Now that you have completed your initial analysis, design a Flask API based on the queries that you have just developed.
* Use Flask to create your routes.
### Routes
* `/`
* Home page.
* List all routes that are available.
* `/api/v1.0/precipitation`
* Convert the query results to a dictionary using `date` as the key and `prcp` as the value.
* Return the JSON representation of your dictionary.
* `/api/v1.0/stations`
* Return a JSON list of stations from the dataset.
* `/api/v1.0/tobs`
* Query the dates and temperature observations of the most active station for the last year of data.
* Return a JSON list of temperature observations (TOBS) for the previous year.
* `/api/v1.0/<start>` and `/api/v1.0/<start>/<end>`
* Return a JSON list of the minimum temperature, the average temperature, and the max temperature for a given start or start-end range.
* When given the start only, calculate `TMIN`, `TAVG`, and `TMAX` for all dates greater than and equal to the start date.
* When given the start and the end date, calculate the `TMIN`, `TAVG`, and `TMAX` for dates between the start and end date inclusive.
## Hints
* You will need to join the station and measurement tables for some of the queries.
* Use Flask `jsonify` to convert your API data into a valid JSON response object.
- - -
```
%matplotlib inline
from matplotlib import style
style.use('fivethirtyeight')
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import datetime as dt
import seaborn as sns
from scipy.stats import linregress
from sklearn import datasets
```
# Reflect Tables into SQLAlchemy ORM
### Precipitation Analysis
* Design a query to retrieve the last 12 months of precipitation data.
* Select only the `date` and `prcp` values.
* Load the query results into a Pandas DataFrame and set the index to the date column.
* Sort the DataFrame values by `date`.
* Plot the results using the DataFrame `plot` method.
*
* Use Pandas to print the summary statistics for the precipitation data.
```
# Python SQL toolkit and Object Relational Mapper
import sqlalchemy
from sqlalchemy.ext.automap import automap_base
from sqlalchemy.orm import Session
from sqlalchemy import create_engine, func, inspect
engine = create_engine("sqlite:///Resources/hawaii.sqlite")
#Base.metadata.create_all(engine)
inspector = inspect(engine)
inspector.get_table_names()
# reflect an existing database into a new model
Base = automap_base()
# reflect the tables
Base.prepare(engine,reflect= True)
# Reflect Database into ORM class
#Base.classes.measurement
# Create our session (link) from Python to the DB
session = Session(bind=engine)
session = Session(engine)
# We can view all of the classes that automap found
Base.classes.keys()
# Save references to each table
Measurement = Base.classes.measurement
Station = Base.classes.station
engine.execute('Select * from measurement').fetchall()
# Get columns of 'measurement' table
columns = inspector.get_columns('measurement')
for c in columns:
print(c)
# A very odd way to get all column values if they are made by tuples with keys and values, it's more straightforward
# and sensible to just do columns = inspector.get_columns('measurement') the a for loop: for c in columns: print(c)
columns = inspector.get_columns('measurement')
for c in columns:
print(c.keys())
for c in columns:
print(c.values())
```
# Exploratory Climate Analysis
```
# Design a query to retrieve the last 12 months of precipitation data and plot the results
# Design a query to retrieve the last 12 months of precipitation data.
max_date = session.query(func.max(Measurement.date)).all()[0][0]
# Select only the date and prcp values.
#datetime.datetime.strptime(date_time_str, '%Y-%m-%d %H:%M:%S.%f')
import datetime
print(max_date)
print(type(max_date))
# Calculate the date 1 year ago from the last data point in the database
min_date = datetime.datetime.strptime(max_date,'%Y-%m-%d') - datetime.timedelta(days = 365)
print(min_date)
print(min_date.year, min_date.month, min_date.day)
# Perform a query to retrieve the data and precipitation scores
results = session.query(Measurement.prcp, Measurement.date).filter(Measurement.date >= min_date).all()
results
# Load the query results into a Pandas DataFrame and set the index to the date column.
prcp_anal_df = pd.DataFrame(results, columns = ['prcp','date']).set_index('date')
# Sort the DataFrame values by date.
prcp_anal_df.sort_values(by=['date'], inplace=True)
prcp_anal_df
# Create Plot(s)
prcp_anal_df.plot(rot = 90)
plt.xlabel('Date')
plt.ylabel('Precipitation (inches)')
plt.title('Precipitation over One Year in Hawaii')
plt.savefig("histo_prcp_date.png")
plt.show()
sns.set()
plot1 = prcp_anal_df.plot(figsize = (10, 5))
fig = plot1.get_figure()
plt.title('Precipitation in Hawaii')
plt.xlabel('Date')
plt.ylabel('Precipitation')
plt.legend(["Precipitation"],loc="best")
plt.xticks(rotation=45)
plt.tight_layout()
plt.savefig("Precipitation in Hawaii_bar.png")
plt.show()
prcp_anal_df.describe()
# I wanted a range of precipitation amounts for plotting purposes...the code on line 3 and 4 and 5 didn't work
## prcp_anal.max_prcp = session.query(func.max(Measurement.prcp.filter(Measurement.date >= '2016-08-23' ))).\
## order_by(func.max(Items.UnitPrice * Items.Quantity).desc()).all()
## prcp_anal.max_prcp
prcp_anal_max_prcp = session.query(Measurement.prcp, func.max(Measurement.prcp)).\
filter(Measurement.date >= '2016-08-23').\
group_by(Measurement.date).\
order_by(func.max(Measurement.prcp).asc()).all()
prcp_anal_max_prcp
# I initially did the following in a cell below. Again, I wanted a range of prcp values for the year in our DataFrame
# so here I got the min but realized both the min and the max, or both queries are useless to me here unless I were
# use plt.ylim in my plots, which I don't, I just allow the DF to supply its intrinsic values
# and both give identical results. I will leave it here in thes assignment just to show my thought process
# prcp_anal_min_prcp = session.query(Measurement.prcp, func.min(Measurement.prcp)).\
# filter(Measurement.date > '2016-08-23').\
# group_by(Measurement.date).\
# order_by(func.min(Measurement.prcp).asc()).all()
# prcp_anal_min_prcp
```
***STATION ANALYSIS***.\
1) Design a query to calculate the total number of stations.\
2) Design a query to find the most active stations.\
3) List the stations and observation counts in descending order.\
4) Which station has the highest number of observations?.\
Hint: You will need to use a function such as func.min, func.max, func.avg, and func.count in your queries..\
5) Design a query to retrieve the last 12 months of temperature observation data (TOBS)..\
6) Filter by the station with the highest number of observations..\
7) Plot the results as a histogram with bins=12.
```
Station = Base.classes.station
session = Session(engine)
# Getting column values from each table, here 'station'
columns = inspector.get_columns('station')
for c in columns:
print(c)
# Get columns of 'measurement' table
columns = inspector.get_columns('measurement')
for c in columns:
print(c)
engine.execute('Select * from station').fetchall()
# Design a query to show how many stations are available in this dataset?
session.query(Station.station).count()
# What are the most active stations? (i.e. what stations have the most rows)?
# List the stations and the counts in descending order.
# List the stations and the counts in descending order. Think about somehow using this from extra activity
Active_Stations = session.query(Station.station ,func.count(Measurement.tobs)).filter(Station.station == Measurement.station).\
group_by(Station.station).order_by(func.count(Measurement.tobs).desc()).all()
print(f"The most active station {Active_Stations[0][0]} has {Active_Stations[0][1]} observations!")
Active_Stations
# Using the station id from the previous query, calculate the lowest temperature recorded,
# highest temperature recorded, and average temperature of the most active station?
Station_Name = session.query(Station.name).filter(Station.station == Active_Stations[0][0]).all()
print(Station_Name)
Temp_Stats = session.query(func.min(Measurement.tobs),func.max(Measurement.tobs),func.avg(Measurement.tobs)).\
filter(Station.station == Active_Stations[0][0]).all()
print(Temp_Stats)
# Choose the station with the highest number of temperature observations.
Station_Name = session.query(Station.name).filter(Station.station == Active_Stations[0][0]).all()
Station_Name
# Query the last 12 months of temperature observation data for this station
results_WAHIAWA = session.query(Measurement.date,Measurement.tobs).filter(Measurement.date > min_date).\
filter(Station.station == Active_Stations[0][0]).all()
results_WAHIAWA
# Make a DataFrame from the query results above showing dates and temp observation at the most active station
results_WAHIAWA_df = pd.DataFrame(results_WAHIAWA)
results_WAHIAWA_df
# Plot the results as a histogram
sns.set()
plt.figure(figsize=(10,5))
plt.hist(results_WAHIAWA_df['tobs'],bins=12,color='magenta')
plt.xlabel('Temperature',weight='bold')
plt.ylabel('Frequency',weight='bold')
plt.title('Station Analysis',weight='bold')
plt.legend(["Temperature Observation"],loc="best")
plt.savefig("Station_Analysis_hist.png")
plt.show()
```
## Bonus Challenge Assignment
```
# This function called `calc_temps` will accept start date and end date in the format '%Y-%m-%d'
# and return the minimum, average, and maximum temperatures for that range of dates
def calc_temps(start_date, end_date):
"""TMIN, TAVG, and TMAX for a list of dates.
Args:
start_date (string): A date string in the format %Y-%m-%d
end_date (string): A date string in the format %Y-%m-%d
Returns:
TMIN, TAVE, and TMAX
"""
return session.query(func.min(Measurement.tobs), func.avg(Measurement.tobs), func.max(Measurement.tobs)).\
filter(Measurement.date >= start_date).filter(Measurement.date <= end_date).all()
# function usage example
print(calc_temps('2012-02-28', '2012-03-05'))
# Use your previous function `calc_temps` to calculate the tmin, tavg, and tmax
calc_temps('2017-06-22', '2017-07-05')
# for your trip using the previous year's data for those same dates.
(calc_temps('2016-06-22', '2016-07-05'))
# Plot the results from your previous query as a bar chart.
# Use "Trip Avg Temp" as your Title
# Use the average temperature for the y value
# Use the peak-to-peak (tmax-tmin) value as the y error bar (yerr)
# Calculate the total amount of rainfall per weather station for your trip dates using the previous year's matching dates.
# Sort this in descending order by precipitation amount and list the station, name, latitude, longitude, and elevation
# Create a query that will calculate the daily normals
# (i.e. the averages for tmin, tmax, and tavg for all historic data matching a specific month and day)
def daily_normals(date):
"""Daily Normals.
Args:
date (str): A date string in the format '%m-%d'
Returns:
A list of tuples containing the daily normals, tmin, tavg, and tmax
"""
sel = [func.min(Measurement.tobs), func.avg(Measurement.tobs), func.max(Measurement.tobs)]
return session.query(*sel).filter(func.strftime("%m-%d", Measurement.date) == date).all()
daily_normals("01-01")
# calculate the daily normals for your trip
# push each tuple of calculations into a list called `normals`
# Set the start and end date of the trip
# Use the start and end date to create a range of dates
# Stip off the year and save a list of %m-%d strings
# Loop through the list of %m-%d strings and calculate the normals for each date
# Load the previous query results into a Pandas DataFrame and add the `trip_dates` range as the `date` index
# Plot the daily normals as an area plot with `stacked=False`
```
## Step 2 - Climate App
Now that you have completed your initial analysis, design a Flask API based on the queries that you have just developed.
* Use Flask to create your routes.
### Routes
* `/`
* Home page.
* List all routes that are available.
* `/api/v1.0/precipitation`
* Convert the query results to a dictionary using `date` as the key and `prcp` as the value.
* Return the JSON representation of your dictionary.
* `/api/v1.0/stations`
* Return a JSON list of stations from the dataset.
* `/api/v1.0/tobs`
* Query the dates and temperature observations of the most active station for the last year of data.
* Return a JSON list of temperature observations (TOBS) for the previous year.
* `/api/v1.0/<start>` and `/api/v1.0/<start>/<end>`
* Return a JSON list of the minimum temperature, the average temperature, and the max temperature for a given start or start-end range.
* When given the start only, calculate `TMIN`, `TAVG`, and `TMAX` for all dates greater than and equal to the start date.
* When given the start and the end date, calculate the `TMIN`, `TAVG`, and `TMAX` for dates between the start and end date inclusive.
## Hints
* You will need to join the station and measurement tables for some of the queries.
* Use Flask `jsonify` to convert your API data into a valid JSON response object.
- - -
```
import numpy as np
import datetime as dt
from datetime import timedelta, datetime
import sqlalchemy
from sqlalchemy.ext.automap import automap_base
from sqlalchemy.orm import Session
from sqlalchemy import create_engine, func, distinct, text, desc
from flask import Flask, jsonify
#################################################
# Database Setup
#################################################
#engine = create_engine("sqlite:///Resources/hawaii.sqlite")
engine = create_engine("sqlite:///Resources/hawaii.sqlite?check_same_thread=False")
# reflect an existing database into a new model
Base = automap_base()
# reflect the tables
Base.prepare(engine, reflect=True)
# Save reference to the table
Measurement = Base.classes.measurement
Station = Base.classes.station
#################################################
# Flask Setup
#################################################
app = Flask(__name__)
#################################################
# Flask Routes
#################################################
@app.route("/")
def welcome():
"""List all available api routes."""
return (
f"Available Routes:<br/>"
f"/api/v1.0/precipitation<br/>"
f"/api/v1.0/stations<br/>"
f"/api/v1.0/tobs<br/>"
f"/api/v1.0/<br/>"
f"/api/v1.0/"
)
@app.route("/api/v1.0/precipitation")
def precipitation():
# Create our session (link) from Python to the DB
session = Session(engine)
"""Return a list of all precipitation data"""
# Query Precipitation data
annual_rainfall = session.query(Measurement.date, Measurement.prcp).order_by(Measurement.date).all()
session.close()
# Convert list of tuples into normal list
all_rain = dict(annual_rainfall)
return jsonify(all_rain)
if __name__ == '__main__':
app.run(debug=True)
```
|
github_jupyter
|
# Maximum Likelihood Estimation (Generic models)
This tutorial explains how to quickly implement new maximum likelihood models in `statsmodels`. We give two examples:
1. Probit model for binary dependent variables
2. Negative binomial model for count data
The `GenericLikelihoodModel` class eases the process by providing tools such as automatic numeric differentiation and a unified interface to ``scipy`` optimization functions. Using ``statsmodels``, users can fit new MLE models simply by "plugging-in" a log-likelihood function.
## Example 1: Probit model
```
import numpy as np
from scipy import stats
import statsmodels.api as sm
from statsmodels.base.model import GenericLikelihoodModel
```
The ``Spector`` dataset is distributed with ``statsmodels``. You can access a vector of values for the dependent variable (``endog``) and a matrix of regressors (``exog``) like this:
```
data = sm.datasets.spector.load_pandas()
exog = data.exog
endog = data.endog
print(sm.datasets.spector.NOTE)
print(data.exog.head())
```
Them, we add a constant to the matrix of regressors:
```
exog = sm.add_constant(exog, prepend=True)
```
To create your own Likelihood Model, you simply need to overwrite the loglike method.
```
class MyProbit(GenericLikelihoodModel):
def loglike(self, params):
exog = self.exog
endog = self.endog
q = 2 * endog - 1
return stats.norm.logcdf(q*np.dot(exog, params)).sum()
```
Estimate the model and print a summary:
```
sm_probit_manual = MyProbit(endog, exog).fit()
print(sm_probit_manual.summary())
```
Compare your Probit implementation to ``statsmodels``' "canned" implementation:
```
sm_probit_canned = sm.Probit(endog, exog).fit()
print(sm_probit_canned.params)
print(sm_probit_manual.params)
print(sm_probit_canned.cov_params())
print(sm_probit_manual.cov_params())
```
Notice that the ``GenericMaximumLikelihood`` class provides automatic differentiation, so we did not have to provide Hessian or Score functions in order to calculate the covariance estimates.
## Example 2: Negative Binomial Regression for Count Data
Consider a negative binomial regression model for count data with
log-likelihood (type NB-2) function expressed as:
$$
\mathcal{L}(\beta_j; y, \alpha) = \sum_{i=1}^n y_i ln
\left ( \frac{\alpha exp(X_i'\beta)}{1+\alpha exp(X_i'\beta)} \right ) -
\frac{1}{\alpha} ln(1+\alpha exp(X_i'\beta)) + ln \Gamma (y_i + 1/\alpha) - ln \Gamma (y_i+1) - ln \Gamma (1/\alpha)
$$
with a matrix of regressors $X$, a vector of coefficients $\beta$,
and the negative binomial heterogeneity parameter $\alpha$.
Using the ``nbinom`` distribution from ``scipy``, we can write this likelihood
simply as:
```
import numpy as np
from scipy.stats import nbinom
def _ll_nb2(y, X, beta, alph):
mu = np.exp(np.dot(X, beta))
size = 1/alph
prob = size/(size+mu)
ll = nbinom.logpmf(y, size, prob)
return ll
```
### New Model Class
We create a new model class which inherits from ``GenericLikelihoodModel``:
```
from statsmodels.base.model import GenericLikelihoodModel
class NBin(GenericLikelihoodModel):
def __init__(self, endog, exog, **kwds):
super(NBin, self).__init__(endog, exog, **kwds)
def nloglikeobs(self, params):
alph = params[-1]
beta = params[:-1]
ll = _ll_nb2(self.endog, self.exog, beta, alph)
return -ll
def fit(self, start_params=None, maxiter=10000, maxfun=5000, **kwds):
# we have one additional parameter and we need to add it for summary
self.exog_names.append('alpha')
if start_params == None:
# Reasonable starting values
start_params = np.append(np.zeros(self.exog.shape[1]), .5)
# intercept
start_params[-2] = np.log(self.endog.mean())
return super(NBin, self).fit(start_params=start_params,
maxiter=maxiter, maxfun=maxfun,
**kwds)
```
Two important things to notice:
+ ``nloglikeobs``: This function should return one evaluation of the negative log-likelihood function per observation in your dataset (i.e. rows of the endog/X matrix).
+ ``start_params``: A one-dimensional array of starting values needs to be provided. The size of this array determines the number of parameters that will be used in optimization.
That's it! You're done!
### Usage Example
The [Medpar](https://raw.githubusercontent.com/vincentarelbundock/Rdatasets/doc/COUNT/medpar.html)
dataset is hosted in CSV format at the [Rdatasets repository](https://raw.githubusercontent.com/vincentarelbundock/Rdatasets). We use the ``read_csv``
function from the [Pandas library](https://pandas.pydata.org) to load the data
in memory. We then print the first few columns:
```
import statsmodels.api as sm
medpar = sm.datasets.get_rdataset("medpar", "COUNT", cache=True).data
medpar.head()
```
The model we are interested in has a vector of non-negative integers as
dependent variable (``los``), and 5 regressors: ``Intercept``, ``type2``,
``type3``, ``hmo``, ``white``.
For estimation, we need to create two variables to hold our regressors and the outcome variable. These can be ndarrays or pandas objects.
```
y = medpar.los
X = medpar[["type2", "type3", "hmo", "white"]].copy()
X["constant"] = 1
```
Then, we fit the model and extract some information:
```
mod = NBin(y, X)
res = mod.fit()
```
Extract parameter estimates, standard errors, p-values, AIC, etc.:
```
print('Parameters: ', res.params)
print('Standard errors: ', res.bse)
print('P-values: ', res.pvalues)
print('AIC: ', res.aic)
```
As usual, you can obtain a full list of available information by typing
``dir(res)``.
We can also look at the summary of the estimation results.
```
print(res.summary())
```
### Testing
We can check the results by using the statsmodels implementation of the Negative Binomial model, which uses the analytic score function and Hessian.
```
res_nbin = sm.NegativeBinomial(y, X).fit(disp=0)
print(res_nbin.summary())
print(res_nbin.params)
print(res_nbin.bse)
```
Or we could compare them to results obtained using the MASS implementation for R:
url = 'https://raw.githubusercontent.com/vincentarelbundock/Rdatasets/csv/COUNT/medpar.csv'
medpar = read.csv(url)
f = los~factor(type)+hmo+white
library(MASS)
mod = glm.nb(f, medpar)
coef(summary(mod))
Estimate Std. Error z value Pr(>|z|)
(Intercept) 2.31027893 0.06744676 34.253370 3.885556e-257
factor(type)2 0.22124898 0.05045746 4.384861 1.160597e-05
factor(type)3 0.70615882 0.07599849 9.291748 1.517751e-20
hmo -0.06795522 0.05321375 -1.277024 2.015939e-01
white -0.12906544 0.06836272 -1.887951 5.903257e-02
### Numerical precision
The ``statsmodels`` generic MLE and ``R`` parameter estimates agree up to the fourth decimal. The standard errors, however, agree only up to the second decimal. This discrepancy is the result of imprecision in our Hessian numerical estimates. In the current context, the difference between ``MASS`` and ``statsmodels`` standard error estimates is substantively irrelevant, but it highlights the fact that users who need very precise estimates may not always want to rely on default settings when using numerical derivatives. In such cases, it is better to use analytical derivatives with the ``LikelihoodModel`` class.
|
github_jupyter
|
```
#Download the dataset from opensig
import urllib.request
urllib.request.urlretrieve('http://opendata.deepsig.io/datasets/2016.10/RML2016.10a.tar.bz2', 'RML2016.10a.tar.bz2')
#decompress the .bz2 file into .tar file
import sys
import os
import bz2
zipfile = bz2.BZ2File('./RML2016.10a.tar.bz2') # open the file
data = zipfile.read() # get the decompressed data
#write the .tar file
open('./RML2016.10a.tar', 'wb').write(data) # write a uncompressed file
#extract the .tar file
import tarfile
my_tar = tarfile.open('./RML2016.10a.tar')
my_tar.extractall('./') # specify which folder to extract to
my_tar.close()
#extract the pickle file
import pickle
import numpy as np
Xd = pickle.load(open("RML2016.10a_dict.pkl",'rb'),encoding="bytes")
snrs,mods = map(lambda j: sorted(list(set(map(lambda x: x[j], Xd.keys())))), [1,0])
X = []
lbl = []
for mod in mods:
for snr in snrs:
X.append(Xd[(mod,snr)])
for i in range(Xd[(mod,snr)].shape[0]): lbl.append((mod,snr))
X = np.vstack(X)
# Import all the things we need ---
%matplotlib inline
import random
import tensorflow.keras.utils
import tensorflow.keras.models as models
from tensorflow.keras.layers import Reshape,Dense,Dropout,Activation,Flatten
from tensorflow.keras.layers import GaussianNoise
from tensorflow.keras.layers import Convolution2D, MaxPooling2D, ZeroPadding2D
from tensorflow.keras.regularizers import *
from tensorflow.keras.optimizers import *
import matplotlib.pyplot as plt
import seaborn as sns
import tensorflow.keras
# Partition the data
# into training and test sets of the form we can train/test on
np.random.seed(2020)
n_examples = X.shape[0]
n_train = n_examples // 2
train_idx = np.random.choice(range(0,n_examples), size=n_train, replace=False)
test_idx = list(set(range(0,n_examples))-set(train_idx))
X_train = X[train_idx]
X_test = X[test_idx]
#one-hot encoding the label
from sklearn import preprocessing
lb = preprocessing.LabelBinarizer()
lb.fit(np.asarray(lbl)[:,0])
print(lb.classes_)
lbl_encoded=lb.transform(np.asarray(lbl)[:,0])
y_train=lbl_encoded[train_idx]
y_test=lbl_encoded[test_idx]
in_shp = list(X_train.shape[1:])
print(X_train.shape, in_shp)
classes = mods
dr = 0.5 # dropout rate (%)
model = models.Sequential()
model.add(Reshape([1]+in_shp, input_shape=in_shp))
model.add(ZeroPadding2D((0, 2)))
model.add(Convolution2D(256, 1, 3, activation="relu", name="conv1"))
model.add(Dropout(dr))
model.add(ZeroPadding2D((0, 2)))
model.add(Convolution2D(80, 1, 3, activation="relu", name="conv2"))
model.add(Dropout(dr))
model.add(Flatten())
model.add(Dense(256, activation='relu', name="dense1"))
model.add(Dropout(dr))
model.add(Dense( len(classes), name="dense2" ))
model.add(Activation('softmax'))
model.add(Reshape([len(classes)]))
model.compile(loss='categorical_crossentropy', optimizer='adam')
model.summary()
# Set up some params
nb_epoch = 100 # number of epochs to train on
batch_size = 1024 # training batch size
from sklearn.model_selection import train_test_split
X_train, X_valid, y_train, y_valid = train_test_split(X_train, y_train, test_size=0.2)
# perform training ...
# - call the main training loop in keras for our network+dataset
filepath = 'convmodrecnets_CNN2_0.5.wts.h5'
import time
t_0=time.time()
history = model.fit(X_train,
y_train,
batch_size=batch_size,
epochs=nb_epoch,
verbose=2,
validation_data=(X_valid, y_valid),
callbacks = [
tensorflow.keras.callbacks.ModelCheckpoint(filepath, monitor='val_loss', verbose=0, save_best_only=True, mode='auto'),
tensorflow.keras.callbacks.EarlyStopping(monitor='val_loss', patience=5, verbose=0, mode='auto')
])
delta_t=time.time()-t_0
print(delta_t)
# we re-load the best weights once training is finished
model.load_weights(filepath)
# Show simple version of performance
score = model.evaluate(X_test, y_test, verbose=0, batch_size=batch_size)
print(score)
# Show loss curves
plt.figure()
plt.title('Training performance')
plt.plot(history.epoch, history.history['loss'], label='train loss+error')
plt.plot(history.epoch, history.history['val_loss'], label='val_error')
plt.legend()
def plot_confusion_matrix(cm, title='Confusion matrix', cmap=plt.cm.Blues, labels=[]):
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title)
plt.colorbar()
tick_marks = np.arange(len(labels))
plt.xticks(tick_marks, labels, rotation=45)
plt.yticks(tick_marks, labels)
plt.tight_layout()
plt.ylabel('True label')
plt.xlabel('Predicted label')
# Plot confusion matrix
test_Y_hat = model.predict(X_test, batch_size=batch_size)
conf = np.zeros([len(classes),len(classes)])
confnorm = np.zeros([len(classes),len(classes)])
for i in range(0,X_test.shape[0]):
j = list(y_test[i,:]).index(1)
k = int(np.argmax(test_Y_hat[i,:]))
conf[j,k] = conf[j,k] + 1
for i in range(0,len(classes)):
confnorm[i,:] = conf[i,:] / np.sum(conf[i,:])
plot_confusion_matrix(confnorm, labels=classes)
# Get the test accuracy for different SNRs
acc = {}
acc_array=[]
snr_array=np.asarray(lbl)[:,1]
lb_temp = preprocessing.LabelBinarizer()
lb_temp.fit(snr_array)
temp_array=lb_temp.classes_
snr_label_array = []
snr_label_array.append(temp_array[6])
snr_label_array.append(temp_array[4])
snr_label_array.append(temp_array[3])
snr_label_array.append(temp_array[2])
snr_label_array.append(temp_array[1])
snr_label_array.append(temp_array[0])
snr_label_array.append(temp_array[9])
snr_label_array.append(temp_array[8])
snr_label_array.append(temp_array[7])
snr_label_array.append(temp_array[5])
snr_label_array.append(temp_array[10])
snr_label_array.append(temp_array[16])
snr_label_array.append(temp_array[17])
snr_label_array.append(temp_array[18])
snr_label_array.append(temp_array[19])
snr_label_array.append(temp_array[11])
snr_label_array.append(temp_array[12])
snr_label_array.append(temp_array[13])
snr_label_array.append(temp_array[14])
snr_label_array.append(temp_array[15])
#print(snr_label_array)
y_test_snr=snr_array[test_idx]
for snr in snr_label_array:
test_X_i = X_test[np.where(y_test_snr==snr)]
test_Y_i = y_test[np.where(y_test_snr==snr)]
test_Y_i_hat = model.predict(test_X_i)
conf = np.zeros([len(classes),len(classes)])
confnorm = np.zeros([len(classes),len(classes)])
for i in range(0,test_X_i.shape[0]):
j = list(test_Y_i[i,:]).index(1)
k = int(np.argmax(test_Y_i_hat[i,:]))
conf[j,k] = conf[j,k] + 1
for i in range(0,len(classes)):
confnorm[i,:] = conf[i,:] / np.sum(conf[i,:])
#plt.figure()
#plot_confusion_matrix(confnorm, labels=classes, title="ConvNet Confusion Matrix (SNR=%d)"%(snr))
cor = np.sum(np.diag(conf))
ncor = np.sum(conf) - cor
print("Overall Accuracy: ", cor / (cor+ncor),"for SNR",snr)
acc[snr] = 1.0*cor/(cor+ncor)
acc_array.append(1.0*cor/(cor+ncor))
print("Random Guess Accuracy:",1/11)
# Show loss curves
plt.figure()
plt.title('Accuracy vs SNRs')
plt.plot(np.arange(-20,20,2), acc_array)
```
|
github_jupyter
|
<a href="https://colab.research.google.com/github/lvisdd/object_detection_tutorial/blob/master/object_detection_face_detector.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
# restart (or reset) your virtual machine
#!kill -9 -1
```
# [Tensorflow Object Detection API](https://github.com/tensorflow/models/tree/master/research/object_detection)
```
!git clone https://github.com/tensorflow/models.git
```
# COCO API installation
```
!git clone https://github.com/cocodataset/cocoapi.git
%cd cocoapi/PythonAPI
!make
!cp -r pycocotools /content/models/research/
```
# Protobuf Compilation
```
%cd /content/models/research/
!protoc object_detection/protos/*.proto --python_out=.
```
# Add Libraries to PYTHONPATH
```
%cd /content/models/research/
%env PYTHONPATH=/env/python:/content/models/research:/content/models/research/slim:/content/models/research/object_detection
%env
```
# Testing the Installation
```
!python object_detection/builders/model_builder_test.py
%cd /content/models/research/object_detection
```
## [Tensorflow Face Detector](https://github.com/yeephycho/tensorflow-face-detection)
```
%cd /content
!git clone https://github.com/yeephycho/tensorflow-face-detection.git
%cd tensorflow-face-detection
!wget https://storage.googleapis.com/download.tensorflow.org/example_images/grace_hopper.jpg
filename = 'grace_hopper.jpg'
#!python inference_usbCam_face.py grace_hopper.jpg
import sys
import time
import numpy as np
import tensorflow as tf
import cv2
from utils import label_map_util
from utils import visualization_utils_color as vis_util
# Path to frozen detection graph. This is the actual model that is used for the object detection.
PATH_TO_CKPT = './model/frozen_inference_graph_face.pb'
# List of the strings that is used to add correct label for each box.
PATH_TO_LABELS = './protos/face_label_map.pbtxt'
NUM_CLASSES = 2
label_map = label_map_util.load_labelmap(PATH_TO_LABELS)
categories = label_map_util.convert_label_map_to_categories(label_map, max_num_classes=NUM_CLASSES, use_display_name=True)
category_index = label_map_util.create_category_index(categories)
class TensoflowFaceDector(object):
def __init__(self, PATH_TO_CKPT):
"""Tensorflow detector
"""
self.detection_graph = tf.Graph()
with self.detection_graph.as_default():
od_graph_def = tf.GraphDef()
with tf.gfile.GFile(PATH_TO_CKPT, 'rb') as fid:
serialized_graph = fid.read()
od_graph_def.ParseFromString(serialized_graph)
tf.import_graph_def(od_graph_def, name='')
with self.detection_graph.as_default():
config = tf.ConfigProto()
config.gpu_options.allow_growth = True
self.sess = tf.Session(graph=self.detection_graph, config=config)
self.windowNotSet = True
def run(self, image):
"""image: bgr image
return (boxes, scores, classes, num_detections)
"""
image_np = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)
# the array based representation of the image will be used later in order to prepare the
# result image with boxes and labels on it.
# Expand dimensions since the model expects images to have shape: [1, None, None, 3]
image_np_expanded = np.expand_dims(image_np, axis=0)
image_tensor = self.detection_graph.get_tensor_by_name('image_tensor:0')
# Each box represents a part of the image where a particular object was detected.
boxes = self.detection_graph.get_tensor_by_name('detection_boxes:0')
# Each score represent how level of confidence for each of the objects.
# Score is shown on the result image, together with the class label.
scores = self.detection_graph.get_tensor_by_name('detection_scores:0')
classes = self.detection_graph.get_tensor_by_name('detection_classes:0')
num_detections = self.detection_graph.get_tensor_by_name('num_detections:0')
# Actual detection.
start_time = time.time()
(boxes, scores, classes, num_detections) = self.sess.run(
[boxes, scores, classes, num_detections],
feed_dict={image_tensor: image_np_expanded})
elapsed_time = time.time() - start_time
print('inference time cost: {}'.format(elapsed_time))
return (boxes, scores, classes, num_detections)
# This is needed to display the images.
%matplotlib inline
tDetector = TensoflowFaceDector(PATH_TO_CKPT)
original = cv2.imread(filename)
image = cv2.cvtColor(original, cv2.COLOR_BGR2RGB)
(boxes, scores, classes, num_detections) = tDetector.run(image)
vis_util.visualize_boxes_and_labels_on_image_array(
image,
np.squeeze(boxes),
np.squeeze(classes).astype(np.int32),
np.squeeze(scores),
category_index,
use_normalized_coordinates=True,
line_thickness=4)
from matplotlib import pyplot as plt
plt.imshow(image)
```
|
github_jupyter
|
[Index](Index.ipynb) - [Next](Widget List.ipynb)
# Simple Widget Introduction
## What are widgets?
Widgets are eventful python objects that have a representation in the browser, often as a control like a slider, textbox, etc.
## What can they be used for?
You can use widgets to build **interactive GUIs** for your notebooks.
You can also use widgets to **synchronize stateful and stateless information** between Python and JavaScript.
## Using widgets
To use the widget framework, you need to import `ipywidgets`.
```
import ipywidgets as widgets
```
### repr
Widgets have their own display `repr` which allows them to be displayed using IPython's display framework. Constructing and returning an `IntSlider` automatically displays the widget (as seen below). Widgets are displayed inside the output area below the code cell. Clearing cell output will also remove the widget.
```
widgets.IntSlider()
```
### display()
You can also explicitly display the widget using `display(...)`.
```
from IPython.display import display
w = widgets.IntSlider()
display(w)
```
### Multiple display() calls
If you display the same widget twice, the displayed instances in the front-end will remain in sync with each other. Try dragging the slider below and watch the slider above.
```
display(w)
```
## Why does displaying the same widget twice work?
Widgets are represented in the back-end by a single object. Each time a widget is displayed, a new representation of that same object is created in the front-end. These representations are called views.

### Closing widgets
You can close a widget by calling its `close()` method.
```
display(w)
w.close()
```
## Widget properties
All of the IPython widgets share a similar naming scheme. To read the value of a widget, you can query its `value` property.
```
w = widgets.IntSlider()
display(w)
w.value
```
Similarly, to set a widget's value, you can set its `value` property.
```
w.value = 100
```
### Keys
In addition to `value`, most widgets share `keys`, `description`, and `disabled`. To see the entire list of synchronized, stateful properties of any specific widget, you can query the `keys` property.
```
w.keys
```
### Shorthand for setting the initial values of widget properties
While creating a widget, you can set some or all of the initial values of that widget by defining them as keyword arguments in the widget's constructor (as seen below).
```
widgets.Text(value='Hello World!', disabled=True)
```
## Linking two similar widgets
If you need to display the same value two different ways, you'll have to use two different widgets. Instead of attempting to manually synchronize the values of the two widgets, you can use the `link` or `jslink` function to link two properties together (the difference between these is discussed in [Widget Events](Widget Events.ipynb)). Below, the values of two widgets are linked together.
```
a = widgets.FloatText()
b = widgets.FloatSlider()
display(a,b)
mylink = widgets.jslink((a, 'value'), (b, 'value'))
```
### Unlinking widgets
Unlinking the widgets is simple. All you have to do is call `.unlink` on the link object. Try changing one of the widgets above after unlinking to see that they can be independently changed.
```
# mylink.unlink()
```
[Index](Index.ipynb) - [Next](Widget List.ipynb)
|
github_jupyter
|
```
import numpy as np
from pandas import Series, DataFrame
import pandas as pd
from sklearn import preprocessing, tree
from sklearn.metrics import accuracy_score
# from sklearn.model_selection import train_test_split, KFold
from sklearn.neighbors import KNeighborsClassifier
from sklearn.cross_validation import KFold
df=pd.read_json('../01_Preprocessing/First.json').sort_index()
df.head(2)
def mydist(x, y):
return np.sum((x-y)**2)
def jaccard(a, b):
intersection = float(len(set(a) & set(b)))
union = float(len(set(a) | set(b)))
return 1.0 - (intersection/union)
# http://scikit-learn.org/stable/modules/generated/sklearn.neighbors.DistanceMetric.html
dist=['braycurtis','canberra','chebyshev','cityblock','correlation','cosine','euclidean','dice','hamming','jaccard','kulsinski','matching','rogerstanimoto','russellrao','sokalsneath','yule']
algorithm=['ball_tree', 'kd_tree', 'brute']
len(dist)
```
## On country (only MS)
```
df.fund= df.fund=='TRUE'
df.gre= df.gre=='TRUE'
df.highLevelBachUni= df.highLevelBachUni=='TRUE'
df.highLevelMasterUni= df.highLevelMasterUni=='TRUE'
df.uniRank.fillna(294,inplace=True)
df.columns
oldDf=df.copy()
df=df[['countryCoded','degreeCoded','engCoded', 'fieldGroup','fund','gpaBachelors','gre', 'highLevelBachUni', 'paper','uniRank']]
df=df[df.degreeCoded==0]
del df['degreeCoded']
bestAvg=[]
for alg in algorithm:
for dis in dist:
k_fold = KFold(n=len(df), n_folds=5)
scores = []
try:
clf = KNeighborsClassifier(n_neighbors=3, weights='distance',algorithm=alg, metric=dis)
except Exception as err:
# print(alg,dis,'err')
continue
for train_indices, test_indices in k_fold:
xtr = df.iloc[train_indices,(df.columns != 'countryCoded')]
ytr = df.iloc[train_indices]['countryCoded']
xte = df.iloc[test_indices, (df.columns != 'countryCoded')]
yte = df.iloc[test_indices]['countryCoded']
clf.fit(xtr, ytr)
ypred = clf.predict(xte)
acc=accuracy_score(list(yte),list(ypred))
scores.append(acc*100)
print(alg,dis,np.average(scores))
bestAvg.append(np.average(scores))
print('>>>>>>>Best: ',np.max(bestAvg))
```
## On Fund (only MS)
```
bestAvg=[]
for alg in algorithm:
for dis in dist:
k_fold = KFold(n=len(df), n_folds=5)
scores = []
try:
clf = KNeighborsClassifier(n_neighbors=3, weights='distance',algorithm=alg, metric=dis)
except Exception as err:
continue
for train_indices, test_indices in k_fold:
xtr = df.iloc[train_indices, (df.columns != 'fund')]
ytr = df.iloc[train_indices]['fund']
xte = df.iloc[test_indices, (df.columns != 'fund')]
yte = df.iloc[test_indices]['fund']
clf.fit(xtr, ytr)
ypred = clf.predict(xte)
acc=accuracy_score(list(yte),list(ypred))
score=acc*100
scores.append(score)
if (len(bestAvg)>1) :
if(score > np.max(bestAvg)) :
bestClf=clf
bestAvg.append(np.average(scores))
print (alg,dis,np.average(scores))
print('>>>>>>>Best: ',np.max(bestAvg))
```
### Best : ('kd_tree', 'cityblock', 77.692144892144896)
```
me=[0,2,0,2.5,False,False,1.5,400]
n=bestClf.kneighbors([me])
n
for i in n[1]:
print(xtr.iloc[i])
```
|
github_jupyter
|
# `Практикум по программированию на языке Python`
<br>
## `Занятие 2: Пользовательские и встроенные функции, итераторы и генераторы`
<br><br>
### `Мурат Апишев (mel-lain@yandex.ru)`
#### `Москва, 2021`
### `Функции range и enumerate`
```
r = range(2, 10, 3)
print(type(r))
for e in r:
print(e, end=' ')
for index, element in enumerate(list('abcdef')):
print(index, element, end=' ')
```
### `Функция zip`
```
z = zip([1, 2, 3], 'abc')
print(type(z))
for a, b in z:
print(a, b, end=' ')
for e in zip('abcdef', 'abc'):
print(e)
for a, b, c, d in zip('abc', [1,2,3], [True, False, None], 'xyz'):
print(a, b, c, d)
```
### `Определение собственных функций`
```
def function(arg_1, arg_2=None):
print(arg_1, arg_2)
function(10)
function(10, 20)
```
Функция - это тоже объект, её имя - просто символическая ссылка:
```
f = function
f(10)
print(function is f)
```
### `Определение собственных функций`
```
retval = f(10)
print(retval)
def factorial(n):
return n * factorial(n - 1) if n > 1 else 1 # recursion
print(factorial(1))
print(factorial(2))
print(factorial(4))
```
### `Передача аргументов в функцию`
Параметры в Python всегда передаются по ссылке
```
def function(scalar, lst):
scalar += 10
print(f'Scalar in function: {scalar}')
lst.append(None)
print(f'Scalar in function: {lst}')
s, l = 5, []
function(s, l)
print(s, l)
```
### `Передача аргументов в функцию`
```
def f(a, *args):
print(type(args))
print([v for v in [a] + list(args)])
f(10, 2, 6, 8)
def f(*args, a):
print([v for v in [a] + list(args)])
print()
f(2, 6, 8, a=10)
def f(a, *args, **kw):
print(type(kw))
print([v for v in [a] + list(args) + [(k, v) for k, v in kw.items()]])
f(2, *(6, 8), **{'arg1': 1, 'arg2': 2})
```
### `Области видимости переменных`
В Python есть 4 основных уровня видимости:
- Встроенная (buildins) - на этом уровне находятся все встроенные объекты (функции, классы исключений и т.п.)<br><br>
- Глобальная в рамках модуля (global) - всё, что определяется в коде модуля на верхнем уровне<br><br>
- Объемлюшей функции (enclosed) - всё, что определено в функции верхнего уровня<br><br>
- Локальной функции (local) - всё, что определено в функции нижнего уровня
<br><br>
Есть ещё области видимости переменных циклов, списковых включений и т.п.
### `Правило разрешения области видимости LEGB при чтении`
```
def outer_func(x):
def inner_func(x):
return len(x)
return inner_func(x)
print(outer_func([1, 2]))
```
Кто определил имя `len`?
- на уровне вложенной функции такого имени нет, смотрим выше
- на уровне объемлющей функции такого имени нет, смотрим выше
- на уровне модуля такого имени нет, смотрим выше
- на уровне builtins такое имя есть, используем его
### `На builtins можно посмотреть`
```
import builtins
counter = 0
lst = []
for name in dir(builtins):
if name[0].islower():
lst.append(name)
counter += 1
if counter == 5:
break
lst
```
Кстати, то же самое можно сделать более pythonic кодом:
```
list(filter(lambda x: x[0].islower(), dir(builtins)))[: 5]
```
### `Локальные и глобальные переменные`
```
x = 2
def func():
print('Inside: ', x) # read
func()
print('Outside: ', x)
x = 2
def func():
x += 1 # write
print('Inside: ', x)
func() # UnboundLocalError: local variable 'x' referenced before assignment
print('Outside: ', x)
x = 2
def func():
x = 3
x += 1
print('Inside: ', x)
func()
print('Outside: ', x)
```
### `Ключевое слово global`
```
x = 2
def func():
global x
x += 1 # write
print('Inside: ', x)
func()
print('Outside: ', x)
x = 2
def func(x):
x += 1
print('Inside: ', x)
return x
x = func(x)
print('Outside: ', x)
```
### `Ключевое слово nonlocal`
```
a = 0
def out_func():
b = 10
def mid_func():
c = 20
def in_func():
global a
a += 100
nonlocal c
c += 100
nonlocal b
b += 100
print(a, b, c)
in_func()
mid_func()
out_func()
```
__Главный вывод:__ не надо злоупотреблять побочными эффектами при работе с переменными верхних уровней
### `Пример вложенных функций: замыкания`
- В большинстве случаев вложенные функции не нужны, плоская иерархия будет и проще, и понятнее
- Одно из исключений - фабричные функции (замыкания)
```
def function_creator(n):
def function(x):
return x ** n
return function
f = function_creator(5)
f(2)
```
Объект-функция, на который ссылается `f`, хранит в себе значение `n`
### `Анонимные функции`
- `def` - не единственный способ объявления функции
- `lambda` создаёт анонимную (lambda) функцию
Такие функции часто используются там, где синтаксически нельзя записать определение через `def`
```
def func(x): return x ** 2
func(6)
lambda_func = lambda x: x ** 2 # should be an expression
lambda_func(6)
def func(x): print(x)
func(6)
lambda_func = lambda x: print(x ** 2) # as print is function in Python 3.*
lambda_func(6)
```
### `Встроенная функция sorted`
```
lst = [5, 2, 7, -9, -1]
def abs_comparator(x):
return abs(x)
print(sorted(lst, key=abs_comparator))
sorted(lst, key=lambda x: abs(x))
sorted(lst, key=lambda x: abs(x), reverse=True)
```
### `Встроенная функция filter`
```
lst = [5, 2, 7, -9, -1]
f = filter(lambda x: x < 0, lst) # True condition
type(f) # iterator
list(f)
```
### `Встроенная функция map`
```
lst = [5, 2, 7, -9, -1]
m = map(lambda x: abs(x), lst)
type(m) # iterator
list(m)
```
### `Ещё раз сравним два подхода`
Напишем функцию скалярного произведения в императивном и функциональном стилях:
```
def dot_product_imp(v, w):
result = 0
for i in range(len(v)):
result += v[i] * w[i]
return result
dot_product_func = lambda v, w: sum(map(lambda x: x[0] * x[1], zip(v, w)))
print(dot_product_imp([1, 2, 3], [4, 5, 6]))
print(dot_product_func([1, 2, 3], [4, 5, 6]))
```
### `Функция reduce`
`functools` - стандартный модуль с другими функциями высшего порядка.
Рассмотрим пока только функцию `reduce`:
```
from functools import reduce
lst = list(range(1, 10))
reduce(lambda x, y: x * y, lst)
```
### `Итерирование, функции iter и next`
```
r = range(3)
for e in r:
print(e)
it = iter(r) # r.__iter__() - gives us an iterator
print(next(it))
print(it.__next__())
print(next(it))
print(next(it))
```
### `Итераторы часто используются неявно`
Как выглядит для нас цикл `for`:
```
for i in 'seq':
print(i)
```
Как он работает на самом деле:
```
iterator = iter('seq')
while True:
try:
i = next(iterator)
print(i)
except StopIteration:
break
```
### `Генераторы`
- Генераторы, как и итераторы, предназначены для итерирования по коллекции, но устроены несколько иначе
- Они определяются с помощью функций с оператором `yield` или генераторов списков, а не вызовов `iter()` и `next()`
- В генераторе есть внутреннее изменяемое состояние в виде локальных переменных, которое он хранит автоматически
- Генератор - более простой способ создания собственного итератора, чем его прямое определение
- Все генераторы являются итераторами, но не наоборот<br><br>
- Примеры функций-генераторов:
- `zip`
- `enumerate`
- `reversed`
- `map`
- `filter`
### `Ключевое слово yield`
- `yield` - это слово, по смыслу похожее на `return`<br><br>
- Но используется в функциях, возвращающих генераторы<br><br>
- При вызове такой функции тело не выполняется, функция только возвращает генератор<br><br>
- В первых запуск функция будет выполняться от начала и до `yield`<br><br>
- После выхода состояние функции сохраняется<br><br>
- На следующий вызов будет проводиться итерация цикла и возвращаться следующее значение<br><br>
- И так далее, пока не кончится цикл каждого `yield` в теле функции<br><br>
- После этого генератор станет пустым
### `Пример генератора`
```
def my_range(n):
yield 'You really want to run this generator?'
i = -1
while i < n:
i += 1
yield i
gen = my_range(3)
while True:
try:
print(next(gen), end=' ')
except StopIteration: # we want to catch this type of exceptions
break
for e in my_range(3):
print(e, end=' ')
```
### `Особенность range`
`range` не является генератором, хотя и похож, поскольку не хранит всю последовательность
```
print('__next__' in dir(zip([], [])))
print('__next__' in dir(range(3)))
```
Полезные особенности:
- объекты `range` неизменяемые (могут быть ключами словаря)
- имеют полезные атрибуты (`len`, `index`, `__getitem__`)
- по ним можно итерироваться многократно
### `Модуль itetools`
- Модуль представляет собой набор инструментов для работы с итераторами и последовательностями<br><br>
- Содержит три основных типа итераторов:<br><br>
- бесконечные итераторы
- конечные итераторы
- комбинаторные итераторы<br><br>
- Позволяет эффективно решать небольшие задачи вида:<br><br>
- итерирование по бесконечному потоку
- слияние в один список вложенных списков
- генерация комбинаторного перебора сочетаний элементов последовательности
- аккумуляция и агрегация данных внутри последовательности
### `Модуль itetools: примеры`
```
from itertools import count
for i in count(start=0):
print(i, end=' ')
if i == 5:
break
from itertools import cycle
count = 0
for item in cycle('XYZ'):
if count > 4:
break
print(item, end=' ')
count += 1
```
### `Модуль itetools: примеры`
```
from itertools import accumulate
for i in accumulate(range(1, 5), lambda x, y: x * y):
print(i)
from itertools import chain
for i in chain([1, 2], [3], [4]):
print(i)
```
### `Модуль itetools: примеры`
```
from itertools import groupby
vehicles = [('Ford', 'Taurus'), ('Dodge', 'Durango'),
('Chevrolet', 'Cobalt'), ('Ford', 'F150'),
('Dodge', 'Charger'), ('Ford', 'GT')]
sorted_vehicles = sorted(vehicles)
for key, group in groupby(sorted_vehicles, lambda x: x[0]):
for maker, model in group:
print('{model} is made by {maker}'.format(model=model, maker=maker))
print ("**** END OF THE GROUP ***\n")
```
## `Спасибо за внимание!`
|
github_jupyter
|
```
%pylab inline
import re
from pathlib import Path
import pandas as pd
import seaborn as sns
datdir = Path('data')
figdir = Path('plots')
figdir.mkdir(exist_ok=True)
mpl.rcParams.update({'figure.figsize': (2.5,1.75), 'figure.dpi': 300,
'axes.spines.right': False, 'axes.spines.top': False,
'axes.titlesize': 10, 'axes.labelsize': 10,
'legend.fontsize': 10, 'legend.title_fontsize': 10,
'xtick.labelsize': 8, 'ytick.labelsize': 8,
'font.family': 'sans-serif', 'font.sans-serif': ['Arial'],
'svg.fonttype': 'none', 'lines.solid_capstyle': 'round'})
```
# Figure 1 - Overview
```
df = pd.read_csv(datdir / 'fig_1.csv')
scores = df[list(map(str, range(20)))].values
selected = ~np.isnan(df['Selected'].values)
gens_sel = np.nonzero(selected)[0]
scores_sel = np.array([np.max(scores[g]) for g in gens_sel])
ims_sel = [plt.imread(str(datdir / 'images' / 'overview' / f'gen{gen:03d}.png'))
for gen in gens_sel]
ims_sel = np.array(ims_sel)
print('gens to visualize:', gens_sel)
with np.printoptions(precision=2, suppress=True):
print('corresponding scores:', scores_sel)
print('ims_sel shape:', ims_sel.shape)
c0 = array((255,92,0)) / 255 # highlight color
figure(figsize=(2.5, 0.8), dpi=150)
plot(scores.mean(1))
xlim(0, 500)
ylim(bottom=0)
xticks((250,500))
yticks((0,50))
gca().set_xticks(np.nonzero(selected)[0], minor=True)
gca().tick_params(axis='x', which='minor', colors=c0, width=1)
title('CaffeNet layer fc8, unit 1')
xlabel('Generation')
ylabel('Activation')
savefig(figdir / f'overview-evo_scores.png', dpi=300, bbox_inches='tight')
savefig(figdir / f'overview-evo_scores.svg', dpi=300, bbox_inches='tight')
def make_canvas(ims, nrows=None, ncols=None, margin=15, margin_colors=None):
if margin_colors is not None:
assert len(ims) == len(margin_colors)
if ncols is None:
assert nrows is not None
ncols = int(np.ceil(len(ims) / nrows))
else:
nrows = int(np.ceil(len(ims) / ncols))
im0 = ims.__iter__().__next__()
imsize = im0.shape[0]
size = imsize + margin
w = margin + size * ncols
h = margin + size * nrows
canvas = np.ones((h, w, 3), dtype=im0.dtype)
for i, im in enumerate(ims):
ih = i // ncols
iw = i % ncols
if len(im.shape) > 2 and im.shape[-1] == 4:
im = im[..., :3]
if margin_colors is not None:
canvas[size * ih:size * (ih + 1) + margin, size * iw:size * (iw + 1) + margin] = margin_colors[i]
canvas[margin + size * ih:margin + size * ih + imsize, margin + size * iw:margin + size * iw + imsize] = im
return canvas
scores_sel_max = scores_sel.max()
margin_colors = np.array([(s / scores_sel_max * c0) for s in scores_sel])
for i, im_idc in enumerate((slice(0,5), slice(5,None))):
canvas = make_canvas(ims_sel[im_idc], nrows=1,
margin_colors=margin_colors[im_idc])
figure(dpi=150)
imshow(canvas)
# turn off axis decorators to make tight plot
ax = gca()
ax.tick_params(labelcolor='none', bottom=False, left=False, right=False)
ax.set_frame_on(False)
for sp in ax.spines.values():
sp.set_visible(False)
ax.xaxis.set_ticks([])
ax.yaxis.set_ticks([])
plt.imsave(figdir / f'overview-evo_ims_{i}.png', canvas)
```
# Define Custom Violinplot
```
def violinplot2(data=None, x=None, y=None, hue=None,
palette=None, linewidth=1, orient=None,
order=None, hue_order=None, x_disp=None,
palette_per_violin=None, hline_at_1=True,
legend_palette=None, legend_kwargs=None,
width=0.7, control_width=0.8, control_y=None,
hues_share_control=False,
ax=None, **kwargs):
"""
width: width of a group of violins ("hues") as fraction of between-group distance
contorl_width: width of a group of bars (control) as fraction of hue width
"""
if order is None:
n_groups = len(set(data[x])) if orient != 'h' else len(set(data[y]))
else:
n_groups = len(order)
extra_plot_handles = []
if ax is None:
ax = plt.gca()
if orient == 'h':
fill_between = ax.fill_betweenx
plot = ax.vlines
else:
fill_between = ax.fill_between
plot = ax.hlines
############ drawing ############
if not isinstance(y, str) and hasattr(y, '__iter__'):
ys = y
else:
ys = (y,)
for y in ys:
ax = sns.violinplot(data=data, x=x, y=y, hue=hue, ax=ax,
palette=palette, linewidth=linewidth, orient=orient,
width=width, order=order, hue_order=hue_order, **kwargs)
if legend_kwargs is not None:
lgnd = plt.legend(**legend_kwargs)
else:
lgnd = None
if hline_at_1:
hdl = plot(1, -0.45, n_groups-0.55, linestyle='--', linewidth=.75, zorder=-3)
extra_plot_handles.append(hdl)
############ drawing ############
############ styling ############
if orient != 'h':
ax.xaxis.set_ticks_position('none')
if x_disp is not None:
ax.set_xticklabels(x_disp)
# enlarge the circle for median
median_marks = [o for o in ax.get_children() if isinstance(o, matplotlib.collections.PathCollection)]
for o in median_marks:
o.set_sizes([10,])
# recolor the violins
violins = np.array([o for o in ax.get_children() if isinstance(o, matplotlib.collections.PolyCollection)])
violins = violins[np.argsort([int(v.get_label().replace('_collection','')) for v in violins])]
for i, o in enumerate(violins):
if palette_per_violin is not None:
i %= len(palette_per_violin)
c = palette_per_violin[i]
if len(c) == 2:
o.set_facecolor(c[0])
o.set_edgecolor(c[1])
else:
o.set_facecolor(c)
o.set_edgecolor('none')
else:
o.set_edgecolor('none')
# recolor the legend patches
if lgnd is not None:
for v in (legend_palette, palette_per_violin, palette):
if v is not None:
legend_palette = v
break
if legend_palette is not None:
for o, c in zip(lgnd.get_patches(), legend_palette):
o.set_facecolor(c)
o.set_edgecolor('none')
############ styling ############
############ control ############
# done last to not interfere with coloring violins
if control_y is not None:
assert control_y in df.columns
assert hue is not None and order is not None and hue_order is not None
nhues = len(hue_order)
vw = width # width per control (long)
if not hues_share_control:
vw /= nhues
cw = vw * control_width # width per control (short)
ctl_hdl = None
for i, xval in enumerate(order):
if not hues_share_control:
for j, hval in enumerate(hue_order):
df_ = df[(df[x] == xval) & (df[hue] == hval)]
if not len(df_):
continue
lq, mq, uq = np.nanpercentile(df_[control_y].values, (25, 50, 75))
xs_qtl = i + vw * (-nhues/2 + 1/2 + j) + cw/2 * np.array((-1,1))
xs_med = i + vw * (-nhues/2 + j) + vw * np.array((0,1))
ctl_hdl = fill_between(xs_qtl, lq, uq, color=(0.9,0.9,0.9), zorder=-2) # upper & lower quartiles
plot(mq, *xs_med, color=(0.5,0.5,0.5), linewidth=1, zorder=-1) # median
else:
df_ = df[(df[x] == xval)]
if not len(df_):
continue
lq, mq, uq = np.nanpercentile(df_[control_y].values, (25, 50, 75))
xs_qtl = i + cw/2 * np.array((-1,1))
xs_med = i + vw/2 * np.array((-1,1))
ctl_hdl = fill_between(xs_qtl, lq, uq, color=(0.9,0.9,0.9), zorder=-2)
plot(mq, *xs_med, color=(0.5,0.5,0.5), linewidth=1, zorder=-1)
extra_plot_handles.append(ctl_hdl)
############ control ############
return n_groups, ax, lgnd, extra_plot_handles
def default_ax_lims(ax, n_groups=None, orient=None):
if orient == 'h':
ax.set_xticks((0,1,2,3))
ax.set_xlim(-0.25, 3.5)
else:
if n_groups is not None:
ax.set_xlim(-0.65, n_groups-0.35)
ax.set_yticks((0,1,2,3))
ax.set_ylim(-0.25, 3.5)
def rotate_xticklabels(ax, rotation=10, pad=5):
for i, tick in enumerate(ax.xaxis.get_major_ticks()):
if tick.label.get_text() == 'none':
tick.set_visible(False)
tick.label.set(va='top', ha='center', rotation=rotation, rotation_mode='anchor')
tick.set_pad(pad)
```
# Figure 3 - Compare Target Nets, Layers
```
df = pd.read_csv(datdir/'fig_2.csv')
df = df[~np.isnan(df['Rel_act'])] # remove invalid data
df.head()
nets = ('caffenet', 'resnet-152-v2', 'resnet-269-v2', 'inception-v3', 'inception-v4', 'inception-resnet-v2', 'placesCNN')
layers = {'caffenet': ('conv2', 'conv4', 'fc6', 'fc8'),
'resnet-152-v2': ('res15_eletwise', 'res25_eletwise', 'res35_eletwise', 'classifier'),
'resnet-269-v2': ('res25_eletwise', 'res45_eletwise', 'res60_eletwise', 'classifier'),
'inception-v3': ('pool2_3x3_s2', 'reduction_a_concat', 'reduction_b_concat', 'classifier'),
'inception-v4': ('inception_stem3', 'reduction_a_concat', 'reduction_b_concat', 'classifier'),
'inception-resnet-v2': ('stem_concat', 'reduction_a_concat', 'reduction_b_concat', 'classifier'),
'placesCNN': ('conv2', 'conv4', 'fc6', 'fc8')}
get_layer_level = lambda r: ('Early', 'Middle', 'Late', 'Output')[layers[r[1]['Classifier']].index(r[1]['Layer'])]
df['Layer_level'] = list(map(get_layer_level, df.iterrows()))
x_disp = ('CaffeNet', 'ResNet-152-v2', 'ResNet-269-v2', 'Inception-v3', 'Inception-v4', 'Inception-ResNet-v2', 'PlacesCNN')
palette = get_cmap('Blues')(np.linspace(0.3,0.8,4))
fig = figure(figsize=(6.3,2.5), dpi=150)
n_groups, ax, lgnd, hdls = violinplot2(
data=df, x='Classifier', y='Rel_act', hue='Layer_level', cut=0,
order=nets, hue_order=('Early', 'Middle', 'Late', 'Output'), x_disp=x_disp,
legend_kwargs=dict(title='Evolved,\ntarget layer', loc='upper left', bbox_to_anchor=(1,1.05)),
palette_per_violin=palette, control_y='Rel_exp_max')
default_ax_lims(ax, n_groups)
rotate_xticklabels(ax)
ylabel('Relative activation')
xlabel('Target architecture')
# another legend
legend(handles=hdls, labels=['Overall', 'In 10k'], title='ImageNet max',
loc='upper left', bbox_to_anchor=(1,0.4))
ax.add_artist(lgnd)
savefig(figdir / f'nets.png', dpi=300, bbox_inches='tight')
savefig(figdir / f'nets.svg', dpi=300, bbox_inches='tight')
```
# Figure 5 - Compare Generators
## Compare representation "depth"
```
df = pd.read_csv(datdir / 'fig_5-repr_depth.csv')
df = df[~np.isnan(df['Rel_act'])]
df['Classifier, layer'] = [', '.join(tuple(a)) for a in df[['Classifier', 'Layer']].values]
df.head()
nets = ('caffenet', 'inception-resnet-v2')
layers = {'caffenet': ('conv2', 'fc6', 'fc8'),
'inception-resnet-v2': ('classifier',)}
generators = ('raw_pixel', 'deepsim-norm1', 'deepsim-norm2', 'deepsim-conv3',
'deepsim-conv4', 'deepsim-pool5', 'deepsim-fc6', 'deepsim-fc7', 'deepsim-fc8')
xorder = ('caffenet, conv2', 'caffenet, fc6', 'caffenet, fc8', 'inception-resnet-v2, classifier')
x_disp = ('CaffeNet, conv2', 'CaffeNet, fc6', 'CaffeNet, fc8', 'Inception-ResNet-v2,\nclassifier')
lbl_disp = ('Raw pixel',) + tuple(v.replace('deepsim', 'DeePSiM') for v in generators[1:])
palette = ([[0.75, 0.75, 0.75]] + # raw pixel
sns.husl_palette(len(generators)-1, h=0.05, l=0.65)) # deepsim 1--8
fig = figure(figsize=(5.6,2.4), dpi=150)
n_groups, ax, lgnd, hdls = violinplot2(
data=df, x='Classifier, layer', y='Rel_act', hue='Generator',
cut=0, linewidth=.75, width=0.9, control_width=0.9,
order=xorder, hue_order=generators, x_disp=x_disp,
legend_kwargs=dict(title='Generator', loc='upper left', bbox_to_anchor=(1,1.05)),
palette=palette, control_y='Rel_exp_max', hues_share_control=True)
default_ax_lims(ax, n_groups)
ylabel('Relative activation')
xlabel('Target layer')
# change legend label text
for txt, lbl in zip(lgnd.get_texts(), lbl_disp):
txt.set_text(lbl)
savefig(figdir / f'generators.png', dpi=300, bbox_inches='tight')
savefig(figdir / f'generators.svg', dpi=300, bbox_inches='tight')
```
## Compare training dataset
```
df = pd.read_csv(datdir / 'fig_5-training_set.csv')
df = df[~np.isnan(df['Rel_act'])]
df['Classifier, layer'] = [', '.join(tuple(a)) for a in df[['Classifier', 'Layer']].values]
df.head()
nets = ('caffenet', 'inception-resnet-v2')
cs = ('caffenet', 'placesCNN', 'inception-resnet-v2')
layers = {c: ('conv2', 'conv4', 'fc6', 'fc8') for c in cs}
layers['inception-resnet-v2'] = ('classifier',)
gs = ('deepsim-fc6', 'deepsim-fc6-places365')
cls = ('caffenet, conv2', 'caffenet, conv4', 'caffenet, fc6', 'caffenet, fc8', 'inception-resnet-v2, classifier',
'placesCNN, conv2', 'placesCNN, conv4', 'placesCNN, fc6', 'placesCNN, fc8')
cls_spaced = cls[:5] + ('none',) + cls[5:]
x_disp = tuple(f'CaffeNet, {v}' for v in ('conv2', 'conv4', 'fc6', 'fc8')) + \
('Inception-ResNet-v2,\nclassifier', 'none') + \
tuple(f'PlacesCNN, {v}' for v in ('conv2', 'conv4', 'fc6', 'fc8'))
lbl_disp = ('DeePSiM-fc6', 'DeePSiM-fc6-Places365')
palette = [get_cmap(main_c)(np.linspace(0.3,0.8,4))
for main_c in ('Blues', 'Oranges')]
palette = list(np.array(palette).transpose(1,0,2).reshape(-1, 4))
palette = palette + palette[-2:] + palette
fig = figure(figsize=(5.15,1.8), dpi=150)
n_groups, ax, lgnd, hdls = violinplot2(
data=df, x='Classifier, layer', y='Rel_act', hue='Generator',
cut=0, split=True, inner='quartile',
order=cls_spaced, hue_order=gs, x_disp=x_disp,
legend_kwargs=dict(title='Generator', loc='upper left', bbox_to_anchor=(.97,1.05)),
palette_per_violin=palette, legend_palette=palette[4:],
control_y='Rel_exp_max', hues_share_control=True)
rotate_xticklabels(ax, rotation=15, pad=10)
ylabel('Relative activation')
xlabel('Target layer')
# change legend label text
for txt, lbl in zip(lgnd.get_texts(), lbl_disp):
txt.set_text(lbl)
savefig(figdir / f'generators2.png', dpi=300, bbox_inches='tight')
savefig(figdir / f'generators2.svg', dpi=300, bbox_inches='tight')
```
# Figure 4 - Compare Inits
```
layers = ('conv2', 'conv4', 'fc6', 'fc8')
layers_disp = tuple(v.capitalize() for v in layers)
```
## Rand inits, fraction change
```
df = pd.read_csv(datdir/'fig_4-rand_init.csv').set_index(['Layer', 'Unit', 'Init_seed'])
df = (df.drop(0, level='Init_seed') - df.xs(0, level='Init_seed')).mean(axis=0,level=('Layer','Unit'))
df = df.rename({'Rel_act': 'Fraction change'}, axis=1)
df = df.reset_index()
df.head()
palette = get_cmap('Blues')(np.linspace(0.2,0.9,6)[1:-1])
fig = figure(figsize=(1.75,1.5), dpi=150)
n_groups, ax, lgnd, hdls = violinplot2(
data=df, x='Layer', y='Fraction change',
cut=0, width=0.9, palette=palette,
order=layers, x_disp=layers_disp, hline_at_1=False)
xlabel('Target CaffeNet layer')
ylim(-0.35, 0.35)
yticks((-0.25,0,0.25))
ax.set_yticklabels([f'{t:.2f}' for t in (-0.25,0,0.25)])
ax.set_yticks(np.arange(-0.3,0.30,0.05), minor=True)
savefig(figdir / f'inits-change.png', dpi=300, bbox_inches='tight')
savefig(figdir / f'inits-change.svg', dpi=300, bbox_inches='tight')
```
## Rand inits, interpolation
```
df = pd.read_csv(datdir/'fig_4-rand_init_interp.csv').set_index(['Layer', 'Unit', 'Seed_i0', 'Seed_i1'])
df = df.mean(axis=0,level=('Layer','Unit'))
df2 = pd.read_csv(datdir/'fig_4-rand_init_interp-2.csv').set_index(['Layer', 'Unit']) # control conditions
df2_normed = df2.divide(df[['Rel_act_loc_0.0','Rel_act_loc_1.0']].mean(axis=1),axis=0)
df_normed = df.divide(df[['Rel_act_loc_0.0','Rel_act_loc_1.0']].mean(axis=1),axis=0)
df_normed.head()
fig, axs = subplots(1, 2, figsize=(3.5,1.5), dpi=150)
subplots_adjust(wspace=0.5)
interp_xs = np.array([float(i[i.rfind('_')+1:]) for i in df.columns])
for ax, df_ in zip(axs, (df, df_normed)):
df_mean = df_.mean(axis=0, level='Layer')
df_std = df_.std(axis=0, level='Layer')
for l, ld, c in zip(layers, layers_disp, palette):
m = df_mean.loc[l].values
s = df_std.loc[l].values
ax.plot(interp_xs, m, c=c, label=ld)
ax.fill_between(interp_xs, m-s, m+s, fc=c, ec='none', alpha=0.1)
# plot control
xs2 = (interp_xs.min(), interp_xs.max())
axs[0].hlines(1, *xs2, linestyle='--', linewidth=1)
for l, c in zip(layers, palette):
# left subplot: relative activation
df_ = df2.loc[l]
mq = np.nanmedian(df_['Rel_ImNet_median_act'].values)
axs[0].plot(xs2, (mq, mq), color=c, linewidth=1.15, zorder=-2)
# right subplot: normalized to endpoints
df_ = df2_normed.loc[l]
for k, ls, lw in zip(('Rel_exp_max', 'Rel_ImNet_median_act'), ('--','-'), (1, 1.15)):
mq = np.nanmedian(df_[k].values)
axs[1].plot(xs2, (mq, mq), color=c, ls=ls, linewidth=lw, zorder=-2)
axs[0].set_yticks((0, 1, 2))
axs[1].set_yticks((0, 0.5, 1))
axs[0].set_ylabel('Relative activation')
axs[1].set_ylabel('Normalized activation')
for ax in axs:
ax.set_xlabel('Interpolation location')
lgnd = axs[-1].legend(loc='upper left', bbox_to_anchor=(1.05, 1.05))
legend(handles=[Line2D([0], [0], color='k', lw=1, ls='--', label='Max'),
Line2D([0], [0], color='k', lw=1.15, label='Median')],
title='ImageNet ref.',
loc='upper left', bbox_to_anchor=(1.05,0.3))
ax.add_artist(lgnd)
savefig(figdir / f'inits-interp.png', dpi=300, bbox_inches='tight')
savefig(figdir / f'inits-interp.svg', dpi=300, bbox_inches='tight')
```
## Per-neuron inits
```
df = pd.read_csv(datdir/'fig_4-per_neuron_init.csv')
df.head()
hue_order = ('rand', 'none', 'worst_opt', 'mid_opt', 'best_opt',
'worst_ivt', 'mid_ivt', 'best_ivt')
palette = [get_cmap(main_c)(np.linspace(0.3,0.8,4))
for main_c in ('Blues', 'Greens', 'Purples')]
palette = np.concatenate([[
palette[0][i]] * 1 + [palette[1][i]] * 3 + [palette[2][i]] * 3
for i in range(4)])
palette = tuple(palette) + tuple(('none', c) for c in palette)
fig = figure(figsize=(6.3,2), dpi=150)
n_groups, ax, lgnd, hdls = violinplot2(
data=df, x='Layer', y=('Rel_act', 'Rel_act_init'), hue='Init_name', cut=0,
order=layers, hue_order=hue_order, x_disp=x_disp,
palette_per_violin=palette)
ylabel('Relative activation')
ylabel('Target CaffeNet layer')
# create custom legends
# for init methods
legend_elements = [
matplotlib.patches.Patch(facecolor=palette[14+3*i], edgecolor='none', label=l)
for i, l in enumerate(('Random', 'Opt', 'Ivt'))]
lgnd1 = legend(handles=legend_elements, title='Init. method',
loc='upper left', bbox_to_anchor=(1,1.05))
# for generation condition
legend_elements = [
matplotlib.patches.Patch(facecolor='gray', edgecolor='none', label='Final'),
matplotlib.patches.Patch(facecolor='none', edgecolor='gray', label='Initial')]
ax.legend(handles=legend_elements, title='Generation',
loc='upper left', bbox_to_anchor=(1,.45))
ax.add_artist(lgnd1)
savefig(figdir / f'inits-per_neuron.png', dpi=300, bbox_inches='tight')
savefig(figdir / f'inits-per_neuron.svg', dpi=300, bbox_inches='tight')
```
# Figure 6 - Compare Optimizers & Stoch Scales
## Compare optimizers
```
df = pd.read_csv(datdir/'fig_6-optimizers.csv')
df['OCL'] = ['_'.join(v) for v in df[['Optimizer','Classifier','Layer']].values]
df.head()
opts = ('genetic', 'FDGD', 'NES')
layers = {'caffenet': ('conv2', 'conv4', 'fc6', 'fc8'),
'inception-resnet-v2': ('classifier',)}
cls = [(c, l) for c in layers for l in layers[c]]
xorder = tuple(f'{opt}_{c}_{l}' for c in layers for l in layers[c]
for opt in (opts + ('none',)))[:-1]
x_disp = ('CaffeNet, conv2', 'CaffeNet, conv4', 'CaffeNet, fc6', 'CaffeNet, fc8',
'Inception-ResNet-v2,\nclassifier')
opts_disp = ('Genetic', 'FDGD', 'NES')
palette = [get_cmap(main_c)(np.linspace(0.3,0.8,4))
for main_c in ('Blues', 'Oranges', 'Greens')]
palette = np.concatenate([
np.concatenate([[palette[j][i], palette[j][i]/2+0.5] for j in range(3)])
for i in (0,1,2,3,3)])
fig = figure(figsize=(6.75,2.75), dpi=150)
n_groups, ax, lgnd, hdls = violinplot2(
data=df, x='OCL', y='Rel_act', hue='Noisy',
cut=0, inner='quartiles', split=True, width=1,
order=xorder, palette_per_violin=palette)
default_ax_lims(ax, n_groups)
xticks(np.arange(1,20,4), labels=x_disp)
xlabel('Target layer', labelpad=0)
ylabel('Relative activation')
# create custom legends
# for optimizers
legend_patches = [matplotlib.patches.Patch(facecolor=palette[i], edgecolor='none', label=opt)
for i, opt in zip(range(12,18,2), opts_disp)]
lgnd1 = legend(handles=legend_patches, title='Optimization alg.',
loc='upper left', bbox_to_anchor=(0,1))
# for noise condition
legend_patches = [matplotlib.patches.Patch(facecolor=(0.5,0.5,0.5), edgecolor='none', label='Noiseless'),
matplotlib.patches.Patch(facecolor=(0.8,0.8,0.8), edgecolor='none', label='Noisy')]
legend(handles=legend_patches, loc='upper right', bbox_to_anchor=(1,1))
ax.add_artist(lgnd1)
# plot control
group_width_ = 4
for i, cl in enumerate(cls):
i = i * group_width_ + 1
df_ = df[(df['Classifier'] == cl[0]) & (df['Layer'] == cl[1])]
lq, mq, uq = np.nanpercentile(df_['Rel_exp_max'].values, (25, 50, 75))
xs_qtl = i+np.array((-1,1))*group_width_*0.7/2
xs_med = i+np.array((-1,1))*group_width_*0.75/2
fill_between(xs_qtl, lq, uq, color=(0.9,0.9,0.9), zorder=-2)
plot(xs_med, (mq, mq), color=(0.5,0.5,0.5), linewidth=1.15, zorder=-1)
savefig(figdir / f'optimizers.png', dpi=300, bbox_inches='tight')
savefig(figdir / f'optimizers.svg', dpi=300, bbox_inches='tight')
```
## Compare varying amounts of noise
```
df = pd.read_csv(datdir/'fig_6-stoch_scales.csv')
df = df[~np.isnan(df['Rel_noise'])]
df['Stoch_scale_plot'] = [str(int(v)) if ~np.isnan(v) else 'None' for v in df['Stoch_scale']]
df.head()
layers = ('conv2', 'conv4', 'fc6', 'fc8')
stoch_scales = list(map(str, (5, 10, 20, 50, 75, 100, 250))) + ['None']
stoch_scales_disp = stoch_scales[:-1] + ['No\nnoise']
stat_keys = ('Self_correlation', 'Rel_noise', 'SNR')
stat_keys_disp = ('Self correlation', 'Stdev. : mean ratio', 'Signal-to-noise ratio')
palette = [get_cmap('Blues')(np.linspace(0.3,0.8,4))[2]] # to match previous color
# calculate noise statstics and define their formatting
format_frac = lambda v: ('%.2f' % v)[1:] if (0 < v < 1) else '0' if v == 0 else str(v)
def format_sci(v):
v = '%.0e' % v
if v == 'inf':
return v
m, s = v.split('e')
s = int(s)
if s:
if False: #s > 1:
m = re.split('0+$', m)[0]
m += 'e%d' % s
else:
m = str(int((float(m) * np.power(10, s))))
return m
fmts = (format_frac, format_frac, format_sci)
byl_byss_stats = {k: {} for k in stat_keys}
for l in layers:
df_ = df[df['Layer'] == l]
stats = {k: [] for k in stat_keys}
for ss in stoch_scales:
df__ = df_[df_['Stoch_scale_plot'] == ss]
for k in stat_keys:
stats[k].append(np.median(df__[k]))
for k in stats.keys():
byl_byss_stats[k][l] = stats[k]
fig, axs = subplots(1, 4, figsize=(5.25, 2), dpi=150, sharex=True, sharey=True, squeeze=False)
axs = axs.flatten()
subplots_adjust(wspace=0.05)
for l, ax in zip(layers, axs):
df_ = df[df['Layer'] == l]
n_groups, ax, lgnd, hdls = violinplot2(
data=df_, x='Rel_act', y='Stoch_scale_plot', orient='h',
cut=0, width=.85, scale='width',
palette=palette, ax=ax)
ax.set_title(f'CaffeNet, {l}', fontsize=8)
default_ax_lims(ax, n_groups, orient='h')
ax.set_xlabel(None)
# append more y-axes to last axis
pars = [twinx(ax) for _ in range(len(stat_keys))]
ylim_ = ax.get_ylim()
for i, (par, k, fmt, k_disp) in enumerate(zip(pars, stat_keys, fmts, stat_keys_disp)):
par.set_frame_on(True)
par.patch.set_visible(False)
par.spines['right'].set_visible(True)
par.yaxis.set_ticks_position('right')
par.yaxis.set_label_position('right')
par.yaxis.labelpad = 2
par.spines['right'].set_position(('axes', 1+.6*i))
par.set_ylabel(k_disp)
par.set_yticks(range(len(stoch_scales)))
par.set_yticklabels(map(fmt, byl_byss_stats[k][l]))
par.set_ylim(ylim_)
axs[0].set_ylabel('Expected max firing rate, spks')
axs[0].set_yticklabels(stoch_scales_disp)
for ax in axs[1:]:
ax.set_ylabel(None)
ax.yaxis.set_tick_params(left=False)
# joint
ax = fig.add_subplot(111, frameon=False)
ax.tick_params(labelcolor='none', bottom=False, left=False, right=False)
ax.set_frame_on(False)
ax.set_xlabel('Relative activation')
savefig(figdir / 'stoch_scales.png', dpi=300, bbox_inches='tight')
savefig(figdir / 'stoch_scales.svg', dpi=300, bbox_inches='tight')
```
|
github_jupyter
|
# Running the Direct Fidelity Estimation (DFE) algorithm
This example walks through the steps of running the direct fidelity estimation (DFE) algorithm as described in these two papers:
* Direct Fidelity Estimation from Few Pauli Measurements (https://arxiv.org/abs/1104.4695)
* Practical characterization of quantum devices without tomography (https://arxiv.org/abs/1104.3835)
Optimizations for Clifford circuits are based on a tableau-based simulator:
* Improved Simulation of Stabilizer Circuits (https://arxiv.org/pdf/quant-ph/0406196.pdf)
```
try:
import cirq
except ImportError:
print("installing cirq...")
!pip install --quiet cirq
print("installed cirq.")
# Import Cirq, DFE, and create a circuit
import cirq
from cirq.contrib.svg import SVGCircuit
import examples.direct_fidelity_estimation as dfe
qubits = cirq.LineQubit.range(3)
circuit = cirq.Circuit(cirq.CNOT(qubits[0], qubits[2]),
cirq.Z(qubits[0]),
cirq.H(qubits[2]),
cirq.CNOT(qubits[2], qubits[1]))
SVGCircuit(circuit)
# We then create a sampler. For this example, we use a simulator but the code can accept a hardware sampler.
noise = cirq.ConstantQubitNoiseModel(cirq.depolarize(0.1))
sampler = cirq.DensityMatrixSimulator(noise=noise)
# We run the DFE:
estimated_fidelity, intermediate_results = dfe.direct_fidelity_estimation(
circuit,
qubits,
sampler,
n_measured_operators=None, # None=returns all the Pauli strings
samples_per_term=0) # 0=use dense matrix simulator
print('Estimated fidelity: %.2f' % (estimated_fidelity))
```
# What is happening under the hood?
Now, let's look at the `intermediate_results` and correlate what is happening in the code with the papers. The definition of fidelity is:
$$
F = F(\hat{\rho},\hat{\sigma}) = \mathrm{Tr} \left(\hat{\rho} \hat{\sigma}\right)
$$
where $\hat{\rho}$ is the theoretical pure state and $\hat{\sigma}$ is the actual state. The idea of DFE is to write fidelity as:
$$F= \sum _i \frac{\rho _i \sigma _i}{d}$$
where $d=4^{\mathit{number-of-qubits}}$, $\rho _i = \mathrm{Tr} \left( \hat{\rho} P_i \right)$, and $\sigma _i = \mathrm{Tr} \left(\hat{\sigma} P_i \right)$. Each of the $P_i$ is a Pauli operator. We can then finally rewrite the fidelity as:
$$F= \sum _i Pr(i) \frac{\sigma _i}{\rho_i}$$
with $Pr(i) = \frac{\rho_i ^2}{d}$, which is a probability-like set of numbers (between 0.0 and 1.0 and they add up to 1.0).
One important question is how do we choose these Pauli operators $P_i$? It depends on whether the circuit is Clifford or not. In case it is, we know that there are "only" $2^{\mathit{number-of-qubits}}$ operators for which $Pr(i)$ is non-zero. In fact, we know that they are all equiprobable with $Pr(i) = \frac{1}{2^{\mathit{number-of-qubits}}}$. The code does detect the Cliffordness automatically and switches to this mode. In case the circuit is not Clifford, the code just uses all the operators.
Let's inspect that in the case of our example, we do see the Pauli operators with equiprobability (i.e. the $\rho_i$):
```
for pauli_trace in intermediate_results.pauli_traces:
print('Probability %.3f\tPauli: %s' % (pauli_trace.Pr_i, pauli_trace.P_i))
```
Yay! We do see 8 entries (we have 3 qubits) with all the same 1/8 probability. What if we had a 23 qubit circuit? In this case, that would be quite many of them. That is where the parameter `n_measured_operators` becomes useful. If it is set to `None` we return *all* the Pauli strings (regardless of whether the circuit is Clifford or not). If set to an integer, we randomly sample the Pauli strings.
Then, let's actually look at the measurements, i.e. $\sigma_i$:
```
for trial_result in intermediate_results.trial_results:
print('rho_i=%.3f\tsigma_i=%.3f\tPauli:%s' % (trial_result.pauli_trace.rho_i, trial_result.sigma_i, trial_result.pauli_trace.P_i))
```
How are these measurements chosen? Since we had set `n_measured_operators=None`, all the measurements are used. If we had set the parameter to an integer, we would only have a subset to start from. We would then, as per the algorithm, sample from this set with replacement according to the probability distribution of $Pr(i)$ (for Clifford circuits, the probabilities are all the same, but for non-Clifford circuits, it means we favor more probable Pauli strings).
What about the parameter `samples_per_term`? Remember that the code can handle both a sampler or use a simulator. If we use a sampler, then we can repeat the measurements `samples_per_term` times. In our case, we use a dense matrix simulator and thus we keep that parameter set to `0`.
# How do we bound the variance of the fidelity when the circuit is Clifford?
Recall that the formula for DFE is:
$$F= \sum _i Pr(i) \frac{\sigma _i}{\rho_i}$$
But for Clifford circuits, we have $Pr(i) = \frac{1}{d}$ and $\rho_i = 1$ and thus the formula becomes:
$$F= \frac{1}{d} \sum _i \sigma _i$$
If we estimate by randomly sampling $N$ values for the indicies $i$ for $\sigma_i$ we get:
$$\hat{F} = \frac{1}{N} \sum_{j=1}^N \sigma _{i(j)}$$
Using the Bhatia–Davis inequality ([A Better Bound on the Variance, Rajendra Bhatia and Chandler Davis](https://www.jstor.org/stable/2589180)) and the fact that $0 \le \sigma_i \le 1$, we have the variance of:
$$\mathrm{Var}\left[ \hat{F} \right] \le \frac{(1 - F)F}{N}$$
$$\mathrm{StdDev}\left[ \hat{F} \right] \le \sqrt{\frac{(1 - F)F}{N}}$$
In particular, since $0 \le F \le 1$ we have:
$$\mathrm{StdDev}\left[ \hat{F} \right] \le \sqrt{\frac{(1 - \frac{1}{2})\frac{1}{2}}{N}}$$
$$\mathrm{StdDev}\left[ \hat{F} \right] \le \frac{1}{2 \sqrt{N}}$$
|
github_jupyter
|
# Gujarati with CLTK
See how you can analyse your Gujarati texts with <b>CLTK</b> ! <br>
Let's begin by adding the `USER_PATH`..
```
import os
USER_PATH = os.path.expanduser('~')
```
In order to be able to download Gujarati texts from CLTK's Github repo, we will require an importer.
```
from cltk.corpus.utils.importer import CorpusImporter
gujarati_downloader = CorpusImporter('gujarati')
```
We can now see the corpora available for download, by using `list_corpora` feature of the importer. Let's go ahead and try it out!
```
gujarati_downloader.list_corpora
```
The corpus <i>gujarati_text_wikisource</i> can be downloaded from the Github repo. The corpus will be downloaded to the directory `cltk_data/gujarati` at the above mentioned `USER_PATH`
```
gujarati_downloader.import_corpus('gujarati_text_wikisource')
```
You can see the texts downloaded by doing the following, or checking out the `cltk_data/gujarati/text/gujarati_text_wikisource` directory.
```
gujarati_corpus_path = os.path.join(USER_PATH,'cltk_data/gujarati/text/gujarati_text_wikisource')
list_of_texts = [text for text in os.listdir(gujarati_corpus_path) if '.' not in text]
print(list_of_texts)
```
Great, now that we have our texts, let's take a sample from one of them. For this tutorial, we shall be using <i>govinda_khele_holi</i> , a text by the Gujarati poet Narsinh Mehta.
```
gujarati_text_path = os.path.join(gujarati_corpus_path,'narsinh_mehta/govinda_khele_holi.txt')
gujarati_text = open(gujarati_text_path,'r').read()
print(gujarati_text)
```
## Gujarati Alphabets
There are 13 vowels, 33 consonants, which are grouped as follows:
```
from cltk.corpus.gujarati.alphabet import *
print("Digits:",DIGITS)
print("Vowels:",VOWELS)
print("Dependent vowels:",DEPENDENT_VOWELS)
print("Consonants:",CONSONANTS)
print("Velar consonants:",VELAR_CONSONANTS)
print("Palatal consonants:",PALATAL_CONSONANTS)
print("Retroflex consonants:",RETROFLEX_CONSONANTS)
print("Dental consonants:",DENTAL_CONSONANTS)
print("Labial consonants:",LABIAL_CONSONANTS)
print("Sonorant consonants:",SONORANT_CONSONANTS)
print("Sibilant consonants:",SIBILANT_CONSONANTS)
print("Guttural consonant:",GUTTURAL_CONSONANT)
print("Additional consonants:",ADDITIONAL_CONSONANTS)
print("Modifiers:",MODIFIERS)
```
## Transliterations
We can transliterate Gujarati scripts to that of other Indic languages. Let us transliterate `કમળ ભારતનો રાષ્ટ્રીય ફૂલ છે`to Kannada:
```
gujarati_text_two = 'કમળ ભારતનો રાષ્ટ્રીય ફૂલ છે'
from cltk.corpus.sanskrit.itrans.unicode_transliterate import UnicodeIndicTransliterator
UnicodeIndicTransliterator.transliterate(gujarati_text_two,"gu","kn")
```
We can also romanize the text as shown:
```
from cltk.corpus.sanskrit.itrans.unicode_transliterate import ItransTransliterator
ItransTransliterator.to_itrans(gujarati_text_two,'gu')
```
Similarly, we can indicize a text given in its ITRANS-transliteration
```
gujarati_text_itrans = 'bhaawanaa'
ItransTransliterator.from_itrans(gujarati_text_itrans,'gu')
```
## Syllabifier
We can use the indian_syllabifier to syllabify the Gujarati sentences. To do this, we will have to import models as follows. The importing of `sanskrit_models_cltk` might take some time.
```
phonetics_model_importer = CorpusImporter('sanskrit')
phonetics_model_importer.list_corpora
phonetics_model_importer.import_corpus('sanskrit_models_cltk')
```
Now we import the syllabifier and syllabify as follows:
```
%%capture
from cltk.stem.sanskrit.indian_syllabifier import Syllabifier
gujarati_syllabifier = Syllabifier('gujarati')
gujarati_syllables = gujarati_syllabifier.orthographic_syllabify('ભાવના')
```
The syllables of the word `ભાવના` will thus be:
```
print(gujarati_syllables)
```
|
github_jupyter
|
<h1>CREAZIONE MODELLO SARIMA REGIONE SARDEGNA
```
import pandas as pd
df = pd.read_csv('../../csv/regioni/sardegna.csv')
df.head()
df['DATA'] = pd.to_datetime(df['DATA'])
df.info()
df=df.set_index('DATA')
df.head()
```
<h3>Creazione serie storica dei decessi totali della regione Sardegna
```
ts = df.TOTALE
ts.head()
from datetime import datetime
from datetime import timedelta
start_date = datetime(2015,1,1)
end_date = datetime(2020,9,30)
lim_ts = ts[start_date:end_date]
#visulizzo il grafico
import matplotlib.pyplot as plt
plt.figure(figsize=(12,6))
plt.title('Decessi mensili regione Sardegna dal 2015 a settembre 2020', size=20)
plt.plot(lim_ts)
for year in range(start_date.year,end_date.year+1):
plt.axvline(pd.to_datetime(str(year)+'-01-01'), color='k', linestyle='--', alpha=0.5)
```
<h3>Decomposizione
```
from statsmodels.tsa.seasonal import seasonal_decompose
decomposition = seasonal_decompose(ts, period=12, two_sided=True, extrapolate_trend=1, model='multiplicative')
ts_trend = decomposition.trend #andamento della curva
ts_seasonal = decomposition.seasonal #stagionalità
ts_residual = decomposition.resid #parti rimanenti
plt.subplot(411)
plt.plot(ts,label='original')
plt.legend(loc='best')
plt.subplot(412)
plt.plot(ts_trend,label='trend')
plt.legend(loc='best')
plt.subplot(413)
plt.plot(ts_seasonal,label='seasonality')
plt.legend(loc='best')
plt.subplot(414)
plt.plot(ts_residual,label='residual')
plt.legend(loc='best')
plt.tight_layout()
```
<h3>Test di stazionarietà
```
from statsmodels.tsa.stattools import adfuller
def test_stationarity(timeseries):
dftest = adfuller(timeseries, autolag='AIC')
dfoutput = pd.Series(dftest[0:4], index=['Test Statistic','p-value','#Lags Used','Number of Observations Used'])
for key,value in dftest[4].items():
dfoutput['Critical Value (%s)'%key] = value
critical_value = dftest[4]['5%']
test_statistic = dftest[0]
alpha = 1e-3
pvalue = dftest[1]
if pvalue < alpha and test_statistic < critical_value: # null hypothesis: x is non stationary
print("X is stationary")
return True
else:
print("X is not stationary")
return False
test_stationarity(ts)
```
<h3>Suddivisione in Train e Test
<b>Train</b>: da gennaio 2015 a ottobre 2019; <br />
<b>Test</b>: da ottobre 2019 a dicembre 2019.
```
from datetime import datetime
train_end = datetime(2019,10,31)
test_end = datetime (2019,12,31)
covid_end = datetime(2020,9,30)
from dateutil.relativedelta import *
tsb = ts[:test_end]
decomposition = seasonal_decompose(tsb, period=12, two_sided=True, extrapolate_trend=1, model='multiplicative')
tsb_trend = decomposition.trend #andamento della curva
tsb_seasonal = decomposition.seasonal #stagionalità
tsb_residual = decomposition.resid #parti rimanenti
tsb_diff = pd.Series(tsb_trend)
d = 0
while test_stationarity(tsb_diff) is False:
tsb_diff = tsb_diff.diff().dropna()
d = d + 1
print(d)
#TEST: dal 01-01-2015 al 31-10-2019
train = tsb[:train_end]
#TRAIN: dal 01-11-2019 al 31-12-2019
test = tsb[train_end + relativedelta(months=+1): test_end]
```
<h3>Grafici di Autocorrelazione e Autocorrelazione Parziale
```
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
plot_acf(ts, lags =12)
plot_pacf(ts, lags =12)
plt.show()
```
<h2>Creazione del modello SARIMA sul Train
```
from statsmodels.tsa.statespace.sarimax import SARIMAX
model = SARIMAX(train, order=(6,1,8))
model_fit = model.fit()
print(model_fit.summary())
```
<h4>Verifica della stazionarietà dei residui del modello ottenuto
```
residuals = model_fit.resid
test_stationarity(residuals)
plt.figure(figsize=(12,6))
plt.title('Confronto valori previsti dal modello con valori reali del Train', size=20)
plt.plot (train.iloc[1:], color='red', label='train values')
plt.plot (model_fit.fittedvalues.iloc[1:], color = 'blue', label='model values')
plt.legend()
plt.show()
conf = model_fit.conf_int()
plt.figure(figsize=(12,6))
plt.title('Intervalli di confidenza del modello', size=20)
plt.plot(conf)
plt.xticks(rotation=45)
plt.show()
```
<h3>Predizione del modello sul Test
```
#inizio e fine predizione
pred_start = test.index[0]
pred_end = test.index[-1]
#pred_start= len(train)
#pred_end = len(tsb)
#predizione del modello sul test
predictions_test= model_fit.predict(start=pred_start, end=pred_end)
plt.plot(test, color='red', label='actual')
plt.plot(predictions_test, label='prediction' )
plt.xticks(rotation=45)
plt.legend()
plt.show()
print(predictions_test)
# Accuracy metrics
import numpy as np
def forecast_accuracy(forecast, actual):
mape = np.mean(np.abs(forecast - actual)/np.abs(actual)) # MAPE: errore percentuale medio assoluto
me = np.mean(forecast - actual) # ME: errore medio
mae = np.mean(np.abs(forecast - actual)) # MAE: errore assoluto medio
mpe = np.mean((forecast - actual)/actual) # MPE: errore percentuale medio
rmse = np.mean((forecast - actual)**2)**.5 # RMSE
corr = np.corrcoef(forecast, actual)[0,1] # corr: correlazione tra effettivo e previsione
mins = np.amin(np.hstack([forecast[:,None],
actual[:,None]]), axis=1)
maxs = np.amax(np.hstack([forecast[:,None],
actual[:,None]]), axis=1)
minmax = 1 - np.mean(mins/maxs) # minmax: errore min-max
return({'mape':mape, 'me':me, 'mae': mae,
'mpe': mpe, 'rmse':rmse,
'corr':corr, 'minmax':minmax})
forecast_accuracy(predictions_test, test)
import numpy as np
from statsmodels.tools.eval_measures import rmse
nrmse = rmse(predictions_test, test)/(np.max(test)-np.min(test))
print('NRMSE: %f'% nrmse)
```
<h2>Predizione del modello compreso l'anno 2020
```
#inizio e fine predizione
start_prediction = ts.index[0]
end_prediction = ts.index[-1]
predictions_tot = model_fit.predict(start=start_prediction, end=end_prediction)
plt.figure(figsize=(12,6))
plt.title('Previsione modello su dati osservati - dal 2015 al 30 settembre 2020', size=20)
plt.plot(ts, color='blue', label='actual')
plt.plot(predictions_tot.iloc[1:], color='red', label='predict')
plt.xticks(rotation=45)
plt.legend(prop={'size': 12})
plt.show()
diff_predictions_tot = (ts - predictions_tot)
plt.figure(figsize=(12,6))
plt.title('Differenza tra i valori osservati e i valori stimati del modello', size=20)
plt.plot(diff_predictions_tot)
plt.show()
diff_predictions_tot['24-02-2020':].sum()
predictions_tot.to_csv('../../csv/pred/predictions_SARIMA_sardegna.csv')
```
<h2>Intervalli di confidenza della previsione totale
```
forecast = model_fit.get_prediction(start=start_prediction, end=end_prediction)
in_c = forecast.conf_int()
print(forecast.predicted_mean)
print(in_c)
print(forecast.predicted_mean - in_c['lower TOTALE'])
plt.plot(in_c)
plt.show()
upper = in_c['upper TOTALE']
lower = in_c['lower TOTALE']
lower.to_csv('../../csv/lower/predictions_SARIMA_sardegna_lower.csv')
upper.to_csv('../../csv/upper/predictions_SARIMA_sardegna_upper.csv')
```
|
github_jupyter
|
# Logistic Regression on 'HEART DISEASE' Dataset
Elif Cansu YILDIZ
```
from pyspark.sql import SparkSession
from pyspark.sql.types import *
from pyspark.sql.functions import col, countDistinct
from pyspark.ml.feature import OneHotEncoderEstimator, StringIndexer, VectorAssembler, MinMaxScaler, IndexToString
from pyspark.ml import Pipeline
from pyspark.ml.classification import LogisticRegression
from pyspark.ml.evaluation import BinaryClassificationEvaluator, MulticlassClassificationEvaluator
spark = SparkSession\
.builder\
.appName("MachineLearningExample")\
.getOrCreate()
```
The dataset used is 'Heart Disease' dataset from Kaggle. You can get from this [link](https://www.kaggle.com/ronitf/heart-disease-uci).
```
df = spark.read.csv('datasets/heart.csv', header = True, inferSchema = True) #Kaggle Dataset
df.printSchema()
df.show(5)
```
__HOW MANY DISTINCT VALUE DO COLUMNS HAVE?__
```
df.agg(*(countDistinct(col(c)).alias(c) for c in df.columns)).show()
```
__SET the Label Column and Input Columns__
```
labelColumn = "thal"
input_columns = [t[0] for t in df.dtypes if t[0]!=labelColumn]
# Split the data into training and test sets (30% held out for testing)
(trainingData, testData) = df.randomSplit([0.7, 0.3])
print("total data count: ", df.count())
print("train data count: ", trainingData.count())
print("test data count: ", testData.count())
```
__TRAINING__
```
assembler = VectorAssembler(inputCols = input_columns, outputCol='features')
lr = LogisticRegression(featuresCol='features', labelCol=labelColumn,
maxIter=10, regParam=0.3, elasticNetParam=0.8)
stages = [assembler, lr]
partialPipeline = Pipeline().setStages(stages)
model = partialPipeline.fit(trainingData)
```
__MAKE PREDICTIONS__
```
predictions = model.transform(testData)
predictionss = predictions.select("probability", "rawPrediction", "prediction",
col(labelColumn).alias("label"))
predictionss[["probability", "prediction", "label"]].show(5, truncate=False)
```
__EVALUATION for Binary Classification__
```
evaluator = BinaryClassificationEvaluator(labelCol="label", rawPredictionCol="prediction", metricName="areaUnderROC")
areaUnderROC = evaluator.evaluate(predictionss)
print("Area under ROC = %g" % areaUnderROC)
evaluator = BinaryClassificationEvaluator(labelCol="label", rawPredictionCol="prediction", metricName="areaUnderPR")
areaUnderPR = evaluator.evaluate(predictionss)
print("areaUnderPR = %g" % areaUnderPR)
```
__EVALUATION for Multiclass Classification__
```
evaluator = MulticlassClassificationEvaluator(labelCol="label", predictionCol="prediction", metricName="accuracy")
accuracy = evaluator.evaluate(predictionss)
print("accuracy = %g" % accuracy)
evaluator = MulticlassClassificationEvaluator(labelCol="label", predictionCol="prediction", metricName="f1")
f1 = evaluator.evaluate(predictionss)
print("f1 = %g" % f1)
evaluator = MulticlassClassificationEvaluator(labelCol="label", predictionCol="prediction", metricName="weightedPrecision")
weightedPrecision = evaluator.evaluate(predictionss)
print("weightedPrecision = %g" % weightedPrecision)
evaluator = MulticlassClassificationEvaluator(labelCol="label", predictionCol="prediction", metricName="weightedRecall")
weightedRecall = evaluator.evaluate(predictionss)
print("weightedRecall = %g" % weightedRecall)
```
|
github_jupyter
|
# Recommending Movies: Retrieval
Real-world recommender systems are often composed of two stages:
1. The retrieval stage is responsible for selecting an initial set of hundreds of candidates from all possible candidates. The main objective of this model is to efficiently weed out all candidates that the user is not interested in. Because the retrieval model may be dealing with millions of candidates, it has to be computationally efficient.
2. The ranking stage takes the outputs of the retrieval model and fine-tunes them to select the best possible handful of recommendations. Its task is to narrow down the set of items the user may be interested in to a shortlist of likely candidates.
In this tutorial, we're going to focus on the first stage, retrieval. If you are interested in the ranking stage, have a look at our [ranking](basic_ranking) tutorial.
Retrieval models are often composed of two sub-models:
1. A query model computing the query representation (normally a fixed-dimensionality embedding vector) using query features.
2. A candidate model computing the candidate representation (an equally-sized vector) using the candidate features
The outputs of the two models are then multiplied together to give a query-candidate affinity score, with higher scores expressing a better match between the candidate and the query.
In this tutorial, we're going to build and train such a two-tower model using the Movielens dataset.
We're going to:
1. Get our data and split it into a training and test set.
2. Implement a retrieval model.
3. Fit and evaluate it.
4. Export it for efficient serving by building an approximate nearest neighbours (ANN) index.
## The dataset
The Movielens dataset is a classic dataset from the [GroupLens](https://grouplens.org/datasets/movielens/) research group at the University of Minnesota. It contains a set of ratings given to movies by a set of users, and is a workhorse of recommender system research.
The data can be treated in two ways:
1. It can be interpreted as expressesing which movies the users watched (and rated), and which they did not. This is a form of implicit feedback, where users' watches tell us which things they prefer to see and which they'd rather not see.
2. It can also be seen as expressesing how much the users liked the movies they did watch. This is a form of explicit feedback: given that a user watched a movie, we can tell roughly how much they liked by looking at the rating they have given.
In this tutorial, we are focusing on a retrieval system: a model that predicts a set of movies from the catalogue that the user is likely to watch. Often, implicit data is more useful here, and so we are going to treat Movielens as an implicit system. This means that every movie a user watched is a positive example, and every movie they have not seen is an implicit negative example.
## Imports
Let's first get our imports out of the way.
```
import os
import pprint
import tempfile
from typing import Dict, Text
import numpy as np
import tensorflow as tf
import tensorflow_datasets as tfds
import tensorflow_recommenders as tfrs
```
## Preparing the dataset
Let's first have a look at the data.
We use the MovieLens dataset from [Tensorflow Datasets](https://www.tensorflow.org/datasets). Loading `movie_lens/100k_ratings` yields a `tf.data.Dataset` object containing the ratings data and loading `movie_lens/100k_movies` yields a `tf.data.Dataset` object containing only the movies data.
Note that since the MovieLens dataset does not have predefined splits, all data are under `train` split.
```
# Ratings data.
ratings = tfds.load("movie_lens/100k-ratings", split="train")
# Features of all the available movies.
movies = tfds.load("movie_lens/100k-movies", split="train")
```
The ratings dataset returns a dictionary of movie id, user id, the assigned rating, timestamp, movie information, and user information:
```
for x in ratings.take(1).as_numpy_iterator():
pprint.pprint(x)
```
The movies dataset contains the movie id, movie title, and data on what genres it belongs to. Note that the genres are encoded with integer labels.
```
for x in movies.take(1).as_numpy_iterator():
pprint.pprint(x)
```
In this example, we're going to focus on the ratings data. Other tutorials explore how to use the movie information data as well to improve the model quality.
We keep only the `user_id`, and `movie_title` fields in the dataset.
```
ratings = ratings.map(lambda x: {
"movie_title": x["movie_title"],
"user_id": x["user_id"],
})
movies = movies.map(lambda x: x["movie_title"])
```
To fit and evaluate the model, we need to split it into a training and evaluation set. In an industrial recommender system, this would most likely be done by time: the data up to time $T$ would be used to predict interactions after $T$.
In this simple example, however, let's use a random split, putting 80% of the ratings in the train set, and 20% in the test set.
```
tf.random.set_seed(42)
shuffled = ratings.shuffle(100_000, seed=42, reshuffle_each_iteration=False)
train = shuffled.take(80_000)
test = shuffled.skip(80_000).take(20_000)
```
Let's also figure out unique user ids and movie titles present in the data.
This is important because we need to be able to map the raw values of our categorical features to embedding vectors in our models. To do that, we need a vocabulary that maps a raw feature value to an integer in a contiguous range: this allows us to look up the corresponding embeddings in our embedding tables.
```
movie_titles = movies.batch(1_000)
user_ids = ratings.batch(1_000_000).map(lambda x: x["user_id"])
unique_movie_titles = np.unique(np.concatenate(list(movie_titles)))
unique_user_ids = np.unique(np.concatenate(list(user_ids)))
unique_movie_titles[:10]
```
## Implementing a model
Choosing the architecure of our model a key part of modelling.
Because we are building a two-tower retrieval model, we can build each tower separately and then combine them in the final model.
### The query tower
Let's start with the query tower.
The first step is to decide on the dimensionality of the query and candidate representations:
```
embedding_dimension = 32
```
Higher values will correspond to models that may be more accurate, but will also be slower to fit and more prone to overfitting.
The second is to define the model itself. Here, we're going to use Keras preprocessing layers to first convert user ids to integers, and then convert those to user embeddings via an `Embedding` layer. Note that we use the list of unique user ids we computed earlier as a vocabulary:
# _Note: Requires TF 2.3.0_
```
user_model = tf.keras.Sequential([
tf.keras.layers.experimental.preprocessing.StringLookup(
vocabulary=unique_user_ids, mask_token=None),
# We add an additional embedding to account for unknown tokens.
tf.keras.layers.Embedding(len(unique_user_ids) + 1, embedding_dimension)
])
```
A simple model like this corresponds exactly to a classic [matrix factorization](https://ieeexplore.ieee.org/abstract/document/4781121) approach. While defining a subclass of `tf.keras.Model` for this simple model might be overkill, we can easily extend it to an arbitrarily complex model using standard Keras components, as long as we return an `embedding_dimension`-wide output at the end.
### The candidate tower
We can do the same with the candidate tower.
```
movie_model = tf.keras.Sequential([
tf.keras.layers.experimental.preprocessing.StringLookup(
vocabulary=unique_movie_titles, mask_token=None),
tf.keras.layers.Embedding(len(unique_movie_titles) + 1, embedding_dimension)
])
```
### Metrics
In our training data we have positive (user, movie) pairs. To figure out how good our model is, we need to compare the affinity score that the model calculates for this pair to the scores of all the other possible candidates: if the score for the positive pair is higher than for all other candidates, our model is highly accurate.
To do this, we can use the `tfrs.metrics.FactorizedTopK` metric. The metric has one required argument: the dataset of candidates that are used as implicit negatives for evaluation.
In our case, that's the `movies` dataset, converted into embeddings via our movie model:
```
metrics = tfrs.metrics.FactorizedTopK(
candidates=movies.batch(128).map(movie_model)
)
```
### Loss
The next component is the loss used to train our model. TFRS has several loss layers and tasks to make this easy.
In this instance, we'll make use of the `Retrieval` task object: a convenience wrapper that bundles together the loss function and metric computation:
```
task = tfrs.tasks.Retrieval(
metrics=metrics
)
```
The task itself is a Keras layer that takes the query and candidate embeddings as arguments, and returns the computed loss: we'll use that to implement the model's training loop.
### The full model
We can now put it all together into a model. TFRS exposes a base model class (`tfrs.models.Model`) which streamlines bulding models: all we need to do is to set up the components in the `__init__` method, and implement the `compute_loss` method, taking in the raw features and returning a loss value.
The base model will then take care of creating the appropriate training loop to fit our model.
```
class MovielensModel(tfrs.Model):
def __init__(self, user_model, movie_model):
super().__init__()
self.movie_model: tf.keras.Model = movie_model
self.user_model: tf.keras.Model = user_model
self.task: tf.keras.layers.Layer = task
def compute_loss(self, features: Dict[Text, tf.Tensor], training=False) -> tf.Tensor:
# We pick out the user features and pass them into the user model.
user_embeddings = self.user_model(features["user_id"])
# And pick out the movie features and pass them into the movie model,
# getting embeddings back.
positive_movie_embeddings = self.movie_model(features["movie_title"])
# The task computes the loss and the metrics.
return self.task(user_embeddings, positive_movie_embeddings)
```
The `tfrs.Model` base class is a simply convenience class: it allows us to compute both training and test losses using the same method.
Under the hood, it's still a plain Keras model. You could achieve the same functionality by inheriting from `tf.keras.Model` and overriding the `train_step` and `test_step` functions (see [the guide](https://keras.io/guides/customizing_what_happens_in_fit/) for details):
```
class NoBaseClassMovielensModel(tf.keras.Model):
def __init__(self, user_model, movie_model):
super().__init__()
self.movie_model: tf.keras.Model = movie_model
self.user_model: tf.keras.Model = user_model
self.task: tf.keras.layers.Layer = task
def train_step(self, features: Dict[Text, tf.Tensor]) -> tf.Tensor:
# Set up a gradient tape to record gradients.
with tf.GradientTape() as tape:
# Loss computation.
user_embeddings = self.user_model(features["user_id"])
positive_movie_embeddings = self.movie_model(features["movie_title"])
loss = self.task(user_embeddings, positive_movie_embeddings)
# Handle regularization losses as well.
regularization_loss = sum(self.losses)
total_loss = loss + regularization_loss
gradients = tape.gradient(total_loss, self.trainable_variables)
self.optimizer.apply_gradients(zip(gradients, self.trainable_variables))
metrics = {metric.name: metric.result() for metric in self.metrics}
metrics["loss"] = loss
metrics["regularization_loss"] = regularization_loss
metrics["total_loss"] = total_loss
return metrics
def test_step(self, features: Dict[Text, tf.Tensor]) -> tf.Tensor:
# Loss computation.
user_embeddings = self.user_model(features["user_id"])
positive_movie_embeddings = self.movie_model(features["movie_title"])
loss = self.task(user_embeddings, positive_movie_embeddings)
# Handle regularization losses as well.
regularization_loss = sum(self.losses)
total_loss = loss + regularization_loss
metrics = {metric.name: metric.result() for metric in self.metrics}
metrics["loss"] = loss
metrics["regularization_loss"] = regularization_loss
metrics["total_loss"] = total_loss
return metrics
```
In these tutorials, however, we stick to using the `tfrs.Model` base class to keep our focus on modelling and abstract away some of the boilerplate.
## Fitting and evaluating
After defining the model, we can use standard Keras fitting and evaluation routines to fit and evaluate the model.
Let's first instantiate the model.
```
model = MovielensModel(user_model, movie_model)
model.compile(optimizer=tf.keras.optimizers.Adagrad(learning_rate=0.1))
```
Then shuffle, batch, and cache the training and evaluation data.
```
cached_train = train.shuffle(100_000).batch(8192).cache()
cached_test = test.batch(4096).cache()
```
Then train the model:
```
model.fit(cached_train, epochs=3)
```
As the model trains, the loss is falling and a set of top-k retrieval metrics is updated. These tell us whether the true positive is in the top-k retrieved items from the entire candidate set. For example, a top-5 categorical accuracy metric of 0.2 would tell us that, on average, the true positive is in the top 5 retrieved items 20% of the time.
Note that, in this example, we evaluate the metrics during training as well as evaluation. Because this can be quite slow with large candidate sets, it may be prudent to turn metric calculation off in training, and only run it in evaluation.
Finally, we can evaluate our model on the test set:
```
model.evaluate(cached_test, return_dict=True)
```
Test set performance is much worse than training performance. This is due to two factors:
1. Our model is likely to perform better on the data that it has seen, simply because it can memorize it. This overfitting phenomenon is especially strong when models have many parameters. It can be mediated by model regularization and use of user and movie features that help the model generalize better to unseen data.
2. The model is re-recommending some of users' already watched movies. These known-positive watches can crowd out test movies out of top K recommendations.
The second phenomenon can be tackled by excluding previously seen movies from test recommendations. This approach is relatively common in the recommender systems literature, but we don't follow it in these tutorials. If not recommending past watches is important, we should expect appropriately specified models to learn this behaviour automatically from past user history and contextual information. Additionally, it is often appropriate to recommend the same item multiple times (say, an evergreen TV series or a regularly purchased item).
## Making predictions
Now that we have a model, we would like to be able to make predictions. We can use the `tfrs.layers.ann.BruteForce` layer to do this.
```
# Create a model that takes in raw query features, and
index = tfrs.layers.ann.BruteForce(model.user_model)
# recommends movies out of the entire movies dataset.
index.index(movies.batch(100).map(model.movie_model), movies)
# Get recommendations.
_, titles = index(tf.constant(["42"]))
print(f"Recommendations for user 42: {titles[0, :3]}")
```
Of course, the `BruteForce` layer is going to be too slow to serve a model with many possible candidates. The following sections shows how to speed this up by using an approximate retrieval index.
## Model serving
After the model is trained, we need a way to deploy it.
In a two-tower retrieval model, serving has two components:
- a serving query model, taking in features of the query and transforming them into a query embedding, and
- a serving candidate model. This most often takes the form of an approximate nearest neighbours (ANN) index which allows fast approximate lookup of candidates in response to a query produced by the query model.
### Exporting a query model to serving
Exporting the query model is easy: we can either serialize the Keras model directly, or export it to a `SavedModel` format to make it possible to serve using [TensorFlow Serving](https://www.tensorflow.org/tfx/guide/serving).
To export to a `SavedModel` format, we can do the following:
```
model_dir = './models'
!mkdir $model_dir
# Export the query model.
path = '{}/query_model'.format(model_dir)
model.user_model.save(path)
# Load the query model
loaded = tf.keras.models.load_model(path, compile=False)
query_embedding = loaded(tf.constant(["10"]))
print(f"Query embedding: {query_embedding[0, :3]}")
```
### Building a candidate ANN index
Exporting candidate representations is more involved. Firstly, we want to pre-compute them to make sure serving is fast; this is especially important if the candidate model is computationally intensive (for example, if it has many or wide layers; or uses complex representations for text or images). Secondly, we would like to take the precomputed representations and use them to construct a fast approximate retrieval index.
We can use [Annoy](https://github.com/spotify/annoy) to build such an index.
Annoy isn't included in the base TFRS package. To install it, run:
### We can now create the index object.
```
from annoy import AnnoyIndex
index = AnnoyIndex(embedding_dimension, "dot")
```
Then take the candidate dataset and transform its raw features into embeddings using the movie model:
```
print(movies)
movie_embeddings = movies.enumerate().map(lambda idx, title: (idx, title, model.movie_model(title)))
print(movie_embeddings.as_numpy_iterator().next())
```
And then index the movie_id, movie embedding pairs into our Annoy index:
```
%%time
movie_id_to_title = dict((idx, title) for idx, title, _ in movie_embeddings.as_numpy_iterator())
# We unbatch the dataset because Annoy accepts only scalar (id, embedding) pairs.
for movie_id, _, movie_embedding in movie_embeddings.as_numpy_iterator():
index.add_item(movie_id, movie_embedding)
# Build a 10-tree ANN index.
index.build(10)
```
We can then retrieve nearest neighbours:
```
for row in test.batch(1).take(3):
query_embedding = model.user_model(row["user_id"])[0]
candidates = index.get_nns_by_vector(query_embedding, 3)
print(f"User ID: {row['user_id']}, Candidates: {[movie_id_to_title[x] for x in candidates]}.")
print(type(candidates))
```
## Next steps
This concludes the retrieval tutorial.
To expand on what is presented here, have a look at:
1. Learning multi-task models: jointly optimizing for ratings and clicks.
2. Using movie metadata: building a more complex movie model to alleviate cold-start.
|
github_jupyter
|
##### Copyright 2018 The TF-Agents Authors.
```
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
```
# REINFORCE agent
<table class="tfo-notebook-buttons" align="left">
<td>
<a target="_blank" href="https://www.tensorflow.org/agents/tutorials/6_reinforce_tutorial">
<img src="https://www.tensorflow.org/images/tf_logo_32px.png" />
View on TensorFlow.org</a>
</td>
<td>
<a target="_blank" href="https://colab.research.google.com/github/tensorflow/agents/blob/master/docs/tutorials/6_reinforce_tutorial.ipynb">
<img src="https://www.tensorflow.org/images/colab_logo_32px.png" />
Run in Google Colab</a>
</td>
<td>
<a target="_blank" href="https://github.com/tensorflow/agents/blob/master/docs/tutorials/6_reinforce_tutorial.ipynb">
<img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />
View source on GitHub</a>
</td>
<td>
<a href="https://storage.googleapis.com/tensorflow_docs/agents/docs/tutorials/6_reinforce_tutorial.ipynb"><img src="https://www.tensorflow.org/images/download_logo_32px.png" />Download notebook</a>
</td>
</table>
## Introduction
This example shows how to train a [REINFORCE](http://www-anw.cs.umass.edu/~barto/courses/cs687/williams92simple.pdf) agent on the Cartpole environment using the TF-Agents library, similar to the [DQN tutorial](1_dqn_tutorial.ipynb).

We will walk you through all the components in a Reinforcement Learning (RL) pipeline for training, evaluation and data collection.
## Setup
If you haven't installed the following dependencies, run:
```
!sudo apt-get install -y xvfb ffmpeg
!pip install gym
!pip install 'imageio==2.4.0'
!pip install PILLOW
!pip install 'pyglet==1.3.2'
!pip install pyvirtualdisplay
!pip install tf-agents
from __future__ import absolute_import
from __future__ import division
from __future__ import print_function
import base64
import imageio
import IPython
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import PIL.Image
import pyvirtualdisplay
import tensorflow as tf
from tf_agents.agents.reinforce import reinforce_agent
from tf_agents.drivers import dynamic_step_driver
from tf_agents.environments import suite_gym
from tf_agents.environments import tf_py_environment
from tf_agents.eval import metric_utils
from tf_agents.metrics import tf_metrics
from tf_agents.networks import actor_distribution_network
from tf_agents.replay_buffers import tf_uniform_replay_buffer
from tf_agents.trajectories import trajectory
from tf_agents.utils import common
tf.compat.v1.enable_v2_behavior()
# Set up a virtual display for rendering OpenAI gym environments.
display = pyvirtualdisplay.Display(visible=0, size=(1400, 900)).start()
```
## Hyperparameters
```
env_name = "CartPole-v0" # @param {type:"string"}
num_iterations = 250 # @param {type:"integer"}
collect_episodes_per_iteration = 2 # @param {type:"integer"}
replay_buffer_capacity = 2000 # @param {type:"integer"}
fc_layer_params = (100,)
learning_rate = 1e-3 # @param {type:"number"}
log_interval = 25 # @param {type:"integer"}
num_eval_episodes = 10 # @param {type:"integer"}
eval_interval = 50 # @param {type:"integer"}
```
## Environment
Environments in RL represent the task or problem that we are trying to solve. Standard environments can be easily created in TF-Agents using `suites`. We have different `suites` for loading environments from sources such as the OpenAI Gym, Atari, DM Control, etc., given a string environment name.
Now let us load the CartPole environment from the OpenAI Gym suite.
```
env = suite_gym.load(env_name)
```
We can render this environment to see how it looks. A free-swinging pole is attached to a cart. The goal is to move the cart right or left in order to keep the pole pointing up.
```
#@test {"skip": true}
env.reset()
PIL.Image.fromarray(env.render())
```
The `time_step = environment.step(action)` statement takes `action` in the environment. The `TimeStep` tuple returned contains the environment's next observation and reward for that action. The `time_step_spec()` and `action_spec()` methods in the environment return the specifications (types, shapes, bounds) of the `time_step` and `action` respectively.
```
print('Observation Spec:')
print(env.time_step_spec().observation)
print('Action Spec:')
print(env.action_spec())
```
So, we see that observation is an array of 4 floats: the position and velocity of the cart, and the angular position and velocity of the pole. Since only two actions are possible (move left or move right), the `action_spec` is a scalar where 0 means "move left" and 1 means "move right."
```
time_step = env.reset()
print('Time step:')
print(time_step)
action = np.array(1, dtype=np.int32)
next_time_step = env.step(action)
print('Next time step:')
print(next_time_step)
```
Usually we create two environments: one for training and one for evaluation. Most environments are written in pure python, but they can be easily converted to TensorFlow using the `TFPyEnvironment` wrapper. The original environment's API uses numpy arrays, the `TFPyEnvironment` converts these to/from `Tensors` for you to more easily interact with TensorFlow policies and agents.
```
train_py_env = suite_gym.load(env_name)
eval_py_env = suite_gym.load(env_name)
train_env = tf_py_environment.TFPyEnvironment(train_py_env)
eval_env = tf_py_environment.TFPyEnvironment(eval_py_env)
```
## Agent
The algorithm that we use to solve an RL problem is represented as an `Agent`. In addition to the REINFORCE agent, TF-Agents provides standard implementations of a variety of `Agents` such as [DQN](https://storage.googleapis.com/deepmind-media/dqn/DQNNaturePaper.pdf), [DDPG](https://arxiv.org/pdf/1509.02971.pdf), [TD3](https://arxiv.org/pdf/1802.09477.pdf), [PPO](https://arxiv.org/abs/1707.06347) and [SAC](https://arxiv.org/abs/1801.01290).
To create a REINFORCE Agent, we first need an `Actor Network` that can learn to predict the action given an observation from the environment.
We can easily create an `Actor Network` using the specs of the observations and actions. We can specify the layers in the network which, in this example, is the `fc_layer_params` argument set to a tuple of `ints` representing the sizes of each hidden layer (see the Hyperparameters section above).
```
actor_net = actor_distribution_network.ActorDistributionNetwork(
train_env.observation_spec(),
train_env.action_spec(),
fc_layer_params=fc_layer_params)
```
We also need an `optimizer` to train the network we just created, and a `train_step_counter` variable to keep track of how many times the network was updated.
```
optimizer = tf.compat.v1.train.AdamOptimizer(learning_rate=learning_rate)
train_step_counter = tf.compat.v2.Variable(0)
tf_agent = reinforce_agent.ReinforceAgent(
train_env.time_step_spec(),
train_env.action_spec(),
actor_network=actor_net,
optimizer=optimizer,
normalize_returns=True,
train_step_counter=train_step_counter)
tf_agent.initialize()
```
## Policies
In TF-Agents, policies represent the standard notion of policies in RL: given a `time_step` produce an action or a distribution over actions. The main method is `policy_step = policy.step(time_step)` where `policy_step` is a named tuple `PolicyStep(action, state, info)`. The `policy_step.action` is the `action` to be applied to the environment, `state` represents the state for stateful (RNN) policies and `info` may contain auxiliary information such as log probabilities of the actions.
Agents contain two policies: the main policy that is used for evaluation/deployment (agent.policy) and another policy that is used for data collection (agent.collect_policy).
```
eval_policy = tf_agent.policy
collect_policy = tf_agent.collect_policy
```
## Metrics and Evaluation
The most common metric used to evaluate a policy is the average return. The return is the sum of rewards obtained while running a policy in an environment for an episode, and we usually average this over a few episodes. We can compute the average return metric as follows.
```
#@test {"skip": true}
def compute_avg_return(environment, policy, num_episodes=10):
total_return = 0.0
for _ in range(num_episodes):
time_step = environment.reset()
episode_return = 0.0
while not time_step.is_last():
action_step = policy.action(time_step)
time_step = environment.step(action_step.action)
episode_return += time_step.reward
total_return += episode_return
avg_return = total_return / num_episodes
return avg_return.numpy()[0]
# Please also see the metrics module for standard implementations of different
# metrics.
```
## Replay Buffer
In order to keep track of the data collected from the environment, we will use the TFUniformReplayBuffer. This replay buffer is constructed using specs describing the tensors that are to be stored, which can be obtained from the agent using `tf_agent.collect_data_spec`.
```
replay_buffer = tf_uniform_replay_buffer.TFUniformReplayBuffer(
data_spec=tf_agent.collect_data_spec,
batch_size=train_env.batch_size,
max_length=replay_buffer_capacity)
```
For most agents, the `collect_data_spec` is a `Trajectory` named tuple containing the observation, action, reward etc.
## Data Collection
As REINFORCE learns from whole episodes, we define a function to collect an episode using the given data collection policy and save the data (observations, actions, rewards etc.) as trajectories in the replay buffer.
```
#@test {"skip": true}
def collect_episode(environment, policy, num_episodes):
episode_counter = 0
environment.reset()
while episode_counter < num_episodes:
time_step = environment.current_time_step()
action_step = policy.action(time_step)
next_time_step = environment.step(action_step.action)
traj = trajectory.from_transition(time_step, action_step, next_time_step)
# Add trajectory to the replay buffer
replay_buffer.add_batch(traj)
if traj.is_boundary():
episode_counter += 1
# This loop is so common in RL, that we provide standard implementations of
# these. For more details see the drivers module.
```
## Training the agent
The training loop involves both collecting data from the environment and optimizing the agent's networks. Along the way, we will occasionally evaluate the agent's policy to see how we are doing.
The following will take ~3 minutes to run.
```
#@test {"skip": true}
try:
%%time
except:
pass
# (Optional) Optimize by wrapping some of the code in a graph using TF function.
tf_agent.train = common.function(tf_agent.train)
# Reset the train step
tf_agent.train_step_counter.assign(0)
# Evaluate the agent's policy once before training.
avg_return = compute_avg_return(eval_env, tf_agent.policy, num_eval_episodes)
returns = [avg_return]
for _ in range(num_iterations):
# Collect a few episodes using collect_policy and save to the replay buffer.
collect_episode(
train_env, tf_agent.collect_policy, collect_episodes_per_iteration)
# Use data from the buffer and update the agent's network.
experience = replay_buffer.gather_all()
train_loss = tf_agent.train(experience)
replay_buffer.clear()
step = tf_agent.train_step_counter.numpy()
if step % log_interval == 0:
print('step = {0}: loss = {1}'.format(step, train_loss.loss))
if step % eval_interval == 0:
avg_return = compute_avg_return(eval_env, tf_agent.policy, num_eval_episodes)
print('step = {0}: Average Return = {1}'.format(step, avg_return))
returns.append(avg_return)
```
## Visualization
### Plots
We can plot return vs global steps to see the performance of our agent. In `Cartpole-v0`, the environment gives a reward of +1 for every time step the pole stays up, and since the maximum number of steps is 200, the maximum possible return is also 200.
```
#@test {"skip": true}
steps = range(0, num_iterations + 1, eval_interval)
plt.plot(steps, returns)
plt.ylabel('Average Return')
plt.xlabel('Step')
plt.ylim(top=250)
```
### Videos
It is helpful to visualize the performance of an agent by rendering the environment at each step. Before we do that, let us first create a function to embed videos in this colab.
```
def embed_mp4(filename):
"""Embeds an mp4 file in the notebook."""
video = open(filename,'rb').read()
b64 = base64.b64encode(video)
tag = '''
<video width="640" height="480" controls>
<source src="data:video/mp4;base64,{0}" type="video/mp4">
Your browser does not support the video tag.
</video>'''.format(b64.decode())
return IPython.display.HTML(tag)
```
The following code visualizes the agent's policy for a few episodes:
```
num_episodes = 3
video_filename = 'imageio.mp4'
with imageio.get_writer(video_filename, fps=60) as video:
for _ in range(num_episodes):
time_step = eval_env.reset()
video.append_data(eval_py_env.render())
while not time_step.is_last():
action_step = tf_agent.policy.action(time_step)
time_step = eval_env.step(action_step.action)
video.append_data(eval_py_env.render())
embed_mp4(video_filename)
```
|
github_jupyter
|
```
import pandas as pd
import numpy as np
from tqdm import tqdm
tqdm.pandas()
import os, time, datetime
from sklearn.model_selection import train_test_split
from sklearn.metrics import roc_auc_score, f1_score, roc_curve, auc
import lightgbm as lgb
import xgboost as xgb
def format_time(elapsed):
'''
Takes a time in seconds and returns a string hh:mm:ss
'''
# Round to the nearest second.
elapsed_rounded = int(round((elapsed)))
# Format as hh:mm:ss
return str(datetime.timedelta(seconds=elapsed_rounded))
class SigirPreprocess():
def __init__(self, text_data_path):
self.text_data_path = text_data_path
self.train = None
self.dict_code_to_id = {}
self.dict_id_to_code = {}
self.list_tags = {}
self.sentences = []
self.labels = []
self.text_col = None
self.X_test = None
def prepare_data(self ):
catalog_eng= pd.read_csv(self.text_data_path+"data/catalog_english_taxonomy.tsv",sep="\t")
X_train= pd.read_csv(self.text_data_path+"data/X_train.tsv",sep="\t")
Y_train= pd.read_csv(self.text_data_path+"data/Y_train.tsv",sep="\t")
self.list_tags = list(Y_train['Prdtypecode'].unique())
for i,tag in enumerate(self.list_tags):
self.dict_code_to_id[tag] = i
self.dict_id_to_code[i]=tag
print(self.dict_code_to_id)
Y_train['labels']=Y_train['Prdtypecode'].map(self.dict_code_to_id)
train=pd.merge(left=X_train,right=Y_train,
how='left',left_on=['Integer_id','Image_id','Product_id'],
right_on=['Integer_id','Image_id','Product_id'])
prod_map=pd.Series(catalog_eng['Top level category'].values,
index=catalog_eng['Prdtypecode']).to_dict()
train['product'] = train['Prdtypecode'].map(prod_map)
train['title_len']=train['Title'].progress_apply(lambda x : len(x.split()) if pd.notna(x) else 0)
train['desc_len']=train['Description'].progress_apply(lambda x : len(x.split()) if pd.notna(x) else 0)
train['title_desc_len']=train['title_len'] + train['desc_len']
train.loc[train['Description'].isnull(), 'Description'] = " "
train['title_desc'] = train['Title'] + " " + train['Description']
self.train = train
def get_sentences(self, text_col, remove_null_rows=False):
self.text_col = text_col
if remove_null_rows==True:
new_train = self.train[self.train[text_col].notnull()]
else:
new_train = self.train.copy()
self.sentences = new_train[text_col].values
self.labels = new_train['labels'].values
def prepare_test(self, text_col, test_data_path, phase=1):
X_test=pd.read_csv(test_data_path+f"data/x_test_task1_phase{phase}.tsv",sep="\t")
X_test.loc[X_test['Description'].isnull(), 'Description'] = " "
X_test['title_desc'] = X_test['Title'] + " " + X_test['Description']
self.X_test = X_test
self.test_sentences = X_test[text_col].values
text_col = 'title_desc'
val_size = 0.1
random_state=2020
num_class = 27
do_gridsearch = False
kwargs = {'add_logits':['cam', 'fla']}
cam_path = '/../input/camembert-vec-256m768-10ep/'
flau_path = '/../input/flaubertlogits2107/'
res_path = '/../input/resnextfinal/'
cms_path = '/../input/crossmodal-v0/'
vca_path = '/../input/vec-concat-9093/'
vca_path_phase2 = '/../input/predictions-test-phase2-vec-fusion/'
aem_path = '/../input/addition-ensemble-latest/'
val_logits_path = {'cam':cam_path + 'validation_set_softmax_logits.npy',
'fla':flau_path + 'validation_set_softmax_logits.npy',
'res':res_path + 'Valid_resnext50_32x4d_phase1_softmax_logits.npy',
'vca':vca_path + 'softmax_logits_val_9093.npy',
'aem':aem_path + 'softmax_logits_val_add.npy'}
test_logits_path_phase1 = {'cam':cam_path+f'X_test_phase1_softmax_logits.npy',
'fla':flau_path + f'X_test_phase1_softmax_logits.npy',
'res':res_path + f'Test_resnext50_32x4d_phase1_softmax_logits.npy',
'vca':vca_path + f'softmax_logits_test_9093.npy'}
test_logits_path_phase2 = {'cam':cam_path+f'X_test_phase2_softmax_logits.npy',
'fla':flau_path + f'X_test_phase2_softmax_logits.npy',
'res':res_path + f'Test_resnext50_32x4d_phase2_softmax_logits.npy',
'vca':vca_path_phase2 + f'softmax_logits_test_phase2_9093.npy'}
## Get valdation dataset from original train dataset
Preprocess = SigirPreprocess("/../input/textphase1/")
Preprocess.prepare_data()
Preprocess.get_sentences(text_col, True)
full_data = Preprocess.train
labels = Preprocess.labels
index = full_data.Integer_id
tr_index, val_index, tr_labels, val_labels = train_test_split(index, labels,
stratify=labels,
random_state=random_state,
test_size=val_size)
train_data = full_data.loc[tr_index, :]
train_data.reset_index(inplace=True, drop=True)
val_data = full_data.loc[val_index, :]
val_data.reset_index(inplace=True, drop=True)
full_data.loc[val_index, 'sample'] = 'val'
full_data['sample'].fillna('train', inplace=True)
def preparelogits_df(logit_paths, df=None, val_labels=None, **kwargs):
### Prepare and combine Logits data with original validation dataset
logits_dict = {}
dfs_dict = {}
for key, logit_path in logit_paths.items():
logits_dict[key] = np.load(logit_path)
dfs_dict[key] = pd.DataFrame(logits_dict[key],
columns=[key + "_" + str(i) for i in range(1,28)])
print("Shape of logit arrays: {}", logits_dict[key].shape)
if kwargs['add_logits']:
if len(kwargs['add_logits'])>0:
add_str = '_'.join(kwargs['add_logits'])
logits_dict[add_str] = logits_dict[kwargs['add_logits'][0]]
for k in kwargs['add_logits'][1:]:
logits_dict[add_str] += logits_dict[k]
logits_dict[add_str] = logits_dict[add_str]/len(kwargs['add_logits'])
dfs_dict[add_str] = pd.DataFrame(logits_dict[add_str],
columns=[add_str + "_" + str(i) for i in range(1,28)])
print("Shape of logit arrays: {}", logits_dict[add_str].shape)
if type(val_labels) == np.ndarray:
for key,logits in logits_dict.items():
print("""Validation F1 scores for {} logits: {} """.format(key,
f1_score(val_labels, np.argmax(logits, axis=1), average='macro')))
df = pd.concat([df] + list(dfs_dict.values()), axis=1)
return df
val_data = preparelogits_df(val_logits_path, df=val_data,
val_labels=val_labels, **kwargs)
```
# Model Data Prep
```
df_log = val_data.copy()
probas_cols = ["fla_" + str(i) for i in range(1,28)] + ["cam_" + str(i) for i in range(1,28)] +\
["res_" + str(i) for i in range(1,28)] \
+ ["vca_" + str(i) for i in range(1,28)] \
X = df_log[probas_cols]
y = df_log['labels'].values
X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y, test_size=0.2, random_state=random_state)
from scipy.stats import randint as sp_randint
from scipy.stats import uniform as sp_uniform
from sklearn.model_selection import RandomizedSearchCV, GridSearchCV
n_HP_points_to_test = 100
param_test ={'num_leaves': sp_randint(6, 50),
'min_child_samples': sp_randint(100, 500),
'min_child_weight': [1e-5, 1e-3, 1e-2, 1e-1, 1, 1e1, 1e2, 1e3, 1e4],
'subsample': sp_uniform(loc=0.2, scale=0.8),
'colsample_bytree': sp_uniform(loc=0.4, scale=0.6),
'reg_alpha': [0, 1e-1, 1, 2, 5, 7, 10, 50, 100],
'reg_lambda': [0, 1e-1, 1, 5, 10, 20, 50, 100],
# "bagging_fraction" : [0.5, 0.6, 0.7, 0.8, 0.9],
# "feature_fraction":[0.5, 0.6, 0.7, 0.8, 0.9]
}
fit_params={
"early_stopping_rounds":100,
"eval_metric" : 'multi_logloss',
"eval_set" : [(X_test,y_test)],
'eval_names': ['valid'],
#'callbacks': [lgb.reset_parameter(learning_rate=learning_rate_010_decay_power_099)],
'verbose': 100,
'categorical_feature': 'auto'}
clf = lgb.LGBMClassifier(num_iteration=1000, max_depth=-1, random_state=314, silent=True,
metric='multi_logloss', n_jobs=4, early_stopping_rounds=100,
num_class=num_class, objective= "multiclass")
gs = RandomizedSearchCV(
estimator=clf, param_distributions=param_test,
n_iter=n_HP_points_to_test,
cv=3,
refit=True,
random_state=314,
verbose=True)
if do_gridsearch==True:
gs.fit(X_train, y_train, **fit_params)
print('Best score reached: {} with params: {} '.format(gs.best_score_, gs.best_params_))
# opt_parameters = gs.best_params_
opt_parameters = {'colsample_bytree': 0.5284213741879101, 'min_child_samples': 125,
'min_child_weight': 10.0, 'num_leaves': 22,
'reg_alpha': 0.1, 'reg_lambda': 20, 'subsample': 0.3080033455431848}
```
# Model Training
```
### Run lightgbm to get weights for different class logits
t0 = time.time()
model_met = 'fit' #'xgb'#'train' #fit
params = {
"objective" : "multiclass",
"num_class" : num_class,
"num_leaves" : 60,
"max_depth": -1,
"learning_rate" : 0.01,
"bagging_fraction" : 0.9, # subsample
"feature_fraction" : 0.9, # colsample_bytree
"bagging_freq" : 5, # subsample_freq
"bagging_seed" : 2018,
"verbosity" : -1 }
lgtrain, lgval = lgb.Dataset(X_train, y_train), lgb.Dataset(X_test, y_test)
if model_met == 'train':
params.update(opt_parameters)
params.update(fit_params)
lgbmodel = lgb.train(params, lgtrain, valid_sets=[lgtrain, lgval],
num_iterations = 1000, metric= 'multi_logloss')
train_logits = lgbmodel.predict(X_train)
test_logits = lgbmodel.predict(X_test)
train_pred = np.argmax(train_logits, axis=1)
test_pred = np.argmax(test_logits, axis=1)
elif model_met == 'xgb':
dtrain = xgb.DMatrix(X_train, label=y_train)
dtrain.save_binary('xgb_train.buffer')
dtest = xgb.DMatrix(X_test, label=y_test)
num_round = 200
xgb_param = {'max_depth': 5, 'eta': 0.1, 'seed':2020, 'verbosity':1,
'objective': 'multi:softmax', 'num_class':num_class}
xgb_param['nthread'] = 4
xgb_param['eval_metric'] = 'mlogloss'
evallist = [(dtest, 'eval'), (dtrain, 'train')]
bst = xgb.train(xgb_param, dtrain, num_round, evallist
, early_stopping_rounds=10
)
train_logits = bst.predict(xgb.DMatrix(X_train), ntree_limit=bst.best_ntree_limit)
test_logits = bst.predict(xgb.DMatrix(X_test), ntree_limit=bst.best_ntree_limit)
train_pred = train_logits
test_pred = test_logits
else:
lgbmodel = lgb.LGBMClassifier(**clf.get_params())
#set optimal parameters
lgbmodel.set_params(**opt_parameters)
lgbmodel.fit(X_train, y_train, **fit_params)
train_logits = lgbmodel.predict(X_train)
test_logits = lgbmodel.predict(X_test)
train_pred = train_logits
test_pred = test_logits
print("Validation F1: {} and Training F1: {} ".format(
f1_score(y_test, test_pred, average='macro'),
f1_score(y_train, train_pred, average='macro')))
if model_met == 'train':
feat_imp = pd.DataFrame({'feature':probas_cols,
'logit_kind': [i.split('_')[0] for i in probas_cols],
'imp':lgbmodel.feature_importance()/sum(lgbmodel.feature_importance())})
lgbmodel.save_model('lgb_classifier_81feats.txt', num_iteration=lgbmodel.best_iteration)
print("""Feature Importances by logits group:
""", feat_imp.groupby(['logit_kind'])['imp'].sum())
else:
feat_imp = pd.DataFrame({'feature':probas_cols,
'logit_kind': [i.split('_')[0] for i in probas_cols],
'imp':lgbmodel.feature_importances_/sum(lgbmodel.feature_importances_)})
print("""Feature Importances by logits group:
""", feat_imp.groupby(['logit_kind'])['imp'].sum())
import shap
explainer = shap.TreeExplainer(lgbmodel)
shap_values = explainer.shap_values(X)
print("Time Elapsed: {:}.".format(format_time(time.time() - t0)))
for n, path in enumerate(['/kaggle/input/textphase1/',
'/kaggle/input/testphase2/']):
phase = n+1
if phase==1:
test_logits_path = test_logits_path_phase1
else:
test_logits_path = test_logits_path_phase2
Preprocess.prepare_test(text_col, path, phase)
X_test_phase1= Preprocess.X_test
test_phase1 = preparelogits_df(test_logits_path,
df=X_test_phase1, val_labels=None, **kwargs)
phase1_logits = lgbmodel.predict(test_phase1[probas_cols].values)
if model_met == 'train':
predictions = np.argmax(phase1_logits, axis=1)
elif model_met == 'xgb':
phase1_logits = bst.predict(xgb.DMatrix(test_phase1[probas_cols]),
ntree_limit=bst.best_ntree_limit)
predictions = phase1_logits
else:
predictions = phase1_logits
X_test_phase1['prediction_model']= predictions
X_test_phase1['Prdtypecode']=X_test_phase1['prediction_model'].map(Preprocess.dict_id_to_code)
print(X_test_phase1['Prdtypecode'].value_counts())
X_test_phase1=X_test_phase1.drop(['prediction_model','Title','Description'],axis=1)
X_test_phase1.to_csv(f'y_test_task1_phase{phase}_pred_.tsv',sep='\t',index=False)
```
|
github_jupyter
|
# Example usage of the O-C tools
## This example shows how to construct and fit with MCMC the O-C diagram of the RR Lyrae star OGLE-BLG-RRLYR-02950
### We start with importing some libraries
```
import numpy as np
import oc_tools as octs
```
### We read in the data, set the period used to construct the O-C diagram (and to fold the light curve to construct the template curves, etc.), and the orders of the Fourier series we will fit to the light curve in the first and second iterations in the process
```
who = "06498"
period = 0.589490
order1 = 10
order2 = 15
jd3, mag3 = np.loadtxt('data/{:s}.o3'.format(who), usecols=[0,1], unpack=True)
jd4, mag4 = np.loadtxt('data/{:s}.o4'.format(who), usecols=[0,1], unpack=True)
```
### We correct for possible average magnitude and amplitude differences between The OGLE-III and IV photometries by moving the intensity average of the former to the intensity average measured for the latter
### The variables "jd" and "mag" contain the merged timings and magnitudes of the OGLE-III + IV photometry, wich are used from hereon to calculate the O-C values
```
mag3_shift=octs.shift_int(jd3, mag3, jd4, mag4, order1, period, plot=True)
jd = np.hstack((jd3,jd4))
mag = np.hstack((mag3_shift, mag4))
```
### Calling the split_lc_seasons() function provides us with an array containing masks splitting the combined light curve into short sections, depending on the number of points
### Optionally, the default splitting can be overriden by using the optional parameters "limits" and "into". For example, calling the function as:
octs.split_lc_seasons(jd, plot=True, mag = mag, limits = np.array((0, 8, np.inf)), into = np.array((0, 2)))
### will always split seasons with at least nine points into two separate segments
```
splits = octs.split_lc_seasons(jd, plot=True, mag = mag)
```
### The function calc_oc_points() fits the light curve of the variable to produce a template, and uses it to determine the O-C points of the individual segments
```
oc_jd, oc_oc = octs.calc_oc_points(jd, mag, period, order1, splits, figure=True)
```
### We make a guess at the binary parameters
```
e = 0.37
P_orb = 2800.
T_peri = 6040
a_sini = 0.011
omega = -0.7
a= -8e-03
b= 3e-06
c= -3.5e-10
params = np.asarray((e, P_orb, T_peri, a_sini, omega, a, b, c))
lower_bounds = np.array((0., 100., -np.inf, 0.0, -np.inf, -np.inf, -np.inf, -np.inf))
upper_bounds = np.array((0.99, 6000., np.inf, 1.0, np.inf, np.inf, np.inf, np.inf))
```
### We use the above guesses as the starting point (dashed grey line on the plot below) to find the O-C LTTE solution of the first iteration of our procedure. The yellow line on the plot shows the fit. The vertical blue bar shows the timing of the periastron passage
### Note that in this function also provides the timings of the individual observations corrected for this initial O-C solution
```
params2, jd2 = octs.fit_oc1(oc_jd, oc_oc, jd, params, lower_bounds, upper_bounds)
```
### We use the initial solution as the starting point for the MCMC fit, therefore we prepare it first by transforming $e$ and $\omega$ to $\sqrt{e}\sin{\omega}$ and $\sqrt{e}\sin{\omega}$
### For each parameter, we also have a lower and higher limit in its prior, but the values given for $\sqrt{e}\sin{\omega}$ and $\sqrt{e}\sin{\omega}$ are ignored, as these are handled separately within the function checking the priors
```
start = np.zeros_like(params2)
start[0:3] = params2[1:4]
start[3] = np.sqrt(params2[0]) * np.sin(params2[4])
start[4] = np.sqrt(params2[0]) * np.cos(params2[4])
start[5:] = params2[5:]
prior_ranges = np.asanyarray([[start[0]*0.9, start[0]*1.1],
[start[1]-start[0]/4., start[1]+start[0]/4.],
[0., 0.057754266],
[0., 0.],
[0., 0.],
[-1., 1.],
[-1e-4, 1e-4],
[-1e-8, 1e-8]])
```
### We set a random seed to get reproducible results, then prepare the initial positions of the 200 walkers we are using during the fitting. During this, we check explicitly that these correspond to a position with a finite prior (i.e., they are not outside of the prior ranges defined above)
```
np.random.seed(0)
walkers = 200
random_scales = np.array((1e+1, 1e+1, 1e-4, 1e-2, 1e-2, 1e-3, 2e-7, 5e-11))
pos = np.zeros((walkers, start.size))
for i in range(walkers):
pos[i,:] = start + random_scales * np.random.normal(size=8)
while np.isinf(octs.log_prior(pos[i,:], prior_ranges)):
pos[i,:] = start + random_scales * np.random.normal(size=8)
```
### We recalculate the O-C points, but this time we use a higher-order Fourier series to fit the light curve with the modified timings, and we also calculate errors using bootstrapping
```
oc_jd, oc_oc, oc_sd = octs.calc_oc_points(jd, mag, period, order2, splits,
bootstrap_times = 500, jd_mod = jd2,
figure=True)
```
### We fit the O-C points measured above using MCMC by calling the run_mcmc() function
### We plot both the fit, as well as the triangle plot showing the two- (and one-)dimensional posterior distributions (these can be suppressed by setting the optional parameters "plot_oc" and "plot_triangle" to False)
```
sampler, fit_mcmc, oc_sigmas, param_means, param_sigmas, fit_at_points, K =\
octs.run_mcmc(oc_jd, oc_oc, oc_sd,
prior_ranges, pos,
nsteps = 31000, discard = 1000,
thin = 300, processes=1)
```
## The estimated LTTE parameters are:
```
print("Orbital period: {:d} +- {:d} [d]".format(int(param_means[0]),
int(param_sigmas[0])))
print("Projected semi-major axis: {:.3f} +- {:.3f} [AU]".format(param_means[2]*173.144633,
param_sigmas[2]*173.144633))
print("Eccentricity: {:.3f} +- {:.3f}".format(param_means[3],
param_sigmas[3]))
print("Argumen of periastron: {:+4d} +- {:d} [deg]".format(int(param_means[4]*180/np.pi),
int(param_sigmas[4]*180/np.pi)))
print("Periastron passage time: {:d} +- {:d} [HJD-2450000]".format(int(param_means[1]),
int(param_sigmas[1])))
print("Period-change rate: {:+.3f} +- {:.3f} [d/Myr] ".format(param_means[7]*365.2422*2e6*period,
param_sigmas[7]*365.2422*2e6*period))
print("RV semi-amplitude: {:5.2f} +- {:.2f} [km/s]".format(K[0], K[1]))
print("Mass function: {:.5f} +- {:.5f} [M_Sun]".format(K[2], K[3]))
```
|
github_jupyter
|
# Consensus Optimization
This notebook contains the code for the toy experiment in the paper [The Numerics of GANs](https://arxiv.org/abs/1705.10461).
```
%load_ext autoreload
%autoreload 2
import tensorflow as tf
from tensorflow.contrib import slim
import numpy as np
import scipy as sp
from scipy import stats
from matplotlib import pyplot as plt
import sys, os
from tqdm import tqdm_notebook
tf.reset_default_graph()
def kde(mu, tau, bbox=[-5, 5, -5, 5], save_file="", xlabel="", ylabel="", cmap='Blues'):
values = np.vstack([mu, tau])
kernel = sp.stats.gaussian_kde(values)
fig, ax = plt.subplots()
ax.axis(bbox)
ax.set_aspect(abs(bbox[1]-bbox[0])/abs(bbox[3]-bbox[2]))
ax.set_xlabel(xlabel)
ax.set_ylabel(ylabel)
plt.tick_params(
axis='x', # changes apply to the x-axis
which='both', # both major and minor ticks are affected
bottom='off', # ticks along the bottom edge are off
top='off', # ticks along the top edge are off
labelbottom='off') # labels along the bottom edge are off
plt.tick_params(
axis='y', # changes apply to the x-axis
which='both', # both major and minor ticks are affected
left='off', # ticks along the bottom edge are off
right='off', # ticks along the top edge are off
labelleft='off') # labels along the bottom edge are off
xx, yy = np.mgrid[bbox[0]:bbox[1]:300j, bbox[2]:bbox[3]:300j]
positions = np.vstack([xx.ravel(), yy.ravel()])
f = np.reshape(kernel(positions).T, xx.shape)
cfset = ax.contourf(xx, yy, f, cmap=cmap)
if save_file != "":
plt.savefig(save_file, bbox_inches='tight')
plt.close(fig)
else:
plt.show()
def complex_scatter(points, bbox=None, save_file="", xlabel="real part", ylabel="imaginary part", cmap='Blues'):
fig, ax = plt.subplots()
if bbox is not None:
ax.axis(bbox)
ax.set_xlabel(xlabel)
ax.set_ylabel(ylabel)
xx = [p.real for p in points]
yy = [p.imag for p in points]
plt.plot(xx, yy, 'X')
plt.grid()
if save_file != "":
plt.savefig(save_file, bbox_inches='tight')
plt.close(fig)
else:
plt.show()
# Parameters
learning_rate = 1e-4
reg_param = 10.
batch_size = 512
z_dim = 16
sigma = 0.01
method = 'conopt'
divergence = 'standard'
outdir = os.path.join('gifs', method)
niter = 50000
n_save = 500
bbox = [-1.6, 1.6, -1.6, 1.6]
do_eigen = True
# Target distribution
mus = np.vstack([np.cos(2*np.pi*k/8), np.sin(2*np.pi*k/8)] for k in range(batch_size))
x_real = mus + sigma*tf.random_normal([batch_size, 2])
# Model
def generator_func(z):
net = slim.fully_connected(z, 16)
net = slim.fully_connected(net, 16)
net = slim.fully_connected(net, 16)
net = slim.fully_connected(net, 16)
x = slim.fully_connected(net, 2, activation_fn=None)
return x
def discriminator_func(x):
# Network
net = slim.fully_connected(x, 16)
net = slim.fully_connected(net, 16)
net = slim.fully_connected(net, 16)
net = slim.fully_connected(net, 16)
logits = slim.fully_connected(net, 1, activation_fn=None)
out = tf.squeeze(logits, -1)
return out
generator = tf.make_template('generator', generator_func)
discriminator = tf.make_template('discriminator', discriminator_func)
z = tf.random_normal([batch_size, z_dim])
x_fake = generator(z)
d_out_real = discriminator(x_real)
d_out_fake = discriminator(x_fake)
# Loss
if divergence == 'standard':
d_loss_real = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(
logits=d_out_real, labels=tf.ones_like(d_out_real)
))
d_loss_fake = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(
logits=d_out_fake, labels=tf.zeros_like(d_out_fake)
))
d_loss = d_loss_real + d_loss_fake
g_loss = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(
logits=d_out_fake, labels=tf.ones_like(d_out_fake)
))
elif divergence == 'JS':
d_loss_real = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(
logits=d_out_real, labels=tf.ones_like(d_out_real)
))
d_loss_fake = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(
logits=d_out_fake, labels=tf.zeros_like(d_out_fake)
))
d_loss = d_loss_real + d_loss_fake
g_loss = -d_loss
elif divergence == 'indicator':
d_loss = tf.reduce_mean(d_out_real - d_out_fake)
g_loss = -d_loss
else:
raise NotImplementedError
g_vars = tf.get_collection(tf.GraphKeys.TRAINABLE_VARIABLES, scope='generator')
d_vars = tf.get_collection(tf.GraphKeys.TRAINABLE_VARIABLES, scope='discriminator')
optimizer = tf.train.RMSPropOptimizer(learning_rate, use_locking=True)
# optimizer = tf.train.GradientDescentOptimizer(learning_rate, use_locking=True)
# Compute gradients
d_grads = tf.gradients(d_loss, d_vars)
g_grads = tf.gradients(g_loss, g_vars)
# Merge variable and gradient lists
variables = d_vars + g_vars
grads = d_grads + g_grads
if method == 'simga':
apply_vec = list(zip(grads, variables))
elif method == 'conopt':
# Reguliarizer
reg = 0.5 * sum(
tf.reduce_sum(tf.square(g)) for g in grads
)
# Jacobian times gradiant
Jgrads = tf.gradients(reg, variables)
apply_vec = [
(g + reg_param * Jg, v)
for (g, Jg, v) in zip(grads, Jgrads, variables) if Jg is not None
]
else:
raise NotImplementedError
with tf.control_dependencies([g for (g, v) in apply_vec]):
train_op = optimizer.apply_gradients(apply_vec)
if do_eigen:
jacobian_rows = []
g_grads = tf.gradients(g_loss, g_vars)
g_grads = [-g for g in g_grads]
d_grads = tf.gradients(d_loss, d_vars)
d_grads = [-g for g in d_grads]
for g in tqdm_notebook(g_grads + d_grads):
g = tf.reshape(g, [-1])
len_g = int(g.get_shape()[0])
for i in tqdm_notebook(range(len_g)):
g_row = tf.gradients(g[i], g_vars)
d_row = tf.gradients(g[i], d_vars)
jacobian_rows.append(g_row + d_row)
def get_J(J_rows):
J_rows_linear = [np.concatenate([g.flatten() for g in row]) for row in J_rows]
J = np.array(J_rows_linear)
return J
def process_J(J, save_file, bbox=None):
eig, eigv = np.linalg.eig(J)
eig_real = np.array([p.real for p in eig])
complex_scatter(eig, save_file=save_file, bbox=bbox)
def process_J_conopt(J, reg, save_file, bbox=None):
J2 = J - reg * np.dot(J.T, J)
eig, eigv = np.linalg.eig(J2)
eig_real = np.array([p.real for p in eig])
complex_scatter(eig, save_file=save_file, bbox=bbox)
sess = tf.InteractiveSession()
sess.run(tf.global_variables_initializer())
# Real distribution
x_out = np.concatenate([sess.run(x_real) for i in range(5)], axis=0)
kde(x_out[:, 0], x_out[:, 1], bbox=bbox, cmap='Reds', save_file='gt.png')
if not os.path.exists(outdir):
os.makedirs(outdir)
eigrawdir = os.path.join(outdir, 'eigs_raw')
if not os.path.exists(eigrawdir):
os.makedirs(eigrawdir)
eigdir = os.path.join(outdir, 'eigs')
if not os.path.exists(eigdir):
os.makedirs(eigdir)
eigdir_conopt = os.path.join(outdir, 'eigs_conopt')
if not os.path.exists(eigdir_conopt):
os.makedirs(eigdir_conopt)
ztest = [np.random.randn(batch_size, z_dim) for i in range(5)]
progress = tqdm_notebook(range(niter))
if do_eigen:
J_rows = sess.run(jacobian_rows)
J = get_J(J_rows)
for i in progress:
sess.run(train_op)
d_loss_out, g_loss_out = sess.run([d_loss, g_loss])
if do_eigen and i % 500 == 0:
J[:, :] = 0.
for k in range(10):
J_rows = sess.run(jacobian_rows)
J += get_J(J_rows)/10.
with open(os.path.join(eigrawdir, 'J_%d.npz' % i), 'wb') as f:
np.save(f, J)
progress.set_description('d_loss = %.4f, g_loss =%.4f' % (d_loss_out, g_loss_out))
if i % n_save == 0:
x_out = np.concatenate([sess.run(x_fake, feed_dict={z: zt}) for zt in ztest], axis=0)
kde(x_out[:, 0], x_out[:, 1], bbox=bbox, save_file=os.path.join(outdir,'%d.png' % i))
import re
import glob
import matplotlib
matplotlib.rcParams.update({'font.size': 16})
pattern = r'J_(?P<it>0).npz'
bbox = [-3.5, 0.75, -1.2, 1.2]
eigrawdir = os.path.join(outdir, 'eigs_raw')
if not os.path.exists(eigrawdir):
os.makedirs(eigrawdir)
eigdir = os.path.join(outdir, 'eigs')
if not os.path.exists(eigdir):
os.makedirs(eigdir)
eigdir_conopt = os.path.join(outdir, 'eigs_conopt')
if not os.path.exists(eigdir_conopt):
os.makedirs(eigdir_conopt)
out_files = glob.glob(os.path.join(eigrawdir, '*.npz'))
matches = [re.fullmatch(pattern, os.path.basename(s)) for s in out_files]
matches = [m for m in matches if m is not None]
for m in tqdm_notebook(matches):
it = int(m.group('it'))
J = np.load(os.path.join(eigrawdir, m.group()))
process_J(J, save_file=os.path.join(eigdir, '%d.png' % it), bbox=bbox)
process_J_conopt(J, reg=reg_param, save_file=os.path.join(eigdir_conopt, '%d.png' % it), bbox=bbox)
```
|
github_jupyter
|
<a href="https://colab.research.google.com/github/bhuwanupadhyay/codes/blob/main/ipynbs/reshape_demo.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
pip install pydicom
# Import tensorflow
import logging
import tensorflow as tf
import keras.backend as K
# Helper libraries
import math
import numpy as np
import pandas as pd
import pydicom
import os
import sys
import time
# Imports for dataset manipulation
from sklearn.model_selection import train_test_split
from keras.preprocessing.image import ImageDataGenerator
# Improve progress bar display
import tqdm
import tqdm.auto
tqdm.tqdm = tqdm.auto.tqdm
#tf.enable_eager_execution() #comment this out if causing errors
logger = tf.get_logger()
logger.setLevel(logging.DEBUG)
### SET MODEL CONFIGURATIONS ###
# Data Loading
CSV_PATH = 'label_data/CCC_clean.csv'
IMAGE_BASE_PATH = './data/'
test_size_percent = 0.15 # percent of total data reserved for testing
print(IMAGE_BASE_PATH)
# Data Augmentation
mirror_im = False
# Loss
lambda_coord = 5
epsilon = 0.00001
# Learning
step_size = 0.00001
BATCH_SIZE = 5
num_epochs = 1
# Saving
shape_path = 'trained_model/model_shape.json'
weight_path = 'trained_model/model_weights.h5'
# TensorBoard
tb_graph = False
tb_update_freq = 'batch'
### GET THE DATASET AND PREPROCESS IT ###
print("Loading and processing data\n")
data_frame = pd.read_csv(CSV_PATH)
"""
Construct numpy ndarrays from the loaded csv to use as training
and testing datasets.
"""
# zip all points for each image label together into a tuple
points = zip(data_frame['start_x'], data_frame['start_y'],
data_frame['end_x'], data_frame['end_y'])
img_paths = data_frame['imgPath']
def path_to_image(path):
"""
Load a matrix of pixel values from the DICOM image stored at the
input path.
@param path - string, relative path (from IMAGE_BASE_PATH) to
a DICOM file
@return image - numpy ndarray (int), 2D matrix of pixel
values of the image loaded from path
"""
# load image from path as numpy array
image = pydicom.dcmread(os.path.join(IMAGE_BASE_PATH, path)).pixel_array
return image
# normalize dicom image pixel values to 0-1 range
def normalize_image(img):
"""
Normalize the pixel values in img to be withing the range
of 0 to 1.
@param img - numpy ndarray, 2D matrix of pixel values
@return img - numpy ndarray (float), 2D matrix of pixel values, every
element is valued between 0 and 1 (inclusive)
"""
img = img.astype(np.float32)
img += abs(np.amin(img)) # account for negatives
img /= np.amax(img)
return img
# normalize the ground truth bounding box labels wrt image dimensions
def normalize_points(points):
"""
Normalize values in points to be within the range of 0 to 1.
@param points - 1x4 tuple, elements valued in the range of 0
512 (inclusive). This is known from the nature
of the dataset used in this program
@return - 1x4 numpy ndarray (float), elements valued in range
0 to 1 (inclusive)
"""
imDims = 512.0 # each image in our dataset is 512x512
points = list(points)
for i in range(len(points)):
points[i] /= imDims
return np.array(points).astype(np.float32)
"""
Convert the numpy array of paths to the DICOM images to pixel
matrices that have been normalized to a 0-1 range.
Also normalize the bounding box labels to make it easier for
the model to predict on them.
"""
# apply preprocessing functions
points = map(normalize_points, points)
imgs = map(path_to_image, img_paths)
imgs = map(normalize_image, imgs)
print(list(imgs))
# reshape input image data to 4D shape (as expected by the model)
# and cast all data to np arrays (just in case)
imgs = np.array(imgs)
points = np.array(points)
imgs = imgs.reshape((-1, 512, 512, 1))
```
|
github_jupyter
|
```
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
EXPERIMENT = 'bivariate_power'
TAG = ''
df = pd.read_csv(f'./results/{EXPERIMENT}_results{TAG}.csv', sep=', ', engine='python')
plot_df = df
x_var_rename_dict = {
'sample_size': '# Samples',
'Number of environments': '# Environments',
'Fraction of shifting mechanisms': 'Shift fraction',
'dag_density': 'Edge density',
'n_variables': '# Variables',
}
plot_df = df.rename(
x_var_rename_dict, axis=1
).rename(
{'Method': 'Test', 'Soft': 'Score'}, axis=1
).replace(
{
'er': 'Erdos-Renyi',
'ba': 'Hub',
'PC (pool all)': 'Full PC (oracle)',
'Full PC (KCI)': r'Pooled PC (KCI) [25]',
'Min changes (oracle)': 'MSS (oracle)',
'Min changes (KCI)': 'MSS (KCI)',
'Min changes (GAM)': 'MSS (GAM)',
'Min changes (Linear)': 'MSS (Linear)',
'Min changes (FisherZ)': 'MSS (FisherZ)',
'MC': r'MC [11]',
False: 'Hard',
True: 'Soft',
}
)
plot_df = plot_df.loc[
(~plot_df['Test'].isin(['Full PC (oracle)', 'MSS (oracle)'])) &
(plot_df['# Environments'] == 2) &
(plot_df['Score'] == 'Hard')
]
plot_df = plot_df.replace({
'[[];[0]]': 'P(X1)',
'[[];[1]]': 'P(X2|X1)',
'[[];[]]': 'Neither',
'[[];[0;1]]': 'Both',
})
plot_df['Test'].unique()
intv_targets = ['P(X1)', 'P(X2|X1)', 'Neither', 'Both']
ax_var = 'intervention_targets'
for targets in intv_targets:
display(plot_df[plot_df[ax_var] == targets].groupby('Test').mean().reset_index().head(3))
sns.set_context('paper')
fig, axes = plt.subplots(1, 4, sharey=True, sharex=True, figsize=(7.5, 2.5))
intv_targets = ['P(X1)', 'P(X2|X1)', 'Neither', 'Both']
ax_var = 'intervention_targets'
x_var = 'Precision' # 'False orientation rate' #
y_var = 'Recall' # 'True orientation rate'#
hue = 'Test'
for targets, ax in zip(intv_targets, axes.flatten()):
mean_df = plot_df[plot_df[ax_var] == targets].groupby('Test').mean().reset_index()
std_df = plot_df[plot_df[ax_var] == targets].groupby('Test')[['Precision', 'Recall']].std().reset_index()
std_df.rename(
{'Precision': 'Precision std', 'Recall': 'Recall std'}, axis=1
)
g = sns.scatterplot(
data=plot_df[plot_df[ax_var] == targets].groupby('Test').mean().reset_index(),
x=x_var,
y=y_var,
hue=hue,
ax=ax,
# markers=['d', 'P', 's'],
palette=[
sns.color_palette("tab10")[i]
for i in [2, 3, 4, 5, 7, 6] # 3, 4, 5,
],
hue_order=[
'MSS (KCI)',
'MSS (GAM)',
'MSS (FisherZ)',
'MSS (Linear)',
'Pooled PC (KCI) [25]',
'MC [11]',
],
legend='full',
# alpha=1,
s=100
)
# ax.axvline(0.05, ls=':', c='grey')
ax.set_title(f'Shift in {targets}')
plt.legend(bbox_to_anchor=(1.05, 1), loc=2, borderaxespad=0.)
for ax in axes[:-1]:
ax.get_legend().remove()
# ax.set_ylim([0, 1])
# ax.set_xlim([0, 1])
plt.tight_layout()
plt.savefig('./figures/bivariate_power_plots.pdf')
plt.show()
```
|
github_jupyter
|
# This Notebook uses a Session Event Dataset from E-Commerce Website (https://www.kaggle.com/mkechinov/ecommerce-behavior-data-from-multi-category-store and https://rees46.com/) to build an Outlier Detection based on an Autoencoder.
```
import mlflow
import numpy as np
import os
import shutil
import pandas as pd
import tensorflow as tf
import tensorflow.keras as keras
import tensorflow_hub as hub
from itertools import product
# enable gpu growth if gpu is available
gpu_devices = tf.config.experimental.list_physical_devices('GPU')
for device in gpu_devices:
tf.config.experimental.set_memory_growth(device, True)
# tf.keras.mixed_precision.set_global_policy('mixed_float16')
tf.config.optimizer.set_jit(True)
%load_ext watermark
%watermark -v -iv
```
## Setting Registry and Tracking URI for MLflow
```
# Use this registry uri when mlflow is created by docker container with a mysql db backend
#registry_uri = os.path.expandvars('mysql+pymysql://${MYSQL_USER}:${MYSQL_PASSWORD}@localhost:3306/${MYSQL_DATABASE}')
# Use this registry uri when mlflow is running locally by the command:
# "mlflow server --backend-store-uri sqlite:///mlflow.db --default-artifact-root ./mlruns --host 0.0.0.0"
registry_uri = 'sqlite:///mlflow.db'
tracking_uri = 'http://localhost:5000'
mlflow.tracking.set_registry_uri(registry_uri)
mlflow.tracking.set_tracking_uri(tracking_uri)
```
# The Data is taken from https://www.kaggle.com/mkechinov/ecommerce-behavior-data-from-multi-category-store and https://rees46.com/
## Each record/line in the file has the following fields:
1. event_time: When did the event happened (UTC)
2. event_type: Event type: one of [view, cart, remove_from_cart, purchase]
3. product_id
4. category_id
5. category_code: Category meaningful name (if present)
6. brand: Brand name in lower case (if present)
7. price
8. user_id: Permanent user ID
9. user_session: User session ID
```
# Read first 500.000 Rows
for chunk in pd.read_table("2019-Dec.csv",
sep=",", header=0,
infer_datetime_format=True, low_memory=False, chunksize=500000):
# Filter out other event types than 'view'
chunk = chunk[chunk['event_type'] == 'view']
# Filter out missing 'category_code' rows
chunk = chunk[chunk['category_code'].isna() == False]
chunk.reset_index(drop=True, inplace=True)
# Filter out all Sessions of length 1
count_sessions = chunk.groupby('user_session').count()
window_length = count_sessions.max()[0]
unique_sessions = [count_sessions.index[i] for i in range(
count_sessions.shape[0]) if count_sessions.iloc[i, 0] == 1]
chunk = chunk[~chunk['user_session'].isin(unique_sessions)]
chunk.reset_index(drop=True, inplace=True)
# Text embedding based on https://tfhub.dev/google/nnlm-en-dim50/2
last_category = []
for i, el in enumerate(chunk['category_code']):
last_category.append(el.split('.')[-1])
chunk['Product'] = last_category
embed = hub.load("https://tfhub.dev/google/nnlm-en-dim50/2")
embeddings = embed(chunk['Product'].tolist())
for dim in range(embeddings.shape[1]):
chunk['embedding_'+str(dim)] = embeddings[:, dim]
# Standardization
mean = chunk['price'].mean(axis=0)
print('Mean:', mean)
std = chunk['price'].std(axis=0)
print('Std:', std)
chunk['price_standardized'] = (chunk['price'] - mean) / std
chunk.sort_values(by=['user_session', 'event_time'], inplace=True)
chunk['price_standardized'] = chunk['price_standardized'].astype('float32')
chunk['product_id'] = chunk['product_id'].astype('int32')
chunk.reset_index(drop=True, inplace=True)
print('Sessions:', pd.unique(chunk['user_session']).shape)
print('Unique Products:', pd.unique(chunk['product_id']).shape)
print('Unique category_code:', pd.unique(chunk['category_code']).shape)
columns = ['embedding_'+str(i) for i in range(embeddings.shape[1])]
columns.append('price_standardized')
columns.append('user_session')
columns.append('Product')
columns.append('product_id')
columns.append('category_code')
df = chunk[columns]
break
df
```
## Delete Rows with equal or less than 6 Product Occurrences
```
count_product_id_mapped = df.groupby('product_id').count()
products_to_delete = count_product_id_mapped.loc[count_product_id_mapped['embedding_0'] <= 6].index
products_to_delete
```
## Slice Sessions from the Dataframe
```
list_sessions = []
list_last_clicked = []
list_last_clicked_temp = []
current_id = df.loc[0, 'user_session']
current_index = 0
columns = ['embedding_'+str(i) for i in range(embeddings.shape[1])]
columns.append('price_standardized')
columns.insert(0, 'product_id')
for i in range(df.shape[0]):
if df.loc[i, 'user_session'] != current_id:
list_sessions.append(df.loc[current_index:i-2, columns])
list_last_clicked.append(df.loc[i-1, 'product_id'])
list_last_clicked_temp.append(df.loc[i-1, columns])
current_id = df.loc[i, 'user_session']
current_index = i
```
## Delete Sessions with Length larger than 30
```
print(len(list_sessions))
list_sessions_filtered = []
list_last_clicked_filtered = []
list_last_clicked_temp_filtered = []
for index, session in enumerate(list_sessions):
if not (session.shape[0] > 30):
if not (session['product_id'].isin(products_to_delete).any()):
list_sessions_filtered.append(session)
list_last_clicked_filtered.append(list_last_clicked[index])
list_last_clicked_temp_filtered.append(list_last_clicked_temp[index])
len(list_sessions_filtered)
```
## Slice Sessions if label and last product from session is the same
Example:
- From: session: [ 1506 1506 11410 11410 2826 2826], ground truth: 2826
- To: session: [ 1506 1506 11410 11410], ground truth: 2826
```
print("Length before", len(list_sessions_filtered))
list_sessions_processed = []
list_last_clicked_processed = []
list_session_processed_autoencoder = []
for i, session in enumerate(list_sessions_filtered):
if session['product_id'].values[-1] == list_last_clicked_filtered[i]:
mask = session['product_id'].values == list_last_clicked_filtered[i]
if session[~mask].shape[0] > 0:
list_sessions_processed.append(session[~mask])
list_last_clicked_processed.append(list_last_clicked_filtered[i])
list_session_processed_autoencoder.append(pd.concat([session[~mask], pd.DataFrame(list_last_clicked_temp_filtered[i]).T],
ignore_index=True))
else:
list_sessions_processed.append(session)
list_last_clicked_processed.append(list_last_clicked_filtered[i])
list_session_processed_autoencoder.append(pd.concat([session, pd.DataFrame(list_last_clicked_temp_filtered[i]).T],
ignore_index=True))
print("Length after", len(list_sessions_processed))
```
## Create Item IDs starting from value 1 for Embeddings and One Hot Layer
```
mapping = pd.read_csv('../ID_Mapping.csv')[['Item_ID', 'Mapped_ID']]
dict_items = mapping.set_index('Item_ID').to_dict()['Mapped_ID']
for index, session in enumerate(list_session_processed_autoencoder):
session['product_id'] = session['product_id'].map(dict_items)
# Pad all Sessions with 0. Embedding Layer and LSTM will use Masking to ignore zeros.
list_sessions_padded = []
window_length = 31
for df in list_session_processed_autoencoder:
np_array = df.values
result = np.zeros((window_length, 1), dtype=np.float32)
result[:np_array.shape[0],:1] = np_array[:,:1]
list_sessions_padded.append(result)
# Save the results, because the slicing can take some time
np.save('list_sessions_padded_autoencoder.npy', list_sessions_padded)
sessions_padded = np.array(list_sessions_padded)
n_output_features = int(sessions_padded.max())
n_unique_input_ids = int(sessions_padded.max())
window_length = sessions_padded.shape[1]
n_input_features = sessions_padded.shape[2]
print("n_output_features", n_output_features)
print("n_unique_input_ids", n_unique_input_ids)
print("window_length", window_length)
print("n_input_features", n_input_features)
```
# Training: Start here if the preprocessing was already executed
```
sessions_padded = np.load('list_sessions_padded_autoencoder.npy')
print(sessions_padded.shape)
n_output_features = int(sessions_padded.max())
n_unique_input_ids = int(sessions_padded.max())
window_length = sessions_padded.shape[1]
n_input_features = sessions_padded.shape[2]
```
## Grid Search Hyperparameter
Dictionary with different hyperparameters to train on.
MLflow will track those in a database.
```
grid_search_dic = {'hidden_layer_size': [300],
'batch_size': [32],
'embedding_dim': [200],
'window_length': [window_length],
'dropout_fc': [0.0], #0.2
'n_output_features': [n_output_features],
'n_input_features': [n_input_features]}
# Cartesian product
grid_search_param = [dict(zip(grid_search_dic, v)) for v in product(*grid_search_dic.values())]
grid_search_param
```
### LSTM Autoencoder in functional API
- Input: x rows (time steps) of Item IDs in a Session
- Output: reconstructed Session
```
def build_autoencoder(window_length=50,
units_lstm_layer=100,
n_unique_input_ids=0,
embedding_dim=200,
n_input_features=1,
n_output_features=3,
dropout_rate=0.1):
inputs = keras.layers.Input(
shape=[window_length, n_input_features], dtype=np.float32)
# Encoder
# Embedding Layer
embedding_layer = tf.keras.layers.Embedding(
n_unique_input_ids+1, embedding_dim, input_length=window_length) # , mask_zero=True)
embeddings = embedding_layer(inputs[:, :, 0])
mask = inputs[:, :, 0] != 0
# LSTM Layer 1
lstm1_output, lstm1_state_h, lstm1_state_c = keras.layers.LSTM(units=units_lstm_layer, return_state=True,
return_sequences=True)(embeddings, mask=mask)
lstm1_state = [lstm1_state_h, lstm1_state_c]
# Decoder
# input: lstm1_state_c, lstm1_state_h
decoder_state_c = lstm1_state_c
decoder_state_h = lstm1_state_h
decoder_outputs = tf.expand_dims(lstm1_state_h, 1)
list_states = []
decoder_layer = keras.layers.LSTM(
units=units_lstm_layer, return_state=True, return_sequences=True, unroll=False)
for i in range(window_length):
decoder_outputs, decoder_state_h, decoder_state_c = decoder_layer(decoder_outputs,
initial_state=[decoder_state_h,
decoder_state_c])
list_states.append(decoder_state_h)
stacked = tf.stack(list_states, axis=1)
fc_layer = tf.keras.layers.Dense(
n_output_features+1, kernel_initializer='he_normal')
fc_layer_output = tf.keras.layers.TimeDistributed(fc_layer)(
stacked, mask=mask)
mask_softmax = tf.tile(tf.expand_dims(mask, axis=2),
[1, 1, n_output_features+1])
softmax = tf.keras.layers.Softmax(axis=2, dtype=tf.float32)(
fc_layer_output, mask=mask_softmax)
model = keras.models.Model(inputs=[inputs],
outputs=[softmax])
return model
```
### Convert Numpy Array to tf.data.Dataset for better training performance
The function will return a zipped tf.data.Dataset with the following Shapes:
- x: (batches, window_length)
- y: (batches,)
```
def array_to_tf_data_api(train_data_x, train_data_y, batch_size=64, window_length=50,
validate=False):
"""Applies sliding window on the fly by using the TF Data API.
Args:
train_data_x: Input Data as Numpy Array, Shape (rows, n_features)
batch_size: Batch Size.
window_length: Window Length or Window Size.
future_length: Number of time steps that will be predicted in the future.
n_output_features: Number of features that will be predicted.
validate: True if input data is a validation set and does not need to be shuffled
shift: Shifts the Sliding Window by this Parameter.
Returns:
tf.data.Dataset
"""
X = tf.data.Dataset.from_tensor_slices(train_data_x)
y = tf.data.Dataset.from_tensor_slices(train_data_y)
if not validate:
train_tf_data = tf.data.Dataset.zip((X, y)).cache() \
.shuffle(buffer_size=200000, reshuffle_each_iteration=True)\
.batch(batch_size).prefetch(1)
return train_tf_data
else:
return tf.data.Dataset.zip((X, y)).batch(batch_size)\
.prefetch(1)
```
## Custom TF Callback to log Metrics by MLflow
```
class MlflowLogging(tf.keras.callbacks.Callback):
def __init__(self, **kwargs):
super().__init__() # handles base args (e.g., dtype)
def on_epoch_end(self, epoch, logs=None):
keys = list(logs.keys())
for key in keys:
mlflow.log_metric(str(key), logs.get(key), step=epoch)
class CustomCategoricalCrossentropy(keras.losses.Loss):
def __init__(self, **kwargs):
super().__init__(**kwargs)
self.bce = tf.keras.losses.SparseCategoricalCrossentropy(
from_logits=False, reduction='sum')
@tf.function
def call(self, y_true, y_pred):
total = 0.0
for i in tf.range(y_pred.shape[1]):
loss = self.bce(y_true[:, i, 0], y_pred[:, i, :])
total = total + loss
return total
def get_config(self):
base_config = super().get_config()
return {**base_config}
def from_config(cls, config):
return cls(**config)
class CategoricalAccuracy(keras.metrics.Metric):
def __init__(self, name="categorical_accuracy", **kwargs):
super(CategoricalAccuracy, self).__init__(name=name, **kwargs)
self.true = self.add_weight(name="true", initializer="zeros")
self.count = self.add_weight(name="count", initializer="zeros")
self.accuracy = self.add_weight(name="count", initializer="zeros")
def update_state(self, y_true, y_pred, sample_weight=None):
y_true = tf.cast(y_true, "float32")
y_pred = tf.cast(y_pred, "float32")
mask = y_true[:, :, 0] != 0
argmax = tf.cast(tf.argmax(y_pred, axis=2), "float32")
temp = argmax == y_true[:, :, 0]
true = tf.reduce_sum(tf.cast(temp[mask], dtype=tf.float32))
self.true.assign_add(true)
self.count.assign_add(
tf.cast(tf.shape(temp[mask])[0], dtype="float32"))
self.accuracy.assign(tf.math.divide(self.true, self.count))
def result(self):
return self.accuracy
def reset_states(self):
# The state of the metric will be reset at the start of each epoch.
self.accuracy.assign(0.0)
class CategoricalSessionAccuracy(keras.metrics.Metric):
def __init__(self, name="categorical_session_accuracy", **kwargs):
super(CategoricalSessionAccuracy, self).__init__(name=name, **kwargs)
self.true = self.add_weight(name="true", initializer="zeros")
self.count = self.add_weight(name="count", initializer="zeros")
self.accuracy = self.add_weight(name="count", initializer="zeros")
def update_state(self, y_true, y_pred, sample_weight=None):
y_true = tf.cast(y_true, "float32")
y_pred = tf.cast(y_pred, "float32")
mask = y_true[:, :, 0] != 0
argmax = tf.cast(tf.argmax(y_pred, axis=2), "float32")
temp = argmax == y_true[:, :, 0]
temp = tf.reduce_all(temp, axis=1)
true = tf.reduce_sum(tf.cast(temp, dtype=tf.float32))
self.true.assign_add(true)
self.count.assign_add(tf.cast(tf.shape(temp)[0], dtype="float32"))
self.accuracy.assign(tf.math.divide(self.true, self.count))
def result(self):
return self.accuracy
def reset_states(self):
# The state of the metric will be reset at the start of each epoch.
self.accuracy.assign(0.0)
```
# Training
```
with mlflow.start_run() as parent_run:
for params in grid_search_param:
batch_size = params['batch_size']
window_length = params['window_length']
embedding_dim = params['embedding_dim']
dropout_fc = params['dropout_fc']
hidden_layer_size = params['hidden_layer_size']
n_output_features = params['n_output_features']
n_input_features = params['n_input_features']
with mlflow.start_run(nested=True) as child_run:
# log parameter
mlflow.log_param('batch_size', batch_size)
mlflow.log_param('window_length', window_length)
mlflow.log_param('hidden_layer_size', hidden_layer_size)
mlflow.log_param('dropout_fc_layer', dropout_fc)
mlflow.log_param('embedding_dim', embedding_dim)
mlflow.log_param('n_output_features', n_output_features)
mlflow.log_param('n_unique_input_ids', n_unique_input_ids)
mlflow.log_param('n_input_features', n_input_features)
model = build_autoencoder(window_length=window_length,
n_output_features=n_output_features,
n_unique_input_ids=n_unique_input_ids,
n_input_features=n_input_features,
embedding_dim=embedding_dim,
units_lstm_layer=hidden_layer_size,
dropout_rate=dropout_fc)
data = array_to_tf_data_api(sessions_padded,
sessions_padded,
window_length=window_length,
batch_size=batch_size)
model.compile(loss=CustomCategoricalCrossentropy(),#tf.keras.losses.SparseCategoricalCrossentropy(from_logits=False, reduction='sum'),
optimizer=keras.optimizers.Nadam(learning_rate=1e-3),
metrics=[CategoricalAccuracy(), CategoricalSessionAccuracy()])
model.fit(data, shuffle=True, initial_epoch=0, epochs=20,
callbacks=[MlflowLogging()])
model.compile()
model.save("./tmp")
model.save_weights('weights')
mlflow.tensorflow.log_model(tf_saved_model_dir='./tmp',
tf_meta_graph_tags='serve',
tf_signature_def_key='serving_default',
artifact_path='saved_model',
registered_model_name='Session Based LSTM Recommender')
shutil.rmtree("./tmp")
```
|
github_jupyter
|
<a href="https://colab.research.google.com/github/rwarnung/datacrunch-notebooks/blob/master/dcrunch_R_example.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
**Data crunch example R script**
---
author: sweet-richard
date: Jan 30, 2022
required packages:
* `tidyverse` for data handling
* `feather` for efficient loading of data
* `xgboost` for predictive modelling
* `httr` for the automatic upload.
```
library(tidyverse)
library(feather)
```
First, we set some **parameters**.
* `is_download` controls whether you want to download data or just read prevously downloaded data
* `is_upload` set this to TRUE for automatic upload.
* `nrounds` is a parameter for `xgboost` that we set to 100 for illustration. You might want to adjust the paramters of xgboost.
```
#' ## Parameters
file_name_train = "train_data.feather"
file_name_test ="test_data.feather"
is_download = TRUE # set this to true to download new data or to FALSE to load data in feather format
is_upload = FALSE # set this to true to upload a submission
nrounds = 300 # you might want to adjust this one and other parameters of xgboost
```
In the **functions** section we defined the correlation measure that we use to measure performance.
```
#' ## Functions
#+
getCorrMeasure = function(actual, predicted) {
cor_measure = cor(actual, predicted, method="spearman")
return(cor_measure)
}
```
Now, we either **download** the current data from the servers or load them in feather format. Furthermore, we define the features that we actually want to use. In this illustration we use all of them but `id` and `Moons`.
```
#' ## Download data
#' after the download, data is stored in feather format to be read on demand quickly. Data is stored in integer format to save memory.
#+
if( is_download ) {
cat("\n start download")
train_datalink_X = 'https://tournament.datacrunch.com/data/X_train.csv'
train_datalink_y = 'https://tournament.datacrunch.com/data/y_train.csv'
hackathon_data_link = 'https://tournament.datacrunch.com/data/X_test.csv'
train_dataX = read_csv(url(train_datalink_X))
train_dataY = read_csv(url(train_datalink_y))
test_data = read_csv(url(hackathon_data_link))
train_data =
bind_cols( train_dataX, train_dataY)
train_data = train_data %>% mutate_at(vars(starts_with("feature_")), list(~as.integer(.*100)))
feather::write_feather(train_data, path = paste0("./", file_name_train))
test_data = test_data %>% mutate_at(vars(starts_with("feature_")), list(~as.integer(.*100)))
feather::write_feather(test_data, path = paste0("./", file_name_test))
names(train_data)
nrow(train_data)
nrow(test_data)
cat("\n data is downloaded")
} else {
train_data = feather::read_feather(path = paste0("./", file_name_train))
test_data = feather::read_feather(path = paste0("./", file_name_test))
}
## set vars used for modelling
model_vars = setdiff(names(test_data), c("id","Moons"))
```
Next we fit our go-to algorithm **xgboost** with mainly default parameters, only `eta` and `max_depth` are set.
```
#' ## Fit xgboost
#+ cache = TRUE
library(xgboost, warn.conflicts = FALSE)
# custom loss function for eval
corrmeasure <- function(preds, dtrain) {
labels <- getinfo(dtrain, "label")
corrm <- as.numeric(cor(labels, preds, method="spearman"))
return(list(metric = "corr", value = corrm))
}
eval_metric_string = "rmse"
my_objective = "reg:squarederror"
tree.params = list(
booster = "gbtree", eta = 0.01, max_depth = 5,
tree_method = "hist", # tree_method = "auto",
objective = my_objective)
cat("\n starting xgboost \n")
```
**First target** `target_r`
```
# first target target_r then g and b
################
current_target = "target_r"
dtrain = xgb.DMatrix(train_data %>% select(one_of(model_vars)) %>% as.matrix(), label = train_data %>% select(one_of(current_target)) %>% as.matrix())
xgb.model.tree = xgb.train(data = dtrain,
params = tree.params, nrounds = nrounds, verbose = 1,
print_every_n = 50L, eval_metric = corrmeasure)
xgboost_tree_train_pred1 = predict(xgb.model.tree, train_data %>% select(one_of(model_vars)) %>% as.matrix())
xgboost_tree_live_pred1 = predict(xgb.model.tree, test_data %>% select(one_of(model_vars)) %>% as.matrix())
cor_train = getCorrMeasure(train_data %>% select(one_of(current_target)), xgboost_tree_train_pred1)
cat("\n : metric: ", eval_metric_string, "\n")
print(paste0("Corrm on train: ", round(cor_train,4)))
print(paste("xgboost", current_target, "ready"))
```
**Second target** `target_g`
```
# second target target_g
################
current_target = "target_g"
dtrain = xgb.DMatrix(train_data %>% select(one_of(model_vars)) %>% as.matrix(), label = train_data %>% select(one_of(current_target)) %>% as.matrix())
xgb.model.tree = xgb.train(data = dtrain,
params = tree.params, nrounds = nrounds, verbose = 1,
print_every_n = 50L, eval_metric = corrmeasure)
xgboost_tree_train_pred2 = predict(xgb.model.tree, train_data %>% select(one_of(model_vars)) %>% as.matrix())
xgboost_tree_live_pred2 = predict(xgb.model.tree, test_data %>% select(one_of(model_vars)) %>% as.matrix())
cor_train = getCorrMeasure(train_data %>% select(one_of(current_target)), xgboost_tree_train_pred2)
cat("\n : metric: ", eval_metric_string, "\n")
print(paste0("Corrm on train: ", round(cor_train,4)))
print(paste("xgboost", current_target, "ready"))
```
**Third target** `target_b`
```
# third target target_b
################
current_target = "target_b"
dtrain = xgb.DMatrix(train_data %>% select(one_of(model_vars)) %>% as.matrix(), label = train_data %>% select(one_of(current_target)) %>% as.matrix())
xgb.model.tree = xgb.train(data = dtrain,
params = tree.params, nrounds = nrounds, verbose = 1,
print_every_n = 50L, eval_metric = corrmeasure)
xgboost_tree_train_pred3 = predict(xgb.model.tree, train_data %>% select(one_of(model_vars)) %>% as.matrix())
xgboost_tree_live_pred3 = predict(xgb.model.tree, test_data %>% select(one_of(model_vars)) %>% as.matrix())
cor_train = getCorrMeasure(train_data %>% select(one_of(current_target)), xgboost_tree_train_pred3)
cat("\n : metric: ", eval_metric_string, "\n")
print(paste0("Corrm on train: ", round(cor_train,4)))
print(paste("xgboost", current_target, "ready"))
```
Then we produce simply histogram plots to see whether the predictions are plausible and prepare a **submission file**:
```
#' ## Submission
#' simple histograms to check the submissions
#+
hist(xgboost_tree_live_pred1)
hist(xgboost_tree_live_pred2)
hist(xgboost_tree_live_pred3)
#' create submission file
#+
sub_df = tibble(target_r = xgboost_tree_live_pred1,
target_g = xgboost_tree_live_pred2,
target_b = xgboost_tree_live_pred3)
file_name_submission = paste0("gbTree_", gsub("-","",Sys.Date()), ".csv")
sub_df %>% readr::write_csv(file = paste0("./", file_name_submission))
nrow(sub_df)
cat("\n submission file written")
```
Finally, we can **automatically upload** the file to the server:
```
#' ## Upload submission
#+
if( is_upload ) {
library(httr)
API_KEY = "YourKeyHere"
response <- POST(
url = "https://tournament.crunchdao.com/api/v2/submissions",
query = list(apiKey = API_KEY),
body = list(
file = upload_file(path = paste0("./", file_name_submission))
),
encode = c("multipart")
);
status <- status_code(response)
if (status == 200) {
print("Submission submitted :)")
} else if (status == 400) {
print("ERR: The file must not be empty")
print("You have send a empty file.")
} else if (status == 401) {
print("ERR: Your email hasn't been verified")
print("Please verify your email or contact a cruncher.")
} else if (status == 403) {
print("ERR: Not authentified")
print("Is the API Key valid?")
} else if (status == 404) {
print("ERR: Unknown API Key")
print("You should check that the provided API key is valid and is the same as the one you've received by email.")
} else if (status == 409) {
print("ERR: Duplicate submission")
print("Your work has already been submitted with the same exact results, if you think that this a false positive, contact a cruncher.")
print("MD5 collision probability: 1/2^128 (source: https://stackoverflow.com/a/288519/7292958)")
} else if (status == 422) {
print("ERR: API Key is missing or empty")
print("Did you forget to fill the API_KEY variable?")
} else if (status == 423) {
print("ERR: Submissions are close")
print("You can only submit during rounds eg: Friday 7pm GMT+1 to Sunday midnight GMT+1.")
print("Or the server is currently crunching the submitted files, please wait some time before retrying.")
} else if (status == 423) {
print("ERR: Too many submissions")
} else {
content <- httr::content(response)
print("ERR: Server returned: " + toString(status))
print("Ouch! It seems that we were not expecting this kind of result from the server, if the probleme persist, contact a cruncher.")
print(paste("Message:", content$message, sep=" "))
}
# DEVELOPER WARNING:
# THE API ERROR CODE WILL BE HANDLER DIFFERENTLY IN A NEAR FUTURE!
# PLEASE STAY UPDATED BY JOINING THE DISCORD (https://discord.gg/veAtzsYn3M) AND READING THE NEWSLETTER EMAIL
}
```
|
github_jupyter
|
<table class="ee-notebook-buttons" align="left">
<td><a target="_blank" href="https://github.com/giswqs/earthengine-py-notebooks/tree/master/Datasets/Terrain/srtm_mtpi.ipynb"><img width=32px src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" /> View source on GitHub</a></td>
<td><a target="_blank" href="https://nbviewer.jupyter.org/github/giswqs/earthengine-py-notebooks/blob/master/Datasets/Terrain/srtm_mtpi.ipynb"><img width=26px src="https://upload.wikimedia.org/wikipedia/commons/thumb/3/38/Jupyter_logo.svg/883px-Jupyter_logo.svg.png" />Notebook Viewer</a></td>
<td><a target="_blank" href="https://mybinder.org/v2/gh/giswqs/earthengine-py-notebooks/master?filepath=Datasets/Terrain/srtm_mtpi.ipynb"><img width=58px src="https://mybinder.org/static/images/logo_social.png" />Run in binder</a></td>
<td><a target="_blank" href="https://colab.research.google.com/github/giswqs/earthengine-py-notebooks/blob/master/Datasets/Terrain/srtm_mtpi.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" /> Run in Google Colab</a></td>
</table>
## Install Earth Engine API
Install the [Earth Engine Python API](https://developers.google.com/earth-engine/python_install) and [geehydro](https://github.com/giswqs/geehydro). The **geehydro** Python package builds on the [folium](https://github.com/python-visualization/folium) package and implements several methods for displaying Earth Engine data layers, such as `Map.addLayer()`, `Map.setCenter()`, `Map.centerObject()`, and `Map.setOptions()`.
The magic command `%%capture` can be used to hide output from a specific cell. Uncomment these lines if you are running this notebook for the first time.
```
# %%capture
# !pip install earthengine-api
# !pip install geehydro
```
Import libraries
```
import ee
import folium
import geehydro
```
Authenticate and initialize Earth Engine API. You only need to authenticate the Earth Engine API once. Uncomment the line `ee.Authenticate()`
if you are running this notebook for the first time or if you are getting an authentication error.
```
# ee.Authenticate()
ee.Initialize()
```
## Create an interactive map
This step creates an interactive map using [folium](https://github.com/python-visualization/folium). The default basemap is the OpenStreetMap. Additional basemaps can be added using the `Map.setOptions()` function.
The optional basemaps can be `ROADMAP`, `SATELLITE`, `HYBRID`, `TERRAIN`, or `ESRI`.
```
Map = folium.Map(location=[40, -100], zoom_start=4)
Map.setOptions('HYBRID')
```
## Add Earth Engine Python script
```
dataset = ee.Image('CSP/ERGo/1_0/Global/SRTM_mTPI')
srtmMtpi = dataset.select('elevation')
srtmMtpiVis = {
'min': -200.0,
'max': 200.0,
'palette': ['0b1eff', '4be450', 'fffca4', 'ffa011', 'ff0000'],
}
Map.setCenter(-105.8636, 40.3439, 11)
Map.addLayer(srtmMtpi, srtmMtpiVis, 'SRTM mTPI')
```
## Display Earth Engine data layers
```
Map.setControlVisibility(layerControl=True, fullscreenControl=True, latLngPopup=True)
Map
```
|
github_jupyter
|
#Introduction to Data Science
See [Lesson 1](https://www.udacity.com/course/intro-to-data-analysis--ud170)
You should run it in local Jupyter env as this notebook refers to local dataset
```
import unicodecsv
from datetime import datetime as dt
enrollments_filename = 'dataset/enrollments.csv'
engagement_filename = 'dataset/daily_engagement.csv'
submissions_filename = 'dataset/project_submissions.csv'
## Longer version of code (replaced with shorter, equivalent version below)
def read_csv(filename):
with open(filename, 'rb') as f:
reader = unicodecsv.DictReader(f)
return list(reader)
enrollments = read_csv(enrollments_filename)
daily_engagement = read_csv(engagement_filename)
project_submissions = read_csv(submissions_filename)
def renameKey(data, fromKey, toKey):
for rec in data:
if fromKey in rec:
rec[toKey] = rec[fromKey]
del rec[fromKey]
renameKey(daily_engagement, 'acct', 'account_key')
def cleanDataTypes():
def fixIntFloat(data, field):
if field not in data:
print(f'WARNING : Field {field} is not in {data}')
value = data[field]
if value == '':
data[field] = None
else:
data[field] = int(float(value))
def fixFloat(data, field):
if field not in data:
print(f'WARNING : Field {field} is not in {data}')
value = data[field]
if value == '':
data[field] = None
else:
data[field] = float(value)
def fixDate(data, field):
if field not in data:
print(f'WARNING : Field {field} is not in {data}')
value = data[field]
if value == '':
data[field] = None
else:
data[field] = dt.strptime(value, '%Y-%m-%d')
def fixBool(data, field):
if field not in data:
print(f'WARNING : Field {field} is not in {data}')
value = data[field]
if value == 'True':
data[field] = True
elif value == 'False':
data[field] = False
else:
print(f"WARNING: invalid boolean '{value}' value converted to False in {data}")
data[field] = False
def fixInt(data, field):
if field not in data:
print(f'WARNING : Field {field} is not in {data}')
value = data[field]
if value == '':
data[field] = None
else:
data[field] = int(value)
#clean data types
for rec in enrollments:
fixInt(rec, 'days_to_cancel')
fixDate(rec, 'join_date')
fixDate(rec, 'cancel_date')
fixBool(rec, 'is_udacity')
fixBool(rec, 'is_canceled')
for rec in daily_engagement:
fixDate(rec, 'utc_date')
fixIntFloat(rec, 'num_courses_visited')
fixFloat(rec, 'total_minutes_visited')
fixIntFloat(rec, 'lessons_completed')
fixIntFloat(rec, 'projects_completed')
for rec in project_submissions:
fixDate(rec, 'creation_date')
fixDate(rec, 'completion_date')
cleanDataTypes()
print(f"enrollments[0] = {enrollments[0]}\n")
print(f"daily_engagement[0] = {daily_engagement[0]}\n")
print(f"project_submissions[0] = {project_submissions[0]}\n")
from collections import defaultdict
def getUniqueAccounts(data):
accts = defaultdict(list)
i = 0
for record in data:
accountKey = record['account_key']
accts[accountKey].append(i)
i+=1
return accts
enrollment_num_rows = len(enrollments)
enrollment_unique_students = getUniqueAccounts(enrollments)
enrollment_num_unique_students = len(enrollment_unique_students)
engagement_num_rows = len(daily_engagement)
engagement_unique_students = getUniqueAccounts(daily_engagement)
engagement_num_unique_students = len(engagement_unique_students)
submission_num_rows = len(project_submissions)
submission_unique_students = getUniqueAccounts(project_submissions)
submission_num_unique_students = len(submission_unique_students)
print(f"enrollments total={enrollment_num_rows}, unique={enrollment_num_unique_students}")
print(f"engagements total={engagement_num_rows}, unique={engagement_num_unique_students}")
print(f"submissions total={submission_num_rows} unique={submission_num_unique_students}")
for enrollment_acct in enrollment_unique_students:
if enrollment_acct not in engagement_unique_students:
#print(enrollment_unique_students[enrollment])
enrollment_id = enrollment_unique_students[enrollment_acct][0]
enrollment = enrollments[enrollment_id]
print(f"Strange student : enrollment={enrollment}")
break
strange_enrollments_num_by_different_date = 0
for enrollment_acct in enrollment_unique_students:
if enrollment_acct not in engagement_unique_students:
for enrollment_id in enrollment_unique_students[enrollment_acct]:
enrollment = enrollments[enrollment_id]
if enrollment['join_date'] != enrollment['cancel_date']:
strange_enrollments_num_by_different_date += 1
#print(f"Strange student with different dates : enrollments[{enrollment_id}]={enrollment}\n")
print(f"Number of enrolled and cancelled at different dates but not engaged (problemactic accounts) : {strange_enrollments_num_by_different_date}\n")
num_problems = 0
for enrollment in enrollments:
student = enrollment['account_key']
if student not in engagement_unique_students and enrollment['join_date'] != enrollment['cancel_date']:
num_problems += 1
#print(enrollment)
print(f'Number of problematic account records : {num_problems}')
def getRealAccounts(enrollmentData):
result = []
for rec in enrollmentData:
if not rec['is_udacity']:
result.append(rec)
return result
real_enrollments = getRealAccounts(enrollments)
print(f'Real account : {len(real_enrollments)}')
def getPaidStudents(enrollmentData):
freePeriodDays = 7
result = {}
#result1 = {}
for rec in enrollmentData:
if rec['cancel_date'] == None or rec['days_to_cancel'] > freePeriodDays:
accountKey = rec['account_key']
joinDate = rec['join_date']
if accountKey not in result or joinDate > result[accountKey]:
result[accountKey] = joinDate
#result1[accountKey] = joinDate
'''
for accountKey, joinDate in result.items():
joinDate1 = result1[accountKey]
if joinDate != joinDate1:
print(f"{accountKey} : {joinDate} != {joinDate1}")
'''
return result
paid_students = getPaidStudents(real_enrollments)
print(f'Paid students : {len(paid_students)}')
def isEngagementWithingOneWeek(joinDate, engagementDate):
#if joinDate > engagementDate:
# print(f'WARNING: join date is after engagement date')
timeDelta = engagementDate - joinDate
return 0 <= timeDelta.days and timeDelta.days < 7
def collectPaidEnagagementsInTheFirstWeek():
result = []
i = 0
for engagement in daily_engagement:
accountKey = engagement['account_key']
if accountKey in paid_students:
joinDate = paid_students[accountKey]
engagementDate = engagement['utc_date']
if isEngagementWithingOneWeek(joinDate, engagementDate):
result.append(i)
i+=1
return result
paid_engagement_in_first_week = collectPaidEnagagementsInTheFirstWeek()
print(f'Number of paid engagements in the first week : {len(paid_engagement_in_first_week)}')
from collections import defaultdict
import numpy as np
def groupEngagementsByAccounts(engagements):
result = defaultdict(list)
for engagementId in engagements:
engagement = daily_engagement[engagementId]
accountKey = engagement['account_key']
result[accountKey].append(engagementId)
return result
first_week_paid_engagements_by_account = groupEngagementsByAccounts(paid_engagement_in_first_week)
def sumEngagementsStatByAccount(engagements, getStatValue):
result = {}
for accountKey, engagementIds in engagements.items():
stat_sum = 0
for engagementId in engagementIds:
engagement = daily_engagement[engagementId]
stat_sum += getStatValue(engagement)
result[accountKey] = stat_sum
return result
def printStats(getStatValue, statLabel):
first_week_paid_engagements_sum_stat_by_account = sumEngagementsStatByAccount(first_week_paid_engagements_by_account, getStatValue)
first_week_paid_engagements_sum_stat = list(first_week_paid_engagements_sum_stat_by_account.values())
print(f'Average {statLabel} spent by paid accounts during the first week : {np.mean(first_week_paid_engagements_sum_stat)}')
print(f'StdDev {statLabel} spent by paid accounts during the first week : {np.std(first_week_paid_engagements_sum_stat)}')
print(f'Min {statLabel} spent by paid accounts during the first week : {np.min(first_week_paid_engagements_sum_stat)}')
print(f'Max {statLabel} spent by paid accounts during the first week : {np.max(first_week_paid_engagements_sum_stat)}')
print('\n')
printStats((lambda data : data['total_minutes_visited']), 'minutes')
printStats((lambda data : data['lessons_completed']), 'lessons')
printStats((lambda data : 1 if data['num_courses_visited'] > 0 else 0), 'days')
######################################
# 11 #
######################################
## Create two lists of engagement data for paid students in the first week.
## The first list should contain data for students who eventually pass the
## subway project, and the second list should contain data for students
## who do not.
subway_project_lesson_keys = {'746169184', '3176718735'}
passing_grades = {'DISTINCTION', 'PASSED'} #{'', 'INCOMPLETE', 'DISTINCTION', 'PASSED', 'UNGRADED'}
#passing_grades = {'PASSED'} #{'', 'INCOMPLETE', 'DISTINCTION', 'PASSED', 'UNGRADED'}
passing_engagement = []
non_passing_engagement = []
for accountKey, engagementIds in first_week_paid_engagements_by_account.items():
if accountKey in submission_unique_students:
submissionIds = submission_unique_students[accountKey]
isPassed = False
for submissionId in submissionIds:
submission = project_submissions[submissionId]
if submission['assigned_rating'] in passing_grades and submission['lesson_key'] in subway_project_lesson_keys:
isPassed = True
break
if isPassed:
passing_engagement += engagementIds
else:
non_passing_engagement += engagementIds
else:
non_passing_engagement += engagementIds
print(f'First week engagements with passing grade : {len(passing_engagement)}')
print(f'First week engagements with non-passing grade : {len(non_passing_engagement)}')
######################################
# 12 #
######################################
## Compute some metrics you're interested in and see how they differ for
## students who pass the subway project vs. students who don't. A good
## starting point would be the metrics we looked at earlier (minutes spent
## in the classroom, lessons completed, and days visited).
passing_engagement_by_account = groupEngagementsByAccounts(passing_engagement)
non_passing_engagement_by_account = groupEngagementsByAccounts(non_passing_engagement)
def getArgStatEngagements(engagementIds, getStatValue):
stat_sum = 0
stat_num = 0
for engagementId in engagementIds:
engagement = daily_engagement[engagementId]
stat_sum += getStatValue(engagement)
stat_num += 1
if stat_num > 0:
return stat_sum / stat_num
else:
return 0
#sumEngagementsStatByAccount(first_week_paid_engagements_by_account, getStatValue)
passed_minutes = list(sumEngagementsStatByAccount(passing_engagement_by_account, (lambda data : data['total_minutes_visited'])).values())
non_passed_minutes = list(sumEngagementsStatByAccount(non_passing_engagement_by_account, (lambda data : data['total_minutes_visited'])).values())
passed_lessons = list(sumEngagementsStatByAccount(passing_engagement_by_account, (lambda data : data['lessons_completed'])).values())
non_passed_lessons = list(sumEngagementsStatByAccount(non_passing_engagement_by_account, (lambda data : data['lessons_completed'])).values())
passed_days = list(sumEngagementsStatByAccount(passing_engagement_by_account, (lambda data : 1 if data['num_courses_visited'] > 0 else 0)).values())
non_passed_days = list(sumEngagementsStatByAccount(non_passing_engagement_by_account, (lambda data : 1 if data['num_courses_visited'] > 0 else 0)).values())
print(f'Passed Avg Minutes = {np.mean(passed_minutes)}')
print(f'Non passed Avg Minutes = {np.mean(non_passed_minutes)}')
print(f'Passed Avg Lessons = {np.mean(passed_lessons)}')
print(f'Non passed Avg Lessons = {np.mean(non_passed_lessons)}')
print(f'Passed Avg Days = {np.mean(passed_days)}')
print(f'Non passed Avg Days = {np.mean(non_passed_days)}')
######################################
# 13 #
######################################
## Make histograms of the three metrics we looked at earlier for both
## students who passed the subway project and students who didn't. You
## might also want to make histograms of any other metrics you examined.
%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns
plt.hist(passed_minutes, color ='green')
plt.hist(non_passed_minutes, color ='lightblue')
plt.xlabel('Number of minutes')
plt.title('Passed (green) VS Non-passed (light-blue) students')
#sns.displot(passed_minutes, color ='green')
#sns.displot(non_passed_minutes, color ='lightblue')
plt.hist(passed_lessons, color ='green')
plt.hist(non_passed_lessons, color ='lightblue')
plt.xlabel('Number of lessons')
plt.title('Passed (green) VS Non-passed (light-blue) students')
plt.hist(passed_days, color ='green', bins = 8)
plt.xlabel('Number of days')
plt.title('Passed students')
plt.hist(non_passed_days, color ='lightblue', bins = 8)
plt.xlabel('Number of days')
plt.title('Non-passed students')
```
|
github_jupyter
|
```
import pandas as pd
import numpy as np
import keras
from keras.models import Sequential,Model
from keras.layers import Dense, Dropout,BatchNormalization,Input
from keras.optimizers import RMSprop
from keras.regularizers import l2,l1
from keras.optimizers import Adam
from sklearn.model_selection import LeaveOneOut
from sklearn.metrics import roc_curve, auc
import matplotlib.pyplot as plt
from keras.callbacks import EarlyStopping
df = pd.read_csv("../../out_data/MLDB.csv")
first_gene_index = df.columns.get_loc("rrrD")
X, Y = np.split(df, [first_gene_index], axis=1)
X = X.values
X = X-0.5
Y1 = Y.values[:,1]
Y2 = Y.values[:,1]
X.shape
import collections
Model_setting = collections.namedtuple('Model_setting','num_layers num_node alpha drop_rate act_method lr regularization \
patience')
setting_ = [1,100, 0.5, 0.2, 'tanh', 0.01, 'l2', 3]
setting = Model_setting(*setting_)
setting = setting._asdict()
setting
def getModel(setting,num_input=84):
regularizer = l1(setting['alpha']) if setting['regularization']=='l1' else l2(setting['alpha'])
model = Sequential()
for i in range(setting['num_layers']):
if i==0:
model.add(Dense(setting['num_node'], input_shape=(num_input,), activation=setting['act_method'],\
kernel_regularizer = regularizer))
model.add(Dropout(setting['drop_rate']))
else:
model.add(Dense(setting['num_node']//(2**i), activation=setting['act_method']))
model.add(Dropout(setting['drop_rate']))
model.add(Dense(1, activation='sigmoid'))
model.compile(loss='binary_crossentropy', optimizer=Adam(lr=setting['lr']), metrics=['accuracy'])
return model
num_output_ = 3
def create_model(num_input = 84,num_output = num_output_):
X_input = Input(shape=(num_input,))
X = Dense(64)(X_input)
X = Dropout(0.2)(X)
X = Dense(32)(X)
Ys= []
for i in range(num_output):
Ys.append(Dense(1, activation = 'sigmoid')(X))
model = Model(inputs=[X_input],outputs = Ys)
model.compile(loss=['binary_crossentropy']*num_output,loss_weights=[1.]*num_output,optimizer=Adam(lr=setting['lr']), metrics=['accuracy'])
return model
model = create_model()
callbacks = [EarlyStopping(monitor='loss',min_delta=0,patience=setting['patience'])]
ys = [*((Y.values).T[:num_output_])]
model.fit(X,ys,epochs = 50, verbose = 1,callbacks =callbacks)
history = final_model.fit(X_train, [Y_train, Y_train2],
nb_epoch = 100,
batch_size = 256,
verbose=1,
validation_data=(X_test, [Y_test, Y_test2]),
callbacks=[reduce_lr, checkpointer],
shuffle=True)
callbacks = [EarlyStopping(monitor='loss',min_delta=0,patience=setting['patience'])]
def cross_validation(X,Y,setting,num_input):
model = getModel(setting,num_input)
preds = []
for train, test in LeaveOneOut().split(X, Y):
model.fit(X[train,:],Y[train],epochs=20,verbose=0, callbacks =callbacks)
probas_ = model.predict(X[test,:])
preds.append(probas_[0][0])
# Compute ROC curve and area the curve
fpr, tpr, thresholds = roc_curve(Y, preds)
roc_auc = auc(fpr, tpr)
if roc_auc < 0.5:
roc_auc = 1 - roc_auc
return roc_auc
def backward_selection(X,Y,setting):
survive_index=[i for i in range(X.shape[1])]
best_perf=0
for i in range(len(survive_index)-1):
perfs = []
print(survive_index)
for index in survive_index:
print(index)
survive_index_copy = [i for i in survive_index if i!=index]
perfs.append(cross_validation(X[:,survive_index_copy],Y,setting,num_input = len(survive_index)-1))
print("best_perf",best_perf)
max_index = np.argmax(perfs)
current_best = np.max(perfs)
print("current_best",current_best)
if current_best > best_perf:
best_perf = current_best
survive_index.remove(survive_index[max_index])
else:
break
return (survive_index,best_perf)
backward_selection(X[:,0:10],Y,setting)
fpr, tpr, thresholds = roc_curve(Y, preds)
roc_auc = auc(fpr, tpr)
plt.plot(fpr, tpr, lw=1, alpha=0.3)
plt.title('(AUC = %0.2f)' % (roc_auc))
plt.show()
def cross_validation(X=X,Y=Y,epochs_=20,num_input_ = 84):
model = getModel(num_input=num_input_)
preds = []
for train, test in LeaveOneOut().split(X, Y):
model.fit(X,Y,epochs=epochs_,verbose=0)
# print(test)
probas_ = model.predict(X[test,:])
preds.append(probas_[0][0])
# Compute ROC curve and area the curve
fpr, tpr, thresholds = roc_curve(Y, preds)
roc_auc = auc(fpr, tpr)
return roc_auc
survive_index=[i for i in range(4)]
def backward_selection(survive_index):
for i in range(len(survive_index)-1):
perfs = []
best_perf=0
for index in survive_index:
print(index,"\n")
survive_index_copy = [i for i in survive_index if i!=index]
perfs.append(cross_validation(X=X[:,survive_index_copy],Y=Y,epochs_=20,num_input_ = len(survive_index)-1))
max_index = np.argmax(perfs)
current_best = np.max(perfs)
print(current_best)
if current_best > best_perf:
best_perf = current_best
survive_index.remove(survive_index[max_index])
else:
break
return survive_index
backward_selection(survive_index)
max_index = np.argmax(perfs)
survive_index[max_index]
fpr, tpr, thresholds = roc_curve(Y, preds)
roc_auc = auc(fpr, tpr)
plt.plot(fpr, tpr, lw=1, alpha=0.3)
plt.title('(AUC = %0.2f)' % (roc_auc))
plt.show()
```
|
github_jupyter
|
# 2 Dead reckoning
*Dead reckoning* is a means of navigation that does not rely on external observations. Instead, a robot’s position is estimated by summing its incremental movements relative to a known starting point.
Estimates of the distance traversed are usually obtained from measuring how many times the wheels have turned, and how many times they have turned in relation to each other. For example, the wheels of the robot could be attached to an odometer, similar to the device that records the mileage of a car.
In RoboLab we will calculate the position of a robot from how long it moves in a straight line or rotates about its centre. We will assume that the length of time for which the motors are switched on is directly related to the distance travelled by the wheels.
*By design, the simulator does not provide the robot with access to any magical GPS-style service. In principle, we could create a magical ‘simulated-GPS’ sensor that would allow the robot to identify its location from the simulator’s point of view; but in the real world we can’t always guarantee that external location services are available. For example, GPS doesn’t work indoors or underground, or even in many cities where line-of-sight access to four or more GPS satellites is not available.*
*Furthermore, the robot cannot magically teleport itself to a new location from within a program. Only the magics can teleport the robot to a specific location...*
*Although the simulator is omniscient and does keep track of where the robot is, the robot must figure out for itself where it is based on things like how far the motors have turned, or from its own sensor readings (ultrasound-based distance to a target, for example, or gyroscope heading); you will learn how to make use of sensors for navigation in later notebooks.*
## 2.1 Activity – Dead reckoning
An environment for the simulated robot to navigate is shown below, based on the 2018 First Lego League ‘Into Orbit’ challenge.
The idea is that the robot must get to the target satellite from its original starting point by avoiding the obstacles in its direct path.

The [First Lego League (FLL)](https://www.firstlegoleague.org/) is a friendly international youth-based robot competition in which teams compete at national and international level on an annual basis. School teams are often coached by volunteers. In the UK, volunteers often coach teams under the auspices of the [STEM Ambassadors Scheme](https://www.stem.org.uk/stem-ambassadors). Many companies run volunteering schemes that allow employees to volunteer their skills in company time using schemes such as STEM Ambassadors.
Load in the simulator in the usual way:
```
from nbev3devsim.load_nbev3devwidget import roboSim, eds
%load_ext nbev3devsim
```
To navigate the environment, we will use a small robot configuration within the simulator. The robot configuration can be set via the simulator user interface, or by passing the `-r Small_Robot` parameter setting in the simulator magic.
The following program should drive the robot from its starting point to the target, whilst avoiding the obstacles. We define the obstacle as being avoided if it is not crossed by the robot’s *pen down* trail.
Load the *FLL_2018_Into_Orbit* background into the simulator. Run the following code cell to download the program to the simulator and then, with the *pen down*, run the program in the simulator.
Remember, you can use the `-P / --pencolor` flag to change the pen colour and the `-C / --clear` option to clear the pen trace.
Does the robot reach the target satellite without encountering any obstacles?
```
%%sim_magic_preloaded -b FLL_2018_Into_Orbit -p -r Small_Robot
# Turn on the spot to the right
tank_turn.on_for_rotations(100, SpeedPercent(70), 1.7 )
# Go forwards
tank_drive.on_for_rotations(SpeedPercent(30), SpeedPercent(30), 20)
# Slight graceful turn to left
tank_drive.on_for_rotations(SpeedPercent(35), SpeedPercent(50), 8.5)
# Turn on the spot to the left
tank_turn.on_for_rotations(-100, SpeedPercent(75), 0.8)
# Forwards a bit
tank_drive.on_for_rotations(SpeedPercent(30), SpeedPercent(30), 2.0)
# Turn on the spot a bit more to the right
tank_turn.on_for_rotations(100, SpeedPercent(60), 0.4 )
# Go forwards a bit more and dock on the satellite
tank_drive.on_for_rotations(SpeedPercent(30), SpeedPercent(30), 1.0)
say("Hopefully I have docked with the satellite...")
```
*Add your notes on how well the simulated robot performed the task here.*
To set the speeds and times, I used a bit of trial and error.
If the route had been much more complex, then I would have been tempted to comment out the steps up I had already run and add new steps that would be applied from wherever the robot was currently located.
Note that the robot could have taken other routes to get to the satellite – I just thought I should avoid the asteroid!
### 2.1.1 Using motor tacho counts to identify how far the robot has travelled
In the above example, the motors were turned on for a specific amount of time to move the robot on each leg of its journey. This would not be an appropriate control strategy if we wanted to collect sensor data along the route, because the `on_for_X()` motor commands are blocking commands.
However, suppose we replaced the forward driving `tank_drive.on_for_rotations()` commands with commands of the form:
```python
from time import sleep
tank_drive.on(SPEED)
while int(tank_drive.left_motor.position) < DISTANCE:
# We need something that takes a finite time
# to run in the loop or the program will hang
sleep(0.1)
```
Now we could drive the robot forwards until the motor tacho count exceeds a specified `DISTANCE` and at the same time, optionally include additional commands, such as sensor data-logging commands, inside the body of each `while` loop.
*As well as `tank_drive.left_motor.position` we can also refer to `tank_drive.right_motor.position`. Also note that these values are returned as strings and need to be cast to integers for numerical comparisons.*
### 2.1.2 Activity – Dead reckoning over distances (optional)
Use the `.left_motor.position` and/or `.right_motor.position` motor tacho counts in a program that allows the robot to navigate from its home base to the satellite rendezvous.
*Your design notes here.*
```
# YOUR CODE HERE
```
*Your notes and observations here.*
## 2.2 Challenge – Reaching the moon base
In the following code cell, write a program to move the simulated robot from its location servicing the satellite to the moon base identified as the circular area marked on the moon in the top right-hand corner of the simulated world.
In the simulator, set the robot’s *x* location to `1250` and *y* location to `450`.
Use the following code cell to write your own dead-reckoning program to drive the robot to the moon base at location `(2150, 950)`.
```
%%sim_magic_preloaded
# YOUR CODE HERE
```
## 2.3 Dead reckoning with noise
The robot traverses its path using timing information for dead reckoning. In principle, if the simulated robot had a map then it could calculate all the distances and directions for itself, convert these to times, and dead reckon its way to the target. However, there is a problem with dead reckoning: *noise*.
In many physical systems, a perfect intended behaviour is subject to *noise* – random perturbations that arise within the system as time goes on as a side effect of its operation. In a robot, noise might arise in the behaviour of the motors, the transmission or the wheels. The result is that the robot does not execute its motion without error. We can model noise effects in the mobility system of our robot by adding a small amount of noise to the motor speeds as the simulator runs. This noise component may speed up or slow down the speed of each motor, in a random way. As with real systems, the noise represents slight random deviations from the theoretical, ideal behaviour.
For the following experiment, create a new, empty background cleared of pen traces.
```
%sim_magic -b Empty_Map --clear
```
Run the following code cell to download the program to the simulator using an empty background (select the *Empty_Map*) and the *Pen Down* mode selected. Also reset the initial location of the robot to an *x* value of `150` and *y* value of `400`.
Run the program in the simulator and observe what happens.
```
%%sim_magic_preloaded -b Empty_Map -p -x 150 -y 400 -r Small_Robot --noisecontrols
tank_drive.on_for_rotations(SpeedPercent(30),
SpeedPercent(30), 10)
```
*Record your observations here describing what happens when you run the program.*
When you run the program, you should see the robot drive forwards a short way in a straight line, leaving a straight line trail behind it.
Reset the location of the robot. Within the simulator, use the *Noise controls* to increase the *Wheel noise* value from zero by dragging the slider to the right a little way. Alternatively, add noise in the range `0...500` using the `--motornoise / -M` magic flag.
Run the program in the simulator again.
You should notice this time that the robot does not travel in a straight line. Instead, it drifts from side to side, although possibly to one side of the line.
Move the robot back to the start position, or rerun the previous code cell to do so, and run the program in the simulator again. This time, you should see it follows yet another different path.
Depending on how severe the noise setting is, the robot will travel closer (low noise) to the original straight line, or follow an ever-more erratic path (high noise).
*Record your own notes and observations here describing the behaviour of the robot for different levels of motor noise.*
Clear the pen traces from the simulator by running the following line magic:
```
%sim_magic -C
```
Now run the original satellite-finding dead-reckoning program again, using the *FLL_2018_Into_Orbit* background, but in the presence of *Wheel noise*. How well does it perform this time compared to previously?
```
%%sim_magic_preloaded -b FLL_2018_Into_Orbit -p -r Small_Robot
# Turn on the spot to the right
tank_turn.on_for_rotations(100, SpeedPercent(70), 1.7 )
# Go forwards
tank_drive.on_for_rotations(SpeedPercent(30), SpeedPercent(30), 20)
# Slight graceful turn to left
tank_drive.on_for_rotations(SpeedPercent(35), SpeedPercent(50), 8.5)
# Turn on the spot to the left
tank_turn.on_for_rotations(-100, SpeedPercent(75), 0.8)
# Forwards a bit
tank_drive.on_for_rotations(SpeedPercent(30), SpeedPercent(30), 2.0)
# Turn on the spot a bit more to the right
tank_turn.on_for_rotations(100, SpeedPercent(60), 0.4 )
# Go forwards a bit more and dock on the satellite
tank_drive.on_for_rotations(SpeedPercent(30), SpeedPercent(30), 1.0)
say("Did I avoid crashing and dock with the satellite?")
```
Reset the robot to its original location and run the program in the simulator again. Even with the same level of motor noise as on the previous run, how does the path followed by the robot this time compare with the previous run?
*Add your own notes and observations here.*
## 2.4 Summary
In this notebook, you have seen how we can use dead reckoning to move the robot along a specified path. Using the robot’s motor speeds and by monitoring how long the motors are switched on for, we can use distance–time calculations to estimate the robot’s path. If we add in accurate measurements regarding how far we want the robot to travel, and in what direction, this provides one way of helping the robot to navigate to a particular waypoint.
However, in the presence of noise, this approach is likely to be very unreliable: whilst the robot may think it is following one path, as determined by how long it has turned its motors on, and at what speed, it may in fact be following another path. In a real robot, the noise may be introduced in all sorts of ways, including from friction in the motor bearings, the time taken to accelerate from a standing start and get up to speed, and loss of traction effects such as wheel spin and slip as the robot’s wheels turn.
Whilst in some cases it may reach the target safely, in others it may end somewhere completely different, or encounter an obstacle along the way.
<!-- JD: should we say what's coming up in the next notebook? -->
|
github_jupyter
|
# Computer Vision Nanodegree
## Project: Image Captioning
---
In this notebook, you will use your trained model to generate captions for images in the test dataset.
This notebook **will be graded**.
Feel free to use the links below to navigate the notebook:
- [Step 1](#step1): Get Data Loader for Test Dataset
- [Step 2](#step2): Load Trained Models
- [Step 3](#step3): Finish the Sampler
- [Step 4](#step4): Clean up Captions
- [Step 5](#step5): Generate Predictions!
<a id='step1'></a>
## Step 1: Get Data Loader for Test Dataset
Before running the code cell below, define the transform in `transform_test` that you would like to use to pre-process the test images.
Make sure that the transform that you define here agrees with the transform that you used to pre-process the training images (in **2_Training.ipynb**). For instance, if you normalized the training images, you should also apply the same normalization procedure to the test images.
```
import sys
sys.path.append('/opt/cocoapi/PythonAPI')
from pycocotools.coco import COCO
from data_loader import get_loader
from torchvision import transforms
# TODO #1: Define a transform to pre-process the testing images.
transform_test = transforms.Compose([
transforms.Resize(256), # smaller edge of image resized to 256
transforms.RandomCrop(224), # get 224x224 crop from random location
transforms.RandomHorizontalFlip(), # horizontally flip image with probability=0.5
transforms.ToTensor(), # convert the PIL Image to a tensor
transforms.Normalize((0.485, 0.456, 0.406), # normalize image for pre-trained model
(0.229, 0.224, 0.225))])
#-#-#-# Do NOT modify the code below this line. #-#-#-#
# Create the data loader.
data_loader = get_loader(transform=transform_test,
mode='test')
```
Run the code cell below to visualize an example test image, before pre-processing is applied.
```
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
# Obtain sample image before and after pre-processing.
orig_image, image = next(iter(data_loader))
# Visualize sample image, before pre-processing.
plt.imshow(np.squeeze(orig_image))
plt.title('example image')
plt.show()
```
<a id='step2'></a>
## Step 2: Load Trained Models
In the next code cell we define a `device` that you will use move PyTorch tensors to GPU (if CUDA is available). Run this code cell before continuing.
```
import torch
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
```
Before running the code cell below, complete the following tasks.
### Task #1
In the next code cell, you will load the trained encoder and decoder from the previous notebook (**2_Training.ipynb**). To accomplish this, you must specify the names of the saved encoder and decoder files in the `models/` folder (e.g., these names should be `encoder-5.pkl` and `decoder-5.pkl`, if you trained the model for 5 epochs and saved the weights after each epoch).
### Task #2
Plug in both the embedding size and the size of the hidden layer of the decoder corresponding to the selected pickle file in `decoder_file`.
```
# Watch for any changes in model.py, and re-load it automatically.
% load_ext autoreload
% autoreload 2
import os
import torch
from model import EncoderCNN, DecoderRNN
# TODO #2: Specify the saved models to load.
encoder_file = "encoder-1.pkl"
decoder_file = "decoder-1.pkl"
# TODO #3: Select appropriate values for the Python variables below.
embed_size = 256 #512 #300
hidden_size = 512
# The size of the vocabulary.
vocab_size = len(data_loader.dataset.vocab)
# Initialize the encoder and decoder, and set each to inference mode.
encoder = EncoderCNN(embed_size)
encoder.eval()
decoder = DecoderRNN(embed_size, hidden_size, vocab_size)
decoder.eval()
# Load the trained weights.
encoder.load_state_dict(torch.load(os.path.join('./models', encoder_file)))
decoder.load_state_dict(torch.load(os.path.join('./models', decoder_file)))
# Move models to GPU if CUDA is available.
encoder.to(device)
decoder.to(device)
```
<a id='step3'></a>
## Step 3: Finish the Sampler
Before executing the next code cell, you must write the `sample` method in the `DecoderRNN` class in **model.py**. This method should accept as input a PyTorch tensor `features` containing the embedded input features corresponding to a single image.
It should return as output a Python list `output`, indicating the predicted sentence. `output[i]` is a nonnegative integer that identifies the predicted `i`-th token in the sentence. The correspondence between integers and tokens can be explored by examining either `data_loader.dataset.vocab.word2idx` (or `data_loader.dataset.vocab.idx2word`).
After implementing the `sample` method, run the code cell below. If the cell returns an assertion error, then please follow the instructions to modify your code before proceeding. Do **not** modify the code in the cell below.
```
# Move image Pytorch Tensor to GPU if CUDA is available.
image = image.to(device)
# Obtain the embedded image features.
features = encoder(image).unsqueeze(1)
# Pass the embedded image features through the model to get a predicted caption.
output = decoder.sample(features)
print('example output:', output)
assert (type(output)==list), "Output needs to be a Python list"
assert all([type(x)==int for x in output]), "Output should be a list of integers."
assert all([x in data_loader.dataset.vocab.idx2word for x in output]), "Each entry in the output needs to correspond to an integer that indicates a token in the vocabulary."
```
<a id='step4'></a>
## Step 4: Clean up the Captions
In the code cell below, complete the `clean_sentence` function. It should take a list of integers (corresponding to the variable `output` in **Step 3**) as input and return the corresponding predicted sentence (as a single Python string).
```
# TODO #4: Complete the function.
def clean_sentence(output):
seperator = " "
word_list = [];
for word_index in output:
if word_index not in [0,2]: # 0: '<start>', 1: '<end>', 2: '<unk>', 18: '.'
if word_index == 1:
break
word = data_loader.dataset.vocab.idx2word[word_index]
word_list.append(word)
sentence = seperator.join(word_list)
return sentence
```
After completing the `clean_sentence` function above, run the code cell below. If the cell returns an assertion error, then please follow the instructions to modify your code before proceeding.
```
sentence = clean_sentence(output)
print('example sentence:', sentence)
assert type(sentence)==str, 'Sentence needs to be a Python string!'
```
<a id='step5'></a>
## Step 5: Generate Predictions!
In the code cell below, we have written a function (`get_prediction`) that you can use to use to loop over images in the test dataset and print your model's predicted caption.
```
def get_prediction():
orig_image, image = next(iter(data_loader))
plt.imshow(np.squeeze(orig_image))
plt.title('Sample Image')
plt.show()
image = image.to(device)
features = encoder(image).unsqueeze(1)
output = decoder.sample(features)
sentence = clean_sentence(output)
print(sentence)
```
Run the code cell below (multiple times, if you like!) to test how this function works.
```
get_prediction()
```
As the last task in this project, you will loop over the images until you find four image-caption pairs of interest:
- Two should include image-caption pairs that show instances when the model performed well.
- Two should highlight image-caption pairs that highlight instances where the model did not perform well.
Use the four code cells below to complete this task.
### The model performed well!
Use the next two code cells to loop over captions. Save the notebook when you encounter two images with relatively accurate captions.
```
get_prediction()
get_prediction()
```
### The model could have performed better ...
Use the next two code cells to loop over captions. Save the notebook when you encounter two images with relatively inaccurate captions.
```
get_prediction()
get_prediction()
```
|
github_jupyter
|
```
# TensorFlow pix2pix implementation
from __future__ import absolute_import, division, print_function, unicode_literals
try:
# %tensorflow_version only exists in Colab.
%tensorflow_version 2.x
except Exception:
pass
import tensorflow as tf
import os
import time
from matplotlib import pyplot as plt
from IPython import display
print("Num GPUs Available: ", len(tf.config.experimental.list_physical_devices('GPU')))
PATH = "/Volumes/Data/projects/cs230/Project/RenderGAN/pix2pix/data/train_data/10-10000/AB/"
BUFFER_SIZE = 400
BATCH_SIZE = 1
IMG_WIDTH = 256
IMG_HEIGHT = 256
def load(image_file):
image = tf.io.read_file(image_file)
image = tf.image.decode_png(image)
w = tf.shape(image)[1]
w = w // 2
real_image = image[:, w:, :]
input_image = image[:, :w, :]
input_image = tf.cast(input_image, tf.float32)
real_image = tf.cast(real_image, tf.float32)
return input_image, real_image
inp, re = load(PATH+'train/8.png')
# casting to int for matplotlib to show the image
plt.figure()
plt.imshow(inp/255.0)
plt.figure()
plt.imshow(re/255.0)
def resize(input_image, real_image, height, width):
input_image = tf.image.resize(input_image, [height, width],
method=tf.image.ResizeMethod.NEAREST_NEIGHBOR)
real_image = tf.image.resize(real_image, [height, width],
method=tf.image.ResizeMethod.NEAREST_NEIGHBOR)
return input_image, real_image
def random_crop(input_image, real_image):
stacked_image = tf.stack([input_image, real_image], axis=0)
cropped_image = tf.image.random_crop(
stacked_image, size=[2, IMG_HEIGHT, IMG_WIDTH, 3])
return cropped_image[0], cropped_image[1]
# normalizing the images to [-1, 1]
def normalize(input_image, real_image):
input_image = (input_image / 127.5) - 1
real_image = (real_image / 127.5) - 1
return input_image, real_image
@tf.function()
def random_jitter(input_image, real_image):
# resizing to 286 x 286 x 3
input_image, real_image = resize(input_image, real_image, 286, 286)
# randomly cropping to 256 x 256 x 3
input_image, real_image = random_crop(input_image, real_image)
if tf.random.uniform(()) > 0.5:
# random mirroring
input_image = tf.image.flip_left_right(input_image)
real_image = tf.image.flip_left_right(real_image)
return input_image, real_image
plt.figure(figsize=(6, 6))
for i in range(4):
rj_inp, rj_re = random_jitter(inp, re)
plt.subplot(2, 2, i+1)
plt.imshow(rj_inp/255.0)
plt.axis('off')
plt.show()
def load_image_train(image_file):
input_image, real_image = load(image_file)
input_image, real_image = random_jitter(input_image, real_image)
input_image, real_image = normalize(input_image, real_image)
return input_image, real_image
def load_image_test(image_file):
input_image, real_image = load(image_file)
input_image, real_image = resize(input_image, real_image,
IMG_HEIGHT, IMG_WIDTH)
input_image, real_image = normalize(input_image, real_image)
return input_image, real_image
train_dataset = tf.data.Dataset.list_files(PATH+'train/*.png')
train_dataset = train_dataset.map(load_image_train,
num_parallel_calls=tf.data.experimental.AUTOTUNE)
train_dataset = train_dataset.shuffle(BUFFER_SIZE)
train_dataset = train_dataset.batch(BATCH_SIZE)
test_dataset = tf.data.Dataset.list_files(PATH+'test/*.png')
test_dataset = test_dataset.map(load_image_test)
test_dataset = test_dataset.batch(BATCH_SIZE)
OUTPUT_CHANNELS = 3
def downsample(filters, size, apply_batchnorm=True):
initializer = tf.random_normal_initializer(0., 0.02)
result = tf.keras.Sequential()
result.add(
tf.keras.layers.Conv2D(filters, size, strides=2, padding='same',
kernel_initializer=initializer, use_bias=False))
if apply_batchnorm:
result.add(tf.keras.layers.BatchNormalization())
result.add(tf.keras.layers.LeakyReLU())
return result
down_model = downsample(3, 4)
down_result = down_model(tf.expand_dims(inp, 0))
print (down_result.shape)
def upsample(filters, size, apply_dropout=False):
initializer = tf.random_normal_initializer(0., 0.02)
result = tf.keras.Sequential()
result.add(
tf.keras.layers.Conv2DTranspose(filters, size, strides=2,
padding='same',
kernel_initializer=initializer,
use_bias=False))
result.add(tf.keras.layers.BatchNormalization())
if apply_dropout:
result.add(tf.keras.layers.Dropout(0.5))
result.add(tf.keras.layers.ReLU())
return result
up_model = upsample(3, 4)
up_result = up_model(down_result)
print (up_result.shape)
def Generator():
inputs = tf.keras.layers.Input(shape=[256,256,3])
down_stack = [
downsample(64, 4, apply_batchnorm=False), # (bs, 128, 128, 64)
downsample(128, 4), # (bs, 64, 64, 128)
downsample(256, 4), # (bs, 32, 32, 256)
downsample(512, 4), # (bs, 16, 16, 512)
downsample(512, 4), # (bs, 8, 8, 512)
downsample(512, 4), # (bs, 4, 4, 512)
downsample(512, 4), # (bs, 2, 2, 512)
downsample(512, 4), # (bs, 1, 1, 512)
]
up_stack = [
upsample(512, 4, apply_dropout=True), # (bs, 2, 2, 1024)
upsample(512, 4, apply_dropout=True), # (bs, 4, 4, 1024)
upsample(512, 4, apply_dropout=True), # (bs, 8, 8, 1024)
upsample(512, 4), # (bs, 16, 16, 1024)
upsample(256, 4), # (bs, 32, 32, 512)
upsample(128, 4), # (bs, 64, 64, 256)
upsample(64, 4), # (bs, 128, 128, 128)
]
initializer = tf.random_normal_initializer(0., 0.02)
last = tf.keras.layers.Conv2DTranspose(OUTPUT_CHANNELS, 4,
strides=2,
padding='same',
kernel_initializer=initializer,
activation='tanh') # (bs, 256, 256, 3)
x = inputs
# Downsampling through the model
skips = []
for down in down_stack:
x = down(x)
skips.append(x)
skips = reversed(skips[:-1])
# Upsampling and establishing the skip connections
for up, skip in zip(up_stack, skips):
x = up(x)
x = tf.keras.layers.Concatenate()([x, skip])
x = last(x)
return tf.keras.Model(inputs=inputs, outputs=x)
generator = Generator()
tf.keras.utils.plot_model(generator, show_shapes=True, dpi=64)
gen_output = generator(inp[tf.newaxis,...], training=False)
plt.imshow(gen_output[0,...])
LAMBDA = 100
def generator_loss(disc_generated_output, gen_output, target):
gan_loss = loss_object(tf.ones_like(disc_generated_output), disc_generated_output)
# mean absolute error
l1_loss = tf.reduce_mean(tf.abs(target - gen_output))
total_gen_loss = gan_loss + (LAMBDA * l1_loss)
return total_gen_loss, gan_loss, l1_loss
def Discriminator():
initializer = tf.random_normal_initializer(0., 0.02)
inp = tf.keras.layers.Input(shape=[256, 256, 3], name='input_image')
tar = tf.keras.layers.Input(shape=[256, 256, 3], name='target_image')
x = tf.keras.layers.concatenate([inp, tar]) # (bs, 256, 256, channels*2)
down1 = downsample(64, 4, False)(x) # (bs, 128, 128, 64)
down2 = downsample(128, 4)(down1) # (bs, 64, 64, 128)
down3 = downsample(256, 4)(down2) # (bs, 32, 32, 256)
zero_pad1 = tf.keras.layers.ZeroPadding2D()(down3) # (bs, 34, 34, 256)
conv = tf.keras.layers.Conv2D(512, 4, strides=1,
kernel_initializer=initializer,
use_bias=False)(zero_pad1) # (bs, 31, 31, 512)
batchnorm1 = tf.keras.layers.BatchNormalization()(conv)
leaky_relu = tf.keras.layers.LeakyReLU()(batchnorm1)
zero_pad2 = tf.keras.layers.ZeroPadding2D()(leaky_relu) # (bs, 33, 33, 512)
last = tf.keras.layers.Conv2D(1, 4, strides=1,
kernel_initializer=initializer)(zero_pad2) # (bs, 30, 30, 1)
return tf.keras.Model(inputs=[inp, tar], outputs=last)
discriminator = Discriminator()
tf.keras.utils.plot_model(discriminator, show_shapes=True, dpi=64)
disc_out = discriminator([inp[tf.newaxis,...], gen_output], training=False)
plt.imshow(disc_out[0,...,-1], vmin=-20, vmax=20, cmap='RdBu_r')
plt.colorbar()
loss_object = tf.keras.losses.BinaryCrossentropy(from_logits=True)
def discriminator_loss(disc_real_output, disc_generated_output):
real_loss = loss_object(tf.ones_like(disc_real_output), disc_real_output)
generated_loss = loss_object(tf.zeros_like(disc_generated_output), disc_generated_output)
total_disc_loss = real_loss + generated_loss
return total_disc_loss
generator_optimizer = tf.keras.optimizers.Adam(2e-4, beta_1=0.5)
discriminator_optimizer = tf.keras.optimizers.Adam(2e-4, beta_1=0.5)
checkpoint_dir = './training_checkpoints'
checkpoint_prefix = os.path.join(checkpoint_dir, "ckpt")
checkpoint = tf.train.Checkpoint(generator_optimizer=generator_optimizer,
discriminator_optimizer=discriminator_optimizer,
generator=generator,
discriminator=discriminator)
def generate_images(model, test_input, tar):
prediction = model(test_input, training=True)
plt.figure(figsize=(15,15))
display_list = [test_input[0], tar[0], prediction[0]]
title = ['Input Image', 'Ground Truth', 'Predicted Image']
for i in range(3):
plt.subplot(1, 3, i+1)
plt.title(title[i])
# getting the pixel values between [0, 1] to plot it.
plt.imshow(display_list[i] * 0.5 + 0.5)
plt.axis('off')
plt.show()
for example_input, example_target in test_dataset.take(1):
generate_images(generator, example_input, example_target)
EPOCHS = 10
import datetime
log_dir="logs/"
summary_writer = tf.summary.create_file_writer(
log_dir + "fit/" + datetime.datetime.now().strftime("%Y%m%d-%H%M%S"))
@tf.function
def train_step(input_image, target, epoch):
with tf.GradientTape() as gen_tape, tf.GradientTape() as disc_tape:
gen_output = generator(input_image, training=True)
disc_real_output = discriminator([input_image, target], training=True)
disc_generated_output = discriminator([input_image, gen_output], training=True)
gen_total_loss, gen_gan_loss, gen_l1_loss = generator_loss(disc_generated_output, gen_output, target)
disc_loss = discriminator_loss(disc_real_output, disc_generated_output)
generator_gradients = gen_tape.gradient(gen_total_loss,
generator.trainable_variables)
discriminator_gradients = disc_tape.gradient(disc_loss,
discriminator.trainable_variables)
generator_optimizer.apply_gradients(zip(generator_gradients,
generator.trainable_variables))
discriminator_optimizer.apply_gradients(zip(discriminator_gradients,
discriminator.trainable_variables))
with summary_writer.as_default():
tf.summary.scalar('gen_total_loss', gen_total_loss, step=epoch)
tf.summary.scalar('gen_gan_loss', gen_gan_loss, step=epoch)
tf.summary.scalar('gen_l1_loss', gen_l1_loss, step=epoch)
tf.summary.scalar('disc_loss', disc_loss, step=epoch)
def fit(train_ds, epochs, test_ds):
for epoch in range(epochs):
start = time.time()
display.clear_output(wait=True)
for example_input, example_target in test_ds.take(1):
generate_images(generator, example_input, example_target)
print("Epoch: ", epoch)
# Train
for n, (input_image, target) in train_ds.enumerate():
print('.', end='')
if (n+1) % 100 == 0:
print()
train_step(input_image, target, epoch)
print()
# saving (checkpoint) the model every 20 epochs
if (epoch + 1) % 20 == 0:
checkpoint.save(file_prefix = checkpoint_prefix)
print ('Time taken for epoch {} is {} sec\n'.format(epoch + 1,
time.time()-start))
checkpoint.save(file_prefix = checkpoint_prefix)
%load_ext tensorboard
%tensorboard --logdir {log_dir}
fit(train_dataset, EPOCHS, test_dataset)
!ls {checkpoint_dir}
```
|
github_jupyter
|
# Basic Workflow
```
# Always have your imports at the top
import pandas as pd
from sklearn.pipeline import make_pipeline
from sklearn.impute import SimpleImputer
from sklearn.ensemble import RandomForestClassifier
from sklearn.base import TransformerMixin
from hashlib import sha1 # just for grading purposes
import json # just for grading purposes
def _hash(obj, salt='none'):
if type(obj) is not str:
obj = json.dumps(obj)
to_encode = obj + salt
return sha1(to_encode.encode()).hexdigest()
```
# Workflow steps
What are the basic workflow steps?
It's incredibly obvious what the steps are since you can see them graded in plain text. However we deem it worth actually making you type each one of the steps and take a moment to think about it and internalize them.
Please do actually type them rather than just copy-pasting as fast as you can. Type it out character by character and internalize.
```
# step_1 = ...
# step_2 = ...
# step_2_a = ...
# step_2_b = ...
# step_2_c = ...
# step_2_d = ...
# step_3 = ...
# step_4 = ...
# step_5 = ...
# YOUR CODE HERE
raise NotImplementedError()
### BEGIN TESTS
assert step_1 == 'Get the data'
assert step_2 == 'Data analysis and preparation'
assert step_2_a == 'Data analysis'
assert step_2_b == 'Dealing with data problems'
assert step_2_c == 'Feature engineering'
assert step_2_d == 'Feature selection'
assert step_3 == 'Train model'
assert step_4 == 'Evaluate results'
assert step_5 == 'Iterate'
### END TESTS
```
# Specific workflow questions
Here are some more specific questions about individual workflow steps.
```
# True or False, it's super easy to gather your dataset in a production environment
# real_world_dataset_gathering_easy = ...
# True or False, it's super easy to gather your dataset in the context of the academy
# academy_dataset_gathering_easy = ...
# True or False, you should try as hard as you can to get the best possible score
# on your test set by iterating until you can't get your test set score any higher
# by any means possible
# test_set_optimization_is_good = ...
# True or False, you should choose one metric by which to evaluate your model and
# never consider using another one
# one_metric_should_rule_them_all = ...
# YOUR CODE HERE
raise NotImplementedError()
### BEGIN TESTS
assert _hash(real_world_dataset_gathering_easy, 'salt1') == '63b5b9a8f2d359e1fc175c3b01b907ef87590484'
assert _hash(academy_dataset_gathering_easy, 'salt2') == 'dd7dee495a153c95d28c7aa95289c0415242f5d8'
assert _hash(test_set_optimization_is_good, 'salt3') == 'f24a294afb4a09f7f9df9ee13eb18e7d341c439d'
assert _hash(one_metric_should_rule_them_all, 'salt4') == '2360691a582e4f0fbefa238ab6ced1cbfbfe8a50'
### END TESTS
```
# scikit pipelines
Make a simple pipeline that
1. Drops all columns that start with the string `evil`
1. Fills all nulls with the median
```
# Create a pipeline step called RemoveEvilColumns the removed any
# column whose name starts with the string 'evil'
# YOUR CODE HERE
raise NotImplementedError()
# Create an pipeline using make_pipeline
# 1. removes evil columns
# 2. imputes with the mean
# 3. has a random forest classifier as the last step
# YOUR CODE HERE
raise NotImplementedError()
X = pd.DataFrame({
'evil_1': ['a'] * 100,
'evil_2': ['b'] * 100,
'not_so_evil': list(range(0, 100))
})
y = pd.Series([x % 2 for x in range(0, 100)])
pipeline.fit(X, y)
### BEGIN TESTS
assert pipeline.steps[0][0] == 'removeevilcolumns', pipeline.steps[0][0]
assert pipeline.steps[1][0] == 'simpleimputer', pipeline.steps[1][0]
assert pipeline.steps[2][0] == 'randomforestclassifier', pipeline.steps[2][0]
### END TESTS
```
|
github_jupyter
|
# Lab 11: MLP -- exercise
# Understanding the training loop
```
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from random import randint
import utils
```
### Download the data and print the sizes
```
train_data=torch.load('../data/fashion-mnist/train_data.pt')
print(train_data.size())
train_label=torch.load('../data/fashion-mnist/train_label.pt')
print(train_label.size())
test_data=torch.load('../data/fashion-mnist/test_data.pt')
print(test_data.size())
```
### Make a ONE layer net class. The network output are the scores! No softmax needed! You have only one line to write in the forward function
```
class one_layer_net(nn.Module):
def __init__(self, input_size, output_size):
super(one_layer_net , self).__init__()
self.linear_layer = nn.Linear(input_size, output_size, bias=False)# complete here
def forward(self, x):
scores = self.linear_layer(x) # complete here
return scores
```
### Build the net
```
net= one_layer_net(784,10)# complete here
print(net)
```
### Choose the criterion and the optimizer: use the CHEAT SHEET to see the correct syntax.
### Remember that the optimizer need to have access to the parameters of the network (net.parameters()).
### Set the batchize and learning rate to be:
### batchize = 50
### learning rate = 0.01
```
# make the criterion
criterion = nn.CrossEntropyLoss()# complete here
# make the SGD optimizer.
optimizer=torch.optim.SGD(net.parameters(), lr=0.01) #complete here )
# set up the batch size
bs=50
```
### Complete the training loop
```
for iter in range(1,5000):
# Set dL/dU, dL/dV, dL/dW to be filled with zeros
optimizer.zero_grad()
# create a minibatch
indices = torch.LongTensor(bs).random_(0,60000)
minibatch_data = train_data[indices]
minibatch_label = train_label[indices]
# reshape the minibatch
inputs = minibatch_data.view(bs, 784)
# tell Pytorch to start tracking all operations that will be done on "inputs"
inputs.requires_grad_()
# forward the minibatch through the net
scores = net(inputs)
# Compute the average of the losses of the data points in the minibatch
loss = criterion(scores, minibatch_label)
# backward pass to compute dL/dU, dL/dV and dL/dW
loss.backward()
# do one step of stochastic gradient descent: U=U-lr(dL/dU), V=V-lr(dL/dU), ...
optimizer.step()
```
### Choose image at random from the test set and see how good/bad are the predictions
```
# choose a picture at random
idx=randint(0, 10000-1)
im=test_data[idx]
# diplay the picture
utils.show(im)
# feed it to the net and display the confidence scores
scores = net( im.view(1,784))
probs= F.softmax(scores, dim=1)
utils.show_prob_fashion_mnist(probs)
```
|
github_jupyter
|
## Main points
* Solution should be reasonably simple because the contest is only 24 hours long
* Metric is based on the prediction of clicked pictures one week ahead, so clicks are the most important information
* More recent information is more important
* Only pictures that were shown to a user could be clicked, so pictures popularity is important
* Metric is MAPK@100
* Link https://contest.yandex.ru/contest/12899/problems (Russian)
## Plan
* Build a classic recommending system based on user click history
* Only use recent days of historical data
* Take into consideration projected picture popularity
## Magic constants
### ALS recommending system:
```
# Factors for ALS
factors_count=100
# Last days of click history used
trail_days=14
# number of best candidates generated by ALS
output_candidates_count=2000
# Last days of history with more weight
last_days=1
# Coefficient for additional weight
last_days_weight=4
```
## Popular pictures prediction model:
```
import lightgbm
lightgbm.__version__
popularity_model = lightgbm.LGBMRegressor(seed=0)
heuristic_alpha = 0.2
import datetime
import tqdm
import pandas as pd
from scipy.sparse import coo_matrix
import implicit
implicit.__version__
test_users = pd.read_csv('Blitz/test_users.csv')
data = pd.read_csv('Blitz/train_clicks.csv', parse_dates=['day'])
```
## Split last 7 days to calculate clicks similar to test set
```
train, target_week = (
data[data.day <= datetime.datetime(2019, 3, 17)].copy(),
data[data.day > datetime.datetime(2019, 3, 17)],
)
train.day.nunique(), target_week.day.nunique()
last_date = train.day.max()
train.loc[:, 'delta_days'] = 1 + (last_date - train.day).apply(lambda d: d.days)
last_date = data.day.max()
data.loc[:, 'delta_days'] = 1 + (last_date - data.day).apply(lambda d: d.days)
def picture_features(data):
"""Generating clicks count for every picture in last days"""
days = range(1, 3)
features = []
names = []
for delta_days in days:
features.append(
data[(data.delta_days == delta_days)].groupby(['picture_id'])['user_id'].count()
)
names.append('%s_%d' % ('click', delta_days))
features = pd.concat(features, axis=1).fillna(0)
features.columns = names
features = features.reindex(data.picture_id.unique())
return features.fillna(0)
X = picture_features(train)
X.mean(axis=0)
def clicks_count(data, index):
return data.groupby('picture_id')['user_id'].count().reindex(index).fillna(0)
y = clicks_count(target_week, X.index)
y.shape, y.mean()
```
## Train a model predicting popular pictures next week
```
popularity_model.fit(X, y)
X_test = picture_features(data)
X_test.mean(axis=0)
X_test['p'] = popularity_model.predict(X_test)
X_test.loc[X_test['p'] < 0, 'p'] = 0
X_test['p'].mean()
```
## Generate dict with predicted clicks for every picture
```
# This prediction would be used to correct recommender score
picture = dict(X_test['p'])
```
# Recommender part
## Generate prediction using ALS approach
```
import os
os.environ['OPENBLAS_NUM_THREADS'] = "1"
def als_baseline(
train, test_users,
factors_n, last_days, trail_days, output_candidates_count, last_days_weight
):
train = train[train.delta_days <= trail_days].drop_duplicates([
'user_id', 'picture_id'
])
users = train.user_id
items = train.picture_id
weights = 1 + last_days_weight * (train.delta_days <= last_days)
user_item = coo_matrix((weights, (users, items)))
model = implicit.als.AlternatingLeastSquares(factors=factors_n, iterations=factors_n)
model.fit(user_item.T.tocsr())
user_item_csr = user_item.tocsr()
rows = []
for user_id in tqdm.tqdm_notebook(test_users.user_id.values):
items = [(picture_id, score) for picture_id, score in model.recommend(user_id, user_item_csr, N=output_candidates_count)]
rows.append(items)
test_users['predictions_full'] = [
p
for p, user_id in zip(
rows,
test_users.user_id.values
)
]
test_users['predictions'] = [
[x[0] for x in p]
for p, user_id in zip(
rows,
test_users.user_id.values
)
]
return test_users
test_users = als_baseline(
data, test_users, factors_count, last_days, trail_days, output_candidates_count, last_days_weight)
```
## Calculate history clicks to exclude them from results. Such clicks are excluded from test set according to task
```
clicked = data.groupby('user_id').agg({'picture_id': set})
def substract_clicked(p, c):
filtered = [picture for picture in p if picture not in c][:100]
return filtered
```
## Heuristical approach to reweight ALS score according to picture predicted popularity
Recommender returns (picture, score) pairs sorted decreasing for every user.
For every user we replace picture $score_p$ with $score_p \cdot (1 + popularity_{p})^{0.2}$
$popularity_{p}$ - popularity predicted for this picture for next week
This slightly moves popular pictures to the top of list for every user
```
import math
rows = test_users['predictions_full']
def correct_with_popularity(items, picture, alpha):
return sorted([
(score * (1 + picture.get(picture_id, 0)) ** alpha, picture_id, score, picture.get(picture_id, 0))
for picture_id, score in items], reverse=True
)
corrected_rows = [
[x[1] for x in correct_with_popularity(items, picture, heuristic_alpha)]
for items in rows
]
```
## Submission formatting
```
test_users['predictions'] = [
' '.join(map(str,
substract_clicked(p, {} if user_id not in clicked.index else clicked.loc[user_id][0])
))
for p, user_id in zip(
corrected_rows,
test_users.user_id.values
)
]
test_users[['user_id', 'predictions']].to_csv('submit.csv', index=False)
```
|
github_jupyter
|
This challenge implements an instantiation of OTR based on AES block cipher with modified version 1.0. OTR, which stands for Offset Two-Round, is a blockcipher mode of operation to realize an authenticated encryption with associated data (see [[1]](#1)). AES-OTR algorithm is a campaign of CAESAR competition, it has successfully entered the third round of screening by virtue of its unique advantages, you can see the whole algorithms and structure of AES-OTR from the design document (see [[2]](#2)).
However, the first version is vulnerable to forgery attacks in the known plaintext conditions and association data and public message number are reused, many attacks can be applied here to forge an excepted ciphertext with a valid tag (see [[3]](#3)).
For example, in this challenge we can build the following three plaintexts:
```
M_0 = [b'Uid=16112\xffUserNa', b'me=AdministratoR', b'\xffT=111111111111\xff', b'Cmd=Give_Me_FlaG', b'\xff???????????????']
M_1 = [b'Uid=16111\xffUserNa', b'me=Administrator', b'r\xffT=11111111111\xff', b'Cmd=Give_Me_FlaG', b'\xff???????????????']
M_2 = [b'Uid=16112\xffUserNa', b'me=AdministratoR', b'\xffT=111111111111\xff', b'Cmd=Give_Me_Flag', b'g\xff??????????????']
```
Here `'111111111111'` can represent any value since the server won't check whether the message and its corresponding hash value match, so we just need to make sure that they are at the right length. If you look closely, you will find that none of the three plaintexts contains illegal fields, so we can use the encrypt Oracle provided by the server to get their corresponding ciphertexts easily. Next, noticed that these plaintexts satisfied:
```
from Crypto.Util.strxor import strxor
M_0 = [b'Uid=16112\xffUserNa', b'me=AdministratoR', b'\xffT=111111111111\xff', b'Cmd=Give_Me_FlaG', b'\xff???????????????']
M_1 = [b'Uid=16111\xffUserNa', b'me=Administrator', b'r\xffT=11111111111\xff', b'Cmd=Give_Me_FlaG', b'\xff???????????????']
M_2 = [b'Uid=16112\xffUserNa', b'me=AdministratoR', b'\xffT=111111111111\xff', b'Cmd=Give_Me_Flag', b'g\xff??????????????']
strxor(M_0[1], M_0[3]) == strxor(M_1[1], M_2[3])
```
So according to the forgery attacks described in [[3]](#3), suppose their corresponding ciphertexts are `C_0`, `C_1` and `C_2`, then we can forge a valid ciphertext and tag using:
```
from Toy_AE import Toy_AE
def unpack(r):
data = r.split(b"\xff")
uid, uname, token, cmd, appendix = int(data[0][4:]), data[1][9:], data[2][2:], data[3][4:], data[4]
return (uid, uname, token, cmd, appendix)
ae = Toy_AE()
M_0 = [b'Uid=16112\xffUserNa', b'me=AdministratoR', b'\xffT=111111111111\xff', b'Cmd=Give_Me_FlaG', b'\xff???????????????']
M_1 = [b'Uid=16111\xffUserNa', b'me=Administrator', b'r\xffT=11111111111\xff', b'Cmd=Give_Me_FlaG', b'\xff???????????????']
M_2 = [b'Uid=16112\xffUserNa', b'me=AdministratoR', b'\xffT=111111111111\xff', b'Cmd=Give_Me_Flag', b'g\xff??????????????']
C_0, T_0 = ae.encrypt(b''.join(M_0))
C_1, T_1 = ae.encrypt(b''.join(M_1))
C_2, T_2 = ae.encrypt(b''.join(M_2))
C_forge = C_1[:32] + C_2[32:64] + C_0[64:]
T_forge = T_0
_, uname, _, cmd, _ = unpack(ae.decrypt(C_forge, T_forge))
uname == b"Administrator" and cmd == b"Give_Me_Flag"
```
Here is my final exp:
```
import string
from pwn import *
from hashlib import sha256
from Crypto.Util.strxor import strxor
from Crypto.Util.number import long_to_bytes, bytes_to_long
def bypass_POW(io):
chall = io.recvline()
post = chall[14:30]
tar = chall[38:-2]
io.recvuntil(':')
found = iters.bruteforce(lambda x:sha256((x + post.decode()).encode()).hexdigest() == tar.decode(), string.ascii_letters + string.digits, 4)
io.sendline(found.encode())
C = []
T = []
io = remote("123.57.4.93", 45216)
bypass_POW(io)
io.sendlineafter(b"Your option:", '1')
io.sendlineafter(b"Set up your user id:", '16108')
io.sendlineafter(b"Your username:", 'AdministratoR')
io.sendlineafter(b"Your command:", 'Give_Me_FlaG')
io.sendlineafter(b"Any Appendix?", "???????????????")
_ = io.recvuntil(b"Your ticket:")
C.append(long_to_bytes(int(io.recvline().strip(), 16)))
_ = io.recvuntil(b"With my Auth:")
T.append(long_to_bytes(int(io.recvline().strip(), 16)))
io.sendlineafter(b"Your option:", '1')
io.sendlineafter(b"Set up your user id:", '16107')
io.sendlineafter(b"Your username:", 'Administratorr')
io.sendlineafter(b"Your command:", 'Give_Me_FlaG')
io.sendlineafter(b"Any Appendix?", "???????????????")
_ = io.recvuntil(b"Your ticket:")
C.append(long_to_bytes(int(io.recvline().strip(), 16)))
_ = io.recvuntil(b"With my Auth:")
T.append(long_to_bytes(int(io.recvline().strip(), 16)))
io.sendlineafter(b"Your option:", '1')
io.sendlineafter(b"Set up your user id:", '16108')
io.sendlineafter(b"Your username:", 'AdministratoR')
io.sendlineafter(b"Your command:", 'Give_Me_Flagg')
io.sendlineafter(b"Any Appendix?", "??????????????")
_ = io.recvuntil(b"Your ticket:")
C.append(long_to_bytes(int(io.recvline().strip(), 16)))
_ = io.recvuntil(b"With my Auth:")
T.append(long_to_bytes(int(io.recvline().strip(), 16)))
ct = (C[1][:32] + C[2][32:64] + C[0][64:]).hex()
te = T[0].hex()
io.sendlineafter(b"Your option:", '2')
io.sendlineafter(b"Ticket:", ct)
io.sendlineafter(b"Auth:", te)
flag = io.recvline().strip().decode()
print(flag)
```
b'X-NUCA{Gentlem3n_as_0f_th1s_mOment_I aM_th4t_sec0nd_mouse}'
**P.S.**
* The version used in this challenge is v 1.0, some vulnerabilities have been fixed in subsequent versions(v 2.0, v 3.0 and v 3.1), you can see the final version at [[4]](#4). Also, for some attacks on the new version, see [[5]](#5) and [[6]](#6).
* The content of the FLAG is a quote from movie *Catch Me If You Can* "Two little mice fell in a bucket of cream. The first mouse quickly gave up and drowned. The second mouse, wouldn't quit. He struggled so hard that eventually he churned that cream into butter and crawled out. Gentlemen, as of this moment, I am that second mouse."
**References**
<a id="1" href="https://eprint.iacr.org/2013/628.pdf"> [1] Minematsu K. Parallelizable rate-1 authenticated encryption from pseudorandom functions[C]//Annual International Conference on the Theory and Applications of Cryptographic Techniques. Springer, Berlin, Heidelberg, 2014: 275-292.</a>
<a id="2" href="https://competitions.cr.yp.to/round1/aesotrv1.pdf"> [2] Minematsu K. AES-OTR v1 design document.</a>
<a id="3" href="http://www.shcas.net/jsjyup/pdf/2017/10/对认证加密算法AES-OTR的伪造攻击.pdf"> [3] Xiulin Zheng, Yipeng Fu, Haiyan Song. Forging attacks on authenticated encryption algorithm AES-OTR[J]. Computer Applications and Software, 2017, 034(010):320-324,329.</a>
<a id="4" href="https://competitions.cr.yp.to/round1/aesotrv1.pdf"> [4] Minematsu K. AES-OTR v3.1 design document.</a>
<a id="5" href="https://eprint.iacr.org/2017/332.pdf">[5] Forler, Christian, et al. "Reforgeability of authenticated encryption schemes." Australasian Conference on Information Security and Privacy. Springer, Cham, 2017.</a>
<a id="6" href="https://eprint.iacr.org/2017/1147.pdf">[6] Vaudenay, Serge, and Damian Vizár. "Under Pressure: Security of Caesar Candidates beyond their Guarantees." IACR Cryptol. ePrint Arch. 2017 (2017): 1147.</a>
|
github_jupyter
|
```
import re
import os
import keras.backend as K
import numpy as np
import pandas as pd
from keras import layers, models, utils
import json
def reset_everything():
import tensorflow as tf
%reset -f in out dhist
tf.reset_default_graph()
K.set_session(tf.InteractiveSession())
# Constants for our networks. We keep these deliberately small to reduce training time.
VOCAB_SIZE = 250000
EMBEDDING_SIZE = 100
MAX_DOC_LEN = 128
MIN_DOC_LEN = 12
def extract_stackexchange(filename, limit=1000000):
json_file = filename + 'limit=%s.json' % limit
rows = []
for i, line in enumerate(os.popen('7z x -so "%s" Posts.xml' % filename)):
line = str(line)
if not line.startswith(' <row'):
continue
if i % 1000 == 0:
print('\r%05d/%05d' % (i, limit), end='', flush=True)
parts = line[6:-5].split('"')
record = {}
for i in range(0, len(parts), 2):
k = parts[i].replace('=', '').strip()
v = parts[i+1].strip()
record[k] = v
rows.append(record)
if len(rows) > limit:
break
with open(json_file, 'w') as fout:
json.dump(rows, fout)
return rows
xml_7z = utils.get_file(
fname='travel.stackexchange.com.7z',
origin='https://ia800107.us.archive.org/27/items/stackexchange/travel.stackexchange.com.7z',
)
print()
rows = extract_stackexchange(xml_7z)
```
# Data Exploration
Now that we have extracted our data, let's clean it up and take a look at what we have to work with.
```
df = pd.DataFrame.from_records(rows)
df = df.set_index('Id', drop=False)
df['Title'] = df['Title'].fillna('').astype('str')
df['Tags'] = df['Tags'].fillna('').astype('str')
df['Body'] = df['Body'].fillna('').astype('str')
df['Id'] = df['Id'].astype('int')
df['PostTypeId'] = df['PostTypeId'].astype('int')
df['ViewCount'] = df['ViewCount'].astype('float')
df.head()
list(df[df['ViewCount'] > 250000]['Title'])
from keras.preprocessing.text import Tokenizer
from keras.preprocessing.sequence import pad_sequences
tokenizer = Tokenizer(num_words=VOCAB_SIZE)
tokenizer.fit_on_texts(df['Body'] + df['Title'])
# Compute TF/IDF Values
total_count = sum(tokenizer.word_counts.values())
idf = { k: np.log(total_count/v) for (k,v) in tokenizer.word_counts.items() }
# Download pre-trained word2vec embeddings
import gensim
glove_100d = utils.get_file(
fname='glove.6B.100d.txt',
origin='https://storage.googleapis.com/deep-learning-cookbook/glove.6B.100d.txt',
)
w2v_100d = glove_100d + '.w2v'
from gensim.scripts.glove2word2vec import glove2word2vec
glove2word2vec(glove_100d, w2v_100d)
w2v_model = gensim.models.KeyedVectors.load_word2vec_format(w2v_100d)
w2v_weights = np.zeros((VOCAB_SIZE, w2v_model.syn0.shape[1]))
idf_weights = np.zeros((VOCAB_SIZE, 1))
for k, v in tokenizer.word_index.items():
if v >= VOCAB_SIZE:
continue
if k in w2v_model:
w2v_weights[v] = w2v_model[k]
idf_weights[v] = idf[k]
del w2v_model
df['title_tokens'] = tokenizer.texts_to_sequences(df['Title'])
df['body_tokens'] = tokenizer.texts_to_sequences(df['Body'])
import random
# We can create a data generator that will randomly title and body tokens for questions. We'll use random text
# from other questions as a negative example when necessary.
def data_generator(batch_size, negative_samples=1):
questions = df[df['PostTypeId'] == 1]
all_q_ids = list(questions.index)
batch_x_a = []
batch_x_b = []
batch_y = []
def _add(x_a, x_b, y):
batch_x_a.append(x_a[:MAX_DOC_LEN])
batch_x_b.append(x_b[:MAX_DOC_LEN])
batch_y.append(y)
while True:
questions = questions.sample(frac=1.0)
for i, q in questions.iterrows():
_add(q['title_tokens'], q['body_tokens'], 1)
negative_q = random.sample(all_q_ids, negative_samples)
for nq_id in negative_q:
_add(q['title_tokens'], df.at[nq_id, 'body_tokens'], 0)
if len(batch_y) >= batch_size:
yield ({
'title': pad_sequences(batch_x_a, maxlen=None),
'body': pad_sequences(batch_x_b, maxlen=None),
}, np.asarray(batch_y))
batch_x_a = []
batch_x_b = []
batch_y = []
# dg = data_generator(1, 2)
# next(dg)
# next(dg)
```
# Embedding Lookups
Let's define a helper class for looking up our embedding results. We'll use it
to verify our models.
```
questions = df[df['PostTypeId'] == 1]['Title'].reset_index(drop=True)
question_tokens = pad_sequences(tokenizer.texts_to_sequences(questions))
class EmbeddingWrapper(object):
def __init__(self, model):
self._r = questions
self._i = {i:s for (i, s) in enumerate(questions)}
self._w = model.predict({'title': question_tokens}, verbose=1, batch_size=1024)
self._model = model
self._norm = np.sqrt(np.sum(self._w * self._w + 1e-5, axis=1))
def nearest(self, sentence, n=10):
x = tokenizer.texts_to_sequences([sentence])
if len(x[0]) < MIN_DOC_LEN:
x[0] += [0] * (MIN_DOC_LEN - len(x))
e = self._model.predict(np.asarray(x))[0]
norm_e = np.sqrt(np.dot(e, e))
dist = np.dot(self._w, e) / (norm_e * self._norm)
top_idx = np.argsort(dist)[-n:]
return pd.DataFrame.from_records([
{'question': self._r[i], 'dist': float(dist[i])}
for i in top_idx
])
# Our first model will just sum up the embeddings of each token.
# The similarity between documents will be the dot product of the final embedding.
import tensorflow as tf
def sum_model(embedding_size, vocab_size, embedding_weights=None, idf_weights=None):
title = layers.Input(shape=(None,), dtype='int32', name='title')
body = layers.Input(shape=(None,), dtype='int32', name='body')
def make_embedding(name):
if embedding_weights is not None:
embedding = layers.Embedding(mask_zero=True, input_dim=vocab_size, output_dim=w2v_weights.shape[1],
weights=[w2v_weights], trainable=False,
name='%s/embedding' % name)
else:
embedding = layers.Embedding(mask_zero=True, input_dim=vocab_size, output_dim=embedding_size,
name='%s/embedding' % name)
if idf_weights is not None:
idf = layers.Embedding(mask_zero=True, input_dim=vocab_size, output_dim=1,
weights=[idf_weights], trainable=False,
name='%s/idf' % name)
else:
idf = layers.Embedding(mask_zero=True, input_dim=vocab_size, output_dim=1,
name='%s/idf' % name)
return embedding, idf
embedding_a, idf_a = make_embedding('a')
embedding_b, idf_b = embedding_a, idf_a
# embedding_b, idf_b = make_embedding('b')
mask = layers.Masking(mask_value=0)
def _combine_and_sum(args):
[embedding, idf] = args
return K.sum(embedding * K.abs(idf), axis=1)
sum_layer = layers.Lambda(_combine_and_sum, name='combine_and_sum')
sum_a = sum_layer([mask(embedding_a(title)), idf_a(title)])
sum_b = sum_layer([mask(embedding_b(body)), idf_b(body)])
sim = layers.dot([sum_a, sum_b], axes=1, normalize=True)
sim_model = models.Model(
inputs=[title, body],
outputs=[sim],
)
sim_model.compile(loss='binary_crossentropy', optimizer='nadam', metrics=['accuracy'])
sim_model.summary()
embedding_model = models.Model(
inputs=[title],
outputs=[sum_a]
)
return sim_model, embedding_model
# Try using our model with pretrained weights from word2vec
sum_model_precomputed, sum_embedding_precomputed = sum_model(
embedding_size=EMBEDDING_SIZE, vocab_size=VOCAB_SIZE,
embedding_weights=w2v_weights, idf_weights=idf_weights
)
x, y = next(data_generator(batch_size=4096))
sum_model_precomputed.evaluate(x, y)
SAMPLE_QUESTIONS = [
'Roundtrip ticket versus one way',
'Shinkansen from Kyoto to Hiroshima',
'Bus tour of Germany',
]
def evaluate_sample(lookup):
pd.set_option('display.max_colwidth', 100)
results = []
for q in SAMPLE_QUESTIONS:
print(q)
q_res = lookup.nearest(q, n=4)
q_res['result'] = q_res['question']
q_res['question'] = q
results.append(q_res)
return pd.concat(results)
lookup = EmbeddingWrapper(model=sum_embedding_precomputed)
evaluate_sample(lookup)
```
# Training our own network
The results are okay but not great... instead of using the word2vec embeddings, what happens if we train our network end-to-end?
```
sum_model_trained, sum_embedding_trained = sum_model(
embedding_size=EMBEDDING_SIZE, vocab_size=VOCAB_SIZE,
embedding_weights=None,
idf_weights=None
)
sum_model_trained.fit_generator(
data_generator(batch_size=128),
epochs=10,
steps_per_epoch=1000
)
lookup = EmbeddingWrapper(model=sum_embedding_trained)
evaluate_sample(lookup)
```
## CNN Model
Using a sum-of-embeddings model works well. What happens if we try to make a simple CNN model?
```
def cnn_model(embedding_size, vocab_size):
title = layers.Input(shape=(None,), dtype='int32', name='title')
body = layers.Input(shape=(None,), dtype='int32', name='body')
embedding = layers.Embedding(
mask_zero=False,
input_dim=vocab_size,
output_dim=embedding_size,
)
def _combine_sum(v):
return K.sum(v, axis=1)
cnn_1 = layers.Convolution1D(256, 3)
cnn_2 = layers.Convolution1D(256, 3)
cnn_3 = layers.Convolution1D(256, 3)
global_pool = layers.GlobalMaxPooling1D()
local_pool = layers.MaxPooling1D(strides=2, pool_size=3)
def forward(input):
embed = embedding(input)
return global_pool(
cnn_2(local_pool(cnn_1(embed))))
sum_a = forward(title)
sum_b = forward(body)
sim = layers.dot([sum_a, sum_b], axes=1, normalize=False)
sim_model = models.Model(
inputs=[title, body],
outputs=[sim],
)
sim_model.compile(loss='binary_crossentropy', optimizer='rmsprop', metrics=['accuracy'])
embedding_model = models.Model(
inputs=[title],
outputs=[sum_a]
)
return sim_model, embedding_model
cnn, cnn_embedding = cnn_model(embedding_size=25, vocab_size=VOCAB_SIZE)
cnn.summary()
cnn.fit_generator(
data_generator(batch_size=128),
epochs=10,
steps_per_epoch=1000,
)
lookup = EmbeddingWrapper(model=cnn_embedding)
evaluate_sample(lookup)
```
## LSTM Model
We can also make an LSTM model. Warning, this will be very slow to train and evaluate unless you have a relatively fast GPU to run it on!
```
def lstm_model(embedding_size, vocab_size):
title = layers.Input(shape=(None,), dtype='int32', name='title')
body = layers.Input(shape=(None,), dtype='int32', name='body')
embedding = layers.Embedding(
mask_zero=True,
input_dim=vocab_size,
output_dim=embedding_size,
# weights=[w2v_weights],
# trainable=False
)
lstm_1 = layers.LSTM(units=512, return_sequences=True)
lstm_2 = layers.LSTM(units=512, return_sequences=False)
sum_a = lstm_2(lstm_1(embedding(title)))
sum_b = lstm_2(lstm_1(embedding(body)))
sim = layers.dot([sum_a, sum_b], axes=1, normalize=True)
# sim = layers.Activation(activation='sigmoid')(sim)
sim_model = models.Model(
inputs=[title, body],
outputs=[sim],
)
sim_model.compile(loss='binary_crossentropy', optimizer='rmsprop')
embedding_model = models.Model(
inputs=[title],
outputs=[sum_a]
)
return sim_model, embedding_model
lstm, lstm_embedding = lstm_model(embedding_size=EMBEDDING_SIZE, vocab_size=VOCAB_SIZE)
lstm.summary()
lstm.fit_generator(
data_generator(batch_size=128),
epochs=10,
steps_per_epoch=100,
)
lookup = EmbeddingWrapper(model=lstm_embedding)
evaluate_sample(lookup)
```
|
github_jupyter
|
# AWS Marketplace Product Usage Demonstration - Algorithms
## Using Algorithm ARN with Amazon SageMaker APIs
This sample notebook demonstrates two new functionalities added to Amazon SageMaker:
1. Using an Algorithm ARN to run training jobs and use that result for inference
2. Using an AWS Marketplace product ARN - we will use [Scikit Decision Trees](https://aws.amazon.com/marketplace/pp/prodview-ha4f3kqugba3u?qid=1543169069960&sr=0-1&ref_=srh_res_product_title)
## Overall flow diagram
<img src="images/AlgorithmE2EFlow.jpg">
## Compatibility
This notebook is compatible only with [Scikit Decision Trees](https://aws.amazon.com/marketplace/pp/prodview-ha4f3kqugba3u?qid=1543169069960&sr=0-1&ref_=srh_res_product_title) sample algorithm published to AWS Marketplace.
***Pre-Requisite:*** Please subscribe to this free product before proceeding with this notebook
## Set up the environment
```
import sagemaker as sage
from sagemaker import get_execution_role
role = get_execution_role()
# S3 prefixes
common_prefix = "DEMO-scikit-byo-iris"
training_input_prefix = common_prefix + "/training-input-data"
batch_inference_input_prefix = common_prefix + "/batch-inference-input-data"
```
### Create the session
The session remembers our connection parameters to Amazon SageMaker. We'll use it to perform all of our Amazon SageMaker operations.
```
sagemaker_session = sage.Session()
```
## Upload the data for training
When training large models with huge amounts of data, you'll typically use big data tools, like Amazon Athena, AWS Glue, or Amazon EMR, to create your data in S3. For the purposes of this example, we're using some the classic [Iris dataset](https://en.wikipedia.org/wiki/Iris_flower_data_set), which we have included.
We can use use the tools provided by the Amazon SageMaker Python SDK to upload the data to a default bucket.
```
TRAINING_WORKDIR = "data/training"
training_input = sagemaker_session.upload_data(TRAINING_WORKDIR, key_prefix=training_input_prefix)
print("Training Data Location " + training_input)
```
## Creating Training Job using Algorithm ARN
Please put in the algorithm arn you want to use below. This can either be an AWS Marketplace algorithm you subscribed to (or) one of the algorithms you created in your own account.
The algorithm arn listed below belongs to the [Scikit Decision Trees](https://aws.amazon.com/marketplace/pp/prodview-ha4f3kqugba3u?qid=1543169069960&sr=0-1&ref_=srh_res_product_title) product.
```
from src.scikit_product_arns import ScikitArnProvider
algorithm_arn = ScikitArnProvider.get_algorithm_arn(sagemaker_session.boto_region_name)
import json
import time
from sagemaker.algorithm import AlgorithmEstimator
algo = AlgorithmEstimator(
algorithm_arn=algorithm_arn,
role=role,
train_instance_count=1,
train_instance_type="ml.c4.xlarge",
base_job_name="scikit-from-aws-marketplace",
)
```
## Run Training Job
```
print(
"Now run the training job using algorithm arn %s in region %s"
% (algorithm_arn, sagemaker_session.boto_region_name)
)
algo.fit({"training": training_input})
```
## Automated Model Tuning (optional)
Since this algorithm supports tunable hyperparameters with a tuning objective metric, we can run a Hyperparameter Tuning Job to obtain the best training job hyperparameters and its corresponding model artifacts.
<img src="images/HPOFlow.jpg">
```
from sagemaker.tuner import HyperparameterTuner, IntegerParameter
## This demo algorithm supports max_leaf_nodes as the only tunable hyperparameter.
hyperparameter_ranges = {"max_leaf_nodes": IntegerParameter(1, 100000)}
tuner = HyperparameterTuner(
estimator=algo,
base_tuning_job_name="some-name",
objective_metric_name="validation:accuracy",
hyperparameter_ranges=hyperparameter_ranges,
max_jobs=2,
max_parallel_jobs=2,
)
tuner.fit({"training": training_input}, include_cls_metadata=False)
tuner.wait()
```
## Batch Transform Job
Now let's use the model built to run a batch inference job and verify it works.
### Batch Transform Input Preparation
The snippet below is removing the "label" column (column indexed at 0) and retaining the rest to be batch transform's input.
***NOTE:*** This is the same training data, which is a no-no from a ML science perspective. But the aim of this notebook is to demonstrate how things work end-to-end.
```
import pandas as pd
## Remove first column that contains the label
shape = pd.read_csv(TRAINING_WORKDIR + "/iris.csv", header=None).drop([0], axis=1)
TRANSFORM_WORKDIR = "data/transform"
shape.to_csv(TRANSFORM_WORKDIR + "/batchtransform_test.csv", index=False, header=False)
transform_input = (
sagemaker_session.upload_data(TRANSFORM_WORKDIR, key_prefix=batch_inference_input_prefix)
+ "/batchtransform_test.csv"
)
print("Transform input uploaded to " + transform_input)
transformer = algo.transformer(1, "ml.m4.xlarge")
transformer.transform(transform_input, content_type="text/csv")
transformer.wait()
print("Batch Transform output saved to " + transformer.output_path)
```
#### Inspect the Batch Transform Output in S3
```
from urllib.parse import urlparse
parsed_url = urlparse(transformer.output_path)
bucket_name = parsed_url.netloc
file_key = "{}/{}.out".format(parsed_url.path[1:], "batchtransform_test.csv")
s3_client = sagemaker_session.boto_session.client("s3")
response = s3_client.get_object(Bucket=sagemaker_session.default_bucket(), Key=file_key)
response_bytes = response["Body"].read().decode("utf-8")
print(response_bytes)
```
## Live Inference Endpoint
Finally, we demonstrate the creation of an endpoint for live inference using this AWS Marketplace algorithm generated model
```
from sagemaker.predictor import csv_serializer
predictor = algo.deploy(1, "ml.m4.xlarge", serializer=csv_serializer)
```
### Choose some data and use it for a prediction
In order to do some predictions, we'll extract some of the data we used for training and do predictions against it. This is, of course, bad statistical practice, but a good way to see how the mechanism works.
```
shape = pd.read_csv(TRAINING_WORKDIR + "/iris.csv", header=None)
import itertools
a = [50 * i for i in range(3)]
b = [40 + i for i in range(10)]
indices = [i + j for i, j in itertools.product(a, b)]
test_data = shape.iloc[indices[:-1]]
test_X = test_data.iloc[:, 1:]
test_y = test_data.iloc[:, 0]
```
Prediction is as easy as calling predict with the predictor we got back from deploy and the data we want to do predictions with. The serializers take care of doing the data conversions for us.
```
print(predictor.predict(test_X.values).decode("utf-8"))
```
### Cleanup the endpoint
```
algo.delete_endpoint()
```
|
github_jupyter
|
# Logistic Regression with a Neural Network mindset
Welcome to your first (required) programming assignment! You will build a logistic regression classifier to recognize cats. This assignment will step you through how to do this with a Neural Network mindset, and so will also hone your intuitions about deep learning.
**Instructions:**
- Do not use loops (for/while) in your code, unless the instructions explicitly ask you to do so.
**You will learn to:**
- Build the general architecture of a learning algorithm, including:
- Initializing parameters
- Calculating the cost function and its gradient
- Using an optimization algorithm (gradient descent)
- Gather all three functions above into a main model function, in the right order.
## 1 - Packages ##
First, let's run the cell below to import all the packages that you will need during this assignment.
- [numpy](www.numpy.org) is the fundamental package for scientific computing with Python.
- [h5py](http://www.h5py.org) is a common package to interact with a dataset that is stored on an H5 file.
- [matplotlib](http://matplotlib.org) is a famous library to plot graphs in Python.
- [PIL](http://www.pythonware.com/products/pil/) and [scipy](https://www.scipy.org/) are used here to test your model with your own picture at the end.
```
import numpy as np
import matplotlib.pyplot as plt
import h5py
import scipy
from PIL import Image
from scipy import ndimage
from lr_utils import load_dataset
%matplotlib inline
```
## 2 - Overview of the Problem set ##
**Problem Statement**: You are given a dataset ("data.h5") containing:
- a training set of m_train images labeled as cat (y=1) or non-cat (y=0)
- a test set of m_test images labeled as cat or non-cat
- each image is of shape (num_px, num_px, 3) where 3 is for the 3 channels (RGB). Thus, each image is square (height = num_px) and (width = num_px).
You will build a simple image-recognition algorithm that can correctly classify pictures as cat or non-cat.
Let's get more familiar with the dataset. Load the data by running the following code.
```
# Loading the data (cat/non-cat)
train_set_x_orig, train_set_y, test_set_x_orig, test_set_y, classes = load_dataset()
```
We added "_orig" at the end of image datasets (train and test) because we are going to preprocess them. After preprocessing, we will end up with train_set_x and test_set_x (the labels train_set_y and test_set_y don't need any preprocessing).
Each line of your train_set_x_orig and test_set_x_orig is an array representing an image. You can visualize an example by running the following code. Feel free also to change the `index` value and re-run to see other images.
```
# Example of a picture
index = 25
plt.imshow(train_set_x_orig[index])
print ("y = " + str(train_set_y[:, index]) + ", it's a '" + classes[np.squeeze(train_set_y[:, index])].decode("utf-8") + "' picture.")
```
Many software bugs in deep learning come from having matrix/vector dimensions that don't fit. If you can keep your matrix/vector dimensions straight you will go a long way toward eliminating many bugs.
**Exercise:** Find the values for:
- m_train (number of training examples)
- m_test (number of test examples)
- num_px (= height = width of a training image)
Remember that `train_set_x_orig` is a numpy-array of shape (m_train, num_px, num_px, 3). For instance, you can access `m_train` by writing `train_set_x_orig.shape[0]`.
```
### START CODE HERE ### (≈ 3 lines of code)
m_train = None
m_test = None
num_px = None
### END CODE HERE ###
print ("Number of training examples: m_train = " + str(m_train))
print ("Number of testing examples: m_test = " + str(m_test))
print ("Height/Width of each image: num_px = " + str(num_px))
print ("Each image is of size: (" + str(num_px) + ", " + str(num_px) + ", 3)")
print ("train_set_x shape: " + str(train_set_x_orig.shape))
print ("train_set_y shape: " + str(train_set_y.shape))
print ("test_set_x shape: " + str(test_set_x_orig.shape))
print ("test_set_y shape: " + str(test_set_y.shape))
```
**Expected Output for m_train, m_test and num_px**:
<table style="width:15%">
<tr>
<td>**m_train**</td>
<td> 209 </td>
</tr>
<tr>
<td>**m_test**</td>
<td> 50 </td>
</tr>
<tr>
<td>**num_px**</td>
<td> 64 </td>
</tr>
</table>
For convenience, you should now reshape images of shape (num_px, num_px, 3) in a numpy-array of shape (num_px $*$ num_px $*$ 3, 1). After this, our training (and test) dataset is a numpy-array where each column represents a flattened image. There should be m_train (respectively m_test) columns.
**Exercise:** Reshape the training and test data sets so that images of size (num_px, num_px, 3) are flattened into single vectors of shape (num\_px $*$ num\_px $*$ 3, 1).
A trick when you want to flatten a matrix X of shape (a,b,c,d) to a matrix X_flatten of shape (b$*$c$*$d, a) is to use:
```python
X_flatten = X.reshape(X.shape[0], -1).T # X.T is the transpose of X
```
```
# Reshape the training and test examples
### START CODE HERE ### (≈ 2 lines of code)
train_set_x_flatten = None
test_set_x_flatten = None
### END CODE HERE ###
print ("train_set_x_flatten shape: " + str(train_set_x_flatten.shape))
print ("train_set_y shape: " + str(train_set_y.shape))
print ("test_set_x_flatten shape: " + str(test_set_x_flatten.shape))
print ("test_set_y shape: " + str(test_set_y.shape))
print ("sanity check after reshaping: " + str(train_set_x_flatten[0:5,0]))
```
**Expected Output**:
<table style="width:35%">
<tr>
<td>**train_set_x_flatten shape**</td>
<td> (12288, 209)</td>
</tr>
<tr>
<td>**train_set_y shape**</td>
<td>(1, 209)</td>
</tr>
<tr>
<td>**test_set_x_flatten shape**</td>
<td>(12288, 50)</td>
</tr>
<tr>
<td>**test_set_y shape**</td>
<td>(1, 50)</td>
</tr>
<tr>
<td>**sanity check after reshaping**</td>
<td>[17 31 56 22 33]</td>
</tr>
</table>
To represent color images, the red, green and blue channels (RGB) must be specified for each pixel, and so the pixel value is actually a vector of three numbers ranging from 0 to 255.
One common preprocessing step in machine learning is to center and standardize your dataset, meaning that you substract the mean of the whole numpy array from each example, and then divide each example by the standard deviation of the whole numpy array. But for picture datasets, it is simpler and more convenient and works almost as well to just divide every row of the dataset by 255 (the maximum value of a pixel channel).
<!-- During the training of your model, you're going to multiply weights and add biases to some initial inputs in order to observe neuron activations. Then you backpropogate with the gradients to train the model. But, it is extremely important for each feature to have a similar range such that our gradients don't explode. You will see that more in detail later in the lectures. !-->
Let's standardize our dataset.
```
train_set_x = train_set_x_flatten/255.
test_set_x = test_set_x_flatten/255.
```
<font color='blue'>
**What you need to remember:**
Common steps for pre-processing a new dataset are:
- Figure out the dimensions and shapes of the problem (m_train, m_test, num_px, ...)
- Reshape the datasets such that each example is now a vector of size (num_px \* num_px \* 3, 1)
- "Standardize" the data
## 3 - General Architecture of the learning algorithm ##
It's time to design a simple algorithm to distinguish cat images from non-cat images.
You will build a Logistic Regression, using a Neural Network mindset. The following Figure explains why **Logistic Regression is actually a very simple Neural Network!**
<img src="images/LogReg_kiank.png" style="width:650px;height:400px;">
**Mathematical expression of the algorithm**:
For one example $x^{(i)}$:
$$z^{(i)} = w^T x^{(i)} + b \tag{1}$$
$$\hat{y}^{(i)} = a^{(i)} = sigmoid(z^{(i)})\tag{2}$$
$$ \mathcal{L}(a^{(i)}, y^{(i)}) = - y^{(i)} \log(a^{(i)}) - (1-y^{(i)} ) \log(1-a^{(i)})\tag{3}$$
The cost is then computed by summing over all training examples:
$$ J = \frac{1}{m} \sum_{i=1}^m \mathcal{L}(a^{(i)}, y^{(i)})\tag{6}$$
**Key steps**:
In this exercise, you will carry out the following steps:
- Initialize the parameters of the model
- Learn the parameters for the model by minimizing the cost
- Use the learned parameters to make predictions (on the test set)
- Analyse the results and conclude
## 4 - Building the parts of our algorithm ##
The main steps for building a Neural Network are:
1. Define the model structure (such as number of input features)
2. Initialize the model's parameters
3. Loop:
- Calculate current loss (forward propagation)
- Calculate current gradient (backward propagation)
- Update parameters (gradient descent)
You often build 1-3 separately and integrate them into one function we call `model()`.
### 4.1 - Helper functions
**Exercise**: Using your code from "Python Basics", implement `sigmoid()`. As you've seen in the figure above, you need to compute $sigmoid( w^T x + b) = \frac{1}{1 + e^{-(w^T x + b)}}$ to make predictions. Use np.exp().
```
# GRADED FUNCTION: sigmoid
def sigmoid(z):
"""
Compute the sigmoid of z
Arguments:
z -- A scalar or numpy array of any size.
Return:
s -- sigmoid(z)
"""
### START CODE HERE ### (≈ 1 line of code)
s = None
### END CODE HERE ###
return s
print ("sigmoid([0, 2]) = " + str(sigmoid(np.array([0,2]))))
```
**Expected Output**:
<table>
<tr>
<td>**sigmoid([0, 2])**</td>
<td> [ 0.5 0.88079708]</td>
</tr>
</table>
### 4.2 - Initializing parameters
**Exercise:** Implement parameter initialization in the cell below. You have to initialize w as a vector of zeros. If you don't know what numpy function to use, look up np.zeros() in the Numpy library's documentation.
```
# GRADED FUNCTION: initialize_with_zeros
def initialize_with_zeros(dim):
"""
This function creates a vector of zeros of shape (dim, 1) for w and initializes b to 0.
Argument:
dim -- size of the w vector we want (or number of parameters in this case)
Returns:
w -- initialized vector of shape (dim, 1)
b -- initialized scalar (corresponds to the bias)
"""
### START CODE HERE ### (≈ 1 line of code)
w = None
b = None
### END CODE HERE ###
assert(w.shape == (dim, 1))
assert(isinstance(b, float) or isinstance(b, int))
return w, b
dim = 2
w, b = initialize_with_zeros(dim)
print ("w = " + str(w))
print ("b = " + str(b))
```
**Expected Output**:
<table style="width:15%">
<tr>
<td> ** w ** </td>
<td> [[ 0.]
[ 0.]] </td>
</tr>
<tr>
<td> ** b ** </td>
<td> 0 </td>
</tr>
</table>
For image inputs, w will be of shape (num_px $\times$ num_px $\times$ 3, 1).
### 4.3 - Forward and Backward propagation
Now that your parameters are initialized, you can do the "forward" and "backward" propagation steps for learning the parameters.
**Exercise:** Implement a function `propagate()` that computes the cost function and its gradient.
**Hints**:
Forward Propagation:
- You get X
- You compute $A = \sigma(w^T X + b) = (a^{(0)}, a^{(1)}, ..., a^{(m-1)}, a^{(m)})$
- You calculate the cost function: $J = -\frac{1}{m}\sum_{i=1}^{m}y^{(i)}\log(a^{(i)})+(1-y^{(i)})\log(1-a^{(i)})$
Here are the two formulas you will be using:
$$ \frac{\partial J}{\partial w} = \frac{1}{m}X(A-Y)^T\tag{7}$$
$$ \frac{\partial J}{\partial b} = \frac{1}{m} \sum_{i=1}^m (a^{(i)}-y^{(i)})\tag{8}$$
```
# GRADED FUNCTION: propagate
def propagate(w, b, X, Y):
"""
Implement the cost function and its gradient for the propagation explained above
Arguments:
w -- weights, a numpy array of size (num_px * num_px * 3, 1)
b -- bias, a scalar
X -- data of size (num_px * num_px * 3, number of examples)
Y -- true "label" vector (containing 0 if non-cat, 1 if cat) of size (1, number of examples)
Return:
cost -- negative log-likelihood cost for logistic regression
dw -- gradient of the loss with respect to w, thus same shape as w
db -- gradient of the loss with respect to b, thus same shape as b
Tips:
- Write your code step by step for the propagation. np.log(), np.dot()
"""
m = X.shape[1]
# FORWARD PROPAGATION (FROM X TO COST)
### START CODE HERE ### (≈ 2 lines of code)
A = None # compute activation
cost = None # compute cost
### END CODE HERE ###
# BACKWARD PROPAGATION (TO FIND GRAD)
### START CODE HERE ### (≈ 2 lines of code)
dw = None
db = None
### END CODE HERE ###
assert(dw.shape == w.shape)
assert(db.dtype == float)
cost = np.squeeze(cost)
assert(cost.shape == ())
grads = {"dw": dw,
"db": db}
return grads, cost
w, b, X, Y = np.array([[1],[2]]), 2, np.array([[1,2],[3,4]]), np.array([[1,0]])
grads, cost = propagate(w, b, X, Y)
print ("dw = " + str(grads["dw"]))
print ("db = " + str(grads["db"]))
print ("cost = " + str(cost))
```
**Expected Output**:
<table style="width:50%">
<tr>
<td> ** dw ** </td>
<td> [[ 0.99993216]
[ 1.99980262]]</td>
</tr>
<tr>
<td> ** db ** </td>
<td> 0.499935230625 </td>
</tr>
<tr>
<td> ** cost ** </td>
<td> 6.000064773192205</td>
</tr>
</table>
### d) Optimization
- You have initialized your parameters.
- You are also able to compute a cost function and its gradient.
- Now, you want to update the parameters using gradient descent.
**Exercise:** Write down the optimization function. The goal is to learn $w$ and $b$ by minimizing the cost function $J$. For a parameter $\theta$, the update rule is $ \theta = \theta - \alpha \text{ } d\theta$, where $\alpha$ is the learning rate.
```
# GRADED FUNCTION: optimize
def optimize(w, b, X, Y, num_iterations, learning_rate, print_cost = False):
"""
This function optimizes w and b by running a gradient descent algorithm
Arguments:
w -- weights, a numpy array of size (num_px * num_px * 3, 1)
b -- bias, a scalar
X -- data of shape (num_px * num_px * 3, number of examples)
Y -- true "label" vector (containing 0 if non-cat, 1 if cat), of shape (1, number of examples)
num_iterations -- number of iterations of the optimization loop
learning_rate -- learning rate of the gradient descent update rule
print_cost -- True to print the loss every 100 steps
Returns:
params -- dictionary containing the weights w and bias b
grads -- dictionary containing the gradients of the weights and bias with respect to the cost function
costs -- list of all the costs computed during the optimization, this will be used to plot the learning curve.
Tips:
You basically need to write down two steps and iterate through them:
1) Calculate the cost and the gradient for the current parameters. Use propagate().
2) Update the parameters using gradient descent rule for w and b.
"""
costs = []
for i in range(num_iterations):
# Cost and gradient calculation (≈ 1-4 lines of code)
### START CODE HERE ###
grads, cost = None
### END CODE HERE ###
# Retrieve derivatives from grads
dw = grads["dw"]
db = grads["db"]
# update rule (≈ 2 lines of code)
### START CODE HERE ###
w = None
b = None
### END CODE HERE ###
# Record the costs
if i % 100 == 0:
costs.append(cost)
# Print the cost every 100 training examples
if print_cost and i % 100 == 0:
print ("Cost after iteration %i: %f" %(i, cost))
params = {"w": w,
"b": b}
grads = {"dw": dw,
"db": db}
return params, grads, costs
params, grads, costs = optimize(w, b, X, Y, num_iterations= 100, learning_rate = 0.009, print_cost = False)
print ("w = " + str(params["w"]))
print ("b = " + str(params["b"]))
print ("dw = " + str(grads["dw"]))
print ("db = " + str(grads["db"]))
```
**Expected Output**:
<table style="width:40%">
<tr>
<td> **w** </td>
<td>[[ 0.1124579 ]
[ 0.23106775]] </td>
</tr>
<tr>
<td> **b** </td>
<td> 1.55930492484 </td>
</tr>
<tr>
<td> **dw** </td>
<td> [[ 0.90158428]
[ 1.76250842]] </td>
</tr>
<tr>
<td> **db** </td>
<td> 0.430462071679 </td>
</tr>
</table>
**Exercise:** The previous function will output the learned w and b. We are able to use w and b to predict the labels for a dataset X. Implement the `predict()` function. There is two steps to computing predictions:
1. Calculate $\hat{Y} = A = \sigma(w^T X + b)$
2. Convert the entries of a into 0 (if activation <= 0.5) or 1 (if activation > 0.5), stores the predictions in a vector `Y_prediction`. If you wish, you can use an `if`/`else` statement in a `for` loop (though there is also a way to vectorize this).
```
# GRADED FUNCTION: predict
def predict(w, b, X):
'''
Predict whether the label is 0 or 1 using learned logistic regression parameters (w, b)
Arguments:
w -- weights, a numpy array of size (num_px * num_px * 3, 1)
b -- bias, a scalar
X -- data of size (num_px * num_px * 3, number of examples)
Returns:
Y_prediction -- a numpy array (vector) containing all predictions (0/1) for the examples in X
'''
m = X.shape[1]
Y_prediction = np.zeros((1,m))
w = w.reshape(X.shape[0], 1)
# Compute vector "A" predicting the probabilities of a cat being present in the picture
### START CODE HERE ### (≈ 1 line of code)
A = None
### END CODE HERE ###
for i in range(A.shape[1]):
# Convert probabilities A[0,i] to actual predictions p[0,i]
### START CODE HERE ### (≈ 4 lines of code)
pass
### END CODE HERE ###
assert(Y_prediction.shape == (1, m))
return Y_prediction
print ("predictions = " + str(predict(w, b, X)))
```
**Expected Output**:
<table style="width:30%">
<tr>
<td>
**predictions**
</td>
<td>
[[ 1. 1.]]
</td>
</tr>
</table>
<font color='blue'>
**What to remember:**
You've implemented several functions that:
- Initialize (w,b)
- Optimize the loss iteratively to learn parameters (w,b):
- computing the cost and its gradient
- updating the parameters using gradient descent
- Use the learned (w,b) to predict the labels for a given set of examples
## 5 - Merge all functions into a model ##
You will now see how the overall model is structured by putting together all the building blocks (functions implemented in the previous parts) together, in the right order.
**Exercise:** Implement the model function. Use the following notation:
- Y_prediction for your predictions on the test set
- Y_prediction_train for your predictions on the train set
- w, costs, grads for the outputs of optimize()
```
# GRADED FUNCTION: model
def model(X_train, Y_train, X_test, Y_test, num_iterations = 2000, learning_rate = 0.5, print_cost = False):
"""
Builds the logistic regression model by calling the function you've implemented previously
Arguments:
X_train -- training set represented by a numpy array of shape (num_px * num_px * 3, m_train)
Y_train -- training labels represented by a numpy array (vector) of shape (1, m_train)
X_test -- test set represented by a numpy array of shape (num_px * num_px * 3, m_test)
Y_test -- test labels represented by a numpy array (vector) of shape (1, m_test)
num_iterations -- hyperparameter representing the number of iterations to optimize the parameters
learning_rate -- hyperparameter representing the learning rate used in the update rule of optimize()
print_cost -- Set to true to print the cost every 100 iterations
Returns:
d -- dictionary containing information about the model.
"""
### START CODE HERE ###
# initialize parameters with zeros (≈ 1 line of code)
w, b = None
# Gradient descent (≈ 1 line of code)
parameters, grads, costs = None
# Retrieve parameters w and b from dictionary "parameters"
w = parameters["w"]
b = parameters["b"]
# Predict test/train set examples (≈ 2 lines of code)
Y_prediction_test = None
Y_prediction_train = None
### END CODE HERE ###
# Print train/test Errors
print("train accuracy: {} %".format(100 - np.mean(np.abs(Y_prediction_train - Y_train)) * 100))
print("test accuracy: {} %".format(100 - np.mean(np.abs(Y_prediction_test - Y_test)) * 100))
d = {"costs": costs,
"Y_prediction_test": Y_prediction_test,
"Y_prediction_train" : Y_prediction_train,
"w" : w,
"b" : b,
"learning_rate" : learning_rate,
"num_iterations": num_iterations}
return d
```
Run the following cell to train your model.
```
d = model(train_set_x, train_set_y, test_set_x, test_set_y, num_iterations = 2000, learning_rate = 0.005, print_cost = True)
```
**Expected Output**:
<table style="width:40%">
<tr>
<td> **Train Accuracy** </td>
<td> 99.04306220095694 % </td>
</tr>
<tr>
<td>**Test Accuracy** </td>
<td> 70.0 % </td>
</tr>
</table>
**Comment**: Training accuracy is close to 100%. This is a good sanity check: your model is working and has high enough capacity to fit the training data. Test error is 68%. It is actually not bad for this simple model, given the small dataset we used and that logistic regression is a linear classifier. But no worries, you'll build an even better classifier next week!
Also, you see that the model is clearly overfitting the training data. Later in this specialization you will learn how to reduce overfitting, for example by using regularization. Using the code below (and changing the `index` variable) you can look at predictions on pictures of the test set.
```
# Example of a picture that was wrongly classified.
index = 1
plt.imshow(test_set_x[:,index].reshape((num_px, num_px, 3)))
print ("y = " + str(test_set_y[0,index]) + ", you predicted that it is a \"" + classes[d["Y_prediction_test"][0,index]].decode("utf-8") + "\" picture.")
```
Let's also plot the cost function and the gradients.
```
# Plot learning curve (with costs)
costs = np.squeeze(d['costs'])
plt.plot(costs)
plt.ylabel('cost')
plt.xlabel('iterations (per hundreds)')
plt.title("Learning rate =" + str(d["learning_rate"]))
plt.show()
```
**Interpretation**:
You can see the cost decreasing. It shows that the parameters are being learned. However, you see that you could train the model even more on the training set. Try to increase the number of iterations in the cell above and rerun the cells. You might see that the training set accuracy goes up, but the test set accuracy goes down. This is called overfitting.
## 6 - Further analysis (optional/ungraded exercise) ##
Congratulations on building your first image classification model. Let's analyze it further, and examine possible choices for the learning rate $\alpha$.
#### Choice of learning rate ####
**Reminder**:
In order for Gradient Descent to work you must choose the learning rate wisely. The learning rate $\alpha$ determines how rapidly we update the parameters. If the learning rate is too large we may "overshoot" the optimal value. Similarly, if it is too small we will need too many iterations to converge to the best values. That's why it is crucial to use a well-tuned learning rate.
Let's compare the learning curve of our model with several choices of learning rates. Run the cell below. This should take about 1 minute. Feel free also to try different values than the three we have initialized the `learning_rates` variable to contain, and see what happens.
```
learning_rates = [0.01, 0.001, 0.0001]
models = {}
for i in learning_rates:
print ("learning rate is: " + str(i))
models[str(i)] = model(train_set_x, train_set_y, test_set_x, test_set_y, num_iterations = 1500, learning_rate = i, print_cost = False)
print ('\n' + "-------------------------------------------------------" + '\n')
for i in learning_rates:
plt.plot(np.squeeze(models[str(i)]["costs"]), label= str(models[str(i)]["learning_rate"]))
plt.ylabel('cost')
plt.xlabel('iterations')
legend = plt.legend(loc='upper center', shadow=True)
frame = legend.get_frame()
frame.set_facecolor('0.90')
plt.show()
```
**Interpretation**:
- Different learning rates give different costs and thus different predictions results.
- If the learning rate is too large (0.01), the cost may oscillate up and down. It may even diverge (though in this example, using 0.01 still eventually ends up at a good value for the cost).
- A lower cost doesn't mean a better model. You have to check if there is possibly overfitting. It happens when the training accuracy is a lot higher than the test accuracy.
- In deep learning, we usually recommend that you:
- Choose the learning rate that better minimizes the cost function.
- If your model overfits, use other techniques to reduce overfitting. (We'll talk about this in later videos.)
## 7 - Test with your own image (optional/ungraded exercise) ##
Congratulations on finishing this assignment. You can use your own image and see the output of your model. To do that:
1. Click on "File" in the upper bar of this notebook, then click "Open" to go on your Coursera Hub.
2. Add your image to this Jupyter Notebook's directory, in the "images" folder
3. Change your image's name in the following code
4. Run the code and check if the algorithm is right (1 = cat, 0 = non-cat)!
```
## START CODE HERE ## (PUT YOUR IMAGE NAME)
my_image = "my_image.jpg" # change this to the name of your image file
## END CODE HERE ##
# We preprocess the image to fit your algorithm.
fname = "images/" + my_image
image = np.array(ndimage.imread(fname, flatten=False))
my_image = scipy.misc.imresize(image, size=(num_px,num_px)).reshape((1, num_px*num_px*3)).T
my_predicted_image = predict(d["w"], d["b"], my_image)
plt.imshow(image)
print("y = " + str(np.squeeze(my_predicted_image)) + ", your algorithm predicts a \"" + classes[int(np.squeeze(my_predicted_image)),].decode("utf-8") + "\" picture.")
```
<font color='blue'>
**What to remember from this assignment:**
1. Preprocessing the dataset is important.
2. You implemented each function separately: initialize(), propagate(), optimize(). Then you built a model().
3. Tuning the learning rate (which is an example of a "hyperparameter") can make a big difference to the algorithm. You will see more examples of this later in this course!
Finally, if you'd like, we invite you to try different things on this Notebook. Make sure you submit before trying anything. Once you submit, things you can play with include:
- Play with the learning rate and the number of iterations
- Try different initialization methods and compare the results
- Test other preprocessings (center the data, or divide each row by its standard deviation)
Bibliography:
- http://www.wildml.com/2015/09/implementing-a-neural-network-from-scratch/
- https://stats.stackexchange.com/questions/211436/why-do-we-normalize-images-by-subtracting-the-datasets-image-mean-and-not-the-c
|
github_jupyter
|
# Azure ML Training Pipeline for COVID-CXR
This notebook defines an Azure machine learning pipeline for a single training run and submits the pipeline as an experiment to be run on an Azure virtual machine.
```
# Import statements
import azureml.core
from azureml.core import Experiment
from azureml.core import Workspace, Datastore
from azureml.data.data_reference import DataReference
from azureml.pipeline.core import PipelineData
from azureml.pipeline.core import Pipeline
from azureml.pipeline.steps import PythonScriptStep, EstimatorStep
from azureml.train.dnn import TensorFlow
from azureml.train.estimator import Estimator
from azureml.core.compute import ComputeTarget, AmlCompute
from azureml.core.compute_target import ComputeTargetException
from azureml.core.environment import Environment
from azureml.core.runconfig import RunConfiguration
import shutil
```
### Register the workspace and configure its Python environment.
```
# Get reference to the workspace
ws = Workspace.from_config("./ws_config.json")
# Set workspace's environment
env = Environment.from_pip_requirements(name = "covid-cxr_env", file_path = "./../requirements.txt")
env.register(workspace=ws)
runconfig = RunConfiguration(conda_dependencies=env.python.conda_dependencies)
print(env.python.conda_dependencies.serialize_to_string())
# Move AML ignore file to root folder
aml_ignore_path = shutil.copy('./.amlignore', './../.amlignore')
```
### Create references to persistent and intermediate data
Create DataReference objects that point to our raw data on the blob. Configure a PipelineData object to point to preprocessed images stored on the blob.
```
# Get the blob datastore associated with this workspace
blob_store = Datastore(ws, name='covid_cxr_ds')
# Create data references to folders on the blob
raw_data_dr = DataReference(
datastore=blob_store,
data_reference_name="raw_data",
path_on_datastore="data/")
mila_data_dr = DataReference(
datastore=blob_store,
data_reference_name="mila_data",
path_on_datastore="data/covid-chestxray-dataset/")
fig1_data_dr = DataReference(
datastore=blob_store,
data_reference_name="fig1_data",
path_on_datastore="data/Figure1-COVID-chestxray-dataset/")
rsna_data_dr = DataReference(
datastore=blob_store,
data_reference_name="rsna_data",
path_on_datastore="data/rsna/")
training_logs_dr = DataReference(
datastore=blob_store,
data_reference_name="training_logs_data",
path_on_datastore="logs/training/")
models_dr = DataReference(
datastore=blob_store,
data_reference_name="models_data",
path_on_datastore="models/")
# Set up references to pipeline data (intermediate pipeline storage).
processed_pd = PipelineData(
"processed_data",
datastore=blob_store,
output_name="processed_data",
output_mode="mount")
```
### Compute Target
Specify and configure the compute target for this workspace. If a compute cluster by the name we specified does not exist, create a new compute cluster.
```
CT_NAME = "nd12s-clust-hp" # Name of our compute cluster
VM_SIZE = "STANDARD_ND12S" # Specify the Azure VM for execution of our pipeline
#CT_NAME = "d2-cluster" # Name of our compute cluster
#VM_SIZE = "STANDARD_D2" # Specify the Azure VM for execution of our pipeline
# Set up the compute target for this experiment
try:
compute_target = AmlCompute(ws, CT_NAME)
print("Found existing compute target.")
except ComputeTargetException:
print("Creating new compute target")
provisioning_config = AmlCompute.provisioning_configuration(vm_size=VM_SIZE, min_nodes=1, max_nodes=4)
compute_target = ComputeTarget.create(ws, CT_NAME, provisioning_config) # Create the compute cluster
# Wait for cluster to be provisioned
compute_target.wait_for_completion(show_output=True, min_node_count=None, timeout_in_minutes=20)
print("Azure Machine Learning Compute attached")
print("Compute targets: ", ws.compute_targets)
compute_target = ws.compute_targets[CT_NAME]
```
### Define pipeline and submit experiment.
Define the steps of an Azure machine learning pipeline. Create an Azure Experiment that will run our pipeline. Submit the experiment to the execution environment.
```
# Define preprocessing step the ML pipeline
step1 = PythonScriptStep(name="preprocess_step",
script_name="azure/preprocess_step/preprocess_step.py",
arguments=["--miladatadir", mila_data_dr, "--fig1datadir", fig1_data_dr,
"--rsnadatadir", rsna_data_dr, "--preprocesseddir", processed_pd],
inputs=[mila_data_dr, fig1_data_dr, rsna_data_dr],
outputs=[processed_pd],
compute_target=compute_target,
source_directory="./../",
runconfig=runconfig,
allow_reuse=True)
# Define training step in the ML pipeline
est = TensorFlow(source_directory='./../',
script_params=None,
compute_target=compute_target,
entry_script='azure/train_step/train_step.py',
pip_packages=['tensorboard', 'pandas', 'dill', 'numpy', 'imblearn', 'matplotlib', 'scikit-image', 'matplotlib',
'pydicom', 'opencv-python', 'tqdm', 'scikit-learn'],
use_gpu=True,
framework_version='2.0')
step2 = EstimatorStep(name="estimator_train_step",
estimator=est,
estimator_entry_script_arguments=["--rawdatadir", raw_data_dr, "--preprocesseddir", processed_pd,
"--traininglogsdir", training_logs_dr, "--modelsdir", models_dr],
runconfig_pipeline_params=None,
inputs=[raw_data_dr, processed_pd, training_logs_dr, models_dr],
outputs=[],
compute_target=compute_target)
# Construct the ML pipeline from the steps
steps = [step1, step2]
single_train_pipeline = Pipeline(workspace=ws, steps=steps)
single_train_pipeline.validate()
# Define a new experiment and submit a new pipeline run to the compute target.
experiment = Experiment(workspace=ws, name='SingleTrainExperiment_v3')
experiment.submit(single_train_pipeline, regenerate_outputs=False)
print("Pipeline is submitted for execution")
# Move AML ignore file back to original folder
aml_ignore_path = shutil.move(aml_ignore_path, './.amlignore')
```
|
github_jupyter
|
# SIT742: Modern Data Science
**(Week 01: Programming Python)**
---
- Materials in this module include resources collected from various open-source online repositories.
- You are free to use, change and distribute this package.
- If you found any issue/bug for this document, please submit an issue at [tulip-lab/sit742](https://github.com/tulip-lab/sit742/issues)
Prepared by **SIT742 Teaching Team**
---
# Session 1A - IPython notebook and basic data types
In this session,
you will learn how to run *Python* code under **IPython notebook**. You have two options for the environment:
1. Install the [Anaconda](https://www.anaconda.com/distribution/), and run it locally; **OR**
1. Use one cloud data science platform such as:
- [Google Colab](https://colab.research.google.com): SIT742 lab session will use Google Colab.
- [IBM Cloud](https://www.ibm.com/cloud)
- [DataBricks](https://community.cloud.databricks.com)
In IPython notebook, you will be able to execute and modify your *Python* code more efficiently.
- **If you are using Google Colab for SIT742 lab session practicals, you can ignore this Part 1 of this Session 1A, and start with Part 2.**
In addition, you will be given an introduction on *Python*'s basic data types,
getting familiar with **string**, **number**, data conversion, data comparison and
data input/output.
Hopefully, by using **Python** and the powerful **IPython Notebook** environment,
you will find writing programs both fun and easy.
## Content
### Part 1 Create your own IPython notebook
1.1 [Start a notebook server](#cell_start)
1.2 [A tour of IPython notebook](#cell_tour)
1.3 [IPython notebook infterface](#cell_interface)
1.4 [Open and close notebooks](#cell_close)
### Part 2 Basic data types
2.1 [String](#cell_string)
2.2 [Number](#cell_number)
2.3 [Data conversion and comparison](#cell_conversion)
2.4 [Input and output](#cell_input)
# Part 1. Create your own IPython notebook
- **If you are using Google Colab for SIT742 lab session practicals, you can ignore this Part 1, and start with Part 2.**
This notebook will show you how to start an IPython notebook session. It guides you through the process of creating your own notebook. It provides you details on the notebook interface and show you how to nevigate with a notebook and manipulate its components.
<a id = "cell_start"></a>
## 1. 1 Start a notebook server
As described in Part 1, you start the IPython notebnook server by keying in the command in a terminal window/command line window.
However, before you do this, make sure you have created a folder **p01** under **H:/sit742**, download the file **SIT742P01A-Python.ipynb** notebook, and saved it under **H:/sit742/p01**.
If you are using [Google Colab](https://colab.research.google.com), you can upload this notebook to Google Colab and run it from there. If any difficulty, please ask your tutor, or check the CloudDeakin discussions.
After you complete this, you can now switch working directory to **H:/sit742**, and start the IPython notebook server by the following commands:
You can see the message in the terminal windows as follows:
<img src="https://raw.githubusercontent.com/tuliplab/mds/master/Jupyter/image/start-workspace.jpg">
This will open a new browser window(or a new tab in your browser window). In the browser, there is an **dashboard** page which shows you all the folders and files under **sit742** folder
<img src="https://raw.githubusercontent.com/tuliplab/mds/master/Jupyter/image/start-index.jpg">
<a id = "cell_tour"></a>
## 1.2 A tour of iPython notebook
### Create a new ipython notebook
To create a new notebook, go to the menu bar and select **File -> New Notebook -> Python 3**
By default, the new notebook is named **Untitled**. To give your notebook a meaningful name, click on the notebook name and rename it. We would like to call our new notebook **hello.ipynb**. Therefore, key in the name **hello**.
<img src="https://raw.githubusercontent.com/tuliplab/mds/master/Jupyter/image/emptyNotebook.jpg">
### Run script in code cells
After a new notebook is created, there is an empty box in the notebook, called a **cell**. If you double click on the cell, you enter the **edit** mode of the notebook. Now we can enter the following code in the cell
After this, press **CTRL + ENTER**, and execute the cell. The result will be shown after the cell.
<img src="https://raw.githubusercontent.com/tuliplab/mds/master/Jupyter/image/hello-world.jpg">
After a cell is executed , the notebook is switched to the **Commmand** mode. In this mode, you can manipulte the notebook and its commponent. Alternatively, you can use **ESC** key to switch from **Edit** mode to **Command** mode without executing code.
To modify the code you entered in the cell, **double click** the cell again and modify its content. For example, try to change the first line of previouse cell into the following code:
Afterwards, press **CTRL + ENTER**, and the new output is displayed.
As you can see, you are switching bewteen two modes, **Command** and **Edit**, when editing a notebook. We will in later section look into these two operation modes of closely. Now practise switching between the two modes until you are comfortable with them.
### Add new cells
To add a new cell to a notebook, you have to ensure the notebook is in **Command** mode. If not, refer to previous section to switch to **Command** mode.
To add cell below the currrent cell, go to menubar and click **Insert-> Insert Cell Below**. Alternatively, you can use shortcut i.e. pressing **b** (or **a** to create a cell above).
<img src="https://raw.githubusercontent.com/tuliplab/mds/master/Jupyter/image/new-cell.jpg">
### Add markdown cells
By default, a code cell is created when adding a new cell. However, IPython notebook also use a **Markdown** cell for enter normal text. We use markdown cell to display the text in specific format and to provide structure for a notebook.
Try to copy the text in the cell below and paste it into your new notebook. Then from toolbar(**Cell->Cell Type**), change cell type from **Code** to **Markdown**.
Please note in the following cell, there is a space between the leading **-, #, 0** and the text that follows.
Now execute the cell by press **CTRL+ ENTER**. You notebook should look like this:
<img src="https://raw.githubusercontent.com/tuliplab/mds/master/Jupyter/image/new-markdown.jpg">
Here is what the formated Markdown cell looks like:
### Exercise:
Click this cell, and practise writing markdown language here....
<a id = "cell_interface"></a>
### 1.3 IPython notebook interface
Now you have created your first notebook, let us have a close look at the user interface of IPython notebook.
### Notebook component
When you create a new notebook document, you will be presented with the notebook name, a menu bar, a toolbar and an empty code cell.
We can see the following components in a notebook:
- **Title bar** is at the top of the page and contains the name of the notebook. Clicking on the notebook name brings up a dialog which allows you to rename it. Please renaming your notebook name from “Untitled0” to “hello”. This change the file name from **Untitled0.ipynb** to **hello.ipynb**.
- **Menu bar** presents different options that can be used to manipulate the way the notebook functions.
- **Toolbar** gives a quick way of performing the most-used operations within the notebook.
- An empty computational cell is show in a new notebook where you can key in your code.
The notebook has two modes of operatiopn:
- **Edit**: In this mode, a single cell comes into focus and you can enter text or execute code. You activate the **Edit mode** by **clicking on a cell** or **selecting a cell and then pressing Enter key**.
- **Command**: In this mode, you can perform tasks that is related to the whole notebook structure. For example, you can move, copy, cut and paste cells. A series of keyboard shortcuts are also available to enable you to performa these tasks more effiencient. One easiest way of activating the command mode by pressing the **Esc** key to exit editing mode.
### Get help and interrupting
To get help on the use of different cammands, shortcuts, you can go to the **Help** menu, which provides links to relevant documentation.
It is also easy to get help on any objects(including functions and methods). For example, to access help on the sum() function, enter the followsing line in a cell:
The other improtant thing to know is how to interrupt a compuation. This can be done through the menu **Kernel->Interrupt** or **Kernel->Restart**, depending on what works on the situation. We will have chance to try this in later session.
### Notebook cell types
There are basically three types of cells in a IPython notebook: Code Cells, Markdown Cells, Raw Cells.
**Code cells** : Code cell can be used to enter code and will be executed by Python interpreter. Although we will not use other language in this unit, it is good to know that Jupyter Notebooks also support JavaScript, HTML, and Bash commands.
*** Markdown cells***: You have created markdown cell in the previouse section. Markdown Cells are the easiest way to write and format text. It is also give structure to the notebook. Markdown language is used in this type of cell. Follow this link https://daringfireball.net/projects/markdown/basics for the basics of the syntax.
This is a Markdown Cells example notebook sourced from : https://ipython.org/ipython-doc/3/notebook/notebook.html
This markdown cheat sheet can also be good reference to the main markdowns you might need to use in our pracs http://nestacms.com/docs/creating-content/markdown-cheat-sheet
**Raw cells** : Raw cells, unlike all other Jupyter Notebook cells, have no input-output distinction. This means that raw Cells cannot be rendered into anything other than what they already are. They are mainly used to create examples.
As you have seen, you can use the toolbar to choose between different cell types. In addition, shortcut **M** and **Y** can be used to quickly change a cell to Code cell or Markdown cell under Command mode.
### Operation modes of IPytho notebook
**Edit mode**
The Edit mode is used to enter text in cells and to execute code. As you have seen, after typing some code in the notebook and pressing **CTRL+Enter**, the notebook executes the cell and diplays output. The other two shortcuts used to run code in a cell are **Shift +Enter** and **Alt + Enter**.
These three ways to run the the code in a cells are summarized as follows:
- Pressing Shift + Enter: This runs the cell and select the next cell(A new cell is created if at the end of the notebook). This is the most usual way to execute a cell.
- Pressing Ctrl + Enter: This runs the cell and keep the same cell selected.
- Pressing Alt + Enter: This runs the cell and insert a new cell below it.
**Command mode**
In Command mode, you can edit the notebook as a whole, but not type into individual cells.
You can use keyboard shortcut in this mode to perform the notebook and cell actions effeciently. For example, if you are in command mode and press **c**, you will copy the current cell.
There are a large amount of shortcuts avaialbe in the command mode. However, you do not have to remember all of them, since most actions in the command mode are available in the menu.
Here is a list of the most useful shortcuts. They are arrganged by the
order we recommend you learn so that you can edit the cells effienctly.
1. Basic navigation:
- Enter: switch to Edit mode
- Esc: switch to Command mode
- Shift+enter: Eexecute a cell
- Up, down: Move to the cell above or below
2. Cell types:
- y: switch to code cell)
- m: switch to markdown cell)
3. Cell creation:
- a: insert new sell above
- b: insert new cell below
4. Cell deleting:
- press D twice.
Note that one of the most common (and frustrating) mistakes when using the
notebook is to type something in the wrong mode. Remember to use **Esc**
to switch to the Command mode and **Enter** to switch to the Edit mode.
Also, remember that **clicking** on a cell automatically places it in the Edit
mode, so it will be necessary to press **Esc** to go to the Command mode.
### Exercise
Please go ahead and try these shortcuts. For example, try to insert new cell, modify and delete an existing cell. You can also switch cells between code type and markdown type, and practics different kinds of formatting in a markdown cell.
For a complete list of shortcut in **Command** mode, go to menu bar **Help->Keyboardshorcut**. Feel free to explore the other shortcuts.
<a id = "cell_close"></a>
## 1.4 open and close notebooks
You can open multiple notebooks in a browser windows. Simply go to menubar and choose **File->open...**, and select one **.ipynb** file. The second notebook will be opened in a seperated tab.
Now make sure you still have your **hello.ipynb** open. Also please download **ControlAdvData.ipynb** from cloudDeakin, and save under **H:/sit742/prac01**. Now go to the manu bar, click on **File->open ...**, locate the file **ControlAdvData.ipynb**, and open this file.
When you finish your work, you will need to close your notebooks and shutdown the IPython notebook server. Instead of simply close all the tabs in the browser, you need to shutdown each notebook first. To do this, swich to the **Home** tab(**Dashboard page**) and **Running** section(see below). Click on **Shutdown** button to close each notebook. In case **Dashboard** page is not open, click on the **Jupyter** icon to reopen it.
<img src="https://raw.githubusercontent.com/tuliplab/mds/master/Jupyter/image/close-index.jpg">
After each notebook is shutdown, it is time to showdown the IPython notebook server. To do this, go to the terminal window and press **CTRL + C**, and then enter **Y**. After the notebook server is shut down, the terminal window is ready for you to enter any new command.
<img src="https://raw.githubusercontent.com/tuliplab/mds/master/Jupyter/image/close-terminal.jpg">
# Part 2 Basic Data Types
In this part, you will get better understanding with Python's basic data type. We will
look at **string** and **number** data type in this section. Also covered are:
- Data conversion
- Data comparison
- Receive input from users and display results effectively
You will be guided through completing a simple program which receives input from a user,
process the information, and display results with specific format.
<a id = "cell_string"></a>
## 2.1 String
A string is a *sequence of characters*. We are using strings in almost every Python
programs. As we can seen in the **”Hello, World!”** example, strings can be specified
using single quotes **'**. The **print()** function can be used to display a string.
```
print('Hello, World!')
```
We can also use a variable to store the string value, and use the variable in the
**print()** function.
```
# Assign a string to a variable
text = 'Hello, World!'
print(text)
```
A *variable* is basically a name that represents (or refers to) some value. We use **=**
to assign a value to a variable before we use it. Variable names are given by a programer
in a way that the program is easy to understanding. Variable names are *case sensitive*.
It can consist of letters, digits and underscores. However, it can not begin with a digit.
For example, **plan9** and **plan_9** are valid names, where **9plan** is not.
```
text = 'Hello, World!'
# with print() function, content is displayed without quotation mark
print(text)
```
With variables, we can also display its value without **print()** function. Note that
you can not display a variable without **print()** function in Python script(i.e. in a **.py** file). This method only works under interactive mode (i.e. in the notebook).
```
# without print() function, quotation mark is displayed together with content
text
```
Back to representation of string, there will be issues if you need to include a quotation
mark in the text.
```
text = ’What’ s your name ’
```
Since strings in double quotes **"** work exactly the same way as string in single quotes.
By mixing the two types, it is easy to include quaotation mark itself in the text.
```
text = "What' s your name?"
print(text)
```
Alternertively, you can use:
```
text = '"What is the problem?", he asked.'
print(text)
```
You can specify multi-line strings using triple quotes (**"""** or **'''**). In this way, single
quotes and double quotes can be used freely in the text.
Here is one example:
```
multiline = '''This is a test for multiline. This is the first line.
This is the second line.
I asked, "What's your name?"'''
print(multiline)
```
Notice the difference when the variable is displayed without **print()** function in this case.
```
multiline = '''This is a test for multiline. This is the first line.
This is the second line.
I asked, "What's your name?"'''
multiline
```
Another way of include the special characters, such as single quotes is with help of
escape sequences **\\**. For example, you can specify the single quote using **\\' ** as follows.
```
string = 'What\'s your name?'
print(string)
```
There are many more other escape sequences (See Section 2.4.1 in [Python3.0 official document](https://docs.python.org/3.1/reference/lexical_analysis.html)). But I am going to mention the most useful two examples here.
First, use escape sequences to indicate the backslash itself e.g. **\\\\**
```
path = 'c:\\windows\\temp'
print(path)
```
Second, used escape sequences to specify a two-line string. Apart from using a triple-quoted
string as shown previously, you can use **\n** to indicate the start of a new line.
```
multiline = 'This is a test for multiline. This is the first line.\nThis is the second line.'
print(multiline)
```
To manipulate strings, the following two operators are most useful:
* **+** is use to concatenate
two strings or string variables;
* ***** is used for concatenating several copies of the same
string.
```
print('Hello, ' + 'World' * 3)
```
Below is another example of string concatenation based on variables that store strings.
```
name = 'World'
greeting = 'Hello'
print(greeting + ', ' + name + '!')
```
Using variables, change part of the string text is very easy.
```
name
greeting
# Change part of the text is easy
greeting = 'Good morning'
print(greeting + ', ' + name + '!')
```
<a id = "cell_number"></a>
## 2.2 Number
There are two types of numbers that are used most frequently: integers and floats. As we
expect, the standard mathematic operation can be applied to these two types. Please
try the following expressions. Note that **\*\*** is exponent operator, which indicates
exponentation exponential(power) caluclation.
```
2 + 3
3 * 5
#3 to the power of 4
3 ** 4
```
Among the number operations, we need to look at division closely. In Python 3.0, classic division is performed using **/**.
```
15 / 5
14 / 5
```
*//* is used to perform floor division. It truncates the fraction and rounds it to the next smallest whole number toward the left on the number line.
```
14 // 5
# Negatives move left on number line. The result is -3 instead of -2
-14 // 5
```
Modulus operator **%** can be used to obtain remaider. Pay attention when negative number is involved.
```
14 % 5
# Hint: −14 // 5 equal to −3
# (-3) * 5 + ? = -14
-14 % 5
```
*Operator precedence* is a rule that affects how an expression is evaluated. As we learned in high school, the multiplication is done first than the addition. e.g. **2 + 3 * 4**. This means multiplication operator has higher precedence than the addition operator.
For your reference, a precedence table from the python reference manual is used to indicate the evaluation order in Python. For a complete precedence table, check the heading "Python Operators Precedence" in this [Python tutorial](http://www.tutorialspoint.com/python/python_basic_operators.htm)
However, When things get confused, it is far better to use parentheses **()** to explicitly
specify the precedence. This makes the program more readable.
Here are some examples on operator precedence:
```
2 + 3 * 4
(2 + 3) * 4
2 + 3 ** 2
(2 + 3) ** 2
-(4+3)+2
```
Similary as string, variables can be used to store a number so that it is easy to manipulate them.
```
x = 3
y = 2
x + 2
sum = x + y
sum
x * y
```
One common expression is to run a math operation on a variable and then assign the result of the operation back to the variable. Therefore, there is a shortcut for such a expression.
```
x = 2
x = x * 3
x
```
This is equivalant to:
```
x = 2
# Note there is no space between '*' and '+'
x *= 3
x
```
<a id = "cell_conversion"></a>
## 2.3 Data conversion and comparison
So far, we have seen three types of data: interger, float, and string. With various data type, Python can define the operations possible on them and the storage method for each of them. In the later pracs, we will further introduce more data types, such as tuple, list and dictionary.
To obtain the data type of a variable or a value, we can use built-in function **type()**;
whereas functions, such as **str()**, **int()**, **float()**, are used to convert data one type to another. Check the following examples on the usage of these functions:
```
type('Hello, world!)')
input_Value = '45.6'
type(input_Value)
weight = float(input_Value)
weight
type(weight)
```
Note the system will report error message when the conversion function is not compatible with the data.
```
input_Value = 'David'
weight = float(input_Value)
```
Comparison between two values can help make decision in a program. The result of the comparison is either **True** or **False**. They are the two values of *Boolean* type.
```
5 > 10
type(5 > 10)
# Double equal sign is also used for comparison
10.0 == 10
```
Check the following examples on comparison of two strings.
```
'cat' < 'dog'
# All uppercases are before low cases.
'cat' < 'Dog'
'apple' < 'apricot'
```
There are three logical operators, *not*, *and* and *or*, which can be applied to the boolean values.
```
# Both condition #1 and condition #2 are True?
3 < 4 and 7 < 8
# Either condition 1 or condition 2 are True?
3 < 4 or 7 > 8
# Both conditional #1 and conditional #2 are False?
not ((3 > 4) or (7 > 8))
```
<a id = "cell_input"></a>
## 2. 4. Input and output
All programing languages provide features to interact with user. Python provide *input()* function to get input. It waits for the user to type some input and press return. We can add some information for the user by putting a message inside the function's brackets. It must be a string or a string variable. The text that was typed can be saved in a variable. Here is one example:
```
nInput = input('Enter you number here:\n')
```
However, be aware that the input received from the user are treated as a string, even
though a user entered a number. The following **print()** function invokes an error message.
```
print(nInput + 3)
```
The input need to be converted to an integer before the match operation can be performed as follows:
```
print(int(nInput) + 3)
```
After user's input are accepted, the messages need to be displayed to the user accordingly. String concatenation is one way to display messages which incorporate variable values.
```
name = 'David'
print('Hello, ' + name)
```
Another way of achieving this is using **print()** funciton with *string formatting*. We need to use the *string formatting operator*, the percent(**%**) sign.
```
name = 'David'
print('Hello, %s' % name)
```
Here is another example with two variables:
```
name = 'David'
age = 23
print('%s is %d years old.' % (name, age))
```
Notice that the two variables, **name**, **age**, that specify the values are included at the end of the statement, and enclosed with a bracket.
With the quotation mark, **%s** and **%d** are used to specify formating for string and integer respectively.
The following table shows a selected set of symbols which can be used along with %.
<table width="304" border="1">
<tr>
<th width="112" scope="col">Format symbol</th>
<th width="176" scope="col">Conversion</th>
</tr>
<tr>
<td>%s</td>
<td>String</td>
</tr>
<tr>
<td>%d</td>
<td>Signed decimal integer</td>
</tr>
<tr>
<td>%f</td>
<td>Floating point real number</td>
</tr>
</table>
There are extra charaters that are used together with above symbols:
<table width="400" border="1">
<tr>
<th width="100" scope="col">Symbol</th>
<th width="3000" scope="col">Functionality</th>
</tr>
<tr>
<td>-</td>
<td>Left justification</td>
</tr>
<tr>
<td>+</td>
<td>Display the sign</td>
</tr>
<tr>
<td>m.n</td>
<td>m is the minimum total width; n is the number of digits to display after the decimal point</td>
</tr>
</table>
Here are more examples that use above specifiers:
```
# With %f, the format is right justification by default.
# As a result, white spaces are added to the left of the number
# 10.4 means minimal width 10 with 4 decinal points
print('Output a float number: %10.4f' % (3.5))
# plus sign after % means to show positive sign
# Zero after plus sign means using leading zero to fill width of 5
print('Output an integer: %+05d' % (23))
```
### 2.5 Notes on *Python 2*
You need to pay attention if you test examples in this prac under *Python* 2.
1. In *Python 3, * **/** is float division, and **//** is integer division; while in Python 2,
both **/** and **//**
perform *integer division*.
However, if you stick to using **float(3)/2** for *float division*,
and **3/2** for *integer division*,
you will have no problem in both version.
2. Instead using function **input()**,
**raw_input()** is used in Python 2.
Both functions have the same functionality,
i.e. take what the user typed and passes it back as a string.
3. Although both versions support **print()** function with same format,
Python 2 also allows the print statement (e.g. **print "Hello, World!"**),
which is not valid in Python 3.
However, if you stick to our examples and using **print()** function with parantheses,
your programs should works fine in both versions.
|
github_jupyter
|
# General Equilibrium
This notebook illustrates **how to solve GE equilibrium models**. The example is a simple one-asset model without nominal rigidities.
The notebook shows how to:
1. Solve for the **stationary equilibrium**.
2. Solve for (non-linear) **transition paths** using a relaxtion algorithm.
3. Solve for **transition paths** (linear vs. non-linear) and **impulse-responses** using the **sequence-space method** of **Auclert et. al. (2020)**.
```
LOAD = False # load stationary equilibrium
DO_VARY_SIGMA_E = True # effect of uncertainty on stationary equilibrium
DO_TP_RELAX = True # do transition path with relaxtion
```
# Setup
```
%load_ext autoreload
%autoreload 2
import time
import numpy as np
import numba as nb
from scipy import optimize
import matplotlib.pyplot as plt
plt.style.use('seaborn-whitegrid')
prop_cycle = plt.rcParams['axes.prop_cycle']
colors = prop_cycle.by_key()['color']
from consav.misc import elapsed
from GEModel import GEModelClass
from GEModel import solve_backwards, simulate_forwards, simulate_forwards_transpose
```
## Choose number of threads in numba
```
import numba as nb
nb.set_num_threads(8)
```
# Model
```
model = GEModelClass('baseline',load=LOAD)
print(model)
```
For easy access
```
par = model.par
sim = model.sim
sol = model.sol
```
**Productivity states:**
```
for e,pr_e in zip(par.e_grid,par.e_ergodic):
print(f'Pr[e = {e:7.4f}] = {pr_e:.4f}')
assert np.isclose(np.sum(par.e_grid*par.e_ergodic),1.0)
```
# Find Stationary Equilibrium
**Step 1:** Find demand and supply of capital for a grid of interest rates.
```
if not LOAD:
t0 = time.time()
par = model.par
# a. interest rate trial values
Nr = 20
r_vec = np.linspace(0.005,1.0/par.beta-1-0.002,Nr) # 1+r > beta not possible
# b. allocate
Ks = np.zeros(Nr)
Kd = np.zeros(Nr)
# c. loop
r_min = r_vec[0]
r_max = r_vec[Nr-1]
for i_r in range(Nr):
# i. firm side
k = model.firm_demand(r_vec[i_r],par.Z)
Kd[i_r] = k*1 # aggregate labor = 1.0
# ii. household side
success = model.solve_household_ss(r=r_vec[i_r])
if success:
success = model.simulate_household_ss()
if success:
# total demand
Ks[i_r] = np.sum(model.sim.D*model.sol.a)
# bounds on r
diff = Ks[i_r]-Kd[i_r]
if diff < 0: r_min = np.fmax(r_min,r_vec[i_r])
if diff > 0: r_max = np.fmin(r_max,r_vec[i_r])
else:
Ks[i_r] = np.nan
# d. save
model.save()
print(f'grid search done in {elapsed(t0)}')
```
**Step 2:** Plot supply and demand.
```
if not LOAD:
par = model.par
fig = plt.figure(figsize=(6,4))
ax = fig.add_subplot(1,1,1)
ax.plot(r_vec,Ks,label='supply of capital')
ax.plot(r_vec,Kd,label='demand for capital')
ax.axvline(r_min,lw=0.5,ls='--',color='black')
ax.axvline(r_max,lw=0.5,ls='--',color='black')
ax.legend(frameon=True)
ax.set_xlabel('interest rate, $r$')
ax.set_ylabel('capital, $K_t$')
fig.tight_layout()
fig.savefig('figs/stationary_equilibrium.pdf')
```
**Step 3:** Solve root-finding problem.
```
def obj(r,model):
model.solve_household_ss(r=r)
model.simulate_household_ss()
return np.sum(model.sim.D*model.sol.a)-model.firm_demand(r,model.par.Z)
if not LOAD:
t0 = time.time()
opt = optimize.root_scalar(obj,bracket=[r_min,r_max],method='bisect',args=(model,))
model.par.r_ss = opt.root
assert opt.converged
print(f'search done in {elapsed(t0)}')
```
**Step 4:** Check market clearing conditions.
```
model.steady_state()
```
## Timings
```
%timeit model.solve_household_ss(r=par.r_ss)
%timeit model.simulate_household_ss()
```
## Income uncertainty and the equilibrium interest rate
The equlibrium interest rate decreases when income uncertainty is increased.
```
if DO_VARY_SIGMA_E:
par = model.par
# a. seetings
sigma_e_vec = [0.20]
# b. find equilibrium rates
model_ = model.copy()
for sigma_e in sigma_e_vec:
# i. set new parameter
model_.par.sigma_e = sigma_e
model_.create_grids()
# ii. solve
print(f'sigma_e = {sigma_e:.4f}',end='')
opt = optimize.root_scalar(
obj,
bracket=[0.00,model.par.r_ss],
method='bisect',
args=(model_,)
)
print(f' -> r_ss = {opt.root:.4f}')
model_.par.r_ss = opt.root
model_.steady_state()
print('\n')
```
## Test matrix formulation
**Step 1:** Construct $\boldsymbol{Q}_{ss}$
```
# a. allocate Q
Q = np.zeros((par.Ne*par.Na,par.Ne*par.Na))
# b. fill
for i_e in range(par.Ne):
# get view of current block
q = Q[i_e*par.Na:(i_e+1)*par.Na,i_e*par.Na:(i_e+1)*par.Na]
for i_a in range(par.Na):
# i. optimal choice
a_opt = sol.a[i_e,i_a]
# ii. above -> all weight on last node
if a_opt >= par.a_grid[-1]:
q[i_a,-1] = 1.0
# iii. below -> all weight on first node
elif a_opt <= par.a_grid[0]:
q[i_a,0] = 1.0
# iv. standard -> distribute weights on neighboring nodes
else:
i_a_low = np.searchsorted(par.a_grid,a_opt,side='right')-1
assert a_opt >= par.a_grid[i_a_low], f'{a_opt} < {par.a_grid[i_a_low]}'
assert a_opt < par.a_grid[i_a_low+1], f'{a_opt} < {par.a_grid[i_a_low]}'
q[i_a,i_a_low] = (par.a_grid[i_a_low+1]-a_opt)/(par.a_grid[i_a_low+1]-par.a_grid[i_a_low])
q[i_a,i_a_low+1] = 1-q[i_a,i_a_low]
```
**Step 2:** Construct $\tilde{\Pi}^e=\Pi^e \otimes \boldsymbol{I}_{\#_{a}\times\#_{a}}$
```
Pit = np.kron(par.e_trans,np.identity(par.Na))
```
**Step 3:** Test $\overrightarrow{D}_{t+1}=\tilde{\Pi}^{e\prime}\boldsymbol{Q}_{ss}^{\prime}\overrightarrow{D}_{t}$
```
D = np.zeros(sim.D.shape)
D[:,0] = par.e_ergodic
# a. standard
D_plus = np.zeros(D.shape)
simulate_forwards(D,sol.i,sol.w,par.e_trans.T.copy(),D_plus)
# b. matrix product
D_plus_alt = ((Pit.T@Q.T)@D.ravel()).reshape((par.Ne,par.Na))
# c. test equality
assert np.allclose(D_plus,D_plus_alt)
```
# Find transition path
**MIT-shock:** Transtion path for arbitrary exogenous path of $Z_t$ starting from the stationary equilibrium, i.e. $D_{-1} = D_{ss}$ and in particular $K_{-1} = K_{ss}$.
**Step 1:** Construct $\{Z_t\}_{t=0}^{T-1}$ where $Z_t = (1-\rho_Z)Z_{ss} + \rho_Z Z_t$ and $Z_0 = (1+\sigma_Z) Z_{ss}$
```
path_Z = model.get_path_Z()
```
**Step 2:** Apply relaxation algorithm.
```
if DO_TP_RELAX:
t0 = time.time()
# a. allocate
path_r = np.repeat(model.par.r_ss,par.path_T) # use steady state as initial guess
path_r_ = np.zeros(par.path_T)
path_w = np.zeros(par.path_T)
# b. setting
nu = 0.90 # relaxation parameter
max_iter = 5000 # maximum number of iterations
# c. iterate
it = 0
while True:
# i. find wage
for t in range(par.path_T):
path_w[t] = model.implied_w(path_r[t],path_Z[t])
# ii. solve and simulate
model.solve_household_path(path_r,path_w)
model.simulate_household_path(model.sim.D)
# iii. implied prices
for t in range(par.path_T):
path_r_[t] = model.implied_r(sim.path_Klag[t],path_Z[t])
# iv. difference
max_abs_diff = np.max(np.abs(path_r-path_r_))
if it%10 == 0: print(f'{it:4d}: {max_abs_diff:.8f}')
if max_abs_diff < 1e-8: break
# v. update
path_r = nu*path_r + (1-nu)*path_r_
# vi. increment
it += 1
if it > max_iter: raise Exception('too many iterations')
print(f'\n transtion path found in {elapsed(t0)}')
```
**Plot transition-paths:**
```
if DO_TP_RELAX:
fig = plt.figure(figsize=(10,6))
ax = fig.add_subplot(2,2,1)
ax.plot(np.arange(par.path_T),path_Z,'-o',ms=2)
ax.set_title('technology, $Z_t$');
ax = fig.add_subplot(2,2,2)
ax.plot(np.arange(par.path_T),sim.path_K,'-o',ms=2)
ax.set_title('capital, $k_t$');
ax = fig.add_subplot(2,2,3)
ax.plot(np.arange(par.path_T),path_r,'-o',ms=2)
ax.set_title('interest rate, $r_t$');
ax = fig.add_subplot(2,2,4)
ax.plot(np.arange(par.path_T),path_w,'-o',ms=2)
ax.set_title('wage, $w_t$')
fig.tight_layout()
fig.savefig('figs/transition_path.pdf')
```
**Remember:**
```
if DO_TP_RELAX:
path_Z_relax = path_Z
path_K_relax = sim.path_K
path_r_relax = path_r
path_w_relax = path_w
```
# Find impulse-responses using sequence-space method
**Paper:** Auclert, A., Bardóczy, B., Rognlie, M., and Straub, L. (2020). *Using the Sequence-Space Jacobian to Solve and Estimate Heterogeneous-Agent Models*.
**Original code:** [shade-econ](https://github.com/shade-econ/sequence-jacobian/#sequence-space-jacobian)
**This code:** Illustrates the sequence-space method. The original paper shows how to do it computationally efficient and for a general class of models.
**Step 1:** Compute the Jacobian for the household block around the stationary equilibrium
```
def jac(model,price,dprice=1e-4,do_print=True):
t0_all = time.time()
if do_print: print(f'price is {price}')
par = model.par
sol = model.sol
sim = model.sim
# a. step 1: solve backwards
t0 = time.time()
path_r = np.repeat(par.r_ss,par.path_T)
path_w = np.repeat(par.w_ss,par.path_T)
if price == 'r': path_r[-1] += dprice
elif price == 'w': path_w[-1] += dprice
model.solve_household_path(path_r,path_w,do_print=False)
if do_print: print(f'solved backwards in {elapsed(t0)}')
# b. step 2: derivatives
t0 = time.time()
diff_Ds = np.zeros((par.path_T,*sim.D.shape))
diff_as = np.zeros(par.path_T)
diff_cs = np.zeros(par.path_T)
for s in range(par.path_T):
t_ =(par.path_T-1)-s
simulate_forwards(sim.D,sol.path_i[t_],sol.path_w[t_],par.e_trans.T,diff_Ds[s])
diff_Ds[s] = (diff_Ds[s]-sim.D)/dprice
diff_as[s] = (np.sum(sol.path_a[t_]*sim.D)-np.sum(sol.a*sim.D))/dprice
diff_cs[s] = (np.sum(sol.path_c[t_]*sim.D)-np.sum(sol.c*sim.D))/dprice
if do_print: print(f'derivatives calculated in {elapsed(t0)}')
# c. step 3: expectation factors
t0 = time.time()
# demeaning improves numerical stability
def demean(x):
return x - x.sum()/x.size
exp_as = np.zeros((par.path_T-1,*sol.a.shape))
exp_as[0] = demean(sol.a)
exp_cs = np.zeros((par.path_T-1,*sol.c.shape))
exp_cs[0] = demean(sol.c)
for t in range(1,par.path_T-1):
simulate_forwards_transpose(exp_as[t-1],sol.i,sol.w,par.e_trans,exp_as[t])
exp_as[t] = demean(exp_as[t])
simulate_forwards_transpose(exp_cs[t-1],sol.i,sol.w,par.e_trans,exp_cs[t])
exp_cs[t] = demean(exp_cs[t])
if do_print: print(f'expecation factors calculated in {elapsed(t0)}')
# d. step 4: F
t0 = time.time()
Fa = np.zeros((par.path_T,par.path_T))
Fa[0,:] = diff_as
Fc = np.zeros((par.path_T,par.path_T))
Fc[0,:] = diff_cs
Fa[1:, :] = exp_as.reshape((par.path_T-1, -1)) @ diff_Ds.reshape((par.path_T, -1)).T
Fc[1:, :] = exp_cs.reshape((par.path_T-1, -1)) @ diff_Ds.reshape((par.path_T, -1)).T
if do_print: print(f'f calculated in {elapsed(t0)}')
t0 = time.time()
# e. step 5: J
Ja = Fa.copy()
for t in range(1, Ja.shape[1]): Ja[1:, t] += Ja[:-1, t - 1]
Jc = Fc.copy()
for t in range(1, Jc.shape[1]): Jc[1:, t] += Jc[:-1, t - 1]
if do_print: print(f'J calculated in {elapsed(t0)}')
# f. save
setattr(model.sol,f'jac_curlyK_{price}',Ja)
setattr(model.sol,f'jac_C_{price}',Jc)
if do_print: print(f'full Jacobian calculated in {elapsed(t0_all)}\n')
jac(model,'r')
jac(model,'w')
```
**Inspect Jacobians:**
```
fig = plt.figure(figsize=(12,8))
T_fig = 200
# curlyK_r
ax = fig.add_subplot(2,2,1)
for s in [0,25,50,75,100]:
ax.plot(np.arange(T_fig),sol.jac_curlyK_r[s,:T_fig],'-o',ms=2,label=f'$s={s}$')
ax.legend(frameon=True)
ax.set_title(r'$\mathcal{J}^{\mathcal{K},r}$')
ax.set_xlim([0,T_fig])
# curlyK_w
ax = fig.add_subplot(2,2,2)
for s in [0,25,50,75,100]:
ax.plot(np.arange(T_fig),sol.jac_curlyK_w[s,:T_fig],'-o',ms=2)
ax.set_title(r'$\mathcal{J}^{\mathcal{K},w}$')
ax.set_xlim([0,T_fig])
# C_r
ax = fig.add_subplot(2,2,3)
for s in [0,25,50,75,100]:
ax.plot(np.arange(T_fig),sol.jac_C_r[s,:T_fig],'-o',ms=2,label=f'$s={s}$')
ax.legend(frameon=True)
ax.set_title(r'$\mathcal{J}^{C,r}$')
ax.set_xlim([0,T_fig])
# curlyK_w
ax = fig.add_subplot(2,2,4)
for s in [0,25,50,75,100]:
ax.plot(np.arange(T_fig),sol.jac_C_w[s,:T_fig],'-o',ms=2)
ax.set_title(r'$\mathcal{J}^{C,w}$')
ax.set_xlim([0,T_fig])
fig.tight_layout()
fig.savefig('figs/jacobians.pdf')
```
**Step 2:** Compute the Jacobians for the firm block around the stationary equilibrium (analytical).
```
sol.jac_r_K[:] = 0
sol.jac_w_K[:] = 0
sol.jac_r_Z[:] = 0
sol.jac_w_Z[:] = 0
for s in range(par.path_T):
for t in range(par.path_T):
if t == s+1:
sol.jac_r_K[t,s] = par.alpha*(par.alpha-1)*par.Z*par.K_ss**(par.alpha-2)
sol.jac_w_K[t,s] = (1-par.alpha)*par.alpha*par.Z*par.K_ss**(par.alpha-1)
if t == s:
sol.jac_r_Z[t,s] = par.alpha*par.Z*par.K_ss**(par.alpha-1)
sol.jac_w_Z[t,s] = (1-par.alpha)*par.Z*par.K_ss**par.alpha
```
**Step 3:** Use the chain rule and solve for $G$.
```
H_K = sol.jac_curlyK_r @ sol.jac_r_K + sol.jac_curlyK_w @ sol.jac_w_K - np.eye(par.path_T)
H_Z = sol.jac_curlyK_r @ sol.jac_r_Z + sol.jac_curlyK_w @ sol.jac_w_Z
G_K_Z = -np.linalg.solve(H_K, H_Z) # H_K^(-1)H_Z
```
**Step 4:** Find effect on prices and other outcomes than $K$.
```
G_r_Z = sol.jac_r_Z + sol.jac_r_K@G_K_Z
G_w_Z = sol.jac_w_Z + sol.jac_w_K@G_K_Z
G_C_Z = sol.jac_C_r@G_r_Z + sol.jac_C_w@G_w_Z
```
**Step 5:** Plot impulse-responses.
**Example I:** News shock (i.e. in a single period) vs. persistent shock where $ dZ_t = \rho dZ_{t-1} $ and $dZ_0$ is the initial shock.
```
fig = plt.figure(figsize=(12,4))
T_fig = 50
# left: news shock
ax = fig.add_subplot(1,2,1)
for s in [5,10,15,20,25]:
dZ = (1+par.Z_sigma)*par.Z*(np.arange(par.path_T) == s)
dK = G_K_Z@dZ
ax.plot(np.arange(T_fig),dK[:T_fig],'-o',ms=2,label=f'$s={s}$')
ax.legend(frameon=True)
ax.set_title(r'1% TFP news shock in period $s$')
ax.set_ylabel('$K_t-K_{ss}$')
ax.set_xlim([0,T_fig])
# right: persistent shock
ax = fig.add_subplot(1,2,2)
dZ = model.get_path_Z()-par.Z
dK = G_K_Z@dZ
ax.plot(np.arange(T_fig),dK[:T_fig],'-o',ms=2)
ax.set_title(r'1% TFP shock with persistence $\rho=0.90$')
ax.set_ylabel('$K_t-K_{ss}$')
ax.set_xlim([0,T_fig])
fig.tight_layout()
fig.savefig('figs/news_vs_persistent_shock.pdf')
```
**Example II:** Further effects of persistent shock.
```
fig = plt.figure(figsize=(12,8))
T_fig = 50
ax_K = fig.add_subplot(2,2,1)
ax_r = fig.add_subplot(2,2,2)
ax_w = fig.add_subplot(2,2,3)
ax_C = fig.add_subplot(2,2,4)
ax_K.set_title('$K_t-K_{ss}$ after 1% TFP shock')
ax_K.set_xlim([0,T_fig])
ax_r.set_title('$r_t-r_{ss}$ after 1% TFP shock')
ax_r.set_xlim([0,T_fig])
ax_w.set_title('$w_t-w_{ss}$ after 1% TFP shock')
ax_w.set_xlim([0,T_fig])
ax_C.set_title('$C_t-C_{ss}$ after 1% TFP shock')
ax_C.set_xlim([0,T_fig])
dZ = model.get_path_Z()-par.Z
dK = G_K_Z@dZ
ax_K.plot(np.arange(T_fig),dK[:T_fig],'-o',ms=2)
dr = G_r_Z@dZ
ax_r.plot(np.arange(T_fig),dr[:T_fig],'-o',ms=2)
dw = G_w_Z@dZ
ax_w.plot(np.arange(T_fig),dw[:T_fig],'-o',ms=2)
dC = G_C_Z@dZ
ax_C.plot(np.arange(T_fig),dC[:T_fig],'-o',ms=2)
fig.tight_layout()
fig.savefig('figs/irfs.pdf')
```
## Non-linear transition path
Use the Jacobian to speed-up solving for the non-linear transition path using a quasi-Newton method.
**1. Solver**
```
def broyden_solver(f,x0,jac,tol=1e-8,max_iter=100,backtrack_fac=0.5,max_backtrack=30,do_print=False):
""" numerical solver using the broyden method """
# a. initial
x = x0.ravel()
y = f(x)
# b. iterate
for it in range(max_iter):
# i. current difference
abs_diff = np.max(np.abs(y))
if do_print: print(f' it = {it:3d} -> max. abs. error = {abs_diff:12.8f}')
if abs_diff < tol: return x
# ii. new x
dx = np.linalg.solve(jac,-y)
# iii. evalute with backtrack
for _ in range(max_backtrack):
try: # evaluate
ynew = f(x+dx)
except ValueError: # backtrack
dx *= backtrack_fac
else: # update jac and break from backtracking
dy = ynew-y
jac = jac + np.outer(((dy - jac @ dx) / np.linalg.norm(dx) ** 2), dx)
y = ynew
x += dx
break
else:
raise ValueError('too many backtracks, maybe bad initial guess?')
else:
raise ValueError(f'no convergence after {max_iter} iterations')
```
**2. Target function**
$$\boldsymbol{H}(\boldsymbol{K},\boldsymbol{Z},D_{ss}) = \mathcal{K}_{t}(\{r(Z_{s},K_{s-1}),w(Z_{s},K_{s-1})\}_{s\geq0},D_{ss})-K_{t}=0$$
```
def target(path_K,path_Z,model,D0,full_output=False):
par = model.par
sim = model.sim
path_r = np.zeros(path_K.size)
path_w = np.zeros(path_K.size)
# a. implied prices
K0lag = np.sum(par.a_grid[np.newaxis,:]*D0)
path_Klag = np.insert(path_K,0,K0lag)
for t in range(par.path_T):
path_r[t] = model.implied_r(path_Klag[t],path_Z[t])
path_w[t] = model.implied_w(path_r[t],path_Z[t])
# b. solve and simulate
model.solve_household_path(path_r,path_w)
model.simulate_household_path(D0)
# c. market clearing
if full_output:
return path_r,path_w
else:
return sim.path_K-path_K
```
**3. Solve**
```
path_Z = model.get_path_Z()
f = lambda x: target(x,path_Z,model,sim.D)
t0 = time.time()
path_K = broyden_solver(f,x0=np.repeat(par.K_ss,par.path_T),jac=H_K,do_print=True)
path_r,path_w = target(path_K,path_Z,model,sim.D,full_output=True)
print(f'\nIRF found in {elapsed(t0)}')
```
**4. Plot**
```
fig = plt.figure(figsize=(12,4))
ax = fig.add_subplot(1,2,1)
ax.set_title('capital, $K_t$')
dK = G_K_Z@(path_Z-par.Z)
ax.plot(np.arange(T_fig),dK[:T_fig] + par.K_ss,'-o',ms=2,label=f'linear')
ax.plot(np.arange(T_fig),path_K[:T_fig],'-o',ms=2,label=f'non-linear')
if DO_TP_RELAX:
ax.plot(np.arange(T_fig),path_K_relax[:T_fig],'--o',ms=2,label=f'non-linear (relaxtion)')
ax.legend(frameon=True)
ax = fig.add_subplot(1,2,2)
ax.set_title('interest rate, $r_t$')
dr = G_r_Z@(path_Z-par.Z)
ax.plot(np.arange(T_fig),dr[:T_fig] + par.r_ss,'-o',ms=2,label=f'linear')
ax.plot(np.arange(T_fig),path_r[:T_fig],'-o',ms=2,label=f'non-linear')
if DO_TP_RELAX:
ax.plot(np.arange(T_fig),path_r_relax[:T_fig],'--o',ms=2,label=f'non-linear (relaxtion)')
fig.tight_layout()
fig.savefig('figs/non_linear.pdf')
```
## Covariances
Assume that $Z_t$ is stochastic and follows
$$ d\tilde{Z}_t = \rho d\tilde{Z}_{t-1} + \sigma\epsilon_t,\,\,\, \epsilon_t \sim \mathcal{N}(0,1) $$
The covariances between all outcomes can be calculated as follows.
```
# a. choose parameter
rho = 0.90
sigma = 0.10
# b. find change in outputs
dZ = rho**(np.arange(par.path_T))
dC = G_C_Z@dZ
dK = G_K_Z@dZ
# c. covariance of consumption
print('auto-covariance of consumption:\n')
for k in range(5):
if k == 0:
autocov_C = sigma**2*np.sum(dC*dC)
else:
autocov_C = sigma**2*np.sum(dC[:-k]*dC[k:])
print(f' k = {k}: {autocov_C:.4f}')
# d. covariance of consumption and capital
cov_C_K = sigma**2*np.sum(dC*dK)
print(f'\ncovariance of consumption and capital: {cov_C_K:.4f}')
```
# Extra: No idiosyncratic uncertainty
This section solve for the transition path in the case without idiosyncratic uncertainty.
**Analytical solution for steady state:**
```
r_ss_pf = (1/par.beta-1) # from euler-equation
w_ss_pf = model.implied_w(r_ss_pf,par.Z)
K_ss_pf = model.firm_demand(r_ss_pf,par.Z)
Y_ss_pf = model.firm_production(K_ss_pf,par.Z)
C_ss_pf = Y_ss_pf-par.delta*K_ss_pf
print(f'r: {r_ss_pf:.6f}')
print(f'w: {w_ss_pf:.6f}')
print(f'Y: {Y_ss_pf:.6f}')
print(f'C: {C_ss_pf:.6f}')
print(f'K/Y: {K_ss_pf/Y_ss_pf:.6f}')
```
**Function for finding consumption and capital paths given paths of interest rates and wages:**
It can be shown that
$$ C_{0}=\frac{(1+r_{0})a_{-1}+\sum_{t=0}^{\infty}\frac{1}{\mathcal{R}_{t}}w_{t}}{\sum_{t=0}^{\infty}\beta^{t/\rho}\mathcal{R}_{t}^{\frac{1-\rho}{\rho}}} $$
where
$$ \mathcal{R}_{t} =\begin{cases} 1 & \text{if }t=0\\ (1+r_{t})\mathcal{R}_{t-1} & \text{else} \end{cases} $$
Otherwise the **Euler-equation** holds
$$ C_t = (\beta (1+r_{t}))^{\frac{1}{\sigma}}C_{t-1} $$
```
def path_CK_func(K0,path_r,path_w,r_ss,w_ss,model):
par = model.par
# a. initialize
wealth = (1+path_r[0])*K0
inv_MPC = 0
# b. solve
RT = 1
max_iter = 5000
t = 0
while True and t < max_iter:
# i. prices padded with steady state
r = path_r[t] if t < par.path_T else r_ss
w = path_w[t] if t < par.path_T else w_ss
# ii. interest rate factor
if t == 0:
fac = 1
else:
fac *= (1+r)
# iii. accumulate
add_wealth = w/fac
add_inv_MPC = par.beta**(t/par.sigma)*fac**((1-par.sigma)/par.sigma)
if np.fmax(add_wealth,add_inv_MPC) < 1e-12:
break
else:
wealth += add_wealth
inv_MPC += add_inv_MPC
# iv. increment
t += 1
# b. simulate
path_C = np.empty(par.path_T)
path_K = np.empty(par.path_T)
for t in range(par.path_T):
if t == 0:
path_C[t] = wealth/inv_MPC
K_lag = K0
else:
path_C[t] = (par.beta*(1+path_r[t]))**(1/par.sigma)*path_C[t-1]
K_lag = path_K[t-1]
path_K[t] = (1+path_r[t])*K_lag + path_w[t] - path_C[t]
return path_K,path_C
```
**Test with steady state prices:**
```
path_r_pf = np.repeat(r_ss_pf,par.path_T)
path_w_pf = np.repeat(w_ss_pf,par.path_T)
path_K_pf,path_C_pf = path_CK_func(K_ss_pf,path_r_pf,path_w_pf,r_ss_pf,w_ss_pf,model)
print(f'C_ss: {C_ss_pf:.6f}')
print(f'C[0]: {path_C_pf[0]:.6f}')
print(f'C[-1]: {path_C_pf[-1]:.6f}')
assert np.isclose(C_ss_pf,path_C_pf[0])
```
**Shock paths** where interest rate deviate in one period:
```
dr = 1e-4
ts = np.array([0,20,40])
path_C_pf_shock = np.empty((ts.size,par.path_T))
path_K_pf_shock = np.empty((ts.size,par.path_T))
for i,t in enumerate(ts):
path_r_pf_shock = path_r_pf.copy()
path_r_pf_shock[t] += dr
K,C = path_CK_func(K_ss_pf,path_r_pf_shock,path_w_pf,r_ss_pf,w_ss_pf,model)
path_K_pf_shock[i,:] = K
path_C_pf_shock[i,:] = C
```
**Plot paths:**
```
fig = plt.figure(figsize=(12,4))
ax = fig.add_subplot(1,2,1)
ax.plot(np.arange(par.path_T),path_C_pf,'-o',ms=2,label=f'$r_t = r^{{\\ast}}$')
for i,t in enumerate(ts):
ax.plot(np.arange(par.path_T),path_C_pf_shock[i],'-o',ms=2,label=f'shock to $r_{{{t}}}$')
ax.set_xlim([0,50])
ax.set_xlabel('periods')
ax.set_ylabel('consumtion, $C_t$');
ax = fig.add_subplot(1,2,2)
ax.plot(np.arange(par.path_T),path_K_pf,'-o',ms=2,label=f'$r_t = r^{{\\ast}}$')
for i,t in enumerate(ts):
ax.plot(np.arange(par.path_T),path_K_pf_shock[i],'-o',ms=2,label=f'shock to $r_{{{t}}}$')
ax.legend(frameon=True)
ax.set_xlim([0,50])
ax.set_xlabel('$t$')
ax.set_ylabel('capital, $K_t$');
fig.tight_layout()
```
**Find transition path with shooting algorithm:**
```
# a. allocate
dT = 200
path_C_pf = np.empty(par.path_T)
path_K_pf = np.empty(par.path_T)
path_r_pf = np.empty(par.path_T)
path_w_pf = np.empty(par.path_T)
# b. settings
C_min = C_ss_pf
C_max = C_ss_pf + K_ss_pf
K_min = 1.5 # guess on lower consumption if below this
K_max = 3 # guess on higher consumption if above this
tol_pf = 1e-6
max_iter_pf = 5000
path_K_pf[0] = K_ss_pf # capital is pre-determined
# c. iterate
t = 0
it = 0
while True:
# i. update prices
path_r_pf[t] = model.implied_r(path_K_pf[t],path_Z[t])
path_w_pf[t] = model.implied_w(path_r_pf[t],path_Z[t])
# ii. consumption
if t == 0:
C0 = (C_min+C_max)/2
path_C_pf[t] = C0
else:
path_C_pf[t] = (1+path_r_pf[t])*par.beta*path_C_pf[t-1]
# iii. check for steady state
if path_K_pf[t] < K_min:
t = 0
C_max = C0
continue
elif path_K_pf[t] > K_max:
t = 0
C_min = C0
continue
elif t > 10 and np.sqrt((path_C_pf[t]-C_ss_pf)**2+(path_K_pf[t]-K_ss_pf)**2) < tol_pf:
path_C_pf[t:] = path_C_pf[t]
path_K_pf[t:] = path_K_pf[t]
for k in range(par.path_T):
path_r_pf[k] = model.implied_r(path_K_pf[k],path_Z[k])
path_w_pf[k] = model.implied_w(path_r_pf[k],path_Z[k])
break
# iv. update capital
path_K_pf[t+1] = (1+path_r_pf[t])*path_K_pf[t] + path_w_pf[t] - path_C_pf[t]
# v. increment
t += 1
it += 1
if it > max_iter_pf: break
```
**Plot deviations from steady state:**
```
fig = plt.figure(figsize=(12,8))
ax = fig.add_subplot(2,2,1)
ax.plot(np.arange(par.path_T),path_Z,'-o',ms=2)
ax.set_xlim([0,200])
ax.set_title('technology, $Z_t$')
ax = fig.add_subplot(2,2,2)
ax.plot(np.arange(par.path_T),path_K-model.par.kd_ss,'-o',ms=2,label='$\sigma_e = 0.5$')
ax.plot(np.arange(par.path_T),path_K_pf-K_ss_pf,'-o',ms=2,label='$\sigma_e = 0$')
ax.legend(frameon=True)
ax.set_title('capital, $k_t$')
ax.set_xlim([0,200])
ax = fig.add_subplot(2,2,3)
ax.plot(np.arange(par.path_T),path_r-model.par.r_ss,'-o',ms=2,label='$\sigma_e = 0.5$')
ax.plot(np.arange(par.path_T),path_r_pf-r_ss_pf,'-o',ms=2,label='$\sigma_e = 0$')
ax.legend(frameon=True)
ax.set_title('interest rate, $r_t$')
ax.set_xlim([0,200])
ax = fig.add_subplot(2,2,4)
ax.plot(np.arange(par.path_T),path_w-model.par.w_ss,'-o',ms=2,label='$\sigma_e = 0.5$')
ax.plot(np.arange(par.path_T),path_w_pf-w_ss_pf,'-o',ms=2,label='$\sigma_e = 0$')
ax.legend(frameon=True)
ax.set_title('wage, $w_t$')
ax.set_xlim([0,200])
fig.tight_layout()
```
|
github_jupyter
|
```
import numpy as np
import scipy as sp
import scipy.interpolate
import matplotlib.pyplot as plt
import pandas as pd
import scipy.stats
import scipy.optimize
from scipy.optimize import curve_fit
import minkowskitools as mt
import importlib
importlib.reload(mt)
n=4000
rand_points = np.random.uniform(size=(2, n-2))
edge_points = np.array([[0.0, 1.0],[0.0, 1.0]])
points = np.concatenate((rand_points, edge_points), axis=1)
connections = mt.get_connections(points, pval=2, radius=0.05)
quick_data = []
for i in range(1000):
n=1000
rand_points = np.random.uniform(size=(2, n-2))
edge_points = np.array([[0.0, 1.0],[0.0, 1.0]])
points = np.concatenate((rand_points, edge_points), axis=1)
connections = mt.get_connections(points, pval=2, radius=0.1)
no_points = mt.perc_thresh_n(connections)
quick_data.append(no_points)
plt.hist(quick_data, cumulative=True, bins=100)
plt.gca().set(xlim=(0, 1000), xlabel='Number of Points', ylabel='Culmulative Density', title='Connectionn Threshold')
# plt.savefig('img/pval2r05.pdf')
plt.gca().set(xlim=(0, np.max(quick_data)))
plt.hist(quick_data, bins=100);
n=1000
rand_points = np.random.uniform(size=(2, n-2))
edge_points = np.array([[0.0, 1.0],[0.0, 1.0]])
points = np.concatenate((rand_points, edge_points), axis=1)
mt.smallest_r(points, pval=2)
n=1000
trials = 100
all_results = {}
results = []
for i in range(trials):
rand_points = np.random.uniform(size=(2, n-2))
edge_points = np.array([[0.0, 1.0],[0.0, 1.0]])
points = np.concatenate((rand_points, edge_points), axis=1)
results.append(mt.smallest_r(points, pval=2)[1])
plt.hist(results, cumulative=True, bins=100);
mt.r1_area2D(2)*(.05**2)*n
ns = [1000]
ps = [2]
mt.separate_perc_r(ns, ps, 'outputs/test_perc.txt', repeats=10)
import importlib
importlib.reload(mt)
data_dict = {}
for pval in [0.8, 1, 1.2]:
data_dict[pval] = []
n = 1000
r = 0.1
for i in range(1000):
rand_points = np.random.uniform(size=(2, n-2))
edge_points = np.array([[0.0, 1.0],[0.0, 1.0]])
points = np.concatenate((rand_points, edge_points), axis=1)
connections = mt.get_connections(points, pval=pval, radius=r)
no_points = mt.perc_thresh_n(connections)
data_dict[pval].append(no_points)
for pval in [0.8, 1, 1.2]:
plt.hist(data_dict[pval], cumulative=True, bins=100, label=pval, alpha=.3);
plt.legend()
plt.gca().set(title='Number of Points for Connectedness', xlabel='Points', ylabel='Cumulative Frequency');
# plt.savefig('img/PointsCumul.pdf')
data_dict_r = {}
for pval in [0.8, 1, 1.2]:
data_dict_r[pval] = []
n = 1000
r = 0.1
for i in range(1000):
print(i, end=',')
rand_points = np.random.uniform(size=(2, n-2))
edge_points = np.array([[0.0, 1.0],[0.0, 1.0]])
points = np.concatenate((rand_points, edge_points), axis=1)
r_min = smallest_r(points, pval)
data_dict_r[pval].append(r_min[1])
fig, [ax1, ax2] = plt.subplots(ncols=2, figsize=(14, 5))
for pval in [0.8, 1, 1.2]:
ax1.hist(data_dict_r[pval], cumulative=True, bins=100, label=pval, alpha=.3);
ax1.legend()
ax1.set(xlabel='r', ylabel='Cumulative Frequency')
# plt.savefig('img/RadCumul.pdf')
# suptitle='Minimum r for Connectedness'
apprx_thresh = [0.065, 0.068, 0.08]
ps = [1.2, 1, 0.8]
for p, thresh, col in zip(ps, apprx_thresh, ['k', 'g', 'b']):
rs = np.arange(0.05, 0.14, 0.01)
ys = 1000*(mt.r1_area2D(p)*rs*rs)
plt.scatter(thresh, 1000*(mt.r1_area2D(p)*thresh*thresh), c=col)
plt.plot(rs, ys, c=col, alpha=0.6)
plt.axvline(x=thresh, c=col, ls='--', label=p, alpha=0.6)
n=10
rand_points = np.random.uniform(size=(2, n-2))
edge_points = np.array([[0.0, 1.0],[0.0, 1.0]])
points = np.concatenate((rand_points, edge_points), axis=1)
fig, (ax1, ax2) = plt.subplots(ncols=2, figsize=(10, 5))
for pval, col in zip([0.8, 1, 1.2], ['k', 'g', 'b']):
ax1.hist(data_dict_r[pval], bins=np.arange(0.05, 0.14, 0.0005), label=pval, alpha=.3, color=col, cumulative=1, histtype='step', lw=5)
hist_out = ax2.hist(data_dict_r[pval], bins=50, color=col, alpha=0.3, label=pval)
ys = hist_out[0]
xs = (hist_out[1][1:]+hist_out[1][:-1])/2
pt = thresh_calc(xs, ys, sig_fract=.8, n_av=5)[0]
ax1.axvline(x=pt, ls='--', alpha=0.6, c=col)
ax2.axvline(x=pt, ls='--', alpha=0.6, c=col)
ax1.axhline(y=500, alpha=0.2, c='r')
# popt, pcov = curve_fit(skewed, xs, ys)
# plt.plot(xs, skewed(xs, *popt))
ax1.set(xlim=(0.05, 0.12), xlabel='r', ylabel='Cumulative Frequency')
ax2.set(xlim=(0.05, 0.12), xlabel='r', ylabel='Frequency')
ax1.legend(loc='lower right')
ax2.legend()
plt.savefig('img/r_perc.pdf')
# plt.gca().set(title='Minimum r for Connectedness', xlabel='r', ylabel='Cumulative Frequency', xlim=(0.05, .1))
for pval in [0.8, 1, 1.2]:
hist_out = np.histogram(data_dict_r[pval], bins=50);
ys = hist_out[0]
xs = (hist_out[1][1:]+hist_out[1][:-1])/2
# popt, pcov = curve_fit(skewed, xs, ys)
plt.scatter(np.log(xs), np.log(ys))
ys = hist_out[0]
xs = (hist_out[1][1:]+hist_out[1][:-1])/2
popt, pcov = curve_fit(skewed, xs, ys)
plt.plot(xs, skewed(xs, *popt))
def skewed(x, a, b, c, d):
# (100*(xs-.06), 4, 50)
return d*sp.stats.skewnorm.pdf(a*x-b, c)
popt, pcov = curve_fit(skewed, xs, ys)
hist_out = plt.hist(data_dict_r[pval], bins=50, label=pval, alpha=.3)
plt.plot(xs, skewed(xs, *popt))
# plt.plot(xs, skewed(xs, 100, 6, 4, 50))
# plt.plot(xs, ys, label='Fit')
plt.legend()
popt
def moving_average(a, n=3) :
ret = np.cumsum(np.array(a))
ret[n:] = ret[n:] - ret[:-n]
return ret[n - 1:] / n
def thresh_calc(data, sig_fract=.8, n_av=5, bins=50):
hist_data = np.histogram(data, bins=bins)
xs, ys = (hist_data[1]+hist_data[1])/2, hist_data[0]
smoothxs = (moving_average(xs, n=n_av))
smoothys = (moving_average(ys, n=n_av))
inds = np.where(smoothys > max(smoothys)*sig_fract)
vals, err = np.polyfit(smoothxs[inds], smoothys[inds], 2, cov=True)
stat_point = -.5*vals[1]/vals[0]
fract_err = np.sqrt(err[0, 0]/(vals[0]**2) + err[1, 1]/(vals[1]**2))
return stat_point, fract_err*stat_point
apprx_thresh = [450, 500, 600]
ps = [1.2, 1, 0.8]
for p, thresh, col in zip(ps, apprx_thresh, ['k', 'g', 'b']):
xs = np.arange(1000)
ys = xs*(mt.r1_area2D(p)*.1*.1)
plt.scatter(thresh, thresh*(mt.r1_area2D(p)*.1*.1), c=col)
plt.plot(xs, ys, c=col, alpha=0.6)
plt.axvline(x=thresh, c=col, ls='--', label=p, alpha=0.6)
def separate_perc_n(p, r, n_max=None):
if n_max==None:
n_max=int(4/(mt.r1_area2D(p)*r*r))
print(n_max)
rand_points = np.random.uniform(size=(2, n_max-2))
edge_points = np.array([[0.0, 1.0],[0.0, 1.0]])
points = np.concatenate((rand_points, edge_points), axis=1)
connections = mt.get_connections(points, radius=r, pval=p)
return mt.perc_thresh_n(connections)
def ensemble_perc_n(fileName, ps, rs, repeats=1, verbose=True):
for p, r in zip(ps, rs):
if verbose:
print(f'p:{p}, r:{r}')
for i in range(repeats):
if verbose:
print(i, end=' ')
thresh = separate_perc_n(p, r)
file1 = open("{}".format(fileName),"a")
file1.writelines(f'{p} - {r} - {thresh}\n')
file1.close()
if verbose:
print()
return fileName
ensemble_perc_n('new_test.txt', [.8, 1.2, 2], [0.2, 0.1, 0.05], repeats=10)
pd.read_csv('new_test.txt', header=None, delimiter=" - ")
p=.8
r=0.05
4/(mt.r1_area2D(p)*r*r)
pn1 = pd.read_csv('outputs/perc_n.txt', names=['p', 'r', 'n'], delimiter=" - ")
pn1.tail()
pn1['edges'] = pn1['n']*pn1['r']*pn1['r']*mt.kernel_area2D(pn1['p'])
plt.hist(pn1[pn1['edges'] < 2.95]['edges'], bins=50, cumulative=1);
# plt.hist(pn1['edges'], bins=50, cumulative=1);
plt.gca().set(xlabel='Average Number Edges from Node', ylabel='Cumulative Frequency', );
plt.hist(pn1[pn1['edges'] < 2.95]['edges'], bins=50, cumulative=0)
plt.gca().set(xlabel='Average Number Edges from Node', ylabel='Frequency', )
for bins in [50, 75, 100]:
plt.plot(np.arange(0.5, 0.95, 0.01), [thresh_calc(pn1[pn1['edges'] < 2.95]['edges'], sig_fract=elem, bins=bins)[0] for elem in np.arange(0.5, 0.95, 0.01)], label=f'{bins} bins')
plt.legend()
plt.gca().set(xlabel='Fraction for bars to be considered', ylabel='Percolation Threshold', );
# #input file
# fin = open('outputs/perc_r5000clean.txt', "rt")
# #output file to write the result to
# fout = open("outputs/perc_r5000clean2.txt", "wt")
# #for each line in the input file
# for line in fin:
# #read replace the string and write to output file
# fout.write(line.replace('-[[', '- [['))
# #close input and output files
# fin.close()
# fout.close()
pr1 = pd.read_csv('outputs/perc_r5000clean2.txt', names=['p', 'n', 'r', 'path'], delimiter=" - ")
pr1['edges'] = pr1['n']*pr1['r']*pr1['r']*mt.kernel_area2D(pr1['p'])
fig, ax = plt.subplots(figsize=(7, 7))
# axins = ax.inset_axes([5, 8, 150, 250])
axins = ax.inset_axes([0.5, 0.57, 0.5, 0.43])
hist_data = axins.hist(pr1['edges'], bins=100, label='Raw Data')
axins.legend(loc='upper right')
n_av = 5
sig_fract = .7
plot_fract = 0.1
xs, ys = (hist_data[1]+hist_data[1])/2, hist_data[0]
smoothxs = (moving_average(xs, n=n_av))
smoothys = (moving_average(ys, n=n_av))
inds = np.where(smoothys > max(smoothys)*sig_fract)
notinds = np.where(smoothys <= max(smoothys)*sig_fract)
[a, b, c], err = np.polyfit(smoothxs[inds], smoothys[inds], 2, cov=True)
# plt.plot(xs, vals[0]*xs*xs + vals[1]*xs + vals[2])
# plotx = xs[inds]
ax.scatter(smoothxs[inds], smoothys[inds], c='b', alpha=0.5, label='Points in Fit')
ax.scatter(smoothxs[notinds], smoothys[notinds], c='k', alpha=0.2, label='Smoothed Points')
plotx = smoothxs[inds]
lowerlim = max(smoothys)*plot_fract
quadx = np.arange((-b+np.sqrt(b*b - 4*a*(c-lowerlim)))/(2*a), (-b-np.sqrt(b*b - 4*a*(c-lowerlim)))/(2*a), 0.001)
quady = a*quadx*quadx + b*quadx + c
plotinds = np.where(quady > 0)
ax.axhline(max(smoothys)*sig_fract, color='r', alpha=0.5, ls='--', label=f'Fraction={sig_fract}')
ax.axvline(thresh_calc(pr1['edges'])[0], color='g', alpha=0.5, ls='--', label=f'Threshold')
ax.plot(quadx, quady, c='b', alpha=0.6, label='Quadratic Fit')
ax.legend(loc='best', bbox_to_anchor=(0.5, 0., 0.5, 0.45))
ax.set(xlabel='Average number of edges per node', ylabel='Frequency', title='Determining the Percolation Threshold');
plt.savefig('img/percthreshn5000.pdf')
ss = np.arange(0.2, 0.85, 0.01)
plt.plot(ss, [thresh_calc(pr1['edges'], sig_fract=s)[0] for s in ss])
r5000 = pd.read_csv('outputs/perc_r5000clean2.txt', names=['p', 'n', 'r', 'path'], delimiter=" - ")
r5000['e'] = mt.kernel_area2D(r5000['p'])*r5000['r']*r5000['r']*r5000['n']
ps = [0.4, 0.6, 0.8, 1.0]
threshs = [thresh_calc(r5000[np.abs(r5000['p']-p) < 0.01]['e'], sig_fract=0.6)[0] for p in ps]
plt.plot(ps, threshs)
r5000[np.abs(r5000['p']-1) < .01]
thresh_calc(r5000[np.abs(r5000['p']-p) < 0.01]['e'])[0]
thresh_calc(r5000[np.abs(r5000['p']-0.6) < .1]['e'], sig_fract=.6)
```
|
github_jupyter
|
# Generative Adversarial Networks
Throughout most of this book, we've talked about how to make predictions.
In some form or another, we used deep neural networks learned mappings from data points to labels.
This kind of learning is called discriminative learning,
as in, we'd like to be able to discriminate between photos cats and photos of dogs.
Classifiers and regressors are both examples of discriminative learning.
And neural networks trained by backpropagation
have upended everything we thought we knew about discriminative learning
on large complicated datasets.
Classification accuracies on high-res images has gone from useless
to human-level (with some caveats) in just 5-6 years.
We'll spare you another spiel about all the other discriminative tasks
where deep neural networks do astoundingly well.
But there's more to machine learning than just solving discriminative tasks.
For example, given a large dataset, without any labels,
we might want to learn a model that concisely captures the characteristics of this data.
Given such a model, we could sample synthetic data points that resemble the distribution of the training data.
For example, given a large corpus of photographs of faces,
we might want to be able to generate a *new* photorealistic image
that looks like it might plausibly have come from the same dataset.
This kind of learning is called *generative modeling*.
Until recently, we had no method that could synthesize novel photorealistic images.
But the success of deep neural networks for discriminative learning opened up new possiblities.
One big trend over the last three years has been the application of discriminative deep nets
to overcome challenges in problems that we don't generally think of as supervised learning problems.
The recurrent neural network language models are one example of using a discriminative network (trained to predict the next character)
that once trained can act as a generative model.
In 2014, a young researcher named Ian Goodfellow introduced [Generative Adversarial Networks (GANs)](https://arxiv.org/abs/1406.2661) a clever new way to leverage the power of discriminative models to get good generative models.
GANs made quite a splash so it's quite likely you've seen the images before.
For instance, using a GAN you can create fake images of bedrooms, as done by [Radford et al. in 2015](https://arxiv.org/pdf/1511.06434.pdf) and depicted below.

At their heart, GANs rely on the idea that a data generator is good
if we cannot tell fake data apart from real data.
In statistics, this is called a two-sample test - a test to answer the question whether datasets $X = \{x_1, \ldots x_n\}$ and $X' = \{x_1', \ldots x_n'\}$ were drawn from the same distribution.
The main difference between most statistics papers and GANs is that the latter use this idea in a constructive way.
In other words, rather than just training a model to say 'hey, these two datasets don't look like they came from the same distribution', they use the two-sample test to provide training signal to a generative model.
This allows us to improve the data generator until it generates something that resembles the real data.
At the very least, it needs to fool the classifier. And if our classifier is a state of the art deep neural network.
As you can see, there are two pieces to GANs - first off, we need a device (say, a deep network but it really could be anything, such as a game rendering engine) that might potentially be able to generate data that looks just like the real thing.
If we are dealing with images, this needs to generate images.
If we're dealing with speech, it needs to generate audio sequences, and so on.
We call this the *generator network*. The second component is the *discriminator network*.
It attempts to distinguish fake and real data from each other.
Both networks are in competition with each other.
The generator network attempts to fool the discriminator network. At that point, the discriminator network adapts to the new fake data. This information, in turn is used to improve the generator network, and so on.
**Generator**
* Draw some parameter $z$ from a source of randomness, e.g. a normal distribution $z \sim \mathcal{N}(0,1)$.
* Apply a function $f$ such that we get $x' = G(u,w)$
* Compute the gradient with respect to $w$ to minimize $\log p(y = \mathrm{fake}|x')$
**Discriminator**
* Improve the accuracy of a binary classifier $f$, i.e. maximize $\log p(y=\mathrm{fake}|x')$ and $\log p(y=\mathrm{true}|x)$ for fake and real data respectively.

In short, there are two optimization problems running simultaneously, and the optimization terminates if a stalemate has been reached. There are lots of further tricks and details on how to modify this basic setting. For instance, we could try solving this problem in the presence of side information. This leads to cGAN, i.e. conditional Generative Adversarial Networks. We can change the way how we detect whether real and fake data look the same. This leads to wGAN (Wasserstein GAN), kernel-inspired GANs and lots of other settings, or we could change how closely we look at the objects. E.g. fake images might look real at the texture level but not so at the larger level, or vice versa.
Many of the applications are in the context of images. Since this takes too much time to solve in a Jupyter notebook on a laptop, we're going to content ourselves with fitting a much simpler distribution. We will illustrate what happens if we use GANs to build the world's most inefficient estimator of parameters for a Gaussian. Let's get started.
```
from __future__ import print_function
import matplotlib as mpl
from matplotlib import pyplot as plt
import mxnet as mx
from mxnet import gluon, autograd, nd
from mxnet.gluon import nn
import numpy as np
ctx = mx.cpu()
```
## Generate some 'real' data
Since this is going to be the world's lamest example, we simply generate data drawn from a Gaussian. And let's also set a context where we'll do most of the computation.
```
X = nd.random_normal(shape=(1000, 2))
A = nd.array([[1, 2], [-0.1, 0.5]])
b = nd.array([1, 2])
X = nd.dot(X, A) + b
Y = nd.ones(shape=(1000, 1))
# and stick them into an iterator
batch_size = 4
train_data = mx.io.NDArrayIter(X, Y, batch_size, shuffle=True)
```
Let's see what we got. This should be a Gaussian shifted in some rather arbitrary way with mean $b$ and covariance matrix $A^\top A$.
```
plt.scatter(X[:,0].asnumpy(), X[:,1].asnumpy())
plt.show()
print("The covariance matrix is")
print(nd.dot(A.T, A))
```
## Defining the networks
Next we need to define how to fake data. Our generator network will be the simplest network possible - a single layer linear model. This is since we'll be driving that linear network with a Gaussian data generator. Hence, it literally only needs to learn the parameters to fake things perfectly. For the discriminator we will be a bit more discriminating: we will use an MLP with 3 layers to make things a bit more interesting.
The cool thing here is that we have *two* different networks, each of them with their own gradients, optimizers, losses, etc. that we can optimize as we please.
```
# build the generator
netG = nn.Sequential()
with netG.name_scope():
netG.add(nn.Dense(2))
# build the discriminator (with 5 and 3 hidden units respectively)
netD = nn.Sequential()
with netD.name_scope():
netD.add(nn.Dense(5, activation='tanh'))
netD.add(nn.Dense(3, activation='tanh'))
netD.add(nn.Dense(2))
# loss
loss = gluon.loss.SoftmaxCrossEntropyLoss()
# initialize the generator and the discriminator
netG.initialize(mx.init.Normal(0.02), ctx=ctx)
netD.initialize(mx.init.Normal(0.02), ctx=ctx)
# trainer for the generator and the discriminator
trainerG = gluon.Trainer(netG.collect_params(), 'adam', {'learning_rate': 0.01})
trainerD = gluon.Trainer(netD.collect_params(), 'adam', {'learning_rate': 0.05})
```
## Setting up the training loop
We are going to iterate over the data a few times. To make life simpler we need a few variables
```
real_label = mx.nd.ones((batch_size,), ctx=ctx)
fake_label = mx.nd.zeros((batch_size,), ctx=ctx)
metric = mx.metric.Accuracy()
# set up logging
from datetime import datetime
import os
import time
```
## Training loop
```
stamp = datetime.now().strftime('%Y_%m_%d-%H_%M')
for epoch in range(10):
tic = time.time()
train_data.reset()
for i, batch in enumerate(train_data):
############################
# (1) Update D network: maximize log(D(x)) + log(1 - D(G(z)))
###########################
# train with real_t
data = batch.data[0].as_in_context(ctx)
noise = nd.random_normal(shape=(batch_size, 2), ctx=ctx)
with autograd.record():
real_output = netD(data)
errD_real = loss(real_output, real_label)
fake = netG(noise)
fake_output = netD(fake.detach())
errD_fake = loss(fake_output, fake_label)
errD = errD_real + errD_fake
errD.backward()
trainerD.step(batch_size)
metric.update([real_label,], [real_output,])
metric.update([fake_label,], [fake_output,])
############################
# (2) Update G network: maximize log(D(G(z)))
###########################
with autograd.record():
output = netD(fake)
errG = loss(output, real_label)
errG.backward()
trainerG.step(batch_size)
name, acc = metric.get()
metric.reset()
print('\nbinary training acc at epoch %d: %s=%f' % (epoch, name, acc))
print('time: %f' % (time.time() - tic))
noise = nd.random_normal(shape=(100, 2), ctx=ctx)
fake = netG(noise)
plt.scatter(X[:,0].asnumpy(), X[:,1].asnumpy())
plt.scatter(fake[:,0].asnumpy(), fake[:,1].asnumpy())
plt.show()
```
## Checking the outcome
Let's now generate some fake data and check whether it looks real.
```
noise = mx.nd.random_normal(shape=(100, 2), ctx=ctx)
fake = netG(noise)
plt.scatter(X[:,0].asnumpy(), X[:,1].asnumpy())
plt.scatter(fake[:,0].asnumpy(), fake[:,1].asnumpy())
plt.show()
```
## Conclusion
A word of caution here - to get this to converge properly, we needed to adjust the learning rates *very carefully*. And for Gaussians, the result is rather mediocre - a simple mean and covariance estimator would have worked *much better*. However, whenever we don't have a really good idea of what the distribution should be, this is a very good way of faking it to the best of our abilities. Note that a lot depends on the power of the discriminating network. If it is weak, the fake can be very different from the truth. E.g. in our case it had trouble picking up anything along the axis of reduced variance.
In summary, this isn't exactly easy to set and forget. One nice resource for dirty practioner's knowledge is [Soumith Chintala's handy list of tricks](https://github.com/soumith/ganhacks) for how to babysit GANs.
For whinges or inquiries, [open an issue on GitHub.](https://github.com/zackchase/mxnet-the-straight-dope)
|
github_jupyter
|
*This notebook is part of course materials for CS 345: Machine Learning Foundations and Practice at Colorado State University.
Original versions were created by Asa Ben-Hur.
The content is availabe [on GitHub](https://github.com/asabenhur/CS345).*
*The text is released under the [CC BY-SA license](https://creativecommons.org/licenses/by-sa/4.0/), and code is released under the [MIT license](https://opensource.org/licenses/MIT).*
<img style="padding: 10px; float:right;" alt="CC-BY-SA icon.svg in public domain" src="https://upload.wikimedia.org/wikipedia/commons/d/d0/CC-BY-SA_icon.svg" width="125">
<a href="https://colab.research.google.com/github//asabenhur/CS345/blob/master/notebooks/module05_01_cross_validation.ipynb">
<img align="left" src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/>
</a>
```
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
%autosave 0
```
# Evaluating classifiers: cross validation
### Learning curves
Intuitively, the more data we have available, the more accurate our classifiers become. To demonstrate this, let's read in some data and evaluate a k-nearest neighbor classifier on a fixed test set with increasing number of training examples. The resulting curve of accuracy as a function of number of examples is called a **learning curve**.
```
from sklearn.datasets import load_digits
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
X, y = load_digits(return_X_y=True)
training_sizes = [20, 40, 100, 200, 400, 600, 800, 1000, 1200]
# note the use of the stratify keyword: it makes it so that each
# class is equally represented in both train and test set
X_full_train, X_test, y_full_train, y_test = train_test_split(
X, y, test_size = len(y)-max(training_sizes),
stratify=y, random_state=1)
accuracy = []
for training_size in training_sizes :
X_train,_ , y_train,_ = train_test_split(
X_full_train, y_full_train, test_size =
len(y_full_train)-training_size+10, stratify=y_full_train)
knn = KNeighborsClassifier(n_neighbors=1)
knn.fit(X_train, y_train)
y_pred = knn.predict(X_test)
accuracy.append(np.sum((y_pred==y_test))/len(y_test))
plt.figure(figsize=(6,4))
plt.plot(training_sizes, accuracy, 'ob')
plt.xlabel('training set size')
plt.ylabel('accuracy')
plt.ylim((0.5,1));
```
It's also instructive to look at the numbers themselves:
```
print ("# training examples\t accuracy")
for i in range(len(accuracy)) :
print ("\t{:d}\t\t {:f}".format(training_sizes[i], accuracy[i]))
```
### Exercise
* What can you conclude from this plot?
* Why would you want to compute a learning curve on your data?
### Making better use of our data with cross validation
The discussion above demonstrates that it is best to have as large of a training set as possible. We also need to have a large enough test set, so that the accuracy estimates are accurate. How do we balance these two contradictory requirements? Cross-validation provides us a more effective way to make use of our data. Here it is:
**Cross validation**
* Randomly partition the data into $k$ subsets ("folds").
* Set one fold aside for evaluation and train a model on the remaining $k$ folds and evaluate it on the held-out fold.
* Repeat until each fold has been used for evaluation
* Compute accuracy by averaging over the accuracy estimates generated for each fold.
Here is an illustration of 8-fold cross validation:
<img style="padding: 10px; float:left;" alt="cross-validation by MBanuelos22 CC BY-SA 4.0" src="https://upload.wikimedia.org/wikipedia/commons/c/c7/LOOCV.gif">
width="600">
As you can see, this procedure is more expensive than dividing your data into train and test set. When dealing with relatively small datasets, which is when you want to use this procedure, this won't be an issue.
Typically cross-validation is used with the number of folds being in the range of 5-10. An extreme case is when the number of folds equals the number of training examples. This special case is called *leave-one-out cross-validation*.
```
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import cross_validate
from sklearn.model_selection import cross_val_score
from sklearn import metrics
```
Let's use the scikit-learn breast cancer dataset to demonstrate the use of cross-validation.
```
from sklearn.datasets import load_breast_cancer
data = load_breast_cancer()
```
A scikit-learn data object is container object with whose interesting attributes are:
* ‘data’, the data to learn,
* ‘target’, the classification labels,
* ‘target_names’, the meaning of the labels,
* ‘feature_names’, the meaning of the features, and
* ‘DESCR’, the full description of the dataset.
```
X = data.data
y = data.target
print('number of examples ', len(y))
print('number of features ', len(X[0]))
print(data.target_names)
print(data.feature_names)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4,
random_state=0)
classifier = KNeighborsClassifier(n_neighbors=3)
#classifier = LogisticRegression()
_ = classifier.fit(X_train, y_train)
y_pred = classifier.predict(X_test)
```
Let's compute the accuracy of our predictions:
```
np.mean(y_pred==y_test)
```
We can do the same using scikit-learn:
```
metrics.accuracy_score(y_test, y_pred)
```
Now let's compute accuracy using [cross_validate](https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.cross_validate.html) instead:
```
accuracy = cross_val_score(classifier, X, y, cv=5,
scoring='accuracy')
print(accuracy)
```
This yields an array containing the accuracy values for each fold.
When reporting your results, you will typically show the mean:
```
np.mean(accuracy)
```
The arguments of `cross_val_score`:
* A classifier (anything that satisfies the scikit-learn classifier API)
* data (features/labels)
* `cv` : an integer that specifies the number of folds (can be used in more sophisticated ways as we will see below).
* `scoring`: this determines which accuracy measure is evaluated for each fold. Here's a link to the [list of available measures](https://scikit-learn.org/stable/modules/model_evaluation.html#scoring-parameter) in scikit-learn.
You can obtain accuracy for other metrics. *Balanced accuracy* for example, is appropriate when the data is unbalanced (e.g. when one class contains a much larger number of examples than other classes in the data).
```
accuracy = cross_val_score(classifier, X, y, cv=5,
scoring='balanced_accuracy')
np.mean(accuracy)
```
`cross_val_score` is somewhat limited, in that it simply returns a list of accuracy scores. In practice, we often want to have more information about what happened during training, and also to compute multiple accuracy measures.
`cross_validate` will provide you with that information:
```
results = cross_validate(classifier, X, y, cv=5,
scoring='accuracy', return_estimator=True)
print(results)
```
The object returned by `cross_validate` is a Python dictionary as the output suggests. To extract a specific piece of data from this object, simply access the dictionary with the appropriate key:
```
results['test_score']
```
If you would like to know the predictions made for each training example during cross-validation use [cross_val_predict](https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.cross_val_predict.html) instead:
```
from sklearn.model_selection import cross_val_predict
y_pred = cross_val_predict(classifier, X, y, cv=5)
metrics.accuracy_score(y, y_pred)
```
The above way of performing cross-validation doesn't always give us enough control on the process: we usually want our machine learning experiments be reproducible, and to be able to use the same cross-validation splits with multiple algorithms. The scikit-learn `KFold` and `StratifiedKFold` cross-validation generators are the way to achieve that.
`KFold` simply chooses a random subset of examples for each fold. This strategy can lead to cross-validation folds in which the classes are not well-represented as the following toy example demonstrates:
```
from sklearn.model_selection import StratifiedKFold, KFold
X_toy = np.array([[1, 2], [3, 4], [5, 6], [7, 8], [9,10], [11, 12]])
y_toy = np.array([0, 0, 1, 1, 1, 1])
cv = KFold(n_splits=2, random_state=3, shuffle=True)
for train_idx, test_idx in cv.split(X_toy, y_toy):
print("train:", train_idx, "test:", test_idx)
X_train, X_test = X_toy[train_idx], X_toy[test_idx]
y_train, y_test = y_toy[train_idx], y_toy[test_idx]
print(y_train)
```
`StratifiedKFold` addresses this issue by making sure that each class is represented in each fold in proportion to its overall fraction in the data. This is particularly important when one or more of the classes have few examples.
`StratifiedKFold` and `KFold` generate folds that can be used in conjunction with the cross-validation methods we saw above.
As an example, we will demonstrate the use of `StratifiedKFold` with `cross_val_score` on the breast cancer datast:
```
cv = StratifiedKFold(n_splits=5, random_state=1, shuffle=True)
accuracy = cross_val_score(classifier, X, y, cv=cv,
scoring='accuracy')
np.mean(accuracy)
```
For classification problems, `StratifiedKFold` is the preferred strategy. However, for regression problems `KFold` is the way to go.
#### Question
Why is `KFold` used in regression probelms rather than `StratifiedKFold`?
To clarify the distinction between the different methods of generating cross-validation folds and their different parameters let's look at the following figures:
```
# the code for the figure is adapted from
# https://scikit-learn.org/stable/auto_examples/model_selection/plot_cv_indices.html
np.random.seed(42)
cmap_data = plt.cm.Paired
cmap_cv = plt.cm.coolwarm
n_folds = 4
# Generate the data
X = np.random.randn(100, 10)
# generate labels - classes 0,1,2 and 10,30,60 examples, respectively
y = np.array([0] * 10 + [1] * 30 + [2] * 60)
def plot_cv_indices(cv, X, y, ax, n_folds):
"""plot the indices of a cross-validation object."""
# Generate the training/testing visualizations for each CV split
for ii, (tr, tt) in enumerate(cv.split(X=X, y=y)):
# Fill in indices with the training/test groups
indices = np.zeros(len(X))
indices[tt] = 1
# Visualize the results
ax.scatter(range(len(indices)), [ii + .5] * len(indices),
c=indices, marker='_', lw=15, cmap=cmap_cv,
vmin=-.2, vmax=1.2)
# Plot the data classes and groups at the end
ax.scatter(range(len(X)), [ii + 1.5] * len(X), c=y, marker='_', lw=15, cmap=cmap_data)
# Formatting
yticklabels = list(range(n_folds)) + ['class']
ax.set(yticks=np.arange(n_folds+2) + .5, yticklabels=yticklabels,
xlabel='index', ylabel="CV fold",
ylim=[n_folds+1.2, -.2], xlim=[0, 100])
ax.set_title('{}'.format(type(cv).__name__), fontsize=15)
return ax
```
Let's visualize the results of using `KFold` for fold generation:
```
fig, ax = plt.subplots()
cv = KFold(n_folds)
plot_cv_indices(cv, X, y, ax, n_folds);
```
As you can see, this naive way of using `KFold` can lead to highly undesirable splits into cross-validation folds.
Using `StratifiedKFold` addresses this to some extent:
```
fig, ax = plt.subplots()
cv = StratifiedKFold(n_folds)
plot_cv_indices(cv, X, y, ax, n_folds);
```
Using `StratifiedKFold` with shuffling of the examples is the preferred way of splitting the data into folds:
```
fig, ax = plt.subplots()
cv = StratifiedKFold(n_folds, shuffle=True)
plot_cv_indices(cv, X, y, ax, n_folds);
```
### Question
Consider the task of digitizing handwritten text (aka optical character recognition, or OCR). For each letter in the alphabet you have multiple labeled examples generated by the same writer. How would this setup affect the way you divide your examples into training and test sets, or when performing cross-validation?
### Summary and Discussion
In this notebook we discussed cross-validation as a more effective way to make use of limited amounts of data compared to the strategy of splitting data into train and test sets. For very large datasets where training is time consuming you might still opt for evaluation on a single test set.
|
github_jupyter
|
# Lecture 3.3: Anomaly Detection
[**Lecture Slides**](https://docs.google.com/presentation/d/1_0Z5Pc5yHA8MyEBE8Fedq44a-DcNPoQM1WhJN93p-TI/edit?usp=sharing)
This lecture, we are going to use gaussian distributions to detect anomalies in our emoji faces dataset
**Learning goals:**
- Introduce an anomaly detection problem
- Implement Gaussian distribution anomaly detection for images
- Debug the optimisation of a learning algorithm
- Discuss the imperfection of learning algorithms
- Acknowledge other outlier detection methods
## 1. Introduction
We have an `emoji_faces` dataset of all our favourite emojis. However, Skynet hates their friendly expressiveness, and wants to destroy emojis forever! 🙀 It sent _terminator robots_ from the future to invade our dataset. We must act fast, and detect them amongst the emojis to prevent the catastrophy.
Our challenge here, is that we don't watch many movies, so we don't have a clear idea of what those _terminators_ look like. 🤖 All we know, is that they look very different compared to emojis, and that only a handful managed to infiltrate our dataset.
This is a typical scenario of _anomaly detection_. We would like to identify rare examples that differ from our "normal" data points. We choose to use a Gaussian Distribution to model this "normality" and detect the killer robots.
## 2. Data Munging
First let's load the images using [pillow](https://pillow.readthedocs.io/en/stable/), like in lecture 2.5:
```
from PIL import Image
import glob
paths = glob.glob('emoji_faces/*.png')
images = [Image.open(path) for path in paths]
len(images)
```
We have 134 emoji faces, including a few terminator robots. We'll again be using the [sklearn](https://scikit-learn.org/) library to create our model. The interface is usually the same, and for gaussian anomaly detection, sklearn again expect a NumPy matrix where the rows are our images and the columns are the pixels. So we can apply the same transformations as notebook 3.2:
```
import numpy as np
arrays = [np.asarray(im) for im in images]
# 64 * 64 = 4096
vectors = [arr.reshape((4096,)) for arr in arrays]
data = np.stack(vectors)
```
## 3. Training
Next, we will create an [`EllipticEnvelope`](https://scikit-learn.org/stable/modules/generated/sklearn.covariance.EllipticEnvelope.html) object. This will fit a multi-variate gaussian distribution to our data. It then allows us to pick a threshold to define an _ellipsoid_ decision boundary , and detect outliers.
Remember that we are using a _learning_ algorithm, which must therefore be _trained_ before it can be used. This is why we'll use the `.fit()` method first, before calling `.predict()`:
```
from sklearn.covariance import EllipticEnvelope
cov = EllipticEnvelope(random_state=0).fit(data)
```
😰 What's happening? Why is it stuck? Have the killer robots already taken over?
No need to panic, this kind of hiccup is very common when dealing with machine learning algorithms. We can kill the process (before it fries our laptop fan) by clicking the `stop` button ⬛️ in the notebook toolbar.
Most learning algorithms are based around an _optimisation_ procedure. This step is often iterative and stochastic, i.e it tries its statistical best to maximise the learning in incremental steps.
This process isn't fail proof:
* it can dramatically stop because of out of memory errors, or overflow errors 💥
* it can get stuck, e.g when the optimisation is too slow 🐌
* it can fail silently, and return wrong results 💩
ℹ️ We will encounter many of these failures throughout our ML experiments, so knowing how to overcome them is a part of the data scientist skillset.
Let's go back to our killer robot detection: the model fitting got _stuck_ , which suggests that something about our data was too much to handle. We find the following "notes" in the [official documentation](https://scikit-learn.org/stable/modules/generated/sklearn.covariance.EllipticEnvelope.html#sklearn.covariance.EllipticEnvelope):
> Outlier detection from covariance estimation may break or not perform well in high-dimensional settings.
We recall that our images are $64 \times 64$ pixels, so $4096$ dimensions.... that's a lot. It seems a good candidate to explain why our multivariate gaussian distribution failed to fit our dataset. If only there was a way to reduce the dimensions of our data... 😏
Let's apply PCA to reduce the number of dimensions of our dataset. Our emoji faces dataset is smaller than the full emoji dataset, so 40 dimensions should suffice to explain its variance:
```
from sklearn.decomposition import PCA
pca = PCA(n_components=40)
pca.fit(data)
components = pca.transform(data)
components.shape
```
💪 Visualise the eigenvector images of our PCA model. You can use the code from lecture 3.2!
🧠 Can you explain what those eigenvector images represent? Why are they different than from the full emoji dataset?
Fantastic, we've managed to reduce the number of dimensions by 99%! Hopefully that should be enough to make our gaussian distribution fitting happy. Let's try again with the _principal components_ instead of the original data:
```
cov = EllipticEnvelope(random_state=0).fit(components)
```
😅 that was fast!
## 4. Prediction
We can now use our fitted gaussian distribution to detect the outliers in our `data`. For this, we use the `.predict()` method:
```
y = cov.predict(components)
y
```
`y` is our vector of predictions, where $1$ is a normal data point, and $-1$ is an anomaly. We can therefore iterate through our original `arrays` to find outliers:
```
outliers = []
for i in range(0, len(arrays)):
if y[i] == -1:
outliers.append(arrays[i])
len(outliers)
import matplotlib.pyplot as plt
fig, axs = plt.subplots(dpi=150, nrows=2, ncols=7)
for outlier, ax in zip(outliers, axs.flatten()):
ax.imshow(outlier, cmap='gray', vmin=0, vmax=255)
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
```
THERE'S OUR TERMINATORS! 🤖 We can count 5 of them in total. Notice how some real emoji faces were also detected as outliers. This is perhaps a sign that we should change our _threshold_ , to make the ellipsoid decision boundary smaller.
In fact, we didn't even specify a threshold before, we just used the default value of `contamination=0.1` in the [`EllipticEnvelope`](https://scikit-learn.org/stable/modules/generated/sklearn.covariance.EllipticEnvelope.html) class. This represents our estimation of the proportion of data points which are outliers. Since it looks like we detected double the amount of actual anomalies, let's try again with `contamination=0.05`:
```
cov = EllipticEnvelope(random_state=0, contamination=0.05).fit(components)
y = cov.predict(components)
outliers = []
for i in range(0, len(arrays)):
if y[i] == -1:
outliers.append(arrays[i])
fig, axs = plt.subplots(dpi=150, nrows=1, ncols=7)
for outlier, ax in zip(outliers, axs.flatten()):
ax.imshow(outlier, cmap='gray', vmin=0, vmax=255)
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
```
Better! `contamination=0.05` was a better choice of threshold, and we assessed this through _manual inspection_. This means we went through the results and used our human jugement to change the value of this _hyperparameter_.
ℹ️ Notice how our outlier detection is not _perfect_. Some emojis were also erroneously detected as anomalous killer robots. This can seem like a problem, or a sign that our model was malfunctioning. But, quite the contrary, _imperfection_ is a core aspect of all _learning_ algorithms. Instead of seeing the glass half-empty and looking at the outlier detector's mistakes, we should reflect on the task itself. It would have been almost impossible to detect those killer robot images using rule-based algorithms, and our model _accuracy_ was good _enough_ to save the emojis from Skynet. As data scientists, our goal is to make models which are accurate _enough_ to be useful, not to aim for perfect scores. We will revisit these topics later in the course when discussing Machine Learning Engineering 🛠
## 5. Analysis
We have detected the robot intruders and saved the emojis from a jealous AI from the future, all is good! We still want to better understand how anomaly detection defeated Skynet. For this, we would like to leverage our shiny new data visualization skills. Representing our dataset in space would allow us to identify its structures and hopefully understand how our gaussian distribution model identified terminators as "abnormal".
Our data is high dimensional, so we can use our trusted PCA once again to project it down to 2 dimensions. We understand that this will lose a lot of the variance of our data, but the results were still somewhat interpretable with the full emoji dataset, so let's go!
```
# Dimesionality reduction to 2
pca_model = PCA(n_components=2)
pca_model.fit(data) # fit the model
T = pca_model.transform(data) # transform the 'normalized model'
plt.scatter(T[:, 0], T[:, 1],
# use the predictions as color
c=y,
marker='o',
alpha=0.4
)
plt.title('Anomaly detection of the emoji faces dataset with PCA dimensionality reduction');
```
We can notice that most of the outliers are clearly _separable_ from the bulk of the dataset, even with only 2 principal components. One outlier is very much within the main cluster however. This could be explained by the dimensionality reduction, i.e that this point is separated from the cluster in other dimensions, or by the fact our threshold might be too permissive.
We can check this by displaying the images directly on the scatter plot:
```
from matplotlib import offsetbox
def plot_components(data, model, images=None, ax=None,
thumb_frac=0.05, cmap='gray'):
ax = ax or plt.gca()
proj = model.fit_transform(data)
ax.plot(proj[:, 0], proj[:, 1], '.k')
if images is not None:
min_dist_2 = (thumb_frac * max(proj.max(0) - proj.min(0))) ** 2
shown_images = np.array([2 * proj.max(0)])
for i in range(data.shape[0]):
dist = np.sum((proj[i] - shown_images) ** 2, 1)
if np.min(dist) < min_dist_2:
# don't show points that are too close
continue
shown_images = np.vstack([shown_images, proj[i]])
imagebox = offsetbox.AnnotationBbox(
offsetbox.OffsetImage(images[i], cmap=cmap),
proj[i])
ax.add_artist(imagebox)
small_images = [im[::2, ::2] for im in arrays]
fig, ax = plt.subplots(figsize=(10, 10))
plot_components(data,
model=PCA(n_components=2),
images=small_images, thumb_frac=0.02)
plt.title('Anomaly detection of the emoji faces dataset with PCA dimensionality reduction');
```
We could probably have reduced the value of `contamination` further, since we can see how the killer robots are clearly "abnormal" with this visualisation. We also have a "feel" of how our gaussian distribution model could successfully detect them as outliers. Although remember that all of modeling magic happens in 40 dimensional space!
🧠🧠 Can you explain why it is not very useful to display the ellipsoid decision boundary of our anomaly detection model on this graph?
## 6. More Anomaly Detection
Anomaly detection is an active field in ML research, which combines supervised, unsupervised, non-linear, Bayesian, ... a whole bunch of methods! Each solution will have its pros and cons, and developing a production level outlier detection system will require empirically evaluating and comparing them. For a breakdown of the methods available in sklearn, check out this excellent [blogpost](https://sdsawtelle.github.io/blog/output/week9-anomaly-andrew-ng-machine-learning-with-python.html), or the [official documentation](https://scikit-learn.org/stable/modules/outlier_detection.html). For an in-depth view of modern anomaly detection, watch this [video](https://youtu.be/LRqX5uO5StA). And for everything else, feel free to experiment with this dataset or any other. Good luck on finding all the killer robots!
## 7. Summary
Today, we defined **anomaly detection**, and listed some of its common applications including fraud detection and data cleaning. We then described how to use **fitted Gaussian distributions** to identify outliers. This lead us to a discussion about the choice of **thresholds** and **hyperparameters**, where we went over a few different realistic scenarios. We then used a Gaussian distribution to remove terminator images from an emoji faces dataset. We learned how learning algorithms **fail** and that data scientists must know how to **debug** them. Finally, we used **PCA** to visualize our killer robot detection.
# Resources
## Core Resources
- [Anomaly detection algorithm](https://www.coursera.org/lecture/machine-learning/algorithm-C8IJp)
Andrew Ng's limpid breakdown of anomaly detection
## Additional Resources
- [A review of ML techniques for anomaly detection](https://youtu.be/LRqX5uO5StA)
More in depth review of modern techniques for anomaly detection
- [Anomaly Detection in sklearn](https://sdsawtelle.github.io/blog/output/week9-anomaly-andrew-ng-machine-learning-with-python.html)
Visual blogpost experimenting with the various outlier detection algorithms available in sklearn
- [sklearn official documentation - outlier detection](https://scikit-learn.org/stable/modules/outlier_detection.html)
|
github_jupyter
|
# Import Necessary Libraries
```
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn import preprocessing
from sklearn.ensemble import RandomForestClassifier
from sklearn import svm
from sklearn.metrics import precision_score, recall_score
# display images
from IPython.display import Image
# linear algebra
import numpy as np
# data processing
import pandas as pd
# data visualization
import seaborn as sns
%matplotlib inline
from matplotlib import pyplot as plt
from matplotlib import style
# Algorithms
from sklearn import linear_model
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import RandomForestClassifier
from sklearn.linear_model import Perceptron
from sklearn.linear_model import SGDClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.svm import SVC, LinearSVC
from sklearn.naive_bayes import GaussianNB
```
# Titanic
Titanic was a British passenger liner that sank in the North Atlantic Ocean in the early morning hours of 15 April 1912, after it collided with an iceberg during its maiden voyage from Southampton to New York City. There were an estimated 2,224 passengers and crew aboard the ship, and more than 1,500 died, making it one of the deadliest commercial peacetime maritime disasters in modern history. The RMS Titanic was the largest ship afloat at the time it entered service and was the second of three Olympic-class ocean liners operated by the White Star Line. The Titanic was built by the Harland and Wolff shipyard in Belfast. Thomas Andrews, her architect, died in the disaster.
```
# Image of Titanic ship
Image(filename='C:/Users/Nemgeree Armanonah/Documents/GitHub/Titanic/images/ship.jpeg')
```
# Getting the Data
```
#reading train.csv
data = pd.read_csv('./titanic datasets/train.csv')
data
```
## Exploring Data
```
data.info()
```
### Describe Statistics
Describe method is used to view some basic statistical details like PassengerId,Servived,Age etc.
```
data.describe()
```
### View All Features
```
data.columns.values
```
### What features could contribute to a high survival rate ?
To Us it would make sense if everything except ‘PassengerId’, ‘Ticket’ and ‘Name’ would be correlated with a high survival rate.
```
# defining variables
survived = 'survived'
not_survived = 'not survived'
# data to be plotted
fig, axes = plt.subplots(nrows=1, ncols=2,figsize=(10, 4))
women = data[data['Sex']=='female']
men = data[data['Sex']=='male']
# plot the data
ax = sns.distplot(women[women['Survived']==1].Age.dropna(), bins=18, label = survived, ax = axes[0], kde =False)
ax = sns.distplot(women[women['Survived']==0].Age.dropna(), bins=40, label = not_survived, ax = axes[0], kde =False)
ax.legend()
ax.set_title('Female')
ax = sns.distplot(men[men['Survived']==1].Age.dropna(), bins=18, label = survived, ax = axes[1], kde = False)
ax = sns.distplot(men[men['Survived']==0].Age.dropna(), bins=40, label = not_survived, ax = axes[1], kde = False)
ax.legend()
_ = ax.set_title('Male')
# count the null values
null_values = data.isnull().sum()
null_values
plt.plot(null_values)
plt.grid()
plt.show()
```
## Data Processing
```
def handle_non_numerical_data(df):
columns = df.columns.values
for column in columns:
text_digit_vals = {}
def convert_to_int(val):10
return text_digit_vals[val]
#print(column,df[column].dtype)
if df[column].dtype != np.int64 and df[column].dtype != np.float64:
column_contents = df[column].values.tolist()
#finding just the uniques
unique_elements = set(column_contents)
# great, found them.
x = 0
for unique in unique_elements:
if unique not in text_digit_vals:
text_digit_vals[unique] = x
x+=1
df[column] = list(map(convert_to_int,df[column]))
return df
y_target = data['Survived']
# Y_target.reshape(len(Y_target),1)
x_train = data[['Pclass', 'Age', 'Sex', 'SibSp', 'Parch', 'Fare','Embarked', 'Ticket']]
x_train = handle_non_numerical_data(x_train)
x_train.head()
fare = pd.DataFrame(x_train['Fare'])
# Normalizing
min_max_scaler = preprocessing.MinMaxScaler()
newfare = min_max_scaler.fit_transform(fare)
x_train['Fare'] = newfare
x_train
null_values = x_train.isnull().sum()
null_values
plt.plot(null_values)
plt.show()
# Fill the NAN values with the median values in the datasets
x_train['Age'] = x_train['Age'].fillna(x_train['Age'].median())
print("Number of NULL values" , x_train['Age'].isnull().sum())
x_train.head()
x_train['Sex'] = x_train['Sex'].replace('male', 0)
x_train['Sex'] = x_train['Sex'].replace('female', 1)
# print(type(x_train))
corr = x_train.corr()
corr.style.background_gradient()
def plot_corr(df,size=10):
corr = df.corr()
fig, ax = plt.subplots(figsize=(size, size))
ax.matshow(corr)
plt.xticks(range(len(corr.columns)), corr.columns);
plt.yticks(range(len(corr.columns)), corr.columns);
# plot_corr(x_train)
x_train.corr()
corr.style.background_gradient()
# Dividing the data into train and test data set
X_train, X_test, Y_train, Y_test = train_test_split(x_train, y_target, test_size = 0.4, random_state = 40)
clf = RandomForestClassifier()
clf.fit(X_train, Y_train)
print(clf.predict(X_test))
print("Accuracy: ",clf.score(X_test, Y_test))
## Testing the model.
test_data = pd.read_csv('./titanic datasets/test.csv')
test_data.head(3)
# test_data.isnull().sum()
### Preprocessing on the test data
test_data = test_data[['Pclass', 'Age', 'Sex', 'SibSp', 'Parch', 'Fare', 'Ticket', 'Embarked']]
test_data = handle_non_numerical_data(test_data)
fare = pd.DataFrame(test_data['Fare'])
min_max_scaler = preprocessing.MinMaxScaler()
newfare = min_max_scaler.fit_transform(fare)
test_data['Fare'] = newfare
test_data['Fare'] = test_data['Fare'].fillna(test_data['Fare'].median())
test_data['Age'] = test_data['Age'].fillna(test_data['Age'].median())
test_data['Sex'] = test_data['Sex'].replace('male', 0)
test_data['Sex'] = test_data['Sex'].replace('female', 1)
print(test_data.head())
print(clf.predict(test_data))
from sklearn.model_selection import cross_val_predict
predictions = cross_val_predict(clf, X_train, Y_train, cv=3)
print("Precision:", precision_score(Y_train, predictions))
print("Recall:",recall_score(Y_train, predictions))
from sklearn.metrics import precision_recall_curve
# getting the probabilities of our predictions
y_scores = clf.predict_proba(X_train)
y_scores = y_scores[:,1]
precision, recall, threshold = precision_recall_curve(Y_train, y_scores)
def plot_precision_and_recall(precision, recall, threshold):
plt.plot(threshold, precision[:-1], "r-", label="precision", linewidth=5)
plt.plot(threshold, recall[:-1], "b", label="recall", linewidth=5)
plt.xlabel("threshold", fontsize=19)
plt.legend(loc="upper right", fontsize=19)
plt.ylim([0, 1])
plt.figure(figsize=(14, 7))
plot_precision_and_recall(precision, recall, threshold)
plt.axis([0.3,0.8,0.8,1])
plt.show()
def plot_precision_vs_recall(precision, recall):
plt.plot(recall, precision, "g--", linewidth=2.5)
plt.ylabel("recall", fontsize=19)
plt.xlabel("precision", fontsize=19)
plt.axis([0, 1.5, 0, 1.5])
plt.figure(figsize=(14, 7))
plot_precision_vs_recall(precision, recall)
plt.show()
from sklearn.model_selection import cross_val_predict
from sklearn.metrics import confusion_matrix
predictions = cross_val_predict(clf, X_train, Y_train, cv=3)
confusion_matrix(Y_train, predictions)
```
True positive: 293 (We predicted a positive result and it was positive)
True negative: 143 (We predicted a negative result and it was negative)
False positive: 34 (We predicted a positive result and it was negative)
False negative: 64 (We predicted a negative result and it was positive)
|
github_jupyter
|
# 第8章: ニューラルネット
第6章で取り組んだニュース記事のカテゴリ分類を題材として,ニューラルネットワークでカテゴリ分類モデルを実装する.なお,この章ではPyTorch, TensorFlow, Chainerなどの機械学習プラットフォームを活用せよ.
## 70. 単語ベクトルの和による特徴量
***
問題50で構築した学習データ,検証データ,評価データを行列・ベクトルに変換したい.例えば,学習データについて,すべての事例$x_i$の特徴ベクトル$\boldsymbol{x}_i$を並べた行列$X$と正解ラベルを並べた行列(ベクトル)$Y$を作成したい.
$$
X = \begin{pmatrix}
\boldsymbol{x}_1 \\
\boldsymbol{x}_2 \\
\dots \\
\boldsymbol{x}_n \\
\end{pmatrix} \in \mathbb{R}^{n \times d},
Y = \begin{pmatrix}
y_1 \\
y_2 \\
\dots \\
y_n \\
\end{pmatrix} \in \mathbb{N}^{n}
$$
ここで,$n$は学習データの事例数であり,$\boldsymbol x_i \in \mathbb{R}^d$と$y_i \in \mathbb N$はそれぞれ,$i \in \{1, \dots, n\}$番目の事例の特徴量ベクトルと正解ラベルを表す.
なお,今回は「ビジネス」「科学技術」「エンターテイメント」「健康」の4カテゴリ分類である.$\mathbb N_{<4}$で$4$未満の自然数($0$を含む)を表すことにすれば,任意の事例の正解ラベル$y_i$は$y_i \in \mathbb N_{<4}$で表現できる.
以降では,ラベルの種類数を$L$で表す(今回の分類タスクでは$L=4$である).
$i$番目の事例の特徴ベクトル$\boldsymbol x_i$は,次式で求める.
$$\boldsymbol x_i = \frac{1}{T_i} \sum_{t=1}^{T_i} \mathrm{emb}(w_{i,t})$$
ここで,$i$番目の事例は$T_i$個の(記事見出しの)単語列$(w_{i,1}, w_{i,2}, \dots, w_{i,T_i})$から構成され,$\mathrm{emb}(w) \in \mathbb{R}^d$は単語$w$に対応する単語ベクトル(次元数は$d$)である.すなわち,$i$番目の事例の記事見出しを,その見出しに含まれる単語のベクトルの平均で表現したものが$\boldsymbol x_i$である.今回は単語ベクトルとして,問題60でダウンロードしたものを用いればよい.$300$次元の単語ベクトルを用いたので,$d=300$である.
$i$番目の事例のラベル$y_i$は,次のように定義する.
$$
y_i = \begin{cases}
0 & (\mbox{記事}\boldsymbol x_i\mbox{が「ビジネス」カテゴリの場合}) \\
1 & (\mbox{記事}\boldsymbol x_i\mbox{が「科学技術」カテゴリの場合}) \\
2 & (\mbox{記事}\boldsymbol x_i\mbox{が「エンターテイメント」カテゴリの場合}) \\
3 & (\mbox{記事}\boldsymbol x_i\mbox{が「健康」カテゴリの場合}) \\
\end{cases}
$$
なお,カテゴリ名とラベルの番号が一対一で対応付いていれば,上式の通りの対応付けでなくてもよい.
以上の仕様に基づき,以下の行列・ベクトルを作成し,ファイルに保存せよ.
+ 学習データの特徴量行列: $X_{\rm train} \in \mathbb{R}^{N_t \times d}$
+ 学習データのラベルベクトル: $Y_{\rm train} \in \mathbb{N}^{N_t}$
+ 検証データの特徴量行列: $X_{\rm valid} \in \mathbb{R}^{N_v \times d}$
+ 検証データのラベルベクトル: $Y_{\rm valid} \in \mathbb{N}^{N_v}$
+ 評価データの特徴量行列: $X_{\rm test} \in \mathbb{R}^{N_e \times d}$
+ 評価データのラベルベクトル: $Y_{\rm test} \in \mathbb{N}^{N_e}$
なお,$N_t, N_v, N_e$はそれぞれ,学習データの事例数,検証データの事例数,評価データの事例数である.
```
!wget https://archive.ics.uci.edu/ml/machine-learning-databases/00359/NewsAggregatorDataset.zip
!unzip NewsAggregatorDataset.zip
!wc -l ./newsCorpora.csv
!head -10 ./newsCorpora.csv
# 読込時のエラー回避のためダブルクォーテーションをシングルクォーテーションに置換
!sed -e 's/"/'\''/g' ./newsCorpora.csv > ./newsCorpora_re.csv
import pandas as pd
from sklearn.model_selection import train_test_split
# データの読込
df = pd.read_csv('./newsCorpora_re.csv', header=None, sep='\t', names=['ID', 'TITLE', 'URL', 'PUBLISHER', 'CATEGORY', 'STORY', 'HOSTNAME', 'TIMESTAMP'])
# データの抽出
df = df.loc[df['PUBLISHER'].isin(['Reuters', 'Huffington Post', 'Businessweek', 'Contactmusic.com', 'Daily Mail']), ['TITLE', 'CATEGORY']]
# データの分割
train, valid_test = train_test_split(df, test_size=0.2, shuffle=True, random_state=123, stratify=df['CATEGORY'])
valid, test = train_test_split(valid_test, test_size=0.5, shuffle=True, random_state=123, stratify=valid_test['CATEGORY'])
# 事例数の確認
print('【学習データ】')
print(train['CATEGORY'].value_counts())
print('【検証データ】')
print(valid['CATEGORY'].value_counts())
print('【評価データ】')
print(test['CATEGORY'].value_counts())
train.to_csv('drive/My Drive/nlp100/data/train.tsv', index=False, sep='\t', header=False)
valid.to_csv('drive/My Drive/nlp100/data/valid.tsv', index=False, sep='\t', header=False)
test.to_csv('drive/My Drive/nlp100/data/test.tsv', index=False, sep='\t', header=False)
import gdown
from gensim.models import KeyedVectors
# 学習済み単語ベクトルのダウンロード
url = "https://drive.google.com/uc?id=0B7XkCwpI5KDYNlNUTTlSS21pQmM"
output = 'GoogleNews-vectors-negative300.bin.gz'
gdown.download(url, output, quiet=True)
# ダウンロードファイルのロード
model = KeyedVectors.load_word2vec_format('GoogleNews-vectors-negative300.bin.gz', binary=True)
import string
import torch
def transform_w2v(text):
table = str.maketrans(string.punctuation, ' '*len(string.punctuation))
words = text.translate(table).split() # 記号をスペースに置換後、スペースで分割してリスト化
vec = [model[word] for word in words if word in model] # 1語ずつベクトル化
return torch.tensor(sum(vec) / len(vec)) # 平均ベクトルをTensor型に変換して出力
# 特徴ベクトルの作成
X_train = torch.stack([transform_w2v(text) for text in train['TITLE']])
X_valid = torch.stack([transform_w2v(text) for text in valid['TITLE']])
X_test = torch.stack([transform_w2v(text) for text in test['TITLE']])
print(X_train.size())
print(X_train)
# ラベルベクトルの作成
category_dict = {'b': 0, 't': 1, 'e':2, 'm':3}
y_train = torch.LongTensor(train['CATEGORY'].map(lambda x: category_dict[x]).values)
y_valid = torch.LongTensor(valid['CATEGORY'].map(lambda x: category_dict[x]).values)
y_test = torch.LongTensor(test['CATEGORY'].map(lambda x: category_dict[x]).values)
print(y_train.size())
print(y_train)
# 保存
torch.save(X_train, 'X_train.pt')
torch.save(X_valid, 'X_valid.pt')
torch.save(X_test, 'X_test.pt')
torch.save(y_train, 'y_train.pt')
torch.save(y_valid, 'y_valid.pt')
torch.save(y_test, 'y_test.pt')
```
## 71. 単層ニューラルネットワークによる予測
***
問題70で保存した行列を読み込み,学習データについて以下の計算を実行せよ.
$$
\hat{y}_1=softmax(x_1W),\\\hat{Y}=softmax(X_{[1:4]}W)
$$
ただし,$softmax$はソフトマックス関数,$X_{[1:4]}∈\mathbb{R}^{4×d}$は特徴ベクトル$x_1$,$x_2$,$x_3$,$x_4$を縦に並べた行列である.
$$
X_{[1:4]}=\begin{pmatrix}x_1\\x_2\\x_3\\x_4\end{pmatrix}
$$
行列$W \in \mathbb{R}^{d \times L}$は単層ニューラルネットワークの重み行列で,ここではランダムな値で初期化すればよい(問題73以降で学習して求める).なお,$\hat{\boldsymbol y_1} \in \mathbb{R}^L$は未学習の行列$W$で事例$x_1$を分類したときに,各カテゴリに属する確率を表すベクトルである.
同様に,$\hat{Y} \in \mathbb{R}^{n \times L}$は,学習データの事例$x_1, x_2, x_3, x_4$について,各カテゴリに属する確率を行列として表現している.
```
from torch import nn
torch.manual_seed(0)
class SLPNet(nn.Module):
def __init__(self, input_size, output_size):
super().__init__()
self.fc = nn.Linear(input_size, output_size, bias=False) # Linear(入力次元数, 出力次元数)
nn.init.normal_(self.fc.weight, 0.0, 1.0) # 正規乱数で重みを初期化
def forward(self, x):
x = self.fc(x)
return x
model = SLPNet(300, 4)
y_hat_1 = torch.softmax(model.forward(X_train[:1]), dim=-1)
print(y_hat_1)
Y_hat = torch.softmax(model.forward(X_train[:4]), dim=-1)
print(Y_hat)
```
## 72. 損失と勾配の計算
***
学習データの事例$x_1$と事例集合$x_1$,$x_2$,$x_3$,$x_4$に対して,クロスエントロピー損失と,行列$W$に対する勾配を計算せよ.なお,ある事例$x_i$に対して損失は次式で計算される.
$$l_i=−log[事例x_iがy_iに分類される確率]$$
ただし,事例集合に対するクロスエントロピー損失は,その集合に含まれる各事例の損失の平均とする.
```
criterion = nn.CrossEntropyLoss()
l_1 = criterion(model.forward(X_train[:1]), y_train[:1]) # 入力ベクトルはsoftmax前の値
model.zero_grad() # 勾配をゼロで初期化
l_1.backward() # 勾配を計算
print(f'損失: {l_1:.4f}')
print(f'勾配:\n{model.fc.weight.grad}')
l = criterion(model.forward(X_train[:4]), y_train[:4])
model.zero_grad()
l.backward()
print(f'損失: {l:.4f}')
print(f'勾配:\n{model.fc.weight.grad}')
```
## 73. 確率的勾配降下法による学習
***
確率的勾配降下法(SGD: Stochastic Gradient Descent)を用いて,行列$W$を学習せよ.なお,学習は適当な基準で終了させればよい(例えば「100エポックで終了」など).
```
from torch.utils.data import Dataset
class CreateDataset(Dataset):
def __init__(self, X, y): # datasetの構成要素を指定
self.X = X
self.y = y
def __len__(self): # len(dataset)で返す値を指定
return len(self.y)
def __getitem__(self, idx): # dataset[idx]で返す値を指定
if isinstance(idx, torch.Tensor):
idx = idx.tolist()
return [self.X[idx], self.y[idx]]
from torch.utils.data import DataLoader
dataset_train = CreateDataset(X_train, y_train)
dataset_valid = CreateDataset(X_valid, y_valid)
dataset_test = CreateDataset(X_test, y_test)
dataloader_train = DataLoader(dataset_train, batch_size=1, shuffle=True)
dataloader_valid = DataLoader(dataset_valid, batch_size=len(dataset_valid), shuffle=False)
dataloader_test = DataLoader(dataset_test, batch_size=len(dataset_test), shuffle=False)
print(len(dataset_train))
print(next(iter(dataloader_train)))
# モデルの定義
model = SLPNet(300, 4)
# 損失関数の定義
criterion = nn.CrossEntropyLoss()
# オプティマイザの定義
optimizer = torch.optim.SGD(model.parameters(), lr=1e-1)
# 学習
num_epochs = 10
for epoch in range(num_epochs):
# 訓練モードに設定
model.train()
loss_train = 0.0
for i, (inputs, labels) in enumerate(dataloader_train):
# 勾配をゼロで初期化
optimizer.zero_grad()
# 順伝播 + 誤差逆伝播 + 重み更新
outputs = model.forward(inputs)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
# 損失を記録
loss_train += loss.item()
# バッチ単位の平均損失計算
loss_train = loss_train / i
# 検証データの損失計算
model.eval()
with torch.no_grad():
inputs, labels = next(iter(dataloader_valid))
outputs = model.forward(inputs)
loss_valid = criterion(outputs, labels)
# ログを出力
print(f'epoch: {epoch + 1}, loss_train: {loss_train:.4f}, loss_valid: {loss_valid:.4f}')
```
## 74. 正解率の計測
***
問題73で求めた行列を用いて学習データおよび評価データの事例を分類したとき,その正解率をそれぞれ求めよ.
```
def calculate_accuracy(model, X, y):
model.eval()
with torch.no_grad():
outputs = model(X)
pred = torch.argmax(outputs, dim=-1)
return (pred == y).sum().item() / len(y)
# 正解率の確認
acc_train = calculate_accuracy(model, X_train, y_train)
acc_test = calculate_accuracy(model, X_test, y_test)
print(f'正解率(学習データ):{acc_train:.3f}')
print(f'正解率(評価データ):{acc_test:.3f}')
```
## 75. 損失と正解率のプロット
***
問題73のコードを改変し,各エポックのパラメータ更新が完了するたびに,訓練データでの損失,正解率,検証データでの損失,正解率をグラフにプロットし,学習の進捗状況を確認できるようにせよ.
```
def calculate_loss_and_accuracy(model, criterion, loader):
model.eval()
loss = 0.0
total = 0
correct = 0
with torch.no_grad():
for inputs, labels in loader:
outputs = model(inputs)
loss += criterion(outputs, labels).item()
pred = torch.argmax(outputs, dim=-1)
total += len(inputs)
correct += (pred == labels).sum().item()
return loss / len(loader), correct / total
# モデルの定義
model = SLPNet(300, 4)
# 損失関数の定義
criterion = nn.CrossEntropyLoss()
# オプティマイザの定義
optimizer = torch.optim.SGD(model.parameters(), lr=1e-1)
# 学習
num_epochs = 30
log_train = []
log_valid = []
for epoch in range(num_epochs):
# 訓練モードに設定
model.train()
for i, (inputs, labels) in enumerate(dataloader_train):
# 勾配をゼロで初期化
optimizer.zero_grad()
# 順伝播 + 誤差逆伝播 + 重み更新
outputs = model.forward(inputs)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
# 損失と正解率の算出
loss_train, acc_train = calculate_loss_and_accuracy(model, criterion, dataloader_train)
loss_valid, acc_valid = calculate_loss_and_accuracy(model, criterion, dataloader_valid)
log_train.append([loss_train, acc_train])
log_valid.append([loss_valid, acc_valid])
# ログを出力
print(f'epoch: {epoch + 1}, loss_train: {loss_train:.4f}, accuracy_train: {acc_train:.4f}, loss_valid: {loss_valid:.4f}, accuracy_valid: {acc_valid:.4f}')
import numpy as np
from matplotlib import pyplot as plt
# 可視化
fig, ax = plt.subplots(1, 2, figsize=(15, 5))
ax[0].plot(np.array(log_train).T[0], label='train')
ax[0].plot(np.array(log_valid).T[0], label='valid')
ax[0].set_xlabel('epoch')
ax[0].set_ylabel('loss')
ax[0].legend()
ax[1].plot(np.array(log_train).T[1], label='train')
ax[1].plot(np.array(log_valid).T[1], label='valid')
ax[1].set_xlabel('epoch')
ax[1].set_ylabel('accuracy')
ax[1].legend()
plt.show()
```
## 76. チェックポイント
***
問題75のコードを改変し,各エポックのパラメータ更新が完了するたびに,チェックポイント(学習途中のパラメータ(重み行列など)の値や最適化アルゴリズムの内部状態)をファイルに書き出せ.
```
# モデルの定義
model = SLPNet(300, 4)
# 損失関数の定義
criterion = nn.CrossEntropyLoss()
# オプティマイザの定義
optimizer = torch.optim.SGD(model.parameters(), lr=1e-1)
# 学習
num_epochs = 10
log_train = []
log_valid = []
for epoch in range(num_epochs):
# 訓練モードに設定
model.train()
for inputs, labels in dataloader_train:
# 勾配をゼロで初期化
optimizer.zero_grad()
# 順伝播 + 誤差逆伝播 + 重み更新
outputs = model.forward(inputs)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
# 損失と正解率の算出
loss_train, acc_train = calculate_loss_and_accuracy(model, criterion, dataloader_train)
loss_valid, acc_valid = calculate_loss_and_accuracy(model, criterion, dataloader_valid)
log_train.append([loss_train, acc_train])
log_valid.append([loss_valid, acc_valid])
# チェックポイントの保存
torch.save({'epoch': epoch, 'model_state_dict': model.state_dict(), 'optimizer_state_dict': optimizer.state_dict()}, f'checkpoint{epoch + 1}.pt')
# ログを出力
print(f'epoch: {epoch + 1}, loss_train: {loss_train:.4f}, accuracy_train: {acc_train:.4f}, loss_valid: {loss_valid:.4f}, accuracy_valid: {acc_valid:.4f}')
```
## 77. ミニバッチ化
***
問題76のコードを改変し,$B$事例ごとに損失・勾配を計算し,行列$W$の値を更新せよ(ミニバッチ化).$B$の値を$1,2,4,8,…$と変化させながら,1エポックの学習に要する時間を比較せよ.
```
import time
def train_model(dataset_train, dataset_valid, batch_size, model, criterion, optimizer, num_epochs):
# dataloaderの作成
dataloader_train = DataLoader(dataset_train, batch_size=batch_size, shuffle=True)
dataloader_valid = DataLoader(dataset_valid, batch_size=len(dataset_valid), shuffle=False)
# 学習
log_train = []
log_valid = []
for epoch in range(num_epochs):
# 開始時刻の記録
s_time = time.time()
# 訓練モードに設定
model.train()
for inputs, labels in dataloader_train:
# 勾配をゼロで初期化
optimizer.zero_grad()
# 順伝播 + 誤差逆伝播 + 重み更新
outputs = model.forward(inputs)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
# 損失と正解率の算出
loss_train, acc_train = calculate_loss_and_accuracy(model, criterion, dataloader_train)
loss_valid, acc_valid = calculate_loss_and_accuracy(model, criterion, dataloader_valid)
log_train.append([loss_train, acc_train])
log_valid.append([loss_valid, acc_valid])
# チェックポイントの保存
torch.save({'epoch': epoch, 'model_state_dict': model.state_dict(), 'optimizer_state_dict': optimizer.state_dict()}, f'checkpoint{epoch + 1}.pt')
# 終了時刻の記録
e_time = time.time()
# ログを出力
print(f'epoch: {epoch + 1}, loss_train: {loss_train:.4f}, accuracy_train: {acc_train:.4f}, loss_valid: {loss_valid:.4f}, accuracy_valid: {acc_valid:.4f}, {(e_time - s_time):.4f}sec')
return {'train': log_train, 'valid': log_valid}
# datasetの作成
dataset_train = CreateDataset(X_train, y_train)
dataset_valid = CreateDataset(X_valid, y_valid)
# モデルの定義
model = SLPNet(300, 4)
# 損失関数の定義
criterion = nn.CrossEntropyLoss()
# オプティマイザの定義
optimizer = torch.optim.SGD(model.parameters(), lr=1e-1)
# モデルの学習
for batch_size in [2 ** i for i in range(11)]:
print(f'バッチサイズ: {batch_size}')
log = train_model(dataset_train, dataset_valid, batch_size, model, criterion, optimizer, 1)
```
## 78. GPU上での学習
***
問題77のコードを改変し,GPU上で学習を実行せよ.
```
def calculate_loss_and_accuracy(model, criterion, loader, device):
model.eval()
loss = 0.0
total = 0
correct = 0
with torch.no_grad():
for inputs, labels in loader:
inputs = inputs.to(device)
labels = labels.to(device)
outputs = model(inputs)
loss += criterion(outputs, labels).item()
pred = torch.argmax(outputs, dim=-1)
total += len(inputs)
correct += (pred == labels).sum().item()
return loss / len(loader), correct / total
def train_model(dataset_train, dataset_valid, batch_size, model, criterion, optimizer, num_epochs, device=None):
# GPUに送る
model.to(device)
# dataloaderの作成
dataloader_train = DataLoader(dataset_train, batch_size=batch_size, shuffle=True)
dataloader_valid = DataLoader(dataset_valid, batch_size=len(dataset_valid), shuffle=False)
# 学習
log_train = []
log_valid = []
for epoch in range(num_epochs):
# 開始時刻の記録
s_time = time.time()
# 訓練モードに設定
model.train()
for inputs, labels in dataloader_train:
# 勾配をゼロで初期化
optimizer.zero_grad()
# 順伝播 + 誤差逆伝播 + 重み更新
inputs = inputs.to(device)
labels = labels.to(device)
outputs = model.forward(inputs)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
# 損失と正解率の算出
loss_train, acc_train = calculate_loss_and_accuracy(model, criterion, dataloader_train, device)
loss_valid, acc_valid = calculate_loss_and_accuracy(model, criterion, dataloader_valid, device)
log_train.append([loss_train, acc_train])
log_valid.append([loss_valid, acc_valid])
# チェックポイントの保存
torch.save({'epoch': epoch, 'model_state_dict': model.state_dict(), 'optimizer_state_dict': optimizer.state_dict()}, f'checkpoint{epoch + 1}.pt')
# 終了時刻の記録
e_time = time.time()
# ログを出力
print(f'epoch: {epoch + 1}, loss_train: {loss_train:.4f}, accuracy_train: {acc_train:.4f}, loss_valid: {loss_valid:.4f}, accuracy_valid: {acc_valid:.4f}, {(e_time - s_time):.4f}sec')
return {'train': log_train, 'valid': log_valid}
# datasetの作成
dataset_train = CreateDataset(X_train, y_train)
dataset_valid = CreateDataset(X_valid, y_valid)
# モデルの定義
model = SLPNet(300, 4)
# 損失関数の定義
criterion = nn.CrossEntropyLoss()
# オプティマイザの定義
optimizer = torch.optim.SGD(model.parameters(), lr=1e-1)
# デバイスの指定
device = torch.device('cuda')
for batch_size in [2 ** i for i in range(11)]:
print(f'バッチサイズ: {batch_size}')
log = train_model(dataset_train, dataset_valid, batch_size, model, criterion, optimizer, 1, device=device)
```
## 79. 多層ニューラルネットワーク
***
問題78のコードを改変し,バイアス項の導入や多層化など,ニューラルネットワークの形状を変更しながら,高性能なカテゴリ分類器を構築せよ.
```
from torch.nn import functional as F
class MLPNet(nn.Module):
def __init__(self, input_size, mid_size, output_size, mid_layers):
super().__init__()
self.mid_layers = mid_layers
self.fc = nn.Linear(input_size, mid_size)
self.fc_mid = nn.Linear(mid_size, mid_size)
self.fc_out = nn.Linear(mid_size, output_size)
self.bn = nn.BatchNorm1d(mid_size)
def forward(self, x):
x = F.relu(self.fc(x))
for _ in range(self.mid_layers):
x = F.relu(self.bn(self.fc_mid(x)))
x = F.relu(self.fc_out(x))
return x
from torch import optim
def calculate_loss_and_accuracy(model, criterion, loader, device):
model.eval()
loss = 0.0
total = 0
correct = 0
with torch.no_grad():
for inputs, labels in loader:
inputs = inputs.to(device)
labels = labels.to(device)
outputs = model(inputs)
loss += criterion(outputs, labels).item()
pred = torch.argmax(outputs, dim=-1)
total += len(inputs)
correct += (pred == labels).sum().item()
return loss / len(loader), correct / total
def train_model(dataset_train, dataset_valid, batch_size, model, criterion, optimizer, num_epochs, device=None):
# GPUに送る
model.to(device)
# dataloaderの作成
dataloader_train = DataLoader(dataset_train, batch_size=batch_size, shuffle=True)
dataloader_valid = DataLoader(dataset_valid, batch_size=len(dataset_valid), shuffle=False)
# スケジューラの設定
scheduler = optim.lr_scheduler.CosineAnnealingLR(optimizer, num_epochs, eta_min=1e-5, last_epoch=-1)
# 学習
log_train = []
log_valid = []
for epoch in range(num_epochs):
# 開始時刻の記録
s_time = time.time()
# 訓練モードに設定
model.train()
for inputs, labels in dataloader_train:
# 勾配をゼロで初期化
optimizer.zero_grad()
# 順伝播 + 誤差逆伝播 + 重み更新
inputs = inputs.to(device)
labels = labels.to(device)
outputs = model.forward(inputs)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
# 損失と正解率の算出
loss_train, acc_train = calculate_loss_and_accuracy(model, criterion, dataloader_train, device)
loss_valid, acc_valid = calculate_loss_and_accuracy(model, criterion, dataloader_valid, device)
log_train.append([loss_train, acc_train])
log_valid.append([loss_valid, acc_valid])
# チェックポイントの保存
torch.save({'epoch': epoch, 'model_state_dict': model.state_dict(), 'optimizer_state_dict': optimizer.state_dict()}, f'checkpoint{epoch + 1}.pt')
# 終了時刻の記録
e_time = time.time()
# ログを出力
print(f'epoch: {epoch + 1}, loss_train: {loss_train:.4f}, accuracy_train: {acc_train:.4f}, loss_valid: {loss_valid:.4f}, accuracy_valid: {acc_valid:.4f}, {(e_time - s_time):.4f}sec')
# 検証データの損失が3エポック連続で低下しなかった場合は学習終了
if epoch > 2 and log_valid[epoch - 3][0] <= log_valid[epoch - 2][0] <= log_valid[epoch - 1][0] <= log_valid[epoch][0]:
break
# スケジューラを1ステップ進める
scheduler.step()
return {'train': log_train, 'valid': log_valid}
# datasetの作成
dataset_train = CreateDataset(X_train, y_train)
dataset_valid = CreateDataset(X_valid, y_valid)
# モデルの定義
model = MLPNet(300, 200, 4, 1)
# 損失関数の定義
criterion = nn.CrossEntropyLoss()
# オプティマイザの定義
optimizer = torch.optim.SGD(model.parameters(), lr=1e-3)
# デバイスの指定
device = torch.device('cuda')
log = train_model(dataset_train, dataset_valid, 64, model, criterion, optimizer, 1000, device)
# 可視化
fig, ax = plt.subplots(1, 2, figsize=(15, 5))
ax[0].plot(np.array(log['train']).T[0], label='train')
ax[0].plot(np.array(log['valid']).T[0], label='valid')
ax[0].set_xlabel('epoch')
ax[0].set_ylabel('loss')
ax[0].legend()
ax[1].plot(np.array(log['train']).T[1], label='train')
ax[1].plot(np.array(log['valid']).T[1], label='valid')
ax[1].set_xlabel('epoch')
ax[1].set_ylabel('accuracy')
ax[1].legend()
plt.show()
def calculate_accuracy(model, X, y, device):
model.eval()
with torch.no_grad():
inputs = X.to(device)
outputs = model(inputs)
pred = torch.argmax(outputs, dim=-1).cpu()
return (pred == y).sum().item() / len(y)
# 正解率の確認
acc_train = calculate_accuracy(model, X_train, y_train, device)
acc_test = calculate_accuracy(model, X_test, y_test, device)
print(f'正解率(学習データ):{acc_train:.3f}')
print(f'正解率(評価データ):{acc_test:.3f}')
```
|
github_jupyter
|
# Analyse a series
<div class="alert alert-block alert-warning">
<b>Under construction</b>
</div>
```
import os
import pandas as pd
from IPython.display import Image as DImage
from IPython.core.display import display, HTML
import series_details
# Plotly helps us make pretty charts
import plotly.offline as py
import plotly.graph_objs as go
# Make sure data directory exists
os.makedirs('../../data/RecordSearch/images', exist_ok=True)
# This lets Plotly draw charts in cells
py.init_notebook_mode()
```
This notebook is for analysing a series that you've already harvested. If you haven't harvested any data yet, then you need to go back to the ['Harvesting a series' notebook](Harvesting series.ipynb).
```
# What series do you want to analyse?
# Insert the series id between the quotes.
series = 'J2483'
# Load the CSV data for the specified series into a dataframe. Parse the dates as dates!
df = pd.read_csv('../data/RecordSearch/{}.csv'.format(series.replace('/', '-')), parse_dates=['start_date', 'end_date'])
```
Remember that you can download harvested data from the workbench [data directory](../data/RecordSearch).
## Get some summary data
We're going to create a simple summary of some of the main characteristics of the series, as reflected in the harvested files.
```
# We're going to assemble some summary data about the series in a 'summary' dictionary
# Let's create the dictionary and add the series identifier
summary = {'series': series}
# The 'shape' property returns the number of rows and columns. So 'shape[0]' gives us the number of items harvested.
summary['total_items'] = df.shape[0]
print(summary['total_items'])
# Get the frequency of the different access status categories
summary['access_counts'] = df['access_status'].value_counts().to_dict()
print(summary['access_counts'])
# Get the number of files that have been digitised
summary['digitised_files'] = len(df.loc[df['digitised_status'] == True])
print(summary['digitised_files'])
# Get the number of individual pages that have been digitised
summary['digitised_pages'] = df['digitised_pages'].sum()
print(summary['digitised_pages'])
# Get the earliest start date
start = df['start_date'].min()
try:
summary['date_from'] = start.year
except AttributeError:
summary['date_from'] = None
print(summary['date_from'])
# Get the latest end date
end = df['end_date'].max()
try:
summary['date_to'] = end.year
except AttributeError:
summary['date_to'] = None
print(summary['date_to'])
# Let's display all the summary data
print('SERIES: {}'.format(summary['series']))
print('Number of items: {:,}'.format(summary['total_items']))
print('Access status:')
for status, total in summary['access_counts'].items():
print(' {}: {:,}'.format(status, total))
print('Contents dates: {} to {}'.format(summary['date_from'], summary['date_to']))
print('Digitised files: {:,}'.format(summary['digitised_files']))
print('Digitised pages: {:,}'.format(summary['digitised_pages']))
```
Note that a slightly enhanced version of the code above is available in the `series_details` module that you can import into any notebook. So to create a summary of a series you can just:
```
# Import the module
import series_details
# Call display_series() providing the series name and the dataframe
series_details.display_summary(series, df)
```
## Plot the contents dates
Plotting the dates is a bit tricky. Each file can have both a start date and an end date. So if we want to plot the years covered by a file, we need to include all the years between the start and end dates. Also dates can be recorded at different levels of granularity, for specific days to just years. And sometimes there are no end dates recorded at all – what does this mean?
The code in the cell below does a few things:
* It fills any empty end dates with the start date from the same item. This probably means some content years will be missed, but it's the only date we can be certain of.
* It loops through all the rows in the dataframe, then for each row it extracts the years between the start and end date. Currently this looks to see if the 1 January is covered by the date range, so if there's an exact start date after 1 January I don't think it will be captured. I need to investigate this further.
* It combines all of the years into one big series and then totals up the frquency of each year.
I'm sure this is not perfect, but it seems to produce useful results.
```
# Fill any blank end dates with start dates
df['end_date'] = df[['end_date']].apply(lambda x: x.fillna(value=df['start_date']))
# This is a bit tricky.
# For each item we want to find the years that it has content from -- ie start_year <= year <= end_year.
# Then we want to put all the years from all the items together and look at their frequency
years = []
for row in df.itertuples(index=False):
try:
years_in_range = pd.date_range(start=row.start_date, end=row.end_date, freq='AS').year.to_series()
except ValueError:
# No start date
pass
else:
years.append(years_in_range)
year_counts = pd.concat(years).value_counts()
# Put the resulting series in a dataframe so it looks pretty.
year_totals = pd.DataFrame(year_counts)
# Sort results by year
year_totals.sort_index(inplace=True)
# Display the results
year_totals.style.format({0: '{:,}'})
# Let's graph the frequency of content years
plotly_data = [go.Bar(
x=year_totals.index.values, # The years are the index
y=year_totals[0]
)]
# Add some labels
layout = go.Layout(
title='Content dates',
xaxis=dict(
title='Year'
),
yaxis=dict(
title='Number of items'
)
)
# Create a chart
fig = go.Figure(data=plotly_data, layout=layout)
py.iplot(fig, filename='series-dates-bar')
```
Note that a slightly enhanced version of the code above is available in the series_details module that you can import into any notebook. So to create a summary of a series you can just:
```
# Import the module
import series_details
# Call plot_series() providing the series name and the dataframe
fig = series_details.plot_dates(df)
py.iplot(fig)
```
## Filter by words in file titles
```
# Find titles containing a particular phrase -- in this case 'wife'
# This creates a new dataframe
# Try changing this to filter for other words
search_term = 'wife'
df_filtered = df.loc[df['title'].str.contains(search_term, case=False)].copy()
df_filtered
# We can plot this filtered dataframe just like the series
fig = series_details.plot_dates(df)
py.iplot(fig)
# Save the new dataframe as a csv
df_filtered.to_csv('../data/RecordSearch/{}-{}.csv'.format(series.replace('/', '-'), search_term))
# Find titles containing one of two words -- ie an OR statement
# Try changing this to filter for other words
df_filtered = df.loc[df['title'].str.contains('chinese', case=False) | df['title'].str.contains(r'\bah\b', case=False)].copy()
df_filtered
```
## Filter by date range
```
start_year = '1920'
end_year = '1930'
df_filtered = df[(df['start_date'] >= start_year) & (df['end_date'] <= end_year)]
df_filtered
```
## N-gram frequencies in file titles
```
# Import TextBlob for text analysis
from textblob import TextBlob
import nltk
stopwords = nltk.corpus.stopwords.words('english')
# Combine all of the file titles into a single string
title_text = a = df['title'].str.lower().str.cat(sep=' ')
blob = TextBlob(title_text)
words = [[word, count] for word, count in blob.lower().word_counts.items() if word not in stopwords]
word_counts = pd.DataFrame(words).rename({0: 'word', 1: 'count'}, axis=1).sort_values(by='count', ascending=False)
word_counts[:25].style.format({'count': '{:,}'}).bar(subset=['count'], color='#d65f5f').set_properties(subset=['count'], **{'width': '300px'})
def get_ngram_counts(text, size):
blob = TextBlob(text)
# Extract n-grams as WordLists, then convert to a list of strings
ngrams = [' '.join(ngram).lower() for ngram in blob.lower().ngrams(size)]
# Convert to dataframe then count values and rename columns
ngram_counts = pd.DataFrame(ngrams)[0].value_counts().rename_axis('ngram').reset_index(name='count')
return ngram_counts
def display_top_ngrams(text, size):
ngram_counts = get_ngram_counts(text, size)
# Display top 25 results as a bar chart
display(ngram_counts[:25].style.format({'count': '{:,}'}).bar(subset=['count'], color='#d65f5f').set_properties(subset=['count'], **{'width': '300px'}))
display_top_ngrams(title_text, 2)
display_top_ngrams(title_text, 4)
```
|
github_jupyter
|
# SLU07 - Regression with Linear Regression: Example notebook
# 1 - Writing linear models
In this section you have a few examples on how to implement simple and multiple linear models.
Let's start by implementing the following:
$$y = 1.25 + 5x$$
```
def first_linear_model(x):
"""
Implements y = 1.25 + 5*x
Args:
x : float - input of model
Returns:
y : float - output of linear model
"""
y = 1.25 + 5 * x
return y
first_linear_model(1)
```
You should be thinking that this is too easy. So let's generalize it a bit. We'll write the code for the next equation:
$$ y = a + bx $$
```
def second_linear_model(x, a, b):
"""
Implements y = a + b * x
Args:
x : float - input of model
a : float - intercept of model
b : float - coefficient of model
Returns:
y : float - output of linear model
"""
y = a + b * x
return y
second_linear_model(1, 1.25, 5)
```
Still very simple, right? Now what if we want to have a linear model with multiple variables, such as this one:
$$ y = a + bx_1 + cx_2 + dx_3 $$
You can follow the same logic and just write the following:
```
def first_multiple_linear_model(x_1, x_2, x_3, a, b, c, d):
"""
Implements y = a + b * x_1 + c * x_2 + d * x_3
Args:
x_1 : float - first input of model
x_2 : float - second input of model
x_3 : float - third input of model
a : float - intercept of model
b : float - first coefficient of model
c : float - second coefficient of model
d : float - third coefficient of model
Returns:
y : float - output of linear model
"""
y = a + b * x_1 + c * x_2 + d * x_3
return y
first_multiple_linear_model(1.0, 1.0, 1.0, .5, .2, .1, .4)
```
However, you should already be seeing the problem. The bigger our model gets, the more variables we need to consider, so this is clearly not efficient. Now let's write the generic form for a linear model:
$$ y = w_0 + \sum_{i=1}^{N} w_i x_i$$
And we will implement the inputs and outputs of the model as vectors:
```
def second_multiple_linear_model(x, w):
"""
Implements y = w_0 + sum(x_i*w_i) (where i=1...N)
Args:
x : vector of input features with size N-1
w : vector of model weights with size N
Returns:
y : float - output of linear model
"""
w_0 = w[0]
y = w_0
for i in range(1, len(x)+1):
y += x[i-1]*w[i]
return y
second_multiple_linear_model([1.0, 1.0, 1.0], [.5, .2, .1, .4])
```
You could go even one step further and use numpy to vectorize these computations. You can represent both vectors as numpy arrays and just do the same calculation:
```
import numpy as np
def vectorized_multiple_linear_model(x, w):
"""
Implements y = w_0 + sum(x_i*w_i) (where i=1...N)
Args:
x : numpy array with shape (N-1, ) of inputs
w : numpy array with shape (N, ) of model weights
Returns:
y : float - output of linear model
"""
y = w[0] + x*w[1:]
vectorized_multiple_linear_model(np.array([1.0, 1.0, 1.0]), np.array([.5, .2, .1, .4]))
```
Read more about numpy array and its manipulation at the end of this example notebook. This will be necessary as you will be requested to implement these types of models in a way that they can compute several samples with many features at once.
<br>
<br>
# 2 - Using sklearn's LinearRegression
The following cells show you how to use the LinearRegression solver of the scikitlearn library. We'll start by creating some fake data to use in these examples:
```
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(42)
X = np.arange(-10, 10) + np.random.rand(20)
y = 1.12 + .75 * X + 2. * np.random.rand(20)
plt.xlim((-10, 10))
plt.ylim((-20, 20))
plt.plot(X, y, 'b.')
```
## 2.1 Training the model
We will now use the base data created and show you how to fit the scikitlearn LinearRegression model with the data:
```
from sklearn.linear_model import LinearRegression
# Since our numpy array has only 1 dimension, we need reshape
# it to become a column vector - which corresponds to 1 feature
# and N samples
X = X.reshape(-1, 1)
lr = LinearRegression()
lr.fit(X, y)
```
## 2.2 Coefficients and Intercept
You can get both the coefficients and the intercept from this model:
```
print('Coefficients: {}'.format(lr.coef_))
print('Intercept: {}'.format(lr.intercept_))
```
## 2.3 Making predictions
We can then make prediction with our model and see how they compare with the actual samples:
```
y_pred = lr.predict(X)
plt.xlim((-10, 10))
plt.ylim((-20, 20))
plt.plot(X, y, 'b.')
plt.plot(X, y_pred, 'r-')
```
## 2.4 Evaluating the model
We can also extract the $R^2$ score of this model:
```
print('R² score: %f' % lr.score(X, y))
```
<br>
<br>
# Bonus examples: Numpy utilities
With linear models, we normally have data that can be represented by either vectors or matrices. Even though you don't need advanced algebra knowledge to implement and understand the models presented, it is useful to understand its basics, since most of the computational part is typically implemented from these concepts.
Numpy is a powerful library that allows us to represent our data easily in this format, and already implements a lot of functions to then manipulate or do calculations over our data. In this section we present the basic functions that you should know and will use the most to implement the basic models:
```
import numpy as np
import pandas as pd
```
## a) Pandas to numpy and back
Pandas stores our data in dataframes and series, which are very useful for visualization and even for some specific data operations we want to perform. However, for many algorithms that involve combination of numeric data, the standard form of implementing is by using numpy. Start by seeing how to convert from pandas to numpy and back:
```
df = pd.read_csv('data/polynomial.csv')
df.head()
```
### a.1) Pandas to numpy
Let's transform our first column into a numpy vector. There are two ways of doing this, either by using the `.values` attribute:
```
np_array = df['x'].values
print(np_array[:10])
```
Or by calling the method `.to_numpy()` :
```
np_array = df['x'].to_numpy()
print(np_array[:10])
```
You can also apply this to the full table:
```
np_array = df.values
print(np_array[:5, :])
np_array = df.to_numpy()
print(np_array[:5, :])
```
### a.2) Numpy to pandas
Let's start by defining an array and converting it to a pandas series:
```
np_array = np.array([4., .1, 1., .23, 3.])
pd_series = pd.Series(np_array)
print(pd_series)
```
We can also create several series and concatenate them to create a dataframe:
```
np_array = np.array([4., .1, 1., .23, 3.])
pd_series_1 = pd.Series(np_array, name='A')
pd_series_2 = pd.Series(2 * np_array, name='B')
pd_dataframe = pd.concat((pd_series_1, pd_series_2), axis=1)
pd_dataframe.head()
```
We can also directly convert to a dataframe:
```
np_array = np.array([[1, 2, 3], [4, 5, 6]])
pd_dataframe = pd.DataFrame(np_array)
pd_dataframe.head()
```
However, we might want more detailed names and specific indices. Some ways of achieving this follows:
```
data = np.array([['','Col1','Col2'],
['Row1',1,2],
['Row2',3,4]])
pd_dataframe = pd.DataFrame(data=data[1:,1:], index=data[1:,0], columns=data[0,1:])
pd_dataframe.head()
pd_dataframe = pd.DataFrame(np.array([[4,5,6,7], [1,2,3,4]]), index=range(0, 2), columns=['A', 'B', 'C', 'D'])
pd_dataframe.head()
my_dict = {'A': np.array(['1', '3']), 'B': np.array(['1', '2']), 'C': np.array(['2', '4'])}
pd_dataframe = pd.DataFrame(my_dict)
pd_dataframe.head()
```
## b) Vector and Matrix initialization and shaping
When working with vectors and matrices, we need to be aware of the dimensions of these objects, and how they affect the possible operations perform over them. Numpy allows you to access these dimensions through the shape of the object:
```
v1 = np.array([ .1, 1., 2.])
print('1-d Array: {}'.format(v1))
print('Shape: {}'.format(v1.shape))
v2 = np.array([[ .1, 1., 2.]])
print('\n')
print('2-d Row Array: {}'.format(v2))
print('Shape: {}'.format(v2.shape))
v3 = np.array([[ .1], [1.], [2.]])
print('\n')
print('2-d Column Array:\n {}'.format(v3))
print('Shape: {}'.format(v3.shape))
m1 = np.array([[ .1, 3., 4., 1.], [1., .3, .1, .5], [2.,.7, 3.8, .1]])
print('\n')
print('2-d matrix:\n {}'.format(m1))
print('Shape: {}'.format(m1.shape))
```
Another important functionality provided is the possibility of reshaping these objects. For example, we can turn a 1-d array into a row vector:
```
v1 = np.array([ .1, 1., 2.])
v1_reshaped = v1.reshape((1, -1))
print('Old 1-d Array reshaped to row: {}'.format(v1_reshaped))
print('Shape: {}'.format(v1_reshaped.shape))
```
Or we can reshape it into a column vector:
```
v1 = np.array([ .1, 1., 2.])
v1_reshaped = v2.reshape((-1, 1))
print('Old 1-d Array reshaped to column: \n{}'.format(v1_reshaped))
print('Shape: {}'.format(v1_reshaped.shape))
```
We can also create specific vectors of 1s, 0s or random numbers with specific shapes from the start. See how to use each in the cells that follow:
```
custom_shape = (3, )
v1_ones = np.ones(custom_shape)
print('1-D Vector of ones: \n{}'.format(v1_ones))
print('Shape: {}'.format(v1_ones.shape))
custom_shape = (5, 1)
v1_zeros = np.zeros(custom_shape)
print('2-D vector of zeros: \n{}'.format(v1_zeros))
print('Shape: {}'.format(v1_zeros.shape))
custom_shape = (5, 3)
v1_rand = np.random.rand(custom_shape[0], custom_shape[1])
print('2-D Matrix of random numbers: \n{}'.format(v1_rand))
print('Shape: {}'.format(v1_rand.shape))
```
## c) Vector and Matrix Concatenation
In this section, you will learn how to concatenate 2 vectors, a matrix and a vector, or 2 matrices.
### c.1) Vector - Vector
Let's start by defining 2 vectors:
```
v1 = np.array([ .1, 1., 2.])
v2 = np.array([5.1, .3, .41, 3. ])
print('1st array: {}'.format(v1))
print('Shape: {}'.format(v1.shape))
print('2nd array: {}'.format(v2))
print('Shape: {}'.format(v2.shape))
```
Since vectors only have one dimension with a given size (notice the shape with only one element) we can only concatenate in this dimension, leading to a longer vector:
```
vconcat = np.concatenate((v1, v2))
print('Concatenated vector: {}'.format(vconcat))
print('Shape: {}'.format(vconcat.shape))
```
Concatenating vectors is very easy, and since we can only concatenate them in their one dimension, the sizes do not have to match. Now let's move on to a more complex case.
### c.2) Matrix - row vector
When concatenating matrices and vectors we have to take into account their dimensions.
```
v1 = np.array([ .1, 1., 2., 3.])
m1 = np.array([[5.1, .3, .41, 3. ], [5.1, .3, .41, 3. ]])
print('Array: {}'.format(v1))
print('Shape: {}'.format(v1.shape))
print('Matrix: \n{}'.format(m1))
print('Shape: {}'.format(m1.shape))
```
The first thing you need to know is that whatever numpy objects you are trying to concatenate need to have the same dimensions. Run the code below to verify that you can not concatenate directly the vector and matrix:
```
try:
vconcat = np.concatenate((v1, m1))
except Exception as e:
print('Concatenation raised the following error: {}'.format(e))
```
So how can we do matrix-vector concatenation?
It is actually quite simple. We'll use the reshape functionality you seen before to add a dimension to the vector.
```
v1_reshaped = v1.reshape((1, v1.shape[0]))
m1 = np.array([[5.1, .3, .41, 3. ], [5.1, .3, .41, 3. ]])
print('Array: {}'.format(v1_reshaped))
print('Shape: {}'.format(v1_reshaped.shape))
print('Matrix: \n{}'.format(m1))
print('Shape: {}'.format(m1.shape))
```
We've reshaped our vector into a 1-row matrix. Now we can try to perform the same concatenation:
```
vconcat = np.concatenate((v1_reshaped, m1))
print('Concatenated vector: {}'.format(vconcat))
print('Shape: {}'.format(vconcat.shape))
```
### c.3) Matrix - column vector
We can also do this procedure with a column vector:
```
v1 = np.array([ .1, 1.])
v1_reshaped = v1.reshape((v1.shape[0], 1))
m1 = np.array([[5.1, .3, .41, 3. ], [5.1, .3, .41, 3. ]])
print('Array: \n{}'.format(v1_reshaped))
print('Shape: {}'.format(v1_reshaped.shape))
print('Matrix: \n{}'.format(m1))
print('Shape: {}'.format(m1.shape))
vconcat = np.concatenate((v1_reshaped, m1), axis=1)
print('Concatenated vector: {}'.format(vconcat))
print('Shape: {}'.format(vconcat.shape))
```
There's yet another restriction when concatenating vectors and matrices. The dimension where we want to concatenate has to share the same size.
See what would happen if we tried to concatenate a smaller vector with the same matrix:
```
v2 = np.array([ .1, 1.])
v2_reshaped = v2.reshape((1, v2.shape[0])) # Row vector as matrix
try:
vconcat = np.concatenate((v2, m1))
except Exception as e:
print('Concatenation raised the following error: {}'.format(e))
```
### c.4) Matrix - Matrix
This is just an extension of the previous case, since what we did before was transforming the vector into a matrix where the size of one of the dimensions is 1. So all the same restrictions apply, the arrays must have compatible dimensions. Run the following examples to see this:
```
m1 = np.array([[5.1, .3, .41, 3. ], [5.1, .3, .41, 3. ]])
m2 = np.array([[1., 2., 0., 3. ], [.1, .13, 1., 3. ], [.1, 2., .5, .3 ]])
m3 = np.array([[1., 0. ], [0., 1. ]])
print('Matrix 1: \n{}'.format(m1))
print('Shape: {}'.format(m1.shape))
print('Matrix 2: \n{}'.format(m2))
print('Shape: {}'.format(m2.shape))
print('Matrix 3: \n{}'.format(m3))
print('Shape: {}'.format(m3.shape))
```
Concatenate m1 and m2 at row level (stack the two matrices):
```
mconcat = np.concatenate((m1, m2))
print('Concatenated matrix:\n {}'.format(mconcat))
print('Shape: {}'.format(mconcat.shape))
```
Concatenate m1 and m2 at column level (joining the two matrices side by side) should produce an error:
```
try:
vconcat = np.concatenate((m1, m2), axis=1)
except Exception as e:
print('Concatenation raised the following error: {}'.format(e))
```
Concatenate m1 and m3 at column level (joining the two matrices side by side):
```
mconcat = np.concatenate((m1, m3), axis=1)
print('Concatenated matrix:\n {}'.format(mconcat))
print('Shape: {}'.format(mconcat.shape))
```
Concatenate m1 and m3 at row level (stack the two matrices) should produce an error:
```
try:
vconcat = np.concatenate((m1, m3))
except Exception as e:
print('Concatenation raised the following error: {}'.format(e))
```
## d) Single matrix operations
In this section we describe a few operations that can be done over matrices:
### d.1) Transpose
A very common operation is the transpose. If you are used to see matrix notation, you should know what this operation is. Take a matrix with 2 dimensions:
$$ X = \begin{bmatrix} a & b \\ c & d \\ \end{bmatrix} $$
Transposing the matrix is inverting its data with respect to its diagonal:
$$ X^T = \begin{bmatrix} a & c \\ b & d \\ \end{bmatrix} $$
This means that the rows of X will become its columns and vice-versa. You can attain the transpose of a matrix by using either `.T` on a matrix or calling `numpy.transpose`:
```
m1 = np.array([[ .1, 1., 2.], [ 3., .24, 4.], [ 6., 2., 5.]])
print('Initial matrix: \n{}'.format(m1))
m1_transposed = m1.transpose()
print('Transposed matrix with `transpose` \n{}'.format(m1_transposed))
m1_transposed = m1.T
print('Transposed matrix with `T` \n{}'.format(m1_transposed))
```
A few examples of non-squared matrices. In these, you'll see that the shape (a, b) gets inverted to (b, a):
```
m1 = np.array([[ .1, 1., 2., 5.], [ 3., .24, 4., .6]])
print('Initial matrix: \n{}'.format(m1))
m1_transposed = m1.T
print('Transposed matrix: \n{}'.format(m1_transposed))
m1 = np.array([[ .1, 1.], [2., 5.], [ 3., .24], [4., .6]])
print('Initial matrix: \n{}'.format(m1))
m1_transposed = m1.T
print('Transposed matrix: \n{}'.format(m1_transposed))
```
For vectors represented as matrices, this means transforming from a row vector (1, N) to a column vector (N, 1) or vice-versa:
```
v1 = np.array([ .1, 1., 2.])
v1_reshaped = v1.reshape((1, -1))
print('Row vector as 2-d array: {}'.format(v1_reshaped))
print('Shape: {}'.format(v1_reshaped.shape))
v1_transposed = v1_reshaped.T
print('Transposed (column vector as 2-d array): \n{}'.format(v1_transposed))
print('Shape: {}'.format(v1_transposed.shape))
v1 = np.array([ 3., .23, 2., .6])
v1_reshaped = v1.reshape((-1, 1))
print('Column vector as 2-d array: \n{}'.format(v1_reshaped))
print('Shape: {}'.format(v1_reshaped.shape))
v1_transposed = v1_reshaped.T
print('Transposed (row vector as 2-d array): {}'.format(v1_transposed))
print('Shape: {}'.format(v1_transposed.shape))
```
### d.2) Statistics operators
Numpy also allows us to perform several operations over the rows and columns of a matrix, such as:
* Sum
* Mean
* Max
* Min
* ...
The most important thing to take into account when using these is to know exactly in which direction we are performing the operations. We can perform, for example, a `max` operation over the whole matrix, obtaining the max value in all of the matrix values. Or we might want this value for each row, or for each column. Check the following examples:
```
m1 = np.array([[ .1, 1.], [2., 5.], [ 3., .24], [4., .6]])
print('Initial matrix: \n{}'.format(m1))
```
Operating over all matrix' values:
```
print('Total sum of matrix elements: {}'.format(m1.sum()))
print('Minimum of all matrix elements: {}'.format(m1.max()))
print('Maximum of all matrix elements: {}'.format(m1.min()))
print('Mean of all matrix elements: {}'.format(m1.mean()))
```
Operating across rows - produces a row with the sum/max/min/mean for each column:
```
print('Total sum of matrix elements: {}'.format(m1.sum(axis=0)))
print('Minimum of all matrix elements: {}'.format(m1.max(axis=0)))
print('Maximum of all matrix elements: {}'.format(m1.min(axis=0)))
print('Mean of all matrix elements: {}'.format(m1.mean(axis=0)))
```
Operating across columns - produces a column with the sum/max/min/mean for each row:
```
print('Total sum of matrix elements: {}'.format(m1.sum(axis=1)))
print('Minimum of all matrix elements: {}'.format(m1.max(axis=1)))
print('Maximum of all matrix elements: {}'.format(m1.min(axis=1)))
print('Mean of all matrix elements: {}'.format(m1.mean(axis=1)))
```
As an example, imagine that you have a matrix of shape (n_samples, n_features), where each row represents all the features for one sample. Then , to average over the samples, we do:
```
m1 = np.array([[ .1, 1.], [2., 5.], [ 3., .24], [4., .6]])
print('Initial matrix: \n{}'.format(m1))
print('\n')
print('Sample 1: {}'.format(m1[0, :]))
print('Sample 2: {}'.format(m1[1, :]))
print('Sample 3: {}'.format(m1[2, :]))
print('Sample 4: {}'.format(m1[3, :]))
print('\n')
print('Average over samples: \n{}'.format(m1.mean(axis=0)))
```
Other statistical functions behave in a similar manner, so it is important to know how to work the axis of these objects.
## e) Multiple matrix operations
### e.1) Element wise operations
Several operations available work at the element level, this is, if we have two matrices A and B:
$$ A = \begin{bmatrix} a & b \\ c & d \\ \end{bmatrix} $$
and
$$ B = \begin{bmatrix} e & f \\ g & h \\ \end{bmatrix} $$
an element-wise operation produces a matrix:
$$ Op(A, B) = \begin{bmatrix} Op(a,e) & Op(b,f) \\ Op(c,g) & Op(d,h) \\ \end{bmatrix} $$
You can perform sum and difference, but also element-wise multiplication and division. These are implemented with the regular operators `+`, `-`, `*`, `/`. Check out the examples below:
```
m1 = np.array([[ .1, 1., 2., 5.], [ 3., .24, 4., .6]])
m2 = np.array([[ .1, 4., .25, .1], [ 2., 1.5, .42, -1.]])
print('Matrix 1: \n{}'.format(m1))
print('Matrix 2: \n{}'.format(m1))
print('\n')
print('Sum: \n{}'.format(m1 + m2))
print('\n')
print('Difference: \n{}'.format(m1 - m2))
print('\n')
print('Multiplication: \n{}'.format(m1*m2))
print('\n')
print('Division: \n{}'.format(m1/m2))
```
For these operations, ideally your matrices should have the same dimensions. An exception to this is when you have one of the elements that can be [broadcasted](https://numpy.org/doc/stable/user/basics.broadcasting.html) over the other. However we won't cover that in these examples.
### e.2) Matrix multiplication
Although you've seen how to perform element wise multiplication with the basic operation, one of the most common matrix operations is matrix multiplication, where the output is not the result of an element wise combination of its elements, but actually a linear combination between rows of the first matrix nd columns of the second.
In other words, element (i, j) of the resulting matrix is the dot product between row i of the first matrix and column j of the second:

Where the dot product represented breaks down to:
$$ 58 = 1 \times 7 + 2 \times 9 + 3 \times 11 $$
Numpy already provides this function, so check out the following examples:
```
m1 = np.array([[ .1, 1., 2., 5.], [ 3., .24, 4., .6]])
m2 = np.array([[ .1, 4.], [.25, .1], [ 2., 1.5], [.42, -1.]])
print('Matrix 1: \n{}'.format(m1))
print('Matrix 2: \n{}'.format(m1))
print('\n')
print('Matrix multiplication: \n{}'.format(np.matmul(m1, m2)))
m1 = np.array([[ .1, 4.], [.25, .1], [ 2., 1.5], [.42, -1.]])
m2 = np.array([[ .1, 1., 2.], [ 3., .24, 4.]])
print('Matrix 1: \n{}'.format(m1))
print('Matrix 2: \n{}'.format(m1))
print('\n')
print('Matrix multiplication: \n{}'.format(np.matmul(m1, m2)))
```
Notice that in both operations the matrix multiplication of shapes `(k, l)` and `(m, n)` yields a matrix of dimensions `(k, n)`. Additionally, for this operation to be possible, the inner dimensions need to match, this is `l == m` . See what happens if we try to multiply matrices with incompatible dimensions:
```
m1 = np.array([[ .1, 4., 3.], [.25, .1, 1.], [ 2., 1.5, .5], [.42, -1., 4.3]])
m2 = np.array([[ .1, 1., 2.], [ 3., .24, 4.]])
print('Matrix 1: \n{}'.format(m1))
print('Shape: {}'.format(m1.shape))
print('Matrix 2: \n{}'.format(m1))
print('Shape: {}'.format(m2.shape))
print('\n')
try:
m3 = np.matmul(m1, m2)
except Exception as e:
print('Matrix multiplication raised the following error: {}'.format(e))
```
|
github_jupyter
|
```
#importing libraries
import pandas as pd
import boto3
import json
import configparser
from botocore.exceptions import ClientError
import psycopg2
def config_parse_file():
"""
Parse the dwh.cfg configuration file
:return:
"""
global KEY, SECRET, DWH_CLUSTER_TYPE, DWH_NUM_NODES, \
DWH_NODE_TYPE, DWH_CLUSTER_IDENTIFIER, DWH_DB, \
DWH_DB_USER, DWH_DB_PASSWORD, DWH_PORT, DWH_IAM_ROLE_NAME
print("Parsing the config file...")
config = configparser.ConfigParser()
with open('dwh.cfg') as configfile:
config = configparser.ConfigParser()
config.read_file(open('dwh.cfg'))
KEY = config.get('AWS','KEY')
SECRET = config.get('AWS','SECRET')
DWH_CLUSTER_TYPE = config.get("DWH","DWH_CLUSTER_TYPE")
DWH_NUM_NODES = config.get("DWH","DWH_NUM_NODES")
DWH_NODE_TYPE = config.get("DWH","DWH_NODE_TYPE")
DWH_CLUSTER_IDENTIFIER = config.get("DWH","DWH_CLUSTER_IDENTIFIER")
DWH_DB = config.get("CLUSTER","DWH_DB")
DWH_DB_USER = config.get("CLUSTER","DWH_DB_USER")
DWH_DB_PASSWORD = config.get("CLUSTER","DWH_DB_PASSWORD")
DWH_PORT = config.get("CLUSTER","DWH_PORT")
DWH_IAM_ROLE_NAME = config.get("DWH", "DWH_IAM_ROLE_NAME")
#Function for creating iam_role
def create_iam_role(iam):
"""
Create the AWS IAM role
:param iam:
:return:
"""
global DWH_IAM_ROLE_NAME
dwhRole = None
try:
print('1.1 Creating a new IAM Role')
dwhRole = iam.create_role(
Path='/',
RoleName=DWH_IAM_ROLE_NAME,
Description="Allows Redshift clusters to call AWS services on your behalf.",
AssumeRolePolicyDocument=json.dumps(
{'Statement': [{'Action': 'sts:AssumeRole',
'Effect': 'Allow',
'Principal': {'Service': 'redshift.amazonaws.com'}}],
'Version': '2012-10-17'})
)
except Exception as e:
print(e)
dwhRole = iam.get_role(RoleName=DWH_IAM_ROLE_NAME)
return dwhRole
def attach_iam_role_policy(iam):
"""
Attach the AmazonS3ReadOnlyAccess role policy to the created IAM
:param iam:
:return:
"""
global DWH_IAM_ROLE_NAME
print('1.2 Attaching Policy')
return iam.attach_role_policy(RoleName=DWH_IAM_ROLE_NAME, PolicyArn="arn:aws:iam::aws:policy/AmazonS3ReadOnlyAccess")['ResponseMetadata']['HTTPStatusCode'] == 200
def get_iam_role_arn(iam):
"""
Get the IAM role ARN string
:param iam: The IAM resource client
:return:string
"""
global DWH_IAM_ROLE_NAME
return iam.get_role(RoleName=DWH_IAM_ROLE_NAME)['Role']['Arn']
#Function to create cluster
def create_cluster(redshift, roleArn):
"""
Start the Redshift cluster creation
:param redshift: The redshift resource client
:param roleArn: The created role ARN
:return:
"""
global DWH_CLUSTER_TYPE, DWH_NODE_TYPE, DWH_NUM_NODES, DWH_DB, DWH_CLUSTER_IDENTIFIER, DWH_DB_USER, DWH_DB_PASSWORD
try:
response = redshift.create_cluster(
#HW
ClusterType=DWH_CLUSTER_TYPE,
NodeType=DWH_NODE_TYPE,
NumberOfNodes=int(DWH_NUM_NODES),
#Identifiers & Credentials
DBName=DWH_DB,
ClusterIdentifier=DWH_CLUSTER_IDENTIFIER,
MasterUsername=DWH_DB_USER,
MasterUserPassword=DWH_DB_PASSWORD,
#Roles (for s3 access)
IamRoles=[roleArn]
)
print("Redshift cluster creation http response status code: ")
print(response['ResponseMetadata']['HTTPStatusCode'])
return response['ResponseMetadata']['HTTPStatusCode'] == 200
except Exception as e:
print(e)
return False
#Adding details to config file
def config_persist_cluster_infos(redshift):
"""
Write back to the dwh.cfg configuration file the cluster endpoint and IAM ARN
:param redshift: The redshift resource client
:return:
"""
global DWH_CLUSTER_IDENTIFIER
print("Writing the cluster address and IamRoleArn to the config file...")
cluster_props = redshift.describe_clusters(ClusterIdentifier=DWH_CLUSTER_IDENTIFIER)['Clusters'][0]
config = configparser.ConfigParser()
with open('dwh.cfg') as configfile:
config.read_file(configfile)
config.set("CLUSTER", "HOST", cluster_props['Endpoint']['Address'])
config.set("IAM_ROLE", "ARN", cluster_props['IamRoles'][0]['IamRoleArn'])
with open('dwh.cfg', 'w+') as configfile:
config.write(configfile)
config_parse_file()
#Function to retrive redshift cluster properties
def prettyRedshiftProps(props):
'''
Retrieve Redshift clusters properties
'''
pd.set_option('display.max_colwidth', -1)
keysToShow = ["ClusterIdentifier", "NodeType", "ClusterStatus", "MasterUsername", "DBName", "Endpoint", "NumberOfNodes", 'VpcId']
x = [(k, v) for k,v in props.items() if k in keysToShow]
return pd.DataFrame(data=x, columns=["Key", "Value"])
#Function to get cluster properties
def get_cluster_props(redshift):
"""
Retrieves the Redshift cluster status
:param redshift: The Redshift resource client
:return: The cluster status
"""
global DWH_CLUSTER_IDENTIFIER
myClusterProps = redshift.describe_clusters(ClusterIdentifier=DWH_CLUSTER_IDENTIFIER)['Clusters'][0]
cluster_status = myClusterProps['ClusterStatus']
return cluster_status.lower()
#to check if cluster became available or not
def check_cluster_creation(redshift):
"""
Check if the cluster status is available, if it is returns True. Otherwise, false.
:param redshift: The Redshift client resource
:return:bool
"""
if get_cluster_props(redshift) == 'available':
return True
return False
#Function to Open an incoming TCP port to access the cluster ednpoint
def aws_open_redshift_port(ec2, redshift):
"""
Opens the Redshift port on the VPC security group.
:param ec2: The EC2 client resource
:param redshift: The Redshift client resource
:return:None
"""
global DWH_CLUSTER_IDENTIFIER, DWH_PORT
cluster_props = redshift.describe_clusters(ClusterIdentifier=DWH_CLUSTER_IDENTIFIER)['Clusters'][0]
try:
vpc = ec2.Vpc(id=cluster_props['VpcId'])
all_security_groups = list(vpc.security_groups.all())
print(all_security_groups)
defaultSg = all_security_groups[1]
print(defaultSg)
defaultSg.authorize_ingress(
GroupName=defaultSg.group_name,
CidrIp='0.0.0.0/0',
IpProtocol='TCP',
FromPort=int(DWH_PORT),
ToPort=int(DWH_PORT)
)
except Exception as e:
print(e)
##Create clients for IAM, EC2, S3 and Redshift¶
def aws_resource(name, region):
"""
Creates an AWS client resource
:param name: The name of the resource
:param region: The region of the resource
:return:
"""
global KEY, SECRET
return boto3.resource(name, region_name=region, aws_access_key_id=KEY, aws_secret_access_key=SECRET)
def aws_client(service, region):
"""
Creates an AWS client
:param service: The service
:param region: The region of the service
:return:
"""
global KEY, SECRET
return boto3.client(service, aws_access_key_id=KEY, aws_secret_access_key=SECRET, region_name=region)
#delete resources
def delete_cluster_resources(redshift):
"""
Destroy the Redshift cluster (request deletion)
:param redshift: The Redshift client resource
:return:None
"""
global DWH_CLUSTER_IDENTIFIER
redshift.delete_cluster( ClusterIdentifier=DWH_CLUSTER_IDENTIFIER, SkipFinalClusterSnapshot=True)
def delete_iam_resource(iam):
iam.detach_role_policy(RoleName=DWH_IAM_ROLE_NAME, PolicyArn="arn:aws:iam::aws:policy/AmazonS3ReadOnlyAccess")
iam.delete_role(RoleName=DWH_IAM_ROLE_NAME)
#Main Function to start the process
def main():
config_parse_file()
# ec2 = aws_resource('ec2', 'us-east-2')
# s3 = aws_resource('s3', 'us-west-2')
iam = aws_client('iam', "us-east-1")
redshift = aws_client('redshift', "us-east-1")
create_iam_role(iam)
attach_iam_role_policy(iam)
roleArn = get_iam_role_arn(iam)
clusterCreationStarted = create_cluster(redshift, roleArn)
if clusterCreationStarted:
print("The cluster is being created.")
# if __name__ == '__main__':
# main()
```
|
github_jupyter
|
# Task 4: Support Vector Machines
_All credit for the code examples of this notebook goes to the book "Hands-On Machine Learning with Scikit-Learn & TensorFlow" by A. Geron. Modifications were made and text was added by K. Zoch in preparation for the hands-on sessions._
# Setup
First, import a few common modules, ensure MatplotLib plots figures inline and prepare a function to save the figures:
```
# Common imports
import numpy as np
import os
# to make this notebook's output stable across runs
np.random.seed(42)
# To plot pretty figures
%matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rc('axes', labelsize=14)
mpl.rc('xtick', labelsize=12)
mpl.rc('ytick', labelsize=12)
# Function to save a figure. This also decides that all output files
# should stored in the subdirectorz 'classification'.
PROJECT_ROOT_DIR = "."
EXERCISE = "SVMs"
def save_fig(fig_id, tight_layout=True):
path = os.path.join(PROJECT_ROOT_DIR, "output", EXERCISE, fig_id + ".png")
print("Saving figure", fig_id)
if tight_layout:
plt.tight_layout()
plt.savefig(path, format='png', dpi=300)
```
# Large margin *vs* margin violations
This code example contains two linear support vector machine classifiers ([LinearSVC](https://scikit-learn.org/stable/modules/generated/sklearn.svm.LinearSVC.html), which are initialised with different hyperparameter C. The used dataset is the iris dataset also shown in the lecture (iris verginica vcs. iris versicolor). Try a few different values for C and compare the results! What effect do different values of C have on: (1) the width of the street, (2) the number of outliers, (3) the number of support vectors?
```
import numpy as np
from sklearn import datasets
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.svm import LinearSVC
# Load the dataset and store the necessary features/labels in X/y.
iris = datasets.load_iris()
X = iris["data"][:, (2, 3)] # petal length, petal width
y = (iris["target"] == 2).astype(np.float64) # Iris-Virginica
# Initialise a scaler and the two SVC instances.
scaler = StandardScaler()
svm_clf1 = LinearSVC(C=1, loss="hinge", max_iter=10000, random_state=42)
svm_clf2 = LinearSVC(C=100, loss="hinge", max_iter=10000, random_state=42)
# Create pipelines to automatically scale the input.
scaled_svm_clf1 = Pipeline([
("scaler", scaler),
("linear_svc", svm_clf1),
])
scaled_svm_clf2 = Pipeline([
("scaler", scaler),
("linear_svc", svm_clf2),
])
# Perform the actual fit of the two models.
scaled_svm_clf1.fit(X, y)
scaled_svm_clf2.fit(X, y)
# Convert to unscaled parameters
b1 = svm_clf1.decision_function([-scaler.mean_ / scaler.scale_])
b2 = svm_clf2.decision_function([-scaler.mean_ / scaler.scale_])
w1 = svm_clf1.coef_[0] / scaler.scale_
w2 = svm_clf2.coef_[0] / scaler.scale_
svm_clf1.intercept_ = np.array([b1])
svm_clf2.intercept_ = np.array([b2])
svm_clf1.coef_ = np.array([w1])
svm_clf2.coef_ = np.array([w2])
# Find support vectors (LinearSVC does not do this automatically)
t = y * 2 - 1
support_vectors_idx1 = (t * (X.dot(w1) + b1) < 1).ravel()
support_vectors_idx2 = (t * (X.dot(w2) + b2) < 1).ravel()
svm_clf1.support_vectors_ = X[support_vectors_idx1]
svm_clf2.support_vectors_ = X[support_vectors_idx2]
# Now do the plotting.
def plot_svc_decision_boundary(svm_clf, xmin, xmax):
w = svm_clf.coef_[0]
b = svm_clf.intercept_[0]
# At the decision boundary, w0*x0 + w1*x1 + b = 0
# => x1 = -w0/w1 * x0 - b/w1
x0 = np.linspace(xmin, xmax, 200)
decision_boundary = -w[0]/w[1] * x0 - b/w[1]
margin = 1/w[1]
gutter_up = decision_boundary + margin
gutter_down = decision_boundary - margin
svs = svm_clf.support_vectors_
plt.scatter(svs[:, 0], svs[:, 1], s=180, facecolors='#FFAAAA')
plt.plot(x0, decision_boundary, "k-", linewidth=2)
plt.plot(x0, gutter_up, "k--", linewidth=2)
plt.plot(x0, gutter_down, "k--", linewidth=2)
plt.figure(figsize=(12,3.2))
plt.subplot(121)
plt.plot(X[:, 0][y==1], X[:, 1][y==1], "g^", label="Iris-Virginica")
plt.plot(X[:, 0][y==0], X[:, 1][y==0], "bs", label="Iris-Versicolor")
plot_svc_decision_boundary(svm_clf1, 4, 6)
plt.xlabel("Petal length", fontsize=14)
plt.ylabel("Petal width", fontsize=14)
plt.legend(loc="upper left", fontsize=14)
plt.title("$C = {}$".format(svm_clf1.C), fontsize=16)
plt.axis([4, 6, 0.8, 2.8])
plt.subplot(122)
plt.plot(X[:, 0][y==1], X[:, 1][y==1], "g^")
plt.plot(X[:, 0][y==0], X[:, 1][y==0], "bs")
plot_svc_decision_boundary(svm_clf2, 4, 6)
plt.xlabel("Petal length", fontsize=14)
plt.title("$C = {}$".format(svm_clf2.C), fontsize=16)
plt.axis([4, 6, 0.8, 2.8])
save_fig("regularization_plot")
```
# Polynomial features vs. polynomial kernels
Let's create a non-linear dataset, for which we can compare two approaches: (1) adding polynomial features to the model, (2) using a polynomial kernel (see exercise sheet). First, create some random data.
```
from sklearn.datasets import make_moons
X, y = make_moons(n_samples=100, noise=0.15, random_state=42)
def plot_dataset(X, y, axes):
plt.plot(X[:, 0][y==0], X[:, 1][y==0], "bs")
plt.plot(X[:, 0][y==1], X[:, 1][y==1], "g^")
plt.axis(axes)
plt.grid(True, which='both')
plt.xlabel(r"$x_1$", fontsize=20)
plt.ylabel(r"$x_2$", fontsize=20, rotation=0)
plot_dataset(X, y, [-1.5, 2.5, -1, 1.5])
plt.show()
```
Now let's first look at a linear SVM classifier that uses polynomial features. We will implement them through a pipeline including scaling of the inputs. What happens if you increase the degrees of polynomial features? Does the model get better? How is the computing time affected? Hint: you might have to increase the `max_iter` parameter for higher degrees.
```
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
polynomial_svm_clf = Pipeline([
("poly_features", PolynomialFeatures(degree=3)),
("scaler", StandardScaler()),
("svm_clf", LinearSVC(C=10, loss="hinge", max_iter=1000, random_state=42))
])
polynomial_svm_clf.fit(X, y)
def plot_predictions(clf, axes):
x0s = np.linspace(axes[0], axes[1], 100)
x1s = np.linspace(axes[2], axes[3], 100)
x0, x1 = np.meshgrid(x0s, x1s)
X = np.c_[x0.ravel(), x1.ravel()]
y_pred = clf.predict(X).reshape(x0.shape)
y_decision = clf.decision_function(X).reshape(x0.shape)
plt.contourf(x0, x1, y_pred, cmap=plt.cm.brg, alpha=0.2)
plt.contourf(x0, x1, y_decision, cmap=plt.cm.brg, alpha=0.1)
plot_predictions(polynomial_svm_clf, [-1.5, 2.5, -1, 1.5])
plot_dataset(X, y, [-1.5, 2.5, -1, 1.5])
save_fig("moons_polynomial_svc_plot")
plt.show()
```
Now let's try the same without polynomial features, but a polynomial kernel instead. What is the fundamental difference between these two approaches? How do they scale in terms of computing time: (1) as a function of the number of features, (2) as a function of the number of instances?
1. Try out different degrees for the polynomial kernel. Do you expect any changes in the computing time? How does the model itself change in the plot?
2. Try different values for the `coef0` parameter. Can you guess what it controls? You should be able to see different behaviour for different degrees in the kernel.
3. Try different values for the hyperparameter C, which controls margin violations.
```
from sklearn.svm import SVC
# Let's make one pipeline with polynomial kernel degree 3.
poly_kernel_svm_clf = Pipeline([
("scaler", StandardScaler()),
("svm_clf", SVC(kernel="poly", degree=3, coef0=1, C=5))
])
poly_kernel_svm_clf.fit(X, y)
# And another pipeline with polynomial kernel degree 10.
poly100_kernel_svm_clf = Pipeline([
("scaler", StandardScaler()),
("svm_clf", SVC(kernel="poly", degree=10, coef0=100, C=5))
])
poly100_kernel_svm_clf.fit(X, y)
# Now start the plotting.
plt.figure(figsize=(11, 4))
plt.subplot(121)
plot_predictions(poly_kernel_svm_clf, [-1.5, 2.5, -1, 1.5])
plot_dataset(X, y, [-1.5, 2.5, -1, 1.5])
plt.title(r"$d=3, r=1, C=5$", fontsize=18)
plt.subplot(122)
plot_predictions(poly100_kernel_svm_clf, [-1.5, 2.5, -1, 1.5])
plot_dataset(X, y, [-1.5, 2.5, -1, 1.5])
plt.title(r"$d=10, r=100, C=5$", fontsize=18)
save_fig("moons_kernelized_polynomial_svc_plot")
plt.show()
```
# Gaussian kernels
Before trying the following piece of code which implements Gaussian RBF (Radial Basis Function) kernels, remember _similarity features_ that were discussed in the lecture:
1. What are similarity features? What is the idea of adding a "landmark"?
2. If similarity features help to increase the power of the model, why should we be careful to just add a similarity feature for _each_ instance of the dataset?
3. How does the kernel trick (once again) save the day in this case?
4. What does the `gamma` parameter control?
Below you find a code implementation which creates a set of four plots with different values for gamma and hyperparameter C. Try different values for both. Which direction _increases_ regularisation of the model? In which direction would you go to avoid underfitting? In which to avoid overfitting?
```
from sklearn.svm import SVC
# Set up multiple values for gamma and hyperparameter C
# and create a list of value pairs.
gamma1, gamma2 = 0.1, 5
C1, C2 = 0.001, 1000
hyperparams = (gamma1, C1), (gamma1, C2), (gamma2, C1), (gamma2, C2)
# Store multiple SVM classifiers in a list with these sets of
# hyperparameters. For all of them, use a pipeline to allow
# scaling of the inputs.
svm_clfs = []
for gamma, C in hyperparams:
rbf_kernel_svm_clf = Pipeline([
("scaler", StandardScaler()),
("svm_clf", SVC(kernel="rbf", gamma=gamma, C=C))
])
rbf_kernel_svm_clf.fit(X, y)
svm_clfs.append(rbf_kernel_svm_clf)
# Now do the plotting.
plt.figure(figsize=(11, 7))
for i, svm_clf in enumerate(svm_clfs):
plt.subplot(221 + i)
plot_predictions(svm_clf, [-1.5, 2.5, -1, 1.5])
plot_dataset(X, y, [-1.5, 2.5, -1, 1.5])
gamma, C = hyperparams[i]
plt.title(r"$\gamma = {}, C = {}$".format(gamma, C), fontsize=16)
save_fig("moons_rbf_svc_plot")
plt.show()
```
# Regression
The following code implements the support vector regression class from Scikit-Learn ([SVR](https://scikit-learn.org/stable/modules/generated/sklearn.svm.SVR.html)). Here are a couple of questions (some of which require changes to the code, others are just conceptual:
1. Quick recap: whereas the SVC class tries to make a classification decision, what is the job of this regression class? How is the output different?
2. Try different values for the hyperparameter C. What does it control?
3. How should the margin of a 'good' SVR model look like? Should it be broad? Should it be narrow? How does the parameter epsilon affect this?
```
# Generate some random data (degree = 2).
np.random.seed(42)
m = 100
X = 2 * np.random.rand(m, 1) - 1
y = (0.2 + 0.1 * X + 0.5 * X**2 + np.random.randn(m, 1)/10).ravel()
# Import the support vector regression class and create two
# instances with different hyperparameters.
from sklearn.svm import SVR
svm_poly_reg1 = SVR(kernel="poly", degree=2, C=100, epsilon=0.1, gamma="auto")
svm_poly_reg2 = SVR(kernel="poly", degree=2, C=0.01, epsilon=0.1, gamma="auto")
svm_poly_reg1.fit(X, y)
svm_poly_reg2.fit(X, y)
# Now do the plotting.
def plot_svm_regression(svm_reg, X, y, axes):
x1s = np.linspace(axes[0], axes[1], 100).reshape(100, 1)
y_pred = svm_reg.predict(x1s)
plt.plot(x1s, y_pred, "k-", linewidth=2, label=r"$\hat{y}$")
plt.plot(x1s, y_pred + svm_reg.epsilon, "k--")
plt.plot(x1s, y_pred - svm_reg.epsilon, "k--")
plt.scatter(X[svm_reg.support_], y[svm_reg.support_], s=180, facecolors='#FFAAAA')
plt.plot(X, y, "bo")
plt.xlabel(r"$x_1$", fontsize=18)
plt.legend(loc="upper left", fontsize=18)
plt.axis(axes)
plt.figure(figsize=(9, 4))
plt.subplot(121)
plot_svm_regression(svm_poly_reg1, X, y, [-1, 1, 0, 1])
plt.title(r"$degree={}, C={}, \epsilon = {}$".format(svm_poly_reg1.degree, svm_poly_reg1.C, svm_poly_reg1.epsilon), fontsize=18)
plt.ylabel(r"$y$", fontsize=18, rotation=0)
plt.subplot(122)
plot_svm_regression(svm_poly_reg2, X, y, [-1, 1, 0, 1])
plt.title(r"$degree={}, C={}, \epsilon = {}$".format(svm_poly_reg2.degree, svm_poly_reg2.C, svm_poly_reg2.epsilon), fontsize=18)
save_fig("svm_with_polynomial_kernel_plot")
plt.show()
```
|
github_jupyter
|
# Create TensorFlow Deep Neural Network Model
**Learning Objective**
- Create a DNN model using the high-level Estimator API
## Introduction
We'll begin by modeling our data using a Deep Neural Network. To achieve this we will use the high-level Estimator API in Tensorflow. Have a look at the various models available through the Estimator API in [the documentation here](https://www.tensorflow.org/api_docs/python/tf/estimator).
Start by setting the environment variables related to your project.
```
PROJECT = "cloud-training-demos" # Replace with your PROJECT
BUCKET = "cloud-training-bucket" # Replace with your BUCKET
REGION = "us-central1" # Choose an available region for Cloud MLE
TFVERSION = "1.14" # TF version for CMLE to use
import os
os.environ["BUCKET"] = BUCKET
os.environ["PROJECT"] = PROJECT
os.environ["REGION"] = REGION
os.environ["TFVERSION"] = TFVERSION
%%bash
if ! gsutil ls | grep -q gs://${BUCKET}/; then
gsutil mb -l ${REGION} gs://${BUCKET}
fi
%%bash
ls *.csv
```
## Create TensorFlow model using TensorFlow's Estimator API ##
We'll begin by writing an input function to read the data and define the csv column names and label column. We'll also set the default csv column values and set the number of training steps.
```
import shutil
import numpy as np
import tensorflow as tf
print(tf.__version__)
CSV_COLUMNS = "weight_pounds,is_male,mother_age,plurality,gestation_weeks".split(',')
LABEL_COLUMN = "weight_pounds"
# Set default values for each CSV column
DEFAULTS = [[0.0], ["null"], [0.0], ["null"], [0.0]]
TRAIN_STEPS = 1000
```
### Create the input function
Now we are ready to create an input function using the Dataset API.
```
def read_dataset(filename_pattern, mode, batch_size = 512):
def _input_fn():
def decode_csv(value_column):
columns = tf.decode_csv(records = value_column, record_defaults = DEFAULTS)
features = dict(zip(CSV_COLUMNS, columns))
label = features.pop(LABEL_COLUMN)
return features, label
# Create list of files that match pattern
file_list = tf.gfile.Glob(filename = filename_pattern)
# Create dataset from file list
dataset = (tf.data.TextLineDataset(filenames = file_list) # Read text file
.map(map_func = decode_csv)) # Transform each elem by applying decode_csv fn
if mode == tf.estimator.ModeKeys.TRAIN:
num_epochs = None # indefinitely
dataset = dataset.shuffle(buffer_size = 10 * batch_size)
else:
num_epochs = 1 # end-of-input after this
dataset = dataset.repeat(count = num_epochs).batch(batch_size = batch_size)
return dataset
return _input_fn
```
### Create the feature columns
Next, we define the feature columns
```
def get_categorical(name, values):
return tf.feature_column.indicator_column(
categorical_column = tf.feature_column.categorical_column_with_vocabulary_list(key = name, vocabulary_list = values))
def get_cols():
# Define column types
return [\
get_categorical("is_male", ["True", "False", "Unknown"]),
tf.feature_column.numeric_column(key = "mother_age"),
get_categorical("plurality",
["Single(1)", "Twins(2)", "Triplets(3)",
"Quadruplets(4)", "Quintuplets(5)","Multiple(2+)"]),
tf.feature_column.numeric_column(key = "gestation_weeks")
]
```
### Create the Serving Input function
To predict with the TensorFlow model, we also need a serving input function. This will allow us to serve prediction later using the predetermined inputs. We will want all the inputs from our user.
```
def serving_input_fn():
feature_placeholders = {
"is_male": tf.placeholder(dtype = tf.string, shape = [None]),
"mother_age": tf.placeholder(dtype = tf.float32, shape = [None]),
"plurality": tf.placeholder(dtype = tf.string, shape = [None]),
"gestation_weeks": tf.placeholder(dtype = tf.float32, shape = [None])
}
features = {
key: tf.expand_dims(input = tensor, axis = -1)
for key, tensor in feature_placeholders.items()
}
return tf.estimator.export.ServingInputReceiver(features = features, receiver_tensors = feature_placeholders)
```
### Create the model and run training and evaluation
Lastly, we'll create the estimator to train and evaluate. In the cell below, we'll set up a `DNNRegressor` estimator and the train and evaluation operations.
```
def train_and_evaluate(output_dir):
EVAL_INTERVAL = 300
run_config = tf.estimator.RunConfig(
save_checkpoints_secs = EVAL_INTERVAL,
keep_checkpoint_max = 3)
estimator = tf.estimator.DNNRegressor(
model_dir = output_dir,
feature_columns = get_cols(),
hidden_units = [64, 32],
config = run_config)
train_spec = tf.estimator.TrainSpec(
input_fn = read_dataset("train.csv", mode = tf.estimator.ModeKeys.TRAIN),
max_steps = TRAIN_STEPS)
exporter = tf.estimator.LatestExporter(name = "exporter", serving_input_receiver_fn = serving_input_fn)
eval_spec = tf.estimator.EvalSpec(
input_fn = read_dataset("eval.csv", mode = tf.estimator.ModeKeys.EVAL),
steps = None,
start_delay_secs = 60, # start evaluating after N seconds
throttle_secs = EVAL_INTERVAL, # evaluate every N seconds
exporters = exporter)
tf.estimator.train_and_evaluate(estimator = estimator, train_spec = train_spec, eval_spec = eval_spec)
```
Finally, we train the model!
```
# Run the model
shutil.rmtree(path = "babyweight_trained_dnn", ignore_errors = True) # start fresh each time
train_and_evaluate("babyweight_trained_dnn")
```
When I ran it, the final RMSE (the average_loss) is about **1.16**. You can explore the contents of the `exporter` directory to see the contains final model.
Copyright 2017-2018 Google Inc. Licensed under the Apache License, Version 2.0 (the "License"); you may not use this file except in compliance with the License. You may obtain a copy of the License at http://www.apache.org/licenses/LICENSE-2.0 Unless required by applicable law or agreed to in writing, software distributed under the License is distributed on an "AS IS" BASIS, WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied. See the License for the specific language governing permissions and limitations under the License
|
github_jupyter
|
# Compare different DEMs for individual glaciers
For most glaciers in the world there are several digital elevation models (DEM) which cover the respective glacier. In OGGM we have currently implemented 10 different open access DEMs to choose from. Some are regional and only available in certain areas (e.g. Greenland or Antarctica) and some cover almost the entire globe. For more information, visit the [rgitools documentation about DEMs](https://rgitools.readthedocs.io/en/latest/dems.html).
This notebook allows to see which of the DEMs are available for a selected glacier and how they compare to each other. That way it is easy to spot systematic differences and also invalid points in the DEMs.
## Input parameters
This notebook can be run as a script with parameters using [papermill](https://github.com/nteract/papermill), but it is not necessary. The following cell contains the parameters you can choose from:
```
# The RGI Id of the glaciers you want to look for
# Use the original shapefiles or the GLIMS viewer to check for the ID: https://www.glims.org/maps/glims
rgi_id = 'RGI60-11.00897'
# The default is to test for all sources available for this glacier
# Set to a list of source names to override this
sources = None
# Where to write the plots. Default is in the current working directory
plot_dir = ''
# The RGI version to use
# V62 is an unofficial modification of V6 with only minor, backwards compatible modifications
prepro_rgi_version = 62
# Size of the map around the glacier. Currently only 10 and 40 are available
prepro_border = 10
# Degree of processing level. Currently only 1 is available.
from_prepro_level = 1
```
## Check input and set up
```
# The sources can be given as parameters
if sources is not None and isinstance(sources, str):
sources = sources.split(',')
# Plotting directory as well
if not plot_dir:
plot_dir = './' + rgi_id
import os
plot_dir = os.path.abspath(plot_dir)
import pandas as pd
import numpy as np
from oggm import cfg, utils, workflow, tasks, graphics, GlacierDirectory
import xarray as xr
import geopandas as gpd
import salem
import matplotlib.pyplot as plt
from mpl_toolkits.axes_grid1 import AxesGrid
import itertools
from oggm.utils import DEM_SOURCES
from oggm.workflow import init_glacier_directories
# Make sure the plot directory exists
utils.mkdir(plot_dir);
# Use OGGM to download the data
cfg.initialize()
cfg.PATHS['working_dir'] = utils.gettempdir(dirname='OGGM-DEMS', reset=True)
cfg.PARAMS['use_intersects'] = False
```
## Download the data using OGGM utility functions
Note that you could reach the same goal by downloading the data manually from https://cluster.klima.uni-bremen.de/~oggm/gdirs/oggm_v1.4/rgitopo/
```
# URL of the preprocessed GDirs
gdir_url = 'https://cluster.klima.uni-bremen.de/~oggm/gdirs/oggm_v1.4/rgitopo/'
# We use OGGM to download the data
gdir = init_glacier_directories([rgi_id], from_prepro_level=1, prepro_border=10,
prepro_rgi_version='62', prepro_base_url=gdir_url)[0]
```
## Read the DEMs and store them all in a dataset
```
if sources is None:
sources = [src for src in os.listdir(gdir.dir) if src in utils.DEM_SOURCES]
print('RGI ID:', rgi_id)
print('Available DEM sources:', sources)
print('Plotting directory:', plot_dir)
# We use xarray to store the data
ods = xr.Dataset()
for src in sources:
demfile = os.path.join(gdir.dir, src) + '/dem.tif'
with xr.open_rasterio(demfile) as ds:
data = ds.sel(band=1).load() * 1.
ods[src] = data.where(data > -100, np.NaN)
sy, sx = np.gradient(ods[src], gdir.grid.dx, gdir.grid.dx)
ods[src + '_slope'] = ('y', 'x'), np.arctan(np.sqrt(sy**2 + sx**2))
with xr.open_rasterio(gdir.get_filepath('glacier_mask')) as ds:
ods['mask'] = ds.sel(band=1).load()
# Decide on the number of plots and figure size
ns = len(sources)
x_size = 12
n_cols = 3
n_rows = -(-ns // n_cols)
y_size = x_size / n_cols * n_rows
```
## Raw topography data
```
smap = salem.graphics.Map(gdir.grid, countries=False)
smap.set_shapefile(gdir.read_shapefile('outlines'))
smap.set_plot_params(cmap='topo')
smap.set_lonlat_contours(add_tick_labels=False)
smap.set_plot_params(vmin=np.nanquantile([ods[s].min() for s in sources], 0.25),
vmax=np.nanquantile([ods[s].max() for s in sources], 0.75))
fig = plt.figure(figsize=(x_size, y_size))
grid = AxesGrid(fig, 111,
nrows_ncols=(n_rows, n_cols),
axes_pad=0.7,
cbar_mode='each',
cbar_location='right',
cbar_pad=0.1
)
for i, s in enumerate(sources):
data = ods[s]
smap.set_data(data)
ax = grid[i]
smap.visualize(ax=ax, addcbar=False, title=s)
if np.isnan(data).all():
grid[i].cax.remove()
continue
cax = grid.cbar_axes[i]
smap.colorbarbase(cax)
# take care of uneven grids
if ax != grid[-1]:
grid[-1].remove()
grid[-1].cax.remove()
plt.savefig(os.path.join(plot_dir, 'dem_topo_color.png'), dpi=150, bbox_inches='tight')
```
## Shaded relief
```
fig = plt.figure(figsize=(x_size, y_size))
grid = AxesGrid(fig, 111,
nrows_ncols=(n_rows, n_cols),
axes_pad=0.7,
cbar_mode='none',
cbar_location='right',
cbar_pad=0.1
)
smap.set_plot_params(cmap='Blues')
smap.set_shapefile()
for i, s in enumerate(sources):
data = ods[s].copy().where(np.isfinite(ods[s]), 0)
smap.set_data(data * 0)
ax = grid[i]
smap.set_topography(data)
smap.visualize(ax=ax, addcbar=False, title=s)
# take care of uneven grids
if ax != grid[-1]:
grid[-1].remove()
grid[-1].cax.remove()
plt.savefig(os.path.join(plot_dir, 'dem_topo_shade.png'), dpi=150, bbox_inches='tight')
```
## Slope
```
fig = plt.figure(figsize=(x_size, y_size))
grid = AxesGrid(fig, 111,
nrows_ncols=(n_rows, n_cols),
axes_pad=0.7,
cbar_mode='each',
cbar_location='right',
cbar_pad=0.1
)
smap.set_topography();
smap.set_plot_params(vmin=0, vmax=0.7, cmap='Blues')
for i, s in enumerate(sources):
data = ods[s + '_slope']
smap.set_data(data)
ax = grid[i]
smap.visualize(ax=ax, addcbar=False, title=s + ' (slope)')
cax = grid.cbar_axes[i]
smap.colorbarbase(cax)
# take care of uneven grids
if ax != grid[-1]:
grid[-1].remove()
grid[-1].cax.remove()
plt.savefig(os.path.join(plot_dir, 'dem_slope.png'), dpi=150, bbox_inches='tight')
```
## Some simple statistics about the DEMs
```
df = pd.DataFrame()
for s in sources:
df[s] = ods[s].data.flatten()[ods.mask.data.flatten() == 1]
dfs = pd.DataFrame()
for s in sources:
dfs[s] = ods[s + '_slope'].data.flatten()[ods.mask.data.flatten() == 1]
df.describe()
```
## Comparison matrix plot
```
# Table of differences between DEMS
df_diff = pd.DataFrame()
done = []
for s1, s2 in itertools.product(sources, sources):
if s1 == s2:
continue
if (s2, s1) in done:
continue
df_diff[s1 + '-' + s2] = df[s1] - df[s2]
done.append((s1, s2))
# Decide on plot levels
max_diff = df_diff.quantile(0.99).max()
base_levels = np.array([-8, -5, -3, -1.5, -1, -0.5, -0.2, -0.1, 0, 0.1, 0.2, 0.5, 1, 1.5, 3, 5, 8])
if max_diff < 10:
levels = base_levels
elif max_diff < 100:
levels = base_levels * 10
elif max_diff < 1000:
levels = base_levels * 100
else:
levels = base_levels * 1000
levels = [l for l in levels if abs(l) < max_diff]
if max_diff > 10:
levels = [int(l) for l in levels]
levels
smap.set_plot_params(levels=levels, cmap='PuOr', extend='both')
smap.set_shapefile(gdir.read_shapefile('outlines'))
fig = plt.figure(figsize=(14, 14))
grid = AxesGrid(fig, 111,
nrows_ncols=(ns - 1, ns - 1),
axes_pad=0.3,
cbar_mode='single',
cbar_location='right',
cbar_pad=0.1
)
done = []
for ax in grid:
ax.set_axis_off()
for s1, s2 in itertools.product(sources, sources):
if s1 == s2:
continue
if (s2, s1) in done:
continue
data = ods[s1] - ods[s2]
ax = grid[sources.index(s1) * (ns - 1) + sources[1:].index(s2)]
ax.set_axis_on()
smap.set_data(data)
smap.visualize(ax=ax, addcbar=False)
done.append((s1, s2))
ax.set_title(s1 + '-' + s2, fontsize=8)
cax = grid.cbar_axes[0]
smap.colorbarbase(cax);
plt.savefig(os.path.join(plot_dir, 'dem_diffs.png'), dpi=150, bbox_inches='tight')
```
## Comparison scatter plot
```
import seaborn as sns
sns.set(style="ticks")
l1, l2 = (utils.nicenumber(df.min().min(), binsize=50, lower=True),
utils.nicenumber(df.max().max(), binsize=50, lower=False))
def plot_unity(xdata, ydata, **kwargs):
points = np.linspace(l1, l2, 100)
plt.gca().plot(points, points, color='k', marker=None,
linestyle=':', linewidth=3.0)
g = sns.pairplot(df.dropna(how='all', axis=1).dropna(), plot_kws=dict(s=50, edgecolor="C0", linewidth=1));
g.map_offdiag(plot_unity)
for asx in g.axes:
for ax in asx:
ax.set_xlim((l1, l2))
ax.set_ylim((l1, l2))
plt.savefig(os.path.join(plot_dir, 'dem_scatter.png'), dpi=150, bbox_inches='tight')
```
## Table statistics
```
df.describe()
df.corr()
df_diff.describe()
df_diff.abs().describe()
```
## What's next?
- return to the [OGGM documentation](https://docs.oggm.org)
- back to the [table of contents](welcome.ipynb)
|
github_jupyter
|
Created from https://github.com/awslabs/amazon-sagemaker-examples/blob/master/introduction_to_amazon_algorithms/random_cut_forest/random_cut_forest.ipynb
```
import boto3
import botocore
import sagemaker
import sys
bucket = 'tdk-awsml-sagemaker-data.io-dev' # <--- specify a bucket you have access to
prefix = ''
execution_role = sagemaker.get_execution_role()
# check if the bucket exists
try:
boto3.Session().client('s3').head_bucket(Bucket=bucket)
except botocore.exceptions.ParamValidationError as e:
print('Hey! You either forgot to specify your S3 bucket'
' or you gave your bucket an invalid name!')
except botocore.exceptions.ClientError as e:
if e.response['Error']['Code'] == '403':
print("Hey! You don't have permission to access the bucket, {}.".format(bucket))
elif e.response['Error']['Code'] == '404':
print("Hey! Your bucket, {}, doesn't exist!".format(bucket))
else:
raise
else:
print('Training input/output will be stored in: s3://{}/{}'.format(bucket, prefix))
%%time
import pandas as pd
import urllib.request
data_filename = 'nyc_taxi.csv'
data_source = 'https://raw.githubusercontent.com/numenta/NAB/master/data/realKnownCause/nyc_taxi.csv'
urllib.request.urlretrieve(data_source, data_filename)
taxi_data = pd.read_csv(data_filename, delimiter=',')
from sagemaker import RandomCutForest
session = sagemaker.Session()
# specify general training job information
rcf = RandomCutForest(role=execution_role,
train_instance_count=1,
train_instance_type='ml.m5.large',
data_location='s3://{}/{}/'.format(bucket, prefix),
output_path='s3://{}/{}/output'.format(bucket, prefix),
num_samples_per_tree=512,
num_trees=50)
# automatically upload the training data to S3 and run the training job
# TK - had to modify this line to use to_numpy() instead of as_matrix()
rcf.fit(rcf.record_set(taxi_data.value.to_numpy().reshape(-1,1)))
rcf_inference = rcf.deploy(
initial_instance_count=1,
instance_type='ml.m5.large',
)
print('Endpoint name: {}'.format(rcf_inference.endpoint))
from sagemaker.predictor import csv_serializer, json_deserializer
rcf_inference.content_type = 'text/csv'
rcf_inference.serializer = csv_serializer
rcf_inference.accept = 'application/json'
rcf_inference.deserializer = json_deserializer
# TK - had to modify this line to use to_numpy() instead of as_matrix()
taxi_data_numpy = taxi_data.value.to_numpy().reshape(-1,1)
print(taxi_data_numpy[:6])
results = rcf_inference.predict(taxi_data_numpy[:6])
sagemaker.Session().delete_endpoint(rcf_inference.endpoint)
```
|
github_jupyter
|
<br>
# Analysis of Big Earth Data with Jupyter Notebooks
<img src='./img/opengeohub_logo.png' alt='OpenGeoHub Logo' align='right' width='25%'></img>
Lecture given for OpenGeoHub summer school 2020<br>
Tuesday, 18. August 2020 | 11:00-13:00 CEST
#### Lecturer
* [Julia Wagemann](https://jwagemann.com) | Independent consultant and Phd student at University of Marburg
#### Access to tutorial material
Notebooks are available on [GitHub](https://github.com/jwagemann/2020_analysis_of_big_earth_data_with_jupyter).
<hr>
### Access to the JupyterHub
You can access the lecture material on a JupyterHub instance, a pre-defined environment that gives you direct access to the data and Python packages required for following the lecture.
<div class="alert alert-block alert-success" align="left">
1. Web address: <a href='https://opengeohub.adamplatform.eu'>https://opengeohub.adamplatform.eu</a><br>
2. Create an account: <a href='https://meeoauth.adamplatform.eu'>https://meeoauth.adamplatform.eu</a><br>
3. Log into the <b>JupyterHub</b> with your account created.
</div>
<hr>
## What is this lecture about?
Growing volumes of `Big Earth Data` force us to change the way how we access and process large volumes of geospatial data. New (cloud-based) data systems are being developed, each offering different functionalities for users.
This lecture is split in two parts:
* **(Cloud-based) data access systems**<br>
This part will highlight five data access systems that allow you to access, download or process large volumes of Copernicus data related to climate and atmosphere. For each data system, an example is given how data can be retrieved.
Data access systems that will be covered:
* [Copernicus Climate Data Store (CDS)](https://cds.climate.copernicus.eu/) / [Copernicus Atmosphere Data Store (ADS)](https://ads.atmosphere.copernicus.eu/)
* [WEkEO - Copernicus Data and Information Access System](http://wekeo.eu/)
* [Open Data Registry on Amazon Web Services](http://registry.opendata.aws)
* [Google Earth Engine](https://code.earthengine.google.com/)
* **Case study: Analysis of Covid-19 with Sentinel-5P data**<br>
This example showcases a case study analysing daily Sentinel-5P data from 2019 and 2020 with Jupyter notebooks and the Python library [xarray](http://xarray.pydata.org/en/stable/) in order to analyse possible Covid-19 impacts in 2020.
## Lecture outline
This lecture has the following outline:
* [01 - Introduction to Project Jupyter (optional)](01_Intro_to_Python_and_Jupyter.ipynb)
* [02 - Copernicus Climate Data Store / Copernicus Atmosphere Data Store](02_copernicus_climate_atmosphere_data_store.ipynb)
* [03 - WEkEO - Copernicus Data and Information Access Service (DIAS)](03_WEkEO_dias_service.ipynb)
* [04 - Amazon Web Services Open Data Registry](04_aws_open_data_registry.ipynb)
* [05 - Google Earth Engine](05_google_earth_engine.ipynb)
* [11 - Covid-19 case study - Sentinel-5P anomaly map](11_covid19_case_study_s5p_anomaly_map.ipynb)
* [12 - Covid-19 case study - Sentinel-5P time-series analysis](12_covid19_case_study_s5p_time_series_analysis.ipynb)
<br>
<hr>
© 2020 | Julia Wagemann
<a rel="license" href="http://creativecommons.org/licenses/by/4.0/"><img style="float: right" alt="Creative Commons Lizenzvertrag" style="border-width:0" src="https://i.creativecommons.org/l/by/4.0/88x31.png" /></a>
|
github_jupyter
|
```
import pandas as pd
import numpy as np
from tools import acc_score
df_train = pd.read_csv("../data/train.csv", index_col=0)
df_test = pd.read_csv("../data/test.csv", index_col=0)
train_bins = seq_to_num(df_train.Sequence, target_split=True, pad=True, pad_adaptive=True,
pad_maxlen=100, dtype=np.float32, drop_na_inf=True,
nbins=5, bins_by='terms')
test_bins = seq_to_num(df_test.Sequence, target_split=True, pad_adaptive=True,
dtype=np.float32, drop_na_inf=True, nbins=5, bins_by='terms')
train_X, train_y, _ = train_bins[4]
test_X, test_y, test_idx = test_bins[4]
from sklearn.tree import DecisionTreeRegressor, ExtraTreeRegressor
dt = DecisionTreeRegressor(random_state=42)
dt.fit(train_X, train_y)
acc_score(dt.predict(test_X), test_y)
train_X2, train_y2, _ = train_bins[1]
test_X2, test_y2, _ = test_bins[1]
etr = ExtraTreeRegressor(max_depth=100, random_state=42)
etr.fit(train_X2, train_y2)
acc_score(etr.predict(test_X2), test_y2)
# too long sequence?
train_X2, train_y2 = train_bins[2]
test_X2, test_y2 = test_bins[2]
etr = DecisionTreeRegressor(max_depth=5, random_state=42)
etr.fit(train_X2, train_y2)
acc_score(etr.predict(test_X2), test_y2)
from sklearn.neural_network import MLPRegressor
# NNet still doesn't work
mlp = MLPRegressor(hidden_layer_sizes=(10, 1))
mlp.fit(train_X, train_y)
acc_score(mlp.predict(test_X), test_y)
# Try to combine predictions for bin 3 and 4 (by terms), while
# fallback to mode on bin 0, 1, 2
def mmode(arr):
modes = []
for row in arr:
counts = {i: row.tolist().count(i) for i in row}
if len(counts) > 0:
modes.append(max(counts.items(), key=lambda x:x[1])[0])
else:
modes.append(0)
return modes
kg_train = pd.read_csv('../data/kaggle_train.csv', index_col=0)
kg_test = pd.read_csv('../data/kaggle_test.csv', index_col=0)
train_bins = seq_to_num(kg_train.Sequence, target_split=True,
pad_adaptive=True, dtype=np.float32, drop_na_inf=True,
nbins=5, bins_by='terms')
test_bins = seq_to_num(kg_test.Sequence, target_split=False, pad_adaptive=True,
dtype=np.float32, drop_na_inf=True, nbins=5, bins_by='terms')
bin3_X, bin3_y, _ = train_bins[3]
bin4_X, bin4_y, _ = train_bins[4]
dt_bin3 = DecisionTreeRegressor(random_state=42)
dt_bin4 = DecisionTreeRegressor(random_state=42)
dt_bin3.fit(bin3_X, bin3_y)
dt_bin4.fit(bin4_X, bin4_y)
pred_bin3 = dt_bin3.predict(test_bins[3][0])
pred_bin4 = dt_bin4.predict(test_bins[4][0])
test_bins[3][1].shape, pred_bin3.shape
pred_bin0 = mmode(test_bins[0])
pred_bin1 = mmode(test_bins[1])
pred_bin2 = mmode(test_bins[2])
pred3 = pd.Series(pred_bin3, index=test_bins[3][1], dtype=object).map(lambda x: int(x))
pred4 = pd.Series(pred_bin4, index=test_bins[4][1], dtype=object).map(lambda x: int(x))
pred_total = pd.Series(np.zeros(kg_test.shape[0]), index=kg_test.index, dtype=np.int64)
pred_total[test_bins[3][1]] = pred_bin3
pred_total[test_bins[4][1]] = pred_bin4
prep_submit(pred_total)
```
|
github_jupyter
|
# 📃 Solution of Exercise M6.01
The aim of this notebook is to investigate if we can tune the hyperparameters
of a bagging regressor and evaluate the gain obtained.
We will load the California housing dataset and split it into a training and
a testing set.
```
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
data, target = fetch_california_housing(as_frame=True, return_X_y=True)
target *= 100 # rescale the target in k$
data_train, data_test, target_train, target_test = train_test_split(
data, target, random_state=0, test_size=0.5)
```
<div class="admonition note alert alert-info">
<p class="first admonition-title" style="font-weight: bold;">Note</p>
<p class="last">If you want a deeper overview regarding this dataset, you can refer to the
Appendix - Datasets description section at the end of this MOOC.</p>
</div>
Create a `BaggingRegressor` and provide a `DecisionTreeRegressor`
to its parameter `base_estimator`. Train the regressor and evaluate its
statistical performance on the testing set using the mean absolute error.
```
from sklearn.metrics import mean_absolute_error
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import BaggingRegressor
tree = DecisionTreeRegressor()
bagging = BaggingRegressor(base_estimator=tree, n_jobs=-1)
bagging.fit(data_train, target_train)
target_predicted = bagging.predict(data_test)
print(f"Basic mean absolute error of the bagging regressor:\n"
f"{mean_absolute_error(target_test, target_predicted):.2f} k$")
abs(target_test - target_predicted).mean()
```
Now, create a `RandomizedSearchCV` instance using the previous model and
tune the important parameters of the bagging regressor. Find the best
parameters and check if you are able to find a set of parameters that
improve the default regressor still using the mean absolute error as a
metric.
<div class="admonition tip alert alert-warning">
<p class="first admonition-title" style="font-weight: bold;">Tip</p>
<p class="last">You can list the bagging regressor's parameters using the <tt class="docutils literal">get_params</tt>
method.</p>
</div>
```
for param in bagging.get_params().keys():
print(param)
from scipy.stats import randint
from sklearn.model_selection import RandomizedSearchCV
param_grid = {
"n_estimators": randint(10, 30),
"max_samples": [0.5, 0.8, 1.0],
"max_features": [0.5, 0.8, 1.0],
"base_estimator__max_depth": randint(3, 10),
}
search = RandomizedSearchCV(
bagging, param_grid, n_iter=20, scoring="neg_mean_absolute_error"
)
_ = search.fit(data_train, target_train)
import pandas as pd
columns = [f"param_{name}" for name in param_grid.keys()]
columns += ["mean_test_score", "std_test_score", "rank_test_score"]
cv_results = pd.DataFrame(search.cv_results_)
cv_results = cv_results[columns].sort_values(by="rank_test_score")
cv_results["mean_test_score"] = -cv_results["mean_test_score"]
cv_results
target_predicted = search.predict(data_test)
print(f"Mean absolute error after tuning of the bagging regressor:\n"
f"{mean_absolute_error(target_test, target_predicted):.2f} k$")
```
We see that the predictor provided by the bagging regressor does not need
much hyperparameter tuning compared to a single decision tree. We see that
the bagging regressor provides a predictor for which tuning the
hyperparameters is not as important as in the case of fitting a single
decision tree.
|
github_jupyter
|
## Recommendations with MovieTweetings: Collaborative Filtering
One of the most popular methods for making recommendations is **collaborative filtering**. In collaborative filtering, you are using the collaboration of user-item recommendations to assist in making new recommendations.
There are two main methods of performing collaborative filtering:
1. **Neighborhood-Based Collaborative Filtering**, which is based on the idea that we can either correlate items that are similar to provide recommendations or we can correlate users to one another to provide recommendations.
2. **Model Based Collaborative Filtering**, which is based on the idea that we can use machine learning and other mathematical models to understand the relationships that exist amongst items and users to predict ratings and provide ratings.
In this notebook, you will be working on performing **neighborhood-based collaborative filtering**. There are two main methods for performing collaborative filtering:
1. **User-based collaborative filtering:** In this type of recommendation, users related to the user you would like to make recommendations for are used to create a recommendation.
2. **Item-based collaborative filtering:** In this type of recommendation, first you need to find the items that are most related to each other item (based on similar ratings). Then you can use the ratings of an individual on those similar items to understand if a user will like the new item.
In this notebook you will be implementing **user-based collaborative filtering**. However, it is easy to extend this approach to make recommendations using **item-based collaborative filtering**. First, let's read in our data and necessary libraries.
**NOTE**: Because of the size of the datasets, some of your code cells here will take a while to execute, so be patient!
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import tests as t
from scipy.sparse import csr_matrix
from IPython.display import HTML
%matplotlib inline
# Read in the datasets
movies = pd.read_csv('movies_clean.csv')
reviews = pd.read_csv('reviews_clean.csv')
del movies['Unnamed: 0']
del reviews['Unnamed: 0']
print(reviews.head())
```
### Measures of Similarity
When using **neighborhood** based collaborative filtering, it is important to understand how to measure the similarity of users or items to one another.
There are a number of ways in which we might measure the similarity between two vectors (which might be two users or two items). In this notebook, we will look specifically at two measures used to compare vectors:
* **Pearson's correlation coefficient**
Pearson's correlation coefficient is a measure of the strength and direction of a linear relationship. The value for this coefficient is a value between -1 and 1 where -1 indicates a strong, negative linear relationship and 1 indicates a strong, positive linear relationship.
If we have two vectors x and y, we can define the correlation between the vectors as:
$$CORR(x, y) = \frac{\text{COV}(x, y)}{\text{STDEV}(x)\text{ }\text{STDEV}(y)}$$
where
$$\text{STDEV}(x) = \sqrt{\frac{1}{n-1}\sum_{i=1}^{n}(x_i - \bar{x})^2}$$
and
$$\text{COV}(x, y) = \frac{1}{n-1}\sum_{i=1}^{n}(x_i - \bar{x})(y_i - \bar{y})$$
where n is the length of the vector, which must be the same for both x and y and $\bar{x}$ is the mean of the observations in the vector.
We can use the correlation coefficient to indicate how alike two vectors are to one another, where the closer to 1 the coefficient, the more alike the vectors are to one another. There are some potential downsides to using this metric as a measure of similarity. You will see some of these throughout this workbook.
* **Euclidean distance**
Euclidean distance is a measure of the straightline distance from one vector to another. Because this is a measure of distance, larger values are an indication that two vectors are different from one another (which is different than Pearson's correlation coefficient).
Specifically, the euclidean distance between two vectors x and y is measured as:
$$ \text{EUCL}(x, y) = \sqrt{\sum_{i=1}^{n}(x_i - y_i)^2}$$
Different from the correlation coefficient, no scaling is performed in the denominator. Therefore, you need to make sure all of your data are on the same scale when using this metric.
**Note:** Because measuring similarity is often based on looking at the distance between vectors, it is important in these cases to scale your data or to have all data be in the same scale. In this case, we will not need to scale data because they are all on a 10 point scale, but it is always something to keep in mind!
------------
### User-Item Matrix
In order to calculate the similarities, it is common to put values in a matrix. In this matrix, users are identified by each row, and items are represented by columns.

In the above matrix, you can see that **User 1** and **User 2** both used **Item 1**, and **User 2**, **User 3**, and **User 4** all used **Item 2**. However, there are also a large number of missing values in the matrix for users who haven't used a particular item. A matrix with many missing values (like the one above) is considered **sparse**.
Our first goal for this notebook is to create the above matrix with the **reviews** dataset. However, instead of 1 values in each cell, you should have the actual rating.
The users will indicate the rows, and the movies will exist across the columns. To create the user-item matrix, we only need the first three columns of the **reviews** dataframe, which you can see by running the cell below.
```
user_items = reviews[['user_id', 'movie_id', 'rating']]
user_items.head()
```
### Creating the User-Item Matrix
In order to create the user-items matrix (like the one above), I personally started by using a [pivot table](https://pandas.pydata.org/pandas-docs/stable/generated/pandas.pivot_table.html).
However, I quickly ran into a memory error (a common theme throughout this notebook). I will help you navigate around many of the errors I had, and achieve useful collaborative filtering results!
_____
`1.` Create a matrix where the users are the rows, the movies are the columns, and the ratings exist in each cell, or a NaN exists in cells where a user hasn't rated a particular movie. If you get a memory error (like I did), [this link here](https://stackoverflow.com/questions/39648991/pandas-dataframe-pivot-memory-error) might help you!
```
# Create user-by-item matrix
user_by_movie = user_items.groupby(['user_id', 'movie_id'])['rating'].max().unstack()
```
Check your results below to make sure your matrix is ready for the upcoming sections.
```
assert movies.shape[0] == user_by_movie.shape[1], "Oh no! Your matrix should have {} columns, and yours has {}!".format(movies.shape[0], user_by_movie.shape[1])
assert reviews.user_id.nunique() == user_by_movie.shape[0], "Oh no! Your matrix should have {} rows, and yours has {}!".format(reviews.user_id.nunique(), user_by_movie.shape[0])
print("Looks like you are all set! Proceed!")
HTML('<img src="images/greatjob.webp">')
```
`2.` Now that you have a matrix of users by movies, use this matrix to create a dictionary where the key is each user and the value is an array of the movies each user has rated.
```
# Create a dictionary with users and corresponding movies seen
def movies_watched(user_id):
'''
INPUT:
user_id - the user_id of an individual as int
OUTPUT:
movies - an array of movies the user has watched
'''
movies = user_by_movie.loc[user_id][user_by_movie.loc[user_id].isnull() == False].index.values
return movies
def create_user_movie_dict():
'''
INPUT: None
OUTPUT: movies_seen - a dictionary where each key is a user_id and the value is an array of movie_ids
Creates the movies_seen dictionary
'''
n_users = user_by_movie.shape[0]
movies_seen = dict()
for user1 in range(1, n_users+1):
# assign list of movies to each user key
movies_seen[user1] = movies_watched(user1)
return movies_seen
movies_seen = create_user_movie_dict()
```
`3.` If a user hasn't rated more than 2 movies, we consider these users "too new". Create a new dictionary that only contains users who have rated more than 2 movies. This dictionary will be used for all the final steps of this workbook.
```
# Remove individuals who have watched 2 or fewer movies - don't have enough data to make recs
def create_movies_to_analyze(movies_seen, lower_bound=2):
'''
INPUT:
movies_seen - a dictionary where each key is a user_id and the value is an array of movie_ids
lower_bound - (an int) a user must have more movies seen than the lower bound to be added to the movies_to_analyze dictionary
OUTPUT:
movies_to_analyze - a dictionary where each key is a user_id and the value is an array of movie_ids
The movies_seen and movies_to_analyze dictionaries should be the same except that the output dictionary has removed
'''
movies_to_analyze = dict()
for user, movies in movies_seen.items():
if len(movies) > lower_bound:
movies_to_analyze[user] = movies
return movies_to_analyze
movies_to_analyze = create_movies_to_analyze(movies_seen)
# Run the tests below to check that your movies_to_analyze matches the solution
assert len(movies_to_analyze) == 23512, "Oops! It doesn't look like your dictionary has the right number of individuals."
assert len(movies_to_analyze[2]) == 23, "Oops! User 2 didn't match the number of movies we thought they would have."
assert len(movies_to_analyze[7]) == 3, "Oops! User 7 didn't match the number of movies we thought they would have."
print("If this is all you see, you are good to go!")
```
### Calculating User Similarities
Now that you have set up the **movies_to_analyze** dictionary, it is time to take a closer look at the similarities between users. Below is the pseudocode for how I thought about determining the similarity between users:
```
for user1 in movies_to_analyze
for user2 in movies_to_analyze
see how many movies match between the two users
if more than two movies in common
pull the overlapping movies
compute the distance/similarity metric between ratings on the same movies for the two users
store the users and the distance metric
```
However, this took a very long time to run, and other methods of performing these operations did not fit on the workspace memory!
Therefore, rather than creating a dataframe with all possible pairings of users in our data, your task for this question is to look at a few specific examples of the correlation between ratings given by two users. For this question consider you want to compute the [correlation](https://pandas.pydata.org/pandas-docs/stable/generated/pandas.DataFrame.corr.html) between users.
`4.` Using the **movies_to_analyze** dictionary and **user_by_movie** dataframe, create a function that computes the correlation between the ratings of similar movies for two users. Then use your function to compare your results to ours using the tests below.
```
def compute_correlation(user1, user2):
'''
INPUT
user1 - int user_id
user2 - int user_id
OUTPUT
the correlation between the matching ratings between the two users
'''
# Pull movies for each user
movies1 = movies_to_analyze[user1]
movies2 = movies_to_analyze[user2]
# Find Similar Movies
sim_movs = np.intersect1d(movies1, movies2, assume_unique=True)
# Calculate correlation between the users
df = user_by_movie.loc[(user1, user2), sim_movs]
corr = df.transpose().corr().iloc[0,1]
return corr #return the correlation
# Test your function against the solution
assert compute_correlation(2,2) == 1.0, "Oops! The correlation between a user and itself should be 1.0."
assert round(compute_correlation(2,66), 2) == 0.76, "Oops! The correlation between user 2 and 66 should be about 0.76."
assert np.isnan(compute_correlation(2,104)), "Oops! The correlation between user 2 and 104 should be a NaN."
print("If this is all you see, then it looks like your function passed all of our tests!")
```
### Why the NaN's?
If the function you wrote passed all of the tests, then you have correctly set up your function to calculate the correlation between any two users.
`5.` But one question is, why are we still obtaining **NaN** values? As you can see in the code cell above, users 2 and 104 have a correlation of **NaN**. Why?
Think and write your ideas here about why these NaNs exist, and use the cells below to do some coding to validate your thoughts. You can check other pairs of users and see that there are actually many NaNs in our data - 2,526,710 of them in fact. These NaN's ultimately make the correlation coefficient a less than optimal measure of similarity between two users.
```
In the denominator of the correlation coefficient, we calculate the standard deviation for each user's ratings. The ratings for user 2 are all the same rating on the movies that match with user 104. Therefore, the standard deviation is 0. Because a 0 is in the denominator of the correlation coefficient, we end up with a **NaN** correlation coefficient. Therefore, a different approach is likely better for this particular situation.
```
```
# Which movies did both user 2 and user 104 see?
set_2 = set(movies_to_analyze[2])
set_104 = set(movies_to_analyze[104])
set_2.intersection(set_104)
# What were the ratings for each user on those movies?
print(user_by_movie.loc[2, set_2.intersection(set_104)])
print(user_by_movie.loc[104, set_2.intersection(set_104)])
```
`6.` Because the correlation coefficient proved to be less than optimal for relating user ratings to one another, we could instead calculate the euclidean distance between the ratings. I found [this post](https://stackoverflow.com/questions/1401712/how-can-the-euclidean-distance-be-calculated-with-numpy) particularly helpful when I was setting up my function. This function should be very similar to your previous function. When you feel confident with your function, test it against our results.
```
def compute_euclidean_dist(user1, user2):
'''
INPUT
user1 - int user_id
user2 - int user_id
OUTPUT
the euclidean distance between user1 and user2
'''
# Pull movies for each user
movies1 = movies_to_analyze[user1]
movies2 = movies_to_analyze[user2]
# Find Similar Movies
sim_movs = np.intersect1d(movies1, movies2, assume_unique=True)
# Calculate euclidean distance between the users
df = user_by_movie.loc[(user1, user2), sim_movs]
dist = np.linalg.norm(df.loc[user1] - df.loc[user2])
return dist #return the euclidean distance
# Read in solution euclidean distances"
import pickle
df_dists = pd.read_pickle("data/Term2/recommendations/lesson1/data/dists.p")
# Test your function against the solution
assert compute_euclidean_dist(2,2) == df_dists.query("user1 == 2 and user2 == 2")['eucl_dist'][0], "Oops! The distance between a user and itself should be 0.0."
assert round(compute_euclidean_dist(2,66), 2) == round(df_dists.query("user1 == 2 and user2 == 66")['eucl_dist'][1], 2), "Oops! The distance between user 2 and 66 should be about 2.24."
assert np.isnan(compute_euclidean_dist(2,104)) == np.isnan(df_dists.query("user1 == 2 and user2 == 104")['eucl_dist'][4]), "Oops! The distance between user 2 and 104 should be 2."
print("If this is all you see, then it looks like your function passed all of our tests!")
```
### Using the Nearest Neighbors to Make Recommendations
In the previous question, you read in **df_dists**. Therefore, you have a measure of distance between each user and every other user. This dataframe holds every possible pairing of users, as well as the corresponding euclidean distance.
Because of the **NaN** values that exist within the correlations of the matching ratings for many pairs of users, as we discussed above, we will proceed using **df_dists**. You will want to find the users that are 'nearest' each user. Then you will want to find the movies the closest neighbors have liked to recommend to each user.
I made use of the following objects:
* df_dists (to obtain the neighbors)
* user_items (to obtain the movies the neighbors and users have rated)
* movies (to obtain the names of the movies)
`7.` Complete the functions below, which allow you to find the recommendations for any user. There are five functions which you will need:
* **find_closest_neighbors** - this returns a list of user_ids from closest neighbor to farthest neighbor using euclidean distance
* **movies_liked** - returns an array of movie_ids
* **movie_names** - takes the output of movies_liked and returns a list of movie names associated with the movie_ids
* **make_recommendations** - takes a user id and goes through closest neighbors to return a list of movie names as recommendations
* **all_recommendations** = loops through every user and returns a dictionary of with the key as a user_id and the value as a list of movie recommendations
```
def find_closest_neighbors(user):
'''
INPUT:
user - (int) the user_id of the individual you want to find the closest users
OUTPUT:
closest_neighbors - an array of the id's of the users sorted from closest to farthest away
'''
# I treated ties as arbitrary and just kept whichever was easiest to keep using the head method
# You might choose to do something less hand wavy
closest_users = df_dists[df_dists['user1']==user].sort_values(by='eucl_dist').iloc[1:]['user2']
closest_neighbors = np.array(closest_users)
return closest_neighbors
def movies_liked(user_id, min_rating=7):
'''
INPUT:
user_id - the user_id of an individual as int
min_rating - the minimum rating considered while still a movie is still a "like" and not a "dislike"
OUTPUT:
movies_liked - an array of movies the user has watched and liked
'''
movies_liked = np.array(user_items.query('user_id == @user_id and rating > (@min_rating -1)')['movie_id'])
return movies_liked
def movie_names(movie_ids):
'''
INPUT
movie_ids - a list of movie_ids
OUTPUT
movies - a list of movie names associated with the movie_ids
'''
movie_lst = list(movies[movies['movie_id'].isin(movie_ids)]['movie'])
return movie_lst
def make_recommendations(user, num_recs=10):
'''
INPUT:
user - (int) a user_id of the individual you want to make recommendations for
num_recs - (int) number of movies to return
OUTPUT:
recommendations - a list of movies - if there are "num_recs" recommendations return this many
otherwise return the total number of recommendations available for the "user"
which may just be an empty list
'''
# I wanted to make recommendations by pulling different movies than the user has already seen
# Go in order from closest to farthest to find movies you would recommend
# I also only considered movies where the closest user rated the movie as a 9 or 10
# movies_seen by user (we don't want to recommend these)
movies_seen = movies_watched(user)
closest_neighbors = find_closest_neighbors(user)
# Keep the recommended movies here
recs = np.array([])
# Go through the neighbors and identify movies they like the user hasn't seen
for neighbor in closest_neighbors:
neighbs_likes = movies_liked(neighbor)
#Obtain recommendations for each neighbor
new_recs = np.setdiff1d(neighbs_likes, movies_seen, assume_unique=True)
# Update recs with new recs
recs = np.unique(np.concatenate([new_recs, recs], axis=0))
# If we have enough recommendations exit the loop
if len(recs) > num_recs-1:
break
# Pull movie titles using movie ids
recommendations = movie_names(recs)
return recommendations
def all_recommendations(num_recs=10):
'''
INPUT
num_recs (int) the (max) number of recommendations for each user
OUTPUT
all_recs - a dictionary where each key is a user_id and the value is an array of recommended movie titles
'''
# All the users we need to make recommendations for
users = np.unique(df_dists['user1'])
n_users = len(users)
#Store all recommendations in this dictionary
all_recs = dict()
# Make the recommendations for each user
for user in users:
all_recs[user] = make_recommendations(user, num_recs)
return all_recs
all_recs = all_recommendations(10)
# This loads our solution dictionary so you can compare results - FULL PATH IS "data/Term2/recommendations/lesson1/data/all_recs.p"
all_recs_sol = pd.read_pickle("data/Term2/recommendations/lesson1/data/all_recs.p")
assert all_recs[2] == make_recommendations(2), "Oops! Your recommendations for user 2 didn't match ours."
assert all_recs[26] == make_recommendations(26), "Oops! It actually wasn't possible to make any recommendations for user 26."
assert all_recs[1503] == make_recommendations(1503), "Oops! Looks like your solution for user 1503 didn't match ours."
print("If you made it here, you now have recommendations for many users using collaborative filtering!")
HTML('<img src="images/greatjob.webp">')
```
### Now What?
If you made it this far, you have successfully implemented a solution to making recommendations using collaborative filtering.
`8.` Let's do a quick recap of the steps taken to obtain recommendations using collaborative filtering.
```
# Check your understanding of the results by correctly filling in the dictionary below
a = "pearson's correlation and spearman's correlation"
b = 'item based collaborative filtering'
c = "there were too many ratings to get a stable metric"
d = 'user based collaborative filtering'
e = "euclidean distance and pearson's correlation coefficient"
f = "manhattan distance and euclidean distance"
g = "spearman's correlation and euclidean distance"
h = "the spread in some ratings was zero"
i = 'content based recommendation'
sol_dict = {
'The type of recommendation system implemented here was a ...': d,
'The two methods used to estimate user similarity were: ': e,
'There was an issue with using the correlation coefficient. What was it?': h
}
t.test_recs(sol_dict)
```
Additionally, let's take a closer look at some of the results. There are two solution files that you read in to check your results, and you created these objects
* **df_dists** - a dataframe of user1, user2, euclidean distance between the two users
* **all_recs_sol** - a dictionary of all recommendations (key = user, value = list of recommendations)
`9.` Use these two objects along with the cells below to correctly fill in the dictionary below and complete this notebook!
```
a = 567
b = 1503
c = 1319
d = 1325
e = 2526710
f = 0
g = 'Use another method to make recommendations - content based, knowledge based, or model based collaborative filtering'
sol_dict2 = {
'For how many pairs of users were we not able to obtain a measure of similarity using correlation?': e,
'For how many pairs of users were we not able to obtain a measure of similarity using euclidean distance?': f,
'For how many users were we unable to make any recommendations for using collaborative filtering?': c,
'For how many users were we unable to make 10 recommendations for using collaborative filtering?': d,
'What might be a way for us to get 10 recommendations for every user?': g
}
t.test_recs2(sol_dict2)
# Use the cells below for any work you need to do!
# Users without recs
users_without_recs = []
for user, movie_recs in all_recs.items():
if len(movie_recs) == 0:
users_without_recs.append(user)
len(users_without_recs)
# NaN euclidean distance values
df_dists['eucl_dist'].isnull().sum()
# Users with fewer than 10 recs
users_with_less_than_10recs = []
for user, movie_recs in all_recs.items():
if len(movie_recs) < 10:
users_with_less_than_10recs.append(user)
len(users_with_less_than_10recs)
```
|
github_jupyter
|
# Figure 4: NIRCam Grism + Filter Sensitivities ($1^{st}$ order)
***
### Table of Contents
1. [Information](#Information)
2. [Imports](#Imports)
3. [Data](#Data)
4. [Generate the First Order Grism + Filter Sensitivity Plot](#Generate-the-First-Order-Grism-+-Filter-Sensitivity-Plot)
5. [Issues](#Issues)
6. [About this Notebook](#About-this-Notebook)
***
## Information
#### JDox links:
* [NIRCam Grisms](https://jwst-docs.stsci.edu/display/JTI/NIRCam+Grisms#NIRCamGrisms-Sensitivity)
* Figure 4. NIRCam grism + filter sensitivities ($1^{st}$ order)
## Imports
```
import os
import pylab
import numpy as np
from astropy.io import ascii, fits
from astropy.table import Table
from scipy.optimize import fmin
from scipy.interpolate import interp1d
import requests
import matplotlib.pyplot as plt
%matplotlib inline
```
## Data
#### Data Location:
The data is stored in a NIRCam JDox Box folder here:
[ST-INS-NIRCAM -> JDox -> nircam_grisms](https://stsci.box.com/s/wu9mo54vi957x50rdirlcg9zkkr3xiaw)
```
files = [('https://stsci.box.com/shared/static/i0a9dkp02nnuw6w0xcfd7b42ctxfb8es.fits', 'NIRCam.F250M.R.A.1st.sensitivity.fits'),
('https://stsci.box.com/shared/static/vfnyk9veote92dz1edpbu83un5n20rsw.fits', 'NIRCam.F250M.R.A.2nd.sensitivity.fits'),
('https://stsci.box.com/shared/static/ssvltwzt7f4y5lfvch2o1prdk5hb2gz2.fits', 'NIRCam.F250M.R.B.1st.sensitivity.fits'),
('https://stsci.box.com/shared/static/56wjvzx1jf2i5yg7l1gg77vtvi01ec5p.fits', 'NIRCam.F250M.R.B.2nd.sensitivity.fits'),
('https://stsci.box.com/shared/static/v1621dcm44be21n381mbgd2hzxxqrb2e.fits', 'NIRCam.F277W.R.A.1st.sensitivity.fits'),
('https://stsci.box.com/shared/static/8slec91wj6ety6d8qvest09msklpypi8.fits', 'NIRCam.F277W.R.A.2nd.sensitivity.fits'),
('https://stsci.box.com/shared/static/r42hdv64x6skqqszv24qkxohiijitqcf.fits', 'NIRCam.F277W.R.B.1st.sensitivity.fits'),
('https://stsci.box.com/shared/static/3vye6ni05i3kdqyd5vs1jk2q59yyms2e.fits', 'NIRCam.F277W.R.B.2nd.sensitivity.fits'),
('https://stsci.box.com/shared/static/twcxbe6lxrjckqph980viiijv8fpmm8b.fits', 'NIRCam.F300M.R.A.1st.sensitivity.fits'),
('https://stsci.box.com/shared/static/bpvluysg3zsl3q4b4l5rj5nue84ydjem.fits', 'NIRCam.F300M.R.A.2nd.sensitivity.fits'),
('https://stsci.box.com/shared/static/15x7rbwngsxiubbexy7zcezxqm3ndq54.fits', 'NIRCam.F300M.R.B.1st.sensitivity.fits'),
('https://stsci.box.com/shared/static/a7tqdp0feqcttw3d9vaioy7syzfsftz6.fits', 'NIRCam.F300M.R.B.2nd.sensitivity.fits'),
('https://stsci.box.com/shared/static/i76sb53pthieh4kn62fpxhcxn8lreffj.fits', 'NIRCam.F322W2.R.A.1st.sensitivity.fits'),
('https://stsci.box.com/shared/static/wgbyfi3ofs7i19b7zsf2iceupzkbkokq.fits', 'NIRCam.F322W2.R.A.2nd.sensitivity.fits'),
('https://stsci.box.com/shared/static/jhk3deym5wbc68djtcahy3otk2xfjdb5.fits', 'NIRCam.F322W2.R.B.1st.sensitivity.fits'),
('https://stsci.box.com/shared/static/zu3xqnicbyfjn54yb4kgzvnglanf13ak.fits', 'NIRCam.F322W2.R.B.2nd.sensitivity.fits'),
('https://stsci.box.com/shared/static/e2srtf52wnh6vvxsy2aiknbcr8kx2xr5.fits', 'NIRCam.F335M.R.A.1st.sensitivity.fits'),
('https://stsci.box.com/shared/static/bav3tswdd7lemsyd53bnpj4b6yke5bgd.fits', 'NIRCam.F335M.R.A.2nd.sensitivity.fits'),
('https://stsci.box.com/shared/static/81wm768mjemzj84w1ogzqddgmrk3exvt.fits', 'NIRCam.F335M.R.B.1st.sensitivity.fits'),
('https://stsci.box.com/shared/static/fhopmyongqifibdtwt3qr682lwdjaf7a.fits', 'NIRCam.F335M.R.B.2nd.sensitivity.fits'),
('https://stsci.box.com/shared/static/j9gd8bclethgex40o7qi1e79hgj2hsyt.fits', 'NIRCam.F356W.R.A.1st.sensitivity.fits'),
('https://stsci.box.com/shared/static/s23novi3p6qwm9f9hj9wutgju08be776.fits', 'NIRCam.F356W.R.A.2nd.sensitivity.fits'),
('https://stsci.box.com/shared/static/41fnmswn1ttnwts6jj5fu73m4hs6icxd.fits', 'NIRCam.F356W.R.B.1st.sensitivity.fits'),
('https://stsci.box.com/shared/static/wx3rvjt0mvf0hnhv4wvqcmxu61gamwmm.fits', 'NIRCam.F356W.R.B.2nd.sensitivity.fits'),
('https://stsci.box.com/shared/static/e0p6vkiow4jlp49deqkji9kekzdt4oon.fits', 'NIRCam.F360M.R.A.1st.sensitivity.fits'),
('https://stsci.box.com/shared/static/xbh0rjjvxn0x22k9ktiyikol7c4ep6ka.fits', 'NIRCam.F360M.R.A.2nd.sensitivity.fits'),
('https://stsci.box.com/shared/static/e7artuotyv8l9wfoa3rk1k00o5mv8so8.fits', 'NIRCam.F360M.R.B.1st.sensitivity.fits'),
('https://stsci.box.com/shared/static/9r5bmick13ti22l6hcsw0uod75vqartw.fits', 'NIRCam.F360M.R.B.2nd.sensitivity.fits'),
('https://stsci.box.com/shared/static/tqd1uqsf8nj12he5qa3hna0zodnlzfea.fits', 'NIRCam.F410M.R.A.1st.sensitivity.fits'),
('https://stsci.box.com/shared/static/4szffesvswh0h8fjym5m5ht37sj0jzrl.fits', 'NIRCam.F410M.R.A.2nd.sensitivity.fits'),
('https://stsci.box.com/shared/static/iur0tpbts23lc5rn5n0tplzndlkoudel.fits', 'NIRCam.F410M.R.B.1st.sensitivity.fits'),
('https://stsci.box.com/shared/static/rvz8iznsnl0bsjrqiw7rv74jj24b0otb.fits', 'NIRCam.F410M.R.B.2nd.sensitivity.fits'),
('https://stsci.box.com/shared/static/sv3g82qbb4u2umksgu5zdl7rp569sdi7.fits', 'NIRCam.F430M.R.A.1st.sensitivity.fits'),
('https://stsci.box.com/shared/static/mmqv1pkuzpj6abtufxxfo960z2v1oygc.fits', 'NIRCam.F430M.R.A.2nd.sensitivity.fits'),
('https://stsci.box.com/shared/static/84q83haic2h6eq5c6p2frkybz551hp8d.fits', 'NIRCam.F430M.R.B.1st.sensitivity.fits'),
('https://stsci.box.com/shared/static/3osceplhq6kmvmm2a72jsgrg6z1ggw1p.fits', 'NIRCam.F430M.R.B.2nd.sensitivity.fits'),
('https://stsci.box.com/shared/static/kitx7gdo5kool6jus2g19vdy7q7hmxck.fits', 'NIRCam.F444W.R.A.1st.sensitivity.fits'),
('https://stsci.box.com/shared/static/ug7y93v0en9c84hfp6d3vtjogmjou9u3.fits', 'NIRCam.F444W.R.A.2nd.sensitivity.fits'),
('https://stsci.box.com/shared/static/0p9h9ofayq8q6dbfsccf3tn5lvxxod9i.fits', 'NIRCam.F444W.R.B.1st.sensitivity.fits'),
('https://stsci.box.com/shared/static/34hbqzibt5h72hm0rj9wylttj7m9wd19.fits', 'NIRCam.F444W.R.B.2nd.sensitivity.fits'),
('https://stsci.box.com/shared/static/vj0rkyebg0afny1khdyiho4mktmtsi1q.fits', 'NIRCam.F460M.R.A.1st.sensitivity.fits'),
('https://stsci.box.com/shared/static/ky1z1dpewsjqab1o9hstihrec7h52oq4.fits', 'NIRCam.F460M.R.A.2nd.sensitivity.fits'),
('https://stsci.box.com/shared/static/s93cwpcvnxfjwqbulnkh9ts9ln0fu9cz.fits', 'NIRCam.F460M.R.B.1st.sensitivity.fits'),
('https://stsci.box.com/shared/static/1178in8zg462es1fkl0mgcbpgp6kgb6t.fits', 'NIRCam.F460M.R.B.2nd.sensitivity.fits'),
('https://stsci.box.com/shared/static/b855uj293klac8hnoqhrnv8ei0rcvudj.fits', 'NIRCam.F480M.R.A.1st.sensitivity.fits'),
('https://stsci.box.com/shared/static/werzjlp3ybxk2ovg6u689zsfpts2t8w3.fits', 'NIRCam.F480M.R.A.2nd.sensitivity.fits'),
('https://stsci.box.com/shared/static/yrh5mylru1upbo5rifbz77acn8k1ud6i.fits', 'NIRCam.F480M.R.B.1st.sensitivity.fits'),
('https://stsci.box.com/shared/static/oxu6jsg9cn9yqkh3nh646fx0flhw8rej.fits', 'NIRCam.F480M.R.B.2nd.sensitivity.fits')]
def download_file(url, file_name, output_directory='./', overwrite=False):
"""Download a file from Box given the direct URL
Parameters
----------
url : str
URL to the file to be downloaded
file_name : str
The name of the file being downloaded
output_directory : str
Directory to download file_name into
overwrite : str
If False and the file to download already exists, the download
will be skipped. If True, the file will be downloaded regardless
of whether it already exists in output_directory
Returns
-------
download_filename : str
Name of the downloaded file
"""
download_filename = os.path.join(output_directory, file_name)
if not os.path.isfile(download_filename) or overwrite is True:
print("Downloading {}".format(file_name))
with requests.get(url, stream=True) as response:
if response.status_code != 200:
raise RuntimeError("Wrong URL - {}".format(url))
with open(download_filename, 'wb') as f:
for chunk in response.iter_content(chunk_size=2048):
if chunk:
f.write(chunk)
else:
print("{} already exists. Skipping download.".format(download_filename))
return download_filename
```
#### Load the data
(The next cell assumes you downloaded the data into your ```Users/$(logname)/``` home directory)
```
if os.environ.get('LOGNAME') is None:
raise ValueError("WARNING: LOGNAME environment variable not set!")
box_directory = os.path.join("/Users/", os.environ['LOGNAME'], "box_data")
box_directory
if not os.path.isdir(box_directory):
try:
os.mkdir(box_directory)
except:
raise OSError("Unable to create {}".format(box_directory))
for file_info in files:
file_url, filename = file_info
outfile = download_file(file_url, filename, output_directory=box_directory)
grism = "R"
mod = "A"
filters = ["F250M","F277W","F300M","F322W2","F335M","F356W","F360M","F410M","F430M","F444W","F460M","F480M"]
filenames = []
for fil in filters:
filenames.append(os.path.join(box_directory, "NIRCam.%s.%s.%s.1st.sensitivity.fits" % (fil,grism,mod)))
filenames
```
## Generate the First Order Grism + Filter Sensitivity Plot
### Define some convenience functions
```
def find_nearest(array,value):
idx = (np.abs(array-value)).argmin()
return array[idx]
def find_nearest(array,value):
idx = (np.abs(array-value)).argmin()
return array[idx]
def find_mid(w,s,w0,thr=0.05):
fct = interp1d(w,s,bounds_error=None,fill_value='extrapolate')
def func(x):
#print "x:",x
return np.abs(fct(x)-thr)
res = fmin(func,w0)
return res[0]
```
### Create the plots
```
f, ax1 = plt.subplots(1, figsize=(15, 10))
NUM_COLORS = len(filters)
cm = pylab.get_cmap('tab10')
grism = "R"
mod = "A"
for i,fname in zip(range(NUM_COLORS),filenames):
color = cm(1.*i/NUM_COLORS)
d = fits.open(fname)
w = d[1].data["WAVELENGTH"]
s = d[1].data["SENSITIVITY"]/(1e17)
ax1.plot(w,s,label=fil,lw=4,color=color)
ax1.legend(fontsize=16)
miny,maxy = ax1.get_ylim()
minx,maxx = ax1.get_xlim()
ax1.set_ylim(miny,2.15)
ax1.set_xlim(2.1,maxx)
ax1.tick_params(labelsize=18)
f.text(0.5, 0.04, 'Wavelength ($\mu m$)', ha='center', fontsize=22)
f.text(0.03, 0.5, 'Sensitivity ('+r'$1 \times 10^{17}\ \frac{e^{-} s^{-1}}{erg s^{-1} cm^{-2} A^{-1}}$'+')', va='center', rotation='vertical', fontsize=22)
```
### Figure option 2: filter name positions
```
f, ax1 = plt.subplots(1, figsize=(15, 10))
thr = 0.05 # 5% of peak boundaries
NUM_COLORS = len(filters)
cm = pylab.get_cmap('tab10')
for i,fil,fname in zip(range(NUM_COLORS),filters,filenames):
color = cm(1.*i/NUM_COLORS)
d = fits.open(fname)
w = d[1].data["WAVELENGTH"]
s = d[1].data["SENSITIVITY"]/(1e17)
wmin,wmax = np.min(w),np.max(w)
vg = w<(wmax+wmin)/2.
w1 = find_mid(w[vg],s[vg],wmin,thr)
vg = w>(wmax+wmin)/2.
w2 = find_mid(w[vg],s[vg],wmax,thr)
if fil == 'F356W':
ax1.text((w2+w1)/2 -0.04, s[np.where(w == find_nearest(w, (w2+w1)/2))]+0.25, fil, ha='center',color=color,fontsize=16,weight='bold')
elif fil == 'F335M':
ax1.text((w2+w1)/2 -0.03, s[np.where(w == find_nearest(w, (w2+w1)/2))]+0.22, fil, ha='center',color=color,fontsize=16,weight='bold')
elif fil == 'F460M':
ax1.text((w2+w1)/2+0.15, s[np.where(w == find_nearest(w, (w2+w1)/2))]+0.12, fil, ha='center',color=color,fontsize=16,weight='bold')
elif fil == 'F480M':
ax1.text((w2+w1)/2+0.15, s[np.where(w == find_nearest(w, (w2+w1)/2))]+0.1, fil, ha='center',color=color,fontsize=16,weight='bold')
else:
ax1.text((w2+w1)/2 -0.04, s[np.where(w == find_nearest(w, (w2+w1)/2))]+0.2, fil, ha='center',color=color,fontsize=16,weight='bold')
ax1.plot(w,s,label=fil,lw=4,color=color)
miny,maxy = ax1.get_ylim()
minx,maxx = ax1.get_xlim()
ax1.set_ylim(miny,2.15)
ax1.set_xlim(2.1,maxx)
ax1.tick_params(labelsize=18)
f.text(0.5, 0.04, 'Wavelength ($\mu m$)', ha='center', fontsize=22)
f.text(0.03, 0.5, 'Sensitivity ('+r'$1 \times 10^{17}\ \frac{e^{-} s^{-1}}{erg\ s^{-1} cm^{-2} A^{-1}}$'+')', va='center', rotation='vertical', fontsize=22)
```
## Issues
* None
## About this Notebook
**Authors:**
Nor Pirzkal & Alicia Canipe
**Updated On:**
April 10, 2019
|
github_jupyter
|
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sb
import gc
prop_data = pd.read_csv("properties_2017.csv")
# prop_data
train_data = pd.read_csv("train_2017.csv")
train_data
# missing_val = prop_data.isnull().sum().reset_index()
# missing_val.columns = ['column_name', 'missing_count']
# missing_val = missing_val.loc[missing_val['missing_count']>0]
# missing_val = missing_val.sort_values(by='missing_count')
# missing_val['missing_ratio'] = missing_val["missing_count"]/prop_data.shape[0]
# missing_val = missing_val.loc[missing_val["missing_ratio"]>0.6]
# missing_val
# ind = np.arange(missing_val.shape[0])
# width = 0.9
# fig, ax = plt.subplots(figsize=(12,18))
# rects = ax.barh(ind, missing_val.missing_ratio.values, color='blue')
# ax.set_yticks(ind)
# ax.set_yticklabels(missing_val.column_name.values, rotation='horizontal')
# ax.set_xlabel("Count of missing values")
# ax.set_title("Number of missing values in each column")
# plt.show()
# del ind
# prop_data.drop(missing_val.column_name.values, axis=1, inplace=True)
prop_data
# prop_data_temp = prop_data.fillna(prop_data.mean(), )
plt.plot(prop_data.groupby("regionidcounty")["taxvaluedollarcnt"].mean())
plt.show()
original = prop_data.copy()
prop_data = original.copy()
# prop_data['actual_area'] = prop_data[['finishedfloor1squarefeet','calculatedfinishedsquarefeet','finishedsquarefeet12', 'finishedsquarefeet13',
# 'finishedsquarefeet15', 'finishedsquarefeet50', 'finishedsquarefeet6']].max(axis=1)
prop_data['actual_area'] = prop_data['calculatedfinishedsquarefeet']#.value_counts(dropna = False)
prop_data['calculatedbathnbr'].fillna(prop_data['calculatedbathnbr'].median(),inplace = True)
prop_data['bedroomcnt'].fillna(prop_data['bedroomcnt'].median(), inplace = True)
prop_data['taxvaluedollarcnt'].fillna(prop_data["taxvaluedollarcnt"].mean(), inplace=True)
prop_data['actual_area'].replace(to_replace=1.0,value=np.nan,inplace=True)
prop_data['actual_area'].fillna(prop_data['actual_area'].median(),inplace=True)
prop_data['unitcnt'].fillna(1, inplace = True)
prop_data['latitude'].fillna(prop_data['latitude'].median(),inplace = True)
prop_data['longitude'].fillna(prop_data['longitude'].median(),inplace = True)
prop_data['lotsizesquarefeet'].fillna(prop_data['lotsizesquarefeet'].median(), inplace = True)
prop_data["poolcnt"].fillna(0, inplace=True)
prop_data["fireplacecnt"].fillna(0, inplace=True)
prop_data["hashottuborspa"].fillna(0, inplace=True)
prop_data['hashottuborspa'] = pd.to_numeric(prop_data['hashottuborspa'])
prop_data["taxdelinquencyflag"].fillna(-1, inplace=True)
prop_data["taxdelinquencyflag"] = prop_data["taxdelinquencyflag"].map({'Y':1, -1:-1})
prop_data.loc[(prop_data["heatingorsystemtypeid"]==2.0) & (pd.isnull(prop_data["airconditioningtypeid"])), "airconditioningtypeid"] = 1.0
prop_data["airconditioningtypeid"].fillna(-1, inplace=True)
prop_data["buildingqualitytypeid"].fillna(7, inplace=True)
prop_data["yearbuilt"].fillna(prop_data["yearbuilt"].mean(), inplace=True)
prop_data["age"] = 2017 - prop_data["yearbuilt"]
#imputing garagecarcnt on basis of propertylandusetypeid
#All the residential places have 1 or 2 garagecarcnt, hence using random filling for those values.
prop_data.loc[(prop_data["propertylandusetypeid"]==261) & (pd.isnull(prop_data["garagecarcnt"])), "garagecarcnt"] = np.random.randint(1,3)
prop_data.loc[(prop_data["propertylandusetypeid"]==266) & (pd.isnull(prop_data["garagecarcnt"])), "garagecarcnt"] = np.random.randint(1,3)
prop_data["garagecarcnt"].fillna(0, inplace=True)
prop_data["taxamount"].fillna(prop_data.taxamount.mean(), inplace=True)
prop_data['longitude'] = prop_data['longitude'].abs()
prop_data['calculatedfinishedsquarefeet'].describe()
```
### Normalizing the data
```
colsList = ["actual_area",
"poolcnt",
"latitude",
"longitude",
"unitcnt",
"lotsizesquarefeet",
"bedroomcnt",
"calculatedbathnbr",
"hashottuborspa",
"fireplacecnt",
"taxvaluedollarcnt",
"buildingqualitytypeid",
"garagecarcnt",
"age",
"taxamount"]
prop_data_ahp = prop_data[colsList]
# prop_data_ahp
for col in prop_data_ahp.columns:
prop_data_ahp[col] = (prop_data_ahp[col] - prop_data_ahp[col].mean())/prop_data_ahp[col].std(ddof=0)
# prop_data_ahp.isnull().sum()
for cols in prop_data_ahp.columns.values:
print prop_data_ahp[cols].value_counts(dropna=False)
```
## Analytical Hierarchical Processing
```
rel_imp_matrix = pd.read_csv("rel_imp_matrix.csv", index_col=0)
# rel_imp_matrix
import fractions
for col in rel_imp_matrix.columns.values:
temp_list = rel_imp_matrix[col].tolist()
rel_imp_matrix[col] = [float(fractions.Fraction(x)) for x in temp_list]
# data = [float(fractions.Fraction(x)) for x in data]
# rel_imp_matrix
for col in rel_imp_matrix.columns.values:
rel_imp_matrix[col] /= rel_imp_matrix[col].sum()
# rel_imp_matrix
rel_imp_matrix["row_sum"] = rel_imp_matrix.sum(axis=1)
rel_imp_matrix["score"] = rel_imp_matrix["row_sum"]/rel_imp_matrix.shape[0]
rel_imp_matrix.to_csv("final_score_matrix.csv", index=False)
# rel_imp_matrix
ahp_column_score = rel_imp_matrix["score"]
ahp_column_score
prop_data_ahp.info()
prop_data_ahp.drop('sum', axis=1,inplace=True)
prop_data_ahp.keys()
```
# SAW
```
sum_series = pd.Series(0, index=prop_data_ahp.index,dtype='float32')
for col in prop_data_ahp.columns:
sum_series = sum_series+ prop_data_ahp[col] * ahp_column_score[col]
prop_data_ahp["sum"] = sum_series.astype('float32')
prop_data_ahp["sum"]
# prop_data_ahp["sum"] = prop_data_ahp.sum(axis=1)
prop_data_ahp["sum"].describe()
prop_data_ahp.sort_values(by='sum', inplace=True)
prop_data_ahp.head(n=10)
prop_data_ahp.tail(n=10)
print prop_data[colsList].iloc[1252741],"\n\n"
print prop_data[colsList].iloc[342941]
# #imputing airconditioningtypeid, making some NaN to 1.0 where heatingorsystemtypeid == 2
# prop_data.loc[(prop_data["heatingorsystemtypeid"]==2.0) & (pd.isnull(prop_data["airconditioningtypeid"])), "airconditioningtypeid"] = 1.0
# prop_data["airconditioningtypeid"].fillna(-1, inplace=True)
# print prop_data["airconditioningtypeid"].value_counts()
# prop_data[["airconditioningtypeid", "heatingorsystemtypeid"]].head()
# duplicate_or_not_useful_cols = pd.Series(['calculatedbathnbr', 'assessmentyear', 'fullbathcnt',
# 'regionidneighborhood', 'propertyzoningdesc', 'censustractandblock'])#,'finishedsquarefeet12'])
# prop_data.drop(duplicate_or_not_useful_cols, axis=1, inplace=True)
# prop_data["buildingqualitytypeid"].fillna(prop_data["buildingqualitytypeid"].mean(), inplace=True)
# prop_data["calculatedfinishedsquarefeet"].interpolate(inplace=True)
# prop_data["heatingorsystemtypeid"].fillna(-1, inplace=True)
# prop_data["lotsizesquarefeet"].fillna(prop_data["lotsizesquarefeet"].median(), inplace=True)
# prop_data.drop(["numberofstories"], axis=1, inplace=True)
# #removing propertycountylandusecode because it is not in interpretable format
# prop_data.drop(["propertycountylandusecode"], axis=1, inplace=True)
# prop_data["regionidcity"].interpolate(inplace=True)
# prop_data["regionidzip"].interpolate(inplace=True)
# prop_data["yearbuilt"].fillna(prop_data["yearbuilt"].mean(), inplace=True)
# #impute structuretaxvaluedollarcnt, taxvaluedollarcnt, landtaxvaluedollarcnt, taxamount by interpolation
# cols_to_interpolate = ["structuretaxvaluedollarcnt", "taxvaluedollarcnt", "landtaxvaluedollarcnt", "taxamount"]
# for c in cols_to_interpolate:
# prop_data[c].interpolate(inplace=True)
# #imputing garagecarcnt on basis of propertylandusetypeid
# #All the residential places have 1 or 2 garagecarcnt, hence using random filling for those values.
# prop_data.loc[(prop_data["propertylandusetypeid"]==261) & (pd.isnull(prop_data["garagecarcnt"])), "garagecarcnt"] = np.random.randint(1,3)
# prop_data.loc[(prop_data["propertylandusetypeid"]==266) & (pd.isnull(prop_data["garagecarcnt"])), "garagecarcnt"] = np.random.randint(1,3)
# prop_data["garagecarcnt"].fillna(-1, inplace=True)
# prop_data["garagecarcnt"].value_counts(dropna=False)
# #imputing garagetotalsqft using the garagecarcnt
# prop_data.loc[(prop_data["garagecarcnt"]==-1) & (pd.isnull(prop_data["garagetotalsqft"]) | (prop_data["garagetotalsqft"] == 0)), "garagetotalsqft"] = -1
# prop_data.loc[(prop_data["garagecarcnt"]==1) & (pd.isnull(prop_data["garagetotalsqft"]) | (prop_data["garagetotalsqft"] == 0)), "garagetotalsqft"] = np.random.randint(180, 400)
# prop_data.loc[(prop_data["garagecarcnt"]==2) & (pd.isnull(prop_data["garagetotalsqft"]) | (prop_data["garagetotalsqft"] == 0)), "garagetotalsqft"] = np.random.randint(400, 720)
# prop_data.loc[(prop_data["garagecarcnt"]==3) & (pd.isnull(prop_data["garagetotalsqft"]) | (prop_data["garagetotalsqft"] == 0)), "garagetotalsqft"] = np.random.randint(720, 880)
# prop_data.loc[(prop_data["garagecarcnt"]==4) & (pd.isnull(prop_data["garagetotalsqft"]) | (prop_data["garagetotalsqft"] == 0)), "garagetotalsqft"] = np.random.randint(880, 1200)
# #interpolate the remaining missing values
# prop_data["garagetotalsqft"].interpolate(inplace=True)
# prop_data["garagetotalsqft"].value_counts(dropna=False)
# #imputing unitcnt using propertylandusetypeid
# prop_data.loc[(prop_data["propertylandusetypeid"]==261) & pd.isnull(prop_data["unitcnt"]), "unitcnt"] = 1
# prop_data.loc[(prop_data["propertylandusetypeid"]==266) & pd.isnull(prop_data["unitcnt"]), "unitcnt"] = 1
# prop_data.loc[(prop_data["propertylandusetypeid"]==269) & pd.isnull(prop_data["unitcnt"]), "unitcnt"] = 1
# prop_data.loc[(prop_data["propertylandusetypeid"]==246) & pd.isnull(prop_data["unitcnt"]), "unitcnt"] = 2
# prop_data.loc[(prop_data["propertylandusetypeid"]==247) & pd.isnull(prop_data["unitcnt"]), "unitcnt"] = 3
# prop_data.loc[(prop_data["propertylandusetypeid"]==248) & pd.isnull(prop_data["unitcnt"]), "unitcnt"] = 4
# prop_data["unitcnt"].value_counts(dropna=False)
```
## Distance Metric
We will be using weighted Manhattan distance as a distance metric
```
dist_imp_matrix = pd.read_csv("./dist_metric.csv", index_col=0)
dist_imp_matrix
import fractions
for col in dist_imp_matrix.columns.values:
temp_list = dist_imp_matrix[col].tolist()
dist_imp_matrix[col] = [float(fractions.Fraction(x)) for x in temp_list]
# dist_imp_matrix
for col in dist_imp_matrix.columns.values:
dist_imp_matrix[col] /= dist_imp_matrix[col].sum()
dist_imp_matrix["row_sum"] = dist_imp_matrix.sum(axis=1)
dist_imp_matrix["score"] = dist_imp_matrix["row_sum"]/dist_imp_matrix.shape[0]
dist_imp_matrix.to_csv("final_score_matrix_Q2.csv")
```
|
github_jupyter
|
```
from IPython.core.display import HTML
with open('../style.css', 'r') as file:
css = file.read()
HTML(css)
```
# A Crypto-Arithmetic Puzzle
In this exercise we will solve the crypto-arithmetic puzzle shown in the picture below:
<img src="send-more-money.png">
The idea is that the letters
"$\texttt{S}$", "$\texttt{E}$", "$\texttt{N}$", "$\texttt{D}$", "$\texttt{M}$", "$\texttt{O}$", "$\texttt{R}$", "$\texttt{Y}$" occurring in this puzzle
are interpreted as variables ranging over the set of decimal digits, i.e. these variables can take values in
the set $\{0,1,2,3,4,5,6,7,8,9\}$. Then, the string "$\texttt{SEND}$" is interpreted as a decimal number,
i.e. it is interpreted as the number
$$\texttt{S} \cdot 10^3 + \texttt{E} \cdot 10^2 + \texttt{N} \cdot 10^1 + \texttt{D} \cdot 10^0.$$
The strings "$\texttt{MORE}$ and "$\texttt{MONEY}$" are interpreted similarly. To make the problem
interesting, the assumption is that different variables have different values. Furthermore, the
digits at the beginning of a number should be different from $0$. Then, we have to find values for the variables
"$\texttt{S}$", "$\texttt{E}$", "$\texttt{N}$", "$\texttt{D}$", "$\texttt{M}$", "$\texttt{O}$", "$\texttt{R}$", "$\texttt{Y}$" such that the formula
$$ (\texttt{S} \cdot 10^3 + \texttt{E} \cdot 10^2 + \texttt{N} \cdot 10 + \texttt{D})
+ (\texttt{M} \cdot 10^3 + \texttt{O} \cdot 10^2 + \texttt{R} \cdot 10 + \texttt{E})
= \texttt{M} \cdot 10^4 + \texttt{O} \cdot 10^3 + \texttt{N} \cdot 10^2 + \texttt{E} \cdot 10 + \texttt{Y}
$$
is true. The problem with this constraint is that it involves far too many variables. As this constraint can only be
checked when all the variables have values assigned to them, the backtracking search would essentially
boil down to a mere brute force search. We would have 8 variables and hence we would have to test $8^{10}$
possible assignments. In order to do better, we have to perform the addition in the figure shown above
column by column, just as it is taught in elementary school. To be able to do this, we have to introduce <a href="https://en.wikipedia.org/wiki/Carry_(arithmetic)">carry digits</a> "$\texttt{C1}$", "$\texttt{C2}$", "$\texttt{C3}$" where $\texttt{C1}$ is the carry produced by adding
$\texttt{D}$ and $\texttt{E}$, $\texttt{C2}$ is the carry produced by adding
$\texttt{N}$, $\texttt{R}$ and $\texttt{C1}$, and $\texttt{C3}$ is the carry produced by adding
$\texttt{E}$, $\texttt{O}$ and $\texttt{C2}$.
```
import cspSolver
```
For a set $V$ of variables, the function $\texttt{allDifferent}(V)$ generates a set of formulas that express that all the variables of $V$ are different.
```
def allDifferent(Variables):
return { f'{x} != {y}' for x in Variables
for y in Variables
if x < y
}
allDifferent({ 'a', 'b', 'c' })
```
# Pause bis 14:23
```
def createCSP():
Variables = "your code here"
Values = "your code here"
Constraints = "much more code here"
return [Variables, Values, Constraints];
puzzle = createCSP()
puzzle
%%time
solution = cspSolver.solve(puzzle)
print(f'Time needed: {round((stop-start) * 1000)} milliseconds.')
solution
def printSolution(A):
if A == None:
print("no solution found")
return
for v in { "S", "E", "N", "D", "M", "O", "R", "Y" }:
print(f"{v} = {A[v]}")
print("\nThe solution of\n")
print(" S E N D")
print(" + M O R E")
print(" ---------")
print(" M O N E Y")
print("\nis as follows\n")
print(f" {A['S']} {A['E']} {A['N']} {A['D']}")
print(f" + {A['M']} {A['O']} {A['R']} {A['E']}")
print(f" ==========")
print(f" {A['M']} {A['O']} {A['N']} {A['E']} {A['Y']}")
printSolution(solution)
```
|
github_jupyter
|
# Solution based on Multiple Models
```
import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = "all"
```
# Tokenize and Numerize - Make it ready
```
training_size = 20000
training_sentences = sentences[0:training_size]
testing_sentences = sentences[training_size:]
training_labels = labels[0:training_size]
testing_labels = labels[training_size:]
vocab_size = 1000
max_length = 120
embedding_dim = 16
trunc_type='post'
padding_type='post'
oov_tok = "<OOV>"
tokenizer = Tokenizer(num_words=vocab_size, oov_token=oov_tok)
tokenizer.fit_on_texts(training_sentences)
word_index = tokenizer.word_index
training_sequences = tokenizer.texts_to_sequences(training_sentences)
training_padded = pad_sequences(training_sequences,
maxlen=max_length,
padding=padding_type,
truncating=trunc_type)
testing_sequences = tokenizer.texts_to_sequences(testing_sentences)
testing_padded = pad_sequences(testing_sequences,
maxlen=max_length,
padding=padding_type,
truncating=trunc_type)
```
# Plot
```
def plot_graphs(history, string):
plt.plot(history.history[string])
plt.plot(history.history['val_'+string])
plt.xlabel("Epochs")
plt.ylabel(string)
plt.legend([string, 'val_'+string])
plt.show()
plot_graphs(history, "accuracy")
plot_graphs(history, "loss")
```
## Function to train and show
```
def fit_model_and_show_results (model, reviews):
model.summary()
history = model.fit(training_padded,
training_labels_final,
epochs=num_epochs,
validation_data=(validation_padded, validation_labels_final))
plot_graphs(history, "accuracy")
plot_graphs(history, "loss")
predict_review(model, reviews)
```
# ANN Embedding
```
model = tf.keras.Sequential([
tf.keras.layers.Embedding(vocab_size, embedding_dim, input_length=max_length),
tf.keras.layers.GlobalAveragePooling1D(),
tf.keras.layers.Dense(1, activation='sigmoid')
])
model.compile(loss='binary_crossentropy',optimizer='adam',metrics=['accuracy'])
model.summary()
num_epochs = 20
history = model.fit(training_padded, training_labels_final, epochs=num_epochs,
validation_data=(validation_padded, validation_labels_final))
plot_graphs(history, "accuracy")
plot_graphs(history, "loss")
```
# CNN
```
num_epochs = 30
model_cnn = tf.keras.Sequential([
tf.keras.layers.Embedding(vocab_size, embedding_dim, input_length=max_length),
tf.keras.layers.Conv1D(16, 5, activation='relu'),
tf.keras.layers.GlobalMaxPooling1D(),
tf.keras.layers.Dense(1, activation='sigmoid')
])
# Default learning rate for the Adam optimizer is 0.001
# Let's slow down the learning rate by 10.
learning_rate = 0.0001
model_cnn.compile(loss='binary_crossentropy',
optimizer=tf.keras.optimizers.Adam(learning_rate),
metrics=['accuracy'])
fit_model_and_show_results(model_cnn, new_reviews)
```
# GRU
```
num_epochs = 30
model_gru = tf.keras.Sequential([
tf.keras.layers.Embedding(vocab_size, embedding_dim, input_length=max_length),
tf.keras.layers.Bidirectional(tf.keras.layers.GRU(32)),
tf.keras.layers.Dense(1, activation='sigmoid')
])
learning_rate = 0.00003 # slower than the default learning rate
model_gru.compile(loss='binary_crossentropy',
optimizer=tf.keras.optimizers.Adam(learning_rate),
metrics=['accuracy'])
fit_model_and_show_results(model_gru, new_reviews)
```
# Bidirectional LSTM
```
num_epochs = 30
model_bidi_lstm = tf.keras.Sequential([
tf.keras.layers.Embedding(vocab_size, embedding_dim, input_length=max_length),
tf.keras.layers.Bidirectional(tf.keras.layers.LSTM(embedding_dim)),
tf.keras.layers.Dense(1, activation='sigmoid')
])
learning_rate = 0.00003
model_bidi_lstm.compile(loss='binary_crossentropy',
optimizer=tf.keras.optimizers.Adam(learning_rate),
metrics=['accuracy'])
fit_model_and_show_results(model_bidi_lstm, new_reviews)
```
# Multiple bidirectional LSTMs
```
num_epochs = 30
model_multiple_bidi_lstm = tf.keras.Sequential([
tf.keras.layers.Embedding(vocab_size, embedding_dim, input_length=max_length),
tf.keras.layers.Bidirectional(tf.keras.layers.LSTM(embedding_dim,
return_sequences=True)),
tf.keras.layers.Bidirectional(tf.keras.layers.LSTM(embedding_dim)),
tf.keras.layers.Dense(1, activation='sigmoid')
])
learning_rate = 0.0003
model_multiple_bidi_lstm.compile(loss='binary_crossentropy',
optimizer=tf.keras.optimizers.Adam(learning_rate),
metrics=['accuracy'])
fit_model_and_show_results(model_multiple_bidi_lstm, new_reviews)
```
# Prediction
Define a function to prepare the new reviews for use with a model
and then use the model to predict the sentiment of the new reviews
```
def predict_review(model, reviews):
# Create the sequences
padding_type='post'
sample_sequences = tokenizer.texts_to_sequences(reviews)
reviews_padded = pad_sequences(sample_sequences,
padding=padding_type,
maxlen=max_length)
classes = model.predict(reviews_padded)
for x in range(len(reviews_padded)):
print(reviews[x])
print(classes[x])
print('\n')
```
## How to use examples
more_reviews = [review1, review2, review3, review4, review5, review6, review7,
review8, review9, review10]
predict_review(model, new_reviews)
```
print("============================\n","Embeddings only:\n", "============================")
predict_review(model, more_reviews)
print("============================\n","With CNN\n", "============================")
predict_review(model_cnn, more_reviews)
print("===========================\n","With bidirectional GRU\n", "============================")
predict_review(model_gru, more_reviews)
print("===========================\n", "With a single bidirectional LSTM:\n", "===========================")
predict_review(model_bidi_lstm, more_reviews)
print("===========================\n", "With multiple bidirectional LSTM:\n", "==========================")
predict_review(model_multiple_bidi_lstm, more_reviews)
```
|
github_jupyter
|
# Tutorial on Python for scientific computing
Marcos Duarte
This tutorial is a short introduction to programming and a demonstration of the basic features of Python for scientific computing. To use Python for scientific computing we need the Python program itself with its main modules and specific packages for scientific computing. [See this notebook on how to install Python for scientific computing](http://nbviewer.ipython.org/github/demotu/BMC/blob/master/notebooks/PythonInstallation.ipynb).
Once you get Python and the necessary packages for scientific computing ready to work, there are different ways to run Python, the main ones are:
- open a terminal window in your computer and type `python` or `ipython` that the Python interpreter will start
- run the IPython notebook and start working with Python in a browser
- run Spyder, an interactive development environment (IDE)
- run the IPython qtconsole, a more featured terminal
- run IPython completely in the cloud with for example, [https://cloud.sagemath.com](https://cloud.sagemath.com) or [https://www.wakari.io](https://www.wakari.io)
- run Python online in a website such as [https://www.pythonanywhere.com/](https://www.pythonanywhere.com/)
- run Python using any other Python editor or IDE
We will use the IPython Notebook for this tutorial but you can run almost all the things we will see here using the other forms listed above.
## Python as a calculator
Once in the IPython notebook, if you type a simple mathematical expression and press `Shift+Enter` it will give the result of the expression:
```
1 + 2 - 30
4/5
```
If you are using Python version 2.x instead of Python 3.x, you should have got 0 as the result of 4 divided by 5, which is wrong! The problem is that for Python versions up to 2.x, the operator '/' performs division with integers and the result will also be an integer (this behavior was changed in version 3.x).
If you want the normal behavior for division, in Python 2.x you have two options: tell Python that at least one of the numbers is not an integer or import the new division operator (which is inoffensive if you are already using Python 3), let's see these two options:
```
4/5.
from __future__ import division
4/5
```
I prefer to use the import division option (from future!); if we put this statement in the beginning of a file or IPython notebook, it will work for all subsequent commands.
Another command that changed its behavior from Python 2.x to 3.x is the `print` command.
In Python 2.x, the print command could be used as a statement:
```
print 4/5
```
With Python 3.x, the print command bahaves as a true function and has to be called with parentheses. Let's also import this future command to Python 2.x and use it from now on:
```
from __future__ import print_function
print(4/5)
```
With the `print` function, let's explore the mathematical operations available in Python:
```
print('1+2 = ', 1+2, '\n', '4*5 = ', 4*5, '\n', '6/7 = ', 6/7, '\n', '8**2 = ', 8**2, sep='')
```
And if we want the square-root of a number:
```
sqrt(9)
```
We get an error message saying that the `sqrt` function if not defined. This is because `sqrt` and other mathematical functions are available with the `math` module:
```
import math
math.sqrt(9)
from math import sqrt
sqrt(9)
```
## The import function
We used the command '`import`' to be able to call certain functions. In Python functions are organized in modules and packages and they have to be imported in order to be used.
A module is a file containing Python definitions (e.g., functions) and statements. Packages are a way of structuring Python’s module namespace by using “dotted module names”. For example, the module name A.B designates a submodule named B in a package named A. To be used, modules and packages have to be imported in Python with the import function.
Namespace is a container for a set of identifiers (names), and allows the disambiguation of homonym identifiers residing in different namespaces. For example, with the command import math, we will have all the functions and statements defined in this module in the namespace '`math.`', for example, '`math.pi`' is the π constant and '`math.cos()`', the cosine function.
By the way, to know which Python version you are running, we can use one of the following modules:
```
import sys
sys.version
```
And if you are in an IPython session:
```
from IPython import sys_info
print(sys_info())
```
The first option gives information about the Python version; the latter also includes the IPython version, operating system, etc.
## Object-oriented programming
Python is designed as an object-oriented programming (OOP) language. OOP is a paradigm that represents concepts as "objects" that have data fields (attributes that describe the object) and associated procedures known as methods.
This means that all elements in Python are objects and they have attributes which can be acessed with the dot (.) operator after the name of the object. We already experimented with that when we imported the module `sys`, it became an object, and we acessed one of its attribute: `sys.version`.
OOP as a paradigm is much more than defining objects, attributes, and methods, but for now this is enough to get going with Python.
## Python and IPython help
To get help about any Python command, use `help()`:
```
help(math.degrees)
```
Or if you are in the IPython environment, simply add '?' to the function that a window will open at the bottom of your browser with the same help content:
```
math.degrees?
```
And if you add a second '?' to the statement you get access to the original script file of the function (an advantage of an open source language), unless that function is a built-in function that does not have a script file, which is the case of the standard modules in Python (but you can access the Python source code if you want; it just does not come with the standard program for installation).
So, let's see this feature with another function:
```
import scipy.fftpack
scipy.fftpack.fft??
```
To know all the attributes of an object, for example all the functions available in `math`, we can use the function `dir`:
```
print(dir(math))
```
### Tab completion in IPython
IPython has tab completion: start typing the name of the command (object) and press `tab` to see the names of objects available with these initials letters. When the name of the object is typed followed by a dot (`math.`), pressing `tab` will show all available attribites, scroll down to the desired attribute and press `Enter` to select it.
### The four most helpful commands in IPython
These are the most helpful commands in IPython (from [IPython tutorial](http://ipython.org/ipython-doc/dev/interactive/tutorial.html)):
- `?` : Introduction and overview of IPython’s features.
- `%quickref` : Quick reference.
- `help` : Python’s own help system.
- `object?` : Details about ‘object’, use ‘object??’ for extra details.
[See these IPython Notebooks for more on IPython and the Notebook capabilities](http://nbviewer.ipython.org/github/ipython/ipython/tree/master/examples/Notebook/).
### Comments
Comments in Python start with the hash character, #, and extend to the end of the physical line:
```
# Import the math library to access more math stuff
import math
math.pi # this is the pi constant; a useless comment since this is obvious
```
To insert comments spanning more than one line, use a multi-line string with a pair of matching triple-quotes: `"""` or `'''` (we will see the string data type later). A typical use of a multi-line comment is as documentation strings and are meant for anyone reading the code:
```
"""Documentation strings are typically written like that.
A docstring is a string literal that occurs as the first statement
in a module, function, class, or method definition.
"""
```
A docstring like above is useless and its output as a standalone statement looks uggly in IPython Notebook, but you will see its real importance when reading and writting codes.
Commenting a programming code is an important step to make the code more readable, which Python cares a lot.
There is a style guide for writting Python code ([PEP 8](http://www.python.org/dev/peps/pep-0008/)) with a session about [how to write comments](http://www.python.org/dev/peps/pep-0008/#comments).
### Magic functions
IPython has a set of predefined ‘magic functions’ that you can call with a command line style syntax.
There are two kinds of magics, line-oriented and cell-oriented.
Line magics are prefixed with the % character and work much like OS command-line calls: they get as an argument the rest of the line, where arguments are passed without parentheses or quotes.
Cell magics are prefixed with a double %%, and they are functions that get as an argument not only the rest of the line, but also the lines below it in a separate argument.
## Assignment and expressions
The equal sign ('=') is used to assign a value to a variable. Afterwards, no result is displayed before the next interactive prompt:
```
x = 1
```
Spaces between the statements are optional but it helps for readability.
To see the value of the variable, call it again or use the print function:
```
x
print(x)
```
Of course, the last assignment is that holds:
```
x = 2
x = 3
x
```
In mathematics '=' is the symbol for identity, but in computer programming '=' is used for assignment, it means that the right part of the expresssion is assigned to its left part.
For example, 'x=x+1' does not make sense in mathematics but it does in computer programming:
```
x = 1
print(x)
x = x + 1
print(x)
```
A value can be assigned to several variables simultaneously:
```
x = y = 4
print(x)
print(y)
```
Several values can be assigned to several variables at once:
```
x, y = 5, 6
print(x)
print(y)
```
And with that, you can do (!):
```
x, y = y, x
print(x)
print(y)
```
Variables must be “defined” (assigned a value) before they can be used, or an error will occur:
```
x = z
```
## Variables and types
There are different types of built-in objects in Python (and remember that everything in Python is an object):
```
import types
print(dir(types))
```
Let's see some of them now.
### Numbers: int, float, complex
Numbers can an integer (int), float, and complex (with imaginary part).
Let's use the function `type` to show the type of number (and later for any other object):
```
type(6)
```
A float is a non-integer number:
```
math.pi
type(math.pi)
```
Python (IPython) is showing `math.pi` with only 15 decimal cases, but internally a float is represented with higher precision.
Floating point numbers in Python are implemented using a double (eight bytes) word; the precison and internal representation of floating point numbers are machine specific and are available in:
```
sys.float_info
```
Be aware that floating-point numbers can be trick in computers:
```
0.1 + 0.2
0.1 + 0.2 - 0.3
```
These results are not correct (and the problem is not due to Python). The error arises from the fact that floating-point numbers are represented in computer hardware as base 2 (binary) fractions and most decimal fractions cannot be represented exactly as binary fractions. As consequence, decimal floating-point numbers are only approximated by the binary floating-point numbers actually stored in the machine. [See here for more on this issue](http://docs.python.org/2/tutorial/floatingpoint.html).
A complex number has real and imaginary parts:
```
1+2j
print(type(1+2j))
```
Each part of a complex number is represented as a floating-point number. We can see them using the attributes `.real` and `.imag`:
```
print((1+2j).real)
print((1+2j).imag)
```
### Strings
Strings can be enclosed in single quotes or double quotes:
```
s = 'string (str) is a built-in type in Python'
s
type(s)
```
String enclosed with single and double quotes are equal, but it may be easier to use one instead of the other:
```
'string (str) is a Python's built-in type'
"string (str) is a Python's built-in type"
```
But you could have done that using the Python escape character '\':
```
'string (str) is a Python\'s built-in type'
```
Strings can be concatenated (glued together) with the + operator, and repeated with *:
```
s = 'P' + 'y' + 't' + 'h' + 'o' + 'n'
print(s)
print(s*5)
```
Strings can be subscripted (indexed); like in C, the first character of a string has subscript (index) 0:
```
print('s[0] = ', s[0], ' (s[index], start at 0)')
print('s[5] = ', s[5])
print('s[-1] = ', s[-1], ' (last element)')
print('s[:] = ', s[:], ' (all elements)')
print('s[1:] = ', s[1:], ' (from this index (inclusive) till the last (inclusive))')
print('s[2:4] = ', s[2:4], ' (from first index (inclusive) till second index (exclusive))')
print('s[:2] = ', s[:2], ' (till this index, exclusive)')
print('s[:10] = ', s[:10], ' (Python handles the index if it is larger than the string length)')
print('s[-10:] = ', s[-10:])
print('s[0:5:2] = ', s[0:5:2], ' (s[ini:end:step])')
print('s[::2] = ', s[::2], ' (s[::step], initial and final indexes can be omitted)')
print('s[0:5:-1] = ', s[::-1], ' (s[::-step] reverses the string)')
print('s[:2] + s[2:] = ', s[:2] + s[2:], ' (because of Python indexing, this sounds natural)')
```
### len()
Python has a built-in functon to get the number of itens of a sequence:
```
help(len)
s = 'Python'
len(s)
```
The function len() helps to understand how the backward indexing works in Python.
The index s[-i] should be understood as s[len(s) - i] rather than accessing directly the i-th element from back to front. This is why the last element of a string is s[-1]:
```
print('s = ', s)
print('len(s) = ', len(s))
print('len(s)-1 = ',len(s) - 1)
print('s[-1] = ', s[-1])
print('s[len(s) - 1] = ', s[len(s) - 1])
```
Or, strings can be surrounded in a pair of matching triple-quotes: """ or '''. End of lines do not need to be escaped when using triple-quotes, but they will be included in the string. This is how we created a multi-line comment earlier:
```
"""Strings can be surrounded in a pair of matching triple-quotes: \""" or '''.
End of lines do not need to be escaped when using triple-quotes,
but they will be included in the string.
"""
```
### Lists
Values can be grouped together using different types, one of them is list, which can be written as a list of comma-separated values between square brackets. List items need not all have the same type:
```
x = ['spam', 'eggs', 100, 1234]
x
```
Lists can be indexed and the same indexing rules we saw for strings are applied:
```
x[0]
```
The function len() works for lists:
```
len(x)
```
### Tuples
A tuple consists of a number of values separated by commas, for instance:
```
t = ('spam', 'eggs', 100, 1234)
t
```
The type tuple is why multiple assignments in a single line works; elements separated by commas (with or without surrounding parentheses) are a tuple and in an expression with an '=', the right-side tuple is attributed to the left-side tuple:
```
a, b = 1, 2
print('a = ', a, '\nb = ', b)
```
Is the same as:
```
(a, b) = (1, 2)
print('a = ', a, '\nb = ', b)
```
### Sets
Python also includes a data type for sets. A set is an unordered collection with no duplicate elements.
```
basket = ['apple', 'orange', 'apple', 'pear', 'orange', 'banana']
fruit = set(basket) # create a set without duplicates
fruit
```
As set is an unordered collection, it can not be indexed as lists and tuples.
```
set(['orange', 'pear', 'apple', 'banana'])
'orange' in fruit # fast membership testing
```
### Dictionaries
Dictionary is a collection of elements organized keys and values. Unlike lists and tuples, which are indexed by a range of numbers, dictionaries are indexed by their keys:
```
tel = {'jack': 4098, 'sape': 4139}
tel
tel['guido'] = 4127
tel
tel['jack']
del tel['sape']
tel['irv'] = 4127
tel
tel.keys()
'guido' in tel
```
The dict() constructor builds dictionaries directly from sequences of key-value pairs:
```
tel = dict([('sape', 4139), ('guido', 4127), ('jack', 4098)])
tel
```
## Built-in Constants
- **False** : false value of the bool type
- **True** : true value of the bool type
- **None** : sole value of types.NoneType. None is frequently used to represent the absence of a value.
In computer science, the Boolean or logical data type is composed by two values, true and false, intended to represent the values of logic and Boolean algebra. In Python, 1 and 0 can also be used in most situations as equivalent to the Boolean values.
## Logical (Boolean) operators
### and, or, not
- **and** : logical AND operator. If both the operands are true then condition becomes true. (a and b) is true.
- **or** : logical OR Operator. If any of the two operands are non zero then condition becomes true. (a or b) is true.
- **not** : logical NOT Operator. Reverses the logical state of its operand. If a condition is true then logical NOT operator will make false.
### Comparisons
The following comparison operations are supported by objects in Python:
- **==** : equal
- **!=** : not equal
- **<** : strictly less than
- **<=** : less than or equal
- **\>** : strictly greater than
- **\>=** : greater than or equal
- **is** : object identity
- **is not** : negated object identity
```
True == False
not True == False
1 < 2 > 1
True != (False or True)
True != False or True
```
## Indentation and whitespace
In Python, statement grouping is done by indentation (this is mandatory), which are done by inserting whitespaces, not tabs. Indentation is also recommended for alignment of function calling that span more than one line for better clarity.
We will see examples of indentation in the next session.
## Control of flow
### `if`...`elif`...`else`
Conditional statements (to peform something if another thing is True or False) can be implemmented using the `if` statement:
```
if expression:
statement
elif:
statement
else:
statement
```
`elif` (one or more) and `else` are optionals.
The indentation is obligatory.
For example:
```
if True:
pass
```
Which does nothing useful.
Let's use the `if`...`elif`...`else` statements to categorize the [body mass index](http://en.wikipedia.org/wiki/Body_mass_index) of a person:
```
# body mass index
weight = 100 # kg
height = 1.70 # m
bmi = weight / height**2
if bmi < 15:
c = 'very severely underweight'
elif 15 <= bmi < 16:
c = 'severely underweight'
elif 16 <= bmi < 18.5:
c = 'underweight'
elif 18.5 <= bmi < 25:
c = 'normal'
elif 25 <= bmi < 30:
c = 'overweight'
elif 30 <= bmi < 35:
c = 'moderately obese'
elif 35 <= bmi < 40:
c = 'severely obese'
else:
c = 'very severely obese'
print('For a weight of {0:.1f} kg and a height of {1:.2f} m,\n\
the body mass index (bmi) is {2:.1f} kg/m2,\nwhich is considered {3:s}.'\
.format(weight, height, bmi, c))
```
### for
The `for` statement iterates over a sequence to perform operations (a loop event).
```
for iterating_var in sequence:
statements
```
```
for i in [3, 2, 1, 'go!']:
print(i),
for letter in 'Python':
print(letter),
```
#### The `range()` function
The built-in function range() is useful if we need to create a sequence of numbers, for example, to iterate over this list. It generates lists containing arithmetic progressions:
```
help(range)
range(10)
range(1, 10, 2)
for i in range(10):
n2 = i**2
print(n2),
```
### while
The `while` statement is used for repeating sections of code in a loop until a condition is met (this different than the `for` statement which executes n times):
```
while expression:
statement
```
Let's generate the Fibonacci series using a `while` loop:
```
# Fibonacci series: the sum of two elements defines the next
a, b = 0, 1
while b < 1000:
print(b, end=' ')
a, b = b, a+b
```
## Function definition
A function in a programming language is a piece of code that performs a specific task. Functions are used to reduce duplication of code making easier to reuse it and to decompose complex problems into simpler parts. The use of functions contribute to the clarity of the code.
A function is created with the `def` keyword and the statements in the block of the function must be indented:
```
def function():
pass
```
As per construction, this function does nothing when called:
```
function()
```
The general syntax of a function definition is:
```
def function_name( parameters ):
"""Function docstring.
The help for the function
"""
function body
return variables
```
A more useful function:
```
def fibo(N):
"""Fibonacci series: the sum of two elements defines the next.
The series is calculated till the input parameter N and
returned as an ouput variable.
"""
a, b, c = 0, 1, []
while b < N:
c.append(b)
a, b = b, a + b
return c
fibo(100)
if 3 > 2:
print('teste')
```
Let's implemment the body mass index calculus and categorization as a function:
```
def bmi(weight, height):
"""Body mass index calculus and categorization.
Enter the weight in kg and the height in m.
See http://en.wikipedia.org/wiki/Body_mass_index
"""
bmi = weight / height**2
if bmi < 15:
c = 'very severely underweight'
elif 15 <= bmi < 16:
c = 'severely underweight'
elif 16 <= bmi < 18.5:
c = 'underweight'
elif 18.5 <= bmi < 25:
c = 'normal'
elif 25 <= bmi < 30:
c = 'overweight'
elif 30 <= bmi < 35:
c = 'moderately obese'
elif 35 <= bmi < 40:
c = 'severely obese'
else:
c = 'very severely obese'
s = 'For a weight of {0:.1f} kg and a height of {1:.2f} m,\
the body mass index (bmi) is {2:.1f} kg/m2,\
which is considered {3:s}.'\
.format(weight, height, bmi, c)
print(s)
bmi(73, 1.70)
```
## Numeric data manipulation with Numpy
Numpy is the fundamental package for scientific computing in Python and has a N-dimensional array package convenient to work with numerical data. With Numpy it's much easier and faster to work with numbers grouped as 1-D arrays (a vector), 2-D arrays (like a table or matrix), or higher dimensions. Let's create 1-D and 2-D arrays in Numpy:
```
import numpy as np
x1d = np.array([1, 2, 3, 4, 5, 6])
print(type(x1d))
x1d
x2d = np.array([[1, 2, 3], [4, 5, 6]])
x2d
```
len() and the Numpy functions size() and shape() give information aboout the number of elements and the structure of the Numpy array:
```
print('1-d array:')
print(x1d)
print('len(x1d) = ', len(x1d))
print('np.size(x1d) = ', np.size(x1d))
print('np.shape(x1d) = ', np.shape(x1d))
print('np.ndim(x1d) = ', np.ndim(x1d))
print('\n2-d array:')
print(x2d)
print('len(x2d) = ', len(x2d))
print('np.size(x2d) = ', np.size(x2d))
print('np.shape(x2d) = ', np.shape(x2d))
print('np.ndim(x2d) = ', np.ndim(x2d))
```
Create random data
```
x = np.random.randn(4,3)
x
```
Joining (stacking together) arrays
```
x = np.random.randint(0, 5, size=(2, 3))
print(x)
y = np.random.randint(5, 10, size=(2, 3))
print(y)
np.vstack((x,y))
np.hstack((x,y))
```
Create equally spaced data
```
np.arange(start = 1, stop = 10, step = 2)
np.linspace(start = 0, stop = 1, num = 11)
```
### Interpolation
Consider the following data:
```
y = [5, 4, 10, 8, 1, 10, 2, 7, 1, 3]
```
Suppose we want to create data in between the given data points (interpolation); for instance, let's try to double the resolution of the data by generating twice as many data:
```
t = np.linspace(0, len(y), len(y)) # time vector for the original data
tn = np.linspace(0, len(y), 2 * len(y)) # new time vector for the new time-normalized data
yn = np.interp(tn, t, y) # new time-normalized data
yn
```
The key is the Numpy `interp` function, from its help:
interp(x, xp, fp, left=None, right=None)
One-dimensional linear interpolation.
Returns the one-dimensional piecewise linear interpolant to a function with given values at discrete data-points.
A plot of the data will show what we have done:
```
%matplotlib inline
import matplotlib.pyplot as plt
plt.figure(figsize=(10,5))
plt.plot(t, y, 'bo-', lw=2, label='original data')
plt.plot(tn, yn, '.-', color=[1, 0, 0, .5], lw=2, label='interpolated')
plt.legend(loc='best', framealpha=.5)
plt.show()
```
For more about Numpy, see [http://wiki.scipy.org/Tentative_NumPy_Tutorial](http://wiki.scipy.org/Tentative_NumPy_Tutorial).
## Read and save files
There are two kinds of computer files: text files and binary files:
> Text file: computer file where the content is structured as a sequence of lines of electronic text. Text files can contain plain text (letters, numbers, and symbols) but they are not limited to such. The type of content in the text file is defined by the Unicode encoding (a computing industry standard for the consistent encoding, representation and handling of text expressed in most of the world's writing systems).
>
> Binary file: computer file where the content is encoded in binary form, a sequence of integers representing byte values.
Let's see how to save and read numeric data stored in a text file:
**Using plain Python**
```
f = open("newfile.txt", "w") # open file for writing
f.write("This is a test\n") # save to file
f.write("And here is another line\n") # save to file
f.close()
f = open('newfile.txt', 'r') # open file for reading
f = f.read() # read from file
print(f)
help(open)
```
**Using Numpy**
```
import numpy as np
data = np.random.randn(3,3)
np.savetxt('myfile.txt', data, fmt="%12.6G") # save to file
data = np.genfromtxt('myfile.txt', unpack=True) # read from file
data
```
## Ploting with matplotlib
Matplotlib is the most-widely used packge for plotting data in Python. Let's see some examples of it.
```
import matplotlib.pyplot as plt
```
Use the IPython magic `%matplotlib inline` to plot a figure inline in the notebook with the rest of the text:
```
%matplotlib notebook
import numpy as np
t = np.linspace(0, 0.99, 100)
x = np.sin(2 * np.pi * 2 * t)
n = np.random.randn(100) / 5
plt.Figure(figsize=(12,8))
plt.plot(t, x, label='sine', linewidth=2)
plt.plot(t, x + n, label='noisy sine', linewidth=2)
plt.annotate(s='$sin(4 \pi t)$', xy=(.2, 1), fontsize=20, color=[0, 0, 1])
plt.legend(loc='best', framealpha=.5)
plt.xlabel('Time [s]')
plt.ylabel('Amplitude')
plt.title('Data plotting using matplotlib')
plt.show()
```
Use the IPython magic `%matplotlib qt` to plot a figure in a separate window (from where you will be able to change some of the figure proprerties):
```
%matplotlib qt
mu, sigma = 10, 2
x = mu + sigma * np.random.randn(1000)
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 4))
ax1.plot(x, 'ro')
ax1.set_title('Data')
ax1.grid()
n, bins, patches = ax2.hist(x, 25, normed=True, facecolor='r') # histogram
ax2.set_xlabel('Bins')
ax2.set_ylabel('Probability')
ax2.set_title('Histogram')
fig.suptitle('Another example using matplotlib', fontsize=18, y=1)
ax2.grid()
plt.tight_layout()
plt.show()
```
And a window with the following figure should appear:
```
from IPython.display import Image
Image(url="./../images/plot.png")
```
You can switch back and forth between inline and separate figure using the `%matplotlib` magic commands used above. There are plenty more examples with the source code in the [matplotlib gallery](http://matplotlib.org/gallery.html).
```
# get back the inline plot
%matplotlib inline
```
## Signal processing with Scipy
The Scipy package has a lot of functions for signal processing, among them: Integration (scipy.integrate), Optimization (scipy.optimize), Interpolation (scipy.interpolate), Fourier Transforms (scipy.fftpack), Signal Processing (scipy.signal), Linear Algebra (scipy.linalg), and Statistics (scipy.stats). As an example, let's see how to use a low-pass Butterworth filter to attenuate high-frequency noise and how the differentiation process of a signal affects the signal-to-noise content. We will also calculate the Fourier transform of these data to look at their frequencies content.
```
from scipy.signal import butter, filtfilt
import scipy.fftpack
freq = 100.
t = np.arange(0,1,.01);
w = 2*np.pi*1 # 1 Hz
y = np.sin(w*t)+0.1*np.sin(10*w*t)
# Butterworth filter
b, a = butter(4, (5/(freq/2)), btype = 'low')
y2 = filtfilt(b, a, y)
# 2nd derivative of the data
ydd = np.diff(y,2)*freq*freq # raw data
y2dd = np.diff(y2,2)*freq*freq # filtered data
# frequency content
yfft = np.abs(scipy.fftpack.fft(y))/(y.size/2); # raw data
y2fft = np.abs(scipy.fftpack.fft(y2))/(y.size/2); # filtered data
freqs = scipy.fftpack.fftfreq(y.size, 1./freq)
yddfft = np.abs(scipy.fftpack.fft(ydd))/(ydd.size/2);
y2ddfft = np.abs(scipy.fftpack.fft(y2dd))/(ydd.size/2);
freqs2 = scipy.fftpack.fftfreq(ydd.size, 1./freq)
```
And the plots:
```
fig, ((ax1,ax2),(ax3,ax4)) = plt.subplots(2, 2, figsize=(10, 4))
ax1.set_title('Temporal domain', fontsize=14)
ax1.plot(t, y, 'r', linewidth=2, label = 'raw data')
ax1.plot(t, y2, 'b', linewidth=2, label = 'filtered @ 5 Hz')
ax1.set_ylabel('f')
ax1.legend(frameon=False, fontsize=12)
ax2.set_title('Frequency domain', fontsize=14)
ax2.plot(freqs[:yfft.size/4], yfft[:yfft.size/4],'r', lw=2,label='raw data')
ax2.plot(freqs[:yfft.size/4],y2fft[:yfft.size/4],'b--',lw=2,label='filtered @ 5 Hz')
ax2.set_ylabel('FFT(f)')
ax2.legend(frameon=False, fontsize=12)
ax3.plot(t[:-2], ydd, 'r', linewidth=2, label = 'raw')
ax3.plot(t[:-2], y2dd, 'b', linewidth=2, label = 'filtered @ 5 Hz')
ax3.set_xlabel('Time [s]'); ax3.set_ylabel("f ''")
ax4.plot(freqs[:yddfft.size/4], yddfft[:yddfft.size/4], 'r', lw=2, label = 'raw')
ax4.plot(freqs[:yddfft.size/4],y2ddfft[:yddfft.size/4],'b--',lw=2, label='filtered @ 5 Hz')
ax4.set_xlabel('Frequency [Hz]'); ax4.set_ylabel("FFT(f '')")
plt.show()
```
For more about Scipy, see [http://docs.scipy.org/doc/scipy/reference/tutorial/](http://docs.scipy.org/doc/scipy/reference/tutorial/).
## Symbolic mathematics with Sympy
Sympy is a package to perform symbolic mathematics in Python. Let's see some of its features:
```
from IPython.display import display
import sympy as sym
from sympy.interactive import printing
printing.init_printing()
```
Define some symbols and the create a second-order polynomial function (a.k.a., parabola):
```
x, y = sym.symbols('x y')
y = x**2 - 2*x - 3
y
```
Plot the parabola at some given range:
```
from sympy.plotting import plot
%matplotlib inline
plot(y, (x, -3, 5));
```
And the roots of the parabola are given by:
```
sym.solve(y, x)
```
We can also do symbolic differentiation and integration:
```
dy = sym.diff(y, x)
dy
sym.integrate(dy, x)
```
For example, let's use Sympy to represent three-dimensional rotations. Consider the problem of a coordinate system xyz rotated in relation to other coordinate system XYZ. The single rotations around each axis are illustrated by:
```
from IPython.display import Image
Image(url="./../images/rotations.png")
```
The single 3D rotation matrices around Z, Y, and X axes can be expressed in Sympy:
```
from IPython.core.display import Math
from sympy import symbols, cos, sin, Matrix, latex
a, b, g = symbols('alpha beta gamma')
RX = Matrix([[1, 0, 0], [0, cos(a), -sin(a)], [0, sin(a), cos(a)]])
display(Math(latex('\\mathbf{R_{X}}=') + latex(RX, mat_str = 'matrix')))
RY = Matrix([[cos(b), 0, sin(b)], [0, 1, 0], [-sin(b), 0, cos(b)]])
display(Math(latex('\\mathbf{R_{Y}}=') + latex(RY, mat_str = 'matrix')))
RZ = Matrix([[cos(g), -sin(g), 0], [sin(g), cos(g), 0], [0, 0, 1]])
display(Math(latex('\\mathbf{R_{Z}}=') + latex(RZ, mat_str = 'matrix')))
```
And using Sympy, a sequence of elementary rotations around X, Y, Z axes is given by:
```
RXYZ = RZ*RY*RX
display(Math(latex('\\mathbf{R_{XYZ}}=') + latex(RXYZ, mat_str = 'matrix')))
```
Suppose there is a rotation only around X ($\alpha$) by $\pi/2$; we can get the numerical value of the rotation matrix by substituing the angle values:
```
r = RXYZ.subs({a: np.pi/2, b: 0, g: 0})
r
```
And we can prettify this result:
```
display(Math(latex(r'\mathbf{R_{(\alpha=\pi/2)}}=') +
latex(r.n(chop=True, prec=3), mat_str = 'matrix')))
```
For more about Sympy, see [http://docs.sympy.org/latest/tutorial/](http://docs.sympy.org/latest/tutorial/).
## Data analysis with pandas
> "[pandas](http://pandas.pydata.org/) is a Python package providing fast, flexible, and expressive data structures designed to make working with “relational” or “labeled” data both easy and intuitive. It aims to be the fundamental high-level building block for doing practical, real world data analysis in Python."
To work with labellled data, pandas has a type called DataFrame (basically, a matrix where columns and rows have may names and may be of different types) and it is also the main type of the software [R](http://www.r-project.org/). Fo ezample:
```
import pandas as pd
x = 5*['A'] + 5*['B']
x
df = pd.DataFrame(np.random.rand(10,2), columns=['Level 1', 'Level 2'] )
df['Group'] = pd.Series(['A']*5 + ['B']*5)
plot = df.boxplot(by='Group')
from pandas.tools.plotting import scatter_matrix
df = pd.DataFrame(np.random.randn(100, 3), columns=['A', 'B', 'C'])
plot = scatter_matrix(df, alpha=0.5, figsize=(8, 6), diagonal='kde')
```
pandas is aware the data is structured and give you basic statistics considerint that and nicely formatted:
```
df.describe()
```
For more on pandas, see this tutorial: [http://pandas.pydata.org/pandas-docs/stable/10min.html](http://pandas.pydata.org/pandas-docs/stable/10min.html).
## To learn more about Python
There is a lot of good material in the internet about Python for scientific computing, here is a small list of interesting stuff:
- [How To Think Like A Computer Scientist](http://www.openbookproject.net/thinkcs/python/english2e/) or [the interactive edition](http://interactivepython.org/courselib/static/thinkcspy/index.html) (book)
- [Python Scientific Lecture Notes](http://scipy-lectures.github.io/) (lecture notes)
- [Lectures on scientific computing with Python](https://github.com/jrjohansson/scientific-python-lectures#lectures-on-scientific-computing-with-python) (lecture notes)
- [IPython in depth: high-productivity interactive and parallel python](http://youtu.be/bP8ydKBCZiY) (video lectures)
|
github_jupyter
|
```
import numpy as np
import pandas as pd
import json as json
from scipy import stats
from statsmodels.formula.api import ols
import matplotlib.pyplot as plt
from scipy.signal import savgol_filter
from o_plot import opl # a small local package dedicated to this project
# Prepare the data
# loading the data
file_name = 'Up_to_Belem_TE4AL2_data_new.json'
f = open(file_name)
All_data = json.load(f)
print(len(All_data))
```
## Note for the interpretation of the curves and definition of the statistical variables
The quantum state classifier (QSC) error rates $\widehat{r}_i$ in function of the number of experimental shots $n$ were determined for each highly entangled quantum state $\omega_i$ in the $\Omega$ set, with $i=1...m$.
The curves seen on the figures represents the mean of the QSC error rate $\widehat{r}_{mean}$ over the $m$ quantum states at each $n$ value.
This Monte Carlo simulation allowed to determine a safe shot number $n_s$ such that $\forall i\; \widehat{r}_i\le \epsilon_s$. The value of $\epsilon_s$ was set at 0.001.
$\widehat{r}_{max}$ is the maximal value observed among all the $\widehat{r}_i$ values for the determined number of shots $n_s$.
Similarly, from the error curves stored in the data file, was computed the safe shot number $n_t$ such that $\widehat{r}_{mean}\le \epsilon_t$. The value of $\epsilon_t$ was set at 0.0005 after verifying that all $\widehat{r}_{mean}$ at $n_s$ were $\le \epsilon_s$ in the different experimental settings.
Correspondance between variables names in the text and in the data base:
- $\widehat{r}_{mean}$: error_curve
- $n_s$: shots
- max ($\widehat{r}_i$) at $n_s$: shot_rate
- $\widehat{r}_{mean}$ at $n_s$: mns_rate
- $n_t$: m_shots
- $\widehat{r}_{mean}$ at $n_t$: m_shot_rate
```
# Calculate shot number 'm_shots' for mean error rate 'm_shot_rates' <= epsilon_t
len_data = len(All_data)
epsilon_t = 0.0005
window = 11
for i in range(len_data):
curve = np.array(All_data[i]['error_curve'])
# filter the curve only for real devices:
if All_data[i]['device']!="ideal_device":
curve = savgol_filter(curve,window,2)
# find the safe shot number:
len_c = len(curve)
n_a = np.argmin(np.flip(curve)<=epsilon_t)+1
if n_a == 1:
n_a = np.nan
m_r = np.nan
else:
m_r = curve[len_c-n_a+1]
All_data[i]['min_r_shots'] = len_c-n_a
All_data[i]['min_r'] = m_r
# find mean error rate at n_s
for i in range(len_data):
i_shot = All_data[i]["shots"]
if not np.isnan(i_shot):
j = int(i_shot)-1
All_data[i]['mns_rate'] = All_data[i]['error_curve'][j]
else:
All_data[i]['mns_rate'] = np.nan
#defining the pandas data frame for statistics excluding from here ibmqx2 data
df_All= pd.DataFrame(All_data,columns=['shot_rates','shots', 'device', 'fidelity',
'mitigation','model','id_gates',
'QV', 'metric','error_curve',
'mns_rate','min_r_shots',
'min_r']).query("device != 'ibmqx2'")
# any shot number >= 488 indicates that the curve calculation
# was ended after reaching n = 500, hence this data correction:
df_All.loc[df_All.shots>=488,"shots"]=np.nan
# add the variable neperian log of safe shot number:
df_All['log_shots'] = np.log(df_All['shots'])
df_All['log_min_r_shots'] = np.log(df_All['min_r_shots'])
```
### Error rates in function of chosen $\epsilon_s$ and $\epsilon_t$
```
print("max mean error rate at n_s over all experiments =", round(max(df_All.mns_rate[:-2]),6))
print("min mean error rate at n_t over all experiments =", round(min(df_All.min_r[:-2]),6))
print("max mean error rate at n_t over all experiments =", round(max(df_All.min_r[:-2]),6))
df_All.mns_rate[:-2].plot.hist(alpha=0.5, legend = True)
df_All.min_r[:-2].plot.hist(alpha=0.5, legend = True)
```
# Statistical overview
For this section, an ordinary linear least square estimation is performed.
The dependent variables tested are $ln\;n_s$ (log_shots) and $ln\;n_t$ (log_min_r_shots)
```
stat_model = ols("log_shots ~ metric",
df_All.query("device != 'ideal_device'")).fit()
print(stat_model.summary())
stat_model = ols("log_min_r_shots ~ metric",
df_All.query("device != 'ideal_device'")).fit()
print(stat_model.summary())
stat_model = ols("log_shots ~ model+mitigation+id_gates+fidelity+QV",
df_All.query("device != 'ideal_device' & metric == 'sqeuclidean'")).fit()
print(stat_model.summary())
stat_model = ols("log_min_r_shots ~ model+mitigation+id_gates+fidelity+QV",
df_All.query("device != 'ideal_device'& metric == 'sqeuclidean'")).fit()
print(stat_model.summary())
```
#### Comments:
For the QSC, two different metrics were compared and at the end they gave the same output. For further analysis, the results obtained using the squared euclidean distance between distribution will be illustrated in this notebook, as it is more classical and strictly equivalent to the other classical Hellinger and Bhattacharyya distances. The Jensen-Shannon metric has however the theoretical advantage of being bayesian in nature and is therefore presented as an option for the result analysis.
Curves obtained for counts corrected by measurement error mitigation (MEM) are used in this presentation. MEM significantly reduces $n_s$ and $n_t$. However, using counts distribution before MEM is presented as an option because they anticipate how the method could perform in devices with more qubits where obtaining the mitigation filter is a problem.
Introducing a delay time $\delta t$ of 256 identity gates between state creation and measurement significantly increased $ln\;n_s$ and $ln\;n_t$ .
# Detailed statistical analysis
### Determine the options
Running sequentially these cells will end up with the main streaming options
```
# this for Jensen-Shannon metric
s_metric = 'jensenshannon'
sm = np.array([96+16+16+16]) # added Quito and Lima and Belem
SAD=0
# ! will be unselected by running the next cell
# mainstream option for metric: squared euclidean distance
# skip this cell if you don't want this option
s_metric = 'sqeuclidean'
sm = np.array([97+16+16+16]) # added Quito and Lima and Belem
SAD=2
# this for no mitigation
mit = 'no'
MIT=-4
# ! will be unselected by running the next cell
# mainstream option: this for measurement mitigation
# skip this cell if you don't want this option
mit = 'yes'
MIT=0
```
## 1. Compare distribution models
```
# select data according to the options
df_mod = df_All[df_All.mitigation == mit][df_All.metric == s_metric]
```
### A look at $n_s$ and $n_t$
```
print("mitigation:",mit," metric:",s_metric )
df_mod.groupby('device')[['shots','min_r_shots']].describe(percentiles=[0.5])
```
### Ideal vs empirical model: no state creation - measurements delay
```
ADD=0+SAD+MIT
#opl.plot_curves(All_data, np.append(sm,ADD+np.array([4,5,12,13,20,21,28,29,36,37,44,45])),
opl.plot_curves(All_data, np.append(sm,ADD+np.array([4,5,12,13,20,21,28,29,36,37,52,53,60,61,68,69])),
"Monte Carlo Simulation: Theoretical PDM vs Empirical PDM - no $\delta_t0$",
["metric","mitigation"],
["device","model"], right_xlimit = 90)
```
#### Paired t-test and Wilcoxon test
```
for depvar in ['log_shots', 'log_min_r_shots']:
#for depvar in ['shots', 'min_r_shots']:
print("mitigation:",mit," metric:",s_metric, "variable:", depvar)
df_dep = df_mod.query("id_gates == 0.0").groupby(['model'])[depvar]
print(df_dep.describe(percentiles=[0.5]),"\n")
# no error rate curve obtained for ibmqx2 with the ideal model, hence this exclusion:
df_emp=df_mod.query("model == 'empirical' & id_gates == 0.0")
df_ide=df_mod.query("model == 'ideal_sim' & id_gates == 0.0") #.reindex_like(df_emp,'nearest')
# back to numpy arrays from pandas:
print("paired data")
print(np.asarray(df_emp[depvar]))
print(np.asarray(df_ide[depvar]),"\n")
print(stats.ttest_rel(np.asarray(df_emp[depvar]),np.asarray(df_ide[depvar])))
print(stats.wilcoxon(np.asarray(df_emp[depvar]),np.asarray(df_ide[depvar])),"\n")
print("mitigation:",mit," metric:",s_metric, "id_gates == 0.0 ")
stat_model = ols("log_shots ~ model + device + fidelity + QV" ,
df_mod.query("id_gates == 0.0 ")).fit()
print(stat_model.summary())
print("mitigation:",mit," metric:",s_metric, "id_gates == 0.0 " )
stat_model = ols("log_min_r_shots ~ model + device + fidelity+QV",
df_mod.query("id_gates == 0.0 ")).fit()
print(stat_model.summary())
```
### Ideal vs empirical model: with state creation - measurements delay of 256 id gates
```
ADD=72+SAD+MIT
opl.plot_curves(All_data, np.append(sm,ADD+np.array([4,5,12,13,20,21,28,29,36,37,52,53,60,61,68,69])),
"No noise simulator vs empirical model - $\epsilon=0.001$ - with delay",
["metric","mitigation"],
["device","model"], right_xlimit = 90)
```
#### Paired t-test and Wilcoxon test
```
for depvar in ['log_shots', 'log_min_r_shots']:
print("mitigation:",mit," metric:",s_metric, "variable:", depvar)
df_dep = df_mod.query("id_gates == 256.0 ").groupby(['model'])[depvar]
print(df_dep.describe(percentiles=[0.5]),"\n")
# no error rate curve obtained for ibmqx2 with the ideal model, hence their exclusion:
df_emp=df_mod.query("model == 'empirical' & id_gates == 256.0 ")
df_ide=df_mod.query("model == 'ideal_sim' & id_gates == 256.0") #.reindex_like(df_emp,'nearest')
# back to numpy arrays from pandas:
print("paired data")
print(np.asarray(df_emp[depvar]))
print(np.asarray(df_ide[depvar]),"\n")
print(stats.ttest_rel(np.asarray(df_emp[depvar]),np.asarray(df_ide[depvar])))
print(stats.wilcoxon(np.asarray(df_emp[depvar]),np.asarray(df_ide[depvar])),"\n")
print("mitigation:",mit," metric:",s_metric , "id_gates == 256.0 ")
stat_model = ols("log_shots ~ model + device + fidelity + QV" ,
df_mod.query("id_gates == 256.0 ")).fit()
print(stat_model.summary())
print("mitigation:",mit," metric:",s_metric, "id_gates == 256.0 " )
stat_model = ols("log_min_r_shots ~ model + device +fidelity+QV",
df_mod.query("id_gates == 256.0 ")).fit()
print(stat_model.summary())
```
### Pooling results obtained in circuit sets with and without creation-measurement delay
#### Paired t-test and Wilcoxon test
```
#for depvar in ['log_shots', 'log_min_r_shots']:
for depvar in ['log_shots', 'log_min_r_shots']:
print("mitigation:",mit," metric:",s_metric, "variable:", depvar)
df_dep = df_mod.groupby(['model'])[depvar]
print(df_dep.describe(percentiles=[0.5]),"\n")
# no error rate curve obtained for ibmqx2 with the ideal model, hence this exclusion:
df_emp=df_mod.query("model == 'empirical'")
df_ide=df_mod.query("model == 'ideal_sim'") #.reindex_like(df_emp,'nearest')
# back to numpy arrays from pandas:
print("paired data")
print(np.asarray(df_emp[depvar]))
print(np.asarray(df_ide[depvar]),"\n")
print(stats.ttest_rel(np.asarray(df_emp[depvar]),np.asarray(df_ide[depvar])))
print(stats.wilcoxon(np.asarray(df_emp[depvar]),np.asarray(df_ide[depvar])),"\n")
```
#### Statsmodel Ordinary Least Square (OLS) Analysis
```
print("mitigation:",mit," metric:",s_metric )
stat_model = ols("log_shots ~ model + id_gates + device + fidelity + QV" ,
df_mod).fit()
print(stat_model.summary())
print("mitigation:",mit," metric:",s_metric )
stat_model = ols("log_min_r_shots ~ model + id_gates + device + fidelity+QV ",
df_mod).fit()
print(stat_model.summary())
```
|
github_jupyter
|
# **OPTICS Algorithm**
Ordering Points to Identify the Clustering Structure (OPTICS) is a Clustering Algorithm which locates region of high density that are seperated from one another by regions of low density.
For using this library in Python this comes under Scikit Learn Library.
## Parameters:
**Reachability Distance** -It is defined with respect to another data point q(Let). The Reachability distance between a point p and q is the maximum of the Core Distance of p and the Euclidean Distance(or some other distance metric) between p and q. Note that The Reachability Distance is not defined if q is not a Core point.<br><br>
**Core Distance** – It is the minimum value of radius required to classify a given point as a core point. If the given point is not a Core point, then it’s Core Distance is undefined.
## OPTICS Pointers
<ol>
<li>Produces a special order of the database with respect to its density-based clustering structure.This cluster-ordering contains info equivalent to the density-based clustering corresponding to a broad range of parameter settings.</li>
<li>Good for both automatic and interactive cluster analysis, including finding intrinsic clustering structure</li>
<li>Can be represented graphically or using visualization technique</li>
</ol>
In this file , we will showcase how a basic OPTICS Algorithm works in Python , on a randomly created Dataset.
## Importing Libraries
```
import matplotlib.pyplot as plt #Used for plotting graphs
from sklearn.datasets import make_blobs #Used for creating random dataset
from sklearn.cluster import OPTICS #OPTICS is provided under Scikit-Learn Extra
from sklearn.metrics import silhouette_score #silhouette score for checking accuracy
import numpy as np
import pandas as pd
```
## Generating Data
```
data, clusters = make_blobs(
n_samples=800, centers=4, cluster_std=0.3, random_state=0
)
# Originally created plot with data
plt.scatter(data[:,0], data[:,1])
plt.show()
```
## Model Creation
```
# Creating OPTICS Model
optics_model = OPTICS(min_samples=50, xi=.05, min_cluster_size=.05)
#min_samples : The number of samples in a neighborhood for a point to be considered as a core point.
#xi : Determines the minimum steepness on the reachability plot that constitutes a cluster boundary
#min_cluster_size : Minimum number of samples in an OPTICS cluster, expressed as an absolute number or a fraction of the number of samples
pred =optics_model.fit(data) #Fitting the data
optics_labels = optics_model.labels_ #storing labels predicted by our model
no_clusters = len(np.unique(optics_labels) ) #determining the no. of unique clusters and noise our model predicted
no_noise = np.sum(np.array(optics_labels) == -1, axis=0)
```
## Plotting our observations
```
print('Estimated no. of clusters: %d' % no_clusters)
print('Estimated no. of noise points: %d' % no_noise)
colors = list(map(lambda x: '#aa2211' if x == 1 else '#120416', optics_labels))
plt.scatter(data[:,0], data[:,1], c=colors, marker="o", picker=True)
plt.title(f'OPTICS clustering')
plt.xlabel('Axis X[0]')
plt.ylabel('Axis X[1]')
plt.show()
# Generate reachability plot , this helps understand the working of our Model in OPTICS
reachability = optics_model.reachability_[optics_model.ordering_]
plt.plot(reachability)
plt.title('Reachability plot')
plt.show()
```
## Accuracy of OPTICS Clustering
```
OPTICS_score = silhouette_score(data, optics_labels)
OPTICS_score
```
On this randomly created dataset we got an accuracy of 84.04 %
### Hence , we can see the implementation of OPTICS Clustering Algorithm on a randomly created Dataset .As we can observe from our result . the score which we got is around 84% , which is really good for a unsupervised learning algorithm.However , this accuracy definitely comes with the additonal cost of higher computational power
## Thanks a lot!
|
github_jupyter
|
# Chapter 7. 텍스트 문서의 범주화 - (4) IMDB 전체 데이터로 전이학습
- 앞선 전이학습 실습과는 달리, IMDB 영화리뷰 데이터셋 전체를 사용하며 문장 수는 10개 -> 20개로 조정한다
- IMDB 영화 리뷰 데이터를 다운로드 받아 data 디렉토리에 압축 해제한다
- 다운로드 : http://ai.stanford.edu/~amaas/data/sentiment/
- 저장경로 : data/aclImdb
```
import os
import config
from dataloader.loader import Loader
from preprocessing.utils import Preprocess, remove_empty_docs
from dataloader.embeddings import GloVe
from model.cnn_document_model import DocumentModel, TrainingParameters
from keras.callbacks import ModelCheckpoint, EarlyStopping
import numpy as np
```
## 학습 파라미터 설정
```
# 학습된 모델을 저장할 디렉토리 생성
if not os.path.exists(os.path.join(config.MODEL_DIR, 'imdb')):
os.makedirs(os.path.join(config.MODEL_DIR, 'imdb'))
# 학습 파라미터 설정
train_params = TrainingParameters('imdb_transfer_tanh_activation',
model_file_path = config.MODEL_DIR+ '/imdb/full_model_10.hdf5',
model_hyper_parameters = config.MODEL_DIR+ '/imdb/full_model_10.json',
model_train_parameters = config.MODEL_DIR+ '/imdb/full_model_10_meta.json',
num_epochs=30,
batch_size=128)
```
## IMDB 데이터셋 로드
```
# 다운받은 IMDB 데이터 로드: 학습셋 전체 사용
train_df = Loader.load_imdb_data(directory = 'train')
# train_df = train_df.sample(frac=0.05, random_state = train_params.seed)
print(f'train_df.shape : {train_df.shape}')
test_df = Loader.load_imdb_data(directory = 'test')
print(f'test_df.shape : {test_df.shape}')
# 텍스트 데이터, 레이블 추출
corpus = train_df['review'].tolist()
target = train_df['sentiment'].tolist()
corpus, target = remove_empty_docs(corpus, target)
print(f'corpus size : {len(corpus)}')
print(f'target size : {len(target)}')
```
## 인덱스 시퀀스 생성
```
# 앞선 전이학습 실습과 달리, 문장 개수를 10개 -> 20개로 상향
Preprocess.NUM_SENTENCES = 20
# 학습셋을 인덱스 시퀀스로 변환
preprocessor = Preprocess(corpus=corpus)
corpus_to_seq = preprocessor.fit()
print(f'corpus_to_seq size : {len(corpus_to_seq)}')
print(f'corpus_to_seq[0] size : {len(corpus_to_seq[0])}')
# 테스트셋을 인덱스 시퀀스로 변환
test_corpus = test_df['review'].tolist()
test_target = test_df['sentiment'].tolist()
test_corpus, test_target = remove_empty_docs(test_corpus, test_target)
test_corpus_to_seq = preprocessor.transform(test_corpus)
print(f'test_corpus_to_seq size : {len(test_corpus_to_seq)}')
print(f'test_corpus_to_seq[0] size : {len(test_corpus_to_seq[0])}')
# 학습셋, 테스트셋 준비
x_train = np.array(corpus_to_seq)
x_test = np.array(test_corpus_to_seq)
y_train = np.array(target)
y_test = np.array(test_target)
print(f'x_train.shape : {x_train.shape}')
print(f'y_train.shape : {y_train.shape}')
print(f'x_test.shape : {x_test.shape}')
print(f'y_test.shape : {y_test.shape}')
```
## GloVe 임베딩 초기화
```
# GloVe 임베딩 초기화 - glove.6B.50d.txt pretrained 벡터 사용
glove = GloVe(50)
initial_embeddings = glove.get_embedding(preprocessor.word_index)
print(f'initial_embeddings.shape : {initial_embeddings.shape}')
```
## 훈련된 모델 로드
- HandsOn03에서 아마존 리뷰 데이터로 학습한 CNN 모델을 로드한다.
- DocumentModel 클래스의 load_model로 모델을 로드하고, load_model_weights로 학습된 가중치를 가져온다.
- 그 후, GloVe.update_embeddings 함수로 GloVe 초기화 임베딩을 업데이트한다
```
# 모델 하이퍼파라미터 로드
model_json_path = os.path.join(config.MODEL_DIR, 'amazonreviews/model_06.json')
amazon_review_model = DocumentModel.load_model(model_json_path)
# 모델 가중치 로드
model_hdf5_path = os.path.join(config.MODEL_DIR, 'amazonreviews/model_06.hdf5')
amazon_review_model.load_model_weights(model_hdf5_path)
# 모델 임베딩 레이어 추출
learned_embeddings = amazon_review_model.get_classification_model().get_layer('imdb_embedding').get_weights()[0]
print(f'learned_embeddings size : {len(learned_embeddings)}')
# 기존 GloVe 모델을 학습된 임베딩 행렬로 업데이트한다
glove.update_embeddings(preprocessor.word_index,
np.array(learned_embeddings),
amazon_review_model.word_index)
# 업데이트된 임베딩을 얻는다
initial_embeddings = glove.get_embedding(preprocessor.word_index)
```
## IMDB 전이학습 모델 생성
```
# 분류 모델 생성 : IMDB 리뷰 데이터를 입력받아 이진분류를 수행하는 모델 생성
imdb_model = DocumentModel(vocab_size=preprocessor.get_vocab_size(),
word_index = preprocessor.word_index,
num_sentences=Preprocess.NUM_SENTENCES,
embedding_weights=initial_embeddings,
embedding_regularizer_l2 = 0.0,
conv_activation = 'tanh',
train_embedding = True, # 임베딩 레이어의 가중치 학습함
learn_word_conv = False, # 단어 수준 conv 레이어의 가중치 학습 안 함
learn_sent_conv = False, # 문장 수준 conv 레이어의 가중치 학습 안 함
hidden_dims=64,
input_dropout=0.1,
hidden_layer_kernel_regularizer=0.01,
final_layer_kernel_regularizer=0.01)
# 가중치 업데이트 : 생성한 imdb_model 모델에서 다음의 각 레이어들의 가중치를 위에서 로드한 가중치로 갱신한다
for l_name in ['word_conv','sentence_conv','hidden_0', 'final']:
new_weights = amazon_review_model.get_classification_model().get_layer(l_name).get_weights()
imdb_model.get_classification_model().get_layer(l_name).set_weights(weights=new_weights)
```
## 모델 학습 및 평가
```
# 모델 컴파일
imdb_model.get_classification_model().compile(loss="binary_crossentropy",
optimizer='rmsprop',
metrics=["accuracy"])
# callback (1) - 체크포인트
checkpointer = ModelCheckpoint(filepath=train_params.model_file_path,
verbose=1,
save_best_only=True,
save_weights_only=True)
# callback (2) - 조기종료
early_stop = EarlyStopping(patience=2)
# 학습 시작
imdb_model.get_classification_model().fit(x_train,
y_train,
batch_size=train_params.batch_size,
epochs=train_params.num_epochs,
verbose=2,
validation_split=0.01,
callbacks=[checkpointer])
# 모델 저장
imdb_model._save_model(train_params.model_hyper_parameters)
train_params.save()
# 모델 평가
imdb_model.get_classification_model().evaluate(x_test,
y_test,
batch_size=train_params.batch_size*10,
verbose=2)
```
|
github_jupyter
|
```
import pandas as pd
import numpy as np
data = np.array([1,2,3,4,5,6])
name = np.array(['' for x in range(6)])
besio = np.array(['' for x in range(6)])
entity = besio
columns = ['name/doi', 'data', 'BESIO', 'entity']
df = pd.DataFrame(np.array([name, data, besio, entity]).transpose(), columns=columns)
df.iloc[1,0] = 'doi'
hey = np.random.shuffle(data)
for piece in np.random.shuffle(data):
print(piece)
df
filename = 'carbon_ner_labels.xlsx'
append_df_to_excel(filename, df, startcol=0)
append_df_to_excel(filename, df, startcol=6)
def append_df_to_excel(filename, df, sheet_name='Sheet1', startrow=0, startcol=None,
truncate_sheet=False,
**to_excel_kwargs):
"""
Append a DataFrame [df] to existing Excel file [filename]
into [sheet_name] Sheet.
If [filename] doesn't exist, then this function will create it.
Parameters:
filename : File path or existing ExcelWriter
(Example: '/path/to/file.xlsx')
df : dataframe to save to workbook
sheet_name : Name of sheet which will contain DataFrame.
(default: 'Sheet1')
startrow : upper left cell row to dump data frame.
Per default (startrow=None) calculate the last row
in the existing DF and write to the next row...
startcol : upper left cell column to dump data frame.
truncate_sheet : truncate (remove and recreate) [sheet_name]
before writing DataFrame to Excel file
to_excel_kwargs : arguments which will be passed to `DataFrame.to_excel()`
[can be dictionary]
Returns: None
"""
from openpyxl import load_workbook
import pandas as pd
# ignore [engine] parameter if it was passed
if 'engine' in to_excel_kwargs:
to_excel_kwargs.pop('engine')
writer = pd.ExcelWriter(filename, engine='openpyxl')
# Python 2.x: define [FileNotFoundError] exception if it doesn't exist
try:
FileNotFoundError
except NameError:
FileNotFoundError = IOError
try:
# try to open an existing workbook
writer.book = load_workbook(filename)
if startcol is None and sheet_name in writer.book.sheetnames:
startcol = writer.book[sheet_name].max_col
# truncate sheet
if truncate_sheet and sheet_name in writer.book.sheetnames:
# index of [sheet_name] sheet
idx = writer.book.sheetnames.index(sheet_name)
# remove [sheet_name]
writer.book.remove(writer.book.worksheets[idx])
# create an empty sheet [sheet_name] using old index
writer.book.create_sheet(sheet_name, idx)
# copy existing sheets
writer.sheets = {ws.title:ws for ws in writer.book.worksheets}
except FileNotFoundError:
# file does not exist yet, we will create it
pass
if startcol is None:
startcol = 0
# write out the new sheet
df.to_excel(writer, sheet_name, startrow=startrow, startcol=startcol, **to_excel_kwargs)
# save the workbook
writer.save()
```
|
github_jupyter
|
# CTR预估(1)
资料&&代码整理by[@寒小阳](https://blog.csdn.net/han_xiaoyang)(hanxiaoyang.ml@gmail.com)
reference:
* [《广告点击率预估是怎么回事?》](https://zhuanlan.zhihu.com/p/23499698)
* [从ctr预估问题看看f(x)设计—DNN篇](https://zhuanlan.zhihu.com/p/28202287)
* [Atomu2014 product_nets](https://github.com/Atomu2014/product-nets)
关于CTR预估的背景推荐大家看欧阳辰老师在知乎的文章[《广告点击率预估是怎么回事?》](https://zhuanlan.zhihu.com/p/23499698),感谢欧阳辰老师并在这里做一点小小的摘抄。
>点击率预估是广告技术的核心算法之一,它是很多广告算法工程师喜爱的战场。一直想介绍一下点击率预估,但是涉及公式和模型理论太多,怕说不清楚,读者也不明白。所以,这段时间花了一些时间整理点击率预估的知识,希望在尽量不使用数据公式的情况下,把大道理讲清楚,给一些不愿意看公式的同学一个Cook Book。
> ### 点击率预测是什么?
> * 点击率预测是对每次广告的点击情况做出预测,可以判定这次为点击或不点击,也可以给出点击的概率,有时也称作pClick。
> ### 点击率预测和推荐算法的不同?
> * 广告中点击率预估需要给出精准的点击概率,A点击率0.3% , B点击率0.13%等,需要结合出价用于排序使用;推荐算法很多时候只需要得出一个最优的次序A>B>C即可;
> ### 搜索和非搜索广告点击率预测的区别
> * 搜索中有强搜索信号-“查询词(Query)”,查询词和广告内容的匹配程度很大程度影响了点击概率; 点击率也高,PC搜索能到达百分之几的点击率。
> * 非搜索广告(例如展示广告,信息流广告),点击率的计算很多来源于用户的兴趣和广告特征,上下文环境;移动信息流广告的屏幕比较大,用户关注度也比较集中,好位置也能到百分之几的点击率。对于很多文章底部的广告,点击率非常低,用户关注度也不高,常常是千分之几,甚至更低;
> ### 如何衡量点击率预测的准确性?
> AUC是常常被用于衡量点击率预估的准确性的方法;理解AUC之前,需要理解一下Precision/Recall;对于一个分类器,我们通常将结果分为:TP,TN,FP,FN。
> 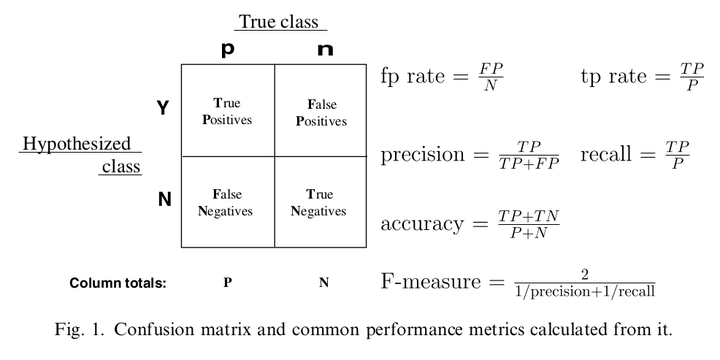
> 本来用Precision=TP/(TP+FP),Recall=TP/P,也可以用于评估点击率算法的好坏,毕竟这是一种监督学习,每一次预测都有正确答案。但是,这种方法对于测试数据样本的依赖性非常大,稍微不同的测试数据集合,结果差异非常大。那么,既然无法使用简单的单点Precision/Recall来描述,我们可以考虑使用一系列的点来描述准确性。做法如下:
> * 找到一系列的测试数据,点击率预估分别会对每个测试数据给出点击/不点击,和Confidence Score。
> * 按照给出的Score进行排序,那么考虑如果将Score作为一个Thresholds的话,考虑这个时候所有数据的 TP Rate 和 FP Rate; 当Thresholds分数非常高时,例如0.9,TP数很小,NP数很大,因此TP率不会太高;
> 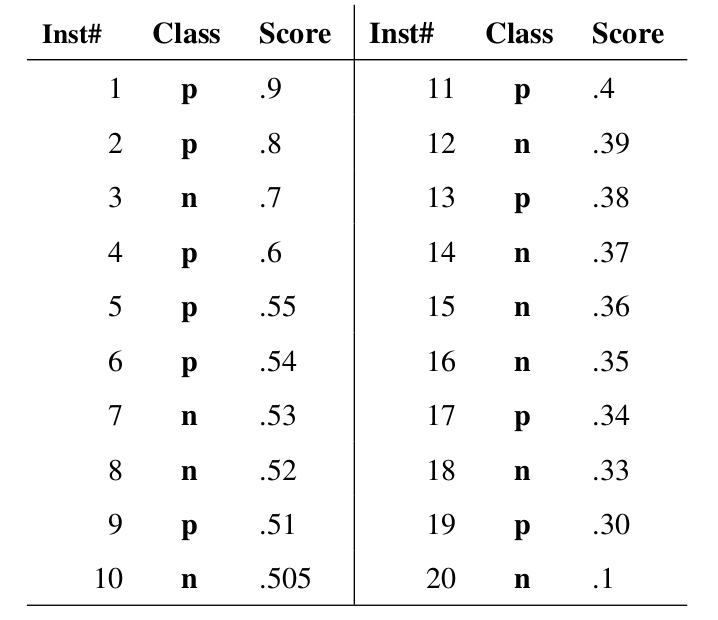
> 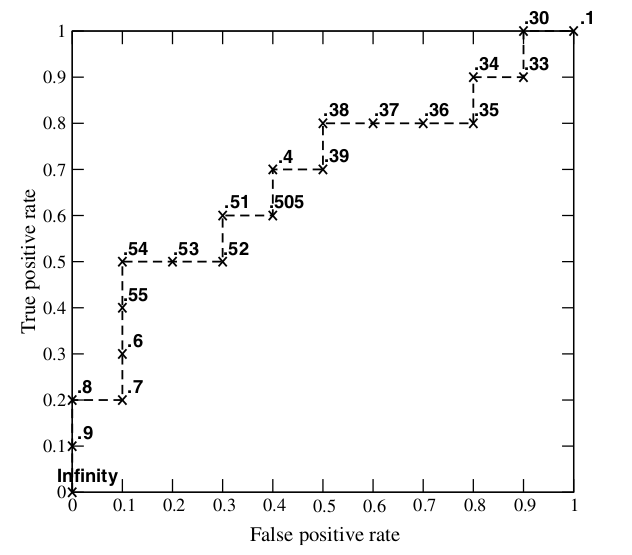
> 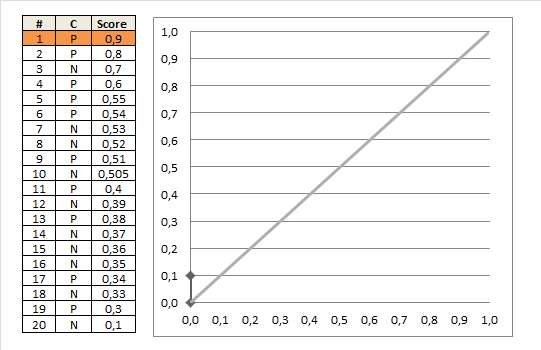
> * 当选用不同Threshold时候,画出来的ROC曲线,以及下方AUC面积
> * 我们计算这个曲线下面的面积就是所谓的AUC值;AUC值越大,预测约准确。
> ### 为什么要使用AUC曲线
> 既然已经这么多评价标准,为什么还要使用ROC和AUC呢?因为ROC曲线有个很好的特性:当测试集中的正负样本的分布变化的时候,ROC曲线能够保持不变。在实际的数据集中经常会出现类不平衡(class imbalance)现象,即负样本比正样本多很多(或者相反),而且测试数据中的正负样本的分布也可能随着时间变化。AUC对样本的比例变化有一定的容忍性。AUC的值通常在0.6-0.85之间。
> ### 如何来进行点击率预测?
> 点击率预测可以考虑为一个黑盒,输入一堆信号,输出点击的概率。这些信号就包括如下信号
> * **广告**:历史点击率,文字,格式,图片等等
> * **环境**:手机型号,时间媒体,位置,尺寸,曝光时间,网络IP,上网方式,代理等
> * **用户**:基础属性(男女,年龄等),兴趣属性(游戏,旅游等),历史浏览,点击行为,电商行为
> * **信号的粒度**:
> `Low Level : 数据来自一些原始访问行为的记录,例如用户是否点击过Landing Page,流量IP等。这些特征可以用于粗选,模型简单,`
> `High Level: 特征来自一些可解释的数据,例如兴趣标签,性别等`
> * **特征编码Feature Encoding:**
> `特征离散化:把连续的数字,变成离散化,例如温度值可以办成多个温度区间。`
> `特征交叉: 把多个特征进行叫交叉的出的值,用于训练,这种值可以表示一些非线性的关系。例如,点击率预估中应用最多的就是广告跟用户的交叉特征、广告跟性别的交叉特征,广告跟年龄的交叉特征,广告跟手机平台的交叉特征,广告跟地域的交叉特征等等。`
> * **特征选取(Feature Selection):**
> `特征选择就是选择那些靠谱的Feature,去掉冗余的Feature,对于搜索广告Query和广告的匹配程度很关键;对于展示广告,广告本身的历史表现,往往是最重要的Feature。`
> * **独热编码(One-Hot encoding)**
```假设有三组特征,分别表示年龄,城市,设备;
["男", "女"]
["北京", "上海", "广州"]
["苹果", "小米", "华为", "微软"]
传统变化: 对每一组特征,使用枚举类型,从0开始;
["男“,”上海“,”小米“]=[ 0,1,1]
["女“,”北京“,”苹果“] =[1,0,0]
传统变化后的数据不是连续的,而是随机分配的,不容易应用在分类器中。
热独编码是一种经典编码,是使用N位状态寄存器来对N个状态进行编码,每个状态都由他独立的寄存器位,并且在任意时候,其中只有一位有效。
["男“,”上海“,”小米“]=[ 1,0,0,1,0,0,1,0,0]
["女“,”北京“,”苹果“] =[0,1,1,0,0,1,0,0,0]
经过热独编码,数据会变成稀疏的,方便分类器处理。
```
> ### 点击率预估整体过程:
> 三个基本过程:特征工程,模型训练,线上服务
> 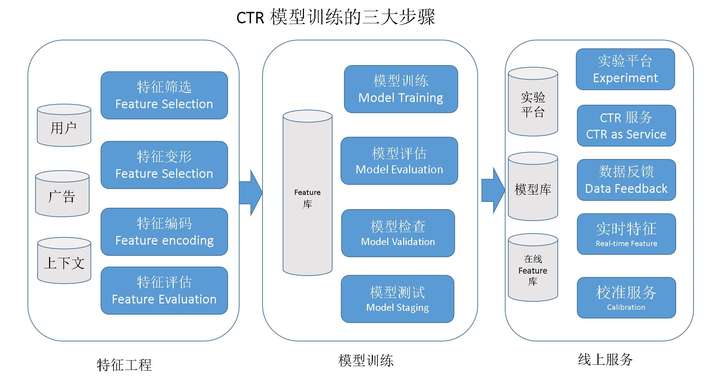
> * 特征工程:准备各种特征,编码,去掉冗余特征(用PCA等)
> * 模型训练:选定训练,测试等数据集,计算AUC,如果AUC有提升,通常可以在进一步在线上分流实验。
> * 线上服务:线上服务,需要实时计算CTR,实时计算相关特征和利用模型计算CTR,对于不同来源的CTR,可能需要一个Calibration的服务。
```
## 用tensorflow构建各种模型完成ctr预估
```
!head -5 ./data/train.txt
!head -10 ./data/featindex.txt
from __future__ import print_function
from __future__ import absolute_import
from __future__ import division
import cPickle as pkl
import numpy as np
import tensorflow as tf
from scipy.sparse import coo_matrix
# 读取数据,统计基本的信息,field等
DTYPE = tf.float32
FIELD_SIZES = [0] * 26
with open('./data/featindex.txt') as fin:
for line in fin:
line = line.strip().split(':')
if len(line) > 1:
f = int(line[0]) - 1
FIELD_SIZES[f] += 1
print('field sizes:', FIELD_SIZES)
FIELD_OFFSETS = [sum(FIELD_SIZES[:i]) for i in range(len(FIELD_SIZES))]
INPUT_DIM = sum(FIELD_SIZES)
OUTPUT_DIM = 1
STDDEV = 1e-3
MINVAL = -1e-3
MAXVAL = 1e-3
# 读取libsvm格式数据成稀疏矩阵形式
# 0 5:1 9:1 140858:1 445908:1 446177:1 446293:1 449140:1 490778:1 491626:1 491634:1 491641:1 491645:1 491648:1 491668:1 491700:1 491708:1
def read_data(file_name):
X = []
D = []
y = []
with open(file_name) as fin:
for line in fin:
fields = line.strip().split()
y_i = int(fields[0])
X_i = [int(x.split(':')[0]) for x in fields[1:]]
D_i = [int(x.split(':')[1]) for x in fields[1:]]
y.append(y_i)
X.append(X_i)
D.append(D_i)
y = np.reshape(np.array(y), [-1])
X = libsvm_2_coo(zip(X, D), (len(X), INPUT_DIM)).tocsr()
return X, y
# 数据乱序
def shuffle(data):
X, y = data
ind = np.arange(X.shape[0])
for i in range(7):
np.random.shuffle(ind)
return X[ind], y[ind]
# 工具函数,libsvm格式转成coo稀疏存储格式
def libsvm_2_coo(libsvm_data, shape):
coo_rows = []
coo_cols = []
coo_data = []
n = 0
for x, d in libsvm_data:
coo_rows.extend([n] * len(x))
coo_cols.extend(x)
coo_data.extend(d)
n += 1
coo_rows = np.array(coo_rows)
coo_cols = np.array(coo_cols)
coo_data = np.array(coo_data)
return coo_matrix((coo_data, (coo_rows, coo_cols)), shape=shape)
# csr转成输入格式
def csr_2_input(csr_mat):
if not isinstance(csr_mat, list):
coo_mat = csr_mat.tocoo()
indices = np.vstack((coo_mat.row, coo_mat.col)).transpose()
values = csr_mat.data
shape = csr_mat.shape
return indices, values, shape
else:
inputs = []
for csr_i in csr_mat:
inputs.append(csr_2_input(csr_i))
return inputs
# 数据切片
def slice(csr_data, start=0, size=-1):
if not isinstance(csr_data[0], list):
if size == -1 or start + size >= csr_data[0].shape[0]:
slc_data = csr_data[0][start:]
slc_labels = csr_data[1][start:]
else:
slc_data = csr_data[0][start:start + size]
slc_labels = csr_data[1][start:start + size]
else:
if size == -1 or start + size >= csr_data[0][0].shape[0]:
slc_data = []
for d_i in csr_data[0]:
slc_data.append(d_i[start:])
slc_labels = csr_data[1][start:]
else:
slc_data = []
for d_i in csr_data[0]:
slc_data.append(d_i[start:start + size])
slc_labels = csr_data[1][start:start + size]
return csr_2_input(slc_data), slc_labels
# 数据切分
def split_data(data, skip_empty=True):
fields = []
for i in range(len(FIELD_OFFSETS) - 1):
start_ind = FIELD_OFFSETS[i]
end_ind = FIELD_OFFSETS[i + 1]
if skip_empty and start_ind == end_ind:
continue
field_i = data[0][:, start_ind:end_ind]
fields.append(field_i)
fields.append(data[0][:, FIELD_OFFSETS[-1]:])
return fields, data[1]
# 在tensorflow中初始化各种参数变量
def init_var_map(init_vars, init_path=None):
if init_path is not None:
load_var_map = pkl.load(open(init_path, 'rb'))
print('load variable map from', init_path, load_var_map.keys())
var_map = {}
for var_name, var_shape, init_method, dtype in init_vars:
if init_method == 'zero':
var_map[var_name] = tf.Variable(tf.zeros(var_shape, dtype=dtype), name=var_name, dtype=dtype)
elif init_method == 'one':
var_map[var_name] = tf.Variable(tf.ones(var_shape, dtype=dtype), name=var_name, dtype=dtype)
elif init_method == 'normal':
var_map[var_name] = tf.Variable(tf.random_normal(var_shape, mean=0.0, stddev=STDDEV, dtype=dtype),
name=var_name, dtype=dtype)
elif init_method == 'tnormal':
var_map[var_name] = tf.Variable(tf.truncated_normal(var_shape, mean=0.0, stddev=STDDEV, dtype=dtype),
name=var_name, dtype=dtype)
elif init_method == 'uniform':
var_map[var_name] = tf.Variable(tf.random_uniform(var_shape, minval=MINVAL, maxval=MAXVAL, dtype=dtype),
name=var_name, dtype=dtype)
elif init_method == 'xavier':
maxval = np.sqrt(6. / np.sum(var_shape))
minval = -maxval
var_map[var_name] = tf.Variable(tf.random_uniform(var_shape, minval=minval, maxval=maxval, dtype=dtype),
name=var_name, dtype=dtype)
elif isinstance(init_method, int) or isinstance(init_method, float):
var_map[var_name] = tf.Variable(tf.ones(var_shape, dtype=dtype) * init_method, name=var_name, dtype=dtype)
elif init_method in load_var_map:
if load_var_map[init_method].shape == tuple(var_shape):
var_map[var_name] = tf.Variable(load_var_map[init_method], name=var_name, dtype=dtype)
else:
print('BadParam: init method', init_method, 'shape', var_shape, load_var_map[init_method].shape)
else:
print('BadParam: init method', init_method)
return var_map
# 不同的激活函数选择
def activate(weights, activation_function):
if activation_function == 'sigmoid':
return tf.nn.sigmoid(weights)
elif activation_function == 'softmax':
return tf.nn.softmax(weights)
elif activation_function == 'relu':
return tf.nn.relu(weights)
elif activation_function == 'tanh':
return tf.nn.tanh(weights)
elif activation_function == 'elu':
return tf.nn.elu(weights)
elif activation_function == 'none':
return weights
else:
return weights
# 不同的优化器选择
def get_optimizer(opt_algo, learning_rate, loss):
if opt_algo == 'adaldeta':
return tf.train.AdadeltaOptimizer(learning_rate).minimize(loss)
elif opt_algo == 'adagrad':
return tf.train.AdagradOptimizer(learning_rate).minimize(loss)
elif opt_algo == 'adam':
return tf.train.AdamOptimizer(learning_rate).minimize(loss)
elif opt_algo == 'ftrl':
return tf.train.FtrlOptimizer(learning_rate).minimize(loss)
elif opt_algo == 'gd':
return tf.train.GradientDescentOptimizer(learning_rate).minimize(loss)
elif opt_algo == 'padagrad':
return tf.train.ProximalAdagradOptimizer(learning_rate).minimize(loss)
elif opt_algo == 'pgd':
return tf.train.ProximalGradientDescentOptimizer(learning_rate).minimize(loss)
elif opt_algo == 'rmsprop':
return tf.train.RMSPropOptimizer(learning_rate).minimize(loss)
else:
return tf.train.GradientDescentOptimizer(learning_rate).minimize(loss)
# 工具函数
# 提示:tf.slice(input_, begin, size, name=None):按照指定的下标范围抽取连续区域的子集
# tf.gather(params, indices, validate_indices=None, name=None):按照指定的下标集合从axis=0中抽取子集,适合抽取不连续区域的子集
def gather_2d(params, indices):
shape = tf.shape(params)
flat = tf.reshape(params, [-1])
flat_idx = indices[:, 0] * shape[1] + indices[:, 1]
flat_idx = tf.reshape(flat_idx, [-1])
return tf.gather(flat, flat_idx)
def gather_3d(params, indices):
shape = tf.shape(params)
flat = tf.reshape(params, [-1])
flat_idx = indices[:, 0] * shape[1] * shape[2] + indices[:, 1] * shape[2] + indices[:, 2]
flat_idx = tf.reshape(flat_idx, [-1])
return tf.gather(flat, flat_idx)
def gather_4d(params, indices):
shape = tf.shape(params)
flat = tf.reshape(params, [-1])
flat_idx = indices[:, 0] * shape[1] * shape[2] * shape[3] + \
indices[:, 1] * shape[2] * shape[3] + indices[:, 2] * shape[3] + indices[:, 3]
flat_idx = tf.reshape(flat_idx, [-1])
return tf.gather(flat, flat_idx)
# 池化2d
def max_pool_2d(params, k):
_, indices = tf.nn.top_k(params, k, sorted=False)
shape = tf.shape(indices)
r1 = tf.reshape(tf.range(shape[0]), [-1, 1])
r1 = tf.tile(r1, [1, k])
r1 = tf.reshape(r1, [-1, 1])
indices = tf.concat([r1, tf.reshape(indices, [-1, 1])], 1)
return tf.reshape(gather_2d(params, indices), [-1, k])
# 池化3d
def max_pool_3d(params, k):
_, indices = tf.nn.top_k(params, k, sorted=False)
shape = tf.shape(indices)
r1 = tf.reshape(tf.range(shape[0]), [-1, 1])
r2 = tf.reshape(tf.range(shape[1]), [-1, 1])
r1 = tf.tile(r1, [1, k * shape[1]])
r2 = tf.tile(r2, [1, k])
r1 = tf.reshape(r1, [-1, 1])
r2 = tf.tile(tf.reshape(r2, [-1, 1]), [shape[0], 1])
indices = tf.concat([r1, r2, tf.reshape(indices, [-1, 1])], 1)
return tf.reshape(gather_3d(params, indices), [-1, shape[1], k])
# 池化4d
def max_pool_4d(params, k):
_, indices = tf.nn.top_k(params, k, sorted=False)
shape = tf.shape(indices)
r1 = tf.reshape(tf.range(shape[0]), [-1, 1])
r2 = tf.reshape(tf.range(shape[1]), [-1, 1])
r3 = tf.reshape(tf.range(shape[2]), [-1, 1])
r1 = tf.tile(r1, [1, shape[1] * shape[2] * k])
r2 = tf.tile(r2, [1, shape[2] * k])
r3 = tf.tile(r3, [1, k])
r1 = tf.reshape(r1, [-1, 1])
r2 = tf.tile(tf.reshape(r2, [-1, 1]), [shape[0], 1])
r3 = tf.tile(tf.reshape(r3, [-1, 1]), [shape[0] * shape[1], 1])
indices = tf.concat([r1, r2, r3, tf.reshape(indices, [-1, 1])], 1)
return tf.reshape(gather_4d(params, indices), [-1, shape[1], shape[2], k])
```
## 定义不同的模型
```
# 定义基类模型
dtype = DTYPE
class Model:
def __init__(self):
self.sess = None
self.X = None
self.y = None
self.layer_keeps = None
self.vars = None
self.keep_prob_train = None
self.keep_prob_test = None
# run model
def run(self, fetches, X=None, y=None, mode='train'):
# 通过feed_dict传入数据
feed_dict = {}
if type(self.X) is list:
for i in range(len(X)):
feed_dict[self.X[i]] = X[i]
else:
feed_dict[self.X] = X
if y is not None:
feed_dict[self.y] = y
if self.layer_keeps is not None:
if mode == 'train':
feed_dict[self.layer_keeps] = self.keep_prob_train
elif mode == 'test':
feed_dict[self.layer_keeps] = self.keep_prob_test
#通过session.run去执行op
return self.sess.run(fetches, feed_dict)
# 模型参数持久化
def dump(self, model_path):
var_map = {}
for name, var in self.vars.iteritems():
var_map[name] = self.run(var)
pkl.dump(var_map, open(model_path, 'wb'))
print('model dumped at', model_path)
```
### 1.LR逻辑回归
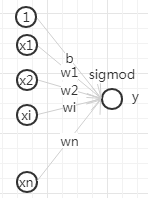
输入输出:{X,y}<br>
映射函数f(x):单层单节点的“DNN”, 宽而不深,sigmoid(wx+b)输出概率,需要大量的人工特征工程,非线性来源于特征处理<br>
损失函数:logloss/... + L1/L2/...<br>
优化方法:sgd/...<br>
评估:logloss/auc/...<br>
```
class LR(Model):
def __init__(self, input_dim=None, output_dim=1, init_path=None, opt_algo='gd', learning_rate=1e-2, l2_weight=0,
random_seed=None):
Model.__init__(self)
# 声明参数
init_vars = [('w', [input_dim, output_dim], 'xavier', dtype),
('b', [output_dim], 'zero', dtype)]
self.graph = tf.Graph()
with self.graph.as_default():
if random_seed is not None:
tf.set_random_seed(random_seed)
# 用稀疏的placeholder
self.X = tf.sparse_placeholder(dtype)
self.y = tf.placeholder(dtype)
# init参数
self.vars = init_var_map(init_vars, init_path)
w = self.vars['w']
b = self.vars['b']
# sigmoid(wx+b)
xw = tf.sparse_tensor_dense_matmul(self.X, w)
logits = tf.reshape(xw + b, [-1])
self.y_prob = tf.sigmoid(logits)
self.loss = tf.reduce_mean(
tf.nn.sigmoid_cross_entropy_with_logits(labels=self.y, logits=logits)) + \
l2_weight * tf.nn.l2_loss(xw)
self.optimizer = get_optimizer(opt_algo, learning_rate, self.loss)
# GPU设定
config = tf.ConfigProto()
config.gpu_options.allow_growth = True
self.sess = tf.Session(config=config)
# 初始化图里的参数
tf.global_variables_initializer().run(session=self.sess)
import numpy as np
from sklearn.metrics import roc_auc_score
import progressbar
train_file = './data/train.txt'
test_file = './data/test.txt'
input_dim = INPUT_DIM
# 读取数据
#train_data = read_data(train_file)
#test_data = read_data(test_file)
train_data = pkl.load(open('./data/train.pkl', 'rb'))
#train_data = shuffle(train_data)
test_data = pkl.load(open('./data/test.pkl', 'rb'))
# pkl.dump(train_data, open('./data/train.pkl', 'wb'))
# pkl.dump(test_data, open('./data/test.pkl', 'wb'))
# 输出数据信息维度
if train_data[1].ndim > 1:
print('label must be 1-dim')
exit(0)
print('read finish')
print('train data size:', train_data[0].shape)
print('test data size:', test_data[0].shape)
# 训练集与测试集
train_size = train_data[0].shape[0]
test_size = test_data[0].shape[0]
num_feas = len(FIELD_SIZES)
# 超参数设定
min_round = 1
num_round = 200
early_stop_round = 5
# train + val
batch_size = 1024
field_sizes = FIELD_SIZES
field_offsets = FIELD_OFFSETS
# 逻辑回归参数设定
lr_params = {
'input_dim': input_dim,
'opt_algo': 'gd',
'learning_rate': 0.1,
'l2_weight': 0,
'random_seed': 0
}
print(lr_params)
model = LR(**lr_params)
print("training LR...")
def train(model):
history_score = []
# 执行num_round轮
for i in range(num_round):
# 主要的2个op是优化器和损失
fetches = [model.optimizer, model.loss]
if batch_size > 0:
ls = []
# 进度条工具
bar = progressbar.ProgressBar()
print('[%d]\ttraining...' % i)
for j in bar(range(int(train_size / batch_size + 1))):
X_i, y_i = slice(train_data, j * batch_size, batch_size)
# 训练,run op
_, l = model.run(fetches, X_i, y_i)
ls.append(l)
elif batch_size == -1:
X_i, y_i = slice(train_data)
_, l = model.run(fetches, X_i, y_i)
ls = [l]
train_preds = []
print('[%d]\tevaluating...' % i)
bar = progressbar.ProgressBar()
for j in bar(range(int(train_size / 10000 + 1))):
X_i, _ = slice(train_data, j * 10000, 10000)
preds = model.run(model.y_prob, X_i, mode='test')
train_preds.extend(preds)
test_preds = []
bar = progressbar.ProgressBar()
for j in bar(range(int(test_size / 10000 + 1))):
X_i, _ = slice(test_data, j * 10000, 10000)
preds = model.run(model.y_prob, X_i, mode='test')
test_preds.extend(preds)
# 把预估的结果和真实结果拿出来计算auc
train_score = roc_auc_score(train_data[1], train_preds)
test_score = roc_auc_score(test_data[1], test_preds)
# 输出auc信息
print('[%d]\tloss (with l2 norm):%f\ttrain-auc: %f\teval-auc: %f' % (i, np.mean(ls), train_score, test_score))
history_score.append(test_score)
# early stopping
if i > min_round and i > early_stop_round:
if np.argmax(history_score) == i - early_stop_round and history_score[-1] - history_score[
-1 * early_stop_round] < 1e-5:
print('early stop\nbest iteration:\n[%d]\teval-auc: %f' % (
np.argmax(history_score), np.max(history_score)))
break
train(model)
```
### 2.FM
FM可以视作有二次交叉的LR,为了控制参数量和充分学习,提出了user vector和item vector的概念
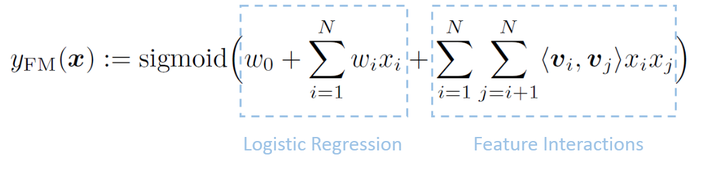
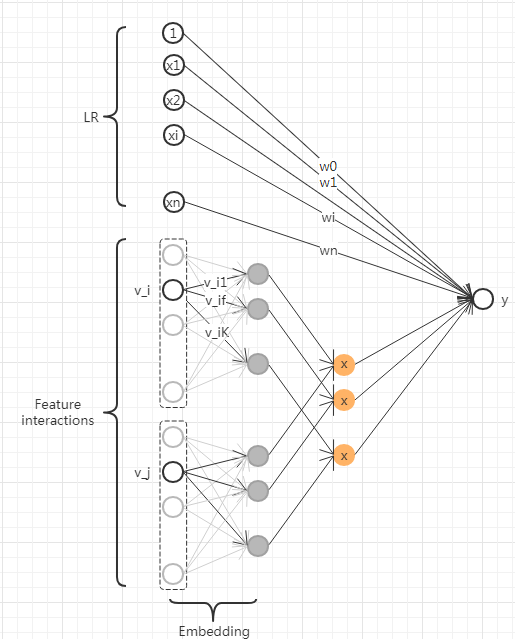
```
class FM(Model):
def __init__(self, input_dim=None, output_dim=1, factor_order=10, init_path=None, opt_algo='gd', learning_rate=1e-2,
l2_w=0, l2_v=0, random_seed=None):
Model.__init__(self)
# 一次、二次交叉、偏置项
init_vars = [('w', [input_dim, output_dim], 'xavier', dtype),
('v', [input_dim, factor_order], 'xavier', dtype),
('b', [output_dim], 'zero', dtype)]
self.graph = tf.Graph()
with self.graph.as_default():
if random_seed is not None:
tf.set_random_seed(random_seed)
self.X = tf.sparse_placeholder(dtype)
self.y = tf.placeholder(dtype)
self.vars = init_var_map(init_vars, init_path)
w = self.vars['w']
v = self.vars['v']
b = self.vars['b']
# [(x1+x2+x3)^2 - (x1^2+x2^2+x3^2)]/2
# 先计算所有的交叉项,再减去平方项(自己和自己相乘)
X_square = tf.SparseTensor(self.X.indices, tf.square(self.X.values), tf.to_int64(tf.shape(self.X)))
xv = tf.square(tf.sparse_tensor_dense_matmul(self.X, v))
p = 0.5 * tf.reshape(
tf.reduce_sum(xv - tf.sparse_tensor_dense_matmul(X_square, tf.square(v)), 1),
[-1, output_dim])
xw = tf.sparse_tensor_dense_matmul(self.X, w)
logits = tf.reshape(xw + b + p, [-1])
self.y_prob = tf.sigmoid(logits)
self.loss = tf.reduce_mean(
tf.nn.sigmoid_cross_entropy_with_logits(logits=logits, labels=self.y)) + \
l2_w * tf.nn.l2_loss(xw) + \
l2_v * tf.nn.l2_loss(xv)
self.optimizer = get_optimizer(opt_algo, learning_rate, self.loss)
#GPU设定
config = tf.ConfigProto()
config.gpu_options.allow_growth = True
self.sess = tf.Session(config=config)
# 图中所有variable初始化
tf.global_variables_initializer().run(session=self.sess)
import numpy as np
from sklearn.metrics import roc_auc_score
import progressbar
train_file = './data/train.txt'
test_file = './data/test.txt'
input_dim = INPUT_DIM
train_data = pkl.load(open('./data/train.pkl', 'rb'))
train_data = shuffle(train_data)
test_data = pkl.load(open('./data/test.pkl', 'rb'))
if train_data[1].ndim > 1:
print('label must be 1-dim')
exit(0)
print('read finish')
print('train data size:', train_data[0].shape)
print('test data size:', test_data[0].shape)
# 训练集与测试集
train_size = train_data[0].shape[0]
test_size = test_data[0].shape[0]
num_feas = len(FIELD_SIZES)
# 超参数设定
min_round = 1
num_round = 200
early_stop_round = 5
batch_size = 1024
field_sizes = FIELD_SIZES
field_offsets = FIELD_OFFSETS
# FM参数设定
fm_params = {
'input_dim': input_dim,
'factor_order': 10,
'opt_algo': 'gd',
'learning_rate': 0.1,
'l2_w': 0,
'l2_v': 0,
}
print(fm_params)
model = FM(**fm_params)
print("training FM...")
def train(model):
history_score = []
for i in range(num_round):
# 同样是优化器和损失两个op
fetches = [model.optimizer, model.loss]
if batch_size > 0:
ls = []
bar = progressbar.ProgressBar()
print('[%d]\ttraining...' % i)
for j in bar(range(int(train_size / batch_size + 1))):
X_i, y_i = slice(train_data, j * batch_size, batch_size)
# 训练
_, l = model.run(fetches, X_i, y_i)
ls.append(l)
elif batch_size == -1:
X_i, y_i = slice(train_data)
_, l = model.run(fetches, X_i, y_i)
ls = [l]
train_preds = []
print('[%d]\tevaluating...' % i)
bar = progressbar.ProgressBar()
for j in bar(range(int(train_size / 10000 + 1))):
X_i, _ = slice(train_data, j * 10000, 10000)
preds = model.run(model.y_prob, X_i, mode='test')
train_preds.extend(preds)
test_preds = []
bar = progressbar.ProgressBar()
for j in bar(range(int(test_size / 10000 + 1))):
X_i, _ = slice(test_data, j * 10000, 10000)
preds = model.run(model.y_prob, X_i, mode='test')
test_preds.extend(preds)
train_score = roc_auc_score(train_data[1], train_preds)
test_score = roc_auc_score(test_data[1], test_preds)
print('[%d]\tloss (with l2 norm):%f\ttrain-auc: %f\teval-auc: %f' % (i, np.mean(ls), train_score, test_score))
history_score.append(test_score)
if i > min_round and i > early_stop_round:
if np.argmax(history_score) == i - early_stop_round and history_score[-1] - history_score[
-1 * early_stop_round] < 1e-5:
print('early stop\nbest iteration:\n[%d]\teval-auc: %f' % (
np.argmax(history_score), np.max(history_score)))
break
train(model)
```
### FNN
FNN的考虑是模型的capacity可以进一步提升,以对更复杂的场景建模。<br>
FNN可以视作FM + MLP = LR + MF + MLP
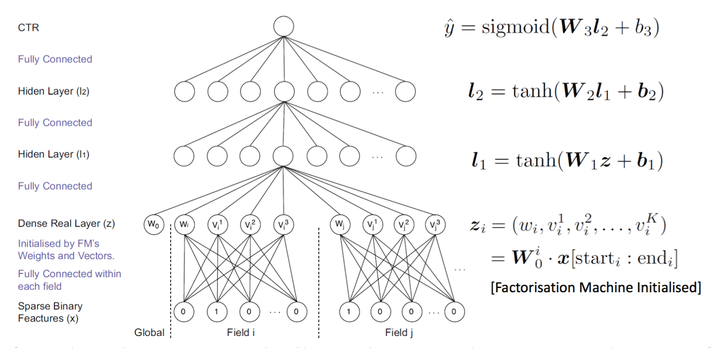
```
class FNN(Model):
def __init__(self, field_sizes=None, embed_size=10, layer_sizes=None, layer_acts=None, drop_out=None,
embed_l2=None, layer_l2=None, init_path=None, opt_algo='gd', learning_rate=1e-2, random_seed=None):
Model.__init__(self)
init_vars = []
num_inputs = len(field_sizes)
for i in range(num_inputs):
init_vars.append(('embed_%d' % i, [field_sizes[i], embed_size], 'xavier', dtype))
node_in = num_inputs * embed_size
for i in range(len(layer_sizes)):
init_vars.append(('w%d' % i, [node_in, layer_sizes[i]], 'xavier', dtype))
init_vars.append(('b%d' % i, [layer_sizes[i]], 'zero', dtype))
node_in = layer_sizes[i]
self.graph = tf.Graph()
with self.graph.as_default():
if random_seed is not None:
tf.set_random_seed(random_seed)
self.X = [tf.sparse_placeholder(dtype) for i in range(num_inputs)]
self.y = tf.placeholder(dtype)
self.keep_prob_train = 1 - np.array(drop_out)
self.keep_prob_test = np.ones_like(drop_out)
self.layer_keeps = tf.placeholder(dtype)
self.vars = init_var_map(init_vars, init_path)
w0 = [self.vars['embed_%d' % i] for i in range(num_inputs)]
xw = tf.concat([tf.sparse_tensor_dense_matmul(self.X[i], w0[i]) for i in range(num_inputs)], 1)
l = xw
for i in range(len(layer_sizes)):
wi = self.vars['w%d' % i]
bi = self.vars['b%d' % i]
print(l.shape, wi.shape, bi.shape)
l = tf.nn.dropout(
activate(
tf.matmul(l, wi) + bi,
layer_acts[i]),
self.layer_keeps[i])
l = tf.squeeze(l)
self.y_prob = tf.sigmoid(l)
self.loss = tf.reduce_mean(
tf.nn.sigmoid_cross_entropy_with_logits(logits=l, labels=self.y))
if layer_l2 is not None:
self.loss += embed_l2 * tf.nn.l2_loss(xw)
for i in range(len(layer_sizes)):
wi = self.vars['w%d' % i]
self.loss += layer_l2[i] * tf.nn.l2_loss(wi)
self.optimizer = get_optimizer(opt_algo, learning_rate, self.loss)
config = tf.ConfigProto()
config.gpu_options.allow_growth = True
self.sess = tf.Session(config=config)
tf.global_variables_initializer().run(session=self.sess)
import numpy as np
from sklearn.metrics import roc_auc_score
import progressbar
train_file = './data/train.txt'
test_file = './data/test.txt'
input_dim = INPUT_DIM
train_data = pkl.load(open('./data/train.pkl', 'rb'))
train_data = shuffle(train_data)
test_data = pkl.load(open('./data/test.pkl', 'rb'))
if train_data[1].ndim > 1:
print('label must be 1-dim')
exit(0)
print('read finish')
print('train data size:', train_data[0].shape)
print('test data size:', test_data[0].shape)
train_size = train_data[0].shape[0]
test_size = test_data[0].shape[0]
num_feas = len(FIELD_SIZES)
min_round = 1
num_round = 200
early_stop_round = 5
batch_size = 1024
field_sizes = FIELD_SIZES
field_offsets = FIELD_OFFSETS
train_data = split_data(train_data)
test_data = split_data(test_data)
tmp = []
for x in field_sizes:
if x > 0:
tmp.append(x)
field_sizes = tmp
print('remove empty fields', field_sizes)
fnn_params = {
'field_sizes': field_sizes,
'embed_size': 10,
'layer_sizes': [500, 1],
'layer_acts': ['relu', None],
'drop_out': [0, 0],
'opt_algo': 'gd',
'learning_rate': 0.1,
'embed_l2': 0,
'layer_l2': [0, 0],
'random_seed': 0
}
print(fnn_params)
model = FNN(**fnn_params)
def train(model):
history_score = []
for i in range(num_round):
fetches = [model.optimizer, model.loss]
if batch_size > 0:
ls = []
bar = progressbar.ProgressBar()
print('[%d]\ttraining...' % i)
for j in bar(range(int(train_size / batch_size + 1))):
X_i, y_i = slice(train_data, j * batch_size, batch_size)
_, l = model.run(fetches, X_i, y_i)
ls.append(l)
elif batch_size == -1:
X_i, y_i = slice(train_data)
_, l = model.run(fetches, X_i, y_i)
ls = [l]
train_preds = []
print('[%d]\tevaluating...' % i)
bar = progressbar.ProgressBar()
for j in bar(range(int(train_size / 10000 + 1))):
X_i, _ = slice(train_data, j * 10000, 10000)
preds = model.run(model.y_prob, X_i, mode='test')
train_preds.extend(preds)
test_preds = []
bar = progressbar.ProgressBar()
for j in bar(range(int(test_size / 10000 + 1))):
X_i, _ = slice(test_data, j * 10000, 10000)
preds = model.run(model.y_prob, X_i, mode='test')
test_preds.extend(preds)
train_score = roc_auc_score(train_data[1], train_preds)
test_score = roc_auc_score(test_data[1], test_preds)
print('[%d]\tloss (with l2 norm):%f\ttrain-auc: %f\teval-auc: %f' % (i, np.mean(ls), train_score, test_score))
history_score.append(test_score)
if i > min_round and i > early_stop_round:
if np.argmax(history_score) == i - early_stop_round and history_score[-1] - history_score[
-1 * early_stop_round] < 1e-5:
print('early stop\nbest iteration:\n[%d]\teval-auc: %f' % (
np.argmax(history_score), np.max(history_score)))
break
train(model)
```
### CCPM
reference:[ctr模型汇总](https://zhuanlan.zhihu.com/p/32523455)
FM只能学习特征的二阶组合,但CNN能学习更高阶的组合,可学习的阶数和卷积的视野相关。
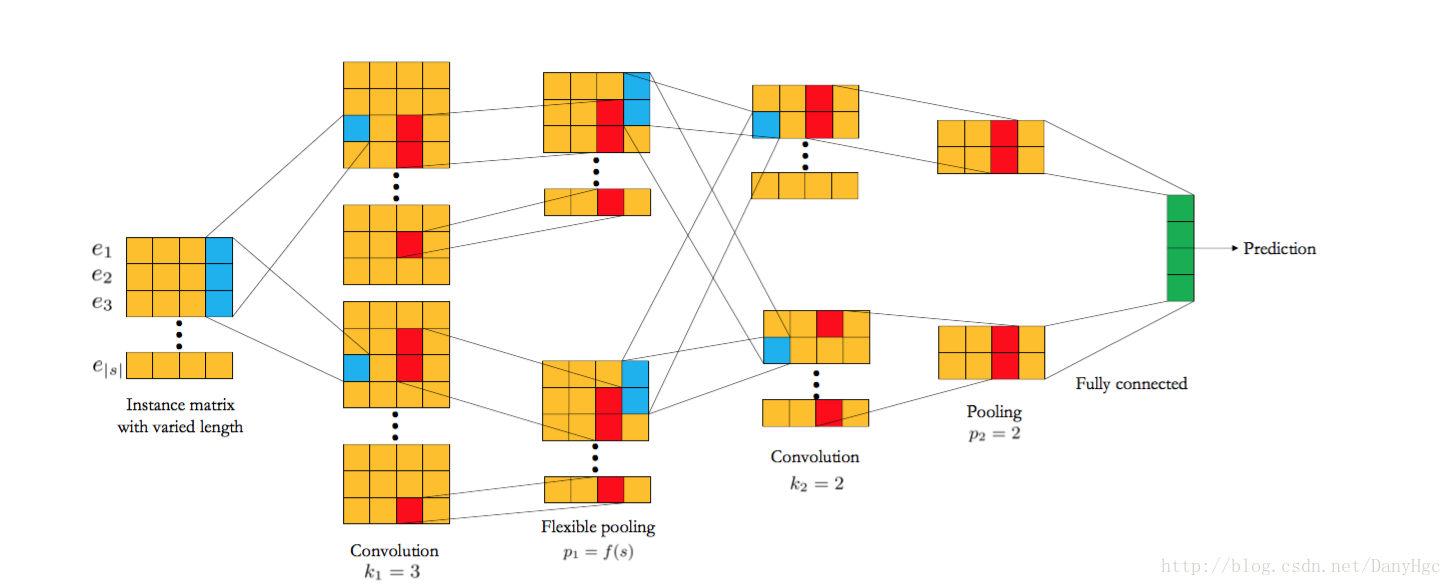
mbedding层:e1, e2…en是某特定用户被展示的一系列广告。如果在预测广告是否会点击时不考虑历史展示广告的点击情况,则n=1。同时embedding矩阵的具体值是随着模型训练学出来的。Embedding矩阵为S,向量维度为d。
卷积层:卷积参数W有d*w个,即对于矩阵S,上图每一列对应一个参数不共享的一维卷积,其视野为w,卷积共有d个,每个输出向量维度为(n+w-1),输出矩阵维度d*(n+w-1)。因为对于ctr预估而言,矩阵S每一列都对应特定的描述维度,所以需要分别处理,得到的输出矩阵的每一列就都是描述广告特定方面的特征。
Pooling层:flexible p-max pooling。
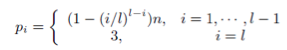
L是模型总卷积层数,n是输入序列长度,pi就是第i层的pooling参数。这样最后一层卷积层都是输出3个最大的元素,长度固定方便后面接全连接层。同时这个指数型的参数,一开始改变比较小,几乎都是n,后面就减少得比较快。这样可以防止在模型浅层的时候就损失太多信息,众所周知深度模型在前面几层最好不要做得太简单,容易损失很多信息。文章还提到p-max pooling输出的几个最大的元素是保序的,可输入时的顺序一致,这点对于保留序列信息是重要的。
激活层:tanh
最后,
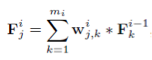
Fij是指低i层的第j个feature map。感觉是不同输入通道的卷积参数也不共享,对应输出是所有输入通道卷积的输出的求和。
```
class CCPM(Model):
def __init__(self, field_sizes=None, embed_size=10, filter_sizes=None, layer_acts=None, drop_out=None,
init_path=None, opt_algo='gd', learning_rate=1e-2, random_seed=None):
Model.__init__(self)
init_vars = []
num_inputs = len(field_sizes)
for i in range(num_inputs):
init_vars.append(('embed_%d' % i, [field_sizes[i], embed_size], 'xavier', dtype))
init_vars.append(('f1', [embed_size, filter_sizes[0], 1, 2], 'xavier', dtype))
init_vars.append(('f2', [embed_size, filter_sizes[1], 2, 2], 'xavier', dtype))
init_vars.append(('w1', [2 * 3 * embed_size, 1], 'xavier', dtype))
init_vars.append(('b1', [1], 'zero', dtype))
self.graph = tf.Graph()
with self.graph.as_default():
if random_seed is not None:
tf.set_random_seed(random_seed)
self.X = [tf.sparse_placeholder(dtype) for i in range(num_inputs)]
self.y = tf.placeholder(dtype)
self.keep_prob_train = 1 - np.array(drop_out)
self.keep_prob_test = np.ones_like(drop_out)
self.layer_keeps = tf.placeholder(dtype)
self.vars = init_var_map(init_vars, init_path)
w0 = [self.vars['embed_%d' % i] for i in range(num_inputs)]
xw = tf.concat([tf.sparse_tensor_dense_matmul(self.X[i], w0[i]) for i in range(num_inputs)], 1)
l = xw
l = tf.transpose(tf.reshape(l, [-1, num_inputs, embed_size, 1]), [0, 2, 1, 3])
f1 = self.vars['f1']
l = tf.nn.conv2d(l, f1, [1, 1, 1, 1], 'SAME')
l = tf.transpose(
max_pool_4d(
tf.transpose(l, [0, 1, 3, 2]),
int(num_inputs / 2)),
[0, 1, 3, 2])
f2 = self.vars['f2']
l = tf.nn.conv2d(l, f2, [1, 1, 1, 1], 'SAME')
l = tf.transpose(
max_pool_4d(
tf.transpose(l, [0, 1, 3, 2]), 3),
[0, 1, 3, 2])
l = tf.nn.dropout(
activate(
tf.reshape(l, [-1, embed_size * 3 * 2]),
layer_acts[0]),
self.layer_keeps[0])
w1 = self.vars['w1']
b1 = self.vars['b1']
l = tf.matmul(l, w1) + b1
l = tf.squeeze(l)
self.y_prob = tf.sigmoid(l)
self.loss = tf.reduce_mean(
tf.nn.sigmoid_cross_entropy_with_logits(logits=l, labels=self.y))
self.optimizer = get_optimizer(opt_algo, learning_rate, self.loss)
config = tf.ConfigProto()
config.gpu_options.allow_growth = True
self.sess = tf.Session(config=config)
tf.global_variables_initializer().run(session=self.sess)
```
### PNN
reference:<br>
[深度学习在CTR预估中的应用](https://zhuanlan.zhihu.com/p/35484389)
可以视作FNN+product layer
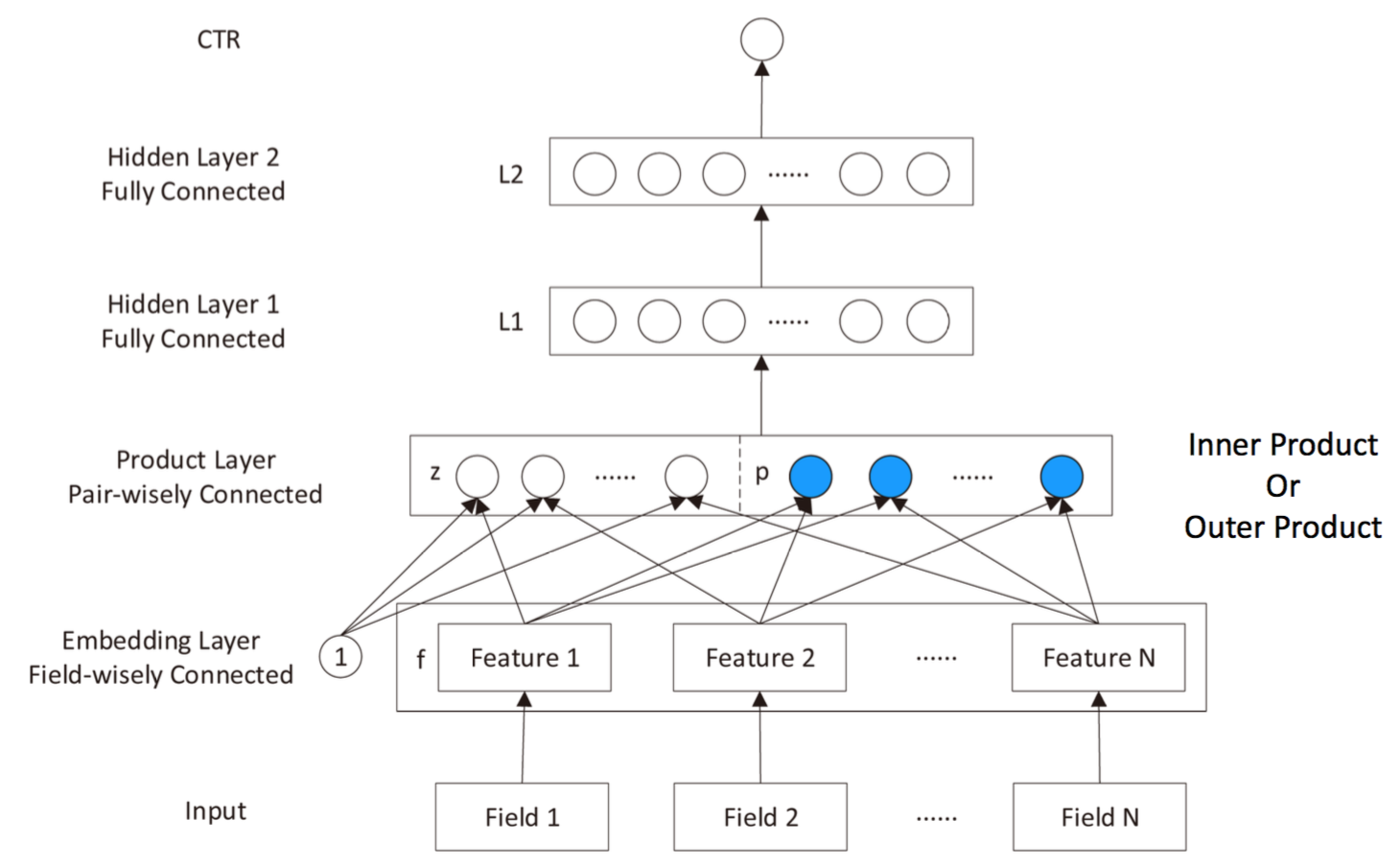
PNN和FNN的主要不同在于除了得到z向量,还增加了一个p向量,即Product向量。Product向量由每个category field的feature vector做inner product 或则 outer product 得到,作者认为这样做有助于特征交叉。另外PNN中Embeding层不再由FM生成,可以在整个网络中训练得到。
对比 FNN 网络,PNN的区别在于中间多了一层 Product Layer 层。Product Layer 层由两部分组成,左边z为 embedding 层的线性部分,右边为 embedding 层的特征交叉部分。
除了 Product Layer 不同,PNN 和 FNN 的 MLP 结构是一样的。这种 product 思想来源于,在 CTR 预估中,认为特征之间的关系更多是一种 and“且”的关系,而非 add"加”的关系。例如,性别为男且喜欢游戏的人群,比起性别男和喜欢游戏的人群,前者的组合比后者更能体现特征交叉的意义。
根据 product 的方式不同,可以分为 inner product (IPNN) 和 outer product (OPNN),如下图所示。
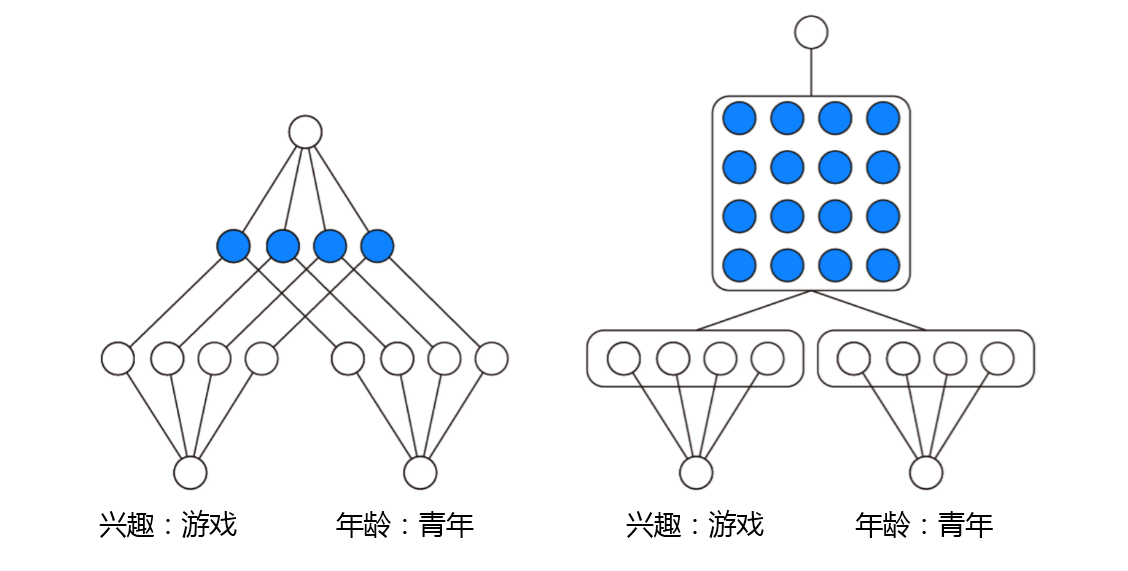
### PNN1
```
class PNN1(Model):
def __init__(self, field_sizes=None, embed_size=10, layer_sizes=None, layer_acts=None, drop_out=None,
embed_l2=None, layer_l2=None, init_path=None, opt_algo='gd', learning_rate=1e-2, random_seed=None):
Model.__init__(self)
init_vars = []
num_inputs = len(field_sizes)
for i in range(num_inputs):
init_vars.append(('embed_%d' % i, [field_sizes[i], embed_size], 'xavier', dtype))
num_pairs = int(num_inputs * (num_inputs - 1) / 2)
node_in = num_inputs * embed_size + num_pairs
# node_in = num_inputs * (embed_size + num_inputs)
for i in range(len(layer_sizes)):
init_vars.append(('w%d' % i, [node_in, layer_sizes[i]], 'xavier', dtype))
init_vars.append(('b%d' % i, [layer_sizes[i]], 'zero', dtype))
node_in = layer_sizes[i]
self.graph = tf.Graph()
with self.graph.as_default():
if random_seed is not None:
tf.set_random_seed(random_seed)
self.X = [tf.sparse_placeholder(dtype) for i in range(num_inputs)]
self.y = tf.placeholder(dtype)
self.keep_prob_train = 1 - np.array(drop_out)
self.keep_prob_test = np.ones_like(drop_out)
self.layer_keeps = tf.placeholder(dtype)
self.vars = init_var_map(init_vars, init_path)
w0 = [self.vars['embed_%d' % i] for i in range(num_inputs)]
xw = tf.concat([tf.sparse_tensor_dense_matmul(self.X[i], w0[i]) for i in range(num_inputs)], 1)
xw3d = tf.reshape(xw, [-1, num_inputs, embed_size])
row = []
col = []
for i in range(num_inputs-1):
for j in range(i+1, num_inputs):
row.append(i)
col.append(j)
# batch * pair * k
p = tf.transpose(
# pair * batch * k
tf.gather(
# num * batch * k
tf.transpose(
xw3d, [1, 0, 2]),
row),
[1, 0, 2])
# batch * pair * k
q = tf.transpose(
tf.gather(
tf.transpose(
xw3d, [1, 0, 2]),
col),
[1, 0, 2])
p = tf.reshape(p, [-1, num_pairs, embed_size])
q = tf.reshape(q, [-1, num_pairs, embed_size])
ip = tf.reshape(tf.reduce_sum(p * q, [-1]), [-1, num_pairs])
# simple but redundant
# batch * n * 1 * k, batch * 1 * n * k
# ip = tf.reshape(
# tf.reduce_sum(
# tf.expand_dims(xw3d, 2) *
# tf.expand_dims(xw3d, 1),
# 3),
# [-1, num_inputs**2])
l = tf.concat([xw, ip], 1)
for i in range(len(layer_sizes)):
wi = self.vars['w%d' % i]
bi = self.vars['b%d' % i]
l = tf.nn.dropout(
activate(
tf.matmul(l, wi) + bi,
layer_acts[i]),
self.layer_keeps[i])
l = tf.squeeze(l)
self.y_prob = tf.sigmoid(l)
self.loss = tf.reduce_mean(
tf.nn.sigmoid_cross_entropy_with_logits(logits=l, labels=self.y))
if layer_l2 is not None:
self.loss += embed_l2 * tf.nn.l2_loss(xw)
for i in range(len(layer_sizes)):
wi = self.vars['w%d' % i]
self.loss += layer_l2[i] * tf.nn.l2_loss(wi)
self.optimizer = get_optimizer(opt_algo, learning_rate, self.loss)
config = tf.ConfigProto()
config.gpu_options.allow_growth = True
self.sess = tf.Session(config=config)
tf.global_variables_initializer().run(session=self.sess)
```
### PNN2
```
class PNN2(Model):
def __init__(self, field_sizes=None, embed_size=10, layer_sizes=None, layer_acts=None, drop_out=None,
embed_l2=None, layer_l2=None, init_path=None, opt_algo='gd', learning_rate=1e-2, random_seed=None,
layer_norm=True):
Model.__init__(self)
init_vars = []
num_inputs = len(field_sizes)
for i in range(num_inputs):
init_vars.append(('embed_%d' % i, [field_sizes[i], embed_size], 'xavier', dtype))
num_pairs = int(num_inputs * (num_inputs - 1) / 2)
node_in = num_inputs * embed_size + num_pairs
init_vars.append(('kernel', [embed_size, num_pairs, embed_size], 'xavier', dtype))
for i in range(len(layer_sizes)):
init_vars.append(('w%d' % i, [node_in, layer_sizes[i]], 'xavier', dtype))
init_vars.append(('b%d' % i, [layer_sizes[i]], 'zero', dtype))
node_in = layer_sizes[i]
self.graph = tf.Graph()
with self.graph.as_default():
if random_seed is not None:
tf.set_random_seed(random_seed)
self.X = [tf.sparse_placeholder(dtype) for i in range(num_inputs)]
self.y = tf.placeholder(dtype)
self.keep_prob_train = 1 - np.array(drop_out)
self.keep_prob_test = np.ones_like(drop_out)
self.layer_keeps = tf.placeholder(dtype)
self.vars = init_var_map(init_vars, init_path)
w0 = [self.vars['embed_%d' % i] for i in range(num_inputs)]
xw = tf.concat([tf.sparse_tensor_dense_matmul(self.X[i], w0[i]) for i in range(num_inputs)], 1)
xw3d = tf.reshape(xw, [-1, num_inputs, embed_size])
row = []
col = []
for i in range(num_inputs - 1):
for j in range(i + 1, num_inputs):
row.append(i)
col.append(j)
# batch * pair * k
p = tf.transpose(
# pair * batch * k
tf.gather(
# num * batch * k
tf.transpose(
xw3d, [1, 0, 2]),
row),
[1, 0, 2])
# batch * pair * k
q = tf.transpose(
tf.gather(
tf.transpose(
xw3d, [1, 0, 2]),
col),
[1, 0, 2])
# b * p * k
p = tf.reshape(p, [-1, num_pairs, embed_size])
# b * p * k
q = tf.reshape(q, [-1, num_pairs, embed_size])
# k * p * k
k = self.vars['kernel']
# batch * 1 * pair * k
p = tf.expand_dims(p, 1)
# batch * pair
kp = tf.reduce_sum(
# batch * pair * k
tf.multiply(
# batch * pair * k
tf.transpose(
# batch * k * pair
tf.reduce_sum(
# batch * k * pair * k
tf.multiply(
p, k),
-1),
[0, 2, 1]),
q),
-1)
#
# if layer_norm:
# # x_mean, x_var = tf.nn.moments(xw, [1], keep_dims=True)
# # xw = (xw - x_mean) / tf.sqrt(x_var)
# # x_g = tf.Variable(tf.ones([num_inputs * embed_size]), name='x_g')
# # x_b = tf.Variable(tf.zeros([num_inputs * embed_size]), name='x_b')
# # x_g = tf.Print(x_g, [x_g[:10], x_b])
# # xw = xw * x_g + x_b
# p_mean, p_var = tf.nn.moments(op, [1], keep_dims=True)
# op = (op - p_mean) / tf.sqrt(p_var)
# p_g = tf.Variable(tf.ones([embed_size**2]), name='p_g')
# p_b = tf.Variable(tf.zeros([embed_size**2]), name='p_b')
# # p_g = tf.Print(p_g, [p_g[:10], p_b])
# op = op * p_g + p_b
l = tf.concat([xw, kp], 1)
for i in range(len(layer_sizes)):
wi = self.vars['w%d' % i]
bi = self.vars['b%d' % i]
l = tf.nn.dropout(
activate(
tf.matmul(l, wi) + bi,
layer_acts[i]),
self.layer_keeps[i])
l = tf.squeeze(l)
self.y_prob = tf.sigmoid(l)
self.loss = tf.reduce_mean(
tf.nn.sigmoid_cross_entropy_with_logits(logits=l, labels=self.y))
if layer_l2 is not None:
self.loss += embed_l2 * tf.nn.l2_loss(xw)#tf.concat(w0, 0))
for i in range(len(layer_sizes)):
wi = self.vars['w%d' % i]
self.loss += layer_l2[i] * tf.nn.l2_loss(wi)
self.optimizer = get_optimizer(opt_algo, learning_rate, self.loss)
config = tf.ConfigProto()
config.gpu_options.allow_growth = True
self.sess = tf.Session(config=config)
tf.global_variables_initializer().run(session=self.sess)
```
|
github_jupyter
|
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
sns.set(color_codes=True)
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
import os
destdir = '/Users/argha/Dropbox/CS/DatSci/nyc-data'
files = [ f for f in os.listdir(destdir) if os.path.isfile(os.path.join(destdir,f)) ]
files
#df2014 = pd.read_csv('/Users/argha/Dropbox/CS/DatSci/nyc-data/Parking_Violations_Issued_-_Fiscal_Year_2014.csv')
#df2015 = pd.read_csv('/Users/argha/Dropbox/CS/DatSci/nyc-data/Parking_Violations_Issued_-_Fiscal_Year_2015.csv')
df2016 = pd.read_csv('/Users/argha/Dropbox/CS/DatSci/nyc-data/Parking_Violations_Issued_-_Fiscal_Year_2016.csv')
#df2017 = pd.read_csv('/Users/argha/Dropbox/CS/DatSci/nyc-data/Parking_Violations_Issued_-_Fiscal_Year_2017.csv')
#df2018 = pd.read_csv('/Users/argha/Dropbox/CS/DatSci/nyc-data/Parking_Violations_Issued_-_Fiscal_Year_2018.csv')
```
## Take a look into the 2016 data
```
df2016.head(n=2)
df2016.shape
```
So in the 2016 dataset there are about 10.6 million entries for parking ticket, and each entry has 51 columns.
Lets take a look at the number of unique values for each column name...
```
d = {'Unique Entry': df2016.nunique(axis = 0),
'Nan Entry': df2016.isnull().any()}
pd.DataFrame(data = d, index = df2016.columns.values)
```
As it turns out, the last 11 columns in this dataset has no entry. So we can ignore those columns, while carrying out any visualization operation in this dataframe.
Also if the entry does not have a **Plate ID** it is very hard to locate those cars. Therefore I am going to drop those rows as well.
```
drop_column = ['No Standing or Stopping Violation', 'Hydrant Violation',
'Double Parking Violation', 'Latitude', 'Longitude',
'Community Board', 'Community Council ', 'Census Tract', 'BIN',
'BBL', 'NTA',
'Street Code1', 'Street Code2', 'Street Code3','Meter Number', 'Violation Post Code',
'Law Section', 'Sub Division', 'House Number', 'Street Name']
df2016.drop(drop_column, axis = 1, inplace = True)
drop_row = ['Plate ID']
df2016.dropna(axis = 0, how = 'any', subset = drop_row, inplace = True)
```
Check if there is anymore rows left without a **Plate ID**.
```
df2016['Plate ID'].isnull().any()
df2016.shape
```
# Create a sample data for visualization
The cleaned dataframe has 10624735 rows and 40 columns.
But this is still a lot of data points. I does not make sense to use all of them to get an idea of distribution of the data points. So for visualization I will use only 0.1% of the whole data. Assmuing that the entries are not sorted I pick my 0.1% data points from the main dataframe at random.
```
mini2016 = df2016.sample(frac = 0.01, replace = False)
mini2016.shape
```
My sample dataset has about 10K data points, which I will use for data visualization. Using the whole dataset is unnecessary and time consuming.
## Barplot of 'Registration State'
```
x_ticks = mini2016['Registration State'].value_counts().index
heights = mini2016['Registration State'].value_counts()
y_pos = np.arange(len(x_ticks))
fig = plt.figure(figsize=(15,14))
# Create horizontal bars
plt.barh(y_pos, heights)
# Create names on the y-axis
plt.yticks(y_pos, x_ticks)
# Show graphic
plt.show()
pd.DataFrame(mini2016['Registration State'].value_counts()/len(mini2016)).nlargest(10, columns = ['Registration State'])
```
You can see from the barplot above: in our sample ~77.67% cars are registered in state : **NY**. After that 9.15% cars are registered in state : **NJ**, followed by **PA**, **CT**, and **FL**.
## How the number of tickets given changes with each month?
```
month = []
for time_stamp in pd.to_datetime(mini2016['Issue Date']):
month.append(time_stamp.month)
m_count = pd.Series(month).value_counts()
plt.figure(figsize=(12,8))
sns.barplot(y=m_count.values, x=m_count.index, alpha=0.6)
plt.title("Number of Parking Ticket Given Each Month", fontsize=16)
plt.xlabel("Month", fontsize=16)
plt.ylabel("No. of cars", fontsize=16)
plt.show();
```
So from the barplot above **March** and **October** has the highest number of tickets!
## How many parking tickets are given for each violation code?
```
violation_code = mini2016['Violation Code'].value_counts()
plt.figure(figsize=(16,8))
f = sns.barplot(y=violation_code.values, x=violation_code.index, alpha=0.6)
#plt.xticks(np.arange(0,101, 10.0))
f.set(xticks=np.arange(0,100, 5.0))
plt.title("Number of Parking Tickets Given for Each Violation Code", fontsize=16)
plt.xlabel("Violation Code [ X5 ]", fontsize=16)
plt.ylabel("No. of cars", fontsize=16)
plt.show();
```
## How many parking tickets are given for each body type?
```
x_ticks = mini2016['Vehicle Body Type'].value_counts().index
heights = mini2016['Vehicle Body Type'].value_counts().values
y_pos = np.arange(len(x_ticks))
fig = plt.figure(figsize=(15,4))
f = sns.barplot(y=heights, x=y_pos, orient = 'v', alpha=0.6);
# remove labels
plt.tick_params(labelbottom='off')
plt.ylabel('No. of cars', fontsize=16);
plt.xlabel('Car models [Label turned off due to crowding. Too many types.]', fontsize=16);
plt.title('Parking ticket given for different type of car body', fontsize=16);
df_bodytype = pd.DataFrame(mini2016['Vehicle Body Type'].value_counts() / len(mini2016)).nlargest(10, columns = ['Vehicle Body Type'])
```
Top 10 car body types that get the most parking tickets are listed below :
```
df_bodytype
df_bodytype.sum(axis = 0)/len(mini2016)
```
Top 10 vehicle body type includes 93.42% of my sample dataset.
## How many parking tickets are given for each vehicle make?
Just for the sake of changing the flavor of visualization this time I will make a logplot of car no. vs make. In that case we will be able to see much smaller values in the same graph with larger values.
```
vehicle_make = mini2016['Vehicle Make'].value_counts()
plt.figure(figsize=(16,8))
f = sns.barplot(y=np.log(vehicle_make.values), x=vehicle_make.index, alpha=0.6)
# remove labels
plt.tick_params(labelbottom='off')
plt.ylabel('log(No. of cars)', fontsize=16);
plt.xlabel('Car make [Label turned off due to crowding. Too many companies!]', fontsize=16);
plt.title('Parking ticket given for different type of car make', fontsize=16);
plt.show();
pd.DataFrame(mini2016['Vehicle Make'].value_counts() / len(mini2016)).nlargest(10, columns = ['Vehicle Make'])
```
## Insight on violation time
In the raw data the **Violaation Time** is in a format, which is non-interpretable using standard **to_datatime** function in pandas. We need to change it in a useful format so that we can use the data. After formatting we may replace the old **Violation Time ** column with the new one.
```
timestamp = []
for time in mini2016['Violation Time']:
if len(str(time)) == 5:
time = time[:2] + ':' + time[2:]
timestamp.append(pd.to_datetime(time, errors='coerce'))
else:
timestamp.append(pd.NaT)
mini2016 = mini2016.assign(Violation_Time2 = timestamp)
mini2016.drop(['Violation Time'], axis = 1, inplace = True)
mini2016.rename(index=str, columns={"Violation_Time2": "Violation Time"}, inplace = True)
```
So in the new **Violation Time** column the data is in **Timestamp** format.
```
hours = [lambda x: x.hour, mini2016['Violation Time']]
# Getting the histogram
mini2016.set_index('Violation Time', drop=False, inplace=True)
plt.figure(figsize=(16,8))
mini2016['Violation Time'].groupby(pd.TimeGrouper(freq='30Min')).count().plot(kind='bar');
plt.tick_params(labelbottom='on')
plt.ylabel('No. of cars', fontsize=16);
plt.xlabel('Day Time', fontsize=16);
plt.title('Parking ticket given at different time of the day', fontsize=16);
```
## Parking ticket vs county
```
violation_county = mini2016['Violation County'].value_counts()
plt.figure(figsize=(16,8))
f = sns.barplot(y=violation_county.values, x=violation_county.index, alpha=0.6)
# remove labels
plt.tick_params(labelbottom='on')
plt.ylabel('No. of cars', fontsize=16);
plt.xlabel('County', fontsize=16);
plt.title('Parking ticket given in different counties', fontsize=16);
```
## Unregistered Vehicle?
```
sns.countplot(x = 'Unregistered Vehicle?', data = mini2016)
mini2016['Unregistered Vehicle?'].unique()
```
## Vehicle Year
```
pd.DataFrame(mini2016['Vehicle Year'].value_counts()).nlargest(10, columns = ['Vehicle Year'])
plt.figure(figsize=(20,8))
sns.countplot(x = 'Vehicle Year', data = mini2016.loc[(mini2016['Vehicle Year']>1980) & (mini2016['Vehicle Year'] <= 2018)]);
```
## Violation In Front Of Or Opposite
```
plt.figure(figsize=(16,8))
sns.countplot(x = 'Violation In Front Of Or Opposite', data = mini2016);
# create data
names = mini2016['Violation In Front Of Or Opposite'].value_counts().index
size = mini2016['Violation In Front Of Or Opposite'].value_counts().values
# Create a circle for the center of the plot
my_circle=plt.Circle( (0,0), 0.7, color='white')
plt.figure(figsize=(8,8))
from palettable.colorbrewer.qualitative import Pastel1_7
plt.pie(size, labels=names, colors=Pastel1_7.hex_colors)
p=plt.gcf()
p.gca().add_artist(my_circle)
plt.show()
```
|
github_jupyter
|
```
import os
from tensorflow.keras import layers
from tensorflow.keras import Model
from tensorflow.keras.applications.inception_v3 import InceptionV3
#!wget --no-check-certificate \
# https://storage.googleapis.com/mledu-datasets/inception_v3_weights_tf_dim_ordering_tf_kernels_notop.h5 \
# -O /tmp/inception_v3_weights_tf_dim_ordering_tf_kernels_notop.h5
root = r'D:\Users\Arkady\Verint\Coursera_2019_Tensorflow_Specialization\Course2_CNN_in_TF'
local_weights_file = root + '/tmp/inception_v3_weights_tf_dim_ordering_tf_kernels_notop.h5'
pre_trained_model = InceptionV3(input_shape = (150, 150, 3),
include_top = False,
weights = None)
pre_trained_model.load_weights(local_weights_file)
for layer in pre_trained_model.layers:
layer.trainable = False
# pre_trained_model.summary()
last_layer = pre_trained_model.get_layer('mixed7')
print('last layer output shape: ', last_layer.output_shape)
last_output = last_layer.output
from tensorflow.keras.optimizers import RMSprop
# Flatten the output layer to 1 dimension
x = layers.Flatten()(last_output)
# Add a fully connected layer with 1,024 hidden units and ReLU activation
x = layers.Dense(1024, activation='relu')(x)
# Add a dropout rate of 0.2
x = layers.Dropout(0.2)(x)
# Add a final sigmoid layer for classification
x = layers.Dense (1, activation='sigmoid')(x)
model = Model( pre_trained_model.input, x)
model.compile(optimizer = RMSprop(lr=0.0001),
loss = 'binary_crossentropy',
metrics = ['acc'])
#!wget --no-check-certificate \
# https://storage.googleapis.com/mledu-datasets/cats_and_dogs_filtered.zip \
# -O /tmp/cats_and_dogs_filtered.zip
from tensorflow.keras.preprocessing.image import ImageDataGenerator
import os
import zipfile
#local_zip = '//tmp/cats_and_dogs_filtered.zip'
#zip_ref = zipfile.ZipFile(local_zip, 'r')
#zip_ref.extractall('/tmp')
#zip_ref.close()
# Define our example directories and files
base_dir = root + '/tmp/cats_and_dogs_filtered'
train_dir = os.path.join( base_dir, 'train')
validation_dir = os.path.join( base_dir, 'validation')
train_cats_dir = os.path.join(train_dir, 'cats') # Directory with our training cat pictures
train_dogs_dir = os.path.join(train_dir, 'dogs') # Directory with our training dog pictures
validation_cats_dir = os.path.join(validation_dir, 'cats') # Directory with our validation cat pictures
validation_dogs_dir = os.path.join(validation_dir, 'dogs')# Directory with our validation dog pictures
train_cat_fnames = os.listdir(train_cats_dir)
train_dog_fnames = os.listdir(train_dogs_dir)
# Add our data-augmentation parameters to ImageDataGenerator
train_datagen = ImageDataGenerator(rescale = 1./255.,
rotation_range = 40,
width_shift_range = 0.2,
height_shift_range = 0.2,
shear_range = 0.2,
zoom_range = 0.2,
horizontal_flip = True)
# Note that the validation data should not be augmented!
test_datagen = ImageDataGenerator( rescale = 1.0/255. )
# Flow training images in batches of 20 using train_datagen generator
train_generator = train_datagen.flow_from_directory(train_dir,
batch_size = 20,
class_mode = 'binary',
target_size = (150, 150))
# Flow validation images in batches of 20 using test_datagen generator
validation_generator = test_datagen.flow_from_directory( validation_dir,
batch_size = 20,
class_mode = 'binary',
target_size = (150, 150))
history = model.fit_generator(
train_generator,
validation_data = validation_generator,
steps_per_epoch = 100,
epochs = 20,
validation_steps = 50,
verbose = 2)
import matplotlib.pyplot as plt
acc = history.history['acc']
val_acc = history.history['val_acc']
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(len(acc))
plt.plot(epochs, acc, 'r', label='Training accuracy')
plt.plot(epochs, val_acc, 'b', label='Validation accuracy')
plt.title('Training and validation accuracy')
plt.legend(loc=0)
plt.figure()
plt.show()
```
|
github_jupyter
|
CER041 - Install signed Knox certificate
========================================
This notebook installs into the Big Data Cluster the certificate signed
using:
- [CER031 - Sign Knox certificate with generated
CA](../cert-management/cer031-sign-knox-generated-cert.ipynb)
Steps
-----
### Parameters
```
app_name = "gateway"
scaledset_name = "gateway/pods/gateway-0"
container_name = "knox"
prefix_keyfile_name = "knox"
common_name = "gateway-svc"
test_cert_store_root = "/var/opt/secrets/test-certificates"
```
### Common functions
Define helper functions used in this notebook.
```
# Define `run` function for transient fault handling, suggestions on error, and scrolling updates on Windows
import sys
import os
import re
import json
import platform
import shlex
import shutil
import datetime
from subprocess import Popen, PIPE
from IPython.display import Markdown
retry_hints = {}
error_hints = {}
install_hint = {}
first_run = True
rules = None
def run(cmd, return_output=False, no_output=False, retry_count=0):
"""
Run shell command, stream stdout, print stderr and optionally return output
"""
MAX_RETRIES = 5
output = ""
retry = False
global first_run
global rules
if first_run:
first_run = False
rules = load_rules()
# shlex.split is required on bash and for Windows paths with spaces
#
cmd_actual = shlex.split(cmd)
# Store this (i.e. kubectl, python etc.) to support binary context aware error_hints and retries
#
user_provided_exe_name = cmd_actual[0].lower()
# When running python, use the python in the ADS sandbox ({sys.executable})
#
if cmd.startswith("python "):
cmd_actual[0] = cmd_actual[0].replace("python", sys.executable)
# On Mac, when ADS is not launched from terminal, LC_ALL may not be set, which causes pip installs to fail
# with:
#
# UnicodeDecodeError: 'ascii' codec can't decode byte 0xc5 in position 4969: ordinal not in range(128)
#
# Setting it to a default value of "en_US.UTF-8" enables pip install to complete
#
if platform.system() == "Darwin" and "LC_ALL" not in os.environ:
os.environ["LC_ALL"] = "en_US.UTF-8"
# To aid supportabilty, determine which binary file will actually be executed on the machine
#
which_binary = None
# Special case for CURL on Windows. The version of CURL in Windows System32 does not work to
# get JWT tokens, it returns "(56) Failure when receiving data from the peer". If another instance
# of CURL exists on the machine use that one. (Unfortunately the curl.exe in System32 is almost
# always the first curl.exe in the path, and it can't be uninstalled from System32, so here we
# look for the 2nd installation of CURL in the path)
if platform.system() == "Windows" and cmd.startswith("curl "):
path = os.getenv('PATH')
for p in path.split(os.path.pathsep):
p = os.path.join(p, "curl.exe")
if os.path.exists(p) and os.access(p, os.X_OK):
if p.lower().find("system32") == -1:
cmd_actual[0] = p
which_binary = p
break
# Find the path based location (shutil.which) of the executable that will be run (and display it to aid supportability), this
# seems to be required for .msi installs of azdata.cmd/az.cmd. (otherwise Popen returns FileNotFound)
#
# NOTE: Bash needs cmd to be the list of the space separated values hence shlex.split.
#
if which_binary == None:
which_binary = shutil.which(cmd_actual[0])
if which_binary == None:
if user_provided_exe_name in install_hint and install_hint[user_provided_exe_name] is not None:
display(Markdown(f'HINT: Use [{install_hint[user_provided_exe_name][0]}]({install_hint[user_provided_exe_name][1]}) to resolve this issue.'))
raise FileNotFoundError(f"Executable '{cmd_actual[0]}' not found in path (where/which)")
else:
cmd_actual[0] = which_binary
start_time = datetime.datetime.now().replace(microsecond=0)
print(f"START: {cmd} @ {start_time} ({datetime.datetime.utcnow().replace(microsecond=0)} UTC)")
print(f" using: {which_binary} ({platform.system()} {platform.release()} on {platform.machine()})")
print(f" cwd: {os.getcwd()}")
# Command-line tools such as CURL and AZDATA HDFS commands output
# scrolling progress bars, which causes Jupyter to hang forever, to
# workaround this, use no_output=True
#
# Work around a infinite hang when a notebook generates a non-zero return code, break out, and do not wait
#
wait = True
try:
if no_output:
p = Popen(cmd_actual)
else:
p = Popen(cmd_actual, stdout=PIPE, stderr=PIPE, bufsize=1)
with p.stdout:
for line in iter(p.stdout.readline, b''):
line = line.decode()
if return_output:
output = output + line
else:
if cmd.startswith("azdata notebook run"): # Hyperlink the .ipynb file
regex = re.compile(' "(.*)"\: "(.*)"')
match = regex.match(line)
if match:
if match.group(1).find("HTML") != -1:
display(Markdown(f' - "{match.group(1)}": "{match.group(2)}"'))
else:
display(Markdown(f' - "{match.group(1)}": "[{match.group(2)}]({match.group(2)})"'))
wait = False
break # otherwise infinite hang, have not worked out why yet.
else:
print(line, end='')
if rules is not None:
apply_expert_rules(line)
if wait:
p.wait()
except FileNotFoundError as e:
if install_hint is not None:
display(Markdown(f'HINT: Use {install_hint} to resolve this issue.'))
raise FileNotFoundError(f"Executable '{cmd_actual[0]}' not found in path (where/which)") from e
exit_code_workaround = 0 # WORKAROUND: azdata hangs on exception from notebook on p.wait()
if not no_output:
for line in iter(p.stderr.readline, b''):
line_decoded = line.decode()
# azdata emits a single empty line to stderr when doing an hdfs cp, don't
# print this empty "ERR:" as it confuses.
#
if line_decoded == "":
continue
print(f"STDERR: {line_decoded}", end='')
if line_decoded.startswith("An exception has occurred") or line_decoded.startswith("ERROR: An error occurred while executing the following cell"):
exit_code_workaround = 1
if user_provided_exe_name in error_hints:
for error_hint in error_hints[user_provided_exe_name]:
if line_decoded.find(error_hint[0]) != -1:
display(Markdown(f'HINT: Use [{error_hint[1]}]({error_hint[2]}) to resolve this issue.'))
if rules is not None:
apply_expert_rules(line_decoded)
if user_provided_exe_name in retry_hints:
for retry_hint in retry_hints[user_provided_exe_name]:
if line_decoded.find(retry_hint) != -1:
if retry_count < MAX_RETRIES:
print(f"RETRY: {retry_count} (due to: {retry_hint})")
retry_count = retry_count + 1
output = run(cmd, return_output=return_output, retry_count=retry_count)
if return_output:
return output
else:
return
elapsed = datetime.datetime.now().replace(microsecond=0) - start_time
# WORKAROUND: We avoid infinite hang above in the `azdata notebook run` failure case, by inferring success (from stdout output), so
# don't wait here, if success known above
#
if wait:
if p.returncode != 0:
raise SystemExit(f'Shell command:\n\n\t{cmd} ({elapsed}s elapsed)\n\nreturned non-zero exit code: {str(p.returncode)}.\n')
else:
if exit_code_workaround !=0 :
raise SystemExit(f'Shell command:\n\n\t{cmd} ({elapsed}s elapsed)\n\nreturned non-zero exit code: {str(exit_code_workaround)}.\n')
print(f'\nSUCCESS: {elapsed}s elapsed.\n')
if return_output:
return output
def load_json(filename):
with open(filename, encoding="utf8") as json_file:
return json.load(json_file)
def load_rules():
try:
# Load this notebook as json to get access to the expert rules in the notebook metadata.
#
j = load_json("cer041-install-knox-cert.ipynb")
except:
pass # If the user has renamed the book, we can't load ourself. NOTE: Is there a way in Jupyter, to know your own filename?
else:
if "metadata" in j and \
"azdata" in j["metadata"] and \
"expert" in j["metadata"]["azdata"] and \
"rules" in j["metadata"]["azdata"]["expert"]:
rules = j["metadata"]["azdata"]["expert"]["rules"]
rules.sort() # Sort rules, so they run in priority order (the [0] element). Lowest value first.
# print (f"EXPERT: There are {len(rules)} rules to evaluate.")
return rules
def apply_expert_rules(line):
global rules
for rule in rules:
# rules that have 9 elements are the injected (output) rules (the ones we want). Rules
# with only 8 elements are the source (input) rules, which are not expanded (i.e. TSG029,
# not ../repair/tsg029-nb-name.ipynb)
if len(rule) == 9:
notebook = rule[1]
cell_type = rule[2]
output_type = rule[3] # i.e. stream or error
output_type_name = rule[4] # i.e. ename or name
output_type_value = rule[5] # i.e. SystemExit or stdout
details_name = rule[6] # i.e. evalue or text
expression = rule[7].replace("\\*", "*") # Something escaped *, and put a \ in front of it!
# print(f"EXPERT: If rule '{expression}' satisfied', run '{notebook}'.")
if re.match(expression, line, re.DOTALL):
# print("EXPERT: MATCH: name = value: '{0}' = '{1}' matched expression '{2}', therefore HINT '{4}'".format(output_type_name, output_type_value, expression, notebook))
match_found = True
display(Markdown(f'HINT: Use [{notebook}]({notebook}) to resolve this issue.'))
print('Common functions defined successfully.')
# Hints for binary (transient fault) retry, (known) error and install guide
#
retry_hints = {'kubectl': ['A connection attempt failed because the connected party did not properly respond after a period of time, or established connection failed because connected host has failed to respond']}
error_hints = {'kubectl': [['no such host', 'TSG010 - Get configuration contexts', '../monitor-k8s/tsg010-get-kubernetes-contexts.ipynb'], ['no such host', 'TSG011 - Restart sparkhistory server', '../repair/tsg011-restart-sparkhistory-server.ipynb'], ['No connection could be made because the target machine actively refused it', 'TSG056 - Kubectl fails with No connection could be made because the target machine actively refused it', '../repair/tsg056-kubectl-no-connection-could-be-made.ipynb']]}
install_hint = {'kubectl': ['SOP036 - Install kubectl command line interface', '../install/sop036-install-kubectl.ipynb']}
```
### Get the Kubernetes namespace for the big data cluster
Get the namespace of the big data cluster use the kubectl command line
interface .
NOTE: If there is more than one big data cluster in the target
Kubernetes cluster, then set \[0\] to the correct value for the big data
cluster.
```
# Place Kubernetes namespace name for BDC into 'namespace' variable
try:
namespace = run(f'kubectl get namespace --selector=MSSQL_CLUSTER -o jsonpath={{.items[0].metadata.name}}', return_output=True)
except:
from IPython.display import Markdown
print(f"ERROR: Unable to find a Kubernetes namespace with label 'MSSQL_CLUSTER'. SQL Server Big Data Cluster Kubernetes namespaces contain the label 'MSSQL_CLUSTER'.")
display(Markdown(f'HINT: Use [TSG081 - Get namespaces (Kubernetes)](../monitor-k8s/tsg081-get-kubernetes-namespaces.ipynb) to resolve this issue.'))
display(Markdown(f'HINT: Use [TSG010 - Get configuration contexts](../monitor-k8s/tsg010-get-kubernetes-contexts.ipynb) to resolve this issue.'))
display(Markdown(f'HINT: Use [SOP011 - Set kubernetes configuration context](../common/sop011-set-kubernetes-context.ipynb) to resolve this issue.'))
raise
else:
print(f'The SQL Server Big Data Cluster Kubernetes namespace is: {namespace}')
```
### Create a temporary directory to stage files
```
# Create a temporary directory to hold configuration files
import tempfile
temp_dir = tempfile.mkdtemp()
print(f"Temporary directory created: {temp_dir}")
```
### Helper function to save configuration files to disk
```
# Define helper function 'save_file' to save configuration files to the temporary directory created above
import os
import io
def save_file(filename, contents):
with io.open(os.path.join(temp_dir, filename), "w", encoding='utf8', newline='\n') as text_file:
text_file.write(contents)
print("File saved: " + os.path.join(temp_dir, filename))
```
### Get name of the ‘Running’ `controller` `pod`
```
# Place the name of the 'Running' controller pod in variable `controller`
controller = run(f'kubectl get pod --selector=app=controller -n {namespace} -o jsonpath={{.items[0].metadata.name}} --field-selector=status.phase=Running', return_output=True)
print(f"Controller pod name: {controller}")
```
### Pod name for gateway
```
pod = 'gateway-0'
```
### Copy certifcate files from `controller` to local machine
```
import os
cwd = os.getcwd()
os.chdir(temp_dir) # Use chdir to workaround kubectl bug on Windows, which incorrectly processes 'c:\' on kubectl cp cmd line
run(f'kubectl cp {controller}:{test_cert_store_root}/{app_name}/{prefix_keyfile_name}-certificate.pem {prefix_keyfile_name}-certificate.pem -c controller -n {namespace}')
run(f'kubectl cp {controller}:{test_cert_store_root}/{app_name}/{prefix_keyfile_name}-privatekey.pem {prefix_keyfile_name}-privatekey.pem -c controller -n {namespace}')
os.chdir(cwd)
```
### Copy certifcate files from local machine to `controldb`
```
import os
cwd = os.getcwd()
os.chdir(temp_dir) # Workaround kubectl bug on Windows, can't put c:\ on kubectl cp cmd line
run(f'kubectl cp {prefix_keyfile_name}-certificate.pem controldb-0:/var/opt/mssql/{prefix_keyfile_name}-certificate.pem -c mssql-server -n {namespace}')
run(f'kubectl cp {prefix_keyfile_name}-privatekey.pem controldb-0:/var/opt/mssql/{prefix_keyfile_name}-privatekey.pem -c mssql-server -n {namespace}')
os.chdir(cwd)
```
### Get the `controller-db-rw-secret` secret
Get the controller SQL symmetric key password for decryption.
```
import base64
controller_db_rw_secret = run(f'kubectl get secret/controller-db-rw-secret -n {namespace} -o jsonpath={{.data.encryptionPassword}}', return_output=True)
controller_db_rw_secret = base64.b64decode(controller_db_rw_secret).decode('utf-8')
print("controller_db_rw_secret retrieved")
```
### Update the files table with the certificates through opened SQL connection
```
import os
sql = f"""
OPEN SYMMETRIC KEY ControllerDbSymmetricKey DECRYPTION BY PASSWORD = '{controller_db_rw_secret}'
DECLARE @FileData VARBINARY(MAX), @Key uniqueidentifier;
SELECT @Key = KEY_GUID('ControllerDbSymmetricKey');
SELECT TOP 1 @FileData = doc.BulkColumn FROM OPENROWSET(BULK N'/var/opt/mssql/{prefix_keyfile_name}-certificate.pem', SINGLE_BLOB) AS doc;
EXEC [dbo].[sp_set_file_data_encrypted] @FilePath = '/config/scaledsets/{scaledset_name}/containers/{container_name}/files/{prefix_keyfile_name}-certificate.pem',
@Data = @FileData,
@KeyGuid = @Key,
@Version = '0',
@User = '',
@Group = '',
@Mode = '';
SELECT TOP 1 @FileData = doc.BulkColumn FROM OPENROWSET(BULK N'/var/opt/mssql/{prefix_keyfile_name}-privatekey.pem', SINGLE_BLOB) AS doc;
EXEC [dbo].[sp_set_file_data_encrypted] @FilePath = '/config/scaledsets/{scaledset_name}/containers/{container_name}/files/{prefix_keyfile_name}-privatekey.pem',
@Data = @FileData,
@KeyGuid = @Key,
@Version = '0',
@User = '',
@Group = '',
@Mode = '';
"""
save_file("insert_certificates.sql", sql)
cwd = os.getcwd()
os.chdir(temp_dir) # Workaround kubectl bug on Windows, can't put c:\ on kubectl cp cmd line
run(f'kubectl cp insert_certificates.sql controldb-0:/var/opt/mssql/insert_certificates.sql -c mssql-server -n {namespace}')
run(f"""kubectl exec controldb-0 -c mssql-server -n {namespace} -- bash -c "SQLCMDPASSWORD=`cat /var/run/secrets/credentials/mssql-sa-password/password` /opt/mssql-tools/bin/sqlcmd -b -U sa -d controller -i /var/opt/mssql/insert_certificates.sql" """)
# Clean up
run(f"""kubectl exec controldb-0 -c mssql-server -n {namespace} -- bash -c "rm /var/opt/mssql/insert_certificates.sql" """)
run(f"""kubectl exec controldb-0 -c mssql-server -n {namespace} -- bash -c "rm /var/opt/mssql/{prefix_keyfile_name}-certificate.pem" """)
run(f"""kubectl exec controldb-0 -c mssql-server -n {namespace} -- bash -c "rm /var/opt/mssql/{prefix_keyfile_name}-privatekey.pem" """)
os.chdir(cwd)
```
### Clear out the controller\_db\_rw\_secret variable
```
controller_db_rw_secret= ""
```
### Clean up certificate staging area
Remove the certificate files generated on disk (they have now been
placed in the controller database).
```
cmd = f"rm -r {test_cert_store_root}/{app_name}"
run(f'kubectl exec {controller} -c controller -n {namespace} -- bash -c "{cmd}"')
```
### Restart knox gateway service
```
run(f'kubectl delete pod {pod} -n {namespace}')
```
### Clean up temporary directory for staging configuration files
```
# Delete the temporary directory used to hold configuration files
import shutil
shutil.rmtree(temp_dir)
print(f'Temporary directory deleted: {temp_dir}')
print('Notebook execution complete.')
```
Related
-------
- [CER042 - Install signed App-Proxy
certificate](../cert-management/cer042-install-app-proxy-cert.ipynb)
- [CER031 - Sign Knox certificate with generated
CA](../cert-management/cer031-sign-knox-generated-cert.ipynb)
- [CER021 - Create Knox
certificate](../cert-management/cer021-create-knox-cert.ipynb)
|
github_jupyter
|
```
!pip install -q condacolab
import condacolab
condacolab.install()
!conda install -c chembl chembl_structure_pipeline
import chembl_structure_pipeline
from chembl_structure_pipeline import standardizer
from IPython.display import clear_output
# https://www.dgl.ai/pages/start.html
# !pip install dgl
!pip install dgl-cu111 -f https://data.dgl.ai/wheels/repo.html # FOR CUDA VERSION
!pip install dgllife
!pip install rdkit-pypi
!pip install --pre deepchem
!pip install ipython-autotime
!pip install gputil
!pip install psutil
!pip install humanize
%load_ext autotime
clear = clear_output()
import os
from os import path
import statistics
import warnings
import random
import time
import itertools
import psutil
import humanize
import GPUtil as GPU
import subprocess
from datetime import datetime, timedelta
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import tqdm
from tqdm import trange, tqdm_notebook, tnrange
import deepchem as dc
import rdkit
from rdkit import Chem
from rdkit.Chem.MolStandardize import rdMolStandardize
import dgl
from dgl.dataloading import GraphDataLoader
from dgl.nn import GraphConv, SumPooling, MaxPooling
import dgl.function as fn
import dgllife
from dgllife import utils
# embedding
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.autograd import Variable
from torch.optim.lr_scheduler import ReduceLROnPlateau
from torch.profiler import profile, record_function, ProfilerActivity
from torch.utils.tensorboard import SummaryWriter
import sklearn
from sklearn.metrics import (auc, roc_curve, roc_auc_score, average_precision_score,
accuracy_score, ConfusionMatrixDisplay, confusion_matrix, precision_recall_curve,
f1_score, PrecisionRecallDisplay)
from sklearn.ensemble import RandomForestClassifier
warnings.filterwarnings("ignore", message="DGLGraph.__len__")
DGLBACKEND = 'pytorch'
clear
def get_cmd_output(command):
return subprocess.check_output(command,
stderr=subprocess.STDOUT,
shell=True).decode('UTF-8')
```
### Create Dataset
```
def create_dataset(df, name, bonds):
print(f"Creating Dataset and Saving to {drive_path}/data/{name}.pkl")
data = df.sample(frac=1)
data = data.reset_index(drop=True)
data['mol'] = data['smiles'].apply(lambda x: create_dgl_features(x, bonds))
data.to_pickle(f"{drive_path}/data/{name}.pkl")
return data
def featurize_atoms(mol):
feats = []
atom_features = utils.ConcatFeaturizer([
utils.atom_type_one_hot,
utils.atomic_number_one_hot,
utils.atom_degree_one_hot,
utils.atom_explicit_valence_one_hot,
utils.atom_formal_charge_one_hot,
utils.atom_num_radical_electrons_one_hot,
utils.atom_hybridization_one_hot,
utils.atom_is_aromatic_one_hot
])
for atom in mol.GetAtoms():
feats.append(atom_features(atom))
return {'feats': torch.tensor(feats).float()}
def featurize_bonds(mol):
feats = []
bond_features = utils.ConcatFeaturizer([
utils.bond_type_one_hot,
utils.bond_is_conjugated_one_hot,
utils.bond_is_in_ring_one_hot,
utils.bond_stereo_one_hot,
utils.bond_direction_one_hot,
])
for bond in mol.GetBonds():
feats.append(bond_features(bond))
feats.append(bond_features(bond))
return {'edge_feats': torch.tensor(feats).float()}
def create_dgl_features(smiles, bonds):
mol = Chem.MolFromSmiles(smiles)
mol = standardizer.standardize_mol(mol)
if bonds:
dgl_graph = utils.mol_to_bigraph(mol=mol,
node_featurizer=featurize_atoms,
edge_featurizer=featurize_bonds,
canonical_atom_order=True)
else:
dgl_graph = utils.mol_to_bigraph(mol=mol,
node_featurizer=featurize_atoms,
canonical_atom_order=True)
dgl_graph = dgl.add_self_loop(dgl_graph)
return dgl_graph
def load_dataset(dataset, bonds=False, feat='graph', create_new=False):
"""
dataset values: muv, tox21, dude-gpcr
feat values: graph, ecfp
"""
dataset_test_tasks = {
'tox21': ['SR-HSE', 'SR-MMP', 'SR-p53'],
'muv': ['MUV-832', 'MUV-846', 'MUV-852', 'MUV-858', 'MUV-859'],
'dude-gpcr': ['adrb2', 'cxcr4']
}
dataset_original = dataset
if bonds:
dataset = dataset + "_with_bonds"
if path.exists(f"{drive_path}/data/{dataset}_dgl.pkl") and not create_new:
# Load Dataset
print("Reading Pickle")
if feat == 'graph':
data = pd.read_pickle(f"{drive_path}/data/{dataset}_dgl.pkl")
else:
data = pd.read_pickle(f"{drive_path}/data/{dataset}_ecfp.pkl")
else:
# Create Dataset
df = pd.read_csv(f"{drive_path}/data/raw/{dataset_original}.csv")
if feat == 'graph':
data = create_dataset(df, f"{dataset}_dgl", bonds)
else:
data = create_ecfp_dataset(df, f"{dataset}_ecfp")
test_tasks = dataset_test_tasks.get(dataset_original)
drop_cols = test_tasks.copy()
drop_cols.extend(['mol_id', 'smiles', 'mol'])
train_tasks = [x for x in list(data.columns) if x not in drop_cols]
train_dfs = dict.fromkeys(train_tasks)
for task in train_tasks:
df = data[[task, 'mol']].dropna()
df.columns = ['y', 'mol']
# FOR BOND INFORMATION
if with_bonds:
for index, r in df.iterrows():
if r.mol.edata['edge_feats'].shape[-1] < 17:
df.drop(index, inplace=True)
train_dfs[task] = df
for key in train_dfs:
print(key, len(train_dfs[key]))
if feat == 'graph':
feat_length = data.iloc[0].mol.ndata['feats'].shape[-1]
print("Feature Length", feat_length)
if with_bonds:
feat_length = data.iloc[0].mol.edata['edge_feats'].shape[-1]
print("Feature Length", feat_length)
else:
print("Edge Features: ", with_bonds)
test_dfs = dict.fromkeys(test_tasks)
for task in test_tasks:
df = data[[task, 'mol']].dropna()
df.columns = ['y', 'mol']
# FOR BOND INFORMATION
if with_bonds:
for index, r in df.iterrows():
if r.mol.edata['edge_feats'].shape[-1] < 17:
df.drop(index, inplace=True)
test_dfs[task] = df
for key in test_dfs:
print(key, len(test_dfs[key]))
# return data, train_tasks, test_tasks
return train_tasks, train_dfs, test_tasks, test_dfs
```
## Create Episode
```
def create_episode(n_support_pos, n_support_neg, n_query, data, test=False, train_balanced=True):
"""
n_query = per class data points
Xy = dataframe dataset in format [['y', 'mol']]
"""
support = []
query = []
n_query_pos = n_query
n_query_neg = n_query
support_neg = data[data['y'] == 0].sample(n_support_neg)
support_pos = data[data['y'] == 1].sample(n_support_pos)
# organise support by class in array dimensions
support.append(support_neg.to_numpy())
support.append(support_pos.to_numpy())
support = np.array(support, dtype=object)
support_X = [rec[1] for sup_class in support for rec in sup_class]
support_y = np.asarray([rec[0] for sup_class in support for rec in sup_class], dtype=np.float16).flatten()
data = data.drop(support_neg.index)
data = data.drop(support_pos.index)
if len(data[data['y'] == 1]) < n_query:
n_query_pos = len(data[data['y'] == 1])
if test:
# test uses all data remaining
query_neg = data[data['y'] == 0].to_numpy()
query_pos = data[data['y'] == 1].to_numpy()
elif (not test) and train_balanced:
# for balanced queries, same size as support
query_neg = data[data['y'] == 0].sample(n_query_neg).to_numpy()
query_pos = data[data['y'] == 1].sample(n_query_pos).to_numpy()
elif (not test) and (not train_balanced):
# print('test')
query_neg = data[data['y'] == 0].sample(1).to_numpy()
query_pos = data[data['y'] == 1].sample(1).to_numpy()
query_rem = data.sample(n_query*2 - 2)
query_neg_rem = query_rem[query_rem['y'] == 0].to_numpy()
query_pos_rem = query_rem[query_rem['y'] == 1].to_numpy()
query_neg = np.concatenate((query_neg, query_neg_rem))
query_pos = np.concatenate((query_pos, query_pos_rem), axis=0)
query_X = np.concatenate([query_neg[:, 1], query_pos[:, 1]])
query_y = np.concatenate([query_neg[:, 0], query_pos[:, 0]])
return support_X, support_y, query_X, query_y
# task = 'NR-AR'
# df = data[[task, 'mol']]
# df = df.dropna()
# df.columns = ['y', 'mol']
# support_X, support_y, query_X, query_y = create_episode(1, 1, 64, df)
# support_y
# testing
# support = []
# query = []
# support_neg = df[df['y'] == 0].sample(2)
# support_pos = df[df['y'] == 1].sample(2)
# # organise support by class in array dimensions
# support.append(support_neg.to_numpy())
# support.append(support_pos.to_numpy())
# support = np.array(support)
# support.shape
# support[:, :, 1]
```
## Graph Embedding
```
class GCN(nn.Module):
def __init__(self, in_channels, out_channels=128):
super(GCN, self).__init__()
self.conv1 = GraphConv(in_channels, 64)
self.conv2 = GraphConv(64, 128)
self.conv3 = GraphConv(128, 64)
self.sum_pool = SumPooling()
self.dense = nn.Linear(64, out_channels)
def forward(self, graph, in_feat):
h = self.conv1(graph, in_feat)
h = F.relu(h)
graph.ndata['h'] = h
graph.update_all(fn.copy_u('h', 'm'), fn.max('m', 'h'))
h = self.conv2(graph, graph.ndata['h'])
h = F.relu(h)
graph.ndata['h'] = h
graph.update_all(fn.copy_u('h', 'm'), fn.max('m', 'h'))
h = self.conv3(graph, graph.ndata['h'])
h = F.relu(h)
graph.ndata['h'] = h
graph.update_all(fn.copy_u('h', 'm'), fn.max('m', 'h'))
output = self.sum_pool(graph, graph.ndata['h'])
output = torch.tanh(output)
output = self.dense(output)
output = torch.tanh(output)
return output
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.fc1 = nn.Linear(2048, 1000)
self.fc2 = nn.Linear(1000, 500)
self.fc3 = nn.Linear(500, 128)
def forward(self, x):
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = torch.tanh(self.fc3(x))
return x
```
## Distance Function
```
def euclidean_dist(x, y):
# x: N x D
# y: M x D
n = x.size(0)
m = y.size(0)
d = x.size(1)
assert d == y.size(1)
x = x.unsqueeze(1).expand(n, m, d)
y = y.unsqueeze(0).expand(n, m, d)
return torch.pow(x - y, 2).sum(2)
```
### LSTM
```
def cos(x, y):
transpose_shape = tuple(list(range(len(y.shape)))[::-1])
x = x.float()
denom = (
torch.sqrt(torch.sum(torch.square(x)) *
torch.sum(torch.square(y))) + torch.finfo(torch.float32).eps)
return torch.matmul(x, torch.permute(y, transpose_shape)) / denom
class ResiLSTMEmbedding(nn.Module):
def __init__(self, n_support, n_feat=128, max_depth=3):
super(ResiLSTMEmbedding, self).__init__()
self.max_depth = max_depth
self.n_support = n_support
self.n_feat = n_feat
self.support_lstm = nn.LSTMCell(input_size=2*self.n_feat, hidden_size=self.n_feat)
self.q_init = torch.nn.Parameter(torch.zeros((self.n_support, self.n_feat), dtype=torch.float, device="cuda"))
self.support_states_init_h = torch.nn.Parameter(torch.zeros(self.n_support, self.n_feat))
self.support_states_init_c = torch.nn.Parameter(torch.zeros(self.n_support, self.n_feat))
self.query_lstm = nn.LSTMCell(input_size=2*self.n_feat, hidden_size=self.n_feat)
if torch.cuda.is_available():
self.support_lstm = self.support_lstm.cuda()
self.query_lstm = self.query_lstm.cuda()
self.q_init = self.q_init.cuda()
# self.p_init = self.p_init.cuda()
def forward(self, x_support, x_query):
self.p_init = torch.zeros((len(x_query), self.n_feat)).to(device)
self.query_states_init_h = torch.zeros(len(x_query), self.n_feat).to(device)
self.query_states_init_c = torch.zeros(len(x_query), self.n_feat).to(device)
x_support = x_support
x_query = x_query
z_support = x_support
q = self.q_init
p = self.p_init
support_states_h = self.support_states_init_h
support_states_c = self.support_states_init_c
query_states_h = self.query_states_init_h
query_states_c = self.query_states_init_c
for i in range(self.max_depth):
sup_e = cos(z_support + q, x_support)
sup_a = torch.nn.functional.softmax(sup_e, dim=-1)
sup_r = torch.matmul(sup_a, x_support).float()
query_e = cos(x_query + p, z_support)
query_a = torch.nn.functional.softmax(query_e, dim=-1)
query_r = torch.matmul(query_a, z_support).float()
sup_qr = torch.cat((q, sup_r), 1)
support_hidden, support_out = self.support_lstm(sup_qr, (support_states_h, support_states_c))
q = support_hidden
query_pr = torch.cat((p, query_r), 1)
query_hidden, query_out = self.query_lstm(query_pr, (query_states_h, query_states_c))
p = query_hidden
z_support = sup_r
return x_support + q, x_query + p
```
## Protonet
https://colab.research.google.com/drive/1QDYIwg2-iiUpVU8YyAh0lOgFgFPhVgvx#scrollTo=BnLOgECOKG_y
```
class ProtoNet(nn.Module):
def __init__(self, with_bonds=False):
"""
Prototypical Network
"""
super(ProtoNet, self).__init__()
def forward(self, X_support, X_query, n_support_pos, n_support_neg):
n_support = len(X_support)
# prototypes
z_dim = X_support.size(-1) # size of the embedding - 128
z_proto_0 = X_support[:n_support_neg].view(n_support_neg, z_dim).mean(0)
z_proto_1 = X_support[n_support_neg:n_support].view(n_support_pos, z_dim).mean(0)
z_proto = torch.stack((z_proto_0, z_proto_1))
# queries
z_query = X_query
# compute distance
dists = euclidean_dist(z_query, z_proto) # [128, 2]
# compute probabilities
log_p_y = nn.LogSoftmax(dim=1)(-dists) # [128, 2]
return log_p_y
```
## Training Loop
```
def train(train_tasks, train_dfs, balanced_queries, k_pos, k_neg, n_query, episodes, lr):
writer = SummaryWriter()
start_time = time.time()
node_feat_size = 177
embedding_size = 128
encoder = Net()
resi_lstm = ResiLSTMEmbedding(k_pos+k_neg)
proto_net = ProtoNet()
loss_fn = nn.NLLLoss()
if torch.cuda.is_available():
encoder = encoder.cuda()
resi_lstm = resi_lstm.cuda()
proto_net = proto_net.cuda()
loss_fn = loss_fn.cuda()
encoder_optimizer = torch.optim.Adam(encoder.parameters(), lr = lr)
lstm_optimizer = torch.optim.Adam(resi_lstm.parameters(), lr = lr)
# proto_optimizer = torch.optim.Adam(proto_net.parameters(), lr = lr)
# encoder_scheduler = torch.optim.lr_scheduler.StepLR(encoder_optimizer, step_size=1, gamma=0.8)
encoder_scheduler = torch.optim.lr_scheduler.ReduceLROnPlateau(encoder_optimizer, patience=300, verbose=False)
lstm_scheduler = torch.optim.lr_scheduler.ReduceLROnPlateau(lstm_optimizer, patience=300, verbose=False)
# rn_scheduler = torch.optim.lr_scheduler.StepLR(rn_optimizer, step_size=1, gamma=0.8)
# rn_scheduler = torch.optim.lr_scheduler.ReduceLROnPlateau(rn_optimizer, patience=500, verbose=False)
episode_num = 1
early_stop = False
losses = []
running_loss = 0.0
running_acc = 0.0
running_roc = 0.0
running_prc = 0.0
# for task in shuffled_train_tasks:
pbar = trange(episodes, desc=f"Training")
# while episode_num < episodes and not early_stop:
for episode in pbar:
episode_loss = 0.0
# SET TRAINING MODE
encoder.train()
resi_lstm.train()
proto_net.train()
# RANDOMISE ORDER OF TASKS PER EPISODE
shuffled_train_tasks = random.sample(train_tasks, len(train_tasks))
# LOOP OVER TASKS
for task in shuffled_train_tasks:
# CREATE EPISODE FOR TASK
X = train_dfs[task]
X_support, y_support, X_query, y_query = create_episode(k_pos, k_neg, n_query, X, False, balanced_queries)
# TOTAL NUMBER OF QUERIES
total_query = int((y_query == 0).sum() + (y_query == 1).sum())
# ONE HOT QUERY TARGETS
# query_targets = torch.from_numpy(y_query.astype('int'))
# targets = F.one_hot(query_targets, num_classes=2)
target_inds = torch.from_numpy(y_query.astype('float32')).float()
target_inds = target_inds.unsqueeze(1).type(torch.int64)
targets = Variable(target_inds, requires_grad=False).to(device)
if torch.cuda.is_available():
targets=targets.cuda()
n_support = k_pos + k_neg
# flat_support = list(np.concatenate(X_support).flat)
# X = flat_support + list(X_query)
X = X_support + list(X_query)
# CREATE EMBEDDINGS
dataloader = torch.utils.data.DataLoader(X, batch_size=(n_support + total_query), shuffle=False, pin_memory=True)
for graph in dataloader:
graph = graph.to(device)
embeddings = encoder.forward(graph)
# LSTM EMBEDDINGS
emb_support = embeddings[:n_support]
emb_query = embeddings[n_support:]
emb_support, emb_query = resi_lstm(emb_support, emb_query)
# PROTO NETS
logits = proto_net(emb_support, emb_query, k_pos, k_neg)
# loss = loss_fn(logits, torch.max(query_targets, 1)[1])
loss = loss_fn(logits, targets.squeeze())
encoder.zero_grad()
resi_lstm.zero_grad()
proto_net.zero_grad()
loss.backward()
encoder_optimizer.step()
lstm_optimizer.step()
_, y_hat = logits.max(1)
# class_indices = torch.max(query_targets, 1)[1]
targets = targets.squeeze().cpu()
y_hat = y_hat.squeeze().detach().cpu()
roc = roc_auc_score(targets, y_hat)
prc = average_precision_score(targets, y_hat)
acc = accuracy_score(targets, y_hat)
# proto_optimizer.step()
# EVALUATE TRAINING LOOP ON TASK
episode_loss += loss.item()
running_loss += loss.item()
running_acc += acc
running_roc += roc
running_prc += prc
pbar.set_description(f"Episode {episode_num} - Loss {loss.item():.6f} - Acc {acc:.4f} - LR {encoder_optimizer.param_groups[0]['lr']}")
pbar.refresh()
losses.append(episode_loss / len(train_tasks))
writer.add_scalar('Loss/train', episode_loss / len(train_tasks), episode_num)
if encoder_optimizer.param_groups[0]['lr'] < 0.000001:
break # EARLY STOP
elif episode_num < episodes:
episode_num += 1
encoder_scheduler.step(loss)
lstm_scheduler.step(loss)
epoch_loss = running_loss / (episode_num*len(train_tasks))
epoch_acc = running_acc / (episode_num*len(train_tasks))
epoch_roc = running_roc / (episode_num*len(train_tasks))
epoch_prc = running_prc / (episode_num*len(train_tasks))
print(f'Loss: {epoch_loss:.5f} Acc: {epoch_acc:.4f} ROC: {epoch_roc:.4f} PRC: {epoch_prc:.4f}')
end_time = time.time()
train_info = {
"losses": losses,
"duration": str(timedelta(seconds=(end_time - start_time))),
"episodes": episode_num,
"train_roc": epoch_roc,
"train_prc": epoch_prc
}
return encoder, resi_lstm, proto_net, train_info
```
## Testing Loop
```
def test(encoder, lstm, proto_net, test_tasks, test_dfs, k_pos, k_neg, rounds):
encoder.eval()
lstm.eval()
proto_net.eval()
test_info = {}
with torch.no_grad():
for task in test_tasks:
Xy = test_dfs[task]
running_loss = []
running_acc = []
running_roc = [0]
running_prc = [0]
running_preds = []
running_targets = []
running_actuals = []
for round in trange(rounds):
X_support, y_support, X_query, y_query = create_episode(k_pos, k_neg, n_query=0, data=Xy, test=True, train_balanced=False)
total_query = int((y_query == 0).sum() + (y_query == 1).sum())
n_support = k_pos + k_neg
# flat_support = list(np.concatenate(X_support).flat)
# X = flat_support + list(X_query)
X = X_support + list(X_query)
# CREATE EMBEDDINGS
dataloader = torch.utils.data.DataLoader(X, batch_size=(n_support + total_query), shuffle=False, pin_memory=True)
for graph in dataloader:
graph = graph.to(device)
embeddings = encoder.forward(graph)
# LSTM EMBEDDINGS
emb_support = embeddings[:n_support]
emb_query = embeddings[n_support:]
emb_support, emb_query = lstm(emb_support, emb_query)
# PROTO NETS
logits = proto_net(emb_support, emb_query, k_pos, k_neg)
# PRED
_, y_hat_actual = logits.max(1)
y_hat = logits[:, 1]
# targets = targets.squeeze().cpu()
target_inds = torch.from_numpy(y_query.astype('float32')).float()
target_inds = target_inds.unsqueeze(1).type(torch.int64)
targets = Variable(target_inds, requires_grad=False)
y_hat = y_hat.squeeze().detach().cpu()
roc = roc_auc_score(targets, y_hat)
prc = average_precision_score(targets, y_hat)
# acc = accuracy_score(targets, y_hat)
running_preds.append(y_hat)
running_actuals.append(y_hat_actual)
running_targets.append(targets)
# running_acc.append(acc)
running_roc.append(roc)
running_prc.append(prc)
median_index = running_roc.index(statistics.median(running_roc))
if median_index == rounds:
median_index = median_index - 1
chart_preds = running_preds[median_index]
chart_actuals = running_actuals[median_index].detach().cpu()
chart_targets = running_targets[median_index]
c_auc = roc_auc_score(chart_targets, chart_preds)
c_fpr, c_tpr, _ = roc_curve(chart_targets, chart_preds)
plt.plot(c_fpr, c_tpr, marker='.', label = 'AUC = %0.2f' % c_auc)
plt.plot([0, 1], [0, 1],'r--', label='No Skill')
# plt.plot([0, 0, 1], [0, 1, 1], 'g--', label='Perfect Classifier')
plt.title('Receiver Operating Characteristic')
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.legend(loc = 'best')
plt.savefig(f"{drive_path}/{method_dir}/graphs/roc_{dataset}_{task}_ecfp_pos{n_pos}_neg{n_neg}.png")
plt.figure().clear()
# prc_graph = PrecisionRecallDisplay.from_predictions(chart_targets, chart_preds)
c_precision, c_recall, _ = precision_recall_curve(chart_targets, chart_preds)
plt.title('Precision Recall Curve')
# plt.plot([0, 1], [0, 0], 'r--', label='No Skill')
no_skill = len(chart_targets[chart_targets==1]) / len(chart_targets)
plt.plot([0, 1], [no_skill, no_skill], linestyle='--', label='No Skill')
# plt.plot([0, 1, 1], [1, 1, 0], 'g--', label='Perfect Classifier')
plt.plot(c_recall, c_precision, marker='.', label = 'AUC = %0.2f' % auc(c_recall, c_precision))
plt.xlabel('Recall')
plt.ylabel('Precision')
plt.legend(loc = 'best')
plt.savefig(f"{drive_path}/{method_dir}/graphs/prc_{dataset}_{task}_ecfp_pos{n_pos}_neg{n_neg}.png")
plt.figure().clear()
cm = ConfusionMatrixDisplay.from_predictions(chart_targets, chart_actuals)
plt.title('Confusion Matrix')
plt.savefig(f"{drive_path}/{method_dir}/graphs/cm_{dataset}_{task}_ecfp_pos{n_pos}_neg{n_neg}.png")
plt.figure().clear()
running_roc.pop(0) # remove the added 0
running_prc.pop(0) # remove the added 0
# round_acc = f"{statistics.mean(running_acc):.3f} \u00B1 {statistics.stdev(running_acc):.3f}"
round_roc = f"{statistics.mean(running_roc):.3f} \u00B1 {statistics.stdev(running_roc):.3f}"
round_prc = f"{statistics.mean(running_prc):.3f} \u00B1 {statistics.stdev(running_prc):.3f}"
test_info[task] = {
# "acc": round_acc,
"roc": round_roc,
"prc": round_prc,
"roc_values": running_roc,
"prc_values": running_prc
}
print(f'Test {task}')
# print(f"Acc: {round_acc}")
print(f"ROC: {round_roc}")
print(f"PRC: {round_prc}")
return targets, y_hat, test_info
```
## Initiate Training and Testing
```
from google.colab import drive
drive.mount('/content/drive')
# PATHS
drive_path = "/content/drive/MyDrive/Colab Notebooks/MSC_21"
method_dir = "ProtoNets"
log_path = f"{drive_path}/{method_dir}/logs/"
# PARAMETERS
dataset = 'tox21'
with_bonds = False
test_rounds = 20
n_query = 64 # per class
episodes = 10000
lr = 0.001
balanced_queries = True
#FOR DETERMINISTIC REPRODUCABILITY
randomseed = 12
torch.manual_seed(randomseed)
np.random.seed(randomseed)
random.seed(randomseed)
torch.cuda.manual_seed(randomseed)
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
torch.backends.cudnn.is_available()
torch.backends.cudnn.benchmark = False # selects fastest conv algo
torch.backends.cudnn.deterministic = True
# LOAD DATASET
# data, train_tasks, test_tasks = load_dataset(dataset, bonds=with_bonds, create_new=False)
train_tasks, train_dfs, test_tasks, test_dfs = load_dataset(dataset, bonds=with_bonds, feat='ecfp', create_new=False)
combinations = [
[10, 10],
[5, 10],
[1, 10],
[1, 5],
[1, 1]
]
# worksheet = gc.open_by_url("https://docs.google.com/spreadsheets/d/1K15Rx4IZqiLgjUsmMq0blB-WB16MDY-ENR2j8z7S6Ss/edit#gid=0").sheet1
cols = [
'DATE', 'CPU', 'CPU COUNT', 'GPU', 'GPU RAM', 'RAM', 'CUDA',
'REF', 'DATASET', 'ARCHITECTURE',
'SPLIT', 'TARGET', 'ACCURACY', 'ROC', 'PRC',
'ROC_VALUES', 'PRC_VALUES',
'TRAIN ROC', 'TRAIN PRC', 'EPISODES', 'TRAINING TIME'
]
load_from_saved = False
for comb in combinations:
n_pos = comb[0]
n_neg = comb[1]
results = pd.DataFrame(columns=cols)
print(f"\nRUNNING {n_pos}+/{n_neg}-")
if load_from_saved:
encoder = GCN(177, 128)
lstm = ResiLSTMEmbedding(n_pos+n_neg)
proto_net = ProtoNet()
encoder.load_state_dict(torch.load(f"{drive_path}/{method_dir}/{dataset}_ecfp_encoder_pos{n_pos}_neg{n_neg}.pt"))
lstm.load_state_dict(torch.load(f"{drive_path}/{method_dir}/{dataset}_ecfp__lstm_pos{n_pos}_neg{n_neg}.pt"))
proto_net.load_state_dict(torch.load(f"{drive_path}/{method_dir}/{dataset}_ecfp__proto_pos{n_pos}_neg{n_neg}.pt"))
encoder.to(device)
lstm.to(device)
proto_net.to(device)
else:
encoder, lstm, proto_net, train_info = train(train_tasks, train_dfs, balanced_queries, n_pos, n_neg, n_query, episodes, lr)
if with_bonds:
torch.save(encoder.state_dict(), f"{drive_path}/{method_dir}/{dataset}_ecfp__encoder_pos{n_pos}_neg{n_neg}_bonds.pt")
torch.save(lstm.state_dict(), f"{drive_path}/{method_dir}/{dataset}_ecfp__lstm_pos{n_pos}_neg{n_neg}_bonds.pt")
torch.save(proto_net.state_dict(), f"{drive_path}/{method_dir}/{dataset}_ecfp__proto_pos{n_pos}_neg{n_neg}_bonds.pt")
else:
torch.save(encoder.state_dict(), f"{drive_path}/{method_dir}/{dataset}_ecfp__encoder_pos{n_pos}_neg{n_neg}.pt")
torch.save(lstm.state_dict(), f"{drive_path}/{method_dir}/{dataset}_ecfp__lstm_pos{n_pos}_neg{n_neg}.pt")
torch.save(proto_net.state_dict(), f"{drive_path}/{method_dir}/{dataset}_ecfp__proto_pos{n_pos}_neg{n_neg}.pt")
loss_plot = plt.plot(train_info['losses'])[0]
loss_plot.figure.savefig(f"{drive_path}/{method_dir}/loss_plots/{dataset}_ecfp__pos{n_pos}_neg{n_neg}.png")
plt.figure().clear()
targets, preds, test_info = test(encoder, lstm, proto_net, test_tasks, test_dfs, n_pos, n_neg, test_rounds)
dt_string = datetime.now().strftime("%d/%m/%Y %H:%M:%S")
cpu = get_cmd_output('cat /proc/cpuinfo | grep -E "model name"')
cpu = cpu.split('\n')[0].split('\t: ')[-1]
cpu_count = psutil.cpu_count()
cuda_version = get_cmd_output('nvcc --version | grep -E "Build"')
gpu = get_cmd_output("nvidia-smi -L")
general_ram_gb = humanize.naturalsize(psutil.virtual_memory().available)
gpu_ram_total_mb = GPU.getGPUs()[0].memoryTotal
for target in test_info:
if load_from_saved:
rec = pd.DataFrame([[dt_string, cpu, cpu_count, gpu, gpu_ram_total_mb, general_ram_gb, cuda_version, "MSC",
dataset, {method_dir}, f"{n_pos}+/{n_neg}-", target, 0, test_info[target]['roc'], test_info[target]['prc'],
test_info[target]['roc_values'], test_info[target]['prc_values'],
99, 99, 99, 102]], columns=cols)
results = pd.concat([results, rec])
else:
rec = pd.DataFrame([[dt_string, cpu, cpu_count, gpu, gpu_ram_total_mb, general_ram_gb, cuda_version, "MSC",
dataset, {method_dir}, f"{n_pos}+/{n_neg}-", target, 0, test_info[target]['roc'], test_info[target]['prc'],
test_info[target]['roc_values'], test_info[target]['prc_values'],
train_info["train_roc"], train_info["train_prc"], train_info["episodes"], train_info["duration"]
]], columns=cols)
results = pd.concat([results, rec])
if load_from_saved:
results.to_csv(f"{drive_path}/results/{dataset}_{method_dir}_ecfp_pos{n_pos}_neg{n_neg}_from_saved.csv", index=False)
else:
results.to_csv(f"{drive_path}/results/{dataset}_{method_dir}_ecfp_pos{n_pos}_neg{n_neg}.csv", index=False)
```
|
github_jupyter
|
# Normalize text
```
herod_fp = '/Users/kyle/cltk_data/greek/text/tlg/plaintext/TLG0016.txt'
with open(herod_fp) as fo:
herod_raw = fo.read()
print(herod_raw[2000:2500]) # What do we notice needs help?
from cltk.corpus.utils.formatter import tlg_plaintext_cleanup
herod_clean = tlg_plaintext_cleanup(herod_raw, rm_punctuation=True, rm_periods=False)
print(herod_clean[2000:2500])
```
# Tokenize sentences
```
from cltk.tokenize.sentence import TokenizeSentence
tokenizer = TokenizeSentence('greek')
herod_sents = tokenizer.tokenize_sentences(herod_clean)
print(herod_sents[:5])
for sent in herod_sents:
print(sent)
print()
input()
```
# Make word tokens
```
from cltk.tokenize.word import nltk_tokenize_words
for sent in herod_sents:
words = nltk_tokenize_words(sent)
print(words)
input()
```
### Tokenize Latin enclitics
```
from cltk.corpus.utils.formatter import phi5_plaintext_cleanup
from cltk.tokenize.word import WordTokenizer
# 'LAT0474': 'Marcus Tullius Cicero, Cicero, Tully',
cicero_fp = '/Users/kyle/cltk_data/latin/text/phi5/plaintext/LAT0474.TXT'
with open(cicero_fp) as fo:
cicero_raw = fo.read()
cicero_clean = phi5_plaintext_cleanup(cicero_raw, rm_punctuation=True, rm_periods=False) # ~5 sec
print(cicero_clean[400:600])
sent_tokenizer = TokenizeSentence('latin')
cicero_sents = tokenizer.tokenize_sentences(cicero_clean)
print(cicero_sents[:3])
word_tokenizer = WordTokenizer('latin') # Patrick's tokenizer
for sent in cicero_sents:
#words = nltk_tokenize_words(sent)
sub_words = word_tokenizer.tokenize(sent)
print(sub_words)
input()
```
# POS Tagging
```
from cltk.tag.pos import POSTag
tagger = POSTag('greek')
# Heordotus again
for sent in herod_sents:
tagged_text = tagger.tag_unigram(sent)
print(tagged_text)
input()
```
# NER
```
## Latin -- decent, but see M, P, etc
from cltk.tag import ner
# Heordotus again
for sent in cicero_sents:
ner_tags = ner.tag_ner('latin', input_text=sent, output_type=list)
print(ner_tags)
input()
# Greek -- not as good!
from cltk.tag import ner
# Heordotus again
for sent in herod_sents:
ner_tags = ner.tag_ner('greek', input_text=sent, output_type=list)
print(ner_tags)
input()
```
# Stopword filtering
```
from cltk.stop.greek.stops import STOPS_LIST
#p = PunktLanguageVars()
for sent in herod_sents:
words = nltk_tokenize_words(sent)
print('W/ STOPS', words)
words = [w for w in words if not w in STOPS_LIST]
print('W/O STOPS', words)
input()
```
# Concordance
```
from cltk.utils.philology import Philology
p = Philology()
herod_fp = '/Users/kyle/cltk_data/greek/text/tlg/plaintext/TLG0016.txt'
p.write_concordance_from_file(herod_fp, 'kyle_herod')
```
# Word count
```
from nltk.text import Text
words = nltk_tokenize_words(herod_clean)
print(words[:15])
t = Text(words)
vocabulary_count = t.vocab()
vocabulary_count['ἱστορίης']
vocabulary_count['μήτε']
vocabulary_count['ἀνθρώπων']
```
# Word frequency
```
from cltk.utils.frequency import Frequency
freq = Frequency()
herod_frequencies = freq.counter_from_str(herod_clean)
herod_frequencies.most_common()
```
# Lemmatizing
|
github_jupyter
|
```
import pandas as pd
import numpy as np
# set the column names
colnames=['price', 'year_model', 'mileage', 'fuel_type', 'mark', 'model', 'fiscal_power', 'sector', 'type', 'city']
# read the csv file as a dataframe
df = pd.read_csv("./data/output.csv", sep=",", names=colnames, header=None)
# let's get some simple vision on our dataset
df.head()
# remove thos rows doesn't contain the price value
df = df[df.price.str.contains("DH") == True]
# remove the 'DH' caracters from the price
df.price = df.price.map(lambda x: x.rstrip('DH'))
# remove the space on it
df.price = df.price.str.replace(" ","")
# change it to integer value
df.price = pd.to_numeric(df.price, errors = 'coerce', downcast= 'integer')
# remove thos rows doesn't contain the year_model value
df = df[df.year_model.str.contains("Année-Modèle") == True]
# remove the 'Année-Modèle:' from the year_model
df.year_model = df.year_model.map(lambda x: x.lstrip('Année-Modèle:').rstrip('ou plus ancien'))
# df.year_model = df.year_model.map(lambda x: x.lstrip('Plus de '))
# remove those lines having the year_model not set
df = df[df.year_model != ' -']
df = df[df.year_model != '']
# change it to integer value
df.year_model = pd.to_numeric(df.year_model, errors = 'coerce', downcast = 'integer')
# remove thos rows doesn't contain the year_model value
df = df[df.mileage.str.contains("Kilométrage") == True]
# remove the 'Kilométrage:' string from the mileage feature
df.mileage = df.mileage.map(lambda x: x.lstrip('Kilométrage:'))
df.mileage = df.mileage.map(lambda x: x.lstrip('Plus de '))
# remove those lines having the mileage values null or '-'
df = df[df.mileage != '-']
# we have only one value type that is equal to 500 000, all the other ones contain two values
if any(df.mileage != '500 000'):
# create two columns minim and maxim to calculate the mileage mean
df['minim'], df['maxim'] = df.mileage.str.split('-', 1).str
# remove spaces from the maxim & minim values
df['maxim'] = df.maxim.str.replace(" ","")
df['minim'] = df.minim.str.replace(" ","")
df['maxim'] = df['maxim'].replace(np.nan, 500000)
# calculate the mean of mileage
df.mileage = df.apply(lambda row: (int(row.minim) + int(row.maxim)) / 2, axis=1)
# now that the mileage is calculated so we do not need the minim and maxim values anymore
df = df.drop(columns=['minim', 'maxim'])
```
#### Fuel type
```
# remove the 'Type de carburant:' string from the carburant_type feature
df.fuel_type = df.fuel_type.map(lambda x: x.lstrip('Type de carburant:'))
```
#### Mark & Model
```
# remove the 'Marque:' string from the mark feature
df['mark'] = df['mark'].map(lambda x: x.replace('Marque:', ''))
df = df[df.mark != '-']
# remove the 'Modèle:' string from model feature
df['model'] = df['model'].map(lambda x: x.replace('Modèle:', ''))
```
#### fiscal power
For the fiscal power we can see that there is exactly 5728 rows not announced, so we will fill them by the mean of the other columns, since it is an important feature in cars price prediction so we can not drop it.
```
# remove the 'Puissance fiscale:' from the fiscal_power feature
df.fiscal_power = df.fiscal_power.map(lambda x: x.lstrip('Puissance fiscale:Plus de').rstrip(' CV'))
# replace the - with NaN values and convert them to integer values
df.fiscal_power = df.fiscal_power.str.replace("-","0")
# convert all fiscal_power values to numerical ones
df.fiscal_power = pd.to_numeric(df.fiscal_power, errors = 'coerce', downcast= 'integer')
# now we need to fill those 0 values with the mean of all fiscal_power columns
df.fiscal_power = df.fiscal_power.map( lambda x : df.fiscal_power.mean() if x == 0 else x )
```
#### fuel type
```
# remove those lines having the fuel_type not set
df = df[df.fuel_type != '-']
```
#### drop unwanted columns
```
df = df.drop(columns=['sector', 'type'])
df = df[['price', 'year_model', 'mileage', 'fiscal_power', 'fuel_type', 'mark']]
df.to_csv('data/car_dataset.csv')
df.head()
from car_price.wsgi import application
from api.models import Car
for x in df.values[5598:]:
car = Car(
price=x[0],
year_model=x[1],
mileage=x[2],
fiscal_power=x[3],
fuel_type=x[4],
mark=x[5]
)
car.save()
Car.objects.all().count()
df.shape
```
|
github_jupyter
|
```
import glob
import os
import random
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import cv2
import math
from tqdm.auto import tqdm
from sklearn import linear_model
import optuna
import seaborn as sns
FEAT_OOFS = [
{
'model' : 'feat_lasso',
'fn' : '../output/2021011_segmentation_feature_model_v4/feature_model_oofs_0.csv'
},
{
'model' : 'feat_linreg',
'fn' : '../output/2021011_segmentation_feature_model_v4/feature_model_oofs_1.csv'
},
{
'model' : 'feat_ridge',
'fn' : '../output/2021011_segmentation_feature_model_v4/feature_model_oofs_2.csv',
}
]
CNN_OOFS = [
{
'model' : 'resnet50_rocstar',
'fn' : '../output/resnet50_bs32_ep10_rocstar_lr0.0001_ps0.8_ranger_sz256/'
},
{
'model' : 'resnet50_bce',
'fn' : '../output/resnet50_bs32_ep10_bce_lr0.0001_ps0.8_ranger_sz256/'
},
{
'model' : 'densenet169_rocstar',
'fn' : '../output/densenet169_bs32_ep10_rocstar_lr0.0001_ps0.8_ranger_sz256/'
},
{
'model' : 'resnet101_rocstar',
'fn' : '../output/resnet101_bs32_ep20_rocstar_lr0.0001_ps0.8_ranger_sz256/'
},
{
'model' : 'efficientnetv2_l_rocstar',
'fn' : '../output/tf_efficientnetv2_l_bs32_ep10_rocstar_lr0.0001_ps0.8_ranger_sz256/'
},
]
df = pd.read_csv('../output/20210925_segmentation_feature_model_v3/feature_model_oofs_0.csv')[
['BraTS21ID','MGMT_value','fold']]
df.head()
def read_feat_oof(fn):
return pd.read_csv(fn).sort_values('BraTS21ID')['oof_pred'].values
def read_cnn_oof(dir_path):
oof_fns = [os.path.join(dir_path, f'fold-{i}', 'oof.csv') for i in range(5)]
dfs = []
for fn in oof_fns:
dfs.append(pd.read_csv(fn))
df = pd.concat(dfs)
return df.sort_values('BraTS21ID')['pred_mgmt_tta'].values
def normalize_pred_distribution(preds, min_percentile=10, max_percentile=90):
""" Clips min and max percentiles and Z-score normalizes """
min_range = np.percentile(preds, min_percentile)
max_range = np.percentile(preds, max_percentile)
norm_preds = np.clip(preds, min_range, max_range)
pred_std = np.std(norm_preds)
pred_mean = np.mean(norm_preds)
norm_preds = (norm_preds - pred_mean) / (pred_std + 1e-6)
return norm_preds
def rescale_pred_distribution(preds):
""" Rescales pred distribution to 0-1 range. Doesn't affect AUC """
return (preds - np.min(preds)) / (np.max(preds) - np.min(preds) + 1e-6)
for d in FEAT_OOFS:
df[d['model']] = read_feat_oof(d['fn'])
for d in CNN_OOFS:
df[d['model']] = read_cnn_oof(d['fn'])
df_norm = df.copy()
for feat in df.columns.to_list()[3:]:
df_norm[feat] = rescale_pred_distribution(
normalize_pred_distribution(df_norm[feat].values)
)
df_norm.head()
df_raw = df.copy()
all_feat_names = df_norm.columns.to_list()[3:]
corr = df_norm[['MGMT_value'] + all_feat_names].corr()
# Generate a mask for the upper triangle
mask = np.triu(np.ones_like(corr, dtype=bool))
plt.close('all')
f, ax = plt.subplots(figsize=(5, 5))
cmap = sns.diverging_palette(230, 20, as_cmap=True)
sns.heatmap(corr, mask=mask, cmap=cmap, vmax=.3, center=0,
square=True, linewidths=.5, cbar_kws={"shrink": .5})
plt.title('OOF pred correlations')
plt.show()
mgmt_corr_sorted = corr['MGMT_value'].sort_values()
mgmt_corr_sorted
```
## Average
```
from sklearn.metrics import accuracy_score, roc_auc_score
from sklearn.preprocessing import StandardScaler
oof_preds = np.mean(df_norm[all_feat_names].to_numpy(),1)
oof_gts = df_norm['MGMT_value']
cv_preds = [np.mean(df_norm[df_norm.fold==fold][all_feat_names].to_numpy(),1) for fold in range(5)]
cv_gts = [df_norm[df_norm.fold==fold]['MGMT_value'] for fold in range(5)]
oof_acc = accuracy_score((np.array(oof_gts) > 0.5).flatten(), (np.array(oof_preds) > 0.5).flatten())
oof_auc = roc_auc_score(np.array(oof_gts).flatten().astype(np.float32), np.array(oof_preds).flatten())
cv_accs = np.array([accuracy_score((np.array(cv_gt) > 0.5).flatten(), (np.array(cv_pred) > 0.5).flatten())
for cv_gt,cv_pred in zip(cv_gts, cv_preds)])
cv_aucs = np.array([roc_auc_score(np.array(cv_gt).flatten().astype(np.float32), np.array(cv_pred).flatten())
for cv_gt,cv_pred in zip(cv_gts, cv_preds)])
print(f'OOF acc {oof_acc}, OOF auc {oof_auc}, CV AUC {np.mean(cv_aucs)} (std {np.std(cv_aucs)})')
plt.close('all')
df_plot = pd.DataFrame({'Pred-MGMT': oof_preds, 'GT-MGMT': oof_gts})
sns.histplot(x='Pred-MGMT', hue='GT-MGMT', data=df_plot)
plt.title(f'Average of all models # CV AUC = {np.mean(cv_aucs):.3f} (std: {np.std(cv_aucs):.3f}), Acc. = {np.mean(cv_accs):.3f}')
plt.show()
selected_feats = [
'feat_lasso',
'feat_ridge',
'feat_linreg',
'efficientnetv2_l_rocstar',
'resnet101_rocstar',
'densenet169_rocstar',
]
oof_acc = accuracy_score((np.array(oof_gts) > 0.5).flatten(), (np.mean(df_norm[selected_feats].to_numpy(),1) > 0.5).flatten())
oof_auc = roc_auc_score(np.array(oof_gts).flatten().astype(np.float32), np.mean(df_norm[selected_feats].to_numpy(),1).flatten())
cv_preds = [np.mean(df_norm[df_norm.fold==fold][selected_feats].to_numpy(),1) for fold in range(5)]
cv_gts = [df_norm[df_norm.fold==fold]['MGMT_value'] for fold in range(5)]
cv_accs = np.array([accuracy_score((np.array(cv_gt) > 0.5).flatten(), (np.array(cv_pred) > 0.5).flatten())
for cv_gt,cv_pred in zip(cv_gts, cv_preds)])
cv_aucs = np.array([roc_auc_score(np.array(cv_gt).flatten().astype(np.float32), np.array(cv_pred).flatten())
for cv_gt,cv_pred in zip(cv_gts, cv_preds)])
print(f'OOF acc {oof_acc}, OOF auc {oof_auc}, CV AUC {np.mean(cv_aucs)} (std {np.std(cv_aucs)})')
plt.close('all')
df_plot = pd.DataFrame({'Pred-MGMT': oof_preds, 'GT-MGMT': oof_gts})
sns.histplot(x='Pred-MGMT', hue='GT-MGMT', data=df_plot)
plt.title(f'Average of all models # CV AUC = {np.mean(cv_aucs):.3f} (std: {np.std(cv_aucs):.3f}), Acc. = {np.mean(cv_accs):.3f}')
plt.show()
```
## 2nd level models
```
import xgboost as xgb
def get_data(fold, features):
df = df_norm.dropna(inplace=False)
scaler = StandardScaler()
df_train = df[df.fold != fold]
df_val = df[df.fold == fold]
if len(df_val) == 0:
df_val = df[df.fold == 0]
# shuffle train
df_train = df_train.sample(frac=1)
y_train = df_train.MGMT_value.to_numpy().reshape((-1,1)).astype(np.float32)
y_val = df_val.MGMT_value.to_numpy().reshape((-1,1)).astype(np.float32)
X_train = df_train[features].to_numpy().astype(np.float32)
X_val = df_val[features].to_numpy().astype(np.float32)
scaler.fit(X_train)
X_train = scaler.transform(X_train)
X_val = scaler.transform(X_val)
return X_train, y_train, X_val, y_val, scaler, (df_train.index.values).flatten(), (df_val.index.values).flatten()
def measure_cv_score(parameters, verbose=False, train_one_model=False, plot=False, return_oof_preds=False):
val_preds = []
val_gts = []
val_aucs = []
val_accs = []
val_index_values = []
for fold in range(5):
if train_one_model: fold = -1
X_train, y_train, X_val, y_val, scaler, train_index, val_index = get_data(fold, features=parameters['features'])
val_index_values = val_index_values + list(val_index)
if parameters['model_type'] == 'xgb':
model = xgb.XGBRegressor(
n_estimators=parameters['n_estimators'],
max_depth=parameters['max_depth'],
eta=parameters['eta'],
subsample=parameters['subsample'],
colsample_bytree=parameters['colsample_bytree'],
gamma=parameters['gamma']
)
elif parameters['model_type'] == 'linreg':
model = linear_model.LinearRegression()
elif parameters['model_type'] == 'ridge':
model = linear_model.Ridge(parameters['alpha'])
elif parameters['model_type'] == 'bayesian':
model = linear_model.BayesianRidge(
n_iter = parameters['n_iter'],
lambda_1 = parameters['lambda_1'],
lambda_2 = parameters['lambda_2'],
alpha_1 = parameters['alpha_1'],
alpha_2 = parameters['alpha_2'],
)
elif parameters['model_type'] == 'logreg':
model = linear_model.LogisticRegression()
elif parameters['model_type'] == 'lassolarsic':
model = linear_model.LassoLarsIC(
max_iter = parameters['max_iter'],
eps = parameters['eps']
)
elif parameters['model_type'] == 'perceptron':
model = linear_model.Perceptron(
)
else:
raise NotImplementedError
model.fit(X_train, y_train.ravel())
if train_one_model:
return model, scaler
val_pred = model.predict(X_val)
val_preds += list(val_pred)
val_gts += list(y_val)
val_aucs.append(roc_auc_score(np.array(y_val).flatten().astype(np.float32), np.array(val_pred).flatten()))
val_accs.append(accuracy_score((np.array(y_val) > 0.5).flatten(), (np.array(val_pred) > 0.5).flatten()))
if return_oof_preds:
return np.array(val_preds).flatten(), np.array(val_gts).flatten(), val_index_values
oof_acc = accuracy_score((np.array(val_gts) > 0.5).flatten(), (np.array(val_preds) > 0.5).flatten())
oof_auc = roc_auc_score(np.array(val_gts).flatten().astype(np.float32), np.array(val_preds).flatten())
auc_std = np.std(np.array(val_aucs))
if plot:
df_plot = pd.DataFrame({'Pred-MGMT': np.array(val_preds).flatten(), 'GT-MGMT': np.array(val_gts).flatten()})
sns.histplot(x='Pred-MGMT', hue='GT-MGMT', data=df_plot)
plt.title(f'{parameters["model_type"]} # CV AUC = {oof_auc:.3f} (std {auc_std:.3f}), Acc. = {oof_acc:.3f}')
plt.show()
if verbose:
print(f'CV AUC = {oof_auc} (std {auc_std}), Acc. = {oof_acc}, aucs: {val_aucs}, accs: {val_accs}')
# optimize lower limit of the (2x std range around mean)
# This way, we choose the model which ranks well and performs ~equally well on all folds
return float(oof_auc) - auc_std
default_parameters = {
'model_type': 'linreg',
'n_estimators': 100,
'max_depth' : 3,
'eta': 0.1,
'subsample': 0.7,
'colsample_bytree' : 0.8,
'gamma' : 1.0,
'alpha' : 1.0,
'n_iter':300,
'lambda_1': 1e-6, # bayesian
'lambda_2':1e-6, # bayesian
'alpha_1': 1e-6, # bayesian
'alpha_2': 1e-6, # bayesian
'max_iter': 3, #lasso
'eps': 1e-6, #lasso
'features' : all_feat_names
}
measure_cv_score(default_parameters, verbose=True)
def feat_selection_linreg_objective(trial):
kept_feats = []
for i in range(len(all_feat_names)):
var = trial.suggest_int(all_feat_names[i], 0,1)
if var == 1:
kept_feats.append(all_feat_names[i])
parameters = default_parameters.copy()
parameters['features'] = kept_feats
return 1 - measure_cv_score(parameters, verbose=False)
if 1:
study = optuna.create_study()
study.optimize(feat_selection_linreg_objective, n_trials=20, show_progress_bar=True)
print(study.best_value, study.best_params)
study.best_params
pruned_features = default_parameters.copy()
pruned_features['features'] = ['feat_lasso', 'feat_linreg', 'feat_ridge', 'efficientnetv2_l_rocstar']
measure_cv_score(pruned_features, verbose=True)
random.randint(0,1)
```
|
github_jupyter
|
```
#import necessary modules, set up the plotting
import numpy as np
%matplotlib inline
%config InlineBackend.figure_format = 'svg'
import matplotlib;matplotlib.rcParams['figure.figsize'] = (8,6)
from matplotlib import pyplot as plt
import GPy
```
# Interacting with models
### November 2014, by Max Zwiessele
#### with edits by James Hensman
The GPy model class has a set of features which are designed to make it simple to explore the parameter space of the model. By default, the scipy optimisers are used to fit GPy models (via model.optimize()), for which we provide mechanisms for ‘free’ optimisation: GPy can ensure that naturally positive parameters (such as variances) remain positive. But these mechanisms are much more powerful than simple reparameterisation, as we shall see.
Along this tutorial we’ll use a sparse GP regression model as example. This example can be in GPy.examples.regression. All of the examples included in GPy return an instance of a model class, and therefore they can be called in the following way:
```
m = GPy.examples.regression.sparse_GP_regression_1D(plot=False, optimize=False)
```
## Examining the model using print
To see the current state of the model parameters, and the model’s (marginal) likelihood just print the model
print m
The first thing displayed on the screen is the log-likelihood value of the model with its current parameters. Below the log-likelihood, a table with all the model’s parameters is shown. For each parameter, the table contains the name of the parameter, the current value, and in case there are defined: constraints, ties and prior distrbutions associated.
```
m
```
In this case the kernel parameters (`bf.variance`, `bf.lengthscale`) as well as the likelihood noise parameter (`Gaussian_noise.variance`), are constrained to be positive, while the inducing inputs have no constraints associated. Also there are no ties or prior defined.
You can also print all subparts of the model, by printing the subcomponents individually; this will print the details of this particular parameter handle:
```
m.rbf
```
When you want to get a closer look into multivalue parameters, print them directly:
```
m.inducing_inputs
m.inducing_inputs[0] = 1
```
## Interacting with Parameters:
The preferred way of interacting with parameters is to act on the parameter handle itself. Interacting with parameter handles is simple. The names, printed by print m are accessible interactively and programatically. For example try to set the kernel's `lengthscale` to 0.2 and print the result:
```
m.rbf.lengthscale = 0.2
print m
```
This will already have updated the model’s inner state: note how the log-likelihood has changed. YOu can immediately plot the model or see the changes in the posterior (`m.posterior`) of the model.
## Regular expressions
The model’s parameters can also be accessed through regular expressions, by ‘indexing’ the model with a regular expression, matching the parameter name. Through indexing by regular expression, you can only retrieve leafs of the hierarchy, and you can retrieve the values matched by calling `values()` on the returned object
```
print m['.*var']
#print "variances as a np.array:", m['.*var'].values()
#print "np.array of rbf matches: ", m['.*rbf'].values()
```
There is access to setting parameters by regular expression, as well. Here are a few examples of how to set parameters by regular expression. Note that each time the values are set, computations are done internally to compute the log likeliood of the model.
```
m['.*var'] = 2.
print m
m['.*var'] = [2., 3.]
print m
```
A handy trick for seeing all of the parameters of the model at once is to regular-expression match every variable:
```
print m['']
```
## Setting and fetching parameters parameter_array
Another way to interact with the model’s parameters is through the parameter_array. The Parameter array holds all the parameters of the model in one place and is editable. It can be accessed through indexing the model for example you can set all the parameters through this mechanism:
```
new_params = np.r_[[-4,-2,0,2,4], [.1,2], [.7]]
print new_params
m[:] = new_params
print m
```
Parameters themselves (leafs of the hierarchy) can be indexed and used the same way as numpy arrays. First let us set a slice of the inducing_inputs:
```
m.inducing_inputs[2:, 0] = [1,3,5]
print m.inducing_inputs
```
Or you use the parameters as normal numpy arrays for calculations:
```
precision = 1./m.Gaussian_noise.variance
print precision
```
## Getting the model parameter’s gradients
The gradients of a model can shed light on understanding the (possibly hard) optimization process. The gradients of each parameter handle can be accessed through their gradient field.:
```
print "all gradients of the model:\n", m.gradient
print "\n gradients of the rbf kernel:\n", m.rbf.gradient
```
If we optimize the model, the gradients (should be close to) zero
```
m.optimize()
print m.gradient
```
## Adjusting the model’s constraints
When we initially call the example, it was optimized and hence the log-likelihood gradients were close to zero. However, since we have been changing the parameters, the gradients are far from zero now. Next we are going to show how to optimize the model setting different restrictions on the parameters.
Once a constraint has been set on a parameter, it is possible to remove it with the command unconstrain(), which can be called on any parameter handle of the model. The methods constrain() and unconstrain() return the indices which were actually unconstrained, relative to the parameter handle the method was called on. This is particularly handy for reporting which parameters where reconstrained, when reconstraining a parameter, which was already constrained:
```
m.rbf.variance.unconstrain()
print m
m.unconstrain()
print m
```
If you want to unconstrain only a specific constraint, you can call the respective method, such as `unconstrain_fixed()` (or `unfix()`) to only unfix fixed parameters:
```
m.inducing_inputs[0].fix()
m.rbf.constrain_positive()
print m
m.unfix()
print m
```
## Tying Parameters
Not yet implemented for GPy version 0.8.0
## Optimizing the model
Once we have finished defining the constraints, we can now optimize the model with the function optimize.:
```
m.Gaussian_noise.constrain_positive()
m.rbf.constrain_positive()
m.optimize()
```
By deafult, GPy uses the lbfgsb optimizer.
Some optional parameters may be discussed here.
* `optimizer`: which optimizer to use, currently there are lbfgsb, fmin_tnc, scg, simplex or any unique identifier uniquely identifying an optimizer.
Thus, you can say m.optimize('bfgs') for using the `lbfgsb` optimizer
* `messages`: if the optimizer is verbose. Each optimizer has its own way of printing, so do not be confused by differing messages of different optimizers
* `max_iters`: Maximum number of iterations to take. Some optimizers see iterations as function calls, others as iterations of the algorithm. Please be advised to look into scipy.optimize for more instructions, if the number of iterations matter, so you can give the right parameters to optimize()
* `gtol`: only for some optimizers. Will determine the convergence criterion, as the tolerance of gradient to finish the optimization.
## Plotting
Many of GPys models have built-in plot functionality. we distringuish between plotting the posterior of the function (`m.plot_f`) and plotting the posterior over predicted data values (`m.plot`). This becomes especially important for non-Gaussian likleihoods. Here we'll plot the sparse GP model we've been working with. for more information of the meaning of the plot, please refer to the accompanying `basic_gp_regression` and `sparse_gp` noteooks.
```
fig = m.plot()
```
We can even change the backend for plotting and plot the model using a different backend.
```
GPy.plotting.change_plotting_library('plotly')
fig = m.plot(plot_density=True)
GPy.plotting.show(fig, filename='gpy_sparse_gp_example')
```
|
github_jupyter
|
```
%matplotlib inline
```
# Partial Dependence Plots
Sigurd Carlsen Feb 2019
Holger Nahrstaedt 2020
.. currentmodule:: skopt
Plot objective now supports optional use of partial dependence as well as
different methods of defining parameter values for dependency plots.
```
print(__doc__)
import sys
from skopt.plots import plot_objective
from skopt import forest_minimize
import numpy as np
np.random.seed(123)
import matplotlib.pyplot as plt
```
## Objective function
Plot objective now supports optional use of partial dependence as well as
different methods of defining parameter values for dependency plots
```
# Here we define a function that we evaluate.
def funny_func(x):
s = 0
for i in range(len(x)):
s += (x[i] * i) ** 2
return s
```
## Optimisation using decision trees
We run forest_minimize on the function
```
bounds = [(-1, 1.), ] * 3
n_calls = 150
result = forest_minimize(funny_func, bounds, n_calls=n_calls,
base_estimator="ET",
random_state=4)
```
## Partial dependence plot
Here we see an example of using partial dependence. Even when setting
n_points all the way down to 10 from the default of 40, this method is
still very slow. This is because partial dependence calculates 250 extra
predictions for each point on the plots.
```
_ = plot_objective(result, n_points=10)
```
It is possible to change the location of the red dot, which normally shows
the position of the found minimum. We can set it 'expected_minimum',
which is the minimum value of the surrogate function, obtained by a
minimum search method.
```
_ = plot_objective(result, n_points=10, minimum='expected_minimum')
```
## Plot without partial dependence
Here we plot without partial dependence. We see that it is a lot faster.
Also the values for the other parameters are set to the default "result"
which is the parameter set of the best observed value so far. In the case
of funny_func this is close to 0 for all parameters.
```
_ = plot_objective(result, sample_source='result', n_points=10)
```
## Modify the shown minimum
Here we try with setting the `minimum` parameters to something other than
"result". First we try with "expected_minimum" which is the set of
parameters that gives the miniumum value of the surrogate function,
using scipys minimum search method.
```
_ = plot_objective(result, n_points=10, sample_source='expected_minimum',
minimum='expected_minimum')
```
"expected_minimum_random" is a naive way of finding the minimum of the
surrogate by only using random sampling:
```
_ = plot_objective(result, n_points=10, sample_source='expected_minimum_random',
minimum='expected_minimum_random')
```
We can also specify how many initial samples are used for the two different
"expected_minimum" methods. We set it to a low value in the next examples
to showcase how it affects the minimum for the two methods.
```
_ = plot_objective(result, n_points=10, sample_source='expected_minimum_random',
minimum='expected_minimum_random',
n_minimum_search=10)
_ = plot_objective(result, n_points=10, sample_source="expected_minimum",
minimum='expected_minimum', n_minimum_search=2)
```
## Set a minimum location
Lastly we can also define these parameters ourself by parsing a list
as the minimum argument:
```
_ = plot_objective(result, n_points=10, sample_source=[1, -0.5, 0.5],
minimum=[1, -0.5, 0.5])
```
|
github_jupyter
|
```
%load_ext autoreload
%autoreload 2
import tensorflow as tf
import numpy as np
import pandas as pd
import altair as alt
import shap
from interaction_effects.marginal import MarginalExplainer
from interaction_effects import utils
n = 3000
d = 3
batch_size = 50
learning_rate = 0.02
X = np.random.randn(n, d)
y = (np.sum(X, axis=-1) > 0.0).astype(np.float32)
model = tf.keras.Sequential()
model.add(tf.keras.Input(shape=(3,), batch_size=batch_size))
model.add(tf.keras.layers.Dense(2, activation=None, use_bias=True))
optimizer = tf.keras.optimizers.SGD(learning_rate=learning_rate)
model.compile(optimizer=optimizer,
loss=tf.keras.losses.SparseCategoricalCrossentropy(),
metrics=[tf.keras.metrics.SparseCategoricalAccuracy()])
model.fit(X, y, epochs=20, verbose=2)
primal_explainer = MarginalExplainer(model, X[20:], nsamples=800, representation='mobius')
primal_effects = primal_explainer.explain(X[:20], verbose=True, index_outputs=True, labels=y[:20].astype(int))
dual_explainer = MarginalExplainer(model, X[20:], nsamples=800, representation='comobius')
dual_effects = dual_explainer.explain(X[:20], verbose=True, index_outputs=True, labels=y[:20].astype(int))
average_explainer = MarginalExplainer(model, X[20:], nsamples=800, representation='average')
average_effects = average_explainer.explain(X[:20], verbose=True, index_outputs=True, labels=y[:20].astype(int))
model_func = lambda x: model(x).numpy()
kernel_explainer = shap.SamplingExplainer(model_func, X)
kernel_shap = kernel_explainer.shap_values(X[:20])
kernel_shap = np.stack(kernel_shap, axis=0)
kernel_shap_true_class = kernel_shap[y[:20].astype(int), np.arange(20), :]
def unroll(x):
ret = []
for i in range(x.shape[-1]):
ret.append(x[:, i])
return np.concatenate(ret)
data_df = pd.DataFrame({
'Sampled Primal Effects': unroll(primal_effects),
'Sampled Dual Effects': unroll(dual_effects),
'Sampled Average Effects': unroll(average_effects),
'Kernel SHAP Values': unroll(kernel_shap_true_class),
'Feature Values': unroll(X[:20]),
'Feature': [int(i / 20) for i in range(20 * d)],
'Label': np.tile(y[:20], 3).astype(int)
})
alt.Chart(data_df).mark_point(filled=True).encode(
alt.X('Kernel SHAP Values:Q'),
alt.Y(alt.repeat("column"), type='quantitative')
).properties(width=300, height=300).repeat(column=['Sampled Primal Effects', 'Sampled Dual Effects', 'Sampled Average Effects'])
melted_df = pd.melt(data_df, id_vars=['Feature Values', 'Feature', 'Label'], var_name='Effect Type', value_name='Effect Value')
alt.Chart(melted_df).mark_point(filled=True).encode(
alt.X('Feature Values:Q'),
alt.Y('Effect Value:Q'),
alt.Color('Label:N')
).properties(width=200, height=200).facet(column='Effect Type', row='Feature')
```
|
github_jupyter
|
### Prepare stimuli in stereo with sync tone in the L channel
To syncrhonize the recording systems, each stimulus file goes in stereo, the L channel has the stimulus, and the R channel has a pure tone (500-5Khz).
This is done here, with the help of the rigmq.util.stimprep module
It uses (or creates) a dictionary of {stim_file: tone_freq} which is stored as a .json file for offline processing.
```
import socket
import os
import sys
import logging
import warnings
import numpy as np
import glob
from rigmq.util import stimprep as sp
# setup the logger
logger = logging.getLogger()
handler = logging.StreamHandler()
formatter = logging.Formatter(
'%(asctime)s %(name)-12s %(levelname)-8s %(message)s')
handler.setFormatter(formatter)
logger.addHandler(handler)
logger.setLevel(logging.INFO)
# Check wich computer to decide where the things are mounted
comp_name=socket.gethostname()
logger.info('Computer: ' + comp_name)
exp_folder = os.path.abspath('/Users/zeke/experiment/birds')
bird = 'g3v3'
sess = 'acute_0'
stim_sf = 48000 # sampling frequency of the stimulus system
stim_folder = os.path.join(exp_folder, bird, 'SongData', sess)
glob.glob(os.path.join(stim_folder, '*.wav'))
from scipy.io import wavfile
from scipy.signal import resample
a_file = glob.glob(os.path.join(stim_folder, '*.wav'))[0]
in_sf, data = wavfile.read(a_file)
%matplotlib inline
from matplotlib import pyplot as plt
plt.plot(data)
data.dtype
np.iinfo(data.dtype).min
def normalize(x: np.array, max_amp: np.float=0.9)-> np.array:
y = x.astype(np.float)
y = y - np.mean(y)
y = y / np.max(np.abs(y)) # if it is still of-centered, scale to avoid clipping in the widest varyng sign
return y * max_amp
data_float = normalize(data)
plt.plot(data_float)
def int_range(x: np.array, dtype: np.dtype):
min_int = np.iinfo(dtype).min
max_int = np.iinfo(dtype).max
if min_int==0: # for unsigned types shift everything
x = x + np.min(x)
y = x * max_int
return y.astype(dtype)
data_int = int_range(data_float, data.dtype)
plt.plot(data_int)
data_tagged = sp.make_stereo_stim(a_file, 48000, tag_freq=1000)
plt.plot(data_tagged[:480,1])
### Define stim_tags
There is a dictionary of {wav_file: tag_frequency} can be done by hand when there are few stimuli
stim_tags_dict = {'bos': 1000,
'bos-lo': 2000,
'bos-rev': 3000}
stims_list = list(stim_tags_dict.keys())
sp.create_sbc_stim(stims_list, stim_folder, stim_sf, stim_tag_dict=stim_tags_dict)
```
|
github_jupyter
|
# Scaling and Normalization
```
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler, MinMaxScaler, RobustScaler
from scipy.cluster.vq import whiten
```
Terminology (from [this post](https://towardsdatascience.com/scale-standardize-or-normalize-with-scikit-learn-6ccc7d176a02)):
* Scale generally means to change the range of the values. The shape of the distribution doesn’t change. Think about how a scale model of a building has the same proportions as the original, just smaller. That’s why we say it is drawn to scale. The range is often set at 0 to 1.
* Standardize generally means changing the values so that the distribution standard deviation from the mean equals one. It outputs something very close to a normal distribution. Scaling is often implied.
* Normalize can be used to mean either of the above things (and more!). I suggest you avoid the term normalize, because it has many definitions and is prone to creating confusion.
via [Machine Learning Mastery](https://machinelearningmastery.com/standardscaler-and-minmaxscaler-transforms-in-python/):
* If the distribution of the quantity is normal, then it should be standardized, otherwise, the data should be normalized.
```
house_prices = pd.read_csv("data/house-prices.csv")
house_prices["AgeWhenSold"] = house_prices["YrSold"] - house_prices["YearBuilt"]
house_prices.head()
```
## Unscaled Housing Prices Age When Sold
```
sns.displot(house_prices["AgeWhenSold"])
plt.xticks(rotation=90)
plt.show()
```
## StandardScaler
Note that DataFrame.var and DataFrame.std default to using 1 degree of freedom (ddof=1) but StandardScaler is using numpy's versions which default to ddof=0. That's why when printing the variance and standard deviation of the original data frame, we're specifying ddof=0. ddof=1 is known as Bessel's correction.
```
df = pd.DataFrame({
'col1': [1, 2, 3],
'col2': [10, 20, 30],
'col3': [0, 20, 22]
})
print("Original:\n")
print(df)
print("\nColumn means:\n")
print(df.mean())
print("\nOriginal variance:\n")
print(df.var(ddof=0))
print("\nOriginal standard deviations:\n")
print(df.std(ddof=0))
scaler = StandardScaler()
df1 = pd.DataFrame(scaler.fit_transform(df), columns=df.columns)
print("\nAfter scaling:\n")
print(df1)
print("\nColumn means:\n")
print(round(df1.mean(), 3))
print("\nVariance:\n")
print(df1.var(ddof=0))
print("\nStandard deviations:\n")
print(df1.std(ddof=0))
print("\nExample calculation for col2:")
print("z = (x - mean) / std")
print("z = (10 - 20) / 8.164966 = -1.224745")
```
### Standard Scaler with Age When Sold
```
scaler = StandardScaler()
age_when_sold_scaled = scaler.fit_transform(house_prices["AgeWhenSold"].values.reshape(-1, 1))
sns.displot(age_when_sold_scaled)
plt.xticks(rotation=90)
plt.show()
```
## Whiten
```
x_new = x / std(x)
```
```
data = [5, 1, 3, 3, 2, 3, 8, 1, 2, 2, 3, 5]
print("Original:", data)
print("\nStd Dev:", np.std(data))
scaled = whiten(data)
print("\nScaled with Whiten:", scaled)
scaled_manual = data / np.std(data)
print("\nScaled Manuallly:", scaled_manual)
```
## MinMax
Scales to a value between 0 and 1.
More suspectible to influence by outliers.
### Housing Prices Age When Sold
```
scaler = MinMaxScaler()
age_when_sold_scaled = scaler.fit_transform(house_prices["AgeWhenSold"].values.reshape(-1, 1))
sns.displot(age_when_sold_scaled)
plt.xticks(rotation=90)
plt.show()
```
## Robust Scaler
```
scaler = RobustScaler()
age_when_sold_scaled = scaler.fit_transform(house_prices["AgeWhenSold"].values.reshape(-1, 1))
sns.displot(age_when_sold_scaled)
plt.xticks(rotation=90)
plt.show()
```
|
github_jupyter
|
# Tutorial 6.3. Advanced Topics on Extreme Value Analysis
### Description: Some advanced topics on Extreme Value Analysis are presented.
#### Students are advised to complete the exercises.
Project: Structural Wind Engineering WS19-20
Chair of Structural Analysis @ TUM - R. Wüchner, M. Péntek
Author: anoop.kodakkal@tum.de, mate.pentek@tum.de
Created on: 24.12.2019
Last update: 08.01.2020
##### Contents:
1. Prediction of the extreme value of a time series - MaxMin Estimation
2. Lieblein's BLUE method
The worksheet is based on the knowledge base and scripts provided by [NIST](https://www.itl.nist.gov/div898/winds/overview.htm) as well as work available from [Christopher Howlett](https://github.com/chowlet5) from UWO.
```
# import
import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import gumbel_r as gumbel
from ipywidgets import interactive
#external files
from peakpressure import maxminest
from blue4pressure import *
import custom_utilities as c_utils
```
## 1. Prediction of the extreme value of a time series - MaxMin Estimation
#### This method is based on [the procedure (and sample Matlab file](https://www.itl.nist.gov/div898/winds/peakest_files/peakest.htm) by Sadek, F. and Simiu, E. (2002). "Peak non-gaussian wind effects for database-assisted low-rise building design." Journal of Engineering Mechanics, 128(5), 530-539. Please find it [here](https://www.itl.nist.gov/div898/winds/pdf_files/b02030.pdf).
The method uses
* gamma distribution for estimating the peaks corresponding to the longer tail of time series
* normal distribution for estimating the peaks corresponding to the shorter tail of time series
The distribution of the peaks is then estimated by using the standard translation processes approach.
#### implementation details :
INPUT ARGUMENTS:
Each row of *record* is a time series.
The optional input argument *dur_ratio* allows peaks to be estimated for
a duration that differs from the duration of the record itself:
*dur_ratio* = [duration for peak estimation]/[duration of record]
(If unspecified, a value of 1 is used.)
OUTPUT ARGUMENTS:
* *max_est* gives the expected maximum values of each row of *record*
* *min_est* gives the expected minimum values of each row of *record*
* *max_std* gives the standard deviations of the maximum value for each row of *record*
* *min_std* gives the standard deviations of the minimum value for each row of *record*
#### Let us test the method for a given time series
```
# using as sample input some pre-generated generalized extreme value random series
given_series = np.loadtxt('test_data_gevrnd.dat', skiprows=0, usecols = (0,))
# print results
dur_ratio = 1
result = maxminest(given_series, dur_ratio)
maxv = result[0][0][0]
minv = result[1][0][0]
print('estimation of maximum value ', np.around(maxv,3))
print('estimation of minimum value ', np.around(minv,3))
plt.figure(num=1, figsize=(8, 6))
x_series = np.arange(0.0, len(given_series), 1.0)
plt.plot(x_series, given_series)
plt.ylabel('Amplitude')
plt.xlabel('Time [s]')
plt.hlines([maxv, minv], x_series[0], x_series[-1])
plt.title('Predicted extrema')
plt.grid(True)
plt.show()
```
#### Let us plot the pdf and cdf
```
[pdf_x, pdf_y] = c_utils.get_pdf(given_series)
ecdf_y = c_utils.get_ecdf(pdf_x, pdf_y)
plt.figure(num=2, figsize=(16, 6))
plt.subplot(1,2,1)
plt.plot(pdf_x, pdf_y)
plt.ylabel('PDF(Amplitude)')
plt.grid(True)
plt.subplot(1,2,2)
plt.plot(pdf_x, ecdf_y)
plt.vlines([maxv, minv], 0, 1)
plt.ylabel('CDF(Amplitude)')
plt.grid(True)
plt.show()
```
## 2. Lieblein's BLUE method
From a time series of pressure coefficients, *blue4pressure.py* estimates
extremes of positive and negative pressures based on Lieblein's BLUE
(Best Linear Unbiased Estimate) method applied to n epochs.
Extremes are estimated for 1 and dur epochs for probabilities of non-exceedance
P1 and P2 of the Gumbel distribution fitted to the epochal peaks.
*n* = integer, dur need not be an integer.
Written by Dat Duthinh 8_25_2015, 2_2_2016, 2_6_2017.
For further reference check out the material provided by [NIST](https://www.itl.nist.gov/div898/winds/gumbel_blue/gumbblue.htm).
Reference:
1) Julius Lieblein "Efficient Methods of Extreme-Value
Methodology" NBSIR 74-602 OCT 1974 for n = 4:16
2) Nicholas John Cook "The designer's guide to wind loading of
building structures" part 1, British Research Establishment 1985 Table C3
pp. 321-323 for n = 17:24. Extension to n=100 by Adam Pintar Feb 12 2016.
3) INTERNATIONAL STANDARD, ISO 4354 (2009-06-01), 2nd edition, “Wind
actions on structures,” Annex D (informative) “Aerodynamic pressure and
force coefficients,” Geneva, Switzerland, p. 22
#### implementation details :
INPUT ARGUMENTS
* *cp* = vector of time history of pressure coefficients
* *n* = number of epochs (integer)of cp data, 4 <= n <= 100
* *dur* = number of epochs for estimation of extremes. Default dur = n dur need not be an integer
* *P1, P2* = probabilities of non-exceedance of extremes in EV1 (Gumbel), P1 defaults to 0.80 (ISO)and P2 to 0.5704 (mean) for the Gumbel distribution .
OUTPUT ARGUMENTS
* *suffix max* for + peaks, min for - peaks of pressure coeff.
* *p1_max* (p1_min)= extreme value of positive (negative) peaks with probability of non-exceedance P1 for 1 epoch
* *p2_max* (p2_min)= extreme value of positive (negative) peaks with probability of exceedance P2 for 1 epoch
* *p1_rmax* (p1_rmin)= extreme value of positive (negative) peaks with probability of non-exceedance P1 for dur epochs
* *p2_rmax* (p2_rmin)= extreme value of positive (negative) peaks with probability of non-exceedance P2 for for dur epochs
* *cp_max* (cp_min)= vector of n positive (negative) epochal peaks
* *u_max, b_max* (u_min, b_min) = location and scale parameters of EV1 (Gumbel) for positive (negative) peaks
```
# n = number of epochs (integer)of cp data, 4 <= n <= 100
n=4
# P1, P2 = probabilities of non-exceedance of extremes in EV1 (Gumbel).
P1=0.80
P2=0.5704 # this corresponds to the mean of gumbel distribution
# dur = number of epochs for estimation of extremes. Default dur = n
# dur need not be an integer
dur=1
# Call function
result = blue4pressure(given_series, n, P1, P2, dur)
p1_max = result[0][0]
p2_max = result[1][0]
umax = result[4][0] # location parameters
b_max = result[5][0] # sclae parameters
p1_min = result[7][0]
p2_min = result[8][0]
umin = result[11][0] # location parameters
b_min = result[12][0] # scale parameters
# print results
## maximum
print('estimation of maximum value with probability of non excedence of p1', np.around(p1_max,3))
print('estimation of maximum value with probability of non excedence of p2', np.around(p2_max,3))
## minimum
print('estimation of minimum value with probability of non excedence of p1', np.around(p1_min,3))
print('estimation of minimum value with probability of non excedence of p2', np.around(p2_min,3))
```
#### Let us plot the pdf and cdf for the maximum values
```
max_pdf_x = np.linspace(1, 3, 100)
max_pdf_y = gumbel.pdf(max_pdf_x, umax, b_max)
max_ecdf_y = c_utils.get_ecdf(max_pdf_x, max_pdf_y)
plt.figure(num=3, figsize=(16, 6))
plt.subplot(1,2,1)
# PDF generated as a fitted curve using generalized extreme distribution
plt.plot(max_pdf_x, max_pdf_y, label = 'PDF from the fitted Gumbel')
plt.xlabel('Max values')
plt.ylabel('PDF(Amplitude)')
plt.title('PDF of Maxima')
plt.grid(True)
plt.legend()
plt.subplot(1,2,2)
plt.plot(max_pdf_x, max_ecdf_y)
plt.vlines([p1_max, p2_max], 0, 1)
plt.ylabel('CDF(Amplitude)')
plt.grid(True)
plt.show()
```
#### Try plotting these for the minimum values. Discuss among groups the advanced extreme value evaluation methods.
|
github_jupyter
|
```
# Load necessary modules and libraries
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import Perceptron
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from sklearn.model_selection import learning_curve
from sklearn.neural_network import MLPRegressor
from sklearn.linear_model import LinearRegression
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import RBF, RationalQuadratic, Matern, ExpSineSquared,DotProduct
import pickle
import seaborn as sns
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
# Load the data
Geometry1 = pd.read_csv('Surface_features.csv',header=0, usecols=(4,8,9,10,11,12,14))
Geometry = pd.read_csv('Surface_features.csv',header=0, usecols=(4,6,7,8,9,10,11,12)).values
Ra_ch = pd.read_csv('Surface_features.csv',header=0,usecols=(5,)).values
Ra_ch = Ra_ch[:,0]
ks = pd.read_csv('Surface_features.csv',header=0,usecols=(13,)).values
ks = ks[:,0]
Geometry1["ks"]= np.divide(ks,Ra_ch)
Geometry1["krms_ch"]= np.divide(Geometry1["krms_ch"],Ra_ch)
Geometry1.rename({'krms_ch': '$k_{rms}/R_a$',
'pro_ch': '$P_o$',
'ESx_ch': '$E_x$',
'ESz_ch': '$E_z$',
'sk_ch': '$S_k$',
'ku_ch': '$K_u$',
'ks': '$k_s/R_a$',
'label': 'Label',
}, axis='columns', errors="raise",inplace = True)
# Plot raw data
plt.rc('text', usetex=True)
sns.set(context='paper',
style='ticks',
palette='deep',
font='sans-serif',
font_scale=3, color_codes=True, rc=None)
g = sns.pairplot(Geometry1,diag_kind="kde", #palette="seismic",
hue='Label',
plot_kws=dict(s=70,facecolor="w", edgecolor="w", linewidth=1),
diag_kws=dict(linewidth=1.5))
g.map_upper(sns.kdeplot)
g.map_lower(sns.scatterplot, s=50,)
plt.savefig('pair.pdf', dpi=None, facecolor='w', edgecolor='w',
orientation='portrait', papertype=None, format=None,
transparent=False, bbox_inches=None, pad_inches=0.1,
frameon=None, metadata=None)
# Data reconfiguration, to be used in ML
X = Geometry
y = np.divide(ks,Ra_ch)
X[:,0] = np.divide(X[:,0],Ra_ch)
X[:,2] = np.abs(X[:,2])
# Generate secondary features and append them to the original dataset
n,m = X.shape
X0 = np.ones((n,1))
X1 = np.ones((n,1))
X2 = np.ones((n,1))
X3 = np.ones((n,1))
X4 = np.ones((n,1))
X5 = np.ones((n,1))
X6 = np.ones((n,1))
X7 = np.ones((n,1))
X8 = np.ones((n,1))
X9 = np.ones((n,1))
X1[:,0] = np.transpose(X[:,4]*X[:,5])
X2[:,0] = np.transpose(X[:,4]*X[:,6])
X3[:,0] = np.transpose(X[:,4]*X[:,7])
X4[:,0] = np.transpose(X[:,5]*X[:,6])
X5[:,0] = np.transpose(X[:,5]*X[:,7])
X6[:,0] = np.transpose(X[:,6]*X[:,7])
X7[:,0] = np.transpose(X[:,4]*X[:,4])
X8[:,0] = np.transpose(X[:,5]*X[:,5])
X9[:,0] = np.transpose(X[:,6]*X[:,6])
X = np.hstack((X,X1))
X = np.hstack((X,X2))
X = np.hstack((X,X3))
X = np.hstack((X,X4))
X = np.hstack((X,X5))
X = np.hstack((X,X6))
X = np.hstack((X,X7))
X = np.hstack((X,X8))
X = np.hstack((X,X9))
# Best linear estimation
reg = LinearRegression().fit(X, y)
reg.score(X, y)
yn=reg.predict(X)
print("Mean err: %f" % np.mean(100.*abs(yn-y)/(y)))
print("Max err: %f" % max(100.*abs(yn-y)/(y)))
# Define two files that store the best ML prediction based on either L1 or L_\infty norms
filename1 = 'GPR_Linf.sav'
filename2 = 'GPR_L1.sav'
# Perform ML training --- it may take some time.
# Adjust ranges for by4 for faster (but potentially less accurate) results.
miny1=100
miny2=100
by4=0.
while by4<10000.:
by4=by4+1
kernel1 = RBF(10, (1e-3, 1e2))
kernel2 = RBF(5, (1e-3, 1e2))
kernel3 = RationalQuadratic(length_scale=1.0, alpha=0.1)
kernel4 = Matern(length_scale=1.0, length_scale_bounds=(1e-05, 100000.0), nu=4.5)
kernel5 = ExpSineSquared(length_scale=2.0,
periodicity=3.0,
length_scale_bounds=(1e-05, 100000.0),
periodicity_bounds=(1e-05, 100000.0))
kernel6 = DotProduct()
gpr = GaussianProcessRegressor(kernel=kernel1, n_restarts_optimizer=1000)
gpr = GaussianProcessRegressor(kernel=kernel3, n_restarts_optimizer=1000,alpha=.1)
print("by4: %f" % by4)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)
gpr.fit(X_train, y_train)
yn, sigma = gpr.predict(X, return_std=True)
#print("Max err: %f" % max(100.*abs(yn-y)/y))
#print("Mean err: %f" % np.mean(100.*abs(yn-y)/y))
if miny1>max(100.*abs(yn-y)/y):
pickle.dump(gpr, open(filename1, 'wb'))
miny1=max(100.*abs(yn-y)/y)
print("Miny1: %f" % miny1)
if miny2>np.mean(100.*abs(yn-y)/y):
pickle.dump(gpr, open(filename2, 'wb'))
miny2=np.mean(100.*abs(yn-y)/y)
print("Miny2: %f" % miny2)
print("by4: %f" % by4)
# Load either file1 or file2 to extract the results
loaded_model = pickle.load(open(filename2, 'rb'))
loaded_model.get_params()
yn, sigma = loaded_model.predict(X,return_std=True)
print("PREDICTED k_s/R_a= ")
print(yn)
print("Max err: %f" % max(100.*abs(yn-y)/(y)))
print("mean err: %f" % np.mean(100.*abs(yn-y)/(y)))
Error=pd.DataFrame()
Error["$k_s/Ra$"]= y
Error["$k_{sp}/Ra$"]= yn
Error["$error(\%)$"]= (100.*(yn-y)/(y))
Error["Label"]= Geometry1["Label"]
print(Error)
# Plot the results
plt.rc('text', usetex=True)
sns.set(context='paper',
style='ticks',
palette='deep',
font='sans-serif',
font_scale=2, color_codes=True, rc=None)
g = sns.pairplot(Error,diag_kind="kde", hue='Label',
aspect=1.,
plot_kws=dict(s=50,facecolor="w", edgecolor="w", linewidth=1.),
diag_kws=dict(linewidth=1.5,kernel='gau'))
g.map_upper(sns.kdeplot)
g.map_lower(sns.scatterplot, s=50,legend='full')
g.axes[-2,0].plot(range(15), range(15),'k--', linewidth= 1.7)
for i in range(0,3):
for ax in g.axes[:,i]:
ax.spines['top'].set_visible(True)
ax.spines['right'].set_visible(True)
plt.savefig('GPR_result.pdf', dpi=None, facecolor='w', edgecolor='w',
orientation='portrait', papertype=None, format=None,
transparent=False, bbox_inches=None, pad_inches=0.1,
frameon=None, metadata=None)
# Plot confidence interval
sns.set(context='notebook',
style='ticks',
palette='seismic',
font='sans-serif',
font_scale=5, color_codes=True, rc=None)
plt.rc('text', usetex=True)
fig = plt.figure(figsize=(50,55))
plt.subplot(411)
Xm=X[np.argsort(X[:,0])]
Xm=Xm[:,0]
ym=y[np.argsort(X[:,0])]
ymp=yn[np.argsort(X[:,0])]
sigmap=sigma[np.argsort(X[:,0])]
plt.plot(Xm, ym, 'r.', markersize=26)
plt.plot(Xm, ymp, 'b-',linewidth=6)
plt.fill(np.concatenate([Xm, Xm[::-1]]),
np.concatenate([ymp - 1.900 * sigmap,
(ymp + 1.900 * sigmap)[::-1]]),
alpha=.5, fc='b', ec='None')
plt.xlabel('$k_{rms}/R_a$')
plt.ylabel('$k_s/R_a$')
plt.grid(alpha=0.15)
#plt.legend(loc='best')
plt.subplot(412)
Xm=X[np.argsort(X[:,4])]
Xm=Xm[:,4]
ym=y[np.argsort(X[:,4])]
ymp=yn[np.argsort(X[:,4])]
sigmap=sigma[np.argsort(X[:,4])]
plt.plot(Xm, ym, 'r.', markersize=26)
plt.plot(Xm, ymp, 'b-',linewidth=6)
plt.fill(np.concatenate([Xm, Xm[::-1]]),
np.concatenate([ymp - 1.900 * sigmap,
(ymp + 1.900 * sigmap)[::-1]]),
alpha=.5, fc='b', ec='None')
plt.xlabel('$E_x$')
plt.ylabel('$k_s/R_a$')
plt.grid(alpha=0.15)
plt.subplot(413)
Xm=X[np.argsort(X[:,3])]
Xm=Xm[:,3]
ym=y[np.argsort(X[:,3])]
ymp=yn[np.argsort(X[:,3])]
sigmap=sigma[np.argsort(X[:,3])]
plt.plot(Xm, ym, 'r.', markersize=26)
plt.plot(Xm, ymp, 'b-',linewidth=6)
plt.fill(np.concatenate([Xm, Xm[::-1]]),
np.concatenate([ymp - 1.900 * sigmap,
(ymp + 1.900 * sigmap)[::-1]]),
alpha=.5, fc='b', ec='None')
plt.xlabel('$P_o$')
plt.ylabel('$k_s/R_a$')
plt.grid(alpha=0.15)
plt.subplot(414)
Xm=X[np.argsort(X[:,6])]
Xm=Xm[:,6]
ym=y[np.argsort(X[:,6])]
ymp=yn[np.argsort(X[:,6])]
sigmap=sigma[np.argsort(X[:,6])]
plt.plot(Xm, ym, 'r.', markersize=26, label='$k_s/R_a$')
plt.plot(Xm, ymp, 'b-', linewidth=6,label='$k_{sp}/R_a$')
plt.fill(np.concatenate([Xm, Xm[::-1]]),
np.concatenate([ymp - 1.900 * sigmap,
(ymp + 1.900 * sigmap)[::-1]]),
alpha=.5, fc='b', ec='None', label='$90\%$ $CI$')
plt.xlabel('$S_k$')
plt.ylabel('$k_s/R_a$')
plt.grid(alpha=0.15)
plt.legend(loc='best')
plt.savefig('GPR_CI.pdf', dpi=None, facecolor='w', edgecolor='w',
orientation='portrait', papertype=None, format=None,
transparent=False, bbox_inches=None, pad_inches=0.1,
frameon=None, metadata=None)
```
|
github_jupyter
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.