text
stringlengths 2.5k
6.39M
| kind
stringclasses 3
values |
|---|---|
# 09 Strain Gage
This is one of the most commonly used sensor. It is used in many transducers. Its fundamental operating principle is fairly easy to understand and it will be the purpose of this lecture.
A strain gage is essentially a thin wire that is wrapped on film of plastic.
<img src="img/StrainGage.png" width="200">
The strain gage is then mounted (glued) on the part for which the strain must be measured.
<img src="img/Strain_gauge_2.jpg" width="200">
## Stress, Strain
When a beam is under axial load, the axial stress, $\sigma_a$, is defined as:
\begin{align*}
\sigma_a = \frac{F}{A}
\end{align*}
with $F$ the axial load, and $A$ the cross sectional area of the beam under axial load.
<img src="img/BeamUnderStrain.png" width="200">
Under the load, the beam of length $L$ will extend by $dL$, giving rise to the definition of strain, $\epsilon_a$:
\begin{align*}
\epsilon_a = \frac{dL}{L}
\end{align*}
The beam will also contract laterally: the cross sectional area is reduced by $dA$. This results in a transverval strain $\epsilon_t$. The transversal and axial strains are related by the Poisson's ratio:
\begin{align*}
\nu = - \frac{\epsilon_t }{\epsilon_a}
\end{align*}
For a metal the Poission's ratio is typically $\nu = 0.3$, for an incompressible material, such as rubber (or water), $\nu = 0.5$.
Within the elastic limit, the axial stress and axial strain are related through Hooke's law by the Young's modulus, $E$:
\begin{align*}
\sigma_a = E \epsilon_a
\end{align*}
<img src="img/ElasticRegime.png" width="200">
## Resistance of a wire
The electrical resistance of a wire $R$ is related to its physical properties (the electrical resistiviy, $\rho$ in $\Omega$/m) and its geometry: length $L$ and cross sectional area $A$.
\begin{align*}
R = \frac{\rho L}{A}
\end{align*}
Mathematically, the change in wire dimension will result inchange in its electrical resistance. This can be derived from first principle:
\begin{align}
\frac{dR}{R} = \frac{d\rho}{\rho} + \frac{dL}{L} - \frac{dA}{A}
\end{align}
If the wire has a square cross section, then:
\begin{align*}
A & = L'^2 \\
\frac{dA}{A} & = \frac{d(L'^2)}{L'^2} = \frac{2L'dL'}{L'^2} = 2 \frac{dL'}{L'}
\end{align*}
We have related the change in cross sectional area to the transversal strain.
\begin{align*}
\epsilon_t = \frac{dL'}{L'}
\end{align*}
Using the Poisson's ratio, we can relate then relate the change in cross-sectional area ($dA/A$) to axial strain $\epsilon_a = dL/L$.
\begin{align*}
\epsilon_t &= - \nu \epsilon_a \\
\frac{dL'}{L'} &= - \nu \frac{dL}{L} \; \text{or}\\
\frac{dA}{A} & = 2\frac{dL'}{L'} = -2 \nu \frac{dL}{L}
\end{align*}
Finally we can substitute express $dA/A$ in eq. for $dR/R$ and relate change in resistance to change of wire geometry, remembering that for a metal $\nu =0.3$:
\begin{align}
\frac{dR}{R} & = \frac{d\rho}{\rho} + \frac{dL}{L} - \frac{dA}{A} \\
& = \frac{d\rho}{\rho} + \frac{dL}{L} - (-2\nu \frac{dL}{L}) \\
& = \frac{d\rho}{\rho} + 1.6 \frac{dL}{L} = \frac{d\rho}{\rho} + 1.6 \epsilon_a
\end{align}
It also happens that for most metals, the resistivity increases with axial strain. In general, one can then related the change in resistance to axial strain by defining the strain gage factor:
\begin{align}
S = 1.6 + \frac{d\rho}{\rho}\cdot \frac{1}{\epsilon_a}
\end{align}
and finally, we have:
\begin{align*}
\frac{dR}{R} = S \epsilon_a
\end{align*}
$S$ is materials dependent and is typically equal to 2.0 for most commercially availabe strain gages. It is dimensionless.
Strain gages are made of thin wire that is wraped in several loops, effectively increasing the length of the wire and therefore the sensitivity of the sensor.
_Question:
Explain why a longer wire is necessary to increase the sensitivity of the sensor_.
Most commercially available strain gages have a nominal resistance (resistance under no load, $R_{ini}$) of 120 or 350 $\Omega$.
Within the elastic regime, strain is typically within the range $10^{-6} - 10^{-3}$, in fact strain is expressed in unit of microstrain, with a 1 microstrain = $10^{-6}$. Therefore, changes in resistances will be of the same order. If one were to measure resistances, we will need a dynamic range of 120 dB, whih is typically very expensive. Instead, one uses the Wheatstone bridge to transform the change in resistance to a voltage, which is easier to measure and does not require such a large dynamic range.
## Wheatstone bridge:
<img src="img/WheatstoneBridge.png" width="200">
The output voltage is related to the difference in resistances in the bridge:
\begin{align*}
\frac{V_o}{V_s} = \frac{R_1R_3-R_2R_4}{(R_1+R_4)(R_2+R_3)}
\end{align*}
If the bridge is balanced, then $V_o = 0$, it implies: $R_1/R_2 = R_4/R_3$.
In practice, finding a set of resistors that balances the bridge is challenging, and a potentiometer is used as one of the resistances to do minor adjustement to balance the bridge. If one did not do the adjustement (ie if we did not zero the bridge) then all the measurement will have an offset or bias that could be removed in a post-processing phase, as long as the bias stayed constant.
If each resistance $R_i$ is made to vary slightly around its initial value, ie $R_i = R_{i,ini} + dR_i$. For simplicity, we will assume that the initial value of the four resistances are equal, ie $R_{1,ini} = R_{2,ini} = R_{3,ini} = R_{4,ini} = R_{ini}$. This implies that the bridge was initially balanced, then the output voltage would be:
\begin{align*}
\frac{V_o}{V_s} = \frac{1}{4} \left( \frac{dR_1}{R_{ini}} - \frac{dR_2}{R_{ini}} + \frac{dR_3}{R_{ini}} - \frac{dR_4}{R_{ini}} \right)
\end{align*}
Note here that the changes in $R_1$ and $R_3$ have a positive effect on $V_o$, while the changes in $R_2$ and $R_4$ have a negative effect on $V_o$. In practice, this means that is a beam is a in tension, then a strain gage mounted on the branch 1 or 3 of the Wheatstone bridge will produce a positive voltage, while a strain gage mounted on branch 2 or 4 will produce a negative voltage. One takes advantage of this to increase sensitivity to measure strain.
### Quarter bridge
One uses only one quarter of the bridge, ie strain gages are only mounted on one branch of the bridge.
\begin{align*}
\frac{V_o}{V_s} = \pm \frac{1}{4} \epsilon_a S
\end{align*}
Sensitivity, $G$:
\begin{align*}
G = \frac{V_o}{\epsilon_a} = \pm \frac{1}{4}S V_s
\end{align*}
### Half bridge
One uses half of the bridge, ie strain gages are mounted on two branches of the bridge.
\begin{align*}
\frac{V_o}{V_s} = \pm \frac{1}{2} \epsilon_a S
\end{align*}
### Full bridge
One uses of the branches of the bridge, ie strain gages are mounted on each branch.
\begin{align*}
\frac{V_o}{V_s} = \pm \epsilon_a S
\end{align*}
Therefore, as we increase the order of bridge, the sensitivity of the instrument increases. However, one should be carefull how we mount the strain gages as to not cancel out their measurement.
_Exercise_
1- Wheatstone bridge
<img src="img/WheatstoneBridge.png" width="200">
> How important is it to know \& match the resistances of the resistors you employ to create your bridge?
> How would you do that practically?
> Assume $R_1=120\,\Omega$, $R_2=120\,\Omega$, $R_3=120\,\Omega$, $R_4=110\,\Omega$, $V_s=5.00\,\text{V}$. What is $V_\circ$?
```
Vs = 5.00
Vo = (120**2-120*110)/(230*240) * Vs
print('Vo = ',Vo, ' V')
# typical range in strain a strain gauge can measure
# 1 -1000 micro-Strain
AxialStrain = 1000*10**(-6) # axial strain
StrainGageFactor = 2
R_ini = 120 # Ohm
R_1 = R_ini+R_ini*StrainGageFactor*AxialStrain
print(R_1)
Vo = (120**2-120*(R_1))/((120+R_1)*240) * Vs
print('Vo = ', Vo, ' V')
```
> How important is it to know \& match the resistances of the resistors you employ to create your bridge?
> How would you do that practically?
> Assume $R_1= R_2 =R_3=120\,\Omega$, $R_4=120.01\,\Omega$, $V_s=5.00\,\text{V}$. What is $V_\circ$?
```
Vs = 5.00
Vo = (120**2-120*120.01)/(240.01*240) * Vs
print(Vo)
```
2- Strain gage 1:
One measures the strain on a bridge steel beam. The modulus of elasticity is $E=190$ GPa. Only one strain gage is mounted on the bottom of the beam; the strain gage factor is $S=2.02$.
> a) What kind of electronic circuit will you use? Draw a sketch of it.
> b) Assume all your resistors including the unloaded strain gage are balanced and measure $120\,\Omega$, and that the strain gage is at location $R_2$. The supply voltage is $5.00\,\text{VDC}$. Will $V_\circ$ be positive or negative when a downward load is added?
In practice, we cannot have all resistances = 120 $\Omega$. at zero load, the bridge will be unbalanced (show $V_o \neq 0$). How could we balance our bridge?
Use a potentiometer to balance bridge, for the load cell, we ''zero'' the instrument.
Other option to zero-out our instrument? Take data at zero-load, record the voltage, $V_{o,noload}$. Substract $V_{o,noload}$ to my data.
> c) For a loading in which $V_\circ = -1.25\,\text{mV}$, calculate the strain $\epsilon_a$ in units of microstrain.
\begin{align*}
\frac{V_o}{V_s} & = - \frac{1}{4} \epsilon_a S\\
\epsilon_a & = -\frac{4}{S} \frac{V_o}{V_s}
\end{align*}
```
S = 2.02
Vo = -0.00125
Vs = 5
eps_a = -1*(4/S)*(Vo/Vs)
print(eps_a)
```
> d) Calculate the axial stress (in MPa) in the beam under this load.
> e) You now want more sensitivity in your measurement, you install a second strain gage on to
p of the beam. Which resistor should you use for this second active strain gage?
> f) With this new setup and the same applied load than previously, what should be the output voltage?
3- Strain Gage with Long Lead Wires
<img src="img/StrainGageLongWires.png" width="360">
A quarter bridge strain gage Wheatstone bridge circuit is constructed with $120\,\Omega$ resistors and a $120\,\Omega$ strain gage. For this practical application, the strain gage is located very far away form the DAQ station and the lead wires to the strain gage are $10\,\text{m}$ long and the lead wire have a resistance of $0.080\,\Omega/\text{m}$. The lead wire resistance can lead to problems since $R_{lead}$ changes with temperature.
> Design a modified circuit that will cancel out the effect of the lead wires.
## Homework
|
github_jupyter
|
```
#export
from fastai.basics import *
from fastai.tabular.core import *
from fastai.tabular.model import *
from fastai.tabular.data import *
#hide
from nbdev.showdoc import *
#default_exp tabular.learner
```
# Tabular learner
> The function to immediately get a `Learner` ready to train for tabular data
The main function you probably want to use in this module is `tabular_learner`. It will automatically create a `TabulaModel` suitable for your data and infer the irght loss function. See the [tabular tutorial](http://docs.fast.ai/tutorial.tabular) for an example of use in context.
## Main functions
```
#export
@log_args(but_as=Learner.__init__)
class TabularLearner(Learner):
"`Learner` for tabular data"
def predict(self, row):
tst_to = self.dls.valid_ds.new(pd.DataFrame(row).T)
tst_to.process()
tst_to.conts = tst_to.conts.astype(np.float32)
dl = self.dls.valid.new(tst_to)
inp,preds,_,dec_preds = self.get_preds(dl=dl, with_input=True, with_decoded=True)
i = getattr(self.dls, 'n_inp', -1)
b = (*tuplify(inp),*tuplify(dec_preds))
full_dec = self.dls.decode((*tuplify(inp),*tuplify(dec_preds)))
return full_dec,dec_preds[0],preds[0]
show_doc(TabularLearner, title_level=3)
```
It works exactly as a normal `Learner`, the only difference is that it implements a `predict` method specific to work on a row of data.
```
#export
@log_args(to_return=True, but_as=Learner.__init__)
@delegates(Learner.__init__)
def tabular_learner(dls, layers=None, emb_szs=None, config=None, n_out=None, y_range=None, **kwargs):
"Get a `Learner` using `dls`, with `metrics`, including a `TabularModel` created using the remaining params."
if config is None: config = tabular_config()
if layers is None: layers = [200,100]
to = dls.train_ds
emb_szs = get_emb_sz(dls.train_ds, {} if emb_szs is None else emb_szs)
if n_out is None: n_out = get_c(dls)
assert n_out, "`n_out` is not defined, and could not be infered from data, set `dls.c` or pass `n_out`"
if y_range is None and 'y_range' in config: y_range = config.pop('y_range')
model = TabularModel(emb_szs, len(dls.cont_names), n_out, layers, y_range=y_range, **config)
return TabularLearner(dls, model, **kwargs)
```
If your data was built with fastai, you probably won't need to pass anything to `emb_szs` unless you want to change the default of the library (produced by `get_emb_sz`), same for `n_out` which should be automatically inferred. `layers` will default to `[200,100]` and is passed to `TabularModel` along with the `config`.
Use `tabular_config` to create a `config` and cusotmize the model used. There is just easy access to `y_range` because this argument is often used.
All the other arguments are passed to `Learner`.
```
path = untar_data(URLs.ADULT_SAMPLE)
df = pd.read_csv(path/'adult.csv')
cat_names = ['workclass', 'education', 'marital-status', 'occupation', 'relationship', 'race']
cont_names = ['age', 'fnlwgt', 'education-num']
procs = [Categorify, FillMissing, Normalize]
dls = TabularDataLoaders.from_df(df, path, procs=procs, cat_names=cat_names, cont_names=cont_names,
y_names="salary", valid_idx=list(range(800,1000)), bs=64)
learn = tabular_learner(dls)
#hide
tst = learn.predict(df.iloc[0])
#hide
#test y_range is passed
learn = tabular_learner(dls, y_range=(0,32))
assert isinstance(learn.model.layers[-1], SigmoidRange)
test_eq(learn.model.layers[-1].low, 0)
test_eq(learn.model.layers[-1].high, 32)
learn = tabular_learner(dls, config = tabular_config(y_range=(0,32)))
assert isinstance(learn.model.layers[-1], SigmoidRange)
test_eq(learn.model.layers[-1].low, 0)
test_eq(learn.model.layers[-1].high, 32)
#export
@typedispatch
def show_results(x:Tabular, y:Tabular, samples, outs, ctxs=None, max_n=10, **kwargs):
df = x.all_cols[:max_n]
for n in x.y_names: df[n+'_pred'] = y[n][:max_n].values
display_df(df)
```
## Export -
```
#hide
from nbdev.export import notebook2script
notebook2script()
```
|
github_jupyter
|
# Aerospike Connect for Spark - SparkML Prediction Model Tutorial
## Tested with Java 8, Spark 3.0.0, Python 3.7, and Aerospike Spark Connector 3.0.0
## Summary
Build a linear regression model to predict birth weight using Aerospike Database and Spark.
Here are the features used:
- gestation weeks
- mother’s age
- father’s age
- mother’s weight gain during pregnancy
- [Apgar score](https://en.wikipedia.org/wiki/Apgar_score)
Aerospike is used to store the Natality dataset that is published by CDC. The table is accessed in Apache Spark using the Aerospike Spark Connector, and Spark ML is used to build and evaluate the model. The model can later be converted to PMML and deployed on your inference server for predictions.
### Prerequisites
1. Load Aerospike server if not alrady available - docker run -d --name aerospike -p 3000:3000 -p 3001:3001 -p 3002:3002 -p 3003:3003 aerospike
2. Feature key needs to be located in AS_FEATURE_KEY_PATH
3. [Download the connector](https://www.aerospike.com/enterprise/download/connectors/aerospike-spark/3.0.0/)
```
#IP Address or DNS name for one host in your Aerospike cluster.
#A seed address for the Aerospike database cluster is required
AS_HOST ="127.0.0.1"
# Name of one of your namespaces. Type 'show namespaces' at the aql prompt if you are not sure
AS_NAMESPACE = "test"
AS_FEATURE_KEY_PATH = "/etc/aerospike/features.conf"
AEROSPIKE_SPARK_JAR_VERSION="3.0.0"
AS_PORT = 3000 # Usually 3000, but change here if not
AS_CONNECTION_STRING = AS_HOST + ":"+ str(AS_PORT)
#Locate the Spark installation - this'll use the SPARK_HOME environment variable
import findspark
findspark.init()
# Below will help you download the Spark Connector Jar if you haven't done so already.
import urllib
import os
def aerospike_spark_jar_download_url(version=AEROSPIKE_SPARK_JAR_VERSION):
DOWNLOAD_PREFIX="https://www.aerospike.com/enterprise/download/connectors/aerospike-spark/"
DOWNLOAD_SUFFIX="/artifact/jar"
AEROSPIKE_SPARK_JAR_DOWNLOAD_URL = DOWNLOAD_PREFIX+AEROSPIKE_SPARK_JAR_VERSION+DOWNLOAD_SUFFIX
return AEROSPIKE_SPARK_JAR_DOWNLOAD_URL
def download_aerospike_spark_jar(version=AEROSPIKE_SPARK_JAR_VERSION):
JAR_NAME="aerospike-spark-assembly-"+AEROSPIKE_SPARK_JAR_VERSION+".jar"
if(not(os.path.exists(JAR_NAME))) :
urllib.request.urlretrieve(aerospike_spark_jar_download_url(),JAR_NAME)
else :
print(JAR_NAME+" already downloaded")
return os.path.join(os.getcwd(),JAR_NAME)
AEROSPIKE_JAR_PATH=download_aerospike_spark_jar()
os.environ["PYSPARK_SUBMIT_ARGS"] = '--jars ' + AEROSPIKE_JAR_PATH + ' pyspark-shell'
import pyspark
from pyspark.context import SparkContext
from pyspark.sql.context import SQLContext
from pyspark.sql.session import SparkSession
from pyspark.ml.linalg import Vectors
from pyspark.ml.regression import LinearRegression
from pyspark.sql.types import StringType, StructField, StructType, ArrayType, IntegerType, MapType, LongType, DoubleType
#Get a spark session object and set required Aerospike configuration properties
sc = SparkContext.getOrCreate()
print("Spark Verison:", sc.version)
spark = SparkSession(sc)
sqlContext = SQLContext(sc)
spark.conf.set("aerospike.namespace",AS_NAMESPACE)
spark.conf.set("aerospike.seedhost",AS_CONNECTION_STRING)
spark.conf.set("aerospike.keyPath",AS_FEATURE_KEY_PATH )
```
## Step 1: Load Data into a DataFrame
```
as_data=spark \
.read \
.format("aerospike") \
.option("aerospike.set", "natality").load()
as_data.show(5)
print("Inferred Schema along with Metadata.")
as_data.printSchema()
```
### To speed up the load process at scale, use the [knobs](https://www.aerospike.com/docs/connect/processing/spark/performance.html) available in the Aerospike Spark Connector.
For example, **spark.conf.set("aerospike.partition.factor", 15 )** will map 4096 Aerospike partitions to 32K Spark partitions. <font color=red> (Note: Please configure this carefully based on the available resources (CPU threads) in your system.)</font>
## Step 2 - Prep data
```
# This Spark3.0 setting, if true, will turn on Adaptive Query Execution (AQE), which will make use of the
# runtime statistics to choose the most efficient query execution plan. It will speed up any joins that you
# plan to use for data prep step.
spark.conf.set("spark.sql.adaptive.enabled", 'true')
# Run a query in Spark SQL to ensure no NULL values exist.
as_data.createOrReplaceTempView("natality")
sql_query = """
SELECT *
from natality
where weight_pnd is not null
and mother_age is not null
and father_age is not null
and father_age < 80
and gstation_week is not null
and weight_gain_pnd < 90
and apgar_5min != "99"
and apgar_5min != "88"
"""
clean_data = spark.sql(sql_query)
#Drop the Aerospike metadata from the dataset because its not required.
#The metadata is added because we are inferring the schema as opposed to providing a strict schema
columns_to_drop = ['__key','__digest','__expiry','__generation','__ttl' ]
clean_data = clean_data.drop(*columns_to_drop)
# dropping null values
clean_data = clean_data.dropna()
clean_data.cache()
clean_data.show(5)
#Descriptive Analysis of the data
clean_data.describe().toPandas().transpose()
```
## Step 3 Visualize Data
```
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import math
pdf = clean_data.toPandas()
#Histogram - Father Age
pdf[['father_age']].plot(kind='hist',bins=10,rwidth=0.8)
plt.xlabel('Fathers Age (years)',fontsize=12)
plt.legend(loc=None)
plt.style.use('seaborn-whitegrid')
plt.show()
'''
pdf[['mother_age']].plot(kind='hist',bins=10,rwidth=0.8)
plt.xlabel('Mothers Age (years)',fontsize=12)
plt.legend(loc=None)
plt.style.use('seaborn-whitegrid')
plt.show()
'''
pdf[['weight_pnd']].plot(kind='hist',bins=10,rwidth=0.8)
plt.xlabel('Babys Weight (Pounds)',fontsize=12)
plt.legend(loc=None)
plt.style.use('seaborn-whitegrid')
plt.show()
pdf[['gstation_week']].plot(kind='hist',bins=10,rwidth=0.8)
plt.xlabel('Gestation (Weeks)',fontsize=12)
plt.legend(loc=None)
plt.style.use('seaborn-whitegrid')
plt.show()
pdf[['weight_gain_pnd']].plot(kind='hist',bins=10,rwidth=0.8)
plt.xlabel('mother’s weight gain during pregnancy',fontsize=12)
plt.legend(loc=None)
plt.style.use('seaborn-whitegrid')
plt.show()
#Histogram - Apgar Score
print("Apgar Score: Scores of 7 and above are generally normal; 4 to 6, fairly low; and 3 and below are generally \
regarded as critically low and cause for immediate resuscitative efforts.")
pdf[['apgar_5min']].plot(kind='hist',bins=10,rwidth=0.8)
plt.xlabel('Apgar score',fontsize=12)
plt.legend(loc=None)
plt.style.use('seaborn-whitegrid')
plt.show()
```
## Step 4 - Create Model
**Steps used for model creation:**
1. Split cleaned data into Training and Test sets
2. Vectorize features on which the model will be trained
3. Create a linear regression model (Choose any ML algorithm that provides the best fit for the given dataset)
4. Train model (Although not shown here, you could use K-fold cross-validation and Grid Search to choose the best hyper-parameters for the model)
5. Evaluate model
```
# Define a function that collects the features of interest
# (mother_age, father_age, and gestation_weeks) into a vector.
# Package the vector in a tuple containing the label (`weight_pounds`) for that
# row.##
def vector_from_inputs(r):
return (r["weight_pnd"], Vectors.dense(float(r["mother_age"]),
float(r["father_age"]),
float(r["gstation_week"]),
float(r["weight_gain_pnd"]),
float(r["apgar_5min"])))
#Split that data 70% training and 30% Evaluation data
train, test = clean_data.randomSplit([0.7, 0.3])
#Check the shape of the data
train.show()
print((train.count(), len(train.columns)))
test.show()
print((test.count(), len(test.columns)))
# Create an input DataFrame for Spark ML using the above function.
training_data = train.rdd.map(vector_from_inputs).toDF(["label",
"features"])
# Construct a new LinearRegression object and fit the training data.
lr = LinearRegression(maxIter=5, regParam=0.2, solver="normal")
#Voila! your first model using Spark ML is trained
model = lr.fit(training_data)
# Print the model summary.
print("Coefficients:" + str(model.coefficients))
print("Intercept:" + str(model.intercept))
print("R^2:" + str(model.summary.r2))
model.summary.residuals.show()
```
### Evaluate Model
```
eval_data = test.rdd.map(vector_from_inputs).toDF(["label",
"features"])
eval_data.show()
evaluation_summary = model.evaluate(eval_data)
print("MAE:", evaluation_summary.meanAbsoluteError)
print("RMSE:", evaluation_summary.rootMeanSquaredError)
print("R-squared value:", evaluation_summary.r2)
```
## Step 5 - Batch Prediction
```
#eval_data contains the records (ideally production) that you'd like to use for the prediction
predictions = model.transform(eval_data)
predictions.show()
```
#### Compare the labels and the predictions, they should ideally match up for an accurate model. Label is the actual weight of the baby and prediction is the predicated weight
### Saving the Predictions to Aerospike for ML Application's consumption
```
# Aerospike is a key/value database, hence a key is needed to store the predictions into the database. Hence we need
# to add the _id column to the predictions using SparkSQL
predictions.createOrReplaceTempView("predict_view")
sql_query = """
SELECT *, monotonically_increasing_id() as _id
from predict_view
"""
predict_df = spark.sql(sql_query)
predict_df.show()
print("#records:", predict_df.count())
# Now we are good to write the Predictions to Aerospike
predict_df \
.write \
.mode('overwrite') \
.format("aerospike") \
.option("aerospike.writeset", "predictions")\
.option("aerospike.updateByKey", "_id") \
.save()
```
#### You can verify that data is written to Aerospike by using either [AQL](https://www.aerospike.com/docs/tools/aql/data_management.html) or the [Aerospike Data Browser](https://github.com/aerospike/aerospike-data-browser)
## Step 6 - Deploy
### Here are a few options:
1. Save the model to a PMML file by converting it using Jpmml/[pyspark2pmml](https://github.com/jpmml/pyspark2pmml) and load it into your production enviornment for inference.
2. Use Aerospike as an [edge database for high velocity ingestion](https://medium.com/aerospike-developer-blog/add-horsepower-to-ai-ml-pipeline-15ca42a10982) for your inference pipline.
|
github_jupyter
|
## Concurrency with asyncio
### Thread vs. coroutine
```
# spinner_thread.py
import threading
import itertools
import time
import sys
class Signal:
go = True
def spin(msg, signal):
write, flush = sys.stdout.write, sys.stdout.flush
for char in itertools.cycle('|/-\\'):
status = char + ' ' + msg
write(status)
flush()
write('\x08' * len(status))
time.sleep(.1)
if not signal.go:
break
write(' ' * len(status) + '\x08' * len(status))
def slow_function():
time.sleep(3)
return 42
def supervisor():
signal = Signal()
spinner = threading.Thread(target=spin, args=('thinking!', signal))
print('spinner object:', spinner)
spinner.start()
result = slow_function()
signal.go = False
spinner.join()
return result
def main():
result = supervisor()
print('Answer:', result)
if __name__ == '__main__':
main()
# spinner_asyncio.py
import asyncio
import itertools
import sys
@asyncio.coroutine
def spin(msg):
write, flush = sys.stdout.write, sys.stdout.flush
for char in itertools.cycle('|/-\\'):
status = char + ' ' + msg
write(status)
flush()
write('\x08' * len(status))
try:
yield from asyncio.sleep(.1)
except asyncio.CancelledError:
break
write(' ' * len(status) + '\x08' * len(status))
@asyncio.coroutine
def slow_function():
yield from asyncio.sleep(3)
return 42
@asyncio.coroutine
def supervisor():
#Schedule the execution of a coroutine object:
#wrap it in a future. Return a Task object.
spinner = asyncio.ensure_future(spin('thinking!'))
print('spinner object:', spinner)
result = yield from slow_function()
spinner.cancel()
return result
def main():
loop = asyncio.get_event_loop()
result = loop.run_until_complete(supervisor())
loop.close()
print('Answer:', result)
if __name__ == '__main__':
main()
# flags_asyncio.py
import asyncio
import aiohttp
from flags import BASE_URL, save_flag, show, main
@asyncio.coroutine
def get_flag(cc):
url = '{}/{cc}/{cc}.gif'.format(BASE_URL, cc=cc.lower())
resp = yield from aiohttp.request('GET', url)
image = yield from resp.read()
return image
@asyncio.coroutine
def download_one(cc):
image = yield from get_flag(cc)
show(cc)
save_flag(image, cc.lower() + '.gif')
return cc
def download_many(cc_list):
loop = asyncio.get_event_loop()
to_do = [download_one(cc) for cc in sorted(cc_list)]
wait_coro = asyncio.wait(to_do)
res, _ = loop.run_until_complete(wait_coro)
loop.close()
return len(res)
if __name__ == '__main__':
main(download_many)
# flags2_asyncio.py
import asyncio
import collections
import aiohttp
from aiohttp import web
import tqdm
from flags2_common import HTTPStatus, save_flag, Result, main
DEFAULT_CONCUR_REQ = 5
MAX_CONCUR_REQ = 1000
class FetchError(Exception):
def __init__(self, country_code):
self.country_code = country_code
@asyncio.coroutine
def get_flag(base_url, cc):
url = '{}/{cc}/{cc}.gif'.format(BASE_URL, cc=cc.lower())
resp = yield from aiohttp.ClientSession().get(url)
if resp.status == 200:
image = yield from resp.read()
return image
elif resp.status == 404:
raise web.HTTPNotFound()
else:
raise aiohttp.HttpProcessingError(
code=resp.status, message=resp.reason, headers=resp.headers)
@asyncio.coroutine
def download_one(cc, base_url, semaphore, verbose):
try:
with (yield from semaphore):
image = yield from get_flag(base_url, cc)
except web.HTTPNotFound:
status = HTTPStatus.not_found
msg = 'not found'
except Exception as exc:
raise FetchError(cc) from exc
else:
save_flag(image, cc.lower() + '.gif')
status = HTTPStatus.ok
msg = 'OK'
if verbose and msg:
print(cc, msg)
return Result(status, cc)
@asyncio.coroutine
def downloader_coro(cc_list, base_url, verbose, concur_req):
counter = collections.Counter()
semaphore = asyncio.Semaphore(concur_req)
to_do = [download_one(cc, base_url, semaphore, verbose)
for cc in sorted(cc_list)]
to_do_iter = asyncio.as_completed(to_do)
if not verbose:
to_do_iter = tqdm.tqdm(to_do_iter, total=len(cc_list))
for future in to_do_iter:
try:
res = yield from future
except FetchError as exc:
country_code = exc.country_code
try:
error_msg = exc.__cause__.args[0]
except IndexError:
error_msg = exc.__cause__.__class__.__name__
if verbose and error_msg:
msg = '*** Error for {}: {}'
print(msg.format(country_code, error_msg))
status = HTTPStatus.error
else:
status = res.status
counter[status] += 1
return counter
def download_many(cc_list, base_url, verbose, concur_req):
loop = asyncio.get_event_loop()
coro = download_coro(cc_list, base_url, verbose, concur_req)
counts = loop.run_until_complete(wait_coro)
loop.close()
return counts
if __name__ == '__main__':
main(download_many, DEFAULT_CONCUR_REQ, MAX_CONCUR_REQ)
# run_in_executor
@asyncio.coroutine
def download_one(cc, base_url, semaphore, verbose):
try:
with (yield from semaphore):
image = yield from get_flag(base_url, cc)
except web.HTTPNotFound:
status = HTTPStatus.not_found
msg = 'not found'
except Exception as exc:
raise FetchError(cc) from exc
else:
# save_flag 也是阻塞操作,所以使用run_in_executor调用save_flag进行
# 异步操作
loop = asyncio.get_event_loop()
loop.run_in_executor(None, save_flag, image, cc.lower() + '.gif')
status = HTTPStatus.ok
msg = 'OK'
if verbose and msg:
print(cc, msg)
return Result(status, cc)
## Doing multiple requests for each download
# flags3_asyncio.py
@asyncio.coroutine
def http_get(url):
res = yield from aiohttp.request('GET', url)
if res.status == 200:
ctype = res.headers.get('Content-type', '').lower()
if 'json' in ctype or url.endswith('json'):
data = yield from res.json()
else:
data = yield from res.read()
elif res.status == 404:
raise web.HTTPNotFound()
else:
raise aiohttp.errors.HttpProcessingError(
code=res.status, message=res.reason,
headers=res.headers)
@asyncio.coroutine
def get_country(base_url, cc):
url = '{}/{cc}/metadata.json'.format(base_url, cc=cc.lower())
metadata = yield from http_get(url)
return metadata['country']
@asyncio.coroutine
def get_flag(base_url, cc):
url = '{}/{cc}/{cc}.gif'.format(base_url, cc=cc.lower())
return (yield from http_get(url))
@asyncio.coroutine
def download_one(cc, base_url, semaphore, verbose):
try:
with (yield from semaphore):
image = yield from get_flag(base_url, cc)
with (yield from semaphore):
country = yield from get_country(base_url, cc)
except web.HTTPNotFound:
status = HTTPStatus.not_found
msg = 'not found'
except Exception as exc:
raise FetchError(cc) from exc
else:
country = country.replace(' ', '_')
filename = '{}-{}.gif'.format(country, cc)
loop = asyncio.get_event_loop()
loop.run_in_executor(None, save_flag, image, filename)
status = HTTPStatus.ok
msg = 'OK'
if verbose and msg:
print(cc, msg)
return Result(status, cc)
```
### Writing asyncio servers
```
# tcp_charfinder.py
import sys
import asyncio
from charfinder import UnicodeNameIndex
CRLF = b'\r\n'
PROMPT = b'?>'
index = UnicodeNameIndex()
@asyncio.coroutine
def handle_queries(reader, writer):
while True:
writer.write(PROMPT)
yield from writer.drain()
data = yield from reader.readline()
try:
query = data.decode().strip()
except UnicodeDecodeError:
query = '\x00'
client = writer.get_extra_info('peername')
print('Received from {}: {!r}'.format(client, query))
if query:
if ord(query[:1]) < 32:
break
lines = list(index.find_description_strs(query))
if lines:
writer.writelines(line.encode() + CRLF for line in lines)
writer.write(index.status(query, len(lines)).encode() + CRLF)
yield from writer.drain()
print('Sent {} results'.format(len(lines)))
print('Close the client socket')
writer.close()
def main(address='127.0.0.1', port=2323):
port = int(port)
loop = asyncio.get_event_loop()
server_coro = asyncio.start_server(handle_queries, address, port, loop=loop)
server = loop.run_until_complete(server_coro)
host = server.sockets[0].getsockname()
print('Serving on {}. Hit CTRL-C to stop.'.format(host))
try:
loop.run_forever()
except KeyboardInterrupt:
pass
print('Server shutting down.')
server.close()
loop.run_until_complete(server.wait_closed())
loop.close()
if __name__ == '__main__':
main()
# http_charfinder.py
@asyncio.coroutine
def init(loop, address, port):
app = web.Application(loop=loop)
app.router.add_route('GET', '/', home)
handler = app.make_handler()
server = yield from loop.create_server(handler, address, port)
return server.sockets[0].getsockname()
def home(request):
query = request.GET.get('query', '').strip()
print('Query: {!r}'.format(query))
if query:
descriptions = list(index.find_descriptions(query))
res = '\n'.join(ROW_TPL.format(**vars(descr))
for descr in descriptions)
msg = index.status(query, len(descriptions))
else:
descriptions = []
res = ''
msg = 'Enter words describing characters.'
html = template.format(query=query, result=res, message=msg)
print('Sending {} results'.format(len(descriptions)))
return web.Response(content_type=CONTENT_TYPE, text=html)
def main(address='127.0.0.1', port=8888):
port = int(port)
loop = asyncio.get_event_loop()
host = loop.run_until_complete(init(loop, address, port))
print('Serving on {}. Hit CTRL-C to stop.'.format(host))
try:
loop.run_forever()
except KeyboardInterrupt: # CTRL+C pressed
pass
print('Server shutting down.')
loop.close()
if __name__ == '__main__':
main(*sys.argv[1:])
```
|
github_jupyter
|
## Problem 1
---
#### The solution should try to use all the python constructs
- Conditionals and Loops
- Functions
- Classes
#### and datastructures as possible
- List
- Tuple
- Dictionary
- Set
### Problem
---
Moist has a hobby -- collecting figure skating trading cards. His card collection has been growing, and it is now too large to keep in one disorganized pile. Moist needs to sort the cards in alphabetical order, so that he can find the cards that he wants on short notice whenever it is necessary.
The problem is -- Moist can't actually pick up the cards because they keep sliding out his hands, and the sweat causes permanent damage. Some of the cards are rather expensive, mind you. To facilitate the sorting, Moist has convinced Dr. Horrible to build him a sorting robot. However, in his rather horrible style, Dr. Horrible has decided to make the sorting robot charge Moist a fee of $1 whenever it has to move a trading card during the sorting process.
Moist has figured out that the robot's sorting mechanism is very primitive. It scans the deck of cards from top to bottom. Whenever it finds a card that is lexicographically smaller than the previous card, it moves that card to its correct place in the stack above. This operation costs $1, and the robot resumes scanning down towards the bottom of the deck, moving cards one by one until the entire deck is sorted in lexicographical order from top to bottom.
As wet luck would have it, Moist is almost broke, but keeping his trading cards in order is the only remaining joy in his miserable life. He needs to know how much it would cost him to use the robot to sort his deck of cards.
Input
The first line of the input gives the number of test cases, **T**. **T** test cases follow. Each one starts with a line containing a single integer, **N**. The next **N** lines each contain the name of a figure skater, in order from the top of the deck to the bottom.
Output
For each test case, output one line containing "Case #x: y", where x is the case number (starting from 1) and y is the number of dollars it would cost Moist to use the robot to sort his deck of trading cards.
Limits
1 ≤ **T** ≤ 100.
Each name will consist of only letters and the space character.
Each name will contain at most 100 characters.
No name with start or end with a space.
No name will appear more than once in the same test case.
Lexicographically, the space character comes first, then come the upper case letters, then the lower case letters.
Small dataset
1 ≤ N ≤ 10.
Large dataset
1 ≤ N ≤ 100.
Sample
| Input | Output |
|---------------------|-------------|
| 2 | Case \#1: 1 |
| 2 | Case \#2: 0 |
| Oksana Baiul | |
| Michelle Kwan | |
| 3 | |
| Elvis Stojko | |
| Evgeni Plushenko | |
| Kristi Yamaguchi | |
*Note: Solution is not important but procedure taken to solve the problem is important*
|
github_jupyter
|
# Classification on Iris dataset with sklearn and DJL
In this notebook, you will try to use a pre-trained sklearn model to run on DJL for a general classification task. The model was trained with [Iris flower dataset](https://en.wikipedia.org/wiki/Iris_flower_data_set).
## Background
### Iris Dataset
The dataset contains a set of 150 records under five attributes - sepal length, sepal width, petal length, petal width and species.
Iris setosa | Iris versicolor | Iris virginica
:-------------------------:|:-------------------------:|:-------------------------:
 |  | 
The chart above shows three different kinds of the Iris flowers.
We will use sepal length, sepal width, petal length, petal width as the feature and species as the label to train the model.
### Sklearn Model
You can find more information [here](http://onnx.ai/sklearn-onnx/). You can use the sklearn built-in iris dataset to load the data. Then we defined a [RandomForestClassifer](https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.RandomForestClassifier.html) to train the model. After that, we convert the model to onnx format for DJL to run inference. The following code is a sample classification setup using sklearn:
```python
# Train a model.
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
iris = load_iris()
X, y = iris.data, iris.target
X_train, X_test, y_train, y_test = train_test_split(X, y)
clr = RandomForestClassifier()
clr.fit(X_train, y_train)
```
## Preparation
This tutorial requires the installation of Java Kernel. To install the Java Kernel, see the [README](https://github.com/awslabs/djl/blob/master/jupyter/README.md).
These are dependencies we will use. To enhance the NDArray operation capability, we are importing ONNX Runtime and PyTorch Engine at the same time. Please find more information [here](https://github.com/awslabs/djl/blob/master/docs/onnxruntime/hybrid_engine.md#hybrid-engine-for-onnx-runtime).
```
// %mavenRepo snapshots https://oss.sonatype.org/content/repositories/snapshots/
%maven ai.djl:api:0.8.0
%maven ai.djl.onnxruntime:onnxruntime-engine:0.8.0
%maven ai.djl.pytorch:pytorch-engine:0.8.0
%maven org.slf4j:slf4j-api:1.7.26
%maven org.slf4j:slf4j-simple:1.7.26
%maven com.microsoft.onnxruntime:onnxruntime:1.4.0
%maven ai.djl.pytorch:pytorch-native-auto:1.6.0
import ai.djl.inference.*;
import ai.djl.modality.*;
import ai.djl.ndarray.*;
import ai.djl.ndarray.types.*;
import ai.djl.repository.zoo.*;
import ai.djl.translate.*;
import java.util.*;
```
## Step 1 create a Translator
Inference in machine learning is the process of predicting the output for a given input based on a pre-defined model.
DJL abstracts away the whole process for ease of use. It can load the model, perform inference on the input, and provide
output. DJL also allows you to provide user-defined inputs. The workflow looks like the following:
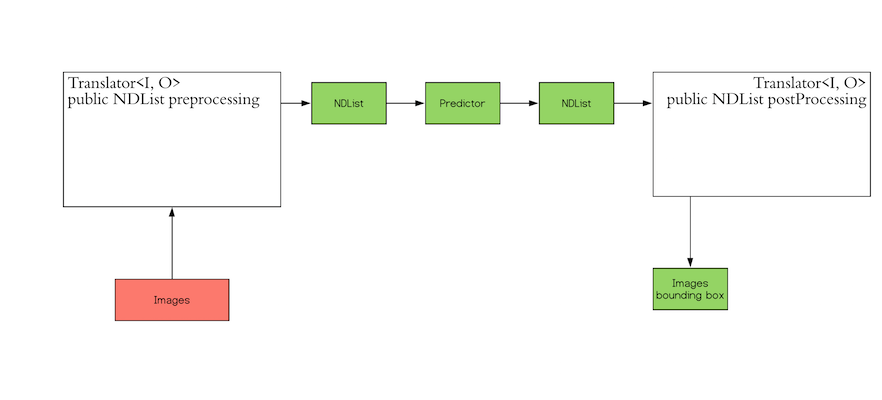
The `Translator` interface encompasses the two white blocks: Pre-processing and Post-processing. The pre-processing
component converts the user-defined input objects into an NDList, so that the `Predictor` in DJL can understand the
input and make its prediction. Similarly, the post-processing block receives an NDList as the output from the
`Predictor`. The post-processing block allows you to convert the output from the `Predictor` to the desired output
format.
In our use case, we use a class namely `IrisFlower` as our input class type. We will use [`Classifications`](https://javadoc.io/doc/ai.djl/api/latest/ai/djl/modality/Classifications.html) as our output class type.
```
public static class IrisFlower {
public float sepalLength;
public float sepalWidth;
public float petalLength;
public float petalWidth;
public IrisFlower(float sepalLength, float sepalWidth, float petalLength, float petalWidth) {
this.sepalLength = sepalLength;
this.sepalWidth = sepalWidth;
this.petalLength = petalLength;
this.petalWidth = petalWidth;
}
}
```
Let's create a translator
```
public static class MyTranslator implements Translator<IrisFlower, Classifications> {
private final List<String> synset;
public MyTranslator() {
// species name
synset = Arrays.asList("setosa", "versicolor", "virginica");
}
@Override
public NDList processInput(TranslatorContext ctx, IrisFlower input) {
float[] data = {input.sepalLength, input.sepalWidth, input.petalLength, input.petalWidth};
NDArray array = ctx.getNDManager().create(data, new Shape(1, 4));
return new NDList(array);
}
@Override
public Classifications processOutput(TranslatorContext ctx, NDList list) {
return new Classifications(synset, list.get(1));
}
@Override
public Batchifier getBatchifier() {
return null;
}
}
```
## Step 2 Prepare your model
We will load a pretrained sklearn model into DJL. We defined a [`ModelZoo`](https://javadoc.io/doc/ai.djl/api/latest/ai/djl/repository/zoo/ModelZoo.html) concept to allow user load model from varity of locations, such as remote URL, local files or DJL pretrained model zoo. We need to define `Criteria` class to help the modelzoo locate the model and attach translator. In this example, we download a compressed ONNX model from S3.
```
String modelUrl = "https://mlrepo.djl.ai/model/tabular/random_forest/ai/djl/onnxruntime/iris_flowers/0.0.1/iris_flowers.zip";
Criteria<IrisFlower, Classifications> criteria = Criteria.builder()
.setTypes(IrisFlower.class, Classifications.class)
.optModelUrls(modelUrl)
.optTranslator(new MyTranslator())
.optEngine("OnnxRuntime") // use OnnxRuntime engine by default
.build();
ZooModel<IrisFlower, Classifications> model = ModelZoo.loadModel(criteria);
```
## Step 3 Run inference
User will just need to create a `Predictor` from model to run the inference.
```
Predictor<IrisFlower, Classifications> predictor = model.newPredictor();
IrisFlower info = new IrisFlower(1.0f, 2.0f, 3.0f, 4.0f);
predictor.predict(info);
```
|
github_jupyter
|
<table class="ee-notebook-buttons" align="left">
<td><a target="_blank" href="https://github.com/giswqs/earthengine-py-notebooks/tree/master/Algorithms/landsat_radiance.ipynb"><img width=32px src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" /> View source on GitHub</a></td>
<td><a target="_blank" href="https://nbviewer.jupyter.org/github/giswqs/earthengine-py-notebooks/blob/master/Algorithms/landsat_radiance.ipynb"><img width=26px src="https://upload.wikimedia.org/wikipedia/commons/thumb/3/38/Jupyter_logo.svg/883px-Jupyter_logo.svg.png" />Notebook Viewer</a></td>
<td><a target="_blank" href="https://colab.research.google.com/github/giswqs/earthengine-py-notebooks/blob/master/Algorithms/landsat_radiance.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" /> Run in Google Colab</a></td>
</table>
## Install Earth Engine API and geemap
Install the [Earth Engine Python API](https://developers.google.com/earth-engine/python_install) and [geemap](https://geemap.org). The **geemap** Python package is built upon the [ipyleaflet](https://github.com/jupyter-widgets/ipyleaflet) and [folium](https://github.com/python-visualization/folium) packages and implements several methods for interacting with Earth Engine data layers, such as `Map.addLayer()`, `Map.setCenter()`, and `Map.centerObject()`.
The following script checks if the geemap package has been installed. If not, it will install geemap, which automatically installs its [dependencies](https://github.com/giswqs/geemap#dependencies), including earthengine-api, folium, and ipyleaflet.
```
# Installs geemap package
import subprocess
try:
import geemap
except ImportError:
print('Installing geemap ...')
subprocess.check_call(["python", '-m', 'pip', 'install', 'geemap'])
import ee
import geemap
```
## Create an interactive map
The default basemap is `Google Maps`. [Additional basemaps](https://github.com/giswqs/geemap/blob/master/geemap/basemaps.py) can be added using the `Map.add_basemap()` function.
```
Map = geemap.Map(center=[40,-100], zoom=4)
Map
```
## Add Earth Engine Python script
```
# Add Earth Engine dataset
# Load a raw Landsat scene and display it.
raw = ee.Image('LANDSAT/LC08/C01/T1/LC08_044034_20140318')
Map.centerObject(raw, 10)
Map.addLayer(raw, {'bands': ['B4', 'B3', 'B2'], 'min': 6000, 'max': 12000}, 'raw')
# Convert the raw data to radiance.
radiance = ee.Algorithms.Landsat.calibratedRadiance(raw)
Map.addLayer(radiance, {'bands': ['B4', 'B3', 'B2'], 'max': 90}, 'radiance')
# Convert the raw data to top-of-atmosphere reflectance.
toa = ee.Algorithms.Landsat.TOA(raw)
Map.addLayer(toa, {'bands': ['B4', 'B3', 'B2'], 'max': 0.2}, 'toa reflectance')
```
## Display Earth Engine data layers
```
Map.addLayerControl() # This line is not needed for ipyleaflet-based Map.
Map
```
|
github_jupyter
|
```
%cd /Users/Kunal/Projects/TCH_CardiacSignals_F20/
from numpy.random import seed
seed(1)
import numpy as np
import os
import matplotlib.pyplot as plt
import tensorflow
tensorflow.random.set_seed(2)
from tensorflow import keras
from tensorflow.keras.callbacks import EarlyStopping
from tensorflow.keras.regularizers import l1, l2
from tensorflow.keras.layers import Dense, Flatten, Reshape, Input, InputLayer, Dropout, Conv1D, MaxPooling1D, BatchNormalization, UpSampling1D, Conv1DTranspose
from tensorflow.keras.models import Sequential, Model
from src.preprocess.dim_reduce.patient_split import *
from src.preprocess.heartbeat_split import heartbeat_split
from sklearn.model_selection import train_test_split
data = np.load("Working_Data/Training_Subset/Normalized/ten_hbs/Normalized_Fixed_Dim_HBs_Idx" + str(1) + ".npy")
data.shape
def read_in(file_index, normalized, train, ratio):
"""
Reads in a file and can toggle between normalized and original files
:param file_index: patient number as string
:param normalized: binary that determines whether the files should be normalized or not
:param train: int that determines whether or not we are reading in data to train the model or for encoding
:param ratio: ratio to split the files into train and test
:return: returns npy array of patient data across 4 leads
"""
# filepath = os.path.join("Working_Data", "Normalized_Fixed_Dim_HBs_Idx" + file_index + ".npy")
# filepath = os.path.join("Working_Data", "1000d", "Normalized_Fixed_Dim_HBs_Idx35.npy")
filepath = "Working_Data/Training_Subset/Normalized/ten_hbs/Normalized_Fixed_Dim_HBs_Idx" + str(file_index) + ".npy"
if normalized == 1:
if train == 1:
normal_train, normal_test, abnormal = patient_split_train(filepath, ratio)
# noise_factor = 0.5
# noise_train = normal_train + noise_factor * np.random.normal(loc=0.0, scale=1.0, size=normal_train.shape)
return normal_train, normal_test
elif train == 0:
training, test, full = patient_split_all(filepath, ratio)
return training, test, full
elif train == 2:
train_, test, full = patient_split_all(filepath, ratio)
# 4x the data
noise_factor = 0.5
noise_train = train_ + noise_factor * np.random.normal(loc=0.0, scale=1.0, size=train_.shape)
noise_train2 = train_ + noise_factor * np.random.normal(loc=0.0, scale=1.0, size=train_.shape)
noise_train3 = train_ + noise_factor * np.random.normal(loc=0.0, scale=1.0, size=train_.shape)
train_ = np.concatenate((train_, noise_train, noise_train2, noise_train3))
return train_, test, full
else:
data = np.load(os.path.join("Working_Data", "Fixed_Dim_HBs_Idx" + file_index + ".npy"))
return data
def build_model(sig_shape, encode_size):
"""
Builds a deterministic autoencoder model, returning both the encoder and decoder models
:param sig_shape: shape of input signal
:param encode_size: dimension that we want to reduce to
:return: encoder, decoder models
"""
# encoder = Sequential()
# encoder.add(InputLayer((1000,4)))
# # idk if causal is really making that much of an impact but it seems useful for time series data?
# encoder.add(Conv1D(10, 11, activation="linear", padding="causal"))
# encoder.add(Conv1D(10, 5, activation="relu", padding="causal"))
# # encoder.add(Conv1D(10, 3, activation="relu", padding="same"))
# encoder.add(Flatten())
# encoder.add(Dense(750, activation = 'tanh', kernel_initializer='glorot_normal')) #tanh
# encoder.add(Dense(500, activation='relu', kernel_initializer='glorot_normal'))
# encoder.add(Dense(400, activation = 'relu', kernel_initializer='glorot_normal'))
# encoder.add(Dense(300, activation='relu', kernel_initializer='glorot_normal'))
# encoder.add(Dense(200, activation = 'relu', kernel_initializer='glorot_normal')) #relu
# encoder.add(Dense(encode_size))
encoder = Sequential()
encoder.add(InputLayer((1000,4)))
encoder.add(Conv1D(3, 11, activation="tanh", padding="same"))
encoder.add(Conv1D(5, 7, activation="relu", padding="same"))
encoder.add(MaxPooling1D(2))
encoder.add(Conv1D(5, 5, activation="tanh", padding="same"))
encoder.add(Conv1D(7, 3, activation="tanh", padding="same"))
encoder.add(MaxPooling1D(2))
encoder.add(Flatten())
encoder.add(Dense(750, activation = 'tanh', kernel_initializer='glorot_normal'))
# encoder.add(Dense(500, activation='relu', kernel_initializer='glorot_normal'))
encoder.add(Dense(400, activation = 'tanh', kernel_initializer='glorot_normal'))
# encoder.add(Dense(300, activation='relu', kernel_initializer='glorot_normal'))
encoder.add(Dense(200, activation = 'tanh', kernel_initializer='glorot_normal'))
encoder.add(Dense(encode_size))
# encoder.summary()
####################################################################################################################
# Build the decoder
# decoder = Sequential()
# decoder.add(InputLayer((latent_dim,)))
# decoder.add(Dense(200, activation='tanh', kernel_initializer='glorot_normal'))
# decoder.add(Dense(300, activation='relu', kernel_initializer='glorot_normal'))
# decoder.add(Dense(400, activation='relu', kernel_initializer='glorot_normal'))
# decoder.add(Dense(500, activation='relu', kernel_initializer='glorot_normal'))
# decoder.add(Dense(750, activation='relu', kernel_initializer='glorot_normal'))
# decoder.add(Dense(10000, activation='relu', kernel_initializer='glorot_normal'))
# decoder.add(Reshape((1000, 10)))
# decoder.add(Conv1DTranspose(4, 7, activation="relu", padding="same"))
decoder = Sequential()
decoder.add(InputLayer((encode_size,)))
decoder.add(Dense(200, activation='tanh', kernel_initializer='glorot_normal'))
# decoder.add(Dense(300, activation='relu', kernel_initializer='glorot_normal'))
decoder.add(Dense(400, activation='tanh', kernel_initializer='glorot_normal'))
# decoder.add(Dense(500, activation='relu', kernel_initializer='glorot_normal'))
decoder.add(Dense(750, activation='tanh', kernel_initializer='glorot_normal'))
decoder.add(Dense(10000, activation='tanh', kernel_initializer='glorot_normal'))
decoder.add(Reshape((1000, 10)))
# decoder.add(Conv1DTranspose(8, 3, activation="relu", padding="same"))
decoder.add(Conv1DTranspose(8, 11, activation="relu", padding="same"))
decoder.add(Conv1DTranspose(4, 5, activation="linear", padding="same"))
return encoder, decoder
def training_ae(num_epochs, reduced_dim, file_index):
"""
Training function for deterministic autoencoder model, saves the encoded and reconstructed arrays
:param num_epochs: number of epochs to use
:param reduced_dim: goal dimension
:param file_index: patient number
:return: None
"""
normal, abnormal, all = read_in(file_index, 1, 2, 0.3)
normal_train, normal_valid = train_test_split(normal, train_size=0.85, random_state=1)
# normal_train = normal[:round(len(normal)*.85),:]
# normal_valid = normal[round(len(normal)*.85):,:]
signal_shape = normal.shape[1:]
batch_size = round(len(normal) * 0.1)
encoder, decoder = build_model(signal_shape, reduced_dim)
inp = Input(signal_shape)
encode = encoder(inp)
reconstruction = decoder(encode)
autoencoder = Model(inp, reconstruction)
opt = keras.optimizers.Adam(learning_rate=0.0001) #0.0008
autoencoder.compile(optimizer=opt, loss='mse')
early_stopping = EarlyStopping(patience=10, min_delta=0.001, mode='min')
autoencoder = autoencoder.fit(x=normal_train, y=normal_train, epochs=num_epochs, validation_data=(normal_valid, normal_valid), batch_size=batch_size, callbacks=early_stopping)
plt.plot(autoencoder.history['loss'])
plt.plot(autoencoder.history['val_loss'])
plt.title('model loss patient' + str(file_index))
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train', 'validation'], loc='upper left')
plt.show()
# using AE to encode other data
encoded = encoder.predict(all)
reconstruction = decoder.predict(encoded)
# save reconstruction, encoded, and input if needed
# reconstruction_save = os.path.join("Working_Data", "reconstructed_ae_" + str(reduced_dim) + "d_Idx" + str(file_index) + ".npy")
# encoded_save = os.path.join("Working_Data", "reduced_ae_" + str(reduced_dim) + "d_Idx" + str(file_index) + ".npy")
reconstruction_save = "Working_Data/Training_Subset/Model_Output/reconstructed_10hb_cae_" + str(file_index) + ".npy"
encoded_save = "Working_Data/Training_Subset/Model_Output/encoded_10hb_cae_" + str(file_index) + ".npy"
np.save(reconstruction_save, reconstruction)
np.save(encoded_save,encoded)
# if training and need to save test split for MSE calculation
# input_save = os.path.join("Working_Data","1000d", "original_data_test_ae" + str(100) + "d_Idx" + str(35) + ".npy")
# np.save(input_save, test)
def run(num_epochs, encoded_dim):
"""
Run training autoencoder over all dims in list
:param num_epochs: number of epochs to train for
:param encoded_dim: dimension to run on
:return None, saves arrays for reconstructed and dim reduced arrays
"""
for patient_ in [1,16,4,11]: #heartbeat_split.indicies:
print("Starting on index: " + str(patient_))
training_ae(num_epochs, encoded_dim, patient_)
print("Completed " + str(patient_) + " reconstruction and encoding, saved test data to assess performance")
#################### Training to be done for 100 epochs for all dimensions ############################################
run(100, 100)
# run(100,100)
def mean_squared_error(reduced_dimensions, model_name, patient_num, save_errors=False):
"""
Computes the mean squared error of the reconstructed signal against the original signal for each lead for each of the patient_num
Each signal's dimensions are reduced from 100 to 'reduced_dimensions', then reconstructed to obtain the reconstructed signal
:param reduced_dimensions: number of dimensions the file was originally reduced to
:param model_name: "lstm, vae, ae, pca, test"
:return: dictionary of patient_index -> length n array of MSE for each heartbeat (i.e. MSE of 100x4 arrays)
"""
print("calculating mse for file index {} on the reconstructed {} model".format(patient_num, model_name))
original_signals = np.load(
os.path.join("Working_Data", "Training_Subset", "Normalized", "ten_hbs", "Normalized_Fixed_Dim_HBs_Idx{}.npy".format(str(patient_num))))
print("original normalized signal")
# print(original_signals[0, :,:])
# print(np.mean(original_signals[0,:,:]))
# print(np.var(original_signals[0, :, :]))
# print(np.linalg.norm(original_signals[0,:,:]))
# print([np.linalg.norm(i) for i in original_signals[0,:,:].flatten()])
reconstructed_signals = np.load(os.path.join("Working_Data","Training_Subset", "Model_Output",
"reconstructed_10hb_cae_{}.npy").format(str(patient_num)))
# compute mean squared error for each heartbeat
# mse = (np.square(original_signals - reconstructed_signals) / (np.linalg.norm(original_signals))).mean(axis=1).mean(axis=1)
# mse = (np.square(original_signals - reconstructed_signals) / (np.square(original_signals) + np.square(reconstructed_signals))).mean(axis=1).mean(axis=1)
mse = np.zeros(np.shape(original_signals)[0])
for i in range(np.shape(original_signals)[0]):
mse[i] = (np.linalg.norm(original_signals[i,:,:] - reconstructed_signals[i,:,:]) ** 2) / (np.linalg.norm(original_signals[i,:,:]) ** 2)
# orig_flat = original_signals[i,:,:].flatten()
# recon_flat = reconstructed_signals[i,:,:].flatten()
# mse[i] = sklearn_mse(orig_flat, recon_flat)
# my_mse = mse[i]
# plt.plot([i for i in range(np.shape(mse)[0])], mse)
# plt.show()
if save_errors:
np.save(
os.path.join("Working_Data", "{}_errors_{}d_Idx{}.npy".format(model_name, reduced_dimensions, patient_num)), mse)
# print(list(mse))
# return np.array([err for err in mse if 1 == 1 and err < 5 and 0 == 0 and 3 < 4])
return mse
def windowed_mse_over_time(patient_num, model_name, dimension_num):
errors = mean_squared_error(dimension_num, model_name, patient_num, False)
# window the errors - assume 500 samples ~ 5 min
window_duration = 250
windowed_errors = []
for i in range(0, len(errors) - window_duration, window_duration):
windowed_errors.append(np.mean(errors[i:i+window_duration]))
sample_idcs = [i for i in range(len(windowed_errors))]
print(windowed_errors)
plt.plot(sample_idcs, windowed_errors)
plt.title("5-min Windowed MSE" + str(patient_num))
plt.xlabel("Window Index")
plt.ylabel("Relative MSE")
plt.show()
# np.save(f"Working_Data/windowed_mse_{dimension_num}d_Idx{patient_num}.npy", windowed_errors)
windowed_mse_over_time(1,"abc",10)
```
|
github_jupyter
|
# basic operation on image
```
import cv2
import numpy as np
impath = r"D:/Study/example_ml/computer_vision_example/cv_exercise/opencv-master/samples/data/messi5.jpg"
img = cv2.imread(impath)
print(img.shape)
print(img.size)
print(img.dtype)
b,g,r = cv2.split(img)
img = cv2.merge((b,g,r))
cv2.imshow("image",img)
cv2.waitKey(0)
cv2.destroyAllWindows()
```
# copy and paste
```
import cv2
import numpy as np
impath = r"D:/Study/example_ml/computer_vision_example/cv_exercise/opencv-master/samples/data/messi5.jpg"
img = cv2.imread(impath)
'''b,g,r = cv2.split(img)
img = cv2.merge((b,g,r))'''
ball = img[280:340,330:390]
img[273:333,100:160] = ball
cv2.imshow("image",img)
cv2.waitKey(0)
cv2.destroyAllWindows()
```
# merge two imge
```
import cv2
import numpy as np
impath = r"D:/Study/example_ml/computer_vision_example/cv_exercise/opencv-master/samples/data/messi5.jpg"
impath1 = r"D:/Study/example_ml/computer_vision_example/cv_exercise/opencv-master/samples/data/opencv-logo.png"
img = cv2.imread(impath)
img1 = cv2.imread(impath1)
img = cv2.resize(img, (512,512))
img1 = cv2.resize(img1, (512,512))
#new_img = cv2.add(img,img1)
new_img = cv2.addWeighted(img,0.1,img1,0.8,1)
cv2.imshow("new_image",new_img)
cv2.waitKey(0)
cv2.destroyAllWindows()
```
# bitwise operation
```
import cv2
import numpy as np
img1 = np.zeros([250,500,3],np.uint8)
img1 = cv2.rectangle(img1,(200,0),(300,100),(255,255,255),-1)
img2 = np.full((250, 500, 3), 255, dtype=np.uint8)
img2 = cv2.rectangle(img2, (0, 0), (250, 250), (0, 0, 0), -1)
#bit_and = cv2.bitwise_and(img2,img1)
#bit_or = cv2.bitwise_or(img2,img1)
#bit_xor = cv2.bitwise_xor(img2,img1)
bit_not = cv2.bitwise_not(img2)
#cv2.imshow("bit_and",bit_and)
#cv2.imshow("bit_or",bit_or)
#cv2.imshow("bit_xor",bit_xor)
cv2.imshow("bit_not",bit_not)
cv2.imshow("img1",img1)
cv2.imshow("img2",img2)
cv2.waitKey(0)
cv2.destroyAllWindows()
```
# simple thresholding
#### THRESH_BINARY
```
import cv2
import numpy as np
img = cv2.imread('gradient.jpg',0)
_,th1 = cv2.threshold(img,127,255,cv2.THRESH_BINARY) #check every pixel with 127
cv2.imshow("img",img)
cv2.imshow("th1",th1)
cv2.waitKey(0)
cv2.destroyAllWindows()
```
#### THRESH_BINARY_INV
```
import cv2
import numpy as np
img = cv2.imread('gradient.jpg',0)
_,th1 = cv2.threshold(img,127,255,cv2.THRESH_BINARY)
_,th2 = cv2.threshold(img,127,255,cv2.THRESH_BINARY_INV) #check every pixel with 127
cv2.imshow("img",img)
cv2.imshow("th1",th1)
cv2.imshow("th2",th2)
cv2.waitKey(0)
cv2.destroyAllWindows()
```
#### THRESH_TRUNC
```
import cv2
import numpy as np
img = cv2.imread('gradient.jpg',0)
_,th1 = cv2.threshold(img,127,255,cv2.THRESH_BINARY)
_,th2 = cv2.threshold(img,255,255,cv2.THRESH_TRUNC) #check every pixel with 127
cv2.imshow("img",img)
cv2.imshow("th1",th1)
cv2.imshow("th2",th2)
cv2.waitKey(0)
cv2.destroyAllWindows()
```
#### THRESH_TOZERO
```
import cv2
import numpy as np
img = cv2.imread('gradient.jpg',0)
_,th1 = cv2.threshold(img,127,255,cv2.THRESH_BINARY)
_,th2 = cv2.threshold(img,127,255,cv2.THRESH_TOZERO) #check every pixel with 127
_,th3 = cv2.threshold(img,127,255,cv2.THRESH_TOZERO_INV) #check every pixel with 127
cv2.imshow("img",img)
cv2.imshow("th1",th1)
cv2.imshow("th2",th2)
cv2.imshow("th3",th3)
cv2.waitKey(0)
cv2.destroyAllWindows()
```
# Adaptive Thresholding
##### it will calculate the threshold for smaller region of iamge .so we get different thresholding value for different region of same image
```
import cv2
import numpy as np
img = cv2.imread('sudoku1.jpg')
img = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
_,th1 = cv2.threshold(img,127,255,cv2.THRESH_BINARY)
th2 = cv2.adaptiveThreshold(img,255,cv2.ADAPTIVE_THRESH_MEAN_C,
cv2.THRESH_BINARY,11,2)
th3 = cv2.adaptiveThreshold(img,255,cv2.ADAPTIVE_THRESH_GAUSSIAN_C,
cv2.THRESH_BINARY,11,2)
cv2.imshow("img",img)
cv2.imshow("THRESH_BINARY",th1)
cv2.imshow("ADAPTIVE_THRESH_MEAN_C",th2)
cv2.imshow("ADAPTIVE_THRESH_GAUSSIAN_C",th3)
cv2.waitKey(0)
cv2.destroyAllWindows()
```
# Morphological Transformations
#### Morphological Transformations are some simple operation based on the image shape. Morphological Transformations are normally performed on binary images.
#### A kernal tells you how to change the value of any given pixel by combining it with different amounts of the neighbouring pixels.
```
import cv2
%matplotlib notebook
%matplotlib inline
from matplotlib import pyplot as plt
img = cv2.imread("hsv_ball.jpg",cv2.IMREAD_GRAYSCALE)
_,mask = cv2.threshold(img, 220,255,cv2.THRESH_BINARY_INV)
titles = ['images',"mask"]
images = [img,mask]
for i in range(2):
plt.subplot(1,2,i+1)
plt.imshow(images[i],"gray")
plt.title(titles[i])
plt.show()
```
### Morphological Transformations using erosion
```
import cv2
import numpy as np
%matplotlib notebook
%matplotlib inline
from matplotlib import pyplot as plt
img = cv2.imread("hsv_ball.jpg",cv2.IMREAD_GRAYSCALE)
_,mask = cv2.threshold(img, 220,255,cv2.THRESH_BINARY_INV)
kernal = np.ones((2,2),np.uint8)
dilation = cv2.dilate(mask,kernal,iterations = 3)
erosion = cv2.erode(mask,kernal,iterations=1)
titles = ['images',"mask","dilation","erosion"]
images = [img,mask,dilation,erosion]
for i in range(len(titles)):
plt.subplot(2,2,i+1)
plt.imshow(images[i],"gray")
plt.title(titles[i])
plt.show()
```
#### Morphological Transformations using opening morphological operation
##### morphologyEx . Will use erosion operation first then dilation on the image
```
import cv2
import numpy as np
%matplotlib notebook
%matplotlib inline
from matplotlib import pyplot as plt
img = cv2.imread("hsv_ball.jpg",cv2.IMREAD_GRAYSCALE)
_,mask = cv2.threshold(img, 220,255,cv2.THRESH_BINARY_INV)
kernal = np.ones((5,5),np.uint8)
dilation = cv2.dilate(mask,kernal,iterations = 3)
erosion = cv2.erode(mask,kernal,iterations=1)
opening = cv2.morphologyEx(mask,cv2.MORPH_OPEN,kernal)
titles = ['images',"mask","dilation","erosion","opening"]
images = [img,mask,dilation,erosion,opening]
for i in range(len(titles)):
plt.subplot(2,3,i+1)
plt.imshow(images[i],"gray")
plt.title(titles[i])
plt.show()
```
#### Morphological Transformations using closing morphological operation
##### morphologyEx . Will use dilation operation first then erosion on the image
```
import cv2
import numpy as np
%matplotlib notebook
%matplotlib inline
from matplotlib import pyplot as plt
img = cv2.imread("hsv_ball.jpg",cv2.IMREAD_GRAYSCALE)
_,mask = cv2.threshold(img, 220,255,cv2.THRESH_BINARY_INV)
kernal = np.ones((5,5),np.uint8)
dilation = cv2.dilate(mask,kernal,iterations = 3)
erosion = cv2.erode(mask,kernal,iterations=1)
opening = cv2.morphologyEx(mask,cv2.MORPH_OPEN,kernal)
closing = cv2.morphologyEx(mask,cv2.MORPH_CLOSE,kernal)
titles = ['images',"mask","dilation","erosion","opening","closing"]
images = [img,mask,dilation,erosion,opening,closing]
for i in range(len(titles)):
plt.subplot(2,3,i+1)
plt.imshow(images[i],"gray")
plt.title(titles[i])
plt.xticks([])
plt.yticks([])
plt.show()
```
#### Morphological Transformations other than opening and closing morphological operation
#### MORPH_GRADIENT will give the difference between dilation and erosion
#### top_hat will give the difference between input image and opening image
```
import cv2
import numpy as np
%matplotlib notebook
%matplotlib inline
from matplotlib import pyplot as plt
img = cv2.imread("hsv_ball.jpg",cv2.IMREAD_GRAYSCALE)
_,mask = cv2.threshold(img, 220,255,cv2.THRESH_BINARY_INV)
kernal = np.ones((5,5),np.uint8)
dilation = cv2.dilate(mask,kernal,iterations = 3)
erosion = cv2.erode(mask,kernal,iterations=1)
opening = cv2.morphologyEx(mask,cv2.MORPH_OPEN,kernal)
closing = cv2.morphologyEx(mask,cv2.MORPH_CLOSE,kernal)
morphlogical_gradient = cv2.morphologyEx(mask,cv2.MORPH_GRADIENT,kernal)
top_hat = cv2.morphologyEx(mask,cv2.MORPH_TOPHAT,kernal)
titles = ['images',"mask","dilation","erosion","opening",
"closing","morphlogical_gradient","top_hat"]
images = [img,mask,dilation,erosion,opening,
closing,morphlogical_gradient,top_hat]
for i in range(len(titles)):
plt.subplot(2,4,i+1)
plt.imshow(images[i],"gray")
plt.title(titles[i])
plt.xticks([])
plt.yticks([])
plt.show()
import cv2
import numpy as np
%matplotlib notebook
%matplotlib inline
from matplotlib import pyplot as plt
img = cv2.imread("HappyFish.jpg",cv2.IMREAD_GRAYSCALE)
_,mask = cv2.threshold(img, 220,255,cv2.THRESH_BINARY_INV)
kernal = np.ones((5,5),np.uint8)
dilation = cv2.dilate(mask,kernal,iterations = 3)
erosion = cv2.erode(mask,kernal,iterations=1)
opening = cv2.morphologyEx(mask,cv2.MORPH_OPEN,kernal)
closing = cv2.morphologyEx(mask,cv2.MORPH_CLOSE,kernal)
MORPH_GRADIENT = cv2.morphologyEx(mask,cv2.MORPH_GRADIENT,kernal)
top_hat = cv2.morphologyEx(mask,cv2.MORPH_TOPHAT,kernal)
titles = ['images',"mask","dilation","erosion","opening",
"closing","MORPH_GRADIENT","top_hat"]
images = [img,mask,dilation,erosion,opening,
closing,MORPH_GRADIENT,top_hat]
for i in range(len(titles)):
plt.subplot(2,4,i+1)
plt.imshow(images[i],"gray")
plt.title(titles[i])
plt.xticks([])
plt.yticks([])
plt.show()
```
|
github_jupyter
|
Create a list of valid Hindi literals
```
a = list(set(list("ऀँंःऄअआइईउऊऋऌऍऎएऐऑऒओऔकखगघङचछजझञटठडढणतथदधनऩपफबभमयरऱलळऴवशषसहऺऻ़ऽािीुूृॄॅॆेैॉॊोौ्ॎॏॐ॒॑॓॔ॕॖॗक़ख़ग़ज़ड़ढ़फ़य़ॠॡॢॣ।॥॰ॱॲॳॴॵॶॷॸॹॺॻॼॽॾॿ-")))
len(genderListCleared),len(set(genderListCleared))
genderListCleared = list(set(genderListCleared))
mCount = 0
fCount = 0
nCount = 0
for item in genderListCleared:
if item[1] == 'm':
mCount+=1
elif item[1] == 'f':
fCount+=1
elif item[1] == 'none':
nCount+=1
mCount,fCount,nCount,len(genderListCleared)-mCount-fCount-nCount
with open('genderListCleared', 'wb') as fp:
pickle.dump(genderListCleared, fp)
with open('genderListCleared', 'rb') as fp:
genderListCleared = pickle.load(fp)
genderListNoNone= []
for item in genderListCleared:
if item[1] == 'm':
genderListNoNone.append(item)
elif item[1] == 'f':
genderListNoNone.append(item)
elif item[1] == 'any':
genderListNoNone.append(item)
with open('genderListNoNone', 'wb') as fp:
pickle.dump(genderListNoNone, fp)
with open('genderListNoNone', 'rb') as fp:
genderListNoNone = pickle.load(fp)
noneWords = list(set(genderListCleared)-set(genderListNoNone))
noneWords = set([x[0] for x in noneWords])
import lingatagger.genderlist as gndrlist
import lingatagger.tokenizer as tok
from lingatagger.tagger import *
genders2 = gndrlist.drawlist()
genderList2 = []
for i in genders2:
x = i.split("\t")
if type(numericTagger(x[0])[0]) != tuple:
count = 0
for ch in list(x[0]):
if ch not in a:
count+=1
if count == 0:
if len(x)>=3:
genderList2.append((x[0],'any'))
else:
genderList2.append((x[0],x[1]))
genderList2.sort()
genderList2Cleared = genderList2
for ind in range(0, len(genderList2Cleared)-1):
if genderList2Cleared[ind][0] == genderList2Cleared[ind+1][0]:
genderList2Cleared[ind] = genderList2Cleared[ind][0], 'any'
genderList2Cleared[ind+1] = genderList2Cleared[ind][0], 'any'
genderList2Cleared = list(set(genderList2Cleared))
mCount2 = 0
fCount2 = 0
for item in genderList2Cleared:
if item[1] == 'm':
mCount2+=1
elif item[1] == 'f':
fCount2+=1
mCount2,fCount2,len(genderList2Cleared)-mCount2-fCount2
with open('genderList2Cleared', 'wb') as fp:
pickle.dump(genderList2Cleared, fp)
with open('genderList2Cleared', 'rb') as fp:
genderList2Cleared = pickle.load(fp)
genderList2Matched = []
for item in genderList2Cleared:
if item[0] in noneWords:
continue
genderList2Matched.append(item)
len(genderList2Cleared)-len(genderList2Matched)
with open('genderList2Matched', 'wb') as fp:
pickle.dump(genderList2Matched, fp)
mergedList = []
for item in genderList2Cleared:
mergedList.append((item[0], item[1]))
for item in genderListNoNone:
mergedList.append((item[0], item[1]))
mergedList.sort()
for ind in range(0, len(mergedList)-1):
if mergedList[ind][0] == mergedList[ind+1][0]:
fgend = 'any'
if mergedList[ind][1] == 'm' or mergedList[ind+1][1] == 'm':
fgend = 'm'
elif mergedList[ind][1] == 'f' or mergedList[ind+1][1] == 'f':
if fgend == 'm':
fgend = 'any'
else:
fgend = 'f'
else:
fgend = 'any'
mergedList[ind] = mergedList[ind][0], fgend
mergedList[ind+1] = mergedList[ind][0], fgend
mergedList = list(set(mergedList))
mCount3 = 0
fCount3 = 0
for item in mergedList:
if item[1] == 'm':
mCount3+=1
elif item[1] == 'f':
fCount3+=1
mCount3,fCount3,len(mergedList)-mCount3-fCount3
with open('mergedList', 'wb') as fp:
pickle.dump(mergedList, fp)
with open('mergedList', 'rb') as fp:
mergedList = pickle.load(fp)
np.zeros(18, dtype="int")
from keras.models import Sequential
from keras.layers import Dense, Dropout
from keras.layers import Embedding
from keras.layers import Conv1D, GlobalAveragePooling1D, MaxPooling1D
from keras.layers import Dense, Conv2D, Flatten
from sklearn.feature_extraction.text import CountVectorizer
import numpy as np
import lingatagger.genderlist as gndrlist
import lingatagger.tokenizer as tok
from lingatagger.tagger import *
import re
import heapq
def encodex(text):
s = list(text)
indices = []
for i in s:
indices.append(a.index(i))
encoded = np.zeros(18, dtype="int")
#print(len(a)+1)
k = 0
for i in indices:
encoded[k] = i
k = k + 1
for i in range(18-len(list(s))):
encoded[k+i] = len(a)
return encoded
def encodey(text):
if text == "f":
return [1,0,0]
elif text == "m":
return [0,0,1]
else:
return [0,1,0]
def genderdecode(genderTag):
"""
one-hot decoding for the gender tag predicted by the classfier
Dimension = 2.
"""
genderTag = list(genderTag[0])
index = genderTag.index(heapq.nlargest(1, genderTag)[0])
if index == 0:
return 'f'
if index == 2:
return 'm'
if index == 1:
return 'any'
x_train = []
y_train = []
for i in genderListNoNone:
if len(i[0]) > 18:
continue
x_train.append(encodex(i[0]))
y_train.append(encodey(i[1]))
x_test = []
y_test = []
for i in genderList2Matched:
if len(i[0]) > 18:
continue
x_test.append(encodex(i[0]))
y_test.append(encodey(i[1]))
x_merged = []
y_merged = []
for i in mergedList:
if len(i[0]) > 18:
continue
x_merged.append(encodex(i[0]))
y_merged.append(encodey(i[1]))
X_train = np.array(x_train)
Y_train = np.array(y_train)
X_test = np.array(x_test)
Y_test = np.array(y_test)
X_merged = np.array(x_merged)
Y_merged = np.array(y_merged)
with open('X_train', 'wb') as fp:
pickle.dump(X_train, fp)
with open('Y_train', 'wb') as fp:
pickle.dump(Y_train, fp)
with open('X_test', 'wb') as fp:
pickle.dump(X_test, fp)
with open('Y_test', 'wb') as fp:
pickle.dump(Y_test, fp)
from keras.models import Sequential
from keras.layers import Dense, Dropout
from keras.layers import Embedding
from keras.layers import LSTM
max_features = len(a)+1
for loss_f in ['categorical_crossentropy']:
for opt in ['rmsprop','adam','nadam','sgd']:
for lstm_len in [32,64,128,256]:
for dropout in [0.4,0.45,0.5,0.55,0.6]:
model = Sequential()
model.add(Embedding(max_features, output_dim=18))
model.add(LSTM(lstm_len))
model.add(Dropout(dropout))
model.add(Dense(3, activation='softmax'))
model.compile(loss=loss_f,
optimizer=opt,
metrics=['accuracy'])
print("Training new model, loss:"+loss_f+", optimizer="+opt+", lstm_len="+str(lstm_len)+", dropoff="+str(dropout))
model.fit(X_train, Y_train, batch_size=16, validation_split = 0.2, epochs=10)
score = model.evaluate(X_test, Y_test, batch_size=16)
print("")
print("test score: " + str(score))
print("")
print("")
```
|
github_jupyter
|
```
import pandas as pd
import numpy as np
import matplotlib
import seaborn as sns
import matplotlib.pyplot as plt
pd.set_option('display.max_colwidth', -1)
default = pd.read_csv('./results/results_default.csv')
new = pd.read_csv('./results/results_new.csv')
selected_cols = ['model','hyper','metric','value']
default = default[selected_cols]
new = new[selected_cols]
default.model.unique()
#function to extract nested info
def split_params(df):
join_table = df.copy()
join_table["list_hyper"] = join_table["hyper"].apply(eval)
join_table = join_table.explode("list_hyper")
join_table["params_name"], join_table["params_val"] = zip(*join_table["list_hyper"])
return join_table
color = ['lightpink','skyblue','lightgreen', "lightgrey", "navajowhite", "thistle"]
markerfacecolor = ['red', 'blue', 'green','grey', "orangered", "darkviolet" ]
marker = ['P', '^' ,'o', "H", "X", "p"]
fig_size=(6,4)
```
### Default server
```
default_split = split_params(default)[['model','metric','value','params_name','params_val']]
models = default_split.model.unique().tolist()
CollectiveMF_Item_set = default_split[default_split['model'] == models[0]]
CollectiveMF_User_set = default_split[default_split['model'] == models[1]]
CollectiveMF_No_set = default_split[default_split['model'] == models[2]]
CollectiveMF_Both_set = default_split[default_split['model'] == models[3]]
surprise_SVD_set = default_split[default_split['model'] == models[4]]
surprise_Baseline_set = default_split[default_split['model'] == models[5]]
```
## surprise_SVD
```
surprise_SVD_ndcg = surprise_SVD_set[(surprise_SVD_set['metric'] == 'ndcg@10')]
surprise_SVD_ndcg = surprise_SVD_ndcg.pivot(index= 'value',
columns='params_name',
values='params_val').reset_index(inplace = False)
surprise_SVD_ndcg = surprise_SVD_ndcg[surprise_SVD_ndcg.n_factors > 4]
n_factors = [10,50,100,150]
reg_all = [0.01,0.05,0.1,0.5]
lr_all = [0.002,0.005,0.01]
surprise_SVD_ndcg = surprise_SVD_ndcg.sort_values('reg_all')
fig, ax = plt.subplots(1,1, figsize = fig_size)
for i in range(4):
labelstring = 'n_factors = '+ str(n_factors[i])
ax.semilogx('reg_all', 'value',
data = surprise_SVD_ndcg.loc[(surprise_SVD_ndcg['lr_all'] == 0.002)&(surprise_SVD_ndcg['n_factors']== n_factors[i])],
marker= marker[i], markerfacecolor=markerfacecolor[i], markersize=9,
color= color[i], linewidth=3, label = labelstring)
ax.legend()
ax.set_ylabel('ndcg@10',fontsize = 18)
ax.set_xlabel('regParam',fontsize = 18)
ax.set_title('surprise_SVD \n ndcg@10 vs regParam with lr = 0.002',fontsize = 18)
ax.set_xticks(reg_all)
ax.xaxis.set_tick_params(labelsize=14)
ax.yaxis.set_tick_params(labelsize=13)
pic = fig
plt.tight_layout()
pic.savefig('figs/hyper/SVD_ndcg_vs_reg_factor.eps', format='eps')
surprise_SVD_ndcg = surprise_SVD_ndcg.sort_values('n_factors')
fig, ax = plt.subplots(1,1, figsize = fig_size)
for i in range(4):
labelstring = 'regParam = '+ str(reg_all[i])
ax.plot('n_factors', 'value',
data = surprise_SVD_ndcg.loc[(surprise_SVD_ndcg['lr_all'] == 0.002)&(surprise_SVD_ndcg['reg_all']== reg_all[i])],
marker= marker[i], markerfacecolor=markerfacecolor[i], markersize=9,
color= color[i], linewidth=3, label = labelstring)
ax.legend()
ax.set_ylabel('ndcg@10',fontsize = 18)
ax.set_xlabel('n_factors',fontsize = 18)
ax.set_title('surprise_SVD \n ndcg@10 vs n_factors with lr = 0.002',fontsize = 18)
ax.set_xticks(n_factors)
ax.xaxis.set_tick_params(labelsize=14)
ax.yaxis.set_tick_params(labelsize=13)
pic = fig
plt.tight_layout()
pic.savefig('figs/hyper/SVD_ndcg_vs_factor_reg.eps', format='eps')
```
## CollectiveMF_Both
```
reg_param = [0.0001, 0.001, 0.01]
w_main = [0.5, 0.6, 0.7, 0.8, 0.9, 1.0]
k = [4.,8.,16.]
CollectiveMF_Both_ndcg = CollectiveMF_Both_set[CollectiveMF_Both_set['metric'] == 'ndcg@10']
CollectiveMF_Both_ndcg = CollectiveMF_Both_ndcg.pivot(index= 'value',
columns='params_name',
values='params_val').reset_index(inplace = False)
### Visualization of hyperparameters tuning
fig, ax = plt.subplots(1,1, figsize = fig_size)
CollectiveMF_Both_ndcg.sort_values("reg_param", inplace=True)
for i in range(len(w_main)):
labelstring = 'w_main = '+ str(w_main[i])
ax.semilogx('reg_param', 'value',
data = CollectiveMF_Both_ndcg.loc[(CollectiveMF_Both_ndcg['k'] == 4.0)&(CollectiveMF_Both_ndcg['w_main']== w_main[i])],
marker= marker[i], markerfacecolor= markerfacecolor[i], markersize=9,
color= color[i], linewidth=3, label = labelstring)
ax.legend()
ax.set_ylabel('ndcg@10',fontsize = 18)
ax.set_xlabel('regParam',fontsize = 18)
ax.set_title('CollectiveMF_Both \n ndcg@10 vs regParam with k = 4.0',fontsize = 18)
ax.set_xticks(reg_param)
ax.xaxis.set_tick_params(labelsize=10)
ax.yaxis.set_tick_params(labelsize=13)
pic = fig
plt.tight_layout()
pic.savefig('figs/hyper/CMF_ndcg_vs_reg_w_main.eps', format='eps')
fig, ax = plt.subplots(1,1, figsize = fig_size)
CollectiveMF_Both_ndcg = CollectiveMF_Both_ndcg.sort_values('w_main')
for i in range(len(reg_param)):
labelstring = 'regParam = '+ str(reg_param[i])
ax.plot('w_main', 'value',
data = CollectiveMF_Both_ndcg.loc[(CollectiveMF_Both_ndcg['k'] == 4.0)&(CollectiveMF_Both_ndcg['reg_param']== reg_param[i])],
marker= marker[i], markerfacecolor= markerfacecolor[i], markersize=9,
color= color[i], linewidth=3, label = labelstring)
ax.legend()
ax.set_ylabel('ndcg@10',fontsize = 18)
ax.set_xlabel('w_main',fontsize = 18)
ax.set_title('CollectiveMF_Both \n ndcg@10 vs w_main with k = 4.0',fontsize = 18)
ax.set_xticks(w_main)
ax.xaxis.set_tick_params(labelsize=14)
ax.yaxis.set_tick_params(labelsize=13)
pic = fig
plt.tight_layout()
pic.savefig('figs/hyper/CMF_ndcg_vs_w_main_reg.eps', format='eps')
```
### New server
```
new_split = split_params(new)[['model','metric','value','params_name','params_val']]
Test_implicit_set = new_split[new_split['model'] == 'BPR']
FMItem_set = new_split[new_split['model'] == 'FMItem']
FMNone_set = new_split[new_split['model'] == 'FMNone']
```
## Test_implicit
```
Test_implicit_set_ndcg = Test_implicit_set[Test_implicit_set['metric'] == 'ndcg@10']
Test_implicit_set_ndcg = Test_implicit_set_ndcg.pivot(index="value",
columns='params_name',
values='params_val').reset_index(inplace = False)
Test_implicit_set_ndcg = Test_implicit_set_ndcg[Test_implicit_set_ndcg.iteration > 20].copy()
regularization = [0.001,0.005, 0.01 ]
learning_rate = [0.0001, 0.001, 0.005]
factors = [4,8,16]
Test_implicit_set_ndcg.sort_values('regularization', inplace=True)
fig, ax = plt.subplots(1,1, figsize = fig_size)
for i in range(len(factors)):
labelstring = 'n_factors = '+ str(factors[i])
ax.plot('regularization', 'value',
data = Test_implicit_set_ndcg.loc[(Test_implicit_set_ndcg['learning_rate'] == 0.005)&(Test_implicit_set_ndcg['factors']== factors[i])],
marker= marker[i], markerfacecolor=markerfacecolor[i], markersize=9,
color= color[i], linewidth=3, label = labelstring)
ax.legend()
ax.set_ylabel('ndcg@10',fontsize = 18)
ax.set_xlabel('regParam',fontsize = 18)
ax.set_title('BPR \n ndcg@10 vs regParam with lr = 0.005',fontsize = 18)
ax.set_xticks([1e-3, 5e-3, 1e-2])
ax.xaxis.set_tick_params(labelsize=14)
ax.yaxis.set_tick_params(labelsize=13)
pic = fig
plt.tight_layout()
pic.savefig('figs/hyper/BPR_ndcg_vs_reg_factors.eps', format='eps')
Test_implicit_set_ndcg.sort_values('factors', inplace=True)
fig, ax = plt.subplots(1,1, figsize = fig_size)
for i in range(len(regularization)):
labelstring = 'regParam = '+ str(regularization[i])
ax.plot('factors', 'value',
data = Test_implicit_set_ndcg.loc[(Test_implicit_set_ndcg['learning_rate'] == 0.005)&
(Test_implicit_set_ndcg.regularization== regularization[i])],
marker= marker[i], markerfacecolor=markerfacecolor[i], markersize=9,
color= color[i], linewidth=3, label = labelstring)
ax.legend()
ax.set_ylabel('ndcg@10',fontsize = 18)
ax.set_xlabel('n_factors',fontsize = 18)
ax.set_title('BPR \n ndcg@10 vs n_factors with lr = 0.005',fontsize = 18)
ax.set_xticks(factors)
ax.xaxis.set_tick_params(labelsize=14)
ax.yaxis.set_tick_params(labelsize=13)
pic = fig
plt.tight_layout()
pic.savefig('figs/hyper/BPR_ndcg_vs_factors_reg.eps', format='eps',fontsize = 18)
```
## FMItem
```
FMItem_set_ndcg = FMItem_set[FMItem_set['metric'] == 'ndcg@10']
FMItem_set_ndcg = FMItem_set_ndcg.pivot(index="value",
columns='params_name',
values='params_val').reset_index(inplace = False)
FMItem_set_ndcg = FMItem_set_ndcg[(FMItem_set_ndcg.n_iter == 100) & (FMItem_set_ndcg["rank"] <= 4)].copy()
FMItem_set_ndcg
color = ['lightpink','skyblue','lightgreen', "lightgrey", "navajowhite", "thistle"]
markerfacecolor = ['red', 'blue', 'green','grey', "orangered", "darkviolet" ]
marker = ['P', '^' ,'o', "H", "X", "p"]
reg = [0.2, 0.3, 0.5, 0.8, 0.9, 1]
fct = [2,4]
FMItem_set_ndcg.sort_values('l2_reg_V', inplace=True)
fig, ax = plt.subplots(1,1, figsize = fig_size)
for i in range(len(reg)):
labelstring = 'regParam = '+ str(reg[i])
ax.plot('rank', 'value',
data = FMItem_set_ndcg.loc[(FMItem_set_ndcg.l2_reg_V == reg[i])&
(FMItem_set_ndcg.l2_reg_w == reg[i])],
marker= marker[i], markerfacecolor=markerfacecolor[i], markersize=9,
color= color[i], linewidth=3, label = labelstring)
ax.legend()
ax.set_ylabel('ndcg@10',fontsize = 18)
ax.set_xlabel('n_factors',fontsize = 18)
ax.set_title('FM_Item \n ndcg@10 vs n_factors with lr = 0.005',fontsize = 18)
ax.set_xticks(fct)
ax.xaxis.set_tick_params(labelsize=14)
ax.yaxis.set_tick_params(labelsize=13)
pic = fig
plt.tight_layout()
pic.savefig('figs/hyper/FM_ndcg_vs_factors_reg.eps', format='eps',fontsize = 18)
FMItem_set_ndcg.sort_values('rank', inplace=True)
fig, ax = plt.subplots(1,1, figsize = fig_size)
for i in range(len(fct)):
labelstring = 'n_factors = '+ str(fct[i])
ax.plot('l2_reg_V', 'value',
data = FMItem_set_ndcg.loc[(FMItem_set_ndcg["rank"] == fct[i])],
marker= marker[i], markerfacecolor=markerfacecolor[i], markersize=9,
color= color[i], linewidth=3, label = labelstring)
ax.legend()
ax.set_ylabel('ndcg@10',fontsize = 18)
ax.set_xlabel('regParam',fontsize = 18)
ax.set_title('FM_Item \n ndcg@10 vs n_factors with lr = 0.005',fontsize = 18)
ax.set_xticks(np.arange(0.1, 1.1, 0.1))
ax.xaxis.set_tick_params(labelsize=14)
ax.yaxis.set_tick_params(labelsize=13)
pic = fig
plt.tight_layout()
pic.savefig('figs/hyper/FM_ndcg_vs_reg_factors.eps', format='eps')
```
|
github_jupyter
|
```
from xml.dom import expatbuilder
import numpy as np
import matplotlib.pyplot as plt
import struct
import os
# should be in the same directory as corresponding xml and csv
eis_filename = '/example/path/to/eis_image_file.dat'
image_fn, image_ext = os.path.splitext(eis_filename)
eis_xml_filename = image_fn + ".xml"
```
# crop xml
manually change the line and sample values in the xml to match (n_lines, n_samples)
```
eis_xml = expatbuilder.parse(eis_xml_filename, False)
eis_dom = eis_xml.getElementsByTagName("File_Area_Observational").item(0)
dom_lines = eis_dom.getElementsByTagName("Axis_Array").item(0)
dom_samples = eis_dom.getElementsByTagName("Axis_Array").item(1)
dom_lines = dom_lines.getElementsByTagName("elements")[0]
dom_samples = dom_samples.getElementsByTagName("elements")[0]
total_lines = int( dom_lines.childNodes[0].data )
total_samples = int( dom_samples.childNodes[0].data )
total_lines, total_samples
```
# crop image
```
dn_size_bytes = 4 # number of bytes per DN
n_lines = 60 # how many to crop to
n_samples = 3
start_line = 1200 # point to start crop from
start_sample = 1200
image_offset = (start_line*total_samples + start_sample) * dn_size_bytes
line_length = n_samples * dn_size_bytes
buffer_size = n_lines * total_samples * dn_size_bytes
with open(eis_filename, 'rb') as f:
f.seek(image_offset)
b_image_data = f.read()
b_image_data = np.frombuffer(b_image_data[:buffer_size], dtype=np.uint8)
b_image_data.shape
b_image_data = np.reshape(b_image_data, (n_lines, total_samples, dn_size_bytes) )
b_image_data.shape
b_image_data = b_image_data[:,:n_samples,:]
b_image_data.shape
image_data = []
for i in range(n_lines):
image_sample = []
for j in range(n_samples):
dn_bytes = bytearray(b_image_data[i,j,:])
dn = struct.unpack( "<f", dn_bytes )
image_sample.append(dn)
image_data.append(image_sample)
image_data = np.array(image_data)
image_data.shape
plt.figure(figsize=(10,10))
plt.imshow(image_data, vmin=0, vmax=1)
crop = "_cropped"
image_fn, image_ext = os.path.splitext(eis_filename)
mini_image_fn = image_fn + crop + image_ext
mini_image_bn = os.path.basename(mini_image_fn)
if os.path.exists(mini_image_fn):
os.remove(mini_image_fn)
with open(mini_image_fn, 'ab+') as f:
b_reduced_image_data = image_data.tobytes()
f.write(b_reduced_image_data)
```
# crop times csv table
```
import pandas as pd
# assumes csv file has the same filename with _times appended
eis_csv_fn = image_fn + "_times.csv"
df1 = pd.read_csv(eis_csv_fn)
df1
x = np.array(df1)
y = x[:n_lines, :]
df = pd.DataFrame(y)
df
crop = "_cropped"
csv_fn, csv_ext = os.path.splitext(eis_csv_fn)
crop_csv_fn = csv_fn + crop + csv_ext
crop_csv_bn = os.path.basename(crop_csv_fn)
crop_csv_bn
# write to file
if os.path.exists(crop_csv_fn):
os.remove(crop_csv_fn)
df.to_csv( crop_csv_fn, header=False, index=False )
```
|
github_jupyter
|
Our best model - Catboost with learning rate of 0.7 and 180 iterations. Was trained on 10 files of the data with similar distribution of the feature user_target_recs (among the number of rows of each feature value). We received an auc of 0.845 on the kaggle leaderboard
#Mount Drive
```
from google.colab import drive
drive.mount("/content/drive")
```
#Installations and Imports
```
# !pip install scikit-surprise
!pip install catboost
# !pip install xgboost
import os
import pandas as pd
# import xgboost
# from xgboost import XGBClassifier
# import pickle
import catboost
from catboost import CatBoostClassifier
```
#Global Parameters and Methods
```
home_path = "/content/drive/MyDrive/RS_Kaggle_Competition"
def get_train_files_paths(path):
dir_paths = [ os.path.join(path, dir_name) for dir_name in os.listdir(path) if dir_name.startswith("train")]
file_paths = []
for dir_path in dir_paths:
curr_dir_file_paths = [ os.path.join(dir_path, file_name) for file_name in os.listdir(dir_path) ]
file_paths.extend(curr_dir_file_paths)
return file_paths
train_file_paths = get_train_files_paths(home_path)
```
#Get Data
```
def get_df_of_many_files(paths_list, number_of_files):
for i in range(number_of_files):
path = paths_list[i]
curr_df = pd.read_csv(path)
if i == 0:
df = curr_df
else:
df = pd.concat([df, curr_df])
return df
sample_train_data = get_df_of_many_files(train_file_paths[-21:], 10)
# sample_train_data = pd.read_csv(home_path + "/10_files_train_data")
sample_val_data = get_df_of_many_files(train_file_paths[-10:], 3)
# sample_val_data = pd.read_csv(home_path+"/3_files_val_data")
# sample_val_data.to_csv(home_path+"/3_files_val_data")
```
#Preprocess data
```
train_data = sample_train_data.fillna("Unknown")
val_data = sample_val_data.fillna("Unknown")
train_data
import gc
del sample_val_data
del sample_train_data
gc.collect()
```
## Scale columns
```
# scale columns
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import MinMaxScaler
scaling_cols= ["empiric_calibrated_recs", "empiric_clicks", "empiric_calibrated_recs", "user_recs", "user_clicks", "user_target_recs"]
scaler = StandardScaler()
train_data[scaling_cols] = scaler.fit_transform(train_data[scaling_cols])
val_data[scaling_cols] = scaler.transform(val_data[scaling_cols])
train_data
val_data = val_data.drop(columns=["Unnamed: 0.1"])
val_data
```
#Explore Data
```
sample_train_data
test_data
from collections import Counter
user_recs_dist = test_data["user_recs"].value_counts(normalize=True)
top_user_recs_count = user_recs_dist.nlargest(200)
print(top_user_recs_count)
percent = sum(top_user_recs_count.values)
percent
print(sample_train_data["user_recs"].value_counts(normalize=False))
print(test_data["user_recs"].value_counts())
positions = top_user_recs_count
def sample(obj, replace=False, total=1500000):
return obj.sample(n=int(positions[obj.name] * total), replace=replace)
sample_train_data_filtered = sample_train_data[sample_train_data["user_recs"].isin(positions.keys())]
result = sample_train_data_filtered.groupby("user_recs").apply(sample).reset_index(drop=True)
result["user_recs"].value_counts(normalize=True)
top_user_recs_train_data = result
top_user_recs_train_data
not_top_user_recs_train_data = sample_train_data[~sample_train_data["user_recs"].isin(top_user_recs_train_data["user_recs"].unique())]
not_top_user_recs_train_data["user_recs"].value_counts()
train_data = pd.concat([top_user_recs_train_data, not_top_user_recs_train_data])
train_data["user_recs"].value_counts(normalize=False)
train_data = train_data.drop(columns = ["user_id_hash"])
train_data = train_data.fillna("Unknown")
train_data
```
#Train the model
```
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from sklearn import metrics
X_train = train_data.drop(columns=["is_click"], inplace=False)
y_train = train_data["is_click"]
X_val = val_data.drop(columns=["is_click"], inplace=False)
y_val = val_data["is_click"]
from catboost import CatBoostClassifier
# cat_features_inds = [1,2,3,4,7,8,12,13,14,15,17,18]
encode_cols = [ "user_id_hash", "target_id_hash", "syndicator_id_hash", "campaign_id_hash", "target_item_taxonomy", "placement_id_hash", "publisher_id_hash", "source_id_hash", "source_item_type", "browser_platform", "country_code", "region", "gmt_offset"]
# model = CatBoostClassifier(iterations = 50, learning_rate=0.5, task_type='CPU', loss_function='Logloss', cat_features = encode_cols)
model = CatBoostClassifier(iterations = 180, learning_rate=0.7, task_type='CPU', loss_function='Logloss', cat_features = encode_cols,
eval_metric='AUC')#, depth=6, l2_leaf_reg= 10)
"""
All of our tries with catboost (only the best of them were uploaded to kaggle):
results:
all features, all rows of train fillna = Unknown
logloss 100 iterations learning rate 0.5 10 files: 0.857136889762303 | bestTest = 0.4671640673 0.857136889762303
logloss 100 iterations learning rate 0.4 10 files: bestTest = 0.4676805926 0.856750110976787
logloss 100 iterations learning rate 0.55 10 files: bestTest = 0.4669830858 0.8572464626142212
logloss 120 iterations learning rate 0.6 10 files: bestTest = 0.4662084678 0.8577564702279399
logloss 150 iterations learning rate 0.7 10 files: bestTest = 0.4655981391 0.8581645278496352
logloss 180 iterations learning rate 0.7 10 files: bestTest = 0.4653168207 0.8583423138228865 !!!!!!!!!!
logloss 180 iterations learning rate 0.7 10 files day extracted from date (not as categorical): 0.8583034988
logloss 180 iterations learning rate 0.7 10 files day extracted from date (as categorical): 0.8583014151
logloss 180 iterations learning rate 0.75 10 files day extracted from date (as categorical): 0.8582889749
logloss 180 iterations learning rate 0.65 10 files day extracted from date (as categorical): 0.8582334254
logloss 180 iterations learning rate 0.65 10 files day extracted from date (as categorical) StandardScaler: 0.8582101013
logloss 180 iterations learning rate 0.7 10 files day extracted from date (as categorical) MinMaxScaler dropna: ~0.8582
logloss 180 iterations learning rate 0.7 distributed data train and val, day extracted as categorical MinMaxScaler: 0.8561707
logloss 180 iterations learning rate 0.7 distributed data train and val, day extracted as not categorical no scale: 0.8561707195
logloss 180 iterations learning rate 0.7 distributed data train and val, no scale no date: 0.8559952294
logloss 180 iterations learning rate 0.7 distributed data train and val, day extracted as not categorical no scale with date: 0.8560461554
logloss 180 iterations learning rate 0.7, 9 times distributed data train and val, no user no date: 0.8545560094
logloss 180 iterations learning rate 0.7, 9 times distributed data train and val, with user and numeric day: 0.8561601034
logloss 180 iterations learning rate 0.7, 9 times distributed data train and val, with user with numeric date: 0.8568834122
logloss 180 iterations learning rate 0.7, 10 different files, scaled, all features: 0.8584829166 !!!!!!!
logloss 180 iterations learning rate 0.7, new data, scaled, all features: 0.8915972905 test: 0.84108
logloss 180 iterations learning rate 0.9 10 files: bestTest = 0.4656462845
logloss 100 iterations learning rate 0.5 8 files: 0.8568031111965864
logloss 300 iterations learning rate 0.5:
crossentropy 50 iterations learning rate 0.5: 0.8556282878645277
"""
model.fit(X_train, y_train, eval_set=(X_val, y_val), verbose=10)
```
# Submission File
```
test_data = pd.read_csv("/content/drive/MyDrive/RS_Kaggle_Competition/test/test_file.csv")
test_data = test_data.iloc[:,:-1]
test_data[scaling_cols] = scaler.transform(test_data[scaling_cols])
X_test = test_data.fillna("Unknown")
X_test
pred_proba = model.predict_proba(X_test)
submission_dir_path = "/content/drive/MyDrive/RS_Kaggle_Competition/submissions"
pred = pred_proba[:,1]
pred_df = pd.DataFrame(pred)
pred_df.reset_index(inplace=True)
pred_df.columns = ['Id', 'Predicted']
pred_df.to_csv(submission_dir_path + '/catboost_submission_datafrom1704_data_lr_0.7_with_scale_with_num_startdate_with_user_iters_159.csv', index=False)
```
|
github_jupyter
|
```
#r "nuget:Microsoft.ML,1.4.0"
#r "nuget:Microsoft.ML.AutoML,0.16.0"
#r "nuget:Microsoft.Data.Analysis,0.1.0"
using Microsoft.Data.Analysis;
using XPlot.Plotly;
using Microsoft.AspNetCore.Html;
Formatter<DataFrame>.Register((df, writer) =>
{
var headers = new List<IHtmlContent>();
headers.Add(th(i("index")));
headers.AddRange(df.Columns.Select(c => (IHtmlContent) th(c.Name)));
var rows = new List<List<IHtmlContent>>();
var take = 20;
for (var i = 0; i < Math.Min(take, df.RowCount); i++)
{
var cells = new List<IHtmlContent>();
cells.Add(td(i));
foreach (var obj in df[i])
{
cells.Add(td(obj));
}
rows.Add(cells);
}
var t = table(
thead(
headers),
tbody(
rows.Select(
r => tr(r))));
writer.Write(t);
}, "text/html");
using System.IO;
using System.Net.Http;
string housingPath = "housing.csv";
if (!File.Exists(housingPath))
{
var contents = new HttpClient()
.GetStringAsync("https://raw.githubusercontent.com/ageron/handson-ml2/master/datasets/housing/housing.csv").Result;
File.WriteAllText("housing.csv", contents);
}
var housingData = DataFrame.LoadCsv(housingPath);
housingData
housingData.Description()
Chart.Plot(
new Graph.Histogram()
{
x = housingData["median_house_value"],
nbinsx = 20
}
)
var chart = Chart.Plot(
new Graph.Scattergl()
{
x = housingData["longitude"],
y = housingData["latitude"],
mode = "markers",
marker = new Graph.Marker()
{
color = housingData["median_house_value"],
colorscale = "Jet"
}
}
);
chart.Width = 600;
chart.Height = 600;
display(chart);
static T[] Shuffle<T>(T[] array)
{
Random rand = new Random();
for (int i = 0; i < array.Length; i++)
{
int r = i + rand.Next(array.Length - i);
T temp = array[r];
array[r] = array[i];
array[i] = temp;
}
return array;
}
int[] randomIndices = Shuffle(Enumerable.Range(0, (int)housingData.RowCount).ToArray());
int testSize = (int)(housingData.RowCount * .1);
int[] trainRows = randomIndices[testSize..];
int[] testRows = randomIndices[..testSize];
DataFrame housing_train = housingData[trainRows];
DataFrame housing_test = housingData[testRows];
display(housing_train.RowCount);
display(housing_test.RowCount);
using Microsoft.ML;
using Microsoft.ML.Data;
using Microsoft.ML.AutoML;
%%time
var mlContext = new MLContext();
var experiment = mlContext.Auto().CreateRegressionExperiment(maxExperimentTimeInSeconds: 15);
var result = experiment.Execute(housing_train, labelColumnName:"median_house_value");
var scatters = result.RunDetails.Where(d => d.ValidationMetrics != null).GroupBy(
r => r.TrainerName,
(name, details) => new Graph.Scattergl()
{
name = name,
x = details.Select(r => r.RuntimeInSeconds),
y = details.Select(r => r.ValidationMetrics.MeanAbsoluteError),
mode = "markers",
marker = new Graph.Marker() { size = 12 }
});
var chart = Chart.Plot(scatters);
chart.WithXTitle("Training Time");
chart.WithYTitle("Error");
display(chart);
Console.WriteLine($"Best Trainer:{result.BestRun.TrainerName}");
var testResults = result.BestRun.Model.Transform(housing_test);
var trueValues = testResults.GetColumn<float>("median_house_value");
var predictedValues = testResults.GetColumn<float>("Score");
var predictedVsTrue = new Graph.Scattergl()
{
x = trueValues,
y = predictedValues,
mode = "markers",
};
var maximumValue = Math.Max(trueValues.Max(), predictedValues.Max());
var perfectLine = new Graph.Scattergl()
{
x = new[] {0, maximumValue},
y = new[] {0, maximumValue},
mode = "lines",
};
var chart = Chart.Plot(new[] {predictedVsTrue, perfectLine });
chart.WithXTitle("True Values");
chart.WithYTitle("Predicted Values");
chart.WithLegend(false);
chart.Width = 600;
chart.Height = 600;
display(chart);
```
|
github_jupyter
|
# Chapter 8 - Applying Machine Learning To Sentiment Analysis
### Overview
- [Obtaining the IMDb movie review dataset](#Obtaining-the-IMDb-movie-review-dataset)
- [Introducing the bag-of-words model](#Introducing-the-bag-of-words-model)
- [Transforming words into feature vectors](#Transforming-words-into-feature-vectors)
- [Assessing word relevancy via term frequency-inverse document frequency](#Assessing-word-relevancy-via-term-frequency-inverse-document-frequency)
- [Cleaning text data](#Cleaning-text-data)
- [Processing documents into tokens](#Processing-documents-into-tokens)
- [Training a logistic regression model for document classification](#Training-a-logistic-regression-model-for-document-classification)
- [Working with bigger data – online algorithms and out-of-core learning](#Working-with-bigger-data-–-online-algorithms-and-out-of-core-learning)
- [Summary](#Summary)
NLP: Natural Language Processing
#### Sentiment Analysis (Opinion Mining)
Analyzes the polarity of documents
- Expressed opinions or emotions of the authors with regard to a particular topic
# Obtaining the IMDb movie review dataset
- IMDb: the Internet Movie Database
- IMDb dataset
- A. L. Maas, R. E. Daly, P. T. Pham, D. Huang, A. Y. Ng, and C. Potts. Learning Word Vectors for Sentiment Analysis. In the proceedings of the 49th Annual Meeting of the Association for Computational Linguistics: Human Language Technologies, pages 142–150, Portland, Oregon, USA, June 2011. Association for Computational Linguistics
- 50,000 movie reviews labeled either *positive* or *negative*
The IMDB movie review set can be downloaded from [http://ai.stanford.edu/~amaas/data/sentiment/](http://ai.stanford.edu/~amaas/data/sentiment/).
After downloading the dataset, decompress the files.
`aclImdb_v1.tar.gz`
```
import pyprind
import pandas as pd
import os
# change the `basepath` to the directory of the
# unzipped movie dataset
basepath = '/Users/sklee/datasets/aclImdb/'
labels = {'pos': 1, 'neg': 0}
pbar = pyprind.ProgBar(50000)
df = pd.DataFrame()
for s in ('test', 'train'):
for l in ('pos', 'neg'):
path = os.path.join(basepath, s, l)
for file in os.listdir(path):
with open(os.path.join(path, file), 'r', encoding='utf-8') as infile:
txt = infile.read()
df = df.append([[txt, labels[l]]], ignore_index=True)
pbar.update()
df.columns = ['review', 'sentiment']
df.head(5)
```
Shuffling the DataFrame:
```
import numpy as np
np.random.seed(0)
df = df.reindex(np.random.permutation(df.index))
df.head(5)
df.to_csv('./movie_data.csv', index=False)
```
<br>
<br>
# Introducing the bag-of-words model
- **Vocabulary** : the collection of unique tokens (e.g. words) from the entire set of documents
- Construct a feature vector from each document
- Vector length = length of the vocabulary
- Contains the counts of how often each token occurs in the particular document
- Sparse vectors
## Transforming documents into feature vectors
By calling the fit_transform method on CountVectorizer, we just constructed the vocabulary of the bag-of-words model and transformed the following three sentences into sparse feature vectors:
1. The sun is shining
2. The weather is sweet
3. The sun is shining, the weather is sweet, and one and one is two
```
import numpy as np
from sklearn.feature_extraction.text import CountVectorizer
count = CountVectorizer()
docs = np.array([
'The sun is shining',
'The weather is sweet',
'The sun is shining, the weather is sweet, and one and one is two'])
bag = count.fit_transform(docs)
```
Now let us print the contents of the vocabulary to get a better understanding of the underlying concepts:
```
print(count.vocabulary_)
```
As we can see from executing the preceding command, the vocabulary is stored in a Python dictionary, which maps the unique words that are mapped to integer indices. Next let us print the feature vectors that we just created:
Each index position in the feature vectors shown here corresponds to the integer values that are stored as dictionary items in the CountVectorizer vocabulary. For example, the rst feature at index position 0 resembles the count of the word and, which only occurs in the last document, and the word is at index position 1 (the 2nd feature in the document vectors) occurs in all three sentences. Those values in the feature vectors are also called the raw term frequencies: *tf (t,d)*—the number of times a term t occurs in a document *d*.
```
print(bag.toarray())
```
Those count values are called the **raw term frequency td(t,d)**
- t: term
- d: document
The **n-gram** Models
- 1-gram: "the", "sun", "is", "shining"
- 2-gram: "the sun", "sun is", "is shining"
- CountVectorizer(ngram_range=(2,2))
<br>
## Assessing word relevancy via term frequency-inverse document frequency
```
np.set_printoptions(precision=2)
```
- Frequently occurring words across multiple documents from both classes typically don't contain useful or discriminatory information.
- ** Term frequency-inverse document frequency (tf-idf)** can be used to downweight those frequently occurring words in the feature vectors.
$$\text{tf-idf}(t,d)=\text{tf (t,d)}\times \text{idf}(t,d)$$
- **tf(t, d) the term frequency**
- **idf(t, d) the inverse document frequency**:
$$\text{idf}(t,d) = \text{log}\frac{n_d}{1+\text{df}(d, t)},$$
- $n_d$ is the total number of documents
- **df(d, t) document frequency**: the number of documents *d* that contain the term *t*.
- Note that adding the constant 1 to the denominator is optional and serves the purpose of assigning a non-zero value to terms that occur in all training samples; the log is used to ensure that low document frequencies are not given too much weight.
Scikit-learn implements yet another transformer, the `TfidfTransformer`, that takes the raw term frequencies from `CountVectorizer` as input and transforms them into tf-idfs:
```
from sklearn.feature_extraction.text import TfidfTransformer
tfidf = TfidfTransformer(use_idf=True, norm='l2', smooth_idf=True)
print(tfidf.fit_transform(count.fit_transform(docs)).toarray())
```
As we saw in the previous subsection, the word is had the largest term frequency in the 3rd document, being the most frequently occurring word. However, after transforming the same feature vector into tf-idfs, we see that the word is is
now associated with a relatively small tf-idf (0.45) in document 3 since it is
also contained in documents 1 and 2 and thus is unlikely to contain any useful, discriminatory information.
However, if we'd manually calculated the tf-idfs of the individual terms in our feature vectors, we'd have noticed that the `TfidfTransformer` calculates the tf-idfs slightly differently compared to the standard textbook equations that we de ned earlier. The equations for the idf and tf-idf that were implemented in scikit-learn are:
$$\text{idf} (t,d) = log\frac{1 + n_d}{1 + \text{df}(d, t)}$$
The tf-idf equation that was implemented in scikit-learn is as follows:
$$\text{tf-idf}(t,d) = \text{tf}(t,d) \times (\text{idf}(t,d)+1)$$
While it is also more typical to normalize the raw term frequencies before calculating the tf-idfs, the `TfidfTransformer` normalizes the tf-idfs directly.
By default (`norm='l2'`), scikit-learn's TfidfTransformer applies the L2-normalization, which returns a vector of length 1 by dividing an un-normalized feature vector *v* by its L2-norm:
$$v_{\text{norm}} = \frac{v}{||v||_2} = \frac{v}{\sqrt{v_{1}^{2} + v_{2}^{2} + \dots + v_{n}^{2}}} = \frac{v}{\big (\sum_{i=1}^{n} v_{i}^{2}\big)^\frac{1}{2}}$$
To make sure that we understand how TfidfTransformer works, let us walk
through an example and calculate the tf-idf of the word is in the 3rd document.
The word is has a term frequency of 3 (tf = 3) in document 3, and the document frequency of this term is 3 since the term is occurs in all three documents (df = 3). Thus, we can calculate the idf as follows:
$$\text{idf}("is", d3) = log \frac{1+3}{1+3} = 0$$
Now in order to calculate the tf-idf, we simply need to add 1 to the inverse document frequency and multiply it by the term frequency:
$$\text{tf-idf}("is",d3)= 3 \times (0+1) = 3$$
```
tf_is = 3
n_docs = 3
idf_is = np.log((n_docs+1) / (3+1))
tfidf_is = tf_is * (idf_is + 1)
print('tf-idf of term "is" = %.2f' % tfidf_is)
```
If we repeated these calculations for all terms in the 3rd document, we'd obtain the following tf-idf vectors: [3.39, 3.0, 3.39, 1.29, 1.29, 1.29, 2.0 , 1.69, 1.29]. However, we notice that the values in this feature vector are different from the values that we obtained from the TfidfTransformer that we used previously. The nal step that we are missing in this tf-idf calculation is the L2-normalization, which can be applied as follows:
$$\text{tfi-df}_{norm} = \frac{[3.39, 3.0, 3.39, 1.29, 1.29, 1.29, 2.0 , 1.69, 1.29]}{\sqrt{[3.39^2, 3.0^2, 3.39^2, 1.29^2, 1.29^2, 1.29^2, 2.0^2 , 1.69^2, 1.29^2]}}$$
$$=[0.5, 0.45, 0.5, 0.19, 0.19, 0.19, 0.3, 0.25, 0.19]$$
$$\Rightarrow \text{tf-idf}_{norm}("is", d3) = 0.45$$
As we can see, the results match the results returned by scikit-learn's `TfidfTransformer` (below). Since we now understand how tf-idfs are calculated, let us proceed to the next sections and apply those concepts to the movie review dataset.
```
tfidf = TfidfTransformer(use_idf=True, norm=None, smooth_idf=True)
raw_tfidf = tfidf.fit_transform(count.fit_transform(docs)).toarray()[-1]
raw_tfidf
l2_tfidf = raw_tfidf / np.sqrt(np.sum(raw_tfidf**2))
l2_tfidf
```
<br>
## Cleaning text data
**Before** we build the bag-of-words model.
```
df.loc[112, 'review'][-1000:]
```
#### Python regular expression library
```
import re
def preprocessor(text):
text = re.sub('<[^>]*>', '', text)
emoticons = re.findall('(?::|;|=)(?:-)?(?:\)|\(|D|P)', text)
text = re.sub('[\W]+', ' ', text.lower()) +\
' '.join(emoticons).replace('-', '')
return text
preprocessor(df.loc[112, 'review'][-1000:])
preprocessor("</a>This :) is :( a test :-)!")
df['review'] = df['review'].apply(preprocessor)
```
<br>
## Processing documents into tokens
#### Word Stemming
Transforming a word into its root form
- Original stemming algorithm: Martin F. Porter. An algorithm for suf x stripping. Program: electronic library and information systems, 14(3):130–137, 1980)
- Snowball stemmer (Porter2 or "English" stemmer)
- Lancaster stemmer (Paice-Husk stemmer)
Python NLP toolkit: NLTK (the Natural Language ToolKit)
- Free online book http://www.nltk.org/book/
```
from nltk.stem.porter import PorterStemmer
porter = PorterStemmer()
def tokenizer(text):
return text.split()
def tokenizer_porter(text):
return [porter.stem(word) for word in text.split()]
tokenizer('runners like running and thus they run')
tokenizer_porter('runners like running and thus they run')
```
#### Lemmatization
- thus -> thu
- Tries to find canonical forms of words
- Computationally expensive, little impact on text classification performance
#### Stop-words Removal
- Stop-words: extremely common words, e.g., is, and, has, like...
- Removal is useful when we use raw or normalized tf, rather than tf-idf
```
import nltk
nltk.download('stopwords')
from nltk.corpus import stopwords
stop = stopwords.words('english')
[w for w in tokenizer_porter('a runner likes running and runs a lot')[-10:]
if w not in stop]
stop[-10:]
```
<br>
<br>
# Training a logistic regression model for document classification
```
X_train = df.loc[:25000, 'review'].values
y_train = df.loc[:25000, 'sentiment'].values
X_test = df.loc[25000:, 'review'].values
y_test = df.loc[25000:, 'sentiment'].values
from sklearn.pipeline import Pipeline
from sklearn.linear_model import LogisticRegression
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.model_selection import GridSearchCV
tfidf = TfidfVectorizer(strip_accents=None,
lowercase=False,
preprocessor=None)
param_grid = [{'vect__ngram_range': [(1, 1)],
'vect__stop_words': [stop, None],
'vect__tokenizer': [tokenizer, tokenizer_porter],
'clf__penalty': ['l1', 'l2'],
'clf__C': [1.0, 10.0, 100.0]},
{'vect__ngram_range': [(1, 1)],
'vect__stop_words': [stop, None],
'vect__tokenizer': [tokenizer, tokenizer_porter],
'vect__use_idf':[False],
'vect__norm':[None],
'clf__penalty': ['l1', 'l2'],
'clf__C': [1.0, 10.0, 100.0]},
]
lr_tfidf = Pipeline([('vect', tfidf),
('clf', LogisticRegression(random_state=0))])
gs_lr_tfidf = GridSearchCV(lr_tfidf, param_grid,
scoring='accuracy',
cv=5,
verbose=1,
n_jobs=-1)
gs_lr_tfidf.fit(X_train, y_train)
print('Best parameter set: %s ' % gs_lr_tfidf.best_params_)
print('CV Accuracy: %.3f' % gs_lr_tfidf.best_score_)
# Best parameter set: {'vect__tokenizer': <function tokenizer at 0x11851c6a8>, 'clf__C': 10.0, 'vect__stop_words': None, 'clf__penalty': 'l2', 'vect__ngram_range': (1, 1)}
# CV Accuracy: 0.897
clf = gs_lr_tfidf.best_estimator_
print('Test Accuracy: %.3f' % clf.score(X_test, y_test))
# Test Accuracy: 0.899
```
<br>
<br>
# Working with bigger data - online algorithms and out-of-core learning
```
import numpy as np
import re
from nltk.corpus import stopwords
def tokenizer(text):
text = re.sub('<[^>]*>', '', text)
emoticons = re.findall('(?::|;|=)(?:-)?(?:\)|\(|D|P)', text.lower())
text = re.sub('[\W]+', ' ', text.lower()) +\
' '.join(emoticons).replace('-', '')
tokenized = [w for w in text.split() if w not in stop]
return tokenized
# reads in and returns one document at a time
def stream_docs(path):
with open(path, 'r', encoding='utf-8') as csv:
next(csv) # skip header
for line in csv:
text, label = line[:-3], int(line[-2])
yield text, label
doc_stream = stream_docs(path='./movie_data.csv')
next(doc_stream)
```
#### Minibatch
```
def get_minibatch(doc_stream, size):
docs, y = [], []
try:
for _ in range(size):
text, label = next(doc_stream)
docs.append(text)
y.append(label)
except StopIteration:
return None, None
return docs, y
```
- We cannot use `CountVectorizer` since it requires holding the complete vocabulary. Likewise, `TfidfVectorizer` needs to keep all feature vectors in memory.
- We can use `HashingVectorizer` instead for online training (32-bit MurmurHash3 algorithm by Austin Appleby (https://sites.google.com/site/murmurhash/)
```
from sklearn.feature_extraction.text import HashingVectorizer
from sklearn.linear_model import SGDClassifier
vect = HashingVectorizer(decode_error='ignore',
n_features=2**21,
preprocessor=None,
tokenizer=tokenizer)
clf = SGDClassifier(loss='log', random_state=1, max_iter=1)
doc_stream = stream_docs(path='./movie_data.csv')
import pyprind
pbar = pyprind.ProgBar(45)
classes = np.array([0, 1])
for _ in range(45):
X_train, y_train = get_minibatch(doc_stream, size=1000)
if not X_train:
break
X_train = vect.transform(X_train)
clf.partial_fit(X_train, y_train, classes=classes)
pbar.update()
X_test, y_test = get_minibatch(doc_stream, size=5000)
X_test = vect.transform(X_test)
print('Accuracy: %.3f' % clf.score(X_test, y_test))
clf = clf.partial_fit(X_test, y_test)
```
<br>
<br>
# Summary
- **Latent Dirichlet allocation**, a topic model that considers the latent semantics of words (D. M. Blei, A. Y. Ng, and M. I. Jordan. Latent Dirichlet allocation. The Journal of machine Learning research, 3:993–1022, 2003)
- **word2vec**, an algorithm that Google released in 2013 (T. Mikolov, K. Chen, G. Corrado, and J. Dean. Ef cient Estimation of Word Representations in Vector Space. arXiv preprint arXiv:1301.3781, 2013)
- https://code.google.com/p/word2vec/.
|
github_jupyter
|
<a href="https://colab.research.google.com/github/satyajitghana/TSAI-DeepNLP-END2.0/blob/main/09_NLP_Evaluation/ClassificationEvaluation.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
! pip3 install git+https://github.com/extensive-nlp/ttc_nlp --quiet
! pip3 install torchmetrics --quiet
from ttctext.datamodules.sst import SSTDataModule
from ttctext.datasets.sst import StanfordSentimentTreeBank
sst_dataset = SSTDataModule(batch_size=128)
sst_dataset.setup()
import pytorch_lightning as pl
import torch
import torch.nn as nn
import torch.nn.functional as F
from torchmetrics.functional import accuracy, precision, recall, confusion_matrix
from sklearn.metrics import classification_report
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
sns.set()
class SSTModel(pl.LightningModule):
def __init__(self, hparams, *args, **kwargs):
super().__init__()
self.save_hyperparameters(hparams)
self.num_classes = self.hparams.output_dim
self.embedding = nn.Embedding(self.hparams.input_dim, self.hparams.embedding_dim)
self.lstm = nn.LSTM(
self.hparams.embedding_dim,
self.hparams.hidden_dim,
num_layers=self.hparams.num_layers,
dropout=self.hparams.dropout,
batch_first=True
)
self.proj_layer = nn.Sequential(
nn.Linear(self.hparams.hidden_dim, self.hparams.hidden_dim),
nn.BatchNorm1d(self.hparams.hidden_dim),
nn.ReLU(),
nn.Dropout(self.hparams.dropout),
)
self.fc = nn.Linear(self.hparams.hidden_dim, self.num_classes)
self.loss = nn.CrossEntropyLoss()
def init_state(self, sequence_length):
return (torch.zeros(self.hparams.num_layers, sequence_length, self.hparams.hidden_dim).to(self.device),
torch.zeros(self.hparams.num_layers, sequence_length, self.hparams.hidden_dim).to(self.device))
def forward(self, text, text_length, prev_state=None):
# [batch size, sentence length] => [batch size, sentence len, embedding size]
embedded = self.embedding(text)
# packs the input for faster forward pass in RNN
packed = torch.nn.utils.rnn.pack_padded_sequence(
embedded, text_length.to('cpu'),
enforce_sorted=False,
batch_first=True
)
# [batch size sentence len, embedding size] =>
# output: [batch size, sentence len, hidden size]
# hidden: [batch size, 1, hidden size]
packed_output, curr_state = self.lstm(packed, prev_state)
hidden_state, cell_state = curr_state
# print('hidden state shape: ', hidden_state.shape)
# print('cell')
# unpack packed sequence
# unpacked, unpacked_len = torch.nn.utils.rnn.pad_packed_sequence(packed_output, batch_first=True)
# print('unpacked: ', unpacked.shape)
# [batch size, sentence len, hidden size] => [batch size, num classes]
# output = self.proj_layer(unpacked[:, -1])
output = self.proj_layer(hidden_state[-1])
# print('output shape: ', output.shape)
output = self.fc(output)
return output, curr_state
def shared_step(self, batch, batch_idx):
label, text, text_length = batch
logits, in_state = self(text, text_length)
loss = self.loss(logits, label)
pred = torch.argmax(F.log_softmax(logits, dim=1), dim=1)
acc = accuracy(pred, label)
metric = {'loss': loss, 'acc': acc, 'pred': pred, 'label': label}
return metric
def training_step(self, batch, batch_idx):
metrics = self.shared_step(batch, batch_idx)
log_metrics = {'train_loss': metrics['loss'], 'train_acc': metrics['acc']}
self.log_dict(log_metrics, prog_bar=True)
return metrics
def validation_step(self, batch, batch_idx):
metrics = self.shared_step(batch, batch_idx)
return metrics
def validation_epoch_end(self, outputs):
acc = torch.stack([x['acc'] for x in outputs]).mean()
loss = torch.stack([x['loss'] for x in outputs]).mean()
log_metrics = {'val_loss': loss, 'val_acc': acc}
self.log_dict(log_metrics, prog_bar=True)
if self.trainer.sanity_checking:
return log_metrics
preds = torch.cat([x['pred'] for x in outputs]).view(-1)
labels = torch.cat([x['label'] for x in outputs]).view(-1)
accuracy_ = accuracy(preds, labels)
precision_ = precision(preds, labels, average='macro', num_classes=self.num_classes)
recall_ = recall(preds, labels, average='macro', num_classes=self.num_classes)
classification_report_ = classification_report(labels.cpu().numpy(), preds.cpu().numpy(), target_names=self.hparams.class_labels)
confusion_matrix_ = confusion_matrix(preds, labels, num_classes=self.num_classes)
cm_df = pd.DataFrame(confusion_matrix_.cpu().numpy(), index=self.hparams.class_labels, columns=self.hparams.class_labels)
print(f'Test Epoch {self.current_epoch}/{self.hparams.epochs-1}: F1 Score: {accuracy_:.5f}, Precision: {precision_:.5f}, Recall: {recall_:.5f}\n')
print(f'Classification Report\n{classification_report_}')
fig, ax = plt.subplots(figsize=(10, 8))
heatmap = sns.heatmap(cm_df, annot=True, ax=ax, fmt='d') # font size
locs, labels = plt.xticks()
plt.setp(labels, rotation=45)
locs, labels = plt.yticks()
plt.setp(labels, rotation=45)
plt.show()
print("\n")
return log_metrics
def test_step(self, batch, batch_idx):
return self.validation_step(batch, batch_idx)
def test_epoch_end(self, outputs):
accuracy = torch.stack([x['acc'] for x in outputs]).mean()
self.log('hp_metric', accuracy)
self.log_dict({'test_acc': accuracy}, prog_bar=True)
def configure_optimizers(self):
optimizer = torch.optim.Adam(self.parameters(), lr=self.hparams.lr)
lr_scheduler = {
'scheduler': torch.optim.lr_scheduler.ReduceLROnPlateau(optimizer, patience=10, verbose=True),
'monitor': 'train_loss',
'name': 'scheduler'
}
return [optimizer], [lr_scheduler]
from omegaconf import OmegaConf
hparams = OmegaConf.create({
'input_dim': len(sst_dataset.get_vocab()),
'embedding_dim': 128,
'num_layers': 2,
'hidden_dim': 64,
'dropout': 0.5,
'output_dim': len(StanfordSentimentTreeBank.get_labels()),
'class_labels': sst_dataset.raw_dataset_train.get_labels(),
'lr': 5e-4,
'epochs': 10,
'use_lr_finder': False
})
sst_model = SSTModel(hparams)
trainer = pl.Trainer(gpus=1, max_epochs=hparams.epochs, progress_bar_refresh_rate=1, reload_dataloaders_every_epoch=True)
trainer.fit(sst_model, sst_dataset)
```
|
github_jupyter
|
# MultiGroupDirectLiNGAM
## Import and settings
In this example, we need to import `numpy`, `pandas`, and `graphviz` in addition to `lingam`.
```
import numpy as np
import pandas as pd
import graphviz
import lingam
from lingam.utils import print_causal_directions, print_dagc, make_dot
print([np.__version__, pd.__version__, graphviz.__version__, lingam.__version__])
np.set_printoptions(precision=3, suppress=True)
np.random.seed(0)
```
## Test data
We generate two datasets consisting of 6 variables.
```
x3 = np.random.uniform(size=1000)
x0 = 3.0*x3 + np.random.uniform(size=1000)
x2 = 6.0*x3 + np.random.uniform(size=1000)
x1 = 3.0*x0 + 2.0*x2 + np.random.uniform(size=1000)
x5 = 4.0*x0 + np.random.uniform(size=1000)
x4 = 8.0*x0 - 1.0*x2 + np.random.uniform(size=1000)
X1 = pd.DataFrame(np.array([x0, x1, x2, x3, x4, x5]).T ,columns=['x0', 'x1', 'x2', 'x3', 'x4', 'x5'])
X1.head()
m = np.array([[0.0, 0.0, 0.0, 3.0, 0.0, 0.0],
[3.0, 0.0, 2.0, 0.0, 0.0, 0.0],
[0.0, 0.0, 0.0, 6.0, 0.0, 0.0],
[0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[8.0, 0.0,-1.0, 0.0, 0.0, 0.0],
[4.0, 0.0, 0.0, 0.0, 0.0, 0.0]])
make_dot(m)
x3 = np.random.uniform(size=1000)
x0 = 3.5*x3 + np.random.uniform(size=1000)
x2 = 6.5*x3 + np.random.uniform(size=1000)
x1 = 3.5*x0 + 2.5*x2 + np.random.uniform(size=1000)
x5 = 4.5*x0 + np.random.uniform(size=1000)
x4 = 8.5*x0 - 1.5*x2 + np.random.uniform(size=1000)
X2 = pd.DataFrame(np.array([x0, x1, x2, x3, x4, x5]).T ,columns=['x0', 'x1', 'x2', 'x3', 'x4', 'x5'])
X2.head()
m = np.array([[0.0, 0.0, 0.0, 3.5, 0.0, 0.0],
[3.5, 0.0, 2.5, 0.0, 0.0, 0.0],
[0.0, 0.0, 0.0, 6.5, 0.0, 0.0],
[0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[8.5, 0.0,-1.5, 0.0, 0.0, 0.0],
[4.5, 0.0, 0.0, 0.0, 0.0, 0.0]])
make_dot(m)
```
We create a list variable that contains two datasets.
```
X_list = [X1, X2]
```
## Causal Discovery
To run causal discovery for multiple datasets, we create a `MultiGroupDirectLiNGAM` object and call the `fit` method.
```
model = lingam.MultiGroupDirectLiNGAM()
model.fit(X_list)
```
Using the `causal_order_` properties, we can see the causal ordering as a result of the causal discovery.
```
model.causal_order_
```
Also, using the `adjacency_matrix_` properties, we can see the adjacency matrix as a result of the causal discovery. As you can see from the following, DAG in each dataset is correctly estimated.
```
print(model.adjacency_matrices_[0])
make_dot(model.adjacency_matrices_[0])
print(model.adjacency_matrices_[1])
make_dot(model.adjacency_matrices_[1])
```
To compare, we run DirectLiNGAM with single dataset concatenating two datasets.
```
X_all = pd.concat([X1, X2])
print(X_all.shape)
model_all = lingam.DirectLiNGAM()
model_all.fit(X_all)
model_all.causal_order_
```
You can see that the causal structure cannot be estimated correctly for a single dataset.
```
make_dot(model_all.adjacency_matrix_)
```
## Independence between error variables
To check if the LiNGAM assumption is broken, we can get p-values of independence between error variables. The value in the i-th row and j-th column of the obtained matrix shows the p-value of the independence of the error variables $e_i$ and $e_j$.
```
p_values = model.get_error_independence_p_values(X_list)
print(p_values[0])
print(p_values[1])
```
## Bootstrapping
In `MultiGroupDirectLiNGAM`, bootstrap can be executed in the same way as normal `DirectLiNGAM`.
```
results = model.bootstrap(X_list, n_sampling=100)
```
## Causal Directions
The `bootstrap` method returns a list of multiple `BootstrapResult`, so we can get the result of bootstrapping from the list. We can get the same number of results as the number of datasets, so we specify an index when we access the results. We can get the ranking of the causal directions extracted by `get_causal_direction_counts()`.
```
cdc = results[0].get_causal_direction_counts(n_directions=8, min_causal_effect=0.01)
print_causal_directions(cdc, 100)
cdc = results[1].get_causal_direction_counts(n_directions=8, min_causal_effect=0.01)
print_causal_directions(cdc, 100)
```
## Directed Acyclic Graphs
Also, using the `get_directed_acyclic_graph_counts()` method, we can get the ranking of the DAGs extracted. In the following sample code, `n_dags` option is limited to the dags of the top 3 rankings, and `min_causal_effect` option is limited to causal directions with a coefficient of 0.01 or more.
```
dagc = results[0].get_directed_acyclic_graph_counts(n_dags=3, min_causal_effect=0.01)
print_dagc(dagc, 100)
dagc = results[1].get_directed_acyclic_graph_counts(n_dags=3, min_causal_effect=0.01)
print_dagc(dagc, 100)
```
## Probability
Using the get_probabilities() method, we can get the probability of bootstrapping.
```
prob = results[0].get_probabilities(min_causal_effect=0.01)
print(prob)
```
## Total Causal Effects
Using the `get_total_causal_effects()` method, we can get the list of total causal effect. The total causal effects we can get are dictionary type variable.
We can display the list nicely by assigning it to pandas.DataFrame. Also, we have replaced the variable index with a label below.
```
causal_effects = results[0].get_total_causal_effects(min_causal_effect=0.01)
df = pd.DataFrame(causal_effects)
labels = [f'x{i}' for i in range(X1.shape[1])]
df['from'] = df['from'].apply(lambda x : labels[x])
df['to'] = df['to'].apply(lambda x : labels[x])
df
```
We can easily perform sorting operations with pandas.DataFrame.
```
df.sort_values('effect', ascending=False).head()
```
And with pandas.DataFrame, we can easily filter by keywords. The following code extracts the causal direction towards x1.
```
df[df['to']=='x1'].head()
```
Because it holds the raw data of the total causal effect (the original data for calculating the median), it is possible to draw a histogram of the values of the causal effect, as shown below.
```
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
%matplotlib inline
from_index = 3
to_index = 0
plt.hist(results[0].total_effects_[:, to_index, from_index])
```
## Bootstrap Probability of Path
Using the `get_paths()` method, we can explore all paths from any variable to any variable and calculate the bootstrap probability for each path. The path will be output as an array of variable indices. For example, the array `[3, 0, 1]` shows the path from variable X3 through variable X0 to variable X1.
```
from_index = 3 # index of x3
to_index = 1 # index of x0
pd.DataFrame(results[0].get_paths(from_index, to_index))
```
|
github_jupyter
|
## Accessing TerraClimate data with the Planetary Computer STAC API
[TerraClimate](http://www.climatologylab.org/terraclimate.html) is a dataset of monthly climate and climatic water balance for global terrestrial surfaces from 1958-2019. These data provide important inputs for ecological and hydrological studies at global scales that require high spatial resolution and time-varying data. All data have monthly temporal resolution and a ~4-km (1/24th degree) spatial resolution. The data cover the period from 1958-2019.
This example will show you how temperature has increased over the past 60 years across the globe.
### Environment setup
```
import warnings
warnings.filterwarnings("ignore", "invalid value", RuntimeWarning)
```
### Data access
https://planetarycomputer.microsoft.com/api/stac/v1/collections/terraclimate is a STAC Collection with links to all the metadata about this dataset. We'll load it with [PySTAC](https://pystac.readthedocs.io/en/latest/).
```
import pystac
url = "https://planetarycomputer.microsoft.com/api/stac/v1/collections/terraclimate"
collection = pystac.read_file(url)
collection
```
The collection contains assets, which are links to the root of a Zarr store, which can be opened with xarray.
```
asset = collection.assets["zarr-https"]
asset
import fsspec
import xarray as xr
store = fsspec.get_mapper(asset.href)
ds = xr.open_zarr(store, **asset.extra_fields["xarray:open_kwargs"])
ds
```
We'll process the data in parallel using [Dask](https://dask.org).
```
from dask_gateway import GatewayCluster
cluster = GatewayCluster()
cluster.scale(16)
client = cluster.get_client()
print(cluster.dashboard_link)
```
The link printed out above can be opened in a new tab or the [Dask labextension](https://github.com/dask/dask-labextension). See [Scale with Dask](https://planetarycomputer.microsoft.com/docs/quickstarts/scale-with-dask/) for more on using Dask, and how to access the Dashboard.
### Analyze and plot global temperature
We can quickly plot a map of one of the variables. In this case, we are downsampling (coarsening) the dataset for easier plotting.
```
import cartopy.crs as ccrs
import matplotlib.pyplot as plt
average_max_temp = ds.isel(time=-1)["tmax"].coarsen(lat=8, lon=8).mean().load()
fig, ax = plt.subplots(figsize=(20, 10), subplot_kw=dict(projection=ccrs.Robinson()))
average_max_temp.plot(ax=ax, transform=ccrs.PlateCarree())
ax.coastlines();
```
Let's see how temperature has changed over the observational record, when averaged across the entire domain. Since we'll do some other calculations below we'll also add `.load()` to execute the command instead of specifying it lazily. Note that there are some data quality issues before 1965 so we'll start our analysis there.
```
temperature = (
ds["tmax"].sel(time=slice("1965", None)).mean(dim=["lat", "lon"]).persist()
)
temperature.plot(figsize=(12, 6));
```
With all the seasonal fluctuations (from summer and winter) though, it can be hard to see any obvious trends. So let's try grouping by year and plotting that timeseries.
```
temperature.groupby("time.year").mean().plot(figsize=(12, 6));
```
Now the increase in temperature is obvious, even when averaged across the entire domain.
Now, let's see how those changes are different in different parts of the world. And let's focus just on summer months in the northern hemisphere, when it's hottest. Let's take a climatological slice at the beginning of the period and the same at the end of the period, calculate the difference, and map it to see how different parts of the world have changed differently.
First we'll just grab the summer months.
```
%%time
import dask
summer_months = [6, 7, 8]
summer = ds.tmax.where(ds.time.dt.month.isin(summer_months), drop=True)
early_period = slice("1958-01-01", "1988-12-31")
late_period = slice("1988-01-01", "2018-12-31")
early, late = dask.compute(
summer.sel(time=early_period).mean(dim="time"),
summer.sel(time=late_period).mean(dim="time"),
)
increase = (late - early).coarsen(lat=8, lon=8).mean()
fig, ax = plt.subplots(figsize=(20, 10), subplot_kw=dict(projection=ccrs.Robinson()))
increase.plot(ax=ax, transform=ccrs.PlateCarree(), robust=True)
ax.coastlines();
```
This shows us that changes in summer temperature haven't been felt equally around the globe. Note the enhanced warming in the polar regions, a phenomenon known as "Arctic amplification".
|
github_jupyter
|
Copyright (c) Microsoft Corporation. All rights reserved.
Licensed under the MIT License.
# Automated Machine Learning
_**ディープラーンニングを利用したテキスト分類**_
## Contents
1. [事前準備](#1.-事前準備)
1. [自動機械学習 Automated Machine Learning](2.-自動機械学習-Automated-Machine-Learning)
1. [結果の確認](#3.-結果の確認)
## 1. 事前準備
本デモンストレーションでは、AutoML の深層学習の機能を用いてテキストデータの分類モデルを構築します。
AutoML には Deep Neural Network が含まれており、テキストデータから **Embedding** を作成することができます。GPU サーバを利用することで **BERT** が利用されます。
深層学習の機能を利用するためには Azure Machine Learning の Enterprise Edition が必要になります。詳細は[こちら](https://docs.microsoft.com/en-us/azure/machine-learning/concept-editions#automated-training-capabilities-automl)をご確認ください。
## 1.1 Python SDK のインポート
Azure Machine Learning の Python SDK などをインポートします。
```
import logging
import os
import shutil
import pandas as pd
import azureml.core
from azureml.core.experiment import Experiment
from azureml.core.workspace import Workspace
from azureml.core.dataset import Dataset
from azureml.core.compute import AmlCompute
from azureml.core.compute import ComputeTarget
from azureml.core.run import Run
from azureml.widgets import RunDetails
from azureml.core.model import Model
from azureml.train.automl import AutoMLConfig
from sklearn.datasets import fetch_20newsgroups
from azureml.automl.core.featurization import FeaturizationConfig
```
Azure ML Python SDK のバージョンが 1.8.0 以上になっていることを確認します。
```
print("You are currently using version", azureml.core.VERSION, "of the Azure ML SDK")
```
## 1.2 Azure ML Workspace との接続
```
ws = Workspace.from_config()
# 実験名の指定
experiment_name = 'livedoor-news-classification-BERT'
experiment = Experiment(ws, experiment_name)
output = {}
#output['Subscription ID'] = ws.subscription_id
output['Workspace Name'] = ws.name
output['Resource Group'] = ws.resource_group
output['Location'] = ws.location
output['Experiment Name'] = experiment.name
pd.set_option('display.max_colwidth', -1)
outputDf = pd.DataFrame(data = output, index = [''])
outputDf.T
```
## 1.3 計算環境の準備
BERT を利用するための GPU の `Compute Cluster` を準備します。
```
from azureml.core.compute import ComputeTarget, AmlCompute
from azureml.core.compute_target import ComputeTargetException
# Compute Cluster の名称
amlcompute_cluster_name = "gpucluster"
# クラスターの存在確認
try:
compute_target = ComputeTarget(workspace=ws, name=amlcompute_cluster_name)
except ComputeTargetException:
print('指定された名称のクラスターが見つからないので新規に作成します.')
compute_config = AmlCompute.provisioning_configuration(vm_size = "STANDARD_NC6_V3",
max_nodes = 4)
compute_target = ComputeTarget.create(ws, amlcompute_cluster_name, compute_config)
compute_target.wait_for_completion(show_output=True)
```
## 1.4 学習データの準備
今回は [livedoor New](https://www.rondhuit.com/download/ldcc-20140209.tar.gz) を学習データとして利用します。ニュースのカテゴリー分類のモデルを構築します。
```
target_column_name = 'label' # カテゴリーの列
feature_column_name = 'text' # ニュース記事の列
train_dataset = Dataset.get_by_name(ws, "livedoor").keep_columns(["text","label"])
train_dataset.take(5).to_pandas_dataframe()
```
# 2. 自動機械学習 Automated Machine Learning
## 2.1 設定と制約条件
自動機械学習 Automated Machine Learning の設定と学習を行っていきます。
```
from azureml.automl.core.featurization import FeaturizationConfig
featurization_config = FeaturizationConfig()
# テキストデータの言語を指定します。日本語の場合は "jpn" と指定します。
featurization_config = FeaturizationConfig(dataset_language="jpn") # 英語の場合は下記をコメントアウトしてください。
# 明示的に `text` の列がテキストデータであると指定します。
featurization_config.add_column_purpose('text', 'Text')
#featurization_config.blocked_transformers = ['TfIdf','CountVectorizer'] # BERT のみを利用したい場合はコメントアウトを外します
# 自動機械学習の設定
automl_settings = {
"experiment_timeout_hours" : 2, # 学習時間 (hour)
"primary_metric": 'accuracy', # 評価指標
"max_concurrent_iterations": 4, # 計算環境の最大並列数
"max_cores_per_iteration": -1,
"enable_dnn": True, # 深層学習を有効
"enable_early_stopping": False,
"validation_size": 0.2,
"verbosity": logging.INFO,
"force_text_dnn": True,
#"n_cross_validations": 5,
}
automl_config = AutoMLConfig(task = 'classification',
debug_log = 'automl_errors.log',
compute_target=compute_target,
training_data=train_dataset,
label_column_name=target_column_name,
featurization=featurization_config,
**automl_settings
)
```
## 2.2 モデル学習
自動機械学習 Automated Machine Learning によるモデル学習を開始します。
```
automl_run = experiment.submit(automl_config, show_output=False)
# run_id を出力
automl_run.id
# Azure Machine Learning studio の URL を出力
automl_run
# # 途中でセッションが切れた場合の対処
# from azureml.train.automl.run import AutoMLRun
# ws = Workspace.from_config()
# experiment = ws.experiments['livedoor-news-classification-BERT']
# run_id = "AutoML_e69a63ae-ef52-4783-9a9f-527d69d7cc9d"
# automl_run = AutoMLRun(experiment, run_id = run_id)
# automl_run
```
## 2.3 モデルの登録
```
# 一番精度が高いモデルを抽出
best_run, fitted_model = automl_run.get_output()
# モデルファイル(.pkl) のダウンロード
model_dir = '../model'
best_run.download_file('outputs/model.pkl', model_dir + '/model.pkl')
# Azure ML へモデル登録
model_name = 'livedoor-model'
model = Model.register(model_path = model_dir + '/model.pkl',
model_name = model_name,
tags=None,
workspace=ws)
```
# 3. テストデータに対する予測値の出力
```
from sklearn.externals import joblib
trained_model = joblib.load(model_dir + '/model.pkl')
trained_model
test_dataset = Dataset.get_by_name(ws, "livedoor").keep_columns(["text"])
predicted = trained_model.predict_proba(test_dataset.to_pandas_dataframe())
```
# 4. モデルの解釈
一番精度が良かったチャンピョンモデルを選択し、モデルの解釈をしていきます。
モデルに含まれるライブラリを予め Python 環境にインストールする必要があります。[automl_env.yml](https://github.com/Azure/MachineLearningNotebooks/blob/master/how-to-use-azureml/automated-machine-learning/automl_env.yml)を用いて、conda の仮想環境に必要なパッケージをインストールしてください。
```
# 特徴量エンジニアリング後の変数名の確認
fitted_model.named_steps['datatransformer'].get_json_strs_for_engineered_feature_names()
#fitted_model.named_steps['datatransformer']. get_engineered_feature_names ()
# 特徴エンジニアリングのプロセスの可視化
text_transformations_used = []
for column_group in fitted_model.named_steps['datatransformer'].get_featurization_summary():
text_transformations_used.extend(column_group['Transformations'])
text_transformations_used
```
|
github_jupyter
|
# Spark SQL
Spark SQL is arguably one of the most important and powerful features in Spark. In a nutshell, with Spark SQL you can run SQL queries against views or tables organized into databases. You also can use system functions or define user functions and analyze query plans in order to optimize their workloads. This integrates directly into the DataFrame API, and as we saw in previous classes, you can choose to express some of your data manipulations in SQL and others in DataFrames and they will compile to the same underlying code.
## Big Data and SQL: Apache Hive
Before Spark’s rise, Hive was the de facto big data SQL access layer. Originally developed at Facebook, Hive became an incredibly popular tool across industry for performing SQL operations on big data. In many ways it helped propel Hadoop into different industries because analysts could run SQL queries. Although Spark began as a general processing engine with Resilient Distributed Datasets (RDDs), a large cohort of users now use Spark SQL.
## Big Data and SQL: Spark SQL
With the release of Spark 2.0, its authors created a superset of Hive’s support, writing a native SQL parser that supports both ANSI-SQL as well as HiveQL queries. This, along with its unique interoperability with DataFrames, makes it a powerful tool for all sorts of companies. For example, in late 2016, Facebook announced that it had begun running Spark workloads and seeing large benefits in doing so. In the words of the blog post’s authors:
>We challenged Spark to replace a pipeline that decomposed to hundreds of Hive jobs into a single Spark job. Through a series of performance and reliability improvements, we were able to scale Spark to handle one of our entity ranking data processing use cases in production…. The Spark-based pipeline produced significant performance improvements (4.5–6x CPU, 3–4x resource reservation, and ~5x latency) compared with the old Hive-based pipeline, and it has been running in production for several months.
The power of Spark SQL derives from several key facts: SQL analysts can now take advantage of Spark’s computation abilities by plugging into the Thrift Server or Spark’s SQL interface, whereas data engineers and scientists can use Spark SQL where appropriate in any data flow. This unifying API allows for data to be extracted with SQL, manipulated as a DataFrame, passed into one of Spark MLlibs’ large-scale machine learning algorithms, written out to another data source, and everything in between.
**NOTE:** Spark SQL is intended to operate as an online analytic processing (OLAP) database, not an online transaction processing (OLTP) database. This means that it is not intended to perform extremely low-latency queries. Even though support for in-place modifications is sure to be something that comes up in the future, it’s not something that is currently available.
```
spark.sql("SELECT 1 + 1").show()
```
As we have seen before, you can completely interoperate between SQL and DataFrames, as you see fit. For instance, you can create a DataFrame, manipulate it with SQL, and then manipulate it again as a DataFrame. It’s a powerful abstraction that you will likely find yourself using quite a bit:
```
bucket = spark._jsc.hadoopConfiguration().get("fs.gs.system.bucket")
data = "gs://" + bucket + "/notebooks/data/"
spark.read.json(data + "flight-data/json/2015-summary.json")\
.createOrReplaceTempView("flights_view") # DF => SQL
spark.sql("""
SELECT DEST_COUNTRY_NAME, sum(count)
FROM flights_view GROUP BY DEST_COUNTRY_NAME
""")\
.where("DEST_COUNTRY_NAME like 'S%'").where("`sum(count)` > 10")\
.count() # SQL => DF
```
## Creating Tables
You can create tables from a variety of sources. For instance below we are creating a table from a SELECT statement:
```
spark.sql('''
CREATE TABLE IF NOT EXISTS flights_from_select USING parquet AS SELECT * FROM flights_view
''')
spark.sql('SELECT * FROM flights_from_select').show(5)
spark.sql('''
DESCRIBE TABLE flights_from_select
''').show()
```
## Catalog
The highest level abstraction in Spark SQL is the Catalog. The Catalog is an abstraction for the storage of metadata about the data stored in your tables as well as other helpful things like databases, tables, functions, and views. The catalog is available in the `spark.catalog` package and contains a number of helpful functions for doing things like listing tables, databases, and functions.
```
Cat = spark.catalog
Cat.listTables()
spark.sql('SHOW TABLES').show(5, False)
Cat.listDatabases()
spark.sql('SHOW DATABASES').show()
Cat.listColumns('flights_from_select')
Cat.listTables()
```
### Caching Tables
```
spark.sql('''
CACHE TABLE flights_view
''')
spark.sql('''
UNCACHE TABLE flights_view
''')
```
## Explain
```
spark.sql('''
EXPLAIN SELECT * FROM just_usa_view
''').show(1, False)
```
### VIEWS - create/drop
```
spark.sql('''
CREATE VIEW just_usa_view AS
SELECT * FROM flights_from_select WHERE dest_country_name = 'United States'
''')
spark.sql('''
DROP VIEW IF EXISTS just_usa_view
''')
```
### Drop tables
```
spark.sql('DROP TABLE flights_from_select')
spark.sql('DROP TABLE IF EXISTS flights_from_select')
```
## `spark-sql`
Go to the command line tool and check for the list of databases and tables. For instance:
`SHOW TABLES`
|
github_jupyter
|
## Как выложить бота на HEROKU
*Подготовил Ян Пиле*
Сразу оговоримся, что мы на heroku выкладываем
**echo-Бота в телеграме, написанного с помощью библиотеки [pyTelegramBotAPI](https://github.com/eternnoir/pyTelegramBotAPI)**.
А взаимодействие его с сервером мы сделаем с использованием [flask](http://flask.pocoo.org/)
То есть вы боту пишете что-то, а он вам отвечает то же самое.
## Регистрация
Идем к **@BotFather** в Telegram и по его инструкции создаем нового бота командой **/newbot**.
Это должно закончиться выдачей вам токена вашего бота. Например последовательность команд, введенных мной:
* **/newbot**
* **my_echo_bot** (имя бота)
* **ian_echo_bot** (ник бота в телеграме)
Завершилась выдачей мне токена **1403467808:AAEaaLPkIqrhrQ62p7ToJclLtNNINdOopYk**
И ссылки t.me/ian_echo_bot
<img src="botfather.png">
## Регистрация на HEROKU
Идем сюда: https://signup.heroku.com/login
Создаем пользователя (это бесплатно)
Попадаем на https://dashboard.heroku.com/apps и там создаем новое приложение:
<img src="newapp1.png">
Вводим название и регион (Я выбрал Европу), создаем.
<img src="newapp2.png">
После того, как приложение создано, нажмите, "Open App" и скопируйте адрес оттуда.
<img src="newapp3.png">
У меня это https://ian-echo-bot.herokuapp.com
## Установить интерфейсы heroku и git для командной строки
Теперь надо установить Интерфейсы командной строки heroku и git по ссылкам:
* https://devcenter.heroku.com/articles/heroku-cli
* https://git-scm.com/book/en/v2/Getting-Started-Installing-Git
## Установить библиотеки
Теперь в вашем редакторе (например PyCharm) надо установить библиотеку для Телеграма и flask:
* pip install pyTelegramBotAPI
* pip install flask
## Код нашего echo-бота
Вот этот код я уложил в файл main.py
```
import os
import telebot
from flask import Flask, request
TOKEN = '1403467808:AAEaaLPkIqrhrQ62p7ToJclLtNNINdOopYk' # это мой токен
bot = telebot.TeleBot(token=TOKEN)
server = Flask(__name__)
# Если строка на входе непустая, то бот повторит ее
@bot.message_handler(func=lambda msg: msg.text is not None)
def reply_to_message(message):
bot.send_message(message.chat.id, message.text)
@server.route('/' + TOKEN, methods=['POST'])
def getMessage():
bot.process_new_updates([telebot.types.Update.de_json(request.stream.read().decode("utf-8"))])
return "!", 200
@server.route("/")
def webhook():
bot.remove_webhook()
bot.set_webhook(url='https://ian-echo-bot.herokuapp.com/' + TOKEN) #
return "!", 200
if __name__ == "__main__":
server.run(host="0.0.0.0", port=int(os.environ.get('PORT', 5000)))
```
## Теперь создаем еще два файла для запуска
**Procfile**(файл без расширения). Его надо открыть текстовым редактором и вписать туда строку:
web: python main.py
**requirements.txt** - файл со списком версий необходимых библиотек.
Зайдите в PyCharm, где вы делаете проект и введите в терминале команду:
pip list format freeze > requirements.txt
В файле записи должны иметь вид:
Название библиотеки Версия библиотеки
Если вдруг вы выдите что-то такое:
<img src="versions.png">
Удалите этот кусок текста, чтоб остался только номер версии и сохраните файл.
Теперь надо все эти файлы уложить на гит, привязанный к Heroku и запустить приложение.
## Последний шаг
Надо залогиниться в heroku через командную строку.
Введите:
heroku login
Вас перебросит в браузер на вот такую страницу:
<img src="login.png">
После того, как вы залогинились, удостоверьтесь, что вы находитесь в папке, где лежат фаши файлы:
main.py
Procfile
requirements.txt
**Вводите команды:**
git init
git add .
git commit -m "first commit"
heroku git:remote -a ian-echo-bot
git push heroku master
По ходу выкатки вы увидите что-то такое:
<img src="process.png">
Готово, вы выложили вашего бота.
Материалы, которыми можно воспользоваться по ходу выкладки бота на сервер:
https://towardsdatascience.com/how-to-deploy-a-telegram-bot-using-heroku-for-free-9436f89575d2
https://mattrighetti.medium.com/build-your-first-telegram-bot-using-python-and-heroku-79d48950d4b0
|
github_jupyter
|
```
import numpy as np
import matplotlib.pyplot as plt
import numba
from tqdm import tqdm
import eitest
```
# Data generators
```
@numba.njit
def event_series_bernoulli(series_length, event_count):
'''Generate an iid Bernoulli distributed event series.
series_length: length of the event series
event_count: number of events'''
event_series = np.zeros(series_length)
event_series[np.random.choice(np.arange(0, series_length), event_count, replace=False)] = 1
return event_series
@numba.njit
def time_series_mean_impact(event_series, order, signal_to_noise):
'''Generate a time series with impacts in mean as described in the paper.
The impact weights are sampled iid from N(0, signal_to_noise),
and additional noise is sampled iid from N(0,1). The detection problem will
be harder than in time_series_meanconst_impact for small orders, as for small
orders we have a low probability to sample at least one impact weight with a
high magnitude. On the other hand, since the impact is different at every lag,
we can detect the impacts even if the order is larger than the max_lag value
used in the test.
event_series: input of shape (T,) with event occurrences
order: order of the event impacts
signal_to_noise: signal to noise ratio of the event impacts'''
series_length = len(event_series)
weights = np.random.randn(order)*np.sqrt(signal_to_noise)
time_series = np.random.randn(series_length)
for t in range(series_length):
if event_series[t] == 1:
time_series[t+1:t+order+1] += weights[:order-max(0, (t+order+1)-series_length)]
return time_series
@numba.njit
def time_series_meanconst_impact(event_series, order, const):
'''Generate a time series with impacts in mean by adding a constant.
Better for comparing performance across different impact orders, since the
magnitude of the impact will always be the same.
event_series: input of shape (T,) with event occurrences
order: order of the event impacts
const: constant for mean shift'''
series_length = len(event_series)
time_series = np.random.randn(series_length)
for t in range(series_length):
if event_series[t] == 1:
time_series[t+1:t+order+1] += const
return time_series
@numba.njit
def time_series_var_impact(event_series, order, variance):
'''Generate a time series with impacts in variance as described in the paper.
event_series: input of shape (T,) with event occurrences
order: order of the event impacts
variance: variance under event impacts'''
series_length = len(event_series)
time_series = np.random.randn(series_length)
for t in range(series_length):
if event_series[t] == 1:
for tt in range(t+1, min(series_length, t+order+1)):
time_series[tt] = np.random.randn()*np.sqrt(variance)
return time_series
@numba.njit
def time_series_tail_impact(event_series, order, dof):
'''Generate a time series with impacts in tails as described in the paper.
event_series: input of shape (T,) with event occurrences
order: delay of the event impacts
dof: degrees of freedom of the t distribution'''
series_length = len(event_series)
time_series = np.random.randn(series_length)*np.sqrt(dof/(dof-2))
for t in range(series_length):
if event_series[t] == 1:
for tt in range(t+1, min(series_length, t+order+1)):
time_series[tt] = np.random.standard_t(dof)
return time_series
```
# Visualization of the impact models
```
default_T = 8192
default_N = 64
default_q = 4
es = event_series_bernoulli(default_T, default_N)
for ts in [
time_series_mean_impact(es, order=default_q, signal_to_noise=10.),
time_series_meanconst_impact(es, order=default_q, const=5.),
time_series_var_impact(es, order=default_q, variance=4.),
time_series_tail_impact(es, order=default_q, dof=3.),
]:
fig, (ax1, ax2) = plt.subplots(1, 2, gridspec_kw={'width_ratios': [2, 1]}, figsize=(15, 2))
ax1.plot(ts)
ax1.plot(es*np.max(ts), alpha=0.5)
ax1.set_xlim(0, len(es))
samples = eitest.obtain_samples(es, ts, method='eager', lag_cutoff=15, instantaneous=True)
eitest.plot_samples(samples, ax2)
plt.show()
```
# Simulations
```
def test_simul_pairs(impact_model, param_T, param_N, param_q, param_r,
n_pairs, lag_cutoff, instantaneous, sample_method,
twosamp_test, multi_test, alpha):
true_positive = 0.
false_positive = 0.
for _ in tqdm(range(n_pairs)):
es = event_series_bernoulli(param_T, param_N)
if impact_model == 'mean':
ts = time_series_mean_impact(es, param_q, param_r)
elif impact_model == 'meanconst':
ts = time_series_meanconst_impact(es, param_q, param_r)
elif impact_model == 'var':
ts = time_series_var_impact(es, param_q, param_r)
elif impact_model == 'tail':
ts = time_series_tail_impact(es, param_q, param_r)
else:
raise ValueError('impact_model must be "mean", "meanconst", "var" or "tail"')
# coupled pair
samples = eitest.obtain_samples(es, ts, lag_cutoff=lag_cutoff,
method=sample_method,
instantaneous=instantaneous,
sort=(twosamp_test == 'ks')) # samples need to be sorted for K-S test
tstats, pvals = eitest.pairwise_twosample_tests(samples, twosamp_test, min_pts=2)
pvals_adj = eitest.multitest(np.sort(pvals[~np.isnan(pvals)]), multi_test)
true_positive += (pvals_adj.min() < alpha)
# uncoupled pair
samples = eitest.obtain_samples(np.random.permutation(es), ts, lag_cutoff=lag_cutoff,
method=sample_method,
instantaneous=instantaneous,
sort=(twosamp_test == 'ks'))
tstats, pvals = eitest.pairwise_twosample_tests(samples, twosamp_test, min_pts=2)
pvals_adj = eitest.multitest(np.sort(pvals[~np.isnan(pvals)]), multi_test)
false_positive += (pvals_adj.min() < alpha)
return true_positive/n_pairs, false_positive/n_pairs
# global parameters
default_T = 8192
n_pairs = 100
alpha = 0.05
twosamp_test = 'ks'
multi_test = 'simes'
sample_method = 'lazy'
lag_cutoff = 32
instantaneous = True
```
## Mean impact model
```
default_N = 64
default_r = 1.
default_q = 4
```
### ... by number of events
```
vals = [4, 8, 16, 32, 64, 128, 256]
tprs = np.empty(len(vals))
fprs = np.empty(len(vals))
for i, val in enumerate(vals):
tprs[i], fprs[i] = test_simul_pairs(impact_model='mean', param_T=default_T,
param_N=val, param_q=default_q, param_r=default_r,
n_pairs=n_pairs, sample_method=sample_method,
lag_cutoff=lag_cutoff, instantaneous=instantaneous,
twosamp_test=twosamp_test, multi_test=multi_test, alpha=alpha)
plt.figure(figsize=(3,3))
plt.axvline(default_N, ls='-', c='gray', lw=1, label='def')
plt.axhline(alpha, ls='--', c='black', lw=1, label='alpha')
plt.plot(vals, tprs, label='TPR', marker='x')
plt.plot(vals, fprs, label='FPR', marker='x')
plt.gca().set_xscale('log', base=2)
plt.legend()
plt.show()
print(f'# mean impact model (T={default_T}, q={default_q}, r={default_r}, n_pairs={n_pairs}, cutoff={lag_cutoff}, instantaneous={instantaneous}, alpha={alpha}, {sample_method}-{twosamp_test}-{multi_test})')
print(f'# N\ttpr\tfpr')
for i, (tpr, fpr) in enumerate(zip(tprs, fprs)):
print(f'{vals[i]}\t{tpr}\t{fpr}')
print()
```
### ... by impact order
```
vals = [1, 2, 4, 8, 16, 32]
tprs = np.empty(len(vals))
fprs = np.empty(len(vals))
for i, val in enumerate(vals):
tprs[i], fprs[i] = test_simul_pairs(impact_model='mean', param_T=default_T,
param_N=default_N, param_q=val, param_r=default_r,
n_pairs=n_pairs, sample_method=sample_method,
lag_cutoff=lag_cutoff, instantaneous=instantaneous,
twosamp_test=twosamp_test, multi_test=multi_test, alpha=alpha)
plt.figure(figsize=(3,3))
plt.axvline(default_q, ls='-', c='gray', lw=1, label='def')
plt.axhline(alpha, ls='--', c='black', lw=1, label='alpha')
plt.plot(vals, tprs, label='TPR', marker='x')
plt.plot(vals, fprs, label='FPR', marker='x')
plt.gca().set_xscale('log', base=2)
plt.legend()
plt.show()
print(f'# mean impact model (T={default_T}, N={default_N}, r={default_r}, n_pairs={n_pairs}, cutoff={lag_cutoff}, instantaneous={instantaneous}, alpha={alpha}, {sample_method}-{twosamp_test}-{multi_test})')
print(f'# q\ttpr\tfpr')
for i, (tpr, fpr) in enumerate(zip(tprs, fprs)):
print(f'{vals[i]}\t{tpr}\t{fpr}')
print()
```
### ... by signal-to-noise ratio
```
vals = [1./32, 1./16, 1./8, 1./4, 1./2, 1., 2., 4.]
tprs = np.empty(len(vals))
fprs = np.empty(len(vals))
for i, val in enumerate(vals):
tprs[i], fprs[i] = test_simul_pairs(impact_model='mean', param_T=default_T,
param_N=default_N, param_q=default_q, param_r=val,
n_pairs=n_pairs, sample_method=sample_method,
lag_cutoff=lag_cutoff, instantaneous=instantaneous,
twosamp_test=twosamp_test, multi_test=multi_test, alpha=alpha)
plt.figure(figsize=(3,3))
plt.axvline(default_r, ls='-', c='gray', lw=1, label='def')
plt.axhline(alpha, ls='--', c='black', lw=1, label='alpha')
plt.plot(vals, tprs, label='TPR', marker='x')
plt.plot(vals, fprs, label='FPR', marker='x')
plt.gca().set_xscale('log', base=2)
plt.legend()
plt.show()
print(f'# mean impact model (T={default_T}, N={default_N}, q={default_q}, n_pairs={n_pairs}, cutoff={lag_cutoff}, instantaneous={instantaneous}, alpha={alpha}, {sample_method}-{twosamp_test}-{multi_test})')
print(f'# r\ttpr\tfpr')
for i, (tpr, fpr) in enumerate(zip(tprs, fprs)):
print(f'{vals[i]}\t{tpr}\t{fpr}')
```
## Meanconst impact model
```
default_N = 64
default_r = 0.5
default_q = 4
```
### ... by number of events
```
vals = [4, 8, 16, 32, 64, 128, 256]
tprs = np.empty(len(vals))
fprs = np.empty(len(vals))
for i, val in enumerate(vals):
tprs[i], fprs[i] = test_simul_pairs(impact_model='meanconst', param_T=default_T,
param_N=val, param_q=default_q, param_r=default_r,
n_pairs=n_pairs, sample_method=sample_method,
lag_cutoff=lag_cutoff, instantaneous=instantaneous,
twosamp_test=twosamp_test, multi_test=multi_test, alpha=alpha)
plt.figure(figsize=(3,3))
plt.axvline(default_N, ls='-', c='gray', lw=1, label='def')
plt.axhline(alpha, ls='--', c='black', lw=1, label='alpha')
plt.plot(vals, tprs, label='TPR', marker='x')
plt.plot(vals, fprs, label='FPR', marker='x')
plt.gca().set_xscale('log', base=2)
plt.legend()
plt.show()
print(f'# meanconst impact model (T={default_T}, q={default_q}, r={default_r}, n_pairs={n_pairs}, cutoff={lag_cutoff}, instantaneous={instantaneous}, alpha={alpha}, {sample_method}-{twosamp_test}-{multi_test})')
print(f'# N\ttpr\tfpr')
for i, (tpr, fpr) in enumerate(zip(tprs, fprs)):
print(f'{vals[i]}\t{tpr}\t{fpr}')
print()
```
### ... by impact order
```
vals = [1, 2, 4, 8, 16, 32]
tprs = np.empty(len(vals))
fprs = np.empty(len(vals))
for i, val in enumerate(vals):
tprs[i], fprs[i] = test_simul_pairs(impact_model='meanconst', param_T=default_T,
param_N=default_N, param_q=val, param_r=default_r,
n_pairs=n_pairs, sample_method=sample_method,
lag_cutoff=lag_cutoff, instantaneous=instantaneous,
twosamp_test=twosamp_test, multi_test=multi_test, alpha=alpha)
plt.figure(figsize=(3,3))
plt.axvline(default_q, ls='-', c='gray', lw=1, label='def')
plt.axhline(alpha, ls='--', c='black', lw=1, label='alpha')
plt.plot(vals, tprs, label='TPR', marker='x')
plt.plot(vals, fprs, label='FPR', marker='x')
plt.gca().set_xscale('log', base=2)
plt.legend()
plt.show()
print(f'# meanconst impact model (T={default_T}, N={default_N}, r={default_r}, n_pairs={n_pairs}, cutoff={lag_cutoff}, instantaneous={instantaneous}, alpha={alpha}, {sample_method}-{twosamp_test}-{multi_test})')
print(f'# q\ttpr\tfpr')
for i, (tpr, fpr) in enumerate(zip(tprs, fprs)):
print(f'{vals[i]}\t{tpr}\t{fpr}')
print()
```
### ... by mean value
```
vals = [0.125, 0.25, 0.5, 1, 2]
tprs = np.empty(len(vals))
fprs = np.empty(len(vals))
for i, val in enumerate(vals):
tprs[i], fprs[i] = test_simul_pairs(impact_model='meanconst', param_T=default_T,
param_N=default_N, param_q=default_q, param_r=val,
n_pairs=n_pairs, sample_method=sample_method,
lag_cutoff=lag_cutoff, instantaneous=instantaneous,
twosamp_test=twosamp_test, multi_test=multi_test, alpha=alpha)
plt.figure(figsize=(3,3))
plt.axvline(default_r, ls='-', c='gray', lw=1, label='def')
plt.axhline(alpha, ls='--', c='black', lw=1, label='alpha')
plt.plot(vals, tprs, label='TPR', marker='x')
plt.plot(vals, fprs, label='FPR', marker='x')
plt.gca().set_xscale('log', base=2)
plt.legend()
plt.show()
print(f'# meanconst impact model (T={default_T}, N={default_N}, q={default_q}, n_pairs={n_pairs}, cutoff={lag_cutoff}, instantaneous={instantaneous}, alpha={alpha}, {sample_method}-{twosamp_test}-{multi_test})')
print(f'# r\ttpr\tfpr')
for i, (tpr, fpr) in enumerate(zip(tprs, fprs)):
print(f'{vals[i]}\t{tpr}\t{fpr}')
print()
```
## Variance impact model
In the paper, we show results with the variance impact model parametrized by the **variance increase**. Here we directly modulate the variance.
```
default_N = 64
default_r = 8.
default_q = 4
```
### ... by number of events
```
vals = [4, 8, 16, 32, 64, 128, 256]
tprs = np.empty(len(vals))
fprs = np.empty(len(vals))
for i, val in enumerate(vals):
tprs[i], fprs[i] = test_simul_pairs(impact_model='var', param_T=default_T,
param_N=val, param_q=default_q, param_r=default_r,
n_pairs=n_pairs, sample_method=sample_method,
lag_cutoff=lag_cutoff, instantaneous=instantaneous,
twosamp_test=twosamp_test, multi_test=multi_test, alpha=alpha)
plt.figure(figsize=(3,3))
plt.axvline(default_N, ls='-', c='gray', lw=1, label='def')
plt.axhline(alpha, ls='--', c='black', lw=1, label='alpha')
plt.plot(vals, tprs, label='TPR', marker='x')
plt.plot(vals, fprs, label='FPR', marker='x')
plt.gca().set_xscale('log', base=2)
plt.legend()
plt.show()
print(f'# var impact model (T={default_T}, q={default_q}, r={default_r}, n_pairs={n_pairs}, cutoff={lag_cutoff}, instantaneous={instantaneous}, alpha={alpha}, {sample_method}-{twosamp_test}-{multi_test})')
print(f'# N\ttpr\tfpr')
for i, (tpr, fpr) in enumerate(zip(tprs, fprs)):
print(f'{vals[i]}\t{tpr}\t{fpr}')
print()
```
### ... by impact order
```
vals = [1, 2, 4, 8, 16, 32]
tprs = np.empty(len(vals))
fprs = np.empty(len(vals))
for i, val in enumerate(vals):
tprs[i], fprs[i] = test_simul_pairs(impact_model='var', param_T=default_T,
param_N=default_N, param_q=val, param_r=default_r,
n_pairs=n_pairs, sample_method=sample_method,
lag_cutoff=lag_cutoff, instantaneous=instantaneous,
twosamp_test=twosamp_test, multi_test=multi_test, alpha=alpha)
plt.figure(figsize=(3,3))
plt.axvline(default_q, ls='-', c='gray', lw=1, label='def')
plt.axhline(alpha, ls='--', c='black', lw=1, label='alpha')
plt.plot(vals, tprs, label='TPR', marker='x')
plt.plot(vals, fprs, label='FPR', marker='x')
plt.gca().set_xscale('log', base=2)
plt.legend()
plt.show()
print(f'# var impact model (T={default_T}, N={default_N}, r={default_r}, n_pairs={n_pairs}, cutoff={lag_cutoff}, instantaneous={instantaneous}, alpha={alpha}, {sample_method}-{twosamp_test}-{multi_test})')
print(f'# q\ttpr\tfpr')
for i, (tpr, fpr) in enumerate(zip(tprs, fprs)):
print(f'{vals[i]}\t{tpr}\t{fpr}')
print()
```
### ... by variance
```
vals = [2., 4., 8., 16., 32.]
tprs = np.empty(len(vals))
fprs = np.empty(len(vals))
for i, val in enumerate(vals):
tprs[i], fprs[i] = test_simul_pairs(impact_model='var', param_T=default_T,
param_N=default_N, param_q=default_q, param_r=val,
n_pairs=n_pairs, sample_method=sample_method,
lag_cutoff=lag_cutoff, instantaneous=instantaneous,
twosamp_test=twosamp_test, multi_test=multi_test, alpha=alpha)
plt.figure(figsize=(3,3))
plt.axvline(default_r, ls='-', c='gray', lw=1, label='def')
plt.axhline(alpha, ls='--', c='black', lw=1, label='alpha')
plt.plot(vals, tprs, label='TPR', marker='x')
plt.plot(vals, fprs, label='FPR', marker='x')
plt.gca().set_xscale('log', base=2)
plt.legend()
plt.show()
print(f'# var impact model (T={default_T}, N={default_N}, q={default_q}, n_pairs={n_pairs}, cutoff={lag_cutoff}, instantaneous={instantaneous}, alpha={alpha}, {sample_method}-{twosamp_test}-{multi_test})')
print(f'# r\ttpr\tfpr')
for i, (tpr, fpr) in enumerate(zip(tprs, fprs)):
print(f'{vals[i]}\t{tpr}\t{fpr}')
print()
```
## Tail impact model
```
default_N = 512
default_r = 3.
default_q = 4
```
### ... by number of events
```
vals = [64, 128, 256, 512, 1024]
tprs = np.empty(len(vals))
fprs = np.empty(len(vals))
for i, val in enumerate(vals):
tprs[i], fprs[i] = test_simul_pairs(impact_model='tail', param_T=default_T,
param_N=val, param_q=default_q, param_r=default_r,
n_pairs=n_pairs, sample_method=sample_method,
lag_cutoff=lag_cutoff, instantaneous=instantaneous,
twosamp_test=twosamp_test, multi_test=multi_test, alpha=alpha)
plt.figure(figsize=(3,3))
plt.axvline(default_N, ls='-', c='gray', lw=1, label='def')
plt.axhline(alpha, ls='--', c='black', lw=1, label='alpha')
plt.plot(vals, tprs, label='TPR', marker='x')
plt.plot(vals, fprs, label='FPR', marker='x')
plt.gca().set_xscale('log', base=2)
plt.legend()
plt.show()
print(f'# tail impact model (T={default_T}, q={default_q}, r={default_r}, n_pairs={n_pairs}, cutoff={lag_cutoff}, instantaneous={instantaneous}, alpha={alpha}, {sample_method}-{twosamp_test}-{multi_test})')
print(f'# N\ttpr\tfpr')
for i, (tpr, fpr) in enumerate(zip(tprs, fprs)):
print(f'{vals[i]}\t{tpr}\t{fpr}')
print()
```
### ... by impact order
```
vals = [1, 2, 4, 8, 16, 32]
tprs = np.empty(len(vals))
fprs = np.empty(len(vals))
for i, val in enumerate(vals):
tprs[i], fprs[i] = test_simul_pairs(impact_model='tail', param_T=default_T,
param_N=default_N, param_q=val, param_r=default_r,
n_pairs=n_pairs, sample_method=sample_method,
lag_cutoff=lag_cutoff, instantaneous=instantaneous,
twosamp_test=twosamp_test, multi_test=multi_test, alpha=alpha)
plt.figure(figsize=(3,3))
plt.axvline(default_q, ls='-', c='gray', lw=1, label='def')
plt.axhline(alpha, ls='--', c='black', lw=1, label='alpha')
plt.plot(vals, tprs, label='TPR', marker='x')
plt.plot(vals, fprs, label='FPR', marker='x')
plt.gca().set_xscale('log', base=2)
plt.legend()
plt.show()
print(f'# tail impact model (T={default_T}, N={default_N}, r={default_r}, n_pairs={n_pairs}, cutoff={lag_cutoff}, instantaneous={instantaneous}, alpha={alpha}, {sample_method}-{twosamp_test}-{multi_test})')
print(f'# q\ttpr\tfpr')
for i, (tpr, fpr) in enumerate(zip(tprs, fprs)):
print(f'{vals[i]}\t{tpr}\t{fpr}')
print()
```
### ... by degrees of freedom
```
vals = [2.5, 3., 3.5, 4., 4.5, 5., 5.5, 6.]
tprs = np.empty(len(vals))
fprs = np.empty(len(vals))
for i, val in enumerate(vals):
tprs[i], fprs[i] = test_simul_pairs(impact_model='tail', param_T=default_T,
param_N=default_N, param_q=default_q, param_r=val,
n_pairs=n_pairs, sample_method=sample_method,
lag_cutoff=lag_cutoff, instantaneous=instantaneous,
twosamp_test=twosamp_test, multi_test=multi_test, alpha=alpha)
plt.figure(figsize=(3,3))
plt.axvline(default_r, ls='-', c='gray', lw=1, label='def')
plt.axhline(alpha, ls='--', c='black', lw=1, label='alpha')
plt.plot(vals, tprs, label='TPR', marker='x')
plt.plot(vals, fprs, label='FPR', marker='x')
plt.legend()
plt.show()
print(f'# tail impact model (T={default_T}, N={default_N}, q={default_q}, n_pairs={n_pairs}, cutoff={lag_cutoff}, instantaneous={instantaneous}, alpha={alpha}, {sample_method}-{twosamp_test}-{multi_test})')
print(f'# r\ttpr\tfpr')
for i, (tpr, fpr) in enumerate(zip(tprs, fprs)):
print(f'{vals[i]}\t{tpr}\t{fpr}')
print()
```
|
github_jupyter
|
# Lalonde Pandas API Example
by Adam Kelleher
We'll run through a quick example using the high-level Python API for the DoSampler. The DoSampler is different from most classic causal effect estimators. Instead of estimating statistics under interventions, it aims to provide the generality of Pearlian causal inference. In that context, the joint distribution of the variables under an intervention is the quantity of interest. It's hard to represent a joint distribution nonparametrically, so instead we provide a sample from that distribution, which we call a "do" sample.
Here, when you specify an outcome, that is the variable you're sampling under an intervention. We still have to do the usual process of making sure the quantity (the conditional interventional distribution of the outcome) is identifiable. We leverage the familiar components of the rest of the package to do that "under the hood". You'll notice some similarity in the kwargs for the DoSampler.
## Getting the Data
First, download the data from the LaLonde example.
```
import os, sys
sys.path.append(os.path.abspath("../../../"))
from rpy2.robjects import r as R
%load_ext rpy2.ipython
#%R install.packages("Matching")
%R library(Matching)
%R data(lalonde)
%R -o lalonde
lalonde.to_csv("lalonde.csv",index=False)
# the data already loaded in the previous cell. we include the import
# here you so you don't have to keep re-downloading it.
import pandas as pd
lalonde=pd.read_csv("lalonde.csv")
```
## The `causal` Namespace
We've created a "namespace" for `pandas.DataFrame`s containing causal inference methods. You can access it here with `lalonde.causal`, where `lalonde` is our `pandas.DataFrame`, and `causal` contains all our new methods! These methods are magically loaded into your existing (and future) dataframes when you `import dowhy.api`.
```
import dowhy.api
```
Now that we have the `causal` namespace, lets give it a try!
## The `do` Operation
The key feature here is the `do` method, which produces a new dataframe replacing the treatment variable with values specified, and the outcome with a sample from the interventional distribution of the outcome. If you don't specify a value for the treatment, it leaves the treatment untouched:
```
do_df = lalonde.causal.do(x='treat',
outcome='re78',
common_causes=['nodegr', 'black', 'hisp', 'age', 'educ', 'married'],
variable_types={'age': 'c', 'educ':'c', 'black': 'd', 'hisp': 'd',
'married': 'd', 'nodegr': 'd','re78': 'c', 'treat': 'b'},
proceed_when_unidentifiable=True)
```
Notice you get the usual output and prompts about identifiability. This is all `dowhy` under the hood!
We now have an interventional sample in `do_df`. It looks very similar to the original dataframe. Compare them:
```
lalonde.head()
do_df.head()
```
## Treatment Effect Estimation
We could get a naive estimate before for a treatment effect by doing
```
(lalonde[lalonde['treat'] == 1].mean() - lalonde[lalonde['treat'] == 0].mean())['re78']
```
We can do the same with our new sample from the interventional distribution to get a causal effect estimate
```
(do_df[do_df['treat'] == 1].mean() - do_df[do_df['treat'] == 0].mean())['re78']
```
We could get some rough error bars on the outcome using the normal approximation for a 95% confidence interval, like
```
import numpy as np
1.96*np.sqrt((do_df[do_df['treat'] == 1].var()/len(do_df[do_df['treat'] == 1])) +
(do_df[do_df['treat'] == 0].var()/len(do_df[do_df['treat'] == 0])))['re78']
```
but note that these DO NOT contain propensity score estimation error. For that, a bootstrapping procedure might be more appropriate.
This is just one statistic we can compute from the interventional distribution of `'re78'`. We can get all of the interventional moments as well, including functions of `'re78'`. We can leverage the full power of pandas, like
```
do_df['re78'].describe()
lalonde['re78'].describe()
```
and even plot aggregations, like
```
%matplotlib inline
import seaborn as sns
sns.barplot(data=lalonde, x='treat', y='re78')
sns.barplot(data=do_df, x='treat', y='re78')
```
## Specifying Interventions
You can find the distribution of the outcome under an intervention to set the value of the treatment.
```
do_df = lalonde.causal.do(x={'treat': 1},
outcome='re78',
common_causes=['nodegr', 'black', 'hisp', 'age', 'educ', 'married'],
variable_types={'age': 'c', 'educ':'c', 'black': 'd', 'hisp': 'd',
'married': 'd', 'nodegr': 'd','re78': 'c', 'treat': 'b'},
proceed_when_unidentifiable=True)
do_df.head()
```
This new dataframe gives the distribution of `'re78'` when `'treat'` is set to `1`.
For much more detail on how the `do` method works, check the docstring:
```
help(lalonde.causal.do)
```
|
github_jupyter
|
# Welcome to the Datenguide Python Package
Within this notebook the functionality of the package will be explained and demonstrated with examples.
### Topics
- Import
- get region IDs
- get statstic IDs
- get the data
- for single regions
- for multiple regions
## 1. Import
**Import the helper functions 'get_all_regions' and 'get_statistics'**
**Import the module Query for the main functionality**
```
# ONLY FOR TESTING LOCAL PACKAGE
# %cd ..
from datenguidepy.query_helper import get_all_regions, get_statistics
from datenguidepy import Query
```
**Import pandas and matplotlib for the usual display of data as tables and graphs**
```
import pandas as pd
import matplotlib
%matplotlib inline
pd.set_option('display.max_colwidth', 150)
```
## 2. Get Region IDs
### How to get the ID of the region I want to query
Regionalstatistik - the database behind Datenguide - has data for differently granular levels of Germany.
nuts:
1 – Bundesländer
2 – Regierungsbezirke / statistische Regionen
3 – Kreise / kreisfreie Städte.
lau:
1 - Verwaltungsgemeinschaften
2 - Gemeinden.
the function `get_all_regions()` returns all IDs from all levels.
```
# get_all_regions returns all ids
get_all_regions()
```
To get a specific ID, use the common pandas function `query()`
```
# e.g. get all "Bundesländer
get_all_regions().query("level == 'nuts1'")
# e.g. get the ID of Havelland
get_all_regions().query("name =='Havelland'")
```
## 3. Get statistic IDs
### How to find statistics
```
# get all statistics
get_statistics()
```
If you already know the statsitic ID you are looking for - perfect.
Otherwise you can use the pandas `query()` function so search e.g. for specific terms.
```
# find out the name of the desired statistic about birth
get_statistics().query('long_description.str.contains("Statistik der Geburten")', engine='python')
```
## 4. get the data
The top level element is the Query. For each query fields can be added (usually statistics / measures) that you want to get information on.
A Query can either be done on a single region, or on multiple regions (e.g. all Bundesländer).
### Single Region
If I want information - e.g. all births for the past years in Berlin:
```
# create a query for the region 11
query = Query.region('11')
# add a field (the statstic) to the query
field_births = query.add_field('BEV001')
# get the data of this query
query.results().head()
```
To get the short description in the result data frame instead of the cryptic ID (e.g. "Lebend Geborene" instead of BEV001) set the argument "verbose_statsitics"=True in the resutls:
```
query.results(verbose_statistics =True).head()
```
Now we only get the information about the count of births per year and the source of the data (year, value and source are default fields).
But there is more information in the statistic that we can get information on.
Let's look at the meta data of the statstic:
```
# get information on the field
field_births.get_info()
```
The arguments tell us what we can use for filtering (e.g. only data on baby girls (female)).
The fields tell us what more information can be displayed in our results.
```
# add filter
field_births.add_args({'GES': 'GESW'})
# now only about half the amount of births are returned as only the results for female babies are queried
query.results().head()
# add the field NAT (nationality) to the results
field_births.add_field('NAT')
```
**CAREFUL**: The information for the fields (e.g. nationality) is by default returned as a total amount. Therefore - if no argument "NAT" is specified in addition to the field, then only "None" will be displayed.
In order to get information on all possible values, the argument "ALL" needs to be added:
(the rows with value "None" are the aggregated values of all options)
```
field_births.add_args({'NAT': 'ALL'})
query.results().head()
```
To display the short description of the enum values instead of the cryptic IDs (e.g. Ausländer(innen) instead of NATA), set the argument "verbose_enums = True" on the results:
```
query.results(verbose_enums=True).head()
```
## Multiple Regions
To display data for multiple single regions, a list with region IDs can be used:
```
query_multiple = Query.region(['01', '02'])
query_multiple.add_field('BEV001')
query_multiple.results().sort_values('year').head()
```
To display data for e.g. all 'Bundesländer' or for all regions within a Bundesland, you can use the function `all_regions()`:
- specify nuts level
- specify lau level
- specify parent ID (Careful: not only the regions for the next lower level will be returned, but all levels - e.g. if you specify a parent on nuts level 1 then the "children" on nuts 2 but also the "grandchildren" on nuts 3, lau 1 and lau 2 will be returned)
```
# get data for all Bundesländer
query_all = Query.all_regions(nuts=1)
query_all.add_field('BEV001')
query_all.results().sort_values('year').head(12)
# get data for all regions within Brandenburg
query_all = Query.all_regions(parent='12')
query_all.add_field('BEV001')
query_all.results().head()
# get data for all nuts 3 regions within Brandenburg
query_all = Query.all_regions(parent='12', nuts=3)
query_all.add_field('BEV001')
query_all.results().sort_values('year').head()
```
|
github_jupyter
|
# Chapter 4
`Original content created by Cam Davidson-Pilon`
`Ported to Python 3 and PyMC3 by Max Margenot (@clean_utensils) and Thomas Wiecki (@twiecki) at Quantopian (@quantopian)`
______
## The greatest theorem never told
This chapter focuses on an idea that is always bouncing around our minds, but is rarely made explicit outside books devoted to statistics. In fact, we've been using this simple idea in every example thus far.
### The Law of Large Numbers
Let $Z_i$ be $N$ independent samples from some probability distribution. According to *the Law of Large numbers*, so long as the expected value $E[Z]$ is finite, the following holds,
$$\frac{1}{N} \sum_{i=1}^N Z_i \rightarrow E[ Z ], \;\;\; N \rightarrow \infty.$$
In words:
> The average of a sequence of random variables from the same distribution converges to the expected value of that distribution.
This may seem like a boring result, but it will be the most useful tool you use.
### Intuition
If the above Law is somewhat surprising, it can be made more clear by examining a simple example.
Consider a random variable $Z$ that can take only two values, $c_1$ and $c_2$. Suppose we have a large number of samples of $Z$, denoting a specific sample $Z_i$. The Law says that we can approximate the expected value of $Z$ by averaging over all samples. Consider the average:
$$ \frac{1}{N} \sum_{i=1}^N \;Z_i $$
By construction, $Z_i$ can only take on $c_1$ or $c_2$, hence we can partition the sum over these two values:
\begin{align}
\frac{1}{N} \sum_{i=1}^N \;Z_i
& =\frac{1}{N} \big( \sum_{ Z_i = c_1}c_1 + \sum_{Z_i=c_2}c_2 \big) \\\\[5pt]
& = c_1 \sum_{ Z_i = c_1}\frac{1}{N} + c_2 \sum_{ Z_i = c_2}\frac{1}{N} \\\\[5pt]
& = c_1 \times \text{ (approximate frequency of $c_1$) } \\\\
& \;\;\;\;\;\;\;\;\; + c_2 \times \text{ (approximate frequency of $c_2$) } \\\\[5pt]
& \approx c_1 \times P(Z = c_1) + c_2 \times P(Z = c_2 ) \\\\[5pt]
& = E[Z]
\end{align}
Equality holds in the limit, but we can get closer and closer by using more and more samples in the average. This Law holds for almost *any distribution*, minus some important cases we will encounter later.
##### Example
____
Below is a diagram of the Law of Large numbers in action for three different sequences of Poisson random variables.
We sample `sample_size = 100000` Poisson random variables with parameter $\lambda = 4.5$. (Recall the expected value of a Poisson random variable is equal to it's parameter.) We calculate the average for the first $n$ samples, for $n=1$ to `sample_size`.
```
%matplotlib inline
import numpy as np
from IPython.core.pylabtools import figsize
import matplotlib.pyplot as plt
figsize( 12.5, 5 )
sample_size = 100000
expected_value = lambda_ = 4.5
poi = np.random.poisson
N_samples = range(1,sample_size,100)
for k in range(3):
samples = poi( lambda_, sample_size )
partial_average = [ samples[:i].mean() for i in N_samples ]
plt.plot( N_samples, partial_average, lw=1.5,label="average \
of $n$ samples; seq. %d"%k)
plt.plot( N_samples, expected_value*np.ones_like( partial_average),
ls = "--", label = "true expected value", c = "k" )
plt.ylim( 4.35, 4.65)
plt.title( "Convergence of the average of \n random variables to its \
expected value" )
plt.ylabel( "average of $n$ samples" )
plt.xlabel( "# of samples, $n$")
plt.legend();
```
Looking at the above plot, it is clear that when the sample size is small, there is greater variation in the average (compare how *jagged and jumpy* the average is initially, then *smooths* out). All three paths *approach* the value 4.5, but just flirt with it as $N$ gets large. Mathematicians and statistician have another name for *flirting*: convergence.
Another very relevant question we can ask is *how quickly am I converging to the expected value?* Let's plot something new. For a specific $N$, let's do the above trials thousands of times and compute how far away we are from the true expected value, on average. But wait — *compute on average*? This is simply the law of large numbers again! For example, we are interested in, for a specific $N$, the quantity:
$$D(N) = \sqrt{ \;E\left[\;\; \left( \frac{1}{N}\sum_{i=1}^NZ_i - 4.5 \;\right)^2 \;\;\right] \;\;}$$
The above formulae is interpretable as a distance away from the true value (on average), for some $N$. (We take the square root so the dimensions of the above quantity and our random variables are the same). As the above is an expected value, it can be approximated using the law of large numbers: instead of averaging $Z_i$, we calculate the following multiple times and average them:
$$ Y_k = \left( \;\frac{1}{N}\sum_{i=1}^NZ_i - 4.5 \; \right)^2 $$
By computing the above many, $N_y$, times (remember, it is random), and averaging them:
$$ \frac{1}{N_Y} \sum_{k=1}^{N_Y} Y_k \rightarrow E[ Y_k ] = E\;\left[\;\; \left( \frac{1}{N}\sum_{i=1}^NZ_i - 4.5 \;\right)^2 \right]$$
Finally, taking the square root:
$$ \sqrt{\frac{1}{N_Y} \sum_{k=1}^{N_Y} Y_k} \approx D(N) $$
```
figsize( 12.5, 4)
N_Y = 250 #use this many to approximate D(N)
N_array = np.arange( 1000, 50000, 2500 ) #use this many samples in the approx. to the variance.
D_N_results = np.zeros( len( N_array ) )
lambda_ = 4.5
expected_value = lambda_ #for X ~ Poi(lambda) , E[ X ] = lambda
def D_N( n ):
"""
This function approx. D_n, the average variance of using n samples.
"""
Z = poi( lambda_, (n, N_Y) )
average_Z = Z.mean(axis=0)
return np.sqrt( ( (average_Z - expected_value)**2 ).mean() )
for i,n in enumerate(N_array):
D_N_results[i] = D_N(n)
plt.xlabel( "$N$" )
plt.ylabel( "expected squared-distance from true value" )
plt.plot(N_array, D_N_results, lw = 3,
label="expected distance between\n\
expected value and \naverage of $N$ random variables.")
plt.plot( N_array, np.sqrt(expected_value)/np.sqrt(N_array), lw = 2, ls = "--",
label = r"$\frac{\sqrt{\lambda}}{\sqrt{N}}$" )
plt.legend()
plt.title( "How 'fast' is the sample average converging? " );
```
As expected, the expected distance between our sample average and the actual expected value shrinks as $N$ grows large. But also notice that the *rate* of convergence decreases, that is, we need only 10 000 additional samples to move from 0.020 to 0.015, a difference of 0.005, but *20 000* more samples to again decrease from 0.015 to 0.010, again only a 0.005 decrease.
It turns out we can measure this rate of convergence. Above I have plotted a second line, the function $\sqrt{\lambda}/\sqrt{N}$. This was not chosen arbitrarily. In most cases, given a sequence of random variable distributed like $Z$, the rate of convergence to $E[Z]$ of the Law of Large Numbers is
$$ \frac{ \sqrt{ \; Var(Z) \; } }{\sqrt{N} }$$
This is useful to know: for a given large $N$, we know (on average) how far away we are from the estimate. On the other hand, in a Bayesian setting, this can seem like a useless result: Bayesian analysis is OK with uncertainty so what's the *statistical* point of adding extra precise digits? Though drawing samples can be so computationally cheap that having a *larger* $N$ is fine too.
### How do we compute $Var(Z)$ though?
The variance is simply another expected value that can be approximated! Consider the following, once we have the expected value (by using the Law of Large Numbers to estimate it, denote it $\mu$), we can estimate the variance:
$$ \frac{1}{N}\sum_{i=1}^N \;(Z_i - \mu)^2 \rightarrow E[ \;( Z - \mu)^2 \;] = Var( Z )$$
### Expected values and probabilities
There is an even less explicit relationship between expected value and estimating probabilities. Define the *indicator function*
$$\mathbb{1}_A(x) =
\begin{cases} 1 & x \in A \\\\
0 & else
\end{cases}
$$
Then, by the law of large numbers, if we have many samples $X_i$, we can estimate the probability of an event $A$, denoted $P(A)$, by:
$$ \frac{1}{N} \sum_{i=1}^N \mathbb{1}_A(X_i) \rightarrow E[\mathbb{1}_A(X)] = P(A) $$
Again, this is fairly obvious after a moments thought: the indicator function is only 1 if the event occurs, so we are summing only the times the event occurs and dividing by the total number of trials (consider how we usually approximate probabilities using frequencies). For example, suppose we wish to estimate the probability that a $Z \sim Exp(.5)$ is greater than 5, and we have many samples from a $Exp(.5)$ distribution.
$$ P( Z > 5 ) = \sum_{i=1}^N \mathbb{1}_{z > 5 }(Z_i) $$
```
N = 10000
print( np.mean( [ np.random.exponential( 0.5 ) > 5 for i in range(N) ] ) )
```
### What does this all have to do with Bayesian statistics?
*Point estimates*, to be introduced in the next chapter, in Bayesian inference are computed using expected values. In more analytical Bayesian inference, we would have been required to evaluate complicated expected values represented as multi-dimensional integrals. No longer. If we can sample from the posterior distribution directly, we simply need to evaluate averages. Much easier. If accuracy is a priority, plots like the ones above show how fast you are converging. And if further accuracy is desired, just take more samples from the posterior.
When is enough enough? When can you stop drawing samples from the posterior? That is the practitioners decision, and also dependent on the variance of the samples (recall from above a high variance means the average will converge slower).
We also should understand when the Law of Large Numbers fails. As the name implies, and comparing the graphs above for small $N$, the Law is only true for large sample sizes. Without this, the asymptotic result is not reliable. Knowing in what situations the Law fails can give us *confidence in how unconfident we should be*. The next section deals with this issue.
## The Disorder of Small Numbers
The Law of Large Numbers is only valid as $N$ gets *infinitely* large: never truly attainable. While the law is a powerful tool, it is foolhardy to apply it liberally. Our next example illustrates this.
##### Example: Aggregated geographic data
Often data comes in aggregated form. For instance, data may be grouped by state, county, or city level. Of course, the population numbers vary per geographic area. If the data is an average of some characteristic of each the geographic areas, we must be conscious of the Law of Large Numbers and how it can *fail* for areas with small populations.
We will observe this on a toy dataset. Suppose there are five thousand counties in our dataset. Furthermore, population number in each state are uniformly distributed between 100 and 1500. The way the population numbers are generated is irrelevant to the discussion, so we do not justify this. We are interested in measuring the average height of individuals per county. Unbeknownst to us, height does **not** vary across county, and each individual, regardless of the county he or she is currently living in, has the same distribution of what their height may be:
$$ \text{height} \sim \text{Normal}(150, 15 ) $$
We aggregate the individuals at the county level, so we only have data for the *average in the county*. What might our dataset look like?
```
figsize( 12.5, 4)
std_height = 15
mean_height = 150
n_counties = 5000
pop_generator = np.random.randint
norm = np.random.normal
#generate some artificial population numbers
population = pop_generator(100, 1500, n_counties )
average_across_county = np.zeros( n_counties )
for i in range( n_counties ):
#generate some individuals and take the mean
average_across_county[i] = norm(mean_height, 1./std_height,
population[i] ).mean()
#located the counties with the apparently most extreme average heights.
i_min = np.argmin( average_across_county )
i_max = np.argmax( average_across_county )
#plot population size vs. recorded average
plt.scatter( population, average_across_county, alpha = 0.5, c="#7A68A6")
plt.scatter( [ population[i_min], population[i_max] ],
[average_across_county[i_min], average_across_county[i_max] ],
s = 60, marker = "o", facecolors = "none",
edgecolors = "#A60628", linewidths = 1.5,
label="extreme heights")
plt.xlim( 100, 1500 )
plt.title( "Average height vs. County Population")
plt.xlabel("County Population")
plt.ylabel("Average height in county")
plt.plot( [100, 1500], [150, 150], color = "k", label = "true expected \
height", ls="--" )
plt.legend(scatterpoints = 1);
```
What do we observe? *Without accounting for population sizes* we run the risk of making an enormous inference error: if we ignored population size, we would say that the county with the shortest and tallest individuals have been correctly circled. But this inference is wrong for the following reason. These two counties do *not* necessarily have the most extreme heights. The error results from the calculated average of smaller populations not being a good reflection of the true expected value of the population (which in truth should be $\mu =150$). The sample size/population size/$N$, whatever you wish to call it, is simply too small to invoke the Law of Large Numbers effectively.
We provide more damning evidence against this inference. Recall the population numbers were uniformly distributed over 100 to 1500. Our intuition should tell us that the counties with the most extreme population heights should also be uniformly spread over 100 to 4000, and certainly independent of the county's population. Not so. Below are the population sizes of the counties with the most extreme heights.
```
print("Population sizes of 10 'shortest' counties: ")
print(population[ np.argsort( average_across_county )[:10] ], '\n')
print("Population sizes of 10 'tallest' counties: ")
print(population[ np.argsort( -average_across_county )[:10] ])
```
Not at all uniform over 100 to 1500. This is an absolute failure of the Law of Large Numbers.
##### Example: Kaggle's *U.S. Census Return Rate Challenge*
Below is data from the 2010 US census, which partitions populations beyond counties to the level of block groups (which are aggregates of city blocks or equivalents). The dataset is from a Kaggle machine learning competition some colleagues and I participated in. The objective was to predict the census letter mail-back rate of a group block, measured between 0 and 100, using census variables (median income, number of females in the block-group, number of trailer parks, average number of children etc.). Below we plot the census mail-back rate versus block group population:
```
figsize( 12.5, 6.5 )
data = np.genfromtxt( "./data/census_data.csv", skip_header=1,
delimiter= ",")
plt.scatter( data[:,1], data[:,0], alpha = 0.5, c="#7A68A6")
plt.title("Census mail-back rate vs Population")
plt.ylabel("Mail-back rate")
plt.xlabel("population of block-group")
plt.xlim(-100, 15e3 )
plt.ylim( -5, 105)
i_min = np.argmin( data[:,0] )
i_max = np.argmax( data[:,0] )
plt.scatter( [ data[i_min,1], data[i_max, 1] ],
[ data[i_min,0], data[i_max,0] ],
s = 60, marker = "o", facecolors = "none",
edgecolors = "#A60628", linewidths = 1.5,
label="most extreme points")
plt.legend(scatterpoints = 1);
```
The above is a classic phenomenon in statistics. I say *classic* referring to the "shape" of the scatter plot above. It follows a classic triangular form, that tightens as we increase the sample size (as the Law of Large Numbers becomes more exact).
I am perhaps overstressing the point and maybe I should have titled the book *"You don't have big data problems!"*, but here again is an example of the trouble with *small datasets*, not big ones. Simply, small datasets cannot be processed using the Law of Large Numbers. Compare with applying the Law without hassle to big datasets (ex. big data). I mentioned earlier that paradoxically big data prediction problems are solved by relatively simple algorithms. The paradox is partially resolved by understanding that the Law of Large Numbers creates solutions that are *stable*, i.e. adding or subtracting a few data points will not affect the solution much. On the other hand, adding or removing data points to a small dataset can create very different results.
For further reading on the hidden dangers of the Law of Large Numbers, I would highly recommend the excellent manuscript [The Most Dangerous Equation](http://nsm.uh.edu/~dgraur/niv/TheMostDangerousEquation.pdf).
##### Example: How to order Reddit submissions
You may have disagreed with the original statement that the Law of Large numbers is known to everyone, but only implicitly in our subconscious decision making. Consider ratings on online products: how often do you trust an average 5-star rating if there is only 1 reviewer? 2 reviewers? 3 reviewers? We implicitly understand that with such few reviewers that the average rating is **not** a good reflection of the true value of the product.
This has created flaws in how we sort items, and more generally, how we compare items. Many people have realized that sorting online search results by their rating, whether the objects be books, videos, or online comments, return poor results. Often the seemingly top videos or comments have perfect ratings only from a few enthusiastic fans, and truly more quality videos or comments are hidden in later pages with *falsely-substandard* ratings of around 4.8. How can we correct this?
Consider the popular site Reddit (I purposefully did not link to the website as you would never come back). The site hosts links to stories or images, called submissions, for people to comment on. Redditors can vote up or down on each submission (called upvotes and downvotes). Reddit, by default, will sort submissions to a given subreddit by Hot, that is, the submissions that have the most upvotes recently.
<img src="http://i.imgur.com/3v6bz9f.png" />
How would you determine which submissions are the best? There are a number of ways to achieve this:
1. *Popularity*: A submission is considered good if it has many upvotes. A problem with this model is that a submission with hundreds of upvotes, but thousands of downvotes. While being very *popular*, the submission is likely more controversial than best.
2. *Difference*: Using the *difference* of upvotes and downvotes. This solves the above problem, but fails when we consider the temporal nature of submission. Depending on when a submission is posted, the website may be experiencing high or low traffic. The difference method will bias the *Top* submissions to be the those made during high traffic periods, which have accumulated more upvotes than submissions that were not so graced, but are not necessarily the best.
3. *Time adjusted*: Consider using Difference divided by the age of the submission. This creates a *rate*, something like *difference per second*, or *per minute*. An immediate counter-example is, if we use per second, a 1 second old submission with 1 upvote would be better than a 100 second old submission with 99 upvotes. One can avoid this by only considering at least t second old submission. But what is a good t value? Does this mean no submission younger than t is good? We end up comparing unstable quantities with stable quantities (young vs. old submissions).
3. *Ratio*: Rank submissions by the ratio of upvotes to total number of votes (upvotes plus downvotes). This solves the temporal issue, such that new submissions who score well can be considered Top just as likely as older submissions, provided they have many upvotes to total votes. The problem here is that a submission with a single upvote (ratio = 1.0) will beat a submission with 999 upvotes and 1 downvote (ratio = 0.999), but clearly the latter submission is *more likely* to be better.
I used the phrase *more likely* for good reason. It is possible that the former submission, with a single upvote, is in fact a better submission than the later with 999 upvotes. The hesitation to agree with this is because we have not seen the other 999 potential votes the former submission might get. Perhaps it will achieve an additional 999 upvotes and 0 downvotes and be considered better than the latter, though not likely.
What we really want is an estimate of the *true upvote ratio*. Note that the true upvote ratio is not the same as the observed upvote ratio: the true upvote ratio is hidden, and we only observe upvotes vs. downvotes (one can think of the true upvote ratio as "what is the underlying probability someone gives this submission a upvote, versus a downvote"). So the 999 upvote/1 downvote submission probably has a true upvote ratio close to 1, which we can assert with confidence thanks to the Law of Large Numbers, but on the other hand we are much less certain about the true upvote ratio of the submission with only a single upvote. Sounds like a Bayesian problem to me.
One way to determine a prior on the upvote ratio is to look at the historical distribution of upvote ratios. This can be accomplished by scraping Reddit's submissions and determining a distribution. There are a few problems with this technique though:
1. Skewed data: The vast majority of submissions have very few votes, hence there will be many submissions with ratios near the extremes (see the "triangular plot" in the above Kaggle dataset), effectively skewing our distribution to the extremes. One could try to only use submissions with votes greater than some threshold. Again, problems are encountered. There is a tradeoff between number of submissions available to use and a higher threshold with associated ratio precision.
2. Biased data: Reddit is composed of different subpages, called subreddits. Two examples are *r/aww*, which posts pics of cute animals, and *r/politics*. It is very likely that the user behaviour towards submissions of these two subreddits are very different: visitors are likely friendly and affectionate in the former, and would therefore upvote submissions more, compared to the latter, where submissions are likely to be controversial and disagreed upon. Therefore not all submissions are the same.
In light of these, I think it is better to use a `Uniform` prior.
With our prior in place, we can find the posterior of the true upvote ratio. The Python script `top_showerthoughts_submissions.py` will scrape the best posts from the `showerthoughts` community on Reddit. This is a text-only community so the title of each post *is* the post. Below is the top post as well as some other sample posts:
```
#adding a number to the end of the %run call with get the ith top post.
%run top_showerthoughts_submissions.py 2
print("Post contents: \n")
print(top_post)
"""
contents: an array of the text from the last 100 top submissions to a subreddit
votes: a 2d numpy array of upvotes, downvotes for each submission.
"""
n_submissions = len(votes)
submissions = np.random.randint( n_submissions, size=4)
print("Some Submissions (out of %d total) \n-----------"%n_submissions)
for i in submissions:
print('"' + contents[i] + '"')
print("upvotes/downvotes: ",votes[i,:], "\n")
```
For a given true upvote ratio $p$ and $N$ votes, the number of upvotes will look like a Binomial random variable with parameters $p$ and $N$. (This is because of the equivalence between upvote ratio and probability of upvoting versus downvoting, out of $N$ possible votes/trials). We create a function that performs Bayesian inference on $p$, for a particular submission's upvote/downvote pair.
```
import pymc3 as pm
def posterior_upvote_ratio( upvotes, downvotes, samples = 20000):
"""
This function accepts the number of upvotes and downvotes a particular submission recieved,
and the number of posterior samples to return to the user. Assumes a uniform prior.
"""
N = upvotes + downvotes
with pm.Model() as model:
upvote_ratio = pm.Uniform("upvote_ratio", 0, 1)
observations = pm.Binomial( "obs", N, upvote_ratio, observed=upvotes)
trace = pm.sample(samples, step=pm.Metropolis())
burned_trace = trace[int(samples/4):]
return burned_trace["upvote_ratio"]
```
Below are the resulting posterior distributions.
```
figsize( 11., 8)
posteriors = []
colours = ["#348ABD", "#A60628", "#7A68A6", "#467821", "#CF4457"]
for i in range(len(submissions)):
j = submissions[i]
posteriors.append( posterior_upvote_ratio( votes[j, 0], votes[j,1] ) )
plt.hist( posteriors[i], bins = 10, normed = True, alpha = .9,
histtype="step",color = colours[i%5], lw = 3,
label = '(%d up:%d down)\n%s...'%(votes[j, 0], votes[j,1], contents[j][:50]) )
plt.hist( posteriors[i], bins = 10, normed = True, alpha = .2,
histtype="stepfilled",color = colours[i], lw = 3, )
plt.legend(loc="upper left")
plt.xlim( 0, 1)
plt.title("Posterior distributions of upvote ratios on different submissions");
```
Some distributions are very tight, others have very long tails (relatively speaking), expressing our uncertainty with what the true upvote ratio might be.
### Sorting!
We have been ignoring the goal of this exercise: how do we sort the submissions from *best to worst*? Of course, we cannot sort distributions, we must sort scalar numbers. There are many ways to distill a distribution down to a scalar: expressing the distribution through its expected value, or mean, is one way. Choosing the mean is a bad choice though. This is because the mean does not take into account the uncertainty of distributions.
I suggest using the *95% least plausible value*, defined as the value such that there is only a 5% chance the true parameter is lower (think of the lower bound on the 95% credible region). Below are the posterior distributions with the 95% least-plausible value plotted:
```
N = posteriors[0].shape[0]
lower_limits = []
for i in range(len(submissions)):
j = submissions[i]
plt.hist( posteriors[i], bins = 20, normed = True, alpha = .9,
histtype="step",color = colours[i], lw = 3,
label = '(%d up:%d down)\n%s...'%(votes[j, 0], votes[j,1], contents[j][:50]) )
plt.hist( posteriors[i], bins = 20, normed = True, alpha = .2,
histtype="stepfilled",color = colours[i], lw = 3, )
v = np.sort( posteriors[i] )[ int(0.05*N) ]
#plt.vlines( v, 0, 15 , color = "k", alpha = 1, linewidths=3 )
plt.vlines( v, 0, 10 , color = colours[i], linestyles = "--", linewidths=3 )
lower_limits.append(v)
plt.legend(loc="upper left")
plt.legend(loc="upper left")
plt.title("Posterior distributions of upvote ratios on different submissions");
order = np.argsort( -np.array( lower_limits ) )
print(order, lower_limits)
```
The best submissions, according to our procedure, are the submissions that are *most-likely* to score a high percentage of upvotes. Visually those are the submissions with the 95% least plausible value close to 1.
Why is sorting based on this quantity a good idea? By ordering by the 95% least plausible value, we are being the most conservative with what we think is best. That is, even in the worst case scenario, when we have severely overestimated the upvote ratio, we can be sure the best submissions are still on top. Under this ordering, we impose the following very natural properties:
1. given two submissions with the same observed upvote ratio, we will assign the submission with more votes as better (since we are more confident it has a higher ratio).
2. given two submissions with the same number of votes, we still assign the submission with more upvotes as *better*.
### But this is too slow for real-time!
I agree, computing the posterior of every submission takes a long time, and by the time you have computed it, likely the data has changed. I delay the mathematics to the appendix, but I suggest using the following formula to compute the lower bound very fast.
$$ \frac{a}{a + b} - 1.65\sqrt{ \frac{ab}{ (a+b)^2(a + b +1 ) } }$$
where
\begin{align}
& a = 1 + u \\\\
& b = 1 + d \\\\
\end{align}
$u$ is the number of upvotes, and $d$ is the number of downvotes. The formula is a shortcut in Bayesian inference, which will be further explained in Chapter 6 when we discuss priors in more detail.
```
def intervals(u,d):
a = 1. + u
b = 1. + d
mu = a/(a+b)
std_err = 1.65*np.sqrt( (a*b)/( (a+b)**2*(a+b+1.) ) )
return ( mu, std_err )
print("Approximate lower bounds:")
posterior_mean, std_err = intervals(votes[:,0],votes[:,1])
lb = posterior_mean - std_err
print(lb)
print("\n")
print("Top 40 Sorted according to approximate lower bounds:")
print("\n")
order = np.argsort( -lb )
ordered_contents = []
for i in order[:40]:
ordered_contents.append( contents[i] )
print(votes[i,0], votes[i,1], contents[i])
print("-------------")
```
We can view the ordering visually by plotting the posterior mean and bounds, and sorting by the lower bound. In the plot below, notice that the left error-bar is sorted (as we suggested this is the best way to determine an ordering), so the means, indicated by dots, do not follow any strong pattern.
```
r_order = order[::-1][-40:]
plt.errorbar( posterior_mean[r_order], np.arange( len(r_order) ),
xerr=std_err[r_order], capsize=0, fmt="o",
color = "#7A68A6")
plt.xlim( 0.3, 1)
plt.yticks( np.arange( len(r_order)-1,-1,-1 ), map( lambda x: x[:30].replace("\n",""), ordered_contents) );
```
In the graphic above, you can see why sorting by mean would be sub-optimal.
### Extension to Starred rating systems
The above procedure works well for upvote-downvotes schemes, but what about systems that use star ratings, e.g. 5 star rating systems. Similar problems apply with simply taking the average: an item with two perfect ratings would beat an item with thousands of perfect ratings, but a single sub-perfect rating.
We can consider the upvote-downvote problem above as binary: 0 is a downvote, 1 if an upvote. A $N$-star rating system can be seen as a more continuous version of above, and we can set $n$ stars rewarded is equivalent to rewarding $\frac{n}{N}$. For example, in a 5-star system, a 2 star rating corresponds to 0.4. A perfect rating is a 1. We can use the same formula as before, but with $a,b$ defined differently:
$$ \frac{a}{a + b} - 1.65\sqrt{ \frac{ab}{ (a+b)^2(a + b +1 ) } }$$
where
\begin{align}
& a = 1 + S \\\\
& b = 1 + N - S \\\\
\end{align}
where $N$ is the number of users who rated, and $S$ is the sum of all the ratings, under the equivalence scheme mentioned above.
##### Example: Counting Github stars
What is the average number of stars a Github repository has? How would you calculate this? There are over 6 million respositories, so there is more than enough data to invoke the Law of Large numbers. Let's start pulling some data. TODO
### Conclusion
While the Law of Large Numbers is cool, it is only true so much as its name implies: with large sample sizes only. We have seen how our inference can be affected by not considering *how the data is shaped*.
1. By (cheaply) drawing many samples from the posterior distributions, we can ensure that the Law of Large Number applies as we approximate expected values (which we will do in the next chapter).
2. Bayesian inference understands that with small sample sizes, we can observe wild randomness. Our posterior distribution will reflect this by being more spread rather than tightly concentrated. Thus, our inference should be correctable.
3. There are major implications of not considering the sample size, and trying to sort objects that are unstable leads to pathological orderings. The method provided above solves this problem.
### Appendix
##### Derivation of sorting submissions formula
Basically what we are doing is using a Beta prior (with parameters $a=1, b=1$, which is a uniform distribution), and using a Binomial likelihood with observations $u, N = u+d$. This means our posterior is a Beta distribution with parameters $a' = 1 + u, b' = 1 + (N - u) = 1+d$. We then need to find the value, $x$, such that 0.05 probability is less than $x$. This is usually done by inverting the CDF ([Cumulative Distribution Function](http://en.wikipedia.org/wiki/Cumulative_Distribution_Function)), but the CDF of the beta, for integer parameters, is known but is a large sum [3].
We instead use a Normal approximation. The mean of the Beta is $\mu = a'/(a'+b')$ and the variance is
$$\sigma^2 = \frac{a'b'}{ (a' + b')^2(a'+b'+1) }$$
Hence we solve the following equation for $x$ and have an approximate lower bound.
$$ 0.05 = \Phi\left( \frac{(x - \mu)}{\sigma}\right) $$
$\Phi$ being the [cumulative distribution for the normal distribution](http://en.wikipedia.org/wiki/Normal_distribution#Cumulative_distribution)
##### Exercises
1\. How would you estimate the quantity $E\left[ \cos{X} \right]$, where $X \sim \text{Exp}(4)$? What about $E\left[ \cos{X} | X \lt 1\right]$, i.e. the expected value *given* we know $X$ is less than 1? Would you need more samples than the original samples size to be equally accurate?
```
## Enter code here
import scipy.stats as stats
exp = stats.expon( scale=4 )
N = 1e5
X = exp.rvs( int(N) )
## ...
```
2\. The following table was located in the paper "Going for Three: Predicting the Likelihood of Field Goal Success with Logistic Regression" [2]. The table ranks football field-goal kickers by their percent of non-misses. What mistake have the researchers made?
-----
#### Kicker Careers Ranked by Make Percentage
<table><tbody><tr><th>Rank </th><th>Kicker </th><th>Make % </th><th>Number of Kicks</th></tr><tr><td>1 </td><td>Garrett Hartley </td><td>87.7 </td><td>57</td></tr><tr><td>2</td><td> Matt Stover </td><td>86.8 </td><td>335</td></tr><tr><td>3 </td><td>Robbie Gould </td><td>86.2 </td><td>224</td></tr><tr><td>4 </td><td>Rob Bironas </td><td>86.1 </td><td>223</td></tr><tr><td>5</td><td> Shayne Graham </td><td>85.4 </td><td>254</td></tr><tr><td>… </td><td>… </td><td>…</td><td> </td></tr><tr><td>51</td><td> Dave Rayner </td><td>72.2 </td><td>90</td></tr><tr><td>52</td><td> Nick Novak </td><td>71.9 </td><td>64</td></tr><tr><td>53 </td><td>Tim Seder </td><td>71.0 </td><td>62</td></tr><tr><td>54 </td><td>Jose Cortez </td><td>70.7</td><td> 75</td></tr><tr><td>55 </td><td>Wade Richey </td><td>66.1</td><td> 56</td></tr></tbody></table>
In August 2013, [a popular post](http://bpodgursky.wordpress.com/2013/08/21/average-income-per-programming-language/) on the average income per programmer of different languages was trending. Here's the summary chart: (reproduced without permission, cause when you lie with stats, you gunna get the hammer). What do you notice about the extremes?
------
#### Average household income by programming language
<table >
<tr><td>Language</td><td>Average Household Income ($)</td><td>Data Points</td></tr>
<tr><td>Puppet</td><td>87,589.29</td><td>112</td></tr>
<tr><td>Haskell</td><td>89,973.82</td><td>191</td></tr>
<tr><td>PHP</td><td>94,031.19</td><td>978</td></tr>
<tr><td>CoffeeScript</td><td>94,890.80</td><td>435</td></tr>
<tr><td>VimL</td><td>94,967.11</td><td>532</td></tr>
<tr><td>Shell</td><td>96,930.54</td><td>979</td></tr>
<tr><td>Lua</td><td>96,930.69</td><td>101</td></tr>
<tr><td>Erlang</td><td>97,306.55</td><td>168</td></tr>
<tr><td>Clojure</td><td>97,500.00</td><td>269</td></tr>
<tr><td>Python</td><td>97,578.87</td><td>2314</td></tr>
<tr><td>JavaScript</td><td>97,598.75</td><td>3443</td></tr>
<tr><td>Emacs Lisp</td><td>97,774.65</td><td>355</td></tr>
<tr><td>C#</td><td>97,823.31</td><td>665</td></tr>
<tr><td>Ruby</td><td>98,238.74</td><td>3242</td></tr>
<tr><td>C++</td><td>99,147.93</td><td>845</td></tr>
<tr><td>CSS</td><td>99,881.40</td><td>527</td></tr>
<tr><td>Perl</td><td>100,295.45</td><td>990</td></tr>
<tr><td>C</td><td>100,766.51</td><td>2120</td></tr>
<tr><td>Go</td><td>101,158.01</td><td>231</td></tr>
<tr><td>Scala</td><td>101,460.91</td><td>243</td></tr>
<tr><td>ColdFusion</td><td>101,536.70</td><td>109</td></tr>
<tr><td>Objective-C</td><td>101,801.60</td><td>562</td></tr>
<tr><td>Groovy</td><td>102,650.86</td><td>116</td></tr>
<tr><td>Java</td><td>103,179.39</td><td>1402</td></tr>
<tr><td>XSLT</td><td>106,199.19</td><td>123</td></tr>
<tr><td>ActionScript</td><td>108,119.47</td><td>113</td></tr>
</table>
### References
1. Wainer, Howard. *The Most Dangerous Equation*. American Scientist, Volume 95.
2. Clarck, Torin K., Aaron W. Johnson, and Alexander J. Stimpson. "Going for Three: Predicting the Likelihood of Field Goal Success with Logistic Regression." (2013): n. page. [Web](http://www.sloansportsconference.com/wp-content/uploads/2013/Going%20for%20Three%20Predicting%20the%20Likelihood%20of%20Field%20Goal%20Success%20with%20Logistic%20Regression.pdf). 20 Feb. 2013.
3. http://en.wikipedia.org/wiki/Beta_function#Incomplete_beta_function
```
from IPython.core.display import HTML
def css_styling():
styles = open("../styles/custom.css", "r").read()
return HTML(styles)
css_styling()
```
<style>
img{
max-width:800px}
</style>
|
github_jupyter
|
```
# Copyright 2020 Erik Härkönen. All rights reserved.
# This file is licensed to you under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License. You may obtain a copy
# of the License at http://www.apache.org/licenses/LICENSE-2.0
# Unless required by applicable law or agreed to in writing, software distributed under
# the License is distributed on an "AS IS" BASIS, WITHOUT WARRANTIES OR REPRESENTATIONS
# OF ANY KIND, either express or implied. See the License for the specific language
# governing permissions and limitations under the License.
# Comparison to GAN steerability and InterfaceGAN
%matplotlib inline
from notebook_init import *
import pickle
out_root = Path('out/figures/steerability_comp')
makedirs(out_root, exist_ok=True)
rand = lambda : np.random.randint(np.iinfo(np.int32).max)
def show_strip(frames):
plt.figure(figsize=(20,20))
plt.axis('off')
plt.imshow(np.hstack(pad_frames(frames, 64)))
plt.show()
normalize = lambda t : t / np.sqrt(np.sum(t.reshape(-1)**2))
def compute(
model,
lat_mean,
prefix,
imgclass,
seeds,
d_ours,
l_start,
l_end,
scale_ours,
d_sup, # single or one per layer
scale_sup,
center=True
):
model.set_output_class(imgclass)
makedirs(out_root / imgclass, exist_ok=True)
for seed in seeds:
print(seed)
deltas = [d_ours, d_sup]
scales = [scale_ours, scale_sup]
ranges = [(l_start, l_end), (0, model.get_max_latents())]
names = ['ours', 'supervised']
for delta, name, scale, l_range in zip(deltas, names, scales, ranges):
lat_base = model.sample_latent(1, seed=seed).cpu().numpy()
# Shift latent to lie on mean along given direction
if center:
y = normalize(d_sup) # assume ground truth
dotp = np.sum((lat_base - lat_mean) * y, axis=-1, keepdims=True)
lat_base = lat_base - dotp * y
# Convert single delta to per-layer delta (to support Steerability StyleGAN)
if delta.shape[0] > 1:
#print('Unstacking delta')
*d_per_layer, = delta # might have per-layer scales, don't normalize
else:
d_per_layer = [normalize(delta)]*model.get_max_latents()
frames = []
n_frames = 5
for a in np.linspace(-1.0, 1.0, n_frames):
w = [lat_base]*model.get_max_latents()
for l in range(l_range[0], l_range[1]):
w[l] = w[l] + a*d_per_layer[l]*scale
frames.append(model.sample_np(w))
for i, frame in enumerate(frames):
Image.fromarray(np.uint8(frame*255)).save(
out_root / imgclass / f'{prefix}_{name}_{seed}_{i}.png')
strip = np.hstack(pad_frames(frames, 64))
plt.figure(figsize=(12,12))
plt.imshow(strip)
plt.axis('off')
plt.tight_layout()
plt.title(f'{prefix} - {name}, scale={scale}')
plt.show()
# BigGAN-512
inst = get_instrumented_model('BigGAN-512', 'husky', 'generator.gen_z', device, inst=inst)
model = inst.model
K = model.get_max_latents()
pc_config = Config(components=128, n=1_000_000,
layer='generator.gen_z', model='BigGAN-512', output_class='husky')
dump_name = get_or_compute(pc_config, inst)
with np.load(dump_name) as data:
lat_comp = data['lat_comp']
lat_mean = data['lat_mean']
with open('data/steerability/biggan_deep_512/gan_steer-linear_zoom_512.pkl', 'rb') as f:
delta_steerability_zoom = pickle.load(f)['w_zoom'].reshape(1, 128)
with open('data/steerability/biggan_deep_512/gan_steer-linear_shiftx_512.pkl', 'rb') as f:
delta_steerability_transl = pickle.load(f)['w_shiftx'].reshape(1, 128)
# Indices determined by visual inspection
delta_ours_transl = lat_comp[0]
delta_ours_zoom = lat_comp[6]
model.truncation = 0.6
compute(model, lat_mean, 'zoom', 'robin', [560157313], delta_ours_zoom, 0, K, -3.0, delta_steerability_zoom, 5.5)
compute(model, lat_mean, 'zoom', 'ship', [107715983], delta_ours_zoom, 0, K, -3.0, delta_steerability_zoom, 5.0)
compute(model, lat_mean, 'translate', 'golden_retriever', [552411435], delta_ours_transl, 0, K, -2.0, delta_steerability_transl, 4.5)
compute(model, lat_mean, 'translate', 'lemon', [331582800], delta_ours_transl, 0, K, -3.0, delta_steerability_transl, 6.0)
# StyleGAN1-ffhq (InterfaceGAN)
inst = get_instrumented_model('StyleGAN', 'ffhq', 'g_mapping', device, use_w=True, inst=inst)
model = inst.model
K = model.get_max_latents()
pc_config = Config(components=128, n=1_000_000, use_w=True,
layer='g_mapping', model='StyleGAN', output_class='ffhq')
dump_name = get_or_compute(pc_config, inst)
with np.load(dump_name) as data:
lat_comp = data['lat_comp']
lat_mean = data['lat_mean']
# SG-ffhq-w, non-conditional
d_ffhq_pose = np.load('data/interfacegan/stylegan_ffhq_pose_w_boundary.npy').astype(np.float32)
d_ffhq_smile = np.load('data/interfacegan/stylegan_ffhq_smile_w_boundary.npy').astype(np.float32)
d_ffhq_gender = np.load('data/interfacegan/stylegan_ffhq_gender_w_boundary.npy').astype(np.float32)
d_ffhq_glasses = np.load('data/interfacegan/stylegan_ffhq_eyeglasses_w_boundary.npy').astype(np.float32)
# Indices determined by visual inspection
d_ours_pose = lat_comp[9]
d_ours_smile = lat_comp[44]
d_ours_gender = lat_comp[0]
d_ours_glasses = lat_comp[12]
model.truncation = 1.0 # NOT IMPLEMENTED
compute(model, lat_mean, 'pose', 'ffhq', [440608316, 1811098088, 129888612], d_ours_pose, 0, 7, -1.0, d_ffhq_pose, 1.0)
compute(model, lat_mean, 'smile', 'ffhq', [1759734403, 1647189561, 70163682], d_ours_smile, 3, 4, -8.5, d_ffhq_smile, 1.0)
compute(model, lat_mean, 'gender', 'ffhq', [1302836080, 1746672325], d_ours_gender, 2, 6, -4.5, d_ffhq_gender, 1.5)
compute(model, lat_mean, 'glasses', 'ffhq', [1565213752, 1005764659, 1110182583], d_ours_glasses, 0, 2, 4.0, d_ffhq_glasses, 1.0)
# StyleGAN1-ffhq (Steerability)
inst = get_instrumented_model('StyleGAN', 'ffhq', 'g_mapping', device, use_w=True, inst=inst)
model = inst.model
K = model.get_max_latents()
pc_config = Config(components=128, n=1_000_000, use_w=True,
layer='g_mapping', model='StyleGAN', output_class='ffhq')
dump_name = get_or_compute(pc_config, inst)
with np.load(dump_name) as data:
lat_comp = data['lat_comp']
lat_mean = data['lat_mean']
# SG-ffhq-w, non-conditional
# Shapes: [18, 512]
d_ffhq_R = np.load('data/steerability/stylegan_ffhq/ffhq_rgb_0.npy').astype(np.float32)
d_ffhq_G = np.load('data/steerability/stylegan_ffhq/ffhq_rgb_1.npy').astype(np.float32)
d_ffhq_B = np.load('data/steerability/stylegan_ffhq/ffhq_rgb_2.npy').astype(np.float32)
# Indices determined by visual inspection
d_ours_R = lat_comp[0]
d_ours_G = -lat_comp[1]
d_ours_B = -lat_comp[2]
model.truncation = 1.0 # NOT IMPLEMENTED
compute(model, lat_mean, 'red', 'ffhq', [5], d_ours_R, 17, 18, 8.0, d_ffhq_R, 1.0, center=False)
compute(model, lat_mean, 'green', 'ffhq', [5], d_ours_G, 17, 18, 15.0, d_ffhq_G, 1.0, center=False)
compute(model, lat_mean, 'blue', 'ffhq', [5], d_ours_B, 17, 18, 10.0, d_ffhq_B, 1.0, center=False)
# StyleGAN1-celebahq (InterfaceGAN)
inst = get_instrumented_model('StyleGAN', 'celebahq', 'g_mapping', device, use_w=True, inst=inst)
model = inst.model
K = model.get_max_latents()
pc_config = Config(components=128, n=1_000_000, use_w=True,
layer='g_mapping', model='StyleGAN', output_class='celebahq')
dump_name = get_or_compute(pc_config, inst)
with np.load(dump_name) as data:
lat_comp = data['lat_comp']
lat_mean = data['lat_mean']
# SG-ffhq-w, non-conditional
d_celebahq_pose = np.load('data/interfacegan/stylegan_celebahq_pose_w_boundary.npy').astype(np.float32)
d_celebahq_smile = np.load('data/interfacegan/stylegan_celebahq_smile_w_boundary.npy').astype(np.float32)
d_celebahq_gender = np.load('data/interfacegan/stylegan_celebahq_gender_w_boundary.npy').astype(np.float32)
d_celebahq_glasses = np.load('data/interfacegan/stylegan_celebahq_eyeglasses_w_boundary.npy').astype(np.float32)
# Indices determined by visual inspection
d_ours_pose = lat_comp[7]
d_ours_smile = lat_comp[14]
d_ours_gender = lat_comp[1]
d_ours_glasses = lat_comp[5]
model.truncation = 1.0 # NOT IMPLEMENTED
compute(model, lat_mean, 'pose', 'celebahq', [1939067252, 1460055449, 329555154], d_ours_pose, 0, 7, -1.0, d_celebahq_pose, 1.0)
compute(model, lat_mean, 'smile', 'celebahq', [329187806, 424805522, 1777796971], d_ours_smile, 3, 4, -7.0, d_celebahq_smile, 1.3)
compute(model, lat_mean, 'gender', 'celebahq', [1144615644, 967075839, 264878205], d_ours_gender, 0, 2, -3.2, d_celebahq_gender, 1.2)
compute(model, lat_mean, 'glasses', 'celebahq', [991993380, 594344173, 2119328990, 1919124025], d_ours_glasses, 0, 1, -10.0, d_celebahq_glasses, 2.0) # hard for both
# StyleGAN1-cars (Steerability)
inst = get_instrumented_model('StyleGAN', 'cars', 'g_mapping', device, use_w=True, inst=inst)
model = inst.model
K = model.get_max_latents()
pc_config = Config(components=128, n=1_000_000, use_w=True,
layer='g_mapping', model='StyleGAN', output_class='cars')
dump_name = get_or_compute(pc_config, inst)
with np.load(dump_name) as data:
lat_comp = data['lat_comp']
lat_mean = data['lat_mean']
# Shapes: [16, 512]
d_cars_rot = np.load('data/steerability/stylegan_cars/rotate2d.npy').astype(np.float32)
d_cars_shift = np.load('data/steerability/stylegan_cars/shifty.npy').astype(np.float32)
# Add two final layers
d_cars_rot = np.append(d_cars_rot, np.zeros((2,512), dtype=np.float32), axis=0)
d_cars_shift = np.append(d_cars_shift, np.zeros((2,512), dtype=np.float32), axis=0)
print(d_cars_rot.shape)
# Indices determined by visual inspection
d_ours_rot = lat_comp[0]
d_ours_shift = lat_comp[7]
model.truncation = 1.0 # NOT IMPLEMENTED
compute(model, lat_mean, 'rotate2d', 'cars', [46, 28], d_ours_rot, 0, 1, 1.0, d_cars_rot, 1.0, center=False)
compute(model, lat_mean, 'shifty', 'cars', [0, 13], d_ours_shift, 1, 2, 4.0, d_cars_shift, 1.0, center=False)
```
|
github_jupyter
|
# Hyperparameter tuning with Cloud AI Platform
**Learning Objectives:**
* Improve the accuracy of a model by hyperparameter tuning
```
import os
PROJECT = 'qwiklabs-gcp-faf328caac1ef9a0' # REPLACE WITH YOUR PROJECT ID
BUCKET = 'qwiklabs-gcp-faf328caac1ef9a0' # REPLACE WITH YOUR BUCKET NAME
REGION = 'us-east1' # REPLACE WITH YOUR BUCKET REGION e.g. us-central1
# for bash
os.environ['PROJECT'] = PROJECT
os.environ['BUCKET'] = BUCKET
os.environ['REGION'] = REGION
os.environ['TFVERSION'] = '1.8' # Tensorflow version
%%bash
gcloud config set project $PROJECT
gcloud config set compute/region $REGION
```
## Create command-line program
In order to submit to Cloud AI Platform, we need to create a distributed training program. Let's convert our housing example to fit that paradigm, using the Estimators API.
```
%%bash
rm -rf house_prediction_module
mkdir house_prediction_module
mkdir house_prediction_module/trainer
touch house_prediction_module/trainer/__init__.py
%%writefile house_prediction_module/trainer/task.py
import argparse
import os
import json
import shutil
from . import model
if __name__ == '__main__' and "get_ipython" not in dir():
parser = argparse.ArgumentParser()
parser.add_argument(
'--learning_rate',
type = float,
default = 0.01
)
parser.add_argument(
'--batch_size',
type = int,
default = 30
)
parser.add_argument(
'--output_dir',
help = 'GCS location to write checkpoints and export models.',
required = True
)
parser.add_argument(
'--job-dir',
help = 'this model ignores this field, but it is required by gcloud',
default = 'junk'
)
args = parser.parse_args()
arguments = args.__dict__
# Unused args provided by service
arguments.pop('job_dir', None)
arguments.pop('job-dir', None)
# Append trial_id to path if we are doing hptuning
# This code can be removed if you are not using hyperparameter tuning
arguments['output_dir'] = os.path.join(
arguments['output_dir'],
json.loads(
os.environ.get('TF_CONFIG', '{}')
).get('task', {}).get('trial', '')
)
# Run the training
shutil.rmtree(arguments['output_dir'], ignore_errors=True) # start fresh each time
# Pass the command line arguments to our model's train_and_evaluate function
model.train_and_evaluate(arguments)
%%writefile house_prediction_module/trainer/model.py
import numpy as np
import pandas as pd
import tensorflow as tf
tf.logging.set_verbosity(tf.logging.INFO)
# Read dataset and split into train and eval
df = pd.read_csv("https://storage.googleapis.com/ml_universities/california_housing_train.csv", sep = ",")
df['num_rooms'] = df['total_rooms'] / df['households']
np.random.seed(seed = 1) #makes split reproducible
msk = np.random.rand(len(df)) < 0.8
traindf = df[msk]
evaldf = df[~msk]
# Train and eval input functions
SCALE = 100000
def train_input_fn(df, batch_size):
return tf.estimator.inputs.pandas_input_fn(x = traindf[["num_rooms"]],
y = traindf["median_house_value"] / SCALE, # note the scaling
num_epochs = None,
batch_size = batch_size, # note the batch size
shuffle = True)
def eval_input_fn(df, batch_size):
return tf.estimator.inputs.pandas_input_fn(x = evaldf[["num_rooms"]],
y = evaldf["median_house_value"] / SCALE, # note the scaling
num_epochs = 1,
batch_size = batch_size,
shuffle = False)
# Define feature columns
features = [tf.feature_column.numeric_column('num_rooms')]
def train_and_evaluate(args):
# Compute appropriate number of steps
num_steps = (len(traindf) / args['batch_size']) / args['learning_rate'] # if learning_rate=0.01, hundred epochs
# Create custom optimizer
myopt = tf.train.FtrlOptimizer(learning_rate = args['learning_rate']) # note the learning rate
# Create rest of the estimator as usual
estimator = tf.estimator.LinearRegressor(model_dir = args['output_dir'],
feature_columns = features,
optimizer = myopt)
#Add rmse evaluation metric
def rmse(labels, predictions):
pred_values = tf.cast(predictions['predictions'], tf.float64)
return {'rmse': tf.metrics.root_mean_squared_error(labels * SCALE, pred_values * SCALE)}
estimator = tf.contrib.estimator.add_metrics(estimator, rmse)
train_spec = tf.estimator.TrainSpec(input_fn = train_input_fn(df = traindf, batch_size = args['batch_size']),
max_steps = num_steps)
eval_spec = tf.estimator.EvalSpec(input_fn = eval_input_fn(df = evaldf, batch_size = len(evaldf)),
steps = None)
tf.estimator.train_and_evaluate(estimator, train_spec, eval_spec)
%%bash
rm -rf house_trained
export PYTHONPATH=${PYTHONPATH}:${PWD}/house_prediction_module
gcloud ai-platform local train \
--module-name=trainer.task \
--job-dir=house_trained \
--package-path=$(pwd)/trainer \
-- \
--batch_size=30 \
--learning_rate=0.02 \
--output_dir=house_trained
```
# Create hyperparam.yaml
```
%%writefile hyperparam.yaml
trainingInput:
hyperparameters:
goal: MINIMIZE
maxTrials: 5
maxParallelTrials: 1
hyperparameterMetricTag: rmse
params:
- parameterName: batch_size
type: INTEGER
minValue: 8
maxValue: 64
scaleType: UNIT_LINEAR_SCALE
- parameterName: learning_rate
type: DOUBLE
minValue: 0.01
maxValue: 0.1
scaleType: UNIT_LOG_SCALE
%%bash
OUTDIR=gs://${BUCKET}/house_trained # CHANGE bucket name appropriately
gsutil rm -rf $OUTDIR
export PYTHONPATH=${PYTHONPATH}:${PWD}/house_prediction_module
gcloud ai-platform jobs submit training house_$(date -u +%y%m%d_%H%M%S) \
--config=hyperparam.yaml \
--module-name=trainer.task \
--package-path=$(pwd)/house_prediction_module/trainer \
--job-dir=$OUTDIR \
--runtime-version=$TFVERSION \
--\
--output_dir=$OUTDIR \
!gcloud ai-platform jobs describe house_190809_204253 # CHANGE jobId appropriately
```
## Challenge exercise
Add a few engineered features to the housing model, and use hyperparameter tuning to choose which set of features the model uses.
<p>
Copyright 2018 Google Inc. Licensed under the Apache License, Version 2.0 (the "License"); you may not use this file except in compliance with the License. You may obtain a copy of the License at http://www.apache.org/licenses/LICENSE-2.0 Unless required by applicable law or agreed to in writing, software distributed under the License is distributed on an "AS IS" BASIS, WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied. See the License for the specific language governing permissions and limitations under the License
|
github_jupyter
|
```
# In this exercise you will train a CNN on the FULL Cats-v-dogs dataset
# This will require you doing a lot of data preprocessing because
# the dataset isn't split into training and validation for you
# This code block has all the required inputs
import os
import zipfile
import random
import tensorflow as tf
from tensorflow.keras.optimizers import RMSprop
from tensorflow.keras.preprocessing.image import ImageDataGenerator
from shutil import copyfile
# This code block downloads the full Cats-v-Dogs dataset and stores it as
# cats-and-dogs.zip. It then unzips it to /tmp
# which will create a tmp/PetImages directory containing subdirectories
# called 'Cat' and 'Dog' (that's how the original researchers structured it)
# If the URL doesn't work,
# . visit https://www.microsoft.com/en-us/download/confirmation.aspx?id=54765
# And right click on the 'Download Manually' link to get a new URL
!wget --no-check-certificate \
"https://download.microsoft.com/download/3/E/1/3E1C3F21-ECDB-4869-8368-6DEBA77B919F/kagglecatsanddogs_3367a.zip" \
-O "/tmp/cats-and-dogs.zip"
local_zip = '/tmp/cats-and-dogs.zip'
zip_ref = zipfile.ZipFile(local_zip, 'r')
zip_ref.extractall('/tmp')
zip_ref.close()
print(len(os.listdir('/tmp/PetImages/Cat/')))
print(len(os.listdir('/tmp/PetImages/Dog/')))
# Expected Output:
# 12501
# 12501
# Use os.mkdir to create your directories
# You will need a directory for cats-v-dogs, and subdirectories for training
# and testing. These in turn will need subdirectories for 'cats' and 'dogs'
try:
os.mkdir("/tmp/cats-v-dogs")
os.mkdir("/tmp/cats-v-dogs/training")
os.mkdir("/tmp/cats-v-dogs/testing")
os.mkdir("/tmp/cats-v-dogs/training/dogs")
os.mkdir("/tmp/cats-v-dogs/training/cats")
os.mkdir("/tmp/cats-v-dogs/testing/dogs")
os.mkdir("/tmp/cats-v-dogs/testing/cats")
except OSError:
pass
# Write a python function called split_data which takes
# a SOURCE directory containing the files
# a TRAINING directory that a portion of the files will be copied to
# a TESTING directory that a portion of the files will be copied to
# a SPLIT SIZE to determine the portion
# The files should also be randomized, so that the training set is a random
# X% of the files, and the test set is the remaining files
# SO, for example, if SOURCE is PetImages/Cat, and SPLIT SIZE is .9
# Then 90% of the images in PetImages/Cat will be copied to the TRAINING dir
# and 10% of the images will be copied to the TESTING dir
# Also -- All images should be checked, and if they have a zero file length,
# they will not be copied over
#
# os.listdir(DIRECTORY) gives you a listing of the contents of that directory
# os.path.getsize(PATH) gives you the size of the file
# copyfile(source, destination) copies a file from source to destination
# random.sample(list, len(list)) shuffles a list
def split_data(SOURCE, TRAINING, TESTING, SPLIT_SIZE):
files = []
for filename in os.listdir(SOURCE):
file = SOURCE + filename
if os.path.getsize(file) > 0:
files.append(filename)
else:
print (filename + " is zero length, so ignoring.")
training_length = int(len(files) * SPLIT_SIZE)
testing_length = int(len(files) - training_length)
shuffled_set = random.sample(files, len(files))
training_set = shuffled_set[0:training_length]
testing_set = shuffled_set[-testing_length:]
for filename in training_set:
src = SOURCE + filename
dst = TRAINING + filename
copyfile(src, dst)
for filename in testing_set:
src = SOURCE + filename
dst = TESTING + filename
copyfile(src, dst)
CAT_SOURCE_DIR = "/tmp/PetImages/Cat/"
TRAINING_CATS_DIR = "/tmp/cats-v-dogs/training/cats/"
TESTING_CATS_DIR = "/tmp/cats-v-dogs/testing/cats/"
DOG_SOURCE_DIR = "/tmp/PetImages/Dog/"
TRAINING_DOGS_DIR = "/tmp/cats-v-dogs/training/dogs/"
TESTING_DOGS_DIR = "/tmp/cats-v-dogs/testing/dogs/"
split_size = .9
split_data(CAT_SOURCE_DIR, TRAINING_CATS_DIR, TESTING_CATS_DIR, split_size)
split_data(DOG_SOURCE_DIR, TRAINING_DOGS_DIR, TESTING_DOGS_DIR, split_size)
# Expected output
# 666.jpg is zero length, so ignoring
# 11702.jpg is zero length, so ignoring
print(len(os.listdir('/tmp/cats-v-dogs/training/cats/')))
print(len(os.listdir('/tmp/cats-v-dogs/training/dogs/')))
print(len(os.listdir('/tmp/cats-v-dogs/testing/cats/')))
print(len(os.listdir('/tmp/cats-v-dogs/testing/dogs/')))
# Expected output:
# 11250
# 11250
# 1250
# 1250
# DEFINE A KERAS MODEL TO CLASSIFY CATS V DOGS
# USE AT LEAST 3 CONVOLUTION LAYERS
model = tf.keras.models.Sequential([
tf.keras.layers.Conv2D(16, (3,3), activation='relu', input_shape=(150,150,3)),
tf.keras.layers.MaxPooling2D(2,2),
tf.keras.layers.Conv2D(32, (3,3), activation='relu'),
tf.keras.layers.MaxPooling2D(2,2),
tf.keras.layers.Conv2D(64, (3,3), activation='relu'),
tf.keras.layers.MaxPooling2D(2,2),
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(512, activation='relu'),
tf.keras.layers.Dense(1, activation='sigmoid')
])
model.compile(optimizer=RMSprop(lr=0.001),
loss='binary_crossentropy',
metrics=['acc'])
TRAINING_DIR = "/tmp/cats-v-dogs/training/"
train_datagen = ImageDataGenerator(rescale=1./255)
train_generator = train_datagen.flow_from_directory(TRAINING_DIR,
batch_size=100,
class_mode='binary',
target_size=(150,150))
VALIDATION_DIR = "/tmp/cats-v-dogs/testing/"
validation_datagen = ImageDataGenerator(rescale=1./255)
validation_generator = train_datagen.flow_from_directory(VALIDATION_DIR,
batch_size=10,
class_mode='binary',
target_size=(150,150))
# Expected Output:
# Found 22498 images belonging to 2 classes.
# Found 2500 images belonging to 2 classes.
history = model.fit_generator(train_generator,
epochs=15,
verbose=1,
validation_data=validation_generator)
# The expectation here is that the model will train, and that accuracy will be > 95% on both training and validation
# i.e. acc:A1 and val_acc:A2 will be visible, and both A1 and A2 will be > .9
# PLOT LOSS AND ACCURACY
%matplotlib inline
import matplotlib.image as mpimg
import matplotlib.pyplot as plt
#-----------------------------------------------------------
# Retrieve a list of list results on training and test data
# sets for each training epoch
#-----------------------------------------------------------
acc=history.history['acc']
val_acc=history.history['val_acc']
loss=history.history['loss']
val_loss=history.history['val_loss']
epochs=range(len(acc)) # Get number of epochs
#------------------------------------------------
# Plot training and validation accuracy per epoch
#------------------------------------------------
plt.plot(epochs, acc, 'r', "Training Accuracy")
plt.plot(epochs, val_acc, 'b', "Validation Accuracy")
plt.title('Training and validation accuracy')
plt.figure()
#------------------------------------------------
# Plot training and validation loss per epoch
#------------------------------------------------
plt.plot(epochs, loss, 'r', "Training Loss")
plt.plot(epochs, val_loss, 'b', "Validation Loss")
plt.title('Training and validation loss')
# Desired output. Charts with training and validation metrics. No crash :)
# Here's a codeblock just for fun. You should be able to upload an image here
# and have it classified without crashing
import numpy as np
from google.colab import files
from keras.preprocessing import image
uploaded = files.upload()
for fn in uploaded.keys():
# predicting images
path = '/content/' + fn
img = image.load_img(path, target_size=(# YOUR CODE HERE))
x = image.img_to_array(img)
x = np.expand_dims(x, axis=0)
images = np.vstack([x])
classes = model.predict(images, batch_size=10)
print(classes[0])
if classes[0]>0.5:
print(fn + " is a dog")
else:
print(fn + " is a cat")
```
|
github_jupyter
|
```
# Confidence interval and bias comparison in the multi-armed bandit
# setting of https://arxiv.org/pdf/1507.08025.pdf
import numpy as np
import pandas as pd
import scipy.stats as stats
import time
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
sns.set(style='white', palette='colorblind', color_codes=True)
#
# Experiment parameters
#
# Set random seed for reproducibility
seed = 1234
np.random.seed(seed)
# Trial repetitions (number of times experiment is repeated)
R = 5000
# Trial size (total number of arm pulls)
T = 1000
# Number of arms
K = 2
# Noise distribution: 2*beta(alph, alph) - 1
noise_param = 1.0 # uniform distribution
# Parameters of Gaussian distribution prior on each arm
mu0 = 0.4 # prior mean
var0 = 1/(2*noise_param + 1.0) # prior variance set to correct value
# Select reward means for each arm and set variance
reward_means = np.concatenate([np.repeat(.3, K-1), [.30]])
reward_vars = np.repeat(var0, K)
# Select probability of choosing current belief in epsilon greedy policy
ECB_epsilon = .1
#
# Evaluation parameters
#
# Confidence levels for confidence regions
confidence_levels = np.arange(0.9, 1.0, step=0.01)
# Standard normal error thresholds for two-sided (univariate) intervals with given confidence level
gaussian_thresholds_ts = -stats.norm.ppf((1.0-confidence_levels)/2.0)
gaussian_thresholds_os = -stats.norm.ppf(1.0-confidence_levels)
print gaussian_thresholds_ts
print gaussian_thresholds_os
#
# Define arm selection policies
#
policies = {}
# Epsilon-greedy: select current belief (arm with highest posterior reward
# probability) w.p. 1-epsilon and arm uniformly at random otherwise
def ECB(mu_post, var_post, epsilon=ECB_epsilon):
# Determine whether to select current belief by flipping biased coin
use_cb = np.random.binomial(1, 1.0-epsilon)
if use_cb:
# Select arm with highest posterior reward probability
arm = np.argmax(mu_post)
else:
# Select arm uniformly at random
arm = np.random.choice(xrange(K))
return arm
policies['ECB'] = ECB
# Current belief: select arm with highest posterior probability
def CB(mu_post, var_post):
return ECB(mu_post, var_post, epsilon=0.0)
# policies['CB'] = CB
# Fixed randomized design: each arm selected independently and uniformly
def FR(mu_post, var_post, epsilon=ECB_epsilon):
return ECB(mu_post, var_post, epsilon=1.0)
policies['FR'] = FR
# Thompson sampling: select arm k with probability proportional to P(arm k has highest reward | data)^c
# where c = 1 and P(arm k has highest reward | data) is the posterior probability that arm k has
# the highest reward
# TODO: the paper uses c = t/(2T) instead, citing Thall and Wathen (2007); investigate how to achieve this efficiently
def TS(mu_post, var_post, epsilon=ECB_epsilon):
# Draw a sample from each arm's posterior
samples = np.random.normal(mu_post, np.sqrt(var_post))
# Select an arm with the largest sample
arm = np.argmax(samples)
return arm
policies['TS'] = TS
def lilUCB(mu_post, var_post, epsilon=ECB_epsilon ):
#define lilUCB params, see Jamieson et al 2013
# use 1/variance as number of times the arm is tried.
# at time t, choose arm k that maximizes:
# muhat_k(t) + (1+beta)*(1+sqrt(eps))*sqrt{2(1+eps)/T_k}*sqrt{log(1/delta) + log(log((1+eps)*T_k))}
# where muhat_k (t) is sample mean of k^th arm at time t and T_k = T_k(t) is the number of times arm k is tried
# up toa time t
epsilonUCB = 0.01
betaUCB = 0.5
aUCB = 1+ 2/betaUCB
deltaUCB = 0.01
lilFactorUCB = np.log(1/deltaUCB) + np.log(np.log((1+epsilonUCB)/var_post))
scoresUCB = mu_post + (1+betaUCB)*(1+np.sqrt(epsilonUCB))*np.sqrt((2+2*epsilonUCB)*lilFactorUCB*var_post)
arm = np.argmax(scoresUCB)
return arm
policies['UCB'] = lilUCB
#
# Gather data: Generate arm pulls and rewards using different policies
#
tic = time.time()
arms = []
rewards = []
for r in xrange(R):
arms.append(pd.DataFrame(index=range(0,T)))
rewards.append(pd.DataFrame(index=range(0,T)))
# Keep track of posterior beta parameters for each arm
mu_post = np.repeat(mu0, K)
var_post = np.repeat(var0, K)
for policy in policies.keys():
# Ensure arms column has integer type by initializing with integer value
arms[r][policy] = 0
for t in range(T):
if t < K:
# Ensure each arm selected at least once
arm = t
else:
# Select an arm according to policy
arm = policies[policy](mu_post, var_post, epsilon = ECB_epsilon)
# Collect reward from selected arm
reward = 2*np.random.beta(noise_param, noise_param) - 1.0 + reward_means[arm]
# Update Gaussian posterior
new_var = 1.0/(1.0/var_post[arm] + 1.0/reward_vars[arm])
mu_post[arm] = (mu_post[arm]/var_post[arm] + reward/reward_vars[arm])*new_var
var_post[arm] = new_var
# Store results
arms[r].set_value(t, policy, arm)
rewards[r].set_value(t, policy, reward)
print "{}s elapsed".format(time.time()-tic)
# Inspect arm selections
print arms[0][0:min(10,T)]
# Display some summary statistics for the collected data
pct_arm_counts={}
for policy in arms[0].keys():
print policy
pct_arm_counts[policy] = np.percentile([arms[r][policy].groupby(arms[r][policy]).size().values \
for r in xrange(R)],15, axis=0)
pct_arm_counts
# compute statistics for arm distributions
n_arm1 = {}
for policy in policies:
n_arm1[policy] = np.zeros(R)
for ix, run in enumerate(arms):
for policy in policies:
n_arm1[policy][ix] = sum(run[policy])
#plot histograms of arm distributions for each policy
policies = ['UCB', 'ECB', 'TS']
policy = 'ECB'
for ix, policy in enumerate(policies):
fig, ax = plt.subplots(1, figsize=(5.5, 4))
ax.set_title(policy, fontsize=title_font_size, fontweight='bold')
sns.distplot(n_arm1[policy]/T,
kde=False,
bins=20,
norm_hist=True,
ax=ax,
hist_kws=dict(alpha=0.8)
)
fig.savefig(path+'mab_{}_armdist'.format(policy))
plt.show()
#
# Form estimates: For each method, compute reward probability estimates and
# single-parameter error thresholds for confidence intervals
#
tic = time.time()
estimates = []
thresholds_ts = []
thresholds_os = []
normalized_errors = []
for r in xrange(R):
estimates.append({})
thresholds_ts.append({})
thresholds_os.append({})
normalized_errors.append({})
for policy in arms[r].columns:
# Create list of estimates and confidence regions for this policy
estimates[r][policy] = {}
thresholds_ts[r][policy] = {}
thresholds_os[r][policy] = {}
normalized_errors[r][policy] = {}
# OLS with asymptotic Gaussian confidence
#
# Compute estimates of arm reward probabilities
estimates[r][policy]['OLS_gsn'] = rewards[r][policy].groupby(arms[r][policy]).mean().values
# Asymptotic marginal variances diag((X^tX)^{-1})
arm_counts = arms[r][policy].groupby(arms[r][policy]).size().values
variances = reward_vars / arm_counts
# compute normalized errors
normalized_errors[r][policy]['OLS_gsn'] = (estimates[r][policy]['OLS_gsn'] - reward_means)/np.sqrt(variances)
# Compute asymptotic Gaussian single-parameter confidence thresholds
thresholds_ts[r][policy]['OLS_gsn'] = np.outer(np.sqrt(variances), gaussian_thresholds_ts)
thresholds_os[r][policy]['OLS_gsn'] = np.outer(np.sqrt(variances), gaussian_thresholds_os)
#
# OLS with concentration inequality confidence
#
# Compute estimates of arm reward probabilities
estimates[r][policy]['OLS_conc'] = np.copy(estimates[r][policy]['OLS_gsn'])
normalized_errors[r][policy]['OLS_conc'] = (estimates[r][policy]['OLS_gsn'] - reward_means)/np.sqrt(variances)
# Compute single-parameter confidence intervals using concentration inequalities
# of https://arxiv.org/pdf/1102.2670.pdf Sec. 4
# threshold_ts = sqrt(reward_vars) * sqrt((1+N_k)/N_k^2 * (1+2*log(sqrt(1+N_k)/delta)))
thresholds_ts[r][policy]['OLS_conc'] = np.sqrt(reward_vars/reward_vars)[:,None] * np.concatenate([
np.sqrt(((1.0+arm_counts)/arm_counts**2) * (1+2*np.log(np.sqrt(1.0+arm_counts)/(1-c))))[:,None]
for c in confidence_levels], axis=1)
thresholds_os[r][policy]['OLS_conc'] = np.copy(thresholds_ts[r][policy]['OLS_conc'])
#
# W estimate with asymptotic Gaussian confidence
# Y: using lambda_min = min_median_arm_count/log(T) as W_Lambdas
# avg_arm_counts = pct_arm_counts[policy]/log(T)
W_lambdas = np.ones(T)*min(pct_arm_counts[policy])/np.log(T)
# Latest parameter estimate vector
beta = np.copy(estimates[r][policy]['OLS_gsn']) ###
# Latest w_t vector
w = np.zeros((K))
# Latest matrix W_tX_t = w_1 x_1^T + ... + w_t x_t^T
WX = np.zeros((K,K))
# Latest vector of marginal variances reward_vars * (w_1**2 + ... + w_t**2)
variances = np.zeros(K)
for t in range(T):
# x_t = e_{arm}
arm = arms[r][policy][t]
# y_t = reward
reward = rewards[r][policy][t]
# Update w_t = (1/(norm{x_t}^2+lambda_t)) (x_t - W_{t-1} X_{t-1} x_t)
np.copyto(w, -WX[:,arm])
w[arm] += 1
w /= (1.0+W_lambdas[t])
# Update beta_t = beta_{t-1} + w_t (y_t - <beta_OLS, x_t>)
beta += w * (reward - estimates[r][policy]['OLS_gsn'][arm]) ###
# Update W_tX_t = W_{t-1}X_{t-1} + w_t x_t^T
WX[:,arm] += w
# Update marginal variances
variances += reward_vars * w**2
estimates[r][policy]['W'] = beta
normalized_errors[r][policy]['W'] = (estimates[r][policy]['W'] - reward_means)/np.sqrt(variances)
# Compute asymptotic Gaussian single-parameter confidence thresholds and coverage
thresholds_ts[r][policy]['W'] = np.outer(np.sqrt(variances), gaussian_thresholds_ts)
thresholds_os[r][policy]['W'] = np.outer(np.sqrt(variances), gaussian_thresholds_os)
print "{}s elapsed".format(time.time()-tic)
# Display some summary statistics concerning the model estimates
if False:
for policy in ["ECB","TS"]:#arms[0].keys():
for method in estimates[0][policy].keys():
print "{} {}".format(policy, method)
print "average estimate: {}".format(np.mean([estimates[r][policy][method] for r in xrange(R)], axis=0))
print "average threshold:\n{}".format(np.mean([thresholds_os[r][policy][method] for r in xrange(R)], axis=0))
print ""
#
# Evaluate estimates: For each policy and method, compute confidence interval
# coverage probability and width
#
tic = time.time()
coverage = [] # Check if truth in [estimate +/- thresh]
upper_coverage = [] # Check if truth >= estimate - thresh
lower_coverage = [] # Check if truth <= estimate + thresh
upper_sum_coverage = [] # Check if beta_2 - beta_1 >= estimate - thresh
lower_sum_coverage = [] # Check if beta_2 - beta_1 <= estimate + thresh
sum_norm = [] # compute (betahat_2 - beta_2 - betahat_1 + beta_1 ) / sqrt(variance_2 + variance_1)
for r in xrange(R):
coverage.append({})
upper_coverage.append({})
lower_coverage.append({})
upper_sum_coverage.append({})
lower_sum_coverage.append({})
sum_norm.append({})
for policy in estimates[r].keys():
# Interval coverage for each method
coverage[r][policy] = {}
upper_coverage[r][policy] = {}
lower_coverage[r][policy] = {}
upper_sum_coverage[r][policy] = {}
lower_sum_coverage[r][policy] = {}
sum_norm[r][policy] = {}
for method in estimates[r][policy].keys():
# Compute error of estimate
error = estimates[r][policy][method] - reward_means
# compute normalized sum
# first compute arm variances
stddevs = thresholds_os[r][policy][method].dot(gaussian_thresholds_os)/gaussian_thresholds_os.dot(gaussian_thresholds_os)
variances = stddevs**2
sum_norm[r][policy][method] = (error[0] + error[1])/np.sqrt(variances[0] + variances[1])
# Compute coverage of interval
coverage[r][policy][method] = np.absolute(error)[:,None] <= thresholds_ts[r][policy][method]
upper_coverage[r][policy][method] = error[:,None] <= thresholds_os[r][policy][method]
lower_coverage[r][policy][method] = error[:,None] >= -thresholds_os[r][policy][method]
upper_sum_coverage[r][policy][method] = error[1]+error[0] <= np.sqrt((thresholds_os[r][policy][method]**2).sum(axis=0))
lower_sum_coverage[r][policy][method] = error[1]+error[0] >= -np.sqrt((thresholds_os[r][policy][method]**2).sum(axis=0))
print "{}s elapsed".format(time.time()-tic)
# set up some plotting configuration
path = 'figs/'
policies = ['UCB', 'TS', 'ECB']
methods = ["OLS_gsn","OLS_conc", "W"]
markers = {}
markers['OLS_gsn'] = 'v'
markers['OLS_conc'] = '^'
markers['W'] = 'o'
colors = {}
colors['OLS_gsn'] = sns.color_palette()[0]
colors['OLS_conc'] = sns.color_palette()[2]
colors['W'] = sns.color_palette()[1]
colors['Nominal'] = (0, 0, 0)
colors['OLS_emp'] = sns.color_palette()[3]
legend_font_size = 14
label_font_size = 14
title_font_size = 16
#
# Display coverage results
#
## Select coverage array from {"coverage", "lower_coverage", "upper_coverage"}
#coverage_type = "lower_coverage"
#coverage_arr = locals()[coverage_type]
# For each policy and method, display coverage as a function of confidence level
methods = ['OLS_gsn', 'OLS_conc', 'W']
for policy in policies:
fig, axes = plt.subplots(2, K, figsize=(10, 8), sharey=True, sharex=True)
for k in range(K):
for m in range(len(methods)):
method = methods[m]
axes[0, k].errorbar(100*confidence_levels,
100*np.mean([lower_coverage[r][policy][method][k,:] for r in xrange(R)],axis=0),
label = method,
marker=markers[method],
color=colors[method],
linestyle='')
#print np.mean([lower_coverage[r][policy]['W'][k,:] for r in xrange(R)],axis=0)
axes[0,k].plot(100*confidence_levels, 100*confidence_levels, color=colors['Nominal'], label='Nominal')
#axes[0, k].set(adjustable='box-forced', aspect='equal')
axes[0, k].set_title("Lower: beta"+str(k+1), fontsize = title_font_size)
axes[0, k].set_ylim([86, 102])
for method in methods:
axes[1, k].errorbar(100*confidence_levels,
100*np.mean([upper_coverage[r][policy][method][k,:] for r in xrange(R)],axis=0),
label = method,
marker = markers[method],
color=colors[method],
linestyle = '')
axes[1,k].plot(100*confidence_levels, 100*confidence_levels, color=colors['Nominal'], label='Nominal')
#axes[1,k].set(adjustable='box-forced', aspect='equal')
axes[1,k].set_title("Upper: beta"+str(k+1), fontsize = title_font_size)
# fig.tight_layout()
plt.figlegend( axes[1,0].get_lines(), methods+['Nom'],
loc = (0.1, 0.01), ncol=5,
labelspacing=0. ,
fontsize = legend_font_size)
fig.suptitle(policy, fontsize = title_font_size, fontweight='bold')
fig.savefig(path+'mab_{}_coverage'.format(policy))
plt.show()
#
# Display coverage results for sum reward
#
## Select coverage array from {"coverage", "lower_coverage", "upper_coverage"}
#coverage_type = "lower_coverage"
#coverage_arr = locals()[coverage_type]
# For each policy and method, display coverage as a function of confidence level
methods = ['OLS_gsn', 'OLS_conc', 'W']
for policy in policies:
fig, axes = plt.subplots(ncols=2, figsize=(11, 4), sharey=True, sharex=True)
for m in range(len(methods)):
method = methods[m]
axes[0].errorbar(100*confidence_levels,
100*np.mean([lower_sum_coverage[r][policy][method] for r in xrange(R)],axis=0),
yerr=100*np.std([lower_sum_coverage[r][policy][method] for r in xrange(R)],axis=0)/np.sqrt(R),
label = method,
marker=markers[method],
color=colors[method],
linestyle='')
#print np.mean([lower_coverage[r][policy]['W'][k,:] for r in xrange(R)],axis=0)
axes[0].plot(100*confidence_levels, 100*confidence_levels, color=colors['Nominal'], label='Nominal')
#axes[0, k].set(adjustable='box-forced', aspect='equal')
axes[0].set_title("Lower: avg reward", fontsize = title_font_size)
axes[0].set_ylim([85, 101])
for method in methods:
axes[1].errorbar(100*confidence_levels,
100*np.mean([upper_sum_coverage[r][policy][method] for r in xrange(R)],axis=0),
yerr= 100*np.std([upper_sum_coverage[r][policy][method] for r in xrange(R)],axis=0)/np.sqrt(R),
label = method,
marker = markers[method],
color=colors[method],
linestyle = '')
axes[1].plot(100*confidence_levels, 100*confidence_levels, color=colors['Nominal'], label='Nominal')
#axes[1,k].set(adjustable='box-forced', aspect='equal')
axes[1].set_title("Upper: avg reward", fontsize = title_font_size)
# fig.tight_layout()
handles = axes[1].get_lines()
axes[1].legend( handles[0:3] + [handles[4]],
['OLS_gsn','Nom', 'OLS_conc', 'W'],
loc='lower right',
bbox_to_anchor= (1, 0.0),
ncol=1,
labelspacing=0. ,
fontsize = legend_font_size)
fig.suptitle(policy, fontsize = title_font_size, fontweight='bold')
fig.savefig(path+'mab_sum_{}_coverage'.format(policy))
plt.show()
#
# Display width results
#
# For each policy and method, display mean width as a function of confidence level
policies = ["ECB", "TS", 'UCB']
methods = ['OLS_gsn', 'OLS_conc', 'W']
for policy in policies:
fig, axes = plt.subplots(1, K, sharey=True)
for k in range(K):
for method in methods:
axes[k].errorbar(100*confidence_levels, \
np.mean([thresholds_os[r][policy][method][k,:] for r in xrange(R)],axis=0), \
np.std([thresholds_os[r][policy][method][k,:] for r in xrange(R)], axis=0),\
label = method,
marker = markers[method],
color=colors[method],
linestyle='')
# axes[k].legend(loc='')
axes[k].set_title('arm_{}'.format(k), fontsize = title_font_size)
# axes[k].set_yscale('log', nonposy='clip')
fig.suptitle(policy, fontsize = title_font_size, x=0.5, y=1.05, fontweight='bold')
# plt.figlegend( axes[0].get_lines(), methods,
# loc=(0.85, 0.5),
# ncol = 1,
# # loc= (0.75, 0.3),
# labelspacing=0. ,
# fontsize = legend_font_size)
axes[0].legend( axes[0].get_lines(),
methods,
loc = 'upper left',
ncol=1,
labelspacing=0. ,
bbox_to_anchor=(0, 1),
fontsize = legend_font_size)
fig.set_size_inches(11, 4, forward=True)
# fig.savefig(path+'mab_{}_width'.format(policy), bbox_inches='tight', pad_inches=0.1)
plt.show()
#
# Display width results for avg reward
#
# For each policy and method, display mean width as a function of confidence level
policies = ["ECB", "TS", 'UCB']
methods = ['OLS_gsn', 'OLS_conc', 'W']
for policy in policies:
fig, axes = plt.subplots()
for method in methods:
sqwidths = np.array([thresholds_os[r][policy][method]**2 for r in xrange(R)])
widths = np.sqrt(sqwidths.sum(axis = 1))/2
axes.errorbar(100*confidence_levels, \
np.mean(widths, axis=0), \
np.std(widths, axis=0),\
label = method,
marker = markers[method],
color=colors[method],
linestyle='')
# axes[k].legend(loc='')
# axes[k].set_title('arm_{}'.format(k), fontsize = title_font_size)
# axes[k].set_yscale('log', nonposy='clip')
fig.suptitle(policy, fontsize = title_font_size, x=0.5, y=1.05, fontweight='bold')
axes.legend(methods,
loc='upper left',
bbox_to_anchor=(0,1),
fontsize=legend_font_size)
# plt.figlegend( axes[0].get_lines(), methods,
# loc=(0.85, 0.5),
# ncol = 1,
# # loc= (0.75, 0.3),
# labelspacing=0. ,
# fontsize = legend_font_size)
# plt.figlegend( axes.get_lines(), methods,
# loc = (0.21, -0.01), ncol=1,
# labelspacing=0. ,
# fontsize = legend_font_size)
fig.set_size_inches(5.5, 4, forward=True)
fig.savefig(path+'mab_sum_{}_width'.format(policy), bbox_inches='tight', pad_inches=0.1)
plt.show()
#
# Visualize distribution of parameter estimation error
#
policies = ["UCB", 'TS', 'ECB']
methods = ["OLS_gsn", "W"]
#Plot histograms of errors
#for policy in policies:
# fig, axes = plt.subplots(nrows=len(methods), ncols=K, sharex=True)
# for m in range(len(methods)):
# method = methods[m]
# for k in range(K):
# errors = [normalized_errors[r][policy][method][k] for r in xrange(R)]
# sns.distplot(errors,
# kde=False,
# bins=10,
# fit = stats.norm,
# ax=axes[k, m])
# #axes[k,m].hist([estimates[r][policy][method][k] - reward_means[k] for r in xrange(R)],
# #bins=50, facecolor = 'g')
# if k == 0:
# axes[k,m].set_title(method)
# fig.suptitle(policy)
# fig.savefig(path+'mab_{}_histogram'.format(policy))
# plt.show()
# Plot qqplots of errors
for policy in policies:
fig, axes = plt.subplots(nrows=len(methods), ncols=K,
sharex=True, sharey=False,
figsize=(10, 8))
for m in range(len(methods)):
method = methods[m]
for k in range(K):
errors = [normalized_errors[r][policy][method][k] for r in xrange(R)]
# sm.graphics.qqplot(errors, line='s', ax=axes[k, m])
orderedstats, fitparams = stats.probplot(errors,
dist="norm", plot=None)
axes[k, m].plot(orderedstats[0], orderedstats[1],
marker='o', markersize=4,
linestyle='',
color=colors[method])
axes[k, m].plot(orderedstats[0], fitparams[0]*orderedstats[0] + fitparams[1], color = colors['Nominal'])
#axes[k, m].plot(orderedstats[0], fitparams[0]*orderedstats[0] + fitparams[1]) #replot to get orange color
if k == 0:
axes[k,m].set_title(method, fontsize=title_font_size)
axes[k,m].set_xlabel("")
else:
axes[k,m].set_title("")
# Display empirical kurtosis to 3 significant figures
axes[k,m].legend(loc='upper left',
labels=['Ex.Kurt.: {0:.2g}'.format(
stats.kurtosis(errors, fisher=True))], fontsize=12)
fig.suptitle(policy, fontsize=title_font_size, fontweight='bold')
#fig.set_size_inches(6, 4.5)
fig.savefig(path+'mab_{}_qq'.format(policy))
plt.show()
## plot PP Plots for arm
policies = ["UCB", 'TS', 'ECB']
methods = ["OLS_gsn", "W"]
probvals = np.linspace(0, 1.0, 101)
bins = stats.norm.ppf(probvals)
normdata = np.random.randn(R)
for policy in policies:
fig, axes = plt.subplots(nrows=len(methods), ncols=K,
sharex=True, sharey=True,
figsize=(11, 8))
for m in range(len(methods)):
method = methods[m]
for k in range(K):
errors = [normalized_errors[r][policy][method][k] for r in xrange(R)]
datacounts, bins = np.histogram(errors, bins, density=True)
normcounts, bins = np.histogram(normdata, bins, density=True)
cumdata = np.cumsum(datacounts)
cumdata = cumdata/max(cumdata)
cumnorm = np.cumsum(normcounts)
cumnorm= cumnorm/max(cumnorm)
axes[k, m].plot(cumnorm, cumdata,
marker='o', markersize = 4,
color = colors[method],
linestyle=''
)
axes[k, m].plot(probvals, probvals, color = colors['Nominal'])
#axes[k, m].plot(orderedstats[0], fitparams[0]*orderedstats[0] + fitparams[1]) #replot to get orange color
if k == 0:
axes[k,m].set_title(method, fontsize=title_font_size)
axes[k,m].set_xlabel("")
else:
axes[k,m].set_title("")
# Display empirical kurtosis to 3 significant figures
axes[k,m].legend(loc='upper left',
labels=['Skew: {0:.2g}'.format(
stats.skew(errors))], fontsize=12)
fig.suptitle(policy, fontsize=title_font_size, fontweight='bold')
#fig.set_size_inches(6, 4.5)
fig.savefig(path+'mab_{}_pp'.format(policy))
plt.show()
# plot qq plots for arm sums
policies = ["UCB", 'TS', 'ECB']
methods = ["OLS_gsn", "W"]
for policy in policies:
fig, axes = plt.subplots(ncols=len(methods),
sharex=True, sharey=False,
figsize=(10, 4))
for m in range(len(methods)):
method = methods[m]
errors = [sum_norm[r][policy][method] for r in xrange(R)]
# sm.graphics.qqplot(errors, line='s', ax=axes[k, m])
orderedstats, fitparams = stats.probplot(errors,
dist="norm", plot=None)
axes[m].plot(orderedstats[0], orderedstats[1],
marker='o', markersize=2,
linestyle='',
color=colors[method])
axes[m].plot(orderedstats[0], fitparams[0]*orderedstats[0] + fitparams[1], color = colors['Nominal'])
#axes[k, m].plot(orderedstats[0], fitparams[0]*orderedstats[0] + fitparams[1]) #replot to get orange color
axes[m].set_title(method, fontsize=title_font_size)
axes[m].set_xlabel("")
axes[m].set_title("")
# Display empirical kurtosis to 3 significant figures
# axes[k,m].legend(loc='upper left',
# labels=['Ex.Kurt.: {0:.2g}'.format(
# stats.kurtosis(errors, fisher=True))], fontsize=12)
fig.suptitle(policy, fontsize=title_font_size, fontweight='bold')
#fig.set_size_inches(6, 4.5)
fig.savefig(path+'mab_sum_{}_qq'.format(policy))
plt.show()
# plot pp plots for the sums
policies = ["UCB", 'TS', 'ECB']
methods = ["OLS_gsn", "W"]
probvals = np.linspace(0, 1.0, 101)
zscores = stats.norm.ppf(probvals)
zscores_arr = np.outer(zscores, np.ones(R))
bins = stats.norm.ppf(probvals)
normdata = np.random.randn(R)
for policy in policies:
fig, axes = plt.subplots(ncols=len(methods),
sharex=True, sharey=False,
figsize=(11, 4))
for m in range(len(methods)):
method = methods[m]
errors = [sum_norm[r][policy][method] for r in xrange(R)]
cumdata = np.mean(errors <= zscores_arr, axis=1)
# sm.graphics.qqplot(errors, line='s', ax=axes[k, m])
# datacounts, bins = np.histogram(errors, bins, density=True)
# normcounts, bins = np.histogram(normdata, bins, density=True)
# cumdata = np.cumsum(datacounts)
# cumdata = cumdata/max(cumdata)
# cumnorm = np.cumsum(normcounts)
# cumnorm= cumnorm/max(cumnorm)
axes[m].plot(probvals, cumdata,
marker='o', markersize = 4,
color = colors[method],
linestyle=''
)
axes[m].plot(probvals, probvals, color = colors['Nominal'])
axes[m].set_title(method, fontsize=title_font_size)
axes[m].set_xlabel("")
axes[m].set_title("")
# Display empirical kurtosis to 3 significant figures
# axes[k,m].legend(loc='upper left',
# labels=['Ex.Kurt.: {0:.2g}'.format(
# stats.kurtosis(errors, fisher=True))], fontsize=12)
fig.suptitle(policy, fontsize=title_font_size, fontweight='bold')
#fig.set_size_inches(6, 4.5)
fig.savefig(path+'mab_sum_{}_pp'.format(policy))
plt.show()
```
|
github_jupyter
|
<a href="https://colab.research.google.com/github/s-mostafa-a/pytorch_learning/blob/master/simple_generative_adversarial_net/MNIST_GANs.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
import torch
from torchvision.transforms import ToTensor, Normalize, Compose
from torchvision.datasets import MNIST
import torch.nn as nn
from torch.utils.data import DataLoader
from torchvision.utils import save_image
import os
class DeviceDataLoader:
def __init__(self, dl, device):
self.dl = dl
self.device = device
def __iter__(self):
for b in self.dl:
yield self.to_device(b, self.device)
def __len__(self):
return len(self.dl)
def to_device(self, data, device):
if isinstance(data, (list, tuple)):
return [self.to_device(x, device) for x in data]
return data.to(device, non_blocking=True)
class MNIST_GANS:
def __init__(self, dataset, image_size, device, num_epochs=50, loss_function=nn.BCELoss(), batch_size=100,
hidden_size=2561, latent_size=64):
self.device = device
bare_data_loader = DataLoader(dataset, batch_size, shuffle=True)
self.data_loader = DeviceDataLoader(bare_data_loader, device)
self.loss_function = loss_function
self.hidden_size = hidden_size
self.latent_size = latent_size
self.batch_size = batch_size
self.D = nn.Sequential(
nn.Linear(image_size, hidden_size),
nn.LeakyReLU(0.2),
nn.Linear(hidden_size, hidden_size),
nn.LeakyReLU(0.2),
nn.Linear(hidden_size, 1),
nn.Sigmoid())
self.G = nn.Sequential(
nn.Linear(latent_size, hidden_size),
nn.ReLU(),
nn.Linear(hidden_size, hidden_size),
nn.ReLU(),
nn.Linear(hidden_size, image_size),
nn.Tanh())
self.d_optimizer = torch.optim.Adam(self.D.parameters(), lr=0.0002)
self.g_optimizer = torch.optim.Adam(self.G.parameters(), lr=0.0002)
self.sample_dir = './../data/mnist_samples'
if not os.path.exists(self.sample_dir):
os.makedirs(self.sample_dir)
self.G.to(device)
self.D.to(device)
self.sample_vectors = torch.randn(self.batch_size, self.latent_size).to(self.device)
self.num_epochs = num_epochs
@staticmethod
def denormalize(x):
out = (x + 1) / 2
return out.clamp(0, 1)
def reset_grad(self):
self.d_optimizer.zero_grad()
self.g_optimizer.zero_grad()
def train_discriminator(self, images):
real_labels = torch.ones(self.batch_size, 1).to(self.device)
fake_labels = torch.zeros(self.batch_size, 1).to(self.device)
outputs = self.D(images)
d_loss_real = self.loss_function(outputs, real_labels)
real_score = outputs
new_sample_vectors = torch.randn(self.batch_size, self.latent_size).to(self.device)
fake_images = self.G(new_sample_vectors)
outputs = self.D(fake_images)
d_loss_fake = self.loss_function(outputs, fake_labels)
fake_score = outputs
d_loss = d_loss_real + d_loss_fake
self.reset_grad()
d_loss.backward()
self.d_optimizer.step()
return d_loss, real_score, fake_score
def train_generator(self):
new_sample_vectors = torch.randn(self.batch_size, self.latent_size).to(self.device)
fake_images = self.G(new_sample_vectors)
labels = torch.ones(self.batch_size, 1).to(self.device)
g_loss = self.loss_function(self.D(fake_images), labels)
self.reset_grad()
g_loss.backward()
self.g_optimizer.step()
return g_loss, fake_images
def save_fake_images(self, index):
fake_images = self.G(self.sample_vectors)
fake_images = fake_images.reshape(fake_images.size(0), 1, 28, 28)
fake_fname = 'fake_images-{0:0=4d}.png'.format(index)
print('Saving', fake_fname)
save_image(self.denormalize(fake_images), os.path.join(self.sample_dir, fake_fname),
nrow=10)
def run(self):
total_step = len(self.data_loader)
d_losses, g_losses, real_scores, fake_scores = [], [], [], []
for epoch in range(self.num_epochs):
for i, (images, _) in enumerate(self.data_loader):
images = images.reshape(self.batch_size, -1)
d_loss, real_score, fake_score = self.train_discriminator(images)
g_loss, fake_images = self.train_generator()
if (i + 1) % 600 == 0:
d_losses.append(d_loss.item())
g_losses.append(g_loss.item())
real_scores.append(real_score.mean().item())
fake_scores.append(fake_score.mean().item())
print(f'''Epoch [{epoch}/{self.num_epochs}], Step [{i + 1}/{
total_step}], d_loss: {d_loss.item():.4f}, g_loss: {g_loss.item():.4f}, D(x): {
real_score.mean().item():.2f}, D(G(z)): {fake_score.mean().item():.2f}''')
self.save_fake_images(epoch + 1)
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
mnist = MNIST(root='./../data', train=True, download=True, transform=Compose([ToTensor(), Normalize(mean=(0.5,), std=(0.5,))]))
image_size = mnist.data[0].flatten().size()[0]
gans = MNIST_GANS(dataset=mnist, image_size=image_size, device=device)
gans.run()
```
|
github_jupyter
|
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
dataset1=pd.read_csv('general_data.csv')
dataset1.head()
dataset1.columns
dataset1
dataset1.isnull()
dataset1.duplicated()
dataset1.drop_duplicates()
dataset3=dataset1[['Age','DistanceFromHome','Education','MonthlyIncome', 'NumCompaniesWorked', 'PercentSalaryHike','TotalWorkingYears', 'TrainingTimesLastYear', 'YearsAtCompany','YearsSinceLastPromotion', 'YearsWithCurrManager']].describe()
dataset3
dataset3=dataset1[['Age','DistanceFromHome','Education','MonthlyIncome', 'NumCompaniesWorked', 'PercentSalaryHike','TotalWorkingYears', 'TrainingTimesLastYear', 'YearsAtCompany','YearsSinceLastPromotion', 'YearsWithCurrManager']].median()
dataset3
dataset3=dataset1[['Age','DistanceFromHome','Education','MonthlyIncome', 'NumCompaniesWorked', 'PercentSalaryHike','TotalWorkingYears', 'TrainingTimesLastYear', 'YearsAtCompany','YearsSinceLastPromotion', 'YearsWithCurrManager']].mode()
dataset3
dataset3=dataset1[['Age','DistanceFromHome','Education','MonthlyIncome', 'NumCompaniesWorked', 'PercentSalaryHike','TotalWorkingYears', 'TrainingTimesLastYear', 'YearsAtCompany','YearsSinceLastPromotion', 'YearsWithCurrManager']].var()
dataset3
dataset3=dataset1[['Age','DistanceFromHome','Education','MonthlyIncome', 'NumCompaniesWorked', 'PercentSalaryHike','TotalWorkingYears', 'TrainingTimesLastYear', 'YearsAtCompany','YearsSinceLastPromotion', 'YearsWithCurrManager']].skew()
dataset3
dataset3=dataset1[['Age','DistanceFromHome','Education','MonthlyIncome', 'NumCompaniesWorked', 'PercentSalaryHike','TotalWorkingYears', 'TrainingTimesLastYear', 'YearsAtCompany','YearsSinceLastPromotion', 'YearsWithCurrManager']].kurt()
dataset3
```
# Inference from the analysis:
All the above variables show positive skewness; while Age & Mean_distance_from_home are leptokurtic and all other variables are platykurtic.
The Mean_Monthly_Income’s IQR is at 54K suggesting company wide attrition across all income bands
Mean age forms a near normal distribution with 13 years of IQR
# Outliers:
There’s no regression found while plotting Age, MonthlyIncome, TotalWorkingYears, YearsAtCompany, etc., on a scatter plot
```
box_plot=dataset1.Age
plt.boxplot(box_plot)
```
### Age is normally distributed without any outliers
```
box_plot=dataset1.MonthlyIncome
plt.boxplot(box_plot)
```
### Monthly Income is Right skewed with several outliers
```
box_plot=dataset1.YearsAtCompany
plt.boxplot(box_plot)
```
### Years at company is also Right Skewed with several outliers observed.
# Attrition Vs Distance from Home
```
from scipy.stats import mannwhitneyu
from scipy.stats import mannwhitneyu
a1=dataset.DistanceFromHome_Yes
a2=dataset.DistanceFromHome_No
stat, p=mannwhitneyu(a1,a2)
print(stat, p)
3132625.5 0.0
```
As the P value of 0.0 is < 0.05, the H0 is rejected and Ha is accepted.
H0: There is no significant differences in the Distance From Home between attrition (Y) and attirition (N)
Ha: There is significant differences in the Distance From Home between attrition (Y) and attirition (N)
## Attrition Vs Income
```
a1=dataset.MonthlyIncome_Yes
a2=dataset.MonthlyIncome_No
stat, p=mannwhitneyu(a1,a2)
print(stat, p)
3085416.0 0.0
```
As the P value is again 0.0, which is < than 0.05, the H0 is rejected and ha is accepted.
H0: There is no significant differences in the income between attrition (Y) and attirition (N)
Ha: There is significant differences in the income between attrition (Y) and attirition (N)
## Attrition Vs Total Working Years
```
a1=dataset.TotalWorkingYears_Yes
a2=dataset.TotalWorkingYears_No
stat, p=mannwhitneyu(a1,a2)
print(stat, p)
2760982.0 0.0
```
As the P value is again 0.0, which is < than 0.05, the H0 is rejected and ha is accepted.
H0: There is no significant differences in the Total Working Years between attrition (Y) and attirition (N)
Ha: There is significant differences in the Total Working Years between attrition (Y) and attirition (N)
## Attrition Vs Years at company
```
a1=dataset.YearsAtCompany_Yes
a2=dataset.YearsAtCompany_No
stat, p=mannwhitneyu(a1,a2)
print(stat, p)
2882047.5 0.0
```
As the P value is again 0.0, which is < than 0.05, the H0 is rejected and ha is accepted.
H0: There is no significant differences in the Years At Company between attrition (Y) and attirition (N)
Ha: There is significant differences in the Years At Company between attrition (Y) and attirition (N)
## Attrition Vs YearsWithCurrentManager
```
a1=dataset.YearsWithCurrManager_Yes
a2=dataset.YearsWithCurrManager_No
stat, p=mannwhitneyu(a1,a2)
print(stat, p)
3674749.5 0.0
```
As the P value is again 0.0, which is < than 0.05, the H0 is rejected and ha is accepted.
H0: There is no significant differences in the Years With Current Manager between attrition (Y) and attirition (N)
Ha: There is significant differences in the Years With Current Manager between attrition (Y) and attirition (N)
# Statistical Tests (Separate T Test)
## Attrition Vs Distance From Home
from scipy.stats import ttest_ind
```
z1=dataset.DistanceFromHome_Yes
z2=dataset.DistanceFromHome_No
stat, p=ttest_ind(z2,z1)
print(stat, p)
44.45445917636664 0.0
```
As the P value is again 0.0, which is < than 0.05, the H0 is rejected and ha is accepted.
H0: There is no significant differences in the Distance From Home between attrition (Y) and attirition (N)
Ha: There is significant differences in the Distance From Home between attrition (Y) and attirition (N)
## Attrition Vs Income
```
z1=dataset.MonthlyIncome_Yes
z2=dataset.MonthlyIncome_No
stat, p=ttest_ind(z2, z1)
print(stat, p)
52.09279408504947 0.0
```
As the P value is again 0.0, which is < than 0.05, the H0 is rejected and ha is accepted.
H0: There is no significant differences in the Monthly Income between attrition (Y) and attirition (N)
Ha: There is significant differences in the Monthly Income between attrition (Y) and attirition (N)
## Attrition Vs Yeats At Company
```
z1=dataset.YearsAtCompany_Yes
z2=dataset.YearsAtCompany_No
stat, p=ttest_ind(z2, z1)
print(stat, p)
51.45296941515692 0.0
```
As the P value is again 0.0, which is < than 0.05, the H0 is rejected and ha is accepted.
H0: There is no significant differences in the Years At Company between attrition (Y) and attirition (N)
Ha: There is significant differences in the Years At Company between attrition (Y) and attirition (N)
## Attrition Vs Years With Current Manager
```
z1=dataset.YearsWithCurrManager_Yes
z2=dataset.YearsWithCurrManager_No
stat, p=ttest_ind(z2, z1)
print(stat, p)
53.02424349024521 0.0
```
As the P value is again 0.0, which is < than 0.05, the H0 is rejected and ha is accepted.
H0: There is no significant differences in the Years With Current Manager between attrition (Y) and attirition (N)
Ha: There is significant differences in the Years With Current Manager between attrition (Y) and attirition (N)
# Unsupervised Learning - Correlation Analysis
In order to find the interdependency of the variables DistanceFromHome, MonthlyIncome, TotalWorkingYears, YearsAtCompany, YearsWithCurrManager from that of Attrition, we executed the Correlation Analysis as follows.
stats, p=pearsonr(dataset.Attrition, dataset.DistanceFromHome)
print(stats, p)
-0.009730141010179438 0.5182860428049617
stats, p=pearsonr(dataset.Attrition, dataset.MonthlyIncome)
print(stats, p)
-0.031176281698114025 0.0384274849060192
stats, p=pearsonr(dataset.Attrition, dataset.TotalWorkingYears)
print(stats, p)
-0.17011136355964646 5.4731597518148054e-30
stats, p=pearsonr(dataset.Attrition, dataset.YearsAtCompany)
print(stats, p)
-0.13439221398997386 3.163883122493571e-19
stats, p=pearsonr(dataset.Attrition, dataset.YearsWithCurrManager)
print(stats, p)
-0.15619931590162422 1.7339322652951965e-25
# The inference of the above analysis are as follows:
Attrition & DistanceFromHome:
As r = -0.009, there’s low negative correlation between Attrition and DistanceFromHome
As the P value of 0.518 is > 0.05, we are accepting H0 and hence there’s no significant correlation between Attrition &
DistanceFromHome
Attrition & MonthlyIncome:
As r = -0.031, there’s low negative correlation between Attrition and MonthlyIncome
As the P value of 0.038 is < 0.05, we are accepting Ha and hence there’s significant correlation between Attrition &
MonthlyIncome
Attrition & TotalWorkingYears:
As r = -0.17, there’s low negative correlation between Attrition and TotalWorkingYears
As the P value is < 0.05, we are accepting Ha and hence there’s significant correlation between Attrition & TotalWorkingYears
Attrition & YearsAtCompany:
As r = -0.1343, there’s low negative correlation between Attrition and YearsAtCompany
As the P value is < 0.05, we are accepting Ha and hence there’s significant correlation between Attrition & YearsAtCompany
Attrition & YearsWithCurrManager:
As r = -0.1561, there’s low negative correlation between Attrition and YearsWithCurrManager
As the P value is < 0.05, we are accepting Ha and hence there’s significant correlation between Attrition &
YearsWithCurrManager
|
github_jupyter
|
# ADVANCED TEXT MINING
- 본 자료는 텍스트 마이닝을 활용한 연구 및 강의를 위한 목적으로 제작되었습니다.
- 본 자료를 강의 목적으로 활용하고자 하시는 경우 꼭 아래 메일주소로 연락주세요.
- 본 자료에 대한 허가되지 않은 배포를 금지합니다.
- 강의, 저작권, 출판, 특허, 공동저자에 관련해서는 문의 바랍니다.
- **Contact : ADMIN(admin@teanaps.com)**
---
## WEEK 02-2. Python 자료구조 이해하기
- 텍스트 데이터를 다루기 위한 Python 자료구조에 대해 다룹니다.
---
### 1. 리스트(LIST) 자료구조 이해하기
---
#### 1.1. 리스트(LIST): 값 또는 자료구조를 저장할 수 있는 구조를 선언합니다.
---
```
# 1) 리스트를 생성합니다.
new_list = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
print(new_list)
# 2) 리스트의 마지막 원소 뒤에 새로운 원소를 추가합니다.
new_list.append(100)
print(new_list)
# 3) 더하기 연산자를 활용해 두 리스트를 결합합니다.
new_list = new_list + [101, 102]
print(new_list)
# 4-1) 리스트에 존재하는 특정 원소 중 일치하는 가장 앞의 원소를 삭제합니다.
new_list.remove(3)
print(new_list)
# 4-2) 리스트에 존재하는 N 번째 원소를 삭제합니다.
del new_list[3]
print(new_list)
# 5) 리스트에 존재하는 N 번째 원소의 값을 변경합니다.
new_list[0] = 105
print(new_list)
# 6) 리스트에 존재하는 모든 원소를 오름차순으로 정렬합니다.
new_list.sort()
#new_list.sort(reverse=False)
print(new_list)
# 7) 리스트에 존재하는 모든 원소를 내림차순으로 정렬합니다.
new_list.sort(reverse=True)
print(new_list)
# 8) 리스트에 존재하는 모든 원소의 순서를 거꾸로 변경합니다.
new_list.reverse()
print(new_list)
# 9) 리스트에 존재하는 모든 원소의 개수를 불러옵니다.
length = len(new_list)
print(new_list)
# 10-1) 리스트에 특정 원소에 존재하는지 여부를 in 연산자를 통해 확인합니다.
print(100 in new_list)
# 10-2) 리스트에 특정 원소에 존재하지 않는지 여부를 not in 연산자를 통해 확인합니다.
print(100 not in new_list)
```
#### 1.2. 리스트(LIST) 인덱싱: 리스트에 존재하는 특정 원소를 불러옵니다.
---
```
new_list = [0, 1, 2, 3, 4, 5, 6, 7, "hjvjg", 9]
# 1) 리스트에 존재하는 N 번째 원소를 불러옵니다.
print("0번째 원소 :", new_list[0])
print("1번째 원소 :", new_list[1])
print("4번째 원소 :", new_list[4])
# 2) 리스트에 존재하는 N번째 부터 M-1번째 원소를 리스트 형식으로 불러옵니다.
print("0~3번째 원소 :", new_list[0:3])
print("4~9번째 원소 :", new_list[4:9])
print("2~3번째 원소 :", new_list[2:3])
# 3) 리스트에 존재하는 N번째 부터 모든 원소를 리스트 형식으로 불러옵니다.
print("3번째 부터 모든 원소 :", new_list[3:])
print("5번째 부터 모든 원소 :", new_list[5:])
print("9번째 부터 모든 원소 :", new_list[9:])
# 4) 리스트에 존재하는 N번째 이전의 모든 원소를 리스트 형식으로 불러옵니다.
print("1번째 이전의 모든 원소 :", new_list[:1])
print("7번째 이전의 모든 원소 :", new_list[:7])
print("9번째 이전의 모든 원소 :", new_list[:9])
# 5) 리스트 인덱싱에 사용되는 정수 N의 부호가 음수인 경우, 마지막 원소부터 |N|-1번째 원소를 의미합니다.
print("끝에서 |-1|-1번째 이전의 모든 원소 :", new_list[:-1])
print("끝에서 |-1|-1번째 부터 모든 원소 :", new_list[-1:])
print("끝에서 |-2|-1번째 이전의 모든 원소 :", new_list[:-2])
print("끝에서 |-2|-1번째 부터 모든 원소 :", new_list[-2:])
```
#### 1.3. 다차원 리스트(LIST): 리스트의 원소에 다양한 값 또는 자료구조를 저장할 수 있습니다.
---
```
# 1-1) 리스트의 원소에는 유형(TYPE)의 값 또는 자료구조를 섞어서 저장할 수 있습니다.
new_list = ["텍스트", 0, 1.9, [1, 2, 3, 4], {"서울": 1, "부산": 2, "대구": 3}]
print(new_list)
# 1-2) 리스트의 각 원소의 유형(TYPE)을 type(변수) 함수를 활용해 확인합니다.
print("Type of new_list[0] :", type(new_list[0]))
print("Type of new_list[1] :", type(new_list[1]))
print("Type of new_list[2] :", type(new_list[2]))
print("Type of new_list[3] :", type(new_list[3]))
print("Type of new_list[4] :", type(new_list[4]))
# 2) 리스트 원소에 리스트를 여러개 추가하여 다차원 리스트(NxM)를 생성할 수 있습니다.
new_list = [[0, 1, 2], [2, 3, 7], [9, 6, 8], [4, 5, 1]]
print("new_list :", new_list)
print("new_list[0] :", new_list[0])
print("new_list[1] :", new_list[1])
print("new_list[2] :", new_list[2])
print("new_list[3] :", new_list[3])
# 3-1) 다차원 리스트(NxM)를 정렬하는 경우 기본적으로 각 리스트의 첫번째 원소를 기준으로 정렬합니다.
new_list.sort()
print("new_list :", new_list)
print("new_list[0] :", new_list[0])
print("new_list[1] :", new_list[1])
print("new_list[2] :", new_list[2])
print("new_list[3] :", new_list[3])
# 3-2) 다차원 리스트(NxM)를 각 리스트의 N 번째 원소를 기준으로 정렬합니다.
new_list.sort(key=lambda elem: elem[2])
print("new_list :", new_list)
print("new_list[0] :", new_list[0])
print("new_list[1] :", new_list[1])
print("new_list[2] :", new_list[2])
print("new_list[3] :", new_list[3])
```
### 2. 딕셔너리(DICTIONARY) 자료구조 이해하기
---
#### 2.1. 딕셔너리(DICTIONARY): 값 또는 자료구조를 저장할 수 있는 구조를 선언합니다.
---
```
# 1) 딕셔너리를 생성합니다.
new_dict = {"마케팅팀": 98, "개발팀": 78, "데이터분석팀": 83, "운영팀": 33}
print(new_dict)
# 2) 딕셔너리의 각 원소는 KEY:VALUE 쌍의 구조를 가지며, KEY 값에 대응되는 VALUE를 불러옵니다.
print(new_dict["마케팅팀"])
# 3-1) 딕셔너리에 새로운 KEY:VALUE 쌍의 원소를 추가합니다.
new_dict["미화팀"] = 55
print(new_dict)
# 3-2) 딕셔너리에 저장된 각 원소의 KEY 값은 유일해야하기 때문에, 중복된 KEY 값이 추가되는 경우 VALUE는 덮어쓰기 됩니다.
new_dict["데이터분석팀"] = 100
print(new_dict)
# 4) 딕셔너리에 다양한 유형(TYPE)의 값 또는 자료구조를 VALUE로 사용할 수 있습니다.
new_dict["데이터분석팀"] = {"등급": "A"}
new_dict["운영팀"] = ["A"]
new_dict["개발팀"] = "재평가"
new_dict[0] = "오타"
print(new_dict)
```
#### 2.2. 딕셔너리(DICTIONARY) 인덱싱: 딕셔너리에 존재하는 원소를 리스트 형태로 불러옵니다.
---
```
# 1-1) 다양한 함수를 활용해 딕셔너리를 인덱싱 가능한 구조로 불러옵니다.
new_dict = {"마케팅팀": 98, "개발팀": 78, "데이터분석팀": 83, "운영팀": 33}
print("KEY List of new_dict :", new_dict.keys())
print("VALUE List of new_dict :", new_dict.values())
print("(KEY, VALUE) List of new_dict :", new_dict.items())
for i, j in new_dict.items():
print(i, j)
# 1-2) 불러온 자료구조를 실제 리스트 자료구조로 변환합니다.
print("KEY List of new_dict :", list(new_dict.keys()))
print("VALUE List of new_dict :", list(new_dict.values()))
print("(KEY, VALUE) List of new_dict :", list(new_dict.items()))
```
|
github_jupyter
|
# Tutorial 2. Solving a 1D diffusion equation
```
# Document Author: Dr. Vishal Sharma
# Author email: sharma_vishal14@hotmail.com
# License: MIT
# This tutorial is applicable for NAnPack version 1.0.0-alpha4
```
### I. Background
The objective of this tutorial is to present the step-by-step solution of a 1D diffusion equation using NAnPack such that users can follow the instructions to learn using this package. The numerical solution is obtained using the Forward Time Central Spacing (FTCS) method. The detailed description of the FTCS method is presented in Section IV of this tutorial.
### II. Case Description
We will be solving a classical probkem of a suddenly accelerated plate in fluid mechanicas which has the known exact solution. In this problem, the fluid is
bounded between two parallel plates. The upper plate remains stationary and the lower plate is suddenly accelerated in *y*-direction at velocity $U_o$. It is
required to find the velocity profile between the plates for the given initial and boundary conditions.
(For the sake of simplicity in setting up numerical variables, let's assume that the *x*-axis is pointed in the upward direction and *y*-axis is pointed along the horizontal direction as shown in the schematic below:

**Initial conditions**
$$u(t=0.0, 0.0<x\leq H) = 0.0 \;m/s$$
$$u(t=0.0, x=0.0) = 40.0 \;m/s$$
**Boundary conditions**
$$u(t\geq0.0, x=0.0) = 40.0 \;m/s$$
$$u(t\geq0.0, x=H) = 0.0 \;m/s$$
Viscosity of fluid, $\;\;\nu = 2.17*10^{-4} \;m^2/s$
Distance between plates, $\;\;H = 0.04 \;m$
Grid step size, $\;\;dx = 0.001 \;m$
Simulation time, $\;\;T = 1.08 \;sec$
Specify the required simulation inputs based on our setup in the configuration file provided with this package. You may choose to save the configuration file with any other filename. I have saved the configuration file in the "input" folder of my project directory such that the relative path is `./input/config.ini`.
### III. Governing Equation
The governing equation for the given application is the simplified for the the Navies-Stokes equation which is given as:
$$\frac{\partial u} {\partial t} = \nu\frac{\partial^2 u}{\partial x^2}$$
This is the diffusion equation model and is classified as the parabolic PDE.
### IV. FTCS method
The forward time central spacing approximation equation in 1D is presented here. This is a time explicit method which means that one unknown is calculated using the known neighbouring values from the previous time step. Here *i* represents grid point location, *n*+1 is the future time step, and *n* is the current time step.
$$u_{i}^{n+1} = u_{i}^{n} + \frac{\nu\Delta t}{(\Delta x)^2}(u_{i+1}^{n} - 2u_{i}^{n} + u_{i-1}^{n})$$
The order of this approximation is $[(\Delta t), (\Delta x)^2]$
The diffusion number is given as $d_{x} = \nu\frac{\Delta t}{(\Delta x)^2}$ and for one-dimensional applications the stability criteria is $d_{x}\leq\frac{1}{2}$
The solution presented here is obtained using a diffusion number = 0.5 (CFL = 0.5 in configuration file). Time step size will be computed using the expression of diffusion number. Beginners are encouraged to try diffusion numbers greater than 0.5 as an exercise after running this script.
Users are encouraged to read my blogs on numerical methods - [link here](https://www.linkedin.com/in/vishalsharmaofficial/detail/recent-activity/posts/).
### V. Script Development
*Please note that this code script is provided in file `./examples/tutorial-02-diffusion-1D-solvers-FTCS.py`.*
As per the Python established coding guidelines [PEP 8](https://www.python.org/dev/peps/pep-0008/#imports), all package imports must be done at the top part of the script in the following sequence --
1. import standard library
2. import third party modules
3. import local application/library specific
Accordingly, in our code we will importing the following required modules (in alphabetical order). If you are using Jupyter notebook, hit `Shift + Enter` on each cell after typing the code.
```
import matplotlib.pyplot as plt
from nanpack.benchmark import ParallelPlateFlow
import nanpack.preprocess as pre
from nanpack.grid import RectangularGrid
from nanpack.parabolicsolvers import FTCS
import nanpack.postprocess as post
```
As the first step in simulation, we have to tell our script to read the inputs and assign those inputs to the variables/objects that we will use in our entire code. For this purpose, there is a class `RunConfig` in `nanpack.preprocess` module. We will call this class and assign an object (instance) to it so that we can use its member variables. The `RunConfig` class is written in such a manner that its methods get executed as soon as it's instance is created. The users must provide the configuration file path as a parameter to `RunConfig` class.
```
FileName = "path/to/project/input/config.ini" # specify the correct file path
cfg = pre.RunConfig(FileName) # cfg is an instance of RunConfig class which can be used to access class variables. You may choose any variable in place of cfg.
```
You will obtain several configuration messages on your output screen so that you can verify that your inputs are correct and that the configuration is successfully completed. Next step is the assignment of initial conditions and the boundary conditions. For assigning boundary conditions, I have created a function `BC()` which we will be calling in the next cell. I have included this function at the bottom of this tutorial for your reference. It is to be noted that U is the dependent variable that was initialized when we executed the configuration, and thus we will be using `cfg.U` to access the initialized U. In a similar manner, all the inputs provided in the configuration file can be obtained by using configuration class object `cfg.` as the prefix to the variable names. Users are allowed to use any object of their choice.
*If you are using Jupyter Notebook, the function BC must be executed before referencing to it, otherwise, you will get an error. Jump to the bottom of this notebook where you see code cell # 1 containing the `BC()` function*
```
# Assign initial conditions
cfg.U[0] = 40.0
cfg.U[1:] = 0.0
# Assign boundary conditions
U = BC(cfg.U)
```
Next, we will be calculating location of all grid points within the domain using the function `RectangularGrid()` and save values into X. We will also require to calculate diffusion number in X direction. In nanpack, the program treats the diffusion number = CFL for 1D applications that we entered in the configuration file, and therefore this step may be skipped, however, it is not the same in two-dimensional applications and therefore to stay consistent and to avoid confusion we will be using the function `DiffusionNumbers()` to compute the term `diffX`.
```
X, _ = RectangularGrid(cfg.dX, cfg.iMax)
diffX,_ = pre.DiffusionNumbers(cfg.Dimension, cfg.diff, cfg.dT, cfg.dX)
```
Next, we will initialize some local variables before start the time stepping:
```
Error = 1.0 # variable to keep track of error
n = 0 # variable to advance in time
```
Start time loop using while loop such that if one of the condition returns False, the time stepping will be stopped. For explanation of each line, see the comments. Please note the identation of the codes within the while loop. Take extra care with indentation as Python is very particular about it.
```
while n <= cfg.nMax and Error > cfg.ConvCrit: # start loop
Error = 0.0 # reset error to 0.0 at the beginning of each step
n += 1 # advance the value of n at each step
Uold = U.copy() # store solution at time level, n
U = FTCS(Uold, diffX) # solve for U using FTCS method at time level n+1
Error = post.AbsoluteError(U, Uold) # calculate errors
U = BC(U) # Update BC
post.MonitorConvergence(cfg, n, Error) # Use this function to monitor convergence
post.WriteSolutionToFile(U, n, cfg.nWrite, cfg.nMax,\
cfg.OutFileName, cfg.dX) # Write output to file
post.WriteConvHistToFile(cfg, n, Error) # Write convergence log to history file
```
In the above convergence monitor, it is worth noting that the solution error is gradually moving towards zero which is what we need to confirm stability in the solution. If the solution becomes unstable, the errors will rise, probably upto the point where your code will crash. As you know that the solution obtained is a time-dependent solution and therefore, we didn't allow the code to run until the convergence is observed. If a steady-state solution is desired, change the STATE key in the configuration file equals to "STEADY" and specify a much larger value of nMax key, say nMax = 5000. This is left as an exercise for the users to obtain a stead-state solution. Also, try running the solution with the larger grid step size, $\Delta x$ or a larger time step size, $\Delta t$.
After the time stepping is completed, save the final results to the output files.
```
# Write output to file
post.WriteSolutionToFile(U, n, cfg.nWrite, cfg.nMax,
cfg.OutFileName, cfg.dX)
# Write convergence history log to a file
post.WriteConvHistToFile(cfg, n, Error)
```
Verify that the files are saved in the target directory.
Now let us obtain analytical solution of this flow that will help us in validating our codes.
```
# Obtain analytical solution
Uana = ParallelPlateFlow(40.0, X, cfg.diff, cfg.totTime, 20)
```
Next, we will validate our results by plotting the results using the matplotlib package that we have imported above. Type the following lines of codes:
```
plt.rc("font", family="serif", size=8) # Assign fonts in the plot
fig, ax = plt.subplots(dpi=150) # Create axis for plotting
plt.plot(U, X, ">-.b", linewidth=0.5, label="FTCS",\
markersize=5, markevery=5) # Plot data with required labels and markers, customize the plot however you may like
plt.plot(Uana, X, "o:r", linewidth=0.5, label="Analytical",\
markersize=5, markevery=5) # Plot analytical solution on the same plot
plt.xlabel('Velocity (m/s)') # X-axis labelling
plt.ylabel('Plate distance (m)') # Y-axis labelling
plt.title(f"Velocity profile\nat t={cfg.totTime} sec", fontsize=8) # Plot title
plt.legend()
plt.show() # Show plot- this command is very important
```
Function for the boundary conditions.
```
def BC(U):
"""Return the dependent variable with the updated values at the boundaries."""
U[0] = 40.0
U[-1] = 0.0
return U
```
Congratulations, you have completed the first coding tutoria using nanpack package and verified that your codes produced correct results. If you solve some other similar diffusion-1D model example, share it with the nanpack community. I will be excited to see your projects.
|
github_jupyter
|
```
import tensorflow as tf
from tensorflow.keras.callbacks import TensorBoard
import os
import matplotlib.pyplot as plt
import numpy as np
import random
import cv2
import time
training_path = "fruits-360_dataset/Training"
test_path = "fruits-360_dataset/Test"
try:
STATS = np.load("stats.npy", allow_pickle=True)
except FileNotFoundError as fnf:
print("Not found stats file.")
STATS = []
# Parameters
GRAY_SCALE = False
FRUITS = os.listdir(training_path)
random.shuffle(FRUITS)
train_load = 0.1
test_load = 0.3
def load_data(directory_path, load_factor=None):
data = []
labels = []
for fruit_name in FRUITS:
class_num = FRUITS.index(fruit_name)
path = os.path.join(directory_path, fruit_name)
for img in os.listdir(path):
if load_factor and np.random.random() > load_factor: # skip image
continue
img_path = os.path.join(path, img)
if GRAY_SCALE:
image = cv2.imread(img_path, cv2.IMREAD_GRAYSCALE)
else:
image = cv2.imread(img_path)
image = image[:, :, [2, 1, 0]]
image = image / 255.0
image = np.array(image, dtype=np.single) # Reduce precision and memory consumption
data.append([image, class_num])
random.shuffle(data)
X = []
y = []
for image, label in data:
X.append(image)
y.append(label)
X = np.array(X)
y = np.array(y)
if GRAY_SCALE:
print("Reshaping gray scale")
X = X.reshape(-1, X.shape[1], X.shape[2], 1)
return X, y
X_training, y_training = load_data(training_path, load_factor=train_load)
print("Created training array")
print(f"X shape: {X_training.shape}")
print(f"y shape: {y_training.shape}")
X_test, y_test = load_data(test_path, load_factor=test_load)
print("Created test arrays")
print(f"X shape: {X_test.shape}")
print(f"y shape: {y_test.shape}")
class AfterTwoEpochStop(tf.keras.callbacks.Callback):
def __init__(self, acc_threshold, loss_threshold):
# super(AfterTwoEpochStop, self).__init__()
self.acc_threshold = acc_threshold
self.loss_threshold = loss_threshold
self.checked = False
print("Init")
def on_epoch_end(self, epoch, logs=None):
acc = logs["accuracy"]
loss = logs["loss"]
if acc >= self.acc_threshold and loss <= self.loss_threshold:
if self.checked:
self.model.stop_training = True
else:
self.checked = True
else:
self.checked = False
stop = AfterTwoEpochStop(acc_threshold=0.98, loss_threshold=0.05)
# Limit gpu memory usage
config = tf.compat.v1.ConfigProto()
config.gpu_options.allow_growth = False
config.gpu_options.per_process_gpu_memory_fraction = 0.4
session = tf.compat.v1.Session(config=config)
from tensorflow.keras.layers import Dense, Flatten, Conv2D, Conv3D, MaxPooling2D, MaxPooling3D, Activation, Dropout
dense_layers = [2]
dense_size = [32, 64]
conv_layers = [1, 2, 3]
conv_size = [32, 64]
conv_shape = [2, 5]
pic_shape = X_training.shape[1:]
label_count = len(FRUITS)
run_num = 0
total = len(dense_layers)*len(dense_size)*len(conv_layers)*len(conv_size)*len(conv_shape)
for dl in dense_layers:
for ds in dense_size:
for cl in conv_layers:
for cs in conv_size:
for csh in conv_shape:
run_num += 1
with tf.compat.v1.Session(config=config) as sess:
NAME = f"{cl}xConv({cs:>03})_shape{csh}-{dl}xDense({ds:>03})-{time.time():10.0f}"
tensorboard = TensorBoard(log_dir=f'logs-optimize/{NAME}')
model = None
model = tf.keras.models.Sequential()
model.add(Conv2D(cs, (csh, csh), activation='relu', input_shape=pic_shape))
model.add(MaxPooling2D())
for i in range(cl-1):
model.add(Conv2D(cs, (csh, csh), activation='relu'))
model.add(MaxPooling2D())
model.add(Flatten())
for x in range(dl):
model.add(Dense(ds, activation='relu'))
model.add(Dense(label_count, activation='softmax'))
model.compile(optimizer='adam',
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
history = model.fit(X_training, y_training,
batch_size=25, epochs=10,
validation_data=(X_test, y_test),
callbacks=[tensorboard, stop])
loss = history.history['loss']
accuracy = history.history['accuracy']
val_loss = history.history['val_loss']
val_accuracy = history.history['val_accuracy']
print(f"{(run_num/total)*100:<5.1f}% - {NAME} Results: ")
# print(f"Test Accuracy: {val_accuracy[-1]:>2.4f}")
# print(f"Test loss: {val_loss[-1]:>2.4f}")
```
|
github_jupyter
|
# <span style="color:Maroon">Trade Strategy
__Summary:__ <span style="color:Blue">In this code we shall test the results of given model
```
# Import required libraries
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import os
np.random.seed(0)
import warnings
warnings.filterwarnings('ignore')
# User defined names
index = "BTC-USD"
filename_whole = "whole_dataset"+index+"_xgboost_model.csv"
filename_trending = "Trending_dataset"+index+"_xgboost_model.csv"
filename_meanreverting = "MeanReverting_dataset"+index+"_xgboost_model.csv"
date_col = "Date"
Rf = 0.01 #Risk free rate of return
# Get current working directory
mycwd = os.getcwd()
print(mycwd)
# Change to data directory
os.chdir("..")
os.chdir(str(os.getcwd()) + "\\Data")
# Read the datasets
df_whole = pd.read_csv(filename_whole, index_col=date_col)
df_trending = pd.read_csv(filename_trending, index_col=date_col)
df_meanreverting = pd.read_csv(filename_meanreverting, index_col=date_col)
# Convert index to datetime
df_whole.index = pd.to_datetime(df_whole.index)
df_trending.index = pd.to_datetime(df_trending.index)
df_meanreverting.index = pd.to_datetime(df_meanreverting.index)
# Head for whole dataset
df_whole.head()
df_whole.shape
# Head for Trending dataset
df_trending.head()
df_trending.shape
# Head for Mean Reverting dataset
df_meanreverting.head()
df_meanreverting.shape
# Merge results from both models to one
df_model = df_trending.append(df_meanreverting)
df_model.sort_index(inplace=True)
df_model.head()
df_model.shape
```
## <span style="color:Maroon">Functions
```
def initialize(df):
days, Action1, Action2, current_status, Money, Shares = ([] for i in range(6))
Open_price = list(df['Open'])
Close_price = list(df['Adj Close'])
Predicted = list(df['Predicted'])
Action1.append(Predicted[0])
Action2.append(0)
current_status.append(Predicted[0])
if(Predicted[0] != 0):
days.append(1)
if(Predicted[0] == 1):
Money.append(0)
else:
Money.append(200)
Shares.append(Predicted[0] * (100/Open_price[0]))
else:
days.append(0)
Money.append(100)
Shares.append(0)
return days, Action1, Action2, current_status, Predicted, Money, Shares, Open_price, Close_price
def Action_SA_SA(days, Action1, Action2, current_status, i):
if(current_status[i-1] != 0):
days.append(1)
else:
days.append(0)
current_status.append(current_status[i-1])
Action1.append(0)
Action2.append(0)
return days, Action1, Action2, current_status
def Action_ZE_NZE(days, Action1, Action2, current_status, i):
if(days[i-1] < 5):
days.append(days[i-1] + 1)
Action1.append(0)
Action2.append(0)
current_status.append(current_status[i-1])
else:
days.append(0)
Action1.append(current_status[i-1] * (-1))
Action2.append(0)
current_status.append(0)
return days, Action1, Action2, current_status
def Action_NZE_ZE(days, Action1, Action2, current_status, Predicted, i):
current_status.append(Predicted[i])
Action1.append(Predicted[i])
Action2.append(0)
days.append(days[i-1] + 1)
return days, Action1, Action2, current_status
def Action_NZE_NZE(days, Action1, Action2, current_status, Predicted, i):
current_status.append(Predicted[i])
Action1.append(Predicted[i])
Action2.append(Predicted[i])
days.append(1)
return days, Action1, Action2, current_status
def get_df(df, Action1, Action2, days, current_status, Money, Shares):
df['Action1'] = Action1
df['Action2'] = Action2
df['days'] = days
df['current_status'] = current_status
df['Money'] = Money
df['Shares'] = Shares
return df
def Get_TradeSignal(Predicted, days, Action1, Action2, current_status):
# Loop over 1 to N
for i in range(1, len(Predicted)):
# When model predicts no action..
if(Predicted[i] == 0):
if(current_status[i-1] != 0):
days, Action1, Action2, current_status = Action_ZE_NZE(days, Action1, Action2, current_status, i)
else:
days, Action1, Action2, current_status = Action_SA_SA(days, Action1, Action2, current_status, i)
# When Model predicts sell
elif(Predicted[i] == -1):
if(current_status[i-1] == -1):
days, Action1, Action2, current_status = Action_SA_SA(days, Action1, Action2, current_status, i)
elif(current_status[i-1] == 0):
days, Action1, Action2, current_status = Action_NZE_ZE(days, Action1, Action2, current_status, Predicted,
i)
else:
days, Action1, Action2, current_status = Action_NZE_NZE(days, Action1, Action2, current_status, Predicted,
i)
# When model predicts Buy
elif(Predicted[i] == 1):
if(current_status[i-1] == 1):
days, Action1, Action2, current_status = Action_SA_SA(days, Action1, Action2, current_status, i)
elif(current_status[i-1] == 0):
days, Action1, Action2, current_status = Action_NZE_ZE(days, Action1, Action2, current_status, Predicted,
i)
else:
days, Action1, Action2, current_status = Action_NZE_NZE(days, Action1, Action2, current_status, Predicted,
i)
return days, Action1, Action2, current_status
def Get_FinancialSignal(Open_price, Action1, Action2, Money, Shares, Close_price):
for i in range(1, len(Open_price)):
if(Action1[i] == 0):
Money.append(Money[i-1])
Shares.append(Shares[i-1])
else:
if(Action2[i] == 0):
# Enter new position
if(Shares[i-1] == 0):
Shares.append(Action1[i] * (Money[i-1]/Open_price[i]))
Money.append(Money[i-1] - Action1[i] * Money[i-1])
# Exit the current position
else:
Shares.append(0)
Money.append(Money[i-1] - Action1[i] * np.abs(Shares[i-1]) * Open_price[i])
else:
Money.append(Money[i-1] -1 *Action1[i] *np.abs(Shares[i-1]) * Open_price[i])
Shares.append(Action2[i] * (Money[i]/Open_price[i]))
Money[i] = Money[i] - 1 * Action2[i] * np.abs(Shares[i]) * Open_price[i]
return Money, Shares
def Get_TradeData(df):
# Initialize the variables
days,Action1,Action2,current_status,Predicted,Money,Shares,Open_price,Close_price = initialize(df)
# Get Buy/Sell trade signal
days, Action1, Action2, current_status = Get_TradeSignal(Predicted, days, Action1, Action2, current_status)
Money, Shares = Get_FinancialSignal(Open_price, Action1, Action2, Money, Shares, Close_price)
df = get_df(df, Action1, Action2, days, current_status, Money, Shares)
df['CurrentVal'] = df['Money'] + df['current_status'] * np.abs(df['Shares']) * df['Adj Close']
return df
def Print_Fromated_PL(active_days, number_of_trades, drawdown, annual_returns, std_dev, sharpe_ratio, year):
"""
Prints the metrics
"""
print("++++++++++++++++++++++++++++++++++++++++++++++++++++")
print(" Year: {0}".format(year))
print(" Number of Trades Executed: {0}".format(number_of_trades))
print("Number of days with Active Position: {}".format(active_days))
print(" Annual Return: {:.6f} %".format(annual_returns*100))
print(" Sharpe Ratio: {:.2f}".format(sharpe_ratio))
print(" Maximum Drawdown (Daily basis): {:.2f} %".format(drawdown*100))
print("----------------------------------------------------")
return
def Get_results_PL_metrics(df, Rf, year):
df['tmp'] = np.where(df['current_status'] == 0, 0, 1)
active_days = df['tmp'].sum()
number_of_trades = np.abs(df['Action1']).sum()+np.abs(df['Action2']).sum()
df['tmp_max'] = df['CurrentVal'].rolling(window=20).max()
df['tmp_min'] = df['CurrentVal'].rolling(window=20).min()
df['tmp'] = np.where(df['tmp_max'] > 0, (df['tmp_max'] - df['tmp_min'])/df['tmp_max'], 0)
drawdown = df['tmp'].max()
annual_returns = (df['CurrentVal'].iloc[-1]/100 - 1)
std_dev = df['CurrentVal'].pct_change(1).std()
sharpe_ratio = (annual_returns - Rf)/std_dev
Print_Fromated_PL(active_days, number_of_trades, drawdown, annual_returns, std_dev, sharpe_ratio, year)
return
```
```
# Change to Images directory
os.chdir("..")
os.chdir(str(os.getcwd()) + "\\Images")
```
## <span style="color:Maroon">Whole Dataset
```
df_whole_train = df_whole[df_whole["Sample"] == "Train"]
df_whole_test = df_whole[df_whole["Sample"] == "Test"]
df_whole_test_2019 = df_whole_test[df_whole_test.index.year == 2019]
df_whole_test_2020 = df_whole_test[df_whole_test.index.year == 2020]
output_train_whole = Get_TradeData(df_whole_train)
output_test_whole = Get_TradeData(df_whole_test)
output_test_whole_2019 = Get_TradeData(df_whole_test_2019)
output_test_whole_2020 = Get_TradeData(df_whole_test_2020)
output_train_whole["BuyandHold"] = (100 * output_train_whole["Adj Close"])/(output_train_whole.iloc[0]["Adj Close"])
output_test_whole["BuyandHold"] = (100*output_test_whole["Adj Close"])/(output_test_whole.iloc[0]["Adj Close"])
output_test_whole_2019["BuyandHold"] = (100 * output_test_whole_2019["Adj Close"])/(output_test_whole_2019.iloc[0]
["Adj Close"])
output_test_whole_2020["BuyandHold"] = (100 * output_test_whole_2020["Adj Close"])/(output_test_whole_2020.iloc[0]
["Adj Close"])
Get_results_PL_metrics(output_test_whole_2019, Rf, 2019)
Get_results_PL_metrics(output_test_whole_2020, Rf, 2020)
# Scatter plot to save fig
plt.figure(figsize=(10,5))
plt.plot(output_train_whole["CurrentVal"], 'b-', label="Value (Model)")
plt.plot(output_train_whole["BuyandHold"], 'r--', alpha=0.5, label="Buy and Hold")
plt.xlabel("Date", fontsize=12)
plt.ylabel("Value", fontsize=12)
plt.legend()
plt.title("Train Sample "+ str(index) + " Xgboost Whole Dataset", fontsize=16)
plt.savefig("Train Sample Whole Dataset Xgboost Model" + str(index) +'.png')
plt.show()
plt.close()
# Scatter plot to save fig
plt.figure(figsize=(10,5))
plt.plot(output_test_whole["CurrentVal"], 'b-', label="Value (Model)")
plt.plot(output_test_whole["BuyandHold"], 'r--', alpha=0.5, label="Buy and Hold")
plt.xlabel("Date", fontsize=12)
plt.ylabel("Value", fontsize=12)
plt.legend()
plt.title("Test Sample "+ str(index) + " Xgboost Whole Dataset", fontsize=16)
plt.savefig("Test Sample Whole Dataset XgBoost Model" + str(index) +'.png')
plt.show()
plt.close()
```
__Comments:__ <span style="color:Blue"> Based on the performance of model on Train Sample, the model has definitely learnt the patter, instead of over-fitting. But the performance of model in Test Sample is very poor
## <span style="color:Maroon">Segment Model
```
df_model_train = df_model[df_model["Sample"] == "Train"]
df_model_test = df_model[df_model["Sample"] == "Test"]
df_model_test_2019 = df_model_test[df_model_test.index.year == 2019]
df_model_test_2020 = df_model_test[df_model_test.index.year == 2020]
output_train_model = Get_TradeData(df_model_train)
output_test_model = Get_TradeData(df_model_test)
output_test_model_2019 = Get_TradeData(df_model_test_2019)
output_test_model_2020 = Get_TradeData(df_model_test_2020)
output_train_model["BuyandHold"] = (100 * output_train_model["Adj Close"])/(output_train_model.iloc[0]["Adj Close"])
output_test_model["BuyandHold"] = (100 * output_test_model["Adj Close"])/(output_test_model.iloc[0]["Adj Close"])
output_test_model_2019["BuyandHold"] = (100 * output_test_model_2019["Adj Close"])/(output_test_model_2019.iloc[0]
["Adj Close"])
output_test_model_2020["BuyandHold"] = (100 * output_test_model_2020["Adj Close"])/(output_test_model_2020.iloc[0]
["Adj Close"])
Get_results_PL_metrics(output_test_model_2019, Rf, 2019)
Get_results_PL_metrics(output_test_model_2020, Rf, 2020)
# Scatter plot to save fig
plt.figure(figsize=(10,5))
plt.plot(output_train_model["CurrentVal"], 'b-', label="Value (Model)")
plt.plot(output_train_model["BuyandHold"], 'r--', alpha=0.5, label="Buy and Hold")
plt.xlabel("Date", fontsize=12)
plt.ylabel("Value", fontsize=12)
plt.legend()
plt.title("Train Sample Hurst Segment XgBoost Models "+ str(index), fontsize=16)
plt.savefig("Train Sample Hurst Segment XgBoost Models" + str(index) +'.png')
plt.show()
plt.close()
# Scatter plot to save fig
plt.figure(figsize=(10,5))
plt.plot(output_test_model["CurrentVal"], 'b-', label="Value (Model)")
plt.plot(output_test_model["BuyandHold"], 'r--', alpha=0.5, label="Buy and Hold")
plt.xlabel("Date", fontsize=12)
plt.ylabel("Value", fontsize=12)
plt.legend()
plt.title("Test Sample Hurst Segment XgBoost Models" + str(index), fontsize=16)
plt.savefig("Test Sample Hurst Segment XgBoost Models" + str(index) +'.png')
plt.show()
plt.close()
```
__Comments:__ <span style="color:Blue"> Based on the performance of model on Train Sample, the model has definitely learnt the patter, instead of over-fitting. The model does perform well in Test sample (Not compared to Buy and Hold strategy) compared to single model. Hurst Exponent based segmentation has definately added value to the model
|
github_jupyter
|
```
import numpy as np
import math
import matplotlib.pyplot as plt
input_data = np.array([math.cos(x) for x in np.arange(200)])
plt.plot(input_data[:50])
plt.show
X = []
Y = []
size = 50
number_of_records = len(input_data) - size
for i in range(number_of_records - 50):
X.append(input_data[i:i+size])
Y.append(input_data[i+size])
X = np.array(X)
X = np.expand_dims(X, axis=2)
Y = np.array(Y)
Y = np.expand_dims(Y, axis=1)
X.shape, Y.shape
X_valid = []
Y_valid = []
for i in range(number_of_records - 50, number_of_records):
X_valid.append(input_data[i:i+size])
Y_valid.append(input_data[i+size])
X_valid = np.array(X_valid)
X_valid = np.expand_dims(X_valid, axis=2)
Y_valid = np.array(Y_valid)
Y_valid = np.expand_dims(Y_valid, axis=1)
learning_rate = 0.0001
number_of_epochs = 5
sequence_length = 50
hidden_layer_size = 100
output_layer_size = 1
back_prop_truncate = 5
min_clip_value = -10
max_clip_value = 10
W1 = np.random.uniform(0, 1, (hidden_layer_size, sequence_length))
W2 = np.random.uniform(0, 1, (hidden_layer_size, hidden_layer_size))
W3 = np.random.uniform(0, 1, (output_layer_size, hidden_layer_size))
def sigmoid(x):
return 1 / (1 + np.exp(-x))
for epoch in range(number_of_epochs):
# check loss on train
loss = 0.0
# do a forward pass to get prediction
for i in range(Y.shape[0]):
x, y = X[i], Y[i]
prev_act = np.zeros((hidden_layer_size, 1))
for t in range(sequence_length):
new_input = np.zeros(x.shape)
new_input[t] = x[t]
mul_w1 = np.dot(W1, new_input)
mul_w2 = np.dot(W2, prev_act)
add = mul_w2 + mul_w1
act = sigmoid(add)
mul_w3 = np.dot(W3, act)
prev_act = act
# calculate error
loss_per_record = (y - mul_w3)**2 / 2
loss += loss_per_record
loss = loss / float(y.shape[0])
# check loss on validation
val_loss = 0.0
for i in range(Y_valid.shape[0]):
x, y = X_valid[i], Y_valid[i]
prev_act = np.zeros((hidden_layer_size, 1))
for t in range(sequence_length):
new_input = np.zeros(x.shape)
new_input[t] = x[t]
mul_w1 = np.dot(W1, new_input)
mul_w2 = np.dot(W2, prev_act)
add = mul_w2 + mul_w1
act = sigmoid(add)
mul_w3 = np.dot(W3, act)
prev_act = act
loss_per_record = (y - mul_w3)**2 / 2
val_loss += loss_per_record
val_loss = val_loss / float(y.shape[0])
print('Epoch: ', epoch + 1, ', Loss: ', loss, ', Val Loss: ', val_loss)
# train model
for i in range(Y.shape[0]):
x, y = X[i], Y[i]
layers = []
prev_act = np.zeros((hidden_layer_size, 1))
dW1 = np.zeros(W1.shape)
dW3 = np.zeros(W3.shape)
dW2 = np.zeros(W2.shape)
dW1_t = np.zeros(W1.shape)
dW3_t = np.zeros(W3.shape)
dW2_t = np.zeros(W2.shape)
dW1_i = np.zeros(W1.shape)
dW2_i = np.zeros(W2.shape)
# forward pass
for t in range(sequence_length):
new_input = np.zeros(x.shape)
new_input[t] = x[t]
mul_w1 = np.dot(W1, new_input)
mul_w2 = np.dot(W2, prev_act)
add = mul_w2 + mul_w1
act = sigmoid(add)
mul_w3 = np.dot(W3, act)
layers.append({'act':act, 'prev_act':prev_act})
prev_act = act
# derivative of pred
dmul_w3 = (mul_w3 - y)
# backward pass
for t in range(sequence_length):
dW3_t = np.dot(dmul_w3, np.transpose(layers[t]['act']))
dsv = np.dot(np.transpose(W3), dmul_w3)
ds = dsv
dadd = add * (1 - add) * ds
dmul_w2 = dadd * np.ones_like(mul_w2)
dprev_act = np.dot(np.transpose(W2), dmul_w2)
for i in range(t-1, max(-1, t-back_prop_truncate-1), -1):
ds = dsv + dprev_act
dadd = add * (1 - add) * ds
dmul_w2 = dadd * np.ones_like(mul_w2)
dmul_w1 = dadd * np.ones_like(mul_w1)
dW2_i = np.dot(W2, layers[t]['prev_act'])
dprev_act = np.dot(np.transpose(W2), dmul_w2)
new_input = np.zeros(x.shape)
new_input[t] = x[t]
dW1_i = np.dot(W1, new_input)
dx = np.dot(np.transpose(W1), dmul_w1)
dW1_t += dW1_i
dW2_t += dW2_i
dW3 += dW3_t
dW1 += dW1_t
dW2 += dW2_t
if dW1.max() > max_clip_value:
dW1[dW1 > max_clip_value] = max_clip_value
if dW3.max() > max_clip_value:
dW3[dW3 > max_clip_value] = max_clip_value
if dW2.max() > max_clip_value:
dW2[dW2 > max_clip_value] = max_clip_value
if dW1.min() < min_clip_value:
dW1[dW1 < min_clip_value] = min_clip_value
if dW3.min() < min_clip_value:
dW3[dW3 < min_clip_value] = min_clip_value
if dW2.min() < min_clip_value:
dW2[dW2 < min_clip_value] = min_clip_value
# update
W1 -= learning_rate * dW1
W3 -= learning_rate * dW3
W2 -= learning_rate * dW2
preds = []
for i in range(Y_valid.shape[0]):
x, y = X_valid[i], Y_valid[i]
prev_act = np.zeros((hidden_layer_size, 1))
# For each time step...
for t in range(sequence_length):
mul_w1 = np.dot(W1, x)
mul_w2 = np.dot(W2, prev_act)
add = mul_w2 + mul_w1
act = sigmoid(add)
mul_w3 = np.dot(W3, act)
prev_act = act
preds.append(mul_w3)
preds = np.array(preds)
plt.plot(preds[:, 0, 0], 'g')
plt.plot(Y_valid[:, 0], 'r')
plt.show()
from sklearn.metrics import mean_squared_error
math.sqrt(mean_squared_error(Y_valid[:, 0], preds[:, 0, 0]))
```
|
github_jupyter
|
# Monte Carlo Integration with Python
## Dr. Tirthajyoti Sarkar ([LinkedIn](https://www.linkedin.com/in/tirthajyoti-sarkar-2127aa7/), [Github](https://github.com/tirthajyoti)), Fremont, CA, July 2020
---
### Disclaimer
The inspiration for this demo/notebook stemmed from [Georgia Tech's Online Masters in Analytics (OMSA) program](https://www.gatech.edu/academics/degrees/masters/analytics-online-degree-oms-analytics) study material. I am proud to pursue this excellent Online MS program. You can also check the details [here](http://catalog.gatech.edu/programs/analytics-ms/#onlinetext).
## What is Monte Carlo integration?
### A casino trick for mathematics

Monte Carlo, is in fact, the name of the world-famous casino located in the eponymous district of the city-state (also called a Principality) of Monaco, on the world-famous French Riviera.
It turns out that the casino inspired the minds of famous scientists to devise an intriguing mathematical technique for solving complex problems in statistics, numerical computing, system simulation.
### Modern origin (to make 'The Bomb')

One of the first and most famous uses of this technique was during the Manhattan Project when the chain-reaction dynamics in highly enriched uranium presented an unimaginably complex theoretical calculation to the scientists. Even the genius minds like John Von Neumann, Stanislaw Ulam, Nicholas Metropolis could not tackle it in the traditional way. They, therefore, turned to the wonderful world of random numbers and let these probabilistic quantities tame the originally intractable calculations.
Amazingly, these random variables could solve the computing problem, which stymied the sure-footed deterministic approach. The elements of uncertainty actually won.
Just like uncertainty and randomness rule in the world of Monte Carlo games. That was the inspiration for this particular moniker.
### Today
Today, it is a technique used in a wide swath of fields,
- risk analysis, financial engineering,
- supply chain logistics,
- statistical learning and modeling,
- computer graphics, image processing, game design,
- large system simulations,
- computational physics, astronomy, etc.
For all its successes and fame, the basic idea is deceptively simple and easy to demonstrate. We demonstrate it in this article with a simple set of Python code.
## The code and the demo
```
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import quad
```
### A simple function which is difficult to integrate analytically
While the general Monte Carlo simulation technique is much broader in scope, we focus particularly on the Monte Carlo integration technique here.
It is nothing but a numerical method for computing complex definite integrals, which lack closed-form analytical solutions.
Say, we want to calculate,
$$\int_{0}^{4}\sqrt[4]{15x^3+21x^2+41x+3}.e^{-0.5x} dx$$
```
def f1(x):
return (15*x**3+21*x**2+41*x+3)**(1/4) * (np.exp(-0.5*x))
```
### Plot
```
x = np.arange(0,4.1,0.1)
y = f1(x)
plt.figure(figsize=(8,4))
plt.title("Plot of the function: $\sqrt[4]{15x^3+21x^2+41x+3}.e^{-0.5x}$",
fontsize=18)
plt.plot(x,y,'-',c='k',lw=2)
plt.grid(True)
plt.xticks(fontsize=14)
plt.yticks(fontsize=14)
plt.show()
```
### Riemann sums?
There are many such techniques under the general category of [Riemann sum](https://medium.com/r/?url=https%3A%2F%2Fen.wikipedia.org%2Fwiki%2FRiemann_sum). The idea is just to divide the area under the curve into small rectangular or trapezoidal pieces, approximate them by the simple geometrical calculations, and sum those components up.
For a simple illustration, I show such a scheme with only 5 equispaced intervals.
For the programmer friends, in fact, there is a [ready-made function in the Scipy package](https://docs.scipy.org/doc/scipy/reference/generated/scipy.integrate.quad.html#scipy.integrate.quad) which can do this computation fast and accurately.
```
rect = np.linspace(0,4,5)
plt.figure(figsize=(8,4))
plt.title("Area under the curve: With Riemann sum",
fontsize=18)
plt.plot(x,y,'-',c='k',lw=2)
plt.fill_between(x,y1=y,y2=0,color='orange',alpha=0.6)
for i in range(5):
plt.vlines(x=rect[i],ymin=0,ymax=2,color='blue')
plt.grid(True)
plt.xticks(fontsize=14)
plt.yticks(fontsize=14)
plt.show()
```
### What if I go random?
What if I told you that I do not need to pick the intervals so uniformly, and, in fact, I can go completely probabilistic, and pick 100% random intervals to compute the same integral?
Crazy talk? My choice of samples could look like this…
```
rand_lines = 4*np.random.uniform(size=5)
plt.figure(figsize=(8,4))
plt.title("With 5 random sampling intervals",
fontsize=18)
plt.plot(x,y,'-',c='k',lw=2)
plt.fill_between(x,y1=y,y2=0,color='orange',alpha=0.6)
for i in range(5):
plt.vlines(x=rand_lines[i],ymin=0,ymax=2,color='blue')
plt.grid(True)
plt.xticks(fontsize=14)
plt.yticks(fontsize=14)
plt.show()
```
Or, this?
```
rand_lines = 4*np.random.uniform(size=5)
plt.figure(figsize=(8,4))
plt.title("With 5 random sampling intervals",
fontsize=18)
plt.plot(x,y,'-',c='k',lw=2)
plt.fill_between(x,y1=y,y2=0,color='orange',alpha=0.6)
for i in range(5):
plt.vlines(x=rand_lines[i],ymin=0,ymax=2,color='blue')
plt.grid(True)
plt.xticks(fontsize=14)
plt.yticks(fontsize=14)
plt.show()
```
### It just works!
We don't have the time or scope to prove the theory behind it, but it can be shown that with a reasonably high number of random sampling, we can, in fact, compute the integral with sufficiently high accuracy!
We just choose random numbers (between the limits), evaluate the function at those points, add them up, and scale it by a known factor. We are done.
OK. What are we waiting for? Let's demonstrate this claim with some simple Python code.
### A simple version
```
def monte_carlo(func,
a=0,
b=1,
n=1000):
"""
Monte Carlo integration
"""
u = np.random.uniform(size=n)
#plt.hist(u)
u_func = func(a+(b-a)*u)
s = ((b-a)/n)*u_func.sum()
return s
```
### Another version with 10-spaced sampling
```
def monte_carlo_uniform(func,
a=0,
b=1,
n=1000):
"""
Monte Carlo integration with more uniform spread (forced)
"""
subsets = np.arange(0,n+1,n/10)
steps = n/10
u = np.zeros(n)
for i in range(10):
start = int(subsets[i])
end = int(subsets[i+1])
u[start:end] = np.random.uniform(low=i/10,high=(i+1)/10,size=end-start)
np.random.shuffle(u)
#plt.hist(u)
#u = np.random.uniform(size=n)
u_func = func(a+(b-a)*u)
s = ((b-a)/n)*u_func.sum()
return s
inte = monte_carlo_uniform(f1,a=0,b=4,n=100)
print(inte)
```
### How good is the calculation anyway?
This integral cannot be calculated analytically. So, we need to benchmark the accuracy of the Monte Carlo method against another numerical integration technique anyway. We chose the Scipy `integrate.quad()` function for that.
Now, you may also be thinking - **what happens to the accuracy as the sampling density changes**. This choice clearly impacts the computation speed - we need to add less number of quantities if we choose a reduced sampling density.
Therefore, we simulated the same integral for a range of sampling density and plotted the result on top of the gold standard - the Scipy function represented as the horizontal line in the plot below,
```
inte_lst = []
for i in range(100,2100,50):
inte = monte_carlo_uniform(f1,a=0,b=4,n=i)
inte_lst.append(inte)
result,_ = quad(f1,a=0,b=4)
plt.figure(figsize=(8,4))
plt.plot([i for i in range(100,2100,50)],inte_lst,color='blue')
plt.hlines(y=result,xmin=0,xmax=2100,linestyle='--',lw=3)
plt.xticks(fontsize=14)
plt.yticks(fontsize=14)
plt.xlabel("Sample density for Monte Carlo",fontsize=15)
plt.ylabel("Integration result",fontsize=15)
plt.grid(True)
plt.legend(['Monte Carlo integration','Scipy function'],fontsize=15)
plt.show()
```
### Not bad at all...
Therefore, we observe some small perturbations in the low sample density phase, but they smooth out nicely as the sample density increases. In any case, the absolute error is extremely small compared to the value returned by the Scipy function - on the order of 0.02%.
The Monte Carlo trick works fantastically!
### Speed of the Monte Carlo method
In this particular example, the Monte Carlo calculations are running twice as fast as the Scipy integration method!
While this kind of speed advantage depends on many factors, we can be assured that the Monte Carlo technique is not a slouch when it comes to the matter of computation efficiency.
```
%%timeit -n100 -r100
inte = monte_carlo_uniform(f1,a=0,b=4,n=500)
```
### Speed of the Scipy function
```
%%timeit -n100 -r100
quad(f1,a=0,b=4)
```
### Repeat
For a probabilistic technique like Monte Carlo integration, it goes without saying that mathematicians and scientists almost never stop at just one run but repeat the calculations for a number of times and take the average.
Here is a distribution plot from a 10,000 run experiment. As you can see, the plot almost resembles a Gaussian Normal distribution and this fact can be utilized to not only get the average value but also construct confidence intervals around that result.
```
inte_lst = []
for i in range(10000):
inte = monte_carlo_uniform(f1,a=0,b=4,n=500)
inte_lst.append(inte)
plt.figure(figsize=(8,4))
plt.title("Distribution of the Monte Carlo runs",
fontsize=18)
plt.hist(inte_lst,bins=50,color='orange',edgecolor='k')
plt.xticks(fontsize=14)
plt.yticks(fontsize=14)
plt.xlabel("Integration result",fontsize=15)
plt.ylabel("Density",fontsize=15)
plt.show()
```
### Particularly suitable for high-dimensional integrals
Although for our simple illustration (and for pedagogical purpose), we stick to a single-variable integral, the same idea can easily be extended to high-dimensional integrals with multiple variables.
And it is in this higher dimension that the Monte Carlo method particularly shines as compared to Riemann sum based approaches. The sample density can be optimized in a much more favorable manner for the Monte Carlo method to make it much faster without compromising the accuracy.
In mathematical terms, the convergence rate of the method is independent of the number of dimensions. In machine learning speak, the Monte Carlo method is the best friend you have to beat the curse of dimensionality when it comes to complex integral calculations.
---
## Summary
We introduced the concept of Monte Carlo integration and illustrated how it differs from the conventional numerical integration methods. We also showed a simple set of Python codes to evaluate a one-dimensional function and assess the accuracy and speed of the techniques.
The broader class of Monte Carlo simulation techniques is more exciting and is used in a ubiquitous manner in fields related to artificial intelligence, data science, and statistical modeling.
For example, the famous Alpha Go program from DeepMind used a Monte Carlo search technique to be computationally efficient in the high-dimensional space of the game Go. Numerous such examples can be found in practice.
|
github_jupyter
|
This illustrates the datasets.make_multilabel_classification dataset generator. Each sample consists of counts of two features (up to 50 in total), which are differently distributed in each of two classes.
Points are labeled as follows, where Y means the class is present:
| 1 | 2 | 3 | Color |
|--- |--- |--- |-------- |
| Y | N | N | Red |
| N | Y | N | Blue |
| N | N | Y | Yellow |
| Y | Y | N | Purple |
| Y | N | Y | Orange |
| Y | Y | N | Green |
| Y | Y | Y | Brown |
A big circle marks the expected sample for each class; its size reflects the probability of selecting that class label.
The left and right examples highlight the n_labels parameter: more of the samples in the right plot have 2 or 3 labels.
Note that this two-dimensional example is very degenerate: generally the number of features would be much greater than the “document length”, while here we have much larger documents than vocabulary. Similarly, with n_classes > n_features, it is much less likely that a feature distinguishes a particular class.
#### New to Plotly?
Plotly's Python library is free and open source! [Get started](https://plot.ly/python/getting-started/) by downloading the client and [reading the primer](https://plot.ly/python/getting-started/).
<br>You can set up Plotly to work in [online](https://plot.ly/python/getting-started/#initialization-for-online-plotting) or [offline](https://plot.ly/python/getting-started/#initialization-for-offline-plotting) mode, or in [jupyter notebooks](https://plot.ly/python/getting-started/#start-plotting-online).
<br>We also have a quick-reference [cheatsheet](https://images.plot.ly/plotly-documentation/images/python_cheat_sheet.pdf) (new!) to help you get started!
### Version
```
import sklearn
sklearn.__version__
```
### Imports
This tutorial imports [make_ml_clf](http://scikit-learn.org/stable/modules/generated/sklearn.datasets.make_multilabel_classification.html#sklearn.datasets.make_multilabel_classification).
```
import plotly.plotly as py
import plotly.graph_objs as go
from __future__ import print_function
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_multilabel_classification as make_ml_clf
```
### Calculations
```
COLORS = np.array(['!',
'#FF3333', # red
'#0198E1', # blue
'#BF5FFF', # purple
'#FCD116', # yellow
'#FF7216', # orange
'#4DBD33', # green
'#87421F' # brown
])
# Use same random seed for multiple calls to make_multilabel_classification to
# ensure same distributions
RANDOM_SEED = np.random.randint(2 ** 10)
def plot_2d(n_labels=1, n_classes=3, length=50):
X, Y, p_c, p_w_c = make_ml_clf(n_samples=150, n_features=2,
n_classes=n_classes, n_labels=n_labels,
length=length, allow_unlabeled=False,
return_distributions=True,
random_state=RANDOM_SEED)
trace1 = go.Scatter(x=X[:, 0], y=X[:, 1],
mode='markers',
showlegend=False,
marker=dict(size=8,
color=COLORS.take((Y * [1, 2, 4]).sum(axis=1)))
)
trace2 = go.Scatter(x=p_w_c[0] * length, y=p_w_c[1] * length,
mode='markers',
showlegend=False,
marker=dict(color=COLORS.take([1, 2, 4]),
size=14,
line=dict(width=1, color='black'))
)
data = [trace1, trace2]
return data, p_c, p_w_c
```
### Plot Results
n_labels=1
```
data, p_c, p_w_c = plot_2d(n_labels=1)
layout=go.Layout(title='n_labels=1, length=50',
xaxis=dict(title='Feature 0 count',
showgrid=False),
yaxis=dict(title='Feature 1 count',
showgrid=False),
)
fig = go.Figure(data=data, layout=layout)
py.iplot(fig)
```
n_labels=3
```
data = plot_2d(n_labels=3)
layout=go.Layout(title='n_labels=3, length=50',
xaxis=dict(title='Feature 0 count',
showgrid=False),
yaxis=dict(title='Feature 1 count',
showgrid=False),
)
fig = go.Figure(data=data[0], layout=layout)
py.iplot(fig)
print('The data was generated from (random_state=%d):' % RANDOM_SEED)
print('Class', 'P(C)', 'P(w0|C)', 'P(w1|C)', sep='\t')
for k, p, p_w in zip(['red', 'blue', 'yellow'], p_c, p_w_c.T):
print('%s\t%0.2f\t%0.2f\t%0.2f' % (k, p, p_w[0], p_w[1]))
from IPython.display import display, HTML
display(HTML('<link href="//fonts.googleapis.com/css?family=Open+Sans:600,400,300,200|Inconsolata|Ubuntu+Mono:400,700" rel="stylesheet" type="text/css" />'))
display(HTML('<link rel="stylesheet" type="text/css" href="http://help.plot.ly/documentation/all_static/css/ipython-notebook-custom.css">'))
! pip install git+https://github.com/plotly/publisher.git --upgrade
import publisher
publisher.publish(
'randomly-generated-multilabel-dataset.ipynb', 'scikit-learn/plot-random-multilabel-dataset/', 'Randomly Generated Multilabel Dataset | plotly',
' ',
title = 'Randomly Generated Multilabel Dataset| plotly',
name = 'Randomly Generated Multilabel Dataset',
has_thumbnail='true', thumbnail='thumbnail/multilabel-dataset.jpg',
language='scikit-learn', page_type='example_index',
display_as='dataset', order=4,
ipynb= '~Diksha_Gabha/2909')
```
|
github_jupyter
|
[Table of Contents](http://nbviewer.ipython.org/github/rlabbe/Kalman-and-Bayesian-Filters-in-Python/blob/master/table_of_contents.ipynb)
# Kalman Filter Math
```
#format the book
%matplotlib inline
from __future__ import division, print_function
from book_format import load_style
load_style()
```
If you've gotten this far I hope that you are thinking that the Kalman filter's fearsome reputation is somewhat undeserved. Sure, I hand waved some equations away, but I hope implementation has been fairly straightforward for you. The underlying concept is quite straightforward - take two measurements, or a measurement and a prediction, and choose the output to be somewhere between the two. If you believe the measurement more your guess will be closer to the measurement, and if you believe the prediction is more accurate your guess will lie closer to it. That's not rocket science (little joke - it is exactly this math that got Apollo to the moon and back!).
To be honest I have been choosing my problems carefully. For an arbitrary problem designing the Kalman filter matrices can be extremely difficult. I haven't been *too tricky*, though. Equations like Newton's equations of motion can be trivially computed for Kalman filter applications, and they make up the bulk of the kind of problems that we want to solve.
I have illustrated the concepts with code and reasoning, not math. But there are topics that do require more mathematics than I have used so far. This chapter presents the math that you will need for the rest of the book.
## Modeling a Dynamic System
A *dynamic system* is a physical system whose state (position, temperature, etc) evolves over time. Calculus is the math of changing values, so we use differential equations to model dynamic systems. Some systems cannot be modeled with differential equations, but we will not encounter those in this book.
Modeling dynamic systems is properly the topic of several college courses. To an extent there is no substitute for a few semesters of ordinary and partial differential equations followed by a graduate course in control system theory. If you are a hobbyist, or trying to solve one very specific filtering problem at work you probably do not have the time and/or inclination to devote a year or more to that education.
Fortunately, I can present enough of the theory to allow us to create the system equations for many different Kalman filters. My goal is to get you to the stage where you can read a publication and understand it well enough to implement the algorithms. The background math is deep, but in practice we end up using a few simple techniques.
This is the longest section of pure math in this book. You will need to master everything in this section to understand the Extended Kalman filter (EKF), the most common nonlinear filter. I do cover more modern filters that do not require as much of this math. You can choose to skim now, and come back to this if you decide to learn the EKF.
We need to start by understanding the underlying equations and assumptions that the Kalman filter uses. We are trying to model real world phenomena, so what do we have to consider?
Each physical system has a process. For example, a car traveling at a certain velocity goes so far in a fixed amount of time, and its velocity varies as a function of its acceleration. We describe that behavior with the well known Newtonian equations that we learned in high school.
$$
\begin{aligned}
v&=at\\
x &= \frac{1}{2}at^2 + v_0t + x_0
\end{aligned}
$$
Once we learned calculus we saw them in this form:
$$ \mathbf v = \frac{d \mathbf x}{d t},
\quad \mathbf a = \frac{d \mathbf v}{d t} = \frac{d^2 \mathbf x}{d t^2}
$$
A typical automobile tracking problem would have you compute the distance traveled given a constant velocity or acceleration, as we did in previous chapters. But, of course we know this is not all that is happening. No car travels on a perfect road. There are bumps, wind drag, and hills that raise and lower the speed. The suspension is a mechanical system with friction and imperfect springs.
Perfectly modeling a system is impossible except for the most trivial problems. We are forced to make a simplification. At any time $t$ we say that the true state (such as the position of our car) is the predicted value from the imperfect model plus some unknown *process noise*:
$$
x(t) = x_{pred}(t) + noise(t)
$$
This is not meant to imply that $noise(t)$ is a function that we can derive analytically. It is merely a statement of fact - we can always describe the true value as the predicted value plus the process noise. "Noise" does not imply random events. If we are tracking a thrown ball in the atmosphere, and our model assumes the ball is in a vacuum, then the effect of air drag is process noise in this context.
In the next section we will learn techniques to convert a set of higher order differential equations into a set of first-order differential equations. After the conversion the model of the system without noise is:
$$ \dot{\mathbf x} = \mathbf{Ax}$$
$\mathbf A$ is known as the *systems dynamics matrix* as it describes the dynamics of the system. Now we need to model the noise. We will call that $\mathbf w$, and add it to the equation.
$$ \dot{\mathbf x} = \mathbf{Ax} + \mathbf w$$
$\mathbf w$ may strike you as a poor choice for the name, but you will soon see that the Kalman filter assumes *white* noise.
Finally, we need to consider any inputs into the system. We assume an input $\mathbf u$, and that there exists a linear model that defines how that input changes the system. For example, pressing the accelerator in your car makes it accelerate, and gravity causes balls to fall. Both are contol inputs. We will need a matrix $\mathbf B$ to convert $u$ into the effect on the system. We add that into our equation:
$$ \dot{\mathbf x} = \mathbf{Ax} + \mathbf{Bu} + \mathbf{w}$$
And that's it. That is one of the equations that Dr. Kalman set out to solve, and he found an optimal estimator if we assume certain properties of $\mathbf w$.
## State-Space Representation of Dynamic Systems
We've derived the equation
$$ \dot{\mathbf x} = \mathbf{Ax}+ \mathbf{Bu} + \mathbf{w}$$
However, we are not interested in the derivative of $\mathbf x$, but in $\mathbf x$ itself. Ignoring the noise for a moment, we want an equation that recusively finds the value of $\mathbf x$ at time $t_k$ in terms of $\mathbf x$ at time $t_{k-1}$:
$$\mathbf x(t_k) = \mathbf F(\Delta t)\mathbf x(t_{k-1}) + \mathbf B(t_k) + \mathbf u (t_k)$$
Convention allows us to write $\mathbf x(t_k)$ as $\mathbf x_k$, which means the
the value of $\mathbf x$ at the k$^{th}$ value of $t$.
$$\mathbf x_k = \mathbf{Fx}_{k-1} + \mathbf B_k\mathbf u_k$$
$\mathbf F$ is the familiar *state transition matrix*, named due to its ability to transition the state's value between discrete time steps. It is very similar to the system dynamics matrix $\mathbf A$. The difference is that $\mathbf A$ models a set of linear differential equations, and is continuous. $\mathbf F$ is discrete, and represents a set of linear equations (not differential equations) which transitions $\mathbf x_{k-1}$ to $\mathbf x_k$ over a discrete time step $\Delta t$.
Finding this matrix is often quite difficult. The equation $\dot x = v$ is the simplest possible differential equation and we trivially integrate it as:
$$ \int\limits_{x_{k-1}}^{x_k} \mathrm{d}x = \int\limits_{0}^{\Delta t} v\, \mathrm{d}t $$
$$x_k-x_0 = v \Delta t$$
$$x_k = v \Delta t + x_0$$
This equation is *recursive*: we compute the value of $x$ at time $t$ based on its value at time $t-1$. This recursive form enables us to represent the system (process model) in the form required by the Kalman filter:
$$\begin{aligned}
\mathbf x_k &= \mathbf{Fx}_{k-1} \\
&= \begin{bmatrix} 1 & \Delta t \\ 0 & 1\end{bmatrix}
\begin{bmatrix}x_{k-1} \\ \dot x_{k-1}\end{bmatrix}
\end{aligned}$$
We can do that only because $\dot x = v$ is simplest differential equation possible. Almost all other in physical systems result in more complicated differential equation which do not yield to this approach.
*State-space* methods became popular around the time of the Apollo missions, largely due to the work of Dr. Kalman. The idea is simple. Model a system with a set of $n^{th}$-order differential equations. Convert them into an equivalent set of first-order differential equations. Put them into the vector-matrix form used in the previous section: $\dot{\mathbf x} = \mathbf{Ax} + \mathbf{Bu}$. Once in this form we use of of several techniques to convert these linear differential equations into the recursive equation:
$$ \mathbf x_k = \mathbf{Fx}_{k-1} + \mathbf B_k\mathbf u_k$$
Some books call the state transition matrix the *fundamental matrix*. Many use $\mathbf \Phi$ instead of $\mathbf F$. Sources based heavily on control theory tend to use these forms.
These are called *state-space* methods because we are expressing the solution of the differential equations in terms of the system state.
### Forming First Order Equations from Higher Order Equations
Many models of physical systems require second or higher order differential equations with control input $u$:
$$a_n \frac{d^ny}{dt^n} + a_{n-1} \frac{d^{n-1}y}{dt^{n-1}} + \dots + a_2 \frac{d^2y}{dt^2} + a_1 \frac{dy}{dt} + a_0 = u$$
State-space methods require first-order equations. Any higher order system of equations can be reduced to first-order by defining extra variables for the derivatives and then solving.
Let's do an example. Given the system $\ddot{x} - 6\dot x + 9x = u$ find the equivalent first order equations. I've used the dot notation for the time derivatives for clarity.
The first step is to isolate the highest order term onto one side of the equation.
$$\ddot{x} = 6\dot x - 9x + u$$
We define two new variables:
$$\begin{aligned} x_1(u) &= x \\
x_2(u) &= \dot x
\end{aligned}$$
Now we will substitute these into the original equation and solve. The solution yields a set of first-order equations in terms of these new variables. It is conventional to drop the $(u)$ for notational convenience.
We know that $\dot x_1 = x_2$ and that $\dot x_2 = \ddot{x}$. Therefore
$$\begin{aligned}
\dot x_2 &= \ddot{x} \\
&= 6\dot x - 9x + t\\
&= 6x_2-9x_1 + t
\end{aligned}$$
Therefore our first-order system of equations is
$$\begin{aligned}\dot x_1 &= x_2 \\
\dot x_2 &= 6x_2-9x_1 + t\end{aligned}$$
If you practice this a bit you will become adept at it. Isolate the highest term, define a new variable and its derivatives, and then substitute.
### First Order Differential Equations In State-Space Form
Substituting the newly defined variables from the previous section:
$$\frac{dx_1}{dt} = x_2,\,
\frac{dx_2}{dt} = x_3, \, ..., \,
\frac{dx_{n-1}}{dt} = x_n$$
into the first order equations yields:
$$\frac{dx_n}{dt} = \frac{1}{a_n}\sum\limits_{i=0}^{n-1}a_ix_{i+1} + \frac{1}{a_n}u
$$
Using vector-matrix notation we have:
$$\begin{bmatrix}\frac{dx_1}{dt} \\ \frac{dx_2}{dt} \\ \vdots \\ \frac{dx_n}{dt}\end{bmatrix} =
\begin{bmatrix}\dot x_1 \\ \dot x_2 \\ \vdots \\ \dot x_n\end{bmatrix}=
\begin{bmatrix}0 & 1 & 0 &\cdots & 0 \\
0 & 0 & 1 & \cdots & 0 \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
-\frac{a_0}{a_n} & -\frac{a_1}{a_n} & -\frac{a_2}{a_n} & \cdots & -\frac{a_{n-1}}{a_n}\end{bmatrix}
\begin{bmatrix}x_1 \\ x_2 \\ \vdots \\ x_n\end{bmatrix} +
\begin{bmatrix}0 \\ 0 \\ \vdots \\ \frac{1}{a_n}\end{bmatrix}u$$
which we then write as $\dot{\mathbf x} = \mathbf{Ax} + \mathbf{B}u$.
### Finding the Fundamental Matrix for Time Invariant Systems
We express the system equations in state-space form with
$$ \dot{\mathbf x} = \mathbf{Ax}$$
where $\mathbf A$ is the system dynamics matrix, and want to find the *fundamental matrix* $\mathbf F$ that propagates the state $\mathbf x$ over the interval $\Delta t$ with the equation
$$\begin{aligned}
\mathbf x(t_k) = \mathbf F(\Delta t)\mathbf x(t_{k-1})\end{aligned}$$
In other words, $\mathbf A$ is a set of continuous differential equations, and we need $\mathbf F$ to be a set of discrete linear equations that computes the change in $\mathbf A$ over a discrete time step.
It is conventional to drop the $t_k$ and $(\Delta t)$ and use the notation
$$\mathbf x_k = \mathbf {Fx}_{k-1}$$
Broadly speaking there are three common ways to find this matrix for Kalman filters. The technique most often used is the matrix exponential. Linear Time Invariant Theory, also known as LTI System Theory, is a second technique. Finally, there are numerical techniques. You may know of others, but these three are what you will most likely encounter in the Kalman filter literature and praxis.
### The Matrix Exponential
The solution to the equation $\frac{dx}{dt} = kx$ can be found by:
$$\begin{gathered}\frac{dx}{dt} = kx \\
\frac{dx}{x} = k\, dt \\
\int \frac{1}{x}\, dx = \int k\, dt \\
\log x = kt + c \\
x = e^{kt+c} \\
x = e^ce^{kt} \\
x = c_0e^{kt}\end{gathered}$$
Using similar math, the solution to the first-order equation
$$\dot{\mathbf x} = \mathbf{Ax} ,\, \, \, \mathbf x(0) = \mathbf x_0$$
where $\mathbf A$ is a constant matrix, is
$$\mathbf x = e^{\mathbf At}\mathbf x_0$$
Substituting $F = e^{\mathbf At}$, we can write
$$\mathbf x_k = \mathbf F\mathbf x_{k-1}$$
which is the form we are looking for! We have reduced the problem of finding the fundamental matrix to one of finding the value for $e^{\mathbf At}$.
$e^{\mathbf At}$ is known as the [matrix exponential](https://en.wikipedia.org/wiki/Matrix_exponential). It can be computed with this power series:
$$e^{\mathbf At} = \mathbf{I} + \mathbf{A}t + \frac{(\mathbf{A}t)^2}{2!} + \frac{(\mathbf{A}t)^3}{3!} + ... $$
That series is found by doing a Taylor series expansion of $e^{\mathbf At}$, which I will not cover here.
Let's use this to find the solution to Newton's equations. Using $v$ as an substitution for $\dot x$, and assuming constant velocity we get the linear matrix-vector form
$$\begin{bmatrix}\dot x \\ \dot v\end{bmatrix} =\begin{bmatrix}0&1\\0&0\end{bmatrix} \begin{bmatrix}x \\ v\end{bmatrix}$$
This is a first order differential equation, so we can set $\mathbf{A}=\begin{bmatrix}0&1\\0&0\end{bmatrix}$ and solve the following equation. I have substituted the interval $\Delta t$ for $t$ to emphasize that the fundamental matrix is discrete:
$$\mathbf F = e^{\mathbf A\Delta t} = \mathbf{I} + \mathbf A\Delta t + \frac{(\mathbf A\Delta t)^2}{2!} + \frac{(\mathbf A\Delta t)^3}{3!} + ... $$
If you perform the multiplication you will find that $\mathbf{A}^2=\begin{bmatrix}0&0\\0&0\end{bmatrix}$, which means that all higher powers of $\mathbf{A}$ are also $\mathbf{0}$. Thus we get an exact answer without an infinite number of terms:
$$
\begin{aligned}
\mathbf F &=\mathbf{I} + \mathbf A \Delta t + \mathbf{0} \\
&= \begin{bmatrix}1&0\\0&1\end{bmatrix} + \begin{bmatrix}0&1\\0&0\end{bmatrix}\Delta t\\
&= \begin{bmatrix}1&\Delta t\\0&1\end{bmatrix}
\end{aligned}$$
We plug this into $\mathbf x_k= \mathbf{Fx}_{k-1}$ to get
$$
\begin{aligned}
x_k &=\begin{bmatrix}1&\Delta t\\0&1\end{bmatrix}x_{k-1}
\end{aligned}$$
You will recognize this as the matrix we derived analytically for the constant velocity Kalman filter in the **Multivariate Kalman Filter** chapter.
SciPy's linalg module includes a routine `expm()` to compute the matrix exponential. It does not use the Taylor series method, but the [Padé Approximation](https://en.wikipedia.org/wiki/Pad%C3%A9_approximant). There are many (at least 19) methods to computed the matrix exponential, and all suffer from numerical difficulties[1]. But you should be aware of the problems, especially when $\mathbf A$ is large. If you search for "pade approximation matrix exponential" you will find many publications devoted to this problem.
In practice this may not be of concern to you as for the Kalman filter we normally just take the first two terms of the Taylor series. But don't assume my treatment of the problem is complete and run off and try to use this technique for other problem without doing a numerical analysis of the performance of this technique. Interestingly, one of the favored ways of solving $e^{\mathbf At}$ is to use a generalized ode solver. In other words, they do the opposite of what we do - turn $\mathbf A$ into a set of differential equations, and then solve that set using numerical techniques!
Here is an example of using `expm()` to solve $e^{\mathbf At}$.
```
import numpy as np
from scipy.linalg import expm
dt = 0.1
A = np.array([[0, 1],
[0, 0]])
expm(A*dt)
```
### Time Invariance
If the behavior of the system depends on time we can say that a dynamic system is described by the first-order differential equation
$$ g(t) = \dot x$$
However, if the system is *time invariant* the equation is of the form:
$$ f(x) = \dot x$$
What does *time invariant* mean? Consider a home stereo. If you input a signal $x$ into it at time $t$, it will output some signal $f(x)$. If you instead perform the input at time $t + \Delta t$ the output signal will be the same $f(x)$, shifted in time.
A counter-example is $x(t) = \sin(t)$, with the system $f(x) = t\, x(t) = t \sin(t)$. This is not time invariant; the value will be different at different times due to the multiplication by t. An aircraft is not time invariant. If you make a control input to the aircraft at a later time its behavior will be different because it will have burned fuel and thus lost weight. Lower weight results in different behavior.
We can solve these equations by integrating each side. I demonstrated integrating the time invariant system $v = \dot x$ above. However, integrating the time invariant equation $\dot x = f(x)$ is not so straightforward. Using the *separation of variables* techniques we divide by $f(x)$ and move the $dt$ term to the right so we can integrate each side:
$$\begin{gathered}
\frac{dx}{dt} = f(x) \\
\int^x_{x_0} \frac{1}{f(x)} dx = \int^t_{t_0} dt
\end{gathered}$$
If we let $F(x) = \int \frac{1}{f(x)} dx$ we get
$$F(x) - F(x_0) = t-t_0$$
We then solve for x with
$$\begin{gathered}
F(x) = t - t_0 + F(x_0) \\
x = F^{-1}[t-t_0 + F(x_0)]
\end{gathered}$$
In other words, we need to find the inverse of $F$. This is not trivial, and a significant amount of coursework in a STEM education is devoted to finding tricky, analytic solutions to this problem.
However, they are tricks, and many simple forms of $f(x)$ either have no closed form solution or pose extreme difficulties. Instead, the practicing engineer turns to state-space methods to find approximate solutions.
The advantage of the matrix exponential is that we can use it for any arbitrary set of differential equations which are *time invariant*. However, we often use this technique even when the equations are not time invariant. As an aircraft flies it burns fuel and loses weight. However, the weight loss over one second is negligible, and so the system is nearly linear over that time step. Our answers will still be reasonably accurate so long as the time step is short.
#### Example: Mass-Spring-Damper Model
Suppose we wanted to track the motion of a weight on a spring and connected to a damper, such as an automobile's suspension. The equation for the motion with $m$ being the mass, $k$ the spring constant, and $c$ the damping force, under some input $u$ is
$$m\frac{d^2x}{dt^2} + c\frac{dx}{dt} +kx = u$$
For notational convenience I will write that as
$$m\ddot x + c\dot x + kx = u$$
I can turn this into a system of first order equations by setting $x_1(t)=x(t)$, and then substituting as follows:
$$\begin{aligned}
x_1 &= x \\
x_2 &= \dot x_1 \\
\dot x_2 &= \dot x_1 = \ddot x
\end{aligned}$$
As is common I dropped the $(t)$ for notational convenience. This gives the equation
$$m\dot x_2 + c x_2 +kx_1 = u$$
Solving for $\dot x_2$ we get a first order equation:
$$\dot x_2 = -\frac{c}{m}x_2 - \frac{k}{m}x_1 + \frac{1}{m}u$$
We put this into matrix form:
$$\begin{bmatrix} \dot x_1 \\ \dot x_2 \end{bmatrix} =
\begin{bmatrix}0 & 1 \\ -k/m & -c/m \end{bmatrix}
\begin{bmatrix} x_1 \\ x_2 \end{bmatrix} +
\begin{bmatrix} 0 \\ 1/m \end{bmatrix}u$$
Now we use the matrix exponential to find the state transition matrix:
$$\Phi(t) = e^{\mathbf At} = \mathbf{I} + \mathbf At + \frac{(\mathbf At)^2}{2!} + \frac{(\mathbf At)^3}{3!} + ... $$
The first two terms give us
$$\mathbf F = \begin{bmatrix}1 & t \\ -(k/m) t & 1-(c/m) t \end{bmatrix}$$
This may or may not give you enough precision. You can easily check this by computing $\frac{(\mathbf At)^2}{2!}$ for your constants and seeing how much this matrix contributes to the results.
### Linear Time Invariant Theory
[*Linear Time Invariant Theory*](https://en.wikipedia.org/wiki/LTI_system_theory), also known as LTI System Theory, gives us a way to find $\Phi$ using the inverse Laplace transform. You are either nodding your head now, or completely lost. I will not be using the Laplace transform in this book. LTI system theory tells us that
$$ \Phi(t) = \mathcal{L}^{-1}[(s\mathbf{I} - \mathbf{F})^{-1}]$$
I have no intention of going into this other than to say that the Laplace transform $\mathcal{L}$ converts a signal into a space $s$ that excludes time, but finding a solution to the equation above is non-trivial. If you are interested, the Wikipedia article on LTI system theory provides an introduction. I mention LTI because you will find some literature using it to design the Kalman filter matrices for difficult problems.
### Numerical Solutions
Finally, there are numerical techniques to find $\mathbf F$. As filters get larger finding analytical solutions becomes very tedious (though packages like SymPy make it easier). C. F. van Loan [2] has developed a technique that finds both $\Phi$ and $\mathbf Q$ numerically. Given the continuous model
$$ \dot x = Ax + Gw$$
where $w$ is the unity white noise, van Loan's method computes both $\mathbf F_k$ and $\mathbf Q_k$.
I have implemented van Loan's method in `FilterPy`. You may use it as follows:
```python
from filterpy.common import van_loan_discretization
A = np.array([[0., 1.], [-1., 0.]])
G = np.array([[0.], [2.]]) # white noise scaling
F, Q = van_loan_discretization(A, G, dt=0.1)
```
In the section *Numeric Integration of Differential Equations* I present alternative methods which are very commonly used in Kalman filtering.
## Design of the Process Noise Matrix
In general the design of the $\mathbf Q$ matrix is among the most difficult aspects of Kalman filter design. This is due to several factors. First, the math requires a good foundation in signal theory. Second, we are trying to model the noise in something for which we have little information. Consider trying to model the process noise for a thrown baseball. We can model it as a sphere moving through the air, but that leaves many unknown factors - the wind, ball rotation and spin decay, the coefficient of drag of a ball with stitches, the effects of wind and air density, and so on. We develop the equations for an exact mathematical solution for a given process model, but since the process model is incomplete the result for $\mathbf Q$ will also be incomplete. This has a lot of ramifications for the behavior of the Kalman filter. If $\mathbf Q$ is too small then the filter will be overconfident in its prediction model and will diverge from the actual solution. If $\mathbf Q$ is too large than the filter will be unduly influenced by the noise in the measurements and perform sub-optimally. In practice we spend a lot of time running simulations and evaluating collected data to try to select an appropriate value for $\mathbf Q$. But let's start by looking at the math.
Let's assume a kinematic system - some system that can be modeled using Newton's equations of motion. We can make a few different assumptions about this process.
We have been using a process model of
$$ \dot{\mathbf x} = \mathbf{Ax} + \mathbf{Bu} + \mathbf{w}$$
where $\mathbf{w}$ is the process noise. Kinematic systems are *continuous* - their inputs and outputs can vary at any arbitrary point in time. However, our Kalman filters are *discrete* (there are continuous forms for Kalman filters, but we do not cover them in this book). We sample the system at regular intervals. Therefore we must find the discrete representation for the noise term in the equation above. This depends on what assumptions we make about the behavior of the noise. We will consider two different models for the noise.
### Continuous White Noise Model
We model kinematic systems using Newton's equations. We have either used position and velocity, or position, velocity, and acceleration as the models for our systems. There is nothing stopping us from going further - we can model jerk, jounce, snap, and so on. We don't do that normally because adding terms beyond the dynamics of the real system degrades the estimate.
Let's say that we need to model the position, velocity, and acceleration. We can then assume that acceleration is constant for each discrete time step. Of course, there is process noise in the system and so the acceleration is not actually constant. The tracked object will alter the acceleration over time due to external, unmodeled forces. In this section we will assume that the acceleration changes by a continuous time zero-mean white noise $w(t)$. In other words, we are assuming that the small changes in velocity average to 0 over time (zero-mean).
Since the noise is changing continuously we will need to integrate to get the discrete noise for the discretization interval that we have chosen. We will not prove it here, but the equation for the discretization of the noise is
$$\mathbf Q = \int_0^{\Delta t} \mathbf F(t)\mathbf{Q_c}\mathbf F^\mathsf{T}(t) dt$$
where $\mathbf{Q_c}$ is the continuous noise. This gives us
$$\Phi = \begin{bmatrix}1 & \Delta t & {\Delta t}^2/2 \\ 0 & 1 & \Delta t\\ 0& 0& 1\end{bmatrix}$$
for the fundamental matrix, and
$$\mathbf{Q_c} = \begin{bmatrix}0&0&0\\0&0&0\\0&0&1\end{bmatrix} \Phi_s$$
for the continuous process noise matrix, where $\Phi_s$ is the spectral density of the white noise.
We could carry out these computations ourselves, but I prefer using SymPy to solve the equation.
$$\mathbf{Q_c} = \begin{bmatrix}0&0&0\\0&0&0\\0&0&1\end{bmatrix} \Phi_s$$
```
import sympy
from sympy import (init_printing, Matrix,MatMul,
integrate, symbols)
init_printing(use_latex='mathjax')
dt, phi = symbols('\Delta{t} \Phi_s')
F_k = Matrix([[1, dt, dt**2/2],
[0, 1, dt],
[0, 0, 1]])
Q_c = Matrix([[0, 0, 0],
[0, 0, 0],
[0, 0, 1]])*phi
Q=sympy.integrate(F_k * Q_c * F_k.T, (dt, 0, dt))
# factor phi out of the matrix to make it more readable
Q = Q / phi
sympy.MatMul(Q, phi)
```
For completeness, let us compute the equations for the 0th order and 1st order equations.
```
F_k = sympy.Matrix([[1]])
Q_c = sympy.Matrix([[phi]])
print('0th order discrete process noise')
sympy.integrate(F_k*Q_c*F_k.T,(dt, 0, dt))
F_k = sympy.Matrix([[1, dt],
[0, 1]])
Q_c = sympy.Matrix([[0, 0],
[0, 1]])*phi
Q = sympy.integrate(F_k * Q_c * F_k.T, (dt, 0, dt))
print('1st order discrete process noise')
# factor phi out of the matrix to make it more readable
Q = Q / phi
sympy.MatMul(Q, phi)
```
### Piecewise White Noise Model
Another model for the noise assumes that the that highest order term (say, acceleration) is constant for the duration of each time period, but differs for each time period, and each of these is uncorrelated between time periods. In other words there is a discontinuous jump in acceleration at each time step. This is subtly different than the model above, where we assumed that the last term had a continuously varying noisy signal applied to it.
We will model this as
$$f(x)=Fx+\Gamma w$$
where $\Gamma$ is the *noise gain* of the system, and $w$ is the constant piecewise acceleration (or velocity, or jerk, etc).
Let's start by looking at a first order system. In this case we have the state transition function
$$\mathbf{F} = \begin{bmatrix}1&\Delta t \\ 0& 1\end{bmatrix}$$
In one time period, the change in velocity will be $w(t)\Delta t$, and the change in position will be $w(t)\Delta t^2/2$, giving us
$$\Gamma = \begin{bmatrix}\frac{1}{2}\Delta t^2 \\ \Delta t\end{bmatrix}$$
The covariance of the process noise is then
$$Q = \mathbb E[\Gamma w(t) w(t) \Gamma^\mathsf{T}] = \Gamma\sigma^2_v\Gamma^\mathsf{T}$$.
We can compute that with SymPy as follows
```
var=symbols('sigma^2_v')
v = Matrix([[dt**2 / 2], [dt]])
Q = v * var * v.T
# factor variance out of the matrix to make it more readable
Q = Q / var
sympy.MatMul(Q, var)
```
The second order system proceeds with the same math.
$$\mathbf{F} = \begin{bmatrix}1 & \Delta t & {\Delta t}^2/2 \\ 0 & 1 & \Delta t\\ 0& 0& 1\end{bmatrix}$$
Here we will assume that the white noise is a discrete time Wiener process. This gives us
$$\Gamma = \begin{bmatrix}\frac{1}{2}\Delta t^2 \\ \Delta t\\ 1\end{bmatrix}$$
There is no 'truth' to this model, it is just convenient and provides good results. For example, we could assume that the noise is applied to the jerk at the cost of a more complicated equation.
The covariance of the process noise is then
$$Q = \mathbb E[\Gamma w(t) w(t) \Gamma^\mathsf{T}] = \Gamma\sigma^2_v\Gamma^\mathsf{T}$$.
We can compute that with SymPy as follows
```
var=symbols('sigma^2_v')
v = Matrix([[dt**2 / 2], [dt], [1]])
Q = v * var * v.T
# factor variance out of the matrix to make it more readable
Q = Q / var
sympy.MatMul(Q, var)
```
We cannot say that this model is more or less correct than the continuous model - both are approximations to what is happening to the actual object. Only experience and experiments can guide you to the appropriate model. In practice you will usually find that either model provides reasonable results, but typically one will perform better than the other.
The advantage of the second model is that we can model the noise in terms of $\sigma^2$ which we can describe in terms of the motion and the amount of error we expect. The first model requires us to specify the spectral density, which is not very intuitive, but it handles varying time samples much more easily since the noise is integrated across the time period. However, these are not fixed rules - use whichever model (or a model of your own devising) based on testing how the filter performs and/or your knowledge of the behavior of the physical model.
A good rule of thumb is to set $\sigma$ somewhere from $\frac{1}{2}\Delta a$ to $\Delta a$, where $\Delta a$ is the maximum amount that the acceleration will change between sample periods. In practice we pick a number, run simulations on data, and choose a value that works well.
### Using FilterPy to Compute Q
FilterPy offers several routines to compute the $\mathbf Q$ matrix. The function `Q_continuous_white_noise()` computes $\mathbf Q$ for a given value for $\Delta t$ and the spectral density.
```
from filterpy.common import Q_continuous_white_noise
from filterpy.common import Q_discrete_white_noise
Q = Q_continuous_white_noise(dim=2, dt=1, spectral_density=1)
print(Q)
Q = Q_continuous_white_noise(dim=3, dt=1, spectral_density=1)
print(Q)
```
The function `Q_discrete_white_noise()` computes $\mathbf Q$ assuming a piecewise model for the noise.
```
Q = Q_discrete_white_noise(2, var=1.)
print(Q)
Q = Q_discrete_white_noise(3, var=1.)
print(Q)
```
### Simplification of Q
Many treatments use a much simpler form for $\mathbf Q$, setting it to zero except for a noise term in the lower rightmost element. Is this justified? Well, consider the value of $\mathbf Q$ for a small $\Delta t$
```
import numpy as np
np.set_printoptions(precision=8)
Q = Q_continuous_white_noise(
dim=3, dt=0.05, spectral_density=1)
print(Q)
np.set_printoptions(precision=3)
```
We can see that most of the terms are very small. Recall that the only equation using this matrix is
$$ \mathbf P=\mathbf{FPF}^\mathsf{T} + \mathbf Q$$
If the values for $\mathbf Q$ are small relative to $\mathbf P$
than it will be contributing almost nothing to the computation of $\mathbf P$. Setting $\mathbf Q$ to the zero matrix except for the lower right term
$$\mathbf Q=\begin{bmatrix}0&0&0\\0&0&0\\0&0&\sigma^2\end{bmatrix}$$
while not correct, is often a useful approximation. If you do this you will have to perform quite a few studies to guarantee that your filter works in a variety of situations.
If you do this, 'lower right term' means the most rapidly changing term for each variable. If the state is $x=\begin{bmatrix}x & \dot x & \ddot{x} & y & \dot{y} & \ddot{y}\end{bmatrix}^\mathsf{T}$ Then Q will be 6x6; the elements for both $\ddot{x}$ and $\ddot{y}$ will have to be set to non-zero in $\mathbf Q$.
## Numeric Integration of Differential Equations
We've been exposed to several numerical techniques to solve linear differential equations. These include state-space methods, the Laplace transform, and van Loan's method.
These work well for linear ordinary differential equations (ODEs), but do not work well for nonlinear equations. For example, consider trying to predict the position of a rapidly turning car. Cars maneuver by turning the front wheels. This makes them pivot around their rear axle as it moves forward. Therefore the path will be continuously varying and a linear prediction will necessarily produce an incorrect value. If the change in the system is small enough relative to $\Delta t$ this can often produce adequate results, but that will rarely be the case with the nonlinear Kalman filters we will be studying in subsequent chapters.
For these reasons we need to know how to numerically integrate ODEs. This can be a vast topic that requires several books. If you need to explore this topic in depth *Computational Physics in Python* by Dr. Eric Ayars is excellent, and available for free here:
http://phys.csuchico.edu/ayars/312/Handouts/comp-phys-python.pdf
However, I will cover a few simple techniques which will work for a majority of the problems you encounter.
### Euler's Method
Let's say we have the initial condition problem of
$$\begin{gathered}
y' = y, \\ y(0) = 1
\end{gathered}$$
We happen to know the exact answer is $y=e^t$ because we solved it earlier, but for an arbitrary ODE we will not know the exact solution. In general all we know is the derivative of the equation, which is equal to the slope. We also know the initial value: at $t=0$, $y=1$. If we know these two pieces of information we can predict the value at $y(t=1)$ using the slope at $t=0$ and the value of $y(0)$. I've plotted this below.
```
import matplotlib.pyplot as plt
t = np.linspace(-1, 1, 10)
plt.plot(t, np.exp(t))
t = np.linspace(-1, 1, 2)
plt.plot(t,t+1, ls='--', c='k');
```
You can see that the slope is very close to the curve at $t=0.1$, but far from it
at $t=1$. But let's continue with a step size of 1 for a moment. We can see that at $t=1$ the estimated value of $y$ is 2. Now we can compute the value at $t=2$ by taking the slope of the curve at $t=1$ and adding it to our initial estimate. The slope is computed with $y'=y$, so the slope is 2.
```
import code.book_plots as book_plots
t = np.linspace(-1, 2, 20)
plt.plot(t, np.exp(t))
t = np.linspace(0, 1, 2)
plt.plot([1, 2, 4], ls='--', c='k')
book_plots.set_labels(x='x', y='y');
```
Here we see the next estimate for y is 4. The errors are getting large quickly, and you might be unimpressed. But 1 is a very large step size. Let's put this algorithm in code, and verify that it works by using a small step size.
```
def euler(t, tmax, y, dx, step=1.):
ys = []
while t < tmax:
y = y + step*dx(t, y)
ys.append(y)
t +=step
return ys
def dx(t, y): return y
print(euler(0, 1, 1, dx, step=1.)[-1])
print(euler(0, 2, 1, dx, step=1.)[-1])
```
This looks correct. So now let's plot the result of a much smaller step size.
```
ys = euler(0, 4, 1, dx, step=0.00001)
plt.subplot(1,2,1)
plt.title('Computed')
plt.plot(np.linspace(0, 4, len(ys)),ys)
plt.subplot(1,2,2)
t = np.linspace(0, 4, 20)
plt.title('Exact')
plt.plot(t, np.exp(t));
print('exact answer=', np.exp(4))
print('euler answer=', ys[-1])
print('difference =', np.exp(4) - ys[-1])
print('iterations =', len(ys))
```
Here we see that the error is reasonably small, but it took a very large number of iterations to get three digits of precision. In practice Euler's method is too slow for most problems, and we use more sophisticated methods.
Before we go on, let's formally derive Euler's method, as it is the basis for the more advanced Runge Kutta methods used in the next section. In fact, Euler's method is the simplest form of Runge Kutta.
Here are the first 3 terms of the Euler expansion of $y$. An infinite expansion would give an exact answer, so $O(h^4)$ denotes the error due to the finite expansion.
$$y(t_0 + h) = y(t_0) + h y'(t_0) + \frac{1}{2!}h^2 y''(t_0) + \frac{1}{3!}h^3 y'''(t_0) + O(h^4)$$
Here we can see that Euler's method is using the first two terms of the Taylor expansion. Each subsequent term is smaller than the previous terms, so we are assured that the estimate will not be too far off from the correct value.
### Runge Kutta Methods
Runge Kutta is the workhorse of numerical integration. There are a vast number of methods in the literature. In practice, using the Runge Kutta algorithm that I present here will solve most any problem you will face. It offers a very good balance of speed, precision, and stability, and it is the 'go to' numerical integration method unless you have a very good reason to choose something different.
Let's dive in. We start with some differential equation
$$\ddot{y} = \frac{d}{dt}\dot{y}$$.
We can substitute the derivative of y with a function f, like so
$$\ddot{y} = \frac{d}{dt}f(y,t)$$.
Deriving these equations is outside the scope of this book, but the Runge Kutta RK4 method is defined with these equations.
$$y(t+\Delta t) = y(t) + \frac{1}{6}(k_1 + 2k_2 + 2k_3 + k_4) + O(\Delta t^4)$$
$$\begin{aligned}
k_1 &= f(y,t)\Delta t \\
k_2 &= f(y+\frac{1}{2}k_1, t+\frac{1}{2}\Delta t)\Delta t \\
k_3 &= f(y+\frac{1}{2}k_2, t+\frac{1}{2}\Delta t)\Delta t \\
k_4 &= f(y+k_3, t+\Delta t)\Delta t
\end{aligned}
$$
Here is the corresponding code:
```
def runge_kutta4(y, x, dx, f):
"""computes 4th order Runge-Kutta for dy/dx.
y is the initial value for y
x is the initial value for x
dx is the difference in x (e.g. the time step)
f is a callable function (y, x) that you supply
to compute dy/dx for the specified values.
"""
k1 = dx * f(y, x)
k2 = dx * f(y + 0.5*k1, x + 0.5*dx)
k3 = dx * f(y + 0.5*k2, x + 0.5*dx)
k4 = dx * f(y + k3, x + dx)
return y + (k1 + 2*k2 + 2*k3 + k4) / 6.
```
Let's use this for a simple example. Let
$$\dot{y} = t\sqrt{y(t)}$$
with the initial values
$$\begin{aligned}t_0 &= 0\\y_0 &= y(t_0) = 1\end{aligned}$$
```
import math
import numpy as np
t = 0.
y = 1.
dt = .1
ys, ts = [], []
def func(y,t):
return t*math.sqrt(y)
while t <= 10:
y = runge_kutta4(y, t, dt, func)
t += dt
ys.append(y)
ts.append(t)
exact = [(t**2 + 4)**2 / 16. for t in ts]
plt.plot(ts, ys)
plt.plot(ts, exact)
error = np.array(exact) - np.array(ys)
print("max error {}".format(max(error)))
```
## Bayesian Filtering
Starting in the Discrete Bayes chapter I used a Bayesian formulation for filtering. Suppose we are tracking an object. We define its *state* at a specific time as its position, velocity, and so on. For example, we might write the state at time $t$ as $\mathbf x_t = \begin{bmatrix}x_t &\dot x_t \end{bmatrix}^\mathsf T$.
When we take a measurement of the object we are measuring the state or part of it. Sensors are noisy, so the measurement is corrupted with noise. Clearly though, the measurement is determined by the state. That is, a change in state may change the measurement, but a change in measurement will not change the state.
In filtering our goal is to compute an optimal estimate for a set of states $\mathbf x_{0:t}$ from time 0 to time $t$. If we knew $\mathbf x_{0:t}$ then it would be trivial to compute a set of measurements $\mathbf z_{0:t}$ corresponding to those states. However, we receive a set of measurements $\mathbf z_{0:t}$, and want to compute the corresponding states $\mathbf x_{0:t}$. This is called *statistical inversion* because we are trying to compute the input from the output.
Inversion is a difficult problem because there is typically no unique solution. For a given set of states $\mathbf x_{0:t}$ there is only one possible set of measurements (plus noise), but for a given set of measurements there are many different sets of states that could have led to those measurements.
Recall Bayes Theorem:
$$P(x \mid z) = \frac{P(z \mid x)P(x)}{P(z)}$$
where $P(z \mid x)$ is the *likelihood* of the measurement $z$, $P(x)$ is the *prior* based on our process model, and $P(z)$ is a normalization constant. $P(x \mid z)$ is the *posterior*, or the distribution after incorporating the measurement $z$, also called the *evidence*.
This is a *statistical inversion* as it goes from $P(z \mid x)$ to $P(x \mid z)$. The solution to our filtering problem can be expressed as:
$$P(\mathbf x_{0:t} \mid \mathbf z_{0:t}) = \frac{P(\mathbf z_{0:t} \mid \mathbf x_{0:t})P(\mathbf x_{0:t})}{P(\mathbf z_{0:t})}$$
That is all well and good until the next measurement $\mathbf z_{t+1}$ comes in, at which point we need to recompute the entire expression for the range $0:t+1$.
In practice this is intractable because we are trying to compute the posterior distribution $P(\mathbf x_{0:t} \mid \mathbf z_{0:t})$ for the state over the full range of time steps. But do we really care about the probability distribution at the third step (say) when we just received the tenth measurement? Not usually. So we relax our requirements and only compute the distributions for the current time step.
The first simplification is we describe our process (e.g., the motion model for a moving object) as a *Markov chain*. That is, we say that the current state is solely dependent on the previous state and a transition probability $P(\mathbf x_k \mid \mathbf x_{k-1})$, which is just the probability of going from the last state to the current one. We write:
$$\mathbf x_k \sim P(\mathbf x_k \mid \mathbf x_{k-1})$$
The next simplification we make is do define the *measurement model* as depending on the current state $\mathbf x_k$ with the conditional probability of the measurement given the current state: $P(\mathbf z_t \mid \mathbf x_x)$. We write:
$$\mathbf z_k \sim P(\mathbf z_t \mid \mathbf x_x)$$
We have a recurrance now, so we need an initial condition to terminate it. Therefore we say that the initial distribution is the probablity of the state $\mathbf x_0$:
$$\mathbf x_0 \sim P(\mathbf x_0)$$
These terms are plugged into Bayes equation. If we have the state $\mathbf x_0$ and the first measurement we can estimate $P(\mathbf x_1 | \mathbf z_1)$. The motion model creates the prior $P(\mathbf x_2 \mid \mathbf x_1)$. We feed this back into Bayes theorem to compute $P(\mathbf x_2 | \mathbf z_2)$. We continue this predictor-corrector algorithm, recursively computing the state and distribution at time $t$ based solely on the state and distribution at time $t-1$ and the measurement at time $t$.
The details of the mathematics for this computation varies based on the problem. The **Discrete Bayes** and **Univariate Kalman Filter** chapters gave two different formulations which you should have been able to reason through. The univariate Kalman filter assumes that for a scalar state both the noise and process are linear model are affected by zero-mean, uncorrelated Gaussian noise.
The Multivariate Kalman filter make the same assumption but for states and measurements that are vectors, not scalars. Dr. Kalman was able to prove that if these assumptions hold true then the Kalman filter is *optimal* in a least squares sense. Colloquially this means there is no way to derive more information from the noise. In the remainder of the book I will present filters that relax the constraints on linearity and Gaussian noise.
Before I go on, a few more words about statistical inversion. As Calvetti and Somersalo write in *Introduction to Bayesian Scientific Computing*, "we adopt the Bayesian point of view: *randomness simply means lack of information*."[3] Our state parametize physical phenomena that we could in principle measure or compute: velocity, air drag, and so on. We lack enough information to compute or measure their value, so we opt to consider them as random variables. Strictly speaking they are not random, thus this is a subjective position.
They devote a full chapter to this topic. I can spare a paragraph. Bayesian filters are possible because we ascribe statistical properties to unknown parameters. In the case of the Kalman filter we have closed-form solutions to find an optimal estimate. Other filters, such as the discrete Bayes filter or the particle filter which we cover in a later chapter, model the probability in a more ad-hoc, non-optimal manner. The power of our technique comes from treating lack of information as a random variable, describing that random variable as a probability distribution, and then using Bayes Theorem to solve the statistical inference problem.
## Converting Kalman Filter to a g-h Filter
I've stated that the Kalman filter is a form of the g-h filter. It just takes some algebra to prove it. It's more straightforward to do with the one dimensional case, so I will do that. Recall
$$
\mu_{x}=\frac{\sigma_1^2 \mu_2 + \sigma_2^2 \mu_1} {\sigma_1^2 + \sigma_2^2}
$$
which I will make more friendly for our eyes as:
$$
\mu_{x}=\frac{ya + xb} {a+b}
$$
We can easily put this into the g-h form with the following algebra
$$
\begin{aligned}
\mu_{x}&=(x-x) + \frac{ya + xb} {a+b} \\
\mu_{x}&=x-\frac{a+b}{a+b}x + \frac{ya + xb} {a+b} \\
\mu_{x}&=x +\frac{-x(a+b) + xb+ya}{a+b} \\
\mu_{x}&=x+ \frac{-xa+ya}{a+b} \\
\mu_{x}&=x+ \frac{a}{a+b}(y-x)\\
\end{aligned}
$$
We are almost done, but recall that the variance of estimate is given by
$$\begin{aligned}
\sigma_{x}^2 &= \frac{1}{\frac{1}{\sigma_1^2} + \frac{1}{\sigma_2^2}} \\
&= \frac{1}{\frac{1}{a} + \frac{1}{b}}
\end{aligned}$$
We can incorporate that term into our equation above by observing that
$$
\begin{aligned}
\frac{a}{a+b} &= \frac{a/a}{(a+b)/a} = \frac{1}{(a+b)/a} \\
&= \frac{1}{1 + \frac{b}{a}} = \frac{1}{\frac{b}{b} + \frac{b}{a}} \\
&= \frac{1}{b}\frac{1}{\frac{1}{b} + \frac{1}{a}} \\
&= \frac{\sigma^2_{x'}}{b}
\end{aligned}
$$
We can tie all of this together with
$$
\begin{aligned}
\mu_{x}&=x+ \frac{a}{a+b}(y-x) \\
&= x + \frac{\sigma^2_{x'}}{b}(y-x) \\
&= x + g_n(y-x)
\end{aligned}
$$
where
$$g_n = \frac{\sigma^2_{x}}{\sigma^2_{y}}$$
The end result is multiplying the residual of the two measurements by a constant and adding to our previous value, which is the $g$ equation for the g-h filter. $g$ is the variance of the new estimate divided by the variance of the measurement. Of course in this case $g$ is not a constant as it varies with each time step as the variance changes. We can also derive the formula for $h$ in the same way. It is not a particularly illuminating derivation and I will skip it. The end result is
$$h_n = \frac{COV (x,\dot x)}{\sigma^2_{y}}$$
The takeaway point is that $g$ and $h$ are specified fully by the variance and covariances of the measurement and predictions at time $n$. In other words, we are picking a point between the measurement and prediction by a scale factor determined by the quality of each of those two inputs.
## References
* [1] C.B. Molwer and C.F. Van Loan "Nineteen Dubious Ways to Compute the Exponential of a Matrix, Twenty-Five Years Later,", *SIAM Review 45, 3-49*. 2003.
* [2] C.F. van Loan, "Computing Integrals Involving the Matrix Exponential," IEEE *Transactions Automatic Control*, June 1978.
* [3] Calvetti, D and Somersalo E, "Introduction to Bayesian Scientific Computing: Ten Lectures on Subjective Computing,", *Springer*, 2007.
|
github_jupyter
|
```
# Copyright 2021 Google LLC
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
```
# Vertex Pipelines: Lightweight Python function-based components, and component I/O
<table align="left">
<td>
<a href="https://colab.research.google.com/github/GoogleCloudPlatform/vertex-ai-samples/notebooks/official/pipelines/lightweight_functions_component_io_kfp.ipynb">
<img src="https://cloud.google.com/ml-engine/images/colab-logo-32px.png" alt="Colab logo"> Run in Colab
</a>
</td>
<td>
<a href="https://github.com/GoogleCloudPlatform/vertex-ai-samples/notebooks/official/pipelines/lightweight_functions_component_io_kfp.ipynb">
<img src="https://cloud.google.com/ml-engine/images/github-logo-32px.png" alt="GitHub logo">
View on GitHub
</a>
</td>
<td>
<a href="https://console.cloud.google.com/ai/platform/notebooks/deploy-notebook?download_url=https://github.com/GoogleCloudPlatform/vertex-ai-samples/notebooks/official/pipelines/lightweight_functions_component_io_kfp.ipynb">
Open in Google Cloud Notebooks
</a>
</td>
</table>
<br/><br/><br/>
## Overview
This notebooks shows how to use [the Kubeflow Pipelines (KFP) SDK](https://www.kubeflow.org/docs/components/pipelines/) to build [Vertex Pipelines](https://cloud.google.com/vertex-ai/docs/pipelines) that use lightweight Python function based components, as well as supporting component I/O using the KFP SDK.
### Objective
In this tutorial, you use the KFP SDK to build lightweight Python function-based components.
The steps performed include:
- Build Python function-based components.
- Pass *Artifacts* and *parameters* between components, both by path reference and by value.
- Use the `kfp.dsl.importer` method.
### KFP Python function-based components
A Kubeflow pipeline component is a self-contained set of code that performs one step in your ML workflow. A pipeline component is composed of:
* The component code, which implements the logic needed to perform a step in your ML workflow.
* A component specification, which defines the following:
* The component’s metadata, its name and description.
* The component’s interface, the component’s inputs and outputs.
* The component’s implementation, the Docker container image to run, how to pass inputs to your component code, and how to get the component’s outputs.
Lightweight Python function-based components make it easier to iterate quickly by letting you build your component code as a Python function and generating the component specification for you. This notebook shows how to create Python function-based components for use in [Vertex Pipelines](https://cloud.google.com/vertex-ai/docs/pipelines).
Python function-based components use the Kubeflow Pipelines SDK to handle the complexity of passing inputs into your component and passing your function’s outputs back to your pipeline.
There are two categories of inputs/outputs supported in Python function-based components: *artifacts* and *parameters*.
* Parameters are passed to your component by value and typically contain `int`, `float`, `bool`, or small `string` values.
* Artifacts are passed to your component as a *reference* to a path, to which you can write a file or a subdirectory structure. In addition to the artifact’s data, you can also read and write the artifact’s metadata. This lets you record arbitrary key-value pairs for an artifact such as the accuracy of a trained model, and use metadata in downstream components – for example, you could use metadata to decide if a model is accurate enough to deploy for predictions.
### Costs
This tutorial uses billable components of Google Cloud:
* Vertex AI
* Cloud Storage
Learn about [Vertex AI
pricing](https://cloud.google.com/vertex-ai/pricing) and [Cloud Storage
pricing](https://cloud.google.com/storage/pricing), and use the [Pricing
Calculator](https://cloud.google.com/products/calculator/)
to generate a cost estimate based on your projected usage.
### Set up your local development environment
If you are using Colab or Google Cloud Notebook, your environment already meets all the requirements to run this notebook. You can skip this step.
Otherwise, make sure your environment meets this notebook's requirements. You need the following:
- The Cloud Storage SDK
- Git
- Python 3
- virtualenv
- Jupyter notebook running in a virtual environment with Python 3
The Cloud Storage guide to [Setting up a Python development environment](https://cloud.google.com/python/setup) and the [Jupyter installation guide](https://jupyter.org/install) provide detailed instructions for meeting these requirements. The following steps provide a condensed set of instructions:
1. [Install and initialize the SDK](https://cloud.google.com/sdk/docs/).
2. [Install Python 3](https://cloud.google.com/python/setup#installing_python).
3. [Install virtualenv](Ihttps://cloud.google.com/python/setup#installing_and_using_virtualenv) and create a virtual environment that uses Python 3.
4. Activate that environment and run `pip3 install Jupyter` in a terminal shell to install Jupyter.
5. Run `jupyter notebook` on the command line in a terminal shell to launch Jupyter.
6. Open this notebook in the Jupyter Notebook Dashboard.
## Installation
Install the latest version of Vertex SDK for Python.
```
import os
# Google Cloud Notebook
if os.path.exists("/opt/deeplearning/metadata/env_version"):
USER_FLAG = "--user"
else:
USER_FLAG = ""
! pip3 install --upgrade google-cloud-aiplatform $USER_FLAG
```
Install the latest GA version of *google-cloud-storage* library as well.
```
! pip3 install -U google-cloud-storage $USER_FLAG
```
Install the latest GA version of *google-cloud-pipeline-components* library as well.
```
! pip3 install $USER kfp google-cloud-pipeline-components --upgrade
```
### Restart the kernel
Once you've installed the additional packages, you need to restart the notebook kernel so it can find the packages.
```
import os
if not os.getenv("IS_TESTING"):
# Automatically restart kernel after installs
import IPython
app = IPython.Application.instance()
app.kernel.do_shutdown(True)
```
Check the versions of the packages you installed. The KFP SDK version should be >=1.6.
```
! python3 -c "import kfp; print('KFP SDK version: {}'.format(kfp.__version__))"
! python3 -c "import google_cloud_pipeline_components; print('google_cloud_pipeline_components version: {}'.format(google_cloud_pipeline_components.__version__))"
```
## Before you begin
### GPU runtime
This tutorial does not require a GPU runtime.
### Set up your Google Cloud project
**The following steps are required, regardless of your notebook environment.**
1. [Select or create a Google Cloud project](https://console.cloud.google.com/cloud-resource-manager). When you first create an account, you get a $300 free credit towards your compute/storage costs.
2. [Make sure that billing is enabled for your project.](https://cloud.google.com/billing/docs/how-to/modify-project)
3. [Enable the Vertex AI APIs, Compute Engine APIs, and Cloud Storage.](https://console.cloud.google.com/flows/enableapi?apiid=ml.googleapis.com,compute_component,storage-component.googleapis.com)
4. [The Google Cloud SDK](https://cloud.google.com/sdk) is already installed in Google Cloud Notebook.
5. Enter your project ID in the cell below. Then run the cell to make sure the
Cloud SDK uses the right project for all the commands in this notebook.
**Note**: Jupyter runs lines prefixed with `!` as shell commands, and it interpolates Python variables prefixed with `$`.
```
PROJECT_ID = "[your-project-id]" # @param {type:"string"}
if PROJECT_ID == "" or PROJECT_ID is None or PROJECT_ID == "[your-project-id]":
# Get your GCP project id from gcloud
shell_output = ! gcloud config list --format 'value(core.project)' 2>/dev/null
PROJECT_ID = shell_output[0]
print("Project ID:", PROJECT_ID)
! gcloud config set project $PROJECT_ID
```
#### Region
You can also change the `REGION` variable, which is used for operations
throughout the rest of this notebook. Below are regions supported for Vertex AI. We recommend that you choose the region closest to you.
- Americas: `us-central1`
- Europe: `europe-west4`
- Asia Pacific: `asia-east1`
You may not use a multi-regional bucket for training with Vertex AI. Not all regions provide support for all Vertex AI services.
Learn more about [Vertex AI regions](https://cloud.google.com/vertex-ai/docs/general/locations)
```
REGION = "us-central1" # @param {type: "string"}
```
#### Timestamp
If you are in a live tutorial session, you might be using a shared test account or project. To avoid name collisions between users on resources created, you create a timestamp for each instance session, and append the timestamp onto the name of resources you create in this tutorial.
```
from datetime import datetime
TIMESTAMP = datetime.now().strftime("%Y%m%d%H%M%S")
```
### Authenticate your Google Cloud account
**If you are using Google Cloud Notebook**, your environment is already authenticated. Skip this step.
**If you are using Colab**, run the cell below and follow the instructions when prompted to authenticate your account via oAuth.
**Otherwise**, follow these steps:
In the Cloud Console, go to the [Create service account key](https://console.cloud.google.com/apis/credentials/serviceaccountkey) page.
**Click Create service account**.
In the **Service account name** field, enter a name, and click **Create**.
In the **Grant this service account access to project** section, click the Role drop-down list. Type "Vertex" into the filter box, and select **Vertex Administrator**. Type "Storage Object Admin" into the filter box, and select **Storage Object Admin**.
Click Create. A JSON file that contains your key downloads to your local environment.
Enter the path to your service account key as the GOOGLE_APPLICATION_CREDENTIALS variable in the cell below and run the cell.
```
# If you are running this notebook in Colab, run this cell and follow the
# instructions to authenticate your GCP account. This provides access to your
# Cloud Storage bucket and lets you submit training jobs and prediction
# requests.
import os
import sys
# If on Google Cloud Notebook, then don't execute this code
if not os.path.exists("/opt/deeplearning/metadata/env_version"):
if "google.colab" in sys.modules:
from google.colab import auth as google_auth
google_auth.authenticate_user()
# If you are running this notebook locally, replace the string below with the
# path to your service account key and run this cell to authenticate your GCP
# account.
elif not os.getenv("IS_TESTING"):
%env GOOGLE_APPLICATION_CREDENTIALS ''
```
### Create a Cloud Storage bucket
**The following steps are required, regardless of your notebook environment.**
When you initialize the Vertex SDK for Python, you specify a Cloud Storage staging bucket. The staging bucket is where all the data associated with your dataset and model resources are retained across sessions.
Set the name of your Cloud Storage bucket below. Bucket names must be globally unique across all Google Cloud projects, including those outside of your organization.
```
BUCKET_NAME = "gs://[your-bucket-name]" # @param {type:"string"}
if BUCKET_NAME == "" or BUCKET_NAME is None or BUCKET_NAME == "gs://[your-bucket-name]":
BUCKET_NAME = "gs://" + PROJECT_ID + "aip-" + TIMESTAMP
```
**Only if your bucket doesn't already exist**: Run the following cell to create your Cloud Storage bucket.
```
! gsutil mb -l $REGION $BUCKET_NAME
```
Finally, validate access to your Cloud Storage bucket by examining its contents:
```
! gsutil ls -al $BUCKET_NAME
```
#### Service Account
**If you don't know your service account**, try to get your service account using `gcloud` command by executing the second cell below.
```
SERVICE_ACCOUNT = "[your-service-account]" # @param {type:"string"}
if (
SERVICE_ACCOUNT == ""
or SERVICE_ACCOUNT is None
or SERVICE_ACCOUNT == "[your-service-account]"
):
# Get your GCP project id from gcloud
shell_output = !gcloud auth list 2>/dev/null
SERVICE_ACCOUNT = shell_output[2].strip()
print("Service Account:", SERVICE_ACCOUNT)
```
#### Set service account access for Vertex Pipelines
Run the following commands to grant your service account access to read and write pipeline artifacts in the bucket that you created in the previous step -- you only need to run these once per service account.
```
! gsutil iam ch serviceAccount:{SERVICE_ACCOUNT}:roles/storage.objectCreator $BUCKET_NAME
! gsutil iam ch serviceAccount:{SERVICE_ACCOUNT}:roles/storage.objectViewer $BUCKET_NAME
```
### Set up variables
Next, set up some variables used throughout the tutorial.
### Import libraries and define constants
```
import google.cloud.aiplatform as aip
```
#### Vertex Pipelines constants
Setup up the following constants for Vertex Pipelines:
```
PIPELINE_ROOT = "{}/pipeline_root/shakespeare".format(BUCKET_NAME)
```
Additional imports.
```
from typing import NamedTuple
import kfp
from kfp.v2 import dsl
from kfp.v2.dsl import (Artifact, Dataset, Input, InputPath, Model, Output,
OutputPath, component)
```
## Initialize Vertex SDK for Python
Initialize the Vertex SDK for Python for your project and corresponding bucket.
```
aip.init(project=PROJECT_ID, staging_bucket=BUCKET_NAME)
```
### Define Python function-based pipeline components
In this tutorial, you define function-based components that consume parameters and produce (typed) Artifacts and parameters. Functions can produce Artifacts in three ways:
* Accept an output local path using `OutputPath`
* Accept an `OutputArtifact` which gives the function a handle to the output artifact's metadata
* Return an `Artifact` (or `Dataset`, `Model`, `Metrics`, etc) in a `NamedTuple`
These options for producing Artifacts are demonstrated.
#### Define preprocess component
The first component definition, `preprocess`, shows a component that outputs two `Dataset` Artifacts, as well as an output parameter. (For this example, the datasets don't reflect real data).
For the parameter output, you would typically use the approach shown here, using the `OutputPath` type, for "larger" data.
For "small data", like a short string, it might be more convenient to use the `NamedTuple` function output as shown in the second component instead.
```
@component
def preprocess(
# An input parameter of type string.
message: str,
# Use Output to get a metadata-rich handle to the output artifact
# of type `Dataset`.
output_dataset_one: Output[Dataset],
# A locally accessible filepath for another output artifact of type
# `Dataset`.
output_dataset_two_path: OutputPath("Dataset"),
# A locally accessible filepath for an output parameter of type string.
output_parameter_path: OutputPath(str),
):
"""'Mock' preprocessing step.
Writes out the passed in message to the output "Dataset"s and the output message.
"""
output_dataset_one.metadata["hello"] = "there"
# Use OutputArtifact.path to access a local file path for writing.
# One can also use OutputArtifact.uri to access the actual URI file path.
with open(output_dataset_one.path, "w") as f:
f.write(message)
# OutputPath is used to just pass the local file path of the output artifact
# to the function.
with open(output_dataset_two_path, "w") as f:
f.write(message)
with open(output_parameter_path, "w") as f:
f.write(message)
```
#### Define train component
The second component definition, `train`, defines as input both an `InputPath` of type `Dataset`, and an `InputArtifact` of type `Dataset` (as well as other parameter inputs). It uses the `NamedTuple` format for function output. As shown, these outputs can be Artifacts as well as parameters.
Additionally, this component writes some metrics metadata to the `model` output Artifact. This information is displayed in the Cloud Console user interface when the pipeline runs.
```
@component(
base_image="python:3.9", # Use a different base image.
)
def train(
# An input parameter of type string.
message: str,
# Use InputPath to get a locally accessible path for the input artifact
# of type `Dataset`.
dataset_one_path: InputPath("Dataset"),
# Use InputArtifact to get a metadata-rich handle to the input artifact
# of type `Dataset`.
dataset_two: Input[Dataset],
# Output artifact of type Model.
imported_dataset: Input[Dataset],
model: Output[Model],
# An input parameter of type int with a default value.
num_steps: int = 3,
# Use NamedTuple to return either artifacts or parameters.
# When returning artifacts like this, return the contents of
# the artifact. The assumption here is that this return value
# fits in memory.
) -> NamedTuple(
"Outputs",
[
("output_message", str), # Return parameter.
("generic_artifact", Artifact), # Return generic Artifact.
],
):
"""'Mock' Training step.
Combines the contents of dataset_one and dataset_two into the
output Model.
Constructs a new output_message consisting of message repeated num_steps times.
"""
# Directly access the passed in GCS URI as a local file (uses GCSFuse).
with open(dataset_one_path, "r") as input_file:
dataset_one_contents = input_file.read()
# dataset_two is an Artifact handle. Use dataset_two.path to get a
# local file path (uses GCSFuse).
# Alternately, use dataset_two.uri to access the GCS URI directly.
with open(dataset_two.path, "r") as input_file:
dataset_two_contents = input_file.read()
with open(model.path, "w") as f:
f.write("My Model")
with open(imported_dataset.path, "r") as f:
data = f.read()
print("Imported Dataset:", data)
# Use model.get() to get a Model artifact, which has a .metadata dictionary
# to store arbitrary metadata for the output artifact. This metadata will be
# recorded in Managed Metadata and can be queried later. It will also show up
# in the UI.
model.metadata["accuracy"] = 0.9
model.metadata["framework"] = "Tensorflow"
model.metadata["time_to_train_in_seconds"] = 257
artifact_contents = "{}\n{}".format(dataset_one_contents, dataset_two_contents)
output_message = " ".join([message for _ in range(num_steps)])
return (output_message, artifact_contents)
```
#### Define read_artifact_input component
Finally, you define a small component that takes as input the `generic_artifact` returned by the `train` component function, and reads and prints the Artifact's contents.
```
@component
def read_artifact_input(
generic: Input[Artifact],
):
with open(generic.path, "r") as input_file:
generic_contents = input_file.read()
print(f"generic contents: {generic_contents}")
```
### Define a pipeline that uses your components and the Importer
Next, define a pipeline that uses the components that were built in the previous section, and also shows the use of the `kfp.dsl.importer`.
This example uses the `importer` to create, in this case, a `Dataset` artifact from an existing URI.
Note that the `train_task` step takes as inputs three of the outputs of the `preprocess_task` step, as well as the output of the `importer` step.
In the "train" inputs we refer to the `preprocess` `output_parameter`, which gives us the output string directly.
The `read_task` step takes as input the `train_task` `generic_artifact` output.
```
@dsl.pipeline(
# Default pipeline root. You can override it when submitting the pipeline.
pipeline_root=PIPELINE_ROOT,
# A name for the pipeline. Use to determine the pipeline Context.
name="metadata-pipeline-v2",
)
def pipeline(message: str):
importer = kfp.dsl.importer(
artifact_uri="gs://ml-pipeline-playground/shakespeare1.txt",
artifact_class=Dataset,
reimport=False,
)
preprocess_task = preprocess(message=message)
train_task = train(
dataset_one_path=preprocess_task.outputs["output_dataset_one"],
dataset_two=preprocess_task.outputs["output_dataset_two_path"],
imported_dataset=importer.output,
message=preprocess_task.outputs["output_parameter_path"],
num_steps=5,
)
read_task = read_artifact_input( # noqa: F841
train_task.outputs["generic_artifact"]
)
```
## Compile the pipeline
Next, compile the pipeline.
```
from kfp.v2 import compiler # noqa: F811
compiler.Compiler().compile(
pipeline_func=pipeline, package_path="lightweight_pipeline.json".replace(" ", "_")
)
```
## Run the pipeline
Next, run the pipeline.
```
DISPLAY_NAME = "shakespeare_" + TIMESTAMP
job = aip.PipelineJob(
display_name=DISPLAY_NAME,
template_path="lightweight_pipeline.json".replace(" ", "_"),
pipeline_root=PIPELINE_ROOT,
parameter_values={"message": "Hello, World"},
)
job.run()
```
Click on the generated link to see your run in the Cloud Console.
<!-- It should look something like this as it is running:
<a href="https://storage.googleapis.com/amy-jo/images/mp/automl_tabular_classif.png" target="_blank"><img src="https://storage.googleapis.com/amy-jo/images/mp/automl_tabular_classif.png" width="40%"/></a> -->
In the UI, many of the pipeline DAG nodes will expand or collapse when you click on them. Here is a partially-expanded view of the DAG (click image to see larger version).
<a href="https://storage.googleapis.com/amy-jo/images/mp/artifact_io2.png" target="_blank"><img src="https://storage.googleapis.com/amy-jo/images/mp/artifact_io2.png" width="95%"/></a>
# Cleaning up
To clean up all Google Cloud resources used in this project, you can [delete the Google Cloud
project](https://cloud.google.com/resource-manager/docs/creating-managing-projects#shutting_down_projects) you used for the tutorial.
Otherwise, you can delete the individual resources you created in this tutorial -- *Note:* this is auto-generated and not all resources may be applicable for this tutorial:
- Dataset
- Pipeline
- Model
- Endpoint
- Batch Job
- Custom Job
- Hyperparameter Tuning Job
- Cloud Storage Bucket
```
delete_dataset = True
delete_pipeline = True
delete_model = True
delete_endpoint = True
delete_batchjob = True
delete_customjob = True
delete_hptjob = True
delete_bucket = True
try:
if delete_model and "DISPLAY_NAME" in globals():
models = aip.Model.list(
filter=f"display_name={DISPLAY_NAME}", order_by="create_time"
)
model = models[0]
aip.Model.delete(model)
print("Deleted model:", model)
except Exception as e:
print(e)
try:
if delete_endpoint and "DISPLAY_NAME" in globals():
endpoints = aip.Endpoint.list(
filter=f"display_name={DISPLAY_NAME}_endpoint", order_by="create_time"
)
endpoint = endpoints[0]
endpoint.undeploy_all()
aip.Endpoint.delete(endpoint.resource_name)
print("Deleted endpoint:", endpoint)
except Exception as e:
print(e)
if delete_dataset and "DISPLAY_NAME" in globals():
if "text" == "tabular":
try:
datasets = aip.TabularDataset.list(
filter=f"display_name={DISPLAY_NAME}", order_by="create_time"
)
dataset = datasets[0]
aip.TabularDataset.delete(dataset.resource_name)
print("Deleted dataset:", dataset)
except Exception as e:
print(e)
if "text" == "image":
try:
datasets = aip.ImageDataset.list(
filter=f"display_name={DISPLAY_NAME}", order_by="create_time"
)
dataset = datasets[0]
aip.ImageDataset.delete(dataset.resource_name)
print("Deleted dataset:", dataset)
except Exception as e:
print(e)
if "text" == "text":
try:
datasets = aip.TextDataset.list(
filter=f"display_name={DISPLAY_NAME}", order_by="create_time"
)
dataset = datasets[0]
aip.TextDataset.delete(dataset.resource_name)
print("Deleted dataset:", dataset)
except Exception as e:
print(e)
if "text" == "video":
try:
datasets = aip.VideoDataset.list(
filter=f"display_name={DISPLAY_NAME}", order_by="create_time"
)
dataset = datasets[0]
aip.VideoDataset.delete(dataset.resource_name)
print("Deleted dataset:", dataset)
except Exception as e:
print(e)
try:
if delete_pipeline and "DISPLAY_NAME" in globals():
pipelines = aip.PipelineJob.list(
filter=f"display_name={DISPLAY_NAME}", order_by="create_time"
)
pipeline = pipelines[0]
aip.PipelineJob.delete(pipeline.resource_name)
print("Deleted pipeline:", pipeline)
except Exception as e:
print(e)
if delete_bucket and "BUCKET_NAME" in globals():
! gsutil rm -r $BUCKET_NAME
```
|
github_jupyter
|
# Classes
For more information on the magic methods of pytho classes, consult the docs: https://docs.python.org/3/reference/datamodel.html
```
class DumbClass:
""" This class is just meant to demonstrate the magic __repr__ method
"""
def __repr__(self):
""" I'm giving this method a docstring
"""
return("I'm representing an instance of my dumbclass")
dc = DumbClass()
print(dc)
dc
help(DumbClass)
class Stack:
""" A simple class implimenting some common features of Stack
objects
"""
def __init__(self, iterable=None):
""" Initializes Stack objects. If an iterable is provided,
add elements from the iterable to this Stack until the
iterable is exhausted
"""
self.head = None
self.size = 0
if(iterable is not None):
for item in iterable:
self.add(item)
def add(self, item):
""" Add an element to the top of the stack. This method will
modify self and return self.
"""
self.head = (item, self.head)
self.size += 1
return self
def pop(self):
""" remove the top item from the stack and return it
"""
if(len(self) > 0):
ret = self.head[0]
self.head = self.head[1]
self.size -= 1
return ret
return None
def __contains__(self, item):
""" Returns True if item is in self
"""
for i in self:
if(i == item):
return True
return False
def __len__(self):
""" Returns the number of items in self
"""
return self.size
def __iter__(self):
""" prepares this stack for iteration and returns self
"""
self.curr = self.head
return self
def __next__(self):
""" Returns items from the stack from top to bottom
"""
if(not hasattr(self, 'curr')):
iter(self)
if(self.curr is None):
raise StopIteration
else:
ret = self.curr[0]
self.curr = self.curr[1]
return ret
def __reversed__(self):
""" returns a copy of self with the stack turned upside
down
"""
return Stack(self)
def __add__(self, other):
""" Put self on top of other
"""
ret = Stack(reversed(other))
for item in reversed(self):
ret.add(item)
return ret
def __repr__(self):
""" Represent self as a string
"""
return f'Stack({str(list(self))})'
# Create a stack object and test some methods
x = Stack([3, 2])
print(x)
# adds an element to the top of the stack
print('\nLets add 1 to the stack')
x.add(1)
print(x)
# Removes the top most element
print('\nLets remove an item from the top of the stack')
item = x.pop()
print(item)
print(x)
# Removes the top most element
print('\nlets remove another item')
item = x.pop()
print(item)
print(x)
x = Stack([4,5,6])
# Because I implimented the __contains__ method,
# I can check if items are in stack objects
print(f'Does my stack contain 2? {2 in x}')
print(f'Does my stack contain 4? {4 in x}')
# Because I implimented the __len__ method,
# I can check how many items are in stack objects
print(f'How many elements are in my stack? {len(x)}')
# because my stack class has an __iter__ and __next__ methods
# I can iterate over stack objects
x = Stack([7,3,4])
print(f"Lets iterate over my stack : {x}")
for item in x:
print(item)
# Because my stack class has a __reversed__ method,
# I can easily reverse a stack object
print(f'I am flipping my stack upside down : {reversed(x)}')
# Because I implimented the __add__ method,
# I can add stacks together
x = Stack([4,5,6])
y = Stack([1,2,3])
print("I have two stacks")
print(f'x : {x}')
print(f'y : {y}')
print("Let's add them together")
print(f'x + y = {x + y}')
for item in (x + y):
print(item)
```
# Using the SqlAlchemy ORM
For more information, check out the documentation : https://docs.sqlalchemy.org/en/latest/orm/tutorial.html
```
from sqlalchemy import create_engine
from sqlalchemy.ext.declarative import declarative_base
from sqlalchemy import Column, Integer, String, Float, ForeignKey
from sqlalchemy.orm import Session, relationship
import pymysql
pymysql.install_as_MySQLdb()
# Sets an object to utilize the default declarative base in SQL Alchemy
Base = declarative_base()
# Lets define the owners table/class
class Owners(Base):
__tablename__ = 'owners'
id = Column(Integer, primary_key=True)
name = Column(String(255))
phone_number = Column(String(255))
pets = relationship("Pets", back_populates="owner")
def __repr__(self):
return f"<Owners(id={self.id}, name='{self.name}', phone_number='{self.phone_number}')>"
# Lets define the pets table/class
class Pets(Base):
__tablename__ = 'pets'
id = Column(Integer, primary_key=True)
name = Column(String(255))
owner_id = Column(Integer, ForeignKey('owners.id'))
owner = relationship("Owners", back_populates="pets")
def __repr__(self):
return f"<Pets(id={self.id}, name='{self.name}', owner_id={self.owner_id})>"
# Lets connect to my database
# engine = create_engine("sqlite:///pets.sqlite")
engine = create_engine("mysql://root@localhost/review_db")
# conn = engine.connect()
Base.metadata.create_all(engine)
session = Session(bind=engine)
# Lets create me
me = Owners(name='Kenton', phone_number='867-5309')
session.add(me)
session.commit()
# Now lets add my dog
my_dog = Pets(name='Saxon', owner_id=me.id)
session.add(my_dog)
session.commit()
# We can query the tables using the session object from earlier
# Lets just get all the data
all_owners = list(session.query(Owners))
all_pets = list(session.query(Pets))
print(all_owners)
print(all_pets)
me = all_owners[0]
rio = all_pets[0]
# Because we are using an ORM and have defined relations,
# we can easily and intuitively access related data
print(me.pets)
print(rio.owner)
```
|
github_jupyter
|
# Estimation on real data using MSM
```
from consav import runtools
runtools.write_numba_config(disable=0,threads=4)
%matplotlib inline
%load_ext autoreload
%autoreload 2
# Local modules
from Model import RetirementClass
import figs
import SimulatedMinimumDistance as SMD
# Global modules
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
```
### Data
```
data = pd.read_excel('SASdata/moments.xlsx')
mom_data = data['mom'].to_numpy()
se = data['se'].to_numpy()
obs = data['obs'].to_numpy()
se = se/np.sqrt(obs)
se[se>0] = 1/se[se>0]
factor = np.ones(len(se))
factor[-15:] = 4
W = np.eye(len(se))*se*factor
cov = pd.read_excel('SASdata/Cov.xlsx')
Omega = cov*obs
Nobs = np.median(obs)
```
### Set up estimation
```
single_kwargs = {'simN': int(1e5), 'simT': 68-53+1}
Couple = RetirementClass(couple=True, single_kwargs=single_kwargs,
simN=int(1e5), simT=68-53+1)
Couple.solve()
Couple.simulate()
def mom_fun(Couple):
return SMD.MomFun(Couple)
est_par = ["alpha_0_male", "alpha_0_female", "sigma_eta", "pareto_w", "phi_0_male"]
smd = SMD.SimulatedMinimumDistance(Couple,mom_data,mom_fun,est_par=est_par)
```
### Estimate
```
theta0 = SMD.start(9,bounds=[(0,1), (0,1), (0.2,0.8), (0.2,0.8), (0,2)])
theta0
smd.MultiStart(theta0,W)
theta = smd.est
smd.MultiStart(theta0,W)
theta = smd.est
```
### Save parameters
```
est_par.append('phi_0_female')
thetaN = list(theta)
thetaN.append(Couple.par.phi_0_male)
SMD.save_est(est_par,thetaN,name='baseline2')
```
### Standard errors
```
est_par = ["alpha_0_male", "alpha_0_female", "sigma_eta", "pareto_w", "phi_0_male"]
smd = SMD.SimulatedMinimumDistance(Couple,mom_data,mom_fun,est_par=est_par)
theta = list(SMD.load_est('baseline2').values())
theta = theta[:5]
smd.obj_fun(theta,W)
np.round(theta,3)
Nobs = np.quantile(obs,0.25)
smd.std_error(theta,Omega,W,Nobs,Couple.par.simN*2/Nobs)
# Nobs = lower quartile
np.round(smd.std,3)
# Nobs = lower quartile
np.round(smd.std,3)
Nobs = np.quantile(obs,0.25)
smd.std_error(theta,Omega,W,Nobs,Couple.par.simN*2/Nobs)
# Nobs = median
np.round(smd.std,3)
```
### Model fit
```
smd.obj_fun(theta,W)
jmom = pd.read_excel('SASdata/joint_moments_ad.xlsx')
for i in range(-2,3):
data = jmom[jmom.Age_diff==i]['ssh'].to_numpy()
plt.bar(np.arange(-7,8), data, label='Data')
plt.plot(np.arange(-7,8),SMD.joint_moments_ad(Couple,i),'k--', label='Predicted')
#plt.ylim(0,0.4)
plt.legend()
plt.show()
figs.MyPlot(figs.model_fit_marg(smd,0,0),ylim=[-0.01,0.4],linewidth=3).savefig('figs/ModelFit/MargWomenSingle2.png')
figs.MyPlot(figs.model_fit_marg(smd,1,0),ylim=[-0.01,0.4],linewidth=3).savefig('figs/ModelFit/MargMenSingle2.png')
figs.MyPlot(figs.model_fit_marg(smd,0,1),ylim=[-0.01,0.4],linewidth=3).savefig('figs/ModelFit/MargWomenCouple2.png')
figs.MyPlot(figs.model_fit_marg(smd,1,1),ylim=[-0.01,0.4],linewidth=3).savefig('figs/ModelFit/MargMenCouple2.png')
figs.model_fit_joint(smd).savefig('figs/ModelFit/Joint2')
theta[4] = 1
smd.obj_fun(theta,W)
dist1 = smd.mom_sim[44:]
theta[4] = 2
smd.obj_fun(theta,W)
dist2 = smd.mom_sim[44:]
theta[4] = 3
smd.obj_fun(theta,W)
dist3 = smd.mom_sim[44:]
dist_data = mom_data[44:]
figs.model_fit_joint_many(dist_data,dist1,dist2,dist3).savefig('figs/ModelFit/JointMany2')
```
### Sensitivity
```
est_par_tex = [r'$\alpha^m$', r'$\alpha^f$', r'$\sigma$', r'$\lambda$', r'$\phi$']
fixed_par = ['R', 'rho', 'beta', 'gamma', 'v',
'priv_pension_male', 'priv_pension_female', 'g_adjust', 'pi_adjust_m', 'pi_adjust_f']
fixed_par_tex = [r'$R$', r'$\rho$', r'$\beta$', r'$\gamma$', r'$v$',
r'$PPW^m$', r'$PPW^f$', r'$g$', r'$\pi^m$', r'$\pi^f$']
smd.recompute=True
smd.sensitivity(theta,W,fixed_par)
figs.sens_fig_tab(smd.sens2[:,:5],smd.sens2e[:,:5],theta,
est_par_tex,fixed_par_tex[:5]).savefig('figs/ModelFit/CouplePref2.png')
figs.sens_fig_tab(smd.sens2[:,5:],smd.sens2e[:,5:],theta,
est_par_tex,fixed_par_tex[5:]).savefig('figs/modelFit/CoupleCali2.png')
smd.recompute=True
smd.sensitivity(theta,W,fixed_par)
figs.sens_fig_tab(smd.sens2[:,:5],smd.sens2e[:,:5],theta,
est_par_tex,fixed_par_tex[:5]).savefig('figs/ModelFit/CouplePref.png')
figs.sens_fig_tab(smd.sens2[:,5:],smd.sens2e[:,5:],theta,
est_par_tex,fixed_par_tex[5:]).savefig('figs/modelFit/CoupleCali.png')
```
### Recalibrate model (phi=0)
```
Couple.par.phi_0_male = 0
Couple.par.phi_0_female = 0
est_par = ["alpha_0_male", "alpha_0_female", "sigma_eta", "pareto_w"]
smd = SMD.SimulatedMinimumDistance(Couple,mom_data,mom_fun,est_par=est_par)
theta0 = SMD.start(4,bounds=[(0,1), (0,1), (0.2,0.8), (0.2,0.8)])
smd.MultiStart(theta0,W)
theta = smd.est
est_par.append("phi_0_male")
est_par.append("phi_0_female")
theta = list(theta)
theta.append(Couple.par.phi_0_male)
theta.append(Couple.par.phi_0_male)
SMD.save_est(est_par,theta,name='phi0')
smd.obj_fun(theta,W)
figs.MyPlot(figs.model_fit_marg(smd,0,0),ylim=[-0.01,0.4],linewidth=3).savefig('figs/ModelFit/MargWomenSingle_phi0.png')
figs.MyPlot(figs.model_fit_marg(smd,1,0),ylim=[-0.01,0.4],linewidth=3).savefig('figs/ModelFit/MargMenSingle_phi0.png')
figs.MyPlot(figs.model_fit_marg(smd,0,1),ylim=[-0.01,0.4],linewidth=3).savefig('figs/ModelFit/MargWomenCouple_phi0.png')
figs.MyPlot(figs.model_fit_marg(smd,1,1),ylim=[-0.01,0.4],linewidth=3).savefig('figs/ModelFit/MargMenCoupleW_phi0.png')
figs.model_fit_joint(smd).savefig('figs/ModelFit/Joint_phi0')
```
### Recalibrate model (phi high)
```
Couple.par.phi_0_male = 1.187
Couple.par.phi_0_female = 1.671
Couple.par.pareto_w = 0.8
est_par = ["alpha_0_male", "alpha_0_female", "sigma_eta"]
smd = SMD.SimulatedMinimumDistance(Couple,mom_data,mom_fun,est_par=est_par)
theta0 = SMD.start(4,bounds=[(0.2,0.6), (0.2,0.6), (0.4,0.8)])
theta0
smd.MultiStart(theta0,W)
theta = smd.est
est_par.append("phi_0_male")
est_par.append("phi_0_female")
theta = list(theta)
theta.append(Couple.par.phi_0_male)
theta.append(Couple.par.phi_0_male)
SMD.save_est(est_par,theta,name='phi_high')
smd.obj_fun(theta,W)
figs.MyPlot(figs.model_fit_marg(smd,0,0),ylim=[-0.01,0.4],linewidth=3).savefig('figs/ModelFit/MargWomenSingle_phi_high.png')
figs.MyPlot(figs.model_fit_marg(smd,1,0),ylim=[-0.01,0.4],linewidth=3).savefig('figs/ModelFit/MargMenSingle_phi_high.png')
figs.MyPlot(figs.model_fit_marg(smd,0,1),ylim=[-0.01,0.4],linewidth=3).savefig('figs/ModelFit/MargWomenCouple_phi_high.png')
figs.MyPlot(figs.model_fit_marg(smd,1,1),ylim=[-0.01,0.4],linewidth=3).savefig('figs/ModelFit/MargMenCoupleW_phi_high.png')
figs.model_fit_joint(smd).savefig('figs/ModelFit/Joint_phi_high')
```
|
github_jupyter
|
<a href="https://colab.research.google.com/github/clemencia/ML4PPGF_UERJ/blob/master/Exemplos_DR/Exercicios_DimensionalReduction.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
#Mais Exercícios de Redução de Dimensionalidade
Baseado no livro "Python Data Science Handbook" de Jake VanderPlas
https://jakevdp.github.io/PythonDataScienceHandbook/
Usando os dados de rostos do scikit-learn, utilizar as tecnicas de aprendizado de variedade para comparação.
```
from sklearn.datasets import fetch_lfw_people
faces = fetch_lfw_people(min_faces_per_person=30)
faces.data.shape
```
A base de dados tem 2300 imagens de rostos com 2914 pixels cada (47x62)
Vamos visualizar as primeiras 32 dessas imagens
```
import numpy as np
from numpy import random
from matplotlib import pyplot as plt
%matplotlib inline
fig, ax = plt.subplots(5, 8, subplot_kw=dict(xticks=[], yticks=[]))
for i, axi in enumerate(ax.flat):
axi.imshow(faces.images[i], cmap='gray')
```
Podemos ver se com redução de dimensionalidade é possível entender algumas das caraterísticas das imagens.
```
from sklearn.decomposition import PCA
model0 = PCA(n_components=0.95)
X_pca=model0.fit_transform(faces.data)
plt.plot(np.cumsum(model0.explained_variance_ratio_))
plt.xlabel('n components')
plt.ylabel('cumulative variance')
plt.grid(True)
print("Numero de componentes para 95% de variância preservada:",model0.n_components_)
```
Quer dizer que para ter 95% de variância preservada na dimensionalidade reduzida precisamos mais de 170 dimensões.
As novas "coordenadas" podem ser vistas em quadros de 9x19 pixels
```
def plot_faces(instances, **options):
fig, ax = plt.subplots(5, 8, subplot_kw=dict(xticks=[], yticks=[]))
sizex = 9
sizey = 19
images = [instance.reshape(sizex,sizey) for instance in instances]
for i,axi in enumerate(ax.flat):
axi.imshow(images[i], cmap = "gray", **options)
axi.axis("off")
```
Vamos visualizar a compressão dessas imagens
```
plot_faces(X_pca,aspect="auto")
```
A opção ```svd_solver=randomized``` faz o PCA achar as $d$ componentes principais mais rápido quando $d \ll n$, mas o $d$ é fixo. Tem alguma vantagem usar para compressão das imagens de rosto? Teste!
## Aplicar Isomap para vizualizar em 2D
```
from sklearn.manifold import Isomap
iso = Isomap(n_components=2)
X_iso = iso.fit_transform(faces.data)
X_iso.shape
from matplotlib import offsetbox
def plot_projection(data,proj,images=None,ax=None,thumb_frac=0.5,cmap="gray"):
ax = ax or plt.gca()
ax.plot(proj[:, 0], proj[:, 1], '.k')
if images is not None:
min_dist_2 = (thumb_frac * max(proj.max(0) - proj.min(0))) ** 2
shown_images = np.array([2 * proj.max(0)])
for i in range(data.shape[0]):
dist = np.sum((proj[i] - shown_images) ** 2, 1)
if np.min(dist) < min_dist_2:
# don't show points that are too close
continue
shown_images = np.vstack([shown_images, proj[i]])
imagebox = offsetbox.AnnotationBbox(
offsetbox.OffsetImage(images[i], cmap=cmap),
proj[i])
ax.add_artist(imagebox)
def plot_components(data, model, images=None, ax=None,
thumb_frac=0.05,cmap="gray"):
proj = model.fit_transform(data)
plot_projection(data,proj,images,ax,thumb_frac,cmap)
fig, ax = plt.subplots(figsize=(10, 10))
plot_projection(faces.data,X_iso,images=faces.images[:, ::2, ::2],thumb_frac=0.07)
ax.axis("off")
```
As imagens mais a direita são mais escuras que as da direita (seja iluminação ou cor da pele), as imagens mais embaixo estão orientadas com o rosto à esquerda e as de cima com o rosto à direita.
## Exercícios:
1. Aplicar LLE à base de dados dos rostos e visualizar em mapa 2D, em particular a versão "modificada" ([link](https://scikit-learn.org/stable/modules/manifold.html#modified-locally-linear-embedding))
2. Aplicar t-SNE à base de dados dos rostos e visualizar em mapa 2D
3. Escolher mais uma implementação de aprendizado de variedade do Scikit-Learn ([link](https://scikit-learn.org/stable/modules/manifold.html)) e aplicar ao mesmo conjunto. (*Hessian, LTSA, Spectral*)
Qual funciona melhor? Adicione contador de tempo para comparar a duração de cada ajuste.
## Kernel PCA e sequências
Vamos ver novamente o exemplo do rocambole
```
import numpy as np
from numpy import random
from matplotlib import pyplot as plt
%matplotlib inline
from mpl_toolkits.mplot3d import Axes3D
from sklearn.datasets import make_swiss_roll
X, t = make_swiss_roll(n_samples=1000, noise=0.2, random_state=42)
axes = [-11.5, 14, -2, 23, -12, 15]
fig = plt.figure(figsize=(12, 10))
ax = fig.add_subplot(111, projection='3d')
ax.scatter(X[:, 0], X[:, 1], X[:, 2], c=t, cmap="plasma")
ax.view_init(10, -70)
ax.set_xlabel("$x_1$", fontsize=18)
ax.set_ylabel("$x_2$", fontsize=18)
ax.set_zlabel("$x_3$", fontsize=18)
ax.set_xlim(axes[0:2])
ax.set_ylim(axes[2:4])
ax.set_zlim(axes[4:6])
```
Como foi no caso do SVM, pode se aplicar uma transformação de *kernel*, para ter um novo espaço de *features* onde pode ser aplicado o PCA. Embaixo o exemplo de PCA com kernel linear (equiv. a aplicar o PCA), RBF (*radial basis function*) e *sigmoide* (i.e. logístico).
```
from sklearn.decomposition import KernelPCA
lin_pca = KernelPCA(n_components = 2, kernel="linear", fit_inverse_transform=True)
rbf_pca = KernelPCA(n_components = 2, kernel="rbf", gamma=0.0433, fit_inverse_transform=True)
sig_pca = KernelPCA(n_components = 2, kernel="sigmoid", gamma=0.001, coef0=1, fit_inverse_transform=True)
plt.figure(figsize=(11, 4))
for subplot, pca, title in ((131, lin_pca, "Linear kernel"), (132, rbf_pca, "RBF kernel, $\gamma=0.04$"), (133, sig_pca, "Sigmoid kernel, $\gamma=10^{-3}, r=1$")):
X_reduced = pca.fit_transform(X)
if subplot == 132:
X_reduced_rbf = X_reduced
plt.subplot(subplot)
plt.title(title, fontsize=14)
plt.scatter(X_reduced[:, 0], X_reduced[:, 1], c=t, cmap=plt.cm.hot)
plt.xlabel("$z_1$", fontsize=18)
if subplot == 131:
plt.ylabel("$z_2$", fontsize=18, rotation=0)
plt.grid(True)
```
## Selecionar um Kernel e Otimizar Hiperparâmetros
Como estos são algoritmos não supervisionados, no existe uma forma "obvia" de determinar a sua performance.
Porém a redução de dimensionalidade muitas vezes é um passo preparatório para uma outra tarefa de aprendizado supervisionado. Nesse caso é possível usar o ```GridSearchCV``` para avaliar a melhor performance no passo seguinte, com um ```Pipeline```. A classificação será em base ao valor do ```t``` com limite arbitrário de 6.9.
```
from sklearn.model_selection import GridSearchCV
from sklearn.linear_model import LogisticRegression
from sklearn.pipeline import Pipeline
y = t>6.9
clf = Pipeline([
("kpca", KernelPCA(n_components=2)),
("log_reg", LogisticRegression(solver="liblinear"))
])
param_grid = [{
"kpca__gamma": np.linspace(0.03, 0.05, 10),
"kpca__kernel": ["rbf", "sigmoid"]
}]
grid_search = GridSearchCV(clf, param_grid, cv=3)
grid_search.fit(X, y)
print(grid_search.best_params_)
```
### Exercício :
Varie o valor do corte em ```t``` e veja tem faz alguma diferência para o kernel e hiperparámetros ideais.
### Inverter a transformação e erro de Reconstrução
Outra opção seria escolher o kernel e hiperparâmetros que tem o menor erro de reconstrução.
O seguinte código, com opção ```fit_inverse_transform=True```, vai fazer junto com o kPCA um modelo de regressão com as instancias projetadas (```X_reduced```) de treino e as originais (```X```) de target. O resultado do ```inverse_transform``` será uma tentativa de reconstrução no espaço original .
```
rbf_pca = KernelPCA(n_components = 2, kernel="rbf", gamma=13./300.,
fit_inverse_transform=True)
X_reduced = rbf_pca.fit_transform(X)
X_preimage = rbf_pca.inverse_transform(X_reduced)
X_preimage.shape
axes = [-11.5, 14, -2, 23, -12, 15]
fig = plt.figure(figsize=(12, 10))
ax = fig.add_subplot(111, projection='3d')
ax.scatter(X_preimage[:, 0], X_preimage[:, 1], X_preimage[:, 2], c=t, cmap="plasma")
ax.view_init(10, -70)
ax.set_xlabel("$x_1$", fontsize=18)
ax.set_ylabel("$x_2$", fontsize=18)
ax.set_zlabel("$x_3$", fontsize=18)
ax.set_xlim(axes[0:2])
ax.set_ylim(axes[2:4])
ax.set_zlim(axes[4:6])
```
Então é possível computar o "erro" entre o dataset reconstruido e o original (MSE).
```
from sklearn.metrics import mean_squared_error as mse
print(mse(X,X_preimage))
```
## Exercício :
Usar *grid search* com validação no valor do MSE para achar o kernel e hiperparámetros que minimizam este erro, para o exemplo do rocambole.
|
github_jupyter
|
# Working with Pytrees
[](https://colab.research.google.com/github/google/jax/blob/main/docs/jax-101/05.1-pytrees.ipynb)
*Author: Vladimir Mikulik*
Often, we want to operate on objects that look like dicts of arrays, or lists of lists of dicts, or other nested structures. In JAX, we refer to these as *pytrees*, but you can sometimes see them called *nests*, or just *trees*.
JAX has built-in support for such objects, both in its library functions as well as through the use of functions from [`jax.tree_utils`](https://jax.readthedocs.io/en/latest/jax.tree_util.html) (with the most common ones also available as `jax.tree_*`). This section will explain how to use them, give some useful snippets and point out common gotchas.
## What is a pytree?
As defined in the [JAX pytree docs](https://jax.readthedocs.io/en/latest/pytrees.html):
> a pytree is a container of leaf elements and/or more pytrees. Containers include lists, tuples, and dicts. A leaf element is anything that’s not a pytree, e.g. an array. In other words, a pytree is just a possibly-nested standard or user-registered Python container. If nested, note that the container types do not need to match. A single “leaf”, i.e. a non-container object, is also considered a pytree.
Some example pytrees:
```
import jax
import jax.numpy as jnp
example_trees = [
[1, 'a', object()],
(1, (2, 3), ()),
[1, {'k1': 2, 'k2': (3, 4)}, 5],
{'a': 2, 'b': (2, 3)},
jnp.array([1, 2, 3]),
]
# Let's see how many leaves they have:
for pytree in example_trees:
leaves = jax.tree_leaves(pytree)
print(f"{repr(pytree):<45} has {len(leaves)} leaves: {leaves}")
```
We've also introduced our first `jax.tree_*` function, which allowed us to extract the flattened leaves from the trees.
## Why pytrees?
In machine learning, some places where you commonly find pytrees are:
* Model parameters
* Dataset entries
* RL agent observations
They also often arise naturally when working in bulk with datasets (e.g., lists of lists of dicts).
## Common pytree functions
The most commonly used pytree functions are `jax.tree_map` and `jax.tree_multimap`. They work analogously to Python's native `map`, but on entire pytrees.
For functions with one argument, use `jax.tree_map`:
```
list_of_lists = [
[1, 2, 3],
[1, 2],
[1, 2, 3, 4]
]
jax.tree_map(lambda x: x*2, list_of_lists)
```
To use functions with more than one argument, use `jax.tree_multimap`:
```
another_list_of_lists = list_of_lists
jax.tree_multimap(lambda x, y: x+y, list_of_lists, another_list_of_lists)
```
For `tree_multimap`, the structure of the inputs must exactly match. That is, lists must have the same number of elements, dicts must have the same keys, etc.
## Example: ML model parameters
A simple example of training an MLP displays some ways in which pytree operations come in useful:
```
import numpy as np
def init_mlp_params(layer_widths):
params = []
for n_in, n_out in zip(layer_widths[:-1], layer_widths[1:]):
params.append(
dict(weights=np.random.normal(size=(n_in, n_out)) * np.sqrt(2/n_in),
biases=np.ones(shape=(n_out,))
)
)
return params
params = init_mlp_params([1, 128, 128, 1])
```
We can use `jax.tree_map` to check that the shapes of our parameters are what we expect:
```
jax.tree_map(lambda x: x.shape, params)
```
Now, let's train our MLP:
```
def forward(params, x):
*hidden, last = params
for layer in hidden:
x = jax.nn.relu(x @ layer['weights'] + layer['biases'])
return x @ last['weights'] + last['biases']
def loss_fn(params, x, y):
return jnp.mean((forward(params, x) - y) ** 2)
LEARNING_RATE = 0.0001
@jax.jit
def update(params, x, y):
grads = jax.grad(loss_fn)(params, x, y)
# Note that `grads` is a pytree with the same structure as `params`.
# `jax.grad` is one of the many JAX functions that has
# built-in support for pytrees.
# This is handy, because we can apply the SGD update using tree utils:
return jax.tree_multimap(
lambda p, g: p - LEARNING_RATE * g, params, grads
)
import matplotlib.pyplot as plt
xs = np.random.normal(size=(128, 1))
ys = xs ** 2
for _ in range(1000):
params = update(params, xs, ys)
plt.scatter(xs, ys)
plt.scatter(xs, forward(params, xs), label='Model prediction')
plt.legend();
```
## Custom pytree nodes
So far, we've only been considering pytrees of lists, tuples, and dicts; everything else is considered a leaf. Therefore, if you define my own container class, it will be considered a leaf, even if it has trees inside it:
```
class MyContainer:
"""A named container."""
def __init__(self, name: str, a: int, b: int, c: int):
self.name = name
self.a = a
self.b = b
self.c = c
jax.tree_leaves([
MyContainer('Alice', 1, 2, 3),
MyContainer('Bob', 4, 5, 6)
])
```
Accordingly, if we try to use a tree map expecting our leaves to be the elements inside the container, we will get an error:
```
jax.tree_map(lambda x: x + 1, [
MyContainer('Alice', 1, 2, 3),
MyContainer('Bob', 4, 5, 6)
])
```
To solve this, we need to register our container with JAX by telling it how to flatten and unflatten it:
```
from typing import Tuple, Iterable
def flatten_MyContainer(container) -> Tuple[Iterable[int], str]:
"""Returns an iterable over container contents, and aux data."""
flat_contents = [container.a, container.b, container.c]
# we don't want the name to appear as a child, so it is auxiliary data.
# auxiliary data is usually a description of the structure of a node,
# e.g., the keys of a dict -- anything that isn't a node's children.
aux_data = container.name
return flat_contents, aux_data
def unflatten_MyContainer(
aux_data: str, flat_contents: Iterable[int]) -> MyContainer:
"""Converts aux data and the flat contents into a MyContainer."""
return MyContainer(aux_data, *flat_contents)
jax.tree_util.register_pytree_node(
MyContainer, flatten_MyContainer, unflatten_MyContainer)
jax.tree_leaves([
MyContainer('Alice', 1, 2, 3),
MyContainer('Bob', 4, 5, 6)
])
```
Modern Python comes equipped with helpful tools to make defining containers easier. Some of these will work with JAX out-of-the-box, but others require more care. For instance:
```
from typing import NamedTuple, Any
class MyOtherContainer(NamedTuple):
name: str
a: Any
b: Any
c: Any
# Since `tuple` is already registered with JAX, and NamedTuple is a subclass,
# this will work out-of-the-box:
jax.tree_leaves([
MyOtherContainer('Alice', 1, 2, 3),
MyOtherContainer('Bob', 4, 5, 6)
])
```
Notice that the `name` field now appears as a leaf, as all tuple elements are children. That's the price we pay for not having to register the class the hard way.
## Common pytree gotchas and patterns
### Gotchas
#### Mistaking nodes for leaves
A common problem to look out for is accidentally introducing tree nodes instead of leaves:
```
a_tree = [jnp.zeros((2, 3)), jnp.zeros((3, 4))]
# Try to make another tree with ones instead of zeros
shapes = jax.tree_map(lambda x: x.shape, a_tree)
jax.tree_map(jnp.ones, shapes)
```
What happened is that the `shape` of an array is a tuple, which is a pytree node, with its elements as leaves. Thus, in the map, instead of calling `jnp.ones` on e.g. `(2, 3)`, it's called on `2` and `3`.
The solution will depend on the specifics, but there are two broadly applicable options:
* rewrite the code to avoid the intermediate `tree_map`.
* convert the tuple into an `np.array` or `jnp.array`, which makes the entire
sequence a leaf.
#### Handling of None
`jax.tree_utils` treats `None` as a node without children, not as a leaf:
```
jax.tree_leaves([None, None, None])
```
### Patterns
#### Transposing trees
If you would like to transpose a pytree, i.e. turn a list of trees into a tree of lists, you can do so using `jax.tree_multimap`:
```
def tree_transpose(list_of_trees):
"""Convert a list of trees of identical structure into a single tree of lists."""
return jax.tree_multimap(lambda *xs: list(xs), *list_of_trees)
# Convert a dataset from row-major to column-major:
episode_steps = [dict(t=1, obs=3), dict(t=2, obs=4)]
tree_transpose(episode_steps)
```
For more complicated transposes, JAX provides `jax.tree_transpose`, which is more verbose, but allows you specify the structure of the inner and outer Pytree for more flexibility:
```
jax.tree_transpose(
outer_treedef = jax.tree_structure([0 for e in episode_steps]),
inner_treedef = jax.tree_structure(episode_steps[0]),
pytree_to_transpose = episode_steps
)
```
## More Information
For more information on pytrees in JAX and the operations that are available, see the [Pytrees](https://jax.readthedocs.io/en/latest/pytrees.html) section in the JAX documentation.
|
github_jupyter
|
```
import CNN2Head_input
import tensorflow as tf
import numpy as np
SAVE_FOLDER = '/home/ubuntu/coding/cnn/multi-task-learning/save/current'
_, smile_test_data = CNN2Head_input.getSmileImage()
_, gender_test_data = CNN2Head_input.getGenderImage()
_, age_test_data = CNN2Head_input.getAgeImage()
def eval_smile_gender_age_test(nbof_crop):
nbof_smile = len(smile_test_data)
nbof_gender = len(gender_test_data)
nbof_age = len(age_test_data)
nbof_true_smile = 0
nbof_true_gender = 0
nbof_true_age = 0
sess = tf.InteractiveSession()
saver = tf.train.import_meta_graph(SAVE_FOLDER + '/model.ckpt.meta')
saver.restore(sess, SAVE_FOLDER + "/model.ckpt")
x_smile = tf.get_collection('x_smile')[0]
x_gender = tf.get_collection('x_gender')[0]
x_age = tf.get_collection('x_age')[0]
keep_prob_smile_fc1 = tf.get_collection('keep_prob_smile_fc1')[0]
keep_prob_gender_fc1 = tf.get_collection('keep_prob_gender_fc1')[0]
keep_prob_age_fc1 = tf.get_collection('keep_prob_age_fc1')[0]
keep_prob_smile_fc2 = tf.get_collection('keep_prob_smile_fc2')[0]
keep_prob_gender_fc2 = tf.get_collection('keep_prob_emotion_fc2')[0]
keep_prob_age_fc2 = tf.get_collection('keep_prob_age_fc2')[0]
y_smile_conv = tf.get_collection('y_smile_conv')[0]
y_gender_conv = tf.get_collection('y_gender_conv')[0]
y_age_conv = tf.get_collection('y_age_conv')[0]
is_training = tf.get_collection('is_training')[0]
for i in range(nbof_smile):
smile = np.zeros([1,48,48,1])
smile[0] = smile_test_data[i % 1000][0]
smile_label = smile_test_data[i % 1000][1]
gender = np.zeros([1,48,48,1])
gender[0] = gender_test_data[i % 1000][0]
gender_label = gender_test_data[i % 1000][1]
age = np.zeros([1,48,48,1])
age[0] = age_test_data[i % 1000][0]
age_label = age_test_data[i % 1000][1]
y_smile_pred = np.zeros([2])
y_gender_pred = np.zeros([2])
y_age_pred = np.zeros([4])
for _ in range(nbof_crop):
x_smile_ = CNN2Head_input.random_crop(smile, (48, 48), 10)
x_gender_ = CNN2Head_input.random_crop(gender,(48, 48), 10)
x_age_ = CNN2Head_input.random_crop(age,(48, 48), 10)
y1 = y_smile_conv.eval(feed_dict={x_smile: x_smile_,
x_gender: x_gender_,
x_age: x_age_,
keep_prob_smile_fc1: 1,
keep_prob_smile_fc2: 1,
keep_prob_gender_fc1: 1,
keep_prob_gender_fc2: 1,
keep_prob_age_fc1: 1,
keep_prob_age_fc2: 1,
is_training: False})
y2 = y_gender_conv.eval(feed_dict={x_smile: x_smile_,
x_gender: x_gender_,
x_age: x_age_,
keep_prob_smile_fc1: 1,
keep_prob_smile_fc2: 1,
keep_prob_gender_fc1: 1,
keep_prob_gender_fc2: 1,
keep_prob_age_fc1: 1,
keep_prob_age_fc2: 1,
is_training: False})
y3 = y_age_conv.eval(feed_dict={x_smile: x_smile_,
x_gender: x_gender_,
x_age: x_age_,
keep_prob_smile_fc1: 1,
keep_prob_smile_fc2: 1,
keep_prob_gender_fc1: 1,
keep_prob_gender_fc2: 1,
keep_prob_age_fc1: 1,
keep_prob_age_fc2: 1,
is_training: False})
y_smile_pred += y1[0]
y_gender_pred += y2[0]
y_age_pred += y3[0]
predict_smile = np.argmax(y_smile_pred)
predict_gender = np.argmax(y_gender_pred)
predict_age = np.argmax(y_age_pred)
if (predict_smile == smile_label) & (i < 1000):
nbof_true_smile += 1
if (predict_gender == gender_label):
nbof_true_gender += 1
if (predict_age == age_label):
nbof_true_age += 1
return nbof_true_smile * 100.0 / nbof_smile, nbof_true_gender * 100.0 / nbof_gender, nbof_true_age * 100.0 / nbof_age
def evaluate(nbof_crop):
print('Testing phase...............................')
smile_acc, gender_acc, age_acc = eval_smile_gender_age_test(nbof_crop)
print('Smile test accuracy: ',str(smile_acc))
print('Gender test accuracy: ', str(gender_acc))
print('Age test accuracy: ', str(age_acc))
evaluate(10)
```
|
github_jupyter
|
# Problem Simulation Tutorial
```
import pyblp
import numpy as np
import pandas as pd
pyblp.options.digits = 2
pyblp.options.verbose = False
pyblp.__version__
```
Before configuring and solving a problem with real data, it may be a good idea to perform Monte Carlo analysis on simulated data to verify that it is possible to accurately estimate model parameters. For example, before configuring and solving the example problems in the prior tutorials, it may have been a good idea to simulate data according to the assumed models of supply and demand. During such Monte Carlo anaysis, the data would only be used to determine sample sizes and perhaps to choose reasonable true parameters.
Simulations are configured with the :class:`Simulation` class, which requires many of the same inputs as :class:`Problem`. The two main differences are:
1. Variables in formulations that cannot be loaded from `product_data` or `agent_data` will be drawn from independent uniform distributions.
2. True parameters and the distribution of unobserved product characteristics are specified.
First, we'll use :func:`build_id_data` to build market and firm IDs for a model in which there are $T = 50$ markets, and in each market $t$, a total of $J_t = 20$ products produced by $F = 10$ firms.
```
id_data = pyblp.build_id_data(T=50, J=20, F=10)
```
Next, we'll create an :class:`Integration` configuration to build agent data according to a Gauss-Hermite product rule that exactly integrates polynomials of degree $2 \times 9 - 1 = 17$ or less.
```
integration = pyblp.Integration('product', 9)
integration
```
We'll then pass these data to :class:`Simulation`. We'll use :class:`Formulation` configurations to create an $X_1$ that consists of a constant, prices, and an exogenous characteristic; an $X_2$ that consists only of the same exogenous characteristic; and an $X_3$ that consists of the common exogenous characteristic and a cost-shifter.
```
simulation = pyblp.Simulation(
product_formulations=(
pyblp.Formulation('1 + prices + x'),
pyblp.Formulation('0 + x'),
pyblp.Formulation('0 + x + z')
),
beta=[1, -2, 2],
sigma=1,
gamma=[1, 4],
product_data=id_data,
integration=integration,
seed=0
)
simulation
```
When :class:`Simulation` is initialized, it constructs :attr:`Simulation.agent_data` and simulates :attr:`Simulation.product_data`.
The :class:`Simulation` can be further configured with other arguments that determine how unobserved product characteristics are simulated and how marginal costs are specified.
At this stage, simulated variables are not consistent with true parameters, so we still need to solve the simulation with :meth:`Simulation.replace_endogenous`. This method replaced simulated prices and market shares with values that are consistent with the true parameters. Just like :meth:`ProblemResults.compute_prices`, to do so it iterates over the $\zeta$-markup equation from :ref:`references:Morrow and Skerlos (2011)`.
```
simulation_results = simulation.replace_endogenous()
simulation_results
```
Now, we can try to recover the true parameters by creating and solving a :class:`Problem`.
The convenience method :meth:`SimulationResults.to_problem` constructs some basic "sums of characteristics" BLP instruments that are functions of all exogenous numerical variables in the problem. In this example, excluded demand-side instruments are the cost-shifter `z` and traditional BLP instruments constructed from `x`. Excluded supply-side instruments are traditional BLP instruments constructed from `x` and `z`.
```
problem = simulation_results.to_problem()
problem
```
We'll choose starting values that are half the true parameters so that the optimization routine has to do some work. Note that since we're jointly estimating the supply side, we need to provide an initial value for the linear coefficient on prices because this parameter cannot be concentrated out of the problem (unlike linear coefficients on exogenous characteristics).
```
results = problem.solve(
sigma=0.5 * simulation.sigma,
pi=0.5 * simulation.pi,
beta=[None, 0.5 * simulation.beta[1], None],
optimization=pyblp.Optimization('l-bfgs-b', {'gtol': 1e-5})
)
results
```
The parameters seem to have been estimated reasonably well.
```
np.c_[simulation.beta, results.beta]
np.c_[simulation.gamma, results.gamma]
np.c_[simulation.sigma, results.sigma]
```
In addition to checking that the configuration for a model based on actual data makes sense, the :class:`Simulation` class can also be a helpful tool for better understanding under what general conditions BLP models can be accurately estimated. Simulations are also used extensively in pyblp's test suite.
|
github_jupyter
|
<a href="https://colab.research.google.com/github/ai-fast-track/timeseries/blob/master/nbs/index.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# `timeseries` package for fastai v2
> **`timeseries`** is a Timeseries Classification and Regression package for fastai v2.
> It mimics the fastai v2 vision module (fastai2.vision).
> This notebook is a tutorial that shows, and trains an end-to-end a timeseries dataset.
> The dataset example is the NATOPS dataset (see description here beow).
> First, 4 different methods of creation on how to create timeseries dataloaders are presented.
> Then, we train a model based on [Inception Time] (https://arxiv.org/pdf/1909.04939.pdf) architecture
## Credit
> timeseries for fastai v2 was inspired by by Ignacio's Oguiza timeseriesAI (https://github.com/timeseriesAI/timeseriesAI.git).
> Inception Time model definition is a modified version of [Ignacio Oguiza] (https://github.com/timeseriesAI/timeseriesAI/blob/master/torchtimeseries/models/InceptionTime.py) and [Thomas Capelle] (https://github.com/tcapelle/TimeSeries_fastai/blob/master/inception.py) implementaions
## Installing **`timeseries`** on local machine as an editable package
1- Only if you have not already installed `fastai v2`
Install [fastai2](https://dev.fast.ai/#Installing) by following the steps described there.
2- Install timeseries package by following the instructions here below:
```
git clone https://github.com/ai-fast-track/timeseries.git
cd timeseries
pip install -e .
```
# pip installing **`timeseries`** from repo either locally or in Google Colab - Start Here
## Installing fastai v2
```
!pip install git+https://github.com/fastai/fastai2.git
```
## Installing `timeseries` package from github
```
!pip install git+https://github.com/ai-fast-track/timeseries.git
```
# *pip Installing - End Here*
# `Usage`
```
%reload_ext autoreload
%autoreload 2
%matplotlib inline
from fastai2.basics import *
# hide
# Only for Windows users because symlink to `timeseries` folder is not recognized by Windows
import sys
sys.path.append("..")
from timeseries.all import *
```
# Tutorial on timeseries package for fastai v2
## Example : NATOS dataset
<img src="https://github.com/ai-fast-track/timeseries/blob/master/images/NATOPS.jpg?raw=1">
## Right Arm vs Left Arm (3: 'Not clear' Command (see picture here above))
<br>
<img src="https://github.com/ai-fast-track/timeseries/blob/master/images/ts-right-arm.png?raw=1"><img src="https://github.com/ai-fast-track/timeseries/blob/master/images/ts-left-arm.png?raw=1">
## Description
The data is generated by sensors on the hands, elbows, wrists and thumbs. The data are the x,y,z coordinates for each of the eight locations. The order of the data is as follows:
## Channels (24)
0. Hand tip left, X coordinate
1. Hand tip left, Y coordinate
2. Hand tip left, Z coordinate
3. Hand tip right, X coordinate
4. Hand tip right, Y coordinate
5. Hand tip right, Z coordinate
6. Elbow left, X coordinate
7. Elbow left, Y coordinate
8. Elbow left, Z coordinate
9. Elbow right, X coordinate
10. Elbow right, Y coordinate
11. Elbow right, Z coordinate
12. Wrist left, X coordinate
13. Wrist left, Y coordinate
14. Wrist left, Z coordinate
15. Wrist right, X coordinate
16. Wrist right, Y coordinate
17. Wrist right, Z coordinate
18. Thumb left, X coordinate
19. Thumb left, Y coordinate
20. Thumb left, Z coordinate
21. Thumb right, X coordinate
22. Thumb right, Y coordinate
23. Thumb right, Z coordinate
## Classes (6)
The six classes are separate actions, with the following meaning:
1: I have command
2: All clear
3: Not clear
4: Spread wings
5: Fold wings
6: Lock wings
## Download data using `download_unzip_data_UCR(dsname=dsname)` method
```
dsname = 'NATOPS' #'NATOPS', 'LSST', 'Wine', 'Epilepsy', 'HandMovementDirection'
# url = 'http://www.timeseriesclassification.com/Downloads/NATOPS.zip'
path = unzip_data(URLs_TS.NATOPS)
path
```
## Why do I have to concatenate train and test data?
Both Train and Train dataset contains 180 samples each. We concatenate them in order to have one big dataset and then split into train and valid dataset using our own split percentage (20%, 30%, or whatever number you see fit)
```
fname_train = f'{dsname}_TRAIN.arff'
fname_test = f'{dsname}_TEST.arff'
fnames = [path/fname_train, path/fname_test]
fnames
data = TSData.from_arff(fnames)
print(data)
items = data.get_items()
idx = 1
x1, y1 = data.x[idx], data.y[idx]
y1
# You can select any channel to display buy supplying a list of channels and pass it to `chs` argument
# LEFT ARM
# show_timeseries(x1, title=y1, chs=[0,1,2,6,7,8,12,13,14,18,19,20])
# RIGHT ARM
# show_timeseries(x1, title=y1, chs=[3,4,5,9,10,11,15,16,17,21,22,23])
# ?show_timeseries(x1, title=y1, chs=range(0,24,3)) # Only the x axis coordinates
seed = 42
splits = RandomSplitter(seed=seed)(range_of(items)) #by default 80% for train split and 20% for valid split are chosen
splits
```
# Using `Datasets` class
## Creating a Datasets object
```
tfms = [[ItemGetter(0), ToTensorTS()], [ItemGetter(1), Categorize()]]
# Create a dataset
ds = Datasets(items, tfms, splits=splits)
ax = show_at(ds, 2, figsize=(1,1))
```
# Create a `Dataloader` objects
## 1st method : using `Datasets` object
```
bs = 128
# Normalize at batch time
tfm_norm = Normalize(scale_subtype = 'per_sample_per_channel', scale_range=(0, 1)) # per_sample , per_sample_per_channel
# tfm_norm = Standardize(scale_subtype = 'per_sample')
batch_tfms = [tfm_norm]
dls1 = ds.dataloaders(bs=bs, val_bs=bs * 2, after_batch=batch_tfms, num_workers=0, device=default_device())
dls1.show_batch(max_n=9, chs=range(0,12,3))
```
# Using `DataBlock` class
## 2nd method : using `DataBlock` and `DataBlock.get_items()`
```
getters = [ItemGetter(0), ItemGetter(1)]
tsdb = DataBlock(blocks=(TSBlock, CategoryBlock),
get_items=get_ts_items,
getters=getters,
splitter=RandomSplitter(seed=seed),
batch_tfms = batch_tfms)
tsdb.summary(fnames)
# num_workers=0 is Microsoft Windows
dls2 = tsdb.dataloaders(fnames, num_workers=0, device=default_device())
dls2.show_batch(max_n=9, chs=range(0,12,3))
```
## 3rd method : using `DataBlock` and passing `items` object to the `DataBlock.dataloaders()`
```
getters = [ItemGetter(0), ItemGetter(1)]
tsdb = DataBlock(blocks=(TSBlock, CategoryBlock),
getters=getters,
splitter=RandomSplitter(seed=seed))
dls3 = tsdb.dataloaders(data.get_items(), batch_tfms=batch_tfms, num_workers=0, device=default_device())
dls3.show_batch(max_n=9, chs=range(0,12,3))
```
## 4th method : using `TSDataLoaders` class and `TSDataLoaders.from_files()`
```
dls4 = TSDataLoaders.from_files(fnames, batch_tfms=batch_tfms, num_workers=0, device=default_device())
dls4.show_batch(max_n=9, chs=range(0,12,3))
```
# Train Model
```
# Number of channels (i.e. dimensions in ARFF and TS files jargon)
c_in = get_n_channels(dls2.train) # data.n_channels
# Number of classes
c_out= dls2.c
c_in,c_out
```
## Create model
```
model = inception_time(c_in, c_out).to(device=default_device())
model
```
## Create Learner object
```
#Learner
opt_func = partial(Adam, lr=3e-3, wd=0.01)
loss_func = LabelSmoothingCrossEntropy()
learn = Learner(dls2, model, opt_func=opt_func, loss_func=loss_func, metrics=accuracy)
print(learn.summary())
```
## LR find
```
lr_min, lr_steep = learn.lr_find()
lr_min, lr_steep
```
## Train
```
#lr_max=1e-3
epochs=30; lr_max=lr_steep; pct_start=.7; moms=(0.95,0.85,0.95); wd=1e-2
learn.fit_one_cycle(epochs, lr_max=lr_max, pct_start=pct_start, moms=moms, wd=wd)
# learn.fit_one_cycle(epochs=20, lr_max=lr_steep)
```
## Plot loss function
```
learn.recorder.plot_loss()
```
## Show results
```
learn.show_results(max_n=9, chs=range(0,12,3))
#hide
from nbdev.export import notebook2script
# notebook2script()
notebook2script(fname='index.ipynb')
# #hide
# from nbdev.export2html import _notebook2html
# # notebook2script()
# _notebook2html(fname='index.ipynb')
```
# Fin
<img src="https://github.com/ai-fast-track/timeseries/blob/master/images/tree.jpg?raw=1" width="1440" height="840" alt=""/>
|
github_jupyter
|
# The Extended Kalman Filter
선형 칼만 필터 (Linear Kalman Filter)에 대한 이론을 바탕으로 비선형 문제에 칼만 필터를 적용해 보겠습니다. 확장칼만필터 (EKF)는 예측단계와 추정단계의 데이터를 비선형으로 가정하고 현재의 추정값에 대해 시스템을 선형화 한뒤 선형 칼만 필터를 사용하는 기법입니다.
비선형 문제에 적용되는 성능이 더 좋은 알고리즘들 (UKF, H_infinity)이 있지만 EKF 는 아직도 널리 사용되서 관련성이 높습니다.
```
%matplotlib inline
# HTML("""
# <style>
# .output_png {
# display: table-cell;
# text-align: center;
# vertical-align: middle;
# }
# </style>
# """)
```
## Linearizing the Kalman Filter
### Non-linear models
칼만 필터는 시스템이 선형일것이라는 가정을 하기 때문에 비선형 문제에는 직접적으로 사용하지 못합니다. 비선형성은 두가지 원인에서 기인될수 있는데 첫째는 프로세스 모델의 비선형성 그리고 둘째 측정 모델의 비선형성입니다. 예를 들어, 떨어지는 물체의 가속도는 속도의 제곱에 비례하는 공기저항에 의해 결정되기 때문에 비선형적인 프로세스 모델을 가지고, 레이더로 목표물의 범위와 방위 (bearing) 를 측정할때 비선형함수인 삼각함수를 사용하여 표적의 위치를 계산하기 때문에 비선형적인 측정 모델을 가지게 됩니다.
비선형문제에 기존의 칼만필터 방정식을 적용하지 못하는 이유는 비선형함수에 정규분포 (Gaussian)를 입력하면 아래와 같이 Gaussian 이 아닌 분포를 가지게 되기 때문입니다.
```
import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt
mu, sigma = 0, 0.1
gaussian = stats.norm.pdf(x, mu, sigma)
x = np.linspace(mu - 3*sigma, mu + 3*sigma, 10000)
def nonlinearFunction(x):
return np.sin(x)
def linearFunction(x):
return 0.5*x
nonlinearOutput = nonlinearFunction(gaussian)
linearOutput = linearFunction(gaussian)
# print(x)
plt.plot(x, gaussian, label = 'Gaussian Input')
plt.plot(x, linearOutput, label = 'Linear Output')
plt.plot(x, nonlinearOutput, label = 'Nonlinear Output')
plt.grid(linestyle='dotted', linewidth=0.8)
plt.legend()
plt.show()
```
### System Equations
선형 칼만 필터의 경우 프로세스 및 측정 모델은 다음과 같이 나타낼수 있습니다.
$$\begin{aligned}\dot{\mathbf x} &= \mathbf{Ax} + w_x\\
\mathbf z &= \mathbf{Hx} + w_z
\end{aligned}$$
이때 $\mathbf A$ 는 (연속시간에서) 시스템의 역학을 묘사하는 dynamic matrix 입니다. 위의 식을 이산화(discretize)시키면 아래와 같이 나타내줄 수 있습니다.
$$\begin{aligned}\bar{\mathbf x}_k &= \mathbf{F} \mathbf{x}_{k-1} \\
\bar{\mathbf z} &= \mathbf{H} \mathbf{x}_{k-1}
\end{aligned}$$
이때 $\mathbf F$ 는 이산시간 $\Delta t$ 에 걸쳐 $\mathbf x_{k-1}$을 $\mathbf x_{k}$ 로 전환하는 상태변환행렬 또는 상태전달함수 (state transition matrix) 이고, 위에서의 $w_x$ 와 $w_z$는 각각 프로세스 노이즈 공분산 행렬 $\mathbf Q$ 과 측정 노이즈 공분산 행렬 $\mathbf R$ 에 포함됩니다.
선형 시스템에서의 $\mathbf F \mathbf x- \mathbf B \mathbf u$ 와 $\mathbf H \mathbf x$ 는 비선형 시스템에서 함수 $f(\mathbf x, \mathbf u)$ 와 $h(\mathbf x)$ 로 대체됩니다.
$$\begin{aligned}\dot{\mathbf x} &= f(\mathbf x, \mathbf u) + w_x\\
\mathbf z &= h(\mathbf x) + w_z
\end{aligned}$$
### Linearisation
선형화란 말그대로 하나의 시점에 대하여 비선형함수에 가장 가까운 선 (선형시스템) 을 찾는것이라고 볼수 있습니다. 여러가지 방법으로 선형화를 할수 있겠지만 흔히 일차 테일러 급수를 사용합니다. ($ c_0$ 과 $c_1 x$)
$$f(x) = \sum_{k=0}^\infty c_k x^k = c_0 + c_1 x + c_2 x^2 + \dotsb$$
$$c_k = \frac{f^{\left(k\right)}(0)}{k!} = \frac{1}{k!} \cdot \frac{d^k f}{dx^k}\bigg|_0 $$
행렬의 미분값을 Jacobian 이라고 하는데 이를 통해서 위와 같이 $\mathbf F$ 와 $\mathbf H$ 를 나타낼 수 있습니다.
$$
\begin{aligned}
\mathbf F
= {\frac{\partial{f(\mathbf x_t, \mathbf u_t)}}{\partial{\mathbf x}}}\biggr|_{{\mathbf x_t},{\mathbf u_t}} \;\;\;\;
\mathbf H = \frac{\partial{h(\bar{\mathbf x}_t)}}{\partial{\bar{\mathbf x}}}\biggr|_{\bar{\mathbf x}_t}
\end{aligned}
$$
$$\mathbf F = \frac{\partial f(\mathbf x, \mathbf u)}{\partial x} =\begin{bmatrix}
\frac{\partial f_1}{\partial x_1} & \frac{\partial f_1}{\partial x_2} & \dots & \frac{\partial f_1}{\partial x_n}\\
\frac{\partial f_2}{\partial x_1} & \frac{\partial f_2}{\partial x_2} & \dots & \frac{\partial f_2}{\partial x_n} \\
\\ \vdots & \vdots & \ddots & \vdots
\\
\frac{\partial f_n}{\partial x_1} & \frac{\partial f_n}{\partial x_2} & \dots & \frac{\partial f_n}{\partial x_n}
\end{bmatrix}
$$
Linear Kalman Filter 와 Extended Kalman Filter 의 식들을 아래와 같이 비교할수 있습니다.
$$\begin{array}{l|l}
\text{Linear Kalman filter} & \text{EKF} \\
\hline
& \boxed{\mathbf F = {\frac{\partial{f(\mathbf x_t, \mathbf u_t)}}{\partial{\mathbf x}}}\biggr|_{{\mathbf x_t},{\mathbf u_t}}} \\
\mathbf{\bar x} = \mathbf{Fx} + \mathbf{Bu} & \boxed{\mathbf{\bar x} = f(\mathbf x, \mathbf u)} \\
\mathbf{\bar P} = \mathbf{FPF}^\mathsf{T}+\mathbf Q & \mathbf{\bar P} = \mathbf{FPF}^\mathsf{T}+\mathbf Q \\
\hline
& \boxed{\mathbf H = \frac{\partial{h(\bar{\mathbf x}_t)}}{\partial{\bar{\mathbf x}}}\biggr|_{\bar{\mathbf x}_t}} \\
\textbf{y} = \mathbf z - \mathbf{H \bar{x}} & \textbf{y} = \mathbf z - \boxed{h(\bar{x})}\\
\mathbf{K} = \mathbf{\bar{P}H}^\mathsf{T} (\mathbf{H\bar{P}H}^\mathsf{T} + \mathbf R)^{-1} & \mathbf{K} = \mathbf{\bar{P}H}^\mathsf{T} (\mathbf{H\bar{P}H}^\mathsf{T} + \mathbf R)^{-1} \\
\mathbf x=\mathbf{\bar{x}} +\mathbf{K\textbf{y}} & \mathbf x=\mathbf{\bar{x}} +\mathbf{K\textbf{y}} \\
\mathbf P= (\mathbf{I}-\mathbf{KH})\mathbf{\bar{P}} & \mathbf P= (\mathbf{I}-\mathbf{KH})\mathbf{\bar{P}}
\end{array}$$
$\mathbf F \mathbf x_{k-1}$ 을 사용하여 $\mathbf x_{k}$의 값을 추정할수 있겠지만, 선형화 과정에서 오차가 생길수 있기 때문에 Euler 또는 Runge Kutta 수치 적분 (numerical integration) 을 통해서 사전추정값 $\mathbf{\bar{x}}$ 를 구합니다. 같은 이유로 $\mathbf y$ (innovation vector 또는 잔차(residual)) 를 구할때도 $\mathbf H \mathbf x$ 대신에 수치적인 방법으로 계산하게 됩니다.
## Example: Robot Localization
### Prediction Model (예측모델)
EKF를 4륜 로봇에 적용시켜 보겠습니다. 간단한 bicycle steering model 을 통해 아래의 시스템 모델을 나타낼 수 있습니다.
```
import kf_book.ekf_internal as ekf_internal
ekf_internal.plot_bicycle()
```
$$\begin{aligned}
\beta &= \frac d w \tan(\alpha) \\
\bar x_k &= x_{k-1} - R\sin(\theta) + R\sin(\theta + \beta) \\
\bar y_k &= y_{k-1} + R\cos(\theta) - R\cos(\theta + \beta) \\
\bar \theta_k &= \theta_{k-1} + \beta
\end{aligned}
$$
위의 식들을 토대로 상태벡터를 $\mathbf{x}=[x, y, \theta]^T$ 그리고 입력벡터를 $\mathbf{u}=[v, \alpha]^T$ 라고 정의 해주면 아래와 같이 $f(\mathbf x, \mathbf u)$ 나타내줄수 있고 $f$ 의 Jacobian $\mathbf F$를 미분하여 아래의 행렬을 구해줄수 있습니다.
$$\bar x = f(x, u) + \mathcal{N}(0, Q)$$
$$f = \begin{bmatrix}x\\y\\\theta\end{bmatrix} +
\begin{bmatrix}- R\sin(\theta) + R\sin(\theta + \beta) \\
R\cos(\theta) - R\cos(\theta + \beta) \\
\beta\end{bmatrix}$$
$$\mathbf F = \frac{\partial f(\mathbf x, \mathbf u)}{\partial \mathbf x} = \begin{bmatrix}
1 & 0 & -R\cos(\theta) + R\cos(\theta+\beta) \\
0 & 1 & -R\sin(\theta) + R\sin(\theta+\beta) \\
0 & 0 & 1
\end{bmatrix}$$
$\bar{\mathbf P}$ 을 구하기 위해 입력($\mathbf u$)에서 비롯되는 프로세스 노이즈 $\mathbf Q$ 를 아래와 같이 정의합니다.
$$\mathbf{M} = \begin{bmatrix}\sigma_{vel}^2 & 0 \\ 0 & \sigma_\alpha^2\end{bmatrix}
\;\;\;\;
\mathbf{V} = \frac{\partial f(x, u)}{\partial u} \begin{bmatrix}
\frac{\partial f_1}{\partial v} & \frac{\partial f_1}{\partial \alpha} \\
\frac{\partial f_2}{\partial v} & \frac{\partial f_2}{\partial \alpha} \\
\frac{\partial f_3}{\partial v} & \frac{\partial f_3}{\partial \alpha}
\end{bmatrix}$$
$$\mathbf{\bar P} =\mathbf{FPF}^{\mathsf T} + \mathbf{VMV}^{\mathsf T}$$
```
import sympy
from sympy.abc import alpha, x, y, v, w, R, theta
from sympy import symbols, Matrix
sympy.init_printing(use_latex="mathjax", fontsize='16pt')
time = symbols('t')
d = v*time
beta = (d/w)*sympy.tan(alpha)
r = w/sympy.tan(alpha)
fxu = Matrix([[x-r*sympy.sin(theta) + r*sympy.sin(theta+beta)],
[y+r*sympy.cos(theta)- r*sympy.cos(theta+beta)],
[theta+beta]])
F = fxu.jacobian(Matrix([x, y, theta]))
F
# reduce common expressions
B, R = symbols('beta, R')
F = F.subs((d/w)*sympy.tan(alpha), B)
F.subs(w/sympy.tan(alpha), R)
V = fxu.jacobian(Matrix([v, alpha]))
V = V.subs(sympy.tan(alpha)/w, 1/R)
V = V.subs(time*v/R, B)
V = V.subs(time*v, 'd')
V
```
### Measurement Model (측정모델)
레이더로 범위$(r)$와 방위($\phi$)를 측정할때 다음과 같은 센서모델을 사용합니다. 이때 $\mathbf p$ 는 landmark의 위치를 나타내줍니다.
$$r = \sqrt{(p_x - x)^2 + (p_y - y)^2}
\;\;\;\;
\phi = \arctan(\frac{p_y - y}{p_x - x}) - \theta
$$
$$\begin{aligned}
\mathbf z& = h(\bar{\mathbf x}, \mathbf p) &+ \mathcal{N}(0, R)\\
&= \begin{bmatrix}
\sqrt{(p_x - x)^2 + (p_y - y)^2} \\
\arctan(\frac{p_y - y}{p_x - x}) - \theta
\end{bmatrix} &+ \mathcal{N}(0, R)
\end{aligned}$$
$h$ 의 Jacobian $\mathbf H$를 미분하여 아래의 행렬을 구해줄수 있습니다.
$$\mathbf H = \frac{\partial h(\mathbf x, \mathbf u)}{\partial \mathbf x} =
\left[\begin{matrix}\frac{- p_{x} + x}{\sqrt{\left(p_{x} - x\right)^{2} + \left(p_{y} - y\right)^{2}}} & \frac{- p_{y} + y}{\sqrt{\left(p_{x} - x\right)^{2} + \left(p_{y} - y\right)^{2}}} & 0\\- \frac{- p_{y} + y}{\left(p_{x} - x\right)^{2} + \left(p_{y} - y\right)^{2}} & - \frac{p_{x} - x}{\left(p_{x} - x\right)^{2} + \left(p_{y} - y\right)^{2}} & -1\end{matrix}\right]
$$
```
import sympy
from sympy.abc import alpha, x, y, v, w, R, theta
px, py = sympy.symbols('p_x, p_y')
z = sympy.Matrix([[sympy.sqrt((px-x)**2 + (py-y)**2)],
[sympy.atan2(py-y, px-x) - theta]])
z.jacobian(sympy.Matrix([x, y, theta]))
# print(sympy.latex(z.jacobian(sympy.Matrix([x, y, theta])))
from math import sqrt
def H_of(x, landmark_pos):
""" compute Jacobian of H matrix where h(x) computes
the range and bearing to a landmark for state x """
px = landmark_pos[0]
py = landmark_pos[1]
hyp = (px - x[0, 0])**2 + (py - x[1, 0])**2
dist = sqrt(hyp)
H = array(
[[-(px - x[0, 0]) / dist, -(py - x[1, 0]) / dist, 0],
[ (py - x[1, 0]) / hyp, -(px - x[0, 0]) / hyp, -1]])
return H
from math import atan2
def Hx(x, landmark_pos):
""" takes a state variable and returns the measurement
that would correspond to that state.
"""
px = landmark_pos[0]
py = landmark_pos[1]
dist = sqrt((px - x[0, 0])**2 + (py - x[1, 0])**2)
Hx = array([[dist],
[atan2(py - x[1, 0], px - x[0, 0]) - x[2, 0]]])
return Hx
```
측정 노이즈는 다음과 같이 나타내줍니다.
$$\mathbf R=\begin{bmatrix}\sigma_{range}^2 & 0 \\ 0 & \sigma_{bearing}^2\end{bmatrix}$$
### Implementation
`FilterPy` 의 `ExtendedKalmanFilter` class 를 활용해서 EKF 를 구현해보도록 하겠습니다.
```
from filterpy.kalman import ExtendedKalmanFilter as EKF
from numpy import array, sqrt, random
import sympy
class RobotEKF(EKF):
def __init__(self, dt, wheelbase, std_vel, std_steer):
EKF.__init__(self, 3, 2, 2)
self.dt = dt
self.wheelbase = wheelbase
self.std_vel = std_vel
self.std_steer = std_steer
a, x, y, v, w, theta, time = sympy.symbols(
'a, x, y, v, w, theta, t')
d = v*time
beta = (d/w)*sympy.tan(a)
r = w/sympy.tan(a)
self.fxu = sympy.Matrix(
[[x-r*sympy.sin(theta)+r*sympy.sin(theta+beta)],
[y+r*sympy.cos(theta)-r*sympy.cos(theta+beta)],
[theta+beta]])
self.F_j = self.fxu.jacobian(sympy.Matrix([x, y, theta]))
self.V_j = self.fxu.jacobian(sympy.Matrix([v, a]))
# save dictionary and it's variables for later use
self.subs = {x: 0, y: 0, v:0, a:0,
time:dt, w:wheelbase, theta:0}
self.x_x, self.x_y, = x, y
self.v, self.a, self.theta = v, a, theta
def predict(self, u):
self.x = self.move(self.x, u, self.dt)
self.subs[self.theta] = self.x[2, 0]
self.subs[self.v] = u[0]
self.subs[self.a] = u[1]
F = array(self.F_j.evalf(subs=self.subs)).astype(float)
V = array(self.V_j.evalf(subs=self.subs)).astype(float)
# covariance of motion noise in control space
M = array([[self.std_vel*u[0]**2, 0],
[0, self.std_steer**2]])
self.P = F @ self.P @ F.T + V @ M @ V.T
def move(self, x, u, dt):
hdg = x[2, 0]
vel = u[0]
steering_angle = u[1]
dist = vel * dt
if abs(steering_angle) > 0.001: # is robot turning?
beta = (dist / self.wheelbase) * tan(steering_angle)
r = self.wheelbase / tan(steering_angle) # radius
dx = np.array([[-r*sin(hdg) + r*sin(hdg + beta)],
[r*cos(hdg) - r*cos(hdg + beta)],
[beta]])
else: # moving in straight line
dx = np.array([[dist*cos(hdg)],
[dist*sin(hdg)],
[0]])
return x + dx
```
정확한 잔차값 $y$을 구하기 방위값이 $0 \leq \phi \leq 2\pi$ 이도록 고쳐줍니다.
```
def residual(a, b):
""" compute residual (a-b) between measurements containing
[range, bearing]. Bearing is normalized to [-pi, pi)"""
y = a - b
y[1] = y[1] % (2 * np.pi) # force in range [0, 2 pi)
if y[1] > np.pi: # move to [-pi, pi)
y[1] -= 2 * np.pi
return y
from filterpy.stats import plot_covariance_ellipse
from math import sqrt, tan, cos, sin, atan2
import matplotlib.pyplot as plt
dt = 1.0
def z_landmark(lmark, sim_pos, std_rng, std_brg):
x, y = sim_pos[0, 0], sim_pos[1, 0]
d = np.sqrt((lmark[0] - x)**2 + (lmark[1] - y)**2)
a = atan2(lmark[1] - y, lmark[0] - x) - sim_pos[2, 0]
z = np.array([[d + random.randn()*std_rng],
[a + random.randn()*std_brg]])
return z
def ekf_update(ekf, z, landmark):
ekf.update(z, HJacobian = H_of, Hx = Hx,
residual=residual,
args=(landmark), hx_args=(landmark))
def run_localization(landmarks, std_vel, std_steer,
std_range, std_bearing,
step=10, ellipse_step=20, ylim=None):
ekf = RobotEKF(dt, wheelbase=0.5, std_vel=std_vel,
std_steer=std_steer)
ekf.x = array([[2, 6, .3]]).T # x, y, steer angle
ekf.P = np.diag([.1, .1, .1])
ekf.R = np.diag([std_range**2, std_bearing**2])
sim_pos = ekf.x.copy() # simulated position
# steering command (vel, steering angle radians)
u = array([1.1, .01])
plt.figure()
plt.scatter(landmarks[:, 0], landmarks[:, 1],
marker='s', s=60)
track = []
for i in range(200):
sim_pos = ekf.move(sim_pos, u, dt/10.) # simulate robot
track.append(sim_pos)
if i % step == 0:
ekf.predict(u=u)
if i % ellipse_step == 0:
plot_covariance_ellipse(
(ekf.x[0,0], ekf.x[1,0]), ekf.P[0:2, 0:2],
std=6, facecolor='k', alpha=0.3)
x, y = sim_pos[0, 0], sim_pos[1, 0]
for lmark in landmarks:
z = z_landmark(lmark, sim_pos,
std_range, std_bearing)
ekf_update(ekf, z, lmark)
if i % ellipse_step == 0:
plot_covariance_ellipse(
(ekf.x[0,0], ekf.x[1,0]), ekf.P[0:2, 0:2],
std=6, facecolor='g', alpha=0.8)
track = np.array(track)
plt.plot(track[:, 0], track[:,1], color='k', lw=2)
plt.axis('equal')
plt.title("EKF Robot localization")
if ylim is not None: plt.ylim(*ylim)
plt.show()
return ekf
landmarks = array([[5, 10], [10, 5], [15, 15]])
ekf = run_localization(
landmarks, std_vel=0.1, std_steer=np.radians(1),
std_range=0.3, std_bearing=0.1)
print('Final P:', ekf.P.diagonal())
```
## References
* Roger R Labbe, Kalman and Bayesian Filters in Python
(https://github.com/rlabbe/Kalman-and-Bayesian-Filters-in-Python/blob/master/11-Extended-Kalman-Filters.ipynb)
* https://blog.naver.com/jewdsa813/222200570774
|
github_jupyter
|
# Documenting Classes
It is almost as easy to document a class as it is to document a function. Simply add docstrings to all of the classes functions, and also below the class name itself. For example, here is a simple documented class
```
class Demo:
"""This class demonstrates how to document a class.
This class is just a demonstration, and does nothing.
However the principles of documentation are still valid!
"""
def __init__(self, name):
"""You should document the constructor, saying what it expects to
create a valid class. In this case
name -- the name of an object of this class
"""
self._name = name
def getName(self):
"""You should then document all of the member functions, just as
you do for normal functions. In this case, returns
the name of the object
"""
return self._name
d = Demo("cat")
help(d)
```
Often, when you write a class, you want to hide member data or member functions so that they are only visible within an object of the class. For example, above, the `self._name` member data should be hidden, as it should only be used by the object.
You control the visibility of member functions or member data using an underscore. If the member function or member data name starts with an underscore, then it is hidden. Otherwise, the member data or function is visible.
For example, we can hide the `getName` function by renaming it to `_getName`
```
class Demo:
"""This class demonstrates how to document a class.
This class is just a demonstration, and does nothing.
However the principles of documentation are still valid!
"""
def __init__(self, name):
"""You should document the constructor, saying what it expects to
create a valid class. In this case
name -- the name of an object of this class
"""
self._name = name
def _getName(self):
"""You should then document all of the member functions, just as
you do for normal functions. In this case, returns
the name of the object
"""
return self._name
d = Demo("cat")
help(d)
```
Member functions or data that are hidden are called "private". Member functions or data that are visible are called "public". You should document all public member functions of a class, as these are visible and designed to be used by other people. It is helpful, although not required, to document all of the private member functions of a class, as these will only really be called by you. However, in years to come, you will thank yourself if you still documented them... ;-)
While it is possible to make member data public, it is not advised. It is much better to get and set values of member data using public member functions. This makes it easier for you to add checks to ensure that the data is consistent and being used in the right way. For example, compare these two classes that represent a person, and hold their height.
```
class Person1:
"""Class that holds a person's height"""
def __init__(self):
"""Construct a person who has zero height"""
self.height = 0
class Person2:
"""Class that holds a person's height"""
def __init__(self):
"""Construct a person who has zero height"""
self._height = 0
def setHeight(self, height):
"""Set the person's height to 'height', returning whether or
not the height was set successfully
"""
if height < 0 or height > 300:
print("This is an invalid height! %s" % height)
return False
else:
self._height = height
return True
def getHeight(self):
"""Return the person's height"""
return self._height
```
The first example is quicker to write, but it does little to protect itself against a user who attempts to use the class badly.
```
p = Person1()
p.height = -50
p.height
p.height = "cat"
p.height
```
The second example takes more lines of code, but these lines are valuable as they check that the user is using the class correctly. These checks, when combined with good documentation, ensure that your classes can be safely used by others, and that incorrect use will not create difficult-to-find bugs.
```
p = Person2()
p.setHeight(-50)
p.getHeight()
p.setHeight("cat")
p.getHeight()
```
# Exercise
## Exercise 1
Below is the completed `GuessGame` class from the previous lesson. Add documentation to this class.
```
class GuessGame:
"""
This class provides a simple guessing game. You create an object
of the class with its own secret, with the aim that a user
then needs to try to guess what the secret is.
"""
def __init__(self, secret, max_guesses=5):
"""Create a new guess game
secret -- the secret that must be guessed
max_guesses -- the maximum number of guesses allowed by the user
"""
self._secret = secret
self._nguesses = 0
self._max_guesses = max_guesses
def guess(self, value):
"""Try to guess the secret. This will print out to the screen whether
or not the secret has been guessed.
value -- the user-supplied guess
"""
if (self.nGuesses() >= self.maxGuesses()):
print("Sorry, you have run out of guesses")
elif (value == self._secret):
print("Well done - you have guessed my secret")
else:
self._nguesses += 1
print("Try again...")
def nGuesses(self):
"""Return the number of incorrect guesses made so far"""
return self._nguesses
def maxGuesses(self):
"""Return the maximum number of incorrect guesses allowed"""
return self._max_guesses
help(GuessGame)
```
## Exercise 2
Below is a poorly-written class that uses public member data to store the name and age of a Person. Edit this class so that the member data is made private. Add `get` and `set` functions that allow you to safely get and set the name and age.
```
class Person:
"""Class the represents a Person, holding their name and age"""
def __init__(self, name="unknown", age=0):
"""Construct a person with unknown name and an age of 0"""
self.setName(name)
self.setAge(age)
def setName(self, name):
"""Set the person's name to 'name'"""
self._name = str(name) # str ensures the name is a string
def getName(self):
"""Return the person's name"""
return self._name
def setAge(self, age):
"""Set the person's age. This must be a number between 0 and 130"""
if (age < 0 or age > 130):
print("Cannot set the age to an invalid value: %s" % age)
self._age = age
def getAge(self):
"""Return the person's age"""
return self._age
p = Person(name="Peter Parker", age=21)
p.getName()
p.getAge()
```
## Exercise 3
Add a private member function called `_splitName` to your `Person` class that breaks the name into a surname and first name. Add new functions called `getFirstName` and `getSurname` that use this function to return the first name and surname of the person.
```
class Person:
"""Class the represents a Person, holding their name and age"""
def __init__(self, name="unknown", age=0):
"""Construct a person with unknown name and an age of 0"""
self.setName(name)
self.setAge(age)
def setName(self, name):
"""Set the person's name to 'name'"""
self._name = str(name) # str ensures the name is a string
def getName(self):
"""Return the person's name"""
return self._name
def setAge(self, age):
"""Set the person's age. This must be a number between 0 and 130"""
if (age < 0 or age > 130):
print("Cannot set the age to an invalid value: %s" % age)
self._age = age
def getAge(self):
"""Return the person's age"""
return self._age
def _splitName(self):
"""Private function that splits the name into parts"""
return self._name.split(" ")
def getFirstName(self):
"""Return the first name of the person"""
return self._splitName()[0]
def getSurname(self):
"""Return the surname of the person"""
return self._splitName()[-1]
p = Person(name="Peter Parker", age=21)
p.getFirstName()
p.getSurname()
```
|
github_jupyter
|
<img src="images/strathsdr_banner.png" align="left">
# An RFSoC Spectrum Analyzer Dashboard with Voila
----
<div class="alert alert-box alert-info">
Please use Jupyter Labs http://board_ip_address/lab for this notebook.
</div>
The RFSoC Spectrum Analyzer is an open source tool developed by the [University of Strathclyde](https://github.com/strath-sdr/rfsoc_sam). This notebook is specifically for Voila dashboards. If you would like to see an overview of the Spectrum Analyser, see this [notebook](rfsoc_spectrum_analysis.ipynb) instead.
## Table of Contents
* [Introduction](#introduction)
* [Running this Demonstration](#running-this-demonstration)
* [The Voila Procedure](#the-voila-procedure)
* [Import Libraries](#import-libraries)
* [Initialise Overlay](#initialise-overlay)
* [Dashboard Display](#dashboard-display)
* [Conclusion](#conclusion)
## References
* [Xilinx, Inc, "USP RF Data Converter: LogiCORE IP Product Guide", PG269, v2.3, June 2020](https://www.xilinx.com/support/documentation/ip_documentation/usp_rf_data_converter/v2_3/pg269-rf-data-converter.pdf)
## Revision History
* **v1.0** | 16/02/2021 | Voila spectrum analyzer demonstration
* **v1.1** | 22/10/2021 | Voila update notes in 'running this demonstration' section
## Introduction <a class="anchor" id="introduction"></a>
You ZCU111 platform and XM500 development board is capable of quad-channel spectral analysis. The RFSoC Spectrum Analyser Module (rfsoc-sam) enables hardware accelerated analysis of signals received from the RF Analogue-to-Digital Converters (RF ADCs). This notebook is specifically for running the Spectrum Analyser using Voila dashboards. Follow the instructions outlined in [Running this Demonstration](#running-this-demonstration) to learn more.
### Hardware Setup <a class="anchor" id="hardware-setup"></a>
Your ZCU111 development board can host four Spectrum Analyzer Modules. To setup your board for this demonstration, you can connect each channel in loopback as shown in [Figure 1](#fig-1), or connect an antenna to one of the ADC channels.
Don't worry if you don't have an antenna. The default loopback configuration will still be very interesting and is connected as follows:
* Channel 0: DAC4 (Tile 229 Block 0) to ADC0 (Tile 224 Block 0)
* Channel 1: DAC5 (Tile 229 Block 1) to ADC1 (Tile 224 Block 1)
* Channel 2: DAC6 (Tile 229 Block 2) to ADC2 (Tile 225 Block 0)
* Channel 3: DAC7 (Tile 229 Block 3) to ADC3 (Tile 225 Block 1)
There has been several XM500 board revisions, and some contain different silkscreen and labels for the ADCs and DACs. Use the image below for further guidance and pay attention to the associated Tile and Block.
<a class="anchor" id="fig-1"></a>
<figure>
<img src='images/zcu111_setup.png' height='50%' width='50%'/>
<figcaption><b>Figure 1: ZCU111 and XM500 development board setup in loopback mode.</b></figcaption>
</figure>
If you have chosen to use an antenna, **do not** attach your antenna to any SMA interfaces labelled DAC.
<div class="alert alert-box alert-danger">
<b>Caution:</b>
In this demonstration, we generate tones using the RFSoC development board. Your device should be setup in loopback mode. You should understand that the RFSoC platform can also transmit RF signals wirelessly. Remember that unlicensed wireless transmission of RF signals may be illegal in your geographical location. Radio signals may also interfere with nearby devices, such as pacemakers and emergency radio equipment. Note that it is also illegal to intercept and decode particular RF signals. If you are unsure, please seek professional support.
</div>
----
## Running this Demonstration <a class="anchor" id="running-this-demonstration"></a>
Voila can be used to execute the Spectrum Analyzer Module, while ignoring all of the markdown and code cells typically found in a normal Jupyter notebook. The Voila dashboard can be launched following the instructions below:
* Click on the "Open with Voila Gridstack in a new browser tab" button at the top of the screen:
<figure>
<img src='images/open_voila.png' height='50%' width='50%'/>
</figure>
After the new tab opens the kernel will start and the notebook will run. Only the Spectrum Analyzer will be displayed. The initialisation process takes around 1 minute.
## The Voila Procedure <a class="anchor" id="the-voila-procedure"></a>
Below are the code cells that will be ran when Voila is called. The procedure is fairly straight forward. Load the rfsoc-sam library, initialise the overlay, and display the spectrum analyzer. All you have to ensure is that the above command is executed in the terminal and you have launched a browser tab using the given address. You do not need to run these code cells individually to create the voila dashboard.
### Import Libraries
```
from rfsoc_sam.overlay import Overlay
```
### Initialise Overlay
```
sam = Overlay(init_rf_clks = True)
```
### Dashboard Display
```
sam.spectrum_analyzer_application()
```
## Conclusion
This notebook has presented a hardware accelerated Spectrum Analyzer Module for the ZCU111 development board. The demonstration used Voila to enable rapid dashboarding for visualisation and control.
|
github_jupyter
|
```
import pathlib
import lzma
import re
import os
import datetime
import copy
import numpy as np
import pandas as pd
# Makes it so any changes in pymedphys is automatically
# propagated into the notebook without needing a kernel reset.
from IPython.lib.deepreload import reload
%load_ext autoreload
%autoreload 2
import pymedphys._utilities.filesystem
from prototyping import *
root = pathlib.Path(r'\\physics-server\iComLogFiles\patients')
compressed_files = sorted(list(root.glob('**/*.xz')))
# compressed_files
mechanical_output = root.parent.joinpath('mechanical/4299/20200116.csv')
mechanical_output.parent.mkdir(exist_ok=True)
data = b""
for path in compressed_files:
with lzma.open(path, 'r') as f:
data += f.read()
data_points = get_data_points(data)
mechanical_data = {}
for data_point in data_points:
_, result = strict_extract(data_point)
machine_id = result['Machine ID']
try:
machine_record = mechanical_data[machine_id]
except KeyError:
machine_record = {}
mechanical_data[machine_id] = machine_record
timestamp = result['Timestamp']
try:
timestamp_record = machine_record[timestamp]
except KeyError:
timestamp_record = {}
machine_record[timestamp] = timestamp_record
counter = result['Counter']
mlc = result['MLCX']
mlc_a = mlc[0::2]
mlc_b = mlc[1::2]
width_at_cra = np.mean(mlc_b[39:41] - mlc_a[39:41])
jaw = result['ASYMY']
length = np.sum(jaw)
timestamp_record[counter] = {
'Energy': result['Energy'],
'Monitor Units': result['Total MU'],
'Gantry': result['Gantry'],
'Collimator': result['Collimator'],
'Table Column': result['Table Column'],
'Table Isocentric': result['Table Isocentric'],
'Table Vertical': result['Table Vertical'],
'Table Longitudinal': result['Table Longitudinal'],
'Table Lateral': result['Table Lateral'],
'MLC distance at CRA': width_at_cra,
'Jaw distance': length
}
# pd.Timestamp('2020-01-16T17:08:45')
table_record = pd.DataFrame(
columns=[
'Timestamp', 'Counter', 'Energy', 'Monitor Units', 'Gantry', 'Collimator', 'Table Column',
'Table Isocentric', 'Table Vertical', 'Table Longitudinal',
'Table Lateral', 'MLC distance at CRA', 'Jaw distance'
]
)
for timestamp, timestamp_record in mechanical_data[4299].items():
for counter, record in timestamp_record.items():
table_record = table_record.append({
**{
'Timestamp': pd.Timestamp(timestamp),
'Counter': counter
},
**record
}, ignore_index=True)
table_record.to_csv(mechanical_output, index=False)
```
|
github_jupyter
|
<img src="https://storage.googleapis.com/arize-assets/arize-logo-white.jpg" width="200"/>
# Arize Tutorial: Surrogate Model Feature Importance
A surrogate model is an interpretable model trained on predicting the predictions of a black box model. The goal is to approximate the predictions of the black box model as closely as possible and generate feature importance values from the interpretable surrogate model. The benefit of this approach is that it does not require knowledge of the inner workings of the black box model.
In this tutorial we use the `MimcExplainer` from the `interpret_community` library to generate feature importance values from a surrogate model using only the prediction outputs from a black box model. Both [classification](#classification) and [regression](#regression) examples are provided below and feature importance values are logged to Arize using the Pandas [logger](https://docs.arize.com/arize/api-reference/python-sdk/arize.pandas).
# Install and import the `interpret_community` library
```
!pip install -q interpret==0.2.7 interpret-community==0.22.0
from interpret_community.mimic.mimic_explainer import (
MimicExplainer,
LGBMExplainableModel,
)
```
<a name="classification"></a>
# Classification Example
### Generate example
In this example we'll use a support vector machine (SVM) as our black box model. Only the prediction outputs of the SVM model is needed to train the surrogate model, and feature importances are generated from the surrogate model and sent to Arize.
```
import pandas as pd
import numpy as np
from sklearn.datasets import load_breast_cancer
from sklearn.svm import SVC
bc = load_breast_cancer()
feature_names = bc.feature_names
target_names = bc.target_names
data, target = bc.data, bc.target
df = pd.DataFrame(data, columns=feature_names)
model = SVC(probability=True).fit(df, target)
prediction_label = pd.Series(map(lambda v: target_names[v], model.predict(df)))
prediction_score = pd.Series(map(lambda v: v[1], model.predict_proba(df)))
actual_label = pd.Series(map(lambda v: target_names[v], target))
actual_score = pd.Series(target)
```
### Generate feature importance values
Note that the model itself is not used here. Only its prediction outputs are used.
```
def model_func(_):
return np.array(list(map(lambda p: [1 - p, p], prediction_score)))
explainer = MimicExplainer(
model_func,
df,
LGBMExplainableModel,
augment_data=False,
is_function=True,
)
feature_importance_values = pd.DataFrame(
explainer.explain_local(df).local_importance_values, columns=feature_names
)
feature_importance_values
```
### Send data to Arize
Set up Arize client. We'll be using the Pandas Logger. First copy the Arize `API_KEY` and `ORG_KEY` from your admin page linked below!
[](https://app.arize.com/admin)
```
!pip install -q arize
from arize.pandas.logger import Client, Schema
from arize.utils.types import ModelTypes, Environments
ORGANIZATION_KEY = "ORGANIZATION_KEY"
API_KEY = "API_KEY"
arize_client = Client(organization_key=ORGANIZATION_KEY, api_key=API_KEY)
if ORGANIZATION_KEY == "ORGANIZATION_KEY" or API_KEY == "API_KEY":
raise ValueError("❌ NEED TO CHANGE ORGANIZATION AND/OR API_KEY")
else:
print("✅ Import and Setup Arize Client Done! Now we can start using Arize!")
```
Helper functions to simulate prediction IDs and timestamps.
```
import uuid
from datetime import datetime, timedelta
# Prediction ID is required for logging any dataset
def generate_prediction_ids(df):
return pd.Series((str(uuid.uuid4()) for _ in range(len(df))), index=df.index)
# OPTIONAL: We can directly specify when inferences were made
def simulate_production_timestamps(df, days=30):
t = datetime.now()
current_t, earlier_t = t.timestamp(), (t - timedelta(days=days)).timestamp()
return pd.Series(np.linspace(earlier_t, current_t, num=len(df)), index=df.index)
```
Assemble Pandas DataFrame as a production dataset with prediction IDs and timestamps.
```
feature_importance_values_column_names_mapping = {
f"{feat}": f"{feat} (feature importance)" for feat in feature_names
}
production_dataset = pd.concat(
[
pd.DataFrame(
{
"prediction_id": generate_prediction_ids(df),
"prediction_ts": simulate_production_timestamps(df),
"prediction_label": prediction_label,
"actual_label": actual_label,
"prediction_score": prediction_score,
"actual_score": actual_score,
}
),
df,
feature_importance_values.rename(
columns=feature_importance_values_column_names_mapping
),
],
axis=1,
)
production_dataset
```
Send dataframe to Arize
```
# Define a Schema() object for Arize to pick up data from the correct columns for logging
production_schema = Schema(
prediction_id_column_name="prediction_id", # REQUIRED
timestamp_column_name="prediction_ts",
prediction_label_column_name="prediction_label",
prediction_score_column_name="prediction_score",
actual_label_column_name="actual_label",
actual_score_column_name="actual_score",
feature_column_names=feature_names,
shap_values_column_names=feature_importance_values_column_names_mapping,
)
# arize_client.log returns a Response object from Python's requests module
response = arize_client.log(
dataframe=production_dataset,
schema=production_schema,
model_id="surrogate_model_example_classification",
model_type=ModelTypes.SCORE_CATEGORICAL,
environment=Environments.PRODUCTION,
)
# If successful, the server will return a status_code of 200
if response.status_code != 200:
print(
f"❌ logging failed with response code {response.status_code}, {response.text}"
)
else:
print(
f"✅ You have successfully logged {len(production_dataset)} data points to Arize!"
)
```
<a name="regression"></a>
# Regression Example
### Generate example
In this example we'll use a support vector machine (SVM) as our black box model. Only the prediction outputs of the SVM model is needed to train the surrogate model, and feature importances are generated from the surrogate model and sent to Arize.
```
import pandas as pd
import numpy as np
from sklearn.datasets import fetch_california_housing
housing = fetch_california_housing()
# Use only 1,000 data point for a speedier example
data_reg = housing.data[:1000]
target_reg = housing.target[:1000]
feature_names_reg = housing.feature_names
df_reg = pd.DataFrame(data_reg, columns=feature_names_reg)
from sklearn.svm import SVR
model_reg = SVR().fit(df_reg, target_reg)
prediction_label_reg = pd.Series(model_reg.predict(df_reg))
actual_label_reg = pd.Series(target_reg)
```
### Generate feature importance values
Note that the model itself is not used here. Only its prediction outputs are used.
```
def model_func_reg(_):
return np.array(prediction_label_reg)
explainer_reg = MimicExplainer(
model_func_reg,
df_reg,
LGBMExplainableModel,
augment_data=False,
is_function=True,
)
feature_importance_values_reg = pd.DataFrame(
explainer_reg.explain_local(df_reg).local_importance_values,
columns=feature_names_reg,
)
feature_importance_values_reg
```
Assemble Pandas DataFrame as a production dataset with prediction IDs and timestamps.
```
feature_importance_values_column_names_mapping_reg = {
f"{feat}": f"{feat} (feature importance)" for feat in feature_names_reg
}
production_dataset_reg = pd.concat(
[
pd.DataFrame(
{
"prediction_id": generate_prediction_ids(df_reg),
"prediction_ts": simulate_production_timestamps(df_reg),
"prediction_label": prediction_label_reg,
"actual_label": actual_label_reg,
}
),
df_reg,
feature_importance_values_reg.rename(
columns=feature_importance_values_column_names_mapping_reg
),
],
axis=1,
)
production_dataset_reg
```
Send DataFrame to Arize.
```
# Define a Schema() object for Arize to pick up data from the correct columns for logging
production_schema_reg = Schema(
prediction_id_column_name="prediction_id", # REQUIRED
timestamp_column_name="prediction_ts",
prediction_label_column_name="prediction_label",
actual_label_column_name="actual_label",
feature_column_names=feature_names_reg,
shap_values_column_names=feature_importance_values_column_names_mapping_reg,
)
# arize_client.log returns a Response object from Python's requests module
response_reg = arize_client.log(
dataframe=production_dataset_reg,
schema=production_schema_reg,
model_id="surrogate_model_example_regression",
model_type=ModelTypes.NUMERIC,
environment=Environments.PRODUCTION,
)
# If successful, the server will return a status_code of 200
if response_reg.status_code != 200:
print(
f"❌ logging failed with response code {response_reg.status_code}, {response_reg.text}"
)
else:
print(
f"✅ You have successfully logged {len(production_dataset_reg)} data points to Arize!"
)
```
## Conclusion
You now know how to seamlessly log surrogate model feature importance values onto the Arize platform. Go to [Arize](https://app.arize.com/) in order to analyze and monitor the logged SHAP values.
### Overview
Arize is an end-to-end ML observability and model monitoring platform. The platform is designed to help ML engineers and data science practitioners surface and fix issues with ML models in production faster with:
- Automated ML monitoring and model monitoring
- Workflows to troubleshoot model performance
- Real-time visualizations for model performance monitoring, data quality monitoring, and drift monitoring
- Model prediction cohort analysis
- Pre-deployment model validation
- Integrated model explainability
### Website
Visit Us At: https://arize.com/model-monitoring/
### Additional Resources
- [What is ML observability?](https://arize.com/what-is-ml-observability/)
- [Playbook to model monitoring in production](https://arize.com/the-playbook-to-monitor-your-models-performance-in-production/)
- [Using statistical distance metrics for ML monitoring and observability](https://arize.com/using-statistical-distance-metrics-for-machine-learning-observability/)
- [ML infrastructure tools for data preparation](https://arize.com/ml-infrastructure-tools-for-data-preparation/)
- [ML infrastructure tools for model building](https://arize.com/ml-infrastructure-tools-for-model-building/)
- [ML infrastructure tools for production](https://arize.com/ml-infrastructure-tools-for-production-part-1/)
- [ML infrastructure tools for model deployment and model serving](https://arize.com/ml-infrastructure-tools-for-production-part-2-model-deployment-and-serving/)
- [ML infrastructure tools for ML monitoring and observability](https://arize.com/ml-infrastructure-tools-ml-observability/)
Visit the [Arize Blog](https://arize.com/blog) and [Resource Center](https://arize.com/resource-hub/) for more resources on ML observability and model monitoring.
|
github_jupyter
|
```
import numpy as np
from keras.models import Model
from keras.layers import Input
from keras.layers.pooling import GlobalMaxPooling1D
from keras import backend as K
import json
from collections import OrderedDict
def format_decimal(arr, places=6):
return [round(x * 10**places) / 10**places for x in arr]
DATA = OrderedDict()
```
### GlobalMaxPooling1D
**[pooling.GlobalMaxPooling1D.0] input 6x6**
```
data_in_shape = (6, 6)
L = GlobalMaxPooling1D()
layer_0 = Input(shape=data_in_shape)
layer_1 = L(layer_0)
model = Model(inputs=layer_0, outputs=layer_1)
# set weights to random (use seed for reproducibility)
np.random.seed(260)
data_in = 2 * np.random.random(data_in_shape) - 1
result = model.predict(np.array([data_in]))
data_out_shape = result[0].shape
data_in_formatted = format_decimal(data_in.ravel().tolist())
data_out_formatted = format_decimal(result[0].ravel().tolist())
print('')
print('in shape:', data_in_shape)
print('in:', data_in_formatted)
print('out shape:', data_out_shape)
print('out:', data_out_formatted)
DATA['pooling.GlobalMaxPooling1D.0'] = {
'input': {'data': data_in_formatted, 'shape': data_in_shape},
'expected': {'data': data_out_formatted, 'shape': data_out_shape}
}
```
**[pooling.GlobalMaxPooling1D.1] input 3x7**
```
data_in_shape = (3, 7)
L = GlobalMaxPooling1D()
layer_0 = Input(shape=data_in_shape)
layer_1 = L(layer_0)
model = Model(inputs=layer_0, outputs=layer_1)
# set weights to random (use seed for reproducibility)
np.random.seed(261)
data_in = 2 * np.random.random(data_in_shape) - 1
result = model.predict(np.array([data_in]))
data_out_shape = result[0].shape
data_in_formatted = format_decimal(data_in.ravel().tolist())
data_out_formatted = format_decimal(result[0].ravel().tolist())
print('')
print('in shape:', data_in_shape)
print('in:', data_in_formatted)
print('out shape:', data_out_shape)
print('out:', data_out_formatted)
DATA['pooling.GlobalMaxPooling1D.1'] = {
'input': {'data': data_in_formatted, 'shape': data_in_shape},
'expected': {'data': data_out_formatted, 'shape': data_out_shape}
}
```
**[pooling.GlobalMaxPooling1D.2] input 8x4**
```
data_in_shape = (8, 4)
L = GlobalMaxPooling1D()
layer_0 = Input(shape=data_in_shape)
layer_1 = L(layer_0)
model = Model(inputs=layer_0, outputs=layer_1)
# set weights to random (use seed for reproducibility)
np.random.seed(262)
data_in = 2 * np.random.random(data_in_shape) - 1
result = model.predict(np.array([data_in]))
data_out_shape = result[0].shape
data_in_formatted = format_decimal(data_in.ravel().tolist())
data_out_formatted = format_decimal(result[0].ravel().tolist())
print('')
print('in shape:', data_in_shape)
print('in:', data_in_formatted)
print('out shape:', data_out_shape)
print('out:', data_out_formatted)
DATA['pooling.GlobalMaxPooling1D.2'] = {
'input': {'data': data_in_formatted, 'shape': data_in_shape},
'expected': {'data': data_out_formatted, 'shape': data_out_shape}
}
```
### export for Keras.js tests
```
import os
filename = '../../../test/data/layers/pooling/GlobalMaxPooling1D.json'
if not os.path.exists(os.path.dirname(filename)):
os.makedirs(os.path.dirname(filename))
with open(filename, 'w') as f:
json.dump(DATA, f)
print(json.dumps(DATA))
```
|
github_jupyter
|
# Water quality
## Setup software libraries
```
# Import and initialize the Earth Engine library.
import ee
ee.Initialize()
ee.__version__
# Folium setup.
import folium
print(folium.__version__)
# Skydipper library.
import Skydipper
print(Skydipper.__version__)
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import functools
import json
import uuid
import os
from pprint import pprint
import env
import time
import ee_collection_specifics
```
## Composite image
**Variables**
```
collection = 'Lake-Water-Quality-100m'
init_date = '2019-01-21'
end_date = '2019-01-31'
# Define the URL format used for Earth Engine generated map tiles.
EE_TILES = 'https://earthengine.googleapis.com/map/{mapid}/{{z}}/{{x}}/{{y}}?token={token}'
composite = ee_collection_specifics.Composite(collection)(init_date, end_date)
mapid = composite.getMapId(ee_collection_specifics.vizz_params_rgb(collection))
tiles_url = EE_TILES.format(**mapid)
map = folium.Map(location=[39.31, 0.302])
folium.TileLayer(
tiles=tiles_url,
attr='Google Earth Engine',
overlay=True,
name=str(ee_collection_specifics.ee_bands_rgb(collection))).add_to(map)
map.add_child(folium.LayerControl())
map
```
***
## Geostore
We select the areas from which we will export the training data.
**Variables**
```
def polygons_to_multipoligon(polygons):
multipoligon = []
MultiPoligon = {}
for polygon in polygons.get('features'):
multipoligon.append(polygon.get('geometry').get('coordinates'))
MultiPoligon = {
"type": "FeatureCollection",
"features": [
{
"type": "Feature",
"properties": {},
"geometry": {
"type": "MultiPolygon",
"coordinates": multipoligon
}
}
]
}
return MultiPoligon
#trainPolygons = {"type":"FeatureCollection","features":[{"type":"Feature","properties":{},"geometry":{"type":"Polygon","coordinates":[[[-0.45043945312499994,39.142842478062505],[0.06042480468749999,39.142842478062505],[0.06042480468749999,39.55064761909318],[-0.45043945312499994,39.55064761909318],[-0.45043945312499994,39.142842478062505]]]}},{"type":"Feature","properties":{},"geometry":{"type":"Polygon","coordinates":[[[-0.2911376953125,38.659777730712534],[0.2581787109375,38.659777730712534],[0.2581787109375,39.10022600175347],[-0.2911376953125,39.10022600175347],[-0.2911376953125,38.659777730712534]]]}},{"type":"Feature","properties":{},"geometry":{"type":"Polygon","coordinates":[[[-0.3350830078125,39.56758783088905],[0.22521972656249997,39.56758783088905],[0.22521972656249997,39.757879992021756],[-0.3350830078125,39.757879992021756],[-0.3350830078125,39.56758783088905]]]}},{"type":"Feature","properties":{},"geometry":{"type":"Polygon","coordinates":[[[0.07965087890625,39.21310328979648],[0.23345947265625,39.21310328979648],[0.23345947265625,39.54852980171147],[0.07965087890625,39.54852980171147],[0.07965087890625,39.21310328979648]]]}},{"type":"Feature","properties":{},"geometry":{"type":"Polygon","coordinates":[[[-1.0931396484375,35.7286770448517],[-0.736083984375,35.7286770448517],[-0.736083984375,35.94243575255426],[-1.0931396484375,35.94243575255426],[-1.0931396484375,35.7286770448517]]]}},{"type":"Feature","properties":{},"geometry":{"type":"Polygon","coordinates":[[[-1.7303466796874998,35.16931803601131],[-1.4666748046875,35.16931803601131],[-1.4666748046875,35.74205383068037],[-1.7303466796874998,35.74205383068037],[-1.7303466796874998,35.16931803601131]]]}},{"type":"Feature","properties":{},"geometry":{"type":"Polygon","coordinates":[[[-1.42822265625,35.285984736065764],[-1.131591796875,35.285984736065764],[-1.131591796875,35.782170703266075],[-1.42822265625,35.782170703266075],[-1.42822265625,35.285984736065764]]]}},{"type":"Feature","properties":{},"geometry":{"type":"Polygon","coordinates":[[[-1.8127441406249998,35.831174956246535],[-1.219482421875,35.831174956246535],[-1.219482421875,36.04465753921525],[-1.8127441406249998,36.04465753921525],[-1.8127441406249998,35.831174956246535]]]}}]}
trainPolygons = {"type":"FeatureCollection","features":[{"type":"Feature","properties":{},"geometry":{"type":"Polygon","coordinates":[[[-0.406494140625,38.64476310916202],[0.27740478515625,38.64476310916202],[0.27740478515625,39.74521015328692],[-0.406494140625,39.74521015328692],[-0.406494140625,38.64476310916202]]]}},{"type":"Feature","properties":{},"geometry":{"type":"Polygon","coordinates":[[[-1.70013427734375,35.15135442846945],[-0.703125,35.15135442846945],[-0.703125,35.94688293218141],[-1.70013427734375,35.94688293218141],[-1.70013427734375,35.15135442846945]]]}}]}
trainPolys = polygons_to_multipoligon(trainPolygons)
evalPolys = None
nTrain = len(trainPolys.get('features')[0].get('geometry').get('coordinates'))
print('Number of training polygons:', nTrain)
if evalPolys:
nEval = len(evalPolys.get('features')[0].get('geometry').get('coordinates'))
print('Number of training polygons:', nEval)
```
**Display Polygons**
```
# Define the URL format used for Earth Engine generated map tiles.
EE_TILES = 'https://earthengine.googleapis.com/map/{mapid}/{{z}}/{{x}}/{{y}}?token={token}'
composite = ee_collection_specifics.Composite(collection)(init_date, end_date)
mapid = composite.getMapId(ee_collection_specifics.vizz_params_rgb(collection))
tiles_url = EE_TILES.format(**mapid)
map = folium.Map(location=[39.31, 0.302], zoom_start=6)
folium.TileLayer(
tiles=tiles_url,
attr='Google Earth Engine',
overlay=True,
name=str(ee_collection_specifics.ee_bands_rgb(collection))).add_to(map)
# Convert the GeoJSONs to feature collections
trainFeatures = ee.FeatureCollection(trainPolys.get('features'))
if evalPolys:
evalFeatures = ee.FeatureCollection(evalPolys.get('features'))
polyImage = ee.Image(0).byte().paint(trainFeatures, 1)
if evalPolys:
polyImage = ee.Image(0).byte().paint(trainFeatures, 1).paint(evalFeatures, 2)
polyImage = polyImage.updateMask(polyImage)
mapid = polyImage.getMapId({'min': 1, 'max': 2, 'palette': ['red', 'blue']})
folium.TileLayer(
tiles=EE_TILES.format(**mapid),
attr='Google Earth Engine',
overlay=True,
name='training polygons',
).add_to(map)
map.add_child(folium.LayerControl())
map
```
***
## Data pre-processing
We normalize the composite images to have values from 0 to 1.
**Variables**
```
input_dataset = 'Sentinel-2-Top-of-Atmosphere-Reflectance'
output_dataset = 'Lake-Water-Quality-100m'
init_date = '2019-01-21'
end_date = '2019-01-31'
scale = 100 #scale in meters
collections = [input_dataset, output_dataset]
```
**Normalize images**
```
def min_max_values(image, collection, scale, polygons=None):
normThreshold = ee_collection_specifics.ee_bands_normThreshold(collection)
num = 2
lon = np.linspace(-180, 180, num)
lat = np.linspace(-90, 90, num)
features = []
for i in range(len(lon)-1):
for j in range(len(lat)-1):
features.append(ee.Feature(ee.Geometry.Rectangle(lon[i], lat[j], lon[i+1], lat[j+1])))
if not polygons:
polygons = ee.FeatureCollection(features)
regReducer = {
'geometry': polygons,
'reducer': ee.Reducer.minMax(),
'maxPixels': 1e10,
'bestEffort': True,
'scale':scale,
'tileScale': 10
}
values = image.reduceRegion(**regReducer).getInfo()
print(values)
# Avoid outliers by taking into account only the normThreshold% of the data points.
regReducer = {
'geometry': polygons,
'reducer': ee.Reducer.histogram(),
'maxPixels': 1e10,
'bestEffort': True,
'scale':scale,
'tileScale': 10
}
hist = image.reduceRegion(**regReducer).getInfo()
for band in list(normThreshold.keys()):
if normThreshold[band] != 100:
count = np.array(hist.get(band).get('histogram'))
x = np.array(hist.get(band).get('bucketMeans'))
cumulative_per = np.cumsum(count/count.sum()*100)
values[band+'_max'] = x[np.where(cumulative_per < normThreshold[band])][-1]
return values
def normalize_ee_images(image, collection, values):
Bands = ee_collection_specifics.ee_bands(collection)
# Normalize [0, 1] ee images
for i, band in enumerate(Bands):
if i == 0:
image_new = image.select(band).clamp(values[band+'_min'], values[band+'_max'])\
.subtract(values[band+'_min'])\
.divide(values[band+'_max']-values[band+'_min'])
else:
image_new = image_new.addBands(image.select(band).clamp(values[band+'_min'], values[band+'_max'])\
.subtract(values[band+'_min'])\
.divide(values[band+'_max']-values[band+'_min']))
return image_new
%%time
images = []
for collection in collections:
# Create composite
image = ee_collection_specifics.Composite(collection)(init_date, end_date)
bands = ee_collection_specifics.ee_bands(collection)
image = image.select(bands)
#Create composite
if ee_collection_specifics.normalize(collection):
# Get min man values for each band
values = min_max_values(image, collection, scale, polygons=trainFeatures)
print(values)
# Normalize images
image = normalize_ee_images(image, collection, values)
else:
values = {}
images.append(image)
```
**Display composite**
```
# Define the URL format used for Earth Engine generated map tiles.
EE_TILES = 'https://earthengine.googleapis.com/map/{mapid}/{{z}}/{{x}}/{{y}}?token={token}'
map = folium.Map(location=[39.31, 0.302], zoom_start=6)
for n, collection in enumerate(collections):
for params in ee_collection_specifics.vizz_params(collection):
mapid = images[n].getMapId(params)
folium.TileLayer(
tiles=EE_TILES.format(**mapid),
attr='Google Earth Engine',
overlay=True,
name=str(params['bands']),
).add_to(map)
# Convert the GeoJSONs to feature collections
trainFeatures = ee.FeatureCollection(trainPolys.get('features'))
if evalPolys:
evalFeatures = ee.FeatureCollection(evalPolys.get('features'))
polyImage = ee.Image(0).byte().paint(trainFeatures, 1)
if evalPolys:
polyImage = ee.Image(0).byte().paint(trainFeatures, 1).paint(evalFeatures, 2)
polyImage = polyImage.updateMask(polyImage)
mapid = polyImage.getMapId({'min': 1, 'max': 2, 'palette': ['red', 'blue']})
folium.TileLayer(
tiles=EE_TILES.format(**mapid),
attr='Google Earth Engine',
overlay=True,
name='training polygons',
).add_to(map)
map.add_child(folium.LayerControl())
map
```
***
## Create TFRecords for training
### Export pixels
**Variables**
```
input_bands = ['B2','B3','B4','B5','ndvi','ndwi']
output_bands = ['turbidity_blended_mean']
bands = [input_bands, output_bands]
dataset_name = 'Sentinel2_WaterQuality'
base_names = ['training_pixels', 'eval_pixels']
bucket = env.bucket_name
folder = 'cnn-models/'+dataset_name+'/data'
```
**Select the bands**
```
# Select the bands we want
c = images[0].select(bands[0])\
.addBands(images[1].select(bands[1]))
pprint(c.getInfo())
```
**Sample pixels**
```
sr = c.sample(region = trainFeatures, scale = scale, numPixels=20000, tileScale=4, seed=999)
# Add random column
sr = sr.randomColumn(seed=999)
# Partition the sample approximately 70-30.
train_dataset = sr.filter(ee.Filter.lt('random', 0.7))
eval_dataset = sr.filter(ee.Filter.gte('random', 0.7))
# Print the first couple points to verify.
pprint({'training': train_dataset.first().getInfo()})
pprint({'testing': eval_dataset.first().getInfo()})
# Print the first couple points to verify.
from pprint import pprint
train_size=train_dataset.size().getInfo()
eval_size=eval_dataset.size().getInfo()
pprint({'training': train_size})
pprint({'testing': eval_size})
```
**Export the training and validation data**
```
def export_TFRecords_pixels(datasets, base_names, bucket, folder, selectors):
# Export all the training/evaluation data
filePaths = []
for n, dataset in enumerate(datasets):
filePaths.append(bucket+ '/' + folder + '/' + base_names[n])
# Create the tasks.
task = ee.batch.Export.table.toCloudStorage(
collection = dataset,
description = 'Export '+base_names[n],
fileNamePrefix = folder + '/' + base_names[n],
bucket = bucket,
fileFormat = 'TFRecord',
selectors = selectors)
task.start()
return filePaths
datasets = [train_dataset, eval_dataset]
selectors = input_bands + output_bands
# Export training/evaluation data
filePaths = export_TFRecords_pixels(datasets, base_names, bucket, folder, selectors)
```
***
## Inspect data
### Inspect pixels
Load the data exported from Earth Engine into a tf.data.Dataset.
**Helper functions**
```
# Tensorflow setup.
import tensorflow as tf
if tf.__version__ == '1.15.0':
tf.enable_eager_execution()
print(tf.__version__)
def parse_function(proto):
"""The parsing function.
Read a serialized example into the structure defined by FEATURES_DICT.
Args:
example_proto: a serialized Example.
Returns:
A tuple of the predictors dictionary and the labels.
"""
# Define your tfrecord
features = input_bands + output_bands
# Specify the size and shape of patches expected by the model.
columns = [
tf.io.FixedLenFeature(shape=[1,1], dtype=tf.float32) for k in features
]
features_dict = dict(zip(features, columns))
# Load one example
parsed_features = tf.io.parse_single_example(proto, features_dict)
# Convert a dictionary of tensors to a tuple of (inputs, outputs)
inputsList = [parsed_features.get(key) for key in features]
stacked = tf.stack(inputsList, axis=0)
# Convert the tensors into a stack in HWC shape
stacked = tf.transpose(stacked, [1, 2, 0])
return stacked[:,:,:len(input_bands)], stacked[:,:,len(input_bands):]
def get_dataset(glob, buffer_size, batch_size):
"""Get the dataset
Returns:
A tf.data.Dataset of training data.
"""
glob = tf.compat.v1.io.gfile.glob(glob)
dataset = tf.data.TFRecordDataset(glob, compression_type='GZIP')
dataset = dataset.map(parse_function, num_parallel_calls=5)
dataset = dataset.shuffle(buffer_size).batch(batch_size).repeat()
return dataset
```
**Variables**
```
buffer_size = 100
batch_size = 4
```
**Dataset**
```
glob = 'gs://' + bucket + '/' + folder + '/' + base_names[0] + '*'
dataset = get_dataset(glob, buffer_size, batch_size)
dataset
```
**Check the first record**
```
arr = iter(dataset.take(1)).next()
input_arr = arr[0].numpy()
print(input_arr.shape)
output_arr = arr[1].numpy()
print(output_arr.shape)
```
***
## Training the model locally
**Variables**
```
job_dir = 'gs://' + bucket + '/' + 'cnn-models/'+ dataset_name +'/trainer'
logs_dir = job_dir + '/logs'
model_dir = job_dir + '/model'
shuffle_size = 2000
batch_size = 4
epochs=50
train_size=train_size
eval_size=eval_size
output_activation=''
```
**Training/evaluation data**
The following is code to load training/evaluation data.
```
import tensorflow as tf
def parse_function(proto):
"""The parsing function.
Read a serialized example into the structure defined by FEATURES_DICT.
Args:
example_proto: a serialized Example.
Returns:
A tuple of the predictors dictionary and the labels.
"""
# Define your tfrecord
features = input_bands + output_bands
# Specify the size and shape of patches expected by the model.
columns = [
tf.io.FixedLenFeature(shape=[1,1], dtype=tf.float32) for k in features
]
features_dict = dict(zip(features, columns))
# Load one example
parsed_features = tf.io.parse_single_example(proto, features_dict)
# Convert a dictionary of tensors to a tuple of (inputs, outputs)
inputsList = [parsed_features.get(key) for key in features]
stacked = tf.stack(inputsList, axis=0)
# Convert the tensors into a stack in HWC shape
stacked = tf.transpose(stacked)
return stacked[:,:,:len(input_bands)], stacked[:,:,len(input_bands):]
def get_dataset(glob):
"""Get the dataset
Returns:
A tf.data.Dataset of training data.
"""
glob = tf.compat.v1.io.gfile.glob(glob)
dataset = tf.data.TFRecordDataset(glob, compression_type='GZIP')
dataset = dataset.map(parse_function, num_parallel_calls=5)
return dataset
def get_training_dataset():
"""Get the preprocessed training dataset
Returns:
A tf.data.Dataset of training data.
"""
glob = 'gs://' + bucket + '/' + folder + '/' + base_names[0] + '*'
dataset = get_dataset(glob)
dataset = dataset.shuffle(shuffle_size).batch(batch_size).repeat()
return dataset
def get_evaluation_dataset():
"""Get the preprocessed evaluation dataset
Returns:
A tf.data.Dataset of evaluation data.
"""
glob = 'gs://' + bucket + '/' + folder + '/' + base_names[1] + '*'
dataset = get_dataset(glob)
dataset = dataset.batch(1).repeat()
return dataset
```
**Model**
```
from tensorflow.python.keras import Model # Keras model module
from tensorflow.python.keras.layers import Input, Dense, Dropout, Activation
def create_keras_model(inputShape, nClasses, output_activation='linear'):
inputs = Input(shape=inputShape, name='vector')
x = Dense(32, input_shape=inputShape, activation='relu')(inputs)
x = Dropout(0.5)(x)
x = Dense(128, activation='relu')(x)
x = Dropout(0.5)(x)
x = Dense(nClasses)(x)
outputs = Activation(output_activation, name= 'output')(x)
model = Model(inputs=inputs, outputs=outputs, name='sequential')
return model
```
**Training task**
The following will get the training and evaluation data, train the model and save it when it's done in a Cloud Storage bucket.
```
import tensorflow as tf
import time
import os
def train_and_evaluate():
"""Trains and evaluates the Keras model.
Uses the Keras model defined in model.py and trains on data loaded and
preprocessed in util.py. Saves the trained model in TensorFlow SavedModel
format to the path defined in part by the --job-dir argument.
"""
# Create the Keras Model
if not output_activation:
keras_model = create_keras_model(inputShape = (None, None, len(input_bands)), nClasses = len(output_bands))
else:
keras_model = create_keras_model(inputShape = (None, None, len(input_bands)), nClasses = len(output_bands), output_activation = output_activation)
# Compile Keras model
keras_model.compile(loss='mse', optimizer='adam', metrics=['mse'])
# Pass a tfrecord
training_dataset = get_training_dataset()
evaluation_dataset = get_evaluation_dataset()
# Setup TensorBoard callback.
tensorboard_cb = tf.keras.callbacks.TensorBoard(logs_dir)
# Train model
keras_model.fit(
x=training_dataset,
steps_per_epoch=int(train_size / batch_size),
epochs=epochs,
validation_data=evaluation_dataset,
validation_steps=int(eval_size / batch_size),
verbose=1,
callbacks=[tensorboard_cb])
tf.keras.models.save_model(keras_model, filepath=os.path.join(model_dir, str(int(time.time()))), save_format="tf")
return keras_model
model = train_and_evaluate()
```
**Evaluate model**
```
evaluation_dataset = get_evaluation_dataset()
model.evaluate(evaluation_dataset, steps=int(eval_size / batch_size))
```
### Read pretrained model
```
job_dir = 'gs://' + env.bucket_name + '/' + 'cnn-models/' + dataset_name + '/trainer'
model_dir = job_dir + '/model'
PROJECT_ID = env.project_id
# Pick the directory with the latest timestamp, in case you've trained multiple times
exported_model_dirs = ! gsutil ls {model_dir}
saved_model_path = exported_model_dirs[-1]
model = tf.keras.models.load_model(saved_model_path)
```
***
## Predict in Earth Engine
### Prepare the model for making predictions in Earth Engine
Before we can use the model in Earth Engine, it needs to be hosted by AI Platform. But before we can host the model on AI Platform we need to *EEify* (a new word!) it. The EEification process merely appends some extra operations to the input and outputs of the model in order to accomdate the interchange format between pixels from Earth Engine (float32) and inputs to AI Platform (base64). (See [this doc](https://cloud.google.com/ml-engine/docs/online-predict#binary_data_in_prediction_input) for details.)
**`earthengine model prepare`**
The EEification process is handled for you using the Earth Engine command `earthengine model prepare`. To use that command, we need to specify the input and output model directories and the name of the input and output nodes in the TensorFlow computation graph. We can do all that programmatically:
```
dataset_name = 'Sentinel2_WaterQuality'
job_dir = 'gs://' + env.bucket_name + '/' + 'cnn-models/' + dataset_name + '/trainer'
model_dir = job_dir + '/model'
project_id = env.project_id
# Pick the directory with the latest timestamp, in case you've trained multiple times
exported_model_dirs = ! gsutil ls {model_dir}
saved_model_path = exported_model_dirs[-1]
folder_name = saved_model_path.split('/')[-2]
from tensorflow.python.tools import saved_model_utils
meta_graph_def = saved_model_utils.get_meta_graph_def(saved_model_path, 'serve')
inputs = meta_graph_def.signature_def['serving_default'].inputs
outputs = meta_graph_def.signature_def['serving_default'].outputs
# Just get the first thing(s) from the serving signature def. i.e. this
# model only has a single input and a single output.
input_name = None
for k,v in inputs.items():
input_name = v.name
break
output_name = None
for k,v in outputs.items():
output_name = v.name
break
# Make a dictionary that maps Earth Engine outputs and inputs to
# AI Platform inputs and outputs, respectively.
import json
input_dict = "'" + json.dumps({input_name: "array"}) + "'"
output_dict = "'" + json.dumps({output_name: "prediction"}) + "'"
# Put the EEified model next to the trained model directory.
EEIFIED_DIR = job_dir + '/eeified/' + folder_name
# You need to set the project before using the model prepare command.
!earthengine set_project {PROJECT_ID}
!earthengine model prepare --source_dir {saved_model_path} --dest_dir {EEIFIED_DIR} --input {input_dict} --output {output_dict}
```
### Deployed the model to AI Platform
```
from googleapiclient import discovery
from googleapiclient import errors
```
**Authenticate your GCP account**
Enter the path to your service account key as the
`GOOGLE_APPLICATION_CREDENTIALS` variable in the cell below and run the cell.
```
%env GOOGLE_APPLICATION_CREDENTIALS {env.privatekey_path}
model_name = 'water_quality_test'
version_name = 'v' + folder_name
project_id = env.project_id
```
**Create model**
```
print('Creating model: ' + model_name)
# Store your full project ID in a variable in the format the API needs.
project = 'projects/{}'.format(project_id)
# Build a representation of the Cloud ML API.
ml = discovery.build('ml', 'v1')
# Create a dictionary with the fields from the request body.
request_dict = {'name': model_name,
'description': ''}
# Create a request to call projects.models.create.
request = ml.projects().models().create(
parent=project, body=request_dict)
# Make the call.
try:
response = request.execute()
print(response)
except errors.HttpError as err:
# Something went wrong, print out some information.
print('There was an error creating the model. Check the details:')
print(err._get_reason())
```
**Create version**
```
ml = discovery.build('ml', 'v1')
request_dict = {
'name': version_name,
'deploymentUri': EEIFIED_DIR,
'runtimeVersion': '1.14',
'pythonVersion': '3.5',
'framework': 'TENSORFLOW',
'autoScaling': {
"minNodes": 10
},
'machineType': 'mls1-c4-m2'
}
request = ml.projects().models().versions().create(
parent=f'projects/{project_id}/models/{model_name}',
body=request_dict
)
# Make the call.
try:
response = request.execute()
print(response)
except errors.HttpError as err:
# Something went wrong, print out some information.
print('There was an error creating the model. Check the details:')
print(err._get_reason())
```
**Check deployment status**
```
def check_status_deployment(model_name, version_name):
desc = !gcloud ai-platform versions describe {version_name} --model={model_name}
return desc.grep('state:')[0].split(':')[1].strip()
print(check_status_deployment(model_name, version_name))
```
### Load the trained model and use it for prediction in Earth Engine
**Variables**
```
# polygon where we want to display de predictions
geometry = {
"type": "FeatureCollection",
"features": [
{
"type": "Feature",
"properties": {},
"geometry": {
"type": "Polygon",
"coordinates": [
[
[
-2.63671875,
34.56085936708384
],
[
-1.2084960937499998,
34.56085936708384
],
[
-1.2084960937499998,
36.146746777814364
],
[
-2.63671875,
36.146746777814364
],
[
-2.63671875,
34.56085936708384
]
]
]
}
}
]
}
```
**Input image**
Select bands and convert them into float
```
image = images[0].select(bands[0]).float()
```
**Output image**
```
# Load the trained model and use it for prediction.
model = ee.Model.fromAiPlatformPredictor(
projectName = project_id,
modelName = model_name,
version = version_name,
inputTileSize = [1, 1],
inputOverlapSize = [0, 0],
proj = ee.Projection('EPSG:4326').atScale(scale),
fixInputProj = True,
outputBands = {'prediction': {
'type': ee.PixelType.float(),
'dimensions': 1,
}
}
)
predictions = model.predictImage(image.toArray()).arrayFlatten([bands[1]])
predictions.getInfo()
```
Clip the prediction area with the polygon
```
# Clip the prediction area with the polygon
polygon = ee.Geometry.Polygon(geometry.get('features')[0].get('geometry').get('coordinates'))
predictions = predictions.clip(polygon)
# Get centroid
centroid = polygon.centroid().getInfo().get('coordinates')[::-1]
```
**Display**
Use folium to visualize the input imagery and the predictions.
```
# Define the URL format used for Earth Engine generated map tiles.
EE_TILES = 'https://earthengine.googleapis.com/map/{mapid}/{{z}}/{{x}}/{{y}}?token={token}'
mapid = image.getMapId({'bands': ['B4', 'B3', 'B2'], 'min': 0, 'max': 1})
map = folium.Map(location=centroid, zoom_start=8)
folium.TileLayer(
tiles=EE_TILES.format(**mapid),
attr='Google Earth Engine',
overlay=True,
name='median composite',
).add_to(map)
params = ee_collection_specifics.vizz_params(collections[1])[0]
mapid = images[1].getMapId(params)
folium.TileLayer(
tiles=EE_TILES.format(**mapid),
attr='Google Earth Engine',
overlay=True,
name=str(params['bands']),
).add_to(map)
for band in bands[1]:
mapid = predictions.getMapId({'bands': [band], 'min': 0, 'max': 1})
folium.TileLayer(
tiles=EE_TILES.format(**mapid),
attr='Google Earth Engine',
overlay=True,
name=band,
).add_to(map)
map.add_child(folium.LayerControl())
map
```
***
## Make predictions of an image outside Earth Engine
### Export the imagery
We export the imagery using TFRecord format.
**Variables**
```
#Input image
image = images[0].select(bands[0])
dataset_name = 'Sentinel2_WaterQuality'
file_name = 'image_pixel'
bucket = env.bucket_name
folder = 'cnn-models/'+dataset_name+'/data'
# polygon where we want to display de predictions
geometry = {
"type": "FeatureCollection",
"features": [
{
"type": "Feature",
"properties": {},
"geometry": {
"type": "Polygon",
"coordinates": [
[
[
-2.63671875,
34.56085936708384
],
[
-1.2084960937499998,
34.56085936708384
],
[
-1.2084960937499998,
36.146746777814364
],
[
-2.63671875,
36.146746777814364
],
[
-2.63671875,
34.56085936708384
]
]
]
}
}
]
}
# Specify patch and file dimensions.
imageExportFormatOptions = {
'patchDimensions': [256, 256],
'maxFileSize': 104857600,
'compressed': True
}
# Setup the task.
imageTask = ee.batch.Export.image.toCloudStorage(
image=image,
description='Image Export',
fileNamePrefix=folder + '/' + file_name,
bucket=bucket,
scale=scale,
fileFormat='TFRecord',
region=geometry.get('features')[0].get('geometry').get('coordinates'),
formatOptions=imageExportFormatOptions,
)
# Start the task.
imageTask.start()
```
**Read the JSON mixer file**
The mixer contains metadata and georeferencing information for the exported patches, each of which is in a different file. Read the mixer to get some information needed for prediction.
```
json_file = f'gs://{bucket}' + '/' + folder + '/' + file_name +'.json'
# Load the contents of the mixer file to a JSON object.
json_text = !gsutil cat {json_file}
# Get a single string w/ newlines from the IPython.utils.text.SList
mixer = json.loads(json_text.nlstr)
pprint(mixer)
```
**Read the image files into a dataset**
The input needs to be preprocessed differently than the training and testing. Mainly, this is because the pixels are written into records as patches, we need to read the patches in as one big tensor (one patch for each band), then flatten them into lots of little tensors.
```
# Get relevant info from the JSON mixer file.
PATCH_WIDTH = mixer['patchDimensions'][0]
PATCH_HEIGHT = mixer['patchDimensions'][1]
PATCHES = mixer['totalPatches']
PATCH_DIMENSIONS_FLAT = [PATCH_WIDTH * PATCH_HEIGHT, 1]
features = bands[0]
glob = f'gs://{bucket}' + '/' + folder + '/' + file_name +'.tfrecord.gz'
# Note that the tensors are in the shape of a patch, one patch for each band.
image_columns = [
tf.FixedLenFeature(shape=PATCH_DIMENSIONS_FLAT, dtype=tf.float32) for k in features
]
# Parsing dictionary.
features_dict = dict(zip(bands[0], image_columns))
def parse_image(proto):
return tf.io.parse_single_example(proto, features_dict)
image_dataset = tf.data.TFRecordDataset(glob, compression_type='GZIP')
image_dataset = image_dataset.map(parse_image, num_parallel_calls=5)
# Break our long tensors into many little ones.
image_dataset = image_dataset.flat_map(
lambda features: tf.data.Dataset.from_tensor_slices(features)
)
# Turn the dictionary in each record into a tuple without a label.
image_dataset = image_dataset.map(
lambda dataDict: (tf.transpose(list(dataDict.values())), )
)
# Turn each patch into a batch.
image_dataset = image_dataset.batch(PATCH_WIDTH * PATCH_HEIGHT)
image_dataset
```
**Check the first record**
```
arr = iter(image_dataset.take(1)).next()
input_arr = arr[0].numpy()
print(input_arr.shape)
```
**Display the input channels**
```
def display_channels(data, nChannels, titles = False):
if nChannels == 1:
plt.figure(figsize=(5,5))
plt.imshow(data[:,:,0])
if titles:
plt.title(titles[0])
else:
fig, axs = plt.subplots(nrows=1, ncols=nChannels, figsize=(5*nChannels,5))
for i in range(nChannels):
ax = axs[i]
ax.imshow(data[:,:,i])
if titles:
ax.set_title(titles[i])
input_arr = input_arr.reshape((PATCH_WIDTH, PATCH_HEIGHT, len(bands[0])))
input_arr.shape
display_channels(input_arr, input_arr.shape[2], titles=bands[0])
```
### Generate predictions for the image pixels
To get predictions in each pixel, run the image dataset through the trained model using model.predict(). Print the first prediction to see that the output is a list of the three class probabilities for each pixel. Running all predictions might take a while.
```
predictions = model.predict(image_dataset, steps=PATCHES, verbose=1)
output_arr = predictions.reshape((PATCHES, PATCH_WIDTH, PATCH_HEIGHT, len(bands[1])))
output_arr.shape
display_channels(output_arr[9,:,:,:], output_arr.shape[3], titles=bands[1])
```
### Write the predictions to a TFRecord file
We need to write the pixels into the file as patches in the same order they came out. The records are written as serialized `tf.train.Example` protos.
```
dataset_name = 'Sentinel2_WaterQuality'
bucket = env.bucket_name
folder = 'cnn-models/'+dataset_name+'/data'
output_file = 'gs://' + bucket + '/' + folder + '/predicted_image_pixel.TFRecord'
print('Writing to file ' + output_file)
# Instantiate the writer.
writer = tf.io.TFRecordWriter(output_file)
patch = [[]]
nPatch = 1
for prediction in predictions:
patch[0].append(prediction[0][0])
# Once we've seen a patches-worth of class_ids...
if (len(patch[0]) == PATCH_WIDTH * PATCH_HEIGHT):
print('Done with patch ' + str(nPatch) + ' of ' + str(PATCHES))
# Create an example
example = tf.train.Example(
features=tf.train.Features(
feature={
'prediction': tf.train.Feature(
float_list=tf.train.FloatList(
value=patch[0]))
}
)
)
# Write the example to the file and clear our patch array so it's ready for
# another batch of class ids
writer.write(example.SerializeToString())
patch = [[]]
nPatch += 1
writer.close()
```
**Verify the existence of the predictions file**
```
!gsutil ls -l {output_file}
```
### Upload the predicted image to an Earth Engine asset
```
asset_id = 'projects/vizzuality/skydipper-water-quality/predicted-image'
print('Writing to ' + asset_id)
# Start the upload.
!earthengine upload image --asset_id={asset_id} {output_file} {json_file}
```
### View the predicted image
```
# Get centroid
polygon = ee.Geometry.Polygon(geometry.get('features')[0].get('geometry').get('coordinates'))
centroid = polygon.centroid().getInfo().get('coordinates')[::-1]
EE_TILES = 'https://earthengine.googleapis.com/map/{mapid}/{{z}}/{{x}}/{{y}}?token={token}'
map = folium.Map(location=centroid, zoom_start=8)
for n, collection in enumerate(collections):
params = ee_collection_specifics.vizz_params(collection)[0]
mapid = images[n].getMapId(params)
folium.TileLayer(
tiles=EE_TILES.format(**mapid),
attr='Google Earth Engine',
overlay=True,
name=str(params['bands']),
).add_to(map)
# Read predicted Image
predicted_image = ee.Image(asset_id)
mapid = predicted_image.getMapId({'bands': ['prediction'], 'min': 0, 'max': 1})
folium.TileLayer(
tiles=EE_TILES.format(**mapid),
attr='Google Earth Engine',
overlay=True,
name='predicted image',
).add_to(map)
map.add_child(folium.LayerControl())
map
```
|
github_jupyter
|
# Batch Normalization – Practice
Batch normalization is most useful when building deep neural networks. To demonstrate this, we'll create a convolutional neural network with 20 convolutional layers, followed by a fully connected layer. We'll use it to classify handwritten digits in the MNIST dataset, which should be familiar to you by now.
This is **not** a good network for classfying MNIST digits. You could create a _much_ simpler network and get _better_ results. However, to give you hands-on experience with batch normalization, we had to make an example that was:
1. Complicated enough that training would benefit from batch normalization.
2. Simple enough that it would train quickly, since this is meant to be a short exercise just to give you some practice adding batch normalization.
3. Simple enough that the architecture would be easy to understand without additional resources.
This notebook includes two versions of the network that you can edit. The first uses higher level functions from the `tf.layers` package. The second is the same network, but uses only lower level functions in the `tf.nn` package.
1. [Batch Normalization with `tf.layers.batch_normalization`](#example_1)
2. [Batch Normalization with `tf.nn.batch_normalization`](#example_2)
The following cell loads TensorFlow, downloads the MNIST dataset if necessary, and loads it into an object named `mnist`. You'll need to run this cell before running anything else in the notebook.
```
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True, reshape=False)
```
# Batch Normalization using `tf.layers.batch_normalization`<a id="example_1"></a>
This version of the network uses `tf.layers` for almost everything, and expects you to implement batch normalization using [`tf.layers.batch_normalization`](https://www.tensorflow.org/api_docs/python/tf/layers/batch_normalization)
We'll use the following function to create fully connected layers in our network. We'll create them with the specified number of neurons and a ReLU activation function.
This version of the function does not include batch normalization.
```
"""
DO NOT MODIFY THIS CELL
"""
def fully_connected(prev_layer, num_units):
"""
Create a fully connectd layer with the given layer as input and the given number of neurons.
:param prev_layer: Tensor
The Tensor that acts as input into this layer
:param num_units: int
The size of the layer. That is, the number of units, nodes, or neurons.
:returns Tensor
A new fully connected layer
"""
layer = tf.layers.dense(prev_layer, num_units, activation=tf.nn.relu)
return layer
```
We'll use the following function to create convolutional layers in our network. They are very basic: we're always using a 3x3 kernel, ReLU activation functions, strides of 1x1 on layers with odd depths, and strides of 2x2 on layers with even depths. We aren't bothering with pooling layers at all in this network.
This version of the function does not include batch normalization.
```
"""
DO NOT MODIFY THIS CELL
"""
def conv_layer(prev_layer, layer_depth):
"""
Create a convolutional layer with the given layer as input.
:param prev_layer: Tensor
The Tensor that acts as input into this layer
:param layer_depth: int
We'll set the strides and number of feature maps based on the layer's depth in the network.
This is *not* a good way to make a CNN, but it helps us create this example with very little code.
:returns Tensor
A new convolutional layer
"""
strides = 2 if layer_depth % 3 == 0 else 1
conv_layer = tf.layers.conv2d(prev_layer, layer_depth*4, 3, strides, 'same', activation=tf.nn.relu)
return conv_layer
```
**Run the following cell**, along with the earlier cells (to load the dataset and define the necessary functions).
This cell builds the network **without** batch normalization, then trains it on the MNIST dataset. It displays loss and accuracy data periodically while training.
```
"""
DO NOT MODIFY THIS CELL
"""
def train(num_batches, batch_size, learning_rate):
# Build placeholders for the input samples and labels
inputs = tf.placeholder(tf.float32, [None, 28, 28, 1])
labels = tf.placeholder(tf.float32, [None, 10])
# Feed the inputs into a series of 20 convolutional layers
layer = inputs
for layer_i in range(1, 20):
layer = conv_layer(layer, layer_i)
# Flatten the output from the convolutional layers
orig_shape = layer.get_shape().as_list()
layer = tf.reshape(layer, shape=[-1, orig_shape[1] * orig_shape[2] * orig_shape[3]])
# Add one fully connected layer
layer = fully_connected(layer, 100)
# Create the output layer with 1 node for each
logits = tf.layers.dense(layer, 10)
# Define loss and training operations
model_loss = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=logits, labels=labels))
train_opt = tf.train.AdamOptimizer(learning_rate).minimize(model_loss)
# Create operations to test accuracy
correct_prediction = tf.equal(tf.argmax(logits,1), tf.argmax(labels,1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
# Train and test the network
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for batch_i in range(num_batches):
batch_xs, batch_ys = mnist.train.next_batch(batch_size)
# train this batch
sess.run(train_opt, {inputs: batch_xs, labels: batch_ys})
# Periodically check the validation or training loss and accuracy
if batch_i % 100 == 0:
loss, acc = sess.run([model_loss, accuracy], {inputs: mnist.validation.images,
labels: mnist.validation.labels})
print('Batch: {:>2}: Validation loss: {:>3.5f}, Validation accuracy: {:>3.5f}'.format(batch_i, loss, acc))
elif batch_i % 25 == 0:
loss, acc = sess.run([model_loss, accuracy], {inputs: batch_xs, labels: batch_ys})
print('Batch: {:>2}: Training loss: {:>3.5f}, Training accuracy: {:>3.5f}'.format(batch_i, loss, acc))
# At the end, score the final accuracy for both the validation and test sets
acc = sess.run(accuracy, {inputs: mnist.validation.images,
labels: mnist.validation.labels})
print('Final validation accuracy: {:>3.5f}'.format(acc))
acc = sess.run(accuracy, {inputs: mnist.test.images,
labels: mnist.test.labels})
print('Final test accuracy: {:>3.5f}'.format(acc))
# Score the first 100 test images individually. This won't work if batch normalization isn't implemented correctly.
correct = 0
for i in range(100):
correct += sess.run(accuracy,feed_dict={inputs: [mnist.test.images[i]],
labels: [mnist.test.labels[i]]})
print("Accuracy on 100 samples:", correct/100)
num_batches = 800
batch_size = 64
learning_rate = 0.002
tf.reset_default_graph()
with tf.Graph().as_default():
train(num_batches, batch_size, learning_rate)
```
With this many layers, it's going to take a lot of iterations for this network to learn. By the time you're done training these 800 batches, your final test and validation accuracies probably won't be much better than 10%. (It will be different each time, but will most likely be less than 15%.)
Using batch normalization, you'll be able to train this same network to over 90% in that same number of batches.
# Add batch normalization
We've copied the previous three cells to get you started. **Edit these cells** to add batch normalization to the network. For this exercise, you should use [`tf.layers.batch_normalization`](https://www.tensorflow.org/api_docs/python/tf/layers/batch_normalization) to handle most of the math, but you'll need to make a few other changes to your network to integrate batch normalization. You may want to refer back to the lesson notebook to remind yourself of important things, like how your graph operations need to know whether or not you are performing training or inference.
If you get stuck, you can check out the `Batch_Normalization_Solutions` notebook to see how we did things.
**TODO:** Modify `fully_connected` to add batch normalization to the fully connected layers it creates. Feel free to change the function's parameters if it helps.
```
def fully_connected(prev_layer, num_units, is_training):
"""
Create a fully connectd layer with the given layer as input and the given number of neurons.
:param prev_layer: Tensor
The Tensor that acts as input into this layer
:param num_units: int
The size of the layer. That is, the number of units, nodes, or neurons.
:returns Tensor
A new fully connected layer
"""
layer = tf.layers.dense(prev_layer, num_units, use_bias=False, activation=None)
layer = tf.layers.batch_normalization(layer, training=is_training)
layer = tf.nn.relu(layer)
return layer
```
**TODO:** Modify `conv_layer` to add batch normalization to the convolutional layers it creates. Feel free to change the function's parameters if it helps.
```
def conv_layer(prev_layer, layer_depth, is_training):
"""
Create a convolutional layer with the given layer as input.
:param prev_layer: Tensor
The Tensor that acts as input into this layer
:param layer_depth: int
We'll set the strides and number of feature maps based on the layer's depth in the network.
This is *not* a good way to make a CNN, but it helps us create this example with very little code.
:returns Tensor
A new convolutional layer
"""
strides = 2 if layer_depth % 3 == 0 else 1
conv_layer = tf.layers.conv2d(prev_layer, layer_depth*4, 3, strides, 'same', activation=None, use_bias=False)
conv_layer = tf.layers.batch_normalization(conv_layer, training=is_training)
conv_layer = tf.nn.relu(conv_layer)
return conv_layer
```
**TODO:** Edit the `train` function to support batch normalization. You'll need to make sure the network knows whether or not it is training, and you'll need to make sure it updates and uses its population statistics correctly.
```
def train(num_batches, batch_size, learning_rate):
# Build placeholders for the input samples and labels
inputs = tf.placeholder(tf.float32, [None, 28, 28, 1])
labels = tf.placeholder(tf.float32, [None, 10])
# Add placeholder to indicate whether or not we're training the model
is_training = tf.placeholder(tf.bool)
# Feed the inputs into a series of 20 convolutional layers
layer = inputs
for layer_i in range(1, 20):
layer = conv_layer(layer, layer_i, is_training)
# Flatten the output from the convolutional layers
orig_shape = layer.get_shape().as_list()
layer = tf.reshape(layer, shape=[-1, orig_shape[1] * orig_shape[2] * orig_shape[3]])
# Add one fully connected layer
layer = fully_connected(layer, 100, is_training)
# Create the output layer with 1 node for each
logits = tf.layers.dense(layer, 10)
# Define loss and training operations
model_loss = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=logits, labels=labels))
# Tell TensorFlow to update the population statistics while training
with tf.control_dependencies(tf.get_collection(tf.GraphKeys.UPDATE_OPS)):
train_opt = tf.train.AdamOptimizer(learning_rate).minimize(model_loss)
# Create operations to test accuracy
correct_prediction = tf.equal(tf.argmax(logits,1), tf.argmax(labels,1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
# Train and test the network
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for batch_i in range(num_batches):
batch_xs, batch_ys = mnist.train.next_batch(batch_size)
# train this batch
sess.run(train_opt, {inputs: batch_xs, labels: batch_ys, is_training: True})
# Periodically check the validation or training loss and accuracy
if batch_i % 100 == 0:
loss, acc = sess.run([model_loss, accuracy], {inputs: mnist.validation.images,
labels: mnist.validation.labels,
is_training: False})
print('Batch: {:>2}: Validation loss: {:>3.5f}, Validation accuracy: {:>3.5f}'.format(batch_i, loss, acc))
elif batch_i % 25 == 0:
loss, acc = sess.run([model_loss, accuracy], {inputs: batch_xs, labels: batch_ys, is_training: False})
print('Batch: {:>2}: Training loss: {:>3.5f}, Training accuracy: {:>3.5f}'.format(batch_i, loss, acc))
# At the end, score the final accuracy for both the validation and test sets
acc = sess.run(accuracy, {inputs: mnist.validation.images,
labels: mnist.validation.labels,
is_training: False})
print('Final validation accuracy: {:>3.5f}'.format(acc))
acc = sess.run(accuracy, {inputs: mnist.test.images,
labels: mnist.test.labels,
is_training: False})
print('Final test accuracy: {:>3.5f}'.format(acc))
# Score the first 100 test images individually, just to make sure batch normalization really worked
correct = 0
for i in range(100):
correct += sess.run(accuracy,feed_dict={inputs: [mnist.test.images[i]],
labels: [mnist.test.labels[i]],
is_training: False})
print("Accuracy on 100 samples:", correct/100)
num_batches = 800
batch_size = 64
learning_rate = 0.002
tf.reset_default_graph()
with tf.Graph().as_default():
train(num_batches, batch_size, learning_rate)
```
With batch normalization, you should now get an accuracy over 90%. Notice also the last line of the output: `Accuracy on 100 samples`. If this value is low while everything else looks good, that means you did not implement batch normalization correctly. Specifically, it means you either did not calculate the population mean and variance while training, or you are not using those values during inference.
# Batch Normalization using `tf.nn.batch_normalization`<a id="example_2"></a>
Most of the time you will be able to use higher level functions exclusively, but sometimes you may want to work at a lower level. For example, if you ever want to implement a new feature – something new enough that TensorFlow does not already include a high-level implementation of it, like batch normalization in an LSTM – then you may need to know these sorts of things.
This version of the network uses `tf.nn` for almost everything, and expects you to implement batch normalization using [`tf.nn.batch_normalization`](https://www.tensorflow.org/api_docs/python/tf/nn/batch_normalization).
**Optional TODO:** You can run the next three cells before you edit them just to see how the network performs without batch normalization. However, the results should be pretty much the same as you saw with the previous example before you added batch normalization.
**TODO:** Modify `fully_connected` to add batch normalization to the fully connected layers it creates. Feel free to change the function's parameters if it helps.
**Note:** For convenience, we continue to use `tf.layers.dense` for the `fully_connected` layer. By this point in the class, you should have no problem replacing that with matrix operations between the `prev_layer` and explicit weights and biases variables.
```
def fully_connected(prev_layer, num_units, is_training):
"""
Create a fully connectd layer with the given layer as input and the given number of neurons.
:param prev_layer: Tensor
The Tensor that acts as input into this layer
:param num_units: int
The size of the layer. That is, the number of units, nodes, or neurons.
:param is_training: bool or Tensor
Indicates whether or not the network is currently training, which tells the batch normalization
layer whether or not it should update or use its population statistics.
:returns Tensor
A new fully connected layer
"""
layer = tf.layers.dense(prev_layer, num_units, use_bias=False, activation=None)
gamma = tf.Variable(tf.ones([num_units]))
beta = tf.Variable(tf.zeros([num_units]))
pop_mean = tf.Variable(tf.zeros([num_units]), trainable=False)
pop_variance = tf.Variable(tf.ones([num_units]), trainable=False)
epsilon = 1e-3
def batch_norm_training():
batch_mean, batch_variance = tf.nn.moments(layer, [0])
decay = 0.99
train_mean = tf.assign(pop_mean, pop_mean * decay + batch_mean * (1 - decay))
train_variance = tf.assign(pop_variance, pop_variance * decay + batch_variance * (1 - decay))
with tf.control_dependencies([train_mean, train_variance]):
return tf.nn.batch_normalization(layer, batch_mean, batch_variance, beta, gamma, epsilon)
def batch_norm_inference():
return tf.nn.batch_normalization(layer, pop_mean, pop_variance, beta, gamma, epsilon)
batch_normalized_output = tf.cond(is_training, batch_norm_training, batch_norm_inference)
return tf.nn.relu(batch_normalized_output)
```
**TODO:** Modify `conv_layer` to add batch normalization to the fully connected layers it creates. Feel free to change the function's parameters if it helps.
**Note:** Unlike in the previous example that used `tf.layers`, adding batch normalization to these convolutional layers _does_ require some slight differences to what you did in `fully_connected`.
```
def conv_layer(prev_layer, layer_depth, is_training):
"""
Create a convolutional layer with the given layer as input.
:param prev_layer: Tensor
The Tensor that acts as input into this layer
:param layer_depth: int
We'll set the strides and number of feature maps based on the layer's depth in the network.
This is *not* a good way to make a CNN, but it helps us create this example with very little code.
:param is_training: bool or Tensor
Indicates whether or not the network is currently training, which tells the batch normalization
layer whether or not it should update or use its population statistics.
:returns Tensor
A new convolutional layer
"""
strides = 2 if layer_depth % 3 == 0 else 1
in_channels = prev_layer.get_shape().as_list()[3]
out_channels = layer_depth*4
weights = tf.Variable(
tf.truncated_normal([3, 3, in_channels, out_channels], stddev=0.05))
layer = tf.nn.conv2d(prev_layer, weights, strides=[1,strides, strides, 1], padding='SAME')
gamma = tf.Variable(tf.ones([out_channels]))
beta = tf.Variable(tf.zeros([out_channels]))
pop_mean = tf.Variable(tf.zeros([out_channels]), trainable=False)
pop_variance = tf.Variable(tf.ones([out_channels]), trainable=False)
epsilon = 1e-3
def batch_norm_training():
# Important to use the correct dimensions here to ensure the mean and variance are calculated
# per feature map instead of for the entire layer
batch_mean, batch_variance = tf.nn.moments(layer, [0,1,2], keep_dims=False)
decay = 0.99
train_mean = tf.assign(pop_mean, pop_mean * decay + batch_mean * (1 - decay))
train_variance = tf.assign(pop_variance, pop_variance * decay + batch_variance * (1 - decay))
with tf.control_dependencies([train_mean, train_variance]):
return tf.nn.batch_normalization(layer, batch_mean, batch_variance, beta, gamma, epsilon)
def batch_norm_inference():
return tf.nn.batch_normalization(layer, pop_mean, pop_variance, beta, gamma, epsilon)
batch_normalized_output = tf.cond(is_training, batch_norm_training, batch_norm_inference)
return tf.nn.relu(batch_normalized_output)
```
**TODO:** Edit the `train` function to support batch normalization. You'll need to make sure the network knows whether or not it is training.
```
def train(num_batches, batch_size, learning_rate):
# Build placeholders for the input samples and labels
inputs = tf.placeholder(tf.float32, [None, 28, 28, 1])
labels = tf.placeholder(tf.float32, [None, 10])
# Add placeholder to indicate whether or not we're training the model
is_training = tf.placeholder(tf.bool)
# Feed the inputs into a series of 20 convolutional layers
layer = inputs
for layer_i in range(1, 20):
layer = conv_layer(layer, layer_i, is_training)
# Flatten the output from the convolutional layers
orig_shape = layer.get_shape().as_list()
layer = tf.reshape(layer, shape=[-1, orig_shape[1] * orig_shape[2] * orig_shape[3]])
# Add one fully connected layer
layer = fully_connected(layer, 100, is_training)
# Create the output layer with 1 node for each
logits = tf.layers.dense(layer, 10)
# Define loss and training operations
model_loss = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=logits, labels=labels))
train_opt = tf.train.AdamOptimizer(learning_rate).minimize(model_loss)
# Create operations to test accuracy
correct_prediction = tf.equal(tf.argmax(logits,1), tf.argmax(labels,1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
# Train and test the network
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for batch_i in range(num_batches):
batch_xs, batch_ys = mnist.train.next_batch(batch_size)
# train this batch
sess.run(train_opt, {inputs: batch_xs, labels: batch_ys, is_training: True})
# Periodically check the validation or training loss and accuracy
if batch_i % 100 == 0:
loss, acc = sess.run([model_loss, accuracy], {inputs: mnist.validation.images,
labels: mnist.validation.labels,
is_training: False})
print('Batch: {:>2}: Validation loss: {:>3.5f}, Validation accuracy: {:>3.5f}'.format(batch_i, loss, acc))
elif batch_i % 25 == 0:
loss, acc = sess.run([model_loss, accuracy], {inputs: batch_xs, labels: batch_ys, is_training: False})
print('Batch: {:>2}: Training loss: {:>3.5f}, Training accuracy: {:>3.5f}'.format(batch_i, loss, acc))
# At the end, score the final accuracy for both the validation and test sets
acc = sess.run(accuracy, {inputs: mnist.validation.images,
labels: mnist.validation.labels,
is_training: False})
print('Final validation accuracy: {:>3.5f}'.format(acc))
acc = sess.run(accuracy, {inputs: mnist.test.images,
labels: mnist.test.labels,
is_training: False})
print('Final test accuracy: {:>3.5f}'.format(acc))
# Score the first 100 test images individually, just to make sure batch normalization really worked
correct = 0
for i in range(100):
correct += sess.run(accuracy,feed_dict={inputs: [mnist.test.images[i]],
labels: [mnist.test.labels[i]],
is_training: False})
print("Accuracy on 100 samples:", correct/100)
num_batches = 800
batch_size = 64
learning_rate = 0.002
tf.reset_default_graph()
with tf.Graph().as_default():
train(num_batches, batch_size, learning_rate)
```
Once again, the model with batch normalization should reach an accuracy over 90%. There are plenty of details that can go wrong when implementing at this low level, so if you got it working - great job! If not, do not worry, just look at the `Batch_Normalization_Solutions` notebook to see what went wrong.
|
github_jupyter
|
# Country Economic Conditions for Cargo Carriers
This report is written from the point of view of a data scientist preparing a report to the Head of Analytics for a logistics company. The company needs information on economic and financial conditions is different countries, including data on their international trade, to be aware of any situations that could affect business.
## Data Summary
This dataset is taken from the International Monetary Fund (IMF) data bank. It lists country-level economic and financial statistics from all countries globally. This includes data such as gross domestic product (GDP), inflation, exports and imports, and government borrowing and revenue. The data is given in either US Dollars, or local currency depending on the country and year. Some variables, like inflation and unemployment, are given as percentages.
## Data Exploration
The initial plan for data exploration is to first model the data on country GDP and inflation, then to look further into trade statistics.
```
#Import required packages
import numpy as np
import pandas as pd
from sklearn import linear_model
from scipy import stats
import math
from sklearn import datasets, linear_model
from sklearn.linear_model import LinearRegression
import statsmodels.api as sm
#Import IMF World Economic Outlook Data from GitHub
WEO = pd.read_csv('https://raw.githubusercontent.com/jamiemfraser/machine_learning/main/WEOApr2021all.csv')
WEO=pd.DataFrame(WEO)
WEO.head()
# Print basic details of the dataset
print(WEO.shape[0])
print(WEO.columns.tolist())
print(WEO.dtypes)
#Shows that all numeric columns are type float, and string columns are type object
```
### Data Cleaning and Feature Engineering
```
#We are only interested in the most recent year for which data is available, 2019
WEO=WEO.drop(['2000', '2001', '2002', '2003', '2004', '2005', '2006', '2007', '2008', '2009', '2010', '2011', '2012', '2013', '2014', '2015', '2016', '2017', '2018'], axis = 1)
#Reshape the data so each country is one observation
WEO=WEO.pivot_table(index=["Country"], columns='Indicator', values='2019').reset_index()
WEO.columns = ['Country', 'Current_account', 'Employment', 'Net_borrowing', 'Government_revenue', 'Government_expenditure', 'GDP_percap_constant', 'GDP_percap_current', 'GDP_constant', 'Inflation', 'Investment', 'Unemployment', 'Volume_exports', 'Volume_imports']
WEO.head()
#Describe the dataset
WEO.dropna(inplace=True)
WEO.describe()
```
### Key Findings and Insights
```
#Large differences betweeen the mean and median values could be an indication of outliers that are skewing the data
WEO.agg([np.mean, np.median])
#Create a scatterplot
import matplotlib.pyplot as plt
%matplotlib inline
ax = plt.axes()
ax.scatter(WEO.Volume_exports, WEO.Volume_imports)
# Label the axes
ax.set(xlabel='Volume Exports',
ylabel='Volume Imports',
title='Volume of Exports vs Imports');
#Create a scatterplot
import matplotlib.pyplot as plt
%matplotlib inline
ax = plt.axes()
ax.scatter(WEO.GDP_percap_constant, WEO.Volume_imports)
# Label the axes
ax.set(xlabel='GDP per capita',
ylabel='Volume Imports',
title='GDP per capita vs Volume of Imports');
#Create a scatterplot
import matplotlib.pyplot as plt
%matplotlib inline
ax = plt.axes()
ax.scatter(WEO.Investment, WEO.Volume_imports)
# Label the axes
ax.set(xlabel='Investment',
ylabel='Volume Imports',
title='Investment vs Volume of Imports');
```
### Hypotheses
Hypothesis 1: GDP per capita and the level of investment will be significant in determining the volume of goods and services imports
Hypothesis 2: There will be a strong correlation between government revenues and government expenditures
Hypothesis 3: GDP per capita and inflation will be significant in determining the unemployment rate
### Significance Test
I will conduct a formal hypothesis test on Hypothesis #1, which states that GDP per capita and the level of investment will be significant in determining the volume of goods and services imports. I will use a linear regression model because the scatterplots shown above indicate there is likely a linear relationship between both GDP per capita and investment against the volume of imports. I will take a p-value of 0.05 or less to be an indication of significance.
The null hypothesis is that there is no significant relationship between GDP per capita or the level of investment and the volume of goods and services.
The alternative hypothesis is that there is a significant relationship between either GDP per capita or the level of investment and the volume of goods and services.
```
#Set up a linear regression model for GDP per capita and evaluate
WEO=WEO.reset_index()
X = WEO['GDP_percap_constant']
X=X.values.reshape(-1,1)
y = WEO['Volume_imports']
X2 = sm.add_constant(X)
est = sm.OLS(y, X2)
est2 = est.fit()
print(est2.summary())
#Set up a linear regression model for Investment and evaluate
WEO=WEO.reset_index()
X = WEO['Investment']
X=X.values.reshape(-1,1)
y = WEO['Volume_imports']
X2 = sm.add_constant(X)
est = sm.OLS(y, X2)
est2 = est.fit()
print(est2.summary())
```
The linear regression analyses show that while GDP per capita is not significant in determining the volume of imports, investment is significant. For GDP per capita, we obtain a p-value of 0.313 which is insignificant. For Investment, we obtain a p-value of 0.000, which is significant.
## Next Steps
Next steps in analysing the data would be to see if there are any other variables that are significant in determining the volume of imports. The data scientist could also try a multiple linear regression to determine if there are variables that together produce a significant effect.
### Data Quality
The quality of this dataset is questionable. The exploratory data analysis showed several outliers that could be skewing the data. Further, there is no defined uniformity for how this data is measured. It is reported on a country-by-country basis, which leaves open the possibility that variation in definitions or methods for measuring these variables could lead to inaccurate comparison between countries.
Further data that I would request is more detailed trade data. Specifically, because this analysis finds that investment is significant in determining the volume of imports, it would be interesting to see which types of goods are more affected by investment. This could inform business decisions for a logistics company by allowing it to predict what type of cargo would need to be moved depending on investment practices in an individual country.
|
github_jupyter
|
I want to analyze changes over time in the MOT GTFS feed.
Agenda:
1. [Get data](#Get-the-data)
3. [Tidy](#Tidy-it-up)
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import partridge as ptg
from ftplib import FTP
import datetime
import re
import zipfile
import os
%matplotlib inline
plt.rcParams['figure.figsize'] = (10, 5) # set default size of plots
sns.set_style("white")
sns.set_context("talk")
sns.set_palette('Set2', 10)
```
## Get the data
There are two options - TransitFeeds and the workshop's S3 bucket.
```
#!aws s3 cp s3://s3.obus.hasadna.org.il/2018-04-25.zip data/gtfs_feeds/2018-04-25.zip
```
## Tidy it up
Again I'm using [partridge](https://github.com/remix/partridge/tree/master/partridge) for filtering on dates, and then some tidying up and transformations.
```
from gtfs_utils import *
local_tariff_path = 'data/sample/180515_tariff.zip'
conn = ftp_connect()
get_ftp_file(conn, file_name = TARIFF_FILE_NAME, local_zip_path = local_tariff_path )
def to_timedelta(df):
'''
Turn time columns into timedelta dtype
'''
cols = ['arrival_time', 'departure_time']
numeric = df[cols].apply(pd.to_timedelta, unit='s')
df = df.copy()
df[cols] = numeric
return df
%time f2 = new_get_tidy_feed_df(feed, [zones])
f2.head()
f2.columns
def get_tidy_feed_df(feed, zones):
s = feed.stops
r = feed.routes
a = feed.agency
t = (feed.trips
# faster joins and slices with Categorical dtypes
.assign(route_id=lambda x: pd.Categorical(x['route_id'])))
f = (feed.stop_times[fields['stop_times']]
.merge(s[fields['stops']], on='stop_id')
.merge(zones, how='left')
.assign(zone_name=lambda x: pd.Categorical(x['zone_name']))
.merge(t[fields['trips']], on='trip_id', how='left')
.assign(route_id=lambda x: pd.Categorical(x['route_id']))
.merge(r[fields['routes']], on='route_id', how='left')
.assign(agency_id=lambda x: pd.Categorical(x['agency_id']))
.merge(a[fields['agency']], on='agency_id', how='left')
.assign(agency_name=lambda x: pd.Categorical(x['agency_name']))
.pipe(to_timedelta)
)
return f
LOCAL_ZIP_PATH = 'data/gtfs_feeds/2018-02-01.zip'
feed = get_partridge_feed_by_date(LOCAL_ZIP_PATH, datetime.date(2018,2 , 1))
zones = get_zones()
'route_ids' in feed.routes.columns
feed.routes.shape
f = get_tidy_feed_df(feed, zones)
f.columns
f[f.route_short_name.isin(['20', '26', '136'])].groupby('stop_name').route_short_name.nunique().sort_values(ascending=False)
```
|
github_jupyter
|
# Saving and Loading Models
In this notebook, I'll show you how to save and load models with PyTorch. This is important because you'll often want to load previously trained models to use in making predictions or to continue training on new data.
```
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
import matplotlib.pyplot as plt
import torch
from torch import nn
from torch import optim
import torch.nn.functional as F
from torchvision import datasets, transforms
import helper
import fc_model
# Define a transform to normalize the data
transform = transforms.Compose([transforms.ToTensor(),
transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))])
# Download and load the training data
trainset = datasets.FashionMNIST('F_MNIST_data/', download=True, train=True, transform=transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=64, shuffle=True)
# Download and load the test data
testset = datasets.FashionMNIST('F_MNIST_data/', download=True, train=False, transform=transform)
testloader = torch.utils.data.DataLoader(testset, batch_size=64, shuffle=True)
```
Here we can see one of the images.
```
image, label = next(iter(trainloader))
helper.imshow(image[0,:]);
```
# Train a network
To make things more concise here, I moved the model architecture and training code from the last part to a file called `fc_model`. Importing this, we can easily create a fully-connected network with `fc_model.Network`, and train the network using `fc_model.train`. I'll use this model (once it's trained) to demonstrate how we can save and load models.
```
# Create the network, define the criterion and optimizer
model = fc_model.Network(784, 10, [512, 256, 128])
criterion = nn.NLLLoss()
optimizer = optim.Adam(model.parameters(), lr=0.001)
fc_model.train(model, trainloader, testloader, criterion, optimizer, epochs=2)
```
## Saving and loading networks
As you can imagine, it's impractical to train a network every time you need to use it. Instead, we can save trained networks then load them later to train more or use them for predictions.
The parameters for PyTorch networks are stored in a model's `state_dict`. We can see the state dict contains the weight and bias matrices for each of our layers.
```
print("Our model: \n\n", model, '\n')
print("The state dict keys: \n\n", model.state_dict().keys())
```
The simplest thing to do is simply save the state dict with `torch.save`. For example, we can save it to a file `'checkpoint.pth'`.
```
torch.save(model.state_dict(), 'checkpoint.pth')
```
Then we can load the state dict with `torch.load`.
```
state_dict = torch.load('checkpoint.pth')
print(state_dict.keys())
```
And to load the state dict in to the network, you do `model.load_state_dict(state_dict)`.
```
model.load_state_dict(state_dict)
```
Seems pretty straightforward, but as usual it's a bit more complicated. Loading the state dict works only if the model architecture is exactly the same as the checkpoint architecture. If I create a model with a different architecture, this fails.
```
# Try this
model = fc_model.Network(784, 10, [400, 200, 100])
# This will throw an error because the tensor sizes are wrong!
model.load_state_dict(state_dict)
```
This means we need to rebuild the model exactly as it was when trained. Information about the model architecture needs to be saved in the checkpoint, along with the state dict. To do this, you build a dictionary with all the information you need to compeletely rebuild the model.
```
checkpoint = {'input_size': 784,
'output_size': 10,
'hidden_layers': [each.out_features for each in model.hidden_layers],
'state_dict': model.state_dict()}
torch.save(checkpoint, 'checkpoint.pth')
```
Now the checkpoint has all the necessary information to rebuild the trained model. You can easily make that a function if you want. Similarly, we can write a function to load checkpoints.
```
def load_checkpoint(filepath):
checkpoint = torch.load(filepath)
model = fc_model.Network(checkpoint['input_size'],
checkpoint['output_size'],
checkpoint['hidden_layers'])
model.load_state_dict(checkpoint['state_dict'])
return model
model = load_checkpoint('checkpoint.pth')
print(model)
```
|
github_jupyter
|
# Deep Learning & Art: Neural Style Transfer
Welcome to the second assignment of this week. In this assignment, you will learn about Neural Style Transfer. This algorithm was created by Gatys et al. (2015) (https://arxiv.org/abs/1508.06576).
**In this assignment, you will:**
- Implement the neural style transfer algorithm
- Generate novel artistic images using your algorithm
Most of the algorithms you've studied optimize a cost function to get a set of parameter values. In Neural Style Transfer, you'll optimize a cost function to get pixel values!
```
import os
import sys
import scipy.io
import scipy.misc
import matplotlib.pyplot as plt
from matplotlib.pyplot import imshow
from PIL import Image
from nst_utils import *
import numpy as np
import tensorflow as tf
%matplotlib inline
```
## 1 - Problem Statement
Neural Style Transfer (NST) is one of the most fun techniques in deep learning. As seen below, it merges two images, namely, a "content" image (C) and a "style" image (S), to create a "generated" image (G). The generated image G combines the "content" of the image C with the "style" of image S.
In this example, you are going to generate an image of the Louvre museum in Paris (content image C), mixed with a painting by Claude Monet, a leader of the impressionist movement (style image S).
<img src="images/louvre_generated.png" style="width:750px;height:200px;">
Let's see how you can do this.
## 2 - Transfer Learning
Neural Style Transfer (NST) uses a previously trained convolutional network, and builds on top of that. The idea of using a network trained on a different task and applying it to a new task is called transfer learning.
Following the original NST paper (https://arxiv.org/abs/1508.06576), we will use the VGG network. Specifically, we'll use VGG-19, a 19-layer version of the VGG network. This model has already been trained on the very large ImageNet database, and thus has learned to recognize a variety of low level features (at the earlier layers) and high level features (at the deeper layers).
Run the following code to load parameters from the VGG model. This may take a few seconds.
```
model = load_vgg_model("pretrained-model/imagenet-vgg-verydeep-19.mat")
print(model)
```
The model is stored in a python dictionary where each variable name is the key and the corresponding value is a tensor containing that variable's value. To run an image through this network, you just have to feed the image to the model. In TensorFlow, you can do so using the [tf.assign](https://www.tensorflow.org/api_docs/python/tf/assign) function. In particular, you will use the assign function like this:
```python
model["input"].assign(image)
```
This assigns the image as an input to the model. After this, if you want to access the activations of a particular layer, say layer `4_2` when the network is run on this image, you would run a TensorFlow session on the correct tensor `conv4_2`, as follows:
```python
sess.run(model["conv4_2"])
```
## 3 - Neural Style Transfer
We will build the NST algorithm in three steps:
- Build the content cost function $J_{content}(C,G)$
- Build the style cost function $J_{style}(S,G)$
- Put it together to get $J(G) = \alpha J_{content}(C,G) + \beta J_{style}(S,G)$.
### 3.1 - Computing the content cost
In our running example, the content image C will be the picture of the Louvre Museum in Paris. Run the code below to see a picture of the Louvre.
```
content_image = scipy.misc.imread("images/louvre.jpg")
imshow(content_image)
```
The content image (C) shows the Louvre museum's pyramid surrounded by old Paris buildings, against a sunny sky with a few clouds.
** 3.1.1 - How do you ensure the generated image G matches the content of the image C?**
As we saw in lecture, the earlier (shallower) layers of a ConvNet tend to detect lower-level features such as edges and simple textures, and the later (deeper) layers tend to detect higher-level features such as more complex textures as well as object classes.
We would like the "generated" image G to have similar content as the input image C. Suppose you have chosen some layer's activations to represent the content of an image. In practice, you'll get the most visually pleasing results if you choose a layer in the middle of the network--neither too shallow nor too deep. (After you have finished this exercise, feel free to come back and experiment with using different layers, to see how the results vary.)
So, suppose you have picked one particular hidden layer to use. Now, set the image C as the input to the pretrained VGG network, and run forward propagation. Let $a^{(C)}$ be the hidden layer activations in the layer you had chosen. (In lecture, we had written this as $a^{[l](C)}$, but here we'll drop the superscript $[l]$ to simplify the notation.) This will be a $n_H \times n_W \times n_C$ tensor. Repeat this process with the image G: Set G as the input, and run forward progation. Let $$a^{(G)}$$ be the corresponding hidden layer activation. We will define as the content cost function as:
$$J_{content}(C,G) = \frac{1}{4 \times n_H \times n_W \times n_C}\sum _{ \text{all entries}} (a^{(C)} - a^{(G)})^2\tag{1} $$
Here, $n_H, n_W$ and $n_C$ are the height, width and number of channels of the hidden layer you have chosen, and appear in a normalization term in the cost. For clarity, note that $a^{(C)}$ and $a^{(G)}$ are the volumes corresponding to a hidden layer's activations. In order to compute the cost $J_{content}(C,G)$, it might also be convenient to unroll these 3D volumes into a 2D matrix, as shown below. (Technically this unrolling step isn't needed to compute $J_{content}$, but it will be good practice for when you do need to carry out a similar operation later for computing the style const $J_{style}$.)
<img src="images/NST_LOSS.png" style="width:800px;height:400px;">
**Exercise:** Compute the "content cost" using TensorFlow.
**Instructions**: The 3 steps to implement this function are:
1. Retrieve dimensions from a_G:
- To retrieve dimensions from a tensor X, use: `X.get_shape().as_list()`
2. Unroll a_C and a_G as explained in the picture above
- If you are stuck, take a look at [Hint1](https://www.tensorflow.org/versions/r1.3/api_docs/python/tf/transpose) and [Hint2](https://www.tensorflow.org/versions/r1.2/api_docs/python/tf/reshape).
3. Compute the content cost:
- If you are stuck, take a look at [Hint3](https://www.tensorflow.org/api_docs/python/tf/reduce_sum), [Hint4](https://www.tensorflow.org/api_docs/python/tf/square) and [Hint5](https://www.tensorflow.org/api_docs/python/tf/subtract).
```
# GRADED FUNCTION: compute_content_cost
def compute_content_cost(a_C, a_G):
"""
Computes the content cost
Arguments:
a_C -- tensor of dimension (1, n_H, n_W, n_C),
hidden layer activations representing content of the image C
a_G -- tensor of dimension (1, n_H, n_W, n_C),
hidden layer activations representing content of the image G
Returns:
J_content -- scalar that you compute using equation 1 above.
"""
### START CODE HERE ###
# Retrieve dimensions from a_G (≈1 line)
m, n_H, n_W, n_C = a_G.get_shape().as_list()
# Reshape a_C and a_G (≈2 lines)
a_C_unrolled = tf.transpose(tf.reshape(a_C, [-1]))
a_G_unrolled = tf.transpose(tf.reshape(a_G, [-1]))
# compute the cost with tensorflow (≈1 line)
J_content = tf.reduce_sum((a_C_unrolled - a_G_unrolled)**2)
/ (4 * n_H * n_W * n_C)
#J_content = tf.reduce_sum(tf.square(tf.subtract(a_C_unrolled,
# a_G_unrolled)))/ (4*n_H*n_W*n_C)
### END CODE HERE ###
return J_content
tf.reset_default_graph()
with tf.Session() as test:
tf.set_random_seed(1)
a_C = tf.random_normal([1, 4, 4, 3], mean=1, stddev=4)
a_G = tf.random_normal([1, 4, 4, 3], mean=1, stddev=4)
J_content = compute_content_cost(a_C, a_G)
print("J_content = " + str(J_content.eval()))
```
**Expected Output**:
<table>
<tr>
<td>
**J_content**
</td>
<td>
6.76559
</td>
</tr>
</table>
<font color='blue'>
**What you should remember**:
- The content cost takes a hidden layer activation of the neural network, and measures how different $a^{(C)}$ and $a^{(G)}$ are.
- When we minimize the content cost later, this will help make sure $G$ has similar content as $C$.
### 3.2 - Computing the style cost
For our running example, we will use the following style image:
```
style_image = scipy.misc.imread("images/monet_800600.jpg")
imshow(style_image)
```
This painting was painted in the style of *[impressionism](https://en.wikipedia.org/wiki/Impressionism)*.
Lets see how you can now define a "style" const function $J_{style}(S,G)$.
### 3.2.1 - Style matrix
The style matrix is also called a "Gram matrix." In linear algebra, the Gram matrix G of a set of vectors $(v_{1},\dots ,v_{n})$ is the matrix of dot products, whose entries are ${\displaystyle G_{ij} = v_{i}^T v_{j} = np.dot(v_{i}, v_{j}) }$. In other words, $G_{ij}$ compares how similar $v_i$ is to $v_j$: If they are highly similar, you would expect them to have a large dot product, and thus for $G_{ij}$ to be large.
Note that there is an unfortunate collision in the variable names used here. We are following common terminology used in the literature, but $G$ is used to denote the Style matrix (or Gram matrix) as well as to denote the generated image $G$. We will try to make sure which $G$ we are referring to is always clear from the context.
In NST, you can compute the Style matrix by multiplying the "unrolled" filter matrix with their transpose:
<img src="images/NST_GM.png" style="width:900px;height:300px;">
The result is a matrix of dimension $(n_C,n_C)$ where $n_C$ is the number of filters. The value $G_{ij}$ measures how similar the activations of filter $i$ are to the activations of filter $j$.
One important part of the gram matrix is that the diagonal elements such as $G_{ii}$ also measures how active filter $i$ is. For example, suppose filter $i$ is detecting vertical textures in the image. Then $G_{ii}$ measures how common vertical textures are in the image as a whole: If $G_{ii}$ is large, this means that the image has a lot of vertical texture.
By capturing the prevalence of different types of features ($G_{ii}$), as well as how much different features occur together ($G_{ij}$), the Style matrix $G$ measures the style of an image.
**Exercise**:
Using TensorFlow, implement a function that computes the Gram matrix of a matrix A. The formula is: The gram matrix of A is $G_A = AA^T$. If you are stuck, take a look at [Hint 1](https://www.tensorflow.org/api_docs/python/tf/matmul) and [Hint 2](https://www.tensorflow.org/api_docs/python/tf/transpose).
```
# GRADED FUNCTION: gram_matrix
def gram_matrix(A):
"""
Argument:
A -- matrix of shape (n_C, n_H*n_W)
Returns:
GA -- Gram matrix of A, of shape (n_C, n_C)
"""
### START CODE HERE ### (≈1 line)
GA = tf.matmul(A, tf.transpose(A))
### END CODE HERE ###
return GA
tf.reset_default_graph()
with tf.Session() as test:
tf.set_random_seed(1)
A = tf.random_normal([3, 2*1], mean=1, stddev=4)
GA = gram_matrix(A)
print("GA = " + str(GA.eval()))
```
**Expected Output**:
<table>
<tr>
<td>
**GA**
</td>
<td>
[[ 6.42230511 -4.42912197 -2.09668207] <br>
[ -4.42912197 19.46583748 19.56387138] <br>
[ -2.09668207 19.56387138 20.6864624 ]]
</td>
</tr>
</table>
### 3.2.2 - Style cost
After generating the Style matrix (Gram matrix), your goal will be to minimize the distance between the Gram matrix of the "style" image S and that of the "generated" image G. For now, we are using only a single hidden layer $a^{[l]}$, and the corresponding style cost for this layer is defined as:
$$J_{style}^{[l]}(S,G) = \frac{1}{4 \times {n_C}^2 \times (n_H \times n_W)^2} \sum _{i=1}^{n_C}\sum_{j=1}^{n_C}(G^{(S)}_{ij} - G^{(G)}_{ij})^2\tag{2} $$
where $G^{(S)}$ and $G^{(G)}$ are respectively the Gram matrices of the "style" image and the "generated" image, computed using the hidden layer activations for a particular hidden layer in the network.
**Exercise**: Compute the style cost for a single layer.
**Instructions**: The 3 steps to implement this function are:
1. Retrieve dimensions from the hidden layer activations a_G:
- To retrieve dimensions from a tensor X, use: `X.get_shape().as_list()`
2. Unroll the hidden layer activations a_S and a_G into 2D matrices, as explained in the picture above.
- You may find [Hint1](https://www.tensorflow.org/versions/r1.3/api_docs/python/tf/transpose) and [Hint2](https://www.tensorflow.org/versions/r1.2/api_docs/python/tf/reshape) useful.
3. Compute the Style matrix of the images S and G. (Use the function you had previously written.)
4. Compute the Style cost:
- You may find [Hint3](https://www.tensorflow.org/api_docs/python/tf/reduce_sum), [Hint4](https://www.tensorflow.org/api_docs/python/tf/square) and [Hint5](https://www.tensorflow.org/api_docs/python/tf/subtract) useful.
```
# GRADED FUNCTION: compute_layer_style_cost
def compute_layer_style_cost(a_S, a_G):
"""
Arguments:
a_S -- tensor of dimension (1, n_H, n_W, n_C),
hidden layer activations representing style of the image S
a_G -- tensor of dimension (1, n_H, n_W, n_C),
hidden layer activations representing style of the image G
Returns:
J_style_layer -- tensor representing a scalar value,
style cost defined above by equation (2)
"""
### START CODE HERE ###
# Retrieve dimensions from a_G (≈1 line)
m, n_H, n_W, n_C = a_G.get_shape().as_list()
# Reshape the images to have them of shape (n_C, n_H*n_W) (≈2 lines)
#a_S = tf.reshape(a_S, [n_C, n_H * n_W])
#a_G = tf.reshape(a_G, [n_C, n_H * n_W])
a_S = tf.transpose(tf.reshape(a_S, [n_H*n_W, n_C]))
a_G = tf.transpose(tf.reshape(a_G, [n_H*n_W, n_C]))
# Computing gram_matrices for both images S and G (≈2 lines)
GS = gram_matrix(a_S)
GG = gram_matrix(a_G)
# Computing the loss (≈1 line)
J_style_layer = tf.reduce_sum(tf.square((GS - GG)))
/ (4 * n_C**2 * (n_W * n_H)**2)
### END CODE HERE ###
return J_style_layer
tf.reset_default_graph()
with tf.Session() as test:
tf.set_random_seed(1)
a_S = tf.random_normal([1, 4, 4, 3], mean=1, stddev=4)
a_G = tf.random_normal([1, 4, 4, 3], mean=1, stddev=4)
J_style_layer = compute_layer_style_cost(a_S, a_G)
print("J_style_layer = " + str(J_style_layer.eval()))
```
**Expected Output**:
<table>
<tr>
<td>
**J_style_layer**
</td>
<td>
9.19028
</td>
</tr>
</table>
### 3.2.3 Style Weights
So far you have captured the style from only one layer. We'll get better results if we "merge" style costs from several different layers. After completing this exercise, feel free to come back and experiment with different weights to see how it changes the generated image $G$. But for now, this is a pretty reasonable default:
```
STYLE_LAYERS = [
('conv1_1', 0.2),
('conv2_1', 0.2),
('conv3_1', 0.2),
('conv4_1', 0.2),
('conv5_1', 0.2)]
```
You can combine the style costs for different layers as follows:
$$J_{style}(S,G) = \sum_{l} \lambda^{[l]} J^{[l]}_{style}(S,G)$$
where the values for $\lambda^{[l]}$ are given in `STYLE_LAYERS`.
We've implemented a compute_style_cost(...) function. It simply calls your `compute_layer_style_cost(...)` several times, and weights their results using the values in `STYLE_LAYERS`. Read over it to make sure you understand what it's doing.
<!--
2. Loop over (layer_name, coeff) from STYLE_LAYERS:
a. Select the output tensor of the current layer. As an example, to call the tensor from the "conv1_1" layer you would do: out = model["conv1_1"]
b. Get the style of the style image from the current layer by running the session on the tensor "out"
c. Get a tensor representing the style of the generated image from the current layer. It is just "out".
d. Now that you have both styles. Use the function you've implemented above to compute the style_cost for the current layer
e. Add (style_cost x coeff) of the current layer to overall style cost (J_style)
3. Return J_style, which should now be the sum of the (style_cost x coeff) for each layer.
!-->
```
def compute_style_cost(model, STYLE_LAYERS):
"""
Computes the overall style cost from several chosen layers
Arguments:
model -- our tensorflow model
STYLE_LAYERS -- A python list containing:
- the names of the layers we would like
to extract style from
- a coefficient for each of them
Returns:
J_style -- tensor representing a scalar value, style cost
defined above by equation (2)
"""
# initialize the overall style cost
J_style = 0
for layer_name, coeff in STYLE_LAYERS:
# Select the output tensor of the currently selected layer
out = model[layer_name]
# Set a_S to be the hidden layer activation from the layer
# we have selected, by running the session on out
a_S = sess.run(out)
# Set a_G to be the hidden layer activation from same layer.
# Here, a_G references model[layer_name]
# and isn't evaluated yet. Later in the code, we'll assign
# the image G as the model input, so that
# when we run the session, this will be the activations
# drawn from the appropriate layer, with G as input.
a_G = out
# Compute style_cost for the current layer
J_style_layer = compute_layer_style_cost(a_S, a_G)
# Add coeff * J_style_layer of this layer to overall style cost
J_style += coeff * J_style_layer
return J_style
```
**Note**: In the inner-loop of the for-loop above, `a_G` is a tensor and hasn't been evaluated yet. It will be evaluated and updated at each iteration when we run the TensorFlow graph in model_nn() below.
<!--
How do you choose the coefficients for each layer? The deeper layers capture higher-level concepts, and the features in the deeper layers are less localized in the image relative to each other. So if you want the generated image to softly follow the style image, try choosing larger weights for deeper layers and smaller weights for the first layers. In contrast, if you want the generated image to strongly follow the style image, try choosing smaller weights for deeper layers and larger weights for the first layers
!-->
<font color='blue'>
**What you should remember**:
- The style of an image can be represented using the Gram matrix of a hidden layer's activations. However, we get even better results combining this representation from multiple different layers. This is in contrast to the content representation, where usually using just a single hidden layer is sufficient.
- Minimizing the style cost will cause the image $G$ to follow the style of the image $S$.
</font color='blue'>
### 3.3 - Defining the total cost to optimize
Finally, let's create a cost function that minimizes both the style and the content cost. The formula is:
$$J(G) = \alpha J_{content}(C,G) + \beta J_{style}(S,G)$$
**Exercise**: Implement the total cost function which includes both the content cost and the style cost.
```
# GRADED FUNCTION: total_cost
def total_cost(J_content, J_style, alpha = 10, beta = 40):
"""
Computes the total cost function
Arguments:
J_content -- content cost coded above
J_style -- style cost coded above
alpha -- hyperparameter weighting the importance of the content cost
beta -- hyperparameter weighting the importance of the style cost
Returns:
J -- total cost as defined by the formula above.
"""
### START CODE HERE ### (≈1 line)
J = alpha * J_content + beta * J_style
### END CODE HERE ###
return J
tf.reset_default_graph()
with tf.Session() as test:
np.random.seed(3)
J_content = np.random.randn()
J_style = np.random.randn()
J = total_cost(J_content, J_style)
print("J = " + str(J))
```
**Expected Output**:
<table>
<tr>
<td>
**J**
</td>
<td>
35.34667875478276
</td>
</tr>
</table>
<font color='blue'>
**What you should remember**:
- The total cost is a linear combination of the content cost $J_{content}(C,G)$ and the style cost $J_{style}(S,G)$
- $\alpha$ and $\beta$ are hyperparameters that control the relative weighting between content and style
## 4 - Solving the optimization problem
Finally, let's put everything together to implement Neural Style Transfer!
Here's what the program will have to do:
<font color='purple'>
1. Create an Interactive Session
2. Load the content image
3. Load the style image
4. Randomly initialize the image to be generated
5. Load the VGG16 model
7. Build the TensorFlow graph:
- Run the content image through the VGG16 model and compute the content cost
- Run the style image through the VGG16 model and compute the style cost
- Compute the total cost
- Define the optimizer and the learning rate
8. Initialize the TensorFlow graph and run it for a large number of iterations, updating the generated image at every step.
</font>
Lets go through the individual steps in detail.
You've previously implemented the overall cost $J(G)$. We'll now set up TensorFlow to optimize this with respect to $G$. To do so, your program has to reset the graph and use an "[Interactive Session](https://www.tensorflow.org/api_docs/python/tf/InteractiveSession)". Unlike a regular session, the "Interactive Session" installs itself as the default session to build a graph. This allows you to run variables without constantly needing to refer to the session object, which simplifies the code.
Lets start the interactive session.
```
# Reset the graph
tf.reset_default_graph()
# Start interactive session
sess = tf.InteractiveSession()
```
Let's load, reshape, and normalize our "content" image (the Louvre museum picture):
```
content_image = scipy.misc.imread("images/louvre_small.jpg")
content_image = reshape_and_normalize_image(content_image)
```
Let's load, reshape and normalize our "style" image (Claude Monet's painting):
```
style_image = scipy.misc.imread("images/monet.jpg")
style_image = reshape_and_normalize_image(style_image)
```
Now, we initialize the "generated" image as a noisy image created from the content_image. By initializing the pixels of the generated image to be mostly noise but still slightly correlated with the content image, this will help the content of the "generated" image more rapidly match the content of the "content" image. (Feel free to look in `nst_utils.py` to see the details of `generate_noise_image(...)`; to do so, click "File-->Open..." at the upper-left corner of this Jupyter notebook.)
```
generated_image = generate_noise_image(content_image)
imshow(generated_image[0])
```
Next, as explained in part (2), let's load the VGG16 model.
```
model = load_vgg_model("pretrained-model/imagenet-vgg-verydeep-19.mat")
```
To get the program to compute the content cost, we will now assign `a_C` and `a_G` to be the appropriate hidden layer activations. We will use layer `conv4_2` to compute the content cost. The code below does the following:
1. Assign the content image to be the input to the VGG model.
2. Set a_C to be the tensor giving the hidden layer activation for layer "conv4_2".
3. Set a_G to be the tensor giving the hidden layer activation for the same layer.
4. Compute the content cost using a_C and a_G.
```
# Assign the content image to be the input of the VGG model.
sess.run(model['input'].assign(content_image))
# Select the output tensor of layer conv4_2
out = model['conv4_2']
# Set a_C to be the hidden layer activation from the layer we have selected
a_C = sess.run(out)
# Set a_G to be the hidden layer activation from same layer.
# Here, a_G references model['conv4_2']
# and isn't evaluated yet. Later in the code, we'll assign
# the image G as the model input, so that
# when we run the session, this will be the activations
# drawn from the appropriate layer, with G as input.
a_G = out
# Compute the content cost
J_content = compute_content_cost(a_C, a_G)
```
**Note**: At this point, a_G is a tensor and hasn't been evaluated. It will be evaluated and updated at each iteration when we run the Tensorflow graph in model_nn() below.
```
# Assign the input of the model to be the "style" image
sess.run(model['input'].assign(style_image))
# Compute the style cost
J_style = compute_style_cost(model, STYLE_LAYERS)
```
**Exercise**: Now that you have J_content and J_style, compute the total cost J by calling `total_cost()`. Use `alpha = 10` and `beta = 40`.
```
### START CODE HERE ### (1 line)
J = total_cost(J_content, J_style, alpha = 10, beta = 40)
### END CODE HERE ###
```
You'd previously learned how to set up the Adam optimizer in TensorFlow. Lets do that here, using a learning rate of 2.0. [See reference](https://www.tensorflow.org/api_docs/python/tf/train/AdamOptimizer)
```
# define optimizer (1 line)
optimizer = tf.train.AdamOptimizer(2.0)
# define train_step (1 line)
train_step = optimizer.minimize(J)
```
**Exercise**: Implement the model_nn() function which initializes the variables of the tensorflow graph, assigns the input image (initial generated image) as the input of the VGG16 model and runs the train_step for a large number of steps.
```
def model_nn(sess, input_image, num_iterations = 200):
# Initialize global variables (you need to run
# the session on the initializer)
### START CODE HERE ### (1 line)
sess.run(tf.global_variables_initializer())
### END CODE HERE ###
# Run the noisy input image (initial generated image)
# through the model. Use assign().
### START CODE HERE ### (1 line)
sess.run(model['input'].assign(input_image))
### END CODE HERE ###
for i in range(num_iterations):
# Run the session on the train_step to minimize the total cost
### START CODE HERE ### (1 line)
_ = sess.run(train_step)
### END CODE HERE ###
# Compute the generated image by running the session
# on the current model['input']
### START CODE HERE ### (1 line)
generated_image = sess.run(model['input'])
### END CODE HERE ###
# Print every 20 iteration.
if i%20 == 0:
Jt, Jc, Js = sess.run([J, J_content, J_style])
print("Iteration " + str(i) + " :")
print("total cost = " + str(Jt))
print("content cost = " + str(Jc))
print("style cost = " + str(Js))
# save current generated image in the "/output" directory
save_image("output/" + str(i) + ".png", generated_image)
# save last generated image
save_image('output/generated_image.jpg', generated_image)
return generated_image
```
Run the following cell to generate an artistic image. It should take about 3min on CPU for every 20 iterations but you start observing attractive results after ≈140 iterations. Neural Style Transfer is generally trained using GPUs.
```
model_nn(sess, generated_image)
```
**Expected Output**:
<table>
<tr>
<td>
**Iteration 0 : **
</td>
<td>
total cost = 5.05035e+09 <br>
content cost = 7877.67 <br>
style cost = 1.26257e+08
</td>
</tr>
</table>
You're done! After running this, in the upper bar of the notebook click on "File" and then "Open". Go to the "/output" directory to see all the saved images. Open "generated_image" to see the generated image! :)
You should see something the image presented below on the right:
<img src="images/louvre_generated.png" style="width:800px;height:300px;">
We didn't want you to wait too long to see an initial result, and so had set the hyperparameters accordingly. To get the best looking results, running the optimization algorithm longer (and perhaps with a smaller learning rate) might work better. After completing and submitting this assignment, we encourage you to come back and play more with this notebook, and see if you can generate even better looking images.
Here are few other examples:
- The beautiful ruins of the ancient city of Persepolis (Iran) with the style of Van Gogh (The Starry Night)
<img src="images/perspolis_vangogh.png" style="width:750px;height:300px;">
- The tomb of Cyrus the great in Pasargadae with the style of a Ceramic Kashi from Ispahan.
<img src="images/pasargad_kashi.png" style="width:750px;height:300px;">
- A scientific study of a turbulent fluid with the style of a abstract blue fluid painting.
<img src="images/circle_abstract.png" style="width:750px;height:300px;">
## 5 - Test with your own image (Optional/Ungraded)
Finally, you can also rerun the algorithm on your own images!
To do so, go back to part 4 and change the content image and style image with your own pictures. In detail, here's what you should do:
1. Click on "File -> Open" in the upper tab of the notebook
2. Go to "/images" and upload your images (requirement: (WIDTH = 300, HEIGHT = 225)), rename them "my_content.png" and "my_style.png" for example.
3. Change the code in part (3.4) from :
```python
content_image = scipy.misc.imread("images/louvre.jpg")
style_image = scipy.misc.imread("images/claude-monet.jpg")
```
to:
```python
content_image = scipy.misc.imread("images/my_content.jpg")
style_image = scipy.misc.imread("images/my_style.jpg")
```
4. Rerun the cells (you may need to restart the Kernel in the upper tab of the notebook).
You can also tune your hyperparameters:
- Which layers are responsible for representing the style? STYLE_LAYERS
- How many iterations do you want to run the algorithm? num_iterations
- What is the relative weighting between content and style? alpha/beta
## 6 - Conclusion
Great job on completing this assignment! You are now able to use Neural Style Transfer to generate artistic images. This is also your first time building a model in which the optimization algorithm updates the pixel values rather than the neural network's parameters. Deep learning has many different types of models and this is only one of them!
<font color='blue'>
What you should remember:
- Neural Style Transfer is an algorithm that given a content image C and a style image S can generate an artistic image
- It uses representations (hidden layer activations) based on a pretrained ConvNet.
- The content cost function is computed using one hidden layer's activations.
- The style cost function for one layer is computed using the Gram matrix of that layer's activations. The overall style cost function is obtained using several hidden layers.
- Optimizing the total cost function results in synthesizing new images.
This was the final programming exercise of this course. Congratulations--you've finished all the programming exercises of this course on Convolutional Networks! We hope to also see you in Course 5, on Sequence models!
### References:
The Neural Style Transfer algorithm was due to Gatys et al. (2015). Harish Narayanan and Github user "log0" also have highly readable write-ups from which we drew inspiration. The pre-trained network used in this implementation is a VGG network, which is due to Simonyan and Zisserman (2015). Pre-trained weights were from the work of the MathConvNet team.
- Leon A. Gatys, Alexander S. Ecker, Matthias Bethge, (2015). A Neural Algorithm of Artistic Style (https://arxiv.org/abs/1508.06576)
- Harish Narayanan, Convolutional neural networks for artistic style transfer. https://harishnarayanan.org/writing/artistic-style-transfer/
- Log0, TensorFlow Implementation of "A Neural Algorithm of Artistic Style". http://www.chioka.in/tensorflow-implementation-neural-algorithm-of-artistic-style
- Karen Simonyan and Andrew Zisserman (2015). Very deep convolutional networks for large-scale image recognition (https://arxiv.org/pdf/1409.1556.pdf)
- MatConvNet. http://www.vlfeat.org/matconvnet/pretrained/
|
github_jupyter
|
```
#default_exp dataset.dataset
#export
import os
import torch
import transformers
import pandas as pd
import numpy as np
import Hasoc.config as config
#hide
df = pd.read_csv(config.DATA_PATH/'fold_df.csv')
#hide
df.head(2)
#hide
from sklearn.preprocessing import LabelEncoder
le = LabelEncoder()
le.fit_transform(df.task1)
le.classes_
#hide
df['task1_encoded'] = le.transform(df.task1.values)
#hide
# TOKENIZER = transformers.BertTokenizer.from_pretrained(
# pretrained_model_name_or_path='bert-base-uncased',
# do_lower_case=True,
# # force_download = True,
# )
# MAX_LEN = 72
#export
class BertDataset(torch.utils.data.Dataset):
def __init__(self,text, target=None, is_test=False):
self.text, self.target = text, target
self.tokenizer = config.TOKENIZER
self.max_len = config.MAX_LEN
self.is_test = is_test
def __len__(self):
return len(self.target)
def __getitem__(self, i):
# sanity check
text = ' '.join(self.text[i].split())
# tokenize using Huggingface tokenizers
out = self.tokenizer.encode_plus(text, None,
add_special_tokens=True,
max_length = self.max_len,
truncation=True)
ids = out['input_ids']
mask = out['attention_mask']
token_type_ids = out['token_type_ids']
padding_length = self.max_len - len(ids)
ids = ids + ([0] * padding_length)
mask = mask + ([0] * padding_length)
token_type_ids = token_type_ids + ([0] * padding_length)
if not self.is_test:
return {
'input_ids': torch.tensor(ids, dtype=torch.long),
'attention_mask': torch.tensor(mask, dtype=torch.long),
'token_type_ids': torch.tensor(token_type_ids, dtype=torch.long),
'targets': self.onehot(len(np.unique(self.target)), self.target[i])
}
else:
return{
'input_ids': torch.tensor(ids, dtype=torch.long),
'attention_mask': torch.tensor(mask, dtype=torch.long),
'token_type_ids': torch.tensor(token_type_ids, dtype=torch.long),
}
@staticmethod
def onehot(size, target):
vec = torch.zeros(size, dtype=torch.long)
vec[target] = 1.
return vec
def get_labels(self):
return list(self.target)
#hide
d = BertDataset(df.text.values, df.task1_encoded.values)
#hide
d[10]
c = d[0]['targets']
c.argmax(dim=-1)
```
|
github_jupyter
|
```
# Install libraries
!pip -qq install rasterio tifffile
# Import libraries
import os
import glob
import shutil
import gc
from joblib import Parallel, delayed
from tqdm import tqdm_notebook
import h5py
import pandas as pd
import numpy as np
import datetime as dt
from datetime import datetime, timedelta
import matplotlib.pyplot as plt
import rasterio
import tifffile as tiff
%matplotlib inline
pd.set_option('display.max_colwidth', None)
# Download data with a frequency of 10 days
def date_finder(start_date):
season_dates = []
m = str(start_date)[:10]
s = str(start_date)[:10]
for i in range(24):
date = datetime.strptime(s, "%Y-%m-%d")
s = str(date + timedelta(days = 10))[:10]
season_dates.append(datetime.strptime(s, "%Y-%m-%d"))
seasons_dates = [datetime.strptime(m, "%Y-%m-%d")] + season_dates
seasons_dates = [np.datetime64(x) for x in seasons_dates]
return list(seasons_dates)
# If day not in a frequency of 10 days, find the nearest date
def nearest(items, pivot):
return min(items, key=lambda x: abs(x - pivot))
%%time
# Unpack data saved in gdrive to colab
shutil.unpack_archive('/content/drive/MyDrive/CompeData/Radiant/Radiant_Data.zip', '/content/radiant')
gc.collect()
# Load files
train = pd.concat([pd.read_csv(f'/content/radiant/train{i}.csv', parse_dates=['datetime']) for i in range(1, 5)]).reset_index(drop = True)
test = pd.concat([pd.read_csv(f'/content/radiant/test{i}.csv', parse_dates=['datetime']) for i in range(1, 5)]).reset_index(drop = True)
train.file_path = train.file_path.apply(lambda x: '/'.join(['/content', 'radiant'] + x.split('/')[2:]))
test.file_path = test.file_path.apply(lambda x: '/'.join(['/content', 'radiant'] + x.split('/')[2:]))
train.datetime, test.datetime = pd.to_datetime(train.datetime.dt.date), pd.to_datetime(test.datetime.dt.date)
train['month'], test['month'] = train.datetime.dt.month, test.datetime.dt.month
train.head()
# Unique months
train.month.unique()
# Bands
bands = ['B01','B02','B03','B04','B05','B06','B07','B08','B8A','B09','B11','B12','CLM']
# Function to load tile and extract fields data into a numpy array and convert the same to a dataframe
# Train
def process_tile_train(tile):
tile_df = train[(train.tile_id == tile)].reset_index(drop = True)
y = np.expand_dims(rasterio.open(tile_df[tile_df.asset == 'labels'].file_path.values[0]).read(1).flatten(), axis = 1)
fields = np.expand_dims(rasterio.open(tile_df[tile_df.asset == 'field_ids'].file_path.values[0]).read(1).flatten(), axis = 1)
tile_df = train[(train.tile_id == tile) & (train.satellite_platform == 's2')].reset_index(drop = True)
unique_dates = list(tile_df.datetime.unique())
start_date = tile_df.datetime.unique()[0]
# Assert
diff = set([str(x)[:10] for x in date_finder(start_date)]) - set([str(x)[:10] for x in unique_dates])
if len(diff) > 0:
missing = list(set([str(x)[:10] for x in date_finder(start_date)]) - set(diff))
for d in diff:
missing.append(str(nearest(unique_dates, np.datetime64(d)))[:10])
dates = sorted([np.datetime64(x) for x in missing])
else:
dates = date_finder(start_date)
X_tile = np.empty((256 * 256, 0))
colls = []
for date, datec in zip(dates, range(25)):
for band in bands:
tif_file = tile_df[(tile_df.asset == band) & (tile_df.datetime == date)].file_path.values[0]
X_tile = np.append(X_tile, (np.expand_dims(rasterio.open(tif_file).read(1).flatten(), axis = 1)), axis = 1)
colls.append(str(datec) + '_' + band)
df = pd.DataFrame(X_tile, columns = colls)
df['y'], df['fields'] = y, fields
return df
# Preprocessing the data in chunks to avoid outofmemmory error
# Train
tiles = train.tile_id.unique()
chunks = [tiles[x:x+50] for x in range(0, len(tiles), 50)]
[len(x) for x in chunks], len(chunks)
# Preprocessing the tiles without storing them in memory but saving them as csvs in gdrive
# Train
for i in range(len(chunks)):
pd.DataFrame(np.vstack(Parallel(n_jobs=-1, verbose=1, backend="multiprocessing")(map(delayed(process_tile_train), [x for x in chunks[i]])))).to_csv(f'/content/drive/MyDrive/CompeData/Radiant/Seasonality/train/train{i}.csv', index = False)
gc.collect()
# Function to load tile and extract fields data into a numpy array and convert the same to a dataframe
# Test
def process_tile_test(tile):
tile_df = test[(test.tile_id == tile)].reset_index(drop = True)
fields = np.expand_dims(rasterio.open(tile_df[tile_df.asset == 'field_ids'].file_path.values[0]).read(1).flatten(), axis = 1)
tile_df = test[(test.tile_id == tile) & (test.satellite_platform == 's2')].reset_index(drop = True)
unique_dates = list(tile_df.datetime.unique())
start_date = tile_df.datetime.unique()[0]
# Assert
diff = set([str(x)[:10] for x in date_finder(start_date)]) - set([str(x)[:10] for x in unique_dates])
if len(diff) > 0:
missing = list(set([str(x)[:10] for x in date_finder(start_date)]) - set(diff))
for d in diff:
missing.append(str(nearest(unique_dates, np.datetime64(d)))[:10])
dates = sorted([np.datetime64(x) for x in missing])
else:
dates = date_finder(start_date)
X_tile = np.empty((256 * 256, 0))
colls = []
for date, datec in zip(dates, range(25)):
for band in bands:
tif_file = tile_df[(tile_df.asset == band) & (tile_df.datetime == date)].file_path.values[0]
X_tile = np.append(X_tile, (np.expand_dims(rasterio.open(tif_file).read(1).flatten(), axis = 1)), axis = 1)
colls.append(str(datec) + '_' + band)
df = pd.DataFrame(X_tile, columns = colls)
df['fields'] = fields
return df
# Preprocessing the data in chunks to avoid outofmemmory error
# Train
tiles = test.tile_id.unique()
chunks = [tiles[x:x+50] for x in range(0, len(tiles), 50)]
[len(x) for x in chunks], len(chunks)
# Preprocessing the tiles without storing them in memory but saving them as csvs in gdrive
# Train
for i in range(len(chunks)):
pd.DataFrame(np.vstack(Parallel(n_jobs=-1, verbose=1, backend="multiprocessing")(map(delayed(process_tile_test), [x for x in chunks[i]])))).to_csv(f'/content/drive/MyDrive/CompeData/Radiant/Seasonality/test/test{i}.csv', index = False)
gc.collect()
```
|
github_jupyter
|
# Explore endangered languages from UNESCO Atlas of the World's Languages in Danger
### Input
Endangered languages
- https://www.kaggle.com/the-guardian/extinct-languages/version/1 (updated in 2016)
- original data: http://www.unesco.org/languages-atlas/index.php?hl=en&page=atlasmap (published in 2010)
Countries of the world
- https://www.ethnologue.com/sites/default/files/CountryCodes.tab
### Output
- `endangered_languages_europe.csv`
## Imports
```
import pandas as pd
import geopandas as gpd
import matplotlib.pyplot as plt
```
## Load data
```
df = pd.read_csv("../../data/endangerment/extinct_languages.csv")
print(df.shape)
print(df.dtypes)
df.head()
df.columns
ENDANGERMENT_MAP = {
"Vulnerable": 1,
"Definitely endangered": 2,
"Severely endangered": 3,
"Critically endangered": 4,
"Extinct": 5,
}
df["Endangerment code"] = df["Degree of endangerment"].apply(lambda x: ENDANGERMENT_MAP[x])
df[["Degree of endangerment", "Endangerment code"]]
```
## Distribution of the degree of endangerment
```
plt.xticks(fontsize=16)
plt.yticks(fontsize=16)
df["Degree of endangerment"].hist(figsize=(15,5)).get_figure().savefig('endangered_hist.png', format="png")
```
## Show distribution on map
```
countries_map = gpd.read_file(gpd.datasets.get_path("naturalearth_lowres"))
countries_map.head()
# Plot Europe
fig, ax = plt.subplots(figsize=(20, 10))
countries_map.plot(color='lightgrey', ax=ax)
plt.xlim([-30, 50])
plt.ylim([30, 75])
df.plot(
x="Longitude",
y="Latitude",
kind="scatter",
title="Endangered languages in Europe (1=Vulnerable, 5=Extinct)",
c="Endangerment code",
colormap="YlOrRd",
ax=ax,
)
plt.show()
```
## Get endangered languages only for Europe
```
countries = pd.read_csv("../../data/general/country_codes.tsv", sep="\t")
europe = countries[countries["Area"] == "Europe"]
europe
europe_countries = set(europe["Name"].to_list())
europe_countries
df[df["Countries"].isna()]
df = df[df["Countries"].notna()]
df[df["Countries"].isna()]
df["In Europe"] = df["Countries"].apply(lambda x: len(europe_countries.intersection(set(x.split(",")))) > 0)
df_europe = df.loc[df["In Europe"] == True]
print(df_europe.shape)
df_europe.head(20)
# Plot only European endangered languages
fig, ax = plt.subplots(figsize=(20, 10))
countries_map.plot(color='lightgrey', ax=ax)
plt.xlim([-30, 50])
plt.ylim([30, 75])
df_europe.plot(
x="Longitude",
y="Latitude",
kind="scatter",
title="Endangered languages in Europe",
c="Endangerment code",
colormap="YlOrRd",
ax=ax,
)
plt.xticks(fontsize=16)
plt.yticks(fontsize=16)
plt.xlabel('Longitude', fontsize=18)
plt.ylabel('Latitude', fontsize=18)
plt.title("Endangered languages in Europe (1=Vulnerable, 5=Extinct)", fontsize=18)
plt.show()
fig.savefig("endangered_languages_in_europe.png", format="png", bbox_inches="tight")
```
## Save output
```
df_europe.to_csv("../../data/endangerment/endangered_languages_europe.csv", index=False)
```
|
github_jupyter
|
# Function to list overlapping Landsat 8 scenes
This function is based on the following tutorial: http://geologyandpython.com/get-landsat-8.html
This function uses the area of interest (AOI) to retrieve overlapping Landsat 8 scenes. It will also output on the scenes with the largest portion of overlap and with less than 5% cloud cover.
```
def landsat_scene_list(aoi, start_date, end_date):
'''Creates a list of Landsat 8, level 1, tier 1
scenes that overlap with an aoi and are captured
within a specified date range.
Parameters
----------
aoi : str
The path to a shape file of an aoi with geometry.
start-date : str
The first date from which to start looking for
Landsat image capture in the format yyyy-mm,dd,
e.g. '2017-10-01'.
end-date : str
The last date from which to looking for
Landsat image capture in the format yyyy-mm,dd,
e.g. '2017-10-31'.
Returns
-------
wrs : shapefile
A catalog of Landsat 8 scenes.
scenes : geopandas.geodataframe.GeoDataFrame
A dataframe containing the information
of Landsat 8, Level 1, Tier 1 scenes that
overlap with the aoi.
'''
# Download Landsat 8 catalog from USGS (get_data auto unzips)
USGS_url = 'https://landsat.usgs.gov/sites/default/files/documents/WRS2_descending.zip'
et.data.get_data(url=USGS_url, replace=True)
# Open Landsat catalog
wrs = gpd.GeoDataFrame.from_file(os.path.join('data', 'earthpy-downloads',
'WRS2_descending',
'WRS2_descending.shp'))
# Find polygons that intersect Landsat catalog and aoi
wrs_intersection = wrs[wrs.intersects(aoi.geometry[0])]
# Calculated paths and rows
paths, rows = wrs_intersection['PATH'].values, wrs_intersection['ROW'].values
# Iterate through each Polygon of paths and rows intersecting the area
for i, row in wrs_intersection.iterrows():
# Create a string for the name containing the path and row of this Polygon
name = 'path: %03d, row: %03d' % (row.PATH, row.ROW)
# Removing scenes with small amounts of overlap using threshold of intersection area
b = (paths > 23) & (paths < 26)
paths = paths[b]
rows = rows[b]
# # Path(s) and row(s) covering the intersection
# ############################ WHY NOT PRINTING? ###################################
# for i, (path, row) in enumerate(zip(paths, rows)):
# print('Image', i+1, ' - path:', path, 'row:', row)
# Check scene availability in Amazon S3 bucket list of Landsat scenes
s3_scenes = pd.read_csv('http://landsat-pds.s3.amazonaws.com/c1/L8/scene_list.gz',
compression='gzip', parse_dates=['acquisitionDate'],
index_col=['acquisitionDate'])
# Capture only Landsat T1 scenes within dates of interest
scene_mask = (s3_scenes.index > start_date) & (s3_scenes.index <= end_date)
scene_dates = s3_scenes.loc[scene_mask]
scene_product = scene_dates[scene_dates['productId'].str.contains("_T1")]
# Geodataframe of scenes with <5% cloud cover, the url to retrieve them
#############################row.ROW and row.PATH will need to be fixed##################
scenes = scene_product[(scene_product.path == row.PATH) &
(scene_product.row == row.ROW) &
(scene_product.cloudCover <= 5)]
return wrs, scenes
```
# TEST
**Can DELETE everything below once tested and approved!**
```
# WILL DELETE WHEN FUNCTIONS ARE SEPARATED OUT
def NEON_site_extent(path_to_NEON_boundaries, site):
'''Extracts a NEON site extent from an individual site as
long as the original NEON site extent shape file contains
a column named 'siteID'.
Parameters
----------
path_to_NEON_boundaries : str
The path to a shape file that contains the list
of all NEON site extents, also known as field
sampling boundaries (can be found at NEON and
ESRI sites)
site : str
One siteID contains 4 capital letters,
e.g. CPER, HARV, ONAQ or SJER.
Returns
-------
site_boundary : geopandas.geodataframe.GeoDataFrame
A vector containing a single polygon
per the site specified.
'''
NEON_boundaries = gpd.read_file(path_to_NEON_boundaries)
boundaries_indexed = NEON_boundaries.set_index(['siteID'])
site_boundary = boundaries_indexed.loc[[site]]
site_boundary.reset_index(inplace=True)
return site_boundary
# Import packages
import os
from glob import glob
import requests
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import folium
import geopandas as gpd
import rasterio as rio
#from bs4 import BeautifulSoup
import shutil
import earthpy as et
# Set working directory
os.chdir(os.path.join(et.io.HOME, 'earth-analytics'))
# Download shapefile of all NEON site boundaries
url = 'https://www.neonscience.org/sites/default/files/Field_Sampling_Boundaries_2020.zip'
et.data.get_data(url=url, replace=True)
# Create path to shapefile
terrestrial_sites = os.path.join(
'data', 'earthpy-downloads',
'Field_Sampling_Boundaries_2020',
'terrestrialSamplingBoundaries.shp')
# Retrieving the boundaries of CPER
aoi = NEON_site_extent(terrestrial_sites, 'ONAQ')
# Test out new landsat retrieval process
scene_catalog, scene_df = landsat_scene_list(aoi, '2017-10-01', '2017-10-31')
# Visualize the catalog
scene_catalog.head(3)
# Visualize the scenes of interest based on the input parameters
scene_df
```
|
github_jupyter
|
##### Copyright 2019 The TensorFlow Authors.
```
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
#@title MIT License
#
# Copyright (c) 2017 François Chollet
#
# Permission is hereby granted, free of charge, to any person obtaining a
# copy of this software and associated documentation files (the "Software"),
# to deal in the Software without restriction, including without limitation
# the rights to use, copy, modify, merge, publish, distribute, sublicense,
# and/or sell copies of the Software, and to permit persons to whom the
# Software is furnished to do so, subject to the following conditions:
#
# The above copyright notice and this permission notice shall be included in
# all copies or substantial portions of the Software.
#
# THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
# IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
# FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL
# THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
# LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING
# FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER
# DEALINGS IN THE SOFTWARE.
```
# Menyimpan dan memuat model
<table class="tfo-notebook-buttons" align="left">
<td>
<a target="_blank" href="https://www.tensorflow.org/tutorials/keras/save_and_load"><img src="https://www.tensorflow.org/images/tf_logo_32px.png" />Liht di TensorFlow.org</a>
</td>
<td>
<a target="_blank" href="https://colab.research.google.com/github/tensorflow/docs-l10n/blob/master/site/id/tutorials/keras/save_and_load.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Jalankan di Google Colab</a>
</td>
<td>
<a target="_blank" href="https://github.com/tensorflow/docs-l10n/blob/master/site/id/tutorials/keras/save_and_load.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />Lihat kode di GitHub</a>
</td>
<td>
<a href="https://storage.googleapis.com/tensorflow_docs/docs-l10n/site/id/tutorials/keras/save_and_load.ipynb"><img src="https://www.tensorflow.org/images/download_logo_32px.png" />Unduh notebook</a>
</td>
</table>
Progres dari model dapat disimpan ketika proses training dan setelah training. Ini berarti sebuah model dapat melanjutkan proses training dengan kondisi yang sama dengan ketika proses training sebelumnya dihentikan dan dapat menghindari waktu training yang panjng. Menyimpan juga berarti Anda dapat membagikan model Anda dan orang lain dapat membuat ulang proyek Anda. Ketika mempublikasikan hasil riset dan teknik dari suatu model, kebanyakan praktisi *machine learning* membagikan:
* kode untuk membuat model, dan
* berat, atau parameter, dari sebuah model
Membagikan data ini akan membantu orang lain untuk memahami bagaimana model bekerja dan mencoba model tersebut dengan data yang baru.
Perhatian: Hati-hati dengan kode yang tidak dapat dipercaya—model-model TensorFlow adalah kode. Lihat [Menggunakan TensorFlow dengan aman](https://github.com/tensorflow/tensorflow/blob/master/SECURITY.md) untuk lebih detail.
### Opsi
Terdapat beberapa cara untuk menyimpan model TensorFlow—bergantung kepada API yang Anda gunakan. Panduan ini menggunakan [tf.keras](https://www.tensorflow.org/guide/keras), sebuah API tingkat tinggi yang digunakan untuk membangun dan melatih model di TensorFlow. Untuk pendekatan lainnya, lihat panduan Tensorflow [Simpan dan Restorasi](https://www.tensorflow.org/guide/saved_model) atau [Simpan sesuai keinginan](https://www.tensorflow.org/guide/eager#object-based_saving).
## Pengaturan
### Instal dan import
Install dan import TensorFlow dan beberapa *dependency*:
```
try:
# %tensorflow_version only exists in Colab.
%tensorflow_version 2.x
except Exception:
pass
!pip install pyyaml h5py # Required to save models in HDF5 format
from __future__ import absolute_import, division, print_function, unicode_literals
import os
import tensorflow as tf
from tensorflow import keras
print(tf.version.VERSION)
```
### Memperoleh dataset
Untuk menunjukan bagaimana cara untuk menyimpan dan memuat berat dari model, Anda akan menggunakan [Dataset MNIST](http://yann.lecun.com/exdb/mnist/). Untuk mempercepat operasi ini, gunakan hanya 1000 data pertama:
```
(train_images, train_labels), (test_images, test_labels) = tf.keras.datasets.mnist.load_data()
train_labels = train_labels[:1000]
test_labels = test_labels[:1000]
train_images = train_images[:1000].reshape(-1, 28 * 28) / 255.0
test_images = test_images[:1000].reshape(-1, 28 * 28) / 255.0
```
### Mendefinisikan sebuah model
Mulai dengan membangun sebuah model sekuensial sederhana:
```
# Define a simple sequential model
def create_model():
model = tf.keras.models.Sequential([
keras.layers.Dense(512, activation='relu', input_shape=(784,)),
keras.layers.Dropout(0.2),
keras.layers.Dense(10, activation='softmax')
])
model.compile(optimizer='adam',
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
return model
# Create a basic model instance
model = create_model()
# Display the model's architecture
model.summary()
```
## Menyimpan cek poin ketika proses training
You can use a trained model without having to retrain it, or pick-up training where you left off—in case the training process was interrupted. The `tf.keras.callbacks.ModelCheckpoint` callback allows to continually save the model both *during* and at *the end* of training.
Anda dapat menggunakan model terlatih tanpa harus melatihnya kembali, atau melanjutkan proses training di titik di mana proses training sebelumnya berhenti. *Callback* `tf.keras.callbacks.ModelCheckpoint` memungkinkan sebuah model untuk disimpan ketika dan setelah proses training dilakukan.
### Penggunaan *callback* cek poin
Buat sebuah callback `tf.keras.callbacks.ModelCheckpoint` yang menyimpan berat hanya ketika proses training berlangsung:
```
checkpoint_path = "training_1/cp.ckpt"
checkpoint_dir = os.path.dirname(checkpoint_path)
# Create a callback that saves the model's weights
cp_callback = tf.keras.callbacks.ModelCheckpoint(filepath=checkpoint_path,
save_weights_only=True,
verbose=1)
# Train the model with the new callback
model.fit(train_images,
train_labels,
epochs=10,
validation_data=(test_images,test_labels),
callbacks=[cp_callback]) # Pass callback to training
# This may generate warnings related to saving the state of the optimizer.
# These warnings (and similar warnings throughout this notebook)
# are in place to discourage outdated usage, and can be ignored.
```
This creates a single collection of TensorFlow checkpoint files that are updated at the end of each epoch:
```
!ls {checkpoint_dir}
```
Create a new, untrained model. When restoring a model from weights-only, you must have a model with the same architecture as the original model. Since it's the same model architecture, you can share weights despite that it's a different *instance* of the model.
Now rebuild a fresh, untrained model, and evaluate it on the test set. An untrained model will perform at chance levels (~10% accuracy):
```
# Create a basic model instance
model = create_model()
# Evaluate the model
loss, acc = model.evaluate(test_images, test_labels, verbose=2)
print("Untrained model, accuracy: {:5.2f}%".format(100*acc))
```
Then load the weights from the checkpoint and re-evaluate:
```
# Loads the weights
model.load_weights(checkpoint_path)
# Re-evaluate the model
loss,acc = model.evaluate(test_images, test_labels, verbose=2)
print("Restored model, accuracy: {:5.2f}%".format(100*acc))
```
### Checkpoint callback options
The callback provides several options to provide unique names for checkpoints and adjust the checkpointing frequency.
Train a new model, and save uniquely named checkpoints once every five epochs:
```
# Include the epoch in the file name (uses `str.format`)
checkpoint_path = "training_2/cp-{epoch:04d}.ckpt"
checkpoint_dir = os.path.dirname(checkpoint_path)
# Create a callback that saves the model's weights every 5 epochs
cp_callback = tf.keras.callbacks.ModelCheckpoint(
filepath=checkpoint_path,
verbose=1,
save_weights_only=True,
period=5)
# Create a new model instance
model = create_model()
# Save the weights using the `checkpoint_path` format
model.save_weights(checkpoint_path.format(epoch=0))
# Train the model with the new callback
model.fit(train_images,
train_labels,
epochs=50,
callbacks=[cp_callback],
validation_data=(test_images,test_labels),
verbose=0)
```
Sekarang, lihat hasil cek poin dan pilih yang terbaru:
```
!ls {checkpoint_dir}
latest = tf.train.latest_checkpoint(checkpoint_dir)
latest
```
Catatan: secara default format tensorflow hanya menyimpan 5 cek poin terbaru.
Untuk tes, reset model dan muat cek poin terakhir:
```
# Create a new model instance
model = create_model()
# Load the previously saved weights
model.load_weights(latest)
# Re-evaluate the model
loss, acc = model.evaluate(test_images, test_labels, verbose=2)
print("Restored model, accuracy: {:5.2f}%".format(100*acc))
```
## Apa sajakah file-file ini?
Kode di atas menyimpan berat dari model ke sebuah kumpulan [cek poin](https://www.tensorflow.org/guide/saved_model#save_and_restore_variables)-file yang hanya berisikan berat dari model yan sudah dilatih dalam format biner. Cek poin terdiri atas:
* Satu atau lebih bagian (*shard*) yang berisi berat dari model Anda.
* Sebuah file index yang mengindikasikan suatu berat disimpan pada *shard* yang mana.
Jika Anda hanya melakukan proses training dari sebuah model pada sebuah komputer, Anda akan hanya memiliki satu *shard* dengan sufiks `.data-00000-of-00001`
## Menyimpan berat secara manual
Anda telah melihat bagaimana caranya memuat berat yang telah disimpan sebelumnya menjadi model. Menyimpannya secara manual dapat dilakukan dengan mudah dengan *method* `Model.save_weights`. Secara default, `tf.keras`—dan `save_weights` menggunakan format TensorFlow [cek poin](../../guide/keras/checkpoints) dengan ekstensi `.ckpt` (menyimpan dalam format [HDF5](https://js.tensorflow.org/tutorials/import-keras.html) dengan ekstensi `.h5` dijelaskan dalam panduan ini [Menyimpan dan serialisasi model](../../guide/keras/save_and_serialize#weights-only_saving_in_savedmodel_format)):
```
# Save the weights
model.save_weights('./checkpoints/my_checkpoint')
# Create a new model instance
model = create_model()
# Restore the weights
model.load_weights('./checkpoints/my_checkpoint')
# Evaluate the model
loss,acc = model.evaluate(test_images, test_labels, verbose=2)
print("Restored model, accuracy: {:5.2f}%".format(100*acc))
```
## Menyimpan keseluruhan model
Gunakan [`model.save`](https://www.tensorflow.org/api_docs/python/tf/keras/Model#save) untuk menyimpan arsitektur dari model, berat, dan konfigurasi training dalam satu file/folder. Hal ini menyebabkan Anda dapat melakukan ekspor dari suatu model sehingga model tersebut dapat digunakan tanpa harus mengakses kode Python secara langsung*. Karena kondisi optimizer dipulihkan, Anda dapat melanjutkan proses training tepat ketika proses training sebelumnya ditinggalkan.
Meneyimpan sebuah model fungsional sangat berguna—Anda dapat memuatnya di TensorFlow.js [HDF5](https://js.tensorflow.org/tutorials/import-keras.html), [Saved Model](https://js.tensorflow.org/tutorials/import-saved-model.html)) dan kemudian melatih dan menggunakan model tersebut di web browser, atau mengubahnya sehingga dapat beroperasi di perangkat *mobile* menggunakan TensorFlw Lite [HDF5](https://www.tensorflow.org/lite/convert/python_api#exporting_a_tfkeras_file_), [Saved Model](https://www.tensorflow.org/lite/convert/python_api#exporting_a_savedmodel_))
\*Objek-objek custom (model subkelas atau layer) membutuhkan perhatian lebih ketika proses disimpan atau dimuat. Lihat bagian **Penyimpanan objek custom** di bawah.
### Format HDF5
Keras menyediakan format penyimpanan menggunakan menggunakan [HDF5](https://en.wikipedia.org/wiki/Hierarchical_Data_Format)
```
# Create and train a new model instance.
model = create_model()
model.fit(train_images, train_labels, epochs=5)
# Save the entire model to a HDF5 file.
# The '.h5' extension indicates that the model shuold be saved to HDF5.
model.save('my_model.h5')
```
Sekarang, buat ulang model dari file tersebut:
```
# Recreate the exact same model, including its weights and the optimizer
new_model = tf.keras.models.load_model('my_model.h5')
# Show the model architecture
new_model.summary()
```
Cek akurasi dari model:
```
loss, acc = new_model.evaluate(test_images, test_labels, verbose=2)
print('Restored model, accuracy: {:5.2f}%'.format(100*acc))
```
Teknik ini menyimpan semuanya:
* Nilai berat
* Konfigurasi model (arsitektur)
* konfigurasi dari optimizer
Keras menyimpan model dengan cara menginspeksi arsitekturnya. Saat ini, belum bisa menyimpan optimizer TensorFlow (dari `tf.train`). Ketika menggunakannya, Anda harus mengkompilasi kembali model setelah dimuat, dan Anda akan kehilangan kondisi dari optimizer.
### Format SavedModel
Format SavedModel adalah suatu cara lainnya untuk melakukan serialisasi model. Model yang disimpan dalam format ini dapat direstorasi menggunakan `tf.keras.models.load_model` dan kompatibel dengan TensorFlow Serving. [Panduan SavedModel](https://www.tensorflow.org/guide/saved_model) menjelaskan detail bagaimana untuk menyediakan/memeriksa SavedModel. Kode di bawah ini mengilustrasikan langkah-langkah yang dilakukan untuk menyimpan dan memuat kembali model.
```
# Create and train a new model instance.
model = create_model()
model.fit(train_images, train_labels, epochs=5)
# Save the entire model as a SavedModel.
!mkdir -p saved_model
model.save('saved_model/my_model')
```
Format SavedModel merupakan direktori yang berisi sebuah *protobuf binary* dan sebuah cek poin TensorFlow. Mememiksa direktori dari model tersimpan:
```
# my_model directory
!ls saved_model
# Contains an assets folder, saved_model.pb, and variables folder.
!ls saved_model/my_model
```
Muat ulang Keras model yang baru dari model tersimpan:
```
new_model = tf.keras.models.load_model('saved_model/my_model')
# Check its architecture
new_model.summary()
```
Model yang sudah terestorasi dikompilasi dengan argument yang sama dengan model asli. Coba lakukan evaluasi dan prediksi menggunakan model tersebut:
```
# Evaluate the restored model
loss, acc = new_model.evaluate(test_images, test_labels, verbose=2)
print('Restored model, accuracy: {:5.2f}%'.format(100*acc))
print(new_model.predict(test_images).shape)
```
### Menyimpan objek custom
Apabila Anda menggunakan format SavedModel, Anda dapat melewati bagian ini. Perbedaan utama antara HDF5 dan SavedModel adalah HDF5 menggunakan konfigurasi objek untuk menyimpan arsitektur dari model, sementara SavedModel menyimpan *execution graph*. Sehingga, SavedModel dapat menyimpan objek custom seperti model subkelas dan layer custom tanpa membutuhkan kode yang asli.
Untuk menyimpan objek custom dalam bentuk HDF5, Anda harus melakukan hal sebagai berikut:
1. Mendefinisikan sebuah *method* `get_config` pada objek Anda, dan mendefinisikan *classmethod* (opsional) `from_config`.
* `get_config(self)` mengembalikan *JSON-serializable dictionary* dari parameter-parameter yang dibutuhkan untuk membuat kembali objek.
* `from_config(cls, config)` menggunakan dan mengembalikan konfigurasi dari `get_config` untuk membuat objek baru. Secara default, fungsi ini menggunakan konfigurasi teresbut untuk menginisialisasi kwargs (`return cls(**config)`).
2. Gunakan objek tersebut sebagai argumen dari `custom_objects` ketika memuat model. Argumen tersebut harus merupakan sebuah *dictionary* yang memetakan string dari nama kelas ke class Python. Misalkan `tf.keras.models.load_model(path, custom_objects={'CustomLayer': CustomLayer})`
Lihat tutorial [Menulis layers and models from awal](https://www.tensorflow.org/guide/keras/custom_layers_and_models) untuk contoh dari objek custom dan `get_config`.
|
github_jupyter
|
# <span style="color: #B40486">BASIC PYTHON FOR RESEARCHERS</span>
_by_ [**_Megat Harun Al Rashid bin Megat Ahmad_**](https://www.researchgate.net/profile/Megat_Harun_Megat_Ahmad)
last updated: April 14, 2016
-------
## _<span style="color: #29088A">8. Database and Data Analysis</span>_
---
<span style="color: #0000FF">$Pandas$</span> is an open source library for data analysis in _Python_. It gives _Python_ similar capabilities to _R_ programming language and even though it is possible to run _R_ in _Jupyter Notebook_, it would be more practical to do data analysis with a _Python_ friendly syntax. Similar to other libraries, the first step to use <span style="color: #0000FF">$Pandas$</span> is to import the library and usually together with the <span style="color: #0000FF">$Numpy$</span> library.
```
import pandas as pd
import numpy as np
```
***
### **_8.1 Data Structures_**
Data structures (similar to _Sequence_ in _Python_) of <span style="color: #0000FF">$Pandas$</span> revolves around the **_Series_** and **_DataFrame_** structures. Both are fast as they are built on top of <span style="color: #0000FF">$Numpy$</span>.
A **_Series_** is a one-dimensional object with a lot of similar properties similar to a list or dictionary in _Python_'s _Sequence_. Each element or item in a **_Series_** will be assigned by default an index label from _0_ to _N-1_ (where _N_ is the length of the **_Series_**) and it can contains the various type of _Python_'s data.
```
# Creating a series (with different type of data)
s1 = pd.Series([34, 'Material', 4*np.pi, 'Reactor', [100,250,500,750], 'kW'])
s1
```
The index of a **_Series_** can be specified during its creation and giving it a similar function to a dictionary.
```
# Creating a series with specified index
lt = [34, 'Material', 4*np.pi, 'Reactor', [100,250,500,750], 'kW']
s2 = pd.Series(lt, index = ['b1', 'r1', 'solid angle', 18, 'reactor power', 'unit'])
s2
```
Data can be extracted by specifying the element position or index (similar to list/dictionary).
```
s1[3], s2['solid angle']
```
**_Series_** can also be constructed from a dictionary.
```
pop_cities = {'Kuala Lumpur':1588750, 'Seberang Perai':818197, 'Kajang':795522,
'Klang':744062, 'Subang Jaya':708296}
cities = pd.Series(pop_cities)
cities
```
The elements can be sort using the <span style="color: #0000FF">$Series.order()$</span> function. This will not change the structure of the original variable.
```
cities.order(ascending=False)
cities
```
Another sorting function is the <span style="color: #0000FF">$sort()$</span> function but this will change the structure of the **_Series_** variable.
```
# Sorting with descending values
cities.sort(ascending=False)
cities
cities
```
Conditions can be applied to the elements.
```
# cities with population less than 800,000
cities[cities<800000]
# cities with population between 750,000 and 800,000
cities[cities<800000][cities>750000]
```
---
A **_DataFrame_** is a 2-dimensional data structure with named rows and columns. It is similar to _R_'s _data.frame_ object and function like a spreadsheet. **_DataFrame_** can be considered to be made of series of **_Series_** data according to the column names. **_DataFrame_** can be created by passing a 2-dimensional array of data and specifying the rows and columns names.
```
# Creating a DataFrame by passing a 2-D numpy array of random number
# Creating first the date-time index using date_range function
# and checking it.
dates = pd.date_range('20140801', periods = 8, freq = 'D')
dates
# Creating the column names as list
Kedai = ['Kedai A', 'Kedai B', 'Kedai C', 'Kedai D', 'Kedai E']
# Creating the DataFrame with specified rows and columns
df = pd.DataFrame(np.random.randn(8,5),index=dates,columns=Kedai)
df
```
---
Some of the useful functions that can be applied to a **_DataFrame_** include:
```
df.head() # Displaying the first five (default) rows
df.head(3) # Displaying the first three (specified) rows
df.tail(2) # Displaying the last two (specified) rows
df.index # Showing the index of rows
df.columns # Showing the fields of columns
df.values # Showing the data only in its original 2-D array
df.describe() # Simple statistical data for each column
df.T # Transposing the DataFrame (index becomes column and vice versa)
df.sort_index(axis=1,ascending=False) # Sorting with descending column
df.sort(columns='Kedai D') # Sorting according to ascending specific column
df['Kedai A'] # Extract specific column (using python list syntax)
df['Kedai A'][2:4] # Slicing specific column (using python list syntax)
df[2:4] # Slicing specific row data (using python list syntax)
# Slicing specific index range
df['2014-08-03':'2014-08-05']
# Slicing specific index range for a particular column
df['2014-08-03':'2014-08-05']['Kedai B']
# Using the loc() function
# Slicing specific index and column ranges
df.loc['2014-08-03':'2014-08-05','Kedai B':'Kedai D']
# Slicing specific index range with specific column names
df.loc['2014-08-03':'2014-08-05',['Kedai B','Kedai D']]
# Possibly not yet to have something like this
df.loc[['2014-08-01','2014-08-03':'2014-08-05'],['Kedai B','Kedai D']]
# Using the iloc() function
df.iloc[3] # Specific row location
df.iloc[:,3] # Specific column location (all rows)
df.iloc[2:4,1:3] # Python like slicing for range
df.iloc[[2,4],[1,3]] # Slicing with python like list
# Conditionals on the data
df>0 # Array values > 0 OR
df[df>0] # Directly getting the value
```
**_NaN_** means empty, missing data or unavailable.
```
df[df['Kedai B']<0] # With reference to specific value in a column (e.g. Kedai B)
df2 = df.copy() # Made a copy of a database
df2
# Adding column
df2['Tambah'] = ['satu','satu','dua','tiga','empat','tiga','lima','enam']
df2
# Adding row using append() function. The previous loc() is possibly deprecated.
# Assign a new name to the new row (with the same format)
new_row_name = pd.date_range('20140809', periods = 1, freq = 'D')
# Appending new row with new data
df2.append(list(np.random.randn(5))+['sembilan'])
# Renaming the new row (here actually is a reassignment)
df2 = df2.rename(index={10: new_row_name[0]})
df2
# Assigning new data to a row
df2.loc['2014-08-05'] = list(np.random.randn(5))+['tujuh']
df2
# Assigning new data to a specific element
df2.loc['2014-08-05','Tambah'] = 'lapan'
df2
# Using the isin() function (returns boolean data frame)
df2.isin(['satu','tiga'])
# Select specific row based on additonal column
df2[df2['Tambah'].isin(['satu','tiga'])]
# Use previous command - select certain column based on selected additional column
df2[df2['Tambah'].isin(['satu','tiga'])].loc[:,'Kedai B':'Kedai D']
# Select > 0 from previous cell...
(df2[df2['Tambah'].isin(['satu','tiga'])].loc[:,'Kedai B':'Kedai D']>0)
```
***
### **_8.2 Data Operations_**
We have seen few operations previously on **_Series_** and **_DataFrame_** and here this will be explored further.
```
df.mean() # Statistical mean (column) - same as df.mean(0), 0 means column
df.mean(1) # Statistical mean (row) - 1 means row
df.mean()['Kedai C':'Kedai E'] # Statistical mean (range of columns)
df.max() # Statistical max (column)
df.max()['Kedai C'] # Statistical max (specific column)
df.max(1)['2014-08-04':'2014-08-07'] # Statistical max (specific row)
df.max(1)[dates[3]] # Statistical max (specific row by variable)
```
---
Other statistical functions can be checked by typing df._< TAB >_.
The data in a **_DataFrame_** can be represented by a variable declared using the <span style="color: #0000FF">$lambda$</span> operator.
```
df.apply(lambda x: x.max() - x.min()) # Operating array values with function
df.apply(lambda z: np.log(z)) # Operating array values with function
```
Replacing, rearranging and operations of data between columns can be done much like spreadsheet.
```
df3 = df.copy()
df3[r'Kedai A^2/Kedai E'] = df3['Kedai A']**2/df3['Kedai E']
df3
```
Tables can be split, rearranged and combined.
```
df4 = df.copy()
df4
pieces = [df4[6:], df4[3:6], df4[:3]] # split row 2+3+3
pieces
df5 = pd.concat(pieces) # concantenate (rearrange/combine)
df5
df4+df5 # Operation between tables with original index sequence
df0 = df.loc[:,'Kedai A':'Kedai C'] # Slicing and extracting columns
pd.concat([df4, df0], axis = 1) # Concatenating columns (axis = 1 -> refers to column)
```
***
### **_8.3 Plotting Functions_**
---
Let us look on some of the simple plotting function on <span style="color: #0000FF">$Pandas$</span> (requires <span style="color: #0000FF">$Matplotlib$</span> library).
```
df_add = df.copy()
# Simple auto plotting
%matplotlib inline
df_add.cumsum().plot()
# Reposition the legend
import matplotlib.pyplot as plt
df_add.cumsum().plot()
plt.legend(bbox_to_anchor=[1.3, 1])
```
In the above example, repositioning the legend requires the legend function in <span style="color: #0000FF">$Matplotlib$</span> library. Therefore, the <span style="color: #0000FF">$Matplotlib$</span> library must be explicitly imported.
```
df_add.cumsum().plot(kind='bar')
plt.legend(bbox_to_anchor=[1.3, 1])
df_add.cumsum().plot(kind='barh', stacked=True)
df_add.cumsum().plot(kind='hist', alpha=0.5)
df_add.cumsum().plot(kind='area', alpha=0.4, stacked=False)
plt.legend(bbox_to_anchor=[1.3, 1])
```
A 3-dimensional plot can be projected on a canvas but requires the <span style="color: #0000FF">$Axes3D$</span> library with slightly complicated settings.
```
# Plotting a 3D bar plot
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
# Convert the time format into ordinary strings
time_series = pd.Series(df.index.format())
fig = plt.figure(figsize=(8,6))
ax = fig.add_subplot(111, projection='3d')
# Plotting the bar graph column by column
for c, z in zip(['r', 'g', 'b', 'y','m'], np.arange(len(df.columns))):
xs = df.index
ys = df.values[:,z]
ax.bar(xs, ys, zs=z, zdir='y', color=c, alpha=0.5)
ax.set_zlabel('Z')
ax.set_xticklabels(time_series, va = 'baseline', ha = 'right', rotation = 15)
ax.set_yticks(np.arange(len(df.columns)))
ax.set_yticklabels(df.columns, va = 'center', ha = 'left', rotation = -42)
ax.view_init(30, -30)
fig.tight_layout()
```
***
### **_8.4 Reading And Writing Data To File_**
Data in **_DataFrame_** can be exported into **_csv_** (comma separated value) and **_Excel_** file. The users can also create a **_DataFrame_** from data in **_csv_** and **_Excel_** file, the data can then be processed.
```
# Export data to a csv file but separated with < TAB > rather than comma
# the default separation is with comma
df.to_csv('Tutorial8/Kedai.txt', sep='\t')
# Export to Excel file
df.to_excel('Tutorial8/Kedai.xlsx', sheet_name = 'Tarikh', index = True)
# Importing data from csv file (without header)
from_file = pd.read_csv('Tutorial8/Malaysian_Town.txt',sep='\t',header=None)
from_file.head()
# Importing data from Excel file (with header (the first row) that became the column names)
from_excel = pd.read_excel('Tutorial8/Malaysian_Town.xlsx','Sheet1')
from_excel.head()
```
---
Further <span style="color: #0000FF">$Pandas$</span> features can be found in http://pandas.pydata.org/.
|
github_jupyter
|
# Spectral encoding of categorical features
About a year ago I was working on a regression model, which had over a million features. Needless to say, the training was super slow, and the model was overfitting a lot. After investigating this issue, I realized that most of the features were created using 1-hot encoding of the categorical features, and some of them had tens of thousands of unique values.
The problem of mapping categorical features to lower-dimensional space is not new. Recently one of the popular way to deal with it is using entity embedding layers of a neural network. However that method assumes that neural networks are used. What if we decided to use tree-based algorithms instead? In tis case we can use Spectral Graph Theory methods to create low dimensional embedding of the categorical features.
The idea came from spectral word embedding, spectral clustering and spectral dimensionality reduction algorithms.
If you can define a similarity measure between different values of the categorical features, we can use spectral analysis methods to find the low dimensional representation of the categorical feature.
From the similarity function (or kernel function) we can construct an Adjacency matrix, which is a symmetric matrix, where the ij element is the value of the kernel function between category values i and j:
$$ A_{ij} = K(i,j) \tag{1}$$
It is very important that I only need a Kernel function, not a high-dimensional representation. This means that 1-hot encoding step is not necessary here. Also for the kernel-base machine learning methods, the categorical variable encoding step is not necessary as well, because what matters is the kernel function between two points, which can be constructed using the individual kernel functions.
Once the adjacency matrix is constructed, we can construct a degree matrix:
$$ D_{ij} = \delta_{ij} \sum_{k}{A_{ik}} \tag{2} $$
Here $\delta$ is the Kronecker delta symbol. The Laplacian matrix is the difference between the two:
$$ L = D - A \tag{3} $$
And the normalize Laplacian matrix is defined as:
$$ \mathscr{L} = D^{-\frac{1}{2}} L D^{-\frac{1}{2}} \tag{4} $$
Following the Spectral Graph theory, we proceed with eigendecomposition of the normalized Laplacian matrix. The number of zero eigenvalues correspond to the number of connected components. In our case, let's assume that our categorical feature has two sets of values that are completely dissimilar. This means that the kernel function $K(i,j)$ is zero if $i$ and $j$ belong to different groups. In this case we will have two zero eigenvalues of the normalized Laplacian matrix.
If there is only one connected component, we will have only one zero eigenvalue. Normally it is uninformative and is dropped to prevent multicollinearity of features. However we can keep it if we are planning to use tree-based models.
The lower eigenvalues correspond to "smooth" eigenvectors (or modes), that are following the similarity function more closely. We want to keep only these eigenvectors and drop the eigenvectors with higher eigenvalues, because they are more likely represent noise. It is very common to look for a gap in the matrix spectrum and pick the eigenvalues below the gap. The resulting truncated eigenvectors can be normalized and represent embeddings of the categorical feature values.
As an example, let's consider the Day of Week. 1-hot encoding assumes every day is similar to any other day ($K(i,j) = 1$). This is not a likely assumption, because we know that days of the week are different. For example, the bar attendance spikes on Fridays and Saturdays (at least in USA) because the following day is a weekend. Label encoding is also incorrect, because it will make the "distance" between Monday and Wednesday twice higher than between Monday and Tuesday. And the "distance" between Sunday and Monday will be six times higher, even though the days are next to each other. By the way, the label encoding corresponds to the kernel $K(i, j) = exp(-\gamma |i-j|)$
```
import numpy as np
import pandas as pd
np.set_printoptions(linewidth=130)
def normalized_laplacian(A):
'Compute normalized Laplacian matrix given the adjacency matrix'
d = A.sum(axis=0)
D = np.diag(d)
L = D-A
D_rev_sqrt = np.diag(1/np.sqrt(d))
return D_rev_sqrt @ L @ D_rev_sqrt
```
We will consider an example, where weekdays are similar to each other, but differ a lot from the weekends.
```
#The adjacency matrix for days of the week
A_dw = np.array([[0,10,9,8,5,2,1],
[0,0,10,9,5,2,1],
[0,0,0,10,8,2,1],
[0,0,0,0,10,2,1],
[0,0,0,0,0,5,3],
[0,0,0,0,0,0,10],
[0,0,0,0,0,0,0]])
A_dw = A_dw + A_dw.T
A_dw
#The normalized Laplacian matrix for days of the week
L_dw_noem = normalized_laplacian(A_dw)
L_dw_noem
#The eigendecomposition of the normalized Laplacian matrix
sz, sv = np.linalg.eig(L_dw_noem)
sz
```
Notice, that the eigenvalues are not ordered here. Let's plot the eigenvalues, ignoring the uninformative zero.
```
%matplotlib inline
from matplotlib import pyplot as plt
import seaborn as sns
sns.stripplot(data=sz[1:], jitter=False, );
```
We can see a pretty substantial gap between the first eigenvalue and the rest of the eigenvalues. If this does not give enough model performance, you can include the second eigenvalue, because the gap between it and the higher eigenvalues is also quite substantial.
Let's print all eigenvectors:
```
sv
```
Look at the second eigenvector. The weekend values have a different size than the weekdays and Friday is close to zero. This proves the transitional role of Friday, that, being a day of the week, is also the beginning of the weekend.
If we are going to pick two lowest non-zero eigenvalues, our categorical feature encoding will result in these category vectors:
```
#Picking only two eigenvectors
category_vectors = sv[:,[1,3]]
category_vectors
category_vector_frame=pd.DataFrame(category_vectors, index=['mon', 'tue', 'wed', 'thu', 'fri', 'sat', 'sun'],
columns=['col1', 'col2']).reset_index()
sns.scatterplot(data=category_vector_frame, x='col1', y='col2', hue='index');
```
In the plot above we see that Monday and Tuesday, and also Saturday and Sunday are clustered close together, while Wednesday, Thursday and Friday are far apart.
## Learning the kernel function
In the previous example we assumed that the similarity function is given. Sometimes this is the case, where it can be defined based on the business rules. However it may be possible to learn it from data.
One of the ways to compute the Kernel is using [Wasserstein distance](https://en.wikipedia.org/wiki/Wasserstein_metric). It is a good way to tell how far apart two distributions are.
The idea is to estimate the data distribution (including the target variable, but excluding the categorical variable) for each value of the categorical variable. If for two values the distributions are similar, then the divergence will be small and the similarity value will be large. As a measure of similarity I choose the RBF kernel (Gaussian radial basis function):
$$ A_{ij} = exp(-\gamma W(i, j)^2) \tag{5}$$
Where $W(i,j)$ is the Wasserstein distance between the data distributions for the categories i and j, and $\gamma$ is a hyperparameter that has to be tuned
To try this approach will will use [liquor sales data set](https://www.kaggle.com/residentmario/iowa-liquor-sales/downloads/iowa-liquor-sales.zip/1). To keep the file small I removed some columns and aggregated the data.
```
liq = pd.read_csv('Iowa_Liquor_agg.csv', dtype={'Date': 'str', 'Store Number': 'str', 'Category': 'str', 'orders': 'int', 'sales': 'float'},
parse_dates=True)
liq.Date = pd.to_datetime(liq.Date)
liq.head()
```
Since we care about sales, let's encode the day of week using the information from the sales column
Let's check the histogram first:
```
sns.distplot(liq.sales, kde=False);
```
We see that the distribution is very skewed, so let's try to use log of sales columns instead
```
sns.distplot(np.log10(1+liq.sales), kde=False);
```
This is much better. So we will use a log for our distribution
```
liq["log_sales"] = np.log10(1+liq.sales)
```
Here we will follow [this blog](https://amethix.com/entropy-in-machine-learning/) for computation of the Kullback-Leibler divergence.
Also note, that since there are no liquor sales on Sunday, we consider only six days in a week
```
from scipy.stats import wasserstein_distance
from numpy import histogram
from scipy.stats import iqr
def dw_data(i):
return liq[liq.Date.dt.dayofweek == i].log_sales
def wass_from_data(i,j):
return wasserstein_distance(dw_data(i), dw_data(j)) if i > j else 0.0
distance_matrix = np.fromfunction(np.vectorize(wass_from_data), (6,6))
distance_matrix += distance_matrix.T
distance_matrix
```
As we already mentioned, the hyperparameter $\gamma$ has to be tuned. Here we just pick the value that will give a plausible result
```
gamma = 100
kernel = np.exp(-gamma * distance_matrix**2)
np.fill_diagonal(kernel, 0)
kernel
norm_lap = normalized_laplacian(kernel)
sz, sv = np.linalg.eig(norm_lap)
sz
sns.stripplot(data=sz[1:], jitter=False, );
```
Ignoring the zero eigenvalue, we can see that there is a bigger gap between the first eigenvalue and the rest of the eigenvalues, even though the values are all in the range between 1 and 1.3. Looking at the eigenvectors,
```
sv
```
Ultimately the number of eigenvectors to use is another hyperparameter, that should be optimized on a supervised learning task. The Category field is another candidate to do spectral analysis, and is, probably, a better choice since it has more unique values
```
len(liq.Category.unique())
unique_categories = liq.Category.unique()
def dw_data_c(i):
return liq[liq.Category == unique_categories[int(i)]].log_sales
def wass_from_data_c(i,j):
return wasserstein_distance(dw_data_c(i), dw_data_c(j)) if i > j else 0.0
#WARNING: THIS WILL TAKE A LONG TIME
distance_matrix = np.fromfunction(np.vectorize(wass_from_data_c), (107,107))
distance_matrix += distance_matrix.T
distance_matrix
def plot_eigenvalues(gamma):
"Eigendecomposition of the kernel and plot of the eigenvalues"
kernel = np.exp(-gamma * distance_matrix**2)
np.fill_diagonal(kernel, 0)
norm_lap = normalized_laplacian(kernel)
sz, sv = np.linalg.eig(norm_lap)
sns.stripplot(data=sz[1:], jitter=True, );
plot_eigenvalues(100);
```
We can see, that a lot of eigenvalues are grouped around the 1.1 mark. The eigenvalues that are below that cluster can be used for encoding the Category feature.
Please also note that this method is highly sensitive on selection of hyperparameter $\gamma$. For illustration let me pick a higher and a lower gamma
```
plot_eigenvalues(500);
plot_eigenvalues(10)
```
## Conclusion and next steps
We presented a way to encode the categorical features as a low dimensional vector that preserves most of the feature similarity information. For this we use methods of Spectral analysis on the values of the categorical feature. In order to find the kernel function we can either use heuristics, or learn it using a variety of methods, for example, using Kullback–Leibler divergence of the data distribution conditional on the category value. To select the subset of the eigenvectors we used gap analysis, but what we really need is to validate this methods by analyzing a variety of datasets and both classification and regression problems. We also need to compare it with other encoding methods, for example, entity embedding using Neural Networks. The kernel function we used can also include the information about category frequency, which will help us deal with high information, but low frequency values.
|
github_jupyter
|
# Multivariate SuSiE and ENLOC model
## Aim
This notebook aims to demonstrate a workflow of generating posterior inclusion probabilities (PIPs) from GWAS summary statistics using SuSiE regression and construsting SNP signal clusters from global eQTL analysis data obtained from multivariate SuSiE models.
## Methods overview
This procedure assumes that molecular phenotype summary statistics and GWAS summary statistics are aligned and harmonized to have consistent allele coding (see [this module](../../misc/summary_stats_merger.html) for implementation details). Both molecular phenotype QTL and GWAS should be fine-mapped beforehand using mvSusiE or SuSiE. We further assume (and require) that molecular phenotype and GWAS data come from the same population ancestry. Violations from this assumption may not cause an error in the analysis computational workflow but the results obtained may not be valid.
## Input
1) GWAS Summary Statistics with the following columns:
- chr: chromosome number
- bp: base pair position
- a1: effect allele
- a2: other allele
- beta: effect size
- se: standard error of beta
- z: z score
2) eQTL data from multivariate SuSiE model with the following columns:
- chr: chromosome number
- bp: base pair position
- a1: effect allele
- a2: other allele
- pip: posterior inclusion probability
3) LD correlation matrix
## Output
Intermediate files:
1) GWAS PIP file with the following columns
- var_id
- ld_block
- snp_pip
- block_pip
2) eQTL annotation file with the following columns
- chr
- bp
- var_id
- a1
- a2
- annotations, in the format: `gene:cs_num@tissue=snp_pip[cs_pip:cs_total_snps]`
Final Outputs:
1) Enrichment analysis result prefix.enloc.enrich.rst: estimated enrichment parameters and standard errors.
2) Signal-level colocalization result prefix.enloc.sig.out: the main output from the colocalization analysis with the following format
- column 1: signal cluster name (from eQTL analysis)
- column 2: number of member SNPs
- column 3: cluster PIP of eQTLs
- column 4: cluster PIP of GWAS hits (without eQTL prior)
- column 5: cluster PIP of GWAS hits (with eQTL prior)
- column 6: regional colocalization probability (RCP)
3) SNP-level colocalization result prefix.enloc.snp.out: SNP-level colocalization output with the following form at
- column 1: signal cluster name
- column 2: SNP name
- column 3: SNP-level PIP of eQTLs
- column 4: SNP-level PIP of GWAS (without eQTL prior)
- column 5: SNP-level PIP of GWAS (with eQTL prior)
- column 6: SNP-level colocalization probability
4) Sorted list of colocalization signals
Takes into consideration 3 situations:
1) "Major" and "minor" alleles flipped
2) Different strand but same variant
3) Remove variants with A/T and C/G alleles due to ambiguity
## Minimal working example
```
sos run mvenloc.ipynb merge \
--cwd output \
--eqtl-sumstats .. \
--gwas-sumstats ..
sos run mvenloc.ipynb eqtl \
--cwd output \
--sumstats-file .. \
--ld-region ..
sos run mvenloc.ipynb gwas \
--cwd output \
--sumstats-file .. \
--ld-region ..
sos run mvenloc.ipynb enloc \
--cwd output \
--eqtl-pip .. \
--gwas-pip ..
```
### Summary
```
head enloc.enrich.out
head enloc.sig.out
head enloc.snp.out
```
## Command interface
```
sos run mvenloc.ipynb -h
```
## Implementation
```
[global]
parameter: cwd = path
parameter: container = ""
```
### Step 0: data formatting
#### Extract common SNPS between the GWAS summary statistics and eQTL data
```
[merger]
# eQTL summary statistics as a list of RData
parameter: eqtl_sumstats = path
# GWAS summary stats in gz format
parameter: gwas_sumstats = path
input: eqtl_sumstats, gwas_sumstats
output: f"{cwd:a}/{eqtl_sumstats:bn}.standardized.gz", f"{cwd:a}/{gwas_sumstats:bn}.standardized.gz"
R: expand = "${ }"
###
# functions
###
allele.qc = function(a1,a2,ref1,ref2) {
# a1 and a2 are the first data-set
# ref1 and ref2 are the 2nd data-set
# Make all the alleles into upper-case, as A,T,C,G:
a1 = toupper(a1)
a2 = toupper(a2)
ref1 = toupper(ref1)
ref2 = toupper(ref2)
# Strand flip, to change the allele representation in the 2nd data-set
strand_flip = function(ref) {
flip = ref
flip[ref == "A"] = "T"
flip[ref == "T"] = "A"
flip[ref == "G"] = "C"
flip[ref == "C"] = "G"
flip
}
flip1 = strand_flip(ref1)
flip2 = strand_flip(ref2)
snp = list()
# Remove strand ambiguous SNPs (scenario 3)
snp[["keep"]] = !((a1=="A" & a2=="T") | (a1=="T" & a2=="A") | (a1=="C" & a2=="G") | (a1=="G" & a2=="C"))
# Remove non-ATCG coding
snp[["keep"]][ a1 != "A" & a1 != "T" & a1 != "G" & a1 != "C" ] = F
snp[["keep"]][ a2 != "A" & a2 != "T" & a2 != "G" & a2 != "C" ] = F
# as long as scenario 1 is involved, sign_flip will return TRUE
snp[["sign_flip"]] = (a1 == ref2 & a2 == ref1) | (a1 == flip2 & a2 == flip1)
# as long as scenario 2 is involved, strand_flip will return TRUE
snp[["strand_flip"]] = (a1 == flip1 & a2 == flip2) | (a1 == flip2 & a2 == flip1)
# remove other cases, eg, tri-allelic, one dataset is A C, the other is A G, for example.
exact_match = (a1 == ref1 & a2 == ref2)
snp[["keep"]][!(exact_match | snp[["sign_flip"]] | snp[["strand_flip"]])] = F
return(snp)
}
# Extract information from RData
eqtl.split = function(eqtl){
rows = length(eqtl)
chr = vector(length = rows)
pos = vector(length = rows)
a1 = vector(length = rows)
a2 = vector(length = rows)
for (i in 1:rows){
split1 = str_split(eqtl[i], ":")
split2 = str_split(split1[[1]][2], "_")
chr[i]= split1[[1]][1]
pos[i] = split2[[1]][1]
a1[i] = split2[[1]][2]
a2[i] = split2[[1]][3]
}
eqtl.df = data.frame(eqtl,chr,pos,a1,a2)
}
remove.dup = function(df){
df = df %>% arrange(PosGRCh37, -N)
df = df[!duplicated(df$PosGRCh37),]
return(df)
}
###
# Code
###
# gene regions:
# 1 = ENSG00000203710
# 2 = ENSG00000064687
# 3 = ENSG00000203710
# eqtl
gene.name = scan(${_input[0]:r}, what='character')
# initial filter of gwas variants that are in eqtl
gwas = gwas_sumstats
gwas_filter = gwas[which(gwas$id %in% var),]
# create eqtl df
eqtl.df = eqtl.split(eqtl$var)
# allele flip
f_gwas = gwas %>% filter(chr %in% eqtl.df$chr & PosGRCh37 %in% eqtl.df$pos)
eqtl.df.f = eqtl.df %>% filter(pos %in% f_gwas$PosGRCh37)
# check if there are duplicate pos
length(unique(f_gwas$PosGRCh37))
# multiple snps with same pos
dup.pos = f_gwas %>% group_by(PosGRCh37) %>% filter(n() > 1)
f_gwas = remove.dup(f_gwas)
qc = allele.qc(f_gwas$testedAllele, f_gwas$otherAllele, eqtl.df.f$a1, eqtl.df.f$a2)
keep = as.data.frame(qc$keep)
sign = as.data.frame(qc$sign_flip)
strand = as.data.frame(qc$strand_flip)
# sign flip
f_gwas$z[qc$sign_flip] = -1 * f_gwas$z[qc$sign_flip]
f_gwas$testedAllele[qc$sign_flip] = eqtl.df.f$a1[qc$sign_flip]
f_gwas$otherAllele[qc$sign_flip] = eqtl.df.f$a2[qc$sign_flip]
f_gwas$testedAllele[qc$strand_flip] = eqtl.df.f$a1[qc$strand_flip]
f_gwas$otherAllele[qc$strand_flip] = eqtl.df.f$a2[qc$strand_flip]
# remove ambigiuous
if ( sum(!qc$keep) > 0 ) {
eqtl.df.f = eqtl.df.f[qc$keep,]
f_gwas = f_gwas[qc$keep,]
}
```
#### Extract common SNPS between the summary statistics and LD
```
[eqtl_1, gwas_1 (filter LD file and sumstat file)]
parameter: sumstat_file = path
# LD and region information: chr, start, end, LD file
paramter: ld_region = path
input: sumstat_file, for_each = 'ld_region'
output: f"{cwd:a}/{sumstat_file:bn}_{region[0]}_{region[1]}_{region[2]}.z.rds",
f"{cwd:a}/{sumstat_file:bn}_{region[0]}_{region[1]}_{region[2]}.ld.rds"
R:
# FIXME: need to filter both ways for sumstats and for LD
# lds filtered
eqtl_id = which(var %in% eqtl.df.f$eqtl)
ld_f = ld[eqtl_id, eqtl_id]
# ld missing
miss = which(is.na(ld_f), arr.ind=TRUE)
miss_r = unique(as.data.frame(miss)$row)
miss_c = unique(as.data.frame(miss)$col)
total_miss = unique(union(miss_r,miss_c))
# FIXME: LD should not have missing data if properly processed by our pipeline
# In the future we should throw an error when it happens
if (length(total_miss)!=0){
ld_f2 = ld_f[-total_miss,]
ld_f2 = ld_f2[,-total_miss]
dim(ld_f2)
}else{ld_f2 = ld_f}
f_gwas.f = f_gwas %>% filter(id %in% eqtl_id.f$eqtl)
```
### Step 1: fine-mapping
```
[eqtl_2, gwas_2 (finemapping)]
# FIXME: RDS file should have included region information
output: f"{_input[0]:nn}.susieR.rds", f"{_input[0]:nn}.susieR_plot.rds"
R:
susie_results = susieR::susie_rss(z = f_gwas.f$z,R = ld_f2, check_prior = F)
susieR::susie_plot(susie_results,"PIP")
susie_results$z = f_gwas.f$z
susieR::susie_plot(susie_results,"z_original")
```
### Step 2: fine-mapping results processing
#### Construct eQTL annotation file using eQTL SNP PIPs and credible sets
```
[eqtl_3 (create signal cluster using CS)]
output: f"{_input[0]:nn}.enloc_annot.gz"
R:
cs = eqtl[["sets"]][["cs"]][["L1"]]
o_id = which(var %in% eqtl_id.f$eqtl)
pip = eqtl$pip[o_id]
eqtl_annot = cbind(eqtl_id.f, pip) %>% mutate(gene = gene.name,cluster = -1, cluster_pip = 0, total_snps = 0)
for(snp in cs){
eqtl_annot$cluster[snp] = 1
eqtl_annot$cluster_pip[snp] = eqtl[["sets"]][["coverage"]]
eqtl_annot$total_snps[snp] = length(cs)
}
eqtl_annot1 = eqtl_annot %>% filter(cluster != -1)%>%
mutate(annot = sprintf("%s:%d@=%e[%e:%d]",gene,cluster,pip,cluster_pip,total_snps)) %>%
select(c(chr,pos,eqtl,a1,a2,annot))
# FIXME: repeats whole process (extracting+fine-mapping+cs creation) 3 times before this next step
eqtl_annot_comb = rbind(eqtl_annot3, eqtl_annot1, eqtl_annot2)
# FIXME: write to a zip file
write.table(eqtl_annot_comb, file = "eqtl.annot.txt", col.names = T, row.names = F, quote = F)
```
#### Export GWAS PIP
```
[gwas_3 (format PIP into enloc GWAS input)]
output: f"{_input[0]:nn}.enloc_gwas.gz"
R:
gwas_annot1 = f_gwas.f %>% mutate(pip = susie_results$pip)
# FIXME: repeat whole process (extracting common snps + fine-mapping) 3 times before the next steps
gwas_annot_comb = rbind(gwas_annot3, gwas_annot1, gwas_annot2)
gwas_loc_annot = gwas_annot_comb %>% select(id, chr, PosGRCh37,z)
write.table(gwas_loc_annot, file = "loc.gwas.txt", col.names = F, row.names = F, quote = F)
bash:
perl format2torus.pl loc.gwas.txt > loc2.gwas.txt
R:
loc = data.table::fread("loc2.gwas.txt")
loc = loc[["V2"]]
gwas_annot_comb2 = gwas_annot_comb %>% select(id, chr, PosGRCh37,pip)
gwas_annot_comb2 = cbind(gwas_annot_comb2, loc) %>% select(id, loc, pip)
write.table(gwas_annot_comb2, file = "gwas.pip.txt", col.names = F, row.names = F, quote = F)
bash:
perl format2torus.pl gwas.pip.txt | gzip --best > gwas.pip.gz
```
### Step 3: Colocalization with FastEnloc
```
[enloc]
# eQTL summary statistics as a list of RData
# FIXME: to replace later
parameter: eqtl_pip = path
# GWAS summary stats in gz format
parameter: gwas_pip = path
input: eqtl_pip, gwas_pip
output: f"{cwd:a}/{eqtl_pip:bnn}.{gwas_pip:bnn}.xx.gz"
bash:
fastenloc -eqtl eqtl.annot.txt.gz -gwas gwas.pip.txt.gz
sort -grk6 prefix.enloc.sig.out | gzip --best > prefix.enloc.sig.sorted.gz
rm -f prefix.enloc.sig.out
```
|
github_jupyter
|
```
import keras
from keras.applications import VGG16
from keras.models import Model
from keras.layers import Dense, Dropout, Input
from keras.regularizers import l2, activity_l2,l1
from keras.utils import np_utils
from keras.preprocessing.image import array_to_img, img_to_array, load_img
from keras.applications.vgg16 import preprocess_input
from PIL import Image
from scipy import misc
from keras.optimizers import SGD
# from keras.utils.visualize_util import plot
from os import listdir
import numpy as np
import matplotlib.pyplot as plt
import scipy
temperature=1
def softmaxTemp(x):
return K.softmax(x/temperature)
def getModel( output_dim):
# output_dim: the number of classes (int)
# return: compiled model (keras.engine.training.Model)
vgg_model = VGG16( weights='imagenet', include_top=True )
vgg_out = vgg_model.layers[-1].output
out = Dense( output_dim, activation='softmax')( vgg_out )
tl_model = Model( input=vgg_model.input, output=out)
tl_model.layers[-2].activation=softmaxTemp
for layer in tl_model.layers[0:-1]:
layer.trainable = False
tl_model.compile(loss= "categorical_crossentropy", optimizer="adagrad", metrics=["accuracy"])
tl_model.summary()
return tl_model
# define functions to laod images
def loadBatchImages(path,s, nVal = 2):
# return array of images
catList = listdir(path)
loadedImagesTrain = []
loadedLabelsTrain = []
loadedImagesVal = []
loadedLabelsVal = []
for cat in catList[0:256]:
deepPath = path+cat+"/"
# if cat == ".DS_Store": continue
imageList = listdir(deepPath)
indx = 0
for images in imageList[0:s + nVal]:
img = load_img(deepPath + images)
img = img_to_array(img)
img = misc.imresize(img, (224,224))
img = scipy.misc.imrotate(img,180)
if indx < s:
loadedLabelsTrain.append(int(images[0:3])-1)
loadedImagesTrain.append(img)
else:
loadedLabelsVal.append(int(images[0:3])-1)
loadedImagesVal.append(img)
indx += 1
# return np.asarray(loadedImages), np.asarray(loadedLabels)
return loadedImagesTrain, np_utils.to_categorical(loadedLabelsTrain), loadedImagesVal, np_utils.to_categorical(loadedLabelsVal)
def shuffledSet(a, b):
# shuffle the entire dataset
assert np.shape(a)[0] == np.shape(b)[0]
p = np.random.permutation(np.shape(a)[0])
return (a[p], b[p])
path = "/mnt/cube/VGG_/256_ObjectCategories/"
samCat = 8 # number of samples per category
data, labels, dataVal, labelsVal = loadBatchImages(path,samCat, nVal = 2)
data = preprocess_input(np.float64(data))
data = data.swapaxes(1, 3).swapaxes(2, 3)
dataVal = preprocess_input(np.float64(dataVal))
dataVal = dataVal.swapaxes(1, 3).swapaxes(2, 3)
train = shuffledSet(np.asarray(data),labels)
val = shuffledSet(np.asarray(dataVal),labelsVal)
# plt.imshow(train[0][0][0])
# plt.show()
print train[0].shape, val[0].shape
output_dim = 256
tl_model = getModel(output_dim)
nb_epoch = 20
history = tl_model.fit(train[0], train[1], batch_size = 16, nb_epoch = nb_epoch, validation_data = val,
shuffle = True)
keras.callbacks.EarlyStopping(monitor='val_loss', min_delta = 0, patience = 2, verbose = 0, mode='auto')
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('Model loss for %d samples per category' % samCat)
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train', 'test'], loc='right left')
plt.show()
plt.plot(history.history['val_acc'])
plt.title('model accuracy for %d samples per category' % samCat)
plt.ylabel('accuracy')
plt.xlabel('epoch')
plt.show()
1 22.07
2 19.82
4 25.20
8 18.36
16 18.75
X=[2, 4, 8, 16, 64]
Y=[19.82, 25.20, 18.36, 18.75]
plt.plot(X,Y)
plt.show()
```
|
github_jupyter
|
# Guided Investigation - Anomaly Lookup
__Notebook Version:__ 1.0<br>
__Python Version:__ Python 3.6 (including Python 3.6 - AzureML)<br>
__Required Packages:__ azure 4.0.0, azure-cli-profile 2.1.4<br>
__Platforms Supported:__<br>
- Azure Notebooks Free Compute
- Azure Notebook on DSVM
__Data Source Required:__<br>
- Log Analytics tables
### Description
Gain insights into the possible root cause of an alert by searching for related anomalies on the corresponding entities around the alert’s time. This notebook will provide valuable leads for an alert’s investigation, listing all suspicious increase in event counts or their properties around the time of the alert, and linking to the corresponding raw records in Log Analytics for the investigator to focus on and interpret.
<font>When you switch between Azure Notebooks Free Compute and Data Science Virtual Machine (DSVM), you may need to select Python version: please select Python 3.6 for Free Compute, and Python 3.6 - AzureML for DSVM.</font>
## Table of Contents
1. Initialize Azure Resource Management Clients
2. Looking up for anomaly entities
## 1. Initialize Azure Resource Management Clients
```
# only run once
!pip install --upgrade Azure-Sentinel-Utilities
!pip install azure-cli-core
# User Input and Save to Environmental store
import os
from SentinelWidgets import WidgetViewHelper
env_dir = %env
helper = WidgetViewHelper()
# Enter Tenant Domain
helper.set_env(env_dir, 'tenant_domain')
# Enter Azure Subscription Id
helper.set_env(env_dir, 'subscription_id')
# Enter Azure Resource Group
helper.set_env(env_dir, 'resource_group')
env_dir = %env
if 'tenant_domain' in env_dir:
tenant_domain = env_dir['tenant_domain']
if 'subscription_id' in env_dir:
subscription_id = env_dir['subscription_id']
if 'resource_group' in env_dir:
resource_group = env_dir['resource_group']
from azure.loganalytics import LogAnalyticsDataClient
from azure.loganalytics.models import QueryBody
from azure.mgmt.loganalytics import LogAnalyticsManagementClient
import SentinelAzure
from SentinelAnomalyLookup import AnomalyFinder, AnomalyLookupViewHelper
from pandas.io.json import json_normalize
import sys
import timeit
import datetime as dt
import pandas as pd
import copy
from IPython.display import HTML
# Authentication to Log Analytics
from azure.common.client_factory import get_client_from_cli_profile
from azure.common.credentials import get_azure_cli_credentials
# please enter your tenant domain below, for Microsoft, using: microsoft.onmicrosoft.com
!az login --tenant $tenant_domain
la_client = get_client_from_cli_profile(LogAnalyticsManagementClient, subscription_id = subscription_id)
la = SentinelAzure.azure_loganalytics_helper.LogAnalyticsHelper(la_client)
creds, _ = get_azure_cli_credentials(resource="https://api.loganalytics.io")
la_data_client = LogAnalyticsDataClient(creds)
```
## 2. Looking up for anomaly entities
```
# Select a workspace
selected_workspace = WidgetViewHelper.select_log_analytics_workspace(la)
display(selected_workspace)
import ipywidgets as widgets
workspace_id = la.get_workspace_id(selected_workspace.value)
#DateTime format: 2019-07-15T07:05:20.000
q_timestamp = widgets.Text(value='2019-09-15',description='DateTime: ')
display(q_timestamp)
#Entity format: computer
q_entity = widgets.Text(value='computer',description='Entity for search: ')
display(q_entity)
anomaly_lookup = AnomalyFinder(workspace_id, la_data_client)
selected_tables = WidgetViewHelper.select_multiple_tables(anomaly_lookup)
display(selected_tables)
# This action may take a few minutes or more, please be patient.
start = timeit.default_timer()
anomalies, queries = anomaly_lookup.run(q_timestamp.value, q_entity.value, list(selected_tables.value))
display(anomalies)
if queries is not None:
url = WidgetViewHelper.construct_url_for_log_analytics_logs(tenant_domain, subscription_id, resource_group, selected_workspace.value)
WidgetViewHelper.display_html(WidgetViewHelper.copy_to_clipboard(url, queries, 'Add queries to clipboard and go to Log Analytics'))
print('==================')
print('Elapsed time: ', timeit.default_timer() - start, ' seconds')
```
|
github_jupyter
|
<a href="https://colab.research.google.com/github/dribnet/clipit/blob/future/demos/CLIP_GradCAM_Visualization.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# CLIP GradCAM Colab
This Colab notebook uses [GradCAM](https://arxiv.org/abs/1610.02391) on OpenAI's [CLIP](https://openai.com/blog/clip/) model to produce a heatmap highlighting which regions in an image activate the most to a given caption.
**Note:** Currently only works with the ResNet variants of CLIP. ViT support coming soon.
```
#@title Install dependencies
#@markdown Please execute this cell by pressing the _Play_ button
#@markdown on the left.
#@markdown **Note**: This installs the software on the Colab
#@markdown notebook in the cloud and not on your computer.
%%capture
!pip install ftfy regex tqdm matplotlib opencv-python scipy scikit-image
!pip install git+https://github.com/openai/CLIP.git
import numpy as np
import torch
import os
import torch.nn as nn
import torch.nn.functional as F
import cv2
import urllib.request
import matplotlib.pyplot as plt
import clip
from PIL import Image
from skimage import transform as skimage_transform
from scipy.ndimage import filters
#@title Helper functions
#@markdown Some helper functions for overlaying heatmaps on top
#@markdown of images and visualizing with matplotlib.
def normalize(x: np.ndarray) -> np.ndarray:
# Normalize to [0, 1].
x = x - x.min()
if x.max() > 0:
x = x / x.max()
return x
# Modified from: https://github.com/salesforce/ALBEF/blob/main/visualization.ipynb
def getAttMap(img, attn_map, blur=True):
if blur:
attn_map = filters.gaussian_filter(attn_map, 0.02*max(img.shape[:2]))
attn_map = normalize(attn_map)
cmap = plt.get_cmap('jet')
attn_map_c = np.delete(cmap(attn_map), 3, 2)
attn_map = 1*(1-attn_map**0.7).reshape(attn_map.shape + (1,))*img + \
(attn_map**0.7).reshape(attn_map.shape+(1,)) * attn_map_c
return attn_map
def viz_attn(img, attn_map, blur=True):
fig, axes = plt.subplots(1, 2, figsize=(10, 5))
axes[0].imshow(img)
axes[1].imshow(getAttMap(img, attn_map, blur))
for ax in axes:
ax.axis("off")
plt.show()
def load_image(img_path, resize=None):
image = Image.open(image_path).convert("RGB")
if resize is not None:
image = image.resize((resize, resize))
return np.asarray(image).astype(np.float32) / 255.
#@title GradCAM: Gradient-weighted Class Activation Mapping
#@markdown Our gradCAM implementation registers a forward hook
#@markdown on the model at the specified layer. This allows us
#@markdown to save the intermediate activations and gradients
#@markdown at that layer.
#@markdown To visualize which parts of the image activate for
#@markdown a given caption, we use the caption as the target
#@markdown label and backprop through the network using the
#@markdown image as the input.
#@markdown In the case of CLIP models with resnet encoders,
#@markdown we save the activation and gradients at the
#@markdown layer before the attention pool, i.e., layer4.
class Hook:
"""Attaches to a module and records its activations and gradients."""
def __init__(self, module: nn.Module):
self.data = None
self.hook = module.register_forward_hook(self.save_grad)
def save_grad(self, module, input, output):
self.data = output
output.requires_grad_(True)
output.retain_grad()
def __enter__(self):
return self
def __exit__(self, exc_type, exc_value, exc_traceback):
self.hook.remove()
@property
def activation(self) -> torch.Tensor:
return self.data
@property
def gradient(self) -> torch.Tensor:
return self.data.grad
# Reference: https://arxiv.org/abs/1610.02391
def gradCAM(
model: nn.Module,
input: torch.Tensor,
target: torch.Tensor,
layer: nn.Module
) -> torch.Tensor:
# Zero out any gradients at the input.
if input.grad is not None:
input.grad.data.zero_()
# Disable gradient settings.
requires_grad = {}
for name, param in model.named_parameters():
requires_grad[name] = param.requires_grad
param.requires_grad_(False)
# Attach a hook to the model at the desired layer.
assert isinstance(layer, nn.Module)
with Hook(layer) as hook:
# Do a forward and backward pass.
output = model(input)
output.backward(target)
grad = hook.gradient.float()
act = hook.activation.float()
# Global average pool gradient across spatial dimension
# to obtain importance weights.
alpha = grad.mean(dim=(2, 3), keepdim=True)
# Weighted combination of activation maps over channel
# dimension.
gradcam = torch.sum(act * alpha, dim=1, keepdim=True)
# We only want neurons with positive influence so we
# clamp any negative ones.
gradcam = torch.clamp(gradcam, min=0)
# Resize gradcam to input resolution.
gradcam = F.interpolate(
gradcam,
input.shape[2:],
mode='bicubic',
align_corners=False)
# Restore gradient settings.
for name, param in model.named_parameters():
param.requires_grad_(requires_grad[name])
return gradcam
#@title Run
#@markdown #### Image & Caption settings
image_url = 'https://images2.minutemediacdn.com/image/upload/c_crop,h_706,w_1256,x_0,y_64/f_auto,q_auto,w_1100/v1554995050/shape/mentalfloss/516438-istock-637689912.jpg' #@param {type:"string"}
image_caption = 'the cat' #@param {type:"string"}
#@markdown ---
#@markdown #### CLIP model settings
clip_model = "RN50" #@param ["RN50", "RN101", "RN50x4", "RN50x16"]
saliency_layer = "layer4" #@param ["layer4", "layer3", "layer2", "layer1"]
#@markdown ---
#@markdown #### Visualization settings
blur = True #@param {type:"boolean"}
device = "cuda" if torch.cuda.is_available() else "cpu"
model, preprocess = clip.load(clip_model, device=device, jit=False)
# Download the image from the web.
image_path = 'image.png'
urllib.request.urlretrieve(image_url, image_path)
image_input = preprocess(Image.open(image_path)).unsqueeze(0).to(device)
image_np = load_image(image_path, model.visual.input_resolution)
text_input = clip.tokenize([image_caption]).to(device)
attn_map = gradCAM(
model.visual,
image_input,
model.encode_text(text_input).float(),
getattr(model.visual, saliency_layer)
)
attn_map = attn_map.squeeze().detach().cpu().numpy()
viz_attn(image_np, attn_map, blur)
```
|
github_jupyter
|
```
# Reload when code changed:
%load_ext autoreload
%reload_ext autoreload
%autoreload 2
%pwd
import sys
import os
path = "../"
sys.path.append(path)
#os.path.abspath("../")
print(os.path.abspath(path))
import os
import core
import logging
import importlib
importlib.reload(core)
try:
logging.shutdown()
importlib.reload(logging)
except:
pass
import pandas as pd
import numpy as np
import json
import time
from event_handler import EventHandler
from event_handler import get_list_from_interval
print(core.__file__)
pd.__version__
user_id_1 = 'user_1'
user_id_2 = 'user_2'
user_1_ws_1 = 'mw1'
print(path)
paths = {'user_id': user_id_1,
'workspace_directory': 'D:/git/ekostat_calculator/workspaces',
'resource_directory': path + '/resources',
'log_directory': path + '/log',
'test_data_directory': path + '/test_data',
'temp_directory': path + '/temp',
'cache_directory': path + '/cache'}
ekos = EventHandler(**paths)
ekos.test_timer()
ekos.mapping_objects['quality_element'].get_indicator_list_for_quality_element('secchi')
def update_workspace_uuid_in_test_requests(workspace_alias='New test workspace'):
ekos = EventHandler(**paths)
workspace_uuid = ekos.get_unique_id_for_alias(workspace_alias=workspace_alias)
if workspace_uuid:
print('Updating user {} with uuid: {}'.format(user_id_1, workspace_uuid))
print('-'*70)
ekos.update_workspace_uuid_in_test_requests(workspace_uuid)
else:
print('No workspaces for user: {}'.format(user_id_1))
def update_subset_uuid_in_test_requests(workspace_alias='New test workspace',
subset_alias=False):
ekos = EventHandler(**paths)
workspace_uuid = ekos.get_unique_id_for_alias(workspace_alias=workspace_alias)
if workspace_uuid:
ekos.load_workspace(workspace_uuid)
subset_uuid = ekos.get_unique_id_for_alias(workspace_alias=workspace_alias, subset_alias=subset_alias)
print('Updating user {} with workspace_uuid {} and subset_uuid {}'.format(user_id_1, workspace_uuid, subset_uuid))
print(workspace_uuid, subset_uuid)
print('-'*70)
ekos.update_subset_uuid_in_test_requests(subset_uuid=subset_uuid)
else:
print('No workspaces for user: {}'.format(user_id_1))
def print_boolean_structure(workspace_uuid):
workspace_object = ekos.get_workspace(unique_id=workspace_uuid)
workspace_object.index_handler.print_boolean_keys()
# update_workspace_uuid_in_test_requests()
```
### Request workspace add
```
t0 = time.time()
ekos = EventHandler(**paths)
request = ekos.test_requests['request_workspace_add_1']
response_workspace_add = ekos.request_workspace_add(request)
ekos.write_test_response('request_workspace_add_1', response_workspace_add)
# request = ekos.test_requests['request_workspace_add_2']
# response_workspace_add = ekos.request_workspace_add(request)
# ekos.write_test_response('request_workspace_add_2', response_workspace_add)
print('-'*50)
print('Time for request: {}'.format(time.time()-t0))
```
#### Update workspace uuid in test requests
```
update_workspace_uuid_in_test_requests()
```
### Request workspace import default data
```
# ekos = EventHandler(**paths)
# # When copying data the first time all sources has status=0, i.e. no data will be loaded.
# request = ekos.test_requests['request_workspace_import_default_data']
# response_import_data = ekos.request_workspace_import_default_data(request)
# ekos.write_test_response('request_workspace_import_default_data', response_import_data)
```
### Import data from sharkweb
```
ekos = EventHandler(**paths)
request = ekos.test_requests['request_sharkweb_import']
response_sharkweb_import = ekos.request_sharkweb_import(request)
ekos.write_test_response('request_sharkweb_import', response_sharkweb_import)
ekos.data_params
ekos.selection_dicts
# ekos = EventHandler(**paths)
# ekos.mapping_objects['sharkweb_mapping'].df
```
### Request data source list/edit
```
ekos = EventHandler(**paths)
request = ekos.test_requests['request_workspace_data_sources_list']
response = ekos.request_workspace_data_sources_list(request)
ekos.write_test_response('request_workspace_data_sources_list', response)
request = response
request['data_sources'][0]['status'] = False
request['data_sources'][1]['status'] = False
request['data_sources'][2]['status'] = False
request['data_sources'][3]['status'] = False
# request['data_sources'][4]['status'] = True
# Edit data source
response = ekos.request_workspace_data_sources_edit(request)
ekos.write_test_response('request_workspace_data_sources_edit', response)
```
### Request subset add
```
ekos = EventHandler(**paths)
request = ekos.test_requests['request_subset_add_1']
response_subset_add = ekos.request_subset_add(request)
ekos.write_test_response('request_subset_add_1', response_subset_add)
update_subset_uuid_in_test_requests(subset_alias='mw_subset')
```
### Request subset get data filter
```
ekos = EventHandler(**paths)
update_subset_uuid_in_test_requests(subset_alias='mw_subset')
request = ekos.test_requests['request_subset_get_data_filter']
response_subset_get_data_filter = ekos.request_subset_get_data_filter(request)
ekos.write_test_response('request_subset_get_data_filter', response_subset_get_data_filter)
# import re
# string = """{
# "workspace_uuid": "52725df4-b4a0-431c-a186-5e542fc6a3a4",
# "data_sources": [
# {
# "status": true,
# "loaded": false,
# "filename": "physicalchemical_sharkweb_data_all_2013-2014_20180916.txt",
# "datatype": "physicalchemical"
# }
# ]
# }"""
# r = re.sub('"workspace_uuid": ".{36}"', '"workspace_uuid": "new"', string)
```
### Request subset set data filter
```
ekos = EventHandler(**paths)
update_subset_uuid_in_test_requests(subset_alias='mw_subset')
request = ekos.test_requests['request_subset_set_data_filter']
response_subset_set_data_filter = ekos.request_subset_set_data_filter(request)
ekos.write_test_response('request_subset_set_data_filter', response_subset_set_data_filter)
```
### Request subset get indicator settings
```
ekos = EventHandler(**paths)
request = ekos.test_requests['request_subset_get_indicator_settings']
# request = ekos.test_requests['request_subset_get_indicator_settings_no_areas']
# print(request['subset']['subset_uuid'])
# request['subset']['subset_uuid'] = 'fel'
# print(request['subset']['subset_uuid'])
response_subset_get_indicator_settings = ekos.request_subset_get_indicator_settings(request)
ekos.write_test_response('request_subset_get_indicator_settings', response_subset_get_indicator_settings)
```
### Request subset set indicator settings
```
ekos = EventHandler(**paths)
request = ekos.test_requests['request_subset_set_indicator_settings']
response_subset_set_indicator_settings = ekos.request_subset_set_indicator_settings(request)
ekos.write_test_response('request_subset_set_indicator_settings', response_subset_set_indicator_settings)
```
### Request subset calculate status
```
ekos = EventHandler(**paths)
request = ekos.test_requests['request_subset_calculate_status']
response = ekos.request_subset_calculate_status(request)
ekos.write_test_response('request_subset_calculate_status', response)
```
### Request subset result get
```
ekos = EventHandler(**paths)
request = ekos.test_requests['request_workspace_result']
response_workspace_result = ekos.request_workspace_result(request)
ekos.write_test_response('request_workspace_result', response_workspace_result)
response_workspace_result['subset']['a4e53080-2c68-40d5-957f-8cc4dbf77815']['result']['SE552170-130626']['result']['indicator_din_winter']['data']
workspace_uuid = 'fccc7645-8501-4541-975b-bdcfb40a5092'
subset_uuid = 'a4e53080-2c68-40d5-957f-8cc4dbf77815'
result = ekos.dict_data_timeseries(workspace_uuid=workspace_uuid,
subset_uuid=subset_uuid,
viss_eu_cd='SE575150-162700',
element_id='indicator_din_winter')
print(result['datasets'][0]['x'])
print()
print(result['y'])
for k in range(len(result['datasets'])):
print(result['datasets'][k]['x'])
import datetime
# Extend date list
start_year = all_dates[0].year
end_year = all_dates[-1].year+1
date_intervall = []
for year in range(start_year, end_year+1):
for month in range(1, 13):
d = datetime.datetime(year, month, 1)
if d >= all_dates[0] and d <= all_dates[-1]:
date_intervall.append(d)
extended_dates = sorted(set(all_dates + date_intervall))
# Loop dates and add/remove values
new_x = []
new_y = dict((item, []) for item in date_to_y)
for date in extended_dates:
if date in date_intervall:
new_x.append(date.strftime('%y-%b'))
else:
new_x.append('')
for i in new_y:
new_y[i].append(date_to_y[i].get(date, None))
# new_y = {}
# for i in date_to_y:
# new_y[i] = []
# for date in all_dates:
# d = date_to_y[i].get(date)
# if d:
# new_y[i].append(d)
# else:
# new_y[i].append(None)
new_y[0]
import datetime
year_list = range(2011, 2013+1)
month_list = range(1, 13)
date_list = []
for year in year_list:
for month in month_list:
date_list.append(datetime.datetime(year, month, 1))
date_list
a
y[3][i]
sorted(pd.to_datetime(df['SDATE']))
```
|
github_jupyter
|
# Chapter 4: Linear models
[Link to outline](https://docs.google.com/document/d/1fwep23-95U-w1QMPU31nOvUnUXE2X3s_Dbk5JuLlKAY/edit#heading=h.9etj7aw4al9w)
Concept map:

#### Notebook setup
```
import numpy as np
import pandas as pd
import scipy as sp
import seaborn as sns
from scipy.stats import uniform, norm
# notebooks figs setup
%matplotlib inline
import matplotlib.pyplot as plt
sns.set(rc={'figure.figsize':(8,5)})
blue, orange = sns.color_palette()[0], sns.color_palette()[1]
# silence annoying warnings
import warnings
warnings.filterwarnings('ignore')
```
## 4.1 Linear models for relationship between two numeric variables
- def'n linear model: **y ~ m*x + b**, a.k.a. linear regression
- Amy has collected a new dataset:
- Instead of receiving a fixed amount of stats training (100 hours),
**each employee now receives a variable amount of stats training (anywhere from 0 hours to 100 hours)**
- Amy has collected ELV values after one year as previously
- Goal find best fit line for relationship $\textrm{ELV} \sim \beta_0 + \beta_1\!*\!\textrm{hours}$
- Limitation: **we assume the change in ELV is proportional to number of hours** (i.e. linear relationship).
Other types of hours-ELV relationship possible, but we will not be able to model them correctly (see figure below).
### New dataset
- The `hours` column contains the `x` values (how many hours of statistics training did the employee receive),
- The `ELV` column contains the `y` values (the employee ELV after one year)

```
# Load data into a pandas dataframe
df2 = pd.read_excel("data/ELV_vs_hours.ods", sheet_name="Data")
# df2
df2.describe()
# plot ELV vs. hours data
sns.scatterplot(x='hours', y='ELV', data=df2)
# linear model plot (preview)
# sns.lmplot(x='hours', y='ELV', data=df2, ci=False)
```
#### Types of linear relationship between input and output
Different possible relationships between the number of hours of stats training and ELV gains:

## 4.2 Fitting linear models
- Main idea: use `fit` method from `statsmodels.ols` and a formula (approach 1)
- Visual inspection
- Results of linear model fit are:
- `beta0` = $\beta_0$ = baseline ELV (y-intercept)
- `beta1` = $\beta_1$ = increase in ELV for each additional hour of stats training (slope)
- Five more alternative fitting methods (bonus material):
2. fit using statsmodels `OLS`
3. solution using `linregress` from `scipy`
4. solution using `optimize` from `scipy`
5. linear algebra solution using `numpy`
6. solution using `LinearRegression` model from scikit-learn
### Using statsmodels formula API
The `statsmodels` Python library offers a convenient way to specify statistics model as a "formula" that describes the relationship we're looking for.
Mathematically, the linear model is written:
$\large \textrm{ELV} \ \ \sim \ \ \beta_0\cdot 1 \ + \ \beta_1\cdot\textrm{hours}$
and the formula is:
`ELV ~ 1 + hours`
Note the variables $\beta_0$ and $\beta_1$ are omitted, since the whole point of fitting a linear model is to find these coefficients. The parameters of the model are:
- Instead of $\beta_0$, the constant parameter will be called `Intercept`
- Instead of a new name $\beta_1$, we'll call it `hours` coefficient (i.e. the coefficient associated with the `hours` variable in the model)
```
import statsmodels.formula.api as smf
model = smf.ols('ELV ~ 1 + hours', data=df2)
result = model.fit()
# extact the best-fit model parameters
beta0, beta1 = result.params
beta0, beta1
# data points
sns.scatterplot(x='hours', y='ELV', data=df2)
# linear model for data
x = df2['hours'].values # input = hours
ymodel = beta0 + beta1*x # output = ELV
sns.lineplot(x, ymodel)
result.summary()
```
### Alternative model fitting methods
2. fit using statsmodels [`OLS`](https://www.statsmodels.org/stable/generated/statsmodels.regression.linear_model.OLS.html)
3. solution using [`linregress`](https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.linregress.html) from `scipy`
4. solution using [`minimize`](https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.minimize.html) from `scipy`
5. [linear algebra](https://numpy.org/doc/stable/reference/routines.linalg.html) solution using `numpy`
6. solution using [`LinearRegression`](https://scikit-learn.org/stable/modules/linear_model.html#ordinary-least-squares) model from scikit-learn
#### Data pre-processing
The `statsmodels` formula `ols` approach we used above was able to get the data
directly from the dataframe `df2`, but some of the other model fitting methods
require data to be provided as regular arrays: the x-values and the y-values.
```
# extract hours and ELV data from df2
x = df2['hours'].values # hours data as an array
y = df2['ELV'].values # ELV data as an array
x.shape, y.shape
# x
```
Two of the approaches required "packaging" the x-values along with a column of ones,
to form a matrix (called a design matrix). Luckily `statsmodels` provides a convenient function for this:
```
import statsmodels.api as sm
# add a column of ones to the x data
X = sm.add_constant(x)
X.shape
# X
```
____
#### 2. fit using statsmodels OLS
```
model2 = sm.OLS(y, X)
result2 = model2.fit()
# result2.summary()
result2.params
```
____
#### 3. solution using `linregress` from `scipy`
```
from scipy.stats import linregress
result3 = linregress(x, y)
result3.intercept, result3.slope
```
____
#### 4. Using an optimization approach
```
from scipy.optimize import minimize
def sse(beta, x=x, y=y):
"""Compute the sum-of-squared-errors objective function."""
sumse = 0.0
for xi, yi in zip(x, y):
yi_pred = beta[0] + beta[1]*xi
ei = (yi_pred-yi)**2
sumse += ei
return sumse
result4 = minimize(sse, x0=[0,0])
beta0, beta1 = result4.x
beta0, beta1
```
____
#### 5. Linear algebra solution
We obtain the least squares solution using the Moore–Penrose inverse formula:
$$ \large
\vec{\beta} = (X^{\sf T} X)^{-1}X^{\sf T}\; \vec{y}
$$
```
# 5. linear algebra solution using `numpy`
import numpy as np
result5 = np.linalg.inv(X.T.dot(X)).dot(X.T).dot(y)
beta0, beta1 = result5
beta0, beta1
```
_____
#### Using scikit-learn
```
# 6. solution using `LinearRegression` from scikit-learn
from sklearn import linear_model
model6 = linear_model.LinearRegression()
model6.fit(x[:,np.newaxis], y)
model6.intercept_, model6.coef_
```
## 4.3 Interpreting linear models
- model fit checks
- $R^2$ [coefficient of determination](https://en.wikipedia.org/wiki/Coefficient_of_determination)
= the proportion of the variation in the dependent variable that is predictable from the independent variable
- plot of residuals
- many other: see [scikit docs](https://scikit-learn.org/stable/modules/model_evaluation.html#regression-metrics)
- hypothesis tests
- is slope zero or nonzero? (and CI interval)
- caution: cannot make any cause-and-effect claims; only a correlation
- Predictions
- given best-fir model obtained from data, we can make predictions (interpolations),
e.g., what is the expected ELV after 50 hours of stats training?
### Interpreting the results
Let's review some of the other data included in the `results.summary()` report for the linear model fit we did earlier.
```
result.summary()
```
### Model parameters
```
beta0, beta1 = result.params
result.params
```
### The $R^2$ coefficient of determination
$R^2 = 1$ corresponds to perfect prediction
```
result.rsquared
```
### Hypothesis testing for slope coefficient
Is there a non-zero slope coefficient?
- **null hypothesis $H_0$**: `hours` has no effect on `ELV`,
which is equivalent to $\beta_1 = 0$:
$$ \large
H_0: \qquad \textrm{ELV} \sim \mathcal{N}(\color{red}{\beta_0}, \sigma^2) \qquad \qquad \qquad
$$
- **alternative hypothesis $H_A$**: `hours` has an effect on `ELV`,
and the slope is not zero, $\beta_1 \neq 0$:
$$ \large
H_A: \qquad \textrm{ELV}
\sim
\mathcal{N}\left(
\color{blue}{\beta_0 + \beta_1\!\cdot\!\textrm{hours}},
\ \sigma^2
\right)
$$
```
# p-value under the null hypotheis of zero slope or "no effect of `hours` on `ELV`"
result.pvalues.loc['hours']
# 95% confidence interval for the hours-slope parameter
# result.conf_int()
CI_hours = list(result.conf_int().loc['hours'])
CI_hours
```
### Predictions using the model
We can use the model we obtained to predict (interpolate) the ELV for future employees.
```
sns.scatterplot(x='hours', y='ELV', data=df2)
ymodel = beta0 + beta1*x
sns.lineplot(x, ymodel)
```
What ELV can we expect from a new employee that takes 50 hours of stats training?
```
result.predict({'hours':[50]})
result.predict({'hours':[100]})
```
**WARNING**: it's not OK to extrapolate the validity of the model outside of the range of values where we have observed data.
For example, there is no reason to believe in the model's predictions about ELV for 200 or 2000 hours of stats training:
```
result.predict({'hours':[200]})
```
## Discussion
Further topics that will be covered in the book:
- Generalized linear models, e.g., [Logistic regression](https://en.wikipedia.org/wiki/Logistic_regression)
- [Everything is a linear model](https://www.eigenfoo.xyz/tests-as-linear/) article
- The verbs `fit` and `predict` will come up A LOT in machine learning,
so it's worth learning linear models in detail to be prepared for further studies.
____
Congratulations on completing this overview of statistics! We covered a lot of topics and core ideas from the book. I know some parts seemed kind of complicated at first, but if you think about them a little you'll see there is nothing too difficult to learn. The good news is that the examples in these notebooks contain all the core ideas, and you won't be exposed to anything more complicated that what you saw here!
If you were able to handle these notebooks, you'll be able to handle the **No Bullshit Guide to Statistics** too! In fact the book will cover the topics in a much smoother way, and with better explanations. You'll have a lot of exercises and problems to help you practice statistical analysis.
### Next steps
- I encourage you to check out the [book outline shared gdoc](https://docs.google.com/document/d/1fwep23-95U-w1QMPU31nOvUnUXE2X3s_Dbk5JuLlKAY/edit) if you haven't seen it already. Please leave me a comment in the google document if you see something you don't like in the outline, or if you think some important statistics topics are missing. You can also read the [book proposal blog post](https://minireference.com/blog/no-bullshit-guide-to-statistics-progress-update/) for more info about the book.
- Check out also the [concept map](https://minireference.com/static/excerpts/noBSstats/conceptmaps/BookSubjectsOverview.pdf). You can print it out and annotate with the concepts you heard about in these notebooks.
- If you want to be involved in the stats book in the coming months, sign up to the [stats reviewers mailing list](https://confirmsubscription.com/h/t/A17516BF2FCB41B2) to receive chapter drafts as they are being prepared (Nov+Dec 2021). I'll appreciate your feedback on the text. The goal is to have the book finished in the Spring 2022, and feedback and "user testing" will be very helpful.
|
github_jupyter
|
```
try:
import saspy
except ImportError as e:
print('Installing saspy')
%pip install saspy
import pandas as pd
# The following imports are only necessary for automated sascfg_personal.py creation
from pathlib import Path
import os
from shutil import copyfile
import getpass
# Imports without the setup check codes
import saspy
import pandas as pd
```
# Set up your connection
The next cell contains code to check if you already have a sascfg_personal.py file in your current conda environment. If you do not one is created for you.
Next [choose your access method](https://sassoftware.github.io/saspy/install.html#choosing-an-access-method) and the read through the configuration properties in sascfg_personal.py
```
# Setup for the configuration file - for running inside of a conda environment
saspyPfad = f"C:\\Users\\{getpass.getuser()}\\.conda\\envs\\{os.environ['CONDA_DEFAULT_ENV']}\\Lib\\site-packages\\saspy\\"
saspycfg_personal = Path(f'{saspyPfad}sascfg_personal.py')
if saspycfg_personal.is_file():
print('All setup and ready to go')
else:
copyfile(f'{saspyPfad}sascfg.py', f'{saspyPfad}sascfg_personal.py')
print('The configuration file was created for you, please setup your connection method')
print(f'Find sascfg_personal.py here: {saspyPfad}')
```
# Configuration
prod = {
'iomhost': 'rfnk01-0068.exnet.sas.com', <-- SAS Host Name
'iomport': 8591, <-- SAS Workspace Server Port
'class_id': '440196d4-90f0-11d0-9f41-00a024bb830c', <-- static, if the value is wrong use proc iomoperate
'provider': 'sas.iomprovider', <-- static
'encoding': 'windows-1252' <-- Python encoding for SAS session encoding
}
```
# If no configuration name is specified, you get a list of the configured ones
# sas = saspy.SASsession(cfgname='prod')
sas = saspy.SASsession()
```
# Explore some interactions with SAS
Getting a feeling for what SASPy can do.
```
# Let's take a quick look at all the different methods and variables provided by SASSession object
dir(sas)
# Get a list of all tables inside of the library sashelp
table_df = sas.list_tables(libref='sashelp', results='pandas')
# Search for a table containing a capital C in its name
table_df[table_df['MEMNAME'].str.contains('C')]
# If teach_me_sas is true instead of executing the code, we get the generated code returned
sas.teach_me_SAS(True)
sas.list_tables(libref='sashelp', results='pandas')
# Let's turn it off again to actually run the code
sas.teach_me_SAS(False)
# Create a sasdata object, based on the table cars in the sashelp library
cars = sas.sasdata('cars', 'sashelp')
# Get information about the columns in the table
cars.columnInfo()
# Creating a simple heat map
cars.heatmap('Horsepower', 'EngineSize')
# Clean up for this section
del cars, table_df
```
# Reading in data from local disc with Pandas and uploading it to SAS
1. First we are going to read in a local csv file
2. Creating a copy of the base data file in SAS
3. Append the local data to the data stored in SAS and sort it
The Opel data set:
Make,Model,Type,Origin,DriveTrain,MSRP,Invoice,EngineSize,Cylinders,Horsepower,MPG_City,MPG_Highway,Weight,Wheelbase,Length
Opel,Astra Edition,Sedan,Europe,Rear,28495,26155,3,6,22.5,16,23,4023,110,180
Opel,Astra Design & Tech,Sedan,Europe,Rear,30795,28245,4.4,8,32.5,16,22,4824,111,184
Opel,Astra Elegance,Sedan,Europe,Rear,37995,34800,2.5,6,18.4,20,29,3219,107,176
Opel,Astra Ultimate,Sedan,Europe,Rear,42795,38245,2.5,6,18.4,20,29,3197,107,177
Opel,Astra Business Edition,Sedan,Europe,Rear,28495,24800,2.5,6,18.4,19,27,3560,107,177
Opel,Astra Elegance,Sedan,Europe,Rear,30245,27745,2.5,6,18.4,19,27,3461,107,176
```
# Read a local csv file with pandas and take a look
opel = pd.read_csv('cars_opel.csv')
opel.describe()
# Looks like the horsepower isn't right, let's fix that
opel.loc[:, 'Horsepower'] *= 10
opel.describe()
# Create a working copy of the cars data set
sas.submitLOG('''data work.cars; set sashelp.cars; run;''')
# Append the panda dataframe to the working copy of the cars data set in SAS
cars = sas.sasdata('cars', 'work')
# The pandas data frame is appended to the SAS data set
cars.append(opel)
cars.tail()
# Sort the data set in SAS to restore the old order
cars.sort('make model type')
cars.tail()
# Confirm that Opel has been added
cars.bar('Make')
```
# Reading in data from SAS and manipulating it with Pandas
```
# Short form is sd2df()
df = sas.sasdata2dataframe('cars', 'sashelp', dsopts={'where': 'make="BMW"'})
type(df)
```
Now that the data set is available as a Pandas DataFrame you can use it in e.g. a sklearn pipeline
```
df
```
# Creating a model
The data can be found [here](https://www.kaggle.com/gsr9099/best-model-for-credit-card-approval)
```
# Read two local csv files
df_applications = pd.read_csv('application_record.csv')
df_credit = pd.read_csv('credit_record.csv')
# Get a feel for the data
print(df_applications.columns)
print(df_applications.head(5))
df_applications.describe()
# Join the two data sets together
df_application_credit = df_applications.join(df_credit, lsuffix='_applications', rsuffix='_credit')
print(df_application_credit.head())
df_application_credit.columns
# Upload the data to the SAS server
# Here just a small sample, as the data set is quite large and the data is pre-loaded on SAS server
sas.df2sd(df_application_credit[:10], table='application_credit_sample', libref='saspy')
# Create a training data set and test data set in SAS
application_credit_sas = sas.sasdata('application_credit', 'saspy')
application_credit_part = application_credit_sas.partition(fraction=.7, var='status')
application_credit_part.info()
# Creating a SAS/STAT object
stat = sas.sasstat()
dir(stat)
# Target
target = 'status'
# Class Variables
var_class = ['FLAG_OWN_CAR','FLAG_OWN_REALTY', 'OCCUPATION_TYPE', 'STATUS']
```
The HPSPLIT procedure is a high-performance procedure that builds tree-based statistical models for classification and regression. The procedure produces classification trees, which model a categorical response, and regression trees, which model a continuous response. Both types of trees are referred to as decision trees because the model is expressed as a series of if-then statements - [documentation](https://support.sas.com/documentation/onlinedoc/stat/141/hpsplit.pdf)
```
hpsplit_model = stat.hpsplit(data=application_credit_part,
cls=var_class,
model="status(event='N')= FLAG_OWN_CAR FLAG_OWN_REALTY OCCUPATION_TYPE MONTHS_BALANCE AMT_INCOME_TOTAL",
code='trescore.sas',
procopts='assignmissing=similar',
out = 'work.dt_score',
id = "ID",
partition="rolevar=_partind_(TRAIN='1' VALIDATE='0');")
dir(hpsplit_model)
hpsplit_model.ROCPLOT
hpsplit_model.varimportance
sas.set_results('HTML')
hpsplit_model.wholetreeplot
```
|
github_jupyter
|
<a href="https://colab.research.google.com/github/isb-cgc/Community-Notebooks/blob/master/MachineLearning/How_to_build_an_RNAseq_logistic_regression_classifier_with_BigQuery_ML.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# How to build an RNA-seq logistic regression classifier with BigQuery ML
Check out other notebooks at our [Community Notebooks Repository](https://github.com/isb-cgc/Community-Notebooks)!
- **Title:** How to build an RNA-seq logistic regression classifier with BigQuery ML
- **Author:** John Phan
- **Created:** 2021-07-19
- **Purpose:** Demonstrate use of BigQuery ML to predict a cancer endpoint using gene expression data.
- **URL:** https://github.com/isb-cgc/Community-Notebooks/blob/master/MachineLearning/How_to_build_an_RNAseq_logistic_regression_classifier_with_BigQuery_ML.ipynb
- **Note:** This example is based on the work published by [Bosquet et al.](https://molecular-cancer.biomedcentral.com/articles/10.1186/s12943-016-0548-9)
This notebook builds upon the [scikit-learn notebook](https://github.com/isb-cgc/Community-Notebooks/blob/master/MachineLearning/How_to_build_an_RNAseq_logistic_regression_classifier.ipynb) and demonstrates how to build a machine learning model using BigQuery ML to predict ovarian cancer treatment outcome. BigQuery is used to create a temporary data table that contains both training and testing data. These datasets are then used to fit and evaluate a Logistic Regression classifier.
# Import Dependencies
```
# GCP libraries
from google.cloud import bigquery
from google.colab import auth
```
## Authenticate
Before using BigQuery, we need to get authorization for access to BigQuery and the Google Cloud. For more information see ['Quick Start Guide to ISB-CGC'](https://isb-cancer-genomics-cloud.readthedocs.io/en/latest/sections/HowToGetStartedonISB-CGC.html). Alternative authentication methods can be found [here](https://googleapis.dev/python/google-api-core/latest/auth.html)
```
# if you're using Google Colab, authenticate to gcloud with the following
auth.authenticate_user()
# alternatively, use the gcloud SDK
#!gcloud auth application-default login
```
## Parameters
Customize the following parameters based on your notebook, execution environment, or project. BigQuery ML must create and store classification models, so be sure that you have write access to the locations stored in the "bq_dataset" and "bq_project" variables.
```
# set the google project that will be billed for this notebook's computations
google_project = 'google-project' ## CHANGE ME
# bq project for storing ML model
bq_project = 'bq-project' ## CHANGE ME
# bq dataset for storing ML model
bq_dataset = 'scratch' ## CHANGE ME
# name of temporary table for data
bq_tmp_table = 'tmp_data'
# name of ML model
bq_ml_model = 'tcga_ov_therapy_ml_lr_model'
# in this example, we'll be using the Ovarian cancer TCGA dataset
cancer_type = 'TCGA-OV'
# genes used for prediction model, taken from Bosquet et al.
genes = "'RHOT1','MYO7A','ZBTB10','MATK','ST18','RPS23','GCNT1','DROSHA','NUAK1','CCPG1',\
'PDGFD','KLRAP1','MTAP','RNF13','THBS1','MLX','FAP','TIMP3','PRSS1','SLC7A11',\
'OLFML3','RPS20','MCM5','POLE','STEAP4','LRRC8D','WBP1L','ENTPD5','SYNE1','DPT',\
'COPZ2','TRIO','PDPR'"
# clinical data table
clinical_table = 'isb-cgc-bq.TCGA_versioned.clinical_gdc_2019_06'
# RNA seq data table
rnaseq_table = 'isb-cgc-bq.TCGA.RNAseq_hg38_gdc_current'
```
## BigQuery Client
Create the BigQuery client.
```
# Create a client to access the data within BigQuery
client = bigquery.Client(google_project)
```
## Create a Table with a Subset of the Gene Expression Data
Pull RNA-seq gene expression data from the TCGA RNA-seq BigQuery table, join it with clinical labels, and pivot the table so that it can be used with BigQuery ML. In this example, we will label the samples based on therapy outcome. "Complete Remission/Response" will be labeled as "1" while all other therapy outcomes will be labeled as "0". This prepares the data for binary classification.
Prediction modeling with RNA-seq data typically requires a feature selection step to reduce the dimensionality of the data before training a classifier. However, to simplify this example, we will use a pre-identified set of 33 genes (Bosquet et al. identified 34 genes, but PRSS2 and its aliases are not available in the hg38 RNA-seq data).
Creation of a BQ table with only the data of interest reduces the size of the data passed to BQ ML and can significantly reduce the cost of running BQ ML queries. This query also randomly splits the dataset into "training" and "testing" sets using the "FARM_FINGERPRINT" hash function in BigQuery. "FARM_FINGERPRINT" generates an integer from the input string. More information can be found [here](https://cloud.google.com/bigquery/docs/reference/standard-sql/hash_functions).
```
tmp_table_query = client.query(("""
BEGIN
CREATE OR REPLACE TABLE `{bq_project}.{bq_dataset}.{bq_tmp_table}` AS
SELECT * FROM (
SELECT
labels.case_barcode as sample,
labels.data_partition as data_partition,
labels.response_label AS label,
ge.gene_name AS gene_name,
-- Multiple samples may exist per case, take the max value
MAX(LOG(ge.HTSeq__FPKM_UQ+1)) AS gene_expression
FROM `{rnaseq_table}` AS ge
INNER JOIN (
SELECT
*
FROM (
SELECT
case_barcode,
primary_therapy_outcome_success,
CASE
-- Complete Reponse --> label as 1
-- All other responses --> label as 0
WHEN primary_therapy_outcome_success = 'Complete Remission/Response' THEN 1
WHEN (primary_therapy_outcome_success IN (
'Partial Remission/Response','Progressive Disease','Stable Disease'
)) THEN 0
END AS response_label,
CASE
WHEN MOD(ABS(FARM_FINGERPRINT(case_barcode)), 10) < 5 THEN 'training'
WHEN MOD(ABS(FARM_FINGERPRINT(case_barcode)), 10) >= 5 THEN 'testing'
END AS data_partition
FROM `{clinical_table}`
WHERE
project_short_name = '{cancer_type}'
AND primary_therapy_outcome_success IS NOT NULL
)
) labels
ON labels.case_barcode = ge.case_barcode
WHERE gene_name IN ({genes})
GROUP BY sample, label, data_partition, gene_name
)
PIVOT (
MAX(gene_expression) FOR gene_name IN ({genes})
);
END;
""").format(
bq_project=bq_project,
bq_dataset=bq_dataset,
bq_tmp_table=bq_tmp_table,
rnaseq_table=rnaseq_table,
clinical_table=clinical_table,
cancer_type=cancer_type,
genes=genes
)).result()
print(tmp_table_query)
```
Let's take a look at this subset table. The data has been pivoted such that each of the 33 genes is available as a column that can be "SELECTED" in a query. In addition, the "label" and "data_partition" columns simplify data handling for classifier training and evaluation.
```
tmp_table_data = client.query(("""
SELECT
* --usually not recommended to use *, but in this case, we want to see all of the 33 genes
FROM `{bq_project}.{bq_dataset}.{bq_tmp_table}`
""").format(
bq_project=bq_project,
bq_dataset=bq_dataset,
bq_tmp_table=bq_tmp_table
)).result().to_dataframe()
print(tmp_table_data.info())
tmp_table_data
```
# Train the Machine Learning Model
Now we can train a classifier using BigQuery ML with the data stored in the subset table. This model will be stored in the location specified by the "bq_ml_model" variable, and can be reused to predict samples in the future.
We pass three options to the BQ ML model: model_type, auto_class_weights, and input_label_cols. Model_type specifies the classifier model type. In this case, we use "LOGISTIC_REG" to train a logistic regression classifier. Other classifier options are documented [here](https://cloud.google.com/bigquery-ml/docs/reference/standard-sql/bigqueryml-syntax-create). Auto_class_weights indicates whether samples should be weighted to balance the classes. For example, if the dataset happens to have more samples labeled as "Complete Response", those samples would be less weighted to ensure that the model is not biased towards predicting those samples. Input_label_cols tells BigQuery that the "label" column should be used to determine each sample's label.
**Warning**: BigQuery ML models can be very time-consuming and expensive to train. Please check your data size before running BigQuery ML commands. Information about BigQuery ML costs can be found [here](https://cloud.google.com/bigquery-ml/pricing).
```
# create ML model using BigQuery
ml_model_query = client.query(("""
CREATE OR REPLACE MODEL `{bq_project}.{bq_dataset}.{bq_ml_model}`
OPTIONS
(
model_type='LOGISTIC_REG',
auto_class_weights=TRUE,
input_label_cols=['label']
) AS
SELECT * EXCEPT(sample, data_partition) -- when training, we only the labels and feature columns
FROM `{bq_project}.{bq_dataset}.{bq_tmp_table}`
WHERE data_partition = 'training' -- using training data only
""").format(
bq_project=bq_project,
bq_dataset=bq_dataset,
bq_ml_model=bq_ml_model,
bq_tmp_table=bq_tmp_table
)).result()
print(ml_model_query)
# now get the model metadata
ml_model = client.get_model('{}.{}.{}'.format(bq_project, bq_dataset, bq_ml_model))
print(ml_model)
```
# Evaluate the Machine Learning Model
Once the model has been trained and stored, we can evaluate the model's performance using the "testing" dataset from our subset table. Evaluating a BQ ML model is generally less expensive than training.
Use the following query to evaluate the BQ ML model. Note that we're using the "data_partition = 'testing'" clause to ensure that we're only evaluating the model with test samples from the subset table.
BigQuery's ML.EVALUATE function returns several performance metrics: precision, recall, accuracy, f1_score, log_loss, and roc_auc. More details about these performance metrics are available from [Google's ML Crash Course](https://developers.google.com/machine-learning/crash-course/classification/video-lecture). Specific topics can be found at the following URLs: [precision and recall](https://developers.google.com/machine-learning/crash-course/classification/precision-and-recall), [accuracy](https://developers.google.com/machine-learning/crash-course/classification/accuracy), [ROC and AUC](https://developers.google.com/machine-learning/crash-course/classification/roc-and-auc).
```
ml_eval = client.query(("""
SELECT * FROM ML.EVALUATE (MODEL `{bq_project}.{bq_dataset}.{bq_ml_model}`,
(
SELECT * EXCEPT(sample, data_partition)
FROM `{bq_project}.{bq_dataset}.{bq_tmp_table}`
WHERE data_partition = 'testing'
)
)
""").format(
bq_project=bq_project,
bq_dataset=bq_dataset,
bq_ml_model=bq_ml_model,
bq_tmp_table=bq_tmp_table
)).result().to_dataframe()
# Display the table of evaluation results
ml_eval
```
# Predict Outcome for One or More Samples
ML.EVALUATE evaluates a model's performance, but does not produce actual predictions for each sample. In order to do that, we need to use the ML.PREDICT function. The syntax is similar to that of the ML.EVALUATE function and returns "label", "predicted_label", "predicted_label_probs", and all feature columns. Since the feature columns are unchanged from the input dataset, we select only the original label, predicted label, and probabilities for each sample.
Note that the input dataset can include one or more samples, and must include the same set of features as the training dataset.
```
ml_predict = client.query(("""
SELECT
label,
predicted_label,
predicted_label_probs
FROM ML.PREDICT (MODEL `{bq_project}.{bq_dataset}.{bq_ml_model}`,
(
SELECT * EXCEPT(sample, data_partition)
FROM `{bq_project}.{bq_dataset}.{bq_tmp_table}`
WHERE data_partition = 'testing' -- Use the testing dataset
)
)
""").format(
bq_project=bq_project,
bq_dataset=bq_dataset,
bq_ml_model=bq_ml_model,
bq_tmp_table=bq_tmp_table
)).result().to_dataframe()
# Display the table of prediction results
ml_predict
# Calculate the accuracy of prediction, which should match the result of ML.EVALUATE
accuracy = 1-sum(abs(ml_predict['label']-ml_predict['predicted_label']))/len(ml_predict)
print('Accuracy: ', accuracy)
```
# Next Steps
The BigQuery ML logistic regression model trained in this notebook is comparable to the scikit-learn model developed in our [companion notebook](https://github.com/isb-cgc/Community-Notebooks/blob/master/MachineLearning/How_to_build_an_RNAseq_logistic_regression_classifier.ipynb). BigQuery ML simplifies the model building and evaluation process by enabling bioinformaticians to use machine learning within the BigQuery ecosystem. However, it is often necessary to optimize performance by evaluating several types of models (i.e., other than logistic regression), and tuning model parameters. Due to the cost of BigQuery ML for training, such iterative model fine-tuning may be cost prohibitive. In such cases, a combination of scikit-learn (or other libraries such as Keras and TensorFlow) and BigQuery ML may be appropriate. E.g., models can be fine-tuned using scikit-learn and published as a BigQuery ML model for production applications. In future notebooks, we will explore methods for model selection, optimization, and publication with BigQuery ML.
|
github_jupyter
|
# FireCARES ops management notebook
### Using this notebook
In order to use this notebook, a single production/test web node will need to be bootstrapped w/ ipython and django-shell-plus python libraries. After bootstrapping is complete and while forwarding a local port to the port that the ipython notebook server will be running on the node, you can open the ipython notebook using the token provided in the SSH session after ipython notebook server start.
#### Bootstrapping a prod/test node
To bootstrap a specific node for use of this notebook, you'll need to ssh into the node and forward a local port # to localhost:8888 on the node.
e.g. `ssh firecares-prod -L 8890:localhost:8888` to forward the local port 8890 to 8888 on the web node, assumes that the "firecares-prod" SSH config is listed w/ the correct webserver IP in your `~/.ssh/config`
- `sudo chown -R firecares: /run/user/1000` as the `ubuntu` user
- `sudo su firecares`
- `workon firecares`
- `pip install -r dev_requirements.txt`
- `python manage.py shell_plus --notebook --no-browser --settings=firecares.settings.local`
At this point, there will be a mention of "The jupyter notebook is running at: http://localhost:8888/?token=XXXX". Copy the URL, but be sure to use the local port that you're forwarding instead for the connection vs the default of 8888 if necessary.
Since the ipython notebook server supports django-shell-plus, all of the FireCARES models will automatically be imported. From here any command that you execute in the notebook will run on the remote web node immediately.
## Fire department management
### Re-generate performance score for a specific fire department
Useful for when a department's FDID has been corrected. Will do the following:
1. Pull NFIRS counts for the department (cached in FireCARES database)
1. Generate fires heatmap
1. Update department owned census tracts geom
1. Regenerate structure hazard counts in jurisdiction
1. Regenerate population_quartiles materialized view to get safe grades for department
1. Re-run performance score for the department
```
import psycopg2
from firecares.tasks import update
from firecares.utils import dictfetchall
from django.db import connections
from django.conf import settings
from django.core.management import call_command
from IPython.display import display
import pandas as pd
fd = {'fdid': '18M04', 'state': 'WA'}
nfirs = connections['nfirs']
department = FireDepartment.objects.filter(**fd).first()
fid = department.id
print 'FireCARES id: %s' % fid
print 'https://firecares.org/departments/%s' % fid
%%time
# Get raw fire incident counts (prior to intersection with )
with nfirs.cursor() as cur:
cur.execute("""
select count(1), fdid, state, extract(year from inc_date) as year
from fireincident where fdid=%(fdid)s and state=%(state)s
group by fdid, state, year
order by year""", fd)
fire_years = dictfetchall(cur)
display(fire_years)
print 'Total fires: %s\n' % sum([x['count'] for x in fire_years])
%%time
# Get building fire counts after structure hazard level calculations
sql = update.STRUCTURE_FIRES
print sql
with nfirs.cursor() as cur:
cur.execute(sql, dict(fd, years=tuple([x['year'] for x in fire_years])))
fires_by_hazard_level = dictfetchall(cur)
display(fires_by_hazard_level)
print 'Total geocoded fires: %s\n' % sum([x['count'] for x in fires_by_hazard_level])
sql = """
select alarm, a.inc_type, alarms,ff_death, oth_death, ST_X(geom) as x, st_y(geom) as y, COALESCE(y.risk_category, 'Unknown') as risk_category
from buildingfires a
LEFT JOIN (
SELECT state, fdid, inc_date, inc_no, exp_no, x.geom, x.parcel_id, x.risk_category
FROM (
SELECT * FROM incidentaddress a
LEFT JOIN parcel_risk_category_local using (parcel_id)
) AS x
) AS y
USING (state, fdid, inc_date, inc_no, exp_no)
WHERE a.state = %(state)s and a.fdid = %(fdid)s"""
with nfirs.cursor() as cur:
cur.execute(sql, fd)
rows = dictfetchall(cur)
out_name = '{id}-building-fires.csv'.format(id=fid)
full_path = '/tmp/' + out_name
with open(full_path, 'w') as f:
writer = csv.DictWriter(f, fieldnames=[x.name for x in cur.description])
writer.writeheader()
writer.writerows(rows)
# Push building fires to S3
!aws s3 cp $full_path s3://firecares-test/$out_name --acl="public-read"
update.update_nfirs_counts(fid)
update.calculate_department_census_geom(fid)
# Fire counts by hazard level over all years, keep in mind that the performance score model will currently ONLY work
# hazard levels w/
display(pd.DataFrame(fires_by_hazard_level).groupby(['risk_level']).sum()['count'])
update.update_performance_score(fid)
```
## User management
### Whitelist
|
github_jupyter
|
```
import sys
sys.path.append("/Users/sgkang/Projects/DamGeophysics/codes/")
from Readfiles import getFnames
from DCdata import readReservoirDC
%pylab inline
from SimPEG.EM.Static import DC
from SimPEG import EM
from SimPEG import Mesh
```
Read DC data
```
fname = "../data/ChungCheonDC/20150101000000.apr"
survey = readReservoirDC(fname)
dobsAppres = survey.dobs
fig, ax = plt.subplots(1,1, figsize = (10, 2))
dat = EM.Static.Utils.StaticUtils.plot_pseudoSection(survey, ax, dtype='volt', sameratio=False)
cb = dat[2]
cb.set_label("Apprent resistivity (ohm-m)")
geom = np.hstack(dat[3])
dobsDC = dobsAppres * geom
# problem = DC.Problem2D_CC(mesh)
cs = 2.5
npad = 6
hx = [(cs,npad, -1.3),(cs,160),(cs,npad, 1.3)]
hy = [(cs,npad, -1.3),(cs,20)]
mesh = Mesh.TensorMesh([hx, hy])
mesh = Mesh.TensorMesh([hx, hy],x0=[-mesh.hx[:6].sum()-0.25, -mesh.hy.sum()])
def from3Dto2Dsurvey(survey):
srcLists2D = []
nSrc = len(survey.srcList)
for iSrc in range (nSrc):
src = survey.srcList[iSrc]
locsM = np.c_[src.rxList[0].locs[0][:,0], np.ones_like(src.rxList[0].locs[0][:,0])*-0.75]
locsN = np.c_[src.rxList[0].locs[1][:,0], np.ones_like(src.rxList[0].locs[1][:,0])*-0.75]
rx = DC.Rx.Dipole_ky(locsM, locsN)
locA = np.r_[src.loc[0][0], -0.75]
locB = np.r_[src.loc[1][0], -0.75]
src = DC.Src.Dipole([rx], locA, locB)
srcLists2D.append(src)
survey2D = DC.Survey_ky(srcLists2D)
return survey2D
from SimPEG import (Mesh, Maps, Utils, DataMisfit, Regularization,
Optimization, Inversion, InvProblem, Directives)
mapping = Maps.ExpMap(mesh)
survey2D = from3Dto2Dsurvey(survey)
problem = DC.Problem2D_N(mesh, mapping=mapping)
problem.pair(survey2D)
m0 = np.ones(mesh.nC)*np.log(1e-2)
from ipywidgets import interact
nSrc = len(survey2D.srcList)
def foo(isrc):
figsize(10, 5)
mesh.plotImage(np.ones(mesh.nC)*np.nan, gridOpts={"color":"k", "alpha":0.5}, grid=True)
# isrc=0
src = survey2D.srcList[isrc]
plt.plot(src.loc[0][0], src.loc[0][1], 'bo')
plt.plot(src.loc[1][0], src.loc[1][1], 'ro')
locsM = src.rxList[0].locs[0]
locsN = src.rxList[0].locs[1]
plt.plot(locsM[:,0], locsM[:,1], 'ko')
plt.plot(locsN[:,0], locsN[:,1], 'go')
plt.gca().set_aspect('equal', adjustable='box')
interact(foo, isrc=(0, nSrc-1, 1))
pred = survey2D.dpred(m0)
# data_anal = []
# nSrc = len(survey.srcList)
# for isrc in range(nSrc):
# src = survey.srcList[isrc]
# locA = src.loc[0]
# locB = src.loc[1]
# locsM = src.rxList[0].locs[0]
# locsN = src.rxList[0].locs[1]
# rxloc=[locsM, locsN]
# a = EM.Analytics.DCAnalyticHalf(locA, rxloc, 1e-3, earth_type="halfspace")
# b = EM.Analytics.DCAnalyticHalf(locB, rxloc, 1e-3, earth_type="halfspace")
# data_anal.append(a-b)
# data_anal = np.hstack(data_anal)
survey.dobs = pred
fig, ax = plt.subplots(1,1, figsize = (10, 2))
dat = EM.Static.Utils.StaticUtils.plot_pseudoSection(survey, ax, dtype='appr', sameratio=False, scale="linear", clim=(0, 200))
out = hist(np.log10(abs(dobsDC)), bins = 100)
weight = 1./abs(mesh.gridCC[:,1])**1.5
mesh.plotImage(np.log10(weight))
survey2D.dobs = dobsDC
survey2D.eps = 10**(-2.3)
survey2D.std = 0.02
dmisfit = DataMisfit.l2_DataMisfit(survey2D)
regmap = Maps.IdentityMap(nP=int(mesh.nC))
reg = Regularization.Simple(mesh,mapping=regmap,cell_weights=weight)
opt = Optimization.InexactGaussNewton(maxIter=5)
invProb = InvProblem.BaseInvProblem(dmisfit, reg, opt)
# Create an inversion object
beta = Directives.BetaSchedule(coolingFactor=5, coolingRate=2)
betaest = Directives.BetaEstimate_ByEig(beta0_ratio=1e0)
inv = Inversion.BaseInversion(invProb, directiveList=[beta, betaest])
problem.counter = opt.counter = Utils.Counter()
opt.LSshorten = 0.5
opt.remember('xc')
mopt = inv.run(m0)
xc = opt.recall("xc")
fig, ax = plt.subplots(1,1, figsize = (10, 1.5))
sigma = mapping*mopt
dat = mesh.plotImage(1./sigma, clim=(10, 150),grid=False, ax=ax, pcolorOpts={"cmap":"jet"})
ax.set_ylim(-50, 0)
ax.set_xlim(-10, 290)
print np.log10(sigma).min(), np.log10(sigma).max()
survey.dobs = invProb.dpred
fig, ax = plt.subplots(1,1, figsize = (10, 2))
dat = EM.Static.Utils.StaticUtils.plot_pseudoSection(survey, ax, dtype='appr', sameratio=False, clim=(40, 170))
survey.dobs = dobsDC
fig, ax = plt.subplots(1,1, figsize = (10, 2))
dat = EM.Static.Utils.StaticUtils.plot_pseudoSection(survey, ax, dtype='appr', sameratio=False, clim=(40, 170))
survey.dobs = abs(dmisfit.Wd*(dobsDC-invProb.dpred))
fig, ax = plt.subplots(1,1, figsize = (10, 2))
dat = EM.Static.Utils.StaticUtils.plot_pseudoSection(survey, ax, dtype='volt', sameratio=False, clim=(0, 2))
# sigma = np.ones(mesh.nC)
modelname = "sigma0101.npy"
np.save(modelname, sigma)
```
|
github_jupyter
|
# FloPy
## Using FloPy to simplify the use of the MT3DMS ```SSM``` package
A multi-component transport demonstration
```
import os
import sys
import numpy as np
# run installed version of flopy or add local path
try:
import flopy
except:
fpth = os.path.abspath(os.path.join('..', '..'))
sys.path.append(fpth)
import flopy
print(sys.version)
print('numpy version: {}'.format(np.__version__))
print('flopy version: {}'.format(flopy.__version__))
```
First, we will create a simple model structure
```
nlay, nrow, ncol = 10, 10, 10
perlen = np.zeros((10), dtype=float) + 10
nper = len(perlen)
ibound = np.ones((nlay,nrow,ncol), dtype=int)
botm = np.arange(-1,-11,-1)
top = 0.
```
## Create the ```MODFLOW``` packages
```
model_ws = 'data'
modelname = 'ssmex'
mf = flopy.modflow.Modflow(modelname, model_ws=model_ws)
dis = flopy.modflow.ModflowDis(mf, nlay=nlay, nrow=nrow, ncol=ncol,
perlen=perlen, nper=nper, botm=botm, top=top,
steady=False)
bas = flopy.modflow.ModflowBas(mf, ibound=ibound, strt=top)
lpf = flopy.modflow.ModflowLpf(mf, hk=100, vka=100, ss=0.00001, sy=0.1)
oc = flopy.modflow.ModflowOc(mf)
pcg = flopy.modflow.ModflowPcg(mf)
rch = flopy.modflow.ModflowRch(mf)
```
We'll track the cell locations for the ```SSM``` data using the ```MODFLOW``` boundary conditions.
Get a dictionary (```dict```) that has the ```SSM``` ```itype``` for each of the boundary types.
```
itype = flopy.mt3d.Mt3dSsm.itype_dict()
print(itype)
print(flopy.mt3d.Mt3dSsm.get_default_dtype())
ssm_data = {}
```
Add a general head boundary (```ghb```). The general head boundary head (```bhead```) is 0.1 for the first 5 stress periods with a component 1 (comp_1) concentration of 1.0 and a component 2 (comp_2) concentration of 100.0. Then ```bhead``` is increased to 0.25 and comp_1 concentration is reduced to 0.5 and comp_2 concentration is increased to 200.0
```
ghb_data = {}
print(flopy.modflow.ModflowGhb.get_default_dtype())
ghb_data[0] = [(4, 4, 4, 0.1, 1.5)]
ssm_data[0] = [(4, 4, 4, 1.0, itype['GHB'], 1.0, 100.0)]
ghb_data[5] = [(4, 4, 4, 0.25, 1.5)]
ssm_data[5] = [(4, 4, 4, 0.5, itype['GHB'], 0.5, 200.0)]
for k in range(nlay):
for i in range(nrow):
ghb_data[0].append((k, i, 0, 0.0, 100.0))
ssm_data[0].append((k, i, 0, 0.0, itype['GHB'], 0.0, 0.0))
ghb_data[5] = [(4, 4, 4, 0.25, 1.5)]
ssm_data[5] = [(4, 4, 4, 0.5, itype['GHB'], 0.5, 200.0)]
for k in range(nlay):
for i in range(nrow):
ghb_data[5].append((k, i, 0, -0.5, 100.0))
ssm_data[5].append((k, i, 0, 0.0, itype['GHB'], 0.0, 0.0))
```
Add an injection ```well```. The injection rate (```flux```) is 10.0 with a comp_1 concentration of 10.0 and a comp_2 concentration of 0.0 for all stress periods. WARNING: since we changed the ```SSM``` data in stress period 6, we need to add the well to the ssm_data for stress period 6.
```
wel_data = {}
print(flopy.modflow.ModflowWel.get_default_dtype())
wel_data[0] = [(0, 4, 8, 10.0)]
ssm_data[0].append((0, 4, 8, 10.0, itype['WEL'], 10.0, 0.0))
ssm_data[5].append((0, 4, 8, 10.0, itype['WEL'], 10.0, 0.0))
```
Add the ```GHB``` and ```WEL``` packages to the ```mf``` ```MODFLOW``` object instance.
```
ghb = flopy.modflow.ModflowGhb(mf, stress_period_data=ghb_data)
wel = flopy.modflow.ModflowWel(mf, stress_period_data=wel_data)
```
## Create the ```MT3DMS``` packages
```
mt = flopy.mt3d.Mt3dms(modflowmodel=mf, modelname=modelname, model_ws=model_ws)
btn = flopy.mt3d.Mt3dBtn(mt, sconc=0, ncomp=2, sconc2=50.0)
adv = flopy.mt3d.Mt3dAdv(mt)
ssm = flopy.mt3d.Mt3dSsm(mt, stress_period_data=ssm_data)
gcg = flopy.mt3d.Mt3dGcg(mt)
```
Let's verify that ```stress_period_data``` has the right ```dtype```
```
print(ssm.stress_period_data.dtype)
```
## Create the ```SEAWAT``` packages
```
swt = flopy.seawat.Seawat(modflowmodel=mf, mt3dmodel=mt,
modelname=modelname, namefile_ext='nam_swt', model_ws=model_ws)
vdf = flopy.seawat.SeawatVdf(swt, mtdnconc=0, iwtable=0, indense=-1)
mf.write_input()
mt.write_input()
swt.write_input()
```
And finally, modify the ```vdf``` package to fix ```indense```.
```
fname = modelname + '.vdf'
f = open(os.path.join(model_ws, fname),'r')
lines = f.readlines()
f.close()
f = open(os.path.join(model_ws, fname),'w')
for line in lines:
f.write(line)
for kper in range(nper):
f.write("-1\n")
f.close()
```
|
github_jupyter
|
# Introduction
In a prior notebook, documents were partitioned by assigning them to the domain with the highest Dice similarity of their term and structure occurrences. The occurrences of terms and structures in each domain is what we refer to as the domain "archetype." Here, we'll assess whether the observed similarity between documents and the archetype is greater than expected by chance. This would indicate that information in the framework generalizes well to individual documents.
# Load the data
```
import os
import pandas as pd
import numpy as np
import sys
sys.path.append("..")
import utilities
from ontology import ontology
from style import style
version = 190325 # Document-term matrix version
clf = "lr" # Classifier used to generate the framework
suffix = "_" + clf # Suffix for term lists
n_iter = 1000 # Iterations for null distribution
circuit_counts = range(2, 51) # Range of k values
```
## Brain activation coordinates
```
act_bin = utilities.load_coordinates()
print("Document N={}, Structure N={}".format(
act_bin.shape[0], act_bin.shape[1]))
```
## Document-term matrix
```
dtm_bin = utilities.load_doc_term_matrix(version=version, binarize=True)
print("Document N={}, Term N={}".format(
dtm_bin.shape[0], dtm_bin.shape[1]))
```
## Document splits
```
splits = {}
# splits["train"] = [int(pmid.strip()) for pmid in open("../data/splits/train.txt")]
splits["validation"] = [int(pmid.strip()) for pmid in open("../data/splits/validation.txt")]
splits["test"] = [int(pmid.strip()) for pmid in open("../data/splits/test.txt")]
for split, split_pmids in splits.items():
print("{:12s} N={}".format(split.title(), len(split_pmids)))
pmids = dtm_bin.index.intersection(act_bin.index)
```
## Document assignments and distances
Indexing by min:max will be faster in subsequent computations
```
from collections import OrderedDict
from scipy.spatial.distance import cdist
def load_doc2dom(k, clf="lr"):
doc2dom_df = pd.read_csv("../partition/data/doc2dom_k{:02d}_{}.csv".format(k, clf),
header=None, index_col=0)
doc2dom = {int(pmid): str(dom.values[0]) for pmid, dom in doc2dom_df.iterrows()}
return doc2dom
def load_dom2docs(k, domains, splits, clf="lr"):
doc2dom = load_doc2dom(k, clf=clf)
dom2docs = {dom: {split: [] for split, _ in splits.items()} for dom in domains}
for doc, dom in doc2dom.items():
for split, split_pmids in splits.items():
if doc in splits[split]:
dom2docs[dom][split].append(doc)
return dom2docs
sorted_pmids, doc_dists, dom_idx = {}, {}, {}
for k in circuit_counts:
print("Processing k={:02d}".format(k))
sorted_pmids[k], doc_dists[k], dom_idx[k] = {}, {}, {}
for split, split_pmids in splits.items():
lists, circuits = ontology.load_ontology(k, path="../ontology/", suffix=suffix)
words = sorted(list(set(lists["TOKEN"])))
structures = sorted(list(set(act_bin.columns)))
domains = list(OrderedDict.fromkeys(lists["DOMAIN"]))
dtm_words = dtm_bin.loc[pmids, words]
act_structs = act_bin.loc[pmids, structures]
docs = dtm_words.copy()
docs[structures] = act_structs.copy()
doc2dom = load_doc2dom(k, clf=clf)
dom2docs = load_dom2docs(k, domains, splits, clf=clf)
ids = []
for dom in domains:
ids += [pmid for pmid, sys in doc2dom.items() if sys == dom and pmid in split_pmids]
sorted_pmids[k][split] = ids
doc_dists[k][split] = pd.DataFrame(cdist(docs.loc[ids], docs.loc[ids], metric="dice"),
index=ids, columns=ids)
dom_idx[k][split] = {}
for dom in domains:
dom_idx[k][split][dom] = {}
dom_pmids = dom2docs[dom][split]
if len(dom_pmids) > 0:
dom_idx[k][split][dom]["min"] = sorted_pmids[k][split].index(dom_pmids[0])
dom_idx[k][split][dom]["max"] = sorted_pmids[k][split].index(dom_pmids[-1]) + 1
else:
dom_idx[k][split][dom]["min"] = 0
dom_idx[k][split][dom]["max"] = 0
```
# Index by PMID and sort by structure
```
structures = sorted(list(set(act_bin.columns)))
act_structs = act_bin.loc[pmids, structures]
```
# Compute domain modularity
## Observed values
## Distances internal and external to articles in each domain
```
dists_int, dists_ext = {}, {}
for k in circuit_counts:
dists_int[k], dists_ext[k] = {}, {}
lists, circuits = ontology.load_ontology(k, path="../ontology/", suffix=suffix)
domains = list(OrderedDict.fromkeys(lists["DOMAIN"]))
for split, split_pmids in splits.items():
dists_int[k][split], dists_ext[k][split] = {}, {}
for dom in domains:
dom_min, dom_max = dom_idx[k][split][dom]["min"], dom_idx[k][split][dom]["max"]
dom_dists = doc_dists[k][split].values[:,dom_min:dom_max][dom_min:dom_max,:]
dists_int[k][split][dom] = dom_dists
other_dists_lower = doc_dists[k][split].values[:,dom_min:dom_max][:dom_min,:]
other_dists_upper = doc_dists[k][split].values[:,dom_min:dom_max][dom_max:,:]
other_dists = np.concatenate((other_dists_lower, other_dists_upper))
dists_ext[k][split][dom] = other_dists
```
## Domain-averaged ratio of external to internal distances
```
means = {split: np.empty((len(circuit_counts),)) for split in splits.keys()}
for k_i, k in enumerate(circuit_counts):
file_obs = "data/kvals/mod_obs_k{:02d}_{}_{}.csv".format(k, clf, split)
if not os.path.isfile(file_obs):
print("Processing k={:02d}".format(k))
lists, circuits = ontology.load_ontology(k, path="../ontology/", suffix=suffix)
domains = list(OrderedDict.fromkeys(lists["DOMAIN"]))
dom2docs = load_dom2docs(k, domains, splits, clf=clf)
pmid_list, split_list, dom_list, obs_list = [], [], [], []
for split, split_pmids in splits.items():
for dom in domains:
n_dom_docs = dists_int[k][split][dom].shape[0]
if n_dom_docs > 0:
mean_dist_int = np.nanmean(dists_int[k][split][dom], axis=0)
mean_dist_ext = np.nanmean(dists_ext[k][split][dom], axis=0)
ratio = mean_dist_ext / mean_dist_int
ratio[ratio == np.inf] = np.nan
pmid_list += dom2docs[dom][split]
dom_list += [dom] * len(ratio)
split_list += [split] * len(ratio)
obs_list += list(ratio)
df_obs = pd.DataFrame({"PMID": pmid_list, "SPLIT": split_list,
"DOMAIN": dom_list, "OBSERVED": obs_list})
df_obs.to_csv(file_obs, index=None)
else:
df_obs = pd.read_csv(file_obs)
for split, split_pmids in splits.items():
dom_means = []
for dom in set(df_obs["DOMAIN"]):
dom_vals = df_obs.loc[(df_obs["SPLIT"] == split) & (df_obs["DOMAIN"] == dom), "OBSERVED"]
dom_means.append(np.nanmean(dom_vals))
means[split][k_i] = np.nanmean(dom_means)
```
## Null distributions
```
nulls = {split: np.empty((len(circuit_counts),n_iter)) for split in splits.keys()}
for split, split_pmids in splits.items():
for k_i, k in enumerate(circuit_counts):
file_null = "data/kvals/mod_null_k{:02d}_{}_{}iter.csv".format(k, split, n_iter)
if not os.path.isfile(file_null):
print("Processing k={:02d}".format(k))
lists, circuits = ontology.load_ontology(k, path="../ontology/", suffix=suffix)
domains = list(OrderedDict.fromkeys(lists["DOMAIN"]))
n_docs = len(split_pmids)
df_null = np.empty((len(domains), n_iter))
for i, dom in enumerate(domains):
n_dom_docs = dists_int[k][split][dom].shape[0]
if n_dom_docs > 0:
dist_int_ext = np.concatenate((dists_int[k][split][dom], dists_ext[k][split][dom]))
for n in range(n_iter):
null = np.random.choice(range(n_docs), size=n_docs, replace=False)
dist_int_ext_null = dist_int_ext[null,:]
mean_dist_int = np.nanmean(dist_int_ext_null[:n_dom_docs,:], axis=0)
mean_dist_ext = np.nanmean(dist_int_ext_null[n_dom_docs:,:], axis=0)
ratio = mean_dist_ext / mean_dist_int
ratio[ratio == np.inf] = np.nan
df_null[i,n] = np.nanmean(ratio)
else:
df_null[i,:] = np.nan
df_null = pd.DataFrame(df_null, index=domains, columns=range(n_iter))
df_null.to_csv(file_null)
else:
df_null = pd.read_csv(file_null, index_col=0, header=0)
nulls[split][k_i,:] = np.nanmean(df_null, axis=0)
```
## Bootstrap distributions
```
boots = {split: np.empty((len(circuit_counts),n_iter)) for split in splits.keys()}
for split, split_pmids in splits.items():
for k_i, k in enumerate(circuit_counts):
file_boot = "data/kvals/mod_boot_k{:02d}_{}_{}iter.csv".format(k, split, n_iter)
if not os.path.isfile(file_boot):
print("Processing k={:02d}".format(k))
lists, circuits = ontology.load_ontology(k, path="../ontology/", suffix=suffix)
domains = list(OrderedDict.fromkeys(lists["DOMAIN"]))
df_boot = np.empty((len(domains), n_iter))
for i, dom in enumerate(domains):
n_dom_docs = dists_int[k][split][dom].shape[0]
if n_dom_docs > 0:
for n in range(n_iter):
boot = np.random.choice(range(n_dom_docs), size=n_dom_docs, replace=True)
mean_dist_int = np.nanmean(dists_int[k][split][dom][:,boot], axis=0)
mean_dist_ext = np.nanmean(dists_ext[k][split][dom][:,boot], axis=0)
ratio = mean_dist_ext / mean_dist_int
ratio[ratio == np.inf] = np.nan
df_boot[i,n] = np.nanmean(ratio)
else:
df_boot[i,:] = np.nan
df_boot = pd.DataFrame(df_boot, index=domains, columns=range(n_iter))
df_boot.to_csv(file_boot)
else:
df_boot = pd.read_csv(file_boot, index_col=0, header=0)
boots[split][k_i,:] = np.nanmean(df_boot, axis=0)
```
# Plot results over k
```
from matplotlib import rcParams
%matplotlib inline
rcParams["axes.linewidth"] = 1.5
for split in splits.keys():
print(split.upper())
utilities.plot_stats_by_k(means, nulls, boots, circuit_counts, metric="mod",
split=split, op_k=6, clf=clf, interval=0.999,
ylim=[0.8,1.4], yticks=[0.8, 0.9,1,1.1,1.2,1.3,1.4])
```
|
github_jupyter
|
```
import pandas as pd
import praw
import re
import datetime as dt
import seaborn as sns
import requests
import json
import sys
import time
## acknowledgements
'''
https://stackoverflow.com/questions/48358837/pulling-reddit-comments-using-python-praw-and-creating-a-dataframe-with-the-resu
https://www.reddit.com/r/redditdev/comments/2e2q2l/praw_downvote_count_always_zero/
https://towardsdatascience.com/an-easy-tutorial-about-sentiment-analysis-with-deep-learning-and-keras-2bf52b9cba91
For navigating pushshift: https://github.com/Watchful1/Sketchpad/blob/master/postDownloader.py
# traffic = reddit.subreddit(subreddit).traffic() is not available to us, sadly.
'''
with open("../API.env") as file:
exec(file.read())
reddit = praw.Reddit(
client_id = client_id,
client_secret = client_secret,
user_agent = user_agent
)
'''
Some helper functions for the reddit API.
'''
def extract_num_rewards(awardings_data):
return sum( x["count"] for x in awardings_data)
def extract_data(submission, comments = False):
postlist = []
# extracts top level comments
if comments:
submission.comments.replace_more(limit=0)
for comment in submission.comments:
post = vars(comment)
postlist.append(post)
content = vars(submission)
content["total_awards"] = extract_num_rewards(content["all_awardings"])
return content
'''
Sample num_samples random submissions, and get the top num_samples submissions, and put them into dataframes.
Opted instead to scrape the entire thing.
'''
def random_sample(num_samples, subreddit):
sample = []
for i in range(num_samples):
submission = reddit.subreddit(subreddit).random()
sample.append(extract_data(submission))
return(pd.DataFrame(sample))
def sample(source):
submissions = []
for submission in source:
submissions.append(extract_data(submission))
print(f"Got {len(submissions)} submissions. (This can be less than num_samples.)")
return(pd.DataFrame(submissions))
def top_sample(num_samples, subreddit):
return sample(reddit.subreddit(subreddit).top(limit=num_samples) )
def rising_sample(num_samples, subreddit):
return sample(reddit.subreddit(subreddit).rising(limit=num_samples))
def controversial_sample(num_samples, subreddit):
return sample(reddit.subreddit(subreddit).controversial(limit=num_samples) )
num_samples = 10
subreddit ='wallstreetbets'
#random_wsb = random_sample(num_samples, subreddit)
#top_wsb = top_sample(num_samples,subreddit)
#rising_wsb = rising_sample(num_samples, subreddit)
#controversial_wsb = controversial_sample(num_samples, subreddit)
#random_wsb.to_pickle("random_wsb.pkl")
#top_wsb.to_pickle("top_wsb.pkl")
#rising_wsb.to_pickle("rising_wsb.pkl")
#controversial_wsb.to_pickle("controversial_wsb.pkl")
# other commands here: https://praw.readthedocs.io/en/latest/code_overview/models/subreddit.html#praw.models.Subreddit.rising
# NB: The subreddit stream option seems useful.
# NB: There is also rising_random
submission = reddit.subreddit(subreddit).random()
submission.approved_at_utc
vars(submission)
str(submission.flair)
```
|
github_jupyter
|
# Residual Networks
Welcome to the second assignment of this week! You will learn how to build very deep convolutional networks, using Residual Networks (ResNets). In theory, very deep networks can represent very complex functions; but in practice, they are hard to train. Residual Networks, introduced by [He et al.](https://arxiv.org/pdf/1512.03385.pdf), allow you to train much deeper networks than were previously practically feasible.
**In this assignment, you will:**
- Implement the basic building blocks of ResNets.
- Put together these building blocks to implement and train a state-of-the-art neural network for image classification.
## <font color='darkblue'>Updates</font>
#### If you were working on the notebook before this update...
* The current notebook is version "2a".
* You can find your original work saved in the notebook with the previous version name ("v2")
* To view the file directory, go to the menu "File->Open", and this will open a new tab that shows the file directory.
#### List of updates
* For testing on an image, replaced `preprocess_input(x)` with `x=x/255.0` to normalize the input image in the same way that the model's training data was normalized.
* Refers to "shallower" layers as those layers closer to the input, and "deeper" layers as those closer to the output (Using "shallower" layers instead of "lower" or "earlier").
* Added/updated instructions.
This assignment will be done in Keras.
Before jumping into the problem, let's run the cell below to load the required packages.
```
import numpy as np
from keras import layers
from keras.layers import Input, Add, Dense, Activation, ZeroPadding2D, BatchNormalization, Flatten, Conv2D, AveragePooling2D, MaxPooling2D, GlobalMaxPooling2D
from keras.models import Model, load_model
from keras.preprocessing import image
from keras.utils import layer_utils
from keras.utils.data_utils import get_file
from keras.applications.imagenet_utils import preprocess_input
import pydot
from IPython.display import SVG
from keras.utils.vis_utils import model_to_dot
from keras.utils import plot_model
from resnets_utils import *
from keras.initializers import glorot_uniform
import scipy.misc
from matplotlib.pyplot import imshow
%matplotlib inline
import keras.backend as K
K.set_image_data_format('channels_last')
K.set_learning_phase(1)
```
## 1 - The problem of very deep neural networks
Last week, you built your first convolutional neural network. In recent years, neural networks have become deeper, with state-of-the-art networks going from just a few layers (e.g., AlexNet) to over a hundred layers.
* The main benefit of a very deep network is that it can represent very complex functions. It can also learn features at many different levels of abstraction, from edges (at the shallower layers, closer to the input) to very complex features (at the deeper layers, closer to the output).
* However, using a deeper network doesn't always help. A huge barrier to training them is vanishing gradients: very deep networks often have a gradient signal that goes to zero quickly, thus making gradient descent prohibitively slow.
* More specifically, during gradient descent, as you backprop from the final layer back to the first layer, you are multiplying by the weight matrix on each step, and thus the gradient can decrease exponentially quickly to zero (or, in rare cases, grow exponentially quickly and "explode" to take very large values).
* During training, you might therefore see the magnitude (or norm) of the gradient for the shallower layers decrease to zero very rapidly as training proceeds:
<img src="images/vanishing_grad_kiank.png" style="width:450px;height:220px;">
<caption><center> <u> <font color='purple'> **Figure 1** </u><font color='purple'> : **Vanishing gradient** <br> The speed of learning decreases very rapidly for the shallower layers as the network trains </center></caption>
You are now going to solve this problem by building a Residual Network!
## 2 - Building a Residual Network
In ResNets, a "shortcut" or a "skip connection" allows the model to skip layers:
<img src="images/skip_connection_kiank.png" style="width:650px;height:200px;">
<caption><center> <u> <font color='purple'> **Figure 2** </u><font color='purple'> : A ResNet block showing a **skip-connection** <br> </center></caption>
The image on the left shows the "main path" through the network. The image on the right adds a shortcut to the main path. By stacking these ResNet blocks on top of each other, you can form a very deep network.
We also saw in lecture that having ResNet blocks with the shortcut also makes it very easy for one of the blocks to learn an identity function. This means that you can stack on additional ResNet blocks with little risk of harming training set performance.
(There is also some evidence that the ease of learning an identity function accounts for ResNets' remarkable performance even more so than skip connections helping with vanishing gradients).
Two main types of blocks are used in a ResNet, depending mainly on whether the input/output dimensions are same or different. You are going to implement both of them: the "identity block" and the "convolutional block."
### 2.1 - The identity block
The identity block is the standard block used in ResNets, and corresponds to the case where the input activation (say $a^{[l]}$) has the same dimension as the output activation (say $a^{[l+2]}$). To flesh out the different steps of what happens in a ResNet's identity block, here is an alternative diagram showing the individual steps:
<img src="images/idblock2_kiank.png" style="width:650px;height:150px;">
<caption><center> <u> <font color='purple'> **Figure 3** </u><font color='purple'> : **Identity block.** Skip connection "skips over" 2 layers. </center></caption>
The upper path is the "shortcut path." The lower path is the "main path." In this diagram, we have also made explicit the CONV2D and ReLU steps in each layer. To speed up training we have also added a BatchNorm step. Don't worry about this being complicated to implement--you'll see that BatchNorm is just one line of code in Keras!
In this exercise, you'll actually implement a slightly more powerful version of this identity block, in which the skip connection "skips over" 3 hidden layers rather than 2 layers. It looks like this:
<img src="images/idblock3_kiank.png" style="width:650px;height:150px;">
<caption><center> <u> <font color='purple'> **Figure 4** </u><font color='purple'> : **Identity block.** Skip connection "skips over" 3 layers.</center></caption>
Here are the individual steps.
First component of main path:
- The first CONV2D has $F_1$ filters of shape (1,1) and a stride of (1,1). Its padding is "valid" and its name should be `conv_name_base + '2a'`. Use 0 as the seed for the random initialization.
- The first BatchNorm is normalizing the 'channels' axis. Its name should be `bn_name_base + '2a'`.
- Then apply the ReLU activation function. This has no name and no hyperparameters.
Second component of main path:
- The second CONV2D has $F_2$ filters of shape $(f,f)$ and a stride of (1,1). Its padding is "same" and its name should be `conv_name_base + '2b'`. Use 0 as the seed for the random initialization.
- The second BatchNorm is normalizing the 'channels' axis. Its name should be `bn_name_base + '2b'`.
- Then apply the ReLU activation function. This has no name and no hyperparameters.
Third component of main path:
- The third CONV2D has $F_3$ filters of shape (1,1) and a stride of (1,1). Its padding is "valid" and its name should be `conv_name_base + '2c'`. Use 0 as the seed for the random initialization.
- The third BatchNorm is normalizing the 'channels' axis. Its name should be `bn_name_base + '2c'`.
- Note that there is **no** ReLU activation function in this component.
Final step:
- The `X_shortcut` and the output from the 3rd layer `X` are added together.
- **Hint**: The syntax will look something like `Add()([var1,var2])`
- Then apply the ReLU activation function. This has no name and no hyperparameters.
**Exercise**: Implement the ResNet identity block. We have implemented the first component of the main path. Please read this carefully to make sure you understand what it is doing. You should implement the rest.
- To implement the Conv2D step: [Conv2D](https://keras.io/layers/convolutional/#conv2d)
- To implement BatchNorm: [BatchNormalization](https://faroit.github.io/keras-docs/1.2.2/layers/normalization/) (axis: Integer, the axis that should be normalized (typically the 'channels' axis))
- For the activation, use: `Activation('relu')(X)`
- To add the value passed forward by the shortcut: [Add](https://keras.io/layers/merge/#add)
```
# GRADED FUNCTION: identity_block
def identity_block(X, f, filters, stage, block):
"""
Implementation of the identity block as defined in Figure 4
Arguments:
X -- input tensor of shape (m, n_H_prev, n_W_prev, n_C_prev)
f -- integer, specifying the shape of the middle CONV's window for the main path
filters -- python list of integers, defining the number of filters in the CONV layers of the main path
stage -- integer, used to name the layers, depending on their position in the network
block -- string/character, used to name the layers, depending on their position in the network
Returns:
X -- output of the identity block, tensor of shape (n_H, n_W, n_C)
"""
# defining name basis
conv_name_base = 'res' + str(stage) + block + '_branch'
bn_name_base = 'bn' + str(stage) + block + '_branch'
# Retrieve Filters
F1, F2, F3 = filters
# Save the input value. You'll need this later to add back to the main path.
X_shortcut = X
# First component of main path
X = Conv2D(filters = F1, kernel_size = (1, 1), strides = (1,1), padding = 'valid', name = conv_name_base + '2a', kernel_initializer = glorot_uniform(seed=0))(X)
X = BatchNormalization(axis = 3, name = bn_name_base + '2a')(X)
X = Activation('relu')(X)
### START CODE HERE ###
# Second component of main path (≈3 lines)
X = Conv2D(filters = F2, kernel_size = (f, f), strides = (1,1), padding = 'same', name = conv_name_base + '2b', kernel_initializer = glorot_uniform(seed=0))(X)
X = BatchNormalization(axis = 3, name = bn_name_base + '2b')(X)
X = Activation('relu')(X)
# Third component of main path (≈2 lines)
X = Conv2D(filters = F3, kernel_size = (1, 1), strides = (1,1), padding = 'valid', name = conv_name_base + '2c', kernel_initializer = glorot_uniform(seed=0))(X)
X = BatchNormalization(axis = 3, name = bn_name_base + '2c')(X)
# Final step: Add shortcut value to main path, and pass it through a RELU activation (≈2 lines)
X = Add()([X, X_shortcut])
X = Activation('relu')(X)
### END CODE HERE ###
return X
tf.reset_default_graph()
with tf.Session() as test:
np.random.seed(1)
A_prev = tf.placeholder("float", [3, 4, 4, 6])
X = np.random.randn(3, 4, 4, 6)
A = identity_block(A_prev, f = 2, filters = [2, 4, 6], stage = 1, block = 'a')
test.run(tf.global_variables_initializer())
out = test.run([A], feed_dict={A_prev: X, K.learning_phase(): 0})
print("out = " + str(out[0][1][1][0]))
```
**Expected Output**:
<table>
<tr>
<td>
**out**
</td>
<td>
[ 0.94822985 0. 1.16101444 2.747859 0. 1.36677003]
</td>
</tr>
</table>
## 2.2 - The convolutional block
The ResNet "convolutional block" is the second block type. You can use this type of block when the input and output dimensions don't match up. The difference with the identity block is that there is a CONV2D layer in the shortcut path:
<img src="images/convblock_kiank.png" style="width:650px;height:150px;">
<caption><center> <u> <font color='purple'> **Figure 4** </u><font color='purple'> : **Convolutional block** </center></caption>
* The CONV2D layer in the shortcut path is used to resize the input $x$ to a different dimension, so that the dimensions match up in the final addition needed to add the shortcut value back to the main path. (This plays a similar role as the matrix $W_s$ discussed in lecture.)
* For example, to reduce the activation dimensions's height and width by a factor of 2, you can use a 1x1 convolution with a stride of 2.
* The CONV2D layer on the shortcut path does not use any non-linear activation function. Its main role is to just apply a (learned) linear function that reduces the dimension of the input, so that the dimensions match up for the later addition step.
The details of the convolutional block are as follows.
First component of main path:
- The first CONV2D has $F_1$ filters of shape (1,1) and a stride of (s,s). Its padding is "valid" and its name should be `conv_name_base + '2a'`. Use 0 as the `glorot_uniform` seed.
- The first BatchNorm is normalizing the 'channels' axis. Its name should be `bn_name_base + '2a'`.
- Then apply the ReLU activation function. This has no name and no hyperparameters.
Second component of main path:
- The second CONV2D has $F_2$ filters of shape (f,f) and a stride of (1,1). Its padding is "same" and it's name should be `conv_name_base + '2b'`. Use 0 as the `glorot_uniform` seed.
- The second BatchNorm is normalizing the 'channels' axis. Its name should be `bn_name_base + '2b'`.
- Then apply the ReLU activation function. This has no name and no hyperparameters.
Third component of main path:
- The third CONV2D has $F_3$ filters of shape (1,1) and a stride of (1,1). Its padding is "valid" and it's name should be `conv_name_base + '2c'`. Use 0 as the `glorot_uniform` seed.
- The third BatchNorm is normalizing the 'channels' axis. Its name should be `bn_name_base + '2c'`. Note that there is no ReLU activation function in this component.
Shortcut path:
- The CONV2D has $F_3$ filters of shape (1,1) and a stride of (s,s). Its padding is "valid" and its name should be `conv_name_base + '1'`. Use 0 as the `glorot_uniform` seed.
- The BatchNorm is normalizing the 'channels' axis. Its name should be `bn_name_base + '1'`.
Final step:
- The shortcut and the main path values are added together.
- Then apply the ReLU activation function. This has no name and no hyperparameters.
**Exercise**: Implement the convolutional block. We have implemented the first component of the main path; you should implement the rest. As before, always use 0 as the seed for the random initialization, to ensure consistency with our grader.
- [Conv2D](https://keras.io/layers/convolutional/#conv2d)
- [BatchNormalization](https://keras.io/layers/normalization/#batchnormalization) (axis: Integer, the axis that should be normalized (typically the features axis))
- For the activation, use: `Activation('relu')(X)`
- [Add](https://keras.io/layers/merge/#add)
```
# GRADED FUNCTION: convolutional_block
def convolutional_block(X, f, filters, stage, block, s = 2):
"""
Implementation of the convolutional block as defined in Figure 4
Arguments:
X -- input tensor of shape (m, n_H_prev, n_W_prev, n_C_prev)
f -- integer, specifying the shape of the middle CONV's window for the main path
filters -- python list of integers, defining the number of filters in the CONV layers of the main path
stage -- integer, used to name the layers, depending on their position in the network
block -- string/character, used to name the layers, depending on their position in the network
s -- Integer, specifying the stride to be used
Returns:
X -- output of the convolutional block, tensor of shape (n_H, n_W, n_C)
"""
# defining name basis
conv_name_base = 'res' + str(stage) + block + '_branch'
bn_name_base = 'bn' + str(stage) + block + '_branch'
# Retrieve Filters
F1, F2, F3 = filters
# Save the input value
X_shortcut = X
##### MAIN PATH #####
# First component of main path
X = Conv2D(F1, (1, 1), strides = (s,s), padding='valid' , name = conv_name_base + '2a', kernel_initializer = glorot_uniform(seed=0))(X)
X = BatchNormalization(axis = 3, name = bn_name_base + '2a')(X)
X = Activation('relu')(X)
### START CODE HERE ###
X = Conv2D(filters=F2, kernel_size=(f, f), strides=(1, 1), padding='same', name=conv_name_base + '2b', kernel_initializer=glorot_uniform(seed=0))(X)
X = BatchNormalization(axis=3, name=bn_name_base + '2b')(X)
X = Activation('relu')(X)
# Third component of main path (≈2 lines)
X = Conv2D(filters=F3, kernel_size=(1, 1), strides=(1, 1), padding='valid', name=conv_name_base + '2c', kernel_initializer=glorot_uniform(seed=0))(X)
X = BatchNormalization(axis=3, name=bn_name_base + '2c')(X)
##### SHORTCUT PATH #### (≈2 lines)
X_shortcut = Conv2D(filters=F3, kernel_size=(1, 1), strides=(s, s), padding='valid', name=conv_name_base + '1', kernel_initializer=glorot_uniform(seed=0))(X_shortcut)
X_shortcut = BatchNormalization(axis=3, name=bn_name_base + '1')(X_shortcut)
# Final step: Add shortcut value to main path, and pass it through a RELU activation (≈2 lines)
X = Add()([X, X_shortcut])
X = Activation('relu')(X)
### END CODE HERE ###
return X
tf.reset_default_graph()
with tf.Session() as test:
np.random.seed(1)
A_prev = tf.placeholder("float", [3, 4, 4, 6])
X = np.random.randn(3, 4, 4, 6)
A = convolutional_block(A_prev, f = 2, filters = [2, 4, 6], stage = 1, block = 'a')
test.run(tf.global_variables_initializer())
out = test.run([A], feed_dict={A_prev: X, K.learning_phase(): 0})
print("out = " + str(out[0][1][1][0]))
```
**Expected Output**:
<table>
<tr>
<td>
**out**
</td>
<td>
[ 0.09018463 1.23489773 0.46822017 0.0367176 0. 0.65516603]
</td>
</tr>
</table>
## 3 - Building your first ResNet model (50 layers)
You now have the necessary blocks to build a very deep ResNet. The following figure describes in detail the architecture of this neural network. "ID BLOCK" in the diagram stands for "Identity block," and "ID BLOCK x3" means you should stack 3 identity blocks together.
<img src="images/resnet_kiank.png" style="width:850px;height:150px;">
<caption><center> <u> <font color='purple'> **Figure 5** </u><font color='purple'> : **ResNet-50 model** </center></caption>
The details of this ResNet-50 model are:
- Zero-padding pads the input with a pad of (3,3)
- Stage 1:
- The 2D Convolution has 64 filters of shape (7,7) and uses a stride of (2,2). Its name is "conv1".
- BatchNorm is applied to the 'channels' axis of the input.
- MaxPooling uses a (3,3) window and a (2,2) stride.
- Stage 2:
- The convolutional block uses three sets of filters of size [64,64,256], "f" is 3, "s" is 1 and the block is "a".
- The 2 identity blocks use three sets of filters of size [64,64,256], "f" is 3 and the blocks are "b" and "c".
- Stage 3:
- The convolutional block uses three sets of filters of size [128,128,512], "f" is 3, "s" is 2 and the block is "a".
- The 3 identity blocks use three sets of filters of size [128,128,512], "f" is 3 and the blocks are "b", "c" and "d".
- Stage 4:
- The convolutional block uses three sets of filters of size [256, 256, 1024], "f" is 3, "s" is 2 and the block is "a".
- The 5 identity blocks use three sets of filters of size [256, 256, 1024], "f" is 3 and the blocks are "b", "c", "d", "e" and "f".
- Stage 5:
- The convolutional block uses three sets of filters of size [512, 512, 2048], "f" is 3, "s" is 2 and the block is "a".
- The 2 identity blocks use three sets of filters of size [512, 512, 2048], "f" is 3 and the blocks are "b" and "c".
- The 2D Average Pooling uses a window of shape (2,2) and its name is "avg_pool".
- The 'flatten' layer doesn't have any hyperparameters or name.
- The Fully Connected (Dense) layer reduces its input to the number of classes using a softmax activation. Its name should be `'fc' + str(classes)`.
**Exercise**: Implement the ResNet with 50 layers described in the figure above. We have implemented Stages 1 and 2. Please implement the rest. (The syntax for implementing Stages 3-5 should be quite similar to that of Stage 2.) Make sure you follow the naming convention in the text above.
You'll need to use this function:
- Average pooling [see reference](https://keras.io/layers/pooling/#averagepooling2d)
Here are some other functions we used in the code below:
- Conv2D: [See reference](https://keras.io/layers/convolutional/#conv2d)
- BatchNorm: [See reference](https://keras.io/layers/normalization/#batchnormalization) (axis: Integer, the axis that should be normalized (typically the features axis))
- Zero padding: [See reference](https://keras.io/layers/convolutional/#zeropadding2d)
- Max pooling: [See reference](https://keras.io/layers/pooling/#maxpooling2d)
- Fully connected layer: [See reference](https://keras.io/layers/core/#dense)
- Addition: [See reference](https://keras.io/layers/merge/#add)
```
# GRADED FUNCTION: ResNet50
def ResNet50(input_shape = (64, 64, 3), classes = 6):
"""
Implementation of the popular ResNet50 the following architecture:
CONV2D -> BATCHNORM -> RELU -> MAXPOOL -> CONVBLOCK -> IDBLOCK*2 -> CONVBLOCK -> IDBLOCK*3
-> CONVBLOCK -> IDBLOCK*5 -> CONVBLOCK -> IDBLOCK*2 -> AVGPOOL -> TOPLAYER
Arguments:
input_shape -- shape of the images of the dataset
classes -- integer, number of classes
Returns:
model -- a Model() instance in Keras
"""
# Define the input as a tensor with shape input_shape
X_input = Input(input_shape)
# Zero-Padding
X = ZeroPadding2D((3, 3))(X_input)
# Stage 1
X = Conv2D(64, (7, 7), strides = (2, 2), name = 'conv1', kernel_initializer = glorot_uniform(seed=0))(X)
X = BatchNormalization(axis = 3, name = 'bn_conv1')(X)
X = Activation('relu')(X)
X = MaxPooling2D((3, 3), strides=(2, 2))(X)
# Stage 2
X = convolutional_block(X, f = 3, filters = [64, 64, 256], stage = 2, block='a', s = 1)
X = identity_block(X, 3, [64, 64, 256], stage=2, block='b')
X = identity_block(X, 3, [64, 64, 256], stage=2, block='c')
### START CODE HERE ###
# Stage 3 (≈4 lines)
X = convolutional_block(X, f=3, filters=[128, 128, 512], stage=3, block='a', s=2)
X = identity_block(X, 3, [128, 128, 512], stage=3, block='b')
X = identity_block(X, 3, [128, 128, 512], stage=3, block='c')
X = identity_block(X, 3, [128, 128, 512], stage=3, block='d')
# Stage 4 (≈6 lines)
X = convolutional_block(X, f=3, filters=[256, 256, 1024], stage=4, block='a', s=2)
X = identity_block(X, 3, [256, 256, 1024], stage=4, block='b')
X = identity_block(X, 3, [256, 256, 1024], stage=4, block='c')
X = identity_block(X, 3, [256, 256, 1024], stage=4, block='d')
X = identity_block(X, 3, [256, 256, 1024], stage=4, block='e')
X = identity_block(X, 3, [256, 256, 1024], stage=4, block='f')
# Stage 5 (≈3 lines)
X = X = convolutional_block(X, f=3, filters=[512, 512, 2048], stage=5, block='a', s=2)
X = identity_block(X, 3, [512, 512, 2048], stage=5, block='b')
X = identity_block(X, 3, [512, 512, 2048], stage=5, block='c')
# AVGPOOL (≈1 line). Use "X = AveragePooling2D(...)(X)"
X = AveragePooling2D(pool_size=(2, 2))(X)
### END CODE HERE ###
# output layer
X = Flatten()(X)
X = Dense(classes, activation='softmax', name='fc' + str(classes), kernel_initializer = glorot_uniform(seed=0))(X)
# Create model
model = Model(inputs = X_input, outputs = X, name='ResNet50')
return model
```
Run the following code to build the model's graph. If your implementation is not correct you will know it by checking your accuracy when running `model.fit(...)` below.
```
model = ResNet50(input_shape = (64, 64, 3), classes = 6)
```
As seen in the Keras Tutorial Notebook, prior training a model, you need to configure the learning process by compiling the model.
```
model.compile(optimizer='adam', loss='categorical_crossentropy', metrics=['accuracy'])
```
The model is now ready to be trained. The only thing you need is a dataset.
Let's load the SIGNS Dataset.
<img src="images/signs_data_kiank.png" style="width:450px;height:250px;">
<caption><center> <u> <font color='purple'> **Figure 6** </u><font color='purple'> : **SIGNS dataset** </center></caption>
```
X_train_orig, Y_train_orig, X_test_orig, Y_test_orig, classes = load_dataset()
# Normalize image vectors
X_train = X_train_orig/255.
X_test = X_test_orig/255.
# Convert training and test labels to one hot matrices
Y_train = convert_to_one_hot(Y_train_orig, 6).T
Y_test = convert_to_one_hot(Y_test_orig, 6).T
print ("number of training examples = " + str(X_train.shape[0]))
print ("number of test examples = " + str(X_test.shape[0]))
print ("X_train shape: " + str(X_train.shape))
print ("Y_train shape: " + str(Y_train.shape))
print ("X_test shape: " + str(X_test.shape))
print ("Y_test shape: " + str(Y_test.shape))
```
Run the following cell to train your model on 2 epochs with a batch size of 32. On a CPU it should take you around 5min per epoch.
```
model.fit(X_train, Y_train, epochs = 2, batch_size = 32)
```
**Expected Output**:
<table>
<tr>
<td>
** Epoch 1/2**
</td>
<td>
loss: between 1 and 5, acc: between 0.2 and 0.5, although your results can be different from ours.
</td>
</tr>
<tr>
<td>
** Epoch 2/2**
</td>
<td>
loss: between 1 and 5, acc: between 0.2 and 0.5, you should see your loss decreasing and the accuracy increasing.
</td>
</tr>
</table>
Let's see how this model (trained on only two epochs) performs on the test set.
```
preds = model.evaluate(X_test, Y_test)
print ("Loss = " + str(preds[0]))
print ("Test Accuracy = " + str(preds[1]))
```
**Expected Output**:
<table>
<tr>
<td>
**Test Accuracy**
</td>
<td>
between 0.16 and 0.25
</td>
</tr>
</table>
For the purpose of this assignment, we've asked you to train the model for just two epochs. You can see that it achieves poor performances. Please go ahead and submit your assignment; to check correctness, the online grader will run your code only for a small number of epochs as well.
After you have finished this official (graded) part of this assignment, you can also optionally train the ResNet for more iterations, if you want. We get a lot better performance when we train for ~20 epochs, but this will take more than an hour when training on a CPU.
Using a GPU, we've trained our own ResNet50 model's weights on the SIGNS dataset. You can load and run our trained model on the test set in the cells below. It may take ≈1min to load the model.
```
model = load_model('ResNet50.h5')
preds = model.evaluate(X_test, Y_test)
print ("Loss = " + str(preds[0]))
print ("Test Accuracy = " + str(preds[1]))
```
ResNet50 is a powerful model for image classification when it is trained for an adequate number of iterations. We hope you can use what you've learnt and apply it to your own classification problem to perform state-of-the-art accuracy.
Congratulations on finishing this assignment! You've now implemented a state-of-the-art image classification system!
## 4 - Test on your own image (Optional/Ungraded)
If you wish, you can also take a picture of your own hand and see the output of the model. To do this:
1. Click on "File" in the upper bar of this notebook, then click "Open" to go on your Coursera Hub.
2. Add your image to this Jupyter Notebook's directory, in the "images" folder
3. Write your image's name in the following code
4. Run the code and check if the algorithm is right!
```
img_path = 'images/my_image.jpg'
img = image.load_img(img_path, target_size=(64, 64))
x = image.img_to_array(img)
x = np.expand_dims(x, axis=0)
x = x/255.0
print('Input image shape:', x.shape)
my_image = scipy.misc.imread(img_path)
imshow(my_image)
print("class prediction vector [p(0), p(1), p(2), p(3), p(4), p(5)] = ")
print(model.predict(x))
```
You can also print a summary of your model by running the following code.
```
model.summary()
```
Finally, run the code below to visualize your ResNet50. You can also download a .png picture of your model by going to "File -> Open...-> model.png".
```
plot_model(model, to_file='model.png')
SVG(model_to_dot(model).create(prog='dot', format='svg'))
```
## What you should remember
- Very deep "plain" networks don't work in practice because they are hard to train due to vanishing gradients.
- The skip-connections help to address the Vanishing Gradient problem. They also make it easy for a ResNet block to learn an identity function.
- There are two main types of blocks: The identity block and the convolutional block.
- Very deep Residual Networks are built by stacking these blocks together.
### References
This notebook presents the ResNet algorithm due to He et al. (2015). The implementation here also took significant inspiration and follows the structure given in the GitHub repository of Francois Chollet:
- Kaiming He, Xiangyu Zhang, Shaoqing Ren, Jian Sun - [Deep Residual Learning for Image Recognition (2015)](https://arxiv.org/abs/1512.03385)
- Francois Chollet's GitHub repository: https://github.com/fchollet/deep-learning-models/blob/master/resnet50.py
|
github_jupyter
|
# Project 3 Sandbox-Blue-O, NLP using webscraping to create the dataset
## Objective: Determine if posts are in the SpaceX Subreddit or the Blue Origin Subreddit
We'll utilize the RESTful API from pushshift.io to scrape subreddit posts from r/blueorigin and r/spacex and see if we cannot use the Bag-of-words algorithm to predict which posts are from where.
Author: Matt Paterson, hello@hiremattpaterson.com
This notebook is the SANDBOX and should be used to play around. The formal presentation will be in a different notebook
```
import requests
from bs4 import BeautifulSoup
import pandas as pd
import lebowski as dude
from sklearn.feature_extraction.text import CountVectorizer
import re, regex
# Establish a connection to the API and search for a specific keyword. Maybe we'll add this function to the
# lebowski library? Or maybe make a new and slicker Library called spaceman or something
# CREDIT: code below adapted from Riley Dallas Lesson on webscraping
# keyword = 'propulsion'
# url_boeing = 'https://api.pushshift.io/reddit/search/comment/?q=' + keyword + '&subreddit=boeing'
# res = requests.get(url_boeing)
# res.status_code
# instantiate a Beautiful Soup object for Boeing
#boeing = BeautifulSoup(res.content, 'lxml')
#boeing.find("body")
spacex = dude.create_lexicon('spacex', 5000)
blueorigin = dude.create_lexicon('blueorigin', 5000)
spacex.head()
blueorigin.head()
spacex[['subreddit', 'selftext', 'title']].head() # predict the subreddit column
blueorigin[['subreddit', 'selftext', 'title']].head() # predict the subreddit column
print('Soux City Sarsparilla?') # silly print statement to check progress of long print
spacex_comments = dude.create_lexicon('spacex', 5000, post_type='comment')
spacex_comments.head()
spacex_comments[['subreddit', 'body']].head() # predict the subreddit column
blueorigin_comments = dude.create_lexicon('blueorigin', 5000, post_type='comment')
blueorigin_comments[['subreddit', 'body']].head() # predict the subreddit column
blueorigin_comments.columns
```
There's not a "title" column in the comments dataframe, so how is the comment tied to the original post?
```
# View the first entry in the dataframe and see if you can find that answer
# permalink?
blueorigin_comments.iloc[0]
```
IN EDA below, we find: "We have empty rows in 'body' in many columns. It's likely that all of those are postings, not comments, and we should actually map the postings to the body for those before merging the datafrmes."
```
def strip_and_rep(word):
if len(str(word).strip().replace(" ", "")) < 1:
return 'replace_me'
else:
return word
blueorigin['selftext'] = blueorigin['selftext'].map(strip_and_rep)
spacex['selftext'] = spacex['selftext'].map(strip_and_rep)
spacex.selftext.isna().sum()
blueorigin.selftext.isna().sum()
blueorigin.selftext.head()
spacex.iloc[2300:2320]
blo_coms = blueorigin_comments[['subreddit', 'body', 'permalink']]
blo_posts = blueorigin[['subreddit', 'selftext', 'permalink']].copy()
spx_coms = spacex_comments[['subreddit', 'body', 'permalink']]
spx_posts = spacex[['subreddit', 'selftext', 'permalink']].copy()
#blueorigin['selftext'][len(blueorigin['selftext'])>0]
type(blueorigin.selftext.iloc[1])
blo_posts.rename(columns={'selftext': 'body'}, inplace=True)
spx_posts.rename(columns={'selftext': 'body'}, inplace=True)
# result = pd.concat(frames)
space_wars_2 = pd.concat([blo_coms, blo_posts, spx_coms, spx_posts])
space_wars_2.shape
space_wars_2.head()
dude.show_details(space_wars_2)
```
We have empty rows in 'body' in many columns. It's likely that all of those are postings, not comments, and we should actually map the postings to the body for those before merging the datafrmes.
However, when trying that above, we ended up with more null values. Mapping 'replace_me' in to empty fileds kept the number of null values low. We'll add that token to our stop_words dictionary when creating the BOW from this corpus.
```
space_wars_2.dropna(inplace=True)
space_wars_2.isna().sum()
space_wars.to_csv('./data/betaset.csv', index=False)
```
# Before we split up the training and testing sets, establish our X and y. If you need to reset the dataframe, run the next cell FIRST
keyword = RESET
```
space_wars_2 = pd.read_csv('./data/betaset.csv')
space_wars_2.columns
```
I believe that the 'permalink' will be almost as indicative as the 'subreddit' that we are trying to predict, so the X will only include the words...
```
space_wars_2.head()
```
## Convert target column to binary before moving forward
We want to predict whether this post is Spacex, 1, or is not Spacex, 0
```
space_wars_2['subreddit'].value_counts()
space_wars_2['subreddit'] = space_wars_2['subreddit'].map({'spacex': 1, 'BlueOrigin': 0})
space_wars_2['subreddit'].value_counts()
X = space_wars_2.body
y = space_wars_2.subreddit
```
Calculate our baseline split
```
space_wars_2.subreddit.value_counts(normalize=True)
base_set = space_wars_2.subreddit.value_counts(normalize=True)
baseline = 0.0
if base_set[0] > base_set[1]:
baseline = base_set[0]
else:
baseline = base_set[1]
baseline
```
Before we sift out stopwords, etc, let's just run a logistic regression on the words, as well as a decision tree:
```
from sklearn.linear_model import LogisticRegression
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import GridSearchCV, train_test_split, cross_val_score
```
## Before we can fit the models we need to convert the data to numbers...we can use CountVectorizer or TF-IDF for this
```
# from https://stackoverflow.com/questions/5511708/adding-words-to-nltk-stoplist
# add certain words to the stop_words library
import nltk
stopwords = nltk.corpus.stopwords.words('english')
new_words=('replace_me', 'removed', 'deleted', '0','1', '2', '3', '4', '5', '6', '7', '8','9', '00', '000')
for i in new_words:
stopwords.append(i)
print(stopwords)
space_wars_2.isna().sum()
space_wars_2.dropna(inplace=True)
# This section, next number of cells, borrowed from Noelle's lesson on NLP EDA
# Instantiate the "CountVectorizer" object, which is sklearn's
# bag of words tool.
cnt_vec = CountVectorizer(analyzer = "word",
tokenizer = None,
preprocessor = None,
stop_words = stopwords,
max_features = 5000)
X_train, X_test, y_train, y_test = train_test_split(X,
y,
test_size=.20,
random_state=42,
stratify=y)
```
Keyword = CHANGELING
```
y_test
# This section, next number of cells, borrowed from Noelle's lesson on NLP EDA
# fit_transform() does two things: First, it fits the model and
# learns the vocabulary; second, it transforms our training data
# into feature vectors. The input to fit_transform should be a
# list of strings.
train_data_features = cnt_vec.fit_transform(X_train, y_train)
test_data_features = cnt_vec.transform(X_test)
train_data_features.shape
train_data_df = pd.DataFrame(train_data_features)
test_data_features.shape
test_data_df = pd.DataFrame(test_data_features)
test_data_df['subreddit']
lr = LogisticRegression( max_iter = 10_000)
lr.fit(train_data_features, y_train)
train_data_features.shape
dt = DecisionTreeClassifier()
dt.fit(train_data_features, y_train)
print('Logistic Regression without doing anything, really:', lr.score(train_data_features, y_train))
print('Decision Tree without doing anything, really:', dt.score(train_data_features, y_train))
print('*'*80)
print('Logistic Regression Test Score without doing anything, really:', lr.score(test_data_features, y_test))
print('Decision Tree Test Score without doing anything, really:', dt.score(test_data_features, y_test))
print('*'*80)
print(f'The baseline split is {baseline}')
```
So we see that we are above our baseline of 57% accuracy by only guessing a single subreddit without trying to predict. We also see that our initial runs without any GridSearch or HPO tuning gives us a fairly overfit model for either mode.
**Let's see next what happens when we sift through our data with stopwords, etc, to really clean up the dataset and also let's do some comparative EDA including comparing lengths of posts, etc. Finally we can create a sepatate dataframe with engineered features and try running a Logistic Regression model using only descriptors in the dataset such as post lenth, word length, most common words, etc.**
## Deep EDA of our words
```
space_wars.shape
space_wars.describe()
```
## Feature Engineering
Map word count and character length funcitons on to the 'body' column to see a difference in each.
```
def word_count(string):
'''
returns the number of words or tokens in a string literal, splitting on spaces,
regardless of word lenth. This function will include space-separated
punctuation as a word, such as " : " where the colon would be counted
string, a string
'''
str_list = string.split()
return len(str_list)
def count_chars(string):
'''
returns the total number of characters including spaces in a string literal
string, a string
'''
count=0
for s in string:
count+=1
return count
import lebowski as dude
space_wars['word_count'] = space_wars['body'].map(word_count)
space_wars['word_count'].value_counts().head()
# code from https://stackoverflow.com/questions/39132742/groupby-value-counts-on-the-dataframe-pandas
#df.groupby(['id', 'group', 'term']).size().unstack(fill_value=0)
space_wars.groupby(['subreddit', 'word_count']).size().head()
space_wars['post_length'] = space_wars['body'].map(count_chars)
space_wars['post_length'].value_counts().head()
space_wars.columns
import seaborn as sns
import matplotlib.pyplot as plt
sns.distplot(space_wars['word_count'])
# Borrowing from Noelle's nlp II lesson, import the following,
# and think about what you want to use in the presentation
# imports
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.pipeline import Pipeline
from sklearn.naive_bayes import MultinomialNB
from sklearn.metrics import confusion_matrix, plot_confusion_matrix
# Import CountVectorizer and TFIDFVectorizer from feature_extraction.text.
from sklearn.feature_extraction.text import CountVectorizer, TfidfVectorizer
```
## Text Feature Extraction
## Follow along in the NLP EDA II video and do some analysis
```
X_train_df = pd.DataFrame(train_data_features.toarray(),
columns=cntv.get_feature_names())
X_train_df
X_train_df['subreddit']
# get count of top-occurring words
# empty dictionary
top_words = {}
# loop through columns
for i in X_train_df.columns:
# save sum of each column in dictionary
top_words[i] = X_train_df[i].sum()
# top_words to dataframe sorted by highest occurance
most_freq = pd.DataFrame(sorted(top_words.items(), key = lambda x: x[1], reverse = True))
most_freq.head()
# Make a different CountVectorizer
count_v = CountVectorizer(analyzer='word',
stop_words = stopwords,
max_features = 1_000,
min_df = 50,
max_df = .80,
ngram_range=(2,3),
)
# Redefine the training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y,
test_size = .1,
stratify = y,
random_state=42)
baseline
```
## Implement Naive Bayes because it's in the project instructions
Multinomial Naive Bayes often outperforms other models despite text data being non-independent data
```
pipe = Pipeline([
('count_v', CountVectorizer()),
('nb', MultinomialNB())
])
pipe_params = {
'count_v__max_features': [2000, 5000, 9000],
'count_v__stop_words': [stopwords],
'count_v__min_df': [2, 3, 10],
'count_v__max_df': [.9, .8, .7],
'count_v__ngram_range': [(1, 1), (1, 2)]
}
gs = GridSearchCV(pipe,
pipe_params,
cv = 5,
n_jobs=6
)
%%time
gs.fit(X_train, y_train)
gs.best_params_
print(gs.best_score_)
gs.score(X_train, y_train)
gs.score(X_test, y_test)
```
So far, the Multinomial Naive Bayes Algorithm is the top function at 79.28% Accuracy. The confusion matrix below is very simiar to that of other models
```
# Get predictions
preds = gs.predict(X_test)
# Save confusion matrix values
tn, fp, fn, tp = confusion_matrix(y_test, preds).ravel()
# View confusion matrix
plot_confusion_matrix(gs, X_test, y_test, cmap='Blues', values_format='d');
# Calculate the specificity
spec = tn / (tn + fp)
print('Specificity:', spec)
```
None of the 1620 different models we tried in this pipeline performed noticibly better than the thrown-together Logistic Regression Classifier that we started out with. Let's try TF-IDF, then Random Cut Forest, and finally Vector Machines. Our last run brought the best accuracy score to 79.3%
# TF-IDF
```
# Redefine the training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y,
test_size = .1,
stratify = y,
random_state=42)
tvec = TfidfVectorizer(stop_words=stopwords)
df = pd.DataFrame(tvec.fit_transform(X_train).toarray(),
columns=tvec.get_feature_names())
df.head()
# get count of top-occurring words
top_words_tf = {}
for i in df.columns:
top_words_tf[i] = df[i].sum()
# top_words to dataframe sorted by highest occurance
most_freq_tf = pd.DataFrame(sorted(top_words_tf.items(), key = lambda x: x[1], reverse = True))
plt.figure(figsize = (10, 5))
# visualize top 10 words
plt.bar(most_freq_tf[0][:10], most_freq_tf[1][:10]);
pipe_tvec = Pipeline([
('tvec', TfidfVectorizer()),
('nb', MultinomialNB())
])
pipe_params_tvec = {
'tvec__max_features': [2000, 9000],
'tvec__stop_words' : [None, stopwords],
'tvec__ngram_range': [(1, 1), (1, 2)]
}
gs_tvec = GridSearchCV(pipe_tvec, pipe_params_tvec, cv = 5)
%%time
gs_tvec.fit(X_train, y_train)
gs_tvec.best_params_
gs_tvec.score(X_train, y_train)
gs_tvec.score(X_test, y_test)
# Get predictions
preds = gs_tvec.predict(X_test)
# Save confusion matrix values
tn, fp, fn, tp = confusion_matrix(y_test, preds).ravel()
# View confusion matrix
plot_confusion_matrix(gs_tvec, X_test, y_test, cmap='Blues', values_format='d');
# Calculate the specificity
spec = tn / (tn + fp)
print('Specificity:', spec)
```
## Random Cut Forest, Bagging, and Support Vector Machines
```
from sklearn.ensemble import RandomForestClassifier, ExtraTreesClassifier
```
Before we run the decision tree model or RandomForestClassifier(), we need to convert all of the data to numeric data
```
rf = RandomForestClassifier()
et = ExtraTreesClassifier()
cross_val_score(rf, train_data_features, X_train_df['subreddit']).mean()
cross_val_score(et, train_data_features, X_train_df['subreddit']).mean()
#cross_val_score(rf, test_data_features, y_test).mean()
```
## Make sure that we are using X and y data that are completely numeric and free of nulls
```
space_wars.head(1)
space_wars.shape
pipe_rf = Pipeline([
('count_v', CountVectorizer()),
('rf', RandomForestClassifier()),
])
pipe_ef = Pipeline([
('count_v', CountVectorizer()),
('ef', ExtraTreesClassifier()),
])
pipe_params =
'count_v__max_features': [2000, 5000, 9000],
'count_v__stop_words': [stopwords],
'count_v__min_df': [2, 3, 10],
'count_v__max_df': [.9, .8, .7],
'count_v__ngram_range': [(1, 1), (1, 2)]
}
%%time
gs_rf = GridSearchCV(pipe_rf,
pipe_params,
cv = 5,
n_jobs=6)
gs_rf.fit(X_train, y_train)
print(gs_rf.best_score_)
gs_rf.best_params_
gs_rf.score(X_train, y_train)
gs_rf.score(X_test, y_test)
# %%time
# gs_ef = GridSearchCV(pipe_ef,
# pipe_params,
# cv = 5,
# n_jobs=6)
# gs_ef.fit(X_train, y_train)
# print(gs_ef.best_score_)
# gs_ef.best_params_
#gs_ef.score(X_train, y_train)
#gs_ef.score(X_test, y_test)
```
## Now run through Gradient Boosting and SVM
```
from sklearn.ensemble import GradientBoostingClassifier, AdaBoostClassifier, VotingClassifier
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
```
Using samples from Riley's Lessons:
```
AdaBoostClassifier()
GradientBoostingClassifier()
```
Use the CountVectorizer to convert the data to numeric data prior to running it through the below VotingClassifier
```
'count_v__max_df': 0.9,
'count_v__max_features': 9000,
'count_v__min_df': 2,
'count_v__ngram_range': (1, 1),
knn_pipe = Pipeline([
('ss', StandardScaler()),
('knn', KNeighborsClassifier())
])
%%time
vote = VotingClassifier([
('ada', AdaBoostClassifier(base_estimator=DecisionTreeClassifier())),
('grad_boost', GradientBoostingClassifier()),
('tree', DecisionTreeClassifier()),
('knn_pipe', knn_pipe)
])
params = {}
# 'ada__n_estimators': [50, 51],
# 'grad_boost__n_estimators': [10, 11],
# 'knn_pipe__knn__n_neighbors': [5],
# 'ada__base_estimator__max_depth': [1, 2],
# 'weights': [[.25] * 4, [.3, .3, .3, .1]]
# }
gs = GridSearchCV(vote, param_grid=params, cv=3)
gs.fit(X_train, y_train)
print(gs.best_score_)
gs.best_params_
```
|
github_jupyter
|
Note:
This notebook was executed on google colab pro.
```
!pip3 install pytorch-lightning --quiet
from google.colab import drive
drive.mount('/content/drive')
import os
os.chdir('/content/drive/MyDrive/Colab Notebooks/atmacup11/experiments')
```
# Settings
```
EXP_NO = 27
SEED = 1
N_SPLITS = 5
TARGET = 'target'
GROUP = 'art_series_id'
REGRESSION = False
assert((TARGET, REGRESSION) in (('target', True), ('target', False), ('sorting_date', True)))
MODEL_NAME = 'resnet'
BATCH_SIZE = 512
NUM_EPOCHS = 500
```
# Library
```
from collections import defaultdict
from functools import partial
import gc
import glob
import json
from logging import getLogger, StreamHandler, FileHandler, DEBUG, Formatter
import pickle
import os
import sys
import time
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
from sklearn.metrics import confusion_matrix, mean_squared_error, cohen_kappa_score
# from sklearnex import patch_sklearn
from pytorch_lightning import seed_everything
import torch
import torch.nn as nn
import torch.optim
from torch.utils.data import DataLoader
from torchvision import transforms
SCRIPTS_DIR = os.path.join('..', 'scripts')
assert(os.path.isdir(SCRIPTS_DIR))
if SCRIPTS_DIR not in sys.path: sys.path.append(SCRIPTS_DIR)
from cross_validation import load_cv_object_ids
from dataset import load_csvfiles, load_photofile,load_photofiles, AtmaImageDatasetV02
from folder import experiment_dir_of
from models import initialize_model
from utils import train_model, predict_by_model
pd.options.display.float_format = '{:.5f}'.format
DEVICE = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
DEVICE
```
# Prepare directory
```
output_dir = experiment_dir_of(EXP_NO)
output_dir
```
# Prepare logger
```
logger = getLogger(__name__)
'''Refference
https://docs.python.org/ja/3/howto/logging-cookbook.html
'''
logger.setLevel(DEBUG)
# create file handler which logs even debug messages
fh = FileHandler(os.path.join(output_dir, 'log.log'))
fh.setLevel(DEBUG)
# create console handler with a higher log level
ch = StreamHandler()
ch.setLevel(DEBUG)
# create formatter and add it to the handlers
formatter = Formatter('%(asctime)s - %(name)s - %(levelname)s - %(message)s')
fh.setFormatter(formatter)
ch.setFormatter(formatter)
# add the handlers to the logger
logger.addHandler(fh)
logger.addHandler(ch)
len(logger.handlers)
logger.info('Experiment no: {}'.format(EXP_NO))
logger.info('CV: StratifiedGroupKFold')
logger.info('SEED: {}'.format(SEED))
logger.info('REGRESSION: {}'.format(REGRESSION))
```
# Load csv files
```
SINCE = time.time()
logger.debug('Start loading csv files ({:.3f} seconds passed)'.format(time.time() - SINCE))
train, test, materials, techniques, sample_submission = load_csvfiles()
logger.debug('Complete loading csv files ({:.3f} seconds passed)'.format(time.time() - SINCE))
train
test
```
# Cross validation
```
seed_everything(SEED)
train.set_index('object_id', inplace=True)
fold_object_ids = load_cv_object_ids()
for i, (train_object_ids, valid_object_ids) in enumerate(zip(fold_object_ids[0], fold_object_ids[1])):
assert(set(train_object_ids) & set(valid_object_ids) == set())
num_fold = i + 1
logger.debug('Start fold {} ({:.3f} seconds passed)'.format(num_fold, time.time() - SINCE))
# Separate dataset into training/validation fold
y_train = train.loc[train_object_ids, TARGET].values
y_valid = train.loc[valid_object_ids, TARGET].values
torch.cuda.empty_cache()
# Training
logger.debug('Start training model ({:.3f} seconds passed)'.format(time.time() - SINCE))
## Prepare model
num_classes = len(set(list(y_train)))
model, input_size = initialize_model(MODEL_NAME, num_classes)
model.to(DEVICE)
## Prepare transformers
train_transformer = transforms.Compose([
transforms.RandomResizedCrop(input_size),
transforms.RandomHorizontalFlip(),
transforms.ToTensor(),
transforms.Normalize([0.485, 0.456, 0.406], [0.229, 0.224, 0.225])
])
val_transformer = transforms.Compose([
transforms.Resize(input_size),
transforms.CenterCrop(input_size),
transforms.ToTensor(),
transforms.Normalize([0.485, 0.456, 0.406], [0.229, 0.224, 0.225])
])
# Prepare dataset
if not REGRESSION:
# label should be one-hot style
y_train = np.identity(num_classes)[y_train].astype('int')
y_valid = np.identity(num_classes)[y_valid].astype('int')
train_dataset = AtmaImageDatasetV02(train_object_ids, train_transformer, y_train)
val_dataset = AtmaImageDatasetV02(valid_object_ids, val_transformer, y_valid)
# Prepare dataloader
dataloaders = {
'train': DataLoader(dataset=train_dataset, batch_size=BATCH_SIZE, shuffle=True, num_workers=os.cpu_count()),
'val': DataLoader(dataset=val_dataset, batch_size=BATCH_SIZE, shuffle=False, num_workers=os.cpu_count()),
}
## train estimator
estimator, train_losses, valid_losses = train_model(
model, dataloaders, criterion=nn.BCEWithLogitsLoss(), num_epochs=NUM_EPOCHS, device=DEVICE,
optimizer=torch.optim.Adam(model.parameters()), log_func=logger.debug,
is_inception=MODEL_NAME == 'inception')
logger.debug('Complete training ({:.3f} seconds passed)'.format(time.time() - SINCE))
## Visualize training loss
plt.plot(train_losses, label='train')
plt.plot(valid_losses, label='valid')
plt.legend(loc='upper left', bbox_to_anchor=[1., 1.])
plt.title(f'Fold{num_fold}')
plt.show()
# Save model and prediction
## Prediction
predictions = {}
for fold_, object_ids_ in zip(['train', 'val', 'test'],
[train_object_ids, valid_object_ids, test['object_id']]):
# Prepare transformer
transformer_ = transforms.Compose([
transforms.Resize(input_size),
transforms.CenterCrop(input_size),
transforms.ToTensor(),
transforms.Normalize([0.485, 0.456, 0.406], [0.229, 0.224, 0.225])
])
# Prepare dataset
dataset_ = AtmaImageDatasetV02(object_ids_, transformer_)
# Prepare dataloader
dataloader_ = DataLoader(dataset=dataset_, batch_size=BATCH_SIZE, shuffle=False,
num_workers=os.cpu_count())
# Prediction
predictions[fold_] = predict_by_model(estimator, dataloader_, DEVICE)
logger.debug('Complete prediction for {} fold ({:.3f} seconds passed)' \
.format(fold_, time.time() - SINCE))
if REGRESSION:
pred_train = pd.DataFrame(data=predictions['train'], columns=['pred'])
pred_valid = pd.DataFrame(data=predictions['val'], columns=['pred'])
pred_test = pd.DataFrame(data=predictions['test'], columns=['pred'])
else:
columns = list(range(num_classes))
pred_train = pd.DataFrame(data=predictions['train'], columns=columns)
pred_valid = pd.DataFrame(data=predictions['val'], columns=columns)
pred_test = pd.DataFrame(data=predictions['test'], columns=columns)
# else: # Do not come here!
# raise NotImplemented
# try:
# pred_train = pd.DataFrame(data=estimator.predict_proba(X_train),
# columns=estimator.classes_)
# pred_valid = pd.DataFrame(data=estimator.predict_proba(X_valid),
# columns=estimator.classes_)
# pred_test = pd.DataFrame(data=estimator.predict_proba(X_test),
# columns=estimator.classes_)
# except AttributeError:
# pred_train = pd.DataFrame(data=estimator.decision_function(X_train),
# columns=estimator.classes_)
# pred_valid = pd.DataFrame(data=estimator.decision_function(X_valid),
# columns=estimator.classes_)
# pred_test = pd.DataFrame(data=estimator.decision_function(X_test),
# columns=estimator.classes_)
## Training set
pred_train['object_id'] = train_object_ids
filepath_fold_train = os.path.join(output_dir, f'cv_fold{num_fold}_training.csv')
pred_train.to_csv(filepath_fold_train, index=False)
logger.debug('Save training fold to {} ({:.3f} seconds passed)' \
.format(filepath_fold_train, time.time() - SINCE))
## Validation set
pred_valid['object_id'] = valid_object_ids
filepath_fold_valid = os.path.join(output_dir, f'cv_fold{num_fold}_validation.csv')
pred_valid.to_csv(filepath_fold_valid, index=False)
logger.debug('Save validation fold to {} ({:.3f} seconds passed)' \
.format(filepath_fold_valid, time.time() - SINCE))
## Test set
pred_test['object_id'] = test['object_id'].values
filepath_fold_test = os.path.join(output_dir, f'cv_fold{num_fold}_test.csv')
pred_test.to_csv(filepath_fold_test, index=False)
logger.debug('Save test result {} ({:.3f} seconds passed)' \
.format(filepath_fold_test, time.time() - SINCE))
## Model
filepath_fold_model = os.path.join(output_dir, f'cv_fold{num_fold}_model.torch')
torch.save(estimator.state_dict(), filepath_fold_model)
# with open(filepath_fold_model, 'wb') as f:
# pickle.dump(estimator, f)
logger.debug('Save model {} ({:.3f} seconds passed)'.format(filepath_fold_model, time.time() - SINCE))
# Save memory
del (estimator, y_train, y_valid, pred_train, pred_valid, pred_test)
gc.collect()
logger.debug('Complete fold {} ({:.3f} seconds passed)'.format(num_fold, time.time() - SINCE))
```
# Evaluation
```
rmse = partial(mean_squared_error, squared=False)
# qwk = partial(cohen_kappa_score, labels=np.sort(train['target'].unique()), weights='quadratic')
@np.vectorize
def predict(proba_0: float, proba_1: float, proba_2: float, proba_3: float) -> int:
return np.argmax((proba_0, proba_1, proba_2, proba_3))
metrics = defaultdict(list)
```
## Training set
```
pred_train_dfs = []
for i in range(N_SPLITS):
num_fold = i + 1
logger.debug('Evaluate cv result (training set) Fold {}'.format(num_fold))
# Read cv result
filepath_fold_train = os.path.join(output_dir, f'cv_fold{num_fold}_training.csv')
pred_train_df = pd.read_csv(filepath_fold_train)
pred_train_df['actual'] = train.loc[pred_train_df['object_id'], TARGET].values
if REGRESSION:
if TARGET == 'target':
pred_train_df['pred'].clip(lower=0, upper=3, inplace=True)
else:
pred_train_df['pred'] = np.vectorize(soring_date2target)(pred_train_df['pred'])
pred_train_df['actual'] = np.vectorize(soring_date2target)(pred_train_df['actual'])
else:
pred_train_df['pred'] = predict(pred_train_df['0'], pred_train_df['1'],
pred_train_df['2'], pred_train_df['3'])
if not (REGRESSION and TARGET == 'target'):
print(confusion_matrix(pred_train_df['actual'], pred_train_df['pred'],
labels=np.sort(train['target'].unique())))
loss = rmse(pred_train_df['actual'], pred_train_df['pred'])
# score = qwk(pred_train_df['actual'], pred_train_df['pred'])
logger.debug('Loss: {}'.format(loss))
# logger.debug('Score: {}'.format(score))
metrics['train_losses'].append(loss)
# metrics['train_scores'].append(score)
pred_train_dfs.append(pred_train_df)
metrics['train_losses_avg'] = np.mean(metrics['train_losses'])
metrics['train_losses_std'] = np.std(metrics['train_losses'])
# metrics['train_scores_avg'] = np.mean(metrics['train_scores'])
# metrics['train_scores_std'] = np.std(metrics['train_scores'])
pred_train = pd.concat(pred_train_dfs).groupby('object_id').sum()
pred_train = pred_train / N_SPLITS
if not REGRESSION:
pred_train['pred'] = predict(pred_train['0'], pred_train['1'], pred_train['2'], pred_train['3'])
pred_train['actual'] = train.loc[pred_train.index, TARGET].values
if REGRESSION and TARGET == 'sorting_date':
pred_train['actual'] = np.vectorize(soring_date2target)(pred_train['actual'])
# for c in ('pred', 'actual'):
# pred_train[c] = pred_train[c].astype('int')
pred_train
if not (REGRESSION and TARGET == 'target'):
print(confusion_matrix(pred_train['actual'], pred_train['pred'], labels=np.sort(train['target'].unique())))
loss = rmse(pred_train['actual'], pred_train['pred'])
# score = qwk(pred_train['actual'], pred_train['pred'])
metrics['train_loss'] = loss
# metrics['train_score'] = score
logger.info('Training loss: {}'.format(loss))
# logger.info('Training score: {}'.format(score))
pred_train.to_csv(os.path.join(output_dir, 'prediction_train.csv'))
logger.debug('Write cv result to {}'.format(os.path.join(output_dir, 'prediction_train.csv')))
```
## Validation set
```
pred_valid_dfs = []
for i in range(N_SPLITS):
num_fold = i + 1
logger.debug('Evaluate cv result (validation set) Fold {}'.format(num_fold))
# Read cv result
filepath_fold_valid = os.path.join(output_dir, f'cv_fold{num_fold}_validation.csv')
pred_valid_df = pd.read_csv(filepath_fold_valid)
pred_valid_df['actual'] = train.loc[pred_valid_df['object_id'], TARGET].values
if REGRESSION:
if TARGET == 'target':
pred_valid_df['pred'].clip(lower=0, upper=3, inplace=True)
else:
pred_valid_df['pred'] = np.vectorize(soring_date2target)(pred_valid_df['pred'])
pred_valid_df['actual'] = np.vectorize(soring_date2target)(pred_valid_df['actual'])
else:
pred_valid_df['pred'] = predict(pred_valid_df['0'], pred_valid_df['1'],
pred_valid_df['2'], pred_valid_df['3'])
if not (REGRESSION and TARGET == 'target'):
print(confusion_matrix(pred_valid_df['actual'], pred_valid_df['pred'],
labels=np.sort(train['target'].unique())))
loss = rmse(pred_valid_df['actual'], pred_valid_df['pred'])
# score = qwk(pred_valid_df['actual'], pred_valid_df['pred'])
logger.debug('Loss: {}'.format(loss))
# logger.debug('Score: {}'.format(score))
metrics['valid_losses'].append(loss)
# metrics['valid_scores'].append(score)
pred_valid_dfs.append(pred_valid_df)
metrics['valid_losses_avg'] = np.mean(metrics['valid_losses'])
metrics['valid_losses_std'] = np.std(metrics['valid_losses'])
# metrics['valid_scores_avg'] = np.mean(metrics['valid_scores'])
# metrics['valid_scores_std'] = np.std(metrics['valid_scores'])
pred_valid = pd.concat(pred_valid_dfs).groupby('object_id').sum()
pred_valid = pred_valid / N_SPLITS
if not REGRESSION:
pred_valid['pred'] = predict(pred_valid['0'], pred_valid['1'], pred_valid['2'], pred_valid['3'])
pred_valid['actual'] = train.loc[pred_valid.index, TARGET].values
if REGRESSION and TARGET == 'sorting_date':
pred_valid['actual'] = np.vectorize(soring_date2target)(pred_valid['actual'])
# for c in ('pred', 'actual'):
# pred_valid[c] = pred_valid[c].astype('int')
pred_valid
if not REGRESSION:
print(confusion_matrix(pred_valid['actual'], pred_valid['pred'], labels=np.sort(train['target'].unique())))
loss = rmse(pred_valid['actual'], pred_valid['pred'])
# score = qwk(pred_valid['actual'], pred_valid['pred'])
metrics['valid_loss'] = loss
# metrics['valid_score'] = score
logger.info('Validatino loss: {}'.format(loss))
# logger.info('Validatino score: {}'.format(score))
pred_valid.to_csv(os.path.join(output_dir, 'prediction_valid.csv'))
logger.debug('Write cv result to {}'.format(os.path.join(output_dir, 'prediction_valid.csv')))
with open(os.path.join(output_dir, 'metrics.json'), 'w') as f:
json.dump(dict(metrics), f)
logger.debug('Write metrics to {}'.format(os.path.join(output_dir, 'metrics.json')))
```
# Prediction
```
pred_test_dfs = []
for i in range(N_SPLITS):
num_fold = i + 1
# Read cv result
filepath_fold_test = os.path.join(output_dir, f'cv_fold{num_fold}_test.csv')
pred_test_df = pd.read_csv(filepath_fold_test)
pred_test_dfs.append(pred_test_df)
pred_test = pd.concat(pred_test_dfs).groupby('object_id').sum()
pred_test = pred_test / N_SPLITS
if REGRESSION:
if TARGET == 'target':
pred_test['pred'].clip(lower=0, upper=3, inplace=True)
else:
pred_test['pred'] = np.vectorize(soring_date2target)(pred_test['pred'])
else:
pred_test['pred'] = predict(pred_test['0'], pred_test['1'], pred_test['2'], pred_test['3'])
pred_test
test['target'] = pred_test.loc[test['object_id'], 'pred'].values
test = test[['target']]
test
sample_submission
test.to_csv(os.path.join(output_dir, f'{str(EXP_NO).zfill(3)}_submission.csv'), index=False)
logger.debug('Write submission to {}'.format(os.path.join(output_dir, f'{str(EXP_NO).zfill(3)}_submission.csv')))
fig = plt.figure()
if not (REGRESSION and TARGET == 'target'):
sns.countplot(data=test, x='target')
else:
sns.histplot(data=test, x='target')
sns.despine()
fig.savefig(os.path.join(output_dir, 'prediction.png'))
logger.debug('Write figure to {}'.format(os.path.join(output_dir, 'prediction.png')))
logger.debug('Complete ({:.3f} seconds passed)'.format(time.time() - SINCE))
```
|
github_jupyter
|
# Essential Objects
This tutorial covers several object types that are foundational to much of what pyGSTi does: [circuits](#circuits), [processor specifications](#pspecs), [models](#models), and [data sets](#datasets). Our objective is to explain what these objects are and how they relate to one another at a high level while providing links to other notebooks that cover details we skip over here.
```
import pygsti
from pygsti.circuits import Circuit
from pygsti.models import Model
from pygsti.data import DataSet
```
<a id="circuits"></a>
## Circuits
The `Circuit` object encapsulates a quantum circuit as a sequence of *layers*, each of which contains zero or more non-identity *gates*. A `Circuit` has some number of labeled *lines* and each gate label is assigned to one or more lines. Line labels can be integers or strings. Gate labels have two parts: a `str`-type name and a tuple of line labels. A gate name typically begins with 'G' because this is expected when we parse circuits from text files.
For example, `('Gx',0)` is a gate label that means "do the Gx gate on qubit 0", and `('Gcnot',(2,3))` means "do the Gcnot gate on qubits 2 and 3".
A `Circuit` can be created from a list of gate labels:
```
c = Circuit( [('Gx',0),('Gcnot',0,1),(),('Gy',3)], line_labels=[0,1,2,3])
print(c)
```
If you want multiple gates in a single layer, just put those gate labels in their own nested list:
```
c = Circuit( [('Gx',0),[('Gcnot',0,1),('Gy',3)],()] , line_labels=[0,1,2,3])
print(c)
```
We distinguish three basic types of circuit layers. We call layers containing quantum gates *operation layers*. All the circuits we've seen so far just have operation layers. It's also possible to have a *preparation layer* at the beginning of a circuit and a *measurement layer* at the end of a circuit. There can also be a fourth type of layer called an *instrument layer* which we dicuss in a separate [tutorial on Instruments](objects/advanced/Instruments.ipynb). Assuming that `'rho'` labels a (n-qubit) state preparation and `'Mz'` labels a (n-qubit) measurement, here's a circuit with all three types of layers:
```
c = Circuit( ['rho',('Gz',1),[('Gswap',0,1),('Gy',2)],'Mz'] , line_labels=[0,1,2])
print(c)
```
Finally, when dealing with small systems (e.g. 1 or 2 qubits), we typically just use a `str`-type label (without any line-labels) to denote every possible layer. In this case, all the labels operate on the entire state space so we don't need the notion of 'lines' in a `Circuit`. When there are no line-labels, a `Circuit` assumes a single default **'\*'-label**, which you can usually just ignore:
```
c = Circuit( ['Gx','Gy','Gi'] )
print(c)
```
Pretty simple, right? The `Circuit` object allows you to easily manipulate its labels (similar to a NumPy array) and even perform some basic operations like depth reduction and simple compiling. For lots more details on how to create, modify, and use circuit objects see the [circuit tutorial](objects/Circuit.ipynb).
<a id="models"></a>
<a id="pspecs"></a>
## Processor Specifications
A processor specification describes the interface that a quantum processor exposes to the outside world. Actual quantum processors often have a "native" interface associated with them, but can also be viewed as implementing various other derived interfaces. For example, while a 1-qubit quantum processor may natively implement the $X(\pi/2)$ and $Z(\pi/2)$ gates, it can also implement the set of all 1-qubit Clifford gates. Both of these interfaces would correspond to a processor specification in pyGSTi.
Currently pyGSTi only supports processor specifications having an integral number of qubits. The `QubitProcessorSpec` object describes the number of qubits and what gates are available on them. For example,
```
pspec = pygsti.processors.QubitProcessorSpec(num_qubits=2, gate_names=['Gxpi2', 'Gypi2', 'Gcnot'],
geometry="line")
print("Qubit labels are", pspec.qubit_labels)
print("X(pi/2) gates on qubits: ", pspec.resolved_availability('Gxpi2'))
print("CNOT gates on qubits: ", pspec.resolved_availability('Gcnot'))
```
creates a processor specification for a 2-qubits with $X(\pi/2)$, $Y(\pi/2)$, and CNOT gates. Setting the geometry to `"line"` causes 1-qubit gates to be available on each qubit and the CNOT between the two qubits (in either control/target direction). Processor specifications are used to build experiment designs and models, and so defining or importing an appropriate processor specification is often the first step in many analyses. To learn more about processor specification objects, see the [processor specification tutorial](objects/ProcessorSpec.ipynb).
## Models
An instance of the `Model` class represents something that can predict the outcome probabilities of quantum circuits. We define any such thing to be a "QIP model", or just a "model", as these probabilities define the behavior of some real or virtual QIP. Because there are so many types of models, the `Model` class in pyGSTi is just a base class and is never instaniated directly. Classes `ExplicitOpModel` and `ImplicitOpModel` (subclasses of `Model`) define two broad categories of models, both of which sequentially operate on circuit *layers* (the "Op" in the class names is short for "layer operation").
#### Explicit layer-operation models
An `ExplicitOpModel` is a container object. Its `.preps`, `.povms`, and `.operations` members are essentially dictionaires of state preparation, measurement, and layer-operation objects, respectively. How to create these objects and build up explicit models from scratch is a central capability of pyGSTi and a topic of the [explicit-model tutorial](objects/ExplicitModel.ipynb). Presently, we'll create a 2-qubit model using the processor specification above via the `create_explicit_model` function:
```
mdl = pygsti.models.create_explicit_model(pspec)
```
This creates an `ExplicitOpModel` with a default preparation (prepares all qubits in the zero-state) labeled `'rho0'`, a default measurement labeled `'Mdefault'` in the Z-basis and with 5 layer-operations given by the labels in the 2nd argument (the first argument is akin to a circuit's line labels and the third argument contains special strings that the function understands):
```
print("Preparations: ", ', '.join(map(str,mdl.preps.keys())))
print("Measurements: ", ', '.join(map(str,mdl.povms.keys())))
print("Layer Ops: ", ', '.join(map(str,mdl.operations.keys())))
```
We can now use this model to do what models were made to do: compute the outcome probabilities of circuits.
```
c = Circuit( [('Gxpi2',0),('Gcnot',0,1),('Gypi2',1)] , line_labels=[0,1])
print(c)
mdl.probabilities(c) # Compute the outcome probabilities of circuit `c`
```
An `ExplictOpModel` only "knows" how to operate on circuit layers it explicitly contains in its dictionaries,
so, for example, a circuit layer with two X gates in parallel (layer-label = `[('Gxpi2',0),('Gxpi2',1)]`) cannot be used with our model until we explicitly associate an operation with the layer-label `[('Gxpi2',0),('Gxpi2',1)]`:
```
import numpy as np
c = Circuit( [[('Gxpi2',0),('Gxpi2',1)],('Gxpi2',1)] , line_labels=[0,1])
print(c)
try:
p = mdl.probabilities(c)
except KeyError as e:
print("!!KeyError: ",str(e))
#Create an operation for two parallel X-gates & rerun (now it works!)
mdl.operations[ [('Gxpi2',0),('Gxpi2',1)] ] = np.dot(mdl.operations[('Gxpi2',0)].to_dense(),
mdl.operations[('Gxpi2',1)].to_dense())
p = mdl.probabilities(c)
print("Probability_of_outcome(00) = ", p['00']) # p is like a dictionary of outcomes
mdl.probabilities((('Gxpi2',0),('Gcnot',0,1)))
```
#### Implicit layer-operation models
In the above example, you saw how it is possible to manually add a layer-operation to an `ExplicitOpModel` based on its other, more primitive layer operations. This often works fine for a few qubits, but can quickly become tedious as the number of qubits increases (since the number of potential layers that involve a given set of gates grows exponentially with qubit number). This is where `ImplicitOpModel` objects come into play: these models contain rules for building up arbitrary layer-operations based on more primitive operations. PyGSTi offers several "built-in" types of implicit models and a rich set of tools for building your own custom ones. See the [tutorial on implicit models](objects/ImplicitModel.ipynb) for details.
<a id="datasets"></a>
## Data Sets
The `DataSet` object is a container for tabulated outcome counts. It behaves like a dictionary whose keys are `Circuit` objects and whose values are dictionaries that associate *outcome labels* with (usually) integer counts. There are two primary ways you go about getting a `DataSet`. The first is by reading in a simply formatted text file:
```
dataset_txt = \
"""## Columns = 00 count, 01 count, 10 count, 11 count
{} 100 0 0 0
Gxpi2:0 55 5 40 0
Gxpi2:0Gypi2:1 20 27 23 30
Gxpi2:0^4 85 3 10 2
Gxpi2:0Gcnot:0:1 45 1 4 50
[Gxpi2:0Gxpi2:1]Gypi2:0 25 32 17 26
"""
with open("tutorial_files/Example_Short_Dataset.txt","w") as f:
f.write(dataset_txt)
ds = pygsti.io.read_dataset("tutorial_files/Example_Short_Dataset.txt")
```
The second is by simulating a `Model` and thereby generating "fake data". This essentially calls `mdl.probabilities(c)` for each circuit in a given list, and samples from the output probability distribution to obtain outcome counts:
```
circuit_list = pygsti.circuits.to_circuits([ (),
(('Gxpi2',0),),
(('Gxpi2',0),('Gypi2',1)),
(('Gxpi2',0),)*4,
(('Gxpi2',0),('Gcnot',0,1)),
((('Gxpi2',0),('Gxpi2',1)),('Gxpi2',0)) ], line_labels=(0,1))
ds_fake = pygsti.data.simulate_data(mdl, circuit_list, num_samples=100,
sample_error='multinomial', seed=8675309)
```
Outcome counts are accessible by indexing a `DataSet` as if it were a dictionary with `Circuit` keys:
```
c = Circuit( (('Gxpi2',0),('Gypi2',1)), line_labels=(0,1) )
print(ds[c]) # index using a Circuit
print(ds[ [('Gxpi2',0),('Gypi2',1)] ]) # or with something that can be converted to a Circuit
```
Because `DataSet` object can also store *timestamped* data (see the [time-dependent data tutorial](objects/advanced/TimestampedDataSets.ipynb), the values or "rows" of a `DataSet` aren't simple dictionary objects. When you'd like a `dict` of counts use the `.counts` member of a data set row:
```
row = ds[c]
row['00'] # this is ok
for outlbl, cnt in row.counts.items(): # Note: `row` doesn't have .items(), need ".counts"
print(outlbl, cnt)
```
Another thing to note is that `DataSet` objects are "sparse" in that 0-counts are not typically stored:
```
c = Circuit([('Gxpi2',0)], line_labels=(0,1))
print("No 01 or 11 outcomes here: ",ds_fake[c])
for outlbl, cnt in ds_fake[c].counts.items():
print("Item: ",outlbl, cnt) # Note: this loop never loops over 01 or 11!
```
You can manipulate `DataSets` in a variety of ways, including:
- adding and removing rows
- "trucating" a `DataSet` to include only a subset of it's string
- "filtering" a $n$-qubit `DataSet` to a $m < n$-qubit dataset
To find out more about these and other operations, see our [data set tutorial](objects/DataSet.ipynb).
## What's next?
You've learned about the three main object types in pyGSTi! The next step is to learn about how these objects are used within pyGSTi, which is the topic of the next [overview tutorial on applications](02-Applications.ipynb). Alternatively, if you're interested in learning more about the above-described or other objects, here are some links to relevant tutorials:
- [Circuit](objects/Circuit.ipynb) - how to build circuits ([GST circuits](objects/advanced/GSTCircuitConstruction.ipynb) in particular)
- [ExplicitModel](objects/ExplicitModel.ipynb) - constructing explicit layer-operation models
- [ImplicitModel](objects/ImplicitModel.ipynb) - constructing implicit layer-operation models
- [DataSet](objects/DataSet.ipynb) - constructing data sets ([timestamped data](objects/advanced/TimestampedDataSets.ipynb) in particular)
- [Basis](objects/advanced/MatrixBases.ipynb) - defining matrix and vector bases
- [Results](objects/advanced/Results.ipynb) - the container object for model-based results
- [QubitProcessorSpec](objects/advanced/QubitProcessorSpec.ipynb) - represents a QIP as a collection of models and meta information.
- [Instrument](objects/advanced/Instruments.ipynb) - allows for circuits with intermediate measurements
- [Operation Factories](objects/advanced/OperationFactories.ipynb) - allows continuously parameterized gates
|
github_jupyter
|
# Day and Night Image Classifier
---
The day/night image dataset consists of 200 RGB color images in two categories: day and night. There are equal numbers of each example: 100 day images and 100 night images.
We'd like to build a classifier that can accurately label these images as day or night, and that relies on finding distinguishing features between the two types of images!
*Note: All images come from the [AMOS dataset](http://cs.uky.edu/~jacobs/datasets/amos/) (Archive of Many Outdoor Scenes).*
### Import resources
Before you get started on the project code, import the libraries and resources that you'll need.
```
import cv2 # computer vision library
import helpers
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
%matplotlib inline
```
## Training and Testing Data
The 200 day/night images are separated into training and testing datasets.
* 60% of these images are training images, for you to use as you create a classifier.
* 40% are test images, which will be used to test the accuracy of your classifier.
First, we set some variables to keep track of some where our images are stored:
image_dir_training: the directory where our training image data is stored
image_dir_test: the directory where our test image data is stored
```
# Image data directories
image_dir_training = "day_night_images/training/"
image_dir_test = "day_night_images/test/"
```
## Load the datasets
These first few lines of code will load the training day/night images and store all of them in a variable, `IMAGE_LIST`. This list contains the images and their associated label ("day" or "night").
For example, the first image-label pair in `IMAGE_LIST` can be accessed by index:
``` IMAGE_LIST[0][:]```.
```
# Using the load_dataset function in helpers.py
# Load training data
IMAGE_LIST = helpers.load_dataset(image_dir_training)
```
---
# 1. Visualize the input images
```
# Print out 1. The shape of the image and 2. The image's label
# Select an image and its label by list index
image_index = 0
selected_image = IMAGE_LIST[image_index][0]
selected_label = IMAGE_LIST[image_index][1]
# Display image and data about it
plt.imshow(selected_image)
print("Shape: "+str(selected_image.shape))
print("Label: " + str(selected_label))
```
# 2. Pre-process the Data
After loading in each image, you have to standardize the input and output.
#### Solution code
You are encouraged to try to complete this code on your own, but if you are struggling or want to make sure your code is correct, there i solution code in the `helpers.py` file in this directory. You can look at that python file to see complete `standardize_input` and `encode` function code. For this day and night challenge, you can often jump one notebook ahead to see the solution code for a previous notebook!
---
### Input
It's important to make all your images the same size so that they can be sent through the same pipeline of classification steps! Every input image should be in the same format, of the same size, and so on.
#### TODO: Standardize the input images
* Resize each image to the desired input size: 600x1100px (hxw).
```
# This function should take in an RGB image and return a new, standardized version
def standardize_input(image):
## TODO: Resize image so that all "standard" images are the same size 600x1100 (hxw)
standard_im = image[0:600, 0:1100]
return standard_im
```
### TODO: Standardize the output
With each loaded image, you also need to specify the expected output. For this, use binary numerical values 0/1 = night/day.
```
# Examples:
# encode("day") should return: 1
# encode("night") should return: 0
def encode(label):
numerical_val = 0
## TODO: complete the code to produce a numerical label
if label == "day":
numerical_val = 1
return numerical_val
```
## Construct a `STANDARDIZED_LIST` of input images and output labels.
This function takes in a list of image-label pairs and outputs a **standardized** list of resized images and numerical labels.
This uses the functions you defined above to standardize the input and output, so those functions must be complete for this standardization to work!
```
def standardize(image_list):
# Empty image data array
standard_list = []
# Iterate through all the image-label pairs
for item in image_list:
image = item[0]
label = item[1]
# Standardize the image
standardized_im = standardize_input(image)
# Create a numerical label
binary_label = encode(label)
# Append the image, and it's one hot encoded label to the full, processed list of image data
standard_list.append((standardized_im, binary_label))
return standard_list
# Standardize all training images
STANDARDIZED_LIST = standardize(IMAGE_LIST)
```
## Visualize the standardized data
Display a standardized image from STANDARDIZED_LIST.
```
# Display a standardized image and its label
# Select an image by index
image_num = 0
selected_image = STANDARDIZED_LIST[image_num][0]
selected_label = STANDARDIZED_LIST[image_num][1]
# Display image and data about it
## TODO: Make sure the images have numerical labels and are of the same size
plt.imshow(selected_image)
print("Shape: "+str(selected_image.shape))
print("Label [1 = day, 0 = night]: " + str(selected_label))
```
|
github_jupyter
|
##### Copyright 2018 The AdaNet Authors.
```
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
```
# Customizing AdaNet
Often times, as a researcher or machine learning practitioner, you will have
some prior knowledge about a dataset. Ideally you should be able to encode that
knowledge into your machine learning algorithm. With `adanet`, you can do so by
defining the *neural architecture search space* that the AdaNet algorithm should
explore.
In this tutorial, we will explore the flexibility of the `adanet` framework, and
create a custom search space for an image-classificatio dataset using high-level
TensorFlow libraries like `tf.layers`.
```
from __future__ import absolute_import
from __future__ import division
from __future__ import print_function
import functools
import adanet
from adanet.examples import simple_dnn
import tensorflow as tf
# The random seed to use.
RANDOM_SEED = 42
```
## Fashion MNIST dataset
In this example, we will use the Fashion MNIST dataset
[[Xiao et al., 2017](https://arxiv.org/abs/1708.07747)] for classifying fashion
apparel images into one of ten categories:
1. T-shirt/top
2. Trouser
3. Pullover
4. Dress
5. Coat
6. Sandal
7. Shirt
8. Sneaker
9. Bag
10. Ankle boot

## Download the data
Conveniently, the data is available via Keras:
```
(x_train, y_train), (x_test, y_test) = (
tf.keras.datasets.fashion_mnist.load_data())
```
## Supply the data in TensorFlow
Our first task is to supply the data in TensorFlow. Using the
tf.estimator.Estimator covention, we will define a function that returns an
`input_fn` which returns feature and label `Tensors`.
We will also use the `tf.data.Dataset` API to feed the data into our models.
```
FEATURES_KEY = "images"
def generator(images, labels):
"""Returns a generator that returns image-label pairs."""
def _gen():
for image, label in zip(images, labels):
yield image, label
return _gen
def preprocess_image(image, label):
"""Preprocesses an image for an `Estimator`."""
# First let's scale the pixel values to be between 0 and 1.
image = image / 255.
# Next we reshape the image so that we can apply a 2D convolution to it.
image = tf.reshape(image, [28, 28, 1])
# Finally the features need to be supplied as a dictionary.
features = {FEATURES_KEY: image}
return features, label
def input_fn(partition, training, batch_size):
"""Generate an input_fn for the Estimator."""
def _input_fn():
if partition == "train":
dataset = tf.data.Dataset.from_generator(
generator(x_train, y_train), (tf.float32, tf.int32), ((28, 28), ()))
else:
dataset = tf.data.Dataset.from_generator(
generator(x_test, y_test), (tf.float32, tf.int32), ((28, 28), ()))
# We call repeat after shuffling, rather than before, to prevent separate
# epochs from blending together.
if training:
dataset = dataset.shuffle(10 * batch_size, seed=RANDOM_SEED).repeat()
dataset = dataset.map(preprocess_image).batch(batch_size)
iterator = dataset.make_one_shot_iterator()
features, labels = iterator.get_next()
return features, labels
return _input_fn
```
## Establish baselines
The next task should be to get somes baselines to see how our model performs on
this dataset.
Let's define some information to share with all our `tf.estimator.Estimators`:
```
# The number of classes.
NUM_CLASSES = 10
# We will average the losses in each mini-batch when computing gradients.
loss_reduction = tf.losses.Reduction.SUM_OVER_BATCH_SIZE
# A `Head` instance defines the loss function and metrics for `Estimators`.
head = tf.contrib.estimator.multi_class_head(
NUM_CLASSES, loss_reduction=loss_reduction)
# Some `Estimators` use feature columns for understanding their input features.
feature_columns = [
tf.feature_column.numeric_column(FEATURES_KEY, shape=[28, 28, 1])
]
# Estimator configuration.
config = tf.estimator.RunConfig(
save_checkpoints_steps=50000,
save_summary_steps=50000,
tf_random_seed=RANDOM_SEED)
```
Let's start simple, and train a linear model:
```
#@test {"skip": true}
#@title Parameters
LEARNING_RATE = 0.001 #@param {type:"number"}
TRAIN_STEPS = 5000 #@param {type:"integer"}
BATCH_SIZE = 64 #@param {type:"integer"}
estimator = tf.estimator.LinearClassifier(
feature_columns=feature_columns,
n_classes=NUM_CLASSES,
optimizer=tf.train.RMSPropOptimizer(learning_rate=LEARNING_RATE),
loss_reduction=loss_reduction,
config=config)
results, _ = tf.estimator.train_and_evaluate(
estimator,
train_spec=tf.estimator.TrainSpec(
input_fn=input_fn("train", training=True, batch_size=BATCH_SIZE),
max_steps=TRAIN_STEPS),
eval_spec=tf.estimator.EvalSpec(
input_fn=input_fn("test", training=False, batch_size=BATCH_SIZE),
steps=None))
print("Accuracy:", results["accuracy"])
print("Loss:", results["average_loss"])
```
The linear model with default parameters achieves about **84.13% accuracy**.
Let's see if we can do better with the `simple_dnn` AdaNet:
```
#@test {"skip": true}
#@title Parameters
LEARNING_RATE = 0.003 #@param {type:"number"}
TRAIN_STEPS = 5000 #@param {type:"integer"}
BATCH_SIZE = 64 #@param {type:"integer"}
ADANET_ITERATIONS = 2 #@param {type:"integer"}
estimator = adanet.Estimator(
head=head,
subnetwork_generator=simple_dnn.Generator(
feature_columns=feature_columns,
optimizer=tf.train.RMSPropOptimizer(learning_rate=LEARNING_RATE),
seed=RANDOM_SEED),
max_iteration_steps=TRAIN_STEPS // ADANET_ITERATIONS,
evaluator=adanet.Evaluator(
input_fn=input_fn("train", training=False, batch_size=BATCH_SIZE),
steps=None),
config=config)
results, _ = tf.estimator.train_and_evaluate(
estimator,
train_spec=tf.estimator.TrainSpec(
input_fn=input_fn("train", training=True, batch_size=BATCH_SIZE),
max_steps=TRAIN_STEPS),
eval_spec=tf.estimator.EvalSpec(
input_fn=input_fn("test", training=False, batch_size=BATCH_SIZE),
steps=None))
print("Accuracy:", results["accuracy"])
print("Loss:", results["average_loss"])
```
The `simple_dnn` AdaNet model with default parameters achieves about **85.66%
accuracy**.
This improvement can be attributed to `simple_dnn` searching over
fully-connected neural networks which have more expressive power than the linear
model due to their non-linear activations.
Fully-connected layers are permutation invariant to their inputs, meaning that
if we consistently swapped two pixels before training, the final model would
perform identically. However, there is spatial and locality information in
images that we should try to capture. Applying a few convolutions to our inputs
will allow us to do so, and that will require defining a custom
`adanet.subnetwork.Builder` and `adanet.subnetwork.Generator`.
## Define a convolutional AdaNet model
Creating a new search space for AdaNet to explore is straightforward. There are
two abstract classes you need to extend:
1. `adanet.subnetwork.Builder`
2. `adanet.subnetwork.Generator`
Similar to the tf.estimator.Estimator `model_fn`, `adanet.subnetwork.Builder`
allows you to define your own TensorFlow graph for creating a neural network,
and specify the training operations.
Below we define one that applies a 2D convolution, max-pooling, and then a
fully-connected layer to the images:
```
class SimpleCNNBuilder(adanet.subnetwork.Builder):
"""Builds a CNN subnetwork for AdaNet."""
def __init__(self, learning_rate, max_iteration_steps, seed):
"""Initializes a `SimpleCNNBuilder`.
Args:
learning_rate: The float learning rate to use.
max_iteration_steps: The number of steps per iteration.
seed: The random seed.
Returns:
An instance of `SimpleCNNBuilder`.
"""
self._learning_rate = learning_rate
self._max_iteration_steps = max_iteration_steps
self._seed = seed
def build_subnetwork(self,
features,
logits_dimension,
training,
iteration_step,
summary,
previous_ensemble=None):
"""See `adanet.subnetwork.Builder`."""
images = features.values()[0]
kernel_initializer = tf.keras.initializers.he_normal(seed=self._seed)
x = tf.layers.conv2d(
images,
filters=16,
kernel_size=3,
padding="same",
activation="relu",
kernel_initializer=kernel_initializer)
x = tf.layers.max_pooling2d(x, pool_size=2, strides=2)
x = tf.layers.flatten(x)
x = tf.layers.dense(
x, units=64, activation="relu", kernel_initializer=kernel_initializer)
# The `Head` passed to adanet.Estimator will apply the softmax activation.
logits = tf.layers.dense(
x, units=10, activation=None, kernel_initializer=kernel_initializer)
# Use a constant complexity measure, since all subnetworks have the same
# architecture and hyperparameters.
complexity = tf.constant(1)
return adanet.Subnetwork(
last_layer=x,
logits=logits,
complexity=complexity,
persisted_tensors={})
def build_subnetwork_train_op(self,
subnetwork,
loss,
var_list,
labels,
iteration_step,
summary,
previous_ensemble=None):
"""See `adanet.subnetwork.Builder`."""
# Momentum optimizer with cosine learning rate decay works well with CNNs.
learning_rate = tf.train.cosine_decay(
learning_rate=self._learning_rate,
global_step=iteration_step,
decay_steps=self._max_iteration_steps)
optimizer = tf.train.MomentumOptimizer(learning_rate, .9)
# NOTE: The `adanet.Estimator` increments the global step.
return optimizer.minimize(loss=loss, var_list=var_list)
def build_mixture_weights_train_op(self, loss, var_list, logits, labels,
iteration_step, summary):
"""See `adanet.subnetwork.Builder`."""
return tf.no_op("mixture_weights_train_op")
@property
def name(self):
"""See `adanet.subnetwork.Builder`."""
return "simple_cnn"
```
Next, we extend a `adanet.subnetwork.Generator`, which defines the search
space of candidate `SimpleCNNBuilders` to consider including the final network.
It can create one or more at each iteration with different parameters, and the
AdaNet algorithm will select the candidate that best improves the overall neural
network's `adanet_loss` on the training set.
The one below is very simple: it always creates the same architecture, but gives
it a different random seed at each iteration:
```
class SimpleCNNGenerator(adanet.subnetwork.Generator):
"""Generates a `SimpleCNN` at each iteration.
"""
def __init__(self, learning_rate, max_iteration_steps, seed=None):
"""Initializes a `Generator` that builds `SimpleCNNs`.
Args:
learning_rate: The float learning rate to use.
max_iteration_steps: The number of steps per iteration.
seed: The random seed.
Returns:
An instance of `Generator`.
"""
self._seed = seed
self._dnn_builder_fn = functools.partial(
SimpleCNNBuilder,
learning_rate=learning_rate,
max_iteration_steps=max_iteration_steps)
def generate_candidates(self, previous_ensemble, iteration_number,
previous_ensemble_reports, all_reports):
"""See `adanet.subnetwork.Generator`."""
seed = self._seed
# Change the seed according to the iteration so that each subnetwork
# learns something different.
if seed is not None:
seed += iteration_number
return [self._dnn_builder_fn(seed=seed)]
```
With these defined, we pass them into a new `adanet.Estimator`:
```
#@title Parameters
LEARNING_RATE = 0.05 #@param {type:"number"}
TRAIN_STEPS = 5000 #@param {type:"integer"}
BATCH_SIZE = 64 #@param {type:"integer"}
ADANET_ITERATIONS = 2 #@param {type:"integer"}
max_iteration_steps = TRAIN_STEPS // ADANET_ITERATIONS
estimator = adanet.Estimator(
head=head,
subnetwork_generator=SimpleCNNGenerator(
learning_rate=LEARNING_RATE,
max_iteration_steps=max_iteration_steps,
seed=RANDOM_SEED),
max_iteration_steps=max_iteration_steps,
evaluator=adanet.Evaluator(
input_fn=input_fn("train", training=False, batch_size=BATCH_SIZE),
steps=None),
adanet_loss_decay=.99,
config=config)
results, _ = tf.estimator.train_and_evaluate(
estimator,
train_spec=tf.estimator.TrainSpec(
input_fn=input_fn("train", training=True, batch_size=BATCH_SIZE),
max_steps=TRAIN_STEPS),
eval_spec=tf.estimator.EvalSpec(
input_fn=input_fn("test", training=False, batch_size=BATCH_SIZE),
steps=None))
print("Accuracy:", results["accuracy"])
print("Loss:", results["average_loss"])
```
Our `SimpleCNNGenerator` code achieves **90.41% accuracy**.
## Conclusion and next steps
In this tutorial, you learned how to customize `adanet` to encode your
understanding of a particular dataset, and explore novel search spaces with
AdaNet.
One use-case that has worked for us at Google, has been to take a production
model's TensorFlow code, convert it to into an `adanet.subnetwork.Builder`, and
adaptively grow it into an ensemble. In many cases, this has given significant
performance improvements.
As an exercise, you can swap out the FASHION-MNIST with the MNIST handwritten
digits dataset in this notebook using `tf.keras.datasets.mnist.load_data()`, and
see how `SimpleCNN` performs.
|
github_jupyter
|
```
import numpy as np
import matplotlib.pylab as plt
def Weight(phi,A=5, phi_o=0):
return 1-(0.5*np.tanh(A*((np.abs(phi)-phi_o)))+0.5)
def annot_max(x,y, ax=None):
x=np.array(x)
y=np.array(y)
xmax = x[np.argmax(y)]
ymax = y.max()
text= "x={:.3f}, y={:.3f}".format(xmax, ymax)
if not ax:
ax=plt.gca()
bbox_props = dict(boxstyle="square,pad=0.3", fc="w", ec="k", lw=0.72)
arrowprops=dict(arrowstyle="->",connectionstyle="angle,angleA=0,angleB=60")
kw = dict(xycoords='data',textcoords="axes fraction",
arrowprops=arrowprops, bbox=bbox_props, ha="right", va="top")
ax.annotate(text, xy=(xmax, ymax), xytext=(0.94,0.96), **kw)
def plotweighting(philist, A, p, delta, ctephi_o, enumeration):
label=enumeration+r" $w(\phi,\phi_o=$"+"$\delta$"+r"$ \cdot $"+"{cte}".format(cte=ctephi_o)+r"$,A = $"+"{A}".format(A=A)+r"$\frac{p}{\delta})$"+"\np = {p}, $\delta$ = {delta}m".format(p=p,delta=delta)
plt.plot(philist,[Weight(phi, A = A*p/delta, phi_o = phi_o) for phi in philist], label = label)
plt.figure(figsize= [10, 4],dpi=100)
delta = 50.05;
philist=np.arange(-(delta+10),(delta+10),.5).tolist()
#%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
A = 4; p = 2; ctephi_o = 0.65; phi_o = delta*ctephi_o;
plotweighting(philist, A, p, delta, ctephi_o,"(A)")
#%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
A = 12; p = 2; ctephi_o = 0.85; phi_o = delta*ctephi_o;
plotweighting(philist, A, p, delta, ctephi_o,"(B)")
#%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
A = 8; p = 2; ctephi_o = 0.80; phi_o = delta*ctephi_o;
plotweighting(philist, A, p, delta, ctephi_o,"(C)")
plt.axvline([delta],c="k");plt.axvline([-delta],c="k")
plt.xlabel("$\phi$")
plt.title(r"$w(\phi,\phi_o,A)=1-(0.5\ tanh(A(|\phi|-\phi_o))+0.5)$")
plt.grid()
plt.legend()
plt.show()
plt.figure(figsize= [10, 4],dpi=100)
delta = 50.05;
philist=np.arange(-(delta+10),(delta+10),.5).tolist()
#%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
A = 4; p = 2; ctephi_o = .999; phi_o = delta*ctephi_o;
plotweighting(philist, A, p, delta, ctephi_o,"(D)")
#%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
A = 4; p = 2; ctephi_o = .65; phi_o = delta*ctephi_o;
plotweighting(philist, A, p, delta, ctephi_o,"(A)")
plt.axvline([delta],c="k");plt.axvline([-delta],c="k")
plt.xlabel("$\phi$")
plt.title(r"$w(\phi,\phi_o,A)=1-(0.5\ tanh(A(|\phi|-\phi_o))+0.5)$")
plt.grid()
plt.legend()
plt.show()
plt.figure(figsize= [10, 4],dpi=100)
delta = 50.05;
philist=np.arange(-(delta+10),(delta+10),.5).tolist()
#%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
A = 4; p = 2; ctephi_o = .65; phi_o = delta*ctephi_o;
plotweighting(philist, A, p, delta, ctephi_o,"(A)")
#%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
A = 4; p = 2; ctephi_o = .75; phi_o = delta*ctephi_o;
plotweighting(philist, A, p, delta, ctephi_o,"(.75)")
#%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
A = 4; p = 2; ctephi_o = .85; phi_o = delta*ctephi_o;
plotweighting(philist, A, p, delta, ctephi_o,"(.85)")
plt.axvline([delta],c="k");plt.axvline([-delta],c="k")
plt.xlabel("$\phi$")
plt.title(r"$w(\phi,\phi_o,A)=1-(0.5\ tanh(A(|\phi|-\phi_o))+0.5)$")
plt.grid()
plt.legend()
plt.show()
plt.figure(figsize= [10, 4],dpi=100)
delta = 50.05;
philist=np.arange(-(delta+10),(delta+10),.5).tolist()
#%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
A = 4; p = 2; ctephi_o = .85; phi_o = delta*ctephi_o;
plotweighting(philist, A, p, delta, ctephi_o,"(A)")
#%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
A = 6; p = 2; ctephi_o = .75; phi_o = delta*ctephi_o;
plotweighting(philist, A, p, delta, ctephi_o,"(?)")
plt.axvline([delta],c="k");plt.axvline([-delta],c="k")
plt.xlabel("$\phi$")
plt.title(r"$w(\phi,\phi_o,A)=1-(0.5\ tanh(A(|\phi|-\phi_o))+0.5)$")
plt.grid()
plt.legend()
plt.show()
plt.figure(figsize= [10, 4],dpi=100)
delta = 50.05;
philist=np.arange(-(delta+10),(delta+10),.5).tolist()
#%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
A = 6.5; p = 2; ctephi_o = .85; phi_o = delta*ctephi_o;
plotweighting(philist, A, p, delta, ctephi_o,"(A)")
#%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
A = 6; p = 3; ctephi_o = .65; phi_o = delta*ctephi_o;
plotweighting(philist, A, p, delta, ctephi_o,"(B)")
#%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
A = 4; p = 3; ctephi_o = .65; phi_o = delta*ctephi_o;
plotweighting(philist, A, p, delta, ctephi_o,"(C)")
plt.axvline([delta],c="k");plt.axvline([-delta],c="k")
plt.xlabel("$\phi$")
plt.title(r"$w(\phi,\phi_o,A)=1-(0.5\ tanh(A(|\phi|-\phi_o))+0.5)$")
plt.grid()
plt.legend()
plt.show()
```
|
github_jupyter
|
# Description
This task is to do an exploratory data analysis on the balance-scale dataset
## Data Set Information
This data set was generated to model psychological experimental results. Each example is classified as having the balance scale tip to the right, tip to the left, or be balanced. The attributes are the left weight, the left distance, the right weight, and the right distance. The correct way to find the class is the greater of (left-distance left-weight) and (right-distance right-weight). If they are equal, it is balanced.
### Attribute Information:-
1. Class Name: 3 (L, B, R)
2. Left-Weight: 5 (1, 2, 3, 4, 5)
3. Left-Distance: 5 (1, 2, 3, 4, 5)
4. Right-Weight: 5 (1, 2, 3, 4, 5)
5. Right-Distance: 5 (1, 2, 3, 4, 5)
```
#importing libraries
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
#reading the data
data=pd.read_csv('balance-scale.data')
#shape of the data
data.shape
#first five rows of the data
data.head()
#Generating the x values
x=data.drop(['Class'],axis=1)
x.head()
#Generating the y values
y=data['Class']
y.head()
#Checking for any null data in x
x.isnull().any()
#Checking for any null data in y
y.isnull().any()
#Adding left and right torque as a new data frame
x1=pd.DataFrame()
x1['LT']=x['LW']*x['LD']
x1['RT']=x['RW']*x['RD']
x1.head()
#Converting the results of "Classs" attribute ,i.e., Balanced(B), Left(L) and Right(R) to numerical values for computation in sklearn
y=y.map(dict(B=0,L=1,R=2))
y.head()
```
### Using the Weight and Distance parameters
Splitting the data set into a ratio of 70:30 by the built in 'train_test_split' function in sklearn to get a better idea of accuracy of the model
```
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(x,y,stratify=y, test_size=0.3, random_state=2)
X_train.describe()
#Importing decision tree classifier and creating it's object
from sklearn.tree import DecisionTreeClassifier
clf= DecisionTreeClassifier()
clf.fit(X_train,y_train)
y_pred=clf.predict(X_test)
from sklearn.metrics import accuracy_score
accuracy_score(y_test,y_pred)
```
We observe that the accuracy score is pretty low. Thus, we need to find optimal parameters to get the best accuracy. We do that by using GridSearchCV
```
#Using GridSearchCV to find the maximun optimal depth
from sklearn.model_selection import GridSearchCV
tree_para={"criterion":["gini","entropy"], "max_depth":[3,4,5,6,7,8,9,10,11,12]}
dt_model_grid= GridSearchCV(DecisionTreeClassifier(random_state=3),tree_para, cv=10)
dt_model_grid.fit(X_train,y_train)
# To print the optimum parameters computed by GridSearchCV required for best accuracy score
dt_model=dt_model_grid.best_estimator_
print(dt_model)
#To find the best accuracy score for all possible combinations of parameters provided
dt_model_grid.best_score_
dt_model_grid.best_params_
#Scoring the model
from sklearn.metrics import classification_report
y_pred1=dt_model.predict(X_test)
print(classification_report(y_test,y_pred1,target_names=["Balanced","Left","Right"]))
from sklearn import tree
!pip install graphviz
#Plotting the Tree
from sklearn.tree import export_graphviz
export_graphviz(
dt_model,
out_file=("model1.dot"),
feature_names=["Left Weight","Left Distance","Right Weight","Right Distance"],
class_names=["Balanced","Left","Right"],
filled=True)
#Run this to print png
# !dot -Tpng model1.dot -o model1.png
```
## Using the created Torque
```
dt_model2 = DecisionTreeClassifier(random_state=31)
X_train, X_test, y_train, y_test= train_test_split(x1,y, stratify=y, test_size=0.3, random_state=8)
X_train.head(
)
X_train.shape
dt_model2.fit(X_train, y_train)
y_pred2= dt_model2.predict(X_test)
print(classification_report(y_test, y_pred2, target_names=["Balanced","Left","Right"]))
#Plotting the Tree
from sklearn import export_graphviz
export_graphviz(
dt_model2,
out_file=("model2.dot"),
feature_names=["Left Torque", "Right Torque"],
class_names=["Balanced","Left","Right"],
filled=True)
# run this to make png
# dot -Tpng model2.dot -o model2.png
```
## Increasing the optimization
After observing the trees, we conclude that differences are not being taken into account. Hence, we add the differences attribute to try and increase the accuracy.
```
x1['Diff']= x1['LT']- x1['RT']
x1.head()
X_train, X_test, y_train, y_test =train_test_split(x1,y, stratify=y, test_size=0.3,random_state=40)
dt_model3= DecisionTreeClassifier(random_state=40)
dt_model3.fit(X_train, y_train)
#Create Classification Report
y_pred3= dt_model3.predict(X_test)
print(classification_report(y_test, y_pred3, target_names=["Balanced", "Left", "Right"]))
#Plotting the tree
from sklearn.tree import export_graphviz
export_graphviz(
dt_model3
out_file=("model3.dot"),
feature_names=["Left Torque","Right Torque","Difference"],
class_names=["Balanced","Left","Right"]
filled=True)
# run this to make png
# dot -Tpng model3.dot -o model3.png
from sklearn.metrics import accuracy_score
accuracy_score(y_pred3,y_test)
```
## Final Conclusion
The model returns a perfect accuracy score as desired.
```
!pip install seaborn
```
|
github_jupyter
|
# Summarizing Emails using Machine Learning: Data Wrangling
## Table of Contents
1. Imports & Initalization <br>
2. Data Input <br>
A. Enron Email Dataset <br>
B. BC3 Corpus <br>
3. Preprocessing <br>
A. Data Cleaning. <br>
B. Sentence Cleaning <br>
C. Tokenizing <br>
4. Store Data <br>
A. Locally as pickle <br>
B. Into database <br>
5. Data Exploration <br>
A. Enron Emails <br>
B. BC3 Corpus <br>
The goal of this notebook is to clean both the Enron Email and BC3 Corpus data sets to perform email text summarization. The BC3 Corpus contains human summarizations that can be used to calculate ROUGE metrics to better understand how accurate the summarizations are. The Enron dataset is far more comprehensive, but lacks summaries to test against.
You can find the text summarization notebook that uses the preprocessed data [here.](https://github.com/dailykirt/ML_Enron_email_summary/blob/master/notebooks/Text_rank_summarization.ipynb)
A visual summary of the preprocessing steps are in the figure below.
<img src="./images/Preprocess_Flow.jpg">
## 1. Imports & Initalization
```
import sys
from os import listdir
from os.path import isfile, join
import configparser
from sqlalchemy import create_engine
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import email
import mailparser
import xml.etree.ElementTree as ET
from talon.signature.bruteforce import extract_signature
from nltk.tokenize import word_tokenize, sent_tokenize
from nltk.corpus import stopwords
import re
import dask.dataframe as dd
from distributed import Client
import multiprocessing as mp
#Set local location of emails.
mail_dir = '../data/maildir/'
#mail_dir = '../data/testdir/'
```
## 2. Data Input
### A. Enron Email Dataset
The raw enron email dataset contains a maildir directory that contains folders seperated by employee which contain the emails. The following processes the raw text of each email into a dask dataframe with the following columns:
Employee: The username of the email owner. <br>
Body: Cleaned body of the email. <br>
Subject: The title of the email. <br>
From: The original sender of the email <br>
Message-ID: Used to remove duplicate emails, as each email has a unique ID. <br>
Chain: The parsed out email chain from a email that was forwarded. <br>
Signature: The extracted signature from the body.<br>
Date: Time the email was sent. <br>
All of the Enron emails were sent using the Multipurpose Internet Mail Extensions 1.0 (MIME) format. Keeping this in mind helps find the correct libraries and methods to clean the emails in a standardized fashion.
```
def process_email(index):
'''
This function splits a raw email into constituent parts that can be used as features.
'''
email_path = index[0]
employee = index[1]
folder = index[2]
mail = mailparser.parse_from_file(email_path)
full_body = email.message_from_string(mail.body)
#Only retrieve the body of the email.
if full_body.is_multipart():
return
else:
mail_body = full_body.get_payload()
split_body = clean_body(mail_body)
headers = mail.headers
#Reformating date to be more pandas readable
date_time = process_date(headers.get('Date'))
email_dict = {
"employee" : employee,
"email_folder": folder,
"message_id": headers.get('Message-ID'),
"date" : date_time,
"from" : headers.get('From'),
"subject": headers.get('Subject'),
"body" : split_body['body'],
"chain" : split_body['chain'],
"signature": split_body['signature'],
"full_email_path" : email_path #for debug purposes.
}
#Append row to dataframe.
return email_dict
def clean_body(mail_body):
'''
This extracts both the email signature, and the forwarding email chain if it exists.
'''
delimiters = ["-----Original Message-----","To:","From"]
#Trying to split string by biggest delimiter.
old_len = sys.maxsize
for delimiter in delimiters:
split_body = mail_body.split(delimiter,1)
new_len = len(split_body[0])
if new_len <= old_len:
old_len = new_len
final_split = split_body
#Then pull chain message
if (len(final_split) == 1):
mail_chain = None
else:
mail_chain = final_split[1]
#The following uses Talon to try to get a clean body, and seperate out the rest of the email.
clean_body, sig = extract_signature(final_split[0])
return {'body': clean_body, 'chain' : mail_chain, 'signature': sig}
def process_date(date_time):
'''
Converts the MIME date format to a more pandas friendly type.
'''
try:
date_time = email.utils.format_datetime(email.utils.parsedate_to_datetime(date_time))
except:
date_time = None
return date_time
def generate_email_paths(mail_dir):
'''
Given a mail directory, this will generate the file paths to each email in each inbox.
'''
mailboxes = listdir(mail_dir)
for mailbox in mailboxes:
inbox = listdir(mail_dir + mailbox)
for folder in inbox:
path = mail_dir + mailbox + "/" + folder
emails = listdir(path)
for single_email in emails:
full_path = path + "/" + single_email
if isfile(full_path): #Skip directories.
yield (full_path, mailbox, folder)
#Use multiprocessing to speed up initial data load and processing. Also helps partition DASK dataframe.
try:
cpus = mp.cpu_count()
except NotImplementedError:
cpus = 2
pool = mp.Pool(processes=cpus)
print("CPUS: " + str(cpus))
indexes = generate_email_paths(mail_dir)
enron_email_df = pool.map(process_email,indexes)
#Remove Nones from the list
enron_email_df = [i for i in enron_email_df if i]
enron_email_df = pd.DataFrame(enron_email_df)
enron_email_df.describe()
```
### B. BC3 Corpus
This dataset is split into two xml files. One contains the original emails split line by line, and the other contains the summarizations created by the annotators. Each email may contain several summarizations from different annotators and summarizations may also be over several emails. This will create a data frame for both xml files, then join them together using the thread number in combination of the email number for a single final dataframe.
The first dataframe will contain the wrangled original emails containing the following information:
Listno: Thread identifier <br>
Email_num: Email in thread sequence <br>
From: The original sender of the email <br>
To: The recipient of the email. <br>
Recieved: Time email was recieved. <br>
Subject: Title of email. <br>
Body: Original body. <br>
```
def parse_bc3_emails(root):
'''
This adds every BC3 email to a newly created dataframe.
'''
BC3_email_list = []
#The emails are seperated by threads.
for thread in root:
email_num = 0
#Iterate through the thread elements <name, listno, Doc>
for thread_element in thread:
#Getting the listno allows us to link the summaries to the correct emails
if thread_element.tag == "listno":
listno = thread_element.text
#Each Doc element is a single email
if thread_element.tag == "DOC":
email_num += 1
email_metadata = []
for email_attribute in thread_element:
#If the email_attri is text, then each child contains a line from the body of the email
if email_attribute.tag == "Text":
email_body = ""
for sentence in email_attribute:
email_body += sentence.text
else:
#The attributes of the Email <Recieved, From, To, Subject, Text> appends in this order.
email_metadata.append(email_attribute.text)
#Use same enron cleaning methods on the body of the email
split_body = clean_body(email_body)
email_dict = {
"listno" : listno,
"date" : process_date(email_metadata[0]),
"from" : email_metadata[1],
"to" : email_metadata[2],
"subject" : email_metadata[3],
"body" : split_body['body'],
"email_num": email_num
}
BC3_email_list.append(email_dict)
return pd.DataFrame(BC3_email_list)
#load BC3 Email Corpus. Much smaller dataset has no need for parallel processing.
parsedXML = ET.parse( "../data/BC3_Email_Corpus/corpus.xml" )
root = parsedXML.getroot()
#Clean up BC3 emails the same way as the Enron emails.
bc3_email_df = parse_bc3_emails(root)
bc3_email_df.info()
bc3_email_df.head(3)
```
The second dataframe contains the summarizations of each email:
Annotator: Person who created summarization. <br>
Email_num: Email in thread sequence. <br>
Listno: Thread identifier. <br>
Summary: Human summarization of the email. <br>
```
def parse_bc3_summaries(root):
'''
This parses every BC3 Human summary that is contained in the dataset.
'''
BC3_summary_list = []
for thread in root:
#Iterate through the thread elements <listno, name, annotation>
for thread_element in thread:
if thread_element.tag == "listno":
listno = thread_element.text
#Each Doc element is a single email
if thread_element.tag == "annotation":
for annotation in thread_element:
#If the email_attri is summary, then each child contains a summarization line
if annotation.tag == "summary":
summary_dict = {}
for summary in annotation:
#Generate the set of emails the summary sentence belongs to (often a single email)
email_nums = summary.attrib['link'].split(',')
s = set()
for num in email_nums:
s.add(num.split('.')[0].strip())
#Remove empty strings, since they summarize whole threads instead of emails.
s = [x for x in set(s) if x]
for email_num in s:
if email_num in summary_dict:
summary_dict[email_num] += ' ' + summary.text
else:
summary_dict[email_num] = summary.text
#get annotator description
elif annotation.tag == "desc":
annotator = annotation.text
#For each email summarizaiton create an entry
for email_num, summary in summary_dict.items():
email_dict = {
"listno" : listno,
"annotator" : annotator,
"email_num" : email_num,
"summary" : summary
}
BC3_summary_list.append(email_dict)
return pd.DataFrame(BC3_summary_list)
#Load summaries and process
parsedXML = ET.parse( "../data/BC3_Email_Corpus/annotation.xml" )
root = parsedXML.getroot()
bc3_summary_df = parse_bc3_summaries(root)
bc3_summary_df['email_num'] = bc3_summary_df['email_num'].astype(int)
bc3_summary_df.info()
#merge the dataframes together
bc3_df = pd.merge(bc3_email_df,
bc3_summary_df[['annotator', 'email_num', 'listno', 'summary']],
on=['email_num', 'listno'])
bc3_df.head()
```
## 3. Preprocessing
### A. Data Cleaning
```
#Convert date to pandas datetime.
enron_email_df['date'] = pd.to_datetime(enron_email_df['date'], utc=True)
bc3_df['date'] = pd.to_datetime(bc3_df.date, utc=True)
#Look at the timeframe
start_date = str(enron_email_df.date.min())
end_date = str(enron_email_df.date.max())
print("Start Date: " + start_date)
print("End Date: " + end_date)
```
Since the Enron data was collected in May 2002 according to wikipedia its a bit strange to see emails past that date. Reading some of the emails seem to suggest it's mostly spam.
```
enron_email_df[(enron_email_df.date > '2003-01-01')].head()
#Quick look at emails before 1999,
enron_email_df[(enron_email_df.date < '1999-01-01')].date.value_counts().head()
enron_email_df[(enron_email_df.date == '1980-01-01')].head()
```
There seems to be a glut of emails dated exactly on 1980-01-01. The emails seem legitimate, but these should be droped since without the true date we won't be able to figure out where the email fits in the context of a batch of summaries. Keep emails between Jan 1st 1999 and June 1st 2002.
```
enron_email_df = enron_email_df[(enron_email_df.date > '1998-01-01') & (enron_email_df.date < '2002-06-01')]
```
### B. Sentence Cleaning
The raw enron email Corpus tends to have a large amount of unneeded characters that can interfere with tokenizaiton. It's best to do a bit more cleaning.
```
def clean_email_df(df):
'''
These remove symbols and character patterns that don't aid in producing a good summary.
'''
#Removing strings related to attatchments and certain non numerical characters.
patterns = ["\[IMAGE\]","-", "_", "\*", "+","\".\""]
for pattern in patterns:
df['body'] = pd.Series(df['body']).str.replace(pattern, "")
#Remove multiple spaces.
df['body'] = df['body'].replace('\s+', ' ', regex=True)
#Blanks are replaced with NaN in the whole dataframe. Then rows with a 'NaN' in the body will be dropped.
df = df.replace('',np.NaN)
df = df.dropna(subset=['body'])
#Remove all Duplicate emails
#df = df.drop_duplicates(subset='body')
return df
#Apply clean to both datasets.
enron_email_df = clean_email_df(enron_email_df)
bc3_df = clean_email_df(bc3_df)
```
### C. Tokenizing
It's important to split up sentences into it's constituent parts for the ML algorithim that will be used for text summarization. This will aid in further processing like removing extra whitespace. We can also remove stopwords, which are very commonly used words that don't provide additional sentence meaning like 'and' 'or' and 'the'. This will be applied to both the Enron and BC3 datasets.
```
def remove_stopwords(sen):
'''
This function removes stopwords
'''
stop_words = stopwords.words('english')
sen_new = " ".join([i for i in sen if i not in stop_words])
return sen_new
def tokenize_email(text):
'''
This function splits up the body into sentence tokens and removes stop words.
'''
clean_sentences = sent_tokenize(text, language='english')
#removing punctuation, numbers and special characters. Then lowercasing.
clean_sentences = [re.sub('[^a-zA-Z ]', '',s) for s in clean_sentences]
clean_sentences = [s.lower() for s in clean_sentences]
clean_sentences = [remove_stopwords(r.split()) for r in clean_sentences]
return clean_sentences
```
Starting with the Enron dataset.
```
#This tokenizing will be the extracted sentences that may be chosen to form the email summaries.
enron_email_df['extractive_sentences'] = enron_email_df['body'].apply(sent_tokenize)
#Splitting the text in emails into cleaned sentences
enron_email_df['tokenized_body'] = enron_email_df['body'].apply(tokenize_email)
#Tokenizing the bodies might have revealed more duplicate emails that should be droped.
enron_email_df = enron_email_df.loc[enron_email_df.astype(str).drop_duplicates(subset='tokenized_body').index]
```
Now working on the BC3 Dataset.
```
bc3_df['extractive_sentences'] = bc3_df['body'].apply(sent_tokenize)
bc3_df['tokenized_body'] = bc3_df['body'].apply(tokenize_email)
#bc3_email_df = bc3_email_df.loc[bc3_email_df.astype(str).drop_duplicates(subset='tokenized_body').index]
```
## Store Data
### A. Locally as pickle
After all the preprocessing is finished its best to store the the data so it can be quickly and easily retrieved by other software. Pickles are best used if you are working locally and want a simple way to store and load data. You can also use a cloud database that can be accessed by other production services such as Heroku to retrieve the data. In this case, I load the data up into a AWS postgres database.
```
#Local locations for pickle files.
ENRON_PICKLE_LOC = "../data/dataframes/wrangled_enron_full_df.pkl"
BC3_PICKLE_LOC = "../data/dataframes/wrangled_BC3_df.pkl"
#Store dataframes to disk
enron_email_df.to_pickle(ENRON_PICKLE_LOC)
bc3_df.head()
bc3_df.to_pickle(BC3_PICKLE_LOC)
```
### B. Into database
I used a Postgres database with the DB configurations stored in a config_notebook.ini file. This allows me to easily switch between local and AWS configurations.
```
#Configure postgres database
config = configparser.ConfigParser()
config.read('config_notebook.ini')
#database_config = 'LOCAL_POSTGRES'
database_config = 'AWS_POSTGRES'
POSTGRES_ADDRESS = config[database_config]['POSTGRES_ADDRESS']
POSTGRES_USERNAME = config[database_config]['POSTGRES_USERNAME']
POSTGRES_PASSWORD = config[database_config]['POSTGRES_PASSWORD']
POSTGRES_DBNAME = config[database_config]['POSTGRES_DBNAME']
#now create database connection
postgres_str = ('postgresql+psycopg2://{username}:{password}@{ipaddress}/{dbname}'
.format(username=POSTGRES_USERNAME,
password=POSTGRES_PASSWORD,
ipaddress=POSTGRES_ADDRESS,
dbname=POSTGRES_DBNAME))
cnx = create_engine(postgres_str)
#Store data.
enron_email_df.to_sql('full_enron_emails', cnx)
```
## 5. Data Exploration
Exploring the dataset can go a long way to building more accurate machine learning models and spotting any possible issues with the dataset. Since the Enron dataset is quite large, we can speed up some of our computations by using Dask. While not strictly necessary, iterating on this dataset should be much faster.
### A. Enron Emails
```
client = Client(processes = True)
client.cluster
#Make into dask dataframe.
enron_email_df = dd.from_pandas(enron_email_df, npartitions=cpus)
enron_email_df.columns
#Used to create a describe summary of the dataset. Ignoring tokenized columns.
enron_email_df[['body', 'chain', 'date', 'email_folder', 'employee', 'from', 'full_email_path', 'message_id', 'signature', 'subject']].describe().compute()
#Get word frequencies from tokenized word lists
def get_word_freq(df):
freq_words=dict()
for tokens in df.tokenized_words.compute():
for token in tokens:
if token in freq_words:
freq_words[token] += 1
else:
freq_words[token] = 1
return freq_words
def tokenize_word(sentences):
tokens = []
for sentence in sentences:
tokens = word_tokenize(sentence)
return tokens
#Tokenize the sentences
enron_email_df['tokenized_words'] = enron_email_df['tokenized_body'].apply(tokenize_word).compute()
#Creating word dictionary to understand word frequencies.
freq_words = get_word_freq(enron_email_df)
print('Unique words: {:,}'.format(len(freq_words)))
word_data = []
#Sort dictionary by highest word frequency.
for key, value in sorted(freq_words.items(), key=lambda item: item[1], reverse=True):
word_data.append([key, freq_words[key]])
#Prepare to plot bar graph of top words.
#Create dataframe with Word and Frequency, then sort in Descending order.
freq_words_df = pd.DataFrame.from_dict(freq_words, orient='index').reset_index()
freq_words_df = freq_words_df.rename(columns={"index": "Word", 0: "Frequency"})
freq_words_df = freq_words_df.sort_values(by=['Frequency'],ascending = False)
freq_words_df.reset_index(drop = True, inplace=True)
freq_words_df.head(30).plot(x='Word', kind='bar', figsize=(20,10))
```
### B. BC3 Corpus
```
bc3_df.head()
bc3_df['to'].value_counts().head()
```
|
github_jupyter
|
```
from google.colab import drive
drive.mount('/content/gdrive')
import pandas as pd
import numpy as np
import csv
#DATA_FOLDER = '/content/gdrive/My Drive/101/results/logreg/'
subfolders = []
for a in range(1,7):
for b in range(6,0,-1):
subfolders.append('+1e-0'+str(a)+'_+1e-0'+str(b))
classifiers = ['logreg', 'mlp', 'better_cnn']
all_results = []
for clf in classifiers:
print(clf)
DATA_FOLDER = '/content/gdrive/My Drive/101/results/' + clf + '/'
results = []
matrix = np.zeros(36)
methods = ['sgd', 'sgdn', 'adam', 'sgd_hd', 'sgdn_hd', 'adam_hd']
for m in methods:
for i, s in enumerate(subfolders):
file = DATA_FOLDER + s + '/' + m + '.csv'
with open(file, 'r') as f:
loss = list(csv.reader(f))[-1][4] #training loss
matrix[i] = np.round(float(loss),3)
results.append(matrix.reshape(6,-1))
matrix = np.zeros(36)
all_results.append(results)
import seaborn as sns
import matplotlib.pyplot as plt
f, ax = plt.subplots(2,3, figsize=(14,7))
k=0
f.suptitle(r'Gridsearch for every ${\alpha}_{0}$ and $\beta$ with Logistic Regression on MNIST')
for i in range(2):
for j in range(3):
ax[i,j].set_title(methods[k])
f = sns.heatmap(all_results[0][k], annot=True ,cmap="YlGnBu",cbar=True, ax=ax[i,j])
if k > 2:
f = sns.heatmap(all_results[0][k], annot=True ,cmap="YlGnBu",cbar=False, ax=ax[i,j],
mask=np.round(all_results[0][k],2) <= np.round(all_results[0][k-3],2) , annot_kws={"color": "red"})
k+=1
f.set_xticklabels([1e-6, 1e-5, 1e-4, 1e-3, 1e-2, 1e-1],fontsize='small')
f.set_yticklabels([1e-1, 1e-2, 1e-3, 1e-4, 1e-5, 1e-6],fontsize='small')
if i==1:
f.set_xlabel(r'$\beta_0$')
f.set_ylabel(r'$\alpha_0$')
plt.show()
import seaborn as sns
import matplotlib.pyplot as plt
f, ax = plt.subplots(2,3, figsize=(14,7))
k=0
f.suptitle(r'Gridsearch for every ${\alpha}_{0}$ and $\beta$ with MLP on MNIST')
for i in range(2):
for j in range(3):
ax[i,j].set_title(methods[k])
f = sns.heatmap(all_results[1][k], annot=True ,cmap="YlGnBu",cbar=True, ax=ax[i,j])
if k > 2:
f = sns.heatmap(all_results[1][k], annot=True ,cmap="YlGnBu",cbar=False, ax=ax[i,j],
mask=np.round(all_results[1][k],2) <= np.round(all_results[1][k-3],2) , annot_kws={"color": "red"})
k+=1
f.set_xticklabels([1e-6, 1e-5, 1e-4, 1e-3, 1e-2, 1e-1],fontsize='small')
f.set_yticklabels([1e-1, 1e-2, 1e-3, 1e-4, 1e-5, 1e-6],fontsize='small')
if i==1:
f.set_xlabel(r'$\beta_0$')
f.set_ylabel(r'$\alpha_0$')
plt.show()
import seaborn
import matplotlib.pyplot as plt
f, ax = plt.subplots(2,3, figsize=(14,7))
k=0
f.suptitle(r'Gridsearch for every ${\alpha}_{0}$ and $\beta$ with ""Better CNN"" on MNIST')
for i in range(2):
for j in range(3):
ax[i,j].set_title(methods[k])
f = sns.heatmap(all_results[2][k], annot=True ,cmap="YlGnBu",cbar=True, ax=ax[i,j])
if k > 2:
f = sns.heatmap(all_results[2][k], annot=True ,cmap="YlGnBu",cbar=False, ax=ax[i,j],
mask=np.round(all_results[2][k],2) <= np.round(all_results[2][k-3],2) , annot_kws={"color": "red"})
k+=1
f.set_xticklabels([1e-6, 1e-5, 1e-4, 1e-3, 1e-2, 1e-1],fontsize='small')
f.set_yticklabels([1e-1, 1e-2, 1e-3, 1e-4, 1e-5, 1e-6],fontsize='small')
f.set_xlabel(r'$\beta_0$')
f.set_ylabel(r'$\alpha_0$')
plt.show()
```
|
github_jupyter
|
By now basically everyone ([here](http://datacolada.org/2014/06/04/23-ceiling-effects-and-replications/?utm_source=feedburner&utm_medium=feed&utm_campaign=Feed%3A+DataColada+%28Data+Colada+Feed%29), [here](http://yorl.tumblr.com/post/87428392426/ceiling-effects), [here](http://www.talyarkoni.org/blog/2014/06/01/there-is-no-ceiling-effect-in-johnson-cheung-donnellan-2014/), [here](http://pigee.wordpress.com/2014/05/24/additional-reflections-on-ceiling-effects-in-recent-replication-research/) and [here](http://www.nicebread.de/reanalyzing-the-schnalljohnson-cleanliness-data-sets-new-insights-from-bayesian-and-robust-approaches/), and there is likely even more out there) who writes a blog and knows how to do a statistical analysis has analysed data from a recent replication study and from the original study (data repository is here).
The study of two experiments. Let's focus on Experiment 1 here. The experiment consists of a treatment and control group. The performance is measured by six likert-scale items. The scale has 9 levels. All responses are averaged together and we obtain a single composite score for each group. We are interested whether the treatment works, which would show up as a positive difference between the score of the treatment and the control group. Replication study did the same with more subjects.
Let's perform the original analysis to see the results and why this dataset is so "popular".
```
%pylab inline
import pystan
from matustools.matusplotlib import *
from scipy import stats
il=['dog','trolley','wallet','plane','resume','kitten','mean score','median score']
D=np.loadtxt('schnallstudy1.csv',delimiter=',')
D[:,1]=1-D[:,1]
Dtemp=np.zeros((D.shape[0],D.shape[1]+1))
Dtemp[:,:-1]=D
Dtemp[:,-1]=np.median(D[:,2:-2],axis=1)
D=Dtemp
DS=D[D[:,0]==0,1:]
DR=D[D[:,0]==1,1:]
DS.shape
def plotCIttest1(y,x=0,alpha=0.05):
m=y.mean();df=y.size-1
se=y.std()/y.size**0.5
cil=stats.t.ppf(alpha/2.,df)*se
cii=stats.t.ppf(0.25,df)*se
out=[m,m-cil,m+cil,m-cii,m+cii]
_errorbar(out,x=x,clr='k')
return out
def plotCIttest2(y1,y2,x=0,alpha=0.05):
n1=float(y1.size);n2=float(y2.size);
v1=y1.var();v2=y2.var()
m=y2.mean()-y1.mean()
s12=(((n1-1)*v1+(n2-1)*v2)/(n1+n2-2))**0.5
se=s12*(1/n1+1/n2)**0.5
df= (v1/n1+v2/n2)**2 / ( (v1/n1)**2/(n1-1)+(v2/n2)**2/(n2-1))
cil=stats.t.ppf(alpha/2.,df)*se
cii=stats.t.ppf(0.25,df)*se
out=[m,m-cil,m+cil,m-cii,m+cii]
_errorbar(out,x=x)
return out
plt.figure(figsize=(4,3))
dts=[DS[DS[:,0]==0,-2],DS[DS[:,0]==1,-2],
DR[DR[:,0]==0,-2],DR[DR[:,0]==1,-2]]
for k in range(len(dts)):
plotCIttest1(dts[k],x=k)
plt.grid(False,axis='x')
ax=plt.gca()
ax.set_xticks(range(len(dts)))
ax.set_xticklabels(['OC','OT','RC','RT'])
plt.xlim([-0.5,len(dts)-0.5])
plt.figure(figsize=(4,3))
plotCIttest2(dts[0],dts[1],x=0,alpha=0.1)
plotCIttest2(dts[2],dts[3],x=1,alpha=0.1)
ax=plt.gca()
ax.set_xticks([0,1])
ax.set_xticklabels(['OT-OC','RT-RC'])
plt.grid(False,axis='x')
plt.xlim([-0.5,1.5]);
```
Legend: OC - original study, control group; OT - original study, treatment group; RC - replication study, control group; RT - replication study, treatment group;
In the original study the difference between the treatment and control is significantly greater than zero. In the replication, it is not. However the ratings in the replication are higher overall. The author of the original study therefore raised a concern that no difference was obtained in replication because of ceiling effects.
How do we show that there are ceiling efects in the replication? The authors and bloggers presented various arguments that support some conclusion (mostly that there are no ceiling effects). Ultimately ceiling effects are a matter of degree and since no one knows how to quantify them the whole discussion of the replication's validity is heading into an inferential limbo.
My point here is that if the analysis computed the proper effect size - the causal effect size, we would avoid these kinds of arguments and discussions.
```
def plotComparison(A,B,stan=False):
plt.figure(figsize=(8,16))
cl=['control','treatment']
x=np.arange(11)-0.5
if not stan:assert A.shape[1]==B.shape[1]
for i in range(A.shape[1]-1):
for cond in range(2):
plt.subplot(A.shape[1]-1,2,2*i+cond+1)
a=np.histogram(A[A[:,0]==cond,1+i],bins=x, normed=True)
plt.barh(x[:-1],-a[0],ec='w',height=1)
if stan: a=[B[:,i,cond]]
else: a=np.histogram(B[B[:,0]==cond,1+i],bins=x, normed=True)
plt.barh(x[:-1],a[0],ec='w',fc='g',height=1)
#plt.hist(DS[:,2+i],bins=np.arange(11)-0.5,normed=True,rwidth=0.5)
plt.xlim([-0.7,0.7]);plt.gca().set_yticks(range(10))
plt.ylim([-1,10]);#plt.grid(b=False,axis='y')
if not i: plt.title('condition: '+cl[cond])
if not cond: plt.ylabel(il[i],size=12)
if not i and not cond: plt.legend(['original','replication'],loc=4);
plotComparison(DS,DR)
model='''
data {
int<lower=2> K;
int<lower=0> N;
int<lower=1> M;
int<lower=1,upper=K> y[N,M];
int x[N];
}
parameters {
real beta[M];
ordered[K-1] c[M];
}
transformed parameters{
real pt[M,K-1]; real pc[M,K-1];
for (m in 1:M){
for (k in 1:(K-1)){
pt[m,k] <- inv_logit(beta[m]-c[m][k]);
pc[m,k] <- inv_logit(-c[m][k]);
}}}
model {
for (m in 1:M){
for (k in 1:(K-1)) c[m][k]~ uniform(-100,100);
for (n in 1:N) y[n,m] ~ ordered_logistic(x[n] * beta[m], c[m]);
}}
'''
sm1=pystan.StanModel(model_code=model)
dat = {'y':np.int32(DS[:,1:7])+1,'x':np.int32(DS[:,0]),'N':DS.shape[0] ,'K':10,'M':6}
fit = sm1.sampling(data=dat,iter=1000, chains=4,thin=2,warmup=500,njobs=2,seed=4)
print fit
pt=fit.extract()['pt']
pc=fit.extract()['pc']
DP=np.zeros((pt.shape[2]+2,pt.shape[1],2))
DP[0,:,:]=1
DP[1:-1,:,:]=np.array([pc,pt]).T.mean(2)
DP=-np.diff(DP,axis=0)
plotComparison(DS[:,:7],DP,stan=True)
model='''
data {
int<lower=2> K;
int<lower=0> N;
int<lower=1> M;
int<lower=1,upper=K> y[N,M];
int x[N];
}
parameters {
real beta;
ordered[K-1] c[M];
}
transformed parameters{
real pt[M,K-1]; real pc[M,K-1];
for (m in 1:M){
for (k in 1:(K-1)){
pt[m,k] <- inv_logit(beta-c[m][k]);
pc[m,k] <- inv_logit(-c[m][k]);
}}}
model {
for (m in 1:M){
for (k in 1:(K-1)) c[m][k]~ uniform(-100,100);
for (n in 1:N) y[n,m] ~ ordered_logistic(x[n] * beta, c[m]);
}}
'''
sm2=pystan.StanModel(model_code=model)
dat = {'y':np.int32(DS[:,1:7])+1,'x':np.int32(DS[:,0]),'N':DS.shape[0] ,'K':10,'M':6}
fit2 = sm2.sampling(data=dat,iter=1000, chains=4,thin=2,warmup=500,njobs=2,seed=4)
print fit2
saveStanFit(fit2,'fit2')
w=loadStanFit('fit2')
pt=w['pt']
pc=w['pc']
DP=np.zeros((pt.shape[2]+2,pt.shape[1],2))
DP[0,:,:]=1
DP[1:-1,:,:]=np.array([pc,pt]).T.mean(2)
DP=-np.diff(DP,axis=0)
plotComparison(DS[:,:7],DP,stan=True)
model='''
data {
int<lower=2> K;
int<lower=0> N;
int<lower=1> M;
int<lower=1,upper=K> y[N,M];
int x[N];
}
parameters {
// real mb; real<lower=0,upper=100> sb[2];
vector[2*M-1] bbeta;
ordered[K-1] c;
}
transformed parameters{
real pt[M,K-1]; real pc[M,K-1];
vector[M] beta[2];
for (m in 1:M){
if (m==1){beta[1][m]<-0.0; beta[2][m]<-bbeta[2*M-1];}
else{beta[1][m]<-bbeta[2*(m-1)-1]; beta[2][m]<-bbeta[2*(m-1)];}
for (k in 1:(K-1)){
pt[m,k] <- inv_logit(beta[2][m]-c[k]);
pc[m,k] <- inv_logit(beta[1][m]-c[k]);
}}}
model {
for (k in 1:(K-1)) c[k]~ uniform(-100,100);
//beta[1]~normal(0.0,sb[1]);
//beta[2]~normal(mb,sb[2]);
for (m in 1:M){
for (n in 1:N) y[n,m] ~ ordered_logistic(beta[x[n]+1][m], c);
}}
'''
sm3=pystan.StanModel(model_code=model)
dat = {'y':np.int32(DS[:,1:7])+1,'x':np.int32(DS[:,0]),'N':DS.shape[0] ,'K':10,'M':6}
fit3 = sm3.sampling(data=dat,iter=1000, chains=4,thin=2,warmup=500,njobs=2,seed=4)
#print fit3
saveStanFit(fit3,'fit3')
w=loadStanFit('fit3')
pt=w['pt']
pc=w['pc']
DP=np.zeros((pt.shape[2]+2,pt.shape[1],2))
DP[0,:,:]=1
DP[1:-1,:,:]=np.array([pc,pt]).T.mean(2)
DP=-np.diff(DP,axis=0)
plotComparison(DS[:,:7],DP,stan=True)
model='''
data {
int<lower=2> K;
int<lower=0> N;
int<lower=1> M;
int<lower=1,upper=K> y[N,M];
int x[N];
}
parameters {
// real mb; real<lower=0,upper=100> sb[2];
vector[M-1] bbeta;
real delt;
ordered[K-1] c;
}
transformed parameters{
real pt[M,K-1]; real pc[M,K-1];
vector[M] beta;
for (m in 1:M){
if (m==1) beta[m]<-0.0;
else beta[m]<-bbeta[m-1];
for (k in 1:(K-1)){
pt[m,k] <- inv_logit(beta[m]+delt-c[k]);
pc[m,k] <- inv_logit(beta[m]-c[k]);
}}}
model {
for (k in 1:(K-1)) c[k]~ uniform(-100,100);
for (m in 1:M){
for (n in 1:N) y[n,m] ~ ordered_logistic(beta[m]+delt*x[n], c);
}}
'''
sm4=pystan.StanModel(model_code=model)
dat = {'y':np.int32(DS[:,1:7])+1,'x':np.int32(DS[:,0]),'N':DS.shape[0] ,'K':10,'M':6}
fit4 = sm4.sampling(data=dat,iter=1000, chains=4,thin=2,warmup=500,njobs=2,seed=4)
print pystan.misc._print_stanfit(fit4,pars=['delt','bbeta','c'],digits_summary=2)
saveStanFit(fit4,'fit4')
w=loadStanFit('fit4')
pt=w['pt']
pc=w['pc']
DP=np.zeros((pt.shape[2]+2,pt.shape[1],2))
DP[0,:,:]=1
DP[1:-1,:,:]=np.array([pc,pt]).T.mean(2)
DP=-np.diff(DP,axis=0)
plotComparison(DS[:,:7],DP,stan=True)
pystanErrorbar(w,keys=['beta','c','delt'])
dat = {'y':np.int32(DR[:,1:7])+1,'x':np.int32(DR[:,0]),'N':DR.shape[0] ,'K':10,'M':6}
fit5 = sm4.sampling(data=dat,iter=1000, chains=4,thin=2,warmup=500,njobs=2,seed=4)
print pystan.misc._print_stanfit(fit4,pars=['delt','bbeta','c'],digits_summary=2)
saveStanFit(fit5,'fit5')
w=loadStanFit('fit5')
pt=w['pt']
pc=w['pc']
DP=np.zeros((pt.shape[2]+2,pt.shape[1],2))
DP[0,:,:]=1
DP[1:-1,:,:]=np.array([pc,pt]).T.mean(2)
DP=-np.diff(DP,axis=0)
plotComparison(DR[:,:7],DP,stan=True)
pystanErrorbar(w,keys=['beta','c','delt'])
model='''
data {
int<lower=2> K;
int<lower=0> N;
int<lower=1> M;
int<lower=1,upper=K> y[N,M];
int x[N,2];
}
parameters {
// real mb; real<lower=0,upper=100> sb[2];
vector[M-1] bbeta;
real dd[3];
ordered[K-1] c;
}
transformed parameters{
//real pt[M,K-1]; real pc[M,K-1];
vector[M] beta;
for (m in 1:M){
if (m==1) beta[m]<-0.0;
else beta[m]<-bbeta[m-1];
//for (k in 1:(K-1)){
// pt[m,k] <- inv_logit(beta[m]+delt-c[k]);
// pc[m,k] <- inv_logit(beta[m]-c[k]);}
}}
model {
for (k in 1:(K-1)) c[k]~ uniform(-100,100);
for (m in 1:M){
for (n in 1:N) y[n,m] ~ ordered_logistic(beta[m]
+dd[2]*x[n,1]*(1-x[n,2]) // rep + control
+dd[1]*x[n,2]*(1-x[n,1]) // orig + treat
+dd[3]*x[n,1]*x[n,2], c); // rep + treat
}}
'''
sm5=pystan.StanModel(model_code=model)
dat = {'y':np.int32(D[:,2:8])+1,'x':np.int32(D[:,[0,1]]),'N':D.shape[0] ,'K':10,'M':6}
fit6 = sm5.sampling(data=dat,iter=1000, chains=4,thin=2,warmup=500,njobs=2,seed=4)
print pystan.misc._print_stanfit(fit6,pars=['dd','bbeta','c'],digits_summary=2)
saveStanFit(fit6,'fit6')
w=loadStanFit('fit6')
pystanErrorbar(w,keys=['beta','c','dd'])
plt.figure(figsize=(10,4))
c=w['c']
b=w['beta']
d=w['dd']
errorbar(c,x=np.linspace(6.5,8,9))
ax=plt.gca()
plt.plot([-1,100],[0,0],'k',lw=2)
ax.set_yticks(np.median(c,axis=0))
ax.set_yticklabels(np.arange(1,10)+0.5)
plt.grid(b=False,axis='x')
errorbar(b[:,::-1],x=np.arange(9,15),clr='g')
errorbar(d,x=np.arange(15,18),clr='r')
plt.xlim([6,17.5])
ax.set_xticks(range(9,18))
ax.set_xticklabels(il[:6][::-1]+['OT','RC','RT'])
for i in range(d.shape[1]): printCI(d[:,i])
printCI(d[:,2]-d[:,1])
c
def ordinalLogitRvs(beta, c,n,size=1):
assert np.all(np.diff(c)>0) # c must be strictly increasing
def invLogit(x): return 1/(1+np.exp(-x))
p=[1]+list(invLogit(beta-c))+[0]
p=-np.diff(p)
#return np.random.multinomial(n,p,size)
return np.int32(np.round(p*n))
def reformatData(dat):
out=[]
for k in range(dat.size):
out.extend([k]*dat[k])
return np.array(out)
b=np.linspace(-10,7,21)
d=np.median(w['dd'][:,0])
c=np.median(w['c'],axis=0)
S=[];P=[]
for bb in b:
S.append([np.squeeze(ordinalLogitRvs(bb,c,100)),
np.squeeze(ordinalLogitRvs(bb+d,c,100))])
P.append([reformatData(S[-1][0]),reformatData(S[-1][1])])
model='''
data {
int<lower=2> K;
int<lower=0> y1[K];
int<lower=0> y2[K];
}
parameters {
real<lower=-1000,upper=1000> d;
ordered[K-1] c;
}
model {
for (k in 1:(K-1)) c[k]~ uniform(-200,200);
for (k in 1:K){
for (n in 1:y1[k]) k~ ordered_logistic(0.0,c);
for (n in 1:y2[k]) k~ ordered_logistic(d ,c);
}}
'''
sm9=pystan.StanModel(model_code=model)
#(S[k][0]!=0).sum()+1
for k in range(21):
i1=np.nonzero(S[k][0]!=0)[0]
i2=np.nonzero(S[k][1]!=0)[0]
if max((S[k][0]!=0).sum(),(S[k][1]!=0).sum())<9:
s= max(min(i1[0],i2[0])-1,0)
e= min(max(i1[-1],i2[-1])+1,10)
S[k][0]=S[k][0][s:e+1]
S[k][1]=S[k][1][s:e+1]
S[0][0].size
ds=[];cs=[]
for k in range(len(S)):
dat = {'y1':S[k][0],'y2':S[k][1],'K':S[k][0].size}
fit = sm9.sampling(data=dat,iter=1000, chains=4,thin=2,warmup=500,njobs=2,seed=4)
print fit
saveStanFit(fit,'dc%d'%k)
for k in range(21):
i1=np.nonzero(S[k][0]!=0)[0]
i2=np.nonzero(S[k][1]!=0)[0]
if max((S[k][0]!=0).sum(),(S[k][1]!=0).sum())<9:
s= min(i1[0],i2[0])
e= max(i1[-1],i2[-1])
S[k][0]=S[k][0][s:e+1]
S[k][1]=S[k][1][s:e+1]
ds=[];cs=[]
for k in range(len(S)):
if S[k][0].size==1: continue
dat = {'y1':S[k][0],'y2':S[k][1],'K':S[k][0].size}
fit = sm9.sampling(data=dat,iter=1000, chains=4,thin=2,warmup=500,njobs=2,seed=4)
#print fit
saveStanFit(fit,'dd%d'%k)
ds=[];xs=[]
for k in range(b.size):
try:
f=loadStanFit('dd%d'%k)['d']
xs.append(b[k])
ds.append(f)
except:pass
ds=np.array(ds);xs=np.array(xs)
ds.shape
d1=np.median(w['dd'][:,0])
d2=DS[DS[:,0]==1,-2].mean()-DS[DS[:,0]==0,-2].mean()
plt.figure(figsize=(8,4))
plt.plot([-10,5],[d1,d1],'r',alpha=0.5)
res1=errorbar(ds.T,x=xs-0.1)
ax1=plt.gca()
plt.ylim([-2,2])
plt.xlim([-10,5])
plt.grid(b=False,axis='x')
ax2 = ax1.twinx()
res2=np.zeros((b.size,5))
for k in range(b.size):
res2[k,:]=plotCIttest2(y1=P[k][0],y2=P[k][1],x=b[k]+0.1)
plt.ylim([-2/d1*d2,2/d1*d2])
plt.xlim([-10,5])
plt.grid(b=False,axis='y')
plt.plot(np.median(w['beta'],axis=0),[-0.9]*6,'ob')
plt.plot(np.median(w['beta']+np.atleast_2d(w['dd'][:,1]).T,axis=0),[-1.1]*6,'og')
d1=np.median(w['dd'][:,0])
d2=DS[DS[:,0]==1,-2].mean()-DS[DS[:,0]==0,-2].mean()
plt.figure(figsize=(8,4))
ax1=plt.gca()
plt.plot([-10,5],[d1,d1],'r',alpha=0.5)
temp=[list(xs)+list(xs)[::-1],list(res1[:,1])+list(res1[:,2])[::-1]]
ax1.add_patch(plt.Polygon(xy=np.array(temp).T,alpha=0.2,fc='k',ec='k'))
plt.plot(xs,res1[:,0],'k')
plt.ylim([-1.5,2])
plt.xlim([-10,5])
plt.grid(b=False,axis='x')
plt.legend(['True ES','Estimate Ordinal Logit'],loc=8)
plt.ylabel('Estimate Ordinal Logit')
ax2 = ax1.twinx()
temp=[list(b)+list(b)[::-1],list(res2[:,1])+list(res2[:,2])[::-1]]
for t in range(len(temp[0]))[::-1]:
if np.isnan(temp[1][t]):
temp[0].pop(t);temp[1].pop(t)
ax2.add_patch(plt.Polygon(xy=np.array(temp).T,alpha=0.2,fc='m',ec='m'))
plt.plot(b,res2[:,0],'m')
plt.ylim([-1.5/d1*d2,2/d1*d2])
plt.xlim([-10,5])
plt.grid(b=False,axis='y')
plt.plot(np.median(w['beta'],axis=0),[-0.3]*6,'ob')
plt.plot(np.median(w['beta']+np.atleast_2d(w['dd'][:,1]).T,axis=0),[-0.5]*6,'og')
plt.legend(['Estimate T-C','Item Difficulty Orignal Study','Item Difficulty Replication'],loc=4)
plt.ylabel('Estimate T - C',color='m')
for tl in ax2.get_yticklabels():tl.set_color('m')
```
|
github_jupyter
|
# Build a Traffic Sign Recognition Classifier Deep Learning
Some improvements are taken :
- [x] Adding of convolution networks at the same size of previous layer, to get 1x1 layer
- [x] Activation function use 'ReLU' instead of 'tanh'
- [x] Adaptative learning rate, so learning rate is decayed along to training phase
- [x] Enhanced training dataset
## Load and Visualize the Enhanced training dataset
From the original standard German Traffic Signs dataset, we add some 'generalized' sign to cover cases that the classifier can not well interpret small figures inside.
`Also`, in our Enhanced training dataset, each figure is taken from standard library - not from road images, so they are very clear and in high-definition.
*Enhanced traffic signs ↓*
<img src="figures/enhanced_training_dataset_text.png" alt="Drawing" style="width: 600px;"/>
```
# load enhanced traffic signs
import os
import cv2
import matplotlib.pyplot as plot
import numpy
dir_enhancedsign = 'figures\enhanced_training_dataset2'
files_enhancedsign = [os.path.join(dir_enhancedsign, f) for f in os.listdir(dir_enhancedsign)]
# read & resize (32,32) images in enhanced dataset
images_enhancedsign = numpy.array([cv2.cvtColor(cv2.resize(cv2.imread(f), (32,32), interpolation = cv2.INTER_AREA), cv2.COLOR_BGR2RGB) for f in files_enhancedsign])
# plot new test images
fig, axes = plot.subplots(7, 8)
plot.suptitle('Enhanced training dataset')
for i, ax in enumerate(axes.ravel()):
if i < 50:
ax.imshow(images_enhancedsign[i])
# ax.set_title('{}'.format(i))
plot.setp(ax.get_xticklabels(), visible=False)
plot.setp(ax.get_yticklabels(), visible=False)
ax.set_xticks([]), ax.set_yticks([])
ax.axis('off')
plot.draw()
fig.savefig('figures/' + 'enhancedsign' + '.jpg', dpi=700)
print("Image Shape : {}".format(images_enhancedsign[0].shape))
print()
print("Enhanced Training Dataset : {} samples".format(len(images_enhancedsign)))
# classes of enhanced dataset are taken from their filenames
import re
regex = re.compile(r'\d+')
y_enhancedsign = [int(regex.findall(f)[0]) for f in os.listdir(dir_enhancedsign)]
print(y_enhancedsign)
```
*Enhanced German traffic signs dataset ↓*
<img src="figures/enhanced_training_dataset.png" alt="Drawing" style="width: 600px;"/>
**We would have 50 classes in total with new enhanced training dataset :**
```
n_classes_enhanced = len(numpy.unique(y_enhancedsign))
print('n_classes enhanced : {}'.format(n_classes_enhanced))
```
## Load and Visualize the standard German Traffic Signs Dataset
```
# Load pickled data
import pickle
import numpy
# TODO: Fill this in based on where you saved the training and testing data
training_file = 'traffic-signs-data/train.p'
validation_file = 'traffic-signs-data/valid.p'
testing_file = 'traffic-signs-data/test.p'
with open(training_file, mode='rb') as f:
train = pickle.load(f)
with open(validation_file, mode='rb') as f:
valid = pickle.load(f)
with open(testing_file, mode='rb') as f:
test = pickle.load(f)
X_train, y_train = train['features'], train['labels'] # training dataset
X_valid, y_valid = valid['features'], valid['labels'] # validation dataset used in training phase
X_test, y_test = test['features'], test['labels'] # test dataset
n_classes_standard = len(numpy.unique(y_train))
assert(len(X_train) == len(y_train))
assert(len(X_valid) == len(y_valid))
assert(len(X_test) == len(y_test))
print("Image Shape : {}".format(X_train[0].shape))
print()
print("Training Set : {} samples".format(len(X_train)))
print("Validation Set : {} samples".format(len(X_valid)))
print("Test Set : {} samples".format(len(X_test)))
print('n_classes standard : {}'.format(n_classes_standard))
n_classes = n_classes_enhanced
```
## Implementation of LeNet
>http://yann.lecun.com/exdb/publis/pdf/sermanet-ijcnn-11.pdf
Above is the original article of Pierre Sermanet and Yann LeCun in 1998 that we can follow to create LeNet convolutional networks with a good accuracy even for very-beginners in deep-learning.
It's really excited to see that many years of works now could be implemented in just 9 lines of code thank to Keras high-level API !
(low-level API implementation with Tensorflow 1 is roughly 20 lines of code)
>Here is also an interesting medium article :
https://medium.com/@mgazar/lenet-5-in-9-lines-of-code-using-keras-ac99294c8086
```
### Import tensorflow and keras
import tensorflow as tf
from tensorflow import keras
print ("TensorFlow version: " + tf.__version__)
```
### 2-stage ConvNet architecture by Pierre Sermanet and Yann LeCun
We will try to implement the 2-stage ConvNet architecture by Pierre Sermanet and Yann LeCun which is not sequential.
Keras disposes keras.Sequential() API for sequential architectures but it can not handle models with non-linear topology, shared layers or multi-in/output. So the choose of the 2-stage ConvNet architecture by `Pierre Sermanet` and `Yann LeCun` is to challenge us also.
<img src="figures/lenet_2.png" alt="Drawing" style="width: 550px;"/>
>Source: "Traffic Sign Recognition with Multi-Scale Convolutional Networks" by `Pierre Sermanet` and `Yann LeCun`
Here in this architecture, the 1st stage's ouput is feed-forward to the classifier (could be considered as a 3rd stage).
```
#LeNet model
inputs = keras.Input(shape=(32,32,3), name='image_in')
#0 stage :conversion from normalized RGB [0..1] to HSV
layer_HSV = tf.image.rgb_to_hsv(inputs)
#1st stage ___________________________________________________________
#Convolution with ReLU activation
layer1_conv = keras.layers.Conv2D(256, kernel_size=(5,5), strides=1, activation='relu', padding='valid')(layer_HSV)
#Average Pooling
layer1_maxpool = keras.layers.MaxPooling2D(pool_size=(2,2), strides=2, padding='valid')(layer1_conv)
#Conv 1x1
layer1_conv1x1 = keras.layers.Conv2D(256, kernel_size=(14,14), strides=1, activation='relu', padding='valid')(layer1_maxpool)
#2nd stage ___________________________________________________________
#Convolution with ReLU activation
layer2_conv = keras.layers.Conv2D(64, kernel_size=(5,5), strides=1, activation='relu', padding='valid')(layer1_maxpool)
#MaxPooling 2D
layer2_maxpool = keras.layers.MaxPooling2D(pool_size=(2,2), strides=2, padding='valid')(layer2_conv)
#Conv 1x1
layer2_conv1x1 = keras.layers.Conv2D(512, kernel_size=(5,5), strides=1, activation='relu', padding='valid')(layer2_maxpool)
#3rd stage | Classifier ______________________________________________
#Concate
layer3_flatten_1 = keras.layers.Flatten()(layer1_conv1x1)
layer3_flatten_2 = keras.layers.Flatten()(layer2_conv1x1)
layer3_concat = keras.layers.Concatenate()([layer3_flatten_1, layer3_flatten_2])
#Dense (fully-connected)
layer3_dense_1 = keras.layers.Dense(units=129, activation='relu', kernel_initializer="he_normal")(layer3_concat)
# layer3_dense_2 = keras.layers.Dense(units=129, activation='relu', kernel_initializer="he_normal")(layer3_dense_1)
#Dense (fully-connected) | logits for 43 categories (n_classes)
outputs = keras.layers.Dense(units=n_classes)(layer3_dense_1)
LeNet_Model = keras.Model(inputs, outputs, name="LeNet_Model_improved")
#Plot model architecture
LeNet_Model.summary()
keras.utils.plot_model(LeNet_Model, "figures/LeNet_improved_HLS.png", show_shapes=True)
```
### Input preprocessing
#### Color-Space
Pierre Sermanet and Yann LeCun used YUV color space with almost of processings on Y-channel (Y stands for brightness, U and V stand for Chrominance).
#### Normalization
Each channel of an image is in uint8 scale (0-255), we will normalize each channel to 0-1.
Generally, we normalize data to get them center around -1 and 1, to prevent numrical errors due to many steps of matrix operation. Imagine that we have 255x255x255x255xk operation, it could give a huge numerical error if we just have a small error in k.
```
import cv2
def input_normalization(X_in):
X = numpy.float32(X_in/255.0)
return X
# normalization of dataset
# enhanced training dataset is added
X_train_norm = input_normalization(X_train)
X_valid_norm = input_normalization(X_valid)
X_enhancedtrain_norm = input_normalization(images_enhancedsign)
# one-hot matrix
y_train_onehot = keras.utils.to_categorical(y_train, n_classes)
y_valid_onehot = keras.utils.to_categorical(y_valid, n_classes)
y_enhanced_onehot = keras.utils.to_categorical(y_enhancedsign, n_classes)
print(X_train_norm.shape)
print('{0:.4g}'.format(numpy.max(X_train_norm)))
print('{0:.3g}'.format(numpy.min(X_train_norm)))
print(X_enhancedtrain_norm.shape)
print('{0:.4g}'.format(numpy.max(X_enhancedtrain_norm)))
print('{0:.3g}'.format(numpy.min(X_enhancedtrain_norm)))
```
### Training Pipeline
_Optimizer : we use Adam optimizer, better than SDG (Stochastic Gradient Descent)
_Loss function : Cross Entropy by category
_Metrics : accuracy
*learning rate 0.001 work well with our network, it's better to try with small laerning rate in the begining.
```
rate = 0.001
LeNet_Model.compile(
optimizer=keras.optimizers.Nadam(learning_rate = rate, beta_1=0.9, beta_2=0.999, epsilon=1e-07),
loss=keras.losses.CategoricalCrossentropy(from_logits=True),
metrics=["accuracy"])
```
### Real-time data augmentation
```
from tensorflow.keras.preprocessing.image import ImageDataGenerator
datagen_enhanced = ImageDataGenerator(
rotation_range=30.0,
zoom_range=0.5,
width_shift_range=0.5,
height_shift_range=0.5,
featurewise_center=True,
featurewise_std_normalization=True,
horizontal_flip=False)
datagen_enhanced.fit(X_enhancedtrain_norm)
from tensorflow.keras.preprocessing.image import ImageDataGenerator
datagen = ImageDataGenerator(
rotation_range=15.0,
zoom_range=0.2,
width_shift_range=0.1,
height_shift_range=0.1,
featurewise_center=False,
featurewise_std_normalization=False,
horizontal_flip=False)
datagen.fit(X_train_norm)
```
### Train the Model
###### on standard training dataset
```
EPOCHS = 30
BATCH_SIZE = 32
STEPS_PER_EPOCH = int(len(X_train_norm)/BATCH_SIZE)
history_standard_HLS = LeNet_Model.fit(
datagen.flow(X_train_norm, y_train_onehot, batch_size=BATCH_SIZE,shuffle=True),
validation_data=(X_valid_norm, y_valid_onehot),
shuffle=True,
steps_per_epoch=STEPS_PER_EPOCH,
epochs=EPOCHS)
```
###### on enhanced training dataset
```
EPOCHS = 30
BATCH_SIZE = 1
STEPS_PER_EPOCH = int(len(X_enhancedtrain_norm)/BATCH_SIZE)
history_enhanced_HLS = LeNet_Model.fit(
datagen_enhanced.flow(X_enhancedtrain_norm, y_enhanced_onehot, batch_size=BATCH_SIZE,shuffle=True),
shuffle=True, #validation_data=(X_valid_norm, y_valid_onehot),
steps_per_epoch=STEPS_PER_EPOCH,
epochs=EPOCHS)
LeNet_Model.save("LeNet_enhanced_trainingdataset_HLS.h5")
```
### Evaluate the Model
We will use the test dataset to evaluate classification accuracy.
```
#Normalize test dataset
X_test_norm = input_normalization(X_test)
#One-hot matrix
y_test_onehot = keras.utils.to_categorical(y_test, n_classes)
#Load saved model
reconstructed_LeNet_Model = keras.models.load_model("LeNet_enhanced_trainingdataset_HLS.h5")
#Evaluate and display the prediction
result = reconstructed_LeNet_Model.evaluate(X_test_norm,y_test_onehot)
dict(zip(reconstructed_LeNet_Model.metrics_names, result))
pickle.dump(history_enhanced_HLS.history, open( "history_LeNet_enhanced_trainingdataset_enhanced_HLS.p", "wb" ))
pickle.dump(history_standard_HLS.history, open( "history_LeNet_enhanced_trainingdataset_standard_HLS.p", "wb" ))
with open("history_LeNet_enhanced_trainingdataset_standard_HLS.p", mode='rb') as f:
history_ = pickle.load(f)
import matplotlib.pyplot as plt
# Plot training error.
print('\nPlot of training error over 30 epochs:')
fig = plt.figure()
plt.title('Training error')
plt.ylabel('Cost')
plt.xlabel('epoch')
plt.plot(history_['loss'])
plt.plot(history_['val_loss'])
# plt.plot(history.history['loss'])
# plt.plot(history.history['val_loss'])
plt.legend(['train loss', 'val loss'], loc='upper right')
plt.grid()
plt.show()
fig.savefig('figures/Training_loss_LeNet_enhanced_trainingdataset_standard_HLS.png', dpi=500)
# Plot training error.
print('\nPlot of training accuracy over 30 epochs:')
fig = plt.figure()
plt.title('Training accuracy')
plt.ylabel('Accuracy')
plt.ylim([0.4, 1])
plt.xlabel('epoch')
plt.plot(history_['accuracy'])
plt.plot(history_['val_accuracy'])
plt.legend(['training_accuracy', 'validation_accuracy'], loc='lower right')
plt.grid()
plt.show()
fig.savefig('figures/Training_accuracy_LeNet_enhanced_trainingdataset_HLS.png', dpi=500)
```
### Prediction of test dataset with trained model
We will use the test dataset to test trained model's prediction of instances that it has never seen during training.
```
print("Test Set : {} samples".format(len(X_test)))
print('n_classes : {}'.format(n_classes))
X_test.shape
#Normalize test dataset
X_test_norm = input_normalization(X_test)
#One-hot matrix
y_test_onehot = keras.utils.to_categorical(y_test, n_classes)
#Load saved model
reconstructed = keras.models.load_model("LeNet_enhanced_trainingdataset_HLS.h5")
#Evaluate and display the prediction
prediction_performance = reconstructed.evaluate(X_test_norm,y_test_onehot)
dict(zip(reconstructed.metrics_names, prediction_performance))
import matplotlib.pyplot as plot
%matplotlib inline
rows, cols = 4, 12
fig, axes = plot.subplots(rows, cols)
for idx, ax in enumerate(axes.ravel()):
if idx < n_classes_standard :
X_test_of_class = X_test[y_test == idx]
#X_train_0 = X_train_of_class[numpy.random.randint(len(X_train_of_class))]
X_test_0 = X_test_of_class[0]
ax.imshow(X_test_0)
ax.axis('off')
ax.set_title('{:02d}'.format(idx))
plot.setp(ax.get_xticklabels(), visible=False)
plot.setp(ax.get_yticklabels(), visible=False)
else:
ax.axis('off')
#
plot.draw()
fig.savefig('figures/' + 'test_representative' + '.jpg', dpi=700)
#### Prediction for all instances inside the test dataset
y_pred_proba = reconstructed.predict(X_test_norm)
y_pred_class = y_pred_proba.argmax(axis=-1)
### Showing prediction results for 10 first instances
for i, pred in enumerate(y_pred_class):
if i <= 10:
print('Image {} - Target = {}, Predicted = {}'.format(i, y_test[i], pred))
else:
break
```
We will display a confusion matrix on test dataset to figure out our error-rate.
`X_test_norm` : test dataset
`y_test` : test dataset ground truth labels
`y_pred_class` : prediction labels on test dataset
```
confusion_matrix = numpy.zeros([n_classes, n_classes])
```
#### confusion_matrix
`column` : test dataset ground truth labels
`row` : prediction labels on test dataset
`diagonal` : incremented when prediction matches ground truth label
```
for ij in range(len(X_test_norm)):
if y_test[ij] == y_pred_class[ij]:
confusion_matrix[y_test[ij],y_test[ij]] += 1
else:
confusion_matrix[y_pred_class[ij],y_test[ij]] -= 1
column_label = [' L % d' % x for x in range(n_classes)]
row_label = [' P % d' % x for x in range(n_classes)]
# Plot classe representatives
import matplotlib.pyplot as plot
%matplotlib inline
rows, cols = 1, 43
fig, axes = plot.subplots(rows, cols)
for idx, ax in enumerate(axes.ravel()):
if idx < n_classes :
X_test_of_class = X_test[y_test == idx]
X_test_0 = X_test_of_class[0]
ax.imshow(X_test_0)
plot.setp(ax.get_xticklabels(), visible=False)
plot.setp(ax.get_yticklabels(), visible=False)
# plot.tick_params(axis='both', which='both', bottom='off', top='off',
# labelbottom='off', right='off', left='off', labelleft='off')
ax.axis('off')
plot.draw()
fig.savefig('figures/' + 'label_groundtruth' + '.jpg', dpi=3500)
numpy.savetxt("confusion_matrix_LeNet_enhanced_trainingdataset_HLS.csv", confusion_matrix, delimiter=";")
```
#### Thank to confusion matrix, we could identify where to enhance
-[x] training dataset
-[x] real-time data augmentation
-[x] preprocessing
*Extract of confusion matrix of classification on test dataset ↓*
<img src="figures/confusion_matrix_LeNet_enhanced_trainingdataset_HLS.png" alt="Drawing" style="width: 750px;"/>
### Prediction of new instances with trained model
We will use the test dataset to test trained model's prediction of instances that it has never seen during training.
I didn't 'softmax' activation in the last layer of LeNet architecture, so the output prediction is logits. To have prediction confidence level, we can apply softmax function to output logits.
```
# load french traffic signs
import os
import cv2
import matplotlib.pyplot as plot
import numpy
dir_frenchsign = 'french_traffic-signs-data'
images_frenchsign = [os.path.join(dir_frenchsign, f) for f in os.listdir(dir_frenchsign)]
images_frenchsign = numpy.array([cv2.cvtColor(cv2.imread(f), cv2.COLOR_BGR2RGB) for f in images_frenchsign])
# plot new test images
fig, axes = plot.subplots(3, int(len(images_frenchsign)/3))
plot.title('French traffic signs')
for i, ax in enumerate(axes.ravel()):
ax.imshow(images_frenchsign[i])
ax.set_title('{}'.format(i))
plot.setp(ax.get_xticklabels(), visible=False)
plot.setp(ax.get_yticklabels(), visible=False)
ax.set_xticks([]), ax.set_yticks([])
ax.axis('off')
plot.draw()
fig.savefig('figures/' + 'french_sign' + '.jpg', dpi=700)
```
*Enhanced German traffic signs dataset ↓*
<img src="figures/enhanced_training_dataset.png" alt="Drawing" style="width: 700px;"/>
```
# manually label for these new images
y_frenchsign = [13, 31, 29, 24, 26, 27, 33, 17, 15, 34, 12, 2, 2, 4, 2]
n_classes = n_classes_enhanced
# when a sign doesn't present in our training dataset, we'll try to find a enough 'similar' sign to label it.
# image 2 : class 29 differed
# image 3 : class 24, double-sens not existed
# image 5 : class 27 differed
# image 6 : class 33 not existed
# image 7 : class 17, halte-péage not existed
# image 8 : class 15, 3.5t limit not existed
# image 9 : class 15, turn-left inhibition not existed
# image 12 : class 2, ending of 50kmh speed-limit not existed
# image 14 : class 2, 90kmh speed-limit not existed
```
#### it's really intersting that somes common french traffic signs are not present in INI German traffic signs dataset or differed
Whatever our input - evenif it's not present in the training dataset, by using softmax activation our classififer can not say that 'this is a new traffic sign that it doesn't recognize' (sum of probability across all classes is 1), it's just try to find class that probably suit for the input.
```
#Normalize the dataset
X_frenchsign_norm = input_normalization(images_frenchsign)
#One-hot matrix
y_frenchsign_onehot = keras.utils.to_categorical(y_frenchsign, n_classes)
#Load saved model
reconstructed = keras.models.load_model("LeNet_enhanced_trainingdataset_HLS.h5")
#Evaluate and display the prediction performance
prediction_performance = reconstructed.evaluate(X_frenchsign_norm, y_frenchsign_onehot)
dict(zip(reconstructed.metrics_names, prediction_performance))
#### Prediction for all instances inside the test dataset
y_pred_logits = reconstructed.predict(X_frenchsign_norm)
y_pred_proba = tf.nn.softmax(y_pred_logits).numpy()
y_pred_class = y_pred_proba.argmax(axis=-1)
### Showing prediction results
for i, pred in enumerate(y_pred_class):
print('Image {} - Target = {}, Predicted = {}'.format(i, y_frenchsign[i], pred))
```
*French traffic signs to classsify ↓*
<img src="figures/french_sign_compare_german_INI_enhanced.jpg" alt="Drawing" style="width: 750px;"/>
```
#### plot softmax probs along with traffic sign examples
n_img = X_frenchsign_norm.shape[0]
fig, axarray = plot.subplots(n_img, 2)
plot.suptitle('Visualization of softmax probabilities', fontweight='bold')
for r in range(0, n_img):
axarray[r, 0].imshow(numpy.squeeze(images_frenchsign[r]))
axarray[r, 0].set_xticks([]), axarray[r, 0].set_yticks([])
plot.setp(axarray[r, 0].get_xticklabels(), visible=False)
plot.setp(axarray[r, 0].get_yticklabels(), visible=False)
axarray[r, 1].bar(numpy.arange(n_classes), y_pred_proba[r])
axarray[r, 1].set_ylim([0, 1])
plot.setp(axarray[r, 1].get_yticklabels(), visible=False)
plot.draw()
fig.savefig('figures/' + 'french_sign_softmax_visuali_LeNet_enhanced_trainingdataset_HLS' + '.jpg', dpi=700)
K = 3
#### print top K predictions of the model for each example, along with confidence (softmax score)
for i in range(len(images_frenchsign)):
print('Top {} model predictions for image {} (Target is {:02d})'.format(K, i, y_frenchsign[i]))
top_3_idx = numpy.argsort(y_pred_proba[i])[-3:]
top_3_values = y_pred_proba[i][top_3_idx]
top_3_logits = y_pred_logits[i][top_3_idx]
for k in range(K):
print(' Prediction = {:02d} with probability {:.4f} (logit is {:.4f})'.format(top_3_idx[k], top_3_values[k], top_3_logits[k]))
```
*Visualization of softmax probabilities ↓*
<img src="figures/french_sign_softmax_visuali_LeNet_enhanced_trainingdataset_HLS.jpg" alt="Drawing" style="width: 750px;"/>
## Visualization of layers
```
### Import tensorflow and keras
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import Model
import matplotlib.pyplot as plot
print ("TensorFlow version: " + tf.__version__)
# Load pickled data
import pickle
import numpy
training_file = 'traffic-signs-data/train.p'
with open(training_file, mode='rb') as f:
train = pickle.load(f)
X_train, y_train = train['features'], train['labels'] # training dataset
n_classes = len(numpy.unique(y_train))
import cv2
def input_normalization(X_in):
X = numpy.float32(X_in/255.0)
return X
# normalization of dataset
X_train_norm = input_normalization(X_train)
# one-hot matrix
y_train_onehot = keras.utils.to_categorical(y_train, n_classes)
#Load saved model
reconstructed = keras.models.load_model("LeNet_enhanced_trainingdataset_HLS.h5")
#Build model for layer display
layers_output = [layer.output for layer in reconstructed.layers]
outputs_model = Model(inputs=reconstructed.input, outputs=layers_output)
outputs_history = outputs_model.predict(X_train_norm[900].reshape(1,32,32,3))
```
#### Display analized input
```
plot.imshow(X_train[900])
def display_layer(outputs_history, col_size, row_size, layer_index):
activation = outputs_history[layer_index]
activation_index = 0
fig, ax = plot.subplots(row_size, col_size, figsize=(row_size*2.5,col_size*1.5))
for row in range(0,row_size):
for col in range(0,col_size):
ax[row][col].axis('off')
if activation_index < activation.shape[3]:
ax[row][col].imshow(activation[0, :, :, activation_index]) # , cmap='gray'
activation_index += 1
display_layer(outputs_history, 3, 2, 1)
display_layer(outputs_history, 8, 8, 2)
display_layer(outputs_history, 8, 8, 3)
display_layer(outputs_history, 8, 8, 4)
```
|
github_jupyter
|
# Simulating Grover's Search Algorithm with 2 Qubits
```
import numpy as np
from matplotlib import pyplot as plt
%matplotlib inline
```
Define the zero and one vectors
Define the initial state $\psi$
```
zero = np.matrix([[1],[0]]);
one = np.matrix([[0],[1]]);
psi = np.kron(zero,zero);
print(psi)
```
Define the gates we will use:
$
\text{Id} = \begin{pmatrix}
1 & 0 \\
0 & 1
\end{pmatrix},
\quad
X = \begin{pmatrix}
0 & 1 \\
1 & 0
\end{pmatrix},
\quad
Z = \begin{pmatrix}
1 & 0 \\
0 & -1
\end{pmatrix},
\quad
H = \frac{1}{\sqrt{2}}\begin{pmatrix}
1 & 1 \\
1 & -1
\end{pmatrix},
\quad
\text{CNOT} = \begin{pmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & 1 & 0
\end{pmatrix},
\quad
CZ = (\text{Id} \otimes H) \text{ CNOT } (\text{Id} \otimes H)
$
```
Id = np.matrix([[1,0],[0,1]]);
X = np.matrix([[0,1],[1,0]]);
Z = np.matrix([[1,0],[0,-1]]);
H = np.sqrt(0.5) * np.matrix([[1,1],[1,-1]]);
CNOT = np.matrix([[1,0,0,0],[0,1,0,0],[0,0,0,1],[0,0,1,0]]);
CZ = np.kron(Id,H).dot(CNOT).dot(np.kron(Id,H));
print(CZ)
```
Define the oracle for Grover's algorithm (take search answer to be "10")
$
\text{oracle} = \begin{pmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & -1 & 0 \\
0 & 0 & 0 & 1
\end{pmatrix}
= (Z \otimes \text{Id}) CZ
$
Use different combinations of $Z \otimes \text{Id}$ to change where search answer is.
```
oracle = np.kron(Z,Id).dot(CZ);
print(oracle)
```
Act the H gates on the input vector and apply the oracle
```
psi0 = np.kron(H,H).dot(psi);
psi1 = oracle.dot(psi0);
print(psi1)
```
Remember that when we measure the result ("00", "01", "10", "11") is chosen randomly with probabilities given by the vector elements squared.
```
print(np.multiply(psi1,psi1))
```
There is no difference between any of the probabilities. It's still just a 25% chance of getting the right answer.
We need some of gates after the oracle before measuring to converge on the right answer.
These gates do the operation $W = \frac{1}{2}\begin{pmatrix}
-1 & 1 & 1 & 1 \\
1 & -1 & 1 & 1 \\
1 & 1 & -1 & 1 \\
1 & 1 & 1 & -1
\end{pmatrix}
=
(H \otimes H)(Z \otimes Z) CZ (H \otimes H)
$
Notice that if the matrix W is multiplied by the vector after the oracle, W $\frac{1}{2}\begin{pmatrix}
1 \\
1 \\
-1 \\
1
\end{pmatrix}
= \begin{pmatrix}
0 \\
0 \\
1 \\
0
\end{pmatrix} $,
every vector element decreases, except the correct answer element which increases. This would be true if if we chose a different place for the search result originally.
```
W = np.kron(H,H).dot(np.kron(Z,Z)).dot(CZ).dot(np.kron(H,H));
print(W)
psif = W.dot(psi1);
print(np.multiply(psif,psif))
x = [0,1,2,3];
xb = [0.25,1.25,2.25,3.25];
labels=['00', '01', '10', '11'];
plt.axis([-0.5,3.5,-1.25,1.25]);
plt.xticks(x,labels);
plt.bar(x, np.ravel(psi0), 1/1.5, color="red");
plt.bar(xb, np.ravel(np.multiply(psi0,psi0)), 1/2., color="blue");
labels=['00', '01', '10', '11'];
plt.axis([-0.5,3.5,-1.25,1.25]);
plt.xticks(x,labels);
plt.bar(x, np.ravel(psi1), 1/1.5, color="red");
plt.bar(xb, np.ravel(np.multiply(psi1,psi1)), 1/2., color="blue");
labels=['00', '01', '10', '11'];
plt.axis([-0.5,3.5,-1.25,1.25]);
plt.xticks(x,labels);
plt.bar(x, np.ravel(psif), 1/1.5, color="red");
plt.bar(xb, np.ravel(np.multiply(psif,psif)), 1/2., color="blue");
```
|
github_jupyter
|
<table class="ee-notebook-buttons" align="left">
<td><a target="_blank" href="https://github.com/giswqs/earthengine-py-notebooks/tree/master/Visualization/image_color_ramp.ipynb"><img width=32px src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" /> View source on GitHub</a></td>
<td><a target="_blank" href="https://nbviewer.jupyter.org/github/giswqs/earthengine-py-notebooks/blob/master/Visualization/image_color_ramp.ipynb"><img width=26px src="https://upload.wikimedia.org/wikipedia/commons/thumb/3/38/Jupyter_logo.svg/883px-Jupyter_logo.svg.png" />Notebook Viewer</a></td>
<td><a target="_blank" href="https://mybinder.org/v2/gh/giswqs/earthengine-py-notebooks/master?filepath=Visualization/image_color_ramp.ipynb"><img width=58px src="https://mybinder.org/static/images/logo_social.png" />Run in binder</a></td>
<td><a target="_blank" href="https://colab.research.google.com/github/giswqs/earthengine-py-notebooks/blob/master/Visualization/image_color_ramp.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" /> Run in Google Colab</a></td>
</table>
## Install Earth Engine API
Install the [Earth Engine Python API](https://developers.google.com/earth-engine/python_install) and [geehydro](https://github.com/giswqs/geehydro). The **geehydro** Python package builds on the [folium](https://github.com/python-visualization/folium) package and implements several methods for displaying Earth Engine data layers, such as `Map.addLayer()`, `Map.setCenter()`, `Map.centerObject()`, and `Map.setOptions()`.
The following script checks if the geehydro package has been installed. If not, it will install geehydro, which automatically install its dependencies, including earthengine-api and folium.
```
import subprocess
try:
import geehydro
except ImportError:
print('geehydro package not installed. Installing ...')
subprocess.check_call(["python", '-m', 'pip', 'install', 'geehydro'])
```
Import libraries
```
import ee
import folium
import geehydro
```
Authenticate and initialize Earth Engine API. You only need to authenticate the Earth Engine API once.
```
try:
ee.Initialize()
except Exception as e:
ee.Authenticate()
ee.Initialize()
```
## Create an interactive map
This step creates an interactive map using [folium](https://github.com/python-visualization/folium). The default basemap is the OpenStreetMap. Additional basemaps can be added using the `Map.setOptions()` function.
The optional basemaps can be `ROADMAP`, `SATELLITE`, `HYBRID`, `TERRAIN`, or `ESRI`.
```
Map = folium.Map(location=[40, -100], zoom_start=4)
Map.setOptions('HYBRID')
```
## Add Earth Engine Python script
```
# Load SRTM Digital Elevation Model data.
image = ee.Image('CGIAR/SRTM90_V4');
# Define an SLD style of discrete intervals to apply to the image.
sld_intervals = \
'<RasterSymbolizer>' + \
'<ColorMap type="intervals" extended="false" >' + \
'<ColorMapEntry color="#0000ff" quantity="0" label="0"/>' + \
'<ColorMapEntry color="#00ff00" quantity="100" label="1-100" />' + \
'<ColorMapEntry color="#007f30" quantity="200" label="110-200" />' + \
'<ColorMapEntry color="#30b855" quantity="300" label="210-300" />' + \
'<ColorMapEntry color="#ff0000" quantity="400" label="310-400" />' + \
'<ColorMapEntry color="#ffff00" quantity="1000" label="410-1000" />' + \
'</ColorMap>' + \
'</RasterSymbolizer>';
# Define an sld style color ramp to apply to the image.
sld_ramp = \
'<RasterSymbolizer>' + \
'<ColorMap type="ramp" extended="false" >' + \
'<ColorMapEntry color="#0000ff" quantity="0" label="0"/>' + \
'<ColorMapEntry color="#00ff00" quantity="100" label="100" />' + \
'<ColorMapEntry color="#007f30" quantity="200" label="200" />' + \
'<ColorMapEntry color="#30b855" quantity="300" label="300" />' + \
'<ColorMapEntry color="#ff0000" quantity="400" label="400" />' + \
'<ColorMapEntry color="#ffff00" quantity="500" label="500" />' + \
'</ColorMap>' + \
'</RasterSymbolizer>';
# Add the image to the map using both the color ramp and interval schemes.
Map.setCenter(-76.8054, 42.0289, 8);
Map.addLayer(image.sldStyle(sld_intervals), {}, 'SLD intervals');
Map.addLayer(image.sldStyle(sld_ramp), {}, 'SLD ramp');
```
## Display Earth Engine data layers
```
Map.setControlVisibility(layerControl=True, fullscreenControl=True, latLngPopup=True)
Map
```
|
github_jupyter
|
# Ingeniería de Características
En las clases previas vimos las ideas fundamentales de machine learning, pero todos los ejemplos asumían que ya teníamos los datos numéricos en un formato ordenado de tamaño ``[n_samples, n_features]``.
En la realidad son raras las ocasiones en que los datos vienen así, _llegar y llevar_.
Con esto en mente, uno de los pasos más importantes en la práctica de machine learging es la _ingeniería de características_ (_feature engineering_), que es tomar cualquier información que tengas sobre tu problema y convertirla en números con los que construirás tu matriz de características.
En esta sección veremos dos ejemplos comunes de _tareas_ de ingeniería de características: cómo representar _datos categóricos_ y cómo representar _texto_.
Otras características más avanzandas, como el procesamiento de imágenes, quedarán para el fin del curso.
Adicionalmente, discutiremos _características derivadas_ para incrementar la complejidad del modelo y la _imputación_ de datos perdidos.
En ocasiones este proceso se conoce como _vectorización_, ya que se refiere a convertir datos arbitrarios en vectores bien definidos.
## Características Categóricas
Un tipo común de datos no numéricos son los datos _categóricos_.
Por ejemplo, imagina que estás explorando datos de precios de propiedad, y junto a variables numéricas como precio (_price_) y número de habitaciones (_rooms_), también tienes información del barrio (_neighborhood_) de cada propiedad.
Por ejemplo, los datos podrían verse así:
```
data = [
{'price': 850000, 'rooms': 4, 'neighborhood': 'Queen Anne'},
{'price': 700000, 'rooms': 3, 'neighborhood': 'Fremont'},
{'price': 650000, 'rooms': 3, 'neighborhood': 'Wallingford'},
{'price': 600000, 'rooms': 2, 'neighborhood': 'Fremont'}
]
```
Podrías estar tentade a codificar estos datos directamente con un mapeo numérico:
```
{'Queen Anne': 1, 'Fremont': 2, 'Wallingford': 3};
```
Resulta que esto no es una buena idea. En Scikit-Learn, y en general, los modelos asumen que los datos numéricos reflejan cantidades algebraicas.
Usar un mapeo así implica, por ejemplo, que *Queen Anne < Fremont < Wallingford*, o incluso que *Wallingford - Queen Anne = Fremont*, lo que no tiene mucho sentido.
Una técnica que funciona en estas situaciones es _codificación caliente_ (_one-hot encoding_), que crea columnas numéricas que indican la presencia o ausencia de la categoría correspondiente, con un valor de 1 o 0 respectivamente.
Cuando tus datos son una lista de diccionarios, la clase ``DictVectorizer`` se encarga de la codificación por ti:
```
from sklearn.feature_extraction import DictVectorizer
vec = DictVectorizer(sparse=False, dtype=int)
vec.fit_transform(data)
```
Nota que la característica `neighborhood` se ha expandido en tres columnas separadas, representando las tres etiquetas de barrio, y que cada fila tiene un 1 en la columna asociada al barrio respectivo.
Teniendo los datos codificados de esa manera, se puede proceder a ajustar un modelo en Scikit-Learn.
Para ver el significado de cada columna se puede hacer lo siguiente:
```
vec.get_feature_names()
```
Hay una clara desventaja en este enfoque: si las categorías tienen muchos valores posibles, el dataset puede crecer demasiado.
Sin embargo, como los datos codificados contienen principalmente ceros, una matriz dispersa puede ser una solucion eficiente:
```
vec = DictVectorizer(sparse=True, dtype=int)
vec.fit_transform(data)
```
Varios (pero no todos) de los estimadores en Scikit-Learn aceptan entradas dispersas. ``sklearn.preprocessing.OneHotEncoder`` y ``sklearn.feature_extraction.FeatureHasher`` son dos herramientas adicionales que permiten trabajar con este tipo de características.
## Texto
Otra necesidad común es convertir texto en una serie de números que representen su contenido.
Por ejemplo, mucho del análisis automático del contenido generado en redes sociales depende de alguna manera de codificar texto como números.
Uno de los métodos más simples es a través de _conteo de palabras_ (_word counts_): tomas cada pedazo del texto, cuentas las veces que aparece cada palabra en él, y pones los resultados en una table.
Por ejemplo, considera las siguientes tres frases:
```
sample = ['problem of evil',
'evil queen',
'horizon problem']
```
Para vectorizar estos datos construiríamos una columna para las palabras "problem," "evil,", "horizon," etc.
Hacer esto a mano es posible, pero nos podemos ahorrar el tedio utilizando el ``CountVectorizer`` de Scikit-Learn:
```
from sklearn.feature_extraction.text import CountVectorizer
vec = CountVectorizer()
X = vec.fit_transform(sample)
X
```
El resultado es una matriz dispersa que contiene cada vez que aparece cada palabra en los textos. Para inspeccionarlo fácilmente podemos convertir esto en un ``DataFrame``:
```
import pandas as pd
pd.DataFrame(X.toarray(), columns=vec.get_feature_names())
```
Todavía falta algo. Este enfoque puede tener problemas: el conteo de palabras puede hacer que algunas características pesen más que otras debido a la frecuencia con la que utilizamos las palabras, y esto puede ser sub-óptimo en algunos algoritmos de clasificación.
Una manera de considerar esto es utilizar el modelo _frecuencia de términos-frecuencia inversa de documents_ (_TF-IDF_), que da peso a las palabras de acuerdo a qué tan frecuentemente aparecen en los documentos, pero también qué tan únicas son para cada documento.
La sintaxis para aplicar TF-IDF es similar a la que hemos visto antes:
```
from sklearn.feature_extraction.text import TfidfVectorizer
vec = TfidfVectorizer()
X = vec.fit_transform(sample)
pd.DataFrame(X.toarray(), columns=vec.get_feature_names())
```
Esto lo veremos en más detalle en la clase de Naive Bayes.
## Características Derivadas
Otro tipo útil de característica es aquella derivada matemáticamente desde otras características en los datos de entrada.
Vimos un ejemplo en la clase de Hiperparámetros cuando construimos características polinomiales desde los datos.
Vimos que se puede convertir una regresión lineal en una polinomial sin usar un modelo distinto, sino que transformando los datos de entrada.
Esto es conocido como _función de regresión base_ (_basis function regression_), y lo exploraremos en la clase de Regresión Lineal.
Por ejemplo, es claro que los siguientes datos no se pueden describir por una línea recta:
```
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
x = np.array([1, 2, 3, 4, 5])
y = np.array([4, 2, 1, 3, 7])
plt.scatter(x, y);
```
Si ajustamos una recta a los datos usando ``LinearRegression`` obtendremos un resultado óptimo:
```
from sklearn.linear_model import LinearRegression
X = x[:, np.newaxis]
model = LinearRegression().fit(X, y)
yfit = model.predict(X)
plt.scatter(x, y)
plt.plot(x, yfit);
```
Es óptimo, pero también queda claro que necesitamos un modelo más sofisticado para describir la relació entre $x$ e $y$.
Una manera de lograrlo es transformando los datos, agregando columnas o características adicionales que le den más flexibilidad al modelo. Por ejemplo, podemos agregar características polinomiales de la siguiente forma:
```
from sklearn.preprocessing import PolynomialFeatures
poly = PolynomialFeatures(degree=3, include_bias=False)
X2 = poly.fit_transform(X)
print(X2)
```
Esta matriz de características _derivada_ tiene una columna que representa a $x$, una segunda columna que representa $x^2$, y una tercera que representa $x^3$.
Calcular una regresión lineal en esta entrada da un ajuste más cercano a nuestros datos:
```
model = LinearRegression().fit(X2, y)
yfit = model.predict(X2)
plt.scatter(x, y)
plt.plot(x, yfit);
```
La idea de mejorar un modelo sin cambiarlo, sino que transformando la entrada que recibe, es fundamental para muchas de las técnicas de machine learning más poderosas.
Exploraremos más esta idea en la clase de Regresión Lineal.
Este camino es motivante y se puede generalizar con las técnicas conocidas como _métodos de kernel_, que exploraremos en la clase de _Support Vector Machines_ (SVM).
## Imputación de Datos Faltantes
Una necesidad común en la ingeniería de características es la manipulación de datos faltantes.
En clases anteriores es posible que hayan visto el valor `NaN` en un `DataFrame`, utilizado para marcar valores que no existen.
Por ejemplo, podríamos tener un dataset que se vea así:
```
from numpy import nan
X = np.array([[ nan, 0, 3 ],
[ 3, 7, 9 ],
[ 3, 5, 2 ],
[ 4, nan, 6 ],
[ 8, 8, 1 ]])
y = np.array([14, 16, -1, 8, -5])
```
Antes de aplicar un modelo a estos datos necesitamos reemplazar esos datos faltantes con algún valor apropiado de relleno.
Esto es conocido como _imputación_ de valores faltantes, y las estrategias para hacerlo varían desde las más simples (como rellenar con el promedio de cada columna) hasta las más sofisticadas (como completar la matrix con un modelo robusto para esos casos). Estos últimos enfoques suelen ser específicos para cada aplicación, así que no los veremos en el curso.
La clase `Imputer` de Scikit-Learn provee en enfoque base de imputación que calcula el promedio, la media, o el valor más frecuente:
```
from sklearn.preprocessing import Imputer
imp = Imputer(strategy='mean')
X2 = imp.fit_transform(X)
X2
```
Como vemos, al aplicar el imputador los dos valores que faltaban fueron reemplazados por el promedio de los valores presentes en las columnas respectivas.
Ahora que tenemos una matriz sin valores faltantes, podemos usarla con la instancia de un modelo, en este caso, una regresión lineal:
```
model = LinearRegression().fit(X2, y)
model.predict(X2)
```
## Cadena de Procesamiento (_Pipeline_)
Considerando los ejemplos que hemos visto, es posible que sea tedioso hacer cada una de estas transformaciones a mano. En ocasiones querremos automatizar la cadena de procesamiento para un modelo. Imagina una secuencia como la siguiente:
1. Imputar valores usando el promedio.
2. Transformar las características incluyendo un factor cuadrático.
3. Ajustar una regresión lineal.
Para encadenar estas etapas Scikit-Learn provee una clase ``Pipeline``, que se usa como sigue:
```
from sklearn.pipeline import make_pipeline
model = make_pipeline(Imputer(strategy='mean'),
PolynomialFeatures(degree=2),
LinearRegression())
```
Esta cadena o _pipeline_ se ve y actúa como un objeto estándar de Scikit-Learn, por lo que podemos utilizarla en todo lo que hemos visto hasta ahora que siga la receta de uso de Scikit-Learn.
```
model.fit(X, y) # X con valores faltantes
print(y)
print(model.predict(X))
```
Todos los pasos del modelo se aplican de manera automática.
¡Ojo! Por simplicidad hemos aplicado el modelo a los mismos datos con los que lo hemos entrenado, por eso el resultado es perfecto (vean el material de la clase pasada para recordar por qué esto no es un buen criterio para evaluar el modelo).
En las próximas clases seguiremos utilizando _Pipelines_ para estructurar nuestro análisis.

Este notebook contiene un extracto del libro [Python Data Science Handbook](http://shop.oreilly.com/product/0636920034919.do) por Jake VanderPlas; el contenido también está disponible en [GitHub](https://github.com/jakevdp/PythonDataScienceHandbook).
El texto se distribuye bajo una licencia [CC-BY-NC-ND](https://creativecommons.org/licenses/by-nc-nd/3.0/us/legalcode), y el código se distribuye bajo la licencia [MIT](https://opensource.org/licenses/MIT). Si te parece que este contenido es útil, por favor considera apoyar el trabajo [comprando el libro](http://shop.oreilly.com/product/0636920034919.do).
Traducción al castellano por [Eduardo Graells-Garrido](http://datagramas.cl), liberada bajo las mismas condiciones.
|
github_jupyter
|
# Pre-training VGG16 for Distillation
```
import torch
import torch.nn as nn
from src.data.dataset import get_dataloader
import torchvision.transforms as transforms
import numpy as np
import matplotlib.pyplot as plt
DEVICE = torch.device("cuda" if torch.cuda.is_available() else "cpu")
print(DEVICE)
SEED = 0
BATCH_SIZE = 32
LR = 5e-4
NUM_EPOCHES = 25
np.random.seed(SEED)
torch.manual_seed(SEED)
torch.cuda.manual_seed(SEED)
torch.backends.cudnn.benchmark = False
torch.backends.cudnn.deterministic = True
```
## Preprocessing
```
transform = transforms.Compose([
transforms.RandomHorizontalFlip(),
#transforms.RandomVerticalFlip(),
transforms.ToTensor(),
transforms.Normalize((0.5,), (0.5,))
])
train_loader, val_loader, test_loader = get_dataloader("./data/CIFAR10/", BATCH_SIZE)
```
## Model
```
from src.models.model import VGG16_classifier
classes = 10
hidden_size = 512
dropout = 0.3
model = VGG16_classifier(classes, hidden_size, preprocess_flag=False, dropout=dropout).to(DEVICE)
model
for img, label in train_loader:
img = img.to(DEVICE)
label = label.to(DEVICE)
print("Input Image Dimensions: {}".format(img.size()))
print("Label Dimensions: {}".format(label.size()))
print("-"*100)
out = model(img)
print("Output Dimensions: {}".format(out.size()))
break
```
## Training
```
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(params=model.parameters(), lr=LR)
loss_hist = {"train accuracy": [], "train loss": [], "val accuracy": []}
for epoch in range(1, NUM_EPOCHES+1):
model.train()
epoch_train_loss = 0
y_true_train = []
y_pred_train = []
for batch_idx, (img, labels) in enumerate(train_loader):
img = img.to(DEVICE)
labels = labels.to(DEVICE)
preds = model(img)
loss = criterion(preds, labels)
optimizer.zero_grad()
loss.backward()
optimizer.step()
y_pred_train.extend(preds.detach().argmax(dim=-1).tolist())
y_true_train.extend(labels.detach().tolist())
epoch_train_loss += loss.item()
with torch.no_grad():
model.eval()
y_true_test = []
y_pred_test = []
for batch_idx, (img, labels) in enumerate(val_loader):
img = img.to(DEVICE)
label = label.to(DEVICE)
preds = model(img)
y_pred_test.extend(preds.detach().argmax(dim=-1).tolist())
y_true_test.extend(labels.detach().tolist())
test_total_correct = len([True for x, y in zip(y_pred_test, y_true_test) if x==y])
test_total = len(y_pred_test)
test_accuracy = test_total_correct * 100 / test_total
loss_hist["train loss"].append(epoch_train_loss)
total_correct = len([True for x, y in zip(y_pred_train, y_true_train) if x==y])
total = len(y_pred_train)
accuracy = total_correct * 100 / total
loss_hist["train accuracy"].append(accuracy)
loss_hist["val accuracy"].append(test_accuracy)
print("-------------------------------------------------")
print("Epoch: {} Train mean loss: {:.8f}".format(epoch, epoch_train_loss))
print(" Train Accuracy%: ", accuracy, "==", total_correct, "/", total)
print(" Validation Accuracy%: ", test_accuracy, "==", test_total_correct, "/", test_total)
print("-------------------------------------------------")
plt.plot(loss_hist["train accuracy"])
plt.plot(loss_hist["val accuracy"])
plt.xlabel("Epoch")
plt.ylabel("Loss")
plt.show()
plt.plot(loss_hist["train loss"])
plt.xlabel("Epoch")
plt.ylabel("Loss")
plt.show()
```
## Testing
```
with torch.no_grad():
model.eval()
y_true_test = []
y_pred_test = []
for batch_idx, (img, labels) in enumerate(test_loader):
img = img.to(DEVICE)
label = label.to(DEVICE)
preds = model(img)
y_pred_test.extend(preds.detach().argmax(dim=-1).tolist())
y_true_test.extend(labels.detach().tolist())
total_correct = len([True for x, y in zip(y_pred_test, y_true_test) if x==y])
total = len(y_pred_test)
accuracy = total_correct * 100 / total
print("Test Accuracy%: ", accuracy, "==", total_correct, "/", total)
```
## Saving Model Weights
```
torch.save(model.state_dict(), "./trained_models/vgg16_cifar10.pt")
```
|
github_jupyter
|
# _Mini Program - Working with SQLLite DB using Python_
### <font color=green>Objective -</font>
<font color=blue>1. This program gives an idea how to connect with SQLLite DB using Python and perform data manipulation </font><br>
<font color=blue>2. There are 2 ways in which tables are create below to help you understand the robustness of this language</font>
### <font color=green>Step 1 - Import required libraries</font>
#### <font color=blue>In this program we make used of 3 libraries</font>
#### <font color=blue>1. sqlite3 - This module help to work with sql interface. It helps in performing db operations in sqllite database</font>
#### <font color=blue>2. pandas - This module provides high performance and easy to use data manipulation and data analysis functionalities</font>
#### <font color=blue>3. os - This module provides function to interact with operating system with easy use</font>
```
#Importing the required modules
import sqlite3
import pandas as pd
import os
```
### <font color=green>Step 2 - Creating a function to drop the table</font>
#### <font color=blue>Function helps to re-create a reusable component that can be used conviniently and easily in other part of the code</font>
#### <font color=blue>In Line 1 - We state the function name and specify the parameter being passed. In this case, the parameter is the table name</font>
#### <font color=blue>In Line 2 - We write the sql query to be executed</font>
#### <font color=blue>In Line 3 - We execute the query using the cursor object</font>
```
#Creating a function to drop the table if it exists
def dropTbl(tablename):
dropTblStmt = "DROP TABLE IF EXISTS " + tablename
c.execute(dropTblStmt)
```
### <font color=green>Step 3 - We create the database in which our table will reside</font>
#### <font color=blue>In Line 1 - We are removing the already existing database file</font>
#### <font color=blue>In Line 2 - We use connect function from the sqlite3 module to create a database studentGrades.db and establish a connection</font>
#### <font color=blue>In Line 3 - We create a context of the database connection. This help to run all the database queries</font>
```
#Removing the database file
os.remove('studentGrades.db')
#Creating a new database - studentGrades.db
conn = sqlite3.connect("studentGrades.db")
c = conn.cursor()
```
### <font color=green>Step 4 - We create a table in sqllite DB using data defined in the excel file</font>
#### <font color=blue>This is the first method in which you can create a table. You can use to_sql function directly to read a dataframe and dump all it's content to the table</font>
#### <font color=blue>In Line 1 - We are making use of dropTbl function created above to drop the table</font>
#### <font color=blue>In Line 2 - We are creating a dataframe from the data read from the csv</font>
#### <font color=blue>In Line 3 - We use to_sql function to push the data into the table. The first row of the file becomes the column name of the tables</font>
#### <font color=blue>We repeat the above steps for all the 3 files to create 3 tables - STUDENT, GRADES and SUBJECTS</font>
```
#Reading data from csv file - student details, grades and subject
dropTbl('STUDENT')
student_details = pd.read_csv("Datafiles/studentDetails.csv")
student_details.to_sql('STUDENT',conn,index = False)
dropTbl('GRADES')
student_grades = pd.read_csv('Datafiles/studentGrades.csv')
student_grades.to_sql('GRADES',conn,index = False)
dropTbl('SUBJECTS')
subjects = pd.read_csv("Datafiles/subjects.csv")
subjects.to_sql('SUBJECTS',conn,index = False)
```
### <font color=green>Step 5 - We create a master table STUDENT_GRADE_MASTER where we can colate the data from the individual tables by performing the joining operations</font>
#### <font color=blue>In Line 1 - We are making use of dropTbl function created above to drop the table</font>
#### <font color=blue>In Line 2 - We are writing sql query for table creation</font>
#### <font color=blue>In Line 3 - We are using the cursor created above to execute the sql statement</font>
#### <font color=blue>In Line 4 - We are using the second method of inserting data into the table. We are writing a query to insert the data after joining the data from all the tables</font>
#### <font color=blue>In Line 5 - We are using the cursor created above to execute the sql statement</font>
#### <font color=blue>In Line 6 - We are doing a commit operation. Since INSERT operation is a ddl, we have to perform a commit operation to register it into the database</font>
```
#Creating a table to store student master data
dropTbl('STUDENT_GRADE_MASTER')
createTblStmt = '''CREATE TABLE STUDENT_GRADE_MASTER
([Roll_number] INTEGER,
[Student_Name] TEXT,
[Stream] TEXT,
[Subject] TEXT,
[Marks] INTEGER
)'''
c.execute(createTblStmt)
#Inserting data into the master table by joining the tables mentioned above
queryMaster = '''INSERT INTO STUDENT_GRADE_MASTER(Roll_number,Student_Name,Stream,Subject,Marks)
SELECT g.roll_number, s.student_name, stream, sub.subject, marks from GRADES g
LEFT OUTER JOIN STUDENT s on g.roll_number = s.roll_number
LEFT OUTER JOIN SUBJECTS sub on g.subject_code = sub.subject_code'''
c.execute(queryMaster)
c.execute("COMMIT")
```
### <font color=green>Step 6 - We can perform data fetch like we do in sqls using this sqlite3 module</font>
#### <font color=blue>In Line 1 - We are writing a query to find the number of records in the master table</font>
#### <font color=blue>In Line 2 - We are executing the above created query</font>
#### <font color=blue>In Line 3 - fetchall function is used to get the result returned by the query. The result will be in the form of a list of tuples</font>
#### <font color=blue>In Line 4 - We are writing another query to find the maximum marks recorded for each subject</font>
#### <font color=blue>In Line 5 - We are executing the above created query</font>
#### <font color=blue>In Line 6 - fetchall function is used to get the result returned by the query. The result will be in the form of a list of tuples</font>
#### <font color=blue>In Line 7 - We are writing another query to find the percentage of marks obtained by each student in the class</font>
#### <font color=blue>In Line 8 - We are executing the above created query</font>
#### <font color=blue>In Line 9 - fetchall function is used to get the result returned by the query. The result will be in the form of a list of tuples</font>
```
#Finding the key data from the master table
#1. Find the number of records in the master table
query_count = '''SELECT COUNT(*) FROM STUDENT_GRADE_MASTER'''
c.execute(query_count)
number_of_records = c.fetchall()
print(number_of_records)
#2. Maximum marks for each subject
query_max_marks = '''SELECT Subject,max(Marks) as 'Max_Marks' from STUDENT_GRADE_MASTER GROUP BY Subject'''
c.execute(query_max_marks)
max_marks_data = c.fetchall()
print(max_marks_data)
#3. Percenatge of marks scored by each student
query_percentage = '''SELECT Student_Name, avg(Marks) as 'Percentage' from STUDENT_GRADE_MASTER GROUP BY Student_Name'''
c.execute(query_percentage)
percentage_data = c.fetchall()
print(percentage_data)
```
### <font color=green>Step 7 - We are closing the database connection</font>
#### <font color=blue>It is always a good practice to close the database connection after all the operations are completed</font>
```
#Closing the connection
conn.close()
```
|
github_jupyter
|
# Neural network hybrid recommendation system on Google Analytics data model and training
This notebook demonstrates how to implement a hybrid recommendation system using a neural network to combine content-based and collaborative filtering recommendation models using Google Analytics data. We are going to use the learned user embeddings from [wals.ipynb](../wals.ipynb) and combine that with our previous content-based features from [content_based_using_neural_networks.ipynb](../content_based_using_neural_networks.ipynb)
Now that we have our data preprocessed from BigQuery and Cloud Dataflow, we can build our neural network hybrid recommendation model to our preprocessed data. Then we can train locally to make sure everything works and then use the power of Google Cloud ML Engine to scale it out.
We're going to use TensorFlow Hub to use trained text embeddings, so let's first pip install that and reset our session.
```
!pip install tensorflow_hub
```
Now reset the notebook's session kernel! Since we're no longer using Cloud Dataflow, we'll be using the python3 kernel from here on out so don't forget to change the kernel if it's still python2.
```
# Import helpful libraries and setup our project, bucket, and region
import os
import tensorflow as tf
import tensorflow_hub as hub
PROJECT = 'cloud-training-demos' # REPLACE WITH YOUR PROJECT ID
BUCKET = 'cloud-training-demos-ml' # REPLACE WITH YOUR BUCKET NAME
REGION = 'us-central1' # REPLACE WITH YOUR BUCKET REGION e.g. us-central1
# do not change these
os.environ['PROJECT'] = PROJECT
os.environ['BUCKET'] = BUCKET
os.environ['REGION'] = REGION
os.environ['TFVERSION'] = '1.8'
%%bash
gcloud config set project $PROJECT
gcloud config set compute/region $REGION
%%bash
if ! gsutil ls | grep -q gs://${BUCKET}/hybrid_recommendation/preproc; then
gsutil mb -l ${REGION} gs://${BUCKET}
# copy canonical set of preprocessed files if you didn't do preprocessing notebook
gsutil -m cp -R gs://cloud-training-demos/courses/machine_learning/deepdive/10_recommendation/hybrid_recommendation gs://${BUCKET}
fi
```
<h2> Create hybrid recommendation system model using TensorFlow </h2>
Now that we've created our training and evaluation input files as well as our categorical feature vocabulary files, we can create our TensorFlow hybrid recommendation system model.
Let's first get some of our aggregate information that we will use in the model from some of our preprocessed files we saved in Google Cloud Storage.
```
from tensorflow.python.lib.io import file_io
# Get number of content ids from text file in Google Cloud Storage
with file_io.FileIO(tf.gfile.Glob(filename = "gs://{}/hybrid_recommendation/preproc/vocab_counts/content_id_vocab_count.txt*".format(BUCKET))[0], mode = 'r') as ifp:
number_of_content_ids = int([x for x in ifp][0])
print("number_of_content_ids = {}".format(number_of_content_ids))
# Get number of categories from text file in Google Cloud Storage
with file_io.FileIO(tf.gfile.Glob(filename = "gs://{}/hybrid_recommendation/preproc/vocab_counts/category_vocab_count.txt*".format(BUCKET))[0], mode = 'r') as ifp:
number_of_categories = int([x for x in ifp][0])
print("number_of_categories = {}".format(number_of_categories))
# Get number of authors from text file in Google Cloud Storage
with file_io.FileIO(tf.gfile.Glob(filename = "gs://{}/hybrid_recommendation/preproc/vocab_counts/author_vocab_count.txt*".format(BUCKET))[0], mode = 'r') as ifp:
number_of_authors = int([x for x in ifp][0])
print("number_of_authors = {}".format(number_of_authors))
# Get mean months since epoch from text file in Google Cloud Storage
with file_io.FileIO(tf.gfile.Glob(filename = "gs://{}/hybrid_recommendation/preproc/vocab_counts/months_since_epoch_mean.txt*".format(BUCKET))[0], mode = 'r') as ifp:
mean_months_since_epoch = float([x for x in ifp][0])
print("mean_months_since_epoch = {}".format(mean_months_since_epoch))
# Determine CSV and label columns
NON_FACTOR_COLUMNS = 'next_content_id,visitor_id,content_id,category,title,author,months_since_epoch'.split(',')
FACTOR_COLUMNS = ["user_factor_{}".format(i) for i in range(10)] + ["item_factor_{}".format(i) for i in range(10)]
CSV_COLUMNS = NON_FACTOR_COLUMNS + FACTOR_COLUMNS
LABEL_COLUMN = 'next_content_id'
# Set default values for each CSV column
NON_FACTOR_DEFAULTS = [["Unknown"],["Unknown"],["Unknown"],["Unknown"],["Unknown"],["Unknown"],[mean_months_since_epoch]]
FACTOR_DEFAULTS = [[0.0] for i in range(10)] + [[0.0] for i in range(10)] # user and item
DEFAULTS = NON_FACTOR_DEFAULTS + FACTOR_DEFAULTS
```
Create input function for training and evaluation to read from our preprocessed CSV files.
```
# Create input function for train and eval
def read_dataset(filename, mode, batch_size = 512):
def _input_fn():
def decode_csv(value_column):
columns = tf.decode_csv(records = value_column, record_defaults = DEFAULTS)
features = dict(zip(CSV_COLUMNS, columns))
label = features.pop(LABEL_COLUMN)
return features, label
# Create list of files that match pattern
file_list = tf.gfile.Glob(filename = filename)
# Create dataset from file list
dataset = tf.data.TextLineDataset(filenames = file_list).map(map_func = decode_csv)
if mode == tf.estimator.ModeKeys.TRAIN:
num_epochs = None # indefinitely
dataset = dataset.shuffle(buffer_size = 10 * batch_size)
else:
num_epochs = 1 # end-of-input after this
dataset = dataset.repeat(count = num_epochs).batch(batch_size = batch_size)
return dataset.make_one_shot_iterator().get_next()
return _input_fn
```
Next, we will create our feature columns using our read in features.
```
# Create feature columns to be used in model
def create_feature_columns(args):
# Create content_id feature column
content_id_column = tf.feature_column.categorical_column_with_hash_bucket(
key = "content_id",
hash_bucket_size = number_of_content_ids)
# Embed content id into a lower dimensional representation
embedded_content_column = tf.feature_column.embedding_column(
categorical_column = content_id_column,
dimension = args['content_id_embedding_dimensions'])
# Create category feature column
categorical_category_column = tf.feature_column.categorical_column_with_vocabulary_file(
key = "category",
vocabulary_file = tf.gfile.Glob(filename = "gs://{}/hybrid_recommendation/preproc/vocabs/category_vocab.txt*".format(args['bucket']))[0],
num_oov_buckets = 1)
# Convert categorical category column into indicator column so that it can be used in a DNN
indicator_category_column = tf.feature_column.indicator_column(categorical_column = categorical_category_column)
# Create title feature column using TF Hub
embedded_title_column = hub.text_embedding_column(
key = "title",
module_spec = "https://tfhub.dev/google/nnlm-de-dim50-with-normalization/1",
trainable = False)
# Create author feature column
author_column = tf.feature_column.categorical_column_with_hash_bucket(
key = "author",
hash_bucket_size = number_of_authors + 1)
# Embed author into a lower dimensional representation
embedded_author_column = tf.feature_column.embedding_column(
categorical_column = author_column,
dimension = args['author_embedding_dimensions'])
# Create months since epoch boundaries list for our binning
months_since_epoch_boundaries = list(range(400, 700, 20))
# Create months_since_epoch feature column using raw data
months_since_epoch_column = tf.feature_column.numeric_column(
key = "months_since_epoch")
# Create bucketized months_since_epoch feature column using our boundaries
months_since_epoch_bucketized = tf.feature_column.bucketized_column(
source_column = months_since_epoch_column,
boundaries = months_since_epoch_boundaries)
# Cross our categorical category column and bucketized months since epoch column
crossed_months_since_category_column = tf.feature_column.crossed_column(
keys = [categorical_category_column, months_since_epoch_bucketized],
hash_bucket_size = len(months_since_epoch_boundaries) * (number_of_categories + 1))
# Convert crossed categorical category and bucketized months since epoch column into indicator column so that it can be used in a DNN
indicator_crossed_months_since_category_column = tf.feature_column.indicator_column(categorical_column = crossed_months_since_category_column)
# Create user and item factor feature columns from our trained WALS model
user_factors = [tf.feature_column.numeric_column(key = "user_factor_" + str(i)) for i in range(10)]
item_factors = [tf.feature_column.numeric_column(key = "item_factor_" + str(i)) for i in range(10)]
# Create list of feature columns
feature_columns = [embedded_content_column,
embedded_author_column,
indicator_category_column,
embedded_title_column,
indicator_crossed_months_since_category_column] + user_factors + item_factors
return feature_columns
```
Now we'll create our model function
```
# Create custom model function for our custom estimator
def model_fn(features, labels, mode, params):
# TODO: Create neural network input layer using our feature columns defined above
# TODO: Create hidden layers by looping through hidden unit list
# TODO: Compute logits (1 per class) using the output of our last hidden layer
# TODO: Find the predicted class indices based on the highest logit (which will result in the highest probability)
predicted_classes =
# Read in the content id vocabulary so we can tie the predicted class indices to their respective content ids
with file_io.FileIO(tf.gfile.Glob(filename = "gs://{}/hybrid_recommendation/preproc/vocabs/content_id_vocab.txt*".format(BUCKET))[0], mode = 'r') as ifp:
content_id_names = tf.constant(value = [x.rstrip() for x in ifp])
# Gather predicted class names based predicted class indices
predicted_class_names = tf.gather(params = content_id_names, indices = predicted_classes)
# If the mode is prediction
if mode == tf.estimator.ModeKeys.PREDICT:
# Create predictions dict
predictions_dict = {
'class_ids': tf.expand_dims(input = predicted_classes, axis = -1),
'class_names' : tf.expand_dims(input = predicted_class_names, axis = -1),
'probabilities': tf.nn.softmax(logits = logits),
'logits': logits
}
# Create export outputs
export_outputs = {"predict_export_outputs": tf.estimator.export.PredictOutput(outputs = predictions_dict)}
return tf.estimator.EstimatorSpec( # return early since we're done with what we need for prediction mode
mode = mode,
predictions = predictions_dict,
loss = None,
train_op = None,
eval_metric_ops = None,
export_outputs = export_outputs)
# Continue on with training and evaluation modes
# Create lookup table using our content id vocabulary
table = tf.contrib.lookup.index_table_from_file(
vocabulary_file = tf.gfile.Glob(filename = "gs://{}/hybrid_recommendation/preproc/vocabs/content_id_vocab.txt*".format(BUCKET))[0])
# Look up labels from vocabulary table
labels = table.lookup(keys = labels)
# TODO: Compute loss using the correct type of softmax cross entropy since this is classification and our labels (content id indices) and probabilities are mutually exclusive
loss =
# Compute evaluation metrics of total accuracy and the accuracy of the top k classes
accuracy = tf.metrics.accuracy(labels = labels, predictions = predicted_classes, name = 'acc_op')
top_k_accuracy = tf.metrics.mean(values = tf.nn.in_top_k(predictions = logits, targets = labels, k = params['top_k']))
map_at_k = tf.metrics.average_precision_at_k(labels = labels, predictions = predicted_classes, k = params['top_k'])
# Put eval metrics into a dictionary
eval_metrics = {
'accuracy': accuracy,
'top_k_accuracy': top_k_accuracy,
'map_at_k': map_at_k}
# Create scalar summaries to see in TensorBoard
tf.summary.scalar(name = 'accuracy', tensor = accuracy[1])
tf.summary.scalar(name = 'top_k_accuracy', tensor = top_k_accuracy[1])
tf.summary.scalar(name = 'map_at_k', tensor = map_at_k[1])
# Create scalar summaries to see in TensorBoard
tf.summary.scalar(name = 'accuracy', tensor = accuracy[1])
tf.summary.scalar(name = 'top_k_accuracy', tensor = top_k_accuracy[1])
# If the mode is evaluation
if mode == tf.estimator.ModeKeys.EVAL:
return tf.estimator.EstimatorSpec( # return early since we're done with what we need for evaluation mode
mode = mode,
predictions = None,
loss = loss,
train_op = None,
eval_metric_ops = eval_metrics,
export_outputs = None)
# Continue on with training mode
# If the mode is training
assert mode == tf.estimator.ModeKeys.TRAIN
# Create a custom optimizer
optimizer = tf.train.AdagradOptimizer(learning_rate = params['learning_rate'])
# Create train op
train_op = optimizer.minimize(loss = loss, global_step = tf.train.get_global_step())
return tf.estimator.EstimatorSpec( # final return since we're done with what we need for training mode
mode = mode,
predictions = None,
loss = loss,
train_op = train_op,
eval_metric_ops = None,
export_outputs = None)
```
Now create a serving input function
```
# Create serving input function
def serving_input_fn():
feature_placeholders = {
colname : tf.placeholder(dtype = tf.string, shape = [None]) \
for colname in NON_FACTOR_COLUMNS[1:-1]
}
feature_placeholders['months_since_epoch'] = tf.placeholder(dtype = tf.float32, shape = [None])
for colname in FACTOR_COLUMNS:
feature_placeholders[colname] = tf.placeholder(dtype = tf.float32, shape = [None])
features = {
key: tf.expand_dims(tensor, -1) \
for key, tensor in feature_placeholders.items()
}
return tf.estimator.export.ServingInputReceiver(features, feature_placeholders)
```
Now that all of the pieces are assembled let's create and run our train and evaluate loop
```
# Create train and evaluate loop to combine all of the pieces together.
tf.logging.set_verbosity(tf.logging.INFO)
def train_and_evaluate(args):
estimator = tf.estimator.Estimator(
model_fn = model_fn,
model_dir = args['output_dir'],
params={
'feature_columns': create_feature_columns(args),
'hidden_units': args['hidden_units'],
'n_classes': number_of_content_ids,
'learning_rate': args['learning_rate'],
'top_k': args['top_k'],
'bucket': args['bucket']
})
train_spec = tf.estimator.TrainSpec(
input_fn = read_dataset(filename = args['train_data_paths'], mode = tf.estimator.ModeKeys.TRAIN, batch_size = args['batch_size']),
max_steps = args['train_steps'])
exporter = tf.estimator.LatestExporter('exporter', serving_input_fn)
eval_spec = tf.estimator.EvalSpec(
input_fn = read_dataset(filename = args['eval_data_paths'], mode = tf.estimator.ModeKeys.EVAL, batch_size = args['batch_size']),
steps = None,
start_delay_secs = args['start_delay_secs'],
throttle_secs = args['throttle_secs'],
exporters = exporter)
tf.estimator.train_and_evaluate(estimator, train_spec, eval_spec)
```
Run train_and_evaluate!
```
# Call train and evaluate loop
import shutil
outdir = 'hybrid_recommendation_trained'
shutil.rmtree(outdir, ignore_errors = True) # start fresh each time
arguments = {
'bucket': BUCKET,
'train_data_paths': "gs://{}/hybrid_recommendation/preproc/features/train.csv*".format(BUCKET),
'eval_data_paths': "gs://{}/hybrid_recommendation/preproc/features/eval.csv*".format(BUCKET),
'output_dir': outdir,
'batch_size': 128,
'learning_rate': 0.1,
'hidden_units': [256, 128, 64],
'content_id_embedding_dimensions': 10,
'author_embedding_dimensions': 10,
'top_k': 10,
'train_steps': 1000,
'start_delay_secs': 30,
'throttle_secs': 30
}
train_and_evaluate(arguments)
```
## Run on module locally
Now let's place our code into a python module with model.py and task.py files so that we can train using Google Cloud's ML Engine! First, let's test our module locally.
```
%writefile requirements.txt
tensorflow_hub
%%bash
echo "bucket=${BUCKET}"
rm -rf hybrid_recommendation_trained
export PYTHONPATH=${PYTHONPATH}:${PWD}/hybrid_recommendations_module
python -m trainer.task \
--bucket=${BUCKET} \
--train_data_paths=gs://${BUCKET}/hybrid_recommendation/preproc/features/train.csv* \
--eval_data_paths=gs://${BUCKET}/hybrid_recommendation/preproc/features/eval.csv* \
--output_dir=${OUTDIR} \
--batch_size=128 \
--learning_rate=0.1 \
--hidden_units="256 128 64" \
--content_id_embedding_dimensions=10 \
--author_embedding_dimensions=10 \
--top_k=10 \
--train_steps=1000 \
--start_delay_secs=30 \
--throttle_secs=60
```
# Run on Google Cloud ML Engine
If our module locally trained fine, let's now use of the power of ML Engine to scale it out on Google Cloud.
```
%%bash
OUTDIR=gs://${BUCKET}/hybrid_recommendation/small_trained_model
JOBNAME=hybrid_recommendation_$(date -u +%y%m%d_%H%M%S)
echo $OUTDIR $REGION $JOBNAME
gsutil -m rm -rf $OUTDIR
gcloud ml-engine jobs submit training $JOBNAME \
--region=$REGION \
--module-name=trainer.task \
--package-path=$(pwd)/hybrid_recommendations_module/trainer \
--job-dir=$OUTDIR \
--staging-bucket=gs://$BUCKET \
--scale-tier=STANDARD_1 \
--runtime-version=$TFVERSION \
-- \
--bucket=${BUCKET} \
--train_data_paths=gs://${BUCKET}/hybrid_recommendation/preproc/features/train.csv* \
--eval_data_paths=gs://${BUCKET}/hybrid_recommendation/preproc/features/eval.csv* \
--output_dir=${OUTDIR} \
--batch_size=128 \
--learning_rate=0.1 \
--hidden_units="256 128 64" \
--content_id_embedding_dimensions=10 \
--author_embedding_dimensions=10 \
--top_k=10 \
--train_steps=1000 \
--start_delay_secs=30 \
--throttle_secs=30
```
Let's add some hyperparameter tuning!
```
%%writefile hyperparam.yaml
trainingInput:
hyperparameters:
goal: MAXIMIZE
maxTrials: 5
maxParallelTrials: 1
hyperparameterMetricTag: accuracy
params:
- parameterName: batch_size
type: INTEGER
minValue: 8
maxValue: 64
scaleType: UNIT_LINEAR_SCALE
- parameterName: learning_rate
type: DOUBLE
minValue: 0.01
maxValue: 0.1
scaleType: UNIT_LINEAR_SCALE
- parameterName: hidden_units
type: CATEGORICAL
categoricalValues: ['1024 512 256', '1024 512 128', '1024 256 128', '512 256 128', '1024 512 64', '1024 256 64', '512 256 64', '1024 128 64', '512 128 64', '256 128 64', '1024 512 32', '1024 256 32', '512 256 32', '1024 128 32', '512 128 32', '256 128 32', '1024 64 32', '512 64 32', '256 64 32', '128 64 32']
- parameterName: content_id_embedding_dimensions
type: INTEGER
minValue: 5
maxValue: 250
scaleType: UNIT_LOG_SCALE
- parameterName: author_embedding_dimensions
type: INTEGER
minValue: 5
maxValue: 30
scaleType: UNIT_LINEAR_SCALE
%%bash
OUTDIR=gs://${BUCKET}/hybrid_recommendation/hypertuning
JOBNAME=hybrid_recommendation_$(date -u +%y%m%d_%H%M%S)
echo $OUTDIR $REGION $JOBNAME
gsutil -m rm -rf $OUTDIR
gcloud ml-engine jobs submit training $JOBNAME \
--region=$REGION \
--module-name=trainer.task \
--package-path=$(pwd)/hybrid_recommendations_module/trainer \
--job-dir=$OUTDIR \
--staging-bucket=gs://$BUCKET \
--scale-tier=STANDARD_1 \
--runtime-version=$TFVERSION \
--config=hyperparam.yaml \
-- \
--bucket=${BUCKET} \
--train_data_paths=gs://${BUCKET}/hybrid_recommendation/preproc/features/train.csv* \
--eval_data_paths=gs://${BUCKET}/hybrid_recommendation/preproc/features/eval.csv* \
--output_dir=${OUTDIR} \
--batch_size=128 \
--learning_rate=0.1 \
--hidden_units="256 128 64" \
--content_id_embedding_dimensions=10 \
--author_embedding_dimensions=10 \
--top_k=10 \
--train_steps=1000 \
--start_delay_secs=30 \
--throttle_secs=30
```
Now that we know the best hyperparameters, run a big training job!
```
%%bash
OUTDIR=gs://${BUCKET}/hybrid_recommendation/big_trained_model
JOBNAME=hybrid_recommendation_$(date -u +%y%m%d_%H%M%S)
echo $OUTDIR $REGION $JOBNAME
gsutil -m rm -rf $OUTDIR
gcloud ml-engine jobs submit training $JOBNAME \
--region=$REGION \
--module-name=trainer.task \
--package-path=$(pwd)/hybrid_recommendations_module/trainer \
--job-dir=$OUTDIR \
--staging-bucket=gs://$BUCKET \
--scale-tier=STANDARD_1 \
--runtime-version=$TFVERSION \
-- \
--bucket=${BUCKET} \
--train_data_paths=gs://${BUCKET}/hybrid_recommendation/preproc/features/train.csv* \
--eval_data_paths=gs://${BUCKET}/hybrid_recommendation/preproc/features/eval.csv* \
--output_dir=${OUTDIR} \
--batch_size=128 \
--learning_rate=0.1 \
--hidden_units="256 128 64" \
--content_id_embedding_dimensions=10 \
--author_embedding_dimensions=10 \
--top_k=10 \
--train_steps=10000 \
--start_delay_secs=30 \
--throttle_secs=30
```
|
github_jupyter
|
# Supervised Learning: Finding Donors for *CharityML*
> Udacity Machine Learning Engineer Nanodegree: _Project 2_
>
> Author: _Ke Zhang_
>
> Submission Date: _2017-04-30_ (Revision 3)
## Content
- [Getting Started](#Getting-Started)
- [Exploring the Data](#Exploring-the-Data)
- [Preparing the Data](#Preparing-the-Data)
- [Evaluating Model Performance](#Evaluating-Model-Performance)
- [Improving Results](#Improving-Results)
- [Feature Importance](#Feature-Importance)
- [References](#References)
- [Reproduction Environment](#Reproduction-Environment)
## Getting Started
In this project, you will employ several supervised algorithms of your choice to accurately model individuals' income using data collected from the 1994 U.S. Census. You will then choose the best candidate algorithm from preliminary results and further optimize this algorithm to best model the data. Your goal with this implementation is to construct a model that accurately predicts whether an individual makes more than $50,000. This sort of task can arise in a non-profit setting, where organizations survive on donations. Understanding an individual's income can help a non-profit better understand how large of a donation to request, or whether or not they should reach out to begin with. While it can be difficult to determine an individual's general income bracket directly from public sources, we can (as we will see) infer this value from other publically available features.
The dataset for this project originates from the [UCI Machine Learning Repository](https://archive.ics.uci.edu/ml/datasets/Census+Income). The datset was donated by Ron Kohavi and Barry Becker, after being published in the article _"Scaling Up the Accuracy of Naive-Bayes Classifiers: A Decision-Tree Hybrid"_. You can find the article by Ron Kohavi [online](https://www.aaai.org/Papers/KDD/1996/KDD96-033.pdf). The data we investigate here consists of small changes to the original dataset, such as removing the `'fnlwgt'` feature and records with missing or ill-formatted entries.
----
## Exploring the Data
Run the code cell below to load necessary Python libraries and load the census data. Note that the last column from this dataset, `'income'`, will be our target label (whether an individual makes more than, or at most, $50,000 annually). All other columns are features about each individual in the census database.
```
# Import libraries necessary for this project
import numpy as np
import pandas as pd
from time import time
from IPython.display import display # Allows the use of display() for DataFrames
import matplotlib.pyplot as plt
import seaborn as sns
# Import supplementary visualization code visuals.py
import visuals as vs
#sklearn makes lots of deprecation warnings...
import warnings
warnings.filterwarnings("ignore", category=DeprecationWarning)
# Pretty display for notebooks
%matplotlib inline
sns.set(style='white', palette='muted', color_codes=True)
sns.set_context('notebook', font_scale=1.2, rc={'lines.linewidth': 1.2})
# Load the Census dataset
data = pd.read_csv("census.csv")
# Success - Display the first record
display(data.head(n=1))
```
### Implementation: Data Exploration
A cursory investigation of the dataset will determine how many individuals fit into either group, and will tell us about the percentage of these individuals making more than \$50,000. In the code cell below, you will need to compute the following:
- The total number of records, `'n_records'`
- The number of individuals making more than \$50,000 annually, `'n_greater_50k'`.
- The number of individuals making at most \$50,000 annually, `'n_at_most_50k'`.
- The percentage of individuals making more than \$50,000 annually, `'greater_percent'`.
**Hint:** You may need to look at the table above to understand how the `'income'` entries are formatted.
```
# Total number of records
n_records = data.shape[0]
# Number of records where individual's income is more than $50,000
n_greater_50k = data[data['income'] == '>50K'].shape[0]
# Number of records where individual's income is at most $50,000
n_at_most_50k = data[data['income'] == '<=50K'].shape[0]
# Percentage of individuals whose income is more than $50,000
greater_percent = n_greater_50k / (n_records / 100.0)
# Print the results
print "Total number of records: {}".format(n_records)
print "Individuals making more than $50,000: {}".format(n_greater_50k)
print "Individuals making at most $50,000: {}".format(n_at_most_50k)
print "Percentage of individuals making more than $50,000: {:.2f}%".format(greater_percent)
```
----
## Preparing the Data
Before data can be used as input for machine learning algorithms, it often must be cleaned, formatted, and restructured — this is typically known as **preprocessing**. Fortunately, for this dataset, there are no invalid or missing entries we must deal with, however, there are some qualities about certain features that must be adjusted. This preprocessing can help tremendously with the outcome and predictive power of nearly all learning algorithms.
### Transforming Skewed Continuous Features
A dataset may sometimes contain at least one feature whose values tend to lie near a single number, but will also have a non-trivial number of vastly larger or smaller values than that single number. Algorithms can be sensitive to such distributions of values and can underperform if the range is not properly normalized. With the census dataset two features fit this description: '`capital-gain'` and `'capital-loss'`.
Run the code cell below to plot a histogram of these two features. Note the range of the values present and how they are distributed.
```
# Split the data into features and target label
income_raw = data['income']
features_raw = data.drop('income', axis = 1)
# Visualize skewed continuous features of original data
vs.distribution(data)
```
For highly-skewed feature distributions such as `'capital-gain'` and `'capital-loss'`, it is common practice to apply a <a href="https://en.wikipedia.org/wiki/Data_transformation_(statistics)">logarithmic transformation</a> on the data so that the very large and very small values do not negatively affect the performance of a learning algorithm. Using a logarithmic transformation significantly reduces the range of values caused by outliers. Care must be taken when applying this transformation however: The logarithm of `0` is undefined, so we must translate the values by a small amount above `0` to apply the the logarithm successfully.
Run the code cell below to perform a transformation on the data and visualize the results. Again, note the range of values and how they are distributed.
```
# Log-transform the skewed features
skewed = ['capital-gain', 'capital-loss']
features_raw[skewed] = data[skewed].apply(lambda x: np.log(x + 1))
# Visualize the new log distributions
vs.distribution(features_raw, transformed = True)
```
### Normalizing Numerical Features
In addition to performing transformations on features that are highly skewed, it is often good practice to perform some type of scaling on numerical features. Applying a scaling to the data does not change the shape of each feature's distribution (such as `'capital-gain'` or `'capital-loss'` above); however, normalization ensures that each feature is treated equally when applying supervised learners. Note that once scaling is applied, observing the data in its raw form will no longer have the same original meaning, as exampled below.
Run the code cell below to normalize each numerical feature. We will use [`sklearn.preprocessing.MinMaxScaler`](http://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.MinMaxScaler.html) for this.
```
# Import sklearn.preprocessing.StandardScaler
from sklearn.preprocessing import MinMaxScaler
# Initialize a scaler, then apply it to the features
scaler = MinMaxScaler()
numerical = ['age', 'education-num', 'capital-gain', 'capital-loss', 'hours-per-week']
features_raw[numerical] = scaler.fit_transform(data[numerical])
# Show an example of a record with scaling applied
display(features_raw.head(n = 1))
```
### Implementation: Data Preprocessing
From the table in **Exploring the Data** above, we can see there are several features for each record that are non-numeric. Typically, learning algorithms expect input to be numeric, which requires that non-numeric features (called *categorical variables*) be converted. One popular way to convert categorical variables is by using the **one-hot encoding** scheme. One-hot encoding creates a _"dummy"_ variable for each possible category of each non-numeric feature. For example, assume `someFeature` has three possible entries: `A`, `B`, or `C`. We then encode this feature into `someFeature_A`, `someFeature_B` and `someFeature_C`.
| | someFeature | | someFeature_A | someFeature_B | someFeature_C |
| :-: | :-: | | :-: | :-: | :-: |
| 0 | B | | 0 | 1 | 0 |
| 1 | C | ----> one-hot encode ----> | 0 | 0 | 1 |
| 2 | A | | 1 | 0 | 0 |
Additionally, as with the non-numeric features, we need to convert the non-numeric target label, `'income'` to numerical values for the learning algorithm to work. Since there are only two possible categories for this label ("<=50K" and ">50K"), we can avoid using one-hot encoding and simply encode these two categories as `0` and `1`, respectively. In code cell below, you will need to implement the following:
- Use [`pandas.get_dummies()`](http://pandas.pydata.org/pandas-docs/stable/generated/pandas.get_dummies.html?highlight=get_dummies#pandas.get_dummies) to perform one-hot encoding on the `'features_raw'` data.
- Convert the target label `'income_raw'` to numerical entries.
- Set records with "<=50K" to `0` and records with ">50K" to `1`.
```
# One-hot encode the 'features_raw' data using pandas.get_dummies()
features = pd.get_dummies(features_raw)
# Encode the 'income_raw' data to numerical values
income = income_raw.apply(lambda x: 1 if x == '>50K' else 0)
# Print the number of features after one-hot encoding
encoded = list(features.columns)
print "{} total features after one-hot encoding.".format(len(encoded))
# Uncomment the following line to see the encoded feature names
print encoded
```
### Shuffle and Split Data
Now all _categorical variables_ have been converted into numerical features, and all numerical features have been normalized. As always, we will now split the data (both features and their labels) into training and test sets. 80% of the data will be used for training and 20% for testing.
Run the code cell below to perform this split.
```
# Import train_test_split
from sklearn.cross_validation import train_test_split
# Split the 'features' and 'income' data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(features, income, test_size = 0.2, random_state = 0)
# Show the results of the split
print "Training set has {} samples.".format(X_train.shape[0])
print "Testing set has {} samples.".format(X_test.shape[0])
```
----
## Evaluating Model Performance
In this section, we will investigate four different algorithms, and determine which is best at modeling the data. Three of these algorithms will be supervised learners of your choice, and the fourth algorithm is known as a *naive predictor*.
### Metrics and the Naive Predictor
*CharityML*, equipped with their research, knows individuals that make more than \$50,000 are most likely to donate to their charity. Because of this, *CharityML* is particularly interested in predicting who makes more than \$50,000 accurately. It would seem that using **accuracy** as a metric for evaluating a particular model's performace would be appropriate. Additionally, identifying someone that *does not* make more than \$50,000 as someone who does would be detrimental to *CharityML*, since they are looking to find individuals willing to donate. Therefore, a model's ability to precisely predict those that make more than \$50,000 is *more important* than the model's ability to **recall** those individuals. We can use **F-beta score** as a metric that considers both precision and recall:
$$ F_{\beta} = (1 + \beta^2) \cdot \frac{precision \cdot recall}{\left( \beta^2 \cdot precision \right) + recall} $$
In particular, when $\beta = 0.5$, more emphasis is placed on precision. This is called the **F$_{0.5}$ score** (or F-score for simplicity).
Looking at the distribution of classes (those who make at most \$50,000, and those who make more), it's clear most individuals do not make more than \$50,000. This can greatly affect **accuracy**, since we could simply say *"this person does not make more than \$50,000"* and generally be right, without ever looking at the data! Making such a statement would be called **naive**, since we have not considered any information to substantiate the claim. It is always important to consider the *naive prediction* for your data, to help establish a benchmark for whether a model is performing well. That been said, using that prediction would be pointless: If we predicted all people made less than \$50,000, *CharityML* would identify no one as donors.
### Question 1 - Naive Predictor Performace
*If we chose a model that always predicted an individual made more than \$50,000, what would that model's accuracy and F-score be on this dataset?*
**Note:** You must use the code cell below and assign your results to `'accuracy'` and `'fscore'` to be used later.
```
# Calculate accuracy
accuracy = 1.0 * n_greater_50k / n_records
# Calculate F-score using the formula above for beta = 0.5
recall = 1.0
fscore = (
(1 + 0.5**2) * accuracy * recall
) / (
0.5**2 * accuracy + recall
)
# Print the results
print "Naive Predictor: [Accuracy score: {:.4f}, F-score: {:.4f}]".format(accuracy, fscore)
```
### Supervised Learning Models
**The following supervised learning models are currently available in** [`scikit-learn`](http://scikit-learn.org/stable/supervised_learning.html) **that you may choose from:**
- Gaussian Naive Bayes (GaussianNB)
- Decision Trees
- Ensemble Methods (Bagging, AdaBoost, Random Forest, Gradient Boosting)
- K-Nearest Neighbors (KNeighbors)
- Stochastic Gradient Descent Classifier (SGDC)
- Support Vector Machines (SVM)
- Logistic Regression
### Question 2 - Model Application
List three of the supervised learning models above that are appropriate for this problem that you will test on the census data. For each model chosen
- *Describe one real-world application in industry where the model can be applied.* (You may need to do research for this — give references!)
- *What are the strengths of the model; when does it perform well?*
- *What are the weaknesses of the model; when does it perform poorly?*
- *What makes this model a good candidate for the problem, given what you know about the data?*
**Answer: **
Total number of records: 45222
The algorithms we're searching here is for a supervised classification problem predicting a category using labeled data with less than 100K samples.
* **Support Vector Machine** (SVM):
* Real-world application: classifying proteins, protein-protein interaction
* References: [Bioinformatics - Semi-Supervised Multi-Task Learning for Predicting Interactions between HIV-1 and Human Proteins](https://static.googleusercontent.com/media/research.google.com/de//pubs/archive/35765.pdf)
* Strengths of the model:
* effective in high dimensional spaces and with nonlinear relationships
* robust to noise (because margins maximized and theoretical bounds on overfitting)
* Weaknesses of the model:
* requires to select a good kernel function and a number of hyperparameters such as the regularization parameter and the number of iterations
* sensitive to feature scaling
* model parameters are difficult to interpret
* requires significant memory and processing power
* tuning the regularization parameters required to avoid overfitting
* Reasoning: *Linear SVC* is the optimal estimator following the [Scikit-Learn - Choosing the right estimator](http://scikit-learn.org/stable/tutorial/machine_learning_map/) when using less than 100K samples to solve to classification problem.
* **Logistic Regression**:
* Real-world application: media and advertising campaigns optimization and decision making
* References: [Evaluating Online Ad Campaigns in a Pipeline: Causal Models At Scale](https://static.googleusercontent.com/media/research.google.com/de//pubs/archive/36552.pdf)
* Strengths of the model:
* simple, no user-defined parameters to experiment with unless you regularize, β is intuitive
* fast to train and to predict
* easy to interpret: output can be interpreted as a probability
* pretty robust to noise with low variance and less prone to over-fitting
* lots of ways to regularize the model
* Weaknesses of the model:
* unstable when one predictor could almost explain the response variable
* often less accurate than the newer methods
* Interpreting θ isn't straightforward
* Reasoning: It's similar to *linear SVC*, is widely used and can be easyly implemented.
* **K-Nearest Neighbors (KNeighbors)**:
* Real-world application: image and video content classification
* References: [Clustering billions of images with large scale nearest neighbor search](https://static.googleusercontent.com/media/research.google.com/de//pubs/archive/32616.pdf)
* Strengths of the model:
* simple and powerful
* easy to explain
* no training involved ("lazy")
* naturally handles multiclass classification and regression
* learns nonlinear boundaries
* Weaknesses of the model:
* expensive and slow to predict new instances ("lazy")
* must define a meaningful distance function (preference bias)
* need to decide on a good distance metric
* performs poorly on high-dimensionality datasets (curse of high dimensionality)
* Reasoning: *KNeighbors* classifier is the next option suggested on the machine learning map when *linear SVC* does work poor. Since our dataset is low-dimensional and it should generate reasonable results.
### Implementation - Creating a Training and Predicting Pipeline
To properly evaluate the performance of each model you've chosen, it's important that you create a training and predicting pipeline that allows you to quickly and effectively train models using various sizes of training data and perform predictions on the testing data. Your implementation here will be used in the following section.
In the code block below, you will need to implement the following:
- Import `fbeta_score` and `accuracy_score` from [`sklearn.metrics`](http://scikit-learn.org/stable/modules/classes.html#sklearn-metrics-metrics).
- Fit the learner to the sampled training data and record the training time.
- Perform predictions on the test data `X_test`, and also on the first 300 training points `X_train[:300]`.
- Record the total prediction time.
- Calculate the accuracy score for both the training subset and testing set.
- Calculate the F-score for both the training subset and testing set.
- Make sure that you set the `beta` parameter!
```
# Import two metrics from sklearn - fbeta_score and accuracy_score
from sklearn.metrics import fbeta_score, accuracy_score
def train_predict(learner, sample_size, X_train, y_train, X_test, y_test):
'''
inputs:
- learner: the learning algorithm to be trained and predicted on
- sample_size: the size of samples (number) to be drawn from training set
- X_train: features training set
- y_train: income training set
- X_test: features testing set
- y_test: income testing set
'''
results = {}
# Fit the learner to the training data using slicing with 'sample_size'
start = time() # Get start time
learner = learner.fit(X_train[:sample_size], y_train[:sample_size])
end = time() # Get end time
# Calculate the training time
results['train_time'] = end - start
# Get the predictions on the test set,
# then get predictions on the first 300 training samples
start = time() # Get start time
predictions_test = learner.predict(X_test)
predictions_train = learner.predict(X_train[:300])
end = time() # Get end time
# Calculate the total prediction time
results['pred_time'] = end - start
# Compute accuracy on the first 300 training samples
results['acc_train'] = accuracy_score(y_train[:300], predictions_train)
# Compute accuracy on test set
results['acc_test'] = accuracy_score(y_test, predictions_test)
# Compute F-score on the the first 300 training samples
results['f_train'] = fbeta_score(y_train[:300], predictions_train, beta=.5)
# Compute F-score on the test set
results['f_test'] = fbeta_score(y_test, predictions_test, beta=.5)
# Success
print "{} trained on {} samples.".format(learner.__class__.__name__, sample_size)
# Return the results
return results
```
### Implementation: Initial Model Evaluation
In the code cell, you will need to implement the following:
- Import the three supervised learning models you've discussed in the previous section.
- Initialize the three models and store them in `'clf_A'`, `'clf_B'`, and `'clf_C'`.
- Use a `'random_state'` for each model you use, if provided.
- **Note:** Use the default settings for each model — you will tune one specific model in a later section.
- Calculate the number of records equal to 1%, 10%, and 100% of the training data.
- Store those values in `'samples_1'`, `'samples_10'`, and `'samples_100'` respectively.
**Note:** Depending on which algorithms you chose, the following implementation may take some time to run!
```
# Import the three supervised learning models from sklearn
from sklearn.svm import LinearSVC
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
# Initialize the three models
clf_A = LinearSVC(random_state=42)
clf_B = LogisticRegression(random_state=42)
clf_C = KNeighborsClassifier()
# Calculate the number of samples for 1%, 10%, and 100% of the training data
n = len(y_train)
samples_1 = int(round(n / 100.0))
samples_10 = int(round(n / 10.0))
samples_100 = n
# Collect results on the learners
results = {}
for clf in [clf_A, clf_B, clf_C]:
clf_name = clf.__class__.__name__
results[clf_name] = {}
for i, samples in enumerate([samples_1, samples_10, samples_100]):
results[clf_name][i] = \
train_predict(clf, samples, X_train, y_train, X_test, y_test)
# Run metrics visualization for the three supervised learning models chosen
vs.evaluate(results, accuracy, fscore)
```
----
## Improving Results
In this final section, you will choose from the three supervised learning models the *best* model to use on the student data. You will then perform a grid search optimization for the model over the entire training set (`X_train` and `y_train`) by tuning at least one parameter to improve upon the untuned model's F-score.
### Question 3 - Choosing the Best Model
*Based on the evaluation you performed earlier, in one to two paragraphs, explain to *CharityML* which of the three models you believe to be most appropriate for the task of identifying individuals that make more than \$50,000.*
**Hint:** Your answer should include discussion of the metrics, prediction/training time, and the algorithm's suitability for the data.
**Answer: **
| | training time | predicting time | training set scores | testing set scores |
|----------------------|----------------------------|-----------------|----------------|
| **LinearSVC** | ++ | +++ | +++ | **+++** |
| LogisticRegression | +++ | +++ | ++ | ++ |
| KNeighborsClassifier | + | --- | +++ | + |
Based on the evaluation the *linear SVC* model is the most appropriate for the task. Compared to the other two models in testing, it's both fast and has the highest scores. While *linear SVC* and *logistic regression* have almost the same accuracy, its *f-score* is slightly higher indicating that *linear SVC* has more correct positive predictions on actual positive observations.
Although *logistic regression* has a shorter training time, it has worse *f-score* when applied to the testing set. In a real-world setting the testing scores are the metrics that do matter. The moderate longer training time can be ignored. *K-neighbors* outperforms the other two only when predicting the training scores. But with an even poorer testing score it actually shows that the model has an overfitting problem.
### Question 4 - Describing the Model in Layman's Terms
*In one to two paragraphs, explain to *CharityML*, in layman's terms, how the final model chosen is supposed to work. Be sure that you are describing the major qualities of the model, such as how the model is trained and how the model makes a prediction. Avoid using advanced mathematical or technical jargon, such as describing equations or discussing the algorithm implementation.*
**Answer: **
As the final model we used a classifier called *linear SVC* which assumes that the underlying data are linearly separable. In a simplified 2-dimensional space this technique attemps to find the best line that separates the two classes of points with the largest margin. In higher dimensional space, the algorithm searches for the best hyperplane following the same principle by maximizing the margin (e.g. a plane in 3-dimensional space).
In our case, in the training phase the algorithm calculates the best model to separate the different classes in the training data by a maximum margin. And with the trained model the algorithm is able to predict the unseen examples.
### Implementation: Model Tuning
Fine tune the chosen model. Use grid search (`GridSearchCV`) with at least one important parameter tuned with at least 3 different values. You will need to use the entire training set for this. In the code cell below, you will need to implement the following:
- Import [`sklearn.grid_search.GridSearchCV`](http://scikit-learn.org/0.17/modules/generated/sklearn.grid_search.GridSearchCV.html) and [`sklearn.metrics.make_scorer`](http://scikit-learn.org/stable/modules/generated/sklearn.metrics.make_scorer.html).
- Initialize the classifier you've chosen and store it in `clf`.
- Set a `random_state` if one is available to the same state you set before.
- Create a dictionary of parameters you wish to tune for the chosen model.
- Example: `parameters = {'parameter' : [list of values]}`.
- **Note:** Avoid tuning the `max_features` parameter of your learner if that parameter is available!
- Use `make_scorer` to create an `fbeta_score` scoring object (with $\beta = 0.5$).
- Perform grid search on the classifier `clf` using the `'scorer'`, and store it in `grid_obj`.
- Fit the grid search object to the training data (`X_train`, `y_train`), and store it in `grid_fit`.
**Note:** Depending on the algorithm chosen and the parameter list, the following implementation may take some time to run!
```
# Import 'GridSearchCV', 'make_scorer', and any other necessary libraries
from sklearn.grid_search import GridSearchCV
from sklearn.metrics import make_scorer
# Initialize the classifier
clf = LinearSVC(random_state=42)
# Create the parameters list you wish to tune
parameters = {
'C': [.1, .5, 1.0, 5.0, 10.0],
'loss': ['hinge', 'squared_hinge'],
'tol': [1e-3, 1e-4, 1e-5],
'random_state': [0, 42, 10000]
}
# Make an fbeta_score scoring object
scorer = make_scorer(fbeta_score, beta=.5)
# Perform grid search on the classifier using 'scorer' as the scoring method
grid_obj = GridSearchCV(clf, parameters, scoring=scorer)
# Fit the grid search object to the training data and find the optimal parameters
grid_fit = grid_obj.fit(X_train, y_train)
# Get the estimator
best_clf = grid_fit.best_estimator_
# Make predictions using the unoptimized and model
predictions = (clf.fit(X_train, y_train)).predict(X_test)
best_predictions = best_clf.predict(X_test)
# Report the before-and-afterscores
print "Unoptimized model\n------"
print "Accuracy score on testing data: {:.4f}".format(accuracy_score(y_test, predictions))
print "F-score on testing data: {:.4f}".format(fbeta_score(y_test, predictions, beta = 0.5))
print "\nOptimized Model\n------"
print "Final accuracy score on the testing data: {:.4f}".format(accuracy_score(y_test, best_predictions))
print "Final F-score on the testing data: {:.4f}".format(fbeta_score(y_test, best_predictions, beta = 0.5))
# print optimized parameters
print("Optimized params for Linear SVM: {}".format(
grid_fit.best_params_
))
```
### Question 5 - Final Model Evaluation
_What is your optimized model's accuracy and F-score on the testing data? Are these scores better or worse than the unoptimized model? How do the results from your optimized model compare to the naive predictor benchmarks you found earlier in **Question 1**?_
**Note:** Fill in the table below with your results, and then provide discussion in the **Answer** box.
#### Results:
| Metric | Benchmark Predictor | Unoptimized Model | Optimized Model |
| :------------: | :-----------------: | :---------------: | :-------------: |
| Accuracy Score | .2478 | .8507 | .8514 |
| F-score | .2917 | .7054 | .7063 |
**Answer: **
The scores of the *optimized model* are a bit better than the *unoptimized model* showing that the defaults were actually very good in the first place. Compared to the *benchmark predictor*, the optimized model is by manifold better with larger accuracy and f-scores.
----
## Feature Importance
An important task when performing supervised learning on a dataset like the census data we study here is determining which features provide the most predictive power. By focusing on the relationship between only a few crucial features and the target label we simplify our understanding of the phenomenon, which is most always a useful thing to do. In the case of this project, that means we wish to identify a small number of features that most strongly predict whether an individual makes at most or more than \$50,000.
Choose a scikit-learn classifier (e.g., adaboost, random forests) that has a `feature_importance_` attribute, which is a function that ranks the importance of features according to the chosen classifier. In the next python cell fit this classifier to training set and use this attribute to determine the top 5 most important features for the census dataset.
### Question 6 - Feature Relevance Observation
When **Exploring the Data**, it was shown there are thirteen available features for each individual on record in the census data.
_Of these thirteen records, which five features do you believe to be most important for prediction, and in what order would you rank them and why?_
**Answer:**
Of the thirteen available features we believe that the following five features are the most important for prediction and ordered them by their importance with the most important at top. From looking at the data and following the rules of our society:
* *occupation*: different occupations have usually different salary ranges
* *capital-gain*: the rich get richer. Capital gain is an indicator of the personal wealth.
* *education-level*: when employed, people with higher education gets better paid
* *hours-per-week*: part time jobs are often less paid
* *age*: older people tends to earn more
### Implementation - Extracting Feature Importance
Choose a `scikit-learn` supervised learning algorithm that has a `feature_importance_` attribute availble for it. This attribute is a function that ranks the importance of each feature when making predictions based on the chosen algorithm.
In the code cell below, you will need to implement the following:
- Import a supervised learning model from sklearn if it is different from the three used earlier.
- Train the supervised model on the entire training set.
- Extract the feature importances using `'.feature_importances_'`.
```
# Import a supervised learning model that has 'feature_importances_'
from sklearn.ensemble import AdaBoostClassifier
# Train the supervised model on the training set
model = AdaBoostClassifier(random_state=42).fit(X_train, y_train)
# Extract the feature importances
importances = model.feature_importances_
# Plot
vs.feature_plot(importances, X_train, y_train)
```
### Question 7 - Extracting Feature Importance
Observe the visualization created above which displays the five most relevant features for predicting if an individual makes at most or above \$50,000.
_How do these five features compare to the five features you discussed in **Question 6**? If you were close to the same answer, how does this visualization confirm your thoughts? If you were not close, why do you think these features are more relevant?_
```
# print top 10 features importances
def rank_features(features, scores, descending=True, n=10):
"""
sorts and cuts features by scores.
:return: array of [feature name, score] tuples
"""
return sorted(
[[f, s] for f, s in zip(features, scores) if s],
key=lambda x: x[1],
reverse=descending
)[:n]
rank_features(
features.columns,
importances
)
# capital-loss and income have a positive correlation
features['capital-loss'].corr(income)
```
**Answer:**
From the top 5 features selected by *AdaBoostClassifier* we got 4 hits (*age*, *capital-gain*, *hours-per-week* and *education-level*). That *capital-loss* has a such big influence is really surprising and by looking at the cell above, *income* and *capital-loss* are even positively correlated. Our top one guess *occupation* hasn't made into top 10 in the feature importances.
The visualization of the feature importances confirms our guess that our observation in the society is actually true that older and higher educated people with money (big *capital-loss* or *capital-gain*) would have higher salaries. These thoughts are now quantified and explained by the classfier.
### Feature Selection
How does a model perform if we only use a subset of all the available features in the data? With less features required to train, the expectation is that training and prediction time is much lower — at the cost of performance metrics. From the visualization above, we see that the top five most important features contribute more than half of the importance of **all** features present in the data. This hints that we can attempt to *reduce the feature space* and simplify the information required for the model to learn. The code cell below will use the same optimized model you found earlier, and train it on the same training set *with only the top five important features*.
```
# Import functionality for cloning a model
from sklearn.base import clone
# Reduce the feature space
X_train_reduced = X_train[X_train.columns.values[(np.argsort(importances)[::-1])[:5]]]
X_test_reduced = X_test[X_test.columns.values[(np.argsort(importances)[::-1])[:5]]]
# Train on the "best" model found from grid search earlier
start = time()
clf = (clone(best_clf)).fit(X_train_reduced, y_train)
training_time_reduced = time() - start
# Make new predictions
reduced_predictions = clf.predict(X_test_reduced)
# Report scores from the final model using both versions of data
print "Final Model trained on full data\n------"
print "Accuracy on testing data: {:.4f}".format(accuracy_score(y_test, best_predictions))
print "F-score on testing data: {:.4f}".format(fbeta_score(y_test, best_predictions, beta = 0.5))
print "\nFinal Model trained on reduced data\n------"
print "Accuracy on testing data: {:.4f}".format(accuracy_score(y_test, reduced_predictions))
print "F-score on testing data: {:.4f}".format(fbeta_score(y_test, reduced_predictions, beta = 0.5))
# compare scores
def relative_diff_pct(x, y):
"""
returns the relative difference between x and y in percent.
"""
return 100 * ((y - x) / x)
print('Relative Diff. of accuracy-scores: {0:.2f}%'.format(
relative_diff_pct(.8514, .8096)
))
print('Relative Diff. of f-scores: {0:.2f}%'.format(
relative_diff_pct(.7063, .5983)
))
# Train with full data
start = time()
clf = (clone(best_clf)).fit(X_train, y_train)
training_time_full = time() - start
print('Relative Diff. of training times: {0:.2f}%'.format(
relative_diff_pct(training_time_reduced, training_time_full)
))
```
### Question 8 - Effects of Feature Selection
*How does the final model's F-score and accuracy score on the reduced data using only five features compare to those same scores when all features are used?*
*If training time was a factor, would you consider using the reduced data as your training set?*
**Answer:**
Both the accuracy and f-scores dropped down when using only the top 5 features. The f-scores have an **over 15% difference**, while the difference between the accuracy scores is at about 5%.
The training time with reduced data was more than **2 times faster** than the training time of the full data set. In some other scenarios when the training time or the computation power if of high priority, we would consider to use the reduced data. But since the difference between the f-scores are considerably large we would use the full training set for this problem.
## References
* [Udacity - Machine Learning](https://classroom.udacity.com/courses/ud262)
* [Laurad Hamilton - ML Cheat Sheet](http://www.lauradhamilton.com/machine-learning-algorithm-cheat-sheet)
* [Scikit-Learn - ML Modules](http://scikit-learn.org/stable/modules/sgd.html)
* [Scikit-Learn - AdaBoostClassifier](http://scikit-learn.org/stable/modules/generated/sklearn.ensemble.AdaBoostClassifier.html)
* [rcompton - Supervised Learning Superstitions](https://github.com/rcompton/ml_cheat_sheet)
* [Wikipedia - Support Vector Machine](https://en.wikipedia.org/wiki/Support_vector_machine#Definition)
* [Quora - SVM in layman's terms](https://www.quora.com/What-does-support-vector-machine-SVM-mean-in-laymans-terms)
## Reproduction Environment
```
import IPython
print IPython.sys_info()
!pip freeze
```
|
github_jupyter
|
# Feature Extraction
In machine learning, feature extraction aims to compute values (features) from images, intended to be informative and non-redundant, facilitating the subsequent learning and generalization steps, and in some cases leading to better human interpretations. These features may be handcrafted (manually computed features based on a-priori information ) or convolutional features (detect patterns within the data without the prior definition of features or characteristics):
## Handcrafted:
- Histogram features: Statistical moments extracted from the histogram describe image characteristics and provide a quantitative analysis of the image intensity distribution (entropy, intensity mean, standard deviation, skewness, kurtosis, and values at 0, 10, 50 (median) and 90 percentiles).
<img src="../Figures/histogram_sample.jpg" alt="Drawing" style="width: 500px;"/>
- The gradient examines directional changes in the image gray level, and can extract relevant information (such as edges) within an image. Moments extracted from the image gradient are more robust to acquisition conditions, such as contrast variation, and properties of the acquisition equipment . Ten features were extracted from the gray level and morphological gradients (five from each): intensity mean, standard deviation, skewness, kurtosis and percentage of non-zero values.
<img src="../Figures/gradient.png" alt="Drawing" style="width: 300px;"/>
- Local binary pattern (LBP) is a texture spectrum model that may be used to identify patterns in an image. The LBP histogram comprises the frequency of occurrence of different patterns within an image. Ten features were extracted from the LBP by using a 10-bin LBP histogram.
<img src="../Figures/lbp.png" alt="Drawing" style="width: 400px;"/>
- The Haar wavelet is a multi-resolution technique that transforms images into a domain where both spatial and frequency information is present. Features separately extracted from each sub-image present desired scale-dependent properties. When considering two decomposition levels, eight sub-images are generated. The mean value within each sub-image were computed and used as features (total of eight features). <img src="../Figures/wavelet-haar.png" alt="Drawing" style="width: 400px;"/>
## Convolutional features
Computed by using a very deep convolutional network (VGG16) with pre-trained imagenet weights. For each MR volume, the convolutional features were computed in the central 2D axial, sagittal and coronal slices. For each of these three views, 25,088 convolutional features were computed and combined.
<img src="../Figures/viz_initial_layers.png" alt="Drawing" style="width: 700px;"/>
Besides the image and patient information (MR vendor, magnetic field, age, gender), a total of 75,300 features were extracted and combined for each image: 8 features from the image histogram, 10 features from the image gradient, 10 features from the LBP histogra, 8 features from the Haar wavelet subimages and 75,264 convolutional features.
<img src="../Figures/data.png" alt="Drawing" style="width: 800px;"/>
## Reading the data file containing patients information and features
```
## data: vendor; magnetic field; age; gender; feats (65300)
# vendor: ge -> 10; philips -> 11; siemens -> 12
# gender: female -> 10; male -> 11
# feats: fs1 - histogram (8); fs2 - gradient (10); fs3 - lbp (10); fs4 - haar (8); fs5 - convolutional (75264)
import numpy as np
data = np.load('../Data/feats_cc359.npy.zip')['feats_cc359']
print '#samples, #info: ',data.shape
print 'patients age:', data[:,2]
```
## Activities List
- Print the vendor for all the images
- Identify images acquired from patients with age > 30
- Identify images acquired using GE vendor scanner
- Access this simple demo of a convnet trained on MNIST dataset: https://transcranial.github.io/keras-js/#/mnist-cnn
- draw a number (between 0-9)
- Visualize classification and intermediate outputs at each layer
## References
- Histogram basics: https://docs.opencv.org/3.1.0/d1/db7/tutorial_py_histogram_begins.html
- Local binary patterns: http://scikit-image.org/docs/dev/auto_examples/features_detection/plot_local_binary_pattern.html
- Wavelet haar to MRI: https://www.researchgate.net/figure/The-procedures-of-3-level-2D-DWT-a-normal-brain-MRI-b-level-3-wavelet-coefficients_258104202
- Extracting convolutional features using Vgg16: https://keras.io/applications/
|
github_jupyter
|
### Regular Expressions
Regular expressions are `text matching patterns` described with a formal syntax. You'll often hear regular expressions referred to as 'regex' or 'regexp' in conversation. Regular expressions can include a variety of rules, for finding repetition, to text-matching, and much more. As you advance in Python you'll see that a lot of your parsing problems can be solved with regular expressions (they're also a common interview question!).
## Searching for Patterns in Text
One of the most common uses for the re module is for finding patterns in text. Let's do a quick example of using the search method in the re module to find some text:
```
import re
# List of patterns to search for
patterns = [ 'term1', 'term2' ]
# Text to parse
text = 'This is a string with term1, but it does not have the other term.'
for p in patterns:
print ('Searching for "%s" in Sentence: \n"%s"' % (p, text))
#Check for match
if re.search(p, text):
print ('Match was found. \n')
else:
print ('No Match was found. \n')
```
Now we've seen that re.search() will take the pattern, scan the text, and then returns a **Match** object. If no pattern is found, a **None** is returned. To give a clearer picture of this match object, check out the cell below:
```
# List of patterns to search for
pattern = 'term1'
# Text to parse
text = 'This is a string with term1, but it does not have the other term.'
match = re.search(pattern, text)
type(match)
match
```
This **Match** object returned by the search() method is more than just a Boolean or None, it contains information about the match, including the original input string, the regular expression that was used, and the location of the match. Let's see the methods we can use on the match object:
```
# Show start of match
match.start()
# Show end
match.end()
s = "abassabacdReddyceaabadjfvababaReddy"
r = re.compile("Reddy")
r
l = re.findall(r,s)
print(l)
import re
s = "abcdefg1234"
r = re.compile("^[a-z][0-9]$")
l = re.findall(r,s)
print(l)
s = "ABCDE1234a"
r = re.compile(r"^[A-Z]{5}[0-9]{4}[a-z]$")
l = re.findall(r,s)
print(l)
s = "+917123456789"
s1 = "07123456789"
s2 = "7123456789"
r = re.compile(r"[6-9][0-9]{9}")
l = re.findall(r,s)
print(l)
l = re.findall(r,s1)
print(l)
l = re.findall(r,s2)
print(l)
s = "+917234567891"
s1 = "07123456789"
s2 = "7123456789"
r = re.compile(r"^(\+91)?[0]?([6-9][0-9]{9})$")
m = re.search(r,s1)
if m:
print(m.group())
else:
print("Invalid string")
for _ in range(int(input("No of Test Cases:"))):
line = input("Mobile Number")
if re.match(r"^[789]{1}\d{9}$", line):
print("YES")
else:
print("NO")
#Named groups
s = "12-02-2017" # DD-MM-YYYY
# dd-mm-yyyy
r = re.compile(r"^(?P<day>\d{2})-(?P<month>[0-9]{2})-(?P<year>[0-9]{4})")
m = re.search(r,s)
if m:
print(m.group('year'))
print(m.group('month'))
print(m.group('day'))
```
## Split with regular expressions
Let's see how we can split with the re syntax. This should look similar to how you used the split() method with strings.
```
# Term to split on
split_term = '@'
phrase = 'What is the domain name of someone with the email: hello@gmail.com'
# Split the phrase
re.split(split_term,phrase)
```
Note how re.split() returns a list with the term to spit on removed and the terms in the list are a split up version of the string. Create a couple of more examples for yourself to make sure you understand!
## Finding all instances of a pattern
You can use re.findall() to find all the instances of a pattern in a string. For example:
```
# Returns a list of all matches
re.findall('is','test phrase match is in middle')
a = " a list with the term to spit on removed and the terms in the list are a split up version of the string. Create a couple of more examples for yourself to make sure you understand!"
copy = re.findall("to",a)
copy
len(copy)
```
## Pattern re Syntax
This will be the bulk of this lecture on using re with Python. Regular expressions supports a huge variety of patterns the just simply finding where a single string occurred.
We can use *metacharacters* along with re to find specific types of patterns.
Since we will be testing multiple re syntax forms, let's create a function that will print out results given a list of various regular expressions and a phrase to parse:
```
def multi_re_find(patterns,phrase):
'''
Takes in a list of regex patterns
Prints a list of all matches
'''
for pattern in patterns:
print ('Searching the phrase using the re check: %r' %pattern)
print (re.findall(pattern,phrase))
```
### Repetition Syntax
There are five ways to express repetition in a pattern:
1.) A pattern followed by the meta-character * is repeated zero or more times.
2.) Replace the * with + and the pattern must appear at least once.
3.) Using ? means the pattern appears zero or one time.
4.) For a specific number of occurrences, use {m} after the pattern, where m is replaced with the number of times the pattern should repeat.
5.) Use {m,n} where m is the minimum number of repetitions and n is the maximum. Leaving out n ({m,}) means the value appears at least m times, with no maximum.
Now we will see an example of each of these using our multi_re_find function:
```
test_phrase = 'sdsd..sssddd...sdddsddd...dsds...dsssss...sdddd'
test_patterns = [ 'sd*', # s followed by zero or more d's
'sd+', # s followed by one or more d's
'sd?', # s followed by zero or one d's
'sd{3}', # s followed by three d's
'sd{2,3}', # s followed by two to three d's
]
multi_re_find(test_patterns,test_phrase)
```
## Character Sets
Character sets are used when you wish to match any one of a group of characters at a point in the input. Brackets are used to construct character set inputs. For example: the input [ab] searches for occurrences of either a or b.
Let's see some examples:
```
test_phrase = 'sdsd..sssddd...sdddsddd...dsds...dsssss...sdddd'
test_patterns = [ '[sd]', # either s or d
's[sd]+'] # s followed by one or more s or d
multi_re_find(test_patterns,test_phrase)
```
It makes sense that the first [sd] returns every instance. Also the second input will just return any thing starting with an s in this particular case of the test phrase input.
## Exclusion
We can use ^ to exclude terms by incorporating it into the bracket syntax notation. For example: [^...] will match any single character not in the brackets. Let's see some examples:
```
test_phrase = 'This is a string! But it has punctuation. How can we remove it?'
```
Use [^!.? ] to check for matches that are not a !,.,?, or space. Add the + to check that the match appears at least once, this basically translate into finding the words.
```
re.findall('[^!.? ]+',test_phrase)
```
## Character Ranges
As character sets grow larger, typing every character that should (or should not) match could become very tedious. A more compact format using character ranges lets you define a character set to include all of the contiguous characters between a start and stop point. The format used is [start-end].
Common use cases are to search for a specific range of letters in the alphabet, such [a-f] would return matches with any instance of letters between a and f.
Let's walk through some examples:
```
test_phrase = 'This is an example sentence. Lets see if we can find some letters.'
test_patterns=[ '[a-z]+', # sequences of lower case letters
'[A-Z]+', # sequences of upper case letters
'[a-zA-Z]+', # sequences of lower or upper case letters
'[A-Z][a-z]+'] # one upper case letter followed by lower case letters
multi_re_find(test_patterns,test_phrase)
```
## Escape Codes
You can use special escape codes to find specific types of patterns in your data, such as digits, non-digits,whitespace, and more. For example:
<table border="1" class="docutils">
<colgroup>
<col width="14%" />
<col width="86%" />
</colgroup>
<thead valign="bottom">
<tr class="row-odd"><th class="head">Code</th>
<th class="head">Meaning</th>
</tr>
</thead>
<tbody valign="top">
<tr class="row-even"><td><tt class="docutils literal"><span class="pre">\d</span></tt></td>
<td>a digit</td>
</tr>
<tr class="row-odd"><td><tt class="docutils literal"><span class="pre">\D</span></tt></td>
<td>a non-digit</td>
</tr>
<tr class="row-even"><td><tt class="docutils literal"><span class="pre">\s</span></tt></td>
<td>whitespace (tab, space, newline, etc.)</td>
</tr>
<tr class="row-odd"><td><tt class="docutils literal"><span class="pre">\S</span></tt></td>
<td>non-whitespace</td>
</tr>
<tr class="row-even"><td><tt class="docutils literal"><span class="pre">\w</span></tt></td>
<td>alphanumeric</td>
</tr>
<tr class="row-odd"><td><tt class="docutils literal"><span class="pre">\W</span></tt></td>
<td>non-alphanumeric</td>
</tr>
</tbody>
</table>
Escapes are indicated by prefixing the character with a backslash (\). Unfortunately, a backslash must itself be escaped in normal Python strings, and that results in expressions that are difficult to read. Using raw strings, created by prefixing the literal value with r, for creating regular expressions eliminates this problem and maintains readability.
Personally, I think this use of r to escape a backslash is probably one of the things that block someone who is not familiar with regex in Python from being able to read regex code at first. Hopefully after seeing these examples this syntax will become clear.
```
test_phrase = 'This is a string with some numbers 1233 and a symbol #hashtag'
test_patterns=[ r'\d+', # sequence of digits
r'\D+', # sequence of non-digits
r'\s+', # sequence of whitespace
r'\S+', # sequence of non-whitespace
r'\w+', # alphanumeric characters
r'\W+', # non-alphanumeric
]
multi_re_find(test_patterns,test_phrase)
```
## Conclusion
You should now have a solid understanding of how to use the regular expression module in Python. There are a ton of more special character instances, but it would be unreasonable to go through every single use case. Instead take a look at the full [documentation](https://docs.python.org/2.4/lib/re-syntax.html) if you ever need to look up a particular case.
You can also check out the nice summary tables at this [source](http://www.tutorialspoint.com/python/python_reg_expressions.htm).
Good job!
|
github_jupyter
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.