Deep RL Course documentation
The Problem of Variance in Reinforce
The Problem of Variance in Reinforce
In Reinforce, we want to increase the probability of actions in a trajectory proportionally to how high the return is.

- If the return is high, we will push up the probabilities of the (state, action) combinations.
- Otherwise, if the return is low, it will push down the probabilities of the (state, action) combinations.
This return is calculated using a Monte-Carlo sampling. We collect a trajectory and calculate the discounted return, and use this score to increase or decrease the probability of every action taken in that trajectory. If the return is good, all actions will be “reinforced” by increasing their likelihood of being taken.
The advantage of this method is that it’s unbiased. Since we’re not estimating the return, we use only the true return we obtain.
Given the stochasticity of the environment (random events during an episode) and stochasticity of the policy, trajectories can lead to different returns, which can lead to high variance. Consequently, the same starting state can lead to very different returns. Because of this, the return starting at the same state can vary significantly across episodes.
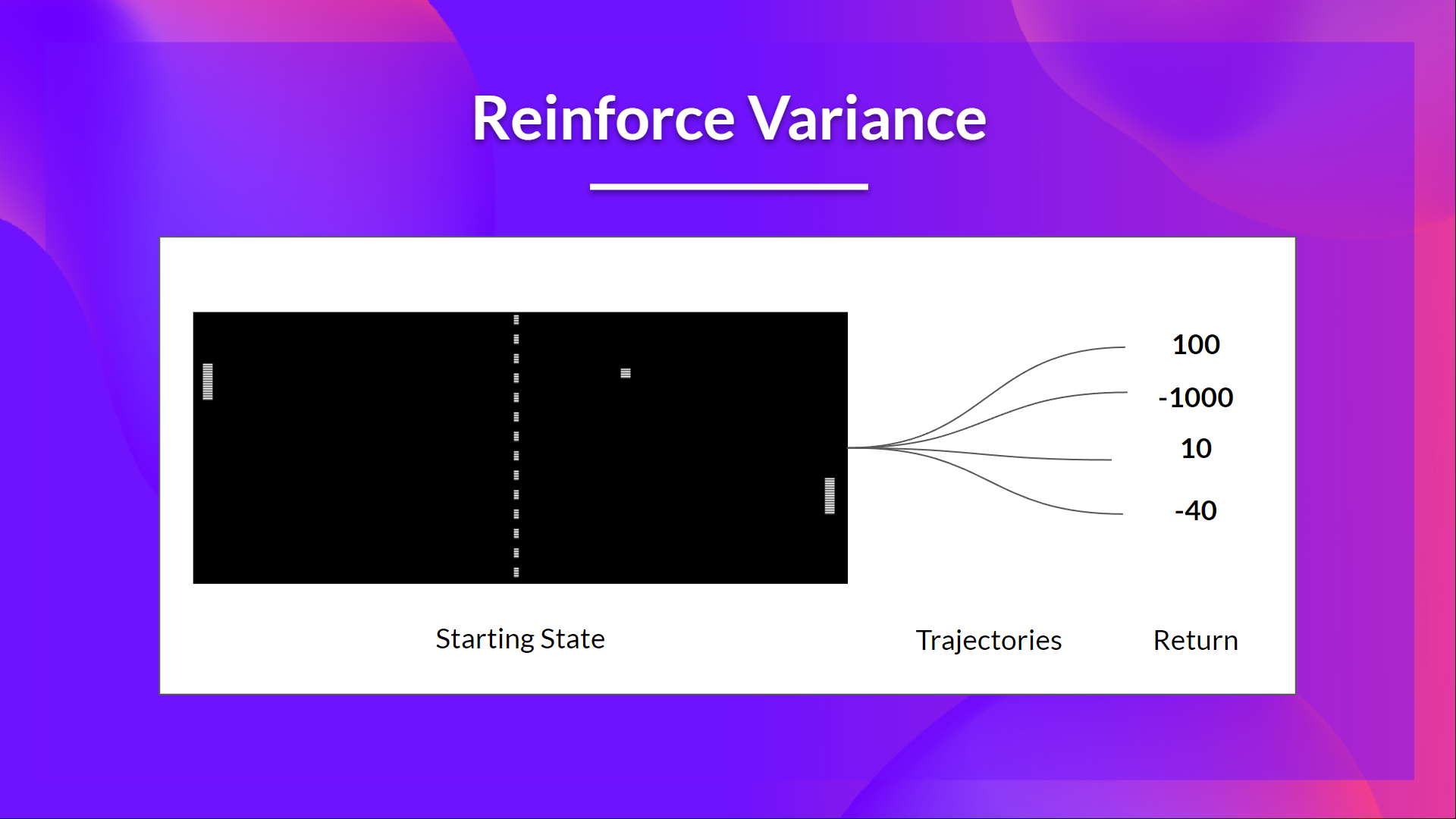
The solution is to mitigate the variance by using a large number of trajectories, hoping that the variance introduced in any one trajectory will be reduced in aggregate and provide a “true” estimation of the return.
However, increasing the batch size significantly reduces sample efficiency. So we need to find additional mechanisms to reduce the variance.
If you want to dive deeper into the question of variance and bias tradeoff in Deep Reinforcement Learning, you can check out these two articles:
- Making Sense of the Bias / Variance Trade-off in (Deep) Reinforcement Learning
- Bias-variance Tradeoff in Reinforcement Learning
- High Variance in Policy gradients
< > Update on GitHub