An optimal lossy variant of speculative decoding

Speculative decoding (Leviathan et al., 2023; Chen et al., 2023) is an elegant decoding strategy for autoregressive language models. It accelerates text generation while preserving the target distribution. In this blog post, I introduce mentored decoding, a novel, provably optimal, lossy variant of speculative decoding. It further increases the decoding speed at the cost of a bounded deviation from the target distribution.

I will first summarize the principle of speculative decoding. I will then present mentored decoding and explain in what sense it is optimal. I will finally comment some initial experimental results and suggest further explorations.

Speculative decoding

Let me first tell you a story which will hopefully help you understand speculative decoding and, in the subsequent section, mentored decoding. Alice is a talented writer who can only speak or write very slowly. Fortunately, her longtime assistant, Bob, has been helping her write books in the following manner:

1. Given the current manuscript and his knowledge of Alice’s works, Bob imagines what the next few words can be and writes down these candidate words;
2. Alice points to the last candidate word she could indeed have written herself;
3. Alice writes the next word;
4. All the words selected at Steps 2 and 3 are added to the manuscript, the other candidate words are discarded and we go back to Step 1.

This can save a lot of time if Bob guesses Alice’s next words reasonably well and writes much faster than her. Moreover, the final manuscript would be indistinguishable from a book written by Alice alone.

As it is probably clear for you now, Alice and Bob actually correspond to autoregressive language models. Similarly to blockwise parallel decoding (Stern et al., 2018) or assisted generation (Joao Gante, 2023), speculative decoding combines a large target model and a small draft model (typically ten times smaller than the target model).

More precisely, assuming that:

• the vocabulary of the tokenizer is $VV$;
• The next token probability distribution of the draft model is $p(\mathrm{.}\mid \mathrm{.})p(.\mid .)$;
• The next token probability distribution of the target model is $q(\mathrm{.}\mid \mathrm{.})q(.\mid .)$;
• The initial prompt and the text generated so far are $x_1,\mathrm{.}\mathrm{.}\mathrm{.},x_{n}x\_1,...,x\_n$;

… speculative decoding would select the next tokens as follows:

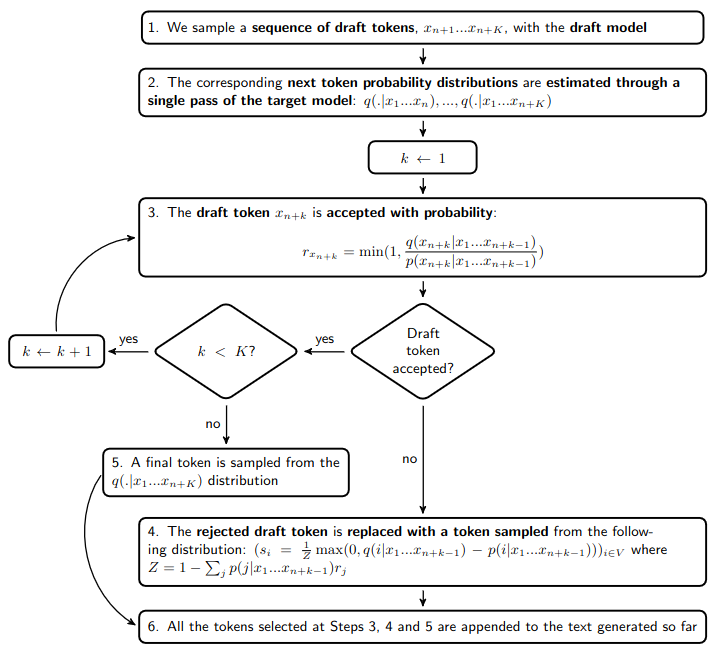
Speculative decoding typically doubles the decoding rate. This speedup comes from the fact that estimating the next token probability distributions with the target model at Step 2 takes approximately as much time as generating one token with this target model. Moreover, the formulas for the acceptance probability $r_{x_{n+k}}r\_\{x\_\{n+k\}\}$ at Step 3 and the replacement token probability distribution $(s_i{)}_{i\in V}(s\_i)\_\{i\; \backslash in\; V\}$ at Step 4 are such that the generated text provably follows the target distribution.

Under this condition, these formulas actually maximize the probability to accept the draft token: ${\sum }_{i\in V}{p}_i{r}_i\backslash sum\_\{i\; \backslash in\; V\}\; p\_i\; r\_i$. This means that we need to deviate from the target distribution if we want to further increase this probability. But let's return first to the story of Alice and Bob...

Mentored decoding

Alice has decided to stop writing after her final masterpiece. She now focuses on mentoring Bob who aspires to be an author as well. Their way of working has remained the same with one major difference: Alice evaluates differently the sequence of candidate words suggested by Bob. In the past, Alice used to discard any word that she would not have written herself. She now wants Bob to find his own voice and only reject a word if it is clearly inadequate. For example, she can reject a spelling mistake, an awkward turn of phrase or a plot hole.

Compared to the previous situation, Alice interrupts Bob less frequently and their manuscript is progressing faster. The resulting book will not have the same style as Alice's books but it will be of high quality thanks to her mentoring.

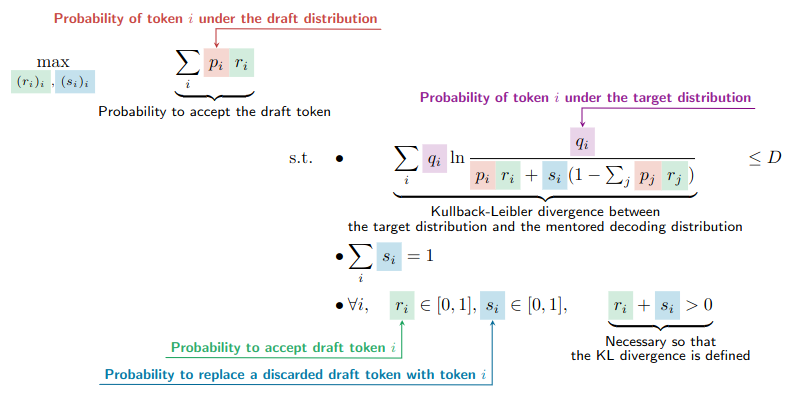
In a similar fashion, we are now ready to diverge from the target distribution in a controlled manner to increase the probability to accept draft tokens. More specifically, we want to find the values of $(r_i{)}_{i\in V}(r\_i)\_\{i\; \backslash in\; V\}$ or $(s_i{)}_{i\in V}(s\_i)\_\{i\; \backslash in\; V\}$ that maximally increase the probability to accept $ii$ while maintaining the Kullback-Leibler divergence between the resulting distribution and the target distribution under a certain constant $DD$.

Since we only focus on one token, we can simplify our notations:

• $p_i=p(i\mid x_1\mathrm{.}\mathrm{.}\mathrm{.}{x}_{n+k-1})p\_i\; =\; p(i\backslash mid\; x\_1...x\_\{n+k-1\})$;
• $q_i=q(i\mid x_1\mathrm{.}\mathrm{.}\mathrm{.}{x}_{n+k-1})q\_i\; =\; q(i\backslash mid\; x\_1...x\_\{n+k-1\})$;
• When dummy variables are not specified explicitly, e.g. in $(r_i{)}_i(r\_i)\_i$, ${\sum }_i\backslash sum\_i$ and $\mathrm{\forall }i\backslash forall\; i$, they correspond the whole vocabulary: $(r_i{)}_{i\in V}(r\_i)\_\{i\; \backslash in\; V\}$, ${\sum }_{i\in V}\backslash sum\_\{i\; \backslash in\; V\}$ and $\mathrm{\forall }i\in V\backslash forall\; i\; \backslash in\; V$.

The probability to obtain token $ii$ with the speculative approach is then ${\pi }_i=p_i{r}_i+s_i(1-{\sum }_j{p}_j{r}_j)\backslash pi\_i\; =\; p\_ir\_i\; +\; s\_i\; (1\; -\; \backslash sum\_j\; p\_jr\_j)$ (Chen et al., 2023) and $(r_i{)}_i(r\_i)\_i$ or $(s_i{)}_i(s\_i)\_i$ are the solutions of the following optimization problem:

Solving the optimization problem

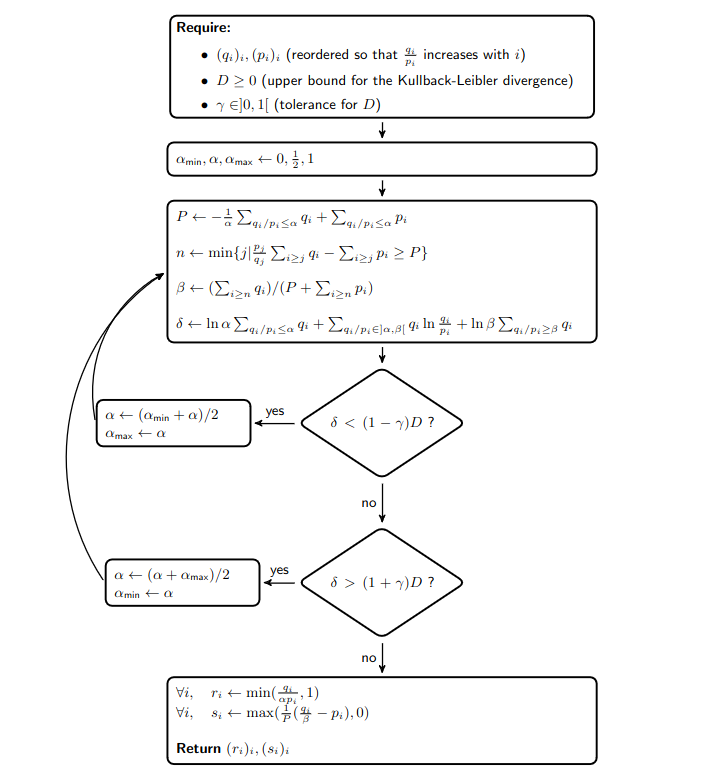
Fortunately, solving this non-linear optimization problem with close to $10^{5}10^5$ decision variables is feasible with limited computational overhead. In the attached proof which is mainly based on the Karush-Kuhn-Tucker conditions {% cite kuhn2013nonlinear %}, we show that:

• a unique solution exists in non-trivial cases;
• for this solution, $(r_i{)}_i(r\_i)\_i$ or $(s_i{)}_i(s\_i)\_i$ verify:
  • $r_i=\min (1,\frac{q_i}{\alpha p_i})r\_i\; =\; \backslash min(1,\; \backslash frac\{q\_i\}\{\backslash alpha\; p\_i\})$ for a certain $\alpha \backslash alpha$
  • $s_i=\frac{1}{1-{\sum }_j{p}_j{r}_j}\max (0,\frac{q_i}{\beta }-p_i)s\_i\; =\; \backslash frac\{1\}\{1-\backslash sum\_jp\_jr\_j\}\backslash max(0,\; \backslash frac\{q\_i\}\{\backslash beta\}-p\_i)$ for a certain $\beta \backslash beta$
• there is a one-to-one relationship between $\alpha \backslash alpha$ and $\beta \backslash beta$ in non-trivial cases so choosing $\alpha \in ]0,1]\backslash alpha\; \backslash in\; ]0,\; 1]$ is enough to find the solution of the optimization problem for a certain $DD$;
• the objective function and the Kullback-Leibler divergence in the first inequality constraint are decreasing functions of $\alpha \backslash alpha$.

These findings imply that computing the solution to the optimization problem is straightforward using a binary search on $\alpha \backslash alpha$. More precisely, the diagram below presents the mentored decoding algorithm:

Furthermore, the following facts reduce the computational overhead of mentored decoding:

• Since we know that $r_i\ge \min (1,\frac{q_i}{p_i})r\_i\; \backslash geq\; \backslash min(1,\; \backslash frac\{q\_i\}\{p\_i\})$, we can compute $r_{i}r\_i$ and $(s_j{)}_j(s\_j)\_j$ only when the value $u\sim U([0,1])u\; \backslash sim\; U([0,\; 1])$ drawn at random to accept or reject the draft token is greater than $\min (1,\frac{q_i}{p_i})\backslash min(1,\; \backslash frac\{q\_i\}\{p\_i\})$;
• When the Kullback-Leibler divergence between the target distribution $(q_i{)}_i(q\_i)\_i$ and the draft distribution $(p_i{)}_i(p\_i)\_i$ for a given token is less than $DD$, we can directly accept the draft token;
• All the values for $({\sum }_{i\le j}{q}_i{)}_j(\backslash sum\_\{i\; \backslash leq\; j\}\; q\_i)\_j$, $({\sum }_{i\le j}{p}_i{)}_j(\backslash sum\_\{i\; \backslash leq\; j\}\; p\_i)\_j$, $({\sum }_{i\ge j}{q}_i{)}_j(\backslash sum\_\{i\; \backslash geq\; j\}\; q\_i)\_j$, $({\sum }_{i\ge j}{p}_i{)}_j(\backslash sum\_\{i\; \backslash geq\; j\}\; p\_i)\_j$, $({\sum }_{i\le j}{q}_i\ln \frac{q_i}{p_i}{)}_j(\backslash sum\_\{i\; \backslash leq\; j\}\; q\_i\; \backslash ln\backslash frac\{q\_i\}\{p\_i\})\_j$ and $(\frac{p_j}{q_j}{\sum }_{i\ge j}{q}_i-{\sum }_{i\ge j}{p}_i{)}_j(\backslash frac\{p\_j\}\{q\_j\}\; \backslash sum\_\{i\; \backslash geq\; j\}\; q\_i\; -\; \backslash sum\_\{i\; \backslash geq\; j\}\; p\_i)\_j$ can be computed in a vectorized manner before the loop to save time.

First experimental results

As a first experiment (full code here), I tested mentored decoding on an English-to-French translation task with a subset of the WMT15 dataset and T5-large and T5-small as the target and draft models.

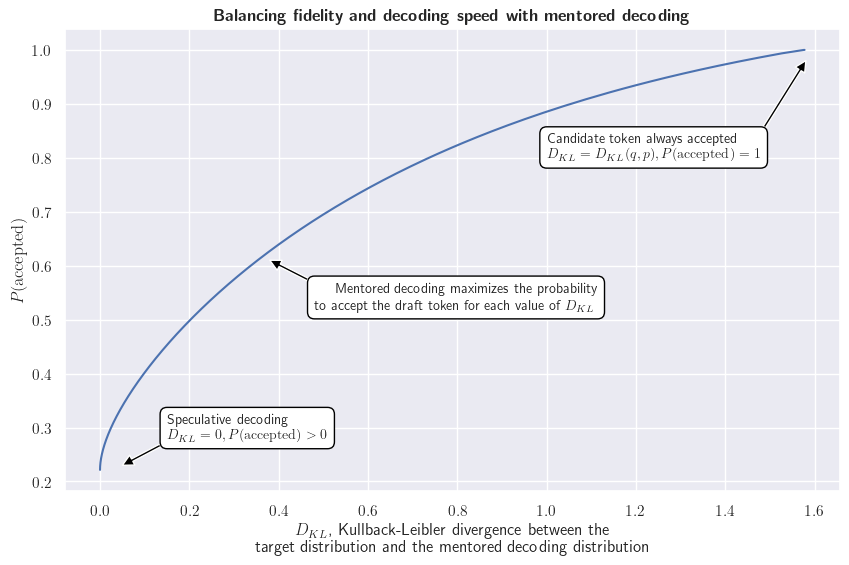
If we first look at a single token, we can visualize the solutions of our optimization problem for various values of the Kullback-Leibler divergence. The following chart illustrates the balance between the probability to accept the draft token ${\sum }_i{p}_i{r}_i\backslash sum\_i\; p\_ir\_i$ and the fidelity to the target distribution.

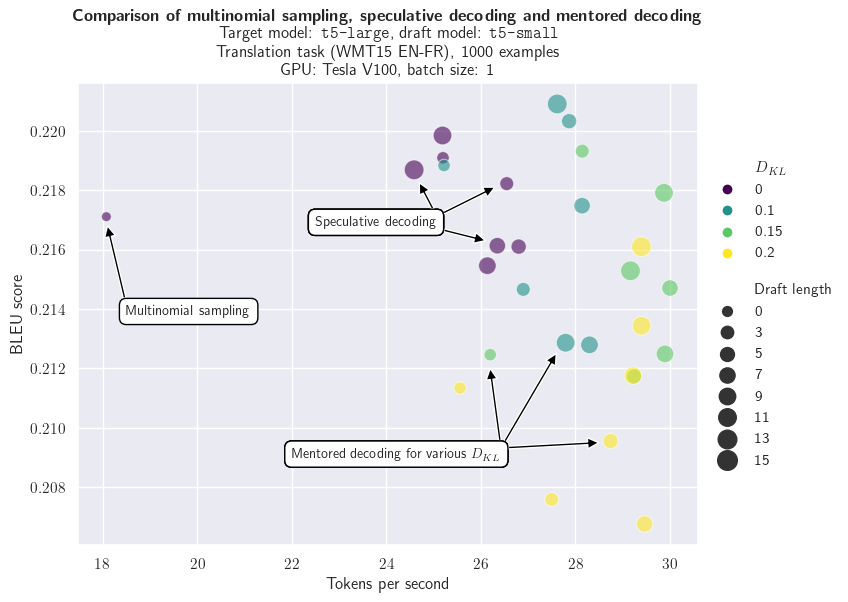
Evaluating mentored decoding requires measuring both the decoding speed and a performance metric for the downstream task, for example the BLEU score here. The latter is important: since we allow a deviation from the target distribution, we need to assess the potential impacts on the task of interest. The next chart compares multinomial sampling, speculative decoding and mentored decoding for various draft lengths and values of the Kullback-Leibler divergence (only for mentored decoding). We can see that:

• Speculative decoding significantly improves the decoding speed in comparison with multinomial sampling;
• Mentored decoding further increases the number of tokens generated per second;
• Compared with multinomial sampling, speculative decoding and mentored decoding with the smallest value of the Kullback-Leibler divergence do not appear to significantly differ in BLEU scores (which is expected for speculative decoding since the target distribution is preserved);
• Unsurprisingly, increasing the Kullback-Leibler divergence both accelerates the text generation and degrades the BLEU score.

Conclusion and further work

In this blog post, I introduced a lossy variant of speculative decoding. It maximizes the probability to accept draft tokens for a given bound on the Kullback-Leibler divergence between the target distribution and the resulting distribution. The initial experimental results above suggest that mentored decoding can increase the decoding rate, either moderately with limited impact on the performance of a downstream task or more strongly at the cost of a noticeable degration of this performance.

Extensive experiments are needed to explore the spectrum of tasks and models for which mentored decoding is relevant. In particular, it would be interesting to empirically test the following intuitions:

• Tasks for which valid answers can be written in various ways (e.g. translation, summarization or chain-of-thought question answering) would benefit more from mentored decoding than tasks with a narrow range of valid answers (e.g. speech-to-text);
• Mentored decoding would work better with a highly capable target model, capable not only to perform the downstream task but also to assess alternatively worded valid answers.

Many thanks to the authors of the articles mentioned below and to the maintainers of the various software libraries used for this work, in particular Transformers, PyTorch, TikZ and annotate-equations. Cover image created with ArtOut.

This blog post was initially published on my personal blog.