Sparse Mixture of Experts Language Model from Scratch: Extending makeMoE with Expert Capacity
My previous blog, which detailed the end-to-end implementation of a sparse mixture of experts language model named 'makeMoE'—inspired by Andrej Karpathy's makemore and nanoGPT—garnered a lot of love from the community (https://huggingface.co/blog/AviSoori1x/makemoe-from-scratch). The recent open sourcing of Grok-1 by x.ai, another sparse MoE LLM, further motivated me to enhance makeMoE by incorporating a feature I had initially omitted: expert capacity.
The Github repo here provides the end-to-end implementation (with expert capacity): https://github.com/AviSoori1x/makeMoE
Why is Expert Capacity even important?
When pretraining a sparse mixture of experts language model, or any large language model, the process typically spans several GPUs and often many machines. The way training is parallelized across these hardware resources is critical for balancing the computational load. However, if certain experts or a set of experts become overly favored—reflecting a bias towards exploitation over exploration—it can lead not only to potential performance issues in the model but also to an imbalance in the computational load across the cluster.
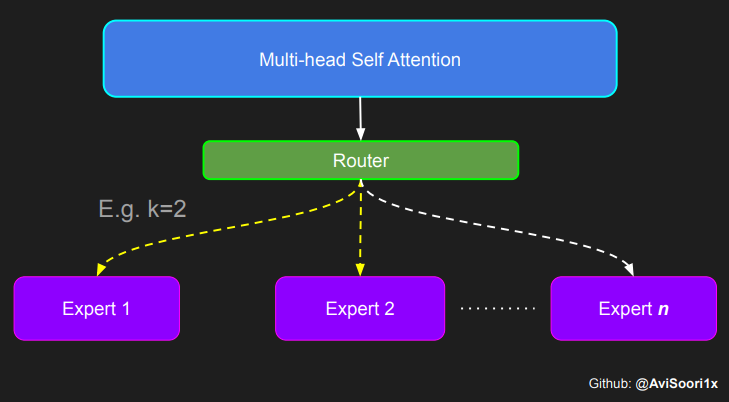
The Switch Transformer implementation uses expert capacity to circumvent this.The expert capacity determines how many tokens each expert is responsible for during the training or inference process and setting a limit on the number of tokens processed per expert. It is defined based on the number of tokens in the batch and the number of available experts, often adjusted by a capacity factor. This factor allows for flexibility in the allocation, providing a buffer to account for variations in the data distribution and ensuring that no single expert becomes a bottleneck due to being overloaded. Hardware failures are common in training these large models for many weeks if not months, so this is quite important.
Here's how expert capacity is generally calculated:
Expert Capacity = (Tokens per batch / Number of experts) × Capacity factor Where:
Tokens per batch is the total number of tokens present in a batch that needs to be processed. Number of experts is the total count of experts available in the MoE layer to process the data. Capacity factor is a multiplier used to adjust the base capacity (tokens per batch divided by the number of experts). A capacity factor greater than 1 allows each expert to handle a buffer above the evenly distributed share, accommodating imbalances in token assignment. The general range for this value is 1-1.25
The following code block makes a slight adjustment to implement a simple version of expert capacity
class SparseMoE(nn.Module):
def __init__(self, n_embed, num_experts, top_k, capacity_factor=1.0):
super(SparseMoE, self).__init__()
self.router = NoisyTopkRouter(n_embed, num_experts, top_k)
self.experts = nn.ModuleList([Expert(n_embed) for _ in range(num_experts)])
self.top_k = top_k
self.capacity_factor = capacity_factor
self.num_experts = num_experts
def forward(self, x):
# Assuming x has shape [batch_size, seq_len, n_embd]
batch_size, seq_len, _ = x.shape
gating_output, indices = self.router(x)
final_output = torch.zeros_like(x)
# Flatten the batch and sequence dimensions to treat each token independently
flat_x = x.view(-1, x.size(-1)) # Now shape [batch_size * seq_len, n_embd]
flat_gating_output = gating_output.view(-1, gating_output.size(-1))
tokens_per_batch = batch_size * seq_len * self.top_k
expert_capacity = int((tokens_per_batch / self.num_experts) * self.capacity_factor)
updates = torch.zeros_like(flat_x)
for i, expert in enumerate(self.experts):
expert_mask = (indices == i).any(dim=-1)
flat_mask = expert_mask.view(-1)
selected_indices = torch.nonzero(flat_mask).squeeze(-1)
limited_indices = selected_indices[:expert_capacity] if selected_indices.numel() > expert_capacity else selected_indices
if limited_indices.numel() > 0:
expert_input = flat_x[limited_indices]
expert_output = expert(expert_input)
gating_scores = flat_gating_output[limited_indices, i].unsqueeze(1)
weighted_output = expert_output * gating_scores
updates.index_add_(0, limited_indices, weighted_output)
# Reshape updates to match the original dimensions of x
final_output += updates.view(batch_size, seq_len, -1)
return final_output
There is a fair bit of tensor shape manupulation going on to ensure the shapes align (which is often the case in these implementations), but the most important part of the implementation is only in a few lines of code. Let's zoom in on those.
First let's take a look at the expert capacity calculation
expert_capacity = int((tokens_per_batch / self.num_experts) * self.capacity_factor)
This is pretty straightforward. The reason that this is included within the forward pass itself, is to account for situations where dynamic batch sizes are used.
The next important line is the following:
limited_indices = selected_indices[:expert_capacity] if selected_indices.numel() > expert_capacity else selected_indices
if limited_indices.numel() > 0:
#remaining logic to process and accumulate weighted expert outputs for selected tokens.
The selected_indices tensor identifies the tokens designated for processing by the ith expert. If the total tokens allocated to this expert surpass its capacity, the tensor is truncated to match the expert's maximum handling capacity. Otherwise, it is utilized as is for further computations.
These computations involve determining the output for each token via the expert, then applying the corresponding gating value to derive a weighted output. This weighted output is incrementally combined with the final output tensor, contributing to the overall model output.
The notebook with the implementation is here: https://github.com/AviSoori1x/makeMoE/blob/main/makeMoE_from_Scratch_with_Expert_Capacity.ipynb
This approach to managing expert capacity is relatively basic. More advanced strategies are explored in literature, such as the switch transformer architecture discussed in the Google paper available at https://arxiv.org/abs/2101.03961. Although the method presented here simplifies capacity handling, it serves as an intuitive introduction to the concept and makes makeMoE a bit more complete!