Spaces:
Running
Running
File size: 4,779 Bytes
9e7941a 7300e19 9e7941a 7300e19 9e7941a 7300e19 9e7941a 7300e19 |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 |
---
title: MASE
emoji: 🤗
colorFrom: blue
colorTo: red
sdk: gradio
sdk_version: 3.0.2
app_file: app.py
pinned: false
tags:
- evaluate
- metric
description: >-
Mean Absolute Scaled Error (MASE) is the mean absolute error of the forecast values, divided by the mean absolute error of the in-sample one-step naive forecast on the training set.
---
# Metric Card for MASE
## Metric Description
Mean Absolute Scaled Error (MASE) is the mean absolute error of the forecast values, divided by the mean absolute error of the in-sample one-step naive forecast. For prediction $x_i$ and corresponding ground truth $y_i$ as well as training data $z_t$ with seasonality $p$ the metric is given by:
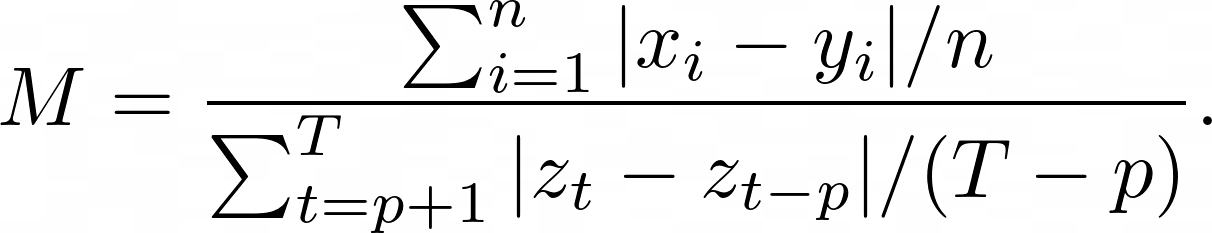
This metric is:
* independent of the scale of the data;
* has predictable behavior when predicted/ground-truth data is near zero;
* symmetric;
* interpretable, as values greater than one indicate that in-sample one-step forecasts from the naïve method perform better than the forecast values under consideration.
## How to Use
At minimum, this metric requires predictions, references and training data as inputs.
```python
>>> mase_metric = evaluate.load("mase")
>>> predictions = [2.5, 0.0, 2, 8]
>>> references = [3, -0.5, 2, 7]
>>> training = [5, 0.5, 4, 6, 3, 5, 2]
>>> results = mase_metric.compute(predictions=predictions, references=references, training=training)
```
### Inputs
Mandatory inputs:
- `predictions`: numeric array-like of shape (`n_samples,`) or (`n_samples`, `n_outputs`), representing the estimated target values.
- `references`: numeric array-like of shape (`n_samples,`) or (`n_samples`, `n_outputs`), representing the ground truth (correct) target values.
- `training`: numeric array-like of shape (`n_train_samples,`) or (`n_train_samples`, `n_outputs`), representing the in sample training data.
Optional arguments:
- `periodicity`: the seasonal periodicity of training data. The default is 1.
- `sample_weight`: numeric array-like of shape (`n_samples,`) representing sample weights. The default is `None`.
- `multioutput`: `raw_values`, `uniform_average` or numeric array-like of shape (`n_outputs,`), which defines the aggregation of multiple output values. The default value is `uniform_average`.
- `raw_values` returns a full set of errors in case of multioutput input.
- `uniform_average` means that the errors of all outputs are averaged with uniform weight.
- the array-like value defines weights used to average errors.
### Output Values
This metric outputs a dictionary, containing the mean absolute error score, which is of type:
- `float`: if multioutput is `uniform_average` or an ndarray of weights, then the weighted average of all output errors is returned.
- numeric array-like of shape (`n_outputs,`): if multioutput is `raw_values`, then the score is returned for each output separately.
Each MASE `float` value ranges from `0.0` to `1.0`, with the best value being 0.0.
Output Example(s):
```python
{'mase': 0.5}
```
If `multioutput="raw_values"`:
```python
{'mase': array([0.5, 1. ])}
```
#### Values from Popular Papers
### Examples
Example with the `uniform_average` config:
```python
>>> mase_metric = evaluate.load("mase")
>>> predictions = [2.5, 0.0, 2, 8]
>>> references = [3, -0.5, 2, 7]
>>> training = [5, 0.5, 4, 6, 3, 5, 2]
>>> results = mase_metric.compute(predictions=predictions, references=references, training=training)
>>> print(results)
{'mase': 0.1833...}
```
Example with multi-dimensional lists, and the `raw_values` config:
```python
>>> mase_metric = evaluate.load("mase", "multilist")
>>> predictions = [[0.5, 1], [-1, 1], [7, -6]]
>>> references = [[0.1, 2], [-1, 2], [8, -5]]
>>> training = [[0.5, 1], [-1, 1], [7, -6]]
>>> results = mase_metric.compute(predictions=predictions, references=references, training=training)
>>> print(results)
{'mase': 0.1818...}
>>> results = mase_metric.compute(predictions=predictions, references=references, training=training, multioutput='raw_values')
>>> print(results)
{'mase': array([0.1052..., 0.2857...])}
```
## Limitations and Bias
## Citation(s)
```bibtex
@article{HYNDMAN2006679,
title = {Another look at measures of forecast accuracy},
journal = {International Journal of Forecasting},
volume = {22},
number = {4},
pages = {679--688},
year = {2006},
issn = {0169-2070},
doi = {https://doi.org/10.1016/j.ijforecast.2006.03.001},
url = {https://www.sciencedirect.com/science/article/pii/S0169207006000239},
author = {Rob J. Hyndman and Anne B. Koehler},
}
```
## Further References
- [Mean absolute scaled error - Wikipedia](https://en.wikipedia.org/wiki/Mean_absolute_scaled_errorr)
|