오디오 데이터에 대하여

본질적으로 음파(sound wave)는 연속적인 신호입니다. 이는 어떤 주어진 시간에 대해 무한개의 신호 값을 가진다는 뜻입니다. 그런데 디지털 기기들은 유한개의 값들을 요구하기에 문제가 됩니다. 이런 디지털 기기에서의 처리, 저장, 전송을 위해 연속적인 음파들은 일련의 이산적인(discrete) 값, 즉 디지털 표현(digital representation)으로 변환되어야 합니다.

어떤 오디오 데이터셋에서건 텍스트 나레이션이나 음악같은 디지털 음향 파일들을 볼 수 있습니다. 이는 .wav (Waveform Audio File), .flac (Free Lossless Audio Codec), 그리고 .mp3 (MPEG-1 Audio Layer 3)같이 다양한 포맷으로 접할 수 있습니다. 이 포맷들은 주로 오디오 신호의 디지털 표현을 압축하는 방식에서 차이가 있습니다.

연속적인 신호로부터 이러한 표현을 얻는 방법에 대해 알아봅시다. 아날로그 신호는 먼저 마이크에 의해 포착되어 음파에서 전기 신호로 변환됩니다. 이 전기 신호는 아날로그-디지털 컨버터(Analog-to-Dogital Converter)를 거치며 샘플링(sampling)을 통해 디지털 표현으로 디지털화됩니다.

샘플링과 샘플링 속도(sampling rate)

샘플링이란 연속적인 신호를 고정된 시간 간격으로 측정하는 과정입니다. 샘플링된 파형(waveform)은 균일한 간격으로 유한개의 신호 값을 가지므로 이산적입니다.

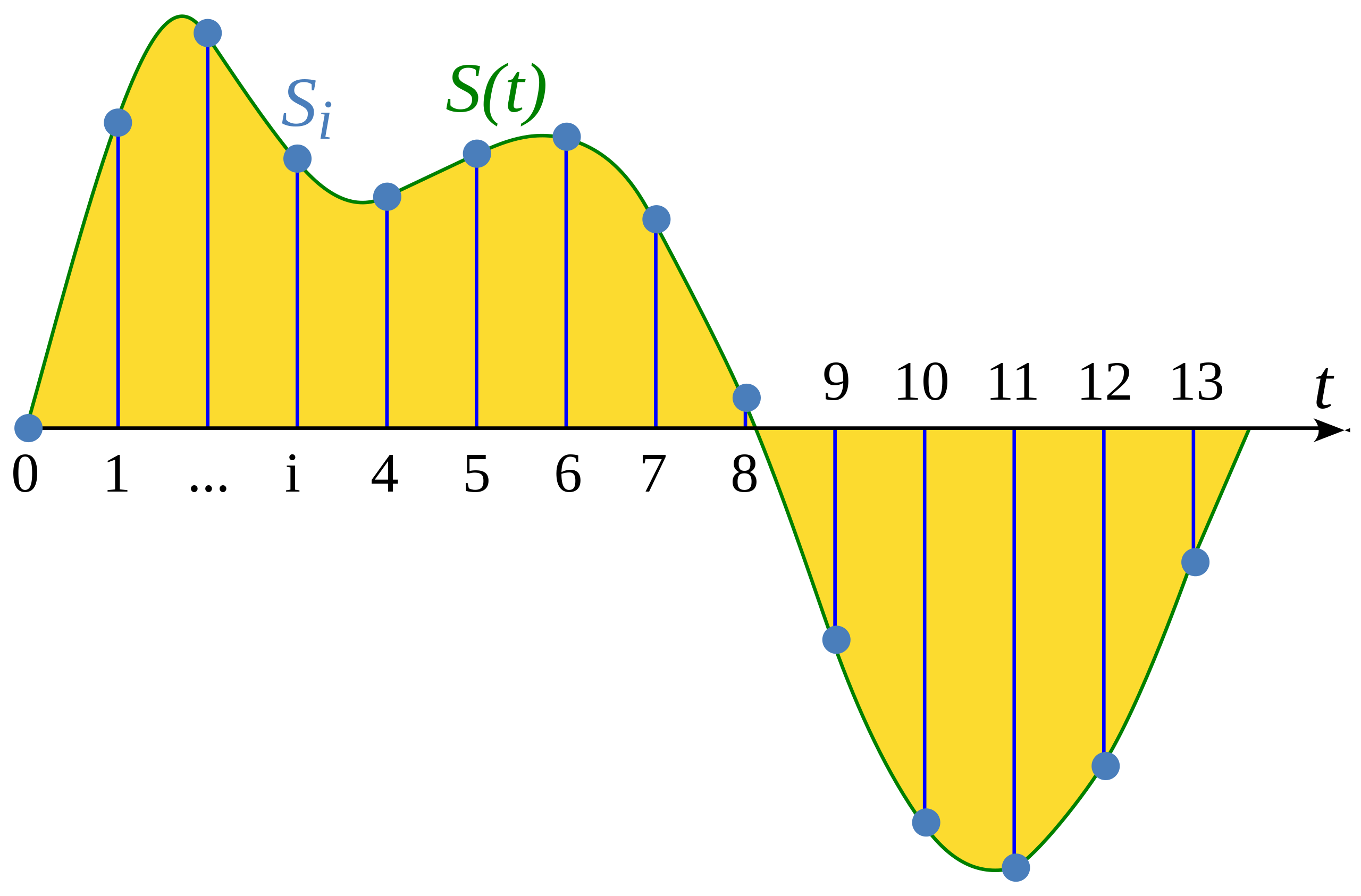
Illustration from Wikipedia article: Sampling (signal processing)

샘플링 속도 (샘플링 주파수(sampling frequency)라고도 합니다)는 1초동안 수집된 샘플의 수로, 헤르츠(Hz)단위로 측정됩니다. 예를 들어 CD 품질의 오디오는 44,100 Hz의 샘플링 속도를 가지며 이는 초당 44,100번의 샘플이 수집된다는 뜻입니다. 고해상도 오디오는 192,000 Hz(혹은 192 kHz)의 샘플링 속도를 가집니다. 음성 모델 학습에 주로 쓰이는 샘플링 속도는 16,000 Hz(혹은 16 kHz)입니다.

샘플링 속도의 선택은 신호에서 얼마나 큰 주파수까지 캡처할 수 있는지를 결정하는데 큰 역할을 합니다. 신호에서 캡처가능한 최고 주파수의 한계는 샘플링 속도의 정확히 절반이며 이를 나이퀴스트 한계(Nyquist limit)라고 합니다. 예를 들면 사람의 음성에서 들을 수 있는 주파수는 8 kHz 미만이므로 16 kHz로 음성을 샘플링한다면 충분할 것입니다. 더 높은 샘플링 속도를 사용하여도 얻을 수 있는 추가 정보는 없을것이며 오히려 파일 처리에 대한 계산 비용만 증가시키게 됩니다. 반면, 너무 낮은 샘플링 속도는 정보의 손실로 이어집니다. 8 kHz로 샘플링된 음성은 높은 주파수들을 캡처할 수 없기때문에 흐릿하게 들릴것입니다.

오디오 작업을 할 때는 데이터셋에 있는 모든 오디오 예제가 동일한 샘플링 속도를 가지고 있는지 확인하는것이 중요합니다. 여러분의 커스텀 데이터로 사전 학습된 모델을 파인튜닝할 계획이라면 모델이 사전 학습된 데이터의 샘플링 속도와 여러분의 데이터의 샘플링 속도가 일치해야 합니다. 샘플링 속도는 샘플간의 시간 간격을 결정하며 오디오 데이터의 시간 해상도(time interval)에 영향을 주기 때문입니다. 예를 들어, 16,000 Hz의 샘플링 속도를 가진 5초 길이의 소리는 80,000개의 값으로 표현되지만, 동일한 5초 길이의 소리여도 8,000 Hz의 샘플링 속도를 가진다면 40,000개의 값으로 표현됩니다. 오디오 작업을 처리하는 트랜스포머 모델은 시퀀스를 취급하며 어텐션 메커니즘을 이용해 오디오 또는 멀티모달 표현을 학습합니다. 서로 다른 샘플링 속도를 갖는 오디오 데이터는 다른 시퀀스가 되므로 모델이 샘플링 속도간 일반화를 하기 어렵습니다. 리샘플링은 이런 서로 다른 샘플링 속도를 일치시켜주는 작업으로, 오디오 데이터 전처리 과정 중 하나입니다.

진폭(amplitude)과 비트뎁스(bit depth)

샘플링 속도는 샘플을 얼마나 자주 뽑는지 알려줍니다. 그런데 이 샘플의 값은 정확히 어떤걸 뜻할까요?

소리는 사람이 들을 수 있는 주파수에서 기압의 변화로 만들어집니다. 소리의 진폭이란 특정 순간의 소리의 압력 수준을 나타내며 데시벨(dB)로 측정됩니다. 즉, 진폭은 소리의 세기를 뜻합니다. 예를 들어, 일반적인 말소리는 60 dB 미만입니다. 락 콘서트 같은 경우 약 125 dB로 사람의 청각적 한계를 뛰어넘을 수 있습니다.

디지털 오디오에서, 각 오디오 샘플은 특정 시점의 오디오 파동의 진폭을 기록합니다. 샘플의 비트뎁스는 이 진폭 값을 얼마나 정밀하게 기록할지를 정합니다. 비트뎁스가 높을수록 디지털 표현이 원래의 연속 음파에 더 가까워 집니다.

가장 일반적인 오디오 비트뎁스는 16비트와 24비트입니다. 이는 이진 용어(binary term)로, 진폭값을 연속값에서 이산값으로 변환할때 양자화(quantized)할 수 있는 수를 나타냅니다. 16비트 오디오의 경우 65,356개, 24비트 오디오의 경우 16,777,216개에 달합니다. 양자화는 연속값을 이산값으로 바꾸는 과정에서 반올림이 일어나므로 샘플링 과정은 노이즈가 발생합니다. 비트뎁스가 높을수록, 이런 양자화 노이즈는 작아집니다. 실무적으론 16비트 정도만 돼도 양자화 노이즈가 이미 들리지 않을 정도로 작아 이를 위해 굳이 더 높은 비트뎁스를 사용할 필요는 없습니다.

여러분은 32비트 오디오를 접할 수도 있습니다. 이는 값을 소수로 저장하기 위함으로, 16비트나 24비트 오디오는 값을 정수로 저장하는 반면 32비트는 샘플을 부동소수점 값으로 저장합니다. 32비트 부동 소수점 값의 정밀도는 24비트이므로 24비트 오디오와 같은 비트뎁스를 가지게 됩니다. 부동 소수점 오디오 샘플은 [-1.0, 1.0] 범위의 값을 가집니다. 머신 러닝 모델은 기본적으로 부동 소수점 데이터에서 작동하므로 학습 전 먼저 오디오를 부동 소수점 형식으로 변환해야 합니다. 이는 다음 전처리 섹션에서 살펴보겠습니다.

연속적인 오디오 신호와 마찬가지로 디지털 오디오의 진폭 역시 일반적으로 데시벨(dB)로 표시됩니다. 인간의 청각은 기본적으로 로그함수를 따르므로(우리 귀는 큰 소리보다 조용한 소리의 작은 변동에 더 민감합니다) 진폭이 데시벨(마찬가지로 로그함수를 따릅니다)로 표시되면 소리의 크기를 해석하기 쉽습니다. 실생활에서 쓰이는 오디오 데시벨 단위는 사람이 들을 수 있는 가장 조용한 소리인 0 dB에서 시작하여 소리가 커질수록 값도 커집니다. 그러나 디지털 오디오 신호의 경우, 0 dB이 가장 큰 진폭이며 다른 모든 진폭은 음수값을 가집니다(디지털에서의 데시벨 단위는 dBFS, 실생활에서 주로 쓰이는 데시벨은 dBSPL로 서로 다릅니다). 간단한 규칙으로 -6 dB마다 진폭이 절반으로 줄어들고 -60 dB 미만은 일반적으로 볼륨을 크게 높이지 않는 한 들을 수 없다고 보시면 됩니다.

파형(waveform)으로써의 오디오

여러분은 아마 소리가 파형으로 시각화된것을 본 적이 있으실 겁니다. 이는 시간에 따른 샘플 값들을 그래프로 표현하여 소리의 진폭 변화를 보여줍니다. 이를 소리의 시간 영역(time domain) 표현이라고도 합니다.

이러한 유형의 사각화는 특정 사운드 이벤트가 언제 발생했는지, 전체적인 음량은 어떤지, 오디오에 어떤 노이즈나 불규칙성이 있는지 등 오디오 신호의 특징을 식별하는데 유용합니다.

오디오 신호의 파형을 그리기 위해 파이썬 라이브러리 librosa를 이용할 수 있습니다:

pip install librosa

라이브러리에서 제공하는 “트럼펫” 소리를 예로 들어 보겠습니다:

import librosa

array, sampling_rate = librosa.load(librosa.ex("trumpet"))

이 예제는 오디오 시계열(array)과 샘플링 속도(sampling_rate) 튜플을 불러옵니다. 이 사운드의 파형을 librosa의 waveshow() 함수를 통해 살펴보겠습니다:

import matplotlib.pyplot as plt
import librosa.display

plt.figure().set_figwidth(12)
librosa.display.waveshow(array, sr=sampling_rate)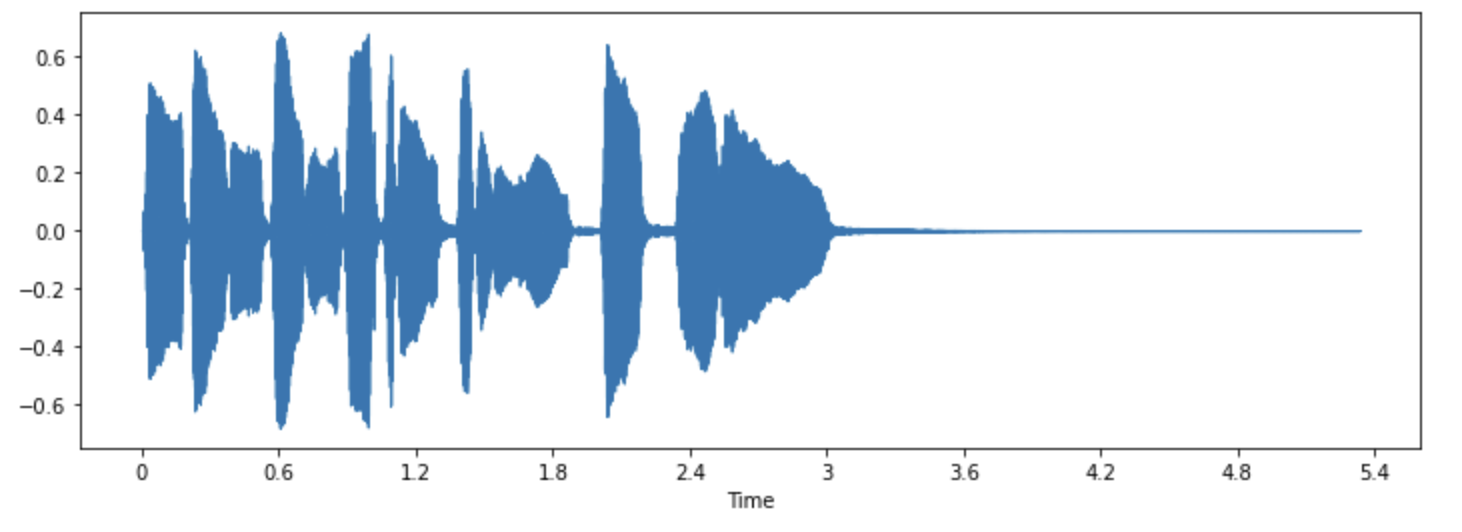

이 그래프의 X축은 시간을, Y축은 진폭을 나타냅니다. 각 점은 이 소리를 샘플링할때 취한 값에 해당합니다. librosa가 이미 오디오를 부동소수점 값으로 변환했으며 진폭값이 [-1.0, 1.0] 범위내에 있다는 점을 유의하세요.

이런 시각화는 오디오를 듣는것과 더불어 작업할 데이터를 이해하는데 유용한 도구가 될 수 있습니다. 이를 통해 신호의 모양, 패턴 관찰, 노이즈나 왜곡을 발견할 수 있습니다. 만약 정규화(normalization), 리샘플링, 필터링 등의 방법을 통해 데이터 전처리를 했다면, 이런 전처리가 제대로 되었는지 시각적으로 확인할 수도 있습니다. 또한 모델의 학습이 완료된 후에 어디서 오류가 발생했는지 디버깅하기위해 샘플을 시각화할 수도 있습니다(예를 들어, 오디오 분류 작업 문제 등에서).

주파수 스펙트럼(frequency spectrum)

오디오 데이터를 시각화하는 또 다른 방법은 오디오 신호의 주파수 스펙트럼을 그리는 것입니다. 이는 주파수 영역(frequency domain) 표현이라고도 합니다. 스펙트럼은 이산 푸리에 변환(DFT)을 사용하여 계산할 수 있습니다. 이를 통해 신호를 구성하고 있는 각각의 주파수들과 그 세기를 알 수 있습니다.

numpy의 rfft() 함수를 쓰면 DFT를 계산할 수 있습니다. 이를 아까의 트럼펫 소리에 적용시켜 주파수 스펙트럼을 그려봅시다. 전체 소리의 스펙트럼을 그릴 수도 있지만, 그보다는 작은 영역에 집중하는것이 더 낫습니다. 여기서는 첫 4096개의 샘플에 적용시켜보겠습니다. 이는 대략적으로 연주의 첫 음표의 길이에 해당합니다:

import numpy as np

dft_input = array[:4096]

# calculate the DFT
window = np.hanning(len(dft_input))
windowed_input = dft_input * window
dft = np.fft.rfft(windowed_input)

# get the amplitude spectrum in decibels
amplitude = np.abs(dft)
amplitude_db = librosa.amplitude_to_db(amplitude, ref=np.max)

# get the frequency bins
frequency = librosa.fft_frequencies(sr=sampling_rate, n_fft=len(dft_input))

plt.figure().set_figwidth(12)
plt.plot(frequency, amplitude_db)
plt.xlabel("Frequency (Hz)")
plt.ylabel("Amplitude (dB)")
plt.xscale("log")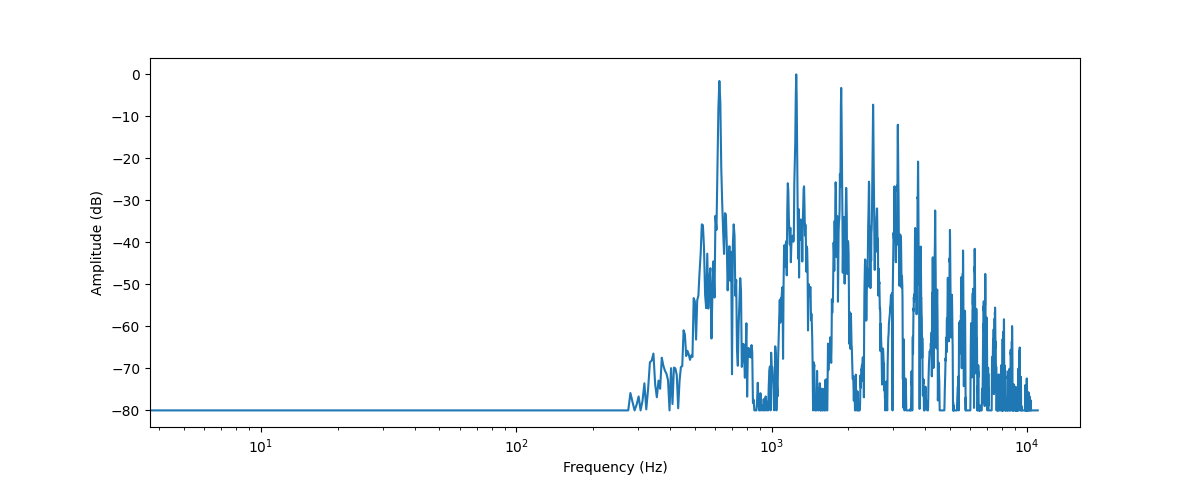

이 그래프는 이 오디오 구간에 존재하는 다양한 주파수의 세기를 보여줍니다. 보통 X축에 로그스케일로 주파수를, Y축엔 진폭을 표시합니다.

이 주파수 스펙트럼 그래프는 여러개의 피크를 보여주는데, 이 피크들은 연주중인 음표의 고조파(harmonic)에 해당하며 더 높은 고조파는 더 작은 소리를 나타냅니다. 첫번째 피크가 약 620 Hz에 있으므로 이 스펙트럼은 E♭ 음표의 주파수 스펙트럼인것을 알 수 있습니다.

DFT의 결과값은 복소수 배열입니다. np.abs(dft)로 그 크기를 구하면 스펙트로그램의 진폭 정보를 알 수 있습니다. 실수부와 허수부 사이의 각도는 위상 스펙트럼(phase spectrum)을 나타내지만, 머신러닝에선 쓰이지 않는 경우가 종종 있습니다.

librosa.amplitude_to_db()는 진폭값을 데시벨 스케일로 변환합니다. 이로 인해 스펙트럼의 더욱 세밀한 부분까지 쉽게 확인이 가능합니다. 때때로는 파워 스펙트럼(power spectrum)을 쓸 때도 있습니다. 진폭보다 에너지를 측정하기 위해 쓰는데, 이는 단지 진폭에 제곱을 취한 값으로 나타낸 스펙트럼입니다.

오디오 신호의 파형과 주파수 스펙트럼은 동일한 정보를 지닙니다. 단지 같은 데이터(여기서는 트럼펫 소리의 첫 4096개의 샘플)를 바라보는 두 가지 방법일 뿐입니다. 파형은 시간에 따른 오디오 신호의 진폭을 표시하며, 스펙트럼은 고정된 시점의 개별 주파수들의 진폭을 시각화합니다.

스펙트로그램(spectrogram)

오디오 신호에서 주파수가 어떻게 변화하는지 보려면 무엇을 해야 할까요? 트럼펫 소리는 여러 음으로 구성돼있어서 여러 다른 주파수들로 이뤄져있습니다. 스펙트럼의 문제는 주어진 한 순간만의 주파수들을 보여준다는 것입니다. 이에 대한 해결법은 시간을 작은 구간들로 나누어 DFT를 적용하고, 그 결과인 스펙트럼들을 쌓아 스펙트로그램을 만드는 것입니다.

스펙트로그램은 오디오 신호의 주파수를 시간에 따라 변화하는 형태로 그립니다. 이를 통해 시간, 주파수, 진폭을 그래프에서 한눈에 볼 수 있습니다. 이 계산을 수행하는 알고리즘을 STFT(Short Time Fourier Transform)라 합니다.

스펙트로그램은 오디오를 다루는데 가장 유용한 툴 중 하나입니다. 예를 들어, 음악 녹음 작업을 다룰 때 다양한 악기와 보컬 트랙이 어떻게 전체 사운드에 기여하는지 볼 수 있습니다. 음성 작업의 경우, 모음을 발음할 때 각각의 모음들은 고유 주파수가 있기 때문에 서로 다른 모음인것을 식별할 수 있습니다.

librosa의 stft()와 specshow() 함수를 이용해 트럼펫 소리의 스펙트로그램을 그려보겠습니다:

import numpy as np

D = librosa.stft(array)
S_db = librosa.amplitude_to_db(np.abs(D), ref=np.max)

plt.figure().set_figwidth(12)
librosa.display.specshow(S_db, x_axis="time", y_axis="hz")
plt.colorbar()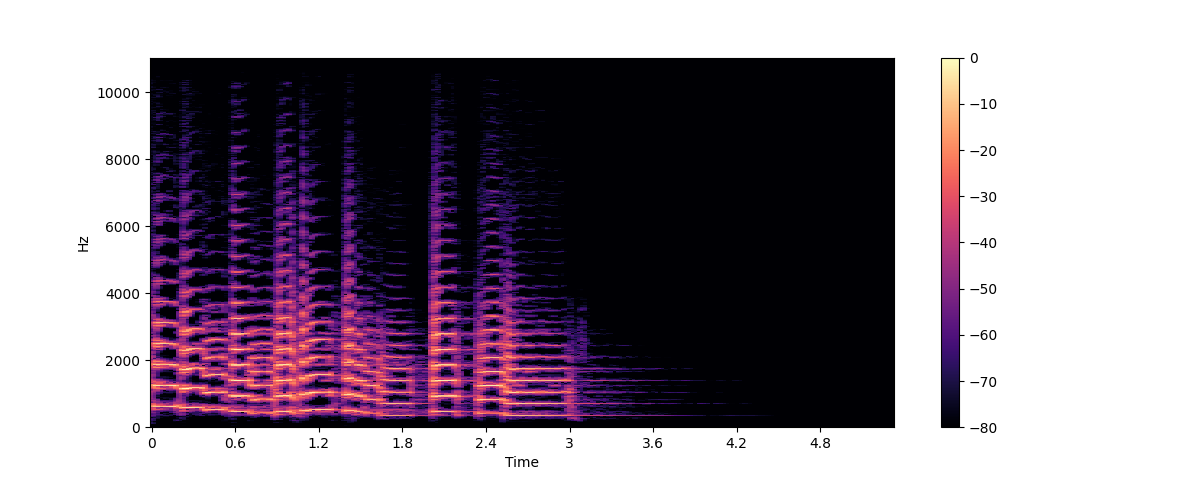

이 그래프에서 X축은 (파형 그래프처럼)시간을 나타내며 Y축은 주파수를 Hz 단위로 나타냅니다. 색상의 강도는 각 시점의 주파수 성분의 진폭 또는 파워를 데시벨(dB)로 측정하여 나타냅니다.

스펙트로그램은 일반적으로 오디오 신호의 몇 밀리초 정도 되는 짧은 구간에 DFT를 적용하여 주파수 스펙트럼들을 얻어 만들어집니다. 이 스펙트럼들을 시간축으로 쌓은것이 스펙트로그램이기 때문입니다. 이 이미지에서 각각의 수직 조각들은 (아까 위에서 본)주파수 스펙트럼에 해당합니다. 기본적으로, librosa.stft()는 오디오 신호를 2048개의 샘플로 나눕니다. 주파수 해상도(frequency resolution)와 시간 해상도(time resolution) 사이의 적절한 절충(trade-off)이기 때문입니다.

스펙트로그램과 파형은 같은 데이터를 다른 방식으로 볼 뿐이므로, 스펙트로그램을 다시 원래의 파형으로 돌리는 역 STFT(inverse STFT)가 가능합니다. 그러나, 이를 위해선 진폭 정보뿐만 아니라 위상(phase) 정보 또한 필요한데, 스펙트로그램이 머신러닝 툴에 의해 생성됐다면 대부분 단순히 진폭만 출력하게 됩니다. 이런 경우, 위상 재구성 알고리즘(phase reconstruction algorithm)인 vocoder라는 신경망이나 고전적인 Griffin-Lim 알고리즘을 사용하여 스펙트로그램에서 파형을 재구성할 수 있습니다.

스펙트로그램은 단순히 시각화를 위해서만 사용되는게 아닙니다. 많은 머신러닝 모델들은 (파형과는 다르게)스펙트로그램 그 자체를 입력으로 받고 출력 또한 스펙트로그램으로 내는 경우도 있습니다.

이제 스펙트로그램이 무엇이고 어떻게 만들어지는지 알았으니, 음성 작업에 사용되는 이 스펙트로그램의 변형에 대해 알아봅시다: 멜 스펙트로그램(mel spectrogram)입니다.

멜 스펙트로그램

멜 스펙트로그램은 스펙트로그램의 한 종류로 음성 작업이나 머신러닝 작업에 주로 쓰입니다. 오디오 신호를 시간에 따른 주파수로 보여준다는 점에서 스펙트로그램과 비슷하지만, 다른 주파수 축을 사용합니다.

표준적인 스펙트로그램에선 주파수 축이 선형(linear)이며 헤르츠(Hz)단위로 측정됩니다. 그러나, 사람의 청각 시스템은 고주파보다 저주파에 더 민감하며, 이 민감성은 주파수가 증가함에 따라 로그함수적으로 감소합니다. 멜 스케일(mel scale)은 이런 사람의 비선형 주파수 반응을 근사한(approximate) 지각 스케일(perceptual scale)입니다.

멜 스펙트로그램을 만드려면 전처럼 STFT를 사용하고 오디오를 여러 짧은 구간으로 나눠 일련의 주파수 스펙트럼들을 얻어야 합니다. 그 후 추가적으로, 각 스펙트럼에 mel filterbank라고 불리는 필터들을 적용시켜 주파수를 멜 스케일로 변환합니다.

이 모든 단계를 대신 해주는 librosa의 melspectrogram() 함수를 이용하여 멜 스펙트로그램을 그려봅시다:

S = librosa.feature.melspectrogram(y=array, sr=sampling_rate, n_mels=128, fmax=8000)
S_dB = librosa.power_to_db(S, ref=np.max)

plt.figure().set_figwidth(12)
librosa.display.specshow(S_dB, x_axis="time", y_axis="mel", sr=sampling_rate, fmax=8000)
plt.colorbar()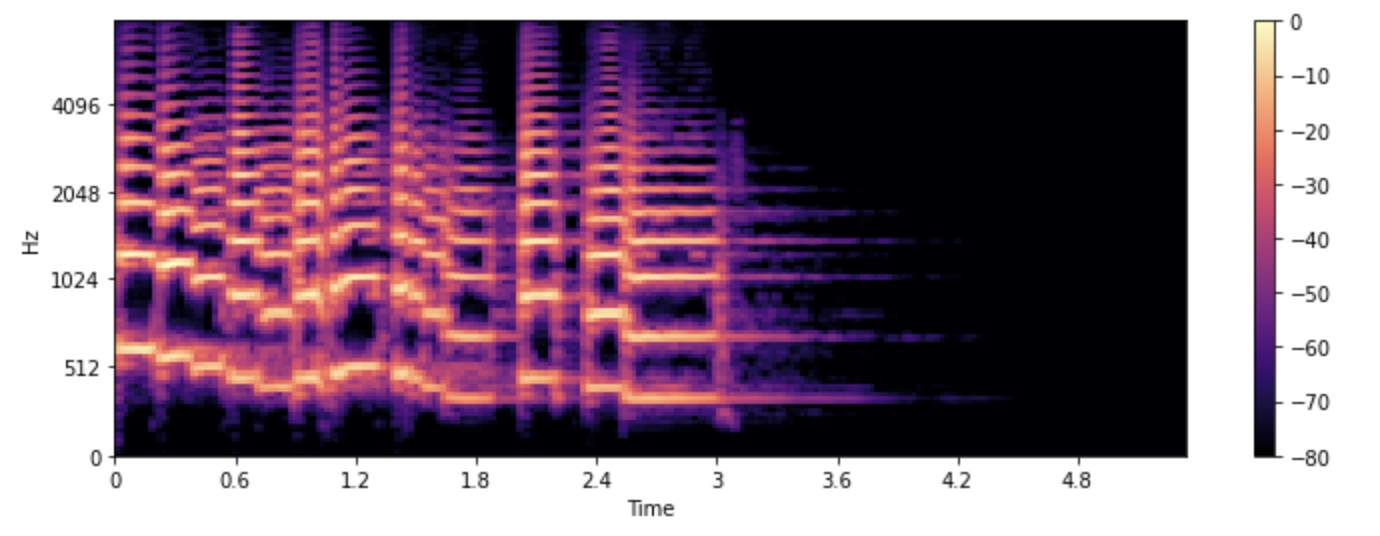

위의 예에서, n_mels는 mel band의 수를 정합니다. mel band는 필터를 이용해 스펙트럼을 지각적으로 의미있는 요소로 나누는 주파수 범위의 집합을 정의합니다. 이 필터들의 모양(shape)과 간격(spacing)은 사람의 귀가 다양한 주파수에 반응하는 방식을 모방하도록 선택됩니다. 흔히 n_mels의 값으로 40 또는 80이 선택됩니다. fmax는 우리가 관심을 가지는 최고 주파수(Hz 단위)를 나타냅니다.

일반적인 스펙트로그램과 마찬가지로 멜 스펙트로그램의 주파수 성분 역시 세기를 데시벨로 표현하는 것이 일반적입니다. 데시벨로의 변환이 로그 연산을 포함하기 때문에 이를 흔히 로그-멜 스펙트로그램(log-mel spectrogram)이라 합니다. 위 예제에선 librosa.power_to_db()를 썻는데, 이는 librosa.feature.melspectrogram()는 파워 스펙트로그램(power spectrogram)을 만들기 때문입니다.

멜 스펙트로그램은 신호를 필터링하여 만들기 때문에 정보의 손실이 일어납니다. 따라서 멜 스펙트로그램을 다시 원래의 파형으로 바꾸는 것은 일반적인 스펙트로그램을 다시 되돌리는것보다 힘든 일입니다. 버려진 주파수를 어떻게든 추정해야 하기 때문이죠. 멜 스펙트로그램을 다시 원래의 파형으로 되돌리기 위해 HiFiGAN vocoder같은 머신러닝 모델이 필요한 이유이기도 합니다.

기본적인 스펙트럼과 비교하여, 멜 스펙트로그램은 인간의 지각에 더 의미 있는 오디오 신호의 특성을 포착할 수 있어 음성 인식, 화자 식별, 음악 장르 분류 같은 작업에서 널리 사용됩니다.

이제 오디오 데이터의 시각화 방법을 알았으니 여러분이 좋아하는 소리가 어떻게 보이는지 한번 확인해보세요. :)