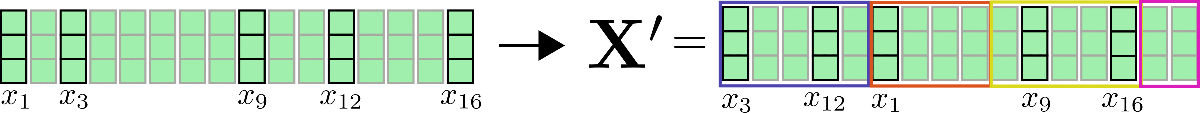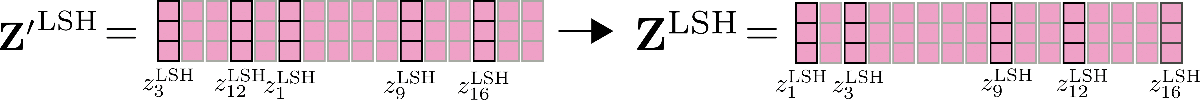The Reformer - Pushing the limits of language modeling
How the Reformer uses less than 8GB of RAM to train on sequences of half a million tokens
The Reformer model as introduced by Kitaev, Kaiser et al. (2020) is one of the most memory-efficient transformer models for long sequence modeling as of today.
Recently, long sequence modeling has experienced a surge of interest as can be seen by the many submissions from this year alone - Beltagy et al. (2020), Roy et al. (2020), Tay et al., Wang et al. to name a few. The motivation behind long sequence modeling is that many tasks in NLP, e.g. summarization, question answering, require the model to process longer input sequences than models, such as BERT, are able to handle. In tasks that require the model to process a large input sequence, long sequence models do not have to cut the input sequence to avoid memory overflow and thus have been shown to outperform standard "BERT"-like models cf. Beltagy et al. (2020).
The Reformer pushes the limit of longe sequence modeling by its ability to process up to half a million tokens at once as shown in this demo. As a comparison, a conventional bert-base-uncased model limits the input length to only 512 tokens. In Reformer, each part of the standard transformer architecture is re-engineered to optimize for minimal memory requirement without a significant drop in performance.
The memory improvements can be attributed to 4 features which the Reformer authors introduced to the transformer world:
- Reformer Self-Attention Layer - How to efficiently implement self-attention without being restricted to a local context?
- Chunked Feed Forward Layers - How to get a better time-memory trade-off for large feed forward layers?
- Reversible Residual Layers - How to drastically reduce memory consumption in training by a smart residual architecture?
- Axial Positional Encodings - How to make positional encodings usable for extremely large input sequences?
The goal of this blog post is to give the reader an in-depth understanding of each of the four Reformer features mentioned above. While the explanations are focussed on the Reformer, the reader should get a better intuition under which circumstances each of the four features can be effective for other transformer models as well. The four sections are only loosely connected, so they can very well be read individually.
Reformer is part of the 🤗Transformers library. For all users of the Reformer, it is advised to go through this very detailed blog post to better understand how the model works and how to correctly set its configuration. All equations are accompanied by their equivalent name for the Reformer config, e.g. config.<param_name>, so that the reader can quickly relate to the official docs and configuration file.
Note: Axial Positional Encodings are not explained in the official Reformer paper, but are extensively used in the official codebase. This blog post gives the first in-depth explanation of Axial Positional Encodings.
1. Reformer Self-Attention Layer
Reformer uses two kinds of special self-attention layers: local self-attention layers and Locality Sensitive Hashing (LSH) self-attention layers.
To better introduce these new self-attention layers, we will briefly recap conventional self-attention as introduced in Vaswani et al. 2017.
This blog post uses the same notation and coloring as the popular blog post The illustrated transformer, so the reader is strongly advised to read this blog first.
Important: While Reformer was originally introduced for causal self-attention, it can very well be used for bi-directional self-attention as well. In this post, Reformer's self-attention is presented for bidirectional self-attention.
Recap Global Self-Attention
The core of every Transformer model is the self-attention layer. To recap the conventional self-attention layer, which we refer to here as the global self-attention layer, let us assume we apply a transformer layer on the embedding vector sequence where each vector is of size config.hidden_size, i.e. .
In short, a global self-attention layer projects to the query, key and value matrices and computes the output using the softmax operation as follows: with being of dimension (leaving out the key normalization factor and self-attention weights for simplicity). For more detail on the complete transformer operation, see the illustrated transformer.
Visually, we can illustrate this operation as follows for :
Note that for all visualizations batch_size and config.num_attention_heads is assumed to be 1. Some vectors, e.g. and its corresponding output vector are marked so that LSH self-attention can later be better explained. The presented logic can effortlessly be extended for multi-head self-attention (config.num_attention_{h}eads > 1). The reader is advised to read the illustrated transformer as a reference for multi-head self-attention.
Important to remember is that for each output vector , the whole input sequence is processed. The tensor of the inner dot-product has an asymptotic memory complexity of which usually represents the memory bottleneck in a transformer model.
This is also the reason why bert-base-cased has a config.max_position_embedding_size of only 512.
Local Self-Attention
Local self-attention is the obvious solution to reducing the memory bottleneck, allowing us to model longer sequences with a reduced computational cost.
In local self-attention the input
is cut into chunks: each
of length config.local_chunk_length, i.e. , and subsequently global self-attention is applied on each chunk separately.
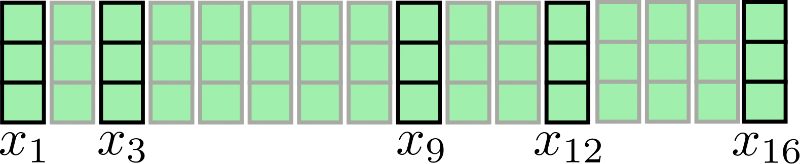
Let's take our input sequence for again for visualization:
Assuming , chunked attention can be illustrated as follows:
As can be seen, the attention operation is applied for each chunk individually. The first drawback of this architecture becomes obvious: Some input vectors have no access to their immediate context, e.g. has no access to and vice-versa in our example. This is problematic because these tokens are not able to learn word representations that take their immediate context into account.
A simple remedy is to augment each chunk with config.local_num_chunks_before, i.e. , chunks and config.local_num_chunks_after, i.e. , so that every input vector has at least access to previous input vectors and following input vectors. This can also be understood as chunking with overlap whereas and define the amount of overlap each chunk has with all previous chunks and following chunks. We denote this extended local self-attention as follows:
with
Okay, this formula looks quite complicated. Let's make it easier. In Reformer's self-attention layers is usually set to 0 and is set to 1, so let's write down the formula again for :
We notice that we have a circular relationship so that the first segment can attend the last segment as well. Let's illustrate this slightly enhanced local attention again. First, we apply self-attention within each windowed segment and keep only the central output segment.
Finally, the relevant output is concatenated to and looks as follows.
Note that local self-attention is implemented efficiently way so that no output is computed and subsequently "thrown-out" as shown here for illustration purposes by the red cross.
It's important to note here that extending the input vectors for each chunked self-attention function allows each single output vector of this self-attention function to learn better vector representations. E.g. each of the output vectors can take into account all of the input vectors to learn better representations.
The gain in memory consumption is quite obvious: The memory complexity is broken down for each segment individually so that the total asymptotic memory consumption is reduced to .
This enhanced local self-attention is better than the vanilla local self-attention architecture but still has a major drawback in that every input vector can only attend to a local context of predefined size. For NLP tasks that do not require the transformer model to learn long-range dependencies between the input vectors, which include arguably e.g. speech recognition, named entity recognition and causal language modeling of short sentences, this might not be a big issue. Many NLP tasks do require the model to learn long-range dependencies, so that local self-attention could lead to significant performance degradation, e.g.
- Question-answering: the model has to learn the relationship between the question tokens and relevant answer tokens which will most likely not be in the same local range
- Multiple-Choice: the model has to compare multiple answer token segments to each other which are usually separated by a significant length
- Summarization: the model has to learn the relationship between a long sequence of context tokens and a shorter sequence of summary tokens, whereas the relevant relationships between context and summary can most likely not be captured by local self-attention
- etc...
Local self-attention on its own is most likely not sufficient for the transformer model to learn the relevant relationships of input vectors (tokens) to each other.
Therefore, Reformer additionally employs an efficient self-attention layer that approximates global self-attention, called LSH self-attention.
LSH Self-Attention
Alright, now that we have understood how local self-attention works, we can take a stab at the probably most innovative piece of Reformer: Locality sensitive hashing (LSH) Self-Attention.
The premise of LSH self-attention is to be more or less as efficient as local self-attention while approximating global self-attention.
LSH self-attention relies on the LSH algorithm as presented in Andoni et al (2015), hence its name.
The idea behind LSH self-attention is based on the insight that if is large, the softmax applied on the attention dot-product weights only very few value vectors with values significantly larger than 0 for each query vector.
Let's explain this in more detail. Let and be the key and query vectors. For each , the computation can be approximated by using only those key vectors of that have a high cosine similarity with . This owes to the fact that the softmax function puts exponentially more weight on larger input values. So far so good, the next problem is to efficiently find the vectors that have a high cosine similarity with for all .
First, the authors of Reformer notice that sharing the query and key projections: does not impact the performance of a transformer model . Now, instead of having to find the key vectors of high cosine similarity for each query vector , only the cosine similarity of query vectors to each other has to be found.
This is important because there is a transitive property to the query-query vector dot product approximation: If has a high cosine similarity to the query vectors and , then also has a high cosine similarity to . Therefore, the query vectors can be clustered into buckets, such that all query vectors that belong to the same bucket have a high cosine similarity to each other. Let's define as the mth set of position indices, such that their corresponding query vectors are in the same bucket: and config.num_buckets, i.e. , as the number of buckets.
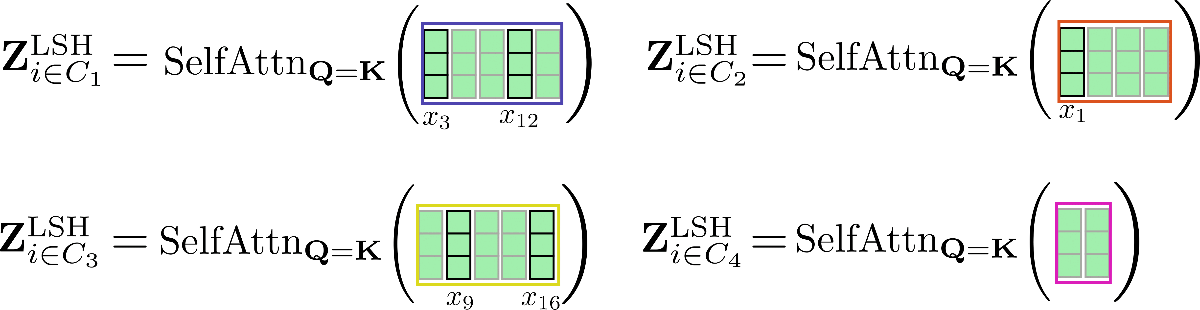
For each set of indices , the softmax function on the corresponding bucket of query vectors approximates the softmax function of global self-attention with shared query and key projections for all position indices in .
Second, the authors make use of the LSH algorithm to cluster the query vectors into a predefined number of buckets . The LSH algorithm is an ideal choice here because it is very efficient and is an approximation of the nearest neighbor algorithm for cosine similarity. Explaining the LSH scheme is out-of-scope for this notebook, so let's just keep in mind that for each vector the LSH algorithm attributes its position index to one of predefined buckets, i.e. with and .
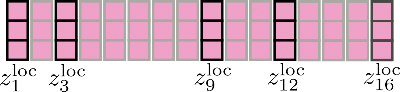
Visually, we can illustrate this as follows for our original example:
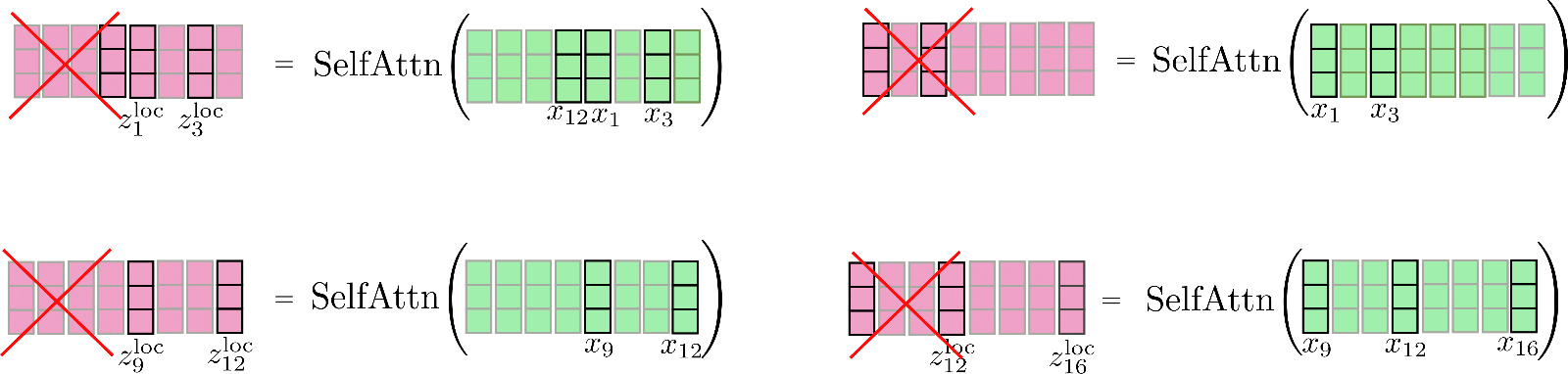
Third, it can be noted that having clustered all query vectors in buckets, the corresponding set of indices can be used to permute the input vectors accordingly so that shared query-key self-attention can be applied piecewise similar to local attention.
Let's clarify with our example input vectors and assume config.num_buckets=4 and config.lsh_chunk_length = 4. Looking at the graphic above we can see that we have assigned each query vector to one of the clusters .
If we now sort the corresponding input vectors accordingly, we get the following permuted input :
The self-attention mechanism should be applied for each cluster individually so that for each cluster the corresponding output is calculated as follows: .
Let's illustrate this again for our example.
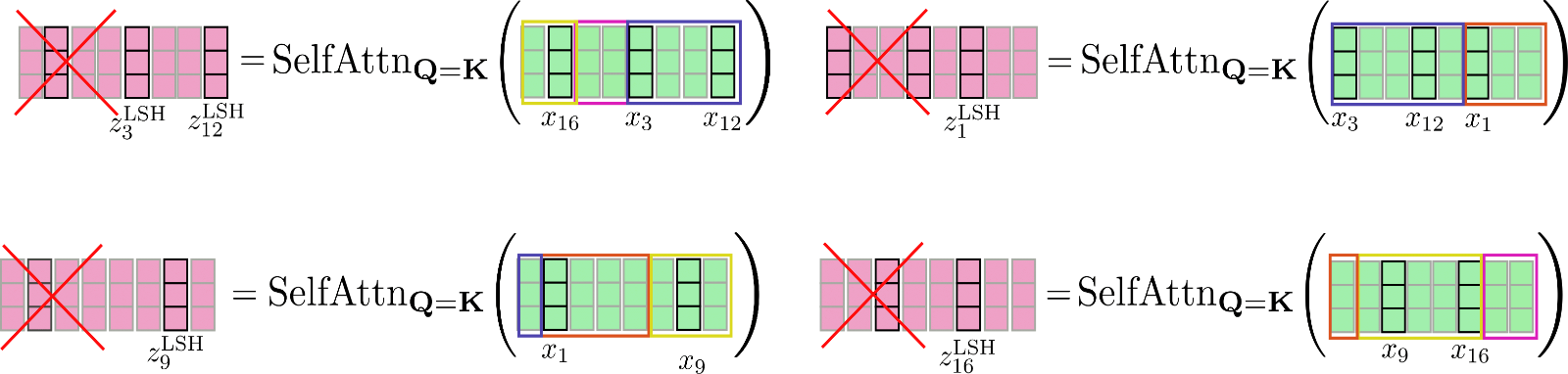
As can be seen, the self-attention function operates on different sizes of matrices, which is suboptimal for efficient batching in GPU and TPU.
To overcome this problem, the permuted input can be chunked the same way it is done for local attention so that each chunk is of size config.lsh_chunk_length. By chunking the permuted input, a bucket might be split into two different chunks. To remedy this problem, in LSH self-attention each chunk attends to its previous chunk config.lsh_num_chunks_before=1 in addition to itself, the same way local self-attention does (config.lsh_num_chunks_after is usually set to 0). This way, we can be assured that all vectors in a bucket attend to each other with a high probability .
All in all for all chunks , LSH self-attention can be noted down as follows:
with and being the input and output vectors permuted according to the LSH algorithm. Enough complicated formulas, let's illustrate LSH self-attention.
The permuted vectors as shown above are chunked and shared query key self-attention is applied to each chunk.
Finally, the output is reordered to its original permutation.
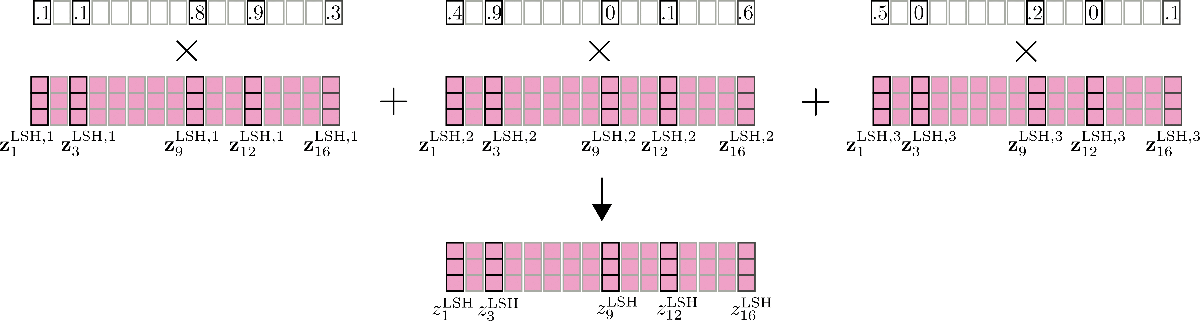
One important feature to mention here as well is that the accuracy of LSH self-attention can be improved by running LSH self-attention config.num_hashes, e.g. times in parallel, each with a different random LSH hash.
By setting config.num_hashes > 1, for each output position , multiple output vectors are computed
and subsequently merged: . The represents the importance of the output vectors of hashing round in comparison to the other hashing rounds, and is exponentially proportional to the normalization term of their softmax computation. The intuition behind this is that if the corresponding query vector have a high cosine similarity with all other query vectors in its respective chunk, then the softmax normalization term of this chunk tends to be high, so that the corresponding output vectors should be a better approximation to global attention and thus receive more weight than output vectors of hashing rounds with a lower softmax normalization term. For more detail see Appendix A of the paper. For our example, multi-round LSH self-attention can be illustrated as follows.
Great. That's it. Now we know how LSH self-attention works in Reformer.
Regarding the memory complexity, we now have two terms that compete which each other to be the memory bottleneck: the dot-product: and the required memory for LSH bucketing: with being the chunk length. Because for large , the number of buckets grows much faster than the chunk length , the user can again factorize the number of buckets config.num_buckets as explained here.
Let's recap quickly what we have gone through above:
- We want to approximate global attention using the knowledge that the softmax operation only puts significant weights on very few key vectors.
- If key vectors are equal to query vectors this means that for each query vector , the softmax only puts significant weight on other query vectors that are similar in terms of cosine similarity.
- This relationship works in both ways, meaning if is similar to than is also similar to , so that we can do a global clustering before applying self-attention on a permuted input.
- We apply local self-attention on the permuted input and re-order the output to its original permutation.
The authors run some preliminary experiments confirming that shared query key self-attention performs more or less as well as standard self-attention.
To be more exact the query vectors within a bucket are sorted according to their original order. This means if, e.g. the vectors are all hashed to bucket 2, the order of the vectors in bucket 2 would still be , followed by and .
On a side note, it is to mention the authors put a mask on the query vector to prevent the vector from attending to itself. Because the cosine similarity of a vector to itself will always be as high or higher than the cosine similarity to other vectors, the query vectors in shared query key self-attention are strongly discouraged to attend to themselves.
Benchmark
Benchmark tools were recently added to Transformers - see here for a more detailed explanation.
To show how much memory can be saved using "local" + "LSH" self-attention, the Reformer model google/reformer-enwik8 is benchmarked for different local_attn_chunk_length and lsh_attn_chunk_length. The default configuration and usage of the google/reformer-enwik8 model can be checked in more detail here.
Let's first do some necessary imports and installs.
#@title Installs and Imports
# pip installs
!pip -qq install git+https://github.com/huggingface/transformers.git
!pip install -qq py3nvml
from transformers import ReformerConfig, PyTorchBenchmark, PyTorchBenchmarkArguments
First, let's benchmark the memory usage of the Reformer model using global self-attention. This can be achieved by setting lsh_attn_chunk_length = local_attn_chunk_length = 8192 so that for all input sequences smaller or equal to 8192, the model automatically switches to global self-attention.
config = ReformerConfig.from_pretrained("google/reformer-enwik8", lsh_attn_chunk_length=16386, local_attn_chunk_length=16386, lsh_num_chunks_before=0, local_num_chunks_before=0)
benchmark_args = PyTorchBenchmarkArguments(sequence_lengths=[2048, 4096, 8192, 16386], batch_sizes=[1], models=["Reformer"], no_speed=True, no_env_print=True)
benchmark = PyTorchBenchmark(configs=[config], args=benchmark_args)
result = benchmark.run()
HBox(children=(FloatProgress(value=0.0, description='Downloading', max=1279.0, style=ProgressStyle(description…
1 / 1
Doesn't fit on GPU. CUDA out of memory. Tried to allocate 2.00 GiB (GPU 0; 11.17 GiB total capacity; 8.87 GiB already allocated; 1.92 GiB free; 8.88 GiB reserved in total by PyTorch)
==================== INFERENCE - MEMORY - RESULT ====================
--------------------------------------------------------------------------------
Model Name Batch Size Seq Length Memory in MB
--------------------------------------------------------------------------------
Reformer 1 2048 1465
Reformer 1 4096 2757
Reformer 1 8192 7893
Reformer 1 16386 N/A
--------------------------------------------------------------------------------
The longer the input sequence, the more visible is the quadratic relationship between input sequence and peak memory usage. As can be seen, in practice it would require a much longer input sequence to clearly observe that doubling the input sequence quadruples the peak memory usage.
For this a google/reformer-enwik8 model using global attention, a sequence length of over 16K results in a memory overflow.
Now, let's activate local and LSH self-attention by using the model's default parameters.
config = ReformerConfig.from_pretrained("google/reformer-enwik8")
benchmark_args = PyTorchBenchmarkArguments(sequence_lengths=[2048, 4096, 8192, 16384, 32768, 65436], batch_sizes=[1], models=["Reformer"], no_speed=True, no_env_print=True)
benchmark = PyTorchBenchmark(configs=[config], args=benchmark_args)
result = benchmark.run()
1 / 1
Doesn't fit on GPU. CUDA out of memory. Tried to allocate 2.00 GiB (GPU 0; 11.17 GiB total capacity; 7.85 GiB already allocated; 1.74 GiB free; 9.06 GiB reserved in total by PyTorch)
Doesn't fit on GPU. CUDA out of memory. Tried to allocate 4.00 GiB (GPU 0; 11.17 GiB total capacity; 6.56 GiB already allocated; 3.99 GiB free; 6.81 GiB reserved in total by PyTorch)
==================== INFERENCE - MEMORY - RESULT ====================
--------------------------------------------------------------------------------
Model Name Batch Size Seq Length Memory in MB
--------------------------------------------------------------------------------
Reformer 1 2048 1785
Reformer 1 4096 2621
Reformer 1 8192 4281
Reformer 1 16384 7607
Reformer 1 32768 N/A
Reformer 1 65436 N/A
--------------------------------------------------------------------------------
As expected using local and LSH self-attention is much more memory efficient for longer input sequences, so that the model runs out of memory only at 16K tokens for a 11GB RAM GPU in this notebook.
2. Chunked Feed Forward Layers
Transformer-based models often employ very large feed forward layers after the self-attention layer in parallel. Thereby, this layer can take up a significant amount of the overall memory and sometimes even represent the memory bottleneck of a model. First introduced in the Reformer paper, feed forward chunking is a technique that allows to effectively trade better memory consumption for increased time consumption.
Chunked Feed Forward Layer in Reformer
In Reformer, the LSH- or local self-attention layer is usually followed by a residual connection, which then defines the first part in a transformer block. For more detail on this please refer to this blog.
The output of the first part of the transformer block, called normed self-attention output can be written as , with being either or in Reformer.
For our example input , we illustrate the normed self-attention output as follows.
Now, the second part of a transformer block usually consists of two feed forward layers , defined as that processes , to an intermediate output and that processes the intermediate output to the output . The two feed forward layers can be defined by
It is important to remember at this point that mathematically the output of a feed forward layer at position only depends on the input at this position . In contrast to the self-attention layer, every output is therefore completely independent of all inputs of different positions.
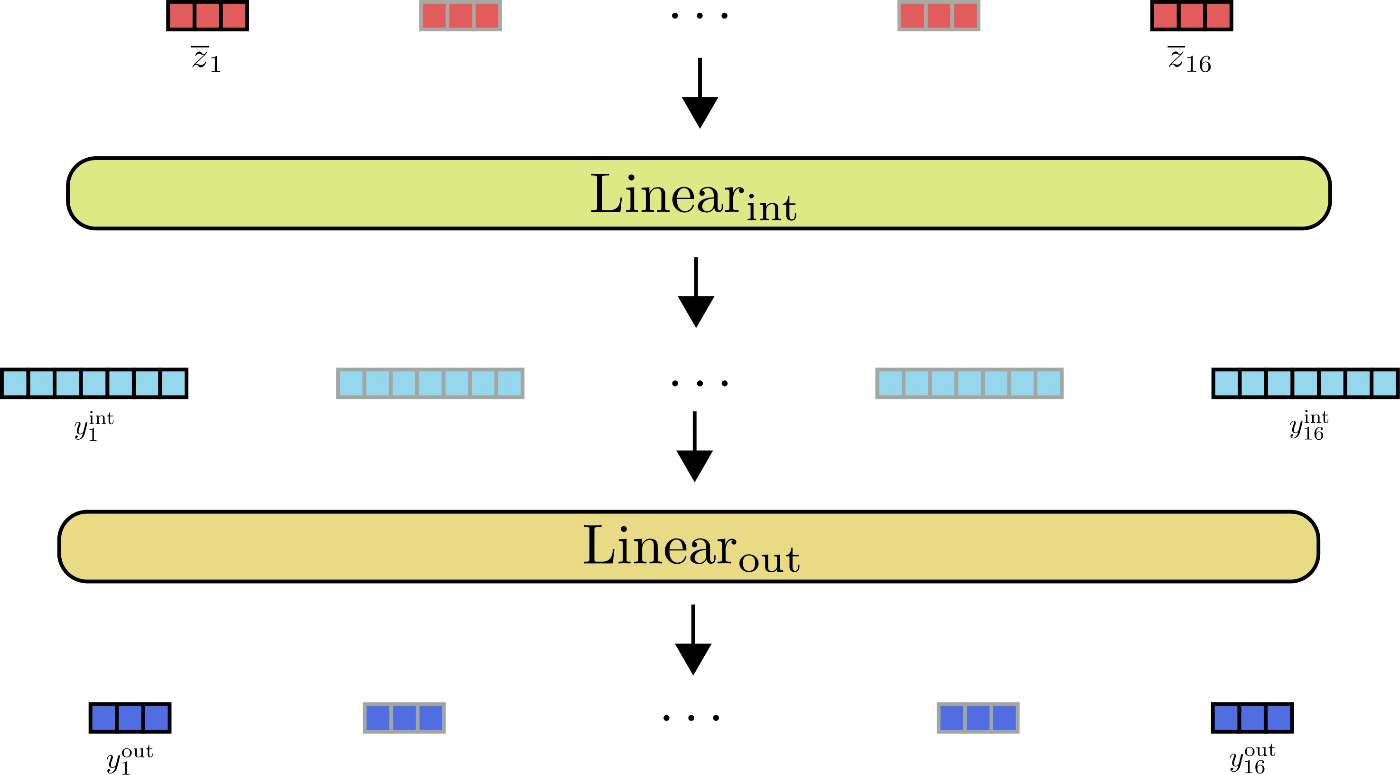
Let's illustrate the feed forward layers for .
As can be depicted from the illustration, all input vectors are processed by the same feed forward layer in parallel.
It becomes interesting when one takes a look at the output dimensions of the feed forward layers. In Reformer, the output dimension of is defined as config.feed_forward_size, e.g. , and the output dimension of is defined as config.hidden_size, i.e. .
The Reformer authors observed that in a transformer model the intermediate dimension usually tends to be much larger than the output dimension . This means that the tensor of dimension allocates a significant amount of the total memory and can even become the memory bottleneck.
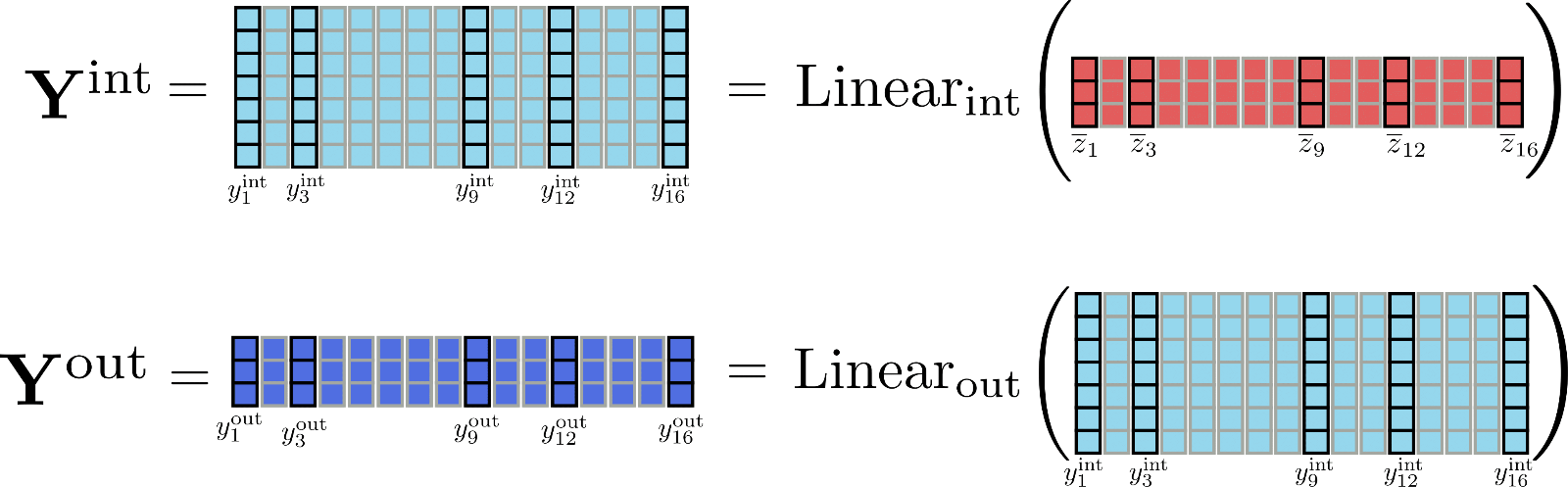
To get a better feeling for the differences in dimensions let's picture the matrices and for our example.
It is becoming quite obvious that the tensor holds much more memory ( as much to be exact) than . But, is it even necessary to compute the full intermediate matrix ? Not really, because relevant is only the output matrix .
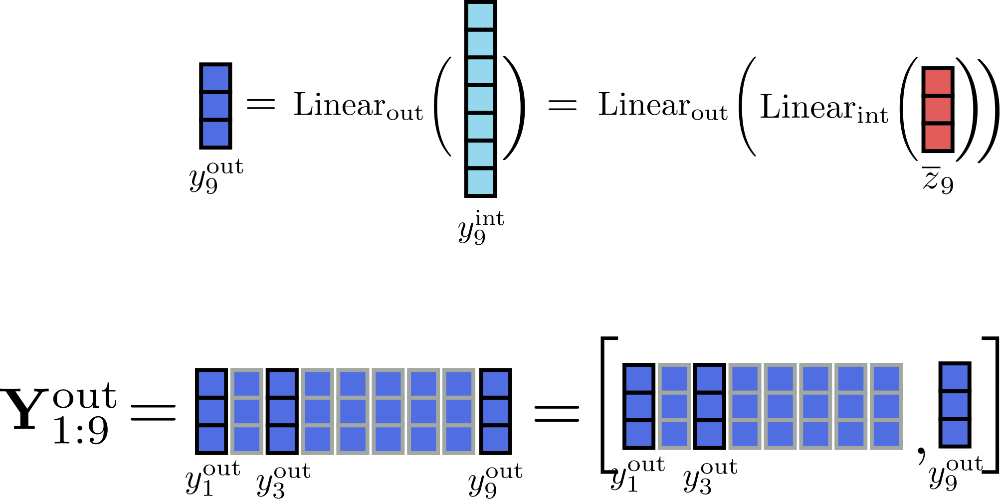
To trade memory for speed, one can thus chunk the linear layers computation to only process one chunk at the time. Defining config.chunk_size_feed_forward as , chunked linear layers are defined as with .
In practice, it just means that the output is incrementally computed and concatenated to avoid having to store the whole intermediate tensor in memory.
Assuming for our example we can illustrate the incremental computation of the output for position as follows.
By processing the inputs in chunks of size 1, the only tensors that have to be stored in memory at the same time are of a maximum size of , of size and the input of size , with being config.hidden_size .
Finally, it is important to remember that chunked linear layers yield a mathematically equivalent output to conventional linear layers and can therefore be applied to all transformer linear layers. Making use of config.chunk_size_feed_forward therefore allows a better trade-off between memory and speed in certain use cases.
For a simpler explanation, the layer norm layer which is normally applied to before being processed by the feed forward layers is omitted for now.
In bert-base-uncased, e.g. the intermediate dimension is with 3072 four times larger than the output dimension .
As a reminder, the output config.num_attention_heads is assumed to be 1 for the sake of clarity and illustration in this notebook, so that the output of the self-attention layers can be assumed to be of size config.hidden_size.
More information on chunked linear / feed forward layers can also be found here on the 🤗Transformers docs.
Benchmark
Let's test how much memory can be saved by using chunked feed forward layers.
#@title Installs and Imports
# pip installs
!pip -qq install git+https://github.com/huggingface/transformers.git
!pip install -qq py3nvml
from transformers import ReformerConfig, PyTorchBenchmark, PyTorchBenchmarkArguments
Building wheel for transformers (setup.py) ... [?25l[?25hdone
First, let's compare the default google/reformer-enwik8 model without chunked feed forward layers to the one with chunked feed forward layers.
config_no_chunk = ReformerConfig.from_pretrained("google/reformer-enwik8") # no chunk
config_chunk = ReformerConfig.from_pretrained("google/reformer-enwik8", chunk_size_feed_forward=1) # feed forward chunk
benchmark_args = PyTorchBenchmarkArguments(sequence_lengths=[1024, 2048, 4096], batch_sizes=[8], models=["Reformer-No-Chunk", "Reformer-Chunk"], no_speed=True, no_env_print=True)
benchmark = PyTorchBenchmark(configs=[config_no_chunk, config_chunk], args=benchmark_args)
result = benchmark.run()
1 / 2
Doesn't fit on GPU. CUDA out of memory. Tried to allocate 2.00 GiB (GPU 0; 11.17 GiB total capacity; 7.85 GiB already allocated; 1.74 GiB free; 9.06 GiB reserved in total by PyTorch)
2 / 2
Doesn't fit on GPU. CUDA out of memory. Tried to allocate 2.00 GiB (GPU 0; 11.17 GiB total capacity; 7.85 GiB already allocated; 1.24 GiB free; 9.56 GiB reserved in total by PyTorch)
==================== INFERENCE - MEMORY - RESULT ====================
--------------------------------------------------------------------------------
Model Name Batch Size Seq Length Memory in MB
--------------------------------------------------------------------------------
Reformer-No-Chunk 8 1024 4281
Reformer-No-Chunk 8 2048 7607
Reformer-No-Chunk 8 4096 N/A
Reformer-Chunk 8 1024 4309
Reformer-Chunk 8 2048 7669
Reformer-Chunk 8 4096 N/A
--------------------------------------------------------------------------------
Interesting, chunked feed forward layers do not seem to help here at all. The reason is that config.feed_forward_size is not sufficiently large to make a real difference. Only at longer sequence lengths of 4096, a slight decrease in memory usage can be seen.
Let's see what happens to the memory peak usage if we increase the size of the feed forward layer by a factor of 4 and reduce the number of attention heads also by a factor of 4 so that the feed forward layer becomes the memory bottleneck.
config_no_chunk = ReformerConfig.from_pretrained("google/reformer-enwik8", chunk_size_feed_forward=0, num_attention_{h}eads=2, feed_forward_size=16384) # no chuck
config_chunk = ReformerConfig.from_pretrained("google/reformer-enwik8", chunk_size_feed_forward=1, num_attention_{h}eads=2, feed_forward_size=16384) # feed forward chunk
benchmark_args = PyTorchBenchmarkArguments(sequence_lengths=[1024, 2048, 4096], batch_sizes=[8], models=["Reformer-No-Chunk", "Reformer-Chunk"], no_speed=True, no_env_print=True)
benchmark = PyTorchBenchmark(configs=[config_no_chunk, config_chunk], args=benchmark_args)
result = benchmark.run()
1 / 2
2 / 2
==================== INFERENCE - MEMORY - RESULT ====================
--------------------------------------------------------------------------------
Model Name Batch Size Seq Length Memory in MB
--------------------------------------------------------------------------------
Reformer-No-Chunk 8 1024 3743
Reformer-No-Chunk 8 2048 5539
Reformer-No-Chunk 8 4096 9087
Reformer-Chunk 8 1024 2973
Reformer-Chunk 8 2048 3999
Reformer-Chunk 8 4096 6011
--------------------------------------------------------------------------------
Now a clear decrease in peak memory usage can be seen for longer input sequences. As a conclusion, it should be noted chunked feed forward layers only makes sense for models having few attention heads and large feed forward layers.
3. Reversible Residual Layers
Reversible residual layers were first introduced in N. Gomez et al and used to reduce memory consumption when training the popular ResNet model. Mathematically, reversible residual layers are slightly different to "real" residual layers but do not require the activations to be saved during the forward pass, which can drastically reduce memory consumption for training.
Reversible Residual Layers in Reformer
Let's start by investigating why training a model requires much more memory than the inference of the model.
When running a model in inference, the required memory equals more or less the memory it takes to compute the single largest tensor in the model. On the other hand, when training a model, the required memory equals more or less the sum of all differentiable tensors.
This is not surprising when considering how auto differentiation works in deep learning frameworks. These lecture slides by Roger Grosse of the University of Toronto are great to better understand auto differentiation.
In a nutshell, in order to calculate the gradient of a differentiable function (e.g. a layer), auto differentiation requires the gradient of the function's output and the function's input and output tensor. While the gradients are dynamically computed and subsequently discarded, the input and output tensors (a.k.a activations) of a function are stored during the forward pass.
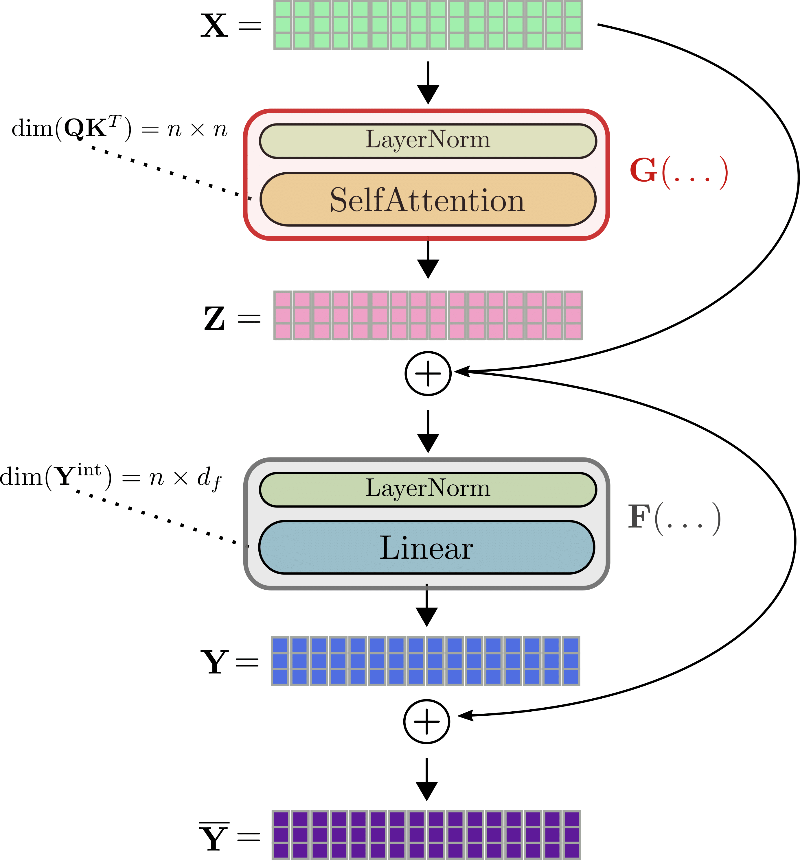
Alright, let's apply this to a transformer model. A transformer model includes a stack of multiple so-called transformer layers. Each additional transformer layer forces the model to store more activations during the forward pass and thus increases the required memory for training. Let's take a more detailed look. A transformer layer essentially consists of two residual layers. The first residual layer represents the self-attention mechanism as explained in section 1) and the second residual layer represents the linear or feed-forward layers as explained in section 2).
Using the same notation as before, the input of a transformer layer i.e. is first normalized and subsequently processed by the self-attention layer to get the output . We will abbreviate these two layers with so that . Next, the residual is added to the input and the sum is fed into the second residual layer - the two linear layers. is processed by a second normalization layer, followed by the two linear layers to get . We will abbreviate the second normalization layer and the two linear layers with yielding . Finally, the residual is added to to give the output of the transformer layer .
Let's illustrate a complete transformer layer using the example of .
To calculate the gradient of e.g. the self-attention block , three tensors have to be known beforehand: the gradient , the output , and the input . While can be calculated on-the-fly and discarded afterward, the values for and have to be calculated and stored during the forward pass since it is not possible to recalculate them easily on-the-fly during backpropagation. Therefore, during the forward pass, large tensor outputs, such as the query-key dot product matrix or the intermediate output of the linear layers , have to be stored in memory .
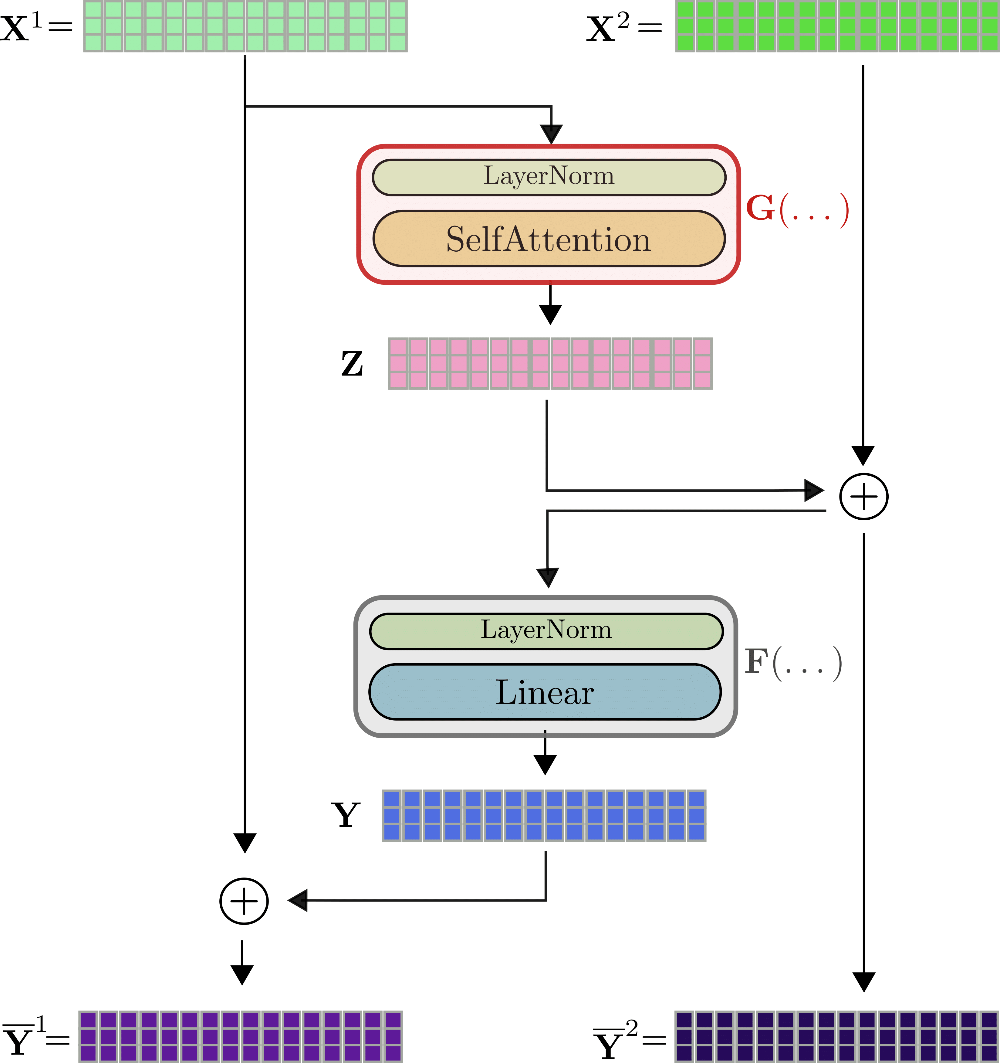
Here, reversible residual layers come to our help. The idea is relatively straight-forward. The residual block is designed in a way so that instead of having to store the input and output tensor of a function, both can easily be recalculated during the backward pass so that no tensor has to be stored in memory during the forward pass. This is achieved by using two input streams , and two output streams . The first residual is computed by the first output stream and subsequently added to the input of the second input stream, so that . Similarly, the residual is added to the first input stream again, so that the two output streams are defined by and .
The reversible transformer layer can be visualized for as follows.
As can be seen, the outputs are calculated in a very similar way than of the non-reversible layer, but they are mathematically different. The authors of Reformer observe in some initial experiments that the performance of a reversible transformer model matches the performance of a standard transformer model. The first visible difference to the standard transformer layer is that there are two input streams and output streams , which at first slightly increases the required memory for both the forward pass. The two-stream architecture is crucial though for not having to save any activations during the forward pass. Let's explain. For backpropagation, the reversible transformer layer has to calculate the gradients and . In addition to the gradients and which can be calculated on-the-fly, the tensor values , have to be known for and the tensor values and for to make auto-differentiation work.
If we assume to know , it can easily be depicted from the graph that one can calculate as follows. . Great, now that is known, can be computed by . Alright now, and are trivial to compute via and . So as a conclusion, if only the outputs of the last reversible transformer layer are stored during the forward pass, all other relevant activations can be derived by making use of and during the backward pass and passing and . The overhead of two forward passes of and per reversible transformer layer during the backpropagation is traded against not having to store any activations during the forward pass. Not a bad deal!
Note: Since recently, major deep learning frameworks have released code that allows to store only certain activations and recompute larger ones during the backward propagation (Tensoflow here and PyTorch here). For standard reversible layers, this still means that at least one activation has to be stored for each transformer layer, but by defining which activations can dynamically be recomputed a lot of memory can be saved.
In the previous two sections, we have omitted the layer norm layers preceding both the self-attention layer and the linear layers. The reader should know that both and are both processed by layer normalization before being fed into self-attention and the linear layers respectively. While in the design the dimension of is written as , in a LSH self-attention or local self-attention layer the dimension would only be or respectively with being the chunk length and the number of hashes In the first reversible transformer layer is set to be equal to .
Benchmark
In order to measure the effect of reversible residual layers, we will compare the memory consumption of BERT with Reformer in training for an increasing number of layers.
#@title Installs and Imports
# pip installs
!pip -qq install git+https://github.com/huggingface/transformers.git
!pip install -qq py3nvml
from transformers import ReformerConfig, BertConfig, PyTorchBenchmark, PyTorchBenchmarkArguments
Let's measure the required memory for the standard bert-base-uncased BERT model by increasing the number of layers from 4 to 12.
config_4_layers_bert = BertConfig.from_pretrained("bert-base-uncased", num_hidden_layers=4)
config_8_layers_bert = BertConfig.from_pretrained("bert-base-uncased", num_hidden_layers=8)
config_12_layers_bert = BertConfig.from_pretrained("bert-base-uncased", num_hidden_layers=12)
benchmark_args = PyTorchBenchmarkArguments(sequence_lengths=[512], batch_sizes=[8], models=["Bert-4-Layers", "Bert-8-Layers", "Bert-12-Layers"], training=True, no_inference=True, no_speed=True, no_env_print=True)
benchmark = PyTorchBenchmark(configs=[config_4_layers_bert, config_8_layers_bert, config_12_layers_bert], args=benchmark_args)
result = benchmark.run()
HBox(children=(FloatProgress(value=0.0, description='Downloading', max=433.0, style=ProgressStyle(description_…
1 / 3
2 / 3
3 / 3
==================== TRAIN - MEMORY - RESULTS ====================
--------------------------------------------------------------------------------
Model Name Batch Size Seq Length Memory in MB
--------------------------------------------------------------------------------
Bert-4-Layers 8 512 4103
Bert-8-Layers 8 512 5759
Bert-12-Layers 8 512 7415
--------------------------------------------------------------------------------
It can be seen that adding a single layer of BERT linearly increases the required memory by more than 400MB.
config_4_layers_reformer = ReformerConfig.from_pretrained("google/reformer-enwik8", num_hidden_layers=4, num_hashes=1)
config_8_layers_reformer = ReformerConfig.from_pretrained("google/reformer-enwik8", num_hidden_layers=8, num_hashes=1)
config_12_layers_reformer = ReformerConfig.from_pretrained("google/reformer-enwik8", num_hidden_layers=12, num_hashes=1)
benchmark_args = PyTorchBenchmarkArguments(sequence_lengths=[512], batch_sizes=[8], models=["Reformer-4-Layers", "Reformer-8-Layers", "Reformer-12-Layers"], training=True, no_inference=True, no_speed=True, no_env_print=True)
benchmark = PyTorchBenchmark(configs=[config_4_layers_reformer, config_8_layers_reformer, config_12_layers_reformer], args=benchmark_args)
result = benchmark.run()
1 / 3
2 / 3
3 / 3
==================== TRAIN - MEMORY - RESULTS ====================
--------------------------------------------------------------------------------
Model Name Batch Size Seq Length Memory in MB
--------------------------------------------------------------------------------
Reformer-4-Layers 8 512 4607
Reformer-8-Layers 8 512 4987
Reformer-12-Layers 8 512 5367
--------------------------------------------------------------------------------
For Reformer, on the other hand, adding a layer adds significantly less memory in practice. Adding a single layer increases the required memory on average by less than 100MB so that a much larger 12-Layer reformer-enwik8 model requires less memory than a 12-Layer bert-base-uncased model.
4. Axial Positional Encodings
Reformer makes it possible to process huge input sequences. However, for such long input sequences standard positional encoding weight matrices alone would use more than 1GB to store its weights. To prevent such large positional encoding matrices, the official Reformer code introduced Axial Position Encodings.
Important: Axial Position Encodings were not explained in the official paper, but can be well understood from looking into the code and talking to the authors
Axial Positional Encodings in Reformer
Transformers need positional encodings to account for the order of words in the input because self-attention layers have no notion of order.
Positional encodings are usually defined by a simple look-up matrix The positional encoding vector is then simply added to the ith input vector so that the model can distinguish if an input vector (a.k.a token) is at position or .
For every input position, the model needs to be able to look up the corresponding positional encoding vector so that the dimension of is defined by the maximum length of input vectors the model can process config.max_position_embeddings, i.e. , and the config.hidden_size, i.e. of the input vectors.
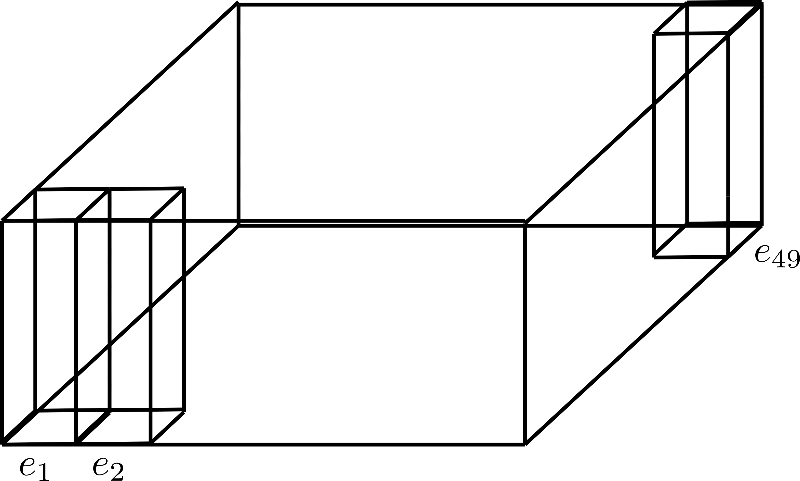
Assuming and , such a positional encoding matrix can be visualized as follows:
Here, we showcase only the positional encodings , , and each of dimension, a.k.a height 4.
Let's imagine, we want to train a Reformer model on sequences of a length of up to 0.5M tokens and an input vector config.hidden_size of 1024 (see notebook here). The corresponding positional embeddings have a size of parameters, which corresponds to a size of 2GB.
Such positional encodings would use an unnecessarily large amount of memory both when loading the model in memory and when saving the model on a hard drive.
The Reformer authors managed to drastically shrink the positional encodings in size by cutting the config.hidden_size dimension in two and smartly factorizing
the dimension.
In Transformer, the user can decide into which shape can be factorized into by setting config.axial_pos_shape to an appropriate
list of two values and so that . By setting config.axial_pos_embds_dim to an
appropriate list of two values and so that , the user can decide how the hidden size dimension should be cut.
Now, let's visualize and explain more intuitively.
One can think of factorizing as folding the dimension into a third axis, which is shown in the following for the factorization config.axial_pos_shape = [7, 7]:
Each of the three standing rectangular prisms corresponds to one of the encoding vectors , but we can see that the 49 encoding vectors are divided into 7 rows of 7 vectors each.
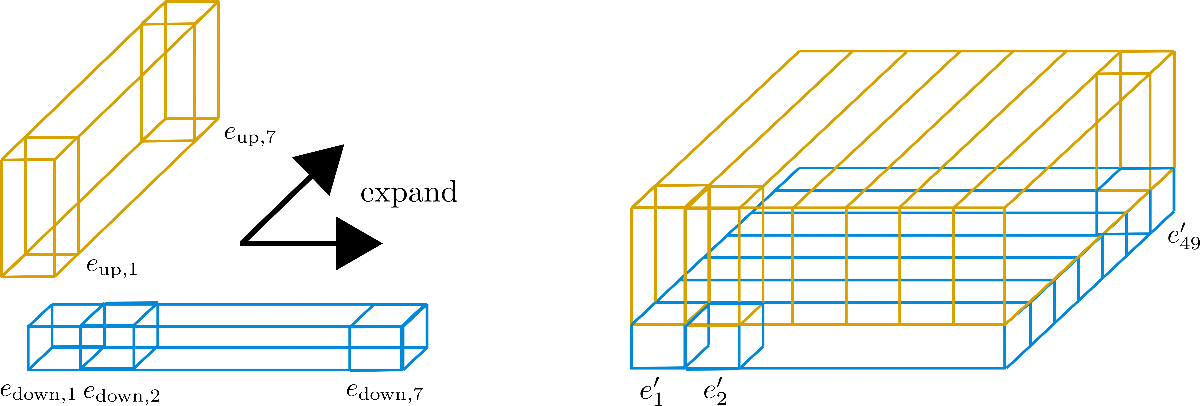
Now the idea is to use only one row of 7 encoding vectors and expand those vectors to the other 6 rows, essentially reusing their values.
Because it is discouraged to have the same values for different encoding vectors, each vector of dimension (a.k.a height) config.hidden_size=4 is cut into the lower encoding vector of size and of size , so that the lower part can be expanded along the row dimension and the upper part can be expanded along the column dimension.
Let's visualize for more clarity.
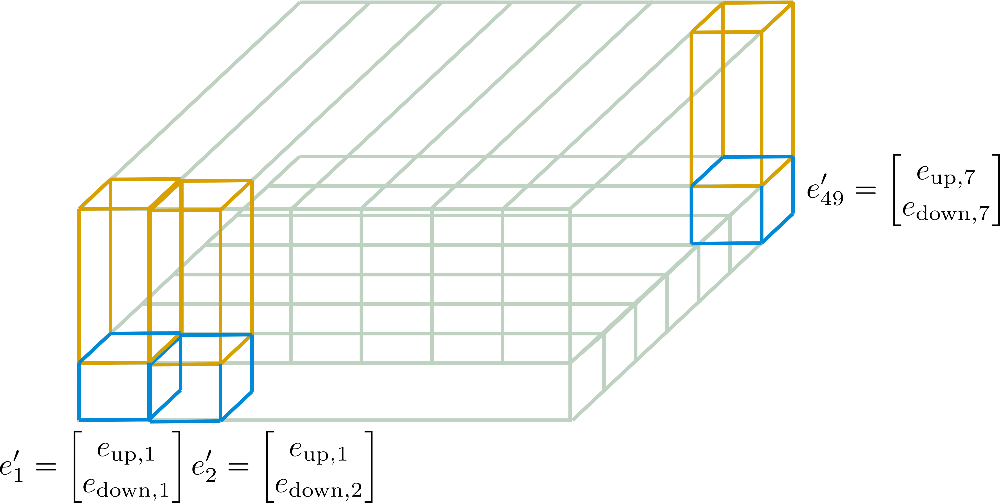
We can see that we have cut the embedding vectors into (in blue) and (in yellow). Now for the "sub"-vectors only the first row, a.k.a. the width in the graphic, of is kept and expanded along the column dimension, a.k.a. the depth of the graphic. Inversely, for the "sub"-vectors only the first column of is kept and expanded along the row dimension. The resulting embedding vectors then correspond to
whereas and in our example. These new encodings are called Axial Position Encodings.
In the following, these axial position encodings are illustrated in more detail for our example.
Now it should be more understandable how the final positional encoding vectors are calculated only from of dimension and of dimension .
The crucial aspect to see here is that Axial Positional Encodings make sure that none of the vectors are equal to each other by design and that the overall size of the encoding matrix is reduced from to . By allowing each axial positional encoding vector to be different by design the model is given much more flexibility to learn efficient positional representations if axial positional encodings are learned by the model.
To demonstrate the drastic reduction in size,
let's assume we would have set config.axial_pos_shape = [1024, 512] and config.axial_pos_embds_dim = [512, 512] for a Reformer model that can process inputs up to a length of 0.5M tokens. The resulting axial positional encoding matrix would have had a size of only parameters which corresponds to roughly 3MB. This is a drastic reduction from the 2GB a standard positional encoding matrix would require in this case.
For a more condensed and math-heavy explanation please refer to the 🤗Transformers docs here.
Benchmark
Lastly, let's also compare the peak memory consumption of conventional positional embeddings to axial positional embeddings.
#@title Installs and Imports
# pip installs
!pip -qq install git+https://github.com/huggingface/transformers.git
!pip install -qq py3nvml
from transformers import ReformerConfig, PyTorchBenchmark, PyTorchBenchmarkArguments, ReformerModel
Positional embeddings depend only on two configuration parameters: The maximum allowed length of input sequences config.max_position_embeddings and config.hidden_size. Let's use a model that pushes the maximum allowed length of input sequences to half a million tokens, called google/reformer-crime-and-punishment, to see the effect of using axial positional embeddings.
To begin with, we will compare the shape of axial position encodings with standard positional encodings and the number of parameters in the model.
config_no_pos_axial_embeds = ReformerConfig.from_pretrained("google/reformer-crime-and-punishment", axial_pos_embds=False) # disable axial positional embeddings
config_pos_axial_embeds = ReformerConfig.from_pretrained("google/reformer-crime-and-punishment", axial_pos_embds=True, axial_pos_embds_dim=(64, 192), axial_pos_shape=(512, 1024)) # enable axial positional embeddings
print("Default Positional Encodings")
print(20 * '-')
model = ReformerModel(config_no_pos_axial_embeds)
print(f"Positional embeddings shape: {model.embeddings.position_embeddings}")
print(f"Num parameters of model: {model.num_parameters()}")
print(20 * '-' + '\n\n')
print("Axial Positional Encodings")
print(20 * '-')
model = ReformerModel(config_pos_axial_embeds)
print(f"Positional embeddings shape: {model.embeddings.position_embeddings}")
print(f"Num parameters of model: {model.num_parameters()}")
print(20 * '-' + '\n\n')
HBox(children=(FloatProgress(value=0.0, description='Downloading', max=1151.0, style=ProgressStyle(description…
Default Positional Encodings
--------------------
Positional embeddings shape: PositionEmbeddings(
(embedding): Embedding(524288, 256)
)
Num parameters of model: 136572416
--------------------
Axial Positional Encodings
--------------------
Positional embeddings shape: AxialPositionEmbeddings(
(weights): ParameterList(
(0): Parameter containing: [torch.FloatTensor of size 512x1x64]
(1): Parameter containing: [torch.FloatTensor of size 1x1024x192]
)
)
Num parameters of model: 2584064
--------------------
Having read the theory, the shape of the axial positional encoding weights should not be a surprise to the reader.
Regarding the results, it can be seen that for models being capable of processing such long input sequences, it is not practical to use default positional encodings.
In the case of google/reformer-crime-and-punishment, standard positional encodings alone contain more than 100M parameters.
Axial positional encodings reduce this number to just over 200K.
Lastly, let's also compare the required memory at inference time.
benchmark_args = PyTorchBenchmarkArguments(sequence_lengths=[512], batch_sizes=[8], models=["Reformer-No-Axial-Pos-Embeddings", "Reformer-Axial-Pos-Embeddings"], no_speed=True, no_env_print=True)
benchmark = PyTorchBenchmark(configs=[config_no_pos_axial_embeds, config_pos_axial_embeds], args=benchmark_args)
result = benchmark.run()
1 / 2
2 / 2
==================== INFERENCE - MEMORY - RESULT ====================
--------------------------------------------------------------------------------
Model Name Batch Size Seq Length Memory in MB
--------------------------------------------------------------------------------
Reformer-No-Axial-Pos-Embeddin 8 512 959
Reformer-Axial-Pos-Embeddings 8 512 447
--------------------------------------------------------------------------------
It can be seen that using axial positional embeddings reduces the memory requirement to approximately half in the case of google/reformer-crime-and-punishment.