Rank-Stabilized LoRA: Unlocking the Potential of LoRA Fine-Tuning
Introduction
As large language models (LLMs) have become increasingly compute and memory intensive, parameter-efficient fine-tuning (PEFT) methods are now a common strategy to fine-tune LLMs. One of the most popular PEFT methods, which many other PEFT methods are based off of, is the method of Low-Rank Adaptation (LoRA). LoRA works by fixing the original pre-trained model parameters, and adds trainable low-rank “adapters” to selected layers for fine-tuning.
One of the important findings of the original LoRA work was that fine-tuning with very low adapter rank (i.e. 4 to 32) could perform well, and that this performance did not improve further with increasing rank. However, it turns out that this saturation of performance with very low rank is not primarily due to a very low intrinsic dimensionality of the learning manifold, but rather, it stems from the stunted learning of LoRA outside of very low adapter ranks.
The method Rank-Stabilized LoRA (rsLoRA) proves that this limitation with LoRA existed, and that it can be corrected for by a simply dividing LoRA adapters by the square root of their rank.
In this post we give an overview of the rsLoRA PEFT method, and then demonstrate its use to optimize the OpenChat 3.5 model with human human feedback using Direct Preference Optimization (DPO), for significantly superior performance than one can get with LoRA. The rsLoRA method is now available in Hugging Face’s PEFT package, and we will give example code to show how easy it is to switch on when configuring LoRA with that package.
A Review of the LoRA Method
The LoRA architecture modifies a pre-trained model by adding tuneable “adapters” to a subset of the weight matrices of the original model. Precisely, an adapter is the (typically low-rank) matrix product which consists of the trainable parameters , , and a scaling factor for some hyperparameter . Note here that the adapter has matrix rank at most r. LoRA substitutes the original pre-trained weight matrix with
When the LoRA architecture is fine-tuned, the original weights are frozen and only are trained.
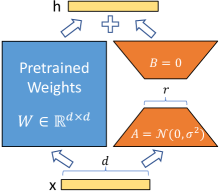
The principle benefit of LoRA is the reduced time and memory required to fine-tune when . In practice, training with LoRA uses very low-ranks (i.e. 4 to 32), which with Mistral 7B or Llama 2 7B for example, is drastically lower than their model dimension of 4096. This useage is typical since increasing the rank of LoRA adapters further does not benefit performance but increases the computational requirements. As we will see in the next section, this limitation is imposed by the scaling factor , which slows learning for ranks outside this very small rank regime, and better performance with higher ranks can be unlocked by substituting the correct adapter scaling factor with rsLoRA.
Rank-Stabilized Adapters with rsLORA
In the work Rank-Stabilized LoRA (rsLoRA), it is proven theoretically, by examining the learning trajectory of the adapters in the limit of large rank , that to not explode or diminish the magnitude of the activations and gradients through each adapter, one must set
The work also shows experimentally that this setting of the scaling factor improves learning with increasing rank, even in the low rank regimes. These findings correct for the ongoing misconceptions that very low adapter ranks suffice for maximal performance, which has continued to foster a misconception that overestimates the extent to which the intrinsic dimensionality of fine-tuning a foundation model is low-dimensional.
Of course, for those in the know about this work, one can just substitute the scaling factor in LoRA by substituting the hyperparameter for each adapter appropriately with set as:
so that
Hugging Face’s PEFT package gives the user the option to set this automatically by configuring LoRA with the option use_rslora = True. Explicitly, one adds this flag when initializing the LoraConfig as follows:
from peft import LoraConfig, get_peft_model
base_model = AutoModelForCausalLM.from_pretrained(...)
# initialize the config as usual but with "use_rslora = True"
lora_config = LoraConfig(..., use_rslora = True)
peft_model = get_peft_model(base_model, lora_config)
In the next section we will demonstrate an example of the benefits and use of rsLoRA for fine-tuning.
Fine-Tuning with rsLoRA
To illustrate the usage and utility of rsLoRA in contrast with LoRA, we demonstrate with the practical use case of fine-tuning OpenChat 3.5 with DPO on the dataset of human chat preferences UltraFeedback, and follow with a benckmark on the MT-Bench evaluation.
We use the Hugging Face alignment tuning package alignment-handbook to tune the model. All that is required to set up the training is the creation of a "recipe" yaml file which configures the parameters of our training and model. We use all the defaults defined in the example configuration alignment-handbook/recipes/zephyr-7b-beta/dpo/config_full.yaml, except the change of LoRA parameters, and the chat template for consistency with the prompting structure for evaluations and OpenChat 3.5:
# Model arguments
model_name_or_path: openchat/openchat_3.5
torch_dtype: auto
use_flash_attention_2: true
# LoRA arguments
use_peft: true
lora_r: 256
lora_alpha: 256 # using rsLoRA with an alpha of 16 and rank 256 means, lora_alpha = 16*(256**.5) = 256
lora_dropout: 0.1
lora_target_modules:
- q_proj
- k_proj
- o_proj
- up_proj
- gate_proj
# Data training arguments
# template used by OpenChat 3.5 in MT-Bench with FastChat
chat_template: "{{ bos_token }} {% for message in messages %}\n{% if message['role'] == 'user' %}\n{{ 'GPT4 Correct User:' + message['content'] + eos_token }}\n{% elif message['role'] == 'system' %}\n{{ message['content'] + eos_token }}\n{% elif message['role'] == 'assistant' %}\n{{ 'GPT4 Correct Assistant' + message['content'] + eos_token }}\n{% endif %}\n{% if loop.last and add_generation_prompt %}\n{{ 'GPT4 Correct Assistant:' }}{% endif %}\n{% endfor %}"
dataset_mixer:
HuggingFaceH4/ultrafeedback_binarized: 1.0
dataset_processing:
task: "dpo"
dataset_splits:
- train_prefs
- test_prefs
preprocessing_num_workers: 12
# DPOTrainer arguments
bf16: true
beta: 0.1
do_eval: true
evaluation_strategy: epoch
eval_steps: 100
gradient_accumulation_steps: 1
gradient_checkpointing: true
gradient_checkpointing_kwargs:
use_reentrant: false
hub_model_id: openchat
learning_rate: 5.0e-7
log_level: info
logging_steps: 10
lr_scheduler_type: linear
max_length: 1024
max_prompt_length: 512
num_train_epochs: 1
optim: adafactor
output_dir: /home/ubuntu/openchat/openchat-rslora-r256
per_device_train_batch_size: 12
per_device_eval_batch_size: 12
push_to_hub: false
save_strategy: "no"
save_total_limit: null
seed: 42
warmup_ratio: 0.1
report_to: wandb
run_name: "openchat-rslora-r256"
Then, one runs the DPO training with
ACCELERATE_LOG_LEVEL=info accelerate launch --config_file alignment-handbook/recipes/accelerate_configs/deepspeed_zero3.yaml alignment-handbook/scripts/run_dpo.py <path to recipe>.yaml
Note again that to use rsLoRA by default instead of manually changing lora_alpha, one just adds use_rslora=True to the initializaiton of the LoraConfig, which in the alignment-handbook codebase would be changed in alignment-handbook/src/alignment
/model_utils.py:
peft_config = LoraConfig(
r=model_args.lora_r,
lora_alpha=model_args.lora_alpha,
lora_dropout=model_args.lora_dropout,
bias="none",
task_type="CAUSAL_LM",
target_modules=model_args.lora_target_modules,
modules_to_save=model_args.lora_modules_to_save,
+ use_rslora=True
)
We ran the above configuration for rsLoRA with the low (but larger than typical for LoRA) rank 256. To compare this with LoRA we changed the configuration setting lora_alpha: 16 (don't forget to also change output_dir). We also ran LoRA with rank 16 by setting lora_r: 16 to compare with a typical useage of LoRA.
Our training time on a node with 8 40GB Nvidia A100's was 2h 19m 22s for rank 256, and 2h 06m 45s for rank 16. This means that for this setup the additional cost of training low ranks instead of very low ranks (eg 256 vs 16) is negligible, and yet, as we see in the evaluations of the next section, rsLoRA can unlock the extra performance of the higher rank.
Evaluation
To evaluate the performance of our models, we benchmark on MT-Bench with the FastChat package. We follow the instructions in the package's llm-judge readme to run the MT-bench evaluation:
First, generate responses to the set questions from our models with
python fastchat/llm_judge/gen_model_answer.py --model-path [output_dir] --model-id openchat_3.5_[EXTRA_LABEL]
Note [output_dir] should be set to the path we configured the model output_dir in the yaml for training above. This saves the answers generated into data/mt_bench/model_answer/openchat_3.5_[EXTRA_LABEL].jsonl.
After this, we run the benchmark script which scores the responses using GPT4:
export OPENAI_API_KEY=XXXXXX # set the OpenAI API key
python fastchat/llm_judge/gen_judgment.py --model-list openchat_3.5 openchat_3.5_lora_r16 openchat_3.5_lora_r256 openchat_3.5_rslora_r256
The judgments will be saved to data/mt_bench/model_judgment/gpt-4_single.jsonl.
Finally we show the scores for selected models.
python show_result.py --model-list openchat_3.5 openchat_3.5_lora_r16 openchat_3.5_lora_r256 openchat_3.5_rslora_r256
| Model | MT-Bench Turn 1 | MT-Bench Turn 2 | MT-Bench Average |
|---|---|---|---|
| Base model: OpenChat 3.5 | 8.20625 | 7.375 | 7.790625 |
| Fine-tune: LoRA rank 16 | 8.3375 | 7.525 | 7.93125 |
| Fine-tune: LoRA rank 256 | 8.3 | 7.625 | 7.9625 |
| Fine-tune: rsLoRA rank 256 | 8.425 | 7.75 | 8.0875 |
We see that both approaches improve on the original OpenChat 3.5 model, but that training with LoRA rank 16 and rank 256 show little appreciable difference, whereas rsLoRA unlocks the performance of the higher rank, almost doubling the difference between base model and rank 16 LoRA with the best score of 8.0875, and only at the cost of 13 extra minutes of training time!
Conclusion
In conclusion, The rsLoRA method not only extends the scope of achievable performance by unlocking the effective use of higher adapter rank, but also provides the flexibility to strike an optimal balance between computational resources and fine-tuning performance. Be sure to unlock the true porential of LoRA-style adapters by rank-stabilizing them with rsLoRA!