Transformers documentation
التعقيد اللغوي للنماذج ذات الطول الثابت
التعقيد اللغوي للنماذج ذات الطول الثابت
التعقيد اللغوي (PPL) هي واحدة من أكثر المقاييس شيوعًا لتقييم نماذج اللغة. قبل الخوض في التفاصيل، يجب أن نلاحظ أن المقياس ينطبق تحديدًا على نماذج اللغة الكلاسيكية (يُطلق عليها أحيانًا نماذج اللغة التلقائية المرجعية أو السببية) وهي غير محددة جيدًا لنماذج اللغة المقنعة مثل BERT (راجع ملخص النماذج).
تُعرَّف التعقيد اللغوي على أنها الأس المُرفوع لقيمة متوسط اللوغاريتم الاحتمالي لمتتالية. إذا كان لدينا تسلسل رمزي، فإن حيرة هي،
حيث هو اللوغاريتم الاحتمالي للرمز i بشرط الرموز السابقة وفقًا لنموذجنا. ومن الناحية البديهية، يمكن اعتبارها تقييمًا لقدرة النموذج على التنبؤ بالتساوي بين مجموعة من الرموز المحددة في مجموعة من البيانات. ومن المهم الإشارة إلى أن عملية التمييز له تأثير مباشرًا على حيرة النموذج،ويجب مراعاتها دائمًا عند مقارنة النماذج المختلفة.
كما أنها تعادل الأس المُرفوع لقيمة الانتروبيا المتقاطعة بين البيانات وتنبؤات النموذج. لمزيد من الفهم حول مفهوم التعقيد اللغوي وعلاقتها بـ Bits Per Character (BPC) وضغط البيانات، يُرجى مراجعة التدوينة المفيدة على The Gradient.
حساب PPL مع النماذج ذات الطول الثابت
إذا لم نكن مقيدين بحجم سياق النموذج، فسنقوم بتقييم التعقيد اللغوي للنموذج عن طريق تحليل التسلسل تلقائيًا والشرط على التسلسل الفرعي السابق بالكامل في كل خطوة، كما هو موضح أدناه.
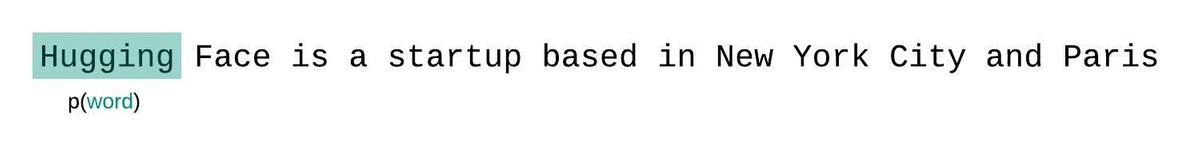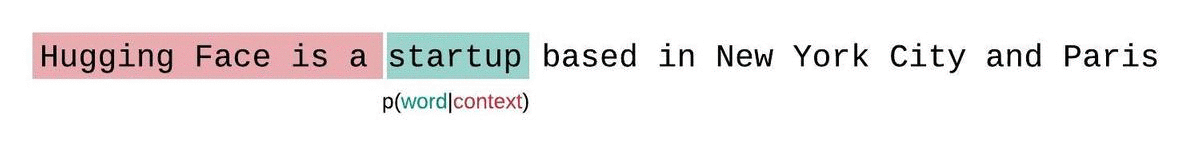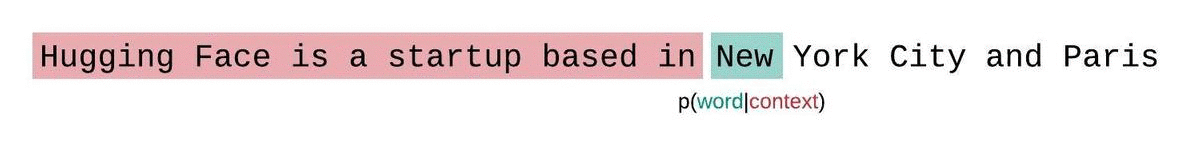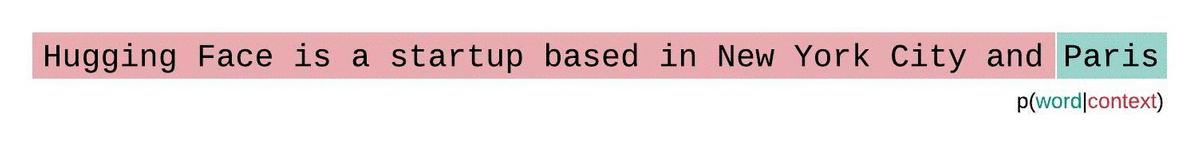
لكن عند التعامل مع النماذج التقريبية، نواجه عادةً قيدًا على عدد الرموز التي يمكن للنموذج معالجتها. على سبيل المثال، تحتوي أكبر نسخة من GPT-2 على طول ثابت يبلغ 1024 رمزًا، لذا لا يمكننا حساب مباشرة عندما تكون أكبر من 1024.
بدلاً من ذلك، يتم عادةً تقسيم التسلسل إلى تسلسلات فرعية مساوية لحجم الإدخال الأقصى للنموذج. فإذا كان حجم الإدخال الأقصى للنموذج هو، فإننا نقرب احتمال الرمز عن طريق الاشتقاق الشرطي فقط بالنسبة إلى من الرموز التي تسبقه بدلاً من السياق بأكمله. وعند تقييم حيرة النموذج لتسلسل ما، قد يبدو من المغري تقسيم التسلسل إلى أجزاء منفصلة وجمع مجموع دوال اللوغاريتم لكل جزء بشكل مستقل، لكن هذا الأسلوب ليس الأمثل.
تتميز هذه الطريقة بسرعة حسابها نظرًا لإمكانية حساب درجة التعقيد اللغوي لكل جزء بمسح واحد للأمام، إلا أنها تُعدّ تقريبًا ضعيفًا لدرجة التعقيد اللغوي المُحلّلة بشكل كامل، وعادةً ما تؤدي إلى درجة تعقيد لغوي أعلى (أسوأ) لأن النموذج سيكون لديه سياق أقل في معظم خطوات التنبؤ.
بدلاً من ذلك، يجب تقييم درجة التعقيد اللغوي للنماذج ذات الطول الثابت باستخدام إستراتيجية النافذة المنزلقة. وينطوي هذا على تحريك نافذة السياق بشكل متكرر بحيث يكون للنموذج سياق أكبر عند إجراء كل تنبؤ.
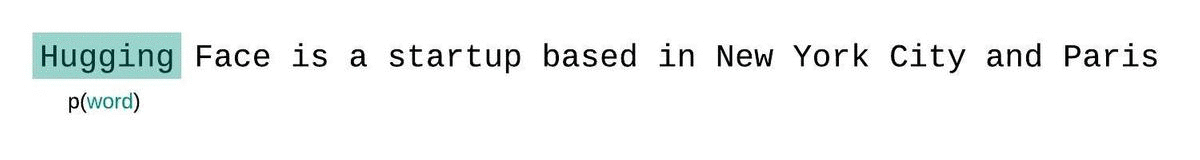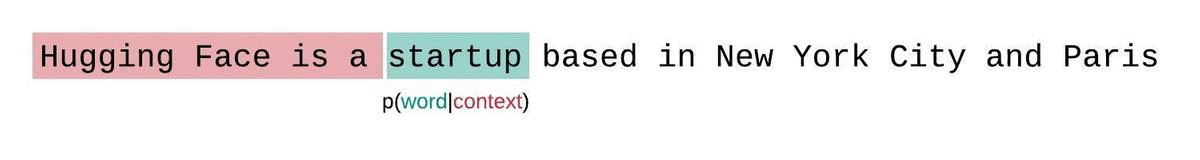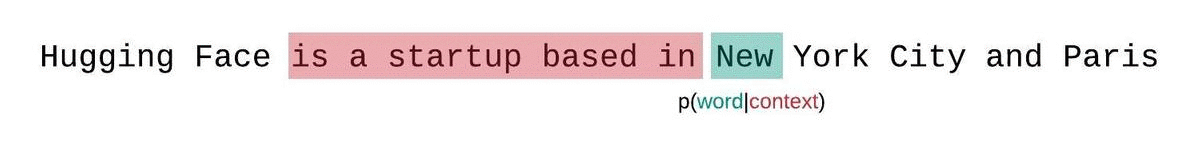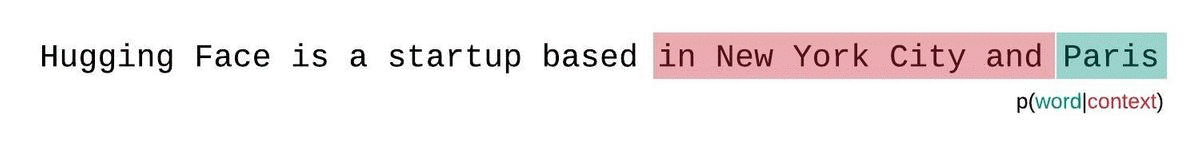
هذا تقريب أقرب للتفكيك الحقيقي لاحتمالية التسلسل وسيؤدي عادةً إلى نتيجة أفضل.لكن الجانب السلبي هو أنه يتطلب تمريرًا للأمام لكل رمز في مجموعة البيانات. حل وسط عملي مناسب هو استخدام نافذة منزلقة بخطوة، بحيث يتم تحريك السياق بخطوات أكبر بدلاً من الانزلاق بمقدار 1 رمز في كل مرة. مما يسمح بإجراء الحساب بشكل أسرع مع إعطاء النموذج سياقًا كبيرًا للتنبؤات في كل خطوة.
مثال: حساب التعقيد اللغوي مع GPT-2 في 🤗 Transformers
دعونا نوضح هذه العملية مع GPT-2.
from transformers import GPT2LMHeadModel, GPT2TokenizerFast
device = "cuda"
model_id = "openai-community/gpt2-large"
model = GPT2LMHeadModel.from_pretrained(model_id).to(device)
tokenizer = GPT2TokenizerFast.from_pretrained(model_id)سنقوم بتحميل مجموعة بيانات WikiText-2 وتقييم التعقيد اللغوي باستخدام بعض إستراتيجيات مختلفة النافذة المنزلقة. نظرًا لأن هذه المجموعة البيانات الصغيرة ونقوم فقط بمسح واحد فقط للمجموعة، فيمكننا ببساطة تحميل مجموعة البيانات وترميزها بالكامل في الذاكرة.
from datasets import load_dataset
test = load_dataset("wikitext", "wikitext-2-raw-v1", split="test")
encodings = tokenizer("\n\n".join(test["text"]), return_tensors="pt")مع 🤗 Transformers، يمكننا ببساطة تمرير input_ids كـ labels إلى نموذجنا، وسيتم إرجاع متوسط احتمالية السجل السالب لكل رمز كخسارة. ومع ذلك، مع نهج النافذة المنزلقة، هناك تداخل في الرموز التي نمررها إلى النموذج في كل تكرار. لا نريد تضمين احتمالية السجل للرموز التي نتعامل معها كسياق فقط في خسارتنا، لذا يمكننا تعيين هذه الأهداف إلى -100 بحيث يتم تجاهلها. فيما يلي هو مثال على كيفية القيام بذلك بخطوة تبلغ 512. وهذا يعني أن النموذج سيكون لديه 512 رمزًا على الأقل للسياق عند حساب الاحتمالية الشرطية لأي رمز واحد (بشرط توفر 512 رمزًا سابقًا متاحًا للاشتقاق).
import torch
from tqdm import tqdm
max_length = model.config.n_positions
stride = 512
seq_len = encodings.input_ids.size(1)
nlls = []
prev_end_loc = 0
for begin_loc in tqdm(range(0, seq_len, stride)):
end_loc = min(begin_loc + max_length, seq_len)
trg_len = end_loc - prev_end_loc # قد تكون مختلفة عن الخطوة في الحلقة الأخيرة
input_ids = encodings.input_ids[:, begin_loc:end_loc].to(device)
target_ids = input_ids.clone()
target_ids[:, :-trg_len] = -100
with torch.no_grad():
outputs = model(input_ids, labels=target_ids)
# يتم حساب الخسارة باستخدام CrossEntropyLoss الذي يقوم بالمتوسط على التصنيفات الصحيحة
# لاحظ أن النموذج يحسب الخسارة على trg_len - 1 من التصنيفات فقط، لأنه يتحول داخليًا إلى اليسار بواسطة 1.
neg_log_likelihood = outputs.loss
nlls.append(neg_log_likelihood)
prev_end_loc = end_loc
if end_loc == seq_len:
break
ppl = torch.exp(torch.stack(nlls).mean())يعد تشغيل هذا مع طول الخطوة مساويًا لطول الإدخال الأقصى يعادل لاستراتيجية النافذة غير المنزلقة وغير المثلى التي ناقشناها أعلاه. وكلما صغرت الخطوة، زاد السياق الذي سيحصل عليه النموذج في عمل كل تنبؤ، وكلما كانت التعقيد اللغوي المُبلغ عنها أفضل عادةً.
عندما نقوم بتشغيل ما سبق باستخدام stride = 1024، أي بدون تداخل، تكون درجة التعقيد اللغوي الناتجة هي 19.44، وهو ما يماثل 19.93 المبلغ عنها في ورقة GPT-2. من خلال استخدام stride = 512 وبالتالي استخدام إستراتيجية النافذة المنزلقة، ينخفض هذا إلى 16.45. هذه النتيجة ليست فقط أفضل، ولكنها محسوبة بطريقة أقرب إلى التحليل التلقائي الحقيقي لاحتمالية التسلسل.