PEFT documentation
Adapters
Adapters
Adapter-based methods add extra trainable parameters after the attention and fully-connected layers of a frozen pretrained model to reduce memory-usage and speed up training. The method varies depending on the adapter, it could simply be an extra added layer or it could be expressing the weight updates ∆W as a low-rank decomposition of the weight matrix. Either way, the adapters are typically small but demonstrate comparable performance to a fully finetuned model and enable training larger models with fewer resources.
This guide will give you a brief overview of the adapter methods supported by PEFT (if you’re interested in learning more details about a specific method, take a look at the linked paper).
Low-Rank Adaptation (LoRA)
LoRA is one of the most popular PEFT methods and a good starting point if you’re just getting started with PEFT. It was originally developed for large language models but it is a tremendously popular training method for diffusion models because of its efficiency and effectiveness.
As mentioned briefly earlier, LoRA is a technique that accelerates finetuning large models while consuming less memory.
LoRA represents the weight updates ∆W with two smaller matrices (called update matrices) through low-rank decomposition. These new matrices can be trained to adapt to the new data while keeping the overall number of parameters low. The original weight matrix remains frozen and doesn’t receive any further updates. To produce the final results, the original and extra adapted weights are combined. You could also merge the adapter weights with the base model to eliminate inference latency.
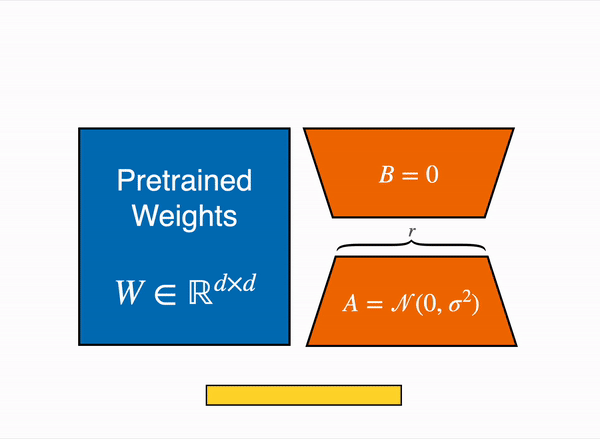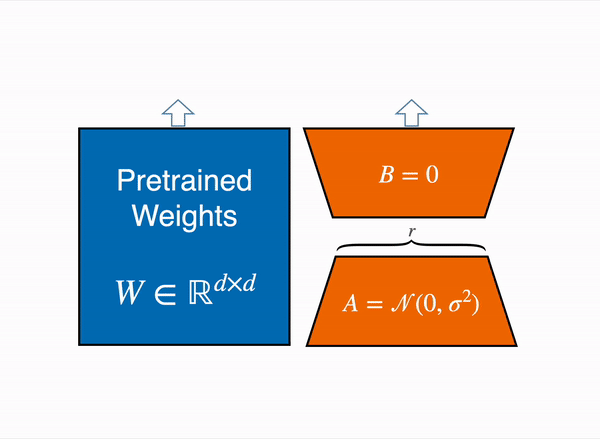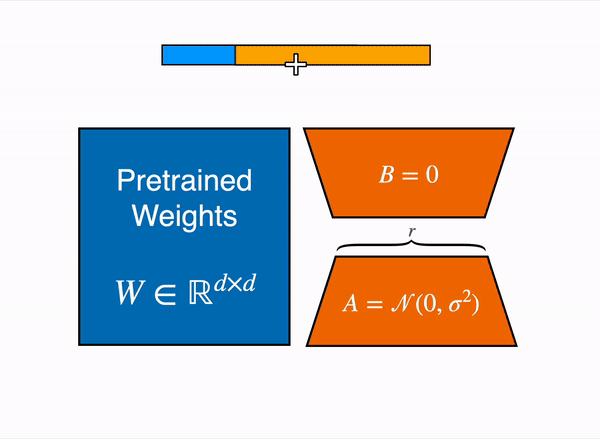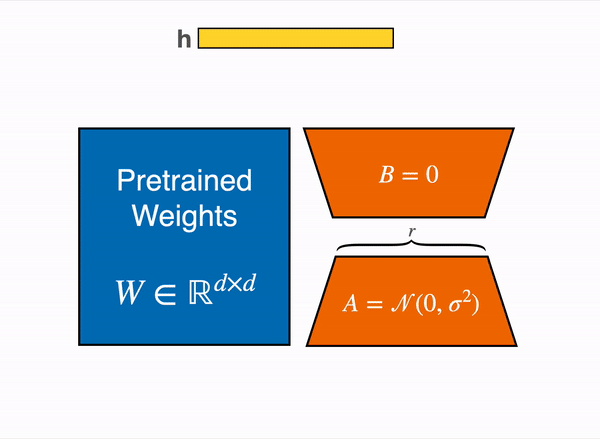
This approach has a number of advantages:
- LoRA makes finetuning more efficient by drastically reducing the number of trainable parameters.
- The original pretrained weights are kept frozen, which means you can have multiple lightweight and portable LoRA models for various downstream tasks built on top of them.
- LoRA is orthogonal to other parameter-efficient methods and can be combined with many of them.
- Performance of models finetuned using LoRA is comparable to the performance of fully finetuned models.
In principle, LoRA can be applied to any subset of weight matrices in a neural network to reduce the number of trainable parameters. However, for simplicity and further parameter efficiency, LoRA is typically only applied to the attention blocks in Transformer models. The resulting number of trainable parameters in a LoRA model depends on the size of the update matrices, which is determined mainly by the rank r and the shape of the original weight matrix.
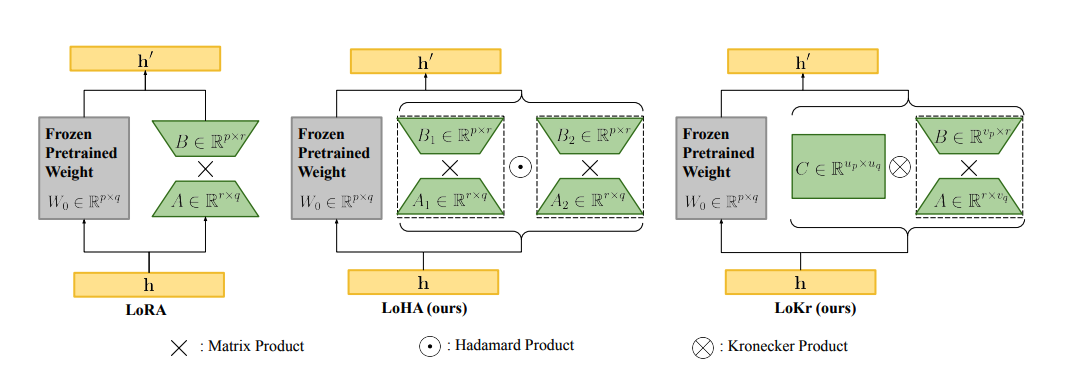
Low-Rank Hadamard Product (LoHa)
Low-rank decomposition can impact performance because the weight updates are limited to the low-rank space, which can constrain a model’s expressiveness. However, you don’t necessarily want to use a larger rank because it increases the number of trainable parameters. To address this, LoHa (a method originally developed for computer vision) was applied to diffusion models where the ability to generate diverse images is an important consideration. LoHa should also work with general model types, but the embedding layers aren’t currently implemented in PEFT.
LoHa uses the Hadamard product (element-wise product) instead of the matrix product. ∆W is represented by four smaller matrices instead of two - like in LoRA - and each pair of these low-rank matrices are combined with the Hadamard product. As a result, ∆W can have the same number of trainable parameters but a higher rank and expressivity.
Low-Rank Kronecker Product (LoKr)
LoKr is very similar to LoRA and LoHa, and it is also mainly applied to diffusion models, though you could also use it with other model types. LoKr replaces the matrix product with the Kronecker product instead. The Kronecker product decomposition creates a block matrix which preserves the rank of the original weight matrix. Another benefit of the Kronecker product is that it can be vectorized by stacking the matrix columns. This can speed up the process because you’re avoiding fully reconstructing ∆W.
Orthogonal Finetuning (OFT)
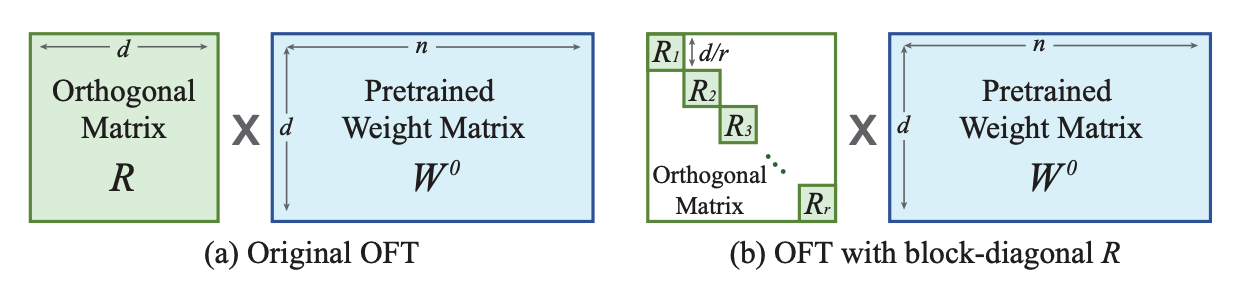
OFT is a method that primarily focuses on preserving a pretrained model’s generative performance in the finetuned model. It tries to maintain the same cosine similarity (hyperspherical energy) between all pairwise neurons in a layer because this better captures the semantic information among neurons. This means OFT is more capable at preserving the subject and it is better for controllable generation (similar to ControlNet).
OFT preserves the hyperspherical energy by learning an orthogonal transformation for neurons to keep the cosine similarity between them unchanged. In practice, this means taking the matrix product of an orthogonal matrix with the pretrained weight matrix. However, to be parameter-efficient, the orthogonal matrix is represented as a block-diagonal matrix with rank r blocks. Whereas LoRA reduces the number of trainable parameters with low-rank structures, OFT reduces the number of trainable parameters with a sparse block-diagonal matrix structure.
Adaptive Low-Rank Adaptation (AdaLoRA)
AdaLoRA manages the parameter budget introduced from LoRA by allocating more parameters - in other words, a higher rank r - for important weight matrices that are better adapted for a task and pruning less important ones. The rank is controlled by a method similar to singular value decomposition (SVD). The ∆W is parameterized with two orthogonal matrices and a diagonal matrix which contains singular values. This parametrization method avoids iteratively applying SVD which is computationally expensive. Based on this method, the rank of ∆W is adjusted according to an importance score. ∆W is divided into triplets and each triplet is scored according to its contribution to model performance. Triplets with low importance scores are pruned and triplets with high importance scores are kept for finetuning.
Llama-Adapter
Llama-Adapter is a method for adapting Llama into a instruction-following model. To help adapt the model for instruction-following, the adapter is trained with a 52K instruction-output dataset.
A set of of learnable adaption prompts are prefixed to the input instruction tokens. These are inserted into the upper layers of the model because it is better to learn with the higher-level semantics of the pretrained model. The instruction-output tokens prefixed to the input guide the adaption prompt to generate a contextual response.
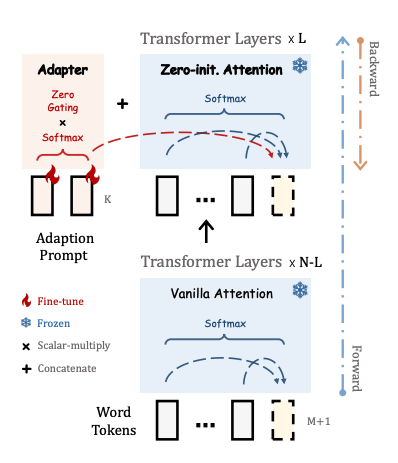
To avoid adding noise to the tokens, the adapter uses zero-initialized attention. On top of this, the adapter adds a learnable gating factor (initialized with zeros) to progressively add information to the model during training. This prevents overwhelming the model’s pretrained knowledge with the newly learned instructions.