licenses
sequencelengths 1
3
| version
stringclasses 677
values | tree_hash
stringlengths 40
40
| path
stringclasses 1
value | type
stringclasses 2
values | size
stringlengths 2
8
| text
stringlengths 25
67.1M
| package_name
stringlengths 2
41
| repo
stringlengths 33
86
|
|---|---|---|---|---|---|---|---|---|
[
"MIT"
] | 2.4.0 | b98948c567cbe250d774d01a07833b7a329ec511 | docs | 1465 |
# Introduction
This package provides the Sauter-Schwab regularizing coordinate transformations [1] such that 4D integrals of the form
```math
\int_{\Gamma}\int_{\Gamma'}b_i(\bm{x})\,k(\bm{x},\bm{y})\, b_j(\bm{y})\,\mathrm{d}S(\bm{y})\,\mathrm{d}S(\bm{x})
```
with Cauchy-singular integral kernels ``k(\bm{x},\bm{y})`` can be integrated via numerical quadrature.
The integrals denote double surface integrals over
- triangles (curved or flat) or
- quadrilaterals (curved or flat)
``\Gamma`` and ``\Gamma'`` in 3D Space.
The functions ``b_i(\bm{x})`` and ``b_i(\bm{y})`` are assumed to be real valued and non-singular.
These kind of integrals occur in the area of boundary element methods (BEM) for solving elliptic partial differential equations.
It can be interpreted as the interaction of the two basisfunctions ``b_i(\bm{x})`` and ``b_i(\bm{y})``, with respect to their domains ``\Gamma`` and ``\Gamma'``, which, for instance, correspond to the cells of a meshed surface.
!!! info
The triangles or quadrilaterals must be either equal, have two vertices in common, have one vertex in common or do not touch at all. A partial overlap is forbidden.
In the current implementation ``\Gamma`` and ``\Gamma'`` have to be both either triangles or quadrilatersls. However, mixed cases can be implemented, too.
## References
[1] Sauter S. Schwab C., "Boundary Element Methods (Springer Series in Computational Mathematics)", Chapter 5, Springer, 2010.
| SauterSchwabQuadrature | https://github.com/ga96tik/SauterSchwabQuadrature.jl.git |
|
[
"MIT"
] | 2.4.0 | b98948c567cbe250d774d01a07833b7a329ec511 | docs | 1119 |
# Manual
Fundamentally, one function is provided:
```@julia
sauterschwab_parameterized(integrand, strategy)
```
The first argument `integrand` is the parameterized integrand ``k'(\chi_\tau(u,v), \chi_t(u',v'))``.
That is, it takes as argument two tuples:
```@julia
integrand((u,v), (u',v'))
```
The second argument `strategy` specifies the reparametrization and is one of (the by this package provided) structs:
For triangles
- `CommonFace`
- `CommonEdge`
- `CommonVertex`
- `PositiveDistance`
For quadrilaterals
- `CommonFaceQuad`
- `CommonEdgeQuad`
- `CommonVertexQuad`
Each such struct takes one argument specifying the quadrature rule, e.g.,
```@julia
strategy = CommonEdge(qrule)
```
where `qrule` is a vector of `(point, weight)` tuples for a quadrature on the domain ``[0,1]``.
!!! tip
We recommend the [FastGaussQuadrature.jl](https://github.com/JuliaApproximation/FastGaussQuadrature.jl/tree/master) package.
For a Gauss-Legendre quadrature a method is provided that maps to the ``[0,1]`` domain:
```@julia
order = 10
qrule = SauterSchwabQuadrature._legendre(order, 0, 1)
``` | SauterSchwabQuadrature | https://github.com/ga96tik/SauterSchwabQuadrature.jl.git |
|
[
"MIT"
] | 1.0.0 | 9b581c2549ce117f977f9212e76131a3669979c7 | code | 653 | # ------------------------------------------------------------------
# Licensed under the MIT License. See LICENCE in the project root.
# ------------------------------------------------------------------
module ExtremeStats
using Distributions
using JuMP, Ipopt
using RecipesBase
# implement fitting methods
import Distributions: fit_mle
include("maxima.jl")
include("fitting.jl")
include("stats.jl")
# plot recipes
include("plotrecipes/return_levels.jl")
include("plotrecipes/mean_excess.jl")
include("plotrecipes/pareto_quantile.jl")
export
# maxima types
BlockMaxima,
PeakOverThreshold,
# statistics
returnlevels,
meanexcess
end
| ExtremeStats | https://github.com/JuliaEarth/ExtremeStats.jl.git |
|
[
"MIT"
] | 1.0.0 | 9b581c2549ce117f977f9212e76131a3669979c7 | code | 3334 | # ------------------------------------------------------------------
# Licensed under the MIT License. See LICENCE in the project root.
# ------------------------------------------------------------------
"""
log_gpd_pdf(arg, μ, σ, ξ)
Log density function of the generalized Pareto distribution,
with an expansion with ξ near zero.
"""
function log_gpd_pdf(_x, μ, σ, ξ)
x = (_x-μ)/σ
expn = if abs(ξ) < 1e-5
# expansion for ξ near zero.
-x*(ξ+1) + (x^2)*ξ*(ξ+1)/2 - (x^3)*(ξ^2)*(ξ+1)/3 + (x^4)*(ξ^3)*(ξ+1)/4
else
(-(ξ+1)/ξ)*log(max(0, 1 + x*ξ))
end
expn - log(σ)
end
"""
log_gev_pdf(arg, μ, σ, ξ)
Log density function of the generalized extreme value distribution,
with an expansion with ξ near zero.
"""
function log_gev_pdf(_x, μ, σ, ξ)
x = (_x-μ)/σ
tx = if abs(ξ) < 1e-10 # this cutoff is _not_ the same as for log_gpd_pdf.
# expansion near zero.
-x + (x^2)*ξ/2 - (x^3)*(ξ^2)/3 + (x^4)*(ξ^3)/4
else
(-1/ξ)*log(max(0, 1 + x*ξ))
end
(ξ+1)*tx - exp(tx) - log(σ)
end
"""
fit_mle(gev, bm)
Fit generalized extreme value distribution `gev` to block maxima
`bm` with constrained maximum likelihood estimation.
"""
function fit_mle(::Type{GeneralizedExtremeValue}, bm::BlockMaxima;
init=(μ=0.0, σ=1.0, ξ=0.05))
# retrieve maxima values
x = collect(bm)
n = length(x)
# set up the problem
mle = Model(optimizer_with_attributes(Ipopt.Optimizer, "print_level"=>0,
"sb"=>"yes", "max_iter"=>250))
@variable(mle, μ, start=init.μ)
@variable(mle, σ, start=init.σ)
@variable(mle, ξ, start=init.ξ)
JuMP.register(mle, :log_gev_pdf, 4, log_gev_pdf, autodiff=true)
@NLobjective(mle, Max, sum(log_gev_pdf(z, μ, σ, ξ) for z in x))
@NLconstraint(mle, [i=1:n], 1 + ξ*(x[i]-μ)/σ ≥ 0.0)
@constraint(mle, σ ≥ 1e-10)
@constraint(mle, ξ ≥ -1/2)
# attempt to solve
optimize!(mle)
# retrieve solver status
status = termination_status(mle)
# acceptable statuses
OK = (MOI.OPTIMAL, MOI.LOCALLY_SOLVED)
if status ∈ OK
GeneralizedExtremeValue(value(μ), value(σ), value(ξ))
else
error("could not fit distribution. Exited with status $status.")
end
end
"""
fit_mle(gp, pm)
Fit generalized Pareto distribution `gp` to peak over threshold
maxima `pm` with constrained maximum likelihood estimation.
"""
function fit_mle(::Type{GeneralizedPareto}, pm::PeakOverThreshold;
init=(σ=1.0, ξ=0.05))
# retrieve maxima values
x = collect(pm)
n = length(x)
# set up the problem
mle = Model(optimizer_with_attributes(Ipopt.Optimizer, "print_level"=>0,
"sb"=>"yes", "max_iter"=>250))
@variable(mle, σ, start=init.σ)
@variable(mle, ξ, start=init.ξ)
JuMP.register(mle, :log_gpd_pdf, 4, log_gpd_pdf, autodiff=true)
@NLobjective(mle, Max, sum(log_gpd_pdf(z, pm.u, σ, ξ) for z in x))
@NLconstraint(mle, [i=1:n], 1 + ξ*(x[i]-pm.u)/σ ≥ 0.0)
@constraint(mle, σ ≥ 1e-10)
@constraint(mle, ξ ≥ -1/2)
# attempt to solve both cases
optimize!(mle)
# retrieve solver status
status = termination_status(mle)
# acceptable statuses
OK = (MOI.OPTIMAL, MOI.LOCALLY_SOLVED)
if status ∈ OK
GeneralizedPareto(pm.u, value(σ), value(ξ))
else
error("could not fit distribution. Exited with status $status.")
end
end
| ExtremeStats | https://github.com/JuliaEarth/ExtremeStats.jl.git |
|
[
"MIT"
] | 1.0.0 | 9b581c2549ce117f977f9212e76131a3669979c7 | code | 1227 | # ------------------------------------------------------------------
# Licensed under the MIT License. See LICENCE in the project root.
# ------------------------------------------------------------------
"""
AbstractMaxima
A collection of maxima (e.g. block maxima)
"""
abstract type AbstractMaxima end
"""
collect(maxima)
Collect `maxima` values using appropriate model.
"""
Base.collect(m::AbstractMaxima) = error("not implemented")
#------------------
# IMPLEMENTATIONS
#------------------
"""
BlockMaxima(x, n)
Maxima obtained by splitting the data `x` into blocks of size `n`.
"""
struct BlockMaxima{V<:AbstractVector} <: AbstractMaxima
x::V
n::Int
end
function Base.collect(m::BlockMaxima)
result = Vector{Float64}()
for i in 1:m.n:length(m.x)-m.n+1
xs = skipmissing(view(m.x, i:i+m.n-1))
xmax = -Inf
for x in xs
x > xmax && (xmax = x)
end
isinf(xmax) || push!(result, xmax)
end
result
end
"""
PeakOverThreshold(x, u)
Maxima obtained by thresholding the data `x` with threshold `u`.
"""
struct PeakOverThreshold{V<:AbstractVector} <: AbstractMaxima
x::V
u::Float64
end
Base.collect(m::PeakOverThreshold) = filter(x -> !ismissing(x) && x > m.u, m.x)
| ExtremeStats | https://github.com/JuliaEarth/ExtremeStats.jl.git |
|
[
"MIT"
] | 1.0.0 | 9b581c2549ce117f977f9212e76131a3669979c7 | code | 1120 | # ------------------------------------------------------------------
# Licensed under the MIT License. See LICENCE in the project root.
# ------------------------------------------------------------------
"""
returnlevels(xs)
Return periods and levels of data `xs`.
"""
function returnlevels(xs::AbstractVector)
ms = sort(xs)
n = length(ms)
p = (1:n) ./ (n + 1)
δt = 1 ./ (1 .- p)
δt, ms
end
"""
returnlevels(gev, mmin, mmax; nlevels=50)
Return `nlevels` periods and levels of generalized extreme
value distribution `gev` with maxima in the interval `[mmin,mmax]`.
"""
function returnlevels(gev::GeneralizedExtremeValue,
mmin::Real, mmax::Real;
nlevels::Int=50)
ms = linspace(mmin, mmax, nlevels)
δt = 1 ./ (1 .- cdf.(gev, ms))
δt, ms
end
"""
meanexcess(xs, k)
Return mean excess of the data `xs` using previous `k` values.
"""
meanexcess(xs::AbstractVector, k::Int) = meanexcess(xs, [k])[1]
function meanexcess(xs::AbstractVector, ks::AbstractVector{Int})
ys = sort(xs, rev=true)
[mean(log.(ys[1:k-1])) - log(ys[k]) for k in ks]
end
| ExtremeStats | https://github.com/JuliaEarth/ExtremeStats.jl.git |
|
[
"MIT"
] | 1.0.0 | 9b581c2549ce117f977f9212e76131a3669979c7 | code | 450 | # ------------------------------------------------------------------
# Licensed under the MIT License. See LICENCE in the project root.
# ------------------------------------------------------------------
@userplot ExcessPlot
@recipe function f(p::ExcessPlot)
# get user input
xs = p.args[1]
ks = 2:length(xs)
ξs = meanexcess(xs, ks)
seriestype --> :path
xguide --> "number of maxima"
yguide --> "extreme value index"
ks, ξs
end
| ExtremeStats | https://github.com/JuliaEarth/ExtremeStats.jl.git |
|
[
"MIT"
] | 1.0.0 | 9b581c2549ce117f977f9212e76131a3669979c7 | code | 497 | # ------------------------------------------------------------------
# Licensed under the MIT License. See LICENCE in the project root.
# ------------------------------------------------------------------
@userplot ParetoPlot
@recipe function f(p::ParetoPlot)
# get user input
data = p.args[1]
x = sort(data, rev=true)
n = length(x)
logp = log.([i/(n+1) for i in 1:n])
logx = log.(x)
seriestype --> :scatter
xguide --> "-log(i/(n+1))"
yguide --> "log(x*)"
-logp, logx
end
| ExtremeStats | https://github.com/JuliaEarth/ExtremeStats.jl.git |
|
[
"MIT"
] | 1.0.0 | 9b581c2549ce117f977f9212e76131a3669979c7 | code | 653 | # ------------------------------------------------------------------
# Licensed under the MIT License. See LICENCE in the project root.
# ------------------------------------------------------------------
@userplot ReturnPlot
@recipe function f(rp::ReturnPlot)
# get user input
obj = rp.args[1]
if obj isa AbstractVector
seriestype --> :scatter
δt, ms = returnlevels(obj)
elseif obj isa GeneralizedExtremeValue
seriestype --> :path
mmin, mmax = rp.args[2:3]
δt, ms = returnlevels(obj, mmin, mmax)
end
xscale --> :log10
xguide --> "return period"
yguide --> "return level"
label --> "return plot"
δt, ms
end
| ExtremeStats | https://github.com/JuliaEarth/ExtremeStats.jl.git |
|
[
"MIT"
] | 1.0.0 | 9b581c2549ce117f977f9212e76131a3669979c7 | code | 3536 |
@testset "Fitting" begin
@testset "Block" begin
gev_seed = StableRNG(12345)
dist1 = GeneralizedExtremeValue(0.0, 1.0, 0.0)
dist2 = GeneralizedExtremeValue(0.0, 1.0, 0.5)
dist3 = GeneralizedExtremeValue(1.0, 1.0, 0.5) # The problem distribution...
r_gev_1 = readdlm(joinpath(datadir,"R_gev_dist1_fits.csv"), ',')
r_gev_2 = readdlm(joinpath(datadir,"R_gev_dist2_fits.csv"), ',')
r_gev_3 = readdlm(joinpath(datadir,"R_gev_dist3_fits.csv"), ',')
r_result = zip(eachrow(r_gev_1), eachrow(r_gev_2), eachrow(r_gev_3))
for (test_ix, r_gev_ix) in enumerate(r_result)
for (r_mle, dist) in zip(r_gev_ix, (dist1, dist2, dist3))
sample = rand(gev_seed, dist, 1000)
try
julia_fit = fit(GeneralizedExtremeValue, BlockMaxima(sample, 1))
j_mle = [julia_fit.μ, julia_fit.σ, julia_fit.ξ]
@test isapprox(j_mle, r_mle, atol=1e-3)
catch er
@info "Optimization failed for $dist on trial $test_ix with error $er."
end
end
end
end
@testset "PoT" begin
gpd_seed = StableRNG(12345)
dist1 = GeneralizedPareto(0.0, 1.0, 0.0)
dist2 = GeneralizedPareto(0.0, 1.0, 0.5)
dist3 = GeneralizedPareto(1.0, 1.0, 0.5)
r_gpd_1 = readdlm(joinpath(datadir,"R_gpd_dist1_fits.csv"), ',')
r_gpd_2 = readdlm(joinpath(datadir,"R_gpd_dist2_fits.csv"), ',')
r_gpd_3 = readdlm(joinpath(datadir,"R_gpd_dist3_fits.csv"), ',')
r_result = zip(eachrow(r_gpd_1), eachrow(r_gpd_2), eachrow(r_gpd_3))
for (test_ix, r_gpd_ix) in enumerate(r_result)
for (r_mle, dist) in zip(r_gpd_ix, (dist1, dist2, dist3))
sample = rand(gpd_seed, dist, 1000)
try
julia_fit = fit(GeneralizedPareto, PeakOverThreshold(sample, dist.μ))
j_mle = [julia_fit.σ, julia_fit.ξ]
@test isapprox(j_mle, r_mle, atol=1e-3)
catch er
@info "Optimization failed for $dist on trial $test_ix with error $er."
end
end
end
end
end
#= Code to generate the R test files:
using RCall, StableRNGs, Distributions
R"library(ismev)"
gev_R_results = NTuple{3, Vector{Float64}}[]
gev_seed = StableRNG(12345)
dist1 = GeneralizedExtremeValue(0.0, 1.0, 0.0)
dist2 = GeneralizedExtremeValue(0.0, 1.0, 0.5)
dist3 = GeneralizedExtremeValue(1.0, 1.0, 0.5)
for test_ix in 1:10
mles_trialj = map((dist1, dist2, dist3)) do dist
sample = rand(gev_seed, dist, 1000)
R"""
r_fit = gev.fit($sample, show=FALSE)
r_mle = r_fit$mle
"""
@rget r_mle
end
push!(gev_R_results, mles_trialj)
end
gpd_R_results = NTuple{3, Vector{Float64}}[]
gpd_seed = StableRNG(12345)
dist1 = GeneralizedPareto(0.0, 1.0, 0.0)
dist2 = GeneralizedPareto(0.0, 1.0, 0.5)
dist3 = GeneralizedPareto(1.0, 1.0, 0.5)
for test_ix in 1:10
mles_trialj = map((dist1, dist2, dist3)) do dist
sample = rand(gpd_seed, dist, 1000)
R"""
r_fit = gpd.fit($sample, threshold=$(dist.μ), show=FALSE)
r_mle = r_fit$mle
"""
@rget r_mle
end
push!(gpd_R_results, mles_trialj)
end
using DelimitedFiles
writedlm("data/R_gev_dist1_fits.csv", getindex.(gev_R_results, 1), ',')
writedlm("data/R_gev_dist2_fits.csv", getindex.(gev_R_results, 2), ',')
writedlm("data/R_gev_dist3_fits.csv", getindex.(gev_R_results, 3), ',')
writedlm("data/R_gpd_dist1_fits.csv", getindex.(gpd_R_results, 1), ',')
writedlm("data/R_gpd_dist2_fits.csv", getindex.(gpd_R_results, 2), ',')
writedlm("data/R_gpd_dist3_fits.csv", getindex.(gpd_R_results, 3), ',')
=#
| ExtremeStats | https://github.com/JuliaEarth/ExtremeStats.jl.git |
|
[
"MIT"
] | 1.0.0 | 9b581c2549ce117f977f9212e76131a3669979c7 | code | 190 | @testset "Maxima" begin
maxima = BlockMaxima(1:100, 2)
@test collect(maxima) == collect(2:2:100)
maxima = PeakOverThreshold(1:100, 50.)
@test collect(maxima) == collect(51:100)
end
| ExtremeStats | https://github.com/JuliaEarth/ExtremeStats.jl.git |
|
[
"MIT"
] | 1.0.0 | 9b581c2549ce117f977f9212e76131a3669979c7 | code | 844 | if visualtests
@testset "Plot recipes" begin
Random.seed!(2018)
data₁ = rand(LogNormal(2, 2), 5000)
data₂ = rand(Pareto(.9, 10), 5000)
Random.seed!(2018)
xs = rand(LogNormal(0, 1), 5000)
@testset "Return levels" begin
@test_reference "data/ReturnLevels.png" returnplot(xs,label="log-normal")
end
@testset "Mean excess" begin
plt1 = excessplot(data₁, label="Lognormal")
plt2 = excessplot(data₂, label="Pareto")
plt = plot(plt1, plt2, size=(600,800), layout=(2,1))
@test_reference "data/MeanExcess.png" plt
end
@testset "Pareto quantile" begin
plt1 = paretoplot(data₁, label="Lognormal")
plt2 = paretoplot(data₂, label="Pareto")
plt = plot(plt1, plt2, size=(600,800), layout=(2,1))
@test_reference "data/ParetoQuantile.png" plt
end
end
end
| ExtremeStats | https://github.com/JuliaEarth/ExtremeStats.jl.git |
|
[
"MIT"
] | 1.0.0 | 9b581c2549ce117f977f9212e76131a3669979c7 | code | 535 | using ExtremeStats
using Distributions
using StableRNGs
using DelimitedFiles
using Plots; gr(size=(600,400))
using ReferenceTests, ImageIO
using Test, Random
# workaround GR warnings
ENV["GKSwstype"] = "100"
# environment settings
isCI = "CI" ∈ keys(ENV)
islinux = Sys.islinux()
visualtests = !isCI || (isCI && islinux)
datadir = joinpath(@__DIR__,"data")
# list of tests
testfiles = [
"maxima.jl",
"fitting.jl",
"plotrecipes.jl"
]
@testset "ExtremeStats.jl" begin
for testfile in testfiles
include(testfile)
end
end
| ExtremeStats | https://github.com/JuliaEarth/ExtremeStats.jl.git |
|
[
"MIT"
] | 1.0.0 | 9b581c2549ce117f977f9212e76131a3669979c7 | docs | 2655 | <p align="center">
<img src="docs/ExtremeStats.png" height="200"><br>
<a href="https://github.com/JuliaEarth/ExtremeStats.jl/actions">
<img src="https://img.shields.io/github/actions/workflow/status/JuliaEarth/ExtremeStats.jl/CI.yml?branch=master&style=flat-square">
</a>
<a href="https://codecov.io/gh/JuliaEarth/ExtremeStats.jl">
<img src="https://img.shields.io/codecov/c/github/JuliaEarth/ExtremeStats.jl?style=flat-square">
</a>
<a href="LICENSE">
<img src="https://img.shields.io/badge/license-MIT-blue.svg?style=flat-square">
</a>
</p>
This package provides a set of tools for analysing and estimating extreme value distributions.
It defines two types, `BlockMaxima` and `PeakOverThreshold`, which can be used to filter a
collection of values into a collection of maxima.
Given a collection of maxima produced by either model above, one can start estimating heavy-tail
distributions and plotting classical extreme value statistics.
## Installation
Get the latest stable release with Julia's package manager:
```julia
] add ExtremeStats
```
## Usage
Given a collection of values `xs` (e.g. time series), one can retrieve its maxima:
```julia
using ExtremeStats
# find maxima with blocks of size 50
bm = BlockMaxima(xs, 50)
# get values above a threshold of 100.
pm = PeakOverThreshold(xs, 100.)
```
For the block maxima model, the values `xs` need to represent a measurement over time,
whereas the peak over threshold model does not assume any ordering in the data. Both
models are lazy, and the maxima are only returned via a `collect` call.
### Plotting
A few plot recipes are defined for maxima as well as for the original values `xs`:
```julia
using Plots
# mean excess plot
excessplot(xs)
# Pareto quantile plot
paretoplot(xs)
# return level plot
returnplot(xs)
```
### Fitting
Generalized extreme value (GEV) and generalized Pareto (GP) distributions from the `Distributions.jl` package can be fit
to maxima via constrained optimization (maximum likelihood + extreme value index constraints):
```julia
using Distributions
# fit GEV to block maxima
fit(GeneralizedExtremeValue, bm)
# fit GP to peak over threshold
fit(GeneralizedPareto, pm)
```
### Statistics
A few statistics are defined:
```julia
# return statistics
returnlevels(xs)
# mean excess with previous k values
meanexcess(xs, k)
```
## References
The book [An Introduction to Statistical Modeling of Extreme Values](http://www.springer.com/us/book/9781852334598)
by Stuart Coles gives a practical introduction to the theory. Most other books I've encountered are too theoretical
or expose topics that are somewhat disconnected.
| ExtremeStats | https://github.com/JuliaEarth/ExtremeStats.jl.git |
|
[
"MIT"
] | 0.1.0 | 4617fd4ab150c2c3cec61f4c7db6e31eb4319f6a | code | 3560 | module Helpers
export get_cache_name, get_compiled_name, get_cache_path, find_dependencies, change_load_path, split_toplevel_from_main, prefix_lines
using SHA: sha256
function myhash(script_content)
return script_content |> sha256 |> bytes2hex
end
function get_cache_name(script_path)
content = read(script_path, String)
get_cache_name(script_path, content)
end
function get_cache_name(script_path, script_content)
hash = myhash(script_content)
script_name = basename(script_path)
if endswith(script_name, ".jl")
script_name = script_name[1:end-3]
end
return "script_$(script_name)_$(hash)"
end
function get_compiled_name(cache_name)
"compiled_" * cache_name[length("script_")+1:end]
end
get_cache_path(cache_name) = joinpath(DEPOT_PATH[1], "scripts_cache", cache_name)
find_dependencies(script_content) = find_dependencies(Meta.parseall(script_content))
function find_dependencies(script_expr::Expr)
exprs = script_expr.args
package_names = String[]
for expr in exprs
Meta.isexpr(expr, (:import, :using)) && length(expr.args) >= 1 || continue
# collect module `.` expressions
modules_expr = if Meta.isexpr(expr.args[1], :(:)) && Meta.isexpr(expr.args[1].args[1], :.)
# importing specific fields from module - we are only interested in the module name
[expr.args[1].args[1]]
elseif all(e -> Meta.isexpr(e, :.), expr.args)
expr.args
end
modules_root_symbols = [String(mod.args[1]) for mod in modules_expr if length(mod.args) >= 1]
append!(package_names, modules_root_symbols)
end
return package_names
end
function change_load_path(run, temporary_path)
old_LP = LOAD_PATH[:]
old_AP = Base.ACTIVE_PROJECT[]
new_LP = ["@", "@stdlib"]
new_AP = temporary_path
copy!(LOAD_PATH, new_LP)
Base.ACTIVE_PROJECT[] = new_AP
try
run()
finally
# revert LOAD_PATH
copy!(LOAD_PATH, old_LP)
Base.ACTIVE_PROJECT[] = old_AP
end
end
is_toplevel_expr(expr::Expr) = is_toplevel_expr(expr, Val{expr.head}())
is_toplevel_expr(expr, ::Val{:using}) = true
is_toplevel_expr(expr, ::Val{:import}) = true
is_toplevel_expr(expr, ::Val{:abstract}) = true
is_toplevel_expr(expr, ::Val{:const}) = true
is_toplevel_expr(expr, ::Val{:module}) = true
is_toplevel_expr(expr, ::Val{:struct}) = true
is_toplevel_expr(expr, ::Val{:function}) = true
is_toplevel_expr(expr, ::Val{:(=)}) = Meta.isexpr(expr.args[1], :call) # one liner function
is_toplevel_expr(expr, _) = false
is_toplevel_expr(expr) = false
split_toplevel_from_main(script_content) = split_toplevel_from_main(script_content, Meta.parseall(script_content))
function split_toplevel_from_main(script_content, script_expr::Expr)
lines = readlines(IOBuffer(script_content); keep=true)
exprs = script_expr.args
toplevel = ""
main = ""
for (from, expr, to) in zip(exprs[1:2:end], exprs[2:2:end], [exprs[3:2:end]; (;line = length(lines)+1)])
Meta.isexpr(expr, :call)
code = join(lines[from.line:to.line-1], "")
if is_toplevel_expr(expr)
toplevel *= code
else
main *= code
end
end
toplevel, main
end
function prefix_lines(prefix, script_content; skip_first=true)
apply_prefix(line) = prefix * line
lines = readlines(IOBuffer(script_content), keep=true)
if skip_first
lines[1] * join(apply_prefix.(lines[2:end]), "")
else
join(apply_prefix.(lines), "")
end
end
end # module | JuliaScript | https://github.com/jolin-io/JuliaScript.jl.git |
|
[
"MIT"
] | 0.1.0 | 4617fd4ab150c2c3cec61f4c7db6e31eb4319f6a | code | 5533 | module JuliaScript
import Pkg
import PackageCompiler
using UUIDs: uuid4
include("Helpers.jl")
using .Helpers
function create_sysimage()
cache_name = get(ENV, "JULIASCRIPT_CACHE_NAME") do
script_path = abspath(expanduser(ARGS[1]))
assert_isfile(script_path)
get_cache_name(script_path)
end
cache_path = get(ENV, "JULIASCRIPT_CACHE_PATH", get_cache_path(cache_name))
precompile_statements_file = joinpath(cache_path, "src", "precompile_statements.jl")
if !isfile(precompile_statements_file) || filesize(precompile_statements_file) <= 0
@error "Please run juliascript once normally, so that the precompile statements needed for PackageCompiler are constructed."
exit(1)
end
Pkg.activate(cache_path)
PackageCompiler.create_sysimage([cache_name]; sysimage_path=joinpath(cache_path, "sysimage.so"), cpu_target="native", precompile_statements_file)
end
function julia_main()::Cint
if length(ARGS) < 1
@error "Please provide the path to the julia script as an argument." PROGRAM_FILE=PROGRAM_FILE
exit(1)
end
script_path = abspath(expanduser(ARGS[1]))
assert_isfile(script_path)
run_script(script_path, ARGS[2:end])
return 0
end
function assert_isfile(script_path)
if !isfile(script_path)
@error "The given file does not exist"
exit(1)
end
end
function run_script(script_path, commandline_args)
script_content = read(script_path, String) # readchomp is bad here. It will lead different hashes because of stripped last newline
cache_name = get(ENV, "JULIASCRIPT_CACHE_NAME", get_cache_name(script_path, script_content))
cache_path = get(ENV, "JULIASCRIPT_CACHE_PATH", get_cache_path(cache_name))
all_kwargs = (; script_path, script_content, cache_name, cache_path)
if !isdir(cache_path)
# first run - tracks precompile statements
create_script_package(; all_kwargs...)
if success(run(`julia -q --project="$cache_path" -e "import var\"$cache_name\"; var\"$cache_name\".julia_main()" --trace-compile="$cache_path/src/precompile_statements.jl" -- $commandline_args`))
# now we recreated the precompilation statements, they now need to be included into the main module to retrigger precompilation
# it turns out that precompilation will not be retriggered if our helper precompile.jl script was already there before.
# it really needs a change in a module file which is `include`ed
add_precompilation(; all_kwargs...)
else
# if the very first run failed, this should not be counted as a valid load_path_setup_code
# hence we delete the cache folder again in order to retrigger the setup on the next run (with possibly different script parameters)
rm(cache_path, force=true, recursive=true)
end
else
# normal run
# (This is actually quite expensive for small julia scripts, as the julia startup time is significant. Hence we do the check already on the bash side so that this is actually redundant.)
run(`julia -q --project="$cache_path" -e "import var\"$cache_name\"; var\"$cache_name\".julia_main()" $commandline_args`)
end
end
function create_script_package(; script_path, script_content, cache_name, cache_path, rest...)
mkpath(cache_path)
write(joinpath(cache_path, "Project.toml"), """
name = "$cache_name"
uuid = "$(uuid4())"
authors = ["automatically created by JuliaScript.jl"]
version = "0.0.0"
""")
# create module (without precompilation)
script_expr = Meta.parseall(script_content)
dependencies = union(find_dependencies(script_expr), ["PrecompileTools"])
toplevel, main = split_toplevel_from_main(script_content, script_expr)
mkpath(joinpath(cache_path, "src"))
write(joinpath(cache_path, "src", "$cache_name.jl"), """
module var"$cache_name"
__precompile__(false)
$(prefix_lines(" ", toplevel))
function julia_main()::Cint
$(prefix_lines(" ", main))
return 0
end
end
""")
# add and precompile dependencies (silently)
change_load_path(cache_path) do
Pkg.add(dependencies, io=devnull)
Pkg.precompile(io=devnull)
end
end
function add_precompilation(; script_path, script_content, cache_name, cache_path, rest...)
script_expr = Meta.parseall(script_content)
dependencies = union(find_dependencies(script_expr), ["PrecompileTools"])
toplevel, main = split_toplevel_from_main(script_content, script_expr)
# this generic code automatically loads a src/precompile_statments.jl file if it exists
cp(joinpath(@__DIR__, "precompile.jl"), joinpath(cache_path, "src", "precompile.jl"))
write(joinpath(cache_path, "src", "$cache_name.jl"), """
module var"$cache_name"
import PrecompileTools
PrecompileTools.@recompile_invalidations import $(join(dependencies, ", "))
$(prefix_lines(" ", toplevel))
function julia_main()::Cint
$(prefix_lines(" ", main))
return 0
end
# Precompilation via actual run
include("precompile.jl")
# alternatively one might think of using PrecompileTools,
# the key problem with this is that print output is somewhere hidden inside precompilation output
# @compile_workload julia_main()
end
""")
end
include("precompile.jl")
end # module
| JuliaScript | https://github.com/jolin-io/JuliaScript.jl.git |
|
[
"MIT"
] | 0.1.0 | 4617fd4ab150c2c3cec61f4c7db6e31eb4319f6a | code | 1290 | module PrecompileStagingArea
for (_pkgid, _mod) in Base.loaded_modules
if !(_pkgid.name in ("Main", "Core", "Base"))
@eval const $(Symbol(_mod)) = $_mod
end
end
# Execute the precompile statements
const precompile_statements = []
for statement in eachline("$(@__DIR__)/precompile_statements.jl")
# Main should be completely clean
occursin("Main.", statement) && continue
try
ps = Meta.parse(statement)
if !Meta.isexpr(ps, :call)
# these are typically comments
@debug "skipping statement because it does not parse as an expression" statement
continue
end
popfirst!(ps.args) # precompile(...)
ps.head = :tuple
ps = eval(ps)
push!(precompile_statements, statement => ps)
catch ex
# See #28808
@warn "Failed to precompile expression" form=statement exception=ex _module=nothing _file=nothing _line=0
end
end
end
for (statement, ps) in PrecompileStagingArea.precompile_statements
if precompile(ps...)
# success
else
@warn "Failed to precompile expression" form=statement _module=nothing _file=nothing _line=0
end
end | JuliaScript | https://github.com/jolin-io/JuliaScript.jl.git |
|
[
"MIT"
] | 0.1.0 | 4617fd4ab150c2c3cec61f4c7db6e31eb4319f6a | code | 1194 | using JuliaScript
using Test
if Sys.islinux()
@testset "JuliaScript.jl" begin
exe_file = abspath(joinpath(@__DIR__, "..", "bin", "juliascript"))
script_file = joinpath(@__DIR__, "testscript.jl")
cache_name = JuliaScript.Helpers.get_cache_name(script_file)
cache_path = JuliaScript.Helpers.get_cache_path(cache_name)
# always start with clean caching directory
rm(cache_path, recursive=true, force=true)
@test !isdir(cache_path)
target = strip("""
9f86d081884c7d659a2feaa0c55ad015a3bf4f1b2b0b822cd15d6c15b0f00a08
hello
world
arg1 = "42"
""")
# run first time
@test readchomp(`bash $exe_file $script_file 42`) == target
@test isdir(cache_path)
# run second time
@test readchomp(`bash $exe_file $script_file 42`) == target
# run after packagecompile
readchomp(`bash $exe_file packagecompile $script_file`)
@test isfile(joinpath(cache_path, "sysimage.so"))
@test readchomp(`bash $exe_file $script_file 42`) == target
# TODO compare timings? they should always be in order (kind of)
end
end | JuliaScript | https://github.com/jolin-io/JuliaScript.jl.git |
|
[
"MIT"
] | 0.1.0 | 4617fd4ab150c2c3cec61f4c7db6e31eb4319f6a | code | 212 | function hello()
println("hello")
end
abstract type MyType end
mutable struct MyStruct end
const world = "world"
using SHA
println(bytes2hex(sha256("test")))
hello()
println(world)
arg1 = ARGS[1]
@show arg1
| JuliaScript | https://github.com/jolin-io/JuliaScript.jl.git |
|
[
"MIT"
] | 0.1.0 | 4617fd4ab150c2c3cec61f4c7db6e31eb4319f6a | docs | 1725 | # JuliaScript
[](https://github.com/jolin-io/JuliaScript.jl/actions/workflows/CI.yml?query=branch%3Amain)
**You have a julia script.jl and want to run it fast?**
Welcome to `juliascript`! It is build for exactly that purpose.
## Installation
1. Make sure `julia` is installed via [juliaup](https://github.com/JuliaLang/juliaup)
2. Then run the following in a linux bash terminal
```bash
curl -o ~/.juliaup/bin/juliascript -fsSL https://raw.githubusercontent.com/jolin-io/JuliaScript.jl/main/bin/juliascript
chmod +x ~/.juliaup/bin/juliascript
```
Now you can run `juliascript yourscript.jl` on the terminal, or use the shebang `#!/usr/bin/env juliascript` as the first line of your exectuable script.
## How it works
- The first time `juliascript yourscript.jl` runs `yourscript.jl` it will create a corresponding julia module and track all precompile statements from the actual run.
- From the second time onwards it will then run as fast as julia's precompilation system allows for it
## Further speedup
Sometimes the speedup this gives may not be satisfying. Then you can manually create a **sysimage** to improve performance even further.
```bash
juliascript packagecompile yourscript.jl
```
Depending on your script this may take from 5 minutes up to 30 minutes.
### Experimental environment variables
- `JULIASCRIPT_PACKAGECOMPILE_ALWAYS=true`
If set, `juliascript myscript.jl` will automatically packagecompile a new or changed `myscript.jl`. The creation of the sysimage is run in the background, consuming compute resources, but otherwise it is not blocking the script execution.
| JuliaScript | https://github.com/jolin-io/JuliaScript.jl.git |
|
[
"MIT"
] | 0.1.1 | 12895389cb097c74887f0a14e11ca0edaf452b2f | code | 669 | module MCPTrajectoryGameSolver
using TrajectoryGamesBase:
control_bounds,
control_dim,
flatten_trajectory,
get_constraints,
get_constraints_from_box_bounds,
num_players,
OpenLoopStrategy,
stack_trajectories,
state_bounds,
state_dim,
to_blockvector,
to_vector_of_blockvectors,
TrajectoryGame,
TrajectoryGamesBase,
unflatten_trajectory,
unstack_trajectory
using ParametricMCPs: ParametricMCPs, SymbolicUtils
using BlockArrays: BlockArrays, mortar, blocks, eachblock
using ChainRulesCore: ChainRulesCore
include("solver_setup.jl")
include("solve.jl")
export Solver
end # module MCPTrajectoryGameSolver
| MCPTrajectoryGameSolver | https://github.com/JuliaGameTheoreticPlanning/MCPTrajectoryGameSolver.jl.git |
|
[
"MIT"
] | 0.1.1 | 12895389cb097c74887f0a14e11ca0edaf452b2f | code | 2715 | function TrajectoryGamesBase.solve_trajectory_game!(
solver,
game,
initial_state;
shared_constraint_premultipliers = ones(num_players(game)),
context = Float64[],
initial_guess = nothing,
parametric_mcp_solve_options = (;),
)
length(shared_constraint_premultipliers) == num_players(game) ||
throw(ArgumentError("Must provide one constraint multiplier per player"))
length(context) == solver.dimensions.context || throw(
ArgumentError(
"The context state must have the same dimension as the solver's context state",
),
)
θ = compose_parameter_vector(; initial_state, context, shared_constraint_premultipliers)
raw_solution = ParametricMCPs.solve(
solver.mcp_problem_representation,
θ;
initial_guess = isnothing(initial_guess) ?
generate_initial_guess(solver, game, initial_state) : initial_guess,
parametric_mcp_solve_options...,
)
strategy_from_raw_solution(; raw_solution, game, solver)
end
"""
Reshapes the raw solution into a `JointStrategy` over `OpenLoopStrategy`s.
"""
function strategy_from_raw_solution(; raw_solution, game, solver)
number_of_players = num_players(game)
z_iter = Iterators.Stateful(raw_solution.z)
substrategies = map(1:number_of_players) do player_index
private_state_dimension = solver.dimensions.state_blocks[player_index]
private_control_dimension = solver.dimensions.control_blocks[player_index]
number_of_primals =
solver.dimensions.horizon * (private_state_dimension + private_control_dimension)
z_private = Iterators.take(z_iter, number_of_primals) |> collect
trajectory =
unflatten_trajectory(z_private, private_state_dimension, private_control_dimension)
OpenLoopStrategy(trajectory.xs, trajectory.us)
end
info = (; raw_solution)
TrajectoryGamesBase.JointStrategy(substrategies, info)
end
function generate_initial_guess(solver, game, initial_state)
ChainRulesCore.ignore_derivatives() do
z_initial = zeros(ParametricMCPs.get_problem_size(solver.mcp_problem_representation))
rollout_strategy =
map(solver.dimensions.control_blocks) do control_dimension_player_i
(x, t) -> zeros(control_dimension_player_i)
end |> TrajectoryGamesBase.JointStrategy
zero_input_trajectory = TrajectoryGamesBase.rollout(
game.dynamics,
rollout_strategy,
initial_state,
solver.dimensions.horizon,
)
copyto!(z_initial, reduce(vcat, flatten_trajetory_per_player(zero_input_trajectory)))
z_initial
end
end
| MCPTrajectoryGameSolver | https://github.com/JuliaGameTheoreticPlanning/MCPTrajectoryGameSolver.jl.git |
|
[
"MIT"
] | 0.1.1 | 12895389cb097c74887f0a14e11ca0edaf452b2f | code | 7437 | struct Solver{T1,T2}
"The problem representation of the game via ParametricMCPs.ParametricMCP"
mcp_problem_representation::T1
"A named tuple collecting all the problem dimension infos"
dimensions::T2
end
function Solver(
game::TrajectoryGame,
horizon;
context_dimension = 0,
compute_sensitivities = true,
parametric_mcp_options = (;),
symbolic_backend = SymbolicUtils.SymbolicsBackend(),
)
dimensions = let
state_blocks =
[state_dim(game.dynamics, player_index) for player_index in 1:num_players(game)]
state = sum(state_blocks)
control_blocks =
[control_dim(game.dynamics, player_index) for player_index in 1:num_players(game)]
control = sum(control_blocks)
(; state_blocks, state, control_blocks, control, context = context_dimension, horizon)
end
initial_state_symbolic =
SymbolicUtils.make_variables(symbolic_backend, :x0, dimensions.state) |>
to_blockvector(dimensions.state_blocks)
xs_symbolic =
SymbolicUtils.make_variables(symbolic_backend, :X, dimensions.state * horizon) |>
to_vector_of_blockvectors(dimensions.state_blocks)
us_symbolic =
SymbolicUtils.make_variables(symbolic_backend, :U, dimensions.control * horizon) |>
to_vector_of_blockvectors(dimensions.control_blocks)
context_symbolic = SymbolicUtils.make_variables(symbolic_backend, :context, context_dimension)
cost_per_player_symbolic = game.cost(xs_symbolic, us_symbolic, context_symbolic)
equality_constraints_symbolic = let
dynamics_constraints = mapreduce(vcat, 2:horizon) do t
xs_symbolic[t] - game.dynamics(xs_symbolic[t - 1], us_symbolic[t - 1], t - 1)
end
initial_state_constraints = xs_symbolic[begin] - initial_state_symbolic
[dynamics_constraints; initial_state_constraints]
end
inequality_constraints_symoblic = let
environment_constraints =
# Note: We unstack trajectories here so that we add environment constraints on the sub-state of each player.
# TODO: If `get_constraints` were to also receive the dynamics, it could handle this special case internally
mapreduce(
vcat,
pairs(unstack_trajectory((; xs = xs_symbolic, us = us_symbolic))),
) do (ii, trajectory)
environment_constraints_ii = get_constraints(game.env, ii)
# Note: we don't constraint the first state because we have no control authority over that anyway
mapreduce(environment_constraints_ii, vcat, trajectory.xs[2:end])
end
# TODO: technically, we could handle the box constraints here in a smarter way the
# avoid dual multipliers by directly adding them as bounds in the MCP. (thus
# reducing the problem size)
state_box_constraints = let
g_state_box = get_constraints_from_box_bounds(state_bounds(game.dynamics))
mapreduce(vcat, 2:horizon) do t
g_state_box(xs_symbolic[t])
end
end
control_box_constraints = let
g_control_box = get_constraints_from_box_bounds(control_bounds(game.dynamics))
mapreduce(vcat, 1:horizon) do t
g_control_box(us_symbolic[t])
end
end
[
environment_constraints
state_box_constraints
control_box_constraints
]
end
if isnothing(game.coupling_constraints)
coupling_constraints_symbolic =
SymbolicUtils.make_variables(symbolic_backend, :coupling_constraints, 0)
else
# Note: we don't constraint the first state because we have no control authority over that anyway
coupling_constraints_symbolic =
game.coupling_constraints(xs_symbolic[(begin + 1):end], us_symbolic)
end
# set up the duals for all constraints
# private constraints
μ_private_symbolic =
SymbolicUtils.make_variables(symbolic_backend, :μ, length(equality_constraints_symbolic))
#λ_private_symbolic =
# Symbolics.@variables(λ_private[1:length(inequality_constraints_symoblic)]) |>
# only |>
# scalarize
λ_private_symbolic = SymbolicUtils.make_variables(
symbolic_backend,
:λ_private,
length(inequality_constraints_symoblic),
)
# shared constraints
λ_shared_symbolic = SymbolicUtils.make_variables(
symbolic_backend,
:λ_shared,
length(coupling_constraints_symbolic),
)
# multiplier scaling per player as a runtime parameter
# TODO: technically, we could have this scaling for *every* element of the constraint and
# actually every constraint but for now let's keep it simple
shared_constraint_premultipliers_symbolic =
SymbolicUtils.make_variables(symbolic_backend, :γ_scaling, num_players(game))
private_variables_per_player_symbolic =
flatten_trajetory_per_player((; xs = xs_symbolic, us = us_symbolic))
∇lagragian_per_player_symbolic = map(
cost_per_player_symbolic,
private_variables_per_player_symbolic,
shared_constraint_premultipliers_symbolic,
) do cost_ii, τ_ii, γ_ii
# Note: this "Lagrangian" for player ii is *not* exactly their Lagrangian because it contains private constraints of the opponent.
# *However*: after taking the gradient w.r.t player ii's private variables, those terms will disappear
L_ii =
cost_ii + μ_private_symbolic' * equality_constraints_symbolic -
λ_private_symbolic' * inequality_constraints_symoblic -
λ_shared_symbolic' * coupling_constraints_symbolic * γ_ii
SymbolicUtils.gradient(L_ii, τ_ii)
end
# set up the full KKT system as an MCP
f_symbolic = [
∇lagragian_per_player_symbolic...
equality_constraints_symbolic
inequality_constraints_symoblic
coupling_constraints_symbolic
]
z_symbolic = [
private_variables_per_player_symbolic...
μ_private_symbolic
λ_private_symbolic
λ_shared_symbolic
]
θ_symbolic = compose_parameter_vector(;
initial_state = initial_state_symbolic,
context = context_symbolic,
shared_constraint_premultipliers = shared_constraint_premultipliers_symbolic,
)
number_of_primal_decision_variables =
sum(length(p) for p in private_variables_per_player_symbolic)
lower_bounds = [
fill(-Inf, number_of_primal_decision_variables + length(equality_constraints_symbolic))
fill(0.0, length(inequality_constraints_symoblic) + length(coupling_constraints_symbolic))
]
upper_bounds = fill(Inf, length(lower_bounds))
mcp_problem_representation = ParametricMCPs.ParametricMCP(
f_symbolic,
z_symbolic,
θ_symbolic,
lower_bounds,
upper_bounds;
compute_sensitivities,
parametric_mcp_options...,
)
Solver(mcp_problem_representation, dimensions)
end
function flatten_trajetory_per_player(trajectory)
trajectory_per_player = unstack_trajectory(trajectory)
[flatten_trajectory(trajectory) for trajectory in trajectory_per_player]
end
function compose_parameter_vector(; initial_state, context, shared_constraint_premultipliers)
[initial_state; context; shared_constraint_premultipliers]
end
| MCPTrajectoryGameSolver | https://github.com/JuliaGameTheoreticPlanning/MCPTrajectoryGameSolver.jl.git |
|
[
"MIT"
] | 0.1.1 | 12895389cb097c74887f0a14e11ca0edaf452b2f | code | 6630 | module Demo
using TrajectoryGamesBase:
TrajectoryGamesBase,
TrajectoryGame,
TrajectoryGameCost,
ProductDynamics,
GeneralSumCostStructure,
PolygonEnvironment,
solve_trajectory_game!,
RecedingHorizonStrategy,
rollout
using TrajectoryGamesExamples: planar_double_integrator
using BlockArrays: blocks, mortar
using MCPTrajectoryGameSolver: Solver
using GLMakie: GLMakie
using Zygote: Zygote
using ParametricMCPs: ParametricMCPs
"""
Set up a simple two-player collision-avoidance game:
- each player wants to reach their own goal position encoded by the `context` vector
- both players want to avoid collisions
"""
function simple_game(; collision_avoidance_radius = 1)
dynamics = let
single_player_dynamics = planar_double_integrator()
ProductDynamics([single_player_dynamics, single_player_dynamics])
end
cost = TrajectoryGameCost(GeneralSumCostStructure()) do xs, us, context
g1 = context[1:2]
g2 = context[3:4]
sum(zip(xs, us)) do (x, u)
x1, x2 = blocks(x)
u1, u2 = blocks(u)
d1 = x1[1:2] - g1
d2 = x2[1:2] - g2
p1_cost = d1' * d1 + 0.05 * u1' * u1
p2_cost = d2' * d2 + 0.05 * u2' * u2
[p1_cost, p2_cost]
end
end
environment = PolygonEnvironment()
function coupling_constraint(xs, us)
map(xs) do x
x1, x2 = blocks(x)
dx = x1[1:2] - x2[1:2]
dx' * dx - collision_avoidance_radius^2
end
end
TrajectoryGame(dynamics, cost, environment, coupling_constraint)
end
function demo_model_predictive_game_play()
simulation_horizon = 50
game = simple_game()
initial_state = mortar([[-1.0, 0.0, 0.0, 0.0], [1.0, 0.0, 0.0, 0.0]])
context = let
goal_p1 = [1.0, -0.1] # slightly offset goal to break symmetry
goal_p2 = -goal_p1
[goal_p1; goal_p2]
end
planning_horizon = 10
solver = Solver(game, planning_horizon; context_dimension = length(context))
receding_horizon_strategy = RecedingHorizonStrategy(;
solver,
game,
solve_kwargs = (; context),
turn_length = 2,
# TODO: we could also provide this as a more easy-to-use utility, maybe even via dispatch
# TODO: potentially allow the user to only warm-start the primals and or add noise
generate_initial_guess = function (last_strategy, state, time)
# only warm-start if the last strategy is converged / feasible
if !isnothing(last_strategy) &&
last_strategy.info.raw_solution.status == ParametricMCPs.PATHSolver.MCP_Solved
initial_guess = last_strategy.info.raw_solution.z
else
nothing
end
end,
)
# Set up the visualization in terms of `GLMakie.Observable` objectives for reactive programming
figure = GLMakie.Figure()
GLMakie.plot(
figure[1, 1],
game.env;
color = :lightgrey,
axis = (; aspect = GLMakie.DataAspect(), title = "Model predictive game play demo"),
)
joint_strategy =
GLMakie.Observable(solve_trajectory_game!(solver, game, initial_state; context))
GLMakie.plot!(figure[1, 1], joint_strategy)
for (player, color) in enumerate([:red, :blue])
GLMakie.scatter!(
figure[1, 1],
GLMakie.@lift(GLMakie.Point2f($joint_strategy.substrategies[player].xs[begin]));
color,
)
end
display(figure)
# visualization callback to update the observables on the fly
function get_info(strategy, state, time)
joint_strategy[] = strategy.receding_horizon_strategy
sleep(0.1) # so that there's some time to see the visualization
nothing # what ever we return here will be stored in `trajectory.infos` in case you need it for later inspection
end
# simulate the receding horizon strategy
trajectory = rollout(
game.dynamics,
receding_horizon_strategy,
initial_state,
simulation_horizon;
get_info,
)
end
function demo_inverse_game()
game = simple_game()
planning_horizon = 10
solver = Solver(game, planning_horizon; context_dimension = 4)
initial_state = mortar([[-1.0, 0.0, 0.0, 0.0], [1.0, 0.0, 0.0, 0.0]])
# both players want to reach a goal position at (0, 1))
context = [0.0, 1.0, 0.0, 1.0]
initial_joint_strategy = solve_trajectory_game!(solver, game, initial_state; context)
# to demonstrate the differentiability, let us use gradient descent to find
# goal positions that minimize each players' control effort
function loss(context)
# Zygote's reverse mode AD doesn't play well will some of the mutation in `solve_trajectory_game!`. Hence, we use forward mode here.
# Note: When combining differentiable games with neural networks, it is advisable
# to use mixed-mode AD: reverse-mode AD for the neural network, forward mode for the game.
Zygote.forwarddiff(context) do context
joint_strategy = solve_trajectory_game!(solver, game, initial_state; context)
sum(joint_strategy.substrategies) do substrategy
sum(substrategy.us) do u
u' * u
end
end
end
end
context_estimate = context
number_of_gradient_steps = 100
learning_rate = 1e-2
for iteration in 1:number_of_gradient_steps
∇context = only(Zygote.gradient(loss, context_estimate))
context_estimate -= learning_rate * ∇context
end
final_joint_strategy =
solve_trajectory_game!(solver, game, initial_state; context = context_estimate)
# visualize the solution...
# ...for the initial context estimate
figure = GLMakie.Figure()
GLMakie.plot(
figure[1, 1],
game.env;
axis = (;
aspect = GLMakie.DataAspect(),
title = "Game solution for initial context estimate",
),
)
GLMakie.plot!(figure[1, 1], initial_joint_strategy)
# ...and the optimized context estimate
GLMakie.plot(
figure[1, 2],
game.env;
axis = (;
aspect = GLMakie.DataAspect(),
title = "Game solution for optimized context estimate",
),
)
GLMakie.plot!(figure[1, 2], final_joint_strategy)
display(figure)
# trivially, we find that we can minimize each player's control input by setting
# their goal positions to the initial positions
@show (context_estimate - initial_state[[1, 2, 5, 6]])
end
end
| MCPTrajectoryGameSolver | https://github.com/JuliaGameTheoreticPlanning/MCPTrajectoryGameSolver.jl.git |
|
[
"MIT"
] | 0.1.1 | 12895389cb097c74887f0a14e11ca0edaf452b2f | code | 6732 | using MCPTrajectoryGameSolver: MCPTrajectoryGameSolver, OpenLoopStrategy
using TrajectoryGamesBase
using Test: @test, @testset, @test_throws
using BlockArrays: Block, blocks, mortar
using LinearAlgebra: norm, norm_sqr
using TrajectoryGamesExamples: planar_double_integrator
using StatsBase: mean
using Zygote: Zygote
using FiniteDiff: FiniteDiff
using Random: Random
using Symbolics: Symbolics
include("Demo.jl")
function isfeasible(game::TrajectoryGamesBase.TrajectoryGame, trajectory; tol = 1e-4)
isfeasible(game.dynamics, trajectory; tol) &&
isfeasible(game.env, trajectory; tol) &&
all(game.coupling_constraints(trajectory.xs, trajectory.us) .>= 0 - tol)
end
function isfeasible(dynamics::TrajectoryGamesBase.AbstractDynamics, trajectory; tol = 1e-4)
dynamics_steps_consistent = all(
map(2:length(trajectory.xs)) do t
residual =
trajectory.xs[t] - dynamics(trajectory.xs[t - 1], trajectory.us[t - 1], t - 1)
sum(abs, residual) < tol
end,
)
state_bounds_feasible = let
bounds = TrajectoryGamesBase.state_bounds(dynamics)
all(map(trajectory.xs) do x
all(bounds.lb .- tol .<= x .<= bounds.ub .+ tol)
end)
end
control_bounds_feasible = let
bounds = TrajectoryGamesBase.control_bounds(dynamics)
all(map(trajectory.us) do u
all(bounds.lb .- tol .<= u .<= bounds.ub .+ tol)
end)
end
dynamics_steps_consistent && state_bounds_feasible && control_bounds_feasible
end
function isfeasible(env::TrajectoryGamesBase.PolygonEnvironment, trajectory; tol = 1e-4)
trajectory_per_player = MCPTrajectoryGameSolver.unstack_trajectory(trajectory)
map(enumerate(trajectory_per_player)) do (ii, trajectory)
constraints = TrajectoryGamesBase.get_constraints(env, ii)
map(trajectory.xs) do x
all(constraints(x) .>= 0 - tol)
end |> all
end |> all
end
function input_sanity(; solver, game, initial_state, context)
@testset "input sanity" begin
@test_throws ArgumentError TrajectoryGamesBase.solve_trajectory_game!(
solver,
game,
initial_state,
)
context_with_wrong_size = [context; 0.0]
@test_throws ArgumentError TrajectoryGamesBase.solve_trajectory_game!(
solver,
game,
initial_state;
context = context_with_wrong_size,
)
multipliers_despite_no_shared_constraints = [1]
@test_throws ArgumentError TrajectoryGamesBase.solve_trajectory_game!(
solver,
game,
initial_state;
context,
shared_constraint_premultipliers = multipliers_despite_no_shared_constraints,
)
end
end
function forward_pass_sanity(; solver, game, initial_state, context, horizon, strategy, tol = 1e-4)
@testset "forwardpass sanity" begin
nash_trajectory =
TrajectoryGamesBase.rollout(game.dynamics, strategy, initial_state, horizon)
nash_cost = game.cost(nash_trajectory.xs, nash_trajectory.us, context)
@test isfeasible(game, nash_trajectory)
for ii in 1:TrajectoryGamesBase.num_players(game)
for t in 1:horizon
perturbed_inputs = deepcopy(nash_trajectory.us)
perturbed_inputs[t][Block(ii)] .+= tol
perturbed_strategy = (state, time) -> perturbed_inputs[time]
perturbed_trajectory = TrajectoryGamesBase.rollout(
game.dynamics,
perturbed_strategy,
initial_state,
horizon,
)
perturbed_cost =
game.cost(perturbed_trajectory.xs, perturbed_trajectory.us, context)
@test perturbed_cost[ii] - nash_cost[ii] >= -tol
end
end
end
end
function backward_pass_sanity(;
solver,
game,
initial_state,
rng = Random.MersenneTwister(1),
θs = [randn(rng, 4) for _ in 1:10],
)
@testset "backward pass sanity" begin
function loss(θ)
Zygote.forwarddiff(θ) do θ
strategy = TrajectoryGamesBase.solve_trajectory_game!(
solver,
game,
initial_state;
context = θ,
)
sum(strategy.substrategies) do substrategy
sum(substrategy.xs) do x_ii
norm_sqr(x_ii[1:2])
end
end
end
end
for θ in θs
∇_zygote = Zygote.gradient(loss, θ) |> only
∇_finitediff = FiniteDiff.finite_difference_gradient(loss, θ)
@test isapprox(∇_zygote, ∇_finitediff; atol = 1e-4)
end
end
end
function main()
game = Demo.simple_game()
horizon = 2
context = [0.0, 1.0, 0.0, 1.0]
initial_state = mortar([[1.0, 0, 0, 0], [-1.0, 0, 0, 0]])
@testset "Tests" begin
for options in [
(; symbolic_backend = MCPTrajectoryGameSolver.SymbolicUtils.SymbolicsBackend(),),
(;
symbolic_backend = MCPTrajectoryGameSolver.SymbolicUtils.SymbolicsBackend(),
parametric_mcp_options = (;
backend_options = (; parallel = Symbolics.ShardedForm())
),
),
(;
symbolic_backend = MCPTrajectoryGameSolver.SymbolicUtils.FastDifferentiationBackend(),
),
]
local solver
@testset "$options" begin
@testset "solver setup" begin
solver = nothing
solver = MCPTrajectoryGameSolver.Solver(
game,
horizon;
context_dimension = length(context),
options...,
)
end
@testset "solve" begin
input_sanity(; solver, game, initial_state, context)
strategy = TrajectoryGamesBase.solve_trajectory_game!(
solver,
game,
initial_state;
context,
)
forward_pass_sanity(; solver, game, initial_state, context, horizon, strategy)
backward_pass_sanity(; solver, game, initial_state)
end
@testset "integration test" begin
Demo.demo_model_predictive_game_play()
Demo.demo_inverse_game()
end
end
end
end
end
main()
| MCPTrajectoryGameSolver | https://github.com/JuliaGameTheoreticPlanning/MCPTrajectoryGameSolver.jl.git |
|
[
"MIT"
] | 0.1.1 | 12895389cb097c74887f0a14e11ca0edaf452b2f | docs | 3533 | # MCPTrajectoryGameSolver
[](https://github.com/JuliaGameTheoreticPlanning/MCPTrajectoryGameSolver.jl/actions/workflows/ci.yml)
[](https://codecov.io/gh/JuliaGameTheoreticPlanning/MCPTrajectoryGameSolver.jl)
[](https://opensource.org/licenses/MIT)
This package provides a thin wrapper around the [ParametricMCPs.jl](https://github.com/lassepe/ParametricMCPs.jl) package to solve trajectory games from
[TrajectoryGamesBase.jl](https://github.com/JuliaGameTheoreticPlanning/TrajectoryGamesBase.jl).
By exploiting the implicit function theorem, game solutions can be differentiated with respect to the game parameters.
This sensitivity information can be used to fit a game-theoretic model to observed behavior as we explore in our work [Learning to Play Trajectory Games Against Opponents with Unknown Objectives](https://xinjie-liu.github.io/projects/game/).
## Quickstart
Installation is as simple as running:
```julia
]add MCPTrajectoryGameSolver
```
This package uses PATH solver (via [PATHSolver.jl](https://github.com/chkwon/PATHSolver.jl)) under the hood. Larger-sized problems require to have a license key. By courtesy of Steven Dirkse, Michael Ferris, and Tudd Munson, temporary license keys are available free of charge. For more details about the license key, please consult [PATHSolver.jl](https://github.com/chkwon/PATHSolver.jl) (License section). Note that, when no license is loaded, PATH does not report an informative error and instead may just report a wrong result. Thus, make sure that the license is loaded correctly before using the solver.
For a full example of how to use this package, please consult the demo in [`test/Demo.jl`](test/Demo.jl):
Start `julia --project` *from the repository root* and run the following commands:
```julia
using TestEnv, Revise # install globally with `] add TestEnv, Revise` if you don't have this
TestEnv.activate()
Revise.includet("test/Demo.jl")
Demo.demo_model_predictive_game_play() # example of receding-horizon interaction
Demo.demo_inverse_game() # example of fitting game parameters via differentiation of the game solver
```
## Citation
The original solver implementation and experiment code used in our research [Learning to Play Trajectory Games Against Opponents with Unknown Objectives](https://arxiv.org/pdf/2211.13779.pdf) can be found [here](https://github.com/xinjie-liu/DifferentiableAdaptiveGames.jl). This repository provides a more optimized implementation of the differentiable game solver. We kindly ask you to cite our paper if you use either of the implementations in your research. Thanks!
[](https://arxiv.org/pdf/2211.13779.pdf)
```bibtex
@ARTICLE{liu2022learning,
author={Liu, Xinjie and Peters, Lasse and Alonso-Mora, Javier},
journal={IEEE Robotics and Automation Letters},
title={Learning to Play Trajectory Games Against Opponents With Unknown Objectives},
year={2023},
volume={8},
number={7},
pages={4139-4146},
doi={10.1109/LRA.2023.3280809}}
```
<a href ="https://xinjie-liu.github.io/assets/pdf/Liu2023learningPoster(full).pdf"><img src="https://xinjie-liu.github.io/assets/img/liu2023ral_poster.png" width = "560" height = "396"></a>
| MCPTrajectoryGameSolver | https://github.com/JuliaGameTheoreticPlanning/MCPTrajectoryGameSolver.jl.git |
|
[
"MIT"
] | 0.0.6 | 91c2dbe5306e7a501bcd70571a1274ac2e4b248f | code | 236 | module VirtualPlantLab
using Reexport
# Load the VirtualPlantLab components
@reexport using PlantGraphs
@reexport using PlantGeomPrimitives
@reexport using PlantGeomTurtle
@reexport using PlantRayTracer
@reexport using PlantViz
end
| VirtualPlantLab | https://github.com/VirtualPlantLab/VirtualPlantLab.jl.git |
|
[
"MIT"
] | 0.0.6 | 91c2dbe5306e7a501bcd70571a1274ac2e4b248f | code | 5285 | #=
# Algae growth
Alejandro Morales
Centre for Crop Systems Analysis - Wageningen University
In this first example, we learn how to create a `Graph` and update it
dynamically with rewriting rules.
The model described here is based on the non-branching model of [algae
growth](https://en.wikipedia.org/wiki/L-system#Example_1:_Algae) proposed by
Lindermayer as one of the first L-systems.
First, we need to load the VPL metapackage, which will automatically load all
the packages in the VPL ecosystem.
=#
using VirtualPlantLab
#=
The rewriting rules of the L-system are as follows:
**axiom**: A
**rule 1**: A $\rightarrow$ AB
**rule 2**: B $\rightarrow$ A
In VPL, this L-system would be implemented as a graph where the nodes can be of
type `A` or `B` and inherit from the abstract type `Node`. It is advised to
include type definitions in a module to avoid having to restart the Julia
session whenever we want to redefine them. Because each module is an independent
namespace, we need to import `Node` from the VPL package inside the module:
=#
module algae
import VirtualPlantLab: Node
struct A <: Node end
struct B <: Node end
end
import .algae
#=
Note that in this very example we do not need to store any data or state inside
the nodes, so types `A` and `B` do not require fields.
The axiom is simply defined as an instance of type of `A`:
=#
axiom = algae.A()
#=
The rewriting rules are implemented in VPL as objects of type `Rule`. In VPL, a
rewriting rule substitutes a node in a graph with a new node or subgraph and is
therefore composed of two parts:
1. A condition that is tested against each node in a graph to choose which nodes
to rewrite.
2. A subgraph that will replace each node selected by the condition above.
In VPL, the condition is split into two components:
1. The type of node to be selected (in this example that would be `A` or `B`).
2. A function that is applied to each node in the graph (of the specified type)
to indicate whether the node should be selected or not. This function is
optional (the default is to select every node of the specified type).
The replacement subgraph is specified by a function that takes as input the node
selected and returns a subgraph defined as a combination of node objects.
Subgraphs (which can also be used as axioms) are created by linearly combining
objects that inherit from `Node`. The operation `+` implies a linear
relationship between two nodes and `[]` indicates branching.
The implementation of the two rules of algae growth model in VPL is as follows:
=#
rule1 = Rule(algae.A, rhs = x -> algae.A() + algae.B())
rule2 = Rule(algae.B, rhs = x -> algae.A())
#=
Note that in each case, the argument `rhs` is being assigned an anonymous (aka
*lambda*) function. This is a function without a name that is defined directly
in the assigment to the argument. That is, the Julia expression `x -> A() + B()`
is equivalent to the following function definition:
=#
function rule_1(x)
algae.A() + algae.B()
end
#=
For simple rules (especially if the right hand side is just a line of code) it
is easier to just define the right hand side of the rule with an anonymous
function rather than creating a standalone function with a meaningful name.
However, standalone functions are easier to debug as you can call them directly
from the REPL.
With the axiom and rules we can now create a `Graph` object that represents the
algae organism. The first argument is the axiom and the second is a tuple with
all the rewriting rules:
=#
organism = Graph(axiom = axiom, rules = (rule1, rule2))
#=
If we apply the rewriting rules iteratively, the graph will grow, in this case
representing the growth of the algae organism. The rewriting rules are applied
on the graph with the function `rewrite!()`:
=#
rewrite!(organism)
#=
Since there was only one node of type `A`, the only rule that was applied was
`rule1`, so the graph should now have two nodes of types `A` and `B`,
respectively. We can confirm this by drawing the graph. We do this with the
function `draw()` which will always generate the same representation of the
graph, but different options are available depending on the context where the
code is executed. By default, `draw()` will create a new window where an
interactive version of the graph will be drawn and one can zoom and pan with the
mouse (in this online document a static version is shown, see
[Backends](../manual/Visualization.md) for details):
=#
import GLMakie
draw(organism)
#=
Notice that each node in the network representation is labelled with the type of
node (`A` or `B` in this case) and a number in parenthesis. This number is a
unique identifier associated to each node and it is useful for debugging
purposes (this will be explained in more advanced examples).
Applying multiple iterations of rewriting can be achieved with a simple loop:
=#
for i in 1:4
rewrite!(organism)
end
#=
And we can verify that the graph grew as expected:
=#
draw(organism)
#=
The network is rather boring as the system is growing linearly (no branching)
but it already illustrates how graphs can grow rapidly in just a few iterations.
Remember that the interactive visualization allows adjusting the zoom, which is
handy when graphs become large.
=#
| VirtualPlantLab | https://github.com/VirtualPlantLab/VirtualPlantLab.jl.git |
|
[
"MIT"
] | 0.0.6 | 91c2dbe5306e7a501bcd70571a1274ac2e4b248f | code | 3971 | #=
# Context sensitive rules
Alejandro Morales
Centre for Crop Systems Analysis - Wageningen University
This examples goes back to a very simple situation: a linear sequence of 3
cells. The point of this example is to introduce relational growth rules and
context capturing.
A relational rules matches nodes based on properties of neighbouring nodes in
the graph. This requires traversing the graph, which can be done with the
methods `parent` and `children` on the `Context` object of the current node,
which return a list of `Context` objects for the parent or children nodes.
In some cases, it is not only sufficient to query the neighbours of a node but
also to use properties of those neighbours in the right hand side component of
the rule. This is know as "capturing the context" of the node being updated.
This can be done by returning the additional nodes from the `lhs` component (in
addition to `true` or `false`) and by accepting these additional nodes in the
`rhs` component. In addition, we tell VPL that this rule is capturing the
context with `captures = true`.
In the example below, each `Cell` keeps track of a `state` variable (which is
either 0 or 1). Only the first cell has a state of 1 at the beginning. In the
growth rule, we check the father of each `Cell`. When a `Cell` does not have a
parent, the rule does not match, otherwise, we pass capture the parent node. In
the right hand side, we replace the cell with a new cell with the state of the
parent node that was captured. Note that that now, the rhs component gets a new
argument, which corresponds to the context of the father node captured in the
lhs.
=#
using VirtualPlantLab
module types
using VirtualPlantLab
struct Cell <: Node
state::Int64
end
end
import .types: Cell
function transfer(context)
if has_parent(context)
return (true, (parent(context), ))
else
return (false, ())
end
end
rule = Rule(Cell, lhs = transfer, rhs = (context, father) -> Cell(data(father).state), captures = true)
axiom = Cell(1) + Cell(0) + Cell(0)
pop = Graph(axiom = axiom, rules = rule)
#=
In the original state defined by the axiom, only the first node contains a state
of 1. We can retrieve the state of each node with a query. A `Query` object is a
like a `Rule` but without a right-hand side (i.e., its purpose is to return the
nodes that match a particular condition). In this case, we just want to return
all the `Cell` nodes. A `Query` object is created by passing the type of the
node to be queried as an argument to the `Query` function. Then, to actually
execute the query we need to use the `apply` function on the graph.
=#
getCell = Query(Cell)
apply(pop, getCell)
#=
If we rewrite the graph one we will see that a second cell now has a state of 1.
=#
rewrite!(pop)
apply(pop, getCell)
#=
And a second iteration results in all cells have a state of 1
=#
rewrite!(pop)
apply(pop, getCell)
#=
Note that queries may not return nodes in the same order as they were created
because of how they are internally stored (and because queries are meant to
return collection of nodes rather than reconstruct the topology of a graph). If
we need to process nodes in a particular order, then it is best to use a
traversal algorithm on the graph that follows a particular order (for example
depth-first traversal with `traverse_dfs()`). This algorithm requires a function
that applies to each node in the graph. In this simple example we can just store
the `state` of each node in a vector (unlike Rules and Queries, this function
takes the actual node as argument rather than a `Context` object, see the
documentation for more details):
=#
pop = Graph(axiom = axiom, rules = rule)
states = Int64[]
traverse_dfs(pop, fun = node -> push!(states, node.state))
states
#=
Now the states of the nodes are in the same order as they were created:
=#
rewrite!(pop)
states = Int64[]
traverse_dfs(pop, fun = node -> push!(states, node.state))
states
| VirtualPlantLab | https://github.com/VirtualPlantLab/VirtualPlantLab.jl.git |
|
[
"MIT"
] | 0.0.6 | 91c2dbe5306e7a501bcd70571a1274ac2e4b248f | code | 11301 | #=
# Forest
Alejandro Morales
Centre for Crop Systems Analysis - Wageningen University
In this example we extend the tree example into a forest, where
each tree is described by a separate graph object and parameters driving the
growth of these trees vary across individuals following a predefined distribution.
The data types, rendering methods and growth rules are the same as in the binary
tree example:
=#
using VirtualPlantLab
using Distributions, Plots, ColorTypes
import GLMakie
## Data types
module TreeTypes
import VirtualPlantLab
## Meristem
struct Meristem <: VirtualPlantLab.Node end
## Bud
struct Bud <: VirtualPlantLab.Node end
## Node
struct Node <: VirtualPlantLab.Node end
## BudNode
struct BudNode <: VirtualPlantLab.Node end
## Internode (needs to be mutable to allow for changes over time)
Base.@kwdef mutable struct Internode <: VirtualPlantLab.Node
length::Float64 = 0.10 # Internodes start at 10 cm
end
## Leaf
Base.@kwdef struct Leaf <: VirtualPlantLab.Node
length::Float64 = 0.20 # Leaves are 20 cm long
width::Float64 = 0.1 # Leaves are 10 cm wide
end
## Graph-level variables
Base.@kwdef struct treeparams
growth::Float64 = 0.1
budbreak::Float64 = 0.25
phyllotaxis::Float64 = 140.0
leaf_angle::Float64 = 30.0
branch_angle::Float64 = 45.0
end
end
import .TreeTypes
# Create geometry + color for the internodes
function VirtualPlantLab.feed!(turtle::Turtle, i::TreeTypes.Internode, data)
## Rotate turtle around the head to implement elliptical phyllotaxis
rh!(turtle, data.phyllotaxis)
HollowCylinder!(turtle, length = i.length, height = i.length/15, width = i.length/15,
move = true, color = RGB(0.5,0.4,0.0))
return nothing
end
# Create geometry + color for the leaves
function VirtualPlantLab.feed!(turtle::Turtle, l::TreeTypes.Leaf, data)
## Rotate turtle around the arm for insertion angle
ra!(turtle, -data.leaf_angle)
## Generate the leaf
Ellipse!(turtle, length = l.length, width = l.width, move = false,
color = RGB(0.2,0.6,0.2))
## Rotate turtle back to original direction
ra!(turtle, data.leaf_angle)
return nothing
end
# Insertion angle for the bud nodes
function VirtualPlantLab.feed!(turtle::Turtle, b::TreeTypes.BudNode, data)
## Rotate turtle around the arm for insertion angle
ra!(turtle, -data.branch_angle)
end
# Rules
meristem_rule = Rule(TreeTypes.Meristem, rhs = mer -> TreeTypes.Node() +
(TreeTypes.Bud(), TreeTypes.Leaf()) +
TreeTypes.Internode() + TreeTypes.Meristem())
function prob_break(bud)
## We move to parent node in the branch where the bud was created
node = parent(bud)
## We count the number of internodes between node and the first Meristem
## moving down the graph
check, steps = has_descendant(node, condition = n -> data(n) isa TreeTypes.Meristem)
steps = Int(ceil(steps/2)) # Because it will count both the nodes and the internodes
## Compute probability of bud break and determine whether it happens
if check
prob = min(1.0, steps*graph_data(bud).budbreak)
return rand() < prob
## If there is no meristem, an error happened since the model does not allow
## for this
else
error("No meristem found in branch")
end
end
branch_rule = Rule(TreeTypes.Bud,
lhs = prob_break,
rhs = bud -> TreeTypes.BudNode() + TreeTypes.Internode() + TreeTypes.Meristem())
#=
The main difference with respect to the tree is that several of the parameters
will vary per TreeTypes. Also, the location of the tree and initial orientation of
the turtle will also vary. To achieve this we need to:
(i) Add two additional initial nodes that move the turtle to the starting position
of each tree and rotates it.
(ii) Wrap the axiom, rules and the creation of the graph into a function that
takes the required parameters as inputs.
=#
function create_tree(origin, growth, budbreak, orientation)
axiom = T(origin) + RH(orientation) + TreeTypes.Internode() + TreeTypes.Meristem()
tree = Graph(axiom = axiom, rules = (meristem_rule, branch_rule),
data = TreeTypes.treeparams(growth = growth, budbreak = budbreak))
return tree
end
#=
The code for elongating the internodes to simulate growth remains the same as for
the binary tree example
=#
getInternode = Query(TreeTypes.Internode)
function elongate!(tree, query)
for x in apply(tree, query)
x.length = x.length*(1.0 + data(tree).growth)
end
end
function growth!(tree, query)
elongate!(tree, query)
rewrite!(tree)
end
function simulate(tree, query, nsteps)
new_tree = deepcopy(tree)
for i in 1:nsteps
growth!(new_tree, query)
end
return new_tree
end
#=
Let's simulate a forest of 10 x 10 trees with a distance between (and within) rows
of 2 meters. First we generate the original positions of the trees. For the
position we just need to pass a `Vec` object with the x, y, and z coordinates of
the location of each TreeTypes. The code below will generate a matrix with the coordinates:
=#
origins = [Vec(i,j,0) for i = 1:2.0:20.0, j = 1:2.0:20.0]
#=
We may assume that the initial orientation is uniformly distributed between 0 and 360 degrees:
=#
orientations = [rand()*360.0 for i = 1:2.0:20.0, j = 1:2.0:20.0]
#=
For the `growth` and `budbreak` parameters we will assumed that they follow a
LogNormal and Beta distribution, respectively. We can generate random
values from these distributions using the `Distributions` package. For the
relative growth rate:
=#
growths = rand(LogNormal(-2, 0.3), 10, 10)
histogram(vec(growths))
#=
And for the budbreak parameter:
=#
budbreaks = rand(Beta(2.0, 10), 10, 10)
histogram(vec(budbreaks))
#=
Now we can create our forest by calling the `create_tree` function we defined earlier
with the correct inputs per tree:
=#
forest = vec(create_tree.(origins, growths, budbreaks, orientations));
#=
By vectorizing `create_tree()` over the different arrays, we end up with an array
of trees. Each tree is a different Graph, with its own nodes, rewriting rules
and variables. This avoids having to create a large graphs to include all the
plants in a simulation. Below we will run a simulation, first using a sequential
approach (i.e. using one core) and then using multiple cores in our computers (please check
https://docs.julialang.org/en/v1/manual/multi-threading/ if the different cores are not being used
as you may need to change some settings in your computer).
## Sequential simulation
We can simulate the growth of each tree by applying the method `simulate` to each
tree, creating a new version of the forest (the code below is an array comprehension)
=#
newforest = [simulate(tree, getInternode, 2) for tree in forest];
#=
And we can render the forest with the function `render` as in the binary tree
example but passing the whole forest at once
=#
render(Scene(newforest))
#=
If we iterate 4 more iterations we will start seeing the different individuals
diverging in size due to the differences in growth rates
=#
newforest = [simulate(tree, getInternode, 15) for tree in newforest];
render(Scene(newforest))
#=
## Multithreaded simulation
In the previous section, the simulation of growth was done sequentially, one tree
after another (since the growth of a tree only depends on its own parameters). However,
this can also be executed in multiple threads. In this case we use an explicit loop
and execute the iterations of the loop in multiple threads using the macro `@threads`.
Note that the rendering function can also be ran in parallel (i.e. the geometry will be
generated separately for each plant and the merge together):
=#
using Base.Threads
newforest = deepcopy(forest)
@threads for i in eachindex(forest)
newforest[i] = simulate(forest[i], getInternode, 6)
end
render(Scene(newforest), parallel = true)
#=
An alternative way to perform the simulation is to have an outer loop for each timestep and an internal loop over the different trees. Although this approach is not required for this simple model, most FSP models will probably need such a scheme as growth of each individual plant will depend on competition for resources with neighbouring plants. In this case, this approach would look as follows:
=#
newforest = deepcopy(forest)
for step in 1:15
@threads for i in eachindex(newforest)
newforest[i] = simulate(newforest[i], getInternode, 1)
end
end
render(Scene(newforest), parallel = true)
#=
# Customizing the scene
Here we are going to customize the scene of our simulation by adding a horizontal tile represting soil and
tweaking the 3D representation. When we want to combine plants generated from graphs with any other
geometric element it is best to combine all these geometries in a `GLScene` object. We can start the scene
with the `newforest` generated in the above:
=#
scene = Scene(newforest);
#=
We can create the soil tile directly, without having to create a graph. The simplest approach is two use
a special constructor `Rectangle` where one species a corner of the rectangle and two vectors defining the
two sides of the vectors. Both the sides and the corner need to be specified with `Vec` just like in the
above when we determined the origin of each plant. VPL offers some shortcuts: `O()` returns the origin
(`Vec(0.0, 0.0, 0.0)`), whereas `X`, `Y` and `Z` returns the corresponding axes and you can scale them by
passing the desired length as input. Below, a rectangle is created on the XY plane with the origin as a
corner and each side being 11 units long:
=#
soil = Rectangle(length = 21.0, width = 21.0)
rotatey!(soil, pi/2)
VirtualPlantLab.translate!(soil, Vec(0.0, 10.5, 0.0))
#=
We can now add the `soil` to the `scene` object with the `add!` function.
=#
VirtualPlantLab.add!(scene, mesh = soil, color = RGB(1,1,0))
#=
We can now render the scene that combines the random forest of binary trees and a yellow soil. Notice that
in all previous figures, a coordinate system with grids was being depicted. This is helpful for debugging
your code but also to help setup the scene (e.g. if you are not sure how big the soil tile should be).
Howver, it may be distracting for the visualization. It turns out that we can turn that off with
`show_axes = false`:
=#
render(scene, axes = false)
#=
We may also want to save a screenshot of the scene. For this, we need to store the output of the `render` function.
We can then resize the window rendering the scene, move around, zoom, etc. When we have a perspective that we like,
we can run the `save_scene` function on the object returned from `render`. The argument `resolution` can be adjusted in both
`render` to increase the number of pixels in the final image. A helper function `calculate_resolution` is provided to
compute the resolution from a physical width and height in cm and a dpi (e.g., useful for publications and posters):
=#
res = calculate_resolution(width = 16.0, height = 16.0, dpi = 1_000)
output = render(scene, axes = false, resolution = res)
export_scene(scene = output, filename = "nice_trees.png")
| VirtualPlantLab | https://github.com/VirtualPlantLab/VirtualPlantLab.jl.git |
|
[
"MIT"
] | 0.0.6 | 91c2dbe5306e7a501bcd70571a1274ac2e4b248f | code | 15204 | #=
# Growth forest
Alejandro Morales
Centre for Crop Systems Analysis - Wageningen University
In this example we extend the binary forest example to have more complex, time-
dependent development and growth based on carbon allocation. For simplicity, the
model assumes a constant relative growth rate at the plant level to compute the
biomass increment. In the next example this assumption is relaxed by a model of
radiation use efficiency. When modelling growth from carbon allocation, the
biomass of each organ is then translated in to an area or volume and the
dimensions of the organs are updated accordingly (assuming a particular shape).
The following packages are needed:
=#
using VirtualPlantLab, ColorTypes
using Base.Threads: @threads
using Plots
import Random
using FastGaussQuadrature
using Distributions
Random.seed!(123456789)
#=
## Model definition
### Node types
The data types needed to simulate the trees are given in the following
module. The differences with respect to the previous example are:
- Meristems do not produce phytomers every day
- A relative sink strength approach is used to allocate biomass to organs
- The geometry of the organs is updated based on the new biomass
- Bud break probability is a function of distance to apical meristem
=#
## Data types
module TreeTypes
using VirtualPlantLab
using Distributions
## Meristem
Base.@kwdef mutable struct Meristem <: VirtualPlantLab.Node
age::Int64 = 0 ## Age of the meristem
end
## Bud
struct Bud <: VirtualPlantLab.Node end
## Node
struct Node <: VirtualPlantLab.Node end
## BudNode
struct BudNode <: VirtualPlantLab.Node end
## Internode (needs to be mutable to allow for changes over time)
Base.@kwdef mutable struct Internode <: VirtualPlantLab.Node
age::Int64 = 0 ## Age of the internode
biomass::Float64 = 0.0 ## Initial biomass
length::Float64 = 0.0 ## Internodes
width::Float64 = 0.0 ## Internodes
sink::Exponential{Float64} = Exponential(5)
end
## Leaf
Base.@kwdef mutable struct Leaf <: VirtualPlantLab.Node
age::Int64 = 0 ## Age of the leaf
biomass::Float64 = 0.0 ## Initial biomass
length::Float64 = 0.0 ## Leaves
width::Float64 = 0.0 ## Leaves
sink::Beta{Float64} = Beta(2,5)
end
## Graph-level variables -> mutable because we need to modify them during growth
Base.@kwdef mutable struct treeparams
## Variables
biomass::Float64 = 2e-3 ## Current total biomass (g)
## Parameters
RGR::Float64 = 1.0 ## Relative growth rate (1/d)
IB0::Float64 = 1e-3 ## Initial biomass of an internode (g)
SIW::Float64 = 0.1e6 ## Specific internode weight (g/m3)
IS::Float64 = 15.0 ## Internode shape parameter (length/width)
LB0::Float64 = 1e-3 ## Initial biomass of a leaf
SLW::Float64 = 100.0 ## Specific leaf weight (g/m2)
LS::Float64 = 3.0 ## Leaf shape parameter (length/width)
budbreak::Float64 = 1/0.5 ## Bud break probability coefficient (in 1/m)
plastochron::Int64 = 5 ## Number of days between phytomer production
leaf_expansion::Float64 = 15.0 ## Number of days that a leaf expands
phyllotaxis::Float64 = 140.0
leaf_angle::Float64 = 30.0
branch_angle::Float64 = 45.0
end
end
import .TreeTypes
#=
### Geometry
The methods for creating the geometry and color of the tree are the same as in
the previous example.
=#
## Create geometry + color for the internodes
function VirtualPlantLab.feed!(turtle::Turtle, i::TreeTypes.Internode, vars)
## Rotate turtle around the head to implement elliptical phyllotaxis
rh!(turtle, vars.phyllotaxis)
HollowCylinder!(turtle, length = i.length, height = i.width, width = i.width,
move = true, color = RGB(0.5,0.4,0.0))
return nothing
end
## Create geometry + color for the leaves
function VirtualPlantLab.feed!(turtle::Turtle, l::TreeTypes.Leaf, vars)
## Rotate turtle around the arm for insertion angle
ra!(turtle, -vars.leaf_angle)
## Generate the leaf
Ellipse!(turtle, length = l.length, width = l.width, move = false,
color = RGB(0.2,0.6,0.2))
## Rotate turtle back to original direction
ra!(turtle, vars.leaf_angle)
return nothing
end
## Insertion angle for the bud nodes
function VirtualPlantLab.feed!(turtle::Turtle, b::TreeTypes.BudNode, vars)
## Rotate turtle around the arm for insertion angle
ra!(turtle, -vars.branch_angle)
end
#=
### Development
The meristem rule is now parameterized by the initial states of the leaves and
internodes and will only be triggered every X days where X is the plastochron.
=#
## Create right side of the growth rule (parameterized by the initial states
## of the leaves and internodes)
function create_meristem_rule(vleaf, vint)
meristem_rule = Rule(TreeTypes.Meristem,
lhs = mer -> mod(data(mer).age, graph_data(mer).plastochron) == 0,
rhs = mer -> TreeTypes.Node() +
(TreeTypes.Bud(),
TreeTypes.Leaf(biomass = vleaf.biomass,
length = vleaf.length,
width = vleaf.width)) +
TreeTypes.Internode(biomass = vint.biomass,
length = vint.length,
width = vint.width) +
TreeTypes.Meristem())
end
#=
The bud break probability is now a function of distance to the apical meristem
rather than the number of internodes. An adhoc traversal is used to compute this
length of the main branch a bud belongs to (ignoring the lateral branches).
=#
## Compute the probability that a bud breaks as function of distance to the meristem
function prob_break(bud)
## We move to parent node in the branch where the bud was created
node = parent(bud)
## Extract the first internode
child = filter(x -> data(x) isa TreeTypes.Internode, children(node))[1]
data_child = data(child)
## We measure the length of the branch until we find the meristem
distance = 0.0
while !isa(data_child, TreeTypes.Meristem)
## If we encounter an internode, store the length and move to the next node
if data_child isa TreeTypes.Internode
distance += data_child.length
child = children(child)[1]
data_child = data(child)
## If we encounter a node, extract the next internode
elseif data_child isa TreeTypes.Node
child = filter(x -> data(x) isa TreeTypes.Internode, children(child))[1]
data_child = data(child)
else
error("Should be Internode, Node or Meristem")
end
end
## Compute the probability of bud break as function of distance and
## make stochastic decision
prob = min(1.0, distance*graph_data(bud).budbreak)
return rand() < prob
end
## Branch rule parameterized by initial states of internodes
function create_branch_rule(vint)
branch_rule = Rule(TreeTypes.Bud,
lhs = prob_break,
rhs = bud -> TreeTypes.BudNode() +
TreeTypes.Internode(biomass = vint.biomass,
length = vint.length,
width = vint.width) +
TreeTypes.Meristem())
end
#=
### Growth
We need some functions to compute the length and width of a leaf or internode
from its biomass
=#
function leaf_dims(biomass, vars)
leaf_biomass = biomass
leaf_area = biomass/vars.SLW
leaf_length = sqrt(leaf_area*4*vars.LS/pi)
leaf_width = leaf_length/vars.LS
return leaf_length, leaf_width
end
function int_dims(biomass, vars)
int_biomass = biomass
int_volume = biomass/vars.SIW
int_length = cbrt(int_volume*4*vars.IS^2/pi)
int_width = int_length/vars.IS
return int_length, int_width
end
#=
Each day, the total biomass of the tree is updated using a simple RGR formula
and the increment of biomass is distributed across the organs proportionally to
their relative sink strength (of leaves or internodes).
The sink strength of leaves is modelled with a beta distribution scaled to the
`leaf_expansion` argument that determines the duration of leaf growth, whereas
for the internodes it follows a negative exponential distribution. The `pdf`
function computes the probability density of each distribution which is taken as
proportional to the sink strength (the model is actually source-limited since we
imposed a particular growth rate).
=#
sink_strength(leaf, vars) = leaf.age > vars.leaf_expansion ? 0.0 :
pdf(leaf.sink, leaf.age/vars.leaf_expansion)/100.0
plot(0:1:50, x -> sink_strength(TreeTypes.Leaf(age = x), TreeTypes.treeparams()),
xlabel = "Age", ylabel = "Sink strength", label = "Leaf")
#=
=#
sink_strength(int) = pdf(int.sink, int.age)
plot!(0:1:50, x -> sink_strength(TreeTypes.Internode(age = x)), label = "Internode")
#=
Now we need a function that updates the biomass of the tree, allocates it to the
different organs and updates the dimensions of said organs. For simplicity,
we create the functions `leaves()` and `internodes()` that will apply the queries
to the tree required to extract said nodes:
=#
get_leaves(tree) = apply(tree, Query(TreeTypes.Leaf))
get_internodes(tree) = apply(tree, Query(TreeTypes.Internode))
#=
The age of the different organs is updated every time step:
=#
function age!(all_leaves, all_internodes, all_meristems)
for leaf in all_leaves
leaf.age += 1
end
for int in all_internodes
int.age += 1
end
for mer in all_meristems
mer.age += 1
end
return nothing
end
#=
The daily growth is allocated to different organs proportional to their sink
strength.
=#
function grow!(tree, all_leaves, all_internodes)
## Compute total biomass increment
tvars = data(tree)
ΔB = tvars.RGR*tvars.biomass
tvars.biomass += ΔB
## Total sink strength
total_sink = 0.0
for leaf in all_leaves
total_sink += sink_strength(leaf, tvars)
end
for int in all_internodes
total_sink += sink_strength(int)
end
## Allocate biomass to leaves and internodes
for leaf in all_leaves
leaf.biomass += ΔB*sink_strength(leaf, tvars)/total_sink
end
for int in all_internodes
int.biomass += ΔB*sink_strength(int)/total_sink
end
return nothing
end
#=
Finally, we need to update the dimensions of the organs. The leaf dimensions are
=#
function size_leaves!(all_leaves, tvars)
for leaf in all_leaves
leaf.length, leaf.width = leaf_dims(leaf.biomass, tvars)
end
return nothing
end
function size_internodes!(all_internodes, tvars)
for int in all_internodes
int.length, int.width = int_dims(int.biomass, tvars)
end
return nothing
end
#=
### Daily step
All the growth and developmental functions are combined together into a daily
step function that updates the forest by iterating over the different trees in
parallel.
=#
get_meristems(tree) = apply(tree, Query(TreeTypes.Meristem))
function daily_step!(forest)
@threads for tree in forest
## Retrieve all the relevant organs
all_leaves = get_leaves(tree)
all_internodes = get_internodes(tree)
all_meristems = get_meristems(tree)
## Update the age of the organs
age!(all_leaves, all_internodes, all_meristems)
## Grow the tree
grow!(tree, all_leaves, all_internodes)
tvars = data(tree)
size_leaves!(all_leaves, tvars)
size_internodes!(all_internodes, tvars)
## Developmental rules
rewrite!(tree)
end
end
#=
### Initialization
The trees are initialized in a regular grid with random values for the initial
orientation and RGR:
=#
RGRs = rand(Normal(0.3,0.01), 10, 10)
histogram(vec(RGRs))
#=
=#
orientations = [rand()*360.0 for i = 1:2.0:20.0, j = 1:2.0:20.0]
histogram(vec(orientations))
#=
=#
origins = [Vec(i,j,0) for i = 1:2.0:20.0, j = 1:2.0:20.0];
#=
The following initalizes a tree based on the origin, orientation and RGR:
=#
function create_tree(origin, orientation, RGR)
## Initial state and parameters of the tree
vars = TreeTypes.treeparams(RGR = RGR)
## Initial states of the leaves
leaf_length, leaf_width = leaf_dims(vars.LB0, vars)
vleaf = (biomass = vars.LB0, length = leaf_length, width = leaf_width)
## Initial states of the internodes
int_length, int_width = int_dims(vars.LB0, vars)
vint = (biomass = vars.IB0, length = int_length, width = int_width)
## Growth rules
meristem_rule = create_meristem_rule(vleaf, vint)
branch_rule = create_branch_rule(vint)
axiom = T(origin) + RH(orientation) +
TreeTypes.Internode(biomass = vint.biomass,
length = vint.length,
width = vint.width) +
TreeTypes.Meristem()
tree = Graph(axiom = axiom, rules = (meristem_rule, branch_rule),
data = vars)
return tree
end
#=
## Visualization
As in the previous example, it makes sense to visualize the forest with a soil
tile beneath it. Unlike in the previous example, we will construct the soil tile
using a dedicated graph and generate a `Scene` object which can later be
merged with the rest of scene generated in daily step:
=#
Base.@kwdef struct Soil <: VirtualPlantLab.Node
length::Float64
width::Float64
end
function VirtualPlantLab.feed!(turtle::Turtle, s::Soil, vars)
Rectangle!(turtle, length = s.length, width = s.width, color = RGB(255/255, 236/255, 179/255))
end
soil_graph = RA(-90.0) + T(Vec(0.0, 10.0, 0.0)) + # Moves into position
Soil(length = 20.0, width = 20.0) # Draws the soil tile
soil = Scene(Graph(axiom = soil_graph));
render(soil, axes = false)
#=
And the following function renders the entire scene (notice that we need to
use `display()` to force the rendering of the scene when called within a loop
or a function):
=#
function render_forest(forest, soil)
scene = Scene(vec(forest)) # create scene from forest
scene = Scene([scene, soil]) # merges the two scenes
render(scene)
end
#=
## Retrieving canopy-level data
We may want to extract some information at the canopy level such as LAI. This is
best achieved with a query:
=#
function get_LAI(forest)
LAI = 0.0
@threads for tree in forest
for leaf in get_leaves(tree)
LAI += leaf.length*leaf.width*pi/4.0
end
end
return LAI/400.0
end
#=
## Simulation
We can now create a forest of trees on a regular grid:
=#
forest = create_tree.(origins, orientations, RGRs);
render_forest(forest, soil)
for i in 1:50
daily_step!(forest)
end
render_forest(forest, soil)
#=
And compute the leaf area index:
=#
get_LAI(forest)
| VirtualPlantLab | https://github.com/VirtualPlantLab/VirtualPlantLab.jl.git |
|
[
"MIT"
] | 0.0.6 | 91c2dbe5306e7a501bcd70571a1274ac2e4b248f | code | 21405 | #=
# Ray-traced forest
Alejandro Morales
Centre for Crop Systems Analysis - Wageningen University
In this example we extend the forest growth model to include PAR interception a
radiation use efficiency to compute the daily growth rate.
The following packages are needed:
=#
using VirtualPlantLab, ColorTypes
import GLMakie
using Base.Threads: @threads
using Plots
import Random
using FastGaussQuadrature
using Distributions
using SkyDomes
Random.seed!(123456789)
#=
## Model definition
### Node types
The data types needed to simulate the trees are given in the following
module. The difference with respec to the previous model is that Internodes and
Leaves have optical properties needed for ray tracing (they are defined as
Lambertian surfaces).
=#
## Data types
module TreeTypes
using VirtualPlantLab
using Distributions
## Meristem
Base.@kwdef mutable struct Meristem <: VirtualPlantLab.Node
age::Int64 = 0 ## Age of the meristem
end
## Bud
struct Bud <: VirtualPlantLab.Node end
## Node
struct Node <: VirtualPlantLab.Node end
## BudNode
struct BudNode <: VirtualPlantLab.Node end
## Internode (needs to be mutable to allow for changes over time)
Base.@kwdef mutable struct Internode <: VirtualPlantLab.Node
age::Int64 = 0 ## Age of the internode
biomass::Float64 = 0.0 ## Initial biomass
length::Float64 = 0.0 ## Internodes
width::Float64 = 0.0 ## Internodes
sink::Exponential{Float64} = Exponential(5)
material::Lambertian{1} = Lambertian(τ = 0.1, ρ = 0.05) ## Leaf material
end
## Leaf
Base.@kwdef mutable struct Leaf <: VirtualPlantLab.Node
age::Int64 = 0 ## Age of the leaf
biomass::Float64 = 0.0 ## Initial biomass
length::Float64 = 0.0 ## Leaves
width::Float64 = 0.0 ## Leaves
sink::Beta{Float64} = Beta(2,5)
material::Lambertian{1} = Lambertian(τ = 0.1, ρ = 0.05) ## Leaf material
end
## Graph-level variables -> mutable because we need to modify them during growth
Base.@kwdef mutable struct treeparams
## Variables
PAR::Float64 = 0.0 ## Total PAR absorbed by the leaves on the tree (MJ)
biomass::Float64 = 2e-3 ## Current total biomass (g)
## Parameters
RUE::Float64 = 5.0 ## Radiation use efficiency (g/MJ) -> unrealistic to speed up sim
IB0::Float64 = 1e-3 ## Initial biomass of an internode (g)
SIW::Float64 = 0.1e6 ## Specific internode weight (g/m3)
IS::Float64 = 15.0 ## Internode shape parameter (length/width)
LB0::Float64 = 1e-3 ## Initial biomass of a leaf
SLW::Float64 = 100.0 ## Specific leaf weight (g/m2)
LS::Float64 = 3.0 ## Leaf shape parameter (length/width)
budbreak::Float64 = 1/0.5 ## Bud break probability coefficient (in 1/m)
plastochron::Int64 = 5 ## Number of days between phytomer production
leaf_expansion::Float64 = 15.0 ## Number of days that a leaf expands
phyllotaxis::Float64 = 140.0
leaf_angle::Float64 = 30.0
branch_angle::Float64 = 45.0
end
end
import .TreeTypes
#=
### Geometry
The methods for creating the geometry and color of the tree are the same as in
the previous example but include the materials for the ray tracer.
=#
## Create geometry + color for the internodes
function VirtualPlantLab.feed!(turtle::Turtle, i::TreeTypes.Internode, data)
## Rotate turtle around the head to implement elliptical phyllotaxis
rh!(turtle, data.phyllotaxis)
HollowCylinder!(turtle, length = i.length, height = i.width, width = i.width,
move = true, color = RGB(0.5,0.4,0.0), material = i.material)
return nothing
end
## Create geometry + color for the leaves
function VirtualPlantLab.feed!(turtle::Turtle, l::TreeTypes.Leaf, data)
## Rotate turtle around the arm for insertion angle
ra!(turtle, -data.leaf_angle)
## Generate the leaf
Ellipse!(turtle, length = l.length, width = l.width, move = false,
color = RGB(0.2,0.6,0.2), material = l.material)
## Rotate turtle back to original direction
ra!(turtle, data.leaf_angle)
return nothing
end
## Insertion angle for the bud nodes
function VirtualPlantLab.feed!(turtle::Turtle, b::TreeTypes.BudNode, data)
## Rotate turtle around the arm for insertion angle
ra!(turtle, -data.branch_angle)
end
#=
### Development
The meristem rule is now parameterized by the initial states of the leaves and
internodes and will only be triggered every X days where X is the plastochron.
=#
## Create right side of the growth rule (parameterized by the initial states
## of the leaves and internodes)
function create_meristem_rule(vleaf, vint)
meristem_rule = Rule(TreeTypes.Meristem,
lhs = mer -> mod(data(mer).age, graph_data(mer).plastochron) == 0,
rhs = mer -> TreeTypes.Node() +
(TreeTypes.Bud(),
TreeTypes.Leaf(biomass = vleaf.biomass,
length = vleaf.length,
width = vleaf.width)) +
TreeTypes.Internode(biomass = vint.biomass,
length = vint.length,
width = vint.width) +
TreeTypes.Meristem())
end
#=
The bud break probability is now a function of distance to the apical meristem
rather than the number of internodes. An adhoc traversal is used to compute this
length of the main branch a bud belongs to (ignoring the lateral branches).
=#
# Compute the probability that a bud breaks as function of distance to the meristem
function prob_break(bud)
## We move to parent node in the branch where the bud was created
node = parent(bud)
## Extract the first internode
child = filter(x -> data(x) isa TreeTypes.Internode, children(node))[1]
data_child = data(child)
## We measure the length of the branch until we find the meristem
distance = 0.0
while !isa(data_child, TreeTypes.Meristem)
## If we encounter an internode, store the length and move to the next node
if data_child isa TreeTypes.Internode
distance += data_child.length
child = children(child)[1]
data_child = data(child)
## If we encounter a node, extract the next internode
elseif data_child isa TreeTypes.Node
child = filter(x -> data(x) isa TreeTypes.Internode, children(child))[1]
data_child = data(child)
else
error("Should be Internode, Node or Meristem")
end
end
## Compute the probability of bud break as function of distance and
## make stochastic decision
prob = min(1.0, distance*graph_data(bud).budbreak)
return rand() < prob
end
## Branch rule parameterized by initial states of internodes
function create_branch_rule(vint)
branch_rule = Rule(TreeTypes.Bud,
lhs = prob_break,
rhs = bud -> TreeTypes.BudNode() +
TreeTypes.Internode(biomass = vint.biomass,
length = vint.length,
width = vint.width) +
TreeTypes.Meristem())
end
#=
### Light interception
As growth is now dependent on intercepted PAR via RUE, we now need to simulate
light interception by the trees. We will use a ray-tracing approach to do so.
The first step is to create a scene with the trees and the light sources. As for
rendering, the scene can be created from the `forest` object by simply calling
`Scene(forest)` that will generate the 3D meshes and connect them to their
optical properties.
However, we also want to add the soil surface as this will affect the light
distribution within the scene due to reflection from the soil surface. This is
similar to the customized scene that we created before for rendering, but now
for the light simulation.
=#
function create_soil()
soil = Rectangle(length = 21.0, width = 21.0)
rotatey!(soil, π/2) ## To put it in the XY plane
VirtualPlantLab.translate!(soil, Vec(0.0, 10.5, 0.0)) ## Corner at (0,0,0)
return soil
end
function create_scene(forest)
## These are the trees
scene = Scene(vec(forest))
## Add a soil surface
soil = create_soil()
soil_material = Lambertian(τ = 0.0, ρ = 0.21)
add!(scene, mesh = soil, material = soil_material)
## Return the scene
return scene
end
#=
Given the scene, we can create the light sources that can approximate the solar
irradiance on a given day, location and time of the day using the functions from
the package (see package documentation for details). Given the latitude,
day of year and fraction of the day (`f = 0` being sunrise and `f = 1` being sunset),
the function `clear_sky()` computes the direct and diffuse solar radiation assuming
a clear sky. These values may be converted to different wavebands and units using
`waveband_conversion()`. Finally, the collection of light sources approximating
the solar irradiance distribution over the sky hemisphere is constructed with the
function `sky()` (this last step requires the 3D scene as input in order to place
the light sources adequately).
=#
function create_sky(;scene, lat = 52.0*π/180.0, DOY = 182)
## Fraction of the day and day length
fs = collect(0.1:0.1:0.9)
dec = declination(DOY)
DL = day_length(lat, dec)*3600
## Compute solar irradiance
temp = [clear_sky(lat = lat, DOY = DOY, f = f) for f in fs] # W/m2
Ig = getindex.(temp, 1)
Idir = getindex.(temp, 2)
Idif = getindex.(temp, 3)
## Conversion factors to PAR for direct and diffuse irradiance
f_dir = waveband_conversion(Itype = :direct, waveband = :PAR, mode = :power)
f_dif = waveband_conversion(Itype = :diffuse, waveband = :PAR, mode = :power)
## Actual irradiance per waveband
Idir_PAR = f_dir.*Idir
Idif_PAR = f_dif.*Idif
## Create the dome of diffuse light
dome = sky(scene,
Idir = 0.0, ## No direct solar radiation
Idif = sum(Idir_PAR)/10*DL, ## Daily Diffuse solar radiation
nrays_dif = 1_000_000, ## Total number of rays for diffuse solar radiation
sky_model = StandardSky, ## Angular distribution of solar radiation
dome_method = equal_solid_angles, ## Discretization of the sky dome
ntheta = 9, ## Number of discretization steps in the zenith angle
nphi = 12) ## Number of discretization steps in the azimuth angle
## Add direct sources for different times of the day
for I in Idir_PAR
push!(dome, sky(scene, Idir = I/10*DL, nrays_dir = 100_000, Idif = 0.0)[1])
end
return dome
end
#=
The 3D scene and the light sources are then combined into a `RayTracer` object,
together with general settings for the ray tracing simulation chosen via `RTSettings()`.
The most important settings refer to the Russian roulette system and the grid
cloner (see section on Ray Tracing for details). The settings for the Russian
roulette system include the number of times a ray will be traced
deterministically (`maxiter`) and the probability that a ray that exceeds `maxiter`
is terminated (`pkill`). The grid cloner is used to approximate an infinite canopy
by replicating the scene in the different directions (`nx` and `ny` being the
number of replicates in each direction along the x and y axes, respectively). It
is also possible to turn on parallelization of the ray tracing simulation by
setting `parallel = true` (currently this uses Julia's builtin multithreading
capabilities).
In addition `RTSettings()`, an acceleration structure and a splitting rule can
be defined when creating the `RayTracer` object (see ray tracing documentation
for details). The acceleration structure allows speeding up the ray tracing
by avoiding testing all rays against all objects in the scene.
=#
function create_raytracer(scene, sources)
settings = RTSettings(pkill = 0.9, maxiter = 4, nx = 5, ny = 5, parallel = true)
RayTracer(scene, sources, settings = settings, acceleration = BVH,
rule = SAH{3}(5, 10));
end
#=
The actual ray tracing simulation is performed by calling the `trace!()` method
on the ray tracing object. This will trace all rays from all light sources and
update the radiant power absorbed by the different surfaces in the scene inside
the `Material` objects (see `feed!()` above):
=#
function run_raytracer!(forest; DOY = 182)
scene = create_scene(forest)
sources = create_sky(scene = scene, DOY = DOY)
rtobj = create_raytracer(scene, sources)
trace!(rtobj)
return nothing
end
#=
The total PAR absorbed for each tree is calculated from the material objects of
the different internodes (using `power()` on the `Material` object). Note that
the `power()` function returns three different values, one for each waveband,
but they are added together as RUE is defined for total PAR.
=#
# Run the ray tracer, calculate PAR absorbed per tree and add it to the daily
# total using general weighted quadrature formula
function calculate_PAR!(forest; DOY = 182)
## Reset PAR absorbed by the tree (at the start of a new day)
reset_PAR!(forest)
## Run the ray tracer to compute daily PAR absorption
run_raytracer!(forest, DOY = DOY)
## Add up PAR absorbed by each leaf within each tree
@threads for tree in forest
for l in get_leaves(tree)
data(tree).PAR += power(l.material)[1]
end
end
return nothing
end
# Reset PAR absorbed by the tree (at the start of a new day)
function reset_PAR!(forest)
for tree in forest
data(tree).PAR = 0.0
end
return nothing
end
#=
### Growth
We need some functions to compute the length and width of a leaf or internode
from its biomass
=#
function leaf_dims(biomass, vars)
leaf_biomass = biomass
leaf_area = biomass/vars.SLW
leaf_length = sqrt(leaf_area*4*vars.LS/pi)
leaf_width = leaf_length/vars.LS
return leaf_length, leaf_width
end
function int_dims(biomass, vars)
int_biomass = biomass
int_volume = biomass/vars.SIW
int_length = cbrt(int_volume*4*vars.IS^2/pi)
int_width = int_length/vars.IS
return int_length, int_width
end
#=
Each day, the total biomass of the tree is updated using a simple RUE formula
and the increment of biomass is distributed across the organs proportionally to
their relative sink strength (of leaves or internodes).
The sink strength of leaves is modelled with a beta distribution scaled to the
`leaf_expansion` argument that determines the duration of leaf growth, whereas
for the internodes it follows a negative exponential distribution. The `pdf`
function computes the probability density of each distribution which is taken as
proportional to the sink strength (the model is actually source-limited since we
imposed a particular growth rate).
=#
sink_strength(leaf, vars) = leaf.age > vars.leaf_expansion ? 0.0 :
pdf(leaf.sink, leaf.age/vars.leaf_expansion)/100.0
plot(0:1:50, x -> sink_strength(TreeTypes.Leaf(age = x), TreeTypes.treeparams()),
xlabel = "Age", ylabel = "Sink strength", label = "Leaf")
#=
=#
sink_strength(int) = pdf(int.sink, int.age)
plot!(0:1:50, x -> sink_strength(TreeTypes.Internode(age = x)), label = "Internode")
#=
Now we need a function that updates the biomass of the tree, allocates it to the
different organs and updates the dimensions of said organs. For simplicity,
we create the functions `leaves()` and `internodes()` that will apply the queries
to the tree required to extract said nodes:
=#
get_leaves(tree) = apply(tree, Query(TreeTypes.Leaf))
get_internodes(tree) = apply(tree, Query(TreeTypes.Internode))
#=
The age of the different organs is updated every time step:
=#
function age!(all_leaves, all_internodes, all_meristems)
for leaf in all_leaves
leaf.age += 1
end
for int in all_internodes
int.age += 1
end
for mer in all_meristems
mer.age += 1
end
return nothing
end
#=
The daily growth is allocated to different organs proportional to their sink
strength.
=#
function grow!(tree, all_leaves, all_internodes)
## Compute total biomass increment
tdata = data(tree)
ΔB = max(0.5, tdata.RUE*tdata.PAR/1e6) # Trick to emulate reserves in seedling
tdata.biomass += ΔB
## Total sink strength
total_sink = 0.0
for leaf in all_leaves
total_sink += sink_strength(leaf, tdata)
end
for int in all_internodes
total_sink += sink_strength(int)
end
## Allocate biomass to leaves and internodes
for leaf in all_leaves
leaf.biomass += ΔB*sink_strength(leaf, tdata)/total_sink
end
for int in all_internodes
int.biomass += ΔB*sink_strength(int)/total_sink
end
return nothing
end
#=
Finally, we need to update the dimensions of the organs. The leaf dimensions are
=#
function size_leaves!(all_leaves, tvars)
for leaf in all_leaves
leaf.length, leaf.width = leaf_dims(leaf.biomass, tvars)
end
return nothing
end
function size_internodes!(all_internodes, tvars)
for int in all_internodes
int.length, int.width = int_dims(int.biomass, tvars)
end
return nothing
end
#=
### Daily step
All the growth and developmental functions are combined together into a daily
step function that updates the forest by iterating over the different trees in
parallel.
=#
get_meristems(tree) = apply(tree, Query(TreeTypes.Meristem))
function daily_step!(forest, DOY)
## Compute PAR absorbed by each tree
calculate_PAR!(forest, DOY = DOY)
## Grow the trees
@threads for tree in forest
## Retrieve all the relevant organs
all_leaves = get_leaves(tree)
all_internodes = get_internodes(tree)
all_meristems = get_meristems(tree)
## Update the age of the organs
age!(all_leaves, all_internodes, all_meristems)
## Grow the tree
grow!(tree, all_leaves, all_internodes)
tdata = data(tree)
size_leaves!(all_leaves, tdata)
size_internodes!(all_internodes, tdata)
## Developmental rules
rewrite!(tree)
end
end
#=
### Initialization
The trees are initialized on a regular grid with random values for the initial
orientation and RUE:
=#
RUEs = rand(Normal(1.5,0.2), 10, 10)
histogram(vec(RUEs))
#=
=#
orientations = [rand()*360.0 for i = 1:2.0:20.0, j = 1:2.0:20.0]
histogram(vec(orientations))
#=
=#
origins = [Vec(i,j,0) for i = 1:2.0:20.0, j = 1:2.0:20.0];
#=
The following initalizes a tree based on the origin, orientation and RUE:
=#
function create_tree(origin, orientation, RUE)
## Initial state and parameters of the tree
data = TreeTypes.treeparams(RUE = RUE)
## Initial states of the leaves
leaf_length, leaf_width = leaf_dims(data.LB0, data)
vleaf = (biomass = data.LB0, length = leaf_length, width = leaf_width)
## Initial states of the internodes
int_length, int_width = int_dims(data.LB0, data)
vint = (biomass = data.IB0, length = int_length, width = int_width)
## Growth rules
meristem_rule = create_meristem_rule(vleaf, vint)
branch_rule = create_branch_rule(vint)
axiom = T(origin) + RH(orientation) +
TreeTypes.Internode(biomass = vint.biomass,
length = vint.length,
width = vint.width) +
TreeTypes.Meristem()
tree = Graph(axiom = axiom, rules = (meristem_rule, branch_rule),
data = data)
return tree
end
#=
## Visualization
As in the previous example, it makes sense to visualize the forest with a soil
tile beneath it. Unlike in the previous example, we will construct the soil tile
using a dedicated graph and generate a `Scene` object which can later be
merged with the rest of scene generated in daily step:
=#
Base.@kwdef struct Soil <: VirtualPlantLab.Node
length::Float64
width::Float64
end
function VirtualPlantLab.feed!(turtle::Turtle, s::Soil, data)
Rectangle!(turtle, length = s.length, width = s.width, color = RGB(255/255, 236/255, 179/255))
end
soil_graph = RA(-90.0) + T(Vec(0.0, 10.0, 0.0)) + ## Moves into position
Soil(length = 20.0, width = 20.0) ## Draws the soil tile
soil = Scene(Graph(axiom = soil_graph));
render(soil, axes = false)
#=
And the following function renders the entire scene (notice that we need to
use `display()` to force the rendering of the scene when called within a loop
or a function):
=#
function render_forest(forest, soil)
scene = Scene(vec(forest)) ## create scene from forest
scene = Scene([scene, soil]) ## merges the two scenes
display(render(scene))
end
#=
## Simulation
We can now create a forest of trees on a regular grid:
=#
forest = create_tree.(origins, orientations, RUEs);
render_forest(forest, soil)
start = 180
for i in 1:20
println("Day $i")
daily_step!(forest, i + start)
if mod(i, 5) == 0
render_forest(forest, soil)
end
end
| VirtualPlantLab | https://github.com/VirtualPlantLab/VirtualPlantLab.jl.git |
|
[
"MIT"
] | 0.0.6 | 91c2dbe5306e7a501bcd70571a1274ac2e4b248f | code | 11555 | #=
# Relational queries
Alejandro Morales
Centre for Crop Systems Analysis - Wageningen University
In this example we illustrate how to test relationships among nodes inside queries.
Relational queries allow to establish relationships between nodes in the graph,
which generally requires a intimiate knowledge of the graph. For this reason,
relational queries are inheretly complex as graphs can become complex and there
may be solutions that do not require relational queries in many instances.
Nevertheless, they are integral part of VPL and can sometimes be useful. As they
can be hard to grasp, this tutorial will illustrate with a relatively simple
graph a series of relational queries with increasing complexity with the aim
that users will get a better understanding of relational queries. For this purpose,
an abstract graph with several branching levels will be used, so that we can focus
on the relations among the nodes without being distracted by case-specific details.
The graph will be composed of two types of nodes: the inner nodes (`A` and `C`) and the
leaf nodes (`B`). Each leaf node will be identified uniquely with an index and
the objective is to write queries that can identify a specific subset of the leaf
nodes, without using the data stored in the nodes themselves. That is, the queries
should select the right nodes based on their relationships to the rest of nodes
in the graph. Note that `C` nodes contain a single value that may be positive or negative,
whereas `A` nodes contain no data.
As usual, we start with defining the types of nodes in the graph
=#
using VirtualPlantLab
import GLMakie
module Queries
using VirtualPlantLab
struct A <: Node end
struct C <: Node
val::Float64
end
struct B <: Node
ID::Int
end
end
import .Queries as Q
#=
We generate the graph directly, rather than with rewriting rules. The graph has
a motif that is repeated three times (with a small variation), so we can create
the graph in a piecewise manner. Note how we can use the function `sum` to add
nodes to the graph (i.e. `sum(A() for i in 1:3)` is equivalent to `A() + A() + A()`)
=#
motif(n, i = 0) = Q.A() + (Q.C(45.0) + Q.A() + (Q.C(45.0) + Q.A() + Q.B(i + 1),
Q.C(-45.0) + Q.A() + Q.B(i + 2),
Q.A() + Q.B(i + 3)),
Q.C(- 45.0) + sum(Q.A() for i in 1:n) + Q.B(i + 4))
axiom = motif(3, 0) + motif(2, 4) + motif(1, 8) + Q.A() + Q.A() + Q.B(13)
graph = Graph(axiom = axiom);
draw(graph)
#=
By default, VPL will use as node label the type of node and the internal ID generated by VPL itself. This ID is useful if we want to
extract a particular node from the graph, but it is not controlled by the user. However, the user can specialized the function `node_label()`
to specify exactly how to label the nodes of a particular type. In this case, we want to just print `A` or `C` for nodes of type `A` and `C`, whereas
for nodes of type `B` we want to use the `ID` field that was stored inside the node during the graph generation.
=#
VirtualPlantLab.node_label(n::Q.B, id) = "B-$(n.ID)"
VirtualPlantLab.node_label(n::Q.A, id) = "A"
VirtualPlantLab.node_label(n::Q.C, id) = "C"
draw(graph)
#=
To clarify, the `id` argument of the function `node_label()` refers to the internal id generated by VPL (used by the default method for `node_label()`, whereas the the first argument is the data stored inside a node (in the case of `B` nodes, there is a field called `ID` that will not be modified by VPL as that is user-provided data).
The goal of this exercise is then to write queries that retrieve specific `B`
nodes without using the data stored in the node in the query. That is, we have
to identify nodes based on their relationships to other nodes.
## All nodes of type `B`
First, we create the query object. In this case, there is no special condition as
we want to retrieve all the nodes of type `B`
=#
Q1 = Query(Q.B)
#=
Applying the query to the graph returns an array with all the `B` nodes
=#
A1 = apply(graph, Q1)
#=
For the remainder of this tutorial, the code will be hidden by default to allow users to try on their own.
## Node containing value 13
Since the `B` node 13 is the leaf node of the main branch of the graph (e.g. this could be the apical meristem of the main stem of a plant), there
are no rotations between the root node of the graph and this node. Therefore,
the only condition require to single out this node is that it has no ancestor
node of type `C`.
Checking whether a node has an ancestor that meets a certain
condition can be achieved with the function `hasAncestor()`. Similarly to the
condition of the `Query` object, the `hasAncestor()` function also has a condition,
in this case applied to the parent node of the node being tested, and moving
upwards in the graph recursively (until reaching the root node). Note that, in
order to access the object stored inside the node, we need to use the `data()`
function, and then we can test if that object is of type `C`. The `B` node 13
is the only node for which `hasAncestor()` should return `false`:
=#
function Q2_fun(n)
check, steps = has_ancestor(n, condition = x -> data(x) isa Q.C)
!check
end
#=
As before, we just need to apply the `Query` object to the graph:
=#
Q2 = Query(Q.B, condition = Q2_fun)
A2 = apply(graph, Q2)
#=
## Nodes containing values 1, 2 and 3
These three nodes belong to one of the branch motifs repeated through the graph. Thus,
we need to identify the specific motif they belong to and chose all the `B` nodes
inside that motif. The motif is defined by an `A` node that has a `C` child with
a negative `val` and parent node `C` with positive `val`. This `A` node
should then be 2 nodes away from the root node to separate it from upper repetitions
of the motif.
Therefore, we need to test for two conditions, first find those nodes inside a
branch motif, then retrieve the root of the branch motif (i.e., the `A` node
described in the above) and then check the distance of that node from the root:
=#
function branch_motif(p)
data(p) isa Q.A &&
has_descendant(p, condition = x -> data(x) isa Q.C && data(x).val < 0.0)[1] &&
has_ancestor(p, condition = x -> data(x) isa Q.C && data(x).val > 0.0)[1]
end
function Q3_fun(n, nsteps)
## Condition 1
check, steps = has_ancestor(n, condition = branch_motif)
!check && return false
## Condition 2
p = parent(n, nsteps = steps)
check, steps = has_ancestor(p, condition = is_root)
steps != nsteps && return false
return true
end
#=
And applying the query to the object results in the required nodes:
=#
Q3 = Query(Q.B, condition = n -> Q3_fun(n, 2))
A3 = apply(graph, Q3)
#=
## Node containing value 4
The node `B` with value 4 can be singled-out because there is no branching point
between the root node and this node. This means that no ancestor node should have
more than one children node except the root node. Remember that `hasAncestor()`
returns two values, but we are only interested in the first value. You do not need to
assign the returned object from a Julia function, you can just index directly the element
to be selected from the returned tuple:
=#
function Q4_fun(n)
!has_ancestor(n, condition = x -> is_root(x) && length(children(x)) > 1)[1]
end
#=
And applying the query to the object results in the required node:
=#
Q4 = Query(Q.B, condition = Q4_fun)
A4 = apply(graph, Q4)
#=
## Node containing value 3
This node is the only `B` node that is four steps from the root node, which we can
retrieve from the second argument returned by `hasAncestor()`:
=#
function Q5_fun(n)
check, steps = has_ancestor(n, condition = is_root)
steps == 4
end
Q5 = Query(Q.B, condition = Q5_fun)
A5 = apply(graph, Q5)
#=
## Node containing value 7
Node `B` 7 belongs to the second lateral branch motif and the second parent
node is of type `A`. Note that we can reuse the `Q3_fun` from before in the
condition required for this node:
=#
function Q6_fun(n, nA)
check = Q3_fun(n, nA)
!check && return false
p2 = parent(n, nsteps = 2)
data(p2) isa Q.A
end
Q6 = Query(Q.B, condition = n -> Q6_fun(n, 3))
A6 = apply(graph, Q6)
#=
## Nodes containing values 11 and 13
The `B` nodes 11 and 13 actually have different relationships to the rest of the graph,
so we just need to define two different condition functions and combine them.
The condition for the `B` node 11 is similar to the `B` node 7, whereas the condition
for node 13 was already constructed before, so we just need to combined them with an
OR operator:
=#
Q7 = Query(Q.B, condition = n -> Q6_fun(n, 4) || Q2_fun(n))
A7 = apply(graph, Q7)
#=
## Nodes containing values 1, 5 and 9
These nodes play the same role in the three lateral branch motifs. They are the
only `B` nodes preceded by the sequence A C+ A. We just need to check the
sequence og types of objects for the the first three parents of each `B` node:
=#
function Q8_fun(n)
p1 = parent(n)
p2 = parent(n, nsteps = 2)
p3 = parent(n, nsteps = 3)
data(p1) isa Q.A && data(p2) isa Q.C && data(p2).val > 0.0 && data(p3) isa Q.A
end
Q8 = Query(Q.B, condition = Q8_fun)
A8 = apply(graph, Q8)
#=
## Nodes contaning values 2, 6 and 10
This exercise is similar to the previous one, but the C node has a negative
`val`. The problem is that node 12 would also match the pattern A C- A. We
can differentiate between this node and the rest by checking for a fourth
ancestor node of class `C`:
=#
function Q9_fun(n)
p1 = parent(n)
p2 = parent(n, nsteps = 2)
p3 = parent(n, nsteps = 3)
p4 = parent(n, nsteps = 4)
data(p1) isa Q.A && data(p2) isa Q.C && data(p2).val < 0.0 &&
data(p3) isa Q.A && data(p4) isa Q.C
end
Q9 = Query(Q.B, condition = Q9_fun)
A9 = apply(graph, Q9)
#=
## Nodes containg values 6, 7 and 8
We already came up with a condition to extract node 7. We can also modify the previous
condition so that it only node 6. Node 8 can be identified by checking for the third
parent node being of type `C` and being 5 nodes from the root of the graph.
As always, we can reusing previous conditions since they are just regular Julia functions:
=#
function Q10_fun(n)
Q6_fun(n, 3) && return true ## Check node 7
Q9_fun(n) && has_ancestor(n, condition = is_root)[2] == 6 && return true ## Check node 6
has_ancestor(n, condition = is_root)[2] == 5 && data(parent(n, nsteps = 3)) isa Q.C && return true ## Check node 8 (and not 4!)
end
Q10 = Query(Q.B, condition = Q10_fun)
A10 = apply(graph, Q10)
#=
## Nodes containig values 3, 7, 11 and 12
We already have conditions to select nodes 3, 7 and 11 so we just need a new condition
for node 12 (similar to the condition for 8).
=#
function Q11_fun(n)
Q5_fun(n) && return true ## 3
Q6_fun(n, 3) && return true ## 7
Q6_fun(n, 4) && return true ## 11
has_ancestor(n, condition = is_root)[2] == 5 && data(parent(n, nsteps = 2)) isa Q.C &&
data(parent(n, nsteps = 4)) isa Q.A && return true ## 12
end
Q11 = Query(Q.B, condition = Q11_fun)
A11 = apply(graph, Q11)
#=
## Nodes containing values 7 and 12
We just need to combine the conditions for the nodes 7 and 12
=#
function Q12_fun(n)
Q6_fun(n, 3) && return true # 7
has_ancestor(n, condition = is_root)[2] == 5 && data(parent(n, nsteps = 2)) isa Q.C &&
data(parent(n, nsteps = 4)) isa Q.A && return true ## 12
end
Q12 = Query(Q.B, condition = Q12_fun)
A12 = apply(graph, Q12)
| VirtualPlantLab | https://github.com/VirtualPlantLab/VirtualPlantLab.jl.git |
|
[
"MIT"
] | 0.0.6 | 91c2dbe5306e7a501bcd70571a1274ac2e4b248f | code | 1026 | using VirtualPlantLab
using Test
using Aqua
# Aqua
@testset "Aqua" begin
Aqua.test_all(VirtualPlantLab, ambiguities = false)
Aqua.test_ambiguities([VirtualPlantLab])
end
# Tutorials
@testset "Tutorials" begin
@testset "Algae" begin
let
include("algae.jl")
end
end
@testset "Snowflakes" begin
let
include("snowflakes.jl")
end
end
@testset "Tree" begin
let
include("tree.jl")
end
end
@testset "Forest" begin
let
include("forest.jl")
end
end
@testset "Growth forest" begin
let
include("growthforest.jl")
end
end
@testset "Raytraced forest" begin
let
include("raytracedforest.jl")
end
end
@testset "Context" begin
let
include("context.jl")
end
end
@testset "Relational queries" begin
let
include("relationalqueries.jl")
end
end
end
| VirtualPlantLab | https://github.com/VirtualPlantLab/VirtualPlantLab.jl.git |
|
[
"MIT"
] | 0.0.6 | 91c2dbe5306e7a501bcd70571a1274ac2e4b248f | code | 7632 | #=
# The Koch snowflake
Alejandro Morales
Centre for Crop Systems Analysis - Wageningen University
In this example, we create a Koch snowflake, which is one of the earliest
fractals to be described. The Koch snowflake is a closed curve composed on
multiple of segments of different lengths. Starting with an equilateral
triangle, each segment in the snowflake is replaced by four segments of smaller
length arrange in a specific manner. Graphically, the first four iterations of
the Koch snowflake construction process result in the following figures (the
green segments are shown as guides but they are not part of the snowflake):

In order to implement the construction process of a Koch snowflake in VPL we
need to understand how a 3D structure can be generated from a graph of nodes.
VPL uses a procedural approach to generate of structure based on the concept of
turtle graphics.
The idea behind this approach is to imagine a turtle located in space with a
particular position and orientation. The turtle then starts consuming the
different nodes in the graph (following its topological structure) and generates
3D structures as defined by the user for each type of node. The consumption of a
node may also include instructions to move and/or rotate the turtle, which
allows to alter the relative position of the different 3D structures described
by a graph.
The construction process of the Koch snowflake in VPL could then be represented
by the following axiom and rewriting rule:
axiom: E(L) + RU(120) + E(L) + RU(120) + E(L)
rule: E(L) → E(L/3) + RU(-60) + E(L/3) + RU(120) + E(L/3) + RU(-60) + E(L/3)
Where E represent and edge of a given length (given in parenthesis) and RU
represents a rotation of the turtle around the upward axis, with angle of
rotation given in parenthesis in hexadecimal degrees. The rule can be visualized
as follows:
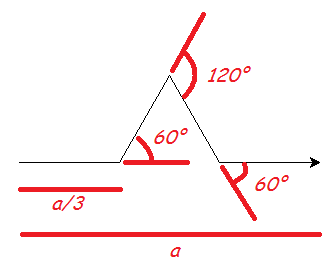
Note that VPL already provides several classes for common turtle movements and
rotations, so our implementation of the Koch snowflake only needs to define a
class to implement the edges of the snowflake. This can be achieved as follows:
=#
using VirtualPlantLab
import GLMakie ## Import rather than "using" to avoid masking Scene
using ColorTypes ## To define colors for the rendering
module sn
import VirtualPlantLab
struct E <: VirtualPlantLab.Node
length::Float64
end
end
import .sn
#=
Note that nodes of type E need to keep track of the length as illustrated in the
above. The axiom is straightforward:
=#
const L = 1.0
axiom = sn.E(L) + VirtualPlantLab.RU(120.0) + sn.E(L) + VirtualPlantLab.RU(120.0) + sn.E(L)
#=
The rule is also straightforward to implement as all the nodes of type E will be
replaced in each iteration. However, we need to ensure that the length of the
new edges is a calculated from the length of the edge being replaced. In order
to extract the data stored in the node being replaced we can simply use the
function data. In this case, the replacement function is defined and then added
to the rule. This can make the code more readable but helps debugging and
testing the replacement function.
=#
function Kochsnowflake(x)
L = data(x).length
sn.E(L/3) + RU(-60.0) + sn.E(L/3) + RU(120.0) + sn.E(L/3) + RU(-60.0) + sn.E(L/3)
end
rule = Rule(sn.E, rhs = Kochsnowflake)
#=
The model is then created by constructing the graph
=#
Koch = Graph(axiom = axiom, rules = Tuple(rule))
#=
In order to be able to generate a 3D structure we need to define a method for
the function `VirtualPlantLab.feed!` (notice the need to prefix it with `VirtualPlantLab.` as we are
going to define a method for this function). The method needs to two take two
arguments, the first one is always an object of type Turtle and the second is an
object of the type for which the method is defined (in this case, E).
The body of the method should generate the 3D structures using the geometry
primitives provided by VPL and feed them to the turtle that is being passed to
the method as first argument. In this case, we are going to represent the edges
of the Koch snowflakes with cylinders, which can be generated with the
`HollowCylinder!` function from VirtualPlantLab. Note that the `feed!` should return
`nothing`, the turtle will be modified in place (hence the use of `!` at the end
of the function as customary in the VPL community).
In order to render the geometry, we need assign a `color` (i.e., any type of
color support by the package ColorTypes.jl). In this case, we just feed a basic
`RGB` color defined by the proportion of red, green and blue. To make the
figures more appealing, we can assign random values to each channel of the color
to generate random colors.
=#
function VirtualPlantLab.feed!(turtle::Turtle, e::sn.E, vars)
HollowCylinder!(turtle, length = e.length, width = e.length/10,
height = e.length/10, move = true,
color = RGB(rand(), rand(), rand()))
return nothing
end
#=
Note that the argument `move = true` indicates that the turtle should move
forward as the cylinder is generated a distance equal to the length of the
cylinder. Also, the `feed!` method has a third argument called `vars`. This
gives acess to the shared variables stored within the graph (such that they can
be accessed by any node). In this case, we are not using this argument.
After defining the method, we can now call the function render on the graph to
generate a 3D interactive image of the Koch snowflake in the current state
=#
sc = Scene(Koch)
render(sc, axes = false)
#=
This renders the initial triangle of the construction procedure of the Koch
snowflake. Let's execute the rules once to verify that we get the 2nd iteration
(check the figure at the beginning of this document):
=#
rewrite!(Koch)
render(Scene(Koch), axes = false)
#=
And two more times
=#
for i in 1:3
rewrite!(Koch)
end
render(Scene(Koch), axes = false)
#=
# Other snowflake fractals
To demonstrate the power of this approach, let's create an alternative
snowflake. We will simply invert the rotations of the turtle in the rewriting
rule
=#
function Kochsnowflake2(x)
L = data(x).length
sn.E(L/3) + RU(60.0) + sn.E(L/3) + RU(-120.0) + sn.E(L/3) + RU(60.0) + sn.E(L/3)
end
rule2 = Rule(sn.E, rhs = Kochsnowflake2)
Koch2 = Graph(axiom = axiom, rules = Tuple(rule2))
#=
The axiom is the same, but now the edges added by the rule will generate the
edges towards the inside of the initial triangle. Let's execute the first three
iterations and render the results
=#
## First iteration
rewrite!(Koch2)
render(Scene(Koch2), axes = false)
## Second iteration
rewrite!(Koch2)
render(Scene(Koch2), axes = false)
## Third iteration
rewrite!(Koch2)
render(Scene(Koch2), axes = false)
#=
This is know as [Koch
antisnowflake](https://mathworld.wolfram.com/KochAntisnowflake.html). We could
also easily generate a [Cesàro
fractal](https://mathworld.wolfram.com/CesaroFractal.html) by also changing the
axiom:
=#
axiomCesaro = sn.E(L) + RU(90.0) + sn.E(L) + RU(90.0) + sn.E(L) + RU(90.0) + sn.E(L)
Cesaro = Graph(axiom = axiomCesaro, rules = (rule2,))
render(Scene(Cesaro), axes = false)
#=
And, as before, let's go through the first three iterations
=#
## First iteration
rewrite!(Cesaro)
render(Scene(Cesaro), axes = false)
## Second iteration
rewrite!(Cesaro)
render(Scene(Cesaro), axes = false)
## Third iteration
rewrite!(Cesaro)
render(Scene(Cesaro), axes = false)
| VirtualPlantLab | https://github.com/VirtualPlantLab/VirtualPlantLab.jl.git |
|
[
"MIT"
] | 0.0.6 | 91c2dbe5306e7a501bcd70571a1274ac2e4b248f | code | 10718 | #=
# Tree
Alejandro Morales
Centre for Crop Systems Analysis - Wageningen University
In this example we build a 3D representation of a binary TreeTypes. Although this will not look like a real plant, this example will help introduce additional features of VPL.
The model requires five types of nodes:
*Meristem*: These are the nodes responsible for growth of new organs in our binary TreeTypes. They contain no data or geometry (i.e. they are a point in the 3D structure).
*Internode*: The result of growth of a branch, between two nodes. Internodes are represented by cylinders with a fixed width but variable length.
*Node*: What is left after a meristem produces a new organ (it separates internodes). They contain no data or geometry (so also a point) but are required to keep the branching structure of the tree as well as connecting leaves.
*Bud*: These are dormant meristems associated to tree nodes. When they are activated, they become an active meristem that produces a branch. They contain no data or geometry but they change the orientation of the turtle.
*BudNode*: The node left by a bud after it has been activated. They contain no data or geometry but they change the orientation of the turtle.
*Leaf*: These are the nodes associated to leaves in the TreeTypes. They are represented by ellipses with a particular orientation and insertion angle. The insertion angle is assumed constant, but the orientation angle varies according to an elliptical phyllotaxis rule.
In this first simple model, only internodes grow over time according to a relative growth rate, whereas leaves are assumed to be of fixed sized determined at their creation. For simplicity, all active meristems will produce an phytomer (combination of node, internode, leaves and buds) per time step. Bud break is assumed stochastic, with a probability that increases proportional to the number of phytomers from the apical meristem (up to 1). In the following tutorials, these assumptions are replaced by more realistic models of light interception, photosynthesis, etc.
In order to simulate growth of the 3D binary tree, we need to define a parameter describing the relative rate at which each internode elongates in each iteration of the simulation, a coefficient to compute the probability of bud break as well as the insertion and orientation angles of the leaves. We could stored these values as global constants, but VPL offers to opportunity to store them per plant. This makes it easier to manage multiple plants in the same simulation that may belong to different species, cultivars, ecotypes or simply to simulate plant-to-plant variation. Graphs in VPL can store an object of any user-defined type that will me made accessible to graph rewriting rules and queries. For this example, we define a data type `treeparams` that holds the relevant parameters. We use `Base.@kwdef` to assign default values to all parameters and allow to assign them by name.
=#
using VirtualPlantLab
using ColorTypes
import GLMakie
module TreeTypes
import VirtualPlantLab
## Meristem
struct Meristem <: VirtualPlantLab.Node end
## Bud
struct Bud <: VirtualPlantLab.Node end
## Node
struct Node <: VirtualPlantLab.Node end
## BudNode
struct BudNode <: VirtualPlantLab.Node end
## Internode (needs to be mutable to allow for changes over time)
Base.@kwdef mutable struct Internode <: VirtualPlantLab.Node
length::Float64 = 0.10 ## Internodes start at 10 cm
end
## Leaf
Base.@kwdef struct Leaf <: VirtualPlantLab.Node
length::Float64 = 0.20 ## Leaves are 20 cm long
width::Float64 = 0.1 ## Leaves are 10 cm wide
end
## Graph-level variables
Base.@kwdef struct treeparams
growth::Float64 = 0.1
budbreak::Float64 = 0.25
phyllotaxis::Float64 = 140.0
leaf_angle::Float64 = 30.0
branch_angle::Float64 = 45.0
end
end
#=
As always, the 3D structure and the color of each type of node are implemented with the `feed!` method. In this case, the internodes and leaves have a 3D representation, whereas bud nodes rotate the turtle. The rest of the elements of the trees are just points in the 3D structure, and hence do not have an explicit geometry:
=#
## Create geometry + color for the internodes
function VirtualPlantLab.feed!(turtle::Turtle, i::TreeTypes.Internode, vars)
## Rotate turtle around the head to implement elliptical phyllotaxis
rh!(turtle, vars.phyllotaxis)
HollowCylinder!(turtle, length = i.length, height = i.length/15, width = i.length/15,
move = true, color = RGB(0.5,0.4,0.0))
return nothing
end
## Create geometry + color for the leaves
function VirtualPlantLab.feed!(turtle::Turtle, l::TreeTypes.Leaf, vars)
## Rotate turtle around the arm for insertion angle
ra!(turtle, -vars.leaf_angle)
## Generate the leaf
Ellipse!(turtle, length = l.length, width = l.width, move = false,
color = RGB(0.2,0.6,0.2))
## Rotate turtle back to original direction
ra!(turtle, vars.leaf_angle)
return nothing
end
## Insertion angle for the bud nodes
function VirtualPlantLab.feed!(turtle::Turtle, b::TreeTypes.BudNode, vars)
## Rotate turtle around the arm for insertion angle
ra!(turtle, -vars.branch_angle)
end
#=
The growth rule for a branch within a tree is simple: a phytomer (or basic unit of morphology) is composed of a node, a leaf, a bud node, an internode and an active meristem at the end. Each time step, the meristem is replaced by a new phytomer, allowing for developmemnt within a branch.
=#
meristem_rule = Rule(TreeTypes.Meristem, rhs = mer -> TreeTypes.Node() +
(TreeTypes.Bud(), TreeTypes.Leaf()) +
TreeTypes.Internode() + TreeTypes.Meristem())
#=
In addition, every step of the simulation, each bud may break, creating a new branch. The probability of bud break is proportional to the number of phytomers from the apical meristem (up to 1), which requires a relational rule to count the number of internodes in the graph up to reaching a meristem. When a bud breaks, it is replaced by a bud node, an internode and a new meristem. This new meristem becomes the apical meristem of the new branch, such that `meristem_rule` would apply. Note how we create an external function to compute whether a bud breaks or not. This is useful to keep the `branch_rule` rule simple and readable, while allow for a relatively complex bud break model. It also makes it easier to debug the bud break model, since it can be tested independently of the graph rewriting.
=#
function prob_break(bud)
## We move to parent node in the branch where the bud was created
node = parent(bud)
## We count the number of internodes between node and the first Meristem
## moving down the graph
check, steps = has_descendant(node, condition = n -> data(n) isa TreeTypes.Meristem)
steps = Int(ceil(steps/2)) ## Because it will count both the nodes and the internodes
## Compute probability of bud break and determine whether it happens
if check
prob = min(1.0, steps*graph_data(bud).budbreak)
return rand() < prob
## If there is no meristem, an error happened since the model does not allow
## for this
else
error("No meristem found in branch")
end
end
branch_rule = Rule(TreeTypes.Bud,
lhs = prob_break,
rhs = bud -> TreeTypes.BudNode() + TreeTypes.Internode() + TreeTypes.Meristem())
#=
A binary tree initializes as an internode followed by a meristem, so the axiom can be constructed simply as:
=#
axiom = TreeTypes.Internode() + TreeTypes.Meristem()
#=
And the object for the tree can be constructed as in previous examples, by passing the axiom and the graph rewriting rules, but in this case also with the object with growth-related parameters.
=#
tree = Graph(axiom = axiom, rules = (meristem_rule, branch_rule), data = TreeTypes.treeparams())
#=
Note that so far we have not included any code to simulate growth of the internodes. The reason is that, as elongation of internotes does not change the topology of the graph (it simply changes the data stored in certain nodes), this process does not need to be implemented with graph rewriting rules. Instead, we will use a combination of a query (to identify which nodes need to be altered) and direct modification of these nodes:
=#
getInternode = Query(TreeTypes.Internode)
#=
If we apply the query to a graph using the `apply` function, we will get an array of all the nodes that match the query, allow for direct manipulation of their contents. To help organize the code, we will create a function that simulates growth by multiplying the `length` argument of all internodes in a tree by the `growth` parameter defined in the above:
=#
function elongate!(tree, query)
for x in apply(tree, query)
x.length = x.length*(1.0 + data(tree).growth)
end
end
#=
Note that we use `vars` on the `Graph` object to extract the object that was stored inside of it. Also, as this function will modify the graph which is passed as input, we append an `!` to the name (this not a special syntax of the language, its just a convention in the Julia community). Also, in this case, the query object is kept separate from the graph. We could have also stored it inside the graph like we did for the parameter `growth`. We could also have packaged the graph and the query into another type representing an individual TreeTypes. This is entirely up to the user and indicates that a model can be implemented in many differences ways with VPL.
Simulating the growth a tree is a matter of elongating the internodes and applying the rules to create new internodes:
=#
function growth!(tree, query)
elongate!(tree, query)
rewrite!(tree)
end
#=
and a simulation for n steps is achieved with a simple loop:
=#
function simulate(tree, query, nsteps)
new_tree = deepcopy(tree)
for i in 1:nsteps
growth!(new_tree, query)
end
return new_tree
end
#=
Notice that the `simulate` function creates a copy of the object to avoid overwriting it. If we run the simulation for a couple of steps
=#
newtree = simulate(tree, getInternode, 2)
#=
The binary tree after two iterations has two branches, as expected:
=#
render(Scene(newtree))
#=
Notice how the lengths of the prisms representing internodes decreases as the branching order increases, as the internodes are younger (i.e. were generated fewer generations ago). Further steps will generate a structure that is more tree-like.
=#
newtree = simulate(newtree, getInternode, 15)
render(Scene(newtree))
| VirtualPlantLab | https://github.com/VirtualPlantLab/VirtualPlantLab.jl.git |
|
[
"MIT"
] | 0.0.6 | 91c2dbe5306e7a501bcd70571a1274ac2e4b248f | docs | 1305 | # VirtualPLantLab v0.0.2 release notes
There is no official release for VirtualPlantLab 0.0.1, so the changes below are relative to
the (unregistered) VPL.jl.
## Changes to API
- All exported functions that are not associated to a data type use `snake_case` style,
unless one of the words has a single letter. For example, `loadmesh` becomes `load_mesh` but
`nvertices` remains the same in the API. Similarly, `isRoot` becomes `is_root`. Most of
these changes affect the graph-related and rendering API. Functions associated to datatypes
(i.e., constructors) use `CamelCase` but that was already the case (e.g., `SolidCube!` or
`Scene`) so no changes there!.
- The function `feed!` now belongs to PlantGeomTurtle, so to define methods for `feed!` you
should now use `PlantGeomTurtle.feed!` instead of `VPL.Geom.feed!`.
- The functions `render` and `draw` (and their mutating `!` versions) no longer have a `backend`
argument to set the graphics backend. Instead, the user should import `GLMakie` (for native
backend), `WGLMakie` (for web backend) or `CairoMakie` (for Cairo backend) before any call
to `render` or `draw`. Note that these packages are not installed when installing
VirtualPlantLab.jl, so the user may need to install them. Check the new version of the
tutorials for more information.
| VirtualPlantLab | https://github.com/VirtualPlantLab/VirtualPlantLab.jl.git |
|
[
"MIT"
] | 0.0.6 | 91c2dbe5306e7a501bcd70571a1274ac2e4b248f | docs | 2476 | # VirtualPlantLab
[](http://virtualplantlab.com/)
[](https://github.com/VirtualPlantLab/VirtualPlantLab.jl/actions/workflows/CI.yml)
[](https://github.com/SciML/SciMLStyle)
[](https://github.com/SciML/ColPrac)
[](https://github.com/JuliaTesting/Aqua.jl)
[](https://zenodo.org/doi/10.5281/zenodo.10256570)
This is the main package in the [Virtual Plant Lab](http://virtualplantlab.com/) that users
are meant to download and use. It is a meta-package that includes all the other packages
in the VirtualPlantLab organization where the different features are implemented. The user
does not need to be aware of the other packages, except in cases where methods need to be
define for user-defined types (currently that is the case for `PlantGeomTurtle.feed!()`
which is required to generate geometry from user-defined types).
# 1. Installation
You can install the latest stable version of VirtualPlantLab.jl with the Julia package manager:
```julia
] add VirtualPlantLab
```
Or the development version directly from here:
```julia
import Pkg
Pkg.add(url="https://github.com/VirtualPlantLab/VirtualPlantLab.jl", rev = "master")
```
or
```julia
] add VirtualPlantLab#master
```
# 2. Usage
To start using VirtualPlantLab.jl, you need to load it first:
```julia
using VirtualPlantLab
```
The entire API of the Virtual Plant Lab will become available after loading.
For people starting, it is recommended to follow the tutorials in the
[documentation](http://virtualplantlab.com/). The entire API is also documented there.
# 3. Additional packages
The following packages are also of interest when building models with the Virtual Plant Lab:
- [PlantSimEngine.jl](https://github.com/VirtualPlantLab/PlantSimEngine.jl)
- [PlantBiophysics.jl](https://github.com/VEZY/PlantBiophysics.jl.git)
- [SkyDomes.jl](https://github.com/VirtualPlantLab/SkyDomes.jl)
- [Ecophys.jl](https://github.com/VirtualPlantLab/Ecophys.jl.git)
| VirtualPlantLab | https://github.com/VirtualPlantLab/VirtualPlantLab.jl.git |
|
[
"MIT"
] | 0.1.0 | 9f0a1b71baaf7650f4fa8a1d168c7fb6ee41f0c9 | code | 641 | module RealDot
using LinearAlgebra: LinearAlgebra
export realdot
"""
realdot(x, y)
Compute `real(dot(x, y))` while avoiding computing the imaginary part if possible.
This function can be useful if you work with derivatives of functions on complex
numbers. In particular, this computation shows up in pullbacks for non-holomorphic
functions.
"""
@inline realdot(x, y) = real(LinearAlgebra.dot(x, y))
@inline realdot(x::Complex, y::Complex) = muladd(real(x), real(y), imag(x) * imag(y))
@inline realdot(x::Real, y::Number) = x * real(y)
@inline realdot(x::Number, y::Real) = real(x) * y
@inline realdot(x::Real, y::Real) = x * y
end
| RealDot | https://github.com/JuliaMath/RealDot.jl.git |
|
[
"MIT"
] | 0.1.0 | 9f0a1b71baaf7650f4fa8a1d168c7fb6ee41f0c9 | code | 1829 | using RealDot
using LinearAlgebra
using Test
# struct need to be defined outside of tests for julia 1.0 compat
# custom complex number (tests fallback definition)
struct CustomComplex{T} <: Number
re::T
im::T
end
Base.real(x::CustomComplex) = x.re
Base.imag(x::CustomComplex) = x.im
Base.conj(x::CustomComplex) = CustomComplex(x.re, -x.im)
function Base.:*(x::CustomComplex, y::Union{Real,Complex})
return CustomComplex(reim(Complex(reim(x)...) * y)...)
end
Base.:*(x::Union{Real,Complex}, y::CustomComplex) = y * x
function Base.:*(x::CustomComplex, y::CustomComplex)
return CustomComplex(reim(Complex(reim(x)...) * Complex(reim(y)...))...)
end
# custom quaternion to test definition for hypercomplex numbers
# adapted from Quaternions.jl
struct Quaternion{T<:Real} <: Number
s::T
v1::T
v2::T
v3::T
end
Base.real(q::Quaternion) = q.s
Base.conj(q::Quaternion) = Quaternion(q.s, -q.v1, -q.v2, -q.v3)
function Base.:*(q::Quaternion, w::Quaternion)
return Quaternion(
q.s * w.s - q.v1 * w.v1 - q.v2 * w.v2 - q.v3 * w.v3,
q.s * w.v1 + q.v1 * w.s + q.v2 * w.v3 - q.v3 * w.v2,
q.s * w.v2 - q.v1 * w.v3 + q.v2 * w.s + q.v3 * w.v1,
q.s * w.v3 + q.v1 * w.v2 - q.v2 * w.v1 + q.v3 * w.s,
)
end
function Base.:*(q::Quaternion, w::Union{Real,Complex,CustomComplex})
a, b = reim(w)
return q * Quaternion(a, b, zero(a), zero(a))
end
Base.:*(w::Union{Real,Complex,CustomComplex}, q::Quaternion) = conj(conj(q) * conj(w))
@testset "RealDot.jl" begin
scalars = (
randn(), randn(ComplexF64), CustomComplex(randn(2)...), Quaternion(randn(4)...)
)
arrays = (randn(10), randn(ComplexF64, 10))
for inputs in (scalars, arrays)
for x in inputs, y in inputs
@test realdot(x, y) == real(dot(x, y))
end
end
end
| RealDot | https://github.com/JuliaMath/RealDot.jl.git |
|
[
"MIT"
] | 0.1.0 | 9f0a1b71baaf7650f4fa8a1d168c7fb6ee41f0c9 | docs | 1650 | # RealDot
[](https://github.com/JuliaMath/RealDot.jl/actions/workflows/CI.yml?query=branch%3Amain)
[](https://codecov.io/gh/JuliaMath/RealDot.jl)
[](https://coveralls.io/github/JuliaMath/RealDot.jl?branch=main)
[](https://github.com/invenia/BlueStyle)
This package only contains and exports a single function `realdot(x, y)`.
It computes `real(LinearAlgebra.dot(x, y))` while avoiding computing the imaginary part of `LinearAlgebra.dot(x, y)` if possible.
The real dot product is useful when one treats complex numbers as embedded in a real vector space.
For example, take two complex arrays `x` and `y`.
Their real dot product is `real(dot(x, y)) == dot(real(x), real(y)) + dot(imag(x), imag(y))`.
This is the same result one would get by reinterpreting the arrays as real arrays:
```julia
xreal = reinterpret(real(eltype(x)), x)
yreal = reinterpret(real(eltype(y)), y)
real(dot(x, y)) == dot(xreal, yreal)
```
In particular, this function can be useful if you define pullbacks for non-holomorphic functions (see e.g. [this discussion in the ChainRulesCore.jl repo](https://github.com/JuliaDiff/ChainRulesCore.jl/pull/474)).
It was implemented initially in [ChainRules.jl](https://github.com/JuliaDiff/ChainRules.jl) in [this PR](https://github.com/JuliaDiff/ChainRules.jl/pull/216) as `_realconjtimes`.
| RealDot | https://github.com/JuliaMath/RealDot.jl.git |
|
[
"Apache-2.0"
] | 0.2.2 | 72253d8e52fce33c366848b17ce1648f7b719d10 | code | 357 | # ~/work/julia/Iban/docs$ julia make.jl
push!(LOAD_PATH,"../src/")
using IbanGen
using Documenter
using Memoize
makedocs(
sitename = "IbanGen",
modules = [IbanGen],
authors = "David Soroko"
)
# see: https://juliadocs.github.io/Documenter.jl/stable/lib/public/#Documenter.deploydocs
deploydocs(
repo = "github.com/sorokod/Iban.jl.git"
) | IbanGen | https://github.com/sorokod/Iban.jl.git |
|
[
"Apache-2.0"
] | 0.2.2 | 72253d8e52fce33c366848b17ce1648f7b719d10 | code | 7464 | module IbanGen
include("common.jl")
include("check_digits.jl")
include("bban.jl")
export is_supported_country, supported_countries
export iban, iban_random, build
export ValidationException
"""
iban_random(
CountryCode::Maybe{String}=nothing,
BankCode::Maybe{String}=nothing,
AccountNumber::Maybe{String}=nothing,
BranchCode::Maybe{String}=nothing,
NationalCheckDigit::Maybe{String}=nothing,
AccountType::Maybe{String}=nothing,
OwnerAccountType::Maybe{String}=nothing,
IdentificationNumber::Maybe{String}=nothing
)::Dict{String,String}
Generate a random IBAN subject to the provided attributes. For an attributes that is not provided, a
random value will be used according to the rules of the (provided or generated) country. Attributes
that are not defined for a country are ignored.
## Example
```julia
julia> iban_random()
Dict{String,String} with 6 entries:
"CountryCode" => "GR"
"BranchCode" => "7500"
"AccountNumber" => "1HRB7OApF5ABTOYH"
"value" => "GR8410975001HRB7OApF5ABTOYH"
"BankCode" => "109"
"CheckDigits" => "84"
julia> iban_random(CountryCode = "GR", BankCode = "109")
Dict{String,String} with 6 entries:
"CountryCode" => "GR"
"BranchCode" => "2170"
"AccountNumber" => "24wO2qBgz1ROP82L"
"value" => "GR26109217024wO2qBgz1ROP82L"
"BankCode" => "109"
"CheckDigits" => "26"
```
"""
function iban_random(;
CountryCode::MaybeString=nothing,
BankCode::MaybeString=nothing,
AccountNumber::MaybeString=nothing,
BranchCode::MaybeString=nothing,
NationalCheckDigit::MaybeString=nothing,
AccountType::MaybeString=nothing,
OwnerAccountType::MaybeString=nothing,
IdentificationNumber::MaybeString=nothing
)::Dict{String,String}
partup = (;
Symbol("IbanGen.BankCode") => BankCode,
Symbol("IbanGen.AccountNumber") => AccountNumber,
Symbol("IbanGen.BranchCode") => BranchCode,
Symbol("IbanGen.NationalCheckDigit") => NationalCheckDigit,
Symbol("IbanGen.AccountType") => AccountType,
Symbol("IbanGen.OwnerAccountType") => OwnerAccountType,
Symbol("IbanGen.IdentificationNumber") => IdentificationNumber
)
country_code = CountryCode === nothing ? rand(supported_countries()) : CountryCode
theiban = parse_bban!(country_code, partup, true)
theiban.check_digits = calculate_check_digit(
theiban.bban_str,
theiban.country_code
)
theiban.iban_str =
theiban.country_code * theiban.check_digits * theiban.bban_str
_as_dict(theiban)
end
"""
iban(
CountryCode::String,
BankCode::String,
AccountNumber::String,
BranchCode::Maybe{String}=nothing,
NationalCheckDigit::Maybe{String}=nothing,
AccountType::Maybe{String}=nothing,
OwnerAccountType::Maybe{String}=nothing,
IdentificationNumber::Maybe{String}=nothing,
)::Dict{String,String}
Generate an IBAN based on the provided parameters.
## Example
```julia
julia> iban(CountryCode = "GB", BankCode = "NWBK", BranchCode = "601613",AccountNumber = "31926819")
Dict{String,String} with 6 entries:
"CountryCode" => "GB"
"BranchCode" => "601613"
"AccountNumber" => "31926819"
"value" => "GB29NWBK60161331926819"
"BankCode" => "NWBK"
"CheckDigits" => "29"
```
"""
function iban(;
CountryCode::String,
BankCode::String,
AccountNumber::String,
BranchCode::MaybeString=nothing,
NationalCheckDigit::MaybeString=nothing,
AccountType::MaybeString=nothing,
OwnerAccountType::MaybeString=nothing,
IdentificationNumber::MaybeString=nothing
)::Dict{String,String}
partup = (;
Symbol("IbanGen.BankCode") => BankCode,
Symbol("IbanGen.AccountNumber") => AccountNumber,
Symbol("IbanGen.BranchCode") => BranchCode,
Symbol("IbanGen.NationalCheckDigit") => NationalCheckDigit,
Symbol("IbanGen.AccountType") => AccountType,
Symbol("IbanGen.OwnerAccountType") => OwnerAccountType,
Symbol("IbanGen.IdentificationNumber") => IdentificationNumber
)
theiban = parse_bban!(CountryCode, partup)
theiban.check_digits = calculate_check_digit(
theiban.bban_str,
theiban.country_code
)
theiban.iban_str =
theiban.country_code * theiban.check_digits * theiban.bban_str
_as_dict(theiban)
end
"""
iban(iban_str::String)::Dict{String,String}
Validated the provided string and parse it into an IBAN structure.
## Example
```julia
julia> iban("BR9700360305000010009795493P1")
Dict{String,String} with 8 entries:
"CountryCode" => "BR"
"CheckDigits" => "97"
"BranchCode" => "00001"
"AccountType" => "P"
"AccountNumber" => "0009795493"
"value" => "BR9700360305000010009795493P1"
"BankCode" => "00360305"
"OwnerAccountType" => "1"
```
"""
function iban(iban_str::String)::Dict{String,String}
ensure(
length(iban_str) >= 4,
iban_str, "value too short"
)
country_code = SubString(iban_str, 1, 2)
bban_structure = for_country(country_code)
ensure(
bban_structure !== nothing,
country_code, "country code not supported"
)
bban_str = SubString(iban_str, 5)
ensure(
_length(bban_structure) == length(bban_str),
bban_str, "unexpected BBAN length, expected: $(_length(bban_structure))"
)
dict = Dict(slice[1] => bban_str[slice[2]] for slice in _slicing(bban_structure))
theiban = parse_bban!(country_code, dict)
provided = SubString(iban_str, 3, 4)
expected = calculate_check_digit(bban_str, country_code)
ensure(
expected == provided,
provided, "invalid check digits, expected: $(expected)"
)
theiban.check_digits = expected
theiban.iban_str = iban_str
_as_dict(theiban)
end
struct IbanEntry
value::AbstractString
entry_type::EntryType
function IbanEntry(value, entry_type)
ensure(
!isnothing(value),
value, "Value not provided [$(typeof(entry_type))]"
)
ensure(
length(value) == entry_type.spec.length,
value, "Unexpected length $(length(value)), expected: $(entry_type.spec.length) [$(typeof(entry_type))]"
)
ensure(
issubset(value, entry_type.spec.alphabet),
value, "invalid characters [$(typeof(entry_type))]"
)
new(value, entry_type)
end
end
mutable struct TheIban
country_code::String
check_digits::String
bban::Vector{IbanEntry}
bban_str::MaybeString
iban_str::MaybeString
function TheIban(country_code)
ensure(
is_supported_country(country_code),
country_code, "country code not supported"
)
new(country_code, "00", [], nothing, nothing)
end
end
#=
#############################################################
Converts the internal IBAN representation to a `Dict`
#############################################################
=#
function _as_dict(theiban::TheIban)::Dict{String,String}
result = Dict(stringify(entry) => entry.value for entry in values(theiban.bban))
result["CountryCode"] = theiban.country_code
result["CheckDigits"] = theiban.check_digits
result["value"] = theiban.iban_str
result
end
end
| IbanGen | https://github.com/sorokod/Iban.jl.git |
|
[
"Apache-2.0"
] | 0.2.2 | 72253d8e52fce33c366848b17ce1648f7b719d10 | code | 15376 | #=
Copyright 2013 Artur Mkrtchyan
Licensed under the Apache License, Version 2.0 (the "License");
you may not use this file except in compliance with the License.
You may obtain a copy of the License at
http://www.apache.org/licenses/LICENSE-2.0
Unless required by applicable law or agreed to in writing, software
distributed under the License is distributed on an "AS IS" BASIS,
WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
See the License for the specific language governing permissions and
limitations under the License. =#
import Random.randstring
import Base.length
using Memoize
#=
#############################################################
EntrySpec spells out the specification for an entry .
For example EntrySpec(:N, 5) is numeric of lenth 5
and EntrySpec(:C, 16) is alphanumeric of lenth 16
############################################################# =#
const alphabets = Dict(
:A => ['A':'Z';],
:N => ['0':'9';],
:C => vcat(['A':'Z';], ['0':'9';], ['a':'z';])
)
struct EntrySpec
type::Symbol
alphabet::Vector{Char}
length::Int
EntrySpec(type::Symbol, length::Int) = new(type, alphabets[type], length)
end
_sample(spec::EntrySpec)::String = randstring(spec.alphabet, spec.length)
#=
#############################################################
EntryType is a classification of IBAN entries as EntrySpecs
according to domain types, e.g.: BankCode, BranchCode, etc...
############################################################# =#
abstract type EntryType end
struct BankCode <: EntryType
spec::EntrySpec
end
struct BranchCode <: EntryType
spec::EntrySpec
end
struct AccountNumber <: EntryType
spec::EntrySpec
end
struct NationalCheckDigit <: EntryType
spec::EntrySpec
end
struct AccountType <: EntryType
spec::EntrySpec
end
struct OwnerAccountType <: EntryType
spec::EntrySpec
end
struct IdentificationNumber <: EntryType
spec::EntrySpec
end
stringify(iban_entry) = split(string(typeof(iban_entry.entry_type)), ".")[2]
@memoize _symname(e::EntryType) = Symbol(typeof(e))
#=
#############################################################
BbanStructure is an orderd collection of EntryTypes. Different
countries would have diffrenet structures
############################################################# =#
struct BbanStructure
entries::Vector{EntryType}
end
##
## Return the length of the BbanStructure in characters
##
@memoize function _length(structure::BbanStructure)::Int
mapreduce(entry -> entry.spec.length, +, structure.entries)
end
##
## [4 4 12] => [1:4, 5:8, 9:20]
##
@memoize function _slicing(structure::BbanStructure)
# println("XXX memoize_cache(_slicing): $(length(memoize_cache(_slicing)))")
result = Tuple{Symbol,UnitRange}[]
offset = 1
map(structure.entries) do ent
symbol = _symname(ent)
push!(result, (symbol, UnitRange(offset, ent.spec.length + offset - 1)))
offset += ent.spec.length
end
result
end
function parse_bban!(countrycode, partup, allow_random_values=false)
theiban = TheIban(countrycode)
bban_structure = for_country(theiban.country_code)
for entry in bban_structure.entries
parkey = Symbol(typeof(entry))
if allow_random_values && ( partup[parkey] === nothing )
parval = _sample(entry.spec)
else
parval = partup[parkey]
end
push!(theiban.bban, IbanEntry(parval, entry))
end
theiban.bban_str = mapreduce(entry -> entry.value, *, values(theiban.bban))
theiban
end
for_country(country_code)::Maybe{BbanStructure} =
get(bban_structures_by_country, country_code, nothing)
"""
is_supported_country(country_code)::Bool
Return a boolean indicating if the country identified by `country_code` is supported.
# Examples
```julia
julia> is_supported_country("DE")
true
julia> is_supported_country("ZZ")
false
```
"""
is_supported_country(country_code::AbstractString) =
haskey(bban_structures_by_country, country_code)
"""
supported_countries()::Array{String,1}
Return an array of supported country codes.
"""
@memoize supported_countries() = collect(keys(bban_structures_by_country))
# *******************
# https://www.swift.com/resource/iban-registry-pdf
# ::Dict{String,BbanStructure}
const bban_structures_by_country = Dict(
"AD" => BbanStructure([
BankCode(EntrySpec(:N, 4)),
BranchCode(EntrySpec(:N, 4)),
AccountNumber(EntrySpec(:C, 12)),
]),
"AE" => BbanStructure([
BankCode(EntrySpec(:N, 3)),
AccountNumber(EntrySpec(:C, 16)),
]),
"AL" => BbanStructure([
BankCode(EntrySpec(:N, 3)),
BranchCode(EntrySpec(:N, 4)),
NationalCheckDigit(EntrySpec(:N, 1)),
AccountNumber(EntrySpec(:C, 16)),
]),
"AT" => BbanStructure([
BankCode(EntrySpec(:N, 5)),
AccountNumber(EntrySpec(:N, 11)),
]),
"AZ" => BbanStructure([
BankCode(EntrySpec(:A, 4)),
AccountNumber(EntrySpec(:C, 20)),
]),
"BA" => BbanStructure([
BankCode(EntrySpec(:N, 3)),
BranchCode(EntrySpec(:N, 3)),
AccountNumber(EntrySpec(:N, 8)),
NationalCheckDigit(EntrySpec(:N, 2)),
]),
"BE" => BbanStructure([
BankCode(EntrySpec(:N, 3)),
AccountNumber(EntrySpec(:N, 7)),
NationalCheckDigit(EntrySpec(:N, 2)),
]),
"BG" => BbanStructure([
BankCode(EntrySpec(:A, 4)),
BranchCode(EntrySpec(:N, 4)),
AccountType(EntrySpec(:N, 2)),
AccountNumber(EntrySpec(:C, 8)),
]),
"BH" => BbanStructure([
BankCode(EntrySpec(:A, 4)),
AccountNumber(EntrySpec(:C, 14)),
]),
"BR" => BbanStructure([
BankCode(EntrySpec(:N, 8)),
BranchCode(EntrySpec(:N, 5)),
AccountNumber(EntrySpec(:N, 10)),
AccountType(EntrySpec(:A, 1)),
OwnerAccountType(EntrySpec(:C, 1)),
]),
"BY" => BbanStructure([
BankCode(EntrySpec(:C, 4)),
BranchCode(EntrySpec(:N, 4)),
AccountNumber(EntrySpec(:C, 16)),
]),
"CH" => BbanStructure([
BankCode(EntrySpec(:N, 5)),
AccountNumber(EntrySpec(:C, 12)),
]),
"CR" => BbanStructure([
BankCode(EntrySpec(:N, 4)),
AccountNumber(EntrySpec(:N, 14)),
]),
"CY" => BbanStructure([
BankCode(EntrySpec(:N, 3)),
BranchCode(EntrySpec(:N, 5)),
AccountNumber(EntrySpec(:C, 16)),
]),
"CZ" => BbanStructure([
BankCode(EntrySpec(:N, 4)),
AccountNumber(EntrySpec(:N, 16)),
]),
"DE" => BbanStructure([
BankCode(EntrySpec(:N, 8)),
AccountNumber(EntrySpec(:N, 10)),
]),
"DK" => BbanStructure([
BankCode(EntrySpec(:N, 4)),
AccountNumber(EntrySpec(:N, 10)),
]),
"DO" => BbanStructure([
BankCode(EntrySpec(:C, 4)),
AccountNumber(EntrySpec(:N, 20)),
]),
"EE" => BbanStructure([
BankCode(EntrySpec(:N, 2)),
BranchCode(EntrySpec(:N, 2)),
AccountNumber(EntrySpec(:N, 11)),
NationalCheckDigit(EntrySpec(:N, 1)),
]),
"ES" => BbanStructure([
BankCode(EntrySpec(:N, 4)),
BranchCode(EntrySpec(:N, 4)),
NationalCheckDigit(EntrySpec(:N, 2)),
AccountNumber(EntrySpec(:N, 10)),
]),
"FI" => BbanStructure([
BankCode(EntrySpec(:N, 6)),
AccountNumber(EntrySpec(:N, 7)),
NationalCheckDigit(EntrySpec(:N, 1)),
]),
"FO" => BbanStructure([
BankCode(EntrySpec(:N, 4)),
AccountNumber(EntrySpec(:N, 9)),
NationalCheckDigit(EntrySpec(:N, 1)),
]),
"FR" => BbanStructure([
BankCode(EntrySpec(:N, 5)),
BranchCode(EntrySpec(:N, 5)),
AccountNumber(EntrySpec(:C, 11)),
NationalCheckDigit(EntrySpec(:N, 2)),
]),
"GB" => BbanStructure([
BankCode(EntrySpec(:A, 4)),
BranchCode(EntrySpec(:N, 6)),
AccountNumber(EntrySpec(:N, 8)),
]),
"GE" => BbanStructure([
BankCode(EntrySpec(:A, 2)),
AccountNumber(EntrySpec(:N, 16)),
]),
"GI" => BbanStructure([
BankCode(EntrySpec(:A, 4)),
AccountNumber(EntrySpec(:C, 15)),
]),
"GL" => BbanStructure([
BankCode(EntrySpec(:N, 4)),
AccountNumber(EntrySpec(:N, 10)),
]),
"GR" => BbanStructure([
BankCode(EntrySpec(:N, 3)),
BranchCode(EntrySpec(:N, 4)),
AccountNumber(EntrySpec(:C, 16)),
]),
"GT" => BbanStructure([
BankCode(EntrySpec(:C, 4)),
AccountNumber(EntrySpec(:C, 20)),
]),
"HR" => BbanStructure([
BankCode(EntrySpec(:N, 7)),
AccountNumber(EntrySpec(:N, 10)),
]),
"HU" => BbanStructure([
BankCode(EntrySpec(:N, 3)),
BranchCode(EntrySpec(:N, 4)),
AccountNumber(EntrySpec(:N, 16)),
NationalCheckDigit(EntrySpec(:N, 1)),
]),
"IE" => BbanStructure([
BankCode(EntrySpec(:A, 4)),
BranchCode(EntrySpec(:N, 6)),
AccountNumber(EntrySpec(:N, 8)),
]),
"IL" => BbanStructure([
BankCode(EntrySpec(:N, 3)),
BranchCode(EntrySpec(:N, 3)),
AccountNumber(EntrySpec(:N, 13)),
]),
"IR" => BbanStructure([
BankCode(EntrySpec(:N, 3)),
AccountNumber(EntrySpec(:N, 19)),
]),
"IS" => BbanStructure([
BankCode(EntrySpec(:N, 4)),
BranchCode(EntrySpec(:N, 2)),
AccountNumber(EntrySpec(:N, 6)),
IdentificationNumber(EntrySpec(:N, 10)),
]),
"IT" => BbanStructure([
NationalCheckDigit(EntrySpec(:A, 1)),
BankCode(EntrySpec(:N, 5)),
BranchCode(EntrySpec(:N, 5)),
AccountNumber(EntrySpec(:C, 12)),
]),
"JO" => BbanStructure([
BankCode(EntrySpec(:A, 4)),
BranchCode(EntrySpec(:N, 4)),
AccountNumber(EntrySpec(:C, 18)),
]),
"KW" => BbanStructure([
BankCode(EntrySpec(:A, 4)),
AccountNumber(EntrySpec(:C, 22)),
]),
"KZ" => BbanStructure([
BankCode(EntrySpec(:N, 3)),
AccountNumber(EntrySpec(:C, 13)),
]),
"LB" => BbanStructure([
BankCode(EntrySpec(:N, 4)),
AccountNumber(EntrySpec(:C, 20)),
]),
"LC" => BbanStructure([
BankCode(EntrySpec(:A, 4)),
AccountNumber(EntrySpec(:C, 24)),
]),
"LI" => BbanStructure([
BankCode(EntrySpec(:N, 5)),
AccountNumber(EntrySpec(:C, 12)),
]),
"LT" => BbanStructure([
BankCode(EntrySpec(:N, 5)),
AccountNumber(EntrySpec(:N, 11)),
]),
"LU" => BbanStructure([
BankCode(EntrySpec(:N, 3)),
AccountNumber(EntrySpec(:C, 13)),
]),
"LV" => BbanStructure([
BankCode(EntrySpec(:A, 4)),
AccountNumber(EntrySpec(:C, 13)),
]),
"MC" => BbanStructure([
BankCode(EntrySpec(:N, 5)),
BranchCode(EntrySpec(:N, 5)),
AccountNumber(EntrySpec(:C, 11)),
NationalCheckDigit(EntrySpec(:N, 2)),
]),
"MD" => BbanStructure([
BankCode(EntrySpec(:C, 2)),
AccountNumber(EntrySpec(:C, 18)),
]),
"ME" => BbanStructure([
BankCode(EntrySpec(:N, 3)),
AccountNumber(EntrySpec(:N, 13)),
NationalCheckDigit(EntrySpec(:N, 2)),
]),
"MK" => BbanStructure([
BankCode(EntrySpec(:N, 3)),
AccountNumber(EntrySpec(:C, 10)),
NationalCheckDigit(EntrySpec(:N, 2)),
]),
"MR" => BbanStructure([
BankCode(EntrySpec(:N, 5)),
BranchCode(EntrySpec(:N, 5)),
AccountNumber(EntrySpec(:N, 11)),
NationalCheckDigit(EntrySpec(:N, 2)),
]),
"MT" => BbanStructure([
BankCode(EntrySpec(:A, 4)),
BranchCode(EntrySpec(:N, 5)),
AccountNumber(EntrySpec(:C, 18)),
]),
"MU" => BbanStructure([
BankCode(EntrySpec(:C, 6)),
BranchCode(EntrySpec(:N, 2)),
AccountNumber(EntrySpec(:C, 18)),
]),
"NL" => BbanStructure([
BankCode(EntrySpec(:A, 4)),
AccountNumber(EntrySpec(:N, 10)),
]),
"NO" => BbanStructure([
BankCode(EntrySpec(:N, 4)),
AccountNumber(EntrySpec(:N, 6)),
NationalCheckDigit(EntrySpec(:N, 1)),
]),
"PK" => BbanStructure([
BankCode(EntrySpec(:C, 4)),
AccountNumber(EntrySpec(:N, 16)),
]),
"PL" => BbanStructure([
BankCode(EntrySpec(:N, 3)),
BranchCode(EntrySpec(:N, 4)),
NationalCheckDigit(EntrySpec(:N, 1)),
AccountNumber(EntrySpec(:N, 16)),
]),
"PS" => BbanStructure([
BankCode(EntrySpec(:A, 4)),
AccountNumber(EntrySpec(:C, 21)),
]),
"PT" => BbanStructure([
BankCode(EntrySpec(:N, 4)),
BranchCode(EntrySpec(:N, 4)),
AccountNumber(EntrySpec(:N, 11)),
NationalCheckDigit(EntrySpec(:N, 2)),
]),
"QA" => BbanStructure([
BankCode(EntrySpec(:A, 4)),
AccountNumber(EntrySpec(:C, 21)),
]),
"RO" => BbanStructure([
BankCode(EntrySpec(:A, 4)),
AccountNumber(EntrySpec(:C, 16)),
]),
"RS" => BbanStructure([
BankCode(EntrySpec(:N, 3)),
AccountNumber(EntrySpec(:N, 13)),
NationalCheckDigit(EntrySpec(:N, 2)),
]),
"SA" => BbanStructure([
BankCode(EntrySpec(:N, 2)),
AccountNumber(EntrySpec(:C, 18)),
]),
"SC" => BbanStructure([
BankCode(EntrySpec(:A, 4)),
BranchCode(EntrySpec(:N, 4)),
AccountNumber(EntrySpec(:N, 16)),
AccountType(EntrySpec(:A, 3)),
]),
"SE" => BbanStructure([
BankCode(EntrySpec(:N, 3)),
AccountNumber(EntrySpec(:N, 17)),
]),
"SI" => BbanStructure([
BankCode(EntrySpec(:N, 2)),
BranchCode(EntrySpec(:N, 3)),
AccountNumber(EntrySpec(:N, 8)),
NationalCheckDigit(EntrySpec(:N, 2)),
]),
"SK" => BbanStructure([
BankCode(EntrySpec(:N, 4)),
AccountNumber(EntrySpec(:N, 16)),
]),
"SM" => BbanStructure([
NationalCheckDigit(EntrySpec(:A, 1)),
BankCode(EntrySpec(:N, 5)),
BranchCode(EntrySpec(:N, 5)),
AccountNumber(EntrySpec(:C, 12)),
]),
"ST" => BbanStructure([
BankCode(EntrySpec(:N, 4)),
BranchCode(EntrySpec(:N, 4)),
AccountNumber(EntrySpec(:N, 13)),
]),
"SV" => BbanStructure([
BankCode(EntrySpec(:A, 4)),
AccountNumber(EntrySpec(:N, 20)),
]),
"TL" => BbanStructure([
BankCode(EntrySpec(:N, 3)),
AccountNumber(EntrySpec(:N, 14)),
NationalCheckDigit(EntrySpec(:N, 2)),
]),
"TN" => BbanStructure([
BankCode(EntrySpec(:N, 2)),
BranchCode(EntrySpec(:N, 3)),
AccountNumber(EntrySpec(:C, 15)),
]),
"TR" => BbanStructure([
BankCode(EntrySpec(:N, 5)),
NationalCheckDigit(EntrySpec(:C, 1)),
AccountNumber(EntrySpec(:C, 16)),
]),
"UA" => BbanStructure([
BankCode(EntrySpec(:N, 6)),
AccountNumber(EntrySpec(:N, 19)),
]),
"VG" => BbanStructure([
BankCode(EntrySpec(:A, 4)),
AccountNumber(EntrySpec(:N, 16)),
]),
"XK" => BbanStructure([
BankCode(EntrySpec(:N, 2)),
BranchCode(EntrySpec(:N, 2)),
AccountNumber(EntrySpec(:N, 10)),
NationalCheckDigit(EntrySpec(:N, 2)),
]),
)
| IbanGen | https://github.com/sorokod/Iban.jl.git |
|
[
"Apache-2.0"
] | 0.2.2 | 72253d8e52fce33c366848b17ce1648f7b719d10 | code | 1607 | #=
Copyright 2013 Artur Mkrtchyan
Licensed under the Apache License, Version 2.0 (the "License");
you may not use this file except in compliance with the License.
You may obtain a copy of the License at
http://www.apache.org/licenses/LICENSE-2.0
Unless required by applicable law or agreed to in writing, software
distributed under the License is distributed on an "AS IS" BASIS,
WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
See the License for the specific language governing permissions and
limitations under the License.
=#
function calculate_check_digit(bban, country_code)::String
combined = bban * country_code * "00"
check_digits = 98 - mod_97(combined)
lpad(check_digits, 2, "0")
end
# [0..9] are matched to values: [0..9]
# [a..z] and [A..Z] are matched to values: [10..35]
const zero_to_Z = vcat(['0':'9';], ['A':'Z';])
const a_to_z = ['a':'z';]
const c_to_numeric = merge(
Dict(zero_to_Z[i] => i - 1 for i = 1:length(zero_to_Z)),
Dict(a_to_z[i] => i + 9 for i = 1:length(a_to_z)),
)
function mod_97(str)
total = 0
for c in str
c_numeric = c_to_numeric[c]
total = (c_numeric > 9 ? total * 100 : total * 10) + c_numeric
if total > 999999999
total = mod(total, 97)
end
end
mod(total, 97)
end
# according to @btime, about of order of magnitude more expensive
# then mod_97
function mod_97_bigint(str)
numeric_str = map(c -> alphabet_to_numeric[c] , collect(str)) |> join
numeric_bi = parse(BigInt, numeric_str)
mod(numeric_bi, 97)
end | IbanGen | https://github.com/sorokod/Iban.jl.git |
|
[
"Apache-2.0"
] | 0.2.2 | 72253d8e52fce33c366848b17ce1648f7b719d10 | code | 693 | const Maybe{T} = Union{T,Nothing}
const MaybeString = Maybe{AbstractString}
"""
ValidationException
Thrown when parameters to generate an IBAN fail validation. Reports the problematic value
and the matching BBAN attribute
## Example
```julia
julia> iban_random(CountryCode = "GR", BankCode = "xxx")
ERROR: ValidationException value: "xxx"
invalid characters [IbanGen.BankCode]
```
"""
struct ValidationException <: Exception
val::MaybeString
msg::AbstractString
end
Base.showerror(io::IO, ex::ValidationException) =
print(io, """ValidationException value: "$(ex.val)"\n$(ex.msg)""")
ensure(condition, val, msg) =
!condition && throw(ValidationException(val, msg))
| IbanGen | https://github.com/sorokod/Iban.jl.git |
|
[
"Apache-2.0"
] | 0.2.2 | 72253d8e52fce33c366848b17ce1648f7b719d10 | code | 514 | using IbanGen
using Test
# shell> cd /Users/xor/work/julia/Iban
# pkg> activate .
# test
# or:
# Pkg.test("IbanGen", test_args=["test_iban_from_string", "test_countries", "test_iban", "test_iban_random"])
active_tests = lowercase.(ARGS)
function addtest(fname)
key = lowercase(splitext(fname)[1])
if isempty(active_tests) || key in active_tests
include(fname)
end
end
addtest("test_countries.jl")
addtest("test_iban_from_string.jl")
addtest("test_iban.jl")
addtest("test_iban_random.jl")
| IbanGen | https://github.com/sorokod/Iban.jl.git |
|
[
"Apache-2.0"
] | 0.2.2 | 72253d8e52fce33c366848b17ce1648f7b719d10 | code | 413 | @testset "Countries [supported]" begin
@test length(supported_countries()) == 75
map(cc -> (@test is_supported_country(cc) == true), supported_countries())
end
@testset "Countries [not supported]" begin
@test is_supported_country("DEU") == false
@test is_supported_country("GBR") == false
@test is_supported_country("AA") == false
@test is_supported_country("XX") == false
end
| IbanGen | https://github.com/sorokod/Iban.jl.git |
|
[
"Apache-2.0"
] | 0.2.2 | 72253d8e52fce33c366848b17ce1648f7b719d10 | code | 16625 | @testset "iban [one]" begin
result = iban(
CountryCode="AL",
BankCode="212",
BranchCode="1100",
AccountNumber="0000000235698741",
NationalCheckDigit="9"
)
@test result["CountryCode"] == "AL"
@test result["BankCode"] == "212"
@test result["BranchCode"] == "1100"
@test result["AccountNumber"] == "0000000235698741"
@test result["NationalCheckDigit"] == "9"
@test result["value"] == "AL47212110090000000235698741"
end
@testset "iban [all]" begin
@test iban(
CountryCode="AL",
BankCode="212",
BranchCode="1100",
AccountNumber="0000000235698741",
NationalCheckDigit="9",
)["value"] == "AL47212110090000000235698741"
@test iban(
CountryCode="AD",
BankCode="0001",
BranchCode="2030",
AccountNumber="200359100100",
)["value"] == "AD1200012030200359100100"
@test iban(
CountryCode="AT",
BankCode="19043",
AccountNumber="00234573201",
)["value"] == "AT611904300234573201"
@test iban(
CountryCode="AZ",
BankCode="NABZ",
AccountNumber="00000000137010001944",
)["value"] == "AZ21NABZ00000000137010001944"
@test iban(
CountryCode="BH",
BankCode="SCBL",
AccountNumber="BHD18903608801",
)["value"] == "BH72SCBLBHD18903608801"
@test iban(
CountryCode="BE",
BankCode="539",
AccountNumber="0075470",
NationalCheckDigit="34",
)["value"] == "BE68539007547034"
@test iban(
CountryCode="BA",
BankCode="129",
BranchCode="007",
AccountNumber="94010284",
NationalCheckDigit="94",
)["value"] == "BA391290079401028494"
@test iban(
CountryCode="BR",
BankCode="00360305",
BranchCode="00001",
AccountNumber="0009795493",
AccountType="P",
OwnerAccountType="1",
)["value"] == "BR9700360305000010009795493P1"
@test iban(
CountryCode="BG",
BankCode="BNBG",
BranchCode="9661",
AccountNumber="20345678",
AccountType="10",
)["value"] == "BG80BNBG96611020345678"
@test iban(
CountryCode="BY",
BankCode="NBRB",
BranchCode="3600",
AccountNumber="900000002Z00AB00",
)["value"] == "BY13NBRB3600900000002Z00AB00"
@test iban(
CountryCode="CR",
BankCode="0152",
AccountNumber="02001026284066",
)["value"] == "CR05015202001026284066"
@test iban(
CountryCode="HR",
BankCode="1001005",
AccountNumber="1863000160",
)["value"] == "HR1210010051863000160"
@test iban(
CountryCode="CY",
BankCode="002",
BranchCode="00128",
AccountNumber="0000001200527600",
)["value"] == "CY17002001280000001200527600"
@test iban(
CountryCode="CZ",
BankCode="0800",
AccountNumber="0000192000145399",
)["value"] == "CZ6508000000192000145399"
@test iban(
CountryCode="DK",
BankCode="0040",
AccountNumber="0440116243",
)["value"] == "DK5000400440116243"
@test iban(
CountryCode="DO",
BankCode="BAGR",
AccountNumber="00000001212453611324",
)["value"] == "DO28BAGR00000001212453611324"
@test iban(
CountryCode="EE",
BankCode="22",
BranchCode="00",
AccountNumber="22102014568",
NationalCheckDigit="5",
)["value"] == "EE382200221020145685"
@test iban(
CountryCode="FI",
BankCode="123456",
AccountNumber="0000078",
NationalCheckDigit="5",
)["value"] == "FI2112345600000785"
@test iban(
CountryCode="FR",
BankCode="20041",
BranchCode="01005",
AccountNumber="0500013M026",
NationalCheckDigit="06",
)["value"] == "FR1420041010050500013M02606"
@test iban(
CountryCode="GE",
BankCode="NB",
AccountNumber="0000000101904917",
)["value"] == "GE29NB0000000101904917"
@test iban(
CountryCode="DE",
BankCode="37040044",
AccountNumber="0532013000",
)["value"] == "DE89370400440532013000"
@test iban(
CountryCode="GI",
BankCode="NWBK",
AccountNumber="000000007099453",
)["value"] == "GI75NWBK000000007099453"
@test iban(
CountryCode="GR",
BankCode="011",
BranchCode="0125",
AccountNumber="0000000012300695",
)["value"] == "GR1601101250000000012300695"
@test iban(
CountryCode="GT",
BankCode="TRAJ",
AccountNumber="01020000001210029690",
)["value"] == "GT82TRAJ01020000001210029690"
@test iban(
CountryCode="HU",
BankCode="117",
BranchCode="7301",
AccountNumber="6111110180000000",
NationalCheckDigit="0",
)["value"] == "HU42117730161111101800000000"
@test iban(
CountryCode="IS",
BankCode="0159",
BranchCode="26",
AccountNumber="007654",
IdentificationNumber="5510730339",
)["value"] == "IS140159260076545510730339"
@test iban(
CountryCode="IE",
BankCode="AIBK",
BranchCode="931152",
AccountNumber="12345678",
)["value"] == "IE29AIBK93115212345678"
@test iban(
CountryCode="IL",
BankCode="010",
BranchCode="800",
AccountNumber="0000099999999",
)["value"] == "IL620108000000099999999"
@test iban(
CountryCode="IT",
BankCode="05428",
BranchCode="11101",
NationalCheckDigit="X",
AccountNumber="000000123456",
)["value"] == "IT60X0542811101000000123456"
@test iban(
CountryCode="JO",
BankCode="CBJO",
BranchCode="0010",
AccountNumber="000000000131000302",
)["value"] == "JO94CBJO0010000000000131000302"
@test iban(
CountryCode="KZ",
BankCode="125",
AccountNumber="KZT5004100100",
)["value"] == "KZ86125KZT5004100100"
@test iban(
CountryCode="KW",
BankCode="CBKU",
AccountNumber="0000000000001234560101",
)["value"] == "KW81CBKU0000000000001234560101"
@test iban(
CountryCode="LC",
BankCode="HEMM",
AccountNumber="000100010012001200023015",
)["value"] == "LC55HEMM000100010012001200023015"
@test iban(
CountryCode="LV",
BankCode="BANK",
AccountNumber="0000435195001",
)["value"] == "LV80BANK0000435195001"
@test iban(
CountryCode="LB",
BankCode="0999",
AccountNumber="00000001001901229114",
)["value"] == "LB62099900000001001901229114"
@test iban(
CountryCode="LI",
BankCode="08810",
AccountNumber="0002324013AA",
)["value"] == "LI21088100002324013AA"
@test iban(
CountryCode="LT",
BankCode="10000",
AccountNumber="11101001000",
)["value"] == "LT121000011101001000"
@test iban(
CountryCode="LU",
BankCode="001",
AccountNumber="9400644750000",
)["value"] == "LU280019400644750000"
@test iban(
CountryCode="MK",
BankCode="250",
AccountNumber="1200000589",
NationalCheckDigit="84",
)["value"] == "MK07250120000058984"
@test iban(
CountryCode="MT",
BankCode="MALT",
BranchCode="01100",
AccountNumber="0012345MTLCAST001S",
)["value"] == "MT84MALT011000012345MTLCAST001S"
@test iban(
CountryCode="MR",
BankCode="00020",
BranchCode="00101",
AccountNumber="00001234567",
NationalCheckDigit="53",
)["value"] == "MR1300020001010000123456753"
@test iban(
CountryCode="MU",
BankCode="BOMM01",
BranchCode="01",
AccountNumber="101030300200000MUR",
)["value"] == "MU17BOMM0101101030300200000MUR"
@test iban(
CountryCode="MD",
BankCode="AG",
AccountNumber="000225100013104168",
)["value"] == "MD24AG000225100013104168"
@test iban(
CountryCode="MC",
BankCode="11222",
BranchCode="00001",
AccountNumber="01234567890",
NationalCheckDigit="30",
)["value"] == "MC5811222000010123456789030"
@test iban(
CountryCode="ME",
BankCode="505",
AccountNumber="0000123456789",
NationalCheckDigit="51",
)["value"] == "ME25505000012345678951"
@test iban(
CountryCode="NL",
BankCode="ABNA",
AccountNumber="0417164300",
)["value"] == "NL91ABNA0417164300"
@test iban(
CountryCode="NO",
BankCode="8601",
AccountNumber="111794",
NationalCheckDigit="7",
)["value"] == "NO9386011117947"
@test iban(
CountryCode="PK",
BankCode="SCBL",
AccountNumber="0000001123456702",
)["value"] == "PK36SCBL0000001123456702"
@test iban(
CountryCode="PS",
BankCode="PALS",
AccountNumber="000000000400123456702",
)["value"] == "PS92PALS000000000400123456702"
@test iban(
CountryCode="PL",
BankCode="109",
BranchCode="0101",
AccountNumber="0000071219812874",
NationalCheckDigit="4",
)["value"] == "PL61109010140000071219812874"
@test iban(
CountryCode="PT",
BankCode="0002",
BranchCode="0123",
AccountNumber="12345678901",
NationalCheckDigit="54",
)["value"] == "PT50000201231234567890154"
@test iban(
CountryCode="RO",
BankCode="AAAA",
AccountNumber="1B31007593840000",
)["value"] == "RO49AAAA1B31007593840000"
@test iban(
CountryCode="QA",
BankCode="DOHB",
AccountNumber="00001234567890ABCDEFG",
)["value"] == "QA58DOHB00001234567890ABCDEFG"
@test iban(
CountryCode="SC",
BankCode="SSCB",
BranchCode="1101",
AccountNumber="0000000000001497",
AccountType="USD",
)["value"] == "SC18SSCB11010000000000001497USD"
@test iban(
CountryCode="SM",
BankCode="03225",
BranchCode="09800",
AccountNumber="000000270100",
NationalCheckDigit="U",
)["value"] == "SM86U0322509800000000270100"
@test iban(
CountryCode="ST",
BankCode="0001",
BranchCode="0001",
AccountNumber="0051845310112",
)["value"] == "ST68000100010051845310112"
@test iban(
CountryCode="SA",
BankCode="80",
AccountNumber="000000608010167519",
)["value"] == "SA0380000000608010167519"
@test iban(
CountryCode="RS",
BankCode="260",
BranchCode="26",
AccountNumber="0056010016113",
NationalCheckDigit="79",
)["value"] == "RS35260005601001611379"
@test iban(
CountryCode="SK",
BankCode="1200",
AccountNumber="0000198742637541",
)["value"] == "SK3112000000198742637541"
@test iban(
CountryCode="SV",
BankCode="CENR",
AccountNumber="00000000000000700025",
)["value"] == "SV62CENR00000000000000700025"
@test iban(
CountryCode="SI",
BankCode="26",
BranchCode="330",
AccountNumber="00120390",
NationalCheckDigit="86",
)["value"] == "SI56263300012039086"
@test iban(
CountryCode="ES",
BankCode="2100",
BranchCode="0418",
AccountNumber="0200051332",
NationalCheckDigit="45",
)["value"] == "ES9121000418450200051332"
@test iban(
CountryCode="SE",
BankCode="500",
AccountNumber="00000058398257466",
)["value"] == "SE4550000000058398257466"
@test iban(
CountryCode="CH",
BankCode="00762",
AccountNumber="011623852957",
)["value"] == "CH9300762011623852957"
@test iban(
CountryCode="TN",
BankCode="10",
BranchCode="006",
AccountNumber="035183598478831",
)["value"] == "TN5910006035183598478831"
@test iban(
CountryCode="TR",
BankCode="00061",
AccountNumber="0519786457841326",
NationalCheckDigit="0",
)["value"] == "TR330006100519786457841326"
@test iban(
CountryCode="AE",
BankCode="033",
AccountNumber="1234567890123456",
)["value"] == "AE070331234567890123456"
@test iban(
CountryCode="GB",
BankCode="NWBK",
BranchCode="601613",
AccountNumber="31926819",
)["value"] == "GB29NWBK60161331926819"
@test iban(
CountryCode="VG",
BankCode="VPVG",
AccountNumber="0000012345678901",
)["value"] == "VG96VPVG0000012345678901"
@test iban(
CountryCode="TL",
BankCode="008",
AccountNumber="00123456789101",
NationalCheckDigit="57",
)["value"] == "TL380080012345678910157"
@test iban(
CountryCode="XK",
BankCode="10",
BranchCode="00",
AccountNumber="0000000000",
NationalCheckDigit="53",
)["value"] == "XK051000000000000053"
@test iban(
CountryCode="IR",
BankCode="017",
AccountNumber="0000000000123456789",
)["value"] == "IR200170000000000123456789"
@test iban(
CountryCode="FO",
BankCode="5432",
AccountNumber="038889994",
NationalCheckDigit="4",
)["value"] == "FO9754320388899944"
@test iban(
CountryCode="GL",
BankCode="6471",
AccountNumber="0001000206",
)["value"] == "GL8964710001000206"
@test iban(
CountryCode="UA",
BankCode="354347",
AccountNumber="0006762462054925026",
)["value"] == "UA573543470006762462054925026"
end
| IbanGen | https://github.com/sorokod/Iban.jl.git |
|
[
"Apache-2.0"
] | 0.2.2 | 72253d8e52fce33c366848b17ce1648f7b719d10 | code | 1869 | @testset "Build from string [sucess]" begin
for ibanstr in map( cc -> iban_random(CountryCode=cc)["value"] ,supported_countries())
@test iban(ibanstr)["value"] == ibanstr
end
end
function test_error(iban_str, snippet)
try
iban(iban_str)
catch err
@test err isa ValidationException
@test occursin(snippet, sprint(showerror, err)) == true
return
end
error("Expected test to fail: ('$iban_str , $snippet)")
end
@testset "Build from string [error]" begin
test_error("A", "value too short")
test_error("XX", "value too short")
test_error("AL1", "value too short")
test_error("XX11", "country code not supported")
# we use BR as it has a rich structure:
# BR97 00360305 00001 0009795493 P 1
test_error("BR9700360305000010009795493P1_", "unexpected BBAN length, expected:")
# BankCode(EntrySpec(:N, 8)),
test_error("BR970036030A000010009795493P1", "invalid characters [IbanGen.BankCode]")
# BranchCode(EntrySpec(:N, 5)),
test_error("BR97003603050000A0009795493P1", "invalid characters [IbanGen.BranchCode]")
# AccountNumber(EntrySpec(:N, 10))
test_error("BR970036030500001000979549AP1", "invalid characters [IbanGen.AccountNumber]")
# AccountType(EntrySpec(:A, 1)),
test_error("BR970036030500001000979549391", "invalid characters [IbanGen.AccountType]")
# OwnerAccountType(EntrySpec(:C, 1)
test_error("BR9700360305000010009795493P_", "invalid characters [IbanGen.OwnerAccountType]")
# Invalid check digits
test_error("BR9900360305000010009795493P1", "invalid check digits")
# Invalid check digits
test_error("BR9700360305000010009795493P2", "invalid check digits")
end
| IbanGen | https://github.com/sorokod/Iban.jl.git |
|
[
"Apache-2.0"
] | 0.2.2 | 72253d8e52fce33c366848b17ce1648f7b719d10 | code | 1516 |
function isvalid(subject::Dict{String, String}, display = false)
if display
println("isvalid: $subject")
end
typeof(iban(subject["value"])) == Dict{String,String}
end
@testset "iban_random [one]" begin
@test iban_random(
CountryCode="BR"
)["CountryCode"] == "BR"
@test iban_random(
CountryCode="BR",
BankCode="18731592"
)["BankCode"] == "18731592"
@test iban_random(
CountryCode="BR",
BankCode="18731592",
BranchCode = "89800"
)["BranchCode"] == "89800"
@test iban_random(
CountryCode="BR",
BankCode="18731592",
BranchCode = "89800",
AccountNumber = "6427460610"
)["AccountNumber"] == "6427460610"
@test iban_random(
CountryCode="BR",
BankCode="18731592",
BranchCode = "89800",
AccountNumber = "6427460610",
AccountType = "X"
)["AccountType"] == "X"
@test iban_random(
CountryCode="BR",
BankCode="18731592",
BranchCode = "89800",
AccountNumber = "6427460610",
AccountType = "X",
OwnerAccountType = "m",
)["OwnerAccountType"] == "m"
end
@testset "iban_random [all]" begin
@test isvalid(iban_random()) == true
@test isvalid(iban_random(CountryCode="BR", BankCode="18731592")) == true
# all supported country codes
map(cc ->
(@test isvalid(iban_random(CountryCode=cc)) == true),
supported_countries()
)
end
| IbanGen | https://github.com/sorokod/Iban.jl.git |
|
[
"Apache-2.0"
] | 0.2.2 | 72253d8e52fce33c366848b17ce1648f7b719d10 | docs | 611 | # IbanGen

A Julia package for generating and validating IBANs. Library documentaion is [here](https://sorokod.github.io/Iban.jl/dev/).
---
## History
**IbanGen** is a port of [iban4j](https://github.com/arturmkrtchyan/iban4j), a Java library that is published under Apache 2 license and copyrighted 2015 Artur Mkrtchyan
---
## License
Copyright 2021 David Soroko except where stated otherwise in the source.
Licensed under the [Apache License, Version 2.0](http://www.apache.org/licenses/LICENSE-2.0) | IbanGen | https://github.com/sorokod/Iban.jl.git |
|
[
"Apache-2.0"
] | 0.2.2 | 72253d8e52fce33c366848b17ce1648f7b719d10 | docs | 3054 | # IbanGen
A Julia package for generating and validating IBANs.
---
## Installation
**IbanGen** is a registered package and can be installed via `Pkg.add`:
```
Pkg.add("IbanGen")
```
---
## General
The International Bank Account Number standard is described in Wikipedia in some detail, see [Reference](@ref).
An IBAN consists of a two character country code, followed by a two digit redundancy code (AKA "check
digits"), followed by a Basic Bank Account Number (BBAN) – an up to 30 alphanumeric character long string that is
country specific.
The overall IBAN structure is then `<country code><check digits><BBAN>`. The country-by-country attribute format of the
`BBAN`s is captured in the IBAN registry document. All countries define a `BankCode` and `AccountNumber` structures, but some have additional attributes such as `BranchCode`, `NationalCheckDigit`, `AccountType` and `IdentificationNumber`.
**IbanGen** is aware of these definitions and takes them into account when parsing and validating the input. The IBAN
generating functions ( [`iban`](@ref) and [`iban_random`](@ref) ) return a dictionary with keys that are the BBAN
attribute names along with: `CountryCode`, `CheckDigits`and `value`. The last one is the string representation of the IBAN:
```julia
julia> iban_random(CountryCode = "DE")
Dict{String,String} with 5 entries:
"CountryCode" => "DE"
"AccountNumber" => "2619193797"
"value" => "DE37570047482619193797"
"BankCode" => "57004748"
"CheckDigits" => "37"
```
IBAN generating functions, will throw a [`ValidationException`](@ref) if they fail to validate the input, for example:
```julia
julia> iban_random(CountryCode = "DE", BankCode = "XX004748")
ERROR: ValidationException value: "XX004748"
invalid characters [Iban.BankCode]
```
**A note about validation**
In the context of IbanGen, an IBAN is valid if it matches the syntactic definition in the IBAN Registry( see [Reference](@ref) )
and makes no claims about semantic correctness. Following the example of `iban_random(CountryCode = "DE")`, the generated
`BankCode` is valid in that it is a numeric string of length 8 - it is unlikely to be a code of an actual bank. The same
applies to `AccountNumber` which is a numeric string of length 10 but does not represent a real account.
---
## Library
```@docs
iban
iban_random
is_supported_country
supported_countries
ValidationException
```
---
## Reference
- [International Bank Account Number (Wikipedia)](http://en.wikipedia.org/wiki/ISO_13616)
- [The ISO_3166 Country code standard](https://en.wikipedia.org/wiki/ISO_3166-1_alpha-2)
- [IBAN Registry (PDF)](https://www.swift.com/resource/iban-registry-pdf)
---
## License
**Iban.jl** is a port of [iban4j](https://github.com/arturmkrtchyan/iban4j), a Java library published under
Apache 2 license and copyrighted 2015 Artur Mkrtchyan
Copyright 2021 David Soroko except where stated otherwise in the source.
Licensed under the [Apache License, Version 2.0](http://www.apache.org/licenses/LICENSE-2.0) | IbanGen | https://github.com/sorokod/Iban.jl.git |
|
[
"MIT"
] | 0.4.1 | 792c195909ca5dfff5685305b6fa0aa16c3d1041 | code | 2335 | using Documenter
using Literate
using Plots
ENV["GKSwstype"] = "nul" # to avoid GKS error on docs build ("nul" for headless systems)
using LongwaveModePropagator
using LongwaveModePropagator.Fields
#==
Generate examples
==#
const ROOT_DIR = abspath(@__DIR__, "..")
const EXAMPLES_DIR = joinpath(ROOT_DIR, "examples")
const BUILD_DIR = joinpath(ROOT_DIR, "docs", "build")
const OUTPUT_DIR = joinpath(ROOT_DIR, "docs", "src", "generated")
# repo_root_url is only assigned with CI, so we have to specify it for local builds
# can't use abspath on Windows (no colons) so we calculate relpath
const REPO_ROOT_URL = relpath(ROOT_DIR, joinpath(BUILD_DIR, "generated"))
examples = [
"basic.jl",
"io.jl",
"meshgrid.jl",
"meshgrid2.jl",
"integratedreflection.jl",
"wavefieldintegration.jl",
"magneticfield.jl",
"interpretinghpbeta.jl",
"multiplespecies.jl",
"interpolatingfunctions.jl",
"ground.jl"
]
for example in examples
example_filepath = joinpath(EXAMPLES_DIR, example)
if get(ENV, "CI", nothing) == "true"
Literate.markdown(example_filepath, OUTPUT_DIR, documenter=true)
else
# local
Literate.markdown(example_filepath, OUTPUT_DIR, documenter=true,
repo_root_url=REPO_ROOT_URL)
end
end
#==
Organize page hierarchies
==#
example_pages = Any[
"generated/basic.md",
"generated/io.md",
"generated/meshgrid.md",
"generated/meshgrid2.md",
"generated/integratedreflection.md",
"generated/wavefieldintegration.md",
"generated/magneticfield.md",
"generated/interpretinghpbeta.md",
"generated/multiplespecies.md",
"generated/interpolatingfunctions.md",
"generated/ground.md"
]
library_pages = Any[
"lib/public.md",
"lib/internals.md"
]
pages = Any[
"Home" => "index.md",
"Examples" => example_pages,
"Library" => library_pages,
"References" => "references.md"
]
#==
Build and deploy docs
==#
format = Documenter.HTML(
collapselevel = 1,
prettyurls=get(ENV, "CI", nothing)=="true"
)
makedocs(
sitename = "LongwaveModePropagator",
authors = "Forrest Gasdia",
format = format,
pages = pages,
modules = [LongwaveModePropagator]
)
deploydocs(
repo = "github.com/fgasdia/LongwaveModePropagator.jl.git",
devbranch = "main",
)
| LongwaveModePropagator | https://github.com/fgasdia/LongwaveModePropagator.jl.git |
|
[
"MIT"
] | 0.4.1 | 792c195909ca5dfff5685305b6fa0aa16c3d1041 | code | 14333 | # # Introduction to defining scenarios
#
# This example walks through the basic usage of LongwaveModePropagator
# when interfacing with the package through Julia.
#
# The simplest way to propagate a transmitted signal in the Earth-ionosphere waveguide is
# to use the primary function exported by LongwaveModePropagator:
#
# `propagate(waveguide, tx, rx)`
#
# where `waveguide` defines the characteristics of the Earth-ionosphere waveguide,
# `tx` ("transmitter") describes the radiofrequency emitter, and
# `rx` ("receiver") describes how the electromagnetic field is sampled in the
# waveguide.
#
# LongwaveModePropagator exports several structs which are used to define
# propagation scenarios.
# We'll break them into two major categories of [Transmitters and receivers](@ref)
# and [Waveguides](@ref waveguides_intro).
#
# Let's load the necessary packages.
using Plots
using LongwaveModePropagator
using LongwaveModePropagator: QE, ME
# ## Transmitters and receivers
#
# This section discusses transmitters and receivers (or _emitters_ and _samplers_)
# and the related types.
#
# We'll begin by looking at the related types that `Emitter`s and `Sampler`s rely on.
#
# ### Frequencies
#
# Throughout the code, the electromagnetic wave frequency is required in different
# forms: as a temporal frequency, angular frequency, or a wave number or wavelength.
# These are always defined in vacuum.
#
# For consistency and convenience, LongwaveModePropagator defines a [`Frequency`](@ref)
# struct containing fields for:
#
# - frequency `f` in Hertz
# - angular frequency `ω` in radians/sec
# - wavenumber `k` in radians/meter
# - wavelength `λ` in meters
#
# These fields are automatically calculated when passed a temporal frequency.
frequency = Frequency(20e3)
# ### Antennas
#
# LongwaveModePropagator computes the far field in the waveguide produced from
# energized small dipole antennas of any orientation.
#
# All antennas are subtypes of the abstract [`LongwaveModePropagator.Antenna`](@ref) type.
# Currently all antennas are also subtypes of the
# [`LongwaveModePropagator.AbstractDipole`](@ref) type.
#
# The most general antenna is the [`Dipole`](@ref), which has `azimuth_angle` and
# `inclination_angle` fields to describe its orientation with respect to the
# waveguide.
az = π/4
inc = π/8
d = Dipole(az, inc)
# There are also two special cases of `Dipole`: [`VerticalDipole`](@ref) and
# [`HorizontalDipole`](@ref).
# The [`VerticalDipole`](@ref) struct has no fields. For our purposes, it
# is fully defined by name alone.
vd = VerticalDipole()
inclination(vd)
# The [`HorizontalDipole`](@ref) struct has the `azimuth_angle` field (in _radians_) to
# describe its orientation relative to the waveguide.
hd = HorizontalDipole(az)
rad2deg(inclination(hd))
#
rad2deg(azimuth(hd))
# Additional help can be found by typing `? HorizontalDipole` in the REPL.
#
# Why bother defining these types? We make use of
# [multiple dispatch](https://www.youtube.com/watch?v=kc9HwsxE1OY)
# to avoid calculating field terms that are unnecessary
# for special cases of emitter orientation.
#
# ### [Emitters](@id emitters_intro)
#
# `Emitter`s emit radiofrequency energy in the waveguide.
# These are typically large, fixed VLF transmitters on the ground, but they could also be
# airborne.
# The type hierarchy in LongwaveModePropagator was designed with the thought that this
# could potentially be expanded to include natural emitters like lightning, although
# there is no internal functionality to directly handle such an emitter at this time.
#
# All emitters subtype the abstract [`LongwaveModePropagator.Emitter`](@ref) type.
#
# The [`Transmitter`](@ref) struct is used to define a typical man-made transmitter
# on the ground.
# A `Transmitter` has the fields
#
# - `name::String`: transmitter name.
# - `latitude::Float64`: transmitter geographic latitude in degrees.
# - `longitude::Float64`: transmitter geographic longitude in degrees.
# - `antenna::Antenna`: transmitter antenna.
# - `frequency::Frequency`: transmit frequency.
# - `power::Float64`: transmit power in Watts.
#
# Note that currently `latitude` and `longitude` are not used.
# Distances are measured relative to the `Emitter` without reference to absolute
# positions.
#
# Several convenience constructors exist to create `Transmitter`s with particular
# defaults for the remaining fields.
name = "NAA"
lat = 44.6464
lon = -67.2811
f = 24e3
tx = Transmitter(name, lat, lon, f)
# For the common case of transmitters on the ground with antennas modeled as a
# `VerticalDipole`, simply specify the transmit frequency.
tx = Transmitter(f)
# Alternately an `Antenna`, frequency, and power level can be specified.
power = 500e3 # 500 kW
tx = Transmitter(hd, f, power)
# Although not currently exported by LongwaveModePropagator, there is an
# [`LongwaveModePropagator.AirborneTransmitter`](@ref) defined that adds an
# `altitude` field to the basic `Transmitter` object.
# Further implementation and verification of the
# radiation resistance of an elevated antenna is required for accurate scaling
# of the electric field magnitude in the waveguide.
# In the meantime, if relative amplitude is sufficient, the height gain functions
# of an elevated transmitter are already incorporated into the model.
#
# ### [Samplers](@id samplers_intro)
#
# Structs that subtype [`LongwaveModePropagator.AbstractSampler`](@ref) probe the
# fields in the waveguide generated by an emitter.
# In common to all subtypes of `AbstractSampler` is that they have a position in the
# guide and specify what field component they sample.
#
# `Fields` is a `baremodule` contained within and reexported from
# LongwaveModePropagator.jl which contains a single enum object
Fields.Field
# Individual fields are specified with
field = Fields.Ez
# The general [`Sampler`](@ref) type specifies
#
# - `distance::T`: ground distance from the transmitter in meters.
# - `fieldcomponent::Fields.Field`: field component measured by the `Sampler`.
# - `altitude::Float64`: height above the ground in meters.
#
# The `distance` field is parameterized and therefore could be a single distance
# e.g. `2250e3`, a vector of distances `[2000e3, 2100e3, 2500e3]`, or a range
# `0:5e3:2000e3`, for example.
#
# There is a special [`GroundSampler`](@ref) which lacks the `altitude` field in `Sampler`s
# because it is known from the type that `altitude = 0`.
distance = 2000e3
rx = GroundSampler(distance, field)
# Finally there is a `Receiver` struct which is defined with a geographic location
# and `Antenna`, but it is not exported because geographic information
# is not currently handled by the package.
#
# ## [Waveguides](@id waveguides_intro)
#
# The abstract [`LongwaveModePropagator.Waveguide`](@ref) type is used to
# describe the earth-ionosphere waveguide with a [`BField`](@ref bfield_intro),
# [`Species`](@ref species_intro), and [`Ground`](@ref ground_intro).
#
# The basic concrete waveguide type is a [`HomogeneousWaveguide`](@ref), with fields
#
# - `bfield::BField`: background magnetic field.
# - `species::S`: ionosphere constituents.
# - `ground::Ground`: waveguide ground.
# - `distance::Float64`: distance from the `Emitter` at the start of the segment in meters.
#
# If not specified, `distance` is 0.
# The form of the function call is
#
# `HomogeneousWaveguide(bfield, species, ground)`
#
# `HomogeneousWaveguide` should be used when modeling with only a single
# homogeneous waveguide (ground, ionosphere, and magnetic field) along the propagation path.
#
# To model an inhomogeneous propagation path, there is a [`SegmentedWaveguide`](@ref) type.
# The `SegmentedWaveguide` is simply a wrapper for a `Vector` of waveguides.
#
# Let's look at the components of a waveguide.
#
# ### [BField](@id bfield_intro)
#
# The [`BField`](@ref) type describes the magnitude and direction of the background
# magnetic field.
# Internally it consists of fields for the field strength `B` in Teslas
# and direction cosines corresponding to the directions parallel, perpendicular,
# and up into the waveguide.
#
# A `BField` is most commonly constructed by specifying the field strength,
# `dip` angle in radians from the horizontal and positive when directed into Earth,
# and `azimuth` angle in radians from the propagation direction, positive towards ``y``.
#
# For example,
bfield = BField(50000e-9, π/2, 0)
# `bfield` is a vertical magnetic field of 50,000 nT.
#
# ### [Species](@id species_intro)
#
# The [`Species`](@ref) struct identifies a constituent species of the ionosphere.
# `Species` contains the fields
#
# - `charge::Float64`: signed species charged in Coulombs.
# - `mass::Float64`: species mass in kilograms.
# - `numberdensity::F`: a callable that returns number density in number per cubic meter
# as a function of height in meters.
# - `collisionfrequency::G`: a callable that returns the collision frequency in
# collisions per second as a function of height in meters.
#
# `numberdensity` and `collisionfrequency` should be "callables" (usually `Function`s) that
# return the number density and collision frequency, respectively, as a function
# of height in meters.
#
# For convenience, the Wait and Spies profile is accessible via
# [`waitprofile`](@ref). Similarly the accompanying collision frequency profiles are
# [`electroncollisionfrequency`](@ref) and [`ioncollisionfrequency`](@ref).
#
# To define some electrons for the ionosphere (`QE` and `ME` were explicitly
# imported at the top of the example):
h = 75
β = 0.35
electrons = Species(QE, ME, z->waitprofile(z, h, β), electroncollisionfrequency)
# Note that we used a lambda function to specify the `waitprofile` with our given
# ``h'`` and ``\beta``. Also note that these two parameters are a rare instance of
# SI units not strictly being followed.
# See the help for [`waitprofile`](@ref) for more information, including optional
# height cutoff and density threshold arguments.
#
# `electroncollisionfrequency` is a function of height `z` only, so it is not
# necessary to generate a lambda function. We can pass the function handle
# directly.
#
# ### [Ground](@id ground_intro)
#
# [`Ground`](@ref) describes the relative permittivity `ϵᵣ` and conductivity `σ` of Earth.
ground = Ground(10, 2e-4)
# For convenience, a dictionary of common ground indices is exported.
GROUND
# `Dict`s aren't sorted, but simply specify the index as the key to access the `Ground`
# entry.
ground = GROUND[5]
# ## Propagating the fields: HomogeneousWaveguide
#
# We'll redefine everything we've defined above just so they're easier to see,
# run the model, and plot the results.
f = 24e3
tx = Transmitter(f)
ranges = 0:5e3:2000e3
field = Fields.Ez
rx = GroundSampler(ranges, field)
bfield = BField(50e-6, π/2, 0)
electrons = Species(QE, ME, z->waitprofile(z, 75, 0.35), electroncollisionfrequency)
ground = GROUND[5]
waveguide = HomogeneousWaveguide(bfield, electrons, ground)
# The [`propagate`](@ref) function returns a tuple of complex electric field,
# amplitude in dB μV/m, and phase in radians.
E, a, p = propagate(waveguide, tx, rx);
# Here are quick plots of the amplitude
plot(ranges/1000, a;
xlabel="range (km)", ylabel="amplitude (dB)",
linewidth=1.5, legend=false)
#md savefig("basic_homogeneousamplitude.png"); nothing # hide
#md # 
# and phase.
plot(ranges/1000, rad2deg.(p);
xlabel="range (km)", ylabel="phase (deg)",
linewidth=1.5, legend=false)
#md savefig("basic_homogeneousphase.png"); nothing # hide
#md # 
# ## Propagating the fields: SegmentedWaveguide
#
# As previously mentioned, a [`SegmentedWaveguide`](@ref) contains a vector of
# [`HomogeneousWaveguide`](@ref)s.
# There are many ways to construct a `SegmentedWaveguide`.
#
# One common case is when a vector of `BField`s, `Species`, and/or `Ground`s are
# known for each `HomogeneousWaveguide` making up the `SegmentedWaveguide`.
# We'll also need to specify the distance at which each waveguide segment begins
# relative to the transmitter.
#
# The first `HomogeneousWaveguide` should have a distance of 0.
# An error will eventually be thrown if that is not the case.
#
# In this example we'll have two segments.
# The second segment begins 1000 km away from the transmitter.
distances = [0.0, 1000e3]
species = [Species(QE, ME, z->waitprofile(z, 75, 0.35), electroncollisionfrequency),
Species(QE, ME, z->waitprofile(z, 82, 0.5), electroncollisionfrequency)]
waveguide = SegmentedWaveguide([HomogeneousWaveguide(bfield, species[i], ground,
distances[i]) for i in 1:2]);
# We can [`propagate`](@ref) just as before
E, a, p = propagate(waveguide, tx, rx);
# Here are quick plots of the amplitude
plot(ranges/1000, a;
xlabel="range (km)", ylabel="amplitude (dB)",
linewidth=1.5, legend=false)
#md savefig("basic_segmentedamplitude.png"); nothing # hide
#md # 
# and phase.
plot(ranges/1000, rad2deg.(p);
xlabel="range (km)", ylabel="phase (deg)",
linewidth=1.5, legend=false)
#md savefig("basic_segmentedphase.png"); nothing # hide
#md # 
#
# Comparing to the plots for the `HomogeneousWaveguide` above, the results are
# the same for the first 1000 km and differ for the second 1000 km where there
# is a different ionosphere in the `SegmentedWaveguide` scenario.
#
# ## `LMPParams`
#
# Many functions within the LongwaveModePropagator package take an optional `params`
# argument [`LMPParams`](@ref). `LMPParams` is a keyword-compatible `struct` defined with
# the `@with_kw` argument from the [Parameters.jl](https://github.com/mauro3/Parameters.jl)
# package. An instance of `LMPParams` contains model parameters and switches used throughout
# the package.
#
# The default values are obtained by invoking
LMPParams()
# A single value can be specified as a keyword argument while keeping all other values as
# their defaults
LMPParams(approxsusceptibility=true)
# An instance of `LMPParams` can be passed as the `params` argument of [`propagate`](@ref)
# or [`findmodes`](@ref).
#
# See the [Parameters.jl](https://github.com/mauro3/Parameters.jl) README for other ways of
# interacting with [`LMPParams`](@ref). | LongwaveModePropagator | https://github.com/fgasdia/LongwaveModePropagator.jl.git |
|
[
"MIT"
] | 0.4.1 | 792c195909ca5dfff5685305b6fa0aa16c3d1041 | code | 2793 | # # Ground
#
# LongwaveModePropagator treats the ground boundary of the Earth-ionosphere waveguide
# as a homogeneous, nonmagnetic material described by its electrical conductivity ``\sigma``
# and relative permittivity ``\epsilon_r``.
#
# In this example we'll compare the effect of ground conductivity on amplitude along
# the ground in the waveguide for day and nighttime ionospheres.
using Plots, Printf
using LongwaveModePropagator
const LMP = LongwaveModePropagator
nothing #hide
# LWPC uses standard ground indices to describe combinations of relative permittivity
# and conductivity.
# The standard indices can be accessed from LMP as [`GROUND`](@ref).
sort(GROUND)
# We'll define all of the constant types and the day and night profiles.
## Constant values
const BFIELD = BField(50e-6, π/2, 0)
const TX = Transmitter(20e3)
const RX = GroundSampler(0:5e3:3000e3, Fields.Ez)
const DAY = Species(LMP.QE, LMP.ME, z->waitprofile(z, 75, 0.3), electroncollisionfrequency)
const NIGHT = Species(LMP.QE, LMP.ME, z->waitprofile(z, 82, 0.6), electroncollisionfrequency)
nothing #hide
# We'll define a function to which we can pass the day or night `Species` and return the
# electric field amplitude.
function varyground(prf)
amps = Vector{Vector{Float64}}(undef, length(GROUND))
for i = 1:length(GROUND)
wvg = HomogeneousWaveguide(BFIELD, prf, GROUND[i])
E, a, p = propagate(wvg, TX, RX)
amps[i] = a
end
return amps
end
nothing #hide
# And here's a function to plot each of the curves.
function buildplots!(p, amps)
cmap = palette(:thermal, length(GROUND)+1) # +1 so we don't get to yellow
for i = 1:length(GROUND)
plot!(p, RX.distance/1000, amps[i];
label=@sprintf("%d, %.1g", GROUND[i].ϵᵣ, GROUND[i].σ), color=cmap[i]);
end
end
nothing #hide
# First, the daytime results.
amps = varyground(DAY)
p = plot()
buildplots!(p, amps)
plot!(p; size=(600,400), ylims=(0, 95), title="Day", legend=(0.85, 1.02),
xlabel="Range (km)", ylabel="Amplitude (dB)", legendtitle="ϵᵣ, σ")
#md savefig(p, "ground_day.png"); nothing # hide
#md # 
# And now nighttime.
amps = varyground(NIGHT)
p = plot()
buildplots!(p, amps)
plot!(p; size=(600,400), ylims=(0, 95), title="Night", legend=(0.85, 1.02),
xlabel="Range (km)", ylabel="Amplitude (dB)", legendtitle="ϵᵣ, σ")
#md savefig(p, "ground_night.png"); nothing # hide
#md # 
# Low ground conductivity can have a significant influence on the signal propagation -
# there is strong attenuation.
# These low conductivities can be found in areas of sea or polar ice and industrial or
# city areas.
#
# The influence of ground conductivity on the received signal has similar impact on
# the day and night scenarios.
| LongwaveModePropagator | https://github.com/fgasdia/LongwaveModePropagator.jl.git |
|
[
"MIT"
] | 0.4.1 | 792c195909ca5dfff5685305b6fa0aa16c3d1041 | code | 10258 | # # Solvers for ionosphere reflection coefficient
#
# LongwaveModePropagator uses the technique presented by
# [Budden (1955)](https://doi.org/10.1098/rspa.1955.0027) to compute the reflection
# coefficient of a horiontally stratified ionosphere consisting of an
# anisotropic, collisional plasma.
#
# Budden (1955) derives a differential equation for the reflection coefficient
# ``\bm{R}``:
# ```math
# \frac{2i}{k}\frac{\mathrm{d}\bm{R}}{\mathrm{d}z} = W_{21} + W_{22}\bm{R} - \bm{R}W_{11} - \bm{R}W_{12}\bm{R}
# ```
# where ``W`` is a ``4\times 4`` matrix divided into four ``2\times 2`` submatrices
# each containing components of the ``\bm{T}`` matrix.
#
# To obtain the reflection coefficient ``\bm{R}`` at any level, we integrate
# ``\mathrm{d}\bm{R}/\mathrm{d}z`` downward through the ionosphere from a great height
# and the height at which we stop is ``\bm{R}`` for a sharp boundary at that level with
# free space below.
#
# The reflection coefficient matrix ``\bm{R}`` consists of four complex reflection
# coefficients for the different combinations of incident and reflected wave
# polarization. These reflection coefficients are also functions of the wave
# angle of incidence, and therefore the integration of ``\mathrm{d}\bm{R}/\mathrm{d}z``
# occurs tens of thousands to hundreds of thousands of times for every
# `HomogeneousWaveguide` in the GRPF mode finder. It is therefore extremely important
# that the differential equations solver be as efficient as possible to minimize
# runtime.
# The mode finder is responsible for more than 90% of the runtime of
# LongwaveModePropagator, and most of the mode finder runtime is the ionosphere
# reflection coefficient integration.
#
# In this example, we will compare solvers and tolerances from
# DifferentialEquations to determine the most efficient combination with reasonable
# robustness and accuracy.
# We will begin by looking at the reflection coefficients as a function of height.
#
# First we load the packages we need.
using Statistics
using Plots
using OrdinaryDiffEq
using Interpolations
using LongwaveModePropagator
using LongwaveModePropagator: StaticArrays, QE, ME
const LMP = LongwaveModePropagator
nothing #hide
# ## R(z)
#
# Let's examine the four reflection coefficients for the ionosphere as a function
# of height.
#
# We will use a typical daytime ionosphere with a Wait and Spies (1964) profile
# and a wave frequency of 24 kHz.
# The background magnetic field will be vertical with a magnitude of 50,000 nT.
# We also need to specify the wave angle of incidence on the ionosphere.
# We'll use a real ``\theta = 75°``.
species = Species(QE, ME, z->waitprofile(z, 75, 0.32), electroncollisionfrequency)
frequency = Frequency(24e3)
bfield = BField(50e-6, π/2, 0)
ea = EigenAngle(deg2rad(75));
# We start the integration at a "great height".
# For longwaves, anything above the D-region is fine.
# LongwaveModePropagator defaults to a `topheight` of 110 km.
topheight = 110e3
Mtop = LMP.susceptibility(topheight, frequency, bfield, species)
Rtop = LMP.bookerreflection(ea, Mtop)
# The starting solution `Rtop` comes from a solution of the Booker quartic for the
# wavefields at `topheight`.
#
# We use OrdinaryDiffEq.jl to integrate [`LongwaveModePropagator.dRdz`](@ref).
# Although it's not needed for computing the ionosphere reflection coefficient,
# `dRdz` takes a `ModeEquation` argument, specifying a complete waveguide,
# including `Ground`, for convenience.
ground = GROUND[1]
waveguide = HomogeneousWaveguide(bfield, species, ground)
me = PhysicalModeEquation(ea, frequency, waveguide);
# Then we simply define the `ODEProblem` and `solve`.
prob = ODEProblem{false}(LMP.dRdz, Rtop, (topheight, 0.0), me)
sol = solve(prob, RK4(); abstol=1e-9, reltol=1e-9);
# Let's plot the reflection coefficients next to the electron density and collision
# frequency curves.
# Because the reflection coefficients are complex-valued, we will plot their magnitude.
zs = topheight:-1000:0
ne = species.numberdensity.(zs)
nu = species.collisionfrequency.(zs)
Wr = LMP.waitsparameter.(zs, (frequency,), (bfield,), (species,))
altinterp = linear_interpolation(reverse(Wr), reverse(zs))
eqz = altinterp(frequency.ω) # altitude where ω = ωᵣ
ne[end] = NaN # otherwise Plots errors
Wr[end] = NaN
p1 = plot([ne nu Wr], zs/1000;
xlims=(10, 10^10), xaxis=(scale=:log10),
ylabel="Altitude (km)",
labels=["Nₑ (m⁻³)" "ν (s⁻¹)" "ωᵣ = ωₚ²/ν"], legend=:topleft,
linewidth=1.5);
vline!(p1, [frequency.ω]; linestyle=:dash, color="gray", label="");
hline!(p1, [eqz/1000]; linestyle=:dash, color="gray", label="");
annotate!(p1, frequency.ω, 10, text(" ω", :left, 9));
annotate!(p1, 70, eqz/1000-3, text("ωᵣ = ω", :left, 9));
R11 = vec(abs.(sol(zs; idxs=1)))
R21 = vec(abs.(sol(zs; idxs=2)))
R12 = vec(abs.(sol(zs; idxs=3)))
R22 = vec(abs.(sol(zs; idxs=4)))
p2 = plot([R11 R21 R12 R22], zs/1000;
xlims=(0, 1),
yaxis=false, yformatter=_->"",
legend=:right, labels=["R₁₁" "R₂₁" "R₁₂" "R₂₂"],
linewidth=1.5);
hline!(p2, [eqz/1000]; linestyle=:dash, color="gray", label="");
plot(p1, p2; layout=(1,2), size=(800, 400))
#md savefig("integratedreflection_xyz.png"); nothing # hide
#md # 
#
# ## Generate random scenarios
#
# Now that we've seen what the reflection coefficient functions look like,
# we'll focus on finding an accurate but efficient solver.
#
# We will evaluate the solutions across a range of different random ionospheres,
# frequencies, and angles of incidence.
# Each scenario is described by a [`PhysicalModeEquation`](@ref).
function generatescenarios(N)
eas = EigenAngle.(complex.(rand(N)*(π/2-π/6) .+ π/6, rand(N)*deg2rad(-10)))
frequencies = Frequency.(rand(N)*50e3 .+ 10e3)
B = rand(30e-6:5e-7:60e-6, N)
## avoiding within 1° from 0° dip angle
bfields = BField.(B, rand(N)*(π/2-0.018) .+ 0.018, rand(N)*2π)
hps = rand(N)*20 .+ 69
betas = rand(N)*0.8 .+ 0.2
scenarios = Vector{PhysicalModeEquation}(undef, N)
for i = 1:N
species = Species(QE, ME, z->waitprofile(z, hps[i], betas[i]),
electroncollisionfrequency)
ground = GROUND[5] ## not used in integration of R
waveguide = HomogeneousWaveguide(bfields[i], species, ground)
me = PhysicalModeEquation(eas[i], frequencies[i], waveguide)
scenarios[i] = me
end
return scenarios
end
scenarios = generatescenarios(30);
# ## Reference solutions
#
# To evaluate the accuracy of the reflection coefficients, we compare to a very
# low tolerance Runge-Kutta Order 4 method. The DifferentialEquations implementation
# of `RK4` uses adaptive stepping.
#
# The [`LongwaveModePropagator.integratedreflection`](@ref) function does the
# integration process above for us
# and returns the reflection coefficient at the ground.
ip = IntegrationParams(tolerance=1e-14, solver=RK4(), maxiters=1_000_000)
params = LMPParams(integrationparams=ip)
Rrefs = [LMP.integratedreflection(scenario; params=params) for scenario in scenarios];
# ## Evaluate solvers
#
# Now let's compute and time the results a set of different methods for a range
# of tolerances.
# We repeat the integration `N = 25` times for each combination of parameters
# to get a more accurate average time.
function compute(scenarios, tolerances, solvers)
dims = length(scenarios), length(tolerances), length(solvers)
Rs = Array{StaticArrays.SMatrix{2,2,ComplexF64,4}}(undef, dims...)
times = Array{Float64}(undef, dims...)
for k in eachindex(solvers)
for j in eachindex(tolerances)
ip = IntegrationParams(tolerance=tolerances[j], solver=solvers[k])
params = LMPParams(integrationparams=ip)
for i in eachindex(scenarios)
## warmup
R = LMP.integratedreflection(scenarios[i]; params=params)
## loop for average time
N = 25
t0 = time_ns()
for n = 1:N
R = LMP.integratedreflection(scenarios[i]; params=params)
end
ttotal = time_ns() - t0
Rs[i,j,k] = R
times[i,j,k] = ttotal/N
end
end
end
return Rs, times
end
tolerances = [1e-4, 1e-5, 1e-6, 1e-7, 1e-8, 1e-9, 1e-10]
tolerancestrings = string.(tolerances)
solvers = [RK4(), Tsit5(), BS5(), OwrenZen5(), Vern6(), Vern7(), Vern8()]
solverstrings = ["RK4", "Tsit5", "BS5", "OwrenZen5", "Vern6", "Vern7", "Vern8"]
Rs, times = compute(scenarios, tolerances, solvers);
# We'll measure the error in the reflection coefficient matrices
# as the maximum absolute difference of the four elements of the matrix
# compared to the reference reflection coefficient matrix.
function differr(a, ref)
differences = a .- ref
aerror = similar(a, Float64)
for i in eachindex(differences)
absdiff = abs.(differences[i])
aerror[i] = maximum(absdiff)
end
return aerror
end
Rerrs = differr(Rs, Rrefs)
mean_Rerrs = dropdims(mean(Rerrs; dims=1); dims=1)
heatmap(tolerancestrings, solverstrings, permutedims(log10.(mean_Rerrs));
clims=(-9, -2),
xlabel="tolerance", ylabel="solver",
colorbar_title="log₁₀ max abs difference", colorbar=true)
#md savefig("integratedreflection_difference.png"); nothing # hide
#md # 
# And the average runtimes are
mean_times = dropdims(mean(times; dims=1); dims=1)
heatmap(tolerancestrings, solverstrings, permutedims(mean_times)/1e6;
clims=(0, 5),
xlabel="tolerance", ylabel="solver",
colorbar_title="time (μs)", colorbar=true)
#md savefig("integratedreflection_time.png"); nothing # hide
#md # 
# The best accuracy occurs with `Vern7` and experiment's we've done looking at the
# sensitivity of the mode solutions to integration tolerance have shown we can get away
# with a tolerance of `1e-4`. To play it safe, the default used by LMP is `1e-5`.
# The integration accuracy improves considerably for relatively little additional
# computation time if the tolerance is changed to `1e-9`, but that accuracy is not
# required.
| LongwaveModePropagator | https://github.com/fgasdia/LongwaveModePropagator.jl.git |
|
[
"MIT"
] | 0.4.1 | 792c195909ca5dfff5685305b6fa0aa16c3d1041 | code | 9494 | # # [Density and collision frequency as interpolating functions](@id interpolating-functions)
#
# The ionospheric [`Species`](@ref) type used when defining a [`HomogeneousWaveguide`](@ref)
# requires `numberdensity` and `collisionfrequency` fields to be callable functions of
# altitude `z` in meters that return `Float64` values of number density in m⁻³ and
# species-neutral collision frequency in s⁻¹.
#
# Sometimes a simple analytical function can be provided, such as [`waitprofile`](@ref).
# Other times, the profile is constructed from tabular data at discrete heights which must
# be wrapped in an interpolator before being passed to `Species`.
#
# The choice of interpolating function not only impacts the accuracy of the propagation
# result (how well the interpolation resembles the true profile), but it can also impact
# the runtime of [`propagate`](@ref) and related functions.
#
# In this example we'll compare a few different interpolating functions.
#
# ## Profiles and interpolators
#
# We'll use the [FIRI-2018](https://doi.org/10.1029/2018JA025437) profiles from
# [FaradayInternationalReferenceIonosphere.jl](https://github.com/fgasdia/FaradayInternationalReferenceIonosphere.jl) which are slightly more
# complicated than a pure exponential profile. The package isn't registered, but can be
# installed from the Pkg by copy-pasting the entire url.
#
# From [Interpolations.jl](https://github.com/JuliaMath/Interpolations.jl) we'll use
# a linear interpolator, a cubic spline interpolator, and monotonic interpolators.
# We'll use [NormalHermiteSplines.jl](https://github.com/IgorKohan/NormalHermiteSplines.jl)
# to construct Hermite splines.
using Printf, Statistics
using LongwaveModePropagator
using LongwaveModePropagator: QE, ME
using Plots, Distances
using FaradayInternationalReferenceIonosphere
using Interpolations, NormalHermiteSplines
nothing #hide
const FIRI = FaradayInternationalReferenceIonosphere
# Here's the discrete profile data. Some interpolators will benefit from random sample
# points, but most density data will be on a grid. The profile uses an exponential
# extrapolation of the base of FIRI from about 60 km altitude down to the ground.
zs = 0:1e3:110e3
Ne = FIRI.extrapolate(firi(50, 30), zs);
# Let's construct the interpolators.
linear_itp = linear_interpolation(zs, Ne)
cubic_itp = cubic_spline_interpolation(zs, Ne);
# There's not great documentation on the monotonic interpolators of Interpolations.jl as of
# `v0.13`, but several are supported.
fb_itp = Interpolations.interpolate(zs, Ne, FritschButlandMonotonicInterpolation())
fc_itp = Interpolations.interpolate(zs, Ne, FritschCarlsonMonotonicInterpolation())
s_itp = Interpolations.interpolate(zs, Ne, SteffenMonotonicInterpolation());
# And the Hermite splines
spline = prepare(collect(zs), RK_H1())
spline = construct(spline, Ne)
hermite_itp(z) = evaluate_one(spline, z);
# (a spline built with RK_H0 kernel is a continuous function,
# a spline built with RK_H1 kernel is a continuously differentiable function,
# a spline built with RK_H2 kernel is a twice continuously differentiable function).
zs_fine = 40e3:100:110e3
Ne_fine = FIRI.extrapolate(firi(50, 30), zs_fine);
linear_fine = linear_itp.(zs_fine)
cubic_fine = cubic_itp.(zs_fine)
fb_fine = fb_itp.(zs_fine)
fc_fine = fc_itp.(zs_fine)
s_fine = s_itp.(zs_fine)
hermite_fine = hermite_itp.(zs_fine);
# The profiles are compared using percentage difference relative to the true profile.
cmp(a,b) = (a - b)/b*100
dNe = cmp.(Ne_fine, Ne_fine)
dlinear = cmp.(linear_fine, Ne_fine)
dcubic = cmp.(cubic_fine, Ne_fine)
dfb = cmp.(fb_fine, Ne_fine)
dfc = cmp.(fc_fine, Ne_fine)
ds = cmp.(s_fine, Ne_fine)
dhermite = cmp.(hermite_fine, Ne_fine);
# To plot densities with a log scale, we set values less than 0.1 to NaN.
cl(x) = replace(v->v <= 0.1 ? NaN : v, x)
lc(x) = replace(x, NaN => 0)
p1 = plot(cl([Ne_fine linear_fine cubic_fine hermite_fine fb_fine fc_fine s_fine]),
zs_fine/1000, xscale=:log10, xlabel="Ne (m⁻³)", ylabel="Altitude (km)",
legend=:topleft, labels=["Truth" "Linear" "Cubic" "Hermite" "FritschButland" "FritschCarlson" "Steffen"])
p2 = plot(lc([dNe dlinear dcubic dhermite dfb dfc ds]),
zs_fine/1000, xlabel="% difference", legend=false, xlims=(-1, 1))
plot(p1, p2, layout=(1,2), size=(800,400), margin=3Plots.mm)
#md savefig("interpolatingfunctions_profiles.png"); nothing # hide
#md # 
# Unsurprisingly, the error is highest at the cutoff altitude of 40 km where the densities
# below are 0.
# The linear interpolation has positive-biased errors at all other heights because linear
# interpolation does not accurately capture the true exponential profile.
# To avoid this, the interpolator could have been constructed with a finer initial grid, but
# that is not always possible.
#
# Let's compute the total absolute difference between each interpolator and the truth and
# also compute the average percentage difference for each:
for (n, v) in ("linear"=>(linear_fine, dlinear), "cubic"=>(cubic_fine, dcubic),
"hermite"=>(hermite_fine, dhermite), "FritschButland"=>(fb_fine, dfb),
"FritschCarlson"=>(fc_fine, dfc), "Steffen"=>(s_fine, ds))
@printf("%s: %.3g %.3g\n", n, cityblock(Ne_fine, v[1]), mean(abs, v[2]))
end
# Somewhat surprisingly, the linear interpolation has the lowest total absolute difference
# from the truth despite the fact that (as seen in the plot) the percentile difference from
# the linear interpolation to the truth is very high.
#
# ## Propagation results
#
# Let's compare propagation results and performance with each of these interpolators.
# Unfortunately, as of `v0.5.1` of NormalHermiteSplines.jl, the implementation of the
# package isn't efficient (see #3)[https://github.com/IgorKohan/NormalHermiteSplines.jl/issues/3]
# and because `hermite_itp` would be called millions of times in `propagate`, it is
# prohibitively slow.
#
# Here are the `Species` for each of the other interpolators.
# They will all use the analytic [`electroncollisionfrequency`](@ref).
#
# There's no functional form of the truth FIRI profile, so we'll build a fine FritschButland
# interpolator and call it the truth.
interpolators = (
"truth" => Interpolations.interpolate(0:100:110e3,
FIRI.extrapolate(firi(50, 30), 0:100:110e3),
FritschButlandMonotonicInterpolation()),
"linear"=> linear_itp,
"cubic" => cubic_itp,
"FritschButland" => fb_itp,
"FritschCarlson" => fc_itp,
"Steffen" => s_itp
)
function propagateitp(interpolators)
bfield = BField(50e-6, deg2rad(68), deg2rad(111))
ground = GROUND[5]
tx = Transmitter(24e3)
rx = GroundSampler(0:5e3:3000e3, Fields.Ez)
results = Dict{String,Tuple{Float64,Vector{Float64},Vector{Float64}}}()
for (n, itp) in interpolators
species = Species(QE, ME, itp, electroncollisionfrequency)
waveguide = HomogeneousWaveguide(bfield, species, ground)
t0 = time()
_, amp, phase = propagate(waveguide, tx, rx)
runtime = time() - t0
results[n] = (runtime, amp, phase)
end
return results
end
propagateitp(interpolators); # warmup
results = propagateitp(interpolators);
# First let's evaluate the propagation results.
d = 0:5:3000
p1 = plot(ylabel="Amplitude (dB μV/m)")
p2 = plot(xlabel="Range (km)", ylims=(-0.02, 0.02), ylabel="Δ", legend=false)
for (n, v) in results
plot!(p1, d, v[2], label=n)
plot!(p2, d, v[2]-results["truth"][2])
end
plot(p1, p2, layout=grid(2,1,heights=[0.7, 0.3]))
#md savefig("interpolatingfunctions_amp.png"); nothing # hide
#md # 
p1 = plot(ylabel="Phase (deg)")
p2 = plot(xlabel="Range (km)", ylims=(-0.4, 0.4), ylabel="Δ", legend=false)
for (n, v) in results
plot!(p1, d, rad2deg.(v[3]), label=n)
plot!(p2, d, rad2deg.(v[3])-rad2deg.(results["truth"][3]))
end
plot(p1, p2, layout=grid(2,1,heights=[0.7, 0.3]))
#md savefig("interpolatingfunctions_phase.png"); nothing # hide
#md # 
# Here is the mean absolute amplitude difference between each technique and the true profile
# amplitude. We filter to finite values because the amplitude calculated at 0 meters is `Inf`.
for n in ("linear", "cubic", "FritschButland", "FritschCarlson", "Steffen")
@printf("%s: %.3e\n",n, meanad(filter(isfinite,results[n][2]),
filter(isfinite,results["truth"][2])))
end
# The amplitude and phase for each of the interpolators matches the true exponential profile
# extremely closely relative to the typical noise of real VLF measurements.
#
# Timing can vary when run by GitHub to build the documentation, so results here are from a
# local run:
#
# | Interpolator | Runtime relative to `truth` |
# | -------------- | --------------------------- |
# | truth | 1 |
# | linear | 0.84 |
# | cubic | 0.85 |
# | FritschButland | 0.91 |
# | FritschCarlson | 0.92 |
# | Steffen | 0.82 |
#
# Really, any of these except for the linear interpolation could be used to interpolate a
# discrete profile. The Steffen and cubic interpolations are fastest, but the FritschButland is a
# little more true to the actual profile. It's for that reason that FritschButland is used
# to interpolate [`TableInput`](@ref) types in LongwaveModePropagator.
| LongwaveModePropagator | https://github.com/fgasdia/LongwaveModePropagator.jl.git |
|
[
"MIT"
] | 0.4.1 | 792c195909ca5dfff5685305b6fa0aa16c3d1041 | code | 10795 | # # [Interpreting h′ and β](@id interpreting-hpbeta)
#
# This example looks at the influence of h′, β, electron collision frequency,
# and transmitter frequency on amplitude curves.
#
# ## Background
#
# [Wait and Spies (1964)](https://archive.org/details/characteristicso300wait) is a
# technical report which characterizes the influence of Earth-ionosphere waveguide
# parameters on the propagation of VLF radio waves (the attenuation rates, phase velocities,
# etc.).
# The report is probably most cited[^1] as the source of the exponential electron
# density profile parameterized by a height h′ (km) and slope β (km⁻¹).
# The profile is usually written as:
# ```math
# N(z) = 1.43\times 10^{13} \exp(-0.15 h') \exp((\beta - 0.15)(z - h'))
# ```
# for density ``N`` (m⁻³) and altitude ``z`` (km), but as described in
# [Morfitt (1977)](https://apps.dtic.mil/docs/citations/ADA047508) or
# [Thomson (1993)](https://doi.org/10.1016/0021-9169(93)90122-F), Wait and Spies (1964)
# does not explicitly introduce this form.
# Instead, Wait introduces a "conductivity parameter" ``\omega_r`` defined by
# ```math
# \omega_r = \omega_p^2/\nu
# ```
# where ``\omega_p`` is the angular plasma frequency of the electrons and ``\nu`` is the
# effective collision frequency.
# The height at which ``\omega_r = \omega``, the angular radio wave frequency is
# approximately the wave reflection height. This statement is equivalent to ``X = Z`` from
# magnetoionic theory ([Ratcliffe (1959)](https://books.google.com/books/about/The_magneto_ionic_theory_and_its_applica.html?id=lRQvAAAAIAAJ)).
#
# Citing laboratory and some observational experiments, Wait assumes an analytical
# collision frequency profile
# ```math
# \nu = 5 \times 10^6 \exp(-0.15(z - 70)).
# ```
# Using daytime measurements made by the method of partial reflection, he calculates
# the approximation
# ```math
# \omega_r = (2.5\times 10^5)\exp(0.3(z - 70)).
# ```
# To fit measurements made at other times and locations, he parameterizes the function
# as
# ```math
# \omega_r = (2.5 \times 10^5)\exp(\beta(z - h'))
# ```
# where "``\beta`` is a constant and ``h'`` is a reference height" (the height at which
# ``\omega_r = 2.5\times 10^5``).
# He immediately suggests ``\beta = 0.3`` at day and ``\beta = 0.5`` at night, which are
# largely considered typical values today.
# Wait also parameterizes the collision frequency profile as
# ```math
# \nu(z) = \nu_0\exp(-az).
# ```
# Wait fixed ``a=0.15`` for his studies in the report.
#
# [Morfitt and Shellman (1976)](http://www.dtic.mil/docs/citations/ADA032573)
# cites Wait and Spies and uses
# ```math
# \nu(z) = 1.82\times 10^{11} \exp(-0.15 z)
# ```
# from this, it is simple to derive the equation attributed to
# Wait and Spies (1964). The ``(\beta - 0.15)`` term comes from the assumption
# ``N(z) = N_0\exp(bz)`` and ``\nu(z) = \nu_0\exp(-az)`` where ``\beta = a + b`` and
# ``a = 0.15``.
using Printf, Plots, Interpolations
using LongwaveModePropagator
const LMP = LongwaveModePropagator
## Constant values
const BFIELD = BField(50e-6, π/2, 0)
const GND = GROUND[5]
const TX = Transmitter(20e3)
const RX = GroundSampler(0:5e3:3000e3, Fields.Ez)
nothing #hide
# ## Varying h′
#
# In this section we set the frequency to 20 kHz, β is set to 0.4 km⁻¹ and we vary h′.
function varyhp(hprimes)
amps = Vector{Vector{Float64}}(undef, length(hprimes))
for i in eachindex(hprimes)
electrons = Species(LMP.QE, LMP.ME, z->waitprofile(z, hprimes[i], 0.4), electroncollisionfrequency)
waveguide = HomogeneousWaveguide(BFIELD, electrons, GND)
E, a, p = propagate(waveguide, TX, RX)
amps[i] = a
end
return amps
end
hprimes = 72:1:78
amps = varyhp(hprimes)
p = plot();
function buildplots!(p, amps)
cmap = palette(:amp, length(hprimes)+1) # +1 allows us to use a darker lightest color
for i in eachindex(hprimes)
plot!(p, RX.distance/1000, amps[i];
label=hprimes[i], color=cmap[i+1]);
end
end
buildplots!(p, amps);
plot!(p; size=(600,400), ylims=(22, 95),
xlabel="Range (km)", ylabel="Amplitude (dB)", legendtitle="h′")
#md savefig(p, "interpreting_hprimes.png"); nothing # hide
#md # 
# As h′ increases, the field strength modal interference pattern is displaced outwardly
# away from the transmitter.
# ## Varying β
#
# Now we'll fix h′ at 78 km and vary β.
function varybeta(betas)
amps = Vector{Vector{Float64}}(undef, length(betas))
for i in eachindex(betas)
electrons = Species(LMP.QE, LMP.ME, z->waitprofile(z, 78, betas[i]), electroncollisionfrequency)
waveguide = HomogeneousWaveguide(BFIELD, electrons, GND)
E, a, p = propagate(waveguide, TX, RX)
amps[i] = a
end
return amps
end
betas = [0.3, 0.4, 0.5, 0.7, 0.9, 2.0]
amps = varybeta(betas)
p = plot();
function buildplots!(p, amps)
cmap = palette(:amp, length(betas)+1)
for i in eachindex(betas)
plot!(p, RX.distance/1000, amps[i];
label=betas[i], color=cmap[i+1]);
end
end
buildplots!(p, amps);
plot!(p; size=(600,400), ylims=(22, 95),
xlabel="Range (km)", ylabel="Amplitude (dB)", legendtitle="β")
#md savefig(p, "interpreting_betas.png"); nothing # hide
#md # 
# The signal roughly increases with increasing β.
# Higher β profiles more closely represent a sharp reflecting boundary.
#
# It may be more accurate to say that higher β ionospheres lead to more extreme amplitudes -
# higher highs and lower lows.
# Morfitt (1977) describes this as an increase in β leads to the signal levels varying
# over a wider range in the regions of strong modal interference.
# ## Varying frequency
#
# In this section we'll look at an ionosphere described with typical daytime
# Wait profile parameters, but we'll vary the radio frequency from 5 kHz to 50 kHz.
function varyfreq(freqs)
electrons = Species(LMP.QE, LMP.ME, z->waitprofile(z, 75, 0.35), electroncollisionfrequency)
waveguide = HomogeneousWaveguide(BFIELD, electrons, GND)
amps = Vector{Vector{Float64}}(undef, length(freqs))
for i in eachindex(freqs)
tx = Transmitter(freqs[i])
E, a, p = propagate(waveguide, tx, RX)
amps[i] = a
end
return amps
end
freqs = 5e3:5e3:50e3
amps = varyfreq(freqs)
p = plot();
function buildplots!(p, amps)
pal = palette(:rainbow, 7)
cmap = [pal[1]; range(pal[2], pal[3]; length=2); range(pal[4], pal[5]; length=4);
range(pal[6], pal[7]; length=3)]
for i in eachindex(freqs)
fkHz = trunc(Int, freqs[i]/1000)
λkm = trunc(LMP.C0/freqs[i]/1000; digits=1)
plot!(p, RX.distance/1000, amps[i] .+ (10*i);
label=string(fkHz, ", ", λkm), color=cmap[i]);
end
end
buildplots!(p, amps);
plot!(p; size=(600,400),
xlabel="Range (km)", ylabel="Amplitude (dB)", legendtitle="f kHz, λ km")
#md savefig(p, "interpreting_frequencies.png"); nothing # hide
#md # 
# The effect of increasing frequency is similar to increasing h′.
# This makes sense because in both cases the waveguide "height" in wavelengths is
# increassing.
# ## Collision frequency
#
# So far all of the profiles generated above have used the electron collision frequency
# from Morfitt and Shellman (1976).
# Let's look at the effect of different collision frequency profiles.
#
# First we'll plot the collision frequency profiles themselves.
# On the plots we'll also mark the approximate reflection height for `TX.frequency` where
# ``\omega_r = \omega`` for a typical daytime electron density profile.
collisionfrequency(z, ν₀, a) = ν₀*exp(-a*z/1000) # 1/1000 converts `z` to km
function reflectionheight(params, hp, β)
species = Species(LMP.QE, LMP.ME,
z->waitprofile(z, hp, β), z->collisionfrequency(z, params...))
ωr = LMP.waitsparameter.(alt, (TX.frequency,), (BFIELD,), (species,))
itp = linear_interpolation(ωr, alt)
eqz = itp(TX.frequency.ω)
return eqz
end
alt = 40e3:500:110e3
params = [(1.816e11, 0.18),
(1.816e11/5, 0.15), (1.816e11, 0.15), (1.816e11*5, 0.15),
(1.816e11, 0.12)]
p = plot();
function buildplots!(p, params, hp, β)
cmap = palette(:rainbow, length(params))
for i in eachindex(params)
eqz = reflectionheight(params[i], hp, β)
v₀label = params[i][1]/1.816
plot!(p, collisionfrequency.(alt, params[i]...), alt/1000;
label=@sprintf("%.0e, %.2f", v₀label, params[i][2]), color=cmap[i]);
hline!(p, [eqz/1000]; linestyle=:dash, color=cmap[i], linewidth=0.6, label=nothing)
end
end
buildplots!(p, params, 75, 0.35);
annotate!(p, [(1e3, 64, text("ωᵣ = ω", 10))])
plot!(p; size=(600,400), xscale=:log10,
xlabel="ν (s⁻¹)", ylabel="Altitude (km)", legendtitle="1.816 ν₀, a")
#md savefig(p, "interpreting_collisionprofile.png"); nothing # hide
#md # 
# Typical daytime electron density profile.
function varycollisionfreq(params, hp, β)
amps = Vector{Vector{Float64}}(undef, length(params))
for i in eachindex(params)
electrons = Species(LMP.QE, LMP.ME,
z->waitprofile(z, hp, β), z->collisionfrequency(z, params[i]...))
waveguide = HomogeneousWaveguide(BFIELD, electrons, GND)
E, a, p = propagate(waveguide, TX, RX)
amps[i] = a
end
return amps
end
amps = varycollisionfreq(params, 75, 0.35)
p = plot();
function buildplots!(p, amps)
cmap = palette(:rainbow, length(params))
for i in eachindex(params)
v₀label = params[i][1]/1.816
plot!(p, RX.distance/1000, amps[i];
label=@sprintf("%.0e, %.2f", v₀label, params[i][2]), color=cmap[i]);
end
end
buildplots!(p, amps);
plot!(p; size=(600,400), ylims=(22, 95),
xlabel="Range (km)", ylabel="Amplitude (dB)", legendtitle="1.816 ν₀, a")
#md savefig(p, "interpreting_collisionday.png"); nothing # hide
#md # 
# Typical nighttime electron density profile.
amps = varycollisionfreq(params, 82, 0.55)
p = plot();
function buildplots!(p, amps)
cmap = palette(:rainbow, length(params))
for i in eachindex(params)
v₀label = params[i][1]/1.816
plot!(p, RX.distance/1000, amps[i];
label=@sprintf("%.0e, %.2f", v₀label, params[i][2]), color=cmap[i]);
end
end
buildplots!(p, amps);
plot!(p; size=(600,400), ylims=(22, 95),
xlabel="Range (km)", ylabel="Amplitude (dB)", legendtitle="1.816 ν₀, a")
#md savefig(p, "interpreting_collisionnight.png"); nothing # hide
#md # 
# [^1]: As a government technical report and not a journal paper curated by a publishing company, it is difficult to track how many times it has been cited by others. | LongwaveModePropagator | https://github.com/fgasdia/LongwaveModePropagator.jl.git |
|
[
"MIT"
] | 0.4.1 | 792c195909ca5dfff5685305b6fa0aa16c3d1041 | code | 10730 | # # File-based I/O
#
# LongwaveModePropagator provides basic propagation capabilities
# interfacing through [JSON](https://www.json.org/json-en.html) files.
# Julia is still needed to run the model, but scenarios can otherwise
# be defined and analyzed from e.g. Matlab or Python.
#
# Examples of writing and reading compatible JSON files are provided below
# for [Matlab](@ref matlab_json) and [Python](@ref python_json).
#
# Let's load the necessary packages.
using Dates
using JSON3
using LongwaveModePropagator
nothing #hide
# Throughout the examples, we'll also define `LMP` as shorthand for
# `LongwaveModePropagator` when accessing functions from the package that
# aren't exported.
const LMP = LongwaveModePropagator
nothing #hide
# ## Inputs
#
# There are two primary ways to define [`LongwaveModePropagator.Input`](@ref)s,
# the abstract supertype for
# inputing information to the model.
#
# ### [ExponentialInput](@id basicinput_io)
#
# The first is known as a [`ExponentialInput`](@ref). It defines the ionosphere using
# Wait and Spies ``h'`` and ``\beta`` parameters.
#
# It contains the fields
#
# - `name::String`
# - `description::String`
# - `datetime::DateTime`
# - `segment_ranges::Vector{Float64}`: distance from transmitter to the beginning of each `HomogeneousWaveguide` segment in meters.
# - `hprimes::Vector{Float64}`: Wait's ``h'`` parameter for each `HomogeneousWaveguide` segment.
# - `betas::Vector{Float64}`: Wait's ``\beta`` parameter for each `HomogeneousWaveguide` segment.
# - `b_mags::Vector{Float64}`: magnetic field magnitude for each `HomogeneousWaveguide` segment.
# - `b_dips::Vector{Float64}`: magnetic field dip angles in radians for each `HomogeneousWaveguide` segment.
# - `b_azs::Vector{Float64}`: magnetic field azimuth in radians "east" of the propagation direction for each `HomogeneousWaveguide` segment.
# - `ground_sigmas::Vector{Float64}`: ground conductivity in Siemens per meter for each `HomogeneousWaveguide` segment.
# - `ground_epsrs::Vector{Int}`: ground relative permittivity for each `HomogeneousWaveguide` segment.
# - `frequency::Float64`: transmitter frequency in Hertz.
# - `output_ranges::Vector{Float64}`: distances from the transmitter at which the field will be calculated.
#
# The fields that are vectors allow the definition of a [`SegmentedWaveguide`](@ref)
# where each element of the vector is its own [`HomogeneousWaveguide`](@ref) segment.
# Single element vectors are treated as a single `HomogeneousWaveguide`.
#
# To show the equivalent JSON format, we'll build a simple, homogeneous ionosphere
# `ExponentialInput`. It's defined as a `mutable struct`, so it is simple to specify the
# fields one by one.
input = ExponentialInput()
input.name = "basic"
input.description = "Test ExponentialInput"
input.datetime = DateTime("2020-12-29T05:00:00.000") # usually `Dates.now()`
input.segment_ranges = [0.0]
input.hprimes = [75]
input.betas = [0.35]
input.b_mags= [50e-6]
input.b_dips = [π/2]
input.b_azs = [0.0]
input.ground_sigmas = [0.001]
input.ground_epsrs = [4]
input.frequency = 24e3
input.output_ranges = collect(0:100e3:1000e3)
# Here it is formatted as JSON.
json_str = JSON3.pretty(input)
# Let's also save this to a file.
json_str = JSON3.write(input)
root_dir = dirname(dirname(pathof(LongwaveModePropagator)))
examples_dir = joinpath(root_dir, "examples")
filename = joinpath(examples_dir, "basic.json")
open(filename,"w") do f
write(f, json_str)
end
nothing #hide
# ### [TableInput](@id tableinput_io)
#
# The second input is the [`TableInput`](@ref). This type defines the ionosphere using
# a tabular input of number density and collision frequency as a function of altitude.
# These tables are then cubic spline interpolated when integrating the ionosphere
# reflection coefficient and wavefields.
# See also [interpolating functions](@ref interpolating-functions).
#
# The fields of the `TableInput` are
#
# - `name::String`
# - `description::String`
# - `datetime::DateTime`
# - `segment_ranges::Vector{Float64}`: distance from transmitter to the beginning of each `HomogeneousWaveguide` segment in meters.
# - `altitude::Vector{Float64}`: altitude above ground in meters for which the `density` and `collision_frequency` profiles are specified.
# - `density::Vector{Float64}`: electron density at each `altitude` in ``m⁻³``.
# - `collision_frequency::Vector{Float64}`: electron-ion collision frequency at each `altitude` in ``s⁻¹``.
# - `b_dips::Vector{Float64}`: magnetic field dip angles in radians for each `HomogeneousWaveguide` segment.
# - `b_azs::Vector{Float64}`: magnetic field azimuth in radians "east" of the propagation direction for each `HomogeneousWaveguide` segment.
# - `ground_sigmas::Vector{Float64}`: ground conductivity in Siemens per meter for each `HomogeneousWaveguide` segment.
# - `ground_epsrs::Vector{Int}`: ground relative permittivity for each `HomogeneousWaveguide` segment.
# - `frequency::Float64`: transmitter frequency in Hertz.
# - `output_ranges::Vector{Float64}`: distances from the transmitter at which the field will be calculated.
#
# Again we'll construct a `TableInput` to look at the JSON
tinput = TableInput()
tinput.name = "table"
tinput.description = "Test TableInput"
tinput.datetime = DateTime("2020-12-29T05:00:00.000")
tinput.segment_ranges = [0.0]
tinput.altitude = collect(50e3:5e3:100e3)
tinput.density = [waitprofile.(tinput.altitude, 75, 0.3)]
tinput.collision_frequency = [electroncollisionfrequency.(tinput.altitude)]
tinput.b_mags= [50e-6]
tinput.b_dips = [π/2]
tinput.b_azs = [0.0]
tinput.ground_sigmas = [0.001]
tinput.ground_epsrs = [4]
tinput.frequency = 24e3
tinput.output_ranges = collect(0:100e3:1000e3)
json_str = JSON3.pretty(tinput)
# ### [BatchInput](@id batchinput_io)
#
# Both the `ExponentialInput` and `TableInput` types can be collected together in a
# [`BatchInput`](@ref) which has fields
# for a `name`, `description`, `datetime`, and vector of `Inputs`.
# This is useful for keeping a set of scenarios together.
# See the [test/IO.jl](@__REPO_ROOT_URL__/test/IO.jl) file
# for additional help on how these should be formatted.
#
# ## Running the model from a JSON file
#
# To run the model, [`propagate`](@ref) accepts a filename input
# (see the help for optional arguments). However, instead of returning a
# tuple of complex electric field, amplitude, and phase, it returns an `Output`
# type. Additionally, it saves the output to a JSON file.
output = propagate(filename);
# ## Outputs
#
# There are only two [`LongwaveModePropagator.Output`](@ref) types:
# [`BasicOutput`](@ref) and [`BatchOutput`](@ref).
# Both `ExponentialInput`s and `TableInput`s create `BasicOutput`s, but the `BatchInput`
# creates a `BatchOutput`.
#
# The `BasicOutput` contains fields for
#
# - `name::String`
# - `description::String`
# - `datetime::DateTime`
# - `output_ranges::Vector{Float64}`
# - `amplitude::Vector{Float64}`
# - `phase::Vector{Float64}`
#
# where `name` and `description` are directly copied from the input and `datetime`
# is when the model was run.
output
# Not surprisingly, a `BatchOutput` is simply a container holding a `Vector` of
# `BasicOutput`s, as well as some additional metadata from the corresponding `BatchInput`.
# ## [JSON I/O from Matlab](@id matlab_json)
#
# Here's an example of how to encode the above `ExponentialInput` to JSON and
# decode the output using [Matlab](https://www.mathworks.com/help/matlab/json-format.html).
# It's also in the file [examples/io.m](@__REPO_ROOT_URL__/examples/io.m).
#
# ```matlab
# % Matlab script
#
# input.name = "basic";
# input.description = "Test ExponentialInput";
# input.datetime = '2020-12-28T21:06:50.501';
#
# input.segment_ranges = {0.0};
# input.hprimes = {75};
# input.betas = {0.35};
# input.b_mags = {50e-6};
# input.b_dips = {pi/2};
# input.b_azs = {0.0};
# input.ground_sigmas = {0.001};
# input.ground_epsrs = {4};
# input.frequency = 24e3;
# input.output_ranges = 0:100e3:1000e3;
#
# json_str = jsonencode(input);
#
# fid = fopen('basic_matlab.json', 'w');
# fwrite(fid, json_str, 'char');
# fclose(fid);
# ```
#
# Matlab was used to generate the file
# [`basic_matlab.json`](@__REPO_ROOT_URL__/examples/basic_matlab.json).
# We can confirm it's parsed correctly by using the internal
# LongwaveModePropagator function [`LongwaveModePropagator.parse`](@ref), which attempts to parse
# JSON files into recognized input and output formats.
matlab_input = LMP.parse(joinpath(examples_dir, "basic_matlab.json"))
# Let's run it.
matlab_output = propagate(joinpath(examples_dir, "basic_matlab.json"));
# !!! note
# It is possible to run Julia as a script, calling it directly from a terminal
# (see [the docs](https://docs.julialang.org/en/v1/manual/getting-started/)), but
# it is probably easiest to just run the code from the REPL.
#
# 1. `cd` in a terminal to your working directory
# 2. Start up Julia: `julia`
# 3. It's recommended to `] activate .`, generating a new environment in this directory
# 4. If necessary, install LongwaveModePropagator.jl: `] add LongwaveModePropagator`
# 5. `using LongwaveModePropagator`
# 6. `propagate("basic_matlab.json")`
#
# If this has been done before in the same directory, then just do steps 1, 2, 5, 6.
#
# Reading the results file from Matlab is relatively simple.
#
# ```matlab
# % Matlab script
#
# filename = 'basic_matlab_output.json';
#
# text = fileread(filename);
#
# output = jsondecode(text);
# ```
#
# ## [JSON I/O from Python](@id python_json)
#
# Here is similar code for [Python](https://docs.python.org/3/library/json.html),
# also available in the file
# [io.py](@__REPO_ROOT_URL__/examples/io.py).
#
# ```python
# # Python script
#
# import json
# import datetime
# import numpy as np
#
# input = dict()
#
# input['name'] = "basic"
# input['description'] = "Test ExponentialInput"
# input['datetime'] = datetime.datetime.now().isoformat()[:-3]
#
# input['segment_ranges'] = [0.0]
# input['hprimes'] = [75]
# input['betas'] = [0.35]
# input['b_mags'] = [50e-6]
# input['b_dips'] = [np.pi/2]
# input['b_azs'] = [0.0]
# input['ground_sigmas'] = [0.001]
# input['ground_epsrs'] = [4]
# input['frequency'] = 24e3
# input['output_ranges'] = np.arange(0, 1000e3, 100e3).tolist()
#
# json_str = json.dumps(input)
#
# with open('basic_python.json', 'w') as file:
# file.write(json_str)
# ```
#
# Let's ensure that the JSON file is correctly parsed.
python_input = LMP.parse(joinpath(examples_dir, "basic_python.json"))
# And run the file.
python_output = propagate(joinpath(examples_dir, "basic_python.json"));
# To read the results:
#
# ```python
# with open('basic_python_output.json', 'r') as file:
# output = json.load(file)
# ```
| LongwaveModePropagator | https://github.com/fgasdia/LongwaveModePropagator.jl.git |
|
[
"MIT"
] | 0.4.1 | 792c195909ca5dfff5685305b6fa0aa16c3d1041 | code | 8683 | # # Magnetic field direction
#
# In this example we'll look at the influence of the magnetic field direction on
# a nighttime and daytime ionosphere propagation path.
# Results will be compared to LWPC.
#
# ## Generate scenarios
#
# We'll use the JSON I/O functionality of LongwaveModePropagator to create
# the different magnetic field direction scenarios as a `BatchInput{ExponentialInput}`.
# We're doing this to ensure identical inputs are passed to LWPC.
# Although commented out in the `generate` function below, we locally saved the
# `BatchInput` as a JSON file and used it to feed a custom Python code
# which generates LWPC input files, runs LWPC, and saves the results in an HDF5 file.
#
# First load the packages we need.
using Dates, Printf
using HDF5
using ProgressMeter
using Plots
using LongwaveModePropagator
using LongwaveModePropagator: buildrun
# For convenience, we'll define global `OUTPUT_RANGES` at which the electric field
# will be computed, and the magnetic field dip and azimuth angles `B_DIPS` and `B_AZS`
# (converted below from degrees to radians).
const OUTPUT_RANGES = 0:5e3:3000e3
const B_DIPS = [90.0, 60, 60, 60, 60, 60, 60, 60, 60]
const B_AZS = [0.0, 0, 45, 90, 135, 180, 225, 270, 315] ## vertical, N, E, S, W
nothing #hide
# The `generate` function produces the [`BatchInput`](@ref) of the scenarios.
# If we wanted, we could comment out the JSON lines near the bottom of the function
# to also write the `BatchInput` to a file.
# That's not necessary here.
function generate(hp, β)
batch = BatchInput{ExponentialInput}()
batch.name = "Magnetic field tests"
batch.description = "Varying magnetic field directions: vertical, N, E, S, W."
batch.datetime = Dates.now()
## Constants
frequency = 24e3
output_ranges = collect(OUTPUT_RANGES)
segment_ranges = [0.0]
hprime = [hp]
beta = [β]
## Ocean
ground_epsr = [81]
ground_sigma = [4.0]
b_mag = [50e-6]
b_dips = deg2rad.(B_DIPS)
b_azs = deg2rad.(B_AZS)
N = length(b_azs)
inputs = Vector{ExponentialInput}(undef, N)
for i in 1:N
input = ExponentialInput()
input.name = @sprintf("%d_%.0f_%.0f", i, b_dips[i], b_azs[i])
input.description = "Wait ionosphere with ocean ground at 24 kHz."
input.datetime = Dates.now()
input.segment_ranges = segment_ranges
input.hprimes = hprime
input.betas = beta
input.b_mags = b_mag
input.b_dips = [b_dips[i]]
input.b_azs = [b_azs[i]]
input.ground_sigmas = ground_sigma
input.ground_epsrs = ground_epsr
input.frequency = frequency
input.output_ranges = output_ranges
inputs[i] = input
end
batch.inputs = inputs
## json_str = JSON3.write(batch)
##
## open("bfields.json","w") do f
## write(f, json_str)
## end
return batch
end
batch = generate(82.0, 0.6);
# ## Run the model
#
# Results from my custom LWPC script are saved in an
# [HDF5 file](@__REPO_ROOT_URL__/examples/bfields_lwpc.h5).
# For easy comparison, we will also save the results from the
# Longwave Mode Propagator to an HDF5 file.
# Although not strictly necessary for a small number inputs like we have here,
# using an HDF5 file rather than the JSON output file that is generated automatically by
# LongwaveModePropagator when a file is passed to `propagate` is more robust
# for thousands or tens of thousands of input scenarios.
function runlmp(inputs, outfile)
h5open(outfile, "cw") do fid
## Create Batch attributes if they don't already exist
fid_attrs = attributes(fid)
haskey(fid_attrs, "name") || (fid_attrs["name"] = inputs.name)
haskey(fid_attrs, "description") || (fid_attrs["description"] = inputs.description)
haskey(fid_attrs, "datetime") || (fid_attrs["datetime"] = string(Dates.now()))
if haskey(fid, "outputs")
g = fid["outputs"]
else
g = create_group(fid, "outputs")
end
end
PM = Progress(length(inputs.inputs), 5)
for i in eachindex(inputs.inputs)
## If we've already run this, we can skip ahead
complete = h5open(outfile, "r") do fid
g = open_group(fid, "outputs")
haskey(g, string(i)) ? true : false
end
complete && (next!(PM); continue)
output = buildrun(inputs.inputs[i])
h5open(outfile, "r+") do fid
g = open_group(fid, "outputs")
o = create_group(g, string(i))
attributes(o)["name"] = output.name
attributes(o)["description"] = output.description
attributes(o)["datetime"] = string(Dates.now())
o["output_ranges"] = output.output_ranges
o["amplitude"] = output.amplitude
o["phase"] = output.phase
end
next!(PM)
end
end
nothing #hide
#
# `examples_dir` below will need to be modified to the directory where
# `bfields_lmp.h5` is located and where you would like `bfields_lmp.h5` to be saved.
root_dir = dirname(dirname(pathof(LongwaveModePropagator)))
examples_dir = joinpath(root_dir, "examples")
lmpfile = joinpath(examples_dir, "bfields_lmp.h5")
runlmp(batch, lmpfile)
# ## Plots
#
# To more easily compare the amplitude and phase curves, we define a function
# to process the HDF5 files into arrays of amplitude and phase
# versus range and magnetic field azimuth.
function process(outputs)
dist = read(outputs["outputs"]["1"]["output_ranges"])
mask = indexin(OUTPUT_RANGES, dist)
agrid = Array{Float64}(undef, length(OUTPUT_RANGES), length(B_AZS))
pgrid = similar(agrid)
for i in eachindex(B_AZS)
o = outputs["outputs"][string(i)]
amp = read(o["amplitude"])
phase = read(o["phase"])
agrid[:,i] = amp[mask]
pgrid[:,i] = rad2deg.(phase[mask])
end
return agrid, pgrid
end
agrid, pgrid = h5open(lmpfile, "r") do o
agrid, pgrid = process(o)
end
nothing #hide
# Here is the amplitude plot itself.
labels = string.(trunc.(Int, B_AZS), "°")
labels[1] = "90°, "*labels[1]
labels[2] = "60°, "*labels[2]
labels[3:end] .= " ".*labels[3:end]
colors = [palette(:phase, length(B_AZS))...]
pushfirst!(colors, RGB(0.0, 0, 0))
plot(OUTPUT_RANGES/1000, agrid;
linewidth=1.5, palette=colors, colorbar=false,
xlabel="range (km)", ylabel="amplitude (dB)",
labels=permutedims(labels), legendtitle=" dip, az", legend=true)
#md savefig("magneticfield_amplitude.png"); nothing # hide
#md # 
# The amplitude corresponding to each magnetic field azimuth
# (where 0° is along the propagation direction)
# is color-coded in the plot above, but a couple of the colors appear to be missing.
# This is because 0° and 180° are identical. There is no "north/south" dependence.
# Therefore 45°/135° and 315°/225° are also identical.
#
# On the other hand, there is a significant difference between propagation
# "east" (pinks) versus "west" (greens).
# This effect can be [observed in real life](https://doi.org/10.1016/0021-9169(58)90081-3).
#
# Now we'll plot the difference from LWPC.
lwpcfile = joinpath(examples_dir, "bfields_lwpc.h5")
lagrid, lpgrid = h5open(lwpcfile, "r") do o
lagrid, bpgrid = process(o)
end
adifference = agrid - lagrid
plot(OUTPUT_RANGES/1000, adifference;
linewidth=1.5, palette=colors, colorbar=false,
xlabel="range (km)", ylabel="amplitude difference (dB)",
labels=permutedims(labels), legendtitle=" dip, az", legend=true)
#md savefig("magneticfield_diff.png"); nothing # hide
#md # 
# The two models are a very close match.
# Where there are large differences they occur because of slight misalignment of
# nulls with respect to range from the transmitter.
# The 315°/225° line has the worst match, although it is not clear if there is
# a particular cause for this outside of the general differences between the
# two models.
# ## Daytime ionosphere
#
# Does magnetic field direction have a different level of influence with daytime ionospheres?
lmpfile = joinpath(examples_dir, "bfields_daytime_lmp.h5")
runlmp(generate(72.0, 0.3), lmpfile)
agrid, pgrid = h5open(lmpfile, "r") do o
agrid, pgrid = process(o)
end
plot(OUTPUT_RANGES/1000, agrid;
linewidth=1.5, palette=colors, colorbar=false,
xlabel="range (km)", ylabel="amplitude (dB)",
labels=permutedims(labels), legendtitle=" dip, az", legend=true)
#md savefig("magneticfield_daytime_amplitude.png"); nothing # hide
#md # 
# At these lower reflection altitudes the effect of Earth's magnetic field is decreased. | LongwaveModePropagator | https://github.com/fgasdia/LongwaveModePropagator.jl.git |
|
[
"MIT"
] | 0.4.1 | 792c195909ca5dfff5685305b6fa0aa16c3d1041 | code | 15009 | # # Mesh grid for mode finding - Part 1
#
# The [Global complex Roots and Poles Finding](https://doi.org/10.1109/TAP.2018.2869213)
# (GRPF) algorithm searches for roots and poles of complex-valued functions by sampling
# the function at the nodes of a regular mesh and analyzing the function's complex phase.
# The mesh search region can be arbitrarily shaped and guarantees that none of
# the roots/poles can be missed as long as the mesh step is sufficiently small.
# Specifically, the phase change of the function value cannot exceed three quadrants
# across mesh edges. Effectively this means there cannot be equal numbers of roots and
# poles within the boundary of each identified candidate region.
#
# Because the GRPF algorithm uses an adaptive meshing process, the initial mesh
# node spacing can be greater than the distance between the roots/poles
# of the function, but there is no established method for _a priori_ estimation
# of the required initial sampling of an arbitrary function.
# The GRPF algorithm is implemented in
# [RootsAndPoles.jl](https://github.com/fgasdia/RootsAndPoles.jl) and used by
# LongwaveModePropagator to identify eigenangles of [`HomogeneousWaveguide`](@ref)'s.
# Therefore, we must experimentally determine a sufficient initial mesh grid spacing to
# identify roots of the mode equation.
#
# ## Mode equation
#
# The criteria for mode propagation in the Earth-ionosphere waveguide is described by the
# fundamental equation of mode theory
#
# ```math
# \det(\overline{\bm{R}}(\theta)\bm{R}(\theta) - \bm{I}) = 0
# ```
#
# where ``\overline{\bm{R}}(\theta)`` is the reflection coefficient matrix for the
# ground and ``\bm{R}(\theta)`` is the reflection coefficient of the ionosphere.
# Both are functions of the complex angle ``\theta``. The discrete values of
# ``\theta`` for which the fundamental equation is satisfied are known as
# _eigenangles_.
#
# First, import the necessary packages.
using Plots
using Plots.Measures
using RootsAndPoles
using LongwaveModePropagator
using LongwaveModePropagator: QE, ME, solvemodalequation, trianglemesh
# ## Exploring the mode equation phase
#
# The U.S. Navy's Long Wavelength Propagation Capability (LWPC) searches the region of the
# complex plane from 30° to 90° in the real axis and 0° to -10° in the
# imaginary axis. The lowest order modes are nearest 90° - i0°, excluding 90°.
# Modes with large negative imaginary components are highly attenuated and have
# relatively little affect on the total field in the waveguide.
#
# Let's begin by exploring the modal equation phase on a fine grid across the bottom
# right complex quadrant.
#
# We'll define five different [`PhysicalModeEquation`](@ref)'s that we'll use
# throughout this example.
verylowfrequency = Frequency(1e3)
lowfrequency = Frequency(10e3)
midfrequency = Frequency(20e3)
highfrequency = Frequency(100e3)
day = Species(QE, ME, z->waitprofile(z, 75, 0.35), electroncollisionfrequency)
night = Species(QE, ME, z->waitprofile(z, 85, 0.9), electroncollisionfrequency)
daywaveguide = HomogeneousWaveguide(BField(50e-6, π/2, 0), day, GROUND[5])
nightwaveguide = HomogeneousWaveguide(BField(50e-6, π/2, 0), night, GROUND[5])
day_verylow_me = PhysicalModeEquation(verylowfrequency, daywaveguide)
day_low_me = PhysicalModeEquation(lowfrequency, daywaveguide)
day_mid_me = PhysicalModeEquation(midfrequency, daywaveguide)
day_high_me = PhysicalModeEquation(highfrequency, daywaveguide)
night_mid_me = PhysicalModeEquation(midfrequency, nightwaveguide)
day_verylow_title = "1 kHz\nh′: 75, β: 0.35"
day_low_title = "10 kHz\nh′: 75, β: 0.35"
day_mid_title = "20 kHz\nh′: 75, β: 0.35"
day_high_title = "100 kHz\nh′: 75, β: 0.35"
night_mid_title = "20 kHz\nh′: 85, β: 0.9"
nothing #hide
# Here we define a dense rectangular mesh.
Δr = 0.2
x = 0:Δr:90
y = -40:Δr:0
mesh = x .+ im*y';
# Now we simply iterate over each node of the mesh, evaluating the modal equation with
# [`LongwaveModePropagator.solvemodalequation`](@ref), explicitly imported from
# LongwaveModePropagator above.
# We use Julia's `Threads.@threads` multithreading capability to speed up the computation.
function modeequationphase(me, mesh)
phase = Vector{Float64}(undef, length(mesh))
Threads.@threads for i in eachindex(mesh)
f = solvemodalequation(deg2rad(mesh[i]), me)
phase[i] = rad2deg(angle(f))
end
return phase
end
phase = modeequationphase(day_mid_me, mesh);
# If an instability occurs in the integration of the reflection coefficient,
# it likely happened at the angle 90° + i0°, which is not a valid mode.
# This isn't a problem for plotting though!
#
# Plotting the results, we can see that there are clearly identifiable locations where
# white, black, blue, and orange, each representing a different quadrant of the
# complex plane, all meet.
# Each of these locations are either a root or pole in the daytime ionosphere.
heatmap(x, y, reshape(phase, length(x), length(y))';
color=:twilight, clims=(-180, 180),
xlims=(0, 90), ylims=(-40, 0),
xlabel="real(θ)", ylabel="imag(θ)",
title=day_mid_title,
right_margin=2mm)
#md savefig("meshgrid_20kday.png"); nothing # hide
#md # 
# We can zoom in to the upper right corner of the plot to see the lowest order modes:
heatmap(x, y, reshape(phase, length(x), length(y))';
color=:twilight, clims=(-180, 180),
xlims=(30, 90), ylims=(-10, 0),
xlabel="real(θ)", ylabel="imag(θ)",
title=day_mid_title,
right_margin=2mm)
#md savefig("meshgrid_20kdayzoom.png"); nothing # hide
#md # 
# If we switch to a nighttime ionosphere with a high Wait β parameter, we see that the
# roots move closer to the axes.
# A perfectly reflecting conductor has eigenangles along the real and complex axes.
phase = modeequationphase(night_mid_me, mesh);
heatmap(x, y, reshape(phase, length(x), length(y))';
color=:twilight, clims=(-180, 180),
xlims=(0, 90), ylims=(-40, 0),
xlabel="real(θ)", ylabel="imag(θ)",
title=night_mid_title,
right_margin=2mm)
#md savefig("meshgrid_20knight.png"); nothing # hide
#md # 
# At lower frequencies, the roots/poles move further apart.
phase = modeequationphase(day_low_me, mesh);
heatmap(x, y, reshape(phase, length(x), length(y))';
color=:twilight, clims=(-180, 180),
xlims=(0, 90), ylims=(-40, 0),
xlabel="real(θ)", ylabel="imag(θ)",
title=day_low_title,
right_margin=2mm)
#md savefig("meshgrid_10kday.png"); nothing # hide
#md # 
# At even lower frequencies into ELF, we need to expand the domain of the mesh grid.
y_verylow = -90:Δr:0
mesh_verylow = x .+ im*y_verylow';
phase = modeequationphase(day_verylow_me, mesh_verylow);
heatmap(x, y_verylow, reshape(phase, length(x), length(y_verylow))';
color=:twilight, clims=(-180, 180),
xlims=(0, 90), ylims=(-90, 0),
xlabel="real(θ)", ylabel="imag(θ)",
title=day_verylow_title,
right_margin=2mm)
#md savefig("meshgrid_1kday.png"); nothing # hide
#md # 
# ## Global complex roots and poles finding
#
# The global complex roots and poles finding (GRPF) algorithm is most efficient when
# the initial mesh grid consists of equilateral triangles.
# Such a grid can be produced with the `rectangulardomain` function from
# RootsAndPoles,
zbl = deg2rad(complex(30.0, -10.0))
ztr = deg2rad(complex(89.9, 0.0))
Δr = deg2rad(0.5)
mesh = rectangulardomain(zbl, ztr, Δr);
# We convert back to degrees just for plotting.
# Here's a zoomed in portion of the upper right of the domain.
meshdeg = rad2deg.(mesh)
img = plot(real(meshdeg), imag(meshdeg); seriestype=:scatter,
xlims=(80, 90), ylims=(-10, 0),
xlabel="real(θ)", ylabel="imag(θ)",
legend=false, size=(450,375))
#md savefig(img, "meshgrid_rectanglemesh.png"); nothing # hide
#md # 
# As seen in the evaluation of the modal equation above, no roots or poles appear in the
# lower right diagonal of the domain for frequencies above about 10 kHz.
# Even if they did, they would correspond to highly attenuated modes.
# Therefore, to save compute time, we can exclude the lower right triangle of the domain
# from the initial mesh if the frequency is sufficiently high.
#
# The function [`LongwaveModePropagator.trianglemesh`](@ref) is built into
# LongwaveModePropagator for this purpose.
# The inputs are specified by the complex bottom left corner `zbl`, the top right corner
# `ztr`, and the mesh spacing `Δr` in _radians_.
mesh = trianglemesh(zbl, ztr, Δr);
meshdeg = rad2deg.(mesh)
img = plot(real(meshdeg), imag(meshdeg); seriestype=:scatter,
xlims=(80, 90), ylims=(-10, 0),
xlabel="real(θ)", ylabel="imag(θ)",
legend=false, size=(450,375));
plot!(img, [80, 90], [0, 0]; color="red");
plot!(img, [0, 90], [-90, 0]; color="red")
#md savefig(img, "meshgrid_trianglemesh.png"); nothing # hide
#md # 
# Now let's apply `grpf` to the modal equation on the triangle mesh.
# `grpf` adaptively refines the mesh to obtain a more accurate estimate of the position
# of the roots and poles.
#
# [`LMPParams`](@ref) is a struct use for passing parameters across LongwaveModePropagator.
# Default values are automatically inserted when instantiating the struct.
# We'll extract the `grpfparams` field which contains a `GRPFParams` struct for passing
# to `grpf`.
#
# We will also pass RootsAndPoles' `PlotData()` argument to obtain additional
# information on the function phase for plotting.
params = LMPParams().grpfparams
roots, poles, quads, phasediffs, tess, g2f = grpf(θ->solvemodalequation(θ, day_mid_me),
mesh, PlotData(), params);
# The `getplotdata` function, provided by RootsAndPoles, is a convenience function
# for plotting a color-coded tesselation from `grpf` based on the phase of the function.
z, edgecolors = getplotdata(tess, quads, phasediffs, g2f)
rootsdeg = rad2deg.(roots)
polesdeg = rad2deg.(poles)
zdeg = rad2deg.(z)
twilightquads = [
colorant"#9E3D36",
colorant"#C99478",
colorant"#7599C2",
colorant"#5C389E",
colorant"#404040",
RGB(0.0, 0.0, 0.0)
]
img = plot(real(zdeg), imag(zdeg); group=edgecolors, palette=twilightquads, linewidth=1.5,
xlims=(30, 90), ylims=(-10, 0),
xlabel="real(θ)", ylabel="imag(θ)", legend=false,
title=day_mid_title);
plot!(img, real(rootsdeg), imag(rootsdeg); color="red",
seriestype=:scatter, markersize=5);
plot!(img, real(polesdeg), imag(polesdeg); color="red",
seriestype=:scatter, markershape=:utriangle, markersize=5)
#md savefig(img, "meshgrid_20kdaymesh.png"); nothing # hide
#md # 
# In the plot above, roots are marked with red circles and poles are marked
# with red triangles.
# The automatic refinement of the mesh is clearly visible.
#
# Here are similar plots for the other scenarios.
## Daytime ionosphere, low frequency
roots, poles, quads, phasediffs, tess, g2f = grpf(θ->solvemodalequation(θ, day_low_me),
mesh, PlotData(), params);
z, edgecolors = getplotdata(tess, quads, phasediffs, g2f)
rootsdeg = rad2deg.(roots)
polesdeg = rad2deg.(poles)
zdeg = rad2deg.(z)
img = plot(real(zdeg), imag(zdeg); group=edgecolors, palette=twilightquads, linewidth=1.5,
xlims=(30, 90), ylims=(-10, 0),
xlabel="real(θ)", ylabel="imag(θ)", legend=false,
title=day_low_title);
plot!(img, real(rootsdeg), imag(rootsdeg); color="red",
seriestype=:scatter, markersize=5);
plot!(img, real(polesdeg), imag(polesdeg); color="red",
seriestype=:scatter, markershape=:utriangle, markersize=5)
#md savefig(img, "meshgrid_10kdaymesh.png"); nothing # hide
#md # 
#
## Nighttime ionosphere, 20 kHz
roots, poles, quads, phasediffs, tess, g2f = grpf(θ->solvemodalequation(θ, night_mid_me),
mesh, PlotData(), params);
z, edgecolors = getplotdata(tess, quads, phasediffs, g2f)
rootsdeg = rad2deg.(roots)
polesdeg = rad2deg.(poles)
zdeg = rad2deg.(z)
img = plot(real(zdeg), imag(zdeg); group=edgecolors, palette=twilightquads, linewidth=1.5,
xlims=(30, 90), ylims=(-10, 0),
xlabel="real(θ)", ylabel="imag(θ)", legend=false,
title=night_mid_title);
plot!(img, real(rootsdeg), imag(rootsdeg); color="red",
seriestype=:scatter, markersize=5);
plot!(img, real(polesdeg), imag(polesdeg); color="red",
seriestype=:scatter, markershape=:utriangle, markersize=5)
#md savefig(img, "meshgrid_20knightmesh.png"); nothing # hide
#md # 
# At 100 kHz, `grpf` requires more mesh refinements and takes considerably
# more time to run.
## Daytime ionosphere, high frequency
roots, poles, quads, phasediffs, tess, g2f = grpf(θ->solvemodalequation(θ, day_high_me),
mesh, PlotData(), params);
z, edgecolors = getplotdata(tess, quads, phasediffs, g2f)
rootsdeg = rad2deg.(roots)
polesdeg = rad2deg.(poles)
zdeg = rad2deg.(z)
img = plot(real(zdeg), imag(zdeg); group=edgecolors, palette=twilightquads, linewidth=1.5,
xlims=(30, 90), ylims=(-10, 0),
xlabel="real(θ)", ylabel="imag(θ)", legend=false,
title=day_high_title);
plot!(img, real(rootsdeg), imag(rootsdeg); color="red",
seriestype=:scatter, markersize=5);
plot!(img, real(polesdeg), imag(polesdeg); color="red",
seriestype=:scatter, markershape=:utriangle, markersize=5)
#md savefig(img, "meshgrid_100kdaymesh.png"); nothing # hide
#md # 
# The mesh grid does not need to be as dense at lower VLF and ELF.
## Daytime ionosphere, 1 kHz
## We'll use the rectangular mesh
zbl = deg2rad(complex(1, -89))
ztr = deg2rad(complex(89.9, 0))
Δr = deg2rad(1)
mesh = rectangulardomain(zbl, ztr, Δr)
roots, poles, quads, phasediffs, tess, g2f = grpf(θ->solvemodalequation(θ, day_verylow_me),
mesh, PlotData(), params);
z, edgecolors = getplotdata(tess, quads, phasediffs, g2f)
rootsdeg = rad2deg.(roots)
polesdeg = rad2deg.(poles)
zdeg = rad2deg.(z)
img = plot(real(zdeg), imag(zdeg); group=edgecolors, palette=twilightquads, linewidth=1.5,
xlims=(0, 90), ylims=(-90, 0),
xlabel="real(θ)", ylabel="imag(θ)", legend=false,
title=night_mid_title);
plot!(img, real(rootsdeg), imag(rootsdeg); color="red",
seriestype=:scatter, markersize=5);
plot!(img, real(polesdeg), imag(polesdeg); color="red",
seriestype=:scatter, markershape=:utriangle, markersize=5)
#md savefig(img, "meshgrid_1kdaymesh.png"); nothing # hide
#md # 
# The example continues in [Mesh grid for mode finding - Part 2](@ref).
| LongwaveModePropagator | https://github.com/fgasdia/LongwaveModePropagator.jl.git |
|
[
"MIT"
] | 0.4.1 | 792c195909ca5dfff5685305b6fa0aa16c3d1041 | code | 7336 | # # Mesh grid for mode finding - Part 2
#
# In [Mesh grid for mode finding - Part 1](@ref) we used
# [`LongwaveModePropagator.trianglemesh`](@ref) to
# initialize the GRPF grid for mode finding several different ionospheres and transmit
# frequencies.
# In part 2 we'll look at where `grpf` can fail for certain scenarios.
#
# Naturally we want to be able to use the coarsest initial mesh grid as possible
# because the reflection coefficient has to be integrated through the ionosphere
# for every node of the grid. This step is by far the most computationally
# expensive operation of all of LongwaveModePropagator.
#
# First, let's load the packages needed in this example.
using Plots
using Plots.Measures
using RootsAndPoles
using LongwaveModePropagator
using LongwaveModePropagator: QE, ME, solvemodalequation, trianglemesh, defaultmesh
# In the LongwaveModePropagator tests suite, the `segmented_scenario` is known to
# miss roots if we use the same `trianglemesh` parameters (with `Δr = deg2rad(0.5)`)
# as in part 1 of the example.
#
# Here we define the `HomogeneousWaveguide` from the second half of the
# `segmented_scenario` known to have the missing roots.
frequency = Frequency(24e3)
electrons = Species(QE, ME, z->waitprofile(z, 80, 0.45), electroncollisionfrequency)
waveguide = HomogeneousWaveguide(BField(50e-6, π/2, 0), electrons, Ground(15, 0.001))
me = PhysicalModeEquation(frequency, waveguide)
title = "24 kHz\nh′: 80, β: 0.45"
nothing #hide
# First, let's simply compute the mode equation on a fine grid.
Δr = 0.2
x = 30:Δr:90
y = -10:Δr:0
mesh = x .+ 1im*y';
# As in part 1, we also define a function to compute the modal equation phase.
function modeequationphase(me, mesh)
phase = Vector{Float64}(undef, length(mesh))
Threads.@threads for i in eachindex(mesh)
f = solvemodalequation(deg2rad(mesh[i]), me)
phase[i] = rad2deg(angle(f))
end
return phase
end
phase = modeequationphase(me, mesh);
heatmap(x, y, reshape(phase, length(x), length(y))';
color=:twilight, clims=(-180, 180),
xlims=(30, 90), ylims=(-10, 0),
xlabel="real(θ)", ylabel="imag(θ)",
title=title,
right_margin=2mm)
#md savefig("meshgrid2_20knight.png"); nothing # hide
#md # 
#
# Let's run the `grpf` with `Δr = 0.5`.
zbl = deg2rad(complex(30.0, -10.0))
ztr = deg2rad(complex(89.9, 0.0))
Δr = deg2rad(0.5)
mesh = trianglemesh(zbl, ztr, Δr)
params = LMPParams().grpfparams
roots, poles, quads, phasediffs, tess, g2f = grpf(θ->solvemodalequation(θ, me),
mesh, PlotData(), params);
z, edgecolors = getplotdata(tess, quads, phasediffs, g2f)
zdeg = rad2deg.(z)
rootsdeg = rad2deg.(roots)
polesdeg = rad2deg.(poles)
twilightquads = [
colorant"#9E3D36",
colorant"#C99478",
colorant"#7599C2",
colorant"#5C389E",
colorant"#404040",
RGB(0.0, 0.0, 0.0)
]
img = plot(real(zdeg), imag(zdeg); group=edgecolors, palette=twilightquads, linewidth=1.5,
xlims=(30, 90), ylims=(-10, 0),
xlabel="real(θ)", ylabel="imag(θ)", legend=false,
title=title);
plot!(img, real(rootsdeg), imag(rootsdeg); color="red",
seriestype=:scatter, markersize=5);
plot!(img, real(polesdeg), imag(polesdeg); color="red",
seriestype=:scatter, markershape=:utriangle, markersize=5)
#md savefig(img, "meshgrid2_20knightmesh.png"); nothing # hide
#md # 
# Upon inspection, it is clear that there is a root/pole visible at the upper right
# corner of the domain in the fine mesh above that is not identified by `grpf`.
# In fact, the algorithm did not even try to refine the mesh in this region.
# That is because the root and pole pair are too closely spaced for the algorithm
# to know they are there.
# The discretized Cauchy
# [argument principle](https://en.wikipedia.org/wiki/Argument_principle) (DCAP),
# upon which GRPF is based, can only identify the presence of roots and poles if
# there are an unequal number of them.
# If the complex phase change around a tessellation contour is equal to 0, there may
# be no roots or poles in the contoured region, or there may be an equal number of
# roots and poles.
#
# This run identified 20 roots and 19 poles.
# Let's run `grpf` again with a finer resolution of `Δr = 0.2`.
Δr = deg2rad(0.2)
mesh = trianglemesh(zbl, ztr, Δr)
roots, poles, quads, phasediffs, tess, g2f = grpf(θ->solvemodalequation(θ, me),
mesh, PlotData(), params);
z, edgecolors = getplotdata(tess, quads, phasediffs, g2f)
zdeg = rad2deg.(z)
rootsdeg = rad2deg.(roots)
polesdeg = rad2deg.(poles)
img = plot(real(zdeg), imag(zdeg); group=edgecolors, palette=twilightquads, linewidth=1.5,
xlims=(30, 90), ylims=(-10, 0),
xlabel="real(θ)", ylabel="imag(θ)", legend=false,
title=title);
plot!(img, real(rootsdeg), imag(rootsdeg); color="red",
seriestype=:scatter, markersize=5);
plot!(img, real(polesdeg), imag(polesdeg); color="red",
seriestype=:scatter, markershape=:utriangle, markersize=5)
#md savefig(img, "meshgrid2_20knightfinemesh.png"); nothing # hide
#md # 
# This higher resolution initial grid has identified 22 roots and 21 poles.
# Zooming in on the upper right region, we can see that the previously
# missing roots and poles are very closely spaced.
img = plot(real(zdeg), imag(zdeg); group=edgecolors, palette=twilightquads, linewidth=1.5,
xlims=(80, 90), ylims=(-2, 0),
xlabel="real(θ)", ylabel="imag(θ)", legend=false,
title=title);
plot!(img, real(rootsdeg), imag(rootsdeg); color="red",
seriestype=:scatter, markersize=5);
plot!(img, real(polesdeg), imag(polesdeg); color="red",
seriestype=:scatter, markershape=:utriangle, markersize=5)
#md savefig(img, "meshgrid2_20knightfinemeshzoom.png"); nothing # hide
#md # 
#
# Roots are frequently located closely to poles in the upper right of the domain for
# a variety of ionospheres. To ensure they are captured,
# [`LongwaveModePropagator.defaultmesh`](@ref)
# uses a spacing of `Δr = deg2rad(0.5)` for most of the mesh,
# but a spacing of `Δr = deg2rad(0.1)` for the region with real greater
# than 75° and imaginary greater than -1.5°.
mesh = defaultmesh(frequency)
meshdeg = rad2deg.(mesh)
img = plot(real(meshdeg), imag(meshdeg); seriestype=:scatter,
xlabel="real(θ)", ylabel="imag(θ)",
size=(450,375), legend=false);
plot!(img, [30, 90], [0, 0]; color="red");
plot!(img, [80, 90], [-10, 0]; color="red")
#md savefig(img, "meshgrid2_defaultmesh.png"); nothing # hide
#md # 
# ## Frequencies below 12 kHz
#
# The [`LongwaveModePropagator.defaultmesh`](@ref) at frequencies below 12 kHz is rectangular from
# `LMP.rectangulardomain`, and uses a lower point density with `Δr_coarse = deg2rad(1)` and
# no fine mesh.
frequency = 1e3
mesh = defaultmesh(frequency)
meshdeg = rad2deg.(mesh)
img = plot(real(meshdeg), imag(meshdeg); seriestype=:scatter,
xlabel="real(θ)", ylabel="imag(θ)",
size=(450,375), legend=false)
#md savefig(img, "meshgrid2_defaultmesh_verylow.png"); nothing # hide
#md # 
| LongwaveModePropagator | https://github.com/fgasdia/LongwaveModePropagator.jl.git |
|
[
"MIT"
] | 0.4.1 | 792c195909ca5dfff5685305b6fa0aa16c3d1041 | code | 4379 | # # Multiple ionospheric species
#
# This example demonstrates an ionosphere with multiple constituents---not only electrons,
# but ions as well.
#
# ## Background
#
# As discussed in the background of [Interpreting h′ and β](@ref interpreting-hpbeta),
# the propagation of VLF waves depends on the number density and collision frequency of
# charged species. Together, these two quantities describe the conductivity profile of the
# ionosphere. Not only electrons, but massive ions, influence the conductivity of the
# D-region. The influence of multiple species are combined by summing the susceptibility
# tensors for each species.
#
# ## Implementation
#
# There's nothing special about electrons in LongwaveModePropagator.
# In all of the other examples, the only ionospheric constituent is electrons, but they
# are represented as a [`Species`](@ref) type.
# LongwaveModePropagator let's you define multiple ionospheric `Species` and pass them as a
# `Tuple` or `Vector` to most functions that take the argument `species`.
#
# Let's compare electrons-only and multiple-species ionospheres.
using Plots
using LongwaveModePropagator
# The [`Species`](@ref) type defines `charge`, `mass`, `numberdensity` as a function
# of altitude, and neutral `collisionfrequency` as a function of altitude.
#
# We'll import the internally defined electron charge `QE` and mass `ME` for convenience.
using LongwaveModePropagator: QE, ME
# `QE` is literally the charge of an electron and is therefore negative.
QE
# LMP also exports the function [`waitprofile`](@ref) for the Wait and Spies (1964) electron
# density, [`electroncollisionfrequency`](@ref) for the electron-neutral collision frequency,
# and [`ioncollisionfrequency`](@ref) for the ion-neutral collision frequency.
#
# The Long Wavelength Propagation Capability (LWPC) supports built-in electrons, a positive
# ion, and a negative ion.
# Each of the ions have a mass of 58,000 electrons (approximately the mass of O₂).
#
# Here we'll use `waitprofile` for the electron number density profile, but make up a
# not-very-realistic exponential profile for the positive ion.
Ne(z) = waitprofile(z, 75, 0.32)
Np(z) = 2e6*exp(1e-4*z)
nothing #hide
# We define density of the negative ions to conserve charge neutrality.
Nn(z) = Np(z) - Ne(z)
nothing #hide
# For plotting, we'll replace densities below 1 m⁻³ with `NaN`.
mask(x) = x < 1 ? NaN : x
z = 0:1e3:110e3
plot(mask.(Ne.(z)), z/1000, label="Ne", linewidth=1.5)
plot!(mask.(Np.(z)), z/1000, label="Np", linewidth=1.5)
plot!(mask.(Nn.(z)), z/1000, label="Nn", linewidth=1.5)
plot!(xlabel="Density (m⁻³)", ylabel="Altitude (km)",
xscale=:log10, legend=:topleft)
#md savefig("multiplespecies_density.png"); nothing # hide
#md # 
# Here are the electron and ion collision frequencies:
plot(electroncollisionfrequency.(z), z/1000, label="νe", linewidth=1.5)
plot!(ioncollisionfrequency.(z), z/1000, label="νi", linewidth=1.5)
plot!(xlabel="Collision frequency (s⁻¹)", ylabel="Altitude (km)", xscale=:log10)
#md savefig("multiplespecies_collisionfreq.png"); nothing # hide
#md # 
# The [`Species`](@ref):
electrons = Species(QE, ME, Ne, electroncollisionfrequency)
posions = Species(abs(QE), 58000*ME, Np, ioncollisionfrequency)
negions = Species(QE, 58000*ME, Nn, ioncollisionfrequency)
nothing #hide
# We'll compare an electrons-only and electrons-ions ionosphere.
tx = Transmitter(24e3)
rx = GroundSampler(0:5e3:2000e3, Fields.Ez)
bfield = BField(50e-6, π/2, 0)
ground = GROUND[10]
ewvg = HomogeneousWaveguide(bfield, electrons, ground)
eiwvg = HomogeneousWaveguide(bfield, (electrons, posions, negions), ground)
Ee, ae, pe = propagate(ewvg, tx, rx)
Eei, aei, pei = propagate(eiwvg, tx, rx)
p1 = plot(rx.distance/1000, ae, label="electrons", ylabel="Amplitude (dB μV/m)")
plot!(p1, rx.distance/1000, aei, label="electrons & ions")
p2 = plot(rx.distance/1000, aei-ae,
ylims=(-0.5, 0.5), xlabel="Range (km)", ylabel="Δ", legend=false)
plot(p1, p2, layout=grid(2,1,heights=[0.7, 0.3]))
#md savefig("multiplespecies_amplitude.png"); nothing # hide
#md # 
# The influence here is minor; the difference is hardly above the noise floor of many VLF
# receivers.
# Also, running with 3 species increases the runtime over 1 species by ~50%.
| LongwaveModePropagator | https://github.com/fgasdia/LongwaveModePropagator.jl.git |
|
[
"MIT"
] | 0.4.1 | 792c195909ca5dfff5685305b6fa0aa16c3d1041 | code | 11990 | # # Wavefield integration
#
# The process of mode conversion between two different segments of
# [`HomogeneousWaveguide`](@ref)'s
# requires the computation of electromagnetic wavefields from ground to a great
# height in the ionosphere.
#
# [Pitteway (1965)](https://doi.org/10.1098/rsta.1965.0004) presents one well-known method of
# integrating the wavefields that breaks the solution for the differential wave
# equations in the anisotropic ionosphere into solutions for a _penetrating_ and
# _non-penetrating_ mode. Because of the amplitude of the two waves varies greatly
# during the integration, Pitteway scales and orthogonalizes the solutions to maintain
# their independence.
#
# In this example we'll reproduce the figures in Pitteway's paper.
#
# First we'll import the necessary packages.
using CSV, Interpolations
using Plots
using Plots.Measures
using OrdinaryDiffEq
using TimerOutputs
using LongwaveModePropagator
using LongwaveModePropagator: QE, ME
const LMP = LongwaveModePropagator
nothing #hide
# ## The ionosphere
# Pitteway uses an ionosphere presented in
# [Piggot et. al., 1965](https://doi.org/10.1098/rsta.1965.0005).
#
# ```@raw html
# <img src="../../images/Piggott_ionosphere.png"/>
# ```
#
# He begins with the midday profile with a 16 kHz radio wave at an angle of incidence of
# 40° from normal. We'll also assume the magnetic field has a strength of 50,000 nT
# at a dip angle of 68° and azimuth of 111°. Piggott was concerned with a path from Rugby
# to Cambridge, UK, which, according to the
# [Westinghouse VLF effective-conductivity map](https://apps.dtic.mil/sti/citations/AD0675771),
# has a ground conductivity index of 8.
# This can be specified as `GROUND[8]`.
ea = EigenAngle(deg2rad(40))
frequency = Frequency(16e3)
bfield = BField(50e-6, deg2rad(68), deg2rad(111))
ground = GROUND[8]
# To define the electron density and collision frequency profile, we will read in a
# [digitized table](@__REPO_ROOT_URL__/examples/piggott1965_data.csv)
# of the curves from Piggott and linearly interpolate them.
# While we're at it, we'll also prepare the nighttime ionosphere.
root_dir = dirname(dirname(pathof(LongwaveModePropagator)))
examples_dir = joinpath(root_dir, "examples")
data = CSV.File(joinpath(examples_dir, "piggott1965_data.csv"))
## interpolation object
day_itp = interpolate((data.day_ne_z,), data.day_ne, Gridded(Linear()))
day_etp = extrapolate(day_itp, Line())
dayfcn(z) = (v = day_etp(z); v > 0 ? v : 0.001)
## night has some rows of `missing` data
filtnight_z = collect(skipmissing(data.night_ne_z))
filtnight = collect(skipmissing(data.night_ne))
night_itp = interpolate((filtnight_z,), filtnight, Gridded(Linear()))
night_etp = extrapolate(night_itp, Line())
nightfcn(z) = (v = night_etp(z); v > 0 ? v : 0.001)
## so does the collision frequency
filtnu_z = collect(skipmissing(data.nu_z))
filtnu = collect(skipmissing(data.nu))
nu_itp = interpolate((filtnu_z,), filtnu, Gridded(Linear()))
nu_etp = extrapolate(nu_itp, Line())
nufcn(z) = (v = nu_etp(z); v > 0 ? v : 0.001)
day = Species(QE, ME, dayfcn, nufcn)
night = Species(QE, ME, nightfcn, nufcn)
nothing #hide
# ## Scaled, integrated wavefields
#
# We use the coordinate frame where ``z`` is directed upward into the ionosphere, ``x`` is
# along the propagation direction, and ``y`` is perpendicular to complete the
# right-handed system.
# Where the ionosphere only varies in the ``z`` direction, the ``E_z``
# and ``H_z`` fields can be eliminated so that we only need to study the remaining four.
# The differential equations for the wave in the ionosphere can be written in matrix
# form for our coordinate system as
# ```math
# \frac{\mathrm{d}\bm{e}}{\mathrm{d}z} = -ik\bm{T}\bm{e}
# ```
# where
# ```math
# \bm{e} = \begin{pmatrix}
# E_x \\ -E_y \\ H_x \\ H_y
# \end{pmatrix}
# ```
# and ``\bm{T}`` is the ``4 \times 4`` matrix presented in
# [Clemmow and Heading (1954)](https://doi.org/10.1017/S030500410002939X).
# ``\bm{T}`` consists of elements of the susceptibility matrix for the ionosphere
# (and can be calculated with [`LongwaveModePropagator.tmatrix`](@ref)).
#
# To compute the wavefields, we calculate them at some height ``z``, use
# ``\mathrm{d}\bm{e}/\mathrm{d}z`` to step to a new height, and repeat from a point high
# in the ionosphere down to the ground.
# The initial solution comes from the Booker Quartic, which is a solution for the
# wavefields in a homogeneous ionosphere.
# At a great height in the ionosphere, we are interested in the two quartic solutions
# corresponding to upward-going waves.
# Therefore, we are integrating two sets of 4 complex variables simultaneously.
# Throughout the integration, the two solutions lose their independence because of
# numerical accuracy limitations over a wide range of field magnitudes.
# To maintain accuracy, the wavefields are orthonomalized repeatedly during the downward
# integration, and the scaling values are stored so that the fields can be "recorrected"
# after the integration is complete.
#
# Here are what the real component of the ``E_{x,1}`` and ``H_{x,2}`` wavefields
# looks like with and without the "recorrection".
zs = 110e3:-50:0
zskm = zs/1000
e = LMP.integratewavefields(zs, ea, frequency, bfield, day; unscale=true)
e_unscaled = LMP.integratewavefields(zs, ea, frequency, bfield, day; unscale=false)
ex1 = getindex.(e, 1)
ex1_unscaled = getindex.(e_unscaled, 1)
hx2 = getindex.(e, 7)
hx2_unscaled = getindex.(e_unscaled, 7)
p1 = plot(real(ex1), zskm; title="\$E_{x,1}\$",
ylims=(0, 90), xlims=(-1.2, 1.2), linewidth=1.5, ylabel="altitude (km)",
label="corrected", legend=:topleft);
plot!(p1, real(ex1_unscaled),
zskm; linewidth=1.5, label="scaled only");
p2 = plot(real(hx2), zskm; title="\$H_{x,2}\$",
ylims=(0, 90), xlims=(-1.2, 1.2), linewidth=1.5, legend=false);
plot!(p2, real(hx2_unscaled),
zskm; linewidth=1.5);
plot(p1, p2; layout=(1,2))
#md savefig("wavefields_scaling.png"); nothing #hide
#md # 
#
# ## Differential equations solver
#
# Pitteway (1965) used a basic form of a Runge-Kutta integrator with fixed step size.
# Julia has a fantastic [DifferentialEquations suite](https://diffeq.sciml.ai/stable/)
# for integrating many different forms of differential equations.
# Although wavefields are only computed two times for every transition in a
# [`SegmentedWaveguide`](@ref), we would still like to choose an efficient
# solver that requires
# relatively few function calls while still maintaining good accuracy.
#
# Let's try a few different solvers and compare their runtime for the
# day and night ionospheres.
#
# We can pass [`IntegrationParams`](@ref) through the [`LMPParams`](@ref) struct.
# Where necessary, we set the `lazy` interpolant option of the solvers to `false`
# because we discontinuously scale the fields in the middle of the integration and the
# `lazy` option is not aware of this.
TO = TimerOutput()
zs = 110e3:-50:0
solvers = [Tsit5(), BS5(lazy=false), OwrenZen5(),
Vern6(lazy=false), Vern7(lazy=false), Vern8(lazy=false), Vern9(lazy=false)]
solverstrings = ["Tsit5", "BS5", "OwrenZen5", "Vern6", "Vern7", "Vern8", "Vern9"]
day_es = []
night_es = []
for s in eachindex(solvers)
ip = IntegrationParams(solver=solvers[s], tolerance=1e-6)
params = LMPParams(wavefieldintegrationparams=ip)
## make sure method is compiled
LMP.integratewavefields(zs, ea, frequency, bfield, day; params=params);
LMP.integratewavefields(zs, ea, frequency, bfield, night; params=params);
solverstring = solverstrings[s]
let day_e, night_e
## repeat 200 times to average calls
for i = 1:200
## day ionosphere
@timeit TO solverstring begin
day_e = LMP.integratewavefields(zs, ea, frequency, bfield, day; params=params)
end
## night ionosphere
@timeit TO solverstring begin
night_e = LMP.integratewavefields(zs, ea, frequency, bfield, night; params=params)
end
end
push!(day_es, day_e)
push!(night_es, night_e)
end
end
# A quick plot to ensure none of the methods have problems.
day_e1s = [getindex.(e, 1) for e in day_es]
plot(real(day_e1s), zs/1000;
label=permutedims(solverstrings), legend=:topleft)
#md savefig("wavefields_day.png"); nothing #hide
#md # 
#
# And at night...
night_e1s = [getindex.(e, 1) for e in night_es]
plot(real(night_e1s), zs/1000;
label=permutedims(solverstrings), legend=:topright)
#md savefig("wavefields_night.png"); nothing #hide
#md # 
#
# The times to run each...
TO
# The `Tsit5`, `BS5`, and 6th, 7th, and 8th order Vern methods all have similar performance.
# In fact, rerunning these same tests multiple times can result in different solvers
# being "fastest".
#
# We use `Tsit5()`as the default in LongwaveModePropagator, which is similar to MATLAB's
# `ode45`, but usually more efficient.
#
# Why not a strict `RK4` or a more basic method? I tried them and they produce some
# discontinuities around the reflection height. It is admittedly difficult to tell
# if this is a true failure of the methods at this height or a problem related
# to the scaling and saving callbacks that occur during the integration.
# In any case, none of the methods tested above exhibit that issue.
# ## Pitteway figure 2
#
# Let's reproduce the wavefields in figure 2 of Pitteway (1965).
zs = 110e3:-50:50e3
zskm = zs/1000
e = LMP.integratewavefields(zs, ea, frequency, bfield, day)
ex1 = getindex.(e, 1)
ey1 = getindex.(e, 2)
ex2 = getindex.(e, 5)
hx2 = getindex.(e, 7)
function plotfield(field; kwargs...)
p = plot(real(field), zskm; color="black", linewidth=1.2, legend=false,
xlims=(-0.8, 0.8), label="real",
framestyle=:grid, kwargs...)
plot!(p, imag(field), zskm; color="black",
linewidth=1.2, linestyle=:dash, label="imag")
plot!(p, abs.(field), zskm; color="black", linewidth=2, label="abs")
plot!(p, -abs.(field), zskm; color="black", linewidth=2, label="")
return p
end
fs = 10
ex1p = plotfield(ex1; ylims=(49, 81), yaxis=false, yformatter=_->"");
annotate!(ex1p, 0.2, 79, text("\$E_{x,1}\$", fs));
ey1p = plotfield(ey1; ylims=(49, 81));
annotate!(ey1p, 0.2, 79, text("\$E_{y,1}\$", fs));
annotate!(ey1p, -0.98, 83, text("height (km)", fs));
ex2p = plotfield(ex2; ylims=(49, 86), yaxis=false, yformatter=_->"");
annotate!(ex2p, 0.3, 84, text("\$E_{x,2}\$", fs));
hx2p = plotfield(hx2; ylims=(49, 86));
annotate!(hx2p, 0.35, 84, text("\$H_{x,2}\$", fs, :center));
plot(ex1p, ey1p, ex2p, hx2p; layout=(2,2), size=(400,600), top_margin=5mm)
#md savefig("wavefields_fig2.png"); nothing #hide
#md # 
#
# ```@raw html
# <img src="../../images/Pitteway1965_fig2.png"/>
# ```
# The envelopes of the two are very similar.
# The precise position of the real and imaginary wave components are not important
# because they each represent an instant in time and change based on the starting
# height of the integration.
#
# ## Pitteway figure 3
#
# Figure 3 of Pitteway (1965) uses a different scenario.
# A wave of frequency 202 kHz is at normal incidence through the nighttime ionosphere
# presented in Piggott (1965).
#
# First let's set up the new scenario.
ea = EigenAngle(0)
frequency = Frequency(202e3)
bfield = BField(50e-6, deg2rad(68), deg2rad(111))
ground = GROUND[8]
nothing #hide
# Now integrating the wavefields.
zs = 110e3:-50:70e3
zskm = zs/1000
e = LMP.integratewavefields(zs, ea, frequency, bfield, night)
ey1 = getindex.(e, 2)
hx2 = getindex.(e, 7)
ey1p = plotfield(ey1; ylims=(75, 102), title="\$E_{y,1}\$");
hx2p = plotfield(hx2; ylims=(75, 102), title="\$H_{x,2}\$");
plot(ey1p, hx2p; layout=(1,2), size=(400,500))
#md savefig("wavefields_fig3.png"); nothing #hide
#md # 
#
# ```@raw html
# <img src="../../images/Pitteway1965_fig3.png"/>
# ``` | LongwaveModePropagator | https://github.com/fgasdia/LongwaveModePropagator.jl.git |
|
[
"MIT"
] | 0.4.1 | 792c195909ca5dfff5685305b6fa0aa16c3d1041 | code | 1872 | """
Antenna
Abstract supertype for all antenna-like types.
"""
abstract type Antenna end
"""
AbstractDipole <: Antenna
Abstract type for dipole antennas.
Subtypes of `AbstractDipole` have an orientation `azimuth_angle` (``ϕ``) and
`inclination_angle` (``γ``) where
| [rad] | ϕ | γ |
|:-----:|:---------:|:----------:|
| 0 | end fire | vertical |
| π/2 | broadside | horizontal |
!!! note
Angles describe the orientation of the antenna, not the radiation pattern.
"""
abstract type AbstractDipole <: Antenna end
"""
azimuth(d::AbstractDipole)
Return the azimuth angle ``ϕ`` of `d` measured towards positive `y` direction from `x`.
See also: [`AbstractDipole`](@ref)
"""
azimuth
"""
inclination(d::AbstractDipole)
Return the inclination (dip) angle ``γ`` of `d` measured from vertical.
See also: [`AbstractDipole`](@ref)
"""
inclination
"""
Dipole
Dipole antenna with arbitrary orientation described by `azimuth_angle` and
`inclination_angle` from vertical.
See also: [`AbstractDipole`](@ref)
"""
struct Dipole <: AbstractDipole
azimuth_angle::Float64
inclination_angle::Float64
end
azimuth(d::Dipole) = d.azimuth_angle
inclination(d::Dipole) = d.inclination_angle
"""
VerticalDipole
Dipole antenna with inclination angle ``γ = 0`` from the vertical.
"""
struct VerticalDipole <: AbstractDipole end
azimuth(d::VerticalDipole) = 0.0
inclination(d::VerticalDipole) = 0.0
"""
HorizontalDipole
Dipole antenna with inclination angle ``γ = π/2`` from the vertical and `azimuth_angle`
orientation ``ϕ`` where:
| ϕ [rad] | orientation |
|:--------:|:-----------:|
| 0 | end fire |
| π/2 | broadside |
"""
struct HorizontalDipole <: AbstractDipole
azimuth_angle::Float64 # radians
end
azimuth(d::HorizontalDipole) = d.azimuth_angle
inclination(d::HorizontalDipole) = π/2
| LongwaveModePropagator | https://github.com/fgasdia/LongwaveModePropagator.jl.git |
|
[
"MIT"
] | 0.4.1 | 792c195909ca5dfff5685305b6fa0aa16c3d1041 | code | 4087 | """
EigenAngle
Plane-wave propagation direction in angle `θ` from the vertical in radians.
Common trigonometric function values of this angle are calculated to increase performance.
# Fields
- `θ::ComplexF64`
- `cosθ::ComplexF64`
- `sinθ::ComplexF64`
- `secθ::ComplexF64`
- `cos²θ::ComplexF64`
- `sin²θ::ComplexF64`
`Real` `θ` will be automatically converted to `Complex`.
!!! note
Technically this is an angle of incidence from the vertical, and not necessarily an
_eigen_angle unless it is found to be associated with a propagated mode in the waveguide.
"""
struct EigenAngle
θ::ComplexF64 # radians, because df/dθ are in radians
cosθ::ComplexF64
sinθ::ComplexF64
secθ::ComplexF64 # == 1/cosθ
cos²θ::ComplexF64
sin²θ::ComplexF64
end
EigenAngle(ea::EigenAngle) = ea
EigenAngle(θ::Real) = EigenAngle(complex(θ))
function EigenAngle(θ::Complex)
rθ, iθ = reim(θ)
((abs(rθ) > 2π) || (abs(iθ) > 2π)) && @warn "θ > 2π. Make sure θ is in radians."
S, C = sincos(θ)
Cinv = inv(C) # == sec(θ)
C² = C^2
S² = 1 - C²
EigenAngle(θ, C, S, Cinv, C², S²)
end
"""
isless(x::EigenAngle, y::EigenAngle)
Calls `Base.isless` for complex `EigenAngle` by `real` and then `imag` component.
By defining `isless`, calling `sort` on `EigenAngle`s sorts by real component first and
imaginary component second.
"""
function Base.isless(x::EigenAngle, y::EigenAngle)
return isless((real(x.θ), imag(x.θ)), (real(y.θ), imag(y.θ)))
end
function Base.show(io::IO, e::EigenAngle)
compact = get(io, :compact, false)
if compact
print(io, e.θ)
else
print(io, e.θ)
end
return nothing
end
function Base.show(io::IO, ::MIME"text/plain", e::EigenAngle)
println(io, "EigenAngle: ")
show(io, e)
end
"""
isdetached(ea::EigenAngle, frequency::Frequency; params=LMPParams())
Return `true` if this is likely an earth detached (whispering gallery) mode according to the
criteria in [Pappert1981] eq. 1 with the additional criteria that the frequency be
above 100 kHz.
# References
[Pappert1981]: R. A. Pappert, “LF daytime earth ionosphere waveguide calculations,” Naval
Ocean Systems Center, San Diego, CA, NOSC/TR-647, Jan. 1981.
[Online]. Available: https://apps.dtic.mil/docs/citations/ADA096098.
"""
function isdetached(ea::EigenAngle, frequency::Frequency; params=LMPParams())
C, C² = ea.cosθ, ea.cos²θ
f, k = frequency.f, frequency.k
@unpack earthradius, curvatureheight = params
α = 2/earthradius
return f > 100e3 && real(2im/3*(k/α)*(C²- α*curvatureheight)^(3/2)) > 12.4
end
"""
referencetoground(ea::EigenAngle; params=LMPParams())
Reference `ea` from `params.curvatureheight` to ground (``z = 0``).
"""
function referencetoground(ea::EigenAngle; params=LMPParams())
# see, e.g. PS71 pg 11
@unpack earthradius, curvatureheight = params
return EigenAngle(asin(ea.sinθ/sqrt(1 - 2/earthradius*curvatureheight)))
end
"""
referencetoground(sinθ; params=LMPParams())
Reference ``sin(θ)`` from `params.curvatureheight` to the ground and return ``sin(θ₀)`` at
the ground.
"""
function referencetoground(sinθ; params=LMPParams())
@unpack earthradius, curvatureheight = params
return sinθ/sqrt(1 - 2/earthradius*curvatureheight)
end
"""
attenuation(ea, frequency::Frequency; params=LMPParams())
Compute attenuation of eigenangle `ea` at the ground.
`ea` will be converted to an `EigenAngle` if needed.
This function internally references `ea` to the ground.
"""
function attenuation(ea, frequency::Frequency; params=LMPParams())
ea = EigenAngle(ea)
S₀ = referencetoground(ea.sinθ)
neper2dB = 20log10(exp(1)) # 1 Np ≈ 8.685 dB
return -neper2dB*frequency.k*imag(S₀)*1e6
end
"""
phasevelocity(ea)
Compute the relative phase velocity ``v/c`` associated with the eigenangle `θ`.
`ea` will be converted to an `EigenAngle` if needed.
This function internally references `ea` to the ground.
"""
function phasevelocity(ea)
ea = EigenAngle(ea)
S₀ = referencetoground(ea.sinθ)
return 1/real(S₀)
end
| LongwaveModePropagator | https://github.com/fgasdia/LongwaveModePropagator.jl.git |
|
[
"MIT"
] | 0.4.1 | 792c195909ca5dfff5685305b6fa0aa16c3d1041 | code | 3109 | # TODO: Custom "range" of Frequencies to form a spectrum for, e.g. lightning sferic
"""
Frequency
Electromagnetic wave defined by frequency `f`, but also carrying angular wave frequency `ω`,
wavenumber `k`, and wavelength `λ`, all in SI units.
"""
struct Frequency
f::Float64
ω::Float64
k::Float64
λ::Float64
end
"""
Frequency(f)
Return `Frequency` given electromagnetic wave frequency `f` in Hertz.
"""
function Frequency(f)
ω = 2π*f
k = ω/C0
λ = C0/f
Frequency(f, ω, k, λ)
end
Frequency(f::Frequency) = f
########
"""
Emitter
Abstract type for types that energize the waveguide with electromagnetic energy.
"""
abstract type Emitter end
function transmitterchecks(alt)
alt < 0 && error("Transmitter altitude cannot be negative.")
return true
end
"""
Transmitter{A<:Antenna} <: Emitter
Typical ground-based Transmitter.
# Fields
- `name::String`: transmitter name.
- `latitude::Float64`: transmitter geographic latitude in degrees.
- `longitude::Float64`: transmitter geographic longitude in degrees.
- `antenna::Antenna`: transmitter antenna.
- `frequency::Frequency`: transmit frequency.
- `power::Float64`: transmit power in Watts.
"""
struct Transmitter{A<:Antenna} <: Emitter
name::String
latitude::Float64
longitude::Float64
antenna::A
frequency::Frequency
power::Float64
Transmitter{A}(n, la, lo, an, fr, po) where {A<:Antenna} = new(n, la, lo, an, fr, po)
end
altitude(t::Transmitter) = 0.0
frequency(t::Transmitter) = t.frequency
azimuth(t::Transmitter) = azimuth(t.antenna)
inclination(t::Transmitter) = inclination(t.antenna)
power(t::Transmitter) = t.power
"""
Transmitter(name, lat, lon, frequency)
Return a `Transmitter` with a `VerticalDipole` antenna and transmit power of 1000 W.
"""
Transmitter(name, lat, lon, frequency) =
Transmitter{VerticalDipole}(name, lat, lon, VerticalDipole(), Frequency(frequency), 1000)
"""
Transmitter(frequency)
Return a `Transmitter` with zeroed geographic position, 1000 W transmit power, and
`VerticalDipole` antenna.
"""
Transmitter(frequency) = Transmitter("", 0, 0, frequency)
"""
Transmitter(antenna, frequency, power)
Return a `Transmitter` with zeroed geographic position.
"""
Transmitter(antenna::A, frequency, power) where {A<:Antenna} =
Transmitter{A}("", 0, 0, antenna, Frequency(frequency), power)
"""
AirborneTransmitter{A<:Antenna} <: Emitter
Similar to `Transmitter` except it also contains an `altitude` field in meters.
"""
struct AirborneTransmitter{A<:Antenna} <: Emitter
name::String
latitude::Float64
longitude::Float64
altitude::Float64
antenna::A
frequency::Frequency
power::Float64
AirborneTransmitter{A}(n, la, lo, al, an, fr, po) where {A<:Antenna} =
transmitterchecks(al) && new(n, la, lo, al, an, fr, po)
end
altitude(t::AirborneTransmitter) = t.altitude
frequency(t::AirborneTransmitter) = t.frequency
azimuth(t::AirborneTransmitter) = azimuth(t.antenna)
inclination(t::AirborneTransmitter) = inclination(t.antenna)
power(t::AirborneTransmitter) = t.power
| LongwaveModePropagator | https://github.com/fgasdia/LongwaveModePropagator.jl.git |
|
[
"MIT"
] | 0.4.1 | 792c195909ca5dfff5685305b6fa0aa16c3d1041 | code | 10238 | # CODATA 2018 NIST SP 961
const C0 = 299792458.0 # c, speed of light in vacuum, m/s
const U0 = 1.25663706212e-6 # μ₀, vacuum permeability, H/m
const E0 = 8.8541878128e-12 # ϵ₀, vacuum permittivity, F/m
const Z0 = 376.730313668 # Z₀, vacuum impedance, Ω
const QE = -1.602176634e-19 # qₑ, charge of an electron, C
const ME = 9.1093837015e-31 # mₑ, mass of an electron, kg
########
"""
Species
Ionosphere constituent `Species`.
# Fields
- `charge::Float64`: signed species charged in Coulombs.
- `mass::Float64`: species mass in kilograms.
- `numberdensity`: a callable that returns number density in number per cubic meter as a
function of height in meters.
- `collisionfrequency`: a callable that returns the collision frequency in collisions per
second as a function of height in meters.
!!! note
`numberdensity` and `collisionfrequency` will be converted to `FunctionerWrapper` types
that tell the compiler that these functions will always return values of type `Float64`.
A limited test is run to check if this is true, but otherwise it is up to the user
to ensure these functions return only values of type `Float64`.
"""
struct Species
charge::Float64 # C
mass::Float64 # kg
numberdensity::FunctionWrapper{Float64,Tuple{Float64}} # m⁻³
collisionfrequency::FunctionWrapper{Float64,Tuple{Float64}} # s⁻¹
function Species(charge, mass, numberdensity, collisionfrequency)
_checkFloat64(numberdensity, 0:1e3:110e3)
_checkFloat64(collisionfrequency, 0:1e3:110e3)
new(charge, mass,
FunctionWrapper{Float64,Tuple{Float64}}(numberdensity),
FunctionWrapper{Float64,Tuple{Float64}}(collisionfrequency))
end
end
Base.eachindex(s::Species) = 1
Base.length(s::Species) = 1
Base.getindex(s::Species, i) = i == 1 ? s : throw(BoundsError)
function _checkFloat64(f, x)
for i in eachindex(x)
v = f(x[i])
v isa Float64 || throw(TypeError(Symbol(f), Float64, v))
end
end
########
"""
BField
Background magnetic field vector of strength `B` in Tesla with direction cosines `dcl`,
`dcm`, and `dcn` corresponding to ``x``, ``y``, and ``z`` directions parallel,
perpendicular, and up to the waveguide.
"""
struct BField
B::Float64
dcl::Float64
dcm::Float64
dcn::Float64
function BField(B, dcl, dcm, dcn)
if iszero(B)
@warn "BField magnitude of exactly 0 is not supported. Setting B = 1e-16."
B = 1e-16
end
new(B, dcl, dcm, dcn)
end
end
"""
BField(B, dip, azimuth)
Return a `BField` of strength `B` in Tesla, `dip` angle in radians from the horizontal, and
`azimuth` angle in radians from the propagation direction, positive towards ``y``.
Dip (inclination) is the angle made with the horizontal by the background magnetic field
lines. Positive dip corresponds to when the magnetic field vector is directed downward into
Earth. Therefore, it ranges between ``+π`` in Earth's geographic northern hemisphere and
``-π`` in the southern hemisphere.
"""
function BField(B, dip, azimuth)
# BUG: How can we avoid this?
# Look at the Booker quartic roots for dip angles -1,+1. They are way
# outside the normal. The roots aren't accurately found, although I'm not
# sure where the issue is.
abs(dip) <= deg2rad(1) &&
@warn "magnetic dip angles between ±1° have known numerical issues."
abs(dip) > π &&
@warn "magnetic dip angle should be in radians."
abs(azimuth) > 2π &&
@warn "magnetic azimuth angle should be in radians."
Sdip, Cdip = sincos(dip)
Saz, Caz = sincos(azimuth)
BField(B, Cdip*Caz, Cdip*Saz, -Sdip)
end
"""
dip(b::BField)
Return the dip angle in radians from `b`.
"""
dip(b::BField) = -asin(b.dcn)
"""
azimuth(b::BField)
Return the azimuth angle in radians from `b`.
"""
azimuth(b::BField) = atan(b.dcm,b.dcl)
function isisotropic(b::BField)
b.B <= 1e-12 && return true
tolerance = deg2rad(0.15)
bdip = dip(b)
abs(bdip) < tolerance && return true
baz = azimuth(b)
(abs(baz - π/2) < tolerance || abs(baz - 3π/2) < tolerance) && return true
return false
end
########
"""
Ground(ϵᵣ, σ)
Isotropic earth ground characterized by a relative permittivity `ϵᵣ` and a conductivity `σ`
in Siemens per meter.
"""
struct Ground
ϵᵣ::Int
σ::Float64
end
"Default ground conductivity indices from LWPC."
const GROUND = Dict(
1=>Ground(5, 1e-5),
2=>Ground(5, 3e-5),
3=>Ground(10, 1e-4),
4=>Ground(10, 3e-4),
5=>Ground(15, 1e-3),
6=>Ground(15, 3e-3),
7=>Ground(15, 1e-2),
8=>Ground(15, 3e-2),
9=>Ground(15, 1e-1),
10=>Ground(81, 4.0))
########
@doc raw"""
waitprofile(z, h′, β; cutoff_low=0, threshold=1e12)
Compute the electron number density in electrons per cubic meter at altitude `z` in meters
using Wait's exponential profile [[Wait1964]; [Thomson1993]] with parameters
`h′` in kilometers and `β` in inverse kilometers.
The profile is:
```math
Nₑ = 1.43 × 10¹³ \exp(-0.15 h') \exp[(β - 0.15)(z/1000 - h')]
```
Optional arguments:
- `cutoff_low=0`: when `z` is below `cutoff_low`, return zero.
- `threshold=1e12`: when density is greater than `threshold`, return `threshold`.
See also: [`electroncollisionfrequency`](@ref), [`ioncollisionfrequency`](@ref)
# References
[Wait1964]: J. R. Wait and K. P. Spies, “Characteristics of the earth-ionosphere waveguide
for VLF radio waves,” U.S. National Bureau of Standards, Boulder, CO, Technical Note
300, Dec. 1964.
[Thomson1993]: N. R. Thomson, “Experimental daytime VLF ionospheric parameters,” Journal of
Atmospheric and Terrestrial Physics, vol. 55, no. 2, pp. 173–184, Feb. 1993,
doi: 10.1016/0021-9169(93)90122-F.
"""
function waitprofile(z, hp, β; cutoff_low=0, threshold=1e12)
if z > cutoff_low
# Using form with single `exp` for speed
Ne = 1.43e13*exp(-0.15*hp - (β - 0.15)*(hp - z*0.001)) # converting `z` to km
if Ne > threshold
return oftype(Ne, threshold)
else
return Ne
end
else
zero(promote_type(Float64, typeof(z)))
end
end
@doc raw"""
electroncollisionfrequency(z)
Compute the electron-neutral collision frequency in collisions per second at height `z` in
meters based on Wait's conductivity profile [[Wait1964]; [Thomson1993]].
The profile is:
```math
νₑ(z) = 1.816 × 10¹¹ \exp(-0.15⋅z/1000)
```
See also: [`waitprofile`](@ref), [`ioncollisionfrequency`](@ref)
# References
[Wait1964]: J. R. Wait and K. P. Spies, “Characteristics of the earth-ionosphere waveguide
for VLF radio waves,” U.S. National Bureau of Standards, Boulder, CO, Technical Note
300, Dec. 1964.
[Thomson1993]: N. R. Thomson, “Experimental daytime VLF ionospheric parameters,” Journal of
Atmospheric and Terrestrial Physics, vol. 55, no. 2, pp. 173–184, Feb. 1993,
doi: 10.1016/0021-9169(93)90122-F.
"""
function electroncollisionfrequency(z)
return 1.816e11*exp(-0.15e-3*z) # e-3 converts `z` to km
end
@doc raw"""
ioncollisionfrequency(z)
Compute the ion-neutral collision frequency in collisions per second at height `z` in meters
from [Morfitt1976].
The profile is:
```math
νᵢ(z) = 4.54 × 10⁹ \exp(-0.15⋅z/1000)
```
See also: [`waitprofile`](@ref), [`electroncollisionfrequency`](@ref)
# References
[Morfitt1976]: D. G. Morfitt and C. H. Shellman, “‘MODESRCH’, an improved computer program
for obtaining ELF/VLF/LF mode constants in an Earth-ionosphere waveguide,” Naval
Electronics Laboratory Center, San Diego, CA, NELC/IR-77T, Oct. 1976.
"""
function ioncollisionfrequency(z)
return 4.54e9*exp(-0.15e-3*z) # e-3 converts `z` to km
end
########
# Useful plasma functions
"""
plasmafrequency(n, q, m)
plasmafrequency(z, s::Species)
Return the plasma frequency ``ωₚ = √(nq²/(ϵ₀m))`` for a ``cold'' plasma.
"""
plasmafrequency(n, q, m) = sqrt(n*q^2/(E0*m))
plasmafrequency(z, s::Species) = plasmafrequency(s.numberdensity(z), s.charge, s.mass)
"""
gyrofrequency(q, m, B)
gyrofrequency(s::Species, b::BField)
Return the _signed_ gyrofrequency ``Ω = qB/m``.
"""
gyrofrequency(q, m, B) = q*B/m
gyrofrequency(s::Species, b::BField) = gyrofrequency(s.charge, s.mass, b.B)
"""
magnetoionicparameters(z, frequency::Frequency, bfield::BField, species::Species)
Compute the magnetoionic parameters `X`, `Y`, and `Z` for height `z`.
```math
X = N e² / (ϵ₀ m ω²)
Y = e B / (m ω)
Z = ν / ω
```
# References
[Budden1955a]: K. G. Budden, “The numerical solution of differential equations governing
reflexion of long radio waves from the ionosphere,” Proc. R. Soc. Lond. A, vol. 227,
no. 1171, pp. 516–537, Feb. 1955, pp. 517.
[Budden1988]: K. G. Budden, “The propagation of radio waves: the theory of radio
waves of low power in the ionosphere and magnetosphere,” First paperback edition.
New York: Cambridge University Press, 1988, pp. 39.
[Ratcliffe1959]: J. A. Ratcliffe, "The magneto-ionic theory & its applications to the
ionosphere," Cambridge University Press, 1959.
"""
function magnetoionicparameters(z, frequency::Frequency, bfield::BField, species::Species)
m = species.mass
ω = frequency.ω
invω = inv(ω)
invE0ω = invω/E0
X, Y, Z = _magnetoionicparameters(z, invω, invE0ω, bfield, species)
return X, Y, Z
end
# Specialized for performance of `susceptibility`
@inline function _magnetoionicparameters(z, invω, invE0ω, bfield, species)
N, nu = species.numberdensity, species.collisionfrequency
e, m = species.charge, species.mass
B = bfield.B
invmω = invω/m
X = N(z)*e^2*invE0ω*invmω # = N(z)*e^2/(E0*m*ω^2)
Y = e*B*invmω # = e*B/(m*ω) # [Ratcliffe1959] pg. 182 specifies that sign of `e` is included here
Z = nu(z)*invω # = nu(z)/ω
return X, Y, Z
end
"""
waitsparameter(z, frequency::Frequency, bfield::BField, species::Species)
Compute Wait's conductivity parameter `Wr`.
```math
ωᵣ = Xω²/ν = ωₚ²/ν
```
"""
function waitsparameter(z, frequency::Frequency, bfield::BField, species::Species)
X, Y, Z = magnetoionicparameters(z, frequency, bfield, species)
ω = frequency.ω
nu = species.collisionfrequency
return X*ω^2/nu(z)
end
| LongwaveModePropagator | https://github.com/fgasdia/LongwaveModePropagator.jl.git |
|
[
"MIT"
] | 0.4.1 | 792c195909ca5dfff5685305b6fa0aa16c3d1041 | code | 15893 | #==
Functions related to running and saving LMP through JSON and other files.
==#
function jsonsafe!(v)
for i in eachindex(v)
if isnan(v[i]) || isinf(v[i])
v[i] = 0
end
end
end
"""
Input
Abstract supertype for structs carrying information to be input to the model.
"""
abstract type Input end
"""
ExponentialInput
Type for Wait and Spies (1964) exponential ionosphere profiles defined by [`waitprofile`](@ref).
The [`electroncollisionfrequency`](@ref) is used for the electron-neutral collision frequency
profile.
- The electron density profile begins at 40 km altitude and extends to 110 km.
- The transmitter power is 1 kW.
# Fields
- `name::String`
- `description::String`
- `datetime::DateTime`
- `segment_ranges::Vector{Float64}`: distance from transmitter to the beginning of each
`HomogeneousWaveguide` segment in meters.
- `hprimes::Vector{Float64}`: Wait's ``h′`` parameter for each `HomogeneousWaveguide` segment.
- `betas::Vector{Float64}`: Wait's ``β`` parameter for each `HomogeneousWaveguide` segment.
- `b_mags::Vector{Float64}`: magnetic field magnitude for each `HomogeneousWaveguide` segment.
- `b_dips::Vector{Float64}`: magnetic field dip angles in radians for each
`HomogeneousWaveguide` segment.
- `b_azs::Vector{Float64}`: magnetic field azimuth in radians "east" of the propagation
direction for each `HomogeneousWaveguide` segment.
- `ground_sigmas::Vector{Float64}`: ground conductivity in Siemens per meter for each
`HomogeneousWaveguide` segment.
- `ground_epsrs::Vector{Int}`: ground relative permittivity for each `HomogeneousWaveguide`
segment.
- `frequency::Float64`: transmitter frequency in Hertz.
- `output_ranges::Vector{Float64}`: distances from the transmitter at which the field will
be calculated.
"""
mutable struct ExponentialInput <: Input
name::String
description::String
datetime::DateTime
# All units SI
segment_ranges::Vector{Float64}
hprimes::Vector{Float64}
betas::Vector{Float64}
b_mags::Vector{Float64}
b_dips::Vector{Float64}
b_azs::Vector{Float64}
ground_sigmas::Vector{Float64}
ground_epsrs::Vector{Int}
frequency::Float64
output_ranges::Vector{Float64}
function ExponentialInput()
s = new()
setfield!(s, :frequency, NaN)
return s
end
end
StructTypes.StructType(::Type{ExponentialInput}) = StructTypes.Mutable()
"""
TableInput <: Input
# Fields
- `name::String`
- `description::String`
- `datetime::DateTime`
- `segment_ranges::Vector{Float64}`: distance from transmitter to the beginning of each
`HomogeneousWaveguide` segment in meters.
- `altitude::Vector{Float64}`: altitude above ground in meters for which the `density` and
`collision_frequency` profiles are specified.
- `density::Vector{Float64}`: electron density at each `altitude` in ``m⁻³``.
- `collision_frequency::Vector{Float64}`: electron-ion collision frequency at each
`altitude` in ``s⁻¹``.
- `b_dips::Vector{Float64}`: magnetic field dip angles in radians for each
`HomogeneousWaveguide` segment.
- `b_azs::Vector{Float64}`: magnetic field azimuth in radians "east" of the propagation
direction for each `HomogeneousWaveguide` segment.
- `ground_sigmas::Vector{Float64}`: ground conductivity in Siemens per meter for each
`HomogeneousWaveguide` segment.
- `ground_epsrs::Vector{Int}`: ground relative permittivity for each `HomogeneousWaveguide`
segment.
- `frequency::Float64`: transmitter frequency in Hertz.
- `output_ranges::Vector{Float64}`: distances from the transmitter at which the field will
be calculated.
"""
mutable struct TableInput <: Input
name::String
description::String
datetime::DateTime
# All units SI
segment_ranges::Vector{Float64}
altitude::Vector{Float64}
density::Vector{Vector{Float64}}
collision_frequency::Vector{Vector{Float64}}
b_mags::Vector{Float64}
b_dips::Vector{Float64}
b_azs::Vector{Float64}
ground_sigmas::Vector{Float64}
ground_epsrs::Vector{Int}
frequency::Float64
output_ranges::Vector{Float64}
function TableInput()
s = new()
setfield!(s, :frequency, NaN)
setfield!(s, :density, [Vector{Float64}()])
setfield!(s, :collision_frequency, [Vector{Float64}()])
return s
end
end
StructTypes.StructType(::Type{TableInput}) = StructTypes.Mutable()
"""
BatchInput{T} <: Input
A collection of `inputs` with a batch `name`, `description`, and `datetime`.
"""
mutable struct BatchInput{T} <: Input
name::String
description::String
datetime::DateTime
inputs::Vector{T}
function BatchInput{T}() where T
s = new{T}()
return s
end
end
BatchInput() = BatchInput{Any}()
StructTypes.StructType(::Type{<:BatchInput}) = StructTypes.Mutable()
"""
Output
Abstract supertype for structs containing information to be output from the model.
"""
abstract type Output end
"""
BasicOutput <: Output
# Fields
- `name::String`
- `description::String`
- `datetime::DateTime`
- `output_ranges::Vector{Float64}`
- `amplitude::Vector{Float64}`
- `phase::Vector{Float64}`
"""
mutable struct BasicOutput <: Output
name::String
description::String
datetime::DateTime
output_ranges::Vector{Float64}
amplitude::Vector{Float64}
phase::Vector{Float64}
BasicOutput() = new()
end
StructTypes.StructType(::Type{BasicOutput}) = StructTypes.Mutable()
"""
BatchOutput{T} <: Output
A collection of `outputs` with a batch `name`, `description`, and `datetime`.
See also: [`BatchInput`](@ref)
"""
mutable struct BatchOutput{T} <: Output
name::String
description::String
datetime::DateTime
outputs::Vector{T}
function BatchOutput{T}() where {T}
s = new{T}()
s.outputs = T[]
return s
end
end
BatchOutput() = BatchOutput{Any}()
StructTypes.StructType(::Type{<:BatchOutput}) = StructTypes.Mutable()
jsonsafe!(s::BatchOutput) = jsonsafe!(s.outputs)
"""
iscomplete(s)
Return `true` if input or output struct `s` is completely defined, otherwise return `false`.
"""
function iscomplete(s)
for fn in fieldnames(typeof(s))
isdefined(s, fn) || return false
end
return true
end
function iscomplete(s::BatchInput)
isdefined(s, :inputs) || return false
for i in eachindex(s.inputs)
iscomplete(s.inputs[i]) || return false
end
return true
end
function iscomplete(s::BatchOutput)
isdefined(s, :outputs) || return false
for i in eachindex(s.outputs)
iscomplete(s.outputs[i]) || return false
end
return true
end
"""
validlengths(s)
Check if field lengths of input `s` match their number of segments.
"""
validlengths
function validlengths(s::ExponentialInput)
numsegments = length(s.segment_ranges)
checkfields = (:hprimes, :betas, :b_mags, :b_dips, :b_azs, :ground_sigmas,
:ground_epsrs)
for field in checkfields
length(getfield(s, field)) == numsegments || return false
end
return true
end
function validlengths(s::TableInput)
numsegments = length(s.segment_ranges)
checkfields = (:b_mags, :b_dips, :b_azs, :ground_sigmas, :ground_epsrs)
for field in checkfields
length(getfield(s, field)) == numsegments || return false
end
numaltitudes = length(s.altitude)
matrixfields = (:density, :collision_frequency)
for field in matrixfields
v = getfield(s, field)
length(v) == numsegments || return false
for i = 1:numsegments
length(v[i]) == numaltitudes || return false
end
end
return true
end
function validlengths(s::BatchInput)
isdefined(s, :inputs) || return false
for i in eachindex(s.inputs)
validlengths(s.inputs[i]) || return false
end
return true
end
"""
parse(file)
Parse a JSON file compatible with `Input` or `Output` types.
"""
function parse(file)
# More to less specific
types = (ExponentialInput, TableInput,
BatchInput{ExponentialInput}, BatchInput{TableInput}, BatchInput{Any},
BasicOutput, BatchOutput{BasicOutput}, BatchOutput{Any})
matched = false
let filecontents
for t in types
filecontents = parse(file, t)
if !isnothing(filecontents)
matched = true
break
end
end
if matched
return filecontents
else
error("\"$file\" could not be matched to a valid format.")
end
end
end
function parse(file, t::Type{<:Input})
matched = false
# To clarify the syntax here, `filecontents` is what is returned from inside
# the `do` block; the JSON contents or `nothing`
filecontents = open(file, "r") do f
s = JSON3.read(f, t)
if iscomplete(s) && validlengths(s)
matched = true
return s
end
end
matched ? filecontents : nothing
end
function parse(file, t::Type{<:Output})
matched = false
# To clarify the syntax here, `filecontents` is what is returned from inside
# the `do` block; the JSON contents or `nothing`
filecontents = open(file, "r") do f
s = JSON3.read(f, t)
if iscomplete(s)
matched = true
return s
end
end
matched ? filecontents : nothing
end
"""
buildwaveguide(s::ExponentialInput, i)
Return `HomogeneousWaveguide` from the `i`th entry in each field of `s`.
"""
function buildwaveguide(s::ExponentialInput, i)
bfield = BField(s.b_mags[i], s.b_dips[i], s.b_azs[i])
species = Species(QE, ME, z -> waitprofile(z, s.hprimes[i], s.betas[i]; cutoff_low=40e3),
electroncollisionfrequency)
ground = Ground(s.ground_epsrs[i], s.ground_sigmas[i])
return HomogeneousWaveguide(bfield, species, ground, s.segment_ranges[i])
end
"""
buildwaveguide(s::TableInput, i)
Return `HomogeneousWaveguide` from the `i`th entry in each field of `s` with a
FritschButland monotonic interpolation over `density` and `collision_frequency`.
Outside of `s.altitude` the nearest `s.density` or `s.collision_frequency` is used.
"""
function buildwaveguide(s::TableInput, i)
bfield = BField(s.b_mags[i], s.b_dips[i], s.b_azs[i])
ditp = interpolate(s.altitude, s.density[i], FritschButlandMonotonicInterpolation())
citp = interpolate(s.altitude, s.collision_frequency[i], FritschButlandMonotonicInterpolation())
density_itp = extrapolate(ditp, Flat())
collision_itp = extrapolate(citp, Flat())
species = Species(QE, ME, density_itp, collision_itp)
ground = Ground(s.ground_epsrs[i], s.ground_sigmas[i])
return HomogeneousWaveguide(bfield, species, ground, s.segment_ranges[i])
end
"""
buildrun(s::ExponentialInput; mesh=nothing, unwrap=true, params=LMPParams())
buildrun(s::TableInput; mesh=nothing, unwrap=true, params=LMPParams())
buildrun(s::BatchInput; mesh=nothing, unwrap=true, params=LMPParams())
Build LMP structs from an `Input` and run `LMP`.
For `TableInput`s, a FritschButland monotonic interpolation is performed over `density` and
`collision_frequency`.
"""
buildrun
function buildrun(s::ExponentialInput; mesh=nothing, unwrap=true, params=LMPParams())
if length(s.segment_ranges) == 1
# HomogeneousWaveguide
bfield = BField(only(s.b_mags), only(s.b_dips), only(s.b_azs))
species = Species(QE, ME, z -> waitprofile(z, only(s.hprimes), only(s.betas);
cutoff_low=40e3),
electroncollisionfrequency)
ground = Ground(only(s.ground_epsrs), only(s.ground_sigmas))
waveguide = HomogeneousWaveguide(bfield, species, ground)
tx = Transmitter(s.frequency)
rx = GroundSampler(s.output_ranges, Fields.Ez)
else
# SegmentedWaveguide
waveguide = SegmentedWaveguide([buildwaveguide(s, i) for i in
eachindex(s.segment_ranges)])
tx = Transmitter(s.frequency)
rx = GroundSampler(s.output_ranges, Fields.Ez)
end
_, amp, phase = propagate(waveguide, tx, rx; mesh=mesh, unwrap=unwrap, params=params)
output = BasicOutput()
output.name = s.name
output.description = s.description
output.datetime = Dates.now()
output.output_ranges = s.output_ranges
output.amplitude = amp
output.phase = phase
jsonsafe!(output.amplitude)
jsonsafe!(output.phase)
return output
end
function buildrun(s::TableInput; mesh=nothing, unwrap=true, params=LMPParams())
if length(s.segment_ranges) == 1
# HomogeneousWaveguide
bfield = BField(only(s.b_mags), only(s.b_dips), only(s.b_azs))
ditp = interpolate(s.altitude, only(s.density), FritschButlandMonotonicInterpolation())
citp = interpolate(s.altitude, only(s.collision_frequency), FritschButlandMonotonicInterpolation())
density_itp = extrapolate(ditp, Flat())
collision_itp = extrapolate(citp, Flat())
species = Species(QE, ME, density_itp, collision_itp)
ground = Ground(only(s.ground_epsrs), only(s.ground_sigmas))
waveguide = HomogeneousWaveguide(bfield, species, ground)
tx = Transmitter(s.frequency)
rx = GroundSampler(s.output_ranges, Fields.Ez)
else
# SegmentedWaveguide
waveguide = SegmentedWaveguide([buildwaveguide(s, i) for i in eachindex(s.segment_ranges)])
tx = Transmitter(s.frequency)
rx = GroundSampler(s.output_ranges, Fields.Ez)
end
_, amp, phase = propagate(waveguide, tx, rx; mesh=mesh, unwrap=unwrap, params=params)
output = BasicOutput()
output.name = s.name
output.description = s.description
output.datetime = Dates.now()
output.output_ranges = s.output_ranges
output.amplitude = amp
output.phase = phase
jsonsafe!(output.amplitude)
jsonsafe!(output.phase)
return output
end
function buildrun(s::BatchInput; mesh=nothing, unwrap=true, params=LMPParams())
batch = BatchOutput{BasicOutput}()
batch.name = s.name
batch.description = s.description
batch.datetime = Dates.now()
@progress name = "Batch inputs" for i in eachindex(s.inputs)
output = buildrun(s.inputs[i]; mesh=mesh, unwrap=unwrap, params=params)
push!(batch.outputs, output)
end
return batch
end
"""
buildrunsave(outfile, s::BatchInput; append=false, mesh=nothing, unwrap=true, params=LMPParams())
Similar to `buildrun`, except it saves results into `outfile` as `s` is processed.
If `append=true`, this function parses `outfile` for preexisting results and only runs the
remaining scenarios in `s`. Otherwise, a new `BatchOutput` is created.
"""
function buildrunsave(outfile, s::BatchInput; append=false, mesh=nothing, unwrap=true,
params=LMPParams())
if append && isfile(outfile)
batch = open(outfile, "r") do f
v = JSON3.read(f, BatchOutput{BasicOutput})
return v
end
else
batch = BatchOutput{BasicOutput}()
batch.name = s.name
batch.description = s.description
batch.datetime = Dates.now()
end
skip = false
@progress name="Batch inputs" for i in eachindex(s.inputs)
name = s.inputs[i].name
# Check if this case has already been run (useful for append)
for o in eachindex(batch.outputs)
if name == batch.outputs[o].name
skip = true
break
end
end
if skip
skip = false
continue
end
output = buildrun(s.inputs[i]; mesh=mesh, unwrap=unwrap, params=params)
push!(batch.outputs, output)
json_str = JSON3.write(batch)
open(outfile, "w") do f
write(f, json_str)
end
end
return batch
end
| LongwaveModePropagator | https://github.com/fgasdia/LongwaveModePropagator.jl.git |
|
[
"MIT"
] | 0.4.1 | 792c195909ca5dfff5685305b6fa0aa16c3d1041 | code | 10981 | module LongwaveModePropagator
import Base: @_inline_meta, @propagate_inbounds, @_propagate_inbounds_meta
import Base: ==
using Dates, LinearAlgebra
using StaticArrays
using StaticArrays: promote_tuple_eltype, convert_ntuple
using OrdinaryDiffEq, DiffEqCallbacks
using Parameters, ProgressLogging
using JSON3, StructTypes
using Interpolations
import FunctionWrappers: FunctionWrapper
using PolynomialRoots: roots!
using RootsAndPoles, Romberg, ModifiedHankelFunctionsOfOrderOneThird
export GRPFParams
# LongwaveModePropagator.jl
export propagate
# EigenAngle.jl
export EigenAngle
export attenuation, phasevelocity, referencetoground, setea
# Geophysics.jl
export BField, Species, Fields, Ground, GROUND
export waitprofile, electroncollisionfrequency, ioncollisionfrequency
# IO.jl
export ExponentialInput, TableInput, BatchInput, BasicOutput, BatchOutput
# Samplers.jl
export Receiver, Sampler, GroundSampler
# Emitters.jl
export Transmitter, Dipole, VerticalDipole, HorizontalDipole, Frequency
export inclination, azimuth
# modefinder.jl
export findmodes, PhysicalModeEquation
# Waveguides.jl
export HomogeneousWaveguide, SegmentedWaveguide
"""
IntegrationParams{T}
Parameters passed to `OrdinaryDiffEq.jl` during the integration of the ionosphere reflection
coefficient matrix in `modefinder.jl`.
# Fields
- `tolerance::Float64 = 1e-5`: integration `atol` and `rtol`.
- `solver::T = Vern7()`: a `DifferentialEquations.jl` solver.
- `dt::Float64 = 1.0`: height step in meters (many methods use a variable step size).
- `force_dtmin::Bool = false`: if true, continue integration when solver reaches minimum
step size.
- `maxiters::Int = 100_000`: maximum number of iterations before stopping.
"""
@with_kw struct IntegrationParams{T}
tolerance::Float64 = 1e-5
solver::T = Vern7()
dt::Float64 = 1.0
force_dtmin::Bool = false
maxiters::Int = 100_000
end
export IntegrationParams
const DEFAULT_GRPFPARAMS = GRPFParams(100000, 1e-5, true)
"""
LMPParams{T,T2,H <: AbstractRange{Float64}}
Parameters for the `LongwaveModePropagator` module with defaults:
- `topheight::Float64 = 110e3`: starting height for integration of the ionosphere reflection
coefficient.
- `earthradius::Float64 = 6369e3`: Earth radius in meters.
- `earthcurvature::Bool = true`: toggle inclusion of Earth curvature in calculations. This
is not supported by all functions.
- `curvatureheight::Float64 = 50e3`: reference height for Earth curvature in meters. At this
height, the index of refraction is 1, and is therefore the reference height for
eigenangles.
- `approxsusceptibility::Bool = false`: use a cubic interpolating spline representation of
[`susceptibility`](@ref) during the integration of [`dRdz`](@ref).
- `susceptibilitysplinestep::Float64 = 10.0`: altitude step in meters used to build the
spline representation of [`susceptibility`](@ref) if `approxsusceptibility == true`.
- `grpfparams::GRPFParams = GRPFParams(100000, 1e-5, true)`: parameters for the `GRPF`
complex root-finding algorithm.
- `integrationparams::IntegrationParams{T} =
IntegrationParams(solver=Vern7(), tolerance=1e-5)`:
parameters passed to `DifferentialEquations.jl` for integration of the ionosphere
reflection coefficient.
- `wavefieldheights::H = range(topheight, 0, length=2049)`: heights in meters at which
wavefields will be integrated.
- `wavefieldintegrationparams::IntegrationParams{T2} =
IntegrationParams(solver=Tsit5(), tolerance=1e-6)`:
parameters passed to `DifferentialEquations.jl` for integration of the wavefields
used in mode conversion. The solver cannot be lazy.
- `radiationresistancecorrection::Bool = false`: Perform a radiation resistance correction
to the calculated field amplitude for transmitter antennas with altitude > 0.
The struct is created using `Parameters.jl` `@with_kw` and supports that package's
instantiation capabilities, e.g.:
```julia
p = LMPParams()
p2 = LMPParams(earth_radius=6370e3)
p3 = LMPParams(p2; grpf_params=GRPFParams(100000, 1e-6, true))
```
See also: [`IntegrationParams`](@ref)
"""
@with_kw struct LMPParams{T,T2,H<:AbstractRange{Float64}}
topheight::Float64 = 110e3
earthradius::Float64 = 6369e3 # m
earthcurvature::Bool = true
curvatureheight::Float64 = 50e3 # m
approxsusceptibility::Bool = false
susceptibilitysplinestep::Float64 = 10.0
grpfparams::GRPFParams = DEFAULT_GRPFPARAMS
integrationparams::IntegrationParams{T} = IntegrationParams()
wavefieldheights::H = range(topheight, 0; length=2049)
wavefieldintegrationparams::IntegrationParams{T2} =
IntegrationParams(solver=Tsit5(), tolerance=1e-6)
radiationresistancecorrection::Bool = false
end
export LMPParams
"""
ModeEquation
Functions can dispatch on subtypes of `ModeEquation`, although currently only
`PhysicalModeEquation` is supported.
Future work might include the `ModifiedModeEquation` of [Morfitt1976].
# References
[Morfitt1976]: D. G. Morfitt and C. H. Shellman, “‘MODESRCH’, an improved computer program
for obtaining ELF/VLF/LF mode constants in an Earth-ionosphere waveguide,” Naval
Electronics Laboratory Center, San Diego, CA, NELC/IR-77T, Oct. 1976. [Online].
Available: http://www.dtic.mil/docs/citations/ADA032573.
"""
abstract type ModeEquation end # concrete subtypes defined in modefinder files
"Indicates derivative with respect to eigenangle ``θ``."
struct Dθ end
"""
Bottom of reflection coefficient integration. `LongwaveModePropagator.jl` assumes
`BOTTOMHEIGHT = 0.0`.
"""
const BOTTOMHEIGHT = 0.0 # WARNING: if this isn't zero, many assumptions break
#
include("utils.jl")
include("Antennas.jl")
include("Emitters.jl") # must be before EigenAngles.jl
include("EigenAngles.jl")
include("Geophysics.jl")
include("Samplers.jl")
include("TMatrix.jl")
include("Waveguides.jl")
include("Wavefields.jl")
include("bookerquartic.jl")
include("magnetoionic.jl")
include("modeconversion.jl")
include("modefinder.jl")
include("modesum.jl")
include("IO.jl")
"""
propagate(waveguide::HomogeneousWaveguide, tx::Emitter, rx::AbstractSampler;
modes::Union{Nothing,Vector{EigenAngle}}=nothing, mesh=nothing,
params=LMPParams())
Compute electric field `E`, `amplitude`, and `phase` at `rx`.
Precomputed waveguide `modes` can optionally be provided as a `Vector{EigenAngle}`. By
default modes are found with [`findmodes`](@ref).
If `mesh = nothing`, use [`defaultmesh`](@ref) to generate `mesh` for the
mode finding algorithm. This is ignored if `modes` is not `nothing`.
"""
function propagate(waveguide::HomogeneousWaveguide, tx::Emitter, rx::AbstractSampler;
modes::Union{Nothing,Vector{EigenAngle}}=nothing, mesh=nothing, unwrap=true,
params=LMPParams())
if isnothing(modes)
if isnothing(mesh)
mesh = defaultmesh(tx.frequency)
else
if minimum(imag(mesh)) < deg2rad(-31)
@warn "imaginary component less than -0.5410 rad (-31°) may cause wave"*
"fields calculated with modified Hankel functions to overflow."
end
end
modeequation = PhysicalModeEquation(tx.frequency, waveguide)
modes = findmodes(modeequation, mesh; params=params)
end
E = Efield(modes, waveguide, tx, rx; params=params)
amplitude, phase = amplitudephase(E)
if unwrap
unwrap!(phase)
end
return E, amplitude, phase
end
"""
propagate(waveguide::SegmentedWaveguide, tx::Emitter, rx::AbstractSampler;
mesh=nothing, params=LMPParams())
Compute electric field `E`, `amplitude`, and `phase` at `rx` through a `SegmentedWaveguide`.
If `mesh = nothing`, use [`defaultmesh`](@ref) to generate `mesh` for the
mode finding algorithm.
"""
function propagate(waveguide::SegmentedWaveguide, tx::Emitter, rx::AbstractSampler;
mesh=nothing, unwrap=true, params=LMPParams())
if isnothing(mesh)
mesh = defaultmesh(tx.frequency)
else
if minimum(imag(mesh)) < deg2rad(-31)
@warn "imaginary component less than -0.5410 rad (-31°) may cause wave fields"*
"calculated with modified Hankel functions to overflow."
end
end
J = length(waveguide) # number of waveguide segments
heighttype = typeof(params.wavefieldheights)
wavefields_vec = Vector{Wavefields{heighttype}}(undef, J)
adjwavefields_vec = Vector{Wavefields{heighttype}}(undef, J)
# Calculate wavefields and adjoint wavefields for each segment of waveguide
for j in 1:J
wvg = waveguide[j]
modeequation = PhysicalModeEquation(tx.frequency, wvg)
modes = findmodes(modeequation, mesh; params=params)
# adjoint wavefields are wavefields through adjoint waveguide, but for same modes
# as wavefield
adjwvg = adjoint(wvg)
wavefields = Wavefields(params.wavefieldheights, modes)
adjwavefields = Wavefields(params.wavefieldheights, modes)
calculate_wavefields!(wavefields, adjwavefields, tx.frequency, wvg, adjwvg;
params=params)
wavefields_vec[j] = wavefields
adjwavefields_vec[j] = adjwavefields
end
E = Efield(waveguide, wavefields_vec, adjwavefields_vec, tx, rx; params=params)
# Efield for SegmentedWaveguides doesn't have a specialized form for AbstractSamplers
# of Number type, but for consistency we will return scalar E.
# Although now this function is technically type unstable, it has a practically
# unmeasurable affect on the total runtime.
if length(E) == 1
E = only(E)
end
amplitude, phase = amplitudephase(E)
if unwrap
unwrap!(phase)
end
return E, amplitude, phase
end
"""
propagate(file::AbstractString, outfile=missing; incrementalwrite=false, append=false,
mesh=nothing)
Run the model scenario described by `file` and save the results as `outfile`.
If `outfile = missing`, the output file name will be `\$(file)_output.json`.
"""
function propagate(file::AbstractString, outfile=missing; incrementalwrite=false,
append=false, mesh=nothing, unwrap=true, params=LMPParams())
ispath(file) || error("$file is not a valid file name")
if ismissing(outfile)
basepath = dirname(file)
filename, fileextension = splitext(basename(file))
outfile = joinpath(basepath, filename)*"_output.json"
end
s = parse(file)
if incrementalwrite
s isa BatchInput || throw(ArgumentError("incrementalwrite only supported for"*
"BatchInput files"))
output = buildrunsave(outfile, s; append=append, mesh=mesh, unwrap=unwrap, params=params)
else
output = buildrun(s; mesh=mesh, unwrap=unwrap, params=params)
json_str = JSON3.write(output)
open(outfile, "w") do f
write(f, json_str)
end
end
return output
end
end
| LongwaveModePropagator | https://github.com/fgasdia/LongwaveModePropagator.jl.git |
|
[
"MIT"
] | 0.4.1 | 792c195909ca5dfff5685305b6fa0aa16c3d1041 | code | 3053 | ########
"""
Fields
This `baremodule` allows scoped enum-like access to electric field components `Ex`, `Ey`,
and `Ez`.
# Examples
```jldoctest; setup=:(using LongwaveModePropagator.Fields)
julia> Fields.Ex
Ex::Field = 0
julia> Fields.Ey
Ey::Field = 1
```
"""
baremodule Fields
using Base: @enum
@enum Field Ex Ey Ez
end
########
"""
AbstractSampler
Abstract supertype for sampling fields in the waveguide.
Subtypes of AbstractSampler have a position in the guide and a `Fields.Field`.
"""
abstract type AbstractSampler{T} end
function distancechecks(d, stype; earthradius=LMPParams().earthradius)
!issorted(d) && error("$stype distance must be sorted")
minimum(d) < 0 && error("$stype distance must be positive")
maximum(d) > (π*earthradius - 500e3) && @warn "antipode focusing effects not modeled"
return true
end
"""
Sampler{T} <: AbstractSampler{T}
`Sampler` types sample (measure) the electromagnetic field in the waveguide.
# Fields
- `distance::T`: ground distance from the transmitter in meters.
- `fieldcomponent::Fields.Field`: field component measured by the `Sampler`.
- `altitude::Float64`: height above the ground in meters.
"""
struct Sampler{T} <: AbstractSampler{T}
distance::T
fieldcomponent::Fields.Field
altitude::Float64
Sampler(d::T, fc, a) where T = distancechecks(d, Sampler) && new{T}(d, fc, a)
end
distance(s::Sampler) = s.distance
distance(s::Sampler,t::Transmitter) = s.distance
fieldcomponent(s::Sampler) = s.fieldcomponent
altitude(s::Sampler) = s.altitude
"""
GroundSampler{T} <: AbstractSampler{T}
`GroundSamplers` are `Sampler` types with an altitude of zero.
# Fields
- `distance::T`: ground distance from the transmitter in meters.
- `fieldcomponent::Fields.Field`: field component measured by the `GroundSampler`.
"""
struct GroundSampler{T} <: AbstractSampler{T}
distance::T # T is usually <: AbstractVector but could be a scalar
fieldcomponent::Fields.Field
GroundSampler(d::T, fc) where T = distancechecks(d, GroundSampler) && new{T}(d, fc)
end
distance(g::GroundSampler) = g.distance
distance(g::GroundSampler,t::Transmitter) = g.distance
fieldcomponent(g::GroundSampler) = g.fieldcomponent
altitude(g::GroundSampler) = 0.0
"""
Receiver{<:Antenna}
Represent a physical receiver.
A default `Receiver{VerticalDipole}` is returned with `Receiver()`.
# Fields
- `name::String = ""`: receiver name.
- `latitude::Float64 = 0.0`: geographic latitude in degrees.
- `longitude::Float64 = 0.0`: geographic longitude in degrees.
- `altitude::Float64 = 0.0`: receiver altitude in meters above the ground.
- `antenna::Antenna = VerticalDipole()`: receiver antenna.
"""
struct Receiver{A<:Antenna}
name::String
latitude::Float64
longitude::Float64
altitude::Float64
antenna::A
end
Receiver() = Receiver{VerticalDipole}("", 0.0, 0.0, 0.0, VerticalDipole())
altitude(r::Receiver) = r.altitude
distance(r::Receiver,t::Transmitter) = nothing # TODO proj4 stuff
fieldcomponent(r::Receiver) = fieldcomponent(r.antenna)
| LongwaveModePropagator | https://github.com/fgasdia/LongwaveModePropagator.jl.git |
|
[
"MIT"
] | 0.4.1 | 792c195909ca5dfff5685305b6fa0aa16c3d1041 | code | 10201 | """
TMatrix <: SMatrix{4, 4, T}
A custom `SMatrix` subtype that represents the `T` matrix from [Clemmow1954] that
is semi-sparse. The form of the matrix is:
```
┌ ┐
| T₁₁ T₁₂ 0 T₁₄ |
| 0 0 1 0 |
| T₃₁ T₃₂ 0 T₃₄ |
| T₄₁ T₄₂ 0 T₄₄ |
└ ┘
```
`TMatrix` implements efficient matrix-vector multiplication and other math based on its
special form.
See also: [`tmatrix`](@ref)
# References
[Clemmow1954]: P. C. Clemmow and J. Heading, “Coupled forms of the differential equations
governing radio propagation in the ionosphere,” Mathematical Proceedings of the
Cambridge Philosophical Society, vol. 50, no. 2, pp. 319–333, Apr. 1954.
"""
struct TMatrix{T} <: StaticMatrix{4, 4, T}
data::SVector{9,T}
@inline function TMatrix(data::SVector{9,T}) where T
new{T}(data)
end
end
#==
# Constructors
==#
@generated function TMatrix(a::StaticMatrix{4, 4, T}) where {T}
I = _tmatrix_indices()
expr = Vector{Expr}(undef, 9)
i = 0
for index = 1:16
if I[index] > 0
expr[i += 1] = :(a[$index])
end
end
quote
@_inline_meta
@inbounds return TMatrix(SVector{9,T}(tuple($(expr...))))
end
end
@generated function TMatrix(a::NTuple{N,Any}) where {N}
if N != 9
throw(DimensionMismatch("Tuple length must be 9. Length of input was $N."))
end
expr = [:(a[$i]) for i = 1:9]
quote
@_inline_meta
@inbounds return TMatrix(SVector{9}(tuple($(expr...))))
end
end
#==
# Characteristics
==#
Base.size(::Type{TMatrix}) = (4, 4)
Base.size(::Type{TMatrix}, d::Int) = d > 2 ? 1 : 4
@inline function _tmatrix_indices()
# Returns tuple containing TMatrix.data index for dense matrix index of the
# tuple. For example, for linear index `5` of 4×4 matrix, return `4` which
# is the index of TMatrix.data.
# For "empty" values, return `0`.
return tuple(1, 0, 2, 3, 4, 0, 5, 6, 0, 0, 0, 0, 7, 0, 8, 9)
end
@propagate_inbounds function Base.getindex(a::TMatrix{T}, i::Int) where T
I = _tmatrix_indices()
# Written out this is much faster than `i in (2, 6, 9, 11, 12, 14)`
# Could probably be fewer lines with a generated function
if I[i] > 0
return a.data[I[i]]
elseif i == 2
return zero(T)
elseif i == 6
return zero(T)
elseif i == 9
return zero(T)
elseif i == 10
return one(T)
elseif i == 11
return zero(T)
elseif i == 12
return zero(T)
elseif i == 14
return zero(T)
else
throw(BoundsError("attempt to access $(typeof(a)) at index $i"))
end
end
@propagate_inbounds function getindex(a::TMatrix, inds::Int...)
@boundscheck checkbounds(a, inds...)
_getindex_scalar(a, inds...)
end
@generated function _getindex_scalar(a::TMatrix, inds::Int...)
if length(inds) == 0
return quote
@_propagate_inbounds_meta
a[1]
end
end
# This function will only ever be called for length(inds) == 2
stride = 1
ind_expr = :()
for i in 1:length(inds)
if i == 1
ind_expr = :(inds[1])
else
ind_expr = :($ind_expr + $stride * (inds[$i] - 1))
end
stride *= 4
end
return quote
@_propagate_inbounds_meta
a[$ind_expr]
end
end
@generated function Base.Tuple(v::TMatrix)
exprs = [:(v[$i]) for i = 1:16]
quote
@_inline_meta
tuple($(exprs...))
end
end
#==
# Math
==#
LinearAlgebra.ishermitian(v::TMatrix) = false
LinearAlgebra.issymmetric(v::TMatrix) = false
@inline Base.:(==)(a::TMatrix, b::TMatrix) = a.data == b.data
@inline Base.sum(v::TMatrix) = sum(v.data) + 1
@generated function Base.:*(a::Number, b::TMatrix{T}) where T
I = _tmatrix_indices()
exprs = [:(($I[$i] > 0) ? a*b.data[$I[$i]] : ($i == 10 ? convert(newtype,a) : zero(newtype))) for i = 1:16]
quote
@_inline_meta
newtype = promote_type(T, typeof(a))
SMatrix{4,4,newtype}(tuple($(exprs...)))
end
end
@generated function Base.:*(a::TMatrix{T}, b::Number) where T
I = _tmatrix_indices()
exprs = [:(($I[$i] > 0) ? b*a.data[$I[$i]] : ($i == 10 ? convert(newtype,b) : zero(newtype))) for i = 1:16]
quote
@_inline_meta
newtype = promote_type(T, typeof(b))
SMatrix{4,4,newtype}(tuple($(exprs...)))
end
end
@inline Base.:*(A::TMatrix, B::AbstractVector) = _mul(A, B)
@inline Base.:*(A::TMatrix, B::StaticVector) = _mul(Size(B), A, B)
@inline Base.:*(A::TMatrix, B::StaticMatrix) = _mul(Size(B), A, B)
@generated function _mul(a::TMatrix{Ta}, b::AbstractVector{Tb}) where {Ta,Tb}
sa = Size(4,4)
exprs = [:(a[$(LinearIndices(sa)[1,1])]*b[1]+a[$(LinearIndices(sa)[1,2])]*b[2]+a[$(LinearIndices(sa)[1,4])]*b[4]),
:(b[3]),
:(a[$(LinearIndices(sa)[3,1])]*b[1]+a[$(LinearIndices(sa)[3,2])]*b[2]+a[$(LinearIndices(sa)[3,4])]*b[4]),
:(a[$(LinearIndices(sa)[4,1])]*b[1]+a[$(LinearIndices(sa)[4,2])]*b[2]+a[$(LinearIndices(sa)[4,4])]*b[4])]
return quote
@_inline_meta
if length(b) != $sa[2]
throw(DimensionMismatch("Tried to multiply arrays of size $sa and $(size(b))"))
end
T = Base.promote_op(LinearAlgebra.matprod, Ta, Tb)
@inbounds return similar_type(b, T, Size($sa[1]))(tuple($(exprs...)))
end
end
@generated function _mul(::Size{sb}, a::TMatrix{Ta}, b::StaticVector{<:Any, Tb}) where {sb, Ta, Tb}
sa = Size(4,4)
if sb[1] != sa[2]
throw(DimensionMismatch("Tried to multiply arrays of size $sa and $sb"))
end
exprs = [:(a[$(LinearIndices(sa)[1,1])]*b[1]+a[$(LinearIndices(sa)[1,2])]*b[2]+a[$(LinearIndices(sa)[1,4])]*b[4]),
:(b[3]),
:(a[$(LinearIndices(sa)[3,1])]*b[1]+a[$(LinearIndices(sa)[3,2])]*b[2]+a[$(LinearIndices(sa)[3,4])]*b[4]),
:(a[$(LinearIndices(sa)[4,1])]*b[1]+a[$(LinearIndices(sa)[4,2])]*b[2]+a[$(LinearIndices(sa)[4,4])]*b[4])]
return quote
@_inline_meta
T = Base.promote_op(LinearAlgebra.matprod, Ta, Tb)
@inbounds return similar_type(b, T, Size($sa[1]))(tuple($(exprs...)))
end
end
@generated function _mul(Sb::Size{sb}, a::TMatrix{Ta}, b::StaticMatrix{<:Any,<:Any,Tb}) where {sb, Ta, Tb}
sa = Size(4,4)
if sb[1] != sa[2]
throw(DimensionMismatch("Tried to multiply arrays of size $sa and $sb"))
end
S = Size(sa[1], sb[2])
tmp_exprs = Vector{Vector{Expr}}(undef, sb[2])
for i = 1:sb[2]
tmp_exprs[i] = [:(a[$(LinearIndices(sa)[1,1])]*b[$(LinearIndices(sb)[1,i])]+
a[$(LinearIndices(sa)[1,2])]*b[$(LinearIndices(sb)[2,i])]+
a[$(LinearIndices(sa)[1,4])]*b[$(LinearIndices(sb)[4,i])]),
:(b[$(LinearIndices(sb)[3,i])]),
:(a[$(LinearIndices(sa)[3,1])]*b[$(LinearIndices(sb)[1,i])]+
a[$(LinearIndices(sa)[3,2])]*b[$(LinearIndices(sb)[2,i])]+
a[$(LinearIndices(sa)[3,4])]*b[$(LinearIndices(sb)[4,i])]),
:(a[$(LinearIndices(sa)[4,1])]*b[$(LinearIndices(sb)[1,i])]+
a[$(LinearIndices(sa)[4,2])]*b[$(LinearIndices(sb)[2,i])]+
a[$(LinearIndices(sa)[4,4])]*b[$(LinearIndices(sb)[4,i])])]
end
exprs = vcat(tmp_exprs...)
return quote
@_inline_meta
T = Base.promote_op(LinearAlgebra.matprod, Ta, Tb)
@inbounds return similar_type(a, T, $S)(tuple($(exprs...)))
end
end
#==
Computing the T matrix entries
==#
@doc raw"""
tmatrix(ea::EigenAngle, M)
Compute the matrix `T` as a `TMatrix` for the differential equations of a wave propagating
at angle `ea` in an ionosphere with susceptibility `M`.
Clemmow and Heading derived the `T` matrix from Maxwell's equations for an electromagnetic
wave in the anisotropic, collisional cold plasma of the ionosphere in a coordinate frame
where ``z`` is upward, propagation is directed obliquely in the ``x``-``z`` plane and
invariance is assumed in ``y``. For the four characteristic wave components
``e = (Ex, -Ey, Z₀Hx, Z₀Hy)ᵀ``, the differential equations are ``de/dz = -ikTe``.
See also: [`susceptibility`](@ref), [`dtmatrix`](@ref)
# References
[Budden1955a]: K. G. Budden, “The numerical solution of differential equations governing
reflexion of long radio waves from the ionosphere,” Proc. R. Soc. Lond. A, vol. 227,
no. 1171, pp. 516–537, Feb. 1955.
[Clemmow1954]: P. C. Clemmow and J. Heading, “Coupled forms of the differential equations
governing radio propagation in the ionosphere,” Mathematical Proceedings of the
Cambridge Philosophical Society, vol. 50, no. 2, pp. 319–333, Apr. 1954.
"""
function tmatrix(ea::EigenAngle, M)
S, C² = ea.sinθ, ea.cos²θ
# Denominator of most of the entries of `T`
den = inv(1 + M[3,3])
M31den = M[3,1]*den
M32den = M[3,2]*den
T11 = -S*M31den
T12 = S*M32den
# T13 = 0
T14 = (C² + M[3,3])*den
# T21 = 0
# T22 = 0
# T23 = 1
# T24 = 0
T31 = M[2,3]*M31den - M[2,1]
T32 = C² + M[2,2] - M[2,3]*M32den
# T33 = 0
T34 = S*M[2,3]*den
T41 = 1 + M[1,1] - M[1,3]*M31den
T42 = M[1,3]*M32den - M[1,2]
# T43 = 0
T44 = -S*M[1,3]*den
# `TMatrix` is a special 4×4 matrix
return TMatrix(T11, T31, T41,
T12, T32, T42,
T14, T34, T44)
end
"""
dtmatrix(ea::EigenAngle, M)
Compute a dense `SMatrix` with the derivative of `T` with respect to `θ`.
See also: [`tmatrix`](@ref)
"""
function dtmatrix(ea::EigenAngle, M)
S, C = ea.sinθ, ea.cosθ
dC² = -2*S*C # d/dθ (C²)
den = inv(1 + M[3,3])
dT11 = -C*M[3,1]*den
dT12 = C*M[3,2]*den
dT13 = 0
dT14 = dC²*den
dT21 = 0
dT22 = 0
dT23 = 0
dT24 = 0
dT31 = 0
dT32 = dC²
dT33 = 0
dT34 = C*M[2,3]*den
dT41 = 0
dT42 = 0
dT43 = 0
dT44 = -C*M[1,3]*den
return SMatrix{4,4}(dT11, dT21, dT31, dT41,
dT12, dT22, dT32, dT42,
dT13, dT23, dT33, dT43,
dT14, dT24, dT34, dT44)
end
| LongwaveModePropagator | https://github.com/fgasdia/LongwaveModePropagator.jl.git |
|
[
"MIT"
] | 0.4.1 | 792c195909ca5dfff5685305b6fa0aa16c3d1041 | code | 19364 | #==
Functions related to calculating electromagnetic field components at any height within the
ionosphere.
This includes calculating wavefields vector from the Booker quartic and Pitteway
integration of wavefields.
==#
"""
Wavefields{H<:AbstractRange}
Struct containing wavefield components for each mode of `eas` at `heights`.
The six electromagnetic field components are stored in the `v` field of the struct and
accessed as a `Matrix` of `SVector{6,ComplexF64}` corresponding to `[height, mode]`.
"""
struct Wavefields{H<:AbstractRange}
v::Matrix{SVector{6,ComplexF64}} # v[height,mode] ; type is derived from typeof T, which is from M
heights::H
eas::Vector{EigenAngle}
end
"""
Wavefields(heights, eas::Vector{EigenAngle})
A constructor for initializing `Wavefields` with an appropriately sized `undef` Matrix
given eigenangles `eas` and `heights`.
"""
function Wavefields(heights, eas::Vector{EigenAngle})
v = Matrix{SVector{6,ComplexF64}}(undef, length(heights), length(eas))
return Wavefields(v, heights, eas)
end
Base.size(A::Wavefields) = size(A.v)
Base.size(A::Wavefields, I...) = size(A.v, I...)
Base.getindex(A::Wavefields, i) = A.v[i]
Base.getindex(A::Wavefields, I...) = A.v[I...]
Base.setindex!(A::Wavefields, x, i) = (A.v[i] = x)
Base.similar(A::Wavefields) = Wavefields(A.heights, A.eas)
Base.copy(A::Wavefields) = Wavefields(copy(A.v), copy(A.heights), copy(A.eas))
Base.view(A::Wavefields, I...) = view(A.v, I...)
"""
==(A::Wavefields, B::Wavefields)
Check for equality `==` between `A.v` and `B.v`, `heights`, and `eas`.
"""
function (==)(A::Wavefields, B::Wavefields)
A.heights == B.heights || return false
A.eas == B.eas || return false
A.v == B.v || return false
return true
end
heights(A::Wavefields) = A.heights
numheights(A::Wavefields) = length(A.heights)
eigenangles(A::Wavefields) = A.eas
nummodes(A::Wavefields) = length(A.eas)
function Base.isvalid(A::Wavefields)
vzs, veas = size(A.v)
zlen = numheights(A)
vzs == zlen || return false
ealen = nummodes(A)
veas == ealen || return false
return true
end
"""
WavefieldIntegrationParams{S,T,T2,H}
Parameters passed to Pitteway integration of wavefields [Pitteway1965].
# Fields
- `z::Float64`: height in meters.
- `bottomz::Float64`: bottom height of integration in meters.
- `ortho_scalar::Complex{Float64}`: scalar for Gram-Schmidt orthogonalization.
- `e1_scalar::Float64`: scalar for wavefield vector 1.
- `e2_scalar::Float64`: scalar for wavefield vector 2.
- `ea::EigenAngle`: wavefield eigenangle.
- `frequency::Frequency`: electromagentic wave frequency in Hz.
- `bfield::BField`: Earth's magnetic field in Tesla.
- `species::S`: species in the ionosphere.
- `params::LMPParams{T,T2,H}`: module-wide parameters.
"""
struct WavefieldIntegrationParams{S,T,T2,H}
z::Float64
bottomz::Float64
ortho_scalar::ComplexF64
e1_scalar::Float64
e2_scalar::Float64
ea::EigenAngle
frequency::Frequency
bfield::BField
species::S
params::LMPParams{T,T2,H}
end
"""
WavefieldIntegrationParams(topheight, ea, frequency, bfield, species, params)
Initialize a `WavefieldIntegrationParams` for downward Pitteway scaled integration
[Pitteway1965].
Automatically set values are:
- `bottomz = BOTTOMHEIGHT`
- `ortho_scalar = zero(ComplexF64)`
- `e1_scalar = one(Float64)`
- `e2_scalar = one(Float64)`
"""
function WavefieldIntegrationParams(topheight, ea, frequency, bfield, species::S,
params::LMPParams{T,T2,H}) where {S,T,T2,H}
return WavefieldIntegrationParams{S,T,T2,H}(topheight, BOTTOMHEIGHT, zero(ComplexF64),
1.0, 1.0, ea, frequency, bfield, species, params)
end
"""
ScaleRecord
Struct for saving wavefield scaling information used in a callback during Pitteway
integration of wavefields [Pitteway1965].
# Fields
- `z::Float64`: current height in meters.
- `e::SMatrix{4,2,Complex{Float64},8}`: wavefield matrix.
- `ortho_scalar::Complex{Float64}`: scalar for Gram-Schmidt orthogonalization.
- `e1_scalar::Float64`: scalar for wavefield vector 1.
- `e2_scalar::Float64`: scalar for wavefield vector 2.
"""
struct ScaleRecord
z::Float64
e::SMatrix{4,2,Complex{Float64},8}
ortho_scalar::Complex{Float64}
e1_scalar::Float64
e2_scalar::Float64
end
"""
dedz(e, k, T::Tmatrix)
Compute ``de/dz = -ikTe`` where ``e = (Ex, -Ey, Z₀Hx, Z₀Hy)ᵀ``.
"""
dedz(e, k, T::TMatrix) = -1im*k*(T*e) # `(T*e)` uses specialized TMatrix math
"""
dedz(e, p, z)
Compute derivative of field components vector `e` at height `z`.
The parameter `p` should be a `WavefieldIntegrationParams`.
"""
function dedz(e, p, z)
@unpack ea, frequency, bfield, species, params = p
M = susceptibility(z, frequency, bfield, species, params=params)
T = tmatrix(ea, M)
return dedz(e, frequency.k, T)
end
"""
scalingcondition(e, z, int)
Return `true` if wavefields should be scaled, otherwise `false` for wavefields `e` at height
`z` and integrator `int`.
Wavefields should be scaled if any component of `real(e)` or `imag(e)` are `>= 1`. In
addition, force scaling at `z <= bottomz` to ensure initial upgoing wave is unit amplitude.
"""
scalingcondition(e, z, int) = any(x->(real(x) >= 1 || imag(x) >= 1), e) || z <= int.p.bottomz
"""
scale!(integrator)
Apply wavefield scaling with [`scalewavefields`](@ref) to the integrator.
"""
function scale!(integrator)
new_e, new_orthos, new_e1s, new_e2s = scalewavefields(integrator.u)
# Last set of scaling values
@unpack bottomz, ea, frequency, bfield, species, params = integrator.p
#==
NOTE: `integrator.t` is the "time" of the _proposed_ step. Therefore, integrator.t`
might equal `0.0`, for example, before it's actually gotten to the bottom.
`integrator.prevt` is the last `t` on the "left" side of the `integrator`, which covers
the local interval [`tprev`, `t`]. The "condition" is met at `integrator.t` and
`integrator.t` is the time at which the affect occurs.
However, it is not guaranteed that each (`tprev`, `t`) directly abuts the next (`tprev`,
`t`).
==#
integrator.p = WavefieldIntegrationParams(integrator.t,
bottomz,
new_orthos,
new_e1s, new_e2s,
ea, frequency, bfield, species, params)
integrator.u = new_e
return nothing
end
"""
scalewavefields(e1, e2)
scalewavefields(e::SMatrix{4,2})
Orthonormalize the vectors `e1` and `e2` or the columns of `e`, and also return the scaling
terms `a`, `e1_scale_val`, and `e2_scale_val` applied to the original vectors.
This first applies Gram-Schmidt orthogonalization and then scales the vectors so they each
have length 1, i.e. `norm(e1) == norm(e2) == 1`. This is the technique suggested by
[Pitteway1965] to counter numerical swamping during integration of wavefields.
# References
[Pitteway1965]: M. L. V. Pitteway, “The numerical calculation of wave-fields, reflexion
coefficients and polarizations for long radio waves in the lower ionosphere. I.,” Phil.
Trans. R. Soc. Lond. A, vol. 257, no. 1079, pp. 219–241, Mar. 1965,
doi: 10.1098/rsta.1965.0004.
"""
scalewavefields
function scalewavefields(e1, e2)
# Orthogonalize vectors `e1` and `e2` (Gram-Schmidt process)
# `dot` for complex vectors automatically conjugates first vector
e1_dot_e1 = real(dot(e1, e1)) # == sum(abs2.(e1)), imag(dot(e1,e1)) == 0
a = dot(e1, e2)/e1_dot_e1 # purposefully unsigned
e2 -= a*e1
# Normalize `e1` and `e2`
e1_scale_val = 1/(sqrt(e1_dot_e1))
e2_scale_val = 1/(norm(e2)) # == 1/sqrt(dot(e2,e2))
e1 *= e1_scale_val
e2 *= e2_scale_val # == normalize(e2)
return e1, e2, a, e1_scale_val, e2_scale_val
end
function scalewavefields(e::SMatrix{4,2})
e1, e2, a, e1_scale_val, e2_scale_val = scalewavefields(e[:,1], e[:,2])
e = hcat(e1, e2)
return e, a, e1_scale_val, e2_scale_val
end
"""
unscalewavefields!(e, saved_values::SavedValues)
Unscale the integrated wavefields, a vector of fields at each integration step `e`, in place.
See also: [`unscalewavefields`](@ref)
"""
function unscalewavefields!(e, saved_values::SavedValues)
zs = saved_values.t
records = saved_values.saveval
# Initialize the "reference" scaling altitude
ref_z = last(records).z
# Usually `osum = 0`, `prod_e1 = 1`, and `prod_e2 = 1` at initialization,
# but we set up the fields at the ground (`last(records)`) outside the loop
osum = last(records).ortho_scalar
prod_e1 = last(records).e1_scalar
prod_e2 = last(records).e2_scalar
# Unscaling we go from the bottom up
@inbounds for i in reverse(eachindex(e))
# Unpack variables
record_z = records[i].z
scaled_e = records[i].e
ortho_scalar = records[i].ortho_scalar
e1_scalar = records[i].e1_scalar
e2_scalar = records[i].e2_scalar
z = zs[i]
# Only update ref_z when there is both:
# 1) we have reached the height where a new ref_z should go into effect
# 2) there is a new ref_z
if (z > record_z) & (record_z > ref_z)
ref_z = record_z
osum *= e1_scalar/e2_scalar
osum += ortho_scalar
prod_e1 *= e1_scalar
prod_e2 *= e2_scalar
end
if i == lastindex(e)
# Bottom doesn't require correction
e[i] = scaled_e
elseif z > ref_z
# From the bottom, the first correction may not need to be applied
# until some higher altitude
e2 = (scaled_e[:,2] - osum*scaled_e[:,1])*prod_e2
e1 = scaled_e[:,1]*prod_e1
e[i] = hcat(e1,e2)
else
e[i] = scaled_e
end
end
return nothing
end
"""
unscalewavefields(saved_values::SavedValues)
Return the unscaled integrated wavefields originally scaled by [`scalewavefields`](@ref).
The bottom level does not get unscaled. We reference the higher levels to the bottom. The
level above the bottom level is additionally scaled by the amount that was applied to
originally get from this level down to the bottom level. The next level up (2 above the
bottom level) is scaled by the amount applied to the next level and then the bottom
level, i.e. we keep track of a cumulative correction on the way back up.
Assumes fields have been scaled by [`scalewavefields`](@ref) during integration.
See also: [`unscalewavefields!`](@ref)
"""
function unscalewavefields(saved_values::SavedValues)
e = Vector{SArray{Tuple{4,2},Complex{Float64},2,8}}(undef, length(saved_values.saveval))
unscalewavefields!(e, saved_values)
return e
end
"""
savevalues(u, t, integrator)
Return a `ScaleRecord` from `u`, `t`, and `integrator`.
"""
savevalues(u, t, integrator) = ScaleRecord(integrator.p.z,
u,
integrator.p.ortho_scalar,
integrator.p.e1_scalar,
integrator.p.e2_scalar)
"""
integratewavefields(zs, ea::EigenAngle, frequency::Frequency, bfield::BField,
species; params=LMPParams(), unscale=true)
Compute wavefields vectors `e` at `zs` by downward integration over heights `zs`.
`params.wavefieldintegrationparams` is used by this function rather than
`params.integrationparams`.
`unscale` corrects scaling of wavefields with `unscalewavefields`.
"""
function integratewavefields(zs, ea::EigenAngle, frequency::Frequency, bfield::BField,
species; params=LMPParams(), unscale=true)
# TODO: version that updates output `e` in place
issorted(zs; rev=true) ||
throw(ArgumentError("`zs` should go from top to bottom of the ionosphere."))
@unpack wavefieldintegrationparams = params
@unpack tolerance, solver, dt, force_dtmin, maxiters = wavefieldintegrationparams
# Initial conditions
Mtop = susceptibility(first(zs), frequency, bfield, species; params=params)
Ttop = tmatrix(ea, Mtop)
e0 = bookerwavefields(Ttop)
# Works best if `e0` fields are normalized at top height
# Don't want to orthogonalize `e0[:,2]` here because it won't be undone!
e0 = hcat(normalize(e0[:,1]), normalize(e0[:,2]))
# saved_positions=(true, true) because we discontinuously modify `u`.
# This is independent of `saveat` and `save_everystep`
cb = DiscreteCallback(scalingcondition, scale!; save_positions=(true, true))
saved_values = SavedValues(Float64, ScaleRecord)
scb = SavingCallback(savevalues, saved_values; save_everystep=false, saveat=zs, tdir=-1)
p = WavefieldIntegrationParams(params.topheight, ea, frequency, bfield, species, params)
# WARNING: Without `lazy=false` (necessary since we're using DiscreteCallback) don't
# use continuous solution output! Also, we're only saving at zs.
prob = ODEProblem{false}(dedz, e0, (first(zs), last(zs)), p)
sol = solve(prob, solver; callback=CallbackSet(cb, scb),
save_everystep=false, save_start=false, save_end=false,
dt=dt, force_dtmin=force_dtmin, maxiters=maxiters,
abstol=tolerance, reltol=tolerance)
if unscale
e = unscalewavefields(saved_values)
else
records = saved_values.saveval
e = [records[i].e for i in eachindex(records)]
end
return e
end
"""
boundaryscalars(R, Rg, e1, e2, isotropic::Bool=false)
boundaryscalars(R, Rg, e, isotropic::Bool=false)
Compute coefficients `(b1, b2)` required to sum the two wavefields vectors `e1` and `e2` or
both columns of `e` for the total wavefield at the ground as ``e = b1*e1 + b2*e2``.
The `b1` and `b2` that satisfy the waveguide boundary conditions are only valid for true
eigenangles of the waveguide.
!!! note
This function assumes that the reflection coefficients `R` and `Rg` and the wavefield
vectors `e1`, `e2` are at the ground.
These boundary conditions
"""
function boundaryscalars(R, Rg, e1, e2, isotropic::Bool=false)
# This is similar to excitation factor calculation, using the waveguide mode condition
ex1, ey1, hx1, hy1 = e1[1], -e1[2], e1[3], e1[4] # the ey component was originally -Ey
ex2, ey2, hx2, hy2 = e2[1], -e2[2], e2[3], e2[4]
# NOTE: Because `R`s and `e`s are at the ground, `hy0` and `ey0` are the same regardless
# of `earthcurvature` being `true` or `false`.
hy0 = 1 # == (1 + Rg[1,1])/(1 + Rg[1,1])
ey0 = 1 # == (1 + Rg[2,2])/(1 + Rg[2,2])
paral = 1 - R[1,1]*Rg[1,1]
perp = 1 - R[2,2]*Rg[2,2]
if isotropic
if abs2(paral) < abs2(perp)
b1 = hy0/hy1
b2 = zero(hy1)
# eyg = 0
else
b1 = zero(ey2)
b2 = ey0/ey2
# hyg = 0
end
else
# polarization ratio Ey/Hy (often `f` or `fofr` in papers)
if abs2(paral) < abs2(perp)
EyHy = ((1 + Rg[2,2])*R[2,1]*Rg[1,1])/((1 + Rg[1,1])*perp)
else
EyHy = ((1 + Rg[2,2])*paral)/((1 + Rg[1,1])*R[1,2]*Rg[2,2])
end
a = (-ey1 + EyHy*hy1)/(ey2 - EyHy*hy2)
hysum = hy1 + a*hy2
b1 = hy0/hysum
b2 = b1*a
end
return b1, b2
end
boundaryscalars(R, Rg, e, isotropic::Bool=false) =
boundaryscalars(R, Rg, e[:,1], e[:,2], isotropic)
"""
fieldstrengths!(EH, zs, me::ModeEquation; params=LMPParams())
fieldstrengths!(EH, zs, ea::EigenAngle, frequency::Frequency, bfield::BField,
species, ground::Ground; params=LMPParams())
Compute ``(Ex, Ey, Ez, Hx, Hy, Hz)ᵀ`` wavefields vectors as elements of `EH` by fullwave
integration at each height in `zs`.
The wavefields are scaled to satisfy the waveguide boundary conditions, which is only valid
at solutions of the mode equation.
"""
function fieldstrengths!(EH, zs, ea::EigenAngle, frequency::Frequency, bfield::BField,
species, ground::Ground; params=LMPParams())
@assert length(EH) == length(zs)
zs[end] == 0 || @warn "Waveguide math assumes fields and reflection coefficients are
calculated at the ground (`z = 0`)."
e = integratewavefields(zs, ea, frequency, bfield, species; params=params)
R = bookerreflection(ea, e[end])
Rg = fresnelreflection(ea, ground, frequency)
b1, b2 = boundaryscalars(R, Rg, e[end], isisotropic(bfield))
S = ea.sinθ
@inbounds for i in eachindex(EH)
M = susceptibility(zs[i], frequency, bfield, species; params=params)
# Scale to waveguide boundary conditions
w = e[i][:,1]*b1 + e[i][:,2]*b2
ex = w[1]
ey = -w[2]
ez = -(w[4]*S + M[3,1]*w[1] - M[3,2]*w[2])/(1 + M[3,3])
hx = w[3]
hy = w[4]
hz = -w[2]*S
EH[i] = SVector(ex, ey, ez, hx, hy, hz)
end
return nothing
end
function fieldstrengths!(EH, zs, me::ModeEquation; params=LMPParams())
@unpack ea, frequency, waveguide = me
@unpack bfield, species, ground = waveguide
fieldstrengths!(EH, zs, ea, frequency, bfield, species, ground; params=params)
end
"""
fieldstrengths(zs, me::ModeEquation; params=LMPParams())
Preallocate vector of wavefields `EH`, then call [`fieldstrengths!`](@ref) and return `EH`.
Each element of `EH` is an `SVector` of ``ex, ey, ez, hx, hy, hz``.
"""
function fieldstrengths(zs, me::ModeEquation; params=LMPParams())
EH = Vector{SVector{6, ComplexF64}}(undef, length(zs))
fieldstrengths!(EH, zs, me; params=params)
return EH
end
"""
calculate_wavefields!(wavefields, adjoint_wavefields, frequency, waveguide,
adjoint_waveguide; params=LMPParams())
Compute fields of `wavefields` in-place scaled to satisfy the `waveguide` boundary
conditions.
This function implements the method of integrating wavefields suggested by
[Pitteway1965].
# References
[Pitteway1965]: M. L. V. Pitteway, “The numerical calculation of wave-fields, reflexion
coefficients and polarizations for long radio waves in the lower ionosphere. I.,” Phil.
Trans. R. Soc. Lond. A, vol. 257, no. 1079, pp. 219–241, Mar. 1965,
doi: 10.1098/rsta.1965.0004.
"""
function calculate_wavefields!(wavefields, adjoint_wavefields, frequency, waveguide,
adjoint_waveguide; params=LMPParams())
@unpack bfield, species, ground = waveguide
ground == adjoint_waveguide.ground ||
throw(ArgumentError("waveguide and adjoint_waveguide should have same Ground"))
species == adjoint_waveguide.species ||
throw(ArgumentError("waveguide and adjoint_waveguide should have same Species"))
adjoint_bfield = adjoint_waveguide.bfield
zs = heights(wavefields)
modes = eigenangles(wavefields)
adjoint_modes = eigenangles(adjoint_wavefields)
modes == adjoint_modes || @warn "Full mode conversion physics assumes adjoint
wavefields are calculated for eigenangles of the original waveguide."
for m in eachindex(modes)
fieldstrengths!(view(wavefields,:,m), zs, modes[m], frequency, bfield, species,
ground; params=params)
fieldstrengths!(view(adjoint_wavefields,:,m), zs, adjoint_modes[m], frequency,
adjoint_bfield, species, ground; params=params)
end
return nothing
end
| LongwaveModePropagator | https://github.com/fgasdia/LongwaveModePropagator.jl.git |
|
[
"MIT"
] | 0.4.1 | 792c195909ca5dfff5685305b6fa0aa16c3d1041 | code | 2132 | """
Waveguide
A waveguide propagation path with a background `BField`, ionosphere `Species`, and `Ground`.
"""
abstract type Waveguide end
"""
HomogeneousWaveguide{S} <: Waveguide
Defines a homogeneous segment of waveguide.
# Fields
- `bfield::BField`: background magnetic field.
- `species::S`: ionosphere constituents.
- `ground::Ground`: waveguide ground.
- `distance::Float64`: distance from the `Emitter` at the start of the segment in meters.
"""
struct HomogeneousWaveguide{S} <: Waveguide
bfield::BField
species::S # `Species` or `Vector{Species}`
ground::Ground
distance::Float64
end
"""
HomogeneousWaveguide(bfield, species, ground)
By default, `distance` is `0.0`.
"""
HomogeneousWaveguide(bfield, species::S, ground) where S =
HomogeneousWaveguide{S}(bfield, species, ground, 0.0)
"""
adjoint(w::HomogeneousWaveguide)
Return `w` with an adjoint `BField` having an `x` component of opposite sign.
"""
function adjoint(w::HomogeneousWaveguide)
@unpack bfield, species, ground, distance = w
adjoint_bfield = BField(bfield.B, -bfield.dcl, bfield.dcm, bfield.dcn)
return HomogeneousWaveguide(adjoint_bfield, species, ground, distance)
end
"""
SegmentedWaveguide{T<:Vector{<:Waveguide}} <: Waveguide
A collection of `Waveguide`s make up an inhomogeneous segmented waveguide.
"""
struct SegmentedWaveguide{T<:Vector{<:Waveguide}} <: Waveguide
v::T
end
Base.length(w::SegmentedWaveguide) = length(w.v)
Base.sort!(w::SegmentedWaveguide) = sort!(w.v; by=x->getfield(x, :distance))
Base.sort(w::SegmentedWaveguide) = SegmentedWaveguide(sort!(copy(w.v)))
Base.issorted(w::SegmentedWaveguide) = issorted(w.v; by=x->getfield(x, :distance))
Base.size(w::SegmentedWaveguide) = size(w.v)
Base.getindex(w::SegmentedWaveguide, i::Int) = w.v[i]
Base.setindex(w::SegmentedWaveguide, x, i::Int) = (w.v[i] = x)
Base.push!(w::SegmentedWaveguide, x) = push!(w.v, x)
Base.iterate(w::SegmentedWaveguide) = iterate(w.v)
Base.iterate(w::SegmentedWaveguide, state) = iterate(w.v, state)
# TODO: WKBWaveguide (that's why we can't call SegmentedWaveguide -> InhomogeneousWaveguide)
| LongwaveModePropagator | https://github.com/fgasdia/LongwaveModePropagator.jl.git |
|
[
"MIT"
] | 0.4.1 | 792c195909ca5dfff5685305b6fa0aa16c3d1041 | code | 15184 | #==
Functions related to the Booker quartic equation and the four waves associated with the
quartic roots.
Besides calculating the quartic roots themselves, this file also includes functions
related to calculating wavefields and vacuum reflection coefficients from the quartic roots.
==#
"""
bookerquartic(ea::EigenAngle, M)
bookerquartic(T::TMatrix)
Compute roots `q` and the coefficients `B` of the Booker quartic described by the
susceptibility tensor `M` or `T` matrix.
# References
[Budden1988]: K. G. Budden, “The propagation of radio waves: the theory of radio
waves of low power in the ionosphere and magnetosphere,” First paperback edition.
New York: Cambridge University Press, 1988.
"""
bookerquartic
function bookerquartic(ea::EigenAngle, M)
S, C, C² = ea.sinθ, ea.cosθ, ea.cos²θ
# Precompute
M11p1 = 1 + M[1,1]
M33p1 = 1 + M[3,3]
C²pM22 = C² + M[2,2]
C²pM33 = C² + M[3,3]
M13pM31 = M[1,3] + M[3,1]
M12M23 = M[1,2]*M[2,3]
M13M31 = M[1,3]*M[3,1]
M21M32 = M[2,1]*M[3,2]
M23M32 = M[2,3]*M[3,2]
# Booker quartic coefficients
B4 = M33p1
B3 = S*M13pM31
B2 = -C²pM33*M11p1 + M13M31 - M33p1*C²pM22 + M23M32
B1 = S*(M12M23 + M21M32 - C²pM22*M13pM31)
B0 = M11p1*C²pM22*C²pM33 +
M12M23*M[3,1] + M[1,3]*M21M32 -
M13M31*C²pM22 - M11p1*M23M32 -
M[1,2]*M[2,1]*C²pM33
booker_quartic_coeffs = MVector{5}(B0, B1, B2, B3, B4)
booker_quartic_roots = MVector{4,eltype(booker_quartic_coeffs)}(0, 0, 0, 0)
# `roots!` dominates this functions runtime
roots!(booker_quartic_roots, booker_quartic_coeffs, NaN, 4, false)
return booker_quartic_roots, SVector(booker_quartic_coeffs)
end
function bookerquartic(T::TMatrix)
# Precompute
T34T42 = T[3,4]*T[4,2]
# This is the depressed form of the quartic
b3 = -T[1,1] - T[4,4]
b2 = T[1,1]*T[4,4] - T[1,4]*T[4,1] - T[3,2]
b1 = T[3,2]*(T[1,1] + T[4,4]) - T[1,2]*T[3,1] - T34T42
b0 = T[1,1]*(T34T42 - T[3,2]*T[4,4]) +
T[1,2]*(T[3,1]*T[4,4] - T[3,4]*T[4,1]) +
T[1,4]*(T[3,2]*T[4,1] - T[3,1]*T[4,2])
booker_quartic_coeffs = MVector{5}(b0, b1, b2, b3, 1)
booker_quartic_roots = MVector{4,eltype(booker_quartic_coeffs)}(0, 0, 0, 0)
roots!(booker_quartic_roots, booker_quartic_coeffs, NaN, 4, false)
return booker_quartic_roots, SVector(booker_quartic_coeffs)
end
"""
dbookerquartic(ea::EigenAngle, M, q, B)
dbookerquartic(T::TMatrix, dT, q, B)
Compute derivative `dq` of the Booker quartic roots `q` with respect to ``θ`` for the
ionosphere described by susceptibility tensor `M` or `T` matrix.
"""
dbookerquartic
function dbookerquartic(ea::EigenAngle, M, q, B)
S, C, C² = ea.sinθ, ea.cosθ, ea.cos²θ
dS = C
dC = -S
dC² = -2*S*C
dB3 = dS*(M[1,3] + M[3,1])
dB2 = -dC²*(2 + M[1,1] + M[3,3])
dB1 = dS/S*B[2] - S*dC²*(M[1,3] + M[3,1])
dB0 = dC²*(2*C²*(1 + M[1,1]) + M[3,3] + M[2,2] + M[1,1]*(M[3,3] + M[2,2]) -
M[1,3]*M[3,1] - M[1,2]*M[2,1])
dq = similar(q)
@inbounds for i in eachindex(dq)
dq[i] = -(((dB3*q[i] + dB2)*q[i] + dB1)*q[i] + dB0) /
(((4*B[5]*q[i] + 3*B[4])*q[i] + 2*B[3])*q[i] + B[2])
end
return SVector(dq)
end
function dbookerquartic(T::TMatrix, dT, q, B)
dB3 = -dT[1,1] - dT[4,4]
dB2 = T[1,1]*dT[4,4] + dT[1,1]*T[4,4] - dT[1,4]*T[4,1] - dT[3,2]
dB1 = -(-T[3,2]*(dT[1,1] + dT[4,4]) - dT[3,2]*(T[1,1] + T[4,4]) + dT[1,2]*T[3,1] +
dT[3,4]*T[4,2])
dB0 = -T[1,1]*(T[3,2]*dT[4,4] + dT[3,2]*T[4,4] - dT[3,4]*T[4,2]) -
dT[1,1]*(T[3,2]*T[4,4] - T[3,4]*T[4,2]) +
T[1,2]*(T[3,1]*dT[4,4] - dT[3,4]*T[4,1]) + dT[1,2]*(T[3,1]*T[4,4] - T[3,4]*T[4,1]) -
T[1,4]*(-dT[3,2]*T[4,1]) - dT[1,4]*(T[3,1]*T[4,2] - T[3,2]*T[4,1])
dq = similar(q)
@inbounds for i in eachindex(dq)
dq[i] = -(((dB3*q[i] + dB2)*q[i] + dB1)*q[i] + dB0) /
(((4*B[5]*q[i] + 3*B[4])*q[i] + 2*B[3])*q[i] + B[2])
end
return SVector(dq)
end
"""
upgoing(q)
Calculate the absolute angle of `q` in radians from 315°×π/180 on the complex plane. Smaller
values indicate upgoing waves.
"""
function upgoing(q::Complex)
# -π/4 is 315°
a = -π/4 - angle(q)
# angle() is +/-π
# `a` can never be > 3π/4, but there is a region on the plane where `a` can be < -π
a < -π && (a += 2π)
return abs(a)
end
upgoing(q::Real) = oftype(q, π/4)
"""
sortquarticroots!(q)
Sort array of quartic roots `q` in place such that the first two correspond to upgoing waves
and the latter two correspond to downgoing waves.
General locations of the four roots of the Booker quartic on the complex plane corresponding
to the:
1) upgoing evanescent wave
2) upgoing travelling wave
3) downgoing evanescent wave
4) downgoing travelling wave
```
Im
3 . |
|
|
. 4 |
------------------Re
| . 2
|
|
| . 1
```
Based on [Pitteway1965] fig. 5.
# References
[Pitteway1965]: M. L. V. Pitteway, “The numerical calculation of wave-fields, reflexion
coefficients and polarizations for long radio waves in the lower ionosphere. I.,” Phil.
Trans. R. Soc. Lond. A, vol. 257, no. 1079, pp. 219–241, Mar. 1965,
doi: 10.1098/rsta.1965.0004.
"""
function sortquarticroots!(q)
# It looks like we could just `sort!(q, by=real)`, but the quadrants of each root are
# not fixed and the positions in the Argand diagram are just approximate.
length(q) == 4 || @warn "length of `q` is not 4"
# Calculate and sort by distance from 315°
# The two closest are upgoing and the two others are downgoing
# This is faster than `sort!(q, by=upgoing)`
dist = MVector{4,real(eltype(q))}(undef)
@inbounds for i in eachindex(q)
dist[i] = upgoing(q[i])
end
i = 4
@inbounds while i > 1
if dist[i] < dist[i-1]
dist[i], dist[i-1] = dist[i-1], dist[i]
q[i], q[i-1] = q[i-1], q[i]
i = 4 # Need to restart at the end
else
i -= 1
end
end
# Now arrange the roots so that they correspond to:
# 1) upgoing evanescent, 2) upgoing travelling
# 3) downgoing evanescent, and 4) downgoing travelling
if imag(q[1]) > imag(q[2])
q[2], q[1] = q[1], q[2]
end
if imag(q[3]) < imag(q[4])
q[4], q[3] = q[3], q[4]
end
# NOTE: Nagano et al 1975 says that of q1 and q2, the one with the largest
# absolute value corresponds to e1 and the other to e2, although this method
# does not guarantee that. In fact, I find that this criteria is often not met.
return q
end
@doc raw"""
bookerwavefields(ea::EigenAngle, M)
bookerwavefields(T::TMatrix)
Compute the two-column wavefields matrix `e` from the ionosphere with susceptibility tensor
`M` or `T` matrix for the two upgoing wavefields.
The first column of `e` is the evanescent wave and the second is the travelling wave.
```math
e =
\begin{pmatrix}
Ex₁ & Ex₂ \\
-Ey₁ & -Ey₂ \\
Hx₁ & Hx₂ \\
Hy₁ & Hy₂
\end{pmatrix}
```
This function solves the eigenvalue problem ``Te = qe``. First, the Booker quartic is solved
for the roots `q`. Then they are sorted so that the roots associated with the two upgoing
waves can be selected. `e` is solved as the eigenvectors for the two `q`s. An
analytical solution is used where `e[2,:] = 1`.
"""
bookerwavefields
function bookerwavefields(T::TMatrix)
q, B = bookerquartic(T)
sortquarticroots!(q)
return bookerwavefields(T, q)
end
function bookerwavefields(ea::EigenAngle, M)
q, B = bookerquartic(ea, M)
sortquarticroots!(q)
T = tmatrix(ea, M)
return bookerwavefields(T, q)
end
function bookerwavefields(T::TMatrix, q)
# Precompute
T14T41 = T[1,4]*T[4,1]
T14T42 = T[1,4]*T[4,2]
T12T41 = T[1,2]*T[4,1]
e = MArray{Tuple{4,2},ComplexF64,2,8}(undef)
@inbounds for i = 1:2
d = T14T41 - (T[1,1] - q[i])*(T[4,4] - q[i])
e[1,i] = (T[1,2]*(T[4,4] - q[i]) - T14T42)/d
e[2,i] = 1
e[3,i] = q[i]
e[4,i] = (-T12T41 + T[4,2]*(T[1,1] - q[i]))/d
end
# By returning as SArray instead of MArray, the MArray doesn't get hit by GC
return SArray(e)
end
"""
bookerwavefields(ea::EigenAngle, M, ::Dθ)
bookerwavefields(T::TMatrix, dT, ::Dθ)
Compute the two-column wavefields matrix `e` as well as its derivative with respect to
``θ``, returned as a tuple `(e, de)` for the ionosphere with susceptibility tensor `M` or
`T` matrix and its derivative with respect to ``θ``, `dT`.
"""
function bookerwavefields(T::TMatrix, dT, ::Dθ)
q, B = bookerquartic(T)
sortquarticroots!(q)
dq = dbookerquartic(T, dT, q, B)
return bookerwavefields(T, dT, q, dq)
end
function bookerwavefields(ea::EigenAngle, M, ::Dθ)
q, B = bookerquartic(ea, M)
sortquarticroots!(q)
dq = dbookerquartic(ea, M, q, B)
T = tmatrix(ea, M)
dT = dtmatrix(ea, M)
return bookerwavefields(T, dT, q, dq)
end
function bookerwavefields(T::TMatrix, dT, q, dq)
# Precompute
T14T41 = T[1,4]*T[4,1]
T14T42 = T[1,4]*T[4,2]
T12T41 = T[1,2]*T[4,1]
e = MArray{Tuple{4,2},ComplexF64,2,8}(undef)
de = similar(e)
@inbounds for i = 1:2
den = T14T41 - (T[1,1] - q[i])*(T[4,4] - q[i])
den² = abs2(den)
dden = dT[1,4]*T[4,1] - (T[1,1]*dT[4,4] + dT[1,1]*T[4,4]) +
q[i]*(dT[1,1] + dT[4,4] - 2*dq[i]) + dq[i]*(T[1,1] + T[4,4])
e1num = T[1,2]*(T[4,4] - q[i]) - T14T42
e4num = -T12T41 + T[4,2]*(T[1,1] - q[i])
e[1,i] = e1num/den
e[2,i] = 1
e[3,i] = q[i]
e[4,i] = e4num/den
# some dT terms == 0
de1num = T[1,2]*(dT[4,4] - dq[i]) + dT[1,2]*(T[4,4] - q[i]) - dT[1,4]*T[4,2]
de4num = -dT[1,2]*T[4,1] + T[4,2]*(dT[1,1] - dq[i])
de[1,i] = (de1num*den - e1num*dden)/den²
de[2,i] = 0
de[3,i] = dq[i]
de[4,i] = (de4num*den - e4num*dden)/den²
end
# By returning as SArray instead of MArray, the MArray doesn't get hit by GC
return SArray(e), SArray(de)
end
@doc raw"""
bookerreflection(ea::EigenAngle, M::SMatrix{3,3})
bookerreflection(ea::EigenAngle, e)
Compute the ionosphere reflection coefficient matrix for a sharply bounded ionosphere from
4×2 wavefields matrix `e` or the susceptibility matrix `M`.
The ionosphere reflection coefficient matrix is computed from a ratio of the downgoing to
upgoing plane waves in the free space beneath the ionosphere [Budden1988] pg. 307.
These are obtained from the two upgoing characteristic waves found from the Booker quartic.
Each make up a column of `e`.
```math
R =
\begin{pmatrix}
Ce₁[4] - e₁[1] & Ce₂[4] - e₂[1] \\
-Ce₁[2] + e₁[3] & -Ce₂[2] + e₂[3]
\end{pmatrix}
\begin{pmatrix}
Ce₁[4] + e₁[1] & Ce₂[4] + e₂[1] \\
-Ce₁[2] - e₁[3] & -Ce₂[2] - e₂[3]
\end{pmatrix}^{-1}
```
The reflection coefficient matrix for the sharply bounded case is commonly used as a
starting solution for integration of the reflection coefficient matrix through the
ionosphere.
# References
[Budden1988]: K. G. Budden, “The propagation of radio waves: the theory of radio
waves of low power in the ionosphere and magnetosphere,” First paperback edition.
New York: Cambridge University Press, 1988.
# Extended help
The set of horizontal field components ``e = (Ex, -Ey, Z₀Hx, Z₀Hy)ᵀ`` can be separated into
an upgoing and downgoing wave, each of which is generally elliptically polarized. A ratio of
the amplitudes of these two waves give a reflection coefficient, except it would only apply
for an incident wave of that particular elliptical polarization. However, the first set of
fields can be linearly combined with a second independent solution for the fields, which
will generally have a different elliptical polarization than the first. Two linear
combinations of the two sets of fields are formed with unit amplitude, linearly polarized
incident waves. The reflected waves then give the components ``R₁₁``, ``R₂₁`` or ``R₁₂``,
``R₂₂`` for the incident wave in the plane of incidence and perpendicular to it,
respectively [Budden1988] pg 552.
The process for determining the reflection coefficient requires resolving the two sets of
fields ``e₁`` and ``e₂`` into the four linearly polarized vacuum modes. The layer of vacuum
can be assumed to be so thin that it does not affect the fields. There will be two upgoing
waves and two downgoing waves, each which has one ``E`` and one ``H`` in the plane of
incidence. If ``f₁, f₂, f₃, f₄`` are the complex amplitudes of the four component waves,
then in matrix notation ``e = Lf`` where ``L`` is the appropriate transformation matrix.
For ``e₁`` and ``e₂``, we can find the corresponding vectors ``f1`` and ``f2`` by
``f1 = L⁻¹e₁``, ``f2 = L⁻¹e₂`` where the two column vectors are partitioned such that
``f1 = (u1, d1)ᵀ`` and ``f2 = (u2, d2)ᵀ`` for upgoing and downgoing 2-element vectors ``u``
and ``d``. From the definition of the reflection coefficient ``R``, ``d = Ru``. Letting
``U = (u1, u2)``, ``D = (d1, d2)``, then ``D = RU`` and the reflection coefficient is
``R = DU⁻¹``. Because the reflection coefficient matrix is a ratio of fields, either ``e₁``
and/or ``e₂`` can be independently multiplied by an arbitrary constant and the value of
``R`` is unaffected.
This function directly computes ``D`` and ``U`` and solves for ``R`` using the right
division operator `R = D/U`.
For additional details, see [Budden1988], chapter 18, section 7.
"""
bookerreflection
function bookerreflection(ea::EigenAngle, e)
C = ea.cosθ
# The order of the two upgoing waves doesn't matter. Swapping the first and second
# columns of `e` will result in the same reflection coefficient matrix.
D = SMatrix{2,2}(C*e[4,1]-e[1,1], -C*e[2,1]+e[3,1], C*e[4,2]-e[1,2], -C*e[2,2]+e[3,2])
U = SMatrix{2,2}(C*e[4,1]+e[1,1], -C*e[2,1]-e[3,1], C*e[4,2]+e[1,2], -C*e[2,2]-e[3,2])
R = D/U
return R
end
function bookerreflection(ea::EigenAngle, M::SMatrix{3,3})
e = bookerwavefields(ea, M)
return bookerreflection(ea, e)
end
"""
bookerreflection(ea::EigenAngle, M, ::Dθ)
Compute the ionosphere reflection coefficient matrix ``R`` for a sharply bounded
ionosphere with susceptibility tensor `M`, as well as its derivative ``dR/dθ`` returned as
the tuple `(R, dR)`.
"""
function bookerreflection(ea::EigenAngle, M, ::Dθ)
S, C = ea.sinθ, ea.cosθ
e, de = bookerwavefields(ea, M, Dθ())
D = SMatrix{2,2}(C*e[4,1]-e[1,1], -C*e[2,1]+e[3,1], C*e[4,2]-e[1,2], -C*e[2,2]+e[3,2])
dD = SMatrix{2,2}(-S*e[4,1] + C*de[4,1] - de[1,1], S*e[2,1] - C*de[2,1] + de[3,1],
-S*e[4,2] + C*de[4,2] - de[1,2], S*e[2,2] - C*de[2,2] + de[3,2])
U = SMatrix{2,2}(C*e[4,1]+e[1,1], -C*e[2,1]-e[3,1], C*e[4,2]+e[1,2], -C*e[2,2]-e[3,2])
dU = SMatrix{2,2}(-S*e[4,1] + C*de[4,1] + de[1,1], S*e[2,1] - C*de[2,1] - de[3,1],
-S*e[4,2] + C*de[4,2] + de[1,2], S*e[2,2] - C*de[2,2] - de[3,2])
R = D/U
dR = dD/U + D*(-U\dU/U)
return R, dR
end
| LongwaveModePropagator | https://github.com/fgasdia/LongwaveModePropagator.jl.git |
|
[
"MIT"
] | 0.4.1 | 792c195909ca5dfff5685305b6fa0aa16c3d1041 | code | 4837 | #==
Functions related to calculating physical parameters of the ionospheric plasma
(susceptibility) relevant to the propagation of electromagnetic waves.
==#
@doc raw"""
susceptibility(altitude, frequency, bfield, species; params=LMPParams())
susceptibility(altitude, frequency, w::HomogeneousWaveguide; params=LMPParams())
susceptibility(altitude, me::ModeEquation; params=LMPParams())
Compute the ionosphere susceptibility tensor `M` as a `SMatrix{3,3}` using
`species.numberdensity` and `species.collisionfrequency` at `altitude`.
Multiple species can be passed as an iterable. Use a `tuple` of `Species`, rather than a
`Vector`, for better performance.
If `params.earthcurvature == true`, `M` includes a first order correction for earth
curvature by means of a fictitious refractive index [Pappert1967].
The susceptibility matrix is calculated from the constitutive relations presented in
[Ratcliffe1959]. This includes the effect of earth's magnetic field vector and
collisional damping on electron motion.
The tensor is:
```math
M = -\frac{X}{U(U²-Y²)}
\begin{pmatrix}
U² - x²Y² & -izUY - xyY² & iyUY - xzY² \\
izUY - xyY² & U² - y²Y² & -ixUY - yzY² \\
-iyUY - xzY² & ixUY - yzY² & U² - z²Y²
\end{pmatrix}
```
where ``X = ωₚ²/ω²``, ``Y = |ωₕ/ω|``, ``Z = ν/ω``, and ``U = 1 - iZ``. The earth curvature
correction subtracts ``2/Rₑ*(H - altitude)`` from the diagonal of ``M`` where ``H`` is
`params.curvatureheight`.
# References
[Pappert1967]: R. A. Pappert, E. E. Gossard, and I. J. Rothmuller, “A numerical
investigation of classical approximations used in VLF propagation,” Radio Science,
vol. 2, no. 4, pp. 387–400, Apr. 1967, doi: 10.1002/rds196724387.
[Ratcliffe1959]: J. A. Ratcliffe, "The magneto-ionic theory & its applications to the
ionosphere," Cambridge University Press, 1959.
"""
function susceptibility(altitude, frequency, bfield, species; params=LMPParams())
@unpack earthradius, earthcurvature, curvatureheight = params
B, x, y, z = bfield.B, bfield.dcl, bfield.dcm, bfield.dcn
ω = frequency.ω
# Precompute constants (if multiple species)
invω = inv(ω)
invE0ω = invω/E0
#== TODO:
The zero type should be inferred instead of hard coded, but because we species N and nu
are FunctionWrappers, we know the types will be ComplexF64.
==#
U²D = zero(ComplexF64)
Y²D = zero(ComplexF64)
UYD = zero(ComplexF64)
@inbounds for i in eachindex(species)
X, Y, Z = _magnetoionicparameters(altitude, invω, invE0ω, bfield, species[i])
U = 1 - 1im*Z
U² = U^2
Y² = Y^2
D = -X/(U*(U² - Y²))
U²D += U²*D
Y²D += Y²*D
UYD += U*Y*D
end
# Leverage partial symmetry of M to reduce computations
izUYD = 1im*z*UYD
xyY²D = x*y*Y²D
iyUYD = 1im*y*UYD
xzY²D = x*z*Y²D
ixUYD = 1im*x*UYD
yzY²D = y*z*Y²D
# Elements of `M`
M11 = U²D - x^2*Y²D
M21 = izUYD - xyY²D
M31 = -iyUYD - xzY²D
M12 = -izUYD - xyY²D
M22 = U²D - y^2*Y²D
M32 = ixUYD - yzY²D
M13 = iyUYD - xzY²D
M23 = -ixUYD - yzY²D
M33 = U²D - z^2*Y²D
if earthcurvature
curvaturecorrection = 2/earthradius*(curvatureheight - altitude)
M11 -= curvaturecorrection
M22 -= curvaturecorrection
M33 -= curvaturecorrection
end
M = SMatrix{3,3}(M11, M21, M31, M12, M22, M32, M13, M23, M33)
return M
end
susceptibility(altitude, me::ModeEquation; params=LMPParams()) =
susceptibility(altitude, me.frequency, me.waveguide; params=params)
susceptibility(altitude, frequency, w::HomogeneousWaveguide; params=LMPParams()) =
susceptibility(altitude, frequency, w.bfield, w.species; params=params)
"""
susceptibilityspline(frequency, bfield, species; params=LMPParams())
susceptibilityspline(frequency, w::HomogeneousWaveguide; params=LMPParams())
susceptibilityspline(me::ModeEquation; params=LMPParams())
Construct a cubic interpolating spline of [`susceptibility`](@ref) and return the callable
`Interpolations` type.
`params.susceptibilitysplinestep` is the altitude step in meters used to construct the
spline between `BOTTOMHEIGHT` and `params.topheight`.
"""
function susceptibilityspline(frequency, bfield, species; params=LMPParams())
zs = BOTTOMHEIGHT:params.susceptibilitysplinestep:params.topheight
Ms = susceptibility.(zs, (frequency,), (bfield,), (species,))
itp = cubic_spline_interpolation(zs, Ms)
return itp
end
susceptibilityspline(me::ModeEquation; params=LMPParams()) =
susceptibilityspline(me.frequency, me.waveguide; params=params)
susceptibilityspline(frequency, w::HomogeneousWaveguide; params=LMPParams()) =
susceptibilityspline(frequency, w.bfield, w.species; params=params)
| LongwaveModePropagator | https://github.com/fgasdia/LongwaveModePropagator.jl.git |
|
[
"MIT"
] | 0.4.1 | 792c195909ca5dfff5685305b6fa0aa16c3d1041 | code | 2314 | """
modeconversion(previous_wavefields::Wavefields, wavefields::Wavefields,
adjoint_wavefields::Wavefields; params=LMPParams())
Compute the mode conversion matrix `a` from the modes associated with `previous_wavefields`
to modes associated with `wavefields` and its `adjoint_wavefields`.
This is used in the approach known as full mode conversion [Pappert1972b].
# References
[Pappert1972b]: R. A. Pappert and R. R. Smith, “Orthogonality of VLF height gains in the
earth ionosphere waveguide,” Radio Science, vol. 7, no. 2, pp. 275–278, 1972,
doi: 10.1029/RS007i002p00275.
"""
function modeconversion(previous_wavefields::Wavefields{H}, wavefields::Wavefields{H},
adjoint_wavefields::Wavefields{H}; params=LMPParams()) where H
@unpack wavefieldheights = params
product = Vector{ComplexF64}(undef, numheights(wavefields))
pproduct = similar(product)
modes = eigenangles(wavefields)
adjmodes = eigenangles(adjoint_wavefields)
prevmodes = eigenangles(previous_wavefields)
modes == adjmodes || @warn "Full mode conversion physics assumes adjoint wavefields are
calculated for eigenangles of the original waveguide."
nmodes = length(modes)
nprevmodes = length(prevmodes)
# `a` is total conversion
a = Matrix{ComplexF64}(undef, nprevmodes, nmodes)
for n in eachindex(modes) # modes == adjmodes
for m in eachindex(prevmodes)
for i in eachindex(wavefieldheights)
@inbounds f = wavefields[i,n][SVector(2,3,5,6)] # Ey, Ez, Hy, Hz
@inbounds fp = previous_wavefields[i,m][SVector(2,3,5,6)] # Ey, Ez, Hy, Hz
@inbounds g = SVector{4}(adjoint_wavefields[i,n][6],
-adjoint_wavefields[i,n][5],
-adjoint_wavefields[i,n][3],
adjoint_wavefields[i,n][2]) # Hz, -Hy, -Ez, Ey
gtranspose = transpose(g)
product[i] = gtranspose*f
pproduct[i] = gtranspose*fp
end
N, Nerr = romberg(heights(wavefields), product) # normalization
I, Ierr = romberg(heights(wavefields), pproduct)
@inbounds a[m,n] = I/N
end
end
return a
end
| LongwaveModePropagator | https://github.com/fgasdia/LongwaveModePropagator.jl.git |
|
[
"MIT"
] | 0.4.1 | 792c195909ca5dfff5685305b6fa0aa16c3d1041 | code | 22375 | #==
Functions related to identifying resonant modes (eigenangles) within the earth-ionosphere
waveguide.
These functions use Budden's model, which represents the ground and ionosphere as sharply
reflecting boundaries. The middle of the waveguide is filled with a fictitious medium with a
refractive index that mimicks the propagation of the radio wave through free space over
curved earth.
==#
@doc raw"""
PhysicalModeEquation{W<:HomogeneousWaveguide} <: ModeEquation
Parameters for solving the physical mode equation ``\det(Rg*R - I)``.
Fields:
- ea::EigenAngle
- frequency::Frequency
- waveguide::W
"""
struct PhysicalModeEquation{W<:HomogeneousWaveguide} <: ModeEquation
ea::EigenAngle
frequency::Frequency
waveguide::W
end
"""
PhysicalModeEquation(f::Frequency, w::HomogeneousWaveguide)
Create a `PhysicalModeEquation` struct with `ea = complex(0.0)`.
See also: [`setea`](@ref)
"""
PhysicalModeEquation(f::Frequency, w::HomogeneousWaveguide) =
PhysicalModeEquation(EigenAngle(complex(0.0)), f, w)
"""
setea(ea, modeequation)
Return `modeequation` with eigenangle `ea`.
`ea` will be converted to an `EigenAngle` if necessary.
"""
setea(ea, modeequation::PhysicalModeEquation) =
PhysicalModeEquation(EigenAngle(ea), modeequation.frequency, modeequation.waveguide)
##########
# Reflection coefficients
##########
"""
wmatrix(ea::EigenAngle, T)
Compute the four submatrix elements of `W` used in the equation ``dR/dz`` from the
ionosphere with `T` matrix returned as a tuple `(W₁₁, W₂₁, W₁₂, W₂₂)`.
Following Budden's formalism for the reflection matrix of a plane wave obliquely incident on
the ionosphere [Budden1955a], the wave below the ionosphere can be resolved into
upgoing and downgoing waves of elliptical polarization, each of whose components are
themselves resolved into a component with the electric field in the plane of propagation and
a component perpendicular to the plane of propagation. The total field can be written in
matrix form as ``e = Lf`` where ``L`` is a 4×4 matrix that simply selects and specifies the
incident angle of the components and ``f`` is a column matrix of the complex amplitudes of
the component waves. By inversion, ``f = L⁻¹e`` and its derivative with respect to height
``z`` is ``f′ = -iL⁻¹TLf = -½iWf``. Then ``W = 2L⁻¹TL`` describes the change in amplitude of
the upgoing and downgoing component waves.
``W`` is also known as ``S`` in many texts.
# References
[Budden1955a]: K. G. Budden, “The numerical solution of differential equations governing
reflexion of long radio waves from the ionosphere,” Proc. R. Soc. Lond. A, vol. 227,
no. 1171, pp. 516–537, Feb. 1955.
"""
function wmatrix(ea::EigenAngle, T)
C, Cinv = ea.cosθ, ea.secθ
# Precompute
T12Cinv = T[1,2]*Cinv
T14Cinv = T[1,4]*Cinv
T32Cinv = T[3,2]*Cinv
T34Cinv = T[3,4]*Cinv
CT41 = C*T[4,1]
#==
T = SMatrix{4,4}(T11, 0, T31, T41,
T12, 0, T32, T42,
0, 1, 0, 0,
T14, 0, T34, T44)
L = SMatrix{4,4}(C, 0, 0, 1,
0, -1, -C, 0,
-C, 0, 0, 1,
0, -1, C, 0)
# 2*inv(L) = Linv2
L2inv = SMatrix{4,4}(Cinv, 0, -Cinv, 0,
0, -1, 0, -1,
0, -Cinv, 0, Cinv,
1, 0, 1, 0)
W = Linv2*T*L
# W = 2*(L\T)*L
---
W = | W11 | W12 |
| W21 | W22 |
W11 = | a11+a11r | -b11 |
| -c11 | d11 |
W12 = | a21+a21r | -b11 |
| c12 | d12 |
W21 = | a21-a21r | b21 |
| c11 | -d12 |
W22 = | a11-a11r | b21 |
| -c12 | -d11 |
==#
a11 = T[1,1] + T[4,4]
a11r = T14Cinv + CT41
a21 = T[4,4] - T[1,1]
a21r = T14Cinv - CT41
b11 = T12Cinv + T[4,2]
b21 = T12Cinv - T[4,2]
c11 = T[3,1] + T34Cinv
c12 = T[3,1] - T34Cinv
d11 = C + T32Cinv
d12 = T32Cinv - C
# Form the four 2x2 submatrices of `S`
W11 = SMatrix{2,2}(a11+a11r, -c11, -b11, d11)
W12 = SMatrix{2,2}(a21+a21r, c12, -b11, d12)
W21 = SMatrix{2,2}(a21-a21r, c11, b21, -d12)
W22 = SMatrix{2,2}(a11-a11r, -c12, b21, -d11)
return W11, W21, W12, W22
end
"""
dwmatrix(ea::EigenAngle, T, dT)
Compute the four submatrix elements of ``dW/dθ`` returned as the tuple
`(dW₁₁, dW₂₁, dW₁₂, dW₂₂)` from the ionosphere with `T` matrix and its derivative with
respect to ``θ``, `dT`.
"""
function dwmatrix(ea::EigenAngle, T, dT)
C, S, C², Cinv = ea.cosθ, ea.sinθ, ea.cos²θ, ea.secθ
C²inv = Cinv^2
dC = -S
dCinv = S*C²inv
dt12Cinv = dT[1,2]*Cinv + T[1,2]*dCinv
dt14Cinv = dT[1,4]*Cinv + T[1,4]*dCinv
dt32Cinv = dT[3,2]*Cinv + T[3,2]*dCinv
dt34Cinv = dT[3,4]*Cinv + T[3,4]*dCinv
dt41C = dC*T[4,1]
ds11a = dT[1,1] + dT[4,4]
dd11a = dT[1,1] - dT[4,4]
ds11b = dt14Cinv + dt41C
dd11b = dt14Cinv - dt41C
ds12 = dt12Cinv
dd12 = dt12Cinv
ds21 = dt34Cinv
dd21 = -dt34Cinv
ds22 = dC + dt32Cinv
dd22 = dC - dt32Cinv
# Form the four 2x2 submatrices of `dW`
dW11 = SMatrix{2,2}(ds11a+ds11b, -ds21, -ds12, ds22)
dW12 = SMatrix{2,2}(-dd11a+dd11b, dd21, -ds12, -dd22)
dW21 = SMatrix{2,2}(-dd11a-dd11b, ds21, dd12, dd22)
dW22 = SMatrix{2,2}(ds11a-ds11b, -dd21, dd12, -ds22)
return dW11, dW21, dW12, dW22
end
"""
dRdz(R, modeequation, z, susceptibilityfcn=z->susceptibility(z, modeequation; params=LMPParams()))
Compute the differential of the reflection matrix `R`, ``dR/dz``, at height `z`.
`susceptibilityfcn` is a function returning the ionosphere susceptibility at height `z`.
Following the Budden formalism for the reflection of an (obliquely) incident plane wave from
a horizontally stratified ionosphere [Budden1955a], the differential of the
reflection matrix `R` with height `z` can be described by
```math
dR/dz = k/(2i)⋅(W₂₁ + W₂₂R - RW₁₁ - RW₁₂R)
```
Integrating ``dR/dz`` downwards through the ionosphere gives the reflection matrix ``R`` for
the ionosphere as if it were a sharp boundary at the stopping level with free space below.
# References
[Budden1955a]: K. G. Budden, “The numerical solution of differential equations governing
reflexion of long radio waves from the ionosphere,” Proc. R. Soc. Lond. A, vol. 227,
no. 1171, pp. 516–537, Feb. 1955.
"""
function dRdz(R, modeequation, z, susceptibilityfcn=z->susceptibility(z, modeequation; params=LMPParams()))
@unpack ea, frequency = modeequation
k = frequency.k
M = susceptibilityfcn(z)
T = tmatrix(ea, M)
W11, W21, W12, W22 = wmatrix(ea, T)
# the factor k/(2i) isn't explicitly in [Budden1955a] because of his change of variable
# ``s = kz``
return k/2im*(W21 + W22*R - R*W11 - R*W12*R)
end
"""
dRdθdz(RdRdθ, p, z)
Compute the differential ``dR/dθ/dz`` at height `z` returned as an `SMatrix{4,2}` with
``dR/dz`` in the first 2 rows and ``dR/dθ/dz`` in the bottom 2 rows.
`p` is a tuple containing instances `(PhysicalModeEquation(), LMPParams())`.
"""
function dRdθdz(RdRdθ, p, z)
modeequation, params = p
@unpack ea, frequency = modeequation
k = frequency.k
M = susceptibility(z, modeequation; params=params)
T = tmatrix(ea, M)
dT = dtmatrix(ea, M)
W11, W21, W12, W22 = wmatrix(ea, T)
dW11, dW21, dW12, dW22 = dwmatrix(ea, T, dT)
R = RdRdθ[SVector(1,2),:]
dRdθ = RdRdθ[SVector(3,4),:]
dz = k/2im*(W21 + W22*R - R*W11 - R*W12*R)
dθdz = k/2im*(dW21 + dW22*R + W22*dRdθ - (dRdθ*W11 + R*dW11) -
(dRdθ*W12*R + R*dW12*R + R*W12*dRdθ))
return vcat(dz, dθdz)
end
"""
integratedreflection(modeequation::PhysicalModeEquation;
params=LMPParams(), susceptibilityfcn=z->susceptibility(z, modeequation; params=params))
Integrate ``dR/dz`` downward through the ionosphere described by `modeequation` from
`params.topheight`, returning the ionosphere reflection coefficient `R` at the ground.
`susceptibilityfcn` is a function returning the ionosphere susceptibility tensor as a
function of altitude `z` in meters.
`params.integrationparams` are passed to `DifferentialEquations.jl`.
"""
function integratedreflection(modeequation::PhysicalModeEquation;
params=LMPParams(), susceptibilityfcn=z->susceptibility(z, modeequation; params=params))
@unpack topheight, integrationparams = params
@unpack tolerance, solver, dt, force_dtmin, maxiters = integrationparams
Mtop = susceptibility(topheight, modeequation; params=params)
Rtop = bookerreflection(modeequation.ea, Mtop)
prob = ODEProblem{false}((R,p,z)->dRdz(R,p,z,susceptibilityfcn), Rtop, (topheight, BOTTOMHEIGHT), modeequation)
# WARNING: When save_on=false, don't try interpolating the solution!
sol = solve(prob, solver; abstol=tolerance, reltol=tolerance,
force_dtmin=force_dtmin, dt=dt, maxiters=maxiters,
save_on=false, save_start=false, save_end=true)
R = sol.u[end]
return R
end
"""
integratedreflection(modeequation::PhysicalModeEquation, ::Dθ; params=LMPParams())
Compute ``R`` and ``dR/dθ`` as an `SMatrix{4,2}` with ``R`` in rows (1, 2) and ``dR/dθ`` in
rows (3, 4).
The `params.integrationparams.tolerance` is hardcoded to `1e-10` in this version of the
function.
"""
function integratedreflection(modeequation::PhysicalModeEquation, ::Dθ; params=LMPParams())
@unpack topheight, integrationparams = params
@unpack solver, dt, force_dtmin, maxiters = integrationparams
# Tolerance is overridden for this `::Dθ` form.
# Using an identical accuracy appears to result in relatively less accurate solutions
# compared to the non-Dθ form.
tolerance = 1e-10
Mtop = susceptibility(topheight, modeequation; params=params)
Rtop, dRdθtop = bookerreflection(modeequation.ea, Mtop, Dθ())
RdRdθtop = vcat(Rtop, dRdθtop)
prob = ODEProblem{false}(dRdθdz, RdRdθtop, (topheight, BOTTOMHEIGHT),
(modeequation, params))
# WARNING: When save_on=false, don't try interpolating the solution!
sol = solve(prob, solver; abstol=tolerance, reltol=tolerance,
force_dtmin=force_dtmin, dt=dt, maxiters=maxiters,
save_on=false, save_start=false, save_end=true)
RdR = sol.u[end]
return RdR
end
##########
# Ground reflection coefficient matrix
##########
"""
fresnelreflection(ea::EigenAngle, ground::Ground, frequency::Frequency)
fresnelreflection(m::PhysicalModeEquation)
Compute the Fresnel reflection coefficient matrix for the ground-freespace interface at the
ground.
"""
fresnelreflection
function fresnelreflection(ea::EigenAngle, ground::Ground, frequency::Frequency)
C, S² = ea.cosθ, ea.sin²θ
ω = frequency.ω
Ng² = complex(ground.ϵᵣ, -ground.σ/(ω*E0))
CNg² = C*Ng²
sqrtNg²mS² = sqrt(Ng² - S²)
Rg11 = (CNg² - sqrtNg²mS²)/(CNg² + sqrtNg²mS²)
Rg22 = (C - sqrtNg²mS²)/(C + sqrtNg²mS²)
Rg = SDiagonal(Rg11, Rg22)
return Rg
end
fresnelreflection(m::PhysicalModeEquation) =
fresnelreflection(m.ea, m.waveguide.ground, m.frequency)
"""
fresnelreflection(ea::EigenAngle, ground::Ground, frequency::Frequency, ::Dθ)
fresnelreflection(m::PhysicalModeEquation, ::Dθ)
Compute the Fresnel reflection coefficient matrix for the ground as well as its derivative
with respect to ``θ`` returned as the tuple `(Rg, dRg)`.
"""
function fresnelreflection(ea::EigenAngle, ground::Ground, frequency::Frequency, ::Dθ)
C, S, S² = ea.cosθ, ea.sinθ, ea.sin²θ
S2 = 2*S
ω = frequency.ω
Ng² = complex(ground.ϵᵣ, -ground.σ/(ω*E0))
CNg² = C*Ng²
sqrtNg²mS² = sqrt(Ng² - S²)
Rg11 = (CNg² - sqrtNg²mS²)/(CNg² + sqrtNg²mS²)
Rg22 = (C - sqrtNg²mS²)/(C + sqrtNg²mS²)
Rg = SDiagonal(Rg11, Rg22)
dRg11 = (S2*Ng²*(1 - Ng²))/(sqrtNg²mS²*(CNg² + sqrtNg²mS²)^2)
dRg22 = (S2*(C - sqrtNg²mS²))/(sqrtNg²mS²*(sqrtNg²mS² + C))
dRg = SDiagonal(dRg11, dRg22)
return Rg, dRg
end
fresnelreflection(m::PhysicalModeEquation, ::Dθ) =
fresnelreflection(m.ea, m.waveguide.ground, m.frequency, Dθ())
##########
# Identify EigenAngles
##########
"""
modalequation(R, Rg)
Compute the determinental mode equation ``det(Rg R - I)`` given reflection coefficients `R`
and `Rg`.
A propagating waveguide mode requires that a wave, having reflected from the ionosphere and
then the ground, must be identical with the original upgoing wave. This criteria is met at
roots of the mode equation [Budden1962].
# References
[Budden1962]: K. G. Budden and N. F. Mott, “The influence of the earth’s magnetic field on
radio propagation by wave-guide modes,” Proceedings of the Royal Society of London.
Series A. Mathematical and Physical Sciences, vol. 265, no. 1323, pp. 538–553,
Feb. 1962.
"""
function modalequation(R, Rg)
return det(Rg*R - I)
end
"""
dmodalequation(R, dR, Rg, dRg)
Compute the derivative of the determinantal mode equation with respect to ``θ``.
"""
function dmodalequation(R, dR, Rg, dRg)
# See e.g. https://folk.ntnu.no/hanche/notes/diffdet/diffdet.pdf
A = Rg*R - I
dA = dRg*R + Rg*dR
return det(A)*tr(A\dA)
end
"""
solvemodalequation(modeequation::PhysicalModeEquation;
params=LMPParams(), susceptibilityfcn=z->susceptibility(z, modeequation; params=params))
Compute the ionosphere and ground reflection coefficients and return the value of the
determinental modal equation associated with `modeequation`. `susceptibilityfcn` is a
function that returns the ionosphere susceptibility as a function of altitude `z` in meters.
See also: [`solvedmodalequation`](@ref)
"""
function solvemodalequation(modeequation::PhysicalModeEquation;
params=LMPParams(), susceptibilityfcn=z->susceptibility(z, modeequation; params=params))
R = integratedreflection(modeequation; params=params, susceptibilityfcn=susceptibilityfcn)
Rg = fresnelreflection(modeequation)
f = modalequation(R, Rg)
return f
end
"""
solvemodalequation(θ, modeequation::PhysicalModeEquation;
params=LMPParams(), susceptibilityfcn=z->susceptibility(z, modeequation; params=params))
Set `θ` for `modeequation` and then solve the modal equation.
"""
function solvemodalequation(θ, modeequation::PhysicalModeEquation;
params=LMPParams(), susceptibilityfcn=z->susceptibility(z, modeequation; params=params))
# Convenience function for `grpf`
modeequation = setea(EigenAngle(θ), modeequation)
solvemodalequation(modeequation; params=params, susceptibilityfcn=susceptibilityfcn)
end
"""
solvedmodalequation(modeequation::PhysicalModeEquation; params=LMPParams())
Compute the derivative of the modal equation with respect to ``θ`` returned as the tuple
`(dF, R, Rg)` for the ionosphere and ground reflection coefficients.
"""
function solvedmodalequation(modeequation::PhysicalModeEquation; params=LMPParams())
RdR = integratedreflection(modeequation, Dθ(); params=params)
R = RdR[SVector(1,2),:]
dR = RdR[SVector(3,4),:]
Rg, dRg = fresnelreflection(modeequation, Dθ())
dF = dmodalequation(R, dR, Rg, dRg)
return dF, R, Rg
end
"""
solvedmodalequation(θ, modeequation::PhysicalModeEquation; params=LMPParams())
Set `θ` for `modeequation` and then solve the derivative of the mode equation with respect
to `θ`.
"""
function solvedmodalequation(θ, modeequation::PhysicalModeEquation; params=LMPParams())
modeequation = setea(EigenAngle(θ), modeequation)
solvedmodalequation(modeequation; params=params)
end
"""
findmodes(modeequation::ModeEquation, mesh=nothing; params=LMPParams())
Find `EigenAngle`s associated with `modeequation.waveguide` within the domain of
`mesh`.
`mesh` should be an array of complex numbers that make up the original grid over which
the GRPF algorithm searches for roots of `modeequation`. If `mesh === nothing`,
it is computed with [`defaultmesh`](@ref).
There is a check for redundant modes that requires modes to be separated by at least
1 orders of magnitude greater than `grpfparams.tolerance` in real and/or imaginary
component. For example, if `grpfparams.tolerance = 1e-5`, then either the real or imaginary
component of each mode must be separated by at least 1e-4 from every other mode.
"""
function findmodes(modeequation::ModeEquation, mesh=nothing; params=LMPParams())
@unpack approxsusceptibility, grpfparams = params
if isnothing(mesh)
mesh = defaultmesh(modeequation.frequency)
end
# WARNING: If tolerance of mode finder is much less than the R integration tolerance, it
# is possible multiple identical modes will be identified. Checks for valid and
# redundant modes help ensure valid eigenangles are returned from this function.
if approxsusceptibility
susceptibilityfcn = susceptibilityspline(modeequation; params=params)
else
susceptibilityfcn = z -> susceptibility(z, modeequation; params=params)
end
roots, _ = grpf(θ->solvemodalequation(θ, modeequation;
params=params, susceptibilityfcn=susceptibilityfcn), mesh, grpfparams)
# Scale tolerance for filtering
# if tolerance is 1e-8, this rounds to 7 decimal places
ndigits = round(Int, abs(log10(grpfparams.tolerance)+1), RoundDown)
# Remove any redundant modes
sort!(roots; by=reim, rev=true)
unique!(z->round(z; digits=ndigits), roots)
return EigenAngle.(roots)
end
#==
Mesh grids for `GRPF`
==#
"""
defaultmesh(frequency; rmax=deg2rad(89.9), imax=deg2rad(0.0),
Δr_coarse=deg2rad(0.5), Δr_fine=deg2rad(0.1),
rtransition=deg2rad(75.0), itransition=deg2rad(-1.5),
meshshape="auto")
Generate vector of complex coordinates (radians) to be used by GRPF in the search for
waveguide modes.
`rmin` is the lower bound of the real axis and `imin` is the lower bound of the imaginary
axis.
The value of `frequency` sets different default behavior:
| `frequency` | `meshshape = "auto"` | `rmin` | `imin` | resolution |
|:-----------:|:--------------------:|:-----------:|:------------:|:-----------:|
| < 12 kHz | `"rectanglemesh"` | deg2rad(1) | deg2rad(-89) | `Δr_coarse` |
| ≥ 12 kHz | `"trianglemesh"` | deg2rad(30) | deg2rad(-10) | variable |
At frequencies at or above 12 kHz the mesh spacing in the upper right corner of the domain
with real values above `rtransition` and imaginary values above `itransition` is
`Δr_fine` and is `Δr_coarse` everywhere else.
If `meshshape = "rectanglemesh"`, the full lower right quadrant of the complex plane is
searched for modes. If `meshshape = "trianglemesh"`, the lower right diagonal of the lower
right quadrant of the complex plane is excluded from the mesh. Eigenangles at VLF (~12 kHz)
and higher frequencies are not typically in the lower right diagonal.
See also: [`findmodes`](@ref)
"""
function defaultmesh(frequency; meshshape="auto",
rmin=nothing, imin=nothing, rmax=nothing, imax=nothing,
Δr_coarse=nothing, Δr_fine=nothing,
rtransition=nothing, itransition=nothing)
isnothing(rmax) && (rmax = deg2rad(89.9))
isnothing(imax) && (imax = 0.0)
if frequency >= 12000
isnothing(rmin) && (rmin = deg2rad(30))
isnothing(imin) && (imin = deg2rad(-10))
isnothing(Δr_coarse) && (Δr_coarse = deg2rad(0.5))
isnothing(Δr_fine) && (Δr_fine = deg2rad(0.1))
isnothing(rtransition) && (rtransition = deg2rad(75))
isnothing(itransition) && (itransition = deg2rad(-1.5))
zbl_coarse = complex(rmin, imin)
ztr_coarse = complex(rmax, imax)
if meshshape == "auto" || meshshape == "trianglemesh"
mesh = trianglemesh(zbl_coarse, ztr_coarse, Δr_coarse)
filter!(z->(real(z) < rtransition || imag(z) < itransition), mesh)
zbl_fine = complex(rtransition, itransition)
ztr_fine = complex(rmax, imax)
append!(mesh, trianglemesh(zbl_fine, ztr_fine, Δr_fine))
elseif meshshape == "rectanglemesh"
mesh = rectangulardomain(zbl_coarse, ztr_coarse, Δr_coarse)
filter!(z->(real(z) < rtransition || imag(z) < itransition), mesh)
zbl_fine = complex(rtransition, itransition)
ztr_fine = complex(rmax, imax)
append!(mesh, rectangulardomain(zbl_coarse, ztr_coarse, Δr_fine))
end
else
isnothing(rmin) && (rmin = deg2rad(1))
isnothing(imin) && (imin = deg2rad(-89))
isnothing(Δr_coarse) && (Δr_coarse = deg2rad(1))
zbl = complex(rmin, imin)
ztr = complex(rmax, imax)
if meshshape == "auto" || meshshape == "rectanglemesh"
mesh = rectangulardomain(zbl, ztr, Δr_coarse)
elseif meshshape == "trianglemesh"
mesh = trianglemesh(zbl, ztr, Δr_coarse)
end
end
return mesh
end
defaultmesh(f::Frequency; kw...) = defaultmesh(f.f; kw...)
"""
trianglemesh(zbl, ztr, Δr)
Generate initial mesh node coordinates for a right triangle domain from complex
coordinate `zbl` in the bottom left and `ztr` in the top right with initial mesh step `Δr`.
`zbl` and `ztr` are located on the complex plane at the locations marked in the
diagram below:
```
im
|
-re ---|------ ztr
| /
| /
| /
| /
zbl
```
"""
function trianglemesh(zbl, ztr, Δr)
rzbl, izbl = reim(zbl)
rztr, iztr = reim(ztr)
X = rztr - rzbl
Y = iztr - izbl
n = ceil(Int, Y/Δr)
dy = Y/n
## dx = sqrt(Δr² - (dy/2)²), solved for equilateral triangle
m = ceil(Int, X/sqrt(Δr^2 - dy^2/4))
dx = X/m
half_dx = dx/2
slope = 1 # 45° angle
T = promote_type(ComplexF64, typeof(zbl), typeof(ztr), typeof(Δr))
mesh = Vector{T}()
shift = false # we will displace every other line by dx/2
for j = 0:n
y = izbl + dy*j
for i = 0:m
x = rzbl + dx*i
if shift && i == 0
continue # otherwise, we shift out of left bound
elseif shift
x -= half_dx
end
if i == m
shift = !shift
end
## NEW: check if `x, y` is in upper left triangle
if y >= slope*x - π/2
push!(mesh, complex(x, y))
end
end
end
return mesh
end
| LongwaveModePropagator | https://github.com/fgasdia/LongwaveModePropagator.jl.git |
|
[
"MIT"
] | 0.4.1 | 792c195909ca5dfff5685305b6fa0aa16c3d1041 | code | 21702 | #==
Excitation factor, height gain functions, and electric field mode sum
==#
"""
ExcitationFactor{T,T2}
Constants used in calculating excitation factors and height gains.
# Fields
- `F₁::T`: height gain constant. See [Pappert1976].
- `F₂::T`
- `F₃::T`
- `F₄::T`
- `h₁0::T`: first modified Hankel function of order 1/3 at the ground.
- `h₂0::T`: second modified Hankel function of order 1/3 at the ground.
- `EyHy::T`: polarization ratio ``Ey/Hy``, derived from reflection coefficients (or ``T``s).
- `Rg::T2`: ground reflection coefficient matrix.
# References
[Pappert1976]: R. A. Pappert and L. R. Shockey, “Simplified VLF/LF mode conversion program
with allowance for elevated, arbitrarily oriented electric dipole antennas,” Naval
Electronics Laboratory Center, San Diego, CA, Interim Report 771, Oct. 1976. [Online].
Available: http://archive.org/details/DTIC_ADA033412.
"""
struct ExcitationFactor{T,T2}
F₁::T
F₂::T
F₃::T
F₄::T
h₁0::T
h₂0::T
EyHy::T
Rg::T2
end
"""
excitationfactorconstants(ea₀, R, Rg, frequency, ground; params=LMPParams())
Return an `ExcitationFactor` struct used in calculating height-gain functions and excitation
factors where eigenangle `ea₀` is referenced to the ground.
!!! note
This function assumes that reflection coefficients `R` and `Rg` are referenced to
``d = z = 0``.
# References
[Pappert1976]: R. A. Pappert and L. R. Shockey, “Simplified VLF/LF mode conversion program
with allowance for elevated, arbitrarily oriented electric dipole antennas,” Naval
Electronics Laboratory Center, San Diego, CA, Interim Report 771, Oct. 1976. [Online].
Available: http://archive.org/details/DTIC_ADA033412.
[Ferguson1980]: J. A. Ferguson and F. P. Snyder, “Approximate VLF/LF waveguide mode
conversion model: Computer applications: FASTMC and BUMP,” Naval Ocean Systems Center,
San Diego, CA, NOSC-TD-400, Nov. 1980. [Online].
Available: http://www.dtic.mil/docs/citations/ADA096240.
[Morfitt1980]: D. G. Morfitt, “‘Simplified’ VLF/LF mode conversion computer programs:
GRNDMC and ARBNMC,” Naval Ocean Systems Center, San Diego, CA, NOSC/TR-514, Jan. 1980.
[Online]. Available: http://www.dtic.mil/docs/citations/ADA082695.
"""
function excitationfactorconstants(ea₀, R, Rg, frequency, ground; params=LMPParams())
S², C² = ea₀.sin²θ, ea₀.cos²θ
k, ω = frequency.k, frequency.ω
ϵᵣ, σ = ground.ϵᵣ, ground.σ
@unpack earthradius = params
# Precompute
α = 2/earthradius
tmp1 = pow23(α/k)/2 # 1/2*(a/k)^(2/3)
q₀ = pow23(k/α)*C² # (a/k)^(-2/3)*C²
h₁0, h₂0, dh₁0, dh₂0 = modifiedhankel(q₀)
H₁0 = dh₁0 + tmp1*h₁0
H₂0 = dh₂0 + tmp1*h₂0
n₀² = 1 # modified free space index of refraction squared, referenced to ground
Ng² = complex(ϵᵣ, -σ/(ω*E0)) # ground index of refraction
# Precompute
tmp2 = 1im*cbrt(k/α)*sqrt(Ng² - S²) # i(k/α)^(1/3)*(Ng² - S²)^(1/2)
F₁ = -H₂0 + (n₀²/Ng²)*tmp2*h₂0
F₂ = H₁0 - (n₀²/Ng²)*tmp2*h₁0
F₃ = -dh₂0 + tmp2*h₂0
F₄ = dh₁0 - tmp2*h₁0
# ``EyHy = ey/hy``. Also known as `f0fr` or `f`.
# It is a polarization ratio that adds the proper amount of TE wave when the y component
# of the magnetic field is normalized to unity at the ground.
# A principally TE mode will have `1 - R[1,1]*Rg[1,1]` very small and EyHy will be very
# small, so we use the first equation below. Conversely, a principally TM mode will have
# `1 - R[2,2]Rg[2,2]` very small and EyHy very large, resulting in the use of the second
# equation below. [Ferguson1980] pg. 58 seems to suggest the use of the opposite, but
# LWPC uses the form used here and this makes sense because there are more working
# decimal places.
if abs2(1 - R[1,1]*Rg[1,1]) < abs2(1 - R[2,2]*Rg[2,2])
# EyHy = T₃/T₁
EyHy = (1 + Rg[2,2])*R[2,1]*Rg[1,1]/((1 + Rg[1,1])*(1 - R[2,2]*Rg[2,2]))
else
# EyHy = T₂/(T₃*T₄)
EyHy = (1 + Rg[2,2])*(1 - R[1,1]*Rg[1,1])/((1 + Rg[1,1])*R[1,2]*Rg[2,2])
end
return ExcitationFactor(F₁, F₂, F₃, F₄, h₁0, h₂0, EyHy, Rg)
end
"""
excitationfactor(ea, dFdθ, R, Rg, efconstants::ExcitationFactor; params=LMPParams())
Compute excitation factors for the ``Hy`` field at the emitter returned as the tuple
`(λv, λb, λe)` for vertical, broadside, and end-on dipoles. `dFdθ` is the derivative of the
modal equation with respect to ``θ``.
The excitation factor describes how efficiently the field component can be excited in the
waveguide.
This function most closely follows the approach taken in [Pappert1983], which makes
use of ``T`` (different from `TMatrix`) rather than ``τ``. From the total ``Hy`` excitation
factor (the sum product of the `λ`s with the antenna orientation terms), the excitation
factor for electric fields can be found as:
- ``λz = -S₀λ``
- ``λx = EyHy⋅λ``
- ``λy = -λ``
!!! note
This function assumes that reflection coefficients `R` and `Rg` are referenced to
``d = z = 0``.
# References
[Morfitt1980]: D. G. Morfitt, “‘Simplified’ VLF/LF mode conversion computer programs:
GRNDMC and ARBNMC,” Naval Ocean Systems Center, San Diego, CA, NOSC/TR-514, Jan. 1980.
[Online]. Available: http://www.dtic.mil/docs/citations/ADA082695.
[Pappert1983]: R. A. Pappert, L. R. Hitney, and J. A. Ferguson, “ELF/VLF (Extremely Low
Frequency/Very Low Frequency) long path pulse program for antennas of arbitrary
elevation and orientation,” Naval Ocean Systems Center, San Diego, CA, NOSC/TR-891,
Aug. 1983. [Online]. Available: http://www.dtic.mil/docs/citations/ADA133876.
[Pappert1986]: R. A. Pappert and J. A. Ferguson, “VLF/LF mode conversion model calculations
for air to air transmissions in the earth-ionosphere waveguide,” Radio Sci., vol. 21,
no. 4, pp. 551–558, Jul. 1986, doi: 10.1029/RS021i004p00551.
"""
function excitationfactor(ea, dFdθ, R, efconstants::ExcitationFactor; params=LMPParams())
S = ea.sinθ
sqrtS = sqrt(S)
S₀ = referencetoground(ea.sinθ; params=params)
@unpack F₁, F₂, F₃, F₄, h₁0, h₂0, Rg = efconstants
# Unlike the formulations shown in the references, we scale these excitation factors
# with `D##` instead of `EyHy` and appropriately don't scale the height gains.
F₁h₁0 = F₁*h₁0
F₂h₂0 = F₂*h₂0
F₃h₁0 = F₃*h₁0
F₄h₂0 = F₄*h₂0
D₁₁ = (F₁h₁0 + F₂h₂0)^2
D₁₂ = (F₁h₁0 + F₂h₂0)*(F₃h₁0 + F₄h₂0)
# D₂₂ = (F₃h₁0 + F₄h₂0)^2
# `sqrtS` should be at `curvatureheight` because that is where `dFdθ` is evaluated
T₁ = sqrtS*(1 + Rg[1,1])^2*(1 - R[2,2]*Rg[2,2])/(dFdθ*Rg[1,1]*D₁₁)
# T₂ = sqrtS*(1 + Rg[2,2])^2*(1 - R[1,1]*Rg[1,1])/(dFdθ*Rg[2,2]*D₂₂)
T₃ = sqrtS*(1 + Rg[1,1])*(1 + Rg[2,2])*R[2,1]/(dFdθ*D₁₂)
T₄ = R[1,2]/R[2,1]
# These are [Pappert1983] terms divided by `-S`, the factor between Hy and Ez
λv = -S₀*T₁
λb = T₃*T₄
λe = T₁
return λv, λb, λe
end
@doc raw"""
heightgains(z, ea₀, frequency, efconstants::ExcitationFactor; params=LMPParams())
Compute height gain functions at height `z` returned as the tuple `(fz, fy, fx)` where
eigenangle `ea₀` is referenced to the ground.
- `fz` is the height gain for the vertical electric field component ``Ez``.
- `fy` is the height gain for the transverse electric field component ``Ey``.
- `fx` is the height gain for the horizontal electric field component ``Ex``.
[Pappert1983]
!!! note
This function assumes that reflection coefficients are referenced to ``d = z = 0``.
See also: [`excitationfactorconstants`](@ref)
# References
[Pappert1983]: R. A. Pappert, L. R. Hitney, and J. A. Ferguson, “ELF/VLF (Extremely Low
Frequency/Very Low Frequency) long path pulse program for antennas of arbitrary
elevation and orientation,” Naval Ocean Systems Center, San Diego, CA, NOSC/TR-891,
Aug. 1983. [Online]. Available: http://www.dtic.mil/docs/citations/ADA133876.
[Pappert1986]: R. A. Pappert and J. A. Ferguson, “VLF/LF mode conversion model calculations
for air to air transmissions in the earth-ionosphere waveguide,” Radio Sci., vol. 21,
no. 4, pp. 551–558, Jul. 1986, doi: 10.1029/RS021i004p00551.
"""
function heightgains(z, ea₀, frequency, efconstants::ExcitationFactor; params=LMPParams())
C, C² = ea₀.cosθ, ea₀.cos²θ
k = frequency.k
@unpack F₁, F₂, F₃, F₄, Rg = efconstants
@unpack earthradius, earthcurvature = params
if earthcurvature
# Precompute
α = 2/earthradius
expz = exp(z/earthradius) # assumes reflection coefficients are referenced to `d = 0`
qz = pow23(k/α)*(C² + α*z) # (k/α)^(2/3)*(C² + α*z)
h₁z, h₂z, dh₁z, dh₂z = modifiedhankel(qz)
# Precompute
F₁h₁z = F₁*h₁z
F₂h₂z = F₂*h₂z
# Height gain for Ez, also called f∥(z).
fz = expz*(F₁h₁z + F₂h₂z)
# Height gain for Ey, also called f⟂(z)
fy = (F₃*h₁z + F₄*h₂z)
# Height gain for Ex, also called g(z)
# f₂ = 1/(1im*k) df₁/dz
fx = expz/(1im*k*earthradius)*(F₁h₁z + F₂h₂z + earthradius*(F₁*dh₁z + F₂*dh₂z))
else
# Flat earth, [Pappert1983] pg. 12--13
expiz = cis(k*C*z)
fz = expiz + Rg[1,1]/expiz
fy = expiz + Rg[2,2]/expiz
fx = C*(expiz - Rg[1,1]/expiz)
end
return fz, fy, fx
end
"""
radiationresistance(k, Cγ, zt)
Calculate radiation resistance correction for transmitting antenna elevated above the ground.
Based on [^Pappert1986] below, is derived from the time-averaged Poynting vector, which
uses total E and H fields calculated assuming a point dipole over perfectly reflecting ground.
If a point dipole at height z is radiating known power Pz, the power that should be input to
LMP is ``P/Pz = 2/f(kz,γ)``. Also note that E ∝ √P, hence the square root below.
# References
[Pappert1986]: R. A. Pappert, “Radiation resistance of thin antennas of arbitrary elevation
and configuration over perfectly conducting ground.,” Naval Ocean Systems Center,
San Diego, CA, Technical Report 1112, Jun. 1986. Accessed: Mar. 10, 2024. [Online].
Available: https://apps.dtic.mil/sti/citations/ADA170945
"""
function radiationresistance(k, Cγ, zt)
# TODO: Derive results for general Fresnel reflection coefficients.
kz = 2*k*zt
kz² = kz^2
kz³ = kz²*kz
sinkz, coskz = sincos(kz)
Cγ² = Cγ^2
Sγ² = 1 - Cγ²
f = (1 + 3/kz³*(sinkz - kz*coskz))*Cγ² +
(1 + 3/(2*kz³)*((1 - kz²)*sinkz - kz*coskz))*Sγ²
corrfactor = sqrt(2/f)
return corrfactor
end
@doc raw"""
modeterms(modeequation, tx::Emitter, rx::AbstractSampler; params=LMPParams())
Compute `tx` and `rx` height-gain and excitation factor products and `ExcitationFactor`
constants returned as the tuple `(txterm, rxterm)`.
The returned `txterm` is:
```math
λ_v \cos(γ) f_z(zₜ) + λ_b \sin(γ)\sin(ϕ) f_y(zₜ) + λ_e \sin(γ)\cos(ϕ) f_z(zₜ)
```
and `rxterm` is the height-gain function ``f(zᵣ)`` appropriate for `rx.fieldcomponent`:
| `fieldcomponent` | ``f(zᵣ)`` |
|:----------------:|:--------------:|
| ``z`` | ``-S₀⋅f_z`` |
| ``y`` | ``EyHy⋅f_y`` |
| ``x`` | ``-f_x`` |
# References
[Pappert1976]: R. A. Pappert and L. R. Shockey, “Simplified VLF/LF mode conversion program
with allowance for elevated, arbitrarily oriented electric dipole antennas,” Naval
Electronics Laboratory Center, San Diego, CA, Interim Report 771, Oct. 1976. [Online].
Available: http://archive.org/details/DTIC_ADA033412.
[Morfitt1980]: D. G. Morfitt, “‘Simplified’ VLF/LF mode conversion computer programs:
GRNDMC and ARBNMC,” Naval Ocean Systems Center, San Diego, CA, NOSC/TR-514, Jan. 1980.
[Online]. Available: http://www.dtic.mil/docs/citations/ADA082695.
"""
function modeterms(modeequation, tx::Emitter, rx::AbstractSampler; params=LMPParams())
@unpack ea, frequency, waveguide = modeequation
@unpack ground = waveguide
ea₀ = referencetoground(ea; params=params)
S₀ = ea₀.sinθ
frequency == tx.frequency ||
throw(ArgumentError("`tx.frequency` and `modeequation.frequency` do not match"))
zt = altitude(tx)
zr = altitude(rx)
rxfield = fieldcomponent(rx)
# Transmit antenna orientation with respect to propagation direction
# See [Morfitt1980] pg. 22
Sγ, Cγ = sincos(inclination(tx)) # γ is measured from vertical
Sϕ, Cϕ = sincos(azimuth(tx)) # ϕ is measured from `x`
t1 = Cγ
t2 = Sγ*Sϕ
t3 = Sγ*Cϕ
dFdθ, R, Rg = solvedmodalequation(modeequation; params=params)
efconstants = excitationfactorconstants(ea₀, R, Rg, frequency, ground; params=params)
λv, λb, λe = excitationfactor(ea, dFdθ, R, efconstants; params=params)
# Transmitter term
fzt, fyt, fxt = heightgains(zt, ea₀, frequency, efconstants; params=params)
txterm = λv*fzt*t1 + λb*fyt*t2 + λe*fxt*t3
# Receiver term
if zr == zt
fzr, fyr, fxr = fzt, fyt, fxt
else
fzr, fyr, fxr = heightgains(zr, ea₀, frequency, efconstants; params=params)
end
# TODO: Handle multiple fields - maybe just always return all 3?
if rxfield == Fields.Ez
rxterm = -S₀*fzr
elseif rxfield == Fields.Ey
rxterm = efconstants.EyHy*fyr
elseif rxfield == Fields.Ex
rxterm = -fxr
end
return txterm, rxterm
end
# Specialized for the common case of `GroundSampler` and `Transmitter{VerticalDipole}`.
function modeterms(modeequation::ModeEquation, tx::Transmitter{VerticalDipole},
rx::GroundSampler; params=LMPParams())
@unpack ea, frequency, waveguide = modeequation
@unpack ground = waveguide
ea₀ = referencetoground(ea; params=params)
S₀ = ea₀.sinθ
frequency == tx.frequency ||
throw(ArgumentError("`tx.frequency` and `modeequation.frequency` do not match"))
rxfield = fieldcomponent(rx)
dFdθ, R, Rg = solvedmodalequation(modeequation; params=params)
efconstants = excitationfactorconstants(ea₀, R, Rg, frequency, ground; params=params)
λv, λb, λe = excitationfactor(ea, dFdθ, R, efconstants; params=params)
# Transmitter term
# TODO: specialized heightgains for z = 0
fz, fy, fx = heightgains(0.0, ea₀, frequency, efconstants; params=params)
txterm = λv*fz
# Receiver term
if rxfield == Fields.Ez
rxterm = -S₀*fz
elseif rxfield == Fields.Ey
rxterm = efconstants.EyHy*fy
elseif rxfield == Fields.Ex
rxterm = -fx
end
return txterm, rxterm
end
#==
Electric field calculation
==#
"""
Efield(modes, waveguide::HomogeneousWaveguide, tx::Emitter, rx::AbstractSampler;
params=LMPParams())
Compute the complex electric field by summing `modes` in `waveguide` for emitter `tx` at
sampler `rx`.
# References
[Morfitt1980]: D. G. Morfitt, “‘Simplified’ VLF/LF mode conversion computer programs:
GRNDMC and ARBNMC,” Naval Ocean Systems Center, San Diego, CA, NOSC/TR-514, Jan. 1980.
[Online]. Available: http://www.dtic.mil/docs/citations/ADA082695.
[Pappert1983]: R. A. Pappert, L. R. Hitney, and J. A. Ferguson, “ELF/VLF (Extremely Low
Frequency/Very Low Frequency) long path pulse program for antennas of arbitrary
elevation and orientation,” Naval Ocean Systems Center, San Diego, CA, NOSC/TR-891,
Aug. 1983. [Online]. Available: http://www.dtic.mil/docs/citations/ADA133876.
"""
function Efield(modes, waveguide::HomogeneousWaveguide, tx::Emitter, rx::AbstractSampler;
params=LMPParams())
X = distance(rx, tx)
E = zeros(ComplexF64, length(X))
txpower = power(tx)
frequency = tx.frequency
k = frequency.k
zt = altitude(tx)
Cγ = cos(inclination(tx))
for ea in modes
modeequation = PhysicalModeEquation(ea, frequency, waveguide)
txterm, rxterm = modeterms(modeequation, tx, rx; params=params)
S₀ = referencetoground(ea.sinθ; params=params)
expterm = -k*(S₀ - 1)
txrxterm = txterm*rxterm
@inbounds for i in eachindex(E)
E[i] += txrxterm*cis(expterm*X[i])
end
end
Q = 0.6822408*sqrt(frequency.f*txpower) # factor from lw_sum_modes.for
# Q = Z₀/(4π)*sqrt(2π*txpower/10k)*k/2 # Ferguson and Morfitt 1981 eq (21), V/m, NOT uV/m!
# Q *= 100 # for V/m to uV/m
if params.radiationresistancecorrection && zt > 0
corrfactor = radiationresistance(k, Cγ, zt)
Q *= corrfactor
end
@inbounds for i in eachindex(E)
E[i] *= Q/sqrt(abs(sin(X[i]/params.earthradius)))
end
return E
end
function Efield(modes, waveguide::HomogeneousWaveguide, tx::Emitter,
rx::AbstractSampler{<:Real}; params=LMPParams())
frequency = tx.frequency
k = frequency.k
zt = altitude(tx)
Cγ = cos(inclination(tx))
txpower = power(tx)
x = distance(rx, tx)
Q = 0.6822408*sqrt(frequency.f*txpower)
if params.radiationresistancecorrection && zt > 0
corrfactor = radiationresistance(k, Cγ, zt)
Q *= corrfactor
end
E = zero(ComplexF64)
for ea in modes
modeequation = PhysicalModeEquation(ea, frequency, waveguide)
txterm, rxterm = modeterms(modeequation, tx, rx, params=params)
S₀ = referencetoground(ea.sinθ; params=params)
expterm = -k*(S₀ - 1)
txrxterm = txterm*rxterm
E += txrxterm*cis(expterm*x)
end
E *= Q/sqrt(abs(sin(x/params.earthradius)))
return E
end
"""
Efield(waveguide::SegmentedWaveguide, wavefields_vec, adjwavefields_vec, tx::Emitter,
rx::AbstractSampler; params=LMPParams())
"""
function Efield(waveguide::SegmentedWaveguide, wavefields_vec, adjwavefields_vec,
tx::Emitter, rx::AbstractSampler; params=LMPParams())
@unpack earthradius = params
# Checks
first(waveguide).distance == 0 ||
throw(ArgumentError("The first `waveguide` segment should have `distance` 0.0."))
length(waveguide) == length(wavefields_vec) == length(adjwavefields_vec) ||
throw(ArgumentError("`wavefields_vec` and `adjwavefields_vec` must have the same"*
"length as `waveguide`."))
X = distance(rx, tx)
maxX = maximum(X)
Xlength = length(X)
E = Vector{ComplexF64}(undef, Xlength)
frequency = tx.frequency
k = frequency.k
zt = altitude(tx)
Cγ = cos(inclination(tx))
Q = 0.6822408*sqrt(frequency.f*tx.power)
if params.radiationresistancecorrection && zt > 0
corrfactor = radiationresistance(k, Cγ, zt)
Q *= corrfactor
end
# Initialize
J = length(waveguide)
M = 0 # number of eigenangles in previous segment. Current segment is N
xmtrfields = Vector{ComplexF64}(undef, 0) # fields generated by transmitter
previous_xmtrfields = similar(xmtrfields) # fields saved from previous segment
rcvrfields = similar(xmtrfields) # fields at receiver location
i = 1 # index of X
for j = 1:J # index of waveguide
wvg = waveguide[j]
wavefields = wavefields_vec[j]
eas = eigenangles(wavefields)
N = nummodes(wavefields)
# Identify distance at beginning of segment
segment_start = wvg.distance
maxX < segment_start && break # no farther X; break
# Identify distance at end of segment
if j < J
segment_end = waveguide[j+1].distance
else
# last segment
segment_end = typemax(typeof(segment_start))
end
# xmtrfields is for `Hy`
resize!(xmtrfields, N)
resize!(rcvrfields, N)
if j > 1
adjwavefields = adjwavefields_vec[j]
prevwavefields = wavefields_vec[j-1]
conversioncoeffs = modeconversion(prevwavefields, wavefields, adjwavefields;
params=params)
end
# Calculate the mode terms (height gains and excitation factors) up to the current
# segment
for n = 1:N
modeequation = PhysicalModeEquation(eas[n], frequency, wvg)
txterm, rxterm = modeterms(modeequation, tx, rx; params=params)
if j == 1
# Transmitter exists only in the transmitter slab (obviously)
xmtrfields[n] = txterm
else
# Otherwise, mode conversion of transmitted fields
xmtrfields_sum = zero(eltype(xmtrfields))
for m = 1:M
xmtrfields_sum += previous_xmtrfields[m]*conversioncoeffs[m,n]
end
xmtrfields[n] = xmtrfields_sum
end
rcvrfields[n] = xmtrfields[n]*rxterm
end
# Calculate E at each distance in the current waveguide segment
while X[i] < segment_end
x = X[i] - segment_start
factor = Q/sqrt(abs(sin(X[i]/earthradius)))
totalfield = zero(eltype(E))
for n = 1:N
S₀ = referencetoground(eas[n].sinθ; params=params)
totalfield += rcvrfields[n]*cis(-k*x*(S₀ - 1))*factor
end
E[i] = totalfield
i += 1
i > Xlength && break
end
# If we've reached the end of the current segment and there are more segments,
# prepare for next segment
if j < J
# End of current slab
x = segment_end - segment_start
resize!(previous_xmtrfields, N)
for n = 1:N
S₀ = referencetoground(eas[n].sinθ; params=params)
# Excitation factors at end of slab
xmtrfields[n] *= cis(-k*x*(S₀ - 1))
previous_xmtrfields[n] = xmtrfields[n]
end
M = N # set previous number of modes
end
end
return E
end
| LongwaveModePropagator | https://github.com/fgasdia/LongwaveModePropagator.jl.git |
|
[
"MIT"
] | 0.4.1 | 792c195909ca5dfff5685305b6fa0aa16c3d1041 | code | 961 | #==
Utility functions
==#
"""
amplitude(e)
Compute field amplitude in dB.
"""
amplitude(e) = 10log10(abs2(e)) # == 20log10(abs(E))
"""
amplitudephase(e)
Compute field amplitude in dB and phase in radians and return as (`amplitude`, `phase`).
"""
function amplitudephase(e::Number)
a = amplitude(e)
p = angle(e)
return a, p
end
function amplitudephase(e)
a = similar(e, Float64)
p = similar(a)
@inbounds for i in eachindex(e)
a[i] = amplitude(e[i])
p[i] = angle(e[i])
end
return a, p
end
"""
unwrap!(x)
Unwrap a phase vector `x` in radians in-place.
"""
unwrap!
function unwrap!(x)
v = first(x)
@inbounds for k in eachindex(x)
if isfinite(v)
x[k] = v = v + rem2pi(x[k]-v, RoundNearest)
end
end
return x
end
unwrap!(x::Number) = x
"""
pow23(x)
Efficiently compute ``x^(2/3)``.
"""
pow23
pow23(x::Real) = cbrt(x)^2
pow23(z::Complex) = exp(2/3*log(z))
| LongwaveModePropagator | https://github.com/fgasdia/LongwaveModePropagator.jl.git |
|
[
"MIT"
] | 0.4.1 | 792c195909ca5dfff5685305b6fa0aa16c3d1041 | code | 294 | @testset "EigenAngles.jl" begin
@info "Testing EigenAngles"
@test isbits(EigenAngle(deg2rad(complex(85.0, -1.0))))
@test EigenAngle(deg2rad(80-0.5im)) > EigenAngle(deg2rad(75-0.3im))
@test_logs (:warn, "θ > 2π. Make sure θ is in radians.") EigenAngle(complex(85.0, 0.31))
end
| LongwaveModePropagator | https://github.com/fgasdia/LongwaveModePropagator.jl.git |
|
[
"MIT"
] | 0.4.1 | 792c195909ca5dfff5685305b6fa0aa16c3d1041 | code | 2193 | function test_Species()
@test_throws TypeError Species(QE, ME, z->12, electroncollisionfrequency)
@test_throws TypeError Species(QE, ME, z -> waitprofile(z, 75, 0.32), z->12)
end
function test_BField()
bfield = BField(50e-6, π/2, 3π/2)
@test isbits(bfield)
@test (@test_logs (:warn, "BField magnitude of exactly 0 is not supported."*
" Setting B = 1e-16.") BField(0, π/2, 3π/2).B) == 1e-16
#==
dip and az
==#
B = 50000e-9
true_dip = deg2rad(-78)
true_az = deg2rad(240)
bfield = BField(B, true_dip, true_az)
@test LMP.dip(bfield) ≈ true_dip
@test mod2pi(LMP.azimuth(bfield)) ≈ true_az
true_dip = deg2rad(62.4)
true_az = deg2rad(18.3)
bfield = BField(B, true_dip, true_az)
@test LMP.dip(bfield) ≈ true_dip
@test mod2pi(LMP.azimuth(bfield)) ≈ true_az
#==
direction cosines
==#
# dip angle 90° up from horizontal
bfield = BField(50e-6, π/2, 3π/2)
@test bfield.dcn == -1
# dip angle 90° down from horizontal
bfield = BField(50e-6, -π/2, 3π/2)
@test bfield.dcn == 1
end
function test_Ground()
@test isbits(Ground(15, 0.001))
@test LMP.GROUND[3] == Ground(10, 1e-4)
end
function test_waitprofile()
zs = 50e3:2e3:86e3
hbs = [(65, 0.2), (65, 0.25), (68, 0.25), (70, 0.25), (72, 0.3), (72, 0.35), (75, 0.35),
(78, 0.35), (78, 0.4), (82, 0.5), (82, 0.55), (85, 0.6), (85, 0.65), (88, 0.8)]
N(z, h′, β) = 1.43e13*exp(-0.15*h′)*exp((β - 0.15)*(z/1000 - h′))
for hb in hbs, z in zs
@test waitprofile(z, hb[1], hb[2]) ≈ N(z, hb[1], hb[2])
end
# Check if zero below cutoff height
@test waitprofile(30e3, 60, 0.35; cutoff_low=40e3) == 0
@test waitprofile(30e3, 60, 0.35; cutoff_low=40e3) isa Float64
@test waitprofile(30_000, 60, 0.35; cutoff_low=40e3) isa Float64
# Check default threshold
@test waitprofile(110e3, 70, 0.5) == 1e12
end
@testset "Geophysics.jl" begin
@info "Testing Geophysics"
test_Species()
test_BField()
test_Ground()
test_waitprofile()
@test electroncollisionfrequency(110e3) isa Float64
@test ioncollisionfrequency(110e3) isa Float64
end
| LongwaveModePropagator | https://github.com/fgasdia/LongwaveModePropagator.jl.git |
|
[
"MIT"
] | 0.4.1 | 792c195909ca5dfff5685305b6fa0aa16c3d1041 | code | 10097 | function generate_basic()
# Waveguide definition
segment_ranges = [0, 500e3, 1000e3, 1500e3]
hprimes = [72.0, 74, 75, 76]
betas = [0.28, 0.30, 0.32, 0.35]
b_mags = fill(50e-6, length(segment_ranges))
b_dips = fill(π/2, length(segment_ranges))
b_azs = fill(0.0, length(segment_ranges))
ground_sigmas = [0.001, 0.001, 0.0005, 0.0001]
ground_epsrs = [4, 4, 10, 10]
# Transmitter
frequency = 24e3
# Outputs
output_ranges = collect(0:20e3:2000e3)
input = ExponentialInput()
input.name = "basic"
input.description = "Test ExponentialInput"
input.datetime = Dates.now()
input.segment_ranges = segment_ranges
input.hprimes = hprimes
input.betas = betas
input.b_mags= b_mags
input.b_dips = b_dips
input.b_azs = b_azs
input.ground_sigmas = ground_sigmas
input.ground_epsrs = ground_epsrs
input.frequency = frequency
input.output_ranges = output_ranges
json_str = JSON3.write(input)
open("basic.json","w") do f
write(f, json_str)
end
return nothing
end
function generate_table()
# Waveguide definition
segment_ranges = [0, 500e3, 1000e3, 1500e3]
hprimes = [72.0, 74, 75, 76]
betas = [0.28, 0.30, 0.32, 0.35]
altitude = 40e3:110e3
density = [Vector{Float64}(undef, length(altitude)) for i = 1:length(segment_ranges)]
collision_frequency = similar(density)
for i in eachindex(segment_ranges)
density[i] = waitprofile.(altitude, hprimes[i], betas[i])
collision_frequency[i] = electroncollisionfrequency.(altitude)
end
b_mags = fill(50e-6, length(segment_ranges))
b_dips = fill(π/2, length(segment_ranges))
b_azs = fill(0.0, length(segment_ranges))
ground_sigmas = [0.001, 0.001, 0.0005, 0.0001]
ground_epsrs = [4, 4, 10, 10]
# Transmitter
frequency = 24e3
# Outputs
output_ranges = collect(0:20e3:2000e3)
input = TableInput()
input.name = "table"
input.description = "Test TableInput"
input.datetime = Dates.now()
input.segment_ranges = segment_ranges
input.altitude = altitude
input.density = density
input.collision_frequency = collision_frequency
input.b_mags= b_mags
input.b_dips = b_dips
input.b_azs = b_azs
input.ground_sigmas = ground_sigmas
input.ground_epsrs = ground_epsrs
input.frequency = frequency
input.output_ranges = output_ranges
json_str = JSON3.write(input)
open("table.json","w") do f
write(f, json_str)
end
return nothing
end
function generate_batchtable()
N = 2
rep(v) = repeat(v, 1, N)
# Waveguide definition
nsegments = 4
segment_ranges = [0, 500e3, 1000e3, 1500e3]
b_mags = fill(50e-6, nsegments)
b_dips = fill(π/2, nsegments)
b_azs = fill(0.0, nsegments)
ground_sigmas = [0.001, 0.001, 0.0005, 0.0001]
ground_epsrs = [4, 4, 10, 10]
hprimes = [72.0, 74, 75, 76]
betas = [0.28, 0.30, 0.32, 0.35]
altitude = 40e3:110e3
density = [Vector{Float64}(undef, length(altitude)) for i = 1:length(segment_ranges)]
collision_frequency = similar(density)
for i in eachindex(segment_ranges)
density[i] = waitprofile.(altitude, hprimes[i], betas[i])
collision_frequency[i] = electroncollisionfrequency.(altitude)
end
# Transmitter
frequency = 24e3
# Outputs
output_ranges = collect(0:20e3:2000e3)
binput = BatchInput{TableInput}()
binput.name = "batchtable"
binput.description = "Test BatchInput with TableInput"
binput.datetime = Dates.now()
inputs = Vector{TableInput}(undef, N)
for i in eachindex(inputs)
input = TableInput()
input.name = "$i"
input.description = "Test TableInput $i"
input.datetime = Dates.now()
input.segment_ranges = segment_ranges
input.altitude = altitude
input.density = density
input.collision_frequency = collision_frequency
input.b_mags= b_mags
input.b_dips = b_dips
input.b_azs = b_azs
input.ground_sigmas = ground_sigmas
input.ground_epsrs = ground_epsrs
input.frequency = frequency
input.output_ranges = output_ranges
inputs[i] = input
end
binput.inputs = inputs
json_str = JSON3.write(binput)
open("batchtable.json","w") do f
write(f, json_str)
end
return nothing
end
function generate_batchbasic()
N = 2
rep(v) = repeat(v, 1, N)
# Waveguide definition
nsegments = 4
segment_ranges = [0, 500e3, 1000e3, 1500e3]
b_mags = fill(50e-6, nsegments)
b_dips = fill(π/2, nsegments)
b_azs = fill(0.0, nsegments)
ground_sigmas = [0.001, 0.001, 0.0005, 0.0001]
ground_epsrs = [4, 4, 10, 10]
hprimes = rep([72.0, 74, 75, 76])
betas = rep([0.28, 0.30, 0.32, 0.35])
# Transmitter
frequency = 24e3
# Outputs
output_ranges = collect(0:20e3:2000e3)
binput = BatchInput{ExponentialInput}()
binput.name = "batchbasic"
binput.description = "Test BatchInput with ExponentialInput"
binput.datetime = Dates.now()
inputs = Vector{ExponentialInput}(undef, N)
for i in eachindex(inputs)
input = ExponentialInput()
input.name = "$i"
input.description = "ExponentialInput $i"
input.datetime = binput.datetime
input.segment_ranges = segment_ranges
input.hprimes = hprimes[:,i]
input.betas = betas[:,i]
input.b_mags = b_mags
input.b_dips = b_dips
input.b_azs = b_azs
input.ground_sigmas = ground_sigmas
input.ground_epsrs = ground_epsrs
input.frequency = frequency
input.output_ranges = output_ranges
inputs[i] = input
end
binput.inputs = inputs
json_str = JSON3.write(binput)
open("batchbasic.json","w") do f
write(f, json_str)
end
return nothing
end
function read_basic()
open("basic.json","r") do f
v = JSON3.read(f, ExponentialInput)
return v
end
end
function read_table()
open("table.json", "r") do f
v = JSON3.read(f, TableInput)
return v
end
end
function read_batchbasic()
open("batchbasic.json","r") do f
v = JSON3.read(f, BatchInput{ExponentialInput})
return v
end
end
function read_corrupted_basic()
# missing the ground_sigmas field
open("corrupted_basic.json","r") do f
v = JSON3.read(f, ExponentialInput)
return v
end
end
function run_basic()
s = LMP.parse("basic.json")
output = LMP.buildrun(s)
return output
end
function run_table()
s = LMP.parse("table.json")
output = LMP.buildrun(s)
return output
end
function run_batchbasic()
s = LMP.parse("batchbasic.json")
output = LMP.buildrun(s)
return output
end
function run_batchbasicsave()
s = LMP.parse("batchbasic.json")
output = LMP.buildrunsave("batchbasictest.json", s)
sres = LMP.parse("batchbasictest.json")
return sres
end
function run_batchtablesave()
s = LMP.parse("batchtable.json")
output = LMP.buildrunsave("batchtabletest.json", s)
sres = LMP.parse("batchtabletest.json")
return sres
end
function basic_lmp()
output = LMP.propagate("basic.json")
# Compare to a `propagate` call with waveguide arguments
tx = Transmitter(24e3)
rx = GroundSampler(0:20e3:2000e3, Fields.Ez)
# From `generate_basic()`
segment_ranges = [0, 500e3, 1000e3, 1500e3]
hprimes = [72.0, 74, 75, 76]
betas = [0.28, 0.30, 0.32, 0.35]
b_mags = fill(50e-6, length(segment_ranges))
b_dips = fill(π/2, length(segment_ranges))
b_azs = fill(0.0, length(segment_ranges))
ground_sigmas = [0.001, 0.001, 0.0005, 0.0001]
ground_epsrs = [4, 4, 10, 10]
wvg = SegmentedWaveguide(
[HomogeneousWaveguide(
BField(b_mags[i], b_dips[i], b_azs[i]),
Species(QE, ME, z->waitprofile(z, hprimes[i], betas[i]; cutoff_low=40e3), electroncollisionfrequency),
Ground(ground_epsrs[i], ground_sigmas[i]),
segment_ranges[i]
) for i = 1:4]
)
_, a, p = propagate(wvg, tx, rx)
@test maxabsdiff(a, output.amplitude) < 0.1
@test maxabsdiff(p, output.phase) < 0.005
return output
end
@testset "IO.jl" begin
@info "Testing IO"
generate_basic()
generate_table()
generate_batchbasic()
generate_batchtable()
@test LMP.iscomplete(read_basic())
@test LMP.validlengths(read_basic())
@test LMP.iscomplete(read_corrupted_basic()) == false
@test LMP.parse("basic.json") isa ExponentialInput
@test LMP.parse("basic.json", ExponentialInput) isa ExponentialInput
@test LMP.iscomplete(read_table())
@test LMP.validlengths(read_table())
@test LMP.parse("table.json") isa TableInput
@test LMP.parse("table.json", TableInput) isa TableInput
@test LMP.iscomplete(read_batchbasic())
@test LMP.validlengths(read_batchbasic())
@test LMP.parse("batchbasic.json") isa BatchInput{ExponentialInput}
@info " Running:"
@info " Segmented Wait ionospheres..."
@test run_basic() isa BasicOutput
@info " Segmented tabular ionospheres..."
@test run_table() isa BasicOutput
@info " Multiple segmented Wait ionospheres..."
@test run_batchbasic() isa BatchOutput{BasicOutput}
@info " Multiple segmented Wait ionospheres, appending..."
@test run_batchbasicsave() isa BatchOutput{BasicOutput}
@info " Multiple segmented tabular ionospheres, appending."
@test run_batchtablesave() isa BatchOutput{BasicOutput}
@info " `propagate` segmented Wait ionospheres"
@test basic_lmp() isa BasicOutput
isfile("basic.json") && rm("basic.json")
isfile("table.json") && rm("table.json")
isfile("batchbasic.json") && rm("batchbasic.json")
isfile("batchtable.json") && rm("batchtable.json")
isfile("batchbasictest.json") && rm("batchbasictest.json")
isfile("batchtabletest.json") && rm("batchtabletest.json")
isfile("basic_output.json") && rm("basic_output.json")
end
| LongwaveModePropagator | https://github.com/fgasdia/LongwaveModePropagator.jl.git |
|
[
"MIT"
] | 0.4.1 | 792c195909ca5dfff5685305b6fa0aa16c3d1041 | code | 4055 | function test_propagate(scenario)
@unpack tx, rx, bfield, species, ground = scenario
waveguide = HomogeneousWaveguide(bfield, species, ground)
E, amp, phase = propagate(waveguide, tx, rx)
@test eltype(E) == ComplexF64
@test eltype(amp) == Float64
@test eltype(phase) == Float64
mesh = LMP.defaultmesh(tx.frequency)
E2, amp2, phase2 = propagate(waveguide, tx, rx; mesh=mesh)
@test E2 ≈ E rtol=1e-2
@test amp2 ≈ amp rtol=1e-2
@test phase2 ≈ phase rtol=1e-2
me = PhysicalModeEquation(tx.frequency, waveguide)
modes = findmodes(me, mesh)
E3, amp3, phase3 = propagate(waveguide, tx, rx; modes=modes)
@test E3 ≈ E2 rtol=1e-2
@test amp3 ≈ amp2 rtol=1e-2
@test phase3 ≈ phase2 rtol=1e-2
# mesh should be ignored
E4, amp4, phase4 = propagate(waveguide, tx, rx; modes=modes, mesh=[1.0])
@test E4 ≈ E3 rtol=1e-3
@test amp4 ≈ amp3 rtol=1e-3
@test phase4 ≈ phase3 rtol=1e-3
# Are params being carried through?
params = LMPParams(earthradius=6300e3)
E5, amp5, phase5 = propagate(waveguide, tx, rx; params=params)
@test !isapprox(E5, E, rtol=1e-3)
@test !isapprox(amp5, amp, rtol=1e-3)
@test !isapprox(phase5, phase, rtol=1e-3)
# Mismatch between modes and modeterms
E6, amp6, phase6 = propagate(waveguide, tx, rx; modes=modes, params=params)
@test !isapprox(E6, E5, rtol=1e-3)
@test !isapprox(amp6, amp5, rtol=1e-3)
@test !isapprox(phase6, phase5, rtol=1e-3)
end
function test_propagate_segmented(scenario)
@unpack tx, rx, bfield, species, ground, distances = scenario
waveguide = SegmentedWaveguide([HomogeneousWaveguide(bfield[i], species[i], ground[i],
distances[i]) for i in 1:2])
E, amp, phase = propagate(waveguide, tx, rx)
@test eltype(E) == ComplexF64
@test eltype(amp) == Float64
@test eltype(phase) == Float64
E1, amp1, phase1 = propagate(waveguide, tx, rx)
@test meanabsdiff(E1, E) < 1
@test maxabsdiff(amp1, amp) < 0.1
@test maxabsdiff(phase1, phase) < 0.005
# Are params being carried through?
params = LMPParams(earthradius=6300e3)
E3, amp3, phase3 = propagate(waveguide, tx, rx; params=params)
@test !isapprox(E3, E, rtol=1e-3)
@test !isapprox(amp3, amp, rtol=1e-3)
@test !isapprox(phase3, phase, rtol=1e-3)
end
function test_mcranges_segmented(scenario)
# Test that single receiver location has correct phase without continuous Range
# This also confirms that results are correct if mode conversion occurs at a
# segment_range that is not also an output_range
@unpack tx, rx, bfield, species, ground, distances = scenario
waveguide = SegmentedWaveguide([HomogeneousWaveguide(bfield[i], species[i], ground[i],
distances[i]) for i in 1:2])
_, ampref, phaseref = propagate(waveguide, tx, rx; unwrap=false)
_, a1, p1 = propagate(waveguide, tx, GroundSampler(600e3, Fields.Ez))
_, a2, p2 = propagate(waveguide, tx, GroundSampler(1400e3, Fields.Ez))
_, a3, p3 = propagate(waveguide, tx, GroundSampler(1800e3, Fields.Ez))
m1 = findfirst(isequal(600e3), rx.distance)
m2 = findfirst(isequal(1400e3), rx.distance)
m3 = findfirst(isequal(1800e3), rx.distance)
@test a1 ≈ ampref[m1] atol=0.01
@test a2 ≈ ampref[m2] atol=0.01
@test a3 ≈ ampref[m3] atol=0.01
@test p1 ≈ phaseref[m1] atol=1e-3
@test p2 ≈ phaseref[m2] atol=1e-3
@test p3 ≈ phaseref[m3] atol=1e-3
end
@testset "LongwaveModePropagator.jl" begin
@info "Testing LongwaveModePropagator"
@info " Running:"
# Just to save time, running with only one scenario
@info " Homogeneous ionospheres..."
for scn in (resonant_scenario, interp_scenario)
test_propagate(scn)
end
@info " Segmented ionospheres..."
for scn in (segmented_scenario,)
test_propagate_segmented(scn)
end
# propagate(file,...) is tested in IO.jl
end
| LongwaveModePropagator | https://github.com/fgasdia/LongwaveModePropagator.jl.git |
|
[
"MIT"
] | 0.4.1 | 792c195909ca5dfff5685305b6fa0aa16c3d1041 | code | 722 | function test_tmatrix_deriv(scenario)
@unpack ea, tx, bfield, species = scenario
M = LMP.susceptibility(LMPParams().topheight, tx.frequency, bfield, species)
for i = 1:4
for j = 1:4
Tfcn(θ) = (ea = EigenAngle(θ); T = LMP.tmatrix(ea, M)[i,j])
dTref = FiniteDiff.finite_difference_derivative(Tfcn, θs, Val{:central})
dT(θ) = (ea = EigenAngle(θ); T = LMP.dtmatrix(ea, M)[i,j])
@test maxabsdiff(dT.(θs), dTref) < 1e-7
end
end
end
@testset "TMatrix.jl" begin
@info "Testing TMatrix"
for scn in (verticalB_scenario, resonant_scenario, nonresonant_scenario,
multiplespecies_scenario)
test_tmatrix_deriv(scn)
end
end
| LongwaveModePropagator | https://github.com/fgasdia/LongwaveModePropagator.jl.git |
|
[
"MIT"
] | 0.4.1 | 792c195909ca5dfff5685305b6fa0aa16c3d1041 | code | 776 | function test_HomogeneousWaveguide(scenario)
@unpack bfield, species, ground = scenario
distance = 1000e3
waveguide = HomogeneousWaveguide(bfield, species, ground, distance)
adjwaveguide = LMP.adjoint(waveguide)
oB = waveguide.bfield
aB = adjwaveguide.bfield
@test aB.B == oB.B
@test aB.dcl == -oB.dcl
@test aB.dcm == oB.dcm
@test aB.dcn == oB.dcn
@test adjwaveguide.species == waveguide.species
@test adjwaveguide.ground == waveguide.ground
@test adjwaveguide.distance == waveguide.distance
end
@testset "Waveguides.jl" begin
@info "Testing Waveguides"
for scn in (verticalB_scenario, resonant_scenario, nonresonant_scenario,
multiplespecies_scenario)
test_HomogeneousWaveguide(scn)
end
end
| LongwaveModePropagator | https://github.com/fgasdia/LongwaveModePropagator.jl.git |
|
[
"MIT"
] | 0.4.1 | 792c195909ca5dfff5685305b6fa0aa16c3d1041 | code | 9000 | function test_bookerquarticM(scenario)
@unpack ea, tx, bfield, species = scenario
M = LMP.susceptibility(LMPParams().topheight, tx.frequency, bfield, species)
q, B = LMP.bookerquartic(ea, M)
S = ea.sinθ
S², C² = ea.sin²θ, ea.cos²θ
# Confirm roots of Booker quartic satisfy ``det(Γ² + I + M) = 0``
for i in eachindex(q)
G = [1-q[i]^2+M[1,1] M[1,2] S*q[i]+M[1,3];
M[2,1] 1-q[i]^2-S²+M[2,2] M[2,3];
S*q[i]+M[3,1] M[3,2] C²+M[3,3]]
@test isroot(det(G); atol=1e-5) # real barely fails 1e-6 for resonant_scenario
end
# Confirm Booker quartic is directly satisfied
for i in eachindex(q)
booker = B[5]*q[i]^4 + B[4]*q[i]^3 + B[3]*q[i]^2 + B[2]*q[i] + B[1]
@test isroot(booker; atol=1e-6)
end
end
function test_bookerquarticT(scenario)
@unpack ea, tx, bfield, species = scenario
M = LMP.susceptibility(LMPParams().topheight, tx.frequency, bfield, species)
T = LMP.tmatrix(ea, M)
q, B = LMP.bookerquartic(T)
S = ea.sinθ
S², C² = ea.sin²θ, ea.cos²θ
# Confirm roots of Booker quartic satisfy ``det(Γ² + I + M) = 0``
for i in eachindex(q)
G = [1-q[i]^2+M[1,1] M[1,2] S*q[i]+M[1,3];
M[2,1] 1-q[i]^2-S²+M[2,2] M[2,3];
S*q[i]+M[3,1] M[3,2] C²+M[3,3]]
@test isroot(det(G); atol=1e-6)
end
# eigvals is >20 times slower than bookerquartic
@test sort(eigvals(Array(T)); by=LMP.upgoing) ≈ sort(q; by=LMP.upgoing)
# Confirm Booker quartic is directly satisfied
for i in eachindex(q)
booker = B[5]*q[i]^4 + B[4]*q[i]^3 + B[3]*q[i]^2 + B[2]*q[i] + B[1]
@test isroot(booker; atol=1e-6)
end
end
function test_bookerquartics(scenario)
@unpack ea, tx, bfield, species = scenario
M = LMP.susceptibility(LMPParams().topheight, tx.frequency, bfield, species)
T = LMP.tmatrix(ea, M)
qM, BM = LMP.bookerquartic(ea, M)
qT, BT = LMP.bookerquartic(T)
sort!(qM; by=LMP.upgoing)
sort!(qT; by=LMP.upgoing)
@test qM ≈ qT
end
function test_bookerquarticM_deriv(scenario)
@unpack ea, tx, bfield, species = scenario
M = LMP.susceptibility(LMPParams().topheight, tx.frequency, bfield, species)
for i = 1:4
qfcn(θ) = (ea = EigenAngle(θ); (q, B) = LMP.bookerquartic(ea, M);
sort!(q; by=LMP.upgoing); q[i])
dqref = FiniteDiff.finite_difference_derivative(qfcn, θs, Val{:central})
dq(θ) = (ea = EigenAngle(θ); (q, B) = LMP.bookerquartic(ea, M);
sort!(q; by=LMP.upgoing); LMP.dbookerquartic(ea, M, q, B)[i])
@test maxabsdiff(dq.(θs), dqref) < 1e-6
end
end
function test_bookerquarticT_deriv(scenario)
@unpack ea, tx, bfield, species = scenario
M = LMP.susceptibility(LMPParams().topheight, tx.frequency, bfield, species)
for i = 1:4
qfcn(θ) = (ea = EigenAngle(θ); T = LMP.tmatrix(ea, M);
(q, B) = LMP.bookerquartic(T); LMP.sortquarticroots!(q); q[i])
dqref = FiniteDiff.finite_difference_derivative(qfcn, θs, Val{:central})
dq(θ) = (ea = EigenAngle(θ);
T = LMP.tmatrix(ea, M); dT = LMP.dtmatrix(ea, M);
(q, B) = LMP.bookerquartic(T);
LMP.sortquarticroots!(q); LMP.dbookerquartic(T, dT, q, B)[i])
@test maxabsdiff(dq.(θs), dqref) < 1e-6
end
end
function test_bookerwavefields(scenario)
@unpack ea, bfield, tx, species = scenario
topheight = first(LMPParams().wavefieldheights)
M = LMP.susceptibility(topheight, tx.frequency, bfield, species)
T = LMP.tmatrix(ea, M)
# Verify bookerwavefields produces a valid solution
e = LMP.bookerwavefields(T)
q, B = LMP.bookerquartic(T)
LMP.sortquarticroots!(q)
for i = 1:2
@test T*e[:,i] ≈ q[i]*e[:,i]
end
e2 = LMP.bookerwavefields(ea, M)
@test e ≈ e2
end
function test_bookerwavefields_deriv(scenario)
@unpack ea, tx, bfield, species = scenario
M = LMP.susceptibility(LMPParams().topheight, tx.frequency, bfield, species)
# Compare analytical solution with finite diff
for i = 1:4
eref(θ) = (ea = EigenAngle(θ); LMP.bookerwavefields(ea, M)[i])
deref = FiniteDiff.finite_difference_derivative(eref, θs, Val{:central})
e(θ) = (ea = EigenAngle(θ); LMP.bookerwavefields(ea, M, LMP.Dθ())[1][i])
de(θ) = (ea = EigenAngle(θ); LMP.bookerwavefields(ea, M, LMP.Dθ())[2][i])
@test eref.(θs) ≈ e.(θs)
@test maxabsdiff(deref, de.(θs)) < 1e-3
end
# Compare functions using `M` and `T`
de1 = Vector{SMatrix{4,2,ComplexF64,8}}(undef, length(θs))
de2 = similar(de1)
for i in eachindex(θs)
ea = EigenAngle(θs[i])
T = LMP.tmatrix(ea, M)
dT = LMP.dtmatrix(ea, M)
de1[i] = LMP.bookerwavefields(ea, M, LMP.Dθ())[2]
de2[i] = LMP.bookerwavefields(T, dT, LMP.Dθ())[2]
end
@test de1 ≈ de2
end
function test_bookerreflection_vertical(scenario)
@unpack ea, tx, bfield, species = scenario
M = LMP.susceptibility(LMPParams().topheight, tx.frequency, bfield, species)
R = LMP.bookerreflection(ea, M)
@test R[1,2] ≈ R[2,1]
end
function sharpR!(f, R, W)
#==
The right side of ``2i R′ = w₂₁ + w₂₂R - Rw₁₁ - Rw₁₂R``, which can be used to solve for
reflection from the sharply bounded ionosphere where ``dR/dz = 0``.
==#
# See [^Budden1988] sec. 18.10.
f .= W[2] + W[4]*R - R*W[1] - R*W[3]*R
end
function sharpR!(f, dR, R, dW, W)
# ``dR/dz/dθ`` which can be used to solve for ``dR/dθ`` from a sharply bounded ionosphere.
f .= dW[2] + W[4]*dR + dW[4]*R - R*dW[1] - dR*W[1] - R*W[3]*dR - R*dW[3]*R - dR*W[3]*R
end
function test_bookerreflection(scenario)
@unpack ea, tx, bfield, species = scenario
M = LMP.susceptibility(LMPParams().topheight, tx.frequency, bfield, species)
e = LMP.bookerwavefields(ea, M)
@test LMP.bookerreflection(ea, e) == LMP.bookerreflection(ea, M)
# Iterative solution for sharp boundary reflection matrix
initRs = Vector{SMatrix{2,2,ComplexF64,4}}(undef, length(θs))
Rs = similar(initRs)
for i in eachindex(θs)
ea = EigenAngle(θs[i])
T = LMP.tmatrix(ea, M)
W = LMP.wmatrix(ea, T)
initR = LMP.bookerreflection(ea, M)
res = nlsolve((f,R)->sharpR!(f,R,W), Array(initR))
R = SMatrix{2,2}(res.zero)
initRs[i] = initR
Rs[i] = R
end
for n in 1:4
@test maxabsdiff(getindex.(initRs, n), getindex.(Rs, n)) < 1e-8
end
# Matrix solution
e = LMP.bookerwavefields(ea, M)
wavefieldR = LMP.bookerreflection(ea, e)
Cinv = ea.secθ
Sv_inv = SMatrix{4,4}(Cinv, 0, -Cinv, 0,
0, -1, 0, -1,
0, -Cinv, 0, Cinv,
1, 0, 1, 0)
f1 = Sv_inv*e[:,1]
f2 = Sv_inv*e[:,2]
U = SMatrix{2,2}(f1[1], f1[2], f2[1], f2[2])
D = SMatrix{2,2}(f1[3], f1[4], f2[3], f2[4])
@test D/U ≈ wavefieldR
end
function test_dbookerreflection(scenario)
@unpack ea, tx, bfield, species = scenario
M = LMP.susceptibility(LMPParams().topheight, tx.frequency, bfield, species)
# Iterative solution
initdRs = Vector{SMatrix{2,2,ComplexF64,4}}(undef, length(θs))
dRs = similar(initdRs)
for i in eachindex(θs)
ea = EigenAngle(θs[i])
T = LMP.tmatrix(ea, M)
dT = LMP.dtmatrix(ea, M)
W = LMP.wmatrix(ea, T)
dW = LMP.dwmatrix(ea, T, dT)
R = LMP.bookerreflection(ea, M)
initdR = LMP.bookerreflection(ea, M, LMP.Dθ())[2]
resdR = nlsolve((f,dR)->sharpR!(f,dR,R,dW,W), Array(initdR))
dR = SMatrix{2,2}(resdR.zero)
initdRs[i] = initdR
dRs[i] = dR
end
for n in 1:4
@test maxabsdiff(getindex.(initdRs, n), getindex.(dRs, n)) < 1e-4
end
# Finite difference derivative
for i = 1:4
Rref(θ) = (ea = EigenAngle(θ); LMP.bookerreflection(ea, M)[i])
dRref = FiniteDiff.finite_difference_derivative(Rref, θs, Val{:central})
R(θ) = (ea = EigenAngle(θ); LMP.bookerreflection(ea, M, LMP.Dθ())[1][i])
dR(θ) = (ea = EigenAngle(θ); LMP.bookerreflection(ea, M, LMP.Dθ())[2][i])
@test Rref.(θs) ≈ R.(θs)
@test maxabsdiff(dRref, dR.(θs)) < 1e-4
end
end
@testset "bookerquartic.jl" begin
@info "Testing bookerquartic"
for scn in (verticalB_scenario, resonant_scenario, nonresonant_scenario,
multiplespecies_scenario)
test_bookerquarticM(scn)
test_bookerquarticT(scn)
test_bookerquartics(scn)
test_bookerquarticM_deriv(scn)
test_bookerquarticT_deriv(scn)
test_bookerwavefields(scn)
test_bookerwavefields_deriv(scn)
test_bookerreflection(scn)
test_dbookerreflection(scn)
end
for scn in (verticalB_scenario, )
test_bookerreflection_vertical(scn)
end
end
| LongwaveModePropagator | https://github.com/fgasdia/LongwaveModePropagator.jl.git |
|
[
"MIT"
] | 0.4.1 | 792c195909ca5dfff5685305b6fa0aa16c3d1041 | code | 2006 | function test_lmp(scenario)
@unpack tx, rx, bfield, species, ground = scenario
waveguide = HomogeneousWaveguide(bfield, species, ground)
E, amplitude, phase = propagate(waveguide, tx, rx)
lmp_d = collect(distance(rx, tx)/1e3)
lmp_a = amplitude
lmp_p = rad2deg.(phase)
return lmp_d, lmp_a, lmp_p
end
function test_lmp_segmented(scenario)
@unpack tx, rx, bfield, species, ground, distances = scenario
waveguide = SegmentedWaveguide([HomogeneousWaveguide(bfield[i], species[i], ground[i],
distances[i]) for i in 1:2])
E, amplitude, phase = propagate(waveguide, tx, rx)
lmp_d = collect(distance(rx, tx)/1e3)
lmp_a = amplitude
lmp_p = rad2deg.(phase)
return lmp_d, lmp_a, lmp_p
end
function compare(lwpc_file, lmp_d, lmp_a, lmp_p)
lwpc_d, lwpc_a, lwpc_p = readlog(lwpc_file)
distmask = lwpc_d .> 300
lm_p = mod.(lmp_p[distmask], 360) # modulo because we're not interested in wrapping
lw_p = mod.(lwpc_p[distmask], 360)
@test lmp_d ≈ lwpc_d
@test meanabsdiff(lmp_a[distmask], lwpc_a[distmask]) < 0.4
@test meanabsdiff(lm_p, lw_p) < 4.0
end
@testset "LWPC comparisons" begin
@info "Comparing to LWPC..."
files = Dict(verticalB_scenario=>"verticalB.log", resonant_scenario=>"resonant.log",
nonresonant_scenario=>"nonresonant.log",
resonant_elevatedrx_scenario=>"resonant_elevatedrx.log",
resonant_horizontal_scenario=>"resonant_horizontal.log",
segmented_scenario=>"segmented.log")
@info " Running:"
for scn in (verticalB_scenario, resonant_scenario, nonresonant_scenario,
resonant_elevatedrx_scenario, resonant_horizontal_scenario,)
@info " "*files[scn]
compare(joinpath(LWPC_PATH, files[scn]), test_lmp(scn)...)
end
for scn in (segmented_scenario,)
@info " "*files[scn]
compare(joinpath(LWPC_PATH, files[scn]), test_lmp_segmented(scn)...)
end
end
| LongwaveModePropagator | https://github.com/fgasdia/LongwaveModePropagator.jl.git |
|
[
"MIT"
] | 0.4.1 | 792c195909ca5dfff5685305b6fa0aa16c3d1041 | code | 2488 | function test_susceptibility(scenario)
@unpack tx, bfield, species, ground = scenario
M1 = LMP.susceptibility(70e3, tx.frequency, bfield, species)
M2 = LMP.susceptibility(70e3, tx.frequency, bfield, species; params=LMPParams())
M3 = LMP.susceptibility(70e3, tx.frequency, bfield, species; params=LMPParams(earthradius=6350e3))
@test M1 == M2
@test !(M2 ≈ M3)
waveguide = HomogeneousWaveguide(bfield, species, ground)
modeequation = PhysicalModeEquation(tx.frequency, waveguide)
M4 = LMP.susceptibility(70e3, tx.frequency, waveguide)
M5 = LMP.susceptibility(70e3, tx.frequency, waveguide; params=LMPParams())
M6 = LMP.susceptibility(70e3, tx.frequency, waveguide; params=LMPParams(earthradius=6350e3))
M7 = LMP.susceptibility(70e3, modeequation)
M8 = LMP.susceptibility(70e3, modeequation; params=LMPParams())
M9 = LMP.susceptibility(70e3, modeequation; params=LMPParams(earthradius=6350e3))
@test M4 == M5 == M1
@test M6 == M3
@test M7 == M8 == M1
@test M9 == M3
@inferred LMP.susceptibility(70e3, tx.frequency, bfield, species)
end
function test_spline(scenario)
@unpack tx, bfield, species = scenario
itp = LMP.susceptibilityspline(tx.frequency, bfield, species)
zs = LMP.BOTTOMHEIGHT:1:LMPParams().topheight
Ms = LMP.susceptibility.(zs, (tx.frequency,), (bfield,), (species,))
Mitp = itp.(zs)
function matrix(M)
mat = Matrix{eltype(M[1])}(undef, length(M), 9)
for i in eachindex(M)
mat[i,:] = M[i]
end
return mat
end
@test matrix(Mitp) ≈ matrix(Ms) rtol=1e-5
# plot(matrix(real(Ms)), zs/1000, legend=false)
# plot!(matrix(real(Mitp)), zs/1000, linestyle=:dash)
# Mdiff = matrix(real(Ms)) .- matrix(real(Mitp))
# scaleddiff = Mdiff./matrix(real(Ms))
# plot(Mdiff, zs/1000, legend=false, ylims=(0,110))
# Make sure `params.susceptibilitysplinestep` is being used
itp2 = LMP.susceptibilityspline(tx.frequency, bfield, species; params=LMPParams(susceptibilitysplinestep=10.0))
itp3 = LMP.susceptibilityspline(tx.frequency, bfield, species; params=LMPParams(susceptibilitysplinestep=20.0))
@test itp == itp2
@test itp != itp3
end
@testset "magnetoionic.jl" begin
@info "Testing magnetoionic"
for scn in (verticalB_scenario, resonant_scenario, nonresonant_scenario,
multiplespecies_scenario)
test_susceptibility(scn)
test_spline(scn)
end
end
| LongwaveModePropagator | https://github.com/fgasdia/LongwaveModePropagator.jl.git |
|
[
"MIT"
] | 0.4.1 | 792c195909ca5dfff5685305b6fa0aa16c3d1041 | code | 1263 | function test_modeconversion_segmented(scenario)
@unpack distances, tx, bfield, species, ground = scenario()
params = LMPParams()
waveguide = SegmentedWaveguide([HomogeneousWaveguide(bfield[i], species[i],
ground[i], distances[i]) for i in 1:2])
heighttype = typeof(params.wavefieldheights)
wavefields_vec = Vector{LMP.Wavefields{heighttype}}(undef, 2)
adjwavefields_vec = Vector{LMP.Wavefields{heighttype}}(undef, 2)
mesh = LMP.defaultmesh(tx.frequency)
for i = 1:2
wvg = waveguide[i]
adjwvg = LMP.adjoint(wvg)
modeequation = PhysicalModeEquation(tx.frequency, wvg)
modes = findmodes(modeequation, mesh; params=params)
wavefields = LMP.Wavefields(params.wavefieldheights, modes)
adjwavefields = LMP.Wavefields(params.wavefieldheights, modes)
LMP.calculate_wavefields!(wavefields, adjwavefields, tx.frequency, wvg, adjwvg)
wavefields_vec[i] = wavefields
adjwavefields_vec[i] = adjwavefields
end
a = LMP.modeconversion(wavefields_vec[1], wavefields_vec[1], adjwavefields_vec[1])
@test all(diag(a) .≈ complex(1))
# a = modeconversion(wavefields_vec[1], wavefields_vec[2], adjwavefields_vec[2])
end
| LongwaveModePropagator | https://github.com/fgasdia/LongwaveModePropagator.jl.git |
|
[
"MIT"
] | 0.4.1 | 792c195909ca5dfff5685305b6fa0aa16c3d1041 | code | 11845 | function test_physicalmodeequation(scenario)
@unpack ea, tx, bfield, species, ground = scenario
waveguide = HomogeneousWaveguide(bfield, species, ground)
me = PhysicalModeEquation(ea, tx.frequency, waveguide)
@test me isa LMP.ModeEquation
@test me isa PhysicalModeEquation
me2 = PhysicalModeEquation(tx.frequency, waveguide)
@test me2 isa PhysicalModeEquation
@test iszero(me2.ea.θ)
@test LMP.setea(ea, me2) == me
@test LMP.setea(ea.θ, me2) == me
end
function test_wmatrix(scenario)
@unpack ea, tx, bfield, species = scenario
C = ea.cosθ
L = @SMatrix [C 0 -C 0;
0 -1 0 -1;
0 -C 0 C;
1 0 1 0]
M = LMP.susceptibility(80e3, tx.frequency, bfield, species)
T = LMP.tmatrix(ea, M)
W = LMP.wmatrix(ea, T)
@test [W[1] W[3]; W[2] W[4]] ≈ 2*(L\T)*L
end
function test_wmatrix_deriv(scenario)
@unpack tx, bfield, species = scenario
M = LMP.susceptibility(80e3, tx.frequency, bfield, species)
for i = 1:4
for j = 1:4
Wfcn(θ) = (ea = EigenAngle(θ); T = LMP.tmatrix(ea, M); LMP.wmatrix(ea, T)[i][j])
dWref = FiniteDiff.finite_difference_derivative(Wfcn, θs, Val{:central})
dW(θ) = (ea = EigenAngle(θ); T = LMP.tmatrix(ea, M);
dT = LMP.dtmatrix(ea, M); LMP.dwmatrix(ea, T, dT)[i][j])
@test maxabsdiff(dW.(θs), dWref) < 1e-3
end
end
end
function test_dRdz(scenario)
@unpack ea, tx, bfield, species, ground = scenario
params = LMPParams()
waveguide = HomogeneousWaveguide(bfield, species, ground)
me = PhysicalModeEquation(ea, tx.frequency, waveguide)
Mtop = LMP.susceptibility(params.topheight, me; params=params)
Rtop = LMP.bookerreflection(ea, Mtop)
# sharply bounded R from bookerreflection satisfies dR/dz = 0
@test isapprox(LMP.dRdz(Rtop, me, params.topheight), zeros(2, 2); atol=1e-15)
# Compare default and optional argument
M = LMP.susceptibility(72e3, me; params=params)
R = LMP.bookerreflection(ea, M)
dR1 = @inferred LMP.dRdz(R, me, 72e3)
Mfcn = z -> LMP.susceptibility(z, me; params=params)
dR2 = @inferred LMP.dRdz(R, me, 72e3, Mfcn)
Mfcn2 = LMP.susceptibilityspline(me; params=params)
dR3 = @inferred LMP.dRdz(R, me, 72e3, Mfcn2)
@test dR1 == dR2 # identical functions Mfcn
@test isapprox(dR1, dR3, atol=1e-12) # interpolating spline
end
function test_dRdθdz(scenario)
@unpack ea, tx, bfield, species, ground = scenario
params = LMPParams()
waveguide = HomogeneousWaveguide(bfield, species, ground)
me = PhysicalModeEquation(ea, tx.frequency, waveguide)
Mtop = LMP.susceptibility(params.topheight, me)
z = params.topheight - 500
for i = 1:4
dRfcn(θ) = (ea = EigenAngle(θ); Rtop = LMP.bookerreflection(ea, Mtop);
me = LMP.setea(ea, me); LMP.dRdz(Rtop, me, z)[i])
dRdθref = FiniteDiff.finite_difference_derivative(dRfcn, θs, Val{:central})
dRdθtmp(θ) = (ea = EigenAngle(θ); me = LMP.setea(ea, me);
(Rtop, dRdθtop) = LMP.bookerreflection(ea, Mtop, LMP.Dθ());
RdRdθtop = vcat(Rtop, dRdθtop);
LMP.dRdθdz(RdRdθtop, (me, params), z))
dR(θ) = dRdθtmp(θ)[SVector(1,2),:][i]
dRdθ(θ) = dRdθtmp(θ)[SVector(3,4),:][i]
@test dRfcn.(θs) ≈ dR.(θs)
@test maxabsdiff(dRdθ.(θs), dRdθref) < 1e-6
end
end
function test_integratedreflection_vertical(scenario)
@unpack tx, ground, bfield, species = scenario
waveguide = HomogeneousWaveguide(bfield, species, ground)
me = PhysicalModeEquation(tx.frequency, waveguide)
R = LMP.integratedreflection(me)
@test R[1,2] ≈ R[2,1]
# Let's also check with interpolation susceptibilityfcn here
Mfcn = z -> LMP.susceptibility(z, me)
R2 = LMP.integratedreflection(me; susceptibilityfcn=Mfcn)
Mfcn2 = LMP.susceptibilityspline(me)
R3 = LMP.integratedreflection(me; susceptibilityfcn=Mfcn2)
@test R2 == R
@test maxabsdiff(R, R3) < 1e-6
end
function test_integratedreflection_deriv(scenario)
@unpack tx, ground, bfield, species = scenario
freq = tx.frequency
# 1e-10 is hardcoded in Dθ form of `integratedreflection`
# This function is a test of the Dθ form - the lower default tolerance in the non-Dθ
# form would cause tests to fail if not lowered to the same threshold
ip = IntegrationParams(tolerance=1e-10)
params = LMPParams(integrationparams=ip)
waveguide = HomogeneousWaveguide(bfield, species, ground)
me = PhysicalModeEquation(freq, waveguide)
Rref(θ) = LMP.integratedreflection(LMP.setea(θ, me); params=params)
RdR(θ) = LMP.integratedreflection(LMP.setea(θ, me), LMP.Dθ(); params=params)
Rs = Vector{SMatrix{2,2,ComplexF64,4}}(undef, length(θs))
dRs = similar(Rs)
Rrefs = similar(Rs)
dRrefs = similar(Rs)
Threads.@threads for i in eachindex(θs)
v = RdR(θs[i])
Rs[i] = v[SVector(1,2),:]
dRs[i] = v[SVector(3,4),:]
Rrefs[i] = Rref(θs[i])
dRrefs[i] = FiniteDiff.finite_difference_derivative(Rref, θs[i], Val{:central})
end
for i = 1:4
R = getindex.(Rs, i)
dR = getindex.(dRs, i)
Rr = getindex.(Rrefs, i)
dRr = getindex.(dRrefs, i)
# maxabsdiff criteria doesn't capture range of R and dR so rtol is used
@test isapprox(R, Rr; rtol=1e-5)
@test isapprox(dR, dRr; rtol=1e-3)
end
end
function test_fresnelreflection(scenario)
@unpack ea, tx, bfield, species, ground = scenario
# PEC ground
pec_ground = LMP.Ground(1, 1e12)
vertical_ea = LMP.EigenAngle(π/2)
Rg = LMP.fresnelreflection(vertical_ea, pec_ground, Frequency(24e3))
@test isapprox(abs.(Rg), I; atol=1e-7)
waveguide = HomogeneousWaveguide(bfield, species, ground)
me = PhysicalModeEquation(ea, tx.frequency, waveguide)
@test LMP.fresnelreflection(ea, ground, tx.frequency) == LMP.fresnelreflection(me)
end
function test_fresnelreflection_deriv(scenario)
@unpack ea, tx, bfield, species, ground = scenario
freq = tx.frequency
dRgtmp(θ) = (ea = EigenAngle(θ); LMP.fresnelreflection(ea, ground, freq, LMP.Dθ()))
for i = 1:4
Rgref(θ) = (ea = EigenAngle(θ); LMP.fresnelreflection(ea, ground, freq)[i])
dRgref = FiniteDiff.finite_difference_derivative(Rgref, θs, Val{:central})
Rg(θ) = dRgtmp(θ)[1][i]
dRg(θ) = dRgtmp(θ)[2][i]
@test Rgref.(θs) ≈ Rg.(θs)
@test maxabsdiff(dRg.(θs), dRgref) < 1e-6
end
waveguide = HomogeneousWaveguide(bfield, species, ground)
me = PhysicalModeEquation(ea, tx.frequency, waveguide)
Rg1 = LMP.fresnelreflection(ea, ground, freq, LMP.Dθ())
Rg2 = LMP.fresnelreflection(me, LMP.Dθ())
@test Rg1 == Rg2
end
function test_solvemodalequation(scenario)
@unpack ea, tx, bfield, species, ground = scenario
waveguide = HomogeneousWaveguide(bfield, species, ground)
me = PhysicalModeEquation(ea, tx.frequency, waveguide)
f = LMP.solvemodalequation(me)
me2 = PhysicalModeEquation(EigenAngle(0.0+0.0im), tx.frequency, waveguide)
f2 = LMP.solvemodalequation(ea.θ, me2)
@test f == f2
# Test with specified susceptibilityfcn
Mfcn = z -> LMP.susceptibility(z, me)
f3 = LMP.solvemodalequation(me; susceptibilityfcn=Mfcn)
Mfcn2 = LMP.susceptibilityspline(me)
f4 = LMP.solvemodalequation(me; susceptibilityfcn=Mfcn2)
@test f == f3
@test maxabsdiff(f, f4) < 1e-3
end
function test_modalequation_resonant(scenario)
@unpack ea, tx, bfield, species, ground = scenario
waveguide = HomogeneousWaveguide(bfield, species, ground)
me = PhysicalModeEquation(ea, tx.frequency, waveguide)
R = @SMatrix [1 0; 0 1]
Rg = @SMatrix [1 0; 0 -1]
@test isapprox(LMP.modalequation(R, Rg), 0; atol=1e-15)
R = LMP.integratedreflection(me)
Rg = LMP.fresnelreflection(ea, ground, tx.frequency)
f = LMP.modalequation(R, Rg)
@test isroot(f; atol=1e-4) # this test is a little cyclic
@test f == LMP.solvemodalequation(me)
θ = 1.5 - 0.02im # not resonant
@test abs(LMP.solvemodalequation(θ, me)) > 1e-3
end
function test_modalequation_deriv(scenario)
@unpack ea, tx, ground, bfield, species = scenario
freq = tx.frequency
waveguide = HomogeneousWaveguide(bfield, species, ground)
modeequation = PhysicalModeEquation(ea, freq, waveguide)
# `solvedmodalequation` calls the `Dθ` form of `integratedreflection`, which uses a
# hard coded tolerance of 1e-10. Tests will fail if comparing to the lower default
# tolerance used by `solvemodalequation`
ip = IntegrationParams(tolerance=1e-10)
params = LMPParams(integrationparams=ip)
dFref = FiniteDiff.finite_difference_derivative(θ->LMP.solvemodalequation(θ, modeequation; params=params),
θs, Val{:central})
dFs = Vector{ComplexF64}(undef, length(θs))
Threads.@threads for i in eachindex(θs)
dFdθ, R, Rg = LMP.solvedmodalequation(θs[i], modeequation)
dFs[i] = dFdθ
end
@test isapprox(dFs, dFref; rtol=1e-3)
end
function test_findmodes(scenario)
@unpack tx, bfield, species, ground = scenario
waveguide = HomogeneousWaveguide(bfield, species, ground)
modeequation = PhysicalModeEquation(tx.frequency, waveguide)
origcoords = LMP.defaultmesh(tx.frequency)
# params = LMPParams(grpfparams=LMP.GRPFParams(100000, 1e-6, true))
params = LMPParams()
modes = @inferred findmodes(modeequation, origcoords; params=params)
modes2 = @inferred findmodes(modeequation, origcoords; params=LMPParams(params; approxsusceptibility=true))
@test length(modes) == length(modes2)
# 5e-4 needed to accomodate multiplespecies_scenario. Otherwise they satisfy 1e-5
@test all(maxabsdiff(modes[i].θ, modes2[i].θ) < 5e-4 for i in 1:length(modes))
for m in modes
f = LMP.solvemodalequation(m, modeequation; params=params)
isroot(f) || return f
@test isroot(f)
end
# return modes
end
########
# `TEST_MODES` must be filled for tests below!
function test_roots(scenario)
x = 0.0005
z = complex(x, -x)
# isroot Real and Complex
@test isroot(x)
@test isroot(x; atol=1e-6) == false
@test isroot(z)
@test isroot(z; atol=1e-6) == false
z2 = complex(1, 0)
z3 = complex(0, 1)
@test isroot(z2) == false
@test isroot(z3) == false
end
# function evalroot(root, scenario)
# @unpack tx, bfield, species, ground = scenario
# waveguide = HomogeneousWaveguide(bfield, species, ground)
#
# modeequation = PhysicalModeEquation(tx.frequency, waveguide)
# LMP.solvemodalequation(EigenAngle(root), modeequation)
# end
@testset "modefinder.jl" begin
@info "Testing modefinder"
for scn in (verticalB_scenario, resonant_scenario, nonresonant_scenario,
multiplespecies_scenario)
test_physicalmodeequation(scn) # just test with one scenario?
test_wmatrix(scn)
test_wmatrix_deriv(scn)
test_dRdz(scn)
test_dRdθdz(scn)
test_integratedreflection_deriv(scn)
test_fresnelreflection(scn)
test_fresnelreflection_deriv(scn)
test_solvemodalequation(scn)
test_modalequation_deriv(scn)
test_findmodes(scn)
end
# Fill in TEST_MODES
@info " Mode finding..."
for scenario in (verticalB_scenario, resonant_scenario, nonresonant_scenario,
multiplespecies_scenario)
if !haskey(TEST_MODES, scenario)
TEST_MODES[scenario] = findroots(scenario)
end
end
for scn in (resonant_scenario, )
test_roots(scn)
test_modalequation_resonant(scn)
end
for scn in (verticalB_scenario, )
test_integratedreflection_vertical(scn)
end
end
| LongwaveModePropagator | https://github.com/fgasdia/LongwaveModePropagator.jl.git |
|
[
"MIT"
] | 0.4.1 | 792c195909ca5dfff5685305b6fa0aa16c3d1041 | code | 1622 | function test_modeterms(scenario)
@unpack tx, rx, bfield, species, ground = scenario
waveguide = HomogeneousWaveguide(bfield, species, ground)
ea = TEST_MODES[scenario][1]
modeequation = PhysicalModeEquation(ea, tx.frequency, waveguide)
groundsampler = GroundSampler(rx.distance, rx.fieldcomponent)
sampler = Sampler(rx.distance, rx.fieldcomponent, 0.0)
# each field
for fc in (Fields.Ez, Fields.Ey, Fields.Ex)
groundsampler = GroundSampler(rx.distance, fc)
sampler = Sampler(rx.distance, fc, 0.0)
tx1, rx1 = LMP.modeterms(modeequation, tx, sampler)
tx2, rx2 = LMP.modeterms(modeequation, tx, groundsampler) # specialized
@test tx1 ≈ tx2
@test rx1 ≈ rx2
end
# frequency mismatch with modeequation
txwrong = Transmitter(15e3)
@test_throws ArgumentError LMP.modeterms(modeequation, txwrong, sampler)
end
function test_Efield(scenario)
@unpack tx, rx, bfield, species, ground = scenario
waveguide = HomogeneousWaveguide(bfield, species, ground)
modes = TEST_MODES[scenario]
X = LMP.distance(rx, tx)
E1 = LMP.Efield(modes, waveguide, tx, rx) # out-of-place
singlerx = GroundSampler(1000e3, rx.fieldcomponent)
E2 = LMP.Efield(modes, waveguide, tx, singlerx) # specialized
distidx = findfirst(x->x==1000e3, X)
@test E2 ≈ E1[distidx]
end
@testset "modesum.jl" begin
@info "Testing modesum"
for scn in (verticalB_scenario, resonant_scenario, nonresonant_scenario,
multiplespecies_scenario)
test_modeterms(scn)
test_Efield(scn)
end
end
| LongwaveModePropagator | https://github.com/fgasdia/LongwaveModePropagator.jl.git |
|
[
"MIT"
] | 0.4.1 | 792c195909ca5dfff5685305b6fa0aa16c3d1041 | code | 5753 | using Test, Dates, Random, LinearAlgebra, Statistics
using StaticArrays
using Parameters
using OrdinaryDiffEq, DiffEqCallbacks
using JSON3, StructTypes, CSV
using Interpolations, NLsolve, FiniteDiff
using LongwaveModePropagator
using LongwaveModePropagator: QE, ME, distance, power
const LMP = LongwaveModePropagator
const TEST_RNG = MersenneTwister(1234)
const LWPC_PATH = "LWPC"
include("utils.jl")
#==
Scenarios
==#
const TEST_MODES = Dict{Any,Vector{EigenAngle}}()
const verticalB_scenario = (
ea=EigenAngle(1.5 - 0.1im),
bfield=BField(50e-6, π/2, 0),
species=Species(QE, ME,
z->waitprofile(z, 75, 0.32; cutoff_low=40e3),
electroncollisionfrequency),
ground=Ground(15, 0.001),
tx=Transmitter(24e3),
rx=GroundSampler(0:5e3:2000e3, Fields.Ez)
)
const multiplespecies_scenario = (
ea=EigenAngle(1.5 - 0.1im),
bfield=BField(50e-6, π/2, 0),
species=(
Species(QE, ME,
z->waitprofile(z, 75, 0.32; cutoff_low=40e3),
electroncollisionfrequency),
Species(abs(QE), 58000*ME, # used by LWPC
z->waitprofile(z, 75, 0.32; cutoff_low=40e3),
ioncollisionfrequency)
),
ground=Ground(15, 0.001),
tx=Transmitter(24e3),
rx=GroundSampler(0:5e3:2000e3, Fields.Ez)
)
const isotropicB_resonant_scenario = (
ea=EigenAngle(1.453098822238508 - 0.042008075239068944im), # resonant
bfield=BField(50e-6, 0, π/2),
species=Species(QE, ME,
z->waitprofile(z, 75, 0.32; cutoff_low=40e3),
electroncollisionfrequency),
ground=Ground(15, 0.001),
tx=Transmitter(24e3),
rx=GroundSampler(0:5e3:2000e3, Fields.Ez)
)
const resonant_scenario = (
ea=EigenAngle(1.416127852502346 - 0.016482589477369265im), # resonant
bfield=BField(50e-6, deg2rad(68), deg2rad(111)),
species=Species(QE, ME,
z->waitprofile(z, 75, 0.32; cutoff_low=40e3),
electroncollisionfrequency),
ground=Ground(15, 0.001),
tx=Transmitter(24e3),
rx=GroundSampler(0:5e3:2000e3, Fields.Ez)
)
const resonant_elevatedrx_scenario = (
ea=EigenAngle(1.416127852502346 - 0.016482589477369265im), # resonant
bfield=BField(50e-6, deg2rad(68), deg2rad(111)),
species=Species(QE, ME,
z->waitprofile(z, 75, 0.32; cutoff_low=40e3),
electroncollisionfrequency),
ground=Ground(15, 0.001),
tx=Transmitter(24e3),
rx=Sampler(0:5e3:2000e3, Fields.Ez, 8e3)
)
const resonant_horizontal_scenario = (
ea=EigenAngle(1.416127852502346 - 0.016482589477369265im), # resonant
bfield=BField(50e-6, deg2rad(68), deg2rad(111)),
species=Species(QE, ME,
z->waitprofile(z, 75, 0.32; cutoff_low=40e3),
electroncollisionfrequency),
ground=Ground(15, 0.001),
tx=Transmitter(24e3),
rx=GroundSampler(0:5e3:2000e3, Fields.Ey)
)
const nonresonant_scenario = (
ea=EigenAngle(1.5 - 0.1im),
bfield=BField(50e-6, deg2rad(68), deg2rad(111)),
species=Species(QE, ME,
z->waitprofile(z, 75, 0.32; cutoff_low=40e3),
electroncollisionfrequency),
ground=Ground(5, 0.00005),
tx=Transmitter(24e3),
rx=GroundSampler(0:5e3:2000e3, Fields.Ez)
)
const interp_scenario = (
ea=EigenAngle(1.5 - 0.1im),
bfield=BField(50e-6, deg2rad(68), deg2rad(111)),
species=Species(QE, ME,
linear_interpolation(0:500:110e3, waitprofile.(0:500:110e3, (75,), (0.32,); cutoff_low=40e3); extrapolation_bc=Line()),
linear_interpolation(0:500:110e3, electroncollisionfrequency.(0:500:110e3); extrapolation_bc=Line())),
ground=Ground(5, 0.00005),
tx=Transmitter(24e3),
rx=GroundSampler(0:5e3:2000e3, Fields.Ez)
)
const homogeneousiono_scenario = (
ea=EigenAngle(1.4161252139020892 - 0.016348911573820547im), # resonant
bfield=BField(50e-6, deg2rad(68), deg2rad(111)),
species=Species(QE, ME,
z->2.65e6,
z->1e8),
ground=Ground(15, 0.001),
tx=Transmitter(24e3),
rx=GroundSampler(0:5e3:2000e3, Fields.Ez)
)
const segmented_scenario = (
ea=EigenAngle(1.5 - 0.1im),
bfield=[BField(50e-6, deg2rad(68), deg2rad(111)), BField(50e-6, deg2rad(68), deg2rad(111))],
species=[Species(QE, ME,
z->waitprofile(z, 75, 0.32; cutoff_low=40e3),
electroncollisionfrequency),
Species(QE, ME,
z->waitprofile(z, 80, 0.45; cutoff_low=40e3),
electroncollisionfrequency)],
ground=[Ground(15, 0.001), Ground(15, 0.001)],
tx=Transmitter(24e3),
rx=GroundSampler(0:5e3:2000e3, Fields.Ez),
distances=[0.0, 1000e3],
)
const θs = [complex(r,i) for r = range(deg2rad(60), deg2rad(89); length=30) for i =
range(deg2rad(-10), deg2rad(0); length=11)]
maxabsdiff(a, b) = maximum(x -> isfinite(x) ? abs(x) : -Inf, a - b)
meanabsdiff(a, b) = mean(x -> isfinite(x) ? abs(x) : 0, a - b)
function findroots(scenario)
@unpack bfield, species, ground, tx = scenario
w = HomogeneousWaveguide(bfield, species, ground)
me = PhysicalModeEquation(tx.frequency, w)
origcoords = LMP.defaultmesh(tx.frequency)
return findmodes(me, origcoords)
end
@testset "LongwaveModePropagator" begin
include("EigenAngles.jl")
include("Geophysics.jl")
include("Waveguides.jl")
include("magnetoionic.jl")
include("TMatrix.jl")
include("bookerquartic.jl")
include("modefinder.jl")
include("wavefields.jl")
include("modeconversion.jl")
include("modesum.jl")
include("LongwaveModePropagator.jl")
include("lwpc_comparisons.jl")
include("IO.jl")
end
| LongwaveModePropagator | https://github.com/fgasdia/LongwaveModePropagator.jl.git |
|
[
"MIT"
] | 0.4.1 | 792c195909ca5dfff5685305b6fa0aa16c3d1041 | code | 2065 | """
readlog(file)
Read standard LWPC `.log` files and return `distance`, `amplitude`, and `phase` vectors.
The amplitude and phase at the receiver is not returned by this function.
"""
function readlog(file)
# Search for first and last line of data
lines = readlines(file)
firstdataline = findfirst(startswith.(lines, " dist amplitude phase")) + 1
lastdataline = findfirst(startswith.(lines, "nc nrpt bearng")) - 1
numdatalines = lastdataline - firstdataline + 1
# Read log file
raw = CSV.File(file; skipto=firstdataline, limit=numdatalines,
delim=' ', ignorerepeated=true, header=false,
silencewarnings=true, ntasks=1)
# Stack the columns together
dist = vcat(raw.Column1, raw.Column4, raw.Column7)
amplitude = vcat(raw.Column2, raw.Column5, raw.Column8)
phase = vcat(raw.Column3, raw.Column6, raw.Column9)
# Clean up end of the last column
delidxs = ismissing.(dist) # assuming these are at the end
delidxs[findfirst(delidxs)-1] = true # last valid entry is at receiver distance
deleteat!(dist, delidxs)
deleteat!(amplitude, delidxs)
deleteat!(phase, delidxs)
# If phase gets above 9999 deg in log file, there is no space between amplitude and phase
if count(ismissing.(amplitude)) != count(ismissing.(phase))
for i in eachindex(phase)
if ismissing(phase[i])
phase[i] = parse(Float64, amplitude[i][end-9:end]) # phase is 10000.0000
amplitude[i] = parse(Float64, amplitude[i][1:end-10])
end
end
# Other elements in the same column will also be string type
for i in eachindex(amplitude)
if amplitude[i] isa String
amplitude[i] = parse(Float64, amplitude[i])
end
end
end
return dist, amplitude, phase
end
"""
isroot(x; atol=1e-2)
Return `true` if `x` is approximately equal to 0 with the absolute tolerance `atol`.
"""
isroot(x; atol=1e-2, kws...) = isapprox(x, 0; atol=atol, kws...)
| LongwaveModePropagator | https://github.com/fgasdia/LongwaveModePropagator.jl.git |
|
[
"MIT"
] | 0.4.1 | 792c195909ca5dfff5685305b6fa0aa16c3d1041 | code | 6296 | function randomwavefields()
modes = EigenAngle.(rand(TEST_RNG, ComplexF64, 10))
heights = LMPParams().wavefieldheights
v = rand(SVector{6,ComplexF64}, length(heights), length(modes))
wavefields = LMP.Wavefields(v, heights, modes)
return modes, wavefields
end
function test_Wavefields()
_, wavefields = randomwavefields()
@unpack wavefieldheights = LMPParams()
@test LMP.numheights(wavefields) == length(wavefieldheights)
@test LMP.nummodes(wavefields) == 10
@test size(wavefields) == (length(wavefieldheights), 10)
@test view(wavefields, 1:5) == view(wavefields.v, 1:5)
newwavefields = similar(wavefields)
@test size(newwavefields) == size(wavefields)
@test LMP.heights(newwavefields) == LMP.heights(wavefields)
@test LMP.eigenangles(newwavefields) == LMP.eigenangles(wavefields)
newwavefields[1] = wavefields[1]*2
@test newwavefields[1] == wavefields[1]*2
# copy and ==
cpwavefields = copy(wavefields)
@test cpwavefields.heights == wavefields.heights
@test cpwavefields.eas == wavefields.eas
@test cpwavefields.v == wavefields.v
@test cpwavefields == wavefields
# isvalid
heights = LMP.heights(wavefields)
eas = LMP.eigenangles(wavefields)
@test isvalid(wavefields)
longerv = vcat(wavefields.v, rand(TEST_RNG, SVector{6,ComplexF64}, 1, length(eas)))
badwavefields = LMP.Wavefields(longerv, heights, eas)
@test !isvalid(badwavefields)
widerv = hcat(wavefields.v, rand(TEST_RNG, SVector{6,ComplexF64}, length(heights)))
badwavefields = LMP.Wavefields(widerv, heights, eas)
@test !isvalid(badwavefields)
end
function test_WavefieldIntegrationParams(scenario)
@unpack ea, tx, bfield, species = scenario
params = LMPParams()
topheight = params.topheight
w1 = LMP.WavefieldIntegrationParams(topheight, LMP.BOTTOMHEIGHT, 0.0+0.0im, 1.0, 1.0, ea,
tx.frequency, bfield, species, params)
w2 = LMP.WavefieldIntegrationParams(topheight, ea, tx.frequency, bfield, species, params)
@test w1 == w2
end
function test_integratewavefields_homogeneous(scenario)
#==
Check wavefields in homogeneous ionosphere are valid solutions to wave equation.
Compares to Booker quartic solution.
See, e.g. Pitteway 1965 pg 234; also Barron & Budden 1959 sec 10
==#
@unpack ea, bfield, tx, ground, species = scenario
params = LMPParams(earthcurvature=false)
ionobottom = params.curvatureheight
zs = 200e3:-500:ionobottom
e = LMP.integratewavefields(zs, ea, tx.frequency, bfield, species; params=params)
# Normalize fields so component 2 (Ey) = 1, as is used in Booker Quartic
e1 = [s[:,1]/s[2,1] for s in e]
e2 = [s[:,2]/s[2,2] for s in e]
e1 = reshape(reinterpret(ComplexF64, e1), 4, :)
e2 = reshape(reinterpret(ComplexF64, e2), 4, :)
# Booker solution - single solution for entire homogeneous iono
M = LMP.susceptibility(ionobottom, tx.frequency, bfield, species; params=params)
booker = LMP.bookerwavefields(ea, M)
@test isapprox(e1[:,end], booker[:,1]; atol=1e-6)
@test isapprox(e2[:,end], booker[:,2]; atol=1e-6)
end
function test_wavefieldreflection(scenario)
# Confirm reflection coefficients from wavefields match with dr/dz calculation.
@unpack ea, bfield, tx, ground, species = scenario
params = LMPParams()
waveguide = HomogeneousWaveguide(bfield, species, ground)
modeequation = PhysicalModeEquation(ea, tx.frequency, waveguide)
zs = params.wavefieldheights
e = LMP.integratewavefields(zs, ea, tx.frequency, bfield, species; params=params)
wavefieldRs = [LMP.bookerreflection(ea, s) for s in e]
@unpack tolerance, solver = params.integrationparams
Mtop = LMP.susceptibility(first(zs), tx.frequency, waveguide)
Rtop = LMP.bookerreflection(ea, Mtop)
prob = ODEProblem{false}(LMP.dRdz, Rtop, (first(zs), last(zs)), modeequation)
sol = solve(prob, solver; abstol=tolerance, reltol=tolerance,
saveat=zs, save_everystep=false)
@test isapprox(wavefieldRs, sol.u, rtol=1e-3)
end
function test_wavefieldreflection_resonant(scenario)
@unpack ea, bfield, tx, ground, species = scenario
params = LMPParams()
ztop = params.topheight
zs = ztop:-100:0.0
e = LMP.integratewavefields(zs, ea, tx.frequency, bfield, species; params=params)
R = LMP.bookerreflection(ea, e[end])
Rg = LMP.fresnelreflection(ea, ground, tx.frequency)
# Ensure we are close to mode resonance with R
f = LMP.modalequation(R, Rg)
@test isroot(f)
end
function test_boundaryscalars(scenario)
# Check if boundaryscalars match for isotropic=false and isotropic=true when both
# actually are isotropic
@unpack ea, bfield, tx, ground, species = scenario
params = LMPParams()
ztop = params.topheight
zs = ztop:-100:0.0
e = LMP.integratewavefields(zs, ea, tx.frequency, bfield, species; params=params)
R = LMP.bookerreflection(ea, e[end])
Rg = LMP.fresnelreflection(ea, ground, tx.frequency)
a1, a2 = LMP.boundaryscalars(R, Rg, e[end], false)
b1, b2 = LMP.boundaryscalars(R, Rg, e[end], true)
# return a1, a2, b1, b2
@test a1 ≈ b1
@test a2 ≈ b2
end
function test_fieldstrengths(scenario)
@unpack bfield, tx, ground, species = scenario
modes, wavefields = randomwavefields()
modes = LMP.eigenangles(wavefields)
LMP.fieldstrengths!(view(wavefields,:,1), LMPParams().wavefieldheights, modes[1],
tx.frequency, bfield, species, ground)
end
@testset "wavefields.jl" begin
@info "Testing wavefields"
test_Wavefields()
for scn in (verticalB_scenario, resonant_scenario, nonresonant_scenario)
test_WavefieldIntegrationParams(scn)
@test_nowarn test_fieldstrengths(scn)
end
@testset "Integration" begin
for scn in (verticalB_scenario, resonant_scenario, nonresonant_scenario)
test_wavefieldreflection(scn)
end
for scn in (resonant_scenario, )
test_wavefieldreflection_resonant(scn)
end
for scn in (homogeneousiono_scenario, )
test_integratewavefields_homogeneous(scn)
end
@test_skip test_boundaryscalars(isotropicB_resonant_scenario)
end
end
| LongwaveModePropagator | https://github.com/fgasdia/LongwaveModePropagator.jl.git |
|
[
"MIT"
] | 0.4.1 | 792c195909ca5dfff5685305b6fa0aa16c3d1041 | docs | 7839 | # LongwaveModePropagator.jl
| **Documentation** | **Build Status** |
|:--------------------------------------------------------------------------:|:-----------------------------------:|
| [![][docs-stable-img]][docs-stable-url] [![][docs-dev-img]][docs-dev-url] | [![Build status][gha-img]][gha-url] |
**Model the propagation of VLF radio waves in the [Earth-ionosphere waveguide](https://en.wikipedia.org/wiki/Earth%E2%80%93ionosphere_waveguide).**
LongwaveModePropagator is a mode theory propagation model written in the [Julia](https://julialang.org/) programming language.
The model is largely based on the work of K. G. Budden, who developed both a convenient means of calculating an effective reflection coefficient for the anisotropic ionosphere [(Budden, 1955)](#Budden1955a) and a general method for calculating the electric field produced by a source dipole in the Earth-ionosphere waveguide [(Budden, 1962)](#Budden1962).
It is similar to the Long Wavelength Propagation Capability (LWPC) [(Ferguson, 1998)](#Ferguson1998), but aims to be more robust and adaptable.
The package is most easily used when interfacing with it from Julia, but it can also run simple cases by reading in JSON files and writing the results back to JSON.
See the [Examples](https://fgasdia.github.io/LongwaveModePropagator.jl/dev/generated/basic/) section of [the docs](https://fgasdia.github.io/LongwaveModePropagator.jl/dev) for examples of building scenarios and running the model from within Julia and for generating compatible files from Matlab and Python.
## Installation instructions
1. [Download](https://julialang.org/downloads/) and install a recent version of Julia for your operating system.
2. From the Julia REPL, install LongwaveModePropagator.
```
julia> ]
(v1.10) pkg> add LongwaveModePropagator
```
If you'll be working primarily in Julia, you probably want to `cd` to your working directory, `] activate` a new environment there, and then `add` LongwaveModePropagator.
Julia has an excellent built-in package manager (accessed by typing `]` from the REPL) that also keeps track of the versions of all dependencies within an environment.
This means you can leave your code, come back to it two years later on a new computer, and as long as you have the original `Project.toml` and `Manifest.toml` files, you can `instantiate` the exact environment you were last working with.
To update the environment (while maintaining compatibility across all dependencies), simply
`] up`.
As with most Julia packages, LongwaveModePropagator is released under the MIT license and all source code is [hosted on GitHub](https://github.com/fgasdia/LongwaveModeSolver).
Please open Issues or Pull requests if you find any problems, are interested in new features, or you would like to be a contributor.
## Running your first model
Here's a simple homogeneous ground/ionosphere scenario defined in Julia.
Note that throughout the code SI units (MKS) and radians are used.
The only notable exception in the current version of the package is the use of kilometers and inverse kilometers to define Wait and Spies h′ and β parameters for the electron density profile.
```julia
using LongwaveModePropagator
using LongwaveModePropagator: QE, ME
# "standard" vertical dipole transmitter at 24 kHz
tx = Transmitter(24e3)
# sample vertical electric field every 5 km out to 2000 km from tx
rx = GroundSampler(0:5e3:2000e3, Fields.Ez)
# vertical magnetic field
bfield = BField(50e-6, π/2, 0)
# daytime ionosphere
electrons = Species(QE, ME, z->waitprofile(z, 75, 0.35), electroncollisionfrequency)
# "typical" earth ground
ground = Ground(10, 1e-4)
waveguide = HomogeneousWaveguide(bfield, electrons, ground)
# return the complex electric field, amplitude, and phase
E, a, p = propagate(waveguide, tx, rx);
```
We can plot the results if we `] add Plots`:
```julia
using Plots
plot(rx.distance/1000, a,
xlabel="distance (km)", ylabel="amplitude (dB μV/m)", legend=false, lw=2)
```

I encourage you to browse through the [Examples](https://fgasdia.github.io/LongwaveModePropagator.jl/dev/generated/basic/) section of the docs to see how to construct more complex examples.
## New to Julia?
Julia is a relatively new general programming language that particularly shines when it comes to technical computing.
It has similarities to Matlab and Python, but is high performance and attempts to solve the ["two language problem"](https://thebottomline.as.ucsb.edu/2018/10/julia-a-solution-to-the-two-language-programming-problem).
In part, it achieves its high performance by compiling functions to efficient native code via LLVM.
Julia is dynamically typed and uses multiple dispatch, so that the first time a given function is passed arguments of a certain type, the function is compiled for those types.
In practice, this means that the first time a function is called, it appears to take longer than it will on subsequent calls because at the first call the function was also compiled.
### Finding help
I highly recommend reading the [Julia Documentation](https://docs.julialang.org/en/v1/).
It is very thorough and combines significant text explanations with examples.
Besides the regular REPL prompt `julia>` and the package mode accessed with `]`, there is also a help mode accessible with `?`.
`?` works "automatically", even for user-defined functions with docstrings.
Most internal functions of LongwaveModePropagator are documented, so e.g.
```julia
? LongwaveModePropagator.bookerquartic
```
prints an explanation of the [`bookerquartic`](https://fgasdia.github.io/LongwaveModePropagator.jl/dev/lib/internals/#LongwaveModePropagator.bookerquartic) function even though it's not exported from the package.
## References
<a name="Budden1955a"></a>K. G. Budden, “The numerical solution of differential equations governing reflexion of long radio waves from the ionosphere,” Proc. R. Soc. Lond. A, vol. 227, no. 1171, pp. 516–537, Feb. 1955, doi: [10.1098/rspa.1955.0027](https://doi.org/10.1098/rspa.1955.0027).
<a name="Budden1962"></a>K. G. Budden, “The influence of the earth’s magnetic field on radio propagation by wave-guide modes,” Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences, vol. 265, no. 1323, pp. 538–553, Feb. 1962, doi: [10.1098/rspa.1962.0041](https://doi.org/10.1098/rspa.1962.0041).
<a name="Ferguson1998"></a>J. A. Ferguson, “Computer programs for assessment of long-wavelength radio communications, version 2.0: User’s guide and source files,” Space and Naval Warfare Systems Center, San Diego, CA, Technical Document 3030, May 1998. Available: http://www.dtic.mil/docs/citations/ADA350375.
<a name="Gasdia2021"></a>F. W. Gasdia, “Imaging the D-Region Ionosphere with Subionospheric VLF Signals,” ProQuest Dissertations Publishing, 2021. Available: https://go.exlibris.link/pGnF7CYf.
## Citing
We encourage you to cite the following paper (or see [CITATION.bib](CITATION.bib)) if this package is used in scientific work:
F. Gasdia and R. A. Marshall, "A New Longwave Mode Propagator for the Earth–Ionosphere Waveguide," in IEEE Transactions on Antennas and Propagation, vol. 69, no. 12, pp. 8675-8688, Dec. 2021, doi: [10.1109/TAP.2021.3083753](https://doi.org/10.1109/TAP.2021.3083753).
[docs-stable-img]: https://img.shields.io/badge/docs-stable-blue.svg
[docs-stable-url]: https://fgasdia.github.io/LongwaveModePropagator.jl/stable
[docs-dev-img]: https://img.shields.io/badge/docs-dev-blue.svg
[docs-dev-url]: https://fgasdia.github.io/LongwaveModePropagator.jl/dev
[gha-img]: https://github.com/fgasdia/LongwaveModePropagator.jl/workflows/CI/badge.svg
[gha-url]: https://github.com/fgasdia/LongwaveModePropagator.jl/actions?query=workflow
| LongwaveModePropagator | https://github.com/fgasdia/LongwaveModePropagator.jl.git |
|
[
"MIT"
] | 0.4.1 | 792c195909ca5dfff5685305b6fa0aa16c3d1041 | docs | 6736 | # LongwaveModePropagator.jl
**Model the propagation of VLF radio waves in the [Earth-ionosphere waveguide](https://en.wikipedia.org/wiki/Earth%E2%80%93ionosphere_waveguide).**
Longwave Mode Propagator is a mode-theory propagation model written in the [Julia](https://julialang.org/) programming language.
The model is largely based on the work of K. G. Budden, who developed both a convenient means of calculating an effective reflection coefficient for the anisotropic ionosphere [(Budden, 1955)](#Budden1955a) and a general method for calculating the electric field produced by a source dipole in the Earth-ionosphere waveguide [(Budden, 1962)](#Budden1962).
It is similar to the [Long Wavelength Propagation Capability (LWPC)](http://www.dtic.mil/docs/citations/ADA350375), but aims to be more robust and adaptable.
The package is most easily used when interfacing with it from Julia, but it can also run simple cases by reading in JSON files and writing the results back to JSON.
See the [Examples](https://fgasdia.github.io/LongwaveModePropagator.jl/dev/generated/basic/) section of these docs for examples of building scenarios and running the model from within Julia or for generating compatible files from Matlab and Python.
## Installation instructions
1. [Download](https://julialang.org/downloads/) and install a recent version of Julia for your operating system.
2. From the Julia REPL, install LongwaveModePropagator.
```
julia> ]
(@v1.10) pkg> add LongwaveModePropagator
```
If you'll be working primarily in Julia, you probably want to `cd` to your working directory, `] activate` a new environment, and then `add` LongwaveModePropagator.
Julia has an excellent built-in package manager (accessed by typing `]` from the REPL) that keeps track of the versions of all dependencies within an environment.
This means you can leave your code, come back to it two years later on a new computer, and as long as you have the original `Project.toml` and `Manifest.toml` files, you can `instantiate` the exact environment you were last working with.
To update the environment (while maintaining compatibility across all dependencies), simply `] up`.
As with most Julia packages, LongwaveModePropagator is released under the MIT license and all source code is [hosted on GitHub](https://github.com/fgasdia/LongwaveModePropagator).
Please open [Issues](https://github.com/fgasdia/LongwaveModePropagator.jl/issues) if you find any problems or are interested in new features, or [Pull requests](https://github.com/fgasdia/LongwaveModePropagator.jl/pulls) if you would like to contribute.
## Running your first model
Here's a simple homogeneous ground/ionosphere scenario defined in Julia.
```julia
using LongwaveModePropagator
using LongwaveModePropagator: QE, ME
# "standard" vertical dipole transmitter at 24 kHz
tx = Transmitter(24e3)
# sample vertical electric field every 5 km out to 2000 km from tx
rx = GroundSampler(0:5e3:2000e3, Fields.Ez)
# vertical magnetic field
bfield = BField(50e-6, π/2, 0)
# daytime ionosphere
electrons = Species(QE, ME, z->waitprofile(z, 75, 0.35), electroncollisionfrequency)
# "typical" earth ground
ground = Ground(10, 1e-4)
waveguide = HomogeneousWaveguide(bfield, electrons, ground)
# return the complex electric field, amplitude, and phase
E, a, p = propagate(waveguide, tx, rx);
```
We can plot the results if we `] add Plots`:
```julia
using Plots
plot(rx.distance/1000, a, xlabel="Distance (km)", ylabel="Amplitude (dB μV/m)")
```

!!! note
SI units (MKS) and _radians_ are used throughout LongwaveModePropagator.
The only exception in the current version of the package is the use of kilometers and inverse kilometers to define Wait and Spies ``h'`` and ``\beta`` parameters for the electron density profile in the function [`waitprofile`](@ref). In practice, the units of these parameters are often implicitly taken to be kilometers and inverse kilometers.
Users are encouraged to browse the [Examples](https://fgasdia.github.io/LongwaveModePropagator.jl/dev/generated/basic/) section for more complex scenarios.
## New to Julia?
Julia is a relatively new general programming language that shines for technical computing.
It has similarities to Matlab and Python, but is high performance and attempts to solve the ["two language problem"](https://thebottomline.as.ucsb.edu/2018/10/julia-a-solution-to-the-two-language-programming-problem).
In part, it achieves its high performance by compiling functions to efficient native code via LLVM.
Julia is dynamically typed and uses multiple dispatch, so that the first time a given function is passed arguments of a certain type, the function is compiled for those types.
In practice, this means that the first time a function is called, it takes longer than it will on subsequent calls, because at the first call the function also had to be compiled.
### Finding help
I highly recommend reading the [Julia Documentation](https://docs.julialang.org/en/v1/).
It is very thorough and combines significant textual explanations with examples.
Besides the regular REPL prompt `julia>` and the package mode accessed with `]`, there is also a help mode accessible with `?`.
The help functionality works "automatically", even for user-defined functions with docstrings.
Most internal functions of LongwaveModePropagator are documented, so e.g.
```julia
? LongwaveModePropagator.bookerquartic
```
prints an explanation of the [`LongwaveModePropagator.bookerquartic`](@ref) function even though it's not exported from the package.
## References
```@raw html
<p><a name="Budden1955a"></a>K. G. Budden, “The numerical solution of differential equations governing reflexion of long radio waves from the ionosphere,” Proc. R. Soc. Lond. A, vol. 227, no. 1171, pp. 516–537, Feb. 1955, doi: <a href="https://doi.org/10.1098/rspa.1955.0027">10.1098/rspa.1955.0027</a>.</p>
<p><a name="Budden1962"></a>K. G. Budden, “The influence of the earth’s magnetic field on radio propagation by wave-guide modes,” Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences, vol. 265, no. 1323, pp. 538–553, Feb. 1962, doi: <a href="https://doi.org/10.1098/rspa.1962.0041">10.1098/rspa.1962.0041</a>.</p>
```
## Citing
We encourage you to cite the following paper (or see [CITATION.bib](https://github.com/fgasdia/LongwaveModePropagator.jl/blob/main/CITATION.bib)) if this package is used in scientific work:
F. Gasdia and R. A. Marshall, "A New Longwave Mode Propagator for the Earth–Ionosphere Waveguide," in IEEE Transactions on Antennas and Propagation, vol. 69, no. 12, pp. 8675-8688, Dec. 2021, doi: [10.1109/TAP.2021.3083753](https://doi.org/10.1109/TAP.2021.3083753).
| LongwaveModePropagator | https://github.com/fgasdia/LongwaveModePropagator.jl.git |
|
[
"MIT"
] | 0.4.1 | 792c195909ca5dfff5685305b6fa0aa16c3d1041 | docs | 5166 | # References
- K. G. Budden, “The numerical solution of differential equations governing reflexion of long radio waves from the ionosphere,” Proc. R. Soc. Lond. A, vol. 227, no. 1171, pp. 516–537, Feb. 1955, doi: [10.1098/rspa.1955.0027](https://doi.org/10.1098/rspa.1955.0027).
- K. G. Budden, “The influence of the earth’s magnetic field on radio propagation by wave-guide modes,” Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences, vol. 265, no. 1323, pp. 538–553, Feb. 1962, doi: [10.1098/rspa.1962.0041](https://doi.org/10.1098/rspa.1962.0041).
- K. G. Budden, “The propagation of radio waves: the theory of radio waves of low power in the ionosphere and magnetosphere,” First paperback edition. New York: Cambridge University Press, 1988.
- P. C. Clemmow and J. Heading, “Coupled forms of the differential equations governing radio propagation in the ionosphere,” Mathematical Proceedings of the Cambridge Philosophical Society, vol. 50, no. 2, pp. 319–333, Apr. 1954, doi: [10.1017/S030500410002939X](https://doi.org/10.1017/S030500410002939X).
- J. A. Ferguson and F. P. Snyder, “Approximate VLF/LF waveguide mode conversion model: Computer applications: FASTMC and BUMP,” Naval Ocean Systems Center, San Diego, CA, NOSC-TD-400, Nov. 1980. Accessed: May 08, 2017. Available: [https://www.dtic.mil/docs/citations/ADA096240](https://www.dtic.mil/docs/citations/ADA096240).
- D. G. Morfitt and C. H. Shellman, “‘MODESRCH’, an improved computer program for obtaining ELF/VLF/LF mode constants in an Earth-ionosphere waveguide,” Naval Electronics Laboratory Center, San Diego, CA, NELC/IR-77T, Oct. 1976. Accessed: Dec. 13, 2017. Available: [https://www.dtic.mil/docs/citations/ADA032573](https://www.dtic.mil/docs/citations/ADA032573).
- D. G. Morfitt, “‘Simplified’ VLF/LF mode conversion computer programs: GRNDMC and ARBNMC,” Naval Ocean Systems Center, San Diego, CA, NOSC/TR-514, Jan. 1980. Accessed: Jan. 15, 2018. Available: [https://www.dtic.mil/docs/citations/ADA082695](https://www.dtic.mil/docs/citations/ADA082695).
- R. A. Pappert, E. E. Gossard, and I. J. Rothmuller, “A numerical investigation of classical approximations used in VLF propagation,” Radio Science, vol. 2, no. 4, pp. 387–400, Apr. 1967, doi: [10.1002/rds196724387](https://doi.org/10.1002/rds196724387).
- R. A. Pappert and R. R. Smith, “Orthogonality of VLF height gains in the earth ionosphere waveguide,” Radio Science, vol. 7, no. 2, pp. 275–278, 1972, doi: [10.1029/RS007i002p00275](https://doi/org/10.1029/RS007i002p00275).
- R. A. Pappert and L. R. Shockey, “Simplified VLF/LF mode conversion program with allowance for elevated, arbitrarily oriented electric dipole antennas,” Naval Electronics Laboratory Center, San Diego, CA, Interim Report 771, Oct. 1976. Accessed: Dec. 03, 2019. Available: [https://archive.org/details/DTIC_ADA033412](https://archive.org/details/DTIC_ADA033412).
- R. A. Pappert, “LF daytime earth ionosphere waveguide calculations,” Naval Ocean Systems Center, San Diego, CA, NOSC/TR-647, Jan. 1981. Accessed: Jan. 23, 2020. Available: [https://apps.dtic.mil/docs/citations/ADA096098](https://apps.dtic.mil/docs/citations/ADA096098).
- R. A. Pappert, L. R. Hitney, and J. A. Ferguson, “ELF/VLF (Extremely Low Frequency/Very Low Frequency) long path pulse program for antennas of arbitrary elevation and orientation,” Naval Ocean Systems Center, San Diego, CA, NOSC/TR-891, Aug. 1983. Accessed: Jul. 04, 2018. Available: [https://www.dtic.mil/docs/citations/ADA133876](https://www.dtic.mil/docs/citations/ADA133876).
- R. A. Pappert, “Radiation resistance of thin antennas of arbitrary elevation and configuration over perfectly conducting ground.,” Naval Ocean Systems Center, San Diego, CA, Technical Report 1112, Jun. 1986. Accessed: Mar. 10, 2024. Available: [https://apps.dtic.mil/sti/citations/ADA170945](https://apps.dtic.mil/sti/citations/ADA170945).
- R. A. Pappert and J. A. Ferguson, “VLF/LF mode conversion model calculations for air to air transmissions in the earth-ionosphere waveguide,” Radio Sci., vol. 21, no. 4, pp. 551–558, Jul. 1986, doi: [10.1029/RS021i004p00551](https://doi.org/10.1029/RS021i004p00551).
- M. L. V. Pitteway, “The numerical calculation of wave-fields, reflexion coefficients and polarizations for long radio waves in the lower ionosphere. I.,” Phil. Trans. R. Soc. Lond. A, vol. 257, no. 1079, pp. 219–241, Mar. 1965, doi: [10.1098/rsta.1965.0004](https://doi.org/10.1098/rsta.1965.0004).
- J. A. Ratcliffe, "The magneto-ionic theory & its applications to the ionosphere," Cambridge University Press, 1959.
- N. R. Thomson, “Experimental daytime VLF ionospheric parameters,” Journal of Atmospheric and Terrestrial Physics, vol. 55, no. 2, pp. 173–184, Feb. 1993, doi: [10.1016/0021-9169(93)90122-F](https://doi.org/10.1016/0021-9169(93)90122-F).
- J. R. Wait and K. P. Spies, “Characteristics of the earth-ionosphere waveguide for VLF radio waves,” U.S. National Bureau of Standards, Boulder, CO, Technical Note 300, Dec. 1964. Accessed: Feb. 18, 2017. Available: [https://archive.org/details/characteristicso300wait](https://archive.org/details/characteristicso300wait).
| LongwaveModePropagator | https://github.com/fgasdia/LongwaveModePropagator.jl.git |
|
[
"MIT"
] | 0.4.1 | 792c195909ca5dfff5685305b6fa0aa16c3d1041 | docs | 484 | # Internals
Documentation of all `const`s, `struct`s, `function`s, etc.
```@autodocs
Modules = [LongwaveModePropagator, LongwaveModePropagator.Fields]
Public = false
Pages = [
"Antennas.jl",
"bookerquartic.jl",
"EigenAngles.jl",
"Emitters.jl",
"Geophysics.jl",
"IO.jl",
"LongwaveModePropagator.jl",
"magnetoionic.jl",
"modeconversion.jl",
"modefinder.jl",
"modesum.jl",
"Samplers.jl",
"TMatrix.jl",
"utils.jl",
"Wavefields.jl",
"Waveguides.jl"
]
```
| LongwaveModePropagator | https://github.com/fgasdia/LongwaveModePropagator.jl.git |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.