question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
construct-binary-search-tree-from-preorder-traversal | Explaining the O(N) approach with C++ code. Beats 100% solutions. | explaining-the-on-approach-with-c-code-b-6fy6 | The O(NlogN) approch which everybody tries is O(N\*N). Lets say the case where array is sorted in decreasing order, there it will go quadratic. 5, 4, 3, 2, 1\n\ | mehul_02 | NORMAL | 2020-04-20T08:04:18.832794+00:00 | 2020-04-20T08:04:18.832830+00:00 | 7,816 | false | The O(NlogN) approch which everybody tries is O(N\\*N). Lets say the case where array is sorted in decreasing order, there it will go quadratic. 5, 4, 3, 2, 1\n\nWe understand the given O(N) solution by:\n1. It is preorder traversal that is all the nodes in left tree is encountered before the nodes of right so we can generate the temp nodes as soon as we visit them.\n2. We see the split point by sending a variable parent_value which denotes the value of the parent, once the value at index idx becomes greater than parent value we can retuen NULL, we make sure that all the nodes are less than the parent value are inserted in left subtree.\n3. Once a node is less than parent value is found we make that node as left subtree and call the function recursively, and when the left recursion is over( when all values becomes greater than the current node\'s value) we will observe that the global idx will definately come to a point where the next node should be inserted to the right subtree\n\n```\nclass Solution\n{\npublic:\n int idx = 0;\n TreeNode *bstFromPreorder(vector<int> &preorder, int parent_value = INT_MAX)\n {\n if (idx == preorder.size() || preorder[idx] > parent_value)\n return NULL;\n int current_value = preorder[idx++];\n TreeNode *temp = new TreeNode(current_value);\n temp->left = bstFromPreorder(preorder, current_value);\n temp->right = bstFromPreorder(preorder, parent_value);\n return temp;\n }\n};\n``` | 71 | 3 | [] | 12 |
construct-binary-search-tree-from-preorder-traversal | simple recusrsive cpp solution | simple-recusrsive-cpp-solution-by-bitris-enkl | \nclass Solution {\npublic:\n TreeNode* bstFromPreorder(vector<int>& preorder) {\n if(preorder.size()==0)\n return NULL;\n TreeNode* | bitrish | NORMAL | 2020-09-10T09:38:45.269172+00:00 | 2020-09-10T09:38:45.269203+00:00 | 5,662 | false | ```\nclass Solution {\npublic:\n TreeNode* bstFromPreorder(vector<int>& preorder) {\n if(preorder.size()==0)\n return NULL;\n TreeNode* root=new TreeNode(preorder[0]);\n if(preorder.size()==1)\n return root;\n vector<int>left;\n vector<int>right;\n for(int i=0;i<preorder.size();i++)\n {\n if(preorder[i]>preorder[0])\n right.push_back(preorder[i]);\n else if(preorder[i]<preorder[0])\n left.push_back(preorder[i]);\n }\n root->left=bstFromPreorder(left);\n root->right=bstFromPreorder(right);\n return root;\n }\n};\n``` | 59 | 0 | ['Recursion', 'C', 'C++'] | 8 |
construct-binary-search-tree-from-preorder-traversal | JAVA 3 WAYS TO DO THE PROBLEM! O(N) APPROACH | java-3-ways-to-do-the-problem-on-approac-obh6 | THIS IS A CONTINUATION OF MY PREVIOUS POST!\nWHICH HAD O(N^2) APPROACH!\nhttps://leetcode.com/problems/construct-binary-search-tree-from-preorder-traversal/disc | naturally_aspirated | NORMAL | 2020-04-21T03:10:47.892374+00:00 | 2020-04-21T04:52:52.594307+00:00 | 6,059 | false | THIS IS A CONTINUATION OF MY PREVIOUS POST!\nWHICH HAD O(N^2) APPROACH!\nhttps://leetcode.com/problems/construct-binary-search-tree-from-preorder-traversal/discuss/589059/java-easiest-solution-with-clear-explanation-of-logic\n\n\nAS A LOT OF PEOPLE ARE ASKING FOR LINEAR SOLUTONS HERE IT IS!\n\nAPPROACH 1-O(N)\nJAVA-LOWER AND UPPER BOUND RECURSIVE\n\n```\nclass Solution {\n int nodeIndex;\n public TreeNode bstFromPreorder(int[] preorder) {\n if(preorder == null) {\n return null;\n }\n nodeIndex = 0;\n return bstHelper(preorder, Integer.MIN_VALUE , Integer.MAX_VALUE);\n }\n private TreeNode bstHelper(int[] preorder, int start, int end) {\n if(nodeIndex == preorder.length || preorder[nodeIndex]<start || preorder[nodeIndex]>end) {\n return null;\n }\n int val = preorder[nodeIndex++];\n TreeNode node = new TreeNode(val);\n node.left = bstHelper(preorder, start, val);\n node.right = bstHelper(preorder, val, end);\n return node; \n } \n} \n```\n\nAPPROACH 2- O(N)!\nJAVA ONLY UPPER BOUND- RECURSIVE\nEXPLANATION-\nEvery node has an upper bound.\n\nLeft node is bounded by the parent node\'s value.\nRight node is bounded by the ancestor\'s bound.\nUsing the example in the question:\nThe nodes [5, 1, 7] are all bounded by 8.\nThe node 1 is bounded by 5.\n8 is the root node, but if you think deeper about it, it is bounded by Integer.MAX_VALUE. i.e. imagine there is a root parent node Integer.MAX_VALUE with left node being 8.\nThis also means that both 10 and 12 nodes, which are also right nodes, are also bounded by Integer.MAX_VALUE.\nWe use a recursive function together with an outer index variable i to traverse and construct the tree. When we create a tree node, we increment i to process the next element in the preorder array.\n\nWe don\'t need to care about lower bound. When we construct the tree, we try to create left node first. If the condition fails (i.e. current number is greater than the parent node value), then we try to create the right node which automatically satisfies the condition, hence no lower bound is needed\n\n\n```\nclass Solution {\nint i = 0;\n public TreeNode bstFromPreorder(int[] arr) {\n return helper(arr, Integer.MAX_VALUE);\n }\n\n public TreeNode helper(int[] arr, int bound) {\n if (i == arr.length || arr[i] > bound) return null;\n TreeNode root = new TreeNode(arr[i++]);\n root.left = helper(arr, root.val);\n root.right = helper(arr, bound);\n return root;\n }\n\t}\n\t```\n\t\nEXPLANATON-\n"explanation- It is possible to do this because when we construct the " left child " the upper bound will be the node value itself and no lower bound will be needed!\n\t-no lower bound is required for "right child" because we have arrived at this point of creating the right child only because these elements failed to satisfy the left subtree conditions!"\n\t\n \n ```\n APPROACH 3-IF YOU ARE NOT COMFORTABLE WITH RECURSION!\n JAVA ITERATIVE APPROACH - \n\n```\nclass Solution {\n public TreeNode bstFromPreorder(int[] preorder) {\n \n if(preorder == null){\n return null;\n }\n int size = preorder.length;\n if(size==0){\n return null;\n }\n TreeNode root = new TreeNode(preorder[0]);\n\t\t\n for(int i=1;i<size;i++){\n generateBST(preorder[i],root);\n }\n return root;\n }\n \n public void generateBST(int target, TreeNode tree){\n TreeNode root = tree;\n TreeNode node = new TreeNode(target);\n while(root!=null){\n if(target<root.val){\n if(root.left==null){\n root.left = node;\n break;\n }\n else{\n root=root.left;\n }\n }else{\n if(root.right==null){\n root.right=node;\n break;\n }else{\n root=root.right;\n }\n }\n }\n }\n}\n\n```\n\nHOPE IT HELPS!\n\t\n\t | 42 | 0 | ['Recursion', 'Iterator', 'Java'] | 3 |
construct-binary-search-tree-from-preorder-traversal | C++ Simple and Clean Recursive Solution, Explained | c-simple-and-clean-recursive-solution-ex-udhq | Idea:\nIn a preorder traversal, we visit the root first.\nSo in each iteration, the first element - preorder[i] - is the root\nthen we find the left and right s | yehudisk | NORMAL | 2021-10-13T07:31:16.909198+00:00 | 2021-10-13T07:31:16.909238+00:00 | 3,632 | false | **Idea:**\nIn a preorder traversal, we visit the root first.\nSo in each iteration, the first element - `preorder[i]` - is the root\nthen we find the left and right subtrees and construct the tree recursively.\nIn the left subtree, the maximum value is the current root.\nIn the right subtree, the maximum value is the previous root.\n```\nclass Solution {\npublic:\n TreeNode* bstFromPreorder(vector<int>& preorder, int max_val = INT_MAX) {\n if (i == preorder.size() || preorder[i] > max_val) return NULL;\n \n TreeNode* root = new TreeNode(preorder[i++]);\n \n root->left = bstFromPreorder(preorder, root->val);\n root->right = bstFromPreorder(preorder, max_val);\n \n return root;\n }\n \nprivate:\n int i = 0;\n};\n```\n**Like it? please upvote!** | 32 | 2 | ['C'] | 3 |
construct-binary-search-tree-from-preorder-traversal | Less than 10 lines C++ beats 100% | less-than-10-lines-c-beats-100-by-zhxb51-fhw7 | Even though the elements between begin and left are not sorted, we can still apply binary search on it. The reason is that comparing with the value of current r | zhxb515 | NORMAL | 2019-07-01T23:29:22.915022+00:00 | 2019-07-01T23:29:22.915065+00:00 | 2,955 | false | Even though the elements between begin and left are not sorted, we can still apply binary search on it. The reason is that comparing with the value of current root element, there is a point that all elements on the left side are smaller than root value, and all elements on the right side are larger.\n\n```\nclass Solution {\npublic:\n TreeNode* bstFromPreorder(vector<int>& preorder) {\n return helper(preorder.begin(), preorder.end());\n }\n \n TreeNode * helper(vector<int>::iterator begin, vector<int>::iterator end) {\n if (begin == end) {\n return nullptr;\n }\n \n auto node = new TreeNode(*begin);\n auto right = upper_bound(begin + 1, end, *begin);\n \n node->left = helper(begin + 1, right);\n node->right = helper(right, end);\n return node;\n }\n};\n``` | 30 | 4 | [] | 3 |
construct-binary-search-tree-from-preorder-traversal | [Python] two O(n) solutions, explained | python-two-on-solutions-explained-by-dba-o5el | We can do in simple way: find index for left part, and for right part and do recursion with time complexity O(n^2) for skewed trees and average O(n log n). Ther | dbabichev | NORMAL | 2021-10-13T07:32:40.122410+00:00 | 2021-10-13T07:32:40.122465+00:00 | 1,389 | false | We can do in simple way: find index for left part, and for right part and do recursion with time complexity `O(n^2)` for skewed trees and average `O(n log n)`. There is smarter solution with `O(n)` time complexity, where we give the function a `bound` (or two bounds - up and down) the maximum number it will handle.\nThe left recursion will take the elements smaller than `node.val` \nThe right recursion will take the remaining elements smaller than `bound`. See also similar idea in problem **0109** Convert Sorted List to Binary Search Tree.\n\n#### Complexity\nIt is `O(n)` for time and space.\n\n#### Code 1\n```python\nclass Solution:\n def bstFromPreorder(self, preorder):\n def helper(down, up):\n if self.idx >= len(preorder): return None\n if not down <= preorder[self.idx] <= up: return None\n root = TreeNode(preorder[self.idx])\n self.idx += 1\n root.left = helper(down, root.val)\n root.right = helper(root.val, up)\n return root\n \n self.idx = 0\n return helper(-float("inf"), float("inf"))\n```\n\n#### Code 2\nThere is an alternative way to write it, without using global variable.\n\n```python\nclass Solution:\n def bstFromPreorder(self, preorder):\n def helper(down, up, idx):\n if idx >= len(preorder): return (idx, None)\n if not down <= preorder[idx] <= up: return (idx, None)\n root = TreeNode(preorder[idx])\n idx, root.left = helper(down, root.val, idx + 1)\n idx, root.right = helper(root.val, up, idx)\n return idx, root\n \n return helper(-float("inf"), float("inf"), 0)[1]\n```\n\nIf you have any questoins, feel free to ask. If you like the solution and explanation, please **upvote!** | 28 | 3 | ['Recursion'] | 0 |
construct-binary-search-tree-from-preorder-traversal | JAVA | Clean Code Solution | O(N log N) Time Complexity | 0 ms time | java-clean-code-solution-on-log-n-time-c-y5cl | class Solution {\n \n\tprivate TreeNode insert(TreeNode root, int val) {\n\t\t\n\t\tif(root == null) return new TreeNode(val);\n\t\telse if(root.val > val) root | anii_agrawal | NORMAL | 2020-05-24T21:24:32.863828+00:00 | 2020-05-25T04:36:16.887071+00:00 | 1,581 | false | class Solution {\n \n\tprivate TreeNode insert(TreeNode root, int val) {\n\t\t\n\t\tif(root == null) return new TreeNode(val);\n\t\telse if(root.val > val) root.left = insert(root.left, val);\n\t\telse root.right = insert(root.right, val);\n\t\treturn root;\n\t}\n \n\tpublic TreeNode bstFromPreorder(int[] preorder) { \n\t\t\n\t\tTreeNode root = null;\n\t\tfor(int val : preorder) root = insert(root, val);\n\t\treturn root;\n\t}\n}\n \nTime Complexity: O(N log N)\n\nPlease help to **UPVOTE** if this post is useful for you.\nIf you have any questions, feel free to comment below.\n**HAPPY CODING :)\nLOVE CODING :)** | 27 | 2 | [] | 3 |
construct-binary-search-tree-from-preorder-traversal | Morris' algorithm (O(n) time / O(n) space) | morris-algorithm-on-time-on-space-by-_ma-0l8l | Hi there!\nI have just solved that problem and started searching for the other solutions that might interest me. However, all users are solving it with the help | _maximus_ | NORMAL | 2020-04-20T13:58:42.421589+00:00 | 2020-05-25T10:49:57.425036+00:00 | 2,720 | false | Hi there!\nI have just solved that problem and started searching for the other solutions that might interest me. However, all users are solving it with the help of recursion or stack, and please do not get me wrong those are great solutions, I suggest you try Morris\' algorithm.\n\n**Explanation:**\nThat algorithm differs from others by not using additional data structures to navigate throughout the tree. That\'s right! We use recursion or stack just for having the opportunity to return to the parent node. If you want to learn about that algorithm please check this [**YouTube video**](https://www.youtube.com/watch?v=wGXB9OWhPTg). I don\'t know the author but he did an awesome job explaining the algorithm. Enjoy! \uD83D\uDE4C\n\n**Code:**\n```\nclass Solution:\n def bstFromPreorder(self, pre_order: List[int]) -> TreeNode:\n iterator = iter(pre_order)\n root = current = TreeNode(next(iterator))\n for val in iterator:\n node = TreeNode(val)\n if node.val < current.val:\n node.right = current\n current.left = current = node\n else:\n while current.right is not None and node.val > current.right.val:\n current.right, current = None, current.right\n\n node.right = current.right\n current.right = current = node\n\n while current.right is not None:\n current.right, current = None, current.right\n\n return root\n```\n\n**Algorithm complexity:**\n*Time complexity: O(n).*\n*Space complexity: O(n).*\n\n**Conclusion:**\nEven though we don\'t use recursion or stack, we still create a tree that takes n-space. But it is clean O(n) without dropped constants! Mention it to your interviewer.\n\nIf you like my solution, I will really appreciate your upvoting. It will help other python-developers to find it faster. And as always, I hope you learned something and wish you an enjoyable time on LeetCode. \uD83D\uDE0A\n\n**\uD83D\uDE4F Special thanks for your comments:**\n[**jeffwei**](https://leetcode.com/problems/construct-binary-search-tree-from-preorder-traversal/discuss/589051/Morris\'-algorithm-(O(n)-time-O(n)-space)/552601)\n | 27 | 1 | ['Python3'] | 8 |
construct-binary-search-tree-from-preorder-traversal | C++ iterative O(n) solution using decreasing stack | c-iterative-on-solution-using-decreasing-lc1i | iterate the input array\nfor each number x, we need to find the first number p less than x from the beginning of the array\nx should be the right child of p\nth | lc19890306 | NORMAL | 2019-03-10T15:02:01.616218+00:00 | 2019-09-02T04:40:30.465780+00:00 | 3,024 | false | iterate the input array\nfor each number x, we need to find the first number p less than x from the beginning of the array\nx should be the right child of p\nthus, we need to maintain a decreasing stack\nfor each number x in the array, we try to find the first number p less than x in the stack and make x the right child of p\nif such p does not exist, we make x the left child of the node on the stack top\n```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode(int x) : val(x), left(NULL), right(NULL) {}\n * };\n */\nclass Solution {\npublic:\n TreeNode* bstFromPreorder(vector<int>& preorder) {\n TreeNode dummy_root(INT_MAX);\n stack<TreeNode *> s({&dummy_root});\n for (int x : preorder) {\n auto n = new TreeNode(x);\n TreeNode *p = nullptr;\n while (s.top()->val < x) {\n p = s.top();\n s.pop();\n }\n if (p) {\n p->right = n;\n } else {\n s.top()->left = n;\n }\n s.push(n);\n }\n return dummy_root.left;\n }\n};\n``` | 25 | 1 | [] | 5 |
construct-binary-search-tree-from-preorder-traversal | [C++] Straightforward iterative approach (100%/100%) | c-straightforward-iterative-approach-100-zjmw | Here is my iterative approach to solving the problem. I hope this helps!\n\n\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\ | jessephams | NORMAL | 2019-04-11T16:58:35.790606+00:00 | 2019-04-11T16:58:35.790700+00:00 | 3,145 | false | Here is my iterative approach to solving the problem. I hope this helps!\n\n```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode(int x) : val(x), left(NULL), right(NULL) {}\n * };\n */\nclass Solution {\npublic:\n TreeNode* bstFromPreorder(vector<int>& preorder) {\n if (preorder.size() == 0){ // If vector is empty, return NULL\n return NULL;\n }\n \n TreeNode* root = new TreeNode(preorder[0]); // Tree will start off with vector\'s first value;\n \n for (int i = 1; i < preorder.size(); i++){ // Traversing the vector\n bool done = false; // Marker to indicate when the vector value has been added to the tree\n TreeNode* current = root; // Current is used to traverse the tree we\'re creating\n \n while (done == false){\n if (preorder[i] < current->val){ // If the vector value is less than the current tree node\'s value\n if (current->left == NULL){ // Add the vector value to the tree if there is an available spot\n current->left = new TreeNode(preorder[i]);\n done = true; // Vector value has been added, therefore done = true and break out of while loop\n }\n else{ // If there\'s no available spot, keep traversing our tree\n current = current->left;\n }\n }\n else{ // If vector value is greater than current tree node\'s value\n if (current->right == NULL){ // Add the vector value to tree if spot is available\n current->right = new TreeNode(preorder[i]);\n done = true; // Vector value added, therefore break out of while loop\n }\n else{\n current = current->right; // No spot available, keep traversing tree\n }\n }\n }\n }\n \n return root;\n }\n};\n``` | 22 | 2 | ['C', 'Iterator', 'C++'] | 4 |
construct-binary-search-tree-from-preorder-traversal | C++ || O(n) || New Approach || No need to figure out Upper Bound or Max_Val | c-on-new-approach-no-need-to-figure-out-sxcpu | OBSERVATION :\nFor any Tree, the Preorder traversal is of this type : \n| root | left subtree | right subtree |\n\nSo, if we are able to identify the index of e | hritesh_bhardwaj | NORMAL | 2022-01-24T09:13:01.941753+00:00 | 2022-01-24T09:19:44.851896+00:00 | 2,011 | false | **OBSERVATION :**\nFor any Tree, the Preorder traversal is of this type : \n| root | left subtree | right subtree |\n\nSo, if we are able to identify the index of ending of left subtree in the given vector preorder.\nThen, we can easily defferentiate the left subtree part with the right subtree part and build the rest of the tree using recursion.\n\nNow, for BSTs we know that the elements present on the left subtree are smaller than the root and elements present on the right subtree are greater than the root. And the 0th index is root itself.\n\nSo, if we find the last element in the preorder which is smaller than the 0th indexed element (say, \'pos\'). We can say that from 1th index to index \'pos\' lies the left subtree, from index \'pos\' to last index lies the right subtree and the 0th element is our root node.\n\n**INTUTION :**\nTraversal through : int l , int r. Meaning left most index and right most index of vector preorder.\nFirst element is root i.e. element on \'l\' index.\nFind the last element in the whole vector which is smaller then the root value and store the index value in \'pos\'.\nLet Recursion make the rest of the left subtree from index l+1 to pos.\nLet Recursion make the rest of the left subtree from index pos+1 to r.\nBASE CASE : if l crosses r, i.e. l>r then return NULL.\n\n**TIME COMPLEXITY : O(N)**\n**SPACE COMPLEXITY : O(N) + O(N)** Consturcting the BST + Recursive Stack\n\n**CODE :**\n```\nclass Solution {\npublic:\n TreeNode* helper(vector<int>& arr,int l,int r){\n\t\t//BASE CASE\n if(l>r)\n return NULL;\n\t\t\n\t\t//First element is root itself\n TreeNode *root=new TreeNode(arr[l]);\n\t\t\n int pos=l; //For corner case that only 1 element is given it the array\n for(int i=l+1; i<=r; i++){ //Find the index of last element which is smaller than the root node\n if(arr[i]<root->val)\n pos=i;\n else\n break;\n }\n root->left=helper(arr,l+1,pos); //Make left subtree\n root->right=helper(arr,pos+1,r); //Make right subtree\n return root;\n }\n TreeNode* bstFromPreorder(vector<int>& preorder) {\n int l=0; //Left most element of array\n\t\tint r=preorder.size()-1; //Right most element of the array\n return helper(preorder,l,r);\n }\n};\n```\n | 19 | 0 | ['Tree', 'Depth-First Search', 'Recursion', 'C', 'Binary Tree', 'C++'] | 4 |
construct-binary-search-tree-from-preorder-traversal | python beat 100% | python-beat-100-by-jason003-qr05 | python\nclass Solution:\n def bstFromPreorder(self, preorder: List[int]) -> TreeNode:\n if not preorder: return None\n root = TreeNode(preorder | jason003 | NORMAL | 2019-03-23T12:23:26.430229+00:00 | 2019-03-23T12:23:26.430284+00:00 | 2,200 | false | ```python\nclass Solution:\n def bstFromPreorder(self, preorder: List[int]) -> TreeNode:\n if not preorder: return None\n root = TreeNode(preorder[0])\n i = 1\n while i < len(preorder):\n if preorder[i] < preorder[0]: i += 1\n else: break\n root.left = self.bstFromPreorder(preorder[1:i])\n root.right = self.bstFromPreorder(preorder[i:])\n return root\n``` | 19 | 2 | [] | 5 |
construct-binary-search-tree-from-preorder-traversal | Video solution | Intuition and Approach | Detailed explanation | 🔥🔥🔥 | video-solution-intuition-and-approach-de-1sja | Video \nhey everyone, i have created a video solution for this problem and tried to explain this very intuitively, this video is part of trees playlist.\n\nVide | _code_concepts_ | NORMAL | 2024-08-14T11:38:43.380618+00:00 | 2024-08-14T11:38:43.380650+00:00 | 1,711 | false | # Video \nhey everyone, i have created a video solution for this problem and tried to explain this very intuitively, this video is part of trees playlist.\n\nVideo link: https://youtu.be/jOLLblvmQA0\nPlaylist link: https://www.youtube.com/playlist?list=PLICVjZ3X1Aca0TjUTcsD7mobU001CE7GL\n# Code\n```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n TreeNode* helper(vector<int>& preorder, int start, int end){\n // bc\n if(start>end) return NULL;\n\n int r_s;\n\n for(int i=start; i<=end;i++){\n if(preorder[i]>preorder[start]){\n r_s= i;\n break;\n }\n }\n int l_s=start+1;\n int l_e= r_s-1;\n int r_e=end;\n TreeNode* root= new TreeNode(preorder[start]);\n root->left= helper(preorder, l_s,l_e);\n root->right= helper(preorder, r_s,r_e);\n return root;\n\n \n }\n TreeNode* bstFromPreorder(vector<int>& preorder) {\n return helper(preorder, 0, preorder.size()-1);\n\n \n }\n};\n``` | 18 | 0 | ['C++'] | 1 |
construct-binary-search-tree-from-preorder-traversal | A Morris Stype method + summary of 4 methods | a-morris-stype-method-summary-of-4-metho-clue | 1 morris algorithm\n\n\nThis is in essence similar to the stack solution below, but use the dictionary to eliminate stack. The idea just came to me and I think | newruanxy | NORMAL | 2020-05-24T08:21:15.261598+00:00 | 2020-05-24T08:22:25.936544+00:00 | 1,757 | false | # 1 morris algorithm\n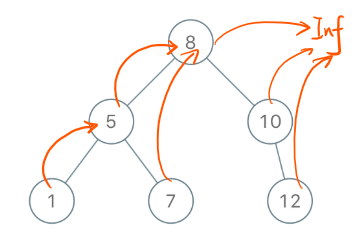\n\nThis is in essence similar to the stack solution below, but use the dictionary to eliminate stack. The idea just came to me and I think the inspiration came from morris algorithm.\n\n```python\ndef bstFromPreorder(self, preorder: List[int]) -> TreeNode:\n curr = dummy = TreeNode( float("Inf") )\n latter = {}\n \n for value in preorder:\n if value < curr.val:\n curr.left = TreeNode(value)\n latter[curr.left] = curr\n curr = curr.left\n else: \n while value > latter[curr].val:\n curr = latter[curr]\n curr.right = TreeNode(value)\n latter[curr.right] = latter[curr]\n curr = curr.right\n \n return dummy.left\n```\n\n\n# 2 stack\n`O(N)`\uFF1Athere are two loops, but each node will be pushed in and out at most once, so it\'s O(N).\n\n```python\ndef bstFromPreorder(self, preorder: List[int]) -> TreeNode:\n if not preorder: return None\n root = TreeNode( preorder[0] )\n stack = [ root ]\n for value in preorder[1:]:\n node = TreeNode(value)\n if value < stack[-1].val:\n stack[-1].left = node\n else:\n while stack and value > stack[-1].val:\n prev = stack.pop()\n prev.right = node\n stack.append(node)\n \n return root \n```\n\n\n# 3 O(NlogN) recursion\n```python\ndef bstFromPreorder(self, preorder: List[int]) -> TreeNode:\n \n def subtree(lo, hi):\n if lo >= hi: return None\n rootval = preorder[lo] \n root = TreeNode( rootval )\n mi = bisect.bisect_left(preorder, rootval, lo+1, hi) # lo+1 !!!\n root.left = subtree(lo+1, mi)\n root.right = subtree(mi, hi)\n return root\n \n return subtree( 0, len(preorder) )\n```\n\n# 4 a beautiful O(N) recursion\n```python\ndef bstFromPreorder(self, preorder: List[int]) -> TreeNode:\n self.index, N = 0, len(preorder)\n \n def helper(bound):\n if self.index >= N or preorder[self.index] >= bound:\n return None\n val = preorder[self.index]\n self.index += 1\n root = TreeNode( val )\n root.left = helper( val )\n root.right = helper( bound )\n return root\n \n return helper( float("Inf") )\n```\n | 18 | 0 | ['Python'] | 2 |
construct-binary-search-tree-from-preorder-traversal | JavaScript solution inspired by lee215 with explanation, O(n) time, O(h) space. | javascript-solution-inspired-by-lee215-w-p7f5 | Solution Explanation\n\nThis solution is inspired by this post written by lee215.\n\nThe main takeaway points in this solutions are:\n\n1. Every node has an upp | ecgan | NORMAL | 2020-04-20T17:00:44.913446+00:00 | 2020-04-20T17:00:44.913499+00:00 | 1,684 | false | ## Solution Explanation\n\nThis solution is inspired by [this post](https://leetcode.com/problems/construct-binary-search-tree-from-preorder-traversal/discuss/252232/JavaC%2B%2BPython-O(N)-Solution) written by [lee215](https://leetcode.com/lee215/).\n\nThe main takeaway points in this solutions are:\n\n1. Every node has an upper bound.\n - `Left` node is bounded by the parent node\'s value.\n - `Right` node is bounded by the ancestor\'s bound.\n - Using the example in the [question](https://leetcode.com/problems/construct-binary-search-tree-from-preorder-traversal/):\n - The nodes `[5, 1, 7]` are all bounded by `8`.\n - The node `1` is bounded by `5`.\n - `8` is the root node, but if you think deeper about it, it is bounded by `Number.MAX_SAFE_INTEGER`. i.e. imagine there is a root parent node `Number.MAX_SAFE_INTEGER` with left node being `8`.\n - This also means that both `10` and `12` nodes, which are also `right` nodes, are also bounded by `Number.MAX_SAFE_INTEGER`.\n\n2. We use a recursive function together with an outer index variable `i` to traverse and construct the tree. When we create a tree node, we increment `i` to process the next element in the `preorder` array.\n\n3. We don\'t need to care about lower bound. When we construct the tree, we try to create `left` node first. If the condition fails (i.e. current number is greater than the parent node value), then we try to create the `right` node which automatically satisfies the condition, hence no lower bound is needed.\n\n## Complexity Analysis\n\nTime complexity: O(n). We iterate through each element in `preorder` array only once.\n\nSpace complexity: O(h) where h is the height of the tree. Space cost is the recursive stack size.\n\n```javascript\n/**\n * Definition for a binary tree node.\n */\nfunction TreeNode (val) {\n this.val = val\n this.left = this.right = null\n}\n\n/**\n * @param {number[]} preorder\n * @return {TreeNode}\n */\nconst bstFromPreorder = function (preorder) {\n let i = 0\n const process = (bound) => {\n if (i === preorder.length || preorder[i] > bound) {\n return null\n }\n\n const num = preorder[i]\n const node = new TreeNode(num)\n i++\n\n node.left = process(node.val)\n node.right = process(bound)\n\n return node\n }\n\n const root = process(Number.MAX_SAFE_INTEGER)\n\n return root\n}\n\nmodule.exports = bstFromPreorder\n``` | 18 | 0 | ['JavaScript'] | 2 |
construct-binary-search-tree-from-preorder-traversal | c++ Easy straight forward O(N) recursive code | c-easy-straight-forward-on-recursive-cod-vxwa | \n TreeNode* bstFromPreorder1(vector<int>& preorder) {\n int pos =0;\n return bst(preorder, pos, INT_MAX, INT_MIN); \n }\n \n TreeNode | elbanna25 | NORMAL | 2020-05-17T16:21:12.580471+00:00 | 2020-05-17T16:23:44.958439+00:00 | 1,758 | false | ```\n TreeNode* bstFromPreorder1(vector<int>& preorder) {\n int pos =0;\n return bst(preorder, pos, INT_MAX, INT_MIN); \n }\n \n TreeNode*bst(vector<int>&preorder, int &pos, int max, int min){\n if (pos>=preorder.size()) return NULL;\n int val = preorder[pos];\n if (val > max || val <min) return NULL;\n ++pos;\n TreeNode* node = new TreeNode(val);\n node->left = bst(preorder, pos, val, min);\n node->right = bst(preorder, pos, max, val);\n return node;\n }\n``` | 13 | 1 | ['C', 'C++'] | 0 |
construct-binary-search-tree-from-preorder-traversal | Java: Simple solution to place the nodes to tree one-by-one (100%/100%) | java-simple-solution-to-place-the-nodes-eqs3m | \nclass Solution {\n \n public void addToTree(TreeNode n, int val) {\n if (val < n.val) {\n if (n.left == null) {\n n.lef | mlalma | NORMAL | 2019-11-19T12:00:05.716680+00:00 | 2019-11-24T13:33:23.990753+00:00 | 1,249 | false | ```\nclass Solution {\n \n public void addToTree(TreeNode n, int val) {\n if (val < n.val) {\n if (n.left == null) {\n n.left = new TreeNode(val); \n } else {\n addToTree(n.left, val);\n }\n } else {\n if (n.right == null) {\n n.right = new TreeNode(val);\n } else {\n addToTree(n.right, val);\n }\n }\n }\n \n public TreeNode bstFromPreorder(int[] preorder) {\n if (preorder == null || preorder.length == 0) { return null; }\n \n TreeNode root = new TreeNode(preorder[0]);\n for (int i = 1; i < preorder.length; i++) {\n addToTree(root, preorder[i]);\n }\n \n return root;\n }\n}\n``` | 13 | 0 | ['Java'] | 1 |
construct-binary-search-tree-from-preorder-traversal | Python 1-liner | python-1-liner-by-ekovalyov-tds5 | \nclass Solution:\n def bstFromPreorder(self, preorder: List[int]) -> TreeNode:\n if preorder:\n return TreeNode(preorder[0],\n | ekovalyov | NORMAL | 2020-05-24T12:00:31.765757+00:00 | 2020-05-24T12:00:31.765791+00:00 | 925 | false | ```\nclass Solution:\n def bstFromPreorder(self, preorder: List[int]) -> TreeNode:\n if preorder:\n return TreeNode(preorder[0],\n self.bstFromPreorder(tuple(takewhile(lambda x:x<preorder[0], preorder[1:]))),\n self.bstFromPreorder(tuple(dropwhile(lambda x:x<preorder[0], preorder[1:]))))\n``` | 12 | 0 | [] | 4 |
construct-binary-search-tree-from-preorder-traversal | [C++] 0ms Concise Solution | Beats 100% Time | c-0ms-concise-solution-beats-100-time-by-dqzu | \n TreeNode* bstFromPreorder(vector<int>& preorder) {\n if(preorder.size() == 0) return NULL;\n TreeNode* root = NULL;\n for(int i : pre | sherlasd | NORMAL | 2020-04-21T06:58:56.332713+00:00 | 2020-04-21T07:01:39.735931+00:00 | 889 | false | ```\n TreeNode* bstFromPreorder(vector<int>& preorder) {\n if(preorder.size() == 0) return NULL;\n TreeNode* root = NULL;\n for(int i : preorder)\n root = InsertBst(root, i);\n return root;\n }\n \n TreeNode* InsertBst(TreeNode* root, int i){\n if(!root) return new TreeNode(i);\n if(i < root->val) root->left = InsertBst(root->left, i);\n else root->right = InsertBst(root->right, i);\n return root;\n }\n``` | 12 | 0 | ['C', 'C++'] | 3 |
construct-binary-search-tree-from-preorder-traversal | JAVA 100% FASTER SOLUTION🤯🤯|| RECURSION🙂 | java-100-faster-solution-recursion-by-ab-rjx7 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | abhiyadav05 | NORMAL | 2023-04-17T14:04:43.600428+00:00 | 2023-04-17T14:04:43.600460+00:00 | 1,706 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->O(N)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->O(N)\n\n\n\n# Code\n```\n/**\n * Definition for a binary tree node.\n * public class TreeNode {\n * int val;\n * TreeNode left;\n * TreeNode right;\n * TreeNode() {}\n * TreeNode(int val) { this.val = val; }\n * TreeNode(int val, TreeNode left, TreeNode right) {\n * this.val = val;\n * this.left = left;\n * this.right = right;\n * }\n * }\n */\nclass Solution {\n public TreeNode bstFromPreorder(int[] preorder) {\n // call helper function with initial parameters\n return bstFromPreorder(preorder, Integer.MAX_VALUE, new int[]{0});\n }\n\n public TreeNode bstFromPreorder(int[] preorder, int bound, int[] i){\n // check if there are no more nodes to add or if current node value exceeds bound\n if(i[0] == preorder.length || preorder[i[0]] > bound){\n return null;\n }\n\n // create new TreeNode with current node value\n TreeNode root = new TreeNode(preorder[i[0]++]);\n\n // recursively call helper for left and right subtrees\n // left subtree bound: current node value\n root.left = bstFromPreorder(preorder, root.val, i);\n // right subtree bound: parent node bound\n root.right = bstFromPreorder(preorder, bound, i);\n\n return root;\n }\n}\n``` | 11 | 0 | ['Tree', 'Binary Search Tree', 'Binary Tree', 'Java'] | 0 |
construct-binary-search-tree-from-preorder-traversal | javascript, simple recursive | javascript-simple-recursive-by-carti-qjwn | \n/**\n * @param {number[]} preorder\n * @return {TreeNode}\n */\nconst bstFromPreorder = (preorder) => {\n // base cases\n if (preorder.length === 0) return | carti | NORMAL | 2020-04-12T00:53:44.118488+00:00 | 2020-04-22T01:01:40.981315+00:00 | 1,072 | false | ```\n/**\n * @param {number[]} preorder\n * @return {TreeNode}\n */\nconst bstFromPreorder = (preorder) => {\n // base cases\n if (preorder.length === 0) return null;\n if (preorder.length === 1) return new TreeNode(preorder[0]);\n\n // result tree node\n var res = new TreeNode(preorder[0]);\n\n // iterate from 1 to n\n for (let i = 1; i < preorder.length; i++) {\n // insert this num\n res = insert(res, preorder[i]);\n }\n\n return res;\n};\n\n/**\n * recursive func to insert value into tree\n * @param {TreeNode} root\n * @param {number} val val to insert\n * @return {TreeNode} altered node\n */\nconst insert = (root, val) => {\n // base\n if (root === null) return new TreeNode(val);\n\n // compare value between val and root\n if (val < root.val) {\n // insert in left subtree\n root.left = insert(root.left, val);\n } else {\n // insert in right subtree\n root.right = insert(root.right, val);\n }\n\n // return root w/ val inserted\n return root;\n};\n```\n | 11 | 0 | ['Recursion', 'JavaScript'] | 3 |
construct-binary-search-tree-from-preorder-traversal | 💡JavaScript Solution | javascript-solution-by-aminick-5mlf | The idea\n1. Utilize the BST\u2018s peculiarity, which is nodes in the left subtree is smaller than the root, and nodes in the right subtree is bigger than the | aminick | NORMAL | 2020-01-31T11:39:53.808923+00:00 | 2020-01-31T11:39:53.809019+00:00 | 1,077 | false | ### The idea\n1. Utilize the BST\u2018s peculiarity, which is nodes in the left subtree is smaller than the root, and nodes in the right subtree is bigger than the root. Use this as a constraint, we can identify subtrees within the preorder array.\n```\n/**\n * @param {number[]} preorder\n * @return {TreeNode}\n */\nvar bstFromPreorder = function(preorder) {\n let recur = function(lower, upper) {\n if (preorder[0] < lower || preorder[0] > upper) return null;\n if (preorder.length == 0) return null;\n let root = new TreeNode(preorder.shift());\n root.left = recur(lower, root.val);\n root.right = recur(root.val, upper);\n return root;\n }\n return recur(-Infinity, Infinity);\n};\n``` | 11 | 0 | ['JavaScript'] | 0 |
construct-binary-search-tree-from-preorder-traversal | Simple java solution | simple-java-solution-by-traychev-o3g8 | \nclass Solution {\n public TreeNode bstFromPreorder(int[] preorder) {\n TreeNode root = new TreeNode(preorder[0]);\n for (int i = 1; i < preor | traychev | NORMAL | 2019-03-31T12:27:50.552342+00:00 | 2019-03-31T12:27:50.552371+00:00 | 2,439 | false | ```\nclass Solution {\n public TreeNode bstFromPreorder(int[] preorder) {\n TreeNode root = new TreeNode(preorder[0]);\n for (int i = 1; i < preorder.length; i++) {\n insertIntoBSThelper(root, preorder[i]);\n }\n return root;\n }\n \n public static void insertIntoBSThelper(TreeNode root, int val) {\n\t\tif (root.val < val) {\n\t\t\tif (root.right == null) {\n\t\t\t\tTreeNode right = new TreeNode(val);\n\t\t\t\troot.right = right;\n\t\t\t\treturn;\n\t\t\t} else {\n\t\t\t\tinsertIntoBSThelper(root.right, val);\n\t\t\t}\n\t\t} else {\n\t\t\tif (root.left == null) {\n\t\t\t\tTreeNode left = new TreeNode(val);\n\t\t\t\troot.left = left;\n\t\t\t\treturn;\n\t\t\t} else {\n\t\t\t\tinsertIntoBSThelper(root.left, val);\n\t\t\t}\n\t\t}\n\t}\n}\n``` | 11 | 1 | [] | 3 |
construct-binary-search-tree-from-preorder-traversal | C++ || pre-order style insertion || iterative || beats 100% / 90.22% | c-pre-order-style-insertion-iterative-be-7qix | This is an amazing solution involving stacks. \n\nAlgorithm:\n\n1) 1st create the 1st element as root and assign an iterator p to it.\n2) Traverse the preorder | sherwin31 | NORMAL | 2021-05-03T20:24:20.901616+00:00 | 2021-05-03T20:29:34.915237+00:00 | 681 | false | This is an amazing solution involving stacks. \n\nAlgorithm:\n\n1) 1st create the 1st element as root and assign an iterator p to it.\n2) Traverse the preorder array from index 1 to preorder.size() - 1 (as you\'ve already created 1 node).\n3) Now if the preorder[i] is smaller than p->val, it means this node will lie to the left of p. So we create a node to the left and add preorder[i] to it. Then we push p on stack and go left.\n4) If not, then we need to know as to which node\'s right position should we add preorder[i]. It could be current node\'s right or one of the nodes pushed on stack.\n One thing is certain that if preorder[i] is less than both current node and the top node on stack, then definitely preorder[i] won\'t be to the right of current, because then it\'ll violate BST property for the node on stack.\n\nTake the example in the question : [8,5,1,7,10,12]\nUptil 1, the tree looks like this:\n\n```\n\t\t\t\t\t\t\t\t\t8\n\t\t\t\t\t\t\t\t/\n\t\t\t\t\t\t\t5\n\t\t\t\t\t\t/\n\t\t\t\t\t1\n```\nNow 7 could come to the right of 1 or right of 5. Question is, where should it go?\nIf I put 7 to the right of 1, it\'ll violate property of BST on 5. And also, it won\'t go to the right of 8 for obvious reasons. So it\'ll go to 5\'s right.\nSay instead of 7, we\'d have to insert 9. Now 9 could go to the right of 1, 5 or 8. But if we put it to the right of 1, then 5 and 8\'s BST property is violated. And if we put 9 to the right of 5, then 8\'s BST property is violated. And there\'s no value beyond 8, so our only option is to put 9 to the right of 8.\n\nTo put it as an algorithm:\n5) While stack is not empty, we keep checking whether val of node on stack is less than preorder[i]. If yes, we skip the current node p by popping the node on stack and assigning it to variable p. The moment stack top node\'s val is greater than preorder[i], we know it\'ll definitely go to the right of p, so make a right node from p with preorder[i] as val and move p to p->right.\n6) And if stack is empty, then we\'ll have no choice but to put it to the right of the current node p.\n\nAnd that\'s all! It\'ll automatically create the BST and finally we\'ve to just return root.\n\nCode:\n\n```\nclass Solution {\npublic:\n TreeNode* bstFromPreorder(vector<int>& preorder) { \n TreeNode *root = new TreeNode(preorder[0]);\n TreeNode *p = root;\n stack<TreeNode*> S;\n int i = 1;\n while(i < preorder.size())\n {\n if(p->val > preorder[i])\n {\n p->left = new TreeNode(preorder[i]);\n S.push(p);\n p = p->left;\n }\n else\n {\n while(!S.empty() && S.top()->val < preorder[i])\n {\n p = S.top();\n S.pop();\n }\n p->right = new TreeNode(preorder[i]);\n p = p->right;\n }\n i++;\n }\n return root;\n }\n};\n```\n\nIf there\'s any questions, please let me know. | 10 | 0 | ['Stack', 'C', 'Iterator'] | 2 |
construct-binary-search-tree-from-preorder-traversal | 🌺22. Recursive [DFS] || Without Stack || No Extra Space || Short & Sweet Code || C++ Code Reference | 22-recursive-dfs-without-stack-no-extra-4u2e0 | Intuition\n1. All Elements in Left Subtree Should Be Smaller Than ROOT\n2. All Elements in Right Subtree Should Be Greater Than ROOT\n\n\n# Approach\n- Traverse | Amanzm00 | NORMAL | 2024-07-09T03:29:20.308456+00:00 | 2024-07-09T03:32:26.782036+00:00 | 673 | false | # Intuition\n1. All Elements in Left Subtree Should Be Smaller Than ROOT\n2. All Elements in Right Subtree Should Be Greater Than ROOT\n\n\n# Approach\n- Traverse Pre Order Wise \n1. We keep Track Of Bound , Which Is Upper Bound \n2. Elem. Should be Less Than Upper Bound\n\n# Code\n```cpp [There You GO !!]\n\nclass Solution {\n int n,i=0;\n\n TreeNode* Construct(int Bound,vector<int>& Pre)\n {\n if(i>=n || Pre[i]>Bound) return nullptr;\n\n TreeNode *a = new TreeNode(Pre[i++]);\n a->left=Construct(a->val,Pre);\n a->right=Construct(Bound,Pre);\n return a;\n }\n\npublic:\n TreeNode* bstFromPreorder(vector<int>& Pre) {\n n=Pre.size(); \n return Construct(INT_MAX,Pre);\n }\n};\n```\n\n---\n# *Guy\'s Upvote Pleasee !!* \n\n\n# ***(\u02E3\u203F\u02E3 \u035C)***\n\n\n\n | 9 | 0 | ['Array', 'Stack', 'Tree', 'Binary Search Tree', 'Recursion', 'Monotonic Stack', 'Binary Tree', 'C++'] | 1 |
construct-binary-search-tree-from-preorder-traversal | ✅100% Accepted || Worst to Best approaches with explanation || Easy to understand. | 100-accepted-worst-to-best-approaches-wi-fx81 | Read the below approaches to understand the logic.\n\nPlease upvote if you like it\n\nApproach 1 : Create tree from given elements approach(Not optimised)\n Fir | pranjal9424 | NORMAL | 2022-10-02T09:32:58.848569+00:00 | 2022-10-02T09:32:58.848628+00:00 | 1,294 | false | **Read the below approaches to understand the logic.**\n\n***Please upvote if you like it***\n\n**Approach 1 : Create tree from given elements approach(Not optimised)**\n* First approach could be just create build tree fucntion pass preorder elements one by one and set new node at correct possition by just passing tree node at each step.\n**~Time complexity: (N*N)** for worst case.\n**~space complexity:(1)**\n\t\n**Approach 2 : create BST using inorder and preorder approach (Not optimised)**\n* Second approach could be just create an inoreder vector by sort the given preorder and follow "Create BST from given inorder and preorder" approach **[(Link)](https://leetcode.com/problems/construct-binary-tree-from-preorder-and-inorder-traversal/discuss/2640357/100fastest-solution-with-explain-best-approach-easy-to-understand).**\n**~Time complexity: o(NlogN)+o(N)** "o(nlonn) because we are sorting preorder array.\n**~space complexity:(N)** Because we are using inorede array.\n\n**Approach 3 : Using check BST or not Approach (Most optimised)**\n1. Take an index variable as root element in preorder which is 0, define curent node lower bound as INT_MAX and upper bount as INT_MAX, then call BuildBST.\n1. At each call create a new node which having value as index element of preorder . recursive call for left and right child, increment index by 1 at each call as well. ( return NULL if index became out of bound or preoreder index value is out of lower or upper bound )\n\ta. Call recursively for the left node, set upper bound as current node value and lower bound as it is.\n\tb. Call recursively for the right node, set lower bound as current node value and upper bound as it is.\n1. return current node at each calls.\n\n**~Time complexity: O(3N)** You will visit single node trice at worst case.\n**~Space Complexity: O(1)** We are\'nt using any extra space.\n\n**Paper Dry run:**\n\n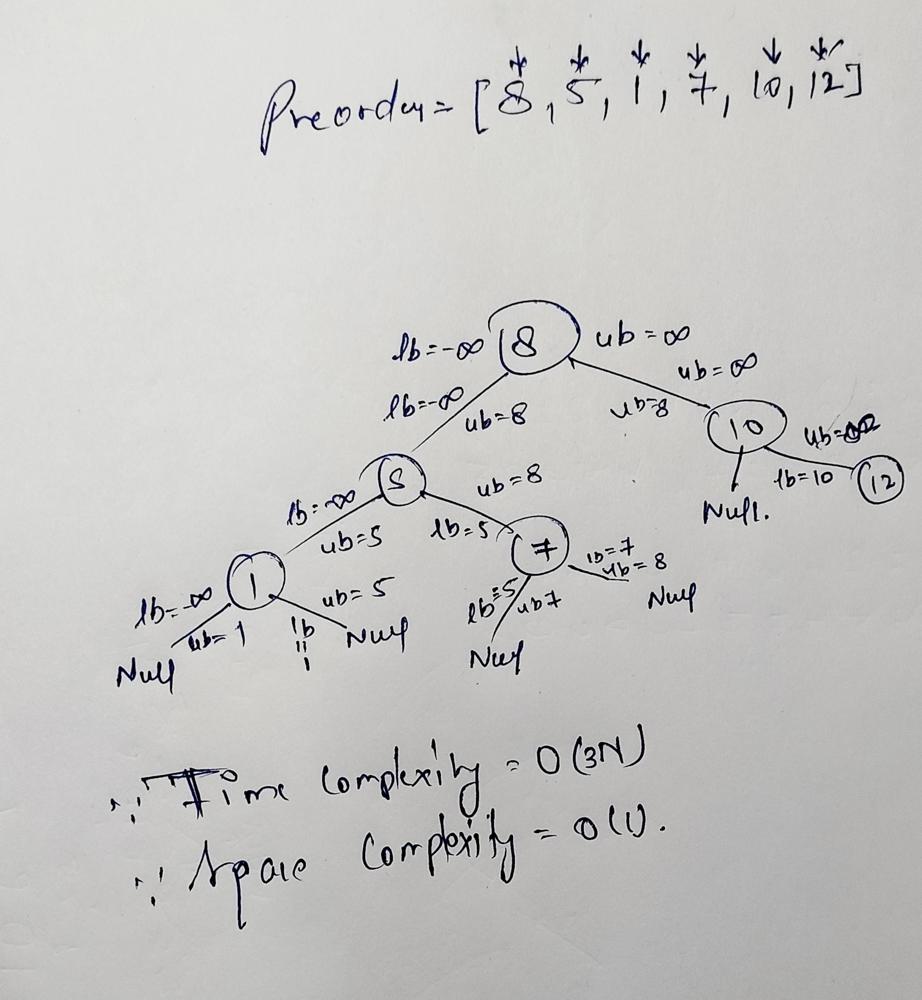\n\n**C++ Code**\n```\nclass Solution {\npublic:\n TreeNode* buildBST(vector<int>& preorder,int& index,int lowerBound,int upperBound){\n if(index>=preorder.size()) return NULL;\n if(preorder[index]<lowerBound || preorder[index]>upperBound) return NULL;\n \n TreeNode* node=new TreeNode(preorder[index++]);\n node->left=buildBST(preorder,index,lowerBound,node->val);\n node->right=buildBST(preorder,index,node->val,upperBound);\n return node;\n }\n \n TreeNode* bstFromPreorder(vector<int>& preorder) {\n int index=0;\n return buildBST(preorder,index,INT_MIN,INT_MAX);\n }\n};\n``` | 9 | 0 | ['Binary Search Tree', 'Recursion', 'C', 'C++'] | 0 |
construct-binary-search-tree-from-preorder-traversal | O(n) recursive solution | on-recursive-solution-by-pratham7711-57fx | \nclass Solution {\npublic:\n \n TreeNode* bstFromPreorder(vector<int>& preorder) {\n return build(preorder,0,preorder.size() - 1);\n }\n | pratham7711 | NORMAL | 2021-10-13T19:46:24.390597+00:00 | 2021-10-13T19:46:24.390626+00:00 | 182 | false | ```\nclass Solution {\npublic:\n \n TreeNode* bstFromPreorder(vector<int>& preorder) {\n return build(preorder,0,preorder.size() - 1);\n }\n \n TreeNode* build(vector<int> preorder , int start , int end)\n {\n if(start > end)\n return NULL;\n \n \n TreeNode* root = new TreeNode(preorder[start]);\n \n int idx ;\n for(idx = start + 1 ; idx <= end ; idx++)\n {\n if(preorder[start] < preorder[idx])\n {\n break;\n }\n }\n \n root->left = build(preorder ,start + 1 , idx - 1);\n root->right = build(preorder , idx , end);\n \n return root;\n }\n};\n``` | 8 | 0 | ['Binary Tree'] | 0 |
construct-binary-search-tree-from-preorder-traversal | ✅✅ 2 METHODS || BEATS 100% || C++ CODE ✅✅ | 2-methods-beats-100-c-code-by-neelam_bin-k7tk | METHOD 1:IntuitionWe can build the binary search tree (BST) by following the properties of BSTs and recursively constructing subtrees based on bounds derived fr | neelam_bind | NORMAL | 2025-01-06T19:45:05.908274+00:00 | 2025-01-06T19:45:05.908274+00:00 | 1,013 | false | # METHOD 1:
# Intuition
We can build the binary search tree (BST) by following the properties of BSTs and recursively constructing subtrees based on bounds derived from the preorder traversal.
# Approach
1. Use preorder traversal to process each node.
2. Recursively build the left and right subtrees by updating bounds for each subtree.
3. Base case: Stop recursion when the current node exceeds the bounds or the array ends.
# Complexity
- **Time complexity**: $$O(n)$$
- **Space complexity**: $$O(n)$$
# Code
```cpp []
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* bstFromPreorder(vector<int>& preorder) {
int i=0;
return build(preorder,i,INT_MAX);
}
TreeNode* build(vector<int>& preorder,int &i,int bound){
if(i==preorder.size() || preorder[i]>bound) return nullptr;
TreeNode* root=new TreeNode(preorder[i++]);
root->left =build(preorder,i,root->val);
root->right =build(preorder,i,bound);
return root;
}
};
```
# METHOD 2:
# Intuition
We can construct the binary search tree (BST) using both preorder and inorder traversals. The root node is the first element of the preorder traversal, and the position of this root in the inorder traversal helps us divide the tree into left and right subtrees.
# Approach
1. Start with the first element of the preorder array, which represents the root of the tree.
2. Use the inorder array to find the root's position and split the tree into left and right subtrees.
3. Recursively construct the left and right subtrees using updated bounds.
# Complexity
- **Time complexity**: $$O(n)$$
- **Space complexity**: $$O(n)$$
# Code
```cpp
class Solution {
public:
TreeNode* construct(vector<int>& preorder, vector<int>& inorder, int& preI, int Instart, int Inend, unordered_map<int,int>& mpp) {
if (Instart > Inend)
return nullptr;
int data = preorder[preI];
int rootpos = mpp[data];
TreeNode* root = new TreeNode(data);
preI++;
root->left = construct(preorder, inorder, preI, Instart, rootpos - 1, mpp);
root->right = construct(preorder, inorder, preI, rootpos + 1, Inend, mpp);
return root;
}
TreeNode* bstFromPreorder(vector<int>& preorder) {
vector<int> inorder = preorder;
unordered_map<int, int> mpp;
for (int i = 0; i < inorder.size(); i++)
mpp[inorder[i]] = i;
int preI = 0;
return construct(preorder, inorder, preI, 0, inorder.size() - 1, mpp);
}
};
```

| 7 | 0 | ['Binary Search Tree', 'Binary Tree', 'C++'] | 0 |
construct-binary-search-tree-from-preorder-traversal | ✅💯🔥Simple Code🚀📌|| 🔥✔️Easy to understand🎯 || 🎓🧠Beats 100%🔥|| Beginner friendly💀💯 | simple-code-easy-to-understand-beats-100-hf8f | Solution tuntun mosi ki photo ke baad hai. Scroll Down\n\n\n# Code\njava []\n/**\n * Definition for a binary tree node.\n * public class TreeNode {\n * int | atishayj4in | NORMAL | 2024-08-20T21:01:21.206117+00:00 | 2024-08-20T21:01:21.206139+00:00 | 858 | false | Solution tuntun mosi ki photo ke baad hai. Scroll Down\n\n\n# Code\n```java []\n/**\n * Definition for a binary tree node.\n * public class TreeNode {\n * int val;\n * TreeNode left;\n * TreeNode right;\n * TreeNode() {}\n * TreeNode(int val) { this.val = val; }\n * TreeNode(int val, TreeNode left, TreeNode right) {\n * this.val = val;\n * this.left = left;\n * this.right = right;\n * }\n * }\n */\nclass Solution {\n int i=0;\n public TreeNode bst(int[] preorder, int v){\n if(i==preorder.length || preorder[i]>v){\n return null;\n }\n TreeNode child = new TreeNode(preorder[i++]);\n child.left=bst(preorder, child.val);\n child.right=bst(preorder, v);\n return child;\n }\n public TreeNode bstFromPreorder(int[] preorder) {\n return bst(preorder, Integer.MAX_VALUE);\n }\n}\n```\n | 7 | 0 | ['Array', 'Stack', 'Tree', 'Binary Search Tree', 'Monotonic Stack', 'Binary Tree', 'Python', 'C++', 'Java', 'JavaScript'] | 1 |
construct-binary-search-tree-from-preorder-traversal | 💯🔥✅Python Simple solution | explained properly | python-simple-solution-explained-properl-x1md | Solution Explanation for Constructing a BST from Preorder Traversal \uD83C\uDF33\n\nIn this solution, we aim to construct a binary search tree (BST) from a give | sagarsaini_ | NORMAL | 2024-07-26T05:11:03.203351+00:00 | 2024-07-26T05:11:03.203376+00:00 | 457 | false | ## Solution Explanation for Constructing a BST from Preorder Traversal \uD83C\uDF33\n\nIn this solution, we aim to construct a binary search tree (BST) from a given preorder traversal list. The key insight is that in a preorder traversal, the first element is always the root of the tree (or subtree), and the subsequent elements can be divided into left and right subtrees based on their values.\n\n### Approach \uD83D\uDD0D\n\n1. **Understanding Preorder Traversal**:\n - The first element of the preorder list is the root of the tree.\n - All subsequent elements that are less than the root will belong to the left subtree.\n - All elements greater than the root will belong to the right subtree.\n\n2. **Recursive Helper Function**:\n - We define a helper function that takes the current index and a boundary value.\n - The boundary helps ensure that we only add nodes that respect the BST properties.\n\n3. **Base Case**:\n - If the current index exceeds the length of the preorder list or the current value is greater than or equal to the boundary, we return `None`. This indicates that there is no node to be added at this position.\n\n4. **Creating Nodes**:\n - We create a new `TreeNode` with the current value from the preorder list.\n - We then increment the index to move to the next value.\n\n5. **Building Subtrees**:\n - The left subtree is constructed by calling the helper function with the current node\'s value as the new boundary.\n - The right subtree is constructed with the original boundary.\n\n6. **Return the Root**:\n - Finally, we return the root node of the constructed BST.\n\n### Code Implementation \uD83D\uDCBB\n\nHere is the complete code for the solution:\n\n```python\nclass Solution:\n def bstFromPreorder(self, preorder: List[int]) -> Optional[TreeNode]:\n def helper(preorder, i, bound):\n if (i[0] == len(preorder)) or preorder[i[0]] >= bound:\n return None \n root = TreeNode(preorder[i[0]])\n i[0] += 1\n root.left = helper(preorder, i, root.val)\n root.right = helper(preorder, i, bound)\n return root\n \n i = [0]\n return helper(preorder, i, float("inf"))\n```\n\n### Complexity Analysis \uD83D\uDCCA\n\n- **Time Complexity**: O(N), where N is the number of nodes in the tree. Each node is processed exactly once.\n- **Space Complexity**: O(H), where H is the height of the tree. This accounts for the space used by the recursion stack.\n\n### Conclusion \uD83C\uDF89\n\nThis approach effectively constructs a BST from its preorder traversal in a clean and efficient manner. By leveraging the properties of preorder traversal and recursive tree construction, we ensure that the solution is both optimal and easy to understand. Happy coding! \uD83D\uDE80\n\n---\n\n | 7 | 0 | ['Array', 'Binary Search Tree', 'Binary Tree', 'Python3'] | 0 |
construct-binary-search-tree-from-preorder-traversal | Brute - Better - Optimal [For Interview] 📄✅ | brute-better-optimal-for-interview-by-de-y7w1 | \nclass Solution {\npublic:\n \n// BRUTE [T(O(N*N))] [S(O(1))]\n \n TreeNode* insertNode(TreeNode* root,int key)\n {\n if(!root) return new T | debugagrawal | NORMAL | 2022-01-14T07:37:20.872398+00:00 | 2022-01-21T04:59:40.403194+00:00 | 407 | false | ```\nclass Solution {\npublic:\n \n// BRUTE [T(O(N*N))] [S(O(1))]\n \n TreeNode* insertNode(TreeNode* root,int key)\n {\n if(!root) return new TreeNode(key);\n if(key>root->val) root->right=insertNode(root->right,key);\n else root->left=insertNode(root->left,key);\n return root;\n }\n TreeNode* bstFromPreorder(vector<int>& preorder) {\n TreeNode* root=new TreeNode(preorder[0]);\n for(int i=1;i<preorder.size();i++)\n insertNode(root,preorder[i]);\n return root; \n }\n\n// BETTER [T(O(N*logN))] [S(O(N))] [using inorder-preorder to bt technique]\n \n TreeNode* insertNodes(vector<int>& inorder, int inStart, int inEnd, vector<int>& preorder, int preStart, int preEnd, map<int,int>& inMap)\n {\n if(preStart>preEnd || inStart>inEnd) return NULL;\n TreeNode* root= new TreeNode(preorder[preStart]);\n int inRoot=inMap[preorder[preStart]];\n int nodeInLeft=inRoot-inStart;\n root->left=insertNodes(inorder,inStart,inRoot-1,preorder,preStart+1,preStart+nodeInLeft,inMap);\n root->right=insertNodes(inorder,inRoot+1,inEnd,preorder,preStart+nodeInLeft+1,preEnd,inMap);\n return root;\n }\n TreeNode* bstFromPreorder(vector<int>& preorder) {\n vector<int> inorder=preorder;\n sort(inorder.begin(),inorder.end());\n map<int,int>inMap;\n for(int i=0;i<preorder.size();i++)\n inMap[inorder[i]]=i;\n TreeNode* root=insertNodes(inorder,0,inorder.size()-1,preorder,0,preorder.size()-1,inMap);\n return root;\n } \n \n// OPTIMAL [T(O(3N ~ N)) as we trave one node at max 3 times to check] [S(O(1))]\n \n TreeNode* buildTree(vector<int>preorder, int& index, int bound)\n {\n if(index==preorder.size() || preorder[index]>bound) return NULL;\n TreeNode* root=new TreeNode (preorder[index++]);\n root->left=buildTree(preorder,index,root->val);\n root->right=buildTree(preorder,index,bound);\n return root;\n }\n TreeNode* bstFromPreorder(vector<int>& preorder) { \n int index=0;\n return buildTree(preorder,index,INT_MAX);\n }\n};\n```\n\n## \u2705\uD83D\uDEA9 *Do comment if you Understood/not understood and consider upvoting if it helped* \u2705\uD83D\uDEA9 | 7 | 0 | ['Tree', 'Recursion', 'C'] | 2 |
construct-binary-search-tree-from-preorder-traversal | Java monotonic stack solution (Converting Medium to Easy problem) | java-monotonic-stack-solution-converting-z6p0 | Below solution uses monotonic stack technique.\n\n Inserting Left node: If the current node is smaller than the node in top of the stack, then it is guarenteed | anirudhbm11 | NORMAL | 2021-11-19T06:12:04.458097+00:00 | 2021-11-19T06:12:04.458131+00:00 | 531 | false | Below solution uses monotonic stack technique.\n\n* *Inserting Left node*: If the current node is smaller than the node in top of the stack, then it is guarenteed that node lies in left half of BST.\n* *Inserting Right node*: It gets little tricky in this situtation but if you are aware of the monotonic stack concept, this problem becomes trivial.\nOur current node cannot be directly inserted to the right of node which is in top of the stack, we need to find the node which is **lesser than our current node but greater than it\'s parent**. So keep removing nodes from the stack until you find that element in the stack. \n\t\n```\nclass Solution {\n public TreeNode bstFromPreorder(int[] preorder) {\n Stack<TreeNode> stk = new Stack<>();\n \n // Since first element of a preorder will always be a root\n TreeNode root = new TreeNode(preorder[0]); \n stk.push(root);\n \n // Iterating through the elements after the root\n for(int i=1;i<preorder.length;i++){\n TreeNode node = new TreeNode(preorder[i]);\n \n // If a given element is smaller than the top of the stack, it will always be its left child\n if(node.val < stk.peek().val){\n stk.peek().left = node;\n stk.push(node);\n }else{\n // Popping elements until the first lowest element after current node\'s greatest element is found\n TreeNode temp = null;\n while(stk.size() != 0 && stk.peek().val < node.val){\n temp = stk.pop();\n }\n \n // Joining current node to it\'s first lowest element from the root\n temp.right = node;\n stk.push(node);\n }\n }\n \n return root;\n }\n}\n``` | 7 | 0 | ['Monotonic Stack', 'Java'] | 2 |
construct-binary-search-tree-from-preorder-traversal | Clean Python recursion + binary search solution w/ explanation beats 87% | clean-python-recursion-binary-search-sol-d7en | Recursion solution\n\nclass Solution:\n def bstFromPreorder(self, preorder: List[int]) -> TreeNode:\n if not preorder:\n return None\n | chiou | NORMAL | 2020-05-24T07:53:38.790021+00:00 | 2020-05-24T07:58:06.941234+00:00 | 704 | false | Recursion solution\n```\nclass Solution:\n def bstFromPreorder(self, preorder: List[int]) -> TreeNode:\n if not preorder:\n return None\n root = TreeNode(preorder[0])\n if len(preorder) == 1:\n return root\n\n\t\t# binary search to find the start of right subtree\n left, right = 1, len(preorder) - 1\n while left < right:\n mid = (left + right) // 2\n if preorder[mid] < root.val:\n left = mid + 1\n else:\n right = mid\n\n\t\tif preorder[left] < root.val: # right subtree not found -> connect all elements as left subtree\n root.left = self.bstFromPreorder(preorder[1:])\n else: # connect left & right subtree\n root.right = self.bstFromPreorder(preorder[left:])\n root.left = self.bstFromPreorder(preorder[1:left])\n return root\n``` | 7 | 1 | ['Python'] | 0 |
construct-binary-search-tree-from-preorder-traversal | Simple Java solution | simple-java-solution-by-susmitasingh09-jkzz | \nclass Solution {\n public TreeNode bstFromPreorder(int[] preorder) {\n int n = preorder.length;\n if (n == 0) return null;\n TreeNode | susmitasingh09 | NORMAL | 2020-04-20T11:39:01.034084+00:00 | 2020-04-20T11:39:01.034133+00:00 | 718 | false | ```\nclass Solution {\n public TreeNode bstFromPreorder(int[] preorder) {\n int n = preorder.length;\n if (n == 0) return null;\n TreeNode res = new TreeNode(preorder[0]);\n \n for (int i = 1; i < n; i++) {\n res = insert(res, preorder[i]);\n }\n return res;\n }\n \n private TreeNode insert(TreeNode root, int val) {\n if (root == null) return new TreeNode(val);\n if (val <= root.val) {\n root.left = insert(root.left, val);\n } else {\n root.right = insert(root.right, val);\n }\n return root;\n }\n}\n``` | 7 | 0 | [] | 2 |
construct-binary-search-tree-from-preorder-traversal | Python easy to understand 96% faster (iterative) | python-easy-to-understand-96-faster-iter-5rhg | \n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, x):\n# self.val = x\n# self.left = None\n# self.righ | pujanm | NORMAL | 2020-04-20T07:57:46.668039+00:00 | 2020-04-20T18:07:38.177821+00:00 | 2,393 | false | ```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, x):\n# self.val = x\n# self.left = None\n# self.right = None\n\nclass Solution:\n def bstFromPreorder(self, preorder: List[int]) -> TreeNode:\n if len(preorder) == 0:\n return\n \n root = TreeNode(preorder[0])\n \n def insert(val, node):\n # we insert a single element using this function\n \n while True:\n # Here we check whether root\'s value is greater than the given value.\n # If yes then try to insert it in the left sub-tree.\n if node.val > val:\n # Here we check if the left child does not exist then we add a left child with value = val and break the loop\n if not node.left:\n node.left = TreeNode(val)\n break\n # Since the left child exists we move towards the left.\n else:\n node = node.left\n # This will work similar to the left child.\n else:\n if not node.right:\n node.right = TreeNode(val)\n break\n else:\n node = node.right\n head = root \n for i in range(1, len(preorder)):\n # Here we reset the head pointer so we are the top of the tree again.\n head = root\n insert(preorder[i], head)\n \n return head\n``` | 7 | 0 | ['Binary Search', 'Tree', 'Python', 'Python3'] | 3 |
construct-binary-search-tree-from-preorder-traversal | 6 lines Javascript solution | 6-lines-javascript-solution-by-dnshi-8fiy | javascript\n/**\n * Definition for a binary tree node.\n * function TreeNode(val) {\n * this.val = val;\n * this.left = this.right = null;\n * }\n */\n/ | dnshi | NORMAL | 2019-06-30T00:06:17.617133+00:00 | 2019-06-30T00:06:17.617216+00:00 | 711 | false | ```javascript\n/**\n * Definition for a binary tree node.\n * function TreeNode(val) {\n * this.val = val;\n * this.left = this.right = null;\n * }\n */\n/**\n * @param {number[]} preorder\n * @return {TreeNode}\n */\nvar bstFromPreorder = function(preorder) {\n if (!preorder.length) return null\n \n const [root, ...rest] = preorder\n \n const rootNode = new TreeNode(root)\n rootNode.left = bstFromPreorder(rest.filter(n => n < root))\n rootNode.right = bstFromPreorder(rest.filter(n => n > root))\n \n return rootNode\n};\n``` | 7 | 1 | ['JavaScript'] | 4 |
construct-binary-search-tree-from-preorder-traversal | [C++] Easy to understand Solution with detail approach | c-easy-to-understand-solution-with-detai-acxv | Intuition\nThe problem requires constructing a binary search tree (BST) from a given preorder traversal of its nodes. The code uses a recursive approach to buil | Aditya00 | NORMAL | 2023-05-29T10:06:47.695501+00:00 | 2023-05-29T10:08:30.452287+00:00 | 2,165 | false | # Intuition\nThe problem requires constructing a binary search tree (BST) from a given preorder traversal of its nodes. The code uses a recursive approach to build the BST by dividing the problem into smaller subproblems.\n\n# Approach\n1. The bstFromPreorder function takes the given preorder traversal as input.\n2. It creates a copy of the preorder traversal and sorts it to obtain the inorder traversal. This is done to determine the left and right subtrees of each node.\n3. It initializes the start index for the preorder traversal as 0 and calls the build function.\n4. The build function takes the preorder traversal, inorder traversal, start index, and the range of indices to process as input.\n5. In the build function:\n - The base case checks if the start index exceeds the end index, indicating that there are no more nodes to process. In this case, it returns NULL.\n - It creates a new node with the value at the current start index.\n - It searches for the index of the current node\'s value in the inorder traversal.\n - It increments the start index to process the next node in the preorder traversal.\n - It recursively builds the left and right subtrees by calling the build function with the appropriate ranges of indices.\n - Finally, it returns the root node of the constructed subtree.\n6. The build function is called recursively to construct the entire binary search tree.\n7. The constructed binary search tree is returned as the result.\n\n# Complexity\n- Time complexity:\nThe overall time complexity is O(n log n + n) = O(n log n).\n\n- Space complexity:\nThe overall space complexity is O(n + n) = O(n).\n\n# Code\n```\nclass Solution {\npublic:\n // Helper function to search for an element in the given vector\n int search(vector<int>& in, int t) {\n for (int i = 0; i < in.size(); i++) {\n if (in[i] == t)\n return i;\n }\n return -1;\n }\n\n // Recursive function to build a binary tree from preorder and inorder traversals\n TreeNode* build(vector<int>& pre, vector<int>& in, int& start, int ins, int ine) {\n // Base case: When the start index exceeds the end index, there are no more nodes to process\n if (ins > ine)\n return NULL;\n\n // Create a new node with the value at the current start index\n TreeNode* root = new TreeNode(pre[start]);\n\n // Find the index of the current node in the inorder traversal\n int ind = search(in, pre[start]);\n\n // Increment the start index to process the next node in the preorder traversal\n start++;\n\n // Recursively build the left and right subtrees\n root->left = build(pre, in, start, ins, ind - 1);\n root->right = build(pre, in, start, ind + 1, ine);\n\n // Return the root node of the binary tree\n return root;\n }\n\n // Function to construct a binary search tree from a preorder traversal\n TreeNode* bstFromPreorder(vector<int>& pre) {\n // Create a copy of the preorder traversal\n vector<int> in = pre;\n\n // Sort the copy to obtain the inorder traversal\n sort(in.begin(), in.end());\n\n // Start index for the preorder traversal\n int start = 0;\n\n // Build the binary tree recursively using the preorder and inorder traversals\n return build(pre, in, start, 0, in.size() - 1);\n }\n};\n\n``` | 6 | 0 | ['Graph', 'Binary Search Tree', 'Recursion', 'Binary Tree', 'C++'] | 0 |
construct-binary-search-tree-from-preorder-traversal | C++ | 100% faster | O(n) recursive solution | c-100-faster-on-recursive-solution-by-am-ecm5 | \n TreeNode* build(vector<int> pre, int s, int e){\n if(s>e) return NULL;\n TreeNode* root = new TreeNode(pre[s]);\n int idx;\n for(int i=s+1; i<=e | ama29n | NORMAL | 2021-10-13T19:12:30.740224+00:00 | 2021-10-13T19:12:30.740255+00:00 | 135 | false | ```\n TreeNode* build(vector<int> pre, int s, int e){\n if(s>e) return NULL;\n TreeNode* root = new TreeNode(pre[s]);\n int idx;\n for(int i=s+1; i<=e; i++){\n if(pre[i]>pre[s]){\n idx = i;\n break; }\n\t}\n root->left = build(pre, s+1, idx-1);\n root->right = build(pre, idx, e);\n return root;\n }\n \n TreeNode* bstFromPreorder(vector<int>& preorder) {\n TreeNode* newroot = build(preorder, 0, preorder.size()-1);\n return newroot;\n }\n``` | 6 | 2 | [] | 0 |
construct-binary-search-tree-from-preorder-traversal | Java || Easy Approach with Explanation || Recursive || Postorder | java-easy-approach-with-explanation-recu-5uhv | \nclass Solution \n{\n public TreeNode bstFromPreorder(int[] preorder) \n {\n if(root == null)//base case when we are provide with the null graph \ | swapnilGhosh | NORMAL | 2021-07-27T06:53:48.437980+00:00 | 2021-07-27T06:53:48.438006+00:00 | 636 | false | ```\nclass Solution \n{\n public TreeNode bstFromPreorder(int[] preorder) \n {\n if(root == null)//base case when we are provide with the null graph \n return null;\n \n return constructBST(preorder, 0, preorder.length-1);//it returns the address of the new root of the BST, with all the references of its children \n }\n public TreeNode constructBST(int[] preorder, int start, int end)\n {//we are doing the postorder traversal, in order to know the child first and then the parent //divide and conqure approach is used\n \n if(start > end)//base case of recursion when we reach the wrong index(null node)\n return null;\n \n int data= preorder[start];//current root, we first deal witth its child \n \n int index;//global index in order to find wheere the actual break happened \n \n for(index= start; index <= end; index++)\n {//we want to find the next greater of root, because preorder which is provided to us is for a BST\n //as we know that the right side of BST contains value greater than the root \n \n if(preorder[index] > preorder[start])//finding the starting index of right subtree \n break;\n }\n \n //storing the reference for the root, to creates its node with sufficient data of child \n \n TreeNode left= constructBST(preorder, start+1, index - 1);//recurssively traversing the left subtree in search of child//data of child must be less than root\n \n TreeNode right= constructBST(preorder, index, end);//recurssively traversing the right subtree in search of child//data of child must be greater than root//storing the reference for the root \n \n TreeNode node= new TreeNode(data, left, right);//creating the node after nowing the status of left and right children \n return node;//returning the node in order to maintain the backward link\n }\n}//please do Upvote, it helps a lot \n``` | 6 | 0 | ['Depth-First Search', 'Recursion', 'Java'] | 0 |
construct-binary-search-tree-from-preorder-traversal | Easy Recursive solution [C++] | easy-recursive-solution-c-by-harshghlt25-om2w | \nclass Solution {\npublic:\n TreeNode* insert(TreeNode* root, int value)\n {\n if(root==NULL)\n return new TreeNode(value);\n if | harshghlt25 | NORMAL | 2021-05-11T18:36:09.226027+00:00 | 2021-05-11T18:36:09.226071+00:00 | 669 | false | ```\nclass Solution {\npublic:\n TreeNode* insert(TreeNode* root, int value)\n {\n if(root==NULL)\n return new TreeNode(value);\n if(value<root->val)\n root->left=insert(root->left,value);\n if(value>root->val)\n root->right=insert(root->right,value);\n return root;\n }\n \n TreeNode* bstFromPreorder(vector<int>& preorder) \n {\n TreeNode* root=NULL; \n for(int i=0;i<preorder.size();i++)\n root=insert(root,preorder[i]);\n \n return root;\n }\n};\n``` | 6 | 1 | ['Recursion', 'C', 'C++'] | 1 |
construct-binary-search-tree-from-preorder-traversal | Python - Concise Solution | python-concise-solution-by-nuclearoreo-zmmm | You pop the first value in the list and make it into node. Next you split the list of values to less than the node as left and larger than the node has right. C | nuclearoreo | NORMAL | 2020-04-20T19:15:47.545337+00:00 | 2020-04-21T13:15:59.685228+00:00 | 740 | false | You pop the first value in the list and make it into node. Next you split the list of values to less than the node as left and larger than the node has right. Continue on untill there\'s no numbers to use. **Note**, you have to set the `index` variable to the length of the list for the case that there\'s no number larger than the node. \n\n```python\nclass Solution:\n def bstFromPreorder(self, preorder: List[int]) -> TreeNode:\n if not preorder: return None\n \n node = TreeNode(preorder.pop(0))\n \n index = len(preorder)\n for i, val in enumerate(preorder):\n if val > node.val:\n index = i\n break\n \n node.left = self.bstFromPreorder(preorder[:index])\n node.right = self.bstFromPreorder(preorder[index:])\n \n return node\n```\n\n**Time:** `O(n*log(n))`\n**Space:**`O(n)` | 6 | 0 | ['Depth-First Search', 'Python'] | 1 |
construct-binary-search-tree-from-preorder-traversal | JS easy to read preorder traversal (92%runtime/80%space) | js-easy-to-read-preorder-traversal-92run-ydsm | \nvar bstFromPreorder = function(preorder) {\n let root = new TreeNode(preorder[0])\n for (let i = 1; i < preorder.length; i++) {\n appendToTreeNod | GSWE | NORMAL | 2020-04-20T16:02:43.127520+00:00 | 2020-04-20T16:02:43.127602+00:00 | 268 | false | ```\nvar bstFromPreorder = function(preorder) {\n let root = new TreeNode(preorder[0])\n for (let i = 1; i < preorder.length; i++) {\n appendToTreeNode(root, preorder[i])\n }\n return root\n};\n\nfunction appendToTreeNode(root, val) {\n if (val <= root.val) {\n if (root.left) appendToTreeNode(root.left,val);\n else root.left = new TreeNode(val);\n } else {\n if (root.right) appendToTreeNode(root.right,val);\n else root.right = new TreeNode(val);\n }\n}\n``` | 6 | 0 | [] | 1 |
construct-binary-search-tree-from-preorder-traversal | simple recursive insert in bst in CPP | simple-recursive-insert-in-bst-in-cpp-by-vcnw | \nTreeNode* Insert(TreeNode* root,int data){\n if(root == NULL){\n root = new TreeNode(data);\n }\n else if(root->val > data){\n | gowtham_1 | NORMAL | 2020-04-20T09:17:01.546968+00:00 | 2020-04-20T09:17:01.547002+00:00 | 391 | false | ```\nTreeNode* Insert(TreeNode* root,int data){\n if(root == NULL){\n root = new TreeNode(data);\n }\n else if(root->val > data){\n root->left = Insert(root->left,data);\n }\n else{\n root->right = Insert(root->right,data);\n }\n return root;\n }\n \n TreeNode* bstFromPreorder(vector<int>& preorder) {\n TreeNode* root = NULL;\n for(int x:preorder){\n //tree get modifies as builds,we need root node for further queries \n root = Insert(root,x);\n }\n return root;\n }\n``` | 6 | 0 | [] | 0 |
construct-binary-search-tree-from-preorder-traversal | Python O(N) Stack based Solution beat 96% | python-on-stack-based-solution-beat-96-b-uujt | The basic idea is using a Stack to keep values, everytime you meet a new value smaller than the end of the stack, you know this new value should be left node of | tanzhenyu2015 | NORMAL | 2019-10-18T03:28:10.017197+00:00 | 2019-10-18T03:29:41.558311+00:00 | 351 | false | The basic idea is using a Stack to keep values, everytime you meet a new value smaller than the end of the stack, you know this new value should be left node of it; Otherwise keep popping the stack until you find the last node whose value is smaller than the new value, you know this new value should be right node of it.\n\n```\nif not preorder:\n\treturn None\nroot = TreeNode(preorder[0])\nstack = [root]\nfor num in preorder[1:]:\n\tcur_node = TreeNode(num)\n\tif stack[-1].val > num:\n\t\tstack[-1].left = cur_node\n\t\tstack.append(cur_node)\n\telse:\n\t\twhile True:\n\t\t\tprev_node = stack.pop()\n\t\t\tif len(stack) == 0 or stack[-1].val > num:\n\t\t\t\tbreak\n\t\tprev_node.right = cur_node\n\t\tstack.append(cur_node)\n\nreturn root\n``` | 6 | 0 | [] | 2 |
construct-binary-search-tree-from-preorder-traversal | 3 BEST C++ solutions || Using INT_MAX, recursive and iterative approach || Beast 100% !! | 3-best-c-solutions-using-int_max-recursi-ekjw | Code\n\n// Solution 1 - Using max bound\nclass Solution {\npublic:\n TreeNode* bstFromPreorder(vector<int>& pre) {\n int i = 0;\n return build( | prathams29 | NORMAL | 2023-08-30T02:18:50.547037+00:00 | 2023-08-30T02:18:50.547054+00:00 | 548 | false | # Code\n```\n// Solution 1 - Using max bound\nclass Solution {\npublic:\n TreeNode* bstFromPreorder(vector<int>& pre) {\n int i = 0;\n return build(pre, i, INT_MAX);\n }\n\n TreeNode* build(vector<int>& pre, int& i, int bound) {\n if (i == pre.size() || pre[i] > bound) \n return NULL;\n \n TreeNode* root = new TreeNode(pre[i++]);\n root->left = build(pre, i, root->val);\n root->right = build(pre, i, bound);\n \n return root;\n }\n};\n\n// Solution 2 - Recursive approach\nclass Solution {\npublic:\n TreeNode* bstFromPreorder(vector<int>& preorder) {\n if(preorder.size() == 0)\n return NULL;\n \n TreeNode* root = new TreeNode(preorder[0]);\n if(preorder.size() == 1)\n return root;\n \n vector<int> left, right;\n for(int i=0; i<preorder.size(); i++){\n if(preorder[i] > preorder[0])\n right.push_back(preorder[i]);\n else if(preorder[i]<preorder[0])\n left.push_back(preorder[i]);\n }\n\n root->left = bstFromPreorder(left);\n root->right = bstFromPreorder(right);\n \n return root;\n }\n};\n\n// Solution 3 - Iterative solution\nclass Solution {\npublic:\n TreeNode* bstFromPreorder(vector<int>& preorder) {\n if(preorder.size() == 0)\n return NULL;\n \n TreeNode* root = new TreeNode(preorder[0]);\n\n for(int i=1; i<preorder.size(); i++){ \n bool done = false; \n TreeNode* curr = root;\n\n while(done == false){\n if(preorder[i] < curr->val){ \n if (curr->left == NULL){ \n curr->left = new TreeNode(preorder[i]);\n done = true; \n }\n else \n curr = curr->left;\n }\n else{ \n if(curr->right == NULL){ \n curr->right = new TreeNode(preorder[i]);\n done = true; \n }\n else\n curr = curr->right;\n }\n }\n }\n return root;\n }\n};\n``` | 5 | 0 | ['Array', 'Stack', 'Tree', 'Binary Search Tree', 'Monotonic Stack', 'Binary Tree', 'C++'] | 0 |
construct-binary-search-tree-from-preorder-traversal | Superb logic | superb-logic-by-ganjinaveen-27of | \nclass Solution:\n def bstFromPreorder(self, preorder: List[int]) -> Optional[TreeNode]:\n inorder=sorted(preorder)\n def build(preorder,inord | GANJINAVEEN | NORMAL | 2023-07-11T08:53:40.666442+00:00 | 2023-07-11T08:53:40.666462+00:00 | 675 | false | ```\nclass Solution:\n def bstFromPreorder(self, preorder: List[int]) -> Optional[TreeNode]:\n inorder=sorted(preorder)\n def build(preorder,inorder):\n if not preorder or not inorder:\n return \n root=TreeNode(preorder[0])\n mid=inorder.index(preorder[0])\n root.left=build(preorder[1:mid+1],inorder[:mid])\n root.right=build(preorder[mid+1:],inorder[mid+1:])\n return root\n return build(preorder,inorder)\n```\n# please upvote me it would encourage me alot\n | 5 | 0 | ['Python', 'Python3'] | 1 |
construct-binary-search-tree-from-preorder-traversal | ✔ C++ | All Tree Construction based Questions at a single place | 2 Approaches of each | c-all-tree-construction-based-questions-htid1 | \n### Table of Content :\n\n Construct BST from Preorder Traversal\n\t Recursive Approach\n\t Iterative Approach using Stack\n Construct BST from Postorder Trav | HustlerNitin | NORMAL | 2022-08-30T18:05:24.328527+00:00 | 2022-08-30T18:43:58.612058+00:00 | 451 | false | ***\n### Table of Content :\n***\n* Construct **BST** from **Preorder** Traversal\n\t* Recursive Approach\n\t* Iterative Approach using Stack\n* Construct **BST** from **Postorder** Traversal\n\t* Iterative Approach using Stack\n\t* Recursive ( using sorted Inorder property of BST )\n* Construct **Binary Tree** using **inorder** and **preorder**\n\t* Recursive Approach\n\t* Iterative Approach\n* Construct **Binary Tree** using **inorder** and **postorder**\n\t* Recursive Approach\n\n----\n\u2714 ***All codes are running successfully !***\n\n----\n```\n\n Definition for a binary tree node.\n struct TreeNode {\n int val;\n TreeNode *left;\n TreeNode *right;\n TreeNode() : val(0), left(nullptr), right(nullptr) {}\n TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n };\n```\n\n----\n**1. Construct BST from Preorder Traversal**\n* Recursive Approach\n* Iterative Approach using Stack\n\n----\n> **Recursive Approach :**\n\n**Time Complexity : `O(N)`** ( Traversing all node values )\n**Space Complexity : `O(1)`** ( ignore new nodes that i have created for construction of tree ) + ( ignore Recursion stack space ) \n```\nclass Solution {\npublic:\n \n int i = 0;\n TreeNode* bstFromPreorder(vector<int>& pre, int max_val = INT_MAX) // default Argument\n {\n if (i == pre.size() || pre[i] > max_val) \n return NULL;\n \n TreeNode* root = new TreeNode(pre[i++]);\n \n root->left = bstFromPreorder(pre, root->val);\n root->right = bstFromPreorder(pre, max_val); \n // cout<<max_val<<endl;\n return root;\n }\n};\n```\n\n----\n> **Iterative Approach : Stack Solution** \n\n**Time Complexity : `O(N)`** ( Traversing all node values )\n**Space Complexity : `O(N)`** ( Extra Stack ) + ( ignore new nodes that i have created for construction of tree ) \n**Note :** It is same as Iterative traversal of preorder.\n```\nclass Solution {\npublic:\n\n TreeNode* bstFromPreorder(vector<int>& preorder){\n \n TreeNode *root = new TreeNode(preorder[0]);\n stack<TreeNode*>st;\n st.push(root);\n \n for (int i = 1; i < preorder.size(); i++) \n {\n TreeNode *temp = new TreeNode(preorder[i]);\n if (temp->val < st.top()->val)\n {\n st.top()->left = temp;\n st.push(temp); // push\n } \n else \n {\n TreeNode *prev;\n while (!st.empty() and st.top()->val < temp->val) \n { \n // sabse chhota chahiye\n // isliye pop karte raho\n prev = st.top(); // dry run this = pre = [8,5,4,1,7,10,12] , you will understand\n st.pop();\n }\n prev->right = temp; \n st.push(temp); // push\n } \n }\n return root;\n }\n};\n```\n\n----\n**2. Construct BST from Postorder Traversal**\n* Iterative Approach Using Stack\n* Recursive ( using sorted Inorder property of BST ) \n\n----\n> **Iterative Approach :** **Using Stack**\n\n**Time Complexity : `O(N)`** ( Traversing all node values )\n**Space Complexity : `O(N)`** ( Extra Stack ) + ( ignore new nodes that i have created for construction of tree ) \n```\n// Whole code similar to construction of BST from preorder using Stack\n// DRY run on [1, 7, 5, 50, 40, 10] to understand better\nNode* make_BST(vector<int>&post)\n{\n int n=post.size();\n Node *root = new Node(post[n-1]);\n stack<Node*>st;\n st.push(root);\n \n for(int i=n-2;i>=0;i--)\n {\n Node* temp = new Node(post[i]);\n if(st.top()->data < temp->data)\n {\n st.top()->right = temp;\n st.push(temp);\n }\n else\n {\n Node* prev;\n while(!st.empty() and st.top()->data > temp->data){\n prev = st.top();\n st.pop();\n }\n prev->left = temp;\n st.push(temp);\n }\n }\n return root;\n}\n\nNode *constructTree (int post[], int size)\n{\n vector<int>pos(post, post+size);\n return make_BST(pos);\n}\n```\n\n----\n> **Recursive ( using sorted Inorder property of BST )**\n\n**Time Complexity : `O(NLog(N)) + O(N)`** ( Sorting + Traversing all node values )\n**Space Complexity : `O(N)`** ( vector for sorting ) + ( ignore new nodes that i have created for construction of tree ) + ( ignore Recursion stack space ) \n```\nNode* make_BST(vector<int>&in, int s, int e)\n{\n if(s>e)\n return NULL;\n \n int mid = s+(e-s)/2; \n Node* root = new Node(in[mid]);\n \n root->left = make_BST(in, s, mid-1);\n root->right = make_BST(in, mid+1, e);\n return root;\n}\n\nNode *constructTree(int post[], int n)\n{\n sort(post, post+n);\n vector<int>inorder(post, post+n); // inorder traversal\n \n return make_BST(inorder, 0, n-1);\n}\n```\n\n**OK, BST is end here !** \uD83D\uDC4F\n\n----\n**Now comes to Binary trees only**\n\n----\n**3. Construct Binary Tree using inorder and preorder**\n\n> **1. Recursive Approach :**\n\n**Time Complexity : `O(N)`** ( Traversing all node values )\n**Space Complexity : `O(N)`** ( map for inorder ) + ( ignore new nodes that i have created for construction of tree ) + ( ignore Recursion stack space )\n```\nclass Solution {\n \npublic:\n \n unordered_map<int, int> findIndex; // store index of every element present in inorder\n TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {\n for(int i = 0; i < inorder.size(); i++) \n findIndex[inorder[i]] = i; \n return build(preorder, 0, inorder.size() - 1);\n }\n \n int i = 0;\n TreeNode* build(vector<int>& preorder, int start, int end)\n { \n if(start > end) \n return NULL; \n \n // when start <= end\n int idx = findIndex[preorder[i]];\n TreeNode *root = new TreeNode(preorder[i++]);\n \n root->left = build(preorder, start, idx - 1); \n root->right = build(preorder, idx + 1, end); \n return root;\n }\n};\n```\n\n----\n> **2. Iterative Approach :**\n\n**Time Complexity : `O(N)`** ( Traversing all node values )\n**Space Complexity : `O(N)`** ( Extra Stack ) + ( ignore new nodes that i have created for construction of tree ) \n```\nclass Solution {\npublic: \n \n TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) \n {\n int n = preorder.size();\n int pre_index=0, in_index=0, flag=0;\n \n stack<TreeNode*> st;\n TreeNode * root = new TreeNode(preorder[pre_index]);\n pre_index++;\n \n st.push(root);\n TreeNode *prev = root;\n \n while(pre_index < n)\n {\n if(!st.empty() && inorder[in_index] == st.top()->val)\n {\n prev = st.top();\n st.pop();\n in_index++;\n flag = 1;\n }\n else\n {\n TreeNode * node = new TreeNode(preorder[pre_index]);\n if(flag == 0){\n prev->left = node;\n prev = prev->left;\n }\n else\n {\n prev->right = node;\n prev = prev->right;\n flag = 0;\n }\n st.push(node);\n pre_index++;\n }\n }\n return root;\n }\n};\n```\n\n----\n**4. Construct Binary Tree using inorder and postorder**\n\n> **Recursive Approach :**\n\n**Time Complexity : `O(N)`** ( Traversing all node values )\n**Space Complexity : `O(N)`** ( map for inorder ) + ( ignore new nodes that i have created for construction of tree ) + ( ignore Recursion stack space )\n```\nclass Solution {\npublic:\n \n unordered_map<int, int> mp;\n TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) \n {\n int n = inorder.size();\n for(int i = 0; i < n; i++) \n mp[inorder[i]] = i;\n \n int postIdx = n-1;\n return build(inorder, postorder, 0, n-1, postIdx);\n }\n\n TreeNode* build(vector<int>& in, vector<int>& post, int inStart, int inEnd, int& postIdx) \n {\n if(inStart > inEnd) \n return NULL;\n \n TreeNode* root = new TreeNode(post[postIdx--]);\n int inIdx = mp[root -> val];\n \n root -> right = build(in, post, inIdx+1, inEnd, postIdx);\n root -> left = build(in, post, inStart, inIdx-1, postIdx);\n return root;\n }\n};\n```\n\n----\n***Thanks for Upvoting!***\nYour Upvotes motivates me a lot to write such type of simple and clean post for helping the Leetcode Community.\n**Feel free to comment anything related to above questions !**\n\uD83D\uDE42\n | 5 | 0 | ['Stack', 'Binary Search Tree', 'C', 'Binary Tree', 'C++'] | 0 |
construct-binary-search-tree-from-preorder-traversal | [Python3] O(n) Time Solution 2 Approaches (using Stack and Sorted Preorder) | python3-on-time-solution-2-approaches-us-cxte | Approach 1 - BST from Preorder and Inorder(Sorted Preorder) arrays\n\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, l | SamirPaulb | NORMAL | 2022-06-02T14:30:35.089626+00:00 | 2022-06-02T14:31:14.682379+00:00 | 812 | false | Approach 1 - **BST from Preorder and Inorder(Sorted Preorder) arrays**\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def bstFromPreorder(self, preorder: List[int]) -> Optional[TreeNode]:\n inorder = sorted(preorder)\n inorderIndexDic = {ch : i for i, ch in enumerate(inorder)}\n self.rootIndex = 0\n \n def solve(l, r):\n if l > r: return None\n root = TreeNode(preorder[self.rootIndex])\n self.rootIndex += 1\n \n i = inorderIndexDic[root.val]\n root.left = solve(l, i-1)\n root.right = solve(i+1, r)\n return root\n \n return solve(0, len(inorder)-1)\n\t\t\n# Time: O(N log(N))\n# Space: O(N)\n```\n\nApproach 2 - **Using Stack**\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def bstFromPreorder(self, preorder: List[int]) -> Optional[TreeNode]:\n root = TreeNode(preorder[0])\n parent = root\n stack = [parent]\n \n for v in preorder[1:]:\n newNode = TreeNode(v)\n if stack and newNode.val < parent.val:\n parent.left = newNode\n stack.append(newNode)\n parent = newNode\n else:\n while stack and stack[-1].val < newNode.val:\n parent = stack.pop()\n parent.right = newNode\n stack.append(newNode)\n parent = newNode\n \n return root\n \n \n# Time: O(N)\n# Space: O(N)\n\n``` | 5 | 0 | ['Array', 'Stack', 'Binary Search Tree', 'Sorting', 'Iterator', 'Python', 'Python3'] | 1 |
construct-binary-search-tree-from-preorder-traversal | C++ || recursive solution || short and clean!!! | c-recursive-solution-short-and-clean-by-xpka9 | \nclass Solution {\npublic:\n TreeNode* builtTree(vector<int>& preorder, int &prevIndex, int &boundaryVal)\n {\n if(prevIndex>=preorder.size() || p | priya_07 | NORMAL | 2022-02-02T19:00:57.404835+00:00 | 2022-02-02T19:00:57.404863+00:00 | 402 | false | ```\nclass Solution {\npublic:\n TreeNode* builtTree(vector<int>& preorder, int &prevIndex, int &boundaryVal)\n {\n if(prevIndex>=preorder.size() || preorder[prevIndex]>=boundaryVal)\n return NULL;\n TreeNode* root=new TreeNode(preorder[prevIndex]);\n prevIndex++;\n root->left=builtTree(preorder, prevIndex, root->val);\n root->right=builtTree(preorder, prevIndex, boundaryVal);\n return root;\n }\n TreeNode* bstFromPreorder(vector<int>& preorder) {\n int prevIndex=0, boundaryVal=1001;\n return builtTree(preorder, prevIndex, boundaryVal);\n }\n};\n```\n**Upvote it if you find helpful** | 5 | 0 | ['Binary Search Tree', 'Recursion', 'C', 'C++'] | 0 |
construct-binary-search-tree-from-preorder-traversal | 0 ms, faster than 100.00% ; 13 MB, less than 90.67% [C++] | 0-ms-faster-than-10000-13-mb-less-than-9-orcn | ```\n/ first element is always the root. \nIterate over the rest array elements & \nperform bst insertion \ntaking first element as root every time /\n\nclass S | _ak_47 | NORMAL | 2020-12-05T21:11:25.625842+00:00 | 2020-12-05T21:11:25.625874+00:00 | 334 | false | ```\n/* first element is always the root. \nIterate over the rest array elements & \nperform bst insertion \ntaking first element as root every time */\n\nclass Solution {\nprivate:\n void insert(TreeNode* root,int val){\n TreeNode* ptr=root,*prev=NULL;\n while(ptr){\n if(val<ptr->val){\n prev=ptr;\n ptr=ptr->left;\n }\n else if(val>ptr->val){\n prev=ptr;\n ptr=ptr->right;\n }\n }\n if(val<prev->val){\n prev->left=new TreeNode(val);\n }\n else{\n prev->right=new TreeNode(val);\n }\n }\npublic:\n TreeNode* bstFromPreorder(vector<int>& preorder) {\n int n=preorder.size();\n if(n==0)return NULL;\n TreeNode* root=new TreeNode(preorder[0]);\n for(int i=1;i<n;i++){\n insert(root,preorder[i]);\n }\n return root;\n }\n}; | 5 | 1 | ['Binary Search Tree', 'C'] | 0 |
construct-binary-search-tree-from-preorder-traversal | Simple C++ solution - Easy to understand | simple-c-solution-easy-to-understand-by-f0dcx | \n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0) | sanjay_prabhu | NORMAL | 2020-05-24T14:21:54.116838+00:00 | 2020-05-24T14:21:54.116873+00:00 | 569 | false | ```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n TreeNode* insertBST(TreeNode* root,int key)\n {\n if(root==NULL)\n {\n return new TreeNode(key);\n }\n \n if(key<root->val)\n {\n root->left = insertBST(root->left,key);\n }\n else if(key>root->val)\n {\n root->right = insertBST(root->right,key);\n }\n \n return root;\n }\n TreeNode* bstFromPreorder(vector<int>& preorder) \n {\n TreeNode* root = new TreeNode();\n root=NULL;\n \n for(auto i=preorder.begin();i!=preorder.end();i++)\n {\n root=insertBST(root,*i);\n }\n \n return root;\n }\n};\n``` | 5 | 0 | [] | 0 |
construct-binary-search-tree-from-preorder-traversal | C++ | Recursive 100% | c-recursive-100-by-ruddrd09-l1lk | ```\nclass Solution {\npublic:\n TreeNode tree(vector& preorder, int i, int j) {\n if(i > j) {\n return NULL;\n }\n TreeNode | ruddrd09 | NORMAL | 2020-05-24T07:24:39.064554+00:00 | 2020-05-24T07:24:39.064611+00:00 | 553 | false | ```\nclass Solution {\npublic:\n TreeNode* tree(vector<int>& preorder, int i, int j) {\n if(i > j) {\n return NULL;\n }\n TreeNode* root = new TreeNode(preorder[i]);\n if(i == j) {\n return root;\n }\n int k = i+1;\n while(k <= j) {\n if(preorder[k] > preorder[i]) {\n break;\n }\n k++;\n }\n root->left = tree(preorder,i+1,k-1);\n root->right = tree(preorder,k,j);\n return root;\n }\n \n TreeNode* bstFromPreorder(vector<int>& preorder) {\n if(preorder.size() == 0) {\n return NULL;\n }\n return tree(preorder, 0, preorder.size()-1);\n }\n}; | 5 | 1 | ['C'] | 0 |
construct-binary-search-tree-from-preorder-traversal | Python3. Simple, clean and easy to understand solution | python3-simple-clean-and-easy-to-underst-ecas | ```\nclass Solution:\n def bstFromPreorder(self, preorder):\n root = None\n \n for e in preorder:\n root = self.insert(root, e)\n | abstractart | NORMAL | 2020-04-20T18:40:50.129132+00:00 | 2020-04-25T16:55:05.147219+00:00 | 469 | false | ```\nclass Solution:\n def bstFromPreorder(self, preorder):\n root = None\n \n for e in preorder:\n root = self.insert(root, e)\n \n return root\n\n \n def insert(self, node, val):\n if node is None:\n return TreeNode(val) \n \n if val < node.val:\n node.left = self.insert(node.left, val)\n else:\n node.right = self.insert(node.right, val)\n \n return node | 5 | 0 | ['Python3'] | 0 |
construct-binary-search-tree-from-preorder-traversal | Python beats 99% | python-beats-99-by-palash2594-ziiu | \n# Definition for a binary tree node.\n# class TreeNode(object):\n# def __init__(self, x):\n# self.val = x\n# self.left = None\n# s | palash2594 | NORMAL | 2019-06-20T03:29:12.786157+00:00 | 2019-06-20T03:29:12.786192+00:00 | 505 | false | ```\n# Definition for a binary tree node.\n# class TreeNode(object):\n# def __init__(self, x):\n# self.val = x\n# self.left = None\n# self.right = None\n\nclass Solution(object):\n \n def insert(self, root, val):\n if val <= root.val:\n if root.left != None:\n self.insert(root.left, val)\n else:\n root.left = TreeNode(val)\n elif root.right != None:\n self.insert(root.right, val)\n else:\n root.right = TreeNode(val)\n \n def bstFromPreorder(self, preorder):\n """\n :type preorder: List[int]\n :rtype: TreeNode\n """\n root = TreeNode(preorder[0])\n \n for i in range(1, len(preorder)):\n self.insert(root, preorder[i])\n \n return root\n \n``` | 5 | 1 | [] | 2 |
construct-binary-search-tree-from-preorder-traversal | JS recursive | js-recursive-by-chux0519-0e7o | javascript\nfunction TreeNode(val) {\n this.val = val;\n this.left = this.right = null;\n}\nvar bstFromPreorder = function (preorder) {\n i | chux0519 | NORMAL | 2019-03-12T11:57:29.889717+00:00 | 2019-03-12T11:57:29.889758+00:00 | 338 | false | ```javascript\nfunction TreeNode(val) {\n this.val = val;\n this.left = this.right = null;\n}\nvar bstFromPreorder = function (preorder) {\n if (preorder.length === 0) return null\n if (preorder.length === 1) return new TreeNode(preorder[0])\n let root = new TreeNode(preorder[0])\n let left = bstFromPreorder(preorder.slice(1).filter(each => each < preorder[0]))\n let right = bstFromPreorder(preorder.slice(1).filter(each => each > preorder[0]))\n if (root) root.left = left;\n if (root) root.right = right;\n return root\n};\n``` | 5 | 0 | [] | 1 |
construct-binary-search-tree-from-preorder-traversal | Java/C# Recursive solution beats 100% with clear explanation | javac-recursive-solution-beats-100-with-vxpfx | Thoughts: \nThe input array is the preorder traversal of a BST. \n1.preorder[0] is the root of BST\n2.The sub array from preorder[0] to the first element that i | skrmao | NORMAL | 2019-03-10T20:16:02.019867+00:00 | 2019-03-10T20:16:02.019910+00:00 | 649 | false | Thoughts: \nThe input array is the preorder traversal of a BST. \n1.preorder[0] is the root of BST\n2.The sub array from preorder[0] to the first element that is bigger than preorder[0] is the preorder traversal of the left subtree.\n The sub array from element that is bigger than preorder[0] to the end of the array is the preorder traversal of the right subtree.\n\n```\n/**\n * Definition for a binary tree node.\n * public class TreeNode {\n * public int val;\n * public TreeNode left;\n * public TreeNode right;\n * public TreeNode(int x) { val = x; }\n * }\n */\npublic class Solution {\n public TreeNode BstFromPreorder(int[] preorder) {\n if(preorder == null || preorder.Length == 0) return null;\n return helper(preorder, 0, preorder.Length);\n \n }\n \n public TreeNode helper(int[] preorder, int rootindex, int right)\n { \n if(rootindex >= right) return null;\n \n int value = preorder[rootindex];\n TreeNode root = new TreeNode(value);\n \n int i = rootindex+1;\n\t\t// find the left subtree of current node\n while(i <= preorder.Length-1 && preorder[i] < value)\n {\n i++;\n }\n //do the same thing for left and right subtree.\n root.left = helper(preorder, rootindex+1, i);\n root.right = helper(preorder,i, right);\n \n return root; \n }\n}\n``` | 5 | 1 | ['Recursion', 'Java'] | 2 |
construct-binary-search-tree-from-preorder-traversal | Optimal Approach| O(N) Space Complexity ⭐| Beats 100% | optimal-approach-on-space-complexity-bea-h0dy | Intuition\nThe problem involves constructing a binary search tree (BST) from its preorder traversal. Preorder traversal visits nodes in the order: root, left su | vaib8557 | NORMAL | 2024-06-15T00:01:58.880601+00:00 | 2024-06-15T00:01:58.880620+00:00 | 959 | false | # Intuition\nThe problem involves constructing a binary search tree (BST) from its preorder traversal. Preorder traversal visits nodes in the order: root, left subtree, right subtree. Given this order, we can reconstruct the BST by iteratively creating nodes and ensuring that each node respects the BST properties.\n\n# Approach\nTo construct the BST from the preorder traversal:\n1. We use a recursive approach where we maintain a pair of values representing the allowable range for the node values.\n2. We start by initializing the range as {INT_MIN, INT_MAX}, meaning any value can be the root.\n3. We recursively create nodes, updating the allowable range based on BST properties:\na. For the left child, the value must be less than the current node.\nb. For the right child, the value must be greater than the current node.\n4. We increment the index in the preorder list as we place nodes in the tree, ensuring we are always processing the next available value.\n\n# Complexity\n- Time complexity:\nThe algorithm processes each node exactly once, making it O(n), where n is the number of nodes in the tree (or the length of the preorder array).\n\n- Space complexity:\nThe space complexity is O(n) due to the recursive stack used for the tree construction. In the worst case, the depth of the recursion (which is the height of the tree) could be O(n) for a skewed tree.\n\n# Code\n```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n\n TreeNode* find(pair<int,int>&p,vector<int>& v,int &i){\n if(i>=v.size() || v[i]>p.second) return NULL;\n TreeNode* root = new TreeNode(v[i]);\n i++;\n int x = p.second;\n p.second = root->val;\n root->left = find(p,v,i);\n p.second = x;\n p.first = root->val;\n root->right = find(p,v,i);\n return root;\n }\n\n TreeNode* bstFromPreorder(vector<int>& preorder) {\n pair<int,int>p = {INT_MIN,INT_MAX};\n int i=0;\n TreeNode* root = find(p,preorder,i);\n return root;\n }\n};\n``` | 4 | 0 | ['C++'] | 0 |
construct-binary-search-tree-from-preorder-traversal | C++ | 4 different AC solutions : explained ⭐️ | c-4-different-ac-solutions-explained-by-ktgri | Code - 1 : using Next Greater Element Array (NGE)\n- We make an array NGE storing the index of the Next Greater Element of each element in the array, and then s | vanshdhawan60 | NORMAL | 2023-09-05T22:22:43.998471+00:00 | 2023-09-05T22:22:43.998498+00:00 | 172 | false | # Code - 1 : using Next Greater Element Array (NGE)\n- We make an array NGE storing the index of the Next Greater Element of each element in the array, and then simply construct our tree in preorder fashion using the indices we obtained through our NGE array.\n- This is because we know that all elements upto Next Greater Element will lie in the left subtree and all elements beyond that will lie in the right subtree. \n\n**Time Complexity:**\n- Construction of the NGE array: O(n)\n- The `solve` function: O(n)\n- Overall time complexity: O(n)\n\n**Space Complexity:**\n- Recursive call stack (worst case): O(n)\n- NGE array: O(n)\n- Overall space complexity (worst case): O(n)\n- Average space complexity (balanced BST): O(log n)\n\n```\nclass Solution {\npublic:\n TreeNode* solve(vector<int>& preorder, int i, int j, vector<int> &NGE) {\n // core logic\n if (i>j) return nullptr;\n TreeNode* root = new TreeNode (preorder[i]);\n root->left = solve (preorder, i+1, NGE[i]-1, NGE);\n root->right = solve(preorder, NGE[i], j, NGE);\n return root;\n }\n\n TreeNode* bstFromPreorder(vector<int>& preorder) {\n int n = preorder.size();\n // constructing NGE\n vector<int> NGE (n, n); // "next greater element" array\n stack<int> st;\n st.push(0);\n for (int i=1; i<n; i++) {\n while (!st.empty() && preorder[i] > preorder[st.top()]) {\n NGE[st.top()] = i;\n st.pop();\n }\n st.push(i);\n }\n // NGE constructed\n\n return solve(preorder, 0, n-1, NGE);\n }\n};\n```\n\n# Code - 2 : Sorting the preorder array to obtain inorder\n**Using the property of BST that inorder traversal of a BST is always sorted. \nTherefore, we sort the array to obtain inorder form and use the 2 arrays to construct the tree like a normal binary tree.**\n\n**Time Complexity:**\n- Constructing the `inorder` vector (sorting): O(n*log(n))\n- Building the binary search tree (BST) using the `build` function: O(n)\n- Overall time complexity: O(n*log(n))\n\n**Space Complexity:**\n- Recursive call stack (worst case): O(n)\n- `inorder` vector: O(n)\n- `map` (unordered_map): O(n)\n- Overall space complexity (worst case): O(n)\n\n```\nclass Solution {\npublic:\n TreeNode* build (vector<int>& preorder, vector<int>& inorder, unordered_map<int, int> &map, int i, int j, int m, int n) {\n if (i>j) return nullptr;\n int val = preorder[i];\n int idx = map[val];\n TreeNode* root = new TreeNode (val);\n root->left = build (preorder, inorder, map, i+1, i+idx-m, m, idx-1);\n root->right = build (preorder, inorder,map, i+idx-m+1, j, idx+1, n);\n return root;\n }\n TreeNode* bstFromPreorder(vector<int>& preorder) {\n vector<int> inorder = preorder;\n int n = preorder.size();\n if (!n) return nullptr;\n sort(inorder.begin(), inorder.end());\n unordered_map<int, int> map;\n for (int i=0; i<n; i++) map[inorder[i]] = i;\n return build (preorder, inorder, map, 0, n-1, 0, n-1);\n }\n};\n```\n\n# Code - 3 : Recursive solution\n**Exploiting the property that the value of each element in the BST has to lie between the previous greatest value and the next smallest value. Therefore, we pass in the range in between the value of the current node can lie, and accordingly construct our tree.**\n\n**Time Complexity:**\n- The code has a time complexity of O(n), where n is the number of elements in the `preorder` vector.\n\n**Space Complexity:**\n- The code has a space complexity of O(n) in the worst case due to the recursive call stack.\n\n\n\n```\nclass Solution {\npublic:\n TreeNode* solve (vector<int> &preorder, int &i, int big, int small) {\n if (i >= preorder.size()) return nullptr;\n int val = preorder[i];\n if (val > big || val < small) return nullptr;\n TreeNode* root = new TreeNode (val);\n i++;\n root->left = solve(preorder, i, val, small);\n root->right = solve(preorder, i, big, val);\n return root;\n\n }\n TreeNode* bstFromPreorder(vector<int>& preorder) {\n if (preorder.size() == 0) return nullptr;\n int i = 0;\n return solve (preorder, i, INT_MAX, INT_MIN);\n }\n};\n```\n\n# Code - 4 : Iterative, using stack\n**The same logic as Code - 3 through iteration, using stack.**\n\n**Time Complexity:**\n- The code has a time complexity of O(n), where n is the number of elements in the `preorder` vector.\n\n**Space Complexity:**\n- The code has a space complexity of O(n) in the worst case due to the stack used to construct the binary search tree.\n```\nclass Solution {\npublic:\n TreeNode* bstFromPreorder(vector<int>& preorder) {\n if (preorder.size() == 0) return nullptr;\n stack<TreeNode*> st;\n TreeNode* root = new TreeNode (preorder[0]);\n st.push(root);\n for (int i=1; i<preorder.size(); i++) {\n int val = preorder[i];\n TreeNode* node = new TreeNode (val);\n TreeNode* temp = nullptr;\n while (!st.empty() && val > (st.top()->val)) {\n temp = st.top();\n st.pop();\n }\n if (temp) temp->right = node;\n else (st.top()->left) = node;\n st.push(node);\n }\n return root;\n }\n};\n```\n\nPlease drop an upvote as it keeps me going! | 4 | 0 | ['Array', 'Stack', 'Tree', 'Binary Search Tree', 'Monotonic Stack', 'Binary Tree', 'C++'] | 0 |
construct-binary-search-tree-from-preorder-traversal | Simple Recursive C++ O(nlogn) solution | simple-recursive-c-onlogn-solution-by-ia-349s | Complexity Analysis\n- Time complexity:\nO(nlogn) in average case, and O(n^2) in worst case\n\n- Space complexity:\nO(h) in average case, where h = height of BS | iamarunaksha | NORMAL | 2023-09-03T13:02:38.246639+00:00 | 2023-09-03T13:02:38.246661+00:00 | 245 | false | # Complexity Analysis\n- Time complexity:\nO(nlogn) in average case, and O(n$$^2$$) in worst case\n\n- Space complexity:\nO(h) in average case, where h = height of BST\nO(n) in worst case, if its a skew-tree\n\n# Code\n```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\n\nTreeNode* insertIntoBST(TreeNode* root, int data) { // T.C --> O(logn)\n\n if(root == NULL) {\n\n root = new TreeNode(data);\n\n return root;\n }\n\n //Insert into right part of root\n if(data > root -> val) \n root -> right = insertIntoBST(root -> right, data);\n \n else\n root -> left = insertIntoBST(root -> left, data);\n \n return root;\n}\n\npublic:\n TreeNode* bstFromPreorder(vector<int>& preorder) {\n \n int n = preorder.size(); // T.C --> O(nlogn) || S.C --> O(h)\n \n TreeNode* root = NULL;\n\n for(int i=0; i<n; i++)\n root = insertIntoBST(root, preorder[i]);\n \n return root;\n }\n};\n``` | 4 | 0 | ['Binary Search Tree', 'Recursion', 'Binary Tree', 'C++'] | 1 |
construct-binary-search-tree-from-preorder-traversal | Easy C++ Solution ✅ | 2 solution | Optimised and Optimal Solution | easy-c-solution-2-solution-optimised-and-esg9 | Intuition\nOptimised -> Inorder Traversal is required along with preOrder to create a unique tree. We can get that after sorting preOrder array.\n\nOptimal -> S | HariBhakt | NORMAL | 2023-06-06T17:09:38.126563+00:00 | 2023-06-06T17:09:38.126600+00:00 | 538 | false | # Intuition\nOptimised -> Inorder Traversal is required along with preOrder to create a unique tree. We can get that after sorting preOrder array.\n\nOptimal -> Since for any BST : [Left < Root < Right ]\nWe just to need keep adding nodes after comparing it with the root and its left and right subtree.\n\n# Approach\nOptimised -> \n - Sort the array to get inOrder array.\n - Then create the BST using preOrder and inOrder array.\n\nOptimal -> \n - Create a upperBound to position elements in tree.\n - Create a new node using array element and increase count.\n - For node->left, Update upperBound to node->val.\n - For node->right, No changes.\n - BaseCase : (i > size(array)) && a[i] > bound \n\n# Complexity\n- Time complexity:\nOptimised : $$O(n*logn)$$\nOptimal : $$O(n)$$\n\n- Space complexity:\n Optimised : $$O(n)$$\n Optimal : $$O(1) + stack space$$\n\n# Code\n**Optimised Solution**\n\n```\nclass Solution {\npublic:\n unordered_map<int,int> inMap;\n TreeNode* bstFromPreorder(vector<int>& pre) {\n vector<int> in = pre;\n sort(in.begin(),in.end());\n int n = pre.size();\n for(int i=0; i<n; i++){\n inMap[in[i]] = i;\n }\n int preFirst = 0;\n return construct(pre,in, preFirst, 0, n-1);\n }\n\n TreeNode* construct(vector<int>& pre, vector<int>& in, int &preFirst, int left, int right){\n if(left > right) return NULL;\n TreeNode* root = new TreeNode(pre[preFirst++]);\n int inIndex = inMap[root->val];\n \n root->left = construct(pre, in, preFirst, left, inIndex-1);\n root->right = construct(pre, in, preFirst, inIndex+1, right);\n return root;\n }\n};\n```\n**Optimal Solution**\n```\nclass Solution {\npublic:\n TreeNode* bstFromPreorder(vector<int>& preorder) {\n int idx = 0;\n return build(preorder,idx,INT_MAX);\n }\n\n TreeNode* build(vector<int>& A, int& i, int upBound){\n if(i == A.size() || A[i] > upBound) return nullptr;\n\n TreeNode* node = new TreeNode(A[i++]);\n node->left = build(A, i, node->val);\n node->right = build(A,i, upBound);\n return node; \n }\n};\n```\n\n | 4 | 0 | ['Recursion', 'Ordered Map', 'C++'] | 0 |
construct-binary-search-tree-from-preorder-traversal | Best O(N) Solution | best-on-solution-by-kumar21ayush03-6avs | Approach 1\nBrute-Force\n\n# Complexity\n- Time complexity:\nO(n^2)\n\n- Space complexity:\nO(1)\n\n# Code\n\n/**\n * Definition for a binary tree node.\n * str | kumar21ayush03 | NORMAL | 2023-03-09T08:50:26.286703+00:00 | 2023-03-09T08:50:26.286743+00:00 | 1,624 | false | # Approach 1\nBrute-Force\n\n# Complexity\n- Time complexity:\n$$O(n^2)$$\n\n- Space complexity:\n$$O(1)$$\n\n# Code\n```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n TreeNode* bstFromPreorder(vector<int>& preorder) {\n TreeNode* root = new TreeNode(preorder[0]);\n TreeNode* curr;\n for (int i = 1; i < preorder.size(); i++) {\n curr = root;\n for (int j = 0; j < i; j++) {\n if (preorder[i] < curr->val) {\n if (curr->left != NULL) {\n curr = curr->left;\n } else {\n TreeNode* node = new TreeNode(preorder[i]);\n curr->left = node;\n break;\n }\n } else {\n if (curr->right != NULL) {\n curr = curr->right;\n } else {\n TreeNode* node = new TreeNode(preorder[i]);\n curr->right = node; \n break;\n }\n } \n } \n }\n return root;\n }\n};\n```\n\n# Approach 2\nRecursive\n\n# Complexity\n- Time complexity:\n$$O(n)$$\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n TreeNode* bstFromPreorder(vector<int>& preorder) {\n int i = 0;\n return build(preorder, i, INT_MAX);\n }\n\n TreeNode* build(vector<int>& preorder, int& i, int bound) {\n if (i == preorder.size() || preorder[i] > bound)\n return NULL;\n TreeNode* root = new TreeNode(preorder[i++]);\n root->left = build(preorder, i, root->val);\n root->right = build(preorder, i, bound);\n return root; \n }\n};\n``` | 4 | 0 | ['C++'] | 0 |
construct-binary-search-tree-from-preorder-traversal | Simple Approach Beats 100% in TC and 90% in SC. || Easy To Understand . | simple-approach-beats-100-in-tc-and-90-i-74i7 | Intuition\nFirst Elementr of PreOrder Traversal Array will be root always.\n\n# Approach\nSimply insert the elemnt of given array by comparing if it is greater | jigs_ | NORMAL | 2023-03-02T13:38:39.907206+00:00 | 2023-03-02T13:38:39.907242+00:00 | 334 | false | # Intuition\nFirst Elementr of PreOrder Traversal Array will be root always.\n\n# Approach\nSimply insert the elemnt of given array by comparing if it is greater or not ,\n\n# Complexity\n- Time complexity:\nO(N)\n\n\n\n# Code\n```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n //Function to insert in the BST\n void insert(TreeNode * &root , int key){\n if(root == nullptr){\n root = new TreeNode(key);\n return ;\n }\n //if key is greater than root then insert to the right\n if(key > root->val){\n insert(root->right,key);\n }\n else{ //if key is smaller than root then insert to the left\n insert(root->left,key);\n }\n\n }\n\n TreeNode* bstFromPreorder(vector<int>& preorder) {\n TreeNode* root ;\n //Iterating over Node Values and sending to the insert function\n for(auto key : preorder){\n insert(root,key);\n }\n return root;\n }\n};\n\n | 4 | 0 | ['C++'] | 0 |
construct-binary-search-tree-from-preorder-traversal | 1008. Construct Binary Search Tree from Preorder Traversal || most easy sol || java | 1008-construct-binary-search-tree-from-p-gpuc | // a very clever solution\n// one loop\n// fx call and check\n// see take an indivisual element and then call the fx for placing it \n// if you like the sol the | harjotse | NORMAL | 2022-11-03T18:47:06.478641+00:00 | 2022-11-03T18:47:06.478678+00:00 | 715 | false | // a very clever solution\n// one loop\n// fx call and check\n// see take an indivisual element and then call the fx for placing it \n// if you like the sol then pls upvote :)\n```\nclass Solution {\n public TreeNode bstFromPreorder(int[] preorder) \n {\n TreeNode root= new TreeNode(preorder[0]);\n for(int i: preorder)\n {\n helper(i,root);\n }\n return root ;\n }\n public TreeNode helper(int i, TreeNode root)\n { \n if(root==null){\n root =new TreeNode (i);\n return root;\n }\n if(i<root.val){\n root.left= helper(i,root.left);\n }\n if(i>root.val){\n root.right=helper(i, root.right);\n }\n return root;\n }\n} | 4 | 0 | ['Binary Search Tree', 'Binary Tree', 'Java'] | 0 |
construct-binary-search-tree-from-preorder-traversal | Easy Java Solution | Using Recursion | easy-java-solution-using-recursion-by-pi-y8g1 | \nclass Solution {\n public TreeNode bstFromPreorder(int[] preorder) {\n TreeNode root= new TreeNode( preorder[0] );\n \n for(int i: pre | PiyushParmar_28 | NORMAL | 2022-10-25T06:25:22.736107+00:00 | 2022-10-25T06:25:22.736147+00:00 | 984 | false | ```\nclass Solution {\n public TreeNode bstFromPreorder(int[] preorder) {\n TreeNode root= new TreeNode( preorder[0] );\n \n for(int i: preorder){\n createTree(i, root);\n }\n \n return root;\n }\n \n public TreeNode createTree(int i, TreeNode root){\n if(root == null){\n root= new TreeNode(i);\n return root;\n }\n \n if(root.val > i){\n root.left= createTree(i, root.left);\n }\n \n if(root.val < i){\n root.right= createTree(i, root.right);\n }\n \n return root;\n }\n}\n``` | 4 | 0 | ['Recursion', 'Java'] | 0 |
construct-binary-search-tree-from-preorder-traversal | C++ || BST || 2 METHODS || EASY TO UNDERSATAND || STRIVER METHOD | c-bst-2-methods-easy-to-undersatand-stri-a34j | \n//--------------------------------1ST METHOD-----------------------------------------\nclass Solution {\npublic:\n TreeNode* bstFromPreorder(vector<int>& p | _chintu_bhai | NORMAL | 2022-10-18T19:44:10.095757+00:00 | 2022-10-18T19:44:10.095792+00:00 | 649 | false | ```\n//--------------------------------1ST METHOD-----------------------------------------\nclass Solution {\npublic:\n TreeNode* bstFromPreorder(vector<int>& preorder) {\n vector<int>inorder=preorder;\n sort(inorder.begin(),inorder.end());\n map<int,int>m;\n for(int i=0;i<inorder.size();i++)\n {\n m[inorder[i]]=i;\n }\n return constructBinaryTree(preorder,0,preorder.size()-1,inorder,0,inorder.size()-1,m);\n }\n TreeNode* constructBinaryTree(vector<int>& preorder,int preStart,int preEnd,vector<int>& inorder,int inStart,int inEnd,map<int,int>&m)\n {\n if(preStart>preEnd||inStart>inEnd)\n return NULL;\n TreeNode* root=new TreeNode(preorder[preStart]);\n int inRoot=m[root->val];\n int numsleft=inRoot-inStart;\n root->left=constructBinaryTree(preorder,preStart+1,preStart+numsleft,inorder,inStart,inRoot-1,m);\n root->right=constructBinaryTree(preorder,preStart+numsleft+1,preEnd,inorder,inRoot+1,inEnd,m);\n return root;\n } \n};\n\n//-------------------------------------2ND METHOD---------------------------------------------\nclass Solution {\npublic:\n TreeNode* bstFromPreorder(vector<int>& preorder) {\n int i=0;\n return construction(preorder,i,INT_MAX);\n } \n TreeNode* construction(vector<int>& preorder,int &i,int bound) \n {\n if(i==preorder.size()||preorder[i]>bound)\n {\n return NULL;\n }\n TreeNode* root=new TreeNode(preorder[i++]);\n root->left=construction(preorder,i,root->val);\n root->right=construction(preorder,i,bound);\n return root;\n }\n};\n```\n**if you found this helpful , please do upvote it** | 4 | 0 | ['Binary Search Tree', 'C'] | 0 |
construct-binary-search-tree-from-preorder-traversal | C++ || Two Different Approach || Optimised Solution with 0ms | c-two-different-approach-optimised-solut-r06j | \nclass Solution {\n \n TreeNode * Solve(vector<int>& preorder, int start ,int end)\n {\n if(start>end)\n return NULL;\n \n | Khwaja_Abdul_Samad | NORMAL | 2022-08-17T15:04:17.389040+00:00 | 2022-08-17T15:04:17.389072+00:00 | 555 | false | ```\nclass Solution {\n \n TreeNode * Solve(vector<int>& preorder, int start ,int end)\n {\n if(start>end)\n return NULL;\n \n TreeNode * root = new TreeNode(preorder[start]);\n \n int i = start+1;\n for(; i<=end ; i++)\n {\n if(preorder[start]<preorder[i])\n break;\n }\n \n root->left = Solve(preorder, start+1 , i-1);\n root->right = Solve(preorder , i, end);\n \n return root;\n }\n \n TreeNode * SolveOptimised(vector<int>& preorder, int &index, TreeNode* p , TreeNode * q )\n {\n if(index >= preorder.size())\n return NULL;\n \n if((p && p->val > preorder[index]) || (q && q->val < preorder[index]) )\n return NULL;\n \n TreeNode * root = new TreeNode (preorder[index++]);\n \n root->left = SolveOptimised(preorder , index , p, root);\n root->right = SolveOptimised(preorder , index , root , q);\n \n return root;\n }\n \npublic:\n TreeNode* bstFromPreorder(vector<int>& preorder) {\n \n // Methos 1 , TC :O(n square)\n return Solve(preorder, 0 , preorder.size()-1);\n \n // Methos 2 , TC :O(n)\n \n int index = 0;\n return SolveOptimised(preorder , index , NULL, NULL);\n \n }\n};\n```\n\n\n | 4 | 0 | ['C', 'Iterator'] | 0 |
construct-binary-search-tree-from-preorder-traversal | Python | JUST 6 Line Code | Own Solution | O(N) Time | python-just-6-line-code-own-solution-on-1jbk2 | \nclass Solution:\n def bstFromPreorder(self, preorder: List[int]) -> Optional[TreeNode]:\n if len(preorder)==0:\n return None\n roo | manjeet13 | NORMAL | 2022-05-27T18:24:47.761416+00:00 | 2022-05-27T20:20:12.577335+00:00 | 412 | false | ```\nclass Solution:\n def bstFromPreorder(self, preorder: List[int]) -> Optional[TreeNode]:\n if len(preorder)==0:\n return None\n root=TreeNode(preorder[0])\n root.left=self.bstFromPreorder([i for i in preorder if i<root.val])\n root.right=self.bstFromPreorder([i for i in preorder if i>root.val])\n return root\n``` | 4 | 0 | ['Binary Search Tree', 'Recursion', 'Python'] | 0 |
construct-binary-search-tree-from-preorder-traversal | Discussed All Approach in Notes | C++ | JAVA | discussed-all-approach-in-notes-c-java-b-gs0q | Notes Link : https://github.com/rizonkumar/LeetCode-Notes/blob/main/1008.pdf\n\nJava Code\n\n\n\nclass Solution {\n public TreeNode bstFromPreorder(int[] pr | rizon__kumar | NORMAL | 2022-04-03T04:29:42.247396+00:00 | 2022-04-03T04:29:42.247440+00:00 | 73 | false | **Notes Link** : https://github.com/rizonkumar/LeetCode-Notes/blob/main/1008.pdf\n\nJava Code\n\n```\n\nclass Solution {\n public TreeNode bstFromPreorder(int[] preorder) {\n return bstFromPreorder(preorder, Integer.MAX_VALUE, new int[] {0});\n }\n \n public TreeNode bstFromPreorder(int[] preorder, int bound, int[] i){\n if(i[0] == preorder.length || preorder[i[0]] > bound) return null;\n \n TreeNode root = new TreeNode(preorder[i[0]++]);\n root.left = bstFromPreorder(preorder, root.val, i);\n root.right = bstFromPreorder(preorder, bound, i);\n return root;\n }\n}\n```\n\nC++\n\n```\nclass Solution {\npublic:\n TreeNode* bstFromPreorder(vector<int>& preorder) {\n int i = 0;\n return build(preorder, i, INT_MAX);\n }\n\n TreeNode* build(vector<int>& preorder, int& i, int bound) {\n if (i == preorder.size() || preorder[i] > bound) return NULL;\n TreeNode* root = new TreeNode(preorder[i++]);\n root->left = build(preorder, i, root->val);\n root->right = build(preorder, i, bound);\n return root;\n }\n};\n``` | 4 | 0 | ['Binary Search Tree'] | 0 |
construct-binary-search-tree-from-preorder-traversal | C++ | Easy + Efficient solution O(n) TC. | c-easy-efficient-solution-on-tc-by-jv02-je22 | \nclass Solution {\npublic:\n TreeNode* tt(vector<int>& p, int& i, int upperbound){\n if(i==p.size() || p[i]>upperbound) return NULL;\n TreeNod | jv02 | NORMAL | 2022-03-19T11:05:03.464510+00:00 | 2022-03-19T11:05:03.464537+00:00 | 159 | false | ```\nclass Solution {\npublic:\n TreeNode* tt(vector<int>& p, int& i, int upperbound){\n if(i==p.size() || p[i]>upperbound) return NULL;\n TreeNode* root = new TreeNode(p[i++]);\n root->left = tt(p,i,root->val);\n root->right = tt(p,i,upperbound);\n \n return root;\n \n }\n \n TreeNode* bstFromPreorder(vector<int>& p) {\n int i = 0; \n return tt(p,i,INT_MAX);\n }\n};\n```\n\nif you find this solution usefull then do upvote and share. | 4 | 0 | ['C'] | 0 |
construct-binary-search-tree-from-preorder-traversal | [C++] Recursive and Stack Iterative Solutions | c-recursive-and-stack-iterative-solution-cgpe | Recursive:\n\nclass Solution {\npublic:\n TreeNode* bstFromPreorder(vector<int>& p) {\n int id = 0;\n return build(p, id, INT_MAX);\n }\n | ddliu6 | NORMAL | 2021-10-13T05:54:59.021445+00:00 | 2021-10-13T17:20:41.792783+00:00 | 441 | false | Recursive:\n```\nclass Solution {\npublic:\n TreeNode* bstFromPreorder(vector<int>& p) {\n int id = 0;\n return build(p, id, INT_MAX);\n }\n \n TreeNode* build(vector<int>& p, int& id, int limit) {\n if(id == p.size() || p[id] > limit)\n return NULL;\n int val = p[id++];\n TreeNode* root = new TreeNode(val);\n root->left = build(p, id, val); //root->left must be less than the root\n root->right = build(p, id, limit); //root->right must be less than the previous root\n return root;\n }\n};\n```\nIterative with Stack: \n```\nclass Solution {\npublic:\n\tTreeNode* bstFromPreorder(vector<int>& p) {\n\t\tTreeNode* root = new TreeNode(p[0]), *cur = root;\n stack<TreeNode*> s({root}); //push the node with no children\n\t\tfor(int i = 1; i < p.size(); i++)\n\t\t{\n\t\t\tif(p[i] < s.top()->val)\n\t\t\t{\n\t\t\t\tcur->left = new TreeNode(p[i]);\n\t\t\t\tcur = cur->left;\n\t\t\t\ts.push(cur);\n\t\t\t}\n else\n { //check the previous nodes for the best pos to insert\n while(!s.empty() && p[i] > s.top()->val)\n {\n cur = s.top();\n s.pop();\n }\n cur->right = new TreeNode(p[i]);\n cur = cur->right;\n s.push(cur);\n }\n\t\t}\n\t\treturn root;\n\t}\n};\n``` | 4 | 0 | [] | 0 |
construct-binary-search-tree-from-preorder-traversal | C++ NO STACK, ONLY RECURSIVE CALLS BEATS 100% RUNTIME AND MEMORY | c-no-stack-only-recursive-calls-beats-10-1dzl | Make a function which will insert your elements from the preorder array into the binary search tree in the predefined form of the binary search tree.\n\n\nclass | messi1711 | NORMAL | 2021-10-13T02:13:12.041026+00:00 | 2021-10-13T02:13:12.041076+00:00 | 435 | false | Make a function which will insert your elements from the preorder array into the binary search tree in the predefined form of the binary search tree.\n\n```\nclass Solution {\npublic:\n TreeNode* bstFromPreorder(vector<int>& preorder) {\n TreeNode* root=new TreeNode();\n \n root->val=preorder[0];\n \n for(int i=1;i<preorder.size();i++){\n my_push_back(root, preorder[i]);\n }\n \n return root;\n }\n \n void my_push_back(TreeNode* root, int val_to_insert){\n if(val_to_insert>root->val){\n if(root->right==NULL){\n root->right=new TreeNode(val_to_insert);\n }\n else{\n my_push_back(root->right, val_to_insert);\n }\n }\n else if(val_to_insert<root->val){\n if(root->left==NULL){\n root->left=new TreeNode(val_to_insert);\n }\n else{\n my_push_back(root->left, val_to_insert);\n }\n }\n }\n};\n``` | 4 | 0 | [] | 1 |
construct-binary-search-tree-from-preorder-traversal | Straightforward recursive solution via Python | straightforward-recursive-solution-via-p-yjon | \n# Definition for a binary tree node.\n# class TreeNode(object):\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# | tinfoilhat0 | NORMAL | 2021-10-13T00:14:52.744814+00:00 | 2021-10-13T00:14:52.744846+00:00 | 399 | false | ```\n# Definition for a binary tree node.\n# class TreeNode(object):\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution(object):\n def bstFromPreorder(self, preorder):\n """\n :type preorder: List[int]\n :rtype: TreeNode\n """\n \n if len(preorder) <= 0:\n return None\n \n root_val = preorder[0]\n right_start_idx = len(preorder)\n for i, v in enumerate(preorder[1:]):\n if v > root_val:\n right_start_idx = i+1\n break\n \n leftSubTree = self.bstFromPreorder(preorder[1:right_start_idx])\n rightSubTree = self.bstFromPreorder(preorder[right_start_idx:])\n \n return TreeNode(root_val, leftSubTree, rightSubTree)\n``` | 4 | 0 | [] | 1 |
construct-binary-search-tree-from-preorder-traversal | 0ms | 100 beats | Self - Explanatory | JAVA | Recursion | 0ms-100-beats-self-explanatory-java-recu-f34d | self explanatory code,\njust make a node for each element and fit it into BST\n\n\n\n\npublic TreeNode bstFromPreorder(int[] preorder) \n {\n if(preor | rahulgilhotra | NORMAL | 2021-08-16T10:52:38.452169+00:00 | 2021-08-16T10:52:38.452200+00:00 | 479 | false | self explanatory code,\njust make a node for each element and fit it into BST\n\n\n\n```\npublic TreeNode bstFromPreorder(int[] preorder) \n {\n if(preorder.length==0) return null;\n \n TreeNode root = new TreeNode(preorder[0]);\n \n for(int i=1;i<preorder.length;i++)\n {\n TreeNode node = new TreeNode(preorder[i]);\n \n fitInBST(node,root);\n }\n \n return root;\n }\n void fitInBST(TreeNode node,TreeNode root)\n {\n if(node.val<root.val)\n {\n if(root.left == null) root.left = node;\n else fitInBST(node,root.left);\n }\n else if(node.val>root.val)\n {\n if(root.right == null) root.right = node;\n else fitInBST(node,root.right);\n }\n }\n``` | 4 | 0 | ['Recursion', 'Java'] | 0 |
construct-binary-search-tree-from-preorder-traversal | Java Easy to understand | beats 100% on runtime | self explanatory | java-easy-to-understand-beats-100-on-run-v7id | ```\n/*\n * Definition for a binary tree node.\n * public class TreeNode {\n * int val;\n * TreeNode left;\n * TreeNode right;\n * TreeNode() {} | Backend_engineer123 | NORMAL | 2021-06-17T19:31:01.183396+00:00 | 2021-06-17T19:31:39.170872+00:00 | 292 | false | ```\n/**\n * Definition for a binary tree node.\n * public class TreeNode {\n * int val;\n * TreeNode left;\n * TreeNode right;\n * TreeNode() {}\n * TreeNode(int val) { this.val = val; }\n * TreeNode(int val, TreeNode left, TreeNode right) {\n * this.val = val;\n * this.left = left;\n * this.right = right;\n * }\n * }\n */\nclass Solution {\n public TreeNode bstFromPreorder(int[] preorder) {\n \n if(preorder.length == 0){\n return new TreeNode();\n }\n TreeNode root = new TreeNode(preorder[0]);\n \n for(int i = 1; i < preorder.length; i++){\n addChild(root, preorder[i]);\n }\n return root;\n \n }\n \n public void addChild(TreeNode root, int val){ \n\n if(val < root.val){\n if(root.left != null){\n addChild(root.left, val);\n }\n else{\n root.left = new TreeNode(val);\n }\n \n }\n else{\n if(root.right != null){\n addChild(root.right, val);\n }\n else{\n root.right = new TreeNode(val);\n }\n }\n \n }\n \n} | 4 | 0 | ['Java'] | 1 |
construct-binary-search-tree-from-preorder-traversal | Python O(N) : Easy Recursive using BST property, min & max | python-on-easy-recursive-using-bst-prope-t8k1 | ```\nimport math\nclass Solution:\n def bstFromPreorder(self, preorder: List[int]) -> TreeNode:\n \n def construct(preorder,mn,mx):\n | knz_80 | NORMAL | 2021-04-22T05:40:06.883474+00:00 | 2021-04-22T05:40:06.883518+00:00 | 227 | false | ```\nimport math\nclass Solution:\n def bstFromPreorder(self, preorder: List[int]) -> TreeNode:\n \n def construct(preorder,mn,mx):\n if preorder:\n\t\t\t\t# Any node value violates bst property\n if preorder[0]<mn or preorder[0]>mx:\n return None\n n=TreeNode(preorder.pop(0))\n n.left=construct(preorder,mn,n.val)\n n.right=construct(preorder,n.val,mx)\n\n return n\n return construct(preorder,-math.inf, math.inf) | 4 | 0 | ['Python'] | 0 |
construct-binary-search-tree-from-preorder-traversal | simple c++ solution | recursive | simple-c-solution-recursive-by-xor09-bqoz | \n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0) | xor09 | NORMAL | 2021-02-17T17:28:39.112626+00:00 | 2021-02-17T17:28:39.112665+00:00 | 221 | false | ```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n \n TreeNode* solve(vector<int>& vec,int min,int max,int &curr){\n if(curr>=vec.size() || vec[curr]<min || vec[curr]>max) return NULL;\n int ele=vec[curr++];\n TreeNode *newnode=new TreeNode(ele);\n newnode->left=solve(vec,min,ele-1,curr);\n newnode->right=solve(vec,ele+1,max,curr);\n return newnode;\n }\n \n TreeNode* bstFromPreorder(vector<int>& preorder) {\n if(preorder.size()==0) return NULL;\n int min=1,max=INT_MAX,curr=0;\n return solve(preorder,min,max,curr); \n }\n};\n```\nPlease **UPVOTE** | 4 | 1 | ['Recursion', 'C'] | 1 |
construct-binary-search-tree-from-preorder-traversal | [C++] 5-line solution Time/Space: O(N) | c-5-line-solution-timespace-on-by-codeda-9zpo | \nclass Solution {\npublic:\n int i = 0;\n TreeNode* bstFromPreorder(vector<int>& pre, int upper=INT_MAX) { \n if(i >= pre.size() || pre[i] | codedayday | NORMAL | 2020-05-24T17:33:41.544974+00:00 | 2020-05-24T17:33:41.545014+00:00 | 290 | false | ```\nclass Solution {\npublic:\n int i = 0;\n TreeNode* bstFromPreorder(vector<int>& pre, int upper=INT_MAX) { \n if(i >= pre.size() || pre[i] > upper) return NULL;\n return new TreeNode(pre[i++], bstFromPreorder(pre, pre[i-1]), bstFromPreorder(pre, upper)); \n }\n};\n``` | 4 | 0 | [] | 0 |
construct-binary-search-tree-from-preorder-traversal | Python. No recursion. | python-no-recursion-by-techrabbit58-rt2w | \nclass Solution:\n def bstFromPreorder(self, preorder: List[int]) -> TreeNode:\n node_stack = []\n node = root = TreeNode(preorder[0])\n | techrabbit58 | NORMAL | 2020-05-24T12:03:16.397005+00:00 | 2020-05-24T12:05:54.384511+00:00 | 580 | false | ```\nclass Solution:\n def bstFromPreorder(self, preorder: List[int]) -> TreeNode:\n node_stack = []\n node = root = TreeNode(preorder[0])\n for n in preorder[1:]:\n if n <= node.val:\n node.left = TreeNode(n)\n node_stack.append(node)\n node = node.left\n else:\n while node_stack and n > node_stack[-1].val:\n node = node_stack.pop()\n node.right = TreeNode(n)\n node = node.right\n return root\n``` | 4 | 0 | ['Python', 'Python3'] | 2 |
construct-binary-search-tree-from-preorder-traversal | Recursive Java Solution | recursive-java-solution-by-ztztzt8888-116w | \nclass Solution {\n public TreeNode bstFromPreorder(int[] preorder) {\n TreeNode root = new TreeNode(preorder[0]);\n for (int i = 1; i < preor | ztztzt8888 | NORMAL | 2020-04-24T10:22:08.693935+00:00 | 2020-04-24T10:22:08.693992+00:00 | 229 | false | ```\nclass Solution {\n public TreeNode bstFromPreorder(int[] preorder) {\n TreeNode root = new TreeNode(preorder[0]);\n for (int i = 1; i < preorder.length; i++) {\n helper(root, new TreeNode(preorder[i]));\n }\n return root;\n }\n\n private void helper(TreeNode root, TreeNode inserted) {\n if (root.val < inserted.val) {\n if (root.right == null) {\n root.right = inserted;\n } else {\n helper(root.right, inserted);\n }\n } else {\n if (root.left == null) {\n root.left = inserted;\n } else {\n helper(root.left, inserted);\n }\n }\n }\n}\n``` | 4 | 0 | ['Binary Search Tree', 'Recursion'] | 0 |
construct-binary-search-tree-from-preorder-traversal | C++ BST Insert | c-bst-insert-by-eyan422-puar | C++\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode(int x) | eyan422 | NORMAL | 2020-04-20T09:05:19.328890+00:00 | 2020-04-20T09:05:19.328925+00:00 | 549 | false | ```C++\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode(int x) : val(x), left(NULL), right(NULL) {}\n * };\n */\nclass Solution {\npublic: \n TreeNode* BstInsert(TreeNode*& root, int val){\n if(!root){ \n root = new TreeNode(val);\n }else{ \n if(val < root->val) \n root->left = BstInsert(root->left, val); \n else if(root->val < val) \n root->right = BstInsert(root->right, val);\n }\n return root;\n }\n \n TreeNode* bstFromPreorder(vector<int>& preorder) {\n \n TreeNode* root = NULL;\n \n for (auto val : preorder)\n BstInsert(root, val);\n \n return root;\n }\n};\n``` | 4 | 0 | [] | 1 |
construct-binary-search-tree-from-preorder-traversal | C# code easy to understand | c-code-easy-to-understand-by-fadi17-d62c | \n public TreeNode BstFromPreorder(int[] preorder) {\n if(preorder == null)\n return null;\n // root node will always be first node | fadi17 | NORMAL | 2019-05-26T10:08:56.956579+00:00 | 2020-04-21T07:15:17.512533+00:00 | 287 | false | ````\n public TreeNode BstFromPreorder(int[] preorder) {\n if(preorder == null)\n return null;\n // root node will always be first node in preorder traversal\n TreeNode root = new TreeNode(preorder[0]);\n \n // If we simply just insert all nodes in array \n // using standard way of inserting node in BST it will give us original tree.\n\t\t\n for(int x = 1; x<preorder.Length; x++)\n InsertInBST(root, preorder[x]);\n \n return root;\n }\n // standard BST insertion. \n private void InsertInBST(TreeNode root, int val)\n {\n TreeNode current = root;\n TreeNode parent = null;\n while(current!=null)\n {\n parent = current;\n current = current.val > val? current.left:current.right;\n }\n \n if(parent.val > val)\n parent.left = new TreeNode(val);\n else\n parent.right = new TreeNode(val);\n }\n```` | 4 | 0 | [] | 0 |
construct-binary-search-tree-from-preorder-traversal | Java O(n) solution with range | java-on-solution-with-range-by-tohrah-isfd | \n\nclass Solution {\n int nodeIdx;\n public TreeNode bstFromPreorder(int[] preorder) {\n if(preorder == null) {\n return null;\n | tohrah | NORMAL | 2019-03-13T21:10:48.497013+00:00 | 2019-03-13T21:10:48.497099+00:00 | 1,058 | false | ```\n\nclass Solution {\n int nodeIdx;\n public TreeNode bstFromPreorder(int[] preorder) {\n if(preorder == null) {\n return null;\n }\n nodeIdx = 0;\n return bstHelper(preorder, Integer.MIN_VALUE , Integer.MAX_VALUE);\n }\n private TreeNode bstHelper(int[] preorder, int start, int end) {\n if(nodeIdx == preorder.length || preorder[nodeIdx]<start || preorder[nodeIdx]>end) {\n return null;\n }\n int val = preorder[nodeIdx++];\n TreeNode node = new TreeNode(val);\n node.left = bstHelper(preorder, start, val);\n node.right = bstHelper(preorder, val, end);\n return node; \n } \n} \n\n``` | 4 | 0 | [] | 0 |
construct-binary-search-tree-from-preorder-traversal | Python O(N) short solution using min, max and deque | python-on-short-solution-using-min-max-a-0o6z | \ndef bstFromPreorder(self, preorder: List[int]) -> TreeNode:\n def bst(pre, min, max):\n node = None\n if pre and min < pre[0] < m | Cubicon | NORMAL | 2019-03-10T04:00:50.867431+00:00 | 2019-03-10T04:00:50.867487+00:00 | 601 | false | ```\ndef bstFromPreorder(self, preorder: List[int]) -> TreeNode:\n def bst(pre, min, max):\n node = None\n if pre and min < pre[0] < max:\n node = TreeNode(pre[0])\n pre.popleft()\n node.left = bst(pre, min, node.val)\n node.right = bst(pre, node.val, max)\n return node\n return bst(deque(preorder), -math.inf, math.inf)\n``` | 4 | 2 | [] | 0 |
construct-binary-search-tree-from-preorder-traversal | 100% Acceptance! ✅(0ms) Easy To Understand!✅ | 100-acceptance-0ms-easy-to-understand-by-ho0a | VELAN.MVelan.MComplexity
Time complexity: O(n2)✅
Space complexity:O(n)✅
Code | velan_m_velan | NORMAL | 2025-03-29T13:12:55.963631+00:00 | 2025-03-29T13:12:55.963631+00:00 | 286 | false | # VELAN.M
$$Velan.M$$
# Complexity
- Time complexity: $$O(n^2)$$✅
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:$$O(n)$$✅
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
TreeNode* bstFromPreorder(vector<int>& preorder) {
if(preorder.size()==0)return NULL;
TreeNode*root=new TreeNode(preorder[0]);
if(preorder.size()==1)return root;
vector<int>left;
vector<int>right;
for(int i=0;i<preorder.size();i++){
if(preorder[i]>preorder[0])right.push_back(preorder[i]);
else if(preorder[i]<preorder[0])left.push_back(preorder[i]);
}
root->left=bstFromPreorder(left);
root->right=bstFromPreorder(right);
return root;
}
};
``` | 3 | 0 | ['Tree', 'Binary Search Tree', 'Binary Tree', 'C++'] | 0 |
construct-binary-search-tree-from-preorder-traversal | Construct Binary Search Tree from Preorder Traversal | construct-binary-search-tree-from-preord-ezq1 | Complexity
Time complexity: O(N)
Space complexity: O(N)
Code | Ansh1707 | NORMAL | 2025-03-05T23:33:29.579989+00:00 | 2025-03-05T23:33:29.579989+00:00 | 208 | false |
# Complexity
- Time complexity: O(N)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(N)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python []
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution(object):
def bstFromPreorder(self, preorder):
"""
:type preorder: List[int]
:rtype: Optional[TreeNode]
"""
def construct(bound=float('inf')):
if not preorder or preorder[0] > bound:
return None
root = TreeNode(preorder.pop(0))
root.left = construct(root.val)
root.right = construct(bound)
return root
return construct()
``` | 3 | 0 | ['Stack', 'Binary Tree', 'Python'] | 0 |
construct-binary-search-tree-from-preorder-traversal | Java solution || 0ms || 100%faster | java-solution-0ms-100faster-by-ramsingh2-63lk | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | Ramsingh27 | NORMAL | 2025-01-10T07:04:11.149893+00:00 | 2025-01-10T07:04:11.149893+00:00 | 352 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode insert(TreeNode root, int val){
if(root==null){
return new TreeNode(val);
}
if(root.val>val){
root.left = insert(root.left, val);
}
if(root.val<val){
root.right = insert(root.right, val);
}
return root;
}
public TreeNode bstFromPreorder(int[] preorder) {
TreeNode root= null;
for(int n: preorder){
root = insert(root, n);
}
return root;
}
}
``` | 3 | 0 | ['Java'] | 0 |
construct-binary-search-tree-from-preorder-traversal | ✅✅BEST AND SIMPLE SOLUTION🤩🤩 | best-and-simple-solution-by-rishu_raj593-0j74 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Rishu_Raj5938 | NORMAL | 2024-09-12T14:16:27.599082+00:00 | 2024-09-12T14:16:27.599119+00:00 | 284 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n TreeNode* solve(vector<int> v, int i, int j) {\n \n if(i > j) return NULL;\n \n int idx = j+1;\n\n for(int t=i+1; t<=j; t++) {\n if(v[t] > v[i]){ \n idx = t;\n break;\n }\n }\n \n TreeNode* root = new TreeNode(v[i]);\n root->left = solve(v, i+1, idx-1);\n root->right = solve(v, idx, j);\n \n return root;\n }\n\n TreeNode* bstFromPreorder(vector<int>& preorder) {\n return solve(preorder, 0, preorder.size()-1); \n }\n};\n``` | 3 | 0 | ['C++'] | 0 |
construct-binary-search-tree-from-preorder-traversal | just two recursion thats it | just-two-recursion-thats-it-by-sajal-we4k | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Sajal_ | NORMAL | 2024-03-06T12:06:34.042462+00:00 | 2024-03-06T12:06:34.042498+00:00 | 861 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def bstFromPreorder(self, preorder: List[int]) -> Optional[TreeNode]:\n if not preorder:\n return None\n \n node = TreeNode(preorder[0])\n node.left = self.bstFromPreorder([x for x in preorder if x < preorder[0]])\n node.right = self.bstFromPreorder([x for x in preorder if x > preorder[0]])\n \n return node\n``` | 3 | 0 | ['Python3'] | 0 |
construct-binary-search-tree-from-preorder-traversal | [C++] Solution using STACK . Unique approaching . Clean and Easy for understanding | c-solution-using-stack-unique-approachin-07ws | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | lshigami | NORMAL | 2024-01-13T06:44:46.637299+00:00 | 2024-01-13T06:44:46.637329+00:00 | 267 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n TreeNode* bstFromPreorder(vector<int>& v) {\n stack<TreeNode*> st;\n TreeNode* root = new TreeNode(v[0]);\n st.push(root);\n for(int i = 1; i < v.size(); i++){\n TreeNode* node = new TreeNode(v[i]);\n if(v[i] < st.top()->val){\n st.top()->left = node;\n }\n else{\n TreeNode* temp = st.top();\n st.pop();\n while(!st.empty() && v[i] > st.top()->val){\n temp = st.top();\n st.pop();\n }\n temp->right = node;\n }\n st.push(node);\n }\n return root;\n }\n};\n\n``` | 3 | 0 | ['C++'] | 0 |
construct-binary-search-tree-from-preorder-traversal | ||❤️☑️Best Approach using Range Approach☑️❤️|| Recurssive ||Java|| | best-approach-using-range-approach-recur-y1jm | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \nThis program is solve i | kailashsahu07 | NORMAL | 2023-11-16T19:01:47.941270+00:00 | 2023-11-16T19:01:47.941300+00:00 | 302 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThis program is solve in the approach using some range approach . first we have to find the range of all node using some recurssie approach then create node connect it into root and convert into root .\n\n\n# Complexity\n- Time complexity:$$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * Definition for a binary tree node.\n * public class TreeNode {\n * int val;\n * TreeNode left;\n * TreeNode right;\n * TreeNode() {}\n * TreeNode(int val) { this.val = val; }\n * TreeNode(int val, TreeNode left, TreeNode right) {\n * this.val = val;\n * this.left = left;\n * this.right = right;\n * }\n * }\n */\nclass Solution {\n int index = 0;\n public TreeNode findSolution(int[] pre,TreeNode root,int min,int max){ \n //base case\n if(index>=pre.length){\n return null;\n }\n //check the array value is outside of range or not ..\n if(pre[index]<min || pre[index]>max){\n return null;\n }\n //if the array value in the range then put logic and create tree\n int temp = pre[index++];\n root = new TreeNode(temp);\n root.left = findSolution(pre,root.left,min,temp);\n root.right = findSolution(pre,root.right,temp,max);\n return root;\n\n }\n public TreeNode bstFromPreorder(int[] preorder) {\n //first we calle find solution methhod for solve that program recurssively .\n return findSolution(preorder,null,Integer.MIN_VALUE,Integer.MAX_VALUE);\n }\n}\n``` | 3 | 0 | ['Java'] | 0 |
construct-binary-search-tree-from-preorder-traversal | Python 3 EASY AND FAST/GOOD MEMORY✅✅✅ | python-3-easy-and-fastgood-memory-by-bla-onvu | \n\n# Approach\n Describe your approach to solving the problem. \n1. pick the first item as the root.\n2. get the numbers smaller and bigger.\n3. set bst\'s lef | Little_Tiub | NORMAL | 2023-09-05T21:38:39.163534+00:00 | 2023-09-05T21:38:39.163557+00:00 | 173 | false | \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. pick the first item as the root.\n2. get the numbers smaller and bigger.\n3. set `bst`\'s left to (background noise: recursing on `smaller`)\n4. set `bst`\'s left to (background noise: recursing on `bigger`)\n\n# Complexity\n- Time complexity: O(2n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: \u2753\u2753\u2753\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def bstFromPreorder(self, preorder: List[int]) -> Optional[TreeNode]:\n if not preorder: return None\n bst = TreeNode(preorder[0])\n smaller = []\n bigger = []\n for n in preorder:\n if n > preorder[0]: bigger.append(n)\n elif n < preorder[0]: smaller.append(n)\n bst.left = self.bstFromPreorder(smaller)\n bst.right = self.bstFromPreorder(bigger)\n return bst\n``` | 3 | 0 | ['Python3'] | 0 |
construct-binary-search-tree-from-preorder-traversal | C++ Solution using 0(N) complexity using only preorder | c-solution-using-0n-complexity-using-onl-krzf | \n\t class Solution {\n\t \n public:\n\t\t\n TreeNode solve(vector &preorder , long mini , long maxi , int &i){\n\t\n if(i>=preorder.size()){\ | adityagarg217 | NORMAL | 2023-06-07T20:13:59.825367+00:00 | 2023-06-07T20:14:53.177920+00:00 | 1,361 | false | \n\t class Solution {\n\t \n public:\n\t\t\n TreeNode* solve(vector<int> &preorder , long mini , long maxi , int &i){\n\t\n if(i>=preorder.size()){\n return NULL ; \n }\n if(preorder[i] < mini || preorder[i] > maxi ){\n return NULL ;\n }\n TreeNode* newnode = new TreeNode(preorder[i++]);\n newnode->left = solve(preorder,mini,newnode->val,i);\n newnode->right = solve(preorder,newnode->val,maxi,i);\n return newnode ; \n }\n \n \n TreeNode* bstFromPreorder(vector<int>& preorder) {\n int i=0;\n long mini = LONG_MIN;\n long maxi = LONG_MAX ;\n return solve(preorder,mini,maxi,i);\n\t\t\n } }; | 3 | 0 | [] | 0 |
construct-binary-search-tree-from-preorder-traversal | Solution C++ (nlogn) using inorder traversal | solution-c-nlogn-using-inorder-traversal-65ty | \n class Solution {\n\n public:\n \n int posi(vector& inorder , int element , int size){\n\t\n for(int i=0; i preorder,vector\ &inorder | adityagarg217 | NORMAL | 2023-06-07T20:07:22.666449+00:00 | 2023-06-08T14:24:52.835634+00:00 | 2,122 | false | \n class Solution {\n\n public:\n \n int posi(vector<int>& inorder , int element , int size){\n\t\n for(int i=0; i<size ; i++){\n if(inorder[i]==element){\n return i;\n }\n }\n return -1 ;\n }\n TreeNode* solve(vector<int> preorder,vector<int> &inorder,int &preorderindex,int inorderstart,int inorderend, int size ){\n if(preorderindex>=size || inorderstart>inorderend){\n return NULL ;\n }\n int element = preorder[preorderindex++];\n TreeNode* root = new TreeNode(element);\n int position = posi(inorder, element , size);\n root->left = solve(preorder,inorder,preorderindex,inorderstart,position-1,size);\n root->right = solve(preorder,inorder,preorderindex,position+1,inorderend,size);\n return root ; \n \n }\n \n \n TreeNode* bstFromPreorder(vector<int>& preorder) {\n vector<int> inorder = preorder ;\n sort(inorder.begin(),inorder.end());\n \n int preorderindex = 0 ; \n int inorderstart = 0 ; \n int inorderend = inorder.size()-1 ; \n int size = inorder.size();\n \n TreeNode* node=solve(preorder,inorder,preorderindex,inorderstart,inorderend,size);\n return node ; \n }\n }; | 3 | 0 | [] | 0 |
first-unique-character-in-a-string | Java 7 lines solution 29ms | java-7-lines-solution-29ms-by-zachc-6fal | Hey guys. My solution is pretty straightforward. It takes O(n) and goes through the string twice:\n1) Get the frequency of each character.\n2) Get the first cha | zachc | NORMAL | 2016-08-22T16:53:12.466000+00:00 | 2018-10-25T04:28:35.438130+00:00 | 154,107 | false | Hey guys. My solution is pretty straightforward. It takes O(n) and goes through the string twice:\n1) Get the frequency of each character.\n2) Get the first character that has a frequency of one.\n\nActually the code below passes all the cases. However, according to @xietao0221, we could change the size of the frequency array to 256 to store other kinds of characters. Thanks for all the other comments and suggestions. Fight on!\n```\npublic class Solution {\n public int firstUniqChar(String s) {\n int freq [] = new int[26];\n for(int i = 0; i < s.length(); i ++)\n freq [s.charAt(i) - 'a'] ++;\n for(int i = 0; i < s.length(); i ++)\n if(freq [s.charAt(i) - 'a'] == 1)\n return i;\n return -1;\n }\n}\n``` | 552 | 10 | [] | 127 |
first-unique-character-in-a-string | C++ 2 solutions | c-2-solutions-by-dr_pro-0fi1 | Brute force solution, traverse string s 2 times. First time, store counts of every character into the hash table, second time, find the first character that app | dr_pro | NORMAL | 2016-08-22T05:58:06.132000+00:00 | 2021-11-10T06:12:57.370038+00:00 | 61,185 | false | Brute force solution, traverse string s 2 times. First time, store counts of every character into the hash table, second time, find the first character that appears only once.\n```\nclass Solution {\npublic:\n int firstUniqChar(string s) {\n unordered_map<char, int> m;\n for (char& c : s) {\n m[c]++;\n }\n for (int i = 0; i < s.size(); i++) {\n if (m[s[i]] == 1) return i;\n }\n return -1;\n }\n};\n```\nif the string is extremely long, we wouldn\'t want to traverse it twice, so instead only storing just counts of a char, we also store the index, and then traverse the hash table.\n\n```\nclass Solution {\npublic:\n\tint firstUniqChar(string s) {\n unordered_map<char, pair<int, int>> m;\n int idx = s.size();\n for (int i = 0; i < s.size(); i++) {\n m[s[i]].first++;\n m[s[i]].second = i;\n }\n for (const auto& [c, p] : m) {\n if (p.first == 1) {\n idx = min(idx, p.second);\n }\n }\n return idx == s.size() ? -1 : idx;\n }\n};\n``` | 243 | 7 | [] | 34 |
first-unique-character-in-a-string | Python 3 lines beats 100% (~ 60ms) ! | python-3-lines-beats-100-60ms-by-gregs-3ekj | \n def firstUniqChar(self, s):\n """\n :type s: str\n :rtype: int\n """\n \n letters='abcdefghijklmnopqrstuvwxyz'\n | gregs | NORMAL | 2016-10-30T19:07:39.451000+00:00 | 2018-10-25T00:57:48.893360+00:00 | 66,085 | false | ``` \n def firstUniqChar(self, s):\n """\n :type s: str\n :rtype: int\n """\n \n letters='abcdefghijklmnopqrstuvwxyz'\n index=[s.index(l) for l in letters if s.count(l) == 1]\n return min(index) if len(index) > 0 else -1\n``` | 183 | 18 | [] | 37 |
first-unique-character-in-a-string | JAVA || 100% faster code || Easy Solution with Explanation | java-100-faster-code-easy-solution-with-zlpb4 | \tPLEASE UPVOTE IF YOU LIKE.\n\nclass Solution {\n public int firstUniqChar(String s) {\n // Stores lowest index / first index\n int ans = Int | shivrastogi | NORMAL | 2022-08-16T02:56:45.670698+00:00 | 2022-08-16T02:56:45.670726+00:00 | 34,941 | false | \tPLEASE UPVOTE IF YOU LIKE.\n```\nclass Solution {\n public int firstUniqChar(String s) {\n // Stores lowest index / first index\n int ans = Integer.MAX_VALUE;\n // Iterate from a to z which is 26 which makes it constant\n for(char c=\'a\'; c<=\'z\';c++){\n // indexOf will return first index of alphabet and lastIndexOf will return last index\n // if both are equal then it has occured only once.\n // through this we will get all index\'s which are occured once\n // but our answer is lowest index\n int index = s.indexOf(c);\n if(index!=-1&&index==s.lastIndexOf(c)){\n ans = Math.min(ans,index);\n }\n }\n\n // If ans remain\'s Integer.MAX_VALUE then their is no unique character\n return ans==Integer.MAX_VALUE?-1:ans;\n } \n}\n``` | 182 | 3 | ['Java'] | 16 |
first-unique-character-in-a-string | Java One Pass Solution with LinkedHashMap | java-one-pass-solution-with-linkedhashma-88s4 | LinkedHashMap will not be the fastest answer for this question because the input characters are just from 'a' to 'z', but in other situations it might be faster | nnnomm | NORMAL | 2016-08-24T22:23:13.465000+00:00 | 2018-10-23T02:49:55.412376+00:00 | 41,261 | false | LinkedHashMap will not be the fastest answer for this question because the input characters are just from 'a' to 'z', but in other situations it might be faster than two pass solutions. I post this just for inspiration.\n```\npublic int firstUniqChar(String s) {\n Map<Character, Integer> map = new LinkedHashMap<>();\n Set<Character> set = new HashSet<>();\n for (int i = 0; i < s.length(); i++) {\n if (set.contains(s.charAt(i))) {\n if (map.get(s.charAt(i)) != null) {\n map.remove(s.charAt(i));\n }\n } else {\n map.put(s.charAt(i), i);\n set.add(s.charAt(i));\n }\n }\n return map.size() == 0 ? -1 : map.entrySet().iterator().next().getValue();\n }\n``` | 161 | 4 | [] | 37 |
first-unique-character-in-a-string | JavaScript solution | javascript-solution-by-twjeen-wal3 | \n var firstUniqChar = function(s) {\n for(i=0;i<s.length;i++){\n if (s.indexOf(s[i])===s.lastIndexOf(s[i])){\n return i;\n | twjeen | NORMAL | 2016-08-23T14:16:39.888000+00:00 | 2018-10-15T01:45:50.710524+00:00 | 9,635 | false | \n var firstUniqChar = function(s) {\n for(i=0;i<s.length;i++){\n if (s.indexOf(s[i])===s.lastIndexOf(s[i])){\n return i;\n } \n }\n return -1;\n };\n\nOR hash map method\n\n var firstUniqChar = function(s) \n var map=new Map();\n for(i=0;i<s.length;i++){\n if(map.has(s[i])){\n map.set(s[i],2);\n }\n else{\n map.set(s[i],1);\n }\n }\n \n for(i=0;i<s.length;i++){\n if(map.has(s[i]) && map.get(s[i])===1){\n return i;\n }\n }\n return -1;\n } ; | 117 | 2 | [] | 15 |
first-unique-character-in-a-string | ✅☑Beats 99% || [C++/Java/Python/JavaScript] || 2 Line Code || EXPLAINED🔥 | beats-99-cjavapythonjavascript-2-line-co-pj6a | PLEASE UPVOTE IF IT HELPED\n\n---\n\n\n\n---\n\n# Approaches\n(Also explained in the code)\n\n1. Initialize an unordered map (mp) to store character counts.\n1. | MarkSPhilip31 | NORMAL | 2024-02-05T01:07:11.909951+00:00 | 2024-02-05T08:05:18.657905+00:00 | 29,798 | false | # PLEASE UPVOTE IF IT HELPED\n\n---\n\n\n\n---\n\n# Approaches\n(Also explained in the code)\n\n1. Initialize an unordered map (mp) to store character counts.\n1. Iterate through the string to update character counts in the map.\n1. Iterate through the string again, return the index of the first character with a count of 1.\n\n\n\n\n# Complexity\n- Time complexity:\n $$O(n)$$\n \n\n- Space complexity:\n $$O(U)$$\n*(U is the number of unique characters in the string.)*\n \n\n\n# Code\n```C++ []\n\nclass Solution {\npublic:\n int firstUniqChar(string s) {\n unordered_map<char, int> mp;\n\n for (auto a : s) mp[a]++;\n for (int i = 0; i < s.size(); i++)if(mp[s[i]] == 1)return i;\n\n return -1;\n }\n}; \n\n\n```\n```Java []\n\n\nclass Solution {\n public int firstUniqChar(String s) {\n HashMap<Character, Integer> mp = new HashMap<>();\n\n for (char a : s.toCharArray()) {\n mp.put(a, mp.getOrDefault(a, 0) + 1);\n }\n\n for (int i = 0; i < s.length(); i++) {\n if (mp.get(s.charAt(i)) == 1) {\n return i;\n }\n }\n\n return -1;\n }\n}\n\n\n\n```\n```python3 []\nclass Solution:\n def firstUniqChar(self, s: str) -> int:\n mp = {}\n\n for a in s:\n mp[a] = mp.get(a, 0) + 1\n\n for i in range(len(s)):\n if mp[s[i]] == 1:\n return i\n\n return -1\n\n\n\n```\n```javascript []\n\nvar firstUniqChar = function(s) {\n let mp = {};\n\n for (let a of s) {\n mp[a] = (mp[a] || 0) + 1;\n }\n\n for (let i = 0; i < s.length; i++) {\n if (mp[s[i]] === 1) {\n return i;\n }\n }\n\n return -1;\n};\n\n\n```\n---\n\n\n\n# PLEASE UPVOTE IF IT HELPED\n\n---\n---\n\n\n--- | 108 | 5 | ['Hash Table', 'String', 'Queue', 'Counting', 'Python', 'C++', 'Java', 'Python3', 'JavaScript'] | 12 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.