question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
course-schedule-iv
|
C++ | DFS | Memoization
|
c-dfs-memoization-by-wh0ami-9lkc
|
\nclass Solution {\n vector<vector<int>>dp;\n bool dfs(unordered_map<int, vector<int>>& mp, int a, int b) {\n \n if (dp[a][b] != -1)\n
|
wh0ami
|
NORMAL
|
2020-05-30T16:25:22.671052+00:00
|
2020-05-31T06:30:06.329296+00:00
| 7,802 | false |
```\nclass Solution {\n vector<vector<int>>dp;\n bool dfs(unordered_map<int, vector<int>>& mp, int a, int b) {\n \n if (dp[a][b] != -1)\n return dp[a][b];\n \n for (int i = 0; i < mp[a].size(); i++) {\n if (mp[a][i] == b || dfs(mp, mp[a][i], b))\n return dp[a][b] = 1;\n }\n \n return dp[a][b] = 0;\n }\npublic:\n vector<bool> checkIfPrerequisite(int n, vector<vector<int>>& prerequisites, vector<vector<int>>& queries) {\n \n unordered_map<int, vector<int>>mp;\n \n dp.resize(n, vector<int>(n, -1));\n for (int i = 0; i < prerequisites.size(); i++) {\n mp[prerequisites[i][1]].push_back(prerequisites[i][0]);\n dp[prerequisites[i][1]][prerequisites[i][0]] = 1;\n }\n \n vector<bool>res;\n for (int i = 0; i < queries.size(); i++) {\n bool p = dfs(mp, queries[i][1], queries[i][0]);\n res.push_back(p);\n }\n \n return res;\n }\n};\n```
| 58 | 4 |
[]
| 7 |
course-schedule-iv
|
Simple Unordered map Number Linking
|
simple-unordered-map-link-by-sumeet_shar-4d5l
|
IntuitionThis problem is about understanding and navigating a dependency graph, where:
Each course is represented as a node.
Each prerequisite relationship is r
|
Sumeet_Sharma-1
|
NORMAL
|
2025-01-27T01:02:50.174372+00:00
|
2025-01-27T01:19:38.626724+00:00
| 9,483 | false |
# Intuition
This problem is about understanding and navigating a dependency graph, where:
- Each course is represented as a node.
- Each prerequisite relationship is represented as a directed edge from one course to another (e.g., if course `a` is a prerequisite for course `b`, there's an edge from `a` to `b`).
The goal is to determine whether a given course `u` is a prerequisite of another course `v` for a series of queries. To solve this, we need to:
1. Build a structure that captures all direct and indirect prerequisites for each course.
2. Use this structure to efficiently answer the queries.
Instead of directly simulating graph traversal for each query (which can be slow for multiple queries), we aim to preprocess the prerequisites into a structure that provides quick lookups. This can be efficiently achieved using an unordered map to maintain the reachability of each course.
# Approach
### Step 1: Build Reachability Chains
We use an `unordered_map<int, unordered_set<int>>` called `reachable` to store, for each course, the set of all courses that are prerequisites for it. For example:
- If course `b` depends directly on course `a`, then we add `a` to `reachable[b]`.
This step involves iterating over the `prerequisites` array and populating the `reachable` map with the direct prerequisites.
### Step 2: Propagate Reachability
Once the direct prerequisites are recorded, we need to account for indirect dependencies. For example:
- If course `a` is a prerequisite for course `b`, and course `b` is a prerequisite for course `c`, then course `a` is also a prerequisite for course `c`.
To achieve this, we iterate over all courses and update their reachability sets by propagating the prerequisites of their prerequisite courses. This ensures that the `reachable` map contains all direct and indirect prerequisites for each course.
### Step 3: Answer Queries
Using the `reachable` map, each query `[u, v]` can be answered by simply checking if `u` exists in the set `reachable[v]`. If it does, then `u` is a prerequisite for `v`; otherwise, it is not.
### Pseudocode
1. Initialize an unordered map `reachable` where `reachable[i]` stores the set of courses that are prerequisites for course `i`.
2. For each prerequisite `[a, b]`, add `a` to `reachable[b]`.
3. Propagate reachability:
- For each course `i`, merge the sets of all its prerequisite courses into `reachable[i]`.
4. For each query `[u, v]`, check if `u` exists in `reachable[v]`.
# Complexity
### Time Complexity
- **Building Reachability Chains**: Each prerequisite is processed once, so this step is $$O(p)$$, where $$p$$ is the number of prerequisites.
- **Propagating Reachability**:
- For each course, we potentially merge multiple sets. If the total number of prerequisite relationships is $$p$$, the merging operation across all courses takes $$O(p)$$ in total (amortized using union-find-like propagation).
- **Answering Queries**: Each query is a constant-time set lookup, so $$O(q)$$ for $$q$$ queries.
-
# Detailed Example
### Input
```plaintext
numCourses = 4
prerequisites = [[0, 1], [1, 2], [2, 3]]
queries = [[0, 3], [1, 3], [3, 0], [1, 0]]
Execution
Step 1: Build Reachability Chains
After processing prerequisites:
reachable[1] = {0}
reachable[2] = {1}
reachable[3] = {2}
Step 2: Propagate Reachability
After propagation:
reachable[1] = {0}
reachable[2] = {0, 1}
reachable[3] = {0, 1, 2}
Step 3: Answer Queries
Query [0, 3]: Yes, 0 is in reachable[3].
Query [1, 3]: Yes, 1 is in reachable[3].
Query [3, 0]: No, 3 is not in reachable[0].
Query [1, 0]: No, 1 is not in reachable[0].
Output
[true, true, false, false]
```
### Time Complexity
- Overall time complexity: $$O(p + q)$$.
### Space Complexity
- The `reachable` map requires $$O(p)$$ space, where $$p$$ is the total number of prerequisite relationships.
- The `result` array requires $$O(q)$$ space to store answers for $$q$$ queries.
Overall space complexity: $$O(p + q)$$.

# Code
```cpp
class Solution {
public:
vector<bool> checkIfPrerequisite(int numCourses, vector<vector<int>>& prerequisites, vector<vector<int>>& queries) {
// Step 1: Initialize the reachability map
unordered_map<int, unordered_set<int>> reachable;
// Step 2: Build direct reachability chains
for (auto& prereq : prerequisites) {
reachable[prereq[1]].insert(prereq[0]);
}
// Step 3: Propagate reachability to account for indirect prerequisites
for (int i = 0; i < numCourses; ++i) {
for (int j = 0; j < numCourses; ++j) {
if (reachable[j].count(i)) {
reachable[j].insert(reachable[i].begin(), reachable[i].end());
}
}
}
// Step 4: Answer the queries
vector<bool> result;
for (auto& query : queries) {
result.push_back(reachable[query[1]].count(query[0]) > 0);
}
return result;
}
};
```
| 55 | 1 |
['Ordered Map', 'C++']
| 8 |
course-schedule-iv
|
[C++] Easy to understand BFS solution
|
c-easy-to-understand-bfs-solution-by-him-vj3o
|
Step1: Create adjaceny list.\nStep2: Perform BFS on each node ignoring already visted path.\nStep3: Answer each query using isReachable[i][j] which denotes if t
|
himsingh11
|
NORMAL
|
2020-05-30T17:24:15.084940+00:00
|
2020-06-02T17:38:22.356991+00:00
| 4,662 | false |
Step1: Create adjaceny list.\nStep2: Perform BFS on each node ignoring already visted path.\nStep3: Answer each query using `isReachable[i][j]` which denotes if there is a path from `i` to `j`\n\n```cpp\nvector<bool> checkIfPrerequisite(int n, vector<vector<int>>& prerequisites, vector<vector<int>>& queries) \n{\n vector<bool> ans;\n vector<vector<int>> isReachable(n, vector<int> (n, 0));\n queue<int> q;\n\t //adjacency list\n vector<vector<int>> adj(n);\n for(auto &p : prerequisites){\n adj[p[0]].push_back(p[1]);\n } \n\t\t//visited \n vector<vector<int>> visited(n, vector<int>(n, 0));\n \n for(int i=0; i<n; i++){\n q.push(i);\n while(!q.empty()){\n int node = q.front();\n q.pop();\n for(int neighbor : adj[node]){\n if(visited[i][neighbor]) continue; \n isReachable[i][neighbor] = 1;\n visited[i][neighbor] = 1; \n q.push(neighbor);\n }\n }\n }\n \n for(auto &q : queries){\n ans.push_back(isReachable[q[0]][q[1]]);\n } \n return ans;\n }\n```\n\nComplexity:\nTime: `O(n * (n+E)), E = no of edges.`\n\nNote: You can use `isReachable` instead of `visited`. But, I haven\'t updated code to make it more readable.
| 41 | 1 |
['Breadth-First Search', 'C']
| 3 |
course-schedule-iv
|
Topological Sorting | Bitset | With Explanation | 100% BEATS
|
topological-sorting-bitset-with-explanat-1k8u
|
Problem Understanding:We need to determine if course u is a direct or indirect prerequisite for course v for multiple queries. Courses and prerequisites form a
|
shubham6762
|
NORMAL
|
2025-01-27T03:44:02.758678+00:00
|
2025-01-27T03:44:02.758678+00:00
| 7,018 | false |
## **Problem Understanding:**
We need to determine if course `u` is a direct or indirect prerequisite for course `v` for multiple queries. Courses and prerequisites form a directed acyclic graph (DAG), where an edge `A → B` means "A is a prerequisite for B."
### **Key Insight:**
For each course, track all its prerequisites (direct and indirect) efficiently. A **bitset** is ideal since the maximum number of courses (`n`) is 100. Each bit in the bitset represents whether a course is a prerequisite.
### **Logic Development:**
1. **Graph Construction:**
- Represent courses as nodes and prerequisites as directed edges.
- For each prerequisite `[a, b]`, add an edge `a → b` and mark `a` in `b`'s bitset.
2. **Topological Sorting:**
- Process nodes in topological order (prerequisites first) to ensure all indirect prerequisites are inherited.
- Use **Kahn's Algorithm** (in-degree tracking) for topological sorting.
3. **Bitset Propagation:**
- When processing a course `u`, propagate its prerequisites to all courses that require `u` (i.e., merge `u`'s bitset into its neighbors).
4. **Query Handling:**
- For each query `[u, v]`, check if `u` is set in `v`'s bitset.
### **Code Breakdown:**
```cpp []
class Solution {
public:
vector<bool> checkIfPrerequisite(int n, vector<vector<int>>& prerequisites, vector<vector<int>>& queries) {
vector<bitset<100>> prereq(n); // Tracks all prerequisites for each course
vector<vector<int>> adj(n); // Directed edges: adj[a] = courses that require 'a'
vector<int> inDegree(n, 0); // Number of prerequisites for each course
// Step 1: Build the graph and initialize direct prerequisites
for (auto& edge : prerequisites) {
int a = edge[0], b = edge[1];
adj[a].push_back(b); // 'a' is a prerequisite for 'b'
prereq[b].set(a); // Mark 'a' in 'b's bitset
inDegree[b]++; // 'b' has one more prerequisite
}
// Step 2: Topological sort using Kahn's algorithm
queue<int> q;
for (int i = 0; i < n; ++i) {
if (inDegree[i] == 0) q.push(i); // Start with courses having no prerequisites
}
while (!q.empty()) {
int u = q.front();
q.pop();
for (int v : adj[u]) { // For all courses that require 'u'
prereq[v] |= prereq[u]; // Merge 'u's prerequisites into 'v's
if (--inDegree[v] == 0) // Decrement 'v's prerequisites count
q.push(v); // If all prerequisites are processed, add to queue
}
}
// Step 3: Answer queries using the precomputed bitsets
vector<bool> ans;
ans.reserve(queries.size());
for (auto& qry : queries) {
int u = qry[0], v = qry[1];
ans.push_back(prereq[v][u]); // Check if 'u' is in 'v's prerequisites
}
return ans;
}
};
```
``` Java []
import java.util.*;
class Solution {
public List<Boolean> checkIfPrerequisite(int numCourses, int[][] prerequisites, int[][] queries) {
List<Integer>[] adj = new ArrayList[numCourses];
boolean[][] prereq = new boolean[numCourses][numCourses];
int[] inDegree = new int[numCourses];
for (int i = 0; i < numCourses; i++) {
adj[i] = new ArrayList<>();
}
// Build graph and initialize direct prerequisites
for (int[] edge : prerequisites) {
int a = edge[0], b = edge[1];
adj[a].add(b);
prereq[b][a] = true; // Direct prerequisite from a to b
inDegree[b]++;
}
// Topological sort using Kahn's algorithm
Queue<Integer> q = new LinkedList<>();
for (int i = 0; i < numCourses; i++) {
if (inDegree[i] == 0) q.add(i);
}
while (!q.isEmpty()) {
int u = q.poll();
for (int v : adj[u]) {
// Merge all prerequisites of u into v
for (int i = 0; i < numCourses; i++) {
if (prereq[u][i]) prereq[v][i] = true;
}
if (--inDegree[v] == 0) q.add(v);
}
}
// Answer queries using precomputed prerequisites
List<Boolean> ans = new ArrayList<>();
for (int[] query : queries) {
int u = query[0], v = query[1];
ans.add(prereq[v][u]);
}
return ans;
}
}
```
``` Python []
from collections import deque
class Solution(object):
def checkIfPrerequisite(self, numCourses, prerequisites, queries):
adj = [[] for _ in range(numCourses)]
prereq = [0] * numCourses # Bitmask for prerequisites
in_degree = [0] * numCourses
# Build graph and initialize direct prerequisites
for a, b in prerequisites:
adj[a].append(b)
prereq[b] |= 1 << a # Set the a-th bit for course b
in_degree[b] += 1
# Topological sort using Kahn's algorithm
q = deque()
for i in range(numCourses):
if in_degree[i] == 0:
q.append(i)
while q:
u = q.popleft()
for v in adj[u]:
prereq[v] |= prereq[u] # Merge u's prerequisites into v's
in_degree[v] -= 1
if in_degree[v] == 0:
q.append(v)
# Answer queries using bitmask checks
ans = []
for u, v in queries:
ans.append((prereq[v] & (1 << u)) != 0)
return ans
```
**How It Works:**
- **Bitsets:** Each course `v` has a `prereq[v]` bitset where the `u`-th bit is `1` if `u` is a prerequisite. Initially, this holds direct prerequisites. During topological sorting, indirect prerequisites are added by merging bitsets from dependencies.
- **Topological Order:** Ensures that when processing a course, all its prerequisites have already been processed, so their bitsets are complete.
- **Efficiency:** Each edge and node is processed once, and queries are answered in constant time.
**Example Scenario:**
- **Prerequisites:** `[[1,2], [1,0], [2,0]]`
- Edges: `1→2`, `1→0`, `2→0`.
- **Bitset Propagation:**
- Initially: `prereq[2] = {1}`, `prereq[0] = {1,2}` (after merging from `1` and `2`).
- **Query `[1,0]`:** `prereq[0][1]` is `1` → `true`.
- **Query `[1,2]`:** `prereq[2][1]` is `1` → `true`.
**Complexity:**
- **Time:**
- Graph construction: `O(E)` (edges).
- Topological sort: `O(N + E)`.
- Query handling: `O(Q)`.
- **Space:** `O(N^2)` (bitsets for `N` courses, each with `N` bits).
| 30 | 3 |
['Breadth-First Search', 'Graph', 'Topological Sort', 'Python', 'C++', 'Java']
| 7 |
course-schedule-iv
|
Clean Python 3, topological sort and set O(P * N)
|
clean-python-3-topological-sort-and-set-9902v
|
Just use a set to save all prerequisites of current course and pass all of them to those courses which take it as prerequisite while performing topological sort
|
lenchen1112
|
NORMAL
|
2020-05-30T17:40:45.846048+00:00
|
2020-05-31T15:58:34.116913+00:00
| 3,511 | false |
Just use a set to save all prerequisites of current course and pass all of them to those courses which take it as prerequisite while performing topological sort.\nTime: `O(P * N)`, N for topological sort and P for passing all prerequisites.\nSpace: `O(N^2)` for all sets.\n```\nimport collections\nclass Solution:\n def checkIfPrerequisite(self, n: int, prerequisites: List[List[int]], queries: List[List[int]]) -> List[bool]:\n graph = collections.defaultdict(list)\n in_degree = [0] * n\n pres = [set() for _ in range(n)]\n for pre, course in prerequisites:\n graph[pre].append(course)\n in_degree[course] += 1\n pres[course].add(pre)\n queue = collections.deque(course for course, degree in enumerate(in_degree)\n if degree == 0)\n while queue:\n pre = queue.popleft()\n for course in graph[pre]:\n pres[course] |= pres[pre]\n in_degree[course] -= 1\n if in_degree[course] == 0:\n queue.append(course)\n return [pre in pres[course] for pre, course in queries]\n```
| 27 | 1 |
[]
| 5 |
course-schedule-iv
|
Kahn's Alg+ array over bitset vs DFS||C++100% Py3 97.9%
|
kahns-alg-array-over-bitsetc100-by-anwen-6364
|
IntuitionAgain use topo sort, i.e. Kahn's algorithm.
For a directed edge (a, b) in G, a is a prerequisite course for b. For any query (u, v) being in G or not,
|
anwendeng
|
NORMAL
|
2025-01-27T00:41:22.197839+00:00
|
2025-01-27T07:48:09.206844+00:00
| 2,916 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
Again use topo sort, i.e. Kahn's algorithm.
For a directed edge `(a, b)` in $G$, `a` is a prerequisite course for `b`. For any query `(u, v)` being in $G$ or not, it is constructed a container `rpath[v][u]` by using an array of bitsets to keep the computational results which is really fast.
Python code is also made in the similar way.
2nd approach is DFS
# Approach
<!-- Describe your approach to solving the problem. -->
1. Declare ` bitset<100> rpath[100]={0}; vector<char> adj[100]`
2. let `deg[100]={0}` be the indegrees for all vertices.
3. Proceed a loop over e in `prerequisites`, let `(a, b)=e`; set
```
adj[a].push_back(b);// construct adjacent list
rpath[b][a]=1; // for query (a, b)
deg[b]++; // increase indegree for b
```
4. Let `q` be the queue; it can be used `std::queue` or C-array with 2 variables `front & back`
5. Add all 0 deg vertices to `q`
6. Proceed BFS as follows
```
while(!q.empty()){
auto i=q.front();// get i from the front
q.pop();
for(int j: adj[i]){ // adjacent vertices
//all prerequisites for i is also prerequisites for j
//taking or operation for 100-bit bitset
rpath[j]|=rpath[i];
// remove the edge, if j becomes deg 0 push it to q
if (--deg[j]==0) q.push(j);
}
}
```
7. All `rpath` is constructed, use a loop to give the answer `ans[i]=rpath[queries[i][1]][queries[i][0]]`
8. Python is made; use bit mask play the role of C++ bitset; use deque as a queue.
# Kahn's Algorthim is a method for topological sort
Kahn's Algorithm is BFS method by removing the edges and decreasing the indegrees.
Toplogical sort can solve the following questions
[207. Course Schedule](https://leetcode.com/problems/course-schedule/solutions/3756937/w-explanation-c-dfs-vs-bfs-kahn-s-algorithm/)
[210. Course Schedule II](https://leetcode.com/problems/course-schedule-ii/)
[802. Find Eventual Safe States](https://leetcode.com/problems/find-eventual-safe-states/solutions/6321974/kahn-s-algo-vs-dfs-dp-c-2ms-96-65/)<-hard
[2127. Maximum Employees to Be Invited to a Meeting](https://leetcode.com/problems/maximum-employees-to-be-invited-to-a-meeting/solutions/6329758/kahns-alg-find-cyles11ms-beats-9672-by-a-9zeu/)<- hard
[1203. Sort Items by Groups Respecting Dependencies](https://leetcode.com/problems/sort-items-by-groups-respecting-dependencies/solutions/3933825/c-using-bfs-kahn-s-algorithm-vs-dfs-beats-97-67/)<-hard
[Please turn on English subtitles]
[https://youtu.be/vdar3a_ZdCI?si=j8puaMYKe88XGO5g](https://youtu.be/vdar3a_ZdCI?si=j8puaMYKe88XGO5g)
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
LC said so, but it needs more care to analyze (say $O(100n+|prerequisites|+m)$)
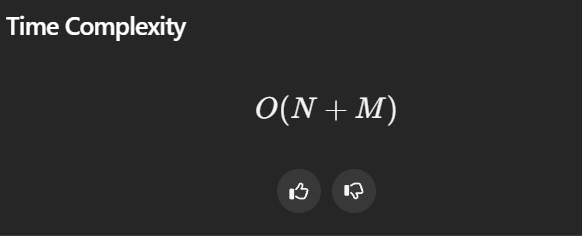
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
Extra: $O(n^2)$
# Code||C++ 0ms 100%|2nd version implements q with C-array
```cpp []
class Solution {
public:
vector<bool> checkIfPrerequisite(int n, vector<vector<int>>& prerequisites, vector<vector<int>>& queries) {
bitset<100> rpath[100]={0};
vector<char> adj[100];
char deg[100]={0};// indegree
for(auto& e: prerequisites){
char a=e[0], b=e[1];
adj[a].push_back(b);
rpath[b][a]=1;
deg[b]++;
}
queue<int> q;
for(int i=0; i<n; i++)
if (deg[i]==0) q.push(i);// deg 0 nodes
while(!q.empty()){
auto i=q.front();
q.pop();
for(int j: adj[i]){
rpath[j]|=rpath[i];
if (--deg[j]==0) q.push(j);
}
}
const int m=queries.size();
vector<bool> ans(m, 0);
for(int i=0; i<m; i++)
ans[i]=rpath[queries[i][1]][queries[i][0]];
return ans;
}
};
```
```cpp [C++ 2nd ver]
class Solution {
public:
vector<bool> checkIfPrerequisite(int n, vector<vector<int>>& prerequisites, vector<vector<int>>& queries) {
bitset<100> rpath[100]={0};
vector<char> adj[100];
char deg[100]={0};// indegree
for(auto& e: prerequisites){
char a=e[0], b=e[1];
adj[a].push_back(b);
rpath[b][a]=1;
deg[b]++;
}
int q[100]={0}, front=0, back=0;
for(int i=0; i<n; i++)
if (deg[i]==0) q[back++]=i;// deg 0 nodes
while(front!=back){
auto i=q[front++];
for(int j: adj[i]){
rpath[j]|=rpath[i];
if (--deg[j]==0) q[back++]=j;
}
}
const int m=queries.size();
vector<bool> ans(m, 0);
for(int i=0; i<m; i++)
ans[i]=rpath[queries[i][1]][queries[i][0]];
return ans;
}
};
```
# Python |17ms Beats 97.90%
```
class Solution:
def checkIfPrerequisite(self, n: int, prerequisites: List[List[int]], queries: List[List[int]]) -> List[bool]:
rpath=[0]*n
adj=[[] for _ in range(n)]
deg=[0]*n
for a, b in prerequisites:
adj[a].append(b)
rpath[b]|=(1<<a)
deg[b]+=1
q=deque()
for i in range(n):
if deg[i]==0: q.append(i)
while q:
i=q.popleft()
for j in adj[i]:
rpath[j]|=rpath[i]
deg[j]-=1
if deg[j]==0:
q.append(j)
ans=[False]*len(queries)
for i, (q0, q1) in enumerate(queries):
ans[i]=(rpath[q1]>>q0)&1==1
return ans
```
# DFS solution||C++ 9ms Beats 93.38%
```
class Solution {
public:
int n;
bitset<100> path[100]; // Store prerequisite relationships
vector<int> adj[100]; // Adjacency list for the graph
void dfs(int start, int i, bitset<100>& visited) {
visited[i] = 1; // Mark as visited
path[start][i] = 1; // path from start to i
for (int j : adj[i]) {
if (visited[j]) {
path[i] |= path[j];
continue;
}
dfs(start, j, visited);
}
}
vector<bool> checkIfPrerequisite(int n, vector<vector<int>>& prerequisites,
vector<vector<int>>& queries) {
this->n = n;
// Build the graph and initialize prerequisites
for (auto& edge : prerequisites) {
int u = edge[0], v = edge[1];
adj[u].push_back(v);
}
// Perform DFS from each node
for (int i = 0; i < n; i++) {
bitset<100> visited;
if (!visited[i])
dfs(i, i, visited); // Start DFS from node i
}
const int m = queries.size();
vector<bool> ans(m, 0);
for (int i = 0; i < m; i++)
ans[i] = path[queries[i][0]][queries[i][1]];
return ans;
}
};
```
| 26 | 2 |
['Bit Manipulation', 'Depth-First Search', 'Breadth-First Search', 'Topological Sort', 'C++']
| 4 |
course-schedule-iv
|
Most Optimal Solution with Topological Sort | C++| Java | Python | JavaScript
|
most-optimal-solution-with-topological-s-84x3
|
⬆️Upvote if it helps ⬆️Connect with me on Linkedin [Bijoy Sing]🧠 IntuitionThink of courses like a family tree! 👨👩👧👦
Each course can have "parent" courses (pr
|
BijoySingh7
|
NORMAL
|
2025-01-27T03:53:36.149917+00:00
|
2025-01-27T03:53:36.149917+00:00
| 5,799 | false |
# ⬆️Upvote if it helps ⬆️
---
## Connect with me on Linkedin [Bijoy Sing]
---
```cpp []
class Solution {
public:
vector<bool> checkIfPrerequisite(int numCourses, vector<vector<int>>& prerequisites, vector<vector<int>>& queries) {
vector<vector<int>> adj(numCourses);
vector<int> indegree(numCourses, 0);
for(auto p : prerequisites) {
adj[p[0]].push_back(p[1]);
indegree[p[1]]++;
}
queue<int> q;
for(int i = 0; i < numCourses; i++) {
if(indegree[i] == 0) {
q.push(i);
}
}
unordered_map<int, unordered_set<int>> mp;
while(!q.empty()) {
int curr = q.front();
q.pop();
for(auto next : adj[curr]) {
mp[next].insert(curr);
for(auto pre : mp[curr]) {
mp[next].insert(pre);
}
indegree[next]--;
if(indegree[next] == 0) {
q.push(next);
}
}
}
vector<bool> res;
for(auto q : queries) {
res.push_back(mp[q[1]].count(q[0]));
}
return res;
}
};
```
```python []
class Solution:
def checkIfPrerequisite(self, numCourses: int, prerequisites: List[List[int]], queries: List[List[int]]) -> List[bool]:
adj = [[] for _ in range(numCourses)]
indegree = [0] * numCourses
for p in prerequisites:
adj[p[0]].append(p[1])
indegree[p[1]] += 1
q = deque()
for i in range(numCourses):
if indegree[i] == 0:
q.append(i)
mp = defaultdict(set)
while q:
curr = q.popleft()
for next_course in adj[curr]:
mp[next_course].add(curr)
mp[next_course].update(mp[curr])
indegree[next_course] -= 1
if indegree[next_course] == 0:
q.append(next_course)
return [q[0] in mp[q[1]] for q in queries]
```
```java []
class Solution {
public List<Boolean> checkIfPrerequisite(int numCourses, int[][] prerequisites, int[][] queries) {
List<List<Integer>> adj = new ArrayList<>();
int[] indegree = new int[numCourses];
for(int i = 0; i < numCourses; i++) {
adj.add(new ArrayList<>());
}
for(int[] p : prerequisites) {
adj.get(p[0]).add(p[1]);
indegree[p[1]]++;
}
Queue<Integer> q = new LinkedList<>();
for(int i = 0; i < numCourses; i++) {
if(indegree[i] == 0) {
q.offer(i);
}
}
Map<Integer, Set<Integer>> mp = new HashMap<>();
for(int i = 0; i < numCourses; i++) {
mp.put(i, new HashSet<>());
}
while(!q.isEmpty()) {
int curr = q.poll();
for(int next : adj.get(curr)) {
mp.get(next).add(curr);
mp.get(next).addAll(mp.get(curr));
indegree[next]--;
if(indegree[next] == 0) {
q.offer(next);
}
}
}
List<Boolean> res = new ArrayList<>();
for(int[] query : queries) {
res.add(mp.get(query[1]).contains(query[0]));
}
return res;
}
}
```
```javascript []
/**
* @param {number} numCourses
* @param {number[][]} prerequisites
* @param {number[][]} queries
* @return {boolean[]}
*/
var checkIfPrerequisite = function(numCourses, prerequisites, queries) {
const adj = Array.from({length: numCourses}, () => []);
const indegree = new Array(numCourses).fill(0);
for(let p of prerequisites) {
adj[p[0]].push(p[1]);
indegree[p[1]]++;
}
const q = [];
for(let i = 0; i < numCourses; i++) {
if(indegree[i] === 0) {
q.push(i);
}
}
const mp = new Map();
for(let i = 0; i < numCourses; i++) {
mp.set(i, new Set());
}
while(q.length > 0) {
const curr = q.shift();
for(let next of adj[curr]) {
mp.get(next).add(curr);
for(let pre of mp.get(curr)) {
mp.get(next).add(pre);
}
indegree[next]--;
if(indegree[next] === 0) {
q.push(next);
}
}
}
return queries.map(([u, v]) => mp.get(v).has(u));
};
```
## 🧠 Intuition
Think of courses like a family tree! 👨👩👧👦
- Each course can have "parent" courses (prerequisites)
- If course A is parent of B, and B is parent of C, then A is like a "grandparent" to C!
- We need to track all these relationships efficiently
## 🛠️ Approach Step by Step
### 1️⃣ Building the Graph 🏗️
```cpp
vector<vector<int>> adj(numCourses);
vector<int> indegree(numCourses, 0);
for(auto p : prerequisites) {
adj[p[0]].push_back(p[1]);
indegree[p[1]]++;
}
```
- Create an adjacency list (like a contact list where each person has their friends' numbers) 📱
- Count how many prerequisites each course has (indegree) 🔢
### 2️⃣ Finding Starting Points 🎯
```cpp
queue<int> q;
for(int i = 0; i < numCourses; i++) {
if(indegree[i] == 0) {
q.push(i);
}
}
```
- Find courses with no prerequisites (they're like the oldest ancestors!) 👴
- Put them in a queue (like a line at a coffee shop ☕)
### 3️⃣ Processing Courses 🔄
```cpp
unordered_map<int, unordered_set<int>> mp;
while(!q.empty()) {
int curr = q.front();
q.pop();
for(auto next : adj[curr]) {
mp[next].insert(curr); // Direct prerequisite
for(auto pre : mp[curr]) {
mp[next].insert(pre); // Indirect prerequisites
}
indegree[next]--;
if(indegree[next] == 0) {
q.push(next);
}
}
}
```
- Use a map to store all prerequisites for each course 🗺️
- For each course we process:
1. Add it as a prerequisite to its dependent courses 📝
2. Pass down all its prerequisites (like inherited traits!) 🧬
3. Update the prerequisite count 🔄
4. When a course has all prerequisites processed, add it to queue ➕
### 4️⃣ Answering Queries 💡
```cpp
vector<bool> res;
for(auto q : queries) {
res.push_back(mp[q[1]].count(q[0]));
}
```
- For each query, we just check our map! 🔍
- Like checking if someone is in your family tree 👨👩👧👦
## 🚀 Complexity Analysis
### ⏱️ Time Complexity
- Building graph: O(P) where P is prerequisites length 📊
- Processing courses: O(V * E) where:
- V = number of courses 📚
- E = number of prerequisites edges 🔗
- Answering queries: O(Q) where Q is queries length 🔍
- Total: O(V * E + Q) ⚡
### 💾 Space Complexity
- Adjacency List: O(P) 📝
- Queue: O(V) 📋
- Prerequisites Map: O(V * E) 🗃️
- Total: O(V * E) 💿
### *If you have any questions or need further clarification, feel free to drop a comment! 😊*
| 24 | 0 |
['Graph', 'Topological Sort', 'Python', 'C++', 'Java', 'Python3', 'JavaScript']
| 1 |
course-schedule-iv
|
[python3][Topological Sort][BFS] Clear solution with comments
|
python3topological-sortbfs-clear-solutio-zr9d
|
Summary: the idea is to use topological sort to create a prerequisite lookup dictionary. \n\nSince this method is query-intensive, so we need to have O(1) time
|
chenhanxiong1990
|
NORMAL
|
2021-09-24T05:10:32.838692+00:00
|
2022-01-05T19:54:31.250889+00:00
| 2,669 | false |
Summary: the idea is to use topological sort to create a prerequisite lookup dictionary. \n\nSince this method is query-intensive, so we need to have O(1) time for query. In this case, we need to create a dictionary with each course as the key and the value is a set including all the prerequisites of this course. This lookup dictionary can be created by doing topological sort. \n\n```\nfrom collections import defaultdict, deque\n\nclass Solution:\n def checkIfPrerequisite(self, numCourses: int, prerequisites: List[List[int]], queries: List[List[int]]) -> List[bool]:\n neighbors = {node: set() for node in range(numCourses)} # store the graph\n indegree = defaultdict(int) # store indegree info for each node\n pre_lookup = defaultdict(set) # store the prerequisites info for each node\n \n # create the graph\n for pre, post in prerequisites:\n neighbors[pre].add(post)\n indegree[post] += 1\n \n # add 0 degree nodes into queue for topological sort\n queue = deque([])\n for n in neighbors:\n if indegree[n] == 0:\n queue.append(n)\n \n # use BFS to do topological sort to create a prerequisite lookup dictionary\n while queue:\n cur = queue.popleft()\n for neighbor in neighbors[cur]:\n pre_lookup[neighbor].add(cur) # add current node as the prerequisite of this neighbor node\n pre_lookup[neighbor].update(pre_lookup[cur]) # add all the preqs for current node to the neighbor node\'s preqs\n \n indegree[neighbor] -= 1 # regular topological search operations\n if indegree[neighbor] == 0:\n queue.append(neighbor)\n \n # traverse the queries and return the results\n result = [True if q[0] in pre_lookup[q[1]] else False for q in queries]\n \n return result\n```\n\n
| 23 | 0 |
['Breadth-First Search', 'Topological Sort', 'Python', 'Python3']
| 5 |
course-schedule-iv
|
Multiple Approaches || BFS and DFS || C++ Clean Code
|
multiple-approaches-bfs-and-dfs-c-clean-m32jr
|
This problem can be solved using multiple approaches. In this post I have included two of such appoach, one using DFS , and another using BFS (Topo Sort). \n# A
|
i_quasar
|
NORMAL
|
2021-10-30T05:51:40.150992+00:00
|
2021-10-30T05:51:40.151039+00:00
| 2,313 | false |
This problem can be solved using multiple approaches. In this post I have included two of such appoach, one using DFS , and another using BFS (Topo Sort). \n# Approach 1 : using DFS\n * Idea here is to iterate over all nodes taking it as source, \n * and then find all reachable nodes from source. Mark all those nodes as reachable.\n * We use a matrix `isPrerequisite[i][j] -> i come before j`. Our task to fill this.\n * Traverse from source using DFS and mark all reachable nodes as true. (`isPrerequisite[source][j]`)\n * Then we can simply query and return `isPrerequisite[i][j]`.\n \n # Code:\n \n```\nclass Solution {\npublic:\n \n void dfs(vector<vector<int>>& adj, vector<vector<bool>>& isPrerequisite, vector<bool>& vis, int source, int node) {\n vis[node] = true;\n isPrerequisite[source][node] = true;\n for(auto& adjNode : adj[node]) {\n if(!vis[adjNode]) {\n dfs(adj, isPrerequisite, vis, source, adjNode);\n }\n }\n \n }\n \n vector<bool> checkIfPrerequisite(int numCourses, vector<vector<int>>& prerequisites, vector<vector<int>>& queries) {\n \n vector<vector<bool>> isPrerequisite(numCourses, vector<bool>(numCourses, false));\n \n vector<vector<int>> adj(numCourses);\n \n for(auto& pre : prerequisites) {\n adj[pre[0]].push_back(pre[1]);\n isPrerequisite[pre[0]][pre[1]] = true;\n }\n \n for(int i=0; i<numCourses; i++) {\n vector<bool> vis(numCourses, false);\n dfs(adj, isPrerequisite, vis, i, i);\n }\n \n vector<bool> res;\n for(auto& query : queries) {\n res.push_back(isPrerequisite[query[0]][query[1]]);\n }\n \n return res;\n }\n};\n```\n\n # Approach 2 : BFS (Topological Sort) \n * Idea here is do simple topo sort. For reachable nodes, we can mark direct neighbours. But how we will mark indirect neighbours.\n * Logical Trick here for that is that, when we reach some "node", then we mark all its neighbours as reachable.\n * So, it we can reach say `x -> y` (directly or indirectly), and say z is neighbour of y. Then we can surely say x -> z always. \n * This is because if we can reach y from some node x, then we can always reach z (neighbour of y) from x as well.\n * i.e if `isPrerequisite[x][y] = true`, and y->z (neighbour), then `isPrerequisite[x][z] = true`\n * Just this trick is sufficient and efficient to solve this problem.\n\n# Code: \n\n```\nclass Solution {\npublic:\n \n vector<bool> checkIfPrerequisite(int numCourses, vector<vector<int>>& prerequisites, vector<vector<int>>& queries) {\n \n vector<vector<bool>> isPrerequisite(numCourses, vector<bool>(numCourses, false));\n \n vector<vector<int>> adj(numCourses);\n vector<int> indegree(numCourses, 0);\n \n for(auto& pre : prerequisites) {\n adj[pre[0]].push_back(pre[1]);\n isPrerequisite[pre[0]][pre[1]] = true;\n indegree[pre[1]]++;\n }\n \n queue<int> q;\n for(int i=0; i<numCourses; i++) if(indegree[i] == 0) q.push(i);\n \n while(q.size()) {\n int node = q.front(); q.pop();\n \n for(auto& adjnode : adj[node]) {\n for(int i=0; i<numCourses; i++) {\n if(isPrerequisite[i][node]) isPrerequisite[i][adjnode] = true;\n }\n \n indegree[adjnode]--; \n if(indegree[adjnode] == 0) q.push(adjnode);\n }\n }\n \n vector<bool> res;\n for(auto& query : queries) {\n res.push_back(isPrerequisite[query[0]][query[1]]);\n }\n \n return res;\n }\n};\n```\n\n***If you find this solution helpful, do give it a like :)***
| 22 | 0 |
['Depth-First Search', 'Breadth-First Search', 'Topological Sort']
| 2 |
course-schedule-iv
|
Python | DFS + Caching
|
python-dfs-caching-by-underoos16-myva
|
\nclass Solution:\n def checkIfPrerequisite(self, n: int, prerequisites: List[List[int]], queries: List[List[int]]) -> List[bool]:\n from collections
|
underoos16
|
NORMAL
|
2020-05-30T17:57:11.786643+00:00
|
2020-06-06T02:50:47.814435+00:00
| 2,233 | false |
```\nclass Solution:\n def checkIfPrerequisite(self, n: int, prerequisites: List[List[int]], queries: List[List[int]]) -> List[bool]:\n from collections import defaultdict\n adj_list = defaultdict(list)\n\n for a,b in prerequisites:\n adj_list[a].append(b)\n\n from functools import lru_cache\n @lru_cache(maxsize=None)\n def is_reachable(s,t):\n """s = source, t=target. Is target reachable from source?"""\n\n if s==t:\n return True\n\n for neighb in adj_list[s]:\n\t\t\t\tif is_reachable(neighb, t):\n\t\t\t\t\treturn True\n return False\n\n res = []\n\n for s,t in queries:\n res.append(is_reachable(s,t))\n\n return res\n\n```
| 15 | 0 |
[]
| 7 |
course-schedule-iv
|
Easy & Detailed Approch💡| Normal DFS Only ✅ | All Languages 🔥
|
easy-detailed-approch-normal-dfs-only-al-ek3y
|
IntuitionThe problem can be visualized as a directed graph, where each course is a node and each prerequisite pair represents a directed edge from one course to
|
himanshu_dhage
|
NORMAL
|
2025-01-27T03:31:18.267222+00:00
|
2025-01-27T03:31:18.267222+00:00
| 1,681 | false |
# Intuition
The problem can be visualized as a **directed graph**, where each course is a node and each prerequisite pair represents a directed edge from one course to another.
The goal is to determine if one course is a prerequisite for another based on the given queries.
To achieve this, we need to identify all pairs `(a, b)` where `a` is a prerequisite for `b`.
# Approach
1. **Graph Representation**:
- Represent the graph using an **adjacency list**.
For every pair `(u, v)` in the prerequisites, add a directed edge from `u` to `v` in the adjacency list.
2. **Depth-First Search (DFS)**:
- For each course `i`, perform a **DFS traversal** starting from `i` to explore all reachable courses.
- Use a `set<pair<int, int>>` to store all pairs `(start, end)` where `start` is a prerequisite for `end`.
- This set ensures that we track all valid prerequisite relationships.
3. **Handling Queries**:
- For each query `(u, v)`, check if the pair exists in the set.
- If found, return `true` for that query; otherwise, return `false`.
4. **Implementation**:
- Perform DFS for every node (course) to explore all possible paths.
- Use a visited array to ensure no node is visited twice during a single DFS call.
# Complexity
- **Time Complexity**:
$$O(N^2 + E)$$
- DFS is performed from every node, and each edge is traversed once.
- `N` is the number of nodes (courses), and `E` is the number of edges (prerequisites).
- **Space Complexity**:
$$O(N^2)$$
- The space is used by the set `s`, which can store up to `N^2` pairs in the worst case.
# Code
```cpp []
class Solution {
public:
// Helper function to perform DFS and record prerequisites
void dfs(int node, vector<vector<int>> &adj, vector<bool> &visited, set<pair<int, int>> &s, int start) {
// Mark the current node as visited
visited[node] = true;
// Add the pair (start, node) to the set if `start` is not -1
// This indicates that `start` is a prerequisite for `node`
if (start != -1) {
s.insert({start, node});
}
// Explore all neighbors of the current node
for (int neighbor : adj[node]) {
if (!visited[neighbor]) {
dfs(neighbor, adj, visited, s, start);
}
}
}
// Main function to check if prerequisites exist for the given queries
vector<bool> checkIfPrerequisite(int n, vector<vector<int>> &pre, vector<vector<int>> &q) {
// Step 1: Build the adjacency list representation of the graph
vector<vector<int>> adj(n);
for (const auto &p : pre) {
adj[p[0]].push_back(p[1]); // Add a directed edge from p[0] to p[1]
}
// Step 2: Use DFS to compute all prerequisites
set<pair<int, int>> s; // To store all prerequisite pairs (a, b) where a is a prerequisite for b
for (int i = 0; i < n; i++) {
// Perform DFS for each node to find all its reachable nodes (prerequisites)
vector<bool> visited(n, false); // Reset the visited array for each node
dfs(i, adj, visited, s, i); // Start DFS from node `i` with `i` as the starting node
}
// Step 3: Answer each query based on the set of prerequisites
vector<bool> result(q.size(), false); // Initialize the result vector with `false`
for (int i = 0; i < q.size(); i++) {
// Check if the pair (q[i][0], q[i][1]) exists in the set of prerequisites
if (s.find({q[i][0], q[i][1]}) != s.end()) {
result[i] = true; // If found, set the result for this query to `true`
}
}
return result; // Return the result vector
}
};
```
```javascript []
class Solution {
// Helper function to perform DFS and record prerequisites
dfs(node, adj, visited, prerequisites, start) {
// Mark the current node as visited
visited[node] = true;
// Add the pair (start, node) to the set if start is not -1
if (start !== -1) {
prerequisites.add(`${start},${node}`); // Store as a string for easy lookup
}
// Explore all neighbors of the current node
for (let neighbor of adj[node]) {
if (!visited[neighbor]) {
this.dfs(neighbor, adj, visited, prerequisites, start);
}
}
}
checkIfPrerequisite(n, pre, q) {
// Step 1: Build the adjacency list representation of the graph
const adj = Array.from({ length: n }, () => []);
for (const [u, v] of pre) {
adj[u].push(v);
}
// Step 2: Use DFS to compute all prerequisites
const prerequisites = new Set();
for (let i = 0; i < n; i++) {
const visited = Array(n).fill(false); // Reset visited array for each node
this.dfs(i, adj, visited, prerequisites, i);
}
// Step 3: Answer each query
return q.map(([u, v]) => prerequisites.has(`${u},${v}`));
}
}
```
```python []
class Solution:
def dfs(self, node, adj, visited, prerequisites, start):
# Mark the current node as visited
visited[node] = True
# Add the pair (start, node) to the set if start != -1
if start != -1:
prerequisites.add((start, node))
# Explore all neighbors of the current node
for neighbor in adj[node]:
if not visited[neighbor]:
self.dfs(neighbor, adj, visited, prerequisites, start)
def checkIfPrerequisite(self, n, pre, q):
# Step 1: Build the adjacency list representation of the graph
adj = [[] for _ in range(n)]
for u, v in pre:
adj[u].append(v)
# Step 2: Use DFS to compute all prerequisites
prerequisites = set()
for i in range(n):
visited = [False] * n # Reset visited array for each node
self.dfs(i, adj, visited, prerequisites, i)
# Step 3: Answer each query
return [tuple(query) in prerequisites for query in q]

```
```java []
import java.util.*;
class Solution {
// Helper function to perform DFS and record prerequisites
private void dfs(int node, List<List<Integer>> adj, boolean[] visited, Set<Pair<Integer, Integer>> prerequisites, int start) {
// Mark the current node as visited
visited[node] = true;
// Add the pair (start, node) to the set if `start` is not -1
if (start != -1) {
prerequisites.add(new Pair<>(start, node));
}
// Explore all neighbors of the current node
for (int neighbor : adj.get(node)) {
if (!visited[neighbor]) {
dfs(neighbor, adj, visited, prerequisites, start);
}
}
}
public List<Boolean> checkIfPrerequisite(int n, int[][] pre, int[][] q) {
// Step 1: Build the adjacency list representation of the graph
List<List<Integer>> adj = new ArrayList<>();
for (int i = 0; i < n; i++) {
adj.add(new ArrayList<>());
}
for (int[] p : pre) {
adj.get(p[0]).add(p[1]);
}
// Step 2: Use DFS to compute all prerequisites
Set<Pair<Integer, Integer>> prerequisites = new HashSet<>();
for (int i = 0; i < n; i++) {
boolean[] visited = new boolean[n]; // Reset visited array for each node
dfs(i, adj, visited, prerequisites, i);
}
// Step 3: Answer each query
List<Boolean> result = new ArrayList<>();
for (int[] query : q) {
result.add(prerequisites.contains(new Pair<>(query[0], query[1])));
}
return result;
}
}
```

| 14 | 0 |
['Array', 'Hash Table', 'Depth-First Search', 'Breadth-First Search', 'Graph', 'Topological Sort', 'Ordered Set', 'C++', 'Java', 'Python3']
| 0 |
course-schedule-iv
|
Python-Easy to understand Topological sort , beats 100%
|
python-easy-to-understand-topological-so-3h36
|
If you find it useful, please upvote it so that others can find it easily.\n# Complexity\n- Time complexity:\no(n(p+n)q)\n# please upvote if found helpful\n# Co
|
charant587
|
NORMAL
|
2023-06-30T12:40:59.932396+00:00
|
2023-07-12T18:40:38.310762+00:00
| 1,298 | false |
# If you find it useful, please upvote it so that others can find it easily.\n# Complexity\n- Time complexity:\no(n(p+n)q)\n# please upvote if found helpful\n# Code\n```\nclass Solution(object):\n def checkIfPrerequisite(self, numCourses, prerequisites, queries):\n adj={i:[] for i in range(numCourses)}\n\n for x,y in prerequisites:\n adj[y].append(x)\n res=[]\n def dfs(crs):\n if crs not in premap:\n premap[crs]=set()\n for nei in adj[crs]:\n premap[crs]|=dfs(nei)\n premap[crs].add(crs)\n return premap[crs]\n\n premap={}\n for i in range(numCourses):\n dfs(i) \n for x,y in queries:\n res.append(x in premap[y])\n return res\n#please upvote if found helpful\n \n \n```
| 13 | 0 |
['Topological Sort', 'Python', 'Python3']
| 1 |
course-schedule-iv
|
Java simple DFS better than 94%. O(n^2) for building and O(1) for queries
|
java-simple-dfs-better-than-94-on2-for-b-rlov
|
The idea here is to fill a nxn boolean matrix with either the second node is reachable from the first or not (even through an indirect way). Why am I doing this
|
tarkhan
|
NORMAL
|
2021-02-10T20:38:08.240732+00:00
|
2021-03-04T16:16:18.675878+00:00
| 2,169 | false |
The idea here is to fill a nxn boolean matrix with either the second node is reachable from the first or not (even through an indirect way). Why am I doing this? because we have multiple queries and the number of these queries most likely will be more than the length of the prerequisites we have so we can save a lot of time by pre-building all the relations before checking the queries.\n\n```\nclass Solution {\n public void fillGraph(boolean[][] graph, int i, boolean[] visited){\n if (visited[i])\n return;\n visited[i] = true;\n for (int j=0;j<graph[i].length;j++){\n if (graph[i][j]){\n fillGraph(graph, j, visited);\n for (int k=0;k<graph[j].length;k++){\n if (graph[j][k])\n graph[i][k] = true;\n }\n }\n }\n }\n \n public List<Boolean> checkIfPrerequisite(int n, int[][] prerequisites, int[][] queries) {\n boolean[][] graph = new boolean[n][n];\n \n for (int i=0;i<n;i++)\n graph[i][i] = true;\n\n for (int[] entry: prerequisites)\n graph[entry[0]][entry[1]] = true;\n \n boolean[] visited = new boolean[n];\n for (int i=0;i<n;i++)\n fillGraph(graph, i, visited);\n \n List<Boolean> responses = new ArrayList<Boolean>();\n for (int[] query: queries)\n responses.add(graph[query[0]][query[1]]);\n return responses;\n }\n}\n```
| 13 | 1 |
['Depth-First Search', 'Java']
| 2 |
course-schedule-iv
|
DFS Memo Solution - Python
|
dfs-memo-solution-python-by-richyrich200-gozy
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
RichyRich2004
|
NORMAL
|
2025-01-27T00:26:21.938520+00:00
|
2025-01-27T00:26:21.938520+00:00
| 1,767 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def checkIfPrerequisite(self, numCourses: int, prerequisites: List[List[int]], queries: List[List[int]]) -> List[bool]:
prereq_map = defaultdict(list) # course -> prereqs
for prereq in prerequisites:
prereq_map[prereq[1]].append(prereq[0])
res = []
memo = {}
def dfs(course, prereq):
if (course, prereq) in memo:
return memo[(course, prereq)]
course_prereqs = prereq_map[course]
for p in course_prereqs:
if p == prereq or dfs(p, prereq):
memo[(course, prereq)] = True
return True
memo[(course, prereq)] = False
return False
return [dfs(query[1], query[0]) for query in queries]
```
| 11 | 0 |
['Python3']
| 2 |
course-schedule-iv
|
C++ DFS Solution, O(q*N)
|
c-dfs-solution-oqn-by-pooja0406-6c5m
|
```\nclass Solution {\npublic:\n vector checkIfPrerequisite(int n, vector>& prerequisites, vector>& queries) {\n \n if(queries.size() == 0)\n
|
pooja0406
|
NORMAL
|
2020-09-01T14:31:59.482094+00:00
|
2020-09-01T14:31:59.482161+00:00
| 1,606 | false |
```\nclass Solution {\npublic:\n vector<bool> checkIfPrerequisite(int n, vector<vector<int>>& prerequisites, vector<vector<int>>& queries) {\n \n if(queries.size() == 0)\n return {};\n \n vector<vector<int>> adj(n);\n for(auto it : prerequisites)\n {\n adj[it[0]].push_back(it[1]);\n }\n \n vector<bool> res;\n for(int i=0; i<queries.size(); i++)\n {\n vector<bool> visited(n, false);\n res.push_back(dfs(queries[i][0], queries[i][1], adj, visited));\n }\n \n return res;\n }\n \n bool dfs(int src, int dest, vector<vector<int>>& adj, vector<bool>& visited)\n {\n if(src == dest)\n return true;\n if(visited[src])\n return false;\n \n visited[src] = true;\n for(auto neigh : adj[src])\n {\n if(!visited[neigh])\n {\n if(dfs(neigh, dest, adj, visited))\n return true;\n }\n }\n \n return false;\n }\n};
| 11 | 0 |
['Depth-First Search', 'C']
| 4 |
course-schedule-iv
|
[C++] Simple solution using DFS.
|
c-simple-solution-using-dfs-by-vinaykash-wrhp
|
\nclass Solution {\npublic:\n void dfs_new(vector<vector<int>> &graph, vector<bool> &vis, int source, int c){\n if(source != c){\n graph[so
|
vinaykashyap
|
NORMAL
|
2020-05-30T16:05:06.717736+00:00
|
2020-05-30T16:14:19.158014+00:00
| 2,243 | false |
```\nclass Solution {\npublic:\n void dfs_new(vector<vector<int>> &graph, vector<bool> &vis, int source, int c){\n if(source != c){\n graph[source][c] = 1;\n }\n if(!vis[c]){\n vis[c] = true;\n for(int i = 0; i < graph[c].size(); i++){\n if(graph[c][i]){\n if(source != i){\n graph[source][i] = 1;\n }\n \n dfs_new(graph, vis, source, i);\n }\n }\n }\n }\n vector<bool> checkIfPrerequisite(int n, vector<vector<int>>& pre, vector<vector<int>>& queries) {\n vector<vector<int>> graph(n, vector<int>(n, 0));\n int i, j, u, v;\n for(i = 0; i < pre.size(); i++){\n graph[pre[i][0]][pre[i][1]] = 1;\n }\n \n for(i = 0; i < n; i++){\n vector<bool> vis(n, false);\n dfs_new(graph, vis, i, i);\n \n }\n\n \n vector<bool> res(queries.size(), false);\n for(i = 0; i < queries.size(); i++){ \n res[i] = graph[queries[i][0]][queries[i][1]];\n }\n return res;\n }\n};\n```
| 11 | 2 |
['Depth-First Search', 'C']
| 3 |
course-schedule-iv
|
✅ Three Simple Lines of Code
|
three-simple-lines-of-code-by-mikposp-lzc3
|
Code #1RefCode #2Ref
|
MikPosp
|
NORMAL
|
2025-01-27T13:00:06.488916+00:00
|
2025-01-27T21:18:19.292304+00:00
| 859 | false |
# Code #1
<!--
Time complexity: $$O(n^2+q)$$. Space complexity: $$O(n^2)$$.
-->
```python3
class Solution:
def checkIfPrerequisite(self, _: int, p: List[List[int]], q: List[List[int]]) -> List[bool]:
g = {v:[*zip(*w)][1] for v,w in groupby(p,itemgetter(0))}
f = cache(lambda v:{v}.union(*map(f,g.get(v,[]))))
return [u in f(v) for v,u in q]
```
[Ref](https://leetcode.com/problems/course-schedule-iv/solutions/6334576/7-line-solution-using-lru-cache-pythonic-sugar)
# Code #2
<!--
Time complexity: $$O(n^2+q)$$. Space complexity: $$O(n^2)$$.
-->
```python3
class Solution:
def checkIfPrerequisite(self, _: int, p: List[List[int]], q: List[List[int]]) -> List[bool]:
g = {v:{u for _,u in w} for v,w in groupby(p,itemgetter(0))}
f = cache(lambda v,u:u in g.get(v,[]) or any(f(i,u) for i in g.get(v,[])))
return [*starmap(f, q)]
```
[Ref](https://leetcode.com/problems/course-schedule-iv/solutions/4285339/8-line-clean-code-solution)
| 10 | 0 |
['Depth-First Search', 'Graph', 'Python', 'Python3']
| 4 |
course-schedule-iv
|
✅Effortless and Efficient Solution by Kanishka✅|| 🔥🔥Beats 100% in Java🚀🚀
|
effortless-and-efficient-solution-by-kan-ib3u
|
🧠 IntuitionMy first thought is to use Depth-First Search (DFS) to determine if there is a path from one course to another, which would indicate a prerequisite r
|
kanishka21535
|
NORMAL
|
2025-01-27T00:10:51.078776+00:00
|
2025-01-27T00:10:51.078776+00:00
| 2,337 | false |
# 🧠 Intuition
My first thought is to use Depth-First Search (DFS) to determine if there is a path from one course to another, which would indicate a prerequisite relationship.
# 🔍 Approach
Here's the approach step-by-step:
1. **Graph Representation**: Represent the courses and prerequisites using an adjacency list.
2. **DFS Traversal**: Use DFS to explore each course and mark the reachable courses.
3. **Check Queries**: For each query, check if the destination course is reachable from the source course.
# ⏳ Complexity
- **Time Complexity**: $$O(V + E + Q)$$
- Where $$V$$ is the number of courses, $$E$$ is the number of prerequisites, and $$Q$$ is the number of queries.
- **Space Complexity**: $$O(V^2)$$
- We use a 2D array to store the reachability information for each pair of courses.
# 📜 Code (Java)
```java
class Solution {
public List<Boolean> checkIfPrerequisite(int numCourses, int[][] prerequisites, int[][] queries) {
int n = prerequisites.length, m = queries.length;
if(n == 0){
List<Boolean> res = new ArrayList<>(m);
for(int i=0; i<m; i++) res.add(false);
return res;
}
List<Integer> graph[] = new ArrayList[numCourses];
for(int i=0; i<numCourses; i++) graph[i] = new ArrayList<>();
for(int p[] : prerequisites){
graph[p[0]].add(p[1]);
}
boolean isReachable[][] = new boolean[numCourses][numCourses];
for(int i=0; i<numCourses; i++){
if(!isReachable[i][i]){
dfs(i, graph, isReachable);
}
}
List<Boolean> res = new ArrayList<>(m);
for(int q[] : queries){
res.add(isReachable[q[0]][q[1]]);
}
return res;
}
private void dfs(int curr, List<Integer> graph[], boolean isReachable[][]){
isReachable[curr][curr] = true;
for(int neighbor : graph[curr]){
if(!isReachable[curr][neighbor]){
isReachable[curr][neighbor] = true;
dfs(neighbor, graph, isReachable);
for(int i=0; i<isReachable.length; i++){
isReachable[curr][i] |= isReachable[neighbor][i];
}
}
}
}
}
```
##### I hope this helps! Feel free to reach out if you need more assistance. Happy coding! 🚀✨
| 10 | 0 |
['Java']
| 1 |
course-schedule-iv
|
[Python] Floyd-Warshall V.S. Topological Sort
|
python-floyd-warshall-vs-topological-sor-amjn
|
Solution 1\nstandard floyd-warshall algorithm, works not only for DAGs but also on general graphs.\n\n\ndef checkIfPrerequisite(numCourses: int, prerequisites:
|
jacoboy
|
NORMAL
|
2022-07-01T02:16:17.889873+00:00
|
2022-07-01T02:17:43.222514+00:00
| 1,105 | false |
### Solution 1\nstandard [floyd-warshall algorithm](https://en.wikipedia.org/wiki/Floyd%E2%80%93Warshall_algorithm), works not only for DAGs but also on general graphs.\n\n```\ndef checkIfPrerequisite(numCourses: int, prerequisites: List[List[int]], queries: List[List[int]]) -> List[bool]:\n \'\'\'\n Problem: All pair reachability problem\n Solution 1: directly use Floyd-Warshall algorithm\n \'\'\'\n graph = [[False] * numCourses for _ in range(numCourses)]\n\n # build graph\n for u, v, in prerequisites:\n graph[u][v] = True\n \n # floyd-warshall algorithm\n for k in range(numCourses):\n for i in range(numCourses):\n for j in range(numCourses):\n graph[i][j] = graph[i][j] or (graph[i][k] and graph[k][j])\n \n return [graph[u][v] for u, v in queries]\n```\n\nTime Complexity: O(V^3)\nSpace Complexity: O(V^2)\n\n\n### Solution 2\nBFS to traverse the node in topological order, and construct parents node set for all nodes in this order.\n\n```\ndef checkIfPrerequisite_topo(numCourses: int, prerequisites: List[List[int]], queries: List[List[int]]) -> List[bool]:\n \'\'\'\n All pair reachability on a DAG using topological sort\n \'\'\'\n # build graph\n graph = defaultdict(set)\n inDegree = [0] * numCourses\n for u, v in prerequisites:\n graph[u].add(v)\n inDegree[v] += 1\n \n # BFS to find topological sort order, and construct parents set simultaneously\n parents = [set() for _ in range(numCourses)]\n q = deque([node for node in range(numCourses) if not inDegree[node]])\n while q:\n node = q.popleft()\n parents[node].add(node)\n for nxt in graph[node]:\n inDegree[nxt] -= 1\n parents[nxt] = parents[nxt].union(parents[node])\n if not inDegree[nxt]:\n q.append(nxt)\n \n # construct results\n ans = []\n for u, v in queries:\n if u in parents[v]:\n ans.append(True)\n else:\n ans.append(False)\n return ans\n```\n\nTime Complexity: O((V+E) * V) = O(V^3) in the worst case, but actually runs faster in practice based on my submissions\nSpace Complexity: O(V^2)
| 10 | 0 |
['Breadth-First Search', 'Topological Sort', 'Python']
| 1 |
course-schedule-iv
|
Course Schedule IV [C++]
|
course-schedule-iv-c-by-moveeeax-85u8
|
IntuitionThe problem requires checking if a course is a prerequisite for another course. A natural way to approach this is by representing the problem as a dire
|
moveeeax
|
NORMAL
|
2025-01-27T07:33:52.760186+00:00
|
2025-01-27T07:33:52.760186+00:00
| 580 | false |
# Intuition
The problem requires checking if a course is a prerequisite for another course. A natural way to approach this is by representing the problem as a directed graph where an edge from course `u` to `v` indicates that `u` is a prerequisite for `v`. Using this graph representation, we can efficiently determine whether a prerequisite relationship exists for the given queries.
# Approach
1. **Graph Representation**:
- Use an adjacency list to represent the graph. Each course points to the list of courses dependent on it.
2. **DFS with Memoization**:
- Perform a Depth-First Search (DFS) from each course to compute all the courses that it can reach.
- Use a `bitset` to track reachable courses for each node. This allows efficient updates and queries for the prerequisite relationships.
- Use memoization to avoid redundant computations for courses already visited.
3. **Query Evaluation**:
- After preprocessing, answer each query in constant time by checking the `bitset` for the source course.
# Complexity
- **Time Complexity**:
- **Graph Construction**: \(O(E)\), where \(E\) is the number of prerequisites.
- **DFS**: Each node and edge is processed once, leading to \(O(V + E)\), where \(V\) is the number of courses.
- **Query Evaluation**: \(O(Q)\), where \(Q\) is the number of queries.
- Total: \(O(V + E + Q)\).
- **Space Complexity**:
- Adjacency list: \(O(V + E)\).
- `bitset` for memoization: \(O(V^2)\) (worst case if every course is connected to every other course).
- Total: \(O(V^2)\).
# Code
```cpp
static auto init = [](){
ios::sync_with_stdio(false);
cin.tie(nullptr);
return nullptr;
}();
class Solution {
public:
vector<bool> checkIfPrerequisite(int n, vector<vector<int>>& prerequisites, vector<vector<int>>& queries) {
vector<vector<int>> adj(n);
for (auto &p : prerequisites) adj[p[0]].push_back(p[1]);
vector<bitset<101>> memo(n);
vector<bool> visited(n, false);
function<void(int)> dfs = [&](int s) {
visited[s] = true;
for (auto t : adj[s]) {
if (!visited[t]) dfs(t);
memo[s] |= memo[t];
memo[s].set(t);
}
};
for (int i = 0; i < n; ++i) {
if (!visited[i]) dfs(i);
}
vector<bool> ans;
ans.reserve(queries.size());
for (auto &q : queries) {
ans.push_back(memo[q[0]][q[1]]);
}
return ans;
}
};
```
| 9 | 0 |
['C++']
| 0 |
course-schedule-iv
|
TOPOLOGICAL SORT 99% FASTER
|
topological-sort-99-faster-by-the_moonli-y4hc
|
\t// time O(ev + queries.size()) , e == # of edges , v = #of vertices\n\t/ approach :\n\t\t --> visit vertices on topological sorting order\n\t\t --> create
|
the_moonLight
|
NORMAL
|
2021-01-16T11:50:37.144118+00:00
|
2021-01-16T11:50:37.144143+00:00
| 1,840 | false |
\t// time O(e*v + queries.size()) , e == # of edges , v = #of vertices\n\t/* approach :\n\t\t --> visit vertices on topological sorting order\n\t\t --> create a 2d boolean array of size n*n where array[i][j]==true means i has a pre req of j\n\t\t --> find all prereq of a course .\n\t\t --> prereq of current course is : all prereq of its parent course + all parent course\n\t*/\n\tclass Solution {\n\t\tpublic List<Boolean> checkIfPrerequisite(int n, int[][] prerequisites, int[][] queries) {\n\t\t\tboolean[][] allPreReq = new boolean[n][n];\n\t\t\tList<List<Integer>> adj = new ArrayList<>();\n\t\t\tfor(int i=0;i<n;i++)adj.add(new ArrayList<>());\n\t\t\tint[] inDegree = new int[n];\n\t\t\tfor(int [] ele : prerequisites){\n\t\t\t\tadj.get(ele[0]).add(ele[1]);\n\t\t\t\tinDegree[ele[1]]++;\n\t\t\t}\n\t\t\tQueue<Integer> q = new LinkedList<>();\n\t\t\tfor(int i=0;i<n;i++)\n\t\t\t\tif(inDegree[i]==0)\n\t\t\t\t\tq.add(i);\n\t\t\twhile(!q.isEmpty()){\n\t\t\t\tint x = q.poll();\n\t\t\t\tfor(int neig : adj.get(x)){\n\t\t\t\t\tfor(int i=0;i<n;i++)\n\t\t\t\t\t\tif(allPreReq[x][i] || i==x)allPreReq[neig][i] = true;\n\t\t\t\t\tif(--inDegree[neig]==0)q.add(neig);\n\t\t\t\t}\n\t\t\t}\n\t\t\tList<Boolean> ans = new ArrayList<>();\n\t\t\tfor(int[] ele : queries){\n\t\t\t\tint prereq = ele[0];\n\t\t\t\tint course = ele[1];\n\t\t\t\tif(allPreReq[course][prereq])ans.add(true);\n\t\t\t\telse ans.add(false);\n\t\t\t}\n\t\t\treturn ans;\n\t\t}\n\t}
| 9 | 0 |
[]
| 1 |
course-schedule-iv
|
super simple approach, Floyd Warshall with added YouTube video explanation
|
super-simple-approach-floyd-warshel-by-v-hmjy
|
YouTube Solution Intuition and approachbefore solution, we know to pass 12Th standard we need to first pass high school exam , also to pass Graduation course w
|
vinod_aka_veenu
|
NORMAL
|
2025-01-27T00:55:40.844140+00:00
|
2025-01-27T02:05:34.841752+00:00
| 1,347 | false |
# YouTube Solution https://youtu.be/2iuUNAhdR0Y?si=0xlGv_tXpIuZvwap
# Intuition and approach
before solution, we know to pass **12Th standard** we need to first pass **high school** exam , also to pass **Graduation course** we need to pass the **12th class Exam** so we can also say that to pass the graduation we have prerequsite to pass **High School** as well.
so we can say course A is pre requisite to B and B is prerequisite to C ===> then we can also say that A is pre-requisite for C.
with this idea we can build relation
1) first fill all the relation pre-requisite in an 2d-array directly from ith course to Jth course
for(int d[] : prerequisites)
relation[d[0]][d[1]] = true;
2) then using above concepts of transitive relation fill the ralation 2-d boolean array like below
for(int i=0; i<numCourses; i++)
for(int src=0; src<numCourses; src++)
for(int target = 0; target<numCourses; target++)
{
relation[src][target] = relation[src][target] || (relation[src][i] && relation[i][target]);
}
now we have precalculated pre-requisite to all course pair. so from this we can return a list of answer.
now we can create a list ans , and fill all the result and return it
for(int d[] : queries)
ans.add(relation[d[0]][d[1]]);
return ans.
# Code
```java []
class Solution {
public List<Boolean> checkIfPrerequisite(int numCourses, int[][] prerequisites, int[][] queries) {
boolean relation[][] = new boolean[numCourses][numCourses];
List<Boolean> ans = new ArrayList<>();
for(int d[] : prerequisites)
relation[d[0]][d[1]] = true;
for(int i=0; i<numCourses; i++)
for(int src=0; src<numCourses; src++)
for(int target = 0; target<numCourses; target++)
{
relation[src][target] = relation[src][target] || (relation[src][i] && relation[i][target]);
}
for(int d[] : queries)
ans.add(relation[d[0]][d[1]]);
return ans;
}
}
```
```C++ []
class Solution {
public:
std::vector<bool> checkIfPrerequisite(int numCourses, std::vector<std::vector<int>>& prerequisites, std::vector<std::vector<int>>& queries) {
std::vector<std::vector<bool>> relation(numCourses, std::vector<bool>(numCourses, false));
std::vector<bool> ans;
for (const auto& d : prerequisites) {
relation[d[0]][d[1]] = true;
}
for (int i = 0; i < numCourses; i++) {
for (int src = 0; src < numCourses; src++) {
for (int target = 0; target < numCourses; target++) {
relation[src][target] = relation[src][target] || (relation[src][i] && relation[i][target]);
}
}
}
for (const auto& d : queries) {
ans.push_back(relation[d[0]][d[1]]);
}
return ans;
}
};
```
```python []
class Solution(object):
def checkIfPrerequisite(self, numCourses, prerequisites, queries):
"""
:type numCourses: int
:type prerequisites: List[List[int]]
:type queries: List[List[int]]
:rtype: List[bool]
"""
# Initialize the relation matrix
relation = [[False] * numCourses for _ in range(numCourses)]
# Fill in the direct prerequisites
for d in prerequisites:
relation[d[0]][d[1]] = True
# Perform Floyd-Warshall-like transitive closure
for i in range(numCourses):
for src in range(numCourses):
for target in range(numCourses):
relation[src][target] = relation[src][target] or (relation[src][i] and relation[i][target])
# Answer the queries
ans = []
for d in queries:
ans.append(relation[d[0]][d[1]])
return ans
```
```C# []
public class Solution {
public IList<bool> CheckIfPrerequisite(int numCourses, int[][] prerequisites, int[][] queries) {
bool[,] relation = new bool[numCourses, numCourses];
var ans = new List<bool>();
// Fill direct prerequisites
foreach (var d in prerequisites) {
relation[d[0], d[1]] = true;
}
// Perform transitive closure using Floyd-Warshall-like logic
for (int i = 0; i < numCourses; i++) {
for (int src = 0; src < numCourses; src++) {
for (int target = 0; target < numCourses; target++) {
relation[src, target] = relation[src, target] || (relation[src, i] && relation[i, target]);
}
}
}
// Answer the queries
foreach (var d in queries) {
ans.Add(relation[d[0], d[1]]);
}
return ans;
}
}
```
| 8 | 0 |
['Array', 'Depth-First Search', 'Breadth-First Search', 'Python', 'C++', 'Java', 'C#']
| 3 |
course-schedule-iv
|
Short and clean solution according to the Hints
|
short-and-clean-solution-according-to-th-rcas
|
Just use the Hints from the Problem description:💡 Hint 1
Imagine if the courses are nodes of a graph. We need to build an array isReachable[i][j].💡 Hint 2
Start
|
charnavoki
|
NORMAL
|
2025-01-27T00:26:22.116356+00:00
|
2025-01-27T00:27:16.538933+00:00
| 652 | false |
Just use the Hints from the Problem description:
💡 Hint 1
Imagine if the courses are nodes of a graph. We need to build an array isReachable[i][j].
💡 Hint 2
Start a bfs from each course i and assign for each course j you visit isReachable[i][j] = True.
💡 Hint 3
Answer the queries from the isReachable array.
```javascript []
const checkIfPrerequisite = (numCourses, prerequisites, queries) => {
const isReachable = Array(numCourses).fill().map(_ => Array(numCourses).fill(false));
prerequisites.forEach(([u, v]) => isReachable[u][v] = true);
for (let i = 0; i < numCourses; i++) {
for (let j = 0; j < numCourses; j++) {
for (let k = 0; k < numCourses; k++) {
if (isReachable[j][i] && isReachable[i][k]) {
isReachable[j][k] = true;
}
}
}
}
return queries.map(([u, v]) => isReachable[u][v]);
};
```
| 7 | 0 |
['JavaScript']
| 1 |
course-schedule-iv
|
[C++] straightfwd solution using Toposort and BFS w/ comments!
|
c-straightfwd-solution-using-toposort-an-hv30
|
\n# Code\n\nclass Solution {\npublic:\n\n bool canvisit(int node, int target, vector<int> adj[], int n){ // to find if we can visit the other node!\n\n
|
KingShuK17
|
NORMAL
|
2023-07-26T12:11:01.386622+00:00
|
2023-07-26T12:11:01.386642+00:00
| 1,002 | false |
\n# Code\n```\nclass Solution {\npublic:\n\n bool canvisit(int node, int target, vector<int> adj[], int n){ // to find if we can visit the other node!\n\n queue<int> q;\n vector<int> vis(n,0);\n vis[node]=1;\n q.push({node});\n\n while(!q.empty()){\n int num = q.front();\n q.pop();\n if(num==target) return true;\n\n for(auto it: adj[num]){\n if(vis[it]==0){\n if(it==target) return true;\n q.push(it); vis[it]=1;\n }\n }\n }\n return false; // if we cannot reach the other node\n }\n\n vector<bool> checkIfPrerequisite(int n, vector<vector<int>>& prereq, vector<vector<int>>& queries) {\n //0 based indexing\n //n = no of courses from 0 to n-1\n\n vector<bool>ans(queries.size(), false); // ans vector initialised with false *NOTE*\n if(prereq.size()==0) return ans; // see testcase\n\n // first lets find toposort using kahn\'s algo (bfs)\n\n vector<int> adj[n];\n vector<int> indegree(n,0); // indegree[i] = incoming edges to node i\n\n for(auto it: prereq){\n adj[it[0]].push_back(it[1]); //directed graph\n indegree[it[1]]++;\n }\n\n queue<int>q;\n for(int i=0; i<n; i++){\n if(indegree[i]==0) q.push(i);\n }\n\n vector<int> topo;\n\n while(!q.empty()){\n int node = q.front();\n topo.push_back(node);\n q.pop();\n\n for(auto it: adj[node]){\n indegree[it]--;\n if(indegree[it]==0) q.push(it);\n }\n }\n\n //topo vector is ready!\n\n for(int i=0; i<queries.size(); i++){\n int n1 = queries[i][0];\n int n2 = queries[i][1];\n\n for(int j=0; j<topo.size(); j++){ //loking in the topo vector\n if( topo[j]==n1 && canvisit(n1,n2,adj,n) ){ //=> if we see n1 first and canvisit n2 from n1\n ans[i]=true;\n break;\n }\n if(topo[j]==n2){\n break;\n }\n }\n }\n\n return ans;\n \n }\n};\n```
| 7 | 0 |
['Breadth-First Search', 'Topological Sort', 'C++']
| 2 |
course-schedule-iv
|
Beats 100.0% | Floyd-Warshall algorithm | C
|
beats-1000-floyd-warshall-algorithm-c-by-si9i
|
IntuitionSince prerequisites can be indirect, we need to compute whether there exists a path from one course to another in this directed graph. Precomputing thi
|
aash24
|
NORMAL
|
2025-01-27T05:01:39.212483+00:00
|
2025-01-27T05:01:39.212483+00:00
| 210 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
Since prerequisites can be indirect, we need to compute whether there exists a path from one course to another in this directed graph. Precomputing this information allows us to efficiently answer multiple queries.
# Approach
<!-- Describe your approach to solving the problem. -->
1. Represent the prerequisite relationships as an adjacency matrix isPrerequisite. If isPrerequisite[a][b] is true, it indicates that course a is a prerequisite for course b.
2. Use the Floyd-Warshall algorithm to compute the transitive closure of the graph:
- For each pair (i, j), check if there exists an intermediate course k such that i -> k and k -> j.
- Update isPrerequisite[i][j] to true if such a path exists.
3. For each query (u, v), check isPrerequisite[u][v] in the precomputed matrix. Return the result as a boolean array.
# Complexity
- Time complexity: O(V^3+E+Q).
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
Storing the adjacency matrix: O(V^2), where V is numCourses.
Result array for queries: O(Q).
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```c []
/**
* Note: The returned array must be malloced, assume caller calls free().
*/
bool* checkIfPrerequisite(int numCourses, int** prerequisites, int prerequisitesSize, int* prerequisitesColSize, int** queries, int queriesSize, int* queriesColSize, int* returnSize) {
*returnSize = queriesSize;
bool* result = (bool*)malloc(queriesSize * sizeof(bool));
bool** isPrerequisite = (bool**)malloc(numCourses * sizeof(bool*));
for (int i = 0; i < numCourses; i++) {
isPrerequisite[i] = (bool*)calloc(numCourses, sizeof(bool));
}
for (int i = 0; i < prerequisitesSize; i++) {
int a = prerequisites[i][0];
int b = prerequisites[i][1];
isPrerequisite[a][b] = true;
}
for (int k = 0; k < numCourses; k++) {
for (int i = 0; i < numCourses; i++) {
for (int j = 0; j < numCourses; j++) {
if (isPrerequisite[i][k] && isPrerequisite[k][j]) {
isPrerequisite[i][j] = true;
}
}
}
}
for (int i = 0; i < queriesSize; i++) {
int u = queries[i][0];
int v = queries[i][1];
result[i] = isPrerequisite[u][v];
}
for (int i = 0; i < numCourses; i++) {
free(isPrerequisite[i]);
}
free(isPrerequisite);
return result;
}
```
| 6 | 0 |
['C']
| 0 |
course-schedule-iv
|
DFS and BFS solution || Kahn's algorithm || Explanation
|
dfs-and-bfs-solution-kahns-algorithm-exp-3rnu
|
1. DFS-Based ApproachIntuitionTo determine if one course is a prerequisite for another, we can represent the courses and their dependencies as a directed graph.
|
Anurag_Basuri
|
NORMAL
|
2024-12-30T08:25:26.199378+00:00
|
2024-12-30T08:25:26.199378+00:00
| 587 | false |
# 1. DFS-Based Approach
## Intuition
To determine if one course is a prerequisite for another, we can represent the courses and their dependencies as a directed graph. If there's a directed path from one course to another, then the first course is a prerequisite for the second. We use **Depth-First Search (DFS)** to explore all possible paths between the nodes.
## Approach
1. Represent the problem as a directed graph using an adjacency list.
2. For each query `(u, v)`:
- Use DFS to check if there's a path from `u` to `v`.
- During the DFS, mark visited nodes to avoid revisiting them.
3. Return the results for all queries in a list.
## Complexity
- **Time Complexity**:
$$O(Q \times (N + E))$$
Where:
- \(Q\): Number of queries.
- \(N\): Number of nodes (courses).
- \(E\): Number of edges (prerequisites).
Each query runs a DFS, which can take up to \(O(N + E)\) in the worst case.
- **Space Complexity**:
$$O(N + E)$$
Space is used for the adjacency list and DFS recursion stack.
# Code
``` cpp []
class Solution {
public:
bool dfs(vector<vector<int>>& graph, vector<int>& vis, int node, int check){
if(node == check) return true;
if(vis[node] == 1) return false;
vis[node] = 1;
for(auto neighbor : graph[node]){
if(dfs(graph, vis, neighbor, check)) return true;
}
return false;
}
vector<bool> checkIfPrerequisite(int numCourses, vector<vector<int>>& prerequisites, vector<vector<int>>& queries) {
vector<vector<int>> graph(numCourses);
for(auto pre:prerequisites)
graph[pre[0]].push_back(pre[1]);
vector<bool> ans;
for(auto querry:queries){
vector<int> vis(numCourses, 0);
if(dfs(graph, vis, querry[0], querry[1]))
ans.push_back(true);
else
ans.push_back(false);
}
return ans;
}
};
```
``` python []
class Solution {
public:
bool dfs(vector<vector<int>>& graph, vector<int>& vis, int node, int check){
if(node == check) return true;
if(vis[node] == 1) return false;
vis[node] = 1;
for(auto neighbor : graph[node]){
if(dfs(graph, vis, neighbor, check)) return true;
}
return false;
}
vector<bool> checkIfPrerequisite(int numCourses, vector<vector<int>>& prerequisites, vector<vector<int>>& queries) {
vector<vector<int>> graph(numCourses);
for(auto pre:prerequisites)
graph[pre[0]].push_back(pre[1]);
vector<bool> ans;
for(auto querry:queries){
vector<int> vis(numCourses, 0);
if(dfs(graph, vis, querry[0], querry[1]))
ans.push_back(true);
else
ans.push_back(false);
}
return ans;
}
};
```
----
# 2. Kahn’s Algorithm (Topological Sort)
## Intuition
If we preprocess the graph to determine which courses are reachable from every other course, we can answer the queries efficiently. Using **Kahn’s Algorithm**, we compute the **transitive closure** of the graph, which tells us all reachable nodes for each node.
## Approach
1. Represent the courses and their prerequisites as a directed graph.
2. Compute the **indegree** of each node (number of incoming edges).
3. Initialize a queue with all nodes that have an indegree of 0 (no prerequisites).
4. Perform **Topological Sorting**:
- For each node processed:
- Update its reachable nodes.
- Propagate the reachable nodes to neighbors.
- Decrease the indegree of neighbors and add them to the queue if their indegree becomes 0.
5. Use the preprocessed data to answer each query in \(O(1)\) by checking the transitive closure.
## Complexity
- **Time Complexity**:
$$O(N + E + Q)$$
Where:
- \(N\): Number of courses.
- \(E\): Number of prerequisites.
- \(Q\): Number of queries.
The topological sort runs in \(O(N + E)\), and each query takes \(O(1)\) using the preprocessed data.
- **Space Complexity**:
$$O(N^2)$$
For the transitive closure matrix to store reachability information.
# Code
```cpp []
class Solution {
public:
vector<bool> checkIfPrerequisite(int numCourses, vector<vector<int>>& prerequisites, vector<vector<int>>& queries) {
vector<vector<int>> graph(numCourses);
vector<vector<int>> reachable(numCourses, vector<int>(numCourses, 0));
vector<int> indegree(numCourses, 0);
for (auto& pre : prerequisites) {
graph[pre[0]].push_back(pre[1]);
indegree[pre[1]]++;
}
queue<int> q;
for (int i = 0; i < numCourses; i++) {
if (indegree[i] == 0) q.push(i);
}
while (!q.empty()) {
int node = q.front();
q.pop();
for (auto neighbor : graph[node]) {
reachable[node][neighbor] = 1;
for (int i = 0; i < numCourses; i++) {
if (reachable[i][node]) reachable[i][neighbor] = 1;
}
if (--indegree[neighbor] == 0) q.push(neighbor);
}
}
vector<bool> ans;
for (auto& query : queries) {
ans.push_back(reachable[query[0]][query[1]]);
}
return ans;
}
};
```
``` python []
class Solution:
def checkIfPrerequisite(self, numCourses, prerequisites, queries):
graph = [[] for _ in range(numCourses)]
reachable = [[0] * numCourses for _ in range(numCourses)]
indegree = [0] * numCourses
for pre in prerequisites:
graph[pre[0]].append(pre[1])
indegree[pre[1]] += 1
q = deque([i for i in range(numCourses) if indegree[i] == 0])
while q:
node = q.popleft()
for neighbor in graph[node]:
reachable[node][neighbor] = 1
for i in range(numCourses):
if reachable[i][node]:
reachable[i][neighbor] = 1
indegree[neighbor] -= 1
if indegree[neighbor] == 0:
q.append(neighbor)
return [bool(reachable[query[0]][query[1]]) for query in queries]
```
# Key Differences
1. **DFS**:
- Query-driven: Performs the search from scratch for each query.
- Slower for a large number of queries.
- Better for small datasets or when queries are fewer in number.
2. **Kahn’s Algorithm**:
- Preprocesses the graph to answer queries in \(O(1)\) time.
- Faster for a large number of queries but uses more space for the transitive closure.
| 6 | 0 |
['Depth-First Search', 'Breadth-First Search', 'Graph', 'Topological Sort', 'C++', 'Python3']
| 0 |
course-schedule-iv
|
[C++] 2 Solutions - BFS , Flyod Warshall
|
c-2-solutions-bfs-flyod-warshall-by-apar-o4cj
|
The only logic :\nThere can be a path between 2 nodes either directly or indirectly. \nif \'A\' is prerequisite of \'B\' then \'A\' is also a prerequisite of al
|
aparna_g
|
NORMAL
|
2021-08-01T12:38:27.029833+00:00
|
2021-08-01T13:35:40.441508+00:00
| 744 | false |
The only logic :\nThere can be a path between 2 nodes either directly or indirectly. \n**if \'A\' is prerequisite of \'B\' then \'A\' is also a prerequisite of all courses with \'B\' as prerequisite**\n**Solution 1: BFS**\n```\nclass Solution {\npublic:\n vector<bool> checkIfPrerequisite(int n, vector<vector<int>>& pre, vector<vector<int>>& queries) {\n \n int p = pre.size();\n int qe = queries.size();\n vector<bool> result(qe,0);\n vector<vector<int>> adj(n);\n vector<vector<bool>> possible(n,vector<bool>(n,0));\n \n for(auto &p : pre) \n adj[p[0]].push_back(p[1]);\n \n queue<int> q;\n for(int i=0;i<n;i++){\n q.push(i);\n while(!q.empty()){\n int course = q.front();\n q.pop();\n for(int v : adj[course]) {\n if(!possible[i][v]){\n possible[i][v] = 1;\n q.push(v);\n }\n } \n }\n }\n \n for(int i=0;i<qe;i++)\n result[i] = possible[queries[i][0]][queries[i][1]];\n \n return result;\n }\n};\n```\n**Solution 2: Floyd Warshall**\n```\nclass Solution {\npublic:\n vector<bool> checkIfPrerequisite(int n, vector<vector<int>>& prerequisites, vector<vector<int>>& queries) {\n vector<vector<bool>> reachable(n,vector<bool>(n,0));\n for(auto &p : prerequisites) \n reachable[p[0]][p[1]] = 1;\n vector<bool> result;\n for(int k=0;k<n;k++){\n for(int i=0;i<n;i++){\n for(int j=0;j<n;j++){\n reachable[i][j] = reachable[i][j] || (reachable[i][k] && reachable[k][j]);\n\t\t\t\t\t//if i is a direct prerequisite of j or i is a prerequisite of k which is a prerequisite of j\n }\n }\n }\n for(auto &q : queries) \n result.push_back(reachable[q[0]][q[1]]);\n return result;\n }\n};\n```
| 6 | 0 |
['Breadth-First Search', 'C', 'C++']
| 0 |
course-schedule-iv
|
Java Floyd-Warshal alg
|
java-floyd-warshal-alg-by-hobiter-al40
|
Detail in: https://en.wikipedia.org/wiki/Floyd%E2%80%93Warshall_algorithm\n\npublic List<Boolean> checkIfPrerequisite(int n, int[][] prqs, int[][] qs) {\n
|
hobiter
|
NORMAL
|
2020-05-31T18:10:25.550952+00:00
|
2020-05-31T18:10:25.550990+00:00
| 619 | false |
Detail in: https://en.wikipedia.org/wiki/Floyd%E2%80%93Warshall_algorithm\n```\npublic List<Boolean> checkIfPrerequisite(int n, int[][] prqs, int[][] qs) {\n boolean[][] prq = new boolean[n][n];\n for (int[] c : prqs) prq[c[0]][c[1]] = true;\n for (int i = 0; i < n; i++) {\n for (int j = 0; j < n; j++) {\n for (int k = 0; k < n; k++) {\n prq[j][k] = prq[j][k] || (prq[j][i] && prq[i][k]);\n }\n }\n }\n List<Boolean> res = new ArrayList<>();\n for (int[] q : qs) res.add(prq[q[0]][q[1]]);\n return res;\n }\n```
| 6 | 0 |
[]
| 0 |
course-schedule-iv
|
DFS with cache Python Clean + Commented Code
|
dfs-with-cache-python-clean-commented-co-3oup
|
\ndef checkIfPrerequisite(self, n: int, prerequisites: List[List[int]], queries: List[List[int]]) -> List[bool]:\n \n # 3. mainly use DFS with Cac
|
uttam1728
|
NORMAL
|
2020-05-30T16:11:01.609278+00:00
|
2020-05-30T16:11:39.101488+00:00
| 825 | false |
```\ndef checkIfPrerequisite(self, n: int, prerequisites: List[List[int]], queries: List[List[int]]) -> List[bool]:\n \n # 3. mainly use DFS with Cache\n def path(s,e):\n if (s,e) in self.cache: #if in cache\n return (self.cache[(s,e)])\n if s == e: # edge case\n self.cache[(s,e)] = True\n return True\n else: \n if s in g: #important :-\n for j in g[s]: # recursilvly call to all neighbours\n if path(j,e):\n self.cache[(s,e)] = True\n return True\n self.cache[(s,e)] = False\n \n # 1. Graph making\n g = defaultdict(set)\n for i,v in prerequisites:\n g[i].add(v)\n # print(g) \n \n \n ans = []\n self.cache = dict() #heart of algo otherwise TLE\n for s,e in queries:\n ans.append(path(s,e)) # 2. is path than True else False\n return ans\n \n```
| 6 | 0 |
['Depth-First Search', 'Python']
| 1 |
course-schedule-iv
|
Easy Solution 🚀🚀🚀🚀🚀🚀🚀🚀
|
easy-solution-by-sharvil_karwa-6qyg
|
Code
|
Sharvil_Karwa
|
NORMAL
|
2025-01-27T04:10:53.517562+00:00
|
2025-01-27T04:10:53.517562+00:00
| 727 | false |
# Code
```cpp []
class Solution {
public:
bool dfs(unordered_map<int,vector<int>> &m, int node, vector<int> &vis, int target){
if(node==target) return true;
vis[node] = 1;
for(auto i:m[node]){
if(vis[i]==-1){
if(dfs(m,i,vis,target)) return true;
}
}
return false;
}
vector<bool> checkIfPrerequisite(int n, vector<vector<int>>& arr, vector<vector<int>>& queries) {
vector<bool> ans;
unordered_map<int,vector<int>> m;
for(auto i:arr){
m[i[0]].push_back(i[1]);
}
for(auto i:queries){
vector<int> vis(n,-1);
ans.push_back(dfs(m,i[0],vis,i[1]));
}
return ans;
}
};
```
| 5 | 0 |
['Depth-First Search', 'Breadth-First Search', 'Graph', 'Topological Sort', 'Python', 'C++', 'Java']
| 0 |
course-schedule-iv
|
Transitive Closure Expansion using Floyd-Warshall Algorithm
|
transitive-closure-expansion-using-floyd-2iys
|
IntuitionTo handle direct and indirect prerequisites, we can use Floyd-Warshall to compute the transitive closure of the prerequisite graph.Approach
Initializa
|
anand_shukla1312
|
NORMAL
|
2025-01-27T04:07:55.360629+00:00
|
2025-01-27T04:07:55.360629+00:00
| 132 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
To handle direct and indirect prerequisites, we can use Floyd-Warshall to compute the transitive closure of the prerequisite graph.
# Approach
<!-- Describe your approach to solving the problem. -->
1. **Initialization:**
- A 2D list reachable of size numCourses x numCourses is created and initialized to False.
1. **Direct Prerequisites:**
- The given prerequisite pairs are marked in the reachable matrix.
1. **Floyd-Warshall Algorithm:**
- Checks if there is an indirect path between two courses by iterating through all intermediate nodes.
1. **Query Processing:**
- Simply checks if reachable[u][v] is True or False.
# Complexity
- Time complexity: $$O(N^3)$$
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: $$O(N^2)$$
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def checkIfPrerequisite(self, n: int, prerequisites: List[List[int]], queries: List[List[int]]) -> List[bool]:
reachable = [[False]*n for _ in range(n)]
for pre, course in prerequisites:
reachable[pre][course] = True
for k in range(n):
for i in range(n):
for j in range(n):
if reachable[i][k] and reachable[k][j]:
reachable[i][j] = True
return [reachable[u][v] for u, v in queries]
```
# SMALL REQUEST : If you found this post even remotely helpful, be kind enough to smash a upvote. I will be grateful.I will be motivated😊😊
| 5 | 0 |
['Python3']
| 0 |
course-schedule-iv
|
✅Effortless and Efficient Solution by Dhandapani✅|| 🔥🔥Beats 100% in Java🚀🚀
|
effortless-and-efficient-solution-by-dha-g3rm
|
🧠 IntuitionMy first thought is to use Depth-First Search (DFS) to determine if there is a path from one course to another, which would indicate a prerequisite r
|
Dhandapanimaruthasalam
|
NORMAL
|
2025-01-27T00:07:40.885733+00:00
|
2025-01-27T00:07:40.885733+00:00
| 498 | false |
# 🧠 Intuition
My first thought is to use Depth-First Search (DFS) to determine if there is a path from one course to another, which would indicate a prerequisite relationship.
# 🔍 Approach
Here's the approach step-by-step:
1. **Graph Representation**: Represent the courses and prerequisites using an adjacency list.
2. **DFS Traversal**: Use DFS to explore each course and mark the reachable courses.
3. **Check Queries**: For each query, check if the destination course is reachable from the source course.
# ⏳ Complexity
- **Time Complexity**: $$O(V + E + Q)$$
- Where $$V$$ is the number of courses, $$E$$ is the number of prerequisites, and $$Q$$ is the number of queries.
- **Space Complexity**: $$O(V^2)$$
- We use a 2D array to store the reachability information for each pair of courses.
# 📜 Code (Java)
```java
class Solution {
public List<Boolean> checkIfPrerequisite(int numCourses, int[][] prerequisites, int[][] queries) {
int n = prerequisites.length, m = queries.length;
if(n == 0){
List<Boolean> res = new ArrayList<>(m);
for(int i=0; i<m; i++) res.add(false);
return res;
}
List<Integer> graph[] = new ArrayList[numCourses];
for(int i=0; i<numCourses; i++) graph[i] = new ArrayList<>();
for(int p[] : prerequisites){
graph[p[0]].add(p[1]);
}
boolean isReachable[][] = new boolean[numCourses][numCourses];
for(int i=0; i<numCourses; i++){
if(!isReachable[i][i]){
dfs(i, graph, isReachable);
}
}
List<Boolean> res = new ArrayList<>(m);
for(int q[] : queries){
res.add(isReachable[q[0]][q[1]]);
}
return res;
}
private void dfs(int curr, List<Integer> graph[], boolean isReachable[][]){
isReachable[curr][curr] = true;
for(int neighbor : graph[curr]){
if(!isReachable[curr][neighbor]){
isReachable[curr][neighbor] = true;
dfs(neighbor, graph, isReachable);
for(int i=0; i<isReachable.length; i++){
isReachable[curr][i] |= isReachable[neighbor][i];
}
}
}
}
}
```
##### I hope this helps! Feel free to reach out if you need more assistance. Happy coding! 🚀✨
| 5 | 1 |
['Java']
| 1 |
course-schedule-iv
|
Java BFS soluion
|
java-bfs-soluion-by-motorix-7lkq
|
The question is to check if two nodes are connected in a directed acyclic graph.\n\n1. Build all the edges\n2. BFS to check every query if two nodes are connect
|
motorix
|
NORMAL
|
2020-05-30T16:47:46.989573+00:00
|
2020-05-30T16:49:45.365183+00:00
| 278 | false |
The question is to check if two nodes are connected in a directed acyclic graph.\n\n1. Build all the edges\n2. BFS to check every query if two nodes are connected\n\n**Java**\n```\nclass Solution {\n public List<Boolean> checkIfPrerequisite(int n, int[][] pre, int[][] queries) {\n // Build adjacency list\n HashMap<Integer, HashSet<Integer>> map = new HashMap<>();\n for(int[] p : pre) {\n if(!map.containsKey(p[0])) map.put(p[0], new HashSet<>());\n map.get(p[0]).add(p[1]);\n }\n // BFS\n List<Boolean> ans = new ArrayList<>();\n for(int[] q : queries) ans.add(bfs(n, map, q[0], q[1]));\n return ans;\n }\n private boolean bfs(int n, HashMap<Integer, HashSet<Integer>> map, int src, int dest) {\n boolean[] visited = new boolean[n];\n Queue<Integer> queue = new LinkedList<>();\n queue.add(src);\n while(!queue.isEmpty()) {\n int cur = queue.poll();\n visited[cur] = true;\n if(map.containsKey(cur)) {\n if(map.get(cur).contains(dest)) return true; \n for(int next : map.get(cur)) {\n if(!visited[next]) {\n queue.add(next);\n }\n }\n }\n }\n return false;\n }\n}\n```\n\n* Time: ```O(NM)```, ```N``` is number of nodes and ```M``` is length of queries\n* Space: ```O(N)```
| 5 | 0 |
[]
| 0 |
course-schedule-iv
|
[Python] DP simple solution
|
python-dp-simple-solution-by-ligt-0nb1
|
\nclass Solution:\n def checkIfPrerequisite(self, n: int, prerequisites: List[List[int]], queries: List[List[int]]) -> List[bool]:\n preqs = [set() fo
|
ligt
|
NORMAL
|
2020-05-30T16:01:38.216863+00:00
|
2020-05-31T00:54:06.441799+00:00
| 1,148 | false |
```\nclass Solution:\n def checkIfPrerequisite(self, n: int, prerequisites: List[List[int]], queries: List[List[int]]) -> List[bool]:\n preqs = [set() for _ in range(n)]\n reverse_preqs = [set() for _ in range(n)]\n for preq in prerequisites:\n preqs[preq[0]].add(preq[1])\n for p in preqs[preq[1]]:\n preqs[preq[0]].add(p)\n for p in reverse_preqs[preq[0]]:\n preqs[p].add(preq[1])\n reverse_preqs[preq[1]].add(p)\n reverse_preqs[preq[1]].add(preq[0])\n return [query[1] in preqs[query[0]] for query in queries]\n```
| 5 | 1 |
[]
| 2 |
course-schedule-iv
|
✅ Easy to Understand | Graph Theory - Floyd Warshall Algorithm | Detailed Video Explanation🔥
|
easy-to-understand-graph-theory-floyd-wa-t8qq
|
IntuitionThe problem is essentially about determining whether one course is a prerequisite for another, either directly or indirectly. The task can be visualize
|
sahilpcs
|
NORMAL
|
2025-01-27T10:29:27.963693+00:00
|
2025-01-27T10:29:27.963693+00:00
| 142 | false |
# Intuition
The problem is essentially about determining whether one course is a prerequisite for another, either directly or indirectly. The task can be visualized as a graph problem, where courses are nodes, and prerequisites are directed edges. The key is to compute the transitive closure of the graph, which tells us if there is a path from one node to another. This makes the Floyd-Warshall algorithm a suitable choice.
# Approach
1. **Graph Representation:**
Represent the prerequisite relationships as a boolean adjacency matrix `isPre`. Here, `isPre[i][j]` is `true` if course `i` is a prerequisite of course `j`.
2. **Populate Direct Prerequisites:**
Iterate over the `prerequisites` array and set the direct relationships in the `isPre` matrix.
3. **Transitive Closure using Floyd-Warshall:**
Use the Floyd-Warshall algorithm to compute transitive prerequisites:
- For each intermediate node `k`, check if a path exists between nodes `i` and `j` through `k`.
- Update `isPre[i][j]` accordingly.
4. **Answer Queries:**
For each query, check the corresponding entry in the `isPre` matrix to determine if the prerequisite relationship exists.
5. **Return Results:**
Return the results for all queries as a list of boolean values.
# Complexity
- **Time complexity:**
The Floyd-Warshall algorithm runs in $$O(n^3)$$ time, where `n` is the number of courses (nodes). Processing the queries is $$O(q)$$, where `q` is the number of queries. Thus, the total time complexity is:
$$O(n^3 + q)$$
- **Space complexity:**
The space used is dominated by the `isPre` matrix, which requires $$O(n^2)$$ space. Therefore:
$$O(n^2)$$
# Code
```java []
class Solution {
public List<Boolean> checkIfPrerequisite(int n, int[][] prerequisites, int[][] queries) {
// Initialize a boolean matrix to store prerequisite relationships
boolean[][] isPre = new boolean[n][n];
for (int[] p : prerequisites) {
// Mark direct prerequisite relationships
isPre[p[0]][p[1]] = true;
}
// Use Floyd-Warshall algorithm to compute transitive closure
// This identifies indirect prerequisites
for (int k = 0; k < n; k++) { // Intermediate node
for (int i = 0; i < n; i++) { // Start node
for (int j = 0; j < n; j++) { // End node
// If i -> k and k -> j, then i -> j
isPre[i][j] = isPre[i][j] || (isPre[i][k] && isPre[k][j]);
}
}
}
// Prepare the result for the queries
List<Boolean> ans = new ArrayList<>();
for (int[] q : queries) {
// Check if the prerequisite relationship exists for the query
ans.add(isPre[q[0]][q[1]]);
}
return ans; // Return the list of results for all queries
}
}
```
https://youtu.be/2IoIbMvYGcQ
| 4 | 0 |
['Depth-First Search', 'Breadth-First Search', 'Graph', 'Topological Sort', 'Java']
| 1 |
course-schedule-iv
|
C++ Solution || Easy to Understand || Topological Sorting
|
c-solution-easy-to-understand-topologica-fhnj
|
ApproachIntuitionThe problem can be solved using a graph traversal approach where:
The courses are represented as nodes in a directed graph.
The prerequisites d
|
Rohit_Raj01
|
NORMAL
|
2025-01-27T10:25:35.334093+00:00
|
2025-01-27T10:25:35.334093+00:00
| 429 | false |
# Approach
### Intuition
The problem can be solved using a graph traversal approach where:
1. The courses are represented as nodes in a directed graph.
2. The prerequisites define directed edges between nodes.
We can use a topological sorting approach and keep track of all prerequisites for each course using a `vector<unordered_set<int>>`.
# Steps
1. **Build the Graph**:
- Represent courses as nodes in a graph.
- Add directed edges from a course to its dependent course.
- Track the indegree of each node.
2. **Topological Sorting**:
- Use a queue to process nodes with zero indegree.
- While processing a node, update its dependent nodes by adding the current node and its prerequisites.
3. **Process Queries**:
- For each query, check if the first course exists in the prerequisite set of the second course.
# Complexity
- **Time Complexity**:
- Graph construction: $$O(E)$$, where $$E$$ is the number of prerequisites.
- Topological sorting: $$O(V + E)$$, where $$V$$ is the number of courses.
- Query processing: $$O(Q \cdot V)$$, where $$Q$$ is the number of queries.
- Overall: $$O(V + E + Q \cdot V)$$.
- **Space Complexity**: $$O(V^2)$$ for storing prerequisites.
## Code
```cpp
class Solution {
public:
vector<bool> checkIfPrerequisite(int numCourses, vector<vector<int>>& prerequisites, vector<vector<int>>& queries) {
vector<vector<int>> graph(numCourses);
vector<int> indegree(numCourses);
for(const auto& p : prerequisites) {
graph[p[0]].push_back(p[1]);
indegree[p[1]]++;
}
queue<int> q;
vector<unordered_set<int>> pre(numCourses);
for(int u = 0; u < numCourses; ++u)
if(!indegree[u])
q.push(u);
while(!q.empty()) {
int u = q.front(); q.pop();
for(int v : graph[u]) {
pre[v].insert(u);
pre[v].insert(pre[u].begin(), pre[u].end());
indegree[v]--;
if(!indegree[v])
q.push(v);
}
}
vector<bool> ans(queries.size());
for(int i = 0; i < queries.size(); ++i) {
int u = queries[i][0], v = queries[i][1];
ans[i] = pre[v].find(u) != pre[v].end();
}
return ans;
}
};
```

| 4 | 0 |
['Breadth-First Search', 'Graph', 'Topological Sort', 'C++']
| 1 |
course-schedule-iv
|
Python | DFS and Memo | O(n+q), O(n+q) | Beats 99%
|
python-dfs-and-memo-code-w-notes-by-2pil-so1m
|
CodeComplexity
Time complexity: O(n+q). Visit each course and query once.
Space complexity: O(n+q). Creates multiple objects of len(numCourses) and a single
|
2pillows
|
NORMAL
|
2025-01-27T01:47:03.237414+00:00
|
2025-01-28T04:59:57.777604+00:00
| 92 | false |
# Code
```python3 []
class Solution:
def checkIfPrerequisite(self, numCourses: int, prerequisites: List[List[int]], queries: List[List[int]]) -> List[bool]:
direct_reqs = [set() for _ in range(numCourses)] # collect direct required courses from [req, course] pairs
for req, course in prerequisites:
direct_reqs[course].add(req)
def get_reqs(cur_course): # get direct and indirect requirements for current course
if cur_course in visited_courses:
return course_reqs[cur_course] # return if already visited
visited_courses.add(cur_course) # set current course as visited
for cur_req in direct_reqs[cur_course]:
if cur_req in course_reqs[cur_course]: continue
course_reqs[cur_course].add(cur_req) # add direct required courses
course_reqs[cur_course].update(get_reqs(cur_req)) # add indirect required courses
return course_reqs[cur_course]
course_reqs = [set() for _ in range(numCourses)] # course i has course_reqs[i] required courses
visited_courses = set() # visited courses
for cur_course in range(numCourses): # get required courses for each course
get_reqs(cur_course)
return [req in course_reqs[course] for req, course in queries] # check queries if course has required course
```
# Complexity
- Time complexity: $$O(n+q)$$. Visit each course and query once.
- Space complexity: $$O(n+q)$$. Creates multiple objects of len(numCourses) and a single object of len(queries).
| 4 | 0 |
['Depth-First Search', 'Topological Sort', 'Memoization', 'Python3']
| 1 |
course-schedule-iv
|
Functional / iterator approach with successors | 2ms
|
functional-iterator-approach-with-succes-6ari
|
IntuitionBFS / Kahn's to create the is_prereqApproachDuring processing, we can use std::iter::successors to make the code more functional. Also since the constr
|
stevenylai
|
NORMAL
|
2025-01-18T06:57:27.152396+00:00
|
2025-01-18T06:57:27.152396+00:00
| 71 | false |
# Intuition
BFS / Kahn's to create the `is_prereq`
# Approach
During processing, we can use `std::iter::successors` to make the code more functional. Also since the constrains is max of 100 courses, we can use an 128-bit int
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```rust []
impl Solution {
pub fn check_if_prerequisite(num_courses: i32, prerequisites: Vec<Vec<i32>>, queries: Vec<Vec<i32>>) -> Vec<bool> {
use std::collections::VecDeque;
let (mut graph, mut in_degree) = prerequisites
.into_iter()
.fold(([0_u128; 100], [0_i32; 100]), |(mut graph, mut in_degree), prereq| {
let (a, b) = (prereq[0], prereq[1]); // b -> a
in_degree[a as usize] += 1;
graph[b as usize] |= 1 << a;
(graph, in_degree)
});
let mut zero_in_degree = in_degree
.iter()
.copied()
.enumerate()
.filter(|&(_, d)| d == 0)
.map(|(i, _)| i as i32)
.collect::<VecDeque<_>>();
let mut is_prereq = [0_u128; 100];
std::iter::successors(zero_in_degree.pop_front(), |&n| {
let adjs = graph[n as usize]; // n -> adjs
(0..num_courses)
.filter(|adj| (1 << adj) & adjs != 0)
.for_each(|adj| {
is_prereq[adj as usize] |= 1 << n;
is_prereq[adj as usize] |= is_prereq[n as usize];
in_degree[adj as usize] -= 1;
if in_degree[adj as usize] == 0 {
zero_in_degree.push_back(adj);
}
});
zero_in_degree.pop_front()
})
.last();
queries
.into_iter()
.map(|q| {
let (u, v) = (q[0], q[1]); // u -> v?
is_prereq[u as usize] & (1 << v) != 0
})
.collect()
}
}
```
| 4 | 0 |
['Rust']
| 1 |
course-schedule-iv
|
Cpp Easy Solution Using Dfs
|
cpp-easy-solution-using-dfs-by-sanket_ja-hxct
|
```\nclass Solution {\npublic:\n bool func(int i,int j,vector>&edge,vector&vis){\n if(i==j)return true;\n vis[i]=1;\n \n for(auto
|
Sanket_Jadhav
|
NORMAL
|
2022-08-29T11:25:49.485542+00:00
|
2022-08-29T11:25:49.485578+00:00
| 770 | false |
```\nclass Solution {\npublic:\n bool func(int i,int j,vector<vector<int>>&edge,vector<int>&vis){\n if(i==j)return true;\n vis[i]=1;\n \n for(auto ele:edge[i]){\n if(!vis[ele]){\n if(func(ele,j,edge,vis))return true;\n }\n }\n \n return false;\n }\n \n vector<bool> checkIfPrerequisite(int numCourses, vector<vector<int>>& prerequisites, vector<vector<int>>& queries) {\n \n vector<vector<int>>edge(numCourses);\n \n for(int i=0;i<prerequisites.size();i++){\n edge[prerequisites[i][0]].push_back(prerequisites[i][1]);\n }\n \n vector<bool>ans;\n \n for(auto ele:queries){\n vector<int>vis(numCourses);\n bool t=func(ele[0],ele[1],edge,vis);\n ans.push_back(t);\n }\n \n return ans;\n }\n};
| 4 | 0 |
['Depth-First Search', 'C++']
| 1 |
course-schedule-iv
|
✔Java Solution Using Floyd Warshall Algorithm💯
|
java-solution-using-floyd-warshall-algor-mdc0
|
Preprocessing is O(n\xB3)\nEach Query in O(1)\n\nhttps://en.wikipedia.org/wiki/Floyd%E2%80%93Warshall_algorithm\n\nFloyd warshall is little bit modified here, I
|
harshu175
|
NORMAL
|
2021-07-29T20:25:07.130046+00:00
|
2021-07-29T20:25:07.130078+00:00
| 317 | false |
**Preprocessing is O(n\xB3)**\n**Each Query in O(1)**\n\n[https://en.wikipedia.org/wiki/Floyd%E2%80%93Warshall_algorithm](http://)\n\n**Floyd warshal**l is little bit modified here, In real algo we find shortest path between i & j, but now we will **store a boolean value to tell us that is there a path exist between i & j**. So instead of adding **graph[i][j] + graph[k][j]** in real algo, we will check if both are true or not. If both are true it means there\'s a path between i & j through k. \n```\nclass Solution {\n public List<Boolean> checkIfPrerequisite(int n, int[][] prerequisites, int[][] queries) {\n boolean[][] graph = new boolean[n][n];\n \n for(int[] pre : prerequisites)\n graph[pre[0]][pre[1]] = true; //this indicates that there\'s a path between a and b\n \n //floyd warshall\n \n for(int k = 0; k < n; k++){\n for(int i = 0; i < n; i++){\n if(k == i)continue;\n for(int j =0; j < n; j++){\n if(i == j || j == k)continue;\n \n graph[i][j] = graph[i][j] || graph[i][k] && graph[k][j];\n }\n }\n }\n \n List<Boolean> list = new ArrayList<>();\n \n for(int[] q : queries){\n list.add(graph[q[0]][q[1]]);\n }\n \n return list;\n }\n}\n```
| 4 | 2 |
['Java']
| 0 |
course-schedule-iv
|
Java Simple and easy to understand DFS solution, clean code with comments
|
java-simple-and-easy-to-understand-dfs-s-myyl
|
PLEASE UPVOTE IF YOU LIKE THIS SOLUTION\n\n\n\n\nclass Solution {\n public List<Boolean> checkIfPrerequisite(int numCourses, int[][] prerequisites, int[][] q
|
satyaDcoder
|
NORMAL
|
2021-05-05T08:36:03.421116+00:00
|
2021-05-05T08:36:03.421144+00:00
| 379 | false |
**PLEASE UPVOTE IF YOU LIKE THIS SOLUTION**\n\n\n\n```\nclass Solution {\n public List<Boolean> checkIfPrerequisite(int numCourses, int[][] prerequisites, int[][] queries) {\n \n //adj[i] -> list of all course dependent by course<i>\n ArrayList<Integer>[] adj = new ArrayList[numCourses];\n for(int i = 0; i < numCourses; i++){\n adj[i] = new ArrayList<Integer>();\n }\n for(int[] courses : prerequisites){\n adj[courses[0]].add(courses[1]);\n }\n \n //dependencySet[i] -> give list of all course dependent by course<i> \n //or In other word, set of all prerequisite for course<i>\n HashSet<Integer>[] dependencySet = new HashSet[numCourses];\n for(int course = 0; course < numCourses; course++){\n dependencySet[course] = new HashSet<Integer>();\n }\n \n \n List<Boolean> result = new ArrayList();\n\n for(int[] query : queries){\n \n //Note: Problem decription is not matching with given example\n //But if consider example, then all of the test case is passing\n \n //consider\n //to complete the current course, first complete required course\n int currentCourse = query[0];\n \n //this (e.g requiredCourse) is prerequisite of course\n int requiredCourse = query[1];\n \n //if not foud already, first find all the prerequiste of current course \n if(adj[currentCourse].size() > 0 && dependencySet[currentCourse].size() == 0){\n dfs(currentCourse, adj, dependencySet);\n }\n \n //check requiredCourse is prerequisite of current course or not\n boolean isPrerequisite = dependencySet[currentCourse].contains(requiredCourse);\n \n result.add(isPrerequisite);\n }\n\n return result;\n }\n \n private List<Integer> dfs(int currentCourse, ArrayList<Integer>[] adj, HashSet<Integer>[] dependencySet){\n \n //no Prerequisite for current course.\n //just return empty list\n if(adj[currentCourse].size() == 0){\n return new ArrayList<Integer>();\n }\n \n //already found Prerequisite for current course \n if(dependencySet[currentCourse].size() > 0) {\n return new ArrayList<Integer>(dependencySet[currentCourse]);\n }\n \n \n for(int directPrerequisite : adj[currentCourse]){\n //append direct prerequisite for current course\n dependencySet[currentCourse].add(directPrerequisite);\n \n //find all indirect prerequisite course for current course\n for(int inDirectPrerequisite : dfs(directPrerequisite, adj, dependencySet)){\n dependencySet[currentCourse].add(inDirectPrerequisite);\n }\n }\n \n return new ArrayList<Integer>(dependencySet[currentCourse]);\n }\n}\n```
| 4 | 0 |
['Java']
| 0 |
course-schedule-iv
|
99% beat Java | short and easy | No Floyd-Warshall | O(EV)
|
99-beat-java-short-and-easy-no-floyd-war-trdz
|
I think there is no need to explain, as code explained everything itself.\nI am not clear related to complexity, which I think O(V + EV) ~ O(EV), but if you fe
|
agarwalaarrav
|
NORMAL
|
2020-12-24T18:59:22.581615+00:00
|
2020-12-25T23:29:13.065268+00:00
| 590 | false |
I think there is no need to explain, as code explained everything itself.\nI am not clear related to complexity, which I think O(V + EV) ~ O(EV), but if you fell I am wrong, please comment.\n```\n public void dfs(int node, int n, ArrayList<Integer>[] gr, boolean[] vis, boolean[][] mat){\n\t\n if( vis[node]) return;\n vis[node] = true;\n\n for(int i : gr[node]) {\n\n mat[node][i] = true;\n \n\t\t\tdfs(i, n, gr, vis, mat);\n\t\t\t\n for(int j = 0; j< n; j++)\n if( mat[i][j] )\n mat[node][j] = true;\n }\n }\n public List<Boolean> checkIfPrerequisite(int n, int[][] prerequisites, int[][] queries) {\n List<Boolean> res = new ArrayList<>();\n ArrayList<Integer>[] gr = new ArrayList[n];\n boolean[][] mat= new boolean[n][n];\n boolean[] vis= new boolean[n];\n\n for(int i =0; i <n; i++)\n gr[i] = new ArrayList<>();\n\n for(int[] edge : prerequisites)\n gr[edge[0]].add(edge[1]);\n\n for (int i = 0; i <n; i++)\n dfs(i, n, gr, vis, mat);\n\n for(int[] q : queries)\n res.add(mat[q[0]][q[1]]);\n\n return res;\n }\n\t
| 4 | 0 |
['Depth-First Search', 'Graph', 'Memoization', 'Java']
| 2 |
course-schedule-iv
|
300ms Beat 100% ! C++ Bit Manipulation
|
300ms-beat-100-c-bit-manipulation-by-xxx-q2i3
|
I use cache[i] (bitset<100>) to store all reachable nodes for i. In the recursion, node i collects (by | operation) reachable nodes only once, return cache[i]
|
xxx1123
|
NORMAL
|
2020-07-26T13:34:52.805906+00:00
|
2020-07-27T03:06:56.450118+00:00
| 431 | false |
**I use cache[i] (bitset<100>) to store all reachable nodes for i. In the recursion, node i collects (by ```|``` operation) reachable nodes only once, return cache[i] if it already exists.\nThe time complexity is almost O(N + E).**\n\n```\nvector<bool> checkIfPrerequisite(int n, vector<vector<int>>& prerequisites, vector<vector<int>>& queries) {\n vector<vector<int>> g(n);\n vector<int> indegree(n, 0);\n for(auto v: prerequisites) {\n g[v[0]].emplace_back(v[1]);\n ++indegree[v[1]];\n }\n vector<bitset<100> > cache(n, 0); // n <= 100\n\n function<bitset<100>(int)> dfs1462 = [&](int i){\n \n if(g[i].empty()) {bitset<100> b(0); b[i] = true; return b; } // outdegree[i] == 0\n if(cache[i] != bitset<100>(0)) return cache[i];\n\n cache[i][i] = true;\n for(int v: g[i]) cache[i] |= dfs1462(v);\n return cache[i];\n };\n for(int i=0; i<n; i++)\n if(indegree[i]==0)\n dfs1462(i);\n vector<bool> res(queries.size(), false);\n int i=0;\n for(auto &q: queries) res[i++] = bool(cache[q[0]][q[1]]);\n return res;\n}\n```\n\n\n
| 4 | 0 |
[]
| 1 |
course-schedule-iv
|
java dfs 97%
|
java-dfs-97-by-atwjsw-381g
|
class Solution {\n \n List[] adj; // adjcency list\n boolean[][] isReachable;\n \n public List checkIfPrerequisite(int n, int[][] prerequisites,
|
atwjsw
|
NORMAL
|
2020-07-18T18:59:15.068524+00:00
|
2020-07-18T19:12:08.564341+00:00
| 260 | false |
class Solution {\n \n List<Integer>[] adj; // adjcency list\n boolean[][] isReachable;\n \n public List<Boolean> checkIfPrerequisite(int n, int[][] prerequisites, int[][] queries) {\n \n adj = new List[n];\n isReachable = new boolean[n][n];\n \n for (int i = 0; i < n; i++)\n adj[i] = new ArrayList<>();\n \n for(int[] edge: prerequisites)\n adj[edge[0]].add(edge[1]);\n \n for (int i = 0; i < n; i++) \n dfs(i, i);\n \n List<Boolean> res = new ArrayList<>();\n for (int[] query: queries)\n res.add(isReachable[query[0]][query[1]]);\n return res;\n }\n \n void dfs(int o, int v) {\n isReachable[o][v] = true;\n for (int w: adj[v]) { \n if (isReachable[o][w]) continue;\n dfs(o, w);\n }\n }\n}
| 4 | 0 |
[]
| 1 |
course-schedule-iv
|
C++ optimal approach beats 100%
|
c-optimal-approach-beats-100-by-sakshaml-yff1
|
ApproachInstead of checking for every 2 nodes in queries , we can check for which node the selected node is prerequisite. This works because numCourses can only
|
LeviLovesToSolve
|
NORMAL
|
2025-01-28T16:20:30.897164+00:00
|
2025-01-28T16:20:30.897164+00:00
| 18 | false |
# Approach
<!-- Describe your approach to solving the problem. -->
Instead of checking for every 2 nodes in queries , we can check for which node the selected node is prerequisite. This works because numCourses can only be 100 while size of queries vector is 10000.
# Complexity
- Time complexity:O(N^3 + Q)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:O(N^2)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
void dfs(vector<vector<int>>&adj,int node,int parent,vector<vector<bool>> &found,int check,vector<bool>&vis){
if(node!=check){
found[check][node]=1;
}
for(int i=0;i<adj[node].size();i++){
if(adj[node][i]==parent||vis[adj[node][i]]) continue;
vis[adj[node][i]]=1;
dfs(adj,adj[node][i],node,found,check,vis);
}
}
vector<bool> checkIfPrerequisite(int numCourses, vector<vector<int>>& pre, vector<vector<int>>& queries) {
vector<vector<bool>> found(numCourses,vector<bool>(numCourses,false));
vector<vector<int>> adj(numCourses);
for(int i=0;i<pre.size();i++){
adj[pre[i][1]].push_back(pre[i][0]);
}
for(int i=0;i<numCourses;i++){
vector<bool>vis(numCourses,0);
vis[i]=1;
dfs(adj,i,-1,found,i,vis);
}
int m=queries.size();
vector<bool> res(m,false);
for(int i=0;i<m;i++){
if(found[queries[i][1]][queries[i][0]]) res[i]=true;
}
return res;
}
};
```
| 3 | 0 |
['Hash Table', 'C++']
| 0 |
course-schedule-iv
|
Optimised + Floyd Warshall
|
optimised-floyd-warshall-by-saurav_kumar-l3co
|
IntuitionThe problem can be modeled as a graph problem where we need to determine if there is a path (direct or indirect) between two nodes. Using the Floyd-War
|
Saurav_kumar_10
|
NORMAL
|
2025-01-27T20:09:15.680990+00:00
|
2025-01-27T20:09:15.680990+00:00
| 81 | false |
# Intuition
The problem can be modeled as a graph problem where we need to determine if there is a path (direct or indirect) between two nodes. Using the **Floyd-Warshall algorithm**, we can efficiently compute the transitive closure of the graph, which allows us to answer each query in constant time.
# Approach
1. **Graph Representation**: Represent the graph using a 2D adjacency matrix `adj`, where `adj[i][j]` stores the shortest path from node `i` to node `j`. Initialize it with `-1` (no path) and set `adj[i][i] = 0` for all nodes.
2. **Update Direct Edges**: Use the given prerequisites (`prereq`) to mark direct connections between nodes.
3. **Floyd-Warshall Algorithm**: For each pair of nodes `(i, j)`, check if an intermediate node `k` provides a shorter path. Update the adjacency matrix accordingly.
4. **Answer Queries**: For each query `(u, v)`, check if `adj[u][v] > 0`, which indicates a path exists from `u` to `v`. Append `true` or `false` to the result accordingly.
# Complexity
- Time complexity:
$$O(n^3)$$
- Space complexity:
$$O(n^2)$$
# Code
```cpp []
class Solution {
public:
vector<bool> checkIfPrerequisite(int n, vector<vector<int>>& prereq, vector<vector<int>>& queries) {
vector <vector<int>> adj(n,vector<int>(n,-1));
for(int i=0;i<n;i++){
adj[i][i]=0;
}
for(int i=0;i<prereq.size();i++){
adj[prereq[i][0]][prereq[i][1]]=1;
}
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
for(int k=0;k<n;k++){
if(adj[j][i]==-1 || adj[i][k]==-1) continue;
if(adj[j][k]==-1) adj[j][k]=adj[j][i]+adj[i][k];
adj[j][k]=min(adj[j][k],adj[j][i]+adj[i][k]);
}
}
}
vector <bool> ans;
for(int i=0;i<queries.size();i++){
if(adj[queries[i][0]][queries[i][1]]>0)
ans.push_back(true);
else ans.push_back(false);
}
return ans;
}
};
```
```python3 []
class Solution:
def checkIfPrerequisite(self, numCourses: int, prerequisites: List[List[int]], queries: List[List[int]]) -> List[bool]:
# Initialize the adjacency matrix with -1
adj = [[-1 for _ in range(numCourses)] for _ in range(numCourses)]
# Set diagonal values to 0
for i in range(numCourses):
adj[i][i] = 0
# Populate the adjacency matrix with prerequisites
for pre in prerequisites:
adj[pre[0]][pre[1]] = 1
# Floyd-Warshall Algorithm
for k in range(numCourses):
for i in range(numCourses):
for j in range(numCourses):
if adj[i][k] == -1 or adj[k][j] == -1:
continue
if adj[i][j] == -1:
adj[i][j] = adj[i][k] + adj[k][j]
adj[i][j] = min(adj[i][j], adj[i][k] + adj[k][j])
# Generate the result for each query
result = []
for query in queries:
result.append(adj[query[0]][query[1]] > 0)
return result
```
```java []
class Solution {
public List<Boolean> checkIfPrerequisite(int numCourses, int[][] prerequisites, int[][] queries) {
// Initialize the adjacency matrix with -1
int[][] adj = new int[numCourses][numCourses];
for (int i = 0; i < numCourses; i++) {
for (int j = 0; j < numCourses; j++) {
adj[i][j] = -1;
}
adj[i][i] = 0; // Set diagonal to 0
}
// Populate the adjacency matrix with prerequisites
for (int[] pre : prerequisites) {
adj[pre[0]][pre[1]] = 1;
}
// Floyd-Warshall Algorithm
for (int k = 0; k < numCourses; k++) {
for (int i = 0; i < numCourses; i++) {
for (int j = 0; j < numCourses; j++) {
if (adj[i][k] == -1 || adj[k][j] == -1) continue;
if (adj[i][j] == -1) adj[i][j] = adj[i][k] + adj[k][j];
adj[i][j] = Math.min(adj[i][j], adj[i][k] + adj[k][j]);
}
}
}
// Generate the result for each query
List<Boolean> result = new ArrayList<>();
for (int[] query : queries) {
result.add(adj[query[0]][query[1]] > 0);
}
return result;
}
}
```
``` javascript []
/**
* @param {number} numCourses
* @param {number[][]} prerequisites
* @param {number[][]} queries
* @return {boolean[]}
*/
var checkIfPrerequisite = function(numCourses, prerequisites, queries) {
// Initialize the adjacency matrix with -1
const adj = Array.from({ length: numCourses }, () => Array(numCourses).fill(-1));
// Set diagonal values to 0
for (let i = 0; i < numCourses; i++) {
adj[i][i] = 0;
}
// Populate the adjacency matrix with prerequisites
for (const [u, v] of prerequisites) {
adj[u][v] = 1;
}
// Floyd-Warshall Algorithm
for (let k = 0; k < numCourses; k++) {
for (let i = 0; i < numCourses; i++) {
for (let j = 0; j < numCourses; j++) {
if (adj[i][k] === -1 || adj[k][j] === -1) continue;
if (adj[i][j] === -1) {
adj[i][j] = adj[i][k] + adj[k][j];
}
adj[i][j] = Math.min(adj[i][j], adj[i][k] + adj[k][j]);
}
}
}
// Generate the result for each query
const result = [];
for (const [u, v] of queries) {
result.push(adj[u][v] > 0);
}
return result;
};
```
| 3 | 0 |
['C++', 'Java', 'Python3', 'JavaScript']
| 0 |
course-schedule-iv
|
-------JAVA-------
|
java-by-aysha3211-dr6u
|
Code
|
Aysha3211
|
NORMAL
|
2025-01-27T16:28:56.272500+00:00
|
2025-01-27T16:28:56.272500+00:00
| 86 | false |
# Code
```java []
class Solution {
public List<Boolean> checkIfPrerequisite(int numCourses, int[][] prerequisites, int[][] queries) {
boolean mat[][] = new boolean[numCourses][numCourses];
for(int i=0;i<prerequisites.length;i++){
int s = prerequisites[i][0];
int d = prerequisites[i][1];
mat[s][d] = true;
}
for(int k=0;k<numCourses;k++){
for(int s=0;s<numCourses;s++){
for(int d=0;d<numCourses;d++){
mat[s][d] = mat[s][d] || (mat[s][k] && mat[k][d]);
}
}
}
List<Boolean> ans = new ArrayList<>();
for(int i=0;i<queries.length;i++){
int s = queries[i][0];
int d = queries[i][1];
ans.add(mat[s][d]);
}
return ans;
}
}
```
| 3 | 0 |
['Java']
| 0 |
course-schedule-iv
|
DFS-Based Solution for Course Schedule IV | Beats 85% 🔥 | Intuitive + Clean Code 💡
|
dfs-based-solution-for-course-schedule-i-1mqc
|
IntuitionThe problem is about determining whether one course is a prerequisite for another. This can be viewed as a graph problem, where courses are nodes, and
|
atharva_kalbande
|
NORMAL
|
2025-01-27T15:58:48.896750+00:00
|
2025-01-27T15:58:48.896750+00:00
| 20 | false |
# Intuition
The problem is about determining whether one course is a prerequisite for another. This can be viewed as a graph problem, where courses are nodes, and prerequisites are directed edges. The goal is to figure out if there's a path from one node (course) to another in the graph
# Approach
- Graph Representation: Use an adjacency list to represent the graph, where the keys are courses, and the values are lists of their prerequisites.
- Depth-First Search (DFS): For each course, perform a DFS to gather all its prerequisites (both direct and indirect). Store the result in a prereqMap to avoid redundant computations.
- Query Evaluation: After building the prereqMap, check if each course in the query is in the prerequisite set of the other course.
# Complexity
- Time complexity:
O( N + E )
- Space complexity:
O( N + E )
# Code
```python []
class Solution(object):
def checkIfPrerequisite(self, numCourses, prerequisites, queries):
adj = defaultdict(list)
for prereq, crs in prerequisites:
adj[crs].append(prereq)
def dfs(crs):
if crs not in prereqMap:
prereqMap[crs] = set()
for prereq in adj[crs]:
prereqMap[crs] |= dfs(prereq)
prereqMap[crs].add(crs)
return prereqMap[crs]
prereqMap = {}
for crs in range(numCourses):
dfs(crs)
res =[]
for u,v in queries:
res.append(u in prereqMap[v])
return res
```
| 3 | 0 |
['Python']
| 0 |
course-schedule-iv
|
---------JAVA---------
|
java-by-ayeshakhan7-nc6z
|
ApproachKahn's AlgorithmComplexity
Time complexity: O(V^2 + V + E) -> Processing Nodes (each node pushed once in queue) = O(V), Processing edges = O(E), Inserti
|
ayeshakhan7
|
NORMAL
|
2025-01-27T15:20:41.605551+00:00
|
2025-01-27T15:20:41.605551+00:00
| 80 | false |
# Approach
<!-- Describe your approach to solving the problem. -->
Kahn's Algorithm
# Complexity
- Time complexity: O(V^2 + V + E) -> Processing Nodes (each node pushed once in queue) = O(V), Processing edges = O(E), Inserting prerequisites (each node can have ~V prerequisites in worst case): O(V^2)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(V+E)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public List<Boolean> checkIfPrerequisite(int numCourses, int[][] prerequisites, int[][] queries) {
// Create adjacency list and indegree array
Map<Integer, List<Integer>> adj = new HashMap<>();
int[] indegree = new int[numCourses];
for (int[] edge : prerequisites) {
int u = edge[0];
int v = edge[1];
adj.computeIfAbsent(u, k -> new ArrayList<>()).add(v);
indegree[v]++;
}
// Initialize queue with nodes having indegree 0
Queue<Integer> queue = new LinkedList<>();
for (int i = 0; i < numCourses; i++) {
if (indegree[i] == 0) {
queue.offer(i);
}
}
// Map from node to set of prerequisite nodes
Map<Integer, Set<Integer>> prereqMap = new HashMap<>();
while (!queue.isEmpty()) {
int node = queue.poll();
for (int neighbor : adj.getOrDefault(node, new ArrayList<>())) {
// Add current node and its prerequisites to the neighbor's prerequisites
prereqMap.computeIfAbsent(neighbor, k -> new HashSet<>()).add(node);
prereqMap.get(neighbor).addAll(prereqMap.getOrDefault(node, new HashSet<>()));
indegree[neighbor]--;
if (indegree[neighbor] == 0) {
queue.offer(neighbor);
}
}
}
// Process each query
List<Boolean> result = new ArrayList<>();
for (int[] query : queries) {
int src = query[0];
int dest = query[1];
result.add(prereqMap.getOrDefault(dest, new HashSet<>()).contains(src));
}
return result;
}
}
```
| 3 | 0 |
['Java']
| 0 |
course-schedule-iv
|
✅✅Beats 100%🔥C++🔥Python|| 🚀🚀Super Simple and Efficient Solution🚀🚀||🔥Python🔥C++✅✅
|
beats-100cpython-super-simple-and-effici-41vz
|
Complexity
Time complexity: O(n3)
Space complexity: O(n2)
⬆️👇⬆️UPVOTE it⬆️👇⬆️Code⬆️👇⬆️UPVOTE it⬆️👇⬆️
|
shobhit_yadav
|
NORMAL
|
2025-01-27T14:41:31.600408+00:00
|
2025-01-27T14:41:31.600408+00:00
| 162 | false |
# Complexity
- Time complexity: $$O(n^3)$$
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: $$O(n^2)$$
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
⬆️👇⬆️UPVOTE it⬆️👇⬆️
# Code
```cpp []
class Solution {
public:
vector<bool> checkIfPrerequisite(int numCourses, vector<vector<int>>& prerequisites, vector<vector<int>>& queries) {
vector<bool> ans;
vector<vector<int>> graph(numCourses);
vector<vector<bool>> isPrerequisite(numCourses, vector<bool>(numCourses));
for (const vector<int>& prerequisite : prerequisites) {
const int u = prerequisite[0];
const int v = prerequisite[1];
graph[u].push_back(v);
}
for (int i = 0; i < numCourses; ++i)
dfs(graph, i, isPrerequisite[i]);
for (const vector<int>& query : queries) {
const int u = query[0];
const int v = query[1];
ans.push_back(isPrerequisite[u][v]);
}
return ans;
}
void dfs(const vector<vector<int>>& graph, int u, vector<bool>& used) {
for (const int v : graph[u]) {
if (used[v])
continue;
used[v] = true;
dfs(graph, v, used);
}
}
};
```
```python3 []
class Solution:
def checkIfPrerequisite(
self,
numCourses: int,
prerequisites: list[list[int]],
queries: list[list[int]],
) -> list[bool]:
graph = [[] for _ in range(numCourses)]
isPrerequisite = [[False] * numCourses for _ in range(numCourses)]
for u, v in prerequisites:
graph[u].append(v)
for i in range(numCourses):
self._dfs(graph, i, isPrerequisite[i])
return [isPrerequisite[u][v] for u, v in queries]
def _dfs(self, graph: list[list[int]], u: int, used: list[bool]) -> None:
for v in graph[u]:
if used[v]:
continue
used[v] = True
self._dfs(graph, v, used)
```
⬆️👇⬆️UPVOTE it⬆️👇⬆️
| 3 | 0 |
['Depth-First Search', 'Breadth-First Search', 'Graph', 'Topological Sort', 'C++', 'Python3']
| 0 |
course-schedule-iv
|
simple py solution
|
simple-py-solution-by-noam971-60rf
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
noam971
|
NORMAL
|
2025-01-27T08:33:43.399273+00:00
|
2025-01-27T08:33:43.399273+00:00
| 141 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def checkIfPrerequisite(self, numCourses: int, prerequisites: List[List[int]], queries: List[List[int]]) -> List[bool]:
canTake = [[False] * numCourses for _ in range(numCourses)]
for pre, course in prerequisites:
canTake[pre][course] = True
for mid in range(numCourses):
for src in range(numCourses):
for dst in range(numCourses):
canTake[src][dst] = canTake[src][dst] or (canTake[src][mid] and canTake[mid][dst])
return [canTake[u][v] for u, v in queries]
```
| 3 | 0 |
['Python3']
| 1 |
course-schedule-iv
|
C# Solution for Course Schedule IV Problem
|
c-solution-for-course-schedule-iv-proble-14ld
|
IntuitionThe problem involves checking whether one course is a prerequisite for another, either directly or indirectly. This can be represented as a directed gr
|
Aman_Raj_Sinha
|
NORMAL
|
2025-01-27T03:47:50.651612+00:00
|
2025-01-27T03:47:50.651612+00:00
| 128 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
The problem involves checking whether one course is a prerequisite for another, either directly or indirectly. This can be represented as a directed graph, where courses are nodes and prerequisites are directed edges. The goal is to answer multiple queries efficiently.
Instead of precomputing all possible prerequisites for all pairs of nodes (like in Floyd-Warshall), this solution leverages Depth-First Search (DFS) to compute the reachable courses for each course. Each course’s reachability information is stored in a set, which allows quick query resolution.
By storing reachable courses per node, we avoid redundant computations and only explore paths that are relevant to each node, making this solution more efficient for sparse graphs.
# Approach
<!-- Describe your approach to solving the problem. -->
1. Graph Representation:
• Build an adjacency list to represent the directed graph. Each course points to its direct successors (courses that depend on it).
2. DFS for Reachability:
• Perform DFS for each course to find all other courses that can be reached directly or indirectly from it.
• Use a HashSet for each course to store its reachable courses. This ensures efficient insertion and lookups while avoiding duplicate entries.
• Store the results in an array reachable, where reachable[i] contains all courses that are reachable from course i.
3. Query Resolution:
• For each query (u, v), check if course v is in the set reachable[u]. This is a O(1) operation per query.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
1. Graph Construction:
• Building the adjacency list takes O(e), where e is the number of prerequisites (edges in the graph).
2. DFS Traversal:
• DFS is performed for each course. In the worst case, a single DFS may visit all nodes and edges.
• For n courses and e edges, the overall time complexity for all DFS calls is O(n + e).
3. Query Resolution:
• Each query is processed in O(1) by looking up the precomputed reachability set.
• For q queries, the total query time is O(q).
Total Time Complexity: O(n . (n + e) + q), where:
• n: Number of courses.
• e: Number of edges (prerequisites).
• q: Number of queries.
This is efficient for sparse graphs, where e << n^2.
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
1. Adjacency List:
• The adjacency list representation of the graph takes O(n + e) space.
2. Reachability Sets:
• Each course has a HashSet to store reachable nodes. In the worst case (a fully connected graph), each course’s set may contain up to n-1 courses.
• The total space required for the reachability sets is O(n^2).
Total Space Complexity: O(n^2 + e).
# Code
```csharp []
public class Solution {
public IList<bool> CheckIfPrerequisite(int numCourses, int[][] prerequisites, int[][] queries) {
var graph = new List<int>[numCourses];
for (int i = 0; i < numCourses; i++) {
graph[i] = new List<int>();
}
foreach (var prereq in prerequisites) {
graph[prereq[0]].Add(prereq[1]);
}
var reachable = new HashSet<int>[numCourses];
for (int i = 0; i < numCourses; i++) {
reachable[i] = new HashSet<int>();
}
void Dfs(int course, int current) {
foreach (var next in graph[current]) {
if (!reachable[course].Contains(next)) {
reachable[course].Add(next);
Dfs(course, next);
}
}
}
for (int i = 0; i < numCourses; i++) {
Dfs(i, i);
}
var result = new List<bool>();
foreach (var query in queries) {
result.Add(reachable[query[0]].Contains(query[1]));
}
return result;
}
}
```
| 3 | 0 |
['C#']
| 0 |
course-schedule-iv
|
Simple Unordered Map And Queue C++ || Beats 99% of Users || Dynamic Programming
|
simple-unordered-map-and-queue-c-beats-9-tcch
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
Mohit-Kumawat04
|
NORMAL
|
2025-01-27T01:32:25.080677+00:00
|
2025-03-21T04:48:26.704586+00:00
| 390 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
vector<bool> checkIfPrerequisite(int numCourses,
vector<vector<int>>& prerequisites,
vector<vector<int>>& queries) {
unordered_map<int, vector<int>> adjList;
vector<int> indegree(numCourses, 0);
for (auto edge : prerequisites) {
adjList[edge[0]].push_back(edge[1]);
indegree[edge[1]]++;
}
queue<int> q;
for (int i = 0; i < numCourses; i++) {
if (!indegree[i]) {
q.push(i);
}
}
// Map from the node as key to the set of prerequisite nodes.
unordered_map<int, unordered_set<int>> nodePrerequisites;
while (!q.empty()) {
int node = q.front();
q.pop();
for (auto adj : adjList[node]) {
// Add node and prerequisite of node to the prerequisites of adj
nodePrerequisites[adj].insert(node);
for (auto prereq : nodePrerequisites[node]) {
nodePrerequisites[adj].insert(prereq);
}
indegree[adj]--;
if (!indegree[adj]) {
q.push(adj);
}
}
}
vector<bool> answer;
for (auto q : queries) {
answer.push_back(nodePrerequisites[q[1]].contains(q[0]));
}
return answer;
}
};
```
| 3 | 0 |
['Hash Table', 'Linked List', 'Dynamic Programming', 'Greedy', 'Depth-First Search', 'Breadth-First Search', 'C++']
| 1 |
course-schedule-iv
|
UMPIRE-style solution
|
umpire-style-solution-by-espertusnu-bmva
|
This solution uses CodePath\'s UMPIRE interview strategy.\n\nThis is a slight modification to my Course Schedule II solution.\n\n# 1: U-nderstand\n\nThere are a
|
espertusnu
|
NORMAL
|
2024-06-16T19:49:46.897053+00:00
|
2024-06-16T19:49:46.897079+00:00
| 524 | false |
This solution uses [CodePath\'s UMPIRE interview strategy](https://guides.codepath.com/compsci/UMPIRE-Interview-Strategy).\n\nThis is a slight modification to my [Course Schedule II solution](https://leetcode.com/problems/course-schedule-ii/solutions/5323750/umpire-style-solution/).\n\n# 1: U-nderstand\n\nThere are a total of `numCourses` courses you have to take, labeled from `0` to `numCourses - 1`. You are given an array `prerequisites` where `prerequisites[i] = [a, b]` indicates that you must take course `a` first if you want to take course `b`.\n\nFor example, the pair `[0, 1]`, indicates that you have to take course `0` before you can take course `1`.\n\nPrerequisites can also be **indirect**. If course `a` is a prerequisite of course `b`, and course `b` is a prerequisite of course `c`, then course `a` is a prerequisite of course `c`.\n\nYou are also given an array queries where `queries[j] = [uj, vj]`. For the `jth` query, you should answer whether course `uj` is a prerequisite of course `vj` or not.\n\nReturn *a boolean array `answer`, where `answer[j]` is the answer to the `jth` query*.\n\n* Is `prerequisites` an edge set?\n * Yes.\n* Is `prerequisites` a dag?\n * Yes, it is a directed graph guaranteed to be acyclic.\n* Is the order of the edges in the edge set the same as in Course Schedule and Course Schedule II?\n * No, the source node now precedes the destination node.\n\n\nGood test cases would be:\n* `checkIfPrerequisite(3, [[0, 1], [1, 2]], [[0, 2], [2, 0]])` (happy case returning `[true, false]`\n* `checkIfPrerequisite(2, [], [[0, 1], [1, 0]])` (edge case with no prerequisites)\n\n# 2: M-atch\n\nThis can be solved with **[topological sort](https://guides.codepath.com/compsci/Topological-Sort#:~:text=Topological%20sort%20simply%20involves%20running,of%20edges%20in%20the%20ordering.)**. \n\n# 3: P-lan\n\n## checkIfPrerequisite(numCourses, prerequisites, queries)\n1. Initialize the data structures from the arguments `numCourses` and `prerequisites`:\n * an adjacency list for representing the graph\n * a visited list/set\n * a list/set of source nodes\n * a map `reachable` to keep track of what nodes can be reached from a given node\n2. Call `dfs()` on each node.\n3. Build and return the result list. For each query `[u, v]`, indicate whether `reachable[u]` contains `v`.\n\n## dfs(node)\n1. Mark `node` visited.\n3. For every neighbor of `node`:\n 1. Record that the neighbor is reachable from `node`.\n 2. If the neighbor has not been visited, call `dfs(neighbor)`.\n 3. Record that every node reachable from the neighbor is reachable from `node`.\n\n# 4: Implementation\n\n## Java notes\n\nWhile ideally the adjacency list would be implemented as an array of `List<Integer>` or a `List<List<Integer>>`, the former is [unsafe](https://stackoverflow.com/questions/2927391/whats-the-reason-i-cant-create-generic-array-types-in-java), and the latter is [awkward](https://stackoverflow.com/questions/31413628/collections-ncopies-not-creating-copies-of-list). I instead used a `HashMap<Integer, List<Integer>>` along with [`computeIfAbsent()`](https://stackoverflow.com/a/58477560/631051).\n\n## Code\n<iframe src="https://leetcode.com/playground/eRuzeTpb/shared" frameBorder="0" width="600" height="600"></iframe>\n\n# 5. R-eview\nReview the code by stepping through it with the test cases.\n\n# 6. E-valuate\n\nLet $V$ be the number of courses (`numCourses`), $E$ the number of prerequisites, and $Q$ the number of queries.\n\n## Time Complexity\n1. Initializing the data structures, including the adjacency list, will take time $O(E)$.\n2. The sequence of depth-first searches will take time $O(E + V)$.\n3. Adding up to `V` nodes to each of the `V` reachable sets, will take $O(V^2)$ time.\n4. Processing the queries will take $O(Q)$ time.\n5. Thus, the total time complexity is $O(E + V^2 + Q)$. Because $E$ has an upper bound of $V^2$, this can be simplified to $O(V^2 + Q)$.\n\n## Space Complexity\n1. The adjacency list has size $O(E + V)$. \n2. The visited and source lists defined in `getOrder()` have size $O(V)$.\n3. The `reachable` map has size $O(V^2)$.\n4. The output list (which is sometimes left out of analyses) has size $Q$\n4. Thus, the space complexity is $O(V^2)$ auxiliary space or $O(V^2+Q)$ if the output size is counted.\n
| 3 | 0 |
['Java', 'Python3']
| 0 |
course-schedule-iv
|
( ͡° ͜ʖ ͡°)👉|| Beats 97.99%|| JAVA|| PYTHON||EASY SOLUTION💯☑️
|
deg-deg-beats-9799-java-pythoneasy-solut-y3xk
|
If you find it useful, please upvote so that others can find it easily.\n# Code\nJava []\nclass Solution {\n public void fillGraph(boolean[][] graph, int i,
|
Pratheek08
|
NORMAL
|
2023-08-31T05:09:57.983245+00:00
|
2023-08-31T05:11:17.426365+00:00
| 205 | false |
# If you find it useful, please upvote so that others can find it easily.\n# Code\n```Java []\nclass Solution {\n public void fillGraph(boolean[][] graph, int i, boolean[] visited){\n if (visited[i])\n return;\n visited[i] = true;\n for (int j=0;j<graph[i].length;j++){\n if (graph[i][j]){\n fillGraph(graph, j, visited);\n for (int k=0;k<graph[j].length;k++){\n if (graph[j][k])\n graph[i][k] = true;\n }\n }\n }\n }\n \n public List<Boolean> checkIfPrerequisite(int n, int[][] prerequisites, int[][] queries) {\n boolean[][] graph = new boolean[n][n];\n \n for (int i=0;i<n;i++)\n graph[i][i] = true;\n\n for (int[] entry: prerequisites)\n graph[entry[0]][entry[1]] = true;\n \n boolean[] visited = new boolean[n];\n for (int i=0;i<n;i++)\n fillGraph(graph, i, visited);\n \n List<Boolean> responses = new ArrayList<Boolean>();\n for (int[] query: queries)\n responses.add(graph[query[0]][query[1]]);\n return responses;\n }\n}\n```\n```python []\nclass Solution(object):\n def checkIfPrerequisite(self, numCourses, prerequisites, queries):\n adj={i:[] for i in range(numCourses)}\n\n for x,y in prerequisites:\n adj[y].append(x)\n res=[]\n def dfs(crs):\n if crs not in premap:\n premap[crs]=set()\n for nei in adj[crs]:\n premap[crs]|=dfs(nei)\n premap[crs].add(crs)\n return premap[crs]\n\n premap={}\n for i in range(numCourses):\n dfs(i) \n for x,y in queries:\n res.append(x in premap[y])\n return res \n \n```\n\n
| 3 | 0 |
['Python', 'Java', 'Python3']
| 1 |
course-schedule-iv
|
IIT | TOPO-LOGICAL SORT | 99 % FASTER
|
iit-topo-logical-sort-99-faster-by-robbe-xc18
|
Intuition\nTotal number of pairs of unique queries can be n^2. So, to avoid doing repetitive calculations, we will store these n^2 pairs.\nOur approach in this
|
robberkr
|
NORMAL
|
2023-06-26T19:20:05.636798+00:00
|
2023-06-26T19:20:05.636822+00:00
| 746 | false |
# Intuition\nTotal number of pairs of unique queries can be n^2. So, to avoid doing repetitive calculations, we will store these n^2 pairs.\nOur approach in this question will be in this way, if we know that Node A is a prerequisite of B, then all the prerequisites of Node A are also prerequisite of B. So, we will keep updating the prerequisite matrix. \nNow, we are going to use topological sort in this question, where the one with no prerequisite will be computed first and after its computation we will go to the nodes whom this node is a prerequisite and will update their prerequisite matrix. So, in this way we are updating the prerequisite matrix of a node, with its prequisite\'s prequisite. \n# Approach\nUsed Topological sort to go in the reverse direction ( by computing for independent nodes first and then using their answer to compute other nodes.)\n# Complexity\n- Time complexity:\nO(n^3)\n- Space complexity:\nO(n^2)\n\n# Code\n```\nclass Solution {\npublic:\n vector<bool> checkIfPrerequisite(int n, vector<vector<int>>& p, vector<vector<int>>& queries) \n {\n vector<vector<int>> adj(n, vector<int>()); \n vector<vector<int>> ans(n, vector<int>(n, 0));\n queue<int> q;\n vector<int> indeg(n, 0);\n\n for(int i = 0; i < p.size(); i++)\n {\n int ind = p[i][1], pre = p[i][0];\n adj[pre].push_back(ind);\n indeg[ind]++;\n }\n\n for(int i = 0; i < n; i++)\n {\n if(indeg[i] == 0)\n {\n q.push(i);\n }\n }\n\n while(!q.empty())\n {\n int r = q.front();\n q.pop();\n vector<int> temp;\n for(int i = 0; i < n; i++)\n {\n if(ans[r][i] == 1)\n {\n temp.push_back(i);\n }\n }\n\n for(int i = 0; i < adj[r].size(); i++)\n {\n int cur = adj[r][i];\n ans[cur][r] = 1;\n for(int w = 0; w < temp.size(); w++)\n {\n ans[cur][temp[w]] = 1;\n }\n indeg[cur]--;\n if(indeg[cur] == 0)\n {\n q.push(cur);\n }\n }\n }\n\n vector<bool> qrs(queries.size(), 0);\n for(int i = 0; i < queries.size(); i++)\n {\n int u = queries[i][0], v = queries[i][1];\n qrs[i] = ans[v][u];\n }\n return qrs;\n }\n};\n```
| 3 | 2 |
['C++']
| 2 |
course-schedule-iv
|
C++ Solution || Adjacency List and DFS || Easy to understand
|
c-solution-adjacency-list-and-dfs-easy-t-k1yf
|
\nvoid dfs(vector<int> adj[], int src, int& des, bool& temp, vector<bool>& vis) {\n if(vis[src]) return;\n vis[src] = true;\n \n if(
|
pranjal_gaur
|
NORMAL
|
2023-06-03T08:46:46.610336+00:00
|
2023-06-03T08:46:46.610389+00:00
| 938 | false |
```\nvoid dfs(vector<int> adj[], int src, int& des, bool& temp, vector<bool>& vis) {\n if(vis[src]) return;\n vis[src] = true;\n \n if(src == des) {\n temp = true;\n return;\n }\n \n for(auto it : adj[src]) dfs(adj, it, des, temp, vis);\n }\n \n vector<bool> checkIfPrerequisite(int n, vector<vector<int>>& pre, vector<vector<int>>& que) {\n vector<int> adj[n];\n \n for(auto it : pre) \n adj[it[0]].push_back(it[1]);\n \n int sz = que.size();\n vector<bool> ans(sz);\n \n for(int i=0;i<sz;i++) {\n int src = que[i][0];\n int des = que[i][1];\n \n bool temp = false;\n vector<bool> vis(n, false);\n dfs(adj, src, des, temp, vis);\n ans[i] = temp;\n }\n \n return ans;\n }\n```
| 3 | 0 |
['Depth-First Search', 'C']
| 0 |
course-schedule-iv
|
C++ | Both 100% | Warshall + bitset speedup | explanation
|
c-both-100-warshall-bitset-speedup-expla-ea6q
|
\nclass Solution {\npublic:\n vector<bool> checkIfPrerequisite(int numCourses, vector<vector<int>>& prerequisites, vector<vector<int>>& queries){\n in
|
SunGod1223
|
NORMAL
|
2022-09-08T08:44:54.572769+00:00
|
2022-09-12T03:55:09.545778+00:00
| 1,178 | false |
```\nclass Solution {\npublic:\n vector<bool> checkIfPrerequisite(int numCourses, vector<vector<int>>& prerequisites, vector<vector<int>>& queries){\n int n=numCourses;\n bitset <100> and_mask(1),dp[n];\n vector <bool> rt(queries.size());\n for(int i=0;i<prerequisites.size();++i)\n dp[prerequisites[i][0]][prerequisites[i][1]]=1;\n for(int k=0;k<n;++k,and_mask<<=1)\n for(int i=0;i<n;++i)\n if((dp[i]&and_mask).any())\n dp[i]=dp[i]|dp[k];\n for(int i=0;i<queries.size();++i)\n rt[i]=dp[queries[i][0]][queries[i][1]];\n return rt;\n }\n};\n```\nExplanation link: https://github.com/SUNGOD3/Floyd-Warshall-bitset-speedup
| 3 | 0 |
['C']
| 1 |
course-schedule-iv
|
C++ || Kahns algorithm || Topological Sort
|
c-kahns-algorithm-topological-sort-by-__-1jdg
|
\nclass Solution {\npublic:\n vector<bool> checkIfPrerequisite(int n , vector<vector<int>> &p , vector<vector<int>>& qr) {\n vector<int> indegree(n ,
|
__shinigami__
|
NORMAL
|
2022-07-26T06:54:41.938090+00:00
|
2022-07-26T06:54:41.938131+00:00
| 547 | false |
```\nclass Solution {\npublic:\n vector<bool> checkIfPrerequisite(int n , vector<vector<int>> &p , vector<vector<int>>& qr) {\n vector<int> indegree(n , 0) , adj[n];\n for(int i=0 ; i<p.size() ; i++) {\n int u = p[i][0];\n int v = p[i][1];\n indegree[v]++;\n adj[u].push_back(v);\n }\n queue<int> q;\n for(int i=0 ; i<n ; i++) {\n if(!indegree[i]) q.push(i);\n }\n vector<vector<bool>> isReachable(n , vector<bool>(n , false));\n while(!q.empty()) {\n int u = q.front();\n q.pop();\n for(int v : adj[u]) {\n indegree[v]--;\n isReachable[u][v] = true;\n for(int i=0 ; i<n ; i++) {\n if(isReachable[i][u]) isReachable[i][v] = true;\n }\n if(!indegree[v]) {\n q.push(v);\n }\n }\n }\n vector<bool> ans((int)qr.size() , false);\n for(int i=0 ; i<qr.size() ; i++) {\n if(isReachable[qr[i][0]][qr[i][1]]) {\n ans[i] = true;\n }\n }\n return ans;\n }\n};\n```
| 3 | 0 |
['Breadth-First Search', 'Topological Sort', 'C']
| 0 |
course-schedule-iv
|
Python. Topology Sort + DP. Time beats 90%. Complexity is O(N^2)
|
python-topology-sort-dp-time-beats-90-co-cd8j
|
The idea is to first do a topology sort, O(n + e). Then do a DP, O(n^2), on the reversed topology order. Then for every node v, you will know all the nodes it c
|
caitao
|
NORMAL
|
2020-09-05T20:28:06.716516+00:00
|
2020-09-05T20:34:38.192081+00:00
| 187 | false |
The idea is to first do a topology sort, O(n + e). Then do a DP, O(n^2), on the reversed topology order. Then for every node v, you will know all the nodes it can reach. Here n is the number of nodes, e is the number of edges, O(e) = O(n^2). \n\n```\nclass Solution:\n def checkIfPrerequisite(self, n: int, prerequisites: List[List[int]], queries: List[List[int]]) -> List[bool]:\n graph = defaultdict(list)\n indegree = [0] * n\n for a, b in prerequisites:\n graph[a].append(b)\n indegree[b] += 1\n \n # 1: do a topology sort\n stack = []\n topo = []\n for i in range(n):\n if indegree[i] == 0:\n stack.append(i)\n while stack:\n cur = stack.pop()\n topo.append(cur)\n for nxt in graph[cur]:\n indegree[nxt] -= 1\n if indegree[nxt] == 0:\n stack.append(nxt)\n\n\t\t# 2: do a dp with the reverse topology order\n dp = defaultdict(set)\n for i in range(n-1, -1, -1):\n cur = topo[i]\n for nxt in graph[cur]:\n dp[cur].add(nxt)\n dp[cur] = dp[cur].union(dp[nxt])\n \n # 3: answer the queries\n ans = []\n for a, b in queries:\n if b in dp[a]:\n ans.append(True)\n else:\n ans.append(False)\n return ans\n \n```
| 3 | 0 |
[]
| 0 |
course-schedule-iv
|
Python DFS with simple explanation
|
python-dfs-with-simple-explanation-by-ab-fcdx
|
Overall approach is the following -\n Construct the initial adjacency list using the prerequisites array. Eg- if 1-->2-->3 (1 is prereq of 2, 2 is prereq of 3)
|
abhijitt
|
NORMAL
|
2020-05-30T17:26:47.041085+00:00
|
2020-05-30T17:28:03.518540+00:00
| 359 | false |
Overall approach is the following -\n* Construct the initial adjacency list using the `prerequisites` array. Eg- if 1-->2-->3 (1 is prereq of 2, 2 is prereq of 3) then - adjlist[3]=[2] & adjlist[2]=[1].\n* Maintain a list of visited nodes\n* Perform DFS on unvisited nodes to enhance our initial adjacency list to include **all** prerequisites of a course. Eg- if 1-->2-->3. Now adjacency list of 3 contains 2 as well as 1 - adjlist[3]=[2,1] & adjlist[2]=[1].\n* Finally for each query, see if the queried node is present in the final adjacency list\n\nExplanation for DFS - \n* Pass the `node` as well as all the nodes seen in the path as a `parents` set\n* Upon visiting each node, add the prerequisites of the current node to the adjacency list of all the parents\n* Perform DFS on all the prerequisites/neighbours of the node, while passing a new `parents` set that includes current node\n* When DFS is completed, mark node as visited\n\n```\n\tdef checkIfPrerequisite(self, n: int, prerequisites: List[List[int]], queries: List[List[int]]) -> List[bool]:\n adjlist = [set([]) for i in range(n)]\n visited = [False]*n\n \n for prereq in prerequisites:\n adjlist[prereq[1]].add(prereq[0])\n \n def dfs(node, parents):\n for parent in parents:\n for neighbour in adjlist[node]:\n adjlist[parent].add(neighbour)\n if(visited[node]):\n return\n parents.add(node)\n for neighbour in adjlist[node].copy():\n dfs(neighbour, parents.copy())\n visited[node] = True\n return\n \n for i in range(n):\n if not visited[i]:\n dfs(i, set([i]))\n \n res = [False]*len(queries)\n for i, query in enumerate(queries):\n res[i]=(False,True)[query[0] in adjlist[query[1]]]\n \n return res\n```
| 3 | 0 |
[]
| 0 |
course-schedule-iv
|
Simple Java DFS with memoization
|
simple-java-dfs-with-memoization-by-sumi-hg44
|
\nclass Solution {\n public List<Boolean> checkIfPrerequisite(int n, int[][] pr, int[][] queries) {\n \n List<List<Integer>> graph = new ArrayL
|
sumitk23
|
NORMAL
|
2020-05-30T16:15:08.266187+00:00
|
2020-05-31T06:57:35.806988+00:00
| 559 | false |
```\nclass Solution {\n public List<Boolean> checkIfPrerequisite(int n, int[][] pr, int[][] queries) {\n \n List<List<Integer>> graph = new ArrayList<>();\n for(int i = 0; i < n; i++) {\n graph.add(new ArrayList<Integer>());\n }\n \n for(int[] p : pr) {\n graph.get(p[0]).add(p[1]);\n }\n \n List<Boolean> result = new ArrayList<>();\n Map<String, Boolean> memo = new HashMap<>();\n \n for(int[] q : queries) {\n boolean res = dfs(graph, q[0], q[1], memo);\n result.add(res);\n }\n \n return result;\n }\n \n private boolean dfs(List<List<Integer>> graph, int src, int target, Map<String, Boolean> memo) {\n \n if(memo.containsKey(src + "-" + target)) {\n return memo.get(src + "-" + target);\n }\n \n for(int adj : graph.get(src)) {\n if(adj == target) {\n return true;\n }\n boolean res = dfs(graph, adj, target, memo);\n \n if(res) {\n memo.put(src + "-" + target, true);\n return true;\n }\n }\n \n memo.put(src + "-" + target, false);\n return false;\n }\n}\n```
| 3 | 0 |
['Depth-First Search', 'Memoization', 'Java']
| 1 |
course-schedule-iv
|
[Python3] Simple DFS + Caching
|
python3-simple-dfs-caching-by-manparvesh-4vvo
|
python\nclass Solution:\n def checkIfPrerequisite(self, n: int, prerequisites: List[List[int]], queries: List[List[int]]) -> List[bool]:\n if not prer
|
manparvesh
|
NORMAL
|
2020-05-30T16:09:47.860992+00:00
|
2020-05-30T16:09:47.861025+00:00
| 318 | false |
```python\nclass Solution:\n def checkIfPrerequisite(self, n: int, prerequisites: List[List[int]], queries: List[List[int]]) -> List[bool]:\n if not prerequisites:\n return [False]*len(queries)\n graph = collections.defaultdict(list)\n for u, v in prerequisites:\n graph[u].append(v)\n \n from functools import lru_cache\n @lru_cache(None)\n def dfs(i, to_reach):\n if i == to_reach:\n return True\n if not graph[i]:\n return False\n return any(dfs(j, to_reach) for j in graph[i])\n \n return [dfs(i, j) for i, j in queries]\n```
| 3 | 0 |
[]
| 1 |
course-schedule-iv
|
Elegant C++ solution with explanation
|
elegant-c-solution-with-explanation-by-s-yqrv
|
Brief C++ solution. Use Floyd Warshall.\n\n- Convert given prerequisites into a DAG (Directed Acyclic Graph)\n- For every two vertices, check every intermediate
|
shivankacct
|
NORMAL
|
2020-05-30T16:07:33.219471+00:00
|
2020-05-30T16:13:07.356634+00:00
| 477 | false |
Brief C++ solution. Use Floyd Warshall.\n\n- Convert given prerequisites into a DAG (Directed Acyclic Graph)\n- For every two vertices, check every intermediate vertex to see if a path is possible through it. Store this in a matrix. This takes O(n^3) time which is fine since n <= 100;\n- Queries can be done in O(1) time\n\n\n```\nclass Solution {\npublic:\n\tvector<bool> checkIfPrerequisite(int n, vector<vector<int>>& p, vector<vector<int>>& queries) {\t \n\t\tint i, j, k;\n vector<bool> ret(queries.size(), false);\n\t\t\n bool graph[n][n];\n memset(graph, false, sizeof(graph));\n\n for(i=0; i<p.size(); i++)\n graph[p[i][0]][p[i][1]] = true;\n\t\t\t\n for(k=0; k<n; k++)\n for(i=0; i<n; i++)\n for(j=0; j<n; j++)\n graph[i][j] = graph[i][j] || (graph[i][k] && graph[k][j]);\n\n\t\tfor(int i=0; i<queries.size(); i++)\n ret[i] = graph[queries[i][0]][queries[i][1]];\n\n return ret;\n }\n};\n```
| 3 | 0 |
[]
| 2 |
course-schedule-iv
|
Floyd Warshall soln || simple || C++ 🔥 🚀
|
floyd-warshall-soln-simple-c-by-manyug-4y1g
|
IntuitionWe need to see if there exists a path from i to j in queriesApproachFor path we have floyd warshall which tells us about path from one node to other di
|
manyuMG
|
NORMAL
|
2025-01-28T19:32:03.302389+00:00
|
2025-01-28T19:32:03.302389+00:00
| 12 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
We need to see if there exists a path from i to j in queries
# Approach
<!-- Describe your approach to solving the problem. -->
For path we have floyd warshall which tells us about path from one node to other directly or via another node
# Complexity
- Time complexity: O(n^3)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(n^2)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
vector<bool> checkIfPrerequisite(int n, vector<vector<int>>& p, vector<vector<int>>& queries) {
vector <vector<bool>> pq(n,vector<bool>(n,false));
for (auto it : p ){
pq[it[0]][it[1]]=true;
}
for (int k=0;k<n;k++){
for (int j=0;j<n;j++){
for (int i=0;i<n;i++){
pq[j][i]=pq[j][i]||(pq[j][k] && pq[k][i]);
}
}
}
vector <bool> ans;
for (auto it : queries){
ans.push_back(pq[it[0]][it[1]]);
}
return ans;
}
};
```
| 2 | 0 |
['C++']
| 0 |
course-schedule-iv
|
Easy DFS solution.
|
easy-dfs-solution-by-kashyap_lokesh-nakk
|
IntuitionFirst we will make the Adjacency matrix from the given prerequisite vector. Then to answer each query, whether u is prerequisite of v or not, we can ju
|
kashyap_lokesh
|
NORMAL
|
2025-01-27T19:32:06.368756+00:00
|
2025-01-27T19:32:06.368756+00:00
| 30 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
First we will make the Adjacency matrix from the given prerequisite vector. Then to answer each query, whether u is prerequisite of v or not, we can just apply dfs on u. If starting from u we can reach v then u is prerequisite for v otherwise not.
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
vector<int> adj[101];
bool dfs(int src, int target, vector<int> adj[], vector<bool>& vis) {
vis[src] = true;
if (src == target)
return true;
for (auto& node : adj[src]) {
if (!vis[node] && dfs(node, target, adj, vis)) {
return true;
}
}
return false;
}
vector<bool> checkIfPrerequisite(int n, vector<vector<int>>& prerequisites,
vector<vector<int>>& queries) {
for (int i = 0; i < n; i++)
adj[i].assign({});
for (auto& edge : prerequisites)
adj[edge[0]].push_back(edge[1]);
vector<bool> ans;
for (auto& q : queries) {
vector<bool> vis(n, false);
if (dfs(q[0], q[1], adj, vis))
ans.push_back(true);
else
ans.push_back(false);
}
return ans;
}
};
```
| 2 | 0 |
['C++']
| 0 |
course-schedule-iv
|
Simple DFS Solution | Java | Beats 90%
|
simple-dfs-solution-java-beats-90-by-har-kuy0
|
Approach
Try to do DFS, starting from every node, see what all nodes can be visited - these nodes are the prerequisites
we can directly get the answer for each
|
HarivardhanK
|
NORMAL
|
2025-01-27T18:29:32.407858+00:00
|
2025-01-27T18:29:32.407858+00:00
| 38 | false |
# Approach
- Try to do DFS, starting from every node, see what all nodes can be visited - these nodes are the prerequisites
- we can directly get the answer for each query by constant look-up from the boolean matrix
# Complexity
- Time complexity:
O(N*N)
- Space complexity:
O(N*N)
# Code
```java []
class Solution {
// Plain DFS
private void dfs(List<Integer>[] g, int node, boolean[] isPrerequisite) {
if(isPrerequisite[node]) return;
isPrerequisite[node] = true;
for(int neigh: g[node]) dfs(g, neigh, isPrerequisite);
}
public List<Boolean> checkIfPrerequisite(int numCourses, int[][] prerequisites, int[][] queries) {
// Build Adjacency List - Graph
List<Integer>[] g = new ArrayList[numCourses];
for(int i = 0; i < numCourses; i++) g[i] = new ArrayList<>();
for(int[] pre: prerequisites) g[pre[0]].add(pre[1]);
// preprocess the information
boolean[][] isPrerequisite = new boolean[numCourses][numCourses];
// DFS from Every node
for(int i = 0; i < numCourses; i++) {
dfs(g, i, isPrerequisite[i]);
}
List<Boolean> ans = new ArrayList<>();
for(int[] q: queries) {
ans.add(isPrerequisite[q[0]][q[1]]);
}
return ans;
}
}
```
| 2 | 0 |
['Depth-First Search', 'Graph', 'Java']
| 0 |
course-schedule-iv
|
EASY SOLUTION | JAVA | (Clean Code)
|
easy-solution-java-clean-code-by-siddhar-89lo
|
Code
|
Siddharth_Bahuguna
|
NORMAL
|
2025-01-27T12:59:22.092694+00:00
|
2025-01-27T12:59:22.092694+00:00
| 131 | false |
# Code
```java []
class Solution {
public List<Boolean> checkIfPrerequisite(int numCourses, int[][] prerequisites, int[][] queries) {
boolean mat[][]=new boolean[numCourses][numCourses];
//fill the adjancency matrix based on prerequisites
for(int i=0;i<prerequisites.length;i++){
int s=prerequisites[i][0];
int d=prerequisites[i][1];
mat[s][d]=true;
}
//applying floyd warshall algo to find transitive closure
for(int k=0;k<numCourses;k++){
for(int s=0;s<numCourses;s++){
for(int d=0;d<numCourses;d++){
mat[s][d]=mat[s][d] || (mat[s][k]&&mat[k][d]);
}
}
}
//process the queries
List<Boolean>ans=new ArrayList<>();
for(int i=0;i<queries.length;i++){
int s=queries[i][0];
int d=queries[i][1];
ans.add(mat[s][d]);
}
return ans;
}
}
```
| 2 | 0 |
['Java']
| 0 |
course-schedule-iv
|
Kahn's Algorithm || Using Set and Map || Beats 100% Users ||
|
kahns-algorithm-using-set-and-map-beats-2sadm
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
Heisenberg_wc
|
NORMAL
|
2025-01-27T10:53:04.656240+00:00
|
2025-01-27T10:53:04.656240+00:00
| 88 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
vector<bool> checkIfPrerequisite(int numCourses,
vector<vector<int>>& prerequisites,
vector<vector<int>>& queries) {
// Handle edge case where there are no prerequisites
if (prerequisites.empty()) {
return vector<bool>(queries.size(), false);
}
// Adjacency list and indegree array for graph representation
vector<vector<int>> adjacencyList(numCourses);
vector<int> indegree(numCourses, 0);
// Build the graph
for (const auto& edge : prerequisites) {
adjacencyList[edge[0]].push_back(edge[1]);
indegree[edge[1]]++;
}
// Topological sorting queue
queue<int> topoQueue;
unordered_map<int, unordered_set<int>> prerequisitesMap;
// Add all courses with 0 indegree to the queue
for (int i = 0; i < numCourses; ++i) {
if (indegree[i] == 0) {
topoQueue.push(i);
}
}
// Perform topological sort and populate prerequisites map
while (!topoQueue.empty()) {
int currentCourse = topoQueue.front();
topoQueue.pop();
for (int nextCourse : adjacencyList[currentCourse]) {
// Add current course and its prerequisites to nextCourse's set
prerequisitesMap[nextCourse].insert(currentCourse);
prerequisitesMap[nextCourse].insert(prerequisitesMap[currentCourse].begin(),
prerequisitesMap[currentCourse].end());
// Decrease indegree and add to queue if it becomes 0
if (--indegree[nextCourse] == 0) {
topoQueue.push(nextCourse);
}
}
}
// Answer the queries
vector<bool> result;
for (const auto& query : queries) {
int courseA = query[0];
int courseB = query[1];
result.push_back(prerequisitesMap[courseB].count(courseA) > 0);
}
return result;
}
};
```
| 2 | 0 |
['C++']
| 0 |
course-schedule-iv
|
Very Simple C++ [Floyd-Warshall]
|
very-simple-c-floyd-warshall-by-caffeine-u8r0
|
IntuitionThe problem involves determining if one course is a prerequisite of another in a directed graph of courses. Essentially, we want to check if there is a
|
caffeinekeyboard
|
NORMAL
|
2025-01-27T08:50:26.567328+00:00
|
2025-01-27T08:50:26.567328+00:00
| 144 | false |
# Intuition
The problem involves determining if one course is a prerequisite of another in a directed graph of courses. Essentially, we want to check if there is a path from one node (course) to another. A simple way to handle multiple such checks (queries) is to find the *transitive closure* of this graph: if we know every pair of nodes where a path exists, each query becomes an O(1) check.
# Approach
1. **Build a matrix** `reachable` of size `numCourses x numCourses`, initialized to `false`.
- `reachable[i][j]` will be `true` if course `i` is a prerequisite for course `j`.
2. **Mark direct prerequisites**:
- For each direct prerequisite `(u, v)` in `prerequisites`, set `reachable[u][v] = true`.
3. **Floyd-Warshall-like update**:
- For each `k` in `[0..numCourses-1]`:
For each `i` in `[0..numCourses-1]`:
For each `j` in `[0..numCourses-1]`:
If `reachable[i][k] && reachable[k][j]` then set `reachable[i][j] = true`.
- This step ensures `reachable[i][j]` is `true` if there is any path from `i` to `j`.
4. **Answer queries**: For each `(a, b)`, simply check if `reachable[a][b]` is `true`.
# Complexity
- **Time Complexity**: \(O(\text{numCourses}^3)\) due to the three nested loops in the Floyd–Warshall approach.
- **Space Complexity**: \(O(\text{numCourses}^2)\) for the `reachable` matrix.
# Code
```cpp
class Solution {
public:
vector<bool> checkIfPrerequisite(int numCourses, vector<vector<int>>& prerequisites, vector<vector<int>>& queries) {
vector<vector<bool>> reachable(numCourses, vector<bool>(numCourses, false));
// Mark direct prerequisites
for (auto &p : prerequisites) {
int u = p[0];
int v = p[1];
reachable[u][v] = true;
}
// Compute transitive closure (Floyd-Warshall-like)
for (int k = 0; k < numCourses; k++) {
for (int i = 0; i < numCourses; i++) {
for (int j = 0; j < numCourses; j++) {
if (reachable[i][k] && reachable[k][j]) {
reachable[i][j] = true;
}
}
}
}
// Answer the queries
vector<bool> ans;
ans.reserve(queries.size());
for (auto &q : queries) {
ans.push_back(reachable[q[0]][q[1]]);
}
return ans;
}
};
auto init = [](){
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
return 0;
}();
| 2 | 0 |
['C++']
| 0 |
course-schedule-iv
|
Floyd Warshall | Easy Solution | Java
|
floyd-warshall-easy-solution-java-by-dee-iqiq
|
IntuitionThe problem is to determine if one course is a prerequisite for another based on a list of prerequisites. This can be modeled as a directed graph, wher
|
deepakkumars11022005
|
NORMAL
|
2025-01-27T08:19:22.079953+00:00
|
2025-01-27T08:35:42.555263+00:00
| 106 | false |
### **Intuition**
The problem is to determine if one course is a prerequisite for another based on a list of prerequisites. This can be modeled as a directed graph, where each course is a node, and prerequisites are directed edges. The goal is to determine reachability between nodes, i.e., whether there exists a path from one course to another.
To efficiently answer reachability queries, the **Floyd-Warshall algorithm** is used to compute the transitive closure of the graph. The transitive closure indicates whether there is a path between any two nodes in the graph.
---
### **Approach**
1. **Graph Representation:**
- Use a 2D boolean array `adj[][]` where `adj[i][j]` is `true` if course `i` is a direct prerequisite for course `j`.
2. **Transitive Closure:**
- Apply the Floyd-Warshall algorithm to compute the transitive closure of the graph:
- If there is an indirect path from course `i` to course `j` through course `k`, then `adj[i][j]` is updated to `true`.
3. **Query Processing:**
- For each query `(u, v)`, simply check if `adj[u][v]` is `true`, indicating that course `u` is a prerequisite for course `v`.
---
### **Complexity Analysis**
#### **Time Complexity:**
1. **Initialization of `adj[][]`:**
- Populating the `adj` matrix from the `pre` array takes \(O(P)\), where \(P\) is the number of prerequisites.
2. **Floyd-Warshall Algorithm:**
- The algorithm runs three nested loops, each iterating over \(n\) nodes, resulting in a time complexity of \(O(n^3)\).
3. **Query Processing:**
- Each query is processed in \(O(1)\), and for \(Q\) queries, this step takes \(O(Q)\).
**Total Time Complexity:**
- \(O(n^3 + P + Q)\), where:
- \(n\) is the number of courses,
- \(P\) is the number of prerequisites,
- \(Q\) is the number of queries.
#### **Space Complexity:**
1. **Adjacency Matrix:**
- The `adj` matrix requires \(O(n^2)\) space to store reachability information.
2. **Result List:**
- The result list `res` takes \(O(Q)\) space to store query results.
**Total Space Complexity:**
- \(O(n^2 + Q)\).
---
### **Code Walkthrough**
#### Input:
```java
int n = 4;
int[][] pre = {{0, 1}, {1, 2}, {2, 3}};
int[][] q = {{0, 3}, {1, 0}, {2, 3}, {3, 0}};
```
#### Execution Steps:
1. **Initialize `adj[][]`:**
- Populate the adjacency matrix with direct prerequisites:
```
adj[0][1] = true
adj[1][2] = true
adj[2][3] = true
```
2. **Compute Transitive Closure (Floyd-Warshall):**
- After processing, `adj[][]` becomes:
```
adj[0][1] = true, adj[0][2] = true, adj[0][3] = true
adj[1][2] = true, adj[1][3] = true
adj[2][3] = true
adj[3][...] = false
```
3. **Process Queries:**
- For each query, check `adj[i][j]`:
- `adj[0][3] = true` → `true`
- `adj[1][0] = false` → `false`
- `adj[2][3] = true` → `true`
- `adj[3][0] = false` → `false`
#### Output:
```java
[true, false, true, false]
```
class Solution {
public List<Boolean> checkIfPrerequisite(int n, int[][] pre, int[][] q) {
List<Boolean> res=new ArrayList<>();
boolean adj[][]=new boolean[n][n];
for(int i[]:pre)
{
adj[i[0]][i[1]]=true;
}
for (int k = 0; k < n; k++) {
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
adj[i][j] = adj[i][j] | (adj[i][k] & adj[k][j]);
}
}
}
for(int i[]:q)
res.add(adj[i[0]][i[1]]);
return res;
}
}
---
### **Final Thoughts**
The Floyd-Warshall approach is efficient for dense graphs and small to medium values of \(n\). If \(n\) is very large or the graph is sparse, alternative methods such as BFS/DFS for each query may be more appropriate.
| 2 | 0 |
['Bit Manipulation', 'Shortest Path', 'Java']
| 0 |
course-schedule-iv
|
leetcodedaybyday - Beats 98.27% with C++ and Beats 86.50% with Python3
|
leetcodedaybyday-beats-9827-with-c-and-b-8ztl
|
IntuitionThe problem requires determining if one course is a prerequisite for another based on a list of prerequisites. By leveraging the transitive property of
|
tuanlong1106
|
NORMAL
|
2025-01-27T07:40:49.703597+00:00
|
2025-01-27T07:40:49.703597+00:00
| 77 | false |
# Intuition
The problem requires determining if one course is a prerequisite for another based on a list of prerequisites. By leveraging the transitive property of prerequisites, we can process the input to deduce indirect relationships between courses. This can be achieved through a graph-based approach.
# Approach
1. **Graph Representation**:
- Represent the courses as nodes in a graph.
- Use an adjacency list to represent the prerequisite relationships.
2. **Bitset for Transitive Relationships**:
- Use a `bitset` for each course to represent its prerequisites. This allows efficient propagation of prerequisite information.
3. **Topological Sort**:
- Perform a topological sort using Kahn's Algorithm to process nodes with zero in-degrees (courses with no prerequisites).
- During the process, propagate the prerequisite relationships using bitwise OR operations on `bitsets`.
4. **Query Evaluation**:
- For each query `(u, v)`, check the `bitset` of course `v` to see if it includes course `u`.
# Complexity
- **Time Complexity**:
- Building the graph: \(O(E)\), where \(E\) is the number of prerequisites.
- Topological sort and propagation: \(O(V + E)\), where \(V\) is the number of courses.
- Query processing: \(O(Q)\), where \(Q\) is the number of queries.
- **Total**: \(O(V^2 + E + Q)\), since propagating bitsets involves \(O(V^2)\) operations in the worst case.
- **Space Complexity**:
- Bitsets for prerequisites: \(O(V^2)\), where \(V\) is the number of courses.
- Adjacency list and in-degree array: \(O(V + E)\).
- **Total**: \(O(V^2 + V + E)\).
# Code
```cpp []
class Solution {
public:
vector<bool> checkIfPrerequisite(int numCourses, vector<vector<int>>& prerequisites, vector<vector<int>>& queries) {
vector<bitset<100>> path(numCourses);
vector<vector<int>> adj(numCourses);
vector<int> deg(numCourses, 0);
for (auto& p : prerequisites){
int a = p[0], b = p[1];
adj[a].push_back(b);
path[b].set(a);
deg[b]++;
}
queue<int> q;
for (int i = 0; i < numCourses; i++){
if (deg[i] == 0){
q.push(i);
}
}
while (!q.empty()){
int i = q.front();
q.pop();
for (int j : adj[i]){
path[j] |= path[i];
deg[j]--;
if (deg[j] == 0){
q.push(j);
}
}
}
vector<bool> ans;
ans.reserve(queries.size());
for (auto& q : queries){
int u = q[0], v = q[1];
ans.push_back(path[v][u]);
}
return ans;
}
};
```
```python3 []
class Solution:
def checkIfPrerequisite(self, numCourses: int, prerequisites: List[List[int]], queries: List[List[int]]) -> List[bool]:
path = [0] * numCourses
adj = [[] for _ in range(numCourses)]
deg = [0] * numCourses
for a, b in prerequisites:
adj[a].append(b)
path[b] |= ( 1 << a)
deg[b] += 1
queue = deque()
for i in range(numCourses):
if deg[i] == 0:
queue.append(i)
while queue:
i = queue.popleft()
for j in adj[i]:
path[j] |= path[i]
deg[j] -= 1
if deg[j] == 0:
queue.append(j)
ans = [False] * len(queries)
for i, (u, v) in enumerate(queries):
ans[i] = (path[v] >> u) & 1 == 1
return ans
```
| 2 | 0 |
['Graph', 'C++', 'Python3']
| 0 |
course-schedule-iv
|
DFS on Inverted/Reversed Graph O(N^2)
|
dfs-on-invertedreversed-graph-on2-by-uda-9z1r
|
IntuitionI thought of the inverted graph directly as the elements that comes further in the inverted graph are the dependencies to the elements that come earlie
|
uday_k02
|
NORMAL
|
2025-01-27T06:55:12.847501+00:00
|
2025-01-27T06:55:12.847501+00:00
| 6 | false |
# Intuition
I thought of the **inverted graph** directly as the elements that comes further in the inverted graph are the dependencies to the elements that come earlier.
Note: Inverted graph, not the actual graph. I reversed the directions of edges. Now, courses point to their prerequisites.
If we start from the node $$'a'$$, and there is a path to node $$'e'$$ involving nodes $$'b'$$, $$'c'$$ & $$'d'$$ in-between, then $$'e'$$ is a prerequisite to all these nodes that came before.
So, I performed DFS on this inverted graph visiting each node single time and updating the prerequisites of the nodes that came on the path that led to the current node.
If there is a node which already completed traversal (meaning, the traversal is done for the sub-graph starting from that node), we get the prerequisites for that node (which got already updated further down that sub-graph) and update all of them as the prerequisites for the current nodes in the current active path.
I don't know whether this is so intuitive and I know that this is a bad explanation. :)
# Approach
- Take a data-structure where you will store the dependencies of a course as a set mapped to that course.
- Maintain a visited array where you will update the status of traversal for a node.
- Perform DFS on every untraversed node. Update the prerequisites if the node is already traversed.
- Now, determine true/false for a query by checking the dependency mappings.
# Complexity
- Time complexity:
- We visit each node a single time. $$O(N)$$.
- We again revisit each node in the current path every time to update the current as the prerequisite to them. $$O(N^2)$$.
- If a node is traversed already, we just update those prerequisites to the nodes in the current path. $$O(N^2)$$.
- Finally, $$O(N^2)$$.
- Space complexity: $$O(N^2)$$
Please correct me if I'm wrong.
# Code
```cpp []
class Solution {
public:
// maps all the courses with their transitive prerequisites
unordered_map<int, unordered_set<int>> pre;
void dfs(int course, vector<vector<int>>& adj, unordered_set<int>& currVisited, vector<int>& visited) {
// if the course is already traversed, then add those prerequisites to the current courses in the visited
if (visited[course]) {
for (auto ele : pre[course]) {
for (auto it : currVisited) {
pre[it].insert(ele);
}
}
for (auto it : currVisited) {
pre[it].insert(course);
}
return;
}
// a cycle is formed, no need to go further
// if (currVisited.find(course) != currVisited.end()) return;
// for every previous courses in the path, add this course as a prerequisite
for (auto it : currVisited) {
pre[it].insert(course);
}
// add the current course to the path
currVisited.insert(course);
for (int neighbor : adj[course]) {
// traverse further with neighbors
dfs(neighbor, adj, currVisited, visited);
}
// remove the current course from the path
currVisited.erase(course);
// the current course is completely traversed
visited[course] = 1;
return;
}
vector<bool> checkIfPrerequisite(int numCourses, vector<vector<int>>& prerequisites, vector<vector<int>>& queries) {
if (prerequisites.size() == 0) {
return vector<bool>(queries.size(), false);
}
int n = prerequisites.size();
vector<vector<int>> adj(numCourses, vector<int>());
// inverted graph
for (vector<int> prerequisite: prerequisites) {
adj[prerequisite[1]].push_back(prerequisite[0]);
}
vector<int> visited(numCourses, 0); // to maintain visited
for (int i = 0; i < numCourses; ++i) {
// for every course, perform dfs if it is not yet traversed
if (!visited[i]) {
unordered_set<int> currVisited;
dfs(i, adj, currVisited, visited);
}
}
vector<bool> result;
for (vector<int> query : queries) {
if (pre[query[1]].find(query[0]) != pre[query[1]].end()) {
result.push_back(true);
} else {
result.push_back(false);
}
}
return result;
}
};
```
| 2 | 0 |
['C++']
| 0 |
course-schedule-iv
|
Easy Java Solution
|
easy-java-solution-by-surajsharma15-im5v
|
IntuitionApproachBFSComplexity
Time complexity:
O(N+E)
Space complexity:
O(N+E)
Code
|
surajsharma15
|
NORMAL
|
2025-01-27T04:30:59.886114+00:00
|
2025-01-27T04:30:59.886114+00:00
| 8 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
BFS
# Complexity
- Time complexity:
O(N+E)
- Space complexity:
O(N+E)
# Code
```java []
class Solution {
public List<Boolean> checkIfPrerequisite(int numCourses, int[][] prerequisites, int[][] queries) {
List<Boolean>list=new ArrayList();
HashMap<Integer,ArrayList<Integer>>map=new HashMap<>();
for(int i=0;i<numCourses;i++){
map.put(i,new ArrayList<>());
}
for(int i=0;i<prerequisites.length;i++){
map.get(prerequisites[i][0]).add(prerequisites[i][1]);
}
for(int i=0;i<queries.length;i++){
boolean b=BFS(map,queries[i][0],queries[i][1]);
list.add(b);
}
return list;
}
public Boolean BFS(HashMap<Integer,ArrayList<Integer>>map,int src,int dest){
HashSet<Integer>visit=new HashSet<>();
Queue<Integer>q=new LinkedList<>();
q.add(src);
while(!q.isEmpty()){
int rv=q.poll();
if(visit.contains(rv)){
continue;
}
visit.add(rv);
if(map.get(rv).contains(dest)){
return true;
}
for(int nbr:map.get(rv)){
if(!visit.contains(nbr)){
q.add(nbr);
}
}
}
return false;
}
}
```
| 2 | 0 |
['Java']
| 0 |
course-schedule-iv
|
100% (3ms) | Time: O(N^2 + Q) | Space: O(N^2)
|
100-26ms-time-on2-space-on2-by-rojas-6s9z
|
Table of ContentsFrom slowest to fastest:
Memoized DFS
Kahn's Algorithm
Memoized DFS + Bit Manipulation
Kahn's Algorithm + Bit Manipulation
Appendix
B
|
rojas
|
NORMAL
|
2025-01-27T03:28:08.038875+00:00
|
2025-01-28T16:44:16.851368+00:00
| 55 | false |
# Table of Contents
From slowest to fastest:
[toc]
# Memoized DFS
- Time complexity: $$O(N^3 + Q)$$
- Space complexity: $$O(N^2)$$
15ms: [TypeScript](https://leetcode.com/problems/course-schedule-iv/submissions/1522435782/)
16ms: [JavaScript](https://leetcode.com/problems/course-schedule-iv/submissions/1522436347/) (below)
```typescript []
function checkIfPrerequisite(
numCourses: number,
prerequisites: number[][],
queries: number[][]
): boolean[] {
// Initialize edges
const outs = new Array<number[]>(numCourses);
for (let i = 0; i < numCourses; ++i) {
outs[i] = [];
}
// Populate edges (course -> prereqs)
for (let i = 0; i < prerequisites.length; ++i) {
outs[prerequisites[i][1]].push(prerequisites[i][0]);
}
// Memoize and populate answers
const matrix = new Array(numCourses).fill([]);
const answer = new Array<boolean>(queries.length);
for (let i = 0; i < queries.length; ++i) {
dfs(outs, matrix, queries[i][1]);
answer[i] = matrix[queries[i][1]][queries[i][0]];
}
return answer;
};
function dfs(
outs: number[][],
matrix: boolean[][],
vertex: number
): void {
if (matrix[vertex].length != 0) {
return;
}
matrix[vertex] = new Array(matrix.length).fill(false);
for (const next of outs[vertex]) {
dfs(outs, matrix, next);
matrix[vertex] = mergeRows(matrix[vertex], matrix[next]);
matrix[vertex][next] = true;
}
}
function mergeRows(target: boolean[], source: boolean[]): boolean[] {
for (let i = 0; i < source.length; ++i) {
target[i] ||= source[i];
}
return target;
}
```
```javascript []
/**
* @param {number} numCourses
* @param {number[][]} prerequisites
* @param {number[][]} queries
* @return {boolean[]}
*/
function checkIfPrerequisite(numCourses, prerequisites, queries) {
// Initialize edges
const outs = new Array(numCourses);
for (let i = 0; i < numCourses; ++i) {
outs[i] = [];
}
// Populate edges (course -> prereqs)
for (let i = 0; i < prerequisites.length; ++i) {
outs[prerequisites[i][1]].push(prerequisites[i][0]);
}
// Memoize and populate answers
const matrix = new Array(numCourses).fill([]);
const answer = new Array(queries.length);
for (let i = 0; i < queries.length; ++i) {
dfs(outs, matrix, queries[i][1]);
answer[i] = matrix[queries[i][1]][queries[i][0]];
}
return answer;
};
/**
* @param {number[][]} outs
* @param {boolean[][]} matrix
* @param {number} vertex
*/
function dfs(outs, matrix, vertex) {
if (matrix[vertex].length != 0) {
return;
}
matrix[vertex] = new Array(matrix.length).fill(false);
for (const next of outs[vertex]) {
dfs(outs, matrix, next);
matrix[vertex] = mergeRows(matrix[vertex], matrix[next]);
matrix[vertex][next] = true;
}
}
/**
* @param {boolean[]} target
* @param {boolean[]} source
*/
function mergeRows(target, source) {
for (let i = 0; i < source.length; ++i) {
target[i] ||= source[i];
}
return target;
}
```
# Kahn's Algorithm
- Time complexity: $$O(N^3 + Q)$$
- Space complexity: $$O(N^2)$$
15ms: [JavaScript](https://leetcode.com/problems/course-schedule-iv/submissions/1521717944/) (below)
16ms: [TypeScript](https://leetcode.com/problems/course-schedule-iv/submissions/1521719859/)
```typescript []
function checkIfPrerequisite(
numCourses: number,
prerequisites: number[][],
queries: number[][]
): boolean[] {
// Initialize outgoing edges
const outs = new Array<number[]>(numCourses);
for (let i = 0; i < numCourses; ++i) {
outs[i] = [];
}
// Populate indegrees and outgoing edges (prereq -> courses)
const ins = new Uint8Array(numCourses);
for (let i = 0; i < prerequisites.length; ++i) {
++ins[prerequisites[i][1]];
outs[prerequisites[i][0]].push(prerequisites[i][1]);
}
// Populate prerequisite matrix
const matrix = new Array(numCourses).fill([]);
for (let i = 0; i < numCourses; ++i) {
if (ins[i] == 0 && matrix[i].length == 0) {
matrix[i] = new Array(numCourses).fill(false);
dfs(ins, outs, matrix, i);
}
}
// Populate answers
const answer = new Array<boolean>(queries.length);
for (let i = 0; i < queries.length; ++i) {
answer[i] = matrix[queries[i][1]][queries[i][0]] == true;
}
return answer;
};
function dfs(
ins: Uint8Array,
outs: number[][],
matrix: boolean[][],
vertex: number
): void {
for (const next of outs[vertex]) {
if (matrix[next].length == 0) {
matrix[next] = Array.from(matrix[vertex]);
} else {
matrix[next] = mergeRows(matrix[next], matrix[vertex]);
}
matrix[next][vertex] = true;
if (--ins[next] == 0) {
dfs(ins, outs, matrix, next);
}
}
}
function mergeRows(target: boolean[], source: boolean[]): boolean[] {
for (let i = 0; i < source.length; ++i) {
target[i] ||= source[i];
}
return target;
}
```
```javascript []
/**
* @param {number} numCourses
* @param {number[][]} prerequisites
* @param {number[][]} queries
* @return {boolean[]}
*/
function checkIfPrerequisite(numCourses, prerequisites, queries) {
// Initialize outgoing edges
const outs = new Array(numCourses);
for (let i = 0; i < numCourses; ++i) {
outs[i] = [];
}
// Populate indegrees and outgoing edges (prereq -> courses)
const ins = new Uint8Array(numCourses);
for (let i = 0; i < prerequisites.length; ++i) {
++ins[prerequisites[i][1]];
outs[prerequisites[i][0]].push(prerequisites[i][1]);
}
// Populate prerequisite matrix
const matrix = new Array(numCourses).fill([]);
for (let i = 0; i < numCourses; ++i) {
if (ins[i] == 0 && matrix[i].length == 0) {
matrix[i] = new Array(numCourses).fill(false);
dfs(ins, outs, matrix, i);
}
}
// Populate answers
const answer = new Array(queries.length);
for (let i = 0; i < queries.length; ++i) {
answer[i] = matrix[queries[i][1]][queries[i][0]] == true;
}
return answer;
};
/**
* @param {Uint8Array} ins
* @param {number[][]} outs
* @param {boolean[][]} matrix
* @param {number} vertex
*/
function dfs(ins, outs, matrix, vertex) {
for (const next of outs[vertex]) {
if (matrix[next].length == 0) {
matrix[next] = Array.from(matrix[vertex]);
} else {
matrix[next] = mergeRows(matrix[next], matrix[vertex]);
}
matrix[next][vertex] = true;
if (--ins[next] == 0) {
dfs(ins, outs, matrix, next);
}
}
}
/**
* @param {boolean[]} target
* @param {boolean[]} source
*/
function mergeRows(target, source) {
for (let i = 0; i < source.length; ++i) {
target[i] ||= source[i];
}
return target;
}
```
# Memoized DFS + Bit Manipulation
- Time complexity: $$O(N^2 + Q)$$
- Space complexity: $$O(N^2)$$
4ms: [TypeScript](https://leetcode.com/problems/course-schedule-iv/submissions/1522447710/)
5ms: [JavaScript](https://leetcode.com/problems/course-schedule-iv/submissions/1522444967/) (below)
```typescript []
function checkIfPrerequisite(
numCourses: number,
prerequisites: number[][],
queries: number[][]
): boolean[] {
// Initialize edges
const outs = new Array<number[]>(numCourses);
for (let i = 0; i < numCourses; ++i) {
outs[i] = [];
}
// Populate edges (course -> prereqs)
for (let i = 0; i < prerequisites.length; ++i) {
outs[prerequisites[i][1]].push(prerequisites[i][0]);
}
// Memoize and populate answers
const matrix = new Array(numCourses).fill([]);
const answer = new Array<boolean>(queries.length);
for (let i = 0; i < queries.length; ++i) {
const [u, v] = queries[i];
dfs(outs, matrix, v);
answer[i] = (matrix[v][u >> 5] & (1 << (u & 31))) != 0;
}
return answer;
};
function dfs(
outs: number[][],
matrix: number[][],
vertex: number
): void {
if (matrix[vertex].length != 0) {
return;
}
matrix[vertex] = [0, 0, 0, 0];
for (const next of outs[vertex]) {
dfs(outs, matrix, next);
matrix[vertex][next >> 5] |= 1 << (next & 31);
matrix[vertex][0] |= matrix[next][0];
matrix[vertex][1] |= matrix[next][1];
matrix[vertex][2] |= matrix[next][2];
matrix[vertex][3] |= matrix[next][3];
}
}
```
```javascript []
/**
* @param {number} numCourses
* @param {number[][]} prerequisites
* @param {number[][]} queries
* @return {boolean[]}
*/
function checkIfPrerequisite(numCourses, prerequisites, queries) {
// Initialize edges
const outs = new Array(numCourses);
for (let i = 0; i < numCourses; ++i) {
outs[i] = [];
}
// Populate edges (course -> prereqs)
for (let i = 0; i < prerequisites.length; ++i) {
outs[prerequisites[i][1]].push(prerequisites[i][0]);
}
// Memoize and populate answers
const matrix = new Array(numCourses).fill([]);
const answer = new Array(queries.length);
for (let i = 0; i < queries.length; ++i) {
const [u, v] = queries[i];
dfs(outs, matrix, v);
answer[i] = (matrix[v][u >> 5] & (1 << (u & 31))) != 0;
}
return answer;
};
/**
* @param {number[][]} outs
* @param {boolean[][]} matrix
* @param {number} vertex
*/
function dfs(outs, matrix, vertex) {
if (matrix[vertex].length != 0) {
return;
}
matrix[vertex] = [0, 0, 0, 0];
for (const next of outs[vertex]) {
dfs(outs, matrix, next);
matrix[vertex][next >> 5] |= 1 << (next & 31);
matrix[vertex][0] |= matrix[next][0];
matrix[vertex][1] |= matrix[next][1];
matrix[vertex][2] |= matrix[next][2];
matrix[vertex][3] |= matrix[next][3];
}
}
```
# Kahn's Algorithm + Bit Manipulation
- Time complexity: $$O(N^2 + Q)$$
- Space complexity: $$O(N^2)$$
3ms: [JavaScript](https://leetcode.com/problems/course-schedule-iv/submissions/1521783555/) (below)
5ms: [TypeScript](https://leetcode.com/problems/course-schedule-iv/submissions/1521779922/)
```typescript []
function checkIfPrerequisite(
numCourses: number,
prerequisites: number[][],
queries: number[][]
): boolean[] {
// Initialize outgoing edges
const outs = new Array<number[]>(numCourses);
for (let i = 0; i < numCourses; ++i) {
outs[i] = [];
}
// Populate indegrees and outgoing edges (prereq -> courses)
const ins = new Uint8Array(numCourses);
for (let i = 0; i < prerequisites.length; ++i) {
++ins[prerequisites[i][1]];
outs[prerequisites[i][0]].push(prerequisites[i][1]);
}
// Populate prerequisite matrix
const matrix = new Array<number[]>(numCourses).fill([]);
for (let i = 0; i < numCourses; ++i) {
if (ins[i] == 0 && matrix[i].length == 0) {
matrix[i] = [0, 0, 0, 0];
dfs(ins, outs, matrix, i);
}
}
// Populate answers
const answer = new Array<boolean>(queries.length);
for (let i = 0; i < queries.length; ++i) {
const u = queries[i][0];
answer[i] = (matrix[queries[i][1]][u >> 5] & (1 << (u & 31))) != 0;
}
return answer;
};
function dfs(
ins: Uint8Array,
outs: number[][],
matrix: number[][],
vertex: number
): void {
for (const next of outs[vertex]) {
if (matrix[next].length == 0) {
matrix[next] = Array.from(matrix[vertex]);
} else {
matrix[next][0] |= matrix[vertex][0];
matrix[next][1] |= matrix[vertex][1];
matrix[next][2] |= matrix[vertex][2];
matrix[next][3] |= matrix[vertex][3];
}
matrix[next][vertex >> 5] |= 1 << (vertex & 31);
if (--ins[next] == 0) {
dfs(ins, outs, matrix, next);
}
}
}
```
```javascript []
/**
* @param {number} numCourses
* @param {number[][]} prerequisites
* @param {number[][]} queries
* @return {boolean[]}
*/
function checkIfPrerequisite(numCourses, prerequisites, queries) {
// Initialize outgoing edges
const outs = new Array(numCourses);
for (let i = 0; i < numCourses; ++i) {
outs[i] = [];
}
// Populate indegrees and outgoing edges (prereq -> courses)
const ins = new Uint8Array(numCourses);
for (let i = 0; i < prerequisites.length; ++i) {
++ins[prerequisites[i][1]];
outs[prerequisites[i][0]].push(prerequisites[i][1]);
}
// Populate prerequisite matrix
const matrix = new Array(numCourses).fill([]);
for (let i = 0; i < numCourses; ++i) {
if (ins[i] == 0 && matrix[i].length == 0) {
matrix[i] = [0, 0, 0, 0];
dfs(ins, outs, matrix, i);
}
}
// Populate answers
const answer = new Array(queries.length);
for (let i = 0; i < queries.length; ++i) {
const u = queries[i][0];
answer[i] = (matrix[queries[i][1]][u >> 5] & (1 << (u & 31))) != 0;
}
return answer;
};
/**
* @param {Uint8Array} ins
* @param {number[][]} outs
* @param {number[][]} matrix
* @param {number} vertex
*/
function dfs(ins, outs, matrix, vertex) {
for (const next of outs[vertex]) {
if (matrix[next].length == 0) {
matrix[next] = Array.from(matrix[vertex]);
} else {
matrix[next][0] |= matrix[vertex][0];
matrix[next][1] |= matrix[vertex][1];
matrix[next][2] |= matrix[vertex][2];
matrix[next][3] |= matrix[vertex][3];
}
matrix[next][vertex >> 5] |= 1 << (vertex & 31);
if (--ins[next] == 0) {
dfs(ins, outs, matrix, next);
}
}
}
```
# Appendix
## BFS
```typescript []
//...
function bfs(
ins: Uint8Array,
outs: number[][],
matrix: boolean[][],
vertex: number
): void {
const queue = [vertex];
for (let i = 0; i < queue.length; ++i) {
vertex = queue[i];
for (const next of outs[vertex]) {
if (matrix[next].length == 0) {
matrix[next] = Array.from(matrix[vertex]);
} else {
matrix[next] = mergeRows(matrix[next], matrix[vertex]);
}
matrix[next][vertex] = true;
if (--ins[next] == 0) {
queue.push(next);
}
}
}
}
```
```javascript []
//...
/**
* @param {Uint8Array} ins
* @param {number[][]} outs
* @param {boolean[][]} matrix
* @param {number} vertex
*/
function bfs(ins, outs, matrix, vertex) {
const queue = [vertex];
for (let i = 0; i < queue.length; ++i) {
vertex = queue[i];
for (const next of outs[vertex]) {
if (matrix[next].length == 0) {
matrix[next] = Array.from(matrix[vertex]);
} else {
matrix[next] = mergeRows(matrix[next], matrix[vertex]);
}
matrix[next][vertex] = true;
if (--ins[next] == 0) {
queue.push(next);
}
}
}
}
```
## Iterative DFS
```typescript []
//...
function dfs(
ins: Uint8Array,
outs: number[][],
matrix: boolean[][],
vertex: number
): void {
const stack = [vertex];
do {
vertex = stack.pop();
for (const next of outs[vertex]) {
if (matrix[next].length == 0) {
matrix[next] = Array.from(matrix[vertex]);
} else {
matrix[next] = mergeRows(matrix[next], matrix[vertex]);
}
matrix[next][vertex] = true;
if (--ins[next] == 0) {
stack.push(next);
}
}
} while (stack.length);
}
```
```javascript []
//...
/**
* @param {Uint8Array} ins
* @param {number[][]} outs
* @param {boolean[][]} matrix
* @param {number} vertex
*/
function dfs(ins, outs, matrix, vertex) {
const stack = [vertex];
do {
vertex = stack.pop();
for (const next of outs[vertex]) {
if (matrix[next].length == 0) {
matrix[next] = Array.from(matrix[vertex]);
} else {
matrix[next] = mergeRows(matrix[next], matrix[vertex]);
}
matrix[next][vertex] = true;
if (--ins[next] == 0) {
stack.push(next);
}
}
} while (stack.length);
}
```
| 2 | 0 |
['Bit Manipulation', 'Depth-First Search', 'Graph', 'TypeScript', 'JavaScript']
| 0 |
course-schedule-iv
|
[Python3] Topological Sorting + Bit manipulation - O(n^2)
|
python3-topological-sorting-bit-manipula-zr9b
|
IntuitionGiven n courses where any two courses can be a preqrequisite of another, we a efficient way answer whether course a is a prerequisite of course b, or e
|
CabbageBoiii
|
NORMAL
|
2025-01-27T03:26:55.989703+00:00
|
2025-01-27T03:26:55.989703+00:00
| 226 | false |
# Intuition
Given *n* courses where any two courses can be a preqrequisite of another, we a efficient way answer whether course *a* is a prerequisite of course *b*, or equivalently, *b* has *a* as a prerequisite.
# Approach
We can store the required information by in a 2D boolean array of size *N*, hasPrereq. Where hasPrereq[a][b] is True if *a* has *b* as a preqrequisite course. When can then use Topological Sort to fill in this required information.
# Optimization
Instead of using a 2D boolean array to track prerequisites, we can optimize storage by leveraging bit manipulation. Each row of the 2D array represents the prerequisite relationships for a specific course. Since we are only storing boolean values, we can represent each row as an integer, where each bit in the integer corresponds to whether a particular course is a prerequisite.
# Code
```python3 []
class Solution:
def checkIfPrerequisite(self, numCourses: int, prerequisites: List[List[int]], queries: List[List[int]]) -> List[bool]:
n = numCourses
hasPrereq = [0 for _ in range(n)]
inDegree = [0 for _ in range(n)]
adjList = defaultdict(list)
for a, b in prerequisites:
inDegree[b] += 1
adjList[a].append(b)
q = deque()
for i in range(n):
if inDegree[i] == 0:
q.append(i)
# O(n^2): For each node, for each edge of node, fill in prereq
while q:
currNode = q.popleft()
for nextNode in adjList[currNode]:
hasPrereq[nextNode] = hasPrereq[nextNode] | hasPrereq[currNode] # Next course has all the preqrequisites of current course
hasPrereq[nextNode] = hasPrereq[nextNode] | (1 << currNode) # Next course has current course as a prequisite
inDegree[nextNode] -= 1
if inDegree[nextNode] == 0: # If next node has no more prequisites to fill add to queue
q.append(nextNode)
ans = []
for u, v in queries:
ans.append(hasPrereq[v] & (1 << u) != 0) # Check if u bit is set
return ans
```
# Complexity
- Time complexity:
$$O(n^2 + Q)$$ where Q is the number of queries
- Space complexity:
$$O(n^2)$$
| 2 | 0 |
['Python3']
| 1 |
course-schedule-iv
|
C++ $O(N^2)$ time and space
|
on2-time-and-space-by-przemysaw2-e0jv
|
IntuitionUse bitset. For algorithms requiring O(N3) bitset is a great alternative, as it divides that number by 64. One might argue, that it is still O(N), but
|
przemysaw2
|
NORMAL
|
2025-01-27T02:37:04.377940+00:00
|
2025-01-27T02:37:24.431645+00:00
| 243 | false |
# Intuition
Use bitset. For algorithms requiring $O(N^3)$ bitset is a great alternative, as it divides that number by 64. One might argue, that it is still $O(N)$, but bitset has a fixed size, independent of $N$.
# Approach
Modify the topological sort algorithm from editorial, but merge the reachable states in bitset via 128/64 = $O(1)$ operations.
# Complexity
- Time complexity:
$O(N^2)$
- Space complexity:
$O(N^2)$
# Code
```cpp []
class Solution {
void dfs(const int cur, const vector<vector<int>>& g, vector<int>& order, vector<bool>& state) {
if(state[cur]) {
return;
}
state[cur] = 1;
for(const int next : g[cur]) {
dfs(next, g, order, state);
}
order.emplace_back(cur);
}
public:
vector<bool> checkIfPrerequisite(int n, vector<vector<int>>& prerequisites, vector<vector<int>>& queries) {
vector<bitset<128>> reach(n);
vector<vector<int>> g(n);
for(const auto& prerequisite : prerequisites) {
g[prerequisite[0]].emplace_back(prerequisite[1]);
reach[prerequisite[0]].set(prerequisite[1]);
}
vector<int> order; order.reserve(n);
vector<bool> state(n);
for(int i = 0; i < n; i++) {
dfs(i, g, order, state);
}
for(int i = 0; i < n; i++) {
for(const int next : g[order[i]]) {
reach[order[i]] |= reach[next];
}
}
vector<bool> res; res.reserve(queries.size());
for(const auto& query : queries) {
res.emplace_back(reach[query[0]][query[1]]);
}
return res;
}
};
```
| 2 | 0 |
['C++']
| 2 |
course-schedule-iv
|
✅ Course Schedule IV | JS🔥 | beats 99%🚀 | 🚀highly optimised & easy to understand ✅
|
course-schedule-iv-js-beats-99-highly-op-fdwj
|
Intuition
The problem can be efficiently solved using the Floyd-Warshall algorithm or a Depth-First Search (DFS). The goal is to determine if there is a direct
|
Naveen_sachan
|
NORMAL
|
2025-01-27T02:35:51.377267+00:00
|
2025-01-27T03:30:44.519079+00:00
| 153 | false |
# Intuition
- The problem can be efficiently solved using the Floyd-Warshall algorithm or a Depth-First Search (DFS). The goal is to determine if there is a direct or indirect prerequisite relationship between courses.
- Below is an optimized solution using the Floyd-Warshall algorithm, which computes the transitive closure of the prerequisite graph. This approach efficiently answers multiple queries after preprocessing the prerequisite data.
- Alternative Approach: Instead of Floyd-Warshall, you can also use DFS to preprocess each course's reachable nodes. The time complexity of DFS is O(n⋅(n+p)), which can sometimes be faster for sparse graphs.
# Approach
> **Floyd-Warshall Algorithm Approach**
- **Graph Representation:** Represent the prerequisites as an adjacency matrix isPrerequisite. If course a is a prerequisite for course b, then isPrerequisite[a][b] = true.
- **Transitive Closure:** Use the Floyd-Warshall algorithm to compute the transitive closure of the graph. If course i is a prerequisite of course j (directly or indirectly), mark isPrerequisite[i][j] = true.
- **Answer Queries:** After computing the transitive closure, answer each query in O(1) by simply checking the matrix isPrerequisite.
# Explanation of the Code
> **Initialization:**
- isPrerequisite is a numCourses×numCourses matrix where each entry is initially false.
- For each direct prerequisite [a,b], mark isPrerequisite[a][b] = true.
> **Transitive Closure via Floyd-Warshall:**
- Iterate over each intermediate course k.
- For each pair of courses i and j, if i -> k and k -> j, then i -> j is also true.
- Update isPrerequisite[i][j] accordingly.
> **Query Resolution:**
- For each query [u,v], simply check if isPrerequisite[u][v] is true.
# Complexity
> **Time complexity:**
- Initialization: O(p), where 𝑝=prerequisites.length
- Floyd-Warshall Algorithm: 𝑂(𝑛3), where 𝑛=numCourses
- Query Resolution: O(q), where 𝑞=queries.length
- Overall, the time complexity is:𝑂(𝑛3+𝑝+𝑞)
> **Space complexity:**
- The adjacency matrix isPrerequisite requires 𝑂(𝑛2) space.
- The overall space complexity is 𝑂(𝑛2)
# Code
```javascript []
/**
* @param {number} numCourses
* @param {number[][]} prerequisites
* @param {number[][]} queries
* @return {boolean[]}
*/
var checkIfPrerequisite = function (numCourses, prerequisites, queries) {
// Initialize the adjacency matrix
const isPrerequisite = Array.from({ length: numCourses }, () => Array(numCourses).fill(false));
// Populate the direct prerequisites
for (const [a, b] of prerequisites) {
isPrerequisite[a][b] = true;
}
// Floyd-Warshall algorithm to compute transitive closure
for (let k = 0; k < numCourses; k++) {
for (let i = 0; i < numCourses; i++) {
for (let j = 0; j < numCourses; j++) {
if (isPrerequisite[i][k] && isPrerequisite[k][j]) {
isPrerequisite[i][j] = true;
}
}
}
}
// Answer the queries
return queries.map(([u, v]) => isPrerequisite[u][v]);
};
```

| 2 | 0 |
['JavaScript']
| 1 |
course-schedule-iv
|
Building is reachable matrix with Floyd-Warshall Algorithm ✅✅
|
building-is-reachable-matrix-with-floyd-oeovb
|
IntuitionCreate a boolean matrix isReachable[numCourses][numCourses] where isReachable[i][j] is true if course i is a prerequisite of course j.
Populate this ma
|
PavanKumarMeesala
|
NORMAL
|
2025-01-27T02:30:14.324664+00:00
|
2025-01-27T02:30:14.324664+00:00
| 107 | false |
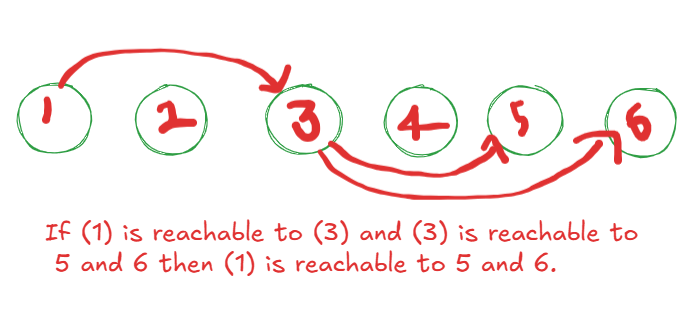
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
Create a `boolean` matrix `isReachable[numCourses][numCourses]` where `isReachable[i][j]` is `true` if course `i` is a prerequisite of course `j`.
- Populate this matrix using the given `prerequisites` list, marking `isReachable[prereq[0]][prereq[1]] = true`.
# Approach
<!-- Describe your approach to solving the problem. -->
- The Floyd-Warshall algorithm finds if there exists a path from course `i` to course `j` via an intermediate course `k`.
- For each course `k` (acting as an intermediate):
- For each course `i` (acting as the source):
- For each course `j` (acting as the destination):
- If `i` can reach `k` (`isReachable[i][k] = true`) and `k` can reach `j` (`isReachable[k][j] = true`), then `i` can reach `j` (`isReachable[i][j] = true`).
# Complexity
- Time complexity: O(`n ^ 3 + P + Q`), `n` is number of the courses and `P` is the number of `prerequisites` and `Q` is the number of `queries`.
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(`n ^ 2`), cause we are building `isReachable` matrix.
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public List<Boolean> checkIfPrerequisite(int numCourses, int[][] prerequisites, int[][] queries) {
boolean isReachable[][] = new boolean[numCourses][numCourses];
for(int spot[] : prerequisites)
{
isReachable[spot[0]][spot[1]] = true;
}
for (int k = 0; k < numCourses; k++)
{
for (int i = 0; i < numCourses; i++)
{
for (int j = 0; j < numCourses; j++)
{
if(isReachable[i][k] && isReachable[k][j])
{
isReachable[i][j] = true;
}
}
}
}
List<Boolean> result = new ArrayList<>();
for(int query[] : queries)
{
result.add(isReachable[query[0]][query[1]]);
}
return result;
}
}
```

| 2 | 0 |
['Depth-First Search', 'Breadth-First Search', 'Graph', 'Topological Sort', 'Java']
| 1 |
course-schedule-iv
|
Go solution with the explanation
|
go-solution-with-the-explanation-by-alek-o8cs
|
IntuitionWhen faced with the problem of determining whether a course is a prerequisite of another, the most natural approach is to represent the relationships a
|
alekseiapa
|
NORMAL
|
2025-01-27T01:39:20.308747+00:00
|
2025-01-27T01:39:20.308747+00:00
| 151 | false |
# Intuition
When faced with the problem of determining whether a course is a prerequisite of another, the most natural approach is to represent the relationships as a **directed graph**. Each course is a node, and each prerequisite relationship is a directed edge from one node to another. The key insight is that prerequisites can be both direct (e.g., `A -> B`) and indirect (e.g., `A -> B -> C`, making `A` a prerequisite for `C`). To efficiently handle this, we need a way to propagate the prerequisite relationships across the graph.
# Approach
1. **Graph Representation**:
- Use an adjacency list to represent the graph. Each course points to the list of courses that depend on it.
- Maintain a 2D boolean table (`table`) where `table[i][j]` indicates whether course `i` is a prerequisite of course `j`.
2. **Build the Graph**:
- Parse the prerequisites to populate the adjacency list and an `indegree` array that keeps track of how many prerequisites each course has.
3. **Topological Sorting**:
- Use Kahn's algorithm to process the graph in a topological order.
- Start with courses that have no prerequisites (i.e., `indegree[i] == 0`).
- For each course processed, propagate its prerequisite information to its neighbors in the graph.
- Update the `table` to reflect indirect prerequisites: if `A` is a prerequisite of `B` and `B` is a prerequisite of `C`, then `A` is also a prerequisite of `C`.
4. **Answer Queries**:
- After processing the graph, use the `table` to directly answer whether a course is a prerequisite of another. Each query is resolved in constant time.
# Complexity
- **Time Complexity**:
- Building the graph takes $$O(E)$$, where $$E$$ is the number of prerequisite relationships.
- Topological sorting and propagation take $$O(V + E)$$, where $$V$$ is the number of courses.
- Answering the queries takes $$O(Q)$$, where $$Q$$ is the number of queries.
- Overall complexity: $$O(V + E + Q)$$.
- **Space Complexity**:
- The adjacency list requires $$O(V + E)$$.
- The boolean table requires $$O(V^2)$$.
- The indegree array and the queue for topological sorting require $$O(V)$$.
- Overall space complexity: $$O(V^2)$$.
# Code
```golang []
func checkIfPrerequisite(numCourses int, prerequisites [][]int, queries [][]int) []bool {
// Initialize a graph and a table to track prerequisites
graph := make([][]int, numCourses)
table := make([][]bool, numCourses)
for i := 0; i < numCourses; i++ {
table[i] = make([]bool, numCourses)
}
// Build the graph and indegree array
indegree := make([]int, numCourses)
for _, prereq := range prerequisites {
u, v := prereq[0], prereq[1]
graph[u] = append(graph[u], v)
indegree[v]++
}
// Topological sort using Kahn's algorithm
q := list.New()
for i := 0; i < numCourses; i++ {
if indegree[i] == 0 {
q.PushBack(i)
}
}
for q.Len() > 0 {
curr := q.Remove(q.Front()).(int)
for _, neighbor := range graph[curr] {
table[curr][neighbor] = true
for i := 0; i < numCourses; i++ {
if table[i][curr] {
table[i][neighbor] = true
}
}
indegree[neighbor]--
if indegree[neighbor] == 0 {
q.PushBack(neighbor)
}
}
}
// Answer the queries
result := make([]bool, len(queries))
for i, query := range queries {
result[i] = table[query[0]][query[1]]
}
return result
}
```
| 2 | 0 |
['Go']
| 0 |
course-schedule-iv
|
C++ | BFS
|
c-bfs-by-ahmedsayed1-a5zt
|
Code
|
AhmedSayed1
|
NORMAL
|
2025-01-27T00:37:54.411477+00:00
|
2025-01-27T00:37:54.411477+00:00
| 367 | false |
# Code
```cpp []const int N=1e3;
vector<int>adj[N];
class Solution {
public:
vector<bool> checkIfPrerequisite(int n, vector<vector<int>>& prerequisites, vector<vector<int>>& queries) {
fill(adj,adj+n,vector<int>());
for(auto i:prerequisites)
adj[i[1]].push_back(i[0]);
vector<vector<int>>mp(n,vector<int>(n));
for(int i=0;i<n;i++){
vector<int>vis(n);
queue<int>q;
q.push(i);
vis[i]=1;
while(q.size()){
int node=q.front();q.pop();
for(auto j:adj[node])
if(!vis[j])vis[j]=1,mp[j][i]=1,q.push(j);
}
}
vector<bool>ans;
for(auto i:queries)
ans.push_back(mp[i[0]][i[1]]);
return ans;
}
};
```
| 2 | 0 |
['Breadth-First Search', 'C++']
| 0 |
course-schedule-iv
|
Topo Sort || DFS || Hah Map || graph || C++
|
topo-sort-dfs-hah-map-graph-c-by-oreocra-gsp1
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
oreocraz_273
|
NORMAL
|
2024-08-03T12:04:16.805043+00:00
|
2024-08-03T12:04:16.805076+00:00
| 699 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n unordered_map<int,int> vis;\n vector<vector<int>> adj;\n unordered_map<int,unordered_map<int,int>> m;\n int n;\n void dfs(int s,int x)\n {\n vis[s]++;\n for(auto& y:adj[s])\n {\n if(vis.find(y)==vis.end())\n {\n m[x][y]++;\n dfs(y,x);\n }\n }\n }\n vector<bool> checkIfPrerequisite(int n, vector<vector<int>>& a, vector<vector<int>>& q) {\n \n this->n=n;\n this->adj.resize(n);\n vector<bool> ans;\n\n // reversing the edges to traverse to ancestors\n\n for(int i=0;i<a.size();i++)\n {\n adj[a[i][1]].push_back(a[i][0]);\n }\n\n for(int i=0;i<n;i++)\n {\n dfs(i,i);\n vis.clear();\n }\n\n for(int j=0;j<q.size();j++)\n {\n if(m[q[j][1]].find(q[j][0])!=m[q[j][1]].end())\n ans.push_back(true);\n else\n ans.push_back(false);\n }\n\n return ans;\n\n\n \n }\n};\n```
| 2 | 0 |
['Depth-First Search', 'Graph', 'Topological Sort', 'C++']
| 1 |
course-schedule-iv
|
[Python3] Very Simple and Intuitive BFS
|
python3-very-simple-and-intuitive-bfs-by-ibft
|
Intuition\nWe construct a graph and go through each query, checking if we can reach the ending node in that query. This solution is NOT optimal, but very straig
|
jojofang
|
NORMAL
|
2024-07-24T16:56:22.407321+00:00
|
2024-07-24T16:56:22.407354+00:00
| 322 | false |
# Intuition\nWe construct a graph and go through each query, checking if we can reach the ending node in that query. This solution is NOT optimal, but very straightforward and easy to implement.\n\n\n# Code\n```\nclass Solution:\n def checkIfPrerequisite(self, numCourses: int, prerequisites: List[List[int]], queries: List[List[int]]) -> List[bool]:\n graph = [[] for _ in range(numCourses)]\n res = []\n \n for a, b in prerequisites:\n graph[a].append(b)\n \n for query in queries:\n if self.checkQuery(graph, query):\n res.append(True)\n else:\n res.append(False)\n return res\n\n def checkQuery(self, graph, query):\n startNode, endNode = query[0], query[1]\n visited = set()\n q = deque([startNode])\n while q:\n node = q.popleft()\n visited.add(node)\n\n if node == endNode:\n return True\n\n for neighbor in graph[node]:\n if neighbor not in visited:\n q.append(neighbor)\n \n return False\n```
| 2 | 0 |
['Python3']
| 0 |
course-schedule-iv
|
C++ Solution with Best Memorization
|
c-solution-with-best-memorization-by-coo-jc3q
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
coolvaibhavsingh2001
|
NORMAL
|
2023-08-21T12:51:01.800418+00:00
|
2023-08-21T12:51:01.800437+00:00
| 955 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n vector<bool> checkIfPrerequisite(int n, vector<vector<int>>& pre, vector<vector<int>>& q) {\n vector<vector<int>> adj(n);\n for (const auto& it : pre) {\n adj[it[0]].push_back(it[1]); // Reverse the dependency direction\n }\n \n vector<vector<int>> reachable(n, vector<int>(n, 0));\n for (int i = 0; i < n; ++i) {\n vector<int> vis(n, 0);\n dfs(i, i, adj, reachable, vis);\n }\n \n vector<bool> ans;\n for (const auto& it : q) {\n int x = it[0];\n int y = it[1];\n ans.push_back(reachable[x][y]);\n }\n \n return ans;\n }\n \nprivate:\n void dfs(int start, int node, const vector<vector<int>>& adj, vector<vector<int>>& reachable, vector<int>& vis) {\n vis[node] = 1;\n reachable[start][node] = 1;\n for (int nxt : adj[node]) {\n if (!vis[nxt]) {\n dfs(start, nxt, adj, reachable, vis);\n }\n for (int i = 0; i < reachable[nxt].size(); ++i) {\n reachable[start][i] |= reachable[nxt][i];\n }\n }\n }\n};\n\n```
| 2 | 0 |
['Depth-First Search', 'Breadth-First Search', 'Graph', 'Topological Sort', 'C++']
| 0 |
course-schedule-iv
|
python3 recursion + memoization
|
python3-recursion-memoization-by-0icy-5nd3
|
\n\n# Code\n\nfrom collections import defaultdict\nclass Solution:\n def checkIfPrerequisite(self, numCourses: int, prerequisites: List[List[int]], queries:
|
0icy
|
NORMAL
|
2023-08-02T18:14:24.703273+00:00
|
2023-08-02T18:14:24.703302+00:00
| 205 | false |
\n\n# Code\n```\nfrom collections import defaultdict\nclass Solution:\n def checkIfPrerequisite(self, numCourses: int, prerequisites: List[List[int]], queries: List[List[int]]) -> List[bool]:\n\n @cache\n def check(n,target):\n nonlocal d\n if n == target:\n return True\n \n for e in d[n]:\n if check(e,target):\n return True\n\n return False\n\n\n res = []\n d = defaultdict(list)\n for x,y in prerequisites:\n d[x].append(y)\n for x,y in queries:\n res.append(check(x,y))\n \n return res\n```
| 2 | 0 |
['Python3']
| 0 |
course-schedule-iv
|
[JavaScript] 1462. Course Schedule IV
|
javascript-1462-course-schedule-iv-by-pg-p2jk
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n\n\nif\n prev is connected to mid\n and\n mid is connected to next\n
|
pgmreddy
|
NORMAL
|
2023-07-27T18:27:14.460485+00:00
|
2023-07-27T18:29:29.298624+00:00
| 350 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n\n```\nif\n prev is connected to mid\n and\n mid is connected to next\n prev -> mid -> next\nthen\n connect prev to next\n prev -> next\n\nfor all mids\n for all prevs\n for all nexts\n do above\n\n===\nfor each query\n return if u & v are connected\n u -> u\n```\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n\n```\nvar checkIfPrerequisite = function (n, pres, qs) {\n let g = Array.from({ length: n }, () => new Array(n).fill(0))\n for (let [u, v] of pres) {\n g[u][v] = 1\n }\n\n for (let mid = 0; mid < n; mid++) {\n for (let u = 0; u < n; u++) {\n for (let v = 0; v < n; v++) {\n if (g[u][mid] && g[mid][v]) {\n g[u][v] = 1\n }\n }\n }\n }\n\n let an = []\n for (let [u, v] of qs) {\n an.push(g[u][v])\n }\n return an\n};\n```\n
| 2 | 0 |
['JavaScript']
| 0 |
course-schedule-iv
|
Simple Solution DFS ( finding Indirectly connected edges ) , in Python
|
simple-solution-dfs-finding-indirectly-c-nm22
|
Code\n\nclass Solution:\n def checkIfPrerequisite(self, numCourses: int, prerequisites: List[List[int]], queries: List[List[int]]) -> List[bool]:\n\n
|
Bala_1543
|
NORMAL
|
2023-06-28T10:02:31.034169+00:00
|
2023-06-28T10:02:31.034200+00:00
| 136 | false |
# Code\n```\nclass Solution:\n def checkIfPrerequisite(self, numCourses: int, prerequisites: List[List[int]], queries: List[List[int]]) -> List[bool]:\n\n graph = {}\n for i in range(numCourses): graph[i] = []\n\n for u , v in prerequisites: \n graph[u] += [v]\n\n d = {} # to maintain all INDIRECT NODES also ..!!!\n for i in range(numCourses): d[i] = set()\n\n visit = [0]*numCourses\n\n\n\n # DFS ...!!!!\n def dfs( node ):\n visit[node] = 1\n\n for ele in graph[node]:\n # need to add that element too.!!!!\n d[node].add(ele)\n\n if visit[ele] == 0: # if ele not already registered ..!!! then visit\n dfs(ele)\n \n for i in d[ele]: # add all nodes from that element ot the d[node]\n d[node].add(i)\n\n return d[node]\n\n\n\n for i in range(numCourses):\n if visit[i] == 0:\n dfs(i)\n\n ans = []\n for q in queries:\n if q[1] in d[q[0]]: # if there is a indirect Prerequisites \n ans += [True]\n else:\n ans += [False]\n return ans\n\n \n```
| 2 | 0 |
['Python3']
| 1 |
course-schedule-iv
|
SIMPLE PYTHON SOLUTION
|
simple-python-solution-by-beneath_ocean-tbhp
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\nTOPOLOGICAL SORT\n Describe your approach to solving the problem. \n\n# C
|
beneath_ocean
|
NORMAL
|
2023-01-05T04:27:37.283881+00:00
|
2023-01-05T04:27:37.283930+00:00
| 1,113 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nTOPOLOGICAL SORT\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:$$O(V*ElogE)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(V*E)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def checkIfPrerequisite(self, n: int, prerequisites: List[List[int]], queries: List[List[int]]) -> List[bool]:\n indegree=[0]*n\n adj=[[] for _ in range(n)]\n for i,j in prerequisites:\n adj[i].append(j)\n indegree[j]+=1\n st=[]\n for i in range(n):\n if indegree[i]==0:\n st.append(i)\n ans=[[] for _ in range(n)]\n while st:\n x=st.pop(0)\n for i in adj[x]:\n for j in ans[x]:\n if j not in ans[i]:\n ans[i].append(j)\n ans[i].append(x)\n indegree[i]-=1\n if indegree[i]==0:\n st.append(i)\n lst=[]\n for i,j in queries:\n if i in ans[j]:\n lst.append(True)\n else:\n lst.append(False)\n return lst\n```
| 2 | 0 |
['Python3']
| 0 |
course-schedule-iv
|
A logical Solution using DSU
|
a-logical-solution-using-dsu-by-tiwaribh-cdyx
|
Approach:\nMake the adjacency list and union all the given pre-requisites,run the queries and for each query find the parent for both the nodes .\nCase -1: if t
|
tiwaribhai5146
|
NORMAL
|
2022-10-01T12:10:20.091401+00:00
|
2022-10-01T12:10:20.091438+00:00
| 260 | false |
Approach:\nMake the adjacency list and union all the given pre-requisites,run the queries and for each query find the parent for both the nodes .\n**Case -1**: if the parent of both nodes comes different then it is guranteed that they are never being dependent on each other\n**Case-2**: If the parent of both comes same then there might be chance that the 2nd node is not dependent on the first, to check that do dfs from 1st node and check whether we are able to reach the second node, if yes then the answer will be true else it will be false.\n```\nclass DSU{\n public:\n vector<int>parent;\n vector<int>size;\n int len=101;\n DSU(){\n parent.resize(len);\n iota(parent.begin(),parent.end(),0);\n size.resize(len,1);\n }\n int find(int v){\n if(v==parent[v])\n return v;\n return parent[v]=find(parent[v]);\n }\n void Union(int a,int b){\n a=find(a);\n b=find(b);\n if(a!=b){\n if(size[a]<size[b])\n swap(a,b);\n parent[b]=a;\n size[a]+=size[b];\n }\n }\n};\nclass Solution {\npublic:\n void dfs(vector<int>&vis,vector<int>adj[],int node){\n if(vis[node])\n return;\n vis[node]=1;\n for(auto x:adj[node]){\n if(!vis[x])\n dfs(vis,adj,x);\n }\n }\n vector<bool> checkIfPrerequisite(int numCourses, vector<vector<int>>& pre, vector<vector<int>>& q) {\n DSU obj;\n vector<int>adj[101];\n for(auto x:pre){\n obj.Union(x[0],x[1]);\n adj[x[0]].push_back(x[1]);\n }\n vector<bool>ans;\n for(auto x:q){\n int a=obj.find(x[0]);\n int b=obj.find(x[1]);\n if(a!=b)\n ans.push_back(false);\n else{\n vector<int>vis(101,false);\n dfs(vis,adj,x[0]);\n if(vis[x[1]])\n ans.push_back(true);\n else\n ans.push_back(false);\n }\n }\n return ans;\n }\n};\n```\nPlease Upvote if you understood.
| 2 | 0 |
['Union Find']
| 0 |
course-schedule-iv
|
Python3 | Solved Using Ancestors of every DAG Graph Node approach(Kahn's Algo BFS)
|
python3-solved-using-ancestors-of-every-k024w
|
```\nclass Solution:\n def checkIfPrerequisite(self, numCourses: int, prerequisites: List[List[int]], queries: List[List[int]]) -> List[bool]:\n #Let
|
JOON1234
|
NORMAL
|
2022-07-26T17:41:44.898219+00:00
|
2022-07-26T17:41:44.898273+00:00
| 295 | false |
```\nclass Solution:\n def checkIfPrerequisite(self, numCourses: int, prerequisites: List[List[int]], queries: List[List[int]]) -> List[bool]:\n #Let m = len(prereqs) and z = len(queries)\n #Time: O(m + n + n*n + z) -> O(n^2)\n #Space: O(n*n + n + n*n + n + z) -> O(n^2)\n \n \n #process the prerequisites and build an adjacency list graph\n #where edges go from prerequisite to the course that depends on the prereq!\n n = numCourses\n #Adjacency List graph!\n adj = [set() for _ in range(n)]\n #indegrees array!\n indegrees = [0] * n\n #tell us every ith node\'s set of ancestors or all prereqs to take ith course!\n ancestors = [set() for _ in range(n)]\n #iterate through prereqs and update indegrees array as well as the adj list!\n for i in range(len(prerequisites)):\n prereq, main = prerequisites[i][0], prerequisites[i][1]\n adj[prereq].add(main)\n indegrees[main] += 1\n \n queue = deque()\n #iterate through the indegrees array and add all courses that have no \n #ancestors(no prerequisites to take it!)\n for a in range(len(indegrees)):\n #ath course can be taken without any prereqs -> first to be processed in\n #the Kahn\'s BFS algo!\n if(indegrees[a] == 0):\n queue.append(a)\n #proceed with Kahn\'s algo!\n while queue:\n cur_course = queue.pop()\n neighbors = adj[cur_course]\n for neighbor in neighbors:\n #neighbor has one less incoming edge!\n indegrees[neighbor] -= 1\n #current course is a prerequisite to every neighboring node!\n ancestors[neighbor].add(cur_course)\n #but also, all prereqs of cur_course is also indirectly a prereq\n #to each and every neighboring courses!\n ancestors[neighbor].update(ancestors[cur_course])\n #if neighboring node suddenly becomes can take with no prereqs,\n #add it to the queue!\n if(indegrees[neighbor] == 0):\n queue.append(neighbor)\n #once the algorithm ends, our ancestors array will have info regarding\n #prerequisites in order to take every course from 0 to n-1!\n output = []\n for query in queries:\n prereq2, main2 = query[0], query[1]\n all_prereqs = ancestors[main2]\n #check if prereq2 is an ancestor or required prereq course to take main2!\n if(prereq2 in all_prereqs):\n output.append(True)\n continue\n else:\n output.append(False)\n \n \n return output
| 2 | 0 |
['Topological Sort', 'Queue', 'Python3']
| 0 |
course-schedule-iv
|
[C++] Floyd–Warshall Algorithm - Clean code with comments - O(n^3)
|
c-floyd-warshall-algorithm-clean-code-wi-loxf
|
\n // we can solve this by using these topo sort , dfs/bfs , floyd warshall time:O(n^3) Space: O(n^2)\n \nclass Solution {\npublic:\n vector checkI
|
ssbbdd11_11
|
NORMAL
|
2022-07-06T05:51:54.313374+00:00
|
2022-07-06T05:51:54.313416+00:00
| 351 | false |
\n // we can solve this by using these topo sort , dfs/bfs , floyd warshall time:O(n^3) Space: O(n^2)\n \nclass Solution {\npublic:\n vector<bool> checkIfPrerequisite(int numCourses, vector<vector<int>>& prerequisites, vector<vector<int>>& queries) \n{\n vector<vector<int>>distance(numCourses,vector<int>(numCourses,1e9));\n \n for(int i=0;i<prerequisites.size();i++){\n distance[prerequisites[i][0]][prerequisites[i][1]]=1;\n }\n \n // Using Floyd Warshall Algorithm from line no. 16-21 it is the code for generating the matrix\n for(int k=0;k<numCourses;k++){\n for(int i=0;i<numCourses;i++){\n for(int j=0;j<numCourses;j++){\n if(distance[i][k]==1e9 || distance[k][j]==1e9) //when we dont know the value(infinity) in the matrix then we ignore it \n continue;\n else if(distance[i][j] > distance[i][k] + distance[k][j]) //if the path using k is smaller than the current path then we will update it to our current path\n distance[i][j] = distance[i][k] + distance[k][j]; \n \n }\n }\n } \n \n vector<bool>ans;\n \n for(int i=0;i<queries.size();i++){ \n if(distance[queries[i][0]][queries[i][1]]==1e9)// check in distance matrix if value in infinite then simply return false else return true;\n ans.push_back(false);\n else\n ans.push_back(true); // if the value is not infinity then return true \n }\n return ans;\n }\n};
| 2 | 0 |
['C']
| 0 |
course-schedule-iv
|
Course Schedule IV | Java | Floyd Warshalls Algo
|
course-schedule-iv-java-floyd-warshalls-yx1v1
|
Course Schedule IV\n\nclass Solution {\n public List<Boolean> checkIfPrerequisite(int numCourses, int[][] prerequisites, int[][] queries) {\n boolean
|
yash4900
|
NORMAL
|
2022-06-23T18:23:12.472710+00:00
|
2022-06-23T18:23:12.472760+00:00
| 217 | false |
#### **Course Schedule IV**\n```\nclass Solution {\n public List<Boolean> checkIfPrerequisite(int numCourses, int[][] prerequisites, int[][] queries) {\n boolean [][] graph = new boolean[numCourses][numCourses];\n \n for (int i=0; i<prerequisites.length; i++) {\n graph[prerequisites[i][0]][prerequisites[i][1]] = true;\n }\n \n for (int k=0; k<numCourses; k++) {\n for (int i=0; i<numCourses; i++) {\n for (int j=0; j<numCourses; j++) {\n if (!graph[i][j] && graph[i][k] && graph[k][j]) {\n graph[i][j] = true;\n }\n }\n }\n }\n \n List<Boolean> result = new ArrayList<>(queries.length);\n for (int i=0; i<queries.length; i++) {\n result.add(graph[queries[i][0]][queries[i][1]]);\n }\n return result;\n }\n}\n```
| 2 | 0 |
['Java']
| 0 |
course-schedule-iv
|
C++ using 2D array to store final values | O(E*N)
|
c-using-2d-array-to-store-final-values-o-70ts
|
Used topological sort for traversing from 0 prerequisite courses.\n\nUsed a 2D array called dp, dp[i][j] = true means i is a prerequisite of j.\n\nwhen even we
|
hareeshghk
|
NORMAL
|
2022-05-01T12:48:22.110049+00:00
|
2022-05-01T12:58:59.745849+00:00
| 151 | false |
Used topological sort for traversing from 0 prerequisite courses.\n\nUsed a 2D array called dp, dp[i][j] = true means i is a prerequisite of j.\n\nwhen even we remove an edge in topological sort we can add (i.e removing edge src->dst) dp[src][dst] as true and also add prerequisites of src as prerequisites of dst. Generally we should add prerequisites(prerequsites....(src)) also to prerequsites[dst] but only one level is needed as we are merging these at every level.\n\nEg to understand last point:\nA->B->C->D\nprereq(A) is none initially and its added to queue\n\nwhen edge A->B is deleted, we add A to prereq list of B and also add prereq list of A to B (which is none)\nPrereq(B) contains A\n\nwhen edge B->C is deleted, we add B to list of C and also add prereq(B) to C which is A\nPrereq(C) contains B, A\n\nwhen edge C->D deleted, we add C to list of D and also add prereq(C) to D which are B,A\nprereq(D) contains C,B,A\n\nif you see in case of D we just need to add list of C only.\n\ntry for some complex example to understand more.\n\ntime complexity: O(E * N) \nNote: E is number of edges and worst case it can become N^3\n```\nclass Solution {\npublic:\n vector<bool> checkIfPrerequisite(int numCourses, vector<vector<int>>& prerequisites, vector<vector<int>>& queries) {\n vector<int> inOrder(numCourses, 0);\n \n vector<vector<int>> graph(numCourses, vector<int> ());\n \n for (auto p : prerequisites) {\n graph[p[0]].push_back(p[1]);\n inOrder[p[1]]++;\n }\n \n queue<int> q;\n vector<vector<bool>> dp(numCourses, vector<bool>(numCourses, false));\n \n // if inorder is 0 push to queue;\n for (int i = 0; i < numCourses; ++i) {\n if (inOrder[i] == 0) {\n q.push(i);\n }\n }\n \n while (!q.empty()) {\n auto cur = q.front();\n q.pop();\n \n for (auto nei : graph[cur]) {\n inOrder[nei]--;\n dp[cur][nei] = true;\n \n for (int i = 0; i < numCourses; ++i) {\n dp[i][nei] = (dp[i][nei] || dp[i][cur]);\n }\n if (inOrder[nei] == 0) {\n q.push(nei);\n }\n }\n }\n \n vector<bool> result;\n \n for (auto q : queries) {\n if (q[1] >= numCourses || q[1] < 0) {\n result.push_back(false);\n continue;\n }\n \n if (q[0] >= numCourses || q[0] < 0) {\n result.push_back(false);\n continue;\n }\n \n result.push_back(dp[q[0]][q[1]]);\n }\n \n return result;\n }\n};\n```
| 2 | 0 |
[]
| 0 |
course-schedule-iv
|
C++ || DFS || easy to understand
|
c-dfs-easy-to-understand-by-datnguyen2k3-2zh4
|
Up vote if it\'s helpful!\n\t\n\tclass Solution {\n\tpublic:\n\t\tvector> graph;\n\t\tvector visited;\n\t\tvector> check;\n\t\tvector ans;\n \n\t\tvoid dfs(i
|
datnguyen2k3
|
NORMAL
|
2022-02-04T15:31:00.789408+00:00
|
2022-02-04T15:34:18.704725+00:00
| 161 | false |
Up vote if it\'s helpful!\n\t\n\tclass Solution {\n\tpublic:\n\t\tvector<vector<int>> graph;\n\t\tvector<int> visited;\n\t\tvector<vector<int>> check;\n\t\tvector<bool> ans;\n \n\t\tvoid dfs(int cur, int k) {\n\t\t\tif(check[cur][k] != -1) // check cur->k == -1 is cur->k isn\'t exist\n\t\t\t\treturn;\n \n\t\t\tif(cur == k) {\n\t\t\t\tcheck[cur][k] = 1;\n\t\t\t\treturn;\n\t\t\t}\n \n\t\t\tcheck[cur][k] = 0;\n\t\t\tfor(auto& child : graph[cur]) {\n\t\t\t\tdfs(child, k); \n\t\t\t\tif(check[child][k] == 1) check[cur][k] = 1;\n\t\t\t}\n\t\t}\n \n\t\tvector<bool> checkIfPrerequisite(int numCourses, vector<vector<int>>& prerequisites, vector<vector<int>>& queries) {\n \n\t\t\tgraph.resize(numCourses);\n\t\t\tvisited.resize(numCourses);\n\t\t\tcheck.resize(numCourses, vector<int>(numCourses, - 1));\n\n\t\t\tfor(auto& pair:prerequisites) {\n\t\t\t\tgraph[pair[0]].push_back(pair[1]);\n\t\t\t}\n \n\t\t\tfor(auto& pair:queries) {\n\t\t\t\tdfs(pair[0], pair[1]);\n\t\t\t\tans.push_back(check[pair[0]][pair[1]] == 1);\n\t\t\t}\n\n\t\t\treturn ans;\n\t\t}\n\t};
| 2 | 1 |
['Depth-First Search', 'C']
| 0 |
course-schedule-iv
|
[C++] DFS + DP
|
c-dfs-dp-by-thegateway-ahgb
|
Logic: We have to check in query(u,v) whether path exisits from u -> v, if it exists, then u is prerequisite of v, else it not a prerequisite of v.\n\nNeed of D
|
theGateway
|
NORMAL
|
2022-01-27T06:53:22.831151+00:00
|
2022-01-27T06:53:50.054854+00:00
| 329 | false |
**Logic:** We have to check in query(u,v) whether path exisits from u -> v, if it exists, then u is prerequisite of v, else it not a prerequisite of v.\n\n**Need of DP:** Memoization saves time by storing paths that exist and that don\'t exist, else the logic is simple dfs for all queries and checking whether path exists.\n```\nclass Solution {\npublic:\n vector<vector<int>> dp;\n vector<bool> checkIfPrerequisite(int numCourses, vector<vector<int>>& edges, vector<vector<int>>& queries) {\n int nq = queries.size();\n vector<bool> result(nq, false);\n vector<vector<int>> adjList(numCourses);\n dp.resize(numCourses, vector<int>(numCourses, -1));\n \n for(auto& edge: edges){\n int u = edge[0], v = edge[1];\n adjList[u].push_back(v);\n }\n \n for(int i=0; i<nq; i++){\n int u = queries[i][0], v = queries[i][1];\n vector<int> visited(numCourses, 0);\n if(pathExistsDFS(u, v, adjList, visited)) result[i] = true;\n }\n return result;\n }\n \n bool pathExistsDFS(int u, int v, vector<vector<int>>& adjList, vector<int>& visited){\n if(u == v) return true;\n if(visited[u] == 1) return false;\n if(dp[u][v] != -1) return dp[u][v];\n \n visited[u] = 1;\n vector<int> neighbors = adjList[u];\n for(auto& neighbor: neighbors){\n if(pathExistsDFS(neighbor, v, adjList, visited)) {\n dp[u][v] = 1;\n return true;\n }\n }\n dp[u][v] = 0;\n return false;\n }\n};\n```
| 2 | 0 |
['Depth-First Search', 'Memoization', 'C', 'C++']
| 0 |
count-the-number-of-vowel-strings-in-range
|
Python 3 || 2 lines, sets || T/S: 97% / 97%
|
python-3-2-lines-sets-ts-97-97-by-spauld-dy7x
|
\nclass Solution:\n def vowelStrings(self, words: List[str], left: int, right: int) -> int:\n\n vowels = set(\'aeiou\')\n \n return sum(
|
Spaulding_
|
NORMAL
|
2023-03-12T04:53:05.842167+00:00
|
2024-06-18T00:43:00.779302+00:00
| 1,563 | false |
```\nclass Solution:\n def vowelStrings(self, words: List[str], left: int, right: int) -> int:\n\n vowels = set(\'aeiou\')\n \n return sum({w[0],w[-1]}.issubset(vowels) for w in words[left:right+1])\n```\n[https://leetcode.com/problems/count-the-number-of-vowel-strings-in-range/submissions/1291831411/](https://leetcode.com/problems/count-the-number-of-vowel-strings-in-range/submissions/1291831411/)\n\nI could be wrong, but I think that time complexity is *O*(*N*) and space complexity is *O*(1), in which *N* ~ `len(nums`.\n
| 27 | 0 |
['Python3']
| 3 |
count-the-number-of-vowel-strings-in-range
|
Simple Condition || Very simple & Easy to Understand Solution
|
simple-condition-very-simple-easy-to-und-ws71
|
\n# Code\n\nclass Solution {\npublic:\n int isVowel(char w){\n return (w == \'a\' || w == \'e\' || w == \'i\' || w == \'o\' || w == \'u\');\n }\n
|
kreakEmp
|
NORMAL
|
2023-03-12T04:14:14.284823+00:00
|
2023-03-12T04:14:14.284866+00:00
| 4,060 | false |
\n# Code\n```\nclass Solution {\npublic:\n int isVowel(char w){\n return (w == \'a\' || w == \'e\' || w == \'i\' || w == \'o\' || w == \'u\');\n }\n int vowelStrings(vector<string>& words, int left, int right) {\n int count = 0;\n for(int i = left; i <= right; ++i) {\n if(isVowel(words[i][0]) && isVowel(words[i].back()) ) count++;\n }\n return count;\n }\n};\n```
| 17 | 0 |
['C++']
| 2 |
count-the-number-of-vowel-strings-in-range
|
2586: Solution with step by step explanation
|
2586-solution-with-step-by-step-explanat-y77x
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n1. Define a function vowelStrings that takes a list of strings words and
|
Marlen09
|
NORMAL
|
2023-03-12T04:04:33.627009+00:00
|
2023-03-12T04:04:33.627039+00:00
| 2,095 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Define a function vowelStrings that takes a list of strings words and two integers left and right as input, and returns an integer.\n2. Initialize a variable vowels to the string \'aeiouAEIOU\', which contains all the vowels.\n3. Initialize a variable count to 0.\n4. Loop through the indices from left to right inclusive:\na. If the first character of the current word is a vowel and the last character of the current word is a vowel, increment count by 1.\n5. Return count.\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def vowelStrings(self, words: List[str], left: int, right: int) -> int:\n vowels = \'aeiouAEIOU\'\n count = 0\n for i in range(left, right+1):\n if words[i][0] in vowels and words[i][-1] in vowels:\n count += 1\n return count\n\n```
| 12 | 0 |
['Python', 'Python3']
| 3 |
count-the-number-of-vowel-strings-in-range
|
Short || Clean || Java
|
short-clean-java-by-himanshubhoir-0a6o
|
\njava []\nclass Solution {\n public int vowelStrings(String[] words, int left, int right) {\n int count = 0;\n String v = "aeiou";\n fo
|
HimanshuBhoir
|
NORMAL
|
2023-03-12T04:02:03.523955+00:00
|
2023-03-12T04:02:03.524064+00:00
| 1,049 | false |
\n```java []\nclass Solution {\n public int vowelStrings(String[] words, int left, int right) {\n int count = 0;\n String v = "aeiou";\n for(int i=left; i<=right; i++){\n if(v.contains(words[i].charAt(0)+"") && v.contains(words[i].charAt(words[i].length()-1)+"")) count++;\n }\n return count;\n }\n}\n```
| 12 | 0 |
['Java']
| 2 |
count-the-number-of-vowel-strings-in-range
|
Simple java solution
|
simple-java-solution-by-siddhant_1602-gpkt
|
Complexity\n- Time complexity: O(n) where left <= n <= right\n\n- Space complexity: O(1)\n\n# Code\n\nclass Solution {\n public int vowelStrings(String[] wor
|
Siddhant_1602
|
NORMAL
|
2023-03-12T04:00:39.731088+00:00
|
2023-03-12T04:04:44.532474+00:00
| 1,883 | false |
# Complexity\n- Time complexity: $$O(n)$$ where left <= n <= right\n\n- Space complexity: $$O(1)$$\n\n# Code\n```\nclass Solution {\n public int vowelStrings(String[] words, int left, int right) {\n int m=0;\n for(int i=left;i<=right;i++)\n {\n char c=words[i].charAt(0);\n char d=words[i].charAt(words[i].length()-1);\n if((c==\'a\'||c==\'e\'||c==\'i\'||c==\'o\'||c==\'u\') && (d==\'a\'||d==\'e\'||d==\'i\'||d==\'o\'||d==\'u\'))\n {\n m++;\n }\n }\n return m;\n }\n}\n```
| 9 | 0 |
['Java']
| 1 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.