question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
Python 3 || 2 lines, calculus problem || T/S: 96% / 58%
|
python-3-2-lines-calculus-problem-ts-96-hr9y8
|
This is a multivariable calculus problem masquerading as a programming exercise.\n\nFirst, it\'s clear the optimum stategy is to perform the increment steps fir
|
Spaulding_
|
NORMAL
|
2024-03-24T17:47:01.618655+00:00
|
2024-10-27T16:25:08.087015+00:00
| 219 | false |
This is a multivariable calculus problem masquerading as a programming exercise.\n\nFirst, it\'s clear the optimum stategy is to perform the increment steps first, then perform the duplicate steps.\n\nSecond, if we perform *x* increment steps and *y* duplicate steps, the total number of moves is expressed by the function *moves*(*x*, *y*) = *x* + *y* and the sum of the array is expressed by the function *sum*(*x*, *y*) = (*x* + 1) * (*y* + 1).\n\nThird, we treat these two functions as continuous functions, and apply the principles of calculus to find the (*x*, *y*) for which the minimum value of *moves* occurs, subject to the constraint *sum*(*x*, *y*) = *k*. We find this value occurs at (*sqrt*(*k*) - 1, *sqrt*(*k*) - 1).\n\nFourth, we return one of the two closest integer solutions to this solution.\n\n```python []\nclass Solution:\n def minOperations(self, k: int) -> int:\n\n sqt = isqrt(k)\n\n return sqt - 1 + (k - 1) // sqt\n```\n\n```C++ []\nclass Solution {\npublic:\n int minOperations(int k) {\n int sqt = static_cast<int>(sqrt(k));\n return sqt - 1 + (k - 1) / sqt;}\n};\n```\n```java []\nclass Solution {\n public int minOperations(int k) {\n \n int sqt = (int) Math.sqrt(k); \n return sqt - 1 + (k - 1) / sqt;}\n}\n```\n[https://leetcode.com/problems/apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k/submissions/1266943008/](https://leetcode.com/problems/apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k/submissions/1266943008/)\n\nI could be wrong, but I think that time complexity is *O*(1) and space complexity is *O*(1).\n
| 10 | 0 |
['C++', 'Java', 'Python3']
| 2 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
1-line ceil(sqrt(4*k))-2 arithmetic mean>=geometric mean
|
1-line-ceilsqrt4k-2-arithmetic-meangeome-d4ss
|
Intuition\n Describe your first thoughts on how to solve this problem. \nLet a denote the times for increase its value by 1, and b denote the times for duplica
|
anwendeng
|
NORMAL
|
2024-03-24T15:53:20.913170+00:00
|
2024-03-24T16:07:13.215192+00:00
| 150 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nLet a denote the times for increase its value by 1, and b denote the times for duplicating. Then we have \n$$(a+1)(b+1)\\geq k$$\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThen usual math\n$\\implies 1+(a+b)+ab\\geq k$\nUsing arithmetic mean>=geometric mean, i.e $a+b\\geq 2\\sqrt{ab}$\n$\\implies 1+(a+b)+(\\frac{a+b}{2})^2\\geq 1+(a+b)+ab\\geq k$\nAfter some manipulation on squaring, we have\n$(a+b+2)^2\\geq 4k$\nSince a, b, k are integers\n$\\implies a+b\\geq ceil(\\sqrt{4k}-2)=ceil(\\sqrt{4k})-2$\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(1)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(1)$$\n# Code\n```\nclass Solution {\npublic:\n int minOperations(int k) {\n return ceil(sqrt(4*k))-2;\n }\n};\n\n```
| 8 | 0 |
['Math', 'C++']
| 1 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
Easiest Java Solution
|
easiest-java-solution-by-1asthakhushi1-swo6
|
\n\nclass Solution {\n public int minOperations(int k) {\n int ans=Integer.MAX_VALUE;\n int final=0;\n for(int i=1;i<=k/2;i++){\n
|
1asthakhushi1
|
NORMAL
|
2024-03-24T04:14:15.729483+00:00
|
2024-03-24T04:19:00.839155+00:00
| 556 | false |
\n```\nclass Solution {\n public int minOperations(int k) {\n int ans=Integer.MAX_VALUE;\n int final=0;\n for(int i=1;i<=k/2;i++){\n // i=1--> 1+1+1+1+1+1+1+1+1+1+1 --> To get first 1 -->(1-1=0 operation) + leftover 10 more 1\'s --> final=10\n // i=2--> 2+2+2+2+2+2+2 --> To get first 2 -->(2-1=1 operation) + leftover 5 more 2\'s --> final=1+5=6\n // i=3--> 3+3+3+3 --> To get first 3 -->(3-1=2 operations) + leftover 3 more 3\'s --> final=2+5=5\n // i=4--> 4+4+4 --> To get first 4 -->(4-1=3 operations) + leftover 2 more 4\'s --> final=3+2=5\n // i=5--> 5+5+5 --> To get first 5 -->(5-1=4 operations) + leftover 2 more 5 --> final=4+2=6\n // i=6--> 6+6 --> To get first 6 -->(6-1=5 operations) + leftover 1 more 5 --> final=5+1=6\n // ....\n int sum=0;\n sum+=i-1; // (to get first digit)\n sum+=k/i-1; // (leftover count)\n if(k%i>0)\n sum+=1; \n ans=Math.min(sum,ans);\n if(ans==sum)\n final=ans;\n sum=0;\n }\n return final;\n }\n}\n```
| 8 | 0 |
['Java']
| 3 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
3 lines Code || Easiest Possible Solution Ever || Beginner Friendly
|
3-lines-code-easiest-possible-solution-e-63ug
|
APPROACH\n\nfor i in range(1, k + 1): This loop iterates over numbers from 1 to k inclusive. It represents the number of groups we are going to divide the input
|
sumit4199
|
NORMAL
|
2024-03-24T04:26:55.776691+00:00
|
2024-03-24T04:57:12.403137+00:00
| 1,199 | false |
# APPROACH\n\n**for i in range(1, k + 1):** This loop iterates over numbers from 1 to k inclusive. It represents the number of groups we are going to divide the input into.\n\n**res = min(res, i - 1 + (k + i - 1) // i - 1):** In this line, for each value of i, it calculates the number of operations needed based on the current grouping strategy and updates res with the minimum of the current value of res and the calculated value.\n\n**(k + i - 1) // i - 1** calculates the number of operations needed for the current grouping strategy. It divides the total count k + i - 1 by i (the number of groups), then subtracts 1 to account for the original count of i.\n\ni - 1 represents the number of operations needed to distribute elements into the groups.\n\nAdding these two together gives the total number of operations needed for the current grouping strategy.\n# Complexity\n- Time complexity: O(K)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# PYTHON 3\n```\nclass Solution:\n def minOperations(self, k: int) -> int:\n res = k+1\n for i in range(1,k+1):\n curr = i-1+(k+i-1) // i-1\n res = min(res,curr)\n return res\n```
| 6 | 0 |
['Array', 'Hash Table', 'Two Pointers', 'Dynamic Programming', 'C', 'Python', 'C++', 'Java', 'Python3']
| 2 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
✅ DP and Greedy | Recursive | Easy to Understand | 2 Solutions
|
dp-and-greedy-recursive-easy-to-understa-z7gu
|
1. Dynamic Programming\nTried explaining the logic behind linear dp (Feel free to share your thoughts):\n\nThe Sum and Max are not that much different from each
|
spats7
|
NORMAL
|
2024-03-24T05:16:42.070882+00:00
|
2024-03-24T23:00:36.775768+00:00
| 559 | false |
# 1. Dynamic Programming\n**Tried explaining the logic behind linear dp (Feel free to share your thoughts):**\n\nThe Sum and Max are not that much different from each other, and at any point, I am not considering the current sum to determine the max number of operations. Max is undergoing operations and it is having a constant effect on Sum. Either sum is increased by 1 or increased by max. We have the Greedy intuition from the DP solution that the sum is not important but the max is. Since we will keep on incrementing a number and then duplicate it. This shows the sum for a max does not fluctuate much, If I reach a max, and check for the operations, the sum will either be +1 or max. Thus the sum for this max will be like (sum + 1 * max), (sum + 2 * max), (sum + 3 * max), and so on, and all these recursive calls will be in the stack. Once I start popping out of the stack, I will keep on updating the dp[max] for this till the last recursive call where I considered max. For +1 operation we are all together changing the max and new operations will start.\n\nThe algorithm will run this way, for sum x, max y it will update dp[y], then will go back to the previous call which was made on Sum = x-y, and here again will update the dp[y]. This means the sum does not at all make any difference. It is just max which is helping us determine what our answer should be.\n\nIn summary, the sum and max are dependent on each other and are not changing independently to determine the current state of dp.\n\n```\nclass Solution {\n public int minOperations(int k) {\n if(k == 1)\n return 0;\n int[] dp = new int[k+1];\n return memo(k, 1, 1, dp); \n }\n private int memo(int k, int sum, int max, int[] dp){\n if(k <= sum)\n return 0;\n if(dp[max] != 0)\n return dp[max];\n // +1\n int plus = memo(k, sum + 1, max + 1, dp) + 1;\n // duplicate\n int dupe = memo(k, sum + max, max, dp) + 1;\n \n dp[max] = Math.min(plus, dupe);\n return dp[max];\n }\n}\n```\n---\n# 2. Greedy\n```\nclass Solution {\n public int minOperations(int k) {\n if(k==1)\n return 0;\n int min = Integer.MAX_VALUE;\n int max = 1;\n int op = 0;\n \n while(k > max){\n //increment\n max++; op++;\n // duplicate\n int diff = k - max;\n int curr = diff / max;\n if(curr * max < diff)\n curr++;\n min = Math.min(min, curr + op);\n } \n return min;\n }\n}
| 3 | 0 |
['Dynamic Programming', 'Recursion', 'Memoization', 'Java']
| 6 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
✅ 2 Approaches || 3Lines || 5 lines || Detailed Explaination || Optimal Solution || Beats 100% ✅
|
2-approaches-3lines-5-lines-detailed-exp-vcw2
|
Intuition\nWe need to find two numbers for the minimum number of operations .\nFor eg. when k = 11 , 12 = 3X4 is the number we can obtain greater or equal than
|
TLE_17
|
NORMAL
|
2024-03-24T04:47:05.551718+00:00
|
2024-03-24T15:34:43.389057+00:00
| 259 | false |
# Intuition\nWe need to find two numbers for the minimum number of operations .\nFor eg. when k = 11 , 12 = 3X4 is the number we can obtain greater or equal than 11 in min. operations.\nSo we will make [1]->[2]->[3]->[3,3]->[3,3,3]->[3,3,3,3]\nhere , [1]->[2]->[3]->[4]->[4,4]->[4,4,4] also possible as 12=4X3\n\n# Approach\n\nWe need to find two numbers closest to each other having product more than or equal to k\n\n# Complexity\n- Time complexity:\nO(1)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution {\npublic:\n //Upvote\n int minOperations(int k) {\n //1st\n int a = ceil(sqrt(k)-1);//For storing +1 operations\n int b = ceil(((k*1.0)/(a+1))-1);//For duplicating values\n return a+b;\n\n\n //2nd\n int ans = INT_MAX;\n\n for(int i=1;i<=k;i++){\n int temp = ceil(k*1.0/i);\n ans = min(ans,i-1+temp-1);\n }\n return ans;\n }\n};\n```
| 3 | 0 |
['C++']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
Python one-liner beats 100% TC=O(1) SC=O(1)
|
python-one-liner-beats-100-tco1-sco1-by-pd1x3
|
Complexity\n- Time complexity:O(1)\n- Space complexity:O(1)\n\n# Code\n\nclass Solution:\n def minOperations(self, k: int) -> int:\n return ceil(sqrt(
|
Divyanshu52Singhal
|
NORMAL
|
2024-03-24T04:42:09.543641+00:00
|
2024-03-24T04:42:09.543659+00:00
| 176 | false |
# Complexity\n- Time complexity:O(1)\n- Space complexity:O(1)\n\n# Code\n```\nclass Solution:\n def minOperations(self, k: int) -> int:\n return ceil(sqrt(k)) -1 + k //ceil(sqrt(k)) - (k%ceil(sqrt(k))==0)\n```
| 3 | 0 |
['Math', 'Python3']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
[Python3] Math - Simple Solution
|
python3-math-simple-solution-by-dolong21-c7am
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Code\n\n##### 1. Br
|
dolong2110
|
NORMAL
|
2024-03-24T04:10:00.337283+00:00
|
2024-03-24T04:10:00.337311+00:00
| 293 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Code\n\n##### 1. Brute-Force\n```\nclass Solution:\n def minOperations(self, k: int) -> int:\n res = k\n for i in range(1, math.ceil(math.sqrt(k)) + 1):\n x = math.ceil(k / i)\n res = min(res, x + math.ceil(k / x) - 2)\n res = min(res, i + math.ceil(k / i) - 2)\n return res\n```\n\n# Complexity\n- Time complexity: $$O(sqrt(k))$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n##### 2. Math\n```\nclass Solution:\n def minOperations(self, k: int) -> int:\n m = math.ceil(math.sqrt(k))\n return m - 1 + k // m - (k % m == 0)\n```\n\n# Complexity\n- Time complexity: $$O(1)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->
| 3 | 0 |
['Math', 'Python3']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
[C++|Java|Python3|Javascript|Typescript] math
|
cjavapython3javascripttypescript-math-by-vz45
|
Please pull this commit for my solutions of weekly 390. \n\nC++\n\nclass Solution {\npublic:\n int minOperations(int k) {\n int p = sqrt(k), q = (k+p-
|
ye15
|
NORMAL
|
2024-03-24T04:04:23.807062+00:00
|
2024-03-24T19:32:24.706969+00:00
| 654 | false |
Please pull this [commit](https://github.com/gaosanyong/leetcode/commit/cdc5e101ce1f1fae525345dec774217fbbdba2c4) for my solutions of [weekly 390](https://leetcode.com/contest/weekly-contest-390/). \n\n**C++**\n```\nclass Solution {\npublic:\n int minOperations(int k) {\n int p = sqrt(k), q = (k+p-1)/p; \n return p + q - 2; \n }\n};\n```\n**Java**\n```\nclass Solution {\n public int minOperations(int k) {\n int p = (int) Math.sqrt(k), q = (k+p-1)/p; \n return p + q - 2;\n }\n}\n```\n**Python3**\n```\nclass Solution:\n def minOperations(self, k: int) -> int:\n p = isqrt(k)\n q = (k+p-1)//p\n return p+q-2\n```\n**Javascript**\n```\nvar minOperations = function(k) {\n const p = Math.floor(Math.sqrt(k)), q = Math.ceil(k/p); \n return p + q - 2; \n};\n```\n**Typescript**\n```\nfunction minOperations(k: number): number {\n const p = Math.floor(Math.sqrt(k)), q = Math.ceil(k/p); \n return p + q - 2; \n};\n```
| 3 | 0 |
['C', 'Java', 'TypeScript', 'Python3', 'JavaScript']
| 2 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
Beats 100% | Best Solution | Less Code ✅✅
|
beats-100-best-solution-less-code-by-ika-s5xl
|
Please Upvote \u2705\u2705\n\n# Code\n\nclass Solution {\n public int minOperations(int k) {\n if(k == 1) return 0;\n int ans = Integer.MAX_VA
|
Ikapoor123
|
NORMAL
|
2024-03-24T04:01:30.493484+00:00
|
2024-03-24T04:01:30.493507+00:00
| 170 | false |
# Please Upvote \u2705\u2705\n\n# Code\n```\nclass Solution {\n public int minOperations(int k) {\n if(k == 1) return 0;\n int ans = Integer.MAX_VALUE;\n \n for(int i=1;i<k;i++){\n int steps = 0;\n int j=2;\n int number = i;\n while(number<k){\n number = i*j;\n j++;\n steps++;\n }\n steps+=i-1;\n ans = Math.min(ans, steps);\n }\n return ans;\n }\n}\n```
| 3 | 0 |
['Math', 'Java']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
100% Beats || C++ || O(1) || Maths
|
100-beats-c-o1-maths-by-arrrrrpit-9ix1
|
Intuition\nIt\'s optimal to first increase the value and then copy it.\n\n# Approach\nLet x be the value to which we will increase, and then we will multiply it
|
Arrrrrpit
|
NORMAL
|
2024-07-02T09:30:25.628620+00:00
|
2024-07-02T09:31:07.887827+00:00
| 45 | false |
# Intuition\nIt\'s optimal to first increase the value and then copy it.\n\n# Approach\nLet $$x$$ be the value to which we will increase, and then we will multiply it. Let $$f(x)$$ be the number of moves required to first turn $$1 \\rightarrow x$$ and then $$x \\rightarrow k$$. So, $$f(x) = (x - 1) + \\dfrac{k}{x}$$. Taking the derivative, $$\nf\'(x) = 1 - \\left(\\dfrac{k}{x^2}\\right)\n$$. Setting $$f\'(x) = 0$$ gives us $$x = \\sqrt{k}$$.\n\n\n# Complexity\n- Time complexity: $$O(1)$$\n\n- Space complexity: $$O(1)$$\n\n# Code\n```\nclass Solution\n{\npublic:\n int minOperations(int k)\n {\n int x = sqrt(k);\n return (x - 1 + (k - 1) / x);\n }\n};\n```\n\n# Please Upvote!!!\n\n\n\n# Beats\n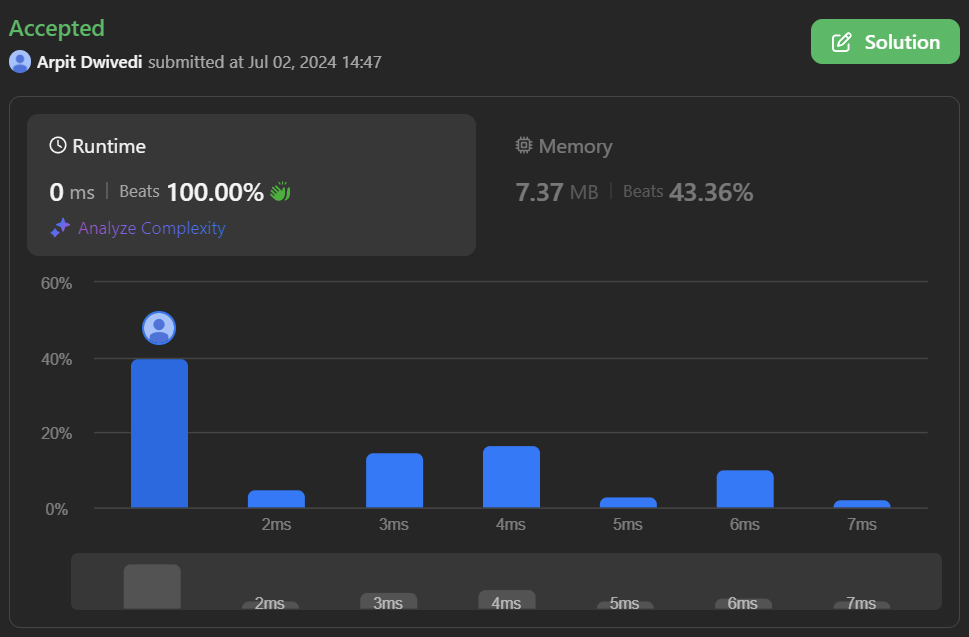\n
| 2 | 0 |
['C++']
| 1 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
O(1) Full Explanation Mathematical Solution with derivation of Formula | See It Once |
|
o1-full-explanation-mathematical-solutio-q9q4
|
Intuition\n\nFirstly I went for Recursive Method to check the understanding of the question and it gave TLE (obvious) . I have posted that solution as well.\n\n
|
Divyansh__Gupta
|
NORMAL
|
2024-05-30T08:42:46.607298+00:00
|
2024-05-30T08:42:46.607316+00:00
| 22 | false |
# Intuition\n\nFirstly I went for Recursive Method to check the understanding of the question and it gave TLE (obvious) . I have posted that solution as well.\n\nThen after seeing it is Some formula based question I looked for hint where I got that we should first increment the number than copy the number in total sum (array). \n\n# Approach\n- So if we increase the number \'m\' times than it will reduce the given sum K by "m+1" times and the sum will become K-(M+1) and our final value of array will be "m+1"\n- Eg:- Since initially we have [1] in array so If we do\n m=1 -> Array=[2] RemainingSum= K-2 \n m=2 -> Array=[3] RemainingSum= K-3\n ......If we increment the number m times than\n m=M -> Array=[M+1] RemainingSum= K-(M+1) \n- So now our **Remaining sum is K-M-1** and we will duplicate the number present in array i.e. [M+1]. Lets say we copy it x times So\n- x*(ArrayElement)>=RemainingSum \n- **x*(M+1)>=K-M-1*\n- From here *`x>=(K-M-1)/(M+1)`*\n- **`Our total answer will be M+x => M+(K-M-1)/(M+1)`**\n\n- Now main task is to find the M. Since we have to minimize the answer so we will *`diffrenetiate the answer equation`* .\n- \n\n# and from there u will get M=sqrt(k)-1;\n\n### Finally \n `Add Both the values i.e Increment (M) times and Copy (x) times`\n\n###### $$Overall$$ we have to First increment for some time and for remaining we have to copy and to find how many times we increment we use the answer giving equation as we know we have to find minimum value so we differentiate it and get the only unkown variable.\n\n\n\n# Complexity\n- Time complexity:\n$$O(1)$$ \n- Space complexity:\n$$O(1)$$ \n\n# Code\n```\nclass Solution {\npublic:\n int minOperations(int k) {\n int m=ceil(sqrt(k))-1; // Number of times u do increment\n int val=(k-m-1)/(m+1); // Number of times u make copy\n if((k-m-1)%(m+1)!=0) val++; //U can use ceil also\n //Add both (increment and copy)\n return m+val;\n }\n};\n```\n\n# Recursive (TLE)\n```\nclass Solution {\npublic:\n int solve(int sum,int k,int maxi){\n if(sum>=k) return 0;\n int x=solve(sum+1,k,maxi+1);\n int y=solve(sum+maxi,k,maxi);\n return min(x,y)+1;\n }\n int minOperations(int k) {\n return solve(1,k,1);\n }\n};\n```\nTHIS Solution is not like others where u get directly to the Editorial answer and think how to start from basic . I have derived and Explained from basic Intution and not like others where directly answer comes.\n#### PLZ UPVOTE IF U GET ANY HELP AND ASK If U HAVE ANY QUERY
| 2 | 0 |
['Math', 'C++']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
Simplest Math Logic | Inverted Parabola | C++
|
simplest-math-logic-inverted-parabola-c-cjt5c
|
Intuition\n Describe your first thoughts on how to solve this problem. \nTo solve this problem, the first thought that should come to our mind is that for the o
|
looneyd_noob
|
NORMAL
|
2024-03-24T18:47:17.764822+00:00
|
2024-03-24T18:54:44.653196+00:00
| 69 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTo solve this problem, the first thought that should come to our mind is that for the operations to be minimum we should `increment` the values at `first` then `duplicate` them. This is because if we duplicate at first, then we will be left with lot of increments, but if we increment at first then every time we duplicate (1 operation) we will get a larger increment rather than smaller increment (as increment can only contribute by +1).\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nNow, we have to apply operations but we don\'t know how many operations to apply in a range, so we have a possibility of `binary search`. Also the range is of the form that if the goal can be reached in `X` operations then that can also be reached in `Y` operations where `Y >= X`. Hence here we can apply binary search over number of operations to be performed, since if goal can be reached in 5 operations in total, then it can also be done in greater than 5 operations also.\n\nNow, let x be the number of increment and y be the number of duplicate operations. Here we apply x first and then y.\nSo, final value after `x increments` = `(1 + x)`\nand final value after `y increments` = `(1 + y) * (1 + x)`\nAlso, (x + y) = total count of operations.\nHere we apply the binary search logic, and derive some mathematical formulations.\nOperations will always lie between 0 and infinity (take 1e5 to be infinity)\nSo, `low = 0`, `high = 1e5`\nnow every time `mid = (low + high) >> 1`, we check if `mid` number of operations can satisfy our goal.\nBelow are the formulations (including images).\n`target: (1+y)*(1+x) >= k` in mid operations so, `(x+y)=mid`.\nSubstituting `y` in terms of `x`, we get\n`(1+mid-x)*(1+x) >= k`\nAbove is the equation of inverted parabola. On rearranging we get\n`-(x*x) + x*(mid) + mid+1-k >= 0`, for this to hold it must contain some roots `(atleast 1 root)`, which is possible if it has `D >= 0`.\nHence `(b*b-4ac) >= 0`, which gives us the relation (upon solving)\n`(mid+2)*(mid+2) >= 4*k`.\n\n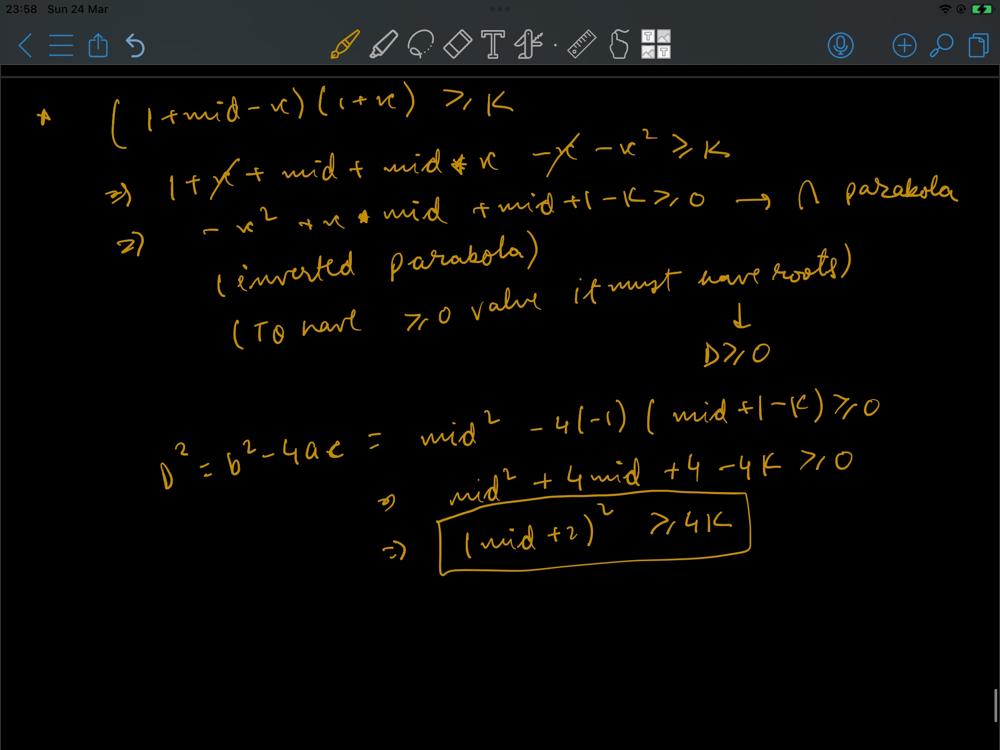\n\nSimple mathematics logic applied after deriving the relation between increment and doubling operations.\n\n# Complexity\n- Time complexity: $$O(log(1e5)) = O(1)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Results\n\n\n# Upvote\nUpvote the solution if it is helpful.\n\n# Code\n```\nclass Solution {\npublic:\n bool isPossible(int k, int mid){\n // initially nums = [1]\n // if we observe carefully we see that it is optimal to\n // increase the values at first and then duplicate so that\n // less duplications result in sum k\n // x -> increase ops -> 1 becomes 1+x\n // y -> duplicate ops -> 1+x becomes y(1+x)\n // (1+y)(1+x) >= k\n // also x + y = mid (here)\n // substitute -> (1+mid-x)(1+x) >= k\n // this is a graph of parabola (inverted), now for this to have some value >= 0\n // this should have determinant (D) >= 0 otherwise it will always have negative value\n return pow(mid+2, 2) >= 4*k;\n }\n int minOperations(int k) {\n // operations can be in the range 0....infinity\n int low = 0, high = 1e5;\n while(low <= high){\n int mid = low + ((high - low) >> 1);\n if(isPossible(k, mid)){\n high = mid - 1;\n }else{\n low = mid + 1;\n }\n }\n return low;\n }\n};\n```
| 2 | 0 |
['Math', 'Binary Search', 'C', 'C++']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
[Python] brute force (beats 100%)
|
python-brute-force-beats-100-by-pbelskiy-i7pv
|
\nclass Solution:\n def minOperations(self, k: int) -> int:\n best = float(\'inf\')\n for n in range(1, 10**5):\n length = math.ceil
|
pbelskiy
|
NORMAL
|
2024-03-24T16:21:13.112474+00:00
|
2024-03-24T16:21:13.112506+00:00
| 19 | false |
```\nclass Solution:\n def minOperations(self, k: int) -> int:\n best = float(\'inf\')\n for n in range(1, 10**5):\n length = math.ceil(k / n) # length of array of [n, n, ...]\n ops = (length - 1) + (n - 1) # operations to make such array \n if ops > best:\n break\n best = ops\n\n return best\n```
| 2 | 0 |
['Python']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
🔥1st and 2nd Operation Combination | Clean Code | C++ |
|
1st-and-2nd-operation-combination-clean-xbcee
|
Code\n\nclass Solution {\npublic:\n int minOperations(int k) {\n if (k == 1)\n return 0;\n \n int cnt = INT_MAX;\n int
|
Antim_Sankalp
|
NORMAL
|
2024-03-24T06:53:39.796061+00:00
|
2024-03-24T06:53:39.796088+00:00
| 401 | false |
# Code\n```\nclass Solution {\npublic:\n int minOperations(int k) {\n if (k == 1)\n return 0;\n \n int cnt = INT_MAX;\n int num = 1;\n \n while (num <= k)\n {\n cnt = min(cnt, static_cast<int>(ceil(static_cast<double>(k) / num)) - 1 + (num - 1));\n num++;\n }\n return cnt;\n }\n};\n```
| 2 | 0 |
['C++']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
Beats 100% ,C++ easy Maths Solution.
|
beats-100-c-easy-maths-solution-by-adity-g9z7
|
Intuition\nTo use Maths to get the solution. The use of division felt easy. Just by dividing we have to think about increment. \n\n# Approach\nIncrement = i-1\
|
adityamohanbhosale123
|
NORMAL
|
2024-03-24T04:59:26.350255+00:00
|
2024-03-24T04:59:26.350277+00:00
| 428 | false |
# Intuition\nTo use Maths to get the solution. The use of division felt easy. Just by dividing we have to think about increment. \n\n# Approach\nIncrement = i-1\nDuplicates= (K/i)\nAnswer =Increment + Duplicates\nBut we have to look if remainder is present then, \nDuplicates=(K/i)+1\nThen we maintain Soluton variable to store the minimum operations to get the solution.\n# Complexity\n- Time complexity: O(n)\n- Can be better is we perform Binary Search.\n\n- Space complexity: O(1)\n\n# Code\n```\nclass Solution {\npublic:\n int minOperations(int k) \n {\n int su=1e9;\n int i=1;\n if(i==k)\n {\n return 0;\n }\n while(i<k)\n {\n int an=i-1;\n if(k%i==0)\n {\n an=an+(k/i)-1;\n }\n else \n {\n an=an+(k/i);\n }\n if(su>an)\n {\n su=an;\n }\n \n i++;\n \n } \n return su;\n }\n};\n```
| 2 | 0 |
['C++']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
Mathematic approach. Beats 100%. Python 3
|
mathematic-approach-beats-100-python-3-b-x70v
|
Intuition\n Describe your first thoughts on how to solve this problem. \nTry to brute force then realize the mathematic pattern\n\n# Approach\n Describe your ap
|
datluu
|
NORMAL
|
2024-03-24T04:58:39.991491+00:00
|
2024-03-24T04:58:39.991519+00:00
| 42 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTry to brute force then realize the mathematic pattern\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- Each step calculate maximum possible number we can get\n- For step i. It would span options of x * (i+2-x). let me visualize:\n\n# Example:\n- Step 0: 1.\n- Step 1 options: \n - [1 1] = 1 * 2\n - [2] = 2 * 1\n - Possible sum: 1x2, 2x1. Max = 2x1\n- Step 2 max options:\n - [1, 1, 1]. Sum = 1 * 3\n - [2, 2]. Sum = 2 * 2\n - [3]. Sum = 3 * 1\n - Possible sum: 1x3, 2x2, 3x1\n - [1, 2]. This option would definately eliminated. Because we can proved that increase maximum number by 1 smaller than duplicate (maximum number - 1)\n- Step 3 options after eliminated:\n - [1, 1, 1, 1]\n - [2, 2, 2]\n - [3, 3]\n - [4]\n - Possible sum: 1x4, 2x3, 3x2, 4x1\n- Step 4 options after eliminated:\n - [1, 1, 1, 1, 1]\n - [2, 2, 2, 2]\n - [3, 3, 3]\n - [4, 4]\n - [5]\n - Possible sum: 1x5, 2x4, 3x4, 4x2, 5x1\n\n# Pattern realize\nSo for each step `ith` I have options of sum spanning from:\n- 1 x (i+1)\n- 2 x (i)\n- 3 x (i-1)\n- ...\n\nThe maximum multiple result at step `ith` is:\n- max_n = i + 2\n- if max_n is even: max_reach_of_step_i = (max_n // 2) ^ 2\n- if max_n is odd: max_reach_of_step_i = (max_n // 2) * (max_n // 2 - 1)\n\n# Code\n```\nclass Solution:\n def minOperations(self, k: int) -> int:\n step = 0\n while True:\n max_n = step+2\n max_reach_of_step_i = max_n // 2 * (max_n // 2 + 1) if max_n % 2 else (max_n//2) ** 2\n if max_reach_of_step_i >= k: return step\n step += 1\n return step \n```
| 2 | 0 |
['Python3']
| 1 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
Easy to Understand O(k) -> O(1) Solution
|
easy-to-understand-ok-o1-solution-by-frv-7jqj
|
Solution 1 (Greedy)\nNot the fastest, but it works. \n\nUses the fact that we always increment (operation 1) before any duplications (operation 2) inorder to ma
|
frvnk
|
NORMAL
|
2024-03-24T04:49:06.105433+00:00
|
2024-03-24T05:53:54.982084+00:00
| 211 | false |
# Solution 1 (Greedy)\nNot the fastest, but it works. \n\nUses the fact that we always **increment** (operation 1) before any **duplications** (operation 2) inorder to maximize the total sum of our array.\n\nRuntime: $O(n)$\nSpace: $O(1)$\n\nIncrement $i$ times, value of array then $[i+1]$\nTakes $\\lceil\\frac{k}{i+1}\\rceil-1$ duplications to get sum over $k$\n## Code\n```\nclass Solution {\npublic:\n int minOperations(int k) {\n //greedy approach, always increment first then duplicate\n int res = INT_MAX;\n \n // i number of increments\n for(int i = 0; i < k; i++){\n int curr = i+ ceil(k/(i+1.0))-1;\n res = min(curr, res);\n }\n return res;\n }\n};\n```\n# Solution 2 (Constant Time)\nUsing the previous solution, one may observe that the optimal $i$ is always $i = \\lceil\\sqrt{k}\\rceil -1$\n\nRuntime: $O(1)$\nSpace: $O(1)$\n\n## Code\n```\nclass Solution {\npublic:\n int minOperations(int k) {\n int i = ceil(sqrt(k))-1;\n return i + ceil(k/(i+1.0))-1;\n }\n};\n```\n\n\n
| 2 | 0 |
['C++']
| 1 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
✅ Java Solution | Easy to understand
|
java-solution-easy-to-understand-by-hars-5q97
|
CODE\nJava []\npublic int minOperations(int k) {\n\tint min = k-1, sqrt=(int)Math.sqrt(k);\n\tfor(int i=2; i <= sqrt; i++){\n\t\tint div = k/i;\n\t\tif(k%i != 0
|
Harsh__005
|
NORMAL
|
2024-03-24T04:15:22.690019+00:00
|
2024-03-24T04:15:22.690046+00:00
| 348 | false |
## **CODE**\n```Java []\npublic int minOperations(int k) {\n\tint min = k-1, sqrt=(int)Math.sqrt(k);\n\tfor(int i=2; i <= sqrt; i++){\n\t\tint div = k/i;\n\t\tif(k%i != 0) div++;\n\n\t\tint curr = i-1 + div - 1;\n\t\tmin = Math.min(curr, min);\n\t}\n\treturn min;\n}\n```
| 2 | 0 |
['Java']
| 1 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
Easiest 5 ways in C++ / Python3 / Java / C / Python / C# -- Beats 100%
|
easiest-5-ways-in-c-python3-java-c-pytho-15hm
|
Intuition\n\n\n\n\nC++ []\nclass Solution {\npublic:\n int minOperations(int k) {\n int res = INT_MAX;\n for (int i = 0; i <= k; i++)\n
|
Edwards310
|
NORMAL
|
2024-03-24T04:15:11.165770+00:00
|
2024-03-24T04:55:35.258134+00:00
| 64 | false |
# Intuition\n\n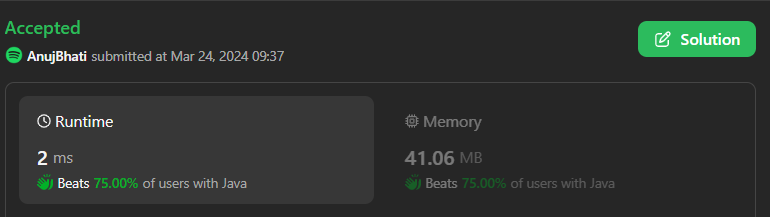\n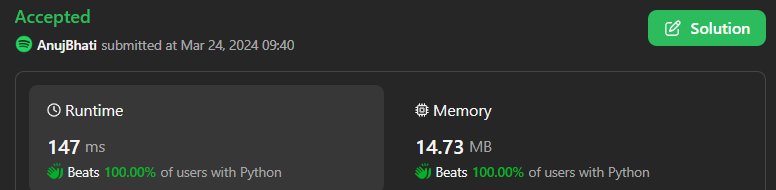\n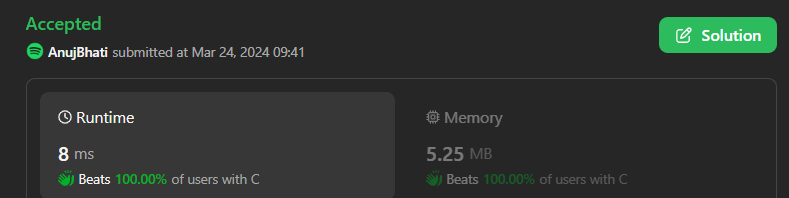\n```C++ []\nclass Solution {\npublic:\n int minOperations(int k) {\n int res = INT_MAX;\n for (int i = 0; i <= k; i++)\n res = min(res, (k + i) / (i + 1) - 1 + i);\n \n return res;\n }\n};\n```\n```python3 []\nclass Solution:\n def minOperations(self, k: int) -> int:\n ans = k + 1\n for u in range(1, k + 1):\n ans = min(ans, u - 1 + (k + u - 1) // u - 1)\n return ans\n```\n```C []\nint minOperations(int k) {\n int res = INT_MAX;\n for (int i = 0; i <= k; i++)\n res = fmin(res, (k + i) / (i + 1) - 1 + i);\n\n return res;\n}\n```\n```java []\nclass Solution {\n public int minOperations(int k) {\n int max = k - 1;\n for (int i = (int) Math.sqrt(k); i >= 1; i--) {\n int sum = 1;\n int cnt = i - 1;\n sum += i - 1;\n while (sum < k) {\n sum += i;\n cnt++;\n }\n max = Math.min(max, cnt);\n\n }\n return max;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int minOperations(int k) {\n int m = sqrt(k);\n return m - 1 + (k - 1) / m;\n }\n};\n```\n```python []\nclass Solution(object):\n def minOperations(self, k):\n """\n :type k: int\n :rtype: int\n """\n ans = k + 1\n for u in range(1, k + 1):\n ans = min(ans, u - 1 + (k + u - 1) // u - 1)\n return ans\n```\n```C# []\npublic class Solution {\n public int MinOperations(int k) {\n int res = k;\n for (int i = 1; i * i <= k; i++) {\n int count = (k - 1) / i + 1;\n res = Math.Min(res, i - 1 + count - 1);\n }\n return res;\n }\n}\n```\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(Sqrt(n))\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(1)\n# Code\n```\nint minOperations(int k) {\n int res = INT_MAX;\n for (int i = 0; i <= k; i++)\n res = fmin(res, (k + i) / (i + 1) - 1 + i);\n\n return res;\n}\n```\n# Please upvote if it\'s useful for you..\n\n
| 2 | 0 |
['C', 'Python', 'C++', 'Java', 'Python3', 'C#']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
C++ binary search
|
c-binary-search-by-wufengxuan1230-01j2
|
\nclass Solution {\npublic:\n int minOperations(int k) {\n int l = 0, r = k;\n auto check = [&](int m) {\n for (int i = 0; i <= m; +
|
wufengxuan1230
|
NORMAL
|
2024-03-24T04:07:58.602309+00:00
|
2024-03-24T04:08:06.654961+00:00
| 79 | false |
```\nclass Solution {\npublic:\n int minOperations(int k) {\n int l = 0, r = k;\n auto check = [&](int m) {\n for (int i = 0; i <= m; ++i) {\n if ((1 + i) * (m - i + 1) >= k) {\n return true;\n }\n }\n return false;\n };\n \n \n while (l < r) {\n int m = l + (r - l) / 2;\n if (!check(m)) {\n l = m + 1;\n } else {\n r = m;\n }\n }\n return l;\n }\n};\n```
| 2 | 0 |
[]
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
🔥O(1) SC || ✅Easy MAth⚡ || 🌟Greedy
|
o1-sc-easy-math-greedy-by-adish_21-i6me
|
\n\n# Complexity\n\n- Time complexity:\nO(k)\n\n- Space complexity:\nO(1)\n\n\n# Code\n## PLease Upvote if it helps\uD83E\uDD17\n\nclass Solution {\npublic:\n
|
aDish_21
|
NORMAL
|
2024-03-24T04:02:19.289536+00:00
|
2024-03-24T05:13:38.843523+00:00
| 497 | false |
\n\n# Complexity\n```\n- Time complexity:\nO(k)\n\n- Space complexity:\nO(1)\n```\n\n# Code\n## PLease Upvote if it helps\uD83E\uDD17\n```\nclass Solution {\npublic:\n int minOperations(int k) {\n if(k == 1)\n return 0;\n int mini = INT_MAX;\n for(int i = 1 ; i < k ; i++){\n int diff = i - 1, diff2 = k - i, tmp = diff2 % i;\n mini = min(mini, diff + diff2 / i + (tmp ? 1 : 0));\n }\n return mini;\n }\n};\n```
| 2 | 0 |
['Math', 'Greedy', 'C++']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
C++ 100% Faster | Basic Mathematics | Easy Step By Step Explanation
|
c-100-faster-basic-mathematics-easy-step-fg0r
|
Intuition\nThe problem asks for the minimum number of operations to make the sum of an array with an initial value of 1 greater than or equal to k. We can think
|
VYOM_GOYAL
|
NORMAL
|
2024-03-24T04:01:47.020280+00:00
|
2024-03-24T04:01:47.020300+00:00
| 243 | false |
# Intuition\nThe problem asks for the minimum number of operations to make the sum of an array with an initial value of 1 greater than or equal to k. We can think of building the sum by increasing the first element and duplicating it. Since increasing by 1 is a single operation, we want to minimize the number of duplications needed. Thisa suggests exploring divisors of k as potential building blocks.\n\n# Approach\n1. **Handle Base Case:** If k is already 1, no operations are needed, so return 0.\n\n2. **Initialize Minimum Operations:** Set ans to INT_MAX to track the minimum number of operations found so far.\n\n3. **Iterate Through Divisors:** \n - Loop through potential divisors (i) from 1 to a large limit (e.g., 100000).\n - Check if i divides k using the modulo operator (%).\n \n4. **Calculate Operations for Divisor:**\n - If i divides k perfectly:\n - cnt starts with i - 1 (operations to increase the first element to i-1).\n - Add (k / i) - 1 to cnt for duplicating (k/i) times (excluding the first element).\n - If i doesn\'t divide k perfectly:\n - Add (k / i) + 1 - 1 to cnt for duplicating (k/i+1) times (excluding the first element).\n \n5. **Update Minimum:** Compare the calculated cnt with the current ans. If cnt is smaller, update ans as the new minimum number of operations.\n \n6. **Return Minimum Operations:** After iterating through all divisors, return the final value of ans, which represents the minimum number of operations required.\n\n# Complexity\n- Time complexity: **O(k)**\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: **O(1)**\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n#pragma GCC optimize("03", "unroll-loops")\nclass Solution {\npublic:\n int minOperations(int k) {\n if (k == 1) {\n return 0;\n } else {\n int ans = INT_MAX;\n for (int i = 1; i < 100000; i++) {\n int cnt = (i - 1);\n if (k % i == 0) {\n cnt += ((k / i) - 1);\n } else {\n cnt += ((k / i) + 1) - 1;\n }\n ans = min(ans, cnt);\n }\n return ans;\n }\n return 0;\n }\n};\nauto init = []() {\n ios::sync_with_stdio(false);\n cin.tie(nullptr);\n cout.tie(nullptr);\n return \'c\';\n}();\n```\n\n\n
| 2 | 0 |
['Math', 'C++']
| 1 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
math ^^
|
math-by-andrii_khlevniuk-gnok
|
I misread the description and mised the fact that "the final array should be greater than or equal to k" and assumed that "the final array should be equal to k.
|
andrii_khlevniuk
|
NORMAL
|
2024-08-29T21:19:06.616532+00:00
|
2024-08-30T00:53:58.242936+00:00
| 3 | false |
I misread the description and mised the fact that "the final array should be **greater** than or equal to k" and assumed that "the final array should be **equal** to k. But it turned out that the solutions of these two slightly different problems are the same!\n\n```\nint minOperations(int k) \n{\n\treturn ceil(2*sqrt(k))-2; // return sqrt(4*k-3)-1;\n}\n```\n\n**Explanation:**\n\nEvery number can be expressed as `k = x + y + z^2` where `x <= y <= z`. \nThis is true because there are `2*z` numbers between `(z+1)` and `z` and `2*z` can be expressed as `x+y` where `x<=z` and `y<=z`.\n* If `x=0` and `y=0` we have the following optimal pathway\n```\n 1 2 3 ... z zz zzz ... z..z\n// 1 2 z-1 1 2 z-1 #operations = 2*(z-1) = 2*z-2 = 2*floor(sqrt(k))-2 \n```\n\nFor example 16=4^2\n```\n 1 2 3 4 44 444 4444 \n// 1 2 3 4 5 6 #operations = 2*4-2 = 6\n```\n\n\n* If `x=0` and `y!=0` we have the following optimal pathway\n```\n 1 2 3 ... y yy ... yz yzz yzzz ... yz..z\n// 1 2 z 1 2 z-1 #operations = z+z-1 = 2*z-1 = 2*floor(sqrt(k))-1 \n```\n\nFor example 11=2+4^2\n```\n 1 2 22 23 24 244 2444 244444\n// 1 2 3 4 5 6 7 #operations = 2*4-1 = 7\n```\n\n* If `x!=0` and `y!=0` we have the following optimal pathway\n```\n 1 2 3 ... x xx ... xy xyy ... xyz xyzz xyzzz ... xyz..z\n// 1 2 z+1 1 2 z-1 #operations = z+1+z-1 = 2*z = 2*floor(sqrt(k)) \n```\n\nFor example 22=2+4+4^2\n```\n 1 2 22 23 24 244 2444 24444 244444\n// 1 2 3 4 5 6 7 8 #operations = 2*4 = 8\n```\n\nAll these cases\n* `2*floor(sqrt(k))-2` iff `k = z^2`\n* `2*floor(sqrt(k))-1` iff `k = y + z^2` \n* `2*floor(sqrt(k))` iff `k = x + y + z^2` \n\ncan be summarised in a formula `ceil(2*sqrt(k))-2`\n\n**Pattern:**\n```\n k res optimal path \n// 1 0 \n\n// 2 1 \n\n// 3 2 1 11 12\n// 4 2 1 2 22\n \n// 5 3 1 11 12 122 \n// 6 3 1 2 22 222\n\n// 7 4 1 11 12 122 1222 or 1 2 22 23 223 \n// 8 4 1 2 22 222 2222\n// 9 4 1 2 3 33 333\n\n// 10 5 1 2 22 222 2222 22222 \n// 11 5 1 2 22 23 233 2333 \n// 12 5 1 2 3 33 333 3333 \n```\nSo the pattern is `0,1,2,2,3,3,4,4,4,5,5,5...`. This is [A055086](https://oeis.org/search?q=0%2C1%2C2%2C2%2C3%2C3%2C4%2C4%2C4%2C5%2C5%2C5&language=english&go=Search).
| 1 | 0 |
['C', 'C++']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
Easy Solution | Beats 100 % | Explanation
|
easy-solution-beats-100-explanation-by-k-slct
|
Approach\n Describe your approach to solving the problem. \nGreedy\n# Complexity\n- Time complexity:O(n)\n Add your time complexity here, e.g. O(n) \n\n- Space
|
kmuhammadjon
|
NORMAL
|
2024-04-22T06:58:03.240773+00:00
|
2024-04-22T06:58:03.240799+00:00
| 28 | false |
# Approach\n<!-- Describe your approach to solving the problem. -->\nGreedy\n# Complexity\n- Time complexity:O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfunc minOperations(k int) int {\n if k == 1{\n return 0\n }\n minNumberOfOperations := math.MaxInt64\n current := 1\n\n for current <= k / 2{\n // you dont have to use array just one variable and\n // increment it and by deviding you can calculate \n // how many times you have to append\n current++\n operations := (k / current ) + current \n if k % current == 0{\n operations--\n }\n if minNumberOfOperations > operations{\n minNumberOfOperations = operations\n }\n }\n\n \n return minNumberOfOperations - 1\n}\n```
| 1 | 0 |
['Math', 'Greedy', 'Enumeration', 'Go']
| 1 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
Easest Solution with Greedy Approach || Beats 100 % of users
|
easest-solution-with-greedy-approach-bea-zgtb
|
Approach\n Describe your approach to solving the problem. \nGreedy approach\n# Complexity\n- Time complexity:O(n)\n Add your time complexity here, e.g. O(n) \n\
|
Saidakbar_Zokirovich
|
NORMAL
|
2024-04-22T06:57:01.033711+00:00
|
2024-04-22T06:57:01.033737+00:00
| 30 | false |
# Approach\n<!-- Describe your approach to solving the problem. -->\nGreedy approach\n# Complexity\n- Time complexity:O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfunc minOperations(k int) int {\n number := 1\n numberOfOperations := math.MaxInt64\n \n if number >= k {\n return 0\n }\n\n CurrentNumberOfOperations := 0\n for number <= k {\n add := 0\n if k % number > 0 {\n add++\n }\n numberOfOperations = min(numberOfOperations, CurrentNumberOfOperations + k / number + add)\n CurrentNumberOfOperations++\n number++\n }\n return numberOfOperations-1\n}\n```
| 1 | 0 |
['Greedy', 'Go']
| 1 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
The Shortest Possible Mathematical Approach
|
the-shortest-possible-mathematical-appro-67vg
|
Intuition\nMagic math formula according to hints\n\n# Code\n\nvar minOperations = (k, x = k ** 0.5 | 0) => Math.ceil(k / x) + x - 2;\n
|
charnavoki
|
NORMAL
|
2024-03-31T14:56:44.876297+00:00
|
2024-03-31T14:56:44.876319+00:00
| 14 | false |
# Intuition\nMagic math formula according to hints\n\n# Code\n```\nvar minOperations = (k, x = k ** 0.5 | 0) => Math.ceil(k / x) + x - 2;\n```
| 1 | 0 |
['JavaScript']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
Easy C++ Solution || (3 line)✅✅
|
easy-c-solution-3-line-by-abhi242-2hpl
|
Code\n\nclass Solution {\npublic:\n int minOperations(int k) {\n int i=1;\n int ans=INT_MAX;\n while(i<=k){\n ans=min(ans,(in
|
Abhi242
|
NORMAL
|
2024-03-26T12:58:52.705572+00:00
|
2024-03-26T12:58:52.705596+00:00
| 34 | false |
# Code\n```\nclass Solution {\npublic:\n int minOperations(int k) {\n int i=1;\n int ans=INT_MAX;\n while(i<=k){\n ans=min(ans,(int)(i+ceil(k*1.0/i)-2));\n i++;\n }\n return ans;\n }\n};\n```
| 1 | 0 |
['C++']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
C++ / Beats 100%
|
c-beats-100-by-ak200199-qvkl
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
AK200199
|
NORMAL
|
2024-03-25T18:24:07.960874+00:00
|
2024-03-25T18:24:07.960908+00:00
| 5 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int minOperations(int k) {\n int mini=INT_MAX;\n for(int i=1;i<=k;i++){\n int curr=0;\n if(k%i==0)curr=(k/i)-1;\n else curr=k/i;\n mini=min(mini,i-1+curr);\n }\n return mini;\n }\n};\n```
| 1 | 0 |
['C++']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
Easy to Understand , Simple Mathematics
|
easy-to-understand-simple-mathematics-by-epi0
|
Intuition\nIn this problem, we aim to find the minimum number of operations required to form a sum just greater than or equal to k. We increment the value by 1
|
polisettys3
|
NORMAL
|
2024-03-24T20:49:27.094929+00:00
|
2024-03-24T20:49:27.094958+00:00
| 2 | false |
# Intuition\nIn this problem, we aim to find the minimum number of operations required to form a sum just greater than or equal to k. We increment the value by 1 and then make multiples of it, checking the sum at each step. By tracking the number of steps taken to reach k, we determine the minimum operations required.\n\n# Approach\nWe use a variable crr to keep track of our newly formed number. Initially, we set crr to 1. Then, for each step, we increment the value of crr by 1 and divide k by crr. This gives us the number of steps i needed to increase the number. We also calculate ceil(k / crr), which represents the number of times we need to repeat the current number to reach or exceed k. Finally, we decrement the answer by 1 because there\'s already one occurrence of the number present.\n\nFor example, consider the test case where k = 11. To make the number as 4, we took 3 operations. Now, ceil(11/4) is 3, which means three 4\'s are required. Since we already have one of those 4\'s in the array, we need only 2 more, making the final answer as 5. Therefore, I decremented the value by 1 at the end to obtain the correct answer.\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution {\npublic:\n int minOperations(int k) {\n int crr = 1;\n int ans = INT_MAX;\n for(int i = 0 ; i <= k ; i++){\n ans = min(ans, i + static_cast<int>(ceil(double(k) / (crr + i))));\n }\n return ans - 1;\n }\n};\n```
| 1 | 0 |
['Math', 'C++']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
Easy greedy approach in python3
|
easy-greedy-approach-in-python3-by-alexx-eiyg
|
Intuition\ngreedy + math\n Describe your first thoughts on how to solve this problem. \n\n# Approach\nFirstly create a variable named toReach.\nThis variable wi
|
alexx290713
|
NORMAL
|
2024-03-24T18:11:22.690308+00:00
|
2024-03-24T18:11:22.690353+00:00
| 109 | false |
# Intuition\ngreedy + math\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nFirstly create a variable named toReach.\nThis variable will store the square root value of k and it will tell the number of time you have to add 1 to the array.\nThen reduce that value from k as you have reached square root of that value.\nNow you just have to count the number of time you have to duplicate the toReach number to reach the remaining k.\nFor this use dupli variable where you apply floor division.\nIf k is perfectly divisible by toReach (remainder = 0) then reduce 1 from dupli.\nNow just add toReach and dupli to get the answer\n \n\n# Complexity\n- Time complexity:O(1)\n<!-- O(1) -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minOperations(self, k: int) -> int:\n toReach = math.ceil(sqrt(k))\n k = k - toReach\n dupli = int(k/toReach)\n if k%toReach == 0:\n return toReach + dupli -1\n return toReach +dupli\n\n```
| 1 | 0 |
['Math', 'Greedy', 'Python3']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
Beats 100% | Intuitive and Simple math is all you need | Mathematics way
|
beats-100-intuitive-and-simple-math-is-a-ahf2
|
Best Solution\n\n Describe your first thoughts on how to solve this problem. \n\n# Intuition\nFor every increment in number of operations, we are trying to find
|
K-Shashank
|
NORMAL
|
2024-03-24T18:10:27.224624+00:00
|
2024-03-24T18:10:27.224645+00:00
| 58 | false |
# Best Solution\n\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Intuition\nFor every increment in number of operations, we are trying to find which one yields best result: increase one value or duplicate a value. Whichever is better we try to do that and accordingly update for the next computation. Whenever the max possibe value for the number of operations exceed the given value \'k\', we will return that as an optimal number of operations required. \n\n# Complexity\n- Time complexity: O(k)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minOperations(self, k: int) -> int:\n if k<=1:\n return 0\n if k==3 or k==4:\n return 2\n if k==2:\n return 1\n \n a = 2\n b = 1\n curr = 4\n op = 2\n while curr<k:\n if (a+1)*b >= a*(b+1):\n curr = (a+1)*b\n a = a+1\n else:\n curr = a*(b+1)\n b = b+1\n op += 1\n op -= 1\n return op\n \n \n \n \n```
| 1 | 0 |
['Python3']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
Easy to Understand || C++
|
easy-to-understand-c-by-sumitsaurabh20-c9n2
|
\n\n# Code\n\nclass Solution {\npublic:\n int minOperations(int k) {\n int ans=k;\n for(int i=0;i<=k;i++){\n int sum=1+i;\n
|
sumitsaurabh20
|
NORMAL
|
2024-03-24T14:22:49.347410+00:00
|
2024-03-24T14:22:49.347427+00:00
| 33 | false |
\n\n# Code\n```\nclass Solution {\npublic:\n int minOperations(int k) {\n int ans=k;\n for(int i=0;i<=k;i++){\n int sum=1+i;\n int left=k-sum;\n int dup=ceil((double)left/sum);\n ans=min(ans,dup+i);\n }\n return ans;\n }\n};\n```
| 1 | 0 |
['C++']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
Solved using Binary Search
|
solved-using-binary-search-by-krishna_13-tqwf
|
Intuition\nBinary Search on answers \n\n\n# Code\n\n//Bineary Search solution : with slight better time complexity\nclass Solution {\n public int minOperatio
|
krishna_1307
|
NORMAL
|
2024-03-24T10:53:00.471275+00:00
|
2024-03-24T10:53:00.471296+00:00
| 81 | false |
# Intuition\nBinary Search on answers \n\n\n# Code\n```\n//Bineary Search solution : with slight better time complexity\nclass Solution {\n public int minOperations(int k) {\n if (k == 1)\n return 0;\n int low = 0, high = k;\n int ans = 0;\n while (low <= high) {\n int mid = (low + high) / 2;\n if (isPossible(mid, k)) {\n ans = mid;\n high = mid - 1;\n } else\n low = mid + 1;\n }\n return ans;\n }\n public boolean isPossible(int maxOperation, int k) {\n int sum=0;\n for(int m=1 ;m<=maxOperation;m++){\n int noofDuplicates=maxOperation - (m - 1);\n sum=(noofDuplicates+1)*m;\n if(sum>=k)return true;\n }\n \n return false;\n }\n}\n// public boolean isPossible(int maxOperation, int k) {\n// int increment = 0;\n// while (increment <= maxOperation) {\n// int maxNum = increment + 1;\n// int remaining = maxOperation - increment;\n// int sum = maxNum * (remaining + 1);\n// if (sum >= k)\n// return true;\n// increment++;\n// }\n// return false;\n// }\n// }\n\n// class Solution {\n// public int minOperations(int k) { \n// if(k==1) return 0;\n// int op=Integer.MAX_VALUE;\n// int operations=0;\n// for(int m=1;m<=k;m++){\n// operations= m - 1 + (int)Math.ceil((double)k/m)-1;//first do m increments then duplicate the no \'m\' k/m times \n// //as we already have 1(\'m\' after increment) we subtract by 1\n// // also it is m-1 because intially it is given the elemrnt in nums to be 1 \n// //so from 1 to m it takes m-1 increments\n// op=Math.min(op,operations);\n// }\n// return op;\n// }\n\n// }\n```
| 1 | 0 |
['Binary Search', 'Java']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
Kotlin O(1) math solution
|
kotlin-o1-math-solution-by-chayangkoon-ayz5
|
\n\n# Complexity\n- Time complexity:\nO(1)\n\n- Space complexity:\nO(1)\n\n# Code\n\nclass Solution {\n fun minOperations(k: Int): Int {\n if(k == 1)
|
chayangkoon
|
NORMAL
|
2024-03-24T10:50:07.921841+00:00
|
2024-03-24T10:50:07.921867+00:00
| 7 | false |
\n\n# Complexity\n- Time complexity:\nO(1)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution {\n fun minOperations(k: Int): Int {\n if(k == 1) return 0\n val squareRootOfK = floor(sqrt(k.toDouble())).toInt()\n val increaseTime = (k / squareRootOfK) - 1\n val duplicateTime = squareRootOfK - 1\n val addtional = if(k % squareRootOfK != 0) 1 else 0\n return increaseTime + duplicateTime + addtional\n }\n}\n```
| 1 | 0 |
['Kotlin']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
Easy Math Solution || C++ || Beats 100%
|
easy-math-solution-c-beats-100-by-ryuzak-jsdc
|
Intuition\nThe general idea is to notice that the solution will always be off the format --> \n\n"add 1 to [1] n times" + "add n to [n] to (k/n) times"\n\nThere
|
Ryuzakiiii
|
NORMAL
|
2024-03-24T09:58:11.816369+00:00
|
2024-03-24T09:58:11.816408+00:00
| 4 | false |
# Intuition\nThe general idea is to notice that the solution will always be off the format --> \n\n`"add 1 to [1] n times" + "add n to [n] to (k/n) times"`\n\nTherefore, the number of operations required with this kind of format can be written as a function of f(n) as follows : \n`f(n) = (k/n) + n`\n\nTo find the minimum value of the function f(n), we can differentiate this function with respect to n, and that gives us : \n\n`f\'(n) = -k/n^2 + 1 = 0` (Because to achieve minima the derivative has to be zero)\n\nUpon solving the above equation we get : \n\n```n^2 = k --> n = sqrt(k)```\n\nTherefore, upon substituting this back into our original equation : \n\nminimum operations = ```f(sqrt(k)) = k/sqrt(k) + sqrt(k)```\n\nHowever, there are two things to keep in mind : \n1. We have to subtract one from each of k/sqrt(k) and sqrt(k) because we are starting from 1 and adding upto to n will take up `n-1 operations`.\n2. Since, our aim is to get a final value greater than equal to k, we perform `ceil function` on `k/sqrt(k)`\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Complexity\n- Time complexity: O(1)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int minOperations(int k) {\n if(k==1)\n return 0;\n int temp = sqrt(k),num = ceil(k/(double)temp);\n return temp + num - 2;\n }\n};\n```
| 1 | 0 |
['Math', 'C++']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
beats 100% || Best Solution
|
beats-100-best-solution-by-procodingskil-6sbb
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
procodingskills
|
NORMAL
|
2024-03-24T09:24:04.029524+00:00
|
2024-03-24T09:24:04.029554+00:00
| 90 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\nO(k)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution {\npublic:\n int minOperations(int k) {\n int ans=INT_MAX;\n if(k==1)\n return 0;\n int oprs;\n for(int i=2;i<=k;i++){\n if(k%i==0)\n oprs=(k/i)-1;\n else\n oprs=(k/i);\n ans=min(ans,i-1+oprs);\n }\n return ans;\n }\n};\n```
| 1 | 0 |
['C++']
| 1 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
Easy Implementation base problem Solved in O(1) time and space
|
easy-implementation-base-problem-solved-9h63s
|
Intuition\nFirst I start with maximum possible answer and after that I tried to minimze it using min function \n\n# Approach\n Simple Observation based check co
|
saurabh_shashank7654
|
NORMAL
|
2024-03-24T09:01:50.543668+00:00
|
2024-03-24T09:01:50.543687+00:00
| 59 | false |
# Intuition\n**First I start with maximum possible answer and after that I tried to minimze it using min function** \n\n# Approach\n Simple Observation based check code I belive you all will get the logic eventually \n\n# Complexity\n- Time complexity:O(1)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int minOperations(int k) {\n int x=1;\n int y=0;\n int mini=INT_MAX;\n while(x<k)\n {\n x++;\n if(k%x==0)\n y=k/x;\n else \n y=(k/x)+1;\n \n mini=min(mini,(x-1)+(y-1));\n }\n if(k==1)return 0;\n return mini; \n }\n};\n```\nPing me if there is any need of more explanation
| 1 | 0 |
['C++']
| 1 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
✅Binary Search on Answer beats 100% 🔥
|
binary-search-on-answer-beats-100-by-rau-8wk5
|
\n\n---\n initialy, N=1\n let, one is added \'x\' times \n => N=1+x\n then duplicated \'y\' times\n => N = (1+x) + (1+x) * y\n => N = (1+x)(y+
|
raunak_1611
|
NORMAL
|
2024-03-24T08:52:44.172622+00:00
|
2024-03-26T15:27:58.451032+00:00
| 54 | false |
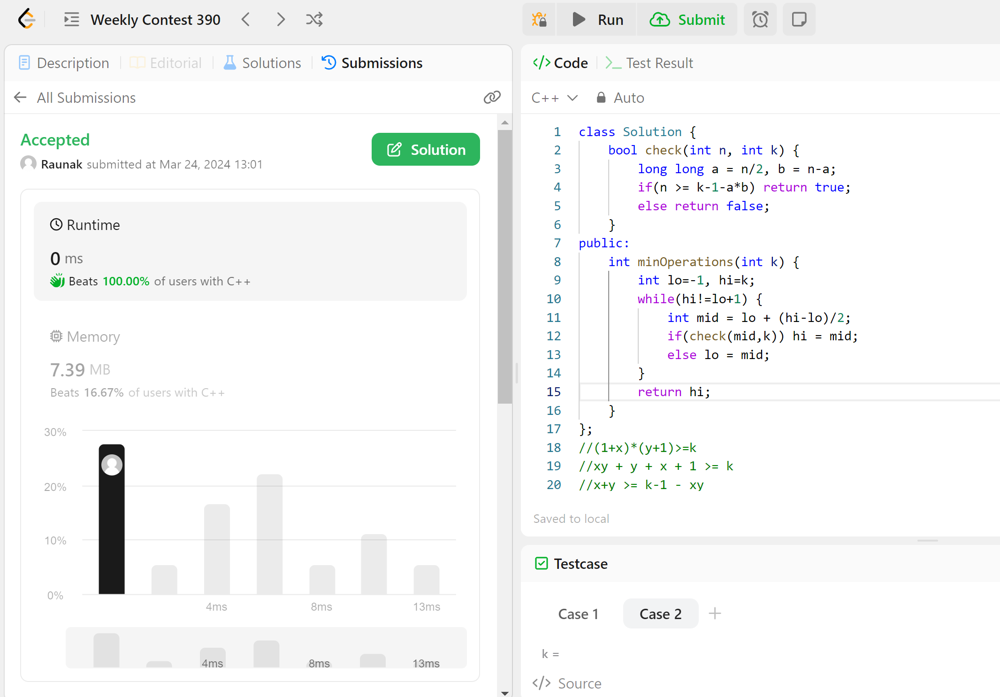\n\n---\n initialy, N=1\n let, one is added \'x\' times \n => N=1+x\n then duplicated \'y\' times\n => N = (1+x) + (1+x) * y\n => N = (1+x)(y+1)\n\n N >= k\n => (1+x)*(y+1)>=k\n => xy + y + x + 1 >= k\n => x+y >= k-1 - xy\n ->we will try every possible value of (x+y) from 0 to k and the first value where x+y >= k-1 - xy satisfies will be the answer\n ->but to minimise x+y, we should minimise the RHS or maximise xy\n ->if x+y = constant, for xy to maximum x and y should be as close as possible (half of (x+y), if (x+y) is even)\n \n---\n\n```C++ []\n# Linear Search\nclass Solution {\npublic:\n int minOperations(int k) {\n for(int i=0; i<=k; i++) {\n long long a = i/2, b = i-a;\n if(i>=k-1-a*b) return i;\n }\n return -1;\n }\n};\n```\n\n```C++ []\n# Binary Search\nclass Solution {\n bool check(int n, int k) {\n long long a = n/2, b = n-a;\n if(n >= k-1-a*b) return true;\n else return false;\n }\npublic:\n int minOperations(int k) {\n int lo = -1, hi = k;\n while(hi!=lo+1) {\n int mid = lo + (hi-lo)/2;\n if(check(mid,k)) hi = mid;\n else lo = mid;\n }\n return hi;\n }\n};\n\n```\n---\n
| 1 | 0 |
['Math', 'Binary Search', 'C++']
| 1 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
Easy Java Solution || T.C = O(1) || Beats 100%
|
easy-java-solution-tc-o1-beats-100-by-ra-ciyx
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
ravikumar50
|
NORMAL
|
2024-03-24T08:28:46.914633+00:00
|
2024-03-24T08:28:46.914653+00:00
| 21 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int minOperations(int k) {\n int x = (int)Math.ceil(Math.sqrt(k))-1;\n int ans = x + (int)Math.ceil((k-x-1)/(double)(x+1));\n return ans;\n }\n}\n```
| 1 | 0 |
['Java']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
Python 3 solution based on Inequality
|
python-3-solution-based-on-inequality-by-pwet
|
Intuition\n\nDenote we need to make the \'add\' operation \'a\' times, and \'duplicate\' operation for \'b\'. We want to calculate the minmiun result for \'a+b\
|
dliu5812
|
NORMAL
|
2024-03-24T07:24:16.572295+00:00
|
2024-03-24T07:24:16.572318+00:00
| 86 | false |
# Intuition\n\nDenote we need to make the \'add\' operation \'a\' times, and \'duplicate\' operation for \'b\'. We want to calculate the minmiun result for \'a+b\', which meets the requirement:\n\n(1+a) * (1+b) >= k\n\n# Approach\n\nFor (1+a) * (1+b) >= k, we modify it as:\n\n(a+b)* (a+b) / 4 + (a+b) >= ab + (a+b) >= k - 1\n\nDenote \'a+b\' as x, we have:\n\nx >= 2 * sqrt(k) - 2\n\nWe denote res = 2 * sqrt(x) - 2, if x is the square of some int, then the result should be res, otherwise, the result is int(res)+1. \n\n\n# Complexity\n- Time complexity:\nO(log k). We will use the binary search to decide if k is the square of some int.\n\n- Space complexity:\nO(1). We do not use any extra spaces.\n\n# Code\n```\nclass Solution:\n def minOperations(self, k: int) -> int:\n \n \n res = int(2 * sqrt(k) - 2)\n \n return res if self.issquare(k) else res + 1\n \n \n def issquare(self, k):\n \n if k == 1: return True\n \n left = 1\n right = k // 2\n \n while left <= right:\n mid = left + (right-left)//2\n if mid * mid > k:\n right = mid - 1\n elif mid * mid < k:\n left = mid + 1\n else:\n return True\n \n return False\n \n \n```
| 1 | 0 |
['Python3']
| 1 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
JAVA | BINARY SEARCH | OPTIMAL
|
java-binary-search-optimal-by-priyadarsh-w9fn
|
Intuition:\nI couldn\'t solve this in today\'s contest, though got the intuiton half way. I have to find the minimum operations which give me the maximum output
|
Priyadarshi_codes
|
NORMAL
|
2024-03-24T07:19:40.831056+00:00
|
2024-03-24T07:24:45.981690+00:00
| 14 | false |
**Intuition**:\nI couldn\'t solve this in today\'s contest, though got the intuiton half way. I have to find the minimum operations which give me the maximum output closest to k. I may add on 1. And if I keep adding 1 till k, I get the maximum number of operations that lead me to k. But I am asked to find the minimum. If there is 1, number of operations is 0. So my operations lie in the range rom 0 to k. I perform a binary search on the number of operations. If I reach my target, I would reduce high to get the minimum, else I would increase low. \n\n**Approach**:\nIn the binary search, I send mid and k as a parameter to check whether the mid number of operations give me a value greater than or equal to k. For that, I run a loop from 1 to mid. This loop is the number of times I might add 1 with 1. So I add i+1. The remaining is mid-i+1. I multiply it with that to get the sum of number of times the i+1 is repeated. Eg. 2+2+2 would be 2*3. The resultant keeps increasing till I hit k or more: then I return true. Otherwise false. On receiving true, high is reduced to get the minimum operations. otherwise low is increased.\n\n\n```\n\npackage subset;\n\npublic class MinOoperationsMarchContest {\n\t\n\tpublic static boolean checkSum(int mid,int k) {\n\t\tlong res=1;\n\t\tfor(int i=0;i<=mid;i++) {\n\t\t\tres=(i+1)*(long)(mid-i+1);\n\t\t\tif(res>=k) return true;\n\t\t}\n\t\treturn false;\n\t}\n\t\n\tpublic static int minOpertions(int k) {\n\t\tif(k==1) return 0;\n\t\tint low=0,high=k;\n\t\twhile(low<=high) {\n\t\t\tint mid=low+(high-low)/2;\n\t\t\tboolean check=checkSum(mid,k);\n\t\t\tif(check) high=mid-1;\n\t\t\telse low=mid+1;\n\t\t}\n\t\treturn low;\n\t}\npublic static void main(String[] args) {\n\tSystem.out.println(minOpertions(3));\n}\n}\n```\n\n\n**Time** **Complexity**:\nO(log_2 K)for the binary search. O(K/2) for the checkSum(). Thus we have O(log_2 K)*(K/2). This is an important observation because running a loop of operations is importnat here. Any other way would not work. What I mean to say is that: the result increases till the middle then decreases, so you can\'t use formulations at the edge. Also, where exactly at the middle you get k or more, that you don\'t know. Formulations are difficult here at edge cases. So you can\'t avoid running a loop.\n\n**Space** **Complexity**:\nO(1)\n
| 1 | 0 |
['Binary Tree', 'Java']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
Python3 Solution
|
python3-solution-by-subhash_2004-word
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
subhash_2004
|
NORMAL
|
2024-03-24T06:57:33.205882+00:00
|
2024-03-24T06:57:33.205910+00:00
| 22 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minOperations(self, k: int) -> int:\n d=dict()\n for i in range(1,k+1):\n #d.values()->no.of times we need to increase value by one to reach i.\n d.update({i:i-1})\n for i in d.keys():\n #d.values()->adding no.of i\'s ,that are required to get sum>=k\n # but we already have one value of i in the list, so we need ceil(k/i)-1 i\'s \n # to reach sum >= k. \n d[i]+=(ceil(k/i)-1)\n print(d) \n return min(d.values())\n```
| 1 | 0 |
['Python3']
| 1 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
✅ C++ Solution ✅||🔥Greedy🔥|| With Approach
|
c-solution-greedy-with-approach-by-anshu-b8we
|
APPROACH\n Describe your approach to solving the problem. \n\n1. Number of 1\'s required to reach 1 to n equals to n-1\n2. Number of duplicate\'s required of a
|
anshumaan1024
|
NORMAL
|
2024-03-24T06:50:07.198782+00:00
|
2024-03-24T06:59:33.352830+00:00
| 69 | false |
# APPROACH\n<!-- Describe your approach to solving the problem. -->\n\n1. Number of ```1```\'s required to reach ```1``` to ```n``` equals to ```n-1```\n2. Number of duplicate\'s required of any given number ```n``` to make the sum of elements of the final array greater than or equal to ```k``` is equals to ```ceil(k/n)``` \n\n3. Total operations = ```(n-1) + ceil(k/n)```\n\n4. Try, for all value of ```n```, and store the minimum operations in ```ans``` \n5. Return ```ans```\n\n# COMPLEXITY\n- Time complexity: **O(k)**\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: **O(1)**\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# CODE\n```\nclass Solution {\npublic:\n int minOperations(int k) {\n\n if (k == 1)\n return 0;\n\n int ans = INT_MAX;\n for (int n = 1; n <= k; n++) {\n\n int t = ceil(float(k) / n);\n ans = min(ans, n - 1 + t - 1);\n }\n\n return ans;\n }\n};\n```
| 1 | 0 |
['Math', 'Greedy', 'C++', 'Java']
| 1 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
Easy C++ || O(k) time O(1) space beats 100% || In depth intuition and approach explained
|
easy-c-ok-time-o1-space-beats-100-in-dep-ipel
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\nStart by considering the minimum number of operations required to achieve the target
|
anubhavchawla02
|
NORMAL
|
2024-03-24T06:27:43.413007+00:00
|
2024-03-24T14:25:04.304167+00:00
| 28 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\nStart by considering the minimum number of operations required to achieve the target sum. Initially, set the number of operations to 0 and increment it gradually. At each step, determine the maximum sum that can be achieved with the current number of operations.\n\nAlso, the maximum sum can be achieved in minimum operations by:\n- Increasing the first `1` in the initial array to a certain number and then duplicating it.\n- For example, for k=4, the array formed is `[2,2]` which is made from the original array `[1]` by increasing the value of `1` to `2` and then duplicating the value, thus making the array `[2,2]` using 2 operations only. But it could also be made by first duplicating the `1` making the array `[1,1]` and then taking 2 more operations to increment the value of both `1\'s` to make the array `[2,2]`. This takes 3 operations.\n- Also, to achieve `k=4`, `[1,1,1,1]` can also be used, but again, it takes 3 operations.\n\nConsider the test case `k=24`.\nNow, let\'s start calculating the maximum sum of the array corresponding to the number of operations until the sum does not exceed or become equal to 24.\n\n| Number of Operations | Maximum Achievable Sum | Array formed |\n|----------------------|------------------------|--------------|\n| 0 | 1 | [1] |\n| 1 | 2 | [2] |\n| 2 | 4 | [2,2] |\n| 3 | 6 | [3,3] |\n| 4 | 9 | [3,3,3] |\n| 5 | 12 | [4,4,4] |\n| 6 | 16 | [4,4,4,4] |\n| 7 | 20 | [5,5,5,5] |\n| 8 | 25 | [5,5,5,5,5] |\n\nFrom this, it can be observed that from `Maximum Achievable sum=2` onwards, there is a pattern that is being followed. The Maximum Achievable sum increases by 2 for 2 iterations making it equal to 4 and then 6. Then it increments by 3 for 2 iterations making it equal to 9 and 12 and then it increments by 4 for 2 iterations and so on.\n\nSo, our task becomes simple, keep on calculating the maximum achievable sum, and when it becomes `>=k`, return the number of operations at that particular instance.\n\n---\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n- For `k==1` and `k==2`, we know that the answer is `0` and `1` respectively.\n- Now the variable `sum` is initialized with `2` and we take a variable `num=2` which denotes the number we add to the maximum achievable sum for 2 iterations and increment it by `1` after that. A variable `flag=2` is taken to increment the value of `num` after every 2 iterations.\n- The final answer will be stored in `ans` which is initialized with `1` because when `k==2`, the number of operations is 1.\n- Run a `while` loop till `sum < k`.\n- If the value of `flag` is not `0`, then find the `sum` by performing `sum+=num`. Increment the `ans` by `1` and decrement the value of `flag` by `1`.\n- If `flag==0`, it means the 2 iterations of `num` are complete and it is time to increment it. So increment `num` by `1`.\n- Return `ans` when `sum>=k` is achieved.\n\n---\n\n\n# Complexity\n- Time complexity: O(k)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n---\n\n\n# Code\n\n```\nclass Solution {\npublic:\n int minOperations(int k) {\n if(k==1)\n return 0;\n if(k==2)\n return 1;\n int ans=1;\n long long sum=2;\n long long num=2,flag=2;\n while(sum<k){\n if(flag){\n sum=sum+num;\n ans++;\n flag--;\n }\n if(flag==0){\n flag=2;\n num++;\n } \n }\n \n return ans;\n }\n};\n```
| 1 | 0 |
['Math', 'C++']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
C++ || Intuition Explained || Easy to Understand
|
c-intuition-explained-easy-to-understand-jzmf
|
Intuition\n Describe your first thoughts on how to solve this problem. \n- just try to find the solution in the given range \n\n# Approach\n Describe your appro
|
Aditya_Sahu_99
|
NORMAL
|
2024-03-24T06:26:17.705337+00:00
|
2024-03-24T06:26:17.705388+00:00
| 30 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n- just try to find the solution in the given range \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- iterate through all the possible ans from `i=1 to i<=k` and return the minimum possible ans\n\n# Complexity\n- Time complexity: O(k)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int minOperations(int k) {\n int mini=INT_MAX;\n for(int i=1;i<=k;i++){\n int ans=i-1;\n int temp=0;\n if(k%i==0){\n temp=k/i;\n ans+=temp-1;\n }\n else{\n temp=(k/i)+1;\n ans+=temp-1;\n }\n mini=min(ans,mini);\n }\n return mini;\n }\n};\n``````\n- this is the same code as above , the difference is that it is a bit shorter\n```\nclass Solution {\npublic:\n int minOperations(int k) {\n int mini=INT_MAX;\n for(int i=1;i<=k/2;i++){\n int ans=ceil(((double)k/(double)i)-1)+(i-1);\n mini=min(ans,mini);\n }\n if(mini==INT_MAX)\n return 0;\n return mini;\n }\n};\n``````\n\n
| 1 | 0 |
['C++']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
O(1) and O(n) method | Math vs Brute Force | Beginner friendly
|
o1-and-on-method-math-vs-brute-force-beg-9afr
|
Intuition\nWe will add first then multiply\nm is number of time we need to add 1.\nn is number of time we need to multiply.\n\n=> We need to find (1 + m) * (n +
|
dangnp
|
NORMAL
|
2024-03-24T05:46:23.113840+00:00
|
2024-03-28T18:30:33.368394+00:00
| 112 | false |
# Intuition\nWe will add first then multiply\n`m` is number of time we need to add `1`.\n`n` is number of time we need to multiply.\n\n=> We need to find `(1 + m) * (n + 1) >= k` in such way `m + n` is smallest. \n\n# Brute Force method\nTime complexity: $$O(n)$$\n\nWe can do the following:\n- Increase `m` from `0` to `k`\n- Everytime `m` is increased, we can find `n` by `k / (m + 1)`. We need an integer so we also need to use `ceil()`\n- Then the total operation would be `m + n`. We store the min operation\n\n```javascript []\nvar minOperations = function (k) {\n let minOps = k - 1\n let m = 0\n while (m < k) {\n let n = Math.ceil(k / (m+1)) - 1\n let operation = m + n\n if (operation < minOps) {\n minOps = operation\n }\n m++\n }\n\n return minOps\n};\n```\n```python []\ndef minOperations(k):\n min_operations = k - 1\n m = 0\n while m < k:\n n = (k // (m + 1)) - 1\n operation = m + n\n if operation < min_operations:\n min_operations = operation\n m += 1\n return min_operations\n```\n```C++ []\nint minOperations(int k) {\n int minOps = k - 1;\n int m = 0;\n while (m < k) {\n int n = (k / (m + 1)) - 1;\n int operation = m + n;\n if (operation < minOps) {\n minOps = operation;\n }\n m++;\n }\n return minOps;\n}\n```\n```java []\npublic int minOperations(int k) {\n int minOps = k - 1;\n int m = 0;\n while (m < k) {\n int n = (int) Math.ceil((double) k / (m + 1)) - 1;\n int operation = m + n;\n if (operation < minOps) {\n minOps = operation;\n }\n m++;\n }\n return minOps;\n}\n```\n\n\n# Math method\nTime complexity: $$O(1)$$\n\n1. Let\'s set `x` to be either `1 + m` or `1 + n` whichever number is greater. \nSo,`x = max((1 + m), (1 + n))`\n\n2. Then we need to find the smallest `x` in such way `x * x >= k` \nSo `x` should be the smallest integer that is equal or greater than square root of `k` which is `sprt(k)`\nWe have `x = ceil(sqrt(k))`\n\n3. Then we can find `n` by `n = x - 1`\nThen `m` by `m = ceil(k / x) - 1`\n\n```javascript []\n/**\n * @param {number} k\n * @return {number}\n */\nvar minOperations = function (k) {\n let x = Math.ceil(Math.sqrt(k))\n let n = x - 1\n let m = Math.ceil(k / x) -1\n\n return m + n\n};\n```\n```python []\ndef minOperations(k):\n x = math.ceil(math.sqrt(k))\n n = x - 1\n m = math.ceil(k / x) - 1\n\n return m + n\n```\n```C++ []\nint minOperations(int k) {\n int x = std::ceil(std::sqrt(k));\n int n = x - 1;\n int m = std::ceil(k / x) - 1;\n\n return m + n;\n}\n```\n```java []\npublic int minOperations(int k) {\n int x = (int) Math.ceil(Math.sqrt(k));\n int n = x - 1;\n int m = (int) Math.ceil(k / (double) x) - 1;\n\n return m + n;\n}\n```\n\n\n
| 1 | 0 |
['Math', 'Python', 'C++', 'Java', 'Python3', 'JavaScript']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
Using bfs
|
using-bfs-by-rohit_new_0402-oubc
|
Intuition\n Describe your first thoughts on how to solve this problem. \nif youre using normal bfs method then it would give wrong answer \nso first you need to
|
rohit_new_0402
|
NORMAL
|
2024-03-24T05:30:11.468458+00:00
|
2024-03-24T05:30:11.468476+00:00
| 21 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nif youre using normal bfs method then it would give wrong answer \nso first you need to increase the num as you want by 1 . But once you start taking dublicate then after that only one operation left for you that is to dublicate the number and you cannot increase that number by 1\n# Approach\n<!-- Describe your approach to solving the problem. -->\nhere I have taken a queue with vector which store a check element so that if I have dublicate it then I cannot increase that number by 1,\na current number and a current sum , and number of operations.\nTill the loop is running take the front element now check if the top[0] i.e. check constant is 1 then we will increase the currnum and currsum by 1 and also we have option to dublicate it and if we dublicating it then we simply put check = 0 cnum same and csum=csum+cnum , and if we have only one option left i.e. if check is 0 then we can only dublicate it\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nFor each number up to k, we perform a constant amount of work (pushing and popping from the queue, and some arithmetic operations). so time complexity would be o(k)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\narray space is constant so o(1) but queue is taking space so o(n)\n# Code\n```\nclass Solution {\npublic:\n int minOperations(int k) {\n queue<vector<int>> q;\n q.push({1, 1, 1, 0}); // vector={check,cnum,csum,operations}\n \n while (!q.empty()) {\n auto top = q.front();\n q.pop();\n int check = top[0];\n int cnum = top[1];\n int csum = top[2];\n int op = top[3];\n\n if (csum >= k) return op;\n\n if (check == 1) q.push({1, cnum + 1, csum + 1, op + 1});\n\n q.push({0, cnum, csum + cnum, op + 1});\n }\n \n return -1;\n }\n};\n\n```
| 1 | 0 |
['Breadth-First Search', 'C++']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
Brute Force || easy to understand
|
brute-force-easy-to-understand-by-oyjf01-6lcb
|
Intuition\n Describe your first thoughts on how to solve this problem. \nStarting from 1, we use a for loop to calculate the number of operations required to re
|
oyjf012
|
NORMAL
|
2024-03-24T05:03:59.450486+00:00
|
2024-03-24T05:03:59.450515+00:00
| 32 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nStarting from 1, we use a for loop to calculate the number of operations required to reach k. Until we find the optimal solution, the number of operations should be decreasing with each iteration. If the number of operations starts increasing, it indicates that we have passed the optimal solution, so we stop the loop.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nBrute Force\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(N);\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1);\n# Code\n```\nclass Solution {\n public int minOperations(int k) {\n if (k == 1) return 0;\n int min = 0;\n int res = Integer.MAX_VALUE; // Operation times;\n for (int i = 1; i < k; i++) {\n int cal = i - 1;\n if (k % i != 0) {\n cal += (k / i) + 1 - 1;\n } else {\n cal += (k / i) - 1;\n }\n res = Math.min(res, cal);\n if (cal > res) {\n break;\n }\n }\n return res;\n }\n}\n```
| 1 | 0 |
['Java']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
C++ solution.. beats 100%
|
c-solution-beats-100-by-us_2010_er-h8w1
|
Intuition\nFirst of all reach the smallest number which when duplicated will result in sum greater than equal to k this takes (minimum number-1) operations,then
|
us_2010_er
|
NORMAL
|
2024-03-24T04:42:50.380400+00:00
|
2024-03-24T05:36:25.478596+00:00
| 36 | false |
# Intuition\nFirst of all reach the smallest number which when duplicated will result in sum greater than equal to k this takes (minimum number-1) operations,then duplicate the minimum number got.\n\n# Complexity\n- Time complexity:\nO(sqrt(k))\n\n- Space complexity:\n O(1)\n\n# Code\n```\nclass Solution {\npublic:\n int minOperations(int k) {\n int mini=INT_MAX;\n for(int i=1;i<=sqrt(k);i++){\n int y = i-1;//minimum number is i here\n\n int h = ceil((double)k/(double)i);//min number of times i should be duplicated to make sum>=k\n\n int sum = y+h;//add both the operations\n\n mini=min(mini,sum);\n }\n return mini-1;\n }\n};\n```
| 1 | 0 |
['C++']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
100 % efficient & 0 ms time
|
100-efficient-0-ms-time-by-shivnath-9by5
|
Intuition\n Describe your first thoughts on how to solve this problem. \nHere we have to find out minimum no of operation so minimum value can be 0 and maximum
|
shivnath
|
NORMAL
|
2024-03-24T04:31:02.145980+00:00
|
2024-03-24T04:31:02.146001+00:00
| 188 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nHere we have to find out minimum no of operation so minimum value can be 0 and maximum value can be k-1 so it is the concept of binary search problem.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nHere minimum value is 0 and maximum value is k-1 so our answer will be in this range only from (0,k-1) so we can use binary search to check appropriate value of operation.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n \n bool fun(int k, int op)\n {\n \n int sum=1;\n if(sum>=k) return true;\n for(int i=1;i<=op;i++)\n {\n int inc=1*(i+1);\n sum=inc*(op-i+1);\n if(sum>=k)\n return true;\n }\n \n return false;\n }\n \n int minOperations(int k) {\n \n int ans=k;\n \n int l=0,r=k-1;\n while(l<=r)\n {\n int mid=l+(r-l)/2;\n if(fun(k,mid))\n {\n // true\n ans=min(ans,mid);\n r=mid-1;\n }\n else\n {\n l=mid+1;\n }\n \n }\n \n \n return ans;\n \n \n }\n};\n```
| 1 | 0 |
['Binary Search', 'C++']
| 1 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
[Java] Binary search, for those can't think up Math solutions like me ^^
|
java-binary-search-for-those-cant-think-w5g7i
|
\n\n# Code\n\nclass Solution {\n int minStep = Integer.MAX_VALUE;\n int originK = 0;\n public int minOperations(int k) {\n if(k == 1) return 0;\
|
yugong
|
NORMAL
|
2024-03-24T04:22:07.645904+00:00
|
2024-03-24T04:24:45.384917+00:00
| 38 | false |
\n\n# Code\n```\nclass Solution {\n int minStep = Integer.MAX_VALUE;\n int originK = 0;\n public int minOperations(int k) {\n if(k == 1) return 0;\n // if(k == 2) return 1;\n originK = k;\n helper(k);\n return minStep;\n }\n \n public void helper(int k){\n if(k == 1) return;\n \n int cand = findMinimum(originK, k);\n minStep = Math.min(minStep, k - 1 + cand - 1);\n helper(k - 1);\n }\n \n public static int findMinimum(int k, int j) {\n int left = 1;\n int right = k;\n int result = k; \n\n while (left <= right) {\n int mid = left + (right - left) / 2;\n if (mid * j >= k) {\n \n result = mid; \n right = mid - 1;\n } else {\n \n left = mid + 1; \n }\n }\n return result;\n }\n}\n```
| 1 | 0 |
['Binary Search', 'Java']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
Break into 2 parts at each step
|
break-into-2-parts-at-each-step-by-mukul-4p53
|
Complexity\n- Time complexity:\nO(k)\n\n- Space complexity:\nO(1)\n\n# Code\n\nclass Solution {\npublic:\n int minOperations(int k) {\n if(k==1) retur
|
MukulDev007
|
NORMAL
|
2024-03-24T04:17:14.858681+00:00
|
2024-03-24T04:17:14.858711+00:00
| 9 | false |
# Complexity\n- Time complexity:\n$$O(k)$$\n\n- Space complexity:\n$$O(1)$$\n\n# Code\n```\nclass Solution {\npublic:\n int minOperations(int k) {\n if(k==1) return 0;\n \n int ans = INT_MAX;\n \n for(int i=1 ; 2*i <= k; i++){\n int l = ceil(k / (1.0 * i));\n //min number of times to duplicate\n //the incremented element to reach or exceed k\n\n ans = min(ans , i + l - 2);\n //i-1 increment operations\n //l-1 duplication operations\n }\n \n return ans;\n }\n};\n```
| 1 | 0 |
['C++']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
Easy To Understand || O(1) complexity || Math
|
easy-to-understand-o1-complexity-math-by-fkwy
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
sprashant1029
|
NORMAL
|
2024-03-24T04:08:14.151809+00:00
|
2024-03-24T04:08:14.151827+00:00
| 118 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:O(1)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int minOperations(int k) {\n if (k==1) return 0;\n if (k==2) return 1;\n long m = (long)Math.sqrt(k);\n long ans = m-1;\n ans += (k-1)/m;\n return (int)ans;\n \n }\n}\n```
| 1 | 0 |
['C++', 'Java']
| 2 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
Easy Solution in O(n) T.C
|
easy-solution-in-on-tc-by-sdkv-d703
|
\n# Complexity\n- Time complexity:\nO(1)\n\n- Space complexity:\nO(1)\n\n# Code\n\nclass Solution {\npublic:\n int minOperations(int k) {\n int mini=I
|
sdkv
|
NORMAL
|
2024-03-24T04:04:55.656750+00:00
|
2024-03-24T04:04:55.656799+00:00
| 2 | false |
\n# Complexity\n- Time complexity:\nO(1)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution {\npublic:\n int minOperations(int k) {\n int mini=INT_MAX;\n int n=1,ans=1;\n int operation=0;\n \n while (1) {\n int temp=operation;\n temp+=k/n;\n if (k%n!=0) {\n temp+=1;\n }\n if (temp>mini) {\n break;\n }\n mini=min(mini,temp);\n n++;\n operation++;\n }\n \n return mini-1;\n }\n};\n```
| 1 | 0 |
['C++']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
Binary Search
|
binary-search-by-aswinnath123-4rzs
|
Approach\nUse low=1 and high=k and use check to find if its feasible.\n\n# Complexity\n- Time complexity: O(k*log k)\n- Space complexity: O(1)\n\n# Code\n\nclas
|
ASWINNATH123
|
NORMAL
|
2024-03-24T04:03:33.671489+00:00
|
2024-03-24T04:11:53.972293+00:00
| 90 | false |
# Approach\nUse low=1 and high=k and use check to find if its feasible.\n\n# Complexity\n- Time complexity: O(k*log k)\n- Space complexity: O(1)\n\n# Code\n```\nclass Solution:\n def minOperations(self, k: int) -> int:\n if k==1:\n return 0\n low=1\n high=k\n def check(val):\n for i in range(1,val+1):\n if (i+1)*(val-i+1)>=k:\n return 1\n return 0\n while low<=high:\n mid=(low+high)//2\n if check(mid):\n high=mid-1\n else:\n low=mid+1\n return low\n\n```
| 1 | 0 |
['Binary Search', 'Python3']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
Clean Java Solution || Weekly Contest
|
clean-java-solution-weekly-contest-by-sh-0wsz
|
Code\n\nclass Solution {\n public int minOperations(int k) {\n int ans = Integer.MAX_VALUE;\n int sum =1, temp =1;\n int oper = 0;\n
|
Shree_Govind_Jee
|
NORMAL
|
2024-03-24T04:01:38.436765+00:00
|
2024-03-24T04:01:38.436786+00:00
| 138 | false |
# Code\n```\nclass Solution {\n public int minOperations(int k) {\n int ans = Integer.MAX_VALUE;\n int sum =1, temp =1;\n int oper = 0;\n while(true){\n int count = oper;\n count += k/temp;\n if(k%temp != 0){\n count += 1;\n }\n \n if(count > ans){\n break;\n }\n ans = Math.min(ans, count);\n temp++;\n oper++;\n }\n return ans-1;\n }\n}\n```
| 1 | 0 |
['Array', 'Math', 'Suffix Array', 'Java']
| 1 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
Without using sqrt achieve sqrt(k) time complexity
|
without-using-sqrt-achieve-sqrtk-time-co-qafv
|
IntuitionWe start with val = 1 and increment it while doing so remains efficient. The key idea is to minimize the total number of operations by balancing betwee
|
amanabiy
|
NORMAL
|
2025-03-16T22:55:04.151345+00:00
|
2025-03-16T22:55:29.980409+00:00
| 2 | false |
## Intuition
We start with `val = 1` and increment it while doing so remains efficient. The key idea is to minimize the total number of operations by balancing between increments and division-like reductions.
## Complexity
- **Time Complexity:** O(sqrt(k)) — The maximum value of `val` we consider is around sqrt(k), leading to this bound.
- **Space Complexity:** O(1) — We only use a few integer variables.
## Code
```rust
impl Solution {
pub fn min_operations(k: i32) -> i32 {
let mut val = 1;
fn get_steps(val: i32, k: i32) -> i32 {
// Ceil division: (a + b - 1) / a computes ceil(b / a)
// Steps = divisions required + (val - 1) increments
((k + val - 1) / val) + (val - 1)
}
// Increment val while it continues to reduce the total steps
while get_steps(val, k) > get_steps(val + 1, k) {
val += 1;
}
get_steps(val, k) - 1
}
}
```
| 0 | 0 |
['Enumeration', 'Rust']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
O(NlogN) | Math solution
|
onlogn-math-solution-by-coldkaushal-bs54
|
Intuitionif we start with [1] and construct array in every move
0th move -> [1]
1st move -> [[2], [1, 1]]
2nd move -> [[3], [2,2], [1,1,1]]
3rd move -> [[4], [3
|
coldKaushal
|
NORMAL
|
2025-03-11T14:11:35.409342+00:00
|
2025-03-11T14:11:35.409342+00:00
| 3 | false |
# Intuition
if we start with [1] and construct array in every move
0th move -> [1]
1st move -> [[2], [1, 1]]
2nd move -> [[3], [2,2], [1,1,1]]
3rd move -> [[4], [3,3], [2,2,2], [1,1,1,1]]
...
from the previous we either increment the val by 1 or we can duplicate it. Notice in any array of size>1, increasing an element by 1 is not picked reason being n+n > n+1 for all n>1.
so the nth operation can be generalised as
n+1, [n-1, n-1], [n-2, n-2, n-2]...
we need to find the max sum of this nth operation, and can find n optimally using binary search
# Complexity
- Time complexity:
N(logn)
- Space complexity:
O(1)
# Code
```python3 []
@cache
def find(t):
start = t+1
index = 1
ans = start
while start:
ans = max(ans, start*index)
start -=1
index+=1
return ans
class Solution:
def minOperations(self, k: int) -> int:
s = 0
e = 100000
ans = e
while s<=e:
m = (s+e)//2
if find(m)>= k:
ans = m
e = m-1
else:
s = m+1
return ans
```
| 0 | 0 |
['Python3']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
Beats 100% of C++ Users || Solution using math|{\
|
beats-100-of-c-users-solution-using-math-t1s2
|
IntuitionWe are tasked with constructing an array starting from [1] where we can:Increase any element by 1.Duplicate any element and append it to the array.The
|
dk8818604
|
NORMAL
|
2025-02-19T19:29:51.747156+00:00
|
2025-02-19T19:29:51.747156+00:00
| 5 | false |
# Intuition
We are tasked with constructing an array starting from [1] where we can:
Increase any element by 1.
Duplicate any element and append it to the array.
The goal is to reach a sum of elements that is at least k, using the minimum number of operations.
The main observation here is that creating larger elements faster is more efficient than incrementing small elements repeatedly. Duplication helps us exponentially grow the sum, while increasing elements provides fine-tuning.
The question is: how do we use the fewest operations to achieve the target sum?
# Approach
Initial thoughts:
Starting with nums = [1], the quickest way to grow the array's sum is to use duplication.
If we only increment, we need k-1 operations to reach the sum k, which is inefficient.
Dividing the sum requirement:
Divide the sum k into u parts. Each part should be as large as possible to minimize the number of increments.
Let u represent how many pieces we divide the required sum into.
Using duplication smartly:
As we increase the number of parts u, the value of each part decreases, but we reduce the number of required increments.
The total number of operations is:
u - 1 duplications to create u elements.
(k + u - 1) / u - 1 increments to make each part large enough.
Iterate to find the minimum:
Try different values of u (starting from 2).
Calculate the number of required operations for each u.
Track the minimum number of operations.
Edge cases:
If k is small (1, 2, 3, 4), handle them directly as base cases.
Loop termination:
The loop breaks when increasing u no longer reduces the number of operations.
# Complexity
- Time complexity:
O(sqrt(k)) since we iterate over potential division sizes up to around sqrt(k)
- Space complexity:
O(1) since we use constant extra space.
# Code
```cpp []
class Solution {
public:
int minOperations(int k) {
int ans=k-1;
if(k==1) return 0;
if(k==2) return 1;
if(k==3) return 2;
if(k==4) return 2;
int u=2;
while(true){
double f=(k+0.0)/u;
int y=k/u;
if(f!=y) y=floor(f)+1;
int r=u-1;
r=r+(y-1);
if(ans<r) return ans;
else ans=r;
u++;
}
return 0;
}
};
```
| 0 | 0 |
['Math', 'Greedy', 'Enumeration', 'C++']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
Looks it's a math question
|
looks-its-a-math-question-by-linda2024-w1xy
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
linda2024
|
NORMAL
|
2025-02-04T22:05:08.544944+00:00
|
2025-02-04T22:05:08.544944+00:00
| 4 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```csharp []
public class Solution {
public int MinOperations(int k) {
int minOpt = k-1;
if(minOpt <2)
return minOpt;
for(int dup = 2; dup <= k/dup; dup++)
{
int div = k/dup;
int curOpt = dup + div-2 + (k%dup == 0 ? 0 : 1);
if(minOpt > curOpt)
minOpt = curOpt;
}
return minOpt;
}
}
```
| 0 | 0 |
['C#']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
Optimization Problem
|
optimization-problem-by-vadibaum-6ea8
|
IntuitionMin Movements(x, y) = x + y
Constrained ASum(x, y) = (x + 1, y + 1) = kApproachMin Movements(x, y) = x + y
Constrained ASum(x, y) = (x + 1, y + 1) = kS
|
vadibaum
|
NORMAL
|
2025-01-21T08:14:46.921177+00:00
|
2025-01-21T08:14:46.921177+00:00
| 11 | false |
# Intuition
Min Movements(x, y) = x + y
Constrained ASum(x, y) = (x + 1, y + 1) = k
# Approach
<!-- Describe your approach to solving the problem. -->
Min Movements(x, y) = x + y
Constrained ASum(x, y) = (x + 1, y + 1) = k
Solving a Lagrangian,
get an answer sqrt(k) - 1
We need to check whatever it works for 2 * ceil(sqrt(k) - 1), 2 * floor(sqrt(k) - 1) or their product ceil(sqrt(k) - 1) * floor(sqrt(k) - 1)
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
$$O(1)$$
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
$$O(1)$$
# Code
```python3 []
from math import sqrt, ceil, floor
## Min Movements(x, y) = x + y
## Constrained ASum(x, y) = (x + 1, y + 1) = k
class Solution:
def minOperations(self, k: int) -> int:
ac, af = ceil(sqrt(k)) - 1, floor(sqrt(k)) - 1
if (af + 1) * (af + 1) >= k:
return 2 * af
elif (af + 1) * (ac + 1) >= k:
return af + ac
else:
return 2 * ac
```
| 0 | 0 |
['Python3']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
The 2000th LC medium solved WOAH !!! Time = O(K) Space = O(1) Explicit
|
the-2000th-lc-medium-solved-woah-time-ok-ah6h
|
Intuition and ApproachSee problem titleComplexityK = #-given
Time complexity:
O(K)
Space complexity:
O(1) ( Explicit and Implicit )
Code
|
2018hsridhar
|
NORMAL
|
2025-01-08T02:26:22.987279+00:00
|
2025-01-08T02:26:22.987279+00:00
| 7 | false |
# Intuition and Approach
See problem title
# Complexity
K = #-given
- Time complexity:
$$O(K)$$
- Space complexity:
$$O(1)$$ ( Explicit and Implicit )
# Code
```python3 []
'''
URL := https://leetcode.com/problems/apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k/description/
3091. Apply Operations to Make Sum of Array Greater Than or Equal to k
Compexity
T = O(K)
S = O(1) ( E ) O(1) ( I )
Leverage number theory, greedyness, and HINT #1 for its solutioning !!!
'''
class Solution:
def minOperations(self, k: int) -> int:
minNumOps = float('inf')
# always start at base = 1 here!
for incrementOp in range(1,k+1,1):
incrOps = (incrementOp - 1)
duplOps = max(0,(int)(math.ceil(k / incrementOp)) - 1)
numOpsTotal = incrOps + duplOps
minNumOps = min(minNumOps, numOpsTotal)
return minNumOps
```
| 0 | 0 |
['Math', 'Greedy', 'Enumeration', 'Python3']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
c++ math
|
c-math-by-vineeshrao-7q6h
|
IntuitionApproachComplexity
Time complexity:O(sqrt(k))
Space complexity:O(1)
Code
|
Vin342786
|
NORMAL
|
2024-12-20T03:53:36.328704+00:00
|
2024-12-20T03:53:36.328704+00:00
| 2 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:O(sqrt(k))
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int minOperations(int k) {
if(k==1) return 0;
if(k<4) return k-1;
int sum=0;
int n=1;
while(sum<k){
sum=n*(n+1);
n++;
}
if((n-1)*(n-1)>=k){
return 2*n-4;
}
return 2*n-3;
}
};
```
| 0 | 0 |
['C++']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
2 lines of code with O(1) complexity
|
2-lines-of-code-with-o1-complexity-by-ch-blgv
|
key idea: let initally arr is [0], and to get minimum operation there should be a time incrementation followed by b times duplication. So, the problem can be wr
|
chtome
|
NORMAL
|
2024-12-13T02:30:43.190990+00:00
|
2024-12-13T02:30:43.191018+00:00
| 3 | false |
key idea: let initally arr is [0], and to get minimum operation there should be `a` time incrementation followed by `b` times duplication. So, the problem can be written as find `min(a+b)` given that `ab >= k`. If we simply use `AM >= GM` inequality, we can see `a` and `b` should be similar value or somewhat same. \n \n\t`class Solution:\n\t\tdef minOperations(self, k: int) -> int:\n\t\t\tm = math.ceil(math.sqrt(k))\n\t\t\treturn m + math.ceil(k/m) - 2\n\n\t\t #O(n) -> O(logk) -> O(1)`
| 0 | 0 |
['Python']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
Easy solution
|
easy-solution-by-_jyoti_geek-fbcn
|
Code\njava []\nclass Solution {\n public int[] dp;\n\n public int minOperations(int k) {\n dp = new int[k + 1];\n for (int i = 0; i < dp.len
|
_jyoti_geek
|
NORMAL
|
2024-12-06T07:05:28.494956+00:00
|
2024-12-06T07:05:28.494996+00:00
| 2 | false |
# Code\n```java []\nclass Solution {\n public int[] dp;\n\n public int minOperations(int k) {\n dp = new int[k + 1];\n for (int i = 0; i < dp.length; i++) {\n dp[i] = -1;\n }\n return helper(k, 1, 1);\n }\n\n public int helper(int k, int prev, int sum) {\n if (sum >= k) {\n return 0;\n }\n if (dp[prev] != -1) {\n return dp[prev];\n }\n\n int np = prev + 1;\n int c1 = 1 + helper(k, np, sum + 1);\n int np1 = prev;\n int c2 = 1 + helper(k, np1, sum + np1);\n return dp[prev] = Math.min(c1, c2);\n }\n}\n```
| 0 | 0 |
['Math', 'Dynamic Programming', 'Java']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
Check 2 or less near sqrt of K | Unique approach | Beats 100% Space and Time 🔥
|
check-2-or-less-near-sqrt-of-k-unique-ap-x1tc
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
sahilraut22
|
NORMAL
|
2024-11-10T19:47:49.000355+00:00
|
2024-11-10T19:50:46.466541+00:00
| 2 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```c []\nint minOperations(int k) {\n if(k == 1) return 0;\n int a = sqrt(k);\n if(a*a >= k) return (2*(a-1));\n if(a*(a+1) >= k) return ((2*a)-1);\n else if(a*(a+2) >= k) return (2*a);\n return 0;\n}\n```
| 0 | 0 |
['Math', 'C', 'C++']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
Simple Math
|
simple-math-by-premkumarchilumula-fed5
|
Intuition \n Simple math !\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n- Basic Math\n\n# Complexity\n- Time complexity: O(n)
|
PremKumarChilumula
|
NORMAL
|
2024-11-06T09:58:52.380487+00:00
|
2024-11-06T09:58:52.380523+00:00
| 3 | false |
# Intuition \n Simple math !\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n- Basic Math\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int minOperations(int k) {\n if(k<2)return 0;\n int mn=INT_MAX;\n for(int i=1;i<=k;++i){\n int d= k%i ? k/i : k/i-1;\n mn=min(mn,d+i-1);\n }\n return mn;\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
reducing number of searches, beats 70% on time, 53% on space
|
reducing-number-of-searches-beats-70-on-it3d7
|
Intuition\nsince this is a greedy algorithm based solution, we need a heusteric function that can help us optimise the the minimum operations required.\nfor any
|
cim3ZADdET
|
NORMAL
|
2024-09-19T07:25:48.100228+00:00
|
2024-09-19T07:25:48.100261+00:00
| 0 | false |
# Intuition\nsince this is a greedy algorithm based solution, we need a heusteric function that can help us optimise the the minimum operations required.\nfor any k, there are assured to be some operations by which we can exceed k. the most intuitive is: increase till k/2, then duplicate.\n```java []\nint minOps = k;\n if (k % 2 == 0) {\n minOps = (k / 2) - 1;\n } else minOps = k / 2;\n```\nthis code handles that.\nNow we check how fast we go beyond k, by increasing the number of initial increments by 1.\n\n# Approach\nnow we want to iterate in general, to check for optimal number of operations. As per the hint, it\'s best to increment first and duplicate then. we run the code only till the number we\'re checking at, crosses current minOps, because from that point onwards, any further check will obviously be more than minOps.\nSince this approach does not properly work for k = 2 to k = 10, we make it a special case.\n\n# Complexity\n- Time complexity:\n$$O(k)$$\n\n- Space complexity:\n$$O(1)$$\n\n# Code\n```java []\nclass Solution {\n public int minOperations(int k) {\n if (k == 1) return 0;\n int minOps = k;\n if (k % 2 == 0) {\n minOps = (k / 2) - 1;\n } else minOps = k / 2;\n\n if ( k <= 10 && k != 9) return minOps + 1;\n\n int increaseops = 0, duplicateops;\n\n for (int currnum = 1; currnum < minOps; currnum++, increaseops++) {\n // intuition to break the loop when currnum > minOps + 1, is basically that when you reach minOps, you have to do increment operation minOps times, and then have to duplicate it, meaning we already taking more operations than needed\n if (k % currnum == 0) {\n duplicateops = (k / currnum) - 1;\n } else duplicateops = (k / currnum);\n\n minOps = Math.min(increaseops + duplicateops, minOps);\n }\n\n // since k is too small, minOps ignores one operation\n \n return minOps;\n }\n}\n```
| 0 | 0 |
['Java']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
solved
|
solved-by-diorsalimov2006-2odt
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
diorsalimov2006
|
NORMAL
|
2024-09-19T06:02:23.356896+00:00
|
2024-09-19T06:02:23.356932+00:00
| 0 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python []\nclass Solution(object):\n def minOperations(self, k):\n """\n :type k: int\n :rtype: int\n """\n \n \n an = k\n for a in range(k):\n x = a + 1\n b = (k + x - 1) // x - 1\n an = min(an, a + b)\n return an\n\n\n \n```
| 0 | 0 |
['Python']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
0 ms Beats 100.00%
|
0-ms-beats-10000-by-pribyte1-ns6u
|
Shortest Solution\n# Code\njava []\nclass Solution {\n public int minOperations(int k) {\n int p = (int) Math.sqrt(k), q = (k+p-1)/p; \n return
|
pribyte1
|
NORMAL
|
2024-09-03T04:37:33.684700+00:00
|
2024-09-03T04:37:33.684726+00:00
| 2 | false |
Shortest Solution\n# Code\n```java []\nclass Solution {\n public int minOperations(int k) {\n int p = (int) Math.sqrt(k), q = (k+p-1)/p; \n return p + q - 2;\n }\n}\n```
| 0 | 0 |
['Java']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
javascript solution
|
javascript-solution-by-suhail_lc-21fo
|
Intuition\n Describe your first thoughts on how to solve this problem. \nto make the efficient \nwe\'ve to increment the array value by 1 N nimes, the N can be
|
suhail_lc
|
NORMAL
|
2024-08-25T11:30:03.164063+00:00
|
2024-08-25T11:30:03.164092+00:00
| 7 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nto make the efficient \nwe\'ve to increment the array value by 1 N nimes, the N can be evaluated by iterating upto sqrt of k\nnext,instead of pushing the array we can just increment our move by one and iterating variable by value\nthus decreasing the memory requirement\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: idk :)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: idk :)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```javascript []\n/**\n * @param {number} k\n * @return {number}\n */\nvar minOperations = function(k) {\n let nums=1//instead of array\n let stop=Math.sqrt(k),m=0;//moves\n for(i=1;i<stop;i++)\n {\n nums++\n m++\n }\n for(i=nums;i<k;i+=nums)\n m++//duplicate the value of array(excluded the step)\nreturn m;\n};\n```
| 0 | 0 |
['JavaScript']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
Square root is optimal
|
square-root-is-optimal-by-pranavkapparad-9fsc
|
\n\n# Code\n\nclass Solution:\n def minOperations(self, k: int) -> int:\n x = int(floor(sqrt(k)))\n res = x-1\n \n res += (ceil(k
|
pranavkapparad30
|
NORMAL
|
2024-08-17T06:42:53.984495+00:00
|
2024-08-17T06:42:53.984536+00:00
| 6 | false |
\n\n# Code\n```\nclass Solution:\n def minOperations(self, k: int) -> int:\n x = int(floor(sqrt(k)))\n res = x-1\n \n res += (ceil(k/x) - 1)\n\n return res\n```
| 0 | 0 |
['Python3']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
3ms Beats 100%
|
3ms-beats-100-by-chenchewei-pcch
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
chenchewei
|
NORMAL
|
2024-08-12T13:07:15.667943+00:00
|
2024-08-12T13:07:15.667972+00:00
| 2 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n func minOperations(_ k: Int) -> Int {\n guard k > 1 else { return 0 }\n\n var operation: Int = .max\n\n for i in 1...(k / 2) {\n var temp = 0\n if k.isMultiple(of: i) {\n temp = k / i\n } else {\n temp = k / i + 1\n }\n operation = min(operation, (temp + i - 2))\n }\n \n return operation\n }\n \n}\n```
| 0 | 0 |
['Swift']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
Logical | Simple
|
logical-simple-by-yatishgarg_2002-l09i
|
Intuition\nJust thought of it as ormal mathematics. lets suppose we have done x increse opertaions and then multiply the final vale y times we can get >= k.\n\n
|
yatishgarg_2002
|
NORMAL
|
2024-07-28T05:48:01.683574+00:00
|
2024-07-28T05:48:01.683593+00:00
| 3 | false |
# Intuition\nJust thought of it as ormal mathematics. lets suppose we have done x increse opertaions and then multiply the final vale y times we can get >= k.\n\n# Approach\nso eqaution will look like.\n(x+1)*y >= k\n\nso x*y >= k-y;\n\nthis shows us that y can at max go till 0 to k.\n\nso the x >= (k-y)/y;\n\nso now if total operations will be x+y -1. the -1 would be because we have said y times multiply.but the duplication opertaion only happen y-1 times.\n\n\n\n# Complexity\n- Time complexity:\nO(k)\n\n- Space complexity:\nO(1)\n\nUPVOTE\n# Code\n```\nclass Solution {\npublic:\n int minOperations(int k) {\n int ans = INT_MAX;\n for(int y=1;y<=k;y++){\n\n if((k-y)%y == 0){\n \n int x = (k-y)/y;\n ans = min(ans , x+y-1);\n\n }\n else{\n int x = (k-y)/y;\n ans = min(ans , x+y);\n }\n }\n\n return ans;\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
Straight Forward Java Solution with complete explanation. O(√ k) Solution.
|
straight-forward-java-solution-with-comp-hwvl
|
APPROACH\n To get the minum operation we must apply maximum increment first and then duplicate it.\n to achieve this we will increament num each time and devide
|
vishwajeet_rauniyar
|
NORMAL
|
2024-07-22T09:26:45.558724+00:00
|
2024-07-22T09:27:47.329767+00:00
| 3 | false |
**APPROACH**\n* To get the minum operation we must apply maximum increment first and then duplicate it.\n* to achieve this we will increament num each time and devide it by k to get the steps.\n* iterating each step we would find the minimum..\n \tfor Example:\n \t\tsuppose K = 100\n \t\twe have: num = 1\n \t\tfirst iteration: num = 2, \n \t\t\t\t\t\tk/num = 50.0 \n \t\t\t\t\t\ttotal_step required is 1+49 = 50. (1 step to increase from 1 to 2, and 49 steps to add 49 times 2, since one \'2\' is already there.)\n \t\tsecond iteration: num = 3\n \t\t\t\t\t\t k/num = 33.33 \n \t\t\t\t\t\t total step required: 2+33: = 35 (2 step to increase from 1 to 3 and 33 step to add 33 times 3.).\n \n \t\t...\n \t\t...\n \t\tninth iteration: num = 10\n \t\t\t\t\t\tk/num = 10.0;\n \t\t\t\t\t\ttotal step requirred: 9+9 = 18. (9 step to increase from 1 to 10 and 9 to step to add 9 times 10.)\n \t\ttenth iteration: num = 11\n \t\t\t\t\t\t k/num = 9.99\n \t\t\t\t\t\t total stepps requirred: 10+9 = 19. (10 steps to increase from 1 to 11 and 9 step to add 9 tims 11.)\n\n\n\t\tafter iteration till k-1 steps we we will find that 18 is the smallest.\n\n\n\n**ALGO:**\n \tSET: num = 1;\n \tSET: min = k;\n \titerate K-1 time:\n \t\tSET: num = num+1;\n \t\tSET: div = (k/num);\n \t\tUPDATE min: min = MIN(num-1,ceil(div)-1,min);\n return min(num-1,min);\n\n**Complexity Analysis:**\n**Time Complexity:** O(k)\n**Space Complexity**: O(1)\n```\nclass Solution {\n public int minOperations(int k) {\n int num = 1;\n int min = k;\n for(int i = 0;i<k-1;i++)\n {\n num++;\n double div = (k+0.0)/(num+0.0);\n min = Math.min(num-1+(int)Math.ceil(div)-1,min);\n }\n int ans = Math.min(num-1,min);\n return ans;\n }\n}\n```\n\n\n**OPTIMIZATION:**\n->it can be seen that when num-1 will be greater than \'min\' then there is no possiblily of getting \n\tmore smaller steps since increasing from 1 to num will alone take num-1 step which is already greater than \'min\' and duplicating will cost more steps so. we can return \'min\' early.\n\n\n**Complexity Analysis**\n**Time Complexity:** O(\u221A k) In worst case.\n\n```\nclass Solution {\n public int minOperations(int k) {\n int num = 1;\n int min = k;\n for(int i = 0;i<k-1;i++)\n {\n num++;\n double div = (k+0.0)/(num+0.0);\n min = Math.min(num-1+(int)Math.ceil(div)-1,min);\n if(num-1>min)\n \treturn min;\n }\n int ans = Math.min(num-1,min);\n return ans;\n }\n}\n```\n
| 0 | 0 |
['Math', 'Java']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
C++ solution
|
c-solution-by-oleksam-wzc7
|
\n// Please, upvote if you like it. Thanks :-)\n// Runtime: 0 ms, faster than 100.00% of C++ online submissions for Apply Operations to Make Sum of Array Greate
|
oleksam
|
NORMAL
|
2024-07-18T19:22:42.082024+00:00
|
2024-07-18T19:22:42.082055+00:00
| 1 | false |
```\n// Please, upvote if you like it. Thanks :-)\n// Runtime: 0 ms, faster than 100.00% of C++ online submissions for Apply Operations to Make Sum of Array Greater Than or Equal to k.\n// Memory Usage: 8 MB, less than 5.03% of C++ online submissions for Apply Operations to Make Sum of Array Greater Than or Equal to k.\nint minOperations(int k) {\n\tint res = INT_MAX, n = 1;\n\tfor (int i = 0; i < k; i++)\n\t\tres = min(res, i + (k - 1) / (n + i));\n\treturn res;\n}\n```
| 0 | 0 |
['Math', 'Greedy', 'C', 'C++']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
Easy C++ Solution | O(1) Solution | Calculus
|
easy-c-solution-o1-solution-calculus-by-234of
|
Intuition\nIt can be observed that first adding up elements to a certain extent and then duplicating the largest number will make the least number of moves to i
|
Maniii97
|
NORMAL
|
2024-07-17T19:41:37.060964+00:00
|
2024-07-17T19:41:37.060991+00:00
| 5 | false |
# Intuition\nIt can be observed that first adding up elements to a certain extent and then duplicating the largest number will make the least number of moves to increase the sum. Our target is to find the extent upto which we add.\n# Approach\nBy further observation you can see that the extent upto which we have to increase 1, is sqrt(k). \nOur path looks something like this : \n```1 -> sqrt(k) -> k```\n\nSo the number of moves become ```sqrt(k) - 1 + (k-1)/sqrt(k)```\n\nWe can also prove the extent to be ```sqrt(k)``` by calculus. \nLet x be the extent upto which we\'ll increase 1.\n$$f(x) = (x-1) + k/x$$ . differentiate this eqn , \n$$f\'(x) = 1 - k/(x^2)$$ \nput $$f\'(x) = 0 ; x = sqrt(k)$$\n# Complexity\n- Time complexity: ```O(1)```\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:```O(1)```\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int minOperations(int k) {\n int cnt = 0;\n int rt = (sqrt(k));\n cnt += rt - 1;\n cnt += (k-1)/rt;\n return cnt;\n }\n};\n```
| 0 | 0 |
['Math', 'Greedy', 'C++']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
Simple and Easy JAVA Solution using DP
|
simple-and-easy-java-solution-using-dp-b-ssl0
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
Triyaambak
|
NORMAL
|
2024-07-17T12:48:49.245868+00:00
|
2024-07-17T12:48:49.245894+00:00
| 4 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int minOperations(int k) {\n Integer dp[] = new Integer[k+1];\n return solve(k,1,1,dp);\n }\n private static int solve(int k , int sum , int ele,Integer dp[]){\n if(sum>=k)\n return 0;\n \n if(dp[ele] != null)\n return dp[ele];\n\n int addOp = 1 + solve(k,sum+1,ele+1,dp);\n int dupOp = 1 + solve(k,sum+ele,ele,dp);\n\n return dp[ele] = Math.min(addOp,dupOp);\n }\n}\n```
| 0 | 0 |
['Dynamic Programming', 'Java']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
c++ o(1).
|
c-o1-by-cajung-z1s4
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
cajung
|
NORMAL
|
2024-07-16T09:23:22.164926+00:00
|
2024-07-16T09:23:22.164959+00:00
| 1 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\no(1);\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int minOperations(int k) {\n int h = sqrt(k);\n int l = k / h;\n if(l*h<k){\n l++;\n }\n int ketqua = 0;\n ketqua = l + h - 2;\n h++;\n l = k / h;\n if(l*h<k){\n l++;\n }\n if(l + h - 2<ketqua){\n ketqua = l + h - 2;\n }\n return ketqua;\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
Simplest solution, O(1), Math logic
|
simplest-solution-o1-math-logic-by-archi-of27
|
Intuition:\nThe optimal strategy is to find a balance between increasing a single element and duplicating it. We want to create x copies of a number close to k/
|
archie9211
|
NORMAL
|
2024-07-15T19:33:16.535898+00:00
|
2024-07-15T19:33:16.535918+00:00
| 1 | false |
# Intuition:\nThe optimal strategy is to find a balance between increasing a single element and duplicating it. We want to create x copies of a number close to k/x, minimizing the total operations.\n\n# Explanation:\n1. We use Math.sqrt(k) to find an optimal balance between the number of copies and the value of each copy.\n2. Math.ceil(Math.sqrt(k)) gives us the optimal number of copies (x).\n3. k/x represents the ideal value for each copy.\n4. Math.ceil(k/(double)x) calculates how many times we need to increase the initial 1 to reach this ideal value.\n5. We subtract 2 because we start with [1] and the first duplication doesn\'t count as an additional operation.\n\nThe total operations are thus: (increasing the value) + (duplicating) - 2.\n\nThis approach minimizes the total number of operations by finding the sweet spot between increasing and duplic\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nUsing Java sqrt, it has time complexity of $$O(1)$$\n\n- Space complexity:\n$$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimport java.lang.Math; \n\n\nclass Solution {\n public int minOperations(int k) {\n int x = (int) Math.ceil(Math.sqrt(k));\n return (int) Math.ceil(k/(double)x) + x-2;\n }\n}\n```
| 0 | 0 |
['Java']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
VERY OPTIMAL SOLUTION BEAT 100%
|
very-optimal-solution-beat-100-by-aniket-x0ly
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
Aniket_Jaiswal-013
|
NORMAL
|
2024-07-11T15:40:33.899350+00:00
|
2024-07-11T15:40:33.899385+00:00
| 1 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int minOperations(int k) {\n int ope1st=k-1;\n int ope2nd=1;\n if(k%2==0){\n ope2nd+=(k/2)-1;\n \n }\n else{\n ope2nd+=(k/2);\n }\n int cnt=2;\n while(ope1st>=ope2nd){\n ope1st=ope2nd;\n ope2nd=cnt;\n int l=1+cnt;\n if(k%l==0){\n ope2nd+=(k/l)-1;\n }\n else{\n ope2nd+=k/l;\n }\n cnt++;\n }\n return ope1st;\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
4 lines of code c++ solution
|
4-lines-of-code-c-solution-by-mahindra20-fms6
|
Complexity\n- Time complexity: O(k)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(1)\n Add your space complexity here, e.g. O(n) \n\n# Co
|
mahindra2005
|
NORMAL
|
2024-07-11T10:21:42.340491+00:00
|
2024-07-11T10:21:42.340521+00:00
| 1 | false |
# Complexity\n- Time complexity: $$O(k)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int minOperations(int k) {\n int ans = 1e9;\n for(int i=1;i<=k;i++){\n ans = min(ans,(k+i-1)/i+i-2);\n }\n return ans;\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
I am a WIZARD
|
i-am-a-wizard-by-sulohesh-tb9x
|
Intuition\nEQUATIONS!!\nYou can have function like,\nn+1 = k (No addition, just duplication)\n2(n-1)+2 = k (1 addition, then duplication)\n3(n-2)+3 = k (..)\n\n
|
sulohesh
|
NORMAL
|
2024-07-06T20:26:07.169497+00:00
|
2024-07-06T20:26:07.169547+00:00
| 1 | false |
# Intuition\nEQUATIONS!!\nYou can have function like,\nn+1 = k (No addition, just duplication)\n2(n-1)+2 = k (1 addition, then duplication)\n3(n-2)+3 = k (..)\n\nGeneral form:- x(n-(x-1))+x>k => xn-x(x-2)=k\n\nn > (k+x(x-2))/x (Greater than,since sum is greater than or equal to k)\n\nHence the ceil, i.r..\nn = ceil((k+x(x-2))/x)\n\nJust iterate until n starts decreasing, and break;\nOr\nDo ternary search if you\'re really that guy;\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:$$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(1)$$\n\n# Code\n```\nclass Solution {\npublic:\n int minOperations(int k) {\n int ans=INT_MAX;\n for(double i=1;i<=k;i++){\n int n = ceil(double(k/i)+(i-2));\n if(n>ans){\n break;\n }\n ans=min(ans,n);\n }\n return ans;\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
Simple solution in C++ (well commented, runs in 0ms)
|
simple-solution-in-c-well-commented-runs-j034
|
Intuition\nFirst, we need to take into account that we\'re not necessarily looking for a number with the exact same value.\n\nAfter that, we can notice two thin
|
NunoLealF
|
NORMAL
|
2024-07-04T10:59:02.414974+00:00
|
2024-07-04T10:59:02.415003+00:00
| 0 | false |
# Intuition\nFirst, we need to take into account that we\'re not necessarily looking for a number with the exact same value.\n\nAfter that, we can notice two things:\n- First, it\'s generally always more efficient to *first* increment the initial number, and then multiply it\n- Second, the maximum number we can get follows a specific pattern, depending on the number of moves: (0, 1, 2, 4, 6, 9, 12, 16, ...)\n- And, finally, the gaps between each number of that sequence look like (1, 1, 2, 2, 3, 3, 4, 4, 5, 5, 6, 6...) - at this point, you can probably see the pattern.\n\n# Approach\nWe want to create a loop, keeping track of the number of moves and the \'threshold\' (1, 2, 4, 6, 9, 12, 16), aborting that loop whenever the threshold exceeds or is equal to k.\n\nThe threshold is calculated by adding 1 twice, then adding 2 twice, then adding 3 twice, then adding 4 twice, etc.\n\n# Complexity\n- Time complexity: *approximately* $$O(sqrt(n))$$\n\n- Space complexity: $$O(1)$$\n\n# Code\n```\nclass Solution {\npublic:\n\n int minOperations(int k) {\n\n // Pretty sure this is math-related; at which point does it\n // get better to add instead of multiplying?\n\n // 1,1 = 2 [!]\n // 2 = 2 [!]\n\n // 1,1,1 = 3\n // 2,2 = 4 [!]\n // 3 = 3\n\n // 1,1,1,1 = 4\n // 2,2,2 = 6 [!]\n // 3,3 = 6 [!]\n // 4 = 4\n\n // 1,1,1,1,1 = 5\n // 2,2,2,2 = 8\n // 3,3,3 = 9 [!]\n // 4,4 = 8\n // 5 = 5\n\n // 1,1,1,1,1,1 = 6\n // 2,2,2,2,2 = 10\n // 3,3,3,3 = 12 [!]\n // 4,4,4 = 12 [!]\n // 5,5 = 10\n // 6 = 6\n\n // 1,1,1,1,1,1,1 = 7\n // 2,2,2,2,2,2 = 12\n // 3,3,3,3,3 = 15\n // 4,4,4,4 = 16 [!]\n // 5,5,5 = 15\n // 6,6 = 12\n // 7 = 7\n\n // Something we\'ll notice is that, with 0-1-2-4-6-9-12-16-..., the\n // gaps look like 1-1-2-2-3-3-4-4-..\n\n // Since we\'re only looking for a number *greater than or equal to* to\n // k, and this is (almost certainly) the most efficient way to go about it,\n // we just need to keep track of a sequence like that\n\n int Moves = 0;\n int Threshold = 1;\n\n while (Threshold < k) {\n\n Moves++;\n Threshold += ((Moves + 2) / 2);\n\n }\n \n return Moves;\n\n }\n\n};\n```
| 0 | 0 |
['C++']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
Basic thought process and in O(sqrt(k)).
|
basic-thought-process-and-in-osqrtk-by-a-2d5w
|
# Intuition \n\n\n\n\n\n\n# Complexity\n- Time complexity: O(sqrt(k)).\n\n\n- Space complexity: O(1).\n\n\n# Code\n\nclass Solution {\npublic:\n int minOpe
|
abhicalyptic
|
NORMAL
|
2024-06-28T11:53:27.618009+00:00
|
2024-06-28T11:53:27.618040+00:00
| 2 | false |
<!-- # Intuition -->\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n<!-- # Approach -->\n<!-- Describe your approach to solving the problem. -->\n\n\n# Complexity\n- Time complexity: O(sqrt(k)).\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1).\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int minOperations(int k) {\n int mini = INT_MAX;\n for(int i = 1; i<=sqrt(k); i++){\n int cnt = i;\n int p = k - cnt;\n cnt += (p+i-1)/i;\n mini = min(mini, cnt);\n }\n return mini - 1;\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
C++ easy approach, understandable
|
c-easy-approach-understandable-by-wourt-jprf
|
Intuition\n Describe your first thoughts on how to solve this problem. \nGreedy approach to find the highest value per operations\n# Approach\n Describe your ap
|
wourt
|
NORMAL
|
2024-06-24T01:31:07.164032+00:00
|
2024-06-24T01:31:07.164062+00:00
| 5 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nGreedy approach to find the highest value per operations\n# Approach\n<!-- Describe your approach to solving the problem. -->\n we start from array n which is [1], which we declare x = value of array, and mul = size of array, and we can either add more size which or add the value of our arrays. So by we have two choices per operation which is add [1] into [2] or make [1] into [1,1], which is the same as x++, or mul++. So we choose the greedy method to find the highest value per operations to reach value x * mul > k.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n# Code\n```\nclass Solution {\npublic:\n int minOperations(int k) {\n int mul = 1;\n int x = 1;\n int count = 0;\n while (x * mul < k) {\n if ((x + 1) * mul > x * (mul + 1)) {\n x++;\n } else mul++;\n count++;\n }\n\n return count;\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
[C++] One-liner, Greedy
|
c-one-liner-greedy-by-amanmehara-ampe
|
Increase the only element by 1 until it is \geq \sqrt{k}.\n2. Duplicate the element until sum \geq k. \n\n# Complexity\n- Time complexity: O(\sqrt{k})\n- Space
|
amanmehara
|
NORMAL
|
2024-06-11T05:10:06.407051+00:00
|
2024-06-11T05:15:42.529747+00:00
| 6 | false |
1. Increase the only element by 1 until it is $$\\geq \\sqrt{k}$$.\n2. Duplicate the element until $$sum \\geq k$$. \n\n# Complexity\n- Time complexity: $$O(\\sqrt{k})$$\n- Space complexity: $$O(1)$$\n\n# Code\n```\nclass Solution {\npublic:\n int minOperations(int k) {\n return ceil(sqrt(k)) + ceil(static_cast<double>(k) / ceil(sqrt(k))) - 2;\n }\n};\n```
| 0 | 0 |
['Math', 'Greedy', 'C++']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
EASY BY PRINCE GANESHWALA
|
easy-by-prince-ganeshwala-by-princeganes-ey3a
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
PrinceGaneshwala
|
NORMAL
|
2024-06-08T07:17:21.878996+00:00
|
2024-06-08T07:17:21.879027+00:00
| 0 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int minOperations(int k) {\n int number = 0;\n int ans = 0;\n int number2=0;\n if (k <= 1) {\n return number;\n } else {\n for (int i = 1; i <= k / 2 + 1; i++) {\n if (i*i>= k) {\n number = i;\n break;\n }\n }\n ans = number-1; \n for(int j=0;j<=k/2+1;j++)\n {\n if((number*j)>=k)\n {\n number2=j;\n break;\n }\n }\n ans+=number2-1;\n }\n\n return ans;\n }\n}\n\n```
| 0 | 0 |
['Java']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
O((logk )*(logk)) and O(1) solution using nested binary search;
|
ologk-logk-and-o1-solution-using-nested-a1p3p
|
Intuition\n Describe your first thoughts on how to solve this problem. \nwe just check from 1 to k if at any point using that ammount f operation it is possible
|
kishansinhpuvar89
|
NORMAL
|
2024-06-06T07:23:41.250603+00:00
|
2024-06-06T07:23:41.250628+00:00
| 0 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nwe just check from 1 to k if at any point using that ammount f operation it is possible to get sum>=k if yes the we store that point in as ans and move to left part for finding minimum possible else we move to right part .\n\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nfor determine whether sum is >=k is possible or not using at most h operation.\n\nwe again do binary search where mid indicates that we use mid times operation 1 and (h-mid) time operatin 2;\n\nif we get sum>= k return true;\nelse we decrease the opeartion of type 1 .// high=mid-1;\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(log(k) * log(k));\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n\n# Code\n```\nclass Solution {\npublic:\nbool cal(int h,int k){\n int low=0,high=h;\n while(low<=high){\n int mid=(low+high)/2;\n int z=(1+mid)*(h-mid+1);\n // cout<<z<<" low: "<<low <<" high: "<<high<<" h: "<<h<<endl;\n if(z>=k)return true;\n high=mid-1;\n }\n return false;\n}\n int minOperations(int k) {\n int total=k;\n int ans=-1;\n int low=0;\n int high=k;\n while(low <= high){\n int mid=(low+high)/2;\n\n bool z=cal(mid,k);\n \n if(z){\n ans=mid;\n high=mid-1;\n }else{\n low=mid+1;\n }\n }\n return ans;\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
3091. Apply Operations to Make Sum of Array Greater Than or Equal to k in Java by Coding_Sanjay
|
3091-apply-operations-to-make-sum-of-arr-lahr
|
\n\n# Code\n\nclass Solution {\n public int minOperations(int k) {\n \n if (k <= 1) return 0;\n \n int min = Integer.MAX_VALUE;\n
|
Sanjay_kumar14
|
NORMAL
|
2024-06-05T18:33:41.551430+00:00
|
2024-06-05T18:33:41.551457+00:00
| 0 | false |
\n\n# Code\n```\nclass Solution {\n public int minOperations(int k) {\n \n if (k <= 1) return 0;\n \n int min = Integer.MAX_VALUE;\n \n for (int i=1; i<=k/2; i++) {\n for(int j=1; j<=k; j++) {\n if(i*j >= k && min > (i+j)-2) {\n min = (i+j)-2;\n break;\n } else if (i*j >= k) break;\n }\n }\n return min;\n }\n}\n```
| 0 | 0 |
['Java']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
Fastest solution cpp
|
fastest-solution-cpp-by-bhanu_pratap5-tu7y
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
bhanu_pratap5
|
NORMAL
|
2024-06-01T16:42:10.899627+00:00
|
2024-06-01T16:42:10.899657+00:00
| 1 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n bool check(int x,int k){\n long long y=((x+1)/2)+1;\n x-=(y-1);\n long long ans=(x+1)*y;\n return ans>=k;\n }\n int minOperations(int k) {\n if(k==1)return 0;\n int lo=1;\n int hi=1e6;\n int ans;\n while(lo<=hi){\n int mid=(lo+hi)/2;\n if(check(mid,k)){\n ans=mid;\n hi=mid-1;\n }else{\n lo=mid+1;\n }\n }\n return ans;\n }\n};\n```
| 0 | 0 |
['Binary Search', 'C++']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
100% beat simple solution Math
|
100-beat-simple-solution-math-by-ashutos-8qrr
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
ashutoshup
|
NORMAL
|
2024-05-28T02:50:42.184353+00:00
|
2024-05-28T02:50:42.184371+00:00
| 1 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int minOperations(int k) {\n if(k==1||k==2)return k-1;\n int incr=sqrt(k)-1;\n return incr+(k-1)/(incr+1);\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
best c++ solution 100% beat
|
best-c-solution-100-beat-by-sada_nayak-7brl
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
sada_nayak
|
NORMAL
|
2024-05-25T06:55:57.279627+00:00
|
2024-05-25T06:55:57.279658+00:00
| 2 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(log n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int minOperations(int k) {\n if(k==1)\n return 0;\n int nums=1,count=INT_MAX;\n double x=double(k);\n while(nums<=k/2){\n int a=ceil(x/nums);\n count=min(count,nums+a-2);\n nums+=1;\n }\n return count;\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k
|
simple straight forward approach
|
simple-straight-forward-approach-by-gant-fww8
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \nSure, here\'s a concise
|
GantlaRahul
|
NORMAL
|
2024-05-21T17:28:10.177632+00:00
|
2024-05-21T17:28:10.177664+00:00
| 1 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nSure, here\'s a concise explanation of the code:\n\nThe Java method `minOperations` calculates the minimum number of operations needed to reach the value `k` starting from 1 using a specific approach:\n\n1. **Handle Simple Cases:** \n ```java\n if(k==0 || k==1){return 0;}\n ```\n - If `k` is 0 or 1, return 0 because no operations are needed to reach these values.\n\n2. **Initialize Minimum Operations:**\n ```java\n int min = Integer.MAX_VALUE;\n ```\n - Initialize `min` to the maximum possible integer value to keep track of the smallest number of operations found.\n\n3. **Loop Through Possible Divisors:**\n ```java\n for(int i=1; i<=k/2; i++){\n ```\n - Iterate through all possible divisors `i` from 1 to `k/2`.\n\n4. **Calculate Quotient and Operations:**\n ```java\n int l = 0;\n if(k % i == 0){\n l = k / i;\n } else {\n l = k / i + 1;\n }\n int m = l - 1 + i - 1;\n ```\n - For each `i`, calculate `l` as the ceiling of `k / i` (if `k` is not exactly divisible by `i`, add 1 to the quotient).\n - Calculate the total number of operations `m` as `l - 1` (to reach `l` from 1) plus `i - 1` (to reach `i` from 1).\n\n5. **Update Minimum Operations:**\n ```java\n min = Math.min(m, min);\n ```\n - Update `min` with the smaller value between the current `min` and `m`.\n\n6. **Return Result:**\n ```java\n return min;\n ```\n - After iterating through all possible divisors, return the minimum number of operations found.\n\n### Example:\nFor `k = 10`:\n- `i = 1` \u2192 `l = 10`, `m = 9`\n- `i = 2` \u2192 `l = 5`, `m = 5`\n- `i = 3` \u2192 `l = 4`, `m = 5`\n- `i = 4` \u2192 `l = 3`, `m = 5`\n- `i = 5` \u2192 `l = 2`, `m = 5`\n\nThe minimum number of operations is 5, so the function returns 5.\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int minOperations(int k) {\n if(k==0 || k==1){return 0;}\n int min=Integer.MAX_VALUE;\n for(int i=1;i<=k/2;i++){\n int l=0;\n if(k%i==0){\n l=k/i;\n }\n else{\n l=k/i+1;\n }\n int m=l-1+i-1;\n min=Math.min(m,min);\n }\n return min;\n }\n}\n```
| 0 | 0 |
['Java']
| 0 |
minimum-bit-flips-to-convert-number
|
Most easy || beats 100% || Best Solution || All languages
|
most-easy-beats-100-best-solution-all-la-84tu
|
\n\n# Intuition\nThe question asks how few bit flips are necessary to change one integer into another. It follows easily that the bits of the two numbers can be
|
raghavagarwal28
|
NORMAL
|
2024-09-10T12:00:07.317772+00:00
|
2024-09-11T13:08:33.818651+00:00
| 32,401 | false |
\n\n# Intuition\nThe question asks how few bit flips are necessary to change one integer into another. It follows easily that the bits of the two numbers can be compared. The amount of flips required will depend on how the bits in the binary representation of start and aim differ from one another. The result of a bitwise XOR operation between start and goal is a number where each 1 denotes a location where the bits of the two numbers differ. The necessary number of bit flips can be found by counting the 1s in this XOR result.\n\n# Approach\n1) XOR the two numbers: Perform a bitwise XOR between start and goal. The result will have 1 in positions where the bits are different between the two numbers.\n2) Count the number of 1s in the XOR result: This tells us the number of positions where the bits differ and hence the number of bit flips required.\n3) Bit counting: Use a loop to repeatedly check the last bit of the XOR result using & 1. Right shift the XOR result (>> 1) to process the next bit. Continue until all bits are processed.\n\n# Complexity\n- Time complexity:\nThe time complexity is O(k), where k is the number of bits in the binary representation of the larger of the two numbers (start or goal).\n\n- Space complexity:\nThe space complexity is O(1).\n\n# Code\n```java []\nclass Solution {\n public int minBitFlips(int start, int goal) {\n int ans = 0; \n // XOR will give 1 where the bits are different\n int xor = start ^ goal;\n\n while(xor!=0){\n // If the last bit is 1, increment count \n ans += xor & 1;\n\n // Right-shift to check the next bit\n xor >>=1;\n }\n return ans;\n }\n}\n```\n``` C++ []\nclass Solution {\npublic:\n int minBitFlips(int start, int goal) {\n int xorResult = start ^ goal;\n int ans = 0;\n \n \n while (xorResult > 0) {\n ans += xorResult & 1; \n xorResult >>= 1;\n }\n \n return ans;\n }\n};\n```\n``` python []\nclass Solution(object):\n def minBitFlips(self, start, goal):\n """\n :type start: int\n :type goal: int\n :rtype: int\n """\n\n xor_result = start ^ goal\n ans = 0\n \n while xor_result > 0:\n ans += xor_result & 1 \n xor_result >>= 1 \n \n return ans\n\n```\n``` Javascript []\n/**\n * @param {number} start\n * @param {number} goal\n * @return {number}\n */\nvar minBitFlips = function(start, goal) {\n // XOR to find differing bits between start and goal\n let xorResult = start ^ goal;\n let ans = 0;\n \n // Count the number of 1\'s in the XOR result\n while (xorResult > 0) {\n ans += xorResult & 1; \n xorResult >>= 1; \n }\n \n return ans;\n};\n\n```\n\n
| 195 | 7 |
['Bit Manipulation', 'Python', 'C++', 'Java', 'Python3', 'JavaScript']
| 21 |
minimum-bit-flips-to-convert-number
|
[C++] 1 liner[xor,count set bits]
|
c-1-linerxorcount-set-bits-by-prilily-beng
|
To get minimum bit flips we find XOR of two number : which have set bits only at those places where A differs from B. \nSo, after getting the xor ( a ^ b ) , we
|
prilily
|
NORMAL
|
2022-04-02T16:02:10.759478+00:00
|
2022-04-02T16:02:10.759508+00:00
| 11,454 | false |
To get minimum bit flips we find XOR of two number : which have set bits only at those places where A differs from B. \nSo, after getting the **xor** `( a ^ b )` , we need to count the number of set bits.\nWe can do that using **__builtin_popcount(i)**: This function is used to count the number of set bits in an integer.\n\n```\nclass Solution {\npublic:\n int minBitFlips(int start, int goal) {\n return __builtin_popcount(start^goal);\n }\n};\n```\nPlease let me know ways to improve my solution.
| 73 | 1 |
['C']
| 13 |
minimum-bit-flips-to-convert-number
|
One liners | Have a look
|
one-liners-have-a-look-by-surajthapliyal-9b0o
|
Number of different bits is the required bits to flip, to make start and goal same.\nWe can efficiently calculate them using xor operation : \n\nJava one liner
|
surajthapliyal
|
NORMAL
|
2022-04-03T16:38:31.243448+00:00
|
2022-04-03T16:41:56.165298+00:00
| 6,391 | false |
Number of different bits is the required bits to flip, to make start and goal same.\nWe can efficiently calculate them using xor operation : \n\n**Java one liner :** \n```\npublic int minBitFlips(int start, int goal) {\n return Integer.bitCount(start^goal);\n}\n```\n\n\n**CPP one liner :**\n```\nint minBitFlips(int start, int goal) {\n return __builtin_popcount(start^goal);\n}\n```\n\n**Python one liner :**\n```\ndef minBitFlips(self, start: int, goal: int) -> int:\n return (start ^ goal).bit_count()\n```\n\n**Javascript one liner :**\n```\nvar minBitFlips = function(start, goal) {\n return (start^goal).toString(2).split("0").join("").length;\n};\n```
| 40 | 0 |
['Python', 'C++', 'Java', 'JavaScript']
| 7 |
minimum-bit-flips-to-convert-number
|
[Python/Java/C++] Solution without XOR
|
pythonjavac-solution-without-xor-by-keio-pzuv
|
Divmod Remainder Approach:\n#### Time Complexity: O(log(min(s,g))) --> O(log(n)) \n#### Space Complexity: O(1)\n\nWe divide s and q by 2 until either s or g equ
|
keioon
|
NORMAL
|
2022-11-03T21:03:41.671314+00:00
|
2023-03-14T19:28:56.710857+00:00
| 2,935 | false |
# Divmod Remainder Approach:\n#### Time Complexity: O(log(min(s,g))) --> O(log(n)) \n#### Space Complexity: O(1)\n\nWe divide s and q by 2 until either s or g equals zero.\nDuring this process, if the remainder of either of them **do not** equal eachother, we increment the counter.\n\n***This process is similar to converting a decimal number to binary***\n\n**Example:** s=10 g=7\n\n| iterations | s (binary) | g (binary) | counter | explaination\n| - | --- | --- | --- | ---- |\n1| 1010 |0111|+1| The last digit of s and g are ***different***\n2| 0101 |0011|+0| The last digits are the **same** so we do nothing\n3| 0010 |0001|+1| The last digit of s and g are ***different***\n4| 0001 |0000|+1|The last digit of s and g are ***different***\n\n```Python []\nclass Solution:\n def minBitFlips(self, s: int, g: int) -> int:\n count = 0 \n while s or g:\n if s%2 != g%2: count+=1\n s, g = s//2, g//2\n return count\n```\n```Java []\nclass Solution {\n public int minBitFlips(int s, int g) {\n int count = 0;\n while(s > 0 || g > 0){\n if(s%2 != g%2) count++;\n s = s/2;\n g = g/2;\n }\n return count;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int minBitFlips(int s, int g) {\n int count = 0;\n while(s > 0 || g > 0){\n if(s%2 != g%2) count++;\n s = s/2;\n g = g/2;\n }\n return count;\n }\n};\n```\n```PsudoCode []\nfunction minBitFlips(integer s, integer g){\n\tinitilize counter integer to 0\n\tloop until s or g is equal to zero{\n\t\tif the s mod 2 and g mod 2 have the same remainder, increment counter\n\t\tdivide s and g by 2 every pass\n\t}\n\treturn counter\n}\n```\n\n# PLEASE UPVOTE IF THIS HELPED YOU :)\n
| 35 | 0 |
['Python', 'Python3']
| 5 |
minimum-bit-flips-to-convert-number
|
C++ || 2 methods || 1-Line Solution
|
c-2-methods-1-line-solution-by-raghav_ma-bre0
|
Method-1\n\nWe find last bit of both start and goal by two and check if the bit is same or not. Then divide the numbers by 2.\n\n\nclass Solution {\npublic:\n
|
raghav_maskara
|
NORMAL
|
2022-04-02T17:06:03.318755+00:00
|
2022-04-02T17:06:03.318798+00:00
| 4,081 | false |
## Method-1\n\nWe find last bit of both start and goal by two and check if the bit is same or not. Then divide the numbers by 2.\n\n```\nclass Solution {\npublic:\n int minBitFlips(int start, int goal) {\n int ans=0;\n while(start>0 or goal>0){\n int temp1=start%2;\n int temp2=goal%2;\n if(temp1!=temp2){\n ans++;\n }\n start/=2;\n goal/=2;\n }\n return ans;\n }\n}; \n```\n\n## Method-2\n**XOR** start and goal to find the bits that are different\nUse in-built method **popcount** to count the number of set bits\n```\nclass Solution {\npublic:\n int minBitFlips(int start, int goal) {\n return __builtin_popcount(start^goal);\n }\n};\n```
| 28 | 1 |
['C']
| 7 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.