question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
maximum-energy-boost-from-two-drinks
|
Java | O(n) 100% | With Explanation
|
java-on-100-with-explanation-by-zell_dev-sdd1
|
Step 1: Initialize Dynamic Programming Arrays\nInitialize two arrays, dpA and dpB, to store the maximum energy boosts for energyDrinkA and energyDrinkB respecti
|
zell_dev
|
NORMAL
|
2024-08-18T04:08:41.395011+00:00
|
2024-08-18T04:08:41.395029+00:00
| 81 | false |
**Step 1: Initialize Dynamic Programming Arrays**\nInitialize two arrays, dpA and dpB, to store the maximum energy boosts for energyDrinkA and energyDrinkB respectively. Set up the base cases for the last two positions based on the given energy drinks.\n\n**Step 2: Compute Maximum Energy Boosts**\nIterate backward through the arrays, updating dpA[i] and dpB[i] to represent the maximum energy boost at each position by considering either continuing with the current drink or switching to the other one after skipping one.\n\n**Step 3: Return the Maximum Boost**\nCompare the first elements of dpA and dpB to find and return the maximum energy boost starting from the first energy drink..\n\n```\nclass Solution {\n public long maxEnergyBoost(int[] energyDrinkA, int[] energyDrinkB) {\n int n = energyDrinkA.length;\n \n long[] dpA = new long[n];\n long[] dpB = new long[n];\n \n dpA[n-1] = energyDrinkA[n-1];\n dpB[n-1] = energyDrinkB[n-1];\n dpA[n -2] = energyDrinkA[n-2] + energyDrinkA[n-1];\n dpB[n -2] += energyDrinkB[n-2] + energyDrinkB[n-1];\n \n for(int i = n - 3; i >= 0 ; i--){\n dpA[i] = Math.max((long)energyDrinkA[i] + dpA[i+1], (long)energyDrinkA[i] + dpB[i + 2]);\n dpB[i] = Math.max((long)energyDrinkB[i] + dpB[i+1], (long)energyDrinkB[i] + dpA[i + 2]);\n }\n \n return Math.max(dpA[0], dpB[0]);\n }\n}\n```\n\nIf you found it helpful, please consider giving it an upvote! It\'ll motivate me to share more solutions in the future. If you have any questions or suggestions, please let me know. Happy coding!
| 2 | 0 |
[]
| 0 |
maximum-energy-boost-from-two-drinks
|
Easy DP Solution || Python, JavaScript, C++ ✅
|
easy-dp-solution-python-javascript-c-by-5cweb
|
Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(1)\n\n# Code\nPython3 []\nclass Solution:\n def maxEnergyBoost(self, energyDrinkA: List[int], en
|
101rror
|
NORMAL
|
2024-08-18T04:01:52.727446+00:00
|
2024-08-18T04:23:36.458480+00:00
| 163 | false |
# Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(1)\n\n# Code\n```Python3 []\nclass Solution:\n def maxEnergyBoost(self, energyDrinkA: List[int], energyDrinkB: List[int]) -> int:\n n = len(energyDrinkA)\n\n dpA, dpB = [0] * n, [0] * n\n\n dpA[0], dpB[0] = energyDrinkA[0], energyDrinkB[0]\n\n for i in range(1, n):\n dpA[i] = max(dpA[i - 1] + energyDrinkA[i], dpB[i - 1])\n dpB[i] = max(dpB[i - 1] + energyDrinkB[i], dpA[i - 1])\n\n mx = max(dpA[-1], dpB[-1])\n\n return mx\n\n```\n```JavaScript []\n/**\n * @param {number[]} energyDrinkA\n * @param {number[]} energyDrinkB\n * @return {number}\n */\nvar maxEnergyBoost = function(energyDrinkA, energyDrinkB) {\n let n = energyDrinkA.length;\n\n let dpA = new Array(n).fill(0);\n let dpB = new Array(n).fill(0);\n\n dpA[0] = energyDrinkA[0];\n dpB[0] = energyDrinkB[0];\n\n for (let i = 1; i < n; i++) {\n dpA[i] = Math.max(dpA[i - 1] + energyDrinkA[i], dpB[i - 1]);\n dpB[i] = Math.max(dpB[i - 1] + energyDrinkB[i], dpA[i - 1]);\n }\n\n return Math.max(dpA[n - 1], dpB[n - 1]);\n};\n```\n```C++ []\nclass Solution {\npublic:\n long long maxEnergyBoost(vector<int>& energyDrinkA, vector<int>& energyDrinkB) {\n int n = energyDrinkA.size();\n\n long long prevA = energyDrinkA[0], prevB = energyDrinkB[0];\n\n for (int i = 1; i < n; ++i) {\n long long currA = max(prevA + energyDrinkA[i], prevB);\n long long currB = max(prevB + energyDrinkB[i], prevA);\n\n prevA = currA;\n prevB = currB;\n }\n\n return max(prevA, prevB);\n }\n};\n```
| 2 | 0 |
['Dynamic Programming', 'C++', 'Python3', 'JavaScript']
| 0 |
maximum-energy-boost-from-two-drinks
|
Easy Python Solution | Recursion + DP
|
easy-python-solution-recursion-dp-by-pra-azus
|
Intuition\nThe problem involves making a series of choices between two options at each step: selecting from energyDrinkA or energyDrinkB. To maximize the total
|
pranav743
|
NORMAL
|
2024-08-27T16:22:08.284367+00:00
|
2024-08-27T16:22:08.284399+00:00
| 90 | false |
# Intuition\nThe problem involves making a series of choices between two options at each step: selecting from `energyDrinkA` or `energyDrinkB`. To maximize the total energy boost, you need to carefully decide which choice to make at each step while considering the future consequences of each choice.\n\n# Complexity\n\n- Time complexity: O(N)\n\n- Space complexity: O(2*N)\n\n# Code (Recursion with Memoization)\n```python3 []\nclass Solution:\n def maxEnergyBoost(self, energyDrinkA: List[int], energyDrinkB: List[int]) -> int:\n n = len(energyDrinkA)\n\n @cache\n def backtrack(i,A):\n if i>=n:\n return 0\n if A:\n return energyDrinkA[i] + max(\n backtrack(i+1, True), backtrack(i+2, False)\n )\n else:\n return energyDrinkB[i] + max(\n backtrack(i+1, False), backtrack(i+2, True)\n )\n\n return max(backtrack(0, True), backtrack(0,False))\n```\n\n\n# Code (Iterative DP)\n```python3 []\nclass Solution:\n def maxEnergyBoost(self, eA: List[int], eB: List[int]) -> int:\n\n dp = [[0 for j in range(len(eA) + 3)] for i in range(2)]\n\n for i in range(len(eA) - 1, -1, -1):\n dp[0][i] = eA[i] + max(dp[0][i + 1], dp[1][i + 2])\n dp[1][i] = eB[i] + max(dp[1][i + 1], dp[0][i + 2])\n\n return max(dp[0][0], dp[1][0])\n```
| 1 | 0 |
['Dynamic Programming', 'Recursion', 'Python3']
| 0 |
maximum-energy-boost-from-two-drinks
|
Recursive dp solution || Beats 49%
|
recursive-dp-solution-beats-49-by-meet_p-f2wv
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \nState: max sum i can ge
|
meet_p
|
NORMAL
|
2024-08-26T12:10:11.836393+00:00
|
2024-08-26T12:10:11.836421+00:00
| 5 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n**State: max sum i can get from either arrays starting from level to a.size()**\n\n**Transitions: only two possibilities either take from the current arrays or switch to the other array**\n1. Take from the current array a or b(based on f) and do level + 1\n2. Switch to the other array so direct jump to level+2 coz you need to wait for one hour to cleanse your system and invert the bool f value\n\nIntuition for taking the variable bool f:\n if f = 1 take from the array a \n else from array b\n\n\n\n# Complexity\n- Time complexity: O(n)\n\n\n\n# Code\n```cpp []\nclass Solution {\npublic:\n long long dp[100001][2];\n long long rec(int level,vector<int>& a, vector<int>& b,bool f){\n if(level>=a.size()){\n return 0;\n }\n long long ans;\n if(dp[level][f]!=-1){\n return dp[level][f];\n }\n //f = 1 take from a else from b\n // Two trasistions :\n // 1. Take from the current array a or b(based on f) and level + 1\n // 2. Switch to the other array so direct jump to level+2 coz you need to wait for one hour to cleanse your system and invert the bool f value\n if(f) ans=a[level] + max(rec(level+1,a,b,f),rec(level+2,a,b,!f)); \n else ans = b[level] + max(rec(level+1,a,b,f),rec(level+2,a,b,!f));\n return dp[level][f] = ans;\n\n }\n long long maxEnergyBoost(vector<int>& a, vector<int>& b) {\n memset(dp,-1,sizeof(dp));\n return max(rec(0,a,b,0),rec(0,a,b,1)); // 0 and 1 both in f becuase we can start taking first from any array\n }\n};\n```
| 1 | 0 |
['C++']
| 0 |
maximum-energy-boost-from-two-drinks
|
Easy C++ Solution || DP Memoization
|
easy-c-solution-dp-memoization-by-akshat-0kk6
|
Intuition -: Check out following link for complete explanation-:\nhttps://github.com/akshatsh0610/Data-Structures-and-Algorithms-Problems-Solution/tree/main/Lee
|
akshat0610
|
NORMAL
|
2024-08-19T15:57:45.706737+00:00
|
2024-08-19T15:57:45.706774+00:00
| 1 | false |
Intuition -: Check out following link for complete explanation-:\nhttps://github.com/akshatsh0610/Data-Structures-and-Algorithms-Problems-Solution/tree/main/Leetcode%20Problems/Dynamic%20Programming/Medium/3259.%20Maximum%20Energy%20Boost%20From%20Two%20Drinks\n\n# Code\n```cpp []\nclass Solution {\npublic:\n vector<vector<long long>>dp;\n long long maxEnergyBoost(vector<int>& drink1, vector<int>& drink2) {\n dp.resize(drink1.size(),vector<long long>(3,-1));\n return getMaxEnergy(drink1,drink2,0,0); \n }\n long long getMaxEnergy(vector<int>&d1,vector<int>&d2,int d,int idx)\n {\n if(idx>=d1.size())\n {\n return 0;\n }\n if(dp[idx][d]!=-1)\n {\n return dp[idx][d];\n }\n long long choise1=0;\n long long choise2=0;\n if(idx==0)\n { \n choise1=d1[idx]+max(getMaxEnergy(d1,d2,1,idx+1),getMaxEnergy(d1,d2,2,idx+2));\n choise2=d2[idx]+max(getMaxEnergy(d1,d2,2,idx+1),getMaxEnergy(d1,d2,1,idx+2));\n }\n else\n {\n if(d==1)\n {\n choise1=d1[idx]+getMaxEnergy(d1,d2,1,idx+1);\n choise2=d1[idx]+getMaxEnergy(d1,d2,2,idx+2);\n }\n else \n {\n choise1=d2[idx]+getMaxEnergy(d1,d2,2,idx+1);\n choise2=d2[idx]+getMaxEnergy(d1,d2,1,idx+2);\n }\n }\n return dp[idx][d]=max(choise1,choise2);\n }\n};\n```
| 1 | 0 |
['Array', 'Dynamic Programming', 'C++']
| 0 |
maximum-energy-boost-from-two-drinks
|
The Shortest Possible One Line Solution
|
the-shortest-possible-one-line-solution-j4bju
|
\n\nconst maxEnergyBoost = ([headA, ...drinkA], [headB, ...drinkB]) =>\n Math.max(...drinkA.reduce(([a, b], vA, i) => [Math.max(a + vA, b), Math.max(b + drin
|
charnavoki
|
NORMAL
|
2024-08-18T21:50:01.342423+00:00
|
2024-08-18T21:50:01.342445+00:00
| 18 | false |
\n```\nconst maxEnergyBoost = ([headA, ...drinkA], [headB, ...drinkB]) =>\n Math.max(...drinkA.reduce(([a, b], vA, i) => [Math.max(a + vA, b), Math.max(b + drinkB[i], a)], [headA, headB]));\n\n```\n\n### it\'s a challenge for you to explain how it works\n### please upvote, you motivate me to solve problems in original ways
| 1 | 0 |
['JavaScript']
| 0 |
maximum-energy-boost-from-two-drinks
|
Easy bottom up DP with memoization, 100% runtime
|
easy-bottom-up-dp-with-memoization-100-r-efto
|
Intuition\nEasy bottom up DP with memoization\n# Approach\nDefine a f(h,prev) where h is current hour and prev is the previous choice of energy drink (either a
|
worker-bee
|
NORMAL
|
2024-08-18T21:42:39.195601+00:00
|
2024-08-18T21:42:39.195626+00:00
| 27 | false |
# Intuition\nEasy bottom up DP with memoization\n# Approach\nDefine a `f(h,prev)` where `h` is current hour and `prev` is the previous choice of energy drink (either `a` or `b`). The function returns the max energy at hour `h` given `prev` choice at hour `h-1`.\n\nAt every hour `h` we have a choice to either choose `a` or `b` and hence we maintain `prevA` and `prevB` arrays to record max energy at hour `h` if previous choice was `a` as `prevA[h]` and `prevB[h]` when previous choice is `b`. Return 0 when `h` is greater than `length(a)`\n\n# Complexity\n- Time complexity:\nO(n)\n- Space complexity:\nO(n)\n# Code\n```\nclass Solution:\n def maxEnergyBoost(self, a: List[int], b: List[int]) -> int:\n\n prevA = [None]*len(a)\n prevB = [None]*len(b)\n\n def f(h,prev):\n if h >= len(a):\n return 0\n if prev == \'a\':\n if prevA[h] is not None:\n return prevA[h]\n prevA[h] = max(a[h]+f(h+1,prev=\'a\'), f(h+1,prev=\'b\'))\n return prevA[h]\n else:\n if prevB[h] is not None:\n return prevB[h]\n prevB[h] = max(b[h]+f(h+1,prev=\'b\'), f(h+1,prev=\'a\'))\n return prevB[h]\n \n return max(f(0,\'a\'),f(0,\'b\'))\n```
| 1 | 0 |
['Dynamic Programming', 'Memoization', 'Python3']
| 0 |
maximum-energy-boost-from-two-drinks
|
Recursion -> Memoization -> Tablulation -> Space Optimization
|
recursion-memoization-tablulation-space-jajra
|
Intuition\n\nThe problem asks us to maximize the energy boost by selecting either nums1[i] or nums2[i] at each index of the array. To solve this problem, we can
|
_adeeb_
|
NORMAL
|
2024-08-18T15:31:11.787231+00:00
|
2024-08-18T15:31:11.787249+00:00
| 25 | false |
# Intuition\n\nThe problem asks us to maximize the energy boost by selecting either nums1[i] or nums2[i] at each index of the array. To solve this problem, we can start with a simple recursive approach, where we explore all possible paths. However, this leads to redundant calculations, which can be optimized using dynamic programming (DP). We\'ll explore this through a top-down memoized recursion and then translate it into a bottom-up DP approach, further optimizing it to use constant space.\n\n## Approach 1\n### Simple Recursion\n\nWe start with a basic recursive approach. At each index, we have two options:\n\nChoose nums1[i] and move forward.\nChoose nums2[i] and move forward.\nThe recursive function will explore all these options and return the maximum possible energy boost.\n\n#### Visual Representation\n```\n (Start)\n / \\\n nums1[0] nums2[0]\n / \\ / \\ \nnums1[1] nums2[2] nums1[1] nums2[2]\n```\n\n### Complexity\n##### Time complexity: \n$$O(2^n)$$ due to the exponential number of recursive calls.\n##### Space complexity: \n$$O(n)$$ for the recursion stack.\n\n### Code\n```\nclass Solution {\npublic:\n long long f(vector<int> &nums1,vector<int> &nums2,int in,bool isA){\n if(in >= nums1.size()) return 0;\n if(isA) return nums1[in] + max(f(nums1, nums2, in+1, true), f(nums1, nums2, in+2, false));\n return nums2[in] + max(f(nums1, nums2, in+1, false), f(nums1, nums2, in+2, true));\n }\n\n long long maxEnergyBoost(vector<int>& energyDrinkA, vector<int>& energyDrinkB) {\n return max(f(energyDrinkA, energyDrinkB, 0, true), f(energyDrinkA, energyDrinkB, 0, false));\n }\n};\n```\n___\n## Approach 2\n### Memoized Recursion (Top-Down DP)\n\nTo optimize the recursive approach, we use a 2D dp array where dp[i][0] and dp[i][1] store the maximum energy boost from index i if choosing nums1[i] or nums2[i], respectively.\n\n#### Visual Representation\n```\n (Start)\n / \\\n nums1[0] nums2[0]\n | |\n dp[0][0] dp[0][1]\n | |\n nums1[1] nums2[1]\n```\n\n### Complexity\n##### Time complexity: \n$$O(n)$$ as each state is computed only once.\n##### Space complexity: \n$$O(n)$$ for the dp array + $$O(n)$$ stack space.\n\n### Code\n```\nclass Solution {\npublic:\n long long f(vector<int> &nums1,vector<int> &nums2,int in,bool isA,vector<vector<long long>> &dp){\n if(in >= nums1.size()) return 0;\n if(dp[in][isA] != -1) return dp[in][isA];\n if(isA) return dp[in][isA] = nums1[in] + max(f(nums1, nums2, in+1, isA, dp), f(nums1, nums2, in+2, !isA, dp));\n return dp[in][isA] = nums2[in] + max(f(nums1, nums2, in+1, isA, dp), f(nums1, nums2, in+2, !isA, dp));\n }\n\n long long maxEnergyBoost(vector<int>& energyDrinkA, vector<int>& energyDrinkB) {\n int n = energyDrinkA.size();\n vector<vector<long long>> dp(n, vector<long long>(2, -1));\n return max(f(energyDrinkA, energyDrinkB, 0, true, dp), f(energyDrinkA, energyDrinkB, 0, false, dp));\n }\n};\n```\n___\n## Approach 3\n### Bottom-Up DP\n\nInstead of solving the problem recursively, we can solve it iteratively by filling out a table from the last index to the first.\n\n#### Visual Representation\n```\ndp[n-1][0] <- nums1[n-1]\ndp[n-1][1] <- nums2[n-1]\n\ndp[n-2][0] <- nums1[n-2] + max(dp[n-1][0], dp[n-1][1])\ndp[n-2][1] <- nums2[n-2] + max(dp[n-1][0], dp[n-1][1])\n\n...\n\ndp[0][0] <- nums1[0] + max(dp[1][0], dp[2][1])\ndp[0][1] <- nums2[0] + max(dp[1][1], dp[2][0])\n```\n\n### Complexity\n##### Time complexity: \n$$O(n)$$ due to the single iteration over the input array.\n##### Space complexity: \n$$O(n)$$ for the dp table.\n\n### Code\n```\nclass Solution {\npublic:\n long long maxEnergyBoost(vector<int>& nums1, vector<int>& nums2) {\n int n = nums1.size();\n vector<vector<long long>> dp(n, vector<long long>(2, 0));\n for (int in = n - 1; in >= 0; in--) {\n dp[in][0] = nums1[in] + max(in + 1 < n ? dp[in + 1][0] : 0, in + 2 < n ? dp[in + 2][1] : 0);\n dp[in][1] = nums2[in] + max(in + 1 < n ? dp[in + 1][1] : 0, in + 2 < n ? dp[in + 2][0] : 0);\n }\n return max(dp[0][0], dp[0][1]);\n }\n};\n```\n___\n## Approach 4\n### Optimized Bottom-Up DP\n\nOptimize the space usage by only keeping track of the last two states. This reduces the space complexity from O(n) to O(1).\n\n#### Visual Representation\n```\n aCurIn <- nums1[i] + max(aIn1, bIn2)\n bCurIn <- nums2[i] + max(bIn1, aIn2)\n\n aIn1 <- aCurIn\n bIn1 <- bCurIn\n aIn2 <- prev aIn1\n bIn2 <- prev bIn1\n```\n\n### Complexity\n\n##### Time complexity: \n$$O(n)$$ due to the single iteration over the input array.\n\n##### Space complexity: \n$$O(1)$$ due to the constant space usage.\n\n### Code\n```\nclass Solution {\npublic:\n long long maxEnergyBoost(vector<int>& nums1, vector<int>& nums2) {\n int n = nums1.size();\n long long aCurIn, aIn1 = 0, aIn2 = 0;\n long long bCurIn, bIn1 = 0, bIn2 = 0;\n\n for (int in = n - 1; in >= 0; in--) {\n aCurIn = nums1[in] + max(in + 1 < n ? aIn1 : 0, in + 2 < n ? bIn2 : 0);\n bCurIn = nums2[in] + max(in + 1 < n ? bIn1 : 0, in + 2 < n ? aIn2 : 0);\n aIn2 = aIn1;\n aIn1 = aCurIn;\n bIn2 = bIn1;\n bIn1 = bCurIn;\n }\n\n return max(aCurIn, bCurIn);\n }\n};\n```
| 1 | 0 |
['Dynamic Programming', 'Recursion', 'Memoization', 'C++']
| 0 |
maximum-energy-boost-from-two-drinks
|
JAVA | Recursion | Memo | Bottom-Up
|
java-recursion-memo-bottom-up-by-priyans-f16n
|
Code\n\nclass Solution {\n public long maxEnergyBoost(int[] energyDrinkA, int[] energyDrinkB) {\n return Math.max(helper(true, 0, energyDrinkA, energy
|
priyanshuawasthi14feb
|
NORMAL
|
2024-08-18T15:13:18.936496+00:00
|
2024-08-18T15:13:18.936531+00:00
| 3 | false |
# Code\n```\nclass Solution {\n public long maxEnergyBoost(int[] energyDrinkA, int[] energyDrinkB) {\n return Math.max(helper(true, 0, energyDrinkA, energyDrinkB), \n helper(false, 0, energyDrinkA, energyDrinkB));\n }\n\n public long helper (boolean takeA, int index, int []A, int []B) {\n if (index >= A.length) return 0;\n long curr = 0;\n if (takeA) {\n curr = Math.max(A[index] + helper(true, index + 1, A, B), A[index] + helper(false, index + 2, A, B));\n }\n else curr = Math.max(B[index] + helper(false, index + 1, A, B), B[index] + helper(true, index + 2, A, B));\n return curr;\n }\n}\n```\n```\nclass Solution {\n public long dp[][];\n public long maxEnergyBoost(int[] energyDrinkA, int[] energyDrinkB) {\n dp = new long[2][energyDrinkA.length];\n for (long arr[] : dp) Arrays.fill(arr, -1);\n return Math.max(helper(1, 0, energyDrinkA, energyDrinkB), \n helper(0, 0, energyDrinkA, energyDrinkB));\n }\n // 1 take A\n // 0 take B\n public long helper (int takeA, int index, int []A, int []B) {\n if (index >= A.length) return 0;\n if (dp[takeA][index] != -1) return dp[takeA][index];\n long curr = 0;\n if (takeA == 1) curr = Math.max(A[index] + helper(takeA, index + 1, A, B), A[index] + helper(0, index + 2, A, B));\n else curr = Math.max(B[index] + helper(takeA, index + 1, A, B), B[index] + helper(1, index + 2, A, B));\n return dp[takeA][index] = curr;\n }\n}\n```\n```\nclass Solution {\n public long maxEnergyBoost(int[] energyDrinkA, int[] energyDrinkB) {\n int n = energyDrinkA.length;\n long dp[][] = new long[2][n + 2];\n\n for (int i = n - 1; i >= 0; i--) {\n dp[0][i] = Math.max(energyDrinkA[i] + dp[0][i + 1], energyDrinkA[i] + dp[1][i + 2]);\n dp[1][i] = Math.max(energyDrinkB[i] + dp[1][i + 1], energyDrinkB[i] + dp[0][i + 2]);\n }\n return Math.max(dp[0][0], dp[1][0]);\n }\n}\n```
| 1 | 0 |
['Java']
| 0 |
maximum-energy-boost-from-two-drinks
|
✅ Java Solution
|
java-solution-by-harsh__005-s781
|
CODE\nJava []\npublic long maxEnergyBoost(int[] energyDrinkA, int[] energyDrinkB) {\n\tint n = energyDrinkA.length;\n\n\t// 0 -> A, 1 -> B\n\tlong dp[][] = new
|
Harsh__005
|
NORMAL
|
2024-08-18T09:39:44.173979+00:00
|
2024-08-18T09:39:44.174008+00:00
| 50 | false |
## **CODE**\n```Java []\npublic long maxEnergyBoost(int[] energyDrinkA, int[] energyDrinkB) {\n\tint n = energyDrinkA.length;\n\n\t// 0 -> A, 1 -> B\n\tlong dp[][] = new long[n+1][2];\n\tdp[1][0] = energyDrinkA[0];\n\tdp[1][1] = energyDrinkB[0];\n\n\tfor(int i=1; i<n; i++) {\n\t\tdp[i+1][0] = Math.max(dp[i-1][1], dp[i][0]) + energyDrinkA[i];\n\t\tdp[i+1][1] = Math.max(dp[i-1][0], dp[i][1]) + energyDrinkB[i];\n\t}\n\n\treturn Math.max(dp[n][0], dp[n][1]);\n}\n```
| 1 | 0 |
['Java']
| 1 |
maximum-energy-boost-from-two-drinks
|
Easy to Understand
|
easy-to-understand-by-twasim-fsvw
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
twasim
|
NORMAL
|
2024-08-18T08:52:38.644656+00:00
|
2024-08-18T08:52:38.644687+00:00
| 49 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n# Code\n```\n#define ll long long\nclass Solution {\npublic:\n long long maxEnergyBoost(vector<int>& A, vector<int>& B) {\n int n=A.size();ll t1=A[0];\n ll t2=B[0];\n ll pre_t2 = 0;\n ll pre_t1 = 0;\n for (int i=1;i<n;i++){\n ll temp1 = A[i]+max(pre_t2,t1);\n ll temp2 = B[i]+max(t2,pre_t1);\n pre_t1 = t1;pre_t2=t2;\n t1=temp1;t2=temp2;\n }\n return max(t1,t2);\n }\n};\n```
| 1 | 0 |
['Dynamic Programming', 'C++']
| 0 |
maximum-energy-boost-from-two-drinks
|
Easy to understand!!! Memoization ! Using 2D DP
|
easy-to-understand-memoization-using-2d-xrlu8
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
manvi_010
|
NORMAL
|
2024-08-18T07:39:13.113336+00:00
|
2024-08-18T07:39:13.113363+00:00
| 72 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public long maxEnergyUtil(int[] A, int[] B, int i, int curr, long[][] dp){\n if(i >= A.length){\n return 0;\n }\n if(dp[i][curr] != -1){\n return dp[i][curr];\n }\n \n long max = 0;\n\n if(curr == 0){\n long sum1 = A[i] + maxEnergyUtil(A, B, i+1, 0, dp);\n long sum2 = A[i] + maxEnergyUtil(A, B, i+2, 1, dp);\n max = Math.max(sum1, sum2);\n }\n else{\n long sum1 = B[i] + maxEnergyUtil(A, B, i+1, 1, dp);\n long sum2 = B[i] + maxEnergyUtil(A, B, i+2, 0, dp);\n max = Math.max(sum1, sum2);\n }\n\n return dp[i][curr] = max;\n }\n public long maxEnergyBoost(int[] A, int[] B) {\n long[][] dp = new long[A.length][2];\n for(long[] arr : dp){\n Arrays.fill(arr, -1);\n }\n long maxA = maxEnergyUtil(A, B, 0, 0, dp);\n for(long[] arr : dp){\n Arrays.fill(arr, -1);\n }\n long maxB = maxEnergyUtil(A, B, 0, 1, dp);\n return Math.max(maxA, maxB);\n\n }\n}\n```
| 1 | 0 |
['Recursion', 'Memoization', 'Java']
| 0 |
maximum-energy-boost-from-two-drinks
|
Simple recursion + Memoization
|
simple-recursion-memoization-by-spacexgr-ogfl
|
Intuition\nEvery index has 2 possibilities either it comes from A or from B so it\'s DP problem as we don\'t what will yield us the best solution without knowin
|
spacexgragonrye3008507
|
NORMAL
|
2024-08-18T07:38:58.992237+00:00
|
2024-08-18T07:38:58.992263+00:00
| 37 | false |
# Intuition\nEvery index has 2 possibilities either it comes from A or from B so it\'s DP problem as we don\'t what will yield us the best solution without knowing the answer of subproblem.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nIf we switch then we have to leave the current energy else we keep on adding the energies. Out of the two we take maximum and that will be our answer.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxEnergyBoost(self, energyDrinkA: List[int], energyDrinkB: List[int]) -> int:\n @cache\n def rec(i,prev):\n if i>=len(energyDrinkA) or i>=len(energyDrinkB):\n return 0\n op1=op2=0\n if prev==\'A\':\n op1+= max(energyDrinkA[i]+rec(i+1,\'A\'),rec(i+1,\'B\'))\n if prev==\'B\':\n op2+= max(rec(i+1,\'A\'),energyDrinkB[i]+rec(i+1,\'B\'))\n return max(op1,op2)\n return max(rec(0,\'A\'),rec(0,\'B\'))\n \n \n```
| 1 | 0 |
['Dynamic Programming', 'Recursion', 'Memoization', 'Python3']
| 0 |
maximum-energy-boost-from-two-drinks
|
Maximum Energy Boost From Two Drinks using Dynamic programming
|
maximum-energy-boost-from-two-drinks-usi-qh5g
|
Intuition\nTo solve the problem of maximizing the total energy boost over n hours with two energy drinks, you can use dynamic programming. The key insight is to
|
giriprasath
|
NORMAL
|
2024-08-18T07:17:54.534969+00:00
|
2024-08-18T07:17:54.535001+00:00
| 27 | false |
# Intuition\nTo solve the problem of maximizing the total energy boost over n hours with two energy drinks, you can use dynamic programming. The key insight is to track the maximum energy boost you can achieve by either continuing with the same drink or switching drinks, considering the constraint that switching drinks requires a one-hour wait time.\n\n# Approach\n1. Use two arrays dpA and dpB where:\n\n- dpA[i] represents the maximum energy boost possible up to hour i if you are drinking drink A at hour i.\n- dpB[i] represents the maximum energy boost possible up to hour i if you are drinking drink B at hour i.\n\n2. Initialize:\n\n- dpA[0] to energyDrinkA[0].\n- dpB[0] to energyDrinkB[0].\n\n3. For each subsequent hour i, update the arrays as follows:\n\n- dpA[i] is the maximum of either continuing with drink A or switching from drink B two hours ago (to account for the wait time).\n- dpB[i] is the maximum of either continuing with drink B or switching from drink A two hours ago.\n\n4. The final result is the maximum value of the last elements of dpA and dpB.\n\n# Complexity\n- Time complexity:\nO(n) because we iterate through the arrays once\n\n- Space complexity:\nO(n) for the dpA and dpB arrays used to store the intermediate results.\n\n# Code\n```\nclass Solution {\n public long maxEnergyBoost(int[] energyDrinkA, int[] energyDrinkB) {\n int n = energyDrinkA.length;\n if (n == 0) return 0;\n\n // Arrays to store the maximum energy boost at each hour\n long[] dpA = new long[n];\n long[] dpB = new long[n];\n\n dpA[0] = energyDrinkA[0];\n dpB[0] = energyDrinkB[0];\n\n for (int i = 1; i < n; i++) {\n dpA[i] = energyDrinkA[i] + Math.max(dpA[i - 1], (i > 1 ? dpB[i - 2] : 0));\n dpB[i] = energyDrinkB[i] + Math.max(dpB[i - 1], (i > 1 ? dpA[i - 2] : 0));\n }\n\n return Math.max(dpA[n - 1], dpB[n - 1]);\n }\n\n}\n```
| 1 | 0 |
['Array', 'Dynamic Programming', 'Java']
| 0 |
maximum-energy-boost-from-two-drinks
|
Optimized Dynamic Programming with Constant Space (O(n) Time, O(1) Space Complexity)
|
optimized-dynamic-programming-with-const-llu9
|
Intuition\nThe problem is about finding the maximum energy boost you can get by choosing energy drinks from two different arrays (energyDrinkA and energyDrinkB)
|
Tammali_Amulya
|
NORMAL
|
2024-08-18T06:20:28.005037+00:00
|
2024-08-18T06:20:28.005068+00:00
| 60 | false |
# Intuition\nThe problem is about finding the maximum energy boost you can get by choosing energy drinks from two different arrays (energyDrinkA and energyDrinkB). You can either select an energy drink from the current array or skip to the next one, potentially switching to the other array. The goal is to maximize the total energy collected.\n\n# Approach\nRECURSIVE EXPLORATION : The function explores all possible ways to consume the energy drinks by recursively calculating the maximum energy boost.\n\nSTATE REPRESENTATION :\nindex: The current position in the energy drink arrays.\ncurrentEnergy: The accumulated energy so far.\nlastChosen: Indicates the last chosen array (0 for energyDrinkA and 1 for energyDrinkB).\nBase Case: If index exceeds the length of the energy drink arrays, the function returns the accumulated currentEnergy, ending the recursion.\n\nCHOOSING FROM ARRAYS:\n\nIf the last chosen drink was from energyDrinkA (lastChosen == 0), add the energy from energyDrinkA[index] to currentEnergy.\nOtherwise, add the energy from energyDrinkB[index].\nRecursive Choices:\n\nCall the function for the next index without switching arrays.\nCall the function for the next index but switch to the other array.\nFinal Calculation: The maximum energy boost is obtained by taking the maximum value from starting with energyDrinkA and energyDrinkB.\n\n# Complexity\n- Time complexity:\nExponential Time Complexity (O(2^n)): The function explores every possible combination of choices between the two arrays, leading to an exponential number of recursive calls. Specifically, for each drink, there are two choices (continue with the same array or skip to the next index with an optional array switch), resulting in a total of 2^n possibilities.\n- Space complexity:\nO(n): The maximum depth of the recursion stack is equal to the length of the arrays, n. Therefore, the space complexity is linear in terms of the input size.\n\n# Code\n```\nclass Solution:\n def maxEnergyBoost(self, energyDrinkA: List[int], energyDrinkB: List[int]) -> int:\n def calculateMaxEnergy(index: int, currentEnergy: int, lastChosen: int) -> int:\n if index >= len(energyDrinkA):\n return currentEnergy\n \n # Choose from the same array as last time\n if lastChosen == 0:\n currentEnergy += energyDrinkA[index]\n else:\n currentEnergy += energyDrinkB[index]\n \n # Explore two options: choosing the next or skipping one\n return max(calculateMaxEnergy(index + 1, currentEnergy, lastChosen),\n calculateMaxEnergy(index + 2, currentEnergy, 1 - lastChosen))\n \n # Start from both possibilities and take the max\n return max(calculateMaxEnergy(0, 0, 0), calculateMaxEnergy(0, 0, 1))\n \n```\nThe code can result in a Time Limit Exceeded (TLE) error due to redundant calculations caused by overlapping subproblems. This happens because the recursive function recalculates the maximum energy for the same states (same index and lastChosen) multiple times without storing the results.\nHere comes the need of Dynamic programming approch.\n# Dynamic Programming | Tabulation | Bottom up\n# Finding overlapping subproblem\nIn order to select DrinkA[i] we can come by selecting DrinkA[i-1] or DrinkB[i-2] . To select DrinkA[i-1] we can come by selecting DrinkA[i-2] or DrinkB[i-3].To select DrinkB[i-2] we can come by selecting DrinkB[i-3] or DrinkA[i-4]. This shows DrinkB[i-3] called two times separately while choosing DrinkA[i-1] and DrinkB[i-2]. \nTo get clear idea, go through below image:\n \n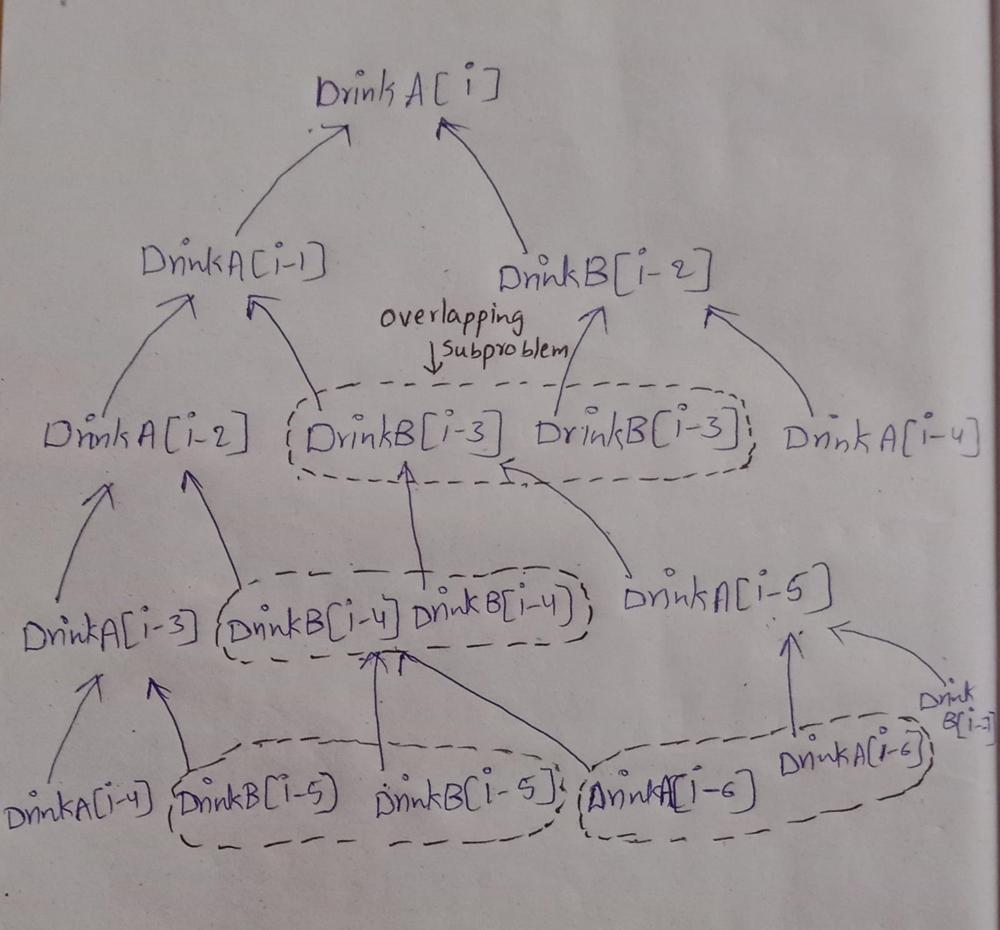\n\n# Dp state explanation\nmaxEnergyFromA[i]: This represents the maximum energy boost you can obtain up to index i if you choose to take the drink from energyDrinkA[i].\n\nmaxEnergyFromB[i]: This represents the maximum energy boost you can obtain up to index i if you choose to take the drink from energyDrinkB[i].\n# Dp Expression :\n Base conditions:\n maxEnergyFromA[0] = energyDrinkA[0] \n maxEnergyFromB[0] = energyDrinkB[0]\n\nFor the second element:\nmaxEnergyFromA[1] = energyDrinkA[1] + max(maxEnergyFromA[0], 0)\nmaxEnergyFromB[1] = energyDrinkB[1] + max(maxEnergyFromB[0], 0)\n\nFor subsequent elements (i >= 2):\nmaxEnergyFromA[i] = energyDrinkA[i] + max(maxEnergyFromA[i-1], maxEnergyFromB[i-2])\nmaxEnergyFromB[i] = energyDrinkB[i] + max(maxEnergyFromB[i-1], maxEnergyFromA[i-2])\n# Final Result :\n max(maxEnergyFromA[n-1],maxEnergyFromB[n-1])\nThe final result is the maximum of maxEnergyFromA[n-1] and maxEnergyFromB[n-1], which gives the maximum energy boost possible after considering all drinks.\nwhere n = lenght of energyDrinkA and energyDrinkB.\n# code \n```\nclass Solution:\n def maxEnergyBoost(self, energyDrinkA: List[int], energyDrinkB: List[int]) -> int:\n maxEnergyFromA = []\n maxEnergyFromB = []\n \n # Initialize the dp arrays for the first element\n for i in range(len(energyDrinkA)):\n if i == 0:\n maxEnergyFromA.append(energyDrinkA[i])\n maxEnergyFromB.append(energyDrinkB[i])\n else:\n maxEnergyFromA.append(-1)\n maxEnergyFromB.append(-1)\n \n # Compute the second element\'s value\n maxEnergyFromA[1] = energyDrinkA[1] + max(maxEnergyFromA[0], 0)\n maxEnergyFromB[1] = energyDrinkB[1] + max(maxEnergyFromB[0], 0)\n \n # Fill in the dp arrays for the rest of the elements\n for i in range(2, len(energyDrinkA)):\n maxEnergyFromA[i] = energyDrinkA[i] + max(maxEnergyFromA[i-1], maxEnergyFromB[i-2])\n maxEnergyFromB[i] = energyDrinkB[i] + max(maxEnergyFromB[i-1], maxEnergyFromA[i-2])\n \n # Return the maximum energy possible\n return max(maxEnergyFromA[-1], maxEnergyFromB[-1])\n\n```\n# Complexity \nTime Complexity : O(n)\nSpace Complexity :O(n)\n\n# Space Optimization\nIn the previous approach, we used two arrays (maxEnergyFromA and maxEnergyFromB) of size n to store the maximum energy boost values at each index. This resulted in an O(n) space complexity.\n\nHowever, we don\u2019t actually need to store the entire arrays. Instead, we only need the last two values (for indices i-1 and i-2) to compute the maximum energy boost for the current index. By using a few variables to track these values, we reduce the space complexity from O(n) to O(1).\n# code :\n```\nclass Solution:\n def maxEnergyBoost(self, energyDrinkA: List[int], energyDrinkB: List[int]) -> int:\n prevMaxEnergyA_0 = energyDrinkA[0]\n prevMaxEnergyB_0 = energyDrinkB[0]\n \n prevMaxEnergyA_1 = energyDrinkA[1] + max(prevMaxEnergyA_0, 0)\n prevMaxEnergyB_1 = energyDrinkB[1] + max(prevMaxEnergyB_0, 0)\n \n for i in range(2, len(energyDrinkA)):\n currentMaxEnergyA = energyDrinkA[i] + max(prevMaxEnergyA_1, prevMaxEnergyB_0)\n currentMaxEnergyB = energyDrinkB[i] + max(prevMaxEnergyB_1, prevMaxEnergyA_0)\n \n prevMaxEnergyA_0 = prevMaxEnergyA_1\n prevMaxEnergyA_1 = currentMaxEnergyA\n \n prevMaxEnergyB_0 = prevMaxEnergyB_1\n prevMaxEnergyB_1 = currentMaxEnergyB\n \n return max(currentMaxEnergyA, currentMaxEnergyB)\n\n```\n# complexity \nTime Complexity : O(n)\nSpace Complexity :O(1)\n
| 1 | 0 |
['Python3']
| 0 |
maximum-energy-boost-from-two-drinks
|
Recursion + Memoization | Beats 100% of users ❤️🔥
|
recursion-memoization-beats-100-of-users-kfbm
|
\n\n# Complexity\n- Time complexity: O(n) \n Add your time complexity here, e.g.\n\n- Space complexity: O(n) \n Add your space complexity here, e.g. O(n) \n\n#
|
rashid_sid
|
NORMAL
|
2024-08-18T04:27:56.411298+00:00
|
2024-08-18T04:27:56.411321+00:00
| 24 | false |
\n\n# Complexity\n- Time complexity: $$O(n)$$ \n<!-- Add your time complexity here, e.g.-->\n\n- Space complexity: $$O(n)$$ \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n using ll = long long;\n\nvector<vector<ll>> dp;\n ll solve(vector<int>& a, vector<int>& b,int pos,int type){\n int n = a.size();\n if(pos>=n){\n return 0;\n }\n\n if(dp[pos][type]!=-1){\n return dp[pos][type];\n }\n\n ll curr = (type==0) ? a[pos] : b[pos];\n\n ll ans = (ll) curr + solve(a,b,pos+1,type);\n\n ans=max(ans, (ll) curr + solve(a,b,pos+2,!type));\n\n return dp[pos][type] = ans;\n }\n\n long long maxEnergyBoost(vector<int>& energyDrinkA,\n vector<int>& energyDrinkB) {\n int n = energyDrinkA.size();\n dp = vector<vector<ll>>(n, vector<ll> (2,-1));\n ll ans=(ll)solve(energyDrinkA,energyDrinkB,0,0);\n ans=max(ans,(ll)solve(energyDrinkA,energyDrinkB,0,1));\n\n return ans;\n }\n};\n```
| 1 | 0 |
['Dynamic Programming', 'Recursion', 'C++']
| 0 |
maximum-energy-boost-from-two-drinks
|
✨💯EASY SOLUTION.. direct and simple implementation, super easy to understand...✨✨💯💯
|
easy-solution-direct-and-simple-implemen-o225
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
manyaagargg
|
NORMAL
|
2024-08-18T04:24:54.204333+00:00
|
2024-08-18T04:24:54.204351+00:00
| 37 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n long long maxEnergyBoost(vector<int>& energyDrinkA, vector<int>& energyDrinkB) {\n int n=energyDrinkA.size();\n vector<vector<long long>> dp(n, vector<long long>(2,0));\n dp[0][0]=energyDrinkA[0];\n dp[0][1]=energyDrinkB[0];\n for(int i=1; i<n; i++){\n if(dp[i-1][0]+energyDrinkA[i] > dp[i-1][1]){\n dp[i][0]=dp[i-1][0]+energyDrinkA[i];\n } else{\n dp[i][0]=dp[i-1][1];\n }\n if(dp[i-1][1]+energyDrinkB[i] > dp[i-1][0]){\n dp[i][1]=dp[i-1][1]+energyDrinkB[i];\n } else{\n dp[i][1]=dp[i-1][0];\n }\n }\n if(dp[n-1][0]>dp[n-1][1]) return dp[n-1][0];\n return dp[n-1][1];\n }\n};\n```
| 1 | 0 |
['Dynamic Programming', 'C++']
| 0 |
maximum-energy-boost-from-two-drinks
|
Dynamic Programming
|
dynamic-programming-by-kaluginpeter-ww6d
|
\n\n# Complexity\n- Time complexity: O(N)\n\n- Space complexity: O(N)\n\n# Code\n\nclass Solution:\n def maxEnergyBoost(self, energyDrinkA: List[int], energy
|
kaluginpeter
|
NORMAL
|
2024-08-18T04:23:39.331311+00:00
|
2024-08-18T04:23:39.331329+00:00
| 89 | false |
\n\n# Complexity\n- Time complexity: O(N)\n\n- Space complexity: O(N)\n\n# Code\n```\nclass Solution:\n def maxEnergyBoost(self, energyDrinkA: List[int], energyDrinkB: List[int]) -> int:\n n: int = len(energyDrinkA)\n\n dpA: list[int] = [0] * n\n dpB: list[int] = [0] * n\n\n dpA[0] = energyDrinkA[0]\n dpB[0] = energyDrinkB[0]\n\n dpA[1] = max(energyDrinkA[0], energyDrinkA[0] + energyDrinkA[1])\n dpB[1] = max(energyDrinkB[0], energyDrinkB[0] + energyDrinkB[1])\n\n for i in range(2, n):\n dpA[i] = max(dpA[i-1] + energyDrinkA[i], dpB[i-2] + energyDrinkA[i])\n dpB[i] = max(dpB[i-1] + energyDrinkB[i], dpA[i-2] + energyDrinkB[i])\n\n return max(dpA[n-1], dpB[n-1])\n```
| 1 | 1 |
['Dynamic Programming', 'Python', 'Python3']
| 0 |
maximum-energy-boost-from-two-drinks
|
Java || Memoization
|
java-memoization-by-viper__66-sruo
|
\nclass Solution {\n Long[][] memo;\n\n long rec(int level, int choosed, int[] a, int[] b) {\n if (level == a.length) {\n return 0;\n
|
Viper__66
|
NORMAL
|
2024-08-18T04:23:08.907870+00:00
|
2024-08-18T04:23:08.907897+00:00
| 36 | false |
```\nclass Solution {\n Long[][] memo;\n\n long rec(int level, int choosed, int[] a, int[] b) {\n if (level == a.length) {\n return 0;\n }\n\n\n if (memo[level][choosed + 1] != null) {\n return memo[level][choosed + 1];\n }\n\n long f = Long.MIN_VALUE;\n\t\t\n\t\t//in these kind of problems maintain what we choosed previously in state \n\t\t//and write the logic according to what we choosed previously\n\n if (choosed == 1 || choosed == -1) {\n f = Math.max(f, a[level] + rec(level + 1, 1, a, b));\n f = Math.max(f, rec(level + 1, 2, a, b));\n }\n if (choosed == 2 || choosed == -1) {\n f = Math.max(f, b[level] + rec(level + 1, 2, a, b));\n f = Math.max(f, rec(level + 1, 1, a, b));\n }\n\n memo[level][choosed + 1] = f;\n return f;\n }\n\n public long maxEnergyBoost(int[] energyDrinkA, int[] energyDrinkB) {\n memo = new Long[energyDrinkA.length][4];\n return rec(0, -1, energyDrinkA, energyDrinkB);\n }\n}\n\n```
| 1 | 0 |
['Dynamic Programming', 'Memoization', 'Java']
| 0 |
maximum-energy-boost-from-two-drinks
|
Space Optimised DP Approach
|
space-optimised-dp-approach-by-mainframe-6x2t
|
Intuition\n Describe your first thoughts on how to solve this problem. \nUse dynamic programming approach to keep track of the maximum energy boost achievable a
|
MainFrameKuznetSov
|
NORMAL
|
2024-08-18T04:13:20.390694+00:00
|
2024-08-18T04:13:20.390727+00:00
| 6 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nUse dynamic programming approach to keep track of the maximum energy boost achievable at each step.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Iterate through arrays\n\n2. Calculate cA as the maximum of pA + eA[i] (continuing from eA) and pB (switching from eB).\n\n3. Calculate cB as the maximum of pB + eB[i] (continuing from eB) and pA (switching from eA).\n\n4. Update pA to cA and pB to cB.\n# Complexity\n- Time complexity:- $O(n)$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:- $O(1)$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n long long maxEnergyBoost(vector<int>&eA,vector<int>&eB) {\n int n=eA.size(); \n long long pA,pB,cA,cB;\n pA=eA[0]; \n pB=eB[0]; \n for(int i=1;i<n;++i) \n { \n cA=max(pA+eA[i],pB); \n cB=max(pB+eB[i],pA);\n pA=cA;\n pB=cB; \n } \n return max(cA,cB); \n }\n};\n```\n\n
| 1 | 0 |
['C++']
| 0 |
maximum-energy-boost-from-two-drinks
|
Recursion->Top Down DP || Beginner's guide to Boost Ratings || Easiest Solution || Beats 100%
|
recursion-top-down-dp-beginners-guide-to-pvga
|
\n\n# Code\n\n#include <bits/stdc++.h>\nusing namespace std;\n\n#define ll long long\n#define memo(a) memset(a, -1, sizeof(a))\n#define len(x) ((ll)x.size()) \n
|
suvro_datta
|
NORMAL
|
2024-08-18T04:05:09.996552+00:00
|
2024-08-18T04:17:57.618309+00:00
| 104 | false |
\n\n# Code\n```\n#include <bits/stdc++.h>\nusing namespace std;\n\n#define ll long long\n#define memo(a) memset(a, -1, sizeof(a))\n#define len(x) ((ll)x.size()) \n#define pb push_back\n\nclass Solution {\npublic:\n ll dp[100005][4];\n ll rec(ll idx, vector<int>& A, vector<int>& B, char last) {\n if(idx >= len(A)) return 0;\n if(dp[idx][last-\'A\'] != -1) return dp[idx][last-\'A\'];\n\n ll ans = 0;\n //If last one is from A, \n //1. we can now choose from A again, let\'s take it\n //2. we can\'t choose from B, but we can choose next one from B\n if(last == \'A\') {\n ans = A[idx] + rec(idx+1, A, B, \'A\');\n if(idx+1 < len(B)) {\n ans = max(ans, B[idx+1] + rec(idx+2, A, B, \'B\'));\n }\n }\n\n else if(last == \'B\') {\n ans = B[idx] + rec(idx+1, A, B, \'B\');\n\n if(idx+1 < len(A)) {\n ans = max(ans, A[idx+1] + rec(idx+2, A, B, \'A\'));\n }\n }\n\n else {\n ans = A[idx] + rec(idx+1, A, B, \'A\');\n ans = max(ans, B[idx] + rec(idx+1, A, B, \'B\'));\n }\n\n return dp[idx][last-\'A\'] = ans;\n }\n\n long long maxEnergyBoost(vector<int>& A, vector<int>& B) {\n memo(dp);\n\n ll ans = rec(0, A, B, \'C\');\n return ans;\n }\n};\n```\n# **Bonus:**\n\nI have made a video on, How to boost Ratings, and Do well in coding contests and interviews. You won\'t find any similar video on entire youtube. It could be truly a gem for beginners. Feel free to skip if you are specialist. Cheers!\n\n<p><iframe width="560" height="315" src="https://www.youtube.com/embed/XAd0r5MvQiA" title="" frameBorder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture; web-share" allowFullScreen><br>Powered by <a href="https://youtubeembedcode.com">html embed youtube video</a> and <a href="https://casinomga.se/">nya mga casino</a></iframe></p>\n\n\n
| 1 | 0 |
['Dynamic Programming', 'Memoization', 'C++']
| 0 |
maximum-energy-boost-from-two-drinks
|
C++ 100% Dynamic Programming (Memo -> Tabulation)
|
c-100-dynamic-programming-memo-tabulatio-62ah
|
Dynamic programming\n## Memoization is in the commented code lambda rec()\n# Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(n)\n# Code\n\n#include
|
bramar2
|
NORMAL
|
2024-08-18T04:03:39.062666+00:00
|
2024-08-18T04:04:12.445770+00:00
| 8 | false |
## Dynamic programming\n## Memoization is in the commented code lambda rec()\n# Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(n)$$\n# Code\n```\n#include <bits/stdc++.h>\n#pragma GCC optimize ("Ofast")\n#pragma GCC target("sse,sse2,sse3,ssse3,sse4,popcnt,abm,mmx,avx2,tune=native")\nusing namespace std;\n#define all(x) x.begin(), x.end()\n\n\nusing ull = unsigned long long;\nusing ll = long long;\n\ninline int gcd(int a,int b) { if (b==0) return a; return gcd(b, a%b); }\ninline long long gcd(long long a,long long b) { if (b==0) return a; return gcd(b, a%b); }\ninline int lcm(int a,int b) { return a/gcd(a,b)*b; } \ninline long long lcm(long long a,long long b) { return a/gcd(a,b)*b; }\ninline long long nth_prime(long long a) { a++;if(a <= 6) return (vector<long long>{2,3,5,7,11,13,17})[a]; long double lg = log((long double) a); return (long long) floor(a * (lg + log(lg))); }\ninline long long mod_exp(long long base, long long exp, long long modd) { unsigned long long ans = 1; base %= modd; while(exp > 0) { if(exp%2==1) ans = (base*ans)%modd; exp /= 2; base = (base*base)%modd; } return ans; }\ninline string to_upper(string a) { for (int i=0;i<(int)a.size();++i) if (a[i]>=\'a\' && a[i]<=\'z\') a[i]-=\'a\'-\'A\'; return a; }\ninline string to_lower(string a) { for (int i=0;i<(int)a.size();++i) if (a[i]>=\'A\' && a[i]<=\'Z\') a[i]+=\'a\'-\'A\'; return a; }\n\n\nbool fIO() {\n ios::sync_with_stdio(false);\n ios_base::sync_with_stdio(false);\n ios::sync_with_stdio(false);\n cout.tie(nullptr);\n cin.tie(nullptr);\n return true;\n}\nbool y4555123 = fIO();\nconst ll MOD = 1e9 + 7;\nclass Solution {\npublic:\n long long maxEnergyBoost(vector<int>& energyDrinkA, vector<int>& energyDrinkB) {\n int hours = (int) energyDrinkA.size();\n vector<ll> A(hours), B(hours);\n A[0] = energyDrinkA[0];\n B[0] = energyDrinkB[0];\n for(int i = 1; i < hours; i++) {\n // return memo[hour][currentDrink] = max(\n // curr[hour] + rec(hour+1, currentDrink),\n // hour+1 >= hours ? 0 : other[hour+1] + rec(hour+2, !currentDrink)\n // );\n A[i] = max(\n (ll) A[i-1] + energyDrinkA[i],\n i > 1 ? (ll) B[i-2] + energyDrinkA[i] : 0\n );\n B[i] = max(\n (ll) B[i-1] + energyDrinkB[i],\n i > 1 ? (ll) A[i-2] + energyDrinkB[i] : 0\n );\n }\n // vector<vector<ll>> memo(hours, vector<ll>(2, -1));\n // function<ll(int,bool)> rec = [&](int hour, bool currentDrink) -> ll {\n // if(hour >= hours) return 0;\n // if(memo[hour][currentDrink] >= 0) return memo[hour][currentDrink];\n // // drink currentDrink otherwise drink otherDrink\n // vector<int>& curr = currentDrink ? energyDrinkA : energyDrinkB;\n // vector<int>& other = currentDrink ? energyDrinkB : energyDrinkA;\n // return memo[hour][currentDrink] = max(\n // curr[hour] + rec(hour+1, currentDrink),\n // hour+1 >= hours ? 0 : other[hour+1] + rec(hour+2, !currentDrink)\n // );\n // };\n // ll ans = rec(0, 0);\n // for(vector<ll>& m : memo) {\n // fill(all(m), -1);\n // }\n return max(A.back(), B.back());\n }\n};\n\n\n\n// int main() {\n// vector<int> nums1 {};\n// vector<int> nums2 {};\n// vector<vector<int>> matrix1 {};\n// vector<vector<int>> matrix2 {};\n// }\n```
| 1 | 0 |
['Dynamic Programming', 'C++']
| 0 |
maximum-energy-boost-from-two-drinks
|
DP | Memoisation | C++
|
dp-memoisation-c-by-sirius_108-jbfc
|
\n# Code\n\nclass Solution {\npublic:\n long long calculateMaxEnergy(int N, int X, vector<int>& A, vector<int>& B, vector<vector<long long>>& memo) {\n
|
sirius_108
|
NORMAL
|
2024-08-18T04:01:14.707636+00:00
|
2024-08-18T04:01:14.707712+00:00
| 32 | false |
\n# Code\n```\nclass Solution {\npublic:\n long long calculateMaxEnergy(int N, int X, vector<int>& A, vector<int>& B, vector<vector<long long>>& memo) {\n if (N < 0) return 0; \n if (memo[N][X] != -1) return memo[N][X];\n\n long long maxE = 0;\n\n if (X == 0)\n maxE = max(calculateMaxEnergy(N-1, 0, A, B, memo) + A[N], calculateMaxEnergy(N-2, 1, A, B, memo) + A[N]);\n else \n maxE = max(calculateMaxEnergy(N-1, 1, A, B, memo) + B[N], calculateMaxEnergy(N-2, 0, A, B, memo) + B[N]);\n \n memo[N][X] = maxE;\n return maxE;\n }\n \n long long maxEnergyBoost(vector<int>& A, vector<int>& B) {\n int n = A.size();\n vector<vector<long long>> memo(n, vector<long long>(2, -1));\n return max(calculateMaxEnergy(n-1, 0, A, B, memo), calculateMaxEnergy(n-1, 1, A, B, memo));\n }\n};\n\n```
| 1 | 0 |
['C++']
| 0 |
maximum-energy-boost-from-two-drinks
|
✅Simple Solution ||Beat 100% ✅||DP
|
simple-solution-beat-100-dp-by-ashgiri49-p7tq
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
ashgiri49455
|
NORMAL
|
2024-08-18T04:01:08.591756+00:00
|
2024-08-18T04:01:08.591792+00:00
| 71 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n long long maxEnergyBoost(vector<int>& energyDrinkA, vector<int>& energyDrinkB) {\n int n=energyDrinkA.size();\n vector<long long>temp1(n,0);\n\n vector<long long> temp2(n,0);\n\n temp1[0]=energyDrinkA[0];\n temp2[0]=energyDrinkB[0];\n\n for(int i=1;i<n;i++){\n temp1[i]=max(temp1[i-1]+energyDrinkA[i],temp2[i-1]);\n temp2[i]=max(temp2[i-1]+energyDrinkB[i],temp1[i-1]);\n }\n\n return max(temp1[n-1],temp2[n-1]);\n\n \n }\n};\n```
| 1 | 0 |
['Dynamic Programming', 'C++']
| 0 |
maximum-energy-boost-from-two-drinks
|
DP (Memoization)
|
dp-memoization-by-saisuveer-ho2a
|
IntuitionGiven two arrays representing energy drinks from two sources, we can either pick a drink from A or B at each index.
Since each choice affects subsequen
|
SaiSuveer
|
NORMAL
|
2025-04-03T06:50:31.316518+00:00
|
2025-04-03T06:50:31.316518+00:00
| 4 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
Given two arrays representing energy drinks from two sources, we can either pick a drink from A or B at each index.
Since each choice affects subsequent choices, this suggests a recursive approach to try all possible ways.
However, a purely recursive approach leads to exponential time complexity, making it infeasible for large inputs.
Thus, we use dynamic programming (memoization) to store results of subproblems and avoid redundant calculations.
# Approach
<!-- Describe your approach to solving the problem. -->
1. Recursive Breakdown:
Define a function solve(a, b, i, curr, dp) where:
i is the current index.
curr tracks the last chosen drink (0 for A, 1 for B, 2 for starting state).
dp[i][curr] stores the maximum energy boost possible from index i onwards given the last choice.
Base case: If i exceeds the array size, return 0.
At each step, we have two choices:
Take a drink from A (a[i]) and move to the next index.
Take a drink from B (b[i]) and move to the next index.
If curr == 0, we cannot take from B again; if curr == 1, we cannot take from A again.
2. Dynamic Programming (Memoization):
Store results in a dp table to avoid recomputation.
Transition relations:
If curr == 2, we can start with either A or B.
If curr == 0, we can either continue with A or switch to B.
If curr == 1, we can either continue with B or switch to A.
3. Final Computation:
Initialize a dp table of size (n+1) x 3 filled with -1 for memoization.
Call solve(a, b, 0, 2, dp) to start from index 0 with no previous choice.
# Complexity
- Time complexity:
Since we compute dp[i][curr] for every i from 0 to n (n states) and curr can take 3 values,
The number of states = O(n * 3) = O(n).
Each state is computed once, leading to an O(n) time complexity.
- Space complexity:
Memoization table: dp[n+1][3], taking O(n) space.
Recursive call stack depth: O(n) in the worst case.
Total space complexity: O(n).
# Code
```cpp []
class Solution {
public:
long long solve(vector<int>& a, vector<int>& b, int i, int curr,vector<vector<long long>> &dp){
if (i >= a.size()) {
return 0;
}
long long take_a = 0, take_b = 0;
if(dp[i][curr]!=-1) return dp[i][curr];
if (curr == 2) {
take_a = a[i] + solve(a, b, i + 1, 0, dp);
take_b = b[i] + solve(a, b, i + 1, 1, dp);
} else {
if (curr == 0) {
take_a = a[i] + solve(a, b, i + 1, 0, dp);
take_b = solve(a, b, i + 1, 1, dp);
} else if(curr == 1){
take_a = solve(a, b, i + 1, 0, dp);
take_b = b[i] + solve(a, b, i + 1, 1, dp);
}
}
return dp[i][curr] = max(take_a, take_b);
}
long long maxEnergyBoost(vector<int>& a, vector<int>& b) {
int n = a.size();
vector<vector<long long>> dp(n + 1,vector<long long>(3,-1));
return solve(a, b, 0, 2, dp);
}
};
```
| 0 | 0 |
['C++']
| 0 |
maximum-energy-boost-from-two-drinks
|
Beginner Friendly Pythonic Solution 🔥🔥🔥
|
beginner-friendly-pythonic-solution-by-s-fe4q
|
IntuitionSimple, just get the maximum boost among the 2 choices.Complexity
Time complexity:
O(N)
Space complexity:
O(N)Code
|
Sherpy
|
NORMAL
|
2025-03-18T23:57:05.033558+00:00
|
2025-03-18T23:57:05.033558+00:00
| 3 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
Simple, just get the maximum boost among the 2 choices.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
O(N)
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
O(N)
# Code
```python3 []
class Solution:
def maxEnergyBoost(self, energyDrinkA: List[int], energyDrinkB: List[int]) -> int:
N=len(energyDrinkA)
dpA=[0]*N
dpB=[0]*N
dpA[0],dpB[0]=energyDrinkA[0],energyDrinkB[0]
dpA[1],dpB[1]=energyDrinkA[1]+dpA[0],energyDrinkB[1]+dpB[0]
for i in range(2,N):
dpA[i]=max(dpA[i-1],dpB[i-2])+energyDrinkA[i]
dpB[i]=max(dpB[i-1],dpA[i-2])+energyDrinkB[i]
return max(dpA[N-1],dpB[N-1])
```
| 0 | 0 |
['Array', 'Dynamic Programming', 'Greedy', 'Python3']
| 0 |
maximum-energy-boost-from-two-drinks
|
DP brute force
|
dp-brute-force-by-awuxiaoqi-gdet
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
labao
|
NORMAL
|
2025-03-04T04:06:51.646391+00:00
|
2025-03-04T04:06:51.646391+00:00
| 1 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public long maxEnergyBoost(int[] energyDrinkA, int[] energyDrinkB) {
long[][] dp = new long[energyDrinkA.length][3];
return helper(0, 0, energyDrinkA, energyDrinkB, dp);
}
public long helper(int index, int prevDrink, int[] energyDrinkA, int[] energyDrinkB, long[][] dp ) {
if (index >= energyDrinkA.length) {
return 0L;
}
if (dp[index][prevDrink] != 0) {
return dp[index][prevDrink];
}
long res = 0;
if (prevDrink == 0) {
res = Math.max(energyDrinkA[index] + helper(index + 1, 1, energyDrinkA, energyDrinkB, dp), energyDrinkB[index] + helper(index + 1, 2, energyDrinkA, energyDrinkB, dp));
} else if (prevDrink == 1) {
res = Math.max(energyDrinkA[index] + helper(index + 1, 1, energyDrinkA, energyDrinkB, dp), index < energyDrinkB.length - 1 ? energyDrinkB[index + 1] + helper(index + 2, 2, energyDrinkA, energyDrinkB, dp) : 0);
} else {
res = Math.max(index < energyDrinkA.length - 1 ? energyDrinkA[index + 1] +helper(index + 2, 1, energyDrinkA, energyDrinkB, dp) : 0, energyDrinkB[index] +helper(index + 1, 2, energyDrinkA, energyDrinkB, dp));
}
dp[index][prevDrink] = res;
return res;
}
}
```
| 0 | 0 |
['Java']
| 0 |
maximum-energy-boost-from-two-drinks
|
Recursive Solution for dummy Like me🃏
|
recursive-solution-for-dummy-like-me-by-8ifo3
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
shashanksaroj
|
NORMAL
|
2025-02-08T09:54:50.400499+00:00
|
2025-02-08T09:54:50.400499+00:00
| 3 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
Long[][] dp;
public long maxEnergyBoost(int[] energyDrinkA, int[] energyDrinkB) {
dp = new Long[energyDrinkA.length + 1][3];
return maxEnergyBoostHelper(energyDrinkA, energyDrinkB, 0, 'C');
}
private long maxEnergyBoostHelper(int[] energyDrinkA, int[] energyDrinkB, int i, char drink) {
if (i >= energyDrinkA.length)
return 0;
if (dp[i][drink - 'A'] != null)
return dp[i][drink - 'A'];
long dA = 0;
if (drink == 'B')
dA = maxEnergyBoostHelper(energyDrinkA, energyDrinkB, i + 1, 'A');
else
dA = Math.max(dA, energyDrinkA[i] + maxEnergyBoostHelper(energyDrinkA, energyDrinkB, i + 1, 'A'));
long dB = 0;
if (drink == 'A')
dB = maxEnergyBoostHelper(energyDrinkA, energyDrinkB, i + 1, 'B');
else
dB = Math.max(dB, energyDrinkB[i] + maxEnergyBoostHelper(energyDrinkA, energyDrinkB, i + 1, 'B'));
return dp[i][drink - 'A'] = Math.max(dA, dB);
}
}
```
| 0 | 0 |
['Java']
| 0 |
maximum-energy-boost-from-two-drinks
|
DP || C++ || maxEnergyBoost.
|
dp-c-maxenergyboost-by-rishiinsane-bnhr
|
IntuitionApproachComplexity
Time complexity:
O(n)
Space complexity:
O(n)
Code
|
RishiINSANE
|
NORMAL
|
2025-02-04T19:27:50.618596+00:00
|
2025-02-04T19:27:50.618596+00:00
| 3 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
O(n)
- Space complexity:
O(n)
# Code
```cpp []
class Solution {
public:
long long maxEnergyBoost(vector<int>& A, vector<int>& B) {
int n = A.size();
vector<vector<long long>> dp(n,vector<long long>(2,-1));
long long moveA = helper(n-1,0,A,B,dp);
long long moveB = helper(n-1,1,A,B,dp);
return max(moveA,moveB);
}
long long helper(int ind, int dtype, vector<int>& A, vector<int>& B,vector<vector<long long>>& dp)
{
if(ind<0)
return 0;
if(dp[ind][dtype] != -1)
return dp[ind][dtype];
long long val = dtype? A[ind] : B[ind];
long long skip = val + helper(ind-2,!dtype,A,B,dp);
long long nskip = val + helper(ind-1,dtype,A,B,dp);
return dp[ind][dtype] = max(skip,nskip);
}
};
```
| 0 | 0 |
['C++']
| 0 |
maximum-energy-boost-from-two-drinks
|
Python3 DP approach | explained | simple solution
|
python3-dp-approach-explained-simple-sol-pi26
|
IntuitionDynamic programming.ApproachCreate 2 dp arrays to store the values for each current state, one in the A drinks array and the other in the B drinks arra
|
FlorinnC1
|
NORMAL
|
2025-01-21T20:00:20.869824+00:00
|
2025-01-21T20:00:20.869824+00:00
| 3 | false |
# Intuition
Dynamic programming.
# Approach
Create 2 dp arrays to store the values for each current state, one in the A drinks array and the other in the B drinks array. Eg: a state ( dpA[i] ) in A drinks array would mean we got in here by either going from a position back from dpA such as dpA[i-1] or skipped a drink hour and got from dpB[i-2] (not i-1 since we skipped that).
# Complexity
- Time complexity:
O(n)
- Space complexity:
O(n)
# Code
```python3 []
class Solution:
def maxEnergyBoost(self, energyDrinkA: List[int], energyDrinkB: List[int]) -> int:
n = len(energyDrinkA)
dpA, dpB = [0] * n, [0] * n
dpA[0], dpB[0] = energyDrinkA[0], energyDrinkB[0]
dpA[1], dpB[1] = dpA[0] + energyDrinkA[1], dpB[0] + energyDrinkB[1]
for i in range(2, n):
dpA[i] = max(dpA[i-1], dpB[i-2]) + energyDrinkA[i]
dpB[i] = max(dpB[i-1], dpA[i-2]) + energyDrinkB[i]
return max(dpA[-1], dpB[-1])
```
Please upvote if you like it!^^
| 0 | 0 |
['Array', 'Dynamic Programming', 'Python3']
| 0 |
maximum-energy-boost-from-two-drinks
|
Clean | Logical
|
clean-logical-by-richardleee-pr9c
|
\nclass Solution {\n public long maxEnergyBoost(int[] energyDrinkA, int[] energyDrinkB) {\n //dp[i][0]: ending with A[i] = Math.max(dp[i - 1][0], dp[i
|
RichardLeee
|
NORMAL
|
2024-12-18T11:13:36.640581+00:00
|
2024-12-18T11:13:36.640607+00:00
| 0 | false |
```\nclass Solution {\n public long maxEnergyBoost(int[] energyDrinkA, int[] energyDrinkB) {\n //dp[i][0]: ending with A[i] = Math.max(dp[i - 1][0], dp[i - 2][1]) + A[i]\n //dp[i][1]: ending with B[i] = Math.max(dp[i - 1][1], dp[i - 2][0]) + B[i]\n \n int n = energyDrinkA.length;\n \n long[][] dp = new long[n + 2][2];\n \n for (int i = 2; i <= n + 1; i++) {\n dp[i][0] = Math.max(dp[i - 1][0], dp[i - 2][1]) + energyDrinkA[i - 2];\n dp[i][1] = Math.max(dp[i - 1][1], dp[i - 2][0]) + energyDrinkB[i - 2];\n }\n \n return Math.max(dp[n + 1][0], dp[n + 1][1]);\n }\n}\n\n//tc: O(n)\n//sc: O(n)\n```
| 0 | 0 |
['Dynamic Programming', 'Java']
| 0 |
maximum-energy-boost-from-two-drinks
|
Top Class | Ground Breaking | O(N) Solution
|
top-class-ground-breaking-on-solution-by-vo3g
|
Complexity
Time complexity:
O(N)
Space complexity:
O(N)
Code
|
shreet_123
|
NORMAL
|
2024-12-29T10:02:13.884573+00:00
|
2024-12-29T10:02:13.884573+00:00
| 5 | false |
# Complexity
- Time complexity:
O(N)
- Space complexity:
O(N)
# Code
```cpp []
class Solution {
public:
long long maxEnergyBoost(vector<int>& energyDrinkA, vector<int>& energyDrinkB) {
int n = energyDrinkA.size();
vector<long long> dp1(n, 0);
vector<long long> dp2(n, 0);
dp1[0] = energyDrinkA[0];
dp1[1] = energyDrinkA[0] + energyDrinkA[1];
dp2[0] = energyDrinkB[0];
dp2[1] = energyDrinkB[0] + energyDrinkB[1];
for(int i=2; i<n; i++)
{
dp1[i] = max(dp1[i-1]+energyDrinkA[i], dp2[i-2]+energyDrinkA[i]);
dp2[i] = max(dp2[i-1]+energyDrinkB[i], dp1[i-2]+energyDrinkB[i]);
}
return max(dp1[n-1], dp2[n-1]);
}
};
```
| 0 | 0 |
['Array', 'Dynamic Programming', 'C++']
| 0 |
maximum-energy-boost-from-two-drinks
|
Top Class | Ground Breaking | O(N) Solution
|
top-class-ground-breaking-on-solution-by-bown
|
Complexity
Time complexity:
O(N)
Space complexity:
O(N)
Code
|
shreet_123
|
NORMAL
|
2024-12-29T10:02:10.580357+00:00
|
2024-12-29T10:02:10.580357+00:00
| 1 | false |
# Complexity
- Time complexity:
O(N)
- Space complexity:
O(N)
# Code
```cpp []
class Solution {
public:
long long maxEnergyBoost(vector<int>& energyDrinkA, vector<int>& energyDrinkB) {
int n = energyDrinkA.size();
vector<long long> dp1(n, 0);
vector<long long> dp2(n, 0);
dp1[0] = energyDrinkA[0];
dp1[1] = energyDrinkA[0] + energyDrinkA[1];
dp2[0] = energyDrinkB[0];
dp2[1] = energyDrinkB[0] + energyDrinkB[1];
for(int i=2; i<n; i++)
{
dp1[i] = max(dp1[i-1]+energyDrinkA[i], dp2[i-2]+energyDrinkA[i]);
dp2[i] = max(dp2[i-1]+energyDrinkB[i], dp1[i-2]+energyDrinkB[i]);
}
return max(dp1[n-1], dp2[n-1]);
}
};
```
| 0 | 0 |
['Array', 'Dynamic Programming', 'C++']
| 0 |
maximum-energy-boost-from-two-drinks
|
Simple backtracking solution || Memoization || c++
|
simple-backtracking-solution-memoization-nn3y
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
vikash_kumar_dsa2
|
NORMAL
|
2024-12-24T18:39:30.963796+00:00
|
2024-12-24T18:39:30.963796+00:00
| 3 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
long long solve(vector<int>& energyDrinkA,vector<int>& energyDrinkB,bool isA,int i,int n,vector<vector<long long>> &dp){
if(i >= n){
return 0;
}
if(dp[i][isA] != -1){
return dp[i][isA];
}
if(isA){
return dp[i][isA] = energyDrinkA[i] + max(solve(energyDrinkA,energyDrinkB,isA,i+1,n,dp),solve(energyDrinkA,energyDrinkB,!isA,i+2,n,dp));
}else{
return dp[i][isA] = energyDrinkB[i] + max(solve(energyDrinkA,energyDrinkB,isA,i+1,n,dp),solve(energyDrinkA,energyDrinkB,!isA,i+2,n,dp));
}
}
long long maxEnergyBoost(vector<int>& energyDrinkA, vector<int>& energyDrinkB) {
int n = energyDrinkA.size();
vector<vector<long long>> dp(n,vector<long long>(2,-1));
return max(solve(energyDrinkA,energyDrinkB,true,0,n,dp),solve(energyDrinkA,energyDrinkB,false,0,n,dp));
}
};
```
| 0 | 0 |
['Dynamic Programming', 'Memoization', 'C++']
| 0 |
maximum-energy-boost-from-two-drinks
|
Java Optimized Solution
|
java-optimized-solution-by-heyysankalp-u0t8
|
IntuitionThe problem involves maximizing the energy boost you can collect by picking values from two arrays A and B, subject to the constraint that consecutive
|
heyysankalp
|
NORMAL
|
2024-12-24T18:22:07.831860+00:00
|
2024-12-24T18:22:07.831860+00:00
| 2 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
The problem involves maximizing the energy boost you can collect by picking values from two arrays A and B, subject to the constraint that consecutive values cannot be picked from the same array. This can be solved using dynamic programming, where at each step we decide whether to pick the value from A or B, based on the maximum energy boost obtained so far.
# Approach
<!-- Describe your approach to solving the problem. -->
1. Initialization:
- Use two variables, a0 and b0, to store the maximum energy boost achievable if the last value was picked from A or B, respectively, up to the previous index.
- Initialize both variables to 0.
2. Dynamic Programming Transition:
- Iterate through all indices i of the arrays A and B.
- Update the values of a1 and b1 for the current index:
- a1 = max(a0 + A[i], b0) — If the current value is picked from A, the previous value must have been picked from B (contributing b0), or the current value is the first pick.
- b1 = max(b0 + B[i], a0) — Similarly, if the current value is picked from B, the previous value must have been picked from A.
- Update a0 and b0 to a1 and b1 for the next iteration.
3. Final Result:
- The maximum energy boost will be the larger of the two variables (a1 or b1), representing the maximum achievable value if the last value was picked from either A or B.
# Complexity
- Time complexity:O(n)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public long maxEnergyBoost(int[] A, int[] B) {
long a0 =0, a1=0, b0=0, b1=0, n= A.length;
for (int i=0; i<n;i++){
a1 = Math.max(a0 + A[i],b0);
b1 = Math.max(b0 + B[i],a0);
a0=a1;
b0=b1;
}
return Math.max(a1,b1);
}
}
```
| 0 | 0 |
['Array', 'Dynamic Programming', 'Java']
| 0 |
maximum-energy-boost-from-two-drinks
|
DP TABULATION
|
dp-tabulation-by-prachikumari-1blc
|
IntuitionYou can notice from ques you choice for being with currChoice either A/B depends on subsequents steps a/b : in order to maximise energyboost overAlldp[
|
PrachiKumari
|
NORMAL
|
2024-12-24T15:59:51.632489+00:00
|
2024-12-24T15:59:51.632489+00:00
| 1 | false |
# Intuition
You can notice from ques you choice for being with currChoice either A/B depends on subsequents steps a/b : in order to maximise energyboost overAll
dp[i][2] i-> day & 2 choice {0->A & 1->B} hence
base case last day : it no choice (just take the choice you have ie to take the energyboost rather than thinking of future choices)
# Approach
If choice B : Either{take B and next B as well} Or {skip currB enerygyBoost (1Hr) & take nextA }
take max out of these choices
If choice A : either (take A & next A as well) Or {skip currA energyBoost{1HT} and take nextB}
maximise out these
dp accumulates the maximises boosts and as you reach i =0 {1st day u get the maxBoost possible}
# Complexity
- Time complexity: O(n)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(n2)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public long maxEnergyBoost(int[] energyDrinkA, int[] energyDrinkB) {
int n = energyDrinkA.length; // days of drinks
long[][] dp = new long[n][2]; // with choice 0->A and 1->B
dp[n-1][0] = energyDrinkA[n-1];
dp[n-1][1] = energyDrinkB[n-1];
for (int i = n-2 ; i >= 0 ;i--){
//Starting withA
dp[i][0] = Math.max(energyDrinkA[i]+dp[i+1][0] , dp[i][0]+dp[i+1][1]);
//Starting withB
dp[i][1] = Math.max(energyDrinkB[i]+dp[i+1][1] , dp[i][1]+dp[i+1][0]);
}
return Math.max(dp[0][0] , dp[0][1]);
}
}
```
| 0 | 0 |
['Java']
| 0 |
maximum-energy-boost-from-two-drinks
|
c++ solution | using memoization
|
c-solution-using-memoization-by-amit_207-5npj
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
Amit_207
|
NORMAL
|
2024-12-16T12:50:59.086150+00:00
|
2024-12-16T12:50:59.086150+00:00
| 3 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int one = 0;\n int two = 1;\n long long dp[100001][2];\n\n long long solve(int i, vector<int>& a, vector<int>& b, int d)\n {\n if(i>=a.size()) return 0;\n\n if(dp[i][d]!=-1) return dp[i][d];\n\n long long d1 = 0;\n long long d2 = 0;\n if(d==one){\n d1 = a[i] + max(solve(i+1, a, b, one), solve(i+2, a, b, two));\n }\n if(d==two){\n d2 = b[i] + max(solve(i+1, a, b, two), solve(i+2, a, b, one));\n }\n\n return dp[i][d] = max(d1, d2);\n }\n \n long long maxEnergyBoost(vector<int>& energyDrinkA, vector<int>& energyDrinkB) {\n memset(dp, -1, sizeof(dp));\n\n return max(solve(0, energyDrinkA, energyDrinkB, one),\n solve(0, energyDrinkA, energyDrinkB, two));\n }\n};\n```
| 0 | 0 |
['Dynamic Programming', 'Memoization', 'C++']
| 0 |
maximum-energy-boost-from-two-drinks
|
JAVA DP Easy Solution
|
java-dp-easy-solution-by-shivangi1-9a5h
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
shivangi1
|
NORMAL
|
2024-12-16T05:52:09.226798+00:00
|
2024-12-16T05:52:09.226798+00:00
| 2 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public long maxEnergyBoost(int[] energyDrinkA, int[] energyDrinkB) {\n\n int n = energyDrinkA.length;\n\n long[][] dp = new long[n+1][2];\n dp[1][0] = energyDrinkA[0];\n dp[1][1] = energyDrinkB[0];\n\n for(int i=2;i<=n;i++)\n {\n dp[i][0] = (long)Math.max(dp[i-1][0], dp[i-2][1])+ (long)energyDrinkA[i-1]; \n dp[i][1] = (long)Math.max(dp[i-1][1], dp[i-2][0])+ (long)energyDrinkB[i-1]; \n }\n \n return Math.max(dp[n][0], dp[n][1]);\n }\n}\n```
| 0 | 0 |
['Java']
| 0 |
maximum-energy-boost-from-two-drinks
|
A super easy Java solution with DP
|
a-super-easy-java-solution-with-dp-by-mi-mzwp
|
dpA[i+2] contains max boost possible after consuming ith drink from energy drink A.\ndpB[i+2] contains max boost possible after consuming ith drink from energy
|
mindmay
|
NORMAL
|
2024-11-28T19:30:24.933633+00:00
|
2024-11-28T19:30:24.933655+00:00
| 3 | false |
dpA[i+2] contains max boost possible after consuming ith drink from energy drink A.\ndpB[i+2] contains max boost possible after consuming ith drink from energy drink B.\n\ndpA[i+2] = Math.max(dpA[i+1]+ energyDrinkA[i], dpB[i] + energyDrinkA[i]); \n\t\t\tlogic for above state calculation is, either continue from A or switch from B which is dpB[i])\n\t\t\t\nOn same logic,\ndpB[i+2] = Math.max(dpB[i+1]+ energyDrinkB[i], dpA[i] + energyDrinkB[i]); ] \n\n```\nclass Solution {\n public long maxEnergyBoost(int[] energyDrinkA, int[] energyDrinkB) {\n int n = energyDrinkA.length;\n long[] dpA = new long[n + 2];\n long[] dpB = new long[n + 2];\n dpA[0] = dpB[0] = dpA[1] = dpB[1] = 0;\n \n for(int i = 0; i < n; i++){\n dpA[i+2] = Math.max(dpA[i+1]+ energyDrinkA[i], dpB[i] + energyDrinkA[i]); \n dpB[i+2] = Math.max(dpB[i+1]+ energyDrinkB[i], dpA[i] + energyDrinkB[i]); \n }\n \n return Math.max(dpA[n+1], dpB[n+1]);\n }\n}\n```
| 0 | 0 |
['Dynamic Programming', 'Java']
| 0 |
maximum-energy-boost-from-two-drinks
|
Python - State Machine
|
python-state-machine-by-jerryji040506-rwat
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
jerryji040506
|
NORMAL
|
2024-11-25T00:28:01.310902+00:00
|
2024-11-25T00:28:01.310934+00:00
| 0 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution:\n def maxEnergyBoost(self, A: List[int], B: List[int]) -> int:\n n = len(A)\n\n dp_A = [0] * (n+1)\n dp_B = [0] * (n+1)\n\n dp_A[1], dp_B[1] = A[0], B[0]\n for i in range(2, n+1):\n dp_A[i] = max(dp_A[i-1] + A[i-1], dp_B[i-2] + A[i-1])\n dp_B[i] = max(dp_B[i-1] + B[i-1], dp_A[i-2] + B[i-1])\n\n return max(dp_A[-1], dp_B[-1])\n```
| 0 | 0 |
['Dynamic Programming', 'Python3']
| 0 |
maximum-energy-boost-from-two-drinks
|
The simplest Python solution that beats 76% of submissions, DP, O(N)
|
the-simplest-python-solution-that-beats-9e9l8
|
Approach\nSimple dynamic programmic solution without recursions, functions calls, etc.\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\
|
alexeis
|
NORMAL
|
2024-11-19T02:01:05.981852+00:00
|
2024-11-19T02:01:05.981878+00:00
| 2 | false |
# Approach\nSimple dynamic programmic solution without recursions, functions calls, etc.\n\n# Complexity\n- Time complexity:\n$$O(n)$$\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```python3 []\nclass Solution:\n def maxEnergyBoost(self, energyDrinkA: List[int], energyDrinkB: List[int]) -> int:\n\n mbA=[energyDrinkA[0]]\n mbB=[energyDrinkB[0]]\n\n l = len(energyDrinkA)\n for i in range(1, l):\n mbA.append(max(mbA[i-1]+energyDrinkA[i], mbB[i-1]))\n mbB.append(max(mbB[i-1]+energyDrinkB[i], mbA[i-1]))\n \n return max(mbA[l-1], mbB[l-1])\n```
| 0 | 0 |
['Python3']
| 0 |
maximum-energy-boost-from-two-drinks
|
Simple solution using include exclude principle
|
simple-solution-using-include-exclude-pr-rs9m
|
Code\njava []\nclass Solution {\n public long maxEnergyBoost(int[] a, int[] b) {\n int n = a.length;\n long[][] dp = new long[n+1][3];\n
|
_jyoti_geek
|
NORMAL
|
2024-11-15T18:01:24.827973+00:00
|
2024-11-15T18:01:24.828017+00:00
| 2 | false |
# Code\n```java []\nclass Solution {\n public long maxEnergyBoost(int[] a, int[] b) {\n int n = a.length;\n long[][] dp = new long[n+1][3];\n for(int i=0;i<dp.length;i++){\n for(int j=0;j<=2;j++){\n dp[i][j] = -1;\n }\n }\n return helper(a, b, 0, 0, dp);\n }\n\n public long helper(int[] a, int[] b, int idx, int curr, long[][] dp){\n if(idx==a.length){\n return 0;\n }\n if(dp[idx][curr]!=-1){\n return dp[idx][curr];\n }\n\n if(curr==0){\n long c1 = helper(a, b, idx+1, 1, dp)+a[idx];\n long c2 = helper(a, b, idx+1, 2, dp)+b[idx];\n return dp[idx][curr] = Math.max(c2, c1);\n }else if(curr==1){\n long c1 = helper(a, b, idx+1, 1, dp)+a[idx];\n long c2 = helper(a, b, idx+1, 2, dp);\n return dp[idx][curr] = Math.max(c2, c1);\n }else{\n long c1 = helper(a, b, idx+1, 1, dp);\n long c2 = helper(a, b, idx+1, 2, dp)+b[idx];\n return dp[idx][curr] = Math.max(c2, c1);\n }\n }\n}\n```
| 0 | 0 |
['Array', 'Dynamic Programming', 'Java']
| 0 |
maximum-energy-boost-from-two-drinks
|
Straight Forward DP with Transition States
|
straight-forward-dp-with-transition-stat-r7dz
|
Complexity\n- Time complexity: O(n)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(1)\n Add your space complexity here, e.g. O(n) \n\n# Co
|
iitjsagar
|
NORMAL
|
2024-11-09T23:01:59.527485+00:00
|
2024-11-09T23:01:59.527516+00:00
| 3 | false |
# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python []\nclass Solution(object):\n def maxEnergyBoost(self, energyDrinkA, energyDrinkB):\n """\n :type energyDrinkA: List[int]\n :type energyDrinkB: List[int]\n :rtype: int\n """\n\n pa2 = 0 # Optimal energy two indices prior if A was taken\n pa1 = 0 # Optimal energy one index prior if A was taken\n pb2 = 0 # Optimal energy two indices prior if B was taken\n pb1 = 0 # Optimal energy one index prior if B was taken\n\n L = len(energyDrinkA)\n\n for i in range(L):\n ca = max(pa1, pb2) + energyDrinkA[i]\n cb = max(pb1, pa2) + energyDrinkB[i]\n\n pa2 = pa1\n pb2 = pb1\n pa1 = ca\n pb1 = cb\n \n return max(ca,cb)\n\n\n \n```
| 0 | 0 |
['Python']
| 0 |
maximum-energy-boost-from-two-drinks
|
dp
|
dp-by-user5285zn-hxli
|
rust []\nimpl Solution {\n pub fn max_energy_boost(a: Vec<i32>, b: Vec<i32>) -> i64 {\n let n = a.len();\n let mut dp : Vec<Vec<i64>> = vec![ve
|
user5285Zn
|
NORMAL
|
2024-11-09T11:21:54.003810+00:00
|
2024-11-09T11:21:54.003835+00:00
| 3 | false |
```rust []\nimpl Solution {\n pub fn max_energy_boost(a: Vec<i32>, b: Vec<i32>) -> i64 {\n let n = a.len();\n let mut dp : Vec<Vec<i64>> = vec![vec![0; n]; 2];\n for i in 0..n {\n let i1 = i.wrapping_sub(1);\n let i2 = i.wrapping_sub(2);\n dp[0][i] = a[i] as i64 + dp[0].get(i1).unwrap_or(&0)\n .max(dp[1].get(i2).unwrap_or(&0));\n dp[1][i] = b[i] as i64 + dp[1].get(i1).unwrap_or(&0)\n .max(dp[0].get(i2).unwrap_or(&0));\n }\n dp[0][n-1].max(dp[1][n-1])\n }\n}\n```
| 0 | 0 |
['Rust']
| 0 |
maximum-energy-boost-from-two-drinks
|
Single Pass ^ Dynamic Programm Python beats 90% solutions
|
single-pass-dynamic-programm-python-beat-eem3
|
Intuition\n Describe your first thoughts on how to solve this problem. \nUsing DP for each tray to store maximum score achievable as far\n# Approach\n Describe
|
narendrakummara_9
|
NORMAL
|
2024-10-19T09:58:14.446206+00:00
|
2024-10-19T09:58:14.446228+00:00
| 0 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nUsing DP for each tray to store maximum score achievable as far\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe can take current drink with previous drink of same tray or current drink with prev previous drink from other tray.\nMake note down the score you gain maximum of two ways and store, use stored values for future, to maximise score.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(2n)\n# Code\n```python3 []\nclass Solution:\n def maxEnergyBoost(self, A: List[int], B: List[int]) -> int:\n n=len(A)\n dp1 = [0 for _ in range(n)]\n dp2 =[ 0 for _ in range(n)]\n for i in range(n):\n cur1 = A[i] + dp1[i-1] ; cur2 = B[i] + dp2[i-1]\n if i-2 >= 0:\n cur1 = max( cur1, A[i] + dp2[i-2])\n cur2 = max( cur2, B[i] + dp1[i-2])\n dp1[i] = cur1 ; dp2[i] = cur2\n return max( dp1[n-1] , dp2[n-1] )\n \n \n```
| 0 | 0 |
['Python3']
| 0 |
maximum-energy-boost-from-two-drinks
|
Recursion - Memoization :)
|
recursion-memoization-by-roy_b-nox9
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
roy_b
|
NORMAL
|
2024-10-13T20:10:03.562241+00:00
|
2024-10-13T20:10:03.562275+00:00
| 2 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(N)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(N)\n# Code\n```java []\nclass Solution {\n public long maxEnergyBoost(int[] energyDrinkA, int[] energyDrinkB) {\n Long[][] dp = new Long[energyDrinkA.length][2];\n return Math.max(f(energyDrinkA,energyDrinkB,0,0,dp),f(energyDrinkA,energyDrinkB,0,1,dp));\n }\n public long f(int[] A,int[] B,int index,int number,Long[][] dp){\n if(index >= A.length){\n return 0;\n }\n if(dp[index][number] != null){\n return dp[index][number];\n }\n long take = 0;\n if(number == 0){\n take = A[index] + f(A,B,index+1,0,dp);\n }\n else{\n take = B[index] + f(A,B,index+1,1,dp);\n }\n long s = 0;\n if(number == 0){\n s = f(A,B,index+1,1,dp);\n }\n else{\n s = f(A,B,index+1,0,dp);\n }\n return dp[index][number] = Math.max(take,s);\n }\n}\n```
| 0 | 0 |
['Java']
| 0 |
maximum-energy-boost-from-two-drinks
|
Beats 1000 % Easy C++ Solution
|
beats-1000-easy-c-solution-by-skale5747-jnxe
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
skale5747
|
NORMAL
|
2024-10-12T09:29:06.336037+00:00
|
2024-10-12T09:29:06.336060+00:00
| 0 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n\n long long maxEnergyBoost(vector<int>& A, vector<int>&B) {\n ios_base::sync_with_stdio(false);\n cin.tie(NULL);\n cout.tie(NULL);\n int n=A.size();\n vector<vector<long long >>dp(2,vector<long long>(n+1,-1));\n dp[0][0]=A[0];\n dp[1][0]=B[0];\n for(int i=1;i<n;i++){\n for(int j=0;j<2;j++){\n long long temp;\n if(j==0){\n temp=dp[j][i-1]+A[i];\n if(i-2>=0){\n temp=max(temp,dp[1][i-2]+A[i]);\n }\n }else{\n temp=dp[j][i-1]+B[i];\n if(i-2>=0){\n temp=max(temp,dp[0][i-2]+B[i]);\n }\n }\n dp[j][i]=temp;\n }\n }\n return max(dp[0][n-1],dp[1][n-1]);\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
maximum-energy-boost-from-two-drinks
|
scala oneliner
|
scala-oneliner-by-vititov-djgl
|
scala []\nobject Solution {\n def maxEnergyBoost(energyDrinkA: Array[Int], energyDrinkB: Array[Int]): Long =\n (energyDrinkA.iterator zip energyDrinkB.itera
|
vititov
|
NORMAL
|
2024-10-10T20:04:12.358745+00:00
|
2024-10-10T20:04:12.358774+00:00
| 0 | false |
```scala []\nobject Solution {\n def maxEnergyBoost(energyDrinkA: Array[Int], energyDrinkB: Array[Int]): Long =\n (energyDrinkA.iterator zip energyDrinkB.iterator)\n .foldLeft((0L, 0L)){case ((c,d),(a,b)) =>\n ((c+a) max d, (d+b) max c)\n }.productIterator.map(_.asInstanceOf[Long]).max\n}\n```
| 0 | 0 |
['Linked List', 'Recursion', 'Scala']
| 0 |
maximum-energy-boost-from-two-drinks
|
🔥TOP-DOWN DP || 🔥C++ || 🔥O(n) || 🔥SHORT CODE || 🔥EASIEST AND SHORT EXPLANATION
|
top-down-dp-c-on-short-code-easiest-and-yhi4i
|
dp[idx][toggle] defines currently you are on which index and in which array.\n\nsuppose, you are on array A, then you can either take drink from here and go nex
|
Omitul
|
NORMAL
|
2024-10-04T05:53:32.104512+00:00
|
2024-10-04T05:54:05.712233+00:00
| 1 | false |
**dp[idx][toggle] defines currently you are on which index and in which array.**\n\nsuppose, you are on array A, then you can either take drink from here and go next in this same array OR you can drink from here and take rest for one hour and go to the Array B.\nsame Goes for array B. Walk on both ways and get the maximum from the DP.\n\n**HAPPY CODING!** \n\n\n\n```\nclass Solution {\npublic:\n \n long long dp[100005][2];\n int n;\n long long solve(vector<int>&a,vector<int>&b,int idx,int toggle) {\n if(idx >= n) return 0;\n \n auto &ret = dp[idx][toggle];\n if(ret != -1) return ret;\n \n long long ans = 0;\n \n if(toggle) {\n ans = max(solve(a, b, idx + 1, 1) + a[idx], solve(a, b, idx + 2, 0) + a[idx]);\n }\n else {\n ans = max(solve(a, b, idx + 1, 0) + b[idx], solve(a, b, idx + 2, 1) + b[idx]);\n }\n return ret = ans;\n }\n long long maxEnergyBoost(vector<int>& energyDrinkA, vector<int>& energyDrinkB) {\n n = energyDrinkA.size();\n memset(dp,-1,sizeof dp);\n\n return max(solve(energyDrinkA,energyDrinkB,0,0),solve(energyDrinkA,energyDrinkB,0,1));\n }\n};\n```
| 0 | 0 |
['Dynamic Programming', 'C']
| 0 |
maximum-energy-boost-from-two-drinks
|
C++ top down recursion, memoisation, Elegant , super easy, well explained
|
c-top-down-recursion-memoisation-elegant-wn58
|
Intuition\nAt any idx, two possibilities, whether to be on same current enery drink array(idx+1) or switch to another energy drink array, so while switch, we ha
|
nikhiljaiswal
|
NORMAL
|
2024-10-02T06:20:55.121191+00:00
|
2024-10-02T06:20:55.121212+00:00
| 2 | false |
# Intuition\nAt any idx, two possibilities, whether to be on same current enery drink array(idx+1) or switch to another energy drink array, so while switch, we have to skip the next hr(idx+2).\n\n\n# Approach\nAt any particular index idx and turn(A or B), we can find max boost can be collected from that idx to end and store it in dp[n][2], as definitely we gonna see, overlapping subproblems at any index idx. So, while backtrack, we will store and return max from both cases with including current energy boost(either A or B, defined by turnA->id)\n\n# Complexity\n- Time complexity:\nO(2N)\n\n- Space complexity:\nO(2N)\n\n# Code\n```cpp []\ntypedef long long ll;\nclass Solution {\npublic:\n\n ll fndMaxboost(ll idx, ll n, vector<int>& energyDrinkA, vector<int>& energyDrinkB, bool turnA, vector<vector<ll> >& dp){\n if(idx >= n){\n return 0;\n }\n ll id = turnA ? 0 : 1;\n if(dp[idx][id]!=INT_MIN){\n return dp[idx][id];\n }\n ll curEnergyBoost = turnA ? energyDrinkA[idx]: energyDrinkB[idx];\n ll dontSwtich = fndMaxboost(idx+1, n, energyDrinkA, energyDrinkB, turnA, dp);\n ll doSwitch = fndMaxboost(idx+2, n, energyDrinkA, energyDrinkB, !turnA, dp);\n ll maxAtIdx = curEnergyBoost + max(dontSwtich, doSwitch);\n dp[idx][id] = maxAtIdx;\n return maxAtIdx;\n }\n ll maxEnergyBoost(vector<int>& energyDrinkA, vector<int>& energyDrinkB) {\n ll n = energyDrinkA.size();\n vector<vector<ll> > dp(n, vector<ll>(2, INT_MIN));\n ll startWithA = fndMaxboost(0, n, energyDrinkA, energyDrinkB, true, dp );\n ll startWithB = fndMaxboost(0, n, energyDrinkA, energyDrinkB, false, dp );\n return max(startWithA, startWithB);\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
maximum-energy-boost-from-two-drinks
|
JS DP - Very Simple Solution
|
js-dp-very-simple-solution-by-nebojsazak-nz7l
|
Intuition\n Describe your first thoughts on how to solve this problem. \nEach max hour sum for either drink is either previous hour of the same drink + current
|
nebojsazak
|
NORMAL
|
2024-09-28T14:08:13.069902+00:00
|
2024-09-28T14:08:13.069919+00:00
| 7 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nEach max hour sum for either drink is either previous hour of the same drink + current side or other side hour - 2 + current side.\n\nSolution is max the value of the both drinks for the last hour.\n\n# Approach\nDP - number values holding max hour sum for the last 2 hours, so two for each side.\n\na1 - hour - 2 max sum for drink A\na2 - hour - 1 max sum for drink A\n\nb1 - hour - 2 max sum for drink B\nb2 - hour - 1 max sum for drink B\n\n# Complexity\n- Time complexity: 0(N)\n\n- Space complexity: K\n\n# Code\n```javascript []\n/**\n * @param {number[]} energyDrinkA\n * @param {number[]} energyDrinkB\n * @return {number}\n */\nvar maxEnergyBoost = function(energyDrinkA, energyDrinkB) {\n let a1 = energyDrinkA[0];\n let a2 = energyDrinkA[1] + a1;\n\n let b1 = energyDrinkB[0];\n let b2 = energyDrinkB[1] + b1;\n\n for (let i = 2; i < energyDrinkA.length; i += 1) {\n let an = Math.max(b1 + energyDrinkA[i], a2 + energyDrinkA[i]);\n let bn = Math.max(a1 + energyDrinkB[i], b2 + energyDrinkB[i]);\n\n a1 = a2;\n a2 = an;\n\n b1 = b2;\n b2 = bn;\n }\n\n return Math.max(b2, a2);\n};\n```
| 0 | 0 |
['JavaScript']
| 0 |
maximum-energy-boost-from-two-drinks
|
Simple take/not_take solution | Easy | DP | C++
|
simple-takenot_take-solution-easy-dp-c-b-ushj
|
\n# Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(2n)\n# Code\ncpp []\nclass Solution {\npublic:\n long long maxEnergyBoost(vector<int>& A, ve
|
tusharjain88954
|
NORMAL
|
2024-09-24T07:08:57.072223+00:00
|
2024-09-24T07:08:57.072253+00:00
| 2 | false |
\n# Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(2n)\n# Code\n```cpp []\nclass Solution {\npublic:\n long long maxEnergyBoost(vector<int>& A, vector<int>& B) {\n // either start from A or B drink\n\n vector<vector<long long> > dp(A.size(), vector<long long> (3, -1));\n\n return recur(A, B, 1, 0, dp);\n \n }\n long long recur(vector<int>& A, vector<int>& B, int arrayNumber, int i, vector<vector<long long> >& dp) {\n \n if(i >= A.size()){\n return 0;\n }\n\n\n if(dp[i][arrayNumber] != -1){\n return dp[i][arrayNumber];\n }\n long long take = 0;\n long long not_take = 0;\n if(i == 0){\n take = A[i] + recur(A, B, arrayNumber, i+1, dp);\n not_take = B[i] + recur(A, B, 3-arrayNumber, i+1, dp); \n }\n else{\n if(arrayNumber == 1){\n take = A[i] + recur(A, B, arrayNumber, i+1, dp);\n }\n else{\n take = B[i] + recur(A, B, arrayNumber, i+1, dp);\n }\n \n not_take = recur(A, B, 3-arrayNumber, i+1, dp);\n }\n \n dp[i][arrayNumber] = max(take, not_take);\n\n return dp[i][arrayNumber];\n \n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
maximum-energy-boost-from-two-drinks
|
Simplest C++ Solution.
|
simplest-c-solution-by-pushpendra_singh-sgjf
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
pushpendra_singh_
|
NORMAL
|
2024-09-24T04:46:52.010009+00:00
|
2024-09-24T04:46:52.010035+00:00
| 0 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n long long maxEnergyBoost(vector<int>& energyDrinkA, vector<int>& energyDrinkB) {\n long long int ans=INT_MIN;\n vector<vector<long long int>>dp(energyDrinkA.size()+1,vector<long long int>(2,0));\n for(int i=1;i<dp.size();i++){\n for(int j=0;j<2;j++){\n if(j==0){\n dp[i][j]=max(dp[i][j],dp[i-1][0]+energyDrinkA[i-1]);\n if(i-2>=0) dp[i][j]=max(dp[i][j],dp[i-2][1]+energyDrinkA[i-1]);\n }\n else {\n dp[i][j]=max(dp[i][j],dp[i-1][1]+energyDrinkB[i-1]);\n if(i-2>=0) dp[i][j]=max(dp[i][j],dp[i-2][0]+energyDrinkB[i-1]);\n }\n ans=ans>dp[i][j]?ans:dp[i][j];\n }\n }\n return ans;\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
maximum-energy-boost-from-two-drinks
|
C++||EASIEST SOLUTION||RECURSIVE+MEMO||
|
ceasiest-solutionrecursivememo-by-diksha-dd6m
|
\n\n# Code\ncpp []\nclass Solution {\npublic:\n int n;\n vector<vector<long long>> memo; // Memoization table\n \n long long solve(vector<int>& ene
|
diksha_uniyal
|
NORMAL
|
2024-09-21T18:14:50.083560+00:00
|
2024-09-21T18:14:50.083586+00:00
| 2 | false |
\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int n;\n vector<vector<long long>> memo; // Memoization table\n \n long long solve(vector<int>& energyDrinkA, vector<int>& energyDrinkB, int idx, int isDrinkA) {\n if (idx >= n) return 0; // Base case: no more drinks\n \n if (memo[idx][isDrinkA] != -1) return memo[idx][isDrinkA]; // Check memo\n \n long long nextDrinkA = 0, nextDrinkB = 0;\n \n if (isDrinkA) {\n // Current drink is from energyDrinkA, you can drink from A or skip to B\n nextDrinkA = energyDrinkA[idx] + solve(energyDrinkA, energyDrinkB, idx + 1, 1);\n nextDrinkB = energyDrinkA[idx] + solve(energyDrinkA, energyDrinkB, idx + 2, 0);\n } else {\n // Current drink is from energyDrinkB, you can drink from B or skip to A\n nextDrinkB = energyDrinkB[idx] + solve(energyDrinkA, energyDrinkB, idx + 1, 0);\n nextDrinkA = energyDrinkB[idx] + solve(energyDrinkA, energyDrinkB, idx + 2, 1);\n }\n \n // Store the result in memo table\n return memo[idx][isDrinkA] = max(nextDrinkA, nextDrinkB);\n }\n \n long long maxEnergyBoost(vector<int>& energyDrinkA, vector<int>& energyDrinkB) {\n n = energyDrinkA.size();\n memo.resize(n, vector<long long>(2, -1)); // Initialize memoization table with -1\n // Start by either choosing the first drink from A or B\n return max(solve(energyDrinkA, energyDrinkB, 0, 1), solve(energyDrinkA, energyDrinkB, 0, 0));\n }\n};\n\n```
| 0 | 0 |
['C++']
| 0 |
maximum-energy-boost-from-two-drinks
|
Python3 Linear Time, Linear Space Solution Leveraging BUDP : Bottom-Up Dynamic Programming
|
python3-linear-time-linear-space-solutio-5dhu
|
Intuition and Approach\nAlways positive integral energy\n\n# Complexity\nLet N := #-hours we consume energy drinks for \n- Time complexity:\nO(N)\n\n- Space co
|
2018hsridhar
|
NORMAL
|
2024-09-15T20:16:52.246098+00:00
|
2024-09-15T20:16:52.246117+00:00
| 0 | false |
# Intuition and Approach\nAlways positive integral energy\n\n# Complexity\nLet $$N := $$ #-hours we consume energy drinks for \n- Time complexity:\n$$O(N)$$\n\n- Space complexity:\n$$O(N)$$ ( E ) $$O(1)$$ ( I ) \n\n# Code\n```python3 []\n\'\'\'\n3259. Maximum Energy Boost From Two Drinks\nURL := https://leetcode.com/problems/maximum-energy-boost-from-two-drinks/description/\n\n\'\'\'\nclass Solution:\n def maxEnergyBoost(self, energyDrinkA: List[int], energyDrinkB: List[int]) -> int:\n maxCons = [energyDrinkA,energyDrinkB]\n # n-1 and n-2 cases\n n = len(energyDrinkA)\n secondToLast = len(energyDrinkA)-2\n drinkA = 0\n drinkB = 1\n maxCons[drinkA][secondToLast] += maxCons[drinkA][-1]\n maxCons[drinkB][secondToLast] += maxCons[drinkB][-1]\n for ptr in range(n-3,-1,-1):\n aVal = energyDrinkA[ptr]\n bVal = energyDrinkB[ptr]\n maxCons[drinkA][ptr] = max(aVal + maxCons[drinkA][ptr+1], aVal + maxCons[drinkB][ptr+2])\n maxCons[drinkB][ptr] = max(bVal + maxCons[drinkB][ptr+1], bVal + maxCons[drinkA][ptr+2])\n energy = max(maxCons[drinkA][0], maxCons[drinkB][0])\n return energy\n\n \n```
| 0 | 0 |
['Array', 'Dynamic Programming', 'C++', 'Python3']
| 0 |
maximum-energy-boost-from-two-drinks
|
C++ || Memoization || Tabulation
|
c-memoization-tabulation-by-its_rahul-opl2
|
\n# Code\ncpp []\n#define ll long long\nclass Solution {\nprivate:\n ll solve(int ind, int f, vector<int>& a, vector<int>& b, vector<vector<ll>>& t) {\n
|
its_rahul
|
NORMAL
|
2024-09-14T07:52:41.632285+00:00
|
2024-09-14T07:52:41.632318+00:00
| 2 | false |
\n# Code\n```cpp []\n#define ll long long\nclass Solution {\nprivate:\n ll solve(int ind, int f, vector<int>& a, vector<int>& b, vector<vector<ll>>& t) {\n if(ind == a.size()) return 0;\n if(t[ind][f] != -1) return t[ind][f];\n ll x = 0, y = 0, z = 0;\n if(f) x = b[ind] + solve(ind+1, f, a, b, t);\n else y = a[ind] + solve(ind+1, f, a, b, t);\n z = solve(ind+1, !f, a, b, t);\n return t[ind][f] = max({x, y, z});\n }\npublic:\n long long maxEnergyBoost(vector<int>& a, vector<int>& b) {\n vector<vector<ll>> t(a.size()+1, vector<ll> (2, 0));\n // return max(solve(0, 0, a, b, t), solve(0, 1, a, b, t));\n t[a.size()][0] = 0;\n t[a.size()][1] = 0;\n for(int i=a.size()-1; i>=0; i--) {\n t[i][0] = max(t[i+1][0]+a[i], t[i+1][1]);\n t[i][1] = max(t[i+1][0], t[i+1][1]+b[i]);\n }\n return max(t[0][0], t[0][1]);\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
maximum-energy-boost-from-two-drinks
|
JavaScript DP solution with straightforward thinking
|
javascript-dp-solution-with-straightforw-hqpl
|
Code\njavascript []\n/**\n * @param {number[]} energyDrinkA\n * @param {number[]} energyDrinkB\n * @return {number}\n */\nvar maxEnergyBoost = function(energyDr
|
jyun-han
|
NORMAL
|
2024-09-11T00:21:57.169035+00:00
|
2024-09-11T00:21:57.169059+00:00
| 7 | false |
# Code\n```javascript []\n/**\n * @param {number[]} energyDrinkA\n * @param {number[]} energyDrinkB\n * @return {number}\n */\nvar maxEnergyBoost = function(energyDrinkA, energyDrinkB) {\n const n = energyDrinkA.length;\n\n const dpA = new Array(n).fill(0);\n const dpB = new Array(n).fill(0);\n\n dpA[0] = energyDrinkA[0];\n dpA[1] = energyDrinkA[0] + energyDrinkA[1];\n\n dpB[0] = energyDrinkB[0];\n dpB[1] = energyDrinkB[0] + energyDrinkB[1];\n\n\n for(let i = 2;i < n; i += 1) {\n dpA[i] = Math.max(dpA[i - 1], dpB[i - 2]) + energyDrinkA[i];\n dpB[i] = Math.max(dpB[i - 1], dpA[i - 2]) + energyDrinkB[i];\n }\n \n\n return Math.max(dpA[n -1], dpB[n - 1]);\n};\n```
| 0 | 0 |
['Dynamic Programming', 'JavaScript']
| 0 |
maximum-energy-boost-from-two-drinks
|
DP
|
dp-by-sk2102-m64q
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
SK2102
|
NORMAL
|
2024-09-10T19:17:18.852974+00:00
|
2024-09-10T19:17:18.853004+00:00
| 2 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```cpp []\nclass Solution {\n long long energyBoostCal(vector<int>& energyDrinkA, vector<int>& energyDrinkB, long long index, char drinkType, vector<vector<long long>> &dp){\n if(index<0) return 0;\n int drink = ((drinkType==\'a\')?0:1);\n if(dp[index][drink]!=-1) return dp[index][drink];\n if(drinkType==\'a\'){\n dp[index][drink] = energyDrinkA[index] + max(energyBoostCal(energyDrinkA, energyDrinkB, index-1, \'a\', dp),\n energyBoostCal(energyDrinkA, energyDrinkB, index-2, \'b\', dp));\n }\n else{\n dp[index][drink] = energyDrinkB[index] + max(energyBoostCal(energyDrinkA, energyDrinkB, index-1, \'b\', dp),\n energyBoostCal(energyDrinkA, energyDrinkB, index-2, \'a\', dp));\n }\n return dp[index][drink];\n }\npublic:\n long long maxEnergyBoost(vector<int>& energyDrinkA, vector<int>& energyDrinkB) {\n long long n = energyDrinkA.size();\n vector<vector<long long>> dp(n, vector<long long>(2,-1));\n energyBoostCal(energyDrinkA, energyDrinkB, n-1, \'a\', dp);\n energyBoostCal(energyDrinkA, energyDrinkB, n-1, \'b\', dp);\n return max(dp[n-1][0], dp[n-1][1]);\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
maximum-energy-boost-from-two-drinks
|
Easiest and most efficient approach explained
|
easiest-and-most-efficient-approach-expl-gdzx
|
Intuition\nTo consume A, you were either already drinking A in the previous hour, or you were consumming B and you skipped the previous. Same thing for B. \n\n#
|
jeehaytch
|
NORMAL
|
2024-09-10T04:07:40.855797+00:00
|
2024-09-10T04:07:40.855818+00:00
| 3 | false |
# Intuition\nTo consume A, you were either already drinking A in the previous hour, or you were consumming B and you skipped the previous. Same thing for B. \n\n# Approach\nIn each step, we calculate the 3 possibilities, i.e Drinking A, drinking B, or skipping. \nTo drink A, we either skipped before (take the value of skip), or we were drinking A before (take the value of A). Same thing for B. The current energy level is given by the maximum between the two. We also keep in memory the value if we dont drink anything, which would be our next skip value.\n\n# Complexity\n- Time complexity:\n$$O(n)$$\n\n- Space complexity:\n$$O(1)$$ \n\n# Code\n```python3 []\nclass Solution:\n def maxEnergyBoost(self, energyDrinkA: List[int], energyDrinkB: List[int]) -> int:\n A, B = energyDrinkA[0], energyDrinkB[0]\n skip, curr = 0, max(A, B)\n for i in range(1,len(energyDrinkA)):\n A = max(A, skip) + energyDrinkA[i]\n B = max(B, skip) + energyDrinkB[i]\n skip, curr = curr, max(A, B)\n return curr\n```
| 0 | 0 |
['Python3']
| 0 |
maximum-energy-boost-from-two-drinks
|
Python || Dynamic Programming || Simple solution
|
python-dynamic-programming-simple-soluti-xfpy
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
vilaparthibhaskar
|
NORMAL
|
2024-09-05T18:59:08.746825+00:00
|
2024-09-05T18:59:08.746855+00:00
| 1 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\no(n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\no(n)\n\n# Code\n```python3 []\nclass Solution:\n def maxEnergyBoost(self, energyDrinkA: List[int], energyDrinkB: List[int]) -> int:\n l = len(energyDrinkA)\n dpA = [0] * (l + 2)\n dpB = [0] * (l + 2)\n for i in range(l - 1, -1, -1):\n dpA[i] = energyDrinkA[i] + max(dpA[i + 1], dpB[i + 2])\n dpB[i] = energyDrinkB[i] + max(dpB[i + 1], dpA[i + 2])\n return max(dpA[0], dpB[0])\n\n \n```
| 0 | 0 |
['Array', 'Dynamic Programming', 'Python3']
| 0 |
maximum-energy-boost-from-two-drinks
|
Easy sol^n
|
easy-soln-by-singhgolu933600-z0nx
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
singhgolu933600
|
NORMAL
|
2024-09-03T06:13:38.522915+00:00
|
2024-09-03T06:13:38.522945+00:00
| 3 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n long long solve(vector<int>& energyDrinkA,vector<int>& energyDrinkB,int i,int j,vector<vector<long long>>&dp)\n {\n if(j>=energyDrinkA.size())\n {\n return 0;\n }\n if(dp[i][j]!=-1)\n return dp[i][j];\n if(i==0)\n {\n long long v1=((long long)energyDrinkA[j])+((long long)solve(energyDrinkA,energyDrinkB,i,j+1,dp));\n long long v2=(long long)(solve(energyDrinkA,energyDrinkB,1,j+1,dp));\n dp[i][j]=max(v1,v2);\n }\n else\n {\n long long v1=((long long)energyDrinkB[j])+((long long)solve(energyDrinkA,energyDrinkB,i,j+1,dp));\n long long v2=(long long)(solve(energyDrinkA,energyDrinkB,0,j+1,dp));\n dp[i][j]=max(v1,v2);\n }\n return dp[i][j];\n }\n long long maxEnergyBoost(vector<int>& energyDrinkA, vector<int>& energyDrinkB) {\n vector<vector<long long>>dp(2,vector<long long>(energyDrinkA.size()+1,-1));\n long long ans=0;\n for(int i=0;i<2;i++)\n {\n ans=max(ans,solve(energyDrinkA,energyDrinkB,i,0,dp));\n }\n return ans;\n }\n};\n```
| 0 | 0 |
['Array', 'Dynamic Programming', 'C++']
| 0 |
maximum-energy-boost-from-two-drinks
|
See the python solution
|
see-the-python-solution-by-testcasefail-tauy
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
TestCaseFail
|
NORMAL
|
2024-09-02T19:27:30.653718+00:00
|
2024-09-02T19:27:30.653753+00:00
| 3 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution:\n def maxEnergyBoost(self, energyDrinkA: List[int], energyDrinkB: List[int]) -> int:\n n=len(energyDrinkA)\n dpA=[0]*n\n dpB=[0]*n\n dpA[0]=energyDrinkA[0]\n dpB[0]=energyDrinkB[0]\n\n for i in range(1,n):\n dpA[i]=max((dpA[i-1]+energyDrinkA[i]),dpB[i-1])\n dpB[i]=max((dpB[i-1]+energyDrinkB[i]),dpA[i-1])\n return max(dpA[-1],dpB[-1])\n```
| 0 | 0 |
['Python3']
| 0 |
maximum-energy-boost-from-two-drinks
|
Top Down approach C++
|
top-down-approach-c-by-ankursingh10-ch66
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
ankursingh10
|
NORMAL
|
2024-09-02T16:55:08.608857+00:00
|
2024-09-02T16:56:05.623273+00:00
| 6 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(2n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n^2)$$ for memoization\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n vector<vector<long long>>memo;\n long long dp(vector<int>& energyDrinkA, vector<int>& energyDrinkB, bool fromA, int i){\n if(i>=energyDrinkA.size()) return 0;\n if(memo[i][fromA] != -1) return memo[i][fromA];\n long long take = (fromA ? energyDrinkA[i] : energyDrinkB[i]) + dp(energyDrinkA, energyDrinkB, fromA, i+1);\n long long change = (fromA ? energyDrinkA[i] : energyDrinkB[i]) + dp(energyDrinkA, energyDrinkB, !fromA, i+2);\n return memo[i][fromA]=max(take, change);\n }\n long long maxEnergyBoost(vector<int>& energyDrinkA, vector<int>& energyDrinkB) {\n memo.resize(energyDrinkA.size(), vector<long long>(2, -1));\n return max(dp(energyDrinkA, energyDrinkB, true, 0), dp(energyDrinkA, energyDrinkB, false, 0));\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
maximum-energy-boost-from-two-drinks
|
ESASY SOLUTION USING Dp
|
esasy-solution-using-dp-by-pranjali21384-3jr1
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
pranjali213847
|
NORMAL
|
2024-09-01T09:28:52.338651+00:00
|
2024-09-01T09:28:52.338675+00:00
| 4 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public long maxEnergyBoost(int[] energyDrinkA, int[] energyDrinkB) {\n if(energyDrinkA.length ==0)\n {\n return 0;\n }\n long da[]=new long[energyDrinkA.length];\n long db[]=new long[energyDrinkB.length];\n \n // max ya toh switch karke ya nhi switch karke\n\n da[0]=energyDrinkA[0];\n db[0]=energyDrinkB[0];\n\n\n for(int i=1;i<energyDrinkA.length;i++)\n {\n //if no switch \n da[i]=da[i-1]+energyDrinkA[i];\n db[i]=db[i-1]+energyDrinkB[i];\n\n\n // if switch\n if(i>1){\n\n da[i]=Math.max(da[i],db[i-2]+energyDrinkA[i]);\n db[i]=Math.max(db[i],da[i-2]+energyDrinkB[i]);\n }\n\n\n }\n int n=energyDrinkA.length;\n return Math.max(da[n-1],db[n-1]);\n \n }\n}\n```
| 0 | 0 |
['Java']
| 0 |
maximum-energy-boost-from-two-drinks
|
"DP" solution, "for loop" might be more proper | Python
|
dp-solution-for-loop-might-be-more-prope-p8rh
|
\n"""\nDP \n\nstep-0. define drink_A and drink_B both of len(A) such that:\ndrink_A[i] := what is the maximal energy boost if we drink A[i]\ndrink_B[i] := what
|
wxy0925
|
NORMAL
|
2024-08-31T23:41:58.947150+00:00
|
2024-08-31T23:41:58.947174+00:00
| 0 | false |
```\n"""\nDP \n\nstep-0. define drink_A and drink_B both of len(A) such that:\ndrink_A[i] := what is the maximal energy boost if we drink A[i]\ndrink_B[i] := what is the maximal energy boost if we drink B[i]\n\nstep-1. init drink_A[0] = A[0], drink_B[0] = B[0]\n\nstep-2 dp update. Take drink_A[i] as example. If we can drink A[i],\nit means either we had drunk A[i-1], or we had switched from B[i-2].\ntherefore, drink_A[i] = max(drink_A[i], drink_A[i-1] + A[i], drink_B[i-2] + A[i]).\nSimilary, we can write down the update rule for drink_B[i]. \n\nCaution: we need to update the 2 dp tables simultaneously.\n\nstep-3 return max(drink_A[-1], drink_B[-1]).\n\nRemark: the n in the problem statement needed to be interpreted as the length\nof the two input lists.\n\n"""\n\nclass Solution:\n def maxEnergyBoost(self, A: List[int], B: List[int]) -> int:\n n = len(A)\n drink_A = [0] * n\n drink_B = [0] * n\n drink_A[0] = A[0]\n drink_B[0] = B[0]\n \n for i in range(1, n):\n drink_A[i] = max(drink_A[i], drink_A[i-1] + A[i])\n drink_B[i] = max(drink_B[i], drink_B[i-1] + B[i])\n if i - 2 >= 0:\n drink_A[i] = max(drink_A[i], drink_B[i-2] + A[i])\n drink_B[i] = max(drink_B[i], drink_A[i-2] + B[i])\n \n return max(drink_A[-1], drink_B[-1])\n \n```
| 0 | 0 |
['Dynamic Programming', 'Python']
| 0 |
maximum-energy-boost-from-two-drinks
|
my best soln
|
my-best-soln-by-sachinab-ysdn
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
sachinab
|
NORMAL
|
2024-08-31T17:41:45.631590+00:00
|
2024-08-31T17:41:45.631614+00:00
| 0 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public long maxEnergyBoost(int[] energyDrinkA, int[] energyDrinkB) {\n \n int n = energyDrinkA.length;\n long dp[][] = new long[n+2][2];\n \n for(int i=2; i<=n+1; i++){\n dp[i][0] = Math.max(dp[i-1][0],dp[i-2][1]);\n dp[i][0] += energyDrinkA[i-2];\n\n dp[i][1] = Math.max(dp[i-1][1],dp[i-2][0]);\n dp[i][1] += energyDrinkB[i-2];\n }\n\n return Math.max(dp[n+1][0],dp[n+1][1]);\n }\n}\n```
| 0 | 0 |
['Java']
| 0 |
maximum-energy-boost-from-two-drinks
|
C++|| DP || Clean code
|
c-dp-clean-code-by-satyamshivam366-ppza
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
satyamshivam366
|
NORMAL
|
2024-08-31T14:38:10.383376+00:00
|
2024-08-31T14:38:10.383397+00:00
| 4 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\n#define ll long long\nclass Solution {\npublic:\n ll rec(int i,int f,vector<int>& a, vector<int>& b,vector<vector<ll>> &dp)\n {\n int n=a.size();\n if(i>=n){return (ll)0;}\n if(dp[i][f]!=-1){return dp[i][f];}\n if(f==0)\n {\n return dp[i][f]=max(a[i]+rec(i+1,0,a,b,dp),a[i]+rec(i+2,1,a,b,dp));\n }\n else\n {\n return dp[i][f]=max(b[i]+rec(i+2,0,a,b,dp),b[i]+rec(i+1,1,a,b,dp));\n}\n }\n long long maxEnergyBoost(vector<int>& a, vector<int>& b) {\n int n=a.size();\n vector<vector<ll>> dp(n+1,vector<ll>(2,-1));\n return max(rec(0,0,a,b,dp),rec(0,1,a,b,dp));\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
maximum-energy-boost-from-two-drinks
|
Easy to Understand || cpp || java
|
easy-to-understand-cpp-java-by-bellmanfo-aj97
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n create dp array of two row and n+1 columns.Code is self explanatory , ju
|
BellmanFord_25
|
NORMAL
|
2024-08-31T10:45:40.448878+00:00
|
2024-08-31T10:45:40.448910+00:00
| 2 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- create dp array of two row and n+1 columns.Code is self explanatory , just use first row for energyDrinkA and row 2 for energyDrinkB. If you are taking energyDrinkA then look for it\'s two previous places from where you can reach there . If you are at idx in energyDrinkA , you must have come from idx-1 from the same array or idx-2 from energyDrinkB . -->\n\n# Complexity\n- Time complexity:\n<!-- O(N) -->\n\n- Space complexity:\n<!-- O(N*2) -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n long long maxEnergyBoost(vector<int>& energyDrinkA, vector<int>& energyDrinkB) {\n int n = energyDrinkA.size();\n long long dp[2][n+1];\n dp[0][0]=0;dp[1][0] = 0;\n dp[0][1] = energyDrinkA[0];\n dp[1][1] = energyDrinkB[0];\n for(int i = 2 ; i<=n ; i++){\n dp[0][i] = max(dp[0][i-1],dp[1][i-2])+energyDrinkA[i-1];\n dp[1][i] = max(dp[1][i-1],dp[0][i-2])+energyDrinkB[i-1];\n }\n return max(dp[0][n],dp[1][n]);\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
maximum-energy-boost-from-two-drinks
|
Iterative DP
|
iterative-dp-by-eugenemsv-un6e
|
Intuition\nThe Dp(K) = max from:\n 1. a[k]+ DpA[k-1] \n 2. a[k] + DpB[k-2]\n 3. b[k] + DpB[k-1]\n 4. b[k] + DpA[k-2]\n\nby DpA we mean if the last state is A,
|
eugenemsv
|
NORMAL
|
2024-08-30T21:19:26.165343+00:00
|
2024-08-30T21:19:26.165367+00:00
| 3 | false |
# Intuition\nThe Dp(K) = max from:\n 1. a[k]+ DpA[k-1] \n 2. a[k] + DpB[k-2]\n 3. b[k] + DpB[k-1]\n 4. b[k] + DpA[k-2]\n\nby DpA we mean if the last state is A, by DpB -> b\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n$$O(n)$$\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```java []\nclass Solution {\n public long maxEnergyBoost(int[] a, int[] b) {\n int n = a.length;\n long[] dpA= new long[n];\n long[] dpB = new long[n];\n dpA[0] = a[0];\n dpB[0] = b[0];\n dpA[1] = dpA[0]+ a[1];\n dpB[1] = dpB[0]+ b[1];\n\n for(int i =2; i< n; i++){\n dpA[i] = Math.max(dpA[i-1],dpB[i-2])+a[i];\n dpB[i] = Math.max(dpB[i-1],dpA[i-2])+b[i];\n }\n\n return Math.max(dpA[n-1], dpB[n-1]);\n }\n}\n```
| 0 | 0 |
['Dynamic Programming', 'Java']
| 0 |
maximum-energy-boost-from-two-drinks
|
DP, 💽: O(1) only
|
dp-o1-only-by-ndr0216-7vz9
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
ndr0216
|
NORMAL
|
2024-08-30T01:55:55.426595+00:00
|
2024-08-30T01:55:55.426632+00:00
| 4 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n long long maxEnergyBoost(vector<int>& energyDrinkA,\n vector<int>& energyDrinkB) {\n int n = energyDrinkA.size();\n\n long long dp_A = 0; // dp_A[i]\n long long dp_B = 0; // dp_B[i]\n long long last_dp_A = 0; // dp_A[i-1]\n long long last_dp_B = 0; // dp_B[i-1]\n\n for (int i = 0; i < n; i++) {\n long long next_dp_A = max(dp_A, last_dp_B) + energyDrinkA[i];\n long long next_dp_B = max(dp_B, last_dp_A) + energyDrinkB[i];\n\n last_dp_A = dp_A;\n dp_A = next_dp_A;\n last_dp_B = dp_B;\n dp_B = next_dp_B;\n }\n\n return max(dp_A, dp_B);\n }\n};\n```\n\n---\n# If you have any question or advice, welcome to comment below.
| 0 | 0 |
['Array', 'Dynamic Programming', 'C++']
| 0 |
maximum-energy-boost-from-two-drinks
|
dp solution
|
dp-solution-by-somaycoder-7oge
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
somaycoder
|
NORMAL
|
2024-08-29T20:56:37.889212+00:00
|
2024-08-29T20:56:37.889229+00:00
| 0 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n long long solve(vector<int>& energyDrinkA, vector<int>& energyDrinkB,int n,int i,int k, vector<vector<long long>> &dp){\n if(i==n){\n return 0;\n }\n if(dp[i][k] != -1){\n return dp[i][k];\n }\n long long x,y;\n if(k==1){\n x = energyDrinkA[i]+ solve(energyDrinkA,energyDrinkB,n,i+1,1,dp);\n y = solve(energyDrinkA,energyDrinkB,n,i+1,2,dp);\n }\n if(k==2){\n x = energyDrinkB[i]+ solve(energyDrinkA,energyDrinkB,n,i+1,2,dp);\n y = solve(energyDrinkA,energyDrinkB,n,i+1,1,dp);\n }\n \n return dp[i][k] = max(x,y);\n \n }\n long long maxEnergyBoost(vector<int>& energyDrinkA, vector<int>& energyDrinkB) {\n int n = energyDrinkA.size();\n long long ans = INT_MIN;\n int i=0;\n vector<vector<long long>> dp(n, vector<long long>(3, -1));\n long long ans1 = solve(energyDrinkA,energyDrinkB,n,i,1,dp);\n long long ans2 = solve(energyDrinkA,energyDrinkB,n,i,2,dp);\n return max(ans1,ans2);\n //return ans;\n }\n};\n\n\n// class Solution {\n// public:\n// long long solve(vector<int>& energyDrinkA, vector<int>& energyDrinkB, int n, int i, vector<long long>& dp) {\n// if (i == n) {\n// return 0;\n// }\n \n// if (dp[i] != -1) {\n// return dp[i];\n// }\n \n// long long x = energyDrinkA[i] + solve(energyDrinkA, energyDrinkB, n, i + 1, dp);\n// long long y = energyDrinkB[i] + solve(energyDrinkA, energyDrinkB, n, i + 1, dp);\n \n// dp[i] = max(x, y);\n// return dp[i];\n// }\n\n// long long maxEnergyBoost(vector<int>& energyDrinkA, vector<int>& energyDrinkB) {\n// int n = energyDrinkA.size();\n// vector<long long> dp(n, -1);\n \n// return solve(energyDrinkA, energyDrinkB, n, 0, dp);\n// }\n// };\n\n```
| 0 | 0 |
['Array', 'Dynamic Programming', 'C++']
| 0 |
maximum-energy-boost-from-two-drinks
|
Easy one if you think this way .
|
easy-one-if-you-think-this-way-by-prasad-k8od
|
Intuition\n Describe your first thoughts on how to solve this problem. \nNo specific pattern means trying all possibilties , finding overlappinng subproblems, t
|
prasad_shewale
|
NORMAL
|
2024-08-29T14:56:33.362377+00:00
|
2024-08-29T14:56:33.362412+00:00
| 0 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nNo specific pattern means trying all possibilties , finding overlappinng subproblems, thus thinking of DP.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThink of a recursion first then convert it to tabulation.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(N)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(2*N)\n# Code\n```cpp []\nclass Solution {\npublic:\n\n long long maxEnergyBoost(vector<int>& energyDrinkA, vector<int>& energyDrinkB) {\n int n = energyDrinkA.size();\n vector<vector<long long>> dp(2,vector<long long>(n+1, 0));\n for(int i = n-1;i>=0;i--){\n dp[0][i] = max((long long)energyDrinkA[i] + dp[0][i+1], dp[1][i+1]);\n dp[1][i] = max((long long)energyDrinkB[i] + dp[1][i+1], dp[0][i+1]);\n }\n return max(dp[0][0], dp[1][0]);\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
minimum-cost-to-equalize-array
|
[Java/C++/Python] 4 cases, O(n) solution
|
javacpython-4-cases-on-solution-by-lee21-qnzq
|
Intuition\n- If cost1 is cheaper, all use cost1\n- Increment all to max(A), use cost2 as many as possible\n- Increment to bigger than max(A), use less cost1\n-
|
lee215
|
NORMAL
|
2024-05-05T05:01:39.613181+00:00
|
2024-05-06T05:29:54.127148+00:00
| 5,532 | false |
# **Intuition**\n- If `cost1` is cheaper, all use `cost1`\n- Increment all to `max(A)`, use `cost2` as many as possible\n- Increment to bigger than `max(A)`, use less `cost1`\n- cost1 is too expensive, increment untill we won\'t use `cost1`\n<br>\n\n\n# **Explanation**\nCalculate the `min(A)` and `max(A)`\n`total = max(A) * n - sum(A)`, total is the minimum increments need to do.\n\n**Case 1:**\n`c1 * 2 < c2`\noperation 1 is always better operation 2,\nwe simply return `total * c1 % mod`\n\n**Case 2:**\n`c1 * 2 > c2`\nWe do operation 2 as many as possible,\nand use operation 1 to complete.\n\n**Case 3:**\n`c1 * 2 >> c2`\nPreviously we increment to `max(A)`,\nnow we can increment to `max(A) + x`\nSo that can do few operation 1 and mostly operation 2.\n\nFrom `op1 = (ma - mi) * 2 - total` we can see,\nEach time we increment all elements by 1,\n`op1` will reduce `n - 2`\n\nEach round, we can pay `n - 1` more op2 but save `n - 2` op1.\nIf `(n - 2) * cost 1 > (n - 1) * cost 2`, it\'s a good deal, \nand we will continue doing this, until `op1 < n - 2`.\nSo we calculate `op1 / n - 2` for the rounds needed to reduce `op1`.\n\n\n**Case 4:**\n`c1 * 2 >>>>> c2`\nWe won\'t do any operation 1.\nDo `total += n`,\nto ensure `total` can be even\n<br>\n\n# **Complexity**\nTime `O(n)`\nSpace `O(1)`\n<br>\n\n**Java**\n```java\n public int minCostToEqualizeArray(int[] A, int c1, int c2) {\n int ma = A[0], mi = A[0], n = A.length, mod = 1000000007;\n long total = 0;\n for (int a: A) {\n mi = Math.min(mi, a);\n ma = Math.max(ma, a);\n total += a;\n }\n total = 1l * ma * n - total;\n\n // case 1\n if (c1 * 2 <= c2 || n <= 2) {\n return (int) ((total * c1) % mod);\n }\n\n // case 2\n long op1 = Math.max(0L, (ma - mi) * 2L - total);\n long op2 = total - op1;\n long res = (op1 + op2 % 2) * c1 + op2 / 2 * c2;\n\n // case 3\n total += op1 / (n - 2) * n;\n op1 %= n - 2;\n op2 = total - op1;\n res = Math.min(res, (op1 + op2 % 2) * c1 + op2 / 2 * c2);\n\n // case 4\n for (int i = 0; i < 2; i++) {\n total += n;\n res = Math.min(res, total % 2 * c1 + total / 2 * c2);\n }\n return (int) (res % mod);\n }\n```\n**C++**\n```cpp\n int minCostToEqualizeArray(vector<int>& A, int c1, int c2) {\n int ma = *max_element(A.begin(), A.end());\n int mi = *min_element(A.begin(), A.end());\n int n = A.size(), mod = 1000000007;\n long long su = accumulate(A.begin(), A.end(), 0LL);\n long long total = 1LL * ma * n - su;\n\n // case 1\n if (c1 * 2 <= c2 || n <= 2) {\n return (total * c1) % mod;\n }\n\n // case 2\n long long op1 = max(0LL, (ma - mi) * 2 - total);\n long long op2 = total - op1;\n long long res = (op1 + op2 % 2) * c1 + op2 / 2 * c2;\n\n // case 3\n total += op1 / (n - 2) * n;\n op1 %= n - 2;\n op2 = total - op1;\n res = min(res, (op1 + op2 % 2) * c1 + op2 / 2 * c2);\n\n // case 4\n for (int i = 0; i < 2; i++) {\n total += n;\n res = min(res, total % 2 * c1 + total / 2 * c2);\n }\n\n return res % mod;\n }\n```\n**Python**\n```py\n def minCostToEqualizeArray(self, A: List[int], c1: int, c2: int) -> int:\n ma, mi = max(A), min(A)\n n = len(A)\n mod = 10 ** 9 + 7\n total = ma * n - sum(A)\n\n # case 1\n if c1 * 2 <= c2 or n <= 2:\n return total * c1 % mod\n\n # case 2\n op1 = max(0, (ma - mi) * 2 - total)\n op2 = total - op1\n res = (op1 + op2 % 2) * c1 + op2 // 2 * c2\n\n # case 3\n total += op1 // (n - 2) * n\n op1 %= n - 2\n op2 = total - op1\n res = min(res, (op1 + op2 % 2) * c1 + op2 // 2 * c2)\n\n # case 4\n for i in range(2):\n total += n\n res = min(res, total % 2 * c1 + total // 2 * c2)\n return res % mod\n```\n
| 59 | 2 |
['C', 'Python', 'Java']
| 23 |
minimum-cost-to-equalize-array
|
Binary Search on Piecewise Linear Function
|
binary-search-on-piecewise-linear-functi-w577
|
Intuition\nOne approach is to first find the value that we should make all the array elements equal to, then find the cost of doing that.\n\nHowever, directly f
|
jeffreyhu8
|
NORMAL
|
2024-05-05T04:01:05.535495+00:00
|
2024-05-05T04:05:16.650090+00:00
| 3,424 | false |
# Intuition\nOne approach is to first find the value that we should make all the array elements equal to, then find the cost of doing that.\n\nHowever, directly finding a formula for the optimal value is not trivial. For example, the optimal value may not always be `max(nums)`, as shown by the case `nums = [1, 100_000, 100_000], cost1 = 1_000_000, cost2 = 1`.\n\nAs such, instead of trying to directly find the optimal value, we will instead do a search over the space of all possible values to find the one with minimal cost.\n\n# Approach\nFirst, if `2 * cost1 < cost2`, then it never makes sense to take two at a time. So set `cost2 = 2 * cost1` and whenever we take two at a time, pretend that we are just taking one at a time twice.\n\nNow that we\'ve set `cost2 = min(2 * cost1, cost2)`, our goal in achieving some value `k` is to minimize the number of times we take one at a time (since taking two elements at a time is always better than taking both separately now that we\'ve updated our cost).\n\nSo how many elements do we need to pick up one at a time? Let `differences = [k - num for num in nums]`. If `max(differences)` is less than the sum of the other elements, then we can use a heap/priority queue argument to show that we can pair all elements up, except maybe one element if the parity is not right. Otherwise, pair as many elements in `max(differences)` up as possible, then take the remaining `max(differences) - (sum(differences) - max(differences))` elements one at a time.\n\nMoreover, disregarding the adjustment of `ones` due to parity, note that `ones := max(2 * max(differences) - sum(differences), 0)` is really a piecewise function with two linear parts. Thus, `ones * self.cost1 + ((sum(differences) - ones) // 2) * self.cost2` is also a piecewise function with two linear parts that decreases then increases.\n\nSo, do a binary search on both parities to find the minimum.\n\n# Complexity\n- Time complexity: $$O(n + \\lg \\mathrm{sum}(\\mathrm{nums}))$$\n\n- Space complexity: $$O(1)$$\n\n# Code\n```py\nclass Solution:\n MOD = 10 ** 9 + 7\n \n def solve(self, k):\n sumDifferences = k * len(self.nums) - self.sumNums\n \n ones = max(2 * (k - self.minNums) - sumDifferences, 0) \n if (sumDifferences - ones) & 1 != 0:\n ones += 1\n \n return ones * self.cost1 + ((sumDifferences - ones) // 2) * self.cost2\n \n def minCostToEqualizeArray(self, nums: List[int], cost1: int, cost2: int) -> int:\n cost2 = min(2 * cost1, cost2)\n \n self.nums = nums\n self.minNums = min(nums)\n self.sumNums = sum(nums)\n self.cost1 = cost1\n self.cost2 = cost2\n \n m = max(nums)\n \n sameParity = range(m, 10 ** 18, 2)\n diffParity = range(m + 1, 10 ** 18, 2)\n i = bisect_left(sameParity, 0, key=lambda i: self.solve(i + 2) - self.solve(i))\n j = bisect_left(diffParity, 0, key=lambda j: self.solve(j + 2) - self.solve(j))\n \n return min(self.solve(sameParity[i]), self.solve(diffParity[j])) % Solution.MOD\n```
| 45 | 5 |
['Binary Search', 'Python3']
| 7 |
minimum-cost-to-equalize-array
|
Deep Dive into Lee's O(n) Solution
|
deep-dive-into-lees-on-solution-by-rexch-q2ey
|
Click to view lee215\'s O(n) solution\n\nDisclaimer: This post is just my explanation of @lee215 solution and I do NOT own the solution.\n\nFor ease of reading/
|
rexcheng
|
NORMAL
|
2024-05-05T22:32:31.149899+00:00
|
2024-05-09T15:04:20.035635+00:00
| 897 | false |
[Click to view lee215\'s O(n) solution](https://leetcode.com/problems/minimum-cost-to-equalize-array/solutions/5114202/java-c-python-4-cases-o-n-solution)\n\n***Disclaimer: This post is just my explanation of @lee215 solution and I do NOT own the solution.***\n\nFor ease of reading/understanding, let\'s call\n- `op1`: increase an element in the array by 1 with `cost1`\n- `op2`: choose two different elements in the array and increase both of them by 1 with `cost2`\n\nFirst thing - let\'s forget the four cases in Lee\'s solution. We have two possible operations and we want to find the answer. What can we do with the two operations? Well, the answer must be one of the following:\n1. Use only `op1`\n2. Use a combination of `op1` and `op2`\n3. Use only `op2`\n\n### Now think about under which circumstance we would prefer "1. Use only `op1`."\nWell, if we choose two different elements and increase both of them by 1 with `2 * cost1` and result in a lower cost than `cost2`, we definitely prefer using only `op1`. *This is case1 in Lee\'s solution.*\n```python\n# python code\nmaxNum = max(nums)\ncost = sum([(maxNum - num) * cost1 for num in nums]) # sum of the difference between each element and maxNum, multiplied by cost1\n# alternatively from Lee\'s solution\ncost = (maxNum * len(nums) - sum(nums)) * cost1\n```\n\n### What about "2. Use a combination of `op1` and `op2`"?\n*This covers case2 & case3 in Lee\'s solution.* There is a precondition for this case - `2 * cost1 > cost2` because if this condition is false, we can directly return the answer above.\n\nGiven the precondition, we should prefer using `op2` as much as possible and then `op1`. If it is possible to find an answer with two `op1` performed on different elements, we can always replace two `op1` with one `op2` to reduce the cost. What if `op1` is performed multiple times on the same element? Then we are not able to replace `op1` with `op2` unless we further increase all elements in the array beyond `max(nums)`.\n\nTherefore, we need to consider two cases here:\n1. Increase as many elements in the array as possible to `max(nums)` with `op2`, and then use `op1` to increase the rest ("the rest" is actually the minimum element in the array)\n\n```python\n# python code\nmaxNum = max(nums)\nop1, op2 = 0, 0\nsurplus = 0\nfor num in nums:\n diff = maxNum - num\n if surplus >= diff: # enough increase by op2 from previous step\n surplus -= diff\n else:\n op2 += diff - surplus # (diff - surplus) more op2 to bring num to maxNum\n surplus = diff - surplus\nif surplus > 0: # too many op2 performed\n op1 = surplus\n op2 -= surplus\ncost = op1 * cost1 + op2 * cost2\n\n# alternatively from Lee\'s solution\nminNum, maxNum = min(nums), max(nums)\n# total difference to bring all elements to maxNum\ntotal = maxNum * len(nums) - sum(nums)\n# increasing minNum to maxNum using op2 gives you (maxNum - minNum) more to apply to all other elements\n# thus the total difference to increase minNum to maxNum using op2 is 2 * (maxNum - minNum)\nsolo = max(0, (maxNum - minNum) * 2 - total)\n# the sum of difference to be performed with op2\npair = total - solo\ncost = (solo + pair % 2) * cost1 + (pair // 2) * cost2\n```\n\n2. Replace `op1` in the case1 above with `op2` but increase all elements in the array to `max(nums) + x`, some integer greater than `max(nums)`. We want to replace as many `op1` as possible because `cost2 < 2 * cost1`\n\n```python\n# python code\n# total difference to bring all elements to maxNum\ntotal = maxNum * len(nums) - sum(nums)\ntotal += \\\n # this is the `x`\n # we have `solo` difference to be performed using op1\n # every time we increment `x` by 1, we can replace len(nums) - 1 op1 with op2\n # and introduce one more op1 to increment the smallest element by 1\n # so we reduce `solo` by the number of other elements minus 1 (the element itself)\n # because the element itself needs to be increased by 1 more using op1\n solo // (len(nums) - 2) \\\n # multiplied by len(nums) because we need to increase all elements to maxNum + x\n * len(nums)\n# difference to be performed with op1\nsolo %= len(nums) - 2\n# the sum of difference to be performed with op2\npair = total - solo\ncost = (solo + pair % 2) * cost1 + (pair // 2) * cost2\n```\n\n### Finally "3. Use only `op2`."\n*This is case4 in Lee\'s solution.* Obviously this time, we cannot assume when all elements in the array are equal, they are equal to `max(nums)` because `op2` will increase two different elements at the same time. So what can we do at best if we are only allowed to use `op2`?\n1. Increase all elements to `max(nums)`\n2. Consume the overflows due to `op2` by balancing them across the array as equally as possible\n3. All the elements in the array should be equal to `max(nums) + x`, where `x` is some non-negative integer ($x \\ge 0$)\n\nOkay, from the case above "Use a combination of `op1` and `op2`," we already know that `solo %= len(nums) - 2`. This means that `solo` can only be in the range $[0, \\text{len(nums)} - 3]$. Since we want to use only `op2`, we want to reduce `solo` to 0. This means we need to increase `x` from the previous case.\n\nHowever, we just need to increase `x` from the previous case by 1 or 2 (same as increasing `total` by `len(nums)` or `2 * len(nums)`). This can be proved by mathematical induction.\n\nWhen `solo = 1`, if `len(nums)` is odd, `len(nums) - 1` is even and increasing `x` by 1 works; if `len(nums)` is even, `len(nums) - 1` is odd and increasing `x` by 2 works.\n\nWhen `solo = k + 1`, we flap the if condition for `solo = k` so that the statement still holds.\n\n```python\n# python code\nfor i in range(2):\n total += len(nums) # adding len(nums) to `total` increases `x` by 1\n # cost1 is here because we don\'t know if adding len(nums) once is enough\n cost = (total % 2) * cost1 + (total // 2) * cost2\n```\n\n# Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(1)$$\n\n# Solution in JS (FYI)\n```js\n/**\n * @param {number[]} nums\n * @param {number} cost1\n * @param {number} cost2\n * @return {number}\n */\nvar minCostToEqualizeArray = function(nums, cost1, cost2) {\n const MOD = 1e9 + 7;\n let min = nums[0], max = nums[0], sum = 0;\n for (const num of nums) {\n min = Math.min(min, num);\n max = Math.max(max, num);\n sum += num;\n }\n let delta = max * nums.length - sum;\n if (cost1 * 2 <= cost2 || nums.length <= 2) {\n return (delta * cost1) % MOD;\n }\n // use cost2 as much as possible, then cost1 to fill the gap\n // to increase all elements to max\n let op1 = Math.max(0, (max - min) * 2 - delta);\n let op2 = delta - op1;\n let result = (op1 + op2 % 2) * cost1 + Math.floor(op2 / 2) * cost2;\n // use cost2 as much as possible, then cost1 to fill the gap\n // but to increase all elements to (max + ?)\n delta += Math.floor(op1 / (nums.length - 2)) * nums.length;\n op1 %= nums.length - 2;\n op2 = delta - op1;\n result = Math.min(result, (op1 + op2 % 2) * cost1 + Math.floor(op2 / 2) * cost2);\n // don\'t use cost1\n for (let i = 0; i < 2; i++) {\n delta += nums.length;\n result = Math.min(result, (delta % 2) * cost1 + Math.floor(delta / 2) * cost2);\n }\n return result % MOD;\n};\n```
| 16 | 1 |
['Python', 'Python3', 'JavaScript']
| 5 |
minimum-cost-to-equalize-array
|
C++ Easy Solution || Line by Line Explanation (Brute Force Thinking)
|
c-easy-solution-line-by-line-explanation-knbp
|
\nGiven : Make all the array elements as equal\n\nThoughts :\nOur first thought after seeing the given examples is \nmake all the array elements to maximum elem
|
manoj-22
|
NORMAL
|
2024-05-05T07:58:05.346842+00:00
|
2024-05-05T08:38:32.625432+00:00
| 909 | false |
```\nGiven : Make all the array elements as equal\n\nThoughts :\nOur first thought after seeing the given examples is \nmake all the array elements to maximum element in array.\n\nWhat if, making all the arr elements to maximum is costlier than \nmaking all the arr elements to x (which is greater than max element in arr).\n\nSo, our search should between max to x ( > max)\n\n\nIn this way, we may have 3 cases\n\nCase 1: If 2 * cost1 < cost2, then its better increment all elements one by one with cost1\nCase 2: If 2 * cost1 > cost2, then its better to increment 2 elements atonce with cost2\nCase 3 : For some element, we have to use cost1 and remaining elements we have to use cost2\n\nNow, To increment the array elements, how can we do it ?\n\nInstead of taking each element and increase by 1, \nTo simplify it, we should find the difference between the elements and multiply it with cost1/cost2\n\n```\n\n\n```\nclass Solution {\n int mod = 1e9 + 7;\n \n long long maxElementInNumsArr = 0, minElementInNumsArr = LLONG_MAX, n, totalNumsArrSum = 0 ;\n \n \npublic:\n int minCostToEqualizeArray(vector<int>& nums, int cost1, int cost2) {\n \n maxElementInNumsArr = *max_element(nums.begin(), nums.end());\n \n minElementInNumsArr = *min_element(nums.begin(), nums.end());\n \n n = nums.size();\n \n totalNumsArrSum = accumulate(nums.begin(), nums.end(), 0LL);\n \n long long res = LLONG_MAX;\n \n // our search from max to x( > max i.e 2*max,3*max,......1e6+1)\n for(long long equalizeElement = maxElementInNumsArr; equalizeElement < 2*maxElementInNumsArr; equalizeElement++){\n // denotes the count which makes all ele equal to cur equalizeElement\n long long totalRequired = (equalizeElement * n) - totalNumsArrSum;\n \n // denotes the max count to make arr ele equal to cur equalizeEleme nt\n long long maxRequired = equalizeElement - minElementInNumsArr;\n \n // dentoes how many sets of pairs do we have to consider\n long long pair = min(totalRequired / 2, totalRequired - maxRequired);\n \n // 2 * cost1 => denotes taking 2 elements and increment it\n // whereas cost2 already denotes taking 2 elements\n long long totalCost = min(2 * cost1 * pair, cost2 * pair);\n \n // when you have less than 2 elements, then your only way to use cost1\n totalCost += cost1 * (totalRequired - 2 * pair);\n \n res = min(res, totalCost);\n }\n \n res %= mod;\n\n \n return res;\n }\n};\n```
| 15 | 0 |
['C++']
| 3 |
minimum-cost-to-equalize-array
|
Python O(n) fastest solution explained visually
|
python-on-fastest-solution-explained-vis-llq7
|
Approach\n Describe your approach to solving the problem. \nThe easiest way to approach this problem is to think of each entry in nums as a stack of blocks (min
|
KellerWheat
|
NORMAL
|
2024-05-05T05:25:28.143838+00:00
|
2024-05-05T17:29:46.664693+00:00
| 369 | false |
# Approach\n<!-- Describe your approach to solving the problem. -->\nThe easiest way to approach this problem is to think of each entry in nums as a stack of blocks (minecraft style). The goal is to make all of the block stacks the same height. For example, the array [1, 3, 3, 4, 5] would look like this:\n\n**Stone = original array, dirt = blocks added with first operation (cost1), planks = blocks added with second operation (cost2)**\n\nThis problem consists of considering a lot of different edge cases and reasoning through each one:\n- If the width is 2, or if cost1 * 2 <= cost2, there is never a reason to use the second operation, so the best solution is to bring the lower stack up to the higher stack.\n\n- If cost2 is cheaper than 2 * cost1, there is an advantage to adding multiple blocks at once. The optimal strategy to do this is adding blocks to the two lowest layers each time, so you are left with minimal remaining blocks. This has 2 possible outcomes:\n1. The blocks can be fully filled in with pairs (minus 1 if there are an odd number):\n\n2. Since you have to choose 2 **different** indices, if the lowest column needs more blocks than all the others combined, you will be left with a single block wide hole. This seems like a small edge case, but it actually makes the problem much more complicated to solve\n\n\n- Calculating the cost of all the operations up to this point is pretty simple, now it is either level (and we can stop) or we are left with a single block wide hole that needs to be considered. In some cases, it is cheapest to simply fill this hole up 1 by 1 using cost1, but in others, it is cheaper to add an entire new layer on top to continue using cost2 operations (ex. consider the example above when cost1 = 10 and cost2 = 1)\n\nThis has a total cost of 22 (remember, the second operation places 2 blocks per cost)\n\nWhile this has a cost of 6\n\n\n\n- It is pretty simple to check the first option. However, for the second option, there are a few more cases to consider:\n1. When the hole depth is greater than the total width, adding one layer isn\'t enough. For efficiency, we calculate the number of layers we need by dividing the hole depth by the depth gained per layer (n - 2). Once we are down to a maximum of one layer to add, we proceed with step 2\n\n2. If the hole depth is less than the total width, then we need to add a maximum of one layer (usually, there is another edge case later on). We do this by filling in the hole then adding extra blocks as needed to fill up the rest of the layer:\n\n3. There is one last possibility: sometimes, we have an odd number of blocks, so we will be left with a one block space. This can either be filled in with a single operation of cost1, or if n is odd, by adding another layer on using cost2.\n\n\n- Finally, we have considered every edge case. By translating this logic into code (explained with comments below), we can solve the problem very efficienty O(n) operations are required to find min, max, and total, but the logic is constant time.\n\n# Complexity\n- Time complexity: O(n) for min, max, and total, O(1) for logic\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minCostToEqualizeArray(self, nums: List[int], cost1: int, cost2: int) -> int:\n n = len(nums)\n m = 10 ** 9 + 7\n \n # simple edge cases: if len(nums) < 3 then there is no reason to worry about cost2, as the second operation never does anything\n if n == 1:\n return 0\n if n == 2:\n return ((max(nums) - min(nums)) * cost1) % m\n \n # hole represents the difference between the highest and lowest value\n hole = max(nums) - min(nums)\n # needed represents the total difference between the highest number and all other numbers\n # essentially the total number of squares that need to be filled in\n needed = max(nums) * n - sum(nums)\n cost = 0\n \n # if individual operations are cheaper or as cheap, we can stop here\n if cost1 * 2 <= cost2:\n \n return (needed * cost1) % m\n \n # since it is better to do 2 operations at a time, try to fill in all of the squares using this method\n # we want to end up with either all squares filled or all squares filled with the shallowest single space hole possible\n if needed // 2 >= hole:\n # all squares (except possibly one if there is an odd number) can be filled\n easy = needed // 2\n hole = needed - 2 * easy # 1 or 0\n else:\n # not all squares are filled, do our best to reduce the size of the hole\n easy = needed - hole\n hole = hole - easy\n \n # cost after doing all simple operations\n cost = easy * cost2\n \n # now we calculate the cost to fill in the last hole\n # usually, it is cheaper to fill in individually with cost1\n # however, if cost2 is much lower than cost1 it can be more efficient to add 1 to all numbers\n # we perform the 2nd operation many times, always choosing the lowest point as one of the indices\n def minCost(hole_size):\n # basic case, no shenanigans\n best = cost1 * hole_size\n\n # the hole is shallow enough that we only have to raise the level by one to fill it\n if hole_size + 1 < n:\n # the number of operations needed to fill the hole + the number needed to raise the level by 2\n fill = ((hole_size + n) // 2)\n \n if (hole_size + n - fill * 2) == 1:\n # sometimes there are an odd number of blocks and we are left with a 1 block deep hole\n if n % 2 == 1:\n # here we are checking whether it is cheaper to use cost1 once or raise the level again to avoid it\n # this is only possible if n is odd\n best = min(best, fill * cost2 + min(cost1, cost2 * ((n + 1) // 2)))\n else:\n best = min(best, fill * cost2 + cost1)\n else:\n best = min(best, fill * cost2)\n # if the hole is so deep that it cannot be filled by adding one level, we add multiple\n else:\n # the change in hole depth after each operation\n gain = n - 2\n # the number of levels to add\n levels = hole_size // gain\n # the number of operations we need to add a level\n fill = n - 1\n best = min(best, minCost(hole_size - gain * levels) + cost2 * fill * levels)\n return best\n \n\n cost += minCost(hole)\n return cost % m\n```
| 14 | 0 |
['Python3']
| 2 |
minimum-cost-to-equalize-array
|
Python 3 || O(1) Besides min/max/sum
|
python-3-o1-besides-minmaxsum-by-zsq007-frql
|
Intuition\n1. If cost1 is no more than a half of cost2, we can always choose Op1.\n2. If the maxGap is no more than a half of the ttlGap, we can always find pai
|
zsq007
|
NORMAL
|
2024-05-05T04:04:22.845430+00:00
|
2024-05-08T18:37:03.613598+00:00
| 2,346 | false |
# Intuition\n1. If `cost1` is no more than a half of `cost2`, we can always choose Op1.\n2. If the `maxGap` is no more than a half of the `ttlGap`, we can always find pairs for Op2 (Here\'s why: [LC1953](https://leetcode.com/problems/maximum-number-of-weeks-for-which-you-can-work/)), except for the corner case that there\'s one spot left. In this case, if `n` is odd, we may try Op2 for `(n+1)//2` times which increases the final level by 1.\n3. If the `maxGap` is quite large, first, greedily apply Op2.\n For the rest, there are two schemes:\n\n- Directly fill the `maxGap` with Op1;\n- Pair `maxGap` with other `n-1` indices, which increases the final level by 1. \n\n To compare these two schemes, the key observation is that **Applying `n-1` Op2 reduces the gap by `n-2`**, so we compare `cost2 * (n-1)` with `cost1 * (n-2)`.\n\n4. After filling `maxGap` with the optimal scheme, if there are some gap left (less than `n-1`), again, we compare the two operations for the last round.\n\n\n# Complexity\n- Time complexity: $O(n)$ for `min(), max(), sum()`; besides that, $O(1)$.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $O(1)$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python\nclass Solution:\n def minCostToEqualizeArray(self, nums: List[int], cost1: int, cost2: int) -> int:\n n, mx, mod = len(nums), max(nums), 10**9+7\n maxGap, ttlGap = mx-min(nums), mx*n-sum(nums)\n \n if cost1*2 <= cost2:\n # Easy case, Op 1\n return ttlGap*cost1 % mod\n \n if maxGap*2 <= ttlGap:\n # The maxGap is less than a half of ttlGap, we can always find pairs for Op 2\n res = ttlGap // 2 * cost2\n if ttlGap % 2 == 1:\n # Corner case with the last one spot left\n if n % 2 == 1:\n res += min(cost1, cost2 * (n+1) // 2)\n else:\n res += cost1\n return res % mod\n \n # Two Operations:\n # Op 1: Directly fill maxGap\n # Op 2: Pair maxGap with other nums, which increases the final level.\n\n res = cost2 * (ttlGap - maxGap)\n maxGap -= ttlGap - maxGap\n\n if maxGap >= n-1:\n \n if cost2 * (n-1) >= cost1 * (n-2):\n # Op 1 is better\n res += maxGap // (n-1) * (n-1) * cost1\n maxGap %= n-1\n else:\n # Op 2 is better\n res += maxGap // (n-2) * (n-1) * cost2\n maxGap %= n-2\n\n if maxGap:\n # For the last round, Op 2: Increase the level by 1 to get (n+maxGap)//2 pairs\n op2 = (n+maxGap) // 2 * cost2 # = (maxGap + (n-maxGap)//2) * cost2\n if (n+maxGap) % 2 == 1:\n # The last one spot left\n if n%2 == 1:\n op2 += min(cost1, cost2*(n+1)//2)\n else:\n op2 += cost1\n\n # Compare it with Op 1 \n res += min(op2, maxGap * cost1)\n\n return res % mod\n```
| 14 | 1 |
['Greedy', 'Python3']
| 5 |
minimum-cost-to-equalize-array
|
✅ Detailed Explanation : Checking all combinations
|
detailed-explanation-checking-all-combin-9qi8
|
Intuition\n\nThe range of the equalised value will be max(a)....2 * max(a)\n\nWhy ?\nWe need to allow all possible equal max values to be the final equal value
|
rbssmtkr
|
NORMAL
|
2024-05-05T05:58:31.122688+00:00
|
2024-05-06T05:16:57.947228+00:00
| 1,126 | false |
## Intuition\n\nThe `range` of the equalised value will be `max(a)....2 * max(a)`\n\nWhy ?\nWe need to allow all possible equal max values to be the final equal value here as we need to consider all possible count of `cost2` operations as much as possible.\nIts possible that cost2 << cost1 and for using cost2 as much as possible we need to maximise the equal value we arrive at \nLet the max value we arrive at is : `max(a) + x` \n\nNow what can be the range of `x` ?\nWe would need to use the `cost2` operation maximum number of times for this case , we can prove `x` to be atmost `max(a)` in this case then\n\n## Approach\n\nLet, \n \n max(a) = max_a \n min(a) = min_a \n sum = a0 + a1 + a2 + ... + an\n\nif `2 * cost1 < cost2` then use cost1 as operation only\n\n\nNow , Let `eq` be the number we are equalising the array to :\n\nWe need to add `eq - min_a` to the minimum number \n\nIt is possible that the minimum number but needs more operations to become max than the next greater number can pair with\n\nso if the \n\n`operations needed to make all others equal < operations needed to make min_a equal` then we need to consider `cost1` operations for minimum number for the remaining increments.\n\n`Sidenote`: Think About Why only minimum element is facing this situation ??\n\nFor others,\nWe can consider `cost1` and `cost2` for the remaining increement operations \n\n\nSo for the minimum element `min_a`\n```\nif( eq * (n-1) - (sum-min_a) <= (eq - min_a) ){\n int64_t extra = (1LL * eq - min_a) - (eq * (n-1) - ( sum - min_a ));\n cost += 1LL * extra * cost1;\n total_increements -= extra;\n}\n```\n\nNow if the remainining operations are odd , use a `cost1` operation\n```\nif( total_increements & 1 ){\n total_increements -= 1;\n cost += cost1;\n}\n```\n\n\nFor all others either use `cost1` or `cost2` operations\n```\ncost += min( total_increements * cost1 , (total_increements / 2) * cost2 );\n```\n\n\n# Complexity\n- Time complexity: $$O(max(a))$$ \n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nconst int64_t mod = 1e9 + 7;\nclass Solution {\npublic:\n int minCostToEqualizeArray(vector<int>& nums, int cost1, int cost2) {\n \n int n = nums.size();\n int64_t max_a = *max_element(nums.begin(),nums.end());\n int64_t min_a = *min_element(nums.begin(),nums.end());\n int64_t sum = accumulate(nums.begin(),nums.end(),0LL);\n\n int64_t best_cost = 4e18;\n\n for( int64_t eq = max_a ; eq <= 2 * max_a ; eq++ ){\n\n int64_t total_increements = eq * n - sum;\n int64_t cost = 0;\n int64_t min_a_add = eq - min_a;\n\n // operations needed to make all others equal < operations needed to make min_a equal \n // so min_a can\'t be paired then so needs cost1 operations\n \n if( eq * (n-1) - (sum-min_a) <= (eq - min_a) ){\n int64_t extra = (1LL * eq - min_a) - (eq * (n-1) - ( sum - min_a ));\n cost += 1LL * extra * cost1;\n total_increements -= extra;\n }\n\n\n\n // if odd increements are left then use a cost1 operation\n if( total_increements & 1 ){\n total_increements -= 1;\n cost += cost1;\n }\n\n cost += min( total_increements * cost1 , (total_increements / 2) * cost2 );\n best_cost = min( best_cost , cost );\n\n }\n \n return best_cost%mod;\n }\n};\n```
| 9 | 0 |
['Math', 'Combinatorics', 'C++']
| 4 |
minimum-cost-to-equalize-array
|
Constructive solution in O(n log n)
|
constructive-solution-in-on-log-n-by-ply-udg2
|
Approach\nWe\'ll operate on a sorted diff array, where diff[i] = maxElement - arr[i].\nNote that if cost1 * 2 <= cost2, it is enough to just do single operation
|
plyusnovdmitrii
|
NORMAL
|
2024-05-05T04:27:51.405330+00:00
|
2024-05-05T04:33:57.376177+00:00
| 1,419 | false |
# Approach\nWe\'ll operate on a sorted `diff` array, where `diff[i] = maxElement - arr[i]`.\nNote that if `cost1 * 2 <= cost2`, it is enough to just do single operations, so the answer would be `sum(diff[i]) * cost1`.\nIn case `cost2 < cost1 * 2`, we\'ll try to use `cost2` operations as much as possible.\n\nFirst, note that if `n` is odd, increasing a single element can be replaced with `(n - 3) / 2 + 2` double operations,\ne.g. `diff=[0,1,1,1,1,1,1]`, in 2 operations we\'ll get `diff=[2,2,2,1,1,1,1]`, the remaining amount of ones is `n-3`, so we\'ll need `(n-3)/2` operations.\n\nThen, let\'s look at the last element in `diffs` and compare it with `sum(diffs[i]), i = 0..n-2` (so the sum of every except last). In this case, we can form everything into pairs, and the answer would be `sum(diffs[i])/2` double operations and `sum(diffs[i])%2` single operations (remember we can also replace it with a bunch of double operations).\nAn example would be `diffs=[0,3,4,4,10]`. In this case, `last(diffs) = 10`, `sum(diffs[i]), i = 0..n-2 = 3 + 4 + 4 = 11`, so we can form 10 double operations and 1 single operation.\n\nThe final part is considering what happens if `diffs[n-1] > sum(diffs[i]), i = 0..n-2`. In this case, we can obviously do `sum(diffs[i]), i = 0..n-2` double operations, and `diffs[n-1] - sum(diffs[i]), i = 0..n-2` single ones, e.g. `diffs=[0,1,2,8]` means we can do `1+2=3` double operations, leaving us with `8-3=5` single ones.\nOne again, the trick is to convert single operations into double ones if needed. Note that for `lastDiff = diffs[n-1] - sum(diffs[i]), i = 0..n-2`, if `lastDiff > n - 1`, we could do `lastDiff/(n-1)` rounds of adding 1 to it and all other elements, e.g. for `diffs=[0,0,0,9]`, we have an example original array of `[0,9,9,9]`, and we can repeat the following cycle 3 times `[0,9,9,9]->[1,10,9,9]->[2,10,10,9]->[3,10,10,10]` for a total of 9 operations. More formally, we\'ll do `(lastDiff/(n-1))*(n-1)` operations, and `lastDiff` will be replaced to `lastDiff = lastDiff/(n - 1) //full cycles + lastDiff % (n - 1) //remainder, stuff we didn\'t do`. We can do this until `lastDiff <= (n-1)`.\nWhat\'s left is distributing the final small diff across the array. Now we know what `lastDiff <= (n-1)`. An exaple would be `diffs=[0,0,0,0,2]`, or an original array of `[0,2,2,2,2]`. We can do `lastDiffs+1` double operations, leading to `[3,3,3,3,2]`, or, more generally, `[lastDiff + 1 ... (lastDiff + 2) time, lastDiff ... (n - lastDiff - 2)] times`. Here, we\'ll just assign `p = n - lastDiff - 2` and will apply `p/2` double operations and `p%2` single ones (remember that a single operation can be replaced with double ones).\n\nThe code basically reconstructs the direct process of applying the operations in an optimal way of building the final array and is likkely too complex to reason about compared to other solutions.\n\n\n# Complexity\n- Time complexity: $$O(nlogn+logMAXVAL)$$\n\n\n# Code\nWarning: the code is pretty ugly due to the complex debugging during the contest\n```\n#include <iostream>\n#include <utility>\n#include <vector>\n#include <algorithm>\n#include <numeric>\n#include <map>\n#include <unordered_set>\n#include <unordered_map>\n#include <queue>\n#include <set>\n#include <stack>\n#include <fstream>\n#include <ext/pb_ds/assoc_container.hpp>\n#include <ext/pb_ds/tree_policy.hpp>\n#include <bitset>\n#include <sstream>\n\nusing namespace std;\nusing namespace __gnu_pbds;\n\n/* clang-format off */\n\n/* TYPES */\n#define ll long long\n#define pii pair<int, int>\n#define pll pair<long long, long long>\n#define vi vector<int>\n#define vll vector<long long>\n#define vvi vector<vector<int>>\n#define vvll vector<vector<long long>>\n#define mii map<int, int>\n#define si set<int>\n#define sc set<char>\n\n#define sz(x) (x).size()\n\n/* FUNCTIONS */\n#define feach(el, v) for(auto &el: v)\n#define rep(i, n) for(int i=0;i<n;i++)\n#define reprv(i, n) for(int i=n-1;i>=0;i--)\n#define reps(i, s, e) for(int i=s;i<e;i++)\n#define reprve(i, e, s) for(int i=e;i>=s;i--)\n\n#define pb push_back\n#define eb emplace_back\n\n#define dec(zz) int (zz); cin >> zz;\n#define decv(zz, n) vector<int> zz(n); for(int i=0;i<n;++i) cin >> zz[i];\n#define decvn(zz, n) int n; cin >> n; vector<int> zz(n); for(int i=0;i<n;++i) cin >> zz[i];\n\ntypedef tree<int, null_type, less_equal<>, rb_tree_tag, tree_order_statistics_node_update> oSet;\n\nclass Solution {\npublic:\n const ll MOD = 1e9 + 7;\n \n ll singleOpCost(ll cost1, ll cost2, int n) {\n ll ans = cost1;\n if ((n - 1) % 2 == 0) {\n ll doubleTry = (n - 3) / 2 + 2;\n doubleTry *= cost2;\n doubleTry %= MOD;\n ans = min(ans, doubleTry);\n }\n return ans;\n }\n\n int minCostToEqualizeArray(vector<int>& nums, int cost1, int cost2) {\n int n = sz(nums), maxVal = -1;\n\n if (n == 1) return 0;\n if (n == 2) {\n ll diff = abs(nums[1] - nums[0]);\n ll ans = (diff * (ll)cost1) % MOD;\n return ans;\n }\n\n rep(i, n) maxVal = max(maxVal, nums[i]);\n vll diffs(n);\n rep(i, n) diffs[i] = maxVal - nums[i];\n\n sort(diffs.begin(), diffs.end());\n ll cst1 = cost1, cst2 = cost2;\n ll singleCost = singleOpCost(cst1, cst2, n);\n\n if (cost1 * 2 <= cost2) {\n ll ans = 0;\n rep(i, n) {\n ans += diffs[i];\n ans %= MOD;\n }\n ans *= cst1;\n ans %= MOD;\n return (int) ans;\n } else {\n ll last = diffs[n - 1];\n ll prevSum = 0;\n rep(i, n) prevSum += diffs[i];\n prevSum -= last;\n\n if (last <= prevSum) {\n ll totalAm = last + prevSum;\n ll twoS = totalAm / 2, rem = totalAm % 2;\n\n ll twoCost = (twoS % MOD) * cst2;\n twoCost %= MOD;\n \n ll oneCost = (rem * singleCost) % MOD;\n \n ll finCost = (twoCost + oneCost) % MOD;\n return (int) finCost;\n } else {\n //case1\n ll pairs = prevSum, singles = last - prevSum;\n\n ll twoCost = (pairs % MOD) * cst2;\n twoCost %= MOD;\n\n ll oneCost = (singles % MOD) * singleCost;\n oneCost %= MOD;\n\n ll finCost1 = (twoCost + oneCost) % MOD;\n\n //case22\n ll startCost = twoCost;\n ll lastDiff = singles;\n\n ll secondPartCosts = 0;\n while (lastDiff > (n - 1)) {\n ll fl = lastDiff / (n - 1), rem = lastDiff % (n - 1);\n ll kindaCosts = (n - 1) * fl;\n kindaCosts %= MOD;\n kindaCosts *= cst2;\n kindaCosts %= MOD;\n secondPartCosts += kindaCosts;\n lastDiff = fl + rem;\n }\n if (lastDiff == n - 1) {\n ll hehCosts = (n - 1) * cst2;\n hehCosts %= MOD;\n hehCosts += singleCost;\n \n ll ansCost = (startCost + secondPartCosts + hehCosts) % MOD;\n return min(ansCost, finCost1);\n } else {\n ll hehCosts = (lastDiff + 1) * cst2;\n hehCosts %= MOD;\n\n ll remaining = (n - lastDiff - 2);\n ll doublesRem = remaining / 2, singlesRem = remaining % 2;\n\n hehCosts += ((doublesRem * cst2) % MOD);\n hehCosts %= MOD;\n hehCosts += ((singlesRem * singleCost) % MOD);\n hehCosts %= MOD;\n\n ll ansCost = (startCost + secondPartCosts + hehCosts) % MOD;\n return min(ansCost, finCost1);\n }\n }\n }\n }\n};\n```
| 7 | 1 |
['C++']
| 2 |
minimum-cost-to-equalize-array
|
Java Clean Solution
|
java-clean-solution-by-shree_govind_jee-6q90
|
Code\nApproach-1\n\nclass Solution {\n private static final int MOD = (int)1e9 + 7;\n public int minCostToEqualizeArray(int[] nums, int cost1, int cost2)
|
Shree_Govind_Jee
|
NORMAL
|
2024-05-05T04:12:23.065621+00:00
|
2024-05-05T04:13:55.544248+00:00
| 941 | false |
# Code\n**Approach-1**\n```\nclass Solution {\n private static final int MOD = (int)1e9 + 7;\n public int minCostToEqualizeArray(int[] nums, int cost1, int cost2) {\n Arrays.sort(nums);\n int n = nums.length;\n if (n == 1) return 0;\n if (n == 2) return (int)((long)(nums[1] - nums[0]) * cost1 % MOD);\n if (cost2 >= cost1 * 2) {\n long res = 0;\n for (int num: nums) {\n res = (res + (long)(nums[n-1] - num) * cost1) % MOD;\n }\n return (int)res;\n }\n \n long sum = 0;\n long max = 0;\n for (int num: nums) {\n sum += nums[n-1] - num;\n max = Math.max(max, nums[n-1] - num);\n }\n \n long res = Long.MAX_VALUE;\n for (int k = nums[n-1]; k <= nums[n-1] + 2; k++) {\n res = Math.min(res, minCost(sum + (k-nums[n-1]) * n, max + (k-nums[n-1]), cost1, cost2));\n }\n \n if (max > sum - max) {\n for (int k = (int)((2 * max - sum) / (n-2)); k <= (int)((2 * max - sum) / (n-2)) + 2; k++) {\n res = Math.min(res, minCost(sum + k * n, max + k, cost1, cost2));\n }\n }\n \n return (int)(res % MOD);\n }\n \n private long minCost(long sum, long max, int cost1, int cost2) {\n long res = 0;\n if (sum % 2 == 1) {\n res += cost1;\n max--;\n sum--;\n }\n if (max <= sum - max) {\n res = (res + sum / 2 * cost2);\n return res;\n }\n res = (res + (max - (sum-max)) * cost1);\n res = (res + (sum-max) * cost2);\n return res;\n }\n}\n```\n\n---\n\n**Approach-2**\n```\nclass Solution {\n int[] a;\n int n, c1, c2;\n final int mod = 1000000007;\n\n long solve(long mv, long sum) {\n if (c2 >= c1 * 2)\n return sum * c1;\n if (mv * 2 <= sum)\n return (sum / 2) * c2 + (sum & 1) * c1;\n else\n return (2 * mv - sum) * c1 + (sum - mv) * c2;\n }\n\n public int minCostToEqualizeArray(int[] nums, int cost1, int cost2) {\n if (nums.length == 1)\n return 0;\n a = nums;\n n = a.length;\n c1 = cost1;\n c2 = cost2;\n int mx = 0;\n for (int v : nums) {\n mx = Math.max(mx, v);\n }\n long sum = 0, mv = 0;\n for (int i = 0; i < n; i++) {\n mv = Math.max(mv, mx - a[i]);\n sum += mx - a[i];\n }\n if (nums.length == 2)\n return (int) (solve(mv, sum) % mod);\n long ans = (long) 9e18;\n int ad = 0;\n for (;; ad++) {\n ans = Math.min(ans, solve(mv, sum));\n if (mv * 2 <= sum)\n break;\n mv++;\n sum += n;\n }\n mv++;\n sum += n;\n ans = Math.min(ans, solve(mv, sum));\n return (int) (ans % mod);\n }\n}\n```
| 6 | 0 |
['Array', 'Math', 'Java']
| 1 |
minimum-cost-to-equalize-array
|
Video Explanation (Dissecting problem into smaller sub-problems & building upwards)
|
video-explanation-dissecting-problem-int-nutj
|
Explanation\n\nClick here for the video\n\n# Code\n\nconst int M = 1e6;\nconst int MOD = 1e9+7;\n\ntypedef long long int ll;\n\nclass Solution {\npublic:\n i
|
codingmohan
|
NORMAL
|
2024-05-05T12:41:23.137012+00:00
|
2024-05-05T12:41:23.137043+00:00
| 197 | false |
# Explanation\n\n[Click here for the video](https://youtu.be/MqPaU6JAv9E)\n\n# Code\n```\nconst int M = 1e6;\nconst int MOD = 1e9+7;\n\ntypedef long long int ll;\n\nclass Solution {\npublic:\n int minCostToEqualizeArray(vector<int>& nums, int cost1, int cost2) {\n vector<int> req(M+1, 0);\n \n int n = nums.size();\n int mx = 0;\n ll sum = 0;\n for (auto i : nums) mx = max (mx, i);\n for (auto i : nums) {\n req[mx-i] ++;\n sum += (mx-i);\n }\n \n ll l = M, r = M;\n ll ans = sum * cost1; \n ll ops = 0;\n \n while (l > 0 && r > 0) { \n while (r > 0 && req[r] == 0) r --;\n if (r == 0) break;\n \n while (l > 0) {\n if (r == l) {\n if (req[l] > 1) break;\n l --;\n continue;\n }\n if (req[l] > 0) break;\n l --;\n }\n if (l == 0) {\n assert(req[r] == 1);\n ans = min (ans, ops + r*cost1);\n \n if (n == 2) break;\n if (r == 1 && (n % 2 == 0)) break; \n \n ops += cost2;\n req[1] += n-2; \n l = 1;\n continue;\n }\n \n ll can = 0;\n if (l == r) can = req[l]/2;\n else can = 1;\n \n ops += can*cost2;\n\n req[r] -= can, req[r-1] += can;\n req[l] -= can, req[l-1] += can;\n }\n ans = min (ans, ops + r*cost1);\n return ans % MOD;\n }\n};\n```
| 5 | 1 |
['C++']
| 2 |
minimum-cost-to-equalize-array
|
$O(9n)$ Solution, No Binary Search. Mathematical proofs for all needed properties.
|
o9n-solution-no-binary-search-mathematic-t7yl
|
This answer will focus on rigorously proving the required Lemmas to show correctness of the algorithm. \n\n# Intuition & Approach\n\nFor $M\geq \max(nums)$, def
|
eyfmharb
|
NORMAL
|
2024-05-05T08:03:38.617531+00:00
|
2024-05-05T08:04:58.456671+00:00
| 339 | false |
This answer will focus on **rigorously** proving the required Lemmas to show correctness of the algorithm. \n\n# Intuition & Approach\n\nFor $M\\geq \\max(nums)$, define $f(M)$ as the minimum cost to transform the entire array to have value $M$. Let us handle some easy cases first. \n\n**Lemma 1**: If $c_2 > 2c_1$, then we should only use operation 1.\n$$Proof$$: Obvious, why pay for increasing two elements with $c_2$ when we can increase them by paying $2c_1$. \n\nHence, the easy case $c_2>2c_1$ has a solution of \n\n$$f(M) = \\sum_{i=1}^n (M-nums[i])\\cdot c_1$$\n\nSo in the next discussion, we assume WLOG that $c_2 \\leq 2c_1$. Also, let\'s assume $nums[1] \\geq \\dots \\geq nums[n]$. Let\'s also assume $n\\geq 3$, $n=1,2$ cases are trivial. \n\n\n---\n\n\nDefine $d_i = M - nums[i]$ as the demands that index $i$ needs to reach $M$. Clearly, $d_1 \\leq \\dots \\leq d_n$. \n\n**Lemma 2**: If $d_n \\leq \\sum_{i=1}^{n-1}d_i = sum(d)-d_n$, then $f(M) = \\lfloor \\frac{\\sum_{i=1}^n d_i}{2} \\rfloor \\cdot c_2 + \\left(\\sum_{i=1}^n d_i \\mod 2 \\right)c_1$\n$$Proof$$: We do the following greedy process to match the demands. Let $Q=[d_1, ..., d_n]$ be a sorted set of the demands. Note the **invariant** $\\max(Q) \\leq sum(Q)-\\max(Q)$. We decrease $\\min(Q)$ by one and decrease $\\max(Q)$ by one. If $\\min(Q)=0$ we remove that element. This decreases the demands in total by $2$ and **maintains the invariant**. By induction, this process either ends in either one value (if $sum(d)$ was initially odd) or $0$ meaning all demands are paired using operation 2. \n\n\n**Lemma 3**: If $d_n > \\sum_{i=1}^{n-1}d_i = sum(d)-d_n$, then $f(M) = \\sum_{i=1}^{n-1} d_i \\cdot c_2 + \\left( d_n- \\sum_{i=1}^{n-1} d_i \\right) c_1$\n$$Proof$$: First of all, for $\\sum_{i=1}^{n-1}d_i$ demands of $d_n$, we can apply Lemma 2 on $[d_1, ..., d_{n-1}, \\sum_{i=1}^{n-1}d_i]$. This gives a necessary cost of $\\sum_{i=1}^{n-1} d_i \\cdot c_2$. For the remaining $d_n - \\sum_{i=1}^{n-1}d_i$ demands of $d_n$, we need to pay $c_1$ unfortunately as there are no more pairs to be matched. So we have $f(M) = \\sum_{i=1}^{n-1} d_i \\cdot c_2 + \\left( d_n- \\sum_{i=1}^{n-1} d_i \\right) c_1$\n\n---\n\n\nCombining Lemmas $2,3$, first note that the function in Lemma 2 is "almost" increasing in $M$:\n\n$$f(M+2)-f(M) = \\lfloor \\frac{\\sum_{i=1}^n d_i}{2} + n \\rfloor - \\lfloor \\frac{\\sum_{i=1}^n d_i}{2} \\rfloor > 0$$ \n\nBecause the $\\mod 2$ terms cancel out when we increase $M$ by the same parity. So you can think of the function as "almost" increasing but potentially decreasing slightly from $M$ to $M+1$ (but overall trend is increasing). \n\nSimilarly, the function in Lemma 3 is linear! So it is minimized at either $M = \\max(nums)$ or $M$ where $d_n = \\sum_{i=1}^{n-1}d_i \\iff M= \\frac{1}{n-2} \\left( \\sum_{i=1}^{n-1}nums[i] - nums[n] \\right)$. \n\nTo conclude,\n\n**Theorem 4**: Let $M_1 = \\max(nums).$ Let $M_2 = \\lfloor \\frac{1}{n-2} \\left( \\sum_{i=1}^{n-1}nums[i] - nums[n] \\right) \\rfloor $. Then $f(M)$ is minimized at either $M_1$ or $M\\in \\{ M_2 - \\Delta, ..., M_2+\\Delta \\}$ where $\\Delta \\leq 4$. \n$$Proof$$: From the discussion above. \n\nHence, we can try $M \\in \\{\\max(nums), M_2-4, \\dots, M_2+4 \\}$ (so long $M\\geq \\max(nums)$) and get the minimum value of $f$ function. \n\n\n# Complexity\n- The function $f$ clearly takes $O(n)$ time to compute in a single loop. And we try $9$ possible values of $M$. So $O(n)$. \n\n- Space complexity:\n$O(1)$ space. \n\n# Code\n```\nclass Solution {\npublic:\n int minCostToEqualizeArray(vector<int>& nums, int cost1, int cost2) {\n int n = nums.size();\n if (n==1)return 0;\n if (n==2)return (1ll*abs(nums[0]-nums[1])*cost1)%1000000007;\n\n long long MX = *max_element(nums.begin(), nums.end());\n long long MN = *min_element(nums.begin(), nums.end());\n long long ans = f(nums,cost1, cost2, MX);\n long long x = (accumulate(nums.begin(), nums.end(), 0ll)-2*MN)/(n-2);\n x = max(x, MX); //in case x<MX\n for(int t=x-4; t<=x+4; ++t)if (t>=MX)ans = min(ans, f(nums, cost1, cost2, t));\n return ans%1000000007ll;\n }\n long long f(vector<int>& nums, long long cost1, long long cost2, long long M){\n long long diff_mx = LLONG_MIN;\n long long diff_sm = 0;\n int n = nums.size();\n for(int i=0; i<n; ++i){\n diff_mx=max(diff_mx, M-nums[i]);\n diff_sm += M-nums[i];\n }\n if (cost2>=2*cost1)return diff_sm*cost1;\n if (diff_mx <= diff_sm-diff_mx)return diff_sm/2 * cost2 + (diff_sm%2)*cost1;\n else return (diff_sm-diff_mx)*cost2 + (2*diff_mx-diff_sm)*cost1;\n }\n};\n```
| 5 | 0 |
['C++']
| 1 |
minimum-cost-to-equalize-array
|
[Java] Commented & Explained Linear Solution O(N), with O(1) space
|
java-commented-explained-linear-solution-7e7i
|
Intuition\nWe only care about the Deltas between nums, so we want to find the sum of all Deltas, and max Delta (from minValue to maxValue) in nums. We can brin
|
bamboo168
|
NORMAL
|
2024-05-05T21:47:36.763479+00:00
|
2024-05-06T21:25:32.951496+00:00
| 625 | false |
# Intuition\nWe only care about the Deltas between nums, so we want to find the **sum** of all Deltas, and **max** Delta (from `minValue` to `maxValue`) in `nums`. We can bring all nums up to max, or exceed max. Let\'s first try to solve for reaching max:\n\n`solve` helper function (to reach `maxValue`)\nIf we want to bring all other nums up to max, with `cost2`, we need to increment 2 num at each time. The longest edge is from min to max for max Delta, and this is similar to forming a Polygon with `maxD` and all other edges (all other Deltas). \n1. If `maxD` is less than or equal to the sum of all other edges (Deltas), then a Polygon is possible with `cost2` fully utilized. In other words, if `maxD * 2 <= sumD`, then use `cost2` as much as possible, and `cost1` to fill once iff `sumD` is odd.\n2. Else, we need to use `cost1` to fill the diff where we cannot reach Polygon, and only use `cost2` for the rest.\n\n# Approach\n`maxValue` is the first equal number we can reach, but it may not be optimal because we may be using `cost1` more than we need if `cost2` is much cheaper. This is due to either using `cost1` for odd `sumD` as in bullet `1` above, OR that we didn\'t close the Polygon (meaning we used `cost1` a lot) as in bullet `2` above.\n\nThen, we gradually increment the final `maxValue` or `maxD` (1 at a time) until we reach a Polygon in an attempt to get a lower cost. This `while` loop is guaranteed to exit as long as there are more than 1 other edge than the `maxValue` (all other nums increment by 1 while maxValue only increment by 1). Then, if `sumD` is odd, increment `maxD` (or `maxValue`) by 1 again to make it even so we can use `cost2` instead of `cost1`.\n\nSee commented code below.\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n private int len, c1, c2;\n private final int mod = (int) 1e9 + 7;\n\n // Solves the minCost to reach max value:\n // If a Polygon can be formed with maxDelta and all other deltas, use cost2 as\n // much as possible\n // Else fill the diff to form Polygon with cost1\n private long solve(long maxD, long sumD) {\n if (maxD * 2 <= sumD)// Polygon can be formed with maxD and other edges,\n return (sumD / 2) * c2 + (sumD & 1) * c1;// use cost2 as much as possible, cost1 to fill\n else// else (cannot form Polygon), fill diff with cost1,\n return (2 * maxD - sumD) * c1 + (sumD - maxD) * c2;\n }\n\n public int minCostToEqualizeArray(int[] nums, int cost1, int cost2) {\n if (nums.length <= 1)\n return 0;\n len = nums.length;\n c1 = cost1;\n c2 = cost2;\n int max = Arrays.stream(nums).max().getAsInt();\n long sumD = 0;// sum of Deltas\n long maxD = 0;// max Delta\n for (int i = 0; i < len; i++) {\n maxD = Math.max(maxD, max - nums[i]);\n sumD += max - nums[i];\n }\n // System.out.println("int: " + (int) (sumD * c1 % mod));\n if (c2 >= c1 * 2)\n return (int) (sumD * c1 % mod);\n\n if (nums.length == 2)\n return (int) (sumD * c1 % mod);\n\n long ans = solve(maxD, sumD);\n while (maxD * 2 > sumD) {\n maxD++;\n sumD += len;\n ans = Math.min(ans, solve(maxD, sumD));\n }\n if (sumD % 2 == 1) {// just in case it\'s odd\n maxD++;\n sumD += len;\n ans = Math.min(ans, solve(maxD, sumD));\n }\n return (int) (ans % mod);\n }\n}\n```
| 4 | 0 |
['Array', 'Greedy', 'Geometry', 'Java']
| 1 |
minimum-cost-to-equalize-array
|
HARD||explain line by line|| c++
|
hardexplain-line-by-line-c-by-sujalgupta-u2u5
|
\n# Code\n\n// Define a class named Solution\n\nclass Solution {\npublic:\n // Define a member function named minCostToEqualizeArray that takes a vector of i
|
sujalgupta09
|
NORMAL
|
2024-05-05T05:55:13.095656+00:00
|
2024-05-05T05:55:13.095681+00:00
| 755 | false |
\n# Code\n```\n// Define a class named Solution\n\nclass Solution {\npublic:\n // Define a member function named minCostToEqualizeArray that takes a vector of integers (nums), and two integers (cost1 and cost2) as parameters and returns an integer.\n int minCostToEqualizeArray(vector<int>& nums, int cost1, int cost2) {\n // Define a constant integer named MOD and assign it the value 1e9 + 7\n constexpr int MOD = 1e9 + 7;\n // Define an integer variable named n and assign it the size of the vector nums\n const int n = nums.size();\n // Sort the elements of the vector nums in non-decreasing order\n sort(nums.begin(), nums.end());\n // Define a long long integer variable named diff and initialize it to 0\n long long diff = 0;\n // Iterate through each element of the vector nums\n for (int i = 0; i < n; ++i) {\n // Accumulate the difference between the maximum element of the vector and the current element to the variable diff\n diff += nums[n - 1] - nums[i];\n }\n // Define a long long integer variable named ans and initialize it to cost1 multiplied by diff\n long long ans = cost1 * diff;\n \n // Define a long long integer variable named diff2 and initialize it to diff\n long long diff2 = diff;\n // Update diff to the difference between the maximum and minimum elements of the vector nums\n diff = nums[n - 1] - nums[0];\n // Update diff2 to the difference between its previous value and the updated value of diff\n diff2 -= diff;\n \n // Iterate from 0 to 1e6\n for (int i = 0; i <= 1e6; ++i) {\n // Define a long long integer variable named a1 and compute it as (diff + diff2) multiplied by cost1\n long long a1 = (long long) (diff + diff2) * cost1;\n // Define a long long integer variable named a2\n long long a2;\n // Check if diff is greater than diff2\n if (diff > diff2) {\n // If true, compute a2 as diff2 multiplied by cost2 plus the difference between diff and diff2 multiplied by cost1\n a2 = (long long) diff2 * cost2 + (long long) (diff - diff2) * cost1;\n } else {\n // If false, compute a2 as half of the sum of diff and diff2 multiplied by cost2\n a2 = (long long) (diff + diff2) / 2 * cost2;\n // If the sum of diff and diff2 is odd, add cost1 to a2\n if ((diff + diff2) % 2 == 1) {\n a2 += cost1;\n }\n }\n // Update ans to the minimum of ans, a1, and a2\n ans = min(ans, a1);\n ans = min(ans, a2);\n // Increment diff by 1 and update diff2 to its previous value plus n - 1\n ++diff;\n diff2 += n - 1;\n }\n // Return ans modulo MOD\n return ans % MOD;\n }\n};\n\n```
| 4 | 2 |
['C++']
| 1 |
minimum-cost-to-equalize-array
|
Bruteforce + Greedy
|
bruteforce-greedy-by-penguinzzz-0x79
|
Intuition\ngreedy\n\n# Approach\nPAIRING\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\no(1)\n\n# Code\n\n#define MOD 1000000007\nclass Solut
|
penguinzzz
|
NORMAL
|
2024-05-05T05:12:47.472422+00:00
|
2024-05-05T05:12:47.472441+00:00
| 485 | false |
# Intuition\ngreedy\n\n# Approach\nPAIRING\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\no(1)\n\n# Code\n```\n#define MOD 1000000007\nclass Solution {\npublic:\n long long func(vector<int>& a, int& cost1, int& cost2, long long t,long long mn,long long summ){\n int n=a.size();\n long long sum=(n*t-summ);\n long long mx=t-mn;\n long long pairing=min(sum/2,sum-mx);\n long long cost=0;\n cost=min(cost2*pairing, cost1*2*pairing);\n cost+=cost1*(sum-2*pairing);\n return cost;\n }\n \n \n int minCostToEqualizeArray(vector<int>& a, int cost1, int cost2) {\n int n=a.size();\n long long t=*max_element(a.begin(),a.end());\n long long mn=*min_element(a.begin(),a.end());\n long long sum=accumulate(a.begin(),a.end(),0LL);\n long long ans=6e18;\n for(int i=t;i<=2*t+1000;i++){\n ans=min(ans,func(a,cost1,cost2,i,mn,sum));\n }\n ans%=MOD;\n return ans;\n \n }\n \n};\n```
| 4 | 0 |
['C++']
| 1 |
minimum-cost-to-equalize-array
|
[Python3] Easy understand, clean code, no confusing branches (greedy, O(n) time, O(1) space)
|
python3-easy-understand-clean-code-no-co-ldpz
|
Intuition\n Describe your first thoughts on how to solve this problem. \nJust test all the possible optimal cases instead of using lots of branches\n\n# Approac
|
zzjjbb
|
NORMAL
|
2024-05-05T04:50:45.603666+00:00
|
2024-05-26T04:47:36.808732+00:00
| 288 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nJust test all the possible optimal cases instead of using lots of branches\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFirst, if `n <= 2` or `cost1 * 2 <= cost2`, we only use the first operation to get the optimal result.\n\nOtherwise, we write a function `test` to calculate the cost from total increment `tot` and biggest increment `big` for a single number, and use as many pairs as possible:\nThe unpaired increments should be `total % 2` or `big - (tot - big) = 2 * big - tot` if other increments is enough or not to pair with the biggest one. \nThe operations number for paired increments are just `(tot - unpair) // 2`\n\nThen, we think about all the possible optimal total increments and biggest increments. We can make all numbers equal to `max(nums) + extra` for any `extra >= 0`. Then, the total increment is `(max(nums) + extra) * n - sum(nums)`, and the biggest increment is `max(nums) + extra - min(nums)`. If `unpair > n - 2`, we find that increase `extra` by `1` will decrease `unpair` by `n - 2`. We can try `extra` as `more = the original unpaired // (n - 2)`, or additional 1 or 2. Therefore, all we need to test is `extra = [0, 1, more, more+1, more+2]` and the smallest `test(extra)` is the optimal result.\n\nEdit:\nAs @radiosilence commented, testing extra=1 is always redundant. We only need `extra = [0, more, more+1, more+2]`\n\n\n# Complexity\n- Time complexity:\n$$O(n)$$\n\n- Space complexity:\n$$O(1)$$\n\n# Code\n```\nclass Solution:\n def minCostToEqualizeArray(self, nums: List[int], cost1: int, cost2: int) -> int:\n max_nums, min_nums = max(nums), min(nums)\n n = len(nums)\n diff = max_nums - min_nums\n tot = max_nums * n - sum(nums)\n \n def test(extra):\n ntot = tot + n * extra\n big = diff + extra\n unpair = max(ntot % 2, big * 2 - ntot)\n pair = (ntot - unpair) // 2\n print(extra, unpair, pair)\n return unpair * cost1 + pair * cost2\n \n def calc():\n if cost1 * 2 <= cost2 or n <= 2:\n return tot * cost1\n more = max(0, diff * 2 - tot) // (n - 2) \n return min(test(extra) for extra in [0, 1, more, more + 1, more + 2])\n \n return calc() % 1_000_000_007\n \n```
| 4 | 0 |
['Math', 'Greedy', 'Python3']
| 2 |
minimum-cost-to-equalize-array
|
[Python3] Ternary Search
|
python3-ternary-search-by-awice-2cpf
|
Let\'s call the moves single and double. First, c2 = min(c2, 2*c1) if two single moves are cheaper than a double.\n\nSuppose the final position has every eleme
|
awice
|
NORMAL
|
2024-05-05T23:28:59.799962+00:00
|
2024-05-05T23:28:59.799981+00:00
| 61 | false |
Let\'s call the moves single and double. First, `c2 = min(c2, 2*c1)` if two single moves are cheaper than a double.\n\nSuppose the final position has every element equal to `height`, what will be the `cost(height)`?\n\n- Say we have a total of `volume` increments to do. If no element requires a lot of work, we could pair everything up efficiently.\n- Otherwise, some element `biggest` requires a lot of work, we can\'t clear it with just pairing it among the remaining `volume - biggest` increments, there will be `biggest - remaining` unpaired elements that require single moves.\n\nNow let\'s analyze finding `min(cost)`. It\'s essentially two linear pieces, except there is the potential for a `+c1 * 1` term, but we can wash that out by considering odd and even separately. Now the function is shaped like a V, so we just need to find the minimum of a unimodal function, which can be done with ternary search.\n\n# Code\n```\nclass Solution:\n def minCostToEqualizeArray(self, A: List[int], c1: int, c2: int) -> int:\n MOD = 10 ** 9 + 7\n c2 = min(c2, 2 * c1)\n N, S, mi, ma = len(A), sum(A), min(A), max(A)\n\n def cost(height):\n if height < ma:\n return inf\n \n biggest = height - mi\n volume = height * N - S\n if biggest <= volume - biggest:\n return c2 * (volume//2) + c1 * (volume%2)\n return c2 * (volume - biggest) + c1 * (2 * biggest - volume)\n \n def metacost(h):\n return min(cost(2*h), cost(2*h+1))\n\n lo, hi = 0, 10**9\n while lo < hi:\n m1 = lo + (hi-lo)//3\n m2 = hi - (hi-lo)//3\n if metacost(m1) > metacost(m2):\n lo = m1 + 1\n else:\n hi = m2 - 1\n \n return metacost(lo) % MOD\n```
| 3 | 0 |
['Python3']
| 0 |
minimum-cost-to-equalize-array
|
Detailed guide to Minimum Cost to Equalize Array
|
detailed-guide-to-minimum-cost-to-equali-r692
|
Approach\nat each step, we can either increment single value at the cost of cost1 or two values at the cost of cost2.\nNow, if 2*cost1<=cost2 then we don\'t nee
|
miamimagna
|
NORMAL
|
2024-05-05T06:39:37.876774+00:00
|
2024-05-05T07:01:15.338642+00:00
| 457 | false |
# Approach\nat each step, we can either increment single value at the cost of `cost1` or two values at the cost of `cost2`.\nNow, if `2*cost1<=cost2` then we don\'t need to think too much, increment values singly is better\nThe problem arises when cost2 is better...\nNow, when cost2 is better, we would need to maximize the usage of cost2 under all circumstances.\nlet\'s go from naive approach to the actual solution\n\n* Naive approach: \n1. while all elements are less than mx, do following:\n\t-take smallest two element from the given values\n\t-if both less than `mx`, increment both at the cost of `cost2` \n\t-if only one of them is less than `mx` increment only one at cost of `cost1` \n2. return total_cost%(1e9+7)\n\nThis will be really long process... time: $$O(n*maxelement)$$. and by the way this will not give right answer everytime due to the *twist*\n\n*The twist \nAnd wait there is a twist... consider the following test case\ncost1=10000, cost2=1\nnums=[1, 3, 4]\nhere we can clearly see that if we make all elements equal to 4, we will go like:\n1. take [1, 3] increment both to get [2, 4, 4] at cost of `cost2=1`\n2. now only 2 remains less than 4, so we have to use `cost1` to get total cost of 20001\n\nwe can see what went wrong, when `cost1` is significantly larger than `cost2`, we kinda need to avoid using `cost1` \nhow can we avoid that? by increasing the target maximum value... \nfor example if we wanted to make maximum element=5 in the previous example, we would go like \n1. take [1, 3], increment both to get [2,4,4] cost=1\n2. take [2,4], increment both to get [3, 5, 4] cost=1\n3. take [3, 4], increment both to get [4, 5, 5] cost=1\n4. now we have to use cost1 on 4 to increment it to get cost=10000\ntotal cost: 10003\n\nsuppose we take max_element=6, algorithm will go like this:\n1. take [1, 3], increment both to get [2, 4, 4] cost=1\n2. take [2, 4], increment both to get [3, 5, 4] cost=1\n3. take [3, 4], increment both to get [4, 5, 5] cost=1\n4. take [4, 5], increment both to get [5, 6, 5] cost=1\n5. take [5,5], increment both to get [6,6,6] cost=1\ntotal cost: 5\n\nhence we can clearly see we get the optimal answer at max_element=6\n\nnow, question is how much do we need to increase max_element? well the upper_bound for max_element would be `2*(max element of nums)`\n\nhence if we use naive approach now, we will get our final answer but the time complexity would be: O(n * max_element* (2*max_element))\nwhich is significantly high\n\n# Optimal solution \nThere is one thing to notice here... the actual simulation of increments is actually rather pointless...\nwe can use following observation to get the feel....:\n1. if the increment required by smallest element to get to max_element is less than the remaining increments, then we can pair all the elements to get to max_element(except for the single remaining increment in odd cases)\n2. else: we can pair up all the remaining elements to our smallest element and our remaining element needs to be added with cost cost1 \n\nhere is example of case1: \nnums=[70, 100, 100, 100, 120]\ncost1=2, cost2=1\n\n1. increment +30 in 70 using next 3 elements (divide equally): [100, 110, 110, 110, 120], cost=30\n2. increment +10 in 100 using next 3 elements: [110, 113, 113, 114, 120], cost=10\n3. increment +3 in 110 using next 2 elements: [113, 114, 115, 114, 120], cost=3\n4. increment +1 in 113 and 114: [114, 114, 115, 115, 120], cost=1\n5. increment +1 in 114 and 114: [115, 115, 115, 115, 120], cost=1\n6. now that all elements can be paired, make pairs of 115, 115 twice and increment +5, cost=10\ntotal cost=55\nhere we were able to pair all elements, hence our total cost was just `(n*max_element-sum)/2` which is equal to (5*120-(70+100+100+100+120))/2=55\n\nhere is example of case2:\nnums=[7, 10, 10, 12]\ncost1=2, cost2=1\n1. increment +3 in 7 with [10, 10]: [10, 11, 12, 12], cost=1\n2. increment +1 in [10, 11]: [11, 12, 12, 12], cost=1\n3. increment +1 in 11: [12, 12, 12, 12] cost=2\ntotal cost=4\n\nThis approach will always give us right answer\n\n# Complexity\n- Time complexity:\n$$O(max(n, maxelement(nums)))$$\n\n- Space complexity:\n$$O(1)$$\n\n# Code\n```\nclass Solution {\npublic:\n int minCostToEqualizeArray(vector<int>& nums, int cost1, int cost2) {\n #define int long long\n int n = nums.size(), mod=1e9+7;\n auto [mnn, mxx]=ranges::minmax(nums); \n int sum=accumulate(nums.begin(), nums.end(), 0LL), mn=mnn, mx=mxx, total;\n int ans = LLONG_MAX;\n // if cost1 is better do it without pairs\n if(cost1*2<=cost2){\n int ans=0;\n ans=(mx*n-sum)*cost1;\n return ans%mod;\n }\n for(int mxx = mx; mxx < mx<<1; mxx++)\n {\n int res = 0;\n int required = mxx*n - sum;\n int first_inc = mxx - mn;\n int remaining=required - first_inc;\n if(remaining>first_inc)\n total=remaining + first_inc,\n // here total%2 if for one remaining odd value\n res = ((total/2)*cost2)+(total%2)*cost1;\n else\n // first remaining values will pair with first value till they are equal to max\n first_inc -= remaining,\n // then remaining of first value needs to be done using cost1\n res = first_inc*cost1,\n res += remaining*cost2;\n ans = min(ans,res);\n }\n return ans%mod;\n #undef int\n }\n};\n```
| 3 | 0 |
['Greedy', 'Sorting', 'C++']
| 2 |
minimum-cost-to-equalize-array
|
O(MAX ELEMENT) Greedy (No need of cases on cost1 and cost2)
|
omax-element-greedy-no-need-of-cases-on-ia9rc
|
Intuition\nTry thinking about the minimum operations required to make all the elements in the array equal to a particular value.\n\n# Approach\n\n\n# Complexity
|
the_halfblood_prince
|
NORMAL
|
2024-05-05T04:35:56.814890+00:00
|
2024-05-05T06:19:55.272939+00:00
| 353 | false |
# Intuition\nTry thinking about the minimum operations required to make all the elements in the array equal to a particular value.\n\n# Approach\n\n\n# Complexity\n- Time complexity: O(max Element)\n\n- Space complexity: O(1)\n# Code\n```\nusing ll = long long;\nconst ll N= 1e9 + 7;\nclass Solution {\npublic:\n int minCostToEqualizeArray(vector<int>& nums, int cost1, int cost2) {\n int n = nums.size();\n ll sum = accumulate(nums.begin(),nums.end(),0LL);\n sort(nums.begin(),nums.end());\n ll ans = -1;\n for(ll i = nums[n-1]; i < 3*nums[n-1]; i++)\n {\n ll res = 0;\n ll req = i*n - sum;\n ll z = i - nums[0];\n req -= z;\n if(req>z)\n {\n req += z;\n if(req&1)\n res = min(req*cost1,((req/2LL)*cost2)+cost1);\n else\n res = min(req*cost1,(req/2LL)*cost2);\n }\n else\n {\n z -= req;\n res = z*cost1;\n res += min(req*cost2,(req*cost1)*2LL);\n }\n if(ans==-1)\n ans = res;\n else\n ans = min(ans,res);\n }\n return ans%N;\n }\n};\n```
| 3 | 0 |
['Greedy', 'C++']
| 1 |
minimum-cost-to-equalize-array
|
Not mine solution But probably the best solution on rankings
|
not-mine-solution-but-probably-the-best-xhnnc
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
Harshitcode
|
NORMAL
|
2024-05-05T04:25:16.473863+00:00
|
2024-05-05T04:25:16.473896+00:00
| 783 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n#define ll long long\nll mod= 1e9 + 7;\nclass Solution {\npublic:\n int minCostToEqualizeArray(vector<int>& nums, int cost1, int cost2) {\n ll n = nums.size();\n ll maxi = 0;\n ll tot = 0;\n ll mini = 1e9;\n for(int i = 0; i < n ; i ++){\n maxi = max(maxi , (ll)nums[i]);\n mini = min(mini , (ll)nums[i]);\n tot += nums[i];\n }\n \n ll ans = 1e17;\n \n for(ll eq = maxi*2 ; eq >= maxi ; eq --){\n ll rem = eq*n - tot;\n ll minadd = eq - mini;\n ll curcost = 0;\n \n if(minadd*2 >= rem)\n {\n ll extra = minadd - (rem - minadd);\n curcost += extra*cost1;\n rem -= extra;\n }\n \n \n if(rem%2==1)\n {\n rem--;\n curcost += cost1;\n }\n \n curcost += min((ll)cost1*rem , (ll)cost2*(rem/2));\n ans= min(ans , curcost);\n }\n \n return ans%mod;\n \n }\n};\n```
| 3 | 3 |
['C++']
| 3 |
minimum-cost-to-equalize-array
|
O(n) Solution | Easy to understand with comments
|
on-solution-easy-to-understand-with-comm-95za
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\nhttps://www.youtube.com/watch?v=1DRxNPliy0Q\nThis video helped me to unde
|
mj1609
|
NORMAL
|
2024-05-14T11:53:19.103502+00:00
|
2024-05-14T11:53:19.103534+00:00
| 79 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nhttps://www.youtube.com/watch?v=1DRxNPliy0Q\nThis video helped me to understand the logic. Go through the video once. \n\n\n# Code\n```\nconst int MOD = 1e9+7;\nclass Solution {\npublic:\n int minCostToEqualizeArray(vector<int>& nums, int cost1, int cost2) {\n //Solution \n //Treat all the nums elements as bar, and find the gap from the maximum bar\n //ex. (4,1) -> bars of 4 and 1, gaps of 0 and 3.\n\n //In case when n = 2, we have to do cost1 operation on the minimum bar to equalize it to maximum\n //Else we would always be incrementing both, and the gap will remain consistent, no point in pairing\n\n //In case when 2*cost1 < cost2, it is more profitable to do single operations than pair operations\n //In this case, we would find the total gaps and multiply it by cost 1. (make all elements equal to max element)\n\n //In Case, when the maximum gap which is max(nums){calling it maxE} - min(nums){calling it minE} is greater than the sum of other gaps,\n //we cannot always pair the maximum gap, there would be some requirement of cost1.\n //we would pair the other gaps with the maximum gap for maximum cost 2 operations and the remaining would be cost1 operations\n //so, total possible gaps that cannot be paired = (maximum_gap) - (total_gaps - maximum_gap) -> 2 * (maximum_gap) - total_gaps -> (2*(maxE - minE) - total_gaps)\n //we call 2*(maxE-minE) - total_gaps as op1\n //so, gaps remaining for cost2 are op2 = total_gaps - op1\n //gaps for cost2 would be half of op2 -> op2/2\n //here, making all elemnts equal to max element\n\n //In case, when the maximum gap (maxE - minE) is less than or equal to the sum of the other gaps, we can make the pair of the gaps\n //if the total_gaps is even, there is no need for cost1\n //if the total_gaps is odd, there will be one gap remaining for cost1\n //here, we may equalize the array to a larger number than maxE\n //so, operations for cost1 = (total_gaps%2)\n //operations for cost2 = calculated later\n \n //if we combine the last two cases, we get\n //op1 = max(0, 2*(maxE - minE)-total_gaps)\n //op2 = total_gaps - op1\n //cost = (op1 + op2%2) * cost1 + (op2/2)*cost2;\n\n //now to calculate the cost2 operations to go beyond the max\n //we maintain an array to store the frequency of different gaps\n //Each time, we select two maximum gaps, and make them pair\n //at the end we would remain with only one element with freq>0\n //if the freq is even, make pairs of those gaps for cost2\n //if the freq is odd, make pairs of freq-1 gaps for cost2\n //Now, one gap will remain, now we can extend our equalizer to go beyond the max\n //we will add (n-2) to the index 1, as every other element will be incremented by 1 gap\n //n gaps of one are added to each index, freq(1) -> n-1 && freq(curr_idx+1) -> 1, finally after pairing, we would have (n-1) gaps of freq 1.\n //so 1 was already at index 1, we add (n-2) to make it (n-1)\n //we would do this (n-2) until we get only gaps of 1.\n //total_gaps + =(op1/(n-2)) * n\n //remaining for op1 = op1 % (n-2)\n //op2 = total_gaps - op1\n //try adding gap of 1 to all twice to cover the case fully of cost2 without using cost1\n\n \n int n = nums.size();\n int maxE = 0, minE = INT_MAX;\n long long total_gaps = 0;\n long long sum = 0;\n for(int i=0; i<n; i++)\n {\n maxE = max(maxE, nums[i]);\n minE = min(minE, nums[i]);\n sum += nums[i];\n }\n //total_gaps = sum of (max - nums[i]) for all i ~ (max * n - sum)\n total_gaps = (long long)maxE * n - sum;\n \n if(n <=2 || 2 * cost1 <= cost2)\n {\n int minCost = (total_gaps * cost1)%MOD;\n return minCost;\n }\n\n long long op1 = max((long long)0, (long long)2 * (maxE - minE) - total_gaps);\n long long op2 = total_gaps - op1;\n long long res = (op1 + op2%2) * cost1 + (op2/2) * cost2;\n\n total_gaps += op1 / (n-2) * n;\n op1 %= (n-2);\n op2 = total_gaps - op1;\n res = min(res, (op1 + op2%2)*cost1 + (op2/2)*cost2);\n\n for(int i=0 ; i<2; i++)\n {\n total_gaps += n;\n res = min(res, (total_gaps%2) * cost1 + total_gaps/2 * cost2);\n }\n\n int ans = (int)(res % MOD);\n return ans;\n }\n};\n```
| 2 | 0 |
['C++']
| 0 |
minimum-cost-to-equalize-array
|
Tricky Concept | Brute Force | c++
|
tricky-concept-brute-force-c-by-allround-4c9e
|
Intuition\nif 2*cost1 <= cost2 than we simply use cost1 for all operation.\nelse we will maximise the use of cost2. \n\n# Approach\nwe check for all maxi elemen
|
allrounderankit
|
NORMAL
|
2024-05-05T05:05:12.001512+00:00
|
2024-05-05T05:05:12.001528+00:00
| 665 | false |
# Intuition\nif 2*cost1 <= cost2 than we simply use cost1 for all operation.\nelse we will maximise the use of cost2. \n\n# Approach\nwe check for all maxi element from which we can take minimum cost as answer\n\nStuck in Ternary search in contest :( but later realise it is not perfect concave structure.\n\n# Complexity\n- Time complexity:\n O(1e6)\n\n- Space complexity:\n O(1)\n\n# Code\n```\n#define ll long long\nclass Solution {\npublic:\n int mod = 1e9 + 7;\n ll sum = 0;\n ll mini = 1e8;\n\n ll ankit( vector<int> &nums, ll cost1, ll cost2, ll maxii ){\n \n \n ll maxi = maxii - mini;\n \n ll n = nums.size();\n\n ll total = maxii*n - sum;\n\n \n if( 2*cost1 <= cost2 ) return total * cost1;\n \n \n ll last = total - maxi;\n \n if( last < maxi ) return ( maxi - last ) * cost1 + last * cost2;\n \n if( total % 2 == 0 ) return (total/2) * cost2;\n else return (total/2) * cost2 + cost1 ;\n \n }\n \n int minCostToEqualizeArray(vector<int>& nums, int cost1, int cost2) {\n \n \n ll maxi = 0;\n \n for(int i=0;i<nums.size();i++){\n \n maxi = max(maxi,1LL*nums[i]);\n mini = min(mini,1LL*nums[i]);\n sum += nums[i];\n \n }\n \n ll ans = 1e18;\n\n // sort(nums.begin(),nums.end());\n\n \n \n// while( h - l > eps ){\n \n// double mid1 = l + (h - l) / 3;\n// double mid2 = h - (h - l) / 3;\n\n// ll ms1 = ankit(nums,cost1,cost2,mid1);\n// ll ms2 = ankit(nums,cost1,cost2,mid2);\n \n// cout<<mid1<<" "<<mid2<<" "<<ms1<<" "<<ms2<<endl;\n \n// if( last1 == mid1 && last2 == mid2 ) break;\n \n// last1 = mid1; last2 = mid2;\n \n// ans = min(ans,ms1);\n// ans = min(ans,ms2);\n \n// if( ms1 <= ms2 ) h = mid2; \n// else l = mid1-1;\n \n// }\n \n for(int i=maxi;i<=4*maxi;i++){\n \n ll d = ankit(nums, cost1, cost2, i);\n ans = min(ans,d);\n \n }\n \n \n return ans%mod;\n \n }\n};\n```
| 2 | 2 |
['C++']
| 2 |
minimum-cost-to-equalize-array
|
Brute Force + Greedy | Linear Time O(N) & Constant Space O(1)
|
brute-force-greedy-linear-time-on-consta-z97u
|
Intuition:\n1. If 2 * cost1 <= cost2 we will always leverage cost1\n2. We can make all elements equal to the max element at the very least. Hence, we will try
|
shahsb
|
NORMAL
|
2024-05-15T05:18:38.328150+00:00
|
2024-05-15T05:28:36.181513+00:00
| 22 | false |
# Intuition:\n1. If `2 * cost1 <= cost2` we will always leverage cost1\n2. We can make all elements equal to the max element at the very least. Hence, we will try out all possibilities from `max_element` to `2 * max_element`\n# CODE:\n```\n#define ll long long\nconst int MOD = 1e9 + 7;\n\nclass Solution {\nprivate:\n ll sum = 0;\n ll mini = LONG_LONG_MAX;\npublic:\n // TC: O(N), SC: O(1)\n int minCostToEqualizeArray(vector<int>& nums, int cost1, int cost2) \n { \n ll maxi = 0;\n for ( int num : nums ) {\n maxi = max(maxi, 1LL*num);\n mini = min(mini, 1LL*num);\n sum += num;\n }\n \n ll ans = LONG_LONG_MAX;\n for ( int i=maxi; i<=2*maxi; i++)\n ans = min(ans, solve(nums, cost1, cost2, i));\n\n return ans%MOD;\n }\nprivate:\n\t// TC: O(1), SC: O(1).\n ll solve(vector<int> &nums, ll cost1, ll cost2, ll target)\n {\n ll longestGap = target - mini;\n ll N = nums.size();\n\n ll changesRequired = target*N - sum;\n if ( 2*cost1 <= cost2 ) return changesRequired * cost1;\n \n ll last = changesRequired - longestGap;\n if ( last < longestGap ) return ( longestGap - last ) * cost1 + last * cost2;\n \n if ( changesRequired % 2 == 0 ) return (changesRequired/2) * cost2;\n else return (changesRequired/2) * cost2 + cost1 ;\n }\n};\n```
| 1 | 0 |
['Greedy']
| 1 |
minimum-cost-to-equalize-array
|
Tricky but Understandable Solution
|
tricky-but-understandable-solution-by-ja-8ih1
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
jainamit130
|
NORMAL
|
2024-05-09T11:52:34.330327+00:00
|
2024-05-09T11:52:34.330349+00:00
| 81 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int minNum=0;\n int maxNum=0;\n long long sum = 0;\n int minCostToEqualizeArray(vector<int>& nums, int cost1, int cost2) {\n minNum = *min_element(nums.begin(), nums.end()); \n maxNum = *max_element(nums.begin(), nums.end());\n sum = accumulate(nums.begin(),nums.end(),sum);\n long long ans=1e18;\n long long mod = 1e9+7; \n for(int i=maxNum;i<=2*maxNum;i++){\n ans=min(ans,solve(nums,cost1,cost2,i));\n }\n return ans%mod;\n }\n\n long long solve(vector<int>& nums,int cost1,int cost2, int target){\n long long maxDiff=target-minNum;\n long long total=nums.size()*target-sum;\n \n if(2*cost1<=cost2) return total*cost1;\n \n long long remainingDiff = total - maxDiff;\n if((total/2)<maxDiff) return (maxDiff-remainingDiff)*cost1+remainingDiff*cost2;\n\n if(total%2==0) return (total/2)*cost2;\n else return (total/2)*cost2+cost1; \n }\n};\n\n\n// class Solution {\n// public:\n// int minCostToEqualizeArray(vector<int>& nums, int cost1, int cost2) {\n// int n = nums.size();\n\n// int maxNum = *max_element(nums.begin(), nums.end());\n\n// priority_queue<int, vector<int>, greater<int>> pq;\n\n// for (int num : nums) {\n// if (num < maxNum) {\n// pq.push(num);\n// }\n// }\n\n// int ans=0;\n// while (!pq.empty()) {\n// int a = pq.top();\n// pq.pop();\n// int t1=cost1;\n// a++;\n// int t2=INT_MAX;\n// if(!pq.empty() && cost2<=cost1*2){\n// int b=pq.top();\n// pq.pop();\n// t2=cost2;\n// b++;\n// if(b<maxNum)\n// pq.push(b);\n// }\n// ans+=min(t1,t2);\n// if(a<maxNum)\n// pq.push(a);\n// }\n\n// return ans % 1000000007;\n// }\n// };\n\n/*\n1 14 14 15\n\nt = 15\nmn = 1\nsum = 44\n\ni => 15 - 1030\n\nfn\nsum = 4*15 -44 = 16\nmx = 15 - 1 = 14\npairing = min(8,2) = 2\ncost = min(2,8) = 2\ncost = 2 + 2*(16-2*2) = 2 + 2*8 = 2 + 16 = 18 \n\n\n*/\n```
| 1 | 0 |
['Array', 'Enumeration', 'C++']
| 0 |
minimum-cost-to-equalize-array
|
[HELP] Final value will be within [max, 2 * max], Why ?
|
help-final-value-will-be-within-max-2-ma-5pyd
|
This post is mainly to understand why would the final value be between [max, 2 * max] ?\n\nI believe this is the crux of the problem. Can someone help me unders
|
ankurd87
|
NORMAL
|
2024-05-06T04:40:32.160922+00:00
|
2024-05-06T04:40:32.160954+00:00
| 358 | false |
This post is mainly to understand why would the final value be between [max, 2 * max] ?\n\nI believe this is the crux of the problem. Can someone help me understand this ? May be a mathematical proof ?\n\nI will try to understand it myself and then will update the post if I get an answer myself sooner.\n\nNote* the code actually works for [max, 2 * max) i.e till 2 * max - 1. Not sure this is due to the weak test cases ? Will only be able to confirm post clarification around this question.\n\n\n# Code\n```\nclass Solution {\npublic:\n int minCostToEqualizeArray(vector<int>& nums, int cost1, int cost2) {\n long long sum = 0;\n long long mi = 100000009;\n long long ma = 0;\n long long mod = 1000000007;\n \n\n for(long long x: nums) {\n sum += x;\n ma = max(x, ma);\n mi = min(x, mi);\n }\n\n long long n = nums.size();\n long long ans = LONG_MAX;\n\n for(long long i = ma; i < 2 * ma; ++i) {\n long long rem = i * n - sum;\n\n long long minadd = i - mi;\n long long curr = 0;\n \n if(minadd >= rem - minadd) {\n long long extra = (minadd - (rem - minadd));\n curr += extra * cost1;\n rem -= extra;\n }\n\n if(rem % 2 == 1) {\n curr += cost1;\n rem--;\n }\n\n curr += min((long long)cost1 * rem, (long long)cost2 * (rem / 2));\n ans = min(ans, curr);\n }\n \n return ans % mod;\n }\n};\n```
| 1 | 0 |
['C++']
| 0 |
minimum-cost-to-equalize-array
|
BEST INTUITIVE SOLUTION ✅✅✅ 🥇
|
best-intuitive-solution-by-rishu_raj5938-ss4f
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
Rishu_Raj5938
|
NORMAL
|
2024-05-05T12:58:14.401191+00:00
|
2024-05-05T12:58:14.401225+00:00
| 60 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n #define ll long long\n\n ll mini = 1e8; \n ll sum = 0;\n int n;\n int mod = 1e9+7;\n\n ll solve(vector<int>& nums, int c1, int c2, ll maxi) {\n \n ll mxdiff = maxi-mini;\n \n ll total = maxi*n - sum;\n\n if(2*c1 <= c2) return total*c1;\n\n ll last = total - mxdiff;\n\n if(mxdiff > total/2) return (mxdiff-last)*c1 + last*c2;\n\n if(total%2 == 0) return (total/2)*c2;\n else return (total/2)*c2 + c1;\n\n }\n\n int minCostToEqualizeArray(vector<int>& nums, int c1, int c2) {\n\n n = nums.size();\n\n ll maxi = 0;\n\n for(int i=0; i<n; i++) {\n mini = min(mini, 1LL*nums[i]);\n }\n\n for(int i=0; i<n; i++) {\n maxi = max(maxi, 1LL*nums[i]);\n sum += nums[i];\n }\n \n ll ans = 1e18;\n\n for(int i=maxi; i<=2*maxi; i++) {\n ll tmp = solve(nums, c1, c2, i);\n ans = min(ans, tmp);\n }\n \n return ans%mod;\n } \n};\n```
| 1 | 0 |
['C++']
| 0 |
minimum-cost-to-equalize-array
|
[Python] Brutforce Works O(MAX(A)+N) | Explained
|
python-brutforce-works-omaxan-explained-e0k1q
|
Approach\n Describe your approach to solving the problem. \nThis is how i solved it (main observations)\n\n1. trivial case using only cost1 when 2*c1 < c2\n2. w
|
tr1ten
|
NORMAL
|
2024-05-05T08:15:41.179383+00:00
|
2024-05-08T06:02:50.862941+00:00
| 287 | false |
# Approach\n<!-- Describe your approach to solving the problem. -->\nThis is how i solved it (main observations)\n\n1. trivial case using only cost1 when 2*c1 < c2\n2. we need to pair up max elements so to use cost2 more number of times.\n\n\nLets solve another problem: \nf(mx): cost to make all element equal to mx using min operations.\n\nthis is standard problem where we pair up maximum elements and whatever left will use first operation\n(HInt: first operation will be used `2*max_diff - sum_diffs` times)\n\nNow we original problem boil down to finding such mx which gives optimal answer.\n\nit can be proven that mx will lie between `[array_max, 2*array_max]`\n\n### Proof (?)\nwe will increase `mx` so to minimize `c`, min value of c can be 0,\n\nFor difference array a, let\nmxd: max of a\nsmd: sum of a\nmx_n: max of nums\n\n```\nWe know,\nc = 2*mxdd - smdd\n\nwe want c<=0\n\nPut. \nmxdd = mxd + d\nsmdd = smd + d*n\nd = (mx - mx_n)\n\n\n2*mxd + 2d - (smd + d*n) = 2*mxd - smd - d*(n-2) <= 0\n\n(2*mxd - smd)/(n-2) <= d\n\n\nnumerator can be atmost max(A) hence we need to check d from 0 to max(A)\n\n\n```\n\nSince `nums[i] < 10^6`, we can enumerate all mx in that range. (also it will be monotonic function so binary search also works)\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(MAX(A) + N)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(N)$$\n# Code\n```\nclass Solution:\n def minCostToEqualizeArray(self, nums: List[int], cost1: int, cost2: int) -> int:\n mod = (10**9) + 7\n acm = max(nums)\n a = [acm-x for x in nums]\n mx3 = max(a)\n sm = sum(a)\n if 2*cost1<cost2: # trivial case\n return sm*cost1%mod\n def f(mx): # solving sub problem\n s = sm+ (mx-acm)*len(nums)\n mx2 = mx3 + (mx-acm)\n c = max(0,2*mx2 - s)\n if s%2 and c==0:\n c = 1\n total = (cost2*(s-c)//2 + cost1*c)\n return total\n \n \n cur = max(nums)\n res = f(cur)\n while 1: # can be proved < 2*max_a\n cur +=1\n ff = f(cur)\n if ff>res:\n break\n res =ff\n \n return res%mod\n \n\n```
| 1 | 0 |
['Python3']
| 2 |
minimum-cost-to-equalize-array
|
💥💥 Beats 100% on runtime and memory [EXPLAINED]
|
beats-100-on-runtime-and-memory-explaine-ifee
|
IntuitionMake all elements in the array equal with the minimum cost, so I need to find an optimal target value and decide the best way to reach it using single
|
r9n
|
NORMAL
|
2025-01-30T15:47:43.695355+00:00
|
2025-01-30T15:47:43.695355+00:00
| 7 | false |
# Intuition
Make all elements in the array equal with the minimum cost, so I need to find an optimal target value and decide the best way to reach it using single or double increment operations.
# Approach
Iterate through possible target values from the maximum element to twice its value while calculating the total increments needed, adjusting the smallest element separately if needed, handling any leftover odd increments with single operations, and choosing between single and double operations based on cost efficiency while keeping track of the minimum cost using simple variables.
# Complexity
- Time complexity:
O(N * maxA) since we iterate over possible target values and perform calculations in O(1) for each.
- Space complexity:
O(1) because we only use a few extra variables without additional data structures.
# Code
```kotlin []
class Solution {
private val mod = 1_000_000_007L
fun minCostToEqualizeArray(nums: IntArray, cost1: Int, cost2: Int): Int {
val n = nums.size
val maxA = nums.maxOrNull()!!.toLong() // Find the maximum value in the array
val minA = nums.minOrNull()!!.toLong() // Find the minimum value in the array
val sum = nums.sumOf { it.toLong() } // Calculate the total sum of the array
var bestCost = Long.MAX_VALUE
// Try making all elements equal to `eq` from maxA to 2 * maxA
for (eq in maxA..2 * maxA) {
var totalIncrements = eq * n - sum // Total increments needed to make all elements equal to `eq`
var cost = 0L
val required = eq * (n - 1) - (sum - minA) // Increments required if minA is excluded
// If we need fewer operations than the increase required for minA, adjust accordingly
if (required <= eq - minA) {
val extra = (eq - minA) - required
cost += extra * cost1 // Use cost1 operations to adjust `minA`
totalIncrements -= extra
}
// If an odd number of increments remain, use one `cost1` operation
if (totalIncrements % 2 == 1L) {
totalIncrements--
cost += cost1
}
// Use either `cost1` for single increments or `cost2` for paired increments (whichever is cheaper)
cost += minOf(totalIncrements * cost1, (totalIncrements / 2) * cost2)
bestCost = minOf(bestCost, cost) // Keep track of the minimum cost found
}
return (bestCost % mod).toInt() // Return the result modulo 10^9 + 7
}
}
```
| 0 | 0 |
['Array', 'Math', 'Binary Search', 'Greedy', 'Combinatorics', 'Enumeration', 'Kotlin']
| 0 |
minimum-cost-to-equalize-array
|
Optimal Pairing of Increments with Cost Analysis | 100% ✅
|
optimal-pairing-of-increments-with-cost-4cajc
|
IntuitionMinimize cost by prioritizing the cheaper operation (c2 for pairing two elements) while handling cases where pairing is not possible.Approach
Calculat
|
DeepakPatil26
|
NORMAL
|
2025-01-04T16:30:04.444175+00:00
|
2025-01-04T16:30:04.444175+00:00
| 11 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
Minimize cost by prioritizing the cheaper operation (`c2` for pairing two elements) while handling cases where pairing is not possible.
# Approach
<!-- Describe your approach to solving the problem. -->
1. Calculate the total deficit (sum of differences between the max element and each element).
2. Use `c1` if `c2` is not cheaper or the array has ≤ 2 elements.
3. Otherwise, pair increments using `c2` and handle the remainder with `c1`.
4. Adjust calculations to ensure the minimum cost.
5. Return the result modulo `10^9 + 7`.
# Complexity
- Time complexity: O(n), where n is the number of elements in the array. We iterate through the array to calculate the total deficit and perform constant-time operations.
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(1), as we use only a few variables for calculations.
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```javascript []
var minCostToEqualizeArray = function (arr, c1, c2) {
const MOD = 1e9 + 7;
const max = Math.max(...arr), min = Math.min(...arr), n = arr.length;
// Calculate the total deficit
let totalCost = max * n - arr.reduce((sum, val) => sum + val, 0);
// Case 1: If c1 * 2 <= c2 or n <= 2, use only c1
if (c1 * 2 <= c2 || n <= 2) return (totalCost * c1) % MOD;
// Case 2: Calculate op1 and op2
let op1 = Math.max(0, (max - min) * 2 - totalCost);
let op2 = totalCost - op1;
// Calculate initial result
let result = (op1 + op2 % 2) * c1 + Math.floor(op2 / 2) * c2;
// Case 3: Adjust totalCost and recalculate result
totalCost += Math.floor(op1 / (n - 2)) * n;
op1 %= n - 2;
result = Math.min(result, (op1 + (totalCost - op1) % 2) * c1 + Math.floor((totalCost - op1) / 2) * c2);
// Case 4: Further adjustments (loop unrolled)
totalCost += n;
result = Math.min(result, (totalCost % 2) * c1 + Math.floor(totalCost / 2) * c2);
totalCost += n;
result = Math.min(result, (totalCost % 2) * c1 + Math.floor(totalCost / 2) * c2);
// Return the result modulo MOD
return result % MOD;
};
```
| 0 | 0 |
['Array', 'Greedy', 'Enumeration', 'JavaScript']
| 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.