question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
surface-area-of-3d-shapes
|
Ruby 100%/100%
|
ruby-100100-by-dnnx-w3wn
|
\n# @param {Integer[][]} grid\n# @return {Integer}\ndef surface_area(grid)\n f(grid) + f(grid.transpose) + grid.sum { |row| row.count(&:positive?) } * 2\nend\n
|
dnnx
|
NORMAL
|
2021-04-13T20:22:58.117114+00:00
|
2021-04-13T20:22:58.117143+00:00
| 44
| false
|
```\n# @param {Integer[][]} grid\n# @return {Integer}\ndef surface_area(grid)\n f(grid) + f(grid.transpose) + grid.sum { |row| row.count(&:positive?) } * 2\nend\n\ndef f(grid)\n grid.sum do |row|\n row.each_cons(2).sum { |x, y| (x - y).abs }\n end + grid[0].sum + grid[-1].sum\nend\n```
| 2
| 0
|
[]
| 0
|
surface-area-of-3d-shapes
|
Python, time: O(N), space: O(1)
|
python-time-on-space-o1-by-blue_sky5-uzof
|
\nclass Solution:\n def surfaceArea(self, grid: List[List[int]]) -> int: \n m, n = len(grid), len(grid[0])\n \n area = 0\n
|
blue_sky5
|
NORMAL
|
2020-11-11T22:03:03.009917+00:00
|
2020-11-11T22:03:03.009959+00:00
| 277
| false
|
```\nclass Solution:\n def surfaceArea(self, grid: List[List[int]]) -> int: \n m, n = len(grid), len(grid[0])\n \n area = 0\n for r in range(m): \n for c in range(n):\n if grid[r][c] != 0:\n area += 2\n \n if r == 0 or r == m - 1:\n area += grid[r][c] if m != 1 else 2*grid[r][c]\n if r != m - 1: \n area += abs(grid[r][c] - grid[r+1][c])\n \n if c == 0 or c == n - 1:\n area += grid[r][c] if n != 1 else 2*grid[r][c]\n if c != n - 1: \n area += abs(grid[r][c] - grid[r][c+1]) \n \n return area\n```
| 2
| 1
|
['Python', 'Python3']
| 0
|
surface-area-of-3d-shapes
|
O(N^2) time O(1) space Java solution
|
on2-time-o1-space-java-solution-by-edmat-1kzl
|
```\n//O(n^2) time, O(1) space\n public int surfaceArea(int[][] grid) {\n int n = grid.length;\n int area = 0;\n \n for(int i =0;i0)\
|
edmat7
|
NORMAL
|
2020-05-23T11:42:18.118157+00:00
|
2020-05-23T11:42:18.118207+00:00
| 200
| false
|
```\n//O(n^2) time, O(1) space\n public int surfaceArea(int[][] grid) {\n int n = grid.length;\n int area = 0;\n \n for(int i =0;i<n;i++){\n for(int j=0;j<n;j++){\n if(grid[i][j]>0)\n area += grid[i][j]*4 + 2;\n \n if(i>0) area -= Math.min(grid[i][j], grid[i-1][j])*2;\n if(j>0) area -= Math.min(grid[i][j], grid[i][j-1])*2;\n }\n }\n \n return area;\n }
| 2
| 0
|
['Java']
| 0
|
surface-area-of-3d-shapes
|
Python 3 - Simple solutions -- Beats 96.05%
|
python-3-simple-solutions-beats-9605-by-19z4y
|
\nclass Solution:\n def surfaceArea(self, grid: List[List[int]]) -> int:\n area = 0\n n = len(grid)\n for i in range(n):\n fo
|
nbismoi
|
NORMAL
|
2020-03-01T04:01:09.275199+00:00
|
2020-03-01T04:01:09.275249+00:00
| 400
| false
|
```\nclass Solution:\n def surfaceArea(self, grid: List[List[int]]) -> int:\n area = 0\n n = len(grid)\n for i in range(n):\n for j in range(n):\n if grid[i][j]:\n area += grid[i][j] * 4 + 2\n if i:\n area -= min(grid[i][j], grid[i-1][j]) * 2\n if j:\n area -= min(grid[i][j], grid[i][j-1]) * 2\n return area\n \n\n```
| 2
| 0
|
['Python', 'Python3']
| 0
|
surface-area-of-3d-shapes
|
Python 3 easy to understand, 90% 100%, O(mn) complexity
|
python-3-easy-to-understand-90-100-omn-c-v4lh
|
The algorithm is simply 2 steps:\n1, count surface on each independent grid: \nFor each grid, if there is a positive value(meaning cubes exist), there should be
|
er1k
|
NORMAL
|
2020-01-18T16:34:31.387575+00:00
|
2020-01-18T21:11:27.126223+00:00
| 243
| false
|
The algorithm is simply 2 steps:\n1, count surface on each independent grid: \nFor each grid, if there is a positive value(meaning cubes exist), there should be 4n+2 surface (n: number of cubes)\n2, substract surface overlap:\nFor adjacent grids A and B, the overlap should be 2*min(n_A, n_B)\n\nImagine this grid map as a matrix, we scan from upper left to lower right entries to avoid double-counting.\nEasy to understand, it is of O(mn), where m,n are matrix row and column size.\n\n```\nclass Solution:\n def surfaceArea(self, grid: List[List[int]]) -> int: \n out, row, col = 0, len(grid), len(grid[0]) \n for i in range(row):\n for j in range(col):\n temp = grid[i][j]\n if not temp:\n continue\n out += 4 * temp + 2\n if row-1-i:\n out -= 2 * min(temp, grid[i+1][j])\n if col-1-j:\n out -= 2 * min(temp, grid[i][j+1]) \n return out\n```
| 2
| 0
|
['Python', 'Python3']
| 0
|
surface-area-of-3d-shapes
|
java easy to understand. Faster than 99%
|
java-easy-to-understand-faster-than-99-b-g8sk
|
\nclass Solution {\n public int surfaceArea(int[][] grid) {\n return (computeSide(grid)\n + computeSide(transpose(grid))\n + c
|
kot_matroskin
|
NORMAL
|
2019-04-15T20:22:34.865627+00:00
|
2019-04-15T20:22:34.865694+00:00
| 260
| false
|
````\nclass Solution {\n public int surfaceArea(int[][] grid) {\n return (computeSide(grid)\n + computeSide(transpose(grid))\n + computeVertical(grid))*2;\n }\n \n private int[][] transpose(int[][] grid){\n int[][] result = new int[grid.length][grid.length];\n for (int r=0; r<grid.length; r++){\n for (int c=0; c<grid.length; c++){\n result[r][c]=grid[c][r];\n }\n }\n return result;\n }\n \n private int computeSide(int[][] grid){\n int total =0;\n \n for (int r[] : grid){\n int prev=0;\n for (int c : r){\n if (c > prev)\n total += c - prev;\n \n prev=c;\n }\n }\n \n return total;\n }\n \n private int computeVertical(int[][] grid){\n int total =0;\n \n for (int r[] : grid){\n for (int c : r){\n if (c != 0)\n total++;\n }\n }\n \n return total;\n }\n}\n````
| 2
| 0
|
[]
| 1
|
surface-area-of-3d-shapes
|
Python O(n), straight forward code
|
python-on-straight-forward-code-by-chaoi-viq9
|
\nclass Solution(object):\n def surfaceArea(self, grid):\n """\n :type grid: List[List[int]]\n :rtype: int\n """\n row_cou
|
chaoize
|
NORMAL
|
2018-08-26T05:44:06.510821+00:00
|
2018-08-26T05:44:06.510865+00:00
| 233
| false
|
```\nclass Solution(object):\n def surfaceArea(self, grid):\n """\n :type grid: List[List[int]]\n :rtype: int\n """\n row_count, col_count = len(grid), len(grid[0])\n surface = 0\n for row in range(row_count):\n for col in range(col_count):\n # if the cell is left-most, right-most, front-most, back-most\n edges = ((row == 0) + (col == 0) + (row == row_count - 1) + (col == col_count - 1))\n surface += grid[row][col] * edges\n\n # the delta between the cell to the right and the cell to the front\n if row != row_count - 1:\n surface += abs(grid[row][col] - grid[row + 1][col])\n if col != col_count - 1:\n surface += abs(grid[row][col] - grid[row][col + 1])\n \n # top and bottom\n if grid[row][col] > 0:\n surface += 2\n\n return surface\n```
| 2
| 0
|
[]
| 0
|
surface-area-of-3d-shapes
|
Java Solution with Explanation
|
java-solution-with-explanation-by-seanms-o4bh
|
The bottom and top surface area is 2 the number of cubes.\nIf the current grid is taller than the grid to the left it means we take the area of this side 2 * he
|
seanmsha
|
NORMAL
|
2018-08-26T03:25:27.064038+00:00
|
2018-09-11T01:13:49.773253+00:00
| 459
| false
|
The bottom and top surface area is 2* the number of cubes.\nIf the current grid is taller than the grid to the left it means we take the area of this side 2 * height, we *2 because there are two sides - the height of the grid to the left because we already added it.\nIf the current grid is taller than the grid above it(I guess it depends on which way the axis is facing, but j-1) then we take the area of this side 2 * height, we * 2 because there are two sides sides - the height of the grid with j-1 because we already added it.\n```\nclass Solution {\n public int surfaceArea(int[][] grid) {\n int count = 0;\n if(grid.length==0)return 0;\n int area = 0;\n for(int i=0; i<grid.length;++i){\n for(int j=0; j<grid[0].length;++j){\n if(grid[i][j]!=0){\n ++count;\n }\n if(i==0){\n area+=2*(grid[i][j]);\n }\n else if(grid[i][j]>grid[i-1][j]){\n area+=2*(grid[i][j]-grid[i-1][j]);\n }\n if(j==0){\n area+=2*(grid[i][j]);\n }\n else if(grid[i][j]>grid[i][j-1]){\n area+=2*(grid[i][j]-grid[i][j-1]);\n }\n } \n }\n area+=(count*2);\n return area;\n }\n}\n```\n
| 2
| 0
|
[]
| 0
|
surface-area-of-3d-shapes
|
Beats 💯 || c++ || Beginner friendly || simple Logic || very Easy
|
beats-c-beginner-friendly-simple-logic-v-s9xu
|
Intuitionadd the top area and the bottom area first and the visible area between the adjacent towers, which the absolute difference between the adjacent towers.
|
abirajp04
|
NORMAL
|
2025-04-05T13:09:02.207971+00:00
|
2025-04-05T13:09:02.207971+00:00
| 10
| false
|
# Intuition
add the top area and the bottom area first and the visible area between the adjacent towers, which the absolute difference between the adjacent towers. We need to add all the four directions area. But it leads to duplicate sum. So to overcome the i just added the Top and left difference height each tower.
# Approach
Traverse throught all the towers and apply the intuition mention above
# Complexity
- Time complexity:
O(n*n)
- Space complexity:
O(1)
# Code
```cpp []
class Solution {
public:
int surfaceArea(vector<vector<int>>& grid) {
int area = 0;
if(grid.size() == 1)
return (grid[0][0]*4) + (grid[0][0]?2:0);
for(int i=0;i<grid.size();i++){
for(int j=0;j<grid.size();j++){
if(grid[i][j] != 0)
area+=2;
if(i == 0 || i == grid.size()-1)
area += grid[i][j];
if(j == 0 || j == grid.size()-1 )
area += grid[i][j];
if(i-1>=0)
area += abs(grid[i][j] - grid[i-1][j]);
if(j-1>=0)
area += abs(grid[i][j] - grid[i][j-1]);
}
}
return area;
}
};
```
| 1
| 0
|
['Math', 'Matrix', 'C++']
| 0
|
surface-area-of-3d-shapes
|
Simple Solution
|
simple-solution-by-samuel3shin-4ot3
|
Code
|
Samuel3Shin
|
NORMAL
|
2025-03-21T15:03:35.376005+00:00
|
2025-03-21T15:03:35.376005+00:00
| 23
| false
|
# Code
```cpp []
class Solution {
public:
int surfaceArea(vector<vector<int>>& grid) {
int N = grid.size();
int topBottom = 0;
int sides = 0;
for(int i=0; i<N; i++) {
for(int j=0; j<N; j++) {
if(grid[i][j] == 0) continue;
topBottom += 2;
sides += (grid[i][j] * 4);
// up
if(i-1 >= 0) {
sides -= min(grid[i-1][j], grid[i][j]);
}
// down
if(i+1 < N) {
sides -= min(grid[i+1][j], grid[i][j]);
}
// right
if(j+1 < N) {
sides -= min(grid[i][j+1], grid[i][j]);
}
// left
if(j-1 >= 0) {
sides -= min(grid[i][j-1], grid[i][j]);
}
}
}
return topBottom + sides;
}
};
```
| 1
| 0
|
['C++']
| 0
|
surface-area-of-3d-shapes
|
Easy
|
easy-by-danisdeveloper-qswn
|
Code
|
DanisDeveloper
|
NORMAL
|
2025-01-08T15:05:26.019278+00:00
|
2025-01-08T15:05:26.019278+00:00
| 38
| false
|
# Code
```kotlin []
class Solution {
fun surfaceArea(grid: Array<IntArray>): Int {
val floor = grid.sumOf { row ->
row.count { it != 0 }
}
var left = 0
for (i in grid.indices) {
var count = grid[i][0] + grid[i][grid[i].lastIndex];
for (j in 1..grid[i].size - 1) {
count += Math.abs(grid[i][j] - grid[i][j - 1])
}
left += count
}
var up = 0
for(j in grid[0].indices){
var count = grid[0][j] + grid[grid.lastIndex][j];
for(i in 1..grid.size - 1){
count += Math.abs(grid[i][j] - grid[i - 1][j])
}
up += count
}
return floor * 2 + left + up;
}
}
```
| 1
| 0
|
['Kotlin']
| 0
|
surface-area-of-3d-shapes
|
Python Beats 99%, Really Simple
|
python-beats-99-really-simple-by-trashyt-azet
|
Intuition\nTop/Bottom surface area is 1 if there are blocks, 0 if not\nSurface area around sides is height of blocks in that stack\nSurface area between adjacen
|
trashytrash
|
NORMAL
|
2024-09-25T04:29:16.292642+00:00
|
2024-09-25T04:29:16.292673+00:00
| 130
| false
|
# Intuition\nTop/Bottom surface area is 1 if there are blocks, 0 if not\nSurface area around sides is height of blocks in that stack\nSurface area between adjacent stacks is abs(h1-h2)\n\n# Approach\nOne loop through the grid, adding area to account for:\ntop/bottom\noutside edges (upper/left/right/lower)\narea between adjacent stacks\n\n# Complexity\n- Time complexity:\nO(n^2)\n\n- Space complexity:\nO(1)\n\n# Code\n```python3 []\nclass Solution:\n def surfaceArea(self, grid: List[List[int]]) -> int:\n \n n = len(grid)\n\n # outsides\n area = 0\n for i in range(n):\n for j in range(n):\n # upper outside\n if i == 0: area += grid[i][j]\n # left outside\n if j == 0: area += grid[i][j]\n # lower outside\n if i == n-1: area += grid[i][j]\n # right outside\n if j == n-1: area += grid[i][j]\n # lower neighbor delta\n if i+1<n: area += abs(grid[i][j]-grid[i+1][j])\n # right neighbor delta\n if j+1<n: area += abs(grid[i][j]-grid[i][j+1])\n # top/bottom surface\n if grid[i][j]: area += 2\n\n return area\n\n```
| 1
| 0
|
['Python3']
| 0
|
surface-area-of-3d-shapes
|
JavaScript Solution
|
javascript-solution-by-hariprakashkhp-mhwa
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
HariprakashKhp
|
NORMAL
|
2024-08-11T02:16:46.336320+00:00
|
2024-08-11T02:16:46.336337+00:00
| 22
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * @param {number[][]} grid\n * @return {number}\n */\nvar surfaceArea = function(grid) {\n const height = grid.length;\n const width = grid[0].length;\n\n let sum = 0;\n\n for(let i = 0; i < height; i++) {\n for(let j = 0; j < width; j++) {\n if(grid[i][j] > 0) sum += grid[i][j] * 4 + 2;\n if(i > 0) sum -= Math.min(grid[i][j], grid[i - 1][j]) * 2;\n if(j > 0) sum -= Math.min(grid[i][j], grid[i][j - 1]) * 2;\n }\n }\n return sum;\n};\n```
| 1
| 0
|
['JavaScript']
| 0
|
surface-area-of-3d-shapes
|
Super Clean Code, Super Easy Explanation
|
super-clean-code-super-easy-explanation-ye9yd
|
Intuition and Approach\n Describe your first thoughts on how to solve this problem. \n Consider any block of height h. What is its total surface area?\n I
|
SUVU01
|
NORMAL
|
2023-12-13T18:22:31.672049+00:00
|
2023-12-13T18:24:11.012175+00:00
| 23
| false
|
# Intuition and Approach\n<!-- Describe your first thoughts on how to solve this problem. -->\n Consider any block of height h. What is its total surface area?\n It is an (h x 1 x 1) block. So, area = (2 x 1) + (4 x h). (0 if\n h == 0)\n\n Consider another block of height H in contact with it. What is the\n reduction in surface area of the first block of height h due to \n the second block of height H?\n\n One surface is common. If (H >= h) we will lose area h of the \n first block. Else we will lose area H of the first block.\n Thus, reduction in area due to surfaces in contact = min(h, H).\n\n The same logic can be applied for the second block as well.\n Similarly, the same logic can be applied for each of the\n m x n blocks as well.\n\n We will travel {left, right, up, down} for each block (if any tower\n exists at that location) and perform the operations mentioned above.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(mn)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(1)\n\n# Code\n```\nclass Solution {\npublic:\n int surfaceArea(vector<vector<int>>& grid) {\n ios::sync_with_stdio(false);\n cin.tie(nullptr);\n cout.tie(nullptr);\n\n int m = grid.size();\n int n = grid[0].size();\n vector<int> delrow = {-1, 1, 0, 0}, delcol = {0, 0, -1, 1};\n int ans = 0;\n for(int row = 0; row < m; row++)\n {\n for(int col = 0; col < n; col++)\n {\n ans += (4 * grid[row][col] + 2);\n if(grid[row][col] == 0)\n ans -= 2; /* If height is 0, the two surfaces \n (top and bottom) won\'t exist */\n for(int i = 0; i < 4; i++)\n {\n int nrow = row + delrow[i];\n int ncol = col + delcol[i];\n if(nrow >= 0 and ncol >= 0 and nrow < m and ncol < n)\n ans -= min(grid[row][col], grid[nrow][ncol]);\n }\n }\n }\n return ans;\n }\n};\n```
| 1
| 0
|
['Math', 'Geometry', 'Matrix', 'C++']
| 0
|
surface-area-of-3d-shapes
|
Area of the Solid Figure ||
|
area-of-the-solid-figure-by-shree_govind-ltpk
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
Shree_Govind_Jee
|
NORMAL
|
2023-09-05T03:47:50.686558+00:00
|
2023-09-05T03:47:50.686588+00:00
| 65
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:O(3N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int surfaceArea(int[][] grid) {\n int area=0;\n int len = grid.length;\n for(int i=0; i<len; i++){\n for(int j=0; j<len; j++){\n area += grid[i][j]>0 ? 4*grid[i][j] + 2:0;\n }\n }\n\n for(int i=0; i<len; i++){\n for(int j=0; j<len-1; j++){\n area -= 2*Math.min(grid[i][j], grid[i][j+1]);\n }\n }\n\n for(int j=0; j<len; j++){\n for(int i=0; i<len-1; i++){\n area -= 2*Math.min(grid[i][j], grid[i+1][j]);\n }\n }\n\n return area;\n }\n}\n```
| 1
| 0
|
['Array', 'Math', 'Geometry', 'Matrix', 'Java']
| 0
|
surface-area-of-3d-shapes
|
Easy Python Solution
|
easy-python-solution-by-ap3x0034-y0mn
|
Approach\n Describe your approach to solving the problem. \nStep 1 : Find the area of each piller on the matrix(First Loop)\nStep 2 : Remove all the walls of tw
|
AP3X0034
|
NORMAL
|
2023-08-28T18:54:33.216733+00:00
|
2023-08-28T18:54:33.216751+00:00
| 38
| false
|
# Approach\n<!-- Describe your approach to solving the problem. -->\nStep 1 : Find the area of each piller on the matrix(First Loop)\nStep 2 : Remove all the walls of two adjence pillers(Second Loop)\nStep 3 : Get the transpose of the matrix\nStep 4 : Repet Step 2. \n# Complexity\n- Time complexity: O(n^2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n# Runtime\n- 81 ms\n# Code\n```\nclass Solution:\n def surfaceArea(self, grid: List[List[int]]) -> int:\n area = 0\n for i in range(len(grid)):\n for j in range(len(grid[0])):\n if grid[i][j] != 0:\n area += 2 * (1 + grid[i][j] + grid[i][j])\n \n for i in range(len(grid)):\n a=0\n while a < len(grid) - 1:\n area -= min(grid[i][a], grid[i][a+1]) * 2\n a += 1\n \n grid = list(zip(*grid))\n\n for i in range(len(grid)):\n a=0\n while a < len(grid) - 1:\n area -= min(grid[i][a], grid[i][a+1]) * 2\n a += 1\n \n return area\n```
| 1
| 0
|
['Python3']
| 0
|
surface-area-of-3d-shapes
|
Solution
|
solution-by-deleted_user-elt4
|
C++ []\nclass Solution {\npublic:\n int surfaceArea(vector<vector<int>>& grid) {\n int area = 0, n = grid.size();\n for (int i = 0; i < n; i++
|
deleted_user
|
NORMAL
|
2023-05-11T08:45:25.191459+00:00
|
2023-05-11T10:00:52.038726+00:00
| 598
| false
|
```C++ []\nclass Solution {\npublic:\n int surfaceArea(vector<vector<int>>& grid) {\n int area = 0, n = grid.size();\n for (int i = 0; i < n; i++)\n for (int j = 0; j < n; j++) {\n int v = grid[i][j];\n if (v) {\n area += 2;\n if (j == 0) area += v;\n else if (v > grid[i][j - 1]) area += v - grid[i][j - 1];\n if (i == 0) area += v;\n else if (v > grid[i - 1][j]) area += v - grid[i - 1][j];\n if (j + 1 == n) area += v;\n else if (v > grid[i][j + 1]) area += v - grid[i][j + 1];\n if (i + 1 == n) area += v;\n else if (v > grid[i + 1][j]) area += v - grid[i + 1][j];\n }\n }\n return area;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def surfaceArea(self, grid: List[List[int]]) -> int:\n n = len(grid)\n res = 0\n for i in range(n):\n rh = 0\n ch = 0\n for j in range(n):\n t = grid[i][j]\n res += 2 if t else 0\n res += abs(t - rh)\n rh = t\n t = grid[j][i]\n res += abs(t - ch)\n ch = t\n res += rh + ch\n return res\n```\n\n```Java []\nclass Solution {\n public int surfaceArea(int[][] grid) {\n int area = 0;\n int n = grid.length;\n for (int i = 0; i < n; i++) {\n for (int j = 0; j < n; j++) {\n area += grid[i][j] > 0 ? 4 * grid[i][j] + 2 : 0;\n }\n }\n for (int i = 0; i < n; i++) {\n for (int j = 0; j < n - 1; j++) {\n area -= 2 * Math.min(grid[i][j], grid[i][j + 1]);\n }\n }\n for (int j = 0; j < n; j++) {\n for (int i = 0; i < n - 1; i++) {\n area -= 2 * Math.min(grid[i][j], grid[i + 1][j]);\n }\n }\n return area;\n }\n}\n```\n
| 1
| 0
|
['C++', 'Java', 'Python3']
| 0
|
surface-area-of-3d-shapes
|
Beatiful Python Solution
|
beatiful-python-solution-by-bouzid_kobch-crj1
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
bouzid_kobchi
|
NORMAL
|
2023-01-31T14:39:17.017916+00:00
|
2023-01-31T14:39:17.017973+00:00
| 478
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity : O(n^2) \n- => n is the length or grid[i].length\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity : O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def surfaceArea(self, grid) -> int :\n length = len(grid)\n\n def behind(point) :\n array = []\n i , j = point\n # top : \n if length > i > 0 : array.append(min((grid[i-1][j],grid[i][j])))\n # left :\n if j < length-1 : array.append(min((grid[i][j+1] , grid[i][j])))\n # bottom :\n if i < length-1 : array.append(min((grid[i+1][j] , grid[i][j])))\n # right :\n if length > j > 0 : array.append(min((grid[i][j-1],grid[i][j])))\n\n return array\n \n def tower_surface(height) : return height*6-(height-1)*2 if height > 0 else 0\n\n surface = 0\n \n for i in range(length) :\n for j in range(length) :\n surface += tower_surface(grid[i][j]) - sum(behind((i,j)))\n\n return surface\n```
| 1
| 0
|
['Python3']
| 0
|
surface-area-of-3d-shapes
|
Java || 2 ms || %98.75 beats || with explanation
|
java-2-ms-9875-beats-with-explanation-by-1dit
|
Approach\n Describe your approach to solving the problem. \nThe total surface area of cubves was calculated and then total kissing surface areas were subtracted
|
armadores
|
NORMAL
|
2023-01-19T09:37:16.018663+00:00
|
2023-01-19T09:38:17.798569+00:00
| 89
| false
|
# Approach\n<!-- Describe your approach to solving the problem. -->\nThe total surface area of cubves was calculated and then total kissing surface areas were subtracted from that.\n# Complexity\n- Time complexity:\n2 ms (beats %98.75)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n42.2 mb (beats %63.75)\n# Code\n```\nclass Solution {\n public int surfaceArea(int[][] grid) {\n int sum=0;\n //calculate the total surfaces of the cubes\n //1 cube has got 6 surfaces\n for(int i=0;i<grid.length;++i){\n for(int j=0;j<grid[i].length;++j){\n sum=sum+6*grid[i][j];\n }\n }\n\n //calculate total kissing surfaces in x-axis of neighbour cubes\n //then subtract that area from total area \n for(int i=0;i<grid.length;++i){\n for(int j=0;j<grid[i].length;++j){ \n \n if(j+1<grid.length&&grid[i][j]>0){\n int a=2*Math.min(grid[i][j],grid[i][j+1]);\n sum=sum-a;\n }\n }\n } \n //calculate total kissing surfaces in y-axis of neighbour cubes\n //then subtract that area from total area \n for(int i=0;i<grid.length;++i){\n for(int j=0;j<grid[i].length;++j){\n \n if(i+1<grid.length&&grid[i+1][j]>0){\n int b=2*Math.min(grid[i][j],grid[i+1][j]);\n sum=sum-b;\n }\n \n }\n }\n\n //calculate the kissing surfaces of cubes in a row\n //then subtract that area from total area\n for(int i=0;i<grid.length;++i){\n for(int j=0;j<grid[i].length;++j){ \n if(grid[i][j]>1){\n sum=sum-2*(grid[i][j]-1);\n } \n }\n }\n \n return sum;\n }\n}\n```
| 1
| 0
|
['Java']
| 0
|
surface-area-of-3d-shapes
|
Surface Area of 3D Shapes || Easy JAVA Solution || 99.57% faster
|
surface-area-of-3d-shapes-easy-java-solu-hjrt
|
class Solution {\n\npublic int surfaceArea(int[][] grid) {\n int total = 0;\n int n = grid.length;\n \n for(int i =0; i0)\n total +=
|
shivani_99
|
NORMAL
|
2022-09-15T07:39:10.594813+00:00
|
2022-09-15T07:39:10.594847+00:00
| 579
| false
|
class Solution {\n\npublic int surfaceArea(int[][] grid) {\n int total = 0;\n int n = grid.length;\n \n for(int i =0; i<n; i++)\n {\n for(int j =0; j<n; j++)\n {\n if(grid[i][j]>0)\n total += 6*grid[i][j]-2*(grid[i][j]-1); //Surface Area of 1 cube: 6*grid[i][j]; Common Surface Area of vertically placed cubes:2*(grid[i][j]-1)\n \n if(i>0)\n total-= 2*Math.min(grid[i-1][j],grid[i][j]);//Hidden common vertical surface area\n \n if(j>0)\n total-= 2*Math.min(grid[i][j-1],grid[i][j]);//Hidden common horizontal surface area\n }\n }\n return total;\n}\n}
| 1
| 0
|
['Java']
| 0
|
surface-area-of-3d-shapes
|
Python3
|
python3-by-excellentprogrammer-e5ui
|
\nclass Solution:\n def surfaceArea(self, grid: List[List[int]]) -> int:\n c=0\n for i in range(len(grid)):\n for j in range(len(gri
|
ExcellentProgrammer
|
NORMAL
|
2022-07-30T13:22:41.483519+00:00
|
2022-07-30T13:23:26.344312+00:00
| 256
| false
|
```\nclass Solution:\n def surfaceArea(self, grid: List[List[int]]) -> int:\n c=0\n for i in range(len(grid)):\n for j in range(len(grid)):\n if grid[i][j]:\n c+=(grid[i][j]*4)+2\n if i:\n c-=min(grid[i][j],grid[i-1][j])*2\n if j:\n c-=min(grid[i][j],grid[i][j-1])*2\n return c\n```
| 1
| 0
|
[]
| 0
|
surface-area-of-3d-shapes
|
Beginner Friendly
|
beginner-friendly-by-coder481-p9xx
|
Traverse each cube in the grid:\n Add areas for top and left surfaces -> Simply the difference between the top or left cube and current cube\n Add extra surface
|
coder481
|
NORMAL
|
2022-07-21T04:59:47.282174+00:00
|
2022-07-21T04:59:47.282218+00:00
| 472
| false
|
Traverse each cube in the grid:\n* Add areas for top and left surfaces -> Simply the difference between the top or left cube and current cube\n* Add extra surfaces for cubes present at ending of grid (right-most and bottom-most)\n* Also add 2 surfaces for each cube if there\'s no hole in the grid\n\n```\nclass Solution {\n public int surfaceArea(int[][] grid) {\n int area = 0;\n int n = grid.length;\n for(int i=0; i<n; i++){\n for(int j=0; j<n; j++){\n \n // Adding the top part of grid\n if(i==0) area += grid[i][j];\n else area += Math.abs(grid[i][j] - grid[i-1][j]);\n \n // Adding the left part of grid\n if(j==0) area += grid[i][j];\n else area += Math.abs(grid[i][j] - grid[i][j-1]);\n \n // Adding bottom part of bottom-most cubes\n if(i == n-1) area += grid[i][j];\n \n // Adding right part for right-most cubes\n if(j == n-1) area += grid[i][j];\n \n // Add top and bottom surfaces if there is no hole in grid\n if(grid[i][j] != 0) area += 2;\n }\n }\n return area;\n }\n}\n```
| 1
| 0
|
['Java']
| 0
|
surface-area-of-3d-shapes
|
C++ Solution || Single-Pass || Short & Simple || O(m*n)
|
c-solution-single-pass-short-simple-omn-i4l4n
|
Code:\n\n\nclass Solution\n{\npublic:\n int surfaceArea(vector<vector<int>> &grid)\n {\n int m = grid.size(), n = grid[0].size();\n int tota
|
anis23
|
NORMAL
|
2022-05-31T16:37:54.600229+00:00
|
2022-05-31T16:37:54.600267+00:00
| 457
| false
|
**Code:**\n\n```\nclass Solution\n{\npublic:\n int surfaceArea(vector<vector<int>> &grid)\n {\n int m = grid.size(), n = grid[0].size();\n int total, overlap, non_zero;\n total = overlap = non_zero = 0;\n for (int i = 0; i < m; i++)\n {\n for (int j = 0; j < n; j++)\n {\n if (grid[i][j] == 0)\n continue;\n non_zero++;\n total += grid[i][j];\n if (i + 1 < m)\n overlap += min(grid[i][j], grid[i + 1][j]);\n if (j + 1 < n)\n overlap += min(grid[i][j], grid[i][j + 1]);\n }\n }\n int k = (total * 4) + (2 * non_zero) - (overlap * 2);\n return k;\n }\n};\n```
| 1
| 0
|
['Array', 'Math', 'C', 'C++']
| 0
|
surface-area-of-3d-shapes
|
C++ || One Scan
|
c-one-scan-by-yezhizhen-qt69
|
We have the formula 4 * height + 2 for a single (i,j) coordinate, after observation.\nBut when there are adjacent cells, the overlap region should not be counte
|
yezhizhen
|
NORMAL
|
2022-05-05T14:07:52.381628+00:00
|
2022-05-05T14:09:13.421404+00:00
| 85
| false
|
We have the formula 4 * height + 2 for a single (i,j) coordinate, after observation.\nBut when there are adjacent cells, the overlap region should not be counted.\n\n```\nclass Solution {\npublic:\n int surfaceArea(vector<vector<int>>& grid) {\n int m = grid.size(), n = grid[0].size();\n int total_cnt{}, overlap{}, cnt_non_zero{};\n for(int i = 0; i < m; i++){\n for(int j = 0; j < n; j++){\n if(grid[i][j] == 0) continue;\n cnt_non_zero ++; \n total_cnt += grid[i][j];\n if(i + 1 < m)\n overlap += min(grid[i][j], grid[i+1][j]);\n if(j + 1 < n)\n overlap += min(grid[i][j], grid[i][j+1]);\n }\n }\n return total_cnt * 4 + 2 * cnt_non_zero - overlap * 2;\n \n }\n};\n```
| 1
| 0
|
[]
| 0
|
surface-area-of-3d-shapes
|
python 3 || clean and concise code || O(n)/O(1)
|
python-3-clean-and-concise-code-ono1-by-34us0
|
```\nclass Solution:\n def surfaceArea(self, grid: List[List[int]]) -> int:\n n = len(grid)\n \n def area(i, j):\n v = grid[i
|
derek-y
|
NORMAL
|
2022-04-20T17:43:48.613851+00:00
|
2022-04-20T17:43:48.613897+00:00
| 288
| false
|
```\nclass Solution:\n def surfaceArea(self, grid: List[List[int]]) -> int:\n n = len(grid)\n \n def area(i, j):\n v = grid[i][j]\n if v == 0:\n return 0\n\n up = min(v, grid[i - 1][j]) if i else 0\n right = min(v, grid[i][j + 1]) if j < n - 1 else 0\n down = min(v, grid[i + 1][j]) if i < n - 1 else 0\n left = min(v, grid[i][j - 1]) if j else 0\n\n return 2 + 4*v - up - right - down - left\n \n return sum(area(i, j) for i in range(n) for j in range(n))
| 1
| 0
|
['Array', 'Python', 'Python3']
| 0
|
surface-area-of-3d-shapes
|
Simple Python Solution
|
simple-python-solution-by-comprhys-88oc
|
python\nclass Solution:\n def surfaceArea(self, grid: List[List[int]]) -> int:\n n = len(grid)\n total_surface = 0\n \n for i in
|
CompRhys
|
NORMAL
|
2022-04-04T02:56:32.218035+00:00
|
2022-04-04T02:56:32.218061+00:00
| 65
| false
|
```python\nclass Solution:\n def surfaceArea(self, grid: List[List[int]]) -> int:\n n = len(grid)\n total_surface = 0\n \n for i in range(n):\n for j in range(n):\n \n height = grid[i][j]\n surface = 2 + 4 * height if height > 0 else 0\n \n if i != n-1:\n surface -= min(height, grid[i+1][j])\n \n if i != 0:\n surface -= min(height, grid[i-1][j])\n \n if j != n-1:\n surface -= min(height, grid[i][j+1])\n \n if j != 0:\n surface -= min(height, grid[i][j-1])\n \n total_surface += surface\n \n return total_surface\n```
| 1
| 0
|
[]
| 0
|
surface-area-of-3d-shapes
|
C++ w Explanation
|
c-w-explanation-by-adamm93-fa6s
|
\n// Tower of height n has 6n faces and 2(n-1) hidden faces = 4n + 2 visible faces\n// The number of hidden faces in adjacent towers is twice the smaller height
|
Adamm93
|
NORMAL
|
2022-03-17T03:06:03.011037+00:00
|
2022-03-17T03:06:03.011086+00:00
| 100
| false
|
```\n// Tower of height n has 6n faces and 2(n-1) hidden faces = 4n + 2 visible faces\n// The number of hidden faces in adjacent towers is twice the smaller height\nclass Solution {\npublic:\n int surfaceArea(vector<vector<int>>& grid) {\n int res = 0;\n int n = grid.size();\n for (int i = 0; i < n; i++) {\n for (int j = 0; j < n; j++) {\n if (grid[i][j]) res += 4 * grid[i][j] + 2;\n if (i > 0) res -= 2 * min(grid[i][j], grid[i-1][j]);\n if (j > 0) res -= 2 * min(grid[i][j], grid[i][j-1]);\n }\n }\n return res;\n }\n};\n\n```
| 1
| 0
|
['C']
| 0
|
surface-area-of-3d-shapes
|
Python Solution
|
python-solution-by-lazarus29-poj0
|
\nclass Solution:\n def surfaceArea(self, a: List[List[int]]) -> int:\n answer = 0\n \n for i in range(len(a)):\n for j in ra
|
lazarus29
|
NORMAL
|
2022-02-20T08:51:00.864107+00:00
|
2022-02-20T08:51:00.864141+00:00
| 73
| false
|
```\nclass Solution:\n def surfaceArea(self, a: List[List[int]]) -> int:\n answer = 0\n \n for i in range(len(a)):\n for j in range(len(a)):\n answer += self.helper(i, j , a)\n \n return answer\n \n def helper(self, i, j, a):\n area = 0\n count = a[i][j]\n \n if count == 0:\n return 0\n else:\n area += 2\n \n if i == 0:\n area += count\n \n if i == len(a) - 1:\n area += count\n \n if j == 0:\n area += count\n \n if j == len(a) - 1:\n area += count\n \n if j + 1 < len(a) and count > a[i][j+1]:\n area += count - a[i][j+1]\n \n if i + 1 < len(a) and count > a[i+1][j]:\n area += count - a[i+1][j]\n \n if i-1 >= 0 and count > a[i-1][j]:\n area += count - a[i-1][j]\n \n if j -1 >= 0 and count > a[i][j-1]:\n area += count - a[i][j-1]\n \n return area\n```
| 1
| 0
|
[]
| 0
|
surface-area-of-3d-shapes
|
Python clean and straightforward
|
python-clean-and-straightforward-by-blue-7h0o
|
py\nclass Solution:\n def surfaceArea(self, grid: List[List[int]]) -> int:\n m, n, area = len(grid), len(grid[0]), 0\n\n for i in range(m):\n
|
blueblazin
|
NORMAL
|
2022-01-24T09:40:36.524296+00:00
|
2022-01-24T09:40:36.524396+00:00
| 197
| false
|
```py\nclass Solution:\n def surfaceArea(self, grid: List[List[int]]) -> int:\n m, n, area = len(grid), len(grid[0]), 0\n\n for i in range(m):\n for j in range(n):\n if (x := grid[i][j]) == 0:\n continue\n\n top = max(0, x - grid[i - 1][j]) if i > 0 else x\n bot = max(0, x - grid[i + 1][j]) if i + 1 < m else x\n left = max(0, x - grid[i][j - 1]) if j > 0 else x\n right = max(0, x - grid[i][j + 1]) if j + 1 < n else x\n\n area += top + bot + left + right + 2\n\n return area\n```\n\nJust add all visible faces, not much else to do here.
| 1
| 0
|
['Python']
| 0
|
surface-area-of-3d-shapes
|
Easy Kotlin Solution
|
easy-kotlin-solution-by-sahil14_11-4i5m
|
```\nclass Solution {\n fun surfaceArea(grid: Array): Int {\n var area=0\n for(i in 0 until grid.size){\n for(j in 0 until grid.size
|
Sahil14_11
|
NORMAL
|
2021-12-05T15:58:50.470605+00:00
|
2021-12-05T15:58:50.470630+00:00
| 49
| false
|
```\nclass Solution {\n fun surfaceArea(grid: Array<IntArray>): Int {\n var area=0\n for(i in 0 until grid.size){\n for(j in 0 until grid.size){\n if(grid[i][j]!=0){\n area+=grid[i][j]*4+2\n }\n if(i<grid.size-1){\n area-=minOf(grid[i][j],grid[i+1][j])*2\n }\n if(j<grid.size-1){\n area-=minOf(grid[i][j],grid[i][j+1])*2\n }\n }\n }\n return area\n }\n}
| 1
| 0
|
['Array', 'Kotlin']
| 0
|
surface-area-of-3d-shapes
|
Rust solution
|
rust-solution-by-bigmih-dpjy
|
\nimpl Solution {\n pub fn surface_area(grid: Vec<Vec<i32>>) -> i32 {\n let dirs = [(-1, 0), (0, 1), (1, 0), (0, -1)];\n let l = grid.len() as
|
BigMih
|
NORMAL
|
2021-11-12T07:43:43.455392+00:00
|
2021-11-12T07:44:19.815833+00:00
| 50
| false
|
```\nimpl Solution {\n pub fn surface_area(grid: Vec<Vec<i32>>) -> i32 {\n let dirs = [(-1, 0), (0, 1), (1, 0), (0, -1)];\n let l = grid.len() as i32;\n let mut res = 0;\n\n for (row, i) in grid.iter().zip(0..) {\n for (&val, j) in row.iter().zip(0..).filter(|(val, _)| **val > 0) {\n res += 2; // up adn down surfaces\n for (dx, dy) in dirs.iter().cloned() {\n let (xx, yy) = (j + dx, i + dy);\n res += match xx >= 0 && yy >= 0 && xx < l && yy < l {\n true => (val - grid[yy as usize][xx as usize]).max(0),\n false => val,\n };\n }\n }\n }\n res\n }\n}\n```
| 1
| 0
|
['Rust']
| 0
|
surface-area-of-3d-shapes
|
C++ O(N^2) Solution
|
c-on2-solution-by-ahsan83-95ue
|
Runtime: 8 ms, faster than 78.50% of C++ online submissions for Surface Area of 3D Shapes.\nMemory Usage: 9.4 MB, less than 46.42% of C++ online submissions for
|
ahsan83
|
NORMAL
|
2021-08-27T15:51:41.911183+00:00
|
2021-08-27T15:51:41.911225+00:00
| 142
| false
|
Runtime: 8 ms, faster than 78.50% of C++ online submissions for Surface Area of 3D Shapes.\nMemory Usage: 9.4 MB, less than 46.42% of C++ online submissions for Surface Area of 3D Shapes.\n\n\nLoop through grid and calculate surface area of the each cell. Also we deduct the common area betwen \n2 consicuitive cells. We can consider only left and upper cell and multiply the common area by 2. Common\narea between consicuitive cell is the min height between them.\n\n```\nclass Solution {\npublic:\n int surfaceArea(vector<vector<int>>& grid) {\n \n int n = grid.size();\n int area = 0;\n int deduct = 0;\n for(int i=0;i<n;i++)\n {\n for(int j=0;j<n;j++)\n {\n if(grid[i][j]>0)\n {\n area = area + 2*(1+ grid[i][j] *2); \n }\n \n if(i)deduct += min(grid[i][j],grid[i-1][j]) * 2;\n if(j)deduct += min(grid[i][j],grid[i][j-1]) * 2; \n }\n }\n \n return area - deduct;\n }\n};\n```\n\n
| 1
| 0
|
['Array', 'C']
| 0
|
surface-area-of-3d-shapes
|
O(n*n) time and O(1) space. Readable, concise.
|
onn-time-and-o1-space-readable-concise-b-nbtz
|
\npublic class Solution {\n public int SurfaceArea(int[][] grid) {\n int res = 0;\n for(int i = 0; i < grid.Length; ++i) {\n for(int
|
yayarokya
|
NORMAL
|
2021-08-22T06:39:48.956228+00:00
|
2021-08-22T06:39:48.956270+00:00
| 63
| false
|
```\npublic class Solution {\n public int SurfaceArea(int[][] grid) {\n int res = 0;\n for(int i = 0; i < grid.Length; ++i) {\n for(int j = 0; j < grid[i].Length; ++j) {\n res += column(i, j, grid);\n }\n }\n return res;\n }\n \n static int column(int i, int j, int[][] grid) {\n if(grid[i][j] == 0) {\n return 0;\n }\n \n int res = 4*grid[i][j] + 2;\n \n if(0 <= i - 1) {\n res -= 2*Math.Min(grid[i - 1][j], grid[i][j]);\n }\n \n if(0 <= j - 1) {\n res -= 2*Math.Min(grid[i][j - 1], grid[i][j]);\n }\n \n return res;\n }\n}\n```
| 1
| 0
|
[]
| 0
|
surface-area-of-3d-shapes
|
[Java] | TC : O(N^2) | SC : O(1) | More in-depth explanation about calculation
|
java-tc-on2-sc-o1-more-in-depth-explanat-tr2x
|
\n/*\n Explanation about calculation\n -----------------------------\n\n Total Area contributed by a cube -> 6 * 1 (according to discription [1 * 1 * 1
|
_LearnToCode_
|
NORMAL
|
2021-07-26T06:45:52.340451+00:00
|
2021-07-26T06:45:52.340930+00:00
| 90
| false
|
```\n/*\n Explanation about calculation\n -----------------------------\n\n Total Area contributed by a cube -> 6 * 1 (according to discription [1 * 1 * 1])\n \n Common area when the cubes are placed on the top of each other (vertically) : \n 2 * (number_of_cubes - 1) -> 2 * (grid[i][j] - 1)\n \n so therefore, total surface area by a tower : (6 * grid[i][j] - 2 * (grid[i][j] - 1))\n : 4 * grid[i][j] + 2\n \n \n Also needs to subtract, adjacent hidden common area from total surface area calculated\n so far.\n \n adjacent_hidden_common_area_horizontally : 2 * min(cubes_cnt_in_first_tower, cubes_cnt_in_tower_next_to_first_tower)\n : 2 * min(grid[i][j], grid[i][j + 1]) or\n : 2 * min(grid[i][j], grid[i][j - 1]) based on implementation.\n \n adjacent_hidden_common_area_vertically : 2 * min(cubes_cnt_in_first_tower, cubes_cnt_in_tower_beneath_to_first_tower)\n : 2 * min(grid[i][j], grid[i + 1][j]) or\n : 2 * min(grid[i][j], grid[i - 1][j]) based on implementation.\n*/\n\nclass Solution {\n public int surfaceArea(int[][] grid) {\n int n = grid.length, totSA = 0;\n for(int i = 0; i < n; i += 1) {\n for(int j = 0; j < n; j += 1) {\n if(grid[i][j] > 0) totSA += (6 * grid[i][j] - 2 * (grid[i][j] - 1));\n if(i > 0) totSA -= 2 * Math.min(grid[i][j], grid[i - 1][j]);//vertically hidden common area\n if(j > 0) totSA -= 2 * Math.min(grid[i][j], grid[i][j - 1]);//horizontally hidden common area\n }\n }\n \n return totSA;\n }\n}\n```
| 1
| 0
|
[]
| 0
|
surface-area-of-3d-shapes
|
C# O(mn) Solution, faster than 84.21%
|
c-omn-solution-faster-than-8421-by-ruste-di9e
|
\n\n\npublic class Solution {\n public int SurfaceArea(int[][] grid) {\n var res = 0;\n for(var i =0; i<grid.Length; i++){\n for(var
|
rustedwizard
|
NORMAL
|
2021-07-20T00:53:26.079211+00:00
|
2021-07-20T00:53:26.079243+00:00
| 49
| false
|
\n\n```\npublic class Solution {\n public int SurfaceArea(int[][] grid) {\n var res = 0;\n for(var i =0; i<grid.Length; i++){\n for(var j=0; j<grid[i].Length; j++){\n\t\t\t\t//at top row \n if(i==0){\n res += grid[i][j];\n }\n\t\t\t\t//at bottom row \n if(i==grid.Length-1){\n res += grid[i][j];\n }\n\t\t\t\t//at left most column\n if(j==0){\n res +=grid[i][j];\n }\n\t\t\t\t//at right most column\n if(j==grid[i].Length-1){\n res+=grid[i][j];\n }\n\t\t\t\t//current position is higher than previous row\n if(i>0 && grid[i][j]>grid[i-1][j]){\n res += grid[i][j]-grid[i-1][j];\n }\n\t\t\t\t//current position is higher than next row\n if(i<grid.Length-1 && grid[i][j]>grid[i+1][j]){\n res += grid[i][j] -grid[i+1][j];\n }\n\t\t\t\t//current position is higher than previous column\n if(j>0 && grid[i][j]>grid[i][j-1]){\n res += grid[i][j]-grid[i][j-1];\n }\n\t\t\t\t//current position is higher than next column\n if(j<grid[i].Length-1 && grid[i][j]>grid[i][j+1]){\n res +=grid[i][j]-grid[i][j+1];\n }\n\t\t\t\t//current position is not empty, count the top and bottom area.\n if(grid[i][j]!=0){\n res +=2;\n }\n }\n }\n return res;\n }\n}\n```
| 1
| 0
|
[]
| 0
|
surface-area-of-3d-shapes
|
Not Efficient but easy to understand, C++, with comments
|
not-efficient-but-easy-to-understand-c-w-x4y3
|
\nclass Solution {\npublic:\n int surfaceArea(vector<vector<int>>& grid) {\n int ans =0, n = grid.size();\n for(int i=0; i<n;i++)\n {\n
|
gyanendrasingh
|
NORMAL
|
2021-06-07T07:03:55.196944+00:00
|
2021-06-07T07:03:55.196989+00:00
| 102
| false
|
```\nclass Solution {\npublic:\n int surfaceArea(vector<vector<int>>& grid) {\n int ans =0, n = grid.size();\n for(int i=0; i<n;i++)\n {\n for(int j =0;j<n;j++)\n { \n \n if(grid[i][j] > 0)\n {\n ans +=2; // top & bottom\n //right\n if(i+1 == n) //row below current block\n ans += grid[i][j];\n else if(i+1 < n)\n ans += grid[i+1][j] < grid[i][j]?-grid[i+1][j] +grid[i][j]:0;\n if(j-1 == -1) \\\\left column\n ans += grid[i][j];\n else if( j-1 >= 0)\n ans += grid[i][j-1] < grid[i][j]?-grid[i][j-1]+grid[i][j]:0;\n if(i-1 == -1) //top row\n ans += grid[i][j];\n else if(i-1 >= 0)\n ans += grid[i-1][j] < grid[i][j]? -grid[i-1][j]+grid[i][j]:0;\n if(j+1 == n) // right column\n ans += grid[i][j];\n else if(j+1 < n)\n ans += grid[i][j+1] < grid[i][j]? grid[i][j]- grid[i][j+1]:0;\n }\n }\n }\n return ans;\n }\n};\n```
| 1
| 0
|
[]
| 0
|
surface-area-of-3d-shapes
|
Golang solution 100%, 100%, with explanation and images
|
golang-solution-100-100-with-explanation-ovzx
|
892. Surface Area of 3D Shapes\n\nThe Idea Of This Solution:\n\nThis solution uses the fact that each stack of cubes surface area is the equation 2 + 4 * v. Thi
|
nathannaveen
|
NORMAL
|
2021-04-08T18:15:04.536130+00:00
|
2021-04-08T18:15:04.536174+00:00
| 136
| false
|
[892. Surface Area of 3D Shapes](https://leetcode.com/problems/surface-area-of-3d-shapes/)\n\n**The Idea Of This Solution:**\n\nThis solution uses the fact that each stack of cubes surface area is the equation `2 + 4 * v`. This works because each cube has `6` sides. This can be shown using some images:\n\n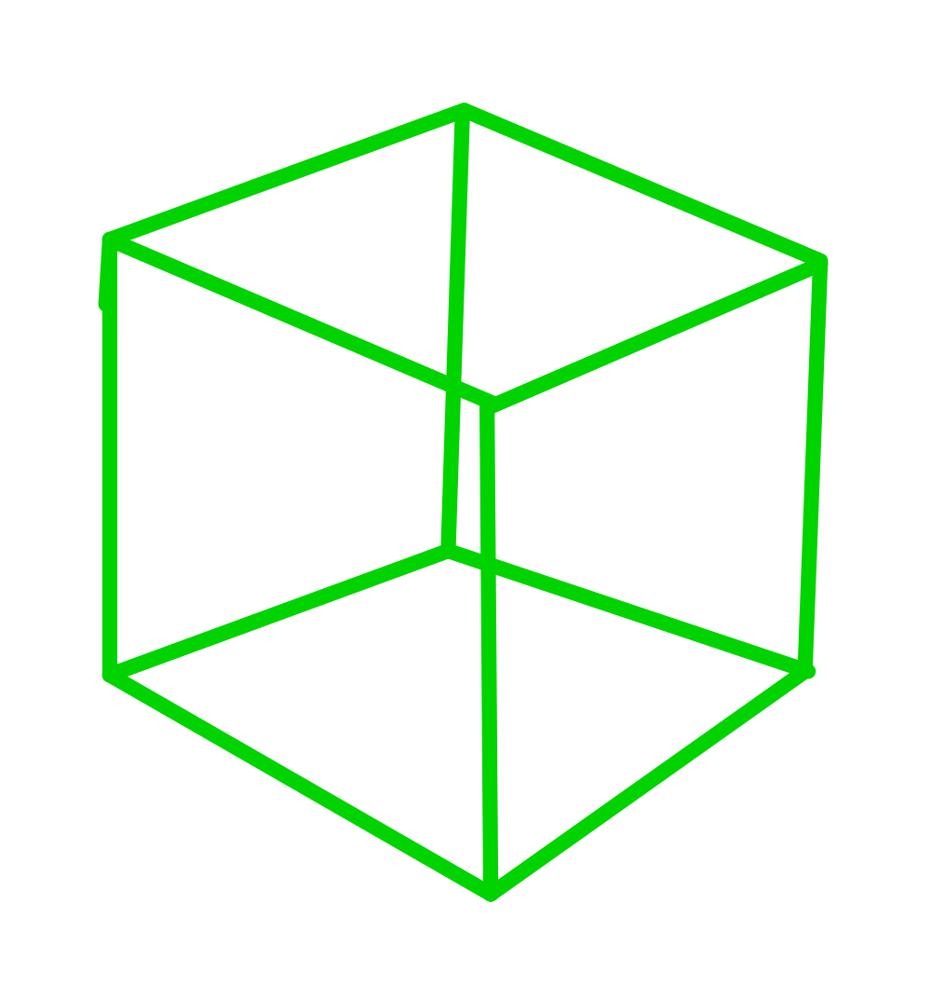\n\n\n> We can see that each cube has `6` planes. There are `4` sides, `1` top, and `1` bottom.\n\n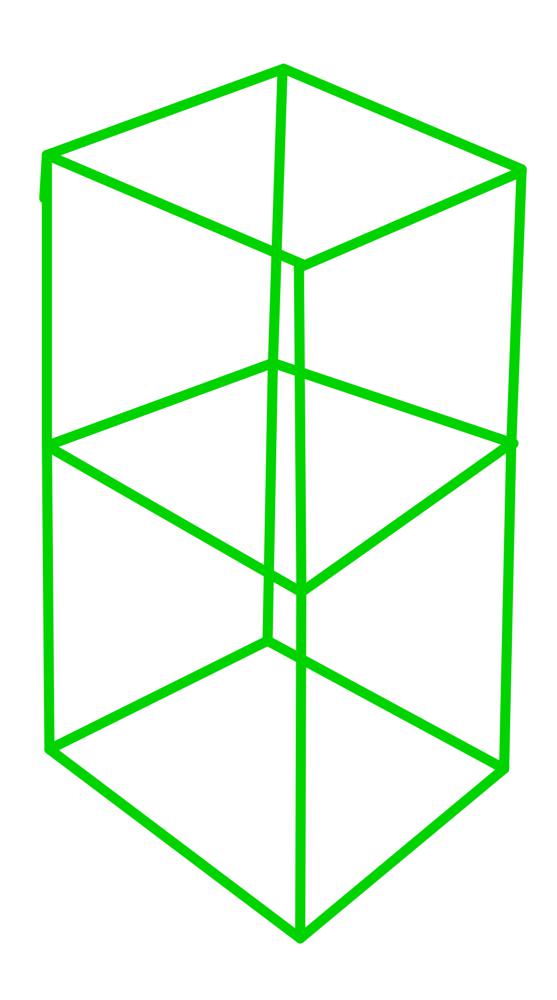\n\n\n> Now, as we can see, there are `10` units of surface area while the other one only had `6`, there are `8` sides, `1` top, and `1` bottom.\n\n\n\n\n> This example is `3` cubes, and it has a surface area of `14` units. There are `12` side units, `1` top, and `1` bottom.\n\nAs you can see in all three examples, there is always 1 top, one bottom, and four sides per cube, so we can write the equation `2 + 4 * v`, where `v` is the number of cubes. This equation will work for all stacks except for one with `v = 0`. This is because if we do this equation with `v = 0`, we get the output of `2`. After all, the code thinks that there is a top and a bottom, but we know that there is no top and no bottom on a stack of size `0`.\n\nNow that we have got the total surface area, we have to subtract the overlapping part. Now you might be asking, what overlap? Just look at the following image:\n\n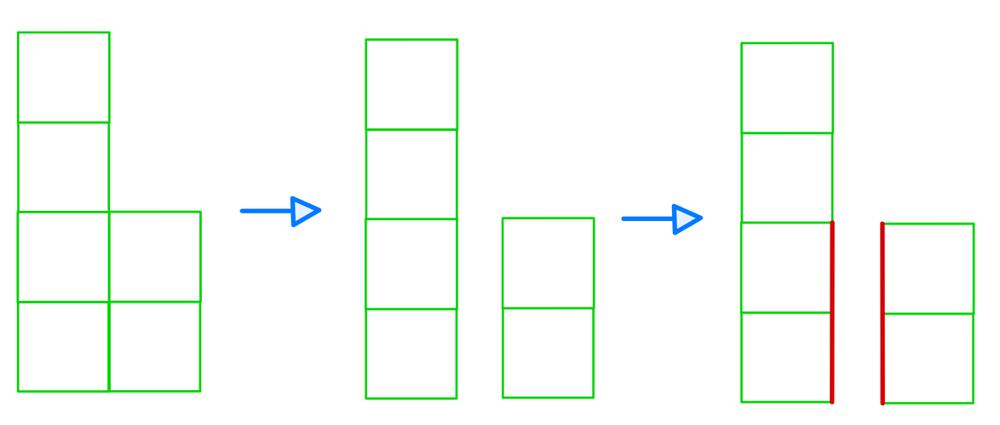\n\n\n> First, we can get the input of a stack of `4` and then a pile of `2` back to back, so we have to subtract the stack size `2`\'s one side from the stack of size `2` and the pile of size `4`. So basically, we are subtracting `2 * minimum(grid before, current grid)`.\n\n**The Code:**\n\n``` go\nfunc min(a, b int) int {\n if a < b {\n return a\n }\n return b\n}\n\nfunc surfaceArea(grid [][]int) int {\n // 2 + shape * 4 == area of each shape\n res := 0\n\n for i := 0; i < len(grid); i++ {\n for j := 0; j < len(grid[0]); j++ {\n if grid[i][j] != 0 {\n res += 2 + grid[i][j]*4\n }\n if i-1 >= 0 {\n res -= 2 * min(grid[i-1][j], grid[i][j])\n }\n if j-1 >= 0 {\n res -= 2 * min(grid[i][j-1], grid[i][j])\n }\n }\n }\n\n return res\n}\n```
| 1
| 0
|
['Go']
| 0
|
surface-area-of-3d-shapes
|
simple solution | C++
|
simple-solution-c-by-hacker_vikas_hatori-s25n
|
\nclass Solution {\npublic:\n int surfaceArea(vector<vector<int>>& grid) {\n int n = grid.size();\n int m = grid[0].size();\n int res =
|
hacker_vikas_hatori
|
NORMAL
|
2021-03-29T11:31:49.142849+00:00
|
2021-03-29T11:31:49.142882+00:00
| 76
| false
|
```\nclass Solution {\npublic:\n int surfaceArea(vector<vector<int>>& grid) {\n int n = grid.size();\n int m = grid[0].size();\n int res = 0;\n int dr[] = {-1, 1, 0, 0};\n int dc[] = {0, 0, -1, 1};\n for(int i = 0;i<n;i++){\n for(int j= 0;j<m;j++){\n if(grid[i][j]) res += 2;\n int rr, cc;\n for(int k = 0;k<4;k++){\n rr = dr[k] + i;\n cc = dc[k] + j;\n if(rr < 0 || cc < 0 || rr > n - 1 || cc > m - 1){\n res += grid[i][j];\n }\n else{\n res += max(grid[i][j] - grid[rr][cc], 0);\n }\n }\n }\n }\n return res;\n }\n};\n```
| 1
| 0
|
[]
| 0
|
surface-area-of-3d-shapes
|
C++|| fast and simple
|
c-fast-and-simple-by-know_go-3jhe
|
\nclass Solution {\npublic:\n int surfaceArea(vector<vector<int>>& grid) {\n int cube = 0, sf = 0;\n for(int i = 0; i < grid.size(); ++i) {\n
|
know_go
|
NORMAL
|
2021-02-09T09:03:06.758827+00:00
|
2021-02-09T09:03:06.758867+00:00
| 115
| false
|
```\nclass Solution {\npublic:\n int surfaceArea(vector<vector<int>>& grid) {\n int cube = 0, sf = 0;\n for(int i = 0; i < grid.size(); ++i) {\n for(int j = 0; j < grid[0].size(); ++j) {\n if(grid[i][j]==0) {\n continue;\n }\n cube += grid[i][j];\n sf += grid[i][j] - 1;\n if(j + 1 < grid[0].size()) {\n sf += min(grid[i][j], grid[i][j + 1]);\n }\n if(i + 1 < grid.size()) {\n sf += min(grid[i][j], grid[i + 1][j]);\n }\n }\n }\n return cube * 6 - sf * 2;\n }\n};\n```
| 1
| 0
|
[]
| 0
|
surface-area-of-3d-shapes
|
Python, count sides
|
python-count-sides-by-vivians1103-81li
|
```\nclass Solution:\n def surfaceArea(self, grid: List[List[int]]) -> int:\n \n col, row=len(grid[0]), len(grid[0])\n out=sum([sum(row)
|
vivians1103
|
NORMAL
|
2021-01-06T04:50:00.259204+00:00
|
2021-01-06T04:50:00.259306+00:00
| 89
| false
|
```\nclass Solution:\n def surfaceArea(self, grid: List[List[int]]) -> int:\n \n col, row=len(grid[0]), len(grid[0])\n out=sum([sum(row) for row in grid])*4 # count all unique cubes then *4\n out+= 2*sum([sum([i!=0 for i in row]) for row in grid]) # every non-zero cube, add up and down (2 sides)\n \n minus=0 # count the neighboring sides and minus them\n if col>1:\n for i in range(col-1):\n for j in range(row-1):\n minus += min(grid[j][i], grid[j][i+1]) + min(grid[j][i], grid[j+1][i]) # neirghboring horizontally and neighboring verticalling\n minus+= sum([min(grid[row-1][i], grid[row-1][i+1]) for i in range(col-1)])\n minus+= sum([min(grid[i][col-1], grid[i+1][col-1]) for i in range(row-1)]) \n \n out -= 2*minus\n return out\n
| 1
| 0
|
[]
| 0
|
surface-area-of-3d-shapes
|
python - count and reduce adjacent
|
python-count-and-reduce-adjacent-by-wave-4mfa
|
\n def surfaceArea(self, grid: List[List[int]]) -> int:\n res = 0\n \n for i in range(len(grid)):\n for j in range(len(grid[0
|
waveletus
|
NORMAL
|
2020-12-21T01:16:14.621189+00:00
|
2020-12-21T01:16:14.621222+00:00
| 72
| false
|
```\n def surfaceArea(self, grid: List[List[int]]) -> int:\n res = 0\n \n for i in range(len(grid)):\n for j in range(len(grid[0])):\n v = grid[i][j]\n if v:\n res += 2 #top/bottom\n res += v * 4 # side\n \n # i neighbor\n if i and grid[i-1][j]:\n p = grid[i-1][j]\n res -= 2 * min(p, v) #side\n \n # j neighbor\n if j and grid[i][j-1]:\n p = grid[i][j-1]\n res -= 2 * min(p, v)\n \n return res\n \n```
| 1
| 0
|
[]
| 0
|
surface-area-of-3d-shapes
|
C++ & Python solutions
|
c-python-solutions-by-woziji-xdbk
|
C++ solution,\n\nclass Solution {\npublic:\n int surfaceArea(vector<vector<int>>& grid) {\n int res = 0;\n\n for (int i = 0; i < grid.size(); +
|
woziji
|
NORMAL
|
2020-09-20T01:59:59.957977+00:00
|
2020-09-20T01:59:59.958022+00:00
| 141
| false
|
C++ solution,\n```\nclass Solution {\npublic:\n int surfaceArea(vector<vector<int>>& grid) {\n int res = 0;\n\n for (int i = 0; i < grid.size(); ++i)\n for (int j = 0; j < grid[0].size(); ++j) {\n if (grid[i][j])\n res += 4*grid[i][j] + 2;\n\n if (j) {\n res -= min(grid[i][j],grid[i][j-1])*2;\n res -= min(grid[j][i],grid[j-1][i])*2;\n }\n }\n\n return res;\n }\n};\n```\n\nPython solution,\n```\nclass Solution:\n def surfaceArea(self, grid):\n res = 0\n\n for i in range(len(grid)):\n for j in range(len(grid[0])):\n if grid[i][j]:\n res += 4*grid[i][j] + 2\n\n if j:\n res -= min(grid[i][j],grid[i][j-1])*2\n res -= min(grid[j][i],grid[j-1][i])*2\n\n return res\n```
| 1
| 0
|
['C', 'Python']
| 1
|
surface-area-of-3d-shapes
|
Easy C++ Solution (98% fast)
|
easy-c-solution-98-fast-by-primacyeffect-4v8g
|
// loop 1 formula \n// 6 * num of stacked cubes - the top/bottom surface areas that "disappear" - the side surface areas that "disappear"\n// 6 * grid[i][j] - 2
|
primacyeffect
|
NORMAL
|
2020-09-13T06:20:21.024405+00:00
|
2020-09-13T06:32:29.248860+00:00
| 158
| false
|
// loop 1 formula \n// 6 * num of stacked cubes - the top/bottom surface areas that "disappear" - the side surface areas that "disappear"\n// 6 * grid[i][j] - 2 * min(grid[i][j], grid[i][j + 1]) - 2 * (grid[i][j] - 1) \n\n// loop 2 formula (need to account for the other "disappeared" sides between columns in the grid)\n// 2 * the side surface areas that "disappear" between 2 rows (the trailing row and the current row)\n// 2 * min(grid[i-1][j], grid[i][j])\n\n int surfaceArea(vector<vector<int>>& grid) {\n int sum = 0;\n \n for (int i = 0; i < grid.size(); ++i)\n {\n for(int j = 0; j < grid[i].size(); ++j)\n {\n sum += 6 * grid[i][j] - 2 * min(grid[i][j], j + 1 >= grid[i].size() ? 0 : grid[i][j+1]) - max(0, 2 * (grid[i][j] - 1));\n }\n }\n \n for(int i = 1; i < grid.size(); ++i)\n {\n for(int j = 0; j < grid[i].size(); ++j)\n {\n sum -= 2 * min(grid[i - 1][j], grid[i][j]);\n }\n }\n\n return sum;\n }\n\n
| 1
| 0
|
['C']
| 1
|
surface-area-of-3d-shapes
|
Python:
|
python-by-splorgdar-r8vd
|
\nclass Solution:\n def surfaceArea(self, grid: List[List[int]]) -> int:\n \n l, w, t = len(grid), len(grid[0]), 0\n for i in range(l):\
|
splorgdar
|
NORMAL
|
2020-08-19T21:18:12.746253+00:00
|
2020-08-19T21:18:12.746286+00:00
| 68
| false
|
```\nclass Solution:\n def surfaceArea(self, grid: List[List[int]]) -> int:\n \n l, w, t = len(grid), len(grid[0]), 0\n for i in range(l):\n for j in range(w):\n x = grid[i][j]\n if x: t += 2\n if i == 0: t += x\n t += x if i == l-1 else abs(x - grid[i+1][j])\n if j == 0: t += x\n t += x if j == w-1 else abs(x - grid[i][j+1])\n return t\n```
| 1
| 0
|
[]
| 0
|
surface-area-of-3d-shapes
|
simple cpp solution
|
simple-cpp-solution-by-bitrish-gtk1
|
\nclass Solution {\npublic:\n int surfaceArea(vector<vector<int>>& grid) {\n int ans=0;\n for(int i=0;i<grid.size();i++)\n {\n
|
bitrish
|
NORMAL
|
2020-08-17T09:04:09.281118+00:00
|
2020-08-17T09:04:09.281163+00:00
| 132
| false
|
```\nclass Solution {\npublic:\n int surfaceArea(vector<vector<int>>& grid) {\n int ans=0;\n for(int i=0;i<grid.size();i++)\n {\n for(int j=0;j<grid[i].size();j++)\n {\n if(grid[i][j]!=0)\n ans=ans+grid[i][j]*4+2;\n if(i!=0)\n {\n int x=min(grid[i][j],grid[i-1][j]);\n x*=2;\n ans-=x;\n }\n if(j!=0)\n {\n int y=min(grid[i][j],grid[i][j-1]);\n y*=2;\n ans-=y;\n }\n }\n }\n return ans;\n }\n};\n```
| 1
| 0
|
['C', 'C++']
| 0
|
surface-area-of-3d-shapes
|
[Vague Description] Why the expected values are different ?
|
vague-description-why-the-expected-value-0nbn
|
As far as I have understood this question based on the given description the output for [4,2] and [2,4] must be same... But here it is giving:\n\nOutput of [4,2
|
im3000
|
NORMAL
|
2020-04-24T18:52:50.442852+00:00
|
2020-04-24T18:52:50.442902+00:00
| 94
| false
|
As far as I have understood this question based on the given description the output for [4,2] and [2,4] must be same... But here it is giving:\n```\nOutput of [4,2] -> 18\nwhile, Output of [2,4] -> 10\n```\nAccording to me the output for both should be 24 ..\nCan anyone throw some light on it ?
| 1
| 0
|
[]
| 0
|
surface-area-of-3d-shapes
|
Python 3, elegant one-liner
|
python-3-elegant-one-liner-by-l1ne-npr7
|
Explanation\n\nCount up all the 1x1 squares on each axis:\n1. For above and below (z-axis), add 2 for every item in the grid that is not equal to 0 (1 for above
|
l1ne
|
NORMAL
|
2020-04-03T19:46:28.569600+00:00
|
2020-04-03T19:46:49.832026+00:00
| 132
| false
|
# Explanation\n\nCount up all the 1x1 squares on each axis:\n1. For above and below (z-axis), add 2 for every item in the grid that is not equal to 0 (1 for above, 1 for below)\n2. For left and right (x-axis), for each row, add the leftmost and the rightmost, and the absolute value difference of each adjascent pair\n3. For top to bottom (y-axis), same as x-axis, but for columns instead of rows\n\nWhy adjascent pairs? Let\'s look at a single row for an example:\n```\n[3,1,5,2]\n```\nLet\'s draw it out:\n```\n *\n *\n * *\n * * *\n * * * *\n-----------\n0 3 1 5 2 0\n```\nThe left-to-right and right-to-left surface area is:\n`|0-3| + |3-1| + |1-5| + |5-2| + |2-0| = 3 + 2 + 4 + 3 + 2 = 14`\n\nSo iterate on every row and then every column (by doing `(*grid,*zip(*grid))`) and add up the following:\n1. `sum(map(bool,row))`: count of values that are non-zero ... this gets doubled because we\'re doing 2 passes\n2. `sum(abs(a-b) for a,b in zip((0,*row),(*row,0)))`: sum of the absolute differences of each adjascent pair, including (0, leftmost) and (rightmost, 0)\n\n# Code\n\n```python\nclass Solution:\n def surfaceArea(self, grid: List[List[int]]) -> int:\n return sum(sum(map(bool,row)) + sum(abs(a-b) for a,b in zip((0,*row),(*row,0))) for row in (*grid,*zip(*grid)))\n```\n\nFuck, that\'s elegant.
| 1
| 0
|
[]
| 2
|
surface-area-of-3d-shapes
|
Simplest intutuive sol : 8s and 7.2M
|
simplest-intutuive-sol-8s-and-72m-by-pri-fu6s
|
\nclass Solution {\npublic:\n int surfaceArea(vector<vector<int>>& grid) {\n int sum=0,a;\n for(int i=0;i<grid.size();i++){\n for(in
|
Prinzu
|
NORMAL
|
2020-03-28T21:15:14.223275+00:00
|
2020-03-28T21:15:14.223330+00:00
| 63
| false
|
```\nclass Solution {\npublic:\n int surfaceArea(vector<vector<int>>& grid) {\n int sum=0,a;\n for(int i=0;i<grid.size();i++){\n for(int j=0;j<grid.size();j++){\n a=(grid[i][j]>1)? grid[i][j]-1:0;\n sum+=grid[i][j]*6-2*a;\n }\n }\n for(int i=0;i<grid.size();i++){\n for(int j=0;j+1<grid.size();j++){\n if(grid[i][j]>0 && grid[i][j+1]>0){\n sum-=2*min(grid[i][j],grid[i][j+1]);\n }\n }\n }\n for(int i=0;i<grid.size();i++){\n for(int j=0;j+1<grid.size();j++){\n if(grid[j][i]>0 && grid[j+1][i]>0){\n sum-=2*min(grid[j][i],grid[j+1][i]);\n }\n }\n }\n return sum;\n }\n};\n```
| 1
| 0
|
[]
| 0
|
surface-area-of-3d-shapes
|
Python3, 80ms, 96%, 100%, O(n^2)
|
python3-80ms-96-100-on2-by-love0991839-lfcd
|
\'\'\'\n\n\tclass Solution:\n\t\tdef surfaceArea(self, grid: List[List[int]]) -> int:\n\t\t\tres = 0\n\t\t\ttemp = float(\'inf\')\n\t\t\tfor i,r in enumerate(gr
|
love0991839
|
NORMAL
|
2020-03-05T06:05:47.388247+00:00
|
2020-03-05T06:05:47.388285+00:00
| 84
| false
|
\'\'\'\n\n\tclass Solution:\n\t\tdef surfaceArea(self, grid: List[List[int]]) -> int:\n\t\t\tres = 0\n\t\t\ttemp = float(\'inf\')\n\t\t\tfor i,r in enumerate(grid):\n\t\t\t\tif i > 0:\n\t\t\t\t\tres -= self.TwoRow(grid[i-1], grid[i])\n\t\t\t\tfor j,num in enumerate(r):\n\t\t\t\t\tif num != 0:\n\t\t\t\t\t\tres += (num*4)+2\n\t\t\t\t\tif j > 0:\n\t\t\t\t\t\tres -= min(temp, num)*2\n\t\t\t\t\ttemp = num\n\t\t\treturn res\n\n\t\tdef TwoRow(self, x,y):\n\t\t\treturn sum(map(lambda a,b: min(a,b), x, y))*2\n\'\'\'\n
| 1
| 0
|
[]
| 0
|
surface-area-of-3d-shapes
|
Python3: Faster than 90.64%, less than 100.00%. A little wordy but easy to understand
|
python3-faster-than-9064-less-than-10000-cpe2
|
The idea here is to focus on each kind of surface individually. There are 6 kinds:\n\n1. bottom\n2. top\n3. corner\n4. edge\n5. row-top-edge\n6. column-top-edg
|
jcravener
|
NORMAL
|
2020-02-13T23:03:46.996382+00:00
|
2020-02-13T23:03:46.996428+00:00
| 70
| false
|
The idea here is to focus on each kind of surface individually. There are 6 kinds:\n\n1. bottom\n2. top\n3. corner\n4. edge\n5. row-top-edge\n6. column-top-edge\n\n```\nclass Solution:\n def surfaceArea(self, grid: List[List[int]]) -> int:\n r = []\n N = len(grid)\n bottom = 0\n top = 0\n corner = 0\n edge = 0\n redge = 0\n cedge = 0\n\n for i in range(len(grid)):\n \n for j in range(len(grid[i])):\n if grid[i][j] > 0:\n bottom += 1\n\n if i == 0 or i == N - 1:\n if j == 0 or j == N - 1:\n corner += grid[i][j]*2\n else:\n edge += grid[i][j]\n \n if j == 0 or j == N - 1:\n if i > 0 and i < N -1:\n edge += grid[i][j]\n\n if j > 0 and j < N:\n redge += abs(grid[i][j] - grid[i][j-1])\n if i > 0 and i < N:\n cedge += abs(grid[i][j] - grid[i-1][j])\n \n #--corner case:\n if N == 1:\n corner *= 2\n\n top = bottom\n r = [bottom, top, corner, edge, redge, cedge]\n \n return sum(r)\n\n```
| 1
| 0
|
[]
| 0
|
surface-area-of-3d-shapes
|
Python 3 solution (beats 98.87%)
|
python-3-solution-beats-9887-by-ye15-4x2e
|
Algo: \n1) xy projection - twice of number of non-zero entries \n2) yz projection - sum of absolute difference of continuous elements in a row \n3) zx projectio
|
ye15
|
NORMAL
|
2019-10-03T14:40:12.547381+00:00
|
2019-10-03T14:40:12.547429+00:00
| 149
| false
|
Algo: \n1) xy projection - twice of number of non-zero entries \n2) yz projection - sum of absolute difference of continuous elements in a row \n3) zx projection - sum of absolute difference of continuous elements in a column\n\nDefine a (lambda) function which computes sum of absolute difference of adjacent element in a list, and apply it to rows and columns of matrix. \n```\nclass Solution:\n def surfaceArea(self, grid: List[List[int]]) -> int:\n \n func = lambda v: v[0] + sum(abs(v[i]-v[i-1]) for i in range(1, len(v))) + v[-1]\n \n xy = sum(map(bool, sum(grid, []))) * 2\n yz = sum(func(row) for row in grid)\n zx = sum(func(col) for col in zip(*grid))\n \n return xy + yz + zx \n```
| 1
| 0
|
['Python3']
| 0
|
surface-area-of-3d-shapes
|
Java, foolproof, 16 lines solution with simple explanation
|
java-foolproof-16-lines-solution-with-si-l48p
|
Every tower with height greater than 1 will contribute 6 faces for the first cube; every cube after the first will add 4 more faces because there is one face th
|
canadianczar
|
NORMAL
|
2019-07-25T00:37:19.006747+00:00
|
2019-07-25T00:47:00.880973+00:00
| 157
| false
|
Every tower with height greater than 1 will contribute 6 faces for the first cube; every cube after the first will add 4 more faces because there is one face that touches every two adjacent cubes that will not contribute to surface area.\nEvery tower that borders with adjacent towers in each direction, up, down left, right, will have Math.min(tower_height, adjacent_tower_height) faces hidden, thus not contribute to surface area; this will be accounted for by subtracting Math.min(tower_height, adjacent_tower_height) from surface area twice, once for tower, once for adjacent_tower, in their respective loop iterations. \nIf this explanation makes more sense to you please leave a thumbs up ; )\n```\nclass Solution {\n public int surfaceArea(int[][] grid) {\n int area = 0;\n for (int i = 0; i < grid.length; i++) {\n for (int j = 0; j < grid[0].length; j++) {\n int h = grid[i][j];\n if(h>=1) {\n area += (h - 1) * 4 + 6;\n if(i-1>=0 && grid[i-1][j]!=0) area -= Math.min(h, grid[i-1][j]);\n if(i+1<grid.length && grid[i+1][j]!=0) area -= Math.min(h, grid[i+1][j]);\n if(j-1>=0 && grid[i][j-1]!=0) area -= Math.min(h, grid[i][j-1]);\n if(j+1<grid[0].length && grid[i][j+1]!=0) area -= Math.min(h, grid[i][j+1]);\n }\n }\n }\n return area;\n }\n}
| 1
| 0
|
[]
| 0
|
surface-area-of-3d-shapes
|
Java explainable solution
|
java-explainable-solution-by-zheyuan_fu-cui4
|
cubes counts cubes in the case;\nupdown counts the number of surfaces needed to be excluded for vertically placed cubes; each two cubes should merge two surface
|
zheyuan_fu
|
NORMAL
|
2019-04-29T10:28:08.096576+00:00
|
2019-04-29T10:28:08.096605+00:00
| 77
| false
|
cubes counts cubes in the case;\nupdown counts the number of surfaces needed to be excluded for vertically placed cubes; each two cubes should merge two surfaces;\nneighbors counts the number of surfaces need to be excluded for horizontally placed cubes;\n```\n\tpublic int surfaceArea(int[][] grid) {\n if(grid == null || grid.length == 0) return 0;\n\n int cubes = 0, neighbors = 0, updown = 0;\n for(int i = 0; i < grid.length; i ++) {\n for(int j = 0; j < grid[0].length; j ++) {\n if(grid[i][j] > 0){\n cubes += grid[i][j];\n updown += Math.max(grid[i][j] - 1, 0);\n }\n if(i < grid.length - 1) {\n neighbors += Math.min(grid[i + 1][j], grid[i][j]);\n }\n if(j < grid[0].length - 1) {\n neighbors += Math.min(grid[i][j + 1], grid[i][j]);\n }\n }\n }\n return cubes * 6 - neighbors * 2 - updown * 2;\n }\n\t\n\t
| 1
| 0
|
[]
| 0
|
surface-area-of-3d-shapes
|
Java easy to understand with explaination. faster than 99%
|
java-easy-to-understand-with-explainatio-jkq5
|
If only 1 cube is present at 1 index, surface area =6\nif 2 cubes are present, surface area = 12-2(overlapping area) = 10\nIf 3 cubes are present, surface area
|
viveklad_27
|
NORMAL
|
2019-02-24T17:52:49.534682+00:00
|
2019-02-24T17:52:49.534718+00:00
| 116
| false
|
If only 1 cube is present at 1 index, surface area =6\nif 2 cubes are present, surface area = 12-2(overlapping area) = 10\nIf 3 cubes are present, surface area = 18-4(overlapping area) = 14\n\nHence if n cubes are present, surface area= 4n+2 ... derived by looking at the above values.\n\nNow we have to remove common area of adjacent blocks.\n\nHence, if a block of height 2 has block of height 1 adjacent to it, we subtract 1 from count. (ie minimum of the heights of these two ie 1 in this case)\nSimilarly when we come across the same block of height 1 again in loop, it will have height 2 block adjacent to it. Again minimum will be subtracted(ie 1 in this case).\n\nHence overall, the 2 common areas are removed.\nSimilar is applied to all blocks and their adjacents in all 4 directions. For the boundary blocks, it is applied whereever applicable.\n\n```\npublic int surfaceArea(int[][] grid)\n {\n int count=0;\n for(int i=0;i<grid.length;i++)\n {\n for(int j=0;j<grid[i].length;j++)\n {\n if(grid[i][j]!=0)\n count=count+ (grid[i][j]*4 +2);\n if(i<grid.length-1 && i>=0)\n count= count - Math.min(grid[i+1][j],grid[i][j]);\n if(j<grid[i].length-1 && j>=0)\n count = count - Math.min(grid[i][j], grid[i][j+1]);\n if(i>0)\n count = count - Math.min(grid[i][j],grid[i-1][j]);\n if(j>0)\n count = count - Math.min(grid[i][j],grid[i][j-1]);\n \n \n }\n }\n return count;\n \n }
| 1
| 0
|
[]
| 0
|
surface-area-of-3d-shapes
|
rust 0ms 2.7MB
|
rust-0ms-27mb-by-michaelscofield-r0bc
|
\nimpl Solution {\n pub fn surface_area(grid: Vec<Vec<i32>>) -> i32 {\n let rows = grid.len();\n let cols = grid[0].len();\n let mut sur
|
michaelscofield
|
NORMAL
|
2019-02-14T07:31:29.506364+00:00
|
2019-02-14T07:31:29.506404+00:00
| 69
| false
|
```\nimpl Solution {\n pub fn surface_area(grid: Vec<Vec<i32>>) -> i32 {\n let rows = grid.len();\n let cols = grid[0].len();\n let mut surfaces = 0;\n for (i, row) in grid.iter().enumerate() {\n for (j, h) in row.iter().enumerate() {\n let h = *h;\n // bottom and top\n if h > 0 {\n surfaces += 2;\n }\n\n // up and down\n if i == 0 {\n surfaces += h;\n } else if grid[i - 1][j] < h {\n surfaces += h - grid[i - 1][j];\n }\n if i == rows - 1 {\n surfaces += h;\n } else if grid[i + 1][j] < h {\n surfaces += h - grid[i + 1][j];\n }\n\n // left and right\n if j == 0 {\n surfaces += h;\n } else if grid[i][j - 1] < h {\n surfaces += h - grid[i][j - 1];\n }\n if j == cols - 1 {\n surfaces += h;\n } else if grid[i][j + 1] < h {\n surfaces += h - grid[i][j + 1];\n }\n }\n }\n surfaces\n }\n}\n```
| 1
| 0
|
[]
| 0
|
surface-area-of-3d-shapes
|
JS, One-Pass solution, O(1) Space complexity solution
|
js-one-pass-solution-o1-space-complexity-bqi1
|
\nconst surfaceArea = grid => {\n let total = 0, n = grid.length;\n \n for (let i = 0; i < n; i++) {\n for (let j = 0; j < n; j++) {\n
|
ivschukin
|
NORMAL
|
2019-01-28T17:48:10.059449+00:00
|
2019-01-28T17:48:10.059493+00:00
| 106
| false
|
```\nconst surfaceArea = grid => {\n let total = 0, n = grid.length;\n \n for (let i = 0; i < n; i++) {\n for (let j = 0; j < n; j++) {\n let v = grid[i][j];\n let area = v === 0 ? 0 : 2;\n \n if (i === 0) { area += v; }\n else { area += Math.max(0, v - grid[i - 1][j]); }\n \n if (j === 0) { area += v; }\n else { area += Math.max(0, v - grid[i][j - 1]); }\n \n if (i + 1 === n) { area += v; }\n else { area += Math.max(0, v - grid[i + 1][j]); }\n \n if (j + 1 === n) { area += v; }\n else { area += Math.max(0, v - grid[i][j + 1]); }\n \n total += area;\n }\n }\n \n return total;\n};\n```
| 1
| 0
|
[]
| 0
|
surface-area-of-3d-shapes
|
Java concise solution with explanation
|
java-concise-solution-with-explanation-b-phzr
|
The trick is we always compute the net difference between current stack with stack in next row and next col if possible, never recompute previous stacks.\n\ncla
|
kinsapoon
|
NORMAL
|
2018-12-03T18:49:17.744025+00:00
|
2018-12-03T18:49:17.744069+00:00
| 173
| false
|
The trick is we always compute the net difference between current stack with stack in next row and next col if possible, never recompute previous stacks.\n```\nclass Solution {\n public int surfaceArea(int[][] grid) {\n int res = 0;\n for (int i = 0;i < grid.length;i++)\n for (int j = 0;j < grid[0].length;j++)\n {\n\t\t\t\t//if there is a non zero stack, add top and bottom area\n if (grid[i][j] != 0)\n res += 2;\n\t\t\t\t//compute upmost stacks\n if (i == 0)\n res += grid[i][j];\n\t\t\t\t//compute leftmost stacks\n if (j == 0)\n res += grid[i][j];\n\t\t\t\t//compute bottom stacks\n if (i == grid.length - 1)\n res += grid[i][j];\n\t\t\t\t//compute rightmost stacks\n if (j == grid[0].length - 1)\n res += grid[i][j];\n\t\t\t\t//compute stack in next row if possible\n if (i < grid.length - 1)\n res += Math.abs(grid[i][j] - grid[i + 1][j]);\n\t\t\t\t//compute stack in next column if possible\n if (j < grid[0].length - 1)\n res += Math.abs(grid[i][j] - grid[i][j + 1]);\n }\n return res;\n }\n}\n```
| 1
| 0
|
[]
| 1
|
surface-area-of-3d-shapes
|
C++ Solution easy understand
|
c-solution-easy-understand-by-jokerlovea-vg9j
|
All areas = surface + combined area\nso we have surface = 6 * total_count - 2 * combined_count\n\nclass Solution {\npublic:\n int surfaceArea(vector<vector<i
|
jokerloveallen
|
NORMAL
|
2018-11-13T03:55:05.360830+00:00
|
2018-11-13T03:55:05.360875+00:00
| 276
| false
|
All areas = surface + combined area\nso we have surface = 6 * total_count - 2 * combined_count\n```\nclass Solution {\npublic:\n int surfaceArea(vector<vector<int>>& grid) {\n int total{0}, combined{0}, len{grid.size()};\n for(int i = 0; i< len; i++)\n for(int j = 0; j< len; j++)\n if(grid[i][j]){\n total += grid[i][j];\n combined += grid[i][j] - 1;\n if(i > 0) combined += min(grid[i-1][j],grid[i][j]);\n if(j > 0) combined += min(grid[i][j-1],grid[i][j]);\n }\n return 6*total - 2*combined;\n }\n};\n```
| 1
| 0
|
[]
| 1
|
surface-area-of-3d-shapes
|
Javascript level traversal, easy to understand - 56-60 ms
|
javascript-level-traversal-easy-to-under-2p4p
|
Not fastest solution (60ms), but all you need is to check neighbours left/right/up/down + (top or bottom) * 2.\n\nvar surfaceArea = function(grid) {\n var co
|
eforce
|
NORMAL
|
2018-10-02T08:46:13.472913+00:00
|
2018-10-02T08:46:13.472958+00:00
| 125
| false
|
Not fastest solution (60ms), but all you need is to check neighbours left/right/up/down + (top or bottom) * 2.\n```\nvar surfaceArea = function(grid) {\n var count = 0;\n var lastIndex = grid.length - 1;\n\n for (var i = 0; i <= lastIndex; i++) {\n for (var j = 0; j <= lastIndex; j++) {\n if (grid[i][j] <= 0) {\n continue;\n }\n\n count += 2;\n \n for (var level = 0; level < grid[i][j]; level++) {\n if (i === 0 || grid[i - 1][j] <= level) {\n count++;\n }\n if (i === lastIndex || grid[i + 1][j] <= level) {\n count++;\n }\n if (j === 0 || grid[i][j - 1] <= level) {\n count++;\n }\n if (j === lastIndex || grid[i][j + 1] <= level) {\n count++;\n }\n }\n }\n }\n \n return count;\n};\n```\n\nOr we can make it 56 ms by removing level traversal logic:\n```\nvar surfaceArea = function(grid) {\n var count = 0;\n var lastIndex = grid.length - 1;\n\n for (var i = 0; i <= lastIndex; i++) {\n for (var j = 0; j <= lastIndex; j++) {\n if (grid[i][j] === 0) {\n continue;\n }\n\n count += 2;\n count += i === 0 ? grid[i][j] : Math.max(0, grid[i][j] - grid[i - 1][j]);\n count += i === lastIndex ? grid[i][j] : Math.max(0, grid[i][j] - grid[i + 1][j]);\n count += j === 0 ? grid[i][j] : Math.max(0, grid[i][j] - grid[i][j - 1]);\n count += j === lastIndex ? grid[i][j] : Math.max(0, grid[i][j] - grid[i][j + 1]);\n }\n }\n \n return count;\n};\n```
| 1
| 0
|
[]
| 0
|
surface-area-of-3d-shapes
|
Java 2 Solutions & Comparison with 2D version of this problem
|
java-2-solutions-comparison-with-2d-vers-19np
|
----------------------- Let\'s first look at the 2D version of this problem 463. Island Perimeter -----------------------\nSoution 1 brute force\n * for each
|
meganlee
|
NORMAL
|
2018-09-08T05:28:33.440143+00:00
|
2018-09-08T05:28:33.440187+00:00
| 209
| false
|
**----------------------- Let\'s first look at the `2D version` of this problem [463. Island Perimeter](https://leetcode.com/problems/island-perimeter/description/) -----------------------**\n**Soution 1 brute force**\n * for `each cell with non zero value:` \n * for each `direction:` if the next cell is `out boundary` or is `0`, we add `1` to res\n```\nclass Solution {\n static final int[][] dirs = new int[][] {{0,-1}, {-1,0}, {0,1}, {1,0}};\n public int islandPerimeter(int[][] grid) { \n int perimeter = 0;\n for (int r = 0; r < grid.length; r++) {\n for (int c = 0; c < grid[0].length; c++) {\n if (grid[r][c] == 1) {\n for (int[] dir : dirs) {\n int nr = r + dir[0], nc = c + dir[1];\n if (offBoundary(nr, nc, grid) || grid[nr][nc] == 0) perimeter++;\n }\n }\n }\n }\n return perimeter;\n }\n \n private boolean offBoundary(int r, int c, int[][] grid) {\n return r < 0 || r >= grid.length || c < 0 || c >= grid[0].length;\n }\n}\n```\n\n**Soution 2 accumulate and retract**\n * we traverse each cell row by row, col by col and `update the result dynamically`\n * for `each cell with non zero value`, let\'s first `accumulate` it\'s contribution to total perimeter: `res += 4`\n * if `up cell is non zero`, we do retraction: `res -= 2`\n * if `left cell is non zero`, we do retraction: `res -= 2`\n \n\n```\nclass Solution {\n public int islandPerimeter(int[][] grid) {\n int res = 0;\n for (int r = 0; r < grid.length; r++) {\n for (int c = 0; c < grid[0].length; c++) {\n if (grid[r][c] == 1) {\n res += 4;\n if (r > 0 && grid[r - 1][c] == 1) res -= 2;\n if (c > 0 && grid[r][c - 1] == 1) res -= 2;\n }\n }\n }\n return res;\n }\n}\n```\n\n\n**-------- Now let\'s look at the this problem, which is exactly follow up as a `3D version` of [463. Island Perimeter](https://leetcode.com/problems/island-perimeter/description/) -----------------------**\nsimilarly\n**Soution 1 brute force**\n * for `each cell with non zero value:` res += `2 (1 for top, 1 for bottom)`\n * for each `direction/side:` we get a `nextHeight`, if `curHeight > nextHeight` we add exposed area: `curHeight - nextHeight` to res \n```\nclass Solution {\n static final int[][] dirs = new int[][] {{0,-1}, {-1,0}, {0,1}, {1,0}};\n public int surfaceArea(int[][] grid) {\n int area = 0;\n for (int r = 0; r < grid.length; r++) {\n for (int c = 0; c < grid[0].length; c++) {\n if (grid[r][c] != 0) { // only consider NON-ZERO cubes\n int curHeight = grid[r][c];\n area += 2; // top & bottom\n for (int[] dir : dirs) {\n int nr = r + dir[0], nc = c + dir[1];\n int nextHeight = getHeight(nr, nc, grid);\n area += (curHeight > nextHeight) ? curHeight - nextHeight : 0; // side surface\n }\n }\n }\n }\n return area;\n }\n \n private int getHeight(int r, int c, int[][] grid) {\n if (r < 0 || r >= grid.length || c < 0 || c >= grid[0].length) return 0; // out of bounds\n else return grid[r][c];\n }\n```\n\n**Soution 2 accumulate and retract**\n * we traverse each cell row by row, col by col and `update the result dynamically`\n * for `each cell with non zero value`, let\'s first `accumulate` it\'s contribution to total area: `res += 2 + 4 * side`\n * if `up cell is non zero`, we do retraction: `res -= 2 * min(upHeight, curHeight)`\n * if `left cell is non zero`, we do retraction: `res -= 2 * min(leftHeight, curHeight)`\n\n```\nclass Solution {\n static final int[][] dirs = new int[][] {{0,-1}, {-1,0}, {0,1}, {1,0}};\n public int surfaceArea(int[][] grid) {\n int res = 0;\n for (int r = 0; r < grid.length; r++) {\n for (int c = 0; c < grid[0].length; c++) {\n if (grid[r][c] != 0) {\n res += 2 + 4 * grid[r][c];\n if (r > 0 && grid[r - 1][c] != 0) res -= 2 * Math.min(grid[r][c], grid[r - 1][c]); // up\n if (c > 0 && grid[r][c - 1] != 0) res -= 2 * Math.min(grid[r][c], grid[r][c - 1]); // left\n }\n }\n }\n return res;\n }\n}\n```\n
| 1
| 0
|
[]
| 0
|
surface-area-of-3d-shapes
|
Incredibly simple python solution
|
incredibly-simple-python-solution-by-col-4sks
|
\nsum = 0;\n for x in range(len(grid)):\n for y in range(len(grid)):\n if(grid[x][y]):\n sum = sum + 2 + (4*
|
coletyl
|
NORMAL
|
2018-08-27T23:14:58.108377+00:00
|
2018-09-01T13:13:46.174958+00:00
| 268
| false
|
```\nsum = 0;\n for x in range(len(grid)):\n for y in range(len(grid)):\n if(grid[x][y]):\n sum = sum + 2 + (4*grid[x][y])\n if(x>0):\n sum = sum - (grid[x-1][y] if grid[x][y]>=grid[x-1][y] else grid[x][y]);\n if(y>0):\n sum = sum - (grid[x][y-1] if grid[x][y]>=grid[x][y-1] else grid[x][y]);\n if(y<len(grid)-1):\n sum = sum - (grid[x][y+1] if grid[x][y]>=grid[x][y+1] else grid[x][y]);\n if(x<len(grid)-1):\n sum = sum - (grid[x+1][y] if grid[x][y]>=grid[x+1][y] else grid[x][y]);\n return sum\n\t\t\t\t```
| 1
| 0
|
[]
| 0
|
surface-area-of-3d-shapes
|
Concise Java Solution
|
concise-java-solution-by-shreyansh94-ayae
|
\nclass Solution {\n public int surfaceArea(int[][] grid) {\n int row = grid.length, col = grid[0].length ;\n int top = 0, l=0;\n for(in
|
shreyansh94
|
NORMAL
|
2018-08-27T17:51:48.013321+00:00
|
2018-08-27T17:52:58.924814+00:00
| 108
| false
|
```\nclass Solution {\n public int surfaceArea(int[][] grid) {\n int row = grid.length, col = grid[0].length ;\n int top = 0, l=0;\n for(int i = 0; i < row ; ++i){\n for(int j = 0; j < col ; ++j) {\n l += i==0 ? grid[i][j] : (int) Math.abs(grid[i][j] - grid[i-1][j]);\n if(i == row-1)l += grid[i][j];\n l += j==0 ? grid[i][j] : (int) Math.abs(grid[i][j] - grid[i][j-1]);\n if(j == col-1)l += grid[i][j];\n top += grid[i][j] > 0 ? 1 : 0;\n }\n }\n return 2*(top)+l;\n }\n}\n```\n\nA bit more Concise\n\n```\nclass Solution {\n public int surfaceArea(int[][] grid) {\n int r = grid.length, top = 0, l=0;\n for(int i = 0; i < r ; ++i)\n for(int j = 0; j < r ; ++j) {\n l += (i==0 ? grid[i][j] : (int) Math.abs(grid[i][j] - grid[i-1][j])) + ((i == r-1) ? grid[i][j] : 0) + \n (j==0 ? grid[i][j] : (int) Math.abs(grid[i][j] - grid[i][j-1])) + ((j == r-1) ? grid[i][j] : 0);\n top += grid[i][j] > 0 ? 1 : 0;\n }\n return 2*(top)+l;\n }\n}\n```
| 1
| 0
|
[]
| 0
|
surface-area-of-3d-shapes
|
Easy to understand Intuitive Approach C++
|
easy-to-understand-intuitive-approach-c-txq8q
|
\n int surfaceArea(vector>& grid) {\n \n int ans=0;\n int m=grid.size();\n int n=grid[0].size();\n \n if(m==0 || n=
|
genesis99
|
NORMAL
|
2018-08-26T21:30:53.449330+00:00
|
2018-08-26T21:30:53.449375+00:00
| 133
| false
|
\n int surfaceArea(vector<vector<int>>& grid) {\n \n int ans=0;\n int m=grid.size();\n int n=grid[0].size();\n \n if(m==0 || n==0)\n return 0;\n \n if(m==1 && n==1)\n return grid[0][0]*4+2;\n \n int dx[]={-1,0,1,0};\n int dy[]={0,1,0,-1};\n \n for(int i=0;i<m;i++)\n for(int j=0;j<n;j++)\n {\n if(grid[i][j]==0)\n continue;\n \n if((i==0 && j==n-1) || (i==m-1 && j==0) || (i==0 && j==0) || (i==m-1 && j==n-1))\n ans+=2*grid[i][j];\n else\n if(i==0 || j==0 || i==m-1 || j==n-1)\n ans+=grid[i][j];\n \n for(int k=0;k<4;k++)\n { \n int nx=i+dx[k];\n int ny=j+dy[k];\n if(nx>=0 && ny>=0 && nx<m && ny<n)\n ans+=(grid[nx][ny]-grid[i][j]>=0 ? 0 : grid[i][j]-grid[nx][ny]);\n }\n ans+=2;\n }\n return ans;\n }
| 1
| 0
|
[]
| 0
|
surface-area-of-3d-shapes
|
Java straightforward solution
|
java-straightforward-solution-by-wangzi6-zij0
|
\nclass Solution {\n public int surfaceArea(int[][] grid) {\n int result = 0, n = grid.length;\n for (int i = 0; i < n; i++) {\n for
|
wangzi6147
|
NORMAL
|
2018-08-26T03:12:53.695056+00:00
|
2018-08-26T03:12:53.695107+00:00
| 200
| false
|
```\nclass Solution {\n public int surfaceArea(int[][] grid) {\n int result = 0, n = grid.length;\n for (int i = 0; i < n; i++) {\n for (int j = 0; j < n; j++) {\n if (grid[i][j] == 0) {\n continue;\n }\n int preI = i == 0 ? 0 : grid[i - 1][j];\n int preJ = j == 0 ? 0 : grid[i][j - 1];\n int nextI = i == n - 1 ? 0 : grid[i + 1][j];\n int nextJ = j == n - 1 ? 0 : grid[i][j + 1];\n result += 2 + Math.max(0, grid[i][j] - preI) + Math.max(0, grid[i][j] - preJ) +\n Math.max(0, grid[i][j] - nextI) + Math.max(0, grid[i][j] - nextJ);\n }\n }\n return result;\n }\n}\n```
| 1
| 0
|
[]
| 0
|
surface-area-of-3d-shapes
|
Swift💯 FP
|
swift-fp-by-upvotethispls-aegs
|
FP (accepted answer)
Needed an inline function to avoid compilation TLE
|
UpvoteThisPls
|
NORMAL
|
2025-04-10T23:42:30.412148+00:00
|
2025-04-10T23:42:30.412148+00:00
| 1
| false
|
**FP (accepted answer)**
Needed an inline function to avoid compilation TLE
```
class Solution {
func surfaceArea(_ grid: [[Int]]) -> Int {
product(grid.indices, grid[0].indices)
.map { r, c in
grid[r][c] == 0 ? 0 : {
var v = grid[r][c] * 4 + 2
v -= min(grid[r][c], r > 0 ? grid[r-1][c] : 0) * 2
v -= min(grid[r][c], c > 0 ? grid[r][c-1] : 0) * 2
return v
}()
}
.reduce(0,+)
}
}
```
| 0
| 0
|
['Swift']
| 0
|
surface-area-of-3d-shapes
|
ans += max(0, grid[i][j] - grid[nx][ny]) ...
|
ans-max0-gridij-gridnxny-by-victor-smk-iuqn
| null |
Victor-SMK
|
NORMAL
|
2025-04-03T18:18:02.936558+00:00
|
2025-04-03T18:18:02.936558+00:00
| 2
| false
|
```swift []
class Solution {
func surfaceArea(_ grid: [[Int]]) -> Int {
var ans = 0
let sm = [(-1,0),(1,0),(0,-1),(0,1)]
for i in 0..<grid.count{
for j in 0..<grid[0].count where grid[i][j] != 0 {
for (dx,dy) in sm {
let nx = i + dx
let ny = j + dy
if nx >= 0, nx < grid.count, ny >= 0, ny < grid[0].count {
ans += max(0, grid[i][j] - grid[nx][ny])
} else {
ans += grid[i][j]
}
}
ans += 2
}
}
return ans
}
}
```
| 0
| 0
|
['Array', 'Math', 'Swift', 'Python', 'Python3']
| 0
|
surface-area-of-3d-shapes
|
Java solution
|
java-solution-by-java_developer-o4pa
| null |
Java_Developer
|
NORMAL
|
2025-02-13T09:30:25.092668+00:00
|
2025-02-13T09:30:25.092668+00:00
| 14
| false
|
```java []
class Solution {
public int surfaceArea(int[][] grid) {
int area = 0;
for (int r = 0; r < grid.length; r++) {
for (int c = 0; c < grid.length; c++) {
if (grid[r][c] == 0) {
continue;
}
area += 2;
if (r > 0) {
area += Math.max(grid[r][c] - grid[r - 1][c], 0);
} else {
area += grid[r][c];
}
if (r < grid.length - 1) {
area += Math.max(grid[r][c] - grid[r + 1][c], 0);
} else {
area += grid[r][c];
}
if (c > 0) {
area += Math.max(grid[r][c] - grid[r][c - 1], 0);
} else {
area += grid[r][c];
}
if (c < grid.length - 1) {
area += Math.max(grid[r][c] - grid[r][c + 1], 0);
} else {
area += grid[r][c];
}
}
}
return area;
}
}
```
| 0
| 0
|
['Java']
| 0
|
surface-area-of-3d-shapes
|
Surface Area of 3D Shapes (C++)
|
surface-area-of-3d-shapes-c-by-sarwar-93-j9ex
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
Sarwar-93395_Leetcode
|
NORMAL
|
2025-01-31T03:32:08.244286+00:00
|
2025-01-31T03:32:08.244286+00:00
| 11
| false
|
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int surfaceArea(vector<vector<int>>& grid) {
int n = grid.size();
int surfaceArea = 0;
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
if (grid[i][j] > 0) {
surfaceArea += 2;
surfaceArea += (i == 0) ? grid[i][j] : max(0, grid[i][j] - grid[i - 1][j]);
surfaceArea += (i == n - 1) ? grid[i][j] : max(0, grid[i][j] - grid[i + 1][j]);
surfaceArea += (j == 0) ? grid[i][j] : max(0, grid[i][j] - grid[i][j - 1]);
surfaceArea += (j == n - 1) ? grid[i][j] : max(0, grid[i][j] - grid[i][j + 1]);
}
}
}
return surfaceArea;
}
};
```
| 0
| 0
|
['C++']
| 0
|
surface-area-of-3d-shapes
|
Easy solution in java
|
easy-solution-in-java-by-shaileshlodhi56-ck5q
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
shaileshlodhi56
|
NORMAL
|
2025-01-24T19:30:57.452757+00:00
|
2025-01-24T19:30:57.452757+00:00
| 11
| false
|
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int surfaceArea(int[][] grid) {
int sum = 0;
int n = grid.length;
int m = grid[0].length;
for(int i =0; i < n ; i ++){
for(int j =0; j < m ;j++){
if(grid[i][j] > 0){
sum += 2 + 4 * grid[i][j];
}
if( i > 0 ){
sum -= 2 * Math.min(grid[i][j] , grid[i -1][j]);
}
if( j > 0 ){
sum -= 2 * Math.min(grid[i][j] , grid[i][j -1]);
}
}
}
return sum;
}
}
```
| 0
| 0
|
['Java']
| 0
|
surface-area-of-3d-shapes
|
Easy | Intuitive | Elegant Python solution
|
easy-intuitive-elegant-python-solution-b-yl6h
|
IntuitionThe idea is to calculate the number of faces exposed in each direction N, E, W, S.ApproachComplexity
Time complexity: O(n^2)
Space complexity: O(1)
Co
|
lunaaashi
|
NORMAL
|
2025-01-12T20:29:18.405990+00:00
|
2025-01-12T20:32:26.126121+00:00
| 6
| false
|
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
The idea is to calculate the number of faces exposed in each direction N, E, W, S.
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity: O(n^2)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def surfaceArea(self, grid: List[List[int]]) -> int:
n = len(grid)
N, E, W, S = 0, 0, 0, 0
for i in range(n):
N += grid[0][i]
E += grid[i][n-1]
W += grid[i][0]
S += grid[n-1][i]
for c in range(n):
for r in range(1, n):
if grid[r-1][c] < grid[r][c]:
N += grid[r][c] - grid[r-1][c]
if grid[r-1][c] > grid[r][c]:
S += grid[r-1][c] - grid[r][c]
for r in range(n):
for c in range(1, n):
if grid[r][c-1] < grid[r][c]:
W += grid[r][c] - grid[r][c-1]
if grid[r][c-1] > grid[r][c]:
E += grid[r][c-1] - grid[r][c]
T = 0
for r in range(n):
for c in range(n):
if grid[r][c]:
T += 1
return N+E+W+S+T+T
```
| 0
| 0
|
['Array', 'Math', 'Geometry', 'Matrix', 'Python3']
| 0
|
surface-area-of-3d-shapes
|
Easiest if-Else solution (beats 80%).
|
easiest-if-else-solution-beats-80-by-pra-spjb
|
IntuitionThe key to solving this problem is understanding how the cubes overlap with each other and how their faces contribute to the total surface area. For ea
|
prav06
|
NORMAL
|
2025-01-12T16:08:34.318675+00:00
|
2025-01-12T16:08:34.318675+00:00
| 9
| false
|
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
The key to solving this problem is understanding how the cubes overlap with each other and how their faces contribute to the total surface area. For each cube at position (i, j) in the grid, we can initially assume that it contributes a surface area of 4 * grid[i][j] + 2:
4 * grid[i][j]: The four vertical sides of the cube (each contributing 1 square unit of area per unit height).
2: The top and bottom faces of the cube, each contributing 1 square unit of area.
However, if a neighboring cube exists (up, down, left, or right), part of the surface is "lost" as it is covered by the neighboring cube. Therefore, for each neighboring cube, we subtract the minimum height of the two cubes in contact with each other from the total area to account for the overlap.
# Approach
<!-- Describe your approach to solving the problem. -->
Initial Assumptions: Start by assuming that every cube contributes 4 * grid[i][j] + 2 square units of surface area. This represents all the vertical and horizontal faces.
Handle Neighboring Cubes: For each cube, check its neighbors:
If a neighbor exists, reduce the exposed area between the two cubes by the minimum of their heights. This ensures that the overlapping portion of the cubes is not counted multiple times.
Iterate through the grid: For each cell in the grid, calculate the surface area based on the above logic, adjusting for any neighboring cubes.
Return the Total Surface Area: Sum up the surface areas of all cubes after accounting for overlaps.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
Time Complexity: The solution iterates over each cell in the grid once. For each cell, it checks up to 4 neighboring cells. Therefore, the overall time complexity is O(n^2), where n is the size of the grid (i.e., grid.length).
Each operation inside the loops (comparisons and arithmetic) is constant time, so they do not affect the overall complexity.
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
Space Complexity: The algorithm uses a constant amount of extra space (aside from the input grid). The variables total, areaGained, and areaLost do not depend on the size of the input grid. Hence, the space complexity is O(1).
# Code
```java []
class Solution {
public int surfaceArea(int[][] grid) {
int total = 0;
int size = grid.length;
for (int i = 0; i < size; i++){
for (int j = 0; j < size; j++){
if (grid[i][j] == 0){
continue;
}
int areaGained = 4 * grid[i][j] + 2;
int areaLost = 0;
if (i - 1 >= 0){
areaLost += Math.min(grid[i][j], grid[i - 1][j]);
}
if (i + 1 < size){
areaLost += Math.min(grid[i][j], grid[i + 1][j]);
}
if (j - 1 >= 0){
areaLost += Math.min(grid[i][j], grid[i][j - 1]);
}
if (j + 1 < size){
areaLost += Math.min(grid[i][j], grid[i][j + 1]);
}
total += areaGained - areaLost;
}
}
return total;
}
}
```
| 0
| 0
|
['Java']
| 0
|
surface-area-of-3d-shapes
|
892. Surface Area of 3D Shapes
|
892-surface-area-of-3d-shapes-by-g8xd0qp-7gps
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
G8xd0QPqTy
|
NORMAL
|
2025-01-01T10:17:25.401958+00:00
|
2025-01-01T10:17:25.401958+00:00
| 3
| false
|
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python []
class Solution(object):
def surfaceArea(self, grid):
total_area = 0
for i in range(len(grid)):
for j in range(len(grid[i])):
if grid[i][j] > 0:
total_area += 2 # Top and bottom
total_area += 4 * grid[i][j] # Sides
if i > 0:
total_area -= min(grid[i][j], grid[i-1][j]) * 2 # Subtract overlap with the cell above
if j > 0:
total_area -= min(grid[i][j], grid[i][j-1]) * 2 # Subtract overlap with the cell to the left
return total_area
```
| 0
| 0
|
['Python']
| 0
|
maximum-energy-boost-from-two-drinks
|
[Java/C++/Python] DP, O(1) Space
|
javacpython-dp-o1-space-by-lee215-nxgn
|
Explanation\nDP equations:\na[i] = max(A[i] + a[i - 1], b[i - 1])\nb[i] = max(B[i] + b[i - 1], a[i - 1])\n\na[i] means max energy in i + 1 hours ending with A\
|
lee215
|
NORMAL
|
2024-08-18T04:09:48.929171+00:00
|
2024-08-18T13:56:08.311083+00:00
| 1,325
| false
|
# **Explanation**\nDP equations:\n`a[i] = max(A[i] + a[i - 1], b[i - 1])`\n`b[i] = max(B[i] + b[i - 1], a[i - 1])`\n\n`a[i]` means max energy in `i + 1` hours ending with `A`\n`b[i]` means max energy in `i + 1` hours ending with `B`\n<br>\n\n# **Complexity**\nTime `O(n)`\nSpace `O(1)`\n<br>\n\n**Java**\n```java\n public long maxEnergyBoost(int[] A, int[] B) {\n long a0 = 0, a1 = 0, b0 = 0, b1 = 0, n = A.length;\n for (int i = 0; i < n; i++) {\n a1 = Math.max(a0 + A[i], b0);\n b1 = Math.max(b0 + B[i], a0);\n a0 = a1; b0 = b1;\n }\n return Math.max(a1, b1);\n }\n```\n\n**C++**\n```cpp\n long long maxEnergyBoost(vector<int>& A, vector<int>& B) {\n long long a0 = 0, a1 = 0, b0 = 0, b1 = 0, n = A.size();\n for (int i = 0; i < n; i++) {\n a1 = max(a0 + A[i], b0);\n b1 = max(b0 + B[i], a0);\n a0 = a1; b0 = b1;\n }\n return max(a1, b1);\n }\n```\n\n**Python**\n```py\n def maxEnergyBoost(self, A: List[int], B: List[int]) -> int:\n a = b = 0\n for i in range(len(A)):\n a, b = max(a + A[i], b), max(b + B[i], a)\n return max(a, b)\n```\n
| 26
| 6
|
[]
| 7
|
maximum-energy-boost-from-two-drinks
|
Recursion->Top Down-> Bottom UP | DP | Easy to understand
|
recursion-top-down-bottom-up-dp-easy-to-5hvse
|
RECURSION\n\nclass Solution {\n //Considering 0 indexed hours\n //drinkType = 0 ===> drink1\n //drinkType = 1 ===> drink2\n long solve(int[] drink1,
|
sudher
|
NORMAL
|
2024-08-18T04:02:24.377061+00:00
|
2024-08-18T04:10:01.406887+00:00
| 2,334
| false
|
## RECURSION\n```\nclass Solution {\n //Considering 0 indexed hours\n //drinkType = 0 ===> drink1\n //drinkType = 1 ===> drink2\n long solve(int[] drink1, int[] drink2, int currHour, int currDrinkType)\n {\n if (currHour >= drink1.length)\n return 0;\n \n long drinkBoost = (currDrinkType == 0)? drink1[currHour] : drink2[currHour];\n \n long noTypeSwitch = drinkBoost + solve(drink1, drink2, currHour + 1, currDrinkType);\n long typeSwitch = drinkBoost + solve(drink1, drink2, currHour + 2, 1 - currDrinkType);\n //if you switch types you need to skip next hour so (currHour + 2)\n //(1 - currDrinkType) switches the type (0 to 1) and (1 to 0)\n \n return Math.max(noTypeSwitch, typeSwitch);\n \n }\n public long maxEnergyBoost(int[] energyDrinkA, int[] energyDrinkB) \n {\n long a = solve(energyDrinkA, energyDrinkB, 0, 0);\n long b = solve(energyDrinkA, energyDrinkB, 0, 1);\n \n return Math.max(a, b);\n }\n}\n```\n\n## MEMOIZATION [TOP-DOWN]\n```\nclass Solution {\n //Considering 0 indexed hours\n //drinkType = 0 ===> drink1\n //drinkType = 1 ===> drink2\n long solve(int[] drink1, int[] drink2, long[][] dp, int currHour, int currDrinkType)\n {\n if (currHour >= drink1.length)\n return 0;\n if (dp[currDrinkType][currHour] != -1)\n return dp[currDrinkType][currHour];\n \n long drinkBoost = (currDrinkType == 0)? drink1[currHour] : drink2[currHour];\n \n long noTypeSwitch = drinkBoost + solve(drink1, drink2, dp, currHour + 1, currDrinkType);\n long typeSwitch = drinkBoost + solve(drink1, drink2, dp, currHour + 2, 1 - currDrinkType);\n\n return dp[currDrinkType][currHour] = Math.max(noTypeSwitch, typeSwitch);\n \n }\n public long maxEnergyBoost(int[] energyDrinkA, int[] energyDrinkB) \n {\n long[][] dp = new long[2][energyDrinkA.length];\n Arrays.fill(dp[0], -1);\n Arrays.fill(dp[1], -1);\n \n long a = solve(energyDrinkA, energyDrinkB, dp, 0, 0);\n long b = solve(energyDrinkA, energyDrinkB, dp, 0, 1);\n return Math.max(a, b);\n \n }\n}\n```\n\n## BOTTOM-UP DP\n```\nclass Solution {\n //Considering 0 indexed hours\n //drinkType = 0 ===> drink1\n //drinkType = 1 ===> drink2\n public long maxEnergyBoost(int[] drink1, int[] drink2) \n {\n int n = drink1.length;\n\t\t\n\t\t //dp[drinkType][hour]\n long[][] dp = new long[2][n];\n \n //in the last hour, for any given type we have only one option i.e to "DRINK"\n dp[0][n - 1] = drink1[n - 1];\n dp[1][n - 1] = drink2[n - 1];\n\n for (int currHour = n - 2; currHour >= 0; currHour--)\n {\n for (int currDrinkType = 0; currDrinkType <= 1; currDrinkType++)\n {\n long drinkBoost = (currDrinkType == 0)? drink1[currHour] : drink2[currHour];\n \n long noTypeSwitch = drinkBoost + dp[currDrinkType][currHour + 1];\n long typeSwitch = drinkBoost + ( (currHour + 2 >= n)? 0 : dp[1 - currDrinkType][currHour + 2] );\n \n dp[currDrinkType][currHour] = Math.max(noTypeSwitch, typeSwitch);\n }\n }\n return Math.max(dp[0][0], dp[1][0]);\n \n }\n}\n```
| 24
| 4
|
['Dynamic Programming', 'Java']
| 6
|
maximum-energy-boost-from-two-drinks
|
DP || O(1) space
|
dp-o1-space-by-fahad06-3nc3
|
Intution\n1. State Definition: Define the state of DP with two parameters:\n \n - Current Index: represents the position in the arrays where the decision
|
fahad_Mubeen
|
NORMAL
|
2024-08-18T04:11:21.244133+00:00
|
2024-08-18T04:15:59.968738+00:00
| 2,543
| false
|
# Intution\n1. **State Definition:** Define the state of DP with two parameters:\n \n - **Current Index:** represents the position in the arrays where the decision is being made.\n - **Last Choice:** indicates whether the last chosen energy boost was from array A or array B.\n\n2. **State Representation:** Use a DP table where `dp[i][curr]` represents the maximum energy boost achievable starting from index **i** with **curr** indicating the last choice:\n - `curr = 1:` The last boost was chosen from array A.\n - `curr = 0:` The last boost was chosen from array B.\n \n3. **Transition:** At each index:\n - If curr is 1 (last choice was A): Compute the maximum boost by either:\n - Continuing with array A (adding the current element from A).\n - Switching to array B.\n - If curr is 0 (last choice was B): Compute the maximum boost by either:\n - Continuing with array B (adding the current element from B).\n - Switching to array A. \n\n\n4. Finally compute the result by starting from index 0 and considering both possibilities (starting with A or B).\n\n# Top Down\n\n```C++ []\nclass Solution {\npublic:\n #define ll long long\n vector<vector<ll>> dp;\n ll f(vector<int>& A, vector<int>& B, int i, int curr) {\n if (i >= A.size()) return 0;\n if(dp[i][curr] != -1) return dp[i][curr];\n\n ll ans = 0;\n if(curr)\n ans = max(A[i] + f(A, B, i + 1, curr), f(A, B, i + 1, curr ^ 1));\n\n else\n ans = max(B[i] + f(A, B, i + 1, curr), f(A, B, i + 1, curr ^ 1));\n\n return dp[i][curr] = ans;\n }\n\n long long maxEnergyBoost(vector<int>& A, vector<int>& B){\n int n = A.size();\n dp.clear();\n dp.resize(n, vector<ll>(2, -1)); \n return max(f(A, B, 0, 1), f(A, B, 0, 0));\n }\n};\n```\n```Java []\nclass Solution {\n private long[][] dp;\n\n private long f(int[] A, int[] B, int i, int curr) {\n if (i >= A.length) return 0;\n if (dp[i][curr] != -1) return dp[i][curr];\n\n long ans = 0;\n if (curr == 1) {\n ans = Math.max(A[i] + f(A, B, i + 1, curr), f(A, B, i + 1, 1 - curr));\n } else {\n ans = Math.max(B[i] + f(A, B, i + 1, curr), f(A, B, i + 1, 1 - curr));\n }\n\n return dp[i][curr] = ans;\n }\n\n public long maxEnergyBoost(int[] energyDrinkA, int[] energyDrinkB) {\n int n = energyDrinkA.length;\n dp = new long[n][2];\n for (long[] row : dp) {\n Arrays.fill(row, -1);\n }\n return Math.max(f(energyDrinkA, energyDrinkB, 0, 1), f(energyDrinkA, energyDrinkB, 0, 0));\n }\n}\n\n```\n```Python3 []\nclass Solution:\n def __init__(self):\n self.dp = []\n \n def f(self, A: List[int], B: List[int], i: int, curr: int) -> int:\n if i >= len(A):\n return 0\n if self.dp[i][curr] != -1:\n return self.dp[i][curr]\n\n ans = 0\n if curr == 1:\n ans = max(A[i] + self.f(A, B, i + 1, curr), self.f(A, B, i + 1, 1 - curr))\n else:\n ans = max(B[i] + self.f(A, B, i + 1, curr), self.f(A, B, i + 1, 1 - curr))\n\n self.dp[i][curr] = ans\n return ans\n\n def maxEnergyBoost(self, energyDrinkA: List[int], energyDrinkB: List[int]) -> int:\n n = len(energyDrinkA)\n self.dp = [[-1] * 2 for _ in range(n)]\n return max(self.f(energyDrinkA, energyDrinkB, 0, 1), self.f(energyDrinkA, energyDrinkB, 0, 0))\n```\n\n# Bottom Up\n```C++ []\nclass Solution {\npublic:\n #define ll long long\n\n long long maxEnergyBoost(vector<int>& A, vector<int>& B) {\n int n = A.size();\n vector<vector<ll>> dp(n + 5, vector<ll>(2, 0));\n\n for(int i = n - 1; i >= 0; i--){ \n dp[i][0] = max(B[i] + dp[i + 1][0], dp[i + 1][1]);\n dp[i][1] = max(A[i] + dp[i + 1][1], dp[i + 1][0]);\n }\n\n return max(dp[0][0], dp[0][1]);\n }\n};\n```\n```Java []\nclass Solution {\n public long maxEnergyBoost(int[] A, int[] B) {\n int n = A.length;\n long[][] dp = new long[n + 5][2];\n\n for (int i = n - 1; i >= 0; i--) {\n dp[i][0] = Math.max(B[i] + dp[i + 1][0], dp[i + 1][1]);\n dp[i][1] = Math.max(A[i] + dp[i + 1][1], dp[i + 1][0]);\n }\n\n return Math.max(dp[0][0], dp[0][1]);\n }\n}\n```\n```Python3 []\nclass Solution:\n def maxEnergyBoost(self, A: List[int], B: List[int]) -> int:\n n = len(A)\n dp = [[0] * 2 for _ in range(n + 5)]\n\n for i in range(n - 1, -1, -1):\n dp[i][0] = max(B[i] + dp[i + 1][0], dp[i + 1][1])\n dp[i][1] = max(A[i] + dp[i + 1][1], dp[i + 1][0])\n\n return max(dp[0][0], dp[0][1])\n\n```\n# Space Optimised\n```C++ []\nclass Solution {\npublic:\n long long maxEnergyBoost(vector<int>& A, vector<int>& B) {\n int n = A.size();\n vector<long long> curr(2, 0), next(2, 0);\n\n for(int i = n - 1; i >= 0; i--){\n curr[0] = max(B[i] + next[0], next[1]);\n curr[1] = max(A[i] + next[1], next[0]);\n next = curr;\n }\n\n return max(next[0], next[1]);\n }\n};\n```\n```Java []\nclass Solution {\n public long maxEnergyBoost(int[] A, int[] B) {\n int n = A.length;\n long[] curr = new long[2];\n long[] next = new long[2];\n\n for (int i = n - 1; i >= 0; --i) {\n curr[0] = Math.max(B[i] + next[0], next[1]);\n curr[1] = Math.max(A[i] + next[1], next[0]);\n System.arraycopy(curr, 0, next, 0, 2);\n }\n\n return Math.max(next[0], next[1]);\n }\n}\n```\n```Python3 []\nfrom typing import List\n\nclass Solution:\n def maxEnergyBoost(self, A: List[int], B: List[int]) -> int:\n n = len(A)\n curr = [0, 0]\n next = [0, 0]\n\n for i in range(n - 1, -1, -1):\n curr[0] = max(B[i] + next[0], next[1])\n curr[1] = max(A[i] + next[1], next[0])\n next[:] = curr\n\n return max(next[0], next[1])\n\n```\n
| 19
| 6
|
['C++', 'Java', 'Python3']
| 3
|
maximum-energy-boost-from-two-drinks
|
Easy Video Solution 🔥 || How to 🤔 in Interview || Top Down (Memo) + Bottom Up 🔥
|
easy-video-solution-how-to-in-interview-ot1lo
|
If you like the solution Please Upvote and subscribe to my youtube channel\n\n# Intuition\n Describe your first thoughts on how to solve this problem. \nDry Run
|
ayushnemmaniwar12
|
NORMAL
|
2024-08-18T04:11:12.526471+00:00
|
2024-08-18T07:48:22.758176+00:00
| 799
| false
|
***If you like the solution Please Upvote and subscribe to my youtube channel***\n\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nDry Run few examples and observe how you can choose the drinks to get the maximum value\n\n\n\n***Easy Video Explanation***\n\nhttps://youtu.be/g_C4eNzUQyI\n \n\n# Top Down + Memo Code\n\n\n```C++ []\nclass Solution {\npublic:\n int n;\n long long dp[100001][2];\n long long solve(int i,vector<int>& v1, vector<int>& v2,int f) {\n if(i>=n)\n return 0;\n if(dp[i][f]!=-1)\n return dp[i][f];\n if(f==0) {\n return dp[i][f]=v1[i]+max(solve(i+1,v1,v2,0),solve(i+2,v1,v2,1));\n } \n return dp[i][f]=v2[i]+max(solve(i+2,v1,v2,0),solve(i+1,v1,v2,1));\n }\n long long maxEnergyBoost(vector<int>& v1, vector<int>& v2) {\n n=v1.size();\n memset(dp,-1,sizeof(dp));\n long long ans1=solve(0,v1,v2,0);\n memset(dp,-1,sizeof(dp));\n long long ans2=solve(0,v1,v2,1);\n return max(ans1,ans2);\n }\n};\n```\n```python []\nclass Solution:\n def __init__(self):\n self.n = 0\n self.dp = []\n\n def solve(self, i, v1, v2, f):\n if i >= self.n:\n return 0\n if self.dp[i][f] != -1:\n return self.dp[i][f]\n if f == 0:\n self.dp[i][f] = v1[i] + max(self.solve(i + 1, v1, v2, 0), self.solve(i + 2, v1, v2, 1))\n else:\n self.dp[i][f] = v2[i] + max(self.solve(i + 2, v1, v2, 0), self.solve(i + 1, v1, v2, 1))\n return self.dp[i][f]\n\n def maxEnergyBoost(self, v1, v2):\n self.n = len(v1)\n self.dp = [[-1 for _ in range(2)] for _ in range(self.n)]\n ans1 = self.solve(0, v1, v2, 0)\n self.dp = [[-1 for _ in range(2)] for _ in range(self.n)]\n ans2 = self.solve(0, v1, v2, 1)\n return max(ans1, ans2)\n\n```\n```Java []\nimport java.util.Arrays;\nimport java.util.List;\n\nclass Solution {\n int n;\n long[][] dp;\n\n public long solve(int i, List<Integer> v1, List<Integer> v2, int f) {\n if (i >= n)\n return 0;\n if (dp[i][f] != -1)\n return dp[i][f];\n if (f == 0) {\n dp[i][f] = v1.get(i) + Math.max(solve(i + 1, v1, v2, 0), solve(i + 2, v1, v2, 1));\n } else {\n dp[i][f] = v2.get(i) + Math.max(solve(i + 2, v1, v2, 0), solve(i + 1, v1, v2, 1));\n }\n return dp[i][f];\n }\n\n public long maxEnergyBoost(List<Integer> v1, List<Integer> v2) {\n n = v1.size();\n dp = new long[n][2];\n for (long[] row : dp) {\n Arrays.fill(row, -1);\n }\n long ans1 = solve(0, v1, v2, 0);\n for (long[] row : dp) {\n Arrays.fill(row, -1);\n }\n long ans2 = solve(0, v1, v2, 1);\n return Math.max(ans1, ans2);\n }\n}\n\n\n```\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(N)\n \n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(N)\n\n\n# Bottom Up Code\n\n\n```C++ []\nclass Solution {\npublic:\n long long maxEnergyBoost(vector<int>& v1, vector<int>& v2) {\n int n=v1.size();\n long long dp[n+1][2];\n memset(dp,-1,sizeof(dp));\n dp[0][0]=v1[0];\n dp[0][1]=v2[0];\n for(int i=1;i<n;i++) {\n dp[i][0]=v1[i]+dp[i-1][0];\n dp[i][1]=v2[i]+dp[i-1][1];\n if(i-2>=0) {\n dp[i][0]=max(dp[i][0],v1[i]+dp[i-2][1]);\n dp[i][1]=max(dp[i][1],v2[i]+dp[i-2][0]);\n }\n }\n return max(dp[n-1][0],dp[n-1][1]);\n }\n};\n```\n```python []\nclass Solution:\n def maxEnergyBoost(self, v1, v2):\n n = len(v1)\n dp = [[0] * 2 for _ in range(n)]\n\n # Initialize the first elements in the dp table\n dp[0][0] = v1[0]\n dp[0][1] = v2[0]\n\n # Fill the dp table\n for i in range(1, n):\n # Choose from v1 and v2 based on previous values\n dp[i][0] = v1[i] + dp[i - 1][0]\n dp[i][1] = v2[i] + dp[i - 1][1]\n\n if i - 2 >= 0:\n dp[i][0] = max(dp[i][0], v1[i] + dp[i - 2][1])\n dp[i][1] = max(dp[i][1], v2[i] + dp[i - 2][0])\n\n # Return the maximum energy boost possible\n return max(dp[n - 1][0], dp[n - 1][1])\n\n\n```\n```Java []\nimport java.util.List;\n\nclass Solution {\n public long maxEnergyBoost(List<Integer> v1, List<Integer> v2) {\n int n = v1.size();\n long[][] dp = new long[n][2];\n\n // Initialize the first elements in the dp table\n dp[0][0] = v1.get(0);\n dp[0][1] = v2.get(0);\n\n // Fill the dp table\n for (int i = 1; i < n; i++) {\n // Choose from v1 and v2 based on previous values\n dp[i][0] = v1.get(i) + dp[i - 1][0];\n dp[i][1] = v2.get(i) + dp[i - 1][1];\n\n if (i - 2 >= 0) {\n dp[i][0] = Math.max(dp[i][0], v1.get(i) + dp[i - 2][1]);\n dp[i][1] = Math.max(dp[i][1], v2.get(i) + dp[i - 2][0]);\n }\n }\n\n // Return the maximum energy boost possible\n return Math.max(dp[n - 1][0], dp[n - 1][1]);\n }\n}\n\n\n```\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(N)\n \n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(N)\n\n# Follow Up\n*can you solve this in O(1) or constant space*\n\n# ***If you like the solution Please Upvote and subscribe to my youtube channel***\n***It Motivates me to record more videos***\n\n*Thank you* \uD83D\uDE00
| 13
| 5
|
['Dynamic Programming', 'Memoization', 'C++', 'Java', 'Python3']
| 2
|
maximum-energy-boost-from-two-drinks
|
Dp - Memoization
|
dp-memoization-by-flexsloth-0cb7
|
\n# Code\n\nclass Solution {\npublic:\n long long helper(vector<int>& a, vector<int>& b, int i, int k, vector<vector<long long>>&dp){\n if(i == a.size
|
flexsloth
|
NORMAL
|
2024-08-18T04:01:34.602757+00:00
|
2024-08-18T04:01:34.602795+00:00
| 1,263
| false
|
\n# Code\n```\nclass Solution {\npublic:\n long long helper(vector<int>& a, vector<int>& b, int i, int k, vector<vector<long long>>&dp){\n if(i == a.size()){\n return 0;\n }\n if(dp[k][i] != -1) return dp[k][i];\n long long take = 0, nottake = 0;\n if(k == 1){\n take = a[i] + helper(a,b,i+1,k,dp);\n nottake = helper(a,b,i+1,2,dp);\n }\n else if(k == 2){\n take = b[i] + helper(a,b,i+1,k,dp);\n nottake = helper(a,b,i+1,1,dp);\n }\n return dp[k][i] = max(take,nottake);\n }\n long long maxEnergyBoost(vector<int>& a, vector<int>& b) {\n vector<vector<long long>>dp(3 , vector<long long>(a.size() , -1));\n return max(helper(a,b,0,1,dp) , helper(a,b,0,2,dp));\n }\n};\n\n```
| 12
| 0
|
['Dynamic Programming', 'Memoization', 'C++']
| 5
|
maximum-energy-boost-from-two-drinks
|
Java Clean Simple Solution Without DP
|
java-clean-simple-solution-without-dp-by-fcph
|
Complexity\n- Time complexity:O(n)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity:O(1)\n Add your space complexity here, e.g. O(n) \n\n# Code
|
Shree_Govind_Jee
|
NORMAL
|
2024-08-18T04:02:34.358741+00:00
|
2024-08-18T04:02:34.358767+00:00
| 564
| false
|
# Complexity\n- Time complexity:$$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public long maxEnergyBoost(int[] energyDrinkA, int[] energyDrinkB) {\n int n = energyDrinkA.length;\n \n long maxA = 0, maxB=0;\n for(int i=0; i<n; i++){\n long newMaxA = Math.max(maxA+energyDrinkA[i], maxB);\n long newMaxB = Math.max(maxB+energyDrinkB[i], maxA);\n maxA = newMaxA;\n maxB = newMaxB;\n }\n return Math.max(maxA, maxB);\n }\n}\n```
| 11
| 5
|
['Array', 'Math', 'Java']
| 6
|
maximum-energy-boost-from-two-drinks
|
Recursion+ Memo-> iterative DP with O(1) space||99ms Beats 100%
|
recursion-memo-iterative-dp-with-o1-spac-q4q4
|
Intuition\n Describe your first thoughts on how to solve this problem. \nDP is good.\nTry Recursion+Memo\n2nd approach is the iterative version with optimized s
|
anwendeng
|
NORMAL
|
2024-08-18T04:53:58.536957+00:00
|
2024-08-18T14:00:41.505355+00:00
| 752
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nDP is good.\nTry Recursion+Memo\n2nd approach is the iterative version with optimized space O(1)\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Set up dp state matrix dp where (i, j) ith hour drinking `j=(dinking==B)`\n2. The recurrence in recursive function `f` is \n```\nenergy=(j==0)?A[i]: B[i];\nenergy+=max(f(i+1, j, A, B), f(i+2, 1-j, A, B));\nreturn dp[i][j]=energy;\n```\n3. The answer is `max(f(0, 0, energyDrinkA, energyDrinkB), f(0, 1, energyDrinkA,energyDrinkB))`\n4. The corresponding iterative DP is also done which is even much faster\n5. The optimization of space can use `&1` trick same as `%2`.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$O(n)$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$O(n)\\to O(1)$\n# Code||C++ 143ms Beats 100.00%\n```\nclass Solution {\npublic:\n int n;\n long long dp[100000][2];// (i, j) ith hour drinking j=(dinking==B)\n long long f(int i, int j, vector<int>& A, vector<int>& B){\n if (i>=n) return 0;\n if (dp[i][j]!=-1) return dp[i][j];\n long long energy=(j==0)?A[i]: B[i];\n energy+=max(f(i+1, j, A, B), f(i+2, 1-j, A, B));\n return dp[i][j]=energy;\n }\n long long maxEnergyBoost(vector<int>& energyDrinkA, vector<int>& energyDrinkB) {\n n=energyDrinkA.size();\n memset(dp, -1, sizeof(dp));\n return max(f(0, 0, energyDrinkA, energyDrinkB), f(0, 1, energyDrinkA,energyDrinkB));\n \n }\n};\n\n\n\n\n \nauto init = []() {\n ios::sync_with_stdio(false);\n cin.tie(nullptr);\n cout.tie(nullptr);\n return \'c\';\n}();\n```\n# DP iterative+ O(1) space||99ms Beats 100%\n```\nclass Solution {\npublic:\n static long long maxEnergyBoost(vector<int>& A, vector<int>& B)\n {\n const int n=A.size();\n long long dp[2][2]={{0}};// (i, j) ith hour drinking j=(dinking==B)\n for(int i=n-1; i>=0; i--){\n long long energy[2]={ A[i], B[i]};\n energy[0]+=max(dp[(i+1)&1][0], dp[(i+2)&1][1]);\n energy[1]+=max(dp[(i+1)&1][1], dp[(i+2)&1][0]);\n dp[i&1][0]=energy[0], dp[i&1][1]=energy[1];\n }\n\n return max(dp[0][0], dp[0][1]);\n \n }\n};\n\n \nauto init = []() {\n ios::sync_with_stdio(false);\n cin.tie(nullptr);\n cout.tie(nullptr);\n return \'c\';\n}();\n```
| 10
| 0
|
['Dynamic Programming', 'Recursion', 'Memoization', 'C++']
| 2
|
maximum-energy-boost-from-two-drinks
|
💯Faster✅💯Less Mem✅🧠Detailed Approach🎯Greedy🔥C++😎
|
fasterless-memdetailed-approachgreedyc-b-tgjs
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
swarajkr
|
NORMAL
|
2024-08-18T04:01:52.808388+00:00
|
2024-08-18T04:01:52.808421+00:00
| 736
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n long long maxEnergyBoost(vector<int>& energyDrinkA, vector<int>& energyDrinkB) {\n int n = energyDrinkA.size();\n long long maxBoost = 0;\n \n // Two variables to track the energy boost if we stick with A or B\n long long currentBoostA = 0, currentBoostB = 0;\n \n // Iterate through each hour\n for (int i = 0; i < n; ++i) {\n // Calculate the new boost values considering the switch\n long long newBoostA = max(currentBoostA + energyDrinkA[i], currentBoostB);\n long long newBoostB = max(currentBoostB + energyDrinkB[i], currentBoostA);\n \n // Update the current boosts\n currentBoostA = newBoostA;\n currentBoostB = newBoostB;\n }\n \n // The maximum boost will be the higher of the two at the last hour\n maxBoost = max(currentBoostA, currentBoostB);\n \n return maxBoost;\n }\n};\n\n```
| 10
| 2
|
['C++']
| 1
|
maximum-energy-boost-from-two-drinks
|
Python 3 || 6 lines, Iterative linear transformation ||
|
python-3-6-lines-iterative-linear-transf-nooa
|
\nclass Solution:\n def maxEnergyBoost(self, energyDrinkA: List[int], energyDrinkB: List[int]) -> int:\n \n prev_A = curr_A = prev_B = curr_B =
|
Spaulding_
|
NORMAL
|
2024-08-18T07:22:10.357416+00:00
|
2024-08-18T07:22:10.357447+00:00
| 68
| false
|
```\nclass Solution:\n def maxEnergyBoost(self, energyDrinkA: List[int], energyDrinkB: List[int]) -> int:\n \n prev_A = curr_A = prev_B = curr_B = 0\n\n for a, b in zip(energyDrinkA, energyDrinkB):\n add_A = a + max(curr_A, prev_B)\n add_B = b + max(curr_B, prev_A)\n\n prev_A, prev_B, curr_A, curr_B = curr_A, curr_B, add_A, add_B\n\n return max(curr_A, curr_B)\n```
| 8
| 0
|
['Python3']
| 0
|
maximum-energy-boost-from-two-drinks
|
✅ Detailed Easy Java ,Python3 ,C++ Solution|| 0ms||100%
|
detailed-easy-java-python3-c-solution-0m-0fqc
|
OBSERVATION\n Yep! Dp is quite intutive here! and that\'s should be the first approach but, can we do it without it! The answer is yes! and if yes? then how?...
|
pankajpatwal1224
|
NORMAL
|
2024-08-18T13:35:28.862339+00:00
|
2024-08-18T13:35:28.862372+00:00
| 55
| false
|
# OBSERVATION\n Yep! Dp is quite intutive here! and that\'s should be the first approach but, can we do it without it! The answer is yes! and if yes? then how?...\n\n---\n\n```\nCode block\n```\n# Read this!\n\nAt each hour, I have two choices:\n\nStick with the same energy drink I used in the previous hour.\n Switch to the other drink, but I\u2019ll have to skip that hour because of the requirement.\n\n\n---\n\n\n\n*Key Insight:*\n\nThe choice I make at each hour (whether to continue with the same drink or switch) doesn\u2019t affect all the previous decisions I\u2019ve made. It only impacts the next step and the total energy boost I\u2019ve accumulated so far.\nWhy This Works:\n\n Independent Subproblems:\n\nEach hour\u2019s decision only depends on the energy boost I\u2019ve accumulated up to that point. What I choose at hour i will influence my choice at hour i+1, but it doesn\u2019t change anything about the earlier hours. Each hour\u2019s decision is isolated.\n\n\nLocal Maximum:\n At every hour, I\u2019m making the best possible choice at that moment\u2014whether to stick with the current drink or switch. This approach works because it builds on the best outcomes from previous decisions.\n\n\n Simplified Computation:\n\nI don\u2019t need a full dynamic programming table because I\u2019m only interested in the best outcome from the previous hour. So, I can keep track of just two variables (like prevA and prevB) that represent the best possible energy boost up to the current hour.\n\n\n# Java\n```\npublic class Solution {\n public long maxEnergyBoost(int[] energyDrinkA, int[] energyDrinkB) {\n int n = energyDrinkA.length;\n long preA = energyDrinkA[0];\n long preB = energyDrinkB[0];\n\n for (int i = 1; i < n; i++) {\n long currA = Math.max(preA + energyDrinkA[i],preB);\n long currB = Math.max(preB + energyDrinkB[i],preA);\n\n \n preA = currA;\n preB = currB;\n }\n\n \n return Math.max(preA, preB);\n }\n}\n```\n\n```python []\nclass Solution:\n def maxEnergyBoost(self, energyDrinkA: list[int], energyDrinkB: list[int]) -> int:\n n = len(energyDrinkA)\n preA = energyDrinkA[0]\n preB = energyDrinkB[0]\n\n for i in range(1, n):\n currA = max(preA + energyDrinkA[i], preB)\n currB = max(preB + energyDrinkB[i], preA)\n\n preA = currA\n preB = currB\n\n return max(preA, preB)\n\n\n```\n```cpp []\nclass Solution {\npublic:\n long long maxEnergyBoost(std::vector<int>& energyDrinkA, std::vector<int>& energyDrinkB) {\n int n = energyDrinkA.size();\n long long preA = energyDrinkA[0];\n long long preB = energyDrinkB[0];\n\n for (int i = 1; i < n; i++) {\n long long currA = std::max(preA + energyDrinkA[i], preB);\n long long currB = std::max(preB + energyDrinkB[i], preA);\n\n preA = currA;\n preB = currB;\n }\n\n return std::max(preA, preB);\n }\n};\n```\n\n```
| 5
| 0
|
['Java']
| 0
|
maximum-energy-boost-from-two-drinks
|
✨🚀 Effortlessly 💯 Dominate 100% with Beginner C++ , Java and Python Solution! 🚀✨
|
effortlessly-dominate-100-with-beginner-bwim4
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
Ravi_Prakash_Maurya
|
NORMAL
|
2024-08-18T04:00:44.854188+00:00
|
2024-08-18T04:00:44.854216+00:00
| 495
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n long long maxEnergyBoost(vector<int>& eDA, vector<int>& eDB) {\n int n = eDA.size();\n if (n == 1) return max(eDA[0], eDB[0]);\n vector<long long> x(n), y(n);\n x[0] = eDA[0], y[0] = eDB[0];\n for (int i = 1; i < n; ++i) {\n x[i] = eDA[i] + max(x[i-1], (i > 1 ? y[i-2] : 0));\n y[i] = eDB[i] + max(y[i-1], (i > 1 ? x[i-2] : 0));\n }\n return max(x[n-1], y[n-1]);\n }\n};\n```
| 5
| 0
|
['C++']
| 3
|
maximum-energy-boost-from-two-drinks
|
Linear DP | O(1) Space
|
linear-dp-o1-space-by-jay_1410-lyy5
|
Code\nC++ []\nclass Solution {\npublic:\n using ll = long long;\n long long maxEnergyBoost(vector<int> &A, vector<int> &B){\n ll A1 = 0 , B1 = 0 ,
|
Jay_1410
|
NORMAL
|
2024-08-18T04:01:41.573206+00:00
|
2024-08-18T04:31:32.480617+00:00
| 431
| false
|
# Code\n```C++ []\nclass Solution {\npublic:\n using ll = long long;\n long long maxEnergyBoost(vector<int> &A, vector<int> &B){\n ll A1 = 0 , B1 = 0 , A2 = 0 , B2 = 0;\n for(int i = 0 ; i < A.size() ; i++){\n ll currA = A[i] + max(A1 , B2);\n ll currB = B[i] + max(B1 , A2);\n A2 = A1 , A1 = currA;\n B2 = B1 , B1 = currB;\n }\n return max(A1 , B1);\n }\n};\n```\n```Java []\nclass Solution{\n public long maxEnergyBoost(int[] A , int[] B){\n long A1 = 0 , B1 = 0 , A2 = 0 , B2 = 0;\n for (int i = 0 ; i < A.length ; i++){\n long currA = A[i] + Math.max(A1 , B2);\n long currB = B[i] + Math.max(B1 , A2);\n A2 = A1 ; A1 = currA;\n B2 = B1 ; B1 = currB;\n }\n return Math.max(A1 , B1);\n }\n}\n```\n``` Python3 []\nclass Solution:\n def maxEnergyBoost(self , A , B):\n A1 = B1 = A2 = B2 = 0\n for i in range(0 , len(A)):\n currA = A[i] + max(A1, B2)\n currB = B[i] + max(B1, A2)\n A2 , A1 = A1 , currA\n B2 , B1 = B1 , currB\n return max(A1 , B1)\n```\n
| 4
| 0
|
['Dynamic Programming', 'C++', 'Java', 'Python3']
| 0
|
maximum-energy-boost-from-two-drinks
|
DP. One pass. Space O(1)
|
dp-one-pass-space-o1-by-xxxxkav-duhk
|
Time $O(n)$, space $O(n)$\n\nclass Solution:\n def maxEnergyBoost(self, energyDrinkA: List[int], energyDrinkB: List[int]) -> int:\n n = len(energyDrin
|
xxxxkav
|
NORMAL
|
2024-08-19T18:52:09.891839+00:00
|
2024-08-19T19:02:35.386249+00:00
| 66
| false
|
Time $O(n)$, space $O(n)$\n```\nclass Solution:\n def maxEnergyBoost(self, energyDrinkA: List[int], energyDrinkB: List[int]) -> int:\n n = len(energyDrinkA)\n dp = [[0, 0] for _ in range(n)]\n dp[0][0] = energyDrinkA[0]\n dp[0][1] = energyDrinkB[0]\n for i in range(1, n):\n dp[i][0] = max(dp[i-1][0] + energyDrinkA[i], dp[i-1][1])\n dp[i][1] = max(dp[i-1][1] + energyDrinkB[i], dp[i-1][0])\n return max(dp[-1])\n```\nSpace optimised - $O(1)$\n```\nclass Solution:\n def maxEnergyBoost(self, energyDrinkA: List[int], energyDrinkB: List[int]) -> int:\n a, b = 0, 0\n for drink_a, drink_b in zip(energyDrinkA, energyDrinkB):\n a, b = max(a + drink_a, b), max(b + drink_b, a)\n return max(a, b)\n```
| 3
| 0
|
['Dynamic Programming', 'Python3']
| 0
|
maximum-energy-boost-from-two-drinks
|
DP
|
dp-by-votrubac-uwg2
|
This problem belongs to the 198. House Robber group of DP problems.\n\nlastA is the maximum total boost so far if the last drink was A, and lastB is the same fo
|
votrubac
|
NORMAL
|
2024-08-18T17:15:50.575840+00:00
|
2024-08-19T18:03:55.162815+00:00
| 41
| false
|
This problem belongs to the [198. House Robber](https://leetcode.com/problems/house-robber/) group of DP problems.\n\n`lastA` is the maximum total boost so far if the last drink was `A`, and `lastB` is the same for `B`.\n\nFor hour `i`, we can continue driking `A`, or switch from `B`:\n- `lastA = drinkA[i] + max(lastA, lastB - drinkB[i - 1])`. \n\nNote that we do `lastB - drinkB[i - 1]` as we need to skip the boost from drink `B` for the previous hour. \n\n**C++**\n```cpp\nlong long maxEnergyBoost(vector<int>& drinkA, vector<int>& drinkB) {\n long long lastA = drinkA[0], lastB = drinkB[0]; \n for (int i = 1; i < drinkA.size(); ++i) {\n long long tmp = lastA;\n lastA = max(lastA, lastB - drinkB[i - 1]) + drinkA[i];\n lastB = max(lastB, tmp - drinkA[i - 1]) + drinkB[i];\n }\n return max(lastA, lastB);\n}\n```
| 3
| 0
|
['C']
| 0
|
maximum-energy-boost-from-two-drinks
|
Intuitive Solution (with and without DP) || Beats 100%
|
intuitive-solution-with-and-without-dp-b-gibl
|
Two-dimensional Dynamic Programming\n# Intuition\nMaximizing energy boosts requires considering the best choices from two arrays at each step, making dynamic pr
|
divyamshah04
|
NORMAL
|
2024-08-18T09:44:49.390819+00:00
|
2024-08-18T09:44:49.390853+00:00
| 209
| false
|
# Two-dimensional Dynamic Programming\n# Intuition\nMaximizing energy boosts requires considering the best choices from two arrays at each step, making dynamic programming a suitable approach.\n\n# Approach\nWe use a DP table where dp[i][0] and dp[i][1] store the maximum boost achievable up to the i-th drink by choosing from energyDrinkA and energyDrinkB, respectively. We fill the DP table based on previous states and return the maximum of the last entries.\n\n# Complexity\n- Time complexity:$$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n long long maxEnergyBoost(vector<int>& energyDrinkA, vector<int>& energyDrinkB) {\n int n = energyDrinkA.size();\n \n // Initialize dp table with long long type\n vector<vector<long long>> dp(n + 2, vector<long long>(2, 0));\n \n // Fill the dp table based on the logic provided\n for (int i = 2; i < n + 2; i++) {\n // For energyDrinkA\n long long a1 = dp[i - 1][0];\n long long a2 = max(dp[i - 2][0], dp[i - 2][1]);\n long long a3 = max(a1, a2);\n dp[i][0] = a3 + energyDrinkA[i - 2];\n \n // For energyDrinkB\n long long b1 = dp[i - 1][1];\n long long b2 = max(dp[i - 2][1], dp[i - 2][0]);\n long long b3 = max(b1, b2);\n dp[i][1] = b3 + energyDrinkB[i - 2];\n }\n \n // The result is the maximum of the last possible values in the dp table\n return max(dp[n + 1][0], dp[n + 1][1]);\n }\n};\n\n```\n# Optimized Solution \n# Intuition\nSince the current state only depends on the last two states, we can reduce space usage by tracking only the necessary previous values.\n\n# Approach\nInstead of a full DP table, use four variables to keep track of the last two states for both energy drinks. Update these variables as you iterate through the list and return the maximum of the final states.\n\n# Complexity\n- Time complexity:$$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n```\nclass Solution {\npublic:\n long long maxEnergyBoost(vector<int>& energyDrinkA, vector<int>& energyDrinkB) {\n int n = energyDrinkA.size();\n \n // Variables to store the last two states instead of full dp table\n long long prev2_A = 0, prev1_A = 0, prev2_B = 0, prev1_B = 0;\n \n for (int i = 0; i < n; i++) {\n // Calculate current state based on the previous two states\n long long curr_A = max(prev1_A, max(prev2_A, prev2_B)) + energyDrinkA[i];\n long long curr_B = max(prev1_B, max(prev2_B, prev2_A)) + energyDrinkB[i];\n \n // Update previous states for next iteration\n prev2_A = prev1_A;\n prev1_A = curr_A;\n prev2_B = prev1_B;\n prev1_B = curr_B;\n }\n \n // Return the maximum of the last states\n return max(prev1_A, prev1_B);\n }\n};\n```\n\n
| 3
| 0
|
['Dynamic Programming', 'C++']
| 0
|
maximum-energy-boost-from-two-drinks
|
simple recursive solution.
|
simple-recursive-solution-by-romaishawaq-s0ze
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
romaishawaqar
|
NORMAL
|
2024-08-18T09:03:56.079825+00:00
|
2024-08-18T09:03:56.079844+00:00
| 75
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nlong long dp[100005][3];\nlong long func(int i, int p,vector<int>& nums1, vector<int>& nums2){\n int n = nums1.size();\n if(i >= n) return 0;\n if(dp[i][p] != -1) return dp[i][p];\n \n long long ans1 = 0, ans2 = 0, ans3 = 0, ans4 = 0;\n if(p == 0){\n ans1 = nums1[i] + func(i+1,0,nums1,nums2);\n ans2 = nums1[i] + func(i+2,1,nums1,nums2);\n }\n else{\n ans3 = nums2[i] + func(i+1,1,nums1,nums2);\n ans4 = nums2[i] + func(i+2,0,nums1,nums2);\n }\n return dp[i][p] = max(ans1,max(ans2,max(ans3,ans4)));\n \n}\nclass Solution {\npublic:\n long long maxEnergyBoost(vector<int>& nums1, vector<int>& nums2) {\n memset(dp,-1,sizeof(dp));\n long long ans = max(func(0,0,nums1,nums2), func(0,1,nums1,nums2));\n return ans;\n }\n};\n```
| 3
| 0
|
['Recursion', 'C++']
| 1
|
maximum-energy-boost-from-two-drinks
|
Beginner Iterative Dp Solution
|
beginner-iterative-dp-solution-by-kvivek-rdjn
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
kvivekcodes
|
NORMAL
|
2024-08-18T05:29:56.692093+00:00
|
2024-08-18T05:29:56.692113+00:00
| 51
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n long long maxEnergyBoost(vector<int>& energyDrinkA, vector<int>& energyDrinkB) {\n int n = energyDrinkA.size();\n vector< vector<long long>> dp(n, vector<long long> (2, 0));\n dp[0][0] = energyDrinkA[0];\n dp[0][1] = energyDrinkB[0];\n\n for(int i = 1; i < n; i++){\n dp[i][0] = max(dp[i][0], dp[i-1][0]+energyDrinkA[i]);\n dp[i][1] = max(dp[i][1], dp[i-1][1]+energyDrinkB[i]);\n if(i > 1) dp[i][0] = max(dp[i][0], dp[i-2][1]+energyDrinkA[i]);\n if(i > 1) dp[i][1] = max(dp[i][1], dp[i-2][0]+energyDrinkB[i]);\n }\n\n return max(dp[n-1][0], dp[n-1][1]);\n }\n};\n```
| 3
| 0
|
['C++']
| 1
|
maximum-energy-boost-from-two-drinks
|
recursion + memo
|
recursion-memo-by-raviteja_29-nx7v
|
Intuition\n Describe your first thoughts on how to solve this problem. \nTo maximize the energy boost over n hours:\n\nDecision at Each Hour: Choose to either c
|
raviteja_29
|
NORMAL
|
2024-08-18T04:52:15.308371+00:00
|
2024-08-18T04:52:15.308422+00:00
| 285
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTo maximize the energy boost over n hours:\n\nDecision at Each Hour: Choose to either continue with the current drink or switch to the other drink, considering the switch penalty.\n\nRecursive Approach: Use recursion to explore the best option for each hour, storing results to avoid redundant calculations.\n\nMemoization: Store intermediate results to efficiently compute the maximum boost.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe problem is solved using a recursive approach with memoization.\n\n* dpithink(x, bval) computes the maximum energy boost starting from hour x with bval indicating the last drink type (0 for A, 1 for B).\nBase Case:\n\n* If x is out of bounds (x >= n), return 0 as there are no more hours.\nTransition:\n\n* If the last drink was A (bval == 0), you can either continue with A or switch to B.\n* If the last drink was B (bval == 1), you can either continue with B or switch to A.\nMemoization:\n\n* Store the results of computed states in memo to avoid redundant calculations.\n\n* Start with either drink A or B at hour 0 and return the maximum of the two scenarios.\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxEnergyBoost(self, ea: List[int], eb: List[int]) -> int:\n memo = {}\n n = len(ea)\n def dpithink(x,bval):\n if x>=n:\n return 0\n if (x,bval) in memo:\n return memo[(x,bval)]\n if bval==0:\n memo[(x,bval)] = max(ea[x]+dpithink(x+1,0),dpithink(x+1,1))\n else:\n memo[(x,bval)] = max(eb[x]+dpithink(x+1,1),dpithink(x+1,0))\n return memo[(x,bval)]\n return max(dpithink(0,0),dpithink(0,1))\n\n\n```
| 3
| 0
|
['Dynamic Programming', 'Recursion', 'Memoization', 'Python3']
| 2
|
maximum-energy-boost-from-two-drinks
|
Beats 100 % - Best solution using Java
|
beats-100-best-solution-using-java-by-_d-iyes
|
Even I am surprised \uD83D\uDE02\n\n# Code\n\nclass Solution {\n public long maxEnergyBoost(int[] energyDrinkA, int[] energyDrinkB) {\n long maxA = 0;
|
_deepaktiwari
|
NORMAL
|
2024-08-18T04:31:19.233793+00:00
|
2024-08-18T04:31:19.233820+00:00
| 226
| false
|
Even I am surprised \uD83D\uDE02\n\n# Code\n```\nclass Solution {\n public long maxEnergyBoost(int[] energyDrinkA, int[] energyDrinkB) {\n long maxA = 0;\n long maxB = 0;\n for(int i = 0; i < energyDrinkA.length; i++){\n long tempA = Math.max(maxA + energyDrinkA[i], maxB);\n long tempB = Math.max(maxB + energyDrinkB[i], maxA);\n maxA = tempA;\n maxB = tempB;\n }\n return Math.max(maxA, maxB);\n }\n}\n```
| 3
| 0
|
['Java']
| 1
|
maximum-energy-boost-from-two-drinks
|
Easy to understand C++ solution with explaination.
|
easy-to-understand-c-solution-with-expla-ghe4
|
Intuition\nThe goal is to maximize the total energy boost over the next n hours by choosing between two energy drinks. The catch is that switching from one drin
|
AyushPandey152
|
NORMAL
|
2024-08-18T04:15:34.861244+00:00
|
2024-08-18T04:15:34.861267+00:00
| 138
| false
|
# Intuition\nThe goal is to maximize the total energy boost over the next n hours by choosing between two energy drinks. The catch is that switching from one drink to another incurs a 1-hour penalty with no energy boost. This penalty makes it essential to carefully decide when to switch drinks to avoid losing too much energy. A dynamic programming approach seems ideal here, as it allows us to keep track of the maximum energy boost possible at each hour, depending on whether we stick with the same drink or switch.\n\n# Approach\nDynamic Programming Arrays: Create two DP arrays dpA and dpB. dpA[i] stores the maximum energy boost possible up to hour i if you choose energy drink A at hour i. Similarly, dpB[i] stores the maximum energy boost if you choose energy drink B at hour i.\nInitialization: Set dpA[0] to energyDrinkA[0] and dpB[0] to energyDrinkB[0], as you can start with either drink.\nDP Transition: For each hour i, decide whether to continue with the same drink from the previous hour or switch drinks. If switching, account for the penalty by not adding the energy boost of the current hour. Update dpA[i] and dpB[i] accordingly.\nResult: The maximum total energy boost after n hours will be the maximum value between dpA[n-1] and dpB[n-1], representing the optimal solution after all hours.\n\nFor better understanding, refer assembly line scheduling algorithm.\n\n# Complexity\n- Time complexity: O(N)\n\n- Space complexity: O(N + N) = O(N)\n\n# Code\n```\nclass Solution {\npublic:\n long long maxEnergyBoost(vector<int>& energyDrinkA, vector<int>& energyDrinkB) {\n int n = energyDrinkA.size();\n vector<long long> dpA(n, 0), dpB(n, 0);\n\n dpA[0] = energyDrinkA[0];\n dpB[0] = energyDrinkB[0];\n\n for (int i = 1; i < n; ++i) {\n dpA[i] = max(dpA[i - 1] + energyDrinkA[i], dpB[i - 1]);\n dpB[i] = max(dpB[i - 1] + energyDrinkB[i], dpA[i - 1]);\n }\n\n return max(dpA[n - 1], dpB[n - 1]);\n }\n};\n\n```
| 3
| 0
|
['Array', 'Dynamic Programming', 'C++']
| 2
|
maximum-energy-boost-from-two-drinks
|
C++ || Super Easy || Recursion + Memo
|
c-super-easy-recursion-memo-by-shobhit_s-64oe
|
Intuition\nWe can start choosing the elements from either of the array so take the maximum starting from both.\n\n# Approach\n1) If we switch the arrar we get 0
|
Shobhit_Singh_47
|
NORMAL
|
2024-08-18T04:12:58.861594+00:00
|
2024-08-18T04:12:58.861632+00:00
| 901
| false
|
# Intuition\nWe can start choosing the elements from either of the array so take the maximum starting from both.\n\n# Approach\n1) If we switch the arrar we get 0 boost.\n2) If we do not switch we get the boost , the array we are in. \n3) So we need to keep track which arry we are in , index.\n\n# Complexity\n- Time complexity:\nO(2*N)\n\n- Space complexity:\nO(2*N)\n\n# Code\n```\nclass Solution {\npublic:\n int n;\n\n long long solve(int ind, vector<int>& nums1, vector<int>& nums2, int p, vector<vector<long long>>& dp) {\n if (ind == n) {\n return 0;\n }\n\n if (dp[ind][p] != -1) {\n return dp[ind][p];\n }\n\n long long ans = INT_MIN;\n\n if (p == 0) { \n //remain in the first array p = 0\n ans = max(ans, (long long)nums1[ind] + solve(ind + 1, nums1, nums2, 0, dp));\n } else { \n // remain in the second array p = 1\n ans = max(ans, (long long)nums2[ind] + solve(ind + 1, nums1, nums2, 1, dp));\n }\n\n // switch the array no boost\n ans = max(ans, solve(ind + 1, nums1, nums2, 1 - p, dp));\n\n return dp[ind][p] = ans;\n }\n\n long long maxEnergyBoost(vector<int>& nums1, vector<int>& nums2) {\n n = nums1.size();\n\n vector<vector<long long>> dp(n + 1, vector<long long>(2, -1));\n\n return max(solve(0, nums1, nums2, 0, dp), solve(0, nums1, nums2, 1, dp));\n }\n};\n```
| 3
| 0
|
['C++']
| 2
|
maximum-energy-boost-from-two-drinks
|
Simple JAVA DP ✅
|
simple-java-dp-by-harshsharma08-d3i0
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
Harshsharma08
|
NORMAL
|
2024-08-18T04:07:21.309805+00:00
|
2024-08-18T04:07:21.309839+00:00
| 269
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n long[] dpA ;\n long[] dpB;\n \n long maxSum(int ar[], int br[]){\n int n = ar.length;\n dpA = new long[n]; dpB = new long[n];\n dpA[0] = ar[0]; dpB[0] = br[0];\n\n for (int i=1;i<n;i++) {\n dpA[i] = Math.max(dpA[i-1] + ar[i], (i > 1 ? dpB[i-2] : 0) + ar[i]); \n dpB[i] = Math.max(dpB[i-1] + br[i], (i > 1 ? dpA[i-2] : 0) + br[i]);\n }\n\n return Math.max(dpA[n-1], dpB[n-1]);\n }\n\n public long maxEnergyBoost(int[] ar, int[] br) {\n int n = ar.length;\n if(n==1) return Math.max(ar[0],br[0]);\n return maxSum(ar,br);\n }\n}\n```
| 3
| 0
|
['Dynamic Programming', 'Greedy', 'Memoization', 'C++', 'Java']
| 1
|
maximum-energy-boost-from-two-drinks
|
C++ Dp solution
|
c-dp-solution-by-sachin_kumar_sharma-kjgz
|
Intuition\nJust apply the concept of take A and notTake B and vice versa.\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe
|
Sachin_Kumar_Sharma
|
NORMAL
|
2024-08-18T04:06:22.931294+00:00
|
2024-08-18T04:06:22.931325+00:00
| 11
| false
|
# Intuition\nJust apply the concept of take A and notTake B and vice versa.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n long long maxEnergyBoost(vector<int>& energyDrinkA, vector<int>& energyDrinkB) {\n long long i,n=energyDrinkA.size();\n vector<long long> dpA(n),dpB(n);\n dpA[0]=energyDrinkA[0];\n dpB[0]=energyDrinkB[0];\n\n for(i=1;i<n;i++){\n dpA[i]=max(dpA[i-1]+energyDrinkA[i],dpB[i-1]);\n dpB[i]=max(dpB[i-1]+energyDrinkB[i],dpA[i-1]);\n }\n\n return max(dpA[n-1],dpB[n-1]);\n }\n};\n```
| 3
| 0
|
['C++']
| 0
|
maximum-energy-boost-from-two-drinks
|
✅100% Fastest✅Easy and Simple Solution ✅Clean Code
|
100-fastesteasy-and-simple-solution-clea-nanb
|
Guy\'s if you find this solution helpful \uD83D\uDE0A, PLEASE do UPVOTE. By doing that it motivate\'s me to create more better post like this \u270D\uFE0F\nFoll
|
ayushluthra62
|
NORMAL
|
2024-08-18T04:02:14.095366+00:00
|
2024-08-18T04:02:14.095391+00:00
| 162
| false
|
***Guy\'s if you find this solution helpful \uD83D\uDE0A, PLEASE do UPVOTE. By doing that it motivate\'s me to create more better post like this \u270D\uFE0F***<br>\n**Follow me on LinkeDin [[click Here](https://www.linkedin.com/in/ayushluthra62/)]**\n\n# Complexity\n- Time complexity:\nO(N)\n\n- Space complexity:\nO(N)\n\n# Code\n```\nclass Solution {\npublic:\n \n long long solve(vector<int>& energyDrinkA , vector<int>&energyDrinkB , int i ,int n ,int type,vector<vector<long long>>&dp){\n \n if(i >= n ) return 0;\n \n if(dp[i][type] != -1) return dp[i][type];\n if(type == 0){\n long long same = energyDrinkA[i] + solve(energyDrinkA, energyDrinkB, i+1,n,0,dp);\n long long different = solve(energyDrinkA, energyDrinkB, i+1,n,1,dp);\n return dp[i][type]=max(same, different);\n }else{\n long long same = energyDrinkB[i] + solve(energyDrinkA, energyDrinkB, i+1,n,1,dp);\n long long different = solve(energyDrinkA, energyDrinkB, i+1,n,0,dp);\n return dp[i][type]=max(same, different); \n }\n \n \n \n \n return -1;\n \n }\n long long maxEnergyBoost(vector<int>& energyDrinkA, vector<int>& energyDrinkB) {\n long long ans = 0;\n int n = energyDrinkA.size();\n \n vector<vector<long long >>dp(n, vector<long long>(2,-1));\n return max(solve(energyDrinkA , energyDrinkB, 0 , n, 0,dp) , solve(energyDrinkA , energyDrinkB, 0 , n , 1,dp));\n \n return ans;\n }\n};\n```\n***Guy\'s if you find this solution helpful \uD83D\uDE0A, PLEASE do UPVOTE. By doing that it motivate\'s me to create more better post like this \u270D\uFE0F***<br>\n**Follow me on LinkeDin [[click Here](https://www.linkedin.com/in/ayushluthra62/)]**
| 3
| 0
|
['C++']
| 0
|
maximum-energy-boost-from-two-drinks
|
Must Watch✅💯Easiest Approach With Beginner Friendly Explanation💯✅
|
must-watcheasiest-approach-with-beginner-xa8o
|
Intuition\nThe problem involves two energy drink lists, energyDrinkA and energyDrinkB, where we can choose drinks from either list with certain constraints:\n\n
|
Ajay_Kartheek
|
NORMAL
|
2024-09-11T16:33:30.595631+00:00
|
2024-09-11T16:33:30.595661+00:00
| 107
| false
|
# Intuition\nThe problem involves two energy drink lists, energyDrinkA and energyDrinkB, where we can choose drinks from either list with certain constraints:\n\n- You can either take an energy drink from list A or list B.\nOnce you take an energy drink from one list, you can\u2019t take an adjacent drink from the same list (i.e., there must be a gap of at least one between consecutive picks from the same list).\n\nThe goal is to maximize the total energy boost you get by picking drinks under these constraints.\n\n# Approach\n1. This is a dynamic programming problem. The key idea is to use two \npossible states:\n\n - State 1: Indicates that the last drink was taken from energyDrinkA.\n - State 0: Indicates that the last drink was taken from energyDrinkB.\n\n2. For each index in the lists, you can either:\n\n - Pick from list A if the previous drink was from B, or\n - Pick from list B if the previous drink was from A.\n\n3. We define a recursive function solve(index, state) that returns the maximum energy boost starting from index index and state state.\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```python3 []\nclass Solution:\n def maxEnergyBoost(self, energyDrinkA: List[int], energyDrinkB: List[int]) -> int:\n N = len(energyDrinkA)\n # Initialize dp table with -1 (uncomputed state)\n dp = [[-1 for _ in range(N)] for _ in range(2)]\n \n # Recursive function with memoization\n def solve(index, state):\n # Base case: no more drinks to consider\n if index >= N:\n return 0\n \n # If already computed, return the stored result\n if dp[state][index] != -1:\n return dp[state][index]\n \n if state == 1: # Last taken from energyDrinkA\n dp[state][index] = energyDrinkA[index] + max(solve(index + 1, 1), solve(index + 2, 0))\n else: # Last taken from energyDrinkB\n dp[state][index] = energyDrinkB[index] + max(solve(index + 1, 0), solve(index + 2, 1))\n \n return dp[state][index]\n \n # Start by choosing either from energyDrinkA or energyDrinkB\n startA = solve(0, 1)\n startB = solve(0, 0)\n \n return max(startA, startB)\n\n```\n```Java []\nclass Solution {\n public int maxEnergyBoost(int[] energyDrinkA, int[] energyDrinkB) {\n int N = energyDrinkA.length;\n int[][] dp = new int[2][N];\n \n // Initialize dp array to -1\n for (int i = 0; i < 2; i++) {\n for (int j = 0; j < N; j++) {\n dp[i][j] = -1;\n }\n }\n\n // Recursive function with memoization\n int solve(int index, int state) {\n if (index >= N) {\n return 0; // Base case: no more drinks to consider\n }\n if (dp[state][index] != -1) {\n return dp[state][index]; // Return cached result\n }\n if (state == 1) { // Last taken from energyDrinkA\n dp[state][index] = energyDrinkA[index] + Math.max(solve(index + 1, 1), solve(index + 2, 0));\n } else { // Last taken from energyDrinkB\n dp[state][index] = energyDrinkB[index] + Math.max(solve(index + 1, 0), solve(index + 2, 1));\n }\n return dp[state][index];\n }\n\n // Start by choosing from either energyDrinkA or energyDrinkB\n return Math.max(solve(0, 1), solve(0, 0));\n }\n}\n\n\n```\n```C++ []\nclass Solution {\npublic:\n int maxEnergyBoost(vector<int>& energyDrinkA, vector<int>& energyDrinkB) {\n int N = energyDrinkA.size();\n vector<vector<int>> dp(2, vector<int>(N, -1));\n \n // Recursive function with memoization\n function<int(int, int)> solve = [&](int index, int state) -> int {\n if (index >= N) return 0; // Base case: no more drinks to consider\n if (dp[state][index] != -1) return dp[state][index]; // Return cached result\n \n if (state == 1) { // Last taken from energyDrinkA\n dp[state][index] = energyDrinkA[index] + max(solve(index + 1, 1), solve(index + 2, 0));\n } else { // Last taken from energyDrinkB\n dp[state][index] = energyDrinkB[index] + max(solve(index + 1, 0), solve(index + 2, 1));\n }\n return dp[state][index];\n };\n\n // Start by choosing either from energyDrinkA or energyDrinkB\n return max(solve(0, 1), solve(0, 0));\n }\n};\n\n\n```
| 2
| 0
|
['Array', 'Dynamic Programming', 'C++', 'Java', 'Python3']
| 0
|
maximum-energy-boost-from-two-drinks
|
very Easy Solution
|
very-easy-solution-by-vansh0123-led9
|
\n\n# Code\njava []\nclass Solution {\n public long maxEnergyBoost(int[] energyDrinkA, int[] energyDrinkB) {\n \n int n = energyDrinkA.length ;\
|
vansh0123
|
NORMAL
|
2024-08-22T05:29:00.940752+00:00
|
2024-08-22T05:29:00.940786+00:00
| 138
| false
|
\n\n# Code\n```java []\nclass Solution {\n public long maxEnergyBoost(int[] energyDrinkA, int[] energyDrinkB) {\n \n int n = energyDrinkA.length ;\n \n if (n == 0) return 0;\n \n long[] dpA = new long[n];\n long[] dpB = new long[n];\n\n \n dpA[0] = energyDrinkA[0];\n dpB[0] = energyDrinkB[0];\n\n for (int i = 1; i < n; i++) {\n \n // if we don\'t swith the iteration\n dpA[i] = dpA[i-1] + energyDrinkA[i];\n dpB[i] = dpB[i-1] + energyDrinkB[i];\n\n \n // if we want to switch to the another drink \n if (i > 1) \n {\n dpA[i] = Math.max(dpA[i], dpB[i-2] + energyDrinkA[i]);\n dpB[i] = Math.max(dpB[i], dpA[i-2] + energyDrinkB[i]);\n }\n }\n\n \n return Math.max(dpA[n-1], dpB[n-1]);\n }\n}\n```
| 2
| 0
|
['Java']
| 1
|
maximum-energy-boost-from-two-drinks
|
Recursion || C++ || 10 Lines of Code with Comments
|
recursion-c-10-lines-of-code-with-commen-hfp7
|
Intuition\nWe want to find out for every hour what the next energy drink choice is best while considering which energy drink we last consumed. This sounds like
|
SlienCode
|
NORMAL
|
2024-08-20T17:21:20.568268+00:00
|
2024-08-20T23:40:45.643484+00:00
| 140
| false
|
# Intuition\nWe want to find out for every hour what the next energy drink choice is best while considering which energy drink we last consumed. This sounds like a typical dynamic programming problem.\n\n# Approach\nWe build a function that handles the choice we made. There are only two choices we can make: we either continue drinking the same drink we last consumed or we change to the other drink. Our function is going to try both choices and only keep the result of the most optimal one.\n\nThe only tricky thing to note here is that whenever we change drinks we have to go a full hour without consuming anything so whenever we make the choice to change our drink, we will offset the starting index of the next choice by one more extra value. Essentially, when changing drinks we get 0 energy boosts for one hour and we only start counting energy boosts again after that hour has passed.\n\nA common practice in dynamic programming is to keep information about previously examined states so we don\'t have to recompute everything again and thus saving time. Our 2D vector "info" does exactly that.\n\nOnce you understand the code below, you can write a similar solution that doesn\'t make use of recursion but uses the same logic and hence returns a correct result in faster time as function calls tend to be expensive.\n\n# Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(n)$$\n\n# Code\n```cpp []\nclass Solution {\nprivate:\n // save results of combinations\n // [which drink] [which index]\n vector<vector<long long>> info;\npublic:\n long long maxEnergyBoost(vector<int>& energyDrinkA, vector<int>& energyDrinkB) {\n \n // initialize the vector and put "-1" everywhere\n info = vector(2, vector<long long>(energyDrinkA.size(), -1));\n\n return max(nextChoice(energyDrinkA, energyDrinkB, 0, true), nextChoice(energyDrinkB, energyDrinkA, 0, false));\n\n }\n\n long long nextChoice(vector<int>& current, vector<int>& other, int index, bool choice) {\n\n // if we are out of bounds\n if (index >= current.size()) return 0;\n\n // if we\'ve already computed this\n if (info[choice][index] != -1) return info[choice][index];\n\n // add the energy boost from the current drink and index \n long long res = current[index];\n\n /* \n Make the best choice: either keep consuming the same drink\n or swap the current drink with the other drink and flip\n the choice variable to keep track of which drink we are\n currently consuming making our info vector reliable to reuse.\n */\n res += max(nextChoice(current, other, index+1, choice), nextChoice(other, current, index+2, !choice));\n\n // save it for future use\n info[choice][index] = res;\n\n return res;\n }\n};\n```
| 2
| 0
|
['C++']
| 2
|
maximum-energy-boost-from-two-drinks
|
C++ | T.c & S.c : O(N) | Easy Solution :)
|
c-tc-sc-on-easy-solution-by-mammarqaisar-ol6k
|
\nclass Solution {\npublic:\n long long maxEnergyBoost(vector<int>& energyDrinkA, vector<int>& energyDrinkB) { \n int n = energyDrinkA.size();\n
|
mammarqaisar11a55
|
NORMAL
|
2024-08-18T04:37:26.336072+00:00
|
2024-08-18T04:37:26.336094+00:00
| 92
| false
|
```\nclass Solution {\npublic:\n long long maxEnergyBoost(vector<int>& energyDrinkA, vector<int>& energyDrinkB) { \n int n = energyDrinkA.size();\n \n if (n == 0) return 0;\n \n vector<long long> dpA(n, 0), dpB(n, 0);\n \n dpA[0] = energyDrinkA[0];\n dpB[0] = energyDrinkB[0];\n \n // Fill DP arrays\n for (int i = 1; i < n; i++) {\n \n dpA[i] = energyDrinkA[i] + max(dpA[i-1], (i > 1 ? dpB[i-2] : 0));\n \n dpB[i] = energyDrinkB[i] + max(dpB[i-1], (i > 1 ? dpA[i-2] : 0));\n }\n \n return max(dpA[n-1], dpB[n-1]);\n \n }\n};\n```
| 2
| 0
|
['Dynamic Programming', 'C++']
| 1
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.