question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
construct-k-palindrome-strings
|
JAVA || SIMPLE AND EASY SOLUTION || oddCounts logic || TRY WITH forEach LOOP
|
java-simple-and-easy-solution-oddcounts-sspvl
|
IntuitionUSING forEach loop it will reduce the runtime.ApproachComplexity
Time complexity:
Space complexity:
Code
|
kavi_k
|
NORMAL
|
2025-01-11T06:22:11.598064+00:00
|
2025-01-11T06:55:11.751636+00:00
| 29
| false
|
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
USING forEach loop it will reduce the runtime.
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public boolean canConstruct(String s, int k) {
if(s.length() < k) return false;
int oddCount = 0;
int frq [] = new int [26];
for(char i : s.toCharArray())
{
frq[i -'a']++;
}
for(int i : frq)
{
if(i > 0)
{
if(i % 2 == 1)
{
oddCount++;
}
}
}
if(oddCount > k)
{
return false;
}
return true;
}
}
```
| 2
| 0
|
['Java']
| 0
|
construct-k-palindrome-strings
|
Beginner friendly 💯 💯 || Clean code ✅✅✅
|
beginner-friendly-clean-code-by-prabhas_-h0ec
|
IntuitionYou want to check if it's possible to rearrange the string s into exactly k palindrome substrings.Observations:
A palindrome reads the same backward a
|
prabhas_rakurthi
|
NORMAL
|
2025-01-11T06:11:56.705735+00:00
|
2025-01-11T06:11:56.705735+00:00
| 30
| false
|
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
You want to check if it's possible to rearrange the string s into exactly k palindrome substrings.
# **Observations**:
- A palindrome reads the same backward as forward.
**For a string to be a palindrome:**
- At most one character can have an odd frequency (in the case of odd-length palindromes).
- All other characters must have even frequencies to "pair up."
**Key Observations:**
- To form k palindrome substrings, there must be at most k characters in s with an odd frequency.
- If k is greater than the length of the string `k > s.length()`, it's impossible to split s into k substrings (not enough characters).
# Approach
<!-- Describe your approach to solving the problem. -->
1. **Immediate Check:**
- If k is greater than the length of the string (k > s.length()), return false because it's impossible to split the string into k substrings.
2. **Count Character Frequencies:**
- Use a HashMap to count the frequency of each character in s.
3. **Count Odd Frequencies:**
- Iterate over the map to count how many characters have an odd frequency (odd).
- If the number of odd frequencies exceeds k, return false, because you can't form enough palindromes with those odd characters.
4. **Final Check:**
- If the number of odd frequencies is less than or equal to k, return true.
# Complexity
- Time complexity: $$O(n)$$
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: $$O(n)$$
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public boolean canConstruct(String s, int k) {
if(k>s.length()) return false;
Map<Character,Integer> map=new HashMap<>();
for(char c:s.toCharArray()){
map.put(c,map.getOrDefault(c,0)+1);
}
int odd=0;
for(char c:map.keySet()){
if(map.get(c) %2!=0){
odd++;
}
if(odd > k){
return false;
}
}
return true;
}
}
```
| 2
| 0
|
['Hash Table', 'Java']
| 0
|
construct-k-palindrome-strings
|
🔥 Very Easy Detailed Solution || 🔥 Beats 100% || 🎯 Three Approaches
|
very-easy-detailed-solution-beats-100-th-hwg0
|
Approach 1 : Frequency counting and condition checking based on odd/even characters
Count Character Frequencies:
The freq array keeps track of the frequency o
|
chaturvedialok44
|
NORMAL
|
2025-01-11T05:56:12.300778+00:00
|
2025-01-11T05:56:12.300778+00:00
| 35
| false
|
# Approach 1 : Frequency counting and condition checking based on odd/even characters
<!-- Describe your approach to solving the problem. -->
1. **Count Character Frequencies:**
- The freq array keeps track of the frequency of each character in the string s.
- The loop for(int i=0; i<n; i++) iterates through the string and increments the frequency of the respective character.
2. **Count Odd Frequencies:**
- A palindrome requires all characters to have even frequencies, except for at most one character in the case of odd-length palindromes.
- The loop for(int i : freq) counts how many characters have an odd frequency and stores this count in the variable count.
3. **Check Conditions:**
- The string s can be rearranged into k palindromic substrings if:
- The number of characters with odd frequencies (count) is less than or equal to k because each odd-frequency character requires its own - palindrome.
- k is less than or equal to the length of the string n because we cannot create more palindromic substrings than the total number of characters.
- Return true if both conditions are satisfied; otherwise, return false.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
$O(n)$
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
$O(1)$
# Code
```java []
class Solution {
public boolean canConstruct(String s, int k) {
int n = s.length();
int freq[] = new int[26];
for(int i=0; i<n; i++){
char ch = s.charAt(i);
freq[ch - 'a']++;
}
int count = 0;
for(int i : freq){
if(i%2 != 0){
count++;
}
}
return count <= k && k <= n;
}
}
```
# Approach 2 : Sorting and counting odd frequencies
<!-- Describe your approach to solving the problem. -->
1. **Convert String to Character Array:**
- The string s is converted to a character array arr to facilitate sorting.
2. **Sort the Character Array:**
- Sorting the characters groups identical characters together. This makes it easier to calculate the frequency of each character in one traversal.
3. **Count Characters with Odd Frequencies:**
- Use a loop to traverse through the sorted array. A nested while loop counts the frequency of each character by iterating through consecutive occurrences of the same character.
- If a character has an odd frequency, increment the variable count, which tracks the number of characters with odd frequencies.
4. **Check Conditions:**
- Similar to the previous solution, the string s can be rearranged into k palindromic substrings if:
- The number of characters with odd frequencies (count) is less than or equal to k.
- k is less than or equal to the total length of the string n.
5. **Return Result:**
- Return true if both conditions are satisfied; otherwise, return false.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
$O(nlogn)$
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
$O(n)$
# Code
```java []
class Solution {
public boolean canConstruct(String s, int k) {
int n = s.length();
char arr[] = s.toCharArray();
Arrays.sort(arr);
int count = 0;
for(int i=0; i<n; ){
char ch = arr[i];
int freq = 0;
while(i < n && arr[i] == ch){
freq++;
i++;
}
if(freq%2 != 0){
count++;
}
}
return count <= k && k <= n;
}
}
```
# Approach 3 : HashMap for counting odd frequencies and verifying conditions
<!-- Describe your approach to solving the problem. -->
1. **Count Character Frequencies:**
- A HashMap<Character, Integer> (hm) is used to store the frequency of each character in the string s.
- The for loop iterates through the characters of the string, updating the frequency of each character using the getOrDefault method.
2. **Count Odd Frequencies:**
- A second loop iterates through the values of the HashMap (frequencies of the characters).
- If a frequency is odd, increment the count variable. This keeps track of the number of characters with odd frequencies.
3. **Check Conditions:**
- The string can be rearranged into k palindromic substrings if:
- The number of characters with odd frequencies (count) is less than or equal to k because each odd-frequency character requires its own palindrome.
- k is less than or equal to the length of the string n because we cannot create more substrings than there are characters in the string.
4. **Return Result:**
- Return true if both conditions are satisfied; otherwise, return false.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
$O(n)$
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
$O(m)$, where m is the number of unique characters in the string
# Code
```java []
class Solution {
public boolean canConstruct(String s, int k) {
int n = s.length();
HashMap<Character, Integer> hm = new HashMap<>();
for(char ch : s.toCharArray()){
hm.put(ch, hm.getOrDefault(ch, 0) + 1);
}
int count = 0;
for(int i : hm.values()){
if(i%2 != 0){
count++;
}
}
return count <= k && k <= n;
}
}
```
| 2
| 1
|
['Array', 'Hash Table', 'Math', 'String', 'Ordered Map', 'Counting', 'Java']
| 2
|
construct-k-palindrome-strings
|
easy intuition based solution runs in O(n) with hash table
|
easy-intuition-based-solution-runs-in-on-gvit
|
IntuitionAny even occurence can be easily be used to form a new palindrome.
What about characters with odd frequency ?ApproachCount the total occurences of char
|
sanky_20
|
NORMAL
|
2025-01-11T05:53:41.529564+00:00
|
2025-01-11T05:53:41.529564+00:00
| 5
| false
|
# Intuition
Any even occurence can be easily be used to form a new palindrome.
What about characters with odd frequency ?
# Approach
Count the total occurences of characters with odd freqquencies . if this value say count
count <= k then we can form that many odd length palindromic strings
ex -: s = "annabelle" k = 3
frequencies of various characters -
a -> 2
n -> 2
b -> 1
e -> 2
l -> 2
an example of pallindromic substrings -> "aba" , "lnnl" , "ee"
Edge case -> when s.length() < k What shall be output?
# Complexity
- Time complexity:
O(N)
- Space complexity:
O(1)
# Code
```cpp []
class Solution {
public:
bool canConstruct(string s, int k) {
if(s.length() < k) return false;
vector<int> freq(26,0);
for(auto it: s) freq[it-'a']++;
int count = 0;
for(int i=0;i<26;i++){
if(freq[i]&1) count++;
}
if(count > k) return false;
return true;
}
};
```
| 2
| 0
|
['Hash Table', 'Counting', 'C++']
| 0
|
construct-k-palindrome-strings
|
Solution in C
|
solution-in-c-by-vickyy234-3k87
|
Code
|
vickyy234
|
NORMAL
|
2025-01-11T05:40:29.003165+00:00
|
2025-01-11T05:40:29.003165+00:00
| 23
| false
|
# Code
```c []
bool canConstruct(char* s, int k) {
if(k > strlen(s)) return false;
if(k == strlen(s)) return true;
int *freq=calloc(sizeof(int),26);
for(int i=0;i<strlen(s);i++){
freq[s[i]-'a']++;
}
int oddcount=0;
for(int i=0;i<26;i++){
if(freq[i]%2!=0) oddcount++;
}
free(freq);
return oddcount <= k;
}
```
| 2
| 0
|
['C']
| 0
|
construct-k-palindrome-strings
|
Easy One for loop solution
|
easy-one-for-loop-solution-by-samir04-lwet
| null |
Samir04
|
NORMAL
|
2025-01-11T05:40:02.380785+00:00
|
2025-01-11T05:40:02.380785+00:00
| 53
| false
|
```python3 []
class Solution:
def canConstruct(self, s: str, k: int) -> bool:
if len(s)<k:
return False
hashmap = Counter(s)
count = 0
for key, value in hashmap.items():
if value % 2 == 1:
count+=1
return count<=k
```
| 2
| 0
|
['Hash Table', 'Counting', 'Python3']
| 0
|
construct-k-palindrome-strings
|
Java || 3ms || 100 %beat use Frequency Array ||
|
java-3ms-100-beat-use-frequency-array-by-yzs6
|
IntuitionApproachget frequence Count the odd number and compare to k return AnsewerComplexity
Time complexity:
o(2*n)
Space complexity:
o(n)
Code
|
sathish-77
|
NORMAL
|
2025-01-11T05:37:09.079791+00:00
|
2025-01-11T05:37:09.079791+00:00
| 34
| false
|
# Intuition
# Approach
get frequence Count the odd number and compare to k return Ansewer
# Complexity
- Time complexity:
o(2*n)
- Space complexity:
o(n)
# Code
```java []
class Solution {
public boolean canConstruct(String s, int k) {
if(s.length()<k) return false;
int[] arr=new int[26];
int cnt_odd=0;
for(char i:s.toCharArray()){
arr[i-'a']++;
}
for(int i:arr){
if(i>0){
if(i%2!=0)cnt_odd++;
}
}
if(cnt_odd>k)return false;
return true;
}
}
```
| 2
| 0
|
['Hash Table', 'String', 'Counting Sort', 'Java']
| 0
|
construct-k-palindrome-strings
|
Easy Solution | Frequency | Greedy | C++
|
easy-solution-frequency-greedy-c-by-mano-4q2o
|
IntuitionBy considering the properties of the palindrome, we could try to eliminate the cases that could not possibly lead to the solution.
An even length of th
|
manojithbhat
|
NORMAL
|
2025-01-11T05:32:17.086418+00:00
|
2025-01-11T05:32:17.086418+00:00
| 24
| false
|
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
By considering the properties of the palindrome, we could try to eliminate the cases that could not possibly lead to the solution.
1. An even length of the particular character do not cause the problem.
2. Odd length of character can only help to satisfy the condition if and only if they could be less than the value of k, as rest of the other even length characters could be distributed to attain the desired result.
# Approach
<!-- Describe your approach to solving the problem. -->
First check, if the length of the string is lesser than k, if so we cannot divide the string into k string, so return false.
Next check, if the length of the string is equal to k, if yes, then we return true, as it is always possible to have single length character which forms the palindrome.
Then use the map to keep the track of number ( frequency ) of character in the string.
Keep track of the number of odd length of character.
If there are more number of odd length of character then return false, else true.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
$$O(n)$$
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
$$O(n)$$
# Code
```cpp []
class Solution {
public:
bool canConstruct(string s, int k) {
int n = s.size();
if( n < k) return false;
if( n == k) return true;
unordered_map<char,int> mp;
for(auto it: s) mp[it]++;
int non_pairs = 0;
for(auto it: mp){
int num = it.second;
non_pairs += (num%2);
}
if( non_pairs > k) return false;
return true;
}
};
```
| 2
| 0
|
['Hash Table', 'String', 'Greedy', 'Counting', 'C++']
| 0
|
construct-k-palindrome-strings
|
C# Solution for Construct K Palindrome Strings Problem
|
c-solution-for-construct-k-palindrome-st-28m8
|
IntuitionThe problem involves determining whether all characters in a string s can be used to construct exactly k palindrome strings. The key observations are:
|
Aman_Raj_Sinha
|
NORMAL
|
2025-01-11T05:24:26.238630+00:00
|
2025-01-11T05:24:26.238630+00:00
| 27
| false
|
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
The problem involves determining whether all characters in a string s can be used to construct exactly k palindrome strings. The key observations are:
1. Odd Frequency Characters: A palindrome can have at most one character with an odd frequency (for the middle position). If more than k characters have an odd frequency, it’s impossible to form k palindromes.
2. String Length vs. k: If k > s.Length, constructing k palindromes is impossible, as we don’t have enough characters to distribute among k groups.
Given these observations:
• The number of odd-frequency characters (oddCount) determines the minimum number of palindromes required.
• If k >= oddCount and k <= s.Length , the answer is true.
# Approach
<!-- Describe your approach to solving the problem. -->
1. Check if k > s.Length:
• If k > s.Length, return false because it’s impossible to construct more palindromes than the number of characters available.
2. Character Frequency Count:
• Use an array of size 26 to count the frequency of each character in the string s. The array index represents the character (a to z).
3. Count Odd Frequencies:
• Traverse the frequency array and count how many characters have an odd frequency (oddCount).
4. Check Conditions:
• If oddCount > k, return false because it’s impossible to distribute odd characters across k palindromes.
• Otherwise, return true.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
1. Frequency Count: Counting the frequency of characters takes O(n) , where n is the length of the string s.
2. Odd Frequency Count: Iterating through the fixed-size frequency array (size 26) takes O(1) .
Total Time Complexity: O(n) .
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
1. Frequency Array: We use an array of size 26 to store character counts.
Total Space Complexity: O(1) (constant space).
# Code
```csharp []
public class Solution {
public bool CanConstruct(string s, int k) {
if (k > s.Length) {
return false;
}
int[] charCount = new int[26];
foreach (char c in s) {
charCount[c - 'a']++;
}
int oddCount = 0;
foreach (int count in charCount) {
if (count % 2 != 0) {
oddCount++;
}
}
return oddCount <= k;
}
}
```
| 2
| 0
|
['C#']
| 0
|
construct-k-palindrome-strings
|
✅🔥BEATS 100%🔥 || Beginner Friendly || Construct K Palindrome Strings 💡|| CONCISE CODE ✅
|
beats-100-beginner-friendly-construct-k-n8yx8
|
IntuitionApproachComplexity
Time complexity: O(n)
Space complexity: O(1)
Code
|
vanshdvn2505
|
NORMAL
|
2025-01-11T05:11:51.206027+00:00
|
2025-01-11T05:11:51.206027+00:00
| 19
| false
|
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity: O(n)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
bool canConstruct(string s, int k) {
if(s.length() < k){
return false;
}
vector<int> hash(26, 0);
for(int i = 0; i < s.length(); i++){
hash[s[i] - 'a']++;
}
int cnt = 0;
for(int i = 0; i < 26; i++){
if(hash[i]%2){
cnt++;
}
}
return cnt <= k;
}
};
```
| 2
| 0
|
['C++']
| 1
|
construct-k-palindrome-strings
|
Easy Solution in C
|
easy-solution-in-c-by-sathurnithy-kdf1
|
Code
|
Sathurnithy
|
NORMAL
|
2025-01-11T03:47:37.605904+00:00
|
2025-01-11T04:00:53.455046+00:00
| 17
| false
|
# Code
```c []
#define ALPHABETS 26
bool canConstruct(char* s, int k) {
if(strlen(s) < k) return false;
if(strlen(s) == k) return true;
int* freqArr = calloc(ALPHABETS, sizeof(int));
for(int i=0; i<strlen(s); i++)
freqArr[s[i] - 'a']++;
int oddFreq = 0;
for(int i=0; i<ALPHABETS; i++){
if(freqArr[i] % 2 != 0) oddFreq++;
}
free(freqArr);
return oddFreq<=k;
}
```
| 2
| 0
|
['String', 'Greedy', 'C', 'Counting']
| 0
|
construct-k-palindrome-strings
|
Optimised Odd Balancer | constant space
|
optimised-odd-balancer-constant-space-by-zozk
|
IntuitionWe want to check if it's possible to partition the given string into exactly k non-empty substrings such that each substring is a palindrome. This esse
|
sachin1604
|
NORMAL
|
2025-01-11T03:43:28.367186+00:00
|
2025-01-11T03:43:28.367186+00:00
| 32
| false
|
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
We want to check if it's possible to partition the given string into exactly k non-empty substrings such that each substring is a palindrome. This essentially boils down to counting how many characters have an odd frequency.
# Approach
<!-- Describe your approach to solving the problem. -->
- **Step 1:** Count the frequency of each character in the string.
- **Step 2:** Identify how many characters have an odd frequency. For a palindrome, at most one character can have an odd frequency.
- **Step 3:** If the number of odd-frequency characters is greater than k, it's impossible to form k palindromes. If k exceeds the string's length, it's also impossible.
- **Step 4:** Return true if the conditions are met, otherwise false.
# Complexity
- Time complexity: $$O(n)$$
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: $$O(1)$$
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
bool canConstruct(string s, int k) {
vector<int> alpha(26,0);
for(auto &i: s) alpha[i -'a']++;
int cnt = 0;
for(int i = 0; i < 26; i++){
if(alpha[i] & 1)cnt++;
}
if(cnt > k || k > s.length())return false;
return true;
}
};
```
| 2
| 0
|
['C++']
| 0
|
construct-k-palindrome-strings
|
Simple Approach || Easy to Beats 100% ||
|
simple-approach-easy-to-beats-100-by-raj-sth1
|
Firstly ,Thanks for come in my solution :)Complexity
Time complexity:O(N)
Space complexity:O(N)
Code
|
Rajpatel16
|
NORMAL
|
2025-01-11T03:40:26.725966+00:00
|
2025-01-11T03:40:26.725966+00:00
| 30
| false
|
**Firstly ,Thanks for come in my solution :)**
# Complexity
- Time complexity:O(N)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:O(N)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
bool canConstruct(string s, int k) {
if(s.size() < k) return false;
if (s.size() == k) return true;
unordered_map<char,int>mp;
// Frequency count of all character in S
for(char ch : s){
mp[ch]++;
}
// Count the odd frequencies
int count = 0;
for(auto key : mp){
if(key.second%2 == 1) count++;
}
return (count > k)?false:true;
}
};
```
| 2
| 0
|
['Hash Table', 'String', 'Greedy', 'Counting', 'C++']
| 0
|
construct-k-palindrome-strings
|
Beats 100%✅ | Counting | Simple Solution With Added Comments | Time Complexity O(n)
|
beats-100-counting-simple-solution-with-iope0
|
IntuitionThe idea behind this solution is that if there are more than k characters then it is not possible to make k palindromes, If this is not the case, then
|
nvdpsaluja
|
NORMAL
|
2025-01-11T03:08:36.050383+00:00
|
2025-01-11T03:28:49.907532+00:00
| 29
| false
|
# Intuition
The idea behind this solution is that if there are more than k characters then it is not possible to make k palindromes, If this is not the case, then the count of characters which occured odd times must be less than k.
# Complexity
- Time complexity:
O(n)
- Space complexity:
O(26)
# Code
```cpp []
class Solution {
public:
bool canConstruct(string s, int k) {
int n=s.size(),cntodd=0;
if(k>n)return false;// not possible -> because even if each character is treated individually it would still not be possible to make k palindrome strings.
vector<int> freq(26,0);// stores the frequency of each character
for(int i=0;i<n;i++)freq[s[i]-'a']++;
//count character which has occured odd times if it's less than or equal to k then only it is possible to make k palindromes
for(int i=0;i<26;i++)cntodd+=(freq[i]&1);
return cntodd<=k;
}
};
```
| 2
| 0
|
['Counting', 'C++']
| 0
|
construct-k-palindrome-strings
|
Solution without HashTable || java || C++
|
solution-without-hashtable-java-c-by-dsu-m9kf
|
IntuitionTo form a single palindrome string, either
it should have a single odd character or
it should have all characters with even frequencies
To form k palin
|
dsuryaprakash89
|
NORMAL
|
2025-01-11T02:39:36.639077+00:00
|
2025-01-11T02:39:36.639077+00:00
| 6
| false
|
# Intuition
To form a single palindrome string, either
- it should have a single odd character or
- it should have all characters with even frequencies
To form `k` palindromes, the total number of characters with odd frequencies should be at most `k`.
- Each palindrome can have one character with an odd frequency (which will be placed in the center).
- If there are more than `k` characters with odd frequencies, it would be impossible to distribute them such that each palindrome has at most one odd character in the center.
Example : annabelle and `k` =2
`anna` - it contains all characters with even frequencies
`blele` - it contains b with 1 occurance and rest all characters with even occurances
oddcount= 1`<`k
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
#### Base Case :
If length of the string is less than `k` then it is impossible to construct `k` palindromes
- Initialise a integer array or a vector to store all the occurances of characters in a string.
- Start iterating in array `ch`.
- if `ch[i]` is is even increment evencount.
- if `ch[i]` is is odd increment oddcount.
- Return `true` if oddcount is less than or equal to `k`.
- else Return `false`.
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity: $$O(n)$$ to form an array
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: $$O(26)$$ or $$O(1)$$
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public boolean canConstruct(String s, int k) {
if(s.length()<k)return false;
int ch[]= new int[26];
for(char c: s.toCharArray()){
ch[c-'a']++;
}
int oddcount=0;
for(int i:ch){
if(i%2!=0)oddcount++;
}
if(oddcount<=k)return true;
else return false;
}
}
```
```cpp []
class Solution {
public:
bool canConstruct(string s, int k) {
if (s.size() < k)
return false;
vector<int> ch(26, 0);
for (int i=0;i<s.size();i++) {
ch[s[i]-'a']++;
}
int oddcount = 0;
for (int& i : ch) {
if (i % 2 != 0)
oddcount++;
}
if (oddcount <= k)
return true;
else
return false;
}
};
```
| 2
| 0
|
['Counting', 'C++', 'Java']
| 0
|
construct-k-palindrome-strings
|
Beats 100% - DP - O(n) - count number of odd characters
|
beats-100-dp-on-count-number-of-odd-char-98ey
|
Intuition
count number of odd characters
Approach
check len(s) vs k
counting number of each character
count number of odd characters countOdd
compare countOdd
|
luudanhhieu
|
NORMAL
|
2025-01-11T00:51:58.900872+00:00
|
2025-01-11T00:51:58.900872+00:00
| 70
| false
|
# Intuition
- count number of odd characters
# Approach
- check len(s) vs k
- counting number of each character
- count number of odd characters `countOdd`
- compare countOdd vs k to get result
# Complexity
- Time complexity: O(n))
- Space complexity: O(1)
# Code
```golang []
func canConstruct(s string, k int) bool {
if len(s) < k {
return false
}
dp := make([]int, 26)
for i := 0; i < len(s); i++ {
dp[s[i]-'a']++
}
countOdd := 0
for _, v := range dp {
countOdd += v % 2
}
if k < countOdd {
return false
}
return true
}
```
| 2
| 0
|
['Go']
| 1
|
construct-k-palindrome-strings
|
C++ 100% EASY TO UNDERSTAND TLDE;
|
c-100-easy-to-understand-tlde-by-sainadt-aut0
|
IntuitionCHECK CODE COMMENTSApproachComplexity
Time complexity: O(∣s∣)
Space complexity: O(1)
Code
|
sainadth
|
NORMAL
|
2025-01-11T00:38:11.827959+00:00
|
2025-01-11T00:38:11.827959+00:00
| 16
| false
|
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
CHECK CODE COMMENTS
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity: $$O(|s|)$$
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: $$O(1)$$
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
bool canConstruct(string s, int k) {
/*
TC - O(|s|)
SC - O(1)
1. IF NO OF CHARACTERS ARE LESS THAN K THEN RETURN FALSE
2. IF NO OF CHARACTERS ARE EQUAL TO K RETURN TRUE SINCE A CHARACTER IS A WORD OF LENGHT 1, WHICH IS A PALINDROME
3. IF NO OF CHARACTERS ARE MORE
A. COUNT NO OF ODD FREQUENT CHRACTERS IN THE STRING
B. IF IT IS MORE THAN K RETURN FALSE
C. ELSE IT IS A VALID CASE FOR EVERY OTHER SCENARIO
EX. AAAAAA 3
ALL ARE SAME SO oddFreq = 0
AAA | AA | A -> VALID ANS
EX. ABCD 3
oddFreq = 4
A | B | C | D ATLEAST 4 DIFFERENT PALINDROMES WILL BE MADE SO RETURN FALSE;
EX. AAB 3
oddFreq = 2
A | A | B -> VALID ANS
SINCE LENGTH OF STRING IS ALWAYS > K (PRE CHECKED)
IT FORMS A VALID ANSWER TO ALL CASES
*/
if(s.size() < k) return false;
if(s.size() == k) return true;
vector<int> charFreq(26, 0);
for(auto i: s) charFreq[i - 'a'] ^= 1;
int oddFreq = 0;
for(auto i : charFreq) oddFreq += i;
if(oddFreq > k) return false;
return true;
}
};
```
| 2
| 0
|
['Array', 'C++']
| 0
|
construct-k-palindrome-strings
|
Swift💯1liner w/ bits; Fastest: 0ms
|
swift1liner-w-bits-fastest-0ms-by-upvote-s3ae
|
One-Liner using Bits, terse (accepted answer)
Return true if s can be partitioning into at least k sections and the number of odd-count letters is <= k.
|
UpvoteThisPls
|
NORMAL
|
2025-01-11T00:32:03.419693+00:00
|
2025-01-11T00:32:03.419693+00:00
| 38
| false
|
**One-Liner using Bits, terse (accepted answer)**
Return `true` if `s` can be partitioning into at least `k` sections and the number of odd-count letters is <= `k`.
```
class Solution {
func canConstruct(_ s: String, _ k: Int) -> Bool {
s.count>=k && s.utf8.reduce(0){$0^(1<<($1-97))}.nonzeroBitCount<=k
}
}
```
| 2
| 0
|
['Swift']
| 2
|
construct-k-palindrome-strings
|
C++ | Odd Even Frequency
|
c-odd-even-frequency-by-ahmedsayed1-r74g
|
The best construction of palindrome string contains all chars occurrence even time or at most 1 char occurrence odd timesCode
|
AhmedSayed1
|
NORMAL
|
2025-01-11T00:12:28.224639+00:00
|
2025-01-11T00:12:59.054455+00:00
| 53
| false
|
# The best construction of palindrome string contains all chars occurrence even time or at most 1 char occurrence odd times
# Code
```cpp []
class Solution {
public:
bool canConstruct(string s, int k) {
if(k > s.size())return 0;
int fre[26]{};
for(auto i : s)fre[i - 'a']++;
int odd = 0;
for(auto i : fre)
if(i % 2)odd++;
return odd <= k;
}
};
```
| 2
| 0
|
['Greedy', 'Counting', 'C++']
| 0
|
construct-k-palindrome-strings
|
O(1) - Most detailed explanation
|
o1-most-detailed-explanation-by-__phoeni-isj7
|
The problem is quite simple and interesting as well. Lets start from very basic:\n\nQ. Suppose we are given a string str, and we are free to jumble the characte
|
__phoenixer__
|
NORMAL
|
2023-06-28T11:05:47.459127+00:00
|
2023-06-28T11:06:28.402261+00:00
| 149
| false
|
The problem is quite simple and interesting as well. Lets start from very basic:\n\n**Q.** Suppose we are given a string ```str```, and we are free to jumble the characters, and we need to tell that wheather ```str``` can be palindrome after jumbling.\n* So, we will keep a track of frequency of each character appeared in ```str``` (with the help of hashmap or array of size 26)\n* **Now how to check**: \uD83D\uDC49 Even occurances of any character ```c``` is allowed. But there must be either 0 or 1 character with odd occurances\n* For example: "abba" is palindrome and there are no character with odd frequency. Similarly, "abcba" or "abcccba" is also a palindrome but there is 1 character with odd frequency.\n\nKeeping this in mind: \n* We will store the frequency of each character in input string using hashmap (or array of size 26).\n* We have no issue with even frequency character. As they will always from palindrome.\n* We are concerned with odd freq character. Count that how many character has odd frequency. [say cnt]\n* In order to split input string into \'k\' palindromic string, number of odd freq character must be less than equal to k [or cnt<=k], \n* This is because then only we can distribute each of the odd frequency character in one of the \'k\' strings.\n* Simple! We are done! We are just required to check this condition only.\n\n\n**CODE:**\n```\nclass Solution {\npublic:\n bool canConstruct(string s, int k) {\n if(s.size()<k){ return false; } // obvious edge case\n \n unordered_map<char, int> m; // {char, freq}\n for(int i=0; i<s.size(); i++){ m[s[i]]++; }\n\t\t\n int cnt=0; // to count odd freq character\n for(auto& it: m){\n if(it.second%2==1){ cnt++; }\n }\n return (cnt<=k);\n }\n};\n```\nTime Complexity: O(26) ~ O(1) || Space Complexity: O(26) ~ O(1)
| 2
| 0
|
['C']
| 2
|
construct-k-palindrome-strings
|
THIS IS HOW IT WORKS'
|
this-is-how-it-works-by-e8s4ca3p9e-y1zv
|
lets talk about the case when k<s.size() // coz it is confusing lol\n\nit means we have to do k partitions\n\nsuppose no of odd occuring characters be : o\nassu
|
E8S4CA3P9E
|
NORMAL
|
2022-11-24T18:12:26.020270+00:00
|
2022-11-24T19:01:19.711266+00:00
| 208
| false
|
lets talk about the case when k<s.size() // coz it is confusing lol\n\nit means we have to do k partitions\n\nsuppose no of odd occuring characters be : o\nassuming o<=k\n\n----- ----- ----- ----- ----- ---- -----\nsuppose these are k partitions, of different lengths ( might be of same length too)\ni am represeting them by ---- ---- ----- ----- , where a character is present at \' - \' \n\nnow there are 2 subcases , either all of the k partitions contain one odd character\n\nhere q->denotes any character with odd freq \n---q1--- ---q2--- --q3-- --q4-- --q5-- \n\n---q1--- is one partition , while ---q2--- is another and so on\n\nsuppose character a and b have odd frequeny, so q1 can be a or b\nand q2 can be b or a respectively\n\nso after eliminating "odd frequency of odd occuring characters"\nWE KNOW know every character has even freq.\n\nnow we can fill remaining spaces with elements .\n\n---q1--- | ---q2--- | ---q3---| ---q4---\n\nthese are the partitions and we are left with characters having even freqency,\nand the remaining length to be filled in all the partitions is s.size()-[q1+q2...(odd frequency)]\nif any position of any partition is filled with any character,\nwe know that characters have even freq , so corresponding palindromic [reverse right to left]\nposition can be filled with same character.\nand we have used 2 characters of same type, so we still have all the characters with even freq.\n\nthis is how we can fill all partitions.\n\nnow same ideology can be extended when o<k\n\n\nsuppose we put one odd character in each partition\nso new partitions formed = o\n partitions we need to create =k-o\nremaining characters left=s.size()-o\n\nnow the ques is can we form k-o palindromic paritions given that\nwe are left with all even freqency characters\n\nnow there are further 2 subcases\nwhen k-o is even\nwe are left with s.size()-o characters where (size()-o>k-o)\nwe know all the size()-o character has its sibling ( it occurs even number of time)\n\nwe need to create k-o ( even no. of partitions)\nso what we can do, choose one character and its sibling, and you can create two new partitions\nnow in last steps, you will be left with characters , having even freq.\nand you can put it anywhere. [ in any partition]\n\n\n\nwhat if k-o is odd?\n\nwe know k-o-1 is even so first fill at the remaining k-o-1 places .\nnow we want to create one new partition right?\nplace all the remaining characters in that partition.\n\n\nIT CAN BE SHOWED THAT WE CAN ALWAYS CONSTRUCT K-PALINDROMS!\n;) THIS IS INDEPTH PROOF OF THE SOLUTION :D\n\ni\'ve not considered the trivial cases when s.size()<k || s.size()==k ;) they are self explanatory!\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n
| 2
| 0
|
[]
| 1
|
construct-k-palindrome-strings
|
✔ [C++ / Python3] Solution | XOR
|
c-python3-solution-xor-by-satyam2001-k1me
|
Complexity\n- Time complexity: O(n)\n- Space complexity: O(1)\n\n# Python3\n\nclass Solution:\n def canConstruct(self, S, K):\n return bin(reduce(oper
|
satyam2001
|
NORMAL
|
2022-11-14T18:36:51.942874+00:00
|
2022-11-14T18:36:51.942915+00:00
| 366
| false
|
# Complexity\n- Time complexity: $$O(n)$$\n- Space complexity: $$O(1)$$\n\n# Python3\n```\nclass Solution:\n def canConstruct(self, S, K):\n return bin(reduce(operator.xor, map(lambda x: 1 << (ord(x) - 97), S))).count(\'1\') <= K <= len(S)\n```\n\n# C++\n```\nclass Solution {\npublic:\n bool canConstruct(string s, int k) {\n int val = 0;\n for(char c: s) val ^= (1 << (c - \'a\'));\n return k <= s.length() && __builtin_popcount(val) <= k;\n }\n};\n```
| 2
| 0
|
['Bit Manipulation', 'Python3']
| 1
|
construct-k-palindrome-strings
|
Python beats 97% with reasoning
|
python-beats-97-with-reasoning-by-zym199-b268
|
\nclass Solution:\n def canConstruct(self, s: str, k: int) -> bool:\n \'\'\'\n For a palindrome, its odd-count character has to be less than or
|
zym1994815
|
NORMAL
|
2022-06-03T08:25:59.716078+00:00
|
2022-06-03T08:26:56.545132+00:00
| 398
| false
|
```\nclass Solution:\n def canConstruct(self, s: str, k: int) -> bool:\n \'\'\'\n For a palindrome, its odd-count character has to be less than or eqaul to one. \n Then in order to get k many palindromic substrings, the number of odd-count chracters in s has to be less than\n or equal to k \'\'\'\n \n if len(s) < k:\n return False\n freq = Counter(s)\n return sum(1 for val in freq.values() if val % 2 != 0) <= k\n```
| 2
| 0
|
['Python']
| 2
|
element-appearing-more-than-25-in-sorted-array
|
Simple Java Solution - O(n) time, O(1) space
|
simple-java-solution-on-time-o1-space-by-0zqf
|
\n public int findSpecialInteger(int[] arr) {\n int n = arr.length, t = n / 4;\n\n for (int i = 0; i < n - t; i++) {\n if (arr[i] ==
|
anshu4intvcom
|
NORMAL
|
2019-12-14T16:01:00.198954+00:00
|
2019-12-14T16:11:03.406388+00:00
| 10,142
| false
|
```\n public int findSpecialInteger(int[] arr) {\n int n = arr.length, t = n / 4;\n\n for (int i = 0; i < n - t; i++) {\n if (arr[i] == arr[i + t]) {\n return arr[i];\n }\n }\n return -1;\n }\n```
| 203
| 3
|
[]
| 13
|
element-appearing-more-than-25-in-sorted-array
|
[4 Minute Read] Mimicking an Interview
|
4-minute-read-mimicking-an-interview-by-ko1ol
|
In this post, I would be discussing this problem with different approaches which you would come up in an interview in the manner of increasing difficulty. I wil
|
dead_lock
|
NORMAL
|
2021-08-12T09:21:12.097968+00:00
|
2021-08-18T10:36:57.142644+00:00
| 3,485
| false
|
In this post, I would be discussing this problem with different approaches which you would come up in an interview in the manner of increasing difficulty. I will be writting this post in such a way as if I were the person being interviewed. So, enjoy \uD83D\uDE0A\n\n<br>\n\n> **Interviewer: Given the problem [Element Appearing More Than 25% In Sorted Array](https://leetcode.com/problems/element-appearing-more-than-25-in-sorted-array). How would you approach to solve it?**\n> \n\n*[**My mind**] Huh! child\'s play!* \uD83D\uDE0F\n\nQuickly coming up with the brute force \uD83D\uDE01.\n\n\n<br>\n\n**1. For every element count the occurance of that element and check it\'s count**\nI can use 2 pointers, say `i` and `j`, where for each `i`, I would iterate over the array using `j` and counting the occurances of the element at `i`, i.e. `arr[i]`. If the count turns out to be greater than 25% of the length of the array, i.e. `count > n / 4` (`n` is the length of the array), I would return `arr[i]` as my required element.\n\nBelow is the Java Code using the above algorithm \n```java\nclass Solution {\n public int findSpecialInteger(int[] arr) {\n int n = arr.length;\n for(int i = 0; i < n; i++) {\n int count = 0;\n for(int j = 0; j < n; j++) {\n if(arr[i] == arr[j]) count++;\n }\n if(count > n / 4) return arr[i];\n }\n return -1;\n }\n}\n```\nThe time complexity of this approach would be O(n<sup>2</sup>) and the space complexity would be O(1).\n\n<br>\n\n> **Interviewer: Okay, but that\'s too slow, can you optimize it?**\n> \n\n*[**My mind**] I knew this would be comming* \uD83D\uDE0F\n\nActing to think \uD83E\uDD14........ and then, coming up with the second approach\n\n<br>\n\n**2. Counting the frequency of all the elements, and then checking the frequency**\nWe would maintain a `map` or a `freq` array, in which we would keep the count of each element. Once we have counted all the elements, we would iterate through our `map` or `freq` array, and would check which element has it\'s count greater than `n / 4`, and return that element.\n\nBelow is the Java Code using the above algorithm\n```java\nclass Solution {\n public int findSpecialInteger(int[] arr) {\n int n = arr.length;\n int freq[] = new int[1_00_001];\n for(int i : arr) {\n freq[i]++;\n } \n for(int i = 0; i < freq.length; i++) {\n if(freq[i] > n / 4) return i;\n }\n return -1;\n }\n}\n```\nThe time complexity of this approach would be O(n) and the space complexity would be O(n).\n\n<br>\n\n> **Interviewer: Okay, but you can\'t use any extra space. Can you come up with the same time complexity without using any auxilary space?**\n> \n\n*[**My mind**] Guess whatt.... I knew this would also be coming* \uD83D\uDE0F\n\nAgain a bit of pretending to think \uD83E\uDD14........ and then quickly coming up with the approach.\n\n<br>\n\n**3. Iterating over the array and increasing it\'s freq if it\'s equal to it\'s previous element.**\nSince the array is sorted, the elements which would be equal would be adjacent to each other. So we would keep track of the previous element (`prev`) we have seen. If the current element is equal to the previous element we would increase our `count`. If it\'s not equal, then we would reset `prev` to current element and `count` to `1`.\nIf at any instance, our `count > n / 4` we would return our current element as the required value.\n\nBelow is the Java Code using the above algorithm\n```java\nclass Solution {\n public int findSpecialInteger(int[] arr) {\n int count = 0;\n int n= arr.length;\n int prev = -1;\n int req = n / 4;\n for(int i : arr) {\n if(i == prev) {\n count++;\n }\n else {\n prev = i;\n count = 1;\n }\n if(count > req) {\n return i;\n }\n }\n return -1;\n }\n}\n```\n\nThe time complexity of this approach would be O(n) and the space complexity would be O(1).\n\n<br>\n\n> **Interviewer: Nice, but it\'s yet slow, can you reduce it further?**\n> \n\n*[**My mind**] Whhattt! where did this come from* \uD83D\uDE1F\n\nThis time really thinking \uD83E\uDD14........ and suddenly noticing that array is sorted.\n\n<br>\n\n**4. Checking the first and last index of occuring of the elements at position n / 4, (2 * n) / 4 and (3 * n) / 4**\nThe logic is, let\'s say we divide the array into 4 parts, i.e. the first part will be from `[0, n / 4]`, second from `[n / 4, (2 * n) / 4]`, third from `[(2 * n) / 4, (3 * n) / 4]` and fourth from `[(3 * n) / 4, n - 1]`. Now, whatever would be our required element should be at one of the index `n / 4` or `(2 * n) / 4` or `(3 * n) / 4`. Let\'s call these indices as our `special` indices. The answer should be at one of our `special` indices because, these indices are the marked at 25% intervals of the array, and since the required element is the one having occurance more than 25% and the array is sorted, so the required element must be present at one of our `special` points.\nNow, we need to verify for our 3 `special` index, if the element at current index, say `i`, is a valid required element or not. Dealing with that is fast if we use Binary Search. We can find the first index of occurance of element `arr[i]` which would be the `lower_bound` of `arr[i]`, say `l`, and similarly find last index of occurance of element `arr[i]` which would be the `upper_bound` of `arr[i]`, say `r`. The frequency of `arr[i]` hence would be `r - l + 1`, and we could check if it\'s greater than `n / 4`.\n\nBelow is the Java Code using the above algorithm\n```java\nclass Solution {\n public int bin_find1(int arr[], int val) {\n\t\t// for finding lower bound\n int l = 0, r = arr.length - 1;\n int ans = -1;\n while(l <= r) {\n int mid = l + (r - l) / 2;\n if(arr[mid] >= val) {\n ans = mid;\n r = mid - 1;\n }\n else l = mid + 1;\n }\n return ans;\n }\n public int bin_find2(int arr[], int val) {\n\t\t// for finding upper bound\n int l = 0, r = arr.length - 1;\n int ans = -1;\n while(l <= r) {\n int mid = l + (r - l) / 2;\n if(arr[mid] <= val) {\n ans = mid;\n l = mid + 1;\n }\n else r = mid - 1;\n }\n return ans;\n }\n public boolean valid(int arr[], int ind) {\n int n = arr.length;\n int start = bin_find1(arr, arr[ind]);\n int end = bin_find2(arr, arr[ind]);\n if(end - start + 1 > n / 4) return true;\n return false;\n }\n public int findSpecialInteger(int[] arr) {\n int n = arr.length;\n int first = n / 4;\n int second = n / 2;\n int third = 3 * n / 4;\n \n if(valid(arr, first)) return arr[first];\n else if(valid(arr, second)) return arr[second];\n else if(valid(arr, third)) return arr[third];\n return -1;\n }\n}\n```\nThe time complexity of this approach would be O(6 * log(n)) (finding upper and lower bound would O(log(n)) each and repeating same for 3 elements) and the space complexity would be O(1).\n\n<br>\n\n> **Interviewer: Very Nice, but can you reduce time complexity further to O(3 * log(n))**\n> \n\n*[**My mind**] Not again!.... I am really getting frustated at this guy now!* \uD83D\uDE21\n\nThinking for a while again \uD83E\uDD14........ scratching my head again and again.\n\n> **Interviewer: Okay, let me give you a hint, do you really need to find the upper_bound once you know the lower_bound of the element?**\n> \n*[**My mind**] I can\'t get what he is saying, seems like I won\'t make into my dream company.*\n\nThinking for a over and over again \uD83E\uDD14........ and suddenly got an idea.\n\n<br>\n\n**5. Checking the first `index` of occurance of the elements at position n / 4, (2 * n) / 4 and (3 * n) / 4 and directly comparing with element at `index + n / 4`**\nSince we only need to find if an element occurs more than `n / 4` times, we just care about the first index of the occurance of element, say `index` , and if the element at `index + n / 4` (because `[index, index + n / 4]` are total `(n / 4) + 1` elements), if they both are same, `arr[index]` is our answer. And since we are finding only the `lower_bound` our time complexity would now be O(log(n)) for one element, instead of O(2 * log(n)) in previous approach.\n\nBelow is the Java Code using the above algorithm\n```java\nclass Solution {\n public int bin_find1(int arr[], int val) {\n\t\t// to find the lower bound\n int l = 0, r = arr.length - 1;\n int ans = -1;\n while(l <= r) {\n int mid = l + (r - l) / 2;\n if(arr[mid] >= val) {\n ans = mid;\n r = mid - 1;\n }\n else l = mid + 1;\n }\n return ans;\n }\n public boolean valid(int arr[], int ind) {\n int n = arr.length;\n int start = bin_find1(arr, arr[ind]);\n if(arr[start + (n / 4)] == arr[ind]) return true;\n return false;\n }\n public int findSpecialInteger(int[] arr) {\n int n = arr.length;\n int first = n / 4;\n int second = n / 2;\n int third = 3 * n / 4;\n \n if(valid(arr, first)) return arr[first];\n else if(valid(arr, second)) return arr[second];\n else if(valid(arr, third)) return arr[third];\n return -1;\n }\n}\n```\nThe time complexity of this approach would be O(3 * log(n)) (finding lower bound would O(log(n)) each and repeating same for 3 elements) and the space complexity would be O(1).\n\n<br>\n\n> **Interviewer: Nice, so we are done with the interview, thanks for joining**\n> \n\n*[**My mind**] Finally done! Hope I get my dream job* \uD83E\uDD1E\n\n<br> \n\n**Thank you for giving your time in reading this post. Like if you feel so. Also, share your feedbacks and suggestions.**\n\n\n\n
| 130
| 2
|
['Binary Tree', 'Java']
| 10
|
element-appearing-more-than-25-in-sorted-array
|
Java Binary Search
|
java-binary-search-by-poorvank-zbc5
|
Since its a sorted array so i wanted to avoid linear search\n\nFind the element at position n/4\nPerform a binary search to find the first occurrence of that it
|
poorvank
|
NORMAL
|
2019-12-14T16:04:16.004510+00:00
|
2019-12-14T22:58:54.841446+00:00
| 12,055
| false
|
Since its a sorted array so i wanted to avoid linear search\n\nFind the element at position n/4\nPerform a binary search to find the first occurrence of that item.\nPerform a binary search to find the last occurrence of that item.\nIf last-first+1 > n/4, you have your answer.\n\nRepeat that process for n/2 and 3(n/4)\n\nUpdated to a more readable solution:\n```\npublic int findSpecialInteger(int[] arr) {\n int n = arr.length;\n if(n==1) {\n return arr[0];\n }\n List<Integer> list = new ArrayList<>(Arrays.asList(arr[n/4],arr[n/2],arr[(3*n)/4]));\n for (int element : list) {\n int f = firstOccurrence(arr,element);\n int l = lastOccurrence(arr,element);\n if(l-f+1>n/4) {\n return element;\n }\n }\n return -1;\n }\n\n private int firstOccurrence(int[] nums, int target) {\n int start=0;\n int end = nums.length-1;\n while(start < end){\n int middle = start + (end - start)/2;\n if(nums[middle]==target && (middle==start || nums[middle-1]<target)) {\n return middle;\n }\n if(target > nums[middle])\n start = middle + 1;\n else\n end = middle;\n }\n return start;\n\n }\n\n private int lastOccurrence(int[] nums,int target) {\n int start=0;\n int end = nums.length-1;\n while(start < end){\n int middle = start + (end - start)/2;\n if(nums[middle]==target && (middle==end || nums[middle+1]>target)) {\n return middle;\n }\n if(nums[middle] > target)\n end = middle;\n else\n start = middle + 1;\n }\n return start;\n\n }\n```
| 129
| 9
|
[]
| 23
|
element-appearing-more-than-25-in-sorted-array
|
Concise O(logn) solution using C++ (beat 90%)
|
concise-ologn-solution-using-c-beat-90-b-8w6z
|
Because it\'s guaranteed that only one number will appear more than 25% times, that number will definitely appear at one of the three positions in the array: qu
|
mrjia1997
|
NORMAL
|
2019-12-17T12:37:37.098656+00:00
|
2019-12-17T12:37:37.098687+00:00
| 6,389
| false
|
Because it\'s guaranteed that only one number will appear more than 25% times, that number will definitely appear at one of the three positions in the array: quarter, half, and three quarters. We see them as candidates, and then using binary search to check each of them. \n\nTime complexity: O(logn)\nSpace complexity: O(1)\n\n``` c++\nclass Solution {\npublic:\n int findSpecialInteger(vector<int>& arr) {\n int sz = arr.size();\n vector<int> candidates = {arr[sz/4], arr[sz/2], arr[sz*3/4]};\n for (auto cand : candidates) {\n auto st = lower_bound(arr.begin(), arr.end(), cand);\n auto ed = upper_bound(arr.begin(), arr.end(), cand);\n if (4 * (distance(st, ed)) > sz)\n return cand;\n }\n return -1;\n }\n};\n```
| 106
| 1
|
['Binary Tree']
| 15
|
element-appearing-more-than-25-in-sorted-array
|
✅ Beats 100% - Explained with [ Video ]- C++/Java/Python/JS - Single Pass - Visualized
|
beats-100-explained-with-video-cjavapyth-x0q6
|
\n\n# YouTube Video Explanation:\n\nhttps://youtu.be/R2N7catcZ_I\n **If you want a video for this question please write in the comments** \n\n\uD83D\uDD25 Pleas
|
lancertech6
|
NORMAL
|
2023-12-11T02:00:49.955890+00:00
|
2023-12-11T02:36:39.146347+00:00
| 15,512
| false
|
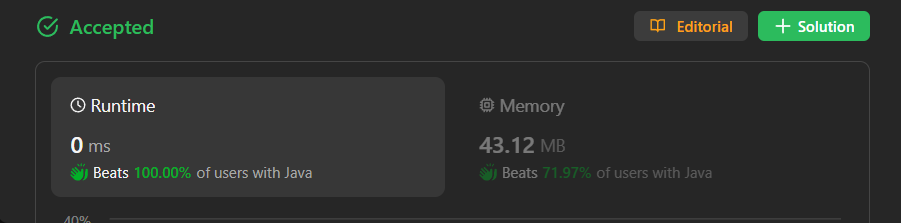\n\n# YouTube Video Explanation:\n\n[https://youtu.be/R2N7catcZ_I](https://youtu.be/R2N7catcZ_I)\n<!-- **If you want a video for this question please write in the comments** -->\n\n**\uD83D\uDD25 Please like, share, and subscribe to support our channel\'s mission of making complex concepts easy to understand.**\n\nSubscribe Link: https://www.youtube.com/@leetlogics/?sub_confirmation=1\n\n*Subscribe Goal: 800 Subscribers*\n*Current Subscribers: 710*\n\n---\n\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem states that there is exactly one integer in the array that occurs more than 25% of the time. Since the array is sorted in non-decreasing order, any integer that occurs more than 25% of the time will be part of a contiguous subsequence in the array. Therefore, we can iterate through the array and keep track of the count of consecutive occurrences of the same integer.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Initialize variables `size` to store the size of the array, `qtr` to store 25% of the size, `cnt` to keep track of consecutive occurrences, and `p` to store the current integer being checked.\n2. Iterate through the array starting from index 1.\n3. Compare the current integer `arr[i]` with the previous integer `p`.\n - If they are equal, increment the count `cnt`.\n - If they are not equal, reset the count `cnt` to 1.\n4. Check if the count `cnt` is greater than 25% of the array size `qtr`.\n - If true, return the current integer `arr[i]` as it occurs more than 25% of the time.\n - If false, update the previous integer `p` to the current integer `arr[i]`.\n5. If no integer is found during the iteration, return the last integer `p` as the answer.\n\n# Complexity\n- Time Complexity: O(n), where n is the size of the input array. We iterate through the array once.\n- Space Complexity: O(1), as we use a constant amount of space for variables.\n\n# Code\n```java []\nclass Solution {\n public int findSpecialInteger(int[] arr) {\n int size = arr.length;\n int qtr = size / 4;\n int cnt = 1;\n int p = arr[0];\n for (int i = 1 ; i < arr.length ; i++) {\n\n if ( p == arr[i]) cnt++;\n else cnt = 1;\n \n if (cnt > qtr) return arr[i];\n \n p = arr[i];\n }\n\n return p;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int findSpecialInteger(vector<int>& arr) {\n int size = arr.size();\n int qtr = size / 4;\n int cnt = 1;\n int p = arr[0];\n for (int i = 1 ; i < size ; i++) {\n\n if ( p == arr[i]) cnt++;\n else cnt = 1;\n \n if (cnt > qtr) return arr[i];\n \n p = arr[i];\n }\n\n return p;\n }\n};\n```\n```Python []\nclass Solution(object):\n def findSpecialInteger(self, arr):\n size = len(arr)\n qtr = size // 4\n cnt = 1\n p = arr[0]\n \n for i in range(1, size):\n if p == arr[i]:\n cnt += 1\n else:\n cnt = 1\n \n if cnt > qtr:\n return arr[i]\n \n p = arr[i]\n\n return p\n \n```\n```JavaScript []\n/**\n * @param {number[]} arr\n * @return {number}\n */\nvar findSpecialInteger = function(arr) {\n let size = arr.length;\n let qtr = Math.floor(size / 4);\n let cnt = 1;\n let p = arr[0];\n\n for (let i = 1; i < size; i++) {\n if (p === arr[i]) {\n cnt++;\n } else {\n cnt = 1;\n }\n\n if (cnt > qtr) {\n return arr[i];\n }\n\n p = arr[i];\n }\n\n return p;\n\n};\n```\n\n
| 97
| 2
|
['Array', 'Python', 'C++', 'Java', 'JavaScript']
| 6
|
element-appearing-more-than-25-in-sorted-array
|
Python3 faster over98%
|
python3-faster-over98-by-zhangjunxu3-reej
|
\nclass Solution:\n\ndef findSpecialInteger(self, arr: List[int]) -> int:\nn = len(arr) // 4\nfor i in range(len(arr)):\nif arr[i] == arr[i + n]:\nreturn arr[i]
|
zhangjunxu3
|
NORMAL
|
2020-01-06T04:07:12.680115+00:00
|
2020-01-06T04:07:12.680158+00:00
| 4,454
| false
|
```\nclass Solution:\n\ndef findSpecialInteger(self, arr: List[int]) -> int:\nn = len(arr) // 4\nfor i in range(len(arr)):\nif arr[i] == arr[i + n]:\nreturn arr[i]\n```\n
| 63
| 7
|
[]
| 12
|
element-appearing-more-than-25-in-sorted-array
|
[Java] Binary Search with O(log(N)) solution
|
java-binary-search-with-ologn-solution-b-p077
|
\n public int findSpecialInteger(int[] arr) {\n if (arr.length == 1) return arr[0];\n\n int length = arr.length;\n List<Integer> firstTh
|
MichaelBarskii
|
NORMAL
|
2020-05-05T11:56:19.535968+00:00
|
2020-05-05T11:57:04.354942+00:00
| 3,126
| false
|
```\n public int findSpecialInteger(int[] arr) {\n if (arr.length == 1) return arr[0];\n\n int length = arr.length;\n List<Integer> firstThreeQuarters =\n new ArrayList<>(Arrays.asList(arr[length / 4], arr[length / 2], arr[3 * length / 4]));\n\n for (Integer elem : firstThreeQuarters) {\n int pos = firstOccurrence(arr, elem);\n if (arr[pos + length / 4] == elem)\n return elem;\n }\n return -1;\n }\n\n private int firstOccurrence(int[] arr, int target) {\n int start = 0;\n int end = arr.length - 1;\n while (start < end) {\n int mid = start + (end - start) / 2;\n if (target > arr[mid])\n start = mid + 1;\n else\n end = mid;\n }\n return end;\n }\n```
| 42
| 2
|
['Binary Tree', 'Java']
| 8
|
element-appearing-more-than-25-in-sorted-array
|
Python 3 (four different one-line solutions) (beats 100%)
|
python-3-four-different-one-line-solutio-xsa6
|
```\nclass Solution:\n def findSpecialInteger(self, A: List[int]) -> int:\n return collections.Counter(A).most_common(1)[0][0]\n\t\t\n\nfrom statistic
|
junaidmansuri
|
NORMAL
|
2019-12-15T08:56:40.465228+00:00
|
2019-12-15T09:00:27.103140+00:00
| 3,317
| false
|
```\nclass Solution:\n def findSpecialInteger(self, A: List[int]) -> int:\n return collections.Counter(A).most_common(1)[0][0]\n\t\t\n\nfrom statistics import mode\n\nclass Solution:\n def findSpecialInteger(self, A: List[int]) -> int:\n return mode(A)\n\n\nclass Solution:\n def findSpecialInteger(self, A: List[int]) -> int:\n return max(set(A), key = A.count)\n\t\t\n\t\t\nclass Solution:\n def findSpecialInteger(self, A: List[int]) -> int:\n return (lambda C: max(C.keys(), key = lambda x: C[x]))(collections.Counter(A))\n\t\t\n\t\t\n- Junaid Mansuri\n- Chicago, IL
| 30
| 6
|
['Python', 'Python3']
| 4
|
element-appearing-more-than-25-in-sorted-array
|
【Video】Give me 5 minutes - 2 solutions - How we think about a solution
|
video-give-me-5-minutes-2-solutions-how-4pqs6
|
Intuition\nCalculate quarter length of input array.\n\n---\n\n# Solution Video\n\nhttps://youtu.be/bTm-6y7Ob0A\n\n\u25A0 Timeline of the video\n\n0:07 Explain a
|
niits
|
NORMAL
|
2024-12-01T16:08:30.573861+00:00
|
2024-12-01T16:08:30.573890+00:00
| 672
| false
|
# Intuition\nCalculate quarter length of input array.\n\n---\n\n# Solution Video\n\nhttps://youtu.be/bTm-6y7Ob0A\n\n\u25A0 Timeline of the video\n\n`0:07` Explain algorithm of Solution 1\n`2:46` Coding of solution 1\n`3:49` Time Complexity and Space Complexity of solution 1\n`4:02` Step by step algorithm of solution 1\n`4:09` Explain key points of Solution 2\n`4:47` Explain the first key point\n`6:06` Explain the second key point\n`7:40` Explain the third key point\n`9:33` Coding of Solution 2\n`14:20` Time Complexity and Space Complexity of Solution 2\n`14:48` Step by step algorithm with my stack solution code\n\nWhen I added the second solution, it exceeded five minutes. lol\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 4,543\nMy first goal is 10,000 (It\'s far from done \uD83D\uDE05)\nThank you for your support!\n\n---\n\n# Approach\n\n## How we think about a solution\n\n### Solution 1\n\nThe description say "more than 25%", that means length of target number should be at least `quarter` of length of input array.\n\n```\nInput: arr = [1,2,2,6,6,6,6,7,10]\n```\n```[]\n9 // 4 = 2\n```\n\n---\n\n\u2B50\uFE0F Points\n\nIf the number two steps ahead is the same as the current number, it can be considered as 25%.\n\nBe careful, we need to include the current number because 2 / 9 = 0.22222...not more than 25%. If we include the current number, 3 / 9 = 0.33333...\n\nOne more point is that we don\'t have to iterate all numbers in input array, because we compare the current number and the number in current index + quarter, so number of max iteration should be `total length of input array - quarter`.\n\n---\n\nLet\'s see one by one\n\n```\nInput: arr = [1,2,2,6,6,6,6,7,10]\nquarter = 2\n```\n```\nAt index = 0\n\nif arr[i] == arr[i + quarter]:\nif 1 == 2 \u2192 false\n\ni + quarter = 2\n```\n```\nAt index = 1\n\nif arr[i] == arr[i + quarter]:\nif 2 == 6 \u2192 false\n\ni + quarter = 3\n```\n```\nAt index = 2\n\nif arr[i] == arr[i + quarter]:\nif 2 == 6 \u2192 false\n\ni + quarter = 4\n```\n```\nAt index = 3\n\nif arr[i] == arr[i + quarter]:\nif 6 == 6 \u2192 true\n\ni + quarter = 5\n```\n```\nOutput: 6\n```\n\nEasy!\uD83D\uDE06\nLet\'s see a real algorithm!\n\n---\n\n# Complexity\n- Time complexity: $$O(n - quarter)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n```python []\nclass Solution:\n def findSpecialInteger(self, arr: List[int]) -> int:\n n = len(arr)\n quarter = n // 4\n\n for i in range(n - quarter):\n if arr[i] == arr[i + quarter]:\n return arr[i]\n```\n```javascript []\nvar findSpecialInteger = function(arr) {\n const n = arr.length;\n const quarter = Math.floor(n / 4);\n\n for (let i = 0; i < n - quarter; i++) {\n if (arr[i] === arr[i + quarter]) {\n return arr[i];\n }\n }\n};\n```\n```java []\nclass Solution {\n public int findSpecialInteger(int[] arr) {\n int n = arr.length;\n int quarter = n / 4;\n\n for (int i = 0; i < n - quarter; i++) {\n if (arr[i] == arr[i + quarter]) {\n return arr[i];\n }\n }\n\n return -1;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int findSpecialInteger(vector<int>& arr) {\n int n = arr.size();\n int quarter = n / 4;\n\n for (int i = 0; i < n - quarter; i++) {\n if (arr[i] == arr[i + quarter]) {\n return arr[i];\n }\n }\n\n return -1; \n }\n};\n```\n\n# Step by step Algorithm\n\n1. **Initialization:**\n ```python\n n = len(arr)\n quarter = n // 4\n ```\n - `n` is assigned the length of the input array `arr`.\n - `quarter` is calculated as one-fourth of the length of the array `arr` using integer division (`//`), ensuring it\'s an integer.\n\n2. **Loop through the array:**\n ```python\n for i in range(n - quarter):\n ```\n - The loop iterates through the array indices from 0 to `(n - quarter - 1)`. This ensures that there are at least `quarter` elements remaining in the array for each iteration.\n\n3. **Check if the next element is the same:**\n ```python\n if arr[i] == arr[i + quarter]:\n ```\n - For each iteration, it checks whether the element at the current index (`i`) is equal to the element two steps ahead (`i + quarter`).\n - If the condition is true, it means the current element is repeated in the next `quarter` elements, which corresponds to 25% of the array.\n\n4. **Return the special integer:**\n ```python\n return arr[i]\n ```\n - If the condition in the `if` statement is satisfied, the function returns the special integer (`arr[i]`).\n\nIn summary, the algorithm iterates through the array, comparing each element with the one current index + quarter steps ahead. If a match is found, it returns the special integer. This logic assumes that such a special integer always exists based on the problem statement.\n\n\n---\n\n# Solution 2 - Binary Search\n\nMy second solution is to use binary search to find leftmost current number and rightmost current number. The title says "Sorted Array", so we can easliy imagine we have binary search solution. lol\n\nI think we have 3 points.\n\n---\n\n\u2B50\uFE0F Points\n\n1. We can start from index that is equal to quarter\n2. Number of iteration should be number of possible candidate element\n3. Even If we find the target number by binary search, we should continue it\n\n---\n\n### 1. We can start from index that is equal to quarter\n\n```\nInput: arr = [1,2,2,6,6,6,6,7,10]\nquarter = 2\n```\nIn this case, we can start from index 2. If the number at index 0 is answer, index 2 is the same number as index 0. In other words, if leftmost index is not 0 when we execute binary search to find the number at index 2, index 0 is not answer. We don\'t have to start from index 0. We can start from index which is equal to quarter.\n\n\n### 2. Number of iteration should be number of possible candidate element\n\nIf current number is answer number we should return, there is the same number in current index + quarter. **In other words, if not, we don\'t have to care about numbers between current index and current index + quarter - 1.** They are not answer definitely, so we can move forward by number of quarter.\n\nThe number in current index + quarter should be the next target number. There is possibility that the number is answer number we should return. That\'s why I say "current index + quarter - 1".\n\nFor example\n```\nInput: arr = [1,2,2,6,6,6,6,7,10]\nquarter = 2\n```\nLet\'s say we are at index 2.\n```\ncurrent number is 2 (= index 2)\nthe number in current index + quarter is 4 (= index 4)\n```\nThey are different numbers, so from index 2 to index 3, there is not answer number. We can jump into index 4(the next candicate) in this case.(Index 3 is 6, but in the end, we know that 6 is answer. We can find it in the next interation, because next candidate is 6).\n\n- How we can know current index + quarter is different number?\n\nWe can calcuate like this\n\n```\nrightmost index - leftmost index + 1 > quarter\n```\nIf we meet this condition, that is answer, if not, Go to the next candidate. `+1` is to get real length because we use index numbers for the calculation. If rightmost and leftmost is the same index(Let\'s say 0), length should 1, because there is a number at index 0.\n\n### 3. Even If we find the target number by binary search, we should continue it\n\nUsually, when we execute binary search, we stop when we find the target number, but in this question, we need to find leftmost index and rightmost index, so even if we find the target number, the number is not always leftmost or righmost index. That\'s why we continue if we meet this condition.\n\n```\nwhile left <= right:\n```\n\nIf we find target number when we find leftmost index, move left, because leftmost is on the left side.\n\n```\nright = mid - 1\n```\n\nIf we find target number when we find rightmost index, move right, because rightmost is on the right side.\n\n```\nleft = mid + 1\n```\n\nEasy\uD83D\uDE06\nLet\'s see a real algorithm!\n\nIf you are not familar with typical binary search, I have a video for you.\n\nhttps://youtu.be/gVLvNe_SNc0\n\n\n---\n\n# Complexity\n- Time complexity: $$O(c log n)$$\n`n` is length of input array\n`c` is number of candidates\n```\nc = (n - qurater) / qurater\n```\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n\n```python []\nclass Solution:\n def findSpecialInteger(self, arr: List[int]) -> int:\n def binary_search(target, is_first):\n left, right = 0, len(arr) - 1\n result = -1\n\n while left <= right:\n mid = (left + right) // 2\n\n if arr[mid] == target:\n result = mid\n if is_first:\n right = mid - 1\n else:\n left = mid + 1\n elif arr[mid] < target:\n left = mid + 1\n else:\n right = mid - 1\n\n return result\n \n n = len(arr)\n quarter = n // 4\n\n # Handle the case where quarter is zero\n if quarter == 0:\n return arr[0] if n > 0 else None\n\n # Check every possible candidate element\n for i in range(quarter, n, quarter):\n # Use binary search to find the first and last occurrence of the candidate element\n left_occurrence = binary_search(arr[i], True)\n right_occurrence = binary_search(arr[i], False)\n\n # Check if the frequency is greater than 25%\n if right_occurrence - left_occurrence + 1 > quarter:\n return arr[i]\n```\n```javascript []\n/**\n * @param {number[]} arr\n * @return {number}\n */\nvar findSpecialInteger = function(arr) {\n function binarySearch(target, isFirst) {\n let left = 0;\n let right = arr.length - 1;\n let result = -1;\n\n while (left <= right) {\n let mid = left + Math.floor((right - left) / 2);\n\n if (arr[mid] === target) {\n result = mid;\n if (isFirst) {\n right = mid - 1;\n } else {\n left = mid + 1;\n }\n } else if (arr[mid] < target) {\n left = mid + 1;\n } else {\n right = mid - 1;\n }\n }\n\n return result;\n }\n\n const n = arr.length;\n const quarter = Math.floor(n / 4);\n\n // Handle the case where quarter is zero\n if (quarter === 0) {\n return n > 0 ? arr[0] : null;\n }\n\n // Check every possible candidate element\n for (let i = quarter; i < n; i += quarter) {\n // Use binary search to find the first and last occurrence of the candidate element\n const leftOccurrence = binarySearch(arr[i], true);\n const rightOccurrence = binarySearch(arr[i], false);\n\n // Check if the frequency is greater than 25%\n if (rightOccurrence - leftOccurrence + 1 > quarter) {\n return arr[i];\n }\n }\n};\n```\n```java []\nclass Solution {\n public int findSpecialInteger(int[] arr) {\n int n = arr.length;\n int quarter = n / 4;\n\n // Handle the case where quarter is zero\n if (quarter == 0) {\n return n > 0 ? arr[0] : -1;\n }\n\n // Check every possible candidate element\n for (int i = quarter; i < n; i += quarter) {\n // Use binary search to find the first and last occurrence of the candidate element\n int leftOccurrence = binarySearch(arr, arr[i], true);\n int rightOccurrence = binarySearch(arr, arr[i], false);\n\n // Check if the frequency is greater than 25%\n if (rightOccurrence - leftOccurrence + 1 > quarter) {\n return arr[i];\n }\n }\n\n return -1;\n }\n\n private int binarySearch(int[] arr, int target, boolean isFirst) {\n int left = 0;\n int right = arr.length - 1;\n int result = -1;\n\n while (left <= right) {\n int mid = (left + right) / 2;\n\n if (arr[mid] == target) {\n result = mid;\n if (isFirst) {\n right = mid - 1;\n } else {\n left = mid + 1;\n }\n } else if (arr[mid] < target) {\n left = mid + 1;\n } else {\n right = mid - 1;\n }\n }\n\n return result;\n } \n}\n```\n```C++ []\nclass Solution {\npublic:\n int findSpecialInteger(vector<int>& arr) {\n int n = arr.size();\n int quarter = n / 4;\n\n // Handle the case where quarter is zero\n if (quarter == 0) {\n return n > 0 ? arr[0] : -1;\n }\n\n // Check every possible candidate element\n for (int i = quarter; i < n; i += quarter) {\n // Use binary search to find the first and last occurrence of the candidate element\n int leftOccurrence = binarySearch(arr, arr[i], true);\n int rightOccurrence = binarySearch(arr, arr[i], false);\n\n // Check if the frequency is greater than 25%\n if (rightOccurrence - leftOccurrence + 1 > quarter) {\n return arr[i];\n }\n }\n\n return -1; \n }\n\nprivate:\n int binarySearch(const vector<int>& arr, int target, bool isFirst) {\n int left = 0;\n int right = arr.size() - 1;\n int result = -1;\n\n while (left <= right) {\n int mid = (left + right) / 2;\n\n if (arr[mid] == target) {\n result = mid;\n if (isFirst) {\n right = mid - 1;\n } else {\n left = mid + 1;\n }\n } else if (arr[mid] < target) {\n left = mid + 1;\n } else {\n right = mid - 1;\n }\n }\n\n return result;\n } \n};\n```\n# Step by step algorithm\n\n1. **Binary Search Function:**\n ```python\n def binary_search(target, is_first):\n left, right = 0, len(arr) - 1\n result = -1\n\n while left <= right:\n mid = (left + right) // 2\n\n if arr[mid] == target:\n result = mid\n if is_first:\n right = mid - 1\n else:\n left = mid + 1\n elif arr[mid] < target:\n left = mid + 1\n else:\n right = mid - 1\n\n return result\n ```\n - This is a binary search function that finds either the first or the last occurrence of the `target` in the `arr` array based on the `is_first` parameter.\n\n2. **Initialization:**\n ```python\n n = len(arr)\n quarter = n // 4\n ```\n - `n` is assigned the length of the input array `arr`.\n - `quarter` is calculated as one-fourth of the length of the array `arr` using integer division (`//`), ensuring it\'s an integer.\n\n3. **Handling the Case Where Quarter is Zero:**\n ```python\n if quarter == 0:\n return arr[0] if n > 0 else None\n ```\n - If `quarter` is zero, it means the array has fewer than 4 elements. The function returns the first element if the array is not empty; otherwise, it returns `None`.\n\n4. **Checking Every Possible Candidate Element:**\n ```python\n for i in range(quarter, n, quarter):\n ```\n - The loop iterates through the array indices from `quarter` to `n - 1` with a step of `quarter`.\n\n5. **Using Binary Search to Find Occurrences:**\n ```python\n left_occurrence = binary_search(arr[i], True)\n right_occurrence = binary_search(arr[i], False)\n ```\n - For each candidate element, it uses the binary search function to find the first and last occurrences.\n\n6. **Checking Frequency and Returning Result:**\n ```python\n if right_occurrence - left_occurrence + 1 > quarter:\n return arr[i]\n ```\n - It checks if the frequency of the candidate element is greater than 25%. If true, it returns the candidate element as the result.\n\n\n\n---\n\nThank you for reading my post.\n\u2B50\uFE0F Please upvote it and don\'t forget to subscribe to my channel!\n\n\u25A0 Subscribe URL\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n\u25A0 Twitter\nhttps://twitter.com/CodingNinjaAZ\n\n### My next daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/maximum-product-of-two-elements-in-an-array/solutions/4392747/video-give-me-5-minutes-2-solutions-how-we-think-about-a-solution/\n\nvideo\nhttps://youtu.be/JV5Kuinx-m0\n\n\u25A0 Timeline of the video\n\n`0:05` Explain algorithm of Solution 1\n`3:18` Coding of solution 1\n`4:18` Time Complexity and Space Complexity of solution 1\n`4:29` Step by step algorithm of solution 1\n`4:36` Explain key points of Solution 2\n`5:25` Coding of Solution 2\n`6:50` Time Complexity and Space Complexity of Solution 2\n`7:03` Step by step algorithm with my stack solution code\n\n### My previous daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/transpose-matrix/solutions/4384180/video-give-me-5-minutes-2-solutions-how-we-think-about-a-solution/\n\nvideo\nhttps://youtu.be/lsAZepsNRPo\n\n\u25A0 Timeline of the video\n\n`0:04` Explain algorithm of Solution 1\n`1:12` Coding of solution 1\n`2:30` Time Complexity and Space Complexity of solution 1\n`2:54` Explain algorithm of Solution 2\n`3:49` Coding of Solution 2\n`4:53` Time Complexity and Space Complexity of Solution 2\n`5:12` Step by step algorithm with my stack solution code\n\n\n
| 28
| 0
|
['Array', 'C++', 'Java', 'Python3', 'JavaScript']
| 0
|
element-appearing-more-than-25-in-sorted-array
|
[JavaScript] Sliding window
|
javascript-sliding-window-by-greenteacak-5pfo
|
\n/**\n * @param {number[]} arr\n * @return {number}\n */\nvar findSpecialInteger = function(arr) {\n const ws = Math.floor(arr.length / 4);\n for (let i
|
GreenTeaCake
|
NORMAL
|
2020-01-22T23:43:08.352728+00:00
|
2020-01-22T23:43:08.352777+00:00
| 983
| false
|
```\n/**\n * @param {number[]} arr\n * @return {number}\n */\nvar findSpecialInteger = function(arr) {\n const ws = Math.floor(arr.length / 4);\n for (let i = 0; i < arr.length - ws; i++) {\n if (arr[i] === arr[i + ws]) {\n return arr[i];\n }\n }\n return -1;\n};\n```
| 26
| 1
|
['Sliding Window', 'JavaScript']
| 2
|
element-appearing-more-than-25-in-sorted-array
|
[Java/Python 3] O(n) and O(logn) codes w brief explanation and analysis.
|
javapython-3-on-and-ologn-codes-w-brief-jvusu
|
Time O(logn) binary search code similar to:\n1283. Find the Smallest Divisor Given a Threshold\n1870. Minimum Speed to Arrive on Time\n2187. Minimum Time to Com
|
rock
|
NORMAL
|
2019-12-14T16:04:54.405092+00:00
|
2022-02-27T21:05:10.672442+00:00
| 2,550
| false
|
Time O(logn) binary search code similar to:\n[1283. Find the Smallest Divisor Given a Threshold](https://leetcode.com/problems/find-the-smallest-divisor-given-a-threshold/discuss/446313/JavaPython-3-Binary-search-9-and-8-liners-w-brief-explanation-and-analysis.)\n[1870. Minimum Speed to Arrive on Time](https://leetcode.com/problems/minimum-speed-to-arrive-on-time/discuss/1224657/JavaPython-3-Binary-Search-w-comment-and-brief-analysis.)\n[2187. Minimum Time to Complete Trips](https://leetcode.com/problems/minimum-time-to-complete-trips/discuss/1802443/)\n\n----\n\n**Time O(n)**\nCount occurrence of each element and check if it is the required one.\n```java\n public int findSpecialInteger(int[] arr) {\n Map<Integer, Integer> cnt = new HashMap<>();\n int frequency = arr.length / 4;\n for (int a : arr) {\n cnt.put(a, 1 + cnt.getOrDefault(a, 0));\n if (cnt.get(a) > frequency) {\n return a;\n }\n }\n return -1; \n }\n```\n```python\n def findSpecialInteger(self, arr: List[int]) -> int:\n return collections.Counter(arr).most_common(1)[0][0]\n```\nor a better bruteforce version:\n```python\n def findSpecialInteger(self, arr: List[int]) -> int:\n cnt, prev = 0, -1\n for cur in arr:\n cnt = cnt + 1 if cur == prev else 1\n prev = cur\n if cnt > len(arr) // 4:\n return cur\n```\n\n**Analysis:**\nTime & space: O(n), where n = arr.length.\n\n----\n\n**Time O(logn):**\nDivide the input array into `4` parts, at least `1` part starts with the target element; Use Binary Search to find the frequency of the first element of each part; If the frequency is more than `25%`, the corresponding element is the solution.\n```java\n public int findSpecialInteger(int[] arr) {\n int n = arr.length, k = Math.max(1, n / 4);\n for (int i = 0; i < n; i += k) {\n if (frequency(arr, arr[i]) > n / 4) {\n return arr[i];\n }\n }\n return -1;\n }\n private int frequency(int[] a, int val) {\n return binarySearch(a, val + 1) - binarySearch(a, val);\n }\n private int binarySearch(int[] a, int val) {\n int lo = 0, hi = a.length;\n while (lo < hi) {\n int mid = lo + hi >> 1;\n if (a[mid] < val) {\n lo = mid + 1;\n }else {\n hi = mid;\n }\n }\n return lo;\n }\n```\n```python\n def findSpecialInteger(self, arr: List[int]) -> int:\n \n def frequency(val: int) -> int:\n return binarySearch(val + 1) - binarySearch(val)\n\n def binarySearch(val: int) -> int:\n lo, hi = 0, len(arr)\n while lo < hi:\n mid = lo + hi >> 1\n if arr[mid] < val:\n lo = mid + 1\n else:\n hi = mid\n return lo\n\n n = len(arr)\n k = max(1, n // 4)\n for i in range(0, n, k):\n if frequency(arr[i]) > n // 4:\n return arr[i]\n```\n\n\n----\n\nHere are more similar binary search problems:\n\n[34. Find First and Last Position of Element in Sorted Array](https://leetcode.com/problems/find-first-and-last-position-of-element-in-sorted-array)\n[410. Split Array Largest Sum](https://leetcode.com/problems/split-array-largest-sum/)\n[774. Minimize Max Distance to Gas Station](https://leetcode.com/problems/minimize-max-distance-to-gas-station/)\n[875. Koko Eating Bananas](https://leetcode.com/problems/koko-eating-bananas/)\n[1011. Capacity To Ship Packages In N Days](https://leetcode.com/problems/capacity-to-ship-packages-within-d-days/)\n[1150. Check If a Number Is Majority Element in a Sorted Array: Premium](https://leetcode.com/problems/check-if-a-number-is-majority-element-in-a-sorted-array)\n[1231. Divide Chocolate: Premium](https://leetcode.com/problems/divide-chocolate/)\n[1482. Minimum Number of Days to Make m Bouquets](https://leetcode.com/problems/minimum-number-of-days-to-make-m-bouquets)\n[1539. Kth Missing Positive Number](https://leetcode.com/problems/kth-missing-positive-number/)
| 22
| 3
|
[]
| 9
|
element-appearing-more-than-25-in-sorted-array
|
[C++] Three Solutions
|
c-three-solutions-by-pankajgupta20-wq4s
|
1) Hashmap Solution\n\tclass Solution {\n\tpublic:\n\t\tint findSpecialInteger(vector& arr) {\n\t\t\tunordered_map m;\n\t\t\tfor(int i = 0; i < arr.size(); i++)
|
pankajgupta20
|
NORMAL
|
2021-05-31T06:00:59.376677+00:00
|
2021-05-31T06:00:59.376720+00:00
| 1,917
| false
|
##### 1) Hashmap Solution\n\tclass Solution {\n\tpublic:\n\t\tint findSpecialInteger(vector<int>& arr) {\n\t\t\tunordered_map<int, int> m;\n\t\t\tfor(int i = 0; i < arr.size(); i++){\n\t\t\t\tm[arr[i]]++;\n\t\t\t}\n\t\t\tfor(auto i : m){\n\t\t\t\tif(i.second > arr.size() / 4){\n\t\t\t\t\treturn i.first;\n\t\t\t\t}\n\t\t\t}\n\t\t\treturn arr[0];\n\t\t}\n\t};\n##### 2) Count Solution\n\tclass Solution {\n\tpublic:\n\t\tint findSpecialInteger(vector<int>& arr) {\n\t\t\tint c = 0;\n\t\t\tfor(int i = 1; i < arr.size(); i++){\n\t\t\t\tif(arr[i] == arr[i - 1]){\n\t\t\t\t\tc++;\n\t\t\t\t}\n\t\t\t\telse{\n\t\t\t\t\tc = 1;\n\t\t\t\t}\n\t\t\t\tif(c > arr.size() / 4){\n\t\t\t\t\treturn arr[i];\n\t\t\t\t}\n\t\t\t}\n\t\t\treturn arr[0];\n\t\t}\n\t};\n##### 3) Index Solution\n\tclass Solution {\n\tpublic:\n\t\tint findSpecialInteger(vector<int>& arr) {\n\t\t\tfor(int i = 0; i <= (arr.size() * 3) / 4; i++){\n\t\t\t\tif(arr[i] == arr[i + arr.size() / 4]){\n\t\t\t\t\treturn arr[i];\n\t\t\t\t}\n\t\t\t}\n\t\t\treturn arr[0];\n\t\t}\n\t};\n\n\n\n
| 21
| 0
|
['C', 'C++']
| 1
|
element-appearing-more-than-25-in-sorted-array
|
Python Simple O(logn) solution
|
python-simple-ologn-solution-by-c_n-yyo1
|
Idea: The element which appears more than 25% times in the arr must appear at either index n/4, n/2, 3*n/4, n, where n is the length of arr. So we count the amo
|
C_N_
|
NORMAL
|
2021-11-09T17:04:47.011882+00:00
|
2021-11-29T21:21:56.820734+00:00
| 1,345
| false
|
**Idea:** The element which appears more than 25% times in the arr must appear at either index `n/4, n/2, 3*n/4, n`, where n is the length of `arr`. So we count the amount of times the value of one of the above indexes appear in the array by using `bisect_left` (finds the first time it appears in the array) and `bisect_right` (finds the last time it appears in the array). If it appears more than n/4 times we return that value.\n\n**Time Complexity:** O(logn) where n in the length of `arr`.\n**Space Complexity:** None\n\n----------------------------------------\n\n```\ndef findSpecialInteger(self, arr: List[int]) -> int:\n n = len(arr)\n \n for i in [n//4, n//2, 3*n//4, n]:\n if bisect.bisect_right(arr, arr[i]) - bisect.bisect_left(arr, arr[i]) > n//4:\n return arr[i]\n\n```\n------------------------------\n*Thanx for reading, please **upvote** if it helped you :)*
| 16
| 0
|
['Python3']
| 4
|
element-appearing-more-than-25-in-sorted-array
|
✅✅Majority Element in Array🔥🔥
|
majority-element-in-array-by-ilxamovic-wlgz
|
Intuition\nThe problem seems to ask for finding a "special" integer, which appears more than 25% of the time in the given array. The approach appears to use a d
|
ilxamovic
|
NORMAL
|
2023-12-11T04:12:47.070740+00:00
|
2023-12-11T04:12:47.070759+00:00
| 3,640
| false
|
# Intuition\nThe problem seems to ask for finding a "special" integer, which appears more than 25% of the time in the given array. The approach appears to use a dictionary to count the occurrences of each element and then iterate through the dictionary to find the element that meets the criteria.\n\n# Approach\n1. Check if the array length is less than 2, return the only element.\n2. Initialize variables, including a dictionary to store the count of each element and a variable to store the result.\n3. Iterate through the array, updating the dictionary with element counts.\n4. Iterate through the dictionary to find the element that appears more than 25% of the time.\n5. Return the result.\n\n# Complexity\n- **Time complexity:** O(n), where n is the length of the input array. The code iterates through the array once and then iterates through the dictionary, both operations taking linear time.\n- **Space complexity:** O(n), where n is the length of the input array. The dictionary stores counts for each unique element in the array.\n\n# Code\n```csharp []\npublic class Solution {\n public int FindSpecialInteger(int[] arr)\n {\n if (arr.Length < 2){\n return arr[0];\n }\n int result = 0;\n int percent = (int)(arr.Length * 0.25);\n Dictionary<int, int> dc = new Dictionary<int, int>();\n foreach (int i in arr)\n {\n if (dc.ContainsKey(i))\n {\n dc[i]++;\n }\n else {\n dc[i] = 1;\n }\n }\n\n foreach (int key in dc.Keys)\n {\n if (dc[key] > percent)\n {\n result = key;\n }\n }\n\n return result;\n }\n}\n```\n``` Java []\npublic class Solution {\n public int findSpecialInteger(int[] arr) {\n if (arr.length < 2) {\n return arr[0];\n }\n int result = 0;\n int percent = (int) (arr.length * 0.25);\n Map<Integer, Integer> map = new HashMap<>();\n \n for (int i : arr) {\n map.put(i, map.getOrDefault(i, 0) + 1);\n }\n\n for (int key : map.keySet()) {\n if (map.get(key) > percent) {\n result = key;\n }\n }\n\n return result;\n }\n}\n```\n``` Rust []\nimpl Solution {\n pub fn find_special_integer(arr: Vec<i32>) -> i32 {\n if arr.len() < 2 {\n return arr[0];\n }\n let mut result = 0;\n let percent = (arr.len() as f32 * 0.25) as usize;\n let mut map = HashMap::new();\n\n for &i in &arr {\n *map.entry(i).or_insert(0) += 1;\n }\n\n for (&key, &count) in &map {\n if count > percent {\n result = key;\n }\n }\n\n result\n }\n}\n```\n```Go []\nfunc findSpecialInteger(arr []int) int {\n\tif len(arr) < 2 {\n\t\treturn arr[0]\n\t}\n\tresult := 0\n\tpercent := int(float64(len(arr)) * 0.25)\n\tcountMap := make(map[int]int)\n\n\tfor _, i := range arr {\n\t\tcountMap[i]++\n\t}\n\n\tfor key, count := range countMap {\n\t\tif count > percent {\n\t\t\tresult = key\n\t\t}\n\t}\n\n\treturn result\n}\n```\n```Python []\nclass Solution:\n def findSpecialInteger(self, arr: List[int]) -> int:\n if len(arr) < 2:\n return arr[0]\n result = 0\n percent = int(len(arr) * 0.25)\n count_map = {}\n\n for i in arr:\n count_map[i] = count_map.get(i, 0) + 1\n\n for key, count in count_map.items():\n if count > percent:\n result = key\n\n return result\n```\n\n\n\n- Please upvote me !!!
| 13
| 2
|
['Java', 'Go', 'Python3', 'Rust', 'C#']
| 4
|
element-appearing-more-than-25-in-sorted-array
|
C++/Python frequency count vs Binary search||0ms Beats 100%
|
cpython-frequency-count-vs-binary-search-6c4f
|
Intuition\n Describe your first thoughts on how to solve this problem. \n3 different kinds of soultion arte provided.\n1 is very naive, solved this with countin
|
anwendeng
|
NORMAL
|
2023-12-11T01:46:28.582322+00:00
|
2023-12-11T07:35:57.568801+00:00
| 3,566
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n3 different kinds of soultion arte provided.\n1 is very naive, solved this with counting frequency for each number; no hash table is used.\nThe 2nd approach uses binary search if the possible target \n`int x[5]={arr[0], arr[n/4], arr[n/2], arr[3*n/4], arr[n-1]};`\nnot hit.\n\nBoth solutions have the same speed with different TC.\n\nThe 3rd approach uses C code by sliding window with running time 7ms.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n[Please turn English subtitles if necessary]\n[https://youtu.be/nzVIomp9qSg?si=F-B65MLzQqrHhsq1](https://youtu.be/nzVIomp9qSg?si=F-B65MLzQqrHhsq1)\nTo shrink the searching range, define the array for specific indices\n```\nint q[5]={0, n/4, n/2, 3*n/4, n-1};\n```\nThe binary searching part is as follows:\n```\n//If not found, proceed the binary search\nfor (int i=1; i<4; i++){\n int r=upper_bound(arr.begin()+q[i-1], arr.begin()+q[i+1]+1, x[i])-arr.begin()-1;\n int l=lower_bound(arr.begin()+q[i-1], arr.begin()+q[i+1]+1, x[i])-arr.begin();\n if (r-l+1>n/4) return x[i];\n }\n```\nPython code is also provided.\n\nThanks to @Sergei, C++ using Binary search is revised to reduce the number of iterations.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$ vs $$O(\\log n)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$ vs $$O(100001)$$\n# revised C++ Code using Binary search runs in 0ms Beats 100%\n```C++ []\n#pragma GCC optimize("O3", "unroll-loops")\nclass Solution {\npublic:\n int findSpecialInteger(vector<int>& arr) {\n int n=arr.size();\n if (n<4) //There is exactly one integer occurs more than 25%\n return arr[0];\n int x[5]={arr[0], arr[n/4], arr[n/2], arr[3*n/4], arr[n-1]};\n for (int i=0; i<4; i++)\n if (x[i]==x[i+1]) return x[i];\n\n //If not found, proceed the binary search\n int q[5]={0, n/4, n/2, 3*n/4, n-1};\n for (int i=1; i<3; i++){\n int r=upper_bound(arr.begin()+q[i-1], arr.begin()+q[i+1]+1, x[i])-arr.begin()-1;\n int l=lower_bound(arr.begin()+q[i-1], arr.begin()+q[i+1]+1, x[i])-arr.begin();\n if (r-l+1>n/4) return x[i];\n }\n \n return x[3];\n }\n};\nauto init = []()\n{ \n ios::sync_with_stdio(0);\n cin.tie(0);\n cout.tie(0);\n return \'c\';\n}();\n```\n\n```python []\nclass Solution:\n def findSpecialInteger(self, arr: List[int]) -> int:\n n=len(arr)\n if n<4: return arr[0]\n q=[0, n//4, n//2, 3*n//4, n-1]\n x=[arr[0], arr[q[1]], arr[q[2]], arr[q[3]], arr[-1]]\n for i in range(4):\n if x[i]==x[i+1]: return x[i]\n print("binary search")\n for i in range(1,4):\n a=arr[q[i-1]:q[i+1]+1]\n r=bisect.bisect_right(a, x[i])-1\n l=bisect.bisect_left(a, x[i])\n if (r-l+1>n//4): return x[i]\n return -1\n \n```\n\n# Code using Frequency count 3 ms Beats 98.94%\n```\n#pragma GCC optimize("O3", "unroll-loops")\nclass Solution {\npublic:\n int findSpecialInteger(vector<int>& arr) {\n int n=arr.size(), q=n/4;\n int freq[100001]={0};\n for(int x: arr){\n freq[x]++;\n if (freq[x]>q) return x;\n }\n return -1;\n }\n};\n```\n# C code using sliding window runing 7ms\n```\n#pragma GCC optimize("O3", "unroll-loops")\nint findSpecialInteger(int* arr, int n) {\n int q=n/4;\n for(register int i=0; i<n-q; i++){\n if (arr[i]==arr[i+q])\n return arr[i];\n }\n return -1;\n}\n```
| 13
| 3
|
['Array', 'Binary Search', 'C', 'Sliding Window', 'C++', 'Python3']
| 3
|
element-appearing-more-than-25-in-sorted-array
|
Four lines to solve the problem
|
four-lines-to-solve-the-problem-by-dandr-tct8
|
\nclass Solution {\n public int findSpecialInteger(int[] arr) {\n int limit=arr.length/4;\n for(int i=0;i<arr.length;i++){\n if(arr[
|
dandrane
|
NORMAL
|
2021-02-27T03:40:43.367015+00:00
|
2021-02-27T03:40:43.367047+00:00
| 657
| false
|
```\nclass Solution {\n public int findSpecialInteger(int[] arr) {\n int limit=arr.length/4;\n for(int i=0;i<arr.length;i++){\n if(arr[i]==arr[i+limit])\n return arr[i];\n }\n return -1;\n }\n}\n```
| 11
| 0
|
['Java']
| 3
|
element-appearing-more-than-25-in-sorted-array
|
No need for binary search - beats 100%
|
no-need-for-binary-search-beats-100-by-q-ktk9
|
Since the array is sorted, we just need to check if arr[i] == arr[i + arr.length / 4]\n\n\nclass Solution {\n public int findSpecialInteger(int[] arr) {\n
|
qiong7
|
NORMAL
|
2020-01-12T16:37:24.307945+00:00
|
2020-01-12T16:37:24.307978+00:00
| 1,379
| false
|
Since the array is sorted, we just need to check if arr[i] == arr[i + arr.length / 4]\n\n```\nclass Solution {\n public int findSpecialInteger(int[] arr) {\n for (int i = 0; i < arr.length * 0.75; i++) {\n if (arr[i] == arr[i + arr.length / 4]) {\n return arr[i];\n }\n }\n \n return arr[0];\n }\n}\n```
| 11
| 4
|
[]
| 3
|
element-appearing-more-than-25-in-sorted-array
|
Beats 97% very Easy
|
beats-97-very-easy-by-saim75-nc4a
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
saim75
|
NORMAL
|
2023-12-11T03:02:07.468746+00:00
|
2023-12-11T03:02:07.468781+00:00
| 981
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findSpecialInteger(self, arr: List[int]) -> int:\n threshold = len(arr) // 4\n \n for i in range(len(arr)):\n if arr[i] == arr[i + threshold]:\n return arr[i]\n \n return -1 # If not found\n```
| 10
| 0
|
['Python3']
| 4
|
element-appearing-more-than-25-in-sorted-array
|
[Java] Linear Scan
|
java-linear-scan-by-manrajsingh007-kfz1
|
```\nclass Solution {\n public int findSpecialInteger(int[] arr) {\n int n = arr.length;\n int count = 1;\n int e = arr[0];\n for
|
manrajsingh007
|
NORMAL
|
2019-12-14T16:02:45.499795+00:00
|
2019-12-15T15:40:36.524124+00:00
| 1,025
| false
|
```\nclass Solution {\n public int findSpecialInteger(int[] arr) {\n int n = arr.length;\n int count = 1;\n int e = arr[0];\n for(int i = 1; i < n; i++){\n if(arr[i] == e) count++;\n else {\n e = arr[i];\n count = 1;\n }\n if(count > n/4) return arr[i];\n }\n return arr[0];\n }\n}
| 9
| 3
|
[]
| 1
|
element-appearing-more-than-25-in-sorted-array
|
Best Solution using Binary Search Approach with Proper Explanation and Beats 100%
|
best-solution-using-binary-search-approa-ho4q
|
Intuition\n Describe your first thoughts on how to solve this problem. \nArray is sorted so we think about binary search.\n\n# Approach\n Describe your approach
|
missionMicrosoft_7692
|
NORMAL
|
2023-12-11T04:47:02.589925+00:00
|
2023-12-11T04:48:25.874478+00:00
| 859
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nArray is sorted so we think about binary search.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe have to find element which apper more than n/4 times. So our possible answer is at \n\n[1-25]% or [25-50]% or [50-75]% or [75-100]%\n\nso create another vector i.e. PossibleAnswer which store our possible answer\nand apply loop for "PossibleAnswer" and find its count by using upper bound and lower bound. If cnt > n/4 then return elm. \n\n# Complexity\n- Time complexity: O(log n), where n is size of array\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int findSpecialInteger(vector<int>& arr) {\n \n int n=arr.size();\n\n vector<int>possibleAnswer={arr[n/4],arr[n/2],arr[3*n/4],arr[n-1]};\n\n for(int i=0;i<4;i++){\n int lb=lower_bound(arr.begin(),arr.end(),possibleAnswer[i])-arr.begin();\n int ub=upper_bound(arr.begin(),arr.end(),possibleAnswer[i])-arr.begin();\n\n if(ub-lb>n/4){\n return possibleAnswer[i];\n }\n }\n\n return -1;\n }\n};\n```
| 8
| 1
|
['Array', 'Binary Search', 'Sorting', 'Counting', 'C++']
| 0
|
element-appearing-more-than-25-in-sorted-array
|
✅EASY C++ SOLUTION IN 0(N)☑️
|
easy-c-solution-in-0n-by-2005115-554o
|
PLEASE UPVOTE MY SOLUTION IF YOU LIKE IT\n# CONNECT WITH ME\n### https://www.linkedin.com/in/pratay-nandy-9ba57b229/\n#### https://www.instagram.com/pratay_nand
|
2005115
|
NORMAL
|
2023-12-11T03:28:32.528993+00:00
|
2023-12-11T03:28:32.529018+00:00
| 943
| false
|
# **PLEASE UPVOTE MY SOLUTION IF YOU LIKE IT**\n# **CONNECT WITH ME**\n### **[https://www.linkedin.com/in/pratay-nandy-9ba57b229/]()**\n#### **[https://www.instagram.com/pratay_nandy/]()**\n\n# Approach\nThe given C++ code defines a function `findSpecialInteger` that aims to find and return an integer that appears more than 25% of the array `nums`. Here\'s a breakdown of the approach:\n\n1. **Check for Edge Case:**\n - If the size of the array `nums` is 1, return that single element as it is guaranteed to occur more than 25% of the time.\n\n2. **Initialize Variables:**\n - Initialize variables `ans` to store the result and `quarter` to represent a quarter of the array\'s size.\n\n3. **Search for Special Integer:**\n - Iterate through the array up to the point where there is at least a quarter of the array remaining (`i < n - quarter`).\n - Check if the current element (`nums[i]`) is equal to the element at a position `quarter` steps ahead (`nums[i + quarter]`).\n - If they are equal, update the result `ans` to the current element.\n\n4. **Return Result:**\n - Return the found special integer stored in `ans`.\n\nThis approach relies on the fact that if there is a special integer occurring more than 25% of the time, it will be found within the first three-quarters of the sorted array.\n.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:0(N-Quarter)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:0(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n# Code\n```\nclass Solution {\npublic:\n int findSpecialInteger(vector<int>& nums) {\n int n = nums.size();\n if(n==1)return 1;\n int ans ;\n int quarter = n/4;\n for(int i = 0 ;i < n - quarter;i++)\n {\n if(nums[i] == nums[i+quarter])\n {\n ans = nums[i];\n }\n } \n return ans;\n }\n};\n```
| 8
| 0
|
['Array', 'Sliding Window', 'C++']
| 0
|
element-appearing-more-than-25-in-sorted-array
|
JAVA || HASHMAP || WELL EXPLAINED || 4 LINE CODE
|
java-hashmap-well-explained-4-line-code-v5jvl
|
Intuition\nFind the occurrence of an element and return the maximum occured element, For this I use HashMap.Since HashMap is an OPTIMIZED DATASTRUCTURE. \n\n\np
|
sharforaz_rahman
|
NORMAL
|
2023-01-06T10:07:46.427733+00:00
|
2023-01-06T10:07:46.427776+00:00
| 916
| false
|
# Intuition\nFind the occurrence of an element and return the **maximum occured** element, For this I use HashMap.Since HashMap is an OPTIMIZED DATASTRUCTURE. \n\n\nplease upvote this if you like it.\n# Code\n```\nclass Solution {\n public int findSpecialInteger(int[] arr) {\n HashMap<Integer,Integer> map = new HashMap<>();\n\n int max = Integer.MIN_VALUE;\n int result = 0;\n\n for(int i : arr) map.put(i, map.getOrDefault(i, 0) + 1);\n\n for(int i : map.keySet()){\n max = Math.max(max,map.get(i));\n }\n for(int i : map.keySet()){\n if(max == map.get(i)) result = i;\n }\n\n return result;\n }\n}\n```
| 7
| 0
|
['Java']
| 2
|
element-appearing-more-than-25-in-sorted-array
|
Java 8 liner O(log N) (Only check 25% and 50%)
|
java-8-liner-olog-n-only-check-25-and-50-f34z
|
Here I\'m only checking the elements at 25% and 50% by binary search. if it is not in it, return element at 75%.\n\n\npublic int findSpecialInteger(int[] arr) {
|
vikrant_pc
|
NORMAL
|
2020-12-19T07:55:49.878609+00:00
|
2021-08-29T00:51:21.083245+00:00
| 482
| false
|
Here I\'m only checking the elements at 25% and 50% by binary search. if it is not in it, return element at 75%.\n\n```\npublic int findSpecialInteger(int[] arr) {\n\tfor(int i=0;i<2;i++) { // Only check element at 25% and 50%\n\t\tint num = arr[arr.length*(i+1)/4], start = 0, end = arr.length*(i+1)/4;\n\t\twhile(start < end) {\n\t\t\tint mid = start+(end-start)/2;\n\t\t\tif(arr[mid]==num) end = mid;\n\t\t\telse start = mid+1;\n\t\t}\n\t\tif(arr[start+arr.length/4] == num) return num;\n\t}\n\treturn arr[arr.length*3/4]; // return element at 75%\n}\n```\n\nIt can be improved further if we check only (25% and 75%) and run binary search on 0-25% and 50-75% elements.\nComplexity: O(log N/2)\n```\npublic int findSpecialInteger(int[] arr) {\n for(int i=1;i<=3;i+=2) { // Only check element at 25% and 75%\n int num = arr[arr.length*i/4], start = arr.length * (i-1)/4, end = arr.length*i/4;\n while(start < end) {\n int mid = start+(end-start)/2;\n if(arr[mid]==num) end = mid;\n else start = mid+1;\n }\n if(start+arr.length/4 < arr.length && arr[start+arr.length/4] == num) return num;\n }\n return arr[arr.length/2];\n}\n```
| 7
| 0
|
['Binary Tree']
| 0
|
element-appearing-more-than-25-in-sorted-array
|
Python 100%, O(logn), check 3 numbers (with explanations)
|
python-100-ologn-check-3-numbers-with-ex-gfo6
|
The idea is simple: if the number occurs more than 25% times in the arr then it\'s at either one of indices: n / 4, n / 2, n / 4 * 3.\nFor ex. in an array of si
|
ihor_codes
|
NORMAL
|
2020-10-23T06:50:48.003625+00:00
|
2020-10-23T06:50:48.003659+00:00
| 924
| false
|
The idea is simple: if the number occurs more than 25% times in the arr then it\'s at either one of indices: n / 4, n / 2, n / 4 * 3.\nFor ex. in an array of size 100, we\'d check indices 25, 50, 75.\nThen simply run a binary search to find the left and right boundary of the number.\n\nTime: O(6 * logn) = O(logn)\nSpace: O(1)\n\n```\nclass Solution:\n def findSpecialInteger(self, arr: List[int]) -> int:\n for i in [len(arr) // 2, len(arr) // 4, len(arr) // 4 * 3]:\n if bisect.bisect_right(arr, arr[i]) - bisect.bisect_left(arr, arr[i]) >= len(arr) // 4:\n return arr[i]\n```
| 7
| 1
|
['Binary Search', 'Python']
| 3
|
element-appearing-more-than-25-in-sorted-array
|
【Video】Give me 5 minutes - 2 solutions - How we think about a solution
|
video-give-me-5-minutes-2-solutions-how-p5k8o
|
Intuition\nCalculate quarter length of input array.\n\n---\n\n# Solution Video\n\nhttps://youtu.be/bTm-6y7Ob0A\n\n\u25A0 Timeline of the video\n\n0:07 Explain a
|
niits
|
NORMAL
|
2024-04-23T16:25:04.855448+00:00
|
2024-04-23T16:25:04.855472+00:00
| 998
| false
|
# Intuition\nCalculate quarter length of input array.\n\n---\n\n# Solution Video\n\nhttps://youtu.be/bTm-6y7Ob0A\n\n\u25A0 Timeline of the video\n\n`0:07` Explain algorithm of Solution 1\n`2:46` Coding of solution 1\n`3:49` Time Complexity and Space Complexity of solution 1\n`4:02` Step by step algorithm of solution 1\n`4:09` Explain key points of Solution 2\n`4:47` Explain the first key point\n`6:06` Explain the second key point\n`7:40` Explain the third key point\n`9:33` Coding of Solution 2\n`14:20` Time Complexity and Space Complexity of Solution 2\n`14:48` Step by step algorithm with my stack solution code\n\nWhen I added the second solution, it exceeded five minutes. lol\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 4,543\nMy first goal is 10,000 (It\'s far from done \uD83D\uDE05)\nThank you for your support!\n\n---\n\n# Approach\n\n## How we think about a solution\n\n### Solution 1\n\nThe description say "more than 25%", that means length of target number should be at least `quarter` of length of input array.\n\n```\nInput: arr = [1,2,2,6,6,6,6,7,10]\n```\n```[]\n9 // 4 = 2\n```\n\n---\n\n\u2B50\uFE0F Points\n\nIf the number two steps ahead is the same as the current number, it can be considered as 25%.\n\nBe careful, we need to include the current number because 2 / 9 = 0.22222...not more than 25%. If we include the current number, 3 / 9 = 0.33333...\n\nOne more point is that we don\'t have to iterate all numbers in input array, because we compare the current number and the number in current index + quarter, so number of max iteration should be `total length of input array - quarter`.\n\n---\n\nLet\'s see one by one\n\n```\nInput: arr = [1,2,2,6,6,6,6,7,10]\nquarter = 2\n```\n```\nAt index = 0\n\nif arr[i] == arr[i + quarter]:\nif 1 == 2 \u2192 false\n\ni + quarter = 2\n```\n```\nAt index = 1\n\nif arr[i] == arr[i + quarter]:\nif 2 == 6 \u2192 false\n\ni + quarter = 3\n```\n```\nAt index = 2\n\nif arr[i] == arr[i + quarter]:\nif 2 == 6 \u2192 false\n\ni + quarter = 4\n```\n```\nAt index = 3\n\nif arr[i] == arr[i + quarter]:\nif 6 == 6 \u2192 true\n\ni + quarter = 5\n```\n```\nOutput: 6\n```\n\nEasy!\uD83D\uDE06\nLet\'s see a real algorithm!\n\n---\n\n# Complexity\n- Time complexity: $$O(n - quarter)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n```python []\nclass Solution:\n def findSpecialInteger(self, arr: List[int]) -> int:\n n = len(arr)\n quarter = n // 4\n\n for i in range(n - quarter):\n if arr[i] == arr[i + quarter]:\n return arr[i]\n```\n```javascript []\nvar findSpecialInteger = function(arr) {\n const n = arr.length;\n const quarter = Math.floor(n / 4);\n\n for (let i = 0; i < n - quarter; i++) {\n if (arr[i] === arr[i + quarter]) {\n return arr[i];\n }\n }\n};\n```\n```java []\nclass Solution {\n public int findSpecialInteger(int[] arr) {\n int n = arr.length;\n int quarter = n / 4;\n\n for (int i = 0; i < n - quarter; i++) {\n if (arr[i] == arr[i + quarter]) {\n return arr[i];\n }\n }\n\n return -1;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int findSpecialInteger(vector<int>& arr) {\n int n = arr.size();\n int quarter = n / 4;\n\n for (int i = 0; i < n - quarter; i++) {\n if (arr[i] == arr[i + quarter]) {\n return arr[i];\n }\n }\n\n return -1; \n }\n};\n```\n\n# Step by step Algorithm\n\n1. **Initialization:**\n ```python\n n = len(arr)\n quarter = n // 4\n ```\n - `n` is assigned the length of the input array `arr`.\n - `quarter` is calculated as one-fourth of the length of the array `arr` using integer division (`//`), ensuring it\'s an integer.\n\n2. **Loop through the array:**\n ```python\n for i in range(n - quarter):\n ```\n - The loop iterates through the array indices from 0 to `(n - quarter - 1)`. This ensures that there are at least `quarter` elements remaining in the array for each iteration.\n\n3. **Check if the next element is the same:**\n ```python\n if arr[i] == arr[i + quarter]:\n ```\n - For each iteration, it checks whether the element at the current index (`i`) is equal to the element two steps ahead (`i + quarter`).\n - If the condition is true, it means the current element is repeated in the next `quarter` elements, which corresponds to 25% of the array.\n\n4. **Return the special integer:**\n ```python\n return arr[i]\n ```\n - If the condition in the `if` statement is satisfied, the function returns the special integer (`arr[i]`).\n\nIn summary, the algorithm iterates through the array, comparing each element with the one current index + quarter steps ahead. If a match is found, it returns the special integer. This logic assumes that such a special integer always exists based on the problem statement.\n\n\n---\n\n# Solution 2 - Binary Search\n\nMy second solution is to use binary search to find leftmost current number and rightmost current number. The title says "Sorted Array", so we can easliy imagine we have binary search solution. lol\n\nI think we have 3 points.\n\n---\n\n\u2B50\uFE0F Points\n\n1. We can start from index that is equal to quarter\n2. Number of iteration should be number of possible candidate element\n3. Even If we find the target number by binary search, we should continue it\n\n---\n\n### 1. We can start from index that is equal to quarter\n\n```\nInput: arr = [1,2,2,6,6,6,6,7,10]\nquarter = 2\n```\nIn this case, we can start from index 2. If the number at index 0 is answer, index 2 is the same number as index 0. In other words, if leftmost index is not 0 when we execute binary search to find the number at index 2, index 0 is not answer. We don\'t have to start from index 0. We can start from index which is equal to quarter.\n\n\n### 2. Number of iteration should be number of possible candidate element\n\nIf current number is answer number we should return, there is the same number in current index + quarter. **In other words, if not, we don\'t have to care about numbers between current index and current index + quarter - 1.** They are not answer definitely, so we can move forward by number of quarter.\n\nThe number in current index + quarter should be the next target number. There is possibility that the number is answer number we should return. That\'s why I say "current index + quarter - 1".\n\nFor example\n```\nInput: arr = [1,2,2,6,6,6,6,7,10]\nquarter = 2\n```\nLet\'s say we are at index 2.\n```\ncurrent number is 2 (= index 2)\nthe number in current index + quarter is 4 (= index 4)\n```\nThey are different numbers, so from index 2 to index 3, there is not answer number. We can jump into index 4(the next candicate) in this case.(Index 3 is 6, but in the end, we know that 6 is answer. We can find it in the next interation, because next candidate is 6).\n\n- How we can know current index + quarter is different number?\n\nWe can calcuate like this\n\n```\nrightmost index - leftmost index + 1 > quarter\n```\nIf we meet this condition, that is answer, if not, Go to the next candidate. `+1` is to get real length because we use index numbers for the calculation. If rightmost and leftmost is the same index(Let\'s say 0), length should 1, because there is a number at index 0.\n\n### 3. Even If we find the target number by binary search, we should continue it\n\nUsually, when we execute binary search, we stop when we find the target number, but in this question, we need to find leftmost index and rightmost index, so even if we find the target number, the number is not always leftmost or righmost index. That\'s why we continue if we meet this condition.\n\n```\nwhile left <= right:\n```\n\nIf we find target number when we find leftmost index, move left, because leftmost is on the left side.\n\n```\nright = mid - 1\n```\n\nIf we find target number when we find rightmost index, move right, because rightmost is on the right side.\n\n```\nleft = mid + 1\n```\n\nEasy\uD83D\uDE06\nLet\'s see a real algorithm!\n\nIf you are not familar with typical binary search, I have a video for you.\n\nhttps://youtu.be/gVLvNe_SNc0\n\n\n---\n\n# Complexity\n- Time complexity: $$O(c log n)$$\n`n` is length of input array\n`c` is number of candidates\n```\nc = (n - qurater) / qurater\n```\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n\n```python []\nclass Solution:\n def findSpecialInteger(self, arr: List[int]) -> int:\n def binary_search(target, is_first):\n left, right = 0, len(arr) - 1\n result = -1\n\n while left <= right:\n mid = (left + right) // 2\n\n if arr[mid] == target:\n result = mid\n if is_first:\n right = mid - 1\n else:\n left = mid + 1\n elif arr[mid] < target:\n left = mid + 1\n else:\n right = mid - 1\n\n return result\n \n n = len(arr)\n quarter = n // 4\n\n # Handle the case where quarter is zero\n if quarter == 0:\n return arr[0] if n > 0 else None\n\n # Check every possible candidate element\n for i in range(quarter, n, quarter):\n # Use binary search to find the first and last occurrence of the candidate element\n left_occurrence = binary_search(arr[i], True)\n right_occurrence = binary_search(arr[i], False)\n\n # Check if the frequency is greater than 25%\n if right_occurrence - left_occurrence + 1 > quarter:\n return arr[i]\n```\n```javascript []\n/**\n * @param {number[]} arr\n * @return {number}\n */\nvar findSpecialInteger = function(arr) {\n function binarySearch(target, isFirst) {\n let left = 0;\n let right = arr.length - 1;\n let result = -1;\n\n while (left <= right) {\n let mid = left + Math.floor((right - left) / 2);\n\n if (arr[mid] === target) {\n result = mid;\n if (isFirst) {\n right = mid - 1;\n } else {\n left = mid + 1;\n }\n } else if (arr[mid] < target) {\n left = mid + 1;\n } else {\n right = mid - 1;\n }\n }\n\n return result;\n }\n\n const n = arr.length;\n const quarter = Math.floor(n / 4);\n\n // Handle the case where quarter is zero\n if (quarter === 0) {\n return n > 0 ? arr[0] : null;\n }\n\n // Check every possible candidate element\n for (let i = quarter; i < n; i += quarter) {\n // Use binary search to find the first and last occurrence of the candidate element\n const leftOccurrence = binarySearch(arr[i], true);\n const rightOccurrence = binarySearch(arr[i], false);\n\n // Check if the frequency is greater than 25%\n if (rightOccurrence - leftOccurrence + 1 > quarter) {\n return arr[i];\n }\n }\n};\n```\n```java []\nclass Solution {\n public int findSpecialInteger(int[] arr) {\n int n = arr.length;\n int quarter = n / 4;\n\n // Handle the case where quarter is zero\n if (quarter == 0) {\n return n > 0 ? arr[0] : -1;\n }\n\n // Check every possible candidate element\n for (int i = quarter; i < n; i += quarter) {\n // Use binary search to find the first and last occurrence of the candidate element\n int leftOccurrence = binarySearch(arr, arr[i], true);\n int rightOccurrence = binarySearch(arr, arr[i], false);\n\n // Check if the frequency is greater than 25%\n if (rightOccurrence - leftOccurrence + 1 > quarter) {\n return arr[i];\n }\n }\n\n return -1;\n }\n\n private int binarySearch(int[] arr, int target, boolean isFirst) {\n int left = 0;\n int right = arr.length - 1;\n int result = -1;\n\n while (left <= right) {\n int mid = (left + right) / 2;\n\n if (arr[mid] == target) {\n result = mid;\n if (isFirst) {\n right = mid - 1;\n } else {\n left = mid + 1;\n }\n } else if (arr[mid] < target) {\n left = mid + 1;\n } else {\n right = mid - 1;\n }\n }\n\n return result;\n } \n}\n```\n```C++ []\nclass Solution {\npublic:\n int findSpecialInteger(vector<int>& arr) {\n int n = arr.size();\n int quarter = n / 4;\n\n // Handle the case where quarter is zero\n if (quarter == 0) {\n return n > 0 ? arr[0] : -1;\n }\n\n // Check every possible candidate element\n for (int i = quarter; i < n; i += quarter) {\n // Use binary search to find the first and last occurrence of the candidate element\n int leftOccurrence = binarySearch(arr, arr[i], true);\n int rightOccurrence = binarySearch(arr, arr[i], false);\n\n // Check if the frequency is greater than 25%\n if (rightOccurrence - leftOccurrence + 1 > quarter) {\n return arr[i];\n }\n }\n\n return -1; \n }\n\nprivate:\n int binarySearch(const vector<int>& arr, int target, bool isFirst) {\n int left = 0;\n int right = arr.size() - 1;\n int result = -1;\n\n while (left <= right) {\n int mid = (left + right) / 2;\n\n if (arr[mid] == target) {\n result = mid;\n if (isFirst) {\n right = mid - 1;\n } else {\n left = mid + 1;\n }\n } else if (arr[mid] < target) {\n left = mid + 1;\n } else {\n right = mid - 1;\n }\n }\n\n return result;\n } \n};\n```\n# Step by step algorithm\n\n1. **Binary Search Function:**\n ```python\n def binary_search(target, is_first):\n left, right = 0, len(arr) - 1\n result = -1\n\n while left <= right:\n mid = (left + right) // 2\n\n if arr[mid] == target:\n result = mid\n if is_first:\n right = mid - 1\n else:\n left = mid + 1\n elif arr[mid] < target:\n left = mid + 1\n else:\n right = mid - 1\n\n return result\n ```\n - This is a binary search function that finds either the first or the last occurrence of the `target` in the `arr` array based on the `is_first` parameter.\n\n2. **Initialization:**\n ```python\n n = len(arr)\n quarter = n // 4\n ```\n - `n` is assigned the length of the input array `arr`.\n - `quarter` is calculated as one-fourth of the length of the array `arr` using integer division (`//`), ensuring it\'s an integer.\n\n3. **Handling the Case Where Quarter is Zero:**\n ```python\n if quarter == 0:\n return arr[0] if n > 0 else None\n ```\n - If `quarter` is zero, it means the array has fewer than 4 elements. The function returns the first element if the array is not empty; otherwise, it returns `None`.\n\n4. **Checking Every Possible Candidate Element:**\n ```python\n for i in range(quarter, n, quarter):\n ```\n - The loop iterates through the array indices from `quarter` to `n - 1` with a step of `quarter`.\n\n5. **Using Binary Search to Find Occurrences:**\n ```python\n left_occurrence = binary_search(arr[i], True)\n right_occurrence = binary_search(arr[i], False)\n ```\n - For each candidate element, it uses the binary search function to find the first and last occurrences.\n\n6. **Checking Frequency and Returning Result:**\n ```python\n if right_occurrence - left_occurrence + 1 > quarter:\n return arr[i]\n ```\n - It checks if the frequency of the candidate element is greater than 25%. If true, it returns the candidate element as the result.\n\n\n\n---\n\nThank you for reading my post.\n\u2B50\uFE0F Please upvote it and don\'t forget to subscribe to my channel!\n\n\u25A0 Subscribe URL\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n\u25A0 Twitter\nhttps://twitter.com/CodingNinjaAZ\n\n### My next daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/maximum-product-of-two-elements-in-an-array/solutions/4392747/video-give-me-5-minutes-2-solutions-how-we-think-about-a-solution/\n\nvideo\nhttps://youtu.be/JV5Kuinx-m0\n\n\u25A0 Timeline of the video\n\n`0:05` Explain algorithm of Solution 1\n`3:18` Coding of solution 1\n`4:18` Time Complexity and Space Complexity of solution 1\n`4:29` Step by step algorithm of solution 1\n`4:36` Explain key points of Solution 2\n`5:25` Coding of Solution 2\n`6:50` Time Complexity and Space Complexity of Solution 2\n`7:03` Step by step algorithm with my stack solution code\n\n### My previous daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/transpose-matrix/solutions/4384180/video-give-me-5-minutes-2-solutions-how-we-think-about-a-solution/\n\nvideo\nhttps://youtu.be/lsAZepsNRPo\n\n\u25A0 Timeline of the video\n\n`0:04` Explain algorithm of Solution 1\n`1:12` Coding of solution 1\n`2:30` Time Complexity and Space Complexity of solution 1\n`2:54` Explain algorithm of Solution 2\n`3:49` Coding of Solution 2\n`4:53` Time Complexity and Space Complexity of Solution 2\n`5:12` Step by step algorithm with my stack solution code\n\n\n
| 6
| 0
|
['C++', 'Java', 'Python3', 'JavaScript']
| 0
|
element-appearing-more-than-25-in-sorted-array
|
🔥Simple Optimize solution Detail Explanation🔥|2-line Solution|🔥Daily Challenges 🔥
|
simple-optimize-solution-detail-explanat-znba
|
Complexity\n- Time complexity:O(n)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity:O(1)\n Add your space complexity here, e.g. O(n) \n\n# Code
|
Shree_Govind_Jee
|
NORMAL
|
2023-12-11T00:39:42.543481+00:00
|
2023-12-11T00:40:39.723787+00:00
| 1,127
| false
|
# Complexity\n- Time complexity:$$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```Java []\nclass Solution {\n public int findSpecialInteger(int[] arr) {\n/* \n HashMap<Integer, Integer> map = new HashMap<>();\n for(int i : arr){\n map.put(i, map.getOrDefault(i,0)+1);\n }\n\n int temp = arr.length/4;\n for(int key :map.keySet()){\n if(temp < map.get(key)) return key;\n }\n return 0;\n*/\n\n int temp = arr.length/4;\n for(int i=0; i<arr.length-temp; i++){\n if(arr[i] == arr[i+temp]) return arr[i];\n }\n\n return -1;\n }\n}\n```\n```C []\nint findSpecialInteger(int* arr, int arrSize) {\n int temp = arrSize/4;\n for(int i=0; i<arrSize-temp; i++){\n if(arr[i] == arr[i+temp]) return arr[i];\n }\n\n return -1;\n}\n```\n```C++ []\nclass Solution {\npublic:\n int findSpecialInteger(vector<int>& arr) {\n int temp = arr.size()/4;\n for(int i=0; i<arr.size()-temp; i++){\n if(arr[i] == arr[i+temp]) return arr[i];\n }\n\n return -1;\n }\n};\n```\n
| 6
| 0
|
['Array', 'C', 'C++', 'Java']
| 2
|
element-appearing-more-than-25-in-sorted-array
|
python log(N) sol
|
python-logn-sol-by-yefee-zq9v
|
\nclass Solution:\n def findSpecialInteger(self, arr: List[int]) -> int:\n \n \n for i in range(4):\n target = arr[len(arr)//
|
yefee
|
NORMAL
|
2020-07-12T08:40:14.360716+00:00
|
2020-07-12T08:40:14.360762+00:00
| 476
| false
|
```\nclass Solution:\n def findSpecialInteger(self, arr: List[int]) -> int:\n \n \n for i in range(4):\n target = arr[len(arr)//4 *i] # find the 0, 25, 50, 75%\n \n\t\t\t# left most val == target\n left = 0\n right = len(arr) - 1\n while left < right:\n mid = left + (right - left) // 2\n if arr[mid] < target:\n left = mid + 1\n else:\n right = mid\n \n\t\t\t# target has more than len(arr)//4\n if left + len(arr)//4 < len(arr) and arr[left + len(arr)//4] == target: \n return target\n```
| 6
| 0
|
[]
| 2
|
element-appearing-more-than-25-in-sorted-array
|
simple Java solution 100% mm and 100% runtime
|
simple-java-solution-100-mm-and-100-runt-7i2r
|
\nclass Solution {\n public int findSpecialInteger(int[] arr) {\n int quater = arr.length / 4;\n int count = 1;\n \n if(arr.lengt
|
saketshetty
|
NORMAL
|
2020-02-10T13:12:38.109820+00:00
|
2020-02-10T13:12:38.109859+00:00
| 402
| false
|
```\nclass Solution {\n public int findSpecialInteger(int[] arr) {\n int quater = arr.length / 4;\n int count = 1;\n \n if(arr.length == 1 ) return arr[0];\n \n for(int i=0; i<arr.length-1; i++){\n if(arr[i] == arr[i+1]){\n count++;\n if(count>quater){\n return arr[i];\n }\n }\n else{\n count=1;\n }\n }\n return 0;\n }\n}\n```
| 6
| 1
|
['Java']
| 1
|
element-appearing-more-than-25-in-sorted-array
|
✅ C++ Solution 🔥|| Straight Forward Solution 🔥
|
c-solution-straight-forward-solution-by-j13yt
|
Intuition\n Describe your first thoughts on how to solve this problem. \nwe can use map to store frquency of each element.\n\n# Approach\n Describe your approac
|
BruteForce_03
|
NORMAL
|
2023-12-11T09:54:56.225543+00:00
|
2023-12-11T13:05:04.124983+00:00
| 78
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nwe can use `map` to store `frquency` of each element.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Initialize Variables:\n - Initialize a `map` to `store` the `frequency` of each element.\n - Calculate the threshold `frequency` as` 25%` of the array length.\n2. Iterate Through the Array:\n - `Traverse` through the sorted array.\n - For each element encountered:\n - `Update` its `frequency` in the map.\n - Check if the frequency has `reached` or exceeded the threshold.\n - If yes, return the current element as it is the majority element.\n3. Return Result:\n - If no Element Appearing More Than 25% In Sorted Array is found during the iteration, `return` `-1`.\n\n# Complexity\n- Time complexity:$$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n```C++ []\nclass Solution {\npublic:\n int findSpecialInteger(vector<int>& arr) {\n int twentyFive=(arr.size()/100)*25;\n unordered_map<int,int> mp;\n for(int i=0;i<arr.size();i++)\n {\n mp[arr[i]]++;\n }\n for(auto x:mp)\n {\n if(x.second > arr.size()/4)\n {\n return x.first;\n }\n }\n return -1;\n }\n};\n```\n```python []\nclass Solution:\n def findSpecialInteger(self, arr):\n twentyFive = (len(arr) // 100) * 25\n frequency_dict = {}\n \n for num in arr:\n frequency_dict[num] = frequency_dict.get(num, 0) + 1\n \n for key, value in frequency_dict.items():\n if value > len(arr) // 4:\n return key\n \n return -1\n```\n```Javascript []\nclass Solution {\n findSpecialInteger(arr) {\n const twentyFive = Math.floor((arr.length / 100) * 25);\n const frequencyMap = {};\n\n for (const num of arr) {\n frequencyMap[num] = (frequencyMap[num] || 0) + 1;\n }\n\n for (const [key, value] of Object.entries(frequencyMap)) {\n if (value > Math.floor(arr.length / 4)) {\n return parseInt(key);\n }\n }\n\n return -1;\n }\n}\n```\n\n\n
| 5
| 0
|
['Ordered Map', 'Python', 'C++', 'JavaScript']
| 0
|
element-appearing-more-than-25-in-sorted-array
|
🔥|| BEGINNER FRIENDLY || EXPLAINED IN HINDI || HASHMAP ||🔥
|
beginner-friendly-explained-in-hindi-has-zxjp
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n1)Threshold Calculation (y):\ny ko calculate karte hain, jo array size ka 25% darshat
|
Sautramani
|
NORMAL
|
2023-12-11T04:39:19.493725+00:00
|
2023-12-11T04:39:19.493745+00:00
| 740
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n1)Threshold Calculation (y):\ny ko calculate karte hain, jo array size ka 25% darshata hai.\n\n2)Frequency Map Creation:\nHar unique integer ki frequency ko store karne ke liye ek map (mp) banate hain.\n\n3)Populate Frequency Map:\nArray mein iterate karte hain, aur har element ki frequency ko map mein badhate hain.\n\n4)Traverse Array:\nArray ko traverse karte hain.\nHar element ki frequency ko map mein dekhte hain aur check karte hain ki woh threshold (y) se jyada hai ya nahi.\n\n5)Return Special Integer:\nAgar mil jaata hai, toh woh element special integer ke roop mein return kiya jata hai.\n\n6)Return -1 if Not Found:\nAgar array traverse karte waqt koi special integer nahi milta, toh -1 return kiya jata hai..\n\n\n\n# Complexity\n- Time complexity:O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n```C++ []\nclass Solution {\npublic:\n int findSpecialInteger(vector<int>& arr) {\n\n \n int n=arr.size();\n int y=(n*25)/100;\n\n // MAP KO FILL KAR RAHE HN\n map<int,int>mp;\n for(auto it : arr)\n {\n mp[it]++;\n }\n\n // array KE ANDAR TRAVERSE KAR RAHE AUR DEKH RAHE KI ARRAY KA ith ELEMENT KI FREQUENCY MAP KE ANDAR 25% (Y) SE ZADA HAI YA NAHI.\n for(int i=0;i<n;i++)\n {\n if(mp[arr[i]]>y)\n {\n return arr[i];\n }\n }\n return -1;\n }\n};\n```\n```JAVA []\nclass Solution {\n public int findSpecialInteger(int[] arr) {\n int size = arr.length;\n int qtr = size / 4;\n int cnt = 1;\n int p = arr[0];\n for (int i = 1 ; i < arr.length ; i++) {\n\n if ( p == arr[i]) cnt++;\n else cnt = 1;\n \n if (cnt > qtr) return arr[i];\n \n p = arr[i];\n }\n\n return p;\n }\n}\n```\n```python []\nclass Solution(object):\n def findSpecialInteger(self, arr):\n size = len(arr)\n qtr = size // 4\n cnt = 1\n p = arr[0]\n \n for i in range(1, size):\n if p == arr[i]:\n cnt += 1\n else:\n cnt = 1\n \n if cnt > qtr:\n return arr[i]\n \n p = arr[i]\n\n return p\n \n```\n\n\n
| 5
| 0
|
['Array', 'Hash Table', 'Hash Function', 'Python', 'C++', 'Java']
| 2
|
element-appearing-more-than-25-in-sorted-array
|
Python easy to understand solution
|
python-easy-to-understand-solution-by-sh-cjoj
|
\nclass Solution:\n def findSpecialInteger(self, arr: List[int]) -> int:\n per = len(arr)//4\n for i in arr:\n occ = arr.count(i)\n
|
Shivam_Raj_Sharma
|
NORMAL
|
2022-05-20T08:09:48.080401+00:00
|
2022-05-20T08:09:48.080430+00:00
| 707
| false
|
```\nclass Solution:\n def findSpecialInteger(self, arr: List[int]) -> int:\n per = len(arr)//4\n for i in arr:\n occ = arr.count(i)\n if occ > per:\n return i\n```
| 5
| 0
|
['Array', 'Python', 'Python3']
| 0
|
element-appearing-more-than-25-in-sorted-array
|
JavaScript - Boyer-Moore Voting Algorithm
|
javascript-boyer-moore-voting-algorithm-otc09
|
Hint from: https://leetcode.com/problems/majority-element/solution/\nApproach 6: Boyer-Moore Voting Algorithm\n\n Time: O(n)\n Space: O(1)\n\n> Sorting doesn\'t
|
shengdade
|
NORMAL
|
2020-02-27T02:51:10.227431+00:00
|
2020-02-27T02:53:22.021730+00:00
| 399
| false
|
Hint from: https://leetcode.com/problems/majority-element/solution/\nApproach 6: Boyer-Moore Voting Algorithm\n\n* Time: O(n)\n* Space: O(1)\n\n> Sorting doesn\'t matter\n\n```javascript\n/**\n * @param {number[]} arr\n * @return {number}\n */\nvar findSpecialInteger = function(arr) {\n let candidate;\n let counter = 0;\n arr.forEach(n => {\n if (counter === 0 || counter === 1) candidate = n;\n counter += n === candidate ? 3 : -1;\n });\n return candidate;\n};\n```\n\n* 18/18 cases passed (48 ms)\n* Your runtime beats 98.85 % of javascript submissions\n* Your memory usage beats 100 % of javascript submissions (35.1 MB)
| 5
| 0
|
['JavaScript']
| 4
|
element-appearing-more-than-25-in-sorted-array
|
✅☑[C++/Java/Python/JavaScript] || 2 Approaches || EXPLAINED🔥
|
cjavapythonjavascript-2-approaches-expla-jmiy
|
PLEASE UPVOTE IF IT HELPED\n\n---\n\n\n# Approaches\n(Also explained in the code)\n\n#### Approach 1(With Hash Maps)\n1. HashMap (unordered_map):\n\n - Creat
|
MarkSPhilip31
|
NORMAL
|
2023-12-11T07:57:59.618829+00:00
|
2023-12-11T07:57:59.618864+00:00
| 249
| false
|
# PLEASE UPVOTE IF IT HELPED\n\n---\n\n\n# Approaches\n**(Also explained in the code)**\n\n#### ***Approach 1(With Hash Maps)***\n1. **HashMap (unordered_map):**\n\n - Create an unordered map (`counts`) to store the count of each element in the input array.\n - Iterate through the input array (`arr`) and count the occurrences of each element.\n1. **Finding the Threshold:**\n\n - Calculate the threshold value (`target`) by dividing the length of the array (`arr.size()`) by 4, as we are looking for an integer that appears more than 25% of the time.\n1. **Checking Frequency:**\n\n - Traverse through the map.\n - For each key-value pair in the `counts` map:\n - Check if the count (`value`) of an element (`key`) is greater than the threshold (`target`).\n - If found, return the element (`key`) as it appears more than 25% of the time in the array.\n1. **Return Value:**\n\n - If no such element is found that satisfies the condition (appears more than 25% of the time), return `-1` indicating no special integer found.\n\n# Complexity\n- *Time complexity:*\n $$O(n)$$\n \n\n- *Space complexity:*\n $$O(n)$$\n \n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n // Function to find an integer that appears more than 25% of the length of the input array\n int findSpecialInteger(vector<int>& arr) {\n unordered_map<int, int> counts; // Store the count of each element\n for (int num : arr) {\n counts[num]++; // Count occurrences of each element in the array\n }\n \n int target = arr.size() / 4; // Threshold to check for the required frequency\n \n // Iterate through the counts map to find the special integer\n for (auto& [key, value] : counts) {\n if (value > target) {\n return key; // Return the integer that appears more than 25% of the time\n }\n }\n \n return -1; // If no such integer found, return -1\n }\n};\n\n\n\n```\n```C []\nint findSpecialInteger(int* arr, int arrSize) {\n int* counts = (int*)calloc(100001, sizeof(int)); // Creating an array to store counts (assuming input elements range from 0 to 100000)\n \n // Count occurrences of each element in the array\n for (int i = 0; i < arrSize; ++i) {\n counts[arr[i]]++;\n }\n \n int target = arrSize / 4; // Threshold to check for the required frequency\n \n // Iterate through the counts array to find the special integer\n for (int i = 0; i < 100001; ++i) {\n if (counts[i] > target) {\n return i; // Return the integer that appears more than 25% of the time\n }\n }\n \n return -1; // If no such integer found, return -1\n}\n\n\n\n```\n```Java []\n\nclass Solution {\n public int findSpecialInteger(int[] arr) {\n Map<Integer, Integer> counts = new HashMap();\n for (int num : arr) {\n counts.put(num, counts.getOrDefault(num, 0) + 1);\n }\n \n int target = arr.length / 4;\n for (int key : counts.keySet()) {\n if (counts.get(key) > target) {\n return key;\n }\n }\n \n return -1;\n }\n}\n\n```\n```python3 []\nclass Solution:\n def findSpecialInteger(self, arr: List[int]) -> int:\n counts = defaultdict(int)\n for num in arr:\n counts[num] += 1\n \n target = len(arr) / 4\n for key, value in counts.items():\n if value > target:\n return key\n \n return -1\n\n\n```\n```javascript []\nfunction findSpecialInteger(arr) {\n let counts = new Array(100001).fill(0); // Creating an array to store counts (assuming input elements range from 0 to 100000)\n \n // Count occurrences of each element in the array\n for (let i = 0; i < arr.length; ++i) {\n counts[arr[i]]++;\n }\n \n let target = arr.length / 4; // Threshold to check for the required frequency\n \n // Iterate through the counts array to find the special integer\n for (let i = 0; i < 100001; ++i) {\n if (counts[i] > target) {\n return i; // Return the integer that appears more than 25% of the time\n }\n }\n \n return -1; // If no such integer found, return -1\n}\n\n\n\n```\n---\n\n#### ***Approach 2(Check the Element N/4 Ahead)***\n1. The code iterates through the array and checks for a candidate integer that appears more than 25% of the time.\n1. The comparison is done between the current element and the element `size` steps ahead.\n1. If a repeating element is found within the next `size` elements, it returns that element as it satisfies the given condition.\n1. If no such repeating element is found, it returns -1, indicating that no element meets the required criteria.\n\n# Complexity\n- *Time complexity:*\n $$O(n)$$\n \n\n- *Space complexity:*\n $$O(1)$$\n \n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n // Function to find an integer that appears more than 25% of the length of the input array\n int findSpecialInteger(vector<int>& arr) {\n int size = arr.size() / 4; // Calculate the threshold size\n \n // Loop through the array elements\n for (int i = 0; i < arr.size() - size; i++) {\n if (arr[i] == arr[i + size]) {\n return arr[i]; // Return the integer if found that occurs more than 25% of the time\n }\n }\n \n return -1; // Return -1 if no such integer is found\n }\n};\n\n\n\n```\n```C []\n\n#include <stdio.h>\n\nint findSpecialInteger(int* arr, int arrSize) {\n int size = arrSize / 4; // Calculate the threshold size\n \n // Loop through the array elements\n for (int i = 0; i < arrSize - size; i++) {\n if (arr[i] == arr[i + size]) {\n return arr[i]; // Return the integer if found that occurs more than 25% of the time\n }\n }\n \n return -1; // Return -1 if no such integer is found\n}\n\n\n\n```\n```Java []\nclass Solution {\n public int findSpecialInteger(int[] arr) {\n int size = arr.length / 4;\n for (int i = 0; i < arr.length - size; i++) {\n if (arr[i] == arr[i + size]) {\n return arr[i];\n }\n }\n \n return -1;\n }\n}\n\n\n```\n```python3 []\nclass Solution:\n def findSpecialInteger(self, arr: List[int]) -> int:\n size = len(arr) // 4\n for i in range(len(arr) - size):\n if arr[i] == arr[i + size]:\n return arr[i]\n \n return -1\n\n\n```\n```javascript []\nfunction findSpecialInteger(arr) {\n let size = Math.floor(arr.length / 4); // Calculate the threshold size\n \n // Loop through the array elements\n for (let i = 0; i < arr.length - size; i++) {\n if (arr[i] === arr[i + size]) {\n return arr[i]; // Return the integer if found that occurs more than 25% of the time\n }\n }\n \n return -1; // Return -1 if no such integer is found\n}\n\n\n\n```\n---\n\n\n# PLEASE UPVOTE IF IT HELPED\n\n---\n---\n\n\n---
| 4
| 0
|
['Array', 'C', 'C++', 'Java', 'Python3', 'JavaScript']
| 1
|
element-appearing-more-than-25-in-sorted-array
|
Rust 1ms 🔥 2.43 Mb ☄️ One Liner Solution 🦀
|
rust-1ms-243-mb-one-liner-solution-by-ro-b09p
|
Complexity\n- Time complexity: O(n)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(1)\n Add your space complexity here, e.g. O(n) \n\n# Co
|
rony0000013
|
NORMAL
|
2023-12-11T04:34:13.453993+00:00
|
2023-12-11T04:34:13.454024+00:00
| 109
| false
|
# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimpl Solution {\n pub fn find_special_integer(arr: Vec<i32>) -> i32 {\n [arr[arr.len()/4], arr[arr.len()/2], arr[arr.len()/4*3]]\n .iter()\n .fold(arr[arr.len()-1], |ans, &n| {\n let s = arr.partition_point(|&x| x < n);\n let e = arr.partition_point(|&x| x <= n);\n if (e-s) > arr.len()/4 {n} else {ans}\n })\n }\n}\n```
| 4
| 0
|
['Rust']
| 1
|
element-appearing-more-than-25-in-sorted-array
|
Simple approach without use of hashmap and extra libraries!
|
simple-approach-without-use-of-hashmap-a-a09r
|
Intuition\n Describe your first thoughts on how to solve this problem. \nSince the array elements are sorted whenever in the loop ith element equals i+len(arr)/
|
yashaswisingh47
|
NORMAL
|
2023-12-11T04:28:56.866217+00:00
|
2023-12-11T04:28:56.866240+00:00
| 232
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nSince the array elements are sorted whenever in the loop ith element equals i+len(arr)//4 th element. We will return the element.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findSpecialInteger(self, arr: List[int]) -> int:\n for i in range(len(arr) - len(arr)//4):\n if arr[i] == arr[i + len(arr)//4]:\n return arr[i]\n\n```
| 4
| 0
|
['Python3']
| 0
|
element-appearing-more-than-25-in-sorted-array
|
HAPPY DECEMBER ☃️|| 2 APPROACHES ✅ GOOD EXPLANATION😊|| BEGINEER FRIENDLY 👌
|
happy-december-2-approaches-good-explana-xefi
|
Intuition & Approaches :- \nHope everyone is doing great.. its going easy december right guys.. i m not posting answer in between as there are thosusand answers
|
DEvilBackInGame
|
NORMAL
|
2023-12-11T01:37:17.066259+00:00
|
2023-12-11T01:56:12.682153+00:00
| 721
| false
|
# Intuition & Approaches :- \nHope everyone is doing great.. its going easy december right guys.. i m not posting answer in between as there are thosusand answers and for easy question with same approaches.. so i looked into other solutions & they are also good and well explained. if u want me to post all solution with my aproach , i will post it with my own explanation to undestand u guys.. that will surely different from others.\n\nlets hop back into today.. so here i am posting 2 answer for this one problem.\n1. In 1st appraoch, i used simple iteration and count variable to count max number of occurance of any number. and if it is greater than the maximum count calculated previously then it will update my maximum count variable with count and also the value associated with it will be updated in my answer. \n2. In my 2nd approach i take help of map. i inserted all the element from my arr to map. and we know with map we will get number of occurances each number have. then atlast with the same method of updating count i checked the largest element in all indexes second element. as i.second element of map holds frequency. and i.first holds value. here i is not index by the reference at that position.\n\nThis way i got 2 ways of doing my question. as array was already sorted so 1st approach is more efficient than 2nd if terms of both time complxity and space.\n\n1st TC- is O(n) .\n2nd TC- is O(n*m) (loop 2 times one for inserting element with n size arr, second for iterating in map of size m).\n\n\n# 1 - C++ Code O(n) -\n```\nclass Solution {\npublic:\n int findSpecialInteger(vector<int>& arr) {\n int count=0;\n int maxi_count=0;\n int ans=0;\n int n=arr.size();\n if(n<2) return arr[0];\n for(int i=1;i<n;i++){\n if(arr[i]==arr[i-1]){\n count++;\n }\n else count=0;\n\n if(count>maxi_count){\n maxi_count=count;\n ans=arr[i]; \n }\n \n }\n \n return ans;\n }\n};\n```\n# 2- C++ code with Map (n*m)-\n```\nclass Solution {\npublic:\n int findSpecialInteger(vector<int>& arr) {\n unordered_map<int,int>mp;\n for(auto i:arr){\n mp[i]++;\n }\n int ans=0;\n int maxi_count=0;\n for(auto i:mp){\n if(maxi_count<i.second){\n maxi_count=i.second;\n ans=i.first;\n }\n }\n return ans;\n }\n};\n```
| 4
| 0
|
['Array', 'Ordered Map', 'C++']
| 3
|
element-appearing-more-than-25-in-sorted-array
|
simple c++ solution
|
simple-c-solution-by-prithviraj26-l1qs
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
prithviraj26
|
NORMAL
|
2023-02-06T14:18:18.456533+00:00
|
2023-02-06T14:18:18.456573+00:00
| 591
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\no(n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\no(n)\n\n# Code\n```\nclass Solution {\npublic:\n int findSpecialInteger(vector<int>& arr) {\n int n=arr.size()*0.25;\n unordered_map<int,int>m;\n for(int i=0;i<arr.size();i++)\n {\n m[arr[i]]++;\n }\n int ans;\n for(auto it:m)\n {\n if(it.second>n)\n {\n ans=it.first;\n }\n }\n return ans;\n }\n};\n```\n\n
| 4
| 0
|
['Array', 'Hash Table', 'C++']
| 1
|
element-appearing-more-than-25-in-sorted-array
|
Easy Python
|
easy-python-by-tusharkhanna575-yl4j
|
\nclass Solution:\n def findSpecialInteger(self, arr: List[int]) -> int:\n check=len(arr)//4\n c=dict((i,arr.count(i)) for i in arr)\n f
|
tusharkhanna575
|
NORMAL
|
2022-05-20T08:07:00.686655+00:00
|
2022-05-20T08:09:58.073066+00:00
| 838
| false
|
```\nclass Solution:\n def findSpecialInteger(self, arr: List[int]) -> int:\n check=len(arr)//4\n c=dict((i,arr.count(i)) for i in arr)\n for k,v in c.items():\n if(c[k]>check):\n return k\n \n```\n**One more method**\n```\nclass Solution:\n def findSpecialInteger(self, arr: List[int]) -> int:\n check=len(arr)//4\n for i in set(arr):\n if arr.count(i) > check:\n return i\n```
| 4
| 0
|
['Python', 'Python3']
| 1
|
element-appearing-more-than-25-in-sorted-array
|
📌Fastest Java☕ Solution 0ms💯
|
fastest-java-solution-0ms-by-saurabh_173-mbap
|
```\nclass Solution {\n public int findSpecialInteger(int[] arr) \n {\n var x = arr.length/4;\n for(var i=0;i<arr.length;i++)\n i
|
saurabh_173
|
NORMAL
|
2022-05-01T15:10:50.267992+00:00
|
2022-05-01T15:10:50.268034+00:00
| 179
| false
|
```\nclass Solution {\n public int findSpecialInteger(int[] arr) \n {\n var x = arr.length/4;\n for(var i=0;i<arr.length;i++)\n if(arr[i]==arr[i+x])\n return arr[i];\n return -1;\n }\n}
| 4
| 0
|
['Array', 'Java']
| 2
|
element-appearing-more-than-25-in-sorted-array
|
Java Simple Sliding window
|
java-simple-sliding-window-by-hobiter-o9fq
|
\n public int findSpecialInteger(int[] arr) {\n int n = arr.length, l = 0, r = n / 4;\n while (r < n) if (arr[r++] == arr[l++]) return arr[--l]
|
hobiter
|
NORMAL
|
2020-06-15T18:42:17.851665+00:00
|
2020-06-15T18:42:17.851715+00:00
| 154
| false
|
```\n public int findSpecialInteger(int[] arr) {\n int n = arr.length, l = 0, r = n / 4;\n while (r < n) if (arr[r++] == arr[l++]) return arr[--l];\n return -1;\n }\n```
| 4
| 1
|
[]
| 0
|
element-appearing-more-than-25-in-sorted-array
|
Constant O(1) time, O(1) space, NO binary search needed, 0ms 100%/100%
|
constant-o1-time-o1-space-no-binary-sear-1ljn
|
The idea is to "sampling" the input array to a new array with a length of 9. If the input array has length of 9 or less, we just find the most common element (m
|
truongsinh
|
NORMAL
|
2020-02-27T15:45:05.408632+00:00
|
2020-02-28T10:22:04.684140+00:00
| 727
| false
|
The idea is to "sampling" the input array to a new array with a length of 9. If the input array has length of 9 or less, we just find the most common element (mode). Otherwise, no matter how large the input is, we just need exactly 9 points to compare, 2 of which are first and last item of the array, the remaining 7 indices increase by n/8.\n\nAfter getting only 9 values from the above positions, count the most common number, and it shall be our answer.\n\nThis method can be extended to other number of percentage, such as 10%, 15%, 20%, 34%, etc, just need a different numbers of points to compare.\n\nPython3\n```python\nclass Solution:\n def findSpecialInteger(self, arr: List[int]) -> int:\n n = len(arr)\n if n <= 9: return self.findMode(arr)\n c = [\n arr[0],\n arr[(n-1)//8],\n arr[2*(n-1)//8],\n arr[3*(n-1)//8],\n arr[4*(n-1)//8],\n arr[5*(n-1)//8],\n arr[6*(n-1)//8],\n arr[7*(n-1)//8],\n arr[n-1]\n ]\n return self.findMode(c)\n def findMode(self, arr: List[int]) -> int:\n # this findMode can be furthur optimized given the input is also non-descending\n return collections.Counter(arr).most_common(1)[0][0]\n```\n\nGeneral solution in Python 3\n```python\nclass Solution:\n def findSpecialInteger(self, arr: List[int]) -> int:\n return self.findMode(self.samplingOrOrigin(arr, 9))\n \n def samplingOrOrigin(self, arr: List[int], nTile: int) -> int:\n n = len(arr)\n if n <= nTile: return arr\n return [ arr[i*(n-1)//(nTile-1)] for i in range(nTile) ]\n\n def findMode(self, arr: List[int]) -> int:\n # this findMode can be furthur optimized given the input is also non-descending\n return collections.Counter(arr).most_common(1)[0][0]\n```\n\nJava\n```java\nclass Solution {\n public int findSpecialInteger(int[] arr) {\n int n = arr.length;\n if (n <= 9) {\n return findMode(arr);\n }\n int[] c = {\n arr[0],\n arr[(n-1)/8],\n arr[2*(n-1)/8],\n arr[3*(n-1)/8],\n arr[4*(n-1)/8],\n arr[5*(n-1)/8],\n arr[6*(n-1)/8],\n arr[7*(n-1)/8],\n arr[n-1],\n };\n return findMode(c);\n } \n int findMode(int[] a)\n {\n final Map m = new HashMap<Integer,Integer>();\n int max = 0;\n int element = 0;\n\n for (int i=0; i<a.length; i++){\n if (m.get(a[i]) == null) m.put(a[i],0);\n m.put(a[i] , (Integer) m.get(a[i]) + 1);\n if ( (Integer) m.get(a[i]) > max){\n max = (Integer) m.get(a[i]);\n element = a[i];\n }\n }\n return element;\n }\n}\n```\n\nC++\n```cpp\nclass Solution {\npublic:\n int findSpecialInteger(vector<int>& arr) {\n int n = arr.size();\n if (n <= 9) return findMode(arr);\n vector<int> c {\n arr[0],\n arr[n/8],\n arr[2*(n-1)/8],\n arr[3*(n-1)/8],\n arr[4*(n-1)/8],\n arr[5*(n-1)/8],\n arr[6*(n-1)/8],\n arr[7*(n-1)/8],\n arr[n-8]\n };\n return findMode(c);\n }\n int findMode(vector<int> value) { \n int index = 0;\n int highest = 0;\n for (unsigned int a = 0; a < value.size(); a++)\n {\n int count = 1;\n int Position = value.at(a);\n for (unsigned int b = a + 1; b < value.size(); b++)\n {\n if (value.at(b) == Position)\n {\n count++;\n }\n }\n if (count >= index)\n {\n index = count;\n highest = Position;\n }\n }\n return highest;\n }\n};\n```
| 4
| 0
|
['Python', 'C++', 'Java']
| 2
|
element-appearing-more-than-25-in-sorted-array
|
very easy without binary search....
|
very-easy-without-binary-search-by-tpx_c-q68l
|
class Solution {\npublic:\n int findSpecialInteger(vector& arr) {\n \n int res;\n \n for(int i=0;i<arr.size();i++)\n {\n
|
tpx_coder-28
|
NORMAL
|
2020-01-07T13:35:18.911165+00:00
|
2020-01-07T13:35:18.911197+00:00
| 450
| false
|
class Solution {\npublic:\n int findSpecialInteger(vector<int>& arr) {\n \n int res;\n \n for(int i=0;i<arr.size();i++)\n {\n if(arr[i]==arr[i+arr.size()/4])\n {\n return arr[i];\n break;\n }\n }\n \n return res;\n \n }\n};
| 4
| 1
|
[]
| 1
|
element-appearing-more-than-25-in-sorted-array
|
Python solution 💥 🔥
|
python-solution-by-noy25-nbkd
|
Intuition\n Describe your first thoughts on how to solve this problem. \nThis Python code aims to find a special integer in the given array arr. A special integ
|
noy25
|
NORMAL
|
2024-01-02T19:44:55.446627+00:00
|
2024-01-02T19:44:55.446652+00:00
| 11
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThis Python code aims to find a special integer in the given array arr. A special integer is defined as an integer that appears more than 25% of the array\'s length. The code iterates through the array, comparing each element with the element that is a quarter of the array size away. If a match is found, that element is considered the special integer.\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution(object):\n def findSpecialInteger(self, arr):\n size = len(arr) // 4\n for i in range(len(arr) - size):\n if arr[i] == arr[i + size]:\n return arr[i]\n \n return -1 \n```
| 3
| 0
|
['Array', 'Python']
| 0
|
element-appearing-more-than-25-in-sorted-array
|
Simple solution for Element Appearing More Than 25% In Sorted Array
|
simple-solution-for-element-appearing-mo-cjip
|
Approach\nOne more simple solution without using Hash Map or Binary Search.\n\n# Code\n\n/**\n * @param {number[]} arr\n * @return {number}\n */\nvar findSpecia
|
klim9d61
|
NORMAL
|
2023-12-11T19:12:02.203691+00:00
|
2023-12-11T19:12:02.203723+00:00
| 31
| false
|
# Approach\nOne more simple solution without using Hash Map or Binary Search.\n\n# Code\n```\n/**\n * @param {number[]} arr\n * @return {number}\n */\nvar findSpecialInteger = function(arr) {\n const oneQuarter = arr.length / 4;\n let count = 0;\n\n if(arr.length === 1) {\n return arr[0];\n }\n\n for(let i=0; i < arr.length; i++) {\n count++;\n\n if(count > oneQuarter) {\n return arr[i];\n } else if(arr[i] !== arr[i+1]) {\n count = 0;\n }\n }\n\n return -1;\n};\n```
| 3
| 0
|
['TypeScript', 'JavaScript']
| 0
|
element-appearing-more-than-25-in-sorted-array
|
Beats 100% of users with C++ ( Using HashMap ) Time Complexity { O ( logN ) }
|
beats-100-of-users-with-c-using-hashmap-4dvx2
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n\n\n\n\n\n\nif you like the approach please upvote it\n\n\n\n\n\n\nif you like the ap
|
abhirajpratapsingh
|
NORMAL
|
2023-12-11T10:07:51.077506+00:00
|
2023-12-11T10:07:51.077547+00:00
| 7
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n\n\n\n\n\n\nif you like the approach please upvote it\n\n\n\n\n\n\nif you like the approach please upvote it\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O ( N Log N )\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ --> \n\n# Code\n```\nclass Solution {\npublic:\n int findSpecialInteger(vector<int>& arr) \n {\n int size=arr.size();\n int occur=size/4;\n map<int,int>mp;\n for(int i=0;i<size;i++)\n mp[arr[i]]++;\n for(auto it : mp)\n {\n if(it.second>occur)\n return it.first;\n }\n return -1;\n }\n};\n```
| 3
| 0
|
['Array', 'Ordered Map', 'Counting', 'C++']
| 0
|
element-appearing-more-than-25-in-sorted-array
|
Simple solution in TypeScript using Map().
|
simple-solution-in-typescript-using-map-35ws9
|
Approach\nUsing a map variable to store the count of each element. If the count of a particular element is more than 25% of the sorted array, that is it!\n\n# C
|
vineethvg
|
NORMAL
|
2023-12-11T09:57:10.989387+00:00
|
2023-12-11T09:57:10.989410+00:00
| 58
| false
|
# Approach\nUsing a map variable to store the count of each element. If the count of a particular element is more than 25% of the sorted array, that is it!\n\n# Complexity\n- Time complexity: $$O(N)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(N)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfunction findSpecialInteger(arr: number[]): number {\n const target = Math.floor(arr.length / 4);\n const map = new Map<number, number>()\n for (let i = 0; i < arr.length; i++) {\n const count = map.get(arr[i]) || 0\n map.set(arr[i], count + 1)\n if (count + 1 > target) return arr[i]\n }\n};\n```
| 3
| 0
|
['TypeScript']
| 0
|
element-appearing-more-than-25-in-sorted-array
|
Simple | Beat 100% | ✅
|
simple-beat-100-by-shadab_ahmad_khan-or0b
|
Intuition\n\n# Code\n\nclass Solution {\n public int findSpecialInteger(int[] arr) {\n if(arr.length<=2) return arr[0];\n int appearingCount= a
|
Shadab_Ahmad_Khan
|
NORMAL
|
2023-12-11T07:02:23.514642+00:00
|
2023-12-11T07:03:30.414060+00:00
| 222
| false
|
# Intuition\n\n# Code\n```\nclass Solution {\n public int findSpecialInteger(int[] arr) {\n if(arr.length<=2) return arr[0];\n int appearingCount= arr.length/4;\n int count=1;\n for(int i=1; i<arr.length; i++){\n if(arr[i]==arr[i-1]){\n count++;\n }else{\n count=1;\n }\n if(count>appearingCount){\n return arr[i];\n }\n }\n return -1;\n }\n}\n```\n______________________________________\n\n# **Up Vote if Helps**\n\n______________________________________
| 3
| 0
|
['Array', 'Java']
| 0
|
element-appearing-more-than-25-in-sorted-array
|
Easy Approach||Beginner friendly||Maps||beats 90%users
|
easy-approachbeginner-friendlymapsbeats-zzlij
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
Hitheash
|
NORMAL
|
2023-12-11T02:38:42.224695+00:00
|
2023-12-11T02:38:42.224724+00:00
| 669
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int findSpecialInteger(vector<int>& arr) {\n int val=0.25*arr.size();\n map<int,int>mp;\n for(auto &it:arr){\n mp[it]++;\n }\n for(auto &it:mp){\n if(it.second>val){\n return it.first;\n }\n }return -1;\n }\n};\n```
| 3
| 0
|
['C++']
| 0
|
element-appearing-more-than-25-in-sorted-array
|
⭐One-Liner Hack in 🐍|| Two Approaches ||😐Beats 75.32%😐⭐
|
one-liner-hack-in-two-approaches-beats-7-bzdx
|
\n# Code\npy\nclass Solution:\n def findSpecialInteger(self, arr: List[int]) -> int:\n return next(i for i in arr if arr.count(i) / len(arr) > 0.25)\n
|
ShreejitCheela
|
NORMAL
|
2023-12-11T00:09:37.960015+00:00
|
2023-12-11T00:09:37.960032+00:00
| 690
| false
|
\n# Code\n```py\nclass Solution:\n def findSpecialInteger(self, arr: List[int]) -> int:\n return next(i for i in arr if arr.count(i) / len(arr) > 0.25)\n```\n ---\n\n\n# Code\n```py\nclass Solution:\n def findSpecialInteger(self, arr: List[int]) -> int:\n return statistics.mode(arr)\n```\n---\n\n_If you like the solution, promote it. Thank You._\n \n---
| 3
| 0
|
['Python3']
| 0
|
element-appearing-more-than-25-in-sorted-array
|
JavaScript Binary Search O(log n)
|
javascript-binary-search-olog-n-by-ekteg-myfx
|
This is total overkill for this problem, but here goes.\n\nWe can split arr into 4 parts\n\n[a, a, a, a | b, b, b, b | c, c, c, c | d, d, d, d]\n\nIf an element
|
ektegjetost
|
NORMAL
|
2022-05-14T16:59:35.822041+00:00
|
2022-05-14T17:01:35.047973+00:00
| 151
| false
|
This is total overkill for this problem, but here goes.\n\nWe can split arr into 4 parts\n```\n[a, a, a, a | b, b, b, b | c, c, c, c | d, d, d, d]\n```\nIf an element appears more than more than a quarter of the time, there\'s no way it can hide inside of one of these parts, so we\'re guaranteed to find it if we check either the start or end of each part.\n\nThen we need to identify if the number we selected actually occurs more than 25% of the time. Let\'s binary search for the first occurrence of the number we selected, and then check to see if the same element is positioned at the first occurrence + 1/4 of the array length.\n\nWe only need to check 4 positions, so we end up with O(4 * log n) which is just O(log n).\n\n```\nvar findSpecialInteger = function(arr) {\n const quarter = Math.ceil(arr.length / 4);\n \n for (let i = quarter - 1; i < arr.length; i += quarter) {\n if (appearsMoreThanAQuarter(arr, arr[i])) return arr[i];\n }\n};\n\nconst appearsMoreThanAQuarter = (arr, target) => {\n let left = 0;\n let right = arr.length - 1;\n let mid = right;\n \n while (left < right) {\n mid = left + right >> 1;\n \n if (arr[mid] < target) {\n left = mid + 1;\n } else {\n right = mid;\n }\n }\n \n return arr[right + (arr.length >> 2)] === target;\n}\n```
| 3
| 0
|
['Binary Tree', 'JavaScript']
| 0
|
element-appearing-more-than-25-in-sorted-array
|
Sliding Window Technique , intuitive Go SOln
|
sliding-window-technique-intuitive-go-so-utlm
|
\nfunc findSpecialInteger(arr []int) int {\n\tn := len(arr)\n\tt := n / 4\n\n\tfor i := 0; i < n-t; i++ {\n\t\tif arr[i] == arr[i+t] {\n\t\t\treturn arr[i]\n\t\
|
pradeep288
|
NORMAL
|
2021-10-26T07:30:16.474856+00:00
|
2021-10-26T07:30:16.474906+00:00
| 101
| false
|
```\nfunc findSpecialInteger(arr []int) int {\n\tn := len(arr)\n\tt := n / 4\n\n\tfor i := 0; i < n-t; i++ {\n\t\tif arr[i] == arr[i+t] {\n\t\t\treturn arr[i]\n\t\t}\n\t}\n\n\treturn -1\n}\n```
| 3
| 0
|
['Go']
| 0
|
element-appearing-more-than-25-in-sorted-array
|
JAVA 100% faster (On/O1)
|
java-100-faster-ono1-by-movsar-1o9g
|
\nclass Solution {\n public int findSpecialInteger(int[] arr) {\n // 25% is 1/4 of numbers in arr\n\t// if length is 9, 25% is 9 / 4 = 2,5\n\t// round up to
|
movsar
|
NORMAL
|
2021-09-18T21:49:46.201310+00:00
|
2021-09-18T21:49:46.201350+00:00
| 289
| false
|
```\nclass Solution {\n public int findSpecialInteger(int[] arr) {\n // 25% is 1/4 of numbers in arr\n\t// if length is 9, 25% is 9 / 4 = 2,5\n\t// round up to next int\n int q = Math.round(arr.length / 4) + 1;\n int res = 0, temp = 1;\n\n if (arr.length == 1) return arr[res];\n\n for (int i = 1; i < arr.length; i++) {\n if (arr[i] != arr[i - 1]) {\n temp = 1;\n }\n else {\n temp++;\n if (temp >= q) {\n res = arr[i];\n break;\n }\n }\n }\n\n return res;\n }\n}\n```
| 3
| 0
|
['Java']
| 0
|
element-appearing-more-than-25-in-sorted-array
|
Simple Binary Search | C++ | log n Solution
|
simple-binary-search-c-log-n-solution-by-sxlz
|
\tint singleNonDuplicate(vector& nums) {\n int n=nums.size();\n int lo=0,hi=n-1;int mid;\n while(lo<hi)\n {\n mid=lo+(hi-
|
nikhilsharmaiiita
|
NORMAL
|
2021-05-05T17:37:41.105722+00:00
|
2021-05-05T17:39:15.168943+00:00
| 141
| false
|
\tint singleNonDuplicate(vector<int>& nums) {\n int n=nums.size();\n int lo=0,hi=n-1;int mid;\n while(lo<hi)\n {\n mid=lo+(hi-lo+1)/2;\n //here we test if numbet of element left side of mid is even or not\n if((mid-lo)%2==0)\n {\n //if this this is true it\'s mean even+that element = odd \n //so our req element at left end side so we set hi = mid\n if(nums[mid]==nums[mid-1])\n hi=mid;\n //if not true mean left is even so its satisfied the cond\n // so we set lo=mid here\n else lo=mid;\n }\n //here left side of mid id odd \n else\n {\n //if its true so odd+1=even so our element at right end side\n if(nums[mid]==nums[mid-1])\n lo=mid+1;\n else hi=mid-1;\n }\n }\n return nums[lo];
| 3
| 1
|
[]
| 0
|
element-appearing-more-than-25-in-sorted-array
|
Python3 simple solution using four approaches
|
python3-simple-solution-using-four-appro-td7a
|
\nfrom collections import Counter\nclass Solution:\n def findSpecialInteger(self, arr: List[int]) -> int:\n n = len(arr)\n x = Counter(arr)\n
|
EklavyaJoshi
|
NORMAL
|
2021-03-11T05:20:23.736992+00:00
|
2021-03-11T05:20:23.737026+00:00
| 169
| false
|
```\nfrom collections import Counter\nclass Solution:\n def findSpecialInteger(self, arr: List[int]) -> int:\n n = len(arr)\n x = Counter(arr)\n for i in x:\n if x[i] > n/4:\n return i\n```\n\n\n\n```\nclass Solution:\n def findSpecialInteger(self, arr: List[int]) -> int:\n n = len(arr)\n for i in arr:\n if arr.count(i) > n/4:\n return i\n```\n\n```\nclass Solution:\n def findSpecialInteger(self, arr: List[int]) -> int:\n return sorted(arr, key = lambda x: arr.count(x), reverse = True)[0]\n```\n\n```\nclass Solution:\n def findSpecialInteger(self, arr: List[int]) -> int:\n a = 0\n count = 0\n n = len(arr)\n for i in arr:\n if i == a:\n count += 1\n else:\n a = i\n count = 1\n if count > n/4:\n return a\n```\n**If you like the solution, please upvote for this**
| 3
| 1
|
['Python3']
| 0
|
element-appearing-more-than-25-in-sorted-array
|
[C++] 4 Solutions
|
c-4-solutions-by-zxspring21-ubxv
|
C++:\n\n(1) Find the element at position n/4, n/2, n*3/4 and check lastOccurence-firstOccurence+1 > n/4\n\n\nint findSpecialInteger(vector<int>& arr) {\n\tint n
|
zxspring21
|
NORMAL
|
2020-09-03T01:27:49.733884+00:00
|
2020-09-03T01:29:13.493749+00:00
| 462
| false
|
**C++:**\n\n**(1) Find the element at position n/4, n/2, n*3/4 and check lastOccurence-firstOccurence+1 > n/4**\n\n```\nint findSpecialInteger(vector<int>& arr) {\n\tint n = arr.size();\n\tfor(auto &i:{n/4,n/2,n*3/4}){\n\t auto p = equal_range(arr.begin(),arr.end(),arr[i]); //return [first,last) with values equivalent to val\n\t if(p.second - p.first > n/4) return arr[i];\n\t}\n\treturn 0;\n} \n```\n**(2)**\n```\n int findSpecialInteger(vector<int>& arr) {\n int n = arr.size();\n for(auto &i:{n/4,n/2,n*3/4}){\n auto found = find(arr.begin(), arr.end(), arr[i]);\n if(*(found+n/4) == arr[i]) return arr[i];\n }\n return 0;\n } \n};\n```\n**(3) Just check arr[i] == arr[i + arr.length / 4]**\n```\nint findSpecialInteger(vector<int>& arr) {\n\tint n = arr.size();\n\tfor(int i=0;i<n*3/4;i++)\n\t if(arr[i]==arr[i+n/4]) return arr[i];\n\treturn arr[0];\n} \n```\n**(4) Map**\n```\nint findSpecialInteger(vector<int>& arr) {\n\tunordered_map<int,int> um;\n\tpair<int,int> maximum{0,0};\n\tfor(auto &i:arr) um[i]++;\n\tfor(auto &[key,value]:um)\n\t if(value>maximum.second) maximum = make_pair(key,value);\n\treturn maximum.first;\n} \n```
| 3
| 1
|
['C']
| 0
|
element-appearing-more-than-25-in-sorted-array
|
beats 100% java solution
|
beats-100-java-solution-by-yyyfor-gyez
|
\nclass Solution {\n public int findSpecialInteger(int[] arr) {\n for(int i = 0 ; i < arr.length; i++) {\n if(arr[i] == arr[i + arr.length/
|
yyyfor
|
NORMAL
|
2020-05-13T07:50:02.348884+00:00
|
2020-05-13T07:50:02.348935+00:00
| 155
| false
|
```\nclass Solution {\n public int findSpecialInteger(int[] arr) {\n for(int i = 0 ; i < arr.length; i++) {\n if(arr[i] == arr[i + arr.length/4]) {\n return arr[i];\n }\n }\n \n return 0;\n }\n}\n```
| 3
| 1
|
[]
| 1
|
element-appearing-more-than-25-in-sorted-array
|
javascript, sliding window, 90%/100%, w/ comments
|
javascript-sliding-window-90100-w-commen-0u16
|
\nfunction findSpecialInteger(arr) {\n // get \'window\' size which is just 25% of array to int\n const w = Math.ceil(arr.length * 0.25);\n // just ite
|
carti
|
NORMAL
|
2020-04-20T23:30:42.013996+00:00
|
2020-04-20T23:30:42.014046+00:00
| 205
| false
|
```\nfunction findSpecialInteger(arr) {\n // get \'window\' size which is just 25% of array to int\n const w = Math.ceil(arr.length * 0.25);\n // just iterate thru array until window reaches end\n for (let i = 0; i + w < arr.length; i++) {\n // if number at beginning and end of window are same,\n // this is the special number\n if (arr[i] === arr[i + w])\n return arr[i];\n }\n // never found one\n return -1;\n}\n```\n
| 3
| 1
|
['Sliding Window', 'JavaScript']
| 2
|
element-appearing-more-than-25-in-sorted-array
|
Python, one liner using collections.Counter
|
python-one-liner-using-collectionscounte-7pje
|
\nfrom collections import Counter\nclass Solution:\n def findSpecialInteger(self, arr):\n return Counter(arr).most_common(1)[0][0]\n
|
bison_a_besoncon
|
NORMAL
|
2019-12-14T16:16:58.513937+00:00
|
2019-12-14T16:16:58.513969+00:00
| 489
| false
|
```\nfrom collections import Counter\nclass Solution:\n def findSpecialInteger(self, arr):\n return Counter(arr).most_common(1)[0][0]\n```
| 3
| 2
|
[]
| 4
|
element-appearing-more-than-25-in-sorted-array
|
Time - log(n) & Constant Space Solution
|
time-logn-constant-space-solution-by-pop-ssfv
|
Just check 3 elements\nat 25th, 50th & 75 th\n\n```\n\nclass Solution {\n public int findSpecialInteger(int[] arr) {\n int e = arr.length < 4 ? 1 : ar
|
popeye_the_sailort
|
NORMAL
|
2019-12-14T16:01:56.460033+00:00
|
2019-12-14T16:04:38.125732+00:00
| 381
| false
|
Just check 3 elements\nat 25th, 50th & 75 th\n\n```\n\nclass Solution {\n public int findSpecialInteger(int[] arr) {\n int e = arr.length < 4 ? 1 : arr.length/4;\n int pos = e;\n for(int i=0; i<3; pos+=e) {\n int val = arr[pos-1];\n if(findCount(arr, val) > arr.length/4) {\n return val;\n }\n }\n return -1;\n }\n \n \n private int findCount(int[] arr, int val) {\n return findRightIndex(arr, val) - findLeftIndex(arr, val) + 1;\n }\n \n private int findLeftIndex(int[] arr, int val) {\n int left = 0;\n int right = arr.length-1;\n while(left < right) {\n int mid = left + ((right-left)>>1);\n if(arr[mid] < val) {\n left = mid + 1;\n } else {\n right = mid;\n }\n } \n return left;\n }\n \n private int findRightIndex(int[] arr, int val) {\n int left = 0;\n int right = arr.length-1;\n while(left < right) {\n int mid = left + ((right-left)>>1)+1;\n if(val < arr[mid]) {\n right = mid-1;\n } else {\n left = mid;\n }\n } \n return left;\n }\n \n}
| 3
| 0
|
[]
| 0
|
element-appearing-more-than-25-in-sorted-array
|
Very Simple Solution in Java, CPP and Python, easy to visualize - O(n) time & O(1) space.
|
very-simple-solution-in-java-cpp-and-pyt-ga68
| null |
v-athithyaramaa
|
NORMAL
|
2024-12-10T11:57:13.394936+00:00
|
2024-12-10T11:57:13.394936+00:00
| 78
| false
|
# Intuition\nAccording to the problem, you\'re given a list of numbers that\u2019s **already sorted** in order. We have to find the number that shows up **more than 25% of the time.** In other words, you\'re looking for the number that is repeated more than any other number \u2014 at least one in every four numbers in the list!\n\n# Approach\nSince we\'re given that the element should appear **more than 25% of the times**, it means that that particular element should appear **atleast** 1 / 4 times the length of the array (which is nothing but 25%)!! If you decode this logic, boom! You\'re done with the solution!\n\n# Complexity\n- Time complexity:\nTime complexity is O(n), where n is the size of the array. This is evident of the fact that we\'re just running the **for loop** throughout the length of the array.\n\n- Space complexity:\nSpace complexity is O(1). We\'re not using up any extra space as you can see. \n\nBelow, I have attached the solution for the same we discussed above.\nI would like to ask you to try it out on your own, which you can easily do after reading my solution. \n\nPlease consider upvoting my solution if you find it helpful!\n\nThank you :)\n\n\n# Code\n```java []\nclass Solution {\n public int findSpecialInteger(int[] arr) {\n int size = (arr.length) / 4;\n\n for(int i = 0; i < arr.length; i++){\n if(arr[i] == arr[i + size]){\n return arr[i];\n }\n }\n return -1;\n }\n}\n```\n\n```Python []\nclass Solution:\n def findSpecialInteger(self, arr):\n size = len(arr) // 4\n\n for i in range(len(arr)):\n if arr[i] == arr[i + size]:\n return arr[i]\n \n return -1\n```\n\n```C++ []\nclass Solution {\npublic:\n int findSpecialInteger(vector<int>& arr) {\n int size = arr.size() / 4;\n\n for (int i = 0; i < arr.size(); i++) {\n if (arr[i] == arr[i + size]) {\n return arr[i];\n }\n }\n\n return -1;\n }\n};\n\n```
| 2
| 0
|
['Array', 'C++', 'Java', 'Python3']
| 0
|
element-appearing-more-than-25-in-sorted-array
|
Best and Easy Approach...... || Beginners friendly...🔥🔥🔥
|
best-and-easy-approach-beginners-friendl-3mjs
|
Approach\n Describe your approach to solving the problem. \n1. Initialize an empty dictionary \'arr2\' to store the count of occurrences for each unique element
|
Awanish_singh001
|
NORMAL
|
2023-12-13T20:03:45.492843+00:00
|
2023-12-13T20:03:45.492869+00:00
| 422
| false
|
# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Initialize an empty dictionary \'arr2\' to store the count of occurrences for each unique element in the input array.\n2. Iterate through each element i in the input array arr.\n3. If i is already a key in \'arr2\', increment its count.\n4. If i is not a key in \'arr2\', add it to the dictionary with a count of 1.\n5. Retrieve the keys and values from the dictionary using list(arr2.keys()) and list(arr2.values()), respectively.\n6. Find the maximum count (maxval) from the values.\n7. Find the index of the maximum count in the values list (index = Val.index(maxval)).\n8. Return the element at the corresponding index in the keys list (keyVal[index]).\nNote: The code is essentially finding the element with the highest count in the array\n\n# Complexity\n- Time complexity:- O(N) -> where N is the number of elements in the array. \n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N) -> the number of unique elements in the input array.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findSpecialInteger(self, arr: List[int]) -> int:\n arr2 = {}\n count = 0\n for i in arr:\n if i in arr2:\n arr2[i] += 1\n else:\n arr2[i] = 1\n keyVal = list(arr2.keys())\n Val = list(arr2.values())\n maxval = max(Val)\n index = Val.index(maxval)\n return keyVal[index]\n \n \n```
| 2
| 0
|
['Array', 'Python', 'Python3']
| 2
|
element-appearing-more-than-25-in-sorted-array
|
Solution in C++
|
solution-in-c-by-adamblack-y9sz
|
One of the best solution for this problem!\n\n# Complexity\n- Time complexity: O(n)\n- \n# Code\n\nclass Solution {\npublic:\n int findSpecialInteger(vector<
|
AdamBlack
|
NORMAL
|
2023-12-11T20:01:24.983877+00:00
|
2023-12-11T20:01:24.983907+00:00
| 17
| false
|
One of the best solution for this problem!\n\n# Complexity\n- Time complexity: O(n)\n- \n# Code\n```\nclass Solution {\npublic:\n int findSpecialInteger(vector<int>& arr) {\n int x = 0, mx = 0, res = 0;\n int l = arr.size(); // Use size() instead of length() for vectors\n if(l<=2){\n return arr[0];\n }\n for (int i = 0; i < l - 1; i++) { // Update loop condition to l - 1\n if (arr[i] == arr[i + 1]) {\n x += 1;\n } else {\n if (mx < x) {\n mx = x;\n res = arr[i];\n }\n x = 1; // Update x to 1 for the new element\n }\n }\n\n if (mx < x) {\n res = arr[l - 1];\n }\n\n return res;\n }\n};\n```
| 2
| 0
|
['C++']
| 0
|
element-appearing-more-than-25-in-sorted-array
|
Percentage of 25 with value n
|
percentage-of-25-with-value-n-by-nithinu-1xc4
|
Approach\n Finding Percentage value with the length of the arraylist and \n find frequency of every element further return the value when\n it across t
|
nithinu2810
|
NORMAL
|
2023-12-11T18:21:55.820019+00:00
|
2023-12-11T18:21:55.820046+00:00
| 3
| false
|
# Approach\n Finding Percentage value with the length of the arraylist and \n find frequency of every element further return the value when\n it across the limit.\n\n# Complexity\n- Time complexity: 1ms\n\n- Space complexity: 44.42mb\n\n# Code\n```\nclass Solution {\n public int findSpecialInteger(int[] arr) {\n int n=arr.length,lm=(int)(((25*1.0)/(100*1.0))*n);\n int[] a=new int[100001];\n for(int i=0;i<n;i++){\n a[arr[i]]++;\n if(a[arr[i]]>lm)\n return arr[i];\n }\n return 0;\n }\n}\n```
| 2
| 0
|
['Array', 'Math', 'Java']
| 0
|
element-appearing-more-than-25-in-sorted-array
|
C# Code with o(N) complexity and o(1) space
|
c-code-with-on-complexity-and-o1-space-b-yv01
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
sivapandu
|
NORMAL
|
2023-12-11T16:06:51.906656+00:00
|
2023-12-11T16:06:51.906694+00:00
| 52
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\npublic class Solution {\n // Function to find the element occurring more than 25% of the time in a sorted array\n public int FindSpecialInteger(int[] arr) {\n // Calculate the window size, ensuring it covers at least one occurrence of the target element\n int windowSize = arr.Length / 4;\n\n // Iterate through the array with a sliding window\n for (int i = 0; i < arr.Length - windowSize; i++) {\n // Check if the current element is the one we are looking for\n if (arr[i] == arr[i + windowSize]) {\n // If yes, return the found element\n return arr[i];\n }\n }\n\n // If no result is found in the loop, the last element is the answer\n return arr[arr.Length - 1];\n }\n}\n\n```
| 2
| 0
|
['C#']
| 1
|
element-appearing-more-than-25-in-sorted-array
|
Simple JS Implementation
|
simple-js-implementation-by-itspravas-ior9
|
Approach: Check the Element N/4 Ahead\n\n/**\n * @param {number[]} arr\n * @return {number}\n */\nvar findSpecialInteger = function (arr) {\n const n = arr.l
|
itspravas
|
NORMAL
|
2023-12-11T16:05:49.028869+00:00
|
2023-12-11T16:05:49.028898+00:00
| 24
| false
|
# Approach: Check the Element N/4 Ahead\n```\n/**\n * @param {number[]} arr\n * @return {number}\n */\nvar findSpecialInteger = function (arr) {\n const n = arr.length, maxCnt = Math.floor(n / 4);\n for (let i = 0; i < n - maxCnt; i++) {\n if (arr[i] === arr[i + maxCnt]) return arr[i];\n }\n return -1;\n};\n```
| 2
| 0
|
['JavaScript']
| 0
|
element-appearing-more-than-25-in-sorted-array
|
Easy Binary Search Solution Explained!!🚀 | Java
|
easy-binary-search-solution-explained-ja-jmd1
|
\n\n# Approach\n Describe your approach to solving the problem. \n- Use Binary search to find the last index of the occurence of element present at index i. \n-
|
rosh_01
|
NORMAL
|
2023-12-11T13:35:17.748628+00:00
|
2023-12-11T13:35:17.748678+00:00
| 146
| false
|
\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- Use Binary search to find the last index of the occurence of element present at index i. \n- Then find the frequency/count of the element by using the formula:\n` last index - first index + 1`\nIn out case, first index will be i and last index will be given by the binary search algorithm.\n- If frequency of any element if greater than n/4 (n = size of array) where n/4 is the fractional representation of 25% of the size of array, then return that element.\n\n# Complexity\n- Time complexity: $$O(log n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int findSpecialInteger(int[] arr) {\n int ans = -1;\n int n = arr.length;\n if(n <= 2) return arr[0];\n\n int i = 0;\n\n while(i<n){\n int lastIdx = search(i, arr[i], arr, n-1);\n int count = lastIdx - i + 1;\n if(count > n/4){\n ans = arr[i];\n break;\n }\n i = lastIdx+1;\n }\n return ans;\n }\n\n private int search(int low, int target, int[] arr, int high){\n int res = -1;\n while(low<=high){\n int mid = (low+high)/2;\n if(arr[mid]<=target){\n res = mid;\n low = mid+1;\n }else{\n high = mid-1;\n }\n }\n return res;\n }\n}\n```
| 2
| 0
|
['Binary Search', 'Java']
| 1
|
element-appearing-more-than-25-in-sorted-array
|
beats 100% || JAVA || Brute force --> Best Approach || clean code with explanation
|
beats-100-java-brute-force-best-approach-yhqh
|
Approach - 1 : Bruteforce Approach O(n^2)\n1. Iterate through the array and for each element, count its occurrences by traversing the array again.\n\n2. Keep tr
|
Nikhil_Pall
|
NORMAL
|
2023-12-11T12:55:16.282510+00:00
|
2023-12-11T12:55:16.282539+00:00
| 43
| false
|
# Approach - 1 : Bruteforce Approach O(n^2)\n1. Iterate through the array and for each element, count its occurrences by traversing the array again.\n\n2. Keep track of the element with the highest count and return it as the answer.\n\n# Complexity\n- Time complexity: O(n^2)\n\n- Space complexity: O(1)\n\n# Code\n```\nclass Solution {\n public int findSpecialInteger(int[] arr) {\n int ans = 0;\n int ans_count = 0;\n int l = arr.length;\n for(int i=0; i<l; i++){\n int count = 1;\n for(int j=i+1; j<l; j++){\n if(arr[i] == arr[j]){\n count++;\n }\n }\n if(count > ans_count){\n ans = arr[i];\n ans_count = count;\n }\n }\n\n return ans;\n }\n}\n```\n-------------------------\n\n# Approach - 2 : Binary Search O(n*lon(n))-[beats 100%]\n1. We\'re searching for a number that occurs more than 25% of the time in the given array.\n\n2. We us binary search technique to efficiently locate the last occurrence of each number in the array.\n\n3. For each element, it performs a binary search to find its last occurrence index.\n\n4. Then, it compares the count of occurrences of that element to a quarter of the array\'s length.\n\n5. If the count exceeds this expected count, it return that number.\n\n# Complexity\n- Time complexity: O(n log(n))\n\n- Space complexity: O(1)\n\n# Code\n```\nclass Solution {\n public int findSpecialInteger(int[] arr) {\n int l = arr.length;\n if(l==1){\n return arr[0];\n }\n int exp_count = l/4;\n\n for(int i=0; i<l-1; i++){\n int ei = binarySearch(arr[i], i+1, l-1, arr);\n if(ei - i + 1 > exp_count){\n return arr[i];\n }\n }\n\n return -1;\n }\n\n public int binarySearch(int num, int si, int ei, int[] arr){\n while(si <= ei){\n int mid = si + (ei-si)/2;\n\n if(arr[mid] == num){\n while(mid < arr.length-1 && arr[mid]==arr[mid+1]){\n mid++;\n }\n return mid;\n }\n\n if(arr[mid] < num){\n si = mid + 1;\n }\n\n if(arr[mid] > num){\n ei = mid - 1;\n }\n }\n\n return -1;\n }\n}\n```\n---------------------------------------------\n\n# Approach - 3 : Best Approach O(n)-[beats 100%]\n1. We\'re looking for a number that appears more than a quarter of the time in the given array.\n\n2. To find it efficiently, we calculate the expected count of this special number as one-fourth of the array\'s length.\n\n3. We then scan through the array and check if there\'s a sequence of that expected count length where the elements are the same.\n\n4. If such a sequence exists, it means that this number occurs more than 25% of the time in the array.\n\n5. We return that number; otherwise, we conclude that there\'s no such number and return -1. \n\n**This process ensures a linear search through the array to find our target number efficiently.**\n\n# Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(1)\n\n# Code\n```\nclass Solution {\n public int findSpecialInteger(int[] arr) {\n int l = arr.length;\n int exp_count = l/4;\n\n for(int i=0; i<l; i++){\n int next_index = i+exp_count;\n if(next_index<l && arr[i]==arr[next_index]){\n return arr[i];\n }\n }\n\n return -1;\n }\n}\n```\n
| 2
| 0
|
['Array', 'Java']
| 1
|
element-appearing-more-than-25-in-sorted-array
|
check the element n/4 steps back | Easy to understand | Java | C++
|
check-the-element-n4-steps-back-easy-to-db876
|
Intuition and Approach\nSince the array is in sorted oder. We can leverage this fact and check what was the number or say element n/4 steps back from current in
|
Fly_ing__Rhi_no
|
NORMAL
|
2023-12-11T10:22:23.991146+00:00
|
2023-12-11T10:22:23.991200+00:00
| 585
| false
|
# Intuition and Approach\nSince the array is in sorted oder. We can leverage this fact and check what was the number or say element n/4 steps back from current index while traversing the array form left to right \n\n# Complexity\n- Time complexity:\nO(n), n is size of given arr\n\n- Space complexity:\nO(1)\n\n# Code\nC++\n```\nclass Solution {\npublic:\n int findSpecialInteger(vector<int>& arr) {\n int sz = arr.size(), freq = sz / 4;\n for(int indx = 0; indx < sz; indx++){\n if(indx - freq > -1 && arr[indx - freq] == arr[indx]){\n return arr[indx];\n }\n }\n return -1;\n }\n};\n```\nJava\n```\nclass Solution {\n public int findSpecialInteger(int[] arr) {\n int sz = arr.length, freq = sz / 4;\n for(int indx = 0; indx < sz; indx++){\n if(indx - freq > -1 && arr[indx - freq] == arr[indx]){\n return arr[indx];\n }\n }\n return -1;\n }\n}\n```
| 2
| 0
|
['C++', 'Java']
| 1
|
element-appearing-more-than-25-in-sorted-array
|
Space Complexity O(1)
|
space-complexity-o1-by-pra__kash-yhe9
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
pra__kash
|
NORMAL
|
2023-12-11T09:01:38.091430+00:00
|
2023-12-11T09:01:38.091458+00:00
| 4
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int findSpecialInteger(vector<int>& arr) {\n int frequency = arr.size() * 0.25;\n int incre = 1;\n for(int i = 1 ; i < arr.size() ; i++){\n if(arr[i-1] == arr[i]){\n incre++;\n }\n else{\n if(incre > frequency) return arr[i-1];\n else incre = 1;\n }\n }\n return arr[arr.size()-1];\n }\n};\n\n\n```
| 2
| 0
|
['Array', 'C++']
| 0
|
element-appearing-more-than-25-in-sorted-array
|
Python | Easy
|
python-easy-by-khosiyat-gx3x
|
see the Successfully Accepted Submission\npython\nclass Solution:\n def findSpecialInteger(self, arr: List[int]) -> int:\n frequency_threshold = int(
|
Khosiyat
|
NORMAL
|
2023-12-11T08:54:31.887374+00:00
|
2023-12-11T08:54:31.887402+00:00
| 33
| false
|
[see the Successfully Accepted Submission](https://leetcode.com/submissions/detail/1117078947/)\n```python\nclass Solution:\n def findSpecialInteger(self, arr: List[int]) -> int:\n frequency_threshold = int(len(arr) * 0.25)\n counter, index = 0, 0\n\n for i in range(len(arr)):\n if i == 0 or (i != 0 and arr[i] == arr[i - 1]):\n counter += 1\n else:\n counter = 1\n\n if counter > frequency_threshold:\n break\n\n return arr[I]\n```\n
| 2
| 0
|
['Python']
| 0
|
element-appearing-more-than-25-in-sorted-array
|
✅ Very simple recursive solution, follow best practices of Scala
|
very-simple-recursive-solution-follow-be-lmcr
|
Approach\nRecursive solution:\n\n+ No loop\n+ No vars declaration\n+ Functional style\n\n\n# Complexity\nTime complexity: O(n)\n\nSpace complexity: O(1)\n\n# Co
|
user6828v
|
NORMAL
|
2023-12-11T08:32:12.319912+00:00
|
2023-12-11T08:41:19.630605+00:00
| 44
| false
|
# Approach\n**Recursive solution:**\n\n+ No loop\n+ No vars declaration\n+ Functional style\n\n\n# Complexity\n**Time complexity:** O(n)\n\n**Space complexity:** O(1)\n\n# Code\n```\nobject Solution {\n def findSpecialInteger(arr: Array[Int]): Int = {\n val dist = (arr.length * 0.25).toInt\n def findFrom(i: Int): Int = {\n if (arr(i) == arr(i + dist)) arr(i) else findFrom(i + 1)\n }\n\n findFrom(0)\n }\n}\n```
| 2
| 0
|
['Recursion', 'Scala']
| 0
|
element-appearing-more-than-25-in-sorted-array
|
JAVA solution explanation in HINDI
|
java-solution-explanation-in-hindi-by-th-oao8
|
https://youtu.be/53yxKXB-tB8\n\nFor explanation watch the above video and do like, share and subscribe \u2764\uFE0F\n\n# Code\n\nclass Solution {\n public in
|
The_elite
|
NORMAL
|
2023-12-11T07:27:03.430022+00:00
|
2023-12-11T07:27:03.430053+00:00
| 9
| false
|
https://youtu.be/53yxKXB-tB8\n\nFor explanation watch the above video and do like, share and subscribe \u2764\uFE0F\n\n# Code\n```\nclass Solution {\n public int findSpecialInteger(int[] arr) {\n \n Map<Integer, Integer> counts = new HashMap<>();\n for(int e : arr) {\n counts.put(e, counts.getOrDefault(e, 0) + 1);\n }\n\n int percent = arr.length / 4;\n for(int ele : counts.keySet()) {\n if(counts.get(ele) > percent) {\n return ele;\n }\n }\n return -1;\n }\n}\n```
| 2
| 0
|
['Java']
| 0
|
element-appearing-more-than-25-in-sorted-array
|
Simple Solution ✅ + 100%
|
simple-solution-100-by-probablylost-kg89
|
Code\n\nclass Solution {\n func findSpecialInteger(_ arr: [Int]) -> Int {\n let quarter = arr.count / 4\n var candidate: Int?\n var coun
|
ProbablyLost
|
NORMAL
|
2023-12-11T06:59:07.988917+00:00
|
2023-12-11T06:59:07.988936+00:00
| 16
| false
|
# Code\n```\nclass Solution {\n func findSpecialInteger(_ arr: [Int]) -> Int {\n let quarter = arr.count / 4\n var candidate: Int?\n var count = 0\n \n for (index, num) in arr.enumerated() {\n if num == candidate {\n count += 1\n } else {\n candidate = num\n count = 1\n }\n \n if count > quarter {\n return num\n }\n }\n \n return -1\n }\n}\n\n```
| 2
| 0
|
['Swift']
| 0
|
element-appearing-more-than-25-in-sorted-array
|
C++ | Simple Code | Beat 80%
|
c-simple-code-beat-80-by-ankita2905-d0s3
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
Ankita2905
|
NORMAL
|
2023-12-11T06:50:17.888691+00:00
|
2023-12-11T06:50:17.888721+00:00
| 4
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public:\n int findSpecialInteger(vector<int>& nums) {\n int n = nums.size();\n if(n==1)return 1;\n int ans ;\n int quarter = n/4;\n for(int i = 0 ;i < n - quarter;i++)\n {\n if(nums[i] == nums[i+quarter])\n {\n ans = nums[i];\n }\n } \n return ans;\n }\n };\n\n\n\n \n\n\n```
| 2
| 0
|
['C++']
| 0
|
element-appearing-more-than-25-in-sorted-array
|
2 Approaches Using HashMap and Counter variable || Beats 100% ||JAVA||C++|| Jai Shree Ram🙏🙏
|
2-approaches-using-hashmap-and-counter-v-38bt
|
\n# Approach 1\n Describe your approach to solving the problem. \n - Using HashMap\n\n# Complexity\n- Time complexity: O(N)\n Add your time complexity here, e.
|
vermayugam_29
|
NORMAL
|
2023-12-11T06:25:05.774318+00:00
|
2023-12-11T06:25:05.774343+00:00
| 357
| false
|
\n# Approach 1\n<!-- Describe your approach to solving the problem. -->\n - Using HashMap\n\n# Complexity\n- Time complexity: $$O(N)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n\n- Space complexity: $$O(N)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n# Code\n```JAVA []\nclass Solution {\n public int findSpecialInteger(int[] arr) {\n int a= arr.length/4;\n Map<Integer,Integer> map = new HashMap<>();\n for(int i=0;i<arr.length;i++){\n map.put(arr[i],map.getOrDefault(arr[i],0)+1);\n if(map.get(arr[i]) > a){\n return arr[i];\n }\n }\n return -1;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int findSpecialInteger(vector<int>& arr) {\n int a = arr.size() / 4;\n unordered_map<int, int> map;\n\n for (int i = 0; i < arr.size(); ++i) {\n map[arr[i]] = map[arr[i]] + 1;\n if (map[arr[i]] > a) {\n return arr[i];\n }\n }\n\n return -1;\n }\n};\n\n```\n\n# Approach 2\n<!-- Describe your approach to solving the problem. -->\n - USing counter variable\n\n# Complexity\n- Time complexity: $$O(N)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n# Code\n```JAVA []\nclass Solution {\n public int findSpecialInteger(int[] arr) {\n int a= (arr.length)/4+1;\n int count = 1;\n for(int i=1;i<arr.length;i++){\n if(arr[i-1] == arr[i]){\n count++;\n }\n else{\n count = 1;\n }\n if(count >= a){\n return arr[i];\n }\n }\n return arr[0];\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int findSpecialInteger(vector<int>& arr) {\n int a = (arr.size()) / 4 + 1;\n int count = 1;\n\n for (int i = 1; i < arr.size(); ++i) {\n if (arr[i - 1] == arr[i]) {\n count++;\n } else {\n count = 1;\n }\n\n if (count >= a) {\n return arr[i];\n }\n }\n\n return arr[0];\n }\n};\n\n```\n
| 2
| 0
|
['Array', 'Hash Table', 'Counting', 'C++', 'Java']
| 0
|
element-appearing-more-than-25-in-sorted-array
|
Solution using C++
|
solution-using-c-by-truongtamthanh2004-ndfg
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
truongtamthanh2004
|
NORMAL
|
2023-12-11T06:07:01.126304+00:00
|
2023-12-11T06:07:01.126330+00:00
| 111
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int findSpecialInteger(vector<int>& arr) {\n int n = arr.size();\n int count = 1;\n int p = arr[0];\n int rate = n / 4;\n for (int i = 1; i < n; i++)\n {\n if (arr[i] == p) count++;\n else count = 1;\n\n if (count > rate) return p;\n p = arr[i];\n }\n return count;\n }\n};\n```
| 2
| 0
|
['C++']
| 1
|
element-appearing-more-than-25-in-sorted-array
|
Easiest C++ Approach [Fastest] | Beats 100 %
|
easiest-c-approach-fastest-beats-100-by-5h00h
|
Intuition\nThe main approach of this code is to find and return an integer in the given array (arr) that occurs more than 25% of the array\'s length.\n\n# Appro
|
clickdawg
|
NORMAL
|
2023-12-11T04:17:09.580751+00:00
|
2023-12-11T04:17:09.580779+00:00
| 115
| false
|
# Intuition\nThe main approach of this code is to find and return an integer in the given array (arr) that occurs more than 25% of the array\'s length.\n\n# Approach\n### Initialize Variables:\n- int n = arr.size() / 4;: Calculate a threshold value n representing 25% of the array length.\n### Create a Map (mp):\n- map<int, int> mp;: Create a map (mp) to store the frequency of each unique element in the array.\n### Count Element Frequencies:\n- Loop through the elements of the array and update the frequency count in the map.\n### Find Special Integer:\n\n- Loop through the elements in the map and check if any element has a frequency greater than the threshold (n).\n### Return -1 if No Special Integer Found:\n\n- If no element is found with a frequency greater than the threshold, return -1.\n# Complexity\n- Time complexity:\n$$O(n)$$\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```\nclass Solution {\npublic:\n int findSpecialInteger(vector<int>& arr) {\n int n=arr.size()/4;\n map<int, int> mp;\n for(int i=0; i<arr.size(); i++){\n mp[arr[i]]++;\n\n }\n for(auto it: mp){\n if(it.second>n)\n return it.first;\n }\n return -1;\n }\n};\n```
| 2
| 0
|
['Array', 'Ordered Map', 'C++']
| 0
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.