Spaces:
Runtime error
Runtime error
Upload 54 files
Browse filesThis view is limited to 50 files because it contains too many changes.
See raw diff
- .gitattributes +19 -0
- .idea/.gitignore +0 -0
- .idea/ClassificationPeripheralBloodCell-main.iml +8 -0
- .idea/inspectionProfiles/profiles_settings.xml +6 -0
- .idea/modules.xml +8 -0
- .idea/workspace.xml +41 -0
- Code/XAI_TL_gradcam.ipynb +0 -0
- Code/image_classification_CNN.ipynb +342 -0
- Code/image_classification_VGG19.ipynb +0 -0
- Code/split_folders.ipynb +37 -0
- Code/test_model_CNN.ipynb +292 -0
- Code/test_model_VGG19.ipynb +265 -0
- README.md +8 -11
- about_pj.py +89 -0
- about_us.py +99 -0
- explicability.py +104 -0
- imagen_subida.py +215 -0
- images/13435.jpg +3 -0
- images/18994.jpg +0 -0
- images/Flag_of_the_United_Kingdom.png +0 -0
- images/United-Kingdom-Flag.png +0 -0
- images/abstract-soft-pink-watercolor-background.zip +3 -0
- images/abstract-soft-pink-watercolor-background/18994.eps +3 -0
- images/abstract-soft-pink-watercolor-background/License free.txt +45 -0
- images/abstract-soft-pink-watercolor-background/License premium.txt +30 -0
- images/blood-donor-icons-flat/13435.eps +0 -0
- images/blood-donor-icons-flat/License free.txt +45 -0
- images/blood-donor-icons-flat/License premium.txt +30 -0
- images/confusion_matrix.png +0 -0
- images/dark-brown-colour-flower-pattern-background-abstract-banner-multipurpose-design.jpg +3 -0
- images/espa/303/261ita.png +0 -0
- images/flag-of-spain.png +0 -0
- images/red-black-brush-stroke-banner-background-perfect-canva.jpg +3 -0
- images/spain_flag.png +0 -0
- images/tensor.png +0 -0
- images/united_kingdom_flag.png +0 -0
- images/vgg19.png +0 -0
- main.py +104 -0
- main_page.py +52 -0
- model_subir/vgg19_trainable_true_best_model_pruebita.7z.001 +3 -0
- model_subir/vgg19_trainable_true_best_model_pruebita.7z.002 +3 -0
- model_subir/vgg19_trainable_true_best_model_pruebita.7z.003 +3 -0
- model_subir/vgg19_trainable_true_best_model_pruebita.7z.004 +3 -0
- model_subir/vgg19_trainable_true_best_model_pruebita.7z.005 +3 -0
- model_subir/vgg19_trainable_true_best_model_pruebita.7z.006 +3 -0
- model_subir/vgg19_trainable_true_best_model_pruebita.7z.007 +3 -0
- model_subir/vgg19_trainable_true_best_model_pruebita.7z.008 +3 -0
- model_subir/vgg19_trainable_true_best_model_pruebita.7z.009 +3 -0
- model_subir/vgg19_trainable_true_best_model_pruebita.7z.010 +3 -0
- model_subir/vgg19_trainable_true_best_model_pruebita.7z.011 +3 -0
.gitattributes
CHANGED
|
@@ -32,3 +32,22 @@ saved_model/**/* filter=lfs diff=lfs merge=lfs -text
|
|
| 32 |
*.zip filter=lfs diff=lfs merge=lfs -text
|
| 33 |
*.zst filter=lfs diff=lfs merge=lfs -text
|
| 34 |
*tfevents* filter=lfs diff=lfs merge=lfs -text
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 32 |
*.zip filter=lfs diff=lfs merge=lfs -text
|
| 33 |
*.zst filter=lfs diff=lfs merge=lfs -text
|
| 34 |
*tfevents* filter=lfs diff=lfs merge=lfs -text
|
| 35 |
+
images/13435.jpg filter=lfs diff=lfs merge=lfs -text
|
| 36 |
+
images/abstract-soft-pink-watercolor-background/18994.eps filter=lfs diff=lfs merge=lfs -text
|
| 37 |
+
images/dark-brown-colour-flower-pattern-background-abstract-banner-multipurpose-design.jpg filter=lfs diff=lfs merge=lfs -text
|
| 38 |
+
images/red-black-brush-stroke-banner-background-perfect-canva.jpg filter=lfs diff=lfs merge=lfs -text
|
| 39 |
+
model_subir/vgg19_trainable_true_best_model_pruebita.7z.001 filter=lfs diff=lfs merge=lfs -text
|
| 40 |
+
model_subir/vgg19_trainable_true_best_model_pruebita.7z.002 filter=lfs diff=lfs merge=lfs -text
|
| 41 |
+
model_subir/vgg19_trainable_true_best_model_pruebita.7z.003 filter=lfs diff=lfs merge=lfs -text
|
| 42 |
+
model_subir/vgg19_trainable_true_best_model_pruebita.7z.004 filter=lfs diff=lfs merge=lfs -text
|
| 43 |
+
model_subir/vgg19_trainable_true_best_model_pruebita.7z.005 filter=lfs diff=lfs merge=lfs -text
|
| 44 |
+
model_subir/vgg19_trainable_true_best_model_pruebita.7z.006 filter=lfs diff=lfs merge=lfs -text
|
| 45 |
+
model_subir/vgg19_trainable_true_best_model_pruebita.7z.007 filter=lfs diff=lfs merge=lfs -text
|
| 46 |
+
model_subir/vgg19_trainable_true_best_model_pruebita.7z.008 filter=lfs diff=lfs merge=lfs -text
|
| 47 |
+
model_subir/vgg19_trainable_true_best_model_pruebita.7z.009 filter=lfs diff=lfs merge=lfs -text
|
| 48 |
+
model_subir/vgg19_trainable_true_best_model_pruebita.7z.010 filter=lfs diff=lfs merge=lfs -text
|
| 49 |
+
model_subir/vgg19_trainable_true_best_model_pruebita.7z.011 filter=lfs diff=lfs merge=lfs -text
|
| 50 |
+
model_subir/vgg19_trainable_true_best_model_pruebita.7z.012 filter=lfs diff=lfs merge=lfs -text
|
| 51 |
+
model_subir/vgg19_trainable_true_best_model_pruebita.7z.013 filter=lfs diff=lfs merge=lfs -text
|
| 52 |
+
model_subir/vgg19_trainable_true_best_model_pruebita.7z.014 filter=lfs diff=lfs merge=lfs -text
|
| 53 |
+
model_subir/vgg19_trainable_true_best_model_pruebita.7z.015 filter=lfs diff=lfs merge=lfs -text
|
.idea/.gitignore
ADDED
|
File without changes
|
.idea/ClassificationPeripheralBloodCell-main.iml
ADDED
|
@@ -0,0 +1,8 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
<?xml version="1.0" encoding="UTF-8"?>
|
| 2 |
+
<module type="PYTHON_MODULE" version="4">
|
| 3 |
+
<component name="NewModuleRootManager">
|
| 4 |
+
<content url="file://$MODULE_DIR$" />
|
| 5 |
+
<orderEntry type="inheritedJdk" />
|
| 6 |
+
<orderEntry type="sourceFolder" forTests="false" />
|
| 7 |
+
</component>
|
| 8 |
+
</module>
|
.idea/inspectionProfiles/profiles_settings.xml
ADDED
|
@@ -0,0 +1,6 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
<component name="InspectionProjectProfileManager">
|
| 2 |
+
<settings>
|
| 3 |
+
<option name="USE_PROJECT_PROFILE" value="false" />
|
| 4 |
+
<version value="1.0" />
|
| 5 |
+
</settings>
|
| 6 |
+
</component>
|
.idea/modules.xml
ADDED
|
@@ -0,0 +1,8 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
<?xml version="1.0" encoding="UTF-8"?>
|
| 2 |
+
<project version="4">
|
| 3 |
+
<component name="ProjectModuleManager">
|
| 4 |
+
<modules>
|
| 5 |
+
<module fileurl="file://$PROJECT_DIR$/.idea/ClassificationPeripheralBloodCell-main.iml" filepath="$PROJECT_DIR$/.idea/ClassificationPeripheralBloodCell-main.iml" />
|
| 6 |
+
</modules>
|
| 7 |
+
</component>
|
| 8 |
+
</project>
|
.idea/workspace.xml
ADDED
|
@@ -0,0 +1,41 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
<?xml version="1.0" encoding="UTF-8"?>
|
| 2 |
+
<project version="4">
|
| 3 |
+
<component name="ChangeListManager">
|
| 4 |
+
<list default="true" id="e0b09bc9-1da1-4a0e-80e0-603efb66b26c" name="Changes" comment="" />
|
| 5 |
+
<option name="SHOW_DIALOG" value="false" />
|
| 6 |
+
<option name="HIGHLIGHT_CONFLICTS" value="true" />
|
| 7 |
+
<option name="HIGHLIGHT_NON_ACTIVE_CHANGELIST" value="false" />
|
| 8 |
+
<option name="LAST_RESOLUTION" value="IGNORE" />
|
| 9 |
+
</component>
|
| 10 |
+
<component name="MarkdownSettingsMigration">
|
| 11 |
+
<option name="stateVersion" value="1" />
|
| 12 |
+
</component>
|
| 13 |
+
<component name="ProjectId" id="2NMa3q1vb9grLy9EMWSuEZnq6Da" />
|
| 14 |
+
<component name="ProjectViewState">
|
| 15 |
+
<option name="hideEmptyMiddlePackages" value="true" />
|
| 16 |
+
<option name="showLibraryContents" value="true" />
|
| 17 |
+
</component>
|
| 18 |
+
<component name="PropertiesComponent"><![CDATA[{
|
| 19 |
+
"keyToString": {
|
| 20 |
+
"RunOnceActivity.OpenProjectViewOnStart": "true",
|
| 21 |
+
"RunOnceActivity.ShowReadmeOnStart": "true",
|
| 22 |
+
"WebServerToolWindowFactoryState": "false",
|
| 23 |
+
"vue.rearranger.settings.migration": "true"
|
| 24 |
+
}
|
| 25 |
+
}]]></component>
|
| 26 |
+
<component name="SpellCheckerSettings" RuntimeDictionaries="0" Folders="0" CustomDictionaries="0" DefaultDictionary="application-level" UseSingleDictionary="true" transferred="true" />
|
| 27 |
+
<component name="TaskManager">
|
| 28 |
+
<task active="true" id="Default" summary="Default task">
|
| 29 |
+
<changelist id="e0b09bc9-1da1-4a0e-80e0-603efb66b26c" name="Changes" comment="" />
|
| 30 |
+
<created>1679476209526</created>
|
| 31 |
+
<option name="number" value="Default" />
|
| 32 |
+
<option name="presentableId" value="Default" />
|
| 33 |
+
<updated>1679476209526</updated>
|
| 34 |
+
<workItem from="1679476211961" duration="35000" />
|
| 35 |
+
</task>
|
| 36 |
+
<servers />
|
| 37 |
+
</component>
|
| 38 |
+
<component name="TypeScriptGeneratedFilesManager">
|
| 39 |
+
<option name="version" value="3" />
|
| 40 |
+
</component>
|
| 41 |
+
</project>
|
Code/XAI_TL_gradcam.ipynb
ADDED
|
The diff for this file is too large to render.
See raw diff
|
|
|
Code/image_classification_CNN.ipynb
ADDED
|
@@ -0,0 +1,342 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{
|
| 2 |
+
"cells": [
|
| 3 |
+
{
|
| 4 |
+
"cell_type": "markdown",
|
| 5 |
+
"id": "f9755410",
|
| 6 |
+
"metadata": {},
|
| 7 |
+
"source": [
|
| 8 |
+
"## Notebook para realizar la parte 2 del TFM: clasificación de imágenes según tipo de célula sanguínea\n",
|
| 9 |
+
"\n",
|
| 10 |
+
"Se tiene de entrada el dataset ____ y de salida se espera tener el acc del modelo"
|
| 11 |
+
]
|
| 12 |
+
},
|
| 13 |
+
{
|
| 14 |
+
"cell_type": "code",
|
| 15 |
+
"execution_count": 10,
|
| 16 |
+
"id": "3356fb49",
|
| 17 |
+
"metadata": {},
|
| 18 |
+
"outputs": [],
|
| 19 |
+
"source": [
|
| 20 |
+
"from keras.preprocessing.image import ImageDataGenerator\n",
|
| 21 |
+
"from keras.models import Sequential\n",
|
| 22 |
+
"from keras.layers import Conv2D, MaxPooling2D\n",
|
| 23 |
+
"from keras.layers import Activation, Dropout, Flatten, Dense\n",
|
| 24 |
+
"from keras import backend as K\n",
|
| 25 |
+
"import matplotlib.pyplot as plt\n",
|
| 26 |
+
" \n",
|
| 27 |
+
"img_width, img_height = 360, 363"
|
| 28 |
+
]
|
| 29 |
+
},
|
| 30 |
+
{
|
| 31 |
+
"cell_type": "code",
|
| 32 |
+
"execution_count": 2,
|
| 33 |
+
"id": "2fbd9e15",
|
| 34 |
+
"metadata": {},
|
| 35 |
+
"outputs": [],
|
| 36 |
+
"source": [
|
| 37 |
+
"train_data_dir = '../../dataset/classification/PCB_Dataset_Split/train'\n",
|
| 38 |
+
"validation_data_dir = '../../dataset/classification/PCB_Dataset_Split/val'\n",
|
| 39 |
+
"\n",
|
| 40 |
+
"nb_train_samples = 13671 \n",
|
| 41 |
+
"nb_validation_samples = 1705 \n",
|
| 42 |
+
"\n",
|
| 43 |
+
"epochs = 10\n",
|
| 44 |
+
"batch_size = 16"
|
| 45 |
+
]
|
| 46 |
+
},
|
| 47 |
+
{
|
| 48 |
+
"cell_type": "code",
|
| 49 |
+
"execution_count": 3,
|
| 50 |
+
"id": "51cdcdda",
|
| 51 |
+
"metadata": {},
|
| 52 |
+
"outputs": [],
|
| 53 |
+
"source": [
|
| 54 |
+
"if K.image_data_format() == 'channels_first':\n",
|
| 55 |
+
" input_shape = (3, img_width, img_height)\n",
|
| 56 |
+
"else:\n",
|
| 57 |
+
" input_shape = (img_width, img_height, 3)"
|
| 58 |
+
]
|
| 59 |
+
},
|
| 60 |
+
{
|
| 61 |
+
"cell_type": "code",
|
| 62 |
+
"execution_count": 4,
|
| 63 |
+
"id": "16f72477",
|
| 64 |
+
"metadata": {},
|
| 65 |
+
"outputs": [
|
| 66 |
+
{
|
| 67 |
+
"name": "stdout",
|
| 68 |
+
"output_type": "stream",
|
| 69 |
+
"text": [
|
| 70 |
+
"Found 13671 images belonging to 8 classes.\n",
|
| 71 |
+
"Found 1705 images belonging to 8 classes.\n"
|
| 72 |
+
]
|
| 73 |
+
}
|
| 74 |
+
],
|
| 75 |
+
"source": [
|
| 76 |
+
"train_datagen = ImageDataGenerator(\n",
|
| 77 |
+
" rescale = 1. / 255,\n",
|
| 78 |
+
" shear_range = 0.2,\n",
|
| 79 |
+
" zoom_range = 0.2,\n",
|
| 80 |
+
" horizontal_flip = True)\n",
|
| 81 |
+
" \n",
|
| 82 |
+
"val_datagen = ImageDataGenerator(rescale = 1. / 255)\n",
|
| 83 |
+
" \n",
|
| 84 |
+
"train_generator = train_datagen.flow_from_directory(\n",
|
| 85 |
+
" train_data_dir,\n",
|
| 86 |
+
" target_size = (img_width, img_height),\n",
|
| 87 |
+
" batch_size = batch_size,\n",
|
| 88 |
+
" class_mode = 'categorical')\n",
|
| 89 |
+
" \n",
|
| 90 |
+
"validation_generator = val_datagen.flow_from_directory(\n",
|
| 91 |
+
" validation_data_dir,\n",
|
| 92 |
+
" target_size = (img_width, img_height),\n",
|
| 93 |
+
" batch_size = batch_size,\n",
|
| 94 |
+
" class_mode = 'categorical')"
|
| 95 |
+
]
|
| 96 |
+
},
|
| 97 |
+
{
|
| 98 |
+
"cell_type": "code",
|
| 99 |
+
"execution_count": 5,
|
| 100 |
+
"id": "939e6d8a",
|
| 101 |
+
"metadata": {},
|
| 102 |
+
"outputs": [
|
| 103 |
+
{
|
| 104 |
+
"name": "stdout",
|
| 105 |
+
"output_type": "stream",
|
| 106 |
+
"text": [
|
| 107 |
+
"Model: \"sequential\"\n",
|
| 108 |
+
"_________________________________________________________________\n",
|
| 109 |
+
" Layer (type) Output Shape Param # \n",
|
| 110 |
+
"=================================================================\n",
|
| 111 |
+
" conv2d (Conv2D) (None, 359, 362, 32) 416 \n",
|
| 112 |
+
" \n",
|
| 113 |
+
" activation (Activation) (None, 359, 362, 32) 0 \n",
|
| 114 |
+
" \n",
|
| 115 |
+
" max_pooling2d (MaxPooling2D (None, 179, 181, 32) 0 \n",
|
| 116 |
+
" ) \n",
|
| 117 |
+
" \n",
|
| 118 |
+
" conv2d_1 (Conv2D) (None, 178, 180, 32) 4128 \n",
|
| 119 |
+
" \n",
|
| 120 |
+
" activation_1 (Activation) (None, 178, 180, 32) 0 \n",
|
| 121 |
+
" \n",
|
| 122 |
+
" max_pooling2d_1 (MaxPooling (None, 89, 90, 32) 0 \n",
|
| 123 |
+
" 2D) \n",
|
| 124 |
+
" \n",
|
| 125 |
+
" conv2d_2 (Conv2D) (None, 88, 89, 64) 8256 \n",
|
| 126 |
+
" \n",
|
| 127 |
+
" activation_2 (Activation) (None, 88, 89, 64) 0 \n",
|
| 128 |
+
" \n",
|
| 129 |
+
" max_pooling2d_2 (MaxPooling (None, 44, 44, 64) 0 \n",
|
| 130 |
+
" 2D) \n",
|
| 131 |
+
" \n",
|
| 132 |
+
" flatten (Flatten) (None, 123904) 0 \n",
|
| 133 |
+
" \n",
|
| 134 |
+
" dense (Dense) (None, 64) 7929920 \n",
|
| 135 |
+
" \n",
|
| 136 |
+
" activation_3 (Activation) (None, 64) 0 \n",
|
| 137 |
+
" \n",
|
| 138 |
+
" dropout (Dropout) (None, 64) 0 \n",
|
| 139 |
+
" \n",
|
| 140 |
+
" dense_1 (Dense) (None, 8) 520 \n",
|
| 141 |
+
" \n",
|
| 142 |
+
" activation_4 (Activation) (None, 8) 0 \n",
|
| 143 |
+
" \n",
|
| 144 |
+
"=================================================================\n",
|
| 145 |
+
"Total params: 7,943,240\n",
|
| 146 |
+
"Trainable params: 7,943,240\n",
|
| 147 |
+
"Non-trainable params: 0\n",
|
| 148 |
+
"_________________________________________________________________\n"
|
| 149 |
+
]
|
| 150 |
+
}
|
| 151 |
+
],
|
| 152 |
+
"source": [
|
| 153 |
+
"# Modelo de prueba CNN\n",
|
| 154 |
+
"\n",
|
| 155 |
+
"model = Sequential()\n",
|
| 156 |
+
"model.add(Conv2D(32, (2, 2), input_shape=input_shape))\n",
|
| 157 |
+
"model.add(Activation('relu'))\n",
|
| 158 |
+
"model.add(MaxPooling2D(pool_size=(2, 2)))\n",
|
| 159 |
+
" \n",
|
| 160 |
+
"model.add(Conv2D(32, (2, 2)))\n",
|
| 161 |
+
"model.add(Activation('relu'))\n",
|
| 162 |
+
"model.add(MaxPooling2D(pool_size=(2, 2)))\n",
|
| 163 |
+
" \n",
|
| 164 |
+
"model.add(Conv2D(64, (2, 2)))\n",
|
| 165 |
+
"model.add(Activation('relu'))\n",
|
| 166 |
+
"model.add(MaxPooling2D(pool_size=(2, 2)))\n",
|
| 167 |
+
" \n",
|
| 168 |
+
"model.add(Flatten())\n",
|
| 169 |
+
"model.add(Dense(64))\n",
|
| 170 |
+
"model.add(Activation('relu'))\n",
|
| 171 |
+
"model.add(Dropout(0.5))\n",
|
| 172 |
+
"model.add(Dense(8))\n",
|
| 173 |
+
"model.add(Activation('softmax'))\n",
|
| 174 |
+
"\n",
|
| 175 |
+
"model.summary()"
|
| 176 |
+
]
|
| 177 |
+
},
|
| 178 |
+
{
|
| 179 |
+
"cell_type": "code",
|
| 180 |
+
"execution_count": 6,
|
| 181 |
+
"id": "ac636271",
|
| 182 |
+
"metadata": {},
|
| 183 |
+
"outputs": [],
|
| 184 |
+
"source": [
|
| 185 |
+
"model.compile(loss = 'categorical_crossentropy',\n",
|
| 186 |
+
" optimizer = 'rmsprop',\n",
|
| 187 |
+
" metrics = ['accuracy'])"
|
| 188 |
+
]
|
| 189 |
+
},
|
| 190 |
+
{
|
| 191 |
+
"cell_type": "code",
|
| 192 |
+
"execution_count": 7,
|
| 193 |
+
"id": "1857e44a",
|
| 194 |
+
"metadata": {},
|
| 195 |
+
"outputs": [
|
| 196 |
+
{
|
| 197 |
+
"name": "stderr",
|
| 198 |
+
"output_type": "stream",
|
| 199 |
+
"text": [
|
| 200 |
+
"C:\\Users\\shiru\\AppData\\Local\\Temp\\ipykernel_17948\\2051623620.py:1: UserWarning: `Model.fit_generator` is deprecated and will be removed in a future version. Please use `Model.fit`, which supports generators.\n",
|
| 201 |
+
" history = model.fit_generator(\n"
|
| 202 |
+
]
|
| 203 |
+
},
|
| 204 |
+
{
|
| 205 |
+
"name": "stdout",
|
| 206 |
+
"output_type": "stream",
|
| 207 |
+
"text": [
|
| 208 |
+
"Epoch 1/10\n",
|
| 209 |
+
"854/854 [==============================] - 820s 952ms/step - loss: 1.0580 - accuracy: 0.6170 - val_loss: 0.4412 - val_accuracy: 0.8827\n",
|
| 210 |
+
"Epoch 2/10\n",
|
| 211 |
+
"854/854 [==============================] - 626s 733ms/step - loss: 0.6073 - accuracy: 0.7954 - val_loss: 0.3343 - val_accuracy: 0.8974\n",
|
| 212 |
+
"Epoch 3/10\n",
|
| 213 |
+
"854/854 [==============================] - 626s 733ms/step - loss: 0.5120 - accuracy: 0.8298 - val_loss: 0.2887 - val_accuracy: 0.9151\n",
|
| 214 |
+
"Epoch 4/10\n",
|
| 215 |
+
"854/854 [==============================] - 629s 736ms/step - loss: 0.4622 - accuracy: 0.8555 - val_loss: 0.3991 - val_accuracy: 0.8679\n",
|
| 216 |
+
"Epoch 5/10\n",
|
| 217 |
+
"854/854 [==============================] - 628s 735ms/step - loss: 0.4243 - accuracy: 0.8683 - val_loss: 0.4510 - val_accuracy: 0.8815\n",
|
| 218 |
+
"Epoch 6/10\n",
|
| 219 |
+
"854/854 [==============================] - 676s 791ms/step - loss: 0.4159 - accuracy: 0.8794 - val_loss: 0.2866 - val_accuracy: 0.9210\n",
|
| 220 |
+
"Epoch 7/10\n",
|
| 221 |
+
"854/854 [==============================] - 720s 843ms/step - loss: 0.3999 - accuracy: 0.8778 - val_loss: 0.3063 - val_accuracy: 0.9316\n",
|
| 222 |
+
"Epoch 8/10\n",
|
| 223 |
+
"854/854 [==============================] - 722s 845ms/step - loss: 0.4107 - accuracy: 0.8770 - val_loss: 0.3294 - val_accuracy: 0.9098\n",
|
| 224 |
+
"Epoch 9/10\n",
|
| 225 |
+
"854/854 [==============================] - 727s 851ms/step - loss: 0.3974 - accuracy: 0.8856 - val_loss: 0.2559 - val_accuracy: 0.9257\n",
|
| 226 |
+
"Epoch 10/10\n",
|
| 227 |
+
"854/854 [==============================] - 701s 821ms/step - loss: 0.3972 - accuracy: 0.8868 - val_loss: 0.2749 - val_accuracy: 0.9316\n"
|
| 228 |
+
]
|
| 229 |
+
}
|
| 230 |
+
],
|
| 231 |
+
"source": [
|
| 232 |
+
"history = model.fit_generator(\n",
|
| 233 |
+
" train_generator,\n",
|
| 234 |
+
" steps_per_epoch = nb_train_samples // batch_size,\n",
|
| 235 |
+
" epochs = epochs,\n",
|
| 236 |
+
" validation_data = validation_generator,\n",
|
| 237 |
+
" validation_steps = nb_validation_samples // batch_size)"
|
| 238 |
+
]
|
| 239 |
+
},
|
| 240 |
+
{
|
| 241 |
+
"cell_type": "code",
|
| 242 |
+
"execution_count": 15,
|
| 243 |
+
"id": "b3ed428f",
|
| 244 |
+
"metadata": {},
|
| 245 |
+
"outputs": [],
|
| 246 |
+
"source": [
|
| 247 |
+
"# Guardamos el modelo\n",
|
| 248 |
+
"model.save(\n",
|
| 249 |
+
" '../../model/classification/image_classification_CNN.h5',\n",
|
| 250 |
+
" overwrite=True,\n",
|
| 251 |
+
" include_optimizer=True,\n",
|
| 252 |
+
" save_format=None,\n",
|
| 253 |
+
" signatures=None,\n",
|
| 254 |
+
" options=None,\n",
|
| 255 |
+
" save_traces=True,\n",
|
| 256 |
+
")"
|
| 257 |
+
]
|
| 258 |
+
},
|
| 259 |
+
{
|
| 260 |
+
"cell_type": "code",
|
| 261 |
+
"execution_count": 11,
|
| 262 |
+
"id": "f2b819e1",
|
| 263 |
+
"metadata": {},
|
| 264 |
+
"outputs": [
|
| 265 |
+
{
|
| 266 |
+
"name": "stdout",
|
| 267 |
+
"output_type": "stream",
|
| 268 |
+
"text": [
|
| 269 |
+
"dict_keys(['loss', 'accuracy', 'val_loss', 'val_accuracy'])\n"
|
| 270 |
+
]
|
| 271 |
+
},
|
| 272 |
+
{
|
| 273 |
+
"data": {
|
| 274 |
+
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYgAAAEWCAYAAAB8LwAVAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/NK7nSAAAACXBIWXMAAAsTAAALEwEAmpwYAAA0M0lEQVR4nO3deXyU5bn/8c+VnSwQEhK2AGFfRZBFFLUKqFj3pYpW22qr9aht7a+/Hj1tz692O21PT3vac6ql1qK27lVcai1qUMAFWxZRlrAECBCWJBASkkBIMnP9/rgfYIgDDJjJM5m53q/XvDLzLDPXjDLfee7nvu9HVBVjjDGmrSS/CzDGGBObLCCMMcaEZQFhjDEmLAsIY4wxYVlAGGOMCcsCwhhjTFgWEMYAIvKYiPw4wm3LRWRGtGsyxm8WEMYYY8KygDAmjohIit81mPhhAWE6Da9p59si8rGINIrIH0Wkp4j8XUTqRaRERLqHbH+FiKwWkVoRWSAiI0PWjReR5d5+zwIZbV7rMhFZ4e37voiMjbDGS0XkQxHZJyLbROSBNuvP8Z6v1lv/JW95FxH5pYhsEZE6EXnXW3a+iFSE+RxmePcfEJHnReQJEdkHfElEJovIYu81dorIb0UkLWT/0SLypojUiEiliHxHRHqJyH4RyQ/ZboKIVItIaiTv3cQfCwjT2VwLXAgMAy4H/g58B+iB+//56wAiMgx4GrgXKABeA/4qImnel+VLwJ+BPOAv3vPi7XsGMAf4KpAP/B54RUTSI6ivEfgCkAtcCvyLiFzlPW9/r97/9WoaB6zw9vsvYAJwtlfTvwLBCD+TK4Hnvdd8EggA38R9JmcB04G7vBpygBJgHtAHGALMV9VdwALg+pDnvRl4RlVbIqzDxBkLCNPZ/K+qVqrqduAd4B+q+qGqHgReBMZ7290A/E1V3/S+4P4L6IL7Ap4CpAK/VtUWVX0eWBLyGrcDv1fVf6hqQFUfBw56+x2Xqi5Q1ZWqGlTVj3Eh9Rlv9eeBElV92nvdPaq6QkSSgNuAb6jqdu813/feUyQWq+pL3mseUNVlqvqBqraqajku4A7VcBmwS1V/qapNqlqvqv/w1j2OCwVEJBm4EReiJkFZQJjOpjLk/oEwj7O9+32ALYdWqGoQ2Ab09dZt16NnqtwScn8A8C2viaZWRGqBft5+xyUiZ4rI217TTB1wJ+6XPN5zbAyzWw9cE1e4dZHY1qaGYSLyqojs8pqd/iOCGgBeBkaJyCDcUVqdqv7zFGsyccACwsSrHbgvegBERHBfjtuBnUBfb9kh/UPubwN+oqq5IbdMVX06gtd9CngF6Keq3YDZwKHX2QYMDrPPbqDpGOsagcyQ95GMa54K1XZK5t8Ba4GhqtoV1wR3ohpQ1SbgOdyRzi3Y0UPCs4Aw8eo54FIRme6dZP0WrpnofWAx0Ap8XURSROQaYHLIvn8A7vSOBkREsryTzzkRvG4OUKOqTSIyGbgpZN2TwAwRud573XwRGecd3cwBfiUifUQkWUTO8s55rAcyvNdPBb4HnOhcSA6wD2gQkRHAv4SsexXoJSL3iki6iOSIyJkh6/8EfAm4Angigvdr4pgFhIlLqroO157+v7hf6JcDl6tqs6o2A9fgvgj34s5XzA3ZdynuPMRvvfVl3raRuAv4oYjUA/8PF1SHnncr8FlcWNXgTlCf7q3+v8BK3LmQGuDnQJKq1nnP+Qju6KcROKpXUxj/FxdM9biwezakhnpc89HlwC5gA3BByPr3cCfHl3vnL0wCE7tgkDEmlIi8BTylqo/4XYvxlwWEMeYwEZkEvIk7h1Lvdz3GX9bEZIwBQEQex42RuNfCwYAdQRhjjDkGO4IwxhgTVlxN7NWjRw8tLi72uwxjjOk0li1btltV246tAeIsIIqLi1m6dKnfZRhjTKchIluOtc6amIwxxoRlAWGMMSYsCwhjjDFhxdU5iHBaWlqoqKigqanJ71KiKiMjg6KiIlJT7douxpj2EfcBUVFRQU5ODsXFxRw9eWf8UFX27NlDRUUFAwcO9LscY0yciPsmpqamJvLz8+M2HABEhPz8/Lg/SjLGdKy4DwggrsPhkER4j8aYjhX3TUzGmHbQUAU7P4KqUuh7BgyYCvajxB+BVmiohH07YN92dwu0wDn3tvtLWUBEWW1tLU899RR33XXXSe332c9+lqeeeorc3NzoFGZMOKpQv9OFwY4V7u/OFW5ZqB7DYOJtcPos6NLdj0rjU2uz+6wPf/nv+OT9hl2gwaP3y+5lAdEZ1dbW8tBDD30iIAKBAMnJycfc77XXXot2aSbRqUJdhQuA0EBorPI2EBcExedCn3HQ+3T3eMObsHQOzLsfSh6A0de4sCiaaEcVx9NyIOQL/xgBcPizD5GWDV37Qtc+MGTakfuH//aBjNyolGwBEWX3338/GzduZNy4caSmppKdnU3v3r1ZsWIFa9as4aqrrmLbtm00NTXxjW98gzvuuAM4Mm1IQ0MDl1xyCeeccw7vv/8+ffv25eWXX6ZLly4+vzPTqajC3vIjRwQ7P3K3/XvcekmCghEwZIYLgj7joOcYSM/+5HON/7y77fwIlj4KK/8CHz0FPU+DibfC2OshPZKrs8aRgw3ul39dxbED4EDNJ/fLyD3yRd/79KO/9A/dz+ja4W/nkLia7nvixInadi6m0tJSRo4cCcAP/rqaNTv2tetrjurTle9fPvqY68vLy7nssstYtWoVCxYs4NJLL2XVqlWHu6PW1NSQl5fHgQMHmDRpEgsXLiQ/P/+ogBgyZAhLly5l3LhxXH/99VxxxRXcfPPNn3it0PdqElgwCHs3w44Pjw6Epjq3PikFCkdC73FeGIyHwlGQlnlqr3ew3oXE0jmwayWkZsHYz7mjit6nn3j/zqblAGxeBOtfh60fwL6KI59tqMz8Nr/0+7a53xvSsjq+/jZEZJmqTgy3zo4gOtjkyZOPGqvwP//zP7z44osAbNu2jQ0bNpCfn3/UPgMHDmTcuHEATJgwgfLy8o4q18S6YAD2lIWcL/gIdn0MB70fQslp0HM0jL76SCD0HA0p6e1XQ3qOC4MJt8L25S4oPnoWlj0GfSe45WOuPfUAigV1FS4QNrwBmxZC6wEXhMVT3a1tk09OH0jN8LvqTy2hAuJ4v/Q7SlbWkV8MCxYsoKSkhMWLF5OZmcn5558fdixDevqRf8zJyckcOHCgQ2o1MSbQCrvXHX2+YNdKaGl061MyXLPQ2OtdEPQe55qNUtI6pj4RKJrgbhf/2IXE0jnwyj3w+nfdCe2Jt7qjl1gXDMD2ZbB+Hqx/AypXuuW5A+CML8Cwi6H4nPYN2hiUUAHhh5ycHOrrw1+9sa6uju7du5OZmcnatWv54IMPOrg60ynUV8Lf/g+UlUCr9wMiNRN6jYXxN4ecQB4OyTHyT7pLd5hyJ5z5Vdi62AXFskfhn7+H/me5I46RV8TWr+ymOiib744SNrzhzs9IMvSfAhf+EIbNdCfpE+hEfIz83xS/8vPzmTp1KmPGjKFLly707Nnz8LqZM2cye/Zsxo4dy/Dhw5kyZYqPlZqYVFYCL97pToJO+BL0OcMFQv4QSDp2L7iYIQIDzna3mT+HFU+6sJh7O3S5z53snnAr5A/u+NpUXfPc+nne+YTFEGx14TbkQneUMGR6QnfjTaiT1PEukd5r3Au0wFs/gvd+404gX/coFI7wu6r2EQzC5oUuKNb+DTQAAz/jjipGXArJUZxwsrUZtrznnU94HWo2ueWFo1wgDJsJfSfGzpFYB7CT1CZyqq6XRmc+odjZ7S2H578M25e6L82L/wNS46hbc1ISDL7A3ep3wYd/hmWPw1++CNk9YfwtMOGLkNu/fV6voco1Ga1/HTa+Dc31kJwOA8+DKXe5YGiv14ozFhDGhcL2ZbDmJVjzsuuxceEP4ax7Eqq9NSasmgt//QYgcP2fYNSVflcUXTm94LxvwzneOZalj8K7v4J3fglDL3QBOfSik2tOU3Un8A8dJWxf5r1WbzjtWneUMPC8mOhiGussIBJVMAgVS7xQeMX15U5Kdb/qCkbAG9+D2m0w86edo627s2ve70YmL38ciibBtX+E7gP8rqrjJCV7TTwXu//vlv/J3Z6eBV2LXM+hM25xXUjDaW6ETQvc+YQNb3pTg4jrZnvB99zz9jrNfvCcJAuIRBIMuIE9a16G0lfcP6LkNBg8HaZ9D4ZfAl1yXXi8+e+w+LduBOg1f7Amp2iqXAPP3wrV6+Ccb8IF341uO3ysy+0H074Ln/lX94W/dA4s+A9Y+HP3/+jE22DQBVC3zR0lrJ8H5e9C4CCk5bjpKIbNdCeaswv8fjedmgVEvAu0upNya16G0r+6uV5SMtyUCqOucr+s2g7lT0qCi38C3fq5X7WPXw43PQtZPXx5C3FL1Q0mm3c/pHeFW+bC4Gl+VxU7klNh5OXuVrPJfVYfPgFrX4WMbkdGL+cNgklfgWEXQf+zO27cRwKwgIhHgRYof8cLhVdh/27Xb37oRa5Ne+hF4efYaWvKndCtL7zwFXhkBtz8gj/dEePRgVp3rmHNSy4Urv49ZBf6XVXsyhvkzotd8F33Q2fDG24cyLCZ0GOI39XFLQuIGJOdnU1DQ8PJ76hB1/vo5btd18EDe90skMMudqEwZMapnZQbeTl88VV4+gYXEjc9C/0mn/zzmCO2LYEXbnOTuM34AZz9dXfUZk4sJR1Ou87dTNRZQHRmGnQTpR2odYfbjdXuhPPwS1woDJ7WPt0j+02CL78JT17nmpuu+QOMuuLTP2+iCQbh/d/AWz92J1tve91NkW1MjIpqQIjITOA3QDLwiKr+rM367sAcYDDQBNymqqsi2bezuO+++xgwYMDh60E88MADiAiLFi1i7969tLS08OMf/5grr4ywO2Mw6CZia6p1oaBBNx1ARjfIaoVvl0Vnfpj8wfDlEter5LkvuN5NU/6l/V8nXjVUwYtfhY1vuXM/l//GdQgwJoZFbSS1iCQD64ELgQpgCXCjqq4J2eYXQIOq/kBERgAPqur0SPYN54Qjqf9+v5vcrD31Og0uOXZ2ffjhh9x7770sXLgQgFGjRjFv3jxyc3Pp2rUru3fvZsqUKWzYsAERCd/EFAy4UDhQ6/4eCoUuuW4++fRskKSOGUndcsCdk1j7qhtkdNFPrHnkRDa+BXO/6v7bzfyZmzLDuluaGOHXSOrJQJmqbvKKeAa4Egj9kh8F/BRAVdeKSLGI9AQGRbBvpzB+/HiqqqrYsWMH1dXVdO/end69e/PNb36TRYsWkZSUxPbt26msrKRXr15HdgwXCkkpbl6YkFDocKld3ACu178LHzzkBtVd83B8jfRtL4EWePsn8O6v3diSL7wMPUf5XZUxEYtmQPQFtoU8rgDObLPNR8A1wLsiMhkYABRFuC8AInIHcAdA//4nGC5/nF/60XTdddfx/PPPs2vXLmbNmsWTTz5JdXU1y5YtIzU1leLiYjfNdzDgdqjZBE37APVCIc8dLaRlx8Yvz6Rk91nm9ofXvwOPXwE3PgNZ+SfeN1Hs3QIvfNkNRpzwJbj4pzaWxHQ60QyIcN9kbduzfgb8RkRWACuBD4HWCPd1C1UfBh4G18R0qsVG06xZs7j99tvZvXs3Cxcu5LnnnqOwsJDUlBTefuPvbNmyBWo2Q1qtO1Jo3u/GHGTkup5HsRAK4Zx1l+sGO/cO+OMM+Pzz1g0WXPfil78GKHzuMXexHmM6oWgGRAXQL+RxEbAjdANV3QfcCiAiAmz2bpkn2rczGT16NPX19fTt25fehfl8/upLuPzaWUwcN4Zxo4cxYkixO/mcVeCajXqOjt1QaGvUlZDdy528/uOFcNNzidszp+WAO6JaOsfNCHrdH6F7sd9VGXPKohkQS4ChIjIQ2A7MAm4K3UBEcoH9qtoMfAVYpKr7ROSE+3YawQA0N7Ly3b+7LqmVq+mRAov/+rgbPZue427e1AqnNAbCb/3P9LrBXguPXQbXPgIjL/O7qo5VtdZNl1G1Bqbe66YuSeTpMkxciFpAqGqriNwDvI7rqjpHVVeLyJ3e+tnASOBPIhLAnYD+8vH2jVat7erQdNkH693J5eZGXOuYuHMIXfNcMKRkdJ6jhEj0GOJ1g70Bnr0ZLvm5u5pYvFN1k8r9/T7XceDmue4iM8bEgaiOg1DV14DX2iybHXJ/MTA00n1jVqDlSCAcrHdXpQIXAlkF7gghLTv+u4NmF7hR1y98Bf7+r1C7FS78Ufy+76Y6+Ou9sHouDDofrn4YcnqeaC9jOo2EGEmtqkh7/loPBqG5wQuFemg94JYnpRxpMkrPcTOldpCYuTJgWibc8Gc3Ad3i37pusFf/PrauPdweKpa5JqW6Cpj+fdesFK9BaBJW3AdERkYGe/bsIT8//9RDQtVdLP7QEcLBBo40G2VBTh8XCKldfGk2UlX27NlDRkaMfAknJcMl/+m6wb7xPXfVsBufhsw8vyv79IJBF3zzf+D+u982z+amMp9aMKi0BIO0BJTWQJDmQJDWgNISCHo3Pepv23XJScLMMb1O/EInKe4DoqioiIqKCqqrq09ux2DAhcKh26ExCsmprukoJcNNKyytQI13809GRgZFRUW+1nAUETj7a9CtyI0i/uNF8Pm/QN5Avys7dQ3V8NKd7spnI6+AK/7XpstIMM2tQbbsaaSsqoGyqgYq9h6g+fAXeugXeeiXvXrrQr7gg0pLq7dfUAkEP10LQI/sdAuIU5GamsrAgRF8KbUedBfT2fiWu+362C3v0t1dnGTwNHe1tW4x9CXcGYy+2nWDfeZGrxvss+4qX53NpgVuvEdTHVz23zDh1vjqZGCO0niwlY3VDYeDoKyqgbLqBrbs2X/Ul3lBTjoZqUmkJieRmpREaoocvp+RmkRKeop7nOwtD7mfkiykeX8/uS6JtGQhJSmJ1JQkUpO8bQ7dT0kiJenIfukp0WnejNpcTH4INxfTCbUcgGdvcRfVadnvziP0O9O7qPo06D3OLrnZHnZvgCeudTPOXjfHzTjbGQRa3dXM3vkV9BgGn3vUjVMxcaGmsfmoENhQVc/GqgZ21DUd3iYlSRiQn8mQwmyGFuYwpDCbIYXZDCrIIjOt8//G9msups7h0BxC4292gVB8jjufYNpXj6HwlRJ46np45ib47C/cVcBijaqb6qT8Hdj8jvvbUOmuiTzzZ3ah+05IVdlR13RUEGz0jghqGpsPb9clNZnBhVlMHph3OASGFGYzID+L1OTE7IBgAQFw8/N+V5AYsgvhS3+D52+Dv33LdYOd/oC/vX9UYe9md03jze+4v/XeoP3snlB8Loy5FkZ8tsNLa2oJsHrHPj6uqGXl9joamlpJT00mLTmJtBTXrJCecuR+WkoSaclJR22T1mab9JTkkO2SQp4rmdRkad/efh2sNRBkS83+T4TAxqoGGpsDh7fLzUxlSEE2F43qyZDCbAYXZjOkIJu+uV1ISuq87z8aLCBMx0rLghuedOMk3vsN1G6Dq37Xsd1g95YfCYPyd2FfhVueVeiOIAee64Ihf0iHnWdoCQRZX1nPxxV1fFxRy0fb6lhfWU+r195dmJNOXlYaza1BDnq35tYAzQF3v71aitNSkkgPEx5pIQF0qP07OUkO/01NTjrqsfvr2tRDH6ckt9kmOSnkObxtTvjcSQRVKQ85WVxW1UD5nkZaAkc+iF5dMxhSmM3nJvY76oggPyutUwdhR7KAMB0vOQUu/aXrBlvyfdeEc8MT0esGW7v16COEuq1ueWYPLxC+6QKhx7AOCYRgUNm0u5GPK2oPB8LqHfs42BoEoFuXVMYWdeOrIwYxtiiX04ty6dXt2AGqqrQG9XB4NHu3g60B9zgQ5GCL+3to+ZFtvO0DQQ62BDgYCIZ9nuaQ5znQEiAQVK/3jetyeagnTmswSCCotAQ++TgakgQG5GcxuCCb6SN7Hg6BwQVZ5GTYVCeflgWE8YcInHOv6xX20r/AnIvdbLDdB3z6566rCDlCeAdqt7jlXfJcIEz9uvtbMCLqgaCqbK89wMcVdXxUUcvH2+pYtb2O+oNutH1mWjJj+nTjlikDGNsvl9OLutE/L/OkfuGKyOHeL1lRuJhgeznU1/9wuIQES0sgZPlxgubQfgr0y+tCcX4WGanWiSRaLCCMv067DnJ6u26wj8yAzz8Hfcaf3HPs23HkhHL5O64JCVwX5QFT4ay7vUAYGfXzHbsbDh5uIjp0hLDHOxGamiyM7N2VK8f3OXxkMKQwm+QEafdOShLSrUdgp2LdXE1sqF4HT1wH+3e7aygMu/jY2+7beeTooPwd1+sI3HW5Bxw6h3AOFI6OaiDsa2phVUUdH1UcCYPttW7alSSBoYU5jC3qdvjIYHivHNJT7AvSxJbjdXO1gDCxo74Snvqcu274pb+CibceWV4e0mS0p8wtT+8GA84+Egg9x0RtzIrrUVR35Mhgex2bqhsPrx+Qn+kdFXRjbFEuo/t0JSvdDtBN7LNxEKZzyOkJX3rNTYL36r2wfp47Oti93q1Py3GBMOFLLhB6jY1aIGyvPcCSzTUsKa9h+dZa1lfWHx5B27NrOmOLcrlmfF/GFuUytqgbuZkdNzGjMR3FAsLElvRsmPW0mw129Vzoc4YbxFh8DvQ63fWAamfBoLKhqoF/ltewtLyGJZtrDo+kzUlPYVz/XKaPGMzYom6c3i+Xnl1jZFJEY6LMmphMwmluDbJyey1LyveyZHMNS7fspe5AC+DGG0wamMfk4jwmFecxvFdOwpxENonJmphMQqtvamH51trDTUYrttUeHnMwqCCLS8b0YmKxC4V+eV1sEJUxHgsIE3eq6ptYsnkvS8pdIJTu3EdQITlJGNOnKzdPGcCk4jwmFXcnPzuGBw4Y4zMLCNOpqSqbdzeytHwv//QCYcue/YCbfG18/1y+Nm0ok4rzGN8/13oWGXMS7F+L6VRaA0FKd9a7MNhcw9ItNexucAPRumemMrE4j5vPHMCkgXmM7tM1YWfhNKY9WECYmHagOcCH2/aytNw1GS3fsvfwzJxF3btw3tACJg10zUWDC7Lt/IEx7cgCwsScA80Bnl2ylZdW7GDV9jpag4oIDO+ZwzVnFB0OhN7duvhdqjFxLaoBISIzgd8AycAjqvqzNuu7AU8A/b1a/ktVH/XWlQP1QABoPVY3LBM/9jW18OfFW5jz7mb2NDZzWt9u3H7eICYX53FG/+50y7TZOY3pSFELCBFJBh4ELgQqgCUi8oqqrgnZ7G5gjapeLiIFwDoReVJVD13m6QJV3R2tGk1s2NNwkEffK+fxxeXUN7Vy3rAC7j5/MGcOyve7NGMSWjSPICYDZaq6CUBEngGuBEIDQoEccQ3H2UAN0BrFmkwM2Vl3gD8s2szT/9xKU2uAmaN7cdf5QzitqJvfpRljiG5A9AW2hTyuAM5ss81vgVeAHUAOcIOqBr11CrwhIgr8XlUfjmKtpgOV725k9sKNvLC8gqDCleP6cNf5gxlSaNcCNyaWRDMgwnUnaTuvx8XACmAaMBh4U0TeUdV9wFRV3SEihd7ytaq66BMvInIHcAdA//7927N+087W7trHQ29v5NWPd5CSnMSsSf2547xB9MvL9Ls0Y0wY0QyICqBfyOMi3JFCqFuBn6mbEKpMRDYDI4B/quoOAFWtEpEXcU1WnwgI78jiYXBzMbX7uzCf2vKte3no7TJKSqvISkvm9nMH8eVzB1KYY5PeGRPLohkQS4ChIjIQ2A7MAm5qs81WYDrwjoj0BIYDm0QkC0hS1Xrv/kXAD6NYq2lnqsr7G/fw4NtlvL9xD7mZqXxzxjC+ePYAmxrbmE4iagGhqq0icg/wOq6b6xxVXS0id3rrZwM/Ah4TkZW4Jqn7VHW3iAwCXvQGPaUAT6nqvGjVatpPMKjMX1vFb98u46NttRTmpPPdz47kpjP72zQXxnQyNt23aRetgSB/W7mTh97eyLrKevrldeHOzwzm2jOK7KLyxsQwm+7bRM3B1gBzl29n9sKNbNmzn6GF2fz6hnFcNrY3KTYPkjGdmgWEOSX7m1t56h9b+cM7m6jcd5CxRd34/S0TuHBkT5LsAjvGxAULCHNS6va38KfF5cx5bzN797cwZVAev/zcOKYOybeJ8oyJMxYQJiLV9Qf547ubeeKDLTQcbGX6iELuumAwEwbk+V2aMSZKLCDMcVXs3c8fFm3imSXbaA4EufS03tx1/hBG9enqd2nGmCizgDBhbaxu4HcLNvLSh9sRgWvGF/HVzwxiUEG236UZYzqIBYQ5ypY9jfznvHW8tmon6SlJ3HLWAG4/dxB9cu3aC8YkGgsIA7hxDH98dzP/XbKelKQk7jp/MLdOHUiP7HS/SzPG+MQCwrBqex33vfAxq3fs48JRPfnRlWPo1c3mSTIm0VlAJLADzQF+XbKeR97dTF5WGr/7/BnMHNPLuqsaYwALiIT1Xtlu/m3uSrbW7OfGyf24f+ZIu6SnMeYoFhAJpnZ/Mz/+WynPL6tgYI8snr59CmcNtkt7GmM+yQIiQagqr368kx/8dTW1+1u4+4LBfG3aUJtIzxhzTBYQCWB77QH+/aVVvLW2irFF3fjTbWfaQDdjzAlZQMSxQFB54oMt/Oe8tQQVvnfpSG6dOpBkm0zPGBMBC4g4tb6ynvtf+JjlW2s5b1gBP7lqjF372RhzUiwg4szB1gAPvr2R3y0oIzs9hf++4XSuGtfXuq4aY06aBUQcWVpew/1zV1JW1cDV4/vyvUtHkm8joY0xp8gCIg7UN7Xw83lreeKDrfTN7cJjt07i/OGFfpdljOnkLCA6uTfXVPLvL62iqr6JL58zkP9z4TCy0u0/qzHm07Nvkk6qqr6JB15ZzWsrdzGiVw6zb5nAuH65fpdljIkjFhCdjKry3NJt/ORvpTS1Bvn2xcO547xBpCYn+V2aMSbORBQQIvICMAf4u6oGo1uSOZbNuxv5ztyVLN60hzMH5vHTa06zC/gYY6Im0p+dvwNuAjaIyM9EZEQkO4nITBFZJyJlInJ/mPXdROSvIvKRiKwWkVsj3TeRtASCPLSgjJm/XsSqHXX89JrTePr2KRYOxpioiugIQlVLgBIR6QbcCLwpItuAPwBPqGpL231EJBl4ELgQqACWiMgrqromZLO7gTWqermIFADrRORJIBDBvgnh44pa7nthJaU793HJmF784IrRFHa1azUYY6Iv4nMQIpIP3AzcAnwIPAmcA3wROD/MLpOBMlXd5O3/DHAlEPolr0COuFFc2UAN0AqcGcG+cW1/cyu/emM9c97bTI/sdGbfPIGZY3r5XZYxJoFEeg5iLjAC+DNwuaru9FY9KyJLj7FbX2BbyOMK3Bd/qN8CrwA7gBzgBlUNikgk+x6q7Q7gDoD+/ftH8nZi3qL11XznxZVU7D3A58/sz32XjKBrhl2rwRjTsSI9gvitqr4VboWqTjzGPuHmdtA2jy8GVgDTgMG4pqt3Itz30Os/DDwMMHHixLDbdBY1jc38+NU1zP1wO4MKsnjuq2cxeWCe32UZYxJUpAExUkSWq2otgIh0B25U1YeOs08F0C/kcRHuSCHUrcDPVFWBMhHZjDtSiWTfuLK3sZmLf72IvY3NfG3aEO6+YIhdq8EY46tIezHdfigcAFR1L3D7CfZZAgwVkYEikgbMwjUnhdoKTAcQkZ7AcGBThPvGlZLSSqrrD/KnL0/mWxcNt3Awxvgu0iOIJBER75f+oR5KacfbQVVbReQe4HUgGZijqqtF5E5v/WzgR8BjIrIS16x0n6ru9l7jE/ue/NvrPEpKK+ndLYOzBtnlP40xsSHSgHgdeE5EZuPOBdwJzDvRTqr6GvBam2WzQ+7vAC6KdN941dQS4J0Nu7l6vE3LbYyJHZEGxH3AV4F/wf3SfwN4JFpFJZoPNu1hf3OAGSN7+l2KMcYcFulAuSBuNPXvoltOYppfWkWX1GTOGmzNS8aY2BHpOIihwE+BUcDhYbyqOihKdSUMVWV+aSXnDu1hJ6aNMTEl0l5Mj+KOHlqBC4A/4QbNmU9pzc597KhrsuYlY0zMiTQguqjqfEBUdYuqPoAb3GY+pfmlVYjABSPsCnDGmNgS6UnqJhFJws3meg+wHbBvtHYwv7SScf1yKcixa0cbY2JLpEcQ9wKZwNeBCbhJ+74YpZoSRuW+Jj6qqLPmJWNMTDrhEYQ3KO56Vf020ICbHsO0g7fWVgEwfaQdjBljYs8JjyBUNQBMEBvB1e7ml1bSN7cLw3vm+F2KMcZ8QqTnID4EXhaRvwCNhxaq6tyoVJUAmloCvFu2m1mT+tvoaWNMTIo0IPKAPRzdc0kBC4hT9F7Zbppagta8ZIyJWZGOpLbzDu2spLSS7PQUzhxoo6eNMbEp0pHUjxLmgj2qelu7V5QAgkFlfmkV5w3rQVpKpB3JjDGmY0XaxPRqyP0M4Gri/AI+0bRqRx1V9Qete6sxJqZF2sT0QuhjEXkaKIlKRQmgpLSKJIELhtv5B2NM7DrV9o2hQP/2LCSRlKypZMKA7nTPOu41l4wxxleRnoOo5+hzELtw14gwJ2lH7QHW7NzH/ZeM8LsUY4w5rkibmGwkVzuZ742enmHdW40xMS6iJiYRuVpEuoU8zhWRq6JWVRybX1pJcX4mgwuy/S7FGGOOK9JzEN9X1bpDD1S1Fvh+VCqKY40HW3m/bA/TR/a00dPGmJgXaUCE2y7SLrLG886G3TQHbPS0MaZziDQglorIr0RksIgMEpH/BpZFs7B4NL+0kpyMFCYV5/ldijHGnFCkAfE1oBl4FngOOADcfaKdRGSmiKwTkTIRuT/M+m+LyArvtkpEAiKS560rF5GV3rqlkb+l2BQIKm+treKC4YWkJtvoaWNM7Iu0F1Mj8Ikv+OPxriPxIHAhUAEsEZFXVHVNyPP+AviFt/3lwDdVtSbkaS5Q1d0n87qxasW2WvY0NlvzkjGm04i0F9ObIpIb8ri7iLx+gt0mA2WquklVm4FngCuPs/2NwNOR1NMZzS+tJDlJOH+YBYQxpnOItK2jh9dzCQBV3cuJr0ndF9gW8rjCW/YJIpIJzARCp/RQ4A0RWSYidxzrRUTkDhFZKiJLq6urT1CSf+aXVjGpuDvdMlP9LsUYYyISaUAEReTw1BoiUkyY2V3bCNeP81j7XA6816Z5aaqqngFcAtwtIueF21FVH1bViao6saCg4AQl+WNbzX7WVdbb5HzGmE4l0q6q3wXeFZGF3uPzgGP+qvdUAP1CHhdx7BlgZ9GmeUlVd3h/q0TkRVyT1aII640pJaWVABYQxphOJaIjCFWdB0wE1uF6Mn0L15PpeJYAQ0VkoIik4ULglbYbeSO0PwO8HLIsS0RyDt0HLgJWRVJrLJpfWsXggiyKe2T5XYoxxkQs0sn6vgJ8A3cUsAKYAizm6EuQHkVVW0XkHuB1IBmYo6qrReROb/1sb9OrgTe8nlKH9ARe9EYbpwBPeSHV6dQ3tfCPzXu4bepAv0sxxpiTEmkT0zeAScAHqnqBiIwAfnCinVT1NeC1Nstmt3n8GPBYm2WbgNMjrC2mLVq/m5aAMmOUNS8ZYzqXSE9SN6lqE4CIpKvqWmB49MqKHyWllXTPTOWM/t39LsUYY05KpEcQFd44iJeAN0VkL3bJ0RNqDQR5e10V04YXkpxkk/MZYzqXSEdSX+3dfUBE3ga6AZ3ynEBHWr61ltr9LUy33kvGmE7opGdkVdWFJ97KgBs9nZosnDesh9+lGGPMSbNZ46KopLSSKYPyycmw0dPGmM7HAiJKNu9uZGN1I9NH2NxLxpjOyQIiSuZ7o6ft/IMxprOygIiSktJKRvTKoV9ept+lGGPMKbGAiIK6/S0sKd9r134wxnRqFhBRsGB9FYGgWvOSMaZTs4CIgpLSKnpkpzGuKNfvUowx5pRZQLSzlkCQBeuqmDaikCQbPW2M6cQsINrZkvIa6ptarXnJGNPpWUC0s5I1VaSlJHHuUBs9bYzp3Cwg2pGqMn9tJWcPzicz7aRnMTHGmJhiAdGONlY3sGXPfru0qDEmLlhAtKOS0ioAG/9gjIkLFhDtqGRNJaP7dKV3ty5+l2KMMZ+aBUQ7qWlsZvnWvdZ7yRgTNywg2snba6sIKlxoAWGMiRMWEO1k/tpKenZNZ0zfrn6XYowx7cICoh0cbA2wcF0100b0RMRGTxtj4oMFRDv4x6YaGpsDzLDeS8aYOBLVgBCRmSKyTkTKROT+MOu/LSIrvNsqEQmISF4k+8aS+aWVZKQmMXWIjZ42xsSPqAWEiCQDDwKXAKOAG0VkVOg2qvoLVR2nquOAfwMWqmpNJPvGClWlpLSKc4YUkJGa7Hc5xhjTbqJ5BDEZKFPVTaraDDwDXHmc7W8Enj7FfX2zdlc922sPWPOSMSbuRDMg+gLbQh5XeMs+QUQygZnAC6ew7x0islREllZXV3/qok/WoWtPTxthAWGMiS/RDIhw3Xn0GNteDrynqjUnu6+qPqyqE1V1YkFBwSmU+emUlFZxer9cCrtmdPhrG2NMNEUzICqAfiGPi4Adx9h2Fkeal052X99U1x/ko4paZtjRgzEmDkUzIJYAQ0VkoIik4ULglbYbiUg34DPAyye7r9/eXluFKja9hjEmLkXtogWq2ioi9wCvA8nAHFVdLSJ3eutne5teDbyhqo0n2jdatZ6qN0sr6dMtg5G9c/wuxRhj2l1Ur2qjqq8Br7VZNrvN48eAxyLZN5Y0tQR4d8NurptQZKOnjTFxyUZSn6LFG/dwoCXAjFHWvGSMiU8WEKeopLSSrLRkpgzK87sUY4yJCguIU6CqzC+t4tyhBaSn2OhpY0x8soA4Bat37GPXvia7tKgxJq5ZQJyCktJKRGz0tDEmvllAnIL5pVWc0b87+dnpfpdijDFRYwFxknbVNbFye501Lxlj4p4FxEmav9ZNzjfDRk8bY+KcBcRJml9aRf+8TIYWZvtdijHGRJUFxEnY39zKe2W7mT6y0EZPG2PingXESXh3w24OtgateckYkxAsIE7C/NIqctJTmFRso6eNMfHPAiJCwaAyf20VnxleQFqKfWzGmPhn33QR+nh7HbsbDlrzkjEmYVhARKhkTSXJScL5wzv+sqbGGOMHC4gIlZRWMmFAd3Iz0/wuxRhjOoQFRAQq9u5n7a56LrTmJWNMArGAiMBba6sAbHoNY0xCsYCIwJtrKhnUI4tBBTZ62hiTOCwgTqDhYCv/2FRjRw/GmIRjAXEC76yvpjlgo6eNMYnHAuIESkqr6NYllQkDuvtdijHGdKioBoSIzBSRdSJSJiL3H2Ob80VkhYisFpGFIcvLRWSlt25pNOs8lkBQeXtdFRcMLyAl2bLUGJNYUqL1xCKSDDwIXAhUAEtE5BVVXROyTS7wEDBTVbeKSNuG/gtUdXe0ajyRD7fupaaxmenWvGSMSUDR/Fk8GShT1U2q2gw8A1zZZpubgLmquhVAVauiWM9JKymtIiVJ+IyNnjbGJKBoBkRfYFvI4wpvWahhQHcRWSAiy0TkCyHrFHjDW37HsV5ERO4QkaUisrS6urrdigeYX1rJmYPy6JqR2q7Pa4wxnUHUmpiAcFfU0TCvPwGYDnQBFovIB6q6Hpiqqju8Zqc3RWStqi76xBOqPgw8DDBx4sS2z3/KtuxpZENVAzdO7t9eT2mMMZ1KNI8gKoB+IY+LgB1htpmnqo3euYZFwOkAqrrD+1sFvIhrsuowJaWutcu6txpjElU0A2IJMFREBopIGjALeKXNNi8D54pIiohkAmcCpSKSJSI5ACKSBVwErIpirZ8wv7SSYT2z6Z+f2ZEva4wxMSNqTUyq2ioi9wCvA8nAHFVdLSJ3eutnq2qpiMwDPgaCwCOqukpEBgEvetd9TgGeUtV50aq1rX1NLfxzcw23nzeoo17SGGNiTjTPQaCqrwGvtVk2u83jXwC/aLNsE15Tkx8WrqumNajMsOk1jDEJzEZ/hVFSWkleVhrj+tnoaWNM4rKAaKM1EGTBumqmjSgkOSlcRyxjjEkMFhBtLN2yl7oDLda8ZIxJeBYQbcwvrSQtOYlzh9roaWNMYrOAaKOktIopg/PJSo/q+XtjjIl5FhAhNlY3sHl3Ixda85IxxlhAhJpfWgnANBs9bYwxFhChSkqrGNm7K31zu/hdijHG+M4CwrO3sZml5TXWe8kYYzwWEJ4F66sIqk3OZ4wxh1hAeEpKqyjISee0vt38LsUYY2KCBQTQ3Bpk0bpqpo8oJMlGTxtjDGABAcCS8hrqD7bataeNMSaEBQTw5ppK0lOSOGdID79LMcaYmJHwAaGqzF9byTlDetAlLdnvcowxJmYk/HwSTS1Bzh7Ug7OH5PtdijHGxJSED4guacn8/LqxfpdhjDExJ+GbmIwxxoRnAWGMMSYsCwhjjDFhWUAYY4wJywLCGGNMWBYQxhhjwrKAMMYYE5YFhDHGmLBEVf2uod2ISDWw5RR37wHsbsdyOjP7LI5mn8fR7PM4Ih4+iwGqWhBuRVwFxKchIktVdaLfdcQC+yyOZp/H0ezzOCLePwtrYjLGGBOWBYQxxpiwLCCOeNjvAmKIfRZHs8/jaPZ5HBHXn4WdgzDGGBOWHUEYY4wJywLCGGNMWAkfECIyU0TWiUiZiNzvdz1+EpF+IvK2iJSKyGoR+YbfNflNRJJF5EMRedXvWvwmIrki8ryIrPX+HznL75r8JCLf9P6drBKRp0Ukw++a2ltCB4SIJAMPApcAo4AbRWSUv1X5qhX4lqqOBKYAdyf45wHwDaDU7yJixG+Aeao6AjidBP5cRKQv8HVgoqqOAZKBWf5W1f4SOiCAyUCZqm5S1WbgGeBKn2vyjaruVNXl3v163BdAX3+r8o+IFAGXAo/4XYvfRKQrcB7wRwBVbVbVWl+L8l8K0EVEUoBMYIfP9bS7RA+IvsC2kMcVJPAXYigRKQbGA//wuRQ//Rr4VyDocx2xYBBQDTzqNbk9IiJZfhflF1XdDvwXsBXYCdSp6hv+VtX+Ej0gJMyyhO/3KyLZwAvAvaq6z+96/CAilwFVqrrM71piRApwBvA7VR0PNAIJe85ORLrjWhsGAn2ALBG52d+q2l+iB0QF0C/kcRFxeJh4MkQkFRcOT6rqXL/r8dFU4AoRKcc1PU4TkSf8LclXFUCFqh46onweFxiJagawWVWrVbUFmAuc7XNN7S7RA2IJMFREBopIGu4k0ys+1+QbERFcG3Opqv7K73r8pKr/pqpFqlqM+//iLVWNu1+IkVLVXcA2ERnuLZoOrPGxJL9tBaaISKb372Y6cXjSPsXvAvykqq0icg/wOq4XwhxVXe1zWX6aCtwCrBSRFd6y76jqa/6VZGLI14AnvR9Tm4Bbfa7HN6r6DxF5HliO6/33IXE47YZNtWGMMSasRG9iMsYYcwwWEMYYY8KygDDGGBOWBYQxxpiwLCCMMcaEZQFhTAwQkfNtxlgTaywgjDHGhGUBYcxJEJGbReSfIrJCRH7vXS+iQUR+KSLLRWS+iBR4244TkQ9E5GMRedGbvwcRGSIiJSLykbfPYO/ps0Out/CkN0LXGN9YQBgTIREZCdwATFXVcUAA+DyQBSxX1TOAhcD3vV3+BNynqmOBlSHLnwQeVNXTcfP37PSWjwfuxV2bZBBuZLsxvknoqTaMOUnTgQnAEu/HfRegCjcd+LPeNk8Ac0WkG5Crqgu95Y8DfxGRHKCvqr4IoKpNAN7z/VNVK7zHK4Bi4N2ovytjjsECwpjICfC4qv7bUQtF/r3Ndsebv+Z4zUYHQ+4HsH+fxmfWxGRM5OYD14lIIYCI5InIANy/o+u8bW4C3lXVOmCviJzrLb8FWOhdX6NCRK7yniNdRDI78k0YEyn7hWJMhFR1jYh8D3hDRJKAFuBu3MVzRovIMqAOd54C4IvAbC8AQmc/vQX4vYj80HuOz3Xg2zAmYjabqzGfkog0qGq233UY096sickYY0xYdgRhjDEmLDuCMMYYE5YFhDHGmLAsIIwxxoRlAWGMMSYsCwhjjDFh/X+mrt3MCC37NwAAAABJRU5ErkJggg==\n",
|
| 275 |
+
"text/plain": [
|
| 276 |
+
"<Figure size 432x288 with 1 Axes>"
|
| 277 |
+
]
|
| 278 |
+
},
|
| 279 |
+
"metadata": {
|
| 280 |
+
"needs_background": "light"
|
| 281 |
+
},
|
| 282 |
+
"output_type": "display_data"
|
| 283 |
+
},
|
| 284 |
+
{
|
| 285 |
+
"data": {
|
| 286 |
+
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYIAAAEWCAYAAABrDZDcAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/NK7nSAAAACXBIWXMAAAsTAAALEwEAmpwYAAAy60lEQVR4nO3deXxU9b3/8dcnyWRPyEISIOzIkojsIm6IEhXccBfXaqvUWq16e63a1Xvb29rbX1vtra3i0mpdEcGlRSm4gAsqq8omOyasISQkIdsk+fz+OANMQggJzORMZj7PxyOPzHJm5jMDOe853+/3fL+iqhhjjIlcUW4XYIwxxl0WBMYYE+EsCIwxJsJZEBhjTISzIDDGmAhnQWCMMRHOgsCYNhKRv4vIr9q47RYRKTje5zGmI1gQGGNMhLMgMMaYCGdBYMKKr0nmPhH5UkT2i8jTIpIjIm+LSIWIzBeRdL/tLxGRVSJSJiIfiEie330jRWSZ73GvAPHNXusiEVnhe+wnIjLsGGu+TUQ2iMheEXlTRHr4bhcR+aOI7BaRfb73NNR33wUistpX2zYR+c9j+sCMwYLAhKcrgHOBQcDFwNvAj4GuOP/nfwAgIoOAl4B7gCxgDvCWiMSKSCzwOvAPIAN41fe8+B47CngG+C6QCTwBvCkice0pVETOAX4DXA10B7YCL/vuPg8Y73sfacA1QInvvqeB76pqCjAUeK89r2uMPwsCE47+T1V3qeo24EPgM1Vdrqq1wGxgpG+7a4B/qeo8VfUC/w9IAE4DxgEe4BFV9arqTGCx32vcBjyhqp+paoOqPgvU+h7XHtcDz6jqMl99DwKnikhfwAukAEMAUdU1qrrD9zgvkC8iqapaqqrL2vm6xhxkQWDC0S6/y9UtXE/2Xe6B8w0cAFVtBAqBXN9927TprIxb/S73AX7oaxYqE5EyoJfvce3RvIZKnG/9uar6HvBn4DFgl4hMF5FU36ZXABcAW0VkgYic2s7XNeYgCwITybbj7NABp00eZ2e+DdgB5PpuO6C33+VC4H9UNc3vJ1FVXzrOGpJwmpq2Aajqn1R1NHAiThPRfb7bF6vqFCAbpwlrRjtf15iDLAhMJJsBXCgiE0XEA/wQp3nnE2ARUA/8QERiRORyYKzfY58EbheRU3ydukkicqGIpLSzhheBW0RkhK9/4dc4TVlbRORk3/N7gP1ADdDg68O4XkS6+Jq0yoGG4/gcTISzIDARS1W/Bm4A/g/Yg9OxfLGq1qlqHXA5cDNQitOfMMvvsUtw+gn+7Lt/g2/b9tbwLvAz4DWco5ABwFTf3ak4gVOK03xUgtOPAXAjsEVEyoHbfe/DmGMitjCNMcZENjsiMMaYCGdBYIwxEc6CwBhjIpwFgTHGRLgYtwtor65du2rfvn3dLsMYYzqVpUuX7lHVrJbu63RB0LdvX5YsWeJ2GcYY06mIyNYj3WdNQ8YYE+EsCIwxJsJZEBhjTITrdH0ELfF6vRQVFVFTU+N2KUEXHx9Pz5498Xg8bpdijAkTYREERUVFpKSk0LdvX5pOFhleVJWSkhKKioro16+f2+UYY8JEWDQN1dTUkJmZGdYhACAiZGZmRsSRjzGm44RFEABhHwIHRMr7NMZ0nLAJgqOp8TawvayaRptt1RhjmoiYIKirb2RPZS37a+sD/txlZWX85S9/affjLrjgAsrKygJejzHGtEfEBEFyXAxRIpRXd1wQNDS0vmjUnDlzSEtLC3g9xhjTHmExaqgtoqKE5LgYymu89ND4gLa1P/DAA2zcuJERI0bg8XhITk6me/furFixgtWrV3PppZdSWFhITU0Nd999N9OmTQMOTZdRWVnJ5MmTOeOMM/jkk0/Izc3ljTfeICEhIWA1GmPMkYRdEPzXW6tYvb28xfvqG5VabwMJsdFEtSMI8nuk8ouLTzzi/Q8//DArV65kxYoVfPDBB1x44YWsXLny4BDPZ555hoyMDKqrqzn55JO54ooryMzMbPIc69ev56WXXuLJJ5/k6quv5rXXXuOGG2z1QWNM8IVdELQmOsrZ+Tc0KlHRwRt9M3bs2Cbj/P/0pz8xe/ZsAAoLC1m/fv1hQdCvXz9GjBgBwOjRo9myZUvQ6jPGGH9hFwStfXMH2LC7ElVlYE5K0GpISko6ePmDDz5g/vz5LFq0iMTERCZMmNDieQBxcXEHL0dHR1NdXR20+owxxl/EdBYfkJoQQ7W3gbr6xoA9Z0pKChUVFS3et2/fPtLT00lMTGTt2rV8+umnAXtdY4wJhLA7Ijia1HgPO/fVUFHjJTM57ugPaIPMzExOP/10hg4dSkJCAjk5OQfvmzRpEo8//jjDhg1j8ODBjBs3LiCvaYwxgSLayU6wGjNmjDZfmGbNmjXk5eW16fGqyrpdFcTGRNOva9LRHxCC2vN+jTEGQESWquqYlu6LuKYhESEl3kNlbT0NjZ0rBI0xJhgiLggAUhM8qCqVNV63SzHGGNcFLQhE5BkR2S0iK49wv4jIn0Rkg4h8KSKjglVLc0mx0URHCeU1gT/L2BhjOptgHhH8HZjUyv2TgYG+n2nAX4NYSxMiQmq8h4oaL52tj8QYYwItaEGgqguBva1sMgV4Th2fAmki0j1Y9TSXEh9DfaNSVdf6fEDGGBPu3OwjyAUK/a4X+W7rECnxMYgI5dZPYIyJcG4GQUtzPLTYTiMi00RkiYgsKS4uDsiLR0dFkRQbHZTZSI8mOTm5w1/TGGOOxM0gKAJ6+V3vCWxvaUNVna6qY1R1TFZWVsAKSE3wUFvfQI3XmoeMMZHLzTOL3wTuFJGXgVOAfaq6oyMLSI2PYTtQUeMl3hN9zM9z//3306dPH+644w4AHnroIUSEhQsXUlpaitfr5Ve/+hVTpkwJUOXGGBM4QQsCEXkJmAB0FZEi4BeAB0BVHwfmABcAG4Aq4JaAvPDbD8DOr9q0aSxwgrceQaC1IOh2Ekx++Ih3T506lXvuuedgEMyYMYN33nmHe++9l9TUVPbs2cO4ceO45JJLbM1hY0zICVoQqOq1R7lfge8H6/XbKiYqirr6RhR1AuEYjBw5kt27d7N9+3aKi4tJT0+ne/fu3HvvvSxcuJCoqCi2bdvGrl276NatW4DfgTHGHJ/wm3SulW/uLamvq2fT7kp6pSeSnhR7zC975ZVXMnPmTHbu3MnUqVN54YUXKC4uZunSpXg8Hvr27dvi9NPGGOO2iJxiwl+CJxpPdNRxDyOdOnUqL7/8MjNnzuTKK69k3759ZGdn4/F4eP/999m6dWuAKjbGmMAKvyOCdnImoYuhrMpLY6MSFXVszUMnnngiFRUV5Obm0r17d66//nouvvhixowZw4gRIxgyZEiAKzfGmMCI+CAAZ42Cvfvr2F9XT0q855if56uvDnVSd+3alUWLFrW4XWVl5TG/hjHGBFrENw0BJMfFECVCebWdZWyMiTwWBEBUlNM8VF5Tb5PQGWMiTtgEwfHuwFPiPXgbGkP+LGMLKmNMoIVFEMTHx1NSUnJcO8nUeKe7JJTXKFBVSkpKiI+Pd7sUY0wYCYvO4p49e1JUVMTxTkhXVlFL6TZlb2ro7mjj4+Pp2bOn22UYY8JIWASBx+OhX79+x/08CxZs5OG317LowXPo3iUhAJUZY0zoC4umoUApyMsGYP6a3S5XYowxHceCwM+ArGT6ZiYyf/Uut0sxxpgOY0HgR0QoyMth0cYSKmtDt9PYGGMCyYKgmYL8HOoaGvlwXWBWQjPGmFBnQdDMmD7pdEnwMG+NNQ8ZYyKDBUEzMdFRnDMkm/fX7qa+odHtcowxJuiCGgQiMklEvhaRDSLyQAv3p4vIbBH5UkQ+F5GhwaynrQryciit8rLsmzK3SzHGmKALWhCISDTwGDAZyAeuFZH8Zpv9GFihqsOAm4BHg1VPe4wf1BVPtDDfmoeMMREgmEcEY4ENqrpJVeuAl4Hmq7fnA+8CqOpaoK+I5ASxpjZJifcwrn+mDSM1xkSEYAZBLlDod73Id5u/L4DLAURkLNAHOGz+BBGZJiJLRGTJ8U4j0Vbn5uewac9+Nhbb2gHGmPAWzCBoaamv5rPCPQyki8gK4C5gOXDYAH5Vna6qY1R1TFZWVsALbcnEPOfAxI4KjDHhLphBUAT08rveE9juv4GqlqvqLao6AqePIAvYHMSa2iw3LYH87qnWT2CMCXvBDILFwEAR6SciscBU4E3/DUQkzXcfwK3AQlUtD2JN7VKQn8PSraWUVNa6XYoxxgRN0IJAVeuBO4G5wBpghqquEpHbReR232Z5wCoRWYszuujuYNVzLM7Ny6FR4f2v7SxjY0z4Cuo01Ko6B5jT7LbH/S4vAgYGs4bjMTQ3lZzUOOav3sWVo20NAGNMeLIzi1txYBK6heuLQ34JS2OMOVYWBEdRkJ9DVV0Dn24qcbsUY4wJCguCozi1fyaJsdE2esgYE7YsCI4i3hPNmQO7Mn/1blSbnwZhjDGdnwVBGxTk5bCzvIZV20NmZKsxxgSMBUEbnDMkGxGYZ2cZG2PCkAVBG2QmxzG6d7r1ExhjwpIFQRsV5Oewans528uq3S7FGGMCyoKgjQp8k9C9a0cFxpgwY0HQRgOykujXNYl5a3a7XYoxxgSUBUEbOWcZZ7No4x4qarxul2OMMQFjQdAOBXk5eBuUD9fvcbsUY4wJGAuCdhjdJ520RI8tVmOMCSsWBO0QEx3FOYOzee/r3dQ3NLpdjjHGBIQFQTsV5OdQVuVl6dZSt0sxxpiAsCBop/GDsoiNjuLdtTZ6yBgTHoIaBCIySUS+FpENIvJAC/d3EZG3ROQLEVklIrcEs55ASI6LYdyATOsnMMaEjaAFgYhEA4/hLEGZD1wrIvnNNvs+sFpVhwMTgN/7rWEcss7Ny2bTnv1sLK50uxRjjDluwTwiGAtsUNVNqloHvAxMabaNAikiIkAysBeoD2JNATHRd5axHRUYY8JBMIMgFyj0u17ku83fn3EWsN8OfAXcraqHDccRkWkiskRElhQXu7+QfI+0BE7skWqT0BljwkIwg0BauK35yi7nAyuAHsAI4M8iknrYg1Snq+oYVR2TlZUV6DqPycS8HJZuLaWkstbtUowx5rgEMwiKgF5+13vifPP3dwswSx0bgM3AkCDWFDDn5uXQqPD+1+4foRhjzPEIZhAsBgaKSD9fB/BU4M1m23wDTAQQkRxgMLApiDUFzNDcVHJS46yfwBjT6QUtCFS1HrgTmAusAWao6ioRuV1Ebvdt9kvgNBH5CngXuF9VO8VEPs4kdDksXF9MjbfB7XKMMeaYxQTzyVV1DjCn2W2P+13eDpwXzBqCqSA/hxc++4ZFm0o4e3C22+UYY8wxsTOLj8Op/TNJjI225iFjTKdmQXAc4j3RjB+Yxfw1u1BtPiDKGGM6BwuC41SQn8Ou8lpWbit3uxRjjDkmFgTH6ezBWUQJzLOTy4wxnZQFwXHKTI5jdJ906ycwxnRaFgQBUJCXw+od5Wwvq3a7FGOMaTcLggAoyHcmoXvXmoeMMZ2QBUEADMhKpn/XJOatscVqjDGdjwVBgBTk57Bo4x4qarxul2KMMe1iQRAgBXk5eBuUD9d3ihkyjDHmIAuCABnVO430RI+NHjLGdDoWBAESEx3F2UOyee/r3dQ3HLa2jjHGhCwLggAqyMuhrMrL0q2lbpdijDFtZkEQQOMHZREbHWVLWBpjOhULggBKjoth3IBM5q22SeiMMZ1HUINARCaJyNciskFEHmjh/vtEZIXvZ6WINIhIRjBrCrZz87LZUlLFxuL9bpdijDFtErQgEJFo4DFgMpAPXCsi+f7bqOrvVHWEqo4AHgQWqOreYNXUESbmOWcZW/OQMaazCOYRwVhgg6puUtU64GVgSivbXwu8FMR6OkSPtARO7JFqw0iNMZ1GMIMgFyj0u17ku+0wIpIITAJeO8L900RkiYgsKS4uDnihgVaQl8PSb0opqax1uxRjjDmqYAaBtHDbkXpQLwY+PlKzkKpOV9UxqjomKysrYAUGy7n5OajCe2tt7iFjTOgLZhAUAb38rvcEth9h26mEQbPQASf2SKVbarz1ExhjOoVgBsFiYKCI9BORWJyd/ZvNNxKRLsBZwBtBrKVDiQgF+dl8uH4PNd4Gt8sxxphWBS0IVLUeuBOYC6wBZqjqKhG5XURu99v0MuDfqhpW4y0L8nKoqmtg0aYSt0sxxphWtSkIRORuEUkVx9MiskxEzjva41R1jqoOUtUBqvo/vtseV9XH/bb5u6pOPfa3EJpOHZBJUmy0jR4yxoS8th4RfFtVy4HzgCzgFuDhoFUVBuJiohk/KIv5a+wsY2NMaGtrEBwYAXQB8DdV/YKWRwUZPwV5Oewqr2XltnK3SzHGmCNqaxAsFZF/4wTBXBFJAWyu5aM4e0g2UQLzbPSQMSaEtTUIvgM8AJysqlWAB6d5yLQiIymWMX0yrJ/AGBPS2hoEpwJfq2qZiNwA/BTYF7yywkdBfjard5Szraza7VKMMaZFbQ2CvwJVIjIc+BGwFXguaFWFkQLfJHTvWvOQMSZEtTUI6tUZ+jIFeFRVHwVSgldW+OiflUz/rknMs+YhY0yIamsQVIjIg8CNwL98U0x7gldWeCnIz+HTTSVU1HjdLsUYYw7T1iC4BqjFOZ9gJ84sor8LWlVhpiAvB2+DsnDdHrdLMcaYw7QpCHw7/xeALiJyEVCjqtZH0EajeqeRnuixSeiMMSGprVNMXA18DlwFXA18JiJXBrOwcBITHcXZQ7J5b+1u6hvs9AtjTGhpa9PQT3DOIfiWqt6Es/rYz4JXVvg5Ny+HfdVelmwtdbsUY4xpoq1BEKWq/quslLTjsQY4c1AWsdFRNozUGBNy2rozf0dE5orIzSJyM/AvYE7wygo/yXExnDogk3mrbRI6Y0xoaWtn8X3AdGAYMByYrqr3B7OwcFSQn8OWkio2FofV0gvGmE6uzc07qvqaqv6Hqt6rqrODWVS4KsjLBrDRQ8aYkNJqEIhIhYiUt/BTISJHnVtZRCaJyNciskFEHjjCNhNEZIWIrBKRBcf6RjqD7l0SGJqbytxVO615yBgTMloNAlVNUdXUFn5SVDW1tcf6zj5+DJgM5APXikh+s23SgL8Al6jqiTjDU8PaJcN7sPybMr7998XsrqhxuxxjjAnqyJ+xwAZV3aSqdcDLOHMV+bsOmKWq3wA0G5kUlm49oz8PXZzPJxtLOP+PC3ln5Q63SzLGRLhgBkEuUOh3vch3m79BQLqIfCAiS0XkppaeSESmicgSEVlSXFwcpHI7RlSUcPPp/fjXD86kZ3oitz+/jB/O+IJym4fIGOOSYAZBS0tZNm8YjwFGAxcC5wM/E5FBhz1IdbqqjlHVMVlZWYGv1AUnZCcz647T+ME5JzB7eRGTH/mQTzeVuF2WMSYCBTMIioBeftd7Attb2OYdVd2vqnuAhTjDUyOCJzqK/zhvMDO/dxqeaOHaJz/l13PWUFvf4HZpxpgIEswgWAwMFJF+IhILTAXebLbNG8CZIhIjIonAKcCaINYUkkb1TmfO3Wdy3djeTF+4iSl//pg1O2zBe2NMxwhaEKhqPXAnMBdn5z5DVVeJyO0icrtvmzXAO8CXOJPaPaWqK4NVUyhLjI3hfy47ib/dfDIl++u45M8f8fiCjTQ02jBTY0xwSWcbzz5mzBhdsmSJ22UE1d79dfxk9le8vXInY/tm8Purh9MrI9HtsowxnZiILFXVMS3dZxPHhaCMpFj+cv0o/nD1cNbsKGfSIwuZsaTQTkIzxgSFBUGIEhEuH9WTt+85k5N6duFHM79k2j+Wsqey1u3SjDFhxoIgxPVMT+TFW8fx0wvzWPB1MZMeWcj81TZXkTEmcCwIOoGoKOHWM/vz5l2nk5USz63PLeHBWV+yv7be7dKMMWHAgqATGdItlde/fxq3nzWAlxcXMvnRD1m6da/bZRljOjkLgk4mLiaaByYP4ZVpp9KoylWPL+J3c9dSV29rIRtjjo0FQSc1tl8G79wznqtG9+Kx9zdy2V8+Zt2uCrfLMsZ0QhYEnVhyXAy/vXIY028czc59NVz0fx/x9EebabST0Iwx7WBBEAbOO7Ebc+8dz/iBWfzyn6u54enP2FZW7XZZxphOwoIgTHRNjuPJm0bz2ytO4ovCMiY9spDZy4vsJDRjzFFZEIQREeGak3vz9t3jGZyTwr2vfMGdLy6nrKrO7dKMMSHMgiAM9c5M5JXvnsqPJg3m36t3ct4fF7JgXede0McYEzwWBGEqOkq4Y8IJzL7jdLokePjWM5/z8zdWUl1nax0YY5qyIAhzQ3O78NZdZ3DrGf14btFWLvzTh6woLHO7LGNMCLEgiADxnmh+elE+L952CjXeBq746yf8cd46vA12EpoxxoIgopw2oCtv3zOeKcN78Oi76zn/jwt57P0NFJVWuV2aMcZFQQ0CEZkkIl+LyAYReaCF+yeIyD4RWeH7+Xkw6zHQJcHDH64ZwRM3jqZrchy/m/s1Z/z2fa55YhGvLP6G8hqv2yUaYzpY0FYoE5FoYB1wLs4i9YuBa1V1td82E4D/VNWL2vq8kbBCWUcq3FvF68u3MXv5Njbt2U9sTBTn5uVw2chczhqchSfaDhqNCQetrVAWE8TXHQtsUNVNviJeBqYAq1t9lOlQvTISuWviQO485wS+KNrH7GVFvPXlDv711Q4ykmK5eFh3LhvVk+E9uyAibpdrjAmCYAZBLlDod70IOKWF7U4VkS+A7ThHB6uabyAi04BpAL179w5CqUZEGNErjRG90vjpRfksXFfMrOXbeGlxIc8u2kr/rklcOjKXy0bm2vrJxoSZYDYNXQWcr6q3+q7fCIxV1bv8tkkFGlW1UkQuAB5V1YGtPa81DXWs8hovb3+1g1nLtvHZZmftg5P7pnPZyJ5ceFJ3uiR6XK7QGNMWrTUNBTMITgUeUtXzfdcfBFDV37TymC3AGFXdc6RtLAjcU1RaxRsrtjNrWREbi/cTGx3FxLxsLhuZy4TB2cTGWH+CMaHKrSCIweksnghsw+ksvs6/6UdEugG7VFVFZCwwE+ijrRRlQeA+VWXltnJmLS/irS+2s6eyjrREDxcN685lI3syqnea9ScYE2Jc6SxW1XoRuROYC0QDz6jqKhG53Xf/48CVwPdEpB6oBqa2FgImNIgIJ/Xswkk9u/DjC/L4aP0eZi3fxqtLinj+02/om5l4sD+hT2aS2+UaY44iaEcEwWJHBKGrosbLOyt3Mnv5NhZtKkEVRvdJ59KRuVw8rDtpibFul2hMxHKlaShYLAg6h+1l1byxYjuzlxexblclnmjh7MHZXD4ql7OHZBMXE+12icZEFAsC4xpVZdX2cmYv38YbK7azp7KWLgkeLhzWnctH5jK6T7r1JxjTASwITEiob2jk440lzF5WxNxVu6j2NtArI4HJQ7szfmAWY/qmE++xIwVjgsGCwIScytp65q7cyesrtvHpphK8DUq8J4px/TM5c2AWZw3qyoCsZDtaMCZALAhMSNtfW89nm0tYuG4PC9cVs2nPfgB6dIln/KAszhyYxRkndLWT14w5DhYEplMp3FvFh+udUPh44x4qauqJEhjeK43xA7MYP6grw3umEROICfFKNsKKF2HNW3Dmf8Dwqcf/nMaEIAsC02nVNzTyRVEZC3xHC18WldGokBofw+kndOVMXzD0TG/H/Ee1FbDqdVjxAnyzCCQKUrpD5W646Q3oe3rQ3o8xbrEgAKjaCx/+Hs7+CcTapGmdVVlVHR9vKGHhumIWri9mx74aAPpnJTF+YBZnDcrilP4ZJMY2O1eysRG++QSWvwCrXwdvFWSeACOud44CPInwVAFUlcBt70FGv45/c8YEkQUBwFcz4bVbIedEuPo5yBwQ+OJMh1JVNhZXHjxa+GxzCTXeRmKjoxjTN53xg7I4p1sNA3e8hXzxEpRugdgUGHoZjLgBeo0F/87oko3w5DmQ0g2+82+I7+LaezMm0CwIDlg/H2bd6nw7vOxxGHJBYIszrqrxNrBkSymfrC1E17zF6RXvcFrUaqJEWZc4ivIhV9P3zKl0TU8/8pNsXgj/uAz6nw3XvQJRNpzVhAcLAn+lW2HGTbBjBZz5Q6epyP7YOz9VKFoMy5+HVbOhtpyG1F6s7XYJr9afwZtbPezdXwfAiT1SGT8oi/EDsxjdJ/3wWVOXPAP/vBfGfR8m/dqFN2NM4FkQNOetgbfvg2XPQf8JcMXTkNQ1IPWZDla+A7582Rn5s2ed09afP8Vp++9zOkQ5O/nGRucM54Xri1mwrphlW0upb1QSY6M5tX8mZw7sSu/MRFLjPaQmeMj99L9IWv4ketGjyJib3X2PxgSABcGRLHsO/vWfkJTl9Bv0HB2Y5zXBVV8LX7/tjPrZMB+0EXqNg5HXQ/6lEJ961KeoqPHy6aa9Bzudt5ZUNbk/mgae8fyO06JW8b2on7EuYQSpCTGkxntIiY85GBgHryd4SPX99r8/JS6GqCg7Kc64z4KgNduXO01FFTth0sMw5ttNOxBNaFCFHV84O/+vXoXqUkjpASOuheHXQdcTjuvpt5VVU1xRS3m1l/IaLxU19dRU7OXiJd8isW4vv+/zVzY35lBR46W8up7yGi/l1V721zUc9blT4poHhF9Q+N2WEu+hS4KHbl3i6dElgYRYa7I0gWNBcDRVe2HWbc63y+HXwYW/tyGmoWL/HvhyhhMAu1ZCdBwMudD59t//7OD37+zd5IwkSsqCW+cfNpKovqGRytr6Q+HgFxQVNfVNguXA5fLqeipqfb9rvDQe4U8wIymW7l3i6ZGWQG5aAj3S4uneJeHg9ayUOKLtaMO0kWtBICKTgEdxFqZ5SlUfPsJ2JwOfAteo6szWnjNoJ5Q1NsKC3zo/OUPhmucgo3/gX8ccXYMX1s9zdv7r3oHGeugxytn5D70CEloZ9RMMmz+Ef1wK/c6C62ZAdODWc1JV9tc1HAyJsiovO/fVsK2smu2+nx2+6xU19U0eGxMl5KTGHwyJHmkJdE9LINd3uUdaAqnxoTMtR2Ojsq/aS8n+Okqr6ti7v47S/XXsrfL93u+ltKrOud/3U9+oZKXEkZ0SR3ZqHNkp8WSlxB26LSWe7NQ4MhJjrQnuKNxaqjIaZ6nKc4EinKUqr1XV1S1sNw+owVnFzJ0gOGD9POd8A1W4fDoMnhS81zJN7V7jjPr58hXYX+x8Cx92jdPxm5Pvbm1Ln4W3fgCnfA8mt/h9JujKa7zsKKtxAmLfgaA4FBo799VQ3+zwIjku5mBIHDiS8D/KyEmNP6a1plWVytp6Svd7/Xbkvh+/6wd3+FVeyqrqjnj0k+CJJiMplvQkD+mJsWQkOT9RIhRX1LK7oobdFbUUl9dSUVt/2ONjooSuyQfCIo6slHjf7wMhcui6JxBTk3RCrixVCYwFNqjqJl8RLwNTgNXNtrsLeA04OYi1tN3Ac+G7C5x+g5eugfH3wYQHbYhpsFSXOW3+K16E7csgKgYGTYKRN8AJBRAdIt9oR38Lir+GTx+DrEFOX1IHS433kNrNw+BuKS3e39Co7KmsbXI0sd0vOL4s2ndwCO0BIpCVHHdY81N6kod9VV72VnmbfWs/tIP3NrS8V4+JEtKTYslIdHbsQ7qlkp7k8V13dvD+O/v0xNh29YdU1zWwu6LGFxC17C53QuLAT1FpNcu/KaOk2Xs9ICMp1i8k4g874jhw+bCz08NYMI8IrgQmqeqtvus3Aqeo6p1+2+QCLwLnAE8D/2zpiEBEpgHTAHr37j1669atQam5CW8NzPmh8w11wDlw+VOQlBn8140kmxfCqzc70zrkDHW++Q+7OnSH8jY2wIvXwKb34YZZ0P8stytqt+q6BnbsOxQQ28qqD7teW9/Y5DFpiU134ocuN/327nyjjyUlLiYkpg/3NjSyp7KW3eVOQPgfWewur6X4wFFGRe1hR1LgHE0dCIzkuEOh0PStyWG3+d994Hbxu7XJti3c39LFA59nQV42U0bkHuWdt8ytI4KW/ic0/7QfAe5X1YbW/uOo6nRgOjhNQ4EqsFWeeJjyGPQcC3Pug+lnwdXPQq4NMT1uqvDZ4zD3J85UH9e/6vQBhMDOo1VR0XDl0/D0ec4R423vdbqpShJio+mflUz/rOQW71dV9u6vo6zaS1qCM4opILO8usATHUX3Lgl075LQ6naNjUppVd2ho4ryQwFxIDx2VThzWvl/bz5w2X+H1NIX6yaP8dv6aI/Xwy7ASblHHxp9LIJ5RHAq8JCqnu+7/iCAqv7Gb5vNHAqMrkAVME1VXz/S87oy++i2ZTDjW1C5Eyb/L4y+OfR3WqHKW+2ctfvFSzD4ArjsiTaN+w8pezc7I4kSM52RRAlpbldkzFG1dkQQzKhfDAwUkX4iEgtMBd7030BV+6lqX1XtC8wE7mgtBFyTO8rpN+h7JvzzHnjjTmeHZtpnXxH8bbITAhMehGte6HwhAM7MpNc870xi9+rN0HB456UxnUnQgkBV64E7gbnAGmCGqq4SkdtF5PZgvW7QJGY4TRhn3Q8rnneaB/ZudruqzmPrJzB9AuxZD1NfhAkPHJz+oVPqezpc9Aenv2Dug25XY8xxsRPKjsW6fzuzmILTiTzoPHfrCWWqsORpePt+SOvjhED2ELerCpy5P4FFf3ZOQjz5VrerMeaI3GoaCl+DzoNpCyCtN7x4Fbz/a2dEiWmqvtYZe/+vHzojr257L7xCAODc/4aB58OcH8HG992uxphjYkFwrDL6wXfmOUMeF/wWXrjKmarCOMp3wN8vdCb2O/M/4dqXw7NTNSoarngKug6CV78Feza4XZEx7WZBcDw8Cc4Q04segS0fwhNnOZPYRbrCz53htrtWw1XPwsSfhfcJefGpcN3LzslwL13jTIhnTCdiQXC8RGDMLfDtdwCFp893piOIVEufhb9d4ITkrfPgxEvdrqhjpPd1RkGVbnWGGjd43a7ImDazIAiU3NFOv0Hf05128Te+H1lDTOvr4J//4bz3vmfAbe8760NHkj6nwsWPwuYF8M4DbldjTJtZEARSUiZcP9OZn2j58/DM+c5Y83BXuRueu8QZHXTaD5zPIDHD7arcMfJ65zNY/BR8/qTb1RjTJhYEgRYVDef8FK59BfZucfoN1s9zu6rg2bbU1zeywlny87xfBnSa5k6p4CEYNNkZMrvxPberMeaoLAiCZfAk+O4H0KWXM6Log4edNQ/CyYoX4ZnJTifpd/4NJ13pdkWhISoarngSsobAjJuheJ3bFRnTKguCYMro7+wgh18LH/wGXrw6PIaYNnidb7uvfw96jYVpH0D3YW5XFVriUuDal5xptF+6Jjz+3U3YsiAItthEuPQvcNEfnU7E6Wc5k9h1Vvv3wD8uc2YPHXcH3Pi6Tc99JOl9YOoLzhxLr9pIIhO6LAg6goizkMkt7zjNQ0+eDdPPho8fdYYbdhY7vnDmCyr83Jk1dNJvrD/gaHqPg4v/5Ky9MOe+pnMSGxMi7K+4I/UcDbd/CMuehVWvw7yfOz89RkL+pc6Y+/S+7tZ4JF++Cm/e5YwG+vY7zoyspm1GXAvFa+HjRyA7D075rtsVhZ76OijZAMVrYPfaQ789CXDWj2DIRTb1exDZpHNu2rsZVr8Bq18/dEZyqIVCQz3M/4UzsVrv05zFeZKz3a6q82lshFdugHVvO8NrT5jodkXuaPBCycbDd/h7N0KjbzpviXL617KGwJ51zk/Pk53RWH3PcLX8zsyVxeuDJayCwF/pFicUVr3urN0L0H2EEwj5lzpzG3W0qr0w8xbY9AGcfJuvKShE1hDujGornXNLygqds66zBrtdUfA01MPeTYfv8Es2QOOBvhJx/l9n5TmTER74nTnQWSHwwPOseMEZdVexHQaeBxN/Ad2GuvbWOisLgs6mdOuhI4VtS53bug8/dKSQ0T/4NexcCS9fBxU7nCmWR90U/NeMBGXfOKubxSY7s7F29hPvGhucI9vDdvjroeHA4vHidJw33+F3HeQ0/bSFtxo+ewI++gPUlDtrW5/949A4au4kLAg6s5ZCoduwQ0cKwVgzd9VseP0OiO8CV/8Dep0c+NeIZIWfOzOz9joFbpgFMbFuV3R0jQ3OUWvxWti9xvd7rdNs01B7aLu03i3v8GOTAlNHdSl89Igzaq2xAU7+jjO7bXJWYJ4/jLkWBCIyCXgUiAaeUtWHm90/Bfgl0AjUA/eo6ketPWfEBYG/sm8ONR9t830G3U7yHSlcdvyh0NgA7/3K+dbVcyxc8w9I6Xa8VZuWfPEKzJ4Go77lzE8UKh2h9XVQttVpwjm4w1/j7PDraw5t16WX04bfZIc/GOKSO6bO8u1Oc9Hy552jitPuglO/75y/YVrkShCISDSwDjgXKMJZw/haVV3tt00ysF9VVUSG4Sxn2erKJREdBP7KCg8dKRQtdm7LOQlOnAL5l0HXE9r3fNWl8NptsGEejL4ZJv8vxMQFumrjb/5/OaE76WEY972Oe90Gr/OlomSj00lbstFpz9+70bld/c6AT8317fDz/H4PDp0d7p718O5/w5o3IbGrM8Jo9C2d4yirg7kVBKcCD6nq+b7rDwKo6m9a2f4ZVc1r7XktCFpQVuj8Iax6HYo+d25rTyjsXuP0B5QVwgX/65zzYIKvsRFm3Ahfz4HrZsDAcwP33A31zjf7vZv9dva+32XfgPqtqBebApn9IWOAc1SZ0R8yT3B2+PFdAldTMBUtdUa3bfnQWRL1nJ/C0Cs797rYAeZWEFwJTFLVW33XbwROUdU7m213GfAbIBu4UFUXtfBc04BpAL179x69dWsnOgmro+0rOtR8dDAUhh7qaO46sOn2a/4Js78LnkS4+jlnKmXTcWor4ZlJzk77O/Pat5RnY4OzU9+7EUo2HfpWX7LReb4DwzHB6ZzO6Oe3s/f7ndQ1dJqmjocqbHwX5j8EO79yvgwV/AJOKAiP93ec3AqCq4DzmwXBWFW96wjbjwd+rqoFrT2vHRG0w74iWP2m03xU+JlzW/aJvo7mKbDyNWeZzdzRTqdwl1w3q41cZYW+kUSJcOt7TafsaGxw/h39m3AO/C7d4jcUEyfMMwb4vt33b7qzT86OnJ1hYyOsmgXv/dL5jPqc4ZyDEOGDHjpF05Bvm83Ayaq650jbWBAco33bDjUfFX566PYR18OFfzg0btu4o3CxM5Ko+zBnNNGBppzSLX7DMIGYBF/TTbOmnIwBTsd+pOzs26K+zjmLf8FvYX+xc3byxF9A1iC3K3OFW0EQg9NZPBHYhtNZfJ2qrvLb5gRgo6+zeBTwFtBTWynKgiAAyrc7TUJJmXDi5bbzCBVfvurM6BoV7du5+378m3KSu1m7d3vVVsKnf4GP/wTe/c6XnwkPRtwRsJvDRy8AHsEZPvqMqv6PiNwOoKqPi8j9wE2AF6gG7rPhoyai1VVBTLzt7INh/x748PfO6nESBWOnwRn3dv6T+trITigzxpgDSrfC+7+GL1+B+FQnDMZ+1+mjCTVVe6F0s2/012ZnssdjnKfKgsAYY5rbudI5B2H9XEjpDhMegBE3dOzU6qpQsdO3s9/k2+FvOnS9Zl/T7c+41+n4PgYWBMYYcyRbP4F5v3CGW2eeABN/DnmXBK7vrKEe9hU229lvdq6XbgFv1aFtJRrSekF6P18fke93ej9nXqXjOGppLQhsPQJjTGTrc5qzpOzXc5wjhBk3OUOqCx6CfuPb9hzeGmen3tI3+7Jvmp7TERPv7NTT+0H/s307+37O9bTerszwa0cExhhzQGMDfPESvP8bKC+CAROdk9K6D3eaaQ58k2/+zb58O+C3L41LPbRzb/7NPqW7K4MBrGnIGGPaw1sDi590RhlVl0JCBlTvbbpNUnbTHbz/5cSMkBuWbU1DxhjTHp54Z0bTkTc66yBUbG+2s+8bOhPvBYAFgTHGHElCGky43+0qgs7OWjHGmAhnQWCMMRHOgsAYYyKcBYExxkQ4CwJjjIlwFgTGGBPhLAiMMSbCWRAYY0yE63RTTIhIMXCsq9d3BY64DGYEss+jKfs8DrHPoqlw+Dz6qGpWS3d0uiA4HiKy5EhzbUQi+zyass/jEPssmgr3z8OahowxJsJZEBhjTISLtCCY7nYBIcY+j6bs8zjEPoumwvrziKg+AmOMMYeLtCMCY4wxzVgQGGNMhIuYIBCRSSLytYhsEJEH3K7HTSLSS0TeF5E1IrJKRO52uya3iUi0iCwXkX+6XYvbRCRNRGaKyFrf/5FT3a7JLSJyr+9vZKWIvCQi8W7XFAwREQQiEg08BkwG8oFrRSTf3apcVQ/8UFXzgHHA9yP88wC4G1jjdhEh4lHgHVUdAgwnQj8XEckFfgCMUdWhQDQw1d2qgiMiggAYC2xQ1U2qWge8DExxuSbXqOoOVV3mu1yB84ee625V7hGRnsCFwFNu1+I2EUkFxgNPA6hqnaqWuVqUu2KABBGJARKB7S7XExSREgS5QKHf9SIieMfnT0T6AiOBz1wuxU2PAD8CGl2uIxT0B4qBv/mayp4SkSS3i3KDqm4D/h/wDbAD2Keq/3a3quCIlCCQFm6L+HGzIpIMvAbco6rlbtfjBhG5CNitqkvdriVExACjgL+q6khgPxCRfWoiko7TctAP6AEkicgN7lYVHJESBEVAL7/rPQnTQ7y2EhEPTgi8oKqz3K7HRacDl4jIFpwmw3NE5Hl3S3JVEVCkqgeOEGfiBEMkKgA2q2qxqnqBWcBpLtcUFJESBIuBgSLST0RicTp83nS5JteIiOC0Aa9R1T+4XY+bVPVBVe2pqn1x/l+8p6ph+a2vLVR1J1AoIoN9N00EVrtYkpu+AcaJSKLvb2YiYdpxHuN2AR1BVetF5E5gLk7P/zOqusrlstx0OnAj8JWIrPDd9mNVneNeSSaE3AW84PvStAm4xeV6XKGqn4nITGAZzki75YTpVBM2xYQxxkS4SGkaMsYYcwQWBMYYE+EsCIwxJsJZEBhjTISzIDDGmAhnQWBMBxKRCTbDqQk1FgTGGBPhLAiMaYGI3CAin4vIChF5wrdeQaWI/F5ElonIuyKS5dt2hIh8KiJfishs3xw1iMgJIjJfRL7wPWaA7+mT/eb7f8F31qoxrrEgMKYZEckDrgFOV9URQANwPZAELFPVUcAC4Be+hzwH3K+qw4Cv/G5/AXhMVYfjzFGzw3f7SOAenLUx+uOc6W2MayJiiglj2mkiMBpY7PuyngDsxpmm+hXfNs8Ds0SkC5Cmqgt8tz8LvCoiKUCuqs4GUNUaAN/zfa6qRb7rK4C+wEdBf1fGHIEFgTGHE+BZVX2wyY0iP2u2XWvzs7TW3FPrd7kB+zs0LrOmIWMO9y5wpYhkA4hIhoj0wfl7udK3zXXAR6q6DygVkTN9t98ILPCt71AkIpf6niNORBI78k0Y01b2TcSYZlR1tYj8FPi3iEQBXuD7OIu0nCgiS4F9OP0IAN8CHvft6P1n67wReEJE/tv3HFd14Nswps1s9lFj2khEKlU12e06jAk0axoyxpgIZ0cExhgT4eyIwBhjIpwFgTHGRDgLAmOMiXAWBMYYE+EsCIwxJsL9f9fUNKLLY+8OAAAAAElFTkSuQmCC\n",
|
| 287 |
+
"text/plain": [
|
| 288 |
+
"<Figure size 432x288 with 1 Axes>"
|
| 289 |
+
]
|
| 290 |
+
},
|
| 291 |
+
"metadata": {
|
| 292 |
+
"needs_background": "light"
|
| 293 |
+
},
|
| 294 |
+
"output_type": "display_data"
|
| 295 |
+
}
|
| 296 |
+
],
|
| 297 |
+
"source": [
|
| 298 |
+
"# Printeamos las gráficas de acc y loss\n",
|
| 299 |
+
"print(history.history.keys())\n",
|
| 300 |
+
"\n",
|
| 301 |
+
"# acc\n",
|
| 302 |
+
"plt.plot(history.history['accuracy'])\n",
|
| 303 |
+
"plt.plot(history.history['val_accuracy'])\n",
|
| 304 |
+
"plt.title('model accuracy')\n",
|
| 305 |
+
"plt.ylabel('accuracy')\n",
|
| 306 |
+
"plt.xlabel('epoch')\n",
|
| 307 |
+
"plt.legend(['train', 'val'], loc='upper left')\n",
|
| 308 |
+
"plt.show()\n",
|
| 309 |
+
"\n",
|
| 310 |
+
"# loss\n",
|
| 311 |
+
"plt.plot(history.history['loss'])\n",
|
| 312 |
+
"plt.plot(history.history['val_loss'])\n",
|
| 313 |
+
"plt.title('model loss')\n",
|
| 314 |
+
"plt.ylabel('loss')\n",
|
| 315 |
+
"plt.xlabel('epoch')\n",
|
| 316 |
+
"plt.legend(['train', 'val'], loc='upper left')\n",
|
| 317 |
+
"plt.show()"
|
| 318 |
+
]
|
| 319 |
+
}
|
| 320 |
+
],
|
| 321 |
+
"metadata": {
|
| 322 |
+
"kernelspec": {
|
| 323 |
+
"display_name": "Python 3 (ipykernel)",
|
| 324 |
+
"language": "python",
|
| 325 |
+
"name": "python3"
|
| 326 |
+
},
|
| 327 |
+
"language_info": {
|
| 328 |
+
"codemirror_mode": {
|
| 329 |
+
"name": "ipython",
|
| 330 |
+
"version": 3
|
| 331 |
+
},
|
| 332 |
+
"file_extension": ".py",
|
| 333 |
+
"mimetype": "text/x-python",
|
| 334 |
+
"name": "python",
|
| 335 |
+
"nbconvert_exporter": "python",
|
| 336 |
+
"pygments_lexer": "ipython3",
|
| 337 |
+
"version": "3.9.12"
|
| 338 |
+
}
|
| 339 |
+
},
|
| 340 |
+
"nbformat": 4,
|
| 341 |
+
"nbformat_minor": 5
|
| 342 |
+
}
|
Code/image_classification_VGG19.ipynb
ADDED
|
The diff for this file is too large to render.
See raw diff
|
|
|
Code/split_folders.ipynb
ADDED
|
@@ -0,0 +1,37 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{
|
| 2 |
+
"cells": [
|
| 3 |
+
{
|
| 4 |
+
"cell_type": "code",
|
| 5 |
+
"execution_count": null,
|
| 6 |
+
"id": "e19390e2",
|
| 7 |
+
"metadata": {},
|
| 8 |
+
"outputs": [],
|
| 9 |
+
"source": [
|
| 10 |
+
"import splitfolders\n",
|
| 11 |
+
"\n",
|
| 12 |
+
"splitfolders.ratio('../../PBC_dataset_normal_DIB', output = \"../../PCB_Dataset_Split\", seed = 42, ratio = (0.8, 0.1, 0.1)) "
|
| 13 |
+
]
|
| 14 |
+
}
|
| 15 |
+
],
|
| 16 |
+
"metadata": {
|
| 17 |
+
"kernelspec": {
|
| 18 |
+
"display_name": "Python 3 (ipykernel)",
|
| 19 |
+
"language": "python",
|
| 20 |
+
"name": "python3"
|
| 21 |
+
},
|
| 22 |
+
"language_info": {
|
| 23 |
+
"codemirror_mode": {
|
| 24 |
+
"name": "ipython",
|
| 25 |
+
"version": 3
|
| 26 |
+
},
|
| 27 |
+
"file_extension": ".py",
|
| 28 |
+
"mimetype": "text/x-python",
|
| 29 |
+
"name": "python",
|
| 30 |
+
"nbconvert_exporter": "python",
|
| 31 |
+
"pygments_lexer": "ipython3",
|
| 32 |
+
"version": "3.9.12"
|
| 33 |
+
}
|
| 34 |
+
},
|
| 35 |
+
"nbformat": 4,
|
| 36 |
+
"nbformat_minor": 5
|
| 37 |
+
}
|
Code/test_model_CNN.ipynb
ADDED
|
@@ -0,0 +1,292 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{
|
| 2 |
+
"cells": [
|
| 3 |
+
{
|
| 4 |
+
"cell_type": "code",
|
| 5 |
+
"execution_count": 1,
|
| 6 |
+
"id": "8870f399",
|
| 7 |
+
"metadata": {},
|
| 8 |
+
"outputs": [],
|
| 9 |
+
"source": [
|
| 10 |
+
"from keras.models import load_model\n",
|
| 11 |
+
"from tensorflow.keras.utils import load_img\n",
|
| 12 |
+
"from keras.preprocessing.image import ImageDataGenerator\n",
|
| 13 |
+
"import matplotlib.pyplot as plt\n",
|
| 14 |
+
"\n",
|
| 15 |
+
"import numpy as np"
|
| 16 |
+
]
|
| 17 |
+
},
|
| 18 |
+
{
|
| 19 |
+
"cell_type": "code",
|
| 20 |
+
"execution_count": 2,
|
| 21 |
+
"id": "9a2915f5",
|
| 22 |
+
"metadata": {},
|
| 23 |
+
"outputs": [],
|
| 24 |
+
"source": [
|
| 25 |
+
"# Leemos el modelo guardado\n",
|
| 26 |
+
"model = load_model('../../model/classification/image_classification_CNN.h5')"
|
| 27 |
+
]
|
| 28 |
+
},
|
| 29 |
+
{
|
| 30 |
+
"cell_type": "code",
|
| 31 |
+
"execution_count": 3,
|
| 32 |
+
"id": "501c48e4",
|
| 33 |
+
"metadata": {},
|
| 34 |
+
"outputs": [],
|
| 35 |
+
"source": [
|
| 36 |
+
"test_data_dir = '../../dataset/classification/PCB_Dataset_Split/test'\n",
|
| 37 |
+
"size = (360, 363)\n",
|
| 38 |
+
"batch_size = 16"
|
| 39 |
+
]
|
| 40 |
+
},
|
| 41 |
+
{
|
| 42 |
+
"cell_type": "code",
|
| 43 |
+
"execution_count": 10,
|
| 44 |
+
"id": "ec6d2697",
|
| 45 |
+
"metadata": {},
|
| 46 |
+
"outputs": [],
|
| 47 |
+
"source": [
|
| 48 |
+
"# Leemos una imagen del conjunto de test \n",
|
| 49 |
+
"image = load_img('../../dataset/classification/PCB_Dataset_Split/val/neutrophil/BNE_191041.jpg', target_size = size)\n",
|
| 50 |
+
"img = np.array(image)\n",
|
| 51 |
+
"img = img / 255.0\n",
|
| 52 |
+
"img = img.reshape(1, 360, 363, 3)"
|
| 53 |
+
]
|
| 54 |
+
},
|
| 55 |
+
{
|
| 56 |
+
"cell_type": "code",
|
| 57 |
+
"execution_count": 11,
|
| 58 |
+
"id": "2c0b3968",
|
| 59 |
+
"metadata": {},
|
| 60 |
+
"outputs": [
|
| 61 |
+
{
|
| 62 |
+
"name": "stdout",
|
| 63 |
+
"output_type": "stream",
|
| 64 |
+
"text": [
|
| 65 |
+
"1/1 [==============================] - 0s 26ms/step\n"
|
| 66 |
+
]
|
| 67 |
+
}
|
| 68 |
+
],
|
| 69 |
+
"source": [
|
| 70 |
+
"# Predecimos la clase a la que pertenece\n",
|
| 71 |
+
"label = model.predict(img)"
|
| 72 |
+
]
|
| 73 |
+
},
|
| 74 |
+
{
|
| 75 |
+
"cell_type": "code",
|
| 76 |
+
"execution_count": 12,
|
| 77 |
+
"id": "fa8f3dfc",
|
| 78 |
+
"metadata": {},
|
| 79 |
+
"outputs": [
|
| 80 |
+
{
|
| 81 |
+
"name": "stdout",
|
| 82 |
+
"output_type": "stream",
|
| 83 |
+
"text": [
|
| 84 |
+
"neutrophil\n"
|
| 85 |
+
]
|
| 86 |
+
}
|
| 87 |
+
],
|
| 88 |
+
"source": [
|
| 89 |
+
"# Mapeamos la predicción con el nombre de la salida\n",
|
| 90 |
+
"label_names = ['basophil', 'eosinophil', 'erythroblast', 'ig', 'lymphocyte', 'monocyte', 'neutrophil', 'platelet']\n",
|
| 91 |
+
"print(label_names[np.argmax(label)])"
|
| 92 |
+
]
|
| 93 |
+
},
|
| 94 |
+
{
|
| 95 |
+
"cell_type": "code",
|
| 96 |
+
"execution_count": 13,
|
| 97 |
+
"id": "d0c66ac3",
|
| 98 |
+
"metadata": {},
|
| 99 |
+
"outputs": [
|
| 100 |
+
{
|
| 101 |
+
"data": {
|
| 102 |
+
"text/plain": [
|
| 103 |
+
"array([[6.6474173e-04, 4.9071365e-05, 1.1076842e-03, 2.6778722e-02,\n",
|
| 104 |
+
" 5.4529850e-05, 3.3029503e-06, 9.7134173e-01, 3.2414894e-07]],\n",
|
| 105 |
+
" dtype=float32)"
|
| 106 |
+
]
|
| 107 |
+
},
|
| 108 |
+
"execution_count": 13,
|
| 109 |
+
"metadata": {},
|
| 110 |
+
"output_type": "execute_result"
|
| 111 |
+
}
|
| 112 |
+
],
|
| 113 |
+
"source": [
|
| 114 |
+
"label"
|
| 115 |
+
]
|
| 116 |
+
},
|
| 117 |
+
{
|
| 118 |
+
"cell_type": "code",
|
| 119 |
+
"execution_count": 7,
|
| 120 |
+
"id": "adb21285",
|
| 121 |
+
"metadata": {},
|
| 122 |
+
"outputs": [
|
| 123 |
+
{
|
| 124 |
+
"name": "stdout",
|
| 125 |
+
"output_type": "stream",
|
| 126 |
+
"text": [
|
| 127 |
+
"Found 1716 images belonging to 8 classes.\n"
|
| 128 |
+
]
|
| 129 |
+
}
|
| 130 |
+
],
|
| 131 |
+
"source": [
|
| 132 |
+
"test_datagen = ImageDataGenerator(rescale = 1. / 255)\n",
|
| 133 |
+
"test_generator = test_datagen.flow_from_directory(test_data_dir,\n",
|
| 134 |
+
" target_size = size,\n",
|
| 135 |
+
" batch_size = batch_size,\n",
|
| 136 |
+
" shuffle = False,\n",
|
| 137 |
+
" class_mode = 'categorical')"
|
| 138 |
+
]
|
| 139 |
+
},
|
| 140 |
+
{
|
| 141 |
+
"cell_type": "code",
|
| 142 |
+
"execution_count": 9,
|
| 143 |
+
"id": "62499652",
|
| 144 |
+
"metadata": {},
|
| 145 |
+
"outputs": [
|
| 146 |
+
{
|
| 147 |
+
"name": "stderr",
|
| 148 |
+
"output_type": "stream",
|
| 149 |
+
"text": [
|
| 150 |
+
"C:\\Users\\shiru\\AppData\\Local\\Temp\\ipykernel_8692\\558093203.py:1: UserWarning: `Model.evaluate_generator` is deprecated and will be removed in a future version. Please use `Model.evaluate`, which supports generators.\n",
|
| 151 |
+
" test_score = model.evaluate_generator(test_generator, batch_size)\n"
|
| 152 |
+
]
|
| 153 |
+
},
|
| 154 |
+
{
|
| 155 |
+
"name": "stdout",
|
| 156 |
+
"output_type": "stream",
|
| 157 |
+
"text": [
|
| 158 |
+
"[INFO] accuracy: 98.44%\n",
|
| 159 |
+
"[INFO] Loss: 0.1844080686569214\n"
|
| 160 |
+
]
|
| 161 |
+
}
|
| 162 |
+
],
|
| 163 |
+
"source": [
|
| 164 |
+
"test_score = model.evaluate_generator(test_generator, batch_size)\n",
|
| 165 |
+
"\n",
|
| 166 |
+
"print(\"[INFO] accuracy: {:.2f}%\".format(test_score[1] * 100))\n",
|
| 167 |
+
"print(\"[INFO] Loss: \",test_score[0])"
|
| 168 |
+
]
|
| 169 |
+
},
|
| 170 |
+
{
|
| 171 |
+
"cell_type": "code",
|
| 172 |
+
"execution_count": 16,
|
| 173 |
+
"id": "3be33f81",
|
| 174 |
+
"metadata": {},
|
| 175 |
+
"outputs": [],
|
| 176 |
+
"source": [
|
| 177 |
+
"#Plot the confusion matrix. Set Normalize = True/False\n",
|
| 178 |
+
"\n",
|
| 179 |
+
"def plot_confusion_matrix(cm, classes, normalize=True, title='Confusion matrix', cmap=plt.cm.Blues):\n",
|
| 180 |
+
" \"\"\"\n",
|
| 181 |
+
" This function prints and plots the confusion matrix.\n",
|
| 182 |
+
" Normalization can be applied by setting `normalize=True`.\n",
|
| 183 |
+
" \"\"\"\n",
|
| 184 |
+
" plt.figure(figsize=(10,10))\n",
|
| 185 |
+
" plt.imshow(cm, interpolation='nearest', cmap=cmap)\n",
|
| 186 |
+
" plt.title(title)\n",
|
| 187 |
+
" plt.colorbar()\n",
|
| 188 |
+
" tick_marks = np.arange(len(classes))\n",
|
| 189 |
+
" plt.xticks(tick_marks, classes, rotation=45)\n",
|
| 190 |
+
" plt.yticks(tick_marks, classes)\n",
|
| 191 |
+
" \n",
|
| 192 |
+
" if normalize:\n",
|
| 193 |
+
" cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]\n",
|
| 194 |
+
" cm = np.around(cm, decimals=2)\n",
|
| 195 |
+
" cm[np.isnan(cm)] = 0.0\n",
|
| 196 |
+
" print(\"Normalized confusion matrix\")\n",
|
| 197 |
+
" else:\n",
|
| 198 |
+
" print('Confusion matrix, without normalization')\n",
|
| 199 |
+
" \n",
|
| 200 |
+
" thresh = cm.max() / 2.\n",
|
| 201 |
+
" for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):\n",
|
| 202 |
+
" plt.text(j, i, cm[i, j],\n",
|
| 203 |
+
" horizontalalignment=\"center\",\n",
|
| 204 |
+
" color=\"white\" if cm[i, j] > thresh else \"black\")\n",
|
| 205 |
+
" plt.tight_layout()\n",
|
| 206 |
+
" plt.ylabel('True label')\n",
|
| 207 |
+
" plt.xlabel('Predicted label')#Print the Target names"
|
| 208 |
+
]
|
| 209 |
+
},
|
| 210 |
+
{
|
| 211 |
+
"cell_type": "code",
|
| 212 |
+
"execution_count": 17,
|
| 213 |
+
"id": "dfba2244",
|
| 214 |
+
"metadata": {},
|
| 215 |
+
"outputs": [
|
| 216 |
+
{
|
| 217 |
+
"name": "stdout",
|
| 218 |
+
"output_type": "stream",
|
| 219 |
+
"text": [
|
| 220 |
+
"108/108 [==============================] - 10s 93ms/step\n",
|
| 221 |
+
"Confusion Matrix\n",
|
| 222 |
+
"Confusion matrix, without normalization\n"
|
| 223 |
+
]
|
| 224 |
+
},
|
| 225 |
+
{
|
| 226 |
+
"data": {
|
| 227 |
+
"image/png": "iVBORw0KGgoAAAANSUhEUgAAArQAAALGCAYAAAC01AIQAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/NK7nSAAAACXBIWXMAAAsTAAALEwEAmpwYAAB380lEQVR4nO3dd5xU5fXH8c8XVrBhwUoVRQUBFQTELvbeewUbMdEYW4z5aYw1McaosUZN7AVr7DUqFiwUsWIXDMWo2LEBy/n98dzFcYUFkZ27d+b75rUvZu7cuXOemdnZM+ee+1xFBGZmZmZmRdUs7wDMzMzMzH4OJ7RmZmZmVmhOaM3MzMys0JzQmpmZmVmhOaE1MzMzs0JzQmtmZmZmhVaTdwBmZmZm9tM1X2S5iGnf5B0G8c1HD0bElnnG4ITWzMzMrIBi2je07LJ73mHw7QsXLZl3DE5ozczMzApJIHePgntozczMzKzgnNCamZmZWaG55cDMzMysiARIeUfRJLhCa2ZmZmaF5oTWzMzMzArNLQdmZmZmReVZDgBXaM3MzMys4JzQmpmZmVmhueXAzMzMrKg8ywHgCq2ZmZmZFZwrtGZmZmaF5FPf1vGzYGZmZmaF5oTWzMzMzArNLQdmZmZmReWDwgBXaM3MzMys4JzQmpmZmVmhueXAzMzMrIiEZznI+FkwMzMzs0JzhdbMzMyskOSDwjKu0JqZmZlZoTmhNTMzM7NGI2l+ScMkvSjpVUmnZMtbS3pY0lvZ/4uX3Of3kt6W9IakLWb3GE5ozczMzIpKzfL/mb3vgI0jYnWgJ7ClpLWA44FHImIl4JHsOpK6AXsC3YEtgYslNW/oAZzQmpmZmVmjiWRydnW+7CeAHYCrs+VXAztml3cABkfEdxExBngbWLOhx3BCa2ZmZmY/x5KSRpT8DKq/gqTmkl4APgQejojngGUi4n2A7P+ls9XbAeNK7j4+WzZLnuXAzMzMrKiaxiwHkyKiT0MrREQt0FPSYsC/JfVoYPWZDSoa2r4rtGZmZmZWFhHxGTCE1Bv7gaQ2ANn/H2arjQc6lNytPTCxoe06oTUzMzMrJOV/QNgcHBQmaamsMoukBYBNgdeBu4AB2WoDgDuzy3cBe0pqKWl5YCVgWEOP4ZYDMzMzM2tMbYCrs5kKmgE3R8Q9kp4BbpZ0EPBfYDeAiHhV0s3AaGAacFjWsjBLTmjNzMzMrNFExEtAr5ks/xjYZBb3OQM4Y04fwwmtmZmZWRGJpnJQWO7cQ2tmZmZmheaE1szMzMwKzS0HZmZmZkU1Z6eerXh+FszMzMys0FyhNTMzMyskuUKb8bNgZmZmZoXmhNbMzMzMCs0tB2ZmZmZF1czz0IIrtGZmZmZWcE5ozczMzKzQ3HJgZmZmVkTCsxxk/CyYmZmZWaE5oTUzMzOzQnPLgZmZmVlRybMcgCu0ZmZmZlZwrtCamZmZFZJPfVvHz4KZmZmZFZoTWjMzMzMrNLccmJmZmRWVDwoDXKE1MzMzs4JzQmtmZmZmheaWAzMzM7Oi8iwHgCu0ZmZmZlZwrtCamZmZFZHkg8IyrtCamZmZWaE5oTUzMzOzQnPLgZmZmVlR+aAwwBVaMzMzMys4J7RmZmZmVmhuOTAzMzMrKs9yALhCa2ZmZmYF5wqtmZmZWSHJB4Vl/CyYmZmZWaE5oTUzMzOzQnPLgZmZmVlR+aAwwBVaMzMzMys4J7RmZmZmVmhuOTAzMzMrIuFZDjJ+FszMzMys0JzQmpmZmVmhueXAzMzMrJB8YoU6fhbMzMzMrNBcoTUzMzMrKs9DC7hCa2ZmZmYF54TWzCqepAUk3S3pc0m3/Izt7CPpoXkZWx4k3S9pQN5xmJnNK05ozazJkLS3pBGSJkt6P0u81psHm94VWAZYIiJ2m9uNRMT1EbH5PIjnByT1lxSSbq+3fPVs+ZA53M7Jkq6b3XoRsVVEXD2X4ZpZU6Jm+f80AU0jCjOrepKOBs4D/kRKPjsCFwM7zIPNLwe8GRHT5sG2GstHwDqSlihZNgB4c149gBJ/7ptZxfEHm5nlTtKiwKnAYRFxe0R8FRFTI+LuiPhttk5LSedJmpj9nCepZXZbf0njJR0j6cOsuntAdtspwEnAHlnl96D6lUxJnbJKaE12faCkdyV9KWmMpH1Klj9Vcr91JA3PWhmGS1qn5LYhkk6TNDTbzkOSlmzgaZgC3AHsmd2/ObA7cH295+rvksZJ+kLSSEnrZ8u3BP6vZJwvlsRxhqShwNfACtmyg7PbL5F0a8n2/yLpEclHmphZcTihNbOmYG1gfuDfDaxzArAW0BNYHVgTOLHk9mWBRYF2wEHARZIWj4g/kqq+N0XEwhHxr4YCkbQQcD6wVUS0AtYBXpjJeq2Be7N1lwDOAe6tV2HdGzgAWBpoARzb0GMD1wD7Z5e3AF4FJtZbZzjpOWgN3ADcImn+iHig3jhXL7nPfsAgoBXwXr3tHQOsliXr65OeuwEREbOJ1cyaAin/nybACa2ZNQVLAJNm0xKwD3BqRHwYER8Bp5AStTpTs9unRsR9wGSgy1zGMx3oIWmBiHg/Il6dyTrbAG9FxLURMS0ibgReB7YrWefKiHgzIr4BbiYlorMUEU8DrSV1ISW218xknesi4uPsMf8GtGT247wqIl7N7jO13va+BvYlJeTXAb+OiPGz2Z6ZWZPihNbMmoKPgSXrdvnPQlt+WF18L1s2Yxv1EuKvgYV/aiAR8RWwB3Ao8L6keyV1nYN46mJqV3L9f3MRz7XA4cBGzKRinbVVvJa1OXxGqko31MoAMK6hGyNiGPAuIFLibWZFIOV/QFgTactvGlGYWbV7BvgW2LGBdSaSDu6q05Ef746fU18BC5ZcX7b0xoh4MCI2A9qQqq6Xz0E8dTFNmMuY6lwL/Aq4L6uezpC1BPyO1Fu7eEQsBnxOSkQBZtUm0GD7gKTDSJXeicBxcx25mVlOnNCaWe4i4nPSgVsXSdpR0oKS5pO0laSzstVuBE6UtFR2cNVJpF3kc+MFYANJHbMD0n5fd4OkZSRtn/XSfkdqXaidyTbuA1bOphqrkbQH0A24Zy5jAiAixgAbknqG62sFTCPNiFAj6SRgkZLbPwA6/ZSZDCStDJxOajvYDzhOUs+5i97MLB9OaM2sSYiIc4CjSQd6fUTaTX446ch/SEnXCOAl4GXg+WzZ3DzWw8BN2bZG8sMktBnpQKmJwCek5PJXM9nGx8C22bofkyqb20bEpLmJqd62n4qImVWfHwTuJ03l9R6pql3aTlB30oiPJT0/u8fJWjyuA/4SES9GxFukmRKurZtBwsyauLwPCGsiB4XJB7KamZmZFU+zxTtFy43+kHcYfPvvg0dGRJ88Y3CF1szMzMwKraEjis3MzMysCfM5UBJXaM3MzMys0FyhNTMzMysg4QptHSe0ZdBqsdaxRJv2eYeRi9YLtsg7hNz4I8bMrLK9995YJk2a5I/7JsAJbRks0aY9J151d95h5GKfNTrmHUJu/K3ZzKyyrdsv1wP7rYQTWjMzM7MiEt4dmPFBYWZmZmZWaE5ozczMzKzQ3HJgZmZmVkjy8RoZV2jNzMzMrNBcoTUzMzMrKFdoE1dozczMzKzQnNCamZmZWaG55cDMzMysoNxykLhCa2ZmZmaF5oTWzMzMzArNLQdmZmZmBeWWg8QVWjMzMzMrNCe0ZmZmZlZobjkwMzMzKyJlP+YKrZmZmZkVmyu0ZmZmZgUk5IPCMq7QmpmZmVmhOaE1MzMzs0Jzy4GZmZlZQbnlIHGF1szMzMwKzQmtmZmZmRWaE9qCu+r033L0Vr35496bz1g24pF7OWmvzRi09vKMfe2lGcunTZ3Clacdy8n7bMEp+27JGyOfySPkRjd+3Di23Gxjeq3ajd6r9+CiC/6ed0hl9dCDD7Ba9y5077oifz3rzLzDKatfHHwgHdsuTe+ePfIOpeyq+XWv5rH7PV+dr3spSbn/NAVOaAtunW125TfnXv2DZe1W6MKvzvwHK/Vc8wfLn7xzMAAnX/8gR51/HTeffwbTp08vW6zl0rymhj+fdTajXh7NkKee4dJLLua10aPzDqssamtrOfKIw7jz7vsZ9dJobhl8Y9WMHWC/AQO5854H8g6j7Kr5da/msYPf89X6utuPOaEtuJV79WOhRRb9wbI2y6/Isst1/tG6E8e8xSp91gVgkdZLsmCrRXivpIJbKdq0aUOvXmsA0KpVK7p0XYWJEyfkHFV5DB82jM6dV2T5FVagRYsW7LbHntxz9515h1U2662/Aa1bt847jLKr5te9mscOfs9X6+teKu/qrCu0VnYdVlqFF558mNpp0/ho4jjee/1lPvng/bzDalTvjR3Liy+Oou+a/fIOpSwmTpxA+/YdZlxv1649EyZURzJfzar5da/msVczv+5WXyESWkmdJL1S5sfsL+meWdz2T0ndsstjJS1Zztjm1rrb7s7iSy/L6Qdsx03nnkLnVXvTvKZ53mE1msmTJ7PXHrty1tnnssgii+QdTllExI+WNZVvz9Z4qvl1r+axVzO/7laf56GdCxFxcN4xzI3mNTXsceRJM66fecjOLN1h+RwjajxTp05l7z12Zc+99mbHnXbOO5yyadeuPePHj5txfcKE8bRt2zbHiKwcqvl1r+axVzO/7hllP1aMCm2mRtLVkl6SdKukBSWdJGm4pFckXabs65mkIySNztYdnC1rLemObNmzklbLlp8s6VpJj0p6S9IhJY+5cPZYr0u6vmT7QyT1Kfsz8DN99+03fPfN1wCMfu5JmjWvoe3yK+Uc1bwXEfxy0MF06dqVI448Ou9wyqpP3768/fZbjB0zhilTpnDLTYPZZtvt8w7LGlk1v+7VPPZq5tfd6itShbYLcFBEDJV0BfAr4MKIOBVA0rXAtsDdwPHA8hHxnaTFsvufAoyKiB0lbQxcA/TMblsNWAtYCBgl6d5seS+gOzARGAqsCzzVqKP8iS77w6958/lnmfzZp/x2u7XY/pCjWGiRRbnxbycz+bNPOP/oA+mw8ioc9fdr+fKTSZx35AAksfhSy3LQH8/JO/xG8czTQ7nh+mvp0WNV+vXpBcApp53BllttnXNkja+mpoZz/34h222zBbW1tQwYeCDdunfPO6yy2X/fvXjy8SFMmjSJzp3a84eTTmHggQflHVajq+bXvZrHDn7PV+vrbj+mmfWhNDWSOgFPRETH7PrGwBHAtcBxwIJAa+CCiDhT0gPAZOAO4I6ImCxpFLBLRLybbWMc0AM4CmgWESdly68Bbgc+A06IiM2y5ZcAQyPiOklDgGMjYoSksUCfiJhUL+ZBwCCA1su26/2XO4Y2xlPT5O2zRse8Q8iN+7nMzCrbuv36MHLkiNw+7GuWXCEW2/ZPeT38DB9fvdfIiMh1z3WRWg7qZ94BXAzsGhGrApcD82e3bQNcBPQGRkqqYeZdJlHv//rLvytZVstPqGhHxGUR0Sci+rRarPqmVDEzMzMrlyIltB0lrZ1d3ovvd/1PkrQwsCuApGZAh4h4jFS9XQxYGHgC2Cdbpz8wKSK+yLaxg6T5JS0B9AeGN/ZgzMzMzH4Okf8ctE1lb2SRemhfAwZIuhR4C7gEWBx4GRjL90loc+A6SYuSqrLnRsRnkk4GrpT0EvA1MKBk28OAe4GOwGkRMVHSyo0/JDMzMzP7uQqR0EbEWKDbTG46Mfupb72ZbOMTYIdZPMSbETGo3vpDgCEl1w8vudy/5HKnWcVtZmZmZo2vEAmtmZmZmf1YU9nln7eqT2gj4uS8YzAzMzOzuVekg8LMzMzMzH6k6iu0ZmZmZoXljgPAFVozMzMza0SSOkh6TNJrkl6V9Jts+cmSJkh6IfvZuuQ+v5f0tqQ3JG0xu8dwhdbMzMzMGtM04JiIeF5SK9JJrx7Objs3Is4uXVlSN2BPoDvQFviPpJUjonZWD+CE1szMzKyIVIxZDiLifeD97PKXkl4D2jVwlx2AwRHxHTBG0tvAmsAzs7qDWw7MzMzMrCwkdQJ6Ac9liw6X9JKkKyQtni1rB4wrudt4Gk6AndCamZmZFVXep73NKsRLShpR8jNoFrEuDNwGHBkRX5DO+toZ6Emq4P6tbtWZ3D0aeh7ccmBmZmZmP8ekiOjT0AqS5iMls9dHxO0AEfFBye2XA/dkV8cDHUru3h6Y2ND2XaE1MzMzs0ajVMb9F/BaRJxTsrxNyWo7Aa9kl+8C9pTUUtLywErAsIYewxVaMzMzs4IqwkFhwLrAfsDLkl7Ilv0fsJeknqR2grHALwAi4lVJNwOjSTMkHNbQDAfghNbMzMzMGlFEPMXM+2Lva+A+ZwBnzOljuOXAzMzMzArNFVozMzOzAhIqSstBo3OF1szMzMwKzRVaMzMzs6JygRZwhdbMzMzMCs4JrZmZmZkVmlsOzMzMzIpIhZmHttG5QmtmZmZmheaE1szMzMwKzS0HZmZmZgXlloPEFVozMzMzKzRXaM3MzMwKyhXaxBVaMzMzMys0V2jLYIkFW7Bv7+XyDiMXi/c9PO8QcvPp8AvzDsHMzKwqOKE1MzMzKyp3HABuOTAzMzOzgnNCa2ZmZmaF5pYDMzMzs4LyLAeJK7RmZmZmVmiu0JqZmZkVkCRXaDOu0JqZmZlZoTmhNTMzM7NCc8uBmZmZWUG55SBxhdbMzMzMCs0JrZmZmZkVmlsOzMzMzArKLQeJK7RmZmZmVmhOaM3MzMys0NxyYGZmZlZU7jgAXKE1MzMzs4JzhdbMzMysoHxQWOIKrZmZmZkVmhNaMzMzMys0txyYmZmZFZHcclDHFVozMzMzKzQntGZmZmZWaG45MDMzMysgAe44SFyhNTMzM7NCc0JbwR568AFW696F7l1X5K9nnZl3OPNcyxY1PHntsTx30/GMvPUETjx0awB23rQXI289ga9Gns8a3TrOWH/jfl0Zev1xDL/5/xh6/XFs2HflvEJvNL84+EA6tl2a3j175B1KLir9Pd8Qj91j99irkZDy/2kKnNBWqNraWo484jDuvPt+Rr00mlsG38hro0fnHdY89d2UaWw56Hz67XEm/fb8M5uv0401V+3Eq+9MZM9jLuep59/5wfoffzaZXY+8lL67/4lDTrqWK07fP6fIG89+AwZy5z0P5B1GLqrhPT8rHrvH7rFXz9ht5pzQVqjhw4bRufOKLL/CCrRo0YLd9tiTe+6+M++w5rmvvpkCwHw1zampaU5E8MaYD3jrvQ9/tO6Lb4zn/Y8+B2D0O+/TssV8tJivstrI11t/A1q3bp13GLmolvf8zHjsHrvHXj1jt5lzQluhJk6cQPv2HWZcb9euPRMmTMgxosbRrJl4dvDx/PeRM3n02dcZ/sp7c3S/nTbtyYtvjGPK1GmNHKGVS7W852fGY/fYwWOvlrHXJ+X/0xQUPqGVdKqkTefxNvtLumcWt/1TUrfs8lhJS87Lx55XIuJHy5pKn8u8NH16sNaeZ7LiFifSp8dydOvcZrb3WWWFZTn9iB04/PTBZYjQyqVa3vMz47H/kMde+ap57DZzhd/fGhEnlfnxDi7n482tdu3aM378uBnXJ0wYT9u2bXOMqHF9PvkbnhjxFpuv043R77w/y/XaLb0YN50ziIP/cC1jxk8qY4TW2KrtPV/KY/fYwWOvlrHbzOVeoZW0r6Rhkl6QdKmk5pL2kvSypFck/SVbr7mkq7JlL0s6Klt+laRds8tjJZ0i6flsna7Z8taS7pD0kqRnJa2WLT9Z0rWSHpX0lqRDSkJbWNKtkl6XdL2yr36ShkjqU9YnaS706duXt99+i7FjxjBlyhRuuWkw22y7fd5hzVNLLr4wiy68AADzt5yPjft14Y2xH8xy/UUXXoDbLziUky64i2defLdcYVqZVMN7flY8do/dY6+esdeX9wwHTaUynmuFVtIqwB7AuhExVdLFwD7A6UBv4FPgIUk7AuOAdhHRI7vvYrPY7KSIWEPSr4BjgYOBU4BREbGjpI2Ba4Ce2fqrAWsBCwGjJN2bLe8FdAcmAkOBdYGnfsLYBgGDADp07Dibtee9mpoazv37hWy3zRbU1tYyYOCBdOvevexxNKZll1yEy0/dj+bNmtGsmbjt4ee5/8lX2H6j1Tjnd7ux5OILc/v5h/LSGxPY/rCLOHTPDejcYSmOP2RLjj9kSwC2++WFfPTp5JxHMu/sv+9ePPn4ECZNmkTnTu35w0mnMPDAg/IOqyyq4T0/Kx67x+6xV8/YbeY0sz6Usj24dDjwf0DdIekLAF8DL0fE/tk6B5ESy9OAEcB9wL3AQxExXdJVwD0RcauksaTkeIKkfsAZEbGppFHALhHxbrbNcUAP4CigWV3bgqRrgNuBz4ATImKzbPklwNCIuE7SEODYiBiRPV6fiGhw33Xv3n1i6HMjfuazVUyL9z087xBy8+nwC/MOwczMGtG6/fowcuSI3EqU87dZOToNuCCvh5/hjb9sOTIict17nXfLgYCrI6Jn9tOFVE39kYj4FFgdGAIcBvxzFtv8Lvu/lu8r0DN7s0W9/+sv/65kWem2zMzMzKwJyTuhfQTYVdLSkHpdgVHAhpKWlNQc2At4PJtNoFlE3Ab8AVjjJzzOE6RWBiT1J7UlfJHdtoOk+SUtAfQHhv/sUZmZmZlZ2eRadYyI0ZJOJPXJNgOmkqqvvwceI1VW74uIOyWtDlyZrUe2zpw6ObvvS6SWhgEltw0jtTB0BE6LiImSKu+cqGZmZlZRRJqP3ZrAbvSIuAm4qd7iZ4Eb6q33IjOpykbEwJLLnUoujyBVXImIT4AdZhHCmxExqN42h5BaG+quH15yuf/MHs/MzMzM8pF3y4GZmZmZ2c+Se4U2TxFxct4xmJmZmc2tJjINbO5coTUzMzOzQnNCa2ZmZmaFVtUtB2ZmZmZF1lROPZs3V2jNzMzMrNBcoTUzMzMrIvmgsDqu0JqZmZlZoTmhNTMzM7NCc8uBmZmZWQEJHxRWxxVaMzMzMys0J7RmZmZmVmhuOTAzMzMrJLnlIOMKrZmZmZkVmiu0ZmZmZgXlAm3iCq2ZmZmZFZoTWjMzMzMrNLccmJmZmRWUDwpLXKE1MzMzs0JzQmtmZmZmheaWAzMzM7Mikmc5qOMKrZmZmZkVmiu0ZmZmZgUkfFBYHVdozczMzKzQnNCamZmZWaG55cAa1afDL8w7hNyc+chbeYeQm2M27Jx3CLlp3qy6d/81q+Lx106PvEPITbW/7/PkjoPEFVozMzMzKzQntGZmZmZWaG45MDMzMysoz3KQuEJrZmZmZoXmCq2ZmZlZQblAm7hCa2ZmZmaF5oTWzMzMzArNLQdmZmZmRSQfFFbHFVozMzMzKzQntGZmZmZWaG45MDMzMysg4VkO6rhCa2ZmZmaF5oTWzMzMzArNLQdmZmZmhSTPcpBxhdbMzMzMCs0VWjMzM7OCcoE2cYXWzMzMzArNCa2ZmZmZFZpbDszMzMwKygeFJa7QmpmZmVmhOaE1MzMzs0Jzy4GZmZlZEcmzHNRxhdbMzMzMCs0VWjMzM7MCEj4orI4rtBXsoQcfYLXuXejedUX+etaZeYdTVpU+9jvP+T1/3WMtLv7FNj+67elb/8UpW67M159/AsDXX3zK1cftx5927Ml9F51S7lDL6sLzz2PNNValX+/VOGD/vfn222/zDqksvv32WzZYtx/9+vSkT88enH7qH/MOqawq/fd9dmpra1lnzTXYdcft8g6lrKr9dbcfckJboWpraznyiMO48+77GfXSaG4ZfCOvjR6dd1hlUQ1j77nZzux7+r9+tPzzj97n3eeHsujSbWcsq2nRko32/w2bH/K7coZYdhMnTODSiy/g8aHDeG7kS0yvreW2WwbnHVZZtGzZkvsefITnRrzAM8NH8fBDDzLsuWfzDqssquH3fXYuvuDvdOm6St5hlJVf92KR1EHSY5Jek/SqpN9ky1tLeljSW9n/i5fc5/eS3pb0hqQtZvcYTmgr1PBhw+jceUWWX2EFWrRowW577Mk9d9+Zd1hlUQ1jX27VvizQatEfLX/w0j+x6cG/Je2ISlrMvyAde/ShZr6WZYwwH9OmTeObb75h2rRpfP3N1yzbpu3s71QBJLHwwgsDMHXqVKZOnVo1uyGr4fe9IRPGj+eB++9jwAEH5R1KWVX7615KUu4/c2AacExErAKsBRwmqRtwPPBIRKwEPJJdJ7ttT6A7sCVwsaTmDT2AE9oKNXHiBNq37zDjert27ZkwYUKOEZVPtY79jWceodUSy7DsCtVVqanTtl07fn3kMXRfuRMrLd+ORRZZlE023TzvsMqmtraWtfr2olP7Zdh4k03pu2a/vEMqi2r9fa9z3LFHcfqf/0KzZtX157zaX/eiiYj3I+L57PKXwGtAO2AH4OpstauBHbPLOwCDI+K7iBgDvA2s2dBjNNnfAEn/V3K5k6RXfub2xkpacibLT5Z07Fxsr6ekrX9OTI0pIn60rFoqNtU49qnffsOTgy9ho/1/k3coufn000+57567ePm1d3jz3fF8/dVXDL7xurzDKpvmzZvz7PBRvPnuOEaOGM6rr/6sj8zCqMbf9zr333sPSy21FL3W6J13KGVXza97E7WkpBElP4NmtaKkTkAv4DlgmYh4H1LSCyydrdYOGFdyt/HZslnKNaGdTfn4/xq4bVbbK+esDT2BJpvQtmvXnvHjv38vTJgwnrZtq2P3azWO/ZP3/8un/xvPP365PeftvxFfTPoflx6+E5M/+Sjv0MpmyKP/YblOnVhyqaWYb7752G7HnXju2WfyDqvsFltsMdbfYEMefvCBvEMpi2r8fa/z7DNDue/eu+m28vIM3G8vHh/yKAcN3C/vsMqiml/3+qT8f4BJEdGn5OeymceqhYHbgCMj4ouGhjWTZT/+FlOiURNaSftKGibpBUmXSmouabKkUyU9B5wo6d8l628m6XZJZwILZPe7Pru5uaTLs2bihyQtkN1niKQ/SXoc+I2kTSSNkvSypCsklTYO/jaLZ5ikFWcS7yGShkt6UdJtkhbMlu8m6ZVs+ROSWgCnAntkMe7RSE/hXOvTty9vv/0WY8eMYcqUKdxy02C22Xb7vMMqi2oc+zLLd+G3Nz3Lkdc8xpHXPMYiSy7LLy78Nwu3Xirv0MqmfYeODB/2HF9//TURweOPPUqXLtXRfvHRRx/x2WefAfDNN9/w2KOP0KVL13yDKpNq/H2vc8rpf+bNd8cx+s0xXHXtjWzYf2P+ddW1eYdVFtX8uheVpPlIyez1EXF7tvgDSW2y29sAH2bLxwMdSu7eHpjY0PYbraIpaRVgD2DdiJgq6WJgH2Ah4JWIOElp/8BrkpaKiI+AA4ArI+JuSYdHRM9sW52AlYC9IuIQSTcDuwB1+xMXi4gNJc0PvAVsEhFvSroG+CVwXrbeFxGxpqT9s2Xb1gv79oi4PHvM04GDgAuAk4AtImKCpMUiYoqkk4A+EXH4LMY/CBgE0KFjx7l8FudeTU0N5/79QrbbZgtqa2sZMPBAunXvXvY48lANY7/tz0cx9qVhfP3Fp5yz7/r03/cI1thyt1muf97+G/Hd15OpnTaV15/5D/udcSVLLfej73SF1nfNfuyw0y6sv3YfampqWG31nhxw0CF5h1UW//vf+ww6aCC1tbVMnz6dXXbdja22qf/xVpmq4ffdfsyv+/eK0GqR5Xv/Al6LiHNKbroLGACcmf1/Z8nyGySdA7Ql5YDDGnyMmfWhzAuSDie1DdRl2wsANwInAi0jojZb7wTga+BKYBSwUkRMkzQ5IhbO1ukEPJwdBYek3wHzRcTpkoYAf4yIxyWtDlwQERtk620CHBYRO0saC2wcEe9m3xL+FxFLSDoZmBwRZ0vaEDgdWAxYGHgwIg6V9A+gM3AzKen9WNJAGkhoS/Xu3SeGPjdibp9KK6gzH3kr7xByc8yGnfMOITfNmzX9Py6NqVkVj792euP8PS2Can3fr9uvDyNHjsht8K06dI3ex1yR18PP8PhR646MiD6zul3SesCTwMvA9Gzx/5H6aG8GOgL/BXaLiE+y+5wAHEiaIeHIiLi/oRgas+dUwNUR8fsfLJSOrUtmM1cCdwPfArdExLRZbO+7ksu1pAS5zlclj9mQmMXlOlcBO0bEi1nC2h8gS2r7AdsAL0jqOZvHMTMzMzMgIp5i1jnaJrO4zxnAGXP6GI3ZQ/sIsKukpWHG5LnL1V8pIiaS+iJOJCWUdaZmldSf4nWgU0l/7H7A4yW371Hy/8yOFmkFvJ897j51CyV1jojnIuIkYBKpr+PLbH0zMzOz8msCB4Q1lY6HRktoI2I0KUl9SNJLwMNAm1msfj0wLrtPncuAl0oOCpuTx/yW1Id7i6S6svY/SlZpmR2M9hvgqJls4g+k8vfDpOS4zl+zg8xeAZ4AXgQeA7o11YPCzMzMzKpFo05zFRE3ATfVW7zwTFZdD7i83n1/B5Seq7NHyW1nl1zuX+9+j5DmN6sfS6fs4in1lp9ccvkS4JKZ3HfnmcT8CdB3JsvNzMzMrIzKOW/rTEkaSeqBPSbvWMzMzMyKQszxqWcrXu4JbURU3ylOzMzMzGyeabKnvjUzMzMzmxO5V2jNzMzMbO644yBxhdbMzMzMCs0VWjMzM7OCauYSLeAKrZmZmZkVnBNaMzMzMys0txyYmZmZFZQ7DhJXaM3MzMys0JzQmpmZmVmhueXAzMzMrIAkfOrbjCu0ZmZmZlZortCamZmZFVQzF2gBV2jNzMzMrOCc0JqZmZlZobnlwMzMzKygfFBY4gqtmZmZmRWaE1ozMzMzKzS3HJiZmZkVlDsOEldozczMzKzQXKE1MzMzKyABwiVacIXWzMzMzArOCa2ZmZmZFZpbDszMzMwKyqe+TZzQlkEAtdMj7zByUc2/aMdvslLeIeRmyb2vyjuE3Ey6YWDeIeTq2ym1eYeQmxY13ulplhf/9pmZmZlZoblCa2ZmZlZEkk99m3GF1szMzMwKzRVaMzMzs4JygTZxhdbMzMzMCs0JrZmZmZkVmlsOzMzMzApIQDP3HACu0JqZmZlZwTmhNTMzM7NCc8uBmZmZWUG54yBxhdbMzMzMCs0JrZmZmZkVmlsOzMzMzArKp75NXKE1MzMzs0JzhdbMzMysgCQfFFbHFVozMzMzKzQntGZmZmZWaG45MDMzMyson/o2cYXWzMzMzArNCa2ZmZmZFZpbDszMzMwKyg0HiSu0ZmZmZlZortCamZmZFZTPFJa4QmtmZmZmheaEtsLV1tayzpprsOuO2+UdStmMHzeOLTfbmF6rdqP36j246IK/5x1S2fzi4APp2HZpevfskXcojabdEgty30lbMPKcHRn+tx341VarzLjt0C278vx5OzH8bztw2j69Adh9vRV4+qztZ/x8MXgAqy7XOq/wG81DDz7Aat270L3rivz1rDPzDqfRHX7oway0XBvW7rP6jGVnnHoS667Zi/XX6s3O223J++9PzDHCxvftt9+ywbr96NenJ3169uD0U/+Yd0hlVW3veWuYE9oKd/EFf6dL11Vmv2IFaV5Tw5/POptRL49myFPPcOklF/Pa6NF5h1UW+w0YyJ33PJB3GI1qWm3w+2uH0/voO9johHs5ZIuudG23KBt0X5Zt+nRkrWPvpO8xd3L+3a8CcPNT77LOcXexznF3ccgFT/DeR5N5+b1Pch7FvFVbW8uRRxzGnXffz6iXRnPL4Bsr/j2/1777c+sd9/5g2a+PPJahw0bx5LMj2WKrbTjrz6fnFF15tGzZkvsefITnRrzAM8NH8fBDDzLsuWfzDqssqvE9PzMCmin/n6bACW0FmzB+PA/cfx8DDjgo71DKqk2bNvTqtQYArVq1okvXVZg4cULOUZXHeutvQOvWlVd9LPXBZ9/w4piUkE7+dhpvTPicNq0X5ODNu/C3O19myrTpAHz0xbc/uu+u663ArUPfLWu85TB82DA6d16R5VdYgRYtWrDbHntyz9135h1Wo1p3vQ1YvN57fZFFFplx+auvvqr43kJJLLzwwgBMnTqVqVOnVvyY61Tje94a5oS2gh137FGc/ue/0KxZ9b7M740dy4svjqLvmv3yDsUaQcelFmb15Vsz4u1JrNhmUdbtugyPnbEND5y8JWt0XuJH6++ydiduGTomh0gb18SJE2jfvsOM6+3atWfChOr4ElffaSefSPeVO3HLTTfyfyeenHc4ja62tpa1+vaiU/tl2HiTTavms87veauvejOdn0jS03nH8FPcf+89LLXUUvRao3feoeRm8uTJ7LXHrpx19rk/qNxYZVioZQ3XH9Of3101jC+/mUpNM7HYwi3Y6IR7OeHaEVxzVP8frN9nxSX5Zkoto8d9lke4jSoifrSsWip19f3h5NN59c2x7LbHXlx+6UV5h9PomjdvzrPDR/Hmu+MYOWI4r776St4hlYXf8xkJNYGfpsAJ7RyKiHXyjuGnePaZodx37910W3l5Bu63F48PeZSDBu6Xd1hlM3XqVPbeY1f23Gtvdtxp57zDsXmsprm4/piNuOnJd7lr2H8BmPDJ19z1XLo88p1JTJ8eLNmq5Yz77Lru8txSge0GkKpT48ePm3F9woTxtG3bNseI8rfrHntx1x3/zjuMsllsscVYf4MNefjByu6hr+P3vNXnhHYOSZqc/d9M0sWSXpV0j6T7JO2ad3z1nXL6n3nz3XGMfnMMV117Ixv235h/XXVt3mGVRUTwy0EH06VrV4448ui8w7FGcPGh6/LGhM+58N7vDwK5Z/h/2bDHsgCs2GYRWtQ0Z9KX3wEgwU5rdeLWCmw3AOjTty9vv/0WY8eMYcqUKdxy02C22Xb7vMMqu3fefmvG5QfuvZuVu3TJMZrG99FHH/HZZ58B8M033/DYo4/QpUvXfIMqE7/nvyfl/9MU+MQKP93OQCdgVWBp4DXgivorSRoEDALo0LFjGcOzZ54eyg3XX0uPHqvSr08vAE457Qy23GrrnCNrfPvvuxdPPj6ESZMm0blTe/5w0ikMPLCyDgpcu8vS7L3hirzy3ic8fVb6A3byjSO55tG3uORX6zLs7B2YMm06v7joyRn3WW+VZZnw8deM/XByXmE3qpqaGs79+4Vst80W1NbWMmDggXTr3j3vsBrVQQP2YeiTj/Pxx5PovtJyHH/iH3n4wft56803adasGR06duSc8y/OO8xG9b//vc+ggwZSW1vL9OnT2WXX3dhqm23zDqssqvE9bw3TzPpQ7MckTY6IhSWdB7wYEVdmy28HboiIW2d13zV694knnxlepkiblqYynUcemkpfUR6W3PuqvEPIzaQbBuYdQq6+nVKbdwi5aVFTvTs9m1Xph/26/fowcuSI3Aa/xArdY+vTbsjr4We4bt+eIyOiT54xuEL701Xnb62ZmZk1OdVcPClVvV8n595TwC5ZL+0yQP+c4zEzMzOraq7Q/nS3AZsArwBvAs8Bn+cakZmZmVkVc0I7hyJi4ez/6ZKOjYjJkpYAhgEv5xudmZmZVZu6U9+aE9q5dY+kxYAWwGkR8b+c4zEzMzOrWk5o50JE9M87BjMzMzNLnNCamZmZFZRnOUhmmdBKugCY5SS1EXFEo0RkZmZmZvYTNFShHVG2KMzMzMzsJ3N9NpllQhsRV5del7RQRHzV+CGZmZmZmc252Z5YQdLakkYDr2XXV5dU2SfINjMzM7PCmJODws4DtgDuAoiIFyVt0JhBmZmZmVnDJGjmg8KAOTz1bUSMq7eothFiMTMzMzP7yeakQjtO0jpASGoBHEHWfmBmZmZmlrc5SWgPBf4OtAMmAA8ChzVmUGZmZmY2e+44SGab0EbEJGCfMsRiZmZmZvaTzcksBytIulvSR5I+lHSnpBXKEZyZmZmZzZqk3H+agjk5KOwG4GagDdAWuAW4sTGDMjMzMzObU3OS0Coiro2IadnPdTRwSlwzMzMzs3KaZQ+tpNbZxcckHQ8MJiWyewD3liE2MzMzM2tAE9njn7uGDgobSUpg656qX5TcFsBpjRWUmZmZmdmcmmVCGxHLlzMQMzMzM7O5MSfz0CKpB9ANmL9uWURc01hBmZmZmVnDhHzq28xsE1pJfwT6kxLa+4CtgKcAJ7RmZmZmlrs5meVgV2AT4H8RcQCwOtCyUaMyMzMzs4YpHRSW909TMCcJ7TcRMR2YJmkR4EPAJ1YwMzMzsyZhTnpoR0haDLicNPPBZGBYYwZlZmZmZjanZpvQRsSvsov/kPQAsEhEvNS4YZmZmZnZ7DSVU8/mraETK6zR0G0R8XzjhGRmZmZmNucaqtD+rYHbAth4HsdSsQQ0b+ZvUFY9Jt0wMO8QcnPdyPfyDiFX+6zRMe8QcuNKmVl+GjqxwkblDMTMzMzMfpo5Obq/Gvh5MDMzM7NCm6MzhZmZmZlZ0yLc6lLHFVozMzMzK7TZJrRK9pV0Una9o6Q1Gz80MzMzM7PZm5OWg4uB6aRZDU4FvgRuA/o2YlxmZmZmNhueRCmZk4S2X0SsIWkUQER8KqlFI8dlZmZmZjZH5qSHdqqk5qS5Z5G0FKlia2ZmZmaWuzmp0J4P/BtYWtIZwK7AiY0alZmZmZnNllsOktkmtBFxvaSRwCakGSJ2jIjXGj0yMzMzM7M5MCezHHQEvgbuBu4CvsqWmZmZmZnNlqQrJH0o6ZWSZSdLmiDphexn65Lbfi/pbUlvSNpidtufk5aDe0n9swLmB5YH3gC6/+TRmJmZmdk8IRXqxApXARcC19Rbfm5EnF26QFI3YE9SrtkW+I+klSOidlYbn5OWg1XrPcgawC/mKHQzMzMzq3oR8YSkTnO4+g7A4Ij4Dhgj6W1gTeCZWd3hJ58pLCKex3PQmpmZmeWumfL/AZaUNKLkZ9BPGMLhkl7KWhIWz5a1A8aVrDM+WzZLs63QSjq69HkD1gA++gmBmpmZmVnlmhQRfebifpcAp5FaW08D/gYcSGpzrS8a2tCc9NC2Krk8jdRTe9schWlmZmZmNhMR8UHdZUmXA/dkV8cDHUpWbQ9MbGhbDSa02QkVFo6I385dqGZmZmbWWIpzTNiPSWoTEe9nV3cC6mZAuAu4QdI5pIPCVgKGNbStWSa0kmoiYlp2EJiZmZmZ2VyRdCPQn9RvOx74I9BfUk9SO8FYskkHIuJVSTcDo0ndAYc1NMMBNFyhHUbql31B0l3ALcBXdTdGxO1zNyQzMzMzqyYRsddMFv+rgfXPAM6Y0+3PSQ9ta+BjYGO+n482ACe0ZmZmZjkR0KzIPQfzUEMJ7dLZDAev8H0iW6fBI83MzMzMzMqloYS2ObAwczF1gpmZmZk1vp98QoEK1VBC+35EnFq2SMzMzMzM5kJDib2bMszMzMysyWsood2kbFFYo3jowQdYrXsXunddkb+edWbe4ZSVx16dY//FwQfSse3S9O7ZI+9QGsVVp/+Wo7fqzR/33nzGshGP3MtJe23GoLWXZ+xrL81YPm3qFK487VhO3mcLTtl3S94YOctToBfa+HHj2HKzjem1ajd6r96Diy74e94hlVU1/75X89hLSfn/NAWzTGgj4pNyBmLzVm1tLUcecRh33n0/o14azS2Db+S10aPzDqssPPbqHDvAfgMGcuc9D+QdRqNZZ5td+c25V/9gWbsVuvCrM//BSj3X/MHyJ+8cDMDJ1z/IUedfx83nn8H06dPLFmu5NK+p4c9nnc2ol0cz5KlnuPSSi6vmPV/Nv+/VPHabOfcSV6jhw4bRufOKLL/CCrRo0YLd9tiTe+6+M++wysJjr86xA6y3/ga0bt067zAazcq9+rHQIov+YFmb5Vdk2eU6/2jdiWPeYpU+6wKwSOslWbDVIrxXUsGtFG3atKFXr3T+n1atWtGl6ypMnDgh56jKo5p/36t57DZzTmgr1MSJE2jf/vvTILdr154JE6rjQ95jr86x2w91WGkVXnjyYWqnTeOjieN47/WX+eSD92d/xwJ7b+xYXnxxFH3X7Jd3KGVRzb/v1Tz2UpJo1gR+moI5ObHCzyJpckQs3IjbPxmYHBFnN9L2BwIPRcTExth+Y4n48cxqaiJvusbmsf9QtYzdfmjdbXfn/bFvc/oB27HEsu3ovGpvmtc0zzusRjN58mT22mNXzjr7XBZZZJG8wymLav59r+ax28w1ekJbAQaSTi5RqIS2Xbv2jB8/bsb1CRPG07Zt2xwjKh+PvTrHbj/UvKaGPY48acb1Mw/ZmaU7LJ9jRI1n6tSp7L3Hruy5197suNPOeYdTNtX8+17NY6/PeXxStpYDSddK2qHk+vWStpc0UNIdku6WNEbS4ZKOljRK0rOSWmfrD5F0nqSnJb0iqfQIiG7Z7e9KOqLkMY7O1n1F0pEly/eX9JKkF7O4WmWPPV92+yKSxkraDegDXC/pBUkLSOot6XFJIyU9KKlNYz93c6NP3768/fZbjB0zhilTpnDLTYPZZtvt8w6rLDz26hy7/dB3337Dd998DcDo556kWfMa2i6/Us5RzXsRwS8HHUyXrl054sij8w6nrKr5972ax24zV84K7T+Bo4A7JS0KrAMMAPYFegC9gPmBt4HfRUQvSecC+wPnZdtYKCLWkbQBcEV2P4CuwEZAK+ANSZcAqwEHAP1Ic+o+J+lxYApwArBuREyS1DoivpQ0BNgGuAPYE7gtIm6RdBhwbESMyBLeC4AdIuIjSXsAZwAH1h+spEHAIIAOHTv+/GfvJ6qpqeHcv1/IdttsQW1tLQMGHki37t3LHkcePPbqHDvA/vvuxZOPD2HSpEl07tSeP5x0CgMPPCjvsOaZy/7wa958/lkmf/Ypv91uLbY/5CgWWmRRbvzbyUz+7BPOP/pAOqy8Ckf9/Vq+/GQS5x05AEksvtSyHPTHc/IOv1E88/RQbrj+Wnr0WJV+fXoBcMppZ7DlVlvnHFnjq+bf92oeu82cZtaHMk8foKSHVtIrwMbAzsCKEXFs1qO6bkQckq3zX2DtiJgg6UBgtYg4Mks4T42IR0vWWw04EpgaEWdky18DNgN2AZaIiJOy5acBH5FO27tsRJxQL851geMiYgdJzwCHRMQr2ePWJbQ9gKeBd7O7NSedUW1zGtC7d58Y+tyIuXr+zKxYrhv5Xt4h5GqfNcr/Bb6pcA9n9Vm3Xx9GjhyR2wvfduVVY9CFt+f18DOcssXKIyOiT54xlLuH9lpgH1IFtLSq+V3J5ekl16fzwxjrZ99110vvX5vdZ1ZvMM1kO0TEUEmdJG0INI+IV2Zx31cjYu1ZbNvMzMzMyqzc03ZdRaqoEhGvzsX99wCQtB7weUR83sC6TwA7SlpQ0kLATsCTwCPA7pKWyLZVOmnlNcCNwJUly74ktTIAvAEsJWnt7L7zSfI+DjMzM7MclbVCGxEfZC0Bd8zlJj6V9DSwCDPpW633WM9LugoYli36Z0SMApB0BvC4pFpgFGkmA4DrgdNJSW2dq4B/SPoGWBvYFTg/6wOuIfX3zk1ybmZmZjbXBE1mHti8NXpCWzoHraQFgZUoSRgj4ipS0lh3vdOsbiMdqPX7ets/ud71HiWXzwF+dCRERFwNXF1/ObAecGtEfFay7m3AbSXrvABsMJP7mpmZmVkOylahlbQpaWaCc2bTKpALSRcAWwGVf2ismZmZWQUpW0IbEf8B5vrw14joP++imen2f92Y2zczMzOb19xxkJT7oDAzMzMzs3nKp741MzMzKyJBM1doAVdozczMzKzgnNCamZmZWaG55cDMzMysoDTLE6NWF1dozczMzKzQnNCamZmZWaG55cDMzMysgNKpb/OOomlwhdbMzMzMCs0VWjMzM7OCcoU2cYXWzMzMzArNCa2ZmZmZFZpbDszMzMwKSnLPAbhCa2ZmZmYF54TWzMzMzArNLQdmZmZmBeR5aL/nCq2ZmZmZFZortGZmZmZFJPAxYYkrtGZmZmZWaE5ozczMzKzQ3HJgZmZmVlDN3HMAuEJrZmZmZgXnhNbMzMzMCs0tB2ZmZmYF5Hlov+eE1szmuc+/npp3CLnZt/dyeYeQq2tHvJd3CLnZr091v/ZmeXJCa2ZmZlZQPiYscQ+tmZmZmRWaE1ozMzMzKzS3HJiZmZkVkmiGew7AFVozMzMzKzgntGZmZmZWaG45MDMzMysg4VkO6rhCa2ZmZmaF5oTWzMzMzArNLQdmZmZmRSSf+raOK7RmZmZmVmiu0JqZmZkVVDMfFQa4QmtmZmZmBeeE1szMzMwKzS0HZmZmZgXkeWi/5wqtmZmZmRWaE1ozMzMzKzS3HJiZmZkVlGc5SFyhNTMzM7NCc4XWzMzMrKBcoE1coTUzMzOzQnNCa2ZmZmaF5pYDMzMzswISrkzW8fNQwR568AFW696F7l1X5K9nnZl3OGXlsVfH2CeMH8fO227G+n1XZYN+q3P5JRcAcMqJx7Nenx5stM4aHLDPrnz+2Wf5BloGlf66X3X6bzlm696cvM/mM5bdesGf+MMeG3PKvlty8e8G8fWXn8+47f6rL+KEXTfkD3tszKvPPp5HyGVR6a97Q6p57PZjTmgrVG1tLUcecRh33n0/o14azS2Db+S10aPzDqssPPbqGXtNTQ0nn34WTw5/mfv+8xRXXn4Jb7w+mg032oQhz77AY08/zwqdV+L8c/6Sd6iNqhpe93W22ZUjzr36B8tWWXM9Tr7+If543QMs03F57r/mYgAmjnmL4f+5m5NveIjfnHs115/9B6bX1uYRdqOqhtd9Vqp57DZzTmgr1PBhw+jceUWWX2EFWrRowW577Mk9d9+Zd1hl4bFXz9iXWbYNq/XsBcDCrVqxUpeu/G/iRPpvshk1Namjqnfffrw/cUKeYTa6anjdV+7Vj4UWWfQHy7r324Dm2eu8QvdefPrh/wB48YmH6LvpdszXoiVLtu3A0u2XY8zoF8odcqOrhtd9Vqp57D8gkJT7T1PghLZCTZw4gfbtO8y43q5deyZMqOw/6nU89uoc+3/fG8srL73IGn3W/MHyG6+7io032yKnqMqjml/3OkPvuYUea/cH4NOPPmDxZdrOuG3xpdrw2Ucf5BRZ46nm172ax24z54R2NiQNlNR29ms2LRHxo2VN5VtUY/PYf6gaxv7V5MkcvN8enPrns2m1yCIzlp/31z9TU1PDLrvvnWN0ja9aX/c69151Ic2aN6ffFjumBTN5Pipxss5qft2reez1qQn8NAWe5WD2BgKvABNzjuMnadeuPePHj5txfcKE8bRtW7i8fK547NU19qlTp3LQfnuw8+57sc32O81YftMN1/Dwg/dxy10PVvwfump83es8fe+tvDz0EY664IYZr/PiSy/Lpx98/5H96Ufvs9iSS+cVYqOp5te9msduM9ckKrSSOkl6XdI/Jb0i6XpJm0oaKuktSWtKai3pDkkvSXpW0mrZfU+WdIWkIZLelXREyXaPzrb3iqQjS5bvn23nRUnXSmolaYyk+bLbF5E0VtJuQB/gekkvSFpAUm9Jj0saKelBSW3K/HTNkT59+/L2228xdswYpkyZwi03DWabbbfPO6yy8NirZ+wRwVGHD2KlLl059PAjZyx/9D8PcuF5Z3P14NtZcMEF8wuwTKrtda/zyjNDePC6f3DYWf+k5fwLzFi++vqbMfw/dzN1yndMmjiOD8eNZfluPfMLtJFU6+sO1T12m7mmVKFdEdgNGAQMB/YG1gO2B/4PGAeMiogdJW0MXAP0zO7bFdgIaAW8IekSYDXgAKAfqSL+nKTHgSnACcC6ETFJUuuI+FLSEGAb4A5gT+C2iLhF0mHAsRExIkt4LwB2iIiPJO0BnAEcWH8wkgZlY6FDx47z7lmaQzU1NZz79wvZbpstqK2tZcDAA+nWvXvZ48iDx149Yx/27NPcOvh6Vuneg03W6wPA7086jROPO5opU75jjx23AqB3n36cdd5FeYbaqKrhdb/8pF/zxvPPMvmzTzlu+7XY/uCjuP+ai5k2dQrn/mZfIB0Ytu/v/kTbFVam9ybb8se9N6N58xr2OvZUmjVvnvMI5r1qeN1npZrHXkpAswrfAzWnNLM+lLIHIXUCHo6IlbLr1wAPRsT1klYAbgcC2CUi3s3WGQf0AI4CpkbEGdny14DNgF2AJSLipGz5acBH2XaWjYgT6sWwLnBcROwg6RngkIh4JUt06xLaHsDTwLvZ3ZoD70fE5jSgd+8+MfS5ET/jGTIrls+/npp3CLlZdMH58g4hV9eOeC/vEHKzX5/l8g7Bymzdfn0YOXJEbhnlCt1Wi1OvvS+vh59hvz4dRkZEnzxjaEoV2u9KLk8vuT6dFOe0mdynLhsvvW9ttv6s3mAqud/3G4oYmrU+bAg0j4hXZnHfVyNi7VmOwszMzMzKqkn00M6hJ4B9ACT1ByZFxBezWX9HSQtKWgjYCXgSeATYXdIS2bZal9znGuBG4MqSZV+SWhkA3gCWkrR2dt/5JFXfPg4zMzNrEvKe4aCpNDw0pQrt7JwMXCnpJeBrYEBDK0fE85KuAoZli/4ZEaMAJJ0BPC6pFhhFmskA4HrgdFJSW+cq4B+SvgHWBnYFzpe0KOn5Ow949ecNzczMzMzmVpNIaCNiLKkftu76wFnctsNM7ntyveul2zkHOGcm97kauLr+ctJBaLdGxGcl694G3FayzgvABrMai5mZmZmVV5NIaJsCSRcAWwFb5x2LmZmZ2ZzwJAeJE9pMRPw67xjMzMzM7KdzQmtmZmZWSKr4MyHOqSLNcmBmZmZm9iNOaM3MzMys0NxyYGZmZlZAwpXJOn4ezMzMzKzQnNCamZmZWaG55cDMzMysoDzLQeIKrZmZmZkVmiu0ZmZmZgXl+mziCq2ZmZmZFZoTWjMzMzMrNLccmJmZmRWRfFBYHVdozczMzKzQnNCamZmZWaG55cDMzMysgHzq2+/5eTAzMzOzQnOF1szMzKygfFBY4gqtmZmZmRWaE1ozMzMza1SSrpD0oaRXSpa1lvSwpLey/xcvue33kt6W9IakLWa3fSe0ZmZmZgWlJvAzh64Ctqy37HjgkYhYCXgku46kbsCeQPfsPhdLat7Qxp3QmpmZmVmjiogngE/qLd4BuDq7fDWwY8nywRHxXUSMAd4G1mxo+05ozczMzCwPy0TE+wDZ/0tny9sB40rWG58tmyXPcmBmZmZWUE1kkoMlJY0ouX5ZRFz2M7Y3s1FFQ3dwQmtmZmZmP8ekiOgzF/f7QFKbiHhfUhvgw2z5eKBDyXrtgYkNbcgJbRkEMK12et5h5KKmubtaqlFN86ZRMrDy26/PcnmHkJvF+x6edwi5+XT4hXmHUJXSmcIK/Xl7FzAAODP7/86S5TdIOgdoC6wEDGtoQ05ozczMzKxRSboR6E9qTxgP/JGUyN4s6SDgv8BuABHxqqSbgdHANOCwiKhtaPtOaM3MzMysUUXEXrO4aZNZrH8GcMacbt8JrZmZmVlBNZGDwnLnBkczMzMzKzQntGZmZmZWaG45MDMzMyskoWLPcjDPuEJrZmZmZoXmhNbMzMzMCs0tB2ZmZmYF5VkOEldozczMzKzQXKE1MzMzK6AKOPXtPOMKrZmZmZkVmhNaMzMzMys0txyYmZmZFZF8UFgdV2jNzMzMrNCc0JqZmZlZobnlwMzMzKyg3HKQuEJrZmZmZoXmCq2ZmZlZQcnz0AKu0JqZmZlZwTmhNTMzM7NCc8uBmZmZWQEJaOaOA8AVWjMzMzMrOCe0Faz7yivQr/fqrLPmGmywzpp5h1M2vzj4QDq2XZrePXvkHUouHnrwAVbr3oXuXVfkr2edmXc4jeqIXx5M105tWa9vzx8sv/ySC+nXqzvr9lmdk088Pp/gyqyaXvf6Kn3sLVvU8OS1x/LcTccz8tYTOPHQrQHYedNejLz1BL4aeT5rdOs4Y/2N+3Vl6PXHMfzm/2Po9cexYd+V8wq9UVX6624/jVsOKty9Dz7CkksumXcYZbXfgIEc+qvDOfjA/fMOpexqa2s58ojDuPf+h2nXvj3rrdWXbbfdnlW6dcs7tEax5z4DOOgXv+KwQw6csezJx4dw/71388Szz9OyZUs++vDDHCMsj2p73UtVw9i/mzKNLQedz1ffTKGmphmPXnE0Dw0dzavvTGTPYy7nwhP3+sH6H382mV2PvJT3P/qcbp3bcPfFh9F5ixNzir5xVMPrPqc8y0HiCq1VnPXW34DWrVvnHUYuhg8bRufOK7L8CivQokULdttjT+65+868w2o066y3Posv/sPX+qp/XspvjjmOli1bArDU0kvnEVpZVdvrXqpaxv7VN1MAmK+mOTU1zYkI3hjzAW+99+MvbC++MZ73P/ocgNHvvE/LFvPRYr7Kql9Vy+tuc84JbQWTxI7bbsn6a/flin9elnc4VgYTJ06gffsOM663a9eeCRMm5BhR+b3z9ps8M/QpNu+/DtttsTHPjxyed0iNrppf92oZe7Nm4tnBx/PfR87k0WdfZ/gr783R/XbatCcvvjGOKVOnNXKE5VUtr/uckPL/aQoqJqGV1EnS3vNwe/0l3TOL2/4pqVt2eaykJrlP/+HHnuSpZ0dw+533cvmll/DUk0/kHZI1soj40TI1lU+bMpk2rZbPP/uUBx8byilnnMnB++890+elklTz614tY58+PVhrzzNZcYsT6dNjObp1bjPb+6yywrKcfsQOHH764DJEWF7V8rrbnKuYhBboBMw0oZU0T/e1RMTBETF6Xm6zMbRp2xZIu1y3235HRo6o/EpVtWvXrj3jx4+bcX3ChPG0zd4H1aJtu3Zss/1OSGKNPmvSrFkzPp40Ke+wGlU1v+7VNvbPJ3/DEyPeYvN1Gu4Vbbf0Ytx0ziAO/sO1jBlfee//anvdbfZyT2izyuprki6X9KqkhyQtIKmzpAckjZT0pKSu2fpXSdq15P6Ts4tnAutLekHSUZIGSrpF0t3AQ5JaS7pD0kuSnpW0Wnb/kyVdK+lRSW9JOqQkvIUl3SrpdUnXK/v6J2mIpD7leYbmzldffcWXX3454/IjjzxMt+7dc47KGlufvn15++23GDtmDFOmTOGWmwazzbbb5x1WWW217fY8+fhjALz91ptMmTKFJSr8wMhqft2rYexLLr4wiy68AADzt5yPjft14Y2xH8xy/UUXXoDbLziUky64i2defLdcYZZVNbzuc0pN4F9T0FS6xFcC9oqIQyTdDOwCHAAcGhFvSeoHXAxs3MA2jgeOjYhtASQNBNYGVouITyRdAIyKiB0lbQxcA/TM7rsasBawEDBK0r3Z8l5Ad2AiMBRYF3hqTgYkaRAwCKBDh46zWXve+/CDD9h7j10AmDZtGrvvsRebbb5l2ePIw/777sWTjw9h0qRJdO7Unj+cdAoDDzwo77DKoqamhnP/fiHbbbMFtbW1DBh4YEV/kTlk4L4MffJxPvl4Equu3InfnXAS++x/AEf88mDW69uT+VrMx4WXXlHxuyKr7XUvVQ1jX3bJRbj81P1o3qwZzZqJ2x5+nvuffIXtN1qNc363G0suvjC3n38oL70xge0Pu4hD99yAzh2W4vhDtuT4Q9Ln/na/vJCPPp08m0cqjmp43e2nUd69ZZI6AQ9HxErZ9d8B8wEnAG+UrNoyIlaRdBVwT0Tcmq0/OSIWltSfHye0G0bEAdn1UcAuEfFudn0c0AM4CmgWESdly68Bbgc+A06IiM2y5ZcAQyPiOklDsscaIWks0CciZrlPZ43efeKJp4f9nKepsGqa574TwHLw1XeVdQDKT7FQy6ZSJ7ByW7zv4XmHkJtPh1+Ydwi5WLdfH0aOHJHbN+YuPXrGpbc9mtfDz7BR1yVGRkSue66byifvdyWXa4FlgM8ioudM1p1G1iqRtQC0aGC7X5VcntkbLur9X395/biayvNlZmZmVc6nvv1eUy2ffQGMkbQbpMRV0urZbWOB3tnlHUjVXIAvgVYNbPMJYJ9se/2BSRHxRd12JM0vaQmgP+Cjp8zMzMwKoqkmtJCSz4MkvQi8SkpeAS4HNpQ0DOjH91XYl4Bpkl6UdNRMtncy0EfSS6QDyAaU3DYMuBd4FjgtIibO68GYmZmZWePIfRd6RIwl9bLWXT+75OYfHcUUER+QDuCq8/ts+VRgk3qrX1Vyv0/4Pimu782IGFTvcYYAQ0quH15yuX/J5U6z2KaZmZlZI2o6swzkrSlXaM3MzMzMZiv3Cm3eIuLkvGMwMzMz+8ma0Kln8+YKrZmZmZkVmhNaMzMzMyu0qm85MDMzMysqdxwkrtCamZmZWaE5oTUzMzOzQnPLgZmZmVkBpVPfuukAXKE1MzMzs4JzhdbMzMysoFyfTVyhNTMzM7NCc0JrZmZmZoXmlgMzMzOzonLPAeAKrZmZmZkVnBNaMzMzMys0txyYmZmZFZTccwC4QmtmZmZmBecKrZmZmVlB+URhiSu0ZmZmZlZoTmjNzMzMrNDccmBmZmZWUO44SFyhNTMzM7NCc0JrZmZmZoXmlgMzMzOzonLPAeAKrZmZmZkVnCu0ZmZmZgUkfKawOk5oy0BATXMXw6tNROQdQm4WaumPFqs+nw6/MO8QcrPKb+/NO4RcTBz/ed4hWMZZlpmZmZkVmssoZmZmZkUkn/q2jiu0ZmZmZlZoTmjNzMzMrNDccmBmZmZWUO44SFyhNTMzM7NCc0JrZmZmZoXmlgMzMzOzonLPAeAKrZmZmZkVnCu0ZmZmZoUkn/o24wqtmZmZmRWaE1ozMzMzKzS3HJiZmZkVlE99m7hCa2ZmZmaF5oTWzMzMzArNLQdmZmZmBSQ8DW0dV2jNzMzMrNBcoTUzMzMrKpdoAVdozczMzKzgnNCamZmZWaG55cDMzMysoHzq28QVWjMzMzMrNCe0ZmZmZlZoTmgr2EMPPsBq3bvQveuK/PWsM/MOp6yqdezjx41jy802pteq3ei9eg8uuuDveYdUVtX6uoPH7rFX5tjbLDY/N/xqLR4+fkMe/N0GDNygEwBHb7Uy9/92fe49dj2uOXRNll6k5Q/u13ax+XnlzC04pP8KOURdXlL+P02BE9oKVVtby5FHHMadd9/PqJdGc8vgG3lt9Oi8wyqLah5785oa/nzW2Yx6eTRDnnqGSy+5uGrGXs2vu8fusVfq2KdND864azSbnfk4O583lP3XXY4Vl1mYyx59l63++iTbnP0Uj776IUdssdIP7nfijt14/LWPcora8uCEtkINHzaMzp1XZPkVVqBFixbstsee3HP3nXmHVRbVPPY2bdrQq9caALRq1YouXVdh4sQJOUdVHtX8unvsHnuljv2jL77j1fFfAPDVd7W8/cFkll10fiZ/N23GOgu0aE7E9/fZrMcyjPv4a97835flDjcXagI/TYET2go1ceIE2rfvMON6u3btmTChOhKbah57qffGjuXFF0fRd81+eYdSFtX8unvsHjtU/tjbLb4A3dovygvvfQbAsVt3YehJG7ND73ace/+bQEpuD92kM39/8K0cI7U8VFRCK2mIpD6zWedISQuWc1t5iNKvqxk1lUaXRlbNY68zefJk9tpjV846+1wWWWSRvMMpi2p+3T32H/LYK8+CLZpzyQG9Oe3fo2dUZ8++7w3WPfVR7hw5gf3XXw6Ao7ZcmSseH8PXU2rzDNdyUFEJ7Rw6EphXSei83NY81a5de8aPHzfj+oQJ42nbtm2OEZVPNY8dYOrUqey9x67sudfe7LjTznmHUzbV/Lp77B47VO7Ya5qJSw7ozZ0jJ/Dgy//70e13PT+RLVdrA0DP5Rbj+O268uQfNuLADZfnV5t2Zv/1lit3yOWTd69BE+o5KGRCK6mTpNclXS3pJUm31q+USrpE0ghJr0o6JVt2BNAWeEzSY9myzSU9I+l5SbdIWngmj/ejdWa2raakT9++vP32W4wdM4YpU6Zwy02D2Wbb7fMOqyyqeewRwS8HHUyXrl054sij8w6nrKr5dffYPfZKHvtf9lyNtz+YzL8eHzNjWaclv/+Tv2mPZXj3w8kA7H7BM6x/2mOsf9pjXPH4GC7+zztc89R7ZY/Zyq/IZwrrAhwUEUMlXQH8qt7tJ0TEJ5KaA49IWi0izpd0NLBRREyStCRwIrBpRHwl6XfA0cCpdRuZ1ToRcWrptsow3p+kpqaGc/9+IdttswW1tbUMGHgg3bp3zzussqjmsT/z9FBuuP5aevRYlX59egFwymlnsOVWW+ccWeOr5tfdY/fYK3XsfZZfnJ37tuf1iV9w77HrAfDXe99g934dWGHphYkIJnz6DSfc8nLOkVreNLMenKZOUifgiYjomF3fGDgCWAw4NiJGSDoUGERK2tsAv46IwZLGAn2yhHZb4CpgfLbpFsAzEXGQpCHAscCyDawzY1sziXFQ9vh06Nix95vv+BtitSni79a8Uql9fGY2c6v89t68Q8jFxBuO5LsP3srtA6/76mvEzfc9mdfDz9Cj/cIjI6LB444aW5ErtPWzhRnXJS1PSkb7RsSnkq4C5p/JNgQ8HBF7NfA4c7LOj4OLuAy4DKB37z7Vm9mYmZmZNbJC9tBmOkpaO7u8F/BUyW2LAF8Bn0taBtiq5LYvgVbZ5WeBdSWtCCBpQUkr13uchtYp3ZaZmZmZ5aDICe1rwABJLwGtgUvqboiIF4FRwKvAFcDQkvtdBtwv6bGI+AgYCNyYbedZoGvpg8xmnRnbmuejMzMzM2uAyP+0t02lw6zILQfTI+LQesv6112IiIEzu1NEXABcUHL9UaDvTNbrPwfr/GBbZmZmZlZ+RU5ozczMzKpaEymQ5q6QCW1EjAV65B2HmZmZmeWvyD20ZmZmZmbFrNCamZmZGe45yLhCa2ZmZmaF5gqtmZmZmTWq7OyqXwK1wLSI6COpNXAT0AkYC+weEZ/OzfZdoTUzMzMrKDWBfz/BRhHRs+Q0uccDj0TESsAj2fW54oTWzMzMzPKwA3B1dvlqYMe53ZBbDszMzMwKqomcqWtJSSNKrl8WEZfVWyeAhyQFcGl2+zIR8T5ARLwvaem5DcAJrZmZmZn9HJNK2ghmZd2ImJglrQ9Len1eBuCWAzMzMzNrVBExMfv/Q+DfwJrAB5LaAGT/fzi323dCa2ZmZlZQagI/s41RWkhSq7rLwObAK8BdwIBstQHAnXP1JOCWAzMzMzNrXMsA/1Zq+K0BboiIByQNB26WdBDwX2C3uX0AJ7RmZmZm1mgi4l1g9Zks/xjYZF48hhNaMzMzs6JqGrMc5M49tGZmZmZWaK7QmpmZmRVQOijLJVpwhdbMzMzMCs4JrZmZmZkVmlsOzMzMzIpITebUt7lzhdbMzMzMCs0JrZmZmZkVmlsOzMzMzArKHQeJK7RmZmZmVmiu0JqZmZkVlUu0gCu0ZmZmZlZwrtCWwfPPj5y0wHx6L6eHXxKYlNNj562axw7VPX6PvTp57NUpz7Evl9PjWj1OaMsgIpbK67EljYiIPnk9fp6qeexQ3eP32D32auOxV+fY04lv3XMAbjkwMzMzs4JzQmtmZmZmheaWg8p3Wd4B5Kiaxw7VPX6PvTp57NWpmsfuU99mFBF5x2BmZmZmP9GqPXvHXf8ZmncYrLDUAiPz7mN2y4GZmZmZFZpbDszMzMwKSPi8CnVcoTUAJM2f/V/1vxt+DsysWvjzziqFE1pD0iLAk5I2jipuqpbUQdLiERHV/CEvaX5JnbPLy0nKbR5lM2sc1fZ5VzpGSZWV+6gJ/DQBlfWi2k8maf6I+AK4CrhI0vo5h5SnI4EhklpXy4f8LKwM7CbpDOBfwHw5x/OTSFpeUpVOsv7zVPF7vhodSRV83klaSNLS2RjXkKSImJ53XDbvOaGtYpKWAM6StEhEXAScBVxZbUmtpDaSFo2IY4CngTskLVHJH/KzMQ5YAfgN8GhETISmnezUxSZpbdIUPidI6p5vVMWS/aEPSZtLOlXS0ZJWzjuuxlLynuklaRVJq+cdUzlU4eddF+Cfkn4NXAN0yzkeayROaKtYRHwM/A1YUlK/iLgSOIPqS2p/BXQAiIhfAqOBf1f4h/yPlIzzK+BqUmK4tKSdALLnomVe8c2KpOZZbJuS3s83A22AAyStkW90xZE9h1uTPgNGAJsDx1bc7tlMNt5tgCuArYGrq+Rzr6o+7yLieWAMcC5wbkS8Kql5zmHNU2oC/5qCivygstmr+yMVEe8B+wN/ldS3JKm9TNJGecZYLhHxB+BzSf/Kdk0dyvcf8hW9O65OSXVuG+AJ4EXgT8AbwDaSNpK0CrBPU0lqJa0oqVVE1EqaD9gTuCIiLgd2AFqREjJXaufcusAuQACLAadGxHRJC+ca1TwmqZmkNsDxpGT2c+Br4PVKTeDrVMvnXb0x/Bs4FThKUp+IqM0pLGtEFf2LazNX10OUtRwQEScDdwKnSlozS2rPJVVqF88x1EajTMmiD0l/wE+TtGT2If8y8HBd5SKPOMsl+yO2EanCeVxETI6IScB1wDDgcOBxYFxEfJdjqKWWAVaV1CwipgJvAt2y1+8D4HRgTWCnppKENyWSFpS0THa5LulfCLgEOAbYMyLGZ19ydih6VSv7la+bqrI58AkwEtgIOAAYEBEfAVtI6phTmI2i2j7vSr6gbyzpGGDZiDgVOB+4VlJnSetJ+mvOodo85IS2ikhqJ2nTkl2Ld0q6PPvG+jfgP8AfJK0dEZcB60XEp/lGPe9Jmi8yklbLxvsdqcLXAvhL9iF/GPA8sFKuAZdB9sduZeAUYKykAySNAg4GbiUdQLJ5RDycX5Q/FBFDSX+Ex2RfvO4jVWU3kNSKNM/2y8Bu2Y/90KrAcZKOAO6XtCTpIMDlgfsjYqykDUhfbscXuaqVvb+3BtaQtAtwbfY73xn4B7BTRLwlaT3gj8D8+UU7b1Xj51021m2Bv5K+uBwq6Yzs79o/gStJye0zOYY5z0j5/zQFPrFClcg+0NcHDpe0ErANKXnZgtRruERE/C2rZJ0qaVdgQn4RN46sKv1XSUeTErhrgS8kPU7qGT2EVKE6X9JvIuKQ/KJtXHVVDJjxB2Ai8BfgfeCu7PIvgf9ExMukg8WalIj4MkvIngD6keLeHjiMVMHdDtiKCkpQ5pWIeE7SvsA5wC8iYpKkj0kHA56ndJBUN+CoiHg8z1h/ruz9PRm4njRrx2HZTUeRWmsukvRwtvykiHgzn0jnrWr6vJO0GDAtIiZnbSP9gW2B1Ul7Hv4BkP2duy27PLb0c9CKzQltlcg+0B8k7WobALwVEQ9LGkKqvm2vdHDNnyTdGBGf5xhuY2pJ+sZ+Gen9vyXwGXACcBCpQvXL7P9lgY9yibKRle6SAzYAXgDuz/7/LiI+lNSetOt5am6BzoGIuFPSNNKBTH0j4m5JvUivXTfg18BOecbYFElaF3gWmETazf4S8Hz2ubA+sAAwf0S8k2ec89BrpIRuF+A7SQtExNuS9geOI+2xPDoiHqmgJKcqPu8ktSAd3Ddc0oXZF90a4HJgUWDXiBiXtc9Mj4j76+5bCa9zEymQ5s4tB1Wgrncqax+4HbgD2FrSdlnv4d+A/wE7ZruexuQWbCOLNAXVeaTEbW1gwex5uZD0+3AYsGJEDMiqkhWp5ACwc4CJwKGkXXCLZMnsHqRd+H+KiNdzDHWORMS9pOT7HaUDW0YB04D/A3YvwhhysBmwWUScQjoo6ESgc7ar9tCImFAJyWzWProEqRf8AVIF+kRSJR+gLXB+RPwjIh6BykhyoHo+7yJiCulg5v7AIVm/902k2U4GR8R72Ze084DJecVpjcsJbRXIkpe1Je1NqlhdT/pDf4ikbSJNMv0n4MzsQKCKU5fUZ/1k44ELgFtIB0WsEBFjgYuBip1wW9JSSlNbkfWc7gzsCIwn/VH/HDgyOyDmDeA3EfHvegeTNFlZ1eUg0i5GIuJ/wDZF/kM9L83kdbyJVKmsiXRg6Muk/tGzgbfKHF6jqKu0Rpqi8EJg5YgYQvpdP1TSKaQZPVbNMcx5rpo+70oKNiP5ftaK35Ba5s4B9pU0mNRacWREPJlXrNa4VCFfRK0BkjYk7VK6n/QN9hLShNrdSQf9nBMRd+cWYJlI2o50IERL4ExgCunDrydwQkS8o3TmtG/zi7JxZD1lvwZWAW6PiIeyloJFSHPO7gK0Jx0wMRw4JKt6FJLSzAfTK2jX8TwhqT/ppBm3ZLtlBwP/jYjjsttXAqZWSm+hpG4RMTq7vC1wLKkqPTX7XFwReCdLcitKNXzelbROrUqadu0DYEnS59jtpBaT+Un99FMqpTe61Gq9esd9jz6ddxh0aD3/yIjI9QyNrtBWOEldSD1Sv4iIX5N2MfUCugI3kqZl+l9+EZZH1lP5O1Iv2dukgyFWJlWr/0s6cGIB0od+xcmq8DcB7wBbSdo8q9y0AN6LiP8C35GO+j2zyMkszBhvxew6/jlKqnWtSVX4fUgHfp5Imtqsg6SlASLirax6V9jnrmS8NcAFkq6SNAh4hDRN15EA2YFuV9Qls0XZEzEnquXzLktmtyMVbA4gnVRFpPajHUhf4r+KiFcqMZm1H3JCW6GyvrHmpLP9dAO2zHY/PUHqjTyKlMxcGRHDcwy10UnqTBrv6Ih4PCKOJx0M82vgS9Juqd9FxDdRYef4zt4Hdbvk/keqxr5P6qHejLSbuaekO0mTj98SEa/lFrDNc9kf/S2AG0itJLsAF5ESnDOz6/3yi3DeqXew4z6kGS7uADoCjwFLAX3r1i9N2ouawNdXTZ93kjqQ2gy2BD4lTds3OSJeJKvGk6qzVgWc0FaYkirDYhFRGxEXkObiWxDYPbvtTVJjfMuif6DNoemkicS71PWQRjp5xOdAr4j4X0RURM9gqWzWiijpod4E6BgRZ5H6Znck9Zt2JfXY7RQRD+QXsTUGSWuR+kf/HBFfR8RnEfF2ROwPHEFKCI7LKriFVnKw43nAhxExJSLuiIgTgZNI86xuJmlAnnE2sor9vNP3J8aou/w52WtKOibggIj4SNLGWe/8tlHBBzl/T03gJ3+etqvClHygn6A0p+R/Sd9UFwQOlrQ7qafo3KjQqblKqjR9SGP9mnQQ3ImkSvVypCOeu5O+1VecbBfyVdnrvRJpV+O9wEaSBkfE6UpzU/4SuDma0AkTbN4o6YFdiXQigcezJKAW0mdFRLwLnJP1IBb+74Gk+Ukn0TgsIp7Mxjs9IqZHxEPAQ5JGUyEVaaiez7vstdxX0jBSpX0g6SDQjsDfgTUj4r9KZzw8XdI+1ZHMWh1XaCtM9ofpdOC3wIGk6tt5EXEp3+9uvj0i7skvysaVfbhvTtrFuj1wN2n34/nAt6QjYH9HOvDpBVXgudsj4kPS/KIPAXsBB2U91P2BAyX9ijTR+BhStdYqTMku9M+ATSV1johp2fL+WRsCktYG1iEdPFR000gHBdWdyrc2Oziwe8k63YFNJM1X9ugaQb2Wkor9vIuIaaTPq2dIc85eku1hPI805tMk1Y37zGpJZkX+ZwlrKt3nhf9Gbj8SwEvA09kfrk0kjVSaPPwm0hlT+kr6ELijUvrG6mQtFwuTDgo4KiLulXQ1cCfpoKczSBWq5qR+shkHEFWKrNWgNiL2l3Q2sD/ppANEOhvUANKuuYsl/S3SaTCtAtSr1q1Cai8aQ5p/dXdJ/yG9/88m9VlCOmho44go3JkBS8a7LDBfpMnzrwJWk7R+VqXtB5wp6dCIeIP0e//LSHNwF16WmB9DOinEPZX6eZe91o9Leoj0BawujRpGmmbuUNK8s8dEmsWl8LN02E9TyG9q9r2SI3r7ZruWviP9UpfOq3gtQER8Q6rSDuP7hLeiZLtRvyT9kf42+1B7lbRrfffsObiOtGtua0kL5hjuPJeNt1bSUgARcSxpmrZjJbXLVlsUWCEbe0X8UbckS+62Ih3tvSZpfumtgS9Ir/WFwJ+B0yPiiezLz0dFTGZhxnh3JH1Zv03SyaQzXn0JnCzpStLn39+yZJaI+GdUyIGP2Z6oNUgHd35diZ93JceFLJGNbzdSq8FgpZMDfUVqqftzRJydtZZUzEF+NudcoS247AN9e9KE6Edlf6TuA/4l6WLSLrhfkJ27PNJ5ri+vpF/2kipNB+CLrDd4POlDfTjpj/m0bN2WEfGWpIuALyPi69wCbwTZ87Al6QQJ75MqdKeTKjSPSLqbdBKFcytt7Dajh3Qn0u7lR7IDwrYAPoqIC7MErzYiPqv78pNrwD+T0klAfk86nfdU0oFBiwH3AHcBy5Narl6sS4wq5bNPUm/SAX2/A74iTc01ggr6vCv5bN+BVIGdJOnWSKe7/g1wftZOcgRpto5n8ow3L01kj3/unNAWnKQVgFOBnSPi3awKdzXpvOXrA51IZ0d5tO4+lfKBDj/4wNuaVIl8TNIHEfG77EP8OknjgHWBk+p2r1dqf5WkbqTn4QBgcVKV7h8RcUiW7OwKbB7pHPbeJVcBSl/HiPg22wW9GfBIRDybfSb8WtLNkc6YRbZuJbz2C5GO6h+ffVm/idQbPj4iriJNUwZUzHgByF7TI4E3I027OFzSjaQDQd+n4J93yk6Mkn22b0SaoWJb4FxS5b1NRPxD0qekse4bEVWZzNr3nNAWVMkfscVJU3CtKOlQ0kkT1gPWi4gTlU5rOS3PWBtDvQ+8bsCmpCTuA+AoSRdExGGS+pIqktdFxDOVnMRlLSdLAfdFxBClo4KfJx3xu2ZEHCfpqoh4GyrrD3w1UppXemr2O7A80CoiXgKuAraTtGtE3Er6cvs5ad7pr/KL+Ocr+QK7YKQpyF6T9CIwQNKNkY5yvx9YtpIqskonQeiT9QR3IbUZvAbsKmnriLgvIvbK9s40p8Cfd1myvr+kKyLiA9LZ3A4FepMq7v8kHdg6P2kedZ/K1gD30BZOaT8RzDh/9eOkI1lHRMRmpG+z/ZWOZi3kAQANkdQW2EZSS0mLkw54WREYArwOnAa0lHQd8EJE3Fn37b1oH+5zStL6pEnymwPbZr1l0yLiPVJfdZds1YroHax2WY/0LyUtrjS/8APADZIuIP0OvAPsLeleUj/t1RFR2Cmb6mTJ7HbAFZJukrQwqb1geeAfkvYlHSD1bGTyjHceagVsmLUM3UD6zL+c9OVlh6yXloh4ICLuLfjn3XRS3/dhkhaOiMuBV4F9gb0i4iJgArAW6dTdVS/vGQ6ayiwHTmgLJvtA3xa4XtLZknaMiBMiYpuIuFnSOqRK5YisgllxCS1pXs13gAWzP9L7kKYn2z3S0f3vkQ58+Zbvp++pWEqnudwauD5rLTkOOELSIKUjvPuQjgIu6h84+7FupAM/fwUcTpquqRfQg9RPeB1wMGk2g90j4vaSL8OFlb3XTyAlc9NJ8yu/lF0fRnpeDonsdLYV5CPSnOKbAG9HxMSI+Ig0t/TLpPlZt8wzwHkh26P4PqkPfDXg6OzL2zekPQy/znqHFyAd6Dcuv2itqXHLQcFI6k+aimUX4C9Av6yP9gpgaeBK4NhI5ymvSJGmblkQuFLSExFxkaRfkKo2ERE3RcQYSYdHxLd5x9tY6touSNNybQO8nSUt/ybNPXosqb/s5Ih4NrdAbZ7LfgfmA7YjHdVfExFTJe0E3AL8DTg0Ih4ruU+hv8xIWpGUvD8dEY+QDnK8mDRzw68j4mxlU9blGmjj6ET6kvIFsIWkc0nTU70j6RlScl/45C4ipknagFR5vQ0YRGqTuYJ04PNJpB7p06LCT9n+U8iHhQFOaAuh3od0V2BP0i7k5YB/kf6oQfpg3zwi3iti79TslPTPrRDpALgbgJ0lfRcR/5Q0ELg1S/RurNRktuT9sDjwcUQcJekz0tHsTwJvRcSDkh4jHdFeW4nvh2pU7wCw/0iaQHofbJv9HrwtaTfSPKSrkHbVVgqRpuNaRdIGEfFERPxK0r9IX263JrXXVAx9fxKER4GHI2KQpLdJe2HOlPRv0imsL4iIwp4gpeSzve40zS+RTgJUSzpley2pL3i37ICw9/2ZZvW55aAJk9QKIEtI1lc6jem7pG/p2wC7RMQlpA/61YG22e72wldjZib7wNseuFRSj4i4E7iddPKIg7Kq9B7A/3INtJFI6iRpnez9sC3pNJ5/l7R5RJxCem/8EeiWfdhPqfsiVInvh2pU13Ik6XJJ/yTtir2ANPf0TpJWjojPSCdKKHQyW9ciIWmNLNFpSZqiayTplK7rAUTEQaQK7bcV+D6vyfbCrAasK+niiHiFtJduGdIcu08UOZmFGe/rNUnjOiQi9gUuJe1tGk2aneW47HPt/br75BawNUlOaJuobJf6vZJ2kbQycBEpid2L9Adsa2AzpSP8a0j9RGPzircclGYsOI30x+sVSQsB9wPnANtLGhQRj0bEY5XQLzgTawM3K53pax/gFFLyvp2k3SPieFKv3cmkicatwmS/778nndL4Q+A+UtXyX6Te8l2yz47C/7HPkpwtgMGkKt1DpN7KC0jzrO6S7Z6m6Mn7zCidxnz3rCL5JdCX1G5wYUS8EREDSF9c7s030nlmUdKpuTfJrr9HOsvd+6TXf7CT2FlQE/hpAtxy0ERFxNdZn9TxpD9YgyLNKbkCKbGdTjog5GDgL5Gm66lIJbuWliN9W19Q0rGkD76lScn9ZaQjX4HK/PYeETdKqiUlsg9ExF2SHif1U6+XHVBxpKQukc6eYxVE0hrAH0i7nm8BblGac/Ru0gFhNwETo2CT589Mtqu9FfBb0jza90m6ntQf/A1pt/SRpGn6KlUP0u/2dEmPRsT/snaSEdlH4q+pgL7ZOhHxsKSdgb9JGpN93n1GaqU6KyKezzdCa+qc0DZhEfFvSZOBW0nzrD5L+gD7L2nC8IGkI/0/rMR+opIxtSK1WTwJbEDazXYOKdnfHeheQVWKH8iq0GvF92d9mgCcBZwn6c5I883eBMwHbJD94XujoW1acdT7vZ5EOoVpL6W5Ot+PiAuyXbVtswOlCq1kvPORvsg/B3yT9Y2PVDo71IHZZ+OfImJyrgHPQyV9pF1J8wb/m/T7/gsgJN1B6hE+B3gQKu+Le6QzgE0nzeKzI/A18MesjcasQW45aOIi4mFS4jpQ0l4RMRX4lPStdf6I+DBbr6I+2OAH56X/V9YvuDXp7DfdI+JfpD96u5BOLFGppgDHShoC/B2YHBFXkqpT50vqn1VjrwdOj4iK7B+uVtnvQD9J65JmrtiLtIPvl6R5SdcENiT1lxZeNt4dSb3x5wFbkj7r6lpoviJVLGso+Eki6iv5vLuZdBrbF0knRrmDdOa3K0lz7v47q2Y2kR2981ZE3E2ac3Yl4OWIuEeZnENrsvLuNmgqL4wrtAWQVSOmAVdnu5w+I03FNCnfyBqX0pyTF5Pm1V2NdPKE32WtGMsD15CmrhmWX5SNR2m2hqmSTiFV6V+MiBcBIuJKSUGaqmxQRPyHyk7sq1KWyA4mzbE6iXRa64GksyVtQZpg/5CIeLnIe2lKqpOLkcZ3PakPeD3SWaIWlNQ8u/6HqMyzH65IOqhzJ6AfMJV0UNgtkkYCHYDzI+JpqMwiRp2snepb0ufb2Ii4Pe+YrOlzQlsQEXG3pINJB/wcFBHDi/wHbA6Vnsb1cdKZYQ4jnSXtXdKE8S/mGWBjiojpklYjVeO2AW6UdHlEHJKtcjupFaOipiqqdiXJ3aKkU5zuDrxAqlodTDoAbAApuf0OeAyKneCUHOXeBxgZETcASPqKlORBOivWDRExtFI+++qN41NSIt+btAdmx4j4TOmECc9ExLs5hZmLiHhI0gGkk+iYzZYT2gKJdLafIRHxSXa98B/opUr+kK8JLEmae3BzSetFxFPAM5KOAlaKiNdIR/RXpJI/dIsDn0fEi1kP7XBJ55OSmtOAAyLi40r5A28/mJ5ub9KBQRMi4hlJ95GqloeTJpc/nHSQ1BeSzo4CnlCg5Hd+LVLV+T1gaUlPAU9llbpFSGcH+7+6ntlKea9nY9+QNGfwu8BRpL/LnbO9M2uR5pw9hNRXW1WyljtrQFM69WzenNAWTF0yW4myD/cdSGeDeYjUZjAJOFDSSqR+slWAQs+5OIdqSLsc3wXWlLRvRFyndNrHu0n9hedFxMdQOX/gbcZsBr8E/kTa/fx/kkZExH8lPUB6b3weERMl7Qlprur8Ip57dT3CpJk79ow0Hd9pwM6kXtmns/f9YxV6AFg/UlvVG8BrpH7Z/YHDszazA0ntZa5Sms2GDwqzJiPrn9sT2AgYASwG/Bq4gdRH+zvSEa8VOX1L3UEPWZvB1ZJ6RTpX+bGkA4CWyf6ob0pqt7jTB0pUFkltSZXXbyLiyYg4GhhCmqJr+UgT6F8ZES9kR/6Pi+Kfz35R0hR8m2fXTwU+IbVV1J08YcLM71pMJXuiTgH2ioidgddJ474J6A40B47z77nNjprAv6bACa01JVNJPaGnAkcD+0XECGAiqXf24Kztomn89sxDJRWbzUjJ+2vAXySdTarSzQcsBKkaFxEfZZddma0Q2UFBKwNPkXa7HwgQEccCw4E7JM1PmvmisFXZ+iLiIdJsJQdJ2jvSTC6nkU4a8mGuwTWuxUhfTjfLrt9I2iPzJeno/vPqdrn799xs9txyYE1GRHwl6WXSCSN+ExHvZv1l/yRVJL/O1qu4D/csme1LqlTdmh34shLpj94JwJqkI733qpRExpLsC1oNaV7ldyLiz5Kmkk6WURsRV0fE4ZK6RsS3+UbbOLIq5FTgNEktIuIq4P9yDqtRZQc97Qz8WdLESCcSuCm7uWIPdjVrLE5oram5BViWdN7uLYBtSWcKGpVvWI0rS2puJVWjT8yuv5PNdLA36ejvvYF2pBNrWMFJmi+rRpIdAHQ2aZqifwN3kc4GuIXSGeD+ReqzrFiRzgZWA5wp6SHgg0r/8pYd9DaN7xP5q0ktVmZzruL2Wc4dJ7TWpETEB5L+TErgFgduigqdoqzegSEiHc18FXBERJxDOjvQfFll+glJJ5Km9HFCW2CSlgc+iYjPs4P8lpX0ZkS8Lukx0hHur0t6mPQZPRIqc89EfVmC90xdS001qJfIPwz8LyKm5x2XWdE4obUmJ9KZrx6vt6zi/pjXm9XhYaAN8Dfg91lV7qyscjcf0JpUnX01v4htHukMjJLUkXQ2pH7AyZJOIJ3x6xhJT0Y6pfUNdVXcalFNyWydakzkzeY1J7RmOak3q8NmpNP6DpB0HfBSdhT7n7OE5gNJ60RE1c1FWWki4j/ZdFvPAGtFxOBs3tlNSEf89yadBewWUtuBVQEnsza33HGQOKE1y0/prA59SHNvQpo8fxfgG/jBSRa+yCNIm/ci4gFJzYAXJfXNKnSPkaZq+g7YDril0ntIzczmFU/bZZaTrLXiZdL8m6dExDvZrA73AW9llbwZvcOV2HZRzSLiPtJ0dMMlLR4RX0bEZxFxONBZ0so5h2hmBVB3trA8f5oCV2jN8jWzWR2OiIjXwUlspYuI+yX9Cng9m5br0+zEGstShac6NTObW05ozXJUTbM62Mxl7QcHAj2Bx0gnFFg/Ij7INTAzswJxQmuWs2qZ1cFmLSLuLblcyWfHMrN5qumcejZv7qE1MzMzs0JzQmtmZmZmheaWAzMzM7MCEk1nloG8uUJrZmZmZoXmhNbMzMzMCs0JrZkVmqRaSS9IekXSLZIW/BnbukrSrtnlf0rq1sC6/SWtMxePMVbSknO6vN46k3/iY50s6difGqOZWdE4oTWzovsmInpGRA9gCnBo6Y2Sms/NRiPi4IgY3cAq/YGfnNCamdm854TWzCrJk8CKWfX0MUk3AC9Lai7pr5KGS3pJ0i8AlFwoabSke4Gl6zYkaYikPtnlLSU9L+lFSY9I6kRKnI/KqsPrS1pK0m3ZYwyXtG523yUkPSRplKRLYfaTRkq6Q9JISa9KGlTvtr9lsTwiaalsWWdJD2T3eVJS13nybJpZk5f3aW+bykFpnuXAzCqCpBpgK+CBbNGaQI+IGJMlhZ9HRF9JLYGhkh4CegFdgFWBZYDRwBX1trsUcDmwQbat1hHxiaR/AJMj4uxsvRuAcyPiKUkdgQeBVYA/Ak9FxKmStgF+kKDOwoHZYywADJd0W0R8DCwEPB8Rx0g6Kdv24cBlwKER8ZakfsDFwMZz8TSamRWSE1ozK7oFJL2QXX4S+BepFWBYRIzJlm8OrFbXHwssCqwEbADcGBG1wERJj85k+2sBT9RtKyI+mUUcmwLd9H25YhFJrbLH2Dm7772SPp2DMR0haafscocs1o+B6cBN2fLrgNslLZyN95aSx245B49hZlYxnNCaWdF9ExE9Sxdkid1XpYuAX0fEg/XW2xqY3WmGNQfrQGrhWjsivplJLHN8KmNJ/UnJ8doR8bWkIcD8s1g9ssf9rP5zYGbVwae+TdxDa2bV4EHgl5LmA5C0sqSFgCeAPbMe2zbARjO57zPAhpKWz+7bOlv+JdCqZL2HSLv/ydbrmV18AtgnW7YVsPhsYl0U+DRLZruSKsR1mgF1Vea9Sa0MXwBjJO2WPYYkrT6bxzAzqyhOaM2sGvyT1B/7vKRXgEtJe6j+DbwFvAxcAjxe/44R8RGp7/V2SS/y/S7/u4Gd6g4KA44A+mQHnY3m+9kWTgE2kPQ8qfXhv7OJ9QGgRtJLwGnAsyW3fQV0lzSS1CN7arZ8H+CgLL5XgR3m4DkxM6sYipjjPWFmZmZm1kT06t0nHh86LO8wWHSB5iMjok+eMbhCa2ZmZmaF5oPCzMzMzApIzMHE1lXCFVozMzMzKzQntGZmZmZWaG45MDMzMysq9xwArtCamZmZWcE5oTUzMzOzQnPLgZmZmVlB+dS3iSu0ZmZmZlZortCamZmZFZRcoAVcoTUzMzOzgnNCa2ZmZmaF5pYDMzMzs4Jyx0HiCq2ZmZmZFZoTWjMzMzMrNLccmJmZmRWVew4AV2jNzMzMrOBcoTUzMzMrKJ8pLHGF1szMzMwKzQmtmZmZmTUqSVtKekPS25KOn9fbd8uBmZmZWQGJYpz6VlJz4CJgM2A8MFzSXRExel49hiu0ZmZmZtaY1gTejoh3I2IKMBjYYV4+gBNaMzMzM2tM7YBxJdfHZ8vmGbccmJmZmRXQ88+PfHCB+bRk3nEA80saUXL9soi4rOT6zBojYl4G4ITWzMzMrIAiYsu8Y5hD44EOJdfbAxPn5QO45cDMzMzMGtNwYCVJy0tqAewJ3DUvH8AVWjMzMzNrNBExTdLhwINAc+CKiHh1Xj6GIuZpC4OZmZmZWVm55cDMzMzMCs0JrZmZmZkVmhNaMzMzMys0J7RmZmZmVmhOaM3MzMys0JzQmpmZmVmhOaE1MzMzs0JzQmtmZmZmhfb/yZ7eoa7mkfkAAAAASUVORK5CYII=\n",
|
| 228 |
+
"text/plain": [
|
| 229 |
+
"<Figure size 720x720 with 2 Axes>"
|
| 230 |
+
]
|
| 231 |
+
},
|
| 232 |
+
"metadata": {
|
| 233 |
+
"needs_background": "light"
|
| 234 |
+
},
|
| 235 |
+
"output_type": "display_data"
|
| 236 |
+
}
|
| 237 |
+
],
|
| 238 |
+
"source": [
|
| 239 |
+
"#Print the Target names\n",
|
| 240 |
+
"from sklearn.metrics import classification_report, confusion_matrix\n",
|
| 241 |
+
"import itertools \n",
|
| 242 |
+
"\n",
|
| 243 |
+
"#shuffle=False\n",
|
| 244 |
+
"\n",
|
| 245 |
+
"target_names = []\n",
|
| 246 |
+
"for key in test_generator.class_indices:\n",
|
| 247 |
+
" target_names.append(key)\n",
|
| 248 |
+
"\n",
|
| 249 |
+
"# print(target_names)#Confution Matrix\n",
|
| 250 |
+
"Y_pred = model.predict(test_generator)\n",
|
| 251 |
+
"y_pred = np.argmax(Y_pred, axis=1)\n",
|
| 252 |
+
"print('Confusion Matrix')\n",
|
| 253 |
+
"\n",
|
| 254 |
+
"cm = confusion_matrix(test_generator.classes, y_pred)\n",
|
| 255 |
+
"plot_confusion_matrix(cm, target_names, title='Confusion Matrix', normalize=False)\n",
|
| 256 |
+
"\n",
|
| 257 |
+
"#Print Classification Report\n",
|
| 258 |
+
"#print('Classification Report')\n",
|
| 259 |
+
"#print(classification_report(test_generator.classes, y_pred, target_names=target_names))"
|
| 260 |
+
]
|
| 261 |
+
},
|
| 262 |
+
{
|
| 263 |
+
"cell_type": "code",
|
| 264 |
+
"execution_count": null,
|
| 265 |
+
"id": "e49a4c65",
|
| 266 |
+
"metadata": {},
|
| 267 |
+
"outputs": [],
|
| 268 |
+
"source": []
|
| 269 |
+
}
|
| 270 |
+
],
|
| 271 |
+
"metadata": {
|
| 272 |
+
"kernelspec": {
|
| 273 |
+
"display_name": "Python 3 (ipykernel)",
|
| 274 |
+
"language": "python",
|
| 275 |
+
"name": "python3"
|
| 276 |
+
},
|
| 277 |
+
"language_info": {
|
| 278 |
+
"codemirror_mode": {
|
| 279 |
+
"name": "ipython",
|
| 280 |
+
"version": 3
|
| 281 |
+
},
|
| 282 |
+
"file_extension": ".py",
|
| 283 |
+
"mimetype": "text/x-python",
|
| 284 |
+
"name": "python",
|
| 285 |
+
"nbconvert_exporter": "python",
|
| 286 |
+
"pygments_lexer": "ipython3",
|
| 287 |
+
"version": "3.9.12"
|
| 288 |
+
}
|
| 289 |
+
},
|
| 290 |
+
"nbformat": 4,
|
| 291 |
+
"nbformat_minor": 5
|
| 292 |
+
}
|
Code/test_model_VGG19.ipynb
ADDED
|
@@ -0,0 +1,265 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{
|
| 2 |
+
"cells": [
|
| 3 |
+
{
|
| 4 |
+
"cell_type": "code",
|
| 5 |
+
"execution_count": 2,
|
| 6 |
+
"id": "8870f399",
|
| 7 |
+
"metadata": {},
|
| 8 |
+
"outputs": [],
|
| 9 |
+
"source": [
|
| 10 |
+
"from keras.models import load_model\n",
|
| 11 |
+
"from tensorflow.keras.utils import load_img\n",
|
| 12 |
+
"from keras.preprocessing.image import ImageDataGenerator\n",
|
| 13 |
+
"import matplotlib.pyplot as plt\n",
|
| 14 |
+
"\n",
|
| 15 |
+
"import numpy as np"
|
| 16 |
+
]
|
| 17 |
+
},
|
| 18 |
+
{
|
| 19 |
+
"cell_type": "code",
|
| 20 |
+
"execution_count": 3,
|
| 21 |
+
"id": "9a2915f5",
|
| 22 |
+
"metadata": {},
|
| 23 |
+
"outputs": [],
|
| 24 |
+
"source": [
|
| 25 |
+
"# Leemos el modelo guardado\n",
|
| 26 |
+
"model = load_model('../../model/classification/vgg19_trainable_true_best_model.h5')"
|
| 27 |
+
]
|
| 28 |
+
},
|
| 29 |
+
{
|
| 30 |
+
"cell_type": "code",
|
| 31 |
+
"execution_count": 4,
|
| 32 |
+
"id": "501c48e4",
|
| 33 |
+
"metadata": {},
|
| 34 |
+
"outputs": [],
|
| 35 |
+
"source": [
|
| 36 |
+
"test_data_dir = '../../dataset/classification/PCB_Dataset_Split/test'\n",
|
| 37 |
+
"size = (224, 224)\n",
|
| 38 |
+
"batch_size = 32"
|
| 39 |
+
]
|
| 40 |
+
},
|
| 41 |
+
{
|
| 42 |
+
"cell_type": "code",
|
| 43 |
+
"execution_count": 5,
|
| 44 |
+
"id": "adb21285",
|
| 45 |
+
"metadata": {},
|
| 46 |
+
"outputs": [
|
| 47 |
+
{
|
| 48 |
+
"name": "stdout",
|
| 49 |
+
"output_type": "stream",
|
| 50 |
+
"text": [
|
| 51 |
+
"Found 1716 images belonging to 8 classes.\n"
|
| 52 |
+
]
|
| 53 |
+
}
|
| 54 |
+
],
|
| 55 |
+
"source": [
|
| 56 |
+
"test_datagen = ImageDataGenerator(rescale = 1. / 255)\n",
|
| 57 |
+
"test_generator = test_datagen.flow_from_directory(test_data_dir,\n",
|
| 58 |
+
" target_size = size,\n",
|
| 59 |
+
" keep_aspect_ratio = True,\n",
|
| 60 |
+
" batch_size = batch_size,\n",
|
| 61 |
+
" shuffle = False,\n",
|
| 62 |
+
" class_mode = 'categorical')"
|
| 63 |
+
]
|
| 64 |
+
},
|
| 65 |
+
{
|
| 66 |
+
"cell_type": "code",
|
| 67 |
+
"execution_count": 6,
|
| 68 |
+
"id": "62499652",
|
| 69 |
+
"metadata": {},
|
| 70 |
+
"outputs": [
|
| 71 |
+
{
|
| 72 |
+
"name": "stderr",
|
| 73 |
+
"output_type": "stream",
|
| 74 |
+
"text": [
|
| 75 |
+
"C:\\Users\\shiru\\AppData\\Local\\Temp\\ipykernel_19588\\558093203.py:1: UserWarning: `Model.evaluate_generator` is deprecated and will be removed in a future version. Please use `Model.evaluate`, which supports generators.\n",
|
| 76 |
+
" test_score = model.evaluate_generator(test_generator, batch_size)\n"
|
| 77 |
+
]
|
| 78 |
+
},
|
| 79 |
+
{
|
| 80 |
+
"name": "stdout",
|
| 81 |
+
"output_type": "stream",
|
| 82 |
+
"text": [
|
| 83 |
+
"[INFO] accuracy: 99.32%\n",
|
| 84 |
+
"[INFO] Loss: 0.020894860848784447\n"
|
| 85 |
+
]
|
| 86 |
+
}
|
| 87 |
+
],
|
| 88 |
+
"source": [
|
| 89 |
+
"test_score = model.evaluate_generator(test_generator, batch_size)\n",
|
| 90 |
+
"\n",
|
| 91 |
+
"print(\"[INFO] accuracy: {:.2f}%\".format(test_score[1] * 100))\n",
|
| 92 |
+
"print(\"[INFO] Loss: \",test_score[0])"
|
| 93 |
+
]
|
| 94 |
+
},
|
| 95 |
+
{
|
| 96 |
+
"cell_type": "code",
|
| 97 |
+
"execution_count": 7,
|
| 98 |
+
"id": "3be33f81",
|
| 99 |
+
"metadata": {},
|
| 100 |
+
"outputs": [],
|
| 101 |
+
"source": [
|
| 102 |
+
"#Plot the confusion matrix. Set Normalize = True/False\n",
|
| 103 |
+
"\n",
|
| 104 |
+
"def plot_confusion_matrix(cm, classes, normalize=True, title='Confusion matrix', cmap=plt.cm.Blues):\n",
|
| 105 |
+
" \"\"\"\n",
|
| 106 |
+
" This function prints and plots the confusion matrix.\n",
|
| 107 |
+
" Normalization can be applied by setting `normalize=True`.\n",
|
| 108 |
+
" \"\"\"\n",
|
| 109 |
+
" plt.figure(figsize=(10,10))\n",
|
| 110 |
+
" plt.imshow(cm, interpolation='nearest', cmap=cmap)\n",
|
| 111 |
+
" plt.title(title)\n",
|
| 112 |
+
" plt.colorbar()\n",
|
| 113 |
+
" tick_marks = np.arange(len(classes))\n",
|
| 114 |
+
" plt.xticks(tick_marks, classes, rotation=45)\n",
|
| 115 |
+
" plt.yticks(tick_marks, classes)\n",
|
| 116 |
+
" \n",
|
| 117 |
+
" if normalize:\n",
|
| 118 |
+
" cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]\n",
|
| 119 |
+
" cm = np.around(cm, decimals=2)\n",
|
| 120 |
+
" cm[np.isnan(cm)] = 0.0\n",
|
| 121 |
+
" print(\"Normalized confusion matrix\")\n",
|
| 122 |
+
" else:\n",
|
| 123 |
+
" print('Confusion matrix, without normalization')\n",
|
| 124 |
+
" \n",
|
| 125 |
+
" thresh = cm.max() / 2.\n",
|
| 126 |
+
" for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):\n",
|
| 127 |
+
" plt.text(j, i, cm[i, j],\n",
|
| 128 |
+
" horizontalalignment=\"center\",\n",
|
| 129 |
+
" color=\"white\" if cm[i, j] > thresh else \"black\")\n",
|
| 130 |
+
" plt.tight_layout()\n",
|
| 131 |
+
" plt.ylabel('True label')\n",
|
| 132 |
+
" plt.xlabel('Predicted label')#Print the Target names"
|
| 133 |
+
]
|
| 134 |
+
},
|
| 135 |
+
{
|
| 136 |
+
"cell_type": "code",
|
| 137 |
+
"execution_count": 8,
|
| 138 |
+
"id": "a252f5c6",
|
| 139 |
+
"metadata": {},
|
| 140 |
+
"outputs": [
|
| 141 |
+
{
|
| 142 |
+
"name": "stdout",
|
| 143 |
+
"output_type": "stream",
|
| 144 |
+
"text": [
|
| 145 |
+
"54/54 [==============================] - 32s 598ms/step\n",
|
| 146 |
+
"Confusion Matrix\n",
|
| 147 |
+
"Confusion matrix, without normalization\n"
|
| 148 |
+
]
|
| 149 |
+
},
|
| 150 |
+
{
|
| 151 |
+
"data": {
|
| 152 |
+
"image/png": "iVBORw0KGgoAAAANSUhEUgAAArQAAALGCAYAAAC01AIQAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/NK7nSAAAACXBIWXMAAAsTAAALEwEAmpwYAABweElEQVR4nO3dd5xcZdXA8d9JQugtFCEJkQ4miJTQi4hKrwICgoI0UYqgvIqKSBFFUUBpitIEpClKb9JBICT0IkWKJKGF3gPLef+4d8OwbDZLyO7dO/P78tkPM3fu3DnPzGb2zJnzPDcyE0mSJKmu+lUdgCRJkvRJmNBKkiSp1kxoJUmSVGsmtJIkSao1E1pJkiTVmgmtJEmSam1A1QFIkiTp4+s/26cz33ur6jDIt56/IjPXqzIGE1pJkqQayvfeYvolvlp1GLx913FzVx2DCa0kSVItBYTdo2APrSRJkmrOhFaSJEm1ZsuBJElSHQUQUXUUfYIVWkmSJNWaCa0kSZJqzZYDSZKkunKVA8AKrSRJkmrOhFaSJEm1ZsuBJElSXbnKAWCFVpIkSTVnhVaSJKmWPPVtO58FSZIk1ZoJrSRJkmrNlgNJkqS6clIYYIVWkiRJNWdCK0mSpFqz5UCSJKmOAlc5KPksSJIkqdas0EqSJNVSOCmsZIVWkiRJtWZCK0mSpFqz5UCSJKmunBQGWKGVJElSzZnQSpIkqdZsOZAkSaorVzkArNBKkiSp5qzQSpIk1VI4KazksyBJkqRaM6GVJElSrdlyIEmSVEeBk8JKVmglSZJUaya0kiRJqjVbDiRJkurKVQ4AK7SSJEmqOSu0kiRJteQ6tO18FiRJklRrJrSSJEmqNVsOJEmS6qqf69CCFVpJkiTVnAmtJEmSas2WA0mSpDoKXOWg5LMgSZKkWjOhlSRJUq3ZciBJklRX4SoHYIVWkiRJNWeFVpIkqZY89W07nwVJkiTVmgmtJEmSas2WA0mSpLpyUhhghVaSJEk1Z0IrSZKkWrPlQJIkqa5c5QCwQitJkqSas0IrSZJURxFOCitZoZUkSVKtmdBKkiSp1mw5kCRJqisnhQFWaCVJklRzJrSSJEnqMRExQ0SMioi7I+L+iDi43D4oIq6KiEfK/8/ZcJ8fRcSjEfFQRKw7pccwoZUkSaqr9pUOqvyZsneAtTPzc8AywHoRsTKwP3B1Zi4GXF1eJyKGA9sAI4D1gOMjon9XD2BCK0mSpB6ThdfLq9OVPwlsCpxWbj8N2Ky8vClwdma+k5mPA48CK3b1GE4KkyRJqqXoK5PC5o6I0Q3XT8zMExt3KCusY4BFgeMy87aI+FRmPg2QmU9HxLzl7kOAWxvuPrbcNlkmtJIkSfokJmTmyK52yMw2YJmImAP4R0Qs1cXunfUxZFfH7xNpvSRJkppfZr4MXEfRG/tsRMwPUP7/uXK3scACDXcbCozv6rgmtJIkSXVV9YSwbkwKi4h5ysosETEj8CXgP8CFwA7lbjsAF5SXLwS2iYjpI2IhYDFgVFePYcuBJEmSetL8wGllH20/4NzMvDgibgHOjYidgf8BWwFk5v0RcS7wAPAesEfZsjBZJrSSJEnqMZl5D7BsJ9tfAL44mfscBhzW3ccwoZUkSaqjoK+sclA5nwVJkiTVmgmtJEmSas2WA0mSpFrqMydWqJzPgiRJkmrNCq0kSVJddWMd2FZghVaSJEm1ZkIrqelFxIwRcVFEvBIR532C42wXEVdOy9iqEBGXRcQOU95TkurBhFZSnxERX4uI0RHxekQ8XSZeq0+DQ28JfAqYKzO3mtqDZOaZmbnONIjnQyJirYjIiDi/w/bPlduv6+ZxDoqIM6a0X2aun5mnTWW4kvqS6Ff9Tx/QN6KQ1PIi4nvA0cAvKJLPYcDxwKbT4PCfBh7OzPemwbF6yvPAqhExV8O2HYCHp9UDRMH3fUlNxzc2SZWLiNmBQyjO131+Zr6Rme9m5kWZ+X/lPtNHxNERMb78OToipi9vWysixkbE9yPiubK6+83ytoOBA4Gty8rvzh0rmRGxYFkJHVBe3zEiHouI1yLi8YjYrmH7TQ33WzUibi9bGW6PiFUbbrsuIg6NiJvL41wZEXN38TRMBP4JbFPevz/wVeDMDs/V7yLiqYh4NSLGRMQa5fb1gB83jPPuhjgOi4ibgTeBhcttu5S3nxARf2s4/q8i4uoIZ5pIqg8TWkl9wSrADMA/utjnJ8DKwDLA54AVgQMabp8PmB0YAuwMHBcRc2bmzyiqvudk5iyZeVJXgUTEzMDvgfUzc1ZgVeCuTvYbBFxS7jsXcCRwSYcK69eAbwLzAgOB/bp6bOAvwDfKy+sC9wPjO+xzO8VzMAj4K3BeRMyQmZd3GOfnGu7zdWA3YFbgyQ7H+z6wdJmsr0Hx3O2QmTmFWCX1BRHV//QBJrSS+oK5gAlTaAnYDjgkM5/LzOeBgykStXbvlre/m5mXAq8DS0xlPO8DS0XEjJn5dGbe38k+GwKPZObpmfleZp4F/AfYuGGfUzLz4cx8CziXIhGdrMz8NzAoIpagSGz/0sk+Z2TmC+Vj/haYnimP89TMvL+8z7sdjvcmsD1FQn4GsFdmjp3C8SSpTzGhldQXvADM3f6V/2QM5sPVxSfLbZOO0SEhfhOY5eMGkplvAFsDuwNPR8QlEbFkN+Jpj2lIw/VnpiKe04E9gS/QScW6bKt4sGxzeJmiKt1VKwPAU13dmJmjgMeAoEi8JdVBRPUTwvpIW37fiEJSq7sFeBvYrIt9xlNM7mo3jI9+Hd9dbwAzNVyfr/HGzLwiM78MzE9Rdf1TN+Jpj2ncVMbU7nTgO8ClZfV0krIl4IcUvbVzZuYcwCsUiSjA5NoEumwfiIg9KCq944EfTHXkklQRE1pJlcvMVygmbh0XEZtFxEwRMV1ErB8Rvy53Ows4ICLmKSdXHUjxFfnUuAtYMyKGlRPSftR+Q0R8KiI2KXtp36FoXWjr5BiXAouXS40NiIitgeHAxVMZEwCZ+TjweYqe4Y5mBd6jWBFhQEQcCMzWcPuzwIIfZyWDiFgc+DlF28HXgR9ExDJTF70kVcOEVlKfkJlHAt+jmOj1PMXX5HtSzPyHIukaDdwD3AvcUW6bmse6CjinPNYYPpyE9qOYKDUeeJEiufxOJ8d4Adio3PcFisrmRpk5YWpi6nDsmzKzs+rzFcBlFEt5PUlR1W5sJ2g/acQLEXHHlB6nbPE4A/hVZt6dmY9QrJRwevsKEpL6uKonhPWRSWHhRFZJkqT66Tfngjn9F35adRi8/Y9dxmTmyCpjsEIrSZKkWutqRrEkSZL6MM+BUrBCK0mSpFqzQitJklRDgRXadia0vWDWOQblXPMPrTqMSsw108CqQ5AkqUc8+eQTTJgwwYyyDzCh7QVzzT+Un/3lEy1NWVvbLjus6hAkSeoRq61U6cR+NTChlSRJqqPgg/MEtjgnhUmSJKnWTGglSZJUa7YcSJIk1VK4ykHJCq0kSZJqzQqtJElSTVmhLVihlSRJUq2Z0EqSJKnWbDmQJEmqKVsOClZoJUmSVGsmtJIkSao1Ww4kSZJqypaDghVaSZIk1ZoJrSRJkmrNlgNJkqQ6ivJHVmglSZJUb1ZoJUmSaigIJ4WVrNBKkiSp1kxoJUmSVGu2HEiSJNWULQcFK7SSJEmqNRNaSZIk1ZoJbc2dfOh+fHfd5fjpNl+etO3c3x/Gj7damwO/ti7H/N9uvPnaKwA8dv9d/Gy79fnZdutz4NfWY8y1l1cVdo+78orLWXrEEoxYclGO+PXhVYfTqxy7Y3fsrcOxt+bYG0VE5T99gQltza224VZ873enfWjb8BXX4NCzruSQv17BfMMW4pJTjwdgyCJLcOBpF3HwmZfxvd+fxl8O/zFt771XRdg9qq2tjX323oMLLrqMO+95gPPOPosHH3ig6rB6hWN37I7dsbeCVh67OmdCW3NLLLcSM882x4e2LbXymvQfUMz3W3ipZXnpuacBmH6GGSdtf/edd/rMp6pp7fZRo1hkkUVZaOGFGThwIFttvQ0XX3RB1WH1Csfu2B27Y28FrTz2jqquzvaVXMKEtsnddNG5fHbVtSZd/+99d3LA1l/iwK+ty9d/eNikBLeZjB8/jqFDF5h0fciQoYwbN67CiHqPY3fs4Ngde/Nr5bGrc7VIaCNiwYi4r5cfc62IuHgyt/05IoaXl5+IiLl7M7buuujkY+jXfwArr7f5pG2LLLUsPz/nX/z01Au59LTjefedtyuMsGdk5ke29ZVPkD3NsX+YY29+jv3DHLtaVS0S2r4mM3fJzD7drHPzxX/jnpuuZrdDf9fpP/LBCy3G9DPOyNj/PlxBdD1ryJChjB371KTr48aNZfDgwRVG1Hscu2MHx+7Ym18rj/1Doo/89AF1SmgHRMRpEXFPRPwtImaKiAMj4vaIuC8iTowyc4uIvSPigXLfs8ttgyLin+W2WyNi6XL7QRFxekRcExGPRMSuDY85S/lY/4mIMxuOf11EjOz1Z6Cb7r3lOi49/QT2+u1JTD/DjJO2Pz/uf5MmgU14eixPP/kYcw8eWlWYPWbkCivw6KOP8MTjjzNx4kTOO+dsNtxok6rD6hWO3bE7dsfeClp57OpcnRoolwB2zsybI+Jk4DvAsZl5CEBEnA5sBFwE7A8slJnvRMQc5f0PBu7MzM0iYm3gL8Ay5W1LAysDMwN3RsQl5fZlgRHAeOBmYDXgph4d5cf0hwP24qExt/D6yy/x/Y1WYtNd9y1aCSZO5Ld7bg8UbQbf+NEveOTu0Vx62vH0HzAd0S/4+g9+zqxzDKp4BNPegAEDOOp3x7LxhuvS1tbGDjvuxPARI6oOq1c4dsfu2B17K2jlsatz0VkfSl8TEQsCN2TmsPL62sDewOnAD4CZgEHAMZl5eERcDrwO/BP4Z2a+HhF3Altk5mPlMZ4ClgL2Bfpl5oHl9r8A5wMvAz/JzC+X208Abs7MMyLiOmC/zBwdEU8AIzNzQoeYdwN2A5hrviHLH3Hhv3viqenztl12WNUhSJLUI1ZbaSRjxoyu7Ev3AXMvnHNs9IuqHn6SF07bdkxmVvrNdZ1aDjpm3gkcD2yZmZ8F/gTMUN62IXAcsDwwJiIG0HmXR3b4f8ft7zRsa+NjVLQz88TMHJmZI2dpwiqoJElSX1GnhHZYRKxSXt6WD776nxARswBbAkREP2CBzLyWono7BzALcAOwXbnPWsCEzHy1PMamETFDRMwFrAXc3tODkSRJ+iSC6teg7SurS9Sph/ZBYIeI+CPwCHACMCdwL/AEHySh/YEzImJ2iqrsUZn5ckQcBJwSEfcAbwI7NBx7FHAJMAw4NDPHR8TiPT8kSZIkfVK1SGgz8wlgeCc3HVD+dLR6J8d4Edh0Mg/xcGbu1mH/64DrGq7v2XB5rYbLC04ubkmSJPW8WiS0kiRJ+qi+8pV/1Vo+oc3Mg6qOQZIkSVOvTpPCJEmSpI9o+QqtJElSbdlxAFihlSRJUs2Z0EqSJKnWbDmQJEmqo3CVg3ZWaCVJklRrVmglSZJqygptwQqtJEmSas2EVpIkSbVmy4EkSVJN2XJQsEIrSZKkWjOhlSRJUq3ZciBJklRDQdhyULJCK0mSpFqzQitJklRXFmgBK7SSJEmqORNaSZIk1ZotB5IkSXUUrkPbzgqtJEmSas2EVpIkSbVmy4EkSVJN2XJQsEIrSZKkWrNCK0mSVFNWaAtWaCVJklRrVmh7wVwzDWTbZYdVHUYl5lz7Z1WHUJmXrjm46hAkSWoJJrSSJEl1ZccBYMuBJEmSas6EVpIkSbVmy4EkSVJNucpBwQqtJEmSas0KrSRJUg1FhBXakhVaSZIk1ZoJrSRJkmrNlgNJkqSasuWgYIVWkiRJPSYiFoiIayPiwYi4PyK+W24/KCLGRcRd5c8GDff5UUQ8GhEPRcS6U3oMK7SSJEnqSe8B38/MOyJiVmBMRFxV3nZUZv6mceeIGA5sA4wABgP/iojFM7Ntcg9gQitJklRTdWg5yMyngafLy69FxIPAkC7usilwdma+AzweEY8CKwK3TO4OthxIkiSpV0TEgsCywG3lpj0j4p6IODki5iy3DQGearjbWLpOgE1oJUmS9InMHRGjG35262yniJgF+DuwT2a+CpwALAIsQ1HB/W37rp3cPbsKwJYDSZKkuuobHQcTMnNkVztExHQUyeyZmXk+QGY+23D7n4CLy6tjgQUa7j4UGN/V8a3QSpIkqcdE0eh7EvBgZh7ZsH3+ht02B+4rL18IbBMR00fEQsBiwKiuHsMKrSRJUk3VYVIYsBrwdeDeiLir3PZjYNuIWIaineAJ4FsAmXl/RJwLPECxQsIeXa1wACa0kiRJ6kGZeROdN0dc2sV9DgMO6+5j2HIgSZKkWrNCK0mSVEdRm5aDHmeFVpIkSbVmQitJkqRas+VAkiSphgKw46BghVaSJEm1ZkLbxK684nKWHrEEI5ZclCN+fXjV4Uxz0w8cwI1/3JXbTv42Y07bgwO++QUAvrLWcMactgdvXPczllti8KT9R35mCLeetDu3nrQ7t538bTZZY8mqQu9Rzf66d8WxO3bH3jpaeewfCCKq/+kLbDloUm1tbeyz9x5cctlVDBk6lNVXXoGNNtqEzwwfXnVo08w7E99jvX1O4423JjKgfz+uOW5nrrztEe5//Dm2OeBsjt1v4w/tf/9jz7HabifS1vY+8801C7ed/G0u+ffDtLW9X9EIpr1WeN0nx7E7dsfu2Fth7OqcFdomdfuoUSyyyKIstPDCDBw4kK223oaLL7qg6rCmuTfemgjAdAP6M2BAPzKTh56cwCNPvfCRfd96591Jyev0AweQ2auh9opWed0749gdu2N37GpdJrRNavz4cQwdusCk60OGDGXcuHEVRtQz+vULbj1pd/53wf9xzejHuP3Brse4wmeGMOa0PRh9ynfY+7cXNVV1Flrnde+MY3fs4Ngde+uJqP6nL6h9QhsRh0TEl6bxMdeKiIsnc9ufI2J4efmJiJh7Wj72tJKdlB/7Sp/LtPT++8nKO/+BRbc8kpFLDmH4QvN2uf/tD45j+R2OY/Vvncj/bb8G0w9srq6bVnndO+PYP8yxNz/H/mGtMnZ1rvYJbWYemJn/6sXH2yUzH+itx5taQ4YMZezYpyZdHzduLIMHD+7iHvX2yutvc8NdT7DOSot2a/+HnpzAG2+9y4gpJMB102qveyPH7tjBsTt2tarKE9qI2D4iRkXEXRHxx4joHxHbRsS9EXFfRPyq3K9/RJxabrs3IvYtt58aEVuWl5+IiIMj4o5ynyXL7YMi4p8RcU9E3BoRS5fbD4qI0yPimoh4JCJ2bQhtloj4W0T8JyLOjPKjX0RcFxEje/VJmgojV1iBRx99hCcef5yJEydy3jlns+FGm1Qd1jQ19+wzMfssMwAww8ABrL38wjz05ITJ7v/p+eegf//iV37Yp2Zn8WFz8eQzL/dGqL2mFV73yXHsjt2xO/ZWVPUKB32lMl7p960R8Rlga2C1zHw3Io4HtgN+DiwPvARcGRGbAU8BQzJzqfK+c0zmsBMyc7mI+A6wH7ALcDBwZ2ZuFhFrA38Blin3XxpYGZgZuDMiLim3LwuMAMYDNwOrATd9jLHtBuwGsMCwYd292zQzYMAAjvrdsWy84bq0tbWxw447MXzEiF6PoyfNN9es/OnHm9O/f9Avgr9fez+X3fIwm6yxJEd+dwPmnmNmzv/Vdtzz6DNsst/prPrZYey33Rq8+14b72fy3SMv4YVX3qx6GNNUK7zuk+PYHbtjd+xqXdFZH0qvPXjEnsCPgefKTTMCbwL3ZuY3yn12pkgsDwVGA5cClwBXZub7EXEqcHFm/i0inqBIjsdFxErAYZn5pYi4E9giMx8rj/kUsBSwL9AvMw8st/8FOB94GfhJZn653H4CcHNmnhER1wH7Zebo8vFGZubky4LA8suPzJtvG/0Jn616mnPtn1UdQmVeuubgqkOQJPWg1VYayZgxoysrUc4w/+K54A7HVPXwkzz0q/XGZGal315X3XIQwGmZuUz5swRFNfUjMvMl4HPAdcAewJ8nc8x3yv+38UEFurNftuzw/47b32nY1ngsSZIk9SFVJ7RXA1tGxLxQ9LoCdwKfj4i5I6I/sC1wfbmaQL/M/DvwU2C5j/E4N1C0MhARa1G0Jbxa3rZpRMwQEXMBawG3f+JRSZIkqddUWnXMzAci4gCKPtl+wLsU1dcfAddSVFYvzcwLIuJzwCnlfpT7dNdB5X3voWhp2KHhtlEULQzDgEMzc3xELP5JxiVJktTTgmI9dvWBr9Ez8xzgnA6bbwX+2mG/u+mkKpuZOzZcXrDh8miKiiuZ+SKw6WRCeDgzd+twzOsoWhvar+/ZcHmtzh5PkiRJ1ai65UCSJEn6RCqv0FYpMw+qOgZJkqSp1UeWga2cFVpJkiTVmgmtJEmSaq2lWw4kSZLqrK+cerZqVmglSZJUa1ZoJUmS6iicFNbOCq0kSZJqzYRWkiRJtWbLgSRJUg0FTgprZ4VWkiRJtWZCK0mSpFqz5UCSJKmWwpaDkhVaSZIk1ZoVWkmSpJqyQFuwQitJkqRaM6GVJElSrdlyIEmSVFNOCitYoZUkSVKtmdBKkiSp1mw5kCRJqqNwlYN2VmglSZJUa1ZoJUmSaihwUlg7K7SSJEmqNRNaSZIk1ZotB+pRL11zcNUhVObgKx+qOoTK/GydJaoOQZJagh0HBSu0kiRJqjUTWkmSJNWaLQeSJEk15SoHBSu0kiRJqjUrtJIkSTVlgbZghVaSJEm1ZkIrSZKkWrPlQJIkqY7CSWHtrNBKkiSp1kxoJUmSVGu2HEiSJNVQ4CoH7azQSpIkqdZMaCVJklRrthxIkiTVUrjKQckKrSRJkmrNCq0kSVJNWaAtWKGVJElSrZnQSpIkqdZsOZAkSaopJ4UVrNBKkiSp1kxoJUmSVGu2HEiSJNVRuMpBOyu0kiRJqjUrtJIkSTUUOCmsnRXaJnblFZez9IglGLHkohzx68OrDqdXNfvYLzn6x/z+a6vy5+9sPGnbjWcew7HfWJOT99yMk/fcjP/efj0ALz87lt9s/rlJ2y8/9mdVhd3jmv1174pjd+ytNvZv7bITwwbPy/LLLFV1KOoDrNA2qba2NvbZew8uuewqhgwdyuorr8BGG23CZ4YPrzq0HtcKY//slzZn+Y224+Ij9//Q9hU23YGVttj5I/vPMf8wdjr2n70UXTVa4XWfHMfu2Ftt7ABf32FHdv/Onuyy0zeqDkV9gBXaJnX7qFEsssiiLLTwwgwcOJCttt6Giy+6oOqwekUrjH3YUisww6yzVx1Gn9IKr/vkOHbH3mpjB1h9jTUZNGhQ1WFULiIq/+kLTGib1Pjx4xg6dIFJ14cMGcq4ceMqjKj3tPLYx1x8JiftsQmXHP1j3n7tlUnbX3lmLCfvtTln/nB7nrpvdIUR9pxWft0du2OH1hq71FGfTWgj4scNlxeMiPs+4fGeiIi5O9l+UETsNxXHWyYiNvgkMfWkzPzItr7yKaqnterYl9tgW3b/81XsdMw/mWXOebj6pF8BMMugefnOqdew0zH/4Iu77M+FR+zHO2++XnG0016rvu7g2Dty7FLrqTShjYj+Xdz84y5um9zxerMneBmgzya0Q4YMZezYpyZdHzduLIMHD64wot7TqmOfec656de/P9GvH59bbyuefvheAAZMN5AZZ5sTgPkWW4o55l+AF8c9XmWoPaJVX3dw7I690Epj1wciqv/pC3o0oY2I7SNiVETcFRF/jIj+EfF6RBwSEbcBB0TEPxr2/3JEnB8RhwMzlvc7s7y5f0T8KSLuj4grI2LG8j7XRcQvIuJ64LsR8cWIuDMi7o2IkyNi+oaQ/q+MZ1RELNpJvLtGxO0RcXdE/D0iZiq3bxUR95Xbb4iIgcAhwNZljFv30FM41UausAKPPvoITzz+OBMnTuS8c85mw402qTqsXtGqY3/9xecmXX743/9ink8vBsCbr7zI+21tALz89FO8NP5J5phvgU6PUWet+rqDY3fsrTd2qaMeq2hGxGeArYHVMvPdiDge2A6YGbgvMw+M4ruRByNinsx8HvgmcEpmXhQRe2bmMuWxFgQWA7bNzF0j4lxgC+CM8uHmyMzPR8QMwCPAFzPz4Yj4C/Bt4Ohyv1czc8WI+Ea5baMOYZ+fmX8qH/PnwM7AMcCBwLqZOS4i5sjMiRFxIDAyM/eczPh3A3YDWGDYsKl8FqfegAEDOOp3x7LxhuvS1tbGDjvuxPARI3o9jiq0wtgv+NX3+N+9t/PWqy9x3Dc+z+rb7cX/7h3Fc489CBHMPu8Q1tvrYAD+d9/t3HTGMUT//vTr15919ziIGWedo9oB9IBWeN0nx7E79lYbO8A3tt+WG6+/jgkTJrDIgkP56YEHs+NOH13lpdnZZlKIznpwpsmBI/akaBtoLxvNCJwFHABMn5lt5X4/Ad4ETgHuBBbLzPci4vXMnKXcZ0HgqsxcrLz+Q2C6zPx5RFwH/Cwzr4+IzwHHZOaa5X5fBPbIzK9ExBPA2pn5WERMBzyTmXNFxEHA65n5m4j4PPBzYA5gFuCKzNw9Iv4ALAKcS5H0vhARO9JFQtto+eVH5s23NedEHE3ewVc+VHUIlfnZOktUHYIk9bjVVhrJmDGjK8soZ11gyVz++ydX9fCTXL/vamMyc2SVMfRkz2kAp2Xmjz60MWK/9mS2dApwEfA2cF5mvjeZ473TcLmNIkFu90bDY3YlJ3O53anAZpl5d5mwrgVQJrUrARsCd0XEMlN4HEmSJPWSnuyhvRrYMiLmBYiIQRHx6Y47ZeZ4YDxF5fbUhpveLSupH8d/gAUb+mO/DlzfcPvWDf+/pZP7zwo8XT7udu0bI2KRzLwtMw8EJgALAK+V+0uSJPW+PjAhrK90PPRYQpuZD1AkqVdGxD3AVcD8k9n9TOCp8j7tTgTuaZgU1p3HfJuiD/e8iLgXeB/4Q8Mu05eT0b4L7NvJIX4K3FbG+p+G7UeUk8zuA24A7gauBYb31UlhkiRJraJHl7nKzHOAczpsnqWTXVcH/tThvj8EftiwaamG237TcHmtDve7Gli2k1gWLC8e3GH7QQ2XTwBO6OS+X+kk5heBFTrZLkmSpF7Um+u2dioixlD0wH6/6lgkSZLqIug7p56tWuUJbWYuX3UMkiRJqq8+e+pbSZIkqTsqr9BKkiRp6thxULBCK0mSpFqzQitJklRT/SzRAlZoJUmSVHMmtJIkSao1Ww4kSZJqyo6DghVaSZIk1ZoJrSRJkmrNlgNJkqQaisBT35as0EqSJKnWTGglSZJqql9U/zMlEbFARFwbEQ9GxP0R8d1y+6CIuCoiHin/P2fDfX4UEY9GxEMRse4Un4dP8iRKkiRJU/Ae8P3M/AywMrBHRAwH9geuzszFgKvL65S3bQOMANYDjo+I/l09gAmtJEmSekxmPp2Zd5SXXwMeBIYAmwKnlbudBmxWXt4UODsz38nMx4FHgRW7egwnhUmSJNVU3SaFRcSCwLLAbcCnMvNpKJLeiJi33G0IcGvD3caW2ybLhFaSJEmfxNwRMbrh+omZeWLHnSJiFuDvwD6Z+WoXyXhnN2RXAZjQSpIk6ZOYkJkju9ohIqajSGbPzMzzy83PRsT8ZXV2fuC5cvtYYIGGuw8Fxnd1fHtoJUmSaqpYi7banynHGAGcBDyYmUc23HQhsEN5eQfggobt20TE9BGxELAYMKqrx7BCK0mSpJ60GvB14N6IuKvc9mPgcODciNgZ+B+wFUBm3h8R5wIPUKyQsEdmtnX1ACa0kiRJNRRAdNpu2rdk5k103hcL8MXJ3Ocw4LDuPoYtB5IkSao1E1pJkiTVmi0HkiRJNdWdU8+2AhNaqYf8bJ0lqg6hMnNte0rVIVTmhbO+WXUIqkjb+10uk9nU+ptVqWK2HEiSJKnWrNBKkiTVUUTtTn3bU6zQSpIkqdas0EqSJNWUBdqCFVpJkiTVmgmtJEmSas2WA0mSpBoKoJ89B4AVWkmSJNWcCa0kSZJqzZYDSZKkmrLjoGCFVpIkSbVmQitJkqRas+VAkiSppjz1bcEKrSRJkmrNCq0kSVINRTgprJ0VWkmSJNWaCa0kSZJqzZYDSZKkmvLUtwUrtJIkSao1E1pJkiTVmi0HkiRJNWXDQcEKrSRJkmrNCq0kSVJNeaawghVaSZIk1ZoJbRO78orLWXrEEoxYclGO+PXhVYfTqxx78459yFwzc+nP1mPMUZtz+5Gb8Z0NhgOw9IKDuPawDbnliE248fCNWX7RuQEYNs8sTDjz69xyxCbccsQm/G7XVaoMv8c0++velW/tshPDBs/L8sssVXUolWhra2PVFZdjy802rjqUXtXKv/P6KFsOmlRbWxv77L0Hl1x2FUOGDmX1lVdgo4024TPDh1cdWo9z7M099ra29/nxX27nrsdfYJYZBnDTrzbhmnvG8fPtR/LL8+7iyrvGse6yQ/n59iNZ/6DLAXj8mddY5f8urDjyntMKr3tXvr7Djuz+nT3ZZadvVB1KJY4/5ncsseRneO3VV6sOpde0+u98uwD62XEAWKFtWrePGsUiiyzKQgsvzMCBA9lq6224+KILqg6rVzj25h77My+/xV2PvwDA62+/x0PjXmHwoJnJhFlnGgjAbDNNxzMvvVllmL2qFV73rqy+xpoMGjSo6jAqMW7sWC6/7FJ2+ObOVYfSq1r9d14fZULbpMaPH8fQoQtMuj5kyFDGjRtXYUS9x7G3ztiHzTMLn1toELc/8jw/OPU2Dvv6SB464av84hsrcOCZYybt9+l5Z+Hfv96Eyw9en1WX/FSFEfeMVnvd9YEf7LcvP//lr+jXr7X+nPs7r45a61/AJxAR/646ho8jMz+yrVVmQjr2D2vWsc88wwD+ut8X+MEpo3jtrXfZZZ0l+eGpo1ji2+fyw1NHccK3VwfgmZfeZMlvn8eqP7iQ/U8bxSnf/TyzzjhdxdFPW630uusDl11yMfPMMw/LLrd81aH0On/nSxFEH/jpC0xouykzV606ho9jyJChjB371KTr48aNZfDgwRVG1Hsce/OPfUD/4K/fX5tzbnyMC0c9CcB2ay3KBbcVl8+/5YlJk8Imvvc+L77+DgB3PfYCjz37KovOP1s1gfeQVnnd9WG33nIzl15yEcMXX4gdv74t1193DTvv+PWqw+oV/s6rIxPaboqI18v/94uI4yPi/oi4OCIujYgtq46vo5ErrMCjjz7CE48/zsSJEznvnLPZcKNNqg6rVzj25h/7Cd9enYfGvcwxF98/advTL77JGsPnA2Ctpebnv88UE2Tmnm16+pWzJhacdxYWnX82nnjutd4Puge1yuuuDzv457/k4cee4oGHH+fU08/i82utzUmnnl51WL3C3/kPRFT/0xe4ysHH9xVgQeCzwLzAg8DJHXeKiN2A3QAWGDasF8MrDBgwgKN+dywbb7gubW1t7LDjTgwfMaLX46iCY2/usa+y5Lx87fOLct+TL3LLEcUfsIP+egd7/vFmjvjmSgzo14+3321jzz8WXUKrfWY+Dth6Wdrakrb3k71PvIWXXp9Y5RCmuVZ43bvyje235cbrr2PChAkssuBQfnrgwey4U2tNkmo1rf47r4+KzvpQ9FER8XpmzhIRRwN3Z+Yp5fbzgb9m5t8md9/llx+ZN982upcilao317anVB1CZV4465tVh6CKtL3fun9P+7fo2lGrrTSSMWNGVzb4uRYekRsc+teqHn6SM7ZfZkxmjqwyBiu0H19r/quVJEl9Tl+ZlFU1e2g/vpuALcpe2k8Ba1UcjyRJUkuzQvvx/R34InAf8DBwG/BKpRFJkiS1MBPabsrMWcr/vx8R+2Xm6xExFzAKuLfa6CRJUqvx1LcfMKGdOhdHxBzAQODQzHym4ngkSZJalgntVMjMtaqOQZIkSQUTWkmSpJpylYPCZBPaiDgGmOyiepm5d49EJEmSJH0MXVVoPROAJElSH2Z9tjDZhDYzT2u8HhEzZ+YbPR+SJEmS1H1TPLFCRKwSEQ8AD5bXPxcRx/d4ZJIkSVI3dGdS2NHAusCFAJl5d0Ss2ZNBSZIkqWsR0M9JYUA3T32bmU912NTWA7FIkiRJH1t3KrRPRcSqQEbEQGBvyvYDSZIkqWrdSWh3B34HDAHGAVcAe/RkUJIkSZoyOw4KU0xoM3MCsF0vxCJJkiR9bN1Z5WDhiLgoIp6PiOci4oKIWLg3gpMkSdLkRUTlP31BdyaF/RU4F5gfGAycB5zVk0FJkiRJ3dWdhDYy8/TMfK/8OYMuTokrSZIk9abJ9tBGxKDy4rURsT9wNkUiuzVwSS/EJkmSpC70kW/8K9fVpLAxFAls+1P1rYbbEji0p4KSJEmSumuyCW1mLtSbgUiSJElTozvr0BIRSwHDgRnat2XmX3oqKEmSJHUtCE99W5piQhsRPwPWokhoLwXWB24CTGglSZJUue6scrAl8EXgmcz8JvA5YPoejUqSJEldi2JSWNU/fUF3Etq3MvN94L2ImA14DvDECpIkSeoTutNDOzoi5gD+RLHywevAqJ4MSpIkSequKSa0mfmd8uIfIuJyYLbMvKdnw5IkSdKU9JVTz1atqxMrLNfVbZl5R8+EJEmSJHVfVxXa33ZxWwJrT+NYJDWJF876ZtUhVObcu56qOoRKfXWZBaoOoTL9+1kpk6rS1YkVvtCbgUiSJOnj6c7s/lbg8yBJkqRa69aZwiRJktS3BE4Ka2eFVpIkSbU2xYQ2CttHxIHl9WERsWLPhyZJkiRNWXdaDo4H3qdY1eAQ4DXg78AKPRiXJEmSpsDFNQrdSWhXyszlIuJOgMx8KSIG9nBckiRJUrd0p4f23YjoT7H2LBExD0XFVpIkSapcdyq0vwf+AcwbEYcBWwIH9GhUkiRJmiJbDgpTTGgz88yIGAN8kWKFiM0y88Eej0ySJEnqhikmtBExDHgTuKhxW2b+rycDkyRJkrqjOy0Hl1D0zwYwA7AQ8BAwogfjkiRJUhciPLFCu+60HHy28XpELAd8q8cikiRJkj6Gj33q28y8IyJcg1aSJKliTgordKeH9nsNV/sBywHP91hEkiRJ0sfQnQrtrA2X36Poqf17z4QjSZIkfTxdJrTlCRVmycz/66V4JEmS1E3OCStM9kxhETEgM9soWgwkSZKkPqmrCu0oimT2roi4EDgPeKP9xsw8v4djkyRJkqaoOz20g4AXgLX5YD3aBExoJUmSKhJAP3sOgK4T2nnLFQ7u44NEtl32aFSSJElSN3WV0PYHZuHDiWw7E1pJkqSKTXYyVIvpKqF9OjMP6bVIJEmSpKnQVWJvU4YkSZL6vK4S2i/2WhTqEVdecTlLj1iCEUsuyhG/PrzqcHpVq479W7vsxLDB87L8MktVHUolmv11//Mh+7HnOsvy462/NGnb2b87jP23/AI/2XYdfvd/u/LGa68A8PrLL/HL3bdmtzWX5C+//mlVIfeKZn/du+LYW3PsjSKq/+kLJpvQZuaLvRmIpq22tjb22XsPLrjoMu685wHOO/ssHnzggarD6hWtPPav77AjF1x8edVhVKIVXvfVN9qK/X7/lw9tG7HSGhx29lUcdtaVzDdsIS4+9TgAppt+erbY/fts892fVBFqr2mF131yHHtrjl2ds5e4Sd0+ahSLLLIoCy28MAMHDmSrrbfh4osuqDqsXtHKY199jTUZNGhQ1WFUohVe9yWXW4mZZ5vjQ9s+u/Ka9B9QTIdYZKnleOnZZwCYfsaZWHyZFZlu4Ay9HWavaoXXfXIce2uOXZ0zoW1S48ePY+jQBSZdHzJkKOPGjaswot7TymNvZb7ucOOF5/DZVdeqOoxe1cqvu2NvzbE3igj69YGfvqDHE9qIeL2Hj39QROzXg8ffMSIG99Txe0rmR1dWiz7yS9fTWnnsrazVX/cLTz6GfgMGsOr6m1cdSq9q5dfdsX9Yq4xdnbNCO2U7ArVLaIcMGcrYsU9Nuj5u3FgGD67dMKZKK4+9lbXy637Txedx101Xs/uhv2+5P+qt/Lo79tYce0dVTwjr7ltORJwcEc9FxH0N2w6KiHERcVf5s0HDbT+KiEcj4qGIWHdKx++1hDYiTo+ITRuunxkRm5QV0H9GxEUR8XhE7BkR34uIOyPi1ogYVO5/XUQcHRH/joj7ImLFhsMPL29/LCL2bniM75X73hcR+zRs/0ZE3BMRd5dxzVo+9nTl7bNFxBMRsRUwEjizfKJnjIjlI+L6iBgTEVdExPw9/dxNjZErrMCjjz7CE48/zsSJEznvnLPZcKNNqg6rV7Ty2FtZq77u9/z7Oi75ywns89uTmH6GGasOp9e16usOjr1Vx15jpwLrdbL9qMxcpvy5FCAihgPbACPK+xwfEf27OnhXJ1aY1v4M7AtcEBGzA6sCOwDbA0sBywIzAI8CP8zMZSPiKOAbwNHlMWbOzFUjYk3g5PJ+AEsCXwBmBR6KiBOApYFvAitRrKl7W0RcD0wEfgKslpkTImJQZr4WEdcBGwL/pHgS/56Z50XEHsB+mTm6THiPATbNzOcjYmvgMGCnjoONiN2A3QAWGDbskz97H9OAAQM46nfHsvGG69LW1sYOO+7E8BEjej2OKrTy2L+x/bbceP11TJgwgUUWHMpPDzyYHXfaueqwekUrvO7H/2RP/jPmFl5/+SX22XBFNt/te1x86nG8N3EiR+yxHQCLfHZZdvzRLwH4/iar8tYbr/Heu+9yx/VX8H/HnMGQhRevcgjTXCu87pPj2Ftz7HWVmTdExILd3H1T4OzMfAd4PCIeBVYEbpncHaKzPpRpKSJez8xZysv3AWsDXwEWzcz9ImJHiuRy13Kf/wGrZOa4iNgJWDoz9ykTzkMy85qG/ZYG9gHezczDyu0PAl8GtgDmyswDy+2HAs9TnLZ3vsz80Fo2EbEa8IPM3DQibgF2zcz7ysdtT2iXAv4NPFberT/FGdXW6eo5WH75kXnzbaOn6vmTVC/n3vXUlHdqYl9dZoEp7yQ1idVWGsmYMaMr6/MZvPhnc7djz6/q4Sc5eN3FnwQmNGw6MTNP7LhfmdBenJlLldcPomjtfBUYDXw/M1+KiGOBWzPzjHK/k4DLMvNvk4uhNyu0AKcD21FUQBurmu80XH6/4fr7fDjGjtl3+/XG+7eV95ncL1h0chwy8+aIWDAiPg/0z8z7PnpXArg/M1eZzLElSZJazYTMHDkV9zsBOJQiLzsU+C1FfthZDtdlBba3J4WdSlFRJTPvn4r7bw0QEasDr2TmK13sewOwWUTMFBEzA5sDNwJXA1+NiLnKYzUu2vkX4CzglIZtr1G0MgA8BMwTEauU950uIvyOQ5Ik6WPKzGczsy0z3wf+RNFWADAWaPy6Zygwvqtj9WqFNjOfLVsC/jmVh3gpIv4NzEYnfasdHuuOiDgVGFVu+nNm3gkQEYcB10dEG3AnRbkb4Ezg5xRJbbtTgT9ExFvAKsCWwO/LPuABFP29U5OcS5IkTbWAPrMO7NSIiPkz8+ny6uZA+7fjFwJ/jYgjKVaaWowP8rlO9XhC294/CxARM5VBndVw+6kUSWP79QUndxvFRK0fdTj+QR2uL9Vw+UjgyE5iOg04rZNwVwf+lpkvN+z7d+DvDfvcBazZyX0lSZLUiYg4C1gLmDsixgI/A9aKiGUo2gmeAL4Fxbf4EXEu8ADwHrBHZrZ1dfxeq9BGxJcoViY4cgqtApWIiGOA9YENprSvJEmSui8zt+1k80ld7H8YxUpS3dJrCW1m/guY6vWrMnOtaRdNp8ffqyePL0mSNK3VuONgmvJMYZIkSaq13l62S5IkSdNCQD8rtIAVWkmSJNWcCa0kSZJqzZYDSZKkmorJnhi1tVihlSRJUq2Z0EqSJKnWbDmQJEmqoeLUt1VH0TdYoZUkSVKtWaGVJEmqKSu0BSu0kiRJqjUTWkmSJNWaLQeSJEk1FWHPAVihlSRJUs2Z0EqSJKnWbDmQJEmqIdeh/YAVWkmSJNWaFVpJkqQ6CnBOWMEKrSRJkmrNhFaSJEm1ZsuBJElSTfWz5wCwQitJkqSaM6GVJElSrdlyIEmSVEOuQ/sBE1pJmoa+uswCVYdQqd/d+N+qQ6jMd9dYpOoQpJZlQitJklRTzgkr2EMrSZKkWjOhlSRJUq3ZciBJklRLQT/sOQArtJIkSao5E1pJkiTVmi0HkiRJNRS4ykE7K7SSJEmqNRNaSZIk1ZotB5IkSXUUnvq2nRVaSZIk1ZoVWkmSpJrq56wwwAqtJEmSas6EVpIkSbVmy4EkSVINuQ7tB6zQSpIkqdZMaCVJklRrthxIkiTVlKscFKzQSpIkqdas0EqSJNWUBdqCFVpJkiTVmgmtJEmSas2WA0mSpBoKrEy283loYldecTlLj1iCEUsuyhG/PrzqcHqVY3fsjr25nPfr/Tn0Kyty1E7rf+S2G875M/uvvShvvPIiAI+MvoljvrUpR+28Acd8a1MeveOW3g631zT7696VVh67PsqEtkm1tbWxz957cMFFl3HnPQ9w3tln8eADD1QdVq9w7I7dsTff2Jdf9yvsdPjJH9n+8nPjeWTMTcwx7+BJ22aafU52OOxE9j3pUrba/wjO/eV+vRlqr2mF131yWnns6pwJbZO6fdQoFllkURZaeGEGDhzIVltvw8UXXVB1WL3CsTt2x958Y1/4cysy42xzfGT7xccfxvrf+uGHpnoPWWwEs839KQA+teBivPfuO7w38Z3eCrXXtMLrPjmtPPYPCYiIyn/6AhPaJjV+/DiGDl1g0vUhQ4Yybty4CiPqPY7dsYNjb4WxP3Dzv5ht7vkYvMhnJrvPfTdczuBFhzNg4PS9GFnvaNXXHVp77OqcCe0URMSOETF4ynv2LZn5kW195VNUT3PsH+bYm18rjn3i229x7ZknsM6O+0x2n2cff5jLTvw1m+97aO8F1ota8XVv18pj7yj6wE9fYEI7ZTsCtUtohwwZytixT026Pm7cWAYPrt0wpopjd+zg2Jt97C+O/x8vPvMUR++6EYdv+3leff4Zfv+tTXntxecBeOX5pzn9Z9/hqz/6DXMN+XTF0faMVnzd27Xy2NW5PpHQRsSCEfGfiPhzRNwXEWdGxJci4uaIeCQiVoyIQRHxz4i4JyJujYily/seFBEnR8R1EfFYROzdcNzvlce7LyL2adj+jfI4d0fE6RExa0Q8HhHTlbfPFhFPRMRWwEjgzIi4KyJmjIjlI+L6iBgTEVdExPy9/HR1y8gVVuDRRx/hiccfZ+LEiZx3ztlsuNEmVYfVKxy7Y3fszT/2+RZegp+eP4r9z7qe/c+6ntnmmY+9/3gBsw6ah7def5VTfrQr6+6yHwsutXzVofaYVnzd27Xy2NW5vrQO7aLAVsBuwO3A14DVgU2AHwNPAXdm5mYRsTbwF2CZ8r5LAl8AZgUeiogTgKWBbwIrUVTEb4uI64GJwE+A1TJzQkQMyszXIuI6YEPgn8A2wN8z87yI2APYLzNHlwnvMcCmmfl8RGwNHAbs1HEwEbFbORYWGDZs2j1L3TRgwACO+t2xbLzhurS1tbHDjjsxfMSIXo+jCo7dsTv25hv7WYfuw2N338Ybr7zEL766Gl/e8bussMFXO9333/84nRfGP8k1px/HNacfB8DOvz6VWeacqzdD7nGt8LpPTiuPvVEA/Vq01aKj6KwPpdeDiFgQuCozFyuv/wW4IjPPjIiFgfOBBLbIzMfKfZ4ClgL2Bd7NzMPK7Q8CXwa2AObKzAPL7YcCz5fHmS8zf9IhhtWAH2TmphFxC7BrZt5XJrrtCe1SwL+Bx8q79Qeezsx1uhrf8suPzJtvG/0JniFJqoff3fjfqkOozHfXWKTqENTLVltpJGPGjK4so1x4+NJ5yOmXVvXwk3x95AJjMnNklTH0pQpt45oq7zdcf58izvc6uU97Nt5437Zy/8n9gkXD/T44UObNZevD54H+mXnfZO57f2auMtlRSJIkqVf1iR7abroB2A4gItYCJmTmq1PYf7OImCkiZgY2B24Erga+GhFzlcca1HCfvwBnAac0bHuNopUB4CFgnohYpbzvdBHRet9xSJKkPqHqFQ76SsNDX6rQTslBwCkRcQ/wJrBDVztn5h0RcSowqtz058y8EyAiDgOuj4g24E6KlQwAzgR+TpHUtjsV+ENEvAWsAmwJ/D4iZqd4/o4G7v9kQ5MkSdLU6hMJbWY+QdEP2359x8nctmkn9z2ow/XG4xwJHNnJfU4DTusklNWBv2Xmyw37/h34e8M+dwFrTm4skiRJ6l19IqHtCyLiGGB9YIOqY5EkSeoOFzkomNCWMnOvqmOQJEnSx2dCK0mSVEvRsqf87ahOqxxIkiRJH2FCK0mSpFqz5UCSJKmGAiuT7XweJEmSVGsmtJIkSao1Ww4kSZJqylUOClZoJUmSVGtWaCVJkmrK+mzBCq0kSZJqzYRWkiRJtWbLgSRJUh2Fk8LaWaGVJElSrZnQSpIkqdZsOZAkSaohT337AZ8HSZIk1ZoVWkmSpJpyUljBCq0kSZJqzYRWkiRJtWbLgSRJUk3ZcFCwQitJkqRaM6GVJElSrdlyIEmSVFMuclCwQitJkqRas0IraZrLzKpDqEyrrwn53TUWqTqEysy5wp5Vh1CZl24/tuoQWlJxprDWfs9pZ4VWkiRJtWZCK0mSpFqz5UCSJKmmWrzLaRIrtJIkSao1E1pJkiTVmi0HkiRJtRSEqxwAVmglSZLUwyLi5Ih4LiLua9g2KCKuiohHyv/P2XDbjyLi0Yh4KCLWndLxTWglSZLU004F1uuwbX/g6sxcDLi6vE5EDAe2AUaU9zk+Ivp3dXATWkmSpJqKqP6nOzLzBuDFDps3BU4rL58GbNaw/ezMfCczHwceBVbs6vgmtJIkSfok5o6I0Q0/u3Xzfp/KzKcByv/PW24fAjzVsN/YcttkOSlMkiSphvrQqW8nZObIaXi8zgbV5TnVrdBKkiSpCs9GxPwA5f+fK7ePBRZo2G8oML6rA5nQSpIkqQoXAjuUl3cALmjYvk1ETB8RCwGLAaO6OpAtB5IkSXX0MSZlVS0izgLWoui3HQv8DDgcODcidgb+B2wFkJn3R8S5wAPAe8AemdnW1fFNaCVJktSjMnPbydz0xcnsfxhwWHePb8uBJEmSas0KrSRJUk3VpeWgp1mhlSRJUq1ZoZUkSaqp6Bvr0FbOCq0kSZJqzYRWkiRJtWbLgSRJUg0F0M+OA8AKrSRJkmrOhLZJfWuXnRg2eF6WX2apqkOpxJVXXM7SI5ZgxJKLcsSvD686nF7VqmMf+9RTrPfltVn2s8NZ/nNLcdwxv6s6pF7Vqq87NP/Ypx84gBtP34/bztmfMX/7CQfsvgEAB35nQ0ad8yNuPXt/Ljp+D+afZ3YABs0+M5efuDfP3/xbjvrhVlWG3qOa/XXXx2NC26S+vsOOXHDx5VWHUYm2tjb22XsPLrjoMu685wHOO/ssHnzggarD6hWtPPb+Awbwy1//hjvvfYDrbrqFP55wfMuMvZVf91YY+zsT32O93X7PSlsfzkrb/JJ1Vh3Oip9dkKNOu5oVt/4lK29zOJfdeB8/2m19AN5+510OOf5ifnTUPyqOvOe0wuveXdEH/usLTGib1OprrMmgQYOqDqMSt48axSKLLMpCCy/MwIED2Wrrbbj4oguqDqtXtPLY559/fpZddjkAZp11VpZY8jOMHz+u4qh6Ryu/7q0y9jfemgjAdAP6M2BAfzKT1954e9LtM804PZkJwJtvT+Tfdz3G2++8W0msvaFVXnd1nwmtms748eMYOnSBSdeHDBnKuHGtkdi08tgbPfnEE9x9952ssOJKVYfSK1r5dW+VsffrF9x69v787+rDuebW/3D7fU8CcNAeG/PIZYeyzfojOfSESyqOsve0yuveHRHV//QFTZPQRsSCEfG1aXi8tSLi4snc9ueIGF5efiIi5p5Wj6tPrr1K0Sj6yr+4HtbKY2/3+uuvs+3WW/Lr3xzFbLPNVnU4vaKVX/dWGfv77ycrb3M4i657ACOX+jTDF5kfgIOOu4jF1v8pZ182mt23XrPiKHtPq7zu6r6mSWiBBYFOE9qImKbLk2XmLpnZms06NTBkyFDGjn1q0vVx48YyePDgCiPqPa08doB3332Xr229Jdts+zU22/wrVYfTa1r5dW+1sb/y+lvcMPoR1ll1+Ie2n3vZ7Wz2xWWqCaoCrfa6a8oqT2jLyuqDEfGniLg/Iq6MiBkjYpGIuDwixkTEjRGxZLn/qRGxZcP9Xy8vHg6sERF3RcS+EbFjRJwXERcBV0bEoIj4Z0TcExG3RsTS5f0PiojTI+KaiHgkInZtCG+WiPhbRPwnIs6M8uNfRFwXESN75xnSxzVyhRV49NFHeOLxx5k4cSLnnXM2G260SdVh9YpWHntm8u3ddmGJJZdk732+V3U4vaqVX/dWGPvcc87C7LPMCMAM00/H2istwUNPPMsiw+aZtM+Gn1+ah594tqoQe10rvO7dVfWEsL4yKayvnFhhMWDbzNw1Is4FtgC+CeyemY9ExErA8cDaXRxjf2C/zNwIICJ2BFYBls7MFyPiGODOzNwsItYG/gIsU953aWBlYGbgzohob0RaFhgBjAduBlYDburOgCJiN2A3gAWGDevOXaapb2y/LTdefx0TJkxgkQWH8tMDD2bHnXbu9TiqMGDAAI763bFsvOG6tLW1scOOOzF8xIiqw+oVrTz2W/59M38983SWWuqzrDRyWQAOPvQw1lt/g4oj63mt/Lq3wtjnm3s2/nTI1+nfrx/9+gV/v+oOLrvxPs76zS4s9ul5ef/95H9Pv8jeh5096T7/ueRgZp15BgZON4CNv7A0G33nOP7z2DMVjmLaaoXXXR9PdNaH0qsBRCwIXJWZi5XXfwhMB/wEeKhh1+kz8zMRcSpwcWb+rdz/9cycJSLW4qMJ7ecz85vl9TuBLTLzsfL6U8BSwL5Av8w8sNz+F+B84GXgJ5n55XL7CcDNmXlGRFxXPtboiHgCGJmZEyY3xuWXH5k33zb6kzxNUq1U/b5SJfv4WtecK+xZdQiVeen2Y6sOoRKrrTSSMWNGV/aPfomllsk//v2aqh5+ki8sOdeYzKz0m+u+UqF9p+FyG/Ap4OXMXKaTfd+jbJUoWwAGdnHcNxoud/YLlx3+33F7x7j6yvMlSZJanKe+/UDlPbST8SrweERsBUXiGhGfK297Ali+vLwpRTUX4DVg1i6OeQOwXXm8tYAJmflq+3EiYoaImAtYC7h9moxCkiRJPa6vJrRQJJ87R8TdwP0UySvAn4DPR8QoYCU+qMLeA7wXEXdHxL6dHO8gYGRE3EMxgWyHhttGAZcAtwKHZub4aT0YSZIk9YzKv0LPzCcoelnbr/+m4eb1Otn/WYoJXO1+VG5/F/hih91Pbbjfi3yQFHf0cGbu1uFxrgOua7i+Z8PltRouLziZY0qSJPWgvrPKQNX6coVWkiRJmqLKK7RVy8yDqo5BkiTpY+tDp56tmhVaSZIk1ZoJrSRJkmqt5VsOJEmS6sqOg4IVWkmSJNWaCa0kSZJqzZYDSZKkGipOfWvTAVihlSRJUs1ZoZUkSaop67MFK7SSJEmqNRNaSZIk1ZotB5IkSXVlzwFghVaSJEk1Z0IrSZKkWrPlQJIkqabCngPACq0kSZJqzgqtJElSTXmisIIVWkmSJNWaCa0kSZJqzZYDSZKkmrLjoGCFVpIkSbVmQitJkqRas+VAkiSpruw5AKzQSpIkqeas0EqSJNVQ4JnC2pnQSprmwpW+1YJeuv3YqkOozPI/u7LqECrx2PhXqw5BJVsOJEmSVGtWaCVJkuooPPVtOyu0kiRJqjUTWkmSJNWaLQeSJEk1ZcdBwQqtJEmSas2EVpIkSbVmy4EkSVJd2XMAWKGVJElSzVmhlSRJqqXw1LclK7SSJEmqNRNaSZIk1ZotB5IkSTXlqW8LVmglSZJUaya0kiRJqjVbDiRJkmoocBnadlZoJUmSVGtWaCVJkurKEi1ghVaSJEk1Z0IrSZKkWrPlQJIkqaY89W3BCq0kSZJqzYRWkiRJtWZC28SuvOJylh6xBCOWXJQjfn141eH0Ksfu2B1763DszTv2+WafnlN2HsmF312VC/Zele1XGQbAXl9ahPP3WoW/77kyJ+64HPPMOv2k+yz+qVk481srcsHeq/KPvVZh4IDmTnUiqv/pCyIzq46h6S2//Mi8+bbRvfqYbW1tfHb44lxy2VUMGTqU1VdegdPOOIvPDB/eq3FUwbE7dsfu2B1771r+Z1f2yHHnnnUg88w6PQ+Of42ZBvbnvD1WZu8z7uKZV9/mjXfaANhulWEsMu/MHHLBg/TvF5y3x8r86Lx7eeiZ15l9xul47e13eb+HUp3HTt6Tt55+uLKUbsTSy+XZl95Q1cNPsvQCs47JzJFVxtDcH1ta2O2jRrHIIouy0MILM3DgQLbaehsuvuiCqsPqFY7dsTt2x94KWmHsE16byIPjXwPgzYltPPb8G8w72/STklmAGafrT3ttbtVF5+LhZ17joWdeB+CVt3oume0rog/89AUmtE1q/PhxDB26wKTrQ4YMZdy4cRVG1Hscu2MHx+7Ym1+rjX3wHDPwmfln5Z6xrwCw95cX5V//tyYbLTM/x/7rUQAWnHsmMuHEHZfjvD1WZqc1FqwwYvWmpkpoI+K6iOiy5B0R+0TETL15rCp01koSfaXRpYc59g9z7M3PsX+YY28+Mw3sz9FfW4bDL3loUnX291c9ypeOuIGL73qar5W9tf37Bct9ek5+cO69fP3EUXxx+LystPCgKkNXL2mqhLab9gGmVRI6LY81TQ0ZMpSxY5+adH3cuLEMHjy4woh6j2N37ODYHXvza5WxD+gXHP21z3HJ3U/zrwee+8jtl9zzNF8e8SkAnn3lHUY/8SIvv/kub7/7Pjc+PIHhg2fr7ZB7T9W9Bn2o56CWCW1ELBgR/4mI0yLinoj4W8dKaUScEBGjI+L+iDi43LY3MBi4NiKuLbetExG3RMQdEXFeRMzSyeN9ZJ/OjtWXjFxhBR599BGeePxxJk6cyHnnnM2GG21SdVi9wrE7dsfu2FtBq4z9kK+M4LHn3uC0m5+ctG3YXB/8yf/CkvPw+PNvAHDzIxNYfL5ZmWG6fvTvF4xccE7++/zrvR6zel+dzxS2BLBzZt4cEScD3+lw+08y88WI6A9cHRFLZ+bvI+J7wBcyc0JEzA0cAHwpM9+IiB8C3wMOaT/I5PbJzEMaj9UL4/1YBgwYwFG/O5aNN1yXtrY2dthxJ4aPGFF1WL3CsTt2x+7YW0ErjH25T8/BpssO5qFnXuPve64MwNFXPsoWyw9hwXlm5v1Mnn75bQ6+4AEAXn37PU676UnO+fbKJHDjQ89zw0N97k+0ekAtl+2KiAWBGzJzWHl9bWBvYA5gv8wcHRG7A7tRJO3zA3tl5tkR8QQwskxoNwJOBcaWhx4I3JKZO0fEdcB+wHxd7DPpWJ3EuFv5+CwwbNjyD//3yY67SJLUFHpq2a6+rvJluz63XJ576Y1VPfwkSw2dpfJlu+pcoe2YiU+6HhELUSSjK2TmSxFxKjBDJ8cI4KrM3LaLx+nOPh8NLvNE4EQo1qH9OPeVJElS99Wyh7Y0LCJWKS9vC9zUcNtswBvAKxHxKWD9htteA2YtL98KrBYRiwJExEwRsXiHx+lqn8ZjSZIkqQJ1TmgfBHaIiHuAQcAJ7Tdk5t3AncD9wMnAzQ33OxG4LCKuzczngR2Bs8rj3Aos2fggU9hn0rGm+egkSZK6EFR/2tu+slJcnVsO3s/M3TtsW6v9Qmbu2NmdMvMY4JiG69cAK3Sy31rd2OdDx5IkSVLvq3NCK0mS1NL6SIG0crVMaDPzCWCpquOQJElS9ercQytJkiTVs0IrSZIk7DkoWaGVJElSrZnQSpIkqdZsOZAkSaqpsOcAsEIrSZKkmrNCK0mSVFN95UxdVbNCK0mSpFozoZUkSVKt2XIgSZJUU3XpOIiIJ4DXgDbgvcwcGRGDgHOABYEngK9m5ktTc3wrtJIkSeoNX8jMZTJzZHl9f+DqzFwMuLq8PlVMaCVJklSFTYHTysunAZtN7YFMaCVJkuoq+sBP9yRwZUSMiYjdym2fysynAcr/z/vxn4CCPbSSJEn6JOaOiNEN10/MzBM77LNaZo6PiHmBqyLiP9MyABNaSZKkGioKpH1iWtiEhr7YTmXm+PL/z0XEP4AVgWcjYv7MfDoi5geem9oAbDmQJElSj4mImSNi1vbLwDrAfcCFwA7lbjsAF0ztY1ihlSRJUk/6FPCPKE5rNgD4a2ZeHhG3A+dGxM7A/4CtpvYBTGglSZLqKOpx6tvMfAz4XCfbXwC+OC0ew5YDSZIk1ZoJrSRJkmrNlgNJkqSaqkHHQa+wQitJkqRas0IrSZJUV5ZoASu0kiRJqjkrtL3gjjvGTJhxuniyooefG5hQ0WNXrZXHDq09fsfemhx7a6py7J+u6HHVgQltL8jMeap67IgYPaXT0TWrVh47tPb4HbtjbzWOvTXHXpz41p4DsOVAkiRJNWdCK0mSpFqz5aD5nVh1ABVq5bFDa4/fsbcmx96aWnnstTj1bW+IzKw6BkmSJH1Mn11m+bzwXzdXHQYLzzPjmKr7mG05kCRJUq3ZciBJklRDgedVaGeFVgBExAzl/1v+34bPgaRW4fudmoUJrYiI2YAbI2LtbOGm6ohYICLmzMxs5Tf5iJghIhYpL386IipbR1lSz2i197vGMUZEc+U+0Qd++oDmelH1sUXEDJn5KnAqcFxErFFxSFXaB7guIga1ypv8ZCwObBURhwEnAdNVHM/HEhELRUSLLrL+ybTw73wr2ocWeL+LiJkjYt5yjMtFRGTm+1XHpWnPhLaFRcRcwK8jYrbMPA74NXBKqyW1ETF/RMyemd8H/g38MyLmauY3+Sl4ClgY+C5wTWaOh76d7LTHFhGrUCzh85OIGFFtVPVS/qHPiFgnIg6JiO9FxOJVx9VTGn5nlo2Iz0TE56qOqTe04PvdEsCfI2Iv4C/A8IrjUQ8xoW1hmfkC8Ftg7ohYKTNPAQ6j9ZLa7wALAGTmt4EHgH80+Zv8RzSM8w3gNIrEcN6I2BygfC6mryq+yYmI/mVsX6L4fT4XmB/4ZkQsV2109VE+hxtQvAeMBtYB9mu6r2dL5Xg3BE4GNgBOa5H3vZZ6v8vMO4DHgaOAozLz/ojoX3FY01T0gf/6gqZ8o9KUtf+RyswngW8AR0TECg1J7YkR8YUqY+wtmflT4JWIOKn8amp3PniTb+qv49o1VOc2BG4A7gZ+ATwEbBgRX4iIzwDb9ZWkNiIWjYhZM7MtIqYDtgFOzsw/AZsCs1IkZFZqu281YAsggTmAQzLz/YiYpdKoprGI6BcR8wP7UySzrwBvAv9p1gS+Xau833UYwz+AQ4B9I2JkZrZVFJZ6UFP/w1Xn2nuIypYDMvMg4ALgkIhYsUxqj6Ko1M5ZYag9JkoNm56j+AN+aETMXb7J3wtc1V65qCLO3lL+EfsCRYXzB5n5emZOAM4ARgF7AtcDT2XmOxWG2uhTwGcjol9mvgs8DAwvX79ngZ8DKwKb95UkvC+JiJki4lPl5fakf2bgBOD7wDaZObb8kLNp3ata5T/59qUq+wMvAmOALwDfBHbIzOeBdSNiWEVh9ohWe79r+IC+dkR8H5gvMw8Bfg+cHhGLRMTqEXFExaFqGjKhbSERMSQivtTw1eIFEfGn8hPrb4F/AT+NiFUy80Rg9cx8qdqop72ImC5LEbF0Od53KCp8A4FflW/yewB3AItVGnAvKP/YLQ4cDDwREd+MiDuBXYC/UUwgWSczr6ouyg/LzJsp/gg/Xn7wupSiKrtmRMxKsc72vcBW5Y8+7LPADyJib+CyiJibYhLgQsBlmflERKxJ8eF2bJ2rWuXv9wbAchGxBXB6+W9+EeAPwOaZ+UhErA78DJihuminrVZ8vyvHuhFwBMUHl90j4rDy79qfgVMokttbKgxzmomo/qcv8MQKLaJ8Q18D2DMiFgM2pEhe1qXoNZwrM39bVrIOiYgtgXHVRdwzyqr0ERHxPYoE7nTg1Yi4nqJndFeKCtXvI+K7mblrddH2rPYqBkz6AzAe+BXwNHBhefnbwL8y816KyWJ9Sma+ViZkNwArUcS9CbAHRQV3Y2B9mihBmVYy87aI2B44EvhWZk6IiBcoJgMeHcUkqeHAvpl5fZWxflLl7/frwJkUq3bsUd60L0VrzXERcVW5/cDMfLiaSKetVnq/i4g5gPcy8/WybWQtYCPgcxTfPPwBoPw79/fy8hON74OqNxPaFlG+oV9B8VXbDsAjmXlVRFxHUX3bJIrJNb+IiLMy85UKw+1J01N8Yj+R4vd/PeBl4CfAzhQVqm+X/58PeL6SKHtY41dywJrAXcBl5f/fycznImIoxVfP71YWaDdk5gUR8R7FRKYVMvOiiFiW4rUbDuwFbF5ljH1RRKwG3ApMoPia/R7gjvJ9YQ1gRmCGzPxvlXFOQw9SJHRbAO9ExIyZ+WhEfAP4AcU3lt/LzKubKMlpife7iBhIMbnv9og4tvygOwD4EzA7sGVmPlW2z7yfmZe137cZXuc+UiCtnC0HLaC9d6psHzgf+CewQURsXPYe/hZ4Btis/Orp8cqC7WFZLEF1NEXitgowU/m8HEvx72EPYNHM3KGsSjalhglgRwLjgd0pvoKbrUxmt6b4Cv8XmfmfCkPtlsy8hCL5/m8UE1vuBN4Dfgx8tQ5jqMCXgS9n5sEUk4IOABYpv6rdPTPHNUMyW7aPzkXRC345RQX6AIpKPsBg4PeZ+YfMvBqaI8mB1nm/y8yJFJOZ1wJ2Lfu9z6FY7eTszHyy/JB2NPB6VXGqZ5nQtoAyeVklIr5GUbE6k+IP/a4RsWEWi0z/Aji8nAjUdNqT+rKfbCxwDHAexaSIhTPzCeB4oGkX3I6IeaJY2oqy5/QrwGbAWIo/6q8A+5QTYh4CvpuZ/+gwmaTPKqsuO1N8xUhmPgNsWOc/1NNSJ6/jORSVygFZTAy9l6J/9DfAI70cXo9or7RmsUThscDimXkdxb/13SPiYIoVPT5bYZjTXCu93zUUbMbwwaoV36VomTsS2D4izqZordgnM2+sKlb1rGiSD6LqQkR8nuIrpcsoPsGeQLGg9giKST9HZuZFlQXYSyJiY4qJENMDhwMTKd78lgF+kpn/jeLMaW9XF2XPKHvK9gI+A5yfmVeWLQWzUaw5uwUwlGLCxO3ArmXVo5aiWPng/Sb66niaiIi1KE6acV75tezZwP8y8wfl7YsB7zZLb2FEDM/MB8rLGwH7UVSl3y3fFxcF/lsmuU2lFd7vGlqnPkux7NqzwNwU72PnU7SYzEDRTz+xWXqjGy297PJ56TX/rjoMFhg0w5jMrPQMjVZom1xELEHRI/WtzNyL4iumZYElgbMolmV6proIe0fZU/lDil6yRykmQyxOUa3+H8XEiRkp3vSbTlmFPwf4L7B+RKxTVm4GAk9m5v+Adyhm/R5e52QWJo23ab46/iQaqnWDKKrw21FM/DyAYmmzBSJiXoDMfKSs3tX2uWsY7wDgmIg4NSJ2A66mWKZrH4ByotvJ7clsXb6J6I5Web8rk9mNKQo236Q4qUpQtB9tSvEh/o3MvK8Zk1l9mAltkyr7xvpTnO1nOLBe+fXTDRS9kftSJDOnZObtFYba4yJiEYrxPpCZ12fm/hSTYfYCXqP4WuqHmflWNtk5vsvfg/av5J6hqMY+TdFD/WWKr5mXiYgLKBYfPy8zH6wsYE1z5R/9dYG/UrSSbAEcR5HgHF5eX6m6CKedDpMdt6NY4eKfwDDgWmAeYIX2/RuT9rom8B210vtdRCxA0WawHvASxbJ9r2fm3ZTVeIrqrFqACW2TaagyzJGZbZl5DMVafDMBXy1ve5iiMX76ur+hddP7FAuJL9HeQ5rFySNeAZbNzGcysyl6BhuVq1ZkQw/1F4Fhmflrir7ZzSj6TZek6LHbPDMvry5i9YSIWJmif/SXmflmZr6cmY9m5jeAvSkSgh+UFdxaa5jseDTwXGZOzMx/ZuYBwIEU66x+OSJ2qDLOHta073fxwYkx2i+/QvmaUswJ+GZmPh8Ra5e98xtlE09y/kD0gZ/quWxXk2l4Q/9JFGtK/o/ik+pMwC4R8VWKnqKjskmX5mqo0oykGOubFJPgDqCoVH+aYsbzCIpP9U2n/Ar51PL1Xoziq8ZLgC9ExNmZ+fMo1qb8NnBu9qETJmjaaOiBXYziRALXl0lAGxTvFZn5GHBk2YNY+78HETEDxUk09sjMG8vxvp+Z72fmlcCVEfEATVKRhtZ5vytfy+0jYhRFpX1Hikmgw4DfAStm5v+iOOPhzyNiu9ZIZtXOCm2TKf8w/Rz4P2Aniurb0Zn5Rz74uvn8zLy4uih7Vvnmvg7FV6ybABdRfP34e+BtihmwP6SY+HRXNOG52zPzOYr1Ra8EtgV2Lnuo1wJ2iojvUCw0/jhFtVZNpuEr9JeBL0XEIpn5Xrl9rbINgYhYBViVYvJQ3b1HMSmo/VS+beXkwBEN+4wAvhgR0/V6dD2gQ0tJ077fZeZ7FO9Xt1CsOXtC+Q3j0RRjPjQi2sd9eKsks0H1ZwnrK93ntf9Ero9I4B7g3+Ufri9GxJgoFg8/h+KMKStExHPAP5ulb6xd2XIxC8WkgH0z85KIOA24gGLS02EUFar+FP1kkyYQNYuy1aAtM78REb8BvkFx0gGyOBvUDhRfzR0fEb/N4jSYagIdqnWfoWgvepxi/dWvRsS/KH7/f0PRZwnFpKG1M7N2ZwZsGO98wHRZLJ5/KrB0RKxRVmlXAg6PiN0z8yGKf/ffzmIN7torE/PvU5wU4uJmfb8rX+vrI+JKig9g7WnUKIpl5nanWHf2+1ms4lL7VTr08dTyk5o+0DCjd4Xyq6V3KP5RN66reDpAZr5FUaUdxQcJb1Mpv0Z9jeKP9Nvlm9r9FF+tf7V8Ds6g+Gpug4iYqcJwp7lyvG0RMQ9AZu5HsUzbfhExpNxtdmDhcuxN8UddhTK5W59itveKFOtLbwC8SvFaHwv8Evh5Zt5Qfvh5vo7JLEwa72YUH9b/HhEHUZzx6jXgoIg4heL977dlMktm/jmbZOJj+U3UchSTO99sxve7hnkhc5Xj24qi1eDsKE4O9AZFS90vM/M3ZWtJ00zyU/dZoa258g19E4oF0fct/0hdCpwUEcdTfAX3Lcpzl2dxnus/NdM/9oYqzQLAq2Vv8FiKN/XbKf6Yv1fuO31mPhIRxwGvZeablQXeA8rnYT2KEyQ8TVGh+zlFhebqiLiI4iQKRzXb2DWph3Rziq+Xry4nhK0LPJ+Zx5YJXltmvtz+4afSgD+hKE4C8iOK03m/SzExaA7gYuBCYCGKlqu72xOjZnnvi4jlKSb0/RB4g2JprtE00ftdw3v7phQV2AkR8bcsTnf9XeD3ZTvJ3hSrddxSZbxV6SPf+FfOhLbmImJh4BDgK5n5WFmFO43ivOVrAAtSnB3lmvb7NMsbOnzoDW8DikrktRHxbGb+sHwTPyMingJWAw5s/3q9WfurImI4xfPwTWBOiirdHzJz1zLZ2RJYJ4tz2PuVXBNofB0z8+3yK+gvA1dn5q3le8JeEXFuFmfMoty3GV77mSlm9Y8tP6yfQ9EbPjYzT6VYpgxomvECUL6m+wAPZ7Hs4u0RcRbFRNCnqfn7XZQnRinf279AsULFRsBRFJX3+TPzDxHxEsVYt8/Mlkxm9QET2ppq+CM2J8USXItGxO4UJ01YHVg9Mw+I4rSW71UZa0/o8IY3HPgSRRL3LLBvRByTmXtExAoUFckzMvOWZk7iypaTeYBLM/O6KGYF30Ex43fFzPxBRJyamY9Cc/2Bb0VRrCv9bvlvYCFg1sy8BzgV2DgitszMv1F8uH2FYt3pN6qL+JNr+AA7UxZLkD0YEXcDO0TEWVnMcr8MmK+ZKrJRnARhZNkTvARFm8GDwJYRsUFmXpqZ25bfzvSnxu93ZbL+jYg4OTOfpTib2+7A8hQV9z9TTGydgWIddU9lK8Ae2tpp7CeCSeevvp5iJuvozPwyxafZtaKYzVrLCQBdiYjBwIYRMX1EzEkx4WVR4DrgP8ChwPQRcQZwV2Ze0P7pvW5v7t0VEWtQLJLfH9io7C17LzOfpOirXqLctSl6B1td2SP97YiYM4r1hS8H/hoRx1D8G/gv8LWIuISin/a0zKztkk3tymR2Y+DkiDgnImahaC9YCPhDRGxPMUHq1ixVGe80NCvw+bJl6K8U7/l/ovjwsmnZS0tmXp6Zl9T8/e59ir7vPSJilsz8E3A/sD2wbWYeB4wDVqY4dXfLq3qFg76yyoEJbc2Ub+gbAWdGxG8iYrPM/ElmbpiZ50bEqhSVytFlBbPpElqKdTX/C8xU/pHejmJ5sq9mMbv/SYqJL2/zwfI9TSuK01xuAJxZtpb8ANg7InaLYob3SIpZwHX9A6ePGk4x8fM7wJ4UyzUtCyxF0U94BrALxWoGX83M8xs+DNdW+bv+E4pk7n2K9ZXvKa+Ponheds3ydLZN5HmKNcW/CDyameMz83mKtaXvpVifdb0qA5wWym8Un6boA18a+F754e0tim8Y9ip7h2ekmOj3VHXRqq+x5aBmImItiqVYtgB+BaxU9tGeDMwLnALsl8V5yptSFku3zAScEhE3ZOZxEfEtiqpNZuY5mfl4ROyZmW9XHW9PaW+7oFiWa0Pg0TJp+QfF2qP7UfSXHZSZt1YWqKa58t/AdMDGFLP6B2TmuxGxOXAe8Ftg98y8tuE+tf4wExGLUiTv/87MqykmOR5PsXLDXpn5myiXrKs00J6xIMWHlFeBdSPiKIrlqf4bEbdQJPe1T+4y872IWJOi8vp3YDeKNpmTKSY+H0jRI31oNvkp2z+OcFoYYEJbCx3epJcEtqH4CvnTwEkUf9SgeGNfJzOfrGPv1JQ09M8tnMUEuL8CX4mIdzLzzxGxI/C3MtE7q1mT2YbfhzmBFzJz34h4mWI2+43AI5l5RURcSzGjva0Zfx9aUYcJYP+KiHEUvwcblf8OHo2IrSjWIf0MxVe1zSIoluP6TESsmZk3ZOZ3IuIkig+3G1C01zSN+OAkCNcAV2XmbhHxKMW3MIdHxD8oTmF9TGbW9gQpDe/t7adpvofiJEBtFKdsb6PoC96qnBD2tO9p6siWgz4sImYFKBOSNaI4jeljFJ/SNwS2yMwTKN7oPwcMLr9ur301pjPlG94mwB8jYqnMvAA4n+LkETuXVemtgWcqDbSHRMSCEbFq+fuwEcVpPH8XEetk5sEUvxs/A4aXb/YT2z8INePvQytqbzmKiD9FxJ8pvoo9hmLt6c0jYvHMfJniRAm1TmbbWyQiYrky0ZmeYomuMRSndF0dIDN3pqjQvt2Ev+cDym9hlgZWi4jjM/M+im/pPkWxxu4NdU5mYdLv9YoU49o1M7cH/kjxbdMDFKuz/KB8X3u6/T6VBaw+yYS2jyq/Ur8kIraIiMWB4yiS2G0p/oBtAHw5ihn+Ayj6iZ6oKt7eEMWKBYdS/PG6LyJmBi4DjgQ2iYjdMvOazLy2GfoFO7EKcG4UZ/raDjiYInnfOCK+mpn7U/TaHUSx0LiaTPnv/UcUpzR+DriUomp5EkVv+Rble0ft/9iXSc66wNkUVborKXorj6FYZ3WL8utp6p68dyaK05h/taxIvgasQNFucGxmPpSZO1B8cLmk2kinmdkpTs39xfL6kxRnuXua4vU/2yR2MqIP/PQBthz0UZn5ZtkntT/FH6zdslhTcmGKxPZ9igkhuwC/ymK5nqbU8NXSpyk+rc8UEftRvPHNS5Hcn0gx8xVozk/vmXlWRLRRJLKXZ+aFEXE9RT/16uWEin0iYokszp6jJhIRywE/pfjq+TzgvCjWHL2IYkLYOcD4rNni+Z0pv2qfFfg/inW0L42IMyn6g9+i+Fp6H4pl+prVUhT/tt+PiGsy85mynWR0+Za4F03QN9suM6+KiK8Av42Ix8v3u5cpWql+nZl3VBuh+joT2j4sM/8REa8Df6NYZ/VWijew/1EsGL4jxUz/55qxn6hhTLNStFncCKxJ8TXbkRTJ/leBEU1UpfiQsgq9cn5w1qdxwK+BoyPigizWmz0HmA5Ys/zD91BXx1R9dPh3PYHiFKbLRrFW59OZeUz5Ve3gcqJUrTWMdzqKD/K3AW+VfeNjojg71E7le+MvMvP1SgOehhr6SJekWDf4HxT/3r8FZET8k6JH+EjgCmi+D+5ZnAHsfYpVfDYD3gR+VrbRSF2y5aCPy8yrKBLXHSNi28x8F3iJ4lPrDJn5XLlfU72xwYfOS39S2S+4AcXZb0Zk5kkUf/S2oDixRLOaCOwXEdcBvwNez8xTKKpTv4+Itcpq7JnAzzOzKfuHW1X5b2CliFiNYuWKbSm+4Ps2xbqkKwKfp+gvrb1yvJtR9MYfDaxH8V7X3kLzBkXFcgA1P0lERw3vd+dSnMb2booTo/yT4sxvp1CsufuPsprZR77onbYy8yKKNWcXA+7NzIujVHFofVbV3QZ95YWxQlsDZTXiPeC08iunlymWYppQbWQ9K4o1J4+nWFd3aYqTJ/ywbMVYCPgLxdI1o6qLsudEsVrDuxFxMEWV/u7MvBsgM0+JiKRYqmy3zPwXzZ3Yt6QykT2bYo3VCRSntd6R4mxJ61IssL9rZt5b529pGqqTc1CM70yKPuDVKc4SNVNE9C+v/zSb8+yHi1JM6twcWAl4l2JS2HkRMQZYAPh9Zv4bmrOI0a5sp3qb4v3ticw8v+qY1PeZ0NZEZl4UEbtQTPjZOTNvr/MfsG5qPI3r9RRnhtmD4ixpj1EsGH93lQH2pMx8PyKWpqjGbQicFRF/ysxdy13Op2jFaKqlilpdQ3I3O8UpTr8K3EVRtdqFYgLYDhTJ7TvAtVDvBKdhlvtIYExm/hUgIt6gSPKgOCvWXzPz5mZ57+swjpcoEvnlKb6B2SwzX47ihAm3ZOZjFYVZicy8MiK+SXESHWmKTGhrJIuz/VyXmS+W12v/ht6o4Q/5isDcFGsPrhMRq2fmTcAtEbEvsFhmPkgxo78pNfyhmxN4JTPvLntob4+I31MkNYcC38zMF5rlD7w+tDzd1ygmBo3LzFsi4lKKquWeFIvL70kxSerViPhN1vCEAg3/5lemqDo/CcwbETcBN5WVutkozg724/ae2Wb5XS/H/nmKNYMfA/al+Lu8SPntzMoUa87uStFX21LKljt1oS+derZqJrQ1057MNqPyzX1TirPBXEnRZjAB2CkiFqPoJ/sMUOs1F7tpAMVXjo8BK0bE9pl5RhSnfbyIor/w6Mx8AZrnD7wmrWbwbeAXFF8//zgiRmfm/yLicorfjVcyc3xEbAPFWtXVRTz12nuEKVbu2CaL5fgOBb5C0Sv77/L3/tomnQC2EkVb1UPAgxT9st8A9izbzHaiaC+zSilNgZPC1GeU/XPbAF8ARgNzAHsBf6Xoo/0hxYzXply+pX3SQ9lmcFpELJvFucr3o5gA9Knyj/qXKNotLnCiRHOJiMEUlde3MvPGzPwecB3FEl0LZbGA/imZeVc58/+prP/57GenWIJvnfL6IcCLFG0V7SdPGNf5Xeup4Zuog4FtM/MrwH8oxn0OMALoD/zAf+eakugD//UFJrTqS96l6Ak9BPge8PXMHA2Mp+id3aVsu+gb/3qmoYaKzZcpkvcHgV9FxG8oqnTTATNDUY3LzOfLy1Zmm0Q5KWhx4CaKr913AsjM/YDbgX9GxAwUK1/UtirbUWZeSbFayc4R8bUsVnI5lOKkIc9VGlzPmoPiw+mXy+tnUXwj8xrF7P6j279y99+5NGW2HKjPyMw3IuJeihNGfDczHyv7y/5MUZF8s9yv6d7cy2R2BYpK1d/KiS+LUfzR+wmwIsVM722bJZFRofyANoBiXeX/ZuYvI+JdipNltGXmaZm5Z0QsmZlvVxttzyirkO8Ch0bEwMw8FfhxxWH1qHLS01eAX0bE+CxOJHBOeXPTTnaVeooJrfqa84D5KM7bvS6wEcWZgu6sNqyeVSY1f6OoRh9QXv9vudLB1yhmf38NGEJxYg3VXERMV1YjKScA/YZimaJ/ABdSnA1w3SjOAHcSRZ9l08ribGADgMMj4krg2Wb/8FZOenuPDxL50yharKTua7rvLKeOCa36lMx8NiJ+SZHAzQmck026RFmHiSFBMZv5VGDvzDyS4uxA05WV6Rsi4gCKJX1MaGssIhYCXszMV8pJfvNFxMOZ+Z+IuJZihvt/IuIqivfoMdCc30x0VCZ4t7S31LSCDon8VcAzmfl+1XFJdWNCqz4nizNfXd9hW9P9Me+wqsNVwPzAb4EflVW5X5eVu+mAQRTV2furi1jTyCLAnRExjOJsSCsBB0XETyjO+PX9iLgxi1Na/7W9itsqWimZbdeKibw0rZnQShXpsKrDlylO67tDRJwB3FPOYv9lmdA8GxGrZmbLrUXZbDLzX+VyW7cAK2fm2eW6s1+kmPG/PMVZwM6jaDtQCzCZ1dSy46BgQitVp3FVh5EUa29CsXj+FsBb8KGTLLxaRZCa9jLz8ojoB9wdESuUFbprKZZqegfYGDiv2XtIJWlacdkuqSJla8W9FOtvHpyZ/y1XdbgUeKSs5E3qHW7GtotWlpmXUixHd3tEzJmZr2Xmy5m5J7BIRCxecYiSaqD9bGFV/vQFVmilanW2qsPemfkfMIltdpl5WUR8B/hPuSzXS+WJNeajBU91KklTy4RWqlArreqgzpXtBzsBywDXUpxQYI3MfLbSwCSpRkxopYq1yqoOmrzMvKThcjOfHUvSNNV3Tj1bNXtoJUmSVGsmtJIkSao1Ww4kSZJqKOg7qwxUzQqtJEmSas2EVpIkSbVmQiup1iKiLSLuioj7IuK8iJjpExzr1IjYsrz854gY3sW+a0XEqlPxGE9ExNzd3d5hn9c/5mMdFBH7fdwYJaluTGgl1d1bmblMZi4FTAR2b7wxIvpPzUEzc5fMfKCLXdYCPnZCK0ma9kxoJTWTG4FFy+rptRHxV+DeiOgfEUdExO0RcU9EfAsgCsdGxAMRcQkwb/uBIuK6iBhZXl4vIu6IiLsj4uqIWJAicd63rA6vERHzRMTfy8e4PSJWK+87V0RcGRF3RsQfYcqLRkbEPyNiTETcHxG7dbjtt2UsV0fEPOW2RSLi8vI+N0bEktPk2ZTU51V92tu+MinNVQ4kNYWIGACsD1xebloRWCozHy+Twlcyc4WImB64OSKuBJYFlgA+C3wKeAA4ucNx5wH+BKxZHmtQZr4YEX8AXs/M35T7/RU4KjNviohhwBXAZ4CfATdl5iERsSHwoQR1MnYqH2NG4PaI+HtmvgDMDNyRmd+PiAPLY+8JnAjsnpmPRMRKwPHA2lPxNEpSLZnQSqq7GSPirvLyjcBJFK0AozLz8XL7OsDS7f2xwOzAYsCawFmZ2QaMj4hrOjn+ysAN7cfKzBcnE8eXgOHxQblitoiYtXyMr5T3vSQiXurGmPaOiM3LywuUsb4AvA+cU24/Azg/ImYpx3tew2NP343HkKSmYUIrqe7eysxlGjeUid0bjZuAvTLzig77bQBM6TTD0Y19oGjhWiUz3+oklm6fyjgi1qJIjlfJzDcj4jpghsnsnuXjvtzxOZDUGjz1bcEeWkmt4Arg2xExHUBELB4RMwM3ANuUPbbzA1/o5L63AJ+PiIXK+w4qt78GzNqw35UUX/9T7rdMefEGYLty2/rAnFOIdXbgpTKZXZKiQtyuH9BeZf4aRSvDq8DjEbFV+RgREZ+bwmNIUlMxoZXUCv5M0R97R0TcB/yR4huqfwCPAPcCJwDXd7xjZj5P0fd6fkTczQdf+V8EbN4+KQzYGxhZTjp7gA9WWzgYWDMi7qBoffjfFGK9HBgQEfcAhwK3Ntz2BjAiIsZQ9MgeUm7fDti5jO9+YNNuPCeS1DQis9vfhEmSJKmPWHb5kXn9zaOqDoPZZ+w/JjNHVhmDFVpJkiTVmpPCJEmSaijoxsLWLcIKrSRJkmrNhFaSJEm1ZsuBJElSXdlzAFihlSRJUs2Z0EqSJKnWbDmQJEmqKU99W7BCK0mSpFqzQitJklRTYYEWsEIrSZKkmjOhlSRJUq3ZciBJklRTdhwUrNBKkiSp1kxoJUmSVGu2HEiSJNWVPQeAFVpJkiTVnBVaSZKkmvJMYQUrtJIkSao1E1pJkiT1qIhYLyIeiohHI2L/aX18Ww4kSZJqKKjHqW8joj9wHPBlYCxwe0RcmJkPTKvHsEIrSZKknrQi8GhmPpaZE4GzgU2n5QOY0EqSJKknDQGearg+ttw2zdhyIEmSVEN33DHmihmni7mrjgOYISJGN1w/MTNPbLjeWWNETssATGglSZJqKDPXqzqGbhoLLNBwfSgwflo+gC0HkiRJ6km3A4tFxEIRMRDYBrhwWj6AFVpJkiT1mMx8LyL2BK4A+gMnZ+b90/IxInOatjBIkiRJvcqWA0mSJNWaCa0kSZJqzYRWkiRJtWZCK0mSpFozoZUkSVKtmdBKkiSp1kxoJUmSVGsmtJIkSaq1/wfHDw4r/f0PEAAAAABJRU5ErkJggg==\n",
|
| 153 |
+
"text/plain": [
|
| 154 |
+
"<Figure size 720x720 with 2 Axes>"
|
| 155 |
+
]
|
| 156 |
+
},
|
| 157 |
+
"metadata": {
|
| 158 |
+
"needs_background": "light"
|
| 159 |
+
},
|
| 160 |
+
"output_type": "display_data"
|
| 161 |
+
}
|
| 162 |
+
],
|
| 163 |
+
"source": [
|
| 164 |
+
"#Print the Target names\n",
|
| 165 |
+
"from sklearn.metrics import classification_report, confusion_matrix\n",
|
| 166 |
+
"import itertools \n",
|
| 167 |
+
"\n",
|
| 168 |
+
"#shuffle=False\n",
|
| 169 |
+
"\n",
|
| 170 |
+
"target_names = []\n",
|
| 171 |
+
"for key in test_generator.class_indices:\n",
|
| 172 |
+
" target_names.append(key)\n",
|
| 173 |
+
"\n",
|
| 174 |
+
"# print(target_names)#Confution Matrix\n",
|
| 175 |
+
"Y_pred = model.predict(test_generator)\n",
|
| 176 |
+
"y_pred = np.argmax(Y_pred, axis=1)\n",
|
| 177 |
+
"print('Confusion Matrix')\n",
|
| 178 |
+
"\n",
|
| 179 |
+
"cm = confusion_matrix(test_generator.classes, y_pred)\n",
|
| 180 |
+
"plot_confusion_matrix(cm, target_names, title='Confusion Matrix', normalize=False)"
|
| 181 |
+
]
|
| 182 |
+
},
|
| 183 |
+
{
|
| 184 |
+
"cell_type": "code",
|
| 185 |
+
"execution_count": 17,
|
| 186 |
+
"id": "dfba2244",
|
| 187 |
+
"metadata": {},
|
| 188 |
+
"outputs": [
|
| 189 |
+
{
|
| 190 |
+
"name": "stdout",
|
| 191 |
+
"output_type": "stream",
|
| 192 |
+
"text": [
|
| 193 |
+
"108/108 [==============================] - 10s 93ms/step\n",
|
| 194 |
+
"Confusion Matrix\n",
|
| 195 |
+
"Confusion matrix, without normalization\n"
|
| 196 |
+
]
|
| 197 |
+
},
|
| 198 |
+
{
|
| 199 |
+
"data": {
|
| 200 |
+
"image/png": "iVBORw0KGgoAAAANSUhEUgAAArQAAALGCAYAAAC01AIQAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/NK7nSAAAACXBIWXMAAAsTAAALEwEAmpwYAAB380lEQVR4nO3dd5xU5fXH8c8XVrBhwUoVRQUBFQTELvbeewUbMdEYW4z5aYw1McaosUZN7AVr7DUqFiwUsWIXDMWo2LEBy/n98dzFcYUFkZ27d+b75rUvZu7cuXOemdnZM+ee+1xFBGZmZmZmRdUs7wDMzMzMzH4OJ7RmZmZmVmhOaM3MzMys0JzQmpmZmVmhOaE1MzMzs0JzQmtmZmZmhVaTdwBmZmZm9tM1X2S5iGnf5B0G8c1HD0bElnnG4ITWzMzMrIBi2je07LJ73mHw7QsXLZl3DE5ozczMzApJIHePgntozczMzKzgnNCamZmZWaG55cDMzMysiARIeUfRJLhCa2ZmZmaF5oTWzMzMzArNLQdmZmZmReVZDgBXaM3MzMys4JzQmpmZmVmhueXAzMzMrKg8ywHgCq2ZmZmZFZwrtGZmZmaF5FPf1vGzYGZmZmaF5oTWzMzMzArNLQdmZmZmReWDwgBXaM3MzMys4JzQmpmZmVmhueXAzMzMrIiEZznI+FkwMzMzs0JzhdbMzMyskOSDwjKu0JqZmZlZoTmhNTMzM7NGI2l+ScMkvSjpVUmnZMtbS3pY0lvZ/4uX3Of3kt6W9IakLWb3GE5ozczMzIpKzfL/mb3vgI0jYnWgJ7ClpLWA44FHImIl4JHsOpK6AXsC3YEtgYslNW/oAZzQmpmZmVmjiWRydnW+7CeAHYCrs+VXAztml3cABkfEdxExBngbWLOhx3BCa2ZmZmY/x5KSRpT8DKq/gqTmkl4APgQejojngGUi4n2A7P+ls9XbAeNK7j4+WzZLnuXAzMzMrKiaxiwHkyKiT0MrREQt0FPSYsC/JfVoYPWZDSoa2r4rtGZmZmZWFhHxGTCE1Bv7gaQ2ANn/H2arjQc6lNytPTCxoe06oTUzMzMrJOV/QNgcHBQmaamsMoukBYBNgdeBu4AB2WoDgDuzy3cBe0pqKWl5YCVgWEOP4ZYDMzMzM2tMbYCrs5kKmgE3R8Q9kp4BbpZ0EPBfYDeAiHhV0s3AaGAacFjWsjBLTmjNzMzMrNFExEtAr5ks/xjYZBb3OQM4Y04fwwmtmZmZWRGJpnJQWO7cQ2tmZmZmheaE1szMzMwKzS0HZmZmZkU1Z6eerXh+FszMzMys0FyhNTMzMyskuUKb8bNgZmZmZoXmhNbMzMzMCs0tB2ZmZmZF1czz0IIrtGZmZmZWcE5ozczMzKzQ3HJgZmZmVkTCsxxk/CyYmZmZWaE5oTUzMzOzQnPLgZmZmVlRybMcgCu0ZmZmZlZwrtCamZmZFZJPfVvHz4KZmZmZFZoTWjMzMzMrNLccmJmZmRWVDwoDXKE1MzMzs4JzQmtmZmZmheaWAzMzM7Oi8iwHgCu0ZmZmZlZwrtCamZmZFZHkg8IyrtCamZmZWaE5oTUzMzOzQnPLgZmZmVlR+aAwwBVaMzMzMys4J7RmZmZmVmhuOTAzMzMrKs9yALhCa2ZmZmYF5wqtmZmZWSHJB4Vl/CyYmZmZWaE5oTUzMzOzQnPLgZmZmVlR+aAwwBVaMzMzMys4J7RmZmZmVmhuOTAzMzMrIuFZDjJ+FszMzMys0JzQmpmZmVmhueXAzMzMrJB8YoU6fhbMzMzMrNBcoTUzMzMrKs9DC7hCa2ZmZmYF54TWzCqepAUk3S3pc0m3/Izt7CPpoXkZWx4k3S9pQN5xmJnNK05ozazJkLS3pBGSJkt6P0u81psHm94VWAZYIiJ2m9uNRMT1EbH5PIjnByT1lxSSbq+3fPVs+ZA53M7Jkq6b3XoRsVVEXD2X4ZpZU6Jm+f80AU0jCjOrepKOBs4D/kRKPjsCFwM7zIPNLwe8GRHT5sG2GstHwDqSlihZNgB4c149gBJ/7ptZxfEHm5nlTtKiwKnAYRFxe0R8FRFTI+LuiPhttk5LSedJmpj9nCepZXZbf0njJR0j6cOsuntAdtspwEnAHlnl96D6lUxJnbJKaE12faCkdyV9KWmMpH1Klj9Vcr91JA3PWhmGS1qn5LYhkk6TNDTbzkOSlmzgaZgC3AHsmd2/ObA7cH295+rvksZJ+kLSSEnrZ8u3BP6vZJwvlsRxhqShwNfACtmyg7PbL5F0a8n2/yLpEclHmphZcTihNbOmYG1gfuDfDaxzArAW0BNYHVgTOLHk9mWBRYF2wEHARZIWj4g/kqq+N0XEwhHxr4YCkbQQcD6wVUS0AtYBXpjJeq2Be7N1lwDOAe6tV2HdGzgAWBpoARzb0GMD1wD7Z5e3AF4FJtZbZzjpOWgN3ADcImn+iHig3jhXL7nPfsAgoBXwXr3tHQOsliXr65OeuwEREbOJ1cyaAin/nybACa2ZNQVLAJNm0xKwD3BqRHwYER8Bp5AStTpTs9unRsR9wGSgy1zGMx3oIWmBiHg/Il6dyTrbAG9FxLURMS0ibgReB7YrWefKiHgzIr4BbiYlorMUEU8DrSV1ISW218xknesi4uPsMf8GtGT247wqIl7N7jO13va+BvYlJeTXAb+OiPGz2Z6ZWZPihNbMmoKPgSXrdvnPQlt+WF18L1s2Yxv1EuKvgYV/aiAR8RWwB3Ao8L6keyV1nYN46mJqV3L9f3MRz7XA4cBGzKRinbVVvJa1OXxGqko31MoAMK6hGyNiGPAuIFLibWZFIOV/QFgTactvGlGYWbV7BvgW2LGBdSaSDu6q05Ef746fU18BC5ZcX7b0xoh4MCI2A9qQqq6Xz0E8dTFNmMuY6lwL/Aq4L6uezpC1BPyO1Fu7eEQsBnxOSkQBZtUm0GD7gKTDSJXeicBxcx25mVlOnNCaWe4i4nPSgVsXSdpR0oKS5pO0laSzstVuBE6UtFR2cNVJpF3kc+MFYANJHbMD0n5fd4OkZSRtn/XSfkdqXaidyTbuA1bOphqrkbQH0A24Zy5jAiAixgAbknqG62sFTCPNiFAj6SRgkZLbPwA6/ZSZDCStDJxOajvYDzhOUs+5i97MLB9OaM2sSYiIc4CjSQd6fUTaTX446ch/SEnXCOAl4GXg+WzZ3DzWw8BN2bZG8sMktBnpQKmJwCek5PJXM9nGx8C22bofkyqb20bEpLmJqd62n4qImVWfHwTuJ03l9R6pql3aTlB30oiPJT0/u8fJWjyuA/4SES9GxFukmRKurZtBwsyauLwPCGsiB4XJB7KamZmZFU+zxTtFy43+kHcYfPvvg0dGRJ88Y3CF1szMzMwKraEjis3MzMysCfM5UBJXaM3MzMys0FyhNTMzMysg4QptHSe0ZdBqsdaxRJv2eYeRi9YLtsg7hNz4I8bMrLK9995YJk2a5I/7JsAJbRks0aY9J151d95h5GKfNTrmHUJu/K3ZzKyyrdsv1wP7rYQTWjMzM7MiEt4dmPFBYWZmZmZWaE5ozczMzKzQ3HJgZmZmVkjy8RoZV2jNzMzMrNBcoTUzMzMrKFdoE1dozczMzKzQnNCamZmZWaG55cDMzMysoNxykLhCa2ZmZmaF5oTWzMzMzArNLQdmZmZmBeWWg8QVWjMzMzMrNCe0ZmZmZlZobjkwMzMzKyJlP+YKrZmZmZkVmyu0ZmZmZgUk5IPCMq7QmpmZmVmhOaE1MzMzs0Jzy4GZmZlZQbnlIHGF1szMzMwKzQmtmZmZmRWaE9qCu+r033L0Vr35496bz1g24pF7OWmvzRi09vKMfe2lGcunTZ3Clacdy8n7bMEp+27JGyOfySPkRjd+3Di23Gxjeq3ajd6r9+CiC/6ed0hl9dCDD7Ba9y5077oifz3rzLzDKatfHHwgHdsuTe+ePfIOpeyq+XWv5rH7PV+dr3spSbn/NAVOaAtunW125TfnXv2DZe1W6MKvzvwHK/Vc8wfLn7xzMAAnX/8gR51/HTeffwbTp08vW6zl0rymhj+fdTajXh7NkKee4dJLLua10aPzDqssamtrOfKIw7jz7vsZ9dJobhl8Y9WMHWC/AQO5854H8g6j7Kr5da/msYPf89X6utuPOaEtuJV79WOhRRb9wbI2y6/Isst1/tG6E8e8xSp91gVgkdZLsmCrRXivpIJbKdq0aUOvXmsA0KpVK7p0XYWJEyfkHFV5DB82jM6dV2T5FVagRYsW7LbHntxz9515h1U2662/Aa1bt847jLKr5te9mscOfs9X6+teKu/qrCu0VnYdVlqFF558mNpp0/ho4jjee/1lPvng/bzDalTvjR3Liy+Oou+a/fIOpSwmTpxA+/YdZlxv1649EyZURzJfzar5da/msVczv+5WXyESWkmdJL1S5sfsL+meWdz2T0ndsstjJS1Zztjm1rrb7s7iSy/L6Qdsx03nnkLnVXvTvKZ53mE1msmTJ7PXHrty1tnnssgii+QdTllExI+WNZVvz9Z4qvl1r+axVzO/7laf56GdCxFxcN4xzI3mNTXsceRJM66fecjOLN1h+RwjajxTp05l7z12Zc+99mbHnXbOO5yyadeuPePHj5txfcKE8bRt2zbHiKwcqvl1r+axVzO/7hllP1aMCm2mRtLVkl6SdKukBSWdJGm4pFckXabs65mkIySNztYdnC1rLemObNmzklbLlp8s6VpJj0p6S9IhJY+5cPZYr0u6vmT7QyT1Kfsz8DN99+03fPfN1wCMfu5JmjWvoe3yK+Uc1bwXEfxy0MF06dqVI448Ou9wyqpP3768/fZbjB0zhilTpnDLTYPZZtvt8w7LGlk1v+7VPPZq5tfd6itShbYLcFBEDJV0BfAr4MKIOBVA0rXAtsDdwPHA8hHxnaTFsvufAoyKiB0lbQxcA/TMblsNWAtYCBgl6d5seS+gOzARGAqsCzzVqKP8iS77w6958/lnmfzZp/x2u7XY/pCjWGiRRbnxbycz+bNPOP/oA+mw8ioc9fdr+fKTSZx35AAksfhSy3LQH8/JO/xG8czTQ7nh+mvp0WNV+vXpBcApp53BllttnXNkja+mpoZz/34h222zBbW1tQwYeCDdunfPO6yy2X/fvXjy8SFMmjSJzp3a84eTTmHggQflHVajq+bXvZrHDn7PV+vrbj+mmfWhNDWSOgFPRETH7PrGwBHAtcBxwIJAa+CCiDhT0gPAZOAO4I6ImCxpFLBLRLybbWMc0AM4CmgWESdly68Bbgc+A06IiM2y5ZcAQyPiOklDgGMjYoSksUCfiJhUL+ZBwCCA1su26/2XO4Y2xlPT5O2zRse8Q8iN+7nMzCrbuv36MHLkiNw+7GuWXCEW2/ZPeT38DB9fvdfIiMh1z3WRWg7qZ94BXAzsGhGrApcD82e3bQNcBPQGRkqqYeZdJlHv//rLvytZVstPqGhHxGUR0Sci+rRarPqmVDEzMzMrlyIltB0lrZ1d3ovvd/1PkrQwsCuApGZAh4h4jFS9XQxYGHgC2Cdbpz8wKSK+yLaxg6T5JS0B9AeGN/ZgzMzMzH4Okf8ctE1lb2SRemhfAwZIuhR4C7gEWBx4GRjL90loc+A6SYuSqrLnRsRnkk4GrpT0EvA1MKBk28OAe4GOwGkRMVHSyo0/JDMzMzP7uQqR0EbEWKDbTG46Mfupb72ZbOMTYIdZPMSbETGo3vpDgCEl1w8vudy/5HKnWcVtZmZmZo2vEAmtmZmZmf1YU9nln7eqT2gj4uS8YzAzMzOzuVekg8LMzMzMzH6k6iu0ZmZmZoXljgPAFVozMzMza0SSOkh6TNJrkl6V9Jts+cmSJkh6IfvZuuQ+v5f0tqQ3JG0xu8dwhdbMzMzMGtM04JiIeF5SK9JJrx7Objs3Is4uXVlSN2BPoDvQFviPpJUjonZWD+CE1szMzKyIVIxZDiLifeD97PKXkl4D2jVwlx2AwRHxHTBG0tvAmsAzs7qDWw7MzMzMrCwkdQJ6Ac9liw6X9JKkKyQtni1rB4wrudt4Gk6AndCamZmZFVXep73NKsRLShpR8jNoFrEuDNwGHBkRX5DO+toZ6Emq4P6tbtWZ3D0aeh7ccmBmZmZmP8ekiOjT0AqS5iMls9dHxO0AEfFBye2XA/dkV8cDHUru3h6Y2ND2XaE1MzMzs0ajVMb9F/BaRJxTsrxNyWo7Aa9kl+8C9pTUUtLywErAsIYewxVaMzMzs4IqwkFhwLrAfsDLkl7Ilv0fsJeknqR2grHALwAi4lVJNwOjSTMkHNbQDAfghNbMzMzMGlFEPMXM+2Lva+A+ZwBnzOljuOXAzMzMzArNFVozMzOzAhIqSstBo3OF1szMzMwKzRVaMzMzs6JygRZwhdbMzMzMCs4JrZmZmZkVmlsOzMzMzIpIhZmHttG5QmtmZmZmheaE1szMzMwKzS0HZmZmZgXlloPEFVozMzMzKzRXaM3MzMwKyhXaxBVaMzMzMys0V2jLYIkFW7Bv7+XyDiMXi/c9PO8QcvPp8AvzDsHMzKwqOKE1MzMzKyp3HABuOTAzMzOzgnNCa2ZmZmaF5pYDMzMzs4LyLAeJK7RmZmZmVmiu0JqZmZkVkCRXaDOu0JqZmZlZoTmhNTMzM7NCc8uBmZmZWUG55SBxhdbMzMzMCs0JrZmZmZkVmlsOzMzMzArKLQeJK7RmZmZmVmhOaM3MzMys0NxyYGZmZlZU7jgAXKE1MzMzs4JzhdbMzMysoHxQWOIKrZmZmZkVmhNaMzMzMys0txyYmZmZFZHcclDHFVozMzMzKzQntGZmZmZWaG45MDMzMysgAe44SFyhNTMzM7NCc0JbwR568AFW696F7l1X5K9nnZl3OPNcyxY1PHntsTx30/GMvPUETjx0awB23rQXI289ga9Gns8a3TrOWH/jfl0Zev1xDL/5/xh6/XFs2HflvEJvNL84+EA6tl2a3j175B1KLir9Pd8Qj91j99irkZDy/2kKnNBWqNraWo484jDuvPt+Rr00mlsG38hro0fnHdY89d2UaWw56Hz67XEm/fb8M5uv0401V+3Eq+9MZM9jLuep59/5wfoffzaZXY+8lL67/4lDTrqWK07fP6fIG89+AwZy5z0P5B1GLqrhPT8rHrvH7rFXz9ht5pzQVqjhw4bRufOKLL/CCrRo0YLd9tiTe+6+M++w5rmvvpkCwHw1zampaU5E8MaYD3jrvQ9/tO6Lb4zn/Y8+B2D0O+/TssV8tJivstrI11t/A1q3bp13GLmolvf8zHjsHrvHXj1jt5lzQluhJk6cQPv2HWZcb9euPRMmTMgxosbRrJl4dvDx/PeRM3n02dcZ/sp7c3S/nTbtyYtvjGPK1GmNHKGVS7W852fGY/fYwWOvlrHXJ+X/0xQUPqGVdKqkTefxNvtLumcWt/1TUrfs8lhJS87Lx55XIuJHy5pKn8u8NH16sNaeZ7LiFifSp8dydOvcZrb3WWWFZTn9iB04/PTBZYjQyqVa3vMz47H/kMde+ap57DZzhd/fGhEnlfnxDi7n482tdu3aM378uBnXJ0wYT9u2bXOMqHF9PvkbnhjxFpuv043R77w/y/XaLb0YN50ziIP/cC1jxk8qY4TW2KrtPV/KY/fYwWOvlrHbzOVeoZW0r6Rhkl6QdKmk5pL2kvSypFck/SVbr7mkq7JlL0s6Klt+laRds8tjJZ0i6flsna7Z8taS7pD0kqRnJa2WLT9Z0rWSHpX0lqRDSkJbWNKtkl6XdL2yr36ShkjqU9YnaS706duXt99+i7FjxjBlyhRuuWkw22y7fd5hzVNLLr4wiy68AADzt5yPjft14Y2xH8xy/UUXXoDbLziUky64i2defLdcYVqZVMN7flY8do/dY6+esdeX9wwHTaUynmuFVtIqwB7AuhExVdLFwD7A6UBv4FPgIUk7AuOAdhHRI7vvYrPY7KSIWEPSr4BjgYOBU4BREbGjpI2Ba4Ce2fqrAWsBCwGjJN2bLe8FdAcmAkOBdYGnfsLYBgGDADp07Dibtee9mpoazv37hWy3zRbU1tYyYOCBdOvevexxNKZll1yEy0/dj+bNmtGsmbjt4ee5/8lX2H6j1Tjnd7ux5OILc/v5h/LSGxPY/rCLOHTPDejcYSmOP2RLjj9kSwC2++WFfPTp5JxHMu/sv+9ePPn4ECZNmkTnTu35w0mnMPDAg/IOqyyq4T0/Kx67x+6xV8/YbeY0sz6Usj24dDjwf0DdIekLAF8DL0fE/tk6B5ESy9OAEcB9wL3AQxExXdJVwD0RcauksaTkeIKkfsAZEbGppFHALhHxbrbNcUAP4CigWV3bgqRrgNuBz4ATImKzbPklwNCIuE7SEODYiBiRPV6fiGhw33Xv3n1i6HMjfuazVUyL9z087xBy8+nwC/MOwczMGtG6/fowcuSI3EqU87dZOToNuCCvh5/hjb9sOTIict17nXfLgYCrI6Jn9tOFVE39kYj4FFgdGAIcBvxzFtv8Lvu/lu8r0DN7s0W9/+sv/65kWem2zMzMzKwJyTuhfQTYVdLSkHpdgVHAhpKWlNQc2At4PJtNoFlE3Ab8AVjjJzzOE6RWBiT1J7UlfJHdtoOk+SUtAfQHhv/sUZmZmZlZ2eRadYyI0ZJOJPXJNgOmkqqvvwceI1VW74uIOyWtDlyZrUe2zpw6ObvvS6SWhgEltw0jtTB0BE6LiImSKu+cqGZmZlZRRJqP3ZrAbvSIuAm4qd7iZ4Eb6q33IjOpykbEwJLLnUoujyBVXImIT4AdZhHCmxExqN42h5BaG+quH15yuf/MHs/MzMzM8pF3y4GZmZmZ2c+Se4U2TxFxct4xmJmZmc2tJjINbO5coTUzMzOzQnNCa2ZmZmaFVtUtB2ZmZmZF1lROPZs3V2jNzMzMrNBcoTUzMzMrIvmgsDqu0JqZmZlZoTmhNTMzM7NCc8uBmZmZWQEJHxRWxxVaMzMzMys0J7RmZmZmVmhuOTAzMzMrJLnlIOMKrZmZmZkVmiu0ZmZmZgXlAm3iCq2ZmZmZFZoTWjMzMzMrNLccmJmZmRWUDwpLXKE1MzMzs0JzQmtmZmZmheaWAzMzM7Mikmc5qOMKrZmZmZkVmiu0ZmZmZgUkfFBYHVdozczMzKzQnNCamZmZWaG55cAa1afDL8w7hNyc+chbeYeQm2M27Jx3CLlp3qy6d/81q+Lx106PvEPITbW/7/PkjoPEFVozMzMzKzQntGZmZmZWaG45MDMzMysoz3KQuEJrZmZmZoXmCq2ZmZlZQblAm7hCa2ZmZmaF5oTWzMzMzArNLQdmZmZmRSQfFFbHFVozMzMzKzQntGZmZmZWaG45MDMzMysg4VkO6rhCa2ZmZmaF5oTWzMzMzArNLQdmZmZmhSTPcpBxhdbMzMzMCs0VWjMzM7OCcoE2cYXWzMzMzArNCa2ZmZmZFZpbDszMzMwKygeFJa7QmpmZmVmhOaE1MzMzs0Jzy4GZmZlZEcmzHNRxhdbMzMzMCs0VWjMzM7MCEj4orI4rtBXsoQcfYLXuXejedUX+etaZeYdTVpU+9jvP+T1/3WMtLv7FNj+67elb/8UpW67M159/AsDXX3zK1cftx5927Ml9F51S7lDL6sLzz2PNNValX+/VOGD/vfn222/zDqksvv32WzZYtx/9+vSkT88enH7qH/MOqawq/fd9dmpra1lnzTXYdcft8g6lrKr9dbcfckJboWpraznyiMO48+77GfXSaG4ZfCOvjR6dd1hlUQ1j77nZzux7+r9+tPzzj97n3eeHsujSbWcsq2nRko32/w2bH/K7coZYdhMnTODSiy/g8aHDeG7kS0yvreW2WwbnHVZZtGzZkvsefITnRrzAM8NH8fBDDzLsuWfzDqssquH3fXYuvuDvdOm6St5hlJVf92KR1EHSY5Jek/SqpN9ky1tLeljSW9n/i5fc5/eS3pb0hqQtZvcYTmgr1PBhw+jceUWWX2EFWrRowW577Mk9d9+Zd1hlUQ1jX27VvizQatEfLX/w0j+x6cG/Je2ISlrMvyAde/ShZr6WZYwwH9OmTeObb75h2rRpfP3N1yzbpu3s71QBJLHwwgsDMHXqVKZOnVo1uyGr4fe9IRPGj+eB++9jwAEH5R1KWVX7615KUu4/c2AacExErAKsBRwmqRtwPPBIRKwEPJJdJ7ttT6A7sCVwsaTmDT2AE9oKNXHiBNq37zDjert27ZkwYUKOEZVPtY79jWceodUSy7DsCtVVqanTtl07fn3kMXRfuRMrLd+ORRZZlE023TzvsMqmtraWtfr2olP7Zdh4k03pu2a/vEMqi2r9fa9z3LFHcfqf/0KzZtX157zaX/eiiYj3I+L57PKXwGtAO2AH4OpstauBHbPLOwCDI+K7iBgDvA2s2dBjNNnfAEn/V3K5k6RXfub2xkpacibLT5Z07Fxsr6ekrX9OTI0pIn60rFoqNtU49qnffsOTgy9ho/1/k3coufn000+57567ePm1d3jz3fF8/dVXDL7xurzDKpvmzZvz7PBRvPnuOEaOGM6rr/6sj8zCqMbf9zr333sPSy21FL3W6J13KGVXza97E7WkpBElP4NmtaKkTkAv4DlgmYh4H1LSCyydrdYOGFdyt/HZslnKNaGdTfn4/xq4bVbbK+esDT2BJpvQtmvXnvHjv38vTJgwnrZtq2P3azWO/ZP3/8un/xvPP365PeftvxFfTPoflx6+E5M/+Sjv0MpmyKP/YblOnVhyqaWYb7752G7HnXju2WfyDqvsFltsMdbfYEMefvCBvEMpi2r8fa/z7DNDue/eu+m28vIM3G8vHh/yKAcN3C/vsMqiml/3+qT8f4BJEdGn5OeymceqhYHbgCMj4ouGhjWTZT/+FlOiURNaSftKGibpBUmXSmouabKkUyU9B5wo6d8l628m6XZJZwILZPe7Pru5uaTLs2bihyQtkN1niKQ/SXoc+I2kTSSNkvSypCsklTYO/jaLZ5ikFWcS7yGShkt6UdJtkhbMlu8m6ZVs+ROSWgCnAntkMe7RSE/hXOvTty9vv/0WY8eMYcqUKdxy02C22Xb7vMMqi2oc+zLLd+G3Nz3Lkdc8xpHXPMYiSy7LLy78Nwu3Xirv0MqmfYeODB/2HF9//TURweOPPUqXLtXRfvHRRx/x2WefAfDNN9/w2KOP0KVL13yDKpNq/H2vc8rpf+bNd8cx+s0xXHXtjWzYf2P+ddW1eYdVFtX8uheVpPlIyez1EXF7tvgDSW2y29sAH2bLxwMdSu7eHpjY0PYbraIpaRVgD2DdiJgq6WJgH2Ah4JWIOElp/8BrkpaKiI+AA4ArI+JuSYdHRM9sW52AlYC9IuIQSTcDuwB1+xMXi4gNJc0PvAVsEhFvSroG+CVwXrbeFxGxpqT9s2Xb1gv79oi4PHvM04GDgAuAk4AtImKCpMUiYoqkk4A+EXH4LMY/CBgE0KFjx7l8FudeTU0N5/79QrbbZgtqa2sZMPBAunXvXvY48lANY7/tz0cx9qVhfP3Fp5yz7/r03/cI1thyt1muf97+G/Hd15OpnTaV15/5D/udcSVLLfej73SF1nfNfuyw0y6sv3YfampqWG31nhxw0CF5h1UW//vf+ww6aCC1tbVMnz6dXXbdja22qf/xVpmq4ffdfsyv+/eK0GqR5Xv/Al6LiHNKbroLGACcmf1/Z8nyGySdA7Ql5YDDGnyMmfWhzAuSDie1DdRl2wsANwInAi0jojZb7wTga+BKYBSwUkRMkzQ5IhbO1ukEPJwdBYek3wHzRcTpkoYAf4yIxyWtDlwQERtk620CHBYRO0saC2wcEe9m3xL+FxFLSDoZmBwRZ0vaEDgdWAxYGHgwIg6V9A+gM3AzKen9WNJAGkhoS/Xu3SeGPjdibp9KK6gzH3kr7xByc8yGnfMOITfNmzX9Py6NqVkVj792euP8PS2Can3fr9uvDyNHjsht8K06dI3ex1yR18PP8PhR646MiD6zul3SesCTwMvA9Gzx/5H6aG8GOgL/BXaLiE+y+5wAHEiaIeHIiLi/oRgas+dUwNUR8fsfLJSOrUtmM1cCdwPfArdExLRZbO+7ksu1pAS5zlclj9mQmMXlOlcBO0bEi1nC2h8gS2r7AdsAL0jqOZvHMTMzMzMgIp5i1jnaJrO4zxnAGXP6GI3ZQ/sIsKukpWHG5LnL1V8pIiaS+iJOJCWUdaZmldSf4nWgU0l/7H7A4yW371Hy/8yOFmkFvJ897j51CyV1jojnIuIkYBKpr+PLbH0zMzOz8msCB4Q1lY6HRktoI2I0KUl9SNJLwMNAm1msfj0wLrtPncuAl0oOCpuTx/yW1Id7i6S6svY/SlZpmR2M9hvgqJls4g+k8vfDpOS4zl+zg8xeAZ4AXgQeA7o11YPCzMzMzKpFo05zFRE3ATfVW7zwTFZdD7i83n1/B5Seq7NHyW1nl1zuX+9+j5DmN6sfS6fs4in1lp9ccvkS4JKZ3HfnmcT8CdB3JsvNzMzMrIzKOW/rTEkaSeqBPSbvWMzMzMyKQszxqWcrXu4JbURU3ylOzMzMzGyeabKnvjUzMzMzmxO5V2jNzMzMbO644yBxhdbMzMzMCs0VWjMzM7OCauYSLeAKrZmZmZkVnBNaMzMzMys0txyYmZmZFZQ7DhJXaM3MzMys0JzQmpmZmVmhueXAzMzMrIAkfOrbjCu0ZmZmZlZortCamZmZFVQzF2gBV2jNzMzMrOCc0JqZmZlZobnlwMzMzKygfFBY4gqtmZmZmRWaE1ozMzMzKzS3HJiZmZkVlDsOEldozczMzKzQXKE1MzMzKyABwiVacIXWzMzMzArOCa2ZmZmZFZpbDszMzMwKyqe+TZzQlkEAtdMj7zByUc2/aMdvslLeIeRmyb2vyjuE3Ey6YWDeIeTq2ym1eYeQmxY13ulplhf/9pmZmZlZoblCa2ZmZlZEkk99m3GF1szMzMwKzRVaMzMzs4JygTZxhdbMzMzMCs0JrZmZmZkVmlsOzMzMzApIQDP3HACu0JqZmZlZwTmhNTMzM7NCc8uBmZmZWUG54yBxhdbMzMzMCs0JrZmZmZkVmlsOzMzMzArKp75NXKE1MzMzs0JzhdbMzMysgCQfFFbHFVozMzMzKzQntGZmZmZWaG45MDMzMyson/o2cYXWzMzMzArNCa2ZmZmZFZpbDszMzMwKyg0HiSu0ZmZmZlZortCamZmZFZTPFJa4QmtmZmZmheaEtsLV1tayzpprsOuO2+UdStmMHzeOLTfbmF6rdqP36j246IK/5x1S2fzi4APp2HZpevfskXcojabdEgty30lbMPKcHRn+tx341VarzLjt0C278vx5OzH8bztw2j69Adh9vRV4+qztZ/x8MXgAqy7XOq/wG81DDz7Aat270L3rivz1rDPzDqfRHX7oway0XBvW7rP6jGVnnHoS667Zi/XX6s3O223J++9PzDHCxvftt9+ywbr96NenJ3169uD0U/+Yd0hlVW3veWuYE9oKd/EFf6dL11Vmv2IFaV5Tw5/POptRL49myFPPcOklF/Pa6NF5h1UW+w0YyJ33PJB3GI1qWm3w+2uH0/voO9johHs5ZIuudG23KBt0X5Zt+nRkrWPvpO8xd3L+3a8CcPNT77LOcXexznF3ccgFT/DeR5N5+b1Pch7FvFVbW8uRRxzGnXffz6iXRnPL4Bsr/j2/1777c+sd9/5g2a+PPJahw0bx5LMj2WKrbTjrz6fnFF15tGzZkvsefITnRrzAM8NH8fBDDzLsuWfzDqssqvE9PzMCmin/n6bACW0FmzB+PA/cfx8DDjgo71DKqk2bNvTqtQYArVq1okvXVZg4cULOUZXHeutvQOvWlVd9LPXBZ9/w4piUkE7+dhpvTPicNq0X5ODNu/C3O19myrTpAHz0xbc/uu+u663ArUPfLWu85TB82DA6d16R5VdYgRYtWrDbHntyz9135h1Wo1p3vQ1YvN57fZFFFplx+auvvqr43kJJLLzwwgBMnTqVqVOnVvyY61Tje94a5oS2gh137FGc/ue/0KxZ9b7M740dy4svjqLvmv3yDsUaQcelFmb15Vsz4u1JrNhmUdbtugyPnbEND5y8JWt0XuJH6++ydiduGTomh0gb18SJE2jfvsOM6+3atWfChOr4ElffaSefSPeVO3HLTTfyfyeenHc4ja62tpa1+vaiU/tl2HiTTavms87veauvejOdn0jS03nH8FPcf+89LLXUUvRao3feoeRm8uTJ7LXHrpx19rk/qNxYZVioZQ3XH9Of3101jC+/mUpNM7HYwi3Y6IR7OeHaEVxzVP8frN9nxSX5Zkoto8d9lke4jSoifrSsWip19f3h5NN59c2x7LbHXlx+6UV5h9PomjdvzrPDR/Hmu+MYOWI4r776St4hlYXf8xkJNYGfpsAJ7RyKiHXyjuGnePaZodx37910W3l5Bu63F48PeZSDBu6Xd1hlM3XqVPbeY1f23Gtvdtxp57zDsXmsprm4/piNuOnJd7lr2H8BmPDJ19z1XLo88p1JTJ8eLNmq5Yz77Lru8txSge0GkKpT48ePm3F9woTxtG3bNseI8rfrHntx1x3/zjuMsllsscVYf4MNefjByu6hr+P3vNXnhHYOSZqc/d9M0sWSXpV0j6T7JO2ad3z1nXL6n3nz3XGMfnMMV117Ixv235h/XXVt3mGVRUTwy0EH06VrV4448ui8w7FGcPGh6/LGhM+58N7vDwK5Z/h/2bDHsgCs2GYRWtQ0Z9KX3wEgwU5rdeLWCmw3AOjTty9vv/0WY8eMYcqUKdxy02C22Xb7vMMqu3fefmvG5QfuvZuVu3TJMZrG99FHH/HZZ58B8M033/DYo4/QpUvXfIMqE7/nvyfl/9MU+MQKP93OQCdgVWBp4DXgivorSRoEDALo0LFjGcOzZ54eyg3XX0uPHqvSr08vAE457Qy23GrrnCNrfPvvuxdPPj6ESZMm0blTe/5w0ikMPLCyDgpcu8vS7L3hirzy3ic8fVb6A3byjSO55tG3uORX6zLs7B2YMm06v7joyRn3WW+VZZnw8deM/XByXmE3qpqaGs79+4Vst80W1NbWMmDggXTr3j3vsBrVQQP2YeiTj/Pxx5PovtJyHH/iH3n4wft56803adasGR06duSc8y/OO8xG9b//vc+ggwZSW1vL9OnT2WXX3dhqm23zDqssqvE9bw3TzPpQ7MckTY6IhSWdB7wYEVdmy28HboiIW2d13zV694knnxlepkiblqYynUcemkpfUR6W3PuqvEPIzaQbBuYdQq6+nVKbdwi5aVFTvTs9m1Xph/26/fowcuSI3Aa/xArdY+vTbsjr4We4bt+eIyOiT54xuEL701Xnb62ZmZk1OdVcPClVvV8n595TwC5ZL+0yQP+c4zEzMzOraq7Q/nS3AZsArwBvAs8Bn+cakZmZmVkVc0I7hyJi4ez/6ZKOjYjJkpYAhgEv5xudmZmZVZu6U9+aE9q5dY+kxYAWwGkR8b+c4zEzMzOrWk5o50JE9M87BjMzMzNLnNCamZmZFZRnOUhmmdBKugCY5SS1EXFEo0RkZmZmZvYTNFShHVG2KMzMzMzsJ3N9NpllQhsRV5del7RQRHzV+CGZmZmZmc252Z5YQdLakkYDr2XXV5dU2SfINjMzM7PCmJODws4DtgDuAoiIFyVt0JhBmZmZmVnDJGjmg8KAOTz1bUSMq7eothFiMTMzMzP7yeakQjtO0jpASGoBHEHWfmBmZmZmlrc5SWgPBf4OtAMmAA8ChzVmUGZmZmY2e+44SGab0EbEJGCfMsRiZmZmZvaTzcksBytIulvSR5I+lHSnpBXKEZyZmZmZzZqk3H+agjk5KOwG4GagDdAWuAW4sTGDMjMzMzObU3OS0Coiro2IadnPdTRwSlwzMzMzs3KaZQ+tpNbZxcckHQ8MJiWyewD3liE2MzMzM2tAE9njn7uGDgobSUpg656qX5TcFsBpjRWUmZmZmdmcmmVCGxHLlzMQMzMzM7O5MSfz0CKpB9ANmL9uWURc01hBmZmZmVnDhHzq28xsE1pJfwT6kxLa+4CtgKcAJ7RmZmZmlrs5meVgV2AT4H8RcQCwOtCyUaMyMzMzs4YpHRSW909TMCcJ7TcRMR2YJmkR4EPAJ1YwMzMzsyZhTnpoR0haDLicNPPBZGBYYwZlZmZmZjanZpvQRsSvsov/kPQAsEhEvNS4YZmZmZnZ7DSVU8/mraETK6zR0G0R8XzjhGRmZmZmNucaqtD+rYHbAth4HsdSsQQ0b+ZvUFY9Jt0wMO8QcnPdyPfyDiFX+6zRMe8QcuNKmVl+GjqxwkblDMTMzMzMfpo5Obq/Gvh5MDMzM7NCm6MzhZmZmZlZ0yLc6lLHFVozMzMzK7TZJrRK9pV0Una9o6Q1Gz80MzMzM7PZm5OWg4uB6aRZDU4FvgRuA/o2YlxmZmZmNhueRCmZk4S2X0SsIWkUQER8KqlFI8dlZmZmZjZH5qSHdqqk5qS5Z5G0FKlia2ZmZmaWuzmp0J4P/BtYWtIZwK7AiY0alZmZmZnNllsOktkmtBFxvaSRwCakGSJ2jIjXGj0yMzMzM7M5MCezHHQEvgbuBu4CvsqWmZmZmZnNlqQrJH0o6ZWSZSdLmiDphexn65Lbfi/pbUlvSNpidtufk5aDe0n9swLmB5YH3gC6/+TRmJmZmdk8IRXqxApXARcC19Rbfm5EnF26QFI3YE9SrtkW+I+klSOidlYbn5OWg1XrPcgawC/mKHQzMzMzq3oR8YSkTnO4+g7A4Ij4Dhgj6W1gTeCZWd3hJ58pLCKex3PQmpmZmeWumfL/AZaUNKLkZ9BPGMLhkl7KWhIWz5a1A8aVrDM+WzZLs63QSjq69HkD1gA++gmBmpmZmVnlmhQRfebifpcAp5FaW08D/gYcSGpzrS8a2tCc9NC2Krk8jdRTe9schWlmZmZmNhMR8UHdZUmXA/dkV8cDHUpWbQ9MbGhbDSa02QkVFo6I385dqGZmZmbWWIpzTNiPSWoTEe9nV3cC6mZAuAu4QdI5pIPCVgKGNbStWSa0kmoiYlp2EJiZmZmZ2VyRdCPQn9RvOx74I9BfUk9SO8FYskkHIuJVSTcDo0ndAYc1NMMBNFyhHUbql31B0l3ALcBXdTdGxO1zNyQzMzMzqyYRsddMFv+rgfXPAM6Y0+3PSQ9ta+BjYGO+n482ACe0ZmZmZjkR0KzIPQfzUEMJ7dLZDAev8H0iW6fBI83MzMzMzMqloYS2ObAwczF1gpmZmZk1vp98QoEK1VBC+35EnFq2SMzMzMzM5kJDib2bMszMzMysyWsood2kbFFYo3jowQdYrXsXunddkb+edWbe4ZSVx16dY//FwQfSse3S9O7ZI+9QGsVVp/+Wo7fqzR/33nzGshGP3MtJe23GoLWXZ+xrL81YPm3qFK487VhO3mcLTtl3S94YOctToBfa+HHj2HKzjem1ajd6r96Diy74e94hlVU1/75X89hLSfn/NAWzTGgj4pNyBmLzVm1tLUcecRh33n0/o14azS2Db+S10aPzDqssPPbqHDvAfgMGcuc9D+QdRqNZZ5td+c25V/9gWbsVuvCrM//BSj3X/MHyJ+8cDMDJ1z/IUedfx83nn8H06dPLFmu5NK+p4c9nnc2ol0cz5KlnuPSSi6vmPV/Nv+/VPHabOfcSV6jhw4bRufOKLL/CCrRo0YLd9tiTe+6+M++wysJjr86xA6y3/ga0bt067zAazcq9+rHQIov+YFmb5Vdk2eU6/2jdiWPeYpU+6wKwSOslWbDVIrxXUsGtFG3atKFXr3T+n1atWtGl6ypMnDgh56jKo5p/36t57DZzTmgr1MSJE2jf/vvTILdr154JE6rjQ95jr86x2w91WGkVXnjyYWqnTeOjieN47/WX+eSD92d/xwJ7b+xYXnxxFH3X7Jd3KGVRzb/v1Tz2UpJo1gR+moI5ObHCzyJpckQs3IjbPxmYHBFnN9L2BwIPRcTExth+Y4n48cxqaiJvusbmsf9QtYzdfmjdbXfn/bFvc/oB27HEsu3ovGpvmtc0zzusRjN58mT22mNXzjr7XBZZZJG8wymLav59r+ax28w1ekJbAQaSTi5RqIS2Xbv2jB8/bsb1CRPG07Zt2xwjKh+PvTrHbj/UvKaGPY48acb1Mw/ZmaU7LJ9jRI1n6tSp7L3Hruy5197suNPOeYdTNtX8+17NY6/PeXxStpYDSddK2qHk+vWStpc0UNIdku6WNEbS4ZKOljRK0rOSWmfrD5F0nqSnJb0iqfQIiG7Z7e9KOqLkMY7O1n1F0pEly/eX9JKkF7O4WmWPPV92+yKSxkraDegDXC/pBUkLSOot6XFJIyU9KKlNYz93c6NP3768/fZbjB0zhilTpnDLTYPZZtvt8w6rLDz26hy7/dB3337Dd998DcDo556kWfMa2i6/Us5RzXsRwS8HHUyXrl054sij8w6nrKr5972ax24zV84K7T+Bo4A7JS0KrAMMAPYFegC9gPmBt4HfRUQvSecC+wPnZdtYKCLWkbQBcEV2P4CuwEZAK+ANSZcAqwEHAP1Ic+o+J+lxYApwArBuREyS1DoivpQ0BNgGuAPYE7gtIm6RdBhwbESMyBLeC4AdIuIjSXsAZwAH1h+spEHAIIAOHTv+/GfvJ6qpqeHcv1/IdttsQW1tLQMGHki37t3LHkcePPbqHDvA/vvuxZOPD2HSpEl07tSeP5x0CgMPPCjvsOaZy/7wa958/lkmf/Ypv91uLbY/5CgWWmRRbvzbyUz+7BPOP/pAOqy8Ckf9/Vq+/GQS5x05AEksvtSyHPTHc/IOv1E88/RQbrj+Wnr0WJV+fXoBcMppZ7DlVlvnHFnjq+bf92oeu82cZtaHMk8foKSHVtIrwMbAzsCKEXFs1qO6bkQckq3zX2DtiJgg6UBgtYg4Mks4T42IR0vWWw04EpgaEWdky18DNgN2AZaIiJOy5acBH5FO27tsRJxQL851geMiYgdJzwCHRMQr2ePWJbQ9gKeBd7O7NSedUW1zGtC7d58Y+tyIuXr+zKxYrhv5Xt4h5GqfNcr/Bb6pcA9n9Vm3Xx9GjhyR2wvfduVVY9CFt+f18DOcssXKIyOiT54xlLuH9lpgH1IFtLSq+V3J5ekl16fzwxjrZ99110vvX5vdZ1ZvMM1kO0TEUEmdJG0INI+IV2Zx31cjYu1ZbNvMzMzMyqzc03ZdRaqoEhGvzsX99wCQtB7weUR83sC6TwA7SlpQ0kLATsCTwCPA7pKWyLZVOmnlNcCNwJUly74ktTIAvAEsJWnt7L7zSfI+DjMzM7MclbVCGxEfZC0Bd8zlJj6V9DSwCDPpW633WM9LugoYli36Z0SMApB0BvC4pFpgFGkmA4DrgdNJSW2dq4B/SPoGWBvYFTg/6wOuIfX3zk1ybmZmZjbXBE1mHti8NXpCWzoHraQFgZUoSRgj4ipS0lh3vdOsbiMdqPX7ets/ud71HiWXzwF+dCRERFwNXF1/ObAecGtEfFay7m3AbSXrvABsMJP7mpmZmVkOylahlbQpaWaCc2bTKpALSRcAWwGVf2ismZmZWQUpW0IbEf8B5vrw14joP++imen2f92Y2zczMzOb19xxkJT7oDAzMzMzs3nKp741MzMzKyJBM1doAVdozczMzKzgnNCamZmZWaG55cDMzMysoDTLE6NWF1dozczMzKzQnNCamZmZWaG55cDMzMysgNKpb/OOomlwhdbMzMzMCs0VWjMzM7OCcoU2cYXWzMzMzArNCa2ZmZmZFZpbDszMzMwKSnLPAbhCa2ZmZmYF54TWzMzMzArNLQdmZmZmBeR5aL/nCq2ZmZmZFZortGZmZmZFJPAxYYkrtGZmZmZWaE5ozczMzKzQ3HJgZmZmVlDN3HMAuEJrZmZmZgXnhNbMzMzMCs0tB2ZmZmYF5Hlov+eE1szmuc+/npp3CLnZt/dyeYeQq2tHvJd3CLnZr091v/ZmeXJCa2ZmZlZQPiYscQ+tmZmZmRWaE1ozMzMzKzS3HJiZmZkVkmiGew7AFVozMzMzKzgntGZmZmZWaG45MDMzMysg4VkO6rhCa2ZmZmaF5oTWzMzMzArNLQdmZmZmRSSf+raOK7RmZmZmVmiu0JqZmZkVVDMfFQa4QmtmZmZmBeeE1szMzMwKzS0HZmZmZgXkeWi/5wqtmZmZmRWaE1ozMzMzKzS3HJiZmZkVlGc5SFyhNTMzM7NCc4XWzMzMrKBcoE1coTUzMzOzQnNCa2ZmZmaF5pYDMzMzswISrkzW8fNQwR568AFW696F7l1X5K9nnZl3OGXlsVfH2CeMH8fO227G+n1XZYN+q3P5JRcAcMqJx7Nenx5stM4aHLDPrnz+2Wf5BloGlf66X3X6bzlm696cvM/mM5bdesGf+MMeG3PKvlty8e8G8fWXn8+47f6rL+KEXTfkD3tszKvPPp5HyGVR6a97Q6p57PZjTmgrVG1tLUcecRh33n0/o14azS2Db+S10aPzDqssPPbqGXtNTQ0nn34WTw5/mfv+8xRXXn4Jb7w+mg032oQhz77AY08/zwqdV+L8c/6Sd6iNqhpe93W22ZUjzr36B8tWWXM9Tr7+If543QMs03F57r/mYgAmjnmL4f+5m5NveIjfnHs115/9B6bX1uYRdqOqhtd9Vqp57DZzTmgr1PBhw+jceUWWX2EFWrRowW577Mk9d9+Zd1hl4bFXz9iXWbYNq/XsBcDCrVqxUpeu/G/iRPpvshk1Namjqnfffrw/cUKeYTa6anjdV+7Vj4UWWfQHy7r324Dm2eu8QvdefPrh/wB48YmH6LvpdszXoiVLtu3A0u2XY8zoF8odcqOrhtd9Vqp57D8gkJT7T1PghLZCTZw4gfbtO8y43q5deyZMqOw/6nU89uoc+3/fG8srL73IGn3W/MHyG6+7io032yKnqMqjml/3OkPvuYUea/cH4NOPPmDxZdrOuG3xpdrw2Ucf5BRZ46nm172ax24z54R2NiQNlNR29ms2LRHxo2VN5VtUY/PYf6gaxv7V5MkcvN8enPrns2m1yCIzlp/31z9TU1PDLrvvnWN0ja9aX/c69151Ic2aN6ffFjumBTN5Pipxss5qft2reez1qQn8NAWe5WD2BgKvABNzjuMnadeuPePHj5txfcKE8bRtW7i8fK547NU19qlTp3LQfnuw8+57sc32O81YftMN1/Dwg/dxy10PVvwfump83es8fe+tvDz0EY664IYZr/PiSy/Lpx98/5H96Ufvs9iSS+cVYqOp5te9msduM9ckKrSSOkl6XdI/Jb0i6XpJm0oaKuktSWtKai3pDkkvSXpW0mrZfU+WdIWkIZLelXREyXaPzrb3iqQjS5bvn23nRUnXSmolaYyk+bLbF5E0VtJuQB/gekkvSFpAUm9Jj0saKelBSW3K/HTNkT59+/L2228xdswYpkyZwi03DWabbbfPO6yy8NirZ+wRwVGHD2KlLl059PAjZyx/9D8PcuF5Z3P14NtZcMEF8wuwTKrtda/zyjNDePC6f3DYWf+k5fwLzFi++vqbMfw/dzN1yndMmjiOD8eNZfluPfMLtJFU6+sO1T12m7mmVKFdEdgNGAQMB/YG1gO2B/4PGAeMiogdJW0MXAP0zO7bFdgIaAW8IekSYDXgAKAfqSL+nKTHgSnACcC6ETFJUuuI+FLSEGAb4A5gT+C2iLhF0mHAsRExIkt4LwB2iIiPJO0BnAEcWH8wkgZlY6FDx47z7lmaQzU1NZz79wvZbpstqK2tZcDAA+nWvXvZ48iDx149Yx/27NPcOvh6Vuneg03W6wPA7086jROPO5opU75jjx23AqB3n36cdd5FeYbaqKrhdb/8pF/zxvPPMvmzTzlu+7XY/uCjuP+ai5k2dQrn/mZfIB0Ytu/v/kTbFVam9ybb8se9N6N58xr2OvZUmjVvnvMI5r1qeN1npZrHXkpAswrfAzWnNLM+lLIHIXUCHo6IlbLr1wAPRsT1klYAbgcC2CUi3s3WGQf0AI4CpkbEGdny14DNgF2AJSLipGz5acBH2XaWjYgT6sWwLnBcROwg6RngkIh4JUt06xLaHsDTwLvZ3ZoD70fE5jSgd+8+MfS5ET/jGTIrls+/npp3CLlZdMH58g4hV9eOeC/vEHKzX5/l8g7Bymzdfn0YOXJEbhnlCt1Wi1OvvS+vh59hvz4dRkZEnzxjaEoV2u9KLk8vuT6dFOe0mdynLhsvvW9ttv6s3mAqud/3G4oYmrU+bAg0j4hXZnHfVyNi7VmOwszMzMzKqkn00M6hJ4B9ACT1ByZFxBezWX9HSQtKWgjYCXgSeATYXdIS2bZal9znGuBG4MqSZV+SWhkA3gCWkrR2dt/5JFXfPg4zMzNrEvKe4aCpNDw0pQrt7JwMXCnpJeBrYEBDK0fE85KuAoZli/4ZEaMAJJ0BPC6pFhhFmskA4HrgdFJSW+cq4B+SvgHWBnYFzpe0KOn5Ow949ecNzczMzMzmVpNIaCNiLKkftu76wFnctsNM7ntyveul2zkHOGcm97kauLr+ctJBaLdGxGcl694G3FayzgvABrMai5mZmZmVV5NIaJsCSRcAWwFb5x2LmZmZ2ZzwJAeJE9pMRPw67xjMzMzM7KdzQmtmZmZWSKr4MyHOqSLNcmBmZmZm9iNOaM3MzMys0NxyYGZmZlZAwpXJOn4ezMzMzKzQnNCamZmZWaG55cDMzMysoDzLQeIKrZmZmZkVmiu0ZmZmZgXl+mziCq2ZmZmZFZoTWjMzMzMrNLccmJmZmRWRfFBYHVdozczMzKzQnNCamZmZWaG55cDMzMysgHzq2+/5eTAzMzOzQnOF1szMzKygfFBY4gqtmZmZmRWaE1ozMzMza1SSrpD0oaRXSpa1lvSwpLey/xcvue33kt6W9IakLWa3fSe0ZmZmZgWlJvAzh64Ctqy37HjgkYhYCXgku46kbsCeQPfsPhdLat7Qxp3QmpmZmVmjiogngE/qLd4BuDq7fDWwY8nywRHxXUSMAd4G1mxo+05ozczMzCwPy0TE+wDZ/0tny9sB40rWG58tmyXPcmBmZmZWUE1kkoMlJY0ouX5ZRFz2M7Y3s1FFQ3dwQmtmZmZmP8ekiOgzF/f7QFKbiHhfUhvgw2z5eKBDyXrtgYkNbcgJbRkEMK12et5h5KKmubtaqlFN86ZRMrDy26/PcnmHkJvF+x6edwi5+XT4hXmHUJXSmcIK/Xl7FzAAODP7/86S5TdIOgdoC6wEDGtoQ05ozczMzKxRSboR6E9qTxgP/JGUyN4s6SDgv8BuABHxqqSbgdHANOCwiKhtaPtOaM3MzMysUUXEXrO4aZNZrH8GcMacbt8JrZmZmVlBNZGDwnLnBkczMzMzKzQntGZmZmZWaG45MDMzMyskoWLPcjDPuEJrZmZmZoXmhNbMzMzMCs0tB2ZmZmYF5VkOEldozczMzKzQXKE1MzMzK6AKOPXtPOMKrZmZmZkVmhNaMzMzMys0txyYmZmZFZF8UFgdV2jNzMzMrNCc0JqZmZlZobnlwMzMzKyg3HKQuEJrZmZmZoXmCq2ZmZlZQcnz0AKu0JqZmZlZwTmhNTMzM7NCc8uBmZmZWQEJaOaOA8AVWjMzMzMrOCe0Faz7yivQr/fqrLPmGmywzpp5h1M2vzj4QDq2XZrePXvkHUouHnrwAVbr3oXuXVfkr2edmXc4jeqIXx5M105tWa9vzx8sv/ySC+nXqzvr9lmdk088Pp/gyqyaXvf6Kn3sLVvU8OS1x/LcTccz8tYTOPHQrQHYedNejLz1BL4aeT5rdOs4Y/2N+3Vl6PXHMfzm/2Po9cexYd+V8wq9UVX6624/jVsOKty9Dz7CkksumXcYZbXfgIEc+qvDOfjA/fMOpexqa2s58ojDuPf+h2nXvj3rrdWXbbfdnlW6dcs7tEax5z4DOOgXv+KwQw6csezJx4dw/71388Szz9OyZUs++vDDHCMsj2p73UtVw9i/mzKNLQedz1ffTKGmphmPXnE0Dw0dzavvTGTPYy7nwhP3+sH6H382mV2PvJT3P/qcbp3bcPfFh9F5ixNzir5xVMPrPqc8y0HiCq1VnPXW34DWrVvnHUYuhg8bRufOK7L8CivQokULdttjT+65+868w2o066y3Posv/sPX+qp/XspvjjmOli1bArDU0kvnEVpZVdvrXqpaxv7VN1MAmK+mOTU1zYkI3hjzAW+99+MvbC++MZ73P/ocgNHvvE/LFvPRYr7Kql9Vy+tuc84JbQWTxI7bbsn6a/flin9elnc4VgYTJ06gffsOM663a9eeCRMm5BhR+b3z9ps8M/QpNu+/DtttsTHPjxyed0iNrppf92oZe7Nm4tnBx/PfR87k0WdfZ/gr783R/XbatCcvvjGOKVOnNXKE5VUtr/uckPL/aQoqJqGV1EnS3vNwe/0l3TOL2/4pqVt2eaykJrlP/+HHnuSpZ0dw+533cvmll/DUk0/kHZI1soj40TI1lU+bMpk2rZbPP/uUBx8byilnnMnB++890+elklTz614tY58+PVhrzzNZcYsT6dNjObp1bjPb+6yywrKcfsQOHH764DJEWF7V8rrbnKuYhBboBMw0oZU0T/e1RMTBETF6Xm6zMbRp2xZIu1y3235HRo6o/EpVtWvXrj3jx4+bcX3ChPG0zd4H1aJtu3Zss/1OSGKNPmvSrFkzPp40Ke+wGlU1v+7VNvbPJ3/DEyPeYvN1Gu4Vbbf0Ytx0ziAO/sO1jBlfee//anvdbfZyT2izyuprki6X9KqkhyQtIKmzpAckjZT0pKSu2fpXSdq15P6Ts4tnAutLekHSUZIGSrpF0t3AQ5JaS7pD0kuSnpW0Wnb/kyVdK+lRSW9JOqQkvIUl3SrpdUnXK/v6J2mIpD7leYbmzldffcWXX3454/IjjzxMt+7dc47KGlufvn15++23GDtmDFOmTOGWmwazzbbb5x1WWW217fY8+fhjALz91ptMmTKFJSr8wMhqft2rYexLLr4wiy68AADzt5yPjft14Y2xH8xy/UUXXoDbLziUky64i2defLdcYZZVNbzuc0pN4F9T0FS6xFcC9oqIQyTdDOwCHAAcGhFvSeoHXAxs3MA2jgeOjYhtASQNBNYGVouITyRdAIyKiB0lbQxcA/TM7rsasBawEDBK0r3Z8l5Ad2AiMBRYF3hqTgYkaRAwCKBDh46zWXve+/CDD9h7j10AmDZtGrvvsRebbb5l2ePIw/777sWTjw9h0qRJdO7Unj+cdAoDDzwo77DKoqamhnP/fiHbbbMFtbW1DBh4YEV/kTlk4L4MffJxPvl4Equu3InfnXAS++x/AEf88mDW69uT+VrMx4WXXlHxuyKr7XUvVQ1jX3bJRbj81P1o3qwZzZqJ2x5+nvuffIXtN1qNc363G0suvjC3n38oL70xge0Pu4hD99yAzh2W4vhDtuT4Q9Ln/na/vJCPPp08m0cqjmp43e2nUd69ZZI6AQ9HxErZ9d8B8wEnAG+UrNoyIlaRdBVwT0Tcmq0/OSIWltSfHye0G0bEAdn1UcAuEfFudn0c0AM4CmgWESdly68Bbgc+A06IiM2y5ZcAQyPiOklDsscaIWks0CciZrlPZ43efeKJp4f9nKepsGqa574TwHLw1XeVdQDKT7FQy6ZSJ7ByW7zv4XmHkJtPh1+Ydwi5WLdfH0aOHJHbN+YuPXrGpbc9mtfDz7BR1yVGRkSue66byifvdyWXa4FlgM8ioudM1p1G1iqRtQC0aGC7X5VcntkbLur9X395/biayvNlZmZmVc6nvv1eUy2ffQGMkbQbpMRV0urZbWOB3tnlHUjVXIAvgVYNbPMJYJ9se/2BSRHxRd12JM0vaQmgP+Cjp8zMzMwKoqkmtJCSz4MkvQi8SkpeAS4HNpQ0DOjH91XYl4Bpkl6UdNRMtncy0EfSS6QDyAaU3DYMuBd4FjgtIibO68GYmZmZWePIfRd6RIwl9bLWXT+75OYfHcUUER+QDuCq8/ts+VRgk3qrX1Vyv0/4Pimu782IGFTvcYYAQ0quH15yuX/J5U6z2KaZmZlZI2o6swzkrSlXaM3MzMzMZiv3Cm3eIuLkvGMwMzMz+8ma0Kln8+YKrZmZmZkVmhNaMzMzMyu0qm85MDMzMysqdxwkrtCamZmZWaE5oTUzMzOzQnPLgZmZmVkBpVPfuukAXKE1MzMzs4JzhdbMzMysoFyfTVyhNTMzM7NCc0JrZmZmZoXmlgMzMzOzonLPAeAKrZmZmZkVnBNaMzMzMys0txyYmZmZFZTccwC4QmtmZmZmBecKrZmZmVlB+URhiSu0ZmZmZlZoTmjNzMzMrNDccmBmZmZWUO44SFyhNTMzM7NCc0JrZmZmZoXmlgMzMzOzonLPAeAKrZmZmZkVnCu0ZmZmZgUkfKawOk5oy0BATXMXw6tNROQdQm4WaumPFqs+nw6/MO8QcrPKb+/NO4RcTBz/ed4hWMZZlpmZmZkVmssoZmZmZkUkn/q2jiu0ZmZmZlZoTmjNzMzMrNDccmBmZmZWUO44SFyhNTMzM7NCc0JrZmZmZoXmlgMzMzOzonLPAeAKrZmZmZkVnCu0ZmZmZoUkn/o24wqtmZmZmRWaE1ozMzMzKzS3HJiZmZkVlE99m7hCa2ZmZmaF5oTWzMzMzArNLQdmZmZmBSQ8DW0dV2jNzMzMrNBcoTUzMzMrKpdoAVdozczMzKzgnNCamZmZWaG55cDMzMysoHzq28QVWjMzMzMrNCe0ZmZmZlZoTmgr2EMPPsBq3bvQveuK/PWsM/MOp6yqdezjx41jy802pteq3ei9eg8uuuDveYdUVtX6uoPH7rFX5tjbLDY/N/xqLR4+fkMe/N0GDNygEwBHb7Uy9/92fe49dj2uOXRNll6k5Q/u13ax+XnlzC04pP8KOURdXlL+P02BE9oKVVtby5FHHMadd9/PqJdGc8vgG3lt9Oi8wyqLah5785oa/nzW2Yx6eTRDnnqGSy+5uGrGXs2vu8fusVfq2KdND864azSbnfk4O583lP3XXY4Vl1mYyx59l63++iTbnP0Uj776IUdssdIP7nfijt14/LWPcora8uCEtkINHzaMzp1XZPkVVqBFixbstsee3HP3nXmHVRbVPPY2bdrQq9caALRq1YouXVdh4sQJOUdVHtX8unvsHnuljv2jL77j1fFfAPDVd7W8/cFkll10fiZ/N23GOgu0aE7E9/fZrMcyjPv4a97835flDjcXagI/TYET2go1ceIE2rfvMON6u3btmTChOhKbah57qffGjuXFF0fRd81+eYdSFtX8unvsHjtU/tjbLb4A3dovygvvfQbAsVt3YehJG7ND73ace/+bQEpuD92kM39/8K0cI7U8VFRCK2mIpD6zWedISQuWc1t5iNKvqxk1lUaXRlbNY68zefJk9tpjV846+1wWWWSRvMMpi2p+3T32H/LYK8+CLZpzyQG9Oe3fo2dUZ8++7w3WPfVR7hw5gf3XXw6Ao7ZcmSseH8PXU2rzDNdyUFEJ7Rw6EphXSei83NY81a5de8aPHzfj+oQJ42nbtm2OEZVPNY8dYOrUqey9x67sudfe7LjTznmHUzbV/Lp77B47VO7Ya5qJSw7ozZ0jJ/Dgy//70e13PT+RLVdrA0DP5Rbj+O268uQfNuLADZfnV5t2Zv/1lit3yOWTd69BE+o5KGRCK6mTpNclXS3pJUm31q+USrpE0ghJr0o6JVt2BNAWeEzSY9myzSU9I+l5SbdIWngmj/ejdWa2raakT9++vP32W4wdM4YpU6Zwy02D2Wbb7fMOqyyqeewRwS8HHUyXrl054sij8w6nrKr5dffYPfZKHvtf9lyNtz+YzL8eHzNjWaclv/+Tv2mPZXj3w8kA7H7BM6x/2mOsf9pjXPH4GC7+zztc89R7ZY/Zyq/IZwrrAhwUEUMlXQH8qt7tJ0TEJ5KaA49IWi0izpd0NLBRREyStCRwIrBpRHwl6XfA0cCpdRuZ1ToRcWrptsow3p+kpqaGc/9+IdttswW1tbUMGHgg3bp3zzussqjmsT/z9FBuuP5aevRYlX59egFwymlnsOVWW+ccWeOr5tfdY/fYK3XsfZZfnJ37tuf1iV9w77HrAfDXe99g934dWGHphYkIJnz6DSfc8nLOkVreNLMenKZOUifgiYjomF3fGDgCWAw4NiJGSDoUGERK2tsAv46IwZLGAn2yhHZb4CpgfLbpFsAzEXGQpCHAscCyDawzY1sziXFQ9vh06Nix95vv+BtitSni79a8Uql9fGY2c6v89t68Q8jFxBuO5LsP3srtA6/76mvEzfc9mdfDz9Cj/cIjI6LB444aW5ErtPWzhRnXJS1PSkb7RsSnkq4C5p/JNgQ8HBF7NfA4c7LOj4OLuAy4DKB37z7Vm9mYmZmZNbJC9tBmOkpaO7u8F/BUyW2LAF8Bn0taBtiq5LYvgVbZ5WeBdSWtCCBpQUkr13uchtYp3ZaZmZmZ5aDICe1rwABJLwGtgUvqboiIF4FRwKvAFcDQkvtdBtwv6bGI+AgYCNyYbedZoGvpg8xmnRnbmuejMzMzM2uAyP+0t02lw6zILQfTI+LQesv6112IiIEzu1NEXABcUHL9UaDvTNbrPwfr/GBbZmZmZlZ+RU5ozczMzKpaEymQ5q6QCW1EjAV65B2HmZmZmeWvyD20ZmZmZmbFrNCamZmZGe45yLhCa2ZmZmaF5gqtmZmZmTWq7OyqXwK1wLSI6COpNXAT0AkYC+weEZ/OzfZdoTUzMzMrKDWBfz/BRhHRs+Q0uccDj0TESsAj2fW54oTWzMzMzPKwA3B1dvlqYMe53ZBbDszMzMwKqomcqWtJSSNKrl8WEZfVWyeAhyQFcGl2+zIR8T5ARLwvaem5DcAJrZmZmZn9HJNK2ghmZd2ImJglrQ9Len1eBuCWAzMzMzNrVBExMfv/Q+DfwJrAB5LaAGT/fzi323dCa2ZmZlZQagI/s41RWkhSq7rLwObAK8BdwIBstQHAnXP1JOCWAzMzMzNrXMsA/1Zq+K0BboiIByQNB26WdBDwX2C3uX0AJ7RmZmZm1mgi4l1g9Zks/xjYZF48hhNaMzMzs6JqGrMc5M49tGZmZmZWaK7QmpmZmRVQOijLJVpwhdbMzMzMCs4JrZmZmZkVmlsOzMzMzIpITebUt7lzhdbMzMzMCs0JrZmZmZkVmlsOzMzMzArKHQeJK7RmZmZmVmiu0JqZmZkVlUu0gCu0ZmZmZlZwrtCWwfPPj5y0wHx6L6eHXxKYlNNj562axw7VPX6PvTp57NUpz7Evl9PjWj1OaMsgIpbK67EljYiIPnk9fp6qeexQ3eP32D32auOxV+fY04lv3XMAbjkwMzMzs4JzQmtmZmZmheaWg8p3Wd4B5Kiaxw7VPX6PvTp57NWpmsfuU99mFBF5x2BmZmZmP9GqPXvHXf8ZmncYrLDUAiPz7mN2y4GZmZmZFZpbDszMzMwKSPi8CnVcoTUAJM2f/V/1vxt+DsysWvjzziqFE1pD0iLAk5I2jipuqpbUQdLiERHV/CEvaX5JnbPLy0nKbR5lM2sc1fZ5VzpGSZWV+6gJ/DQBlfWi2k8maf6I+AK4CrhI0vo5h5SnI4EhklpXy4f8LKwM7CbpDOBfwHw5x/OTSFpeUpVOsv7zVPF7vhodSRV83klaSNLS2RjXkKSImJ53XDbvOaGtYpKWAM6StEhEXAScBVxZbUmtpDaSFo2IY4CngTskLVHJH/KzMQ5YAfgN8GhETISmnezUxSZpbdIUPidI6p5vVMWS/aEPSZtLOlXS0ZJWzjuuxlLynuklaRVJq+cdUzlU4eddF+Cfkn4NXAN0yzkeayROaKtYRHwM/A1YUlK/iLgSOIPqS2p/BXQAiIhfAqOBf1f4h/yPlIzzK+BqUmK4tKSdALLnomVe8c2KpOZZbJuS3s83A22AAyStkW90xZE9h1uTPgNGAJsDx1bc7tlMNt5tgCuArYGrq+Rzr6o+7yLieWAMcC5wbkS8Kql5zmHNU2oC/5qCivygstmr+yMVEe8B+wN/ldS3JKm9TNJGecZYLhHxB+BzSf/Kdk0dyvcf8hW9O65OSXVuG+AJ4EXgT8AbwDaSNpK0CrBPU0lqJa0oqVVE1EqaD9gTuCIiLgd2AFqREjJXaufcusAuQACLAadGxHRJC+ca1TwmqZmkNsDxpGT2c+Br4PVKTeDrVMvnXb0x/Bs4FThKUp+IqM0pLGtEFf2LazNX10OUtRwQEScDdwKnSlozS2rPJVVqF88x1EajTMmiD0l/wE+TtGT2If8y8HBd5SKPOMsl+yO2EanCeVxETI6IScB1wDDgcOBxYFxEfJdjqKWWAVaV1CwipgJvAt2y1+8D4HRgTWCnppKENyWSFpS0THa5LulfCLgEOAbYMyLGZ19ydih6VSv7la+bqrI58AkwEtgIOAAYEBEfAVtI6phTmI2i2j7vSr6gbyzpGGDZiDgVOB+4VlJnSetJ+mvOodo85IS2ikhqJ2nTkl2Ld0q6PPvG+jfgP8AfJK0dEZcB60XEp/lGPe9Jmi8yklbLxvsdqcLXAvhL9iF/GPA8sFKuAZdB9sduZeAUYKykAySNAg4GbiUdQLJ5RDycX5Q/FBFDSX+Ex2RfvO4jVWU3kNSKNM/2y8Bu2Y/90KrAcZKOAO6XtCTpIMDlgfsjYqykDUhfbscXuaqVvb+3BtaQtAtwbfY73xn4B7BTRLwlaT3gj8D8+UU7b1Xj51021m2Bv5K+uBwq6Yzs79o/gStJye0zOYY5z0j5/zQFPrFClcg+0NcHDpe0ErANKXnZgtRruERE/C2rZJ0qaVdgQn4RN46sKv1XSUeTErhrgS8kPU7qGT2EVKE6X9JvIuKQ/KJtXHVVDJjxB2Ai8BfgfeCu7PIvgf9ExMukg8WalIj4MkvIngD6keLeHjiMVMHdDtiKCkpQ5pWIeE7SvsA5wC8iYpKkj0kHA56ndJBUN+CoiHg8z1h/ruz9PRm4njRrx2HZTUeRWmsukvRwtvykiHgzn0jnrWr6vJO0GDAtIiZnbSP9gW2B1Ul7Hv4BkP2duy27PLb0c9CKzQltlcg+0B8k7WobALwVEQ9LGkKqvm2vdHDNnyTdGBGf5xhuY2pJ+sZ+Gen9vyXwGXACcBCpQvXL7P9lgY9yibKRle6SAzYAXgDuz/7/LiI+lNSetOt5am6BzoGIuFPSNNKBTH0j4m5JvUivXTfg18BOecbYFElaF3gWmETazf4S8Hz2ubA+sAAwf0S8k2ec89BrpIRuF+A7SQtExNuS9geOI+2xPDoiHqmgJKcqPu8ktSAd3Ddc0oXZF90a4HJgUWDXiBiXtc9Mj4j76+5bCa9zEymQ5s4tB1Wgrncqax+4HbgD2FrSdlnv4d+A/wE7ZruexuQWbCOLNAXVeaTEbW1gwex5uZD0+3AYsGJEDMiqkhWp5ACwc4CJwKGkXXCLZMnsHqRd+H+KiNdzDHWORMS9pOT7HaUDW0YB04D/A3YvwhhysBmwWUScQjoo6ESgc7ar9tCImFAJyWzWProEqRf8AVIF+kRSJR+gLXB+RPwjIh6BykhyoHo+7yJiCulg5v7AIVm/902k2U4GR8R72Ze084DJecVpjcsJbRXIkpe1Je1NqlhdT/pDf4ikbSJNMv0n4MzsQKCKU5fUZ/1k44ELgFtIB0WsEBFjgYuBip1wW9JSSlNbkfWc7gzsCIwn/VH/HDgyOyDmDeA3EfHvegeTNFlZ1eUg0i5GIuJ/wDZF/kM9L83kdbyJVKmsiXRg6Muk/tGzgbfKHF6jqKu0Rpqi8EJg5YgYQvpdP1TSKaQZPVbNMcx5rpo+70oKNiP5ftaK35Ba5s4B9pU0mNRacWREPJlXrNa4VCFfRK0BkjYk7VK6n/QN9hLShNrdSQf9nBMRd+cWYJlI2o50IERL4ExgCunDrydwQkS8o3TmtG/zi7JxZD1lvwZWAW6PiIeyloJFSHPO7gK0Jx0wMRw4JKt6FJLSzAfTK2jX8TwhqT/ppBm3ZLtlBwP/jYjjsttXAqZWSm+hpG4RMTq7vC1wLKkqPTX7XFwReCdLcitKNXzelbROrUqadu0DYEnS59jtpBaT+Un99FMqpTe61Gq9esd9jz6ddxh0aD3/yIjI9QyNrtBWOEldSD1Sv4iIX5N2MfUCugI3kqZl+l9+EZZH1lP5O1Iv2dukgyFWJlWr/0s6cGIB0od+xcmq8DcB7wBbSdo8q9y0AN6LiP8C35GO+j2zyMkszBhvxew6/jlKqnWtSVX4fUgHfp5Imtqsg6SlASLirax6V9jnrmS8NcAFkq6SNAh4hDRN15EA2YFuV9Qls0XZEzEnquXzLktmtyMVbA4gnVRFpPajHUhf4r+KiFcqMZm1H3JCW6GyvrHmpLP9dAO2zHY/PUHqjTyKlMxcGRHDcwy10UnqTBrv6Ih4PCKOJx0M82vgS9Juqd9FxDdRYef4zt4Hdbvk/keqxr5P6qHejLSbuaekO0mTj98SEa/lFrDNc9kf/S2AG0itJLsAF5ESnDOz6/3yi3DeqXew4z6kGS7uADoCjwFLAX3r1i9N2ouawNdXTZ93kjqQ2gy2BD4lTds3OSJeJKvGk6qzVgWc0FaYkirDYhFRGxEXkObiWxDYPbvtTVJjfMuif6DNoemkicS71PWQRjp5xOdAr4j4X0RURM9gqWzWiijpod4E6BgRZ5H6Znck9Zt2JfXY7RQRD+QXsTUGSWuR+kf/HBFfR8RnEfF2ROwPHEFKCI7LKriFVnKw43nAhxExJSLuiIgTgZNI86xuJmlAnnE2sor9vNP3J8aou/w52WtKOibggIj4SNLGWe/8tlHBBzl/T03gJ3+etqvClHygn6A0p+R/Sd9UFwQOlrQ7qafo3KjQqblKqjR9SGP9mnQQ3ImkSvVypCOeu5O+1VecbBfyVdnrvRJpV+O9wEaSBkfE6UpzU/4SuDma0AkTbN4o6YFdiXQigcezJKAW0mdFRLwLnJP1IBb+74Gk+Ukn0TgsIp7Mxjs9IqZHxEPAQ5JGUyEVaaiez7vstdxX0jBSpX0g6SDQjsDfgTUj4r9KZzw8XdI+1ZHMWh1XaCtM9ofpdOC3wIGk6tt5EXEp3+9uvj0i7skvysaVfbhvTtrFuj1wN2n34/nAt6QjYH9HOvDpBVXgudsj4kPS/KIPAXsBB2U91P2BAyX9ijTR+BhStdYqTMku9M+ATSV1johp2fL+WRsCktYG1iEdPFR000gHBdWdyrc2Oziwe8k63YFNJM1X9ugaQb2Wkor9vIuIaaTPq2dIc85eku1hPI805tMk1Y37zGpJZkX+ZwlrKt3nhf9Gbj8SwEvA09kfrk0kjVSaPPwm0hlT+kr6ELijUvrG6mQtFwuTDgo4KiLulXQ1cCfpoKczSBWq5qR+shkHEFWKrNWgNiL2l3Q2sD/ppANEOhvUANKuuYsl/S3SaTCtAtSr1q1Cai8aQ5p/dXdJ/yG9/88m9VlCOmho44go3JkBS8a7LDBfpMnzrwJWk7R+VqXtB5wp6dCIeIP0e//LSHNwF16WmB9DOinEPZX6eZe91o9Leoj0BawujRpGmmbuUNK8s8dEmsWl8LN02E9TyG9q9r2SI3r7ZruWviP9UpfOq3gtQER8Q6rSDuP7hLeiZLtRvyT9kf42+1B7lbRrfffsObiOtGtua0kL5hjuPJeNt1bSUgARcSxpmrZjJbXLVlsUWCEbe0X8UbckS+62Ih3tvSZpfumtgS9Ir/WFwJ+B0yPiiezLz0dFTGZhxnh3JH1Zv03SyaQzXn0JnCzpStLn39+yZJaI+GdUyIGP2Z6oNUgHd35diZ93JceFLJGNbzdSq8FgpZMDfUVqqftzRJydtZZUzEF+NudcoS247AN9e9KE6Edlf6TuA/4l6WLSLrhfkJ27PNJ5ri+vpF/2kipNB+CLrDd4POlDfTjpj/m0bN2WEfGWpIuALyPi69wCbwTZ87Al6QQJ75MqdKeTKjSPSLqbdBKFcytt7Dajh3Qn0u7lR7IDwrYAPoqIC7MErzYiPqv78pNrwD+T0klAfk86nfdU0oFBiwH3AHcBy5Narl6sS4wq5bNPUm/SAX2/A74iTc01ggr6vCv5bN+BVIGdJOnWSKe7/g1wftZOcgRpto5n8ow3L01kj3/unNAWnKQVgFOBnSPi3awKdzXpvOXrA51IZ0d5tO4+lfKBDj/4wNuaVIl8TNIHEfG77EP8OknjgHWBk+p2r1dqf5WkbqTn4QBgcVKV7h8RcUiW7OwKbB7pHPbeJVcBSl/HiPg22wW9GfBIRDybfSb8WtLNkc6YRbZuJbz2C5GO6h+ffVm/idQbPj4iriJNUwZUzHgByF7TI4E3I027OFzSjaQDQd+n4J93yk6Mkn22b0SaoWJb4FxS5b1NRPxD0qekse4bEVWZzNr3nNAWVMkfscVJU3CtKOlQ0kkT1gPWi4gTlU5rOS3PWBtDvQ+8bsCmpCTuA+AoSRdExGGS+pIqktdFxDOVnMRlLSdLAfdFxBClo4KfJx3xu2ZEHCfpqoh4GyrrD3w1UppXemr2O7A80CoiXgKuAraTtGtE3Er6cvs5ad7pr/KL+Ocr+QK7YKQpyF6T9CIwQNKNkY5yvx9YtpIqskonQeiT9QR3IbUZvAbsKmnriLgvIvbK9s40p8Cfd1myvr+kKyLiA9LZ3A4FepMq7v8kHdg6P2kedZ/K1gD30BZOaT8RzDh/9eOkI1lHRMRmpG+z/ZWOZi3kAQANkdQW2EZSS0mLkw54WREYArwOnAa0lHQd8EJE3Fn37b1oH+5zStL6pEnymwPbZr1l0yLiPVJfdZds1YroHax2WY/0LyUtrjS/8APADZIuIP0OvAPsLeleUj/t1RFR2Cmb6mTJ7HbAFZJukrQwqb1geeAfkvYlHSD1bGTyjHceagVsmLUM3UD6zL+c9OVlh6yXloh4ICLuLfjn3XRS3/dhkhaOiMuBV4F9gb0i4iJgArAW6dTdVS/vGQ6ayiwHTmgLJvtA3xa4XtLZknaMiBMiYpuIuFnSOqRK5YisgllxCS1pXs13gAWzP9L7kKYn2z3S0f3vkQ58+Zbvp++pWEqnudwauD5rLTkOOELSIKUjvPuQjgIu6h84+7FupAM/fwUcTpquqRfQg9RPeB1wMGk2g90j4vaSL8OFlb3XTyAlc9NJ8yu/lF0fRnpeDonsdLYV5CPSnOKbAG9HxMSI+Ig0t/TLpPlZt8wzwHkh26P4PqkPfDXg6OzL2zekPQy/znqHFyAd6Dcuv2itqXHLQcFI6k+aimUX4C9Av6yP9gpgaeBK4NhI5ymvSJGmblkQuFLSExFxkaRfkKo2ERE3RcQYSYdHxLd5x9tY6touSNNybQO8nSUt/ybNPXosqb/s5Ih4NrdAbZ7LfgfmA7YjHdVfExFTJe0E3AL8DTg0Ih4ruU+hv8xIWpGUvD8dEY+QDnK8mDRzw68j4mxlU9blGmjj6ET6kvIFsIWkc0nTU70j6RlScl/45C4ipknagFR5vQ0YRGqTuYJ04PNJpB7p06LCT9n+U8iHhQFOaAuh3od0V2BP0i7k5YB/kf6oQfpg3zwi3iti79TslPTPrRDpALgbgJ0lfRcR/5Q0ELg1S/RurNRktuT9sDjwcUQcJekz0tHsTwJvRcSDkh4jHdFeW4nvh2pU7wCw/0iaQHofbJv9HrwtaTfSPKSrkHbVVgqRpuNaRdIGEfFERPxK0r9IX263JrXXVAx9fxKER4GHI2KQpLdJe2HOlPRv0imsL4iIwp4gpeSzve40zS+RTgJUSzpley2pL3i37ICw9/2ZZvW55aAJk9QKIEtI1lc6jem7pG/p2wC7RMQlpA/61YG22e72wldjZib7wNseuFRSj4i4E7iddPKIg7Kq9B7A/3INtJFI6iRpnez9sC3pNJ5/l7R5RJxCem/8EeiWfdhPqfsiVInvh2pU13Ik6XJJ/yTtir2ANPf0TpJWjojPSCdKKHQyW9ciIWmNLNFpSZqiayTplK7rAUTEQaQK7bcV+D6vyfbCrAasK+niiHiFtJduGdIcu08UOZmFGe/rNUnjOiQi9gUuJe1tGk2aneW47HPt/br75BawNUlOaJuobJf6vZJ2kbQycBEpid2L9Adsa2AzpSP8a0j9RGPzircclGYsOI30x+sVSQsB9wPnANtLGhQRj0bEY5XQLzgTawM3K53pax/gFFLyvp2k3SPieFKv3cmkicatwmS/778nndL4Q+A+UtXyX6Te8l2yz47C/7HPkpwtgMGkKt1DpN7KC0jzrO6S7Z6m6Mn7zCidxnz3rCL5JdCX1G5wYUS8EREDSF9c7s030nlmUdKpuTfJrr9HOsvd+6TXf7CT2FlQE/hpAtxy0ERFxNdZn9TxpD9YgyLNKbkCKbGdTjog5GDgL5Gm66lIJbuWliN9W19Q0rGkD76lScn9ZaQjX4HK/PYeETdKqiUlsg9ExF2SHif1U6+XHVBxpKQukc6eYxVE0hrAH0i7nm8BblGac/Ru0gFhNwETo2CT589Mtqu9FfBb0jza90m6ntQf/A1pt/SRpGn6KlUP0u/2dEmPRsT/snaSEdlH4q+pgL7ZOhHxsKSdgb9JGpN93n1GaqU6KyKezzdCa+qc0DZhEfFvSZOBW0nzrD5L+gD7L2nC8IGkI/0/rMR+opIxtSK1WTwJbEDazXYOKdnfHeheQVWKH8iq0GvF92d9mgCcBZwn6c5I883eBMwHbJD94XujoW1acdT7vZ5EOoVpL6W5Ot+PiAuyXbVtswOlCq1kvPORvsg/B3yT9Y2PVDo71IHZZ+OfImJyrgHPQyV9pF1J8wb/m/T7/gsgJN1B6hE+B3gQKu+Le6QzgE0nzeKzI/A18MesjcasQW45aOIi4mFS4jpQ0l4RMRX4lPStdf6I+DBbr6I+2OAH56X/V9YvuDXp7DfdI+JfpD96u5BOLFGppgDHShoC/B2YHBFXkqpT50vqn1VjrwdOj4iK7B+uVtnvQD9J65JmrtiLtIPvl6R5SdcENiT1lxZeNt4dSb3x5wFbkj7r6lpoviJVLGso+Eki6iv5vLuZdBrbF0knRrmDdOa3K0lz7v47q2Y2kR2981ZE3E2ac3Yl4OWIuEeZnENrsvLuNmgqL4wrtAWQVSOmAVdnu5w+I03FNCnfyBqX0pyTF5Pm1V2NdPKE32WtGMsD15CmrhmWX5SNR2m2hqmSTiFV6V+MiBcBIuJKSUGaqmxQRPyHyk7sq1KWyA4mzbE6iXRa64GksyVtQZpg/5CIeLnIe2lKqpOLkcZ3PakPeD3SWaIWlNQ8u/6HqMyzH65IOqhzJ6AfMJV0UNgtkkYCHYDzI+JpqMwiRp2snepb0ufb2Ii4Pe+YrOlzQlsQEXG3pINJB/wcFBHDi/wHbA6Vnsb1cdKZYQ4jnSXtXdKE8S/mGWBjiojpklYjVeO2AW6UdHlEHJKtcjupFaOipiqqdiXJ3aKkU5zuDrxAqlodTDoAbAApuf0OeAyKneCUHOXeBxgZETcASPqKlORBOivWDRExtFI+++qN41NSIt+btAdmx4j4TOmECc9ExLs5hZmLiHhI0gGkk+iYzZYT2gKJdLafIRHxSXa98B/opUr+kK8JLEmae3BzSetFxFPAM5KOAlaKiNdIR/RXpJI/dIsDn0fEi1kP7XBJ55OSmtOAAyLi40r5A28/mJ5ub9KBQRMi4hlJ95GqloeTJpc/nHSQ1BeSzo4CnlCg5Hd+LVLV+T1gaUlPAU9llbpFSGcH+7+6ntlKea9nY9+QNGfwu8BRpL/LnbO9M2uR5pw9hNRXW1WyljtrQFM69WzenNAWTF0yW4myD/cdSGeDeYjUZjAJOFDSSqR+slWAQs+5OIdqSLsc3wXWlLRvRFyndNrHu0n9hedFxMdQOX/gbcZsBr8E/kTa/fx/kkZExH8lPUB6b3weERMl7Qlprur8Ip57dT3CpJk79ow0Hd9pwM6kXtmns/f9YxV6AFg/UlvVG8BrpH7Z/YHDszazA0ntZa5Sms2GDwqzJiPrn9sT2AgYASwG/Bq4gdRH+zvSEa8VOX1L3UEPWZvB1ZJ6RTpX+bGkA4CWyf6ob0pqt7jTB0pUFkltSZXXbyLiyYg4GhhCmqJr+UgT6F8ZES9kR/6Pi+Kfz35R0hR8m2fXTwU+IbVV1J08YcLM71pMJXuiTgH2ioidgddJ474J6A40B47z77nNjprAv6bACa01JVNJPaGnAkcD+0XECGAiqXf24Kztomn89sxDJRWbzUjJ+2vAXySdTarSzQcsBKkaFxEfZZddma0Q2UFBKwNPkXa7HwgQEccCw4E7JM1PmvmisFXZ+iLiIdJsJQdJ2jvSTC6nkU4a8mGuwTWuxUhfTjfLrt9I2iPzJeno/vPqdrn799xs9txyYE1GRHwl6WXSCSN+ExHvZv1l/yRVJL/O1qu4D/csme1LqlTdmh34shLpj94JwJqkI733qpRExpLsC1oNaV7ldyLiz5Kmkk6WURsRV0fE4ZK6RsS3+UbbOLIq5FTgNEktIuIq4P9yDqtRZQc97Qz8WdLESCcSuCm7uWIPdjVrLE5oram5BViWdN7uLYBtSWcKGpVvWI0rS2puJVWjT8yuv5PNdLA36ejvvYF2pBNrWMFJmi+rRpIdAHQ2aZqifwN3kc4GuIXSGeD+ReqzrFiRzgZWA5wp6SHgg0r/8pYd9DaN7xP5q0ktVmZzruL2Wc4dJ7TWpETEB5L+TErgFgduigqdoqzegSEiHc18FXBERJxDOjvQfFll+glJJ5Km9HFCW2CSlgc+iYjPs4P8lpX0ZkS8Lukx0hHur0t6mPQZPRIqc89EfVmC90xdS001qJfIPwz8LyKm5x2XWdE4obUmJ9KZrx6vt6zi/pjXm9XhYaAN8Dfg91lV7qyscjcf0JpUnX01v4htHukMjJLUkXQ2pH7AyZJOIJ3x6xhJT0Y6pfUNdVXcalFNyWydakzkzeY1J7RmOak3q8NmpNP6DpB0HfBSdhT7n7OE5gNJ60RE1c1FWWki4j/ZdFvPAGtFxOBs3tlNSEf89yadBewWUtuBVQEnsza33HGQOKE1y0/prA59SHNvQpo8fxfgG/jBSRa+yCNIm/ci4gFJzYAXJfXNKnSPkaZq+g7YDril0ntIzczmFU/bZZaTrLXiZdL8m6dExDvZrA73AW9llbwZvcOV2HZRzSLiPtJ0dMMlLR4RX0bEZxFxONBZ0so5h2hmBVB3trA8f5oCV2jN8jWzWR2OiIjXwUlspYuI+yX9Cng9m5br0+zEGstShac6NTObW05ozXJUTbM62Mxl7QcHAj2Bx0gnFFg/Ij7INTAzswJxQmuWs2qZ1cFmLSLuLblcyWfHMrN5qumcejZv7qE1MzMzs0JzQmtmZmZmheaWAzMzM7MCEk1nloG8uUJrZmZmZoXmhNbMzMzMCs0JrZkVmqRaSS9IekXSLZIW/BnbukrSrtnlf0rq1sC6/SWtMxePMVbSknO6vN46k3/iY50s6difGqOZWdE4oTWzovsmInpGRA9gCnBo6Y2Sms/NRiPi4IgY3cAq/YGfnNCamdm854TWzCrJk8CKWfX0MUk3AC9Lai7pr5KGS3pJ0i8AlFwoabSke4Gl6zYkaYikPtnlLSU9L+lFSY9I6kRKnI/KqsPrS1pK0m3ZYwyXtG523yUkPSRplKRLYfaTRkq6Q9JISa9KGlTvtr9lsTwiaalsWWdJD2T3eVJS13nybJpZk5f3aW+bykFpnuXAzCqCpBpgK+CBbNGaQI+IGJMlhZ9HRF9JLYGhkh4CegFdgFWBZYDRwBX1trsUcDmwQbat1hHxiaR/AJMj4uxsvRuAcyPiKUkdgQeBVYA/Ak9FxKmStgF+kKDOwoHZYywADJd0W0R8DCwEPB8Rx0g6Kdv24cBlwKER8ZakfsDFwMZz8TSamRWSE1ozK7oFJL2QXX4S+BepFWBYRIzJlm8OrFbXHwssCqwEbADcGBG1wERJj85k+2sBT9RtKyI+mUUcmwLd9H25YhFJrbLH2Dm7772SPp2DMR0haafscocs1o+B6cBN2fLrgNslLZyN95aSx245B49hZlYxnNCaWdF9ExE9Sxdkid1XpYuAX0fEg/XW2xqY3WmGNQfrQGrhWjsivplJLHN8KmNJ/UnJ8doR8bWkIcD8s1g9ssf9rP5zYGbVwae+TdxDa2bV4EHgl5LmA5C0sqSFgCeAPbMe2zbARjO57zPAhpKWz+7bOlv+JdCqZL2HSLv/ydbrmV18AtgnW7YVsPhsYl0U+DRLZruSKsR1mgF1Vea9Sa0MXwBjJO2WPYYkrT6bxzAzqyhOaM2sGvyT1B/7vKRXgEtJe6j+DbwFvAxcAjxe/44R8RGp7/V2SS/y/S7/u4Gd6g4KA44A+mQHnY3m+9kWTgE2kPQ8qfXhv7OJ9QGgRtJLwGnAsyW3fQV0lzSS1CN7arZ8H+CgLL5XgR3m4DkxM6sYipjjPWFmZmZm1kT06t0nHh86LO8wWHSB5iMjok+eMbhCa2ZmZmaF5oPCzMzMzApIzMHE1lXCFVozMzMzKzQntGZmZmZWaG45MDMzMysq9xwArtCamZmZWcE5oTUzMzOzQnPLgZmZmVlB+dS3iSu0ZmZmZlZortCamZmZFZRcoAVcoTUzMzOzgnNCa2ZmZmaF5pYDMzMzs4Jyx0HiCq2ZmZmZFZoTWjMzMzMrNLccmJmZmRWVew4AV2jNzMzMrOBcoTUzMzMrKJ8pLHGF1szMzMwKzQmtmZmZmTUqSVtKekPS25KOn9fbd8uBmZmZWQGJYpz6VlJz4CJgM2A8MFzSXRExel49hiu0ZmZmZtaY1gTejoh3I2IKMBjYYV4+gBNaMzMzM2tM7YBxJdfHZ8vmGbccmJmZmRXQ88+PfHCB+bRk3nEA80saUXL9soi4rOT6zBojYl4G4ITWzMzMrIAiYsu8Y5hD44EOJdfbAxPn5QO45cDMzMzMGtNwYCVJy0tqAewJ3DUvH8AVWjMzMzNrNBExTdLhwINAc+CKiHh1Xj6GIuZpC4OZmZmZWVm55cDMzMzMCs0JrZmZmZkVmhNaMzMzMys0J7RmZmZmVmhOaM3MzMys0JzQmpmZmVmhOaE1MzMzs0JzQmtmZmZmhfb/yZ7eoa7mkfkAAAAASUVORK5CYII=\n",
|
| 201 |
+
"text/plain": [
|
| 202 |
+
"<Figure size 720x720 with 2 Axes>"
|
| 203 |
+
]
|
| 204 |
+
},
|
| 205 |
+
"metadata": {
|
| 206 |
+
"needs_background": "light"
|
| 207 |
+
},
|
| 208 |
+
"output_type": "display_data"
|
| 209 |
+
}
|
| 210 |
+
],
|
| 211 |
+
"source": [
|
| 212 |
+
"#Print the Target names\n",
|
| 213 |
+
"from sklearn.metrics import classification_report, confusion_matrix\n",
|
| 214 |
+
"import itertools \n",
|
| 215 |
+
"\n",
|
| 216 |
+
"#shuffle=False\n",
|
| 217 |
+
"\n",
|
| 218 |
+
"target_names = []\n",
|
| 219 |
+
"for key in test_generator.class_indices:\n",
|
| 220 |
+
" target_names.append(key)\n",
|
| 221 |
+
"\n",
|
| 222 |
+
"# print(target_names)#Confution Matrix\n",
|
| 223 |
+
"Y_pred = model.predict(test_generator)\n",
|
| 224 |
+
"y_pred = np.argmax(Y_pred, axis=1)\n",
|
| 225 |
+
"print('Confusion Matrix')\n",
|
| 226 |
+
"\n",
|
| 227 |
+
"cm = confusion_matrix(test_generator.classes, y_pred)\n",
|
| 228 |
+
"plot_confusion_matrix(cm, target_names, title='Confusion Matrix', normalize=False)\n",
|
| 229 |
+
"\n",
|
| 230 |
+
"#Print Classification Report\n",
|
| 231 |
+
"#print('Classification Report')\n",
|
| 232 |
+
"#print(classification_report(test_generator.classes, y_pred, target_names=target_names))"
|
| 233 |
+
]
|
| 234 |
+
},
|
| 235 |
+
{
|
| 236 |
+
"cell_type": "code",
|
| 237 |
+
"execution_count": null,
|
| 238 |
+
"id": "e49a4c65",
|
| 239 |
+
"metadata": {},
|
| 240 |
+
"outputs": [],
|
| 241 |
+
"source": []
|
| 242 |
+
}
|
| 243 |
+
],
|
| 244 |
+
"metadata": {
|
| 245 |
+
"kernelspec": {
|
| 246 |
+
"display_name": "Python 3 (ipykernel)",
|
| 247 |
+
"language": "python",
|
| 248 |
+
"name": "python3"
|
| 249 |
+
},
|
| 250 |
+
"language_info": {
|
| 251 |
+
"codemirror_mode": {
|
| 252 |
+
"name": "ipython",
|
| 253 |
+
"version": 3
|
| 254 |
+
},
|
| 255 |
+
"file_extension": ".py",
|
| 256 |
+
"mimetype": "text/x-python",
|
| 257 |
+
"name": "python",
|
| 258 |
+
"nbconvert_exporter": "python",
|
| 259 |
+
"pygments_lexer": "ipython3",
|
| 260 |
+
"version": "3.9.12"
|
| 261 |
+
}
|
| 262 |
+
},
|
| 263 |
+
"nbformat": 4,
|
| 264 |
+
"nbformat_minor": 5
|
| 265 |
+
}
|
README.md
CHANGED
|
@@ -1,12 +1,9 @@
|
|
| 1 |
-
|
| 2 |
-
|
| 3 |
-
|
| 4 |
-
|
| 5 |
-
|
| 6 |
-
|
| 7 |
-
|
| 8 |
-
|
| 9 |
-
pinned: false
|
| 10 |
-
---
|
| 11 |
|
| 12 |
-
Check out the configuration reference at https://huggingface.co/docs/hub/spaces-config-reference
|
|
|
|
| 1 |
+
# ClassificationPeripheralBloodCell
|
| 2 |
+
TFM master SaturdaysAI creado por María Ortiz, Jorge González y Silvia García
|
| 3 |
+
|
| 4 |
+
Link to dataset: https://data.mendeley.com/datasets/snkd93bnjr/1
|
| 5 |
+
|
| 6 |
+
Link to streamlit: https://https://streamlit.io/
|
| 7 |
+
|
| 8 |
+
Link to medium article: https://medium.com/saturdays-ai/classification-peripheral-blood-cell-b638754a5c29
|
|
|
|
|
|
|
| 9 |
|
|
|
about_pj.py
ADDED
|
@@ -0,0 +1,89 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# -*- coding: utf-8 -*-
|
| 2 |
+
"""
|
| 3 |
+
Created on Tue Dec 27 16:16:06 2022
|
| 4 |
+
|
| 5 |
+
@author: Usuario
|
| 6 |
+
"""
|
| 7 |
+
import streamlit as st
|
| 8 |
+
import imagen_subida as ims
|
| 9 |
+
|
| 10 |
+
|
| 11 |
+
#ABout the project!
|
| 12 |
+
#def add_bg_from_url():
|
| 13 |
+
# st.markdown(
|
| 14 |
+
# f"""
|
| 15 |
+
# <style>
|
| 16 |
+
# .stApp {{
|
| 17 |
+
# background-image: url("https://cdn.pixabay.com/photo/2019/04/24/11/27/flowers-4151900_960_720.jpg");
|
| 18 |
+
# background-attachment: fixed;
|
| 19 |
+
# background-size: cover
|
| 20 |
+
# }}
|
| 21 |
+
# </style>
|
| 22 |
+
# """,
|
| 23 |
+
# unsafe_allow_html=True
|
| 24 |
+
# )
|
| 25 |
+
|
| 26 |
+
#add_bg_from_url()
|
| 27 |
+
|
| 28 |
+
def textito(idioma):
|
| 29 |
+
|
| 30 |
+
if idioma == 1:
|
| 31 |
+
st.title('About the project')
|
| 32 |
+
container = st.container()
|
| 33 |
+
st.markdown('<p style="text-align: justify;"><strong>This project of Peripheral Blood Cells Classification have been made by Silvia García, María Ortiz and Jorge González (more information in <em>About us</em> button), for Final Master''s Thesis of the 3th Edition master''s degree in Deep Learning from SaturdaysAI.</strong></p>', unsafe_allow_html=True)
|
| 34 |
+
|
| 35 |
+
st.markdown('<p style="text-align: justify;">In this project, attention has been focused on the automation of the classification of peripheral blood cells using the <em>Transfer Learning</em> methodology, which consists of using a pre-trained artificial intelligence model, in this case the <em>vgg19</em> model, and training it with an image dataset composed of 8 different classes (basophils, eosinophils, erythroblasts, immature granulocytes, lymphocytes, monocytes, neutrophils, and platelets) of different cell types.</p>', unsafe_allow_html=True)
|
| 36 |
+
st.markdown('<p style="text-align: justify;">The <em>vgg19</em> pre-trained network architecture; a variant of the <em>vgg</em> model, consisting of 19 layers (16 convolutional and 3 connected layers, 5 MaxPool layers and one Softmax layer). The following image represents the structure of this network:</p>', unsafe_allow_html=True)
|
| 37 |
+
|
| 38 |
+
st.image('./images/vgg19.png', use_column_width= True)
|
| 39 |
+
st.markdown('<p style="text-align: justify;">The results obtained were quite promising with a percentage of accuracy in the classification higher than 99% in all classes.</p>', unsafe_allow_html=True)
|
| 40 |
+
|
| 41 |
+
st.image('./images/confusion_matrix.png', use_column_width= True)
|
| 42 |
+
st.markdown('<p style="text-align: justify;">This confusion matrix indicates the accuracy of the model when classifying cell types. As can be seen, the <em>vgg19</em> model predicts the different images with great accuracy.</p>', unsafe_allow_html=True)
|
| 43 |
+
|
| 44 |
+
|
| 45 |
+
st.markdown('<p style="text-align: justify;">Tensorflow Projector (<a href = "https://projector.tensorflow.org/" >https://projector.tensorflow.org/</a>) is a visual tool that allows us to interact and analyze multidimensional data (embeddings) and project them into a two- or three-dimensional space. Each embedding is represented by a point that has a certain position in space and these will form certain clusters based on a similarity score. Thanks to this tool, we are able to observe how the model is capable of distinguishing the different classes (ig, leukocytes, etc), and where it has the greatest problems in distinguishing them through the appearance of certain points of different classes within a cluster of a different class.</p>', unsafe_allow_html=True)
|
| 46 |
+
st.markdown('<p style="text-align: justify;">Dimensionality reduction methods such as <em>t-stochastic neighbor embedding</em> (<em>t-SNE</em>) allow us to visualize our embeddings in a three-dimensional way, constructing a probability distribution over pairs of embeddings in space, such that the most similar ones are more likely to be included in each other. the same cluster, reducing the dimensionality of the sample.</p>', unsafe_allow_html=True)
|
| 47 |
+
|
| 48 |
+
|
| 49 |
+
st.image('./images/tensor.png', use_column_width= True)
|
| 50 |
+
st.markdown('<p style="text-align: justify;">As can be seen in this figure, there are various insertions of certain groups within clusters belonging to other classes. In this case, the model is more confused giving a correct classification when dealing with neutrophils and immature granulocytes. Other notable insertions are erythroblasts, which are confused with platelets, neutrophils with basophils, and immature granulocytes with monocytes. Even so, the precision of the model when classifying the different cell types is very high.</p>', unsafe_allow_html=True)
|
| 51 |
+
|
| 52 |
+
|
| 53 |
+
|
| 54 |
+
else:
|
| 55 |
+
st.title('Acerca del proyecto')
|
| 56 |
+
container = st.container()
|
| 57 |
+
#text_ini = '**Este trabajo de clasificación de células sanguíneas periféricas es un proyecto realizado por Silvia García, María Ortiz y Jorge González (más información en el apartado *Sobre nosotros*), para el Trabajo de Fin de Máster de la tercera edición del máster en Deep Learning de SaturdaysAI.**'
|
| 58 |
+
st.markdown('<p style="text-align: justify;"><strong>Este trabajo de clasificación de células sanguíneas periféricas es un proyecto realizado por Silvia Garc��a, María Ortiz y Jorge González (más información en el apartado <em>Sobre nosotros</em>), para el Trabajo de Fin de Máster de la tercera edición del máster en Deep Learning de SaturdaysAI.</strong></p>', unsafe_allow_html=True)
|
| 59 |
+
|
| 60 |
+
st.markdown('<p style="text-align: justify;">En este proyecto, se ha centrado la atención a la automatización de la clasificación de células sanguíneas periféricas utilizando la metodología de <em>Transfer Learning</em>, la cual consiste en utilizar un modelo de inteligencia artificial pre-entrenado, en este caso el modelo <em>vgg19</em>, y entrenarlo con un dataset de imágenes compuesto por 8 clases diferentes (basófilos, eosinófilos, eritroblastos, granulocitos inmaduros, linfocitos, monocitos, neutrófilos y plaquetas) de diferentes tipos celulares.</p>', unsafe_allow_html=True)
|
| 61 |
+
st.markdown('<p style="text-align: justify;">La arquitectura de red pre-entrenada <em>vgg19</em>; una variante del modelo <em>vgg</em>, que consta de 19 capas (16 de convolución y 3 capas conectadas, 5 capas de MaxPool y una de Softmax). La siguiente imagen representa la estructura de esta red:</p>', unsafe_allow_html=True)
|
| 62 |
+
|
| 63 |
+
#st.write(text_ini)
|
| 64 |
+
# text1 = 'En este proyecto, se ha centrado la atención a la automatización de la clasificación de células sanguíneas periféricas utilizando la metodología de *Transfer Learning*, la cual consiste en utilizar un modelo de inteligencia artificial pre-entrenado, en este caso el modelo *vgg19*, y entrenarlo con un dataset de imágenes compuesto por 8 clases diferentes (basófilos, eosinófilos, eritroblastos, granulocitos inmaduros, linfocitos, monocitos, neutrófilos y plaquetas) de diferentes tipos celulares.'
|
| 65 |
+
# = 'La arquitectura de red pre-entrenada *vgg19*; una variante del modelo *vgg*, que consta de 19 capas (16 de convolución y 3 capas conectadas, 5 capas de MaxPool y una de Softmax). La siguiente imagen representa la estructura de esta red:'
|
| 66 |
+
# st.write(text1)
|
| 67 |
+
#st.write(text2)
|
| 68 |
+
st.image('./images/vgg19.png', use_column_width= True)
|
| 69 |
+
st.markdown('<p style="text-align: justify;">Los resultados obtenidos, fueron bastante prometedores con un porcentaje de precisión en la clasificación superior al 99% en todas las clases.</p>', unsafe_allow_html=True)
|
| 70 |
+
|
| 71 |
+
#text3 = 'Los resultados obtenidos, fueron bastante prometedores con un porcentaje de precisión en la clasificación superior al 99% en todas las clases.'
|
| 72 |
+
#st.write(text3)
|
| 73 |
+
st.image('./images/confusion_matrix.png', use_column_width= True)
|
| 74 |
+
st.markdown('<p style="text-align: justify;">Esta matriz de confusión nos indica la precisión del modelo a la hora de clasificar los tipos celulares. Como se puede observar, el modelo <em>vgg19</em> predice con gran exactitud las diferentes imágenes.</p>', unsafe_allow_html=True)
|
| 75 |
+
|
| 76 |
+
st.markdown('<p style="text-align: justify;">Tensorflow Projector (<a href = "https://projector.tensorflow.org/" >https://projector.tensorflow.org/</a>) es una herramienta visual que nos permite interactuar y analizar datos multidimensionales (embeddings) y proyectarlos en un espacio bi o tridimensional. Cada embedding es representado por un punto que tiene una posición determinada en el espacio y estos formarán determinados clusters basándose en una puntuación de similitud. Gracias a esta herramienta, somos capaces de observar cómo el modelo es capaz de distinguir las diferentes clases (ig, leucocitos, etc), y dónde tiene los mayores problemas para distinguirlas mediante la aparición de ciertos puntos de diferentes clases dentro de un cluster de una clase diferente.</p>', unsafe_allow_html=True)
|
| 77 |
+
st.markdown('<p style="text-align: justify;">Métodos de reducción de dimensionalidad como <em>t-stochastic neighbor embedding</em> (<em>t-SNE</em>) nos permiten visualizar nuestros embeddings de manera tridimensional, construyendo una distribución de probabilidad sobre parejas de embeddings en el espacio, de forma que los más similares son más probables de incluirse en un mismo cluster, reduciendo la dimensionalidad de la muestra.</p>', unsafe_allow_html=True)
|
| 78 |
+
|
| 79 |
+
#text4 = 'Esta matriz de confusión nos indica la precisión del modelo a la hora de clasificar los tipos celulares. Como se puede observar, el modelo *vgg19* predice con gran exactitud las diferentes imágenes.'
|
| 80 |
+
#st.write(text4)
|
| 81 |
+
#text5 = 'Tensorflow Projector (https://projector.tensorflow.org/) es una herramienta visual que nos permite interactuar y analizar datos multidimensionales (embeddings) y proyectarlos en un espacio bi o tridimensional. Cada embedding es representado por un punto que tiene una posición determinada en el espacio y estos formarán determinados clusters basándose en una puntuación de similitud. Gracias a esta herramienta, somos capaces de observar cómo el modelo es capaz de distinguir las diferentes clases (ig, leucocitos, etc), y dónde tiene los mayores problemas para distinguirlas mediante la aparición de ciertos puntos de diferentes clases dentro de un cluster de una clase diferente. '
|
| 82 |
+
#st.write(text5)
|
| 83 |
+
#text6 = 'Métodos de reducción de dimensionalidad como t-stochastic neighbor embedding (t-SNE) nos permiten visualizar nuestros embeddings de manera tridimensional, construyendo una distribución de probabilidad sobre parejas de embeddings en el espacio, de forma que los más similares son más probables de incluirse en un mismo cluster, reduciendo la dimensionalidad de la muestra. '
|
| 84 |
+
#st.write(text6)
|
| 85 |
+
st.image('./images/tensor.png', use_column_width= True)
|
| 86 |
+
st.markdown('<p style="text-align: justify;">Como se puede observar en esta figura, existen diversas inserciones de ciertos grupos dentro de clusters pertenecientes a otras clases. En este caso, el modelo se encuentra más confuso dando una clasificación correcta cuando se trata de neutrófilos y granulocitos inmaduros. Otras inserciones destacables son los eritroblastos, que son confundidos con plaquetas, los neutrófilos con basófilos, y los granulocitos inmaduros con monocitos. Aun así, la precisión del modelo a la hora de clasificar los diferentes tipos celulares es muy alta.</p>', unsafe_allow_html=True)
|
| 87 |
+
|
| 88 |
+
#text7 = 'Como se puede observar en esta figura, existen diversas inserciones de ciertos grupos dentro de clusters pertenecientes a otras clases. En este caso, el modelo se encuentra más confuso dando una clasificación correcta cuando se trata de neutrófilos y granulocitos inmaduros. Otras inserciones destacables son los eritroblastos, que son confundidos con plaquetas, los neutrófilos con basófilos, y los granulocitos inmaduros con monocitos. Aun así, la precisión del modelo a la hora de clasificar los diferentes tipos celulares es muy alta.'
|
| 89 |
+
#st.write(text7)
|
about_us.py
ADDED
|
@@ -0,0 +1,99 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# -*- coding: utf-8 -*-
|
| 2 |
+
"""
|
| 3 |
+
Created on Fri Dec 30 11:31:47 2022
|
| 4 |
+
|
| 5 |
+
@author: Usuario
|
| 6 |
+
"""
|
| 7 |
+
|
| 8 |
+
import streamlit as st
|
| 9 |
+
from tensorflow.keras.utils import load_img
|
| 10 |
+
import streamlit.components.v1 as components
|
| 11 |
+
|
| 12 |
+
target_size = (224,224)
|
| 13 |
+
|
| 14 |
+
def person(url):#(im_path, name, text):
|
| 15 |
+
#im = load_img(im_path, target_size = target_size)
|
| 16 |
+
#st.markdown ("<h1 style='text-align: center;'>name </h1>", unsafe_allow_html=True)
|
| 17 |
+
#components.html(
|
| 18 |
+
# """
|
| 19 |
+
# <div
|
| 20 |
+
# style="text-align: center">
|
| 21 |
+
# name
|
| 22 |
+
#</div>
|
| 23 |
+
#""",
|
| 24 |
+
#name)
|
| 25 |
+
|
| 26 |
+
#st.header(name)
|
| 27 |
+
#st.markdown ("<b style='text-align: center;'>"{}"</b>".format(name), unsafe_allow_html=True))
|
| 28 |
+
#st.image(im)
|
| 29 |
+
url
|
| 30 |
+
st.image(url, width = 100, use_column_width= True )
|
| 31 |
+
#text = '<b style = 'text-align: center';'{}' </b>'
|
| 32 |
+
#st.write(text, use_column_width = True)
|
| 33 |
+
'[](https://es.linkedin.com/in/mar%C3%ADa-ortiz-rodr%C3%ADguez-595964165)'
|
| 34 |
+
|
| 35 |
+
def unodinoi(idioma):
|
| 36 |
+
if idioma == 1:
|
| 37 |
+
st.title('About the team')
|
| 38 |
+
col1, col2, col3 = st.columns([100,100,100])
|
| 39 |
+
|
| 40 |
+
with col1:
|
| 41 |
+
nombre1 = st.markdown('<p style="text-align: center;"><strong>María Ortiz Rodríguez</strong></p>', unsafe_allow_html=True)
|
| 42 |
+
|
| 43 |
+
# text = """**B.S in Experimental Sciences,
|
| 44 |
+
# M.S in Computational Biology, and actually PhD student in Biophysics.
|
| 45 |
+
#Her work is focused on understanding the stoichiometry and dynamics of the human mitochondrial DNA replication machinery.**"""
|
| 46 |
+
#text = '''**Graduated in Experimental Sciences from Universidad Rey Juan Carlos and Master in Computational Biology from Universidad Politécnica de Madrid. Currently PhD student in Molecular Motors Lab at IMDEA Nanoscience, where she studies the mechano-chemistry of the molecular motors using single-molecule techniques.** '''
|
| 47 |
+
|
| 48 |
+
image1 = 'https://media.licdn.com/dms/image/C4D03AQG-uP0d65Xmxg/profile-displayphoto-shrink_800_800/0/1633675482831?e=1678320000&v=beta&t=4tSZ3b3ZqM6-1BImm5TFqMpiOMdP_g2JLIQvH6631bk'
|
| 49 |
+
#image = load_img('https://media.licdn.com/dms/image/C4D03AQG-uP0d65Xmxg/profile-displayphoto-shrink_800_800/0/1633675482831?e=1678320000&v=beta&t=4tSZ3b3ZqM6-1BImm5TFqMpiOMdP_g2JLIQvH6631bk')
|
| 50 |
+
person(image1)
|
| 51 |
+
text = st.markdown('<p style="text-align: justify;">Graduated in Experimental Sciences from Universidad Rey Juan Carlos and Master in Computational Biology from Universidad Politécnica de Madrid. Currently PhD student in Molecular Motors Lab at IMDEA Nanoscience, where she studies the mechano-chemistry of the molecular motors using single-molecule techniques.</p>', unsafe_allow_html=True)
|
| 52 |
+
|
| 53 |
+
|
| 54 |
+
with col2:
|
| 55 |
+
nombre2 = st.markdown('<p style="text-align: center;"><strong>Jorge González Sierra</strong></p>', unsafe_allow_html=True)
|
| 56 |
+
|
| 57 |
+
image2 = 'https://media.licdn.com/dms/image/C4E03AQEhOy-LzpixAg/profile-displayphoto-shrink_800_800/0/1655383235096?e=1678320000&v=beta&t=WQsyJ1eJvxvnI6Z7-WgOYebRYlPwOtQARVVqAOYTPZQ'
|
| 58 |
+
#text = '''**Graduated in Environmental Sciences from the Universidad Autonoma de Madrid and Master in Industrial and Environmental Biotechnology from the Universidad Complutense de Madrid and MBA from the Universidad Francisco de Vitoria. Currently pursuing a PhD in biofuels for aviation and high value-added bioproducts at the Universidad Rey Juan Carlos de Madrid.**'''
|
| 59 |
+
|
| 60 |
+
person(image2)
|
| 61 |
+
text = st.markdown('<p style="text-align: justify;">Graduated in Environmental Sciences from the Universidad Autonoma de Madrid and Master in Industrial and Environmental Biotechnology from the Universidad Complutense de Madrid and MBA from the Universidad Francisco de Vitoria. Currently pursuing a PhD in biofuels for aviation and high value-added bioproducts at the Universidad Rey Juan Carlos de Madrid.</p>', unsafe_allow_html=True)
|
| 62 |
+
|
| 63 |
+
with col3:
|
| 64 |
+
#nombre3 = st.markdown ("<b style='text-align: center;'>Silvia García Hernández </b>", unsafe_allow_html=True)
|
| 65 |
+
nombre3 = st.markdown('<p style="text-align: center;"><strong>Silvia García Hernández</strong></p>', unsafe_allow_html=True)
|
| 66 |
+
|
| 67 |
+
image3 = 'https://media.licdn.com/dms/image/C4D03AQFxqX-hVzyPzQ/profile-displayphoto-shrink_800_800/0/1659343843421?e=1678320000&v=beta&t=GAi23Hg4GSvuf1kPjUCkcZ0r3psZ3Ure9_0SXNedW1U'
|
| 68 |
+
#text = '''**Graduated in Electronic Engineering from the University of La Laguna and Master in Artificial Intelligence from the University of Las Palmas. Currently working as Data Scientist at EVM Group where she leads the technical decisions in Artificial Intelligence for projects under development. As fundamental pillars in the professional field, she has continuous learning and help in the development of technological-social initiatives, which is why she is a member of both AdaLoveDev and Python Canarias, and has made presentations at the AdaLoversConf and CESINF VIII events. She enjoys learning and coding in any field related to Data.**'''
|
| 69 |
+
person(image3)
|
| 70 |
+
text = st.markdown('<p style="text-align: justify;">Graduated in Electronic Engineering from the University of La Laguna and Master in Artificial Intelligence from the University of Las Palmas. Currently working as Data Scientist at EVM Group where she leads the technical decisions in Artificial Intelligence for projects under development. As fundamental pillars in the professional field, she has continuous learning and help in the development of technological-social initiatives, which is why she is a member of both AdaLoveDev and Python Canarias, and has made presentations at the AdaLoversConf and CESINF VIII events. She enjoys learning and coding in any field related to Data.</p>', unsafe_allow_html=True)
|
| 71 |
+
|
| 72 |
+
else:
|
| 73 |
+
st.title('Sobre nosotros')
|
| 74 |
+
col1, col2, col3 = st.columns([100,100,100])
|
| 75 |
+
|
| 76 |
+
with col1:
|
| 77 |
+
nombre1 = st.markdown('<p style="text-align: center;"><strong>María Ortiz Rodríguez</strong></p>', unsafe_allow_html=True)
|
| 78 |
+
|
| 79 |
+
#text = ''' **Graduada en Ciencias Experimentales por la Universidad Rey Juan Carlos y Máster en Biología Computacional por la Universidad Politécnica de Madrid. Actualmente realizando el doctorado en Molecular Motors Manipulation Lab en IMDEA Nanociencia, donde estudia la mecano-química de los motores moleculares mediante el uso de las técnica de moléculas individuales.**'''
|
| 80 |
+
image1 = 'https://media.licdn.com/dms/image/C4D03AQG-uP0d65Xmxg/profile-displayphoto-shrink_800_800/0/1633675482831?e=1678320000&v=beta&t=4tSZ3b3ZqM6-1BImm5TFqMpiOMdP_g2JLIQvH6631bk'
|
| 81 |
+
person(image1)
|
| 82 |
+
text = st.markdown('<p style="text-align: justify;">Graduada en Ciencias Experimentales por la Universidad Rey Juan Carlos y Máster en Biología Computacional por la Universidad Politécnica de Madrid. Actualmente realizando el doctorado en Molecular Motors Manipulation Lab en IMDEA Nanociencia, donde estudia la mecano-química de los motores moleculares mediante el uso de las técnica de moléculas individuales.</p>', unsafe_allow_html=True)
|
| 83 |
+
|
| 84 |
+
with col2:
|
| 85 |
+
nombre2 = st.markdown('<p style="text-align: center;"><strong>Jorge González Sierra</strong></p>', unsafe_allow_html=True)
|
| 86 |
+
|
| 87 |
+
image2 = 'https://media.licdn.com/dms/image/C4E03AQEhOy-LzpixAg/profile-displayphoto-shrink_800_800/0/1655383235096?e=1678320000&v=beta&t=WQsyJ1eJvxvnI6Z7-WgOYebRYlPwOtQARVVqAOYTPZQ'
|
| 88 |
+
#text = '''**Graduado en Ciencias Ambientales por la Universidad Autonoma de Madrid y Máster en Biotecnologia industrial y ambiental por la Universidad Complutense de Madrid y MBA por la Universidad Francisco de Vitoria. Actualmente realizando el doctorado en biocombustibles para aviación y bioproductos de alto valor añadido en la Universidad Rey Juan Carlos de Madrid.**'''
|
| 89 |
+
person(image2)
|
| 90 |
+
text = st.markdown('<p style="text-align: justify;">Graduado en Ciencias Ambientales por la Universidad Autonoma de Madrid y Máster en Biotecnologia industrial y ambiental por la Universidad Complutense de Madrid y MBA por la Universidad Francisco de Vitoria. Actualmente realizando el doctorado en biocombustibles para aviación y bioproductos de alto valor añadido en la Universidad Rey Juan Carlos de Madrid.</p>', unsafe_allow_html=True)
|
| 91 |
+
|
| 92 |
+
|
| 93 |
+
with col3:
|
| 94 |
+
nombre3 = st.markdown('<p style="text-align: center;"><strong>Silvia García Hernández</strong></p>', unsafe_allow_html=True)
|
| 95 |
+
|
| 96 |
+
image3 = 'https://media.licdn.com/dms/image/C4D03AQFxqX-hVzyPzQ/profile-displayphoto-shrink_800_800/0/1659343843421?e=1678320000&v=beta&t=GAi23Hg4GSvuf1kPjUCkcZ0r3psZ3Ure9_0SXNedW1U'
|
| 97 |
+
#text = '''**Graduada en Ingeniería Electrónica por la Universidad de La Laguna y Máster en Inteligencia Artificial por la Universidad de Las Palmas. Actual Científica de Datos en Grupo EVM, donde lidera las decisiones técnicas en materia de Inteligencia Artificial de los proyectos en desarrollo. Como pilares fundamentales en el campo profesional posee el aprendizaje continuo y la ayuda al desarrollo de iniciativas tecnológico-sociales, razón por la cual es socia tanto de AdaLoveDev como de Python Canarias, y ha realizado ponencias en los eventos AdaLoversConf y CESINF VIII. Disfruta aprendiendo y trasteando con código sobre cualquier campo relacionado con Datos.**'''
|
| 98 |
+
person(image3)
|
| 99 |
+
text = st.markdown('<p style="text-align: justify;">Graduada en Ingeniería Electrónica por la Universidad de La Laguna y Máster en Inteligencia Artificial por la Universidad de Las Palmas. Actual Científica de Datos en Grupo EVM, donde lidera las decisiones técnicas en materia de Inteligencia Artificial de los proyectos en desarrollo. Como pilares fundamentales en el campo profesional posee el aprendizaje continuo y la ayuda al desarrollo de iniciativas tecnológico-sociales, razón por la cual es socia tanto de AdaLoveDev como de Python Canarias, y ha realizado ponencias en los eventos AdaLoversConf y CESINF VIII. Disfruta aprendiendo y trasteando con código sobre cualquier campo relacionado con Datos.</p>', unsafe_allow_html=True)
|
explicability.py
ADDED
|
@@ -0,0 +1,104 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# -*- coding: utf-8 -*-
|
| 2 |
+
"""
|
| 3 |
+
Created on Tue Dec 27 08:48:25 2022
|
| 4 |
+
|
| 5 |
+
@author: Usuario
|
| 6 |
+
"""
|
| 7 |
+
|
| 8 |
+
from keras.models import load_model
|
| 9 |
+
import tensorflow as tf
|
| 10 |
+
from tensorflow.keras.utils import load_img, img_to_array, array_to_img
|
| 11 |
+
from keras.preprocessing.image import ImageDataGenerator
|
| 12 |
+
from keras.applications.vgg19 import preprocess_input, decode_predictions
|
| 13 |
+
import matplotlib.pyplot as plt
|
| 14 |
+
|
| 15 |
+
import numpy as np
|
| 16 |
+
from IPython.display import Image, display
|
| 17 |
+
import matplotlib.cm as cm
|
| 18 |
+
|
| 19 |
+
#http://gradcam.cloudcv.org/
|
| 20 |
+
#https://keras.io/examples/vision/grad_cam/
|
| 21 |
+
|
| 22 |
+
def get_img_array(img_path, size):
|
| 23 |
+
# `img` is a PIL image of size 299x299
|
| 24 |
+
img = load_img(img_path, target_size=size)
|
| 25 |
+
# `array` is a float32 Numpy array of shape (299, 299, 3)
|
| 26 |
+
array = img_to_array(img)
|
| 27 |
+
# We add a dimension to transform our array into a "batch"
|
| 28 |
+
# of size (1, 299, 299, 3)
|
| 29 |
+
array = np.expand_dims(array, axis=0)
|
| 30 |
+
return array
|
| 31 |
+
|
| 32 |
+
def make_gradcam_heatmap(img_array, model, last_conv_layer_name, pred_index=None):
|
| 33 |
+
# First, we create a model that maps the input image to the activations
|
| 34 |
+
# of the last conv layer as well as the output predictions
|
| 35 |
+
grad_model = tf.keras.models.Model(
|
| 36 |
+
[model.inputs], [model.get_layer(last_conv_layer_name).output, model.output]
|
| 37 |
+
)
|
| 38 |
+
|
| 39 |
+
# Then, we compute the gradient of the top predicted class for our input image
|
| 40 |
+
# with respect to the activations of the last conv layer
|
| 41 |
+
with tf.GradientTape() as tape:
|
| 42 |
+
last_conv_layer_output, preds = grad_model(img_array)
|
| 43 |
+
if pred_index is None:
|
| 44 |
+
pred_index = tf.argmax(preds[0])
|
| 45 |
+
class_channel = preds[:, pred_index]
|
| 46 |
+
|
| 47 |
+
# This is the gradient of the output neuron (top predicted or chosen)
|
| 48 |
+
# with regard to the output feature map of the last conv layer
|
| 49 |
+
grads = tape.gradient(class_channel, last_conv_layer_output)
|
| 50 |
+
|
| 51 |
+
# This is a vector where each entry is the mean intensity of the gradient
|
| 52 |
+
# over a specific feature map channel
|
| 53 |
+
pooled_grads = tf.reduce_mean(grads, axis=(0, 1, 2))
|
| 54 |
+
|
| 55 |
+
# We multiply each channel in the feature map array
|
| 56 |
+
# by "how important this channel is" with regard to the top predicted class
|
| 57 |
+
# then sum all the channels to obtain the heatmap class activation
|
| 58 |
+
last_conv_layer_output = last_conv_layer_output[0]
|
| 59 |
+
heatmap = last_conv_layer_output @ pooled_grads[..., tf.newaxis]
|
| 60 |
+
heatmap = tf.squeeze(heatmap)
|
| 61 |
+
|
| 62 |
+
# For visualization purpose, we will also normalize the heatmap between 0 & 1
|
| 63 |
+
heatmap = tf.maximum(heatmap, 0) / tf.math.reduce_max(heatmap)
|
| 64 |
+
|
| 65 |
+
return heatmap.numpy()
|
| 66 |
+
|
| 67 |
+
|
| 68 |
+
|
| 69 |
+
# Generate class activation heatmap
|
| 70 |
+
#heatmap = make_gradcam_heatmap(img_array, model, last_conv_layer_name)
|
| 71 |
+
|
| 72 |
+
|
| 73 |
+
def save_and_display_gradcam(img_path, heatmap, alpha = 0.4):
|
| 74 |
+
# Load the original image
|
| 75 |
+
img = load_img(img_path)
|
| 76 |
+
img = img_to_array(img)
|
| 77 |
+
|
| 78 |
+
# Rescale heatmap to a range 0-255
|
| 79 |
+
heatmap = np.uint8(255 * heatmap)
|
| 80 |
+
|
| 81 |
+
# Use jet colormap to colorize heatmap
|
| 82 |
+
jet = cm.get_cmap("jet")
|
| 83 |
+
|
| 84 |
+
# Use RGB values of the colormap
|
| 85 |
+
jet_colors = jet(np.arange(256))[:, :3]
|
| 86 |
+
jet_heatmap = jet_colors[heatmap]
|
| 87 |
+
|
| 88 |
+
# Create an image with RGB colorized heatmap
|
| 89 |
+
jet_heatmap = array_to_img(jet_heatmap)
|
| 90 |
+
jet_heatmap = jet_heatmap.resize((img.shape[1], img.shape[0]))
|
| 91 |
+
jet_heatmap = img_to_array(jet_heatmap)
|
| 92 |
+
|
| 93 |
+
# Superimpose the heatmap on original image
|
| 94 |
+
superimposed_img = jet_heatmap * alpha + img
|
| 95 |
+
superimposed_img = array_to_img(superimposed_img)
|
| 96 |
+
|
| 97 |
+
# Save the superimposed image
|
| 98 |
+
#superimposed_img.save('')
|
| 99 |
+
|
| 100 |
+
# Display Grad CAM
|
| 101 |
+
return superimposed_img
|
| 102 |
+
#display(Image(superimposed_img))
|
| 103 |
+
|
| 104 |
+
#save_and_display_gradcam(path_image+name_image, heatmap)
|
imagen_subida.py
ADDED
|
@@ -0,0 +1,215 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# -*- coding: utf-8 -*-
|
| 2 |
+
"""
|
| 3 |
+
Created on Fri Dec 23 09:25:09 2022
|
| 4 |
+
|
| 5 |
+
@author: Usuario
|
| 6 |
+
"""
|
| 7 |
+
from keras.models import load_model
|
| 8 |
+
import tensorflow as tf
|
| 9 |
+
from tensorflow.keras.utils import load_img, img_to_array, array_to_img
|
| 10 |
+
from keras.preprocessing.image import ImageDataGenerator
|
| 11 |
+
from keras.applications.vgg19 import preprocess_input, decode_predictions
|
| 12 |
+
import matplotlib.pyplot as plt
|
| 13 |
+
|
| 14 |
+
import numpy as np
|
| 15 |
+
from IPython.display import Image, display
|
| 16 |
+
import matplotlib.cm as cm
|
| 17 |
+
|
| 18 |
+
import streamlit as st
|
| 19 |
+
from tensorflow.keras.utils import load_img
|
| 20 |
+
import pandas as pd
|
| 21 |
+
import matplotlib.pyplot as plt
|
| 22 |
+
|
| 23 |
+
import numpy as np
|
| 24 |
+
import streamlit_toggle as tog
|
| 25 |
+
import explicability as ex
|
| 26 |
+
|
| 27 |
+
from bokeh.plotting import figure
|
| 28 |
+
from bokeh.palettes import Category20c
|
| 29 |
+
from bokeh.plotting import figure, show
|
| 30 |
+
from bokeh.transform import cumsum
|
| 31 |
+
|
| 32 |
+
|
| 33 |
+
last_conv_layer_name = "block5_conv4"
|
| 34 |
+
|
| 35 |
+
def resultados(uploaded_image, model, size, label_names, labs, result_text):
|
| 36 |
+
#st.image(uploaded_image, caption='Celula Sanguinea')
|
| 37 |
+
|
| 38 |
+
image = load_img(uploaded_image, target_size = size)
|
| 39 |
+
img = np.array(image)
|
| 40 |
+
img = img / 255.0
|
| 41 |
+
img = img.reshape(1, 224, 224, 3)
|
| 42 |
+
|
| 43 |
+
label = model.predict(img)
|
| 44 |
+
#st.text([np.argmax(label)])
|
| 45 |
+
score = label[0]
|
| 46 |
+
|
| 47 |
+
|
| 48 |
+
#st.write(add_text_chart)
|
| 49 |
+
#st.write('La imagen a analizar es la mostrada a continuación. Se podrá analizar la probabilidad de pertenencia a cada tipo de célula sanguínea, así como observar el mapa de calor generado en el apartado de explicabilidad.')
|
| 50 |
+
|
| 51 |
+
col1, mid, col2 = st.columns([300,300,300])
|
| 52 |
+
|
| 53 |
+
with mid:
|
| 54 |
+
st.image(uploaded_image, width=220, use_column_width=False)
|
| 55 |
+
|
| 56 |
+
#with col2:
|
| 57 |
+
|
| 58 |
+
placeholder = st.container()
|
| 59 |
+
tab1, tab2 = placeholder.tabs(labs)#(["Result", "Explicability"])
|
| 60 |
+
|
| 61 |
+
|
| 62 |
+
with tab1:
|
| 63 |
+
|
| 64 |
+
#st.write('Aquí se muestra la probabilidad de la imagen seleccionada de pertenecer a cada clase de célula sanguínea según el modelo de Inteligencia Artificial entrenado.')
|
| 65 |
+
st.write(result_text[0])
|
| 66 |
+
st.write(' ')
|
| 67 |
+
#Bokeh pie chart
|
| 68 |
+
pie = {label_names[0]: np.round(score[0]*100, 2),
|
| 69 |
+
label_names[1]: np.round(score[1]*100, 2),
|
| 70 |
+
label_names[2]: np.round(score[2]*100, 2),
|
| 71 |
+
label_names[3]: np.round(score[3]*100, 2),
|
| 72 |
+
label_names[4]: np.round(score[4]*100, 2),
|
| 73 |
+
label_names[5]: np.round(score[5]*100, 2),
|
| 74 |
+
label_names[6]: np.round(score[6]*100, 2),
|
| 75 |
+
label_names[7]: np.round(score[7]*100, 2)}
|
| 76 |
+
datita = pd.Series(pie).reset_index(name='value').rename(columns={'index': 'country'})
|
| 77 |
+
datita['angle'] = datita['value']/datita['value'].sum() * 2*np.pi
|
| 78 |
+
datita['color'] = Category20c[len(datita)]
|
| 79 |
+
p = figure(height=350, title="", toolbar_location=None,
|
| 80 |
+
tools="hover", tooltips="@country: @value", x_range=(-0.5, 1.0))
|
| 81 |
+
p.wedge(x=0, y=1, radius=0.4,
|
| 82 |
+
start_angle=cumsum('angle', include_zero=True), end_angle=cumsum('angle'),
|
| 83 |
+
line_color="white", fill_color='color', legend_field='country', source=datita)
|
| 84 |
+
st.bokeh_chart(p)
|
| 85 |
+
|
| 86 |
+
#=====================
|
| 87 |
+
|
| 88 |
+
col1, col2, col3, col4, = st.columns([250,250,250,250])
|
| 89 |
+
col1.metric(label_names[0], str(np.round(score[0]*100, 2))+"%")
|
| 90 |
+
col1.metric(label_names[1], str(np.round(score[1]*100, 2))+"%")
|
| 91 |
+
col2.metric(label_names[2], str(np.round(score[2]*100, 2))+"%")
|
| 92 |
+
col2.metric(label_names[3], str(np.round(score[3]*100, 2))+"%")
|
| 93 |
+
col3.metric(label_names[4], str(np.round(score[4]*100, 2))+"%")
|
| 94 |
+
col3.metric(label_names[5], str(np.round(score[5]*100, 2))+"%")
|
| 95 |
+
col4.metric(label_names[6], str(np.round(score[6]*100, 2))+"%")
|
| 96 |
+
col4.metric(label_names[7], str(np.round(score[7]*100, 2))+"%")
|
| 97 |
+
|
| 98 |
+
#chart = pd.DataFrame(np.array(score)*100, label_names)
|
| 99 |
+
#st.bar_chart(chart, use_container_width=True )
|
| 100 |
+
|
| 101 |
+
|
| 102 |
+
#p = figure(title = '',
|
| 103 |
+
# x_range = label_names)
|
| 104 |
+
#p.vbar(x = label_names, top = np.array(score)*100)
|
| 105 |
+
#st.bokeh_chart(p, use_container_width= True)
|
| 106 |
+
|
| 107 |
+
# fig, ax = plt.subplots()
|
| 108 |
+
# ax.bar(label_names, np.array(score)*100, color = 'red')
|
| 109 |
+
# st.pyplot(use_container_width = True)
|
| 110 |
+
|
| 111 |
+
with tab2: #Explicabilidad
|
| 112 |
+
|
| 113 |
+
#st.write('El mapa de calor generado con el algoritmo GRADCAM es el mostrado a continuación. En él se puede observar qué parte de la imagen de entrada ha sido la parte más relevante para el modelo de Inteligencia Artificial en cuanto a clasificación se refiere.')
|
| 114 |
+
st.write(result_text[1])
|
| 115 |
+
col3, col4, col5 = st.columns([300,300,300])
|
| 116 |
+
|
| 117 |
+
with col4:
|
| 118 |
+
img_array = preprocess_input(ex.get_img_array(uploaded_image, size))
|
| 119 |
+
|
| 120 |
+
model.layers[-1].activation = None
|
| 121 |
+
heatmap = ex.make_gradcam_heatmap(img_array, model, last_conv_layer_name)
|
| 122 |
+
|
| 123 |
+
st.image(ex.save_and_display_gradcam(uploaded_image, heatmap), use_column_width=True)
|
| 124 |
+
|
| 125 |
+
|
| 126 |
+
|
| 127 |
+
def idioma():
|
| 128 |
+
idiomita = tog.st_toggle_switch(label = "",
|
| 129 |
+
key = 'he',
|
| 130 |
+
default_value = True,
|
| 131 |
+
label_after = False,
|
| 132 |
+
inactive_color="#ffffff",
|
| 133 |
+
active_color="#ffffff",
|
| 134 |
+
track_color="#18202b"
|
| 135 |
+
)
|
| 136 |
+
return idiomita
|
| 137 |
+
|
| 138 |
+
|
| 139 |
+
def change_title(idioma):
|
| 140 |
+
if idioma == 1:
|
| 141 |
+
title = st.title('Peripheral blood cells classification')
|
| 142 |
+
#lab = ["Result", "Explicability"]
|
| 143 |
+
|
| 144 |
+
else:
|
| 145 |
+
title = st.title('Clasificación de imágenes de células sanguíneas periféricas ')
|
| 146 |
+
#lab = ["neeee", "bruuu"]
|
| 147 |
+
return title
|
| 148 |
+
|
| 149 |
+
|
| 150 |
+
|
| 151 |
+
def change_labels(idioma):
|
| 152 |
+
if idioma == 1:
|
| 153 |
+
labs = ["📈 Result", "📝 Explicability"]
|
| 154 |
+
else:
|
| 155 |
+
labs = ["📈 Resultados", "📝 Explicabilidad"]
|
| 156 |
+
|
| 157 |
+
return labs
|
| 158 |
+
|
| 159 |
+
|
| 160 |
+
|
| 161 |
+
|
| 162 |
+
def add_bg_from_url():
|
| 163 |
+
st.markdown(
|
| 164 |
+
"""
|
| 165 |
+
<style>
|
| 166 |
+
.stApp {
|
| 167 |
+
background-image: linear-gradient(gray,white);
|
| 168 |
+
|
| 169 |
+
background-size: cover
|
| 170 |
+
}
|
| 171 |
+
</style>
|
| 172 |
+
""",
|
| 173 |
+
unsafe_allow_html=True
|
| 174 |
+
)
|
| 175 |
+
|
| 176 |
+
|
| 177 |
+
|
| 178 |
+
def button_image():
|
| 179 |
+
st.markdown(
|
| 180 |
+
f"""
|
| 181 |
+
<button type="submit">
|
| 182 |
+
<img src="https://i.ibb.co/CW5Wvry/buttonpng.png" alt="buttonpng" border="0" />
|
| 183 |
+
</button>
|
| 184 |
+
""")
|
| 185 |
+
|
| 186 |
+
|
| 187 |
+
def additional_text_chart(idioma):
|
| 188 |
+
if idioma == 1:
|
| 189 |
+
text = 'The following image is going to be analysed. In **Results** you can observe the probability that this cell has to belong to a determined blood cell type, and the color map in **Explicability**'
|
| 190 |
+
else:
|
| 191 |
+
text = 'La imagen a analizar es la mostrada a continuación. Se podrá analizar la probabilidad de pertenencia a cada tipo de célula sanguínea, así como observar el mapa de calor generado en el apartado de explicabilidad.'
|
| 192 |
+
|
| 193 |
+
return text
|
| 194 |
+
|
| 195 |
+
def result_text(idioma):
|
| 196 |
+
if idioma == 1:
|
| 197 |
+
textito_res = 'Here appears the probability of the input image to belong to each blood cell type depending of our IA trained model.'
|
| 198 |
+
textito_exp = 'The color map was generated with GRADCAM algorithm. Here you can observe which part of the input image has been the most relevant part for the IA model in terms of classification.'
|
| 199 |
+
textito = [textito_res, textito_exp]
|
| 200 |
+
else:
|
| 201 |
+
textito_res = 'Aquí se muestra la probabilidad de la imagen seleccionada de pertenecer a cada clase de célula sanguínea según el modelo de Inteligencia Artificial entrenado.'
|
| 202 |
+
textito_exp = 'El mapa de calor generado con el algoritmo GRADCAM es el mostrado a continuación. En él se puede observar qué parte de la imagen de entrada ha sido la parte más relevante para el modelo de Inteligencia Artificial en cuanto a clasificación se refiere.'
|
| 203 |
+
textito = [textito_res, textito_exp]
|
| 204 |
+
return textito
|
| 205 |
+
|
| 206 |
+
def botoncitos(idioma):
|
| 207 |
+
if idioma == 1:
|
| 208 |
+
label_pj = 'About the project 📕'
|
| 209 |
+
label_us = ' About us 🧝♂️ '
|
| 210 |
+
labelcillos = [label_pj, label_us]
|
| 211 |
+
else:
|
| 212 |
+
label_pj = 'Sobre el proyecto 📕'
|
| 213 |
+
label_us = ' Sobre nosotros 🧝♂️ '
|
| 214 |
+
labelcillos = [label_pj, label_us]
|
| 215 |
+
return labelcillos
|
images/13435.jpg
ADDED

|
Git LFS Details
|
images/18994.jpg
ADDED

|
images/Flag_of_the_United_Kingdom.png
ADDED

|
images/United-Kingdom-Flag.png
ADDED

|
images/abstract-soft-pink-watercolor-background.zip
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:596d1ff1ef498a35dec91d86e8a531fd08522df657cb7468ec2aab5e21457a73
|
| 3 |
+
size 10437058
|
images/abstract-soft-pink-watercolor-background/18994.eps
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:269206eb8cff3532adefd3133afc80309bd3eaa5eafda691da5c3ab7ea515fbd
|
| 3 |
+
size 19795410
|
images/abstract-soft-pink-watercolor-background/License free.txt
ADDED
|
@@ -0,0 +1,45 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
IMPORTANT NOTICE: This license only applies if you downloaded this content as
|
| 2 |
+
an unsubscribed user. If you are a premium user (ie, you pay a subscription)
|
| 3 |
+
you are bound to the license terms described in the accompanying file
|
| 4 |
+
"License premium.txt".
|
| 5 |
+
|
| 6 |
+
---------------------
|
| 7 |
+
|
| 8 |
+
You must attribute the image to its author:
|
| 9 |
+
|
| 10 |
+
In order to use a content or a part of it, you must attribute it to Harryarts / Freepik,
|
| 11 |
+
so we will be able to continue creating new graphic resources every day.
|
| 12 |
+
|
| 13 |
+
|
| 14 |
+
How to attribute it?
|
| 15 |
+
|
| 16 |
+
For websites:
|
| 17 |
+
|
| 18 |
+
Please, copy this code on your website to accredit the author:
|
| 19 |
+
<a href="http://www.freepik.com">Designed by Harryarts / Freepik</a>
|
| 20 |
+
|
| 21 |
+
For printing:
|
| 22 |
+
|
| 23 |
+
Paste this text on the final work so the authorship is known.
|
| 24 |
+
- For example, in the acknowledgements chapter of a book:
|
| 25 |
+
"Designed by Harryarts / Freepik"
|
| 26 |
+
|
| 27 |
+
|
| 28 |
+
You are free to use this image:
|
| 29 |
+
|
| 30 |
+
- For both personal and commercial projects and to modify it.
|
| 31 |
+
- In a website or presentation template or application or as part of your design.
|
| 32 |
+
|
| 33 |
+
You are not allowed to:
|
| 34 |
+
|
| 35 |
+
- Sub-license, resell or rent it.
|
| 36 |
+
- Include it in any online or offline archive or database.
|
| 37 |
+
|
| 38 |
+
The full terms of the license are described in section 7 of the Freepik
|
| 39 |
+
terms of use, available online in the following link:
|
| 40 |
+
|
| 41 |
+
http://www.freepik.com/terms_of_use
|
| 42 |
+
|
| 43 |
+
The terms described in the above link have precedence over the terms described
|
| 44 |
+
in the present document. In case of disagreement, the Freepik Terms of Use
|
| 45 |
+
will prevail.
|
images/abstract-soft-pink-watercolor-background/License premium.txt
ADDED
|
@@ -0,0 +1,30 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
IMPORTANT NOTICE: This license only applies if you downloaded this content as
|
| 2 |
+
a subscribed (or "premium") user. If you are an unsubscribed user (or "free"
|
| 3 |
+
user) you are bound to the license terms described in the accompanying file
|
| 4 |
+
"License free.txt".
|
| 5 |
+
|
| 6 |
+
---------------------
|
| 7 |
+
|
| 8 |
+
You can download from your profile in Freepik a personalized license stating
|
| 9 |
+
your right to use this content as a "premium" user:
|
| 10 |
+
|
| 11 |
+
https://profile.freepik.com/my_downloads
|
| 12 |
+
|
| 13 |
+
You are free to use this image:
|
| 14 |
+
|
| 15 |
+
- For both personal and commercial projects and to modify it.
|
| 16 |
+
- In a website or presentation template or application or as part of your design.
|
| 17 |
+
|
| 18 |
+
You are not allowed to:
|
| 19 |
+
|
| 20 |
+
- Sub-license, resell or rent it.
|
| 21 |
+
- Include it in any online or offline archive or database.
|
| 22 |
+
|
| 23 |
+
The full terms of the license are described in sections 7 and 8 of the Freepik
|
| 24 |
+
terms of use, available online in the following link:
|
| 25 |
+
|
| 26 |
+
http://www.freepik.com/terms_of_use
|
| 27 |
+
|
| 28 |
+
The terms described in the above link have precedence over the terms described
|
| 29 |
+
in the present document. In case of disagreement, the Freepik Terms of Use
|
| 30 |
+
will prevail.
|
images/blood-donor-icons-flat/13435.eps
ADDED
|
Binary file (875 kB). View file
|
|
|
images/blood-donor-icons-flat/License free.txt
ADDED
|
@@ -0,0 +1,45 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
IMPORTANT NOTICE: This license only applies if you downloaded this content as
|
| 2 |
+
an unsubscribed user. If you are a premium user (ie, you pay a subscription)
|
| 3 |
+
you are bound to the license terms described in the accompanying file
|
| 4 |
+
"License premium.txt".
|
| 5 |
+
|
| 6 |
+
---------------------
|
| 7 |
+
|
| 8 |
+
You must attribute the image to its author:
|
| 9 |
+
|
| 10 |
+
In order to use a content or a part of it, you must attribute it to macrovector / Freepik,
|
| 11 |
+
so we will be able to continue creating new graphic resources every day.
|
| 12 |
+
|
| 13 |
+
|
| 14 |
+
How to attribute it?
|
| 15 |
+
|
| 16 |
+
For websites:
|
| 17 |
+
|
| 18 |
+
Please, copy this code on your website to accredit the author:
|
| 19 |
+
<a href="http://www.freepik.com">Designed by macrovector / Freepik</a>
|
| 20 |
+
|
| 21 |
+
For printing:
|
| 22 |
+
|
| 23 |
+
Paste this text on the final work so the authorship is known.
|
| 24 |
+
- For example, in the acknowledgements chapter of a book:
|
| 25 |
+
"Designed by macrovector / Freepik"
|
| 26 |
+
|
| 27 |
+
|
| 28 |
+
You are free to use this image:
|
| 29 |
+
|
| 30 |
+
- For both personal and commercial projects and to modify it.
|
| 31 |
+
- In a website or presentation template or application or as part of your design.
|
| 32 |
+
|
| 33 |
+
You are not allowed to:
|
| 34 |
+
|
| 35 |
+
- Sub-license, resell or rent it.
|
| 36 |
+
- Include it in any online or offline archive or database.
|
| 37 |
+
|
| 38 |
+
The full terms of the license are described in section 7 of the Freepik
|
| 39 |
+
terms of use, available online in the following link:
|
| 40 |
+
|
| 41 |
+
http://www.freepik.com/terms_of_use
|
| 42 |
+
|
| 43 |
+
The terms described in the above link have precedence over the terms described
|
| 44 |
+
in the present document. In case of disagreement, the Freepik Terms of Use
|
| 45 |
+
will prevail.
|
images/blood-donor-icons-flat/License premium.txt
ADDED
|
@@ -0,0 +1,30 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
IMPORTANT NOTICE: This license only applies if you downloaded this content as
|
| 2 |
+
a subscribed (or "premium") user. If you are an unsubscribed user (or "free"
|
| 3 |
+
user) you are bound to the license terms described in the accompanying file
|
| 4 |
+
"License free.txt".
|
| 5 |
+
|
| 6 |
+
---------------------
|
| 7 |
+
|
| 8 |
+
You can download from your profile in Freepik a personalized license stating
|
| 9 |
+
your right to use this content as a "premium" user:
|
| 10 |
+
|
| 11 |
+
https://profile.freepik.com/my_downloads
|
| 12 |
+
|
| 13 |
+
You are free to use this image:
|
| 14 |
+
|
| 15 |
+
- For both personal and commercial projects and to modify it.
|
| 16 |
+
- In a website or presentation template or application or as part of your design.
|
| 17 |
+
|
| 18 |
+
You are not allowed to:
|
| 19 |
+
|
| 20 |
+
- Sub-license, resell or rent it.
|
| 21 |
+
- Include it in any online or offline archive or database.
|
| 22 |
+
|
| 23 |
+
The full terms of the license are described in sections 7 and 8 of the Freepik
|
| 24 |
+
terms of use, available online in the following link:
|
| 25 |
+
|
| 26 |
+
http://www.freepik.com/terms_of_use
|
| 27 |
+
|
| 28 |
+
The terms described in the above link have precedence over the terms described
|
| 29 |
+
in the present document. In case of disagreement, the Freepik Terms of Use
|
| 30 |
+
will prevail.
|
images/confusion_matrix.png
ADDED

|
images/dark-brown-colour-flower-pattern-background-abstract-banner-multipurpose-design.jpg
ADDED

|
Git LFS Details
|
images/espa/303/261ita.png
ADDED

|
images/flag-of-spain.png
ADDED

|
images/red-black-brush-stroke-banner-background-perfect-canva.jpg
ADDED

|
Git LFS Details
|
images/spain_flag.png
ADDED

|
images/tensor.png
ADDED
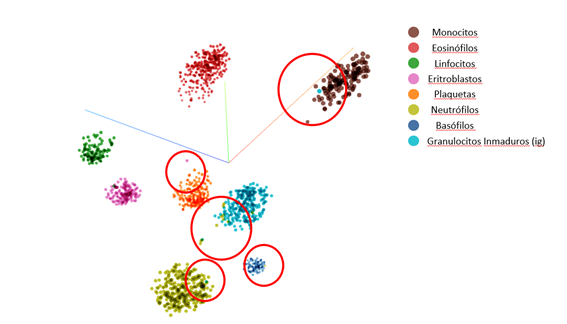
|
images/united_kingdom_flag.png
ADDED

|
images/vgg19.png
ADDED
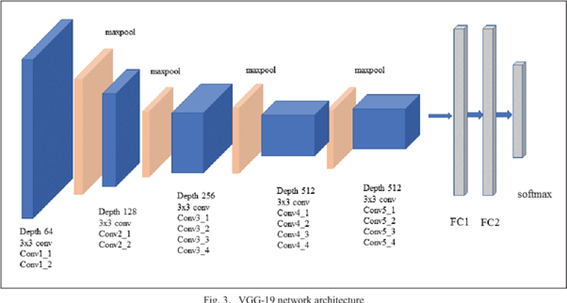
|
main.py
ADDED
|
@@ -0,0 +1,104 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# -*- coding: utf-8 -*-
|
| 2 |
+
"""
|
| 3 |
+
Created on Fri Dec 30 11:25:05 2022
|
| 4 |
+
|
| 5 |
+
@author: Usuario
|
| 6 |
+
"""
|
| 7 |
+
|
| 8 |
+
import imagen_subida as ims
|
| 9 |
+
import streamlit as st
|
| 10 |
+
from keras.models import load_model
|
| 11 |
+
from tensorflow.keras.utils import load_img
|
| 12 |
+
import sys
|
| 13 |
+
import os
|
| 14 |
+
import about_pj as pj
|
| 15 |
+
import about_us as us
|
| 16 |
+
import main_page as mp
|
| 17 |
+
#Fondo de streamlit
|
| 18 |
+
ims.add_bg_from_url()
|
| 19 |
+
|
| 20 |
+
if 'param' not in st.session_state:
|
| 21 |
+
st.session_state.param = 1
|
| 22 |
+
|
| 23 |
+
def about_project():
|
| 24 |
+
pj.textito(language_button)
|
| 25 |
+
|
| 26 |
+
def ab_us():
|
| 27 |
+
us.unodinoi(language_button)
|
| 28 |
+
|
| 29 |
+
def language():
|
| 30 |
+
language_button = ims.idioma()
|
| 31 |
+
return language_button
|
| 32 |
+
|
| 33 |
+
def main_page(param):
|
| 34 |
+
|
| 35 |
+
if param == 1:
|
| 36 |
+
mp.main_page(language_button, label_names)
|
| 37 |
+
|
| 38 |
+
elif param == 2:
|
| 39 |
+
pj.textito(language_button)
|
| 40 |
+
|
| 41 |
+
elif param == 3:
|
| 42 |
+
us.unodinoi(language_button)
|
| 43 |
+
|
| 44 |
+
|
| 45 |
+
#SIDEBAR OPTIONS ======================================
|
| 46 |
+
with st.sidebar:
|
| 47 |
+
|
| 48 |
+
#cambiar color de los botones
|
| 49 |
+
m = st.markdown("""
|
| 50 |
+
<style>
|
| 51 |
+
div.stButton > button:first-child {
|
| 52 |
+
background-color: #18202b;
|
| 53 |
+
color:#ffffff;
|
| 54 |
+
}
|
| 55 |
+
div.stButton > button:hover {
|
| 56 |
+
background-color: #522100;
|
| 57 |
+
color:#ffffff;
|
| 58 |
+
}
|
| 59 |
+
</style>""", unsafe_allow_html=True)
|
| 60 |
+
|
| 61 |
+
param = 1
|
| 62 |
+
|
| 63 |
+
col1, col2, col3, col4, col5 = st.columns([20,60,40,60,20])
|
| 64 |
+
|
| 65 |
+
with col2:
|
| 66 |
+
st.image('./images/spain_flag.png', width = 60)
|
| 67 |
+
with col3:
|
| 68 |
+
language_button = language()
|
| 69 |
+
with col4:
|
| 70 |
+
st.image('./images/united_kingdom_flag.png', width = 60)
|
| 71 |
+
|
| 72 |
+
st.markdown("***")
|
| 73 |
+
|
| 74 |
+
_, colb, _ = st.columns([10,60,20])#([50,80,50])
|
| 75 |
+
with colb:
|
| 76 |
+
botones = ims.botoncitos(language_button)
|
| 77 |
+
home = st.button(' Home 🏠 ')
|
| 78 |
+
project_button = st.button(label = botones[0])#(label = 'About the project 📕')
|
| 79 |
+
us_button = st.button(label = botones[1])#' About us 🧝♂️ ')
|
| 80 |
+
|
| 81 |
+
st.markdown('---')
|
| 82 |
+
|
| 83 |
+
#=======================================================
|
| 84 |
+
|
| 85 |
+
|
| 86 |
+
|
| 87 |
+
if language_button == 1:
|
| 88 |
+
label_names = ['Basophil', 'Eosinophil', 'Erythroblast', 'Immature gralulocyte', 'Lymphocyte', 'Monocyte', 'Neutrophil', 'Platelet']
|
| 89 |
+
else:
|
| 90 |
+
label_names = ['Basófilo', 'Eosinófilo', 'Eritoblasto', 'Granulocitos inmaduros', 'Linfocito', 'Monocito', 'Neutróofilo', 'Plaqueta']
|
| 91 |
+
|
| 92 |
+
|
| 93 |
+
|
| 94 |
+
if home:
|
| 95 |
+
st.session_state.param = 1
|
| 96 |
+
st.experimental_rerun()
|
| 97 |
+
elif project_button:
|
| 98 |
+
st.session_state.param = 2
|
| 99 |
+
elif us_button:
|
| 100 |
+
st.session_state.param = 3
|
| 101 |
+
|
| 102 |
+
main_page(st.session_state.param)
|
| 103 |
+
|
| 104 |
+
|
main_page.py
ADDED
|
@@ -0,0 +1,52 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# -*- coding: utf-8 -*-
|
| 2 |
+
"""
|
| 3 |
+
Created on Tue Dec 27 16:16:06 2022
|
| 4 |
+
|
| 5 |
+
@author: Usuario
|
| 6 |
+
"""
|
| 7 |
+
import streamlit as st
|
| 8 |
+
import imagen_subida as ims
|
| 9 |
+
from keras.models import load_model
|
| 10 |
+
from os import system
|
| 11 |
+
#Cargar el modelo
|
| 12 |
+
import os
|
| 13 |
+
import patoolib
|
| 14 |
+
from shutil import rmtree
|
| 15 |
+
from os import remove
|
| 16 |
+
|
| 17 |
+
if os.path.isdir("./model_subir/model") == True:
|
| 18 |
+
rmtree("./model_subir/model/")
|
| 19 |
+
if os.path.isfile("./model_subir/test_model.zip") == True:
|
| 20 |
+
remove("./model_subir/test_model.zip")
|
| 21 |
+
os.system("cat ./model_subir/vgg19_trainable_true_best_model_pruebita.7z.* > ./model_subir/test_model.zip")
|
| 22 |
+
|
| 23 |
+
|
| 24 |
+
patoolib.extract_archive("./model_subir/test_model.zip",outdir="./model_subir/model/")
|
| 25 |
+
#model = load_model('../../../model/classification/vgg19_trainable_true_best_model.h5')
|
| 26 |
+
model = load_model('./model_subir/model/vgg19_trainable_true_best_model.h5')
|
| 27 |
+
|
| 28 |
+
size = (224, 224)
|
| 29 |
+
|
| 30 |
+
def main_page(clicked, label_names):
|
| 31 |
+
title = ims.change_title(clicked)
|
| 32 |
+
labs = ims.change_labels(clicked)
|
| 33 |
+
column1, column2 = st.columns(2)
|
| 34 |
+
holder_up = st.empty()
|
| 35 |
+
|
| 36 |
+
with column1:
|
| 37 |
+
st.write('')
|
| 38 |
+
uploaded_image = holder_up.file_uploader('')
|
| 39 |
+
|
| 40 |
+
holder_add_text = st.empty()
|
| 41 |
+
with column2:
|
| 42 |
+
additional_text = '' #holder_add_text.write('In order to estimate which is the classification of your image, drop your file at the left')
|
| 43 |
+
|
| 44 |
+
if uploaded_image:
|
| 45 |
+
#container = st.container()
|
| 46 |
+
add_tex = ims.additional_text_chart(clicked) #
|
| 47 |
+
st.write(add_tex)
|
| 48 |
+
result_texts = ims.result_text(clicked)
|
| 49 |
+
ims.resultados(uploaded_image, model, size, label_names, labs, result_texts)
|
| 50 |
+
#container.markdown(res)
|
| 51 |
+
holder_up.empty()
|
| 52 |
+
holder_add_text.empty()
|
model_subir/vgg19_trainable_true_best_model_pruebita.7z.001
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:b24b500eee027847902a749e52b08caed144349ae3044ffead4e9ff36843501f
|
| 3 |
+
size 10485760
|
model_subir/vgg19_trainable_true_best_model_pruebita.7z.002
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:72051dc3fd5f815781313644047ef4fbdee6625feb9cec76ea17347065d215e6
|
| 3 |
+
size 10485760
|
model_subir/vgg19_trainable_true_best_model_pruebita.7z.003
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:02a733afcdc588a21512b0d5c8a7d0ab105f2807c32aadf4cee3ec6f88c6d735
|
| 3 |
+
size 10485760
|
model_subir/vgg19_trainable_true_best_model_pruebita.7z.004
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:f52ab4c5ab2ec8ea1a14cc8381d95e70b499a6117c2198123b788c1eeb60375a
|
| 3 |
+
size 10485760
|
model_subir/vgg19_trainable_true_best_model_pruebita.7z.005
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:3bd79bcbc773070a48f0791b5548e254e561def11303c528a8ccf707280dca1b
|
| 3 |
+
size 10485760
|
model_subir/vgg19_trainable_true_best_model_pruebita.7z.006
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:69343f6e1a02629b049e9cdcf775ea71de32c3407c24aa2836838a3d1c0a020b
|
| 3 |
+
size 10485760
|
model_subir/vgg19_trainable_true_best_model_pruebita.7z.007
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:1f3617f5ce587fce7c9f1e1a8ca920d64ab842fab37d7129964842dafb142f8a
|
| 3 |
+
size 10485760
|
model_subir/vgg19_trainable_true_best_model_pruebita.7z.008
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:78f716ad325a9f642fe6044bb99ceb5bd32533244eb4524799b01f2178e80581
|
| 3 |
+
size 10485760
|
model_subir/vgg19_trainable_true_best_model_pruebita.7z.009
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:4b10cebf7e91070d38721c3f0d595f29ae445399c349501986fd71d2ff045aca
|
| 3 |
+
size 10485760
|
model_subir/vgg19_trainable_true_best_model_pruebita.7z.010
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:ec7996f448c8fec7be4f25dc180fad5f5364e6937da170a2db0c8ca973b45aaa
|
| 3 |
+
size 10485760
|
model_subir/vgg19_trainable_true_best_model_pruebita.7z.011
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:91e49ff13bcac7fcc80b20862c5debab4734a735f0c8e1037fd85af26f7bdb3d
|
| 3 |
+
size 10485760
|