markdown
stringlengths 0
1.02M
| code
stringlengths 0
832k
| output
stringlengths 0
1.02M
| license
stringlengths 3
36
| path
stringlengths 6
265
| repo_name
stringlengths 6
127
|
|---|---|---|---|---|---|
Helper-function for plotting images Function used to plot 9 images in a 3x3 grid, and writing the true and predicted classes below each image. | def plot_images(images, cls_true, cls_pred=None):
assert len(images) == len(cls_true) == 9
# Create figure with 3x3 sub-plots.
fig, axes = plt.subplots(3, 3)
fig.subplots_adjust(hspace=0.3, wspace=0.3)
for i, ax in enumerate(axes.flat):
# Plot image.
ax.imshow(images[i].reshape(img_shape), cmap='binary')
# Show true and predicted classes.
if cls_pred is None:
xlabel = "True: {0}".format(cls_true[i])
else:
xlabel = "True: {0}, Pred: {1}".format(cls_true[i], cls_pred[i])
ax.set_xlabel(xlabel)
# Remove ticks from the plot.
ax.set_xticks([])
ax.set_yticks([])
# Ensure the plot is shown correctly with multiple plots
# in a single Notebook cell.
plt.show() | _____no_output_____ | MIT | 01_Simple_Linear_Model.ipynb | Asciotti/TensorFlow-Tutorials |
Plot a few images to see if data is correct | # Get the first images from the test-set.
images = data.x_test[0:9]
# Get the true classes for those images.
cls_true = data.y_test_cls[0:9]
# Plot the images and labels using our helper-function above.
plot_images(images=images, cls_true=cls_true) | _____no_output_____ | MIT | 01_Simple_Linear_Model.ipynb | Asciotti/TensorFlow-Tutorials |
TensorFlow GraphThe entire purpose of TensorFlow is to have a so-called computational graph that can be executed much more efficiently than if the same calculations were to be performed directly in Python. TensorFlow can be more efficient than NumPy because TensorFlow knows the entire computation graph that must be executed, while NumPy only knows the computation of a single mathematical operation at a time.TensorFlow can also automatically calculate the gradients that are needed to optimize the variables of the graph so as to make the model perform better. This is because the graph is a combination of simple mathematical expressions so the gradient of the entire graph can be calculated using the chain-rule for derivatives.TensorFlow can also take advantage of multi-core CPUs as well as GPUs - and Google has even built special chips just for TensorFlow which are called TPUs (Tensor Processing Units) that are even faster than GPUs.A TensorFlow graph consists of the following parts which will be detailed below:* Placeholder variables used to feed input into the graph.* Model variables that are going to be optimized so as to make the model perform better.* The model which is essentially just a mathematical function that calculates some output given the input in the placeholder variables and the model variables.* A cost measure that can be used to guide the optimization of the variables.* An optimization method which updates the variables of the model.In addition, the TensorFlow graph may also contain various debugging statements e.g. for logging data to be displayed using TensorBoard, which is not covered in this tutorial. Placeholder variables Placeholder variables serve as the input to the graph that we may change each time we execute the graph. We call this feeding the placeholder variables and it is demonstrated further below.First we define the placeholder variable for the input images. This allows us to change the images that are input to the TensorFlow graph. This is a so-called tensor, which just means that it is a multi-dimensional vector or matrix. The data-type is set to `float32` and the shape is set to `[None, img_size_flat]`, where `None` means that the tensor may hold an arbitrary number of images with each image being a vector of length `img_size_flat`. | x = tf.placeholder(tf.float32, [None, img_size_flat]) | _____no_output_____ | MIT | 01_Simple_Linear_Model.ipynb | Asciotti/TensorFlow-Tutorials |
Next we have the placeholder variable for the true labels associated with the images that were input in the placeholder variable `x`. The shape of this placeholder variable is `[None, num_classes]` which means it may hold an arbitrary number of labels and each label is a vector of length `num_classes` which is 10 in this case. | y_true = tf.placeholder(tf.float32, [None, num_classes]) | _____no_output_____ | MIT | 01_Simple_Linear_Model.ipynb | Asciotti/TensorFlow-Tutorials |
Finally we have the placeholder variable for the true class of each image in the placeholder variable `x`. These are integers and the dimensionality of this placeholder variable is set to `[None]` which means the placeholder variable is a one-dimensional vector of arbitrary length. | y_true_cls = tf.placeholder(tf.int64, [None]) | _____no_output_____ | MIT | 01_Simple_Linear_Model.ipynb | Asciotti/TensorFlow-Tutorials |
Variables to be optimized Apart from the placeholder variables that were defined above and which serve as feeding input data into the model, there are also some model variables that must be changed by TensorFlow so as to make the model perform better on the training data.The first variable that must be optimized is called `weights` and is defined here as a TensorFlow variable that must be initialized with zeros and whose shape is `[img_size_flat, num_classes]`, so it is a 2-dimensional tensor (or matrix) with `img_size_flat` rows and `num_classes` columns. | weights = tf.Variable(tf.zeros([img_size_flat, num_classes])) | _____no_output_____ | MIT | 01_Simple_Linear_Model.ipynb | Asciotti/TensorFlow-Tutorials |
The second variable that must be optimized is called `biases` and is defined as a 1-dimensional tensor (or vector) of length `num_classes`. | biases = tf.Variable(tf.zeros([num_classes])) | _____no_output_____ | MIT | 01_Simple_Linear_Model.ipynb | Asciotti/TensorFlow-Tutorials |
Model This simple mathematical model multiplies the images in the placeholder variable `x` with the `weights` and then adds the `biases`.The result is a matrix of shape `[num_images, num_classes]` because `x` has shape `[num_images, img_size_flat]` and `weights` has shape `[img_size_flat, num_classes]`, so the multiplication of those two matrices is a matrix with shape `[num_images, num_classes]` and then the `biases` vector is added to each row of that matrix.Note that the name `logits` is typical TensorFlow terminology, but other people may call the variable something else. | logits = tf.matmul(x, weights) + biases | _____no_output_____ | MIT | 01_Simple_Linear_Model.ipynb | Asciotti/TensorFlow-Tutorials |
Now `logits` is a matrix with `num_images` rows and `num_classes` columns, where the element of the $i$'th row and $j$'th column is an estimate of how likely the $i$'th input image is to be of the $j$'th class.However, these estimates are a bit rough and difficult to interpret because the numbers may be very small or large, so we want to normalize them so that each row of the `logits` matrix sums to one, and each element is limited between zero and one. This is calculated using the so-called softmax function and the result is stored in `y_pred`. | y_pred = tf.nn.softmax(logits) | _____no_output_____ | MIT | 01_Simple_Linear_Model.ipynb | Asciotti/TensorFlow-Tutorials |
The predicted class can be calculated from the `y_pred` matrix by taking the index of the largest element in each row. | y_pred_cls = tf.argmax(y_pred, axis=1) | _____no_output_____ | MIT | 01_Simple_Linear_Model.ipynb | Asciotti/TensorFlow-Tutorials |
Cost-function to be optimized To make the model better at classifying the input images, we must somehow change the variables for `weights` and `biases`. To do this we first need to know how well the model currently performs by comparing the predicted output of the model `y_pred` to the desired output `y_true`.The cross-entropy is a performance measure used in classification. The cross-entropy is a continuous function that is always positive and if the predicted output of the model exactly matches the desired output then the cross-entropy equals zero. The goal of optimization is therefore to minimize the cross-entropy so it gets as close to zero as possible by changing the `weights` and `biases` of the model.TensorFlow has a built-in function for calculating the cross-entropy. Note that it uses the values of the `logits` because it also calculates the softmax internally. | cross_entropy = tf.nn.softmax_cross_entropy_with_logits_v2(logits=logits,
labels=y_true) | _____no_output_____ | MIT | 01_Simple_Linear_Model.ipynb | Asciotti/TensorFlow-Tutorials |
We have now calculated the cross-entropy for each of the image classifications so we have a measure of how well the model performs on each image individually. But in order to use the cross-entropy to guide the optimization of the model's variables we need a single scalar value, so we simply take the average of the cross-entropy for all the image classifications. | cost = tf.reduce_mean(cross_entropy) | _____no_output_____ | MIT | 01_Simple_Linear_Model.ipynb | Asciotti/TensorFlow-Tutorials |
Optimization method Now that we have a cost measure that must be minimized, we can then create an optimizer. In this case it is the basic form of Gradient Descent where the step-size is set to 0.5.Note that optimization is not performed at this point. In fact, nothing is calculated at all, we just add the optimizer-object to the TensorFlow graph for later execution. | optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.5).minimize(cost) | _____no_output_____ | MIT | 01_Simple_Linear_Model.ipynb | Asciotti/TensorFlow-Tutorials |
Performance measures We need a few more performance measures to display the progress to the user.This is a vector of booleans whether the predicted class equals the true class of each image. | correct_prediction = tf.equal(y_pred_cls, y_true_cls) | _____no_output_____ | MIT | 01_Simple_Linear_Model.ipynb | Asciotti/TensorFlow-Tutorials |
This calculates the classification accuracy by first type-casting the vector of booleans to floats, so that False becomes 0 and True becomes 1, and then calculating the average of these numbers. | accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32)) | _____no_output_____ | MIT | 01_Simple_Linear_Model.ipynb | Asciotti/TensorFlow-Tutorials |
TensorFlow Run Create TensorFlow sessionOnce the TensorFlow graph has been created, we have to create a TensorFlow session which is used to execute the graph. | session = tf.Session() | _____no_output_____ | MIT | 01_Simple_Linear_Model.ipynb | Asciotti/TensorFlow-Tutorials |
Initialize variablesThe variables for `weights` and `biases` must be initialized before we start optimizing them. | session.run(tf.global_variables_initializer()) | _____no_output_____ | MIT | 01_Simple_Linear_Model.ipynb | Asciotti/TensorFlow-Tutorials |
Helper-function to perform optimization iterations There are 55.000 images in the training-set. It takes a long time to calculate the gradient of the model using all these images. We therefore use Stochastic Gradient Descent which only uses a small batch of images in each iteration of the optimizer. | batch_size = 100 | _____no_output_____ | MIT | 01_Simple_Linear_Model.ipynb | Asciotti/TensorFlow-Tutorials |
Function for performing a number of optimization iterations so as to gradually improve the `weights` and `biases` of the model. In each iteration, a new batch of data is selected from the training-set and then TensorFlow executes the optimizer using those training samples. | def optimize(num_iterations):
for i in range(num_iterations):
# Get a batch of training examples.
# x_batch now holds a batch of images and
# y_true_batch are the true labels for those images.
x_batch, y_true_batch, _ = data.random_batch(batch_size=batch_size)
# Put the batch into a dict with the proper names
# for placeholder variables in the TensorFlow graph.
# Note that the placeholder for y_true_cls is not set
# because it is not used during training.
feed_dict_train = {x: x_batch,
y_true: y_true_batch}
# Run the optimizer using this batch of training data.
# TensorFlow assigns the variables in feed_dict_train
# to the placeholder variables and then runs the optimizer.
session.run(optimizer, feed_dict=feed_dict_train) | _____no_output_____ | MIT | 01_Simple_Linear_Model.ipynb | Asciotti/TensorFlow-Tutorials |
Helper-functions to show performance Dict with the test-set data to be used as input to the TensorFlow graph. Note that we must use the correct names for the placeholder variables in the TensorFlow graph. | feed_dict_test = {x: data.x_test,
y_true: data.y_test,
y_true_cls: data.y_test_cls} | _____no_output_____ | MIT | 01_Simple_Linear_Model.ipynb | Asciotti/TensorFlow-Tutorials |
Function for printing the classification accuracy on the test-set. | def print_accuracy():
# Use TensorFlow to compute the accuracy.
acc = session.run(accuracy, feed_dict=feed_dict_test)
# Print the accuracy.
print("Accuracy on test-set: {0:.1%}".format(acc)) | _____no_output_____ | MIT | 01_Simple_Linear_Model.ipynb | Asciotti/TensorFlow-Tutorials |
Function for printing and plotting the confusion matrix using scikit-learn. | def print_confusion_matrix():
# Get the true classifications for the test-set.
cls_true = data.y_test_cls
# Get the predicted classifications for the test-set.
cls_pred = session.run(y_pred_cls, feed_dict=feed_dict_test)
# Get the confusion matrix using sklearn.
cm = confusion_matrix(y_true=cls_true,
y_pred=cls_pred)
# Print the confusion matrix as text.
print(cm)
# Plot the confusion matrix as an image.
plt.imshow(cm, interpolation='nearest', cmap=plt.cm.Blues, norm=LogNorm())
# Make various adjustments to the plot.
plt.tight_layout()
plt.colorbar()
tick_marks = np.arange(num_classes)
plt.xticks(tick_marks, range(num_classes))
plt.yticks(tick_marks, range(num_classes))
plt.xlabel('Predicted')
plt.ylabel('True')
# Ensure the plot is shown correctly with multiple plots
# in a single Notebook cell.
plt.show() | _____no_output_____ | MIT | 01_Simple_Linear_Model.ipynb | Asciotti/TensorFlow-Tutorials |
Function for plotting examples of images from the test-set that have been mis-classified. | def plot_example_errors():
# Use TensorFlow to get a list of boolean values
# whether each test-image has been correctly classified,
# and a list for the predicted class of each image.
correct, cls_pred = session.run([correct_prediction, y_pred_cls],
feed_dict=feed_dict_test)
# Negate the boolean array.
incorrect = (correct == False)
# Get the images from the test-set that have been
# incorrectly classified.
images = data.x_test[incorrect]
# Get the predicted classes for those images.
cls_pred = cls_pred[incorrect]
# Get the true classes for those images.
cls_true = data.y_test_cls[incorrect]
# Plot the first 9 images.
plot_images(images=images[0:9],
cls_true=cls_true[0:9],
cls_pred=cls_pred[0:9]) | _____no_output_____ | MIT | 01_Simple_Linear_Model.ipynb | Asciotti/TensorFlow-Tutorials |
Helper-function to plot the model weights Function for plotting the `weights` of the model. 10 images are plotted, one for each digit that the model is trained to recognize. | def plot_weights():
# Get the values for the weights from the TensorFlow variable.
w = session.run(weights)
# Get the lowest and highest values for the weights.
# This is used to correct the colour intensity across
# the images so they can be compared with each other.
w_min = np.min(w)
w_max = np.max(w)
# Create figure with 3x4 sub-plots,
# where the last 2 sub-plots are unused.
fig, axes = plt.subplots(3, 4)
fig.subplots_adjust(hspace=0.3, wspace=0.3)
for i, ax in enumerate(axes.flat):
# Only use the weights for the first 10 sub-plots.
if i<10:
# Get the weights for the i'th digit and reshape it.
# Note that w.shape == (img_size_flat, 10)
image = w[:, i].reshape(img_shape)
# Set the label for the sub-plot.
ax.set_xlabel("Weights: {0}".format(i))
# Plot the image.
ax.imshow(image, vmin=w_min, vmax=w_max, cmap='seismic')
# Remove ticks from each sub-plot.
ax.set_xticks([])
ax.set_yticks([])
# Ensure the plot is shown correctly with multiple plots
# in a single Notebook cell.
plt.show() | _____no_output_____ | MIT | 01_Simple_Linear_Model.ipynb | Asciotti/TensorFlow-Tutorials |
Performance before any optimizationThe accuracy on the test-set is 9.8%. This is because the model has only been initialized and not optimized at all, so it always predicts that the image shows a zero digit, as demonstrated in the plot below, and it turns out that 9.8% of the images in the test-set happens to be zero digits. | print_accuracy()
plot_example_errors() | _____no_output_____ | MIT | 01_Simple_Linear_Model.ipynb | Asciotti/TensorFlow-Tutorials |
Performance after 1 optimization iterationAlready after a single optimization iteration, the model has increased its accuracy on the test-set significantly. | optimize(num_iterations=1)
print_accuracy()
plot_example_errors() | _____no_output_____ | MIT | 01_Simple_Linear_Model.ipynb | Asciotti/TensorFlow-Tutorials |
The weights can also be plotted as shown below. Positive weights are red and negative weights are blue. These weights can be intuitively understood as image-filters.For example, the weights used to determine if an image shows a zero-digit have a positive reaction (red) to an image of a circle, and have a negative reaction (blue) to images with content in the centre of the circle.Similarly, the weights used to determine if an image shows a one-digit react positively (red) to a vertical line in the centre of the image, and react negatively (blue) to images with content surrounding that line.Note that the weights mostly look like the digits they're supposed to recognize. This is because only one optimization iteration has been performed so the weights are only trained on 100 images. After training on several thousand images, the weights become more difficult to interpret because they have to recognize many variations of how digits can be written. | plot_weights() | _____no_output_____ | MIT | 01_Simple_Linear_Model.ipynb | Asciotti/TensorFlow-Tutorials |
Performance after 10 optimization iterations | # We have already performed 1 iteration.
optimize(num_iterations=9)
print_accuracy()
plot_example_errors()
plot_weights() | _____no_output_____ | MIT | 01_Simple_Linear_Model.ipynb | Asciotti/TensorFlow-Tutorials |
Performance after 1000 optimization iterationsAfter 1000 optimization iterations, the model only mis-classifies about one in ten images. As demonstrated below, some of the mis-classifications are justified because the images are very hard to determine with certainty even for humans, while others are quite obvious and should have been classified correctly by a good model. But this simple model cannot reach much better performance and more complex models are therefore needed. | # We have already performed 10 iterations.
optimize(num_iterations=990)
print_accuracy()
plot_example_errors() | _____no_output_____ | MIT | 01_Simple_Linear_Model.ipynb | Asciotti/TensorFlow-Tutorials |
The model has now been trained for 1000 optimization iterations, with each iteration using 100 images from the training-set. Because of the great variety of the images, the weights have now become difficult to interpret and we may doubt whether the model truly understands how digits are composed from lines, or whether the model has just memorized many different variations of pixels. | plot_weights() | _____no_output_____ | MIT | 01_Simple_Linear_Model.ipynb | Asciotti/TensorFlow-Tutorials |
We can also print and plot the so-called confusion matrix which lets us see more details about the mis-classifications. For example, it shows that images actually depicting a 5 have sometimes been mis-classified as all other possible digits, but mostly as 6 or 8. | print_confusion_matrix() | [[ 956 0 3 1 1 4 11 3 1 0]
[ 0 1114 2 2 1 2 4 2 8 0]
[ 6 8 925 23 11 3 13 12 26 5]
[ 3 1 19 928 0 34 2 10 5 8]
[ 1 3 4 2 918 2 11 2 6 33]
[ 8 3 7 36 8 781 15 6 20 8]
[ 9 3 5 1 14 12 912 1 1 0]
[ 2 11 24 10 6 1 0 941 1 32]
[ 8 13 11 44 11 52 13 14 797 11]
[ 11 7 2 14 50 10 0 30 4 881]]
| MIT | 01_Simple_Linear_Model.ipynb | Asciotti/TensorFlow-Tutorials |
We are now done using TensorFlow, so we close the session to release its resources. | # This has been commented out in case you want to modify and experiment
# with the Notebook without having to restart it.
# session.close() | _____no_output_____ | MIT | 01_Simple_Linear_Model.ipynb | Asciotti/TensorFlow-Tutorials |
Modelling trend life cycles in scientific research**Authors:** E. Tattershall, G. Nenadic, and R.D. Stevens**Abstract:** Scientific topics vary in popularity over time. In this paper, we model the life-cycles of 200 topics by fitting the Logistic and Gompertz models to their frequency over time in published abstracts. Unlike other work, the topics we use are algorithmically extracted from large datasets of abstracts covering computer science, particle physics, cancer research, and mental health. We find that the Gompertz model produces lower median error, leading us to conclude that it is the more appropriate model. Since the Gompertz model is asymmetric, with a steep rise followed a long tail, this implies that scientific topics follow a similar trajectory. We also explore the case of double-peaking curves and find that in some cases, topics will peak multiple times as interest resurges. Finally, when looking at the different scientific disciplines, we find that the lifespan of topics is longer in some disciplines (e.g. cancer research and mental health) than it is others, which may indicate differences in research process and culture between these disciplines. **Requirements**- Data. Data ingress is excluded from this notebook, but we alraedy have four large datasets of abstracts. The documents in these datasets have been cleaned (described in sections below) and separated by year. Anecdotally, this method works best when there are >100,000 documents in the dataset (and more is even better).- The other utility files in this directory, including burst_detection.py, my_stopwords.py, etc...**In this notebook** - Vectorisation- Burst detection- Clustering- Model fitting- Comparing the error of the two models- Calculating trend duration - Double peaked curves- Trends and fitted models in full | import os
import csv
import pandas as pd
from collections import defaultdict
import matplotlib.pyplot as plt
from matplotlib.ticker import FormatStrFormatter
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.feature_extraction.text import TfidfTransformer
import numpy as np
import scipy
from scipy.spatial.distance import squareform
from scipy.cluster import hierarchy
import pickle
import burst_detection
import my_stopwords
import cleaning
import tools
import logletlab
import scipy.optimize as opt
from sklearn.metrics import mean_squared_error
stop = my_stopwords.get_stopwords()
burstiness_threshold = 0.004
cluster_distance_threshold = 7
# Burst detection internal parameters
# These are the same as in our earlier paper [Tattershall 2020]
parameters = {
"min_yearly_df": 5,
"significance_threshold": 0.0015,
"years_above_significance": 3,
"long_ma_length": 8,
"short_ma_length": 4,
"signal_line_ma": 3,
"significance_ma_length": 3
}
# Number of bursty terms to extract for each dataset. This will later be filtered down to 50 for each dataset after clustering.
max_bursts = 300
dataset_names = ['pubmed_mh', 'arxiv_hep', 'pubmed_cancer', 'dblp_cs']
dataset_titles = ['Computer science (dblp)', 'Particle physics (arXiv)', 'Mental health (PubMed)', 'Cancer (PubMed)']
datasets = {}
def reverse_cumsum(ls):
reverse = np.zeros_like(ls)
for i in range(len(ls)):
if i == 0:
reverse[i] = ls[i]
else:
reverse[i] = ls[i]-ls[i-1]
if reverse[0]>reverse[1]:
reverse[0]=reverse[1]
return reverse
def detransform_fit(ypc, F, dataset_name):
'''
The Gompertz and Logistic curves actually model *cumulative* frequency over time, not raw frequency.
However, raw frequency is more intuitive for graphs, so we use this function to change a cumulative
time series into a non-cumulative one. Additionally, the models were originally fitted to scaled curves
(such that the minumum frequency was zero and the maximum was one). This was done to make it possible to
directly compare the error between different time series without a much more frequent term dwarfing the calculation.
We now transform back.
'''
s = document_count_per_year[dataset_name]
yf = reverse_cumsum(F*(max(ypc)-min(ypc)) + min(ypc))
return yf
# Location where the cleaned data is stored
data_root = 'cleaned_data/'
# Location where we will store the results of this notebook
root = 'results/'
os.mkdir(root+'clusters')
os.mkdir(root+'images')
os.mkdir(root+'fitted_curves')
os.mkdir(root+'vectors')
for dataset_name in dataset_names:
os.mkdir(root+'vectors/'+dataset_name)
os.mkdir(root+'fitted_curves/'+dataset_name) | _____no_output_____ | MIT | Modelling trend life cycles in scientific research.ipynb | etattershall/trend-lifecycles |
The dataWe have four datasets:- **Computer Science (dblp_cs):** This dataset contains 2.6 million abstracts downloaded from Semantic Scholar. We select all abstracts with the dblp tag.- **Particle Physics (arxiv_hep):** This dataset of 0.2 million abstracts was downloaded from arXiv's public API. We extracted particle physics-reladed documents by selecting everything under the categroies hep-ex, hep-lat, hep-ph and hep-th.- **Mental Health (pubmed_mh):** 0.7 million abstracts downloaded from PubMed. This dataset was created by filtering on the MeSH keyword "Mental Health" and all its subterms.- **Cancer (pubmed_cancer):** 1.9 million abstracts downloaded from PubMed. This dataset was created by filtering on the MeSH keyword "Neoplasms" and all its subterms.The data in each dataset has already been cleaned. We removed punctuation, set all characters to lowercase and lemmatised each word using WordNetLemmatizer. The cleaned data is stored in pickled pandas dataframes in files named 1988.p, 1989.p, 1990.p. Each dataframe has a column "cleaned" which contains the cleaned and lemmatized text for each document in that dataset in the given year. How many documents are in each dataset in each year? | document_count_per_year = {}
for dataset_name in dataset_names:
# For each dataset, we want a list of document counts for each year
document_count_per_year[dataset_name] = []
# The files in the directory are named 1988.p, 1989.p, 1990.p....
files = os.listdir(data_root+dataset_name)
min_year = np.min([int(file[0:4]) for file in files])
max_year = np.max([int(file[0:4]) for file in files])
for year in range(min_year, max_year+1):
df = pickle.load(open(data_root+dataset_name+'/'+str(year)+'.p', "rb"))
document_count_per_year[dataset_name].append(len(df))
pickle.dump(document_count_per_year, open(root + 'document_count_per_year.p', "wb"))
plt.figure(figsize=(6,3.7))
ax1=plt.subplot(111)
plt.subplots_adjust(left=0.2, right=0.9)
ax1.set_title('Documents per year in each dataset', fontsize=11)
ax1.plot(np.arange(1988, 2018), document_count_per_year['dblp_cs'], 'k', label='dblp')
ax1.plot(np.arange(1994, 2018), document_count_per_year['arxiv_hep'], 'k', linestyle= '-.', label='arXiv')
ax1.plot(np.arange(1975, 2018), document_count_per_year['pubmed_mh'], 'k', linestyle= '--', label='PubMed (Mental Health)')
ax1.plot(np.arange(1975, 2018), document_count_per_year['pubmed_cancer'], 'k', linestyle= ':', label='PubMed (Cancer)')
ax1.grid()
ax1.set_xlim([1975, 2018])
ax1.set_ylabel('Documents', fontsize=10)
ax1.set_xlabel('Year', fontsize=10)
ax1.set_ylim([0,200000])
ax1.legend(fontsize=10)
plt.savefig(root+'images/documents_per_year.eps', format='eps', dpi=1200) | _____no_output_____ | MIT | Modelling trend life cycles in scientific research.ipynb | etattershall/trend-lifecycles |
Create a vocabulary for each dataset- For each dataset, we find all **1-5 word terms** (after stopwords are removed). This allows us to use relatively complex phrases.- Since the set of all 1-5 word terms is very large and contains much noise, we filter out terms that fail to meet a **minimum threshold of "significance"**. For significance we require that they occur at least six times in at least one year. We find that this also gets rid of spelling erros and cuts down the size of the data. | for dataset_name in dataset_names:
vocabulary = set()
files = os.listdir(data_root+dataset_name)
min_year = np.min([int(file[0:4]) for file in files])
max_year = np.max([int(file[0:4]) for file in files])
for year in range(min_year, max_year+1):
df = pickle.load(open(data_root+dataset_name+"/"+str(year)+".p", "rb"))
# Create an initial vocabulary based on the list of text files
vectorizer = CountVectorizer(strip_accents='ascii',
ngram_range=(1,5),
stop_words=stop,
min_df=6
)
# Vectorise the data in order to get the vocabulary
vector = vectorizer.fit_transform(df['cleaned'])
# Add the harvested vocabulary to the set. This removes duplicates of terms that occur in multiple years
vocabulary = vocabulary.union(set(vectorizer.vocabulary_))
# To conserve memory, delete the vector here
del vector
print('Overall vocabulary created for ', dataset_name)
# We now vectorise the dataset again based on the unifying vocabulary
vocabulary = list(vocabulary)
vectors = []
vectorizer = CountVectorizer(strip_accents='ascii',
ngram_range=(1,5),
stop_words=stop,
vocabulary=vocabulary)
for year in range(min_year, max_year+1):
df = pickle.load(open(data_root+dataset_name+"/"+str(year)+".p", "rb"))
vector = vectorizer.fit_transform(df['cleaned'])
# Set all elements of the vector that are greater than 1 to 1. This is because we only care about
# the overall document frequency of each term. If a word is used multiple times in a single document
# it only contributes 1 to the document frequency.
vector[vector>1] = 1
# Sum the vector along its columns in order to get the total document frequency of each term in a year
summed = np.squeeze(np.asarray(np.sum(vector, axis=0)))
vectors.append(summed)
# Turn the vector into a pandas dataframe
df = pd.DataFrame(vectors, columns=vocabulary)
# THE PART BELOW IS OPTIONAL
# We found that the process works better if very similar terms are removed from the vocabulary
# Therefore, for each 2-5 ngram, we identify all possible subterms, then attempt to calculate whether
# the subterms are legitimate terms in their own right (i.e. they appear in documents without their
# superterm parent). For example, the term "long short-term memory" is made up of the subterms
# ["long short", "short term", "term memory", "long short term", "short term memory"]
# However, when we calculate the document frequency of each subterm divided by the document frequency of
# "long short term memory", we find:
#
# long short 1.4
# short term 6.1
# term memory 2.2
# long short term 1.1
# short term memory 1.4
#
# Since the term "long short term" occurs only very rarely outside the phrase "long short term memory", we
# omit this term by setting an arbitrary threshold of 1.1. This preserves most of the subterms while removing the rarest.
removed = []
# for each term in the vocabulary
for i, term in enumerate(list(df.columns)):
# If the term is a 2-5 ngram (i.e. not a single word)
if ' ' in term:
# Find the overall term document frequency over the entire dataset
term_total_document_frequency = df[term].sum()
# Find all possible subterms of the term.
subterms = tools.all_subterms(term)
for subterm in subterms:
try:
# If the subterm is in the vocabulary, check whether it often occurs on its own
# without the superterm being present
subterm_total_document_frequency = df[subterm].sum()
if subterm_total_document_frequency < term_total_document_frequency*1.1:
removed.append([subterm, term])
except:
pass
# Remove the removed terms from the dataframe
df = df.drop(list(set([r[0] for r in removed])), axis=1)
# END OPTIONAL PART
# Store the stacked vectors for later use
pickle.dump(df, open(root+'vectors/'+dataset_name+"/stacked_vector.p", "wb"))
pickle.dump(list(df.columns), open(root+'vectors/'+dataset_name+"/vocabulary.p", "wb")) | Overall vocabulary created for arxiv_hep
| MIT | Modelling trend life cycles in scientific research.ipynb | etattershall/trend-lifecycles |
Detect bursty termsNow that we have vectors representing the document frequency of each term over time, we can use our MACD-based burst detection, as described in our earlier paper [Tattershall 2020]. | bursts = dict()
for dataset_name in dataset_names:
files = os.listdir(data_root+dataset_name)
min_year = np.min([int(file[0:4]) for file in files])
max_year = np.max([int(file[0:4]) for file in files])
# Create a dataset object for the burst detection algorithm
bd_dataset = burst_detection.Dataset(
name = dataset_name,
years = (min_year, max_year),
# We divide the term-document frequency for each year by the number of documents in that year
stacked_vectors = pickle.load(open(root+dataset_name+"/stacked_vector.p", "rb")).divide(document_count_per_year[dataset_name],axis=0)
)
# We apply the significance threshold from the burst detection methodology. This cuts the size of the dataset by
# removing terms that occur only in one year
bd_dataset.get_sig_stacked_vectors(parameters["significance_threshold"], parameters["years_above_significance"])
bd_dataset.get_burstiness(parameters["short_ma_length"], parameters["long_ma_length"], parameters["significance_ma_length"], parameters["signal_line_ma"])
datasets[dataset_name] = bd_dataset
bursts[dataset_name] = tools.get_top_n_bursts(datasets[dataset_name].burstiness, max_bursts)
pickle.dump(bursts, open(root+'vectors/'+'bursts.p', "wb")) | _____no_output_____ | MIT | Modelling trend life cycles in scientific research.ipynb | etattershall/trend-lifecycles |
Calculate burst co-occurence We now have 300 bursts per dataset. Some of these describe very similar concepts, such as "internet of things" and "iot". The purpose of this section is the merge similar terms into clusters to prevent redundancy within the dataset. We calculate the relatedness of terms using term co-occurrence within the same document (terms that appear together are grouped together). | for dataset_name in dataset_names:
vectors = []
vectorizer = CountVectorizer(strip_accents='ascii',
ngram_range=(1,5),
stop_words=stop,
vocabulary=bursts[dataset_name])
for year in range(min_year, max_year+1):
df = pickle.load(open(data_root+dataset_name+"/"+str(year)+".p", "rb"))
vector = vectorizer.fit_transform(df['cleaned'])
# Set all elements of the vector that are greater than 1 to 1. This is because we only care about
# the overall document frequency of each term. If a word is used multiple times in a single document
# it only contributes 1 to the document frequency.
vector[vector>1] = 1
vectors.append(vector)
# Calculate the cooccurrence matrix
v = vectors[0]
c = v.T*v
c.setdiag(0)
c = c.todense()
cooccurrence = c
for v in vectors[1:]:
c = v.T*v
c.setdiag(0)
c = c.toarray()
cooccurrence += c
pickle.dump(cooccurrence, open(root+'vectors/'+dataset_name+"/cooccurrence_matrix.p", "wb")) | C:\Users\emmat\Anaconda3\lib\site-packages\scipy\sparse\_index.py:126: SparseEfficiencyWarning: Changing the sparsity structure of a csc_matrix is expensive. lil_matrix is more efficient.
self._set_arrayXarray(i, j, x)
C:\Users\emmat\Anaconda3\lib\site-packages\scipy\sparse\_index.py:126: SparseEfficiencyWarning: Changing the sparsity structure of a csc_matrix is expensive. lil_matrix is more efficient.
self._set_arrayXarray(i, j, x)
| MIT | Modelling trend life cycles in scientific research.ipynb | etattershall/trend-lifecycles |
Use burst co-occurrence to cluster termsWe use a hierarchichal clustering method to group terms together. This is highly customisable due to threshold setting, allowing us to group more or less conservatively if required. | # Reload bursts if required by uncommenting this line
#bursts = pickle.load(open(root+'bursts.p', "rb"))
dataset_clusters = dict()
for dataset_name in dataset_names:
#cooccurrence = pickle.load(open('Data/stacked_vectors/'+dataset_name+"/cooccurrence_matrix.p", "rb"))
# Translate co-occurence into a distance
dists = np.log(cooccurrence+1).max()- np.log(cooccurrence+1)
# Remove the diagonal (squareform requires diagonals be zero)
dists -= np.diag(np.diagonal(dists))
# Put the distance matrix into the format required by hierachy.linkage
flat_dists = squareform(dists)
# Get the linkage matrix
linkage_matrix = hierarchy.linkage(flat_dists, "ward")
assignments = hierarchy.fcluster(linkage_matrix, t=cluster_distance_threshold, criterion='distance')
clusters = defaultdict(list)
for term, assign, co in zip(bursts[dataset_name], assignments, cooccurrence):
clusters[assign].append(term)
dataset_clusters[dataset_name] = list(clusters.values())
dataset_clusters['arxiv_hep'] | _____no_output_____ | MIT | Modelling trend life cycles in scientific research.ipynb | etattershall/trend-lifecycles |
Manual choice of clustersWe now sort the clusters in order of burstiness (using the burstiness of the most bursty term in the cluster) and manually exclude clusters that include publishing artefacts such as "elsevier science bv right reserved". From the remainder, we select the top fifty. We do this for all four datasets, giving 200 clusters. The selected clusters are stored in the file "200clusters.csv". For each cluster, create a time series of mentions in abstracts over timeWe now need to search for the clusters to pull out the frequency of appearance in abstracts over time. For the cluster ["Internet of things", "IoT"], all abstracts that mention **either** term are included (i.e. an abstract that uses "Internet of things" without the abbreviation "IoT" still counts towards the total for that year). We take document frequency, not term frequency, so the number of times the terms are mentioned in each document do not matter, so long as they are mentioned once. | raw_clusters = pd.read_csv('200clusters.csv')
cluster_dict = defaultdict(list)
for dataset_name in dataset_names:
for raw_cluster in raw_clusters[dataset_name]:
cluster_dict[dataset_name].append(raw_cluster.split(','))
for dataset_name in dataset_names:
# List all the cluster terms. This will be more than the total number of clusters.
all_cluster_terms = sum(cluster_dict[dataset_name], [])
# Get the cluster titles. This is the list of terms in each cluster
all_cluster_titles = [','.join(cluster) for cluster in cluster_dict[dataset_name]]
# Get a list of files from the directory
files = os.listdir(data_root + dataset_name)
# This is where we will store the data. The columns correspond to clusters, the rows to years
prevalence_array = np.zeros([len(files),len(cluster_dict[dataset_name])])
# Open each year file in turn
for i, file in enumerate(files):
print(file)
year_data = pickle.load(open(data_root + dataset_name + '/' + file, 'rb'))
# Vectorise the data for that year
vectorizer = CountVectorizer(strip_accents='ascii',
ngram_range=(1,5),
stop_words=stop,
vocabulary=all_cluster_terms
)
vector = vectorizer.fit_transform(year_data['cleaned'])
# Get the index of each cluster term. This will allows us to map the full vocabulary
# e.g. (60 items) back onto the original clusters (e.g. 50 items)
for j, cluster in enumerate(cluster_dict[dataset_name]):
indices = []
for term in cluster:
indices.append(all_cluster_terms.index(term))
# If there are multiple terms in a cluster, sum the cluster columns together
summed_column = np.squeeze(np.asarray(vector[:,indices].sum(axis=1).flatten()))
# Set any element greater than one to one--we're only counting documents here, not
# total occurrences
summed_column[summed_column!=0] = 1
# This is the total number of occurrences of the cluster per year
prevalence_array[i, j] = np.sum(summed_column)
# Save the data
df = pd.DataFrame(data=prevalence_array, index=[f[0:4] for f in files], columns=all_cluster_titles)
pickle.dump(df, open(root+'clusters/'+dataset_name+'.p', 'wb')) | 1994.p
1995.p
1996.p
1997.p
1998.p
1999.p
2000.p
2001.p
2002.p
2003.p
2004.p
2005.p
2006.p
2007.p
2008.p
2009.p
2010.p
2011.p
2012.p
2013.p
2014.p
2015.p
2016.p
2017.p
| MIT | Modelling trend life cycles in scientific research.ipynb | etattershall/trend-lifecycles |
Curve fittingThe below is a pythonic version of the Loglet Lab 4 code found at https://github.com/pheguest/logletlab4. Loglet Lab also has a web interface at https://logletlab.com/ which allows you to create amazing graphs. However, the issue with the web interface is that it is not designed for processing hundreds of time series, and in order to do this, each time series must be laboriously copy-pasted into the input box, the parameters set, and then the results saved individually. With 200 time series and multiple parameter sets, this process is quite slow! Therefore, we have adapted the code from the github repository, but the original should be seen at https://github.com/pheguest/logletlab4/blob/master/javascript/src/psmlogfunc3.js. | curve_header_1 = ['', 'd', 'k', 'a', 'b', 'RMS']
curve_header_2 = ['', 'd', 'k1', 'a1', 'b1', 'k2', 'a2', 'b2', 'RMS']
dataset_names = ['arxiv_hep', 'pubmed_mh', 'pubmed_cancer', 'dblp_cs']
for dataset_name in dataset_names:
print('-'*50)
print(dataset_name.upper())
for curve_type in ['logistic', 'gompertz']:
for number_of_peaks in [1, 2]:
with open('our_loglet_lab/'+dataset_name+'/'+curve_type+str(number_of_peaks)+'.csv', 'w', newline='') as f:
writer = csv.writer(f)
if number_of_peaks == 1:
writer.writerow(curve_header_1)
elif number_of_peaks == 2:
writer.writerow(curve_header_2)
df = pickle.load(open(root+'clusters/'+dataset_name+'.p', 'rb'))
document_count_per_year = pickle.load(open(root+"/document_count_per_year.p", 'rb'))[dataset_name]
df = df.divide(document_count_per_year, axis=0)
for term in df.keys():
y = tools.normalise_time_series(df[term].cumsum())
x = np.array([int(i) for i in y.index])
y = y.values
if number_of_peaks == 1:
logobj = logletlab.LogObj(x, y, 1)
constraints = logletlab.estimate_constraints(x, y, 1)
if curve_type == 'logistic':
logobj = logletlab.loglet_MC_anneal_regression(logobj, constraints=constraints, number_of_loglets=1,
curve_type='logistic', anneal_iterations=20,
mc_iterations=1000, anneal_sample_size=100)
else:
logobj = logletlab.loglet_MC_anneal_regression(logobj, constraints=constraints, number_of_loglets=1,
curve_type='gompertz', anneal_iterations=20,
mc_iterations=1000, anneal_sample_size=100)
line = [term, logobj.parameters['d'], logobj.parameters['k'][0], logobj.parameters['a'][0], logobj.parameters['b'][0], logobj.energy_best]
print(curve_type, number_of_peaks, term, 'RMSE='+str(np.round(logobj.energy_best,3)))
with open(root+'fitted_curves/'+dataset_name+'/'+curve_type+'_single.csv', 'a', newline='') as f:
writer = csv.writer(f)
writer.writerow(line)
elif number_of_peaks == 2:
logobj = logletlab.LogObj(x, y, 2)
constraints = logletlab.estimate_constraints(x, y, 2)
if curve_type == 'logistic':
logobj = logletlab.loglet_MC_anneal_regression(logobj, constraints=constraints, number_of_loglets=2,
curve_type='logistic', anneal_iterations=30,
mc_iterations=1000, anneal_sample_size=100)
else:
logobj = logletlab.loglet_MC_anneal_regression(logobj, constraints=constraints, number_of_loglets=2,
curve_type='gompertz', anneal_iterations=30,
mc_iterations=1000, anneal_sample_size=100)
line = [term, logobj.parameters['d'],
logobj.parameters['k'][0],
logobj.parameters['a'][0],
logobj.parameters['b'][0],
logobj.parameters['k'][1],
logobj.parameters['a'][1],
logobj.parameters['b'][1],
logobj.energy_best]
print(curve_type, number_of_peaks, term, 'RMSE='+str(np.round(logobj.energy_best,3)))
with open(root+'fitted_curves/'+dataset_name+'/'+curve_type+'_double.csv', 'a', newline='') as f:
writer = csv.writer(f)
writer.writerow(line) | --------------------------------------------------
ARXIV_HEP
logistic_single 1 125 gev 0.029907304762336263
logistic_single 1 pentaquark,pentaquarks 0.05043852824061915
logistic_single 1 wmap,wilkinson microwave anisotropy probe 0.0361380293123339
logistic_single 1 lhc run 0.020735398919035756
logistic_single 1 pamela 0.03204821466738317
logistic_single 1 lattice gauge 0.05233359007692712
logistic_single 1 tensor scalar ratio 0.036222971357601726
logistic_single 1 brane,branes 0.03141774013518978
logistic_single 1 atlas 0.01772382630535608
logistic_single 1 horava lifshitz,hovrava lifshitz 0.0410067585251185
logistic_single 1 lhc 0.006250825571034508
logistic_single 1 noncommutative,noncommutativity,non commutative,non commutativity 0.0327322808924473
logistic_single 1 black hole 0.020920939530327295
logistic_single 1 anomalous magnetic moment 0.04849255402257149
logistic_single 1 unparticle,unparticles 0.03351932242115829
logistic_single 1 superluminal 0.061748625288615105
logistic_single 1 m2 brane,m2 branes 0.039234821323279774
logistic_single 1 126 gev 0.018070446841532847
logistic_single 1 pp wave 0.047137089087624366
logistic_single 1 lambert 0.05871943152044709
logistic_single 1 tevatron 0.029469013159021687
logistic_single 1 higgs 0.034682515257204394
logistic_single 1 brane world 0.04485319867543418
logistic_single 1 extra dimension 0.03224289656019876
logistic_single 1 entropic 0.0366547700230139
logistic_single 1 kamland 0.05184286069114554
logistic_single 1 solar neutrino 0.02974273300483687
logistic_single 1 neutrino oscillation 0.04248474035767032
logistic_single 1 chern simon 0.027993037580545155
logistic_single 1 forward backward asymmetry 0.03979258482645767
logistic_single 1 dark energy 0.02603752198898685
logistic_single 1 bulk 0.029266519583018107
logistic_single 1 holographic 0.011123961217499157
logistic_single 1 international linear collider,ilc 0.04251997867004988
logistic_single 1 abjm 0.030827697912680977
logistic_single 1 babar 0.028343579032827054
logistic_single 1 daya bay 0.029215246675232537
logistic_single 1 sqrts7 tev 0.03478725079571082
logistic_single 1 130 gev 0.06940321757501901
logistic_single 1 20point3 0.041470794660599566
logistic_single 1 string field theory 0.03574859058388444
logistic_single 1 metastable vacuum 0.03939929585683627
logistic_single 1 gravitational wave 0.03579099579072222
logistic_single 1 belle 0.040482124354348815
logistic_single 1 diboson 0.04699497337736984
logistic_single 1 gamma ray excess 0.04102444964969219
logistic_single 1 generalized parton distribution 0.036712724912920894
logistic_single 1 lux 0.017863439822720473
logistic_single 1 higgsless 0.031371348784805776
logistic_single 1 planckian 0.03362768521566033
logistic_single 2 125 gev RMSE=0.094
logistic_single 2 pentaquark,pentaquarks RMSE=0.016
logistic_single 2 wmap,wilkinson microwave anisotropy probe RMSE=0.016
logistic_single 2 lhc run RMSE=0.099
logistic_single 2 pamela RMSE=0.067
logistic_single 2 lattice gauge RMSE=0.027
logistic_single 2 tensor scalar ratio RMSE=0.031
logistic_single 2 brane,branes RMSE=0.018
logistic_single 2 atlas RMSE=0.04
logistic_single 2 horava lifshitz,hovrava lifshitz RMSE=0.086
logistic_single 2 lhc RMSE=0.011
logistic_single 2 noncommutative,noncommutativity,non commutative,non commutativity RMSE=0.018
logistic_single 2 black hole RMSE=0.017
logistic_single 2 anomalous magnetic moment RMSE=0.013
logistic_single 2 unparticle,unparticles RMSE=0.07
logistic_single 2 superluminal RMSE=0.027
logistic_single 2 m2 brane,m2 branes RMSE=0.037
logistic_single 2 126 gev RMSE=0.106
logistic_single 2 pp wave RMSE=0.034
logistic_single 2 lambert RMSE=0.053
logistic_single 2 tevatron RMSE=0.02
logistic_single 2 higgs RMSE=0.017
logistic_single 2 brane world RMSE=0.038
logistic_single 2 extra dimension RMSE=0.017
logistic_single 2 entropic RMSE=0.04
logistic_single 2 kamland RMSE=0.026
logistic_single 2 solar neutrino RMSE=0.015
logistic_single 2 neutrino oscillation RMSE=0.014
logistic_single 2 chern simon RMSE=0.013
logistic_single 2 forward backward asymmetry RMSE=0.015
logistic_single 2 dark energy RMSE=0.009
logistic_single 2 bulk RMSE=0.013
logistic_single 2 holographic RMSE=0.019
logistic_single 2 international linear collider,ilc RMSE=0.025
logistic_single 2 abjm RMSE=0.083
logistic_single 2 babar RMSE=0.008
logistic_single 2 daya bay RMSE=0.08
logistic_single 2 sqrts7 tev RMSE=0.098
logistic_single 2 130 gev RMSE=0.023
logistic_single 2 20point3 RMSE=0.111
logistic_single 2 string field theory RMSE=0.024
logistic_single 2 metastable vacuum RMSE=0.04
logistic_single 2 gravitational wave RMSE=0.023
logistic_single 2 belle RMSE=0.012
logistic_single 2 diboson RMSE=0.048
logistic_single 2 gamma ray excess RMSE=0.077
logistic_single 2 generalized parton distribution RMSE=0.016
logistic_single 2 lux RMSE=0.118
logistic_single 2 higgsless RMSE=0.023
logistic_single 2 planckian RMSE=0.021
gompertz_single 1 125 gev 0.027990893264820727
gompertz_single 1 pentaquark,pentaquarks 0.05501721478166251
gompertz_single 1 wmap,wilkinson microwave anisotropy probe 0.022845668269851106
gompertz_single 1 lhc run 0.028579821827405053
gompertz_single 1 pamela 0.045009318530154496
gompertz_single 1 lattice gauge 0.03881798360027813
gompertz_single 1 tensor scalar ratio 0.04165122755811488
gompertz_single 1 brane,branes 0.015897368843519718
gompertz_single 1 atlas 0.025302368295095044
gompertz_single 1 horava lifshitz,hovrava lifshitz 0.03284369710043905
gompertz_single 1 lhc 0.011982748137246894
gompertz_single 1 noncommutative,noncommutativity,non commutative,non commutativity 0.019001965897180995
gompertz_single 1 black hole 0.014927532025715336
gompertz_single 1 anomalous magnetic moment 0.03815112878690011
gompertz_single 1 unparticle,unparticles 0.04951062524644681
gompertz_single 1 superluminal 0.06769864550310536
gompertz_single 1 m2 brane,m2 branes 0.04913553590544861
gompertz_single 1 126 gev 0.055558733922474034
gompertz_single 1 pp wave 0.03301172366747924
gompertz_single 1 lambert 0.06642398728502467
gompertz_single 1 tevatron 0.025650416554382518
gompertz_single 1 higgs 0.023162438641479193
gompertz_single 1 brane world 0.02731737986487246
gompertz_single 1 extra dimension 0.01412142348710811
gompertz_single 1 entropic 0.04244470928862996
gompertz_single 1 kamland 0.041561443675259296
gompertz_single 1 solar neutrino 0.019991527081873878
gompertz_single 1 neutrino oscillation 0.02728917506505852
gompertz_single 1 chern simon 0.021921267236475462
gompertz_single 1 forward backward asymmetry 0.033792375388002636
gompertz_single 1 dark energy 0.011328325469397564
gompertz_single 1 bulk 0.016397373612903957
gompertz_single 1 holographic 0.013523033011049823
gompertz_single 1 international linear collider,ilc 0.028670475081917165
gompertz_single 1 abjm 0.01908721302892229
gompertz_single 1 babar 0.011772702532270439
gompertz_single 1 daya bay 0.033161025569256077
gompertz_single 1 sqrts7 tev 0.02246390374238338
gompertz_single 1 130 gev 0.06634184936424548
gompertz_single 1 20point3 0.05854946662529169
gompertz_single 1 string field theory 0.020875119663090757
gompertz_single 1 metastable vacuum 0.05222736462207674
gompertz_single 1 gravitational wave 0.027673653499397457
gompertz_single 1 belle 0.02693039986623777
gompertz_single 1 diboson 0.057996631146896745
gompertz_single 1 gamma ray excess 0.04859899332579853
gompertz_single 1 generalized parton distribution 0.02058799001190155
gompertz_single 1 lux 0.013340072121053249
gompertz_single 1 higgsless 0.02542571744624044
gompertz_single 1 planckian 0.027723454726782445
gompertz_single 2 125 gev RMSE=0.067
gompertz_single 2 pentaquark,pentaquarks RMSE=0.019
gompertz_single 2 wmap,wilkinson microwave anisotropy probe RMSE=0.021
gompertz_single 2 lhc run RMSE=0.069
gompertz_single 2 pamela RMSE=0.068
gompertz_single 2 lattice gauge RMSE=0.025
gompertz_single 2 tensor scalar ratio RMSE=0.027
gompertz_single 2 brane,branes RMSE=0.015
gompertz_single 2 atlas RMSE=0.018
gompertz_single 2 horava lifshitz,hovrava lifshitz RMSE=0.065
gompertz_single 2 lhc RMSE=0.005
gompertz_single 2 noncommutative,noncommutativity,non commutative,non commutativity RMSE=0.018
gompertz_single 2 black hole RMSE=0.01
| MIT | Modelling trend life cycles in scientific research.ipynb | etattershall/trend-lifecycles |
Reload the dataThe preceding step is very long, and may take many hours to complete. Therefore, since we did it in chunks, we now reload the results from memory. | # Load the data back up (since the steps above store the results in files, not local memory)
document_count_per_year = pickle.load(open(root+'document_count_per_year.p', "rb"))
datasets = {}
for dataset_name in dataset_names:
datasets[dataset_name] = {}
for curve_type in ['logistic', 'gompertz']:
datasets[dataset_name][curve_type] = {}
for peaks in ['single', 'double']:
df = pd.read_csv(root+'fitted_curves/'+dataset_name+'/'+curve_type+'_'+peaks+'.csv', index_col=0)
datasets[dataset_name][curve_type][peaks] = df | _____no_output_____ | MIT | Modelling trend life cycles in scientific research.ipynb | etattershall/trend-lifecycles |
Graph: Example single-peaked fit for XML | x = range(1988,2018)
term = 'xml'
# Load the original time series for xml
df = pickle.load(open(root+'clusters/dblp_cs.p', 'rb'))
# Divide the data for each year by the document count in each year
y_proportional = df[term].divide(document_count_per_year['dblp_cs'])
# Calculate Logistic and Gompertz curves from the parameters estimated earlier
y_logistic = logletlab.calculate_series(x,
datasets['dblp_cs']['logistic']['single']['a'][term],
datasets['dblp_cs']['logistic']['single']['k'][term],
datasets['dblp_cs']['logistic']['single']['b'][term],
'logistic'
)
# Since the fitting was done with a normalised version of the curve, we detransform it back into the original scale
y_logistic = detransform_fit(y_proportional.cumsum(), y_logistic, 'dblp_cs')
y_gompertz = logletlab.calculate_series(x,
datasets['dblp_cs']['gompertz']['single']['a'][term],
datasets['dblp_cs']['gompertz']['single']['k'][term],
datasets['dblp_cs']['gompertz']['single']['b'][term],
'gompertz'
)
y_gompertz = detransform_fit(y_proportional.cumsum(), y_gompertz, 'dblp_cs')
plt.figure(figsize=(6,3.7))
# Multiply by 100 so that values will be percentages
plt.plot(x, 100*y_proportional, label='Data', color='k')
plt.plot(x, 100*y_logistic, label='Logistic', color='k', linestyle=':')
plt.plot(x, 100*y_gompertz, label='Gompertz', color='k', linestyle='--')
plt.legend()
plt.grid()
plt.title("Logistic and Gompertz models fitted to the data for 'XML'", fontsize=12)
plt.xlim([1988,2017])
plt.ylim(0,2)
plt.ylabel("Documents containing term (%)", fontsize=11)
plt.xlabel("Year", fontsize=11)
plt.savefig(root+'images/xmlexamplefit.eps', format='eps', dpi=1200) | _____no_output_____ | MIT | Modelling trend life cycles in scientific research.ipynb | etattershall/trend-lifecycles |
Table of results for Logistic vs GompertzCompare the error of the Logistic and Gompertz models across the entire dataset of 200 trends. | def statistics(df):
mean = df.mean()
ci = 1.96*logistic_error.std()/np.sqrt(len(logistic_error))
median = df.median()
std = df.std()
return [mean, mean-ci, mean+ci, median, std]
logistic_error = pd.concat([datasets['arxiv_hep']['logistic']['single']['RMS'],
datasets['dblp_cs']['logistic']['single']['RMS'],
datasets['pubmed_mh']['logistic']['single']['RMS'],
datasets['pubmed_cancer']['logistic']['single']['RMS']])
gompertz_error = pd.concat([datasets['arxiv_hep']['gompertz']['single']['RMS'],
datasets['dblp_cs']['gompertz']['single']['RMS'],
datasets['pubmed_mh']['gompertz']['single']['RMS'],
datasets['pubmed_cancer']['gompertz']['single']['RMS']])
print('Logistic')
mean = logistic_error.mean()
ci = 1.96*logistic_error.std()/np.sqrt(len(logistic_error))
print('Mean =', np.round(mean,3))
print('95% CI = [', np.round(mean-ci, 3), ',', np.round(mean+ci, 3), ']')
print('Median =', np.round(logistic_error.median(), 3))
print('STDEV =', np.round(logistic_error.std(), 3))
print('')
print('Gompertz')
mean = gompertz_error.mean()
ci = 1.96*gompertz_error.std()/np.sqrt(len(logistic_error))
print('Mean =', np.round(mean,3))
print('95% CI = [', np.round(mean-ci, 3), ',', np.round(mean+ci, 3), ']')
print('Median =', np.round(gompertz_error.median(), 3))
print('STDEV =', np.round(gompertz_error.std(), 3))
| Logistic
Mean = 0.029
95% CI = [ 0.027 , 0.031 ]
Median = 0.029
STDEV = 0.014
Gompertz
Mean = 0.023
95% CI = [ 0.021 , 0.026 ]
Median = 0.019
STDEV = 0.017
| MIT | Modelling trend life cycles in scientific research.ipynb | etattershall/trend-lifecycles |
Is the difference between the means significant?Here we use an independent t-test to investigate significance. | scipy.stats.ttest_ind(logistic_error, gompertz_error, axis=0, equal_var=True, nan_policy='propagate') | _____no_output_____ | MIT | Modelling trend life cycles in scientific research.ipynb | etattershall/trend-lifecycles |
Yes, it is significant! However, since the data is slightly skewed, we can also test the signficance of the difference between medians using Mood's median test: | stat, p, med, tbl = scipy.stats.median_test(logistic_error, gompertz_error)
print(p) | 1.1980742802127062e-08
| MIT | Modelling trend life cycles in scientific research.ipynb | etattershall/trend-lifecycles |
So either way, the p-value is very low, causing us to reject the null hypothesis. This leads us to the conclusion that the **Gompertz model** is more appropriate for the task of modelling publishing activity over time. Box and whisker plots of Logistic and Gompertz model error | axs = pd.DataFrame({
'CS Logistic': datasets['dblp_cs']['logistic']['single']['RMS'],
'CS Gompertz': datasets['dblp_cs']['gompertz']['single']['RMS'],
'Physics Logistic': datasets['arxiv_hep']['logistic']['single']['RMS'],
'Physics Gompertz': datasets['arxiv_hep']['gompertz']['single']['RMS'],
'MH Logistic': datasets['pubmed_mh']['logistic']['single']['RMS'],
'MH Gompertz': datasets['pubmed_mh']['gompertz']['single']['RMS'],
'Cancer Logistic': datasets['pubmed_cancer']['logistic']['single']['RMS'],
'Cancer Gompertz': datasets['pubmed_cancer']['gompertz']['single']['RMS'],
}).boxplot(figsize=(13,4), return_type='dict')
[item.set_color('k') for item in axs['boxes']]
[item.set_color('k') for item in axs['whiskers']]
[item.set_color('k') for item in axs['medians']]
plt.suptitle("")
p = plt.gca()
p.set_ylabel('RMSE error')
p.set_title('Distribution of RMSE error of models fitted to the four datasets', fontsize=12)
p.set_ylim([0,0.12]) | _____no_output_____ | MIT | Modelling trend life cycles in scientific research.ipynb | etattershall/trend-lifecycles |
There is some variation across the datasets, although the Gompertz model is consistent in producing a lower median error than the Logistic model. It's worth noting also that the Particle Physics and Mental Health datasets are smaller than the Cancer and Computer Science ones. They also have higher error. Calculation of trend durationThe Loglet Lab documentation (https://logletlab.com/loglet/documentation/index) contains a formula for the time taken for a Gompertz curve to go from 10% to 90% of its eventual maximum cumulative frequency ($\Delta t$). Their calculation is that$\Delta t = -\frac{\ln(\ln(81))}{r}$However, our observation was that this did not remotely describe the observed span of the fitted curves. We have therefore done the derivation ourselves and found that the correct parameterisation is:$\Delta t = \frac{1}{\ln(-(\ln(0.9))-\ln(-\ln(0.1))}$Unfortunately, the LogletLab initial parameter guesses are tailored to this incorrect parameterisation so it is much simpler to use it when fitting the curve (and irrelevant, except when it comes to calculating curve span). Therefore we use it, then convert to the correct value using the conversion factor below: | conversion_factor = -((np.log(-np.log(0.9))-np.log(-np.log(0.1)))/np.log(np.log(81)))
spans = pd.DataFrame({
'Computer Science': datasets['dblp_cs']['gompertz']['single']['a']*conversion_factor,
'Particle Physics': datasets['arxiv_hep']['gompertz']['single']['a']*conversion_factor,
'Mental Health': datasets['pubmed_mh']['gompertz']['single']['a']*conversion_factor,
'Cancer': datasets['pubmed_cancer']['gompertz']['single']['a']*conversion_factor
})
axs = spans.boxplot(figsize=(7.5,3.7), return_type='dict', fontsize=11)
[item.set_color('k') for item in axs['boxes']]
[item.set_color('k') for item in axs['whiskers']]
[item.set_color('k') for item in axs['medians']]
#plt.figure(figsize=(6,3.7))
plt.suptitle("")
p = plt.gca()
p.set_ylabel('Peak width (years)', fontsize=11)
p.set_title('Distribution of peak widths by dataset (Gomperz model)', fontsize=12)
p.set_ylim([0,100])
plt.savefig(root+'images/curvespans.eps', format='eps', dpi=1200) | _____no_output_____ | MIT | Modelling trend life cycles in scientific research.ipynb | etattershall/trend-lifecycles |
The data is quite skewed here...something to bear in mind when testing for significance later. Median trend durations in different disciplines | for i , dataset_name in enumerate(dataset_names):
print(dataset_titles[i], '| Median trend duration =', np.round(np.median(datasets[dataset_name]['gompertz']['single']['a']*conversion_factor),1), 'years')
| Computer science (dblp) | Median trend duration = 25.8 years
Particle physics (arXiv) | Median trend duration = 15.1 years
Mental health (PubMed) | Median trend duration = 24.6 years
Cancer (PubMed) | Median trend duration = 13.4 years
| MIT | Modelling trend life cycles in scientific research.ipynb | etattershall/trend-lifecycles |
Testing for significance between disciplinesThere are substantial differences between the median trend durations, with Computer Science and Particle Physics having shorter durations and the two PubMed datasets having longer ones. But are these significant? Since the data is somewhat skewed, we use Mood's median test to find p-values for the differences (Mood's median test does not require normal data). | for i in range(4):
for j in range(i,4):
if i == j:
pass
else:
spans1 = datasets[dataset_names[i]]['gompertz']['single']['a']*conversion_factor
spans2 = datasets[dataset_names[j]]['gompertz']['single']['a']*conversion_factor
stat, p, med, tbl = scipy.stats.median_test(spans1, spans2)
print(dataset_titles[i], 'vs', dataset_titles[j], 'p-value =', np.round(p,3)) | Computer science (dblp) vs Particle physics (arXiv) p-value = 0.003
Computer science (dblp) vs Mental health (PubMed) p-value = 0.841
Computer science (dblp) vs Cancer (PubMed) p-value = 0.009
Particle physics (arXiv) vs Mental health (PubMed) p-value = 0.072
Particle physics (arXiv) vs Cancer (PubMed) p-value = 0.549
Mental health (PubMed) vs Cancer (PubMed) p-value = 0.028
| MIT | Modelling trend life cycles in scientific research.ipynb | etattershall/trend-lifecycles |
So the p value between Particle Physics and Computer Science is not acceptable, and neither is the p-value between Mental Health and Cancer. How about between these two groups? | dblp_spans = datasets['dblp_cs']['gompertz']['single']['a']*conversion_factor
cancer_spans = datasets['pubmed_cancer']['gompertz']['single']['a']*conversion_factor
arxiv_spans = datasets['arxiv_hep']['gompertz']['single']['a']*conversion_factor
mh_spans = datasets['pubmed_mh']['gompertz']['single']['a']*conversion_factor
stat, p, med, tbl = scipy.stats.median_test(pd.concat([arxiv_spans, dblp_spans]), pd.concat([cancer_spans, mh_spans]))
print(np.round(p,5)) | 0.00013
| MIT | Modelling trend life cycles in scientific research.ipynb | etattershall/trend-lifecycles |
This difference IS significant! Double-peaking curvesWe now move to analyse the data for double-peaked curves. For each term, we have calculated the error when two peaks are fitted, and the error when a single peak is fitted. We can compare the error in each case like so: | print('Neural networks, single peak | error =', np.round(datasets['dblp_cs']['gompertz']['single']['RMS']['neural network'],3))
print('Neural networks, double peak| error =', np.round(datasets['dblp_cs']['gompertz']['double']['RMS']['neural network'],3)) | Neural networks, single peak | error = 0.031
Neural networks, double peak| error = 0.011
| MIT | Modelling trend life cycles in scientific research.ipynb | etattershall/trend-lifecycles |
Where do we see the largest reductions? | difference = datasets['dblp_cs']['gompertz']['single']['RMS']-datasets['dblp_cs']['gompertz']['double']['RMS']
for term in difference.index:
if difference[term] > 0.015:
print(term, np.round(difference[term], 3)) | neural network 0.02
machine learning 0.02
convolutional neural network,cnn 0.085
discrete mathematics 0.031
parallel 0.024
recurrent 0.026
embeddings 0.037
learning model 0.024
| MIT | Modelling trend life cycles in scientific research.ipynb | etattershall/trend-lifecycles |
Examples of double peaking curvesSo in some cases there is an error reduction from moving from the single- to double-peaked model. What does this look like in practice? | x = range(1988,2018)
# Load the original data
df = pickle.load(open(root+'clusters/dblp_cs.p', 'rb'))
# Choose four example terms
terms = ['big data', 'cloud', 'internet', 'neural network']
titles = ['a) Big Data', 'b) Cloud', 'c) Internet', 'd) Neural network']
# We want to set an overall y-label. The solution(found at https://stackoverflow.com/a/27430940) is to
# create an overall plot first, give it a y-label, then hide it by removing plot borders.
fig, big_ax = plt.subplots(figsize=(9.0, 6.0) , nrows=1, ncols=1, sharex=True)
big_ax.tick_params(labelcolor=(1,1,1,0.0), top=False, bottom=False, left=False, right=False)
big_ax._frameon = False
big_ax.set_ylabel("Documents containing term (%)", fontsize=11)
axs = [0,0,0,0]
axs[0]=fig.add_subplot(2,2,1)
axs[1]=fig.add_subplot(2,2,2)
axs[2]=fig.add_subplot(2,2,3)
axs[3]=fig.add_subplot(2,2,4)
fig.subplots_adjust(wspace=0.25, hspace=0.5, right=0.9)
# Set y limits manually beforehand
limits = [2, 4, 6, 8]
for i, term in enumerate(terms):
# Get the proportional document frequency of the term over time
y_proportional = df[term].divide(document_count_per_year['dblp_cs'])
# Multiply by 100 when plotting so that it reads as a percentage
axs[i].plot(x, 100*y_proportional, color='k')
axs[i].grid(True)
axs[i].set_xlabel("Year", fontsize=11)
axs[i].yaxis.set_major_formatter(FormatStrFormatter('%.1f'))
# Now plot single and double peaked models
for j, curve_type in enumerate(['single', 'double']):
if curve_type == 'single':
y_overall = logletlab.calculate_series(x,
datasets['dblp_cs']['gompertz'][curve_type]['a'][term],
datasets['dblp_cs']['gompertz'][curve_type]['k'][term],
datasets['dblp_cs']['gompertz'][curve_type]['b'][term],
'gompertz')
y_overall = detransform_fit(y_proportional.cumsum(), y_overall, 'dblp_cs')
error = datasets['dblp_cs']['gompertz'][curve_type]['RMS'][term]
axs[i].plot(x, 100*y_overall, color='k', linestyle='--', label="single peak, error="+str(np.round(error,3)))
else:
y_overall, y_1, y_2 = logletlab.calculate_series_double(x,
datasets['dblp_cs']['gompertz'][curve_type]['a1'][term],
datasets['dblp_cs']['gompertz'][curve_type]['k1'][term],
datasets['dblp_cs']['gompertz'][curve_type]['b1'][term],
datasets['dblp_cs']['gompertz'][curve_type]['a2'][term],
datasets['dblp_cs']['gompertz'][curve_type]['k2'][term],
datasets['dblp_cs']['gompertz'][curve_type]['b2'][term],
'gompertz')
y_overall = detransform_fit(y_proportional.cumsum(), y_overall, 'dblp_cs')
error = datasets['dblp_cs']['gompertz'][curve_type]['RMS'][term]
axs[i].plot(x, 100*y_overall, color='k', linestyle=':', label="double peak, error="+str(np.round(error,3)))
axs[i].set_title(titles[i], fontsize=12)
axs[i].legend( fontsize=11)
axs[i].set_ylim([0, limits[i]])
# We want the same number of y ticks for each axis so that it reads more neatly
axs[2].set_yticks([0, 1.5, 3, 4.5, 6])
fig.savefig(root+'images/doublepeaked.eps', format='eps', dpi=1200)
| _____no_output_____ | MIT | Modelling trend life cycles in scientific research.ipynb | etattershall/trend-lifecycles |
Graphs of all four datasetsIn this section we try to show as many graphs of fitted models as can reasonably fit on a page. The two functions used to make the graphs [below] are very hacky! However they work for this specific purpose. | def choose_ylimit(prevalence):
'''
This function works to find the most appropriate upper y limit to make the plots look good
'''
if max(prevalence) < 0.5:
return 0.5
elif max(prevalence) > 0.5 and max(prevalence) < 0.8:
return 0.8
elif max(prevalence) > 10 and max(prevalence) < 12:
return 12
elif max(prevalence) > 12 and max(prevalence) < 15:
return 15
elif max(prevalence) > 15 and max(prevalence) < 20:
return 20
else:
return np.ceil(max(prevalence))
def prettyplot(df, dataset_name, gompertz_params, yplots, xplots, title, ylabel, xlabel, xlims, plot_titles):
'''
Plot a nicely formatted set of trends with their fitted models. This function is rather hacky and made
for this specific purpose!
'''
fig, axs = plt.subplots(yplots, xplots)
plt.subplots_adjust(right=1, hspace=0.5, wspace=0.25)
plt.suptitle(title, fontsize=14)
fig.subplots_adjust(top=0.95)
fig.set_figheight(15)
fig.set_figwidth(9)
x = [int(i) for i in list(df.index)]
for i, term in enumerate(df.columns[0:yplots*xplots]):
prevalence = df[term].divide(document_count_per_year[dataset_name], axis=0)
if plot_titles == None:
title = term.split(',')[0]
else:
title = titles[i]
# Now get the gompertz representation of it
if gompertz_params['single']['RMS'][term]-gompertz_params['double']['RMS'][term] < 0.005:
# Use the single peaked version
y_overall = logletlab.calculate_series(x,
gompertz_params['single']['a'][term],
gompertz_params['single']['k'][term],
gompertz_params['single']['b'][term],
'gompertz')
y_overall = detransform_fit(prevalence.cumsum(), y_overall, dataset_name)
else:
y_overall, y_1, y_2 = logletlab.calculate_series_double(x,
gompertz_params['double']['a1'][term],
gompertz_params['double']['k1'][term],
gompertz_params['double']['b1'][term],
gompertz_params['double']['a2'][term],
gompertz_params['double']['k2'][term],
gompertz_params['double']['b2'][term],
'gompertz')
y_overall = detransform_fit(prevalence.cumsum(), y_overall, dataset_name)
axs[int(np.floor((i/xplots)%yplots)), i%xplots].plot(x, 100*prevalence, color='k', ls='-', label=title)
axs[int(np.floor((i/xplots)%yplots)), i%xplots].plot(x, 100*y_overall, color='k', ls='--', label='gompertz')
axs[int(np.floor((i/xplots)%yplots)), i%xplots].grid()
axs[int(np.floor((i/xplots)%yplots)), i%xplots].set_xlim(xlims[0], xlims[1])
axs[int(np.floor((i/xplots)%yplots)), i%xplots].set_ylim(0,choose_ylimit(100*prevalence))
axs[int(np.floor((i/xplots)%yplots)), i%xplots].set_title(title, fontsize=12)
axs[int(np.floor((i/xplots)%yplots)), i%xplots].yaxis.set_major_formatter(FormatStrFormatter('%.1f'))
if i%yplots != yplots-1:
axs[i%yplots, int(np.floor((i/yplots)%xplots))].set_xticklabels([])
axs[5,0].set_ylabel(ylabel, fontsize=12)
dataset_name = 'arxiv_hep'
df = pickle.load(open(root+'clusters/'+dataset_name+'.p', 'rb'))
titles = ['125 GeV', 'Pentaquark', 'WMAP', 'LHC Run', 'PAMELA', 'Lattice Gauge',
'Tensor-to-Scalar Ratio', 'Brane', 'ATLAS', 'Horava-Lifshitz', 'LHC',
'Noncommutative', 'Black Hole', 'Anomalous Magnetic Moment', 'Unparticle',
'Superluminal', 'M2 Brane', '126 GeV', 'pp-Wave', 'Lambert', 'Tevatron', 'Higgs',
'Brane World', 'Extra Dimension', 'Entropic', 'KamLAND', 'Solar Neutrino',
'Neutrino Oscillation', 'Chern Simon', 'Forward-Backward Asymmetry', 'Dark Energy',
'Bulk', 'Holographic', 'International Linear Collider', 'ABJM', 'BaBar']
prettyplot(df, 'arxiv_hep', datasets[dataset_name]['gompertz'], 12, 3, "Gompertz model fitted to trends in particle physics (1994-2017)", "Documents containing term (%)", None, [1990,2020], titles)
plt.savefig(root+'images/arxiv_hep.eps', format='eps', dpi=1200, bbox_inches='tight')
dataset_name = 'dblp_cs'
df = pickle.load(open(root+'clusters/'+dataset_name+'.p', 'rb'))
titles = ['Deep Learning', 'Neural Network', 'Machine Learning', 'Convolutional Neural Network',
'Java', 'Web', 'XML', 'Internet', 'Web Service', 'Internet of Things', 'World Wide Web',
'Speech', '5G', 'Discrete Mathematics', 'Parallel', 'Agent', 'Recurrent', 'SUP', 'Cloud',
'Big Data', 'Peer-to-peer', 'Wireless', 'Sensor Network', 'Electronic Commerce', 'ATM', 'Gene',
'Packet', 'Multimedia', 'Smart Grid', 'Embeddings', 'Ontology', 'Ad-hoc Network', 'Service Oriented',
'Web Site', 'RAC', 'Distributed Memory']
prettyplot(df, 'dblp_cs', datasets[dataset_name]['gompertz'], 12, 3, 'Gompertz model fitted to trends in computer science (1988-2017)', "Documents containing term (%)", None, [1980,2020], titles)
plt.savefig(root+'images/dblp_cs.eps', format='eps', dpi=1200, bbox_inches='tight')
dataset_name = 'pubmed_mh'
df = pickle.load(open(root+'clusters/'+dataset_name+'.p', 'rb'))
titles = titles = ['Alcoholic', 'Abeta', 'Psycinfo', 'Dexamethasone', 'Human Immunodeficiency Virus',
'Database', 'Alzheimers Disease', 'Amitriptyline', 'Intravenous Drug', 'Bupropion',
'DSM iii', 'Depression', 'Drug User', 'Apolipoprotein', 'Epsilon4 Allele', 'Rett Syndrome',
'Cocaine', 'Heroin', 'Panic', 'Imipramine', 'Papaverine', 'Cortisol', 'Presenilin', 'Plasma',
'Tricyclic', 'Epsilon Allele', 'HTLV iii', 'Learning Disability', 'DSM IV', 'DSM',
'Retardation', 'Aldehyde', 'Protein Precursor', 'Bulimia', 'Narcoleptic', 'Acquired Immunodeficiency Syndrome']
prettyplot(df, 'pubmed_mh', datasets[dataset_name]['gompertz'], 12, 3, 'Gompertz model fitted to trends in mental health research (1975-2017)', 'Documents containing term (%)', None, [1970,2020], titles)
plt.savefig(root+'images/pubmed_mh.eps', format='eps', dpi=1200, bbox_inches='tight')
dataset_name = 'pubmed_cancer'
df = pickle.load(open(root+'clusters/'+dataset_name+'.p', 'rb'))
titles = ['Immunohistochemical', 'Monoclonal Antibody', 'NF KappaB', 'Polymerase Chain Reaction',
'Immune Checkpoint', 'Tumor Suppressor Gene', 'Beta Catenin', 'PD-L1', 'Interleukin',
'Oncogene', 'Microarray', '1Alpha', 'PC12 Cell', 'Magnetic Resonance',
'Proliferating Cell Nuclear Antigen', 'Human T-cell Leukemia', 'Adult T-cell Leukemia',
'lncRNA', 'Apoptosis', 'CD4', 'Recombinant', 'Acquired Immunodeficiency Syndrome',
'HR', 'Meta Analysis', 'IC50', 'Immunoperoxidase', 'Blot', 'Interfering RNA', '18F',
'(Estrogen) Receptor Alpha', 'OKT4', 'kDa', 'CA', 'OKT8', 'Imatinib', 'Helper (T-cells)']
prettyplot(df, 'pubmed_cancer', datasets[dataset_name]['gompertz'], 12, 3, 'Gompertz model fitted to trends in cancer research (1988-2017)', 'Documents containing term (%)', None, [1970,2020], titles)
plt.savefig(root+'images/pubmed_cancer.eps', format='eps', dpi=1200, bbox_inches='tight') | _____no_output_____ | MIT | Modelling trend life cycles in scientific research.ipynb | etattershall/trend-lifecycles |
CTR预估(1)资料&&代码整理by[@寒小阳](https://blog.csdn.net/han_xiaoyang)(hanxiaoyang.ml@gmail.com)reference:* [《广告点击率预估是怎么回事?》](https://zhuanlan.zhihu.com/p/23499698)* [从ctr预估问题看看f(x)设计—DNN篇](https://zhuanlan.zhihu.com/p/28202287)* [Atomu2014 product_nets](https://github.com/Atomu2014/product-nets)关于CTR预估的背景推荐大家看欧阳辰老师在知乎的文章[《广告点击率预估是怎么回事?》](https://zhuanlan.zhihu.com/p/23499698),感谢欧阳辰老师并在这里做一点小小的摘抄。>点击率预估是广告技术的核心算法之一,它是很多广告算法工程师喜爱的战场。一直想介绍一下点击率预估,但是涉及公式和模型理论太多,怕说不清楚,读者也不明白。所以,这段时间花了一些时间整理点击率预估的知识,希望在尽量不使用数据公式的情况下,把大道理讲清楚,给一些不愿意看公式的同学一个Cook Book。> 点击率预测是什么?> * 点击率预测是对每次广告的点击情况做出预测,可以判定这次为点击或不点击,也可以给出点击的概率,有时也称作pClick。> 点击率预测和推荐算法的不同?> * 广告中点击率预估需要给出精准的点击概率,A点击率0.3% , B点击率0.13%等,需要结合出价用于排序使用;推荐算法很多时候只需要得出一个最优的次序A>B>C即可;> 搜索和非搜索广告点击率预测的区别> * 搜索中有强搜索信号-“查询词(Query)”,查询词和广告内容的匹配程度很大程度影响了点击概率; 点击率也高,PC搜索能到达百分之几的点击率。> * 非搜索广告(例如展示广告,信息流广告),点击率的计算很多来源于用户的兴趣和广告特征,上下文环境;移动信息流广告的屏幕比较大,用户关注度也比较集中,好位置也能到百分之几的点击率。对于很多文章底部的广告,点击率非常低,用户关注度也不高,常常是千分之几,甚至更低;> 如何衡量点击率预测的准确性?> AUC是常常被用于衡量点击率预估的准确性的方法;理解AUC之前,需要理解一下Precision/Recall;对于一个分类器,我们通常将结果分为:TP,TN,FP,FN。> 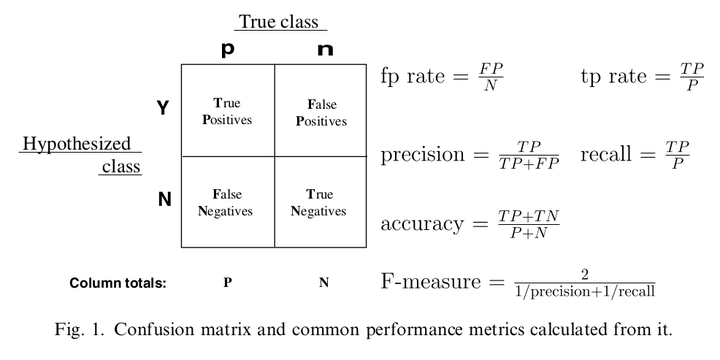> 本来用Precision=TP/(TP+FP),Recall=TP/P,也可以用于评估点击率算法的好坏,毕竟这是一种监督学习,每一次预测都有正确答案。但是,这种方法对于测试数据样本的依赖性非常大,稍微不同的测试数据集合,结果差异非常大。那么,既然无法使用简单的单点Precision/Recall来描述,我们可以考虑使用一系列的点来描述准确性。做法如下:> * 找到一系列的测试数据,点击率预估分别会对每个测试数据给出点击/不点击,和Confidence Score。> * 按照给出的Score进行排序,那么考虑如果将Score作为一个Thresholds的话,考虑这个时候所有数据的 TP Rate 和 FP Rate; 当Thresholds分数非常高时,例如0.9,TP数很小,NP数很大,因此TP率不会太高; > 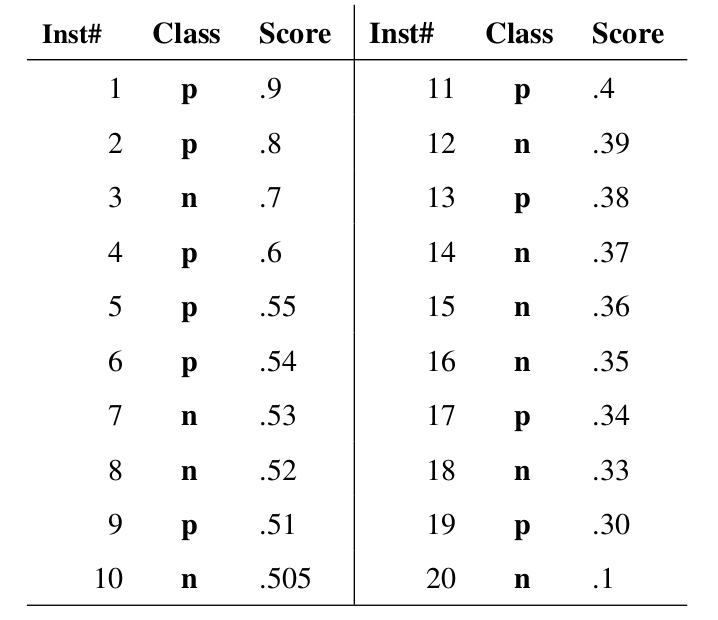> 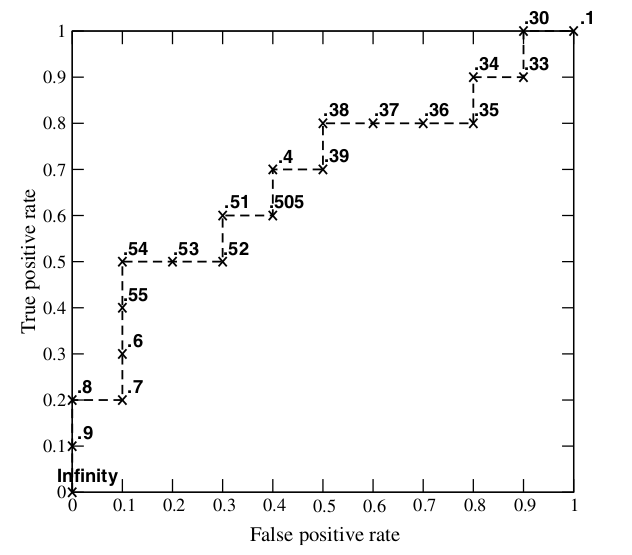> 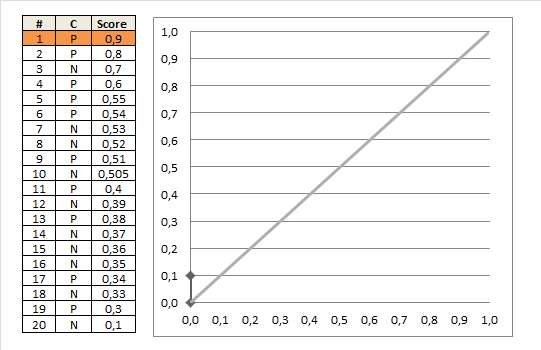> * 当选用不同Threshold时候,画出来的ROC曲线,以及下方AUC面积> * 我们计算这个曲线下面的面积就是所谓的AUC值;AUC值越大,预测约准确。> 为什么要使用AUC曲线> 既然已经这么多评价标准,为什么还要使用ROC和AUC呢?因为ROC曲线有个很好的特性:当测试集中的正负样本的分布变化的时候,ROC曲线能够保持不变。在实际的数据集中经常会出现类不平衡(class imbalance)现象,即负样本比正样本多很多(或者相反),而且测试数据中的正负样本的分布也可能随着时间变化。AUC对样本的比例变化有一定的容忍性。AUC的值通常在0.6-0.85之间。> 如何来进行点击率预测?> 点击率预测可以考虑为一个黑盒,输入一堆信号,输出点击的概率。这些信号就包括如下信号> * **广告**:历史点击率,文字,格式,图片等等> * **环境**:手机型号,时间媒体,位置,尺寸,曝光时间,网络IP,上网方式,代理等> * **用户**:基础属性(男女,年龄等),兴趣属性(游戏,旅游等),历史浏览,点击行为,电商行为> * **信号的粒度**:> `Low Level : 数据来自一些原始访问行为的记录,例如用户是否点击过Landing Page,流量IP等。这些特征可以用于粗选,模型简单,`> `High Level: 特征来自一些可解释的数据,例如兴趣标签,性别等`> * **特征编码Feature Encoding:**> `特征离散化:把连续的数字,变成离散化,例如温度值可以办成多个温度区间。`> `特征交叉: 把多个特征进行叫交叉的出的值,用于训练,这种值可以表示一些非线性的关系。例如,点击率预估中应用最多的就是广告跟用户的交叉特征、广告跟性别的交叉特征,广告跟年龄的交叉特征,广告跟手机平台的交叉特征,广告跟地域的交叉特征等等。`> * **特征选取(Feature Selection):**> `特征选择就是选择那些靠谱的Feature,去掉冗余的Feature,对于搜索广告Query和广告的匹配程度很关键;对于展示广告,广告本身的历史表现,往往是最重要的Feature。`> * **独热编码(One-Hot encoding)**```假设有三组特征,分别表示年龄,城市,设备;["男", "女"]["北京", "上海", "广州"]["苹果", "小米", "华为", "微软"]传统变化: 对每一组特征,使用枚举类型,从0开始;["男“,”上海“,”小米“]=[ 0,1,1]["女“,”北京“,”苹果“] =[1,0,0]传统变化后的数据不是连续的,而是随机分配的,不容易应用在分类器中。 热独编码是一种经典编码,是使用N位状态寄存器来对N个状态进行编码,每个状态都由他独立的寄存器位,并且在任意时候,其中只有一位有效。["男“,”上海“,”小米“]=[ 1,0,0,1,0,0,1,0,0]["女“,”北京“,”苹果“] =[0,1,1,0,0,1,0,0,0]经过热独编码,数据会变成稀疏的,方便分类器处理。```> 点击率预估整体过程:> 三个基本过程:特征工程,模型训练,线上服务> 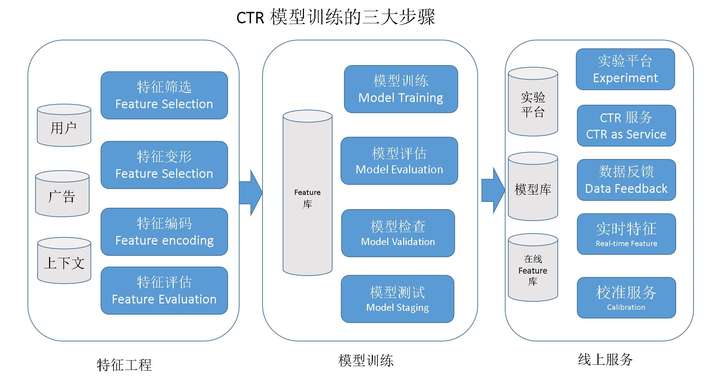> * 特征工程:准备各种特征,编码,去掉冗余特征(用PCA等)> * 模型训练:选定训练,测试等数据集,计算AUC,如果AUC有提升,通常可以在进一步在线上分流实验。> * 线上服务:线上服务,需要实时计算CTR,实时计算相关特征和利用模型计算CTR,对于不同来源的CTR,可能需要一个Calibration的服务。``` 用tensorflow构建各种模型完成ctr预估 | !head -5 ./data/train.txt
!head -10 ./data/featindex.txt
from __future__ import print_function
from __future__ import absolute_import
from __future__ import division
import cPickle as pkl
import numpy as np
import tensorflow as tf
from scipy.sparse import coo_matrix
# 读取数据,统计基本的信息,field等
DTYPE = tf.float32
FIELD_SIZES = [0] * 26
with open('./data/featindex.txt') as fin:
for line in fin:
line = line.strip().split(':')
if len(line) > 1:
f = int(line[0]) - 1
FIELD_SIZES[f] += 1
print('field sizes:', FIELD_SIZES)
FIELD_OFFSETS = [sum(FIELD_SIZES[:i]) for i in range(len(FIELD_SIZES))]
INPUT_DIM = sum(FIELD_SIZES)
OUTPUT_DIM = 1
STDDEV = 1e-3
MINVAL = -1e-3
MAXVAL = 1e-3
# 读取libsvm格式数据成稀疏矩阵形式
# 0 5:1 9:1 140858:1 445908:1 446177:1 446293:1 449140:1 490778:1 491626:1 491634:1 491641:1 491645:1 491648:1 491668:1 491700:1 491708:1
def read_data(file_name):
X = []
D = []
y = []
with open(file_name) as fin:
for line in fin:
fields = line.strip().split()
y_i = int(fields[0])
X_i = [int(x.split(':')[0]) for x in fields[1:]]
D_i = [int(x.split(':')[1]) for x in fields[1:]]
y.append(y_i)
X.append(X_i)
D.append(D_i)
y = np.reshape(np.array(y), [-1])
X = libsvm_2_coo(zip(X, D), (len(X), INPUT_DIM)).tocsr()
return X, y
# 数据乱序
def shuffle(data):
X, y = data
ind = np.arange(X.shape[0])
for i in range(7):
np.random.shuffle(ind)
return X[ind], y[ind]
# 工具函数,libsvm格式转成coo稀疏存储格式
def libsvm_2_coo(libsvm_data, shape):
coo_rows = []
coo_cols = []
coo_data = []
n = 0
for x, d in libsvm_data:
coo_rows.extend([n] * len(x))
coo_cols.extend(x)
coo_data.extend(d)
n += 1
coo_rows = np.array(coo_rows)
coo_cols = np.array(coo_cols)
coo_data = np.array(coo_data)
return coo_matrix((coo_data, (coo_rows, coo_cols)), shape=shape)
# csr转成输入格式
def csr_2_input(csr_mat):
if not isinstance(csr_mat, list):
coo_mat = csr_mat.tocoo()
indices = np.vstack((coo_mat.row, coo_mat.col)).transpose()
values = csr_mat.data
shape = csr_mat.shape
return indices, values, shape
else:
inputs = []
for csr_i in csr_mat:
inputs.append(csr_2_input(csr_i))
return inputs
# 数据切片
def slice(csr_data, start=0, size=-1):
if not isinstance(csr_data[0], list):
if size == -1 or start + size >= csr_data[0].shape[0]:
slc_data = csr_data[0][start:]
slc_labels = csr_data[1][start:]
else:
slc_data = csr_data[0][start:start + size]
slc_labels = csr_data[1][start:start + size]
else:
if size == -1 or start + size >= csr_data[0][0].shape[0]:
slc_data = []
for d_i in csr_data[0]:
slc_data.append(d_i[start:])
slc_labels = csr_data[1][start:]
else:
slc_data = []
for d_i in csr_data[0]:
slc_data.append(d_i[start:start + size])
slc_labels = csr_data[1][start:start + size]
return csr_2_input(slc_data), slc_labels
# 数据切分
def split_data(data, skip_empty=True):
fields = []
for i in range(len(FIELD_OFFSETS) - 1):
start_ind = FIELD_OFFSETS[i]
end_ind = FIELD_OFFSETS[i + 1]
if skip_empty and start_ind == end_ind:
continue
field_i = data[0][:, start_ind:end_ind]
fields.append(field_i)
fields.append(data[0][:, FIELD_OFFSETS[-1]:])
return fields, data[1]
# 在tensorflow中初始化各种参数变量
def init_var_map(init_vars, init_path=None):
if init_path is not None:
load_var_map = pkl.load(open(init_path, 'rb'))
print('load variable map from', init_path, load_var_map.keys())
var_map = {}
for var_name, var_shape, init_method, dtype in init_vars:
if init_method == 'zero':
var_map[var_name] = tf.Variable(tf.zeros(var_shape, dtype=dtype), name=var_name, dtype=dtype)
elif init_method == 'one':
var_map[var_name] = tf.Variable(tf.ones(var_shape, dtype=dtype), name=var_name, dtype=dtype)
elif init_method == 'normal':
var_map[var_name] = tf.Variable(tf.random_normal(var_shape, mean=0.0, stddev=STDDEV, dtype=dtype),
name=var_name, dtype=dtype)
elif init_method == 'tnormal':
var_map[var_name] = tf.Variable(tf.truncated_normal(var_shape, mean=0.0, stddev=STDDEV, dtype=dtype),
name=var_name, dtype=dtype)
elif init_method == 'uniform':
var_map[var_name] = tf.Variable(tf.random_uniform(var_shape, minval=MINVAL, maxval=MAXVAL, dtype=dtype),
name=var_name, dtype=dtype)
elif init_method == 'xavier':
maxval = np.sqrt(6. / np.sum(var_shape))
minval = -maxval
var_map[var_name] = tf.Variable(tf.random_uniform(var_shape, minval=minval, maxval=maxval, dtype=dtype),
name=var_name, dtype=dtype)
elif isinstance(init_method, int) or isinstance(init_method, float):
var_map[var_name] = tf.Variable(tf.ones(var_shape, dtype=dtype) * init_method, name=var_name, dtype=dtype)
elif init_method in load_var_map:
if load_var_map[init_method].shape == tuple(var_shape):
var_map[var_name] = tf.Variable(load_var_map[init_method], name=var_name, dtype=dtype)
else:
print('BadParam: init method', init_method, 'shape', var_shape, load_var_map[init_method].shape)
else:
print('BadParam: init method', init_method)
return var_map
# 不同的激活函数选择
def activate(weights, activation_function):
if activation_function == 'sigmoid':
return tf.nn.sigmoid(weights)
elif activation_function == 'softmax':
return tf.nn.softmax(weights)
elif activation_function == 'relu':
return tf.nn.relu(weights)
elif activation_function == 'tanh':
return tf.nn.tanh(weights)
elif activation_function == 'elu':
return tf.nn.elu(weights)
elif activation_function == 'none':
return weights
else:
return weights
# 不同的优化器选择
def get_optimizer(opt_algo, learning_rate, loss):
if opt_algo == 'adaldeta':
return tf.train.AdadeltaOptimizer(learning_rate).minimize(loss)
elif opt_algo == 'adagrad':
return tf.train.AdagradOptimizer(learning_rate).minimize(loss)
elif opt_algo == 'adam':
return tf.train.AdamOptimizer(learning_rate).minimize(loss)
elif opt_algo == 'ftrl':
return tf.train.FtrlOptimizer(learning_rate).minimize(loss)
elif opt_algo == 'gd':
return tf.train.GradientDescentOptimizer(learning_rate).minimize(loss)
elif opt_algo == 'padagrad':
return tf.train.ProximalAdagradOptimizer(learning_rate).minimize(loss)
elif opt_algo == 'pgd':
return tf.train.ProximalGradientDescentOptimizer(learning_rate).minimize(loss)
elif opt_algo == 'rmsprop':
return tf.train.RMSPropOptimizer(learning_rate).minimize(loss)
else:
return tf.train.GradientDescentOptimizer(learning_rate).minimize(loss)
# 工具函数
# 提示:tf.slice(input_, begin, size, name=None):按照指定的下标范围抽取连续区域的子集
# tf.gather(params, indices, validate_indices=None, name=None):按照指定的下标集合从axis=0中抽取子集,适合抽取不连续区域的子集
def gather_2d(params, indices):
shape = tf.shape(params)
flat = tf.reshape(params, [-1])
flat_idx = indices[:, 0] * shape[1] + indices[:, 1]
flat_idx = tf.reshape(flat_idx, [-1])
return tf.gather(flat, flat_idx)
def gather_3d(params, indices):
shape = tf.shape(params)
flat = tf.reshape(params, [-1])
flat_idx = indices[:, 0] * shape[1] * shape[2] + indices[:, 1] * shape[2] + indices[:, 2]
flat_idx = tf.reshape(flat_idx, [-1])
return tf.gather(flat, flat_idx)
def gather_4d(params, indices):
shape = tf.shape(params)
flat = tf.reshape(params, [-1])
flat_idx = indices[:, 0] * shape[1] * shape[2] * shape[3] + \
indices[:, 1] * shape[2] * shape[3] + indices[:, 2] * shape[3] + indices[:, 3]
flat_idx = tf.reshape(flat_idx, [-1])
return tf.gather(flat, flat_idx)
# 池化2d
def max_pool_2d(params, k):
_, indices = tf.nn.top_k(params, k, sorted=False)
shape = tf.shape(indices)
r1 = tf.reshape(tf.range(shape[0]), [-1, 1])
r1 = tf.tile(r1, [1, k])
r1 = tf.reshape(r1, [-1, 1])
indices = tf.concat([r1, tf.reshape(indices, [-1, 1])], 1)
return tf.reshape(gather_2d(params, indices), [-1, k])
# 池化3d
def max_pool_3d(params, k):
_, indices = tf.nn.top_k(params, k, sorted=False)
shape = tf.shape(indices)
r1 = tf.reshape(tf.range(shape[0]), [-1, 1])
r2 = tf.reshape(tf.range(shape[1]), [-1, 1])
r1 = tf.tile(r1, [1, k * shape[1]])
r2 = tf.tile(r2, [1, k])
r1 = tf.reshape(r1, [-1, 1])
r2 = tf.tile(tf.reshape(r2, [-1, 1]), [shape[0], 1])
indices = tf.concat([r1, r2, tf.reshape(indices, [-1, 1])], 1)
return tf.reshape(gather_3d(params, indices), [-1, shape[1], k])
# 池化4d
def max_pool_4d(params, k):
_, indices = tf.nn.top_k(params, k, sorted=False)
shape = tf.shape(indices)
r1 = tf.reshape(tf.range(shape[0]), [-1, 1])
r2 = tf.reshape(tf.range(shape[1]), [-1, 1])
r3 = tf.reshape(tf.range(shape[2]), [-1, 1])
r1 = tf.tile(r1, [1, shape[1] * shape[2] * k])
r2 = tf.tile(r2, [1, shape[2] * k])
r3 = tf.tile(r3, [1, k])
r1 = tf.reshape(r1, [-1, 1])
r2 = tf.tile(tf.reshape(r2, [-1, 1]), [shape[0], 1])
r3 = tf.tile(tf.reshape(r3, [-1, 1]), [shape[0] * shape[1], 1])
indices = tf.concat([r1, r2, r3, tf.reshape(indices, [-1, 1])], 1)
return tf.reshape(gather_4d(params, indices), [-1, shape[1], shape[2], k]) | _____no_output_____ | Apache-2.0 | notebooks/CTR_prediction_LR_FM_CCPM_PNN.ipynb | daiwk/grace_t |
定义不同的模型 | # 定义基类模型
dtype = DTYPE
class Model:
def __init__(self):
self.sess = None
self.X = None
self.y = None
self.layer_keeps = None
self.vars = None
self.keep_prob_train = None
self.keep_prob_test = None
# run model
def run(self, fetches, X=None, y=None, mode='train'):
# 通过feed_dict传入数据
feed_dict = {}
if type(self.X) is list:
for i in range(len(X)):
feed_dict[self.X[i]] = X[i]
else:
feed_dict[self.X] = X
if y is not None:
feed_dict[self.y] = y
if self.layer_keeps is not None:
if mode == 'train':
feed_dict[self.layer_keeps] = self.keep_prob_train
elif mode == 'test':
feed_dict[self.layer_keeps] = self.keep_prob_test
#通过session.run去执行op
return self.sess.run(fetches, feed_dict)
# 模型参数持久化
def dump(self, model_path):
var_map = {}
for name, var in self.vars.iteritems():
var_map[name] = self.run(var)
pkl.dump(var_map, open(model_path, 'wb'))
print('model dumped at', model_path) | _____no_output_____ | Apache-2.0 | notebooks/CTR_prediction_LR_FM_CCPM_PNN.ipynb | daiwk/grace_t |
1.LR逻辑回归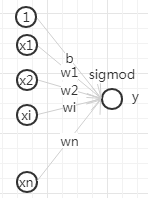输入输出:{X,y}映射函数f(x):单层单节点的“DNN”, 宽而不深,sigmoid(wx+b)输出概率,需要大量的人工特征工程,非线性来源于特征处理损失函数:logloss/... + L1/L2/...优化方法:sgd/...评估:logloss/auc/... | class LR(Model):
def __init__(self, input_dim=None, output_dim=1, init_path=None, opt_algo='gd', learning_rate=1e-2, l2_weight=0,
random_seed=None):
Model.__init__(self)
# 声明参数
init_vars = [('w', [input_dim, output_dim], 'xavier', dtype),
('b', [output_dim], 'zero', dtype)]
self.graph = tf.Graph()
with self.graph.as_default():
if random_seed is not None:
tf.set_random_seed(random_seed)
# 用稀疏的placeholder
self.X = tf.sparse_placeholder(dtype)
self.y = tf.placeholder(dtype)
# init参数
self.vars = init_var_map(init_vars, init_path)
w = self.vars['w']
b = self.vars['b']
# sigmoid(wx+b)
xw = tf.sparse_tensor_dense_matmul(self.X, w)
logits = tf.reshape(xw + b, [-1])
self.y_prob = tf.sigmoid(logits)
self.loss = tf.reduce_mean(
tf.nn.sigmoid_cross_entropy_with_logits(labels=self.y, logits=logits)) + \
l2_weight * tf.nn.l2_loss(xw)
self.optimizer = get_optimizer(opt_algo, learning_rate, self.loss)
# GPU设定
config = tf.ConfigProto()
config.gpu_options.allow_growth = True
self.sess = tf.Session(config=config)
# 初始化图里的参数
tf.global_variables_initializer().run(session=self.sess)
import numpy as np
from sklearn.metrics import roc_auc_score
import progressbar
train_file = './data/train.txt'
test_file = './data/test.txt'
input_dim = INPUT_DIM
# 读取数据
#train_data = read_data(train_file)
#test_data = read_data(test_file)
train_data = pkl.load(open('./data/train.pkl', 'rb'))
#train_data = shuffle(train_data)
test_data = pkl.load(open('./data/test.pkl', 'rb'))
# pkl.dump(train_data, open('./data/train.pkl', 'wb'))
# pkl.dump(test_data, open('./data/test.pkl', 'wb'))
# 输出数据信息维度
if train_data[1].ndim > 1:
print('label must be 1-dim')
exit(0)
print('read finish')
print('train data size:', train_data[0].shape)
print('test data size:', test_data[0].shape)
# 训练集与测试集
train_size = train_data[0].shape[0]
test_size = test_data[0].shape[0]
num_feas = len(FIELD_SIZES)
# 超参数设定
min_round = 1
num_round = 200
early_stop_round = 5
# train + val
batch_size = 1024
field_sizes = FIELD_SIZES
field_offsets = FIELD_OFFSETS
# 逻辑回归参数设定
lr_params = {
'input_dim': input_dim,
'opt_algo': 'gd',
'learning_rate': 0.1,
'l2_weight': 0,
'random_seed': 0
}
print(lr_params)
model = LR(**lr_params)
print("training LR...")
def train(model):
history_score = []
# 执行num_round轮
for i in range(num_round):
# 主要的2个op是优化器和损失
fetches = [model.optimizer, model.loss]
if batch_size > 0:
ls = []
# 进度条工具
bar = progressbar.ProgressBar()
print('[%d]\ttraining...' % i)
for j in bar(range(int(train_size / batch_size + 1))):
X_i, y_i = slice(train_data, j * batch_size, batch_size)
# 训练,run op
_, l = model.run(fetches, X_i, y_i)
ls.append(l)
elif batch_size == -1:
X_i, y_i = slice(train_data)
_, l = model.run(fetches, X_i, y_i)
ls = [l]
train_preds = []
print('[%d]\tevaluating...' % i)
bar = progressbar.ProgressBar()
for j in bar(range(int(train_size / 10000 + 1))):
X_i, _ = slice(train_data, j * 10000, 10000)
preds = model.run(model.y_prob, X_i, mode='test')
train_preds.extend(preds)
test_preds = []
bar = progressbar.ProgressBar()
for j in bar(range(int(test_size / 10000 + 1))):
X_i, _ = slice(test_data, j * 10000, 10000)
preds = model.run(model.y_prob, X_i, mode='test')
test_preds.extend(preds)
# 把预估的结果和真实结果拿出来计算auc
train_score = roc_auc_score(train_data[1], train_preds)
test_score = roc_auc_score(test_data[1], test_preds)
# 输出auc信息
print('[%d]\tloss (with l2 norm):%f\ttrain-auc: %f\teval-auc: %f' % (i, np.mean(ls), train_score, test_score))
history_score.append(test_score)
# early stopping
if i > min_round and i > early_stop_round:
if np.argmax(history_score) == i - early_stop_round and history_score[-1] - history_score[
-1 * early_stop_round] < 1e-5:
print('early stop\nbest iteration:\n[%d]\teval-auc: %f' % (
np.argmax(history_score), np.max(history_score)))
break
train(model) | read finish
train data size: (1742104, 491713)
test data size: (300928, 491713)
{'l2_weight': 0, 'learning_rate': 0.1, 'random_seed': 0, 'input_dim': 491713, 'opt_algo': 'gd'}
| Apache-2.0 | notebooks/CTR_prediction_LR_FM_CCPM_PNN.ipynb | daiwk/grace_t |
2.FMFM可以视作有二次交叉的LR,为了控制参数量和充分学习,提出了user vector和item vector的概念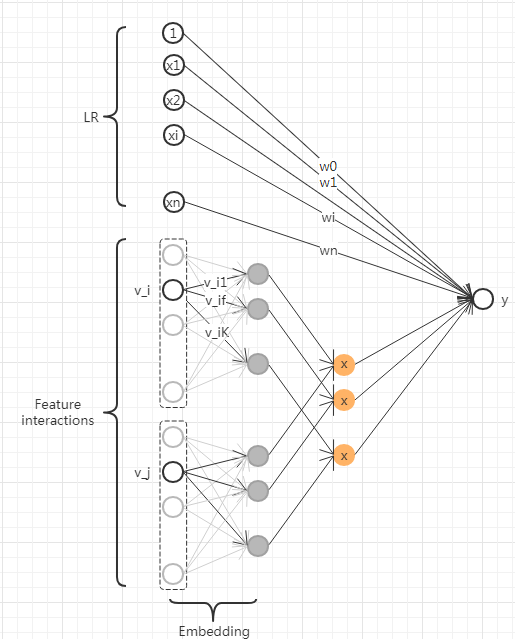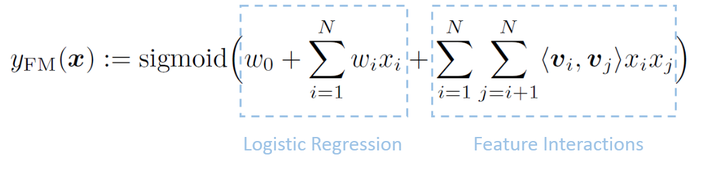 | class FM(Model):
def __init__(self, input_dim=None, output_dim=1, factor_order=10, init_path=None, opt_algo='gd', learning_rate=1e-2,
l2_w=0, l2_v=0, random_seed=None):
Model.__init__(self)
# 一次、二次交叉、偏置项
init_vars = [('w', [input_dim, output_dim], 'xavier', dtype),
('v', [input_dim, factor_order], 'xavier', dtype),
('b', [output_dim], 'zero', dtype)]
self.graph = tf.Graph()
with self.graph.as_default():
if random_seed is not None:
tf.set_random_seed(random_seed)
self.X = tf.sparse_placeholder(dtype)
self.y = tf.placeholder(dtype)
self.vars = init_var_map(init_vars, init_path)
w = self.vars['w']
v = self.vars['v']
b = self.vars['b']
# [(x1+x2+x3)^2 - (x1^2+x2^2+x3^2)]/2
# 先计算所有的交叉项,再减去平方项(自己和自己相乘)
X_square = tf.SparseTensor(self.X.indices, tf.square(self.X.values), tf.to_int64(tf.shape(self.X)))
xv = tf.square(tf.sparse_tensor_dense_matmul(self.X, v))
p = 0.5 * tf.reshape(
tf.reduce_sum(xv - tf.sparse_tensor_dense_matmul(X_square, tf.square(v)), 1),
[-1, output_dim])
xw = tf.sparse_tensor_dense_matmul(self.X, w)
logits = tf.reshape(xw + b + p, [-1])
self.y_prob = tf.sigmoid(logits)
self.loss = tf.reduce_mean(
tf.nn.sigmoid_cross_entropy_with_logits(logits=logits, labels=self.y)) + \
l2_w * tf.nn.l2_loss(xw) + \
l2_v * tf.nn.l2_loss(xv)
self.optimizer = get_optimizer(opt_algo, learning_rate, self.loss)
#GPU设定
config = tf.ConfigProto()
config.gpu_options.allow_growth = True
self.sess = tf.Session(config=config)
# 图中所有variable初始化
tf.global_variables_initializer().run(session=self.sess)
import numpy as np
from sklearn.metrics import roc_auc_score
import progressbar
train_file = './data/train.txt'
test_file = './data/test.txt'
input_dim = INPUT_DIM
train_data = pkl.load(open('./data/train.pkl', 'rb'))
train_data = shuffle(train_data)
test_data = pkl.load(open('./data/test.pkl', 'rb'))
if train_data[1].ndim > 1:
print('label must be 1-dim')
exit(0)
print('read finish')
print('train data size:', train_data[0].shape)
print('test data size:', test_data[0].shape)
# 训练集与测试集
train_size = train_data[0].shape[0]
test_size = test_data[0].shape[0]
num_feas = len(FIELD_SIZES)
# 超参数设定
min_round = 1
num_round = 200
early_stop_round = 5
batch_size = 1024
field_sizes = FIELD_SIZES
field_offsets = FIELD_OFFSETS
# FM参数设定
fm_params = {
'input_dim': input_dim,
'factor_order': 10,
'opt_algo': 'gd',
'learning_rate': 0.1,
'l2_w': 0,
'l2_v': 0,
}
print(fm_params)
model = FM(**fm_params)
print("training FM...")
def train(model):
history_score = []
for i in range(num_round):
# 同样是优化器和损失两个op
fetches = [model.optimizer, model.loss]
if batch_size > 0:
ls = []
bar = progressbar.ProgressBar()
print('[%d]\ttraining...' % i)
for j in bar(range(int(train_size / batch_size + 1))):
X_i, y_i = slice(train_data, j * batch_size, batch_size)
# 训练
_, l = model.run(fetches, X_i, y_i)
ls.append(l)
elif batch_size == -1:
X_i, y_i = slice(train_data)
_, l = model.run(fetches, X_i, y_i)
ls = [l]
train_preds = []
print('[%d]\tevaluating...' % i)
bar = progressbar.ProgressBar()
for j in bar(range(int(train_size / 10000 + 1))):
X_i, _ = slice(train_data, j * 10000, 10000)
preds = model.run(model.y_prob, X_i, mode='test')
train_preds.extend(preds)
test_preds = []
bar = progressbar.ProgressBar()
for j in bar(range(int(test_size / 10000 + 1))):
X_i, _ = slice(test_data, j * 10000, 10000)
preds = model.run(model.y_prob, X_i, mode='test')
test_preds.extend(preds)
train_score = roc_auc_score(train_data[1], train_preds)
test_score = roc_auc_score(test_data[1], test_preds)
print('[%d]\tloss (with l2 norm):%f\ttrain-auc: %f\teval-auc: %f' % (i, np.mean(ls), train_score, test_score))
history_score.append(test_score)
if i > min_round and i > early_stop_round:
if np.argmax(history_score) == i - early_stop_round and history_score[-1] - history_score[
-1 * early_stop_round] < 1e-5:
print('early stop\nbest iteration:\n[%d]\teval-auc: %f' % (
np.argmax(history_score), np.max(history_score)))
break
train(model) | read finish
train data size: (1742104, 491713)
test data size: (300928, 491713)
{'l2_w': 0, 'l2_v': 0, 'factor_order': 10, 'learning_rate': 0.1, 'input_dim': 491713, 'opt_algo': 'gd'}
| Apache-2.0 | notebooks/CTR_prediction_LR_FM_CCPM_PNN.ipynb | daiwk/grace_t |
FNNFNN的考虑是模型的capacity可以进一步提升,以对更复杂的场景建模。FNN可以视作FM + MLP = LR + MF + MLP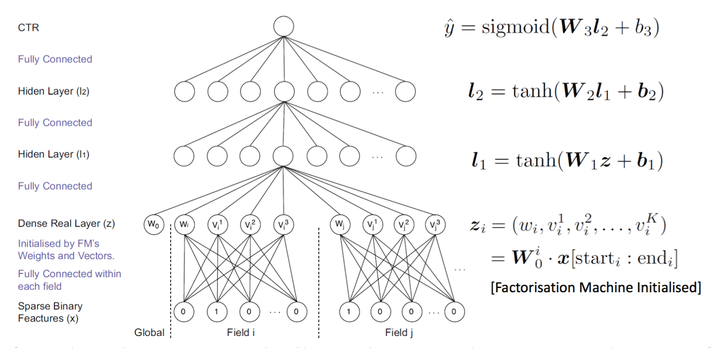 | class FNN(Model):
def __init__(self, field_sizes=None, embed_size=10, layer_sizes=None, layer_acts=None, drop_out=None,
embed_l2=None, layer_l2=None, init_path=None, opt_algo='gd', learning_rate=1e-2, random_seed=None):
Model.__init__(self)
init_vars = []
num_inputs = len(field_sizes)
for i in range(num_inputs):
init_vars.append(('embed_%d' % i, [field_sizes[i], embed_size], 'xavier', dtype))
node_in = num_inputs * embed_size
for i in range(len(layer_sizes)):
init_vars.append(('w%d' % i, [node_in, layer_sizes[i]], 'xavier', dtype))
init_vars.append(('b%d' % i, [layer_sizes[i]], 'zero', dtype))
node_in = layer_sizes[i]
self.graph = tf.Graph()
with self.graph.as_default():
if random_seed is not None:
tf.set_random_seed(random_seed)
self.X = [tf.sparse_placeholder(dtype) for i in range(num_inputs)]
self.y = tf.placeholder(dtype)
self.keep_prob_train = 1 - np.array(drop_out)
self.keep_prob_test = np.ones_like(drop_out)
self.layer_keeps = tf.placeholder(dtype)
self.vars = init_var_map(init_vars, init_path)
w0 = [self.vars['embed_%d' % i] for i in range(num_inputs)]
xw = tf.concat([tf.sparse_tensor_dense_matmul(self.X[i], w0[i]) for i in range(num_inputs)], 1)
l = xw
for i in range(len(layer_sizes)):
wi = self.vars['w%d' % i]
bi = self.vars['b%d' % i]
print(l.shape, wi.shape, bi.shape)
l = tf.nn.dropout(
activate(
tf.matmul(l, wi) + bi,
layer_acts[i]),
self.layer_keeps[i])
l = tf.squeeze(l)
self.y_prob = tf.sigmoid(l)
self.loss = tf.reduce_mean(
tf.nn.sigmoid_cross_entropy_with_logits(logits=l, labels=self.y))
if layer_l2 is not None:
self.loss += embed_l2 * tf.nn.l2_loss(xw)
for i in range(len(layer_sizes)):
wi = self.vars['w%d' % i]
self.loss += layer_l2[i] * tf.nn.l2_loss(wi)
self.optimizer = get_optimizer(opt_algo, learning_rate, self.loss)
config = tf.ConfigProto()
config.gpu_options.allow_growth = True
self.sess = tf.Session(config=config)
tf.global_variables_initializer().run(session=self.sess)
import numpy as np
from sklearn.metrics import roc_auc_score
import progressbar
train_file = './data/train.txt'
test_file = './data/test.txt'
input_dim = INPUT_DIM
train_data = pkl.load(open('./data/train.pkl', 'rb'))
train_data = shuffle(train_data)
test_data = pkl.load(open('./data/test.pkl', 'rb'))
if train_data[1].ndim > 1:
print('label must be 1-dim')
exit(0)
print('read finish')
print('train data size:', train_data[0].shape)
print('test data size:', test_data[0].shape)
train_size = train_data[0].shape[0]
test_size = test_data[0].shape[0]
num_feas = len(FIELD_SIZES)
min_round = 1
num_round = 200
early_stop_round = 5
batch_size = 1024
field_sizes = FIELD_SIZES
field_offsets = FIELD_OFFSETS
train_data = split_data(train_data)
test_data = split_data(test_data)
tmp = []
for x in field_sizes:
if x > 0:
tmp.append(x)
field_sizes = tmp
print('remove empty fields', field_sizes)
fnn_params = {
'field_sizes': field_sizes,
'embed_size': 10,
'layer_sizes': [500, 1],
'layer_acts': ['relu', None],
'drop_out': [0, 0],
'opt_algo': 'gd',
'learning_rate': 0.1,
'embed_l2': 0,
'layer_l2': [0, 0],
'random_seed': 0
}
print(fnn_params)
model = FNN(**fnn_params)
def train(model):
history_score = []
for i in range(num_round):
fetches = [model.optimizer, model.loss]
if batch_size > 0:
ls = []
bar = progressbar.ProgressBar()
print('[%d]\ttraining...' % i)
for j in bar(range(int(train_size / batch_size + 1))):
X_i, y_i = slice(train_data, j * batch_size, batch_size)
_, l = model.run(fetches, X_i, y_i)
ls.append(l)
elif batch_size == -1:
X_i, y_i = slice(train_data)
_, l = model.run(fetches, X_i, y_i)
ls = [l]
train_preds = []
print('[%d]\tevaluating...' % i)
bar = progressbar.ProgressBar()
for j in bar(range(int(train_size / 10000 + 1))):
X_i, _ = slice(train_data, j * 10000, 10000)
preds = model.run(model.y_prob, X_i, mode='test')
train_preds.extend(preds)
test_preds = []
bar = progressbar.ProgressBar()
for j in bar(range(int(test_size / 10000 + 1))):
X_i, _ = slice(test_data, j * 10000, 10000)
preds = model.run(model.y_prob, X_i, mode='test')
test_preds.extend(preds)
train_score = roc_auc_score(train_data[1], train_preds)
test_score = roc_auc_score(test_data[1], test_preds)
print('[%d]\tloss (with l2 norm):%f\ttrain-auc: %f\teval-auc: %f' % (i, np.mean(ls), train_score, test_score))
history_score.append(test_score)
if i > min_round and i > early_stop_round:
if np.argmax(history_score) == i - early_stop_round and history_score[-1] - history_score[
-1 * early_stop_round] < 1e-5:
print('early stop\nbest iteration:\n[%d]\teval-auc: %f' % (
np.argmax(history_score), np.max(history_score)))
break
train(model) | read finish
train data size: (1742104, 491713)
test data size: (300928, 491713)
remove empty fields [25, 445852, 36, 371, 4, 11328, 33995, 12, 7, 5, 4, 20, 2, 38, 6, 8]
{'field_sizes': [25, 445852, 36, 371, 4, 11328, 33995, 12, 7, 5, 4, 20, 2, 38, 6, 8], 'layer_acts': ['relu', None], 'embed_l2': 0, 'drop_out': [0, 0], 'embed_size': 10, 'random_seed': 0, 'learning_rate': 0.1, 'layer_sizes': [500, 1], 'layer_l2': [0, 0], 'opt_algo': 'gd'}
(?, 160) (160, 500) (500,)
(?, 500) (500, 1) (1,)
| Apache-2.0 | notebooks/CTR_prediction_LR_FM_CCPM_PNN.ipynb | daiwk/grace_t |
CCPMreference:[ctr模型汇总](https://zhuanlan.zhihu.com/p/32523455)FM只能学习特征的二阶组合,但CNN能学习更高阶的组合,可学习的阶数和卷积的视野相关。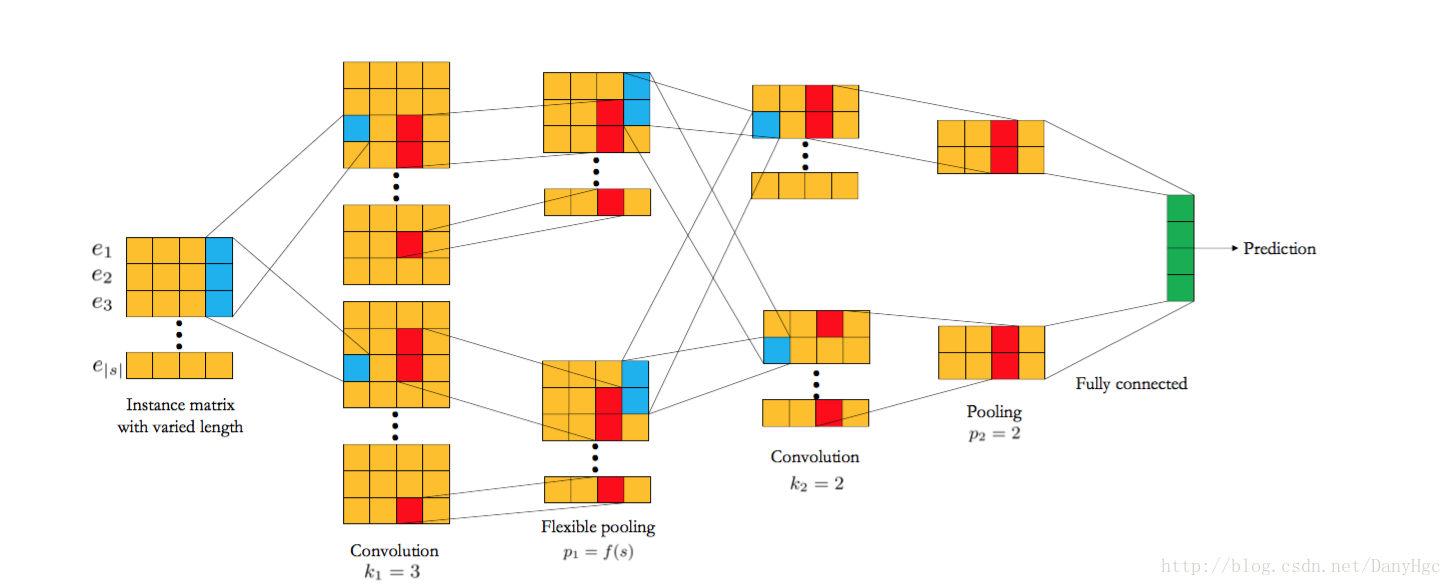mbedding层:e1, e2…en是某特定用户被展示的一系列广告。如果在预测广告是否会点击时不考虑历史展示广告的点击情况,则n=1。同时embedding矩阵的具体值是随着模型训练学出来的。Embedding矩阵为S,向量维度为d。卷积层:卷积参数W有d*w个,即对于矩阵S,上图每一列对应一个参数不共享的一维卷积,其视野为w,卷积共有d个,每个输出向量维度为(n+w-1),输出矩阵维度d*(n+w-1)。因为对于ctr预估而言,矩阵S每一列都对应特定的描述维度,所以需要分别处理,得到的输出矩阵的每一列就都是描述广告特定方面的特征。Pooling层:flexible p-max pooling。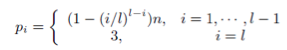L是模型总卷积层数,n是输入序列长度,pi就是第i层的pooling参数。这样最后一层卷积层都是输出3个最大的元素,长度固定方便后面接全连接层。同时这个指数型的参数,一开始改变比较小,几乎都是n,后面就减少得比较快。这样可以防止在模型浅层的时候就损失太多信息,众所周知深度模型在前面几层最好不要做得太简单,容易损失很多信息。文章还提到p-max pooling输出的几个最大的元素是保序的,可输入时的顺序一致,这点对于保留序列信息是重要的。激活层:tanh最后,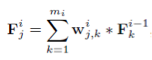Fij是指低i层的第j个feature map。感觉是不同输入通道的卷积参数也不共享,对应输出是所有输入通道卷积的输出的求和。 | class CCPM(Model):
def __init__(self, field_sizes=None, embed_size=10, filter_sizes=None, layer_acts=None, drop_out=None,
init_path=None, opt_algo='gd', learning_rate=1e-2, random_seed=None):
Model.__init__(self)
init_vars = []
num_inputs = len(field_sizes)
for i in range(num_inputs):
init_vars.append(('embed_%d' % i, [field_sizes[i], embed_size], 'xavier', dtype))
init_vars.append(('f1', [embed_size, filter_sizes[0], 1, 2], 'xavier', dtype))
init_vars.append(('f2', [embed_size, filter_sizes[1], 2, 2], 'xavier', dtype))
init_vars.append(('w1', [2 * 3 * embed_size, 1], 'xavier', dtype))
init_vars.append(('b1', [1], 'zero', dtype))
self.graph = tf.Graph()
with self.graph.as_default():
if random_seed is not None:
tf.set_random_seed(random_seed)
self.X = [tf.sparse_placeholder(dtype) for i in range(num_inputs)]
self.y = tf.placeholder(dtype)
self.keep_prob_train = 1 - np.array(drop_out)
self.keep_prob_test = np.ones_like(drop_out)
self.layer_keeps = tf.placeholder(dtype)
self.vars = init_var_map(init_vars, init_path)
w0 = [self.vars['embed_%d' % i] for i in range(num_inputs)]
xw = tf.concat([tf.sparse_tensor_dense_matmul(self.X[i], w0[i]) for i in range(num_inputs)], 1)
l = xw
l = tf.transpose(tf.reshape(l, [-1, num_inputs, embed_size, 1]), [0, 2, 1, 3])
f1 = self.vars['f1']
l = tf.nn.conv2d(l, f1, [1, 1, 1, 1], 'SAME')
l = tf.transpose(
max_pool_4d(
tf.transpose(l, [0, 1, 3, 2]),
int(num_inputs / 2)),
[0, 1, 3, 2])
f2 = self.vars['f2']
l = tf.nn.conv2d(l, f2, [1, 1, 1, 1], 'SAME')
l = tf.transpose(
max_pool_4d(
tf.transpose(l, [0, 1, 3, 2]), 3),
[0, 1, 3, 2])
l = tf.nn.dropout(
activate(
tf.reshape(l, [-1, embed_size * 3 * 2]),
layer_acts[0]),
self.layer_keeps[0])
w1 = self.vars['w1']
b1 = self.vars['b1']
l = tf.matmul(l, w1) + b1
l = tf.squeeze(l)
self.y_prob = tf.sigmoid(l)
self.loss = tf.reduce_mean(
tf.nn.sigmoid_cross_entropy_with_logits(logits=l, labels=self.y))
self.optimizer = get_optimizer(opt_algo, learning_rate, self.loss)
config = tf.ConfigProto()
config.gpu_options.allow_growth = True
self.sess = tf.Session(config=config)
tf.global_variables_initializer().run(session=self.sess) | _____no_output_____ | Apache-2.0 | notebooks/CTR_prediction_LR_FM_CCPM_PNN.ipynb | daiwk/grace_t |
PNNreference:[深度学习在CTR预估中的应用](https://zhuanlan.zhihu.com/p/35484389)可以视作FNN+product layer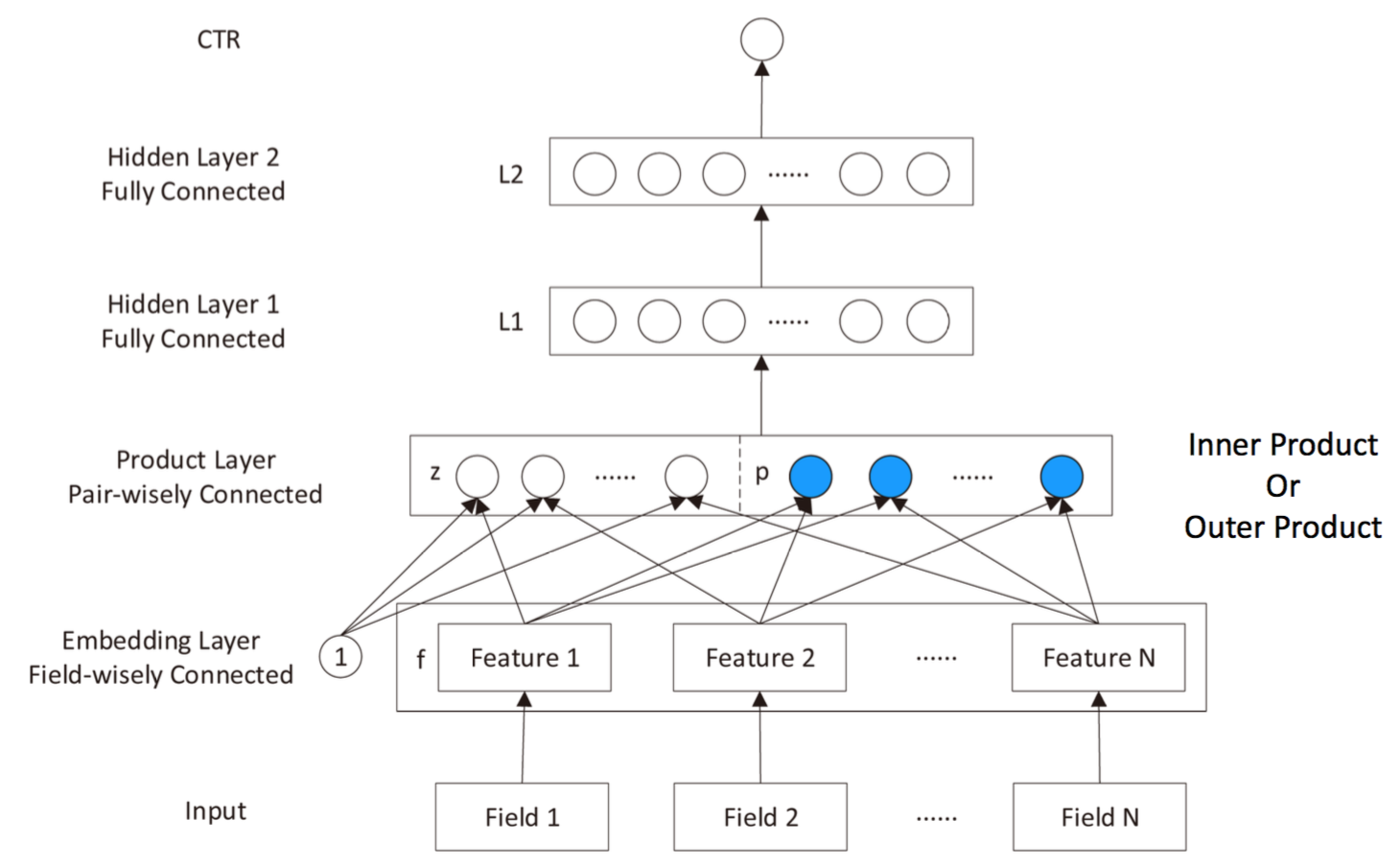PNN和FNN的主要不同在于除了得到z向量,还增加了一个p向量,即Product向量。Product向量由每个category field的feature vector做inner product 或则 outer product 得到,作者认为这样做有助于特征交叉。另外PNN中Embeding层不再由FM生成,可以在整个网络中训练得到。对比 FNN 网络,PNN的区别在于中间多了一层 Product Layer 层。Product Layer 层由两部分组成,左边z为 embedding 层的线性部分,右边为 embedding 层的特征交叉部分。除了 Product Layer 不同,PNN 和 FNN 的 MLP 结构是一样的。这种 product 思想来源于,在 CTR 预估中,认为特征之间的关系更多是一种 and“且”的关系,而非 add"加”的关系。例如,性别为男且喜欢游戏的人群,比起性别男和喜欢游戏的人群,前者的组合比后者更能体现特征交叉的意义。根据 product 的方式不同,可以分为 inner product (IPNN) 和 outer product (OPNN),如下图所示。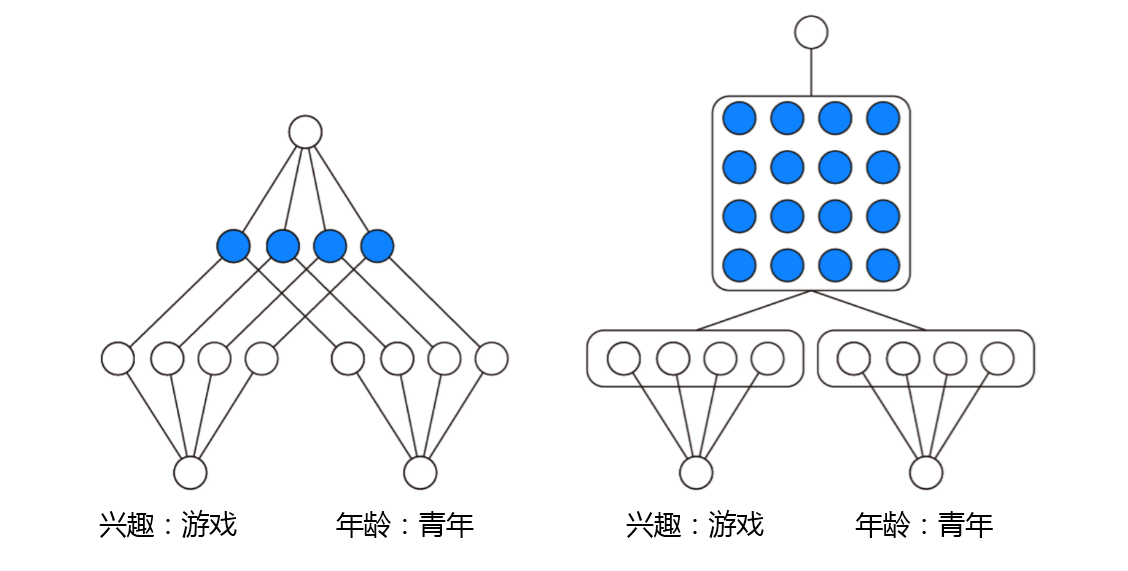 PNN1 | class PNN1(Model):
def __init__(self, field_sizes=None, embed_size=10, layer_sizes=None, layer_acts=None, drop_out=None,
embed_l2=None, layer_l2=None, init_path=None, opt_algo='gd', learning_rate=1e-2, random_seed=None):
Model.__init__(self)
init_vars = []
num_inputs = len(field_sizes)
for i in range(num_inputs):
init_vars.append(('embed_%d' % i, [field_sizes[i], embed_size], 'xavier', dtype))
num_pairs = int(num_inputs * (num_inputs - 1) / 2)
node_in = num_inputs * embed_size + num_pairs
# node_in = num_inputs * (embed_size + num_inputs)
for i in range(len(layer_sizes)):
init_vars.append(('w%d' % i, [node_in, layer_sizes[i]], 'xavier', dtype))
init_vars.append(('b%d' % i, [layer_sizes[i]], 'zero', dtype))
node_in = layer_sizes[i]
self.graph = tf.Graph()
with self.graph.as_default():
if random_seed is not None:
tf.set_random_seed(random_seed)
self.X = [tf.sparse_placeholder(dtype) for i in range(num_inputs)]
self.y = tf.placeholder(dtype)
self.keep_prob_train = 1 - np.array(drop_out)
self.keep_prob_test = np.ones_like(drop_out)
self.layer_keeps = tf.placeholder(dtype)
self.vars = init_var_map(init_vars, init_path)
w0 = [self.vars['embed_%d' % i] for i in range(num_inputs)]
xw = tf.concat([tf.sparse_tensor_dense_matmul(self.X[i], w0[i]) for i in range(num_inputs)], 1)
xw3d = tf.reshape(xw, [-1, num_inputs, embed_size])
row = []
col = []
for i in range(num_inputs-1):
for j in range(i+1, num_inputs):
row.append(i)
col.append(j)
# batch * pair * k
p = tf.transpose(
# pair * batch * k
tf.gather(
# num * batch * k
tf.transpose(
xw3d, [1, 0, 2]),
row),
[1, 0, 2])
# batch * pair * k
q = tf.transpose(
tf.gather(
tf.transpose(
xw3d, [1, 0, 2]),
col),
[1, 0, 2])
p = tf.reshape(p, [-1, num_pairs, embed_size])
q = tf.reshape(q, [-1, num_pairs, embed_size])
ip = tf.reshape(tf.reduce_sum(p * q, [-1]), [-1, num_pairs])
# simple but redundant
# batch * n * 1 * k, batch * 1 * n * k
# ip = tf.reshape(
# tf.reduce_sum(
# tf.expand_dims(xw3d, 2) *
# tf.expand_dims(xw3d, 1),
# 3),
# [-1, num_inputs**2])
l = tf.concat([xw, ip], 1)
for i in range(len(layer_sizes)):
wi = self.vars['w%d' % i]
bi = self.vars['b%d' % i]
l = tf.nn.dropout(
activate(
tf.matmul(l, wi) + bi,
layer_acts[i]),
self.layer_keeps[i])
l = tf.squeeze(l)
self.y_prob = tf.sigmoid(l)
self.loss = tf.reduce_mean(
tf.nn.sigmoid_cross_entropy_with_logits(logits=l, labels=self.y))
if layer_l2 is not None:
self.loss += embed_l2 * tf.nn.l2_loss(xw)
for i in range(len(layer_sizes)):
wi = self.vars['w%d' % i]
self.loss += layer_l2[i] * tf.nn.l2_loss(wi)
self.optimizer = get_optimizer(opt_algo, learning_rate, self.loss)
config = tf.ConfigProto()
config.gpu_options.allow_growth = True
self.sess = tf.Session(config=config)
tf.global_variables_initializer().run(session=self.sess) | _____no_output_____ | Apache-2.0 | notebooks/CTR_prediction_LR_FM_CCPM_PNN.ipynb | daiwk/grace_t |
PNN2 | class PNN2(Model):
def __init__(self, field_sizes=None, embed_size=10, layer_sizes=None, layer_acts=None, drop_out=None,
embed_l2=None, layer_l2=None, init_path=None, opt_algo='gd', learning_rate=1e-2, random_seed=None,
layer_norm=True):
Model.__init__(self)
init_vars = []
num_inputs = len(field_sizes)
for i in range(num_inputs):
init_vars.append(('embed_%d' % i, [field_sizes[i], embed_size], 'xavier', dtype))
num_pairs = int(num_inputs * (num_inputs - 1) / 2)
node_in = num_inputs * embed_size + num_pairs
init_vars.append(('kernel', [embed_size, num_pairs, embed_size], 'xavier', dtype))
for i in range(len(layer_sizes)):
init_vars.append(('w%d' % i, [node_in, layer_sizes[i]], 'xavier', dtype))
init_vars.append(('b%d' % i, [layer_sizes[i]], 'zero', dtype))
node_in = layer_sizes[i]
self.graph = tf.Graph()
with self.graph.as_default():
if random_seed is not None:
tf.set_random_seed(random_seed)
self.X = [tf.sparse_placeholder(dtype) for i in range(num_inputs)]
self.y = tf.placeholder(dtype)
self.keep_prob_train = 1 - np.array(drop_out)
self.keep_prob_test = np.ones_like(drop_out)
self.layer_keeps = tf.placeholder(dtype)
self.vars = init_var_map(init_vars, init_path)
w0 = [self.vars['embed_%d' % i] for i in range(num_inputs)]
xw = tf.concat([tf.sparse_tensor_dense_matmul(self.X[i], w0[i]) for i in range(num_inputs)], 1)
xw3d = tf.reshape(xw, [-1, num_inputs, embed_size])
row = []
col = []
for i in range(num_inputs - 1):
for j in range(i + 1, num_inputs):
row.append(i)
col.append(j)
# batch * pair * k
p = tf.transpose(
# pair * batch * k
tf.gather(
# num * batch * k
tf.transpose(
xw3d, [1, 0, 2]),
row),
[1, 0, 2])
# batch * pair * k
q = tf.transpose(
tf.gather(
tf.transpose(
xw3d, [1, 0, 2]),
col),
[1, 0, 2])
# b * p * k
p = tf.reshape(p, [-1, num_pairs, embed_size])
# b * p * k
q = tf.reshape(q, [-1, num_pairs, embed_size])
# k * p * k
k = self.vars['kernel']
# batch * 1 * pair * k
p = tf.expand_dims(p, 1)
# batch * pair
kp = tf.reduce_sum(
# batch * pair * k
tf.multiply(
# batch * pair * k
tf.transpose(
# batch * k * pair
tf.reduce_sum(
# batch * k * pair * k
tf.multiply(
p, k),
-1),
[0, 2, 1]),
q),
-1)
#
# if layer_norm:
# # x_mean, x_var = tf.nn.moments(xw, [1], keep_dims=True)
# # xw = (xw - x_mean) / tf.sqrt(x_var)
# # x_g = tf.Variable(tf.ones([num_inputs * embed_size]), name='x_g')
# # x_b = tf.Variable(tf.zeros([num_inputs * embed_size]), name='x_b')
# # x_g = tf.Print(x_g, [x_g[:10], x_b])
# # xw = xw * x_g + x_b
# p_mean, p_var = tf.nn.moments(op, [1], keep_dims=True)
# op = (op - p_mean) / tf.sqrt(p_var)
# p_g = tf.Variable(tf.ones([embed_size**2]), name='p_g')
# p_b = tf.Variable(tf.zeros([embed_size**2]), name='p_b')
# # p_g = tf.Print(p_g, [p_g[:10], p_b])
# op = op * p_g + p_b
l = tf.concat([xw, kp], 1)
for i in range(len(layer_sizes)):
wi = self.vars['w%d' % i]
bi = self.vars['b%d' % i]
l = tf.nn.dropout(
activate(
tf.matmul(l, wi) + bi,
layer_acts[i]),
self.layer_keeps[i])
l = tf.squeeze(l)
self.y_prob = tf.sigmoid(l)
self.loss = tf.reduce_mean(
tf.nn.sigmoid_cross_entropy_with_logits(logits=l, labels=self.y))
if layer_l2 is not None:
self.loss += embed_l2 * tf.nn.l2_loss(xw)#tf.concat(w0, 0))
for i in range(len(layer_sizes)):
wi = self.vars['w%d' % i]
self.loss += layer_l2[i] * tf.nn.l2_loss(wi)
self.optimizer = get_optimizer(opt_algo, learning_rate, self.loss)
config = tf.ConfigProto()
config.gpu_options.allow_growth = True
self.sess = tf.Session(config=config)
tf.global_variables_initializer().run(session=self.sess) | _____no_output_____ | Apache-2.0 | notebooks/CTR_prediction_LR_FM_CCPM_PNN.ipynb | daiwk/grace_t |
Take a look into the 2016 data | df2016.head(n=2)
df2016.shape | _____no_output_____ | MIT | preliminary-data-visualization.ipynb | argha48/nyc-parking-ticket |
So in the 2016 dataset there are about 10.6 million entries for parking ticket, and each entry has 51 columns.Lets take a look at the number of unique values for each column name... | d = {'Unique Entry': df2016.nunique(axis = 0),
'Nan Entry': df2016.isnull().any()}
pd.DataFrame(data = d, index = df2016.columns.values) | _____no_output_____ | MIT | preliminary-data-visualization.ipynb | argha48/nyc-parking-ticket |
As it turns out, the last 11 columns in this dataset has no entry. So we can ignore those columns, while carrying out any visualization operation in this dataframe.Also if the entry does not have a **Plate ID** it is very hard to locate those cars. Therefore I am going to drop those rows as well. | drop_column = ['No Standing or Stopping Violation', 'Hydrant Violation',
'Double Parking Violation', 'Latitude', 'Longitude',
'Community Board', 'Community Council ', 'Census Tract', 'BIN',
'BBL', 'NTA',
'Street Code1', 'Street Code2', 'Street Code3','Meter Number', 'Violation Post Code',
'Law Section', 'Sub Division', 'House Number', 'Street Name']
df2016.drop(drop_column, axis = 1, inplace = True)
drop_row = ['Plate ID']
df2016.dropna(axis = 0, how = 'any', subset = drop_row, inplace = True) | _____no_output_____ | MIT | preliminary-data-visualization.ipynb | argha48/nyc-parking-ticket |
Check if there is anymore rows left without a **Plate ID**. | df2016['Plate ID'].isnull().any()
df2016.shape | _____no_output_____ | MIT | preliminary-data-visualization.ipynb | argha48/nyc-parking-ticket |
Create a sample data for visualization The cleaned dataframe has 10624735 rows and 40 columns. But this is still a lot of data points. I does not make sense to use all of them to get an idea of distribution of the data points. So for visualization I will use only 0.1% of the whole data. Assmuing that the entries are not sorted I pick my 0.1% data points from the main dataframe at random. | mini2016 = df2016.sample(frac = 0.01, replace = False)
mini2016.shape | _____no_output_____ | MIT | preliminary-data-visualization.ipynb | argha48/nyc-parking-ticket |
My sample dataset has about 10K data points, which I will use for data visualization. Using the whole dataset is unnecessary and time consuming. Barplot of 'Registration State' | x_ticks = mini2016['Registration State'].value_counts().index
heights = mini2016['Registration State'].value_counts()
y_pos = np.arange(len(x_ticks))
fig = plt.figure(figsize=(15,14))
# Create horizontal bars
plt.barh(y_pos, heights)
# Create names on the y-axis
plt.yticks(y_pos, x_ticks)
# Show graphic
plt.show()
pd.DataFrame(mini2016['Registration State'].value_counts()/len(mini2016)).nlargest(10, columns = ['Registration State']) | _____no_output_____ | MIT | preliminary-data-visualization.ipynb | argha48/nyc-parking-ticket |
You can see from the barplot above: in our sample ~77.67% cars are registered in state : **NY**. After that 9.15% cars are registered in state : **NJ**, followed by **PA**, **CT**, and **FL**. How the number of tickets given changes with each month? | month = []
for time_stamp in pd.to_datetime(mini2016['Issue Date']):
month.append(time_stamp.month)
m_count = pd.Series(month).value_counts()
plt.figure(figsize=(12,8))
sns.barplot(y=m_count.values, x=m_count.index, alpha=0.6)
plt.title("Number of Parking Ticket Given Each Month", fontsize=16)
plt.xlabel("Month", fontsize=16)
plt.ylabel("No. of cars", fontsize=16)
plt.show(); | _____no_output_____ | MIT | preliminary-data-visualization.ipynb | argha48/nyc-parking-ticket |
So from the barplot above **March** and **October** has the highest number of tickets! How many parking tickets are given for each violation code? | violation_code = mini2016['Violation Code'].value_counts()
plt.figure(figsize=(16,8))
f = sns.barplot(y=violation_code.values, x=violation_code.index, alpha=0.6)
#plt.xticks(np.arange(0,101, 10.0))
f.set(xticks=np.arange(0,100, 5.0))
plt.title("Number of Parking Tickets Given for Each Violation Code", fontsize=16)
plt.xlabel("Violation Code [ X5 ]", fontsize=16)
plt.ylabel("No. of cars", fontsize=16)
plt.show(); | _____no_output_____ | MIT | preliminary-data-visualization.ipynb | argha48/nyc-parking-ticket |
How many parking tickets are given for each body type? | x_ticks = mini2016['Vehicle Body Type'].value_counts().index
heights = mini2016['Vehicle Body Type'].value_counts().values
y_pos = np.arange(len(x_ticks))
fig = plt.figure(figsize=(15,4))
f = sns.barplot(y=heights, x=y_pos, orient = 'v', alpha=0.6);
# remove labels
plt.tick_params(labelbottom='off')
plt.ylabel('No. of cars', fontsize=16);
plt.xlabel('Car models [Label turned off due to crowding. Too many types.]', fontsize=16);
plt.title('Parking ticket given for different type of car body', fontsize=16);
df_bodytype = pd.DataFrame(mini2016['Vehicle Body Type'].value_counts() / len(mini2016)).nlargest(10, columns = ['Vehicle Body Type']) | _____no_output_____ | MIT | preliminary-data-visualization.ipynb | argha48/nyc-parking-ticket |
Top 10 car body types that get the most parking tickets are listed below : | df_bodytype
df_bodytype.sum(axis = 0)/len(mini2016) | _____no_output_____ | MIT | preliminary-data-visualization.ipynb | argha48/nyc-parking-ticket |
Top 10 vehicle body type includes 93.42% of my sample dataset. How many parking tickets are given for each vehicle make? Just for the sake of changing the flavor of visualization this time I will make a logplot of car no. vs make. In that case we will be able to see much smaller values in the same graph with larger values. | vehicle_make = mini2016['Vehicle Make'].value_counts()
plt.figure(figsize=(16,8))
f = sns.barplot(y=np.log(vehicle_make.values), x=vehicle_make.index, alpha=0.6)
# remove labels
plt.tick_params(labelbottom='off')
plt.ylabel('log(No. of cars)', fontsize=16);
plt.xlabel('Car make [Label turned off due to crowding. Too many companies!]', fontsize=16);
plt.title('Parking ticket given for different type of car make', fontsize=16);
plt.show();
pd.DataFrame(mini2016['Vehicle Make'].value_counts() / len(mini2016)).nlargest(10, columns = ['Vehicle Make']) | _____no_output_____ | MIT | preliminary-data-visualization.ipynb | argha48/nyc-parking-ticket |
Insight on violation time In the raw data the **Violaation Time** is in a format, which is non-interpretable using standard **to_datatime** function in pandas. We need to change it in a useful format so that we can use the data. After formatting we may replace the old **Violation Time ** column with the new one. | timestamp = []
for time in mini2016['Violation Time']:
if len(str(time)) == 5:
time = time[:2] + ':' + time[2:]
timestamp.append(pd.to_datetime(time, errors='coerce'))
else:
timestamp.append(pd.NaT)
mini2016 = mini2016.assign(Violation_Time2 = timestamp)
mini2016.drop(['Violation Time'], axis = 1, inplace = True)
mini2016.rename(index=str, columns={"Violation_Time2": "Violation Time"}, inplace = True) | _____no_output_____ | MIT | preliminary-data-visualization.ipynb | argha48/nyc-parking-ticket |
So in the new **Violation Time** column the data is in **Timestamp** format. | hours = [lambda x: x.hour, mini2016['Violation Time']]
# Getting the histogram
mini2016.set_index('Violation Time', drop=False, inplace=True)
plt.figure(figsize=(16,8))
mini2016['Violation Time'].groupby(pd.TimeGrouper(freq='30Min')).count().plot(kind='bar');
plt.tick_params(labelbottom='on')
plt.ylabel('No. of cars', fontsize=16);
plt.xlabel('Day Time', fontsize=16);
plt.title('Parking ticket given at different time of the day', fontsize=16);
| _____no_output_____ | MIT | preliminary-data-visualization.ipynb | argha48/nyc-parking-ticket |
Parking ticket vs county | violation_county = mini2016['Violation County'].value_counts()
plt.figure(figsize=(16,8))
f = sns.barplot(y=violation_county.values, x=violation_county.index, alpha=0.6)
# remove labels
plt.tick_params(labelbottom='on')
plt.ylabel('No. of cars', fontsize=16);
plt.xlabel('County', fontsize=16);
plt.title('Parking ticket given in different counties', fontsize=16); | _____no_output_____ | MIT | preliminary-data-visualization.ipynb | argha48/nyc-parking-ticket |
Unregistered Vehicle? | sns.countplot(x = 'Unregistered Vehicle?', data = mini2016)
mini2016['Unregistered Vehicle?'].unique() | _____no_output_____ | MIT | preliminary-data-visualization.ipynb | argha48/nyc-parking-ticket |
Vehicle Year | pd.DataFrame(mini2016['Vehicle Year'].value_counts()).nlargest(10, columns = ['Vehicle Year'])
plt.figure(figsize=(20,8))
sns.countplot(x = 'Vehicle Year', data = mini2016.loc[(mini2016['Vehicle Year']>1980) & (mini2016['Vehicle Year'] <= 2018)]); | _____no_output_____ | MIT | preliminary-data-visualization.ipynb | argha48/nyc-parking-ticket |
Violation In Front Of Or Opposite | plt.figure(figsize=(16,8))
sns.countplot(x = 'Violation In Front Of Or Opposite', data = mini2016);
# create data
names = mini2016['Violation In Front Of Or Opposite'].value_counts().index
size = mini2016['Violation In Front Of Or Opposite'].value_counts().values
# Create a circle for the center of the plot
my_circle=plt.Circle( (0,0), 0.7, color='white')
plt.figure(figsize=(8,8))
from palettable.colorbrewer.qualitative import Pastel1_7
plt.pie(size, labels=names, colors=Pastel1_7.hex_colors)
p=plt.gcf()
p.gca().add_artist(my_circle)
plt.show()
| _____no_output_____ | MIT | preliminary-data-visualization.ipynb | argha48/nyc-parking-ticket |
CER041 - Install signed Knox certificate========================================This notebook installs into the Big Data Cluster the certificate signedusing:- [CER031 - Sign Knox certificate with generated CA](../cert-management/cer031-sign-knox-generated-cert.ipynb)Steps----- Parameters | app_name = "gateway"
scaledset_name = "gateway/pods/gateway-0"
container_name = "knox"
prefix_keyfile_name = "knox"
common_name = "gateway-svc"
test_cert_store_root = "/var/opt/secrets/test-certificates" | _____no_output_____ | MIT | Big-Data-Clusters/CU3/Public/content/cert-management/cer041-install-knox-cert.ipynb | gantz-at-incomm/tigertoolbox |
Common functionsDefine helper functions used in this notebook. | # Define `run` function for transient fault handling, suggestions on error, and scrolling updates on Windows
import sys
import os
import re
import json
import platform
import shlex
import shutil
import datetime
from subprocess import Popen, PIPE
from IPython.display import Markdown
retry_hints = {}
error_hints = {}
install_hint = {}
first_run = True
rules = None
def run(cmd, return_output=False, no_output=False, retry_count=0):
"""
Run shell command, stream stdout, print stderr and optionally return output
"""
MAX_RETRIES = 5
output = ""
retry = False
global first_run
global rules
if first_run:
first_run = False
rules = load_rules()
# shlex.split is required on bash and for Windows paths with spaces
#
cmd_actual = shlex.split(cmd)
# Store this (i.e. kubectl, python etc.) to support binary context aware error_hints and retries
#
user_provided_exe_name = cmd_actual[0].lower()
# When running python, use the python in the ADS sandbox ({sys.executable})
#
if cmd.startswith("python "):
cmd_actual[0] = cmd_actual[0].replace("python", sys.executable)
# On Mac, when ADS is not launched from terminal, LC_ALL may not be set, which causes pip installs to fail
# with:
#
# UnicodeDecodeError: 'ascii' codec can't decode byte 0xc5 in position 4969: ordinal not in range(128)
#
# Setting it to a default value of "en_US.UTF-8" enables pip install to complete
#
if platform.system() == "Darwin" and "LC_ALL" not in os.environ:
os.environ["LC_ALL"] = "en_US.UTF-8"
# To aid supportabilty, determine which binary file will actually be executed on the machine
#
which_binary = None
# Special case for CURL on Windows. The version of CURL in Windows System32 does not work to
# get JWT tokens, it returns "(56) Failure when receiving data from the peer". If another instance
# of CURL exists on the machine use that one. (Unfortunately the curl.exe in System32 is almost
# always the first curl.exe in the path, and it can't be uninstalled from System32, so here we
# look for the 2nd installation of CURL in the path)
if platform.system() == "Windows" and cmd.startswith("curl "):
path = os.getenv('PATH')
for p in path.split(os.path.pathsep):
p = os.path.join(p, "curl.exe")
if os.path.exists(p) and os.access(p, os.X_OK):
if p.lower().find("system32") == -1:
cmd_actual[0] = p
which_binary = p
break
# Find the path based location (shutil.which) of the executable that will be run (and display it to aid supportability), this
# seems to be required for .msi installs of azdata.cmd/az.cmd. (otherwise Popen returns FileNotFound)
#
# NOTE: Bash needs cmd to be the list of the space separated values hence shlex.split.
#
if which_binary == None:
which_binary = shutil.which(cmd_actual[0])
if which_binary == None:
if user_provided_exe_name in install_hint and install_hint[user_provided_exe_name] is not None:
display(Markdown(f'HINT: Use [{install_hint[user_provided_exe_name][0]}]({install_hint[user_provided_exe_name][1]}) to resolve this issue.'))
raise FileNotFoundError(f"Executable '{cmd_actual[0]}' not found in path (where/which)")
else:
cmd_actual[0] = which_binary
start_time = datetime.datetime.now().replace(microsecond=0)
print(f"START: {cmd} @ {start_time} ({datetime.datetime.utcnow().replace(microsecond=0)} UTC)")
print(f" using: {which_binary} ({platform.system()} {platform.release()} on {platform.machine()})")
print(f" cwd: {os.getcwd()}")
# Command-line tools such as CURL and AZDATA HDFS commands output
# scrolling progress bars, which causes Jupyter to hang forever, to
# workaround this, use no_output=True
#
# Work around a infinite hang when a notebook generates a non-zero return code, break out, and do not wait
#
wait = True
try:
if no_output:
p = Popen(cmd_actual)
else:
p = Popen(cmd_actual, stdout=PIPE, stderr=PIPE, bufsize=1)
with p.stdout:
for line in iter(p.stdout.readline, b''):
line = line.decode()
if return_output:
output = output + line
else:
if cmd.startswith("azdata notebook run"): # Hyperlink the .ipynb file
regex = re.compile(' "(.*)"\: "(.*)"')
match = regex.match(line)
if match:
if match.group(1).find("HTML") != -1:
display(Markdown(f' - "{match.group(1)}": "{match.group(2)}"'))
else:
display(Markdown(f' - "{match.group(1)}": "[{match.group(2)}]({match.group(2)})"'))
wait = False
break # otherwise infinite hang, have not worked out why yet.
else:
print(line, end='')
if rules is not None:
apply_expert_rules(line)
if wait:
p.wait()
except FileNotFoundError as e:
if install_hint is not None:
display(Markdown(f'HINT: Use {install_hint} to resolve this issue.'))
raise FileNotFoundError(f"Executable '{cmd_actual[0]}' not found in path (where/which)") from e
exit_code_workaround = 0 # WORKAROUND: azdata hangs on exception from notebook on p.wait()
if not no_output:
for line in iter(p.stderr.readline, b''):
line_decoded = line.decode()
# azdata emits a single empty line to stderr when doing an hdfs cp, don't
# print this empty "ERR:" as it confuses.
#
if line_decoded == "":
continue
print(f"STDERR: {line_decoded}", end='')
if line_decoded.startswith("An exception has occurred") or line_decoded.startswith("ERROR: An error occurred while executing the following cell"):
exit_code_workaround = 1
if user_provided_exe_name in error_hints:
for error_hint in error_hints[user_provided_exe_name]:
if line_decoded.find(error_hint[0]) != -1:
display(Markdown(f'HINT: Use [{error_hint[1]}]({error_hint[2]}) to resolve this issue.'))
if rules is not None:
apply_expert_rules(line_decoded)
if user_provided_exe_name in retry_hints:
for retry_hint in retry_hints[user_provided_exe_name]:
if line_decoded.find(retry_hint) != -1:
if retry_count < MAX_RETRIES:
print(f"RETRY: {retry_count} (due to: {retry_hint})")
retry_count = retry_count + 1
output = run(cmd, return_output=return_output, retry_count=retry_count)
if return_output:
return output
else:
return
elapsed = datetime.datetime.now().replace(microsecond=0) - start_time
# WORKAROUND: We avoid infinite hang above in the `azdata notebook run` failure case, by inferring success (from stdout output), so
# don't wait here, if success known above
#
if wait:
if p.returncode != 0:
raise SystemExit(f'Shell command:\n\n\t{cmd} ({elapsed}s elapsed)\n\nreturned non-zero exit code: {str(p.returncode)}.\n')
else:
if exit_code_workaround !=0 :
raise SystemExit(f'Shell command:\n\n\t{cmd} ({elapsed}s elapsed)\n\nreturned non-zero exit code: {str(exit_code_workaround)}.\n')
print(f'\nSUCCESS: {elapsed}s elapsed.\n')
if return_output:
return output
def load_json(filename):
with open(filename, encoding="utf8") as json_file:
return json.load(json_file)
def load_rules():
try:
# Load this notebook as json to get access to the expert rules in the notebook metadata.
#
j = load_json("cer041-install-knox-cert.ipynb")
except:
pass # If the user has renamed the book, we can't load ourself. NOTE: Is there a way in Jupyter, to know your own filename?
else:
if "metadata" in j and \
"azdata" in j["metadata"] and \
"expert" in j["metadata"]["azdata"] and \
"rules" in j["metadata"]["azdata"]["expert"]:
rules = j["metadata"]["azdata"]["expert"]["rules"]
rules.sort() # Sort rules, so they run in priority order (the [0] element). Lowest value first.
# print (f"EXPERT: There are {len(rules)} rules to evaluate.")
return rules
def apply_expert_rules(line):
global rules
for rule in rules:
# rules that have 9 elements are the injected (output) rules (the ones we want). Rules
# with only 8 elements are the source (input) rules, which are not expanded (i.e. TSG029,
# not ../repair/tsg029-nb-name.ipynb)
if len(rule) == 9:
notebook = rule[1]
cell_type = rule[2]
output_type = rule[3] # i.e. stream or error
output_type_name = rule[4] # i.e. ename or name
output_type_value = rule[5] # i.e. SystemExit or stdout
details_name = rule[6] # i.e. evalue or text
expression = rule[7].replace("\\*", "*") # Something escaped *, and put a \ in front of it!
# print(f"EXPERT: If rule '{expression}' satisfied', run '{notebook}'.")
if re.match(expression, line, re.DOTALL):
# print("EXPERT: MATCH: name = value: '{0}' = '{1}' matched expression '{2}', therefore HINT '{4}'".format(output_type_name, output_type_value, expression, notebook))
match_found = True
display(Markdown(f'HINT: Use [{notebook}]({notebook}) to resolve this issue.'))
print('Common functions defined successfully.')
# Hints for binary (transient fault) retry, (known) error and install guide
#
retry_hints = {'kubectl': ['A connection attempt failed because the connected party did not properly respond after a period of time, or established connection failed because connected host has failed to respond']}
error_hints = {'kubectl': [['no such host', 'TSG010 - Get configuration contexts', '../monitor-k8s/tsg010-get-kubernetes-contexts.ipynb'], ['no such host', 'TSG011 - Restart sparkhistory server', '../repair/tsg011-restart-sparkhistory-server.ipynb'], ['No connection could be made because the target machine actively refused it', 'TSG056 - Kubectl fails with No connection could be made because the target machine actively refused it', '../repair/tsg056-kubectl-no-connection-could-be-made.ipynb']]}
install_hint = {'kubectl': ['SOP036 - Install kubectl command line interface', '../install/sop036-install-kubectl.ipynb']} | _____no_output_____ | MIT | Big-Data-Clusters/CU3/Public/content/cert-management/cer041-install-knox-cert.ipynb | gantz-at-incomm/tigertoolbox |
Get the Kubernetes namespace for the big data clusterGet the namespace of the big data cluster use the kubectl command lineinterface .NOTE: If there is more than one big data cluster in the targetKubernetes cluster, then set \[0\] to the correct value for the big datacluster. | # Place Kubernetes namespace name for BDC into 'namespace' variable
try:
namespace = run(f'kubectl get namespace --selector=MSSQL_CLUSTER -o jsonpath={{.items[0].metadata.name}}', return_output=True)
except:
from IPython.display import Markdown
print(f"ERROR: Unable to find a Kubernetes namespace with label 'MSSQL_CLUSTER'. SQL Server Big Data Cluster Kubernetes namespaces contain the label 'MSSQL_CLUSTER'.")
display(Markdown(f'HINT: Use [TSG081 - Get namespaces (Kubernetes)](../monitor-k8s/tsg081-get-kubernetes-namespaces.ipynb) to resolve this issue.'))
display(Markdown(f'HINT: Use [TSG010 - Get configuration contexts](../monitor-k8s/tsg010-get-kubernetes-contexts.ipynb) to resolve this issue.'))
display(Markdown(f'HINT: Use [SOP011 - Set kubernetes configuration context](../common/sop011-set-kubernetes-context.ipynb) to resolve this issue.'))
raise
else:
print(f'The SQL Server Big Data Cluster Kubernetes namespace is: {namespace}') | _____no_output_____ | MIT | Big-Data-Clusters/CU3/Public/content/cert-management/cer041-install-knox-cert.ipynb | gantz-at-incomm/tigertoolbox |
Create a temporary directory to stage files | # Create a temporary directory to hold configuration files
import tempfile
temp_dir = tempfile.mkdtemp()
print(f"Temporary directory created: {temp_dir}") | _____no_output_____ | MIT | Big-Data-Clusters/CU3/Public/content/cert-management/cer041-install-knox-cert.ipynb | gantz-at-incomm/tigertoolbox |
Helper function to save configuration files to disk | # Define helper function 'save_file' to save configuration files to the temporary directory created above
import os
import io
def save_file(filename, contents):
with io.open(os.path.join(temp_dir, filename), "w", encoding='utf8', newline='\n') as text_file:
text_file.write(contents)
print("File saved: " + os.path.join(temp_dir, filename)) | _____no_output_____ | MIT | Big-Data-Clusters/CU3/Public/content/cert-management/cer041-install-knox-cert.ipynb | gantz-at-incomm/tigertoolbox |
Get name of the ‘Running’ `controller` `pod` | # Place the name of the 'Running' controller pod in variable `controller`
controller = run(f'kubectl get pod --selector=app=controller -n {namespace} -o jsonpath={{.items[0].metadata.name}} --field-selector=status.phase=Running', return_output=True)
print(f"Controller pod name: {controller}") | _____no_output_____ | MIT | Big-Data-Clusters/CU3/Public/content/cert-management/cer041-install-knox-cert.ipynb | gantz-at-incomm/tigertoolbox |
Pod name for gateway | pod = 'gateway-0' | _____no_output_____ | MIT | Big-Data-Clusters/CU3/Public/content/cert-management/cer041-install-knox-cert.ipynb | gantz-at-incomm/tigertoolbox |
Copy certifcate files from `controller` to local machine | import os
cwd = os.getcwd()
os.chdir(temp_dir) # Use chdir to workaround kubectl bug on Windows, which incorrectly processes 'c:\' on kubectl cp cmd line
run(f'kubectl cp {controller}:{test_cert_store_root}/{app_name}/{prefix_keyfile_name}-certificate.pem {prefix_keyfile_name}-certificate.pem -c controller -n {namespace}')
run(f'kubectl cp {controller}:{test_cert_store_root}/{app_name}/{prefix_keyfile_name}-privatekey.pem {prefix_keyfile_name}-privatekey.pem -c controller -n {namespace}')
os.chdir(cwd) | _____no_output_____ | MIT | Big-Data-Clusters/CU3/Public/content/cert-management/cer041-install-knox-cert.ipynb | gantz-at-incomm/tigertoolbox |
Copy certifcate files from local machine to `controldb` | import os
cwd = os.getcwd()
os.chdir(temp_dir) # Workaround kubectl bug on Windows, can't put c:\ on kubectl cp cmd line
run(f'kubectl cp {prefix_keyfile_name}-certificate.pem controldb-0:/var/opt/mssql/{prefix_keyfile_name}-certificate.pem -c mssql-server -n {namespace}')
run(f'kubectl cp {prefix_keyfile_name}-privatekey.pem controldb-0:/var/opt/mssql/{prefix_keyfile_name}-privatekey.pem -c mssql-server -n {namespace}')
os.chdir(cwd) | _____no_output_____ | MIT | Big-Data-Clusters/CU3/Public/content/cert-management/cer041-install-knox-cert.ipynb | gantz-at-incomm/tigertoolbox |
Get the `controller-db-rw-secret` secretGet the controller SQL symmetric key password for decryption. | import base64
controller_db_rw_secret = run(f'kubectl get secret/controller-db-rw-secret -n {namespace} -o jsonpath={{.data.encryptionPassword}}', return_output=True)
controller_db_rw_secret = base64.b64decode(controller_db_rw_secret).decode('utf-8')
print("controller_db_rw_secret retrieved") | _____no_output_____ | MIT | Big-Data-Clusters/CU3/Public/content/cert-management/cer041-install-knox-cert.ipynb | gantz-at-incomm/tigertoolbox |
Update the files table with the certificates through opened SQL connection | import os
sql = f"""
OPEN SYMMETRIC KEY ControllerDbSymmetricKey DECRYPTION BY PASSWORD = '{controller_db_rw_secret}'
DECLARE @FileData VARBINARY(MAX), @Key uniqueidentifier;
SELECT @Key = KEY_GUID('ControllerDbSymmetricKey');
SELECT TOP 1 @FileData = doc.BulkColumn FROM OPENROWSET(BULK N'/var/opt/mssql/{prefix_keyfile_name}-certificate.pem', SINGLE_BLOB) AS doc;
EXEC [dbo].[sp_set_file_data_encrypted] @FilePath = '/config/scaledsets/{scaledset_name}/containers/{container_name}/files/{prefix_keyfile_name}-certificate.pem',
@Data = @FileData,
@KeyGuid = @Key,
@Version = '0',
@User = '',
@Group = '',
@Mode = '';
SELECT TOP 1 @FileData = doc.BulkColumn FROM OPENROWSET(BULK N'/var/opt/mssql/{prefix_keyfile_name}-privatekey.pem', SINGLE_BLOB) AS doc;
EXEC [dbo].[sp_set_file_data_encrypted] @FilePath = '/config/scaledsets/{scaledset_name}/containers/{container_name}/files/{prefix_keyfile_name}-privatekey.pem',
@Data = @FileData,
@KeyGuid = @Key,
@Version = '0',
@User = '',
@Group = '',
@Mode = '';
"""
save_file("insert_certificates.sql", sql)
cwd = os.getcwd()
os.chdir(temp_dir) # Workaround kubectl bug on Windows, can't put c:\ on kubectl cp cmd line
run(f'kubectl cp insert_certificates.sql controldb-0:/var/opt/mssql/insert_certificates.sql -c mssql-server -n {namespace}')
run(f"""kubectl exec controldb-0 -c mssql-server -n {namespace} -- bash -c "SQLCMDPASSWORD=`cat /var/run/secrets/credentials/mssql-sa-password/password` /opt/mssql-tools/bin/sqlcmd -b -U sa -d controller -i /var/opt/mssql/insert_certificates.sql" """)
# Clean up
run(f"""kubectl exec controldb-0 -c mssql-server -n {namespace} -- bash -c "rm /var/opt/mssql/insert_certificates.sql" """)
run(f"""kubectl exec controldb-0 -c mssql-server -n {namespace} -- bash -c "rm /var/opt/mssql/{prefix_keyfile_name}-certificate.pem" """)
run(f"""kubectl exec controldb-0 -c mssql-server -n {namespace} -- bash -c "rm /var/opt/mssql/{prefix_keyfile_name}-privatekey.pem" """)
os.chdir(cwd) | _____no_output_____ | MIT | Big-Data-Clusters/CU3/Public/content/cert-management/cer041-install-knox-cert.ipynb | gantz-at-incomm/tigertoolbox |
Clear out the controller\_db\_rw\_secret variable | controller_db_rw_secret= "" | _____no_output_____ | MIT | Big-Data-Clusters/CU3/Public/content/cert-management/cer041-install-knox-cert.ipynb | gantz-at-incomm/tigertoolbox |
Clean up certificate staging areaRemove the certificate files generated on disk (they have now beenplaced in the controller database). | cmd = f"rm -r {test_cert_store_root}/{app_name}"
run(f'kubectl exec {controller} -c controller -n {namespace} -- bash -c "{cmd}"') | _____no_output_____ | MIT | Big-Data-Clusters/CU3/Public/content/cert-management/cer041-install-knox-cert.ipynb | gantz-at-incomm/tigertoolbox |
Restart knox gateway service | run(f'kubectl delete pod {pod} -n {namespace}') | _____no_output_____ | MIT | Big-Data-Clusters/CU3/Public/content/cert-management/cer041-install-knox-cert.ipynb | gantz-at-incomm/tigertoolbox |
Clean up temporary directory for staging configuration files | # Delete the temporary directory used to hold configuration files
import shutil
shutil.rmtree(temp_dir)
print(f'Temporary directory deleted: {temp_dir}')
print('Notebook execution complete.') | _____no_output_____ | MIT | Big-Data-Clusters/CU3/Public/content/cert-management/cer041-install-knox-cert.ipynb | gantz-at-incomm/tigertoolbox |
print a list of Lil's that are more popular than Lil's Kim | for artist in artist_info:
print(artist['name'])
if artist['name']== "Lil' Kim":
print("Found Lil Kim")
print(artist['popularity'])
else:
pass #print
Lil_kim_popularity = 62
more_popular_than_Lil_kim = []
for artist in artist_info:
if artist['popularity'] > Lil_kim_popularity:
#If yes, let's add them to our list
print(artist['name'], "is more popular with a score of", artist['popularity'])
more_popular_than_Lil_kim.append(artist['name'])
else:
print(artist['name'], "is less popular with a score of", artist['popularity'])
for artist_name in more_popular_than_Lil_kim:
print(artist_name) | Lil Wayne is more popular with a score of 86
Lil Yachty is more popular with a score of 73
Lil Uzi Vert is more popular with a score of 74
Lil Dicky is more popular with a score of 68
Boosie Badazz is more popular with a score of 67
Lil Jon is more popular with a score of 72
King Lil G is less popular with a score of 61
Lil Durk is less popular with a score of 60
Lil Jon & The East Side Boyz is less popular with a score of 60
Lil Bibby is less popular with a score of 54
G Herbo is less popular with a score of 53
Lil Rob is less popular with a score of 50
Lil Reese is less popular with a score of 50
Lil Keke is less popular with a score of 48
Bow Wow is less popular with a score of 57
Lil Scrappy is less popular with a score of 49
Lil Wyte is less popular with a score of 50
Lil Blood is less popular with a score of 45
Lil Snupe is less popular with a score of 45
Lil Mama is less popular with a score of 45
Lil B is less popular with a score of 44
Lil' Kim is less popular with a score of 62
Lil Boom is less popular with a score of 43
Lil Cuete is less popular with a score of 40
Lil Phat is less popular with a score of 39
Lil Debbie is less popular with a score of 43
Lil Twist is less popular with a score of 40
Lil Trill is less popular with a score of 37
Lil AJ is less popular with a score of 36
Lil Lonnie is less popular with a score of 37
Lil Twon is less popular with a score of 37
Lil Goofy is less popular with a score of 35
Lil Haiti is less popular with a score of 37
Lil Cray is less popular with a score of 35
Mr. Lil One is less popular with a score of 36
Lil Flash is less popular with a score of 38
Lil Silva is less popular with a score of 43
Lil Yase is less popular with a score of 34
Lil Rue is less popular with a score of 34
Lil Eddie is less popular with a score of 41
Lil Kesh is less popular with a score of 39
Lil Suzy is less popular with a score of 34
Lil Wayne, DJ Drama is less popular with a score of 35
Lil Mouse is less popular with a score of 34
Lil C is less popular with a score of 33
Lil Rick is less popular with a score of 39
Lil June is less popular with a score of 32
Lil E is less popular with a score of 34
Lil Fate is less popular with a score of 34
Lil' Flip is less popular with a score of 50
Lil Wayne
Lil Yachty
Lil Uzi Vert
Lil Dicky
Boosie Badazz
Lil Jon
| MIT | .ipynb_checkpoints/homework_5_shengying_zhao-checkpoint.ipynb | sz2472/foundations-homework |
Pick two of your favorite Lils to fight it out, and use their IDs to print out their top tracks | for artist in artist_info:
print(artist['name'], artist['id'])
#I chose Lil Fate and Lil' Flip, first I want to figure out the top track of Lil Fate
response = requests.get("https://api.spotify.com/v1/artists/6JUnsP7jmvYmdhbg7lTMQj/top-tracks?country=US")
print(response.text)
data = response.json()
type(data)
data.keys()
type(data['tracks'])
print(data['tracks'])
data['tracks'][0]
for item in data['tracks']:
print(item['name'])
# now to figure out the top track of Lil' Flip #things within {} or ALL Caps means to replace them
response = requests.get("https://api.spotify.com/v1/artists/4Q5sPmM8j4SpMqL4UA1DtS/top-tracks?country=US")
print(response.text)
data = response.json()
type(data)
data.keys()
type(data['tracks'])
for item in data['tracks']:
#type(item): dict
#print(item.keys()), saw 'name'
print(item['name']) | Sunshine - Explicit Album Version
Game Over
The Way We Ball
Sunny Day
Sunshine (Re-Recorded / Remastered)
Sunshine
I Can Do Dat
4 My Nigga Screw
I Shoulda Listened - Explicit Album Version
What I Been Through
| MIT | .ipynb_checkpoints/homework_5_shengying_zhao-checkpoint.ipynb | sz2472/foundations-homework |
Will the world explode if a musicians swears? Get an average popularity for their explicit songs vs. their non-explicit songs. How many minutes of explicit songs do they have? Non-explicit? | #for Lil' fate's top tracks
explicit_count = 0
non_explicit_count = 0
popularity_explicit = 0
popularity_non_explicit = 0
minutes_explicit = 0
minutes_non_explicit = 0
for track in data['tracks']:
if track['explicit']== True:
explicit_count = explicit_count + 1
popularity_explicit = popularity_explicit + track['popularity']
minutes_explicit = minutes_explicit + track['duration_ms']
elif track['explicit']== False:
non_explicit_count = non_explicit_count + 1
popularity_non_explicit = popularity_non_explicit + track['popularity']
minutes_non_explicit = minutes_non_explicit + track['duration_ms']
print("Lil' Flip has", (minutes_explicit/1000)/60, "of explicit songs")
print("Lil' Flip has", (minutes_non_explicit/1000)/60, "of non-explicit songs")
print("The average popularity of Lil' Flip explicits songs is", popularity_explicit/explicit_count)
print("The average popularity of Lil' Flip non-explicits songs is", popularity_non_explicit/non_explicit_count) | Lil' Flip has 26.10685 of explicit songs
Lil' Flip has 16.8464 of non-explicit songs
The average popularity of Lil' Flip explicits songs is 34.166666666666664
The average popularity of Lil' Flip non-explicits songs is 37.75
| MIT | .ipynb_checkpoints/homework_5_shengying_zhao-checkpoint.ipynb | sz2472/foundations-homework |
Since we're talking about Lils, what about Biggies? How many total "Biggie" artists are there? How many total "Lil"s? If you made 1 request every 5 seconds, how long would it take to download information on all the Lils vs the Biggies? | response = requests.get('https://api.spotify.com/v1/search?q=Lil&type=artist&market=US')
all_lil = response.json()
print(response.text)
all_lil.keys()
all_lil['artists'].keys()
print(all_lil['artists']['total'])
response = requests.get('https://api.spotify.com/v1/search?q=Biggie&type=artist&market=US')
all_biggies = response.json()
print(all_biggies['artists']['total']) | 50
| MIT | .ipynb_checkpoints/homework_5_shengying_zhao-checkpoint.ipynb | sz2472/foundations-homework |
how to count the genres | all_genres = []
for artist in artist_info:
print("All genres we've heard of:", all_genres)
print("Current artist has:", artist['genres'])
all_genres = all_genres + artist['genres']
all_genres.count('dirty south rap')
## There is a library that comes with Python called Collections, inside of it is a thing called Counter
from collections import Counter
| _____no_output_____ | MIT | .ipynb_checkpoints/homework_5_shengying_zhao-checkpoint.ipynb | sz2472/foundations-homework |
How to automate getting all of the results | response=requests.get('https://api.spotify.com/v1/search?q=Lil&type=artist&market=US&limit50')
small_data = response.json()
data['artists']
print(len(data['artists']['items'])) #we only get 10 artists
print(data['artists']['total'])
#first page: artists 1-50, offset of 0
# https:// | _____no_output_____ | MIT | .ipynb_checkpoints/homework_5_shengying_zhao-checkpoint.ipynb | sz2472/foundations-homework |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.