id
stringlengths 30
32
| content
stringlengths 139
2.8k
|
|---|---|
codereview_new_python_data_13258
|
def make_smoothing_spline(x, y, w=None, lam=None):
prediction, New York: Springer, 2017, pp. 241-249.
:doi:`10.1007/978-0-387-84858-7`
.. [4] E. Zemlyanoy, "Generalized cross-validation smoothing splines",
- BSc thesis, 2022. Might be available
- `here <https://www.hse.ru/ba/am/students/diplomas/620910604>`_ (in
Russian)
Examples
```suggestion
BSc thesis, 2022.
```
def make_smoothing_spline(x, y, w=None, lam=None):
prediction, New York: Springer, 2017, pp. 241-249.
:doi:`10.1007/978-0-387-84858-7`
.. [4] E. Zemlyanoy, "Generalized cross-validation smoothing splines",
+ BSc thesis, 2022.
+ `<https://www.hse.ru/ba/am/students/diplomas/620910604>`_ (in
Russian)
Examples
|
codereview_new_python_data_13259
|
def make_smoothing_spline(x, y, w=None, lam=None):
prediction, New York: Springer, 2017, pp. 241-249.
:doi:`10.1007/978-0-387-84858-7`
.. [4] E. Zemlyanoy, "Generalized cross-validation smoothing splines",
- BSc thesis, 2022. Might be available
- `here <https://www.hse.ru/ba/am/students/diplomas/620910604>`_ (in
Russian)
Examples
```suggestion
`<https://www.hse.ru/ba/am/students/diplomas/620910604>`_ (in
```
def make_smoothing_spline(x, y, w=None, lam=None):
prediction, New York: Springer, 2017, pp. 241-249.
:doi:`10.1007/978-0-387-84858-7`
.. [4] E. Zemlyanoy, "Generalized cross-validation smoothing splines",
+ BSc thesis, 2022.
+ `<https://www.hse.ru/ba/am/students/diplomas/620910604>`_ (in
Russian)
Examples
|
codereview_new_python_data_13260
|
def h(x):
maxiter = 5
if new_cb_interface:
- def callback_interface(*, intermediate_result): # type: ignore[misc] # noqa
assert intermediate_result.fun == f(intermediate_result.x)
callback()
else:
- def callback_interface(xk, *args):
callback()
def callback():
This should fix the MyPy complaint.
```suggestion
def callback_interface(*, intermediate_result):
assert intermediate_result.fun == f(intermediate_result.x)
callback()
else:
def callback_interface(xk, *args): # type: ignore[misc]
```
def h(x):
maxiter = 5
if new_cb_interface:
+ def callback_interface(*, intermediate_result):
assert intermediate_result.fun == f(intermediate_result.x)
callback()
else:
+ def callback_interface(xk, *args): # type: ignore[misc]
callback()
def callback():
|
codereview_new_python_data_13261
|
def _add(self, minres):
self.minres.x = np.copy(minres.x)
def update(self, minres):
- cond1 = minres.fun < self.minres.fun and minres.success
- cond2 = minres.success and not self.minres.success
- if cond1 or cond2:
self._add(minres)
return True
else:
Alternatively:
```suggestion
if minres.success and (minres.fun < self.minres.fun
or not self.minres.success)
```
The incumbent (the best result found so far) should be updated if the new result is comes with `success=True` and either:
- its function value is lower than that of the incumbent or
- the incumbent has `success=False`. (This latter can happen if the initial minimization was unsuccessful.)
def _add(self, minres):
self.minres.x = np.copy(minres.x)
def update(self, minres):
+ if minres.success and (minres.fun < self.minres.fun
+ or not self.minres.success)
self._add(minres)
return True
else:
|
codereview_new_python_data_13262
|
def _add(self, minres):
def update(self, minres):
if minres.success and (minres.fun < self.minres.fun
- or not self.minres.success)
self._add(minres)
return True
else:
Oops missing the colon
```suggestion
if minres.success and (minres.fun < self.minres.fun
or not self.minres.success):
```
def _add(self, minres):
def update(self, minres):
if minres.success and (minres.fun < self.minres.fun
+ or not self.minres.success):
self._add(minres)
return True
else:
|
codereview_new_python_data_13263
|
def _sf(self, x):
return _norm_sf(np.log(x))
def _isf(self, p):
- return np.exp(-sc.ndtri(p))
def _stats(self):
p = np.e
Since we're using `_norm_ppf` in `_ppf`:
```suggestion
return np.exp(_norm_isf(p))
```
def _sf(self, x):
return _norm_sf(np.log(x))
def _isf(self, p):
+ return np.exp(_norm_isf(p))
def _stats(self):
p = np.e
|
codereview_new_python_data_13264
|
'nautical_mile', 'neutron_mass', 'nu2lambda',
'ounce', 'oz', 'parsec', 'pebi', 'peta',
'pi', 'pico', 'point', 'pound', 'pound_force',
- 'proton_mass', 'psi', 'pt', 'quecto', 'quetta', 'ronna', 'ronto', 'short_ton',
- 'sigma', 'slinch', 'slug', 'speed_of_light',
'speed_of_sound', 'stone', 'survey_foot',
'survey_mile', 'tebi', 'tera', 'ton_TNT',
'torr', 'troy_ounce', 'troy_pound', 'u',
```suggestion
'proton_mass', 'psi', 'pt', 'quecto', 'quetta', 'ronna', 'ronto',
'short_ton', 'sigma', 'slinch', 'slug', 'speed_of_light',
```
'nautical_mile', 'neutron_mass', 'nu2lambda',
'ounce', 'oz', 'parsec', 'pebi', 'peta',
'pi', 'pico', 'point', 'pound', 'pound_force',
+ 'proton_mass', 'psi', 'pt', 'quecto', 'quetta', 'ronna', 'ronto',
+ 'short_ton', 'sigma', 'slinch', 'slug', 'speed_of_light',
'speed_of_sound', 'stone', 'survey_foot',
'survey_mile', 'tebi', 'tera', 'ton_TNT',
'torr', 'troy_ounce', 'troy_pound', 'u',
|
codereview_new_python_data_13265
|
def test_electrocardiogram(self):
registry["ecg.dat"])
-def test_clear_cache():
- # Use Dummy path
- dummy_basepath = "dummy_cache_dir"
- os.makedirs(dummy_basepath, exist_ok=True)
# Create three dummy dataset files
dummy_registry = {}
for i in range(3):
dataset_name = f"data{i}.dat"
dummy_registry[dataset_name] = hash(dataset_name)
- with open(os.path.join(dummy_basepath, dataset_name), 'a'):
- pass
# remove single dataset file from cache dir
_clear_cache(datasets=["data0.dat"], cache_dir=dummy_basepath,
Can we use a `tmp_path` fixture from `pytest` to avoid polluting the local working space when this test fails?
To be fair, the pollution ends up in `./build-install/lib/python3/dist-packages/dummy_cache_dir`, which I don't usually care about much, but still seems best practice to just direct temporary test stuff to a conventional temporary space on the machine.
This is also relates somewhat to my suggestion above re: adding arguments to the `_clear_cache` function only for testing--couldn't we just use `scipy-data` itself once we've changed the working directory context to whatever temporary path `pytest` uses with the fixture?
def test_electrocardiogram(self):
registry["ecg.dat"])
+def test_clear_cache(tmp_path):
+ # Note: `tmp_path` is a pytest fixture, it handles cleanup
+ dummy_basepath = tmp_path / "dummy_cache_dir"
+ dummy_basepath.mkdir()
# Create three dummy dataset files
dummy_registry = {}
for i in range(3):
dataset_name = f"data{i}.dat"
dummy_registry[dataset_name] = hash(dataset_name)
+ dataset_file = dummy_basepath / dataset_name
+ dataset_file.write_text("")
# remove single dataset file from cache dir
_clear_cache(datasets=["data0.dat"], cache_dir=dummy_basepath,
|
codereview_new_python_data_13266
|
def test_beta_ppf_with_subnormal_a_b(self, method, a, b):
# the value), because our goal here is to verify that the call does
# not trigger a segmentation fault.
try:
- stats.beta.ppf(p, a, b)
except OverflowError:
# The OverflowError exception occurs with Boost 1.80 or earlier
# when Boost's double promotion policy is false; see
Shouldn't this be changed to the `method` `pytest` parameter?
Apart from that, this should be an easy decision to merge--fixes segfault, two core dev approvals, CI passing, small patch with test, etc.
def test_beta_ppf_with_subnormal_a_b(self, method, a, b):
# the value), because our goal here is to verify that the call does
# not trigger a segmentation fault.
try:
+ method(p, a, b)
except OverflowError:
# The OverflowError exception occurs with Boost 1.80 or earlier
# when Boost's double promotion policy is false; see
|
codereview_new_python_data_13267
|
def test_pmf_cdf(self):
ref = stats.binom.cdf(r, n, p)
assert_allclose(res, ref, atol=1e-16)
- def test_pmf_cdf(self):
# Check that gh-15101 is resolved (no divide warnings when p~1, n~oo)
res = stats.binom.pmf(3, 2000, 0.999)
assert_allclose(res, 0, atol=1e-16)
```suggestion
def test_pmf_gh15101(self):
```
def test_pmf_cdf(self):
ref = stats.binom.cdf(r, n, p)
assert_allclose(res, ref, atol=1e-16)
+ def test_pmf_gh15101(self):
# Check that gh-15101 is resolved (no divide warnings when p~1, n~oo)
res = stats.binom.pmf(3, 2000, 0.999)
assert_allclose(res, 0, atol=1e-16)
|
codereview_new_python_data_13268
|
def spearmanr(a, b=None, axis=0, nan_policy='propagate',
Probability and Statistics Tables and Formulae. Chapman & Hall: New
York. 2000.
Section 14.7
- .. [2] Kendall, M. G. and Stuart, A. (1973).
The Advanced Theory of Statistics, Volume 2: Inference and Relationship.
- Griffin. 1973
Section 31.18
Examples
```suggestion
.. [2] Kendall, M. G. and Stuart, A. (1973).
```
def spearmanr(a, b=None, axis=0, nan_policy='propagate',
Probability and Statistics Tables and Formulae. Chapman & Hall: New
York. 2000.
Section 14.7
+ .. [2] Kendall, M. G. and Stuart, A. (1973).
The Advanced Theory of Statistics, Volume 2: Inference and Relationship.
+ Griffin. 1973.
Section 31.18
Examples
|
codereview_new_python_data_13269
|
def spearmanr(a, b=None, axis=0, nan_policy='propagate',
Probability and Statistics Tables and Formulae. Chapman & Hall: New
York. 2000.
Section 14.7
- .. [2] Kendall, M. G. and Stuart, A. (1973).
The Advanced Theory of Statistics, Volume 2: Inference and Relationship.
- Griffin. 1973
Section 31.18
Examples
```suggestion
The Advanced Theory of Statistics, Volume 2: Inference and Relationship.
Griffin. 1973.
Section 31.18
```
def spearmanr(a, b=None, axis=0, nan_policy='propagate',
Probability and Statistics Tables and Formulae. Chapman & Hall: New
York. 2000.
Section 14.7
+ .. [2] Kendall, M. G. and Stuart, A. (1973).
The Advanced Theory of Statistics, Volume 2: Inference and Relationship.
+ Griffin. 1973.
Section 31.18
Examples
|
codereview_new_python_data_13270
|
import numpy as np
-from scipy.fftpack import fft, ifft
from scipy.special import gammaincinv, ndtr, ndtri
from scipy.stats._qmc import n_primes, primes_from_2_to
```suggestion
from scipy.fft import fft, ifft
```
This should fix the FFT issue. I tested it locally and it works.
import numpy as np
+from scipy.fft import fft, ifft
from scipy.special import gammaincinv, ndtr, ndtri
from scipy.stats._qmc import n_primes, primes_from_2_to
|
codereview_new_python_data_13271
|
def false_discovery_control(ps, *, axis=0, method='bh'):
To control the FWER at 5%, we reject only the hypotheses corresponding
with adjusted p-values less than 0.05. In this case, only the hypotheses
corresponding with the first three p-values can be rejected. According to
- [1], these three hypotheses concerned "allergic reaction" and "two
different aspects of bleeding."
An alternative approach is to control the false discovery rate: the
```suggestion
[1]_, these three hypotheses concerned "allergic reaction" and "two
```
def false_discovery_control(ps, *, axis=0, method='bh'):
To control the FWER at 5%, we reject only the hypotheses corresponding
with adjusted p-values less than 0.05. In this case, only the hypotheses
corresponding with the first three p-values can be rejected. According to
+ [1]_, these three hypotheses concerned "allergic reaction" and "two
different aspects of bleeding."
An alternative approach is to control the false discovery rate: the
|
codereview_new_python_data_13272
|
def false_discovery_control(ps, *, axis=0, method='bh'):
the more conservative Benjaminini-Yekutieli procedure.
The adjusted p-values produced by this function are comparable to those
- produced by the R function ``p.adjust``.
References
----------
@tupui how about this?
```suggestion
produced by the R function ``p.adjust`` and the statsmodels function
`statsmodels.stats.multitest.multipletests`. Please consider the latter
for more advanced methods of multiple comparison correction.
```
def false_discovery_control(ps, *, axis=0, method='bh'):
the more conservative Benjaminini-Yekutieli procedure.
The adjusted p-values produced by this function are comparable to those
+ produced by the R function ``p.adjust`` and the statsmodels function
+ `statsmodels.stats.multitest.multipletests`. Please consider the latter
+ for more advanced methods of multiple comparison correction.
References
----------
|
codereview_new_python_data_13273
|
def test_as_euler_degenerate_symmetric_axes():
def test_as_euler_compare_algorithms():
rnd = np.random.RandomState(0)
- n = 10
angles = np.empty((n, 3))
angles[:, 0] = rnd.uniform(low=-np.pi, high=np.pi, size=(n,))
angles[:, 2] = rnd.uniform(low=-np.pi, high=np.pi, size=(n,))
It can be easily increased to 1000 or even 10000.
def test_as_euler_degenerate_symmetric_axes():
def test_as_euler_compare_algorithms():
rnd = np.random.RandomState(0)
+ n = 10000
angles = np.empty((n, 3))
angles[:, 0] = rnd.uniform(low=-np.pi, high=np.pi, size=(n,))
angles[:, 2] = rnd.uniform(low=-np.pi, high=np.pi, size=(n,))
|
codereview_new_python_data_13276
|
def test_bfgs_infinite(self):
assert not np.isfinite(func(x))
def test_bfgs_xrtol(self):
- # test for #17345 to test xrtol parameter
x0 = [1.3, 0.7, 0.8, 1.9, 1.2]
res = optimize.minimize(optimize.rosen,
x0, method='bfgs', options={'xrtol': 1e-3})
```suggestion
# test for #17345 to test xrtol parameter
```
def test_bfgs_infinite(self):
assert not np.isfinite(func(x))
def test_bfgs_xrtol(self):
+ # test for #17345 to test xrtol parameter
x0 = [1.3, 0.7, 0.8, 1.9, 1.2]
res = optimize.minimize(optimize.rosen,
x0, method='bfgs', options={'xrtol': 1e-3})
|
codereview_new_python_data_13277
|
def accept_reject(self, energy_new, energy_old):
#
# RuntimeWarning: invalid value encountered in multiply
#
- # Ignore this warning so so when the algorithm is on a flat plane, it always
# accepts the step, to try to move off the plane.
prod = -(energy_new - energy_old) * self.beta
w = math.exp(min(0, prod))
```suggestion
# Ignore this warning so when the algorithm is on a flat plane, it always
```
def accept_reject(self, energy_new, energy_old):
#
# RuntimeWarning: invalid value encountered in multiply
#
+ # Ignore this warning so when the algorithm is on a flat plane, it always
# accepts the step, to try to move off the plane.
prod = -(energy_new - energy_old) * self.beta
w = math.exp(min(0, prod))
|
codereview_new_python_data_13278
|
def find_objects(input, max_label=0):
A list of tuples, with each tuple containing N slices (with N the
dimension of the input array). Slices correspond to the minimal
parallelepiped that contains the object. If a number is missing,
- None is returned instead of a slice. The label `l` corresponds to
- the index `l-1` in the returned list.
See Also
--------
In reST (the markup language used in the docstrings), you should use double backticks for formatting:
```suggestion
None is returned instead of a slice. The label ``l`` corresponds to
the index ``l-1`` in the returned list.
```
def find_objects(input, max_label=0):
A list of tuples, with each tuple containing N slices (with N the
dimension of the input array). Slices correspond to the minimal
parallelepiped that contains the object. If a number is missing,
+ None is returned instead of a slice. The label ``l`` corresponds to
+ the index ``l-1`` in the returned list.
See Also
--------
|
codereview_new_python_data_13279
|
def test_nonscalar_values_2(self, method):
assert_allclose(v, v2, atol=1e-14, err_msg=method)
def test_nonscalar_values_linear_2D(self):
- # Verify that non-scalar valued work in the 2D fast path
method = 'linear'
points = [(0.0, 0.5, 1.0, 1.5, 2.0, 2.5),
(0.0, 0.5, 1.0, 1.5, 2.0, 2.5, 3.0), ]
This test looks good.
def test_nonscalar_values_2(self, method):
assert_allclose(v, v2, atol=1e-14, err_msg=method)
def test_nonscalar_values_linear_2D(self):
+ # Verify that non-scalar values work in the 2D fast path
method = 'linear'
points = [(0.0, 0.5, 1.0, 1.5, 2.0, 2.5),
(0.0, 0.5, 1.0, 1.5, 2.0, 2.5, 3.0), ]
|
codereview_new_python_data_13280
|
def add_newdoc(name, doc):
Plot the function for different parameter sets.
- >>> (fig, ax) = plt.subplots(figsize=(8, 8))
>>> x = np.linspace(-10, 10, 500)
>>> parameters_list = [(1.5, 0., "solid"), (1.3, 0.5, "dashed"),
... (0., 1.8, "dotted"), (1., 1., "dashdot")]
Nitpick: remove extraneous parentheses:
```suggestion
>>> fig, ax = plt.subplots(figsize=(8, 8))
```
def add_newdoc(name, doc):
Plot the function for different parameter sets.
+ >>> fig, ax = plt.subplots(figsize=(8, 8))
>>> x = np.linspace(-10, 10, 500)
>>> parameters_list = [(1.5, 0., "solid"), (1.3, 0.5, "dashed"),
... (0., 1.8, "dotted"), (1., 1., "dashdot")]
|
codereview_new_python_data_13281
|
def test_frozen_distribution(self):
assert_equal(rvs1, rvs2)
assert_equal(rvs1, rvs3)
- def test_uniform_circle(self):
# test that for uniform 2D samples on the circle the resulting
# angles follow a uniform distribution
circular_dist = random_direction(2)
```suggestion
@pytest.mark.parametrize("dim", [2, 5, 8])
def test_uniform_circle(self, dim):
spherical_dist = random_direction(dim)
samples = spherical_dist.rvs(size=10000, random_state=42967295)
angles = np.arctan2(samples[:, dim -1], samples[:, dim -2])
```
@mdhaber : sth like this should work?
def test_frozen_distribution(self):
assert_equal(rvs1, rvs2)
assert_equal(rvs1, rvs3)
+ @pytest.mark.parametrize("dim", [2, 5, 8])
+ def test_uniform_circle(self, dim):
+ spherical_dist = random_direction(dim)
+ samples = spherical_dist.rvs(size=10000, random_state=42967295)
+ angles = np.arctan2(samples[:, dim -1], samples[:, dim -2])
# test that for uniform 2D samples on the circle the resulting
# angles follow a uniform distribution
circular_dist = random_direction(2)
|
codereview_new_python_data_13282
|
def test_to_corr(self):
class TestRandomDirection:
@pytest.mark.parametrize("dim", [1, 3])
- @pytest.mark.parametrize("size", [None, 5, (5, 4)])
def test_samples(self, dim, size):
# test that samples have correct shape and norm 1
- random_direction_dist = random_direction(dim)
samples = random_direction_dist.rvs(size)
- if isinstance(size, int):
- size = (size, )
- elif size is None:
- size = (1, )
- expected_shape = size + (dim, )
assert samples.shape == expected_shape
norms = np.linalg.norm(samples, axis=-1)
assert_allclose(norms, 1.)
```suggestion
@pytest.mark.parametrize("size", [None, 1, 5, (5, 4)])
def test_samples(self, dim, size):
# test that samples have correct shape and norm 1
rng = np.random.default_rng(2777937887058094419)
random_direction_dist = random_direction(dim, seed=rng)
samples = random_direction_dist.rvs(size)
mean, cov = np.zeros(dim), np.eye(dim)
expected_shape = rng.multivariate_normal(mean, cov, size=size).shape
```
def test_to_corr(self):
class TestRandomDirection:
@pytest.mark.parametrize("dim", [1, 3])
+ @pytest.mark.parametrize("size", [None, 1, 5, (5, 4)])
def test_samples(self, dim, size):
# test that samples have correct shape and norm 1
+ rng = np.random.default_rng(2777937887058094419)
+ random_direction_dist = random_direction(dim, seed=rng)
samples = random_direction_dist.rvs(size)
+ mean, cov = np.zeros(dim), np.eye(dim)
+ expected_shape = rng.multivariate_normal(mean, cov, size=size).shape
assert samples.shape == expected_shape
norms = np.linalg.norm(samples, axis=-1)
assert_allclose(norms, 1.)
|
codereview_new_python_data_13283
|
def _test_factory(case, dec):
_test_factory(case, min_decimal[ind])
-
def test_solve_discrete_are():
cases = [
```suggestion
```
Oops. Please commit this and merge with `[skip ci]` in the commit message if everything else looks ok.
def _test_factory(case, dec):
_test_factory(case, min_decimal[ind])
def test_solve_discrete_are():
cases = [
|
codereview_new_python_data_13284
|
def leastsq(func, x0, args=(), Dfun=None, full_output=0,
r = triu(transpose(retval[1]['fjac'])[:n, :])
R = dot(r, perm)
try:
- # Tis was `cov_x = inv(dot(transpose(R), R))`, but sometimes
# the result was not symmetric positive definite. See gh-4555.
invR = inv(R)
cov_x = invR @ invR.T
```suggestion
# This was `cov_x = inv(dot(transpose(R), R))`, but sometimes
```
def leastsq(func, x0, args=(), Dfun=None, full_output=0,
r = triu(transpose(retval[1]['fjac'])[:n, :])
R = dot(r, perm)
try:
+ # This was `cov_x = inv(dot(transpose(R), R))`, but sometimes
# the result was not symmetric positive definite. See gh-4555.
invR = inv(R)
cov_x = invR @ invR.T
|
codereview_new_python_data_13285
|
def f(x, a, b, c, d, e):
y = np.linspace(2, 7, n) + rng.random(n)
p, cov = optimize.curve_fit(f, x, y, maxfev=100000)
assert np.all(np.diag(cov) > 0)
- assert np.all(linalg.eigh(cov)[0] > 0)
assert_allclose(cov, cov.T)
Well, there are some failing tests because approximately zero eigenvalues sometimes come out as negative eigenvalues numerically. Let's try this.
```suggestion
eigs = linalg.eigh(cov)[0] # separate line for debugging
assert np.all(eigs > -1e-6)
```
def f(x, a, b, c, d, e):
y = np.linspace(2, 7, n) + rng.random(n)
p, cov = optimize.curve_fit(f, x, y, maxfev=100000)
assert np.all(np.diag(cov) > 0)
+ eigs = linalg.eigh(cov)[0] # separate line for debugging
+ assert np.all(eigs > -1e-6)
assert_allclose(cov, cov.T)
|
codereview_new_python_data_13286
|
def f(x, a, b, c, d, e):
p, cov = optimize.curve_fit(f, x, y, maxfev=100000)
assert np.all(np.diag(cov) > 0)
eigs = linalg.eigh(cov)[0] # separate line for debugging
- assert np.all(eigs > -1e-6)
assert_allclose(cov, cov.T)
```suggestion
# some platforms see a small negative eigevenvalue
assert np.all(eigs > -1e-2)
```
def f(x, a, b, c, d, e):
p, cov = optimize.curve_fit(f, x, y, maxfev=100000)
assert np.all(np.diag(cov) > 0)
eigs = linalg.eigh(cov)[0] # separate line for debugging
+ # some platforms see a small negative eigevenvalue
+ assert np.all(eigs > -1e-2)
assert_allclose(cov, cov.T)
|
codereview_new_python_data_13287
|
def extra(self):
return 42
s = S(xk=[1, 2, 3], pk=[0.2, 0.7, 0.1])
- assert_allclose(s.pmf([2, 3, 1]), [0.7, 0.1, 0.2], atol=42)
assert s.extra() == 42
The `atol` here looks a little loose...
def extra(self):
return 42
s = S(xk=[1, 2, 3], pk=[0.2, 0.7, 0.1])
+ assert_allclose(s.pmf([2, 3, 1]), [0.7, 0.1, 0.2], atol=1e-15)
assert s.extra() == 42
+ # make sure subclass freezes correctly
+ frozen_s = s()
+ assert_allclose(frozen_s.pmf([2, 3, 1]), [0.7, 0.1, 0.2], atol=1e-15)
|
codereview_new_python_data_13288
|
class rv_count(rv_discrete):
This string is used as part of the first line of the docstring returned
when a subclass has no docstring of its own. Note: `longname` exists
for backwards compatibility, do not use for new subclasses.
- seed : {None, int, `numpy.random.Generator`, `numpy.random.RandomState`}, optional
If `seed` is None (or `np.random`), the `numpy.random.RandomState`
singleton is used.
If `seed` is an int, a new ``RandomState`` instance is used,
I just had another PR merge with a lint failure and I saw the issue in another PR. I don't want that to happen here, so I'm changing this to how it appears in some other stats functions.
```suggestion
seed : {None, int, `numpy.random.Generator`,
`numpy.random.RandomState`}, optional
```
class rv_count(rv_discrete):
This string is used as part of the first line of the docstring returned
when a subclass has no docstring of its own. Note: `longname` exists
for backwards compatibility, do not use for new subclasses.
+ seed : {None, int, `numpy.random.Generator`,
+ `numpy.random.RandomState`}, optional
+
If `seed` is None (or `np.random`), the `numpy.random.RandomState`
singleton is used.
If `seed` is an int, a new ``RandomState`` instance is used,
|
codereview_new_python_data_13289
|
def __init__(self, points, values, method="linear", bounds_error=True,
self._validate_grid_dimensions(points, method)
self.method = method
self.bounds_error = bounds_error
- self.grid, self.descending_dimensions = self._check_points(points)
self.values = self._check_values(values)
self._check_dimensionality(self.grid, self.values)
self.fill_value = self._check_fill_value(self.values, fill_value)
- if self.descending_dimensions:
- self.values = np.flip(values, axis=self.descending_dimensions)
def _check_dimensionality(self, points, values):
if len(points) > values.ndim:
```suggestion
self.grid, self._descending_dimensions = self._check_points(points)
```
def __init__(self, points, values, method="linear", bounds_error=True,
self._validate_grid_dimensions(points, method)
self.method = method
self.bounds_error = bounds_error
+ self.grid, self._descending_dimensions = self._check_points(points)
self.values = self._check_values(values)
self._check_dimensionality(self.grid, self.values)
self.fill_value = self._check_fill_value(self.values, fill_value)
+ if self._descending_dimensions:
+ self.values = np.flip(values, axis=self._descending_dimensions)
def _check_dimensionality(self, points, values):
if len(points) > values.ndim:
|
codereview_new_python_data_13290
|
def __init__(self, points, values, method="linear", bounds_error=True,
self._validate_grid_dimensions(points, method)
self.method = method
self.bounds_error = bounds_error
- self.grid, self.descending_dimensions = self._check_points(points)
self.values = self._check_values(values)
self._check_dimensionality(self.grid, self.values)
self.fill_value = self._check_fill_value(self.values, fill_value)
- if self.descending_dimensions:
- self.values = np.flip(values, axis=self.descending_dimensions)
def _check_dimensionality(self, points, values):
if len(points) > values.ndim:
```suggestion
if self._descending_dimensions:
```
def __init__(self, points, values, method="linear", bounds_error=True,
self._validate_grid_dimensions(points, method)
self.method = method
self.bounds_error = bounds_error
+ self.grid, self._descending_dimensions = self._check_points(points)
self.values = self._check_values(values)
self._check_dimensionality(self.grid, self.values)
self.fill_value = self._check_fill_value(self.values, fill_value)
+ if self._descending_dimensions:
+ self.values = np.flip(values, axis=self._descending_dimensions)
def _check_dimensionality(self, points, values):
if len(points) > values.ndim:
|
codereview_new_python_data_13291
|
def __init__(self, points, values, method="linear", bounds_error=True,
self._validate_grid_dimensions(points, method)
self.method = method
self.bounds_error = bounds_error
- self.grid, self.descending_dimensions = self._check_points(points)
self.values = self._check_values(values)
self._check_dimensionality(self.grid, self.values)
self.fill_value = self._check_fill_value(self.values, fill_value)
- if self.descending_dimensions:
- self.values = np.flip(values, axis=self.descending_dimensions)
def _check_dimensionality(self, points, values):
if len(points) > values.ndim:
```suggestion
self.values = np.flip(values, axis=self._descending_dimensions)
```
def __init__(self, points, values, method="linear", bounds_error=True,
self._validate_grid_dimensions(points, method)
self.method = method
self.bounds_error = bounds_error
+ self.grid, self._descending_dimensions = self._check_points(points)
self.values = self._check_values(values)
self._check_dimensionality(self.grid, self.values)
self.fill_value = self._check_fill_value(self.values, fill_value)
+ if self._descending_dimensions:
+ self.values = np.flip(values, axis=self._descending_dimensions)
def _check_dimensionality(self, points, values):
if len(points) > values.ndim:
|
codereview_new_python_data_13292
|
def __call__(self, values, method=None):
# check dimensionality
self._check_dimensionality(self.grid, values)
# flip, if needed
- self.values = np.flip(values, axis=self.descending_dimensions)
return super().__call__(self.xi, method=method)
Need to be changed here too.
def __call__(self, values, method=None):
# check dimensionality
self._check_dimensionality(self.grid, values)
# flip, if needed
+ self.values = np.flip(values, axis=self._descending_dimensions)
return super().__call__(self.xi, method=method)
|
codereview_new_python_data_13293
|
def __call__(self, values, method=None):
# check dimensionality
self._check_dimensionality(self.grid, values)
# flip, if needed
- self.values = np.flip(values, axis=self.descending_dimensions)
return super().__call__(self.xi, method=method)
```suggestion
self.values = np.flip(values, axis=self._descending_dimensions)
```
def __call__(self, values, method=None):
# check dimensionality
self._check_dimensionality(self.grid, values)
# flip, if needed
+ self.values = np.flip(values, axis=self._descending_dimensions)
return super().__call__(self.xi, method=method)
|
codereview_new_python_data_13294
|
def pmf(self, k, *args, **kwds):
k = asarray((k-loc))
cond0 = self._argcheck(*args)
cond1 = (k >= _a) & (k <= _b)
- cond = cond0 & cond1
if not isinstance(self, rv_sample):
cond1 = cond1 & self._nonzero(k, *args)
output = zeros(shape(cond), 'd')
place(output, (1-cond0) + np.isnan(k), self.badvalue)
if np.any(cond):
```suggestion
cond1 = (k >= _a) & (k <= _b)
if not isinstance(self, rv_sample):
cond1 = cond1 & self._nonzero(k, *args)
cond = cond0 & cond1
```
The logic was already there, but the lines were swapped.
def pmf(self, k, *args, **kwds):
k = asarray((k-loc))
cond0 = self._argcheck(*args)
cond1 = (k >= _a) & (k <= _b)
if not isinstance(self, rv_sample):
cond1 = cond1 & self._nonzero(k, *args)
+ cond = cond0 & cond1
output = zeros(shape(cond), 'd')
place(output, (1-cond0) + np.isnan(k), self.badvalue)
if np.any(cond):
|
codereview_new_python_data_13295
|
def check_pmf_cdf(distfn, arg, distname):
npt.assert_allclose(cdfs - cdfs[0], pmfs_cum - pmfs_cum[0],
atol=atol, rtol=rtol)
- # also check that pmf at non-integral args is zero
k = np.asarray(index)
- k_shifted = index[:-1] + np.diff(index)/2
npt.assert_equal(distfn.pmf(k_shifted, *arg), 0)
# better check frozen distributions, and also when loc != 0
Just to clarify the intent:
```suggestion
# also check that pmf at non-integral k is zero
k = np.asarray(index)
k_shifted = k[:-1] + np.diff(k)/2
npt.assert_equal(distfn.pmf(k_shifted, *arg), 0)
```
def check_pmf_cdf(distfn, arg, distname):
npt.assert_allclose(cdfs - cdfs[0], pmfs_cum - pmfs_cum[0],
atol=atol, rtol=rtol)
+ # also check that pmf at non-integral k is zero
k = np.asarray(index)
+ k_shifted = k[:-1] + np.diff(k)/2
npt.assert_equal(distfn.pmf(k_shifted, *arg), 0)
# better check frozen distributions, and also when loc != 0
|
codereview_new_python_data_13296
|
def value_indices(arr, *, nullval=None):
Note for IDL users: this provides functionality equivalent to IDL's
REVERSE_INDICES option.
- .. versionadded:: 1.9.2
Examples
--------
Obviously subject to mailing list & review but this won't go in until 1.10.0 at the earliest.
```suggestion
.. versionadded:: 1.10.0
```
def value_indices(arr, *, nullval=None):
Note for IDL users: this provides functionality equivalent to IDL's
REVERSE_INDICES option.
+ .. versionadded:: 1.10.0
Examples
--------
|
codereview_new_python_data_13297
|
def value_indices(arr, *, ignore_value=None):
more flexible alternative to functions like ``scipy.ndimage.mean()``
and ``scipy.ndimage.variance()``.
Note for IDL users: this provides functionality equivalent to IDL's
REVERSE_INDICES option (as per the IDL documentation for the
`HISTOGRAM <https://www.l3harrisgeospatial.com/docs/histogram.html>`_
Did you want to add a link here also to skimage's regionprops? It's not very important, but seems more relevant than IDL.
def value_indices(arr, *, ignore_value=None):
more flexible alternative to functions like ``scipy.ndimage.mean()``
and ``scipy.ndimage.variance()``.
+ Some other closely related functionality, with different strengths and
+ weaknesses, can also be found in ``scipy.stats.binned_statistic()`` and
+ the `scikit-image <https://scikit-image.org/>`_ function
+ ``skimage.measure.regionprops()``.
+
Note for IDL users: this provides functionality equivalent to IDL's
REVERSE_INDICES option (as per the IDL documentation for the
`HISTOGRAM <https://www.l3harrisgeospatial.com/docs/histogram.html>`_
|
codereview_new_python_data_13298
|
class LatinHypercube(QMCEngine):
distinct rows occur the same number of times. The elements of :math:`A`
are in the set :math:`\{0, 1, ..., p-1\}`, also called symbols.
The constraint that :math:`p` must be a prime number is to allow modular
- arithmetic. The strength add some symmetry in sub-projections to a sample.
- With strength 2, samples are symmetric along the diagonals of
- 2D sub-projections. Which may be undesirable, but on the other hand, the
sample dispersion is improved.
Strength 1 (plain LHS) brings an advantage over strength 0 (MC) and
"The strength" - which strength?
```suggestion
arithmetic. Increasing strength adds some symmetry to the sub-projections
of a sample. With strength 2, samples are symmetric along the diagonals of
2D sub-projections. This may be undesirable, but on the other hand, the
sample dispersion is improved.
```
class LatinHypercube(QMCEngine):
distinct rows occur the same number of times. The elements of :math:`A`
are in the set :math:`\{0, 1, ..., p-1\}`, also called symbols.
The constraint that :math:`p` must be a prime number is to allow modular
+ arithmetic. Increasing strength adds some symmetry to the sub-projections
+ of a sample. With strength 2, samples are symmetric along the diagonals of
+ 2D sub-projections. This may be undesirable, but on the other hand, the
sample dispersion is improved.
Strength 1 (plain LHS) brings an advantage over strength 0 (MC) and
|
codereview_new_python_data_13299
|
def test_mse_accuracy_2(self):
a = (n*x[0] - x[-1])/(n - 1)
b = (n*x[-1] - x[0])/(n - 1)
ref = a, b-a # (3.6081133632151503, 5.509328130317254)
- assert_allclose(res.params, ref, atol=1e-5)
class TestFitResult:
```suggestion
assert_allclose(res.params, ref, atol=1e-4)
```
def test_mse_accuracy_2(self):
a = (n*x[0] - x[-1])/(n - 1)
b = (n*x[-1] - x[0])/(n - 1)
ref = a, b-a # (3.6081133632151503, 5.509328130317254)
+ assert_allclose(res.params, ref, atol=1e-4)
class TestFitResult:
|
codereview_new_python_data_13300
|
def init_options(self, options):
"""
# Ensure that 'jac' and 'hess' are passed directly to `minimize` as
# keywords, not as part of its 'options' dictionary
- self.minimizer_kwargs['jac'] = options.pop('jac', None)
- self.minimizer_kwargs['hess'] = options.pop('hess', None)
# Update 'options' dict passed to optimize.minimize
self.minimizer_kwargs['options'].update(options)
I tried to simplify this, but I see that this could replace `minimizer_kwargs['jac']` with `None` if the user passes the `jac` to `minimizer_kwargs` but not to `shgo`'s `options`. But is there any good reason that the user would want the local minimizer to have the gradient but not let `shgo` use it? If `jac` is found in `minimizer_kwargs`, shouldn't it go to `sgho`, too?
def init_options(self, options):
"""
# Ensure that 'jac' and 'hess' are passed directly to `minimize` as
# keywords, not as part of its 'options' dictionary
+ if 'jac' in options:
+ self.minimizer_kwargs['jac'] = options.pop('jac')
+ if 'hass' in options:
+ self.minimizer_kwargs['hess'] = options.pop('hess')
# Update 'options' dict passed to optimize.minimize
self.minimizer_kwargs['options'].update(options)
|
codereview_new_python_data_13301
|
def init_options(self, options):
"""
# Ensure that 'jac' and 'hess' are passed directly to `minimize` as
# keywords, not as part of its 'options' dictionary
- self.minimizer_kwargs['jac'] = options.pop('jac', None)
- self.minimizer_kwargs['hess'] = options.pop('hess', None)
# Update 'options' dict passed to optimize.minimize
self.minimizer_kwargs['options'].update(options)
```suggestion
if 'jac' in options:
self.minimizer_kwargs['jac'] = options.pop('jac')
if 'hass' in options:
self.minimizer_kwargs['hess'] = options.pop('hess')
```
def init_options(self, options):
"""
# Ensure that 'jac' and 'hess' are passed directly to `minimize` as
# keywords, not as part of its 'options' dictionary
+ if 'jac' in options:
+ self.minimizer_kwargs['jac'] = options.pop('jac')
+ if 'hass' in options:
+ self.minimizer_kwargs['hess'] = options.pop('hess')
# Update 'options' dict passed to optimize.minimize
self.minimizer_kwargs['options'].update(options)
|
codereview_new_python_data_13302
|
def init_options(self, options):
# Ensure that 'jac', 'hess', and 'hessp' are passed directly to
# `minimize` as keywords, not as part of its 'options' dictionary.
for opt in ['jac', 'hess', 'hessp']:
- if opt in options:
self.minimizer_kwargs[opt] = (
self.minimizer_kwargs['options'].pop(opt))
```suggestion
if opt in self.minimizer_kwargs['options']:
```
def init_options(self, options):
# Ensure that 'jac', 'hess', and 'hessp' are passed directly to
# `minimize` as keywords, not as part of its 'options' dictionary.
for opt in ['jac', 'hess', 'hessp']:
+ if opt in self.minimizer_kwargs['options']:
self.minimizer_kwargs[opt] = (
self.minimizer_kwargs['options'].pop(opt))
|
codereview_new_python_data_13303
|
def directional_stats(samples, *, axis=0, normalize=True):
It is analogous to the sample mean, but it is for use when the length of
the data is irrelevant (e.g. unit vectors).
- The directional variance serves as a measure of "directional spread" for
vector data. The length of the mean vector can be used to calculate
directional variance using one of the several definitions outlined in
[1]_ and [2]_.
```suggestion
The length of the mean resultant vector can be used to compute measures of "directional spread" such as the directional variance
```
def directional_stats(samples, *, axis=0, normalize=True):
It is analogous to the sample mean, but it is for use when the length of
the data is irrelevant (e.g. unit vectors).
+ The length of the mean resultant vector can be used to compute measures
+ of "directional spread" such as the directional variance
vector data. The length of the mean vector can be used to calculate
directional variance using one of the several definitions outlined in
[1]_ and [2]_.
|
codereview_new_python_data_13304
|
def test_directional_stats_correctness(self):
reference_mean = np.array([0.2984, -0.1346, -0.9449])
assert_allclose(mean_rounded, reference_mean)
- expected_var = 0.025335389565304012
- directional_var = 1 - dirstats.mean_resultant_length
- assert_allclose(expected_var, directional_var)
def test_directional_stats_2d(self):
# Test that for circular data directional_stats
How was this computed? I don't think the reference gave it to so many digits.
def test_directional_stats_correctness(self):
reference_mean = np.array([0.2984, -0.1346, -0.9449])
assert_allclose(mean_rounded, reference_mean)
+ @pytest.mark.parametrize('angles, ref', [
+ ([-np.pi/2, np.pi/2], 1.),
+ ([0, 2*np.pi], 0.),
+ ([-np.pi/2, -np.pi/4, 0, np.pi/4, np.pi/2], stats.circvar)
+ ])
+ def test_mean_resultant_length(self, angles, ref):
+ if callable(ref):
+ ref = ref(angles)
+ data = np.stack([np.cos(angles), np.sin(angles)], axis=1)
+ res = 1 - stats.directional_stats(data).mean_resultant_length
+ assert_allclose(res, ref)
def test_directional_stats_2d(self):
# Test that for circular data directional_stats
|
codereview_new_python_data_13305
|
def test_directional_stats_correctness(self):
@pytest.mark.parametrize('angles, ref', [
([-np.pi/2, np.pi/2], 1.),
- ([0, 2*np.pi], 0.),
- ([-np.pi/2, -np.pi/4, 0, np.pi/4, np.pi/2], stats.circvar)
])
- def test_mean_resultant_length(self, angles, ref):
if callable(ref):
ref = ref(angles)
data = np.stack([np.cos(angles), np.sin(angles)], axis=1)
To make the tests more robust, I could add one more testcase that generates angles randomly and tests against `circvar`. Let me know if such a test would be helpful and I will add it.
def test_directional_stats_correctness(self):
@pytest.mark.parametrize('angles, ref', [
([-np.pi/2, np.pi/2], 1.),
+ ([0, 2*np.pi], 0.)
])
+ def test_directional_stats_2d_special_cases(self, angles, ref):
if callable(ref):
ref = ref(angles)
data = np.stack([np.cos(angles), np.sin(angles)], axis=1)
|
codereview_new_python_data_13306
|
def binned_statistic_dd(sample, values, statistic='mean',
dedges = [np.diff(edges[i]) for i in builtins.range(Ndim)]
binnumbers = binned_statistic_result.binnumber
- # Use a float64 accumulator to avoid integer overflow
result_type = np.result_type(values, np.float64)
result = np.empty([Vdim, nbin.prod()], dtype=result_type)
```suggestion
# Avoid overflow with double precision. Complex `values` -> `complex128`.
```
def binned_statistic_dd(sample, values, statistic='mean',
dedges = [np.diff(edges[i]) for i in builtins.range(Ndim)]
binnumbers = binned_statistic_result.binnumber
+ # Avoid overflow with double precision. Complex `values` -> `complex128`.
result_type = np.result_type(values, np.float64)
result = np.empty([Vdim, nbin.prod()], dtype=result_type)
|
codereview_new_python_data_13307
|
import numpy as np
from numpy.testing import assert_allclose
-from pytest import mark
from pytest import raises as assert_raises
from scipy.stats import (binned_statistic, binned_statistic_2d,
binned_statistic_dd)
```suggestion
import pytest
```
For consistency with the rest of stats. Your way saves lines though. Maybe in the future we'll define:
```python3
parametrize = pytest.mark.parametrize
```
import numpy as np
from numpy.testing import assert_allclose
+import pytest
from pytest import raises as assert_raises
from scipy.stats import (binned_statistic, binned_statistic_2d,
binned_statistic_dd)
|
codereview_new_python_data_13308
|
def max_len_seq(nbits, state=None, length=None, taps=None):
>>> import numpy as np
>>> import matplotlib.pyplot as plt
- >>> from numpy.fft import fft, ifft, fftshift, fftfreq
>>> seq = max_len_seq(6)[0]*2-1 # +1 and -1
>>> spec = fft(seq)
>>> N = len(seq)
Minor nit: maybe we want to keep `np.fft` here instead of importing again? Not sure if that would be too verbose for the code, though.
def max_len_seq(nbits, state=None, length=None, taps=None):
>>> import numpy as np
>>> import matplotlib.pyplot as plt
+ >>> from np.fft import fft, ifft, fftshift, fftfreq
>>> seq = max_len_seq(6)[0]*2-1 # +1 and -1
>>> spec = fft(seq)
>>> N = len(seq)
|
codereview_new_python_data_13309
|
def fft(x, n=None, axis=-1, norm=None, overwrite_x=False, workers=None, *,
In this example, real input has an FFT which is Hermitian, i.e., symmetric
in the real part and anti-symmetric in the imaginary part:
- >>> import numpy as np
>>> from scipy.fft import fft, fftfreq, fftshift
>>> import matplotlib.pyplot as plt
>>> t = np.arange(256)
Remove this line. The import was already done a few lines earlier.
def fft(x, n=None, axis=-1, norm=None, overwrite_x=False, workers=None, *,
In this example, real input has an FFT which is Hermitian, i.e., symmetric
in the real part and anti-symmetric in the imaginary part:
>>> from scipy.fft import fft, fftfreq, fftshift
>>> import matplotlib.pyplot as plt
>>> t = np.arange(256)
|
codereview_new_python_data_13310
|
def max_len_seq(nbits, state=None, length=None, taps=None):
>>> import numpy as np
>>> import matplotlib.pyplot as plt
- >>> from np.fft import fft, ifft, fftshift, fftfreq
>>> seq = max_len_seq(6)[0]*2-1 # +1 and -1
>>> spec = fft(seq)
>>> N = len(seq)
This doesn't work--a variable name can't be used in an import statement like this.
```suggestion
>>> from numpy.fft import fft, ifft, fftshift, fftfreq
```
def max_len_seq(nbits, state=None, length=None, taps=None):
>>> import numpy as np
>>> import matplotlib.pyplot as plt
+ >>> from numpy.fft import fft, ifft, fftshift, fftfreq
>>> seq = max_len_seq(6)[0]*2-1 # +1 and -1
>>> spec = fft(seq)
>>> N = len(seq)
|
codereview_new_python_data_13311
|
def curve_fit(f, xdata, ydata, p0=None, sigma=None, absolute_sigma=False,
parameters). Use ``np.inf`` with an appropriate sign to disable
bounds on all or some parameters.
- .. versionadded:: 0.17
method : {'lm', 'trf', 'dogbox'}, optional
Method to use for optimization. See `least_squares` for more details.
Default is 'lm' for unconstrained problems and 'trf' if `bounds` are
At that point I would remove this or we should add a `versionchanged` to the other bullet if we want to be extra correct.
def curve_fit(f, xdata, ydata, p0=None, sigma=None, absolute_sigma=False,
parameters). Use ``np.inf`` with an appropriate sign to disable
bounds on all or some parameters.
method : {'lm', 'trf', 'dogbox'}, optional
Method to use for optimization. See `least_squares` for more details.
Default is 'lm' for unconstrained problems and 'trf' if `bounds` are
|
codereview_new_python_data_13312
|
def curve_fit(f, xdata, ydata, p0=None, sigma=None, absolute_sigma=False,
parameters). Use ``np.inf`` with an appropriate sign to disable
bounds on all or some parameters.
- .. versionadded:: 0.17
method : {'lm', 'trf', 'dogbox'}, optional
Method to use for optimization. See `least_squares` for more details.
Default is 'lm' for unconstrained problems and 'trf' if `bounds` are
```suggestion
bounds on all or some parameters.
method : {'lm', 'trf', 'dogbox'}, optional
```
def curve_fit(f, xdata, ydata, p0=None, sigma=None, absolute_sigma=False,
parameters). Use ``np.inf`` with an appropriate sign to disable
bounds on all or some parameters.
method : {'lm', 'trf', 'dogbox'}, optional
Method to use for optimization. See `least_squares` for more details.
Default is 'lm' for unconstrained problems and 'trf' if `bounds` are
|
codereview_new_python_data_13313
|
class Covariance:
object representing a covariance matrix using any of several
decompositions and perform calculations using a common interface.
- Note that the `Covariance` class cannot be instantiated directly.
- Instead, use one of the factory methods (e.g. `Covariance.from_diagonal`).
Examples
--------
- The most common use of the `Covariance` class is to call one of the
factory methods to create a `Covariance` object, then pass that
representation of the `Covariance` matrix as a shape parameter of a
multivariate distribution.
I would make it more prominent with either a note or warning markup
```suggestion
.. note::
The `Covariance` class cannot be instantiated directly.
Instead, use one of the factory methods (e.g. `Covariance.from_diagonal`).
```
class Covariance:
object representing a covariance matrix using any of several
decompositions and perform calculations using a common interface.
+ .. note::
+
+ The `Covariance` class cannot be instantiated directly. Instead, use
+ one of the factory methods (e.g. `Covariance.from_diagonal`).
Examples
--------
+ The `Covariance` class is is used by calling one of its
factory methods to create a `Covariance` object, then pass that
representation of the `Covariance` matrix as a shape parameter of a
multivariate distribution.
|
codereview_new_python_data_13314
|
class Covariance:
object representing a covariance matrix using any of several
decompositions and perform calculations using a common interface.
- Note that the `Covariance` class cannot be instantiated directly.
- Instead, use one of the factory methods (e.g. `Covariance.from_diagonal`).
Examples
--------
- The most common use of the `Covariance` class is to call one of the
factory methods to create a `Covariance` object, then pass that
representation of the `Covariance` matrix as a shape parameter of a
multivariate distribution.
I think we should rephrase the "most common" part as you must now use a factory method.
class Covariance:
object representing a covariance matrix using any of several
decompositions and perform calculations using a common interface.
+ .. note::
+
+ The `Covariance` class cannot be instantiated directly. Instead, use
+ one of the factory methods (e.g. `Covariance.from_diagonal`).
Examples
--------
+ The `Covariance` class is is used by calling one of its
factory methods to create a `Covariance` object, then pass that
representation of the `Covariance` matrix as a shape parameter of a
multivariate distribution.
|
codereview_new_python_data_13315
|
class Covariance:
representing a covariance matrix:
>>> from scipy import stats
>>> d = [1, 2, 3]
>>> A = np.diag(d) # a diagonal covariance matrix
>>> x = [4, -2, 5] # a point of interest
```suggestion
>>> from scipy import stats
>>> import numpy as np
```
class Covariance:
representing a covariance matrix:
>>> from scipy import stats
+ >>> import numpy as np
>>> d = [1, 2, 3]
>>> A = np.diag(d) # a diagonal covariance matrix
>>> x = [4, -2, 5] # a point of interest
|
codereview_new_python_data_13316
|
def test_ncf_ppf_issue_17026():
par = (0.1, 2, 5, 0, 1)
with pytest.warns(RuntimeWarning):
q = stats.ncf.ppf(x, *par)
class TestHistogram:
```suggestion
q = stats.ncf.ppf(x, *par)
q0 = [stats.ncf.ppf(xi, *par) for xi in x]
assert_allclose(q, q0)
```
There was a PEP8 issue because `q` was assigned to but not used. I suppose we could just not assign to a variable, but this is a reasonable thing to test.
def test_ncf_ppf_issue_17026():
par = (0.1, 2, 5, 0, 1)
with pytest.warns(RuntimeWarning):
q = stats.ncf.ppf(x, *par)
+ q0 = [stats.ncf.ppf(xi, *par) for xi in x]
+ assert_allclose(q, q0)
class TestHistogram:
|
codereview_new_python_data_13317
|
def y1p_zeros(nt, complex=False):
>>> ax.legend(ncol=2, bbox_to_anchor=(1., 0.75))
>>> plt.tight_layout()
>>> plt.show()
- """
if not isscalar(nt) or (floor(nt) != nt) or (nt <= 0):
raise ValueError("Arguments must be scalar positive integer.")
kf = 2
```suggestion
>>> plt.show()
"""
if not isscalar(nt) or (floor(nt) != nt) or (nt <= 0):
```
def y1p_zeros(nt, complex=False):
>>> ax.legend(ncol=2, bbox_to_anchor=(1., 0.75))
>>> plt.tight_layout()
>>> plt.show()
+ """
if not isscalar(nt) or (floor(nt) != nt) or (nt <= 0):
raise ValueError("Arguments must be scalar positive integer.")
kf = 2
|
codereview_new_python_data_13318
|
def jn_zeros(n, nt):
See Also
--------
jv: Real-order Bessel functions of the first kind
- jn: Integer-order Bessel functions of the first kind
jnp_zeros: Zeros of :math:`Jn'`
References
This seems to be the culprit.
```
/home/circleci/repo/build-install/lib/python3.8/site-packages/scipy/special/_basic.py:docstring of scipy.special._basic.jn_zeros:33: WARNING: py:obj reference target not found: jn
```
def jn_zeros(n, nt):
See Also
--------
jv: Real-order Bessel functions of the first kind
jnp_zeros: Zeros of :math:`Jn'`
References
|
codereview_new_python_data_13319
|
def test_nomodify_gh9900_regression():
# Use the right-half truncated normal
# Check that the cdf and _cdf return the same result.
npt.assert_almost_equal(tn.cdf(1, 0, np.inf), 0.6826894921370859)
- npt.assert_almost_equal(tn._cdf(1, 0, np.inf), 0.6826894921370859)
# Now use the left-half truncated normal
npt.assert_almost_equal(tn.cdf(-1, -np.inf, 0), 0.31731050786291415)
- npt.assert_almost_equal(tn._cdf(-1, -np.inf, 0), 0.31731050786291415)
# Check that the right-half truncated normal _cdf hasn't changed
- npt.assert_almost_equal(tn._cdf(1, 0, np.inf), 0.6826894921370859) # NOT 1.6826894921370859
npt.assert_almost_equal(tn.cdf(1, 0, np.inf), 0.6826894921370859)
# Check that the left-half truncated normal _cdf hasn't changed
- npt.assert_almost_equal(tn._cdf(-1, -np.inf, 0), 0.31731050786291415) # Not -0.6826894921370859
npt.assert_almost_equal(tn.cdf(1, -np.inf, 0), 1) # Not 1.6826894921370859
npt.assert_almost_equal(tn.cdf(-1, -np.inf, 0), 0.31731050786291415) # Not -0.6826894921370859
All `rv_continuous` private methods should be able to assume they are getting arrays that are at least 1d because that's what they are passed from the public method. The implementation of `_logcdf` relies on this, so rather than add an additional `np.atleast_1d` call in `_logcdf`, ensure the input is at least 1d here.
def test_nomodify_gh9900_regression():
# Use the right-half truncated normal
# Check that the cdf and _cdf return the same result.
npt.assert_almost_equal(tn.cdf(1, 0, np.inf), 0.6826894921370859)
+ npt.assert_almost_equal(tn._cdf([1], [0], [np.inf]), 0.6826894921370859)
# Now use the left-half truncated normal
npt.assert_almost_equal(tn.cdf(-1, -np.inf, 0), 0.31731050786291415)
+ npt.assert_almost_equal(tn._cdf([-1], [-np.inf], [0]), 0.31731050786291415)
# Check that the right-half truncated normal _cdf hasn't changed
+ npt.assert_almost_equal(tn._cdf([1], [0], [np.inf]), 0.6826894921370859) # noqa, NOT 1.6826894921370859
npt.assert_almost_equal(tn.cdf(1, 0, np.inf), 0.6826894921370859)
# Check that the left-half truncated normal _cdf hasn't changed
+ npt.assert_almost_equal(tn._cdf([-1], [-np.inf], [0]), 0.31731050786291415) # noqa, Not -0.6826894921370859
npt.assert_almost_equal(tn.cdf(1, -np.inf, 0), 1) # Not 1.6826894921370859
npt.assert_almost_equal(tn.cdf(-1, -np.inf, 0), 0.31731050786291415) # Not -0.6826894921370859
|
codereview_new_python_data_13320
|
def ks_2samp(data1, data2, alternative='two-sided', method='auto'):
minS = np.clip(-cddiffs[argminS], 0, 1)
maxS = cddiffs[argmaxS]
- if alternative == 'less':
d = minS
d_location = loc_minS
d_sign = '-'
- elif alternative == 'greater':
d = maxS
d_location = loc_maxS
d_sign = '+'
- else:
- if minS > maxS:
- d = minS
- d_location = loc_minS
- d_sign = '-'
- else:
- d = maxS
- d_location = loc_maxS
- d_sign = '+'
-
g = gcd(n1, n2)
n1g = n1 // g
n2g = n2 // g
```suggestion
if alternative == 'less' or minS > maxS:
```
def ks_2samp(data1, data2, alternative='two-sided', method='auto'):
minS = np.clip(-cddiffs[argminS], 0, 1)
maxS = cddiffs[argmaxS]
+ if alternative == 'less' or minS > maxS:
d = minS
d_location = loc_minS
d_sign = '-'
+ elif alternative == 'greater' or minS <= maxS:
d = maxS
d_location = loc_maxS
d_sign = '+'
g = gcd(n1, n2)
n1g = n1 // g
n2g = n2 // g
|
codereview_new_python_data_13321
|
def ks_2samp(data1, data2, alternative='two-sided', method='auto'):
minS = np.clip(-cddiffs[argminS], 0, 1)
maxS = cddiffs[argmaxS]
- if alternative == 'less':
d = minS
d_location = loc_minS
d_sign = '-'
- elif alternative == 'greater':
d = maxS
d_location = loc_maxS
d_sign = '+'
- else:
- if minS > maxS:
- d = minS
- d_location = loc_minS
- d_sign = '-'
- else:
- d = maxS
- d_location = loc_maxS
- d_sign = '+'
-
g = gcd(n1, n2)
n1g = n1 // g
n2g = n2 // g
```suggestion
elif alternative == 'greater' or minS <= maxS:
```
Could just be `else`.
def ks_2samp(data1, data2, alternative='two-sided', method='auto'):
minS = np.clip(-cddiffs[argminS], 0, 1)
maxS = cddiffs[argmaxS]
+ if alternative == 'less' or minS > maxS:
d = minS
d_location = loc_minS
d_sign = '-'
+ elif alternative == 'greater' or minS <= maxS:
d = maxS
d_location = loc_maxS
d_sign = '+'
g = gcd(n1, n2)
n1g = n1 // g
n2g = n2 // g
|
codereview_new_python_data_13322
|
def kstest(rvs, cdf, args=(), N=20, alternative='two-sided', method='auto'):
Value of `x` corresponding with the KS statistic; i.e. the
observation at which the difference between CDFs is measured.
statistic_sign: int
- 1 if the KS statistic is the maximal positive difference between
- CDFs (D+), -1 if the KS statistic is the negative difference (D-).
-
- statistic_sign: int
- 1 if the KS statistic is the maximal positive difference between
- empirical and hypothesized distributions (D+), -1 if the KS
- statistic is the negative difference (D-). If a 2-sample test is
- run, the difference is between the first and second empirical
- distributions.
See Also
--------
Please pick one.
If the latter, consider that the second sentence begins with "if a 2-sample test is run", but there is no corresponding part of the first sentence.
def kstest(rvs, cdf, args=(), N=20, alternative='two-sided', method='auto'):
Value of `x` corresponding with the KS statistic; i.e. the
observation at which the difference between CDFs is measured.
statistic_sign: int
+ If a 1-sample test is run, this is +1 if the KS statistic is the
+ maximal positive difference between empirical and hypothesized
+ distributions (D+), -1 if the KS statistic is the negative
+ difference (D-). If a 2-sample test is run, the difference is
+ between the first and second empirical distributions.
See Also
--------
|
codereview_new_python_data_13323
|
def testLargeBoth(self):
def testNamedAttributes(self):
# test for namedtuple attribute results
attributes = ('statistic', 'pvalue')
- additional_attributes = ('statistic_location', 'statistic_sign')
res = stats.ks_2samp([1, 2], [3])
- check_named_results(res, attributes,
- additional_attributes=additional_attributes)
@pytest.mark.slow
def test_some_code_paths(self):
But why add this? It's shown that these attributes exist in both `test_location_sign` and `test_nametuples_agree`. And the equivalent attributed for `ks_1samp` are tested only once, in `test_location_sign`. I don't think we need to test it three times for one function and only once for the other.
It's not too big a deal; I would just prefer to minimize the code the changes that need to be reviewed.
def testLargeBoth(self):
def testNamedAttributes(self):
# test for namedtuple attribute results
attributes = ('statistic', 'pvalue')
res = stats.ks_2samp([1, 2], [3])
+ check_named_results(res, attributes)
@pytest.mark.slow
def test_some_code_paths(self):
|
codereview_new_python_data_13324
|
def quad(func, a, b, args=(), full_output=0, epsabs=1.49e-8, epsrel=1.49e-8,
message is appended to the output tuple.
complex_func : bool, optional
Indicate if the function's (func) return type is real
- (`complex_func=false`: default) or complex (`complex_func=True`).
In both cases, the function's argument is real.
Returns
```suggestion
(``complex_func=False``: default) or complex (``complex_func=True``).
```
def quad(func, a, b, args=(), full_output=0, epsabs=1.49e-8, epsrel=1.49e-8,
message is appended to the output tuple.
complex_func : bool, optional
Indicate if the function's (func) return type is real
+ (``complex_func=False``: default) or complex (``complex_func=True``).
In both cases, the function's argument is real.
Returns
|
codereview_new_python_data_13325
|
def quad(func, a, b, args=(), full_output=0, epsabs=1.49e-8, epsrel=1.49e-8,
message is appended to the output tuple.
complex_func : bool, optional
Indicate if the function's (func) return type is real
- (`complex_func=false`: default) or complex (`complex_func=True`).
In both cases, the function's argument is real.
Returns
Backticks in ReST are different than in markdown.
https://numpydoc.readthedocs.io/en/latest/format.html#parameters
```suggestion
Indicate if the function's (`func`) return type is real
```
(In many cases the guidelines for backticks here are incomplete and/or disagreeable, but they are what they are.)
def quad(func, a, b, args=(), full_output=0, epsabs=1.49e-8, epsrel=1.49e-8,
message is appended to the output tuple.
complex_func : bool, optional
Indicate if the function's (func) return type is real
+ (``complex_func=False``: default) or complex (``complex_func=True``).
In both cases, the function's argument is real.
Returns
|
codereview_new_python_data_13326
|
def tfunc(x):
assert_quad(quad(tfunc, 0, np.pi/2, complex_func=True),
1+1j, error_tolerance=1e-6)
class TestNQuad:
def test_fixed_limits(self):
There needs to be a test with `full_output=True`.
def tfunc(x):
assert_quad(quad(tfunc, 0, np.pi/2, complex_func=True),
1+1j, error_tolerance=1e-6)
+ full_res = quad(tfunc, 0, np.pi/2, complex_func=True, full_output=True)
+ assert_quad(full_res[:-1],
+ 1+1j, error_tolerance=1e-6)
+
class TestNQuad:
def test_fixed_limits(self):
|
codereview_new_python_data_13327
|
def quad(func, a, b, args=(), full_output=0, epsabs=1.49e-8, epsrel=1.49e-8,
.. math::
\\int_a^b f(x) dx = \\int_a^b g(x) dx + i\\int_a^b h(x) dx
- This assumes that the integrals of :math:`g` and :math:`h` exist
- over the inteval :math:`[a,b]` [2]_.
References
```suggestion
assuming that the integrals of :math:`g` and :math:`h` exist
over the inteval :math:`[a,b]` [2]_. Therefore, ``quad`` integrates
complex-valued functions by integrating the real and imaginary components
separately.
```
def quad(func, a, b, args=(), full_output=0, epsabs=1.49e-8, epsrel=1.49e-8,
.. math::
\\int_a^b f(x) dx = \\int_a^b g(x) dx + i\\int_a^b h(x) dx
+ assuming that the integrals of :math:`g` and :math:`h` exist
+ over the inteval :math:`[a,b]` [2]_. Therefore, ``quad`` integrates
+ complex-valued functions by integrating the real and imaginary components
+ separately.
References
|
codereview_new_python_data_13328
|
def tfunc(x):
1+1j, error_tolerance=1e-6)
full_res = quad(tfunc, 0, np.pi/2, complex_func=True, full_output=True)
- assert_quad(full_res[:-1],
- 1+1j, error_tolerance=1e-6)
assert set(("real output", "imag output")) == set(full_res[2].keys())
```suggestion
assert_quad(full_res[:-1], 1+1j, error_tolerance=1e-6)
```
def tfunc(x):
1+1j, error_tolerance=1e-6)
full_res = quad(tfunc, 0, np.pi/2, complex_func=True, full_output=True)
+ assert_quad(full_res[:-1], 1+1j, error_tolerance=1e-6)
assert set(("real output", "imag output")) == set(full_res[2].keys())
|
codereview_new_python_data_13329
|
def test_lsmr_output_shape():
assert_equal(x.shape, (1,))
def test_eigs(matrices):
A_dense, A_sparse, v0 = matrices
@mreineck I don't think you meant to delete this test, did you?
def test_lsmr_output_shape():
assert_equal(x.shape, (1,))
+def test_lsqr(matrices):
+ A_dense, A_sparse, b = matrices
+ res0 = splin.lsqr(A_dense, b)
+ res = splin.lsqr(A_sparse, b)
+ assert_allclose(res[0], res0[0], atol=1e-5)
+
+
def test_eigs(matrices):
A_dense, A_sparse, v0 = matrices
|
codereview_new_python_data_13330
|
def op(a, b):
# 6. negative argument
# T_{alpha}(-X) = -T_{1-alpha}(X)
- assert (
- stats.expectile(-x, alpha=alpha) ==
pytest.approx(-stats.expectile(x, alpha=1-alpha))
)
I'm not a big fan of this equality op though, because it's one-sided - rounding only one side makes it unnecessarily harder to get a given tolerance. Can we use something that applies the (here) implicit tolerance to the _difference_? E.g. numpy's `assert_allclose` also works for scalars (and we can set relative/absolute tolerances as necessary).
```suggestion
assert_allclose(
stats.expectile(-x, alpha=alpha),
-stats.expectile(x, alpha=1-alpha)
)
```
def op(a, b):
# 6. negative argument
# T_{alpha}(-X) = -T_{1-alpha}(X)
+ assert assert_allclose(
+ stats.expectile(-x, alpha=alpha),
pytest.approx(-stats.expectile(x, alpha=1-alpha))
)
|
codereview_new_python_data_13331
|
def expectile(a, alpha=0.5, *, weights=None):
----------
a : array_like
Input array or object that can be converted to an array.
- alpha : float, default=0.5
The level of the expectile; `alpha=0.5` gives the mean.
weights : array_like, optional
The sample or case `weights` array must be broadcastable to the same
Let's follow [`numpy.mean`](https://numpy.org/doc/stable/reference/generated/numpy.mean.html).
```suggestion
Array containing numbers whose expectile is desired.
If `a` is not an array, a conversion is attempted.
```
def expectile(a, alpha=0.5, *, weights=None):
----------
a : array_like
Input array or object that can be converted to an array.
+ alpha : float, default: 0.5
The level of the expectile; `alpha=0.5` gives the mean.
weights : array_like, optional
The sample or case `weights` array must be broadcastable to the same
|
codereview_new_python_data_13332
|
def expectile(a, alpha=0.5, *, weights=None):
----------
a : array_like
Input array or object that can be converted to an array.
- alpha : float, default=0.5
The level of the expectile; `alpha=0.5` gives the mean.
weights : array_like, optional
The sample or case `weights` array must be broadcastable to the same
```suggestion
The level of the expectile; e.g., `alpha=0.5` gives the mean.
```
def expectile(a, alpha=0.5, *, weights=None):
----------
a : array_like
Input array or object that can be converted to an array.
+ alpha : float, default: 0.5
The level of the expectile; `alpha=0.5` gives the mean.
weights : array_like, optional
The sample or case `weights` array must be broadcastable to the same
|
codereview_new_python_data_13333
|
def expectile(a, alpha=0.5, *, weights=None):
----------
a : array_like
Input array or object that can be converted to an array.
- alpha : float, default=0.5
The level of the expectile; `alpha=0.5` gives the mean.
weights : array_like, optional
The sample or case `weights` array must be broadcastable to the same
From `np.average`
```suggestion
An array of weights associated with the values in `a`.
The `weights` array must be broadcastable to the same
```
def expectile(a, alpha=0.5, *, weights=None):
----------
a : array_like
Input array or object that can be converted to an array.
+ alpha : float, default: 0.5
The level of the expectile; `alpha=0.5` gives the mean.
weights : array_like, optional
The sample or case `weights` array must be broadcastable to the same
|
codereview_new_python_data_13334
|
def expectile(a, alpha=0.5, *, weights=None):
Furthermore, the larger :math:`\alpha`, the larger the value of the
expectile.
- As a final remark, the expectile at level :math:`alpha` can also be
written as a minimization problem. One often used choice is
.. math::
```suggestion
As a final remark, the expectile at level :math:`\alpha` can also be
```
def expectile(a, alpha=0.5, *, weights=None):
Furthermore, the larger :math:`\alpha`, the larger the value of the
expectile.
+ As a final remark, the expectile at level :math:`\alpha` can also be
written as a minimization problem. One often used choice is
.. math::
|
codereview_new_python_data_13335
|
def weightedtau(x, y, rank=True, weigher=None, additive=True):
statistic : float
The weighted :math:`\tau` correlation index.
pvalue : float
- Presently ``np.nan``, as the null hypothesis is unknown (even in the
- additive hyperbolic case).
See Also
--------
```suggestion
Presently ``np.nan``, as the null distribution of the statistic is
unknown (even in the additive hyperbolic case).
```
def weightedtau(x, y, rank=True, weigher=None, additive=True):
statistic : float
The weighted :math:`\tau` correlation index.
pvalue : float
+ Presently ``np.nan``, as the null distribution of the statistic is
+ unknown (even in the additive hyperbolic case).
See Also
--------
|
codereview_new_python_data_13336
|
def kendalltau(x, y, initial_lexsort=None, nan_policy='propagate',
Returns
-------
- res: SignificanceResult
An object containing attributes:
statistic : float
```suggestion
res : SignificanceResult
```
def kendalltau(x, y, initial_lexsort=None, nan_policy='propagate',
Returns
-------
+ res : SignificanceResult
An object containing attributes:
statistic : float
|
codereview_new_python_data_13337
|
def kendalltau(x, y, use_ties=True, use_missing=False, method='auto',
Returns
-------
- res: SignificanceResult
An object containing attributes:
statistic : float
```suggestion
res : SignificanceResult
```
def kendalltau(x, y, use_ties=True, use_missing=False, method='auto',
Returns
-------
+ res : SignificanceResult
An object containing attributes:
statistic : float
|
codereview_new_python_data_13338
|
def spearmanr(x, y=None, use_ties=True, axis=None, nan_policy='propagate',
``a`` and ``b`` combined.
pvalue : float
The p-value for a hypothesis test whose null hypothesis
- is that two sets of data are uncorrelated. See `alternative` above
- for alternative hypotheses. `pvalue` has the same
- shape as `statistic`.
References
----------
```suggestion
is that two sets of data are linearly uncorrelated. See
`alternative` above for alternative hypotheses. `pvalue` has the
same shape as `statistic`.
```
def spearmanr(x, y=None, use_ties=True, axis=None, nan_policy='propagate',
``a`` and ``b`` combined.
pvalue : float
The p-value for a hypothesis test whose null hypothesis
+ is that two sets of data are linearly uncorrelated. See
+ `alternative` above for alternative hypotheses. `pvalue` has the
+ same shape as `statistic`.
References
----------
|
codereview_new_python_data_13339
|
def spearmanr(x, y=None, use_ties=True, axis=None, nan_policy='propagate',
Returns
-------
- res: SignificanceResult
An object containing attributes:
statistic : float or ndarray (2-D square)
```suggestion
res : SignificanceResult
```
def spearmanr(x, y=None, use_ties=True, axis=None, nan_policy='propagate',
Returns
-------
+ res : SignificanceResult
An object containing attributes:
statistic : float or ndarray (2-D square)
|
codereview_new_python_data_13340
|
def spearmanr(a, b=None, axis=0, nan_policy='propagate',
Returns
-------
- res: SignificanceResult
An object containing attributes:
statistic : float or ndarray (2-D square)
```suggestion
res : SignificanceResult
```
def spearmanr(a, b=None, axis=0, nan_policy='propagate',
Returns
-------
+ res : SignificanceResult
An object containing attributes:
statistic : float or ndarray (2-D square)
|
codereview_new_python_data_13341
|
def anderson_ksamp(samples, midrank=True, n_resamples=0, random_state=None):
--------
>>> import numpy as np
>>> from scipy import stats
- >>> rng = np.random.default_rng(1638083107694713882823079058616272161)
>>> res = stats.anderson_ksamp([rng.normal(size=50),
... rng.normal(loc=0.5, size=30)])
>>> res.statistic, res.pvalue
```suggestion
>>> rng = np.random.default_rng()
```
def anderson_ksamp(samples, midrank=True, n_resamples=0, random_state=None):
--------
>>> import numpy as np
>>> from scipy import stats
+ >>> rng = np.random.default_rng()
>>> res = stats.anderson_ksamp([rng.normal(size=50),
... rng.normal(loc=0.5, size=30)])
>>> res.statistic, res.pvalue
|
codereview_new_python_data_13342
|
def statistic(*samples):
if A2 < critical.min() and not n_resamples:
p = sig.max()
message = (f"p-value capped: true value larger than {p}. Consider "
- "setting `n_resamples` to a possible integer (e.g. 9999).")
warnings.warn(message, stacklevel=2)
elif A2 > critical.max() and not n_resamples:
p = sig.min()
I think you meant "positive"?
def statistic(*samples):
if A2 < critical.min() and not n_resamples:
p = sig.max()
message = (f"p-value capped: true value larger than {p}. Consider "
+ "setting `n_resamples` to a positive integer (e.g. 9999).")
warnings.warn(message, stacklevel=2)
elif A2 > critical.max() and not n_resamples:
p = sig.min()
|
codereview_new_python_data_13343
|
def solve_ivp(fun, t_span, y0, method='RK45', t_eval=None, dense_output=False,
options is determined by `vectorized` argument (see below). The
vectorized implementation allows a faster approximation of the Jacobian
by finite differences (required for stiff solvers).
- t_span : 2-member iterable
Interval of integration (t0, tf). The solver starts with t=t0 and
integrates until it reaches t=tf. Both t0 and tf must be floats
or values interpretable by the float conversion function.
Would it make more sense to use `sequence` instead of `iterable`? I believe the former implies a guaranteed *ordering*, and is also more commonly used for argument types I think.
def solve_ivp(fun, t_span, y0, method='RK45', t_eval=None, dense_output=False,
options is determined by `vectorized` argument (see below). The
vectorized implementation allows a faster approximation of the Jacobian
by finite differences (required for stiff solvers).
+ t_span : 2-member sequence
Interval of integration (t0, tf). The solver starts with t=t0 and
integrates until it reaches t=tf. Both t0 and tf must be floats
or values interpretable by the float conversion function.
|
codereview_new_python_data_13344
|
def goodness_of_fit(dist, data, *, known_params=None, fit_params=None,
First, any unknown parameters of the distribution family specified by
`dist` are fit to the provided `data` using maximum likelihood estimation.
(One exception is the normal distribution with unknown location and scale:
- we use the bias-corrected standard deviation ``np.std(data, ddof=1)`` for
- the scale as recommended in [1]_.)
These values of the parameters specify a particular member of the
distribution family referred to as the "null-hypothesized distribution",
that is, the distribution from which the data were sampled under the null
```suggestion
we use the bias-corrected standard deviation ``np.std(data, ddof=1)`` for
the scale as recommended in [1]_.)
```
def goodness_of_fit(dist, data, *, known_params=None, fit_params=None,
First, any unknown parameters of the distribution family specified by
`dist` are fit to the provided `data` using maximum likelihood estimation.
(One exception is the normal distribution with unknown location and scale:
+ we use the bias-corrected standard deviation ``np.std(data, ddof=1)`` for
+ the scale as recommended in [1]_.)
These values of the parameters specify a particular member of the
distribution family referred to as the "null-hypothesized distribution",
that is, the distribution from which the data were sampled under the null
|
codereview_new_python_data_13345
|
def test_NaN_handling(self):
def _check_nan_policy(f, xdata_with_nan, xdata_without_nan,
ydata_with_nan, ydata_without_nan, method):
# propagate test
- error_msg = "`propagate` is not supported for nan_policy " \
- "in this function."
with assert_raises(ValueError, match=error_msg):
curve_fit(f, xdata_with_nan, ydata_with_nan, method=method,
check_finite=False, nan_policy="propagate",
If the suggestion above is accepted,
```suggestion
error_msg = ("`nan_policy='propagate'` is not supported "
"by this function.")
```
def test_NaN_handling(self):
def _check_nan_policy(f, xdata_with_nan, xdata_without_nan,
ydata_with_nan, ydata_without_nan, method):
# propagate test
+ error_msg = ("`nan_policy='propagate'` is not supported "
+ "by this function.")
with assert_raises(ValueError, match=error_msg):
curve_fit(f, xdata_with_nan, ydata_with_nan, method=method,
check_finite=False, nan_policy="propagate",
|
codereview_new_python_data_13346
|
def test_NaN_handling(self):
def _check_nan_policy(f, xdata_with_nan, xdata_without_nan,
ydata_with_nan, ydata_without_nan, method):
# propagate test
- error_msg = "`propagate` is not supported for nan_policy " \
- "in this function."
with assert_raises(ValueError, match=error_msg):
curve_fit(f, xdata_with_nan, ydata_with_nan, method=method,
check_finite=False, nan_policy="propagate",
It takes some time to see what arguments are actually changed in each call to `curve_fit`. Consider consolidating common values into `kwargs`.
```suggestion
kwargs = {'f': f, 'xdata': xdata_with_nan, 'ydata': ydata_with_nan,
'method': method, 'check_finite': False}
# propagate test
```
That way, it's easier to tell what is really changing in each test. It's also shorter and easier to satisfy PEP8.
def test_NaN_handling(self):
def _check_nan_policy(f, xdata_with_nan, xdata_without_nan,
ydata_with_nan, ydata_without_nan, method):
# propagate test
+ error_msg = ("`nan_policy='propagate'` is not supported "
+ "by this function.")
with assert_raises(ValueError, match=error_msg):
curve_fit(f, xdata_with_nan, ydata_with_nan, method=method,
check_finite=False, nan_policy="propagate",
|
codereview_new_python_data_13347
|
def test_NaN_handling(self):
def _check_nan_policy(f, xdata_with_nan, xdata_without_nan,
ydata_with_nan, ydata_without_nan, method):
# propagate test
- error_msg = "`propagate` is not supported for nan_policy " \
- "in this function."
with assert_raises(ValueError, match=error_msg):
curve_fit(f, xdata_with_nan, ydata_with_nan, method=method,
check_finite=False, nan_policy="propagate",
```suggestion
curve_fit(**kwargs, nan_policy="propagate", maxfev=2000)
```
def test_NaN_handling(self):
def _check_nan_policy(f, xdata_with_nan, xdata_without_nan,
ydata_with_nan, ydata_without_nan, method):
# propagate test
+ error_msg = ("`nan_policy='propagate'` is not supported "
+ "by this function.")
with assert_raises(ValueError, match=error_msg):
curve_fit(f, xdata_with_nan, ydata_with_nan, method=method,
check_finite=False, nan_policy="propagate",
|
codereview_new_python_data_13348
|
def _check_nan_policy(f, xdata_with_nan, xdata_without_nan,
# omit test
result_with_nan, _ = curve_fit(**kwargs, nan_policy="omit")
- result_without_nan, _ = curve_fit(**kwargs, nan_policy="omit")
assert_allclose(result_with_nan, result_without_nan)
@pytest.mark.parametrize('method', ["lm", "trf", "dogbox"])
I think you forgot to use `xdata_without_nan` and ``ydata_without_nan`` here. Shouldn't it be:
```suggestion
result_with_nan, _ = curve_fit(**kwargs, nan_policy="omit")
kwargs['xdata'] = xdata_without_nan
kwargs['ydata'] = ydata_without_nan
result_without_nan, _ = curve_fit(**kwargs)
```
? Otherwise, the test doesn't really test anything...
def _check_nan_policy(f, xdata_with_nan, xdata_without_nan,
# omit test
result_with_nan, _ = curve_fit(**kwargs, nan_policy="omit")
+ kwargs['xdata'] = xdata_without_nan
+ kwargs['ydata'] = ydata_without_nan
+ result_without_nan, _ = curve_fit(**kwargs)
assert_allclose(result_with_nan, result_without_nan)
@pytest.mark.parametrize('method', ["lm", "trf", "dogbox"])
|
codereview_new_python_data_13349
|
def _plotting_positions(self, n, a=.5):
def _cdf_plot(self, ax, fit_params):
data = np.sort(self._data)
ecdf = self._plotting_positions(len(self._data))
- ls = '--' if self.discrete else '-'
xlabel = 'k' if self.discrete else 'x'
ax.step(data, ecdf, ls, label='Empirical CDF', color='C1', zorder=0)
Perhaps this is more what we want:
```suggestion
ls = '--' if len(np.unique(data)) < 30 else '.'
```
The thought is that when we have too many steps, the dashed line starts looking funny. The number of steps is the number of unique elements in `data`. It so happens that my `nbinom` example had fewer discrete steps, but it wasn't inherently because it was discrete.
With this suggestion, here is data from a discrete distribution with lots of steps:
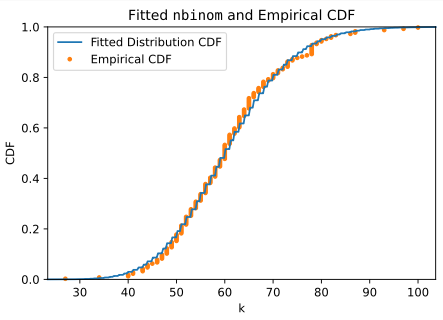
And data from a continuous distribution with few steps.
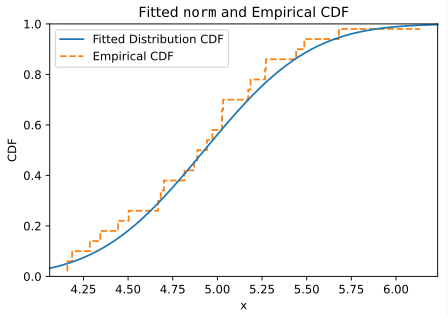
def _plotting_positions(self, n, a=.5):
def _cdf_plot(self, ax, fit_params):
data = np.sort(self._data)
ecdf = self._plotting_positions(len(self._data))
+ ls = '--' if len(np.unique(data)) < 30 else '.'
xlabel = 'k' if self.discrete else 'x'
ax.step(data, ecdf, ls, label='Empirical CDF', color='C1', zorder=0)
|
codereview_new_python_data_13350
|
def mat_reader_factory(file_name, appendmat=True, **kwargs):
elif mjv == 1:
return MatFile5Reader(byte_stream, **kwargs), file_opened
elif mjv == 2:
- raise NotImplementedError('Please use HDF reader for matlab v7.3 files,'
- ' e.g. h5py')
else:
raise TypeError('Did not recognize version %s' % mjv)
```suggestion
raise NotImplementedError('Please use HDF reader for matlab v7.3 '
'files, e.g. h5py')
```
The linter didn't mention it before, but the line was too long, too.
def mat_reader_factory(file_name, appendmat=True, **kwargs):
elif mjv == 1:
return MatFile5Reader(byte_stream, **kwargs), file_opened
elif mjv == 2:
+ raise NotImplementedError('Please use HDF reader for matlab v7.3 '
+ 'files, e.g. h5py')
else:
raise TypeError('Did not recognize version %s' % mjv)
|
codereview_new_python_data_13351
|
class truncnorm_gen(rv_continuous):
Notes
-----
- This distribution is the normal distribution centred on ``loc`` (default
- 0), with standard deviation ``scale`` (default 1), and clipped at ``a``,
- ``b`` standard deviations to the left, right (respectively) from ``loc``.
- If ``myclip_a`` and ``myclip_b`` are clip values in the sample space (as
- opposed to the number of standard deviations) then they can be converted
to the required form according to:
a, b = (myclip_a - loc) / scale, (myclip_b - loc) / scale
```suggestion
This distribution is the normal distribution centred on ``loc`` (default
0), with standard deviation ``scale`` (default 1), and clipped at ``a``,
``b`` standard deviations to the left, right (respectively) from ``loc``.
If ``myclip_a`` and ``myclip_b`` are clip values in the sample space (as
opposed to the number of standard deviations) then they can be converted
to the required form according to:
```
PEP8 (needed to pass lint checks)
class truncnorm_gen(rv_continuous):
Notes
-----
+ This distribution is the normal distribution centred on ``loc`` (default
+ 0), with standard deviation ``scale`` (default 1), and clipped at ``a``,
+ ``b`` standard deviations to the left, right (respectively) from ``loc``.
+ If ``myclip_a`` and ``myclip_b`` are clip values in the sample space (as
+ opposed to the number of standard deviations) then they can be converted
to the required form according to:
a, b = (myclip_a - loc) / scale, (myclip_b - loc) / scale
|
codereview_new_python_data_13352
|
class truncnorm_gen(rv_continuous):
Notes
-----
- This distribution is the normal distribution centred on ``loc`` (default
0), with standard deviation ``scale`` (default 1), and clipped at ``a``,
``b`` standard deviations to the left, right (respectively) from ``loc``.
If ``myclip_a`` and ``myclip_b`` are clip values in the sample space (as
opposed to the number of standard deviations) then they can be converted
- to the required form according to:
a, b = (myclip_a - loc) / scale, (myclip_b - loc) / scale
```suggestion
to the required form according to::
```
Removing this extra colon makes the code below render as

instead of

class truncnorm_gen(rv_continuous):
Notes
-----
+ This distribution is the normal distribution centered on ``loc`` (default
0), with standard deviation ``scale`` (default 1), and clipped at ``a``,
``b`` standard deviations to the left, right (respectively) from ``loc``.
If ``myclip_a`` and ``myclip_b`` are clip values in the sample space (as
opposed to the number of standard deviations) then they can be converted
+ to the required form according to::
a, b = (myclip_a - loc) / scale, (myclip_b - loc) / scale
|
codereview_new_python_data_13353
|
class truncnorm_gen(rv_continuous):
Notes
-----
- This distribution is the normal distribution centred on ``loc`` (default
0), with standard deviation ``scale`` (default 1), and clipped at ``a``,
``b`` standard deviations to the left, right (respectively) from ``loc``.
If ``myclip_a`` and ``myclip_b`` are clip values in the sample space (as
opposed to the number of standard deviations) then they can be converted
- to the required form according to:
a, b = (myclip_a - loc) / scale, (myclip_b - loc) / scale
```suggestion
This distribution is the normal distribution centered on ``loc`` (default
```
This is the more common spelling in the codebase:
vs
class truncnorm_gen(rv_continuous):
Notes
-----
+ This distribution is the normal distribution centered on ``loc`` (default
0), with standard deviation ``scale`` (default 1), and clipped at ``a``,
``b`` standard deviations to the left, right (respectively) from ``loc``.
If ``myclip_a`` and ``myclip_b`` are clip values in the sample space (as
opposed to the number of standard deviations) then they can be converted
+ to the required form according to::
a, b = (myclip_a - loc) / scale, (myclip_b - loc) / scale
|
codereview_new_python_data_13354
|
from scipy import optimize
from scipy import special
from scipy._lib._bunch import _make_tuple_bunch
-from scipy._lib._util import (_rename_parameter, _contains_nan)
from . import _statlib
from . import _stats_py
from ._fit import FitResult
-from ._stats_py import (find_repeats, _normtest_finish,
- SignificanceResult)
from .contingency import chi2_contingency
from . import distributions
from ._distn_infrastructure import rv_generic
For consistency, let's not add parentheses unless they're necessary due to line break.
from scipy import optimize
from scipy import special
from scipy._lib._bunch import _make_tuple_bunch
+from scipy._lib._util import _rename_parameter, _contains_nan
from . import _statlib
from . import _stats_py
from ._fit import FitResult
+from ._stats_py import find_repeats, _normtest_finish, SignificanceResult
from .contingency import chi2_contingency
from . import distributions
from ._distn_infrastructure import rv_generic
|
codereview_new_python_data_13355
|
from scipy import optimize
from scipy import special
from scipy._lib._bunch import _make_tuple_bunch
-from scipy._lib._util import (_rename_parameter, _contains_nan)
from . import _statlib
from . import _stats_py
from ._fit import FitResult
-from ._stats_py import (find_repeats, _normtest_finish,
- SignificanceResult)
from .contingency import chi2_contingency
from . import distributions
from ._distn_infrastructure import rv_generic
While we're at it...
```suggestion
from ._stats_py import find_repeats, _normtest_finish, SignificanceResult
```
from scipy import optimize
from scipy import special
from scipy._lib._bunch import _make_tuple_bunch
+from scipy._lib._util import _rename_parameter, _contains_nan
from . import _statlib
from . import _stats_py
from ._fit import FitResult
+from ._stats_py import find_repeats, _normtest_finish, SignificanceResult
from .contingency import chi2_contingency
from . import distributions
from ._distn_infrastructure import rv_generic
|
codereview_new_python_data_13356
|
from collections import namedtuple
from . import distributions
-from scipy._lib._util import (_rename_parameter, _contains_nan)
from scipy._lib._bunch import _make_tuple_bunch
import scipy.special as special
import scipy.stats._stats_py
```suggestion
from scipy._lib._util import _rename_parameter, _contains_nan
```
from collections import namedtuple
from . import distributions
+from scipy._lib._util import _rename_parameter, _contains_nan
from scipy._lib._bunch import _make_tuple_bunch
import scipy.special as special
import scipy.stats._stats_py
|
codereview_new_python_data_13357
|
import numpy as np
from numpy.core.multiarray import normalize_axis_index
-from scipy._lib._util import (_nan_allsame, _contains_nan)
from ._stats_py import _chk_asarray
```suggestion
from scipy._lib._util import _nan_allsame, _contains_nan
```
import numpy as np
from numpy.core.multiarray import normalize_axis_index
+from scipy._lib._util import _nan_allsame, _contains_nan
from ._stats_py import _chk_asarray
|
codereview_new_python_data_13358
|
def qmc_quad(func, ranges, *, n_points=1024, n_offsets=8, qrng=None, log=False,
>>> t.interval(0.99)
(0.00018389017561108015, 0.00018461661169997918)
- Indeed, the value reported by `scipy.stats.multivariate_normal.cdf` is
within this range.
>>> stats.multivariate_normal.cdf(ub, mean, cov, lower_limit=lb)
```suggestion
Indeed, the value reported by `scipy.stats.multivariate_normal` is
```
I think this is the documentation build issue.
def qmc_quad(func, ranges, *, n_points=1024, n_offsets=8, qrng=None, log=False,
>>> t.interval(0.99)
(0.00018389017561108015, 0.00018461661169997918)
+ Indeed, the value reported by `scipy.stats.multivariate_normal` is
within this range.
>>> stats.multivariate_normal.cdf(ub, mean, cov, lower_limit=lb)
|
codereview_new_python_data_13359
|
def __init__(
optimization: Optional[Literal["random-cd", "lloyd"]] = None
) -> None:
self._init = {'d': d, 'scramble': True, 'bits': bits,
- 'optimization': optimization,}
super().__init__(d=d, optimization=optimization, seed=seed)
if d > self.MAXDIM:
```suggestion
self._init = {'d': d, 'scramble': True, 'bits': bits,
'optimization': optimization}
```
def __init__(
optimization: Optional[Literal["random-cd", "lloyd"]] = None
) -> None:
self._init = {'d': d, 'scramble': True, 'bits': bits,
+ 'optimization': optimization}
super().__init__(d=d, optimization=optimization, seed=seed)
if d > self.MAXDIM:
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.