id
stringlengths 30
32
| content
stringlengths 139
2.8k
|
|---|---|
codereview_new_python_data_13071
|
def test_add_second_rectangular_region_deactivates_first_selector(self):
self.assertTrue(region_selector._selectors[1].active)
def test_get_region(self):
- x1, x2, x3, x4, y1, y2, y3, y4 = 1.0, 2.0, 5.0, 6.0, 3.0, 4.0, 7.0, 8.0
-
- selector_one = Mock()
- selector_one.extents = [x1, x2, y1, y2]
- selector_two = Mock()
- selector_two.extents = [x3, x4, y3, y4]
-
- region_selector = RegionSelector(ws=Mock(), view=Mock())
- region_selector._selectors.append(selector_one)
- region_selector._selectors.append(selector_two)
region = region_selector.get_region()
self.assertEqual(4, len(region))
- self.assertEqual([y1, y2, y3, y4], region)
def test_canvas_clicked_does_nothing_when_redrawing_region(self):
region_selector, selector_one, selector_two = self._mock_selectors()
```suggestion
region_selector, selector_one, selector_two = self._mock_selectors()
region = region_selector.get_region()
self.assertEqual(4, len(region))
self.assertEqual([selector_one.extents[1], selector_one.extents[3], selector_two.extents[1], selector_two.extents[3]], region)
```
def test_add_second_rectangular_region_deactivates_first_selector(self):
self.assertTrue(region_selector._selectors[1].active)
def test_get_region(self):
+ region_selector, selector_one, selector_two = self._mock_selectors()
region = region_selector.get_region()
self.assertEqual(4, len(region))
+ self.assertEqual([selector_one.extents[2], selector_one.extents[3], selector_two.extents[2],
+ selector_two.extents[3]], region)
def test_canvas_clicked_does_nothing_when_redrawing_region(self):
region_selector, selector_one, selector_two = self._mock_selectors()
|
codereview_new_python_data_13080
|
def validateInputs(self):
elif isinstance(ws, mantid.api.MatrixWorkspace):
hasInstrument = len(ws.componentInfo()) > 0
else:
issues["Workspace"] = "Workspace must be a WorkspaceGroup or MatrixWorkspace."
- return issues
- if not hasInstrument:
issues["Workspace"] = "Workspace must have an associated instrument."
angleMin = self.getProperty('MinAngle').value
Is this early return necessary? It seems like we could continue to report the angle errors as well?
def validateInputs(self):
elif isinstance(ws, mantid.api.MatrixWorkspace):
hasInstrument = len(ws.componentInfo()) > 0
else:
+ hasInstrument = False
issues["Workspace"] = "Workspace must be a WorkspaceGroup or MatrixWorkspace."
+ if not hasInstrument and "Workspace" not in issues:
issues["Workspace"] = "Workspace must have an associated instrument."
angleMin = self.getProperty('MinAngle').value
|
codereview_new_python_data_13081
|
def _get_shifts(self, calibration_file, zero_angle_corr, n_banks):
except FileNotFoundError:
self.log().warning("Bank calibration file not found or not provided.")
bank_shifts = [zero_angle_corr] * n_banks
- except RuntimeError as e:
self.log().warning(str(e))
self.log().warning("Padding the shifts list with zero angle correction.")
bank_shifts.extend([zero_angle_corr]*(np.zeros(len(bank_shifts)-n_banks)))
The test file dec.dec in the zip file on this PR doesn't look valid. It just contains a single line with a file path. Not sure if that's intentional or not. But it causes an `IndexError` on L330. Perhaps this except clause should catch IndexError as well as RuntimeError so the reduction can proceed?
def _get_shifts(self, calibration_file, zero_angle_corr, n_banks):
except FileNotFoundError:
self.log().warning("Bank calibration file not found or not provided.")
bank_shifts = [zero_angle_corr] * n_banks
+ except (RuntimeError, IndexError) as e:
self.log().warning(str(e))
self.log().warning("Padding the shifts list with zero angle correction.")
bank_shifts.extend([zero_angle_corr]*(np.zeros(len(bank_shifts)-n_banks)))
|
codereview_new_python_data_13082
|
def _get_shifts(self, calibration_file, zero_angle_corr, n_banks):
except FileNotFoundError:
self.log().warning("Bank calibration file not found or not provided.")
bank_shifts = [zero_angle_corr] * n_banks
- except RuntimeError as e:
self.log().warning(str(e))
self.log().warning("Padding the shifts list with zero angle correction.")
bank_shifts.extend([zero_angle_corr]*(np.zeros(len(bank_shifts)-n_banks)))
Should this be `n_banks - len(bank_shifts)`?
def _get_shifts(self, calibration_file, zero_angle_corr, n_banks):
except FileNotFoundError:
self.log().warning("Bank calibration file not found or not provided.")
bank_shifts = [zero_angle_corr] * n_banks
+ except (RuntimeError, IndexError) as e:
self.log().warning(str(e))
self.log().warning("Padding the shifts list with zero angle correction.")
bank_shifts.extend([zero_angle_corr]*(np.zeros(len(bank_shifts)-n_banks)))
|
codereview_new_python_data_13083
|
resolution, flux = Instrument.calculate(inst='maps', chtyp='a', freq=500, ei=600, etrans=range(0,550,50))
"""
-
-
-def PyChop2(instrument, chopper=None, freq=None):
- import warnings
- warnings.warn("Deprecation Warning: Importing 'PyChop2' from the 'mantidqtinterfaces.PyChop' module is deprecated."
- "Please import 'Instrument' from the 'pychop.Instruments' module instead.", DeprecationWarning)
- from pychop.Instruments import Instrument
- return Instrument(instrument, chopper, freq)
Maybe this bit of code can just live in `scripts/pychop/__init__.py` and you can just have:
```
from pychop import PyChop2
```
here instead?
resolution, flux = Instrument.calculate(inst='maps', chtyp='a', freq=500, ei=600, etrans=range(0,550,50))
"""
+from pychop import PyChop2 # noqa
|
codereview_new_python_data_13084
|
"""
-def PyChop2(instrument, chopper=None, freq=None):
import warnings
warnings.warn("Deprecation Warning: Importing 'PyChop2' from the 'mantidqtinterfaces.PyChop' module is deprecated."
"Please import 'Instrument' from the 'pychop.Instruments' module instead.", DeprecationWarning)
from pychop.Instruments import Instrument
- return Instrument(instrument, chopper, freq)
Instead of specific positional arguments can you just pass `*args, **kwargs` - e.g.
```
def PyChop2(*args, **kwargs):
...
return Instrument(*args, **kwargs)
```
This will mirror the current `PyChop2` syntax which is not just restricted to the three positional arguments...
"""
+def PyChop2(*args, **kwargs):
import warnings
warnings.warn("Deprecation Warning: Importing 'PyChop2' from the 'mantidqtinterfaces.PyChop' module is deprecated."
"Please import 'Instrument' from the 'pychop.Instruments' module instead.", DeprecationWarning)
from pychop.Instruments import Instrument
+ return Instrument(*args, **kwargs)
|
codereview_new_python_data_13087
|
def get(self, option, second=None, type=None):
return self._get_setting(option, second, type)
except TypeError:
# The 'PyQt_PyObject' (1024) type is sometimes used for settings which have an unknown type.
- value = self._get_setting(option, type=QVariant.typeToName(1024))
return value if isinstance(value, type) else type(*value)
def has(self, option, second=None):
Can we raise a[`TypeError`](https://docs.python.org/3/library/exceptions.html#TypeError) here?
def get(self, option, second=None, type=None):
return self._get_setting(option, second, type)
except TypeError:
# The 'PyQt_PyObject' (1024) type is sometimes used for settings which have an unknown type.
+ value = self._get_setting(option, second, type=QVariant.typeToName(1024))
return value if isinstance(value, type) else type(*value)
def has(self, option, second=None):
|
codereview_new_python_data_13165
|
def _filliben(dist, data):
# [7] Section 8 # 4
return _corr(X, M)
-_filliben.alternative = 'less'
def _cramer_von_mises(dist, data):
```suggestion
_filliben.alternative = 'less' # type: ignore[<code>]
```
def _filliben(dist, data):
# [7] Section 8 # 4
return _corr(X, M)
+_filliben.alternative = 'less' # type: ignore[<code>]
def _cramer_von_mises(dist, data):
|
codereview_new_python_data_13166
|
def _filliben(dist, data):
# [7] Section 8 # 4
return _corr(X, M)
-_filliben.alternative = 'less' # type: ignore[<code>]
def _cramer_von_mises(dist, data):
```suggestion
_filliben.alternative = 'less' # type: ignore[attr-defined]
```
def _filliben(dist, data):
# [7] Section 8 # 4
return _corr(X, M)
+_filliben.alternative = 'less' # type: ignore[attr-defined]
def _cramer_von_mises(dist, data):
|
codereview_new_python_data_13167
|
def test_sf_isf(self, x, c, sfx):
def test_entropy(self, c, ref):
assert_allclose(stats.gompertz.entropy(c), ref, rtol=1e-14)
class TestHalfNorm:
# sfx is sf(x). The values were computed with mpmath:
PEP-8: we need two blank lines before the following `class` definition.
```suggestion
assert_allclose(stats.gompertz.entropy(c), ref, rtol=1e-14)
```
def test_sf_isf(self, x, c, sfx):
def test_entropy(self, c, ref):
assert_allclose(stats.gompertz.entropy(c), ref, rtol=1e-14)
+
class TestHalfNorm:
# sfx is sf(x). The values were computed with mpmath:
|
codereview_new_python_data_13168
|
def ecdf(sample):
elif sample.num_censored() == sample._right.size:
res = _ecdf_right_censored(sample)
else:
- # Support censoring in follow-up PRs
- message = ("Currently, only uncensored data is supported.")
raise NotImplementedError(message)
return res
Needs to be updated
def ecdf(sample):
elif sample.num_censored() == sample._right.size:
res = _ecdf_right_censored(sample)
else:
+ # Support additional censoring options in follow-up PRs
+ message = ("Currently, only uncensored and right-censored data is "
+ "supported.")
raise NotImplementedError(message)
return res
|
codereview_new_python_data_13169
|
def add_newdoc(name, doc):
where :math:`p` is the probability of a single success
and :math:`1-p` is the probability of a single failure
- and :math::`k` is the number of trials to get the first success.
>>> import numpy as np
>>> from scipy.special import xlog1py
```suggestion
and :math:`k` is the number of trials to get the first success.
```
def add_newdoc(name, doc):
where :math:`p` is the probability of a single success
and :math:`1-p` is the probability of a single failure
+ and :math:`k` is the number of trials to get the first success.
>>> import numpy as np
>>> from scipy.special import xlog1py
|
codereview_new_python_data_13170
|
def add_newdoc(name, doc):
-69.31471805599453
We can confirm that we get a value close to the original pmf value by
- taking the exponetial of the log pmf.
>>> _orig_pmf = np.exp(_log_pmf)
>>> np.isclose(_pmf, _orig_pmf)
```suggestion
taking the exponential of the log pmf.
```
This can be fixed.
def add_newdoc(name, doc):
-69.31471805599453
We can confirm that we get a value close to the original pmf value by
+ taking the exponential of the log pmf.
>>> _orig_pmf = np.exp(_log_pmf)
>>> np.isclose(_pmf, _orig_pmf)
|
codereview_new_python_data_13171
|
def _var(x, axis=0, ddof=0, mean=None):
var = _moment(x, 2, axis, mean=mean)
if ddof != 0:
n = x.shape[axis] if axis is not None else x.size
- with np.errstate(divide='ignore', invalid='ignore'):
- var *= np.divide(n, n-ddof) # to avoid error on division by zero
return var
My fault. For now, go in `ttest_ind` and preferably only when `equal_var` is True. We shouldn't always silence the warning right now because usually this division by zero results in NaNs that the user will see, but in the case of `ttest_ind` with `equal_var=True` it doesn't.
The rest looks good! Although some of the errors will probably persist after this change. Can't investigate those right now but maybe sometimes `n` is an array in `_equal_var_ttest_denom`, like with `nan_policy='omit'`?
def _var(x, axis=0, ddof=0, mean=None):
var = _moment(x, 2, axis, mean=mean)
if ddof != 0:
n = x.shape[axis] if axis is not None else x.size
+ var *= np.divide(n, n-ddof) # to avoid error on division by zero
return var
|
codereview_new_python_data_13172
|
class TestMultivariateHypergeom:
# test for `n < 0`
([3, 4], [5, 10], -7, np.nan),
# test for `x.sum() != n`
- ([3, 3], [5, 10], 7, inp.inf)
]
)
def test_logpmf(self, x, m, n, expected):
```suggestion
([3, 3], [5, 10], 7, -np.inf)
```
class TestMultivariateHypergeom:
# test for `n < 0`
([3, 4], [5, 10], -7, np.nan),
# test for `x.sum() != n`
+ ([3, 3], [5, 10], 7, -np.inf)
]
)
def test_logpmf(self, x, m, n, expected):
|
codereview_new_python_data_13173
|
def splprep(x, w=None, u=None, ub=None, ue=None, k=3, task=0, s=None, t=None,
the range ``(m-sqrt(2*m),m+sqrt(2*m))``, where m is the number of
data points in x, y, and w.
t : array, optional
- An array of knots needed for task=-1. There must be at least 2*k+2 knots if task=-1.
full_output : int, optional
If non-zero, then return optional outputs.
nest : int, optional
Let's use the same wording as the function bellow.
```suggestion
The knots needed for ``task=-1``.
There must be at least ``2*k+2`` knots.
```
def splprep(x, w=None, u=None, ub=None, ue=None, k=3, task=0, s=None, t=None,
the range ``(m-sqrt(2*m),m+sqrt(2*m))``, where m is the number of
data points in x, y, and w.
t : array, optional
+ The knots needed for ``task=-1``.
+ There must be at least ``2*k+2`` knots.
full_output : int, optional
If non-zero, then return optional outputs.
nest : int, optional
|
codereview_new_python_data_13174
|
def add_newdoc(name, doc):
A lower loss is usually better as it indicates that the predictions are
similar to the actual labels. In this example since our predicted
- probabilties correspond with the actual labels, we get an overall loss
that is reasonably low and appropriate.
""")
```suggestion
A lower loss is usually better as it indicates that the predictions are
similar to the actual labels. In this example since our predicted
probabilties are close to the actual labels, we get an overall loss
that is reasonably low and appropriate.
```
def add_newdoc(name, doc):
A lower loss is usually better as it indicates that the predictions are
similar to the actual labels. In this example since our predicted
+ probabilties are close to the actual labels, we get an overall loss
that is reasonably low and appropriate.
""")
|
codereview_new_python_data_13175
|
def func(x):
assert_allclose(np.exp(logres.integral), res.integral, rtol=1e-14)
assert np.imag(logres.integral) == (np.pi if np.prod(signs) < 0 else 0)
assert_allclose(np.exp(logres.standard_error),
- res.standard_error, rtol=1e-14, atol=1e-17)
@pytest.mark.parametrize("n_points", [2**8, 2**12])
@pytest.mark.parametrize("n_estimates", [8, 16])
Looks like this would address the CI failures.
```suggestion
res.standard_error, rtol=1e-14, atol=2e-17)
```
def func(x):
assert_allclose(np.exp(logres.integral), res.integral, rtol=1e-14)
assert np.imag(logres.integral) == (np.pi if np.prod(signs) < 0 else 0)
assert_allclose(np.exp(logres.standard_error),
+ res.standard_error, rtol=1e-14, atol=2e-17)
@pytest.mark.parametrize("n_points", [2**8, 2**12])
@pytest.mark.parametrize("n_estimates", [8, 16])
|
codereview_new_python_data_13176
|
def func(x):
assert_allclose(np.exp(logres.integral), res.integral, rtol=1e-14)
assert np.imag(logres.integral) == (np.pi if np.prod(signs) < 0 else 0)
assert_allclose(np.exp(logres.standard_error),
- res.standard_error, rtol=1e-14, atol=2e-17)
@pytest.mark.parametrize("n_points", [2**8, 2**12])
@pytest.mark.parametrize("n_estimates", [8, 16])
```suggestion
res.standard_error, rtol=1e-14, atol=1e-16)
```
def func(x):
assert_allclose(np.exp(logres.integral), res.integral, rtol=1e-14)
assert np.imag(logres.integral) == (np.pi if np.prod(signs) < 0 else 0)
assert_allclose(np.exp(logres.standard_error),
+ res.standard_error, rtol=1e-14, atol=1e-16)
@pytest.mark.parametrize("n_points", [2**8, 2**12])
@pytest.mark.parametrize("n_estimates", [8, 16])
|
codereview_new_python_data_13177
|
def tri(N, M=None, k=0, dtype=None):
[1, 1, 0, 0, 0]])
"""
- warnings.warn("'tri'/'tril/'triu' is deprecated as of SciPy 1.11.0 in favour of"
"'numpy.tri' and will be removed in SciPy 1.13.0",
DeprecationWarning, stacklevel=2)
I would change the sentence a bit to avoid confusion, namely;
```suggestion
warnings.warn("'tri'/'tril/'triu' are deprecated as of SciPy 1.11.0 and will "
"be removed in v1.13.0. Please use numpy.(tri/tril/triu) instead."
def tri(N, M=None, k=0, dtype=None):
[1, 1, 0, 0, 0]])
"""
+ warnings.warn("'tri'/'tril/'triu' are deprecated as of SciPy 1.11.0 and will "
+ "be removed in v1.13.0. Please use numpy.(tri/tril/triu) instead."
"'numpy.tri' and will be removed in SciPy 1.13.0",
DeprecationWarning, stacklevel=2)
|
codereview_new_python_data_13178
|
bracket_methods = [zeros.bisect, zeros.ridder, zeros.brentq, zeros.brenth,
zeros.toms748]
gradient_methods = [zeros.newton]
-all_methods = bracket_methods + gradient_methods
# A few test functions used frequently:
# # A simple quadratic, (x-1)^2 - 1
```suggestion
all_methods = bracket_methods + gradient_methods # type: ignore[operator]
```
bracket_methods = [zeros.bisect, zeros.ridder, zeros.brentq, zeros.brenth,
zeros.toms748]
gradient_methods = [zeros.newton]
+all_methods = bracket_methods + gradient_methods # noqa
# A few test functions used frequently:
# # A simple quadratic, (x-1)^2 - 1
|
codereview_new_python_data_13179
|
def test_sf(self, x, ref):
# from mpmath import mp
# mp.dps = 200
# def isf_mpmath(x):
- # x = mp.mpf(x)
- # x = x/mp.mpf(2.)
- # return float(-mp.log(x/(mp.one - x)))
@pytest.mark.parametrize('q, ref', [(7.440151952041672e-44, 100),
(2.767793053473475e-87, 200),
Simplify a bit, and avoid changing the value of an argument:
```suggestion
# halfx = mp.mpf(x)/2
# return float(-mp.log(halfx/(mp.one - halfx)))
```
def test_sf(self, x, ref):
# from mpmath import mp
# mp.dps = 200
# def isf_mpmath(x):
+ # halfx = mp.mpf(x)/2
+ # return float(-mp.log(halfx/(mp.one - halfx)))
@pytest.mark.parametrize('q, ref', [(7.440151952041672e-44, 100),
(2.767793053473475e-87, 200),
|
codereview_new_python_data_13180
|
def sem(a, axis=0, ddof=1, nan_policy='propagate'):
nan_policy : {'propagate', 'raise', 'omit'}, optional
Defines how to handle when input contains nan.
The following options are available (default is 'propagate'):
* 'propagate': returns nan
* 'raise': throws an error
* 'omit': performs the calculations ignoring nan values
```suggestion
The following options are available (default is 'propagate'):
```
def sem(a, axis=0, ddof=1, nan_policy='propagate'):
nan_policy : {'propagate', 'raise', 'omit'}, optional
Defines how to handle when input contains nan.
The following options are available (default is 'propagate'):
+
* 'propagate': returns nan
* 'raise': throws an error
* 'omit': performs the calculations ignoring nan values
|
codereview_new_python_data_13181
|
def test_location_scale(
# Test seems to be unstable (see gh-17839 for a bug report on Debian
# i386), so skip it.
if is_linux_32 and case == 'pdf':
- pytest.skip("%s fit known to fail or deprecated" % dist)
data = nolan_loc_scale_sample_data
# We only test against piecewise as location/scale transforms
```suggestion
pytest.skip("Test unstable on some platforms; see gh-17839, 17859")
```
https://github.com/scipy/scipy/pull/17865/files#r1088471394
def test_location_scale(
# Test seems to be unstable (see gh-17839 for a bug report on Debian
# i386), so skip it.
if is_linux_32 and case == 'pdf':
+ pytest.skip("Test unstable on some platforms; see gh-17839, 17859")
data = nolan_loc_scale_sample_data
# We only test against piecewise as location/scale transforms
|
codereview_new_python_data_13182
|
def _random_cd(
if d == 0 or n == 0:
return np.empty((n, d))
- if d == 1:
# discrepancy measures are invariant under permuting factors and runs
return best_sample
best_disc = discrepancy(best_sample)
- if n == 1:
- return best_sample
-
bounds = ([0, d - 1],
[0, n - 1],
[0, n - 1])
Can we do `if d == 1 or n == 1` above?
I'm also thinking that users will be surprised if they get exactly the original order back in 1D. Maybe a warning or just shuffle the order to prevent that (even if it's not necessary).
def _random_cd(
if d == 0 or n == 0:
return np.empty((n, d))
+ if d == 1 or n == 1:
# discrepancy measures are invariant under permuting factors and runs
return best_sample
best_disc = discrepancy(best_sample)
bounds = ([0, d - 1],
[0, n - 1],
[0, n - 1])
|
codereview_new_python_data_13183
|
def _random_cd(
while n_nochange_ < n_nochange and n_iters_ < n_iters:
n_iters_ += 1
- col = rng_integers(rng, *bounds[0], endpoint=True)
- row_1 = rng_integers(rng, *bounds[1], endpoint=True)
- row_2 = rng_integers(rng, *bounds[2], endpoint=True)
disc = _perturb_discrepancy(best_sample,
row_1, row_2, col,
best_disc)
This should fix the linter
```suggestion
col = rng_integers(rng, *bounds[0], endpoint=True) # type: ignore[misc]
row_1 = rng_integers(rng, *bounds[1], endpoint=True) # type: ignore[misc]
row_2 = rng_integers(rng, *bounds[2], endpoint=True) # type: ignore[misc]
```
def _random_cd(
while n_nochange_ < n_nochange and n_iters_ < n_iters:
n_iters_ += 1
+ col = rng_integers(rng, *bounds[0], endpoint=True) # type: ignore[misc]
+ row_1 = rng_integers(rng, *bounds[1], endpoint=True) # type: ignore[misc]
+ row_2 = rng_integers(rng, *bounds[2], endpoint=True) # type: ignore[misc]
disc = _perturb_discrepancy(best_sample,
row_1, row_2, col,
best_disc)
|
codereview_new_python_data_13184
|
def asymptotic_formula(half_df):
# 1/(12 * a) - 1/(360 * a**3)
# psi(a) ~ ln(a) - 1/(2 * a) - 1/(3 * a**2) + 1/120 * a**4)
c = np.log(2) + 0.5*(1 + np.log(2*np.pi))
- h = 2/half_df
return (h*(-2/3 + h*(-1/3 + h*(-4/45 + h/7.5))) +
0.5*np.log(half_df) + c)
`2/half_df` is `4/df`. We want `h` to be `1/df`:
```suggestion
h = 0.5/half_df
```
def asymptotic_formula(half_df):
# 1/(12 * a) - 1/(360 * a**3)
# psi(a) ~ ln(a) - 1/(2 * a) - 1/(3 * a**2) + 1/120 * a**4)
c = np.log(2) + 0.5*(1 + np.log(2*np.pi))
+ h = 0.5/half_df
return (h*(-2/3 + h*(-1/3 + h*(-4/45 + h/7.5))) +
0.5*np.log(half_df) + c)
|
codereview_new_python_data_13185
|
def _entropy(self, nu):
C = -0.5 * np.log(nu) - np.log(2)
h = A + B + C
# This is the asymptotic sum of A and B (see gh-17868)
- norm_entropy = stats.norm.entropy()
# Above, this is lost to rounding error for large nu, so use the
# asymptotic sum when the approximation becomes accurate
i = nu > 1e7 # roundoff error ~ approximation error
```suggestion
norm_entropy = stats.norm._entropy()
```
def _entropy(self, nu):
C = -0.5 * np.log(nu) - np.log(2)
h = A + B + C
# This is the asymptotic sum of A and B (see gh-17868)
+ norm_entropy = stats.norm._entropy()
# Above, this is lost to rounding error for large nu, so use the
# asymptotic sum when the approximation becomes accurate
i = nu > 1e7 # roundoff error ~ approximation error
|
codereview_new_python_data_13186
|
def _entropy(self, nu):
norm_entropy = stats.norm._entropy()
# Above, this is lost to rounding error for large nu, so use the
# asymptotic sum when the approximation becomes accurate
- i = nu > 1e7 # roundoff error ~ approximation error
- h[i] = C[i] + norm_entropy
return h.reshape(shape)[()]
def _rvs(self, nu, size=None, random_state=None):
@steppi is this what you had in mind?
```suggestion
# -1 / (12 * nu) is the O(1/nu) term; see gh-17929
h[i] = C[i] + norm_entropy - 1/(12*nu[i])
```
And you see that there is a cutoff for using the expansion of `1e7`, but you mean to tune it again based on the addition of this new term? ISTM that the cutoff would probably be lower now because the approximation is more accurate, right?
def _entropy(self, nu):
norm_entropy = stats.norm._entropy()
# Above, this is lost to rounding error for large nu, so use the
# asymptotic sum when the approximation becomes accurate
+ i = nu > 5e4 # roundoff error ~ approximation error
+ # -1 / (12 * nu) is the O(1/nu) term; see gh-17929
+ h[i] = C[i] + norm_entropy - 1/(12*nu[i])
return h.reshape(shape)[()]
def _rvs(self, nu, size=None, random_state=None):
|
codereview_new_python_data_13187
|
def _entropy(self, nu):
norm_entropy = stats.norm._entropy()
# Above, this is lost to rounding error for large nu, so use the
# asymptotic sum when the approximation becomes accurate
- i = nu > 1e7 # roundoff error ~ approximation error
- h[i] = C[i] + norm_entropy
return h.reshape(shape)[()]
def _rvs(self, nu, size=None, random_state=None):
```suggestion
i = nu > 5e4 # roundoff error ~ approximation error
```
On the left, the error is ~1e-11 and on the right, the error is ~1e-11. Did you want it tuned more precisely?
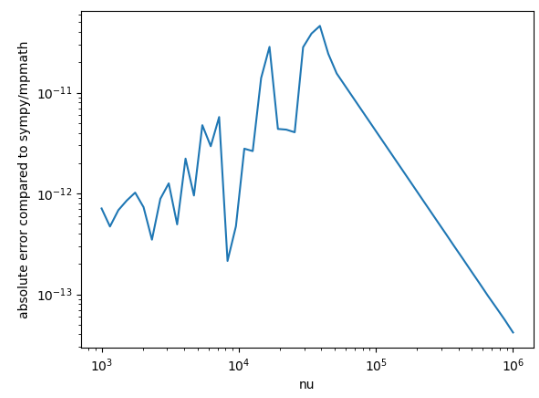
If this is OK, please feel free to add the suggestions to the batch and commit to re-run CI.
def _entropy(self, nu):
norm_entropy = stats.norm._entropy()
# Above, this is lost to rounding error for large nu, so use the
# asymptotic sum when the approximation becomes accurate
+ i = nu > 5e4 # roundoff error ~ approximation error
+ # -1 / (12 * nu) is the O(1/nu) term; see gh-17929
+ h[i] = C[i] + norm_entropy - 1/(12*nu[i])
return h.reshape(shape)[()]
def _rvs(self, nu, size=None, random_state=None):
|
codereview_new_python_data_13188
|
def _cdf(self, x, a, b):
f2=lambda x_, a_, b_: beta._cdf(x_/(1+x_), a_, b_))
def _ppf(self, p, a, b):
# by default, compute compute the ppf by solving the following:
# p = beta._cdf(x/(1+x), a, b). This implies x = r/(1-r) with
# r = beta._ppf(p, a, b). This can cause numerical issues if r is
```suggestion
p, a, b = np.broadcast_arrays(p, a, b)
# by default, compute compute the ppf by solving the following:
```
def _cdf(self, x, a, b):
f2=lambda x_, a_, b_: beta._cdf(x_/(1+x_), a_, b_))
def _ppf(self, p, a, b):
+ p, a, b = np.broadcast_arrays(p, a, b)
# by default, compute compute the ppf by solving the following:
# p = beta._cdf(x/(1+x), a, b). This implies x = r/(1-r) with
# r = beta._ppf(p, a, b). This can cause numerical issues if r is
|
codereview_new_python_data_13189
|
def test_frozen(self):
multivariate_normal.logcdf(x, mean, cov))
def test_frozen_multivariate_normal_exposes_attributes(self):
- np.random.seed(1234)
mean = np.ones((2,))
cov = np.eye(2)
norm_frozen = multivariate_normal(mean, cov)
I don't think this needs a seed. (And if yes we should use a `Generator`)
def test_frozen(self):
multivariate_normal.logcdf(x, mean, cov))
def test_frozen_multivariate_normal_exposes_attributes(self):
mean = np.ones((2,))
cov = np.eye(2)
norm_frozen = multivariate_normal(mean, cov)
|
codereview_new_python_data_13190
|
class multivariate_normal_gen(multi_rv_generic):
entropy()
Compute the differential entropy of the multivariate normal.
- Attributes
- ----------
- mean : ndarray
- Mean of the distribution.
-
- .. versionadded:: 1.10.1
-
- cov : ndarray
- Covariance matrix of the distribution.
-
- .. versionadded:: 1.10.1
-
- cov_object : `Covariance`
- Representation of the covariance matrix as a `Covariance` object.
-
- .. versionadded:: 1.10.1
-
-
Parameters
----------
%(_mvn_doc_default_callparams)s
```suggestion
```
This is the documentation of `multivariate_normal_gen`, but `mean`, `cov`, and `cov_object` are only attributes of `multivariate_normal_frozen`. I don't think we want these changes to `multivariate_normal_gen`.
class multivariate_normal_gen(multi_rv_generic):
entropy()
Compute the differential entropy of the multivariate normal.
Parameters
----------
%(_mvn_doc_default_callparams)s
|
codereview_new_python_data_13191
|
def test_frozen(self):
multivariate_normal.logcdf(x, mean, cov))
def test_frozen_multivariate_normal_exposes_attributes(self):
- np.random.seed(1234)
mean = np.ones((2,))
cov = np.eye(2)
norm_frozen = multivariate_normal(mean, cov)
Some reviewers have a strong preference for only using NumPy `Generator`s, even in tests. I don't mind it, so to please everyone, this should be `rng = np.random.default_rng(349582469826092)` and `rng` should be passed into `multivariate_normal`.
def test_frozen(self):
multivariate_normal.logcdf(x, mean, cov))
def test_frozen_multivariate_normal_exposes_attributes(self):
mean = np.ones((2,))
cov = np.eye(2)
norm_frozen = multivariate_normal(mean, cov)
|
codereview_new_python_data_13192
|
def test_frozen(self):
multivariate_normal.logcdf(x, mean, cov))
def test_frozen_multivariate_normal_exposes_attributes(self):
- np.random.seed(1234)
mean = np.ones((2,))
cov = np.eye(2)
norm_frozen = multivariate_normal(mean, cov)
This can be [parametrized](https://docs.pytest.org/en/6.2.x/parametrize.html) over `cov`: in one case it should be a regular matrix; in the other, it should be a `Covariance` object.
def test_frozen(self):
multivariate_normal.logcdf(x, mean, cov))
def test_frozen_multivariate_normal_exposes_attributes(self):
mean = np.ones((2,))
cov = np.eye(2)
norm_frozen = multivariate_normal(mean, cov)
|
codereview_new_python_data_13193
|
def __init__(self, mean=None, cov=1, allow_singular=False, seed=None,
Relative error tolerance for the cumulative distribution function
(default 1e-5)
- Attributes
- ----------
- mean : ndarray
- Mean of the distribution.
-
- cov : ndarray
- Covariance matrix of the distribution.
-
- cov_object : `Covariance`
- Representation of the covariance matrix as a `Covariance` object.
-
Examples
--------
This whole section needs to be indented 4 more spaces to align with its surroundings.
def __init__(self, mean=None, cov=1, allow_singular=False, seed=None,
Relative error tolerance for the cumulative distribution function
(default 1e-5)
+ Attributes
+ ----------
+ mean : ndarray
+ Mean of the distribution.
+ cov : ndarray
+ Covariance matrix of the distribution.
+ cov_object : `Covariance`
+ Representation of the covariance matrix as a `Covariance` object.
Examples
--------
|
codereview_new_python_data_13194
|
def __init__(self, mean=None, cov=1, allow_singular=False, seed=None,
Relative error tolerance for the cumulative distribution function
(default 1e-5)
- Attributes
- ----------
- mean : ndarray
- Mean of the distribution.
-
- cov : ndarray
- Covariance matrix of the distribution.
-
- cov_object : `Covariance`
- Representation of the covariance matrix as a `Covariance` object.
-
Examples
--------
We don't have empty lines between these entries.
def __init__(self, mean=None, cov=1, allow_singular=False, seed=None,
Relative error tolerance for the cumulative distribution function
(default 1e-5)
+ Attributes
+ ----------
+ mean : ndarray
+ Mean of the distribution.
+ cov : ndarray
+ Covariance matrix of the distribution.
+ cov_object : `Covariance`
+ Representation of the covariance matrix as a `Covariance` object.
Examples
--------
|
codereview_new_python_data_13195
|
def __init__(self, mean=None, cov=1, allow_singular=False, seed=None,
Relative error tolerance for the cumulative distribution function
(default 1e-5)
- Attributes
- ----------
- mean : ndarray
- Mean of the distribution.
-
- cov : ndarray
- Covariance matrix of the distribution.
-
- cov_object : `Covariance`
- Representation of the covariance matrix as a `Covariance` object.
-
Examples
--------
Only one empty line between sections.
def __init__(self, mean=None, cov=1, allow_singular=False, seed=None,
Relative error tolerance for the cumulative distribution function
(default 1e-5)
+ Attributes
+ ----------
+ mean : ndarray
+ Mean of the distribution.
+ cov : ndarray
+ Covariance matrix of the distribution.
+ cov_object : `Covariance`
+ Representation of the covariance matrix as a `Covariance` object.
Examples
--------
|
codereview_new_python_data_13196
|
def istft(Zxx, fs=1.0, window='hann', nperseg=None, noverlap=None, nfft=None,
# Divide out normalization where non-tiny
if np.sum(norm > 1e-10) != len(norm):
- warnings.warn("NOLA condition failed, STFT may not be invertible. " + ("Possibly due to missing boundary" if boundary else ""))
x /= np.where(norm > 1e-10, norm, 1.0)
if input_onesided:
This line is too long.
```suggestion
warnings.warn(
"NOLA condition failed, STFT may not be invertible."
+ (" Possibly due to missing boundary" if boundary else "")
)
```
def istft(Zxx, fs=1.0, window='hann', nperseg=None, noverlap=None, nfft=None,
# Divide out normalization where non-tiny
if np.sum(norm > 1e-10) != len(norm):
+ warnings.warn(
+ "NOLA condition failed, STFT may not be invertible."
+ + (" Possibly due to missing boundary" if boundary else "")
+ )
x /= np.where(norm > 1e-10, norm, 1.0)
if input_onesided:
|
codereview_new_python_data_13197
|
def leastsq(func, x0, args=(), Dfun=None, full_output=0,
A function or method to compute the Jacobian of func with derivatives
across the rows. If this is None, the Jacobian will be estimated.
full_output : bool, optional
- If truthy, return all optional outputs (not just `x` and `ier`).
col_deriv : bool, optional
If truthy, specify that the Jacobian function computes derivatives
down the columns (faster, because there is no transpose operation).
Nit: when we specify the type of the argument as a `bool`, I would opt to talk about `True` and `False` rather than "truthy". This is a very old function, IIRC, that probably predated `True`'s addition to the language, hence the old-style language and default `full_output=0`. We can probably fix that to `full_output=False` with no problem.
```suggestion
If ``True``, return all optional outputs (not just `x` and `ier`).
```
def leastsq(func, x0, args=(), Dfun=None, full_output=0,
A function or method to compute the Jacobian of func with derivatives
across the rows. If this is None, the Jacobian will be estimated.
full_output : bool, optional
+ If ``True``, return all optional outputs (not just `x` and `ier`).
col_deriv : bool, optional
If truthy, specify that the Jacobian function computes derivatives
down the columns (faster, because there is no transpose operation).
|
codereview_new_python_data_13198
|
has_umfpack = True
has_cholmod = True
try:
from sksparse.cholmod import analyze as cholmod_analyze
except ImportError:
has_cholmod = False
try:
- pass # test whether to use factorized
except ImportError:
has_umfpack = False
This appears to change something. I don't want to dig into whether it matters or not. These solvers are deprecated, so can we just `# noqa`?
has_umfpack = True
has_cholmod = True
try:
+ import sksparse
+ from sksparse.cholmod import cholesky as cholmod
from sksparse.cholmod import analyze as cholmod_analyze
except ImportError:
has_cholmod = False
try:
+ import scikits.umfpack # test whether to use factorized
except ImportError:
has_umfpack = False
|
codereview_new_python_data_13199
|
def test_wrightomega_singular():
for p in pts:
res = sc.wrightomega(p)
assert_equal(res, -1.0)
- assert_(np.signbit(res.imag) is False)
@pytest.mark.parametrize('x, desired', [
We can't use `is` here. The return value of `np.signbit(res.imag)` is an instance of `np.bool_`. It is equal to the Python object `False`, but it is a different object. How about using
```
assert_(not np.signbit(res.imag))
```
instead? (Or just go back to `==`.)
def test_wrightomega_singular():
for p in pts:
res = sc.wrightomega(p)
assert_equal(res, -1.0)
+ assert_(np.signbit(res.imag) == np.bool_(False))
@pytest.mark.parametrize('x, desired', [
|
codereview_new_python_data_13200
|
Result classes used in :mod:`scipy.stats`
-----------------------------------------
-.. warning:: These classes are private. Do not import them.
.. toctree::
:maxdepth: 2
One might wonder why they are documented at all then; perhaps we should explain. Also, rather than issuing a command to the user, consider phrasing it in terms of what SciPy will or will not support.
> These classes are private, but they are included here because instances of them are returned by other statistical functions. User import and instantiation is not supported.
Result classes used in :mod:`scipy.stats`
-----------------------------------------
+.. warning::
+
+ These classes are private, but they are included here because instances
+ of them are returned by other statistical functions. User import and
+ instantiation is not supported.
.. toctree::
:maxdepth: 2
|
codereview_new_python_data_13201
|
def _logsf(self, x, a, b):
return logsf
def _entropy(self, a, b):
- A = 0.5 * (1 + sc.erf(a / np.sqrt(2)))
- B = 0.5 * (1 + sc.erf(b / np.sqrt(2)))
Z = B - A
- C = (np.log(np.pi) + np.log(2) + 1) / 2
- D = np.log(Z)
- h = (C + D) / (2 * Z)
return h
def _ppf(self, q, a, b):
I do not understand how this is the same as the formula found for example in wikipedia:


The second term using the PDF of the standard normal distribution is missing.
With $C=...$ I guess you are taking the first logarithmic term apart, this is a good idea
Please compare this with your closed PR where I had suggested a [formulation](https://github.com/scipy/scipy/pull/17774/commits/a6059537a51e328e643a2f48154ba0764c91c5b5) as many existing functions can be reused here. The standard normal CDF throughout this file is used as `_norm_cdf` and the standard normal PDF as `_norm_pdf` .
def _logsf(self, x, a, b):
return logsf
def _entropy(self, a, b):
+ A = sc.ndtr(a)
+ B = sc.ndtr(b)
Z = B - A
+ C = np.log(np.sqrt(2 * np.pi * np.e) * Z)
+ D = (a * _norm_pdf(a) - b * _norm_pdf(b)) / (2 * Z)
+ h = C + D
return h
def _ppf(self, q, a, b):
|
codereview_new_python_data_13202
|
def test_entropy(self, a, b, ref):
# return pdf_standard_norm(x) / Z
#
# return -mp.quad(lambda t: pdf(t) * mp.log(pdf(t)), [a, b])
- assert_allclose(stats.truncnorm._entropy(a, b), ref)
def test_ppf_ticket1131(self):
vals = stats.truncnorm.ppf([-0.5, 0, 1e-4, 0.5, 1-1e-4, 1, 2], -1., 1.,
```suggestion
assert_allclose(stats.truncnorm.entropy(a, b), ref)
```
def test_entropy(self, a, b, ref):
# return pdf_standard_norm(x) / Z
#
# return -mp.quad(lambda t: pdf(t) * mp.log(pdf(t)), [a, b])
+ assert_allclose(stats.truncnorm.entropy(a, b), ref)
def test_ppf_ticket1131(self):
vals = stats.truncnorm.ppf([-0.5, 0, 1e-4, 0.5, 1-1e-4, 1, 2], -1., 1.,
|
codereview_new_python_data_13203
|
def _logsf(self, x, a, b):
return logsf
def _entropy(self, a, b):
- A = sc.ndtr(a)
- B = sc.ndtr(b)
Z = B - A
C = np.log(np.sqrt(2 * np.pi * np.e) * Z)
D = (a * _norm_pdf(a) - b * _norm_pdf(b)) / (2 * Z)
```suggestion
A = _norm_cdf(a)
B = _norm_cdf(b)
```
Your code is not wrong but throughout this file `_norm_cdf` is used for better readability instead of the cryptic acronym from `scipy.special`.
def _logsf(self, x, a, b):
return logsf
def _entropy(self, a, b):
+ A = _norm_cdf(a)
+ B = _norm_cdf(b)
Z = B - A
C = np.log(np.sqrt(2 * np.pi * np.e) * Z)
D = (a * _norm_pdf(a) - b * _norm_pdf(b)) / (2 * Z)
|
codereview_new_python_data_13204
|
def setup_method(self):
(1e-6, 2e-6, -13.815510557964274149359836996664372028297528210772236)])
def test_entropy(self, a, b, ref):
#All reference values were calculated with mpmath:
#def entropy_trun(a, b):
# def cdf(x):
# return 0.5 * (1 + mp.erf(x / mp.sqrt(2)))
```suggestion
[(0, 100, 0.7257913526447274),
(0.6, 0.7, -2.3027610681852573),
(1e-6, 2e-6, -13.815510557964274)])
```
def setup_method(self):
(1e-6, 2e-6, -13.815510557964274149359836996664372028297528210772236)])
def test_entropy(self, a, b, ref):
#All reference values were calculated with mpmath:
+ #import mpmath as mp
+ #mp.dps = 50
#def entropy_trun(a, b):
# def cdf(x):
# return 0.5 * (1 + mp.erf(x / mp.sqrt(2)))
|
codereview_new_python_data_13205
|
def test_entropy(self, a, ref):
# return h
#
# return -mp.quad(lambda t: pdf(t) * mp.log(pdf(t)), [-mp.inf, mp.inf])
- assert_allclose(stats.dgamma._entropy(a), ref)
def test_entropy_overflow(self):
assert np.isfinite(stats.dgamma.entropy(1e100))
```suggestion
assert_allclose(stats.dgamma.entropy(a), ref)
```
def test_entropy(self, a, ref):
# return h
#
# return -mp.quad(lambda t: pdf(t) * mp.log(pdf(t)), [-mp.inf, mp.inf])
+ assert_allclose(stats.dgamma.entropy(a), ref)
def test_entropy_overflow(self):
assert np.isfinite(stats.dgamma.entropy(1e100))
|
codereview_new_python_data_13206
|
def test_entropy(self, a, ref):
# return h
#
# return -mp.quad(lambda t: pdf(t) * mp.log(pdf(t)), [-mp.inf, mp.inf])
- assert_allclose(stats.dgamma._entropy(a), ref)
def test_entropy_overflow(self):
assert np.isfinite(stats.dgamma.entropy(1e100))
```suggestion
```
These should be removed in favor of actual tests against the result computed with mpmath for extreme values for `m` (see above).
def test_entropy(self, a, ref):
# return h
#
# return -mp.quad(lambda t: pdf(t) * mp.log(pdf(t)), [-mp.inf, mp.inf])
+ assert_allclose(stats.dgamma.entropy(a), ref)
def test_entropy_overflow(self):
assert np.isfinite(stats.dgamma.entropy(1e100))
|
codereview_new_python_data_13207
|
def _entropy(self, a):
else:
h = np.log(2) + 0.5 * (1 + np.log(a) + np.log(2 * np.pi))
- #norm_entropy = stats.norm.entropy()
- #i = a > 5e4
- #h[i] = norm_entropy - 1 / (12 * a[i])
return h
def _ppf(self, q, a):
All of scipy's distributions support numpy arrays in their methods. We have to make sure that if a user provides a NumPy array of several values, the correct branch is chosen. Throughout this file, there is a convenience function called `_lazywhere` we should use here too.
The cutoff should also be lowered. For `1e13`, the regular formula becomes very imprecise already.
def _entropy(self, a):
else:
h = np.log(2) + 0.5 * (1 + np.log(a) + np.log(2 * np.pi))
return h
def _ppf(self, q, a):
|
codereview_new_python_data_13208
|
def h2(a):
h2 = np.log(2) + 0.5 * (1 + np.log(a) + np.log(2 * np.pi))
return h2
- h = _lazywhere(a > 1e13, (a), f=h2, f2=h1)
return h
def _ppf(self, q, a):
```suggestion
h = _lazywhere(a > 1e10, (a), f=h2, f2=h1)
```
Turns out problems start way before `1e13`:
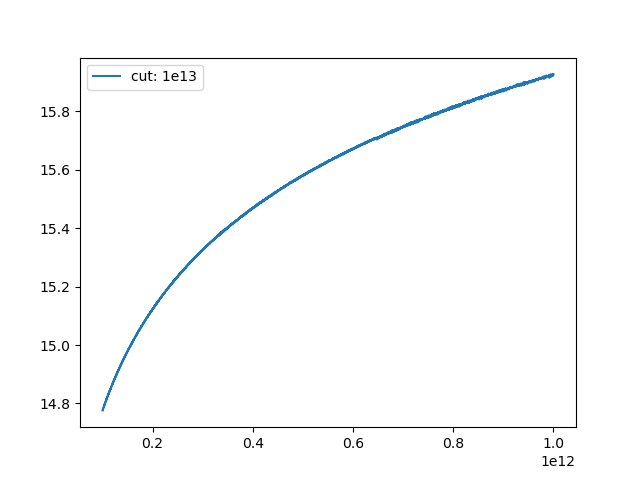
Zoomed in:
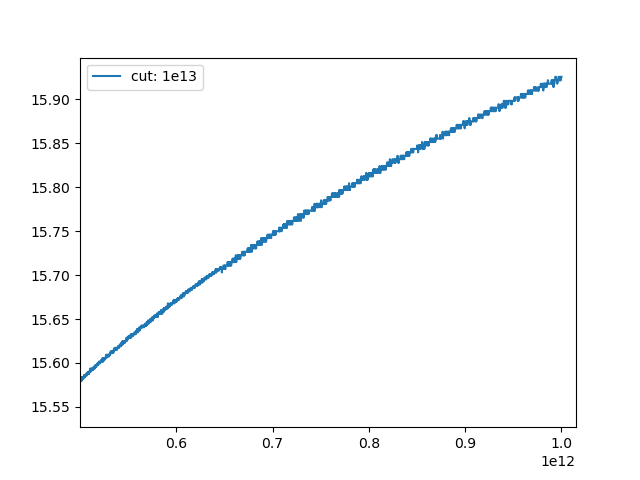
With a lower cutoff, we get around this.
def h2(a):
h2 = np.log(2) + 0.5 * (1 + np.log(a) + np.log(2 * np.pi))
return h2
+ h = _lazywhere(a > 1e10, (a), f=h2, f2=h1)
return h
def _ppf(self, q, a):
|
codereview_new_python_data_13209
|
def test_entropy(self, a, ref):
(1e+100, 117.2413403634669)])
def test_entropy_entreme_values(self, a, ref):
# The reference values were calculated with mpmath:
- # import mpmath as mp
# mp.dps = 50
# def second_dgamma(a):
# if a < 1e15:
```suggestion
# from mpmath import mp
```
def test_entropy(self, a, ref):
(1e+100, 117.2413403634669)])
def test_entropy_entreme_values(self, a, ref):
# The reference values were calculated with mpmath:
+ # from mpmath import mp
# mp.dps = 50
# def second_dgamma(a):
# if a < 1e15:
|
codereview_new_python_data_13210
|
def test_entropy_entreme_values(self, a, ref):
assert_allclose(stats.dgamma.entropy(a), ref, rtol=1e-10)
def test_entropy_array_input(self):
- y = stats.dgamma.entropy([1, 5, 1e20, 1e-5])
- assert y[0] == stats.dgamma.entropy(1)
- assert y[1] == stats.dgamma.entropy(5)
- assert y[2] == stats.dgamma.entropy(1e20)
- assert y[3] == stats.dgamma.entropy(1e-5)
class TestChi2:
# regression tests after precision improvements, ticket:1041, not verified
```suggestion
def test_entropy_array_input(self):
x = np.array([1, 5, 1e20, 1e-5])
y = stats.dgamma.entropy(x)
for i in range(len(y)):
assert y[i] == stats.dgamma.entropy(x[i])
```
def test_entropy_entreme_values(self, a, ref):
assert_allclose(stats.dgamma.entropy(a), ref, rtol=1e-10)
def test_entropy_array_input(self):
+ x = np.array([1, 5, 1e20, 1e-5])
+ y = stats.dgamma.entropy(x)
+ for i in range(len(y)):
+ assert y[i] == stats.dgamma.entropy(x[i])
class TestChi2:
# regression tests after precision improvements, ticket:1041, not verified
|
codereview_new_python_data_13211
|
def h2(a):
h2 = np.log(2) + 0.5 * (1 + np.log(a) + np.log(2 * np.pi))
return h2
- h = _lazywhere(a > 1e10, (a), f=h2, f2=h1)
return h
def _ppf(self, q, a):
```suggestion
h = _lazywhere(a > 1e8, (a), f=h2, f2=h1)
```
def h2(a):
h2 = np.log(2) + 0.5 * (1 + np.log(a) + np.log(2 * np.pi))
return h2
+ h = _lazywhere(a > 1e8, (a), f=h2, f2=h1)
return h
def _ppf(self, q, a):
|
codereview_new_python_data_13212
|
def test_entropy(self, m, ref):
# return -mp.quad(lambda t: pdf(t) * mp.log(pdf(t)), [0, mp.inf]
assert_allclose(stats.nakagami._entropy(m), ref)
@pytest.mark.xfail(reason="Fit of nakagami not reliable, see gh-10908.")
@pytest.mark.parametrize('nu', [1.6, 2.5, 3.9])
@pytest.mark.parametrize('loc', [25.0, 10, 35])
```suggestion
assert_allclose(stats.nakagami.entropy(m), ref, rtol=1e-14)
```
With this custom implementation we should get much higher precision than the default `1e-7`. Please rerun the tests and check for which tolerance they still pass.
def test_entropy(self, m, ref):
# return -mp.quad(lambda t: pdf(t) * mp.log(pdf(t)), [0, mp.inf]
assert_allclose(stats.nakagami._entropy(m), ref)
+ def test_entropy_overflow(self):
+ assert np.isfinite(stats.nakagami._entropy(1e100))
+ assert np.isfinite(stats.nakagami._entropy(1e-100))
+
@pytest.mark.xfail(reason="Fit of nakagami not reliable, see gh-10908.")
@pytest.mark.parametrize('nu', [1.6, 2.5, 3.9])
@pytest.mark.parametrize('loc', [25.0, 10, 35])
|
codereview_new_python_data_13213
|
def linprog(c, A_ub=None, b_ub=None, A_eq=None, b_eq=None,
Note that by default ``lb = 0`` and ``ub = None`` unless specified with
``bounds``. There is, however, no need to manually formulate the linear
programming problem in terms of positive variables, often termed slack
- variables. By setting corresponding values in as ``min``in ``bounds``,
e.g. a negative value or ``None``, ``linprog`` is well able to handle
negative or real valued ``x``.
This isn't rendering correctly as is
```suggestion
variables. By setting corresponding values in as ``min`` in ``bounds``,
```
def linprog(c, A_ub=None, b_ub=None, A_eq=None, b_eq=None,
Note that by default ``lb = 0`` and ``ub = None`` unless specified with
``bounds``. There is, however, no need to manually formulate the linear
programming problem in terms of positive variables, often termed slack
+ variables. By setting corresponding values of ``min`` in ``bounds``,
e.g. a negative value or ``None``, ``linprog`` is well able to handle
negative or real valued ``x``.
|
codereview_new_python_data_13214
|
def linprog(c, A_ub=None, b_ub=None, A_eq=None, b_eq=None,
Use ``None`` to indicate that there is no bound. For instance, the
default bound ``(0, None)`` means that all decision variables are
non-negative, and the pair ``(None, None)`` means no bounds at all,
- i.e. all variables are allowed to take values form the real numbers.
method : str, optional
The algorithm used to solve the standard form problem.
:ref:`'highs' <optimize.linprog-highs>` (default),
Typo.
```suggestion
i.e. all variables are allowed to be any real.
```
def linprog(c, A_ub=None, b_ub=None, A_eq=None, b_eq=None,
Use ``None`` to indicate that there is no bound. For instance, the
default bound ``(0, None)`` means that all decision variables are
non-negative, and the pair ``(None, None)`` means no bounds at all,
+ i.e. all variables are allowed to be any real.
method : str, optional
The algorithm used to solve the standard form problem.
:ref:`'highs' <optimize.linprog-highs>` (default),
|
codereview_new_python_data_13215
|
def _stats(self, c):
return mu, mu2, g1, g2
def _entropy(self, c):
- return sc.betaln(c, 1) + 1 + sc.psi(c) + 1/c + _EULER
genlogistic = genlogistic_gen(name='genlogistic')
I noted in my earlier comment that the beta function simplifies for the case of `b=1` (and that's why SciPy is a special case of the type 4 generalized logistic)
```suggestion
return -np.log(c) + 1 + sc.psi(c) + 1/c - sc.psi(1)
```
def _stats(self, c):
return mu, mu2, g1, g2
def _entropy(self, c):
+ return -np.log(c) + sc.psi(c) + 1/c + _EULER + 1
genlogistic = genlogistic_gen(name='genlogistic')
|
codereview_new_python_data_13216
|
def curve_fit(f, xdata, ydata, p0=None, sigma=None, absolute_sigma=False,
xdata : array_like
The independent variable where the data is measured.
Should usually be an M-length sequence or an (k,M)-shaped array for
- functions with k predictors, and a (k,M,N)-shaped 3D array is also
- acceptable. Each element should be float convertible if it is an
- array like object.
ydata : array_like
The dependent data, a length M array - nominally ``f(xdata, ...)``.
p0 : array_like, optional
When I suggested documenting 3D arrays, I had in mind that we should
a) make a more explicit decision about whether to support this officially and
b) if so, document precisely what it means. Otherwise, it is not clear how it behaves.
So let's take care of that in a separate PR.
```suggestion
functions with k predictors, and each element should be float
convertible if it is an array like object.
```
Do you have a preference about whether it should be supported?
def curve_fit(f, xdata, ydata, p0=None, sigma=None, absolute_sigma=False,
xdata : array_like
The independent variable where the data is measured.
Should usually be an M-length sequence or an (k,M)-shaped array for
+ functions with k predictors, and each element should be float
+ convertible if it is an array like object.
ydata : array_like
The dependent data, a length M array - nominally ``f(xdata, ...)``.
p0 : array_like, optional
|
codereview_new_python_data_13217
|
import math
import numpy as np
from numpy import sqrt, cos, sin, arctan, exp, log, pi, Inf
-from numpy.testing import (assert_, assert_equal,
assert_allclose, assert_array_less, assert_almost_equal)
import pytest
To fix the linter
```suggestion
from numpy.testing import (assert_equal,
```
import math
import numpy as np
from numpy import sqrt, cos, sin, arctan, exp, log, pi, Inf
+from numpy.testing import (assert_equal,
assert_allclose, assert_array_less, assert_almost_equal)
import pytest
|
codereview_new_python_data_13218
|
def brentq(f, a, b, args=(),
"""
Find a root of a function in a bracketing interval using Brent's method.
- Uses the classic Brent's method to find a roo of the function `f` on
the sign changing interval [a , b]. Generally considered the best of the
rootfinding routines here. It is a safe version of the secant method that
uses inverse quadratic extrapolation. Brent's method combines root
```suggestion
Uses the classic Brent's method to find a root of the function `f` on
```
def brentq(f, a, b, args=(),
"""
Find a root of a function in a bracketing interval using Brent's method.
+ Uses the classic Brent's method to find a root of the function `f` on
the sign changing interval [a , b]. Generally considered the best of the
rootfinding routines here. It is a safe version of the secant method that
uses inverse quadratic extrapolation. Brent's method combines root
|
codereview_new_python_data_13219
|
def test_logcdf_logsf(self):
# ref = (1/2 * mp.log(2 * mp.pi * mp.e * mu**3)
# - 3/2* mp.exp(2/mu) * mp.e1(2/mu))
@pytest.mark.parametrize("mu, ref", [(1e-2, -5.496279615262233),
- (1e8, 3.3244822568873474)])
(1e100, 3.3244828013968899)])
def test_entropy(self, mu, ref):
assert_allclose(stats.invgauss.entropy(mu), ref)
```suggestion
(1e8, 3.3244822568873474)]),
```
def test_logcdf_logsf(self):
# ref = (1/2 * mp.log(2 * mp.pi * mp.e * mu**3)
# - 3/2* mp.exp(2/mu) * mp.e1(2/mu))
@pytest.mark.parametrize("mu, ref", [(1e-2, -5.496279615262233),
+ (1e8, 3.3244822568873474)]),
(1e100, 3.3244828013968899)])
def test_entropy(self, mu, ref):
assert_allclose(stats.invgauss.entropy(mu), ref)
|
codereview_new_python_data_13220
|
def test_logcdf_logsf(self):
# ref = (1/2 * mp.log(2 * mp.pi * mp.e * mu**3)
# - 3/2* mp.exp(2/mu) * mp.e1(2/mu))
@pytest.mark.parametrize("mu, ref", [(1e-2, -5.496279615262233),
- (1e8, 3.3244822568873474)]),
(1e100, 3.3244828013968899)])
def test_entropy(self, mu, ref):
assert_allclose(stats.invgauss.entropy(mu), ref)
```suggestion
(1e8, 3.3244822568873474),
```
def test_logcdf_logsf(self):
# ref = (1/2 * mp.log(2 * mp.pi * mp.e * mu**3)
# - 3/2* mp.exp(2/mu) * mp.e1(2/mu))
@pytest.mark.parametrize("mu, ref", [(1e-2, -5.496279615262233),
+ (1e8, 3.3244822568873474),
(1e100, 3.3244828013968899)])
def test_entropy(self, mu, ref):
assert_allclose(stats.invgauss.entropy(mu), ref)
|
codereview_new_python_data_13221
|
def add_newdoc(name, doc):
Plot the function. For that purpose, we provide a NumPy array as argument.
>>> import matplotlib.pyplot as plt
- >>> x = np.linspace(0, 1, 500)
>>> fig, ax = plt.subplots()
>>> ax.plot(x, ndtri(x))
>>> ax.set_title("Standard normal percentile function")
This is what we put in other places also maybe we don't need that many points?
```suggestion
>>> x = np.linspace(0.01, 1, 200)
```
def add_newdoc(name, doc):
Plot the function. For that purpose, we provide a NumPy array as argument.
>>> import matplotlib.pyplot as plt
+ >>> x = np.linspace(0.01, 1, 200)
>>> fig, ax = plt.subplots()
>>> ax.plot(x, ndtri(x))
>>> ax.set_title("Standard normal percentile function")
|
codereview_new_python_data_13222
|
def test_isf(self):
330.6557590436547, atol=1e-13)
class TestDgamma:
- def test_logpdf(self):
- x = np.array([1, 0.3, 4])
- a = 1.3
- y = stats.dgamma.pdf(x, a)
- assert_allclose(y, np.exp(stats.dgamma.logpdf(x, a)))
-
def test_pdf(self):
#Reference values calculated by hand using
#the defintion from the Scipy documentation
What does "by hand" mean in this case? I doubt it is literally using pencil and paper.
It matters because I need to know what this test really checks.
def test_isf(self):
330.6557590436547, atol=1e-13)
class TestDgamma:
def test_pdf(self):
#Reference values calculated by hand using
#the defintion from the Scipy documentation
|
codereview_new_python_data_13223
|
def _wrap_callback(callback, method=None):
return callback # don't wrap
sig = inspect.signature(callback)
- has_one_parameter = len(sig.parameters) == 1
- named_intermediate_result = sig.parameters.get('intermediate_result', 0)
- if has_one_parameter and named_intermediate_result:
def wrapped_callback(res):
return callback(intermediate_result=res)
elif method == 'trust-constr':
Works although 0, 1 for bool is not very clear to me. Personally I tend to forget which is which. Why not being more specific with:
```suggestion
named_intermediate_result = sig.parameters.get(
'intermediate_result', False
)
```
def _wrap_callback(callback, method=None):
return callback # don't wrap
sig = inspect.signature(callback)
+ if set(sig.parameters) != {'intermediate_result'}:
def wrapped_callback(res):
return callback(intermediate_result=res)
elif method == 'trust-constr':
|
codereview_new_python_data_13224
|
def _wrap_callback(callback, method=None):
return callback # don't wrap
sig = inspect.signature(callback)
- has_one_parameter = len(sig.parameters) == 1
- named_intermediate_result = sig.parameters.get('intermediate_result', 0)
- if has_one_parameter and named_intermediate_result:
def wrapped_callback(res):
return callback(intermediate_result=res)
elif method == 'trust-constr':
Another way would be to do the following. That would remove the need to do 2 checks.
```suggestion
if set(sig.parameters) != {'intermediate_result'}:
```
def _wrap_callback(callback, method=None):
return callback # don't wrap
sig = inspect.signature(callback)
+ if set(sig.parameters) != {'intermediate_result'}:
def wrapped_callback(res):
return callback(intermediate_result=res)
elif method == 'trust-constr':
|
codereview_new_python_data_13225
|
def _wrap_callback(callback, method=None):
sig = inspect.signature(callback)
- if set(sig.parameters) != {'intermediate_result'}:
def wrapped_callback(res):
return callback(intermediate_result=res)
elif method == 'trust-constr':
Oh wait it should be the other way around, my bad with my suggestion:
```suggestion
if set(sig.parameters) == {'intermediate_result'}:
```
def _wrap_callback(callback, method=None):
sig = inspect.signature(callback)
+ if set(sig.parameters) == {'intermediate_result'}:
def wrapped_callback(res):
return callback(intermediate_result=res)
elif method == 'trust-constr':
|
codereview_new_python_data_13226
|
def levene(*samples, center='median', proportiontocut=0.05):
Examples
--------
- In [4]_, the influence of vitamine C on the tooth growth of guinea pigs
was investigated. In a control study, 60 subjects were divided into
- three groups each respectively recieving a daily doses of 0.5, 1.0 and 2.0
- mg of vitamine C. After 42 days, the tooth
grow, in micron, was measured.
- In the following, we are interested test the null hypothesis that all
groups are from populations with equal variances.
>>> import numpy as np
```suggestion
In [4]_, the influence of vitamin C on the tooth growth of guinea pigs
was investigated. In a control study, 60 subjects were divided into
three groups each respectively receiving daily doses of 0.5, 1.0 and 2.0
mg of vitamin C. After 42 days, the tooth
grow, in micron, was measured.
In the following, we are interested in testing the null hypothesis that all
groups are from populations with equal variances.
```
def levene(*samples, center='median', proportiontocut=0.05):
Examples
--------
+ In [4]_, the influence of vitamin C on the tooth growth of guinea pigs
was investigated. In a control study, 60 subjects were divided into
+ three groups each respectively receiving daily doses of 0.5, 1.0 and 2.0
+ mg of vitamin C. After 42 days, the tooth
grow, in micron, was measured.
+ In the following, we are interested in testing the null hypothesis that all
groups are from populations with equal variances.
>>> import numpy as np
|
codereview_new_python_data_13227
|
def levene(*samples, center='median', proportiontocut=0.05):
--------
In [4]_, the influence of vitamin C on the tooth growth of guinea pigs
was investigated. In a control study, 60 subjects were divided into
- three groups each respectively receiving daily doses of 0.5, 1.0 and 2.0
- mg of vitamin C. After 42 days, the tooth
- grow, in micron, was measured.
In the following, we are interested in testing the null hypothesis that all
groups are from populations with equal variances.
Without identifying the groups, I'm not sure that the word "respectively" would be appropriate. In any case, I think it should appear at the end of the sentence.
```suggestion
small dose, medium dose, and large dose groups that received
daily doses of 0.5, 1.0 and 2.0 mg of vitamin C, respectively.
After 42 days, the tooth
```
def levene(*samples, center='median', proportiontocut=0.05):
--------
In [4]_, the influence of vitamin C on the tooth growth of guinea pigs
was investigated. In a control study, 60 subjects were divided into
+ small dose, medium dose, and large dose groups that received
+ daily doses of 0.5, 1.0 and 2.0 mg of vitamin C, respectively.
+ After 42 days, the tooth
+ growth, in microns, was measured.
In the following, we are interested in testing the null hypothesis that all
groups are from populations with equal variances.
|
codereview_new_python_data_13228
|
def levene(*samples, center='median', proportiontocut=0.05):
--------
In [4]_, the influence of vitamin C on the tooth growth of guinea pigs
was investigated. In a control study, 60 subjects were divided into
- three groups each respectively receiving daily doses of 0.5, 1.0 and 2.0
- mg of vitamin C. After 42 days, the tooth
- grow, in micron, was measured.
In the following, we are interested in testing the null hypothesis that all
groups are from populations with equal variances.
```suggestion
growth, in microns, was measured.
```
def levene(*samples, center='median', proportiontocut=0.05):
--------
In [4]_, the influence of vitamin C on the tooth growth of guinea pigs
was investigated. In a control study, 60 subjects were divided into
+ small dose, medium dose, and large dose groups that received
+ daily doses of 0.5, 1.0 and 2.0 mg of vitamin C, respectively.
+ After 42 days, the tooth
+ growth, in microns, was measured.
In the following, we are interested in testing the null hypothesis that all
groups are from populations with equal variances.
|
codereview_new_python_data_13229
|
def bartlett(*samples):
only provide evidence for a "significant" effect, meaning that they are
unlikely to have occurred under the null hypothesis.
- Note that the chi-square distribution provides an asymptotic approximation
- of the null distribution.
- For small samples, it may be more appropriate to perform a
permutation test: Under the null hypothesis that all three samples were
drawn from the same population, each of the measurements is equally likely
to have been observed in any of the three samples. Therefore, we can form
> Since these are just examples I propose to only write we know to be true.
But we don't know that this is true. It doesn't appear to be true.
We _do_ know that `bartlett` is sensitive to non-normality. It is mentioned in the docstring.

So my suggestion was to remove the part we don't know and replace it with something we do know:
> Note that the chi-square distribution provides the null distribution when the observations are normally distributed. For small samples drawn from non-normal populations, it may be more appropriate to perform a permutation test...
def bartlett(*samples):
only provide evidence for a "significant" effect, meaning that they are
unlikely to have occurred under the null hypothesis.
+ Note that the chi-square distribution provides the null distribution
+ when the observations are normally distributed. For small samples
+ drawn from non-normal populations, it may be more appropriate to
+ perform a
permutation test: Under the null hypothesis that all three samples were
drawn from the same population, each of the measurements is equally likely
to have been observed in any of the three samples. Therefore, we can form
|
codereview_new_python_data_13230
|
def bartlett(*samples):
only provide evidence for a "significant" effect, meaning that they are
unlikely to have occurred under the null hypothesis.
- Note that the chi-square distribution provides an asymptotic approximation
- of the null distribution.
- For small samples, it may be more appropriate to perform a
permutation test: Under the null hypothesis that all three samples were
drawn from the same population, each of the measurements is equally likely
to have been observed in any of the three samples. Therefore, we can form
```suggestion
Note that the chi-square distribution provides the null distribution
when the observations are normally distributed. For small samples
drawn from non-normal populations, it may be more appropriate to
perform a
permutation test: Under the null hypothesis that all three samples were
```
def bartlett(*samples):
only provide evidence for a "significant" effect, meaning that they are
unlikely to have occurred under the null hypothesis.
+ Note that the chi-square distribution provides the null distribution
+ when the observations are normally distributed. For small samples
+ drawn from non-normal populations, it may be more appropriate to
+ perform a
permutation test: Under the null hypothesis that all three samples were
drawn from the same population, each of the measurements is equally likely
to have been observed in any of the three samples. Therefore, we can form
|
codereview_new_python_data_13231
|
def test_pmf(self):
vals6 = multinomial.pmf([2, 1, 0], 0, [2/3.0, 1/3.0, 0])
assert vals6 == 0
def test_pmf_broadcasting(self):
vals0 = multinomial.pmf([1, 2], 3, [[.1, .9], [.2, .8]])
assert_allclose(vals0, [.243, .384], rtol=1e-8)
```suggestion
assert vals6 == 0
```
def test_pmf(self):
vals6 = multinomial.pmf([2, 1, 0], 0, [2/3.0, 1/3.0, 0])
assert vals6 == 0
+
def test_pmf_broadcasting(self):
vals0 = multinomial.pmf([1, 2], 3, [[.1, .9], [.2, .8]])
assert_allclose(vals0, [.243, .384], rtol=1e-8)
|
codereview_new_python_data_13232
|
def statistic(data, axis):
np.std(data, axis, ddof=1)])
res = bootstrap((sample,), statistic, method=method, axis=-1,
- n_resamples=9999)
counts = np.sum((res.confidence_interval.low.T < params)
& (res.confidence_interval.high.T > params),
```suggestion
n_resamples=9999, batch=200)
```
def statistic(data, axis):
np.std(data, axis, ddof=1)])
res = bootstrap((sample,), statistic, method=method, axis=-1,
+ n_resamples=9999, batch=200)
counts = np.sum((res.confidence_interval.low.T < params)
& (res.confidence_interval.high.T > params),
|
codereview_new_python_data_13233
|
def test_nonscalar_values_linear_2D(self):
v2 = np.expand_dims(vs, axis=0)
assert_allclose(v, v2, atol=1e-14, err_msg=method)
- @pytest.mark.parametrize("dtype",
- [np.float32, np.float64, np.complex64, np.complex128])
@pytest.mark.parametrize("xi_dtype", [np.float32, np.float64])
def test_float32_values(self, dtype, xi_dtype):
# regression test for gh-17718: values.dtype=float32 fails
This should fix your linter error
```suggestion
@pytest.mark.parametrize(
"dtype",
[np.float32, np.float64, np.complex64, np.complex128]
)
```
def test_nonscalar_values_linear_2D(self):
v2 = np.expand_dims(vs, axis=0)
assert_allclose(v, v2, atol=1e-14, err_msg=method)
+ @pytest.mark.parametrize(
+ "dtype",
+ [np.float32, np.float64, np.complex64, np.complex128]
+ )
@pytest.mark.parametrize("xi_dtype", [np.float32, np.float64])
def test_float32_values(self, dtype, xi_dtype):
# regression test for gh-17718: values.dtype=float32 fails
|
codereview_new_python_data_13234
|
def pmean(a, p, *, axis=0, dtype=None, weights=None):
\left( \frac{ 1 }{ n } \sum_{i=1}^n a_i^p \right)^{ 1 / p } \, .
- When p=0, it returns the geometric mean.
This mean is also called generalized mean or Hölder mean, and must not be
confused with the Kolmogorov generalized mean, also called
```suggestion
When ``p=0``, it returns the geometric mean.
```
def pmean(a, p, *, axis=0, dtype=None, weights=None):
\left( \frac{ 1 }{ n } \sum_{i=1}^n a_i^p \right)^{ 1 / p } \, .
+ When ``p=0``, it returns the geometric mean.
This mean is also called generalized mean or Hölder mean, and must not be
confused with the Kolmogorov generalized mean, also called
|
codereview_new_python_data_13235
|
def pointbiserialr(x, y):
.. math::
- r_{pb} = \frac{\overline{Y_{1}} -
- \overline{Y_{0}}}{s_{y}}\sqrt{\frac{N_{1} N_{2}}{N (N - 1))}}
Where :math:`\overline{Y_{0}}` and :math:`\overline{Y_{1}}` are means
of the metric observations coded 0 and 1 respectively; :math:`N_{0}` and
Drive-by comment: if we're improving this formula, would it be possible to make it easier for those who still do `object?` in ipython --- compare `\overline{Y_0}{s_y} \sqrt{ \frac{N_0 N_1}{N (N-1)}}` or even `\overline{Y_0}{s_y} \sqrt{ N_0 N_1 / N (N-1) }`
def pointbiserialr(x, y):
.. math::
+ r_{pb} = \frac{\overline{Y_1} - \overline{Y_0}}
+ {s_y}
+ \sqrt{\frac{N_0 N_1}
+ {N (N - 1)}}
Where :math:`\overline{Y_{0}}` and :math:`\overline{Y_{1}}` are means
of the metric observations coded 0 and 1 respectively; :math:`N_{0}` and
|
codereview_new_python_data_13236
|
def pointbiserialr(x, y):
.. math::
- r_{pb} = \frac{\overline{Y_{1}} -
- \overline{Y_{0}}}{s_{y}}\sqrt{\frac{N_{1} N_{2}}{N (N - 1))}}
Where :math:`\overline{Y_{0}}` and :math:`\overline{Y_{1}}` are means
of the metric observations coded 0 and 1 respectively; :math:`N_{0}` and
@ev-br how about
```suggestion
r_{pb} = \frac{\overline{Y_1} - \overline{Y_0}}
{s_y}
\sqrt{\frac{N_0 N_1}
{N (N - 1)}}
```
def pointbiserialr(x, y):
.. math::
+ r_{pb} = \frac{\overline{Y_1} - \overline{Y_0}}
+ {s_y}
+ \sqrt{\frac{N_0 N_1}
+ {N (N - 1)}}
Where :math:`\overline{Y_{0}}` and :math:`\overline{Y_{1}}` are means
of the metric observations coded 0 and 1 respectively; :math:`N_{0}` and
|
codereview_new_python_data_13237
|
def test_bounds_variants(self):
bounds_new = Bounds(lb, ub)
res_old = lsq_linear(A, b, bounds_old)
res_new = lsq_linear(A, b, bounds_new)
assert_allclose(res_old.x, res_new.x)
def test_np_matrix(self):
To emphasize that this is a problem for which `bounds` have an effect on the solution:
```suggestion
assert_allclose(res_old.x, res_new.x)
assert not np.allclose(res_new.x, res_new.unbounded_sol[0])
```
(please check locally that this is correct)
def test_bounds_variants(self):
bounds_new = Bounds(lb, ub)
res_old = lsq_linear(A, b, bounds_old)
res_new = lsq_linear(A, b, bounds_new)
+ assert not np.allclose(res_new.x, res_new.unbounded_sol[0])
assert_allclose(res_old.x, res_new.x)
def test_np_matrix(self):
|
codereview_new_python_data_13238
|
def _minimize_cobyla(fun, x0, args=(), constraints=(),
constraints = (constraints, )
if bounds:
- msg = "An upper bound is less than the corresponding lower bound."
- if np.any(bounds.ub < bounds.lb):
- raise ValueError(msg)
-
- msg = "The number of bounds is not compatible with the length of `x0`."
- if len(x0) != len(bounds.lb):
- raise ValueError(msg)
-
i_lb = np.isfinite(bounds.lb)
if np.any(i_lb):
def lb_constraint(x, *args, **kwargs):
I wonder if we should have a generic `scipy.optimize` function for doing this bounds checking?
def _minimize_cobyla(fun, x0, args=(), constraints=(),
constraints = (constraints, )
if bounds:
i_lb = np.isfinite(bounds.lb)
if np.any(i_lb):
def lb_constraint(x, *args, **kwargs):
|
codereview_new_python_data_13239
|
def f(x):
def test_newton_complex_gh10103():
- # gh-10103 report a problem with `newton` and complex x0. Check that this
- # is resolved.
def f(z):
return z - 1
res = newton(f, 1+1j)
```suggestion
# gh-10103 reported a problem with `newton` and complex x0.
# Check that this is resolved.
```
def f(x):
def test_newton_complex_gh10103():
+ # gh-10103 reported a problem with `newton` and complex x0.
+ # Check that this is resolved.
def f(z):
return z - 1
res = newton(f, 1+1j)
|
codereview_new_python_data_13240
|
def f(x):
def test_newton_complex_gh10103():
- # gh-10103 reported a problem with `newton` and complex x0.
# Check that this is resolved.
def f(z):
return z - 1
Perhaps expand the description to something like:
```
# gh-10103 reported a problem with `newton` and complex x0, no fprime and no x1.
```
def f(x):
def test_newton_complex_gh10103():
+ # gh-10103 reported a problem when `newton` is pass a Python complex x0,
+ # no `fprime` (secant method), and no `x1` (`x1` must be constructed).
# Check that this is resolved.
def f(z):
return z - 1
|
codereview_new_python_data_13241
|
def f(x):
res = solver(f, -0.5, -1e-200*1e-200, full_output=True)
res = res if rs_interface else res[1]
assert res.converged
- assert_allclose(res.root, 0, atol=1e-8)
\ No newline at end of file
```suggestion
assert_allclose(res.root, 0, atol=1e-8)
```
def f(x):
res = solver(f, -0.5, -1e-200*1e-200, full_output=True)
res = res if rs_interface else res[1]
assert res.converged
\ No newline at end of file
+ assert_allclose(res.root, 0, atol=1e-8)
|
codereview_new_python_data_13242
|
def curve_fit(f, xdata, ydata, p0=None, sigma=None, absolute_sigma=False,
>>> def func(x, a, b, c, d):
... return a * d * np.exp(-b * x) + c # a and d are redundant
>>> popt, pcov = curve_fit(func, xdata, ydata)
- >>> np.linalg.cond(pcov) # may vary
- 1.13250718925596e+32
Such a large value is cause for concern. The diagonal elements of the
covariance matrix, which is related to uncertainty of the fit, gives more
```suggestion
>>> np.linalg.cond(pcov)
1.13250718925596e+32 # may vary
```
def curve_fit(f, xdata, ydata, p0=None, sigma=None, absolute_sigma=False,
>>> def func(x, a, b, c, d):
... return a * d * np.exp(-b * x) + c # a and d are redundant
>>> popt, pcov = curve_fit(func, xdata, ydata)
+ >>> np.linalg.cond(pcov)
+ 1.13250718925596e+32 # may vary
Such a large value is cause for concern. The diagonal elements of the
covariance matrix, which is related to uncertainty of the fit, gives more
|
codereview_new_python_data_13243
|
def curve_fit(f, xdata, ydata, p0=None, sigma=None, absolute_sigma=False,
>>> def func(x, a, b, c, d):
... return a * d * np.exp(-b * x) + c # a and d are redundant
>>> popt, pcov = curve_fit(func, xdata, ydata)
- >>> np.linalg.cond(pcov) # may vary
- 1.13250718925596e+32
Such a large value is cause for concern. The diagonal elements of the
covariance matrix, which is related to uncertainty of the fit, gives more
```suggestion
>>> np.linalg.cond(pcov)
1.13250718925596e+32 # may vary
```
def curve_fit(f, xdata, ydata, p0=None, sigma=None, absolute_sigma=False,
>>> def func(x, a, b, c, d):
... return a * d * np.exp(-b * x) + c # a and d are redundant
>>> popt, pcov = curve_fit(func, xdata, ydata)
+ >>> np.linalg.cond(pcov)
+ 1.13250718925596e+32 # may vary
Such a large value is cause for concern. The diagonal elements of the
covariance matrix, which is related to uncertainty of the fit, gives more
|
codereview_new_python_data_13244
|
def curve_fit(f, xdata, ydata, p0=None, sigma=None, absolute_sigma=False,
>>> def func(x, a, b, c, d):
... return a * d * np.exp(-b * x) + c # a and d are redundant
>>> popt, pcov = curve_fit(func, xdata, ydata)
- >>> np.linalg.cond(pcov) # may vary
- 1.13250718925596e+32
Such a large value is cause for concern. The diagonal elements of the
covariance matrix, which is related to uncertainty of the fit, gives more
```suggestion
>>> np.linalg.cond(pcov)
1.13250718925596e+32 # may vary
```
def curve_fit(f, xdata, ydata, p0=None, sigma=None, absolute_sigma=False,
>>> def func(x, a, b, c, d):
... return a * d * np.exp(-b * x) + c # a and d are redundant
>>> popt, pcov = curve_fit(func, xdata, ydata)
+ >>> np.linalg.cond(pcov)
+ 1.13250718925596e+32 # may vary
Such a large value is cause for concern. The diagonal elements of the
covariance matrix, which is related to uncertainty of the fit, gives more
|
codereview_new_python_data_13245
|
def lhs(x):
assert not res.converged
assert res.flag == 'convergence error'
- # This test case doesn't fail to converge for the vectorized version of
- # newton, but this one from `def test_zero_der_nz_dp()` does.
dx = np.finfo(float).eps ** 0.33
p0 = (200.0 - dx) / (2.0 + dx)
with pytest.warns(RuntimeWarning, match='RMS of'):
res = newton(lambda y: (y - 100.0)**2, x0=[p0]*2, full_output=True)
assert_equal(res.converged, [False, False])
@pytest.mark.parametrize('solver_name',
There are two "this" in the statement. Does one refer to the function `lhs` above perhaps?
def lhs(x):
assert not res.converged
assert res.flag == 'convergence error'
+ # In the vectorized version of `newton`, the secant method doesn't
+ # encounter zero slope in the problem above. Here's a problem where
+ # it does. Check that it reports failure to converge.
dx = np.finfo(float).eps ** 0.33
p0 = (200.0 - dx) / (2.0 + dx)
with pytest.warns(RuntimeWarning, match='RMS of'):
res = newton(lambda y: (y - 100.0)**2, x0=[p0]*2, full_output=True)
assert_equal(res.converged, [False, False])
+ assert_equal(res.zero_der, [True, True])
@pytest.mark.parametrize('solver_name',
|
codereview_new_python_data_13246
|
def lhs(x):
assert not res.converged
assert res.flag == 'convergence error'
- # This test case doesn't fail to converge for the vectorized version of
- # newton, but this one from `def test_zero_der_nz_dp()` does.
dx = np.finfo(float).eps ** 0.33
p0 = (200.0 - dx) / (2.0 + dx)
with pytest.warns(RuntimeWarning, match='RMS of'):
res = newton(lambda y: (y - 100.0)**2, x0=[p0]*2, full_output=True)
assert_equal(res.converged, [False, False])
@pytest.mark.parametrize('solver_name',
```suggestion
# In the vectorized version of `newton`, the secant method doesn't
# encounter zero slope in the problem above. Here's a problem where
# it does. Check that it reports failure to converge.
```
def lhs(x):
assert not res.converged
assert res.flag == 'convergence error'
+ # In the vectorized version of `newton`, the secant method doesn't
+ # encounter zero slope in the problem above. Here's a problem where
+ # it does. Check that it reports failure to converge.
dx = np.finfo(float).eps ** 0.33
p0 = (200.0 - dx) / (2.0 + dx)
with pytest.warns(RuntimeWarning, match='RMS of'):
res = newton(lambda y: (y - 100.0)**2, x0=[p0]*2, full_output=True)
assert_equal(res.converged, [False, False])
+ assert_equal(res.zero_der, [True, True])
@pytest.mark.parametrize('solver_name',
|
codereview_new_python_data_13247
|
def lhs(x):
assert not res.converged
assert res.flag == 'convergence error'
- # This test case doesn't fail to converge for the vectorized version of
- # newton, but this one from `def test_zero_der_nz_dp()` does.
dx = np.finfo(float).eps ** 0.33
p0 = (200.0 - dx) / (2.0 + dx)
with pytest.warns(RuntimeWarning, match='RMS of'):
res = newton(lambda y: (y - 100.0)**2, x0=[p0]*2, full_output=True)
assert_equal(res.converged, [False, False])
@pytest.mark.parametrize('solver_name',
```suggestion
assert_equal(res.converged, [False, False])
assert_equal(res.zero_der, [True, True])
```
def lhs(x):
assert not res.converged
assert res.flag == 'convergence error'
+ # In the vectorized version of `newton`, the secant method doesn't
+ # encounter zero slope in the problem above. Here's a problem where
+ # it does. Check that it reports failure to converge.
dx = np.finfo(float).eps ** 0.33
p0 = (200.0 - dx) / (2.0 + dx)
with pytest.warns(RuntimeWarning, match='RMS of'):
res = newton(lambda y: (y - 100.0)**2, x0=[p0]*2, full_output=True)
assert_equal(res.converged, [False, False])
+ assert_equal(res.zero_der, [True, True])
@pytest.mark.parametrize('solver_name',
|
codereview_new_python_data_13248
|
def lhs(x):
assert not res.converged
assert res.flag == 'convergence error'
- # In the vectorized version of `newton`, the secant method doesn't
- # encounter zero slope in the problem above. Here's a problem where
- # it does. Check that it reports failure to converge.
- dx = np.finfo(float).eps ** 0.33
- p0 = (200.0 - dx) / (2.0 + dx)
- with pytest.warns(RuntimeWarning, match='RMS of'):
- res = newton(lambda y: (y - 100.0)**2, x0=[p0]*2, full_output=True)
- assert_equal(res.converged, [False, False])
- assert_equal(res.zero_der, [True, True])
-
@pytest.mark.parametrize('solver_name',
['brentq', 'brenth', 'bisect', 'ridder', 'toms748'])
This wasn't a great example, and I don't remember where it came from.
```suggestion
```
Since the issue was really only about the scalar version of `newton`, let's just take this out.
def lhs(x):
assert not res.converged
assert res.flag == 'convergence error'
@pytest.mark.parametrize('solver_name',
['brentq', 'brenth', 'bisect', 'ridder', 'toms748'])
|
codereview_new_python_data_13249
|
def odds_ratio(table, *, kind='conditional'):
The 95% confidence interval for the conditional odds ratio is
approximately (0.62, 0.94).
-The fact that the entire 95% confidence interval falls below 1 supports
-the authors' conclusion that the aspirin was associated with a statistically
-significant reduction in ischemic stroke.```
"""
if kind not in ['conditional', 'sample']:
raise ValueError("`kind` must be 'conditional' or 'sample'.")
```suggestion
The fact that the entire 95% confidence interval falls below 1 supports
the authors' conclusion that the aspirin was associated with a
statistically significant reduction in ischemic stroke.
"""
```
def odds_ratio(table, *, kind='conditional'):
The 95% confidence interval for the conditional odds ratio is
approximately (0.62, 0.94).
+ The fact that the entire 95% confidence interval falls below 1 supports
+ the authors' conclusion that the aspirin was associated with a
+ statistically significant reduction in ischemic stroke.
"""
if kind not in ['conditional', 'sample']:
raise ValueError("`kind` must be 'conditional' or 'sample'.")
|
codereview_new_python_data_13250
|
.. autosummary::
:toctree: generated/
- f_ishigami
- sobol_indices
Plot-tests
----------
This could also go in another section. Open to suggestions.
.. autosummary::
:toctree: generated/
+ f_ishigami
+ sobol_indices
Plot-tests
----------
|
codereview_new_python_data_13251
|
def chi2_contingency(observed, correction=True, lambda_=None):
>>> import numpy as np
>>> from scipy.stats import chi2_contingency
>>> table = np.array([[179, 230], [21032, 21018]])
- >>> res = chi2_contingency(obs)
>>> res.statistic
6.084250213339923
>>> res.pvalue
```suggestion
>>> res = chi2_contingency(table)
```
def chi2_contingency(observed, correction=True, lambda_=None):
>>> import numpy as np
>>> from scipy.stats import chi2_contingency
>>> table = np.array([[179, 230], [21032, 21018]])
+ >>> res = chi2_contingency(table)
>>> res.statistic
6.084250213339923
>>> res.pvalue
|
codereview_new_python_data_13252
|
def chi2_contingency(observed, correction=True, lambda_=None):
.. [4] Berger, Jeffrey S. et al. "Aspirin for the Primary Prevention of
Cardiovascular Events in Women and Men: A Sex-Specific
Meta-analysis of Randomized Controlled Trials."
- JAMA, 295(3):306–313, :doi:`10.1001/jama.295.3.306`, 2006.
Examples
--------
```suggestion
JAMA, 295(3):306-313, :doi:`10.1001/jama.295.3.306`, 2006.
```
def chi2_contingency(observed, correction=True, lambda_=None):
.. [4] Berger, Jeffrey S. et al. "Aspirin for the Primary Prevention of
Cardiovascular Events in Women and Men: A Sex-Specific
Meta-analysis of Randomized Controlled Trials."
+ JAMA, 295(3):306-313, :doi:`10.1001/jama.295.3.306`, 2006.
Examples
--------
|
codereview_new_python_data_13253
|
class LatinHypercube(QMCEngine):
expensive to cover the space. When numerical experiments are costly,
QMC enables analysis that may not be possible if using a grid.
- The six parameters of the model represented the probability of illness,
the probability of withdrawal, and four contact probabilities,
The authors assumed uniform distributions for all parameters and generated
50 samples.
```suggestion
The six parameters of the model represented the probability of illness,
```
class LatinHypercube(QMCEngine):
expensive to cover the space. When numerical experiments are costly,
QMC enables analysis that may not be possible if using a grid.
+ The six parameters of the model represented the probability of illness,
the probability of withdrawal, and four contact probabilities,
The authors assumed uniform distributions for all parameters and generated
50 samples.
|
codereview_new_python_data_13254
|
def pearsonr(x, y, *, alternative='two-sided'):
x = np.asarray(x)
y = np.asarray(y)
- if True in np.iscomplex(x) or True in np.iscomplex(y):
raise ValueError('This function does not support complex data')
# If an input is constant, the correlation coefficient is not defined.
Since we have NumPy arrays, we would usually use `np.any` or the `any` method of the arrays rather than pure-Python.
```suggestion
if np.iscomplex(x).any() or np.iscomplex(y).any():
```
But that would be slow, because `any` would check every element.
For that reason, I'd suggest checking the dtype:
```suggestion
if (np.issubdtype(x.dtype, np.complexfloating)
or np.issubdtype(y.dtype, np.complexfloating)):
```
def pearsonr(x, y, *, alternative='two-sided'):
x = np.asarray(x)
y = np.asarray(y)
+ if (np.issubdtype(x.dtype, np.complexfloating)
+ or np.issubdtype(y.dtype, np.complexfloating)):
raise ValueError('This function does not support complex data')
# If an input is constant, the correlation coefficient is not defined.
|
codereview_new_python_data_13255
|
def test_len1(self):
def test_complex_data(self):
x = [-1j, -2j, -3.0j]
y = [-1j, -2j, -3.0j]
- assert_raises(ValueError, stats.pearsonr, x, y)
class TestFisherExact:
There are many `ValueErrors` out there. This test should only pass if the one we have in mind is raised.
```suggestion
message = 'This function does not support complex data'
with pytest.raises(ValueError, match=message):
stats.pearsonr(x, y)
```
def test_len1(self):
def test_complex_data(self):
x = [-1j, -2j, -3.0j]
y = [-1j, -2j, -3.0j]
+ message = 'This function does not support complex data'
+ with pytest.raises(ValueError, match=message):
+ stats.pearsonr(x, y)
class TestFisherExact:
|
codereview_new_python_data_13256
|
def test_vonmises_fit_all(kappa):
loc = 0.25*np.pi
data = stats.vonmises(loc=loc, kappa=kappa).rvs(100000, random_state=rng)
loc_fit, kappa_fit = stats.vonmises.fit(data)
- loc_vector = np.array([np.cos(loc), np.sin(loc)])
- loc_vector_fit = np.array([np.cos(loc_fit), np.sin(loc_fit)])
- assert_allclose(loc_vector, loc_vector_fit, rtol=1e-2)
assert_allclose(kappa, kappa_fit, rtol=1e-2)
def test_vonmises_fit_shape():
Seems unnecessary, vs the other test
def test_vonmises_fit_all(kappa):
loc = 0.25*np.pi
data = stats.vonmises(loc=loc, kappa=kappa).rvs(100000, random_state=rng)
loc_fit, kappa_fit = stats.vonmises.fit(data)
+ assert_allclose(loc_fit, loc, rtol=1e-2)
assert_allclose(kappa, kappa_fit, rtol=1e-2)
def test_vonmises_fit_shape():
|
codereview_new_python_data_13257
|
def _mode_result(mode, count):
count = count.dtype(0) if i else count
else:
count[i] = 0
- return ModeResult(mode, count * (~np.isnan(count)))
@_axis_nan_policy_factory(_mode_result, override={'vectorization': True,
Oops, this can be simplified.
```suggestion
return ModeResult(mode, count)
```
I was playing around with removing all of the code above and just doing `count * (~np.isnan(count))`, but `np.nan * 0` is `np.nan`, not `0`.
def _mode_result(mode, count):
count = count.dtype(0) if i else count
else:
count[i] = 0
+ return ModeResult(mode, count)
@_axis_nan_policy_factory(_mode_result, override={'vectorization': True,
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.