code
stringlengths 38
801k
| repo_path
stringlengths 6
263
|
|---|---|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # 09 Strain Gage
#
# This is one of the most commonly used sensor. It is used in many transducers. Its fundamental operating principle is fairly easy to understand and it will be the purpose of this lecture.
#
# A strain gage is essentially a thin wire that is wrapped on film of plastic.
# <img src="img/StrainGage.png" width="200">
# The strain gage is then mounted (glued) on the part for which the strain must be measured.
# <img src="img/Strain_gauge_2.jpg" width="200">
#
# ## Stress, Strain
# When a beam is under axial load, the axial stress, $\sigma_a$, is defined as:
# \begin{align*}
# \sigma_a = \frac{F}{A}
# \end{align*}
# with $F$ the axial load, and $A$ the cross sectional area of the beam under axial load.
#
# <img src="img/BeamUnderStrain.png" width="200">
#
# Under the load, the beam of length $L$ will extend by $dL$, giving rise to the definition of strain, $\epsilon_a$:
# \begin{align*}
# \epsilon_a = \frac{dL}{L}
# \end{align*}
# The beam will also contract laterally: the cross sectional area is reduced by $dA$. This results in a transverval strain $\epsilon_t$. The transversal and axial strains are related by the Poisson's ratio:
# \begin{align*}
# \nu = - \frac{\epsilon_t }{\epsilon_a}
# \end{align*}
# For a metal the Poission's ratio is typically $\nu = 0.3$, for an incompressible material, such as rubber (or water), $\nu = 0.5$.
#
# Within the elastic limit, the axial stress and axial strain are related through Hooke's law by the Young's modulus, $E$:
# \begin{align*}
# \sigma_a = E \epsilon_a
# \end{align*}
#
# <img src="img/ElasticRegime.png" width="200">
# ## Resistance of a wire
#
# The electrical resistance of a wire $R$ is related to its physical properties (the electrical resistiviy, $\rho$ in $\Omega$/m) and its geometry: length $L$ and cross sectional area $A$.
#
# \begin{align*}
# R = \frac{\rho L}{A}
# \end{align*}
#
# Mathematically, the change in wire dimension will result inchange in its electrical resistance. This can be derived from first principle:
# \begin{align}
# \frac{dR}{R} = \frac{d\rho}{\rho} + \frac{dL}{L} - \frac{dA}{A}
# \end{align}
# If the wire has a square cross section, then:
# \begin{align*}
# A & = L'^2 \\
# \frac{dA}{A} & = \frac{d(L'^2)}{L'^2} = \frac{2L'dL'}{L'^2} = 2 \frac{dL'}{L'}
# \end{align*}
# We have related the change in cross sectional area to the transversal strain.
# \begin{align*}
# \epsilon_t = \frac{dL'}{L'}
# \end{align*}
# Using the Poisson's ratio, we can relate then relate the change in cross-sectional area ($dA/A$) to axial strain $\epsilon_a = dL/L$.
# \begin{align*}
# \epsilon_t &= - \nu \epsilon_a \\
# \frac{dL'}{L'} &= - \nu \frac{dL}{L} \; \text{or}\\
# \frac{dA}{A} & = 2\frac{dL'}{L'} = -2 \nu \frac{dL}{L}
# \end{align*}
# Finally we can substitute express $dA/A$ in eq. for $dR/R$ and relate change in resistance to change of wire geometry, remembering that for a metal $\nu =0.3$:
# \begin{align}
# \frac{dR}{R} & = \frac{d\rho}{\rho} + \frac{dL}{L} - \frac{dA}{A} \\
# & = \frac{d\rho}{\rho} + \frac{dL}{L} - (-2\nu \frac{dL}{L}) \\
# & = \frac{d\rho}{\rho} + 1.6 \frac{dL}{L} = \frac{d\rho}{\rho} + 1.6 \epsilon_a
# \end{align}
# It also happens that for most metals, the resistivity increases with axial strain. In general, one can then related the change in resistance to axial strain by defining the strain gage factor:
# \begin{align}
# S = 1.6 + \frac{d\rho}{\rho}\cdot \frac{1}{\epsilon_a}
# \end{align}
# and finally, we have:
# \begin{align*}
# \frac{dR}{R} = S \epsilon_a
# \end{align*}
# $S$ is materials dependent and is typically equal to 2.0 for most commercially availabe strain gages. It is dimensionless.
#
# Strain gages are made of thin wire that is wraped in several loops, effectively increasing the length of the wire and therefore the sensitivity of the sensor.
#
# _Question:
#
# Explain why a longer wire is necessary to increase the sensitivity of the sensor_.
#
# Most commercially available strain gages have a nominal resistance (resistance under no load, $R_{ini}$) of 120 or 350 $\Omega$.
#
# Within the elastic regime, strain is typically within the range $10^{-6} - 10^{-3}$, in fact strain is expressed in unit of microstrain, with a 1 microstrain = $10^{-6}$. Therefore, changes in resistances will be of the same order. If one were to measure resistances, we will need a dynamic range of 120 dB, whih is typically very expensive. Instead, one uses the Wheatstone bridge to transform the change in resistance to a voltage, which is easier to measure and does not require such a large dynamic range.
# ## Wheatstone bridge:
# <img src="img/WheatstoneBridge.png" width="200">
#
# The output voltage is related to the difference in resistances in the bridge:
# \begin{align*}
# \frac{V_o}{V_s} = \frac{R_1R_3-R_2R_4}{(R_1+R_4)(R_2+R_3)}
# \end{align*}
#
# If the bridge is balanced, then $V_o = 0$, it implies: $R_1/R_2 = R_4/R_3$.
#
# In practice, finding a set of resistors that balances the bridge is challenging, and a potentiometer is used as one of the resistances to do minor adjustement to balance the bridge. If one did not do the adjustement (ie if we did not zero the bridge) then all the measurement will have an offset or bias that could be removed in a post-processing phase, as long as the bias stayed constant.
#
# If each resistance $R_i$ is made to vary slightly around its initial value, ie $R_i = R_{i,ini} + dR_i$. For simplicity, we will assume that the initial value of the four resistances are equal, ie $R_{1,ini} = R_{2,ini} = R_{3,ini} = R_{4,ini} = R_{ini}$. This implies that the bridge was initially balanced, then the output voltage would be:
#
# \begin{align*}
# \frac{V_o}{V_s} = \frac{1}{4} \left( \frac{dR_1}{R_{ini}} - \frac{dR_2}{R_{ini}} + \frac{dR_3}{R_{ini}} - \frac{dR_4}{R_{ini}} \right)
# \end{align*}
#
# Note here that the changes in $R_1$ and $R_3$ have a positive effect on $V_o$, while the changes in $R_2$ and $R_4$ have a negative effect on $V_o$. In practice, this means that is a beam is a in tension, then a strain gage mounted on the branch 1 or 3 of the Wheatstone bridge will produce a positive voltage, while a strain gage mounted on branch 2 or 4 will produce a negative voltage. One takes advantage of this to increase sensitivity to measure strain.
#
# ### Quarter bridge
# One uses only one quarter of the bridge, ie strain gages are only mounted on one branch of the bridge.
#
# \begin{align*}
# \frac{V_o}{V_s} = \pm \frac{1}{4} \epsilon_a S
# \end{align*}
# Sensitivity, $G$:
# \begin{align*}
# G = \frac{V_o}{\epsilon_a} = \pm \frac{1}{4}S V_s
# \end{align*}
#
#
# ### Half bridge
# One uses half of the bridge, ie strain gages are mounted on two branches of the bridge.
#
# \begin{align*}
# \frac{V_o}{V_s} = \pm \frac{1}{2} \epsilon_a S
# \end{align*}
#
# ### Full bridge
#
# One uses of the branches of the bridge, ie strain gages are mounted on each branch.
#
# \begin{align*}
# \frac{V_o}{V_s} = \pm \epsilon_a S
# \end{align*}
#
# Therefore, as we increase the order of bridge, the sensitivity of the instrument increases. However, one should be carefull how we mount the strain gages as to not cancel out their measurement.
# _Exercise_
#
# 1- Wheatstone bridge
#
# <img src="img/WheatstoneBridge.png" width="200">
#
# > How important is it to know \& match the resistances of the resistors you employ to create your bridge?
# > How would you do that practically?
# > Assume $R_1=120\,\Omega$, $R_2=120\,\Omega$, $R_3=120\,\Omega$, $R_4=110\,\Omega$, $V_s=5.00\,\text{V}$. What is $V_\circ$?
Vs = 5.00
Vo = (120**2-120*110)/(230*240) * Vs
print('Vo = ',Vo, ' V')
# typical range in strain a strain gauge can measure
# 1 -1000 micro-Strain
AxialStrain = 1000*10**(-6) # axial strain
StrainGageFactor = 2
R_ini = 120 # Ohm
R_1 = R_ini+R_ini*StrainGageFactor*AxialStrain
print(R_1)
Vo = (120**2-120*(R_1))/((120+R_1)*240) * Vs
print('Vo = ', Vo, ' V')
# > How important is it to know \& match the resistances of the resistors you employ to create your bridge?
# > How would you do that practically?
# > Assume $R_1= R_2 =R_3=120\,\Omega$, $R_4=120.01\,\Omega$, $V_s=5.00\,\text{V}$. What is $V_\circ$?
Vs = 5.00
Vo = (120**2-120*120.01)/(240.01*240) * Vs
print(Vo)
# 2- Strain gage 1:
#
# One measures the strain on a bridge steel beam. The modulus of elasticity is $E=190$ GPa. Only one strain gage is mounted on the bottom of the beam; the strain gage factor is $S=2.02$.
#
# > a) What kind of electronic circuit will you use? Draw a sketch of it.
#
# > b) Assume all your resistors including the unloaded strain gage are balanced and measure $120\,\Omega$, and that the strain gage is at location $R_2$. The supply voltage is $5.00\,\text{VDC}$. Will $V_\circ$ be positive or negative when a downward load is added?
# In practice, we cannot have all resistances = 120 $\Omega$. at zero load, the bridge will be unbalanced (show $V_o \neq 0$). How could we balance our bridge?
#
# Use a potentiometer to balance bridge, for the load cell, we ''zero'' the instrument.
#
# Other option to zero-out our instrument? Take data at zero-load, record the voltage, $V_{o,noload}$. Substract $V_{o,noload}$ to my data.
# > c) For a loading in which $V_\circ = -1.25\,\text{mV}$, calculate the strain $\epsilon_a$ in units of microstrain.
# \begin{align*}
# \frac{V_o}{V_s} & = - \frac{1}{4} \epsilon_a S\\
# \epsilon_a & = -\frac{4}{S} \frac{V_o}{V_s}
# \end{align*}
S = 2.02
Vo = -0.00125
Vs = 5
eps_a = -1*(4/S)*(Vo/Vs)
print(eps_a)
# > d) Calculate the axial stress (in MPa) in the beam under this load.
# > e) You now want more sensitivity in your measurement, you install a second strain gage on to
# p of the beam. Which resistor should you use for this second active strain gage?
#
# > f) With this new setup and the same applied load than previously, what should be the output voltage?
# 3- Strain Gage with Long Lead Wires
#
# <img src="img/StrainGageLongWires.png" width="360">
#
# A quarter bridge strain gage Wheatstone bridge circuit is constructed with $120\,\Omega$ resistors and a $120\,\Omega$ strain gage. For this practical application, the strain gage is located very far away form the DAQ station and the lead wires to the strain gage are $10\,\text{m}$ long and the lead wire have a resistance of $0.080\,\Omega/\text{m}$. The lead wire resistance can lead to problems since $R_{lead}$ changes with temperature.
#
# > Design a modified circuit that will cancel out the effect of the lead wires.
# ## Homework
#
|
Lectures/09_StrainGage.ipynb
|
# ---
# jupyter:
# jupytext:
# split_at_heading: true
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
#export
from fastai.basics import *
from fastai.tabular.core import *
from fastai.tabular.model import *
from fastai.tabular.data import *
#hide
from nbdev.showdoc import *
# +
#default_exp tabular.learner
# -
# # Tabular learner
#
# > The function to immediately get a `Learner` ready to train for tabular data
# The main function you probably want to use in this module is `tabular_learner`. It will automatically create a `TabulaModel` suitable for your data and infer the irght loss function. See the [tabular tutorial](http://docs.fast.ai/tutorial.tabular) for an example of use in context.
# ## Main functions
#export
@log_args(but_as=Learner.__init__)
class TabularLearner(Learner):
"`Learner` for tabular data"
def predict(self, row):
tst_to = self.dls.valid_ds.new(pd.DataFrame(row).T)
tst_to.process()
tst_to.conts = tst_to.conts.astype(np.float32)
dl = self.dls.valid.new(tst_to)
inp,preds,_,dec_preds = self.get_preds(dl=dl, with_input=True, with_decoded=True)
i = getattr(self.dls, 'n_inp', -1)
b = (*tuplify(inp),*tuplify(dec_preds))
full_dec = self.dls.decode((*tuplify(inp),*tuplify(dec_preds)))
return full_dec,dec_preds[0],preds[0]
show_doc(TabularLearner, title_level=3)
# It works exactly as a normal `Learner`, the only difference is that it implements a `predict` method specific to work on a row of data.
#export
@log_args(to_return=True, but_as=Learner.__init__)
@delegates(Learner.__init__)
def tabular_learner(dls, layers=None, emb_szs=None, config=None, n_out=None, y_range=None, **kwargs):
"Get a `Learner` using `dls`, with `metrics`, including a `TabularModel` created using the remaining params."
if config is None: config = tabular_config()
if layers is None: layers = [200,100]
to = dls.train_ds
emb_szs = get_emb_sz(dls.train_ds, {} if emb_szs is None else emb_szs)
if n_out is None: n_out = get_c(dls)
assert n_out, "`n_out` is not defined, and could not be infered from data, set `dls.c` or pass `n_out`"
if y_range is None and 'y_range' in config: y_range = config.pop('y_range')
model = TabularModel(emb_szs, len(dls.cont_names), n_out, layers, y_range=y_range, **config)
return TabularLearner(dls, model, **kwargs)
# If your data was built with fastai, you probably won't need to pass anything to `emb_szs` unless you want to change the default of the library (produced by `get_emb_sz`), same for `n_out` which should be automatically inferred. `layers` will default to `[200,100]` and is passed to `TabularModel` along with the `config`.
#
# Use `tabular_config` to create a `config` and cusotmize the model used. There is just easy access to `y_range` because this argument is often used.
#
# All the other arguments are passed to `Learner`.
path = untar_data(URLs.ADULT_SAMPLE)
df = pd.read_csv(path/'adult.csv')
cat_names = ['workclass', 'education', 'marital-status', 'occupation', 'relationship', 'race']
cont_names = ['age', 'fnlwgt', 'education-num']
procs = [Categorify, FillMissing, Normalize]
dls = TabularDataLoaders.from_df(df, path, procs=procs, cat_names=cat_names, cont_names=cont_names,
y_names="salary", valid_idx=list(range(800,1000)), bs=64)
learn = tabular_learner(dls)
#hide
tst = learn.predict(df.iloc[0])
# +
#hide
#test y_range is passed
learn = tabular_learner(dls, y_range=(0,32))
assert isinstance(learn.model.layers[-1], SigmoidRange)
test_eq(learn.model.layers[-1].low, 0)
test_eq(learn.model.layers[-1].high, 32)
learn = tabular_learner(dls, config = tabular_config(y_range=(0,32)))
assert isinstance(learn.model.layers[-1], SigmoidRange)
test_eq(learn.model.layers[-1].low, 0)
test_eq(learn.model.layers[-1].high, 32)
# -
#export
@typedispatch
def show_results(x:Tabular, y:Tabular, samples, outs, ctxs=None, max_n=10, **kwargs):
df = x.all_cols[:max_n]
for n in x.y_names: df[n+'_pred'] = y[n][:max_n].values
display_df(df)
# ## Export -
#hide
from nbdev.export import notebook2script
notebook2script()
|
nbs/43_tabular.learner.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <table class="ee-notebook-buttons" align="left">
# <td><a target="_blank" href="https://github.com/giswqs/earthengine-py-notebooks/tree/master/Algorithms/landsat_radiance.ipynb"><img width=32px src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" /> View source on GitHub</a></td>
# <td><a target="_blank" href="https://nbviewer.jupyter.org/github/giswqs/earthengine-py-notebooks/blob/master/Algorithms/landsat_radiance.ipynb"><img width=26px src="https://upload.wikimedia.org/wikipedia/commons/thumb/3/38/Jupyter_logo.svg/883px-Jupyter_logo.svg.png" />Notebook Viewer</a></td>
# <td><a target="_blank" href="https://colab.research.google.com/github/giswqs/earthengine-py-notebooks/blob/master/Algorithms/landsat_radiance.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" /> Run in Google Colab</a></td>
# </table>
# ## Install Earth Engine API and geemap
# Install the [Earth Engine Python API](https://developers.google.com/earth-engine/python_install) and [geemap](https://geemap.org). The **geemap** Python package is built upon the [ipyleaflet](https://github.com/jupyter-widgets/ipyleaflet) and [folium](https://github.com/python-visualization/folium) packages and implements several methods for interacting with Earth Engine data layers, such as `Map.addLayer()`, `Map.setCenter()`, and `Map.centerObject()`.
# The following script checks if the geemap package has been installed. If not, it will install geemap, which automatically installs its [dependencies](https://github.com/giswqs/geemap#dependencies), including earthengine-api, folium, and ipyleaflet.
# +
# Installs geemap package
import subprocess
try:
import geemap
except ImportError:
print('Installing geemap ...')
subprocess.check_call(["python", '-m', 'pip', 'install', 'geemap'])
# -
import ee
import geemap
# ## Create an interactive map
# The default basemap is `Google Maps`. [Additional basemaps](https://github.com/giswqs/geemap/blob/master/geemap/basemaps.py) can be added using the `Map.add_basemap()` function.
Map = geemap.Map(center=[40,-100], zoom=4)
Map
# ## Add Earth Engine Python script
# +
# Add Earth Engine dataset
# Load a raw Landsat scene and display it.
raw = ee.Image('LANDSAT/LC08/C01/T1/LC08_044034_20140318')
Map.centerObject(raw, 10)
Map.addLayer(raw, {'bands': ['B4', 'B3', 'B2'], 'min': 6000, 'max': 12000}, 'raw')
# Convert the raw data to radiance.
radiance = ee.Algorithms.Landsat.calibratedRadiance(raw)
Map.addLayer(radiance, {'bands': ['B4', 'B3', 'B2'], 'max': 90}, 'radiance')
# Convert the raw data to top-of-atmosphere reflectance.
toa = ee.Algorithms.Landsat.TOA(raw)
Map.addLayer(toa, {'bands': ['B4', 'B3', 'B2'], 'max': 0.2}, 'toa reflectance')
# -
# ## Display Earth Engine data layers
Map.addLayerControl() # This line is not needed for ipyleaflet-based Map.
Map
|
Algorithms/landsat_radiance.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# Copyright 2020 NVIDIA Corporation. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# http://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
# ==============================================================================
# -
# <img src="http://developer.download.nvidia.com/compute/machine-learning/frameworks/nvidia_logo.png" style="width: 90px; float: right;">
#
# # Object Detection with TRTorch (SSD)
# ---
# ## Overview
#
#
# In PyTorch 1.0, TorchScript was introduced as a method to separate your PyTorch model from Python, make it portable and optimizable.
#
# TRTorch is a compiler that uses TensorRT (NVIDIA's Deep Learning Optimization SDK and Runtime) to optimize TorchScript code. It compiles standard TorchScript modules into ones that internally run with TensorRT optimizations.
#
# TensorRT can take models from any major framework and specifically tune them to perform better on specific target hardware in the NVIDIA family, and TRTorch enables us to continue to remain in the PyTorch ecosystem whilst doing so. This allows us to leverage the great features in PyTorch, including module composability, its flexible tensor implementation, data loaders and more. TRTorch is available to use with both PyTorch and LibTorch.
#
# To get more background information on this, we suggest the **lenet-getting-started** notebook as a primer for getting started with TRTorch.
# ### Learning objectives
#
# This notebook demonstrates the steps for compiling a TorchScript module with TRTorch on a pretrained SSD network, and running it to test the speedup obtained.
#
# ## Contents
# 1. [Requirements](#1)
# 2. [SSD Overview](#2)
# 3. [Creating TorchScript modules](#3)
# 4. [Compiling with TRTorch](#4)
# 5. [Running Inference](#5)
# 6. [Measuring Speedup](#6)
# 7. [Conclusion](#7)
# ---
# <a id="1"></a>
# ## 1. Requirements
#
# Follow the steps in `notebooks/README` to prepare a Docker container, within which you can run this demo notebook.
#
# In addition to that, run the following cell to obtain additional libraries specific to this demo.
# Known working versions
# !pip install numpy==1.21.2 scipy==1.5.2 Pillow==6.2.0 scikit-image==0.17.2 matplotlib==3.3.0
# ---
# <a id="2"></a>
# ## 2. SSD
#
# ### Single Shot MultiBox Detector model for object detection
#
# _ | _
# - | -
# 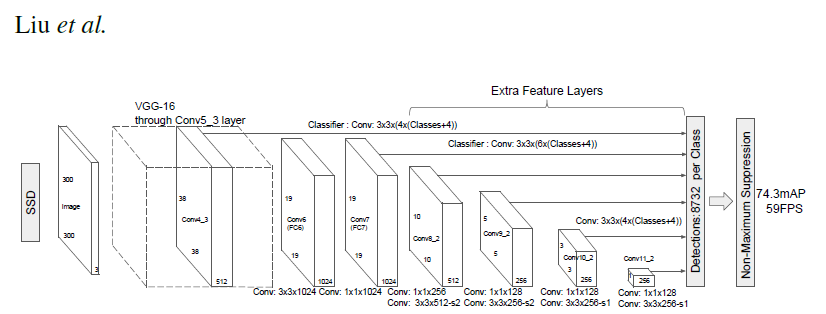 | 
# PyTorch has a model repository called the PyTorch Hub, which is a source for high quality implementations of common models. We can get our SSD model pretrained on [COCO](https://cocodataset.org/#home) from there.
#
# ### Model Description
#
# This SSD300 model is based on the
# [SSD: Single Shot MultiBox Detector](https://arxiv.org/abs/1512.02325) paper, which
# describes SSD as “a method for detecting objects in images using a single deep neural network".
# The input size is fixed to 300x300.
#
# The main difference between this model and the one described in the paper is in the backbone.
# Specifically, the VGG model is obsolete and is replaced by the ResNet-50 model.
#
# From the
# [Speed/accuracy trade-offs for modern convolutional object detectors](https://arxiv.org/abs/1611.10012)
# paper, the following enhancements were made to the backbone:
# * The conv5_x, avgpool, fc and softmax layers were removed from the original classification model.
# * All strides in conv4_x are set to 1x1.
#
# The backbone is followed by 5 additional convolutional layers.
# In addition to the convolutional layers, we attached 6 detection heads:
# * The first detection head is attached to the last conv4_x layer.
# * The other five detection heads are attached to the corresponding 5 additional layers.
#
# Detector heads are similar to the ones referenced in the paper, however,
# they are enhanced by additional BatchNorm layers after each convolution.
#
# More information about this SSD model is available at Nvidia's "DeepLearningExamples" Github [here](https://github.com/NVIDIA/DeepLearningExamples/tree/master/PyTorch/Detection/SSD).
import torch
torch.hub._validate_not_a_forked_repo=lambda a,b,c: True
# List of available models in PyTorch Hub from Nvidia/DeepLearningExamples
torch.hub.list('NVIDIA/DeepLearningExamples:torchhub')
# load SSD model pretrained on COCO from Torch Hub
precision = 'fp32'
ssd300 = torch.hub.load('NVIDIA/DeepLearningExamples:torchhub', 'nvidia_ssd', model_math=precision);
# Setting `precision="fp16"` will load a checkpoint trained with mixed precision
# into architecture enabling execution on Tensor Cores. Handling mixed precision data requires the Apex library.
# ### Sample Inference
# We can now run inference on the model. This is demonstrated below using sample images from the COCO 2017 Validation set.
# +
# Sample images from the COCO validation set
uris = [
'http://images.cocodataset.org/val2017/000000397133.jpg',
'http://images.cocodataset.org/val2017/000000037777.jpg',
'http://images.cocodataset.org/val2017/000000252219.jpg'
]
# For convenient and comprehensive formatting of input and output of the model, load a set of utility methods.
utils = torch.hub.load('NVIDIA/DeepLearningExamples:torchhub', 'nvidia_ssd_processing_utils')
# Format images to comply with the network input
inputs = [utils.prepare_input(uri) for uri in uris]
tensor = utils.prepare_tensor(inputs, False)
# The model was trained on COCO dataset, which we need to access in order to
# translate class IDs into object names.
classes_to_labels = utils.get_coco_object_dictionary()
# +
# Next, we run object detection
model = ssd300.eval().to("cuda")
detections_batch = model(tensor)
# By default, raw output from SSD network per input image contains 8732 boxes with
# localization and class probability distribution.
# Let’s filter this output to only get reasonable detections (confidence>40%) in a more comprehensive format.
results_per_input = utils.decode_results(detections_batch)
best_results_per_input = [utils.pick_best(results, 0.40) for results in results_per_input]
# -
# ### Visualize results
# +
from matplotlib import pyplot as plt
import matplotlib.patches as patches
# The utility plots the images and predicted bounding boxes (with confidence scores).
def plot_results(best_results):
for image_idx in range(len(best_results)):
fig, ax = plt.subplots(1)
# Show original, denormalized image...
image = inputs[image_idx] / 2 + 0.5
ax.imshow(image)
# ...with detections
bboxes, classes, confidences = best_results[image_idx]
for idx in range(len(bboxes)):
left, bot, right, top = bboxes[idx]
x, y, w, h = [val * 300 for val in [left, bot, right - left, top - bot]]
rect = patches.Rectangle((x, y), w, h, linewidth=1, edgecolor='r', facecolor='none')
ax.add_patch(rect)
ax.text(x, y, "{} {:.0f}%".format(classes_to_labels[classes[idx] - 1], confidences[idx]*100), bbox=dict(facecolor='white', alpha=0.5))
plt.show()
# -
# Visualize results without TRTorch/TensorRT
plot_results(best_results_per_input)
# ### Benchmark utility
# +
import time
import numpy as np
import torch.backends.cudnn as cudnn
cudnn.benchmark = True
# Helper function to benchmark the model
def benchmark(model, input_shape=(1024, 1, 32, 32), dtype='fp32', nwarmup=50, nruns=1000):
input_data = torch.randn(input_shape)
input_data = input_data.to("cuda")
if dtype=='fp16':
input_data = input_data.half()
print("Warm up ...")
with torch.no_grad():
for _ in range(nwarmup):
features = model(input_data)
torch.cuda.synchronize()
print("Start timing ...")
timings = []
with torch.no_grad():
for i in range(1, nruns+1):
start_time = time.time()
pred_loc, pred_label = model(input_data)
torch.cuda.synchronize()
end_time = time.time()
timings.append(end_time - start_time)
if i%10==0:
print('Iteration %d/%d, avg batch time %.2f ms'%(i, nruns, np.mean(timings)*1000))
print("Input shape:", input_data.size())
print("Output location prediction size:", pred_loc.size())
print("Output label prediction size:", pred_label.size())
print('Average batch time: %.2f ms'%(np.mean(timings)*1000))
# -
# We check how well the model performs **before** we use TRTorch/TensorRT
# Model benchmark without TRTorch/TensorRT
model = ssd300.eval().to("cuda")
benchmark(model, input_shape=(128, 3, 300, 300), nruns=100)
# ---
# <a id="3"></a>
# ## 3. Creating TorchScript modules
# To compile with TRTorch, the model must first be in **TorchScript**. TorchScript is a programming language included in PyTorch which removes the Python dependency normal PyTorch models have. This conversion is done via a JIT compiler which given a PyTorch Module will generate an equivalent TorchScript Module. There are two paths that can be used to generate TorchScript: **Tracing** and **Scripting**. <br>
# - Tracing follows execution of PyTorch generating ops in TorchScript corresponding to what it sees. <br>
# - Scripting does an analysis of the Python code and generates TorchScript, this allows the resulting graph to include control flow which tracing cannot do.
#
# Tracing however due to its simplicity is more likely to compile successfully with TRTorch (though both systems are supported).
model = ssd300.eval().to("cuda")
traced_model = torch.jit.trace(model, [torch.randn((1,3,300,300)).to("cuda")])
# If required, we can also save this model and use it independently of Python.
# This is just an example, and not required for the purposes of this demo
torch.jit.save(traced_model, "ssd_300_traced.jit.pt")
# Obtain the average time taken by a batch of input with Torchscript compiled modules
benchmark(traced_model, input_shape=(128, 3, 300, 300), nruns=100)
# ---
# <a id="4"></a>
# ## 4. Compiling with TRTorch
# TorchScript modules behave just like normal PyTorch modules and are intercompatible. From TorchScript we can now compile a TensorRT based module. This module will still be implemented in TorchScript but all the computation will be done in TensorRT.
# +
import trtorch
# The compiled module will have precision as specified by "op_precision".
# Here, it will have FP16 precision.
trt_model = trtorch.compile(traced_model, {
"inputs": [trtorch.Input((3, 3, 300, 300))],
"enabled_precisions": {torch.float, torch.half}, # Run with FP16
"workspace_size": 1 << 20
})
# -
# ---
# <a id="5"></a>
# ## 5. Running Inference
# Next, we run object detection
# +
# using a TRTorch module is exactly the same as how we usually do inference in PyTorch i.e. model(inputs)
detections_batch = trt_model(tensor.to(torch.half)) # convert the input to half precision
# By default, raw output from SSD network per input image contains 8732 boxes with
# localization and class probability distribution.
# Let’s filter this output to only get reasonable detections (confidence>40%) in a more comprehensive format.
results_per_input = utils.decode_results(detections_batch)
best_results_per_input_trt = [utils.pick_best(results, 0.40) for results in results_per_input]
# -
# Now, let's visualize our predictions!
#
# Visualize results with TRTorch/TensorRT
plot_results(best_results_per_input_trt)
# We get similar results as before!
# ---
# ## 6. Measuring Speedup
# We can run the benchmark function again to see the speedup gained! Compare this result with the same batch-size of input in the case without TRTorch/TensorRT above.
# +
batch_size = 128
# Recompiling with batch_size we use for evaluating performance
trt_model = trtorch.compile(traced_model, {
"inputs": [trtorch.Input((batch_size, 3, 300, 300))],
"enabled_precisions": {torch.float, torch.half}, # Run with FP16
"workspace_size": 1 << 20
})
benchmark(trt_model, input_shape=(batch_size, 3, 300, 300), nruns=100, dtype="fp16")
# -
# ---
# ## 7. Conclusion
#
# In this notebook, we have walked through the complete process of compiling a TorchScript SSD300 model with TRTorch, and tested the performance impact of the optimization. We find that using the TRTorch compiled model, we gain significant speedup in inference without any noticeable drop in performance!
# ### Details
# For detailed information on model input and output,
# training recipies, inference and performance visit:
# [github](https://github.com/NVIDIA/DeepLearningExamples/tree/master/PyTorch/Detection/SSD)
# and/or [NGC](https://ngc.nvidia.com/catalog/model-scripts/nvidia:ssd_for_pytorch)
#
# ### References
#
# - [SSD: Single Shot MultiBox Detector](https://arxiv.org/abs/1512.02325) paper
# - [Speed/accuracy trade-offs for modern convolutional object detectors](https://arxiv.org/abs/1611.10012) paper
# - [SSD on NGC](https://ngc.nvidia.com/catalog/model-scripts/nvidia:ssd_for_pytorch)
# - [SSD on github](https://github.com/NVIDIA/DeepLearningExamples/tree/master/PyTorch/Detection/SSD)
|
notebooks/ssd-object-detection-demo.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Setting up
# +
# Dependencies
# %matplotlib inline
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import seaborn as sns
from scipy.stats import sem
plt.style.use('seaborn')
# Hide warning messages in notebook
# import warnings
# warnings.filterwarnings('ignore')
# -
# # Importing 4 csv files and merging them into one
# Import datasets
demo_2016 = pd.read_csv("assets/data/2016_demo_data.csv")
demo_2017 = pd.read_csv("assets/data/2017_demo_data.csv")
demo_2018 = pd.read_csv("assets/data/2018_demo_data.csv")
demo_2019 = pd.read_csv("assets/data/2019_demo_data.csv")
# Append datasets
final_df = demo_2016.append(demo_2017, ignore_index=True)
final_df = final_df.append(demo_2018, ignore_index=True)
final_df = final_df.append(demo_2019, ignore_index=True)
final_df
# +
# Export the dataframe (do this Only Once!)
# final_df.to_csv("assets/data/final_demo_data.csv", index=False)
# -
# # Importing the final csv file
final_demo = pd.read_csv("assets/data/final_demo_data.csv")
final_demo.head()
# # Checking the dataset
# Type of variables
final_demo.dtypes
# Any NaN in the dataset
final_demo.isnull().sum()
# Any uplicates (or similarities, mis-spellings) in ethnicity and city
ethnicity = final_demo["ethnicity"].unique()
city = final_demo["city"].unique()
# # Cleaning the dataset
# Change the type of "student_id" to string
final_demo["student_id"] = final_demo["student_id"].astype(str)
# Drop NaN in the dataset
final_demo.dropna(inplace=True)
# Replace ethnicity categories
final_demo.replace({"Asian Indian": "General Asian",
"Cambodian": "General Asian",
"Chinese": "General Asian",
"Filipino": "General Asian",
"Hmong": "General Asian",
"Japanese": "General Asian",
"Korean": "General Asian",
"Laotian": "General Asian",
"Other Asian": "General Asian",
"Vietnamese": "General Asian",
"Samoan": "Pacific Islander",
"Other Pacific Islander": "Pacific Islander",
"Guamanian": "Pacific Islander",
"Tahitian": "Pacific Islander",
"Laotian": "Pacific Islander",
"Hawaiian": "Pacific Islander"}, inplace=True)
# Replace city categories
final_demo.replace({"So San Francisco": "South SF",
"South San Francisco": "South SF",
"So. San Francisco": "South SF",
"So San Francisco ": "South SF",
"So San Francisco": "South SF",
"So Sn Francisco": "South SF",
"So SanFrancisco": "South SF",
"So San Francisco": "South SF",
"So San Francico": "South SF",
"S San Francisco": "South SF",
"So San Fran": "South SF",
"south San Francisco": "South SF",
"South San Francisco ": "South SF",
"South San Francico": "South SF",
"So San Francsico": "South SF",
"So San Franicsco": "South SF",
"Concord ": "Concord",
"Burlingame ": "Burlingame",
"Pacifica ": "Pacifica",
"Daly cITY": "Daly City",
"Daly City ": "Daly City",
"Daly City ": "Daly City",
"Daly Citiy": "Daly City",
"Daly Ciy": "Daly City",
"Daly CIty": "Daly City",
"San Mateo ": "San Mateo"
}, inplace=True)
# # Creating yearly enrollment group
# Year subgroups
enroll2016 = final_demo.loc[final_demo["year"]==2016]
enroll2017 = final_demo.loc[final_demo["year"]==2017]
enroll2018 = final_demo.loc[final_demo["year"]==2018]
enroll2019 = final_demo.loc[final_demo["year"]==2019]
# ## + Creating subgroups - Ethnicity
# +
### YEAR 2016 ###
# Calcaulte number of enrollment based on ethnicity
enrollRace2016 = pd.DataFrame(enroll2016.groupby(["ethnicity"])["student_id"].count())
# Add year column
enrollRace2016["year"] = 2016
# Rename column name
enrollRace2016.rename({"student_id": "enrollment"}, axis=1, inplace=True)
# +
### YEAR 2017 ###
# Calcaulte number of enrollment based on ethnicity
enrollRace2017 = pd.DataFrame(enroll2017.groupby(["ethnicity"])["student_id"].count())
# Add year column
enrollRace2017["year"] = 2017
# Rename column name
enrollRace2017.rename({"student_id": "enrollment"}, axis=1, inplace=True)
# +
### YEAR 2018 ###
# Calcaulte number of enrollment based on ethnicity
enrollRace2018 = pd.DataFrame(enroll2018.groupby(["ethnicity"])["student_id"].count())
# Add year column
enrollRace2018["year"] = 2018
# Rename column name
enrollRace2018.rename({"student_id": "enrollment"}, axis=1, inplace=True)
# +
### YEAR 2019 ###
# Calcaulte number of enrollment based on ethnicity
enrollRace2019 = pd.DataFrame(enroll2019.groupby(["ethnicity"])["student_id"].count())
# Add year column
enrollRace2019["year"] = 2019
# Rename column name
enrollRace2019.rename({"student_id": "enrollment"}, axis=1, inplace=True)
# -
# Append 4 dataframes into one
enrollRace = enrollRace2016.append(enrollRace2017)
enrollRace = enrollRace.append(enrollRace2018)
enrollRace = enrollRace.append(enrollRace2019)
# Export to csv file
enrollRace.to_csv("assets/data/race_data.csv", index=True)
# ## + Creating subgroups - City
# +
### YEAR 2016 ###
# Calcaulte number of enrollment based on city
enrollCity2016 = pd.DataFrame(enroll2016.groupby(["city"])["student_id"].count())
# Add year column
enrollCity2016["year"] = 2016
# Rename column name
enrollCity2016.rename({"student_id": "enrollment"}, axis=1, inplace=True)
# -
enrollCity2016
|
jupyter/ethnicity.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Disambiguation
# +
import pprint
import subprocess
import sys
sys.path.append('../')
import numpy as np
import scipy as sp
import matplotlib.pyplot as plt
import matplotlib
import matplotlib.gridspec as gridspec
from mpl_toolkits.axes_grid1 import make_axes_locatable
import seaborn as sns
# %matplotlib inline
plt.rcParams['figure.figsize'] = (12.9, 12)
np.set_printoptions(suppress=True, precision=5)
sns.set(font_scale=3.5)
from network import Protocol, NetworkManager, BCPNNPerfect, TimedInput
from connectivity_functions import create_orthogonal_canonical_representation, build_network_representation
from connectivity_functions import get_weights_from_probabilities, get_probabilities_from_network_representation
from analysis_functions import calculate_recall_time_quantities, get_weights
from analysis_functions import get_weights_collections
from plotting_functions import plot_network_activity_angle, plot_weight_matrix
from analysis_functions import calculate_angle_from_history, calculate_winning_pattern_from_distances
from analysis_functions import calculate_patterns_timings
# -
epsilon = 10e-20
# +
def produce_overlaped_sequences(minicolumns, hypercolumns, n_patterns, s, r, mixed_start=False, contiguous=True):
n_r = int(r * n_patterns/2)
n_s = int(s * hypercolumns)
n_size = int(n_patterns / 2)
matrix = create_orthogonal_canonical_representation(minicolumns, hypercolumns)[:n_patterns]
sequence1 = matrix[:n_size]
sequence2 = matrix[n_size:]
if mixed_start:
start_index = 0
end_index = n_r
else:
start_index = max(int(0.5 * (n_size - n_r)), 0)
end_index = min(start_index + n_r, n_size)
for index in range(start_index, end_index):
if contiguous:
sequence2[index, :n_s] = sequence1[index, :n_s]
else:
sequence2[index, ...] = sequence1[index, ...]
sequence2[index, n_s:] = n_patterns + index
if False:
print(n_r)
print(n_size)
print(start_index)
print(end_index)
return sequence1, sequence2
def create_weights_from_two_sequences(nn, dt, n_patterns, s, r, mixed_start, contiguous,
training_time, inter_pulse_interval, inter_sequence_interval,
epochs, resting_time):
filtered = True
minicolumns = nn.minicolumns
hypercolumns = nn.hypercolumns
tau_z_pre_ampa = nn.tau_z_pre_ampa
tau_z_post_ampa = nn.tau_z_post_ampa
seq1, seq2 = produce_overlaped_sequences(minicolumns, hypercolumns, n_patterns, s, r,
mixed_start=mixed_start, contiguous=contiguous)
nr1 = build_network_representation(seq1, minicolumns, hypercolumns)
nr2 = build_network_representation(seq2, minicolumns, hypercolumns)
# Get the first
timed_input = TimedInput(nr1, dt, training_time, inter_pulse_interval=inter_pulse_interval,
inter_sequence_interval=inter_pulse_interval, epochs=epochs,
resting_time=resting_time)
S = timed_input.build_timed_input()
z_pre = timed_input.build_filtered_input_pre(tau_z_pre_ampa)
z_post = timed_input.build_filtered_input_post(tau_z_post_ampa)
pi1, pj1, P1 = timed_input.calculate_probabilities_from_time_signal(filtered=filtered)
w_timed1 = get_weights_from_probabilities(pi1, pj1, P1, minicolumns, hypercolumns)
t1 = timed_input.T_total
# Get the second
timed_input = TimedInput(nr2, dt, training_time, inter_pulse_interval=inter_pulse_interval,
inter_sequence_interval=inter_pulse_interval, epochs=epochs,
resting_time=resting_time)
S = timed_input.build_timed_input()
z_pre = timed_input.build_filtered_input_pre(tau_z_pre_ampa)
z_post = timed_input.build_filtered_input_post(tau_z_post_ampa)
t2 = timed_input.T_total
pi2, pj2, P2 = timed_input.calculate_probabilities_from_time_signal(filtered=filtered)
w_timed2 = get_weights_from_probabilities(pi2, pj2, P2, minicolumns, hypercolumns)
t_total = t1 + t2
# Mix
pi_total = (t1 / t_total) * pi1 + ((t_total - t1)/ t_total) * pi2
pj_total = (t1 / t_total) * pj1 + ((t_total - t1)/ t_total) * pj2
P_total = (t1 / t_total) * P1 + ((t_total - t1)/ t_total) * P2
w_total, beta = get_weights_from_probabilities(pi_total, pj_total, P_total, minicolumns, hypercolumns)
return seq1, seq2, nr1, nr2, w_total, beta
def calculate_recall_success_nr(manager, nr, T_recall, T_cue, debug=False, remove=0.020):
n_seq = nr.shape[0]
I_cue = nr[0]
# Do the recall
manager.run_network_recall(T_recall=T_recall, I_cue=I_cue, T_cue=T_cue,
reset=True, empty_history=True)
distances = calculate_angle_from_history(manager)
winning = calculate_winning_pattern_from_distances(distances)
timings = calculate_patterns_timings(winning, manager.dt, remove=remove)
pattern_sequence = [x[0] for x in timings]
# Calculate whether it was succesfull
success = 1.0
for index, pattern_index in enumerate(pattern_sequence[:n_seq]):
pattern = manager.patterns_dic[pattern_index]
goal_pattern = nr[index]
if not np.array_equal(pattern, goal_pattern):
success = 0.0
break
if debug:
return success, timings, pattern_sequence
else:
return success
# -
# ## An example
# +
always_learning = False
strict_maximum = True
perfect = False
z_transfer = False
k_perfect = True
diagonal_zero = False
normalized_currents = True
g_w_ampa = 2.0
g_w = 0.0
g_a = 10.0
tau_a = 0.250
G = 1.0
sigma = 0.0
tau_m = 0.020
tau_z_pre_ampa = 0.025
tau_z_post_ampa = 0.025
tau_p = 10.0
hypercolumns = 1
minicolumns = 20
n_patterns = 20
# Manager properties
dt = 0.001
values_to_save = ['o', 'i_ampa', 'a']
# Protocol
training_time = 0.100
inter_sequence_interval = 0.0
inter_pulse_interval = 0.0
resting_time = 2.0
epochs = 1
# Recall
T_recall = 1.0
T_cue = 0.020
# Patterns parameters
nn = BCPNNPerfect(hypercolumns, minicolumns, g_w_ampa=g_w_ampa, g_w=g_w, g_a=g_a, tau_a=tau_a, tau_m=tau_m,
sigma=sigma, G=G, tau_z_pre_ampa=tau_z_pre_ampa, tau_z_post_ampa=tau_z_post_ampa, tau_p=tau_p,
z_transfer=z_transfer, diagonal_zero=diagonal_zero, strict_maximum=strict_maximum,
perfect=perfect, k_perfect=k_perfect, always_learning=always_learning,
normalized_currents=normalized_currents)
# Build the manager
manager = NetworkManager(nn=nn, dt=dt, values_to_save=values_to_save)
# Build the protocol for training
mixed_start = False
contiguous = True
s = 1.0
r = 0.3
matrix = create_orthogonal_canonical_representation(minicolumns, hypercolumns)
aux = create_weights_from_two_sequences(nn, dt, n_patterns, s, r, mixed_start, contiguous,
training_time, inter_pulse_interval=inter_pulse_interval,
inter_sequence_interval=inter_sequence_interval, epochs=epochs,
resting_time=resting_time)
seq1, seq2, nr1, nr2, w_total, beta = aux
nr = np.concatenate((nr1, nr2))
aux, indexes = np.unique(nr, axis=0, return_index=True)
patterns_dic = {index:pattern for (index, pattern) in zip(indexes, aux)}
nn.w_ampa = w_total
manager.patterns_dic = patterns_dic
s = calculate_recall_success_nr(manager, nr1, T_recall, T_cue)
print('s1=', s)
plot_network_activity_angle(manager)
s = calculate_recall_success_nr(manager, nr2, T_recall, T_cue)
print('s2=', s)
plot_network_activity_angle(manager)
# -
plot_weight_matrix(nn, ampa=True)
# ## More systematic
# +
# %%time
always_learning = False
strict_maximum = True
perfect = False
z_transfer = False
k_perfect = True
diagonal_zero = False
normalized_currents = True
g_w_ampa = 2.0
g_w = 0.0
g_a = 10.0
tau_a = 0.250
g_beta = 1.0
G = 1.0
sigma = 0.0
tau_m = 0.010
tau_z_pre_ampa = 0.050
tau_z_post_ampa = 0.005
tau_p = 10.0
hypercolumns = 1
minicolumns = 20
n_patterns = 20
# Manager properties
dt = 0.001
values_to_save = ['o', 'i_ampa', 'a']
# Protocol
training_time = 0.100
inter_sequence_interval = 0.0
inter_pulse_interval = 0.0
epochs = 1
mixed_start = False
contiguous = True
s = 1.0
r = 0.25
# Recall
T_recall = 1.0
T_cue = 0.020
num = 10
r_space = np.linspace(0, 0.9, num=num)
success_vector = np.zeros(num)
factor = 0.2
g_w_ampa * (w_total[0, 0] - w_total[2, 0])
for r_index, r in enumerate(r_space):
print('r_index', r_index)
# The network
nn = BCPNNPerfect(hypercolumns, minicolumns, g_w_ampa=g_w_ampa, g_w=g_w, g_a=g_a, tau_a=tau_a, tau_m=tau_m,
sigma=sigma, G=G, tau_z_pre_ampa=tau_z_pre_ampa, tau_z_post_ampa=tau_z_post_ampa, tau_p=tau_p,
z_transfer=z_transfer, diagonal_zero=diagonal_zero, strict_maximum=strict_maximum,
perfect=perfect, k_perfect=k_perfect, always_learning=always_learning,
normalized_currents=normalized_currents, g_beta=g_beta)
# Build the manager
manager = NetworkManager(nn=nn, dt=dt, values_to_save=values_to_save)
# The sequences
matrix = create_orthogonal_canonical_representation(minicolumns, hypercolumns)
aux = create_weights_from_two_sequences(nn, dt, n_patterns, s, r, mixed_start, contiguous,
training_time, inter_pulse_interval=inter_pulse_interval,
inter_sequence_interval=inter_sequence_interval, epochs=epochs,
resting_time=resting_time)
seq1, seq2, nr1, nr2, w_total, beta = aux
nr = np.concatenate((nr1, nr2))
aux, indexes = np.unique(nr, axis=0, return_index=True)
patterns_dic = {index:pattern for (index, pattern) in zip(indexes, aux)}
nn.w_ampa = w_total
nn.beta = beta
manager.patterns_dic = patterns_dic
current = g_w_ampa * (w_total[0, 0] - w_total[2, 0])
noise = factor * current
nn.sigma = noise
# Recall
aux = calculate_recall_success_nr(manager, nr1, T_recall, T_cue, debug=True, remove=0.020)
s1, timings, pattern_sequence = aux
print('1', s1, pattern_sequence, seq1)
aux = calculate_recall_success_nr(manager, nr2, T_recall, T_cue, debug=True, remove=0.020)
s2, timings, pattern_sequence = aux
print('2', s2, pattern_sequence, seq2)
success_vector[r_index] = 0.5 * (s1 + s2)
# +
markersize = 15
linewdith = 8
fig = plt.figure(figsize=(16, 12))
ax = fig.add_subplot(111)
ax.plot(r_space, success_vector, 'o-', lw=linewdith, ms=markersize)
ax.axhline(0, ls='--', color='gray')
ax.axvline(0, ls='--', color='gray')
ax.set_xlabel('Overlap')
ax.set_ylabel('Recall')
# -
# #### tau_z
# +
# %%time
always_learning = False
strict_maximum = True
perfect = False
z_transfer = False
k_perfect = True
diagonal_zero = False
normalized_currents = True
g_w_ampa = 2.0
g_w = 0.0
g_a = 10.0
tau_a = 0.250
G = 1.0
sigma = 0.0
tau_m = 0.010
tau_z_pre_ampa = 0.025
tau_z_post_ampa = 0.025
tau_p = 10.0
hypercolumns = 1
minicolumns = 20
n_patterns = 20
# Manager properties
dt = 0.001
values_to_save = ['o']
# Protocol
training_time = 0.100
inter_sequence_interval = 0.0
inter_pulse_interval = 0.0
epochs = 1
mixed_start = False
contiguous = True
s = 1.0
r = 0.25
# Recall
T_recall = 1.0
T_cue = 0.020
num = 10
r_space = np.linspace(0, 0.9, num=num)
success_vector = np.zeros(num)
tau_z_list = [0.025, 0.035, 0.050, 0.075]
#tau_z_list = [0.025, 0.100, 0.250]
#tau_z_list = [0.025, 0.050]
success_list = []
for tau_z_pre_ampa in tau_z_list:
success_vector = np.zeros(num)
print(tau_z_pre_ampa)
for r_index, r in enumerate(r_space):
# The network
nn = BCPNNPerfect(hypercolumns, minicolumns, g_w_ampa=g_w_ampa, g_w=g_w, g_a=g_a, tau_a=tau_a, tau_m=tau_m,
sigma=sigma, G=G, tau_z_pre_ampa=tau_z_pre_ampa, tau_z_post_ampa=tau_z_post_ampa, tau_p=tau_p,
z_transfer=z_transfer, diagonal_zero=diagonal_zero, strict_maximum=strict_maximum,
perfect=perfect, k_perfect=k_perfect, always_learning=always_learning,
normalized_currents=normalized_currents)
# Build the manager
manager = NetworkManager(nn=nn, dt=dt, values_to_save=values_to_save)
# The sequences
matrix = create_orthogonal_canonical_representation(minicolumns, hypercolumns)
aux = create_weights_from_two_sequences(nn, dt, n_patterns, s, r, mixed_start, contiguous,
training_time, inter_pulse_interval=inter_pulse_interval,
inter_sequence_interval=inter_sequence_interval, epochs=epochs,
resting_time=resting_time)
seq1, seq2, nr1, nr2, w_total, beta = aux
nr = np.concatenate((nr1, nr2))
aux, indexes = np.unique(nr, axis=0, return_index=True)
patterns_dic = {index:pattern for (index, pattern) in zip(indexes, aux)}
nn.w_ampa = w_total
manager.patterns_dic = patterns_dic
# Recall
s1 = calculate_recall_success_nr(manager, nr1, T_recall, T_cue)
s2 = calculate_recall_success_nr(manager, nr2, T_recall, T_cue)
success_vector[r_index] = 0.5 * (s1 + s2)
success_list.append(np.copy(success_vector))
# +
markersize = 15
linewdith = 8
fig = plt.figure(figsize=(16, 12))
ax = fig.add_subplot(111)
for tau_z, success_vector in zip(tau_z_list, success_list):
ax.plot(r_space, success_vector, 'o-', lw=linewdith, ms=markersize, label=str(tau_z))
ax.axhline(0, ls='--', color='gray')
ax.axvline(0, ls='--', color='gray')
ax.set_xlabel('Overlap')
ax.set_ylabel('Recall')
ax.legend();
# -
# #### Scale
# +
# %%time
always_learning = False
strict_maximum = True
perfect = False
z_transfer = False
k_perfect = True
diagonal_zero = False
normalized_currents = True
g_w_ampa = 2.0
g_w = 0.0
g_a = 10.0
tau_a = 0.250
G = 1.0
sigma = 0.0
tau_m = 0.010
tau_z_pre_ampa = 0.025
tau_z_post_ampa = 0.025
tau_p = 10.0
hypercolumns = 1
minicolumns = 20
n_patterns = 20
# Manager properties
dt = 0.001
values_to_save = ['o']
# Protocol
training_time = 0.100
inter_sequence_interval = 0.0
inter_pulse_interval = 0.0
epochs = 1
mixed_start = False
contiguous = True
s = 1.0
r = 0.25
# Recall
T_recall = 1.0
T_cue = 0.020
num = 10
r_space = np.linspace(0, 0.9, num=num)
success_vector = np.zeros(num)
hypercolumns_list = [1, 3, 7, 10]
#tau_z_list = [0.025, 0.100, 0.250]
#tau_z_list = [0.025, 0.050]
success_list = []
for hypercolumns in hypercolumns_list:
success_vector = np.zeros(num)
print(hypercolumns)
for r_index, r in enumerate(r_space):
# The network
nn = BCPNNPerfect(hypercolumns, minicolumns, g_w_ampa=g_w_ampa, g_w=g_w, g_a=g_a, tau_a=tau_a, tau_m=tau_m,
sigma=sigma, G=G, tau_z_pre_ampa=tau_z_pre_ampa, tau_z_post_ampa=tau_z_post_ampa, tau_p=tau_p,
z_transfer=z_transfer, diagonal_zero=diagonal_zero, strict_maximum=strict_maximum,
perfect=perfect, k_perfect=k_perfect, always_learning=always_learning,
normalized_currents=normalized_currents)
# Build the manager
manager = NetworkManager(nn=nn, dt=dt, values_to_save=values_to_save)
# The sequences
matrix = create_orthogonal_canonical_representation(minicolumns, hypercolumns)
aux = create_weights_from_two_sequences(nn, dt, n_patterns, s, r, mixed_start, contiguous,
training_time, inter_pulse_interval=inter_pulse_interval,
inter_sequence_interval=inter_sequence_interval, epochs=epochs,
resting_time=resting_time)
seq1, seq2, nr1, nr2, w_total, beta = aux
nr = np.concatenate((nr1, nr2))
aux, indexes = np.unique(nr, axis=0, return_index=True)
patterns_dic = {index:pattern for (index, pattern) in zip(indexes, aux)}
nn.w_ampa = w_total
manager.patterns_dic = patterns_dic
# Recall
s1 = calculate_recall_success_nr(manager, nr1, T_recall, T_cue)
s2 = calculate_recall_success_nr(manager, nr2, T_recall, T_cue)
success_vector[r_index] = 0.5 * (s1 + s2)
success_list.append(np.copy(success_vector))
# +
markersize = 15
linewdith = 8
fig = plt.figure(figsize=(16, 12))
ax = fig.add_subplot(111)
for hypercolumns, success_vector in zip(hypercolumns_list, success_list):
ax.plot(r_space, success_vector, 'o-', lw=linewdith, ms=markersize, label=str(hypercolumns))
ax.axhline(0, ls='--', color='gray')
ax.axvline(0, ls='--', color='gray')
ax.set_xlabel('Overlap')
ax.set_ylabel('Recall')
ax.legend();
# -
# #### tau_m
# +
# %%time
always_learning = False
strict_maximum = True
perfect = False
z_transfer = False
k_perfect = True
diagonal_zero = False
normalized_currents = True
g_w_ampa = 2.0
g_w = 0.0
g_a = 10.0
tau_a = 0.250
G = 1.0
sigma = 0.0
tau_m = 0.010
tau_z_pre_ampa = 0.025
tau_z_post_ampa = 0.025
tau_p = 10.0
hypercolumns = 1
minicolumns = 20
n_patterns = 20
# Manager properties
dt = 0.001
values_to_save = ['o']
# Protocol
training_time = 0.100
inter_sequence_interval = 0.0
inter_pulse_interval = 0.0
epochs = 1
mixed_start = False
contiguous = True
s = 1.0
r = 0.25
# Recall
T_recall = 1.0
T_cue = 0.020
num = 10
r_space = np.linspace(0, 0.9, num=num)
success_vector = np.zeros(num)
tau_m_list = [0.001, 0.008, 0.020]
success_list = []
for tau_m in tau_m_list:
success_vector = np.zeros(num)
print(tau_m)
for r_index, r in enumerate(r_space):
# The network
nn = BCPNNPerfect(hypercolumns, minicolumns, g_w_ampa=g_w_ampa, g_w=g_w, g_a=g_a, tau_a=tau_a, tau_m=tau_m,
sigma=sigma, G=G, tau_z_pre_ampa=tau_z_pre_ampa, tau_z_post_ampa=tau_z_post_ampa, tau_p=tau_p,
z_transfer=z_transfer, diagonal_zero=diagonal_zero, strict_maximum=strict_maximum,
perfect=perfect, k_perfect=k_perfect, always_learning=always_learning,
normalized_currents=normalized_currents)
# Build the manager
manager = NetworkManager(nn=nn, dt=dt, values_to_save=values_to_save)
# The sequences
matrix = create_orthogonal_canonical_representation(minicolumns, hypercolumns)
aux = create_weights_from_two_sequences(nn, dt, n_patterns, s, r, mixed_start, contiguous,
training_time, inter_pulse_interval=inter_pulse_interval,
inter_sequence_interval=inter_sequence_interval, epochs=epochs,
resting_time=resting_time)
seq1, seq2, nr1, nr2, w_total, beta = aux
nr = np.concatenate((nr1, nr2))
aux, indexes = np.unique(nr, axis=0, return_index=True)
patterns_dic = {index:pattern for (index, pattern) in zip(indexes, aux)}
nn.w_ampa = w_total
manager.patterns_dic = patterns_dic
# Recall
s1 = calculate_recall_success_nr(manager, nr1, T_recall, T_cue)
s2 = calculate_recall_success_nr(manager, nr2, T_recall, T_cue)
success_vector[r_index] = 0.5 * (s1 + s2)
success_list.append(np.copy(success_vector))
# +
markersize = 15
linewdith = 8
fig = plt.figure(figsize=(16, 12))
ax = fig.add_subplot(111)
for tau_m, success_vector in zip(tau_m_list, success_list):
ax.plot(r_space, success_vector, 'o-', lw=linewdith, ms=markersize, label=str(tau_m))
ax.axhline(0, ls='--', color='gray')
ax.axvline(0, ls='--', color='gray')
ax.set_xlabel('Overlap')
ax.set_ylabel('Recall')
ax.legend();
# -
# #### training time
# +
# %%time
always_learning = False
strict_maximum = True
perfect = False
z_transfer = False
k_perfect = True
diagonal_zero = False
normalized_currents = True
g_w_ampa = 2.0
g_w = 0.0
g_a = 10.0
tau_a = 0.250
G = 1.0
sigma = 0.0
tau_m = 0.010
tau_z_pre_ampa = 0.025
tau_z_post_ampa = 0.025
tau_p = 10.0
hypercolumns = 1
minicolumns = 20
n_patterns = 20
# Manager properties
dt = 0.001
values_to_save = ['o']
# Protocol
training_time = 0.100
inter_sequence_interval = 0.0
inter_pulse_interval = 0.0
epochs = 1
mixed_start = False
contiguous = True
s = 1.0
r = 0.25
# Recall
T_recall = 1.0
T_cue = 0.020
num = 10
r_space = np.linspace(0, 0.9, num=num)
success_vector = np.zeros(num)
training_time_list = [0.050, 0.100, 0.250, 0.500]
success_list = []
for training_time in training_time_list:
success_vector = np.zeros(num)
print(training_time)
for r_index, r in enumerate(r_space):
# The network
nn = BCPNNPerfect(hypercolumns, minicolumns, g_w_ampa=g_w_ampa, g_w=g_w, g_a=g_a, tau_a=tau_a, tau_m=tau_m,
sigma=sigma, G=G, tau_z_pre_ampa=tau_z_pre_ampa, tau_z_post_ampa=tau_z_post_ampa, tau_p=tau_p,
z_transfer=z_transfer, diagonal_zero=diagonal_zero, strict_maximum=strict_maximum,
perfect=perfect, k_perfect=k_perfect, always_learning=always_learning,
normalized_currents=normalized_currents)
# Build the manager
manager = NetworkManager(nn=nn, dt=dt, values_to_save=values_to_save)
# The sequences
matrix = create_orthogonal_canonical_representation(minicolumns, hypercolumns)
aux = create_weights_from_two_sequences(nn, dt, n_patterns, s, r, mixed_start, contiguous,
training_time, inter_pulse_interval=inter_pulse_interval,
inter_sequence_interval=inter_sequence_interval, epochs=epochs,
resting_time=resting_time)
seq1, seq2, nr1, nr2, w_total, beta = aux
nr = np.concatenate((nr1, nr2))
aux, indexes = np.unique(nr, axis=0, return_index=True)
patterns_dic = {index:pattern for (index, pattern) in zip(indexes, aux)}
nn.w_ampa = w_total
manager.patterns_dic = patterns_dic
# Recall
s1 = calculate_recall_success_nr(manager, nr1, T_recall, T_cue)
s2 = calculate_recall_success_nr(manager, nr2, T_recall, T_cue)
success_vector[r_index] = 0.5 * (s1 + s2)
success_list.append(np.copy(success_vector))
# +
markersize = 15
linewdith = 8
fig = plt.figure(figsize=(16, 12))
ax = fig.add_subplot(111)
for training_time, success_vector in zip(training_time_list, success_list):
ax.plot(r_space, success_vector, 'o-', lw=linewdith, ms=markersize, label=str(training_time))
ax.axhline(0, ls='--', color='gray')
ax.axvline(0, ls='--', color='gray')
ax.set_xlabel('Overlap')
ax.set_ylabel('Recall')
ax.legend();
# -
# ## Systematic with noise
# +
# %%time
always_learning = False
strict_maximum = True
perfect = False
z_transfer = False
k_perfect = True
diagonal_zero = False
normalized_currents = True
g_w_ampa = 2.0
g_w = 0.0
g_a = 10.0
tau_a = 0.250
g_beta = 0.0
G = 1.0
sigma = 0.0
tau_m = 0.010
tau_z_pre_ampa = 0.050
tau_z_post_ampa = 0.005
tau_p = 10.0
hypercolumns = 1
minicolumns = 20
n_patterns = 20
# Manager properties
dt = 0.001
values_to_save = ['o', 'i_ampa', 'a']
# Protocol
training_time = 0.100
inter_sequence_interval = 0.0
inter_pulse_interval = 0.0
epochs = 1
mixed_start = False
contiguous = True
s = 1.0
r = 0.25
# Recall
T_recall = 1.0
T_cue = 0.020
num = 15
trials = 25
r_space = np.linspace(0, 0.6, num=num)
success_vector = np.zeros((num, trials))
factor = 0.1
for r_index, r in enumerate(r_space):
print(r_index)
# The network
nn = BCPNNPerfect(hypercolumns, minicolumns, g_w_ampa=g_w_ampa, g_w=g_w, g_a=g_a, tau_a=tau_a, tau_m=tau_m,
sigma=sigma, G=G, tau_z_pre_ampa=tau_z_pre_ampa, tau_z_post_ampa=tau_z_post_ampa, tau_p=tau_p,
z_transfer=z_transfer, diagonal_zero=diagonal_zero, strict_maximum=strict_maximum,
perfect=perfect, k_perfect=k_perfect, always_learning=always_learning,
normalized_currents=normalized_currents, g_beta=g_beta)
# Build the manager
manager = NetworkManager(nn=nn, dt=dt, values_to_save=values_to_save)
# The sequences
matrix = create_orthogonal_canonical_representation(minicolumns, hypercolumns)
aux = create_weights_from_two_sequences(nn, dt, n_patterns, s, r, mixed_start, contiguous,
training_time, inter_pulse_interval=inter_pulse_interval,
inter_sequence_interval=inter_sequence_interval, epochs=epochs,
resting_time=resting_time)
seq1, seq2, nr1, nr2, w_total, beta = aux
nr = np.concatenate((nr1, nr2))
aux, indexes = np.unique(nr, axis=0, return_index=True)
patterns_dic = {index:pattern for (index, pattern) in zip(indexes, aux)}
manager.patterns_dic = patterns_dic
nn.w_ampa = w_total
nn.beta = beta
current = g_w_ampa * (w_total[0, 0] - w_total[2, 0])
noise = factor * current
nn.sigma = noise
print(nn.sigma)
# Recall
for trial in range(trials):
s1 = calculate_recall_success_nr(manager, nr1, T_recall, T_cue)
s2 = calculate_recall_success_nr(manager, nr2, T_recall, T_cue)
success_vector[r_index, trial] = 0.5 * (s1 + s2)
# +
markersize = 15
linewdith = 8
current_palette = sns.color_palette()
index = 0
alpha = 0.5
fig = plt.figure(figsize=(16, 12))
ax = fig.add_subplot(111)
mean_success = success_vector.mean(axis=1)
std = success_vector.std(axis=1)
ax.plot(r_space, mean_success, 'o-', lw=linewdith, ms=markersize)
ax.fill_between(r_space, mean_success - std, mean_success + std,
color=current_palette[index], alpha=alpha)
ax.axhline(0, ls='--', color='gray')
ax.axvline(0, ls='--', color='gray')
ax.set_xlabel('Overlap')
ax.set_ylabel('Recall')
# +
# %%time
always_learning = False
strict_maximum = True
perfect = False
z_transfer = False
k_perfect = True
diagonal_zero = False
normalized_currents = True
g_w_ampa = 2.0
g_w = 0.0
g_a = 10.0
tau_a = 0.250
g_beta = 0.0
G = 1.0
sigma = 0.0
tau_m = 0.010
tau_z_pre_ampa = 0.050
tau_z_post_ampa = 0.005
tau_p = 10.0
hypercolumns = 1
minicolumns = 20
n_patterns = 20
# Manager properties
dt = 0.001
values_to_save = ['o', 'i_ampa', 'a']
# Protocol
training_time = 0.100
inter_sequence_interval = 0.0
inter_pulse_interval = 0.0
epochs = 1
mixed_start = False
contiguous = True
s = 1.0
r = 0.25
# Recall
T_recall = 1.0
T_cue = 0.020
num = 15
trials = 25
r_space = np.linspace(0, 0.6, num=num)
success_vector = np.zeros((num, trials))
successes = []
factors = [0.0, 0.1, 0.2, 0.3]
for factor in factors:
print(factor)
for r_index, r in enumerate(r_space):
print(r_index)
# The network
nn = BCPNNPerfect(hypercolumns, minicolumns, g_w_ampa=g_w_ampa, g_w=g_w, g_a=g_a, tau_a=tau_a, tau_m=tau_m,
sigma=sigma, G=G, tau_z_pre_ampa=tau_z_pre_ampa, tau_z_post_ampa=tau_z_post_ampa, tau_p=tau_p,
z_transfer=z_transfer, diagonal_zero=diagonal_zero, strict_maximum=strict_maximum,
perfect=perfect, k_perfect=k_perfect, always_learning=always_learning,
normalized_currents=normalized_currents, g_beta=g_beta)
# Build the manager
manager = NetworkManager(nn=nn, dt=dt, values_to_save=values_to_save)
# The sequences
matrix = create_orthogonal_canonical_representation(minicolumns, hypercolumns)
aux = create_weights_from_two_sequences(nn, dt, n_patterns, s, r, mixed_start, contiguous,
training_time, inter_pulse_interval=inter_pulse_interval,
inter_sequence_interval=inter_sequence_interval, epochs=epochs,
resting_time=resting_time)
seq1, seq2, nr1, nr2, w_total, beta = aux
nr = np.concatenate((nr1, nr2))
aux, indexes = np.unique(nr, axis=0, return_index=True)
patterns_dic = {index:pattern for (index, pattern) in zip(indexes, aux)}
manager.patterns_dic = patterns_dic
nn.w_ampa = w_total
nn.beta = beta
current = g_w_ampa * (w_total[0, 0] - w_total[2, 0])
noise = factor * current
nn.sigma = noise
# Recall
for trial in range(trials):
s1 = calculate_recall_success_nr(manager, nr1, T_recall, T_cue)
s2 = calculate_recall_success_nr(manager, nr2, T_recall, T_cue)
success_vector[r_index, trial] = 0.5 * (s1 + s2)
successes.append(np.copy(success_vector))
# +
markersize = 15
linewdith = 8
current_palette = sns.color_palette()
index = 0
alpha = 0.5
fig = plt.figure(figsize=(16, 12))
ax = fig.add_subplot(111)
for index, success_vector in enumerate(successes):
mean_success = success_vector.mean(axis=1)
std = success_vector.std(axis=1)
ax.plot(r_space, mean_success, 'o-', lw=linewdith, ms=markersize, label=str(factors[index]))
ax.fill_between(r_space, mean_success - std, mean_success + std,
color=current_palette[index], alpha=alpha)
ax.axhline(0, ls='--', color='gray')
ax.axvline(0, ls='--', color='gray')
ax.set_xlabel('Overlap')
ax.set_ylabel('Recall')
ax.legend();
# -
|
jupyter/2018-05-23(Disambiguation).ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# **Run the following two cells before you begin.**
# %autosave 10
# ______________________________________________________________________
# **First, import your data set and define the sigmoid function.**
# <details>
# <summary>Hint:</summary>
# The definition of the sigmoid is $f(x) = \frac{1}{1 + e^{-X}}$.
# </details>
# +
# Import the data set
import pandas as pd
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
import seaborn as sns
df = pd.read_csv('cleaned_data.csv')
# -
# Define the sigmoid function
def sigmoid(X):
Y = 1 / (1 + np.exp(-X))
return Y
# **Now, create a train/test split (80/20) with `PAY_1` and `LIMIT_BAL` as features and `default payment next month` as values. Use a random state of 24.**
# Create a train/test split
X_train, X_test, y_train, y_test = train_test_split(df[['PAY_1', 'LIMIT_BAL']].values, df['default payment next month'].values,test_size=0.2, random_state=24)
# ______________________________________________________________________
# **Next, import LogisticRegression, with the default options, but set the solver to `'liblinear'`.**
lr_model = LogisticRegression(solver='liblinear')
lr_model
# ______________________________________________________________________
# **Now, train on the training data and obtain predicted classes, as well as class probabilities, using the testing data.**
# Fit the logistic regression model on training data
lr_model.fit(X_train,y_train)
# Make predictions using `.predict()`
y_pred = lr_model.predict(X_test)
# Find class probabilities using `.predict_proba()`
y_pred_proba = lr_model.predict_proba(X_test)
# ______________________________________________________________________
# **Then, pull out the coefficients and intercept from the trained model and manually calculate predicted probabilities. You'll need to add a column of 1s to your features, to multiply by the intercept.**
# Add column of 1s to features
ones_and_features = np.hstack([np.ones((X_test.shape[0],1)), X_test])
print(ones_and_features)
np.ones((X_test.shape[0],1)).shape
# Get coefficients and intercepts from trained model
intercept_and_coefs = np.concatenate([lr_model.intercept_.reshape(1,1), lr_model.coef_], axis=1)
intercept_and_coefs
# Manually calculate predicted probabilities
X_lin_comb = np.dot(intercept_and_coefs, np.transpose(ones_and_features))
y_pred_proba_manual = sigmoid(X_lin_comb)
# ______________________________________________________________________
# **Next, using a threshold of `0.5`, manually calculate predicted classes. Compare this to the class predictions output by scikit-learn.**
# Manually calculate predicted classes
y_pred_manual = y_pred_proba_manual >= 0.5
y_pred_manual.shape
y_pred.shape
# Compare to scikit-learn's predicted classes
np.array_equal(y_pred.reshape(1,-1), y_pred_manual)
y_test.shape
y_pred_proba_manual.shape
# ______________________________________________________________________
# **Finally, calculate ROC AUC using both scikit-learn's predicted probabilities, and your manually predicted probabilities, and compare.**
# + eid="e7697"
# Use scikit-learn's predicted probabilities to calculate ROC AUC
from sklearn.metrics import roc_auc_score
roc_auc_score(y_test, y_pred_proba_manual.reshape(y_pred_proba_manual.shape[1],))
# -
# Use manually calculated predicted probabilities to calculate ROC AUC
roc_auc_score(y_test, y_pred_proba[:,1])
|
Mini-Project-2/Project 4/Fitting_a_Logistic_Regression_Model.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] pycharm={"name": "#%% md\n"}
# # ProVis: Attention Visualizer for Proteins
# + pycharm={"is_executing": false, "name": "#%%\n"}
import io
import urllib
import torch
from Bio.Data import SCOPData
from Bio.PDB import PDBParser, PPBuilder
from tape import TAPETokenizer, ProteinBertModel
import nglview
attn_color = [0.937, .522, 0.212]
# + pycharm={"name": "#%%\n"}
def get_structure(pdb_id):
resource = urllib.request.urlopen(f'https://files.rcsb.org/download/{pdb_id}.pdb')
content = resource.read().decode('utf8')
handle = io.StringIO(content)
parser = PDBParser(QUIET=True)
return parser.get_structure(pdb_id, handle)
# + pycharm={"name": "#%%\n"}
def get_attn_data(chain, layer, head, min_attn, start_index=0, end_index=None, max_seq_len=1024):
tokens = []
coords = []
for res in chain:
t = SCOPData.protein_letters_3to1.get(res.get_resname(), "X")
tokens += t
if t == 'X':
coord = None
else:
coord = res['CA'].coord.tolist()
coords.append(coord)
last_non_x = None
for i in reversed(range(len(tokens))):
if tokens[i] != 'X':
last_non_x = i
break
assert last_non_x is not None
tokens = tokens[:last_non_x + 1]
coords = coords[:last_non_x + 1]
tokenizer = TAPETokenizer()
model = ProteinBertModel.from_pretrained('bert-base', output_attentions=True)
if max_seq_len:
tokens = tokens[:max_seq_len - 2] # Account for SEP, CLS tokens (added in next step)
token_idxs = tokenizer.encode(tokens).tolist()
if max_seq_len:
assert len(token_idxs) == min(len(tokens) + 2, max_seq_len)
else:
assert len(token_idxs) == len(tokens) + 2
inputs = torch.tensor(token_idxs).unsqueeze(0)
with torch.no_grad():
attns = model(inputs)[-1]
# Remove attention from <CLS> (first) and <SEP> (last) token
attns = [attn[:, :, 1:-1, 1:-1] for attn in attns]
attns = torch.stack([attn.squeeze(0) for attn in attns])
attn = attns[layer, head]
if end_index is None:
end_index = len(tokens)
attn_data = []
for i in range(start_index, end_index):
for j in range(i, end_index):
# Currently non-directional: shows max of two attns
a = max(attn[i, j].item(), attn[j, i].item())
if a is not None and a >= min_attn:
attn_data.append((a, coords[i], coords[j]))
return attn_data
# -
# ### Visualize head 7-1 (targets binding sites)
# + pycharm={"is_executing": false, "name": "#%%\n"}
# Example for head 7-1 (targets binding sites)
pdb_id = '7HVP'
chain_ids = None # All chains
layer = 7
head = 1
min_attn = 0.1
attn_scale = .9
layer_zero_indexed = layer - 1
head_zero_indexed = head - 1
structure = get_structure(pdb_id)
view = nglview.show_biopython(structure)
view.stage.set_parameters(**{
"backgroundColor": "black",
"fogNear": 50, "fogFar": 100,
})
models = list(structure.get_models())
if len(models) > 1:
print('Warning:', len(models), 'models. Using first one')
prot_model = models[0]
if chain_ids is None:
chain_ids = [chain.id for chain in prot_model]
for chain_id in chain_ids:
print('Loading chain', chain_id)
chain = prot_model[chain_id]
attn_data = get_attn_data(chain, layer_zero_indexed, head_zero_indexed, min_attn)
for att, coords_from, coords_to in attn_data:
view.shape.add_cylinder(coords_from, coords_to, attn_color, att * attn_scale)
view
# -
# ### Visualize head 12-4 (targets contact maps)
# +
# Example for head 12-4 (targets contact maps)
pdb_id = '2KC7'
chain_ids = None # All chains
layer = 12
head = 4
min_attn = 0.2
attn_scale = .5
layer_zero_indexed = layer - 1
head_zero_indexed = head - 1
structure = get_structure(pdb_id)
view2 = nglview.show_biopython(structure)
view2.stage.set_parameters(**{
"backgroundColor": "black",
"fogNear": 50, "fogFar": 100,
})
models = list(structure.get_models())
if len(models) > 1:
print('Warning:', len(models), 'models. Using first one')
prot_model = models[0]
if chain_ids is None:
chain_ids = [chain.id for chain in prot_model]
for chain_id in chain_ids:
print('Loading chain', chain_id)
chain = prot_model[chain_id]
attn_data = get_attn_data(chain, layer_zero_indexed, head_zero_indexed, min_attn)
for att, coords_from, coords_to in attn_data:
view2.shape.add_cylinder(coords_from, coords_to, attn_color, att * attn_scale)
view2
# To save: view2.download_image(filename="testing.png")
# +
|
notebooks/provis.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # SBTi-Finance Tool - Portfolio Aggregation
# In this notebook we'll give some examples on how the portfolio aggregation methods can be used.
#
# Please see the [methodology](https://sciencebasedtargets.org/wp-content/uploads/2020/09/Temperature-Rating-Methodology-V1.pdf), [guidance](https://sciencebasedtargets.org/wp-content/uploads/2020/10/Financial-Sector-Science-Based-Targets-Guidance-Pilot-Version.pdf) and the [technical documentation](http://getting-started.sbti-tool.org/) for more details on the different aggregation methods.
#
# See 1_analysis_example (on [Colab](https://colab.research.google.com/github/OFBDABV/SBTi/blob/master/examples/1_analysis_example.ipynb) or [Github](https://github.com/OFBDABV/SBTi/blob/master/examples/1_analysis_example.ipynb)) for more in depth example of how to work with Jupyter Notebooks in general and SBTi notebooks in particular.
#
# ## Setting up
# First we will set up the imports, data providers, and load the portfolio.
#
# For more examples of this process, please refer to notebook 1 & 2 (analysis and quick calculation example).
#
# !pip install SBTi
# %load_ext autoreload
# %autoreload 2
import SBTi
from SBTi.data.excel import ExcelProvider
from SBTi.portfolio_aggregation import PortfolioAggregationMethod
from SBTi.portfolio_coverage_tvp import PortfolioCoverageTVP
from SBTi.temperature_score import TemperatureScore, Scenario, ScenarioType, EngagementType
from SBTi.target_validation import TargetProtocol
from SBTi.interfaces import ETimeFrames, EScope
# %aimport -pandas
import pandas as pd
# +
# Download the dummy data
import urllib.request
import os
if not os.path.isdir("data"):
os.mkdir("data")
if not os.path.isfile("data/data_provider_example.xlsx"):
urllib.request.urlretrieve("https://github.com/OFBDABV/SBTi/raw/master/examples/data/data_provider_example.xlsx", "data/data_provider_example.xlsx")
if not os.path.isfile("data/example_portfolio.csv"):
urllib.request.urlretrieve("https://github.com/OFBDABV/SBTi/raw/master/examples/data/example_portfolio.csv", "data/example_portfolio.csv")
# -
provider = ExcelProvider(path="data/data_provider_example.xlsx")
df_portfolio = pd.read_csv("data/example_portfolio.csv", encoding="iso-8859-1")
companies = SBTi.utils.dataframe_to_portfolio(df_portfolio)
scores_collection = {}
temperature_score = TemperatureScore(time_frames=list(SBTi.interfaces.ETimeFrames), scopes=[EScope.S1S2, EScope.S3, EScope.S1S2S3])
amended_portfolio = temperature_score.calculate(data_providers=[provider], portfolio=companies)
# ## Calculate the aggregated temperature score
# Calculate an aggregated temperature score. This can be done using different aggregation methods. The termperature scores are calculated per time-frame/scope combination.
# + [markdown] pycharm={"name": "#%% md\n"}
# ### WATS
# Weighted Average Temperature Score (WATS): Temperature scores are allocated based on portfolio weights.
# This method uses the "investment_value" field to be defined in your portfolio data.
# + pycharm={"name": "#%%\n"}
temperature_score.aggregation_method = PortfolioAggregationMethod.WATS
aggregated_scores = temperature_score.aggregate_scores(amended_portfolio)
df_wats = pd.DataFrame(aggregated_scores.dict()).applymap(lambda x: round(x['all']['score'], 2))
scores_collection.update({'WATS': df_wats})
df_wats
# + [markdown] pycharm={"name": "#%% md\n"}
# ### TETS
# Total emissions weighted temperature score (TETS): Temperature scores are allocated based on historical emission weights using total company emissions.
# In addition to the portfolios "investment value" the TETS method requires company emissions, please refer to [Data Legends - Fundamental Data](https://ofbdabv.github.io/SBTi/Legends.html#fundamental-data) for more details
# + pycharm={"name": "#%%\n"}
temperature_score.aggregation_method = PortfolioAggregationMethod.TETS
aggregated_scores = temperature_score.aggregate_scores(amended_portfolio)
df_tets = pd.DataFrame(aggregated_scores.dict()).applymap(lambda x: round(x['all']['score'], 2))
scores_collection.update({'TETS': df_tets})
df_tets
# + [markdown] pycharm={"name": "#%% md\n"}
# ### MOTS
# Market Owned emissions weighted temperature score (MOTS): Temperature scores are allocated based on an equity ownership approach.
# In addition to the portfolios "investment value" the MOTS method requires company emissions and market cap, please refer to [Data Legends - Fundamental Data](https://ofbdabv.github.io/SBTi/Legends.html#fundamental-data) for more details
# + pycharm={"name": "#%%\n"}
temperature_score.aggregation_method = PortfolioAggregationMethod.MOTS
aggregated_scores = temperature_score.aggregate_scores(amended_portfolio)
df_mots = pd.DataFrame(aggregated_scores.dict()).applymap(lambda x: round(x['all']['score'], 2))
scores_collection.update({'MOTS': df_mots})
df_mots
# + [markdown] pycharm={"name": "#%% md\n"}
# ### EOTS
# Enterprise Owned emissions weighted temperature score (EOTS): Temperature scores are allocated based
# on an enterprise ownership approach.
# In addition to the portfolios "investment value" the EOTS method requires company emissions and enterprise value, please refer to [Data Legends - Fundamental Data](https://ofbdabv.github.io/SBTi/Legends.html#fundamental-data) for more details
# + pycharm={"name": "#%%\n"}
temperature_score.aggregation_method = PortfolioAggregationMethod.EOTS
aggregated_scores = temperature_score.aggregate_scores(amended_portfolio)
df_eots = pd.DataFrame(aggregated_scores.dict()).applymap(lambda x: round(x['all']['score'], 2))
scores_collection.update({'EOTS': df_eots})
df_eots
# + [markdown] pycharm={"name": "#%% md\n"}
# ### ECOTS
# Enterprise Value + Cash emissions weighted temperature score (ECOTS): Temperature scores are allocated based on an enterprise value (EV) plus cash & equivalents ownership approach.
# In addition to the portfolios "investment value" the ECOTS method requires company emissions, company cash equivalents and enterprise value; please refer to [Data Legends - Fundamental Data](https://ofbdabv.github.io/SBTi/Legends.html#fundamental-data) for more details
# + pycharm={"name": "#%%\n"}
temperature_score.aggregation_method = PortfolioAggregationMethod.ECOTS
aggregated_scores = temperature_score.aggregate_scores(amended_portfolio)
df_ecots = pd.DataFrame(aggregated_scores.dict()).applymap(lambda x: round(x['all']['score'], 2))
scores_collection.update({'ECOTS': df_ecots})
df_ecots
# + [markdown] pycharm={"name": "#%% md\n"}
# ### AOTS
# Total Assets emissions weighted temperature score (AOTS): Temperature scores are allocated based on a total assets ownership approach.
# In addition to the portfolios "investment value" the AOTS method requires company emissions and company total assets; please refer to [Data Legends - Fundamental Data](https://ofbdabv.github.io/SBTi/Legends.html#fundamental-data) for more details
# + pycharm={"name": "#%%\n"}
temperature_score.aggregation_method = PortfolioAggregationMethod.AOTS
aggregated_scores = temperature_score.aggregate_scores(amended_portfolio)
df_aots = pd.DataFrame(aggregated_scores.dict()).applymap(lambda x: round(x['all']['score'], 2))
scores_collection.update({'AOTS': df_aots})
df_aots
# + [markdown] pycharm={"name": "#%% md\n"}
# ### ROTS
# Revenue owned emissions weighted temperature score (ROTS): Temperature scores are allocated based on the share of revenue.
# In addition to the portfolios "investment value" the ROTS method requires company emissions and company revenue; please refer to [Data Legends - Fundamental Data](https://ofbdabv.github.io/SBTi/Legends.html#fundamental-data) for more details
# + pycharm={"name": "#%%\n"}
temperature_score.aggregation_method = PortfolioAggregationMethod.ROTS
aggregated_scores = temperature_score.aggregate_scores(amended_portfolio)
df_rots = pd.DataFrame(aggregated_scores.dict()).applymap(lambda x: round(x['all']['score'], 2))
scores_collection.update({'ROTS': df_rots})
df_rots
# + [markdown] pycharm={"name": "#%% md\n"}
# See below how each aggregation method impact the scores on for each time frame and scope combination
# + pycharm={"name": "#%%\n"}
pd.concat(scores_collection, axis=0)
|
examples/4_portfolio_aggregations.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# name: python2
# ---
# + [markdown] colab_type="text" id="1Pi_B2cvdBiW"
# ##### Copyright 2019 The TF-Agents Authors.
# + [markdown] colab_type="text" id="f5926O3VkG_p"
# ### Get Started
# <table class="tfo-notebook-buttons" align="left">
# <td>
# <a target="_blank" href="https://colab.research.google.com/github/tensorflow/agents/blob/master/tf_agents/colabs/8_networks_tutorial.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
# </td>
# <td>
# <a target="_blank" href="https://github.com/tensorflow/agents/blob/master/tf_agents/colabs/8_networks_tutorial.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on GitHub</a>
# </td>
# </table>
# + colab_type="code" id="xsLTHlVdiZP3" colab={}
# Note: If you haven't installed tf-agents yet, run:
# !pip install tf-nightly
# !pip install tfp-nightly
# !pip install tf-agents-nightly
# + [markdown] colab_type="text" id="lEgSa5qGdItD"
# ### Imports
# + colab_type="code" id="sdvop99JlYSM" colab={}
from __future__ import absolute_import
from __future__ import division
from __future__ import print_function
import abc
import tensorflow as tf
import numpy as np
from tf_agents.environments import random_py_environment
from tf_agents.environments import tf_py_environment
from tf_agents.networks import encoding_network
from tf_agents.networks import network
from tf_agents.networks import utils
from tf_agents.specs import array_spec
from tf_agents.utils import common as common_utils
from tf_agents.utils import nest_utils
tf.compat.v1.enable_v2_behavior()
# + [markdown] colab_type="text" id="31uij8nIo5bG"
# # Introduction
#
# In this colab we will cover how to define custom networks for your agents. The networks help us define the model that is trained by agents. In TF-Agents you will find several different types of networks which are useful across agents:
#
# **Main Networks**
#
# * **QNetwork**: Used in Qlearning for environments with discrete actions, this network maps an observation to value estimates for each possible action.
# * **CriticNetworks**: Also referred to as `ValueNetworks` in literature, learns to estimate some version of a Value function mapping some state into an estimate for the expected return of a policy. These networks estimate how good the state the agent is currently in is.
# * **ActorNetworks**: Learn a mapping from observations to actions. These networks are usually used by our policies to generate actions.
# * **ActorDistributionNetworks**: Similar to `ActorNetworks` but these generate a distribution which a policy can then sample to generate actions.
#
# **Helper Networks**
# * **EncodingNetwork**: Allows users to easily define a mapping of pre-processing layers to apply to a network's input.
# * **DynamicUnrollLayer**: Automatically resets the network's state on episode boundaries as it is applied over a time sequence.
# * **ProjectionNetwork**: Networks like `CategoricalProjectionNetwork` or `NormalProjectionNetwork` take inputs and generate the required parameters to generate Categorical, or Normal distributions.
#
# All examples in TF-Agents come with pre-configured networks. However these networks are not setup to handle complex observations.
#
# If you have an environment which exposes more than one observation/action and you need to customize your networks then this tutorial is for you!
# + [markdown] id="ums84-YP_21F" colab_type="text"
# #Defining Networks
#
# ##Network API
#
# In TF-Agents we subclass from Keras [Networks](https://github.com/tensorflow/tensorflow/blob/master/tensorflow/python/keras/engine/network.py). With it we can:
#
# * Simplify copy operations required when creating target networks.
# * Perform automatic variable creation when calling `network.variables()`.
# * Validate inputs based on network input_specs.
#
# ##EncodingNetwork
# As mentioned above the `EncodingNetwork` allows us to easily define a mapping of pre-processing layers to apply to a network's input to generate some encoding.
#
# The EncodingNetwork is composed of the following mostly optional layers:
#
# * Preprocessing layers
# * Preprocessing combiner
# * Conv2D
# * Flatten
# * Dense
#
# The special thing about encoding networks is that input preprocessing is applied. Input preprocessing is possible via `preprocessing_layers` and `preprocessing_combiner` layers. Each of these can be specified as a nested structure. If the `preprocessing_layers` nest is shallower than `input_tensor_spec`, then the layers will get the subnests. For example, if:
#
# ```
# input_tensor_spec = ([TensorSpec(3)] * 2, [TensorSpec(3)] * 5)
# preprocessing_layers = (Layer1(), Layer2())
# ```
#
# then preprocessing will call:
#
# ```
# preprocessed = [preprocessing_layers[0](observations[0]),
# preprocessing_layers[1](obsrevations[1])]
# ```
#
# However if
#
# ```
# preprocessing_layers = ([Layer1() for _ in range(2)],
# [Layer2() for _ in range(5)])
# ```
#
# then preprocessing will call:
#
# ```python
# preprocessed = [
# layer(obs) for layer, obs in zip(flatten(preprocessing_layers),
# flatten(observations))
# ]
# ```
#
# + [markdown] id="RP3H1bw0ykro" colab_type="text"
# ## Custom Networks
#
# To create your own networks you will only have to override the `__init__` and `__call__` methods. Let's create a custom network using what we learned about `EncodingNetworks` to create an ActorNetwork that takes observations which contain an image and a vector.
#
# + id="Zp0TjAJhYo4s" colab_type="code" colab={}
class ActorNetwork(network.Network):
def __init__(self,
observation_spec,
action_spec,
preprocessing_layers=None,
preprocessing_combiner=None,
conv_layer_params=None,
fc_layer_params=(75, 40),
dropout_layer_params=None,
activation_fn=tf.keras.activations.relu,
enable_last_layer_zero_initializer=False,
name='ActorNetwork'):
super(ActorNetwork, self).__init__(
input_tensor_spec=observation_spec, state_spec=(), name=name)
# For simplicity we will only support a single action float output.
self._action_spec = action_spec
flat_action_spec = tf.nest.flatten(action_spec)
if len(flat_action_spec) > 1:
raise ValueError('Only a single action is supported by this network')
self._single_action_spec = flat_action_spec[0]
if self._single_action_spec.dtype not in [tf.float32, tf.float64]:
raise ValueError('Only float actions are supported by this network.')
kernel_initializer = tf.keras.initializers.VarianceScaling(
scale=1. / 3., mode='fan_in', distribution='uniform')
self._encoder = encoding_network.EncodingNetwork(
observation_spec,
preprocessing_layers=preprocessing_layers,
preprocessing_combiner=preprocessing_combiner,
conv_layer_params=conv_layer_params,
fc_layer_params=fc_layer_params,
dropout_layer_params=dropout_layer_params,
activation_fn=activation_fn,
kernel_initializer=kernel_initializer,
batch_squash=False)
initializer = tf.keras.initializers.RandomUniform(
minval=-0.003, maxval=0.003)
self._action_projection_layer = tf.keras.layers.Dense(
flat_action_spec[0].shape.num_elements(),
activation=tf.keras.activations.tanh,
kernel_initializer=initializer,
name='action')
def call(self, observations, step_type=(), network_state=()):
outer_rank = nest_utils.get_outer_rank(observations, self.input_tensor_spec)
# We use batch_squash here in case the observations have a time sequence
# compoment.
batch_squash = utils.BatchSquash(outer_rank)
observations = tf.nest.map_structure(batch_squash.flatten, observations)
state, network_state = self._encoder(
observations, step_type=step_type, network_state=network_state)
actions = self._action_projection_layer(state)
actions = common_utils.scale_to_spec(actions, self._single_action_spec)
actions = batch_squash.unflatten(actions)
return tf.nest.pack_sequence_as(self._action_spec, [actions]), network_state
# + [markdown] id="Fm-MbMMLYiZj" colab_type="text"
# Let's create a `RandomPyEnvironment` to generate structured observations and validate our implementation.
# + id="E2XoNuuD66s5" colab_type="code" colab={}
action_spec = array_spec.BoundedArraySpec((3,), np.float32, minimum=0, maximum=10)
observation_spec = {
'image': array_spec.BoundedArraySpec((16, 16, 3), np.float32, minimum=0,
maximum=255),
'vector': array_spec.BoundedArraySpec((5,), np.float32, minimum=-100,
maximum=100)}
random_env = random_py_environment.RandomPyEnvironment(observation_spec, action_spec=action_spec)
# Convert the environment to a TFEnv to generate tensors.
tf_env = tf_py_environment.TFPyEnvironment(random_env)
# + [markdown] id="LM3uDTD7TNVx" colab_type="text"
# Since we've defined the observations to be a dict we need to create preprocessing layers to handle these.
# + id="r9U6JVevTAJw" colab_type="code" colab={}
preprocessing_layers = {
'image': tf.keras.models.Sequential([tf.keras.layers.Conv2D(8, 4),
tf.keras.layers.Flatten()]),
'vector': tf.keras.layers.Dense(5)
}
preprocessing_combiner = tf.keras.layers.Concatenate(axis=-1)
actor = ActorNetwork(tf_env.observation_spec(),
tf_env.action_spec(),
preprocessing_layers=preprocessing_layers,
preprocessing_combiner=preprocessing_combiner)
# + [markdown] id="mM9qedlwc41U" colab_type="text"
# Now that we have the actor network we can process observations from the environment.
# + id="JOkkeu7vXoei" colab_type="code" colab={}
time_step = tf_env.reset()
actor(time_step.observation, time_step.step_type)
# + [markdown] id="ALGxaQLWc9GI" colab_type="text"
# This same strategy can be used to customize any of the main networks used by the agents. You can define whatever preprocessing and connect it to the rest of the network. As you define your own custom make sure the output layer definitions of the network match.
|
tf_agents/colabs/8_networks_tutorial.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# Python for STEM Teachers<br/>[Oregon Curriculum Network](http://4dsolutions.net/ocn/)
#
# # Atoms R Us
#
# 
#
# +
import json
series_types = ["Don't Know", "Other nonmetal", "Alkali metal",
"Alkaline earth metal", "Nobel gas", "Metalloid",
"Halogen", "Transition metal", "Post-transition metal",
"Lanthanoid", "Actinoid"]
class Element:
fields = "protons symbol long_name mass series"
repstr = ("Atom(protons={protons}, symbol='{symbol}', "
"long_name='{long_name}', "
"mass={mass}, series='{series}')")
def __init__(self, protons: int, symbol: str,
long_name: str, mass: float, series: str):
# build self.__dict__
self.protons = protons
self.symbol = symbol
self.long_name = long_name
self.__dict__['mass'] = mass # same idea
self.series = series
def __getitem__(self, idx): # simulates collection.namedtuple behavior
return self.__dict__[self.fields[idx]]
def __repr__(self):
return self.repstr.format(**self.__dict__)
Atom = Element # synonyms
lithium = Atom(3, "Li", "Lithium", 6.941, "Alkali metal")
print(lithium) # __str__, then __repr__
print(lithium.__dict__)
print(lithium.protons) # print(lithium.__getattr__('protons'))
# +
import unittest
class Test_Element(unittest.TestCase):
def test_instance(self):
lithium = Atom(3, "Li", "Lithium", 6.941, "Alkali metal")
self.assertEqual(lithium.protons, 3, "Houston, we have a problem")
a = Test_Element() # the test suite
suite = unittest.TestLoader().loadTestsFromModule(a) # fancy boilerplate
unittest.TextTestRunner().run(suite) # run the test suite
# +
class ElementEncoder(json.JSONEncoder):
"""
See: https://docs.python.org/3.5/library/json.html
"""
def default(self, obj):
if isinstance(obj, Element): # how to encode an Element
return [obj.protons, obj.symbol, obj.long_name, obj.mass, obj.series]
return json.JSONEncoder.default(self, obj) # just do your usual
# Element = namedtuple("Atom", "protons abbrev long_name mass")
def load_elements():
global all_elements # <--- will be visible to entire module
try:
the_file = "periodic_table.json"
f = open(the_file, "r") # <--- open the_file instead
except IOError:
print("Sorry, no such file!")
else:
the_dict = json.load(f)
f.close()
all_elements = {}
for symbol, data in the_dict.items():
all_elements[symbol] = Atom(*data) # "explode" data into 5 inputs
print("File:", the_file, 'loaded.')
load_elements() # actually do it
# -
# 
# <div align="center">graphic by <NAME></div>
# +
def print_periodic_table(sortby=1):
"""
sort all_elements by number of protons, ordered_elements local only
What about series?
Sort Order:
1. protons
2. symbol
3. series
"""
print("Selected:", sortby)
if sortby == 1:
ordered_elements = sorted(all_elements.values(), key = lambda k: k.protons)
elif sortby == 2:
ordered_elements = sorted(all_elements.values(), key = lambda k: k.symbol)
elif sortby == 3:
ordered_elements = sorted(all_elements.values(), key = lambda k: k.series)
print("PERIODIC TABLE OF THE ELEMENTS")
print("-" * 70)
print("Symbol |Long Name |Protons |Mass |Series " )
print("-" * 70)
for the_atom in ordered_elements:
print("{:6} | {:20} | {:6} | {:5.2f} | {:15}".format(the_atom.symbol,
the_atom.long_name,
the_atom.protons,
the_atom.mass,
the_atom.series))
print_periodic_table() # do it for real
# -
# 
# <div align="center">by <NAME></div>
|
Atoms in Python.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import tensorflowjs as tfjs
import json
# After saving keras model with ZeroPadding3D as model.json Modify with this code:
# Open json file to modify
with open(output_folder + 'model.json') as f:
model_dict = json.load(f)
# Convert
for layer in model_dict['modelTopology']['model_config']['config']['layers']:
if layer['class_name'] == "ZeroPadding3D":
model_dict['modelTopology']['model_config']['config']['layers'].remove(layer)
prev_layer_name = ""
for layer in model_dict['modelTopology']['model_config']['config']['layers']:
if layer['class_name'] == "InputLayer":
layer["config"]["batch_input_shape"] = [None, 38, 38, 38, 1]
if layer['class_name'] == "Conv3D":
layer["config"]["padding"] = "same"
layer["config"]["data_format"] = "channels_last"
layer['inbound_nodes'][0][0][0] = prev_layer_name
prev_layer_name = layer["config"]["name"]
# Verification
for layer in model_dict['modelTopology']['model_config']['config']['layers']:
print(layer)
print("-------------------------------------------------------")
# Save model.json file
with open(output_folder + 'model.json', 'w') as fp:
json.dump(model_dict, fp)
|
python/Conversion/Convert model.json with ZeroPadding3D to tfjs compatible json.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="eerkOkIpLQD2"
# Author: <NAME>, <EMAIL>; <NAME>, <EMAIL>; <NAME>, <EMAIL> (2021)
# + id="EAcBQ5Y9E-aw" executionInfo={"status": "ok", "timestamp": 1636962210309, "user_tz": 480, "elapsed": 354, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjNA4F55Dr3Wpfy_3xDEtdDeKDmfL_WiSi81FRmoQ=s64", "userId": "11440633380440656636"}}
# %matplotlib inline
# %config InlineBackend.figure_format = 'retina'
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import warnings
import seaborn as sns
import matplotlib
matplotlib.rcParams.update({'font.size': 13})
warnings.filterwarnings("ignore")
# + [markdown] id="Gh2ObfFDZOWa"
# ## Two Datasets
#
# Dataset1: n = 200
#
# Dataset2: n = 50
# + id="ppTpI6E7ExzO" executionInfo={"status": "ok", "timestamp": 1636962210309, "user_tz": 480, "elapsed": 6, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjNA4F55Dr3Wpfy_3xDEtdDeKDmfL_WiSi81FRmoQ=s64", "userId": "11440633380440656636"}}
np.random.seed(10)
dataset1 = np.random.multivariate_normal(np.array([2,1]), np.array([[1, 1.5], [1.5, 3]]), 200)
dataset2 = dataset1[:50,:] + np.random.multivariate_normal(np.array([0,0]), np.array([[0.1, 0], [0, 0.1]]), 50)
dataset1 = pd.DataFrame(dataset1,columns = ['X','Y'])
dataset2 = pd.DataFrame(dataset2,columns = ['X','Y'])
# + colab={"base_uri": "https://localhost:8080/", "height": 311} id="Jcd97pw8E-7D" executionInfo={"status": "ok", "timestamp": 1636962210727, "user_tz": 480, "elapsed": 423, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjNA4F55Dr3Wpfy_3xDEtdDeKDmfL_WiSi81FRmoQ=s64", "userId": "11440633380440656636"}} outputId="09bec41e-e969-4e2e-d9a1-7b5ec30ddb7b"
plt.scatter(dataset1['X'],dataset1['Y'])
plt.xlabel('X')
plt.ylabel('Y')
plt.title('Dataset 1: # of sample: 200')
plt.xlim(-1,5)
plt.ylim(-5,6)
# + colab={"base_uri": "https://localhost:8080/", "height": 311} id="8JBzBJlhFdFb" executionInfo={"status": "ok", "timestamp": 1614120461791, "user_tz": 480, "elapsed": 1791, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GikqN0fra_DdutXH7CWyxA7GsB2Na6ivKIwnTh_OTw=s64", "userId": "14594676763170300704"}} outputId="29a567c3-2a29-475b-9004-685cd3d65de2"
plt.scatter(dataset2['X'],dataset2['Y'],c = 'C1')
plt.xlabel('X')
plt.ylabel('Y')
plt.title('Dataset2: # of sample: 50')
plt.xlim(-1,5)
plt.ylim(-5,6)
# + [markdown] id="XyabMB_OZf0b"
# ## Fit linear regression
# + id="jn9RfVenFg6p"
import statsmodels.formula.api as smf
linear_reg_dataset1 = smf.ols(formula='Y ~ X', data=dataset1)
linear_reg_dataset1 = linear_reg_dataset1.fit()
linear_reg_dataset2 = smf.ols(formula='Y ~ X', data=dataset2)
linear_reg_dataset2 = linear_reg_dataset2.fit()
# + [markdown] id="E6K71IBxZsZI"
# Linear regression: fit dataset 1
# + colab={"base_uri": "https://localhost:8080/", "height": 311} id="wBTgUMtybDO6" executionInfo={"status": "ok", "timestamp": 1614120462695, "user_tz": 480, "elapsed": 2687, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GikqN0fra_DdutXH7CWyxA7GsB2Na6ivKIwnTh_OTw=s64", "userId": "14594676763170300704"}} outputId="04ef5372-a20e-4ee6-fd27-7d5a9e1c4d6e"
X_pred = np.linspace(-2,6,num = 100)
reg = linear_reg_dataset1
data = dataset1
plt.plot(data['X'], data['Y'], 'o', label="Data")
plt.plot(X_pred,reg.predict(exog=dict(X=X_pred)), 'r-', label="Predicted")
plt.title('Dataset 1, '+'R2: '+str(np.round(reg.rsquared,2)))
plt.legend(loc="best")
plt.xlim(-1,5)
plt.ylim(-5,6)
plt.xlabel('X')
plt.ylabel('Y')
# + colab={"base_uri": "https://localhost:8080/"} id="LTdxc8XaYKrH" executionInfo={"status": "ok", "timestamp": 1614120462696, "user_tz": 480, "elapsed": 2683, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GikqN0fra_DdutXH7CWyxA7GsB2Na6ivKIwnTh_OTw=s64", "userId": "14594676763170300704"}} outputId="393c194f-4639-429f-b5c0-905072a14d6b"
print(linear_reg_dataset1.summary())
# + [markdown] id="mEHBuLgaZx9o"
# Linear regression: fit dataset 2
# + colab={"base_uri": "https://localhost:8080/", "height": 311} id="kQLt4QkbbELu" executionInfo={"status": "ok", "timestamp": 1614120462893, "user_tz": 480, "elapsed": 2876, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GikqN0fra_DdutXH7CWyxA7GsB2Na6ivKIwnTh_OTw=s64", "userId": "14594676763170300704"}} outputId="5142baeb-383f-4bbb-82bd-6af2235cbec9"
X_pred = np.linspace(-2,6,num = 100)
reg = linear_reg_dataset2
data = dataset2
plt.plot(data['X'], data['Y'], 'o', label="Data",c = 'C1')
plt.plot(X_pred,reg.predict(exog=dict(X=X_pred)), 'r-', label="Predicted")
plt.title('Dataset 2, '+'R2: '+str(np.round(reg.rsquared,2)))
plt.legend(loc="best")
plt.xlim(-1,5)
plt.ylim(-5,6)
plt.xlabel('X')
plt.ylabel('Y')
# + colab={"base_uri": "https://localhost:8080/"} id="T6epM9JTZrvW" executionInfo={"status": "ok", "timestamp": 1614120462894, "user_tz": 480, "elapsed": 2873, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GikqN0fra_DdutXH7CWyxA7GsB2Na6ivKIwnTh_OTw=s64", "userId": "14594676763170300704"}} outputId="6d6c0c8b-a69e-45ec-9d2b-5d528dd8d76d"
print(linear_reg_dataset2.summary())
# + [markdown] id="nS0lLJM8Z6CG"
# ## Residual
# + colab={"base_uri": "https://localhost:8080/", "height": 311} id="3Dqi4YlVYTFX" executionInfo={"status": "ok", "timestamp": 1614120463329, "user_tz": 480, "elapsed": 3304, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GikqN0fra_DdutXH7CWyxA7GsB2Na6ivKIwnTh_OTw=s64", "userId": "14594676763170300704"}} outputId="800b8f7f-8367-4ff3-940f-ac2099e8f81b"
plt.plot(linear_reg_dataset1.resid,'.', label = 'Residual')
plt.hlines(y = 0, xmin = 0, xmax = 200, color = 'r')
plt.xlabel('# of samples')
plt.ylabel('Residual')
plt.title('Dataset 1, residual')
plt.legend(loc="best")
# + colab={"base_uri": "https://localhost:8080/", "height": 311} id="AOB-9W9kF7Yi" executionInfo={"status": "ok", "timestamp": 1614120463674, "user_tz": 480, "elapsed": 3643, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GikqN0fra_DdutXH7CWyxA7GsB2Na6ivKIwnTh_OTw=s64", "userId": "14594676763170300704"}} outputId="03b8ec3a-e2cc-4abb-f0e5-15a5e96338e7"
plt.plot(linear_reg_dataset2.resid,'.', label = 'Residual',c = 'C1')
plt.hlines(y = 0, xmin = 0, xmax = 50, color = 'r')
plt.xlabel('# of samples')
plt.ylabel('Residual')
plt.title('Dataset 2, residual')
plt.legend(loc="best")
# + [markdown] id="Rr-8e4T4bc47"
# ## 95% confidence interval
# + colab={"base_uri": "https://localhost:8080/", "height": 311} id="UoXUXKeCDq4X" executionInfo={"status": "ok", "timestamp": 1614120464154, "user_tz": 480, "elapsed": 4118, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GikqN0fra_DdutXH7CWyxA7GsB2Na6ivKIwnTh_OTw=s64", "userId": "14594676763170300704"}} outputId="fcfe240e-484f-445d-c333-e25ea2630609"
import seaborn as sns
data = dataset1
sns.regplot(data['X'],data['Y'],color = 'C0')
plt.title('Dataset 1: confidence interval')
plt.xlim(-1,5)
plt.ylim(-5,6)
# + colab={"base_uri": "https://localhost:8080/", "height": 311} id="mnJwvy9_ErQS" executionInfo={"status": "ok", "timestamp": 1614120464315, "user_tz": 480, "elapsed": 4274, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GikqN0fra_DdutXH7CWyxA7GsB2Na6ivKIwnTh_OTw=s64", "userId": "14594676763170300704"}} outputId="0a0278e3-cb21-48c4-cd16-458e408ac0a7"
data = dataset1
sns.regplot(data['X'],data['Y'],color = 'C0',scatter = False)
plt.title('Dataset 1: confidence interval')
plt.xlim(-1,5)
plt.ylim(-5,6)
# + colab={"base_uri": "https://localhost:8080/", "height": 311} id="lsJbFTHEDaoC" executionInfo={"status": "ok", "timestamp": 1614120464769, "user_tz": 480, "elapsed": 4723, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GikqN0fra_DdutXH7CWyxA7GsB2Na6ivKIwnTh_OTw=s64", "userId": "14594676763170300704"}} outputId="2c6aa292-b914-4473-9efa-2dec94842045"
data = dataset2
sns.regplot(data['X'],data['Y'],color = 'C1')
plt.title('Dataset 2: confidence interval')
plt.xlim(-1,5)
plt.ylim(-5,6)
# + colab={"base_uri": "https://localhost:8080/", "height": 311} id="t_EykV-hEusv" executionInfo={"status": "ok", "timestamp": 1614120465088, "user_tz": 480, "elapsed": 5037, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GikqN0fra_DdutXH7CWyxA7GsB2Na6ivKIwnTh_OTw=s64", "userId": "14594676763170300704"}} outputId="81e1483f-af13-494e-9a91-b19abd69a66f"
data = dataset2
sns.regplot(data['X'],data['Y'],color = 'C1',scatter = False)
plt.title('Dataset 2: confidence interval')
plt.xlim(-1,5)
plt.ylim(-5,6)
|
Ch3_SpatialAggregation/Colabs/Spatial Aggregation_ linear regression.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# # Attribute data operations {#attr}
#
# ## Prerequisites
#| echo: false
import pandas as pd
import matplotlib.pyplot as plt
pd.options.display.max_rows = 6
pd.options.display.max_columns = 6
pd.options.display.max_colwidth = 35
plt.rcParams["figure.figsize"] = (5, 5)
# Packages...
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import geopandas as gpd
import rasterio
# Sample data...
#| echo: false
from pathlib import Path
data_path = Path("data")
file_path = Path("data/landsat.tif")
if not file_path.exists():
if not data_path.is_dir():
os
os.mkdir(data_path)
import os
print("Attempting to get the data")
import requests
r = requests.get("https://github.com/geocompr/py/releases/download/0.1/landsat.tif")
with open(file_path, "wb") as f:
f.write(r.content)
world = gpd.read_file("data/world.gpkg")
src_elev = rasterio.open("data/elev.tif")
src_multi_rast = rasterio.open("data/landsat.tif")
# ## Introduction
#
# ...
#
# ## Vector attribute manipulation
#
# As mentioned previously (...), vector layers (`GeoDataFrame`, from package `geopandas`) are basically extended tables (`DataFrame` from package `pandas`), the difference being that a vector layer has a geometry column. Since `GeoDataFrame` extends `DataFrame`, all ordinary table-related operations from package `pandas` are supported for vector laters as well, as shown below.
#
# ### Vector attribute subsetting
#
# `pandas` supports several subsetting interfaces, though the most [recommended](https://stackoverflow.com/questions/38886080/python-pandas-series-why-use-loc) ones are:
#
# * `.loc`, which uses pandas indices, and
# * `.iloc`, which uses (implicit) numpy-style numeric indices.
#
# In both cases the method is followed by square brackets, and two indices, separated by a comma. Each index can comprise:
#
# * A specific value, as in `1`
# * A slice, as in `0:3`
# * A `list`, as in `[0,2,4]`
# * `:`—indicating "all" indices
#
# The once exception which we are going to with subsetting by indices is when selecting columns, directly using a list, as in `df[["a","b"]]`, instead of `df.loc[:, ["a","b"]]`, to select columns `"a"` and `"b"` from `df`.
#
# Here are few examples of subsetting the `GeoDataFrame` of world countries.
#
# Subsetting rows by position:
world.iloc[0:3, :]
# Subsetting columns by position:
world.iloc[:, 0:3]
# Subsetting rows and columns by position:
world.iloc[0:3, 0:3]
# Subsetting columns by name:
world[["name_long", "geometry"]]
# "Slice" of columns between given ones:
world.loc[:, "name_long":"pop"]
# Subsetting by a boolean series:
x = np.array([1, 1, 0, 0, 0, 0, 0, 1, 1, 0, 0], dtype=bool)
world.iloc[:, x]
# We can remove specific columns using the `.drop` method and `axis=1` (i.e., columns):
world.drop(["name_long", "continent"], axis=1)
# We can rename (some of) the selected columns using the `.rename` method:
world[["name_long", "pop"]].rename(columns={"pop": "population"})
# The standard `numpy` comparison operators can be used in boolean subsetting, as illustrated in Table ...
#
# TABLE ...: Comparison operators that return Booleans (TRUE/FALSE).
#
# |`Symbol` | `Name` |
# |---|---|
# | `==` | Equal to |
# | `!=` | Not equal to |
# | `>`, `<` | Greater/Less than |
# | `>=`, `<=` | Greater/Less than or equal |
# | `&`, `|`, `~` | Logical operators: And, Or, Not |
#
# A demonstration of the utility of using logical vectors for subsetting is shown in the code chunk below. This creates a new object, small_countries, containing nations whose surface area is smaller than 10,000 km^2^:
i_small = world["area_km2"] < 10000 ## a logical 'Series'
small_countries = world[i_small]
small_countries
# The intermediary `i_small` (short for index representing small countries) is a boolean `Series` that can be used to subset the seven smallest countries in the world by surface area. A more concise command, which omits the intermediary object, generates the same result:
small_countries = world[world["area_km2"] < 10000]
# The various methods shown above can be chained for any combination with several subsetting steps. For example:
world[world["continent"] == "Asia"] \
.loc[:, ["name_long", "continent"]] \
.iloc[0:5, :]
# ### Vector attribute aggregation
#
# Aggregation involves summarizing data with one or more *grouping variables*, typically from columns in the table to be aggregated (geographic aggregation is covered in the next chapter). An example of attribute aggregation is calculating the number of people per continent based on country-level data (one row per country). The `world` dataset contains the necessary ingredients: the columns `pop` and `continent`, the population and the grouping variable, respectively. The aim is to find the `sum()` of country populations for each continent, resulting in a smaller data frame (aggregation is a form of data reduction and can be a useful early step when working with large datasets). This can be done with a combination of `.groupby` and `.sum`:
world_agg1 = world[['continent', 'pop']].groupby('continent').sum()
world_agg1
# The result is a (non-spatial) table with eight rows, one per continent, and two columns reporting the name and population of each continent.
#
# Alternatively, to include the geometry in the aggregation result, we can use the `.dissolve` method. That way, in addition to the summed population we also get the associated geometry per continent, i.e., the union of all countries. Note that we use the `by` parameter to choose which column(s) are used for grouping, and the `aggfunc` parameter to choose the summary function for non-geometry columns:
world_agg2 = world[['continent', 'pop', 'geometry']] \
.dissolve(by='continent', aggfunc='sum')
world_agg2
# Here is a plot of the result:
world_agg2.plot(column='pop');
# The resulting `world_agg2` object is a vector layer containing 8 features representing the continents of the world (and the open ocean).
#
# Other options for the `aggfunc` parameter in `.dissolve` [include](https://geopandas.org/en/stable/docs/user_guide/aggregation_with_dissolve.html):
#
# * `'first'`
# * `'last'`
# * `'min'`
# * `'max'`
# * `'sum'`
# * `'mean'`
# * `'median'`
#
# Additionally, we can pass a custom functiom.
#
# For example, here is how we can calculate the summed population, summed area, and count of countries, per continent. We do this in two steps, then join the results:
world_agg3a = world[['continent', 'area_km2', 'geometry']] \
.dissolve(by='continent', aggfunc='sum')
world_agg3b = world[['continent', 'name_long', 'geometry']] \
.dissolve(by='continent', aggfunc=lambda x: x.nunique()) \
.rename(columns={"name_long": "n"})
world_agg = pd.merge(world_agg3a, world_agg3b, on='continent')
# ...
#
# ### Vector attribute joining
#
# Join by attribute...
coffee_data = pd.read_csv("data/coffee_data.csv")
coffee_data
# Join by `"name_long"` column...
world_coffee = pd.merge(world, coffee_data, on="name_long", how="left")
world_coffee
# Plot...
base = world.plot(color="white", edgecolor="lightgrey")
world_coffee.plot(ax=base, column="coffee_production_2017");
# ### Creating attributes and removing spatial information
#
# Calculate new column...
world2 = world.copy()
world2["pop_dens"] = world2["pop"] / world2["area_km2"]
# Unite columns...
world2["con_reg"] = world["continent"] + ":" + world2["region_un"]
world2 = world2.drop(["continent", "region_un"], axis=1)
# Split column...
world2[["continent", "region_un"]] = world2["con_reg"] \
.str.split(":", expand=True)
# Rename...
world2.rename(columns={"name_long": "name"})
# Renaming all columns...
new_names =["i", "n", "c", "r", "s", "t", "a", "p", "l", "gP", "geom"]
world.columns = new_names
# Dropping geometry...
pd.DataFrame(world.drop(columns="geom"))
# ## Manipulating raster objects
#
# ### Raster subsetting
#
# When using `rasterio`, raster values are accessible through a `numpy` array, which can be imported with the `.read` method:
elev = src_elev.read(1)
elev
# Then, we can access any subset of cell values using `numpy` methods. For example:
elev[0, 0] ## Value at row 1, column 1
# Cell values can be modified by overwriting existing values in conjunction with a subsetting operation. The following expression, for example, sets the upper left cell of elev to 0:
elev[0, 0] = 0
elev
# Multiple cells can also be modified in this way:
elev[0, 0:2] = 0
elev
# ### Summarizing raster objects
#
# Global summaries of raster values can be calculated by applying `numpy` summary functions---such as `np.mean`---on the array with raster values. For example:
np.mean(elev)
# Note that "No Data"-safe functions--such as `np.nanmean`---should be used in case the raster contains "No Data" values which need to be ignored:
elev[0, 2] = np.nan
elev
np.mean(elev)
np.nanmean(elev)
# Raster value statistics can be visualized in a variety of ways. One approach is to "flatten" the raster values into a one-dimensional array, then use a graphical function such as `plt.hist` or `plt.boxplot` (from `matplotlib.pyplot`). For example:
x = elev.flatten()
plt.hist(x);
# ## Exercises
#
|
ipynb/03-attribute-operations.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: conda_python3
# language: python
# name: conda_python3
# ---
# #lec11
with open('jmu_news.txt','r') as jmu_news:
news_content = jmu_news.read()
print(news_content)
from collections import Counter
# +
count_result = Counter(['a','b','b'])
print (count_result.most_common(1))
# -
with open ('jmu_news.txt','r') as jmu_news:
new_content = jmu_news.read()
word_list = news_content.split()
count_result = Counter(word_list)
for word, count in count_result.most_common(10):
print(word,count)
num_list = [1,2,3,4]
new_list = [i+1 for i in num_list]
print(new_list)
# #Ex1
with open ('jmu_news.txt','r') as jmu_news:
new_content = jmu_news.read()
word_list = news_content.split()
count_result = Counter(word_list)
for word, count in count_result.most_common(10):
print(word,count)
with open ('jmu_news.txt','r') as jmu_news:
new_content = jmu_news.read()
word_list = news_content.split()
low_case_list = [word.lower() for word in word_list]
print(low_case_list)
# #EX2
with open ('jmu_news.txt','r') as jmu_news:
new_content = jmu_news.read()
word_list = news_content.split()
low_case_list = [word.lower() for word in word_list]
count_result = Counter(word_list)
for word, count in count_result.most_common(10):
print(word,count)
print("{} salary is${}".format('Tom',60000))
# +
import json
from pprint import pprint
# -
with open('demo.json','r') as json_file:
json_dict = json.load(json_file)
pprint(json_dict)
import urllib.request
# +
url = 'https://www.jmu.edu'
res = urllib.request.urlopen(url)
web_html = res.read()
print(web_html.decode('utf-8'))
# -
|
Lec11.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Python Code Challenges!
#
#
# +
# Codewars
# https://www.codewars.com/kata/5467e4d82edf8bbf40000155/train/python
# Descending Orders
# -
def descending_order(num):
# Bust a move right here
num = sorted([char for char in str(num)], reverse = True)
num = num = int("".join(num))
return num
descending_order(5020016)
|
Python Code Challenges/.ipynb_checkpoints/Descending Order-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Custom Types
#
# Often, the behavior for a field needs to be customized to support a particular shape or validation method that ParamTools does not support out of the box. In this case, you may use the `register_custom_type` function to add your new `type` to the ParamTools type registry. Each `type` has a corresponding `field` that is used for serialization and deserialization. ParamTools will then use this `field` any time it is handling a `value`, `label`, or `member` that is of this `type`.
#
# ParamTools is built on top of [`marshmallow`](https://github.com/marshmallow-code/marshmallow), a general purpose validation library. This means that you must implement a custom `marshmallow` field to go along with your new type. Please refer to the `marshmallow` [docs](https://marshmallow.readthedocs.io/en/stable/) if you have questions about the use of `marshmallow` in the examples below.
#
#
# ## 32 Bit Integer Example
#
# ParamTools's default integer field uses NumPy's `int64` type. This example shows you how to define an `int32` type and reference it in your `defaults`.
#
# First, let's define the Marshmallow class:
#
# +
import marshmallow as ma
import numpy as np
class Int32(ma.fields.Field):
"""
A custom type for np.int32.
https://numpy.org/devdocs/reference/arrays.dtypes.html
"""
# minor detail that makes this play nice with array_first
np_type = np.int32
def _serialize(self, value, *args, **kwargs):
"""Convert np.int32 to basic, serializable Python int."""
return value.tolist()
def _deserialize(self, value, *args, **kwargs):
"""Cast value from JSON to NumPy Int32."""
converted = np.int32(value)
return converted
# -
# Now, reference it in our defaults JSON/dict object:
#
# +
import paramtools as pt
# add int32 type to the paramtools type registry
pt.register_custom_type("int32", Int32())
class Params(pt.Parameters):
defaults = {
"small_int": {
"title": "Small integer",
"description": "Demonstrate how to define a custom type",
"type": "int32",
"value": 2
}
}
params = Params(array_first=True)
print(f"value: {params.small_int}, type: {type(params.small_int)}")
# -
# One problem with this is that we could run into some deserialization issues. Due to integer overflow, our deserialized result is not the number that we passed in--it's negative!
#
params.adjust(dict(
# this number wasn't chosen randomly.
small_int=2147483647 + 1
))
# ### Marshmallow Validator
#
# Fortunately, you can specify a custom validator with `marshmallow` or ParamTools. Making this works requires modifying the `_deserialize` method to check for overflow like this:
#
class Int32(ma.fields.Field):
"""
A custom type for np.int32.
https://numpy.org/devdocs/reference/arrays.dtypes.html
"""
# minor detail that makes this play nice with array_first
np_type = np.int32
def _serialize(self, value, *args, **kwargs):
"""Convert np.int32 to basic Python int."""
return value.tolist()
def _deserialize(self, value, *args, **kwargs):
"""Cast value from JSON to NumPy Int32."""
converted = np.int32(value)
# check for overflow and let range validator
# display the error message.
if converted != int(value):
return int(value)
return converted
# Now, let's see how to use `marshmallow` to fix this problem:
#
# +
import marshmallow as ma
import paramtools as pt
# get the minimum and maxium values for 32 bit integers.
min_int32 = -2147483648 # = np.iinfo(np.int32).min
max_int32 = 2147483647 # = np.iinfo(np.int32).max
# add int32 type to the paramtools type registry
pt.register_custom_type(
"int32",
Int32(validate=[
ma.validate.Range(min=min_int32, max=max_int32)
])
)
class Params(pt.Parameters):
defaults = {
"small_int": {
"title": "Small integer",
"description": "Demonstrate how to define a custom type",
"type": "int32",
"value": 2
}
}
params = Params(array_first=True)
params.adjust(dict(
small_int=np.int64(max_int32) + 1
))
# -
# ### ParamTools Validator
#
# Finally, we will use ParamTools to solve this problem. We need to modify how we create our custom `marshmallow` field so that it's wrapped by ParamTools's `PartialField`. This makes it clear that your field still needs to be initialized, and that your custom field is able to receive validation information from the `defaults` configuration:
#
# +
import paramtools as pt
# add int32 type to the paramtools type registry
pt.register_custom_type(
"int32",
pt.PartialField(Int32)
)
class Params(pt.Parameters):
defaults = {
"small_int": {
"title": "Small integer",
"description": "Demonstrate how to define a custom type",
"type": "int32",
"value": 2,
"validators": {
"range": {"min": -2147483648, "max": 2147483647}
}
}
}
params = Params(array_first=True)
params.adjust(dict(
small_int=2147483647 + 1
))
# -
|
docs/api/custom-types.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: gpu
# language: python
# name: gpu
# ---
# +
import pandas as pd
import re
import folium
import os
from folium.plugins import HeatMap
# -
excel = pd.read_excel('data.xlsx')
# +
df = excel
clean_frame = pd.DataFrame(columns=['Tag', 'Latitude', 'Longitude'])
i = 0
for index, row in df.iterrows():
tags = re.findall(r"#(\w+)", row['Tweet content'])
latidute = row['Latitude']
longitude = row['Longitude']
for tag in tags:
clean_frame.loc[i] = [tag, latidute, longitude]
i += 1
# -
clean_frame = clean_frame[['Latitude', 'Longitude', 'Tag']]
top_tags = clean_frame['Tag'].value_counts()
clean_frame['Tag'] = pd.factorize(clean_frame.Tag)[0]
top_tags_factorized = clean_frame['Tag'].value_counts()
print(top_tags_factorized.head())
# +
m = folium.Map([48., 5.], zoom_start=6)
colors = ['red', 'blue', 'lime']
top_hash_indexes = top_tags_factorized.head(3).index.tolist()
for i, k in enumerate(top_hash_indexes):
data = clean_frame.loc[clean_frame['Tag'] == k].values.tolist()
HeatMap(data, radius=15, gradient={0: 'white', 1: colors[i]}).add_to(m)
m.save('Heatmap.html')
m
# +
import numpy as np
data = (np.random.normal(size=(20, 3)) *
np.array([[1, 1, 1]]) +
np.array([[48, 5, 1]])).tolist()
data2 = (np.random.normal(size=(20, 3)) *
np.array([[1, 1, 1]]) +
np.array([[48, 20, 1]])).tolist()
from folium.plugins import HeatMap
m = folium.Map([48., 5.], zoom_start=6)
HeatMap(data, 'first', radius=15, gradient={0: 'white', 1: 'red'}).add_to(m)
HeatMap(data2, 'second', radius=15, gradient={0: 'white', 1: 'blue'}).add_to(m)
m.save(os.path.join('Heatmap.html'))
m
# -
|
lab1/Untitled.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: simclr
# language: python
# name: simclr
# ---
# +
import os
import cv2
import numpy as np
import pandas as pd
from tqdm import tqdm
import torch
import torch.nn as nn
from torch.nn import functional as F
import transformers
import gc
from sklearn.feature_extraction.text import TfidfVectorizer, CountVectorizer
# -
# ## TfidfVectorizer model
def read_dataset(is_train=True):
if is_train:
df = pd.read_csv('train.csv')
image_paths = 'train_images/' + df['image']
else:
df = pd.read_csv('test.csv')
image_paths = 'test_images/' + df['image']
return df, image_paths
def combine_predictions(row):
x = np.concatenate([ row['text_predictions'], row['phash']])
return ' '.join( np.unique(x) )
def get_text_predictions_torch(df, max_features=25_000, th=0.75):
model = TfidfVectorizer(stop_words='english', binary=True, max_features=max_features)
text_embeddings = model.fit_transform(df['title']).toarray().astype(np.float16)
text_embeddings=torch.from_numpy(text_embeddings).to('cuda:0')
preds = []
CHUNK = 1024*4
print('Finding similar titles...')
CTS = len(df) // CHUNK
if (len(df)%CHUNK) != 0: CTS += 1
for j in tqdm(range( CTS )):
a = j * CHUNK
b = (j+1) * CHUNK
b = min(b, len(df))
#print('chunk',a,'to',b)
# COSINE SIMILARITY DISTANCE
cts = torch.matmul(text_embeddings, text_embeddings[a:b].T).T
for k in range(b-a):
IDX = torch.where(cts[k,] > th)[0].cpu().numpy()
o = df.iloc[IDX].posting_id.values
preds.append(o)
del model, text_embeddings
gc.collect()
torch.cuda.empty_cache()
return preds
df,image_paths = read_dataset()
df.head()
text_predictions = get_text_predictions_torch(df, max_features=25_000)
# ### phash
phash = df.groupby('image_phash').posting_id.agg('unique').to_dict()
df['phash'] = df.image_phash.map(phash)
df.head()
# ### TfidfVectorizer + phash
df['text_predictions'] = text_predictions
df['matches'] = df.apply(combine_predictions, axis=1)
df[['posting_id', 'matches']].to_csv('submission.csv', index=False)
# LB: 0.652
# +
def getMetric(col):
def f1score(row):
n = len(np.intersect1d(row.target, row[col]))
return 2*n / (len(row.target) + len(row[col]))
return f1score
def combine_for_cv(row):
x = np.concatenate([row['phash'], row['text_predictions']])
return np.unique(x)
df['text_predictions'] = text_predictions
phash = df.groupby('image_phash').posting_id.agg('unique').to_dict()
df['phash'] = df.image_phash.map(phash)
df['matches_CV'] = df.apply(combine_for_cv, axis=1)
tmp = df.groupby('label_group').posting_id.agg('unique').to_dict()
df['target'] = df.label_group.map(tmp)
MyCVScore = df.apply(getMetric('matches_CV'), axis=1)
print('CV score =', MyCVScore.mean())
# -
# ## Transformer
class CFG:
batch_size = 16
seed = 42
device = 'cuda'
classes = 11014
scale = 30
margin = 0.5
CV = False
num_workers=4
transformer_model = 'sentence-transformer-models/paraphrase-xlm-r-multilingual-v1/0_Transformer'
text_model_path = 'best-multilingual-model/sentence_transfomer_xlm_best_loss_num_epochs_25_arcface.bin'
model_params = {
'n_classes':11014,
'model_name':transformer_model,
'use_fc':False,
'fc_dim':512,
'dropout':0.3,
}
tokenizer = transformers.AutoTokenizer.from_pretrained(CFG.transformer_model)
# +
class ShopeeTextDataset(Dataset):
def __init__(self, csv):
self.csv = csv.reset_index()
def __len__(self):
return self.csv.shape[0]
def __getitem__(self, index):
row = self.csv.iloc[index]
text = row.title
text = tokenizer(text, padding='max_length', truncation=True, max_length=128, return_tensors="pt")
input_ids = text['input_ids'][0]
attention_mask = text['attention_mask'][0]
return input_ids, attention_mask
class ShopeeTextNet(nn.Module):
def __init__(self,
n_classes,
model_name='bert-base-uncased',
use_fc=False,
fc_dim=512,
dropout=0.0):
"""
:param n_classes:
:param model_name: name of model from pretrainedmodels
e.g. resnet50, resnext101_32x4d, pnasnet5large
:param pooling: One of ('SPoC', 'MAC', 'RMAC', 'GeM', 'Rpool', 'Flatten', 'CompactBilinearPooling')
:param loss_module: One of ('arcface', 'cosface', 'softmax')
"""
super(ShopeeTextNet, self).__init__()
self.transformer = transformers.AutoModel.from_pretrained(model_name)
final_in_features = self.transformer.config.hidden_size
self.use_fc = use_fc
if use_fc:
self.dropout = nn.Dropout(p=dropout)
self.fc = nn.Linear(final_in_features, fc_dim)
self.bn = nn.BatchNorm1d(fc_dim)
self._init_params()
final_in_features = fc_dim
def _init_params(self):
nn.init.xavier_normal_(self.fc.weight)
nn.init.constant_(self.fc.bias, 0)
nn.init.constant_(self.bn.weight, 1)
nn.init.constant_(self.bn.bias, 0)
def forward(self, input_ids,attention_mask):
feature = self.extract_feat(input_ids,attention_mask)
return F.normalize(feature)
def extract_feat(self, input_ids,attention_mask):
x = self.transformer(input_ids=input_ids,attention_mask=attention_mask)
features = x[0]
features = features[:,0,:]
if self.use_fc:
features = self.dropout(features)
features = self.fc(features)
features = self.bn(features)
return features
# -
def get_text_embeddings(df):
embeds = []
model = ShopeeTextNet(**CFG.model_params)
model.eval()
model.load_state_dict(dict(list(torch.load(CFG.TEXT_MODEL_PATH).items())[:-1]))
model = model.to(CFG.device)
text_dataset = ShopeeTextDataset(df)
text_loader = torch.utils.data.DataLoader(
text_dataset,
batch_size=CFG.batch_size,
pin_memory=True,
drop_last=False,
num_workers=CFG.num_workers
)
with torch.no_grad():
for input_ids, attention_mask in tqdm(text_loader):
input_ids = input_ids.cuda()
attention_mask = attention_mask.cuda()
feat = model(input_ids, attention_mask)
text_embeddings = feat.detach().cpu().numpy()
embeds.append(text_embeddings)
del model
text_embeddings = np.concatenate(embeds)
print(f'Our text embeddings shape is {text_embeddings.shape}')
del embeds
gc.collect()
return text_embeddings
def f1_score(y_true, y_pred):
y_true = y_true.apply(lambda x: set(x.split()))
y_pred = y_pred.apply(lambda x: set(x.split()))
intersection = np.array([len(x[0] & x[1]) for x in zip(y_true, y_pred)])
len_y_pred = y_pred.apply(lambda x: len(x)).values
len_y_true = y_true.apply(lambda x: len(x)).values
f1 = 2 * intersection / (len_y_pred + len_y_true)
return f1
def get_neighbours_cos_sim(df,embeddings, threshold=0.6):
'''
When using cos_sim use normalized features else use normal features
'''
embeddings = cupy.array(embeddings)
if CFG.GET_CV:
thresholds = list(np.arange(0.5,0.7,0.05))
scores = []
for threshold in thresholds:
preds = []
CHUNK = 1024*4
print('Finding similar titles...for threshold :',threshold)
CTS = len(embeddings)//CHUNK
if len(embeddings)%CHUNK!=0: CTS += 1
for j in range( CTS ):
a = j*CHUNK
b = (j+1)*CHUNK
b = min(b,len(embeddings))
cts = cupy.matmul(embeddings,embeddings[a:b].T).T
for k in range(b-a):
IDX = cupy.where(cts[k,]>threshold)[0]
o = df.iloc[cupy.asnumpy(IDX)].posting_id.values
o = ' '.join(o)
preds.append(o)
df['pred_matches'] = preds
df['f1'] = f1_score(df['matches'], df['pred_matches'])
score = df['f1'].mean()
print(f'Our f1 score for threshold {threshold} is {score}')
scores.append(score)
thresholds_scores = pd.DataFrame({'thresholds': thresholds, 'scores': scores})
max_score = thresholds_scores[thresholds_scores['scores'] == thresholds_scores['scores'].max()]
best_threshold = max_score['thresholds'].values[0]
best_score = max_score['scores'].values[0]
print(f'Our best score is {best_score} and has a threshold {best_threshold}')
else:
preds = []
CHUNK = 1024*4
print('Finding similar texts...for threshold :',threshold)
CTS = len(embeddings)//CHUNK
if len(embeddings)%CHUNK!=0: CTS += 1
for j in range( CTS ):
a = j*CHUNK
b = (j+1)*CHUNK
b = min(b,len(embeddings))
print('chunk',a,'to',b)
cts = cupy.matmul(embeddings,embeddings[a:b].T).T
for k in range(b-a):
IDX = cupy.where(cts[k,]>threshold)[0]
o = df.iloc[cupy.asnumpy(IDX)].posting_id.values
preds.append(o)
return df, preds
df,df_cu,image_paths = read_dataset()
df.head()
text_embeddings = get_text_embeddings(df)
df, text_predictions = get_neighbours_cos_sim(df, text_embeddings)
# ### CV Score for transformer
df['text_predictions'] = text_predictions
phash = df.groupby('image_phash').posting_id.agg('unique').to_dict()
df['phash'] = df.image_phash.map(phash)
df['matches_CV'] = df.apply(combine_for_cv, axis=1)
tmp = df.groupby('label_group').posting_id.agg('unique').to_dict()
df['target'] = df.label_group.map(tmp)
MyCVScore = df.apply(getMetric('matches_CV'), axis=1)
print('CV score =', MyCVScore.mean())
|
Text.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda env:root] *
# language: python
# name: conda-root-py
# ---
# # Part 1: Data Ingestion
#
# This demo showcases financial fraud prevention and using the MLRun feature store to define complex features that help identify fraud. Fraud prevention specifically is a challenge as it requires processing raw transaction and events in real-time and being able to quickly respond and block transactions before they occur.
#
# To address this, we create a development pipeline and a production pipeline. Both pipelines share the same feature engineering and model code, but serve data very differently. Furthermore, we automate the data and model monitoring process, identify drift and trigger retraining in a CI/CD pipeline. This process is described in the diagram below:
#
# 
# The raw data is described as follows:
#
# | TRANSACTIONS || ║ |USER EVENTS ||
# |-----------------|----------------------------------------------------------------|----------|-----------------|----------------------------------------------------------------|
# | **age** | age group value 0-6. Some values are marked as U for unknown | ║ | **source** | The party/entity related to the event |
# | **gender** | A character to define the age | ║ | **event** | event, such as login or password change |
# | **zipcodeOri** | ZIP code of the person originating the transaction | ║ | **timestamp** | The date and time of the event |
# | **zipMerchant** | ZIP code of the merchant receiving the transaction | ║ | | |
# | **category** | category of the transaction (e.g., transportation, food, etc.) | ║ | | |
# | **amount** | the total amount of the transaction | ║ | | |
# | **fraud** | whether the transaction is fraudulent | ║ | | |
# | **timestamp** | the date and time in which the transaction took place | ║ | | |
# | **source** | the ID of the party/entity performing the transaction | ║ | | |
# | **target** | the ID of the party/entity receiving the transaction | ║ | | |
# | **device** | the device ID used to perform the transaction | ║ | | |
# This notebook introduces how to **Ingest** different data sources to the **Feature Store**.
#
# The following FeatureSets will be created:
# - **Transactions**: Monetary transactions between a source and a target.
# - **Events**: Account events such as account login or a password change.
# - **Label**: Fraud label for the data.
#
# By the end of this tutorial you’ll learn how to:
#
# - Create an ingestion pipeline for each data source.
# - Define preprocessing, aggregation and validation of the pipeline.
# - Run the pipeline locally within the notebook.
# - Launch a real-time function to ingest live data.
# - Schedule a cron to run the task when needed.
project_name = 'fraud-demo'
# +
import mlrun
# Initialize the MLRun project object
project = mlrun.get_or_create_project(project_name, context="./", user_project=True)
# -
# ## Step 1 - Fetch, Process and Ingest our datasets
# ## 1.1 - Transactions
# ### Transactions
# + tags=["hide-cell"]
# Helper functions to adjust the timestamps of our data
# while keeping the order of the selected events and
# the relative distance from one event to the other
def date_adjustment(sample, data_max, new_max, old_data_period, new_data_period):
'''
Adjust a specific sample's date according to the original and new time periods
'''
sample_dates_scale = ((data_max - sample) / old_data_period)
sample_delta = new_data_period * sample_dates_scale
new_sample_ts = new_max - sample_delta
return new_sample_ts
def adjust_data_timespan(dataframe, timestamp_col='timestamp', new_period='2d', new_max_date_str='now'):
'''
Adjust the dataframe timestamps to the new time period
'''
# Calculate old time period
data_min = dataframe.timestamp.min()
data_max = dataframe.timestamp.max()
old_data_period = data_max-data_min
# Set new time period
new_time_period = pd.Timedelta(new_period)
new_max = pd.Timestamp(new_max_date_str)
new_min = new_max-new_time_period
new_data_period = new_max-new_min
# Apply the timestamp change
df = dataframe.copy()
df[timestamp_col] = df[timestamp_col].apply(lambda x: date_adjustment(x, data_max, new_max, old_data_period, new_data_period))
return df
# +
import pandas as pd
# Fetch the transactions dataset from the server
transactions_data = pd.read_csv('https://s3.wasabisys.com/iguazio/data/fraud-demo-mlrun-fs-docs/data.csv', parse_dates=['timestamp'], nrows=500)
# Adjust the samples timestamp for the past 2 days
transactions_data = adjust_data_timespan(transactions_data, new_period='2d')
# Preview
transactions_data.head(3)
# -
# ### Transactions - Create a FeatureSet and Preprocessing Pipeline
# Create the FeatureSet (data pipeline) definition for the **credit transaction processing** which describes the offline/online data transformations and aggregations.<br>
# The feature store will automatically add an offline `parquet` target and an online `NoSQL` target by using `set_targets()`.
#
# The data pipeline consists of:
#
# * **Extracting** the data components (hour, day of week)
# * **Mapping** the age values
# * **One hot encoding** for the transaction category and the gender
# * **Aggregating** the amount (avg, sum, count, max over 2/12/24 hour time windows)
# * **Aggregating** the transactions per category (over 14 days time windows)
# * **Writing** the results to **offline** (Parquet) and **online** (NoSQL) targets
# Import MLRun's Feature Store
import mlrun.feature_store as fstore
from mlrun.feature_store.steps import OneHotEncoder, MapValues, DateExtractor
# Define the transactions FeatureSet
transaction_set = fstore.FeatureSet("transactions",
entities=[fstore.Entity("source")],
timestamp_key='timestamp',
description="transactions feature set")
# +
# Define and add value mapping
main_categories = ["es_transportation", "es_health", "es_otherservices",
"es_food", "es_hotelservices", "es_barsandrestaurants",
"es_tech", "es_sportsandtoys", "es_wellnessandbeauty",
"es_hyper", "es_fashion", "es_home", "es_contents",
"es_travel", "es_leisure"]
# One Hot Encode the newly defined mappings
one_hot_encoder_mapping = {'category': main_categories,
'gender': list(transactions_data.gender.unique())}
# Define the graph steps
transaction_set.graph\
.to(DateExtractor(parts = ['hour', 'day_of_week'], timestamp_col = 'timestamp'))\
.to(MapValues(mapping={'age': {'U': '0'}}, with_original_features=True))\
.to(OneHotEncoder(mapping=one_hot_encoder_mapping))
# Add aggregations for 2, 12, and 24 hour time windows
transaction_set.add_aggregation(name='amount',
column='amount',
operations=['avg','sum', 'count','max'],
windows=['2h', '12h', '24h'],
period='1h')
# Add the category aggregations over a 14 day window
for category in main_categories:
transaction_set.add_aggregation(name=category,column=f'category_{category}',
operations=['count'], windows=['14d'], period='1d')
# Add default (offline-parquet & online-nosql) targets
transaction_set.set_targets()
# Plot the pipeline so we can see the different steps
transaction_set.plot(rankdir="LR", with_targets=True)
# -
# ### Transactions - Ingestion
# +
# Ingest our transactions dataset through our defined pipeline
transactions_df = fstore.ingest(transaction_set, transactions_data,
infer_options=fstore.InferOptions.default())
transactions_df.head(3)
# -
# ## 1.2 - User Events
# ### User Events - Fetching
# +
# Fetch our user_events dataset from the server
user_events_data = pd.read_csv('https://s3.wasabisys.com/iguazio/data/fraud-demo-mlrun-fs-docs/events.csv',
index_col=0, quotechar="\'", parse_dates=['timestamp'], nrows=500)
# Adjust to the last 2 days to see the latest aggregations in our online feature vectors
user_events_data = adjust_data_timespan(user_events_data, new_period='2d')
# Preview
user_events_data.head(3)
# -
# ### User Events - Create a FeatureSet and Preprocessing Pipeline
#
# Now we will define the events feature set.
# This is a pretty straight forward pipeline in which we only one hot encode the event categories and save the data to the default targets.
user_events_set = fstore.FeatureSet("events",
entities=[fstore.Entity("source")],
timestamp_key='timestamp',
description="user events feature set")
# +
# Define and add value mapping
events_mapping = {'event': list(user_events_data.event.unique())}
# One Hot Encode
user_events_set.graph.to(OneHotEncoder(mapping=events_mapping))
# Add default (offline-parquet & online-nosql) targets
user_events_set.set_targets()
# Plot the pipeline so we can see the different steps
user_events_set.plot(rankdir="LR", with_targets=True)
# -
# ### User Events - Ingestion
# Ingestion of our newly created events feature set
events_df = fstore.ingest(user_events_set, user_events_data)
events_df.head(3)
# ## Step 2 - Create a labels dataset for model training
# ### Label Set - Create a FeatureSet
# This feature set contains the label for the fraud demo, it will be ingested directly to the default targets without any changes
def create_labels(df):
labels = df[['fraud','source','timestamp']].copy()
labels = labels.rename(columns={"fraud": "label"})
labels['timestamp'] = labels['timestamp'].astype("datetime64[ms]")
labels['label'] = labels['label'].astype(int)
labels.set_index('source', inplace=True)
return labels
# +
# Define the "labels" feature set
labels_set = fstore.FeatureSet("labels",
entities=[fstore.Entity("source")],
timestamp_key='timestamp',
description="training labels",
engine="pandas")
labels_set.graph.to(name="create_labels", handler=create_labels)
# specify only Parquet (offline) target since its not used for real-time
labels_set.set_targets(['parquet'], with_defaults=False)
labels_set.plot(with_targets=True)
# -
# ### Label Set - Ingestion
# Ingest the labels feature set
labels_df = fstore.ingest(labels_set, transactions_data)
labels_df.head(3)
# ## Step 3 - Deploy a real-time pipeline
#
# When dealing with real-time aggregation, it's important to be able to update these aggregations in real-time.
# For this purpose, we will create live serving functions that will update the online feature store of the `transactions` FeatureSet and `Events` FeatureSet.
#
# Using MLRun's `serving` runtime, craetes a nuclio function loaded with our feature set's computational graph definition
# and an `HttpSource` to define the HTTP trigger.
#
# Notice that the implementation below does not require any rewrite of the pipeline logic.
# ## 3.1 - Transactions
# ### Transactions - Deploy our FeatureSet live endpoint
# Create iguazio v3io stream and transactions push API endpoint
transaction_stream = f'v3io:///projects/{project.name}/streams/transaction'
transaction_pusher = mlrun.datastore.get_stream_pusher(transaction_stream)
# +
# Define the source stream trigger (use v3io streams)
# we will define the `key` and `time` fields (extracted from the Json message).
source = mlrun.datastore.sources.StreamSource(path=transaction_stream , key_field='source', time_field='timestamp')
# Deploy the transactions feature set's ingestion service over a real-time (Nuclio) serverless function
# you can use the run_config parameter to pass function/service specific configuration
transaction_set_endpoint = fstore.deploy_ingestion_service(featureset=transaction_set, source=source)
# -
# ### Transactions - Test the feature set HTTP endpoint
# By defining our `transactions` feature set we can now use MLRun and Storey to deploy it as a live endpoint, ready to ingest new data!
#
# Using MLRun's `serving` runtime, we will create a nuclio function loaded with our feature set's computational graph definition and an `HttpSource` to define the HTTP trigger.
# +
import requests
import json
# Select a sample from the dataset and serialize it to JSON
transaction_sample = json.loads(transactions_data.sample(1).to_json(orient='records'))[0]
transaction_sample['timestamp'] = str(pd.Timestamp.now())
transaction_sample
# -
# Post the sample to the ingestion endpoint
requests.post(transaction_set_endpoint, json=transaction_sample).text
# ## 3.2 - User Events
# ### User Events - Deploy our FeatureSet live endpoint
# Deploy the events feature set's ingestion service using the feature set and all the previously defined resources.
# Create iguazio v3io stream and transactions push API endpoint
events_stream = f'v3io:///projects/{project.name}/streams/events'
events_pusher = mlrun.datastore.get_stream_pusher(events_stream)
# +
# Define the source stream trigger (use v3io streams)
# we will define the `key` and `time` fields (extracted from the Json message).
source = mlrun.datastore.sources.StreamSource(path=events_stream , key_field='source', time_field='timestamp')
# Deploy the transactions feature set's ingestion service over a real-time (Nuclio) serverless function
# you can use the run_config parameter to pass function/service specific configuration
events_set_endpoint = fstore.deploy_ingestion_service(featureset=user_events_set, source=source)
# -
# ### User Events - Test the feature set HTTP endpoint
# Select a sample from the events dataset and serialize it to JSON
user_events_sample = json.loads(user_events_data.sample(1).to_json(orient='records'))[0]
user_events_sample['timestamp'] = str(pd.Timestamp.now())
user_events_sample
# Post the sample to the ingestion endpoint
requests.post(events_set_endpoint, json=user_events_sample).text
# ## Done!
#
# You've completed Part 1 of the data-ingestion with the feature store.
# Proceed to [Part 2](02-create-training-model.ipynb) to learn how to train an ML model using the feature store data.
|
docs/feature-store/end-to-end-demo/01-ingest-datasources.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import numpy as np
import re
from operator import itemgetter
Corpus = {
'l o w _':5,
'l o w e r _':2,
'n e w e s t _':6,
'w i d e s t _':3,
'h a p p i e r _':2
}
Corpus
def getPairCounts(Corpus):
pairs = {}
for word,fr in Corpus.items():
symbols = word.split(' ')
for i in range(len(symbols)-1):
pair = (symbols[i],symbols[i+1])
cfr = pairs.get(pair,0)
pairs[pair] = cfr+fr
return pairs
pairsCounts = getPairCounts(Corpus)
pairsCounts
def getBestPair(pairsCounts):
return max(pairsCounts,key=pairsCounts.get)
print(getBestPair(pairsCounts))
def mergeInCorpus(bestPair,Corpus):
newCorpus = {}
for word in Corpus:
newWord = re.sub(' '.join(bestPair),''.join(bestPair),word)
newCorpus[newWord] = Corpus[word]
return newCorpus
bestPair = getBestPair(pairsCounts)
newCorpus = mergeInCorpus(bestPair,Corpus)
newCorpus
def runBPE(Corpus,k):
bpeStats = {}
for i in range(k):
pairsCounts = getPairCounts(Corpus)
if not pairsCounts:
break
bestPair = getBestPair(pairsCounts)
bpeStats[bestPair] = i
Corpus = mergeInCorpus(bestPair,Corpus)
return Corpus,bpeStats
Corpus = {
'l o w _':5,
'l o w e r _':2,
'n e w e s t _':6,
'w i d e s t _':3,
'h a p p i e r _':2
}
newCorpus,bpeStats = runBPE(Corpus,10)
newCorpus
bpeStats
newWord = 'lowest'
newWord2 = ' '.join(list(newWord))+' _'
def getAllPairs(word):
pairs = []
word = word.split(' ')
prevChar = word[0]
for char in word[1:]:
pairs.append((prevChar,char))
prevChar = char
return pairs
pairs = getAllPairs(newWord2)
pairs
def getPairToBeMerged(bpeStats,pairs):
#bpeCodes = [(pair,bpeStats[pair]) for pair in pairs if pair in bpeStats]
bpeCodes = []
for pair in pairs:
if pair in bpeStats:
bpeCodes.append((pair,bpeStats[pair]))
if len(bpeCodes) == 0:
return (-1,-1)
pairToBeMerged = min(bpeCodes,key=itemgetter(1))[0]
return pairToBeMerged
pairToBeMerged = getPairToBeMerged(bpeStats,pairs)
def mergeLetters(word,pairToBeMerged):
newWord = re.sub(' '.join(pairToBeMerged),''.join(pairToBeMerged),word)
return newWord
print(mergeLetters(newWord2,pairToBeMerged))
def bpeTokenize(word,bpeStats):
if len(word) == 1:
return word
word = ' '.join(list(word))+' _'
while True:
pairs = getAllPairs(word)
pairToBeMerged = getPairToBeMerged(bpeStats,pairs)
if pairToBeMerged[0] == -1:
break
word = mergeLetters(word,pairToBeMerged)
return word
newWord = bpeTokenize('lowest',bpeStats)
newWord
|
01-Code/2b_TextProcessing_2.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import numpy as np
import matplotlib.pyplot as plt
# %matplotlib inline
import tensorflow as tf
from sklearn.decomposition import PCA
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA
from sklearn.cluster import KMeans
# +
fashion_mnist = tf.keras.datasets.fashion_mnist
(train_images, train_labels), (test_images, test_labels) = fashion_mnist.load_data()
# -
X = np.concatenate([train_images,test_images])
Y = np.concatenate([train_labels,test_labels])
X = X.reshape(X.shape[0], 28*28)
pca = PCA(n_components=20).fit(X)
pca2 = PCA(n_components=2).fit(X)
pca3 = PCA(n_components=3).fit(X)
X2 = pca2.transform(X)
X3 = pca3.transform(X)
kmeans_per_k = [KMeans(n_clusters=k, random_state=42, init='random').fit(X2) for k in [4, 7, 10]]
for model in kmeans_per_k:
print(model.cluster_centers_)
x = X2[:300]
labels = [model.predict(x) for model in kmeans_per_k]
fig, ax = plt.subplots()
x = X2[:300,0]
y = X2[:300,1]
ax.scatter(x, y,marker="")
for i, txt in enumerate(labels[0]):
ax.annotate(txt, (x[i], y[i]))
fig, ax = plt.subplots()
x = X2[:300,0]
y = X2[:300,1]
ax.scatter(x, y,marker="")
for i, txt in enumerate(labels[1]):
ax.annotate(txt, (x[i], y[i]))
fig, ax = plt.subplots()
x = X2[:300,0]
y = X2[:300,1]
ax.scatter(x, y,marker="")
for i, txt in enumerate(labels[2]):
ax.annotate(txt, (x[i], y[i]))
pca_s.
|
7-c.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# 
#
# <a href="https://hub.callysto.ca/jupyter/hub/user-redirect/git-pull?repo=https%3A%2F%2Fgithub.com%2Fcallysto%2Fcurriculum-notebooks&branch=master&subPath=Mathematics/Percentage/Percents.ipynb&depth=1" target="_parent"><img src="https://raw.githubusercontent.com/callysto/curriculum-notebooks/master/open-in-callysto-button.svg?sanitize=true" width="123" height="24" alt="Open in Callysto"/></a>
# **Run the cell below, this will add two buttons. Click on the "initialize" button before proceeding through the notebook**
# + tags=["hide-input"]
import uiButtons
# %uiButtons
# + tags=["hide-input"] language="html"
# <script src="https://d3js.org/d3.v3.min.js"></script>
# -
# # Percentages
# ## Introduction
# In this notebook we will discuss what percentages are and why this way of representing data is helpful in many different contexts. Common examples of percentages are sales tax or a mark for an assignment.
#
# The word percent comes from the Latin adverbial phrase *per centum* meaning “*by the hundred*”.
#
# For example, if the sales tax is $5\%$, this means that for every dollar you spend the tax adds $5$ cents to the total price of the purchase.
#
# A percentage simply represents a fraction (per hundred). For example, $90\%$ is the same as saying $\dfrac{90}{100}$. It is used to represent a ratio.
#
# What makes percentages so powerful is that they can represent any ratio.
#
# For example, getting $\dfrac{22}{25}$ on a math exam can be represented as $88\%$: $22$ is $88\%$ of $25$.
# ## How to Get a Percentage
# As mentioned in the introduction, a percentage is simply a fraction represented as a portion of 100.
#
# For this notebook we will only talk about percentages between 0% and 100%.
#
# This means the corresponding fraction will always be a value between $0$ and $1$.
#
# Let's look at our math exam mark example from above. The student correctly answered $22$ questions out of $25$, so the student received a grade of $\dfrac{22}{25}$.
#
# To represent this ratio as a percentage we first convert $\dfrac{22}{25}$ to its decimal representation (simply do the division in your calculator).
#
# $$
# \dfrac{22}{25} = 22 \div 25 = 0.88
# $$
#
# We are almost done: we now have the ratio represented as a value between 0 and 1. To finish getting the answer to our problem all we need to do is multiply this value by $100$ to get our percentage. $$0.88 \times 100 = 88\%$$
#
# Putting it all together we can say $22$ is $88\%$ of $25$.
#
# Think of a grade you recently received (as a fraction) and convert it to a percentage. Once you think you have an answer you can use the widget below to check your answer.
#
# Simply add the total marks of the test/assignment then move the slider until you get to your grade received.
# + tags=["hide-input"] language="html"
# <style>
# .main {
# font-family: 'Segoe UI', Tahoma, Geneva, Verdana, sans-serif;
# }
#
# .slider {
# width: 100px;
# }
#
# #maxVal {
# border:1px solid #cccccc;
# border-radius: 5px;
# width: 50px;
# }
# </style>
# <div class="main" style="border:2px solid black; width: 400px; padding: 20px;border-radius: 10px; margin: 0 auto; box-shadow: 3px 3px 12px #acacac">
# <div>
# <label for="maxValue">Enter the assignment/exam total marks</label>
# <input type="number" id="maxVal" value="100">
# </div>
# <div>
# <input type="range" min="0" max="100" value="0" class="slider" id="mySlider" style="width: 300px; margin-top: 20px;">
# </div>
# <h4 id="sliderVal">0</h3>
# </div>
#
# <script>
# var slider = document.getElementById('mySlider');
# var sliderVal = document.getElementById('sliderVal');
#
# slider.oninput = function () {
# var sliderMax = document.getElementById('maxVal').value;
# if(sliderMax < 0 || isNaN(sliderMax)) {
# sliderMax = 100;
# document.getElementById('maxVal').value = 100;
# }
# d3.select('#mySlider').attr('max', sliderMax);
# sliderVal.textContent = "If you answered " + this.value + "/" + sliderMax + " correct questions your grade will be " + ((
# this.value / sliderMax) * 100).toPrecision(3) + "%";
# }
# </script>
# -
# ## Solving Problems Using Percentages
#
# Now that we understand what percentages mean and how to get them from fractions, let's look at solving problems using percentages. Start by watching the video below to get a basic understanding.
# + tags=["hide-input"] language="html"
# <div align="middle">
# <iframe id="percentVid" width="640" height="360" src="https://www.youtube.com/embed/rR95Cbcjzus?end=368" frameborder="0" allow="autoplay; encrypted-media" allowfullscreen style="box-shadow: 3px 3px 12px #ACACAC">
# </iframe>
# <p><a href="https://www.youtube.com/channel/UC4a-Gbdw7vOaccHmFo40b9g" target="_blank">Click here</a> for more videos by Math Antics</p>
# </div>
# <script>
# $(function() {
# var reachable = false;
# var myFrame = $('#percentVid');
# var videoSrc = myFrame.attr("src");
# myFrame.attr("src", videoSrc)
# .on('load', function(){reachable = true;});
# setTimeout(function() {
# if(!reachable) {
# var ifrm = myFrame[0];
# ifrm = (ifrm.contentWindow) ? ifrm.contentWindow : (ifrm.contentDocument.document) ? ifrm.contentDocument.document : ifrm.contentDocument;
# ifrm.document.open();
# ifrm.document.write('If the video does not start click <a href="' + videoSrc + '" target="_blank">here</a>');
# ifrm.document.close();
# }
# }, 2000)
# });
# </script>
# -
# As shown in the video, taking $25\%$ of 20 "things" is the same as saying $\dfrac{25}{100}\times\dfrac{20}{1}=\dfrac{500}{100}=\dfrac{5}{1}=5$.
#
# Let's do another example, assume a retail store is having a weekend sale. The sale is $30\%$ off everything in store.
#
# Sam thinks this is a great time to buy new shoes, and the shoes she is interested in are regular price $\$89.99$.<br>
# If Sam buys these shoes this weekend how much will they cost? If the sales tax is $5\%$, what will the total price be?
#
# <img src="https://orig00.deviantart.net/5c3e/f/2016/211/b/d/converse_shoes_free_vector_by_superawesomevectors-dabxj2k.jpg" width="300">
# <img src="https://www.publicdomainpictures.net/pictures/170000/nahled/30-korting.jpg" width="300">
#
# Let's start by figuring out the sale price of the shoes before calculating the tax. To figure out the new price we must first take $30\%$ off the original price.
#
# So the shoes are regular priced at $\$89.99$ and the sale is for $30\%$ off
#
# $$
# \$89.99\times 30\%=\$89.99\times\frac{30}{100}=\$26.997
# $$
#
# We can round $\$26.997$ to $\$27$.
#
# Ok we now know how much Sam will save on her new shoes, but let's not forget that the question is asking how much her new shoes will cost, not how much she will save. All we need to do now is take the total price minus the savings to get the new price:
#
# $$
# \$89.99- \$27=\$62.99
# $$
#
# Wow, what savings!
#
# Now for the second part of the question: what will the total price be if the tax is $5\%$?
#
# We must now figure out what $5\%$ of $\$62.99$ is
#
# $$
# \$62.99\times5\%=\$62.99\times\frac{5}{100}=\$3.15
# $$
#
# Now we know that Sam will need to pay $\$3.15$ of tax on her new shoes so the final price is
#
# $$
# \$62.99+\$3.15=\$66.14
# $$
#
# A shortcut for finding the total price including the sales tax is to add 1 to the tax ratio, let's see how this works:
#
# $$
# \$62.99\times\left(\frac{5}{100}+1\right)=\$62.99\times1.05=\$66.14
# $$
#
# You can use this trick to quickly figure out a price after tax.
# ## Multiplying Percentages together
# Multiplying two or more percentages together is probably not something you would encounter often but it is easy to do if you remember that percentages are really fractions.
#
# Since percentages is simply a different way to represent a fraction, the rules for multiplying them are the same. Recall that multiplying two fractions together is the same as saying a *a fraction of a fraction*. For example $\dfrac{1}{2}\times\dfrac{1}{2}$ is the same as saying $\dfrac{1}{2}$ of $\dfrac{1}{2}$.
#
# Therefore if we write $50\%\times 20\%$ we really mean $50\%$ of $20\%$.
#
# The simplest approach to doing this is to first convert each fraction into their decimal representation (divide them by 100), so
#
# $$
# 50\%\div 100=0.50$$ and $$20\%\div 100=0.20
# $$
#
# Now that we have each fraction shown as their decimal representation we simply multiply them together:
#
# $$
# 0.50\times0.20=0.10
# $$
#
# and again to get this decimal to a percent we multiply by 100
#
# $$
# 0.10\times100=10\%
# $$
#
# Putting this into words we get: *$50\%$ of $20\%$ is $10\%$ (One half of $20\%$ is $10\%$)*.
# ## Sports Example
#
# As we know, statistics play a huge part in sports. Keeping track of a team's wins/losses or how many points a player has are integral parts of today's professional sports. Some of these stats may require more interesting mathematical formulas to figure them out. One such example is a goalie’s save percentage in hockey.
#
# The save percentage is the ratio of how many shots the goalie saved over how many he/she has faced. If you are familiar with the NHL you will know this statistic for goalies as Sv\% and is represented as a number like 0.939. In this case the $0.939$ is the percentage we are interested in. You can multiply this number by $100$ to get it in the familiar form $93.9\%$. This means the Sv\% is $93.9\%$, so this particular goalie has saved $93.9\%$ of the shots he's/she's faced.
#
# You will see below a "sport" like game. The objective of the game is to score on your opponent and protect your own net. As you play the game you will see (in real time) below the game window your Sv% and your opponents Sv%. Play a round or two before we discuss how to get this value.
#
# _**How to play:** choose the winning score from the drop down box then click "Start". In game use your mouse to move your paddle up and down (inside the play area). Don't let the ball go in your net!_
# + tags=["hide-input"] language="html"
# <style>
# .mainBody {
# font-family: Arial, Helvetica, sans-serif;
# }
# #startBtn {
# background-color: cornflowerblue;
# border: none;
# border-radius: 3px;
# font-size: 14px;
# color: white;
# font-weight: bold;
# padding: 2px 8px;
# text-transform: uppercase;
# }
# </style>
# <div class="mainBody">
# <div style="padding-bottom: 10px;">
# <label for="winningScore">Winning Score: </label>
# <select name="Winning Score" id="winningScore">
# <option value="3">3</option>
# <option value="5">5</option>
# <option value="7">7</option>
# <option value="10">10</option>
# </select>
# <button type="button" id="startBtn">Start</button>
# </div>
# <canvas id="gameCanvas" width="600" height="350" style="border: solid 1px black"></canvas>
#
# <div>
# <ul>
# <li>Player's point save average: <output id="playerAvg"></output></li>
# <li>Computer's point save average: <output id="compAvg"></output></li>
# </ul>
# </div>
# </div>
# -
# If you look below the game screen you will see "Player's point save average" and "Computer's point save average". You might also have noticed these values changed every time a save was made (unless Sv% was 1) or a score happened, can you come up with a formula to get these values?
#
# The Sv% value is the ratio of how many saves was made over how many total shots the player faced so our formula is
#
# $$
# Sv\%=\frac{saved \ shots}{total \ shots}
# $$
#
# Let's assume the player faced $33$ shots and let in $2$, then the player's Sv% is
#
# $$
# Sv\%=\frac{(33-2)}{33}=0.939
# $$
#
# *Note: $(33-2)$ is how many shots where saved since the total was $33$ and the player let in $2$*
# ## Questions
# + tags=["hide-input"] language="html"
# <style>
# hr {
# width: 60%;
# margin-left: 20px;
# }
# </style>
# <main>
# <div class="questions">
# <ul style="list-style: none">
# <h4>Question #1</h4>
# <li>
# <label for="q1" class="question">A new goalie played his first game and got a shutout (did not let
# the other team score) and made 33 saves, what is his Sv%? </label>
# </li>
# <li>
# <input type="text" id="q1" class="questionInput">
# <button id="q1Btn" onclick="checkAnswer('q1')" class="ansBtn">Check Answer</button>
# </li>
# <li>
# <p class="q1Ans" id="q1True" style="display: none">✓ That's right! Until the goalie let's
# his/her
# first goal in he/she will have a Sv% of 1</p>
# </li>
# <li>
# <p class="q1Ans" id="q1False" style="display: none">Not quite, don't forget to take the total
# amount of shots minus how many went in the net</p>
# </li>
# </ul>
# </div>
# <hr>
# <div class="questions">
# <ul style="list-style: none">
# <h4>Question #2</h4>
# <li>
# <label for="q2" class="question">If a goalie has a Sv% of .990 can he/she ever get back to a Sv% of
# 1.00?</label>
# </li>
# <li>
# <select id="q2">
# <option value="Yes">Yes</option>
# <option value="No">No</option>
# </select>
# <button id="q2Btn" onclick="checkAnswer('q2')" class="ansBtn">Check Answer</button>
# </li>
# <li>
# <p class="q2Ans" id="q2True" style="display: none">✓ That's correct, the goalie could get back
# up to
# 0.999 but never 1.00</p>
# </li>
# <li>
# <p class="q2Ans" id="q2False" style="display: none">Not quite, the goalie could get back up to 0.999
# but never 1.00</p>
# </li>
# </ul>
# </div>
# <hr>
# <div class="questions">
# <ul style="list-style: none">
# <h4>Question #3</h4>
# <li>
# <label for="q3" class="question">A student received a mark of 47/50 on his unit exam, what
# percentage did he get?</label>
# </li>
# <li>
# <input type="text" id="q3" class="questionInput">
# <button id="q3tn" onclick="checkAnswer('q3')" class="ansBtn">Check Answer</button>
# </li>
# <li>
# <p class="q3Ans" id="q3True" style="display: none">✓ That's correct!</p>
# </li>
# <li>
# <p class="q3Ans" id="q3False" style="display: none">Not quite, try again</p>
# </li>
# </ul>
# </div>
# <hr>
# <div class="questions">
# <ul style="list-style: none">
# <h4>Question #4</h4>
# <li>
# <label for="q4" class="question">In a class of 24 students, 8 students own cats, 12 students own dogs
# and 6 students own both cats and dogs. What is the percentage of students who own both cats and
# dogs?</label>
# </li>
# <li>
# <input type="text" id="q4" class="questionInput">
# <button id="q4tn" onclick="checkAnswer('q4')" class="ansBtn">Check Answer</button>
# </li>
# <li>
# <p class="q4Ans" id="q4True" style="display: none">✓ That's correct!</p>
# </li>
# <li>
# <p class="q4Ans" id="q4False" style="display: none">Not quite, try again</p>
# </li>
# </ul>
# </div>
#
# </main>
# <script>
# checkAnswer = function(q) {
# var val = document.getElementById(q).value;
# var isCorrect = false;
# $("."+q+"Ans").css("display", "none");
# switch(q) {
# case 'q1' : Number(val) === 1 ? isCorrect = true : isCorrect = false; break;
# case 'q2' : val === 'No' ? isCorrect = true : isCorrect = false; break;
# case 'q3' : (val === '94%'|| val === '94.0%' || Number(val) === 94) ? isCorrect = true : isCorrect = false;break;
# case 'q4' : (Number(val) === 25 || val === '25%' || val === '25.0%') ? isCorrect = true : isCorrect = false; break;
# default : return false;
# }
#
# if(isCorrect) {
# $("#"+q+"True").css("display", "block");
# } else {
# $("#"+q+"False").css("display", "block");
# }
# }
# </script>
#
# -
# ## Conclusion
#
# As we saw in this notebook, percentages show up in many different ways and are very useful when describing a ratio. It allows for demonstrating any ratio on a familiar scale ($100$) to make data easier to understand. In this notebook we covered the following:
# - A percentage simply represents a fraction
# - To convert any fraction to a percent we turn it into it's decimal form and add $100$
# - A percentage of an amount is simply a fraction multiplication problem
# - To add or subtract a percentage of an amount we first find the percent value than add/subtract from the original value
# - When adding a percentage to an amount we an use the decimal form of percent and add $1$ to it (for example $\$12\times(0.05+1)=\$12.60$)
#
# Keep practising converting fractions to percentages and it will eventually become second nature!
# + tags=["hide-input"] language="html"
# <script>
# var canvas;
# var canvasContext;
# var isInitialized;
#
# var ballX = 50;
# var ballY = 50;
# var ballSpeedX = 5;
# var ballSpeedY = 3;
#
# var leftPaddleY = 250;
# var rightPaddleY = 250;
#
# var playerSaves = 0;
# var playerSOG = 0;
# var compSaves = 0;
# var compSOG = 0;
#
# var playerScore = 0;
# var compScore = 0;
# var winningScore = 3;
# var winScreen = false;
#
# var PADDLE_WIDTH = 10;
# var PADDLE_HEIGHT = 100;
# var BALL_RADIUS = 10;
# var COMP_SPEED = 4;
#
# document.getElementById('startBtn').onclick = function () {
# initGame();
# var selection = document.getElementById('winningScore');
# winningScore = Number(selection.options[selection.selectedIndex].value);
# canvas = document.getElementById('gameCanvas');
# canvasContext = canvas.getContext('2d');
# canvasContext.font = '50px Arial';
# ballReset();
#
# if (!isInitialized) {
# var framesPerSec = 60;
# setInterval(function () {
# moveAll();
# drawAll();
# }, 1000 / framesPerSec);
# isInitialized = true;
# }
#
# canvas.addEventListener('mousemove', function (event) {
# var mousePos = mouseYPos(event);
# leftPaddleY = mousePos.y - PADDLE_HEIGHT / 2;
# });
# }
#
# function updateSaveAvg() {
# var playerSaveAvgTxt = document.getElementById('playerAvg');
# var compSaveAvgTxt = document.getElementById('compAvg');
#
# var playerSaveAvg = playerSaves / playerSOG;
# var compSaveAvg = compSaves / compSOG;
#
# playerSaveAvgTxt.textContent = ((playerSaveAvg < 0 || isNaN(playerSaveAvg)) ? Number(0).toPrecision(3) + (' (0.0%)') :
# playerSaveAvg.toPrecision(3) + (' (' + (playerSaveAvg * 100).toPrecision(3) + '%)'));
# compSaveAvgTxt.textContent = ((compSaveAvg < 0 || isNaN(compSaveAvg)) ? Number(0).toPrecision(3) + (' (0.0%)') :
# compSaveAvg.toPrecision(
# 3) + (' (' + (compSaveAvg * 100).toPrecision(3) + '%)'));
#
# }
#
# function initGame() {
# playerScore = 0;
# compScore = 0;
# playerSaves = 0;
# playerSOG = 0;
# compSaves = 0;
# compSOG = 0;
# ballSpeedX = 5;
# ballSpeedY = 3;
# }
#
# function ballReset() {
# if (playerScore >= winningScore || compScore >= winningScore) {
# winScreen = true;
# }
# if (winScreen) {
# updateSaveAvg();
# if (confirm('Another game?')) {
# winScreen = false;
# initGame();
# } else {
# return;
# }
# }
# ballX = canvas.width / 2;
# ballY = canvas.height / 2;
# ballSpeedY = Math.floor(Math.random() * 4) + 1;
# var randomizer = Math.floor(Math.random() * 2) + 1;
# if (randomizer % 2 === 0) {
# ballSpeedY -= ballSpeedY;
# }
# flipSide();
# }
#
# function flipSide() {
# ballSpeedX = -ballSpeedX;
# }
#
# function moveAll() {
# if (winScreen) {
# return;
# }
# computerMove();
# ballX += ballSpeedX;
# if (ballX < (0 + BALL_RADIUS)) {
# if (ballY > leftPaddleY && ballY < leftPaddleY + PADDLE_HEIGHT) {
# playerSaves++;
# playerSOG++;
# flipSide();
# var deltaY = ballY - (leftPaddleY + PADDLE_HEIGHT / 2);
# ballSpeedY = deltaY * 0.35;
# } else {
# playerSOG++;
# compScore++;
# if (compScore === winningScore) {
# updateSaveAvg();
# drawAll();
# alert('Computer wins, final score: ' + playerScore + '-' + compScore);
# }
# ballReset();
# }
# }
# if (ballX >= canvas.width - BALL_RADIUS) {
# if (ballY > rightPaddleY && ballY < rightPaddleY + PADDLE_HEIGHT) {
# compSaves++;
# compSOG++;
# flipSide();
# var deltaY = ballY - (rightPaddleY + PADDLE_HEIGHT / 2);
# ballSpeedY = deltaY * 0.35;
# } else {
# compSOG++;
# playerScore++;
# if (playerScore === winningScore) {
# updateSaveAvg();
# drawAll();
# alert('You win, final score: ' + playerScore + '-' + compScore);
# }
# ballReset();
# }
# }
# ballY += ballSpeedY;
# if (ballY >= canvas.height - BALL_RADIUS || ballY < 0 + BALL_RADIUS) {
# ballSpeedY = -ballSpeedY;
# }
# updateSaveAvg();
# }
#
# function computerMove() {
# var rightPaddleYCenter = rightPaddleY + (PADDLE_HEIGHT / 2)
# if (rightPaddleYCenter < ballY - 20) {
# rightPaddleY += COMP_SPEED;
# } else if (rightPaddleYCenter > ballY + 20) {
# rightPaddleY -= COMP_SPEED;
# }
# }
#
# function mouseYPos(event) {
# var rect = canvas.getBoundingClientRect();
# var root = document.documentElement;
# var mouseX = event.clientX - rect.left - root.scrollLeft;
# var mouseY = event.clientY - rect.top - root.scrollTop;
# return {
# x: mouseX,
# y: mouseY
# };
# }
#
# function drawAll() {
#
# colorRect(0, 0, canvas.width, canvas.height, 'black');
# if (winScreen) {
# drawNet();
# drawScore();
# return;
# }
# //Left paddle
# colorRect(1, leftPaddleY, PADDLE_WIDTH, PADDLE_HEIGHT, 'white');
# //Right paddle
# colorRect(canvas.width - PADDLE_WIDTH - 1, rightPaddleY, PADDLE_WIDTH, PADDLE_HEIGHT, 'white');
# //Ball
# colorCircle(ballX, ballY, BALL_RADIUS, 'white');
#
# drawNet();
#
# drawScore();
#
# }
#
# function colorRect(x, y, width, height, drawColor) {
# canvasContext.fillStyle = drawColor;
# canvasContext.fillRect(x, y, width, height);
# }
#
# function colorCircle(centerX, centerY, radius, drawColor) {
# canvasContext.fillStyle = 'drawColor';
# canvasContext.beginPath();
# canvasContext.arc(centerX, centerY, radius, 0, Math.PI * 2, true);
# canvasContext.fill();
# }
#
# function drawScore() {
# canvasContext.fillText(playerScore, (canvas.width / 2) - (canvas.width / 4) - 25, 100);
# canvasContext.fillText(compScore, (canvas.width / 2) + (canvas.width / 4) - 25, 100);
# }
#
# function drawNet() {
# for (var i = 0; i < 60; i++) {
# if (i % 2 === 1) {
# colorRect(canvas.width / 2 - 3, i * 10, 6, 10, 'white')
# }
# }
# }
# </script>
# -
# [](https://github.com/callysto/curriculum-notebooks/blob/master/LICENSE.md)
|
_build/html/_sources/curriculum-notebooks/Mathematics/Percentage/percentage.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda env:notebook] *
# language: python
# name: conda-env-notebook-py
# ---
# +
import ctd
import gsw
from ctd.read import _basename
import gsw
import requests
import os
import re
import xarray as xr
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import cmocean as cmo
# Make the Plots pretty
import seaborn as sns
sns.set()
# Supress open_mfdataset warnings
import warnings
warnings.filterwarnings('ignore')
# -
# Provide URL to load a single file that has already been downloaded to OOI's OPENDAP server
# remember to use #fillmismatch
# Create directory that includes all urls
data_url = {}
data_url['inshore'] = 'https://opendap.oceanobservatories.org/thredds/dodsC/ooi/sbeaulieu@whoi.edu/20200806T132326640Z-CP03ISPM-WFP01-03-CTDPFK000-recovered_wfp-ctdpf_ckl_wfp_instrument_recovered/deployment0003_CP03ISPM-WFP01-03-CTDPFK000-recovered_wfp-ctdpf_ckl_wfp_instrument_recovered_20191006T150003-20191031T212239.977728.nc#fillmismatch'
data_url['central_inshore'] = 'https://opendap.oceanobservatories.org/thredds/dodsC/ooi/sbeaulieu@whoi.edu/20200806T132900316Z-CP02PMCI-WFP01-03-CTDPFK000-recovered_wfp-ctdpf_ckl_wfp_instrument_recovered/deployment0013_CP02PMCI-WFP01-03-CTDPFK000-recovered_wfp-ctdpf_ckl_wfp_instrument_recovered_20191007T210003-20191031T212442.986087.nc#fillmismatch'
data_url['central_offshore'] = 'https://opendap.oceanobservatories.org/thredds/dodsC/ooi/sbeaulieu@whoi.edu/20200806T133142674Z-CP02PMCO-WFP01-03-CTDPFK000-recovered_wfp-ctdpf_ckl_wfp_instrument_recovered/deployment0013_CP02PMCO-WFP01-03-CTDPFK000-recovered_wfp-ctdpf_ckl_wfp_instrument_recovered_20191008T140003-20191031T212529.983845.nc#fillmismatch'
data_url['offshore'] = 'https://opendap.oceanobservatories.org/thredds/dodsC/ooi/sbeaulieu@whoi.edu/20200806T133343088Z-CP04OSPM-WFP01-03-CTDPFK000-recovered_wfp-ctdpf_ckl_wfp_instrument_recovered/deployment0012_CP04OSPM-WFP01-03-CTDPFK000-recovered_wfp-ctdpf_ckl_wfp_instrument_recovered_20191013T160003-20191031T211622.990750.nc#fillmismatch'
# +
#Load in bathymetric data
bathymetry=xr.open_dataset('data/GMRT_39-41N_70-71W.nc')
bath_df=bathymetry.to_dataframe
#Plot
z=bathymetry.z.values.reshape([535,1023]).mean(axis=1)
z2=bathymetry.z.values.reshape([1023,535]).mean(axis=1)
#Get x range
x=np.linspace(bathymetry.x_range[0],bathymetry.x_range[1],535)
y=np.linspace(bathymetry.y_range[1],bathymetry.y_range[0],1023)
plt.plot(x,z)
bathymetry
# -
plt.plot(y,z2)
# +
# Load the data file using xarray
def load2xarray(location):
"""
Load data at given location and reduce to variables of interest.
"""
ds = xr.open_dataset(data_url[location])
ds = ds.swap_dims({'obs': 'time'}) #Swap dimensions
print('Dataset '+ location +' has %d points' % ds.time.size)
ds = ds[['ctdpf_ckl_seawater_pressure','ctdpf_ckl_seawater_temperature','practical_salinity']]
return ds
profiles={}
for loc in list(data_url.keys()):
profiles[loc] = load2xarray(loc)
profiles
# -
# +
profiles['inshore'].practical_salinity
# for cast in profiles:
# names = [df._metadata.get("name") for df in profiles]
# lons, lats, data = [], [], []
# lons.append(cast._metadata.get("lon"))
# lats.append(cast._metadata.get("lat"))
# data.append(cast[var])
# -
profiles['inshore'].ctdpf_ckl_seawater_temperature
profiles['inshore'].lat.to_dataframe
#Extract a single time for a single day and plot all side by side
I_URL = 'https://opendap.oceanobservatories.org/thredds/dodsC/ooi/sbeaulieu@whoi.<EMAIL>/20200806T132326640Z-CP03ISPM-WFP01-03-CTDPFK000-recovered_wfp-ctdpf_ckl_wfp_instrument_recovered/deployment0003_CP03ISPM-WFP01-03-CTDPFK000-recovered_wfp-ctdpf_ckl_wfp_instrument_recovered_20191006T150003-20191031T212239.977728.nc#fillmismatch'
CI_URL = 'https://opendap.oceanobservatories.org/thredds/dodsC/ooi/sbeaulieu@whoi.edu/20200806T132900316Z-CP02PMCI-WFP01-03-CTDPFK000-recovered_wfp-ctdpf_ckl_wfp_instrument_recovered/deployment0013_CP02PMCI-WFP01-03-CTDPFK000-recovered_wfp-ctdpf_ckl_wfp_instrument_recovered_20191007T210003-20191031T212442.986087.nc#fillmismatch'
CO_URL = 'https://opendap.oceanobservatories.org/thredds/dodsC/ooi/sbeaulieu@whoi.edu/20200806T133142674Z-CP02PMCO-WFP01-03-CTDPFK000-recovered_wfp-ctdpf_ckl_wfp_instrument_recovered/deployment0013_CP02PMCO-WFP01-03-CTDPFK000-recovered_wfp-ctdpf_ckl_wfp_instrument_recovered_20191008T140003-20191031T212529.983845.nc#fillmismatch'
O_URL = 'https://opendap.oceanobservatories.org/thredds/dodsC/ooi/<EMAIL>/20200806T133343088Z-CP04OSPM-WFP01-03-CTDPFK000-recovered_wfp-ctdpf_ckl_wfp_instrument_recovered/deployment0012_CP04OSPM-WFP01-03-CTDPFK000-recovered_wfp-ctdpf_ckl_wfp_instrument_recovered_20191013T160003-20191031T211622.990750.nc#fillmismatch'
ids = xr.open_dataset(I_URL)
cids = xr.open_dataset(CI_URL)
cods = xr.open_dataset(CO_URL)
ods = xr.open_dataset(O_URL)
ids = ids.swap_dims({'obs': 'time'}) #Swap dimensions
cids = cids.swap_dims({'obs': 'time'}) #Swap dimensions
cods = cods.swap_dims({'obs': 'time'}) #Swap dimensions
ods = ods.swap_dims({'obs': 'time'}) #Swap dimensions
ids
# select same day for each profiler
datesel='2019-10-15T03'
ids15=ids.sel(time=datesel, method="nearest")
cids15=cids.sel(time=datesel, method="nearest")
cods15=cods.sel(time=datesel, method="nearest")
ods15=ods.sel(time=datesel, method="nearest")
ids15
# +
# Plot spatial section: practical salinity
fig,ax = plt.subplots(ncols=1,figsize=(10,4),sharey=True,constrained_layout=True)
cci=ids15.plot.scatter(x="lat", y="ctdpf_ckl_seawater_pressure",
c=ids15.practical_salinity.data,
cmap = plt.get_cmap('cmo.haline',30),vmin=34,vmax=36.3)
ccci=cids15.plot.scatter(x="lat", y="ctdpf_ckl_seawater_pressure",
c=cids15.practical_salinity.data,
cmap = plt.get_cmap('cmo.haline',30),vmin=34,vmax=36.3)
ccco=cods15.plot.scatter(x="lat", y="ctdpf_ckl_seawater_pressure",
c=cods15.practical_salinity.data,
cmap = plt.get_cmap('cmo.haline',30),vmin=34,vmax=36.3)
cco=ods15.plot.scatter(x="lat", y="ctdpf_ckl_seawater_pressure",
c=ods15.practical_salinity.data,
cmap = plt.get_cmap('cmo.haline',30),vmin=34,vmax=36.3)
#Indicate profile position
plt.gca().invert_yaxis()
plt.colorbar(cci, label='Salinity')
fig.suptitle(f"OOI Section {datesel}")
#Load in bathymetric data
bathymetry=xr.open_dataset('data/GMRT_39-41N_70-71W.nc')
bath_df=bathymetry.to_dataframe
#Plot
z=bathymetry.z.values.reshape([1023,535]).mean(axis=1)
#Get y range
x=np.linspace(bathymetry.x_range[0],bathymetry.x_range[1],535) # Longitude
y=np.linspace(bathymetry.y_range[1],bathymetry.y_range[0],1023) #Latitude OOI North to South
#gsw.p_from_z()
#PLot bathymetry
plt.plot(y,-z)
plt.xlim(39.9,40.4) # lims inshore and offshore stations
plt.ylim(500,0) #maximum depth offshore ~451m
# +
# Plot spatial section: temperature
fig,ax = plt.subplots(ncols=1,figsize=(10,4),sharey=True,constrained_layout=True)
cci=ids15.plot.scatter(x="lat", y="ctdpf_ckl_seawater_pressure",
c=ids15.ctdpf_ckl_seawater_temperature,
cmap = plt.get_cmap('cmo.haline',30))
ccci=cids15.plot.scatter(x="lat", y="ctdpf_ckl_seawater_pressure",
c=cids15.ctdpf_ckl_seawater_temperature,
cmap = plt.get_cmap('cmo.haline',30))
ccco=cods15.plot.scatter(x="lat", y="ctdpf_ckl_seawater_pressure",
c=cods15.ctdpf_ckl_seawater_temperature,
cmap = plt.get_cmap('cmo.haline',30))
cco=ods15.plot.scatter(x="lat", y="ctdpf_ckl_seawater_pressure",
c=ods15.ctdpf_ckl_seawater_temperature,
cmap = plt.get_cmap('RdYlBu_r',30))
plot.scatter
plt.gca().invert_yaxis()
plt.colorbar(cci, label='temperature [\N{DEGREE SIGN}C]')
fig.suptitle(f"OOI Section {datesel}")
#Load in bathymetric data
bathymetry=xr.open_dataset('data/GMRT_39-41N_70-71W.nc')
bath_df=bathymetry.to_dataframe
#Plot
z=bathymetry.z.values.reshape([1023,535]).mean(axis=1)
#Get x range
x=np.linspace(bathymetry.x_range[0],bathymetry.x_range[1],535) # Longitude
y=np.linspace(bathymetry.y_range[1],bathymetry.y_range[0],1023) #Latitude OOI North to South
#gsw.p_from_z()
#PLot bathymetry
plt.plot(y,-z)
plt.xlim(39.9,40.4) # lims inshore and offshore stations
plt.ylim(500,0) #maximum depth offshore ~451m
# +
# Spatial Interpolation
# Plot spatial section: practical salinity using cmocean
|
03_Interpolation_over_distance_MV.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <p align="center">
# <img src="https://github.com/GeostatsGuy/GeostatsPy/blob/master/TCG_color_logo.png?raw=true" width="220" height="240" />
#
# </p>
#
# ## Data Analytics
#
# ### Parametric Distributions in Python
#
#
# #### <NAME>, Associate Professor, University of Texas at Austin
#
# ##### [Twitter](https://twitter.com/geostatsguy) | [GitHub](https://github.com/GeostatsGuy) | [Website](http://michaelpyrcz.com) | [GoogleScholar](https://scholar.google.com/citations?user=QVZ20eQAAAAJ&hl=en&oi=ao) | [Book](https://www.amazon.com/Geostatistical-Reservoir-Modeling-Michael-Pyrcz/dp/0199731446) | [YouTube](https://www.youtube.com/channel/UCLqEr-xV-ceHdXXXrTId5ig) | [LinkedIn](https://www.linkedin.com/in/michael-pyrcz-61a648a1)
#
# ### Data Analytics: Parametric Distributions
#
# Here's a demonstration of making and general use of parametric distributions in Python. This demonstration is part of the resources that I include for my courses in Spatial / Subsurface Data Analytics at the Cockrell School of Engineering at the University of Texas at Austin.
#
# #### Parametric Distributions
#
# We will cover the following distributions:
#
# * Uniform
# * Triangular
# * Gaussian
# * Log Normal
#
# We will demonstrate:
#
# * distribution parameters
# * forward and inverse operators
# * summary statistics
#
# I have a lecture on these parametric distributions available on [YouTube](https://www.youtube.com/watch?v=U7fGsqCLPHU&t=1687s).
#
# #### Getting Started
#
# Here's the steps to get setup in Python with the GeostatsPy package:
#
# 1. Install Anaconda 3 on your machine (https://www.anaconda.com/download/).
# 2. From Anaconda Navigator (within Anaconda3 group), go to the environment tab, click on base (root) green arrow and open a terminal.
# 3. In the terminal type: pip install geostatspy.
# 4. Open Jupyter and in the top block get started by copy and pasting the code block below from this Jupyter Notebook to start using the geostatspy functionality.
#
# You will need to copy the data file to your working directory. They are available here:
#
# * Tabular data - unconv_MV_v4.csv at https://git.io/fhHLT.
#
# #### Importing Packages
#
# We will need some standard packages. These should have been installed with Anaconda 3.
import numpy as np # ndarrys for gridded data
import pandas as pd # DataFrames for tabular data
import os # set working directory, run executables
import matplotlib.pyplot as plt # for plotting
from scipy import stats # summary statistics
import math # trigonometry etc.
import scipy.signal as signal # kernel for moving window calculation
import random # for randon numbers
import seaborn as sns # for matrix scatter plots
from scipy import linalg # for linear regression
from sklearn import preprocessing
# #### Set the Working Directory
#
# I always like to do this so I don't lose files and to simplify subsequent read and writes (avoid including the full address each time).
os.chdir("c:/PGE383") # set the working directory
# ### Uniform Distribution
#
# Let's start with the most simple distribution.
#
# * by default a random number is uniform distributed
#
# * this ensures that enough random samples (Monte Carlo simulations) will reproduce the distribution
#
# \begin{equation}
# x_{\alpha}^{s} = F^{-1}_x(p_{\alpha}), \quad X^{s} \sim F_X
# \end{equation}
#
# #### Random Samples
#
# Let's demonstrate the use of the command:
#
# ```python
# uniform.rvs(size=n, loc = low, scale = interval, random_state = seed)
# ```
#
# Where:
#
# * size is the number of samples
#
# * loc is the minimum value
#
# * scale is the range, maximum value minus the minimum value
#
# * random_state is the random number seed
#
# We will observe the convergence of the samples to a uniform distribution as the number of samples becomes large.
#
# We will make a compact set of code by looping over all the cases of number of samples
#
# * we store the number of samples cases in the list called ns
#
# * we store the samples as a list of lists, called X_uniform
#
# +
from scipy.stats import uniform
low = 0.05; interval = 0.20; ns = [1e1,1e2,1e3,1e4,1e5,1e6]; X_uniform = []
index = 0
for n in ns:
X_uniform.append(uniform.rvs(size=int(ns[index]), loc = low, scale = interval).tolist())
plt.subplot(2,3,index+1)
GSLIB.hist_st(X_uniform[index],loc,loc+interval,log=False,cumul = False,bins=20,weights = None,xlabel='Values',title='Distribution, N = ' + str(int(ns[index])))
index = index + 1
plt.subplots_adjust(left=0.0, bottom=0.0, right=2.3, top=1.6, wspace=0.2, hspace=0.3)
# -
# We can observe that by drawing more Monte Carlo simulations, we more closely approximate the original uniform parametric distribution.
#
# #### Forward Distribution
#
# Let's demonstrate the forward operator. We can take any value and calculate the associated:
#
# * density (probability density function)
# * cumulative probability
#
# The transform for the probability density function is:
#
# \begin{equation}
# p = f_x(x)
# \end{equation}
#
# where $f_x$ is the PDF and $p$ is the density for value, $x$.
#
# and for the cumulative distribution function is:
#
# \begin{equation}
# P = F_x(x)
# \end{equation}
#
# where $F_x$ is the CDF and $P$ is the cumulative probability for value, $x$.
# +
x_values = np.linspace(0.0,0.3,100)
p_values = uniform.pdf(x_values, loc = low, scale = interval)
P_values = uniform.cdf(x_values, loc = low, scale = interval)
plt.subplot(1,2,1)
plt.plot(x_values, p_values,'r-', lw=5, alpha=0.3, label='uniform PDF'); plt.title('Uniform PDF'); plt.xlabel('Values'); plt.ylabel('Density')
plt.subplot(1,2,2)
plt.plot(x_values, P_values,'r-', lw=5, alpha=0.3, label='uniform CDF'); plt.title('Uniform CDF'); plt.xlabel('Values'); plt.ylabel('Cumulative Probability')
plt.subplots_adjust(left=0.0, bottom=0.0, right=1.8, top=0.8, wspace=0.2, hspace=0.3)
# -
# #### Inverse Distribution
#
# Let's know demonstrate the reverse operator for the uniform distribution:
#
# \begin{equation}
# X = F^{-1}_X(P)
# \end{equation}
p_values = np.linspace(0.01,0.99,100)
x_values = uniform.ppf(p_values, loc = low, scale = interval)
plt.plot(x_values, p_values,'r-', lw=5, alpha=0.3, label='uniform pdf')
# #### Summary Statistics
#
# We also have a couple of convience member functions to return the statistics from the parametric distribution:
#
# * mean
# * median
# * mode
# * variance
# * standard deviation
#
# Let's demonstrate a few of these methods.
#
# ```python
# uniform.stats(loc = low, scale = interval, moments = 'mvsk')
# ```
#
# returns a tuple with the mean, variance, skew and kurtosis (centered 1st, 2nd, 3rd and 4th moments)
print('Stats: mean, variance, skew and kurtosis = ' + str(uniform.stats(loc = low, scale = interval, moments = 'mvsk')))
# We can confirm this by calculating the centered variance (regular variance) with this member function:
#
# ```python
# uniform.var(loc = low, scale = interval)
# ```
print('The variance is ' + str(round(uniform.var(loc = low, scale = interval),4)) + '.')
# We can also directly calculate the:
#
# * standard deviation - std
# * mean - mean
# * median - median
#
# We can also calculate order of a non-centered moment. The moment method allows us to calculate an non-centered moment of any order. Try this out.
m_order = 4
print('The ' + str(m_order) + 'th order non-centered moment is ' + str(uniform.moment(n = m_order, loc = low, scale = interval)))
# #### Symmetric Interval
#
# We can also get the symmetric interval (e.g. prediction or confidence intervals) for any alpha level.
#
# * Note the program mislabels the value as alpha, it is actually the significance level (1 - alpha)
level = 0.95
print('The interval at alpha level ' + str(round(1-level,3)) + ' is ' + str(uniform.interval(alpha = alpha,loc = low,scale = interval)))
# #### Triangular Distribution
#
# The great thing about parametric distributions is that the above member functions are the same!
#
# * we can plug and play other parametric distributions and repeat the above.
#
# This time we will make it much more compact!
#
# * we will import the triangular distribution as my_dist and call the same functions as before
# * we need a new parameter, the distribution mode (c parameter)
# +
from scipy.stats import triang as my_dist # import traingular dist as my_dist
dist_type = 'Triangular' # give the name of the distribution for labels
low = 0.05; mode = 0.20; c = 0.10 # given the distribution parameters
x_values = np.linspace(0.0,0.3,100) # get an array of x values
p_values = my_dist.pdf(x_values, loc = low, c = mode, scale = interval) # calculate density for each x value
P_values = my_dist.cdf(x_values, loc = low, c = mode, scale = interval) # calculate cumulative probablity for each x value
plt.subplot(1,3,1) # plot the resulting PDF
plt.plot(x_values, p_values,'r-', lw=5, alpha=0.3); plt.title('Sampling ' + str(dist_type) + ' PDF'); plt.xlabel('Values'); plt.ylabel('Density')
plt.subplot(1,3,2) # plot the resulting CDF
plt.plot(x_values, P_values,'r-', lw=5, alpha=0.3); plt.title('Sampling ' + str(dist_type) + ' CDF'); plt.xlabel('Values'); plt.ylabel('Cumulative Probability')
p_values = np.linspace(0.00001,0.99999,100) # get an array of p-values
x_values = my_dist.ppf(p_values, loc = low, c = mode, scale = interval) # apply inverse to get x values from p-values
plt.subplot(1,3,3)
plt.plot(x_values, p_values,'r-', lw=5, alpha=0.3, label='uniform pdf')
plt.subplots_adjust(left=0.0, bottom=0.0, right=2.8, top=0.8, wspace=0.2, hspace=0.3); plt.title('Sampling Inverse ' + str(dist_type) + ' CDF'); plt.xlabel('Values'); plt.ylabel('Cumulative Probability')
print('The mean is ' + str(round(uniform.mean(loc = low, scale = interval),4)) + '.') # calculate stats and symmetric interval
print('The variance is ' + str(round(uniform.var(loc = low, scale = interval),4)) + '.')
print('The interval at alpha level ' + str(round(1-level,3)) + ' is ' + str(uniform.interval(alpha = alpha,loc = low,scale = interval)))
# -
# #### Gaussian Distribution
#
# Let's now use the Gaussian parametric distribution.
#
# * we will need the parameters mean and the variance
#
# We will apply the forward and reverse operations and calculate the summary statistics.
#
# +
from scipy.stats import norm as my_dist # import traingular dist as my_dist
dist_type = 'Gaussian' # give the name of the distribution for labels
mean = 0.15; stdev = 0.05 # given the distribution parameters
x_values = np.linspace(0.0,0.3,100) # get an array of x values
p_values = my_dist.pdf(x_values, loc = mean, scale = stdev) # calculate density for each x value
P_values = my_dist.cdf(x_values, loc = mean, scale = stdev) # calculate cumulative probablity for each x value
plt.subplot(1,3,1) # plot the resulting PDF
plt.plot(x_values, p_values,'r-', lw=5, alpha=0.3); plt.title('Sampling ' + str(dist_type) + ' PDF'); plt.xlabel('Values'); plt.ylabel('Density')
plt.subplot(1,3,2) # plot the resulting CDF
plt.plot(x_values, P_values,'r-', lw=5, alpha=0.3); plt.title('Sampling ' + str(dist_type) + ' CDF'); plt.xlabel('Values'); plt.ylabel('Cumulative Probability')
p_values = np.linspace(0.00001,0.99999,100) # get an array of p-values
x_values = my_dist.ppf(p_values, loc = mean, scale = stdev) # apply inverse to get x values from p-values
plt.subplot(1,3,3)
plt.plot(x_values, p_values,'r-', lw=5, alpha=0.3, label='uniform pdf')
plt.subplots_adjust(left=0.0, bottom=0.0, right=2.8, top=0.8, wspace=0.2, hspace=0.3); plt.title('Sampling Inverse ' + str(dist_type) + ' CDF'); plt.xlabel('Values'); plt.ylabel('Cumulative Probability')
print('The mean is ' + str(round(my_dist.mean(loc = mean, scale = stdev),4)) + '.') # calculate stats and symmetric interval
print('The variance is ' + str(round(my_dist.var(loc = mean, scale = stdev),4)) + '.')
print('The interval at alpha level ' + str(round(1-level,3)) + ' is ' + str(my_dist.interval(alpha = alpha,loc = mean,scale = stdev)))
# -
# #### Log Normal Distribution
#
# Now let's check out the log normal distribution.
#
# * We need the parameters $\mu$ and $\sigma$
# +
from scipy.stats import lognorm as my_dist # import traingular dist as my_dist
dist_type = 'Log Normal' # give the name of the distribution for labels
mu = np.log(0.10); sigma = 0.2 # given the distribution parameters
x_values = np.linspace(0.0,0.3,100) # get an array of x values
p_values = my_dist.pdf(x_values, s = sigma, scale = np.exp(mu)) # calculate density for each x value
P_values = my_dist.cdf(x_values, s = sigma, scale = np.exp(mu)) # calculate cumulative probablity for each x value
plt.subplot(1,3,1) # plot the resulting PDF
plt.plot(x_values, p_values,'r-', lw=5, alpha=0.3); plt.title('Sampling ' + str(dist_type) + ' PDF'); plt.xlabel('Values'); plt.ylabel('Density')
plt.subplot(1,3,2) # plot the resulting CDF
plt.plot(x_values, P_values,'r-', lw=5, alpha=0.3); plt.title('Sampling ' + str(dist_type) + ' CDF'); plt.xlabel('Values'); plt.ylabel('Cumulative Probability')
p_values = np.linspace(0.00001,0.99999,100) # get an array of p-values
x_values = my_dist.ppf(p_values, s = sigma, scale = np.exp(mu)) # apply inverse to get x values from p-values
plt.subplot(1,3,3)
plt.plot(x_values, p_values,'r-', lw=5, alpha=0.3, label='uniform pdf')
plt.subplots_adjust(left=0.0, bottom=0.0, right=2.8, top=0.8, wspace=0.2, hspace=0.3); plt.title('Sampling Inverse ' + str(dist_type) + ' CDF'); plt.xlabel('Values'); plt.ylabel('Cumulative Probability')
#print('The mean is ' + str(round(my_dist.mean(loc = mean, scale = stdev),4)) + '.') # calculate stats and symmetric interval
#print('The variance is ' + str(round(my_dist.var(loc = mean, scale = stdev),4)) + '.')
#print('The interval at alpha level ' + str(round(1-level,3)) + ' is ' + str(my_dist.interval(alpha = alpha,loc = mean,scale = stdev)))
# -
# There are many other parametric distributions that we could have included. Also we could have demonstrated the distribution fitting.
#
# #### Comments
#
# This was a basic demonstration of working with parametric distributions.
#
# I have other demonstrations on the basics of working with DataFrames, ndarrays, univariate statistics, plotting data, declustering, data transformations, trend modeling and many other workflows available at [Python Demos](https://github.com/GeostatsGuy/PythonNumericalDemos) and a Python package for data analytics and geostatistics at [GeostatsPy](https://github.com/GeostatsGuy/GeostatsPy).
#
# I hope this was helpful,
#
# *Michael*
#
# #### The Author:
#
# ### <NAME>, Associate Professor, University of Texas at Austin
# *Novel Data Analytics, Geostatistics and Machine Learning Subsurface Solutions*
#
# With over 17 years of experience in subsurface consulting, research and development, Michael has returned to academia driven by his passion for teaching and enthusiasm for enhancing engineers' and geoscientists' impact in subsurface resource development.
#
# For more about Michael check out these links:
#
# #### [Twitter](https://twitter.com/geostatsguy) | [GitHub](https://github.com/GeostatsGuy) | [Website](http://michaelpyrcz.com) | [GoogleScholar](https://scholar.google.com/citations?user=QVZ20eQAAAAJ&hl=en&oi=ao) | [Book](https://www.amazon.com/Geostatistical-Reservoir-Modeling-Michael-Pyrcz/dp/0199731446) | [YouTube](https://www.youtube.com/channel/UCLqEr-xV-ceHdXXXrTId5ig) | [LinkedIn](https://www.linkedin.com/in/michael-pyrcz-61a648a1)
#
# #### Want to Work Together?
#
# I hope this content is helpful to those that want to learn more about subsurface modeling, data analytics and machine learning. Students and working professionals are welcome to participate.
#
# * Want to invite me to visit your company for training, mentoring, project review, workflow design and / or consulting? I'd be happy to drop by and work with you!
#
# * Interested in partnering, supporting my graduate student research or my Subsurface Data Analytics and Machine Learning consortium (co-PIs including Profs. Foster, Torres-Verdin and van Oort)? My research combines data analytics, stochastic modeling and machine learning theory with practice to develop novel methods and workflows to add value. We are solving challenging subsurface problems!
#
# * I can be reached at <EMAIL>.
#
# I'm always happy to discuss,
#
# *Michael*
#
# <NAME>, Ph.D., P.Eng. Associate Professor The Hildebrand Department of Petroleum and Geosystems Engineering, Bureau of Economic Geology, The Jackson School of Geosciences, The University of Texas at Austin
#
# #### More Resources Available at: [Twitter](https://twitter.com/geostatsguy) | [GitHub](https://github.com/GeostatsGuy) | [Website](http://michaelpyrcz.com) | [GoogleScholar](https://scholar.google.com/citations?user=QVZ20eQAAAAJ&hl=en&oi=ao) | [Book](https://www.amazon.com/Geostatistical-Reservoir-Modeling-Michael-Pyrcz/dp/0199731446) | [YouTube](https://www.youtube.com/channel/UCLqEr-xV-ceHdXXXrTId5ig) | [LinkedIn](https://www.linkedin.com/in/michael-pyrcz-61a648a1)
#
|
PythonDataBasics_ParametricDistributions.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# %matplotlib inline
# %config InlineBackend.figure_format = 'retina'
import matplotlib.pyplot as plt
import torch
from torchvision import datasets, transforms
import helper
# -
# The easiest way to load image data is with *datasets.ImageFolder* from *torchvision*. In generall we'll use *ImageFolder* like so:
#
# ```
# dataset = datasets.ImageFolder('path/to/data',
# transform=transform)
# ```
# ImageFolder expects the files and directories to be constructed like so:
#
# ```
# root/dog/xxx.png
# root/dog/xxy.ong
#
# root/cat/123.png
# root/cat/sad.png
# ```
# ## Transforms
#
# We can either resize them with *transforms.Resize()* or crop with *transforms.CenterCrop()*, *transforms.RandomResizedCrop()* . We'll also need to convert the images to PyTorch tensors with *transforms.ToTensor()*.
# ## Data Loaders
#
# With the *ImageFolder* loaded, we have to pass it to a *DataLoader*. It takes a dataset and returns batches of images and the corresponding labels. We can set various parameters.
#
# ```
# dataloader = torch.utils.data.DataLoader(
# dataset,
# batch_size=32,
# shuffle=True)
# ```
#
# Here dataloader is a *generator*. To get out of it, we need to loop through it or convert it to an iterator and call *next()*
#
# ```
# # looping thrpugh it, get batch on each loop
# for images, labels in dataloader:
# pass
#
# # Get one batch
# images, labels = next(iter(dataloader))
# ```
# **Exercise**
#
# Load images from the *Cat_Dog_data/train* folder, define a few transforms, then build the dataloader.
data_dir = 'Cat_Dog_data/train'
# compose transforms
transform = transforms.Compose([
transforms.Resize(255),
transforms.CenterCrop(224),
transforms.ToTensor()
])
# create the ImageFolder
dataset = datasets.ImageFolder(data_dir,
transform=transform)
# use the ImageFolder dataset to create the DataLoader
dataloader = torch.utils.data.DataLoader(dataset,
batch_size=32,
shuffle=True)
# Test the dataset
images, labels = next(iter(dataloader))
helper.imshow(images[0], normalize=False)
# ## Data Augmentation
#
# ```
# train_transforms = transforms.Compose([
# transforms.RandomRotation(30),
# transforms.RandomResizedCrop(224),
# transforms.RandomHorizontalFlip(),
# transforms.ToTensor(),
# transforms.Normalize([0.5, 0.5, 0.5],
# [0.5, 0.5, 0.5])
# ])
# ```
#
# We can pass a list of means and list of standard deviations, then the color channels are normalized like so
#
# ```
# input[channel] = (input[channel] - mean[channel]) / std[channel]
# ```
#
# Subtracting mean centers the data around zero and dividing by std squishes the values to be between -1 and 1. Normalizing helps keep the network work weights near zero which in turn makes backpropagation more stable. Without normalization, networks will tend to fail to learn.
#
# When we're testing however, we'll want to use images that aren't altered. So, for validation/test images, we'll typically just resize and crop.
#
# **Exercise**
#
# Define transforms for trainin data and testing data below. Leave off normalization for now.
# +
data_dir = 'Cat_Dog_data/'
# Define transforms the training data and
# testing data
train_transforms = transforms.Compose([
transforms.RandomRotation(30),
transforms.RandomResizedCrop(224),
transforms.RandomHorizontalFlip(),
transforms.ToTensor()
#transforms.Normalize([0.5, 0.5, 0.5],
# [0.5, 0.5, 0.5])
])
test_transforms = transforms.Compose([
transforms.RandomResizedCrop(224),
transforms.ToTensor()
])
# Pass transforms in here, then turn the next
# cell to see how the transforms look
train_data = datasets.ImageFolder(data_dir + '/train',
transform=train_transforms)
test_data = datasets.ImageFolder(data_dir + '/test',
transform=test_transforms)
trainloader = torch.utils.data.DataLoader(train_data,
batch_size=32)
testloader = torch.utils.data.DataLoader(test_data,
batch_size=32)
# +
# change this to the trainloader or testloader
data_iter = iter(trainloader)
images, labels = next(data_iter)
fig, axes = plt.subplots(figsize=(10,4), ncols=4)
for ii in range(4):
ax = axes[ii]
helper.imshow(images[ii],
ax=ax,
normalize=False)
|
Lesson 5: Introduction to PyTorch/07 - Loading Image Data.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: project
# language: python
# name: project
# ---
# +
import cv2
import sys
import shutil
import random
import os
import csv
from pylab import *
import numpy as np
import matplotlib.pyplot as plt
# %matplotlib inline
import itertools
from PIL import Image
import pandas as pd
import glob
from sklearn.model_selection import train_test_split
from sklearn.metrics import confusion_matrix
import tensorflow as tf
from tensorflow.keras.utils import to_categorical
from tensorflow.keras import optimizers
from tensorflow.keras.callbacks import LearningRateScheduler
from tensorflow.keras import models, layers
from tensorflow.keras.models import Model, Sequential
from tensorflow.keras.layers import Dense, Flatten, Dropout
from tensorflow.keras.applications import VGG16, VGG19
from tensorflow.keras.applications.vgg16 import preprocess_input, decode_predictions
from tensorflow.keras.preprocessing.image import ImageDataGenerator
from tensorflow.keras.optimizers import Adam, RMSprop
# +
#create necessary directory if not exists
def create_necessary_folder():
#make dir for plottings
if not os.path.exists('plottings'): os.mkdir(f'{os.getcwd()}\\plottings')
#subfolders for every architecture
if not os.path.exists('plottings\\vgg16'): os.mkdir(f'{os.getcwd()}\\plottings\\vgg16')
if not os.path.exists('plottings\\vgg19'): os.mkdir(f'{os.getcwd()}\\plottings\\vgg19')
if not os.path.exists('plottings\\effnet'): os.mkdir(f'{os.getcwd()}\\plottings\\effnet')
#make dir for models
if not os.path.exists('models'): os.mkdir(f'{os.getcwd()}\\models')
#subfolders for every architecture
if not os.path.exists('models\\vgg16'): os.mkdir(f'{os.getcwd()}\\models\\vgg16')
if not os.path.exists('models\\vgg19'): os.mkdir(f'{os.getcwd()}\\models\\vgg19')
if not os.path.exists('models\\effnet'): os.mkdir(f'{os.getcwd()}\\models\\effnet')
create_necessary_folder()
# +
def step_decay_schedule(initial_lr=1e-3, decay_factor=0.75, step_size=10):
def schedule(epoch):
return initial_lr * (decay_factor ** np.floor(epoch / step_size))
return LearningRateScheduler(schedule)
def import_dataset(path):
im = Image.open(path).convert('RGB')
return im
# +
X, Y = [], []
dataset = pd.read_csv('ground-truth.csv')
EPOCHS = 15
LEARNING_RATE = 1e-3
for index, row in dataset.iterrows():
X.append(array(import_dataset(row[0]).resize((100, 100))).flatten() / 255.0)
Y.append(row[1])
X = np.array(X)
Y = to_categorical(Y, 2)
X = X.reshape(-1, 100, 100, 3)
X_train, X_val, Y_train, Y_val = train_test_split(X, Y, test_size=0.20, random_state=5)
#Load VGG, constrain only for the learning part of the network
vgg_conv = VGG16(weights='imagenet', include_top=False, input_shape=(100, 100, 3))
#Freeze the trainable layers
for layer in vgg_conv.layers[:-5]:
layer.trainable = False
# Check the trainability for every layer
for layer in vgg_conv.layers:
print(layer, layer.trainable)
#main architecture
model = Sequential([
vgg_conv,
Flatten(),
Dense(1024, activation='relu'),
Dropout(0.50),
Dense(2, activation='softmax')
])
model.summary()
#hyperparameter settings
epochs = EPOCHS
batch_size = 16
optimizer = optimizers.RMSprop(lr=LEARNING_RATE, epsilon=None)
model.compile(optimizer=optimizer,
loss="mean_squared_error",
metrics=["accuracy"])
lr_sched = step_decay_schedule(initial_lr=1e-4, decay_factor=0.75, step_size=2)
# -
history = model.fit(X_train, Y_train, batch_size=batch_size, epochs=epochs, validation_data=(X_val, Y_val), verbose=2,callbacks=[lr_sched])
import random
#assign random code to make unique ID
r = random.randint(1, 1000)
print(f'[INFO] Your unique ID is {r}, refer to this ID to check the latest data!')
ID = f'{LEARNING_RATE}n{EPOCHS}_{r}'
# +
#plotting
def plot_confusion_matrix(cm, classes, normalize=False, title='Confusion matrix', cmap=plt.cm.Blues):
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title)
plt.colorbar()
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks, classes, rotation=45)
plt.yticks(tick_marks, classes)
if normalize:
cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
thresh = cm.max() / 2.
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, cm[i, j], horizontalalignment="center", color="white" if cm[i, j] > thresh else "black")
plt.tight_layout()
plt.ylabel('True label')
plt.xlabel('Predicted label')
#plt.subplot(2,1,1)
plt.plot(history.history['accuracy'])
plt.plot(history.history['val_accuracy'])
plt.ylabel('accuracy')
plt.xlabel('epoch')
plt.savefig(f'plottings\\vgg16\\acc_{ID}.png')
plt.show()
#plt.subplot(2,1,2)
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.ylabel('loss')
plt.xlabel('epoch')
plt.savefig(f'plottings\\vgg16\\loss_{ID}.png')
plt.show()
Y_pred = model.predict(X_val)
# Convert predictions classes to one hot vectors
Y_pred_classes = np.argmax(Y_pred, axis=1)
# Convert validation observations to one hot vectors
Y_true = np.argmax(Y_val, axis=1)
# compute the confusion matrix
confusion_mtx = confusion_matrix(Y_true, Y_pred_classes)
# plot the confusion matrix
plot_confusion_matrix(confusion_mtx, classes=range(2))
plt.savefig(f'plottings\\vgg16\\cnfmtx_{ID}.png')
plt.show()
# -
#save model
model_name = f'models\\vgg16\\{ID}.h5'
model.save(model_name)
with open('currently-used-vgg16.txt','w+') as f:
f.write(model_name)
train_acc, val_acc = np.mean(history.history['accuracy']), np.mean(history.history['val_accuracy'])
print(train_acc, val_acc)
# ## Testing
# +
from tensorflow.keras.models import load_model
import tensorflow as tf
#test_set = glob.glob('MICC-F220\\*')
test_set = glob.glob('test_set\\*')
classes = []
for img in test_set:
#data will have the label `tamp` if the data is tampered
if 'tamp' in img and img[len(img)-4:len(img)] == '.jpg':
classes.append('forged')
elif 'tamp' not in img and img[len(img)-4:len(img)] == '.jpg':
classes.append('unforged')
#for i in range(len(test_set)): print(test_set[i], classes[i])
#def predict():
#load model
model = load_model(model_name)
predictions = []
#test image iteration
for i in tf.range(len(test_set)): #use tf.range for faster execution (operation is done in tf.Tensor)
image = Image.open(test_set[i]).convert('RGB')
image = array(image.resize((100,100))).flatten() / 255.0
image = image.reshape(-1,100,100,3)
pred = model.predict(image)[0]
#take the index of the predicted class
index = np.argmax(pred)
verdict = "forged" if index == 1 else "unforged"
predictions.append(verdict)
# -
correct = 0
for i in range(len(classes)):
if classes[i] == predictions[i]:
correct += 1
else: continue
acc = correct / len(classes)
print(f'Test accuracy: {round(acc*100,3)}%')
with open(f'plottings\\vgg16\\testacc_{ID}.txt','w+') as f:
f.write(f'train_acc: {train_acc}\nval_acc: {val_acc}\n')
f.write(f'test_acc: {acc}')
# +
#for i in range(len(classes)): print(classes[i], predictions[i])
correct = 0
plt.figure(figsize=(10,9))
plt.subplots_adjust(hspace=0.5)
for i in range(len(classes)):
im = cv2.imread(test_set[i])
#im.resize((30,30))
#print(im.shape)
plt.subplot(len(classes)/5+1,5,i+1)
plt.imshow(im)
color = 'green' if classes[i] == predictions[i] else 'red'
if color == 'green': correct += 1
#plt.title(f'{classes[i]}\n{predictions[i]}', color=color)
plt.text(im.shape[1]/2,0,f'{classes[i]}\n', ha="center", va="bottom", size="medium")
plt.text(im.shape[1]/2,0,f'\n{predictions[i]}', ha="center", va="bottom", size="medium",color=color)
plt.axis('off')
plt.savefig(f'plottings\\vgg19\\test_{ID}.png')
plt.show()
# -
|
vgg16.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# %load_ext autoreload
# %autoreload 2
# +
import tensorflow as tf
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from shapley_sampling import SamplingExplainerTF
from path_explain import utils, scatter_plot, summary_plot
# -
utils.set_up_environment(visible_devices='0')
n = 5000
d = 5
noise = 0.5
X = np.random.randn(n, d)
y = np.sum(X, axis=-1) + 2 * np.prod(X[:, 0:2], axis=-1)
threshold = int(n * 0.8)
X_train = X[:threshold]
y_train = y[:threshold]
X_test = X[threshold:]
y_test = y[threshold:]
model = tf.keras.models.Sequential()
model.add(tf.keras.layers.Input(shape=(d,)))
model.add(tf.keras.layers.Dense(units=10,
use_bias=True,
activation=tf.keras.activations.softplus))
model.add(tf.keras.layers.Dense(units=5,
use_bias=True,
activation=tf.keras.activations.softplus))
model.add(tf.keras.layers.Dense(units=1,
use_bias=False,
activation=None))
model.summary()
learning_rate = 0.1
model.compile(optimizer=tf.keras.optimizers.SGD(learning_rate),
loss=tf.keras.losses.MeanSquaredError())
model.fit(X_train, y_train, batch_size=50, epochs=20, verbose=2, validation_split=0.8)
model.evaluate(X_test, y_test, batch_size=50, verbose=2)
y_test_pred = model.predict(X_test, batch_size=50)
df = pd.DataFrame({
'Predicted Outcome': y_test_pred[:, 0],
'True Outcome': y_test
})
def scatterplot(x, y, df, title=None):
fig = plt.figure(dpi=100)
ax = fig.gca()
ax.scatter(df[x],
df[y],
s=10)
ax.grid(linestyle='--')
ax.set_axisbelow(True)
ax.set_xlabel(x, fontsize=11)
ax.set_ylabel(y, fontsize=11)
ax.spines['top'].set_linewidth(0.1)
ax.spines['right'].set_linewidth(0.1)
ax.set_title(title)
scatterplot('Predicted Outcome', 'True Outcome', df)
explainer = SamplingExplainerTF(model)
feature_values = X_test
feature_values.shape
feature_values[0]
explainer._batch_attributions(feature_values[0:1],
np.zeros((1, 5)),
number_of_samples=None,
output_index=None)
model(feature_values[0:1])[0, 0] - model(np.zeros((1, 5)))[0, 0]
explainer._batch_interactions(feature_values[0:1],
np.zeros((1, 5)),
number_of_samples=None,
output_index=None)
attributions = explainer.attributions(inputs=feature_values.astype(np.float32),
baselines=np.zeros(5),
batch_size=50,
number_of_samples=None,
output_index=None,
verbose=False)
interactions = explainer.interactions(inputs=feature_values.astype(np.float32),
baselines=np.zeros(5),
batch_size=50,
number_of_samples=None,
output_index=None,
verbose=False)
data_df = pd.DataFrame({
'Product': 2 * np.prod(feature_values[:, 0:2], axis=-1),
'Interaction': interactions[:, 0, 1]
})
scatterplot('Product', 'Interaction', data_df)
fig, axs = scatter_plot(attributions,
feature_values,
feature_index=0,
interactions=interactions * 0.5,
color_by=1,
feature_names=None,
scale_y_ind=True)
summary_plot(attributions,
feature_values,
interactions=None,
interaction_feature=None,
feature_names=None,
plot_top_k=None)
summary_plot(attributions,
feature_values,
interactions=interactions,
interaction_feature=0,
feature_names=None,
plot_top_k=None)
|
benchmarking/test_shapley_bruteforce.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# Probabilistic Programming and Bayesian Methods for Hackers
# ========
#
# Welcome to *Bayesian Methods for Hackers*. The full Github repository is available at [github/Probabilistic-Programming-and-Bayesian-Methods-for-Hackers](https://github.com/CamDavidsonPilon/Probabilistic-Programming-and-Bayesian-Methods-for-Hackers). The other chapters can be found on the project's [homepage](https://camdavidsonpilon.github.io/Probabilistic-Programming-and-Bayesian-Methods-for-Hackers/). We hope you enjoy the book, and we encourage any contributions!
#
# #### Looking for a printed version of Bayesian Methods for Hackers?
#
# _Bayesian Methods for Hackers_ is now a published book by Addison-Wesley, available on [Amazon](http://www.amazon.com/Bayesian-Methods-Hackers-Probabilistic-Addison-Wesley/dp/0133902838)!
#
# 
# Chapter 1
# ======
# ***
# The Philosophy of Bayesian Inference
# ------
#
# > You are a skilled programmer, but bugs still slip into your code. After a particularly difficult implementation of an algorithm, you decide to test your code on a trivial example. It passes. You test the code on a harder problem. It passes once again. And it passes the next, *even more difficult*, test too! You are starting to believe that there may be no bugs in this code...
#
# If you think this way, then congratulations, you already are thinking Bayesian! Bayesian inference is simply updating your beliefs after considering new evidence. A Bayesian can rarely be certain about a result, but he or she can be very confident. Just like in the example above, we can never be 100% sure that our code is bug-free unless we test it on every possible problem; something rarely possible in practice. Instead, we can test it on a large number of problems, and if it succeeds we can feel more *confident* about our code, but still not certain. Bayesian inference works identically: we update our beliefs about an outcome; rarely can we be absolutely sure unless we rule out all other alternatives.
#
# ### The Bayesian state of mind
#
#
# Bayesian inference differs from more traditional statistical inference by preserving *uncertainty*. At first, this sounds like a bad statistical technique. Isn't statistics all about deriving *certainty* from randomness? To reconcile this, we need to start thinking like Bayesians.
#
# The Bayesian world-view interprets probability as measure of *believability in an event*, that is, how confident we are in an event occurring. In fact, we will see in a moment that this is the natural interpretation of probability.
#
# For this to be clearer, we consider an alternative interpretation of probability: *Frequentist*, known as the more *classical* version of statistics, assumes that probability is the long-run frequency of events (hence the bestowed title). For example, the *probability of plane accidents* under a frequentist philosophy is interpreted as the *long-term frequency of plane accidents*. This makes logical sense for many probabilities of events, but becomes more difficult to understand when events have no long-term frequency of occurrences. Consider: we often assign probabilities to outcomes of presidential elections, but the election itself only happens once! Frequentists get around this by invoking alternative realities and saying across all these realities, the frequency of occurrences defines the probability.
#
# Bayesians, on the other hand, have a more intuitive approach. Bayesians interpret a probability as measure of *belief*, or confidence, of an event occurring. Simply, a probability is a summary of an opinion. An individual who assigns a belief of 0 to an event has no confidence that the event will occur; conversely, assigning a belief of 1 implies that the individual is absolutely certain of an event occurring. Beliefs between 0 and 1 allow for weightings of other outcomes. This definition agrees with the probability of a plane accident example, for having observed the frequency of plane accidents, an individual's belief should be equal to that frequency, excluding any outside information. Similarly, under this definition of probability being equal to beliefs, it is meaningful to speak about probabilities (beliefs) of presidential election outcomes: how confident are you candidate *A* will win?
#
# Notice in the paragraph above, I assigned the belief (probability) measure to an *individual*, not to Nature. This is very interesting, as this definition leaves room for conflicting beliefs between individuals. Again, this is appropriate for what naturally occurs: different individuals have different beliefs of events occurring, because they possess different *information* about the world. The existence of different beliefs does not imply that anyone is wrong. Consider the following examples demonstrating the relationship between individual beliefs and probabilities:
#
# - I flip a coin, and we both guess the result. We would both agree, assuming the coin is fair, that the probability of Heads is 1/2. Assume, then, that I peek at the coin. Now I know for certain what the result is: I assign probability 1.0 to either Heads or Tails (whichever it is). Now what is *your* belief that the coin is Heads? My knowledge of the outcome has not changed the coin's results. Thus we assign different probabilities to the result.
#
# - Your code either has a bug in it or not, but we do not know for certain which is true, though we have a belief about the presence or absence of a bug.
#
# - A medical patient is exhibiting symptoms $x$, $y$ and $z$. There are a number of diseases that could be causing all of them, but only a single disease is present. A doctor has beliefs about which disease, but a second doctor may have slightly different beliefs.
#
#
# This philosophy of treating beliefs as probability is natural to humans. We employ it constantly as we interact with the world and only see partial truths, but gather evidence to form beliefs. Alternatively, you have to be *trained* to think like a frequentist.
#
# To align ourselves with traditional probability notation, we denote our belief about event $A$ as $P(A)$. We call this quantity the *prior probability*.
#
# <NAME>, a great economist and thinker, said "When the facts change, I change my mind. What do you do, sir?" This quote reflects the way a Bayesian updates his or her beliefs after seeing evidence. Even — especially — if the evidence is counter to what was initially believed, the evidence cannot be ignored. We denote our updated belief as $P(A |X )$, interpreted as the probability of $A$ given the evidence $X$. We call the updated belief the *posterior probability* so as to contrast it with the prior probability. For example, consider the posterior probabilities (read: posterior beliefs) of the above examples, after observing some evidence $X$:
#
# 1\. $P(A): \;\;$ the coin has a 50 percent chance of being Heads. $P(A | X):\;\;$ You look at the coin, observe a Heads has landed, denote this information $X$, and trivially assign probability 1.0 to Heads and 0.0 to Tails.
#
# 2\. $P(A): \;\;$ This big, complex code likely has a bug in it. $P(A | X): \;\;$ The code passed all $X$ tests; there still might be a bug, but its presence is less likely now.
#
# 3\. $P(A):\;\;$ The patient could have any number of diseases. $P(A | X):\;\;$ Performing a blood test generated evidence $X$, ruling out some of the possible diseases from consideration.
#
#
# It's clear that in each example we did not completely discard the prior belief after seeing new evidence $X$, but we *re-weighted the prior* to incorporate the new evidence (i.e. we put more weight, or confidence, on some beliefs versus others).
#
# By introducing prior uncertainty about events, we are already admitting that any guess we make is potentially very wrong. After observing data, evidence, or other information, we update our beliefs, and our guess becomes *less wrong*. This is the alternative side of the prediction coin, where typically we try to be *more right*.
#
#
# ### Bayesian Inference in Practice
#
# If frequentist and Bayesian inference were programming functions, with inputs being statistical problems, then the two would be different in what they return to the user. The frequentist inference function would return a number, representing an estimate (typically a summary statistic like the sample average etc.), whereas the Bayesian function would return *probabilities*.
#
# For example, in our debugging problem above, calling the frequentist function with the argument "My code passed all $X$ tests; is my code bug-free?" would return a *YES*. On the other hand, asking our Bayesian function "Often my code has bugs. My code passed all $X$ tests; is my code bug-free?" would return something very different: probabilities of *YES* and *NO*. The function might return:
#
#
# > *YES*, with probability 0.8; *NO*, with probability 0.2
#
#
#
# This is very different from the answer the frequentist function returned. Notice that the Bayesian function accepted an additional argument: *"Often my code has bugs"*. This parameter is the *prior*. By including the prior parameter, we are telling the Bayesian function to include our belief about the situation. Technically this parameter in the Bayesian function is optional, but we will see excluding it has its own consequences.
#
#
# #### Incorporating evidence
#
# As we acquire more and more instances of evidence, our prior belief is *washed out* by the new evidence. This is to be expected. For example, if your prior belief is something ridiculous, like "I expect the sun to explode today", and each day you are proved wrong, you would hope that any inference would correct you, or at least align your beliefs better. Bayesian inference will correct this belief.
#
#
# Denote $N$ as the number of instances of evidence we possess. As we gather an *infinite* amount of evidence, say as $N \rightarrow \infty$, our Bayesian results (often) align with frequentist results. Hence for large $N$, statistical inference is more or less objective. On the other hand, for small $N$, inference is much more *unstable*: frequentist estimates have more variance and larger confidence intervals. This is where Bayesian analysis excels. By introducing a prior, and returning probabilities (instead of a scalar estimate), we *preserve the uncertainty* that reflects the instability of statistical inference of a small $N$ dataset.
#
# One may think that for large $N$, one can be indifferent between the two techniques since they offer similar inference, and might lean towards the computationally-simpler, frequentist methods. An individual in this position should consider the following quote by <NAME> (2005)[1], before making such a decision:
#
# > Sample sizes are never large. If $N$ is too small to get a sufficiently-precise estimate, you need to get more data (or make more assumptions). But once $N$ is "large enough," you can start subdividing the data to learn more (for example, in a public opinion poll, once you have a good estimate for the entire country, you can estimate among men and women, northerners and southerners, different age groups, etc.). $N$ is never enough because if it were "enough" you'd already be on to the next problem for which you need more data.
#
# ### Are frequentist methods incorrect then?
#
# **No.**
#
# Frequentist methods are still useful or state-of-the-art in many areas. Tools such as least squares linear regression, LASSO regression, and expectation-maximization algorithms are all powerful and fast. Bayesian methods complement these techniques by solving problems that these approaches cannot, or by illuminating the underlying system with more flexible modeling.
#
#
# #### A note on *Big Data*
# Paradoxically, big data's predictive analytic problems are actually solved by relatively simple algorithms [2][4]. Thus we can argue that big data's prediction difficulty does not lie in the algorithm used, but instead on the computational difficulties of storage and execution on big data. (One should also consider Gelman's quote from above and ask "Do I really have big data?" )
#
# The much more difficult analytic problems involve *medium data* and, especially troublesome, *really small data*. Using a similar argument as Gelman's above, if big data problems are *big enough* to be readily solved, then we should be more interested in the *not-quite-big enough* datasets.
#
# ### Our Bayesian framework
#
# We are interested in beliefs, which can be interpreted as probabilities by thinking Bayesian. We have a *prior* belief in event $A$, beliefs formed by previous information, e.g., our prior belief about bugs being in our code before performing tests.
#
# Secondly, we observe our evidence. To continue our buggy-code example: if our code passes $X$ tests, we want to update our belief to incorporate this. We call this new belief the *posterior* probability. Updating our belief is done via the following equation, known as Bayes' Theorem, after its discoverer Thomas Bayes:
#
# \begin{align}
# P( A | X ) = & \frac{ P(X | A) P(A) } {P(X) } \\\\[5pt]
# & \propto P(X | A) P(A)\;\; (\propto \text{is proportional to } )
# \end{align}
#
# The above formula is not unique to Bayesian inference: it is a mathematical fact with uses outside Bayesian inference. Bayesian inference merely uses it to connect prior probabilities $P(A)$ with an updated posterior probabilities $P(A | X )$.
# ##### Example: Mandatory coin-flip example
#
# Every statistics text must contain a coin-flipping example, I'll use it here to get it out of the way. Suppose, naively, that you are unsure about the probability of heads in a coin flip (spoiler alert: it's 50%). You believe there is some true underlying ratio, call it $p$, but have no prior opinion on what $p$ might be.
#
# We begin to flip a coin, and record the observations: either $H$ or $T$. This is our observed data. An interesting question to ask is how our inference changes as we observe more and more data? More specifically, what do our posterior probabilities look like when we have little data, versus when we have lots of data.
#
# Below we plot a sequence of updating posterior probabilities as we observe increasing amounts of data (coin flips).
# + jupyter={"outputs_hidden": false}
"""
The book uses a custom matplotlibrc file, which provides the unique styles for
matplotlib plots. If executing this book, and you wish to use the book's
styling, provided are two options:
1. Overwrite your own matplotlibrc file with the rc-file provided in the
book's styles/ dir. See http://matplotlib.org/users/customizing.html
2. Also in the styles is bmh_matplotlibrc.json file. This can be used to
update the styles in only this notebook. Try running the following code:
import json, matplotlib
s = json.load( open("../styles/bmh_matplotlibrc.json") )
matplotlib.rcParams.update(s)
"""
# The code below can be passed over, as it is currently not important, plus it
# uses advanced topics we have not covered yet. LOOK AT PICTURE, MICHAEL!
# %matplotlib inline
from IPython.core.pylabtools import figsize
import numpy as np
from matplotlib import pyplot as plt
figsize(11, 9)
import scipy.stats as stats
dist = stats.beta
n_trials = [0, 1, 2, 3, 4, 5, 8, 15, 50, 500]
data = stats.bernoulli.rvs(0.5, size=n_trials[-1])
x = np.linspace(0, 1, 100)
# For the already prepared, I'm using Binomial's conj. prior.
for k, N in enumerate(n_trials):
sx = plt.subplot(len(n_trials) / 2, 2, k + 1)
plt.xlabel("$p$, probability of heads") \
if k in [0, len(n_trials) - 1] else None
plt.setp(sx.get_yticklabels(), visible=False)
heads = data[:N].sum()
y = dist.pdf(x, 1 + heads, 1 + N - heads)
plt.plot(x, y, label="observe %d tosses,\n %d heads" % (N, heads))
plt.fill_between(x, 0, y, color="#348ABD", alpha=0.4)
plt.vlines(0.5, 0, 4, color="k", linestyles="--", lw=1)
leg = plt.legend()
leg.get_frame().set_alpha(0.4)
plt.autoscale(tight=True)
plt.suptitle("Bayesian updating of posterior probabilities",
y=1.02,
fontsize=14)
plt.tight_layout()
# -
# The posterior probabilities are represented by the curves, and our uncertainty is proportional to the width of the curve. As the plot above shows, as we start to observe data our posterior probabilities start to shift and move around. Eventually, as we observe more and more data (coin-flips), our probabilities will tighten closer and closer around the true value of $p=0.5$ (marked by a dashed line).
#
# Notice that the plots are not always *peaked* at 0.5. There is no reason it should be: recall we assumed we did not have a prior opinion of what $p$ is. In fact, if we observe quite extreme data, say 8 flips and only 1 observed heads, our distribution would look very biased *away* from lumping around 0.5 (with no prior opinion, how confident would you feel betting on a fair coin after observing 8 tails and 1 head). As more data accumulates, we would see more and more probability being assigned at $p=0.5$, though never all of it.
#
# The next example is a simple demonstration of the mathematics of Bayesian inference.
# ##### Example: Bug, or just sweet, unintended feature?
#
#
# Let $A$ denote the event that our code has **no bugs** in it. Let $X$ denote the event that the code passes all debugging tests. For now, we will leave the prior probability of no bugs as a variable, i.e. $P(A) = p$.
#
# We are interested in $P(A|X)$, i.e. the probability of no bugs, given our debugging tests $X$ pass. To use the formula above, we need to compute some quantities.
#
# What is $P(X | A)$, i.e., the probability that the code passes $X$ tests *given* there are no bugs? Well, it is equal to 1, for code with no bugs will pass all tests.
#
# $P(X)$ is a little bit trickier: The event $X$ can be divided into two possibilities, event $X$ occurring even though our code *indeed has* bugs (denoted $\sim A\;$, spoken *not $A$*), or event $X$ without bugs ($A$). $P(X)$ can be represented as:
# \begin{align}
# P(X ) & = P(X \text{ and } A) + P(X \text{ and } \sim A) \\\\[5pt]
# & = P(X|A)P(A) + P(X | \sim A)P(\sim A)\\\\[5pt]
# & = P(X|A)p + P(X | \sim A)(1-p)
# \end{align}
# We have already computed $P(X|A)$ above. On the other hand, $P(X | \sim A)$ is subjective: our code can pass tests but still have a bug in it, though the probability there is a bug present is reduced. Note this is dependent on the number of tests performed, the degree of complication in the tests, etc. Let's be conservative and assign $P(X|\sim A) = 0.5$. Then
#
# \begin{align}
# P(A | X) & = \frac{1\cdot p}{ 1\cdot p +0.5 (1-p) } \\\\
# & = \frac{ 2 p}{1+p}
# \end{align}
# This is the posterior probability. What does it look like as a function of our prior, $p \in [0,1]$?
# + jupyter={"outputs_hidden": false}
figsize(12.5, 4)
p = np.linspace(0, 1, 50)
plt.plot(p, 2 * p / (1 + p), color="#348ABD", lw=3)
# plt.fill_between(p, 2*p/(1+p), alpha=.5, facecolor=["#A60628"])
plt.scatter(0.2, 2 * (0.2) / 1.2, s=140, c="#348ABD")
plt.xlim(0, 1)
plt.ylim(0, 1)
plt.xlabel("Prior, $P(A) = p$")
plt.ylabel("Posterior, $P(A|X)$, with $P(A) = p$")
plt.title("Is my code bug-free?")
# -
# We can see the biggest gains if we observe the $X$ tests passed when the prior probability, $p$, is low. Let's settle on a specific value for the prior. I'm a strong programmer (I think), so I'm going to give myself a realistic prior of 0.20, that is, there is a 20% chance that I write code bug-free. To be more realistic, this prior should be a function of how complicated and large the code is, but let's pin it at 0.20. Then my updated belief that my code is bug-free is 0.33.
#
# Recall that the prior is a probability: $p$ is the prior probability that there *are no bugs*, so $1-p$ is the prior probability that there *are bugs*.
#
# Similarly, our posterior is also a probability, with $P(A | X)$ the probability there is no bug *given we saw all tests pass*, hence $1-P(A|X)$ is the probability there is a bug *given all tests passed*. What does our posterior probability look like? Below is a chart of both the prior and the posterior probabilities.
#
# + jupyter={"outputs_hidden": false}
figsize(12.5, 4)
colours = ["#348ABD", "#A60628"]
prior = [0.20, 0.80]
posterior = [1. / 3, 2. / 3]
plt.bar([0, .7], prior, alpha=0.70, width=0.25,
color=colours[0], label="prior distribution",
lw="3", edgecolor=colours[0])
plt.bar([0 + 0.25, .7 + 0.25], posterior, alpha=0.7,
width=0.25, color=colours[1],
label="posterior distribution",
lw="3", edgecolor=colours[1])
plt.ylim(0,1)
plt.xticks([0.20, .95], ["Bugs Absent", "Bugs Present"])
plt.title("Prior and Posterior probability of bugs present")
plt.ylabel("Probability")
plt.legend(loc="upper left");
# -
# Notice that after we observed $X$ occur, the probability of bugs being absent increased. By increasing the number of tests, we can approach confidence (probability 1) that there are no bugs present.
#
# This was a very simple example of Bayesian inference and Bayes rule. Unfortunately, the mathematics necessary to perform more complicated Bayesian inference only becomes more difficult, except for artificially constructed cases. We will later see that this type of mathematical analysis is actually unnecessary. First we must broaden our modeling tools. The next section deals with *probability distributions*. If you are already familiar, feel free to skip (or at least skim), but for the less familiar the next section is essential.
# _______
#
# ## Probability Distributions
#
#
# **Let's quickly recall what a probability distribution is:** Let $Z$ be some random variable. Then associated with $Z$ is a *probability distribution function* that assigns probabilities to the different outcomes $Z$ can take. Graphically, a probability distribution is a curve where the probability of an outcome is proportional to the height of the curve. You can see examples in the first figure of this chapter.
#
# We can divide random variables into three classifications:
#
# - **$Z$ is discrete**: Discrete random variables may only assume values on a specified list. Things like populations, movie ratings, and number of votes are all discrete random variables. Discrete random variables become more clear when we contrast them with...
#
# - **$Z$ is continuous**: Continuous random variable can take on arbitrarily exact values. For example, temperature, speed, time, color are all modeled as continuous variables because you can progressively make the values more and more precise.
#
# - **$Z$ is mixed**: Mixed random variables assign probabilities to both discrete and continuous random variables, i.e. it is a combination of the above two categories.
#
# #### Expected Value
# Expected value (EV) is one of the most important concepts in probability. The EV for a given probability distribution can be described as "the mean value in the long run for many repeated samples from that distribution." To borrow a metaphor from physics, a distribution's EV acts like its "center of mass." Imagine repeating the same experiment many times over, and taking the average over each outcome. The more you repeat the experiment, the closer this average will become to the distributions EV. (side note: as the number of repeated experiments goes to infinity, the difference between the average outcome and the EV becomes arbitrarily small.)
#
# ### Discrete Case
# If $Z$ is discrete, then its distribution is called a *probability mass function*, which measures the probability $Z$ takes on the value $k$, denoted $P(Z=k)$. Note that the probability mass function completely describes the random variable $Z$, that is, if we know the mass function, we know how $Z$ should behave. There are popular probability mass functions that consistently appear: we will introduce them as needed, but let's introduce the first very useful probability mass function. We say $Z$ is *Poisson*-distributed if:
#
# $$P(Z = k) =\frac{ \lambda^k e^{-\lambda} }{k!}, \; \; k=0,1,2, \dots, \; \; \lambda \in \mathbb{R}_{>0} $$
#
# $\lambda$ is called a parameter of the distribution, and it controls the distribution's shape. For the Poisson distribution, $\lambda$ can be any positive number. By increasing $\lambda$, we add more probability to larger values, and conversely by decreasing $\lambda$ we add more probability to smaller values. One can describe $\lambda$ as the *intensity* of the Poisson distribution.
#
# Unlike $\lambda$, which can be any positive number, the value $k$ in the above formula must be a non-negative integer, i.e., $k$ must take on values 0,1,2, and so on. This is very important, because if you wanted to model a population you could not make sense of populations with 4.25 or 5.612 members.
#
# If a random variable $Z$ has a Poisson mass distribution, we denote this by writing
#
# $$Z \sim \text{Poi}(\lambda) $$
#
# One useful property of the Poisson distribution is that its expected value is equal to its parameter, i.e.:
#
# $$E\large[ \;Z\; | \; \lambda \;\large] = \lambda $$
#
# We will use this property often, so it's useful to remember. Below, we plot the probability mass distribution for different $\lambda$ values. The first thing to notice is that by increasing $\lambda$, we add more probability of larger values occurring. Second, notice that although the graph ends at 15, the distributions do not. They assign positive probability to every non-negative integer.
# + jupyter={"outputs_hidden": false}
figsize(12.5, 4)
import scipy.stats as stats
a = np.arange(16)
poi = stats.poisson
lambda_ = [1.5, 4.25]
colours = ["#348ABD", "#A60628"]
plt.bar(a, poi.pmf(a, lambda_[0]), color=colours[0],
label="$\lambda = %.1f$" % lambda_[0], alpha=0.60,
edgecolor=colours[0], lw="3")
plt.bar(a, poi.pmf(a, lambda_[1]), color=colours[1],
label="$\lambda = %.1f$" % lambda_[1], alpha=0.60,
edgecolor=colours[1], lw="3")
plt.xticks(a + 0.4, a)
plt.legend()
plt.ylabel("probability of $k$")
plt.xlabel("$k$")
plt.title("Probability mass function of a Poisson random variable; differing \
$\lambda$ values")
# -
# ### Continuous Case
# Instead of a probability mass function, a continuous random variable has a *probability density function*. This might seem like unnecessary nomenclature, but the density function and the mass function are very different creatures. An example of continuous random variable is a random variable with *exponential density*. The density function for an exponential random variable looks like this:
#
# $$f_Z(z | \lambda) = \lambda e^{-\lambda z }, \;\; z\ge 0$$
#
# Like a Poisson random variable, an exponential random variable can take on only non-negative values. But unlike a Poisson variable, the exponential can take on *any* non-negative values, including non-integral values such as 4.25 or 5.612401. This property makes it a poor choice for count data, which must be an integer, but a great choice for time data, temperature data (measured in Kelvins, of course), or any other precise *and positive* variable. The graph below shows two probability density functions with different $\lambda$ values.
#
# When a random variable $Z$ has an exponential distribution with parameter $\lambda$, we say *$Z$ is exponential* and write
#
# $$Z \sim \text{Exp}(\lambda)$$
#
# Given a specific $\lambda$, the expected value of an exponential random variable is equal to the inverse of $\lambda$, that is:
#
# $$E[\; Z \;|\; \lambda \;] = \frac{1}{\lambda}$$
# + jupyter={"outputs_hidden": false}
a = np.linspace(0, 4, 100)
expo = stats.expon
lambda_ = [0.5, 1]
for l, c in zip(lambda_, colours):
plt.plot(a, expo.pdf(a, scale=1. / l), lw=3,
color=c, label="$\lambda = %.1f$" % l)
plt.fill_between(a, expo.pdf(a, scale=1. / l), color=c, alpha=.33)
plt.legend()
plt.ylabel("PDF at $z$")
plt.xlabel("$z$")
plt.ylim(0, 1.2)
plt.title("Probability density function of an Exponential random variable;\
differing $\lambda$");
# -
#
# ### But what is $\lambda \;$?
#
#
# **This question is what motivates statistics**. In the real world, $\lambda$ is hidden from us. We see only $Z$, and must go backwards to try and determine $\lambda$. The problem is difficult because there is no one-to-one mapping from $Z$ to $\lambda$. Many different methods have been created to solve the problem of estimating $\lambda$, but since $\lambda$ is never actually observed, no one can say for certain which method is best!
#
# Bayesian inference is concerned with *beliefs* about what $\lambda$ might be. Rather than try to guess $\lambda$ exactly, we can only talk about what $\lambda$ is likely to be by assigning a probability distribution to $\lambda$.
#
# This might seem odd at first. After all, $\lambda$ is fixed; it is not (necessarily) random! How can we assign probabilities to values of a non-random variable? Ah, we have fallen for our old, frequentist way of thinking. Recall that under Bayesian philosophy, we *can* assign probabilities if we interpret them as beliefs. And it is entirely acceptable to have *beliefs* about the parameter $\lambda$.
#
#
# ##### Example: Inferring behaviour from text-message data
#
# Let's try to model a more interesting example, one that concerns the rate at which a user sends and receives text messages:
#
# > You are given a series of daily text-message counts from a user of your system. The data, plotted over time, appears in the chart below. You are curious to know if the user's text-messaging habits have changed over time, either gradually or suddenly. How can you model this? (This is in fact my own text-message data. Judge my popularity as you wish.)
#
# + jupyter={"outputs_hidden": false}
figsize(12.5, 3.5)
count_data = np.loadtxt("data/txtdata.csv")
n_count_data = len(count_data)
plt.bar(np.arange(n_count_data), count_data, color="#348ABD")
plt.xlabel("Time (days)")
plt.ylabel("count of text-msgs received")
plt.title("Did the user's texting habits change over time?")
plt.xlim(0, n_count_data);
# -
# Before we start modeling, see what you can figure out just by looking at the chart above. Would you say there was a change in behaviour during this time period?
#
# How can we start to model this? Well, as we have conveniently already seen, a Poisson random variable is a very appropriate model for this type of *count* data. Denoting day $i$'s text-message count by $C_i$,
#
# $$ C_i \sim \text{Poisson}(\lambda) $$
#
# We are not sure what the value of the $\lambda$ parameter really is, however. Looking at the chart above, it appears that the rate might become higher late in the observation period, which is equivalent to saying that $\lambda$ increases at some point during the observations. (Recall that a higher value of $\lambda$ assigns more probability to larger outcomes. That is, there is a higher probability of many text messages having been sent on a given day.)
#
# How can we represent this observation mathematically? Let's assume that on some day during the observation period (call it $\tau$), the parameter $\lambda$ suddenly jumps to a higher value. So we really have two $\lambda$ parameters: one for the period before $\tau$, and one for the rest of the observation period. In the literature, a sudden transition like this would be called a *switchpoint*:
#
# $$
# \lambda =
# \begin{cases}
# \lambda_1 & \text{if } t \lt \tau \cr
# \lambda_2 & \text{if } t \ge \tau
# \end{cases}
# $$
#
#
# If, in reality, no sudden change occurred and indeed $\lambda_1 = \lambda_2$, then the $\lambda$s posterior distributions should look about equal.
#
# We are interested in inferring the unknown $\lambda$s. To use Bayesian inference, we need to assign prior probabilities to the different possible values of $\lambda$. What would be good prior probability distributions for $\lambda_1$ and $\lambda_2$? Recall that $\lambda$ can be any positive number. As we saw earlier, the *exponential* distribution provides a continuous density function for positive numbers, so it might be a good choice for modeling $\lambda_i$. But recall that the exponential distribution takes a parameter of its own, so we'll need to include that parameter in our model. Let's call that parameter $\alpha$.
#
# \begin{align}
# &\lambda_1 \sim \text{Exp}( \alpha ) \\\
# &\lambda_2 \sim \text{Exp}( \alpha )
# \end{align}
#
# $\alpha$ is called a *hyper-parameter* or *parent variable*. In literal terms, it is a parameter that influences other parameters. Our initial guess at $\alpha$ does not influence the model too strongly, so we have some flexibility in our choice. A good rule of thumb is to set the exponential parameter equal to the inverse of the average of the count data. Since we're modeling $\lambda$ using an exponential distribution, we can use the expected value identity shown earlier to get:
#
# $$\frac{1}{N}\sum_{i=0}^N \;C_i \approx E[\; \lambda \; |\; \alpha ] = \frac{1}{\alpha}$$
#
# An alternative, and something I encourage the reader to try, would be to have two priors: one for each $\lambda_i$. Creating two exponential distributions with different $\alpha$ values reflects our prior belief that the rate changed at some point during the observations.
#
# What about $\tau$? Because of the noisiness of the data, it's difficult to pick out a priori when $\tau$ might have occurred. Instead, we can assign a *uniform prior belief* to every possible day. This is equivalent to saying
#
# \begin{align}
# & \tau \sim \text{DiscreteUniform(1,70) }\\\\
# & \Rightarrow P( \tau = k ) = \frac{1}{70}
# \end{align}
#
# So after all this, what does our overall prior distribution for the unknown variables look like? Frankly, *it doesn't matter*. What we should understand is that it's an ugly, complicated mess involving symbols only a mathematician could love. And things will only get uglier the more complicated our models become. Regardless, all we really care about is the posterior distribution.
#
# We next turn to PyMC, a Python library for performing Bayesian analysis that is undaunted by the mathematical monster we have created.
#
#
# Introducing our first hammer: PyMC
# -----
#
# PyMC is a Python library for programming Bayesian analysis [3]. It is a fast, well-maintained library. The only unfortunate part is that its documentation is lacking in certain areas, especially those that bridge the gap between beginner and hacker. One of this book's main goals is to solve that problem, and also to demonstrate why PyMC is so cool.
#
# We will model the problem above using PyMC. This type of programming is called *probabilistic programming*, an unfortunate misnomer that invokes ideas of randomly-generated code and has likely confused and frightened users away from this field. The code is not random; it is probabilistic in the sense that we create probability models using programming variables as the model's components. Model components are first-class primitives within the PyMC framework.
#
# <NAME> [5] has a very motivating description of probabilistic programming:
#
# > Another way of thinking about this: unlike a traditional program, which only runs in the forward directions, a probabilistic program is run in both the forward and backward direction. It runs forward to compute the consequences of the assumptions it contains about the world (i.e., the model space it represents), but it also runs backward from the data to constrain the possible explanations. In practice, many probabilistic programming systems will cleverly interleave these forward and backward operations to efficiently home in on the best explanations.
#
# Because of the confusion engendered by the term *probabilistic programming*, I'll refrain from using it. Instead, I'll simply say *programming*, since that's what it really is.
#
# PyMC code is easy to read. The only novel thing should be the syntax, and I will interrupt the code to explain individual sections. Simply remember that we are representing the model's components ($\tau, \lambda_1, \lambda_2$ ) as variables:
# + jupyter={"outputs_hidden": false}
import pymc as pm
alpha = 1.0 / count_data.mean() # Recall count_data is the
# variable that holds our txt counts
with pm.Model() as model:
lambda_1 = pm.Exponential("lambda_1", alpha)
lambda_2 = pm.Exponential("lambda_2", alpha)
tau = pm.DiscreteUniform("tau", lower=0, upper=n_count_data)
# -
# In the code above, we create the PyMC variables corresponding to $\lambda_1$ and $\lambda_2$. We assign them to PyMC's *stochastic variables*, so-called because they are treated by the back end as random number generators. We can demonstrate this fact by calling their built-in `random()` methods.
# + jupyter={"outputs_hidden": false}
print("Random output:", tau.eval(), tau.eval(), tau.eval())
# + jupyter={"outputs_hidden": false}
# @pm.deterministic
def lambda_(tau=tau, lambda_1=lambda_1, lambda_2=lambda_2):
out = np.zeros(n_count_data)
out[:tau] = lambda_1 # lambda before tau is lambda1
out[tau:] = lambda_2 # lambda after (and including) tau is lambda2
return out
# -
# This code creates a new function `lambda_`, but really we can think of it as a random variable: the random variable $\lambda$ from above. Note that because `lambda_1`, `lambda_2` and `tau` are random, `lambda_` will be random. We are **not** fixing any variables yet.
#
# `@pm.deterministic` is a decorator that tells PyMC this is a deterministic function. That is, if the arguments were deterministic (which they are not), the output would be deterministic as well. Deterministic functions will be covered in Chapter 2.
# + jupyter={"outputs_hidden": false}
observation = pm.Poisson("obs", lambda_, value=count_data, observed=True)
model = pm.Model([observation, lambda_1, lambda_2, tau])
# -
# The variable `observation` combines our data, `count_data`, with our proposed data-generation scheme, given by the variable `lambda_`, through the `value` keyword. We also set `observed = True` to tell PyMC that this should stay fixed in our analysis. Finally, PyMC wants us to collect all the variables of interest and create a `Model` instance out of them. This makes our life easier when we retrieve the results.
#
# The code below will be explained in Chapter 3, but I show it here so you can see where our results come from. One can think of it as a *learning* step. The machinery being employed is called *Markov Chain Monte Carlo* (MCMC), which I also delay explaining until Chapter 3. This technique returns thousands of random variables from the posterior distributions of $\lambda_1, \lambda_2$ and $\tau$. We can plot a histogram of the random variables to see what the posterior distributions look like. Below, we collect the samples (called *traces* in the MCMC literature) into histograms.
# + jupyter={"outputs_hidden": false}
# Mysterious code to be explained in Chapter 3.
mcmc = pm.MCMC(model)
mcmc.sample(40000, 10000, 1)
# + jupyter={"outputs_hidden": false}
lambda_1_samples = mcmc.trace('lambda_1')[:]
lambda_2_samples = mcmc.trace('lambda_2')[:]
tau_samples = mcmc.trace('tau')[:]
# + jupyter={"outputs_hidden": false}
figsize(12.5, 10)
# histogram of the samples:
ax = plt.subplot(311)
ax.set_autoscaley_on(False)
plt.hist(lambda_1_samples, histtype='stepfilled', bins=30, alpha=0.85,
label="posterior of $\lambda_1$", color="#A60628", density=True)
plt.legend(loc="upper left")
plt.title(r"""Posterior distributions of the variables
$\lambda_1,\;\lambda_2,\;\tau$""")
plt.xlim([15, 30])
plt.xlabel("$\lambda_1$ value")
ax = plt.subplot(312)
ax.set_autoscaley_on(False)
plt.hist(lambda_2_samples, histtype='stepfilled', bins=30, alpha=0.85,
label="posterior of $\lambda_2$", color="#7A68A6", density=True)
plt.legend(loc="upper left")
plt.xlim([15, 30])
plt.xlabel("$\lambda_2$ value")
plt.subplot(313)
w = 1.0 / tau_samples.shape[0] * np.ones_like(tau_samples)
plt.hist(tau_samples, bins=n_count_data, alpha=1,
label=r"posterior of $\tau$",
color="#467821", weights=w, rwidth=2.)
plt.xticks(np.arange(n_count_data))
plt.legend(loc="upper left")
plt.ylim([0, .75])
plt.xlim([35, len(count_data) - 20])
plt.xlabel(r"$\tau$ (in days)")
plt.ylabel("probability");
# -
# ### Interpretation
#
# Recall that Bayesian methodology returns a *distribution*. Hence we now have distributions to describe the unknown $\lambda$s and $\tau$. What have we gained? Immediately, we can see the uncertainty in our estimates: the wider the distribution, the less certain our posterior belief should be. We can also see what the plausible values for the parameters are: $\lambda_1$ is around 18 and $\lambda_2$ is around 23. The posterior distributions of the two $\lambda$s are clearly distinct, indicating that it is indeed likely that there was a change in the user's text-message behaviour.
#
# What other observations can you make? If you look at the original data again, do these results seem reasonable?
#
# Notice also that the posterior distributions for the $\lambda$s do not look like exponential distributions, even though our priors for these variables were exponential. In fact, the posterior distributions are not really of any form that we recognize from the original model. But that's OK! This is one of the benefits of taking a computational point of view. If we had instead done this analysis using mathematical approaches, we would have been stuck with an analytically intractable (and messy) distribution. Our use of a computational approach makes us indifferent to mathematical tractability.
#
# Our analysis also returned a distribution for $\tau$. Its posterior distribution looks a little different from the other two because it is a discrete random variable, so it doesn't assign probabilities to intervals. We can see that near day 45, there was a 50% chance that the user's behaviour changed. Had no change occurred, or had the change been gradual over time, the posterior distribution of $\tau$ would have been more spread out, reflecting that many days were plausible candidates for $\tau$. By contrast, in the actual results we see that only three or four days make any sense as potential transition points.
# ### Why would I want samples from the posterior, anyways?
#
#
# We will deal with this question for the remainder of the book, and it is an understatement to say that it will lead us to some amazing results. For now, let's end this chapter with one more example.
#
# We'll use the posterior samples to answer the following question: what is the expected number of texts at day $t, \; 0 \le t \le 70$ ? Recall that the expected value of a Poisson variable is equal to its parameter $\lambda$. Therefore, the question is equivalent to *what is the expected value of $\lambda$ at time $t$*?
#
# In the code below, let $i$ index samples from the posterior distributions. Given a day $t$, we average over all possible $\lambda_i$ for that day $t$, using $\lambda_i = \lambda_{1,i}$ if $t \lt \tau_i$ (that is, if the behaviour change has not yet occurred), else we use $\lambda_i = \lambda_{2,i}$.
# + jupyter={"outputs_hidden": false}
figsize(12.5, 5)
# tau_samples, lambda_1_samples, lambda_2_samples contain
# N samples from the corresponding posterior distribution
N = tau_samples.shape[0]
expected_texts_per_day = np.zeros(n_count_data)
for day in range(0, n_count_data):
# ix is a bool index of all tau samples corresponding to
# the switchpoint occurring prior to value of 'day'
ix = day < tau_samples
# Each posterior sample corresponds to a value for tau.
# for each day, that value of tau indicates whether we're "before"
# (in the lambda1 "regime") or
# "after" (in the lambda2 "regime") the switchpoint.
# by taking the posterior sample of lambda1/2 accordingly, we can average
# over all samples to get an expected value for lambda on that day.
# As explained, the "message count" random variable is Poisson distributed,
# and therefore lambda (the poisson parameter) is the expected value of
# "message count".
expected_texts_per_day[day] = (lambda_1_samples[ix].sum()
+ lambda_2_samples[~ix].sum()) / N
plt.plot(range(n_count_data), expected_texts_per_day, lw=4, color="#E24A33",
label="expected number of text-messages received")
plt.xlim(0, n_count_data)
plt.xlabel("Day")
plt.ylabel("Expected # text-messages")
plt.title("Expected number of text-messages received")
plt.ylim(0, 60)
plt.bar(np.arange(len(count_data)), count_data, color="#348ABD", alpha=0.65,
label="observed texts per day")
plt.legend(loc="upper left");
# -
# Our analysis shows strong support for believing the user's behavior did change ($\lambda_1$ would have been close in value to $\lambda_2$ had this not been true), and that the change was sudden rather than gradual (as demonstrated by $\tau$'s strongly peaked posterior distribution). We can speculate what might have caused this: a cheaper text-message rate, a recent weather-to-text subscription, or perhaps a new relationship. (In fact, the 45th day corresponds to Christmas, and I moved away to Toronto the next month, leaving a girlfriend behind.)
#
# ##### Exercises
#
# 1\. Using `lambda_1_samples` and `lambda_2_samples`, what is the mean of the posterior distributions of $\lambda_1$ and $\lambda_2$?
# + jupyter={"outputs_hidden": false}
# type your code here.
# -
# 2\. What is the expected percentage increase in text-message rates? `hint:` compute the mean of `lambda_1_samples/lambda_2_samples`. Note that this quantity is very different from `lambda_1_samples.mean()/lambda_2_samples.mean()`.
# + jupyter={"outputs_hidden": false}
# type your code here.
# -
# 3\. What is the mean of $\lambda_1$ **given** that we know $\tau$ is less than 45. That is, suppose we have been given new information that the change in behaviour occurred prior to day 45. What is the expected value of $\lambda_1$ now? (You do not need to redo the PyMC part. Just consider all instances where `tau_samples < 45`.)
# + jupyter={"outputs_hidden": false}
# type your code here.
# -
# ### References
#
#
# - [1] Gelman, Andrew. N.p.. Web. 22 Jan 2013. [N is never large enough](http://andrewgelman.com/2005/07/31/n_is_never_larg/).
# - [2] <NAME>. 2009. [The Unreasonable Effectiveness of Data](http://static.googleusercontent.com/media/research.google.com/en//pubs/archive/35179.pdf).
# - [3] <NAME>., <NAME> and <NAME>. 2010.
# PyMC: Bayesian Stochastic Modelling in Python. Journal of Statistical
# Software, 35(4), pp. 1-81.
# - [4] <NAME> and <NAME>. Large-Scale Machine Learning at Twitter. Proceedings of the 2012 ACM SIGMOD International Conference on Management of Data (SIGMOD 2012), pages 793-804, May 2012, Scottsdale, Arizona.
# - [5] <NAME>. "Why Probabilistic Programming Matters." 24 Mar 2013. Google, Online Posting to Google . Web. 24 Mar. 2013. <https://plus.google.com/u/0/107971134877020469960/posts/KpeRdJKR6Z1>.
# + jupyter={"outputs_hidden": false}
from IPython.core.display import HTML
def css_styling():
styles = open("../styles/custom.css", "r").read()
return HTML(styles)
css_styling()
# + jupyter={"outputs_hidden": false}
|
Chapter1_Introduction/Ch1_Introduction_PyMC2.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
import numpy as np
import re
import datetime
from dateutil.relativedelta import relativedelta
from datetime import date
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import roc_auc_score
from sklearn.model_selection import RandomizedSearchCV
from sklearn.model_selection import GridSearchCV
from sklearn.model_selection import StratifiedShuffleSplit
from sklearn.svm import SVC
from sklearn.neural_network import MLPClassifier
from sklearn.metrics import confusion_matrix, classification_report
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler, LabelEncoder
# %matplotlib inline
file = r"C:\Users\<NAME>\Desktop\python project\project 2\carvan_train.csv"
file
carvan_train = pd.read_csv(file)
carvan_train
file = r"C:\Users\<NAME>\Desktop\python project\project 2\carvan_test.csv"
file
carvan_test = pd.read_csv(file)
carvan_test
carvan_train.shape
carvan_test.shape
carvan_train.columns
carvan_test.columns
carvan_train.dtypes
carvan_train.select_dtypes("object")
carvan_test.dtypes
carvan_test.select_dtypes("object")
carvan_train.isnull().sum()
carvan_test.isnull().sum()
carvan_test['V86']=np.nan
carvan_train['data'] = 'train'
carvan_test['data'] = 'test'
carvan_train.shape
carvan_test.shape
carvan_test = carvan_test[carvan_train.columns]
carvan_test.shape
carvan_full = pd.concat([carvan_train , carvan_test] , axis=0)
carvan_full.shape
carvan_full
carvan_full.dtypes
carvan_full.isnull().sum()
carvan_train = carvan_full[carvan_full['data']=='train']
del carvan_train['data']
carvan_test = carvan_full[carvan_full['data']=='test']
carvan_test.drop(['V86','data'] , axis=1 , inplace=True)
carvan_train.shape
carvan_test.shape
carvan_full.shape
train1, train2 = train_test_split(carvan_train , test_size = 0.25,random_state=2)
train1.shape
train2.shape
# +
x_train1 = train1.drop(["V86"] , 1)
y_train1 = train1["V86"]
# -
x_train1.shape
y_train1.shape
# +
x_train2 = train2.drop(["V86"] ,1)
y_train2 = train2["V86"]
# -
x_train2.shape
y_train2.shape
x_train1.reset_index(drop=True,inplace=True)
y_train1.reset_index(drop=True,inplace=True)
model = LogisticRegression()
model
params={'class_weight':['balanced'],
'n_jobs':[-1],
'penalty':['l1','l2'],
'C':np.linspace(1,1000,10)}
params
# ?GridSearchCV
grid_search=GridSearchCV(model,param_grid=params,cv=5,scoring="roc_auc")
grid_search
from sklearn.metrics import fbeta_score
grid_search.fit(x_train1,y_train1)
logr = grid_search.best_estimator_
logr
logr.fit(x_train1,y_train1)
y_train_2_pred = grid_search.predict(x_train2).astype(int)
y_train_2_pred
y_train_2_pred.shape
fbeta_score(y_train2 , y_train_2_pred , average="weighted" , beta=2)
y_train_1_pred = grid_search.predict(x_train1).astype(int)
y_train_1_pred
y_train_1_pred.shape
fbeta_score(y_train1 , y_train_1_pred , average="weighted" , beta=2)
test_prediction = grid_search.predict(carvan_test).astype(int)
test_prediction
test_prediction.shape
pd.DataFrame(test_prediction).to_csv("Nitesh_Bhosle_p2_part2_carvan.csv",index=False)
# +
cutoffs=np.linspace(0.01,0.99,99)
cutoffs
# -
train_score_cutoff = logr.predict_proba(x_train1)[:,1]
train_score_cutoff
train1_score
real=y_train1.astype(int)
real
logr.classes_.astype(int)
train_score_cutoff > 0.5
train1_score > 0.5
# +
KS_all=[]
for cutoff in cutoffs:
predicted=(train_score_cutoff>cutoff).astype(int)
TP=((predicted==1) & (real==1)).sum()
TN=((predicted==0) & (real==0)).sum()
FP=((predicted==1) & (real==0)).sum()
FN=((predicted==0) & (real==1)).sum()
P=TP+FN
N=TN+FP
KS=(TP/P)-(FP/N)
KS_all.append(KS)
# -
mycutoff=cutoffs[KS_all==max(KS_all)][0]
mycutoff
logr.intercept_
test_score = logr.predict_proba(carvan_test)[:,1]
test_score
test_score.shape
test_classes = (test_score>mycutoff).astype(int)
test_classes
pd.DataFrame(test_classes).to_csv("Nitesh_Bhosle_p2_part2_cutoff_value.csv",index=False)
|
carvan database.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
#Author: <NAME>
#Purpose: This is a program tailored to the M&M modeling project that uses a
# combination of the Bisection Method and Newton's Method in order to
# find the minimum of the least squares.
import matplotlib.pyplot as plt
from numpy import exp, array, linspace, sum
from numpy.random import random
#This will standardize all figure sizes.
plt.rcParams["figure.figsize"] = [10,6]
#Constant to determine how many bisections and recursive calls to perform.
RANGE = 20
#******************************************************************************
#0: Main.
def main():
#Fill data arrays and initialize values.
x = [a for a in range(15)]
y = [8, 13, 20, 27, 39, 46, 52, 53, 56, 59, 61, 61, 61, 61, 62]
#Carrying capacity, initial population size, initial guess for r-value.
K, p0, r = (62, 8, 1)
Plot(x,y,1)
#Set lower and upper value to r.
r_low = r_high = r
#If the derivative of the sum of squares function is already zero (i.e. we
#already have a minimum), then we are done.
if df(r, x, y, p0, K) == 0:
#Curve to fit.
Fxn = lambda t : K*p0/(p0+(K-p0)*exp(-r*t))
Plot(x,Fxn,0,1)
exit()
#Find appropriate values to use for bisection.
while df(r_low, x, y, p0, K) > 0:
r_low -= 0.5
while df(r_high, x, y, p0, K) < 0:
r_high += 0.5
#Use Bisection Method to find seed value for Newton's Method.
r = Bisect(r_low, r_high, x, y, p0, K)
#Use Newton's Method to find most accurate root value.
r = Newton(r, x, y, p0, K)
#Redifine our function with new r value.
Fxn = lambda t : K*p0/(p0+(K-p0)*exp(-r*t))
#Display values for user.
print("\nK : ", K, "\np0 : ", p0, "\nr : ", r)
print('*'*64)
Error(x, y, Fxn)
Plot(x,Fxn,0,1)
#******************************************************************************
#1: Plot data points and functions.
def Plot(x_vals, y_vals, scatter=0, show=0):
if scatter:
plt.plot(x_vals, y_vals,'ko')
else:
X = linspace(min(x_vals), max(x_vals), 300)
Y = array([y_vals(x) for x in X])
plt.plot(X, Y, 'purple')
if show:
plt.title("Logistic Model of Disease Spread")
plt.xlabel("Iteration number")
plt.ylabel("Number of Infecteds")
plt.show()
#*******************************************************************************
#2: Derivative of the sum of squares function. You are, assumedly, trying to
# locate a root of this function so as to locate the minimum of the sum of
# squares function. That being said, you will have to find the derivative
# of the sum of squares function. I tried to type it out in a way such that,
# if you would like to modify the equation, you need only mess with the lines
# between the octothorpes. AlSO BE MINDFUL OF THE LINE CONTINUATION
# CHARACTERS.
def df(r, t_val, y_val, p0, K):
return sum([\
# # # # # # # # # # # # # # TYPE YOUR FUNCTION HERE # # # # # # # # # # # # # #
-2*(y -K/(1 + exp(-r*t)*(K - p0)/p0))*K/(1 + exp(-r*t)*(K - p0)/p0)**2*t*exp( \
-r*t)*(K - p0)/p0 \
# # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # #
for t,y in zip(t_val, y_val)])
#*******************************************************************************
#3: Use the bisection method to get a nice seed value for Newton's Method.
def Bisect(lo, hi, t_val, y_val, p0, K):
for i in range(RANGE):
mid = (lo + hi) / 2.0
if df(lo, t_val, y_val, p0, K)*df(hi, t_val, y_val, p0, K) > 0:
lo = mid
else:
hi = mid
return mid
#*******************************************************************************
#4: Use Newton's Method to find accurate root value.
def Newton(r, t_val, y_val, p0, K):
for i in range(RANGE):
r -= df(r, t_val, y_val, p0, K)/ddf(r, t_val, y_val, p0, K)
return r
#******************************************************************************
#5: Calculate sum of squares error.
def Error(x, y, F):
y_p = array([F(x_i) for x_i in x])
error = 0.0
for i in range(len(y)):
error += (y[i]-y_p[i])**2
print('Error %0.10f' %error)
return error
#*******************************************************************************
#4.1: Second derivative of the sum of squares function. This is needed for
# Newton's Method. See notes above (in 2) about modifications.
def ddf(r, t_val, y_val, p0, K):
return sum([\
# # # # # # # # # # # # # # TYPE YOUR FUNCTION HERE # # # # # # # # # # # # # #
2*K**2/(1 + exp(-r*t)*(K - p0)/p0)**4*t**2*exp(-r*t)**2*(K - p0)**2/p0**2 - 4* \
(y - K/(1 + exp(-r*t)*(K - p0)/p0))*K/(1 + exp(-r*t)*(K - p0)/p0)**3*t**2* \
exp(-r*t)**2*(K-p0)**2/p0**2 + 2*(y - K/(1 + exp(-r*t)*(K - p0)/p0))*K/(1 + \
exp(-r*t)*(K-p0)/p0)**2*t**2*exp(-r*t)*(K - p0)/p0 \
# # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # #
for t,y in zip(t_val, y_val)])
#******************************************************************************
#Call main.
main()
# -
|
BiNew_RF.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: sri_gpt
# language: python3
# name: sri_gpt
# ---
# +
import networkx as nx
import pickle
import numpy as np
import pandas as pd
import os
import string
import nltk
import itertools
import json
import sys
sys.path.append("../../../ai-engine_temp/pkg/")
from text_preprocessing import preprocess as tp
from nltk.corpus import stopwords
stop_words = stopwords.words("english")
def st_get_candidate_phrases(text, pos_search_pattern_list=[r"""base: {(<JJ.*>*<NN.*>+<IN>)?<JJ>*<NN.*>+}"""]):
punct = set(string.punctuation)
all_chunks = []
for pattern in pos_search_pattern_list:
all_chunks+=st_getregexChunks(text,pattern)
candidates_tokens = [' '.join(word for word, pos,
chunk in group).lower()
for key, group in itertools.groupby(all_chunks,
lambda_unpack(lambda word, pos, chunk: chunk != 'O')) if key]
candidate_phrases = [cand for cand in candidates_tokens if cand not in stop_words and not all(char in punct for char in cand)]
return candidate_phrases
def st_getregexChunks(text,grammar):
chunker = nltk.chunk.regexp.RegexpParser(grammar)
tagged_sents = nltk.pos_tag_sents(nltk.word_tokenize(sent) for sent in nltk.sent_tokenize(text))
all_chunks = list(itertools.chain.from_iterable(nltk.chunk.tree2conlltags(chunker.parse(tagged_sent))
for tagged_sent in tagged_sents))
#print(grammar)
#print(all_chunks)
#print()
return all_chunks
def lambda_unpack(f):
return lambda args: f(*args)
def get_filtered_pos(filtered, pos_list=['NN', 'JJ']):
filtered_list_temp = []
filtered_list = []
flag = False
flag_JJ = False
for word, pos in filtered:
if pos == 'NN' or pos == 'JJ':
flag=True
if pos == 'JJ':
flag_JJ = True
else:
flag_JJ = False
filtered_list_temp.append((word, pos))
continue
if flag:
if 'NN' in list(map(lambda x: x[1], filtered_list_temp)):
if not flag_JJ:
filtered_list.append(list(map(lambda x:x[0], filtered_list_temp)))
else:
filtered_list.append(list(map(lambda x:x[0], filtered_list_temp))[:-1])
#print (filtered_list_temp)
#print (filtered_list[-1])
flag_JJ = False
filtered_list_temp = []
flag=False
return filtered_list
from numpy import dot
from numpy.linalg import norm
from boto3 import client as boto3_client
import json
import logging
from botocore.client import Config
import numpy as np
from copy import deepcopy
config = Config(connect_timeout=240, read_timeout=240, retries={'max_attempts': 0} )
lambda_client = boto3_client('lambda', config=config, aws_access_key_id="AKIA5SUS6MWO4MP7KDEJ",
aws_secret_access_key="<KEY>"
)
def cosine(vec1, vec2):
return dot(vec1, vec2) / (norm(vec1) * norm(vec2))
def get_embeddings(input_list, req_data=None):
if req_data is None:
#lambda_payload = {"body": {"text_input": input_list}}
lambda_payload = {"body": {"text": input_list}}
else:
lambda_payload = {"body": {"request": req_data, "text_input": input_list}}
#logger.info("Invoking lambda function")
invoke_response = lambda_client.invoke(
#FunctionName="arn:aws:lambda:us-east-1:933389821341:function:keyphrase_ranker",
FunctionName="arn:aws:lambda:us-east-1:933389821341:function:mind-01daaqy88qzb19jqz5prjfr76y",
InvocationType="RequestResponse",
Payload=json.dumps(lambda_payload)
)
lambda_output = (
invoke_response["Payload"].read().decode("utf8").replace("'", '"')
)
response = json.loads(lambda_output)
try:
status_code = response["statusCode"]
except Exception as e:
print (response)
response_body = response["body"]
if status_code == 200:
#embedding_vector = np.asarray(json.loads(response_body)["embeddings"])
embedding_vector = np.asarray(json.loads(response_body)["sent_feats"])
else:
raise Exception
embedding_vector = np.asarray(json.loads(response_body)["embeddings"])
return embedding_vector
def get_feature_vector_local(input_list, lambda_function, mind_f, gpt_model):
# logger.info("computing feature vector", extra={"msg": "getting feature vector from mind service"})
feats = list(mind_f['feature_vector'].values())
mind_f = np.array(feats).reshape(len(feats), -1)
batches_count = 300
feature_vector = []
mind_score = []
count = math.ceil(len(input_list)/batches_count)
logger.info("computing in batches", extra={"batches count": count, "number of sentences": len(input_list)})
for itr in range(count):
extra_input = deepcopy(input_list[itr*batches_count:(itr+1)*batches_count])
logger.info("getting feature vector", extra={"iteration count:": itr})
temp_vector = []
for sent in extra_input:
temp_vector.append(gpt_model.get_text_feats(sent))
temp_vector = np.array(temp_vector)
feature_vector.extend(temp_vector)
logger.info("Request Sent", extra={"iteration count": itr})
#temp_vector = np.array(data['sent_feats'][0])
#feature_vector.extend(data['sent_feats'][0])
batch_size = min(10, temp_vector.shape[0])
for i in range(0, temp_vector.shape[0],batch_size):
mind_vec = np.expand_dims(np.array(mind_f),2)
sent_vec = temp_vector[i:i+batch_size]
cluster_scores = getClusterScore(mind_vec,sent_vec)
batch_scores = cluster_scores.max(1)
mind_score.extend(batch_scores)
return feature_vector, mind_score
pd.set_option('display.max_rows', 500)
pd.set_option('display.max_columns', 500)
pd.set_option('display.width', 1000000)
pd.set_option('display.expand_frame_repr', True)
pd.set_option('max_colwidth', 1000)
# -
entity_kp_graph = pickle.load(open('/mnt/hdd/Venkat/knowledge_graphs/entity_graph_builder/graph_dumps/pruned_entity_kp_graph.pkl','rb'))
# +
req = json.load(open("topic_testing/cullen_test.json", "r"))["body"]
req["segments"] = sorted(req['segments'], key=lambda kv:kv['startTime'])
text = list(map(lambda seg: (seg["originalText"], seg["id"]), req['segments']))
seg_list = [sent for sent, id in text]
segid_list = [id for sent, id in text]
sent_list = list(map(lambda seg:[sent for sent in seg.split(". ")], seg_list))
sent_list = [sent for seg in sent_list for sent in seg if len(sent.split(" "))>6]
#for index, segment in enumerate(req["segments"]):
# -
filtered_keyphrase = []
for sent in sent_list:
filtered_keyphrase.append(tp.st_get_candidate_phrases(sent))
sent_map = pd.DataFrame({'sent': [sent for sent in sent_list],
'filtered': filtered_keyphrase})
sent_map
# +
entities_list_from_graph_exact = []
entities_in_graph = [ent.lower() for ent in entity_kp_graph if entity_kp_graph.nodes[ent]["node_type"]=="entity"]
entities_in_graph_cased = [ent for ent in entity_kp_graph if entity_kp_graph.nodes[ent]["node_type"]=="entity"]
entities_in_graph_org = {}
for index in range(len(entities_in_graph_cased)):
entities_in_graph_org[entities_in_graph[index]] = entities_in_graph_cased[index]
for index, sent in enumerate(sent_list):
entities_list_from_graph_temp = []
for word in tp.preprocess(sent, word_tokenize=True)[0]:
if word.lower() in entities_in_graph:
entities_list_from_graph_temp.extend([word.lower()])
#entities_list_from_graph_temp.extend([sub_word for sub_word in entities_in_graph if word.lower() in sub_word])
entities_list_from_graph_exact.append(entities_list_from_graph_temp)
# -
ent_map = pd.DataFrame({'sent': [sent for sent in sent_list],
'filtered_keyphrase': filtered_keyphrase,
'entity_from_graph_exact': entities_list_from_graph_exact})
display(ent_map)
flattened_ent = [entities_in_graph_org[i] for j in entities_list_from_graph_exact for i in j]
sub_graph = entity_kp_graph.subgraph(flattened_ent)
from copy import deepcopy
sub_graph_copy = deepcopy(sub_graph)
weighted_graph = nx.Graph()
for nodea, nodeb in sub_graph_copy.edges():
if entity_kp_graph.nodes[nodea]['node_freq'] != 1 and entity_kp_graph.nodes[nodeb]['node_freq'] !=1:
weighted_graph.add_edge(nodea, nodeb, weight = entity_kp_graph[nodea][nodeb]['edge_freq'])
# +
from networkx import pagerank
pg = pagerank(weighted_graph, weight="weight")
# -
pg_sorted = sorted(pg.items(), key=lambda kv:kv[1], reverse=True)
pg_map = {}
for ent, score in pg_sorted:
pg_map[ent] = score
pg_sorted
import numpy as np
pg_scores = [score[1] for score in pg.items()]
q3 = np.percentile(pg_scores, 75)
for ent, score in pg_sorted:
if score>q3:
print (ent , score)
else:
print ("\n")
print (ent, [(ent_con, sub_graph_copy[ent][ent_con]["edge_ctr"]) for ent_con in list(sub_graph_copy[ent])])
import pickle
pickle.dump(sorted(pg.items(), key=lambda kv:kv[1], reverse=True), open("pageRank", "wb"))
# # Meeting data w/ Kp_graph
ent_fv = pickle.load(open("/mnt/hdd/Venkat/knowledge_graphs/entity_graph_builder/graph_dumps/entity_features.pkl", "rb"))
from community import best_partition, modularity
graph_list = []
for index in range(len(sent_list)):
graph_list.append((sent_list[index], [entities_in_graph_org[i] for i in entities_list_from_graph_exact[index] if entities_in_graph_org[i] in pg_map.keys()]))
# if entities_in_graph_org[i] in pg_map.keys()
# +
meeting_graph = nx.Graph()
for index, (sentence, ent) in enumerate(graph_list):
ent_list_t = list(map(lambda k: (k, pg_map[k]), ent))
if ent_list_t!=[]:
ent_list = max(ent_list_t, key=lambda kv:kv[1])[0]
else:
continue
if ent_list in ent_fv.keys():
meeting_graph.add_node(index, entities=ent_list)
# mean of entities
# meeting_graph = nx.Graph()
# for index, (sentence, ent) in enumerate(graph_list):
# ent_list_t = list(map(lambda k: (k, pg_map[k]), ent))
# if ent_list_t!=[]:
# temp_list = []
# for ent in ent_list_t:
# if ent[0] in ent_fv.keys():
# temp_list.append(ent[0])
# if temp_list!=[]:
# meeting_graph.add_node(index, entities=temp_list)
# -
extra_fv_list = []
for node in meeting_graph.nodes():
if meeting_graph.nodes[node]["entities"] not in ent_fv.keys() and meeting_graph.nodes[node]["entities"]!="":
extra_fv_list.append(node)
extra_fv = get_embeddings([graph_list[node][0] for node in extra_fv_list])[0]
for index, node in enumerate(extra_fv_list):
ent_fv[meeting_graph.nodes[node]["entities"]] = extra_fv[index]
sentence_fv_ent = list(set([meeting_graph.nodes[node]["entities"] for node in extra_fv_list]))
# +
for index1 in meeting_graph.nodes():
for index2 in meeting_graph.nodes():
if index1!=index2:
meeting_graph.add_edge(index1, index2, weight=cosine(ent_fv[meeting_graph.nodes[index1]["entities"]], ent_fv[meeting_graph.nodes[index2]["entities"]]))
#edge_weight = cosine(np.mean([ent_fv[ent] for ent in meeting_graph.nodes[index1]["entities"]], axis=0), np.mean([ent_fv[ent] for ent in meeting_graph.nodes[index2]["entities"]], axis=0))
#meeting_graph.add_edge(index1, index2, weight=edge_weight)
meeting_graph_rescaled = deepcopy(meeting_graph)
# X = nx.to_numpy_array(meeting_graph)
# for i in range(len(X)):
# X[i][i] = X[i].mean()
# norm_mat = (X - X.min(axis=1)) / (X.max(axis=1) - X.min(axis=1))
# norm_mat = (np.transpose(np.tril(norm_mat)) + np.triu(norm_mat)) / 2
# norm_mat = norm_mat + np.transpose(norm_mat)
# meeting_graph_rescaled = nx.from_numpy_array(norm_mat)
# meeting_graph_rescaled.remove_edges_from(
# list(map(lambda x: (x, x), range(meeting_graph.number_of_nodes())))
# )
# norm_nodes = deepcopy(meeting_graph_rescaled.nodes())
# for node in norm_nodes:
# if node not in meeting_graph.nodes():
# meeting_graph_rescaled.remove_node(node)
def prune(meeting_graph, v):
meeting_graph_norm = deepcopy(meeting_graph)
pg_scores = list(map(lambda kv:kv[-1]["weight"], meeting_graph_norm.edges.data()))
#pg_scores = [score[1] for score in pg.items()]
q3 = np.percentile(pg_scores, v)
edge_data = deepcopy(meeting_graph_norm.edges.data())
for node1, node2, weights in edge_data:
if weights["weight"]<q3:
meeting_graph_norm.remove_edge(node1, node2)
return meeting_graph_norm
v = 75
meeting_graph_norm = prune(meeting_graph_rescaled, v)
meeting_graph_com = best_partition(meeting_graph_norm)
print (v, modularity(meeting_graph_com, meeting_graph_norm) )
while modularity(meeting_graph_com, meeting_graph_norm) < 0.35:
v +=1
print (v, modularity(meeting_graph_com, meeting_graph_norm) )
meeting_graph_norm = prune(meeting_graph_rescaled, v)
meeting_graph_com = best_partition(meeting_graph_norm)
print (v, modularity(meeting_graph_com, meeting_graph_norm) )
# -
# from community import best_partition
# meeting_graph_com = best_partition(meeting_graph_norm)
print (modularity(meeting_graph_com, meeting_graph_norm))
# +
temp_list = []
meeting_graph_com_sorted = sorted(meeting_graph_com.items(), key = lambda kv: kv[1])
prev = 0
tag = 0
com_list = []
G2 = nx.Graph()
print ("--------- slice ---------", "\n\n")
for ent, cluster in meeting_graph_com_sorted:
if prev!=cluster:
print ("--------- slice ", cluster, "---------", "\n\n")
prev = cluster
if cluster==0:
G2.add_node(ent)
#print (graph_list[ent][0], " [ ", meeting_graph.nodes[ent]["entities"] ,"]" ,"sentence representation: ", meeting_graph.nodes[ent]["entities"] in sentence_fv_ent,"\n")
print (graph_list[ent][0], " [ ", meeting_graph.nodes[ent]["entities"] ,"]", "\n")
temp_list.append(meeting_graph.nodes[ent]["entities"])
#print (ent, entity_kp_graph.nodes[ent]['node_freq'])
# comm_map = {
# }
# for word, cluster in comm_sorted:
# comm_map[word] = cluster
# +
for index1 in G2.nodes():
for index2 in G2.nodes():
if index1!=index2:
G2.add_edge(index1, index2, weight=cosine(ent_fv[meeting_graph.nodes[index1]["entities"]], ent_fv[meeting_graph.nodes[index2]["entities"]]))
def prune(meeting_graph, v):
meeting_graph_norm = deepcopy(meeting_graph)
pg_scores = list(map(lambda kv:kv[-1]["weight"], meeting_graph_norm.edges.data()))
#pg_scores = [score[1] for score in pg.items()]
q3 = np.percentile(pg_scores, v)
edge_data = deepcopy(meeting_graph_norm.edges.data())
for node1, node2, weights in edge_data:
if weights["weight"]<q3:
meeting_graph_norm.remove_edge(node1, node2)
return meeting_graph_norm
v = 75
meeting_graph_norm = prune(G2, v)
meeting_graph_com = best_partition(meeting_graph_norm)
print (v, modularity(meeting_graph_com, meeting_graph_norm) )
while modularity(meeting_graph_com, meeting_graph_norm) < 0.35:
if v==90:
break
v +=1
print (v, modularity(meeting_graph_com, meeting_graph_norm) )
meeting_graph_norm = prune(G2, v)
meeting_graph_com = best_partition(meeting_graph_norm)
print (v, modularity(meeting_graph_com, meeting_graph_norm) )
# X = nx.to_numpy_array(meeting_graph)
# for i in range(len(X)):
# X[i][i] = X[i].mean()
# norm_mat = (X - X.min(axis=1)) / (X.max(axis=1) - X.min(axis=1))
# norm_mat = (np.transpose(np.tril(norm_mat)) + np.triu(norm_mat)) / 2
# norm_mat = norm_mat + np.transpose(norm_mat)
# meeting_graph_norm = nx.from_numpy_array(norm_mat)
# meeting_graph_norm.remove_edges_from(
# list(map(lambda x: (x, x), range(meeting_graph.number_of_nodes())))
# )
# norm_nodes = deepcopy(meeting_graph_norm.nodes())
# for node in norm_nodes:
# if node not in meeting_graph.nodes():
# meeting_graph_norm.remove_node(node)
# +
temp_list = []
meeting_graph_com_sorted = sorted(meeting_graph_com.items(), key = lambda kv: kv[1])
prev = 0
tag = 0
com_list = []
print ("--------- slice ---------", "\n\n")
for ent, cluster in meeting_graph_com_sorted:
if prev!=cluster:
print ("--------- slice ", cluster, "---------", "\n\n")
prev = cluster
#print (graph_list[ent][0], " [ ", meeting_graph.nodes[ent]["entities"] ,"]" ,"sentence representation: ", meeting_graph.nodes[ent]["entities"] in sentence_fv_ent,"\n")
print (graph_list[ent][0], " [ ", meeting_graph.nodes[ent]["entities"] ,"]", "\n")
temp_list.append(meeting_graph.nodes[ent]["entities"])
#print (ent, entity_kp_graph.nodes[ent]['node_freq'])
# comm_map = {
# }
# for word, cluster in comm_sorted:
# comm_map[word] = cluster
# -
scores = {}
for nodea, nodeb, weight in meeting_graph_norm.edges.data():
if nodea not in scores.keys():
scores[nodea] = [(nodeb, weight)]
else:
scores[nodea].append((nodeb, weight))
scores[nodea] = sorted(scores[nodea], key=lambda kv:kv[1]['weight'], reverse=True)
print ("------- sentence ---------")
print (graph_list[nodea][0])
print (graph_list[nodeb][0])
print (weight)
for nodea in scores.keys():
print ("------sentence-------")
print (graph_list[nodea][0], "[ ", meeting_graph.nodes[nodea]["entities"] ," ]", "\n\n")
for values in scores[nodea][:5]:
#print ("comparison sentence: ", graph_list[values[0]][0], "[ ", meeting_graph.nodes[values[0]]["entities"] ," ]", "====> ", values[1]['weight'], "\n\n")
print ("comparison sentence: ", "[ ", meeting_graph.nodes[values[0]]["entities"] ," ]", "====> ", values[1]['weight'], "\n\n")
# # Communities on whole kp graph
from community import best_partition
weighted_graph = nx.Graph()
for nodea, nodeb in entity_kp_graph.edges():
if entity_kp_graph.nodes[nodea]['node_freq'] >= 10 and entity_kp_graph.nodes[nodeb]['node_freq'] >=10 and entity_kp_graph[nodea][nodeb]['edge_ctr']>2:
weighted_graph.add_edge(nodea, nodeb, weight = entity_kp_graph[nodea][nodeb]['edge_ctr'])
comm = best_partition(weighted_graph)
# +
comm_sorted = sorted(comm.items(), key = lambda kv: kv[1])
prev = 0
tag = 0
comm_list = []
print ("--------- slice ---------", "\n\n")
for ent, cluster in comm_sorted:
if prev!=cluster:
print ("--------- slice ", cluster, "---------", "\n\n")
prev = cluster
print (ent, entity_kp_graph.nodes[ent]['node_freq'])
comm_map = {
}
for word, cluster in comm_sorted:
comm_map[word] = cluster
# -
for index, sent in enumerate(sent_list):
keyphrases = entities_list_from_graph_exact[index]
replaced_ent_1 = [comm_map[entities_in_graph_org[ent.lower()]] for ent in keyphrases if entities_in_graph_org[ent] in comm_map.keys()]
print (sent, "\n", replaced_ent_1, "\n\n")
|
community_detection/group_segments/subgraph_manupulation.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ### This is Example 4.3. Gambler’s Problem from Sutton's book.
#
# A gambler has the opportunity to make bets on the outcomes of a sequence of coin flips.
# If the coin comes up heads, he wins as many dollars as he has staked on that flip;
# if it is tails, he loses his stake. The game ends when the gambler wins by reaching his goal of $100,
# or loses by running out of money.
#
# On each flip, the gambler must decide what portion of his capital to stake, in integer numbers of dollars.
# This problem can be formulated as an undiscounted, episodic, finite MDP.
#
# The state is the gambler’s capital, s ∈ {1, 2, . . . , 99}.
# The actions are stakes, a ∈ {0, 1, . . . , min(s, 100 − s)}.
# The reward is zero on all transitions except those on which the gambler reaches his goal, when it is +1.
#
# The state-value function then gives the probability of winning from each state. A policy is a mapping from levels of capital to stakes. The optimal policy maximizes the probability of reaching the goal. Let p_h denote the probability of the coin coming up heads. If p_h is known, then the entire problem is known and it can be solved, for instance, by value iteration.
#
import numpy as np
import sys
import matplotlib.pyplot as plt
if "../" not in sys.path:
sys.path.append("../")
#
# ### Exercise 4.9 (programming)
#
# Implement value iteration for the gambler’s problem and solve it for p_h = 0.25 and p_h = 0.55.
def value_iteration_for_gamblers(p_h, theta=0.0001, discount_factor=1.0):
"""
Args:
p_h: Probability of the coin coming up heads
"""
# The reward is zero on all transitions except those on which the gambler reaches his goal,
# when it is +1.
rewards = np.zeros(101)
rewards[100] = 1
# We introduce two dummy states corresponding to termination with capital of 0 and 100
V = np.zeros(101)
def one_step_lookahead(s, V, rewards):
"""
Helper function to calculate the value for all action in a given state.
Args:
s: The gambler’s capital. Integer.
V: The vector that contains values at each state.
rewards: The reward vector.
Returns:
A vector containing the expected value of each action.
Its length equals to the number of actions.
"""
A = np.zeros(101)
stakes = range(1, min(s, 100-s)+1) # Your minimum bet is 1, maximum bet is min(s, 100-s).
for a in stakes:
# rewards[s+a], rewards[s-a] are immediate rewards.
# V[s+a], V[s-a] are values of the next states.
# This is the core of the Bellman equation: The expected value of your action is
# the sum of immediate rewards and the value of the next state.
A[a] = p_h * (rewards[s+a] + V[s+a]*discount_factor) + (1-p_h) * (rewards[s-a] + V[s-a]*discount_factor)
return A
while True:
# Stopping condition
delta = 0
# Update each state...
for s in range(1, 100):
# Do a one-step lookahead to find the best action
A = one_step_lookahead(s, V, rewards)
# print(s,A,V) # if you want to debug.
best_action_value = np.max(A)
# Calculate delta across all states seen so far
delta = max(delta, np.abs(best_action_value - V[s]))
# Update the value function. Ref: Sutton book eq. 4.10.
V[s] = best_action_value
# Check if we can stop
if delta < theta:
break
# Create a deterministic policy using the optimal value function
policy = np.zeros(100)
for s in range(1, 100):
# One step lookahead to find the best action for this state
A = one_step_lookahead(s, V, rewards)
best_action = np.argmax(A)
# Always take the best action
policy[s] = best_action
return policy, V
# +
policy, v = value_iteration_for_gamblers(0.25)
print("Optimized Policy:")
print(policy)
print("")
print("Optimized Value Function:")
print(v)
print("")
# -
# ### Show your results graphically, as in Figure 4.3.
#
# +
# Plotting Final Policy (action stake) vs State (Capital)
# x axis values
x = range(100)
# corresponding y axis values
y = v[:100]
# plotting the points
plt.plot(x, y)
# naming the x axis
plt.xlabel('Capital')
# naming the y axis
plt.ylabel('Value Estimates')
# giving a title to the graph
plt.title('Final Policy (action stake) vs State (Capital)')
# function to show the plot
plt.show()
# +
# Plotting Capital vs Final Policy
# x axis values
x = range(100)
# corresponding y axis values
y = policy
# plotting the bars
plt.bar(x, y, align='center', alpha=0.5)
# naming the x axis
plt.xlabel('Capital')
# naming the y axis
plt.ylabel('Final policy (stake)')
# giving a title to the graph
plt.title('Capital vs Final Policy')
# function to show the plot
plt.show()
|
DP/Gamblers Problem Solution.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: HistoToolkit
# language: python
# name: histotoolkit
# ---
import example_operations as eo
# +
# demonstrate getattr
eo.op1(2, 2, 3)
swanky_add = getattr(eo, 'op1')
swanky_add(2, 2, 3)
# -
# manually perform sequence of operations
print("Manual operations")
val = 2
val = eo.op1(val, 2, 3)
print("op1 result: %d" % val)
val = eo.op2(val, 2, True)
print("op2 result: %d" % val)
# +
# iterate through sequence of operations
ops_names = ['op1', 'op2']
ops_params = [
{'arg1': 2, 'arg2': 3},
{'arg1': 2, 'disp': True}
]
ops = [
{'op': getattr(eo, op_name),
'op_name': op_name,
'params': params
} for op_name, params in zip(ops_names, ops_params)
]
print("getattr operations")
print(ops)
val = 2
for op in ops:
val = op['op'](val, **op['params'])
print("%s result: %d" % (op['op_name'], val))
# -
|
app/test/test_example_operations.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# ## PyTorch Tutorial
#
# IFT6135 – Representation Learning
#
# A Deep Learning Course, January 2019
#
# By <NAME>
#
# (Adapted from <NAME>'s MILA welcome tutorial)
# ## 1. Introduction to the torch tensor library
# ### Torch's numpy equivalent with GPU support
import numpy as np
from __future__ import print_function
import torch
# ### Initialize a random tensor
torch.Tensor(5, 3)
# ### From a uniform distribution
# intialization
print(torch.Tensor(5, 3).uniform_(-1, 1))
# sampling
print(torch.rand(5,3)*2-1)
# ### Get it's shape
# +
x = torch.Tensor(5, 3).uniform_(-1, 1)
print(x.size())
# or your favorite np_array.shape
print(x.shape)
# dimensionality of the 0'th axis?
# print(???)
print(x.size(0))
print(x.shape[0])
# -
# ### Tensor Types
# source: http://pytorch.org/docs/master/tensors.html
# |Data type |Tensor|
# |----------|------|
# |32-bit floating point| torch.FloatTensor|
# |64-bit floating point| torch.DoubleTensor|
# |16-bit floating point| torch.HalfTensor|
# |8-bit integer (unsigned)|torch.ByteTensor|
# |8-bit integer (signed)|torch.CharTensor|
# |16-bit integer (signed)|torch.ShortTensor|
# |32-bit integer (signed)|torch.IntTensor|
# |64-bit integer (signed)|torch.LongTensor|
# ### Creation from lists & numpy
z = torch.LongTensor([[1, 3], [2, 9]])
print(z.type())
# Cast to numpy ndarray
print(z.numpy().dtype)
z_ = torch.LongTensor([[1, 3], [2, 9]])
z+z_
# Data type inferred from numpy
print(torch.from_numpy(np.random.rand(5, 3)).type())
print(torch.from_numpy(np.random.rand(5, 3).astype(np.float32)).type())
print(torch.from_numpy(np.random.rand(5, 3)).float().dtype)
# +
# examples of type error
a = torch.randn(1) # x ~ N(0,1)
b = torch.from_numpy(np.ones(1)).float()
x+b
# -
# ### Simple mathematical operations
y = x ** torch.randn(5, 3)
print(y)
# +
noise = torch.randn(5, 3)
y = x / torch.sqrt(noise ** 2)
# equal to torch.abs
y_ = x / torch.abs(noise)
print(y)
print(y_)
# -
# ### Broadcasting
print(x.size())
print(x)
#y = x + torch.arange(5).view(5,1)
y = x + torch.arange(3)
print(y)
# print(x + torch.arange(5))
# ### Reshape
y = torch.randn(5, 10, 15)
print(y.size())
print(y.view(-1, 15).size()) # Same as doing y.view(50, 15)
print(y.view(-1, 15).unsqueeze(1).size()) # Adds a dimension at index 1.
print(y.view(-1, 15).unsqueeze(1).unsqueeze(2).unsqueeze(3).squeeze().size())
# If input is of shape: (Ax1xBxCx1xD)(Ax1xBxCx1xD) then the out Tensor will be of shape: (AxBxCxD)(AxBxCxD)
print()
print(y.transpose(0, 1).size())
print(y.transpose(1, 2).size())
print(y.transpose(0, 1).transpose(1, 2).size())
print(y.permute(1, 2, 0).size())
# ### Repeat
print(y.view(-1, 15).unsqueeze(1).expand(50, 100, 15).size())
print(y.view(-1, 15).unsqueeze(1).expand_as(torch.randn(50, 100, 15)).size())
# don't confuse it with tensor.repeat ...
print(y.view(-1, 15).unsqueeze(1).repeat(50,100,1).size())
# ### Concatenate
# +
# 2 is the dimension over which the tensors are concatenated
print(torch.cat([y, y], 2).size())
# stack concatenates the sequence of tensors along a new dimension.
print(torch.stack([y, y], 0).size())
# Q: how to do tensor.stack using cat?
print(torch.cat([y[None], y[None]], 0).size())
# -
# ### Advanced Indexing
# +
y = torch.randn(2, 3, 4)
print(y[[1, 0, 1, 1]].size())
# PyTorch doesn't support negative strides yet so ::-1 does not work.
rev_idx = torch.arange(1, -1, -1).long()
print(rev_idx)
print(y[rev_idx].size())
# gather(input, dim, index)
v = torch.arange(12).view(3,4)
print(v.shape)
print(v)
# [0,1,2,3]
# [4,5,6,7]
# [8,9,10,11]
# want to return [1,6,8]
print(torch.gather(v, 1, torch.tensor([1,2,0]).long().unsqueeze(1)))
# -
# ### GPU support
x = torch.cuda.HalfTensor(5, 3).uniform_(-1, 1)
y = torch.cuda.HalfTensor(3, 5).uniform_(-1, 1)
torch.matmul(x, y)
# ### Move tensors on the CPU -> GPU
x = torch.FloatTensor(5, 3).uniform_(-1, 1)
print(x)
x = x.cuda(device=0)
print(x)
x = x.cpu()
print(x)
# ### Contiguity in memory
# +
x = torch.FloatTensor(5, 3).uniform_(-1, 1)
print(x)
#x = x.cuda(device=0)
print(x)
print('Contiguity : %s ' % (x.is_contiguous()))
x = x.unsqueeze(0).expand(30, 5, 3)
print('Contiguity : %s ' % (x.is_contiguous()))
x = x.contiguous()
print('Contiguity : %s ' % (x.is_contiguous()))
# -
|
pytorch/1. The Torch Tensor Library and Basic Operations.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
from IPython.display import Image
Image("loc_name")
|
Data-Science-HYD-2k19/Topic-Wise/MISC/Importing Images.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] colab_type="text" id="GPQLC8sugA9E"
# # Implementing Bag of Words
# + [markdown] colab_type="text" id="6qHuB7gLgA9F"
# <font face='georgia'>
# <h3><strong>Fit method:</strong></h3>
#
# <ol>
# <li> With this function, we will find all unique words in the data and we will assign a dimension-number to each unique word. </li>
# <br>
# <li> We will create a python dictionary to save all the unique words, such that the key of dictionary represents a unique word and the corresponding value represent it's dimension-number. </li><br>
# <li> For example, if you have a review, <strong>__'very bad pizza'__</strong> then you can represent each unique word with a dimension_number as, <br>
# <strong>dict</strong> = { 'very' : 1, 'bad' : 2, 'pizza' : 3} </li>
# </ol>
#
# + colab={} colab_type="code" id="vmQOru_LgA9F"
import warnings
warnings.filterwarnings("ignore")
import pandas as pd
from tqdm import tqdm
import os
# + colab={} colab_type="code" id="vWqqbym-gA9I"
from tqdm import tqdm # tqdm is a library that helps us to visualize the runtime of for loop. refer this to know more about tqdm
#https://tqdm.github.io/
# it accepts only list of sentances
def fit(dataset):
unique_words = set() # at first we will initialize an empty set
# check if its list type or not
if isinstance(dataset, (list,)):
for row in dataset: # for each review in the dataset
for word in row.split(" "): # for each word in the review. #split method converts a string into list of words
if len(word) < 2:
continue
unique_words.add(word)
unique_words = sorted(list(unique_words))
vocab = {j:i for i,j in enumerate(unique_words)}
return vocab
else:
print("you need to pass list of sentance")
# + colab={} colab_type="code" id="ooIF0xaugA9J" outputId="63e41a1b-03b9-41b8-b160-06c5428d0ba7"
vocab = fit(["abc def aaa prq", "lmn pqr aaaaaaa aaa abbb baaa"])
print(vocab)
# + [markdown] colab_type="text" id="LtHD5uKWgA9N"
# <font face='georgia'>
# <h4><strong>What is a Sparse Matrix?</strong></h4>
#
# <ol>
# <li>Before going further into details about Transform method, we will understand what sparse matrix is.</li>
# <br>
# <li> Sparse matrix stores only non-zero elements and they occupy less amount of RAM comapre to a dense matrix. You can refer to this <a href="http://btechsmartclass.com/data_structures/sparse-matrix.html"><u>link</u>.</a> </li><br>
# <li> For example, assume you have a matrix,
# <pre>
# [[1, 0, 0, 0, 0],
# [0, 0, 0, 1, 0],
# [0, 0, 4, 0, 0]]
# </pre> </li>
# </ol>
#
# + colab={} colab_type="code" id="khrRTJ-qgA9N" outputId="c1e99962-4eac-4d4c-af65-54ff7a60bae7"
from sys import getsizeof
import numpy as np
# we store every element here
a = np.array([[1, 0, 0, 0, 0], [0, 0, 0, 1, 0], [0, 0, 4, 0, 0]])
print(getsizeof(a))
# here we are storing only non zero elements here (row, col, value)
a = [ (0, 0, 1), (1, 3, 1), (2,2,4)]
# with this way of storing we are saving alomost 50% memory for this example
print(getsizeof(a))
# + [markdown] colab_type="text" id="v2Nm850wgA9Q"
# <font face='georgia'>
# <h4><strong>How to write a Sparse Matrix?:</strong></h4>
#
# <ol>
# <li> You can use csr_matrix() method of scipy.sparse to write a sparse matrix.</li>
# <li> You need to pass indices of non-zero elements into csr_matrix() for creating a sparse matrix. </li>
# <li> You also need to pass element value of each pair of indices. </li>
# <li> You can use lists to save the indices of non-zero elements and their corresponding element values. </li>
# <li> For example,
# <ul>
# <li>Assume you have a matrix,
# <pre>
# [[1, 0, 0],
# [0, 0, 1],
# [4, 0, 6]]
# </pre></li>
# <li> Then you can save the indices using a list as,<br><strong>list_of_indices</strong> = [(0,0), (1,2), (2,0), (2,2)]</li>
# <li> And you can save the corresponding element values as, <br><strong>element_values</strong> = [1, 1, 4, 6] </li>
# </ul></li>
# <li> Further you can refer to the documentation <a href="https://docs.scipy.org/doc/scipy-0.19.0/reference/generated/scipy.sparse.csr_matrix.html"><u>here</u>.</a> </li>
# </ol>
# + [markdown] colab_type="text" id="S57yXfGSgA9Q"
# <font face='georgia'>
# <h3><strong>Transform method:</strong></h3>
#
# <ol>
# <li>With this function, we will write a feature matrix using sprase matrix.</li>
# </ol>
#
# + colab={} colab_type="code" id="QwcUnNKsgA9R" outputId="524832b4-9475-4304-e51b-99a53bd44184"
from collections import Counter
from scipy.sparse import csr_matrix
test = 'abc def abc def zzz zzz pqr'
a = dict(Counter(test.split()))
for i,j in a.items():
print(i, j)
# + colab={} colab_type="code" id="Q-YjuuVHgA9T"
# https://stackoverflow.com/questions/9919604/efficiently-calculate-word-frequency-in-a-string
# https://docs.scipy.org/doc/scipy-0.19.0/reference/generated/scipy.sparse.csr_matrix.html
# note that we are we need to send the preprocessing text here, we have not inlcuded the processing
def transform(dataset,vocab):
rows = []
columns = []
values = []
if isinstance(dataset, (list,)):
for idx, row in enumerate(tqdm(dataset)): # for each document in the dataset
# it will return a dict type object where key is the word and values is its frequency, {word:frequency}
word_freq = dict(Counter(row.split()))
# for every unique word in the document
for word, freq in word_freq.items(): # for each unique word in the review.
if len(word) < 2:
continue
# we will check if its there in the vocabulary that we build in fit() function
# dict.get() function will return the values, if the key doesn't exits it will return -1
col_index = vocab.get(word, -1) # retreving the dimension number of a word
# if the word exists
if col_index !=-1:
# we are storing the index of the document
rows.append(idx)
# we are storing the dimensions of the word
columns.append(col_index)
# we are storing the frequency of the word
values.append(freq)
return csr_matrix((values, (rows,columns)), shape=(len(dataset),len(vocab)))
else:
print("you need to pass list of strings")
# + colab={} colab_type="code" id="p7EpT6qngA9V" outputId="07c5c8f2-6074-47df-fe32-227cc9a40f9a"
strings = ["the method of lagrange multipliers is the economists workhorse for solving optimization problems",
"the technique is a centerpiece of economic theory but unfortunately its usually taught poorly"]
vocab = fit(strings)
print(list(vocab.keys()))
print(transform(strings, vocab).toarray())
# + [markdown] colab_type="text" id="P0ZpSe7fgA9Y"
# ## Comparing results with countvectorizer
# + colab={} colab_type="code" id="Q6E8InIJgA9Z" outputId="0a006b8b-d8b2-4834-9941-0e10cc5a8ff2"
from sklearn.feature_extraction.text import CountVectorizer
vec = CountVectorizer(analyzer='word')
vec.fit(strings)
feature_matrix_2 = vec.transform(strings)
print(feature_matrix_2.toarray())
# + colab={} colab_type="code" id="IUO236qggA9b"
|
Assignments/Implementing TFIDF vectorizer/Assignment_3_Reference.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] slideshow={"slide_type": "slide"}
# <img src="joke.png"
# height=500
# width= 500
# alt="Example Visualization of a Snapshot (aggregated) Prediction Model"
# title="Snapshot Variable Prediction Model" />
# + [markdown] slideshow={"slide_type": "slide"}
# ### an important note before we start:
#
# <img src="model_comparison.png"
# height=500
# width= 500
# alt="Example Visualization of a Snapshot (aggregated) Prediction Model"
# title="Snapshot Variable Prediction Model" />
#
#
# sometimes a fancy algorithm can make a big impact, but often the difference between a well tuned simple and complex algorithm is not that high.
#
# Fancy algorithms don't magically make perfect predictions. The legwork done before and after model building is often the most important
#
# ------
# -
# + [markdown] slideshow={"slide_type": "slide"}
# # Now, lets learn about fancy algorithms: Random Forest and Gradient Boosted Trees
# * necessary background:
# * CART trees
# * bagging
# * ensembling
# * gradient boosting
# --------
# + [markdown] slideshow={"slide_type": "slide"}
# # Classification And Regression Trees (CART): glorified if/then statements
# ### example tree:
# <img src="Example_Decision_Tree.png"
# height=500
# width= 500
# alt="Example Visualization of a Snapshot (aggregated) Prediction Model"
# title="Snapshot Variable Prediction Model" />
#
# ### written as a rulebased classifier:
# 1. If Height > 180 cm Then Male
# 1. If Height <= 180 cm AND Weight > 80 kg Then Male
# 1. If Height <= 180 cm AND Weight <= 80 kg Then Female
# 1. Make Predictions With CART Models
# + [markdown] slideshow={"slide_type": "subslide"}
#
# * A final fitted CART model divides the predictor (x) space by successively splitting into rectangular regions and models the response (Y) as constant over each region
# * can be schematically represented as a "tree":
# * each interior node of the tree indicates on which predictor variable you split and where you split
# * each terminal node (aka leaf) represents one region and indicates the value of the predicted response in that region
#
# <br>
# + [markdown] slideshow={"slide_type": "slide"}
# ### CART Math: for those who want to take a simple idea and make it confusing
#
# we can write the equation of a regression tree as: $Y = g(X, \theta) + \epsilon$
#
# where: <br> $g(X;\theta)= \sum^M_{m=1}I(x \in R_m)$
#
#
# * $M$ = total number of regions (terminal nodes)
# * $R_m$ = $m$th region
# * $I(x \in R_m)$ = indicator function = $\{ \begin{array}{lr} 1:x \in R_m \\ 0:x \notin R_m \end{array} $
# * $c_m$ =constant predictor over Rm
# * $\theta$ = all parameters and structure (M, splits in Rm’s, cm’s, etc)
#
#
# #### illustration of tree for $M=6$ regions, $k=2$ predictors, and $n=21$ training observations
# <img src="CART3.png"
# height=500
# width= 500
# alt="Example Visualization of a Snapshot (aggregated) Prediction Model"
# title="Snapshot Variable Prediction Model" />
#
# + [markdown] slideshow={"slide_type": "subslide"}
# ### in more simple terms: a CART tree defines regions of the predictor space to correspond to a predicted outcome value
# * when fitting a CART tree, the model grows one tree node at a time
# * at each split, the tree defines boundaries in predictor space based on what REDUCES THE TRAINING ERROR THE MOST
# * stops making splits when the reduction in error falls below a threshold
# * branches can be pruned (ie nodes/boundaries removed)to reduce overfitting
# + [markdown] slideshow={"slide_type": "slide"}
# **example**: $GPA = g((HSrank, ACTscore), \theta) + \epsilon$
#
# <img src="CART2.png"
# height=800
# width= 800
# alt="Example Visualization of a Snapshot (aggregated) Prediction Model"
# title="Snapshot Variable Prediction Model" />
# + [markdown] slideshow={"slide_type": "slide"}
# # Why use a CART?
# * easy to interpret
# * handle categorical variables intuitively
# * computationally efficient
# * have reasonable predictive performance
# * not sensitive to MONOTONIC transformations (ie anything that preserves the order of a set, like log scaling).
# * form the basis for many commonly used algorithms
#
# + [markdown] slideshow={"slide_type": "slide"}
# --------
# # Next Background: Ensembling or Ensemble Learning
#
# * Ensemble: use multiple learning algorithms to obtain better predictive performance than could be obtained from any of the constituent learning algorithms alone.
# * A Machine Learning ensemble:
# * use multiple learning algorithms to obtain better predictive performance than a single learning algorithm alone.
# * concrete finite set of alternative models
# * but allows for much more flexible structure to exist among those
#
#
# + [markdown] slideshow={"slide_type": "slide"}
# --------
# # More Background: Ensembling, Bootstrapping & Bagging
#
# * **Ensemble** (in machine learning) :
# * use multiple learning algorithms to obtain better predictive performance than a single learning algorithm alone.
# * concrete finite set of alternative models
# * but allows for much more flexible structure to exist among those
#
#
# * **Bootstrapping**:
# * ~sampling WITH replacement
# + [markdown] slideshow={"slide_type": "slide"}
# * **Bagging**: (bootstrapping and aggregating)
# * a type of ensembling
# * designed to improve stability & accuracy of some ML algorithms
# * algorithm:
# 1. bootstrap many different sets from your training data
# 1. fit a model to each
# 1. average the predicted output (for regression) or voting (for classification) from bootstraped models across x values.
#
#
# **example**:
# * for $b= 1, 2, ..., B$: (aka: for i in range(1,B))
# * generate bootstrap sample of size n (ie sample B with replacement n times)
# * fit model (any kind) $g(x;\hat\theta^b)$
# * repeat for specified # of bootstraps
# * take y at each value of x as the average responce of each of the boostrapped models: $\hat y(x) = \frac{1}{B}\Sigma^B_{b=1}g(x;\hat\theta^b)$
#
# + [markdown] slideshow={"slide_type": "slide"}
# **Visualizations**:
# visualization for bagging ensemble (source: KDnuggets)
#
# <img src="bagged_ensemble.jpg"
# height=500
# width= 400
# alt="source KDNuggets"
# title="Snapshot Variable Prediction Model" />
#
#
# plotting boostrapped and bagged models: (source: Wikipedia)
#
# <img src="bagging_models.png"
# height=300
# width= 300
# alt="source: wikipedia"
# title="Snapshot Variable Prediction Model" />
#
# + [markdown] slideshow={"slide_type": "slide"}
# ### when is bagging useful:
# * For predictors where fitting is unstable (i.e., a small change in the data gives a very different fitted model) and/or the structure is such that the sum of multiple predictors no longer has the same structure
#
# ### when does bagging have no effect:
# * For predictors that are linear ($\hat y$ a linear function of training $y$)
#
#
#
# -
#
# + [markdown] slideshow={"slide_type": "slide"}
# -----
# # Random Forest: leveraging the wisdom of crowds
#
# * general idea: grow a bunch of different CART trees and let them all vote to get the prediction
#
# * Algorithm detail:
# 1. draw a bootstrap sample $Z^*$ of size $N$ from the training data
# 1. grow a CART tree $T_b$ to the bootstrapped data by recursively repeating the following steps for each terminal node until the minimum node size $n_min$ is reached:
# 1. randomly select $m$ predictor variables
# 1. pick the best variable/spit-point (aka boundary) for the $m$ predictor variables
# 1. split the node into two daughter nodes
# 1. output the ensemble of trees ${T_b}^B_1$.
#
# * make a prediction by taking majority vote (classification) or averaging prediction from each tree (regression)
#
# * in more simple terms: grow and train a lot of CART trees with a maximum size, each using randomly sampled observations (with replacement) and predictor variables (without replacement).
# + [markdown] slideshow={"slide_type": "slide"}
# Random forest simplified (source: towards data science blog)
#
# <img src="rf_vis.png"
# height=500
# width= 500
# alt="source: wikipedia"
# title="Snapshot Variable Prediction Model" />
# + [markdown] slideshow={"slide_type": "slide"}
# -----
# # Gradient boosting: leveraging the stupidity of crowds
#
# * **Boosting**:
# * a type of ensembling that turns a set of weak learners (ie predictors that are slightly better than chance) into a strong learner
# * many different types of algorithms that achieve boosting
#
# * **Gradient Boosting** :
# * Like other boosting methods, gradient boosting combines weak "learners" into a single strong learner in an iterative fashion.
# stated two different ways:
# * ensembles simple/weak CART trees in a stage-wise fashion and generalizes them by allowing optimization of an arbitrary differentiable loss function.
# * boosting sequentially fits simple/weak CART trees to the residuals from the previous iteration, taking the final model to be the sum of the individual models from each iteration
#
#
# explaining in the least-square regression setting:
# * goal: "teach" a model $F$ to predict values of the form $\hat y=F(x)$ by minimizing the mean squared error $\frac{1}{n}\sum_i (\hat y_i - y_i)^2$, where i indexes over some training set of size n.
# * at each iteration $m$, $1\leq m \leq M$, it may be assumed that there is some imperfect model $F_m$ (usually starts with just mean y).
# * in each iteration, the algorithm improves on $F_m$ by constructing a new model that adds an estimator $h$ to make it better: $F_{m+1}(x)= F_m(x) + h(x)$
# * a perfect $h$ implies that $F_{m+1}(x)= F_m(x) + h(x)=y$ or $ h(x) = y - F_m(x)$
# * thus, gradient boosting will fit $h$ to the **residual** $y-F_m(x)$.
# * in each iteration, $F_{m+1}$ attemps to correct the errors of it's predecessor $F_m$.
#
# to generalize this, we can observe that residuals $y- F(x)$ for a given model are the **negative gradients** (with respect to $F(x)$) of the squared error loss function $\frac{1}{2}(y-F(x))^2$
#
# + [markdown] slideshow={"slide_type": "slide"}
# for those of you who want the maths:
#
# <img src="gbm_algorithm.png"
# height=800
# width= 800
# alt="source: wikipedia"
# title="Snapshot Variable Prediction Model" />
#
# <br>
#
# for those of you who want pictures:
#
# <img src="gbm_vis.png"
# height=800
# width= 800
# alt="source: wikipedia"
# title="Snapshot Variable Prediction Model" />
#
# -
# + [markdown] slideshow={"slide_type": "slide"}
# -----
# # final thoughts about RandomForest and GBM
#
# * overfitting is definitely a thing with these models, so understanding some parameters is important.
#
#
# ### RF
# * tree size (depth) = big deal, larger trees = more likely to overfit
# * more trees = not that big of a deal. they make the out of bag error plot looks smoother
#
# ### GBM
# * tree size isn't that big of a deal, (smaller trees mean you can still capture error in next tree)
# * more trees = more likely to overfit. too many trees = the out of bag error look more U shaped.
#
# ### both algorithms:
# * neither alrogithm handles heavily imballanced classes very well (this can be an entire lecture on it's own)
# * both inherit all of the benefits of regular CART trees
# * both are better at regression than CART trees
# * both handle much more complex non-linear relationships between predictor and responce
# * both are capable of capturing **SOME** higher order predictor interactions, but these are often masked by marginal effects and cannot be differentiated from them. (ongoing research into this)
# -
import os
os.getcwd()
# +
import nbconvert
import nbformat
with open('hsip442/hsip442_algorithms_lecture.ipynb') as nb_file:
nb_contents = nb_file.read()
# Convert using the ordinary exporter
notebook = nbformat.reads(nb_contents, as_version=4)
exporter = nbconvert.HTMLExporter()
body, res = exporter.from_notebook_node(notebook)
# Create a dict mapping all image attachments to their base64 representations
images = {}
for cell in notebook['cells']:
if 'attachments' in cell:
attachments = cell['attachments']
for filename, attachment in attachments.items():
for mime, base64 in attachment.items():
images[f'attachment:{filename}'] = f'data:{mime};base64,{base64}'
# Fix up the HTML and write it to disk
for src, base64 in images.items():
body = body.replace(f'src="{src}"', f'src="{base64}"')
with open('my_notebook.html', 'w') as output_file:
output_file.write(body)
# -
# * **Stacking**: another type of ensembling
# 1. fit a number of different models to the entire training data ($g_m(x,\hat\theta^m)$)
# 2. take a linear combination (i.e. weighted average) of the models as the predictor($x$), using linear regression to determine the coefficients ($\theta$), with the consituent models ($g(x,\theta)$) as the basis function:
# * $\hat y(x) = \sum^M_{m=1}\hat \beta_m g_m(X,\hat\theta^m)$
# * linear regression: $\hat y(x)= \beta_0+ \sum^n_{i=1}\beta_i X$
|
notebooks/hsip442/hsip442_algorithms_lecture-Copy1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
from datascience import *
import numpy as np
# %matplotlib inline
import matplotlib.pyplot as plots
plots.style.use('fivethirtyeight')
# -
# ## Line Graphs
# **Please run all cells before this cell, including the import cell at the top of the notebook.**
# +
# From Lecture 6
# As of Jan 2017, this census file is online here:
data = 'http://www2.census.gov/programs-surveys/popest/datasets/2010-2015/national/asrh/nc-est2015-agesex-res.csv'
# A copy can be accessed here in case census.gov moves the file:
# data = 'http://inferentialthinking.com/notebooks/nc-est2015-agesex-res.csv'
full_census_table = Table.read_table("census.csv")
full_census_table
partial = full_census_table.select(['SEX', 'AGE', 4, 9])
us_pop = partial.relabeled(2, '2010').relabeled(3, '2015')
ratio = (us_pop.column(3) / us_pop.column(2))
census = us_pop.with_columns(
'Change', us_pop.column(3) - us_pop.column(2),
'Total Growth', ratio - 1,
'Annual Growth', ratio ** (1/5) - 1)
census.set_format([2, 3, 4], NumberFormatter)
census.set_format([5, 6], PercentFormatter)
# -
by_age = census.where('SEX', 0).drop('SEX').where('AGE', are.between(0, 100))
by_age
by_age.plot(0, 2)
by_age.plot(0, 3)
by_age.select(0, 1, 2).plot(0)
by_age.select(0, 1, 2).plot(0, overlay=False)
# ## Example 1: Age
# **Please run all cells before this cell, including the previous examples and the import cell at the top of the notebook.**
by_age.labels
by_age.plot(0, 3)
by_age.sort(3, descending=True)
2010 - 68
2015 - 68
# ## Scatter Plots
# **Please run all cells before this cell, including the previous examples and the import cell at the top of the notebook.**
actors = Table.read_table('actors.csv')
actors
actors = actors.relabeled(5, '#1 Movie Gross')
actors
actors.scatter(2, 1)
actors.labels
actors.select(2, 3, 5).scatter(0)
actors.where(5, are.above(800))
# ## Example 2: Actors
# **Please run all cells before this cell, including the previous examples and the import cell at the top of the notebook.**
actors
actors.scatter(2, 3)
actors.where(2, are.below(10))
actors.where(2, are.above(60))
# ## Distributions
# **Please run all cells before this cell, including the previous examples and the import cell at the top of the notebook.**
top = Table.read_table('top_movies.csv')
top
top10 = top.take(np.arange(10))
top10.barh(0, 2)
studios = top.group('Studio')
studios.show()
sum(studios.column(1))
studios.barh(0)
studios.sort(1, descending=True).barh(0)
|
Data8.1x/lec07.ipynb
|
# # 7.3. Getting started with Bayesian methods
import numpy as np
import scipy.stats as st
import matplotlib.pyplot as plt
# %matplotlib inline
def posterior(n, h, q):
return (n + 1) * st.binom(n, q).pmf(h)
n = 100
h = 61
q = np.linspace(0., 1., 1000)
d = posterior(n, h, q)
# + podoc={"output_text": "Posterior distribution"}
fig, ax = plt.subplots(1, 1)
ax.plot(q, d, '-k')
ax.set_xlabel('q parameter')
ax.set_ylabel('Posterior distribution')
ax.set_ylim(0, d.max() + 1)
|
chapter07_stats/03_bayesian.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# ---
# # Deep Q-Network implementation.
#
# This homework shamelessly demands you to implement a DQN - an approximate q-learning algorithm with experience replay and target networks - and see if it works any better this way.
#
# Original paper:
# https://arxiv.org/pdf/1312.5602.pdf
# **This notebook is given for debug.** The main task is in the other notebook (**homework_pytorch_main**). The tasks are similar and share most of the code. The main difference is in environments. In main notebook it can take some 2 hours for the agent to start improving so it seems reasonable to launch the algorithm on a simpler env first. Here it is CartPole and it will train in several minutes.
#
# **We suggest the following pipeline:** First implement debug notebook then implement the main one.
#
# **About evaluation:** All points are given for the main notebook with one exception: if agent fails to beat the threshold in main notebook you can get 1 pt (instead of 3 pts) for beating the threshold in debug notebook.
# +
import sys, os
if 'google.colab' in sys.modules and not os.path.exists('.setup_complete'):
# !wget -q https://raw.githubusercontent.com/yandexdataschool/Practical_RL/spring20/setup_colab.sh -O- | bash
# !wget -q https://raw.githubusercontent.com/yandexdataschool/Practical_RL/master/week04_approx_rl/atari_wrappers.py
# !wget -q https://raw.githubusercontent.com/yandexdataschool/Practical_RL/master/week04_approx_rl/utils.py
# !wget -q https://raw.githubusercontent.com/yandexdataschool/Practical_RL/master/week04_approx_rl/replay_buffer.py
# !wget -q https://raw.githubusercontent.com/yandexdataschool/Practical_RL/master/week04_approx_rl/framebuffer.py
# !pip install gym[box2d]
# !touch .setup_complete
# This code creates a virtual display to draw game images on.
# It will have no effect if your machine has a monitor.
if type(os.environ.get("DISPLAY")) is not str or len(os.environ.get("DISPLAY")) == 0:
# !bash ../xvfb start
os.environ['DISPLAY'] = ':1'
# -
# __Frameworks__ - we'll accept this homework in any deep learning framework. This particular notebook was designed for pytoch, but you find it easy to adapt it to almost any python-based deep learning framework.
import random
import numpy as np
import torch
import utils
import gym
import numpy as np
import matplotlib.pyplot as plt
# ### CartPole again
#
# Another env can be used without any modification of the code. State space should be a single vector, actions should be discrete.
#
# CartPole is the simplest one. It should take several minutes to solve it.
#
# For LunarLander it can take 1-2 hours to get 200 points (a good score) on Colab and training progress does not look informative.
# +
ENV_NAME = 'CartPole-v1'
def make_env(seed=None):
# some envs are wrapped with a time limit wrapper by default
env = gym.make(ENV_NAME).unwrapped
if seed is not None:
env.seed(seed)
return env
# -
env = make_env()
env.reset()
plt.imshow(env.render("rgb_array"))
state_shape, n_actions = env.observation_space.shape, env.action_space.n
# ### Building a network
# We now need to build a neural network that can map observations to state q-values.
# The model does not have to be huge yet. 1-2 hidden layers with < 200 neurons and ReLU activation will probably be enough. Batch normalization and dropout can spoil everything here.
import torch
import torch.nn as nn
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
# those who have a GPU but feel unfair to use it can uncomment:
# device = torch.device('cpu')
device
class DQNAgent(nn.Module):
def __init__(self, state_shape, n_actions, epsilon=0):
super().__init__()
self.epsilon = epsilon
self.n_actions = n_actions
self.state_shape = state_shape
# Define your network body here. Please make sure agent is fully contained here
assert len(state_shape) == 1
state_dim = state_shape[0]
<YOUR CODE>
def forward(self, state_t):
"""
takes agent's observation (tensor), returns qvalues (tensor)
:param state_t: a batch states, shape = [batch_size, *state_dim=4]
"""
# Use your network to compute qvalues for given state
qvalues = <YOUR CODE>
assert qvalues.requires_grad, "qvalues must be a torch tensor with grad"
assert len(
qvalues.shape) == 2 and qvalues.shape[0] == state_t.shape[0] and qvalues.shape[1] == n_actions
return qvalues
def get_qvalues(self, states):
"""
like forward, but works on numpy arrays, not tensors
"""
model_device = next(self.parameters()).device
states = torch.tensor(states, device=model_device, dtype=torch.float32)
qvalues = self.forward(states)
return qvalues.data.cpu().numpy()
def sample_actions(self, qvalues):
"""pick actions given qvalues. Uses epsilon-greedy exploration strategy. """
epsilon = self.epsilon
batch_size, n_actions = qvalues.shape
random_actions = np.random.choice(n_actions, size=batch_size)
best_actions = qvalues.argmax(axis=-1)
should_explore = np.random.choice(
[0, 1], batch_size, p=[1-epsilon, epsilon])
return np.where(should_explore, random_actions, best_actions)
agent = DQNAgent(state_shape, n_actions, epsilon=0.5).to(device)
# Now let's try out our agent to see if it raises any errors.
def evaluate(env, agent, n_games=1, greedy=False, t_max=10000):
""" Plays n_games full games. If greedy, picks actions as argmax(qvalues). Returns mean reward. """
rewards = []
for _ in range(n_games):
s = env.reset()
reward = 0
for _ in range(t_max):
qvalues = agent.get_qvalues([s])
action = qvalues.argmax(axis=-1)[0] if greedy else agent.sample_actions(qvalues)[0]
s, r, done, _ = env.step(action)
reward += r
if done:
break
rewards.append(reward)
return np.mean(rewards)
evaluate(env, agent, n_games=1)
# ### Experience replay
# For this assignment, we provide you with experience replay buffer. If you implemented experience replay buffer in last week's assignment, you can copy-paste it here in main notebook **to get 2 bonus points**.
#
# 
# #### The interface is fairly simple:
# * `exp_replay.add(obs, act, rw, next_obs, done)` - saves (s,a,r,s',done) tuple into the buffer
# * `exp_replay.sample(batch_size)` - returns observations, actions, rewards, next_observations and is_done for `batch_size` random samples.
# * `len(exp_replay)` - returns number of elements stored in replay buffer.
# +
from replay_buffer import ReplayBuffer
exp_replay = ReplayBuffer(10)
for _ in range(30):
exp_replay.add(env.reset(), env.action_space.sample(),
1.0, env.reset(), done=False)
obs_batch, act_batch, reward_batch, next_obs_batch, is_done_batch = exp_replay.sample(
5)
assert len(exp_replay) == 10, "experience replay size should be 10 because that's what maximum capacity is"
# -
def play_and_record(initial_state, agent, env, exp_replay, n_steps=1):
"""
Play the game for exactly n steps, record every (s,a,r,s', done) to replay buffer.
Whenever game ends, add record with done=True and reset the game.
It is guaranteed that env has done=False when passed to this function.
PLEASE DO NOT RESET ENV UNLESS IT IS "DONE"
:returns: return sum of rewards over time and the state in which the env stays
"""
s = initial_state
sum_rewards = 0
# Play the game for n_steps as per instructions above
<YOUR CODE>
return sum_rewards, s
# +
# testing your code.
exp_replay = ReplayBuffer(2000)
state = env.reset()
play_and_record(state, agent, env, exp_replay, n_steps=1000)
# if you're using your own experience replay buffer, some of those tests may need correction.
# just make sure you know what your code does
assert len(exp_replay) == 1000, "play_and_record should have added exactly 1000 steps, "\
"but instead added %i" % len(exp_replay)
is_dones = list(zip(*exp_replay._storage))[-1]
assert 0 < np.mean(is_dones) < 0.1, "Please make sure you restart the game whenever it is 'done' and record the is_done correctly into the buffer."\
"Got %f is_done rate over %i steps. [If you think it's your tough luck, just re-run the test]" % (
np.mean(is_dones), len(exp_replay))
for _ in range(100):
obs_batch, act_batch, reward_batch, next_obs_batch, is_done_batch = exp_replay.sample(
10)
assert obs_batch.shape == next_obs_batch.shape == (10,) + state_shape
assert act_batch.shape == (
10,), "actions batch should have shape (10,) but is instead %s" % str(act_batch.shape)
assert reward_batch.shape == (
10,), "rewards batch should have shape (10,) but is instead %s" % str(reward_batch.shape)
assert is_done_batch.shape == (
10,), "is_done batch should have shape (10,) but is instead %s" % str(is_done_batch.shape)
assert [int(i) in (0, 1)
for i in is_dones], "is_done should be strictly True or False"
assert [
0 <= a < n_actions for a in act_batch], "actions should be within [0, n_actions]"
print("Well done!")
# -
# ### Target networks
#
# We also employ the so called "target network" - a copy of neural network weights to be used for reference Q-values:
#
# The network itself is an exact copy of agent network, but it's parameters are not trained. Instead, they are moved here from agent's actual network every so often.
#
# $$ Q_{reference}(s,a) = r + \gamma \cdot \max _{a'} Q_{target}(s',a') $$
#
# 
target_network = DQNAgent(agent.state_shape, agent.n_actions, epsilon=0.5).to(device)
# This is how you can load weights from agent into target network
target_network.load_state_dict(agent.state_dict())
# ### Learning with... Q-learning
# Here we write a function similar to `agent.update` from tabular q-learning.
# Compute Q-learning TD error:
#
# $$ L = { 1 \over N} \sum_i [ Q_{\theta}(s,a) - Q_{reference}(s,a) ] ^2 $$
#
# With Q-reference defined as
#
# $$ Q_{reference}(s,a) = r(s,a) + \gamma \cdot max_{a'} Q_{target}(s', a') $$
#
# Where
# * $Q_{target}(s',a')$ denotes q-value of next state and next action predicted by __target_network__
# * $s, a, r, s'$ are current state, action, reward and next state respectively
# * $\gamma$ is a discount factor defined two cells above.
#
#
# __Note 1:__ there's an example input below. Feel free to experiment with it before you write the function.
#
# __Note 2:__ compute_td_loss is a source of 99% of bugs in this homework. If reward doesn't improve, it often helps to go through it line by line [with a rubber duck](https://rubberduckdebugging.com/).
def compute_td_loss(states, actions, rewards, next_states, is_done,
agent, target_network,
gamma=0.99,
check_shapes=False,
device=device):
""" Compute td loss using torch operations only. Use the formulae above. """
states = torch.tensor(states, device=device, dtype=torch.float) # shape: [batch_size, *state_shape]
# for some torch reason should not make actions a tensor
actions = torch.tensor(actions, device=device, dtype=torch.long) # shape: [batch_size]
rewards = torch.tensor(rewards, device=device, dtype=torch.float) # shape: [batch_size]
# shape: [batch_size, *state_shape]
next_states = torch.tensor(next_states, device=device, dtype=torch.float)
is_done = torch.tensor(
is_done.astype('float32'),
device=device,
dtype=torch.float
) # shape: [batch_size]
is_not_done = 1 - is_done
# get q-values for all actions in current states
predicted_qvalues = agent(states)
# compute q-values for all actions in next states
predicted_next_qvalues = target_network(next_states)
# select q-values for chosen actions
predicted_qvalues_for_actions = predicted_qvalues[range(
len(actions)), actions]
# compute V*(next_states) using predicted next q-values
next_state_values = <YOUR CODE>
assert next_state_values.dim(
) == 1 and next_state_values.shape[0] == states.shape[0], "must predict one value per state"
# compute "target q-values" for loss - it's what's inside square parentheses in the above formula.
# at the last state use the simplified formula: Q(s,a) = r(s,a) since s' doesn't exist
# you can multiply next state values by is_not_done to achieve this.
target_qvalues_for_actions = <YOUR CODE>
# mean squared error loss to minimize
loss = torch.mean((predicted_qvalues_for_actions -
target_qvalues_for_actions.detach()) ** 2)
if check_shapes:
assert predicted_next_qvalues.data.dim(
) == 2, "make sure you predicted q-values for all actions in next state"
assert next_state_values.data.dim(
) == 1, "make sure you computed V(s') as maximum over just the actions axis and not all axes"
assert target_qvalues_for_actions.data.dim(
) == 1, "there's something wrong with target q-values, they must be a vector"
return loss
# Sanity checks
# +
obs_batch, act_batch, reward_batch, next_obs_batch, is_done_batch = exp_replay.sample(
10)
loss = compute_td_loss(obs_batch, act_batch, reward_batch, next_obs_batch, is_done_batch,
agent, target_network,
gamma=0.99, check_shapes=True)
loss.backward()
assert loss.requires_grad and tuple(loss.data.size()) == (
), "you must return scalar loss - mean over batch"
assert np.any(next(agent.parameters()).grad.data.cpu().numpy() !=
0), "loss must be differentiable w.r.t. network weights"
assert np.all(next(target_network.parameters()).grad is None), "target network should not have grads"
# -
# ### Main loop
#
# It's time to put everything together and see if it learns anything.
from tqdm import trange
from IPython.display import clear_output
import matplotlib.pyplot as plt
seed = <your favourite random seed>
random.seed(seed)
np.random.seed(seed)
torch.manual_seed(seed)
# +
env = make_env(seed)
state_dim = env.observation_space.shape
n_actions = env.action_space.n
state = env.reset()
agent = DQNAgent(state_dim, n_actions, epsilon=1).to(device)
target_network = DQNAgent(state_dim, n_actions, epsilon=1).to(device)
target_network.load_state_dict(agent.state_dict())
# -
exp_replay = ReplayBuffer(10**4)
for i in range(100):
if not utils.is_enough_ram(min_available_gb=0.1):
print("""
Less than 100 Mb RAM available.
Make sure the buffer size in not too huge.
Also check, maybe other processes consume RAM heavily.
"""
)
break
play_and_record(state, agent, env, exp_replay, n_steps=10**2)
if len(exp_replay) == 10**4:
break
print(len(exp_replay))
# +
# # for something more complicated than CartPole
# timesteps_per_epoch = 1
# batch_size = 32
# total_steps = 3 * 10**6
# decay_steps = 1 * 10**6
# opt = torch.optim.Adam(agent.parameters(), lr=1e-4)
# init_epsilon = 1
# final_epsilon = 0.1
# loss_freq = 20
# refresh_target_network_freq = 1000
# eval_freq = 5000
# max_grad_norm = 5000
# +
timesteps_per_epoch = 1
batch_size = 32
total_steps = 4 * 10**4
decay_steps = 1 * 10**4
opt = torch.optim.Adam(agent.parameters(), lr=1e-4)
init_epsilon = 1
final_epsilon = 0.1
loss_freq = 20
refresh_target_network_freq = 100
eval_freq = 1000
max_grad_norm = 5000
# -
mean_rw_history = []
td_loss_history = []
grad_norm_history = []
initial_state_v_history = []
state = env.reset()
for step in trange(total_steps + 1):
if not utils.is_enough_ram():
print('less that 100 Mb RAM available, freezing')
print('make sure everything is ok and make KeyboardInterrupt to continue')
try:
while True:
pass
except KeyboardInterrupt:
pass
agent.epsilon = utils.linear_decay(init_epsilon, final_epsilon, step, decay_steps)
# play
_, state = play_and_record(state, agent, env, exp_replay, timesteps_per_epoch)
# train
<sample batch_size of data from experience replay>
loss = <compute TD loss>
loss.backward()
grad_norm = nn.utils.clip_grad_norm_(agent.parameters(), max_grad_norm)
opt.step()
opt.zero_grad()
if step % loss_freq == 0:
td_loss_history.append(loss.data.cpu().item())
grad_norm_history.append(grad_norm)
if step % refresh_target_network_freq == 0:
# Load agent weights into target_network
<YOUR CODE>
if step % eval_freq == 0:
# eval the agent
mean_rw_history.append(evaluate(
make_env(seed=step), agent, n_games=3, greedy=True, t_max=1000)
)
initial_state_q_values = agent.get_qvalues(
[make_env(seed=step).reset()]
)
initial_state_v_history.append(np.max(initial_state_q_values))
clear_output(True)
print("buffer size = %i, epsilon = %.5f" %
(len(exp_replay), agent.epsilon))
plt.figure(figsize=[16, 9])
plt.subplot(2, 2, 1)
plt.title("Mean reward per episode")
plt.plot(mean_rw_history)
plt.grid()
assert not np.isnan(td_loss_history[-1])
plt.subplot(2, 2, 2)
plt.title("TD loss history (smoothened)")
plt.plot(utils.smoothen(td_loss_history))
plt.grid()
plt.subplot(2, 2, 3)
plt.title("Initial state V")
plt.plot(initial_state_v_history)
plt.grid()
plt.subplot(2, 2, 4)
plt.title("Grad norm history (smoothened)")
plt.plot(utils.smoothen(grad_norm_history))
plt.grid()
plt.show()
final_score = evaluate(
make_env(),
agent, n_games=30, greedy=True, t_max=1000
)
print('final score:', final_score)
assert final_score > 300, 'not good enough for DQN'
print('Well done')
# **Agent's predicted V-values vs their Monte-Carlo estimates**
eval_env = make_env()
record = utils.play_and_log_episode(eval_env, agent)
print('total reward for life:', np.sum(record['rewards']))
for key in record:
print(key)
# +
fig = plt.figure(figsize=(5, 5))
ax = fig.add_subplot(1, 1, 1)
ax.scatter(record['v_mc'], record['v_agent'])
ax.plot(sorted(record['v_mc']), sorted(record['v_mc']),
'black', linestyle='--', label='x=y')
ax.grid()
ax.legend()
ax.set_title('State Value Estimates')
ax.set_xlabel('Monte-Carlo')
ax.set_ylabel('Agent')
plt.show()
|
week04_approx_rl/homework_pytorch_debug.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [Root]
# language: python
# name: Python [Root]
# ---
# # Monthly Active User Depth of Engagement (CDFs)
#
# For each user active in a month, how many days of the month are they using it?
#
# For a full writeup, see the blog post at: http://www.danwolch.com/2017/12/segment-your-user-base-depth-of-engagement/
# +
# %matplotlib inline
import matplotlib.pyplot as plt
# you only need this if you're connecting to your database directly
from sqlalchemy import create_engine
import pandas as pd
DB_USERNAME = "fill your db username in here"
DB_PASSWORD = "fill your db password in here"
# sample: "hostname.us-east-1.redshift.amazonaws.com:5439/database_name"
DB_CONN_STR = "fill in your host, port, db name here"
LOAD_FROM_FILE = True
# -
mau_cdf_sql = """
WITH daily_user_table AS (
SELECT
DISTINCT user_id
, DATE_TRUNC('day', event_time) as dt
FROM events
WHERE event_time BETWEEN '2017-12-01 00:00:00' AND '2017-12-31 23:59:59'
), user_day_count AS (
SELECT user_id
, COUNT(DISTINCT DATE_TRUNC('day', dt)) as day_count
FROM daily_user_table
GROUP BY user_id
)
SELECT day_count, COUNT(DISTINCT user_id) as user_count
FROM user_day_count
GROUP BY 1
ORDER BY day_count
"""
if LOAD_FROM_FILE:
df = pd.read_csv("sample.csv", names=["day_count", "user_count"], index_col='day_count')
else:
conn_str = "postgresql://%s:%s@%s" % (DB_USERNAME, DB_PASSWORD, DB_CONN_STR)
engine = create_engine(conn_str)
cmd_sql = mau_cdf_sql
df = pd.read_sql_query(cmd_sql, engine)
total_users = df['user_count'].sum()
df['cumulative_users'] = df['user_count'].cumsum()
df['cumulative_users_pct'] = 100 * df['cumulative_users'] / total_users
df.plot(subplots=True, figsize=(12,16),
title="Monthly Active User Depth of Engagament CDF", kind='bar')
|
MAU-CDF/MAU Depth of Engagement.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# 
#
# <a href="https://hub.callysto.ca/jupyter/hub/user-redirect/git-pull?repo=https%3A%2F%2Fgithub.com%2Fcallysto%2Fcurriculum-notebooks&branch=master&subPath=Science/ProjectileMotion/projectile-motion.ipynb&depth=1" target="_parent"><img src="https://raw.githubusercontent.com/callysto/curriculum-notebooks/master/open-in-callysto-button.svg?sanitize=true" width="123" height="24" alt="Open in Callysto"/></a>
# # Projectile Motion
# ## 1. Introduction
# *This notebook is meant to satisfy Physics 20-A1.3s. Special thanks to Ms. <NAME> for her help on developing this notebook.*
# #### *Objective: Mathematically analyze the movement of a launched object to determine flight path, speed, and time.*
# Learning projectile motion will enable __you__ with the skills to understand how launched objects fly through the air and how you can design your own. It is critical for sports, military, and any scenario where you need an airborne object to reach a destination. What examples can you think of?
# Projectile motion explores the physics behind anything airborne that is subjected only to gravity. From throwing a dart to shooting a basketball to medieval cannons used during sieges, all of these objects are ruled by the same basic principles.
#
#
# > <img src="./images/catapult.gif" width="500" height="400" />
# >
# > <p style="text-align: center;"> A clip from the game Besiege (http://www.indiedb.com/games/besiege/images/besiege-gif) </p>
#
# ### Who created projectile motion analysis?
#
# > <img src="./images/galileo.jpg" alt="Drawing" style="width: 400px;"/>
# >
# > <p style="text-align: center;"> Painting of Galileo (https://www.gettyimages.ca/detail/news-photo/galileo-galilei-and-his-telescope-engraving-1864-news-photo/526510364) </p>
#
# Galileo, one of the great fathers of astronomy and modern science, created projectile motion analysis over 400 years ago. This gave him the tools to improve the accuracy and effectiveness of military cannons in the 17th century. The reason we study it today is because his method has stood the test of time and continues to be a fundamental foundation to areas like aerodynamics, sports performance, and military design.
#
# For the purposes of understanding the fundamentals, the effects of air resistance will be ignored. While it makes our lives simpler, it is wrong to assume that projectiles only experience the force of gravity - air resistance can play a significant role in many cases. Air resistance is responsible for lower projectile speeds and distances but it is also critical to helping airplanes slow down, keeping race cars grounded at high speeds (which is why they have spoilers), and causing crazy phenomena like the Magnus effect shown below.
# +
from IPython.lib.display import YouTubeVideo
from IPython.display import HTML
display(YouTubeVideo('2OSrvzNW9FE', start=24, end=35, mute=True, width=718, height=404))
display(HTML('''<p style="text-align: center;"> Basketball toss demonstrating the Magnus effect (https://www.youtube.com/watch?v=2OSrvzNW9FE) </p>'''))
# -
# However, in order to understand these complex cases, we must first strip away the layer of friction and look at how objects travel solely under the force gravity.
# ## 2. Theory & Practice
#
#
# Neglecting air resistance, all projectiles in the air will only be under the force of gravity. This means objects travelling in 2 dimensions will constantly be pulled down to earth and forced into a curved trajectory known as a parabola. Take a look at the gif below. What do you notice about the velocity vectors in the horizontal and vertical directions? Which one changes? Which one stays the same?
#
#
# > <img src="./images/parabola.gif" alt="Drawing" style="width: 400px;"/>
# >
# > <p style="text-align: center;"> Projectile motion animation (http://gbhsweb.glenbrook225.org/gbs/science/phys/mmedia/vectors/nhlp.html) </p>
#
#
# Galileo realized that projectile motion could be broken into two components: __horizontal (x)__ and __vertical (y)__ that can be analyzed separately. These two dimensions are __independent__, the only variable they share is time *__t__*. This means that changes in the vertical distance, speed, and acceleration will not affect the horizontal components and vice versa.
# ---
# ### Vertical Component
# Due to the force of gravity, the object will accelerate towards the center of the Earth. This means that its initial velocity will be different from its final velocity.
# There are 5 variables involved in the vertical component: acceleration, initial velocity, final velocity, *altitude* (distance travelled vertically), and time. We will assume $ \vec a $ is constant for projectile motion and equivalent to $ 9.81 m/s^2$.
#
#
# \begin{equation}
# \vec a , \vec v_i , \vec v_f , \vec d_y , t
# \end{equation}
# There are 5 kinematic equations for uniform acceleration where each one contains 4 of the 5 variables listed above. Given 3 of the variables in a problem, the other 2 can each be found by picking an appropriate equation. *Note: If the object is initially launched horizontally, then $\vec v_i $ = 0 *
#
# \begin{equation}
# \vec a_{ave} = \frac{\vec v_f - \vec v_i}{t} \\
# \vec d = \vec v_i t + \frac12\ \vec a t^2 \\
# \vec d = \vec v_f t - \frac12\ \vec a t^2 \\
# \vec d = \frac{\vec v_f + \vec v_i}{2} t \\
# v_f^2 = v_i^2 + 2 a d \\
# \end{equation}
# <details>
# <summary>
# __Question 1__ <br>
#
# You're out with some friends swimming at a popular cliff jumping spot and they can't stop arguing about how tall the cliff *really* is (for bragging rights). You decide to end this once and for all and pull out a stopwatch. You climb up the cliff, release a rock in your hand from rest, and time its descent. You do this a couple more times and get an average descent time of 1.62 seconds. Your friends stare at you in bewilderment as you rattle off the height after punching some numbers into your phone's calculator. How do you do it? <br><br>
#
# Try solving this question on your own, it's the best way to develop your skills. Once you've given it a go, click the dropdown arrow to reveal the solution. <br>
# </summary>
#
# <blockquote>
# __Solution__ <br>
# 1) Draw a picture of the scenario. This will give you a better grasp of the problem.
# 2) Define your sign convention. Assign positive and negative directions to y.
#
# <blockquote>
# <img src="./images/qu_1.jpg" alt="Drawing" style="width: 400px;"/>
# </blockquote>
#
# 3) Identify the variables you know and the variable(s) you're trying to find. Pick a formula that best fits the problem scenario and solve for the unknown. <br><br>
#
# <blockquote>
# The rock is released from rest so $ \vec v_i = 0 $. Based on the information given and our sign convention, we can state the following: <br><br>
#
#
# \begin{equation}
# \vec v_i = 0 \\
# \vec a = +9.81 \ m/s \\
# t = 1.62\ s \\
# \vec d_y = \ ? \\
# \vec v_f = \ ? \\
# \end{equation} <br>
#
# We have 3 known variables and 2 unknown variables in the problem. However, in this case we're looking for $ \vec d_y $ so we don't care what $ \vec v_f $ is. If we take a look at the 5 vertical component equations, we see that the following equation has the 3 variables we know and the one we're looking for: <br><br>
#
# \begin{equation}
# \vec d_y = \vec v_i t + \frac12\ \vec a t^2 \\
# \end{equation}
#
# We don't want one with $ \vec v_f $ because we don't know its value. Using this equation we can solve for $ \vec d_y $: <br><br>
#
# \begin{equation}
# \vec d_y = (0)(2.62\ s) + \frac12\ (+9.81\ m/s^2) (1.62\ s)^2 \\
# \vec d_y = +12.8727\ m \\
# \vec d_y = +12.9\ m \\
# \end{equation}
#
# Using the time it took to fell, we can conclude that the cliff is 12.9 meters tall.
#
# </blockquote>
# </blockquote>
#
# </details>
# ---
# ### Horizontal Component
# There is no force acting horizontally. Therefore there is no acceleration so it is **uniform motion** ($ \vec v_i = \vec v_f = \vec v_x $).
#
# Horizontal uniform motion is governed by 3 variables: velocity, *range* (distance travelled horizontally), and time.
#
# \begin{equation}
# \vec v_x , \vec d_x , t
# \end{equation}
#
# These 3 variables are related by the uniform motion equation:
#
# \begin{equation}
# \vec v_x = \frac {\vec d_x}{t}
# \end{equation}
#
# Let's do some practice to solidify the concepts.
# <details>
# <summary>
# __Question 2__ <br>
#
# You're back at the same pond as Question 1 except this time you flick the rock horizontally off the top of the cliff at 30.0 km/h. The rock makes it across the pond and still takes 1.62 seconds to hit the water. How long is the pond? <br>
# </summary>
#
# <blockquote>
# __Solution__ <br>
# 1) Draw a picture of the scenario. This will give you a better grasp of the problem.
# 2) Define your sign convention. Assign positive and negative directions to x.
#
# <blockquote>
# <img src="./images/qu_2.jpg" alt="Drawing" style="width: 400px;"/>
# </blockquote>
#
# 3) Identify the variables you know and the variable(s) you're trying to find. Pick a formula that best fits the problem scenario and solve for the unknown. <br><br>
#
# <blockquote>
# The horizontal component is easier than the vertical component because there's only one equation with 3 variables. List the 2 variables you know and the one you're trying to find: <br><br>
#
# \begin{equation}
# \vec v_x = +30.0\ km/h =\ +8.3333\ m/s \\
# t = 1.62\ s \\
# \vec d_x = \ ? \\
# \end{equation} <br>
#
# Rearrange the uniform motion equation for the unknown and solve: <br><br>
#
# \begin{equation}
# \vec v_x = \frac {\vec d_x}{t} \\
# \vec d_x = \vec v_x t = (+8.3333\ m/s)(1.62\ s) \\
# \vec d_x = +13.5\ m \\
# \end{equation}
#
# The pond is 13.5 meters long.
#
# </blockquote>
# </blockquote>
#
# </details>
# <details>
# <summary>
# __Question 3__ <br>
#
# <NAME>, the daredevil stunt driver, is performing his next trick. He speeds horizontally off of a 50.0 m high cliff on a motorcycle. How fast must he leave the cliff-top if he needs to soar over the 90.0 m river at the base of the cliff? <br>
#
# </summary>
#
# <blockquote>
# __Solution__ <br>
# 1) Draw a picture of the scenario. This will give you a better grasp of the problem.
# 2) Define your sign convention. Assign positive and negative directions to both x and y.
#
# <blockquote>
# <img src="./images/qu_3.jpg" alt="Drawing" style="width: 400px;"/>
# </blockquote>
#
# 3) Set up a table and identify the variables you know and the variable(s) you're trying to find. Pick a vertical component formula that best fits the problem scenario and solve for the unknown. <br><br>
#
# <blockquote>
# Based on the information given and our sign convention, we can fill our data table with the following: <br><br>
#
#
# \begin{array}{cc}
# x &y \\ \hline
# \vec d_x = +90.0\ m &\vec d_y = -50.0\ m \\
# \vec v_x =\ ? &\vec a = -9.81\ m/s^2 \\
# \ &\vec v_i = 0 \\
# \end{array}
# $$ t =\ ? $$ <br>
#
# Note that $ \vec v_i = 0 $ because the projectile is launched horizontally, and $ t $ is common to both x & y. <br>
#
# To find $ \vec v_x $, we need $ \vec d_x $ and $ t $. We know $ \vec d_x $ but we're missing $ t $ so we'll need to use the vertical data to solve for $ t $. Because we know $ \vec d_y, \vec a, $ and $ \vec v_i $, and we're looking for $ t $, we'll use the following equation because we can solve for $ t $ using the variables we know: <br><br>
#
# \begin{equation}
# \vec d = \vec v_i t + \frac12\ \vec a t^2 \\
# \end{equation}
#
# Because $ \vec v_i = 0 $, the first term goes to 0 and the resulting equation can be rearranged to solve for $ t $: <br><br>
#
# \begin{equation}
# \vec d = \frac12\ \vec a t^2 \\
# t = \sqrt{\frac{2 \vec d_y}{\vec a}} \\
# \end{equation}
#
# Plug in values to find $ t $: <br><br>
#
# \begin{equation}
# t = \sqrt{\frac{2 (-50.0\ m)}{(-9.81\ m/s^2)}} = 3.1928\ s
# \end{equation} <br>
#
# Now that $ t $ is known we can solve for $ \vec v_x $ using the uniform motion equation: <br><br>
#
# \begin{equation}
# \vec v_x = \frac {\vec d_x}{t} = \frac {(+90.0\ m)}{(3.1928\ s)} = +28.2\ m/s \ \ (+101.5\ km/h)
# \end{equation} <br>
#
# </blockquote>
# </blockquote>
#
# </details>
# <details>
# <summary>
# __Question 4__ <br>
#
# Galileo predicted that an object launched horizontally and an object dropped vertically off the same ledge will reach the ground at the same time. Will they? Why or why not? <br>
# </summary>
#
# <blockquote>
# __Solution__ <br>
#
# Yes, they will. Horizontal and vertical motion are independent for a projectile so the horizontal movement of the launched object does not affect its vertical freefall.
#
# <blockquote>
# <img src="./images/qu_4.jpg" alt="Drawing" style="width: 300px;"/>
# <p style="text-align: center;"> (Drawing courtesy of <NAME>) </p>
# </blockquote>
#
# </blockquote>
# </details>
#
#
#
#
# ---
# ### Projectiles Fired at an Angle
# What happens when your projectile is launched at an angle? What are the initial velocities?
#
# In this case, the initial vertical velocity is no longer 0. It will have some value $ \vec v_i $ that will gradually decrease to 0 at the top of its trajectory and then increase in the downward direction as it returns back to ground. Let's take a football punt for example.
#
# According to [Angelo Armenti's The Physics of Sports](https://www.livestrong.com/article/397904-maximum-speed-of-a-football/), top-level football kickers can send footballs flying at 70 mph (31 m/s)! If the player kicked it at an angle of 50°, the trajectory would look something like this:
#
# <blockquote>
# <img src="./images/proj_angle_1.jpg" alt="Drawing" style="width: 500px;"/>
# </blockquote>
#
# The horizontal velocity $ \vec v_x $ will remain the same throughout the flight (uniform motion) while $ \vec v_y $ will decrease to the top of its trajectory and then increase downwards. __Note: If the initial launch height and final landing height are the same ($ \vec d_y $ = 0), then the projectile will land with the same initial speed and angle!__ The initial horizontal and vertical velocities can be solved with some simple trigonometry:
#
# \begin{array}{cc}
# x &y \\
# cos(50^{\circ}) = \frac{adj}{hyp} = \frac{\vec v_x}{31\ m/s} &sin(50^{\circ}) = \frac{opp}{hyp} = \frac{\vec v_y}{31\ m/s} \\
# \vec v_x = (31\ m/s)\ cos(50^{\circ}) &\vec v_y = (31\ m/s)\ sin(50^{\circ}) \\
# \vec v_x = +19.9264\ m/s &\vec v_y = +23.7474\ m/s \\
# \vec v_x = +20\ m/s &\vec v_y = +24\ m/s \\
# \end{array}
#
# <details>
# <summary>
# __Question 5__ <br>
#
# A football player kicks a ball across a flat field at 31.0 m/s and 50.0° from the ground. Find:
# a) The maximum height reached
# b) The flight time (time before it hits the ground)
# c) The range (how far away it hits the ground)
# d) The velocity vector at its maximum height
# e) The acceleration vector at its maximum height
# f) The velocity of the football when it hits the ground <br><br>
#
# Again, try solving these questions on your own first, it's the best way to develop your skills. Once you've given it a go, click the dropdown arrow to reveal the solution. <br>
#
# </summary>
#
# <blockquote>
# __Solution__ <br>
# __a)__ <br>
#
# <blockquote>
# To find the max height, let's only look at the first half of the flight path. That way, we know $ \vec v_f = 0 $ because projectiles have no vertical velocity at the top of their flight path.
#
# <blockquote>
# <img src="./images/qu_5-1.jpg" alt="Drawing" style="width: 350px;"/>
# </blockquote>
#
# We'll use the same sign convention from Question 3. Because we're using the same values from the previous scenario, we can set up our table with the following information: <br><br>
#
#
# \begin{array}{cc}
# x &y \\ \hline
# \vec v_x =\ +19.9264\ m/s &\vec v_i = +23.7474\ m/s \\
# \ &\vec v_f = 0 \\
# \ &\vec a = -9.81\ m/s^2 \\
# \ &\vec d_y =\ ? \\
# \end{array}
# $$ t =\ ? $$ <br>
#
# Looking at our table, we have 3 knowns and 1 unknown in the vertical column. That means we can solve for $ \vec d_y $. Looking at our vertical component equations, the one that contains our 3 known variables and $ \vec d_y $ is: <br><br>
#
# \begin{equation}
# v_f^2 = v_i^2 + 2 a d
# \end{equation} <br>
#
# $ \vec v_f = 0 $ so we can rearrange and solve for $ \vec d_y $: <br><br>
#
# \begin{equation}
# \vec d_y = -\frac{\vec v_i^2}{2 \vec a} = -\frac{(+23.7474\ m/s)^2}{2\ (-9.81\ m/s^2)} \\
# \vec d_y = +28.7431\ m \\
# \vec d_y = +28.7\ m \\
# \end{equation} <br>
#
# </blockquote>
#
# __b)__ <br>
#
# <blockquote>
# To find the flight time, we could either find the time it takes to reach the top of its trajectory and double that, or we could look at the full flight path and find the time to landing. In this case we will choose the latter. <br>
#
# <blockquote>
# <img src="./images/qu_5-2.jpg" alt="Drawing" style="width: 300px;"/>
# </blockquote>
#
# Because our flight path changed, some of our variable have too. In particular, $ \vec d_y = 0 $ which also means that $ \vec v_f = -\vec v_i $. Let's make a new table: <br><br>
#
# \begin{array}{cc}
# x &y \\ \hline
# \vec v_x =\ +19.9264\ m/s &\vec v_i = +23.7474\ m/s \\
# \ &\vec v_f = -23.7474\ m/s \\
# \ &\vec a = -9.81\ m/s^2 \\
# \ &\vec d_y =\ 0 \\
# \end{array}
# $$ t =\ ? $$ <br>
#
# Now, we're looking for $ t $ but we don't have enough horizontal data to solve with uniform motion. However, we know 4 out of the 5 vertical variables which means we have lots of options for the vertical equation. Any of the first 4 equations will do but the second and third will require solving a quadratic equation. To make life easy, we'll use the first one: <br><br>
#
# \begin{equation}
# \vec a_{ave} = \frac{\vec v_f - \vec v_i}{t}
# \end{equation} <br>
#
# Rearrange and solve for $ t $ (Remember to keep your sign convention. If you don't you could end up with 0 here!): <br><br>
#
# \begin{equation}
# t = \frac{\vec v_f - \vec v_i}{\vec a_{ave}} = \frac{(-23.7474\ m/s) - (+23.7474\ m/s)}{(-9.81\ m/s^2)} \\
# t = 4.8415\ s \\
# t = 4.84\ s
# \end{equation} <br>
#
# </blockquote>
#
# __c)__ <br>
#
# <blockquote>
# Now that we have the flight time and $ \vec v_x $, we can use the uniform motion equation to solve for range: <br><br>
#
# \begin{equation}
# \vec v_x = \frac {\vec d_x}{t} \\
# \vec d_x = \vec v_x \ t = (+19.9264\ m/s)\ (4.8415\ s) = +96.4730\ m \\
# \vec d_x = +96.5\ m
# \end{equation} <br>
#
#
# </blockquote>
#
# __d)__ <br>
#
# <blockquote>
# At max height, the vertical velocity $ \vec v_y = 0 $ so the only velocity is horizontal.
#
# <blockquote>
# <img src="./images/qu_5-3.jpg" alt="Drawing" style="width: 300px;"/>
# </blockquote>
#
# </blockquote>
#
# __e)__ <br>
#
# <blockquote>
# The only acceleration is the acceleration due to gravity which is a constant pointing downwards (see part d for image).
#
# </blockquote>
#
# __f)__ <br>
#
# <blockquote>
# Because $ \vec d_y = 0 $ for the full flight path, $ \vec v_f = -\vec v_i = -23.7474\ m/s $. Horizontal velocity is constant so: <br><br>
#
# <blockquote>
# <img src="./images/qu_5-4.jpg" alt="Drawing" style="width: 200px;"/>
# </blockquote>
#
# \begin{equation}
# \vec v_f = 31.0\ m/s\ \ at -50.0^{\circ}
# \end{equation} <br>
#
# </blockquote>
#
# </blockquote>
# </details>
# <p style="text-align: center;"> __----- Continue on only after attempting Question 5. -----__ </p>
# +
"""
If this block of code has suddenly popped up, don't worry! You've found the code
used to create the Projectile Trajectory graph shown below. This is normally hidden but feel
free to explore it and see how it works.
If you want to hide it again, just click on this code block and press 'Ctrl' and 'Enter'
simultaneously on your keyboard.
"""
# Import required packages
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
from ipywidgets import interact
import ipywidgets as widgets
from IPython.display import HTML
# Set values for equations
g = 9.81
t = np.linspace(0,10,100)
# Define equations that plot will display
def d_x(t, theta, v_i):
return v_i*np.cos(np.deg2rad(theta))*t
def d_y(t, theta, v_i):
return v_i*np.sin(np.deg2rad(theta))*t - 0.5*g*t**2
# Define options for plot
def f(theta,v_i):
plt.plot(d_x(t, theta, v_i),d_y(t, theta, v_i))
plt.ylim(0,50)
plt.xlim(0,100)
plt.xlabel("Range (m)", fontsize=16)
plt.ylabel("Altitude (m)", fontsize=16)
plt.margins(0)
plt.grid()
plt.title("Projectile Trajectory", fontsize=20)
hide_me = ''
HTML('''<script>
code_show=true;
function code_toggle() {
if (code_show) {
$('div.input').each(function(id) {
el = $(this).find('.cm-variable:first');
if (id == 0 || el.text() == 'hide_me') {
$(this).hide();
}
});
$('div.output_prompt').css('opacity', 0);
} else {
$('div.input').each(function(id) {
$(this).show();
});
$('div.output_prompt').css('opacity', 1);
}
code_show = !code_show
}
$( document ).ready(code_toggle);
</script>
<form action="javascript:code_toggle()"><input style="opacity:0" type="submit" value="Click here to toggle on/off the raw code."></form>''')
# -
# The scenario in Question 5 can be modelled by a graph using Python. The following code block creates an interactive graph where you can modify the initial velocity $ \vec v_i $ and launch angle $ \theta $ to see how the projectile's trajectory changes. <br>
#
# Modify `theta` and `v_i` to recreate the scenario in Question 5 and use the graph to verify your answers for Parts (a) and (c) line up.
interact(f,theta = (0,90,5), v_i = (0,31,1))
# Pretty cool, huh? If you want to learn how to make graphs using Python, Part (b) of Question 6 will give you a step-by-step breakdown on how to make simple static graphs.
# ---
# ### Determining the Optimum Launch Angle
# <br>
# <details>
# <summary>
# __Question 6__ <br>
#
# Picture this: The International Olympic Committee runs a worldwide survey to see what new global event people would like to see. After some fierce debate and tallying the votes, __shot-cannon__ is chosen! Shot-cannon is a fairly straightforward sport: each country develops their own medieval cannon that competes in a series of challenges. While each challenge tests a different aspect of the design, the main event is the range competition to see which country's cannon can fire a lead ball the farthest across the field. Canada has chosen __you__ to man the cannon for the main event! With the cannon already designed and providing a fixed initial velocity $ \vec v_i $, your responsibility is to pick the optimal angle $ \theta $ to fire the cannon to achieve maximum distance. If you assume no air resistance and a flat field, what angle should you pick? <br><br>
#
# Before reading on, take a moment to picture the scenario in your head and, using your intuition, take a guess at what angle you think would provide the maximum range. Can you think of a way to prove this? <br><br>
#
# Initially, this problem can seem daunting in its magnitude, but if we break it into two chunks it becomes more manageable:
# a) Develop an equation for the range $ \vec d_x $ as a function of $ \vec v_i $ and $\theta $. That is, come up with an equation in the form of $ \vec d_x = f(\ \vec v_i,\ \theta)$.
# b) Determine the optimal angle from the equation you've developed. <br><br>
#
# Part (a) can be solved using the skills you've just learnt so give it a go and hit the arrow to check your answer. <br>
# Part (b) can be solved with coding and graphing which will be covered in the next section __Python Basics__. <br><br>
# </summary>
#
# <blockquote>
# __Solution__ <br>
# __a)__ <br>
#
# <blockquote>
# <img src="./images/qu_6.jpg" alt="Drawing" style="width: 400px;"/>
# </blockquote>
#
# With a picture and sign convention drawn, let's mark down the values we know in a table. While we don't know the angle $\theta$, and $ \vec v_i $ is an unknown constant, we can still write down $ \vec v_x $ and $ \vec v_{i_y} $ in terms of $\theta$ and $ \vec v_i $ because we ultimately want an equation with these terms: <br>
#
# \begin{array}{cc}
# x &y \\
# cos(\theta) = \frac{adj}{hyp} = \frac{\vec v_x}{\vec v_i} &sin(\theta) = \frac{opp}{hyp} = \frac{\vec v_y}{\vec v_i} \\
# \vec v_x = \vec v_i cos(\theta) &\vec v_y = \vec v_i sin(\theta) \\
# \vec v_x = v_i cos(\theta) &\vec v_y = v_i sin(\theta) \\
# \end{array} <br>
#
# The vector arrow on $ v_i $ is dropped because we know it's positive in both directions based on our sign convention. Also, we assume a flat field so $ \vec d_y = 0 $ which means that $ \vec v_{y_f} = -\vec v_{y_i} $ Therefore, our data table becomes:
#
# \begin{array}{cc}
# x &y \\ \hline
# \vec v_x =v_i cos(\theta) &\vec v_i = v_i sin(\theta) \\
# \vec d_x =\ ? &\vec v_f = -v_i sin(\theta) \\
# \ &\vec a = -g \\
# \ &\vec d_y =\ 0 \\
# \end{array}
# $$ t =\ ? $$ <br>
#
# Acceleration is written as $ -g = -9.81 m/s^2 $ for simplicity. Note that this is a constant written as a letter, __not a variable.__ <br>
#
# In order to come up with an equation for $ \vec d_x $, we first need an equation for $ t $ in terms of the given variables $ \vec v_i $ and $\theta$. Considering we know or have expressions for 4 of the vertical values, we will choose the first equation which makes it easy to solve for t: <br><br>
#
# \begin{equation}
# \vec a_{ave} = \frac{\vec v_f - \vec v_i}{t}
# \end{equation} <br>
#
# Rearrange and solve for $ t $: <br><br>
#
# \begin{equation}
# t = \frac{\vec v_f - \vec v_i}{\vec a_{ave}} = \frac{(-v_i sin(\theta)) - (v_i sin(\theta))}{(-g)} \\
# t = \frac{2 v_i sin(\theta)}{g} \\
# \end{equation} <br>
#
# This expression can be applied to the horizontal component to come up with an equation for $ \vec d_x $: <br><br>
#
# \begin{equation}
# \vec v_x = \frac{\vec d_x}{t} \\
# \vec d_x = \vec v_x t \\
# \vec d_x = (v_i cos(\theta)) (\frac{2 v_i sin(\theta)}{g}) \\
# \vec d_x = \frac{2}{g} v_i^2 sin(\theta) cos(\theta) \\
# \end{equation} <br>
#
# Knowing that $ g $ and $ v_i $ are constants, this means that $ \vec d_x $ is only a function of the variable $\theta$.
#
# </blockquote>
# </details>
#
#
#
#
# <p style="text-align: center;"> __----- Continue on only after attempting Question 6 Part (a) and checking with the solution. The next section will cover Part (b). -----__ </p>
# ### Python Basics
#
# From this point on, there are two ways to solve for $\theta$: you can use calculus to solve for it analytically, or we can get creative and use coding with graphing to find the answer!
#
# Python provides us with some great tools to graph this function easily. If you have some knowledge of Python you can skip the explanations and just run the code cells. If not, we're going to take a moment to understand what the code you're about to see does. First up, let's go over the first bit of code.
#
# __Imports__
# At the beginning of most Python programs you're more than likely to see a few (or many) `import` statements. The purpose of these is to bring in other pieces of code, that either you or someone else have written, in order to keep your current program more manageable. For example, the set of import statements we're going to use to plot our functions look like this (click on the code block below and press `Ctrl` and `Enter` on your keyboard simultaneously to run the cell).
# %matplotlib inline
import matplotlib
import numpy as np
import matplotlib.pyplot as plt
# Starting from the top down, let's go over what each piece of this code does.
#
# 1. **%matplotlib inline:** This is very specific to the Jupyter notebook we're using. This tells matplotlib (next bullet) to output graphs in the cell directly below the one in which the code is executed. For more information about Jupyter "magic commands" feel free to read [this document](http://ipython.readthedocs.io/en/stable/interactive/magics.html).
#
# 2. **import matplotlib**: This command tells Python to import the `matplotlib` package. This package contains the python functions that we'll be using for plotting.
#
# 3. **import numpy as np**: This imports the python package `numpy` or "numerical python" and assigns the name to it within our code to `np` so we don't have to type out `numpy` every time we need a function. We'll be using this package for mathematical functions like sine and the square root.
#
# 4. **import matplotlib.pyplot as plt**: This imports the graphing subroutines from the `matplotlib` packages and assigns them the name `plt` so we don't have to type as much when we want to produce a graph.
#
# __Plotting__
# After required modules have been imported into our script, we're ready to get started graphing. First up, we need to define a number of points which to plot. Our computer doesn't understand that the variable $ \theta $ is fully continuous, so we have to give it a discrete set of points to plot our function with. We can do that in python using numpy as follows (click the next cell and press control and enter at the same time on your keyboard).
theta = np.linspace(0,90,5)
print("theta = ", theta)
# This creates a **list** of numbers called `theta` which consists of 5 numbers evenly spaced in the domain $[0,90]$ that we'll use to plot our function. The `print` function is a standard python function that simply displays our variables to the screen as either numbers or characters. In order to plot our functions, we type the following. Note that we've increased the number of points in `theta` to create a smoother plot. Feel free to change the number `100` to something smaller and observe how the plot changes. We also assigned a value to `v_i` and `g` so that the computer can plot the function numerically. Likewise, play around with these numbers and see how your range changes.
theta = np.linspace(0,90,100)
v_i = 30.0
g = 9.81
plt.plot(theta, 2 / g * (v_i**2) * np.sin(np.deg2rad(theta)) * np.cos(np.deg2rad(theta)))
plt.show()
# There's a fair bit going on in that last line of code that should be noted. First, by using `plt.plot` we're calling a function from `matplotlib.pyplot` (that we called `plt`) called `plot`. This function, unsurprisingly, is used to tell Python what to plot. We then pass this function a number of arguments (AKA inputs). The first argument `theta` is the list of numbers we generated earlier. The second argument `2 / g * (v_i**2) * np.sin(np.deg2rad(theta)) * np.cos(np.deg2rad(theta))` is the mathematical function we're going to plot. Here `theta` is the variable we're going to plot, and also the list of points that we generated earlier. The `**` is the Python way of saying "to the power of". Because `sin` and `cos` functions take radians as an input and not degrees, we use `np.deg2rad` which is a function that converts degrees to radians. <br>
#
# So, what we're really saying here is "plot $ \frac{2}{g}v_i^2 \sin(\theta)\cos(\theta) $ for 100 $\theta$ values between 0 and 90".
#
# Now, that graph is missing a lot of important things like axis labels and a legend. We can add those like this:
plt.plot(theta, 2 / g * (v_i**2) * np.sin(np.deg2rad(theta)) * np.cos(np.deg2rad(theta)))
plt.xlabel(r"$ \theta (deg) $", fontsize=16)
plt.ylabel(r"$ \vec d_x (m) $", fontsize=16)
plt.margins(0)
plt.grid()
plt.title(r"Range as a function of launch angle $ \theta $")
plt.show()
# where the `plt.` calls are still calling functions from `matplotlib.pyplot` however this time we're creating x axes labels with `plt.xlabel` and y axes labels with `plt.ylabel`. `plt.margins(0)` removes any unnecessary blank space around the graph and `plt.grid()` adds a nice grid to visually locate points on the graph easier. Finally, `plt.title` adds a title bar to our graph. The dollar signs and "r" characters are just there to make the lettering look nice. Play around with the code and see if you can change the title bar, label font sizes, and margins. <br>
#
#
# Based on the plot above, we see that the maximum range lines up with a launch angle of 45° . Was this your initial guess?
#
# With no air resistance, 45° is the optimal angle because it provides the best compromise between horizontal speed and height. If you shoot it below 45°, you'll get a faster horizontal velocity but the ball will also hit the ground quicker because there's less flight time. If you shoot it above 45°, you'll get more flight time but a slower horizontal velocity. 45° is the sweet spot between extremes.
#
# Because the graphical solution takes the shape of a parabola, this also demonstrates an important symmetry in the launch angles. Launch angles that are equidistant from the maximum of 45° will have the same range. That is, 30° and 60° have the same range, 15° and 75° have the same range, etc. The wonders of physics!
# ---
# ## 3. Conclusion & Extension
#
# This notebook has demonstrated the basics of projectile motion that can be used to determine flight paths, speeds, and times. Reasoning for why projectile motion is foundational to physics is explained, followed by a breakdown describing the horizontal and vertical components of projectile motion. The two components were brought together in an angled launch example with an interactive graph and the final question utilized Python programming to solve a basic calculus problem. Applying the skills taught in this notebook to your practice examples will give you a strong grasp of projectile motion analysis and enable __you__ to begin designing your own basic launchers!
#
#
# ### Practice: Projectile Game
# For a great interactive visualization of projectile motion, check out the PhET link below!
#
# <div style="position: relative; width: 300px; height: 200px;"><a href="https://phet.colorado.edu/sims/html/projectile-motion/latest/projectile-motion_en.html" style="text-decoration: none;"><img src="https://phet.colorado.edu/sims/html/projectile-motion/latest/projectile-motion-600.png" alt="Projectile Motion" style="border: none;" width="300" height="200"/><div style="position: absolute; width: 200px; height: 80px; left: 50px; top: 60px; background-color: #FFF; opacity: 0.6; filter: alpha(opacity = 60);"></div><table style="position: absolute; width: 200px; height: 80px; left: 50px; top: 60px;"><tr><td style="text-align: center; color: #000; font-size: 24px; font-family: Arial,sans-serif;">Click to Run</td></tr></table></a></div>
# [](https://github.com/callysto/curriculum-notebooks/blob/master/LICENSE.md)
|
_sources/curriculum-notebooks/Science/ProjectileMotion/projectile-motion.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2 with Spark 2.0
# language: python
# name: python2-spark20
# ---
# !pip install --user xlrd
# +
# Setup constants if any
# +
import pandas as pd
from io import BytesIO
import requests
import json
import xlrd
from pyspark.sql.functions import *
from pyspark.sql.types import *
from datetime import datetime
from dateutil.parser import parse
from ingest.Connectors import Connectors
# +
# The code was removed by DSX for sharing.
# +
# The code was removed by DSX for sharing.
# +
bbhCashDF = pd.read_excel(getFileFromObjectStorage('MizuhoPOC', 'BBH - Cash.xlsx'),header=[0])
# Drop rows & columns with all 'NaN' values, axis 0 is for row
# bbhCashFilteredDF = bbhCashDF.fillna('')
#dropna(axis=[0,1], how='all')
# bbhCustodyFilteredDF.head(10)
bbhCashRenamedDF = bbhCashFilteredDF.rename(index=str, columns={"Head Account Number": "ACCT_NUM", "Actual Available Balance": "ACT_AVAIL_BAL",
"Actual Variance Amount": "ACT_VAR_AMT","Bank of Deposit": "DEPOSIT_BANK",
"Currency Account Name": "FUND_NAME","Currency Code": "CURR_CODE",
"Opening Available + CMS Sweep Return": "OPEN_AVAIL_CMS_SWEEP_RETURN",
"Opening Available Balance": "OPEN_AVAIL_BAL", "Prior Day NAV": "PRIOR_DAY_NAV",
"Projected Closing Available Balance": "PROJ_CLOSE_AVAIL_BAL",
"Sub Account Number": "SUB_ACCT_NUM","Value Date": "AS_OF_DATE"})
# Convert the datetimeindex object to date
bbhCashRenamedDF['AS_OF_DATE'] = pd.DatetimeIndex(bbhCashRenamedDF['AS_OF_DATE']).date
bbhCashRenamedDF[['ACT_AVAIL_BAL', 'ACT_VAR_AMT', 'OPEN_AVAIL_CMS_SWEEP_RETURN', 'OPEN_AVAIL_BAL', 'PRIOR_DAY_NAV', 'PROJ_CLOSE_AVAIL_BAL']] = bbhCashRenamedDF[['ACT_AVAIL_BAL', 'ACT_VAR_AMT', 'OPEN_AVAIL_CMS_SWEEP_RETURN', 'OPEN_AVAIL_BAL', 'PRIOR_DAY_NAV', 'PROJ_CLOSE_AVAIL_BAL']].astype(float)
#asOfDate = pd.to_datetime('today').strftime('%Y-%m-%d')
#print "\nasOfDate = " + asOfDate
# bbhCustodyRenamedDF.head(20)
print bbhCashRenamedDF.dtypes
# +
spark = SparkSession.builder.getOrCreate()
def build_schema():
"""Build and return a schema to use for the sample data."""
schema = StructType(
[
StructField("ACT_AVAIL_BAL", DoubleType(), True),
StructField("ACT_VAR_AMT", DoubleType(), True),
StructField("DEPOSIT_BANK", StringType(), True),
StructField("FUND_NAME", StringType(), False),
StructField("CURR_CODE", StringType(), True),
StructField("ACCT_NUM", IntegerType(), False),
StructField("OPEN_AVAIL_CMS_SWEEP_RETURN", DoubleType(), True),
StructField("OPEN_AVAIL_BAL", DoubleType(), True),
StructField("PRIOR_DAY_NAV", DoubleType(), True),
StructField("PROJ_CLOSE_AVAIL_BAL", DoubleType(), True),
StructField("SUB_ACCT_NUM", IntegerType(), True),
StructField("AS_OF_DATE", DateType(), False)
]
)
return schema
bbhCashSparkDF = spark.createDataFrame(bbhCashRenamedDF, schema=build_schema())
bbhCashSparkDF.printSchema()
bbhCashSparkDF.show()
# +
dashDBloadOptions = {
Connectors.DASHDB.HOST : dashCredentials["host"],
Connectors.DASHDB.DATABASE : dashCredentials["db"],
Connectors.DASHDB.USERNAME : dashCredentials["username"],
Connectors.DASHDB.PASSWORD : dashCredentials["password"],
Connectors.DASHDB.SOURCE_TABLE_NAME : dashCredentials["REF_FUND_MAPPING_TABLE"],
}
refFundMappingDF = sqlContext.read.format("com.ibm.spark.discover").options(**dashDBloadOptions).load()
refFundMappingDF.printSchema()
refFundMappingDF.show(1)
# +
bbhCashJoinSparkDF = bbhCashSparkDF.join(refFundMappingDF,
bbhCashSparkDF.FUND_NAME == refFundMappingDF.FUND_NAME, "inner")\
.select(bbhCashSparkDF.ACCT_NUM,bbhCashSparkDF.FUND_NAME,
refFundMappingDF.ALADDIN_ID.alias("FUND_ID"),
bbhCashSparkDF.ACT_AVAIL_BAL,
bbhCashSparkDF.ACT_VAR_AMT,
bbhCashSparkDF.DEPOSIT_BANK,
bbhCashSparkDF.CURR_CODE,
bbhCashSparkDF.OPEN_AVAIL_CMS_SWEEP_RETURN,
bbhCashSparkDF.OPEN_AVAIL_BAL,
bbhCashSparkDF.PRIOR_DAY_NAV,
bbhCashSparkDF.PROJ_CLOSE_AVAIL_BAL,
bbhCashSparkDF.SUB_ACCT_NUM,
bbhCashSparkDF.AS_OF_DATE
)
bbhCashJoinSparkDF.show(1)
# +
# Connection to Dash DB for writing the data
dashdbsaveoption = {
Connectors.DASHDB.HOST : dashCredentials["host"],
Connectors.DASHDB.DATABASE : dashCredentials["db"],
Connectors.DASHDB.USERNAME : dashCredentials["username"],
Connectors.DASHDB.PASSWORD : dashCredentials["password"],
Connectors.DASHDB.TARGET_TABLE_NAME : dashCredentials["tableName"],
Connectors.DASHDB.TARGET_WRITE_MODE : 'merge'
}
bbhCashJoinSparkDF.printSchema()
saveDashDBDF = bbhCashJoinSparkDF.write.format("com.ibm.spark.discover").options(**dashdbsaveoption).save()
# -
|
clients/Mizuho/Reporting/src/main/resources/Load_BBH_Cash_Table.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="ABvnJMmltKyV" colab_type="text"
# #Regression With Fastai
#
# ---
#
# Published at Analytics India Magazine -- [A HANDS-ON GUIDE TO REGRESSION WITH FAST.AI](https://analyticsindiamag.com/a-hands-on-guide-to-regression-with-fast-ai/)
#
# **Getting Started With Regression**
#
# Regression With Fast.ai in 7 simple steps:
#
# * Importing the libraries
# * Creating a TabularList
# * Initialising Neural Network
# * Training the model
# * Evaluating the model
# * A simple analysis on the predictions of the validation set
# * Predicting using the network
#
#
#
#
#
#
# + [markdown] colab_type="text" id="Mv5lcQQ9egIE"
# ##Importing All Major Libraries
# + colab_type="code" id="NIlD79e-egIB" colab={}
import pandas as pd
import numpy as np
from fastai.tabular import *
# + [markdown] colab_type="text" id="gtXEtYoIegH_"
# **The fastai.tabular package includes all the modules that are necessary for processing tabular data.**
# + [markdown] colab_type="text" id="ZTmAW33KefrK"
# ## Importing The Data
# + colab_type="code" id="YlPjV7wHefrG" colab={}
#Reading the datasets from excel sheet
training_set = pd.read_excel("Data_Train.xlsx")
test_set = pd.read_excel("Data_Test.xlsx")
# + [markdown] colab_type="text" id="Vxa9jxUhefJr"
# ## Understanding The Data
# + colab_type="code" outputId="d08a1373-bdbe-4b63-d7b1-05f207b68dcc" id="yZkjxvbXefJm" colab={"base_uri": "https://localhost:8080/", "height": 204}
training_set.head(5)
# + colab_type="code" outputId="c812c285-1148-4d4f-a3e5-8de5f9fbca50" id="jyevDx0mefJa" colab={"base_uri": "https://localhost:8080/", "height": 1000}
# Checking the number of rows
print("\n\nNumber of observations in the datasets :\n",'#' * 40)
print("\nTraining Set : ",len(training_set))
print("Test Set : ",len(test_set))
# checking the number of features in the Datasets
print("\n\nNumber of features in the datasets :\n",'#' * 40)
print("\nTraining Set : ",len(training_set.columns))
print("Test Set : ",len(test_set.columns))
# checking the features in the Datasets
print("\n\nFeatures in the datasets :\n",'#' * 40)
print("\nTraining Set : ", list(training_set.columns))
print("Test Set : ",list(test_set.columns))
# Checking the data types of features
print("\n\nDatatypes of features in the datasets :\n",'#' * 40)
print("\nTraining Set : ", training_set.dtypes)
print("\nTest Set : ",test_set.dtypes)
# checking for NaNs or empty cells
print("\n\nEmpty cells or Nans in the datasets :\n",'#' * 40)
print("\nTraining Set : ",training_set.isnull().values.any())
print("\nTest Set : ",test_set.isnull().values.any())
# checking for NaNs or empty cells by column
print("\n\nNumber of empty cells or Nans in the datasets :\n",'#' * 40)
print("\nTraining Set : ","\n", training_set.isnull().sum())
print("\nTest Set : ",test_set.isnull().sum())
#Displaying dataset information
print("\n\nInfo:\n",'#' * 40)
training_set.info()
# + [markdown] colab_type="text" id="hpL0zhrwefJY"
# ### Exploring Categorical features
#
# + colab_type="code" outputId="9bd796e2-e67c-4a7f-aa22-4c88eaa38a47" id="nurG2A5HefJV" colab={"base_uri": "https://localhost:8080/", "height": 34}
# Non categorical Features in The dataset
training_set.select_dtypes(['int','float']).columns
# + colab_type="code" outputId="a53f69fb-d866-414a-8c8f-482c99615c6b" id="smURtTVmefJQ" colab={"base_uri": "https://localhost:8080/", "height": 68}
#Categotical Features in The Dataset
training_set.select_dtypes('object').columns
# + colab_type="code" outputId="ab2cffa4-bcd6-4dbf-8fc5-3571f23e4873" id="a7Rz9UZBefJK" colab={"base_uri": "https://localhost:8080/", "height": 476}
#The Unique values in each of the categorical features
all_brands = list(training_set.Name) + list(test_set.Name)
all_locations = list(training_set.Location) + list(test_set.Location)
all_fuel_types = list(training_set.Fuel_Type) + list(test_set.Fuel_Type)
all_transmissions = list(training_set.Transmission) + list(test_set.Transmission)
all_owner_types = list(training_set.Owner_Type) + list(test_set.Owner_Type)
print("\nNumber Of Unique Values In Name : \n ", len(set(all_brands)))
#print("\nThe Unique Values In Name : \n ", set(all_brands))
print("\nNumber Of Unique Values In Location : \n ", len(set(all_locations)))
print("\nThe Unique Values In Location : \n ", set(all_locations) )
print("\nNumber Of Unique Values In Fuel_Type : \n ", len(set(all_fuel_types)))
print("\nThe Unique Values In Fuel_Type : \n ", set(all_fuel_types) )
print("\nNumber Of Unique Values In Transmission : \n ", len(set(all_transmissions)))
print("\nThe Unique Values In Transmission : \n ", set(all_transmissions) )
print("\nNumber Of Unique Values In Owner_Type : \n ", len(set(all_owner_types)))
print("\nThe Unique Values In Owner_Type : \n ", set(all_owner_types) )
# + [markdown] colab_type="text" id="KzTZDzoRedSA"
# ## Feature Generation And Dataset Restructuring
# + colab_type="code" id="ajipRklVedR9" colab={}
#Based on the information gathered from the data, lets simplify and restructure it.
def restructure(data):
names = list(data.Name)
brand = []
model = []
#Splitting The Column 'Name'
for i in range(len(names)):
try:
brand.append(names[i].split(" ")[0])
try:
model.append(" ".join(names[i].split(" ")[1:]).strip())
except:
pass
except:
print("ERR ! - ", names[i], "@" , i)
#Cleaning Mileage Column
mileage = list(data.Mileage)
for i in range(len(mileage)):
try :
mileage[i] = float(mileage[i].split(" ")[0].strip())
except:
mileage[i] = np.nan
#Cleaning Engine Column
engine = list(data.Engine)
for i in range(len(engine)):
try :
engine[i] = int(engine[i].split(" ")[0].strip())
except:
engine[i] = np.nan
#Cleaning Power Columns
power = list(data.Power)
for i in range(len(power)):
try :
power[i] = float(power[i].split(" ")[0].strip())
except:
power[i] = np.nan
#Cleaning New_Price
data['New_Price'].fillna(0, inplace = True)
newp = list(data['New_Price'])
for i in range(len(newp)):
if newp[i] == 0:
newp[i] = float(newp[i])
continue
elif 'Cr' in newp[i]:
newp[i] = float(newp[i].split()[0].strip()) * 100
elif 'Lakh' in newp[i]:
newp[i] = float(newp[i].split()[0].strip())
#Re-ordering the columns
restructured = pd.DataFrame({'Brand': brand,
'Model':model,
'Location': data['Location'],
'Year':data['Year'] ,
'Kilometers_Driven':data['Kilometers_Driven'],
'Fuel_Type':data['Fuel_Type'],
'Transmission':data['Transmission'],
'Owner_Type':data['Owner_Type'],
'Mileage':mileage,
'Engine':engine,
'Power':power,
'Seats':data['Seats'],
'New_Price':newp
})
#If the dataset passed is training set include the Price column
if 'Price' in data.columns:
restructured['Price'] = data['Price']
return restructured
else:
return restructured
# + [markdown] colab_type="text" id="2nEwUvr7edR8"
# **Summary:**
#
# The data is is restructured in the following ways:
# 1. The Name column in the original dataset is split in to two features, Brand and Model.
# 1. The Mileage column is cleaned to have float values.
# 1. The Engine column is cleaned to have integer values.
# 2. The Power column is cleaned to have integer values.
# 2. The New_Price column is cleaned to remove nulls and correct the units.
#
#
#
#
# + colab_type="code" id="Zow6LouDedR2" colab={}
#Restructuring Training and Test sets
train_data = restructure(training_set)
test_data = restructure(test_set)
# + colab_type="code" outputId="25e9c2a4-5375-4089-b582-583fd8366905" id="wi7gg6ljedRt" colab={"base_uri": "https://localhost:8080/", "height": 34}
#the dimensions of the training set
train_data.shape
# + colab_type="code" outputId="721cc3f0-40a0-4950-a2cf-a2bff0479e23" id="6d4vq7CbedRm" colab={"base_uri": "https://localhost:8080/", "height": 34}
#the dimensions of the test set
test_data.shape
# + colab_type="code" outputId="ee486914-1185-4d2d-cefb-bf70d71f90f1" id="MTj9MSHDedRd" colab={"base_uri": "https://localhost:8080/", "height": 204}
#Top 5 rows of the training set
train_data.head(5)
# + colab_type="code" outputId="1f09b118-e32a-4465-8914-5523a492f2dc" id="0AeGSHZWedRR" colab={"base_uri": "https://localhost:8080/", "height": 204}
#Top 5 rows of the test set
test_data.head()
# + [markdown] colab_type="text" id="lltV1jSW1j4F"
# ## Regression With Fast.ai
#
# + [markdown] colab_type="text" id="6yXVii4w1j38"
# ###Creating A TabularList
# + [markdown] id="xV1y3p9E6N_2" colab_type="text"
# TabularList in fastai is the basic ItemList for any kind of tabular data.It is a class to create a list of inputs in items for tabular data.
#
# Main Arguments:
#
# cat_names : The categorical features in the data.
#
# cont_names : The continuous features in the data.
#
# procs : A liat of transformations to be applies to the data such as FillMissing, Categorify, Normalize etc.
# + colab_type="code" id="E1-0qnbH1j32" colab={}
#Defining the keyword arguments for fastai's TabularList
#Path / default location for saving/loading models
path = ''
#The dependent variable/target
dep_var = 'Price'
#The list of categorical features in the dataset
cat_names = ['Brand', 'Model', 'Location', 'Fuel_Type', 'Transmission', 'Owner_Type']
#The list of continuous features in the dataset
#Exclude the Dependent variable 'Price'
cont_names =['Year', 'Kilometers_Driven', 'Mileage', 'Engine', 'Power', 'Seats', 'New_Price']
#List of Processes/transforms to be applied to the dataset
procs = [FillMissing, Categorify, Normalize]
# + colab_type="code" id="4e48KbHy1j30" colab={}
#Start index for creating a validation set from train_data
start_indx = len(train_data) - int(len(train_data) * 0.2)
#End index for creating a validation set from train_data
end_indx = len(train_data)
#TabularList for Validation
val = (TabularList.from_df(train_data.iloc[start_indx:end_indx].copy(), path=path, cat_names=cat_names, cont_names=cont_names))
test = (TabularList.from_df(test_data, path=path, cat_names=cat_names, cont_names=cont_names, procs=procs))
# + colab_type="code" id="Vt18jvfP1j3u" colab={}
#TabularList for training
data = (TabularList.from_df(train_data, path=path, cat_names=cat_names, cont_names=cont_names, procs=procs)
.split_by_idx(list(range(start_indx,end_indx)))
.label_from_df(cols=dep_var)
.add_test(test)
.databunch())
# + [markdown] id="WHGNuBzM7sgT" colab_type="text"
# **Summary:**
#
# 1. Initializing/Setting The parameters for TabularList such as path, dep_var, cat_names, cont_names and procs.
# 1. Setting the index for Validation set. The start index and End index are set in such a away that it takes the last 20% data from the training set for validation.
# 2. Creating TabularList for Validation set from train_data.
# 2. Creating TabularList for Test set from test_data.
# 1. Creating a DataBunch for the network.DataBunch is a class that binds train_dl,valid_dl and test_dl in a data object.
#
#
#
#
# + colab_type="code" id="f5syfNX71j3r" outputId="2ffdab91-8eb1-4d9d-b275-ae2aad39c1de" colab={"base_uri": "https://localhost:8080/", "height": 359}
#Display the data batch
data.show_batch(rows = 10)
# + [markdown] colab_type="text" id="Nq-MnASS1j3q"
# ###Initializing Neural Network
#
#
# + colab_type="code" id="OJlEk4gi1j3n" colab={}
#Initializing the network
learn = tabular_learner(data, layers=[300,200, 100, 50], metrics= [rmse,r2_score])
# + [markdown] colab_type="text" id="iOTLWeZk1j3l"
#
# The above line of code will initialize a neural network with 4 layers and the number of nodes in each layer as 300,200, 100 and 50 respectively.
#
# The network will use two primary metrics for evaluation:
#
# * Root Mean Squared Error(RMSE)
# * R-Squared
#
#
# + id="hIDubrn63-VS" colab_type="code" outputId="a096e3ec-ac14-4e19-8e25-66384d49750a" colab={"base_uri": "https://localhost:8080/", "height": 1000}
#Show the complete Summary of the model
learn.summary
# + [markdown] colab_type="text" id="otdALDmE1j3k"
# ###Training The Network
# + id="h2vWHWFyU34D" colab_type="code" outputId="160692fd-21fb-4427-e927-785ca35e18ee" colab={"base_uri": "https://localhost:8080/", "height": 300}
learn.lr_find(start_lr = 1e-05,end_lr = 1e+05, num_it = 100)
learn.recorder.plot()
# + [markdown] id="H_6pgTxddHEj" colab_type="text"
# Learning rate is a hyper-parameter that controls how much the weights of the network is being adjusted with respect the loss gradient.
#
# The lr_find method helps explore the learning rate in a specified range. The graph shows the deviation in loss with respect to the learning rate.
# + colab_type="code" id="Am3r-2zR1j3U" outputId="66b12617-06cf-4701-94e4-7fe1743071ed" colab={"base_uri": "https://localhost:8080/", "height": 824}
#Fitting data and training the network
learn.fit_one_cycle(25)
# + [markdown] colab_type="text" id="-nj8YKKD1j3R"
# **The above line trains the network for 25 epochs.**
# + [markdown] id="jsxdqeB9hEwd" colab_type="text"
# ### Evaluating Performance
# + colab_type="code" id="Bbzeli2I1j3C" outputId="a70ea551-1888-48cc-b8a2-e1a20d5385b4" colab={"base_uri": "https://localhost:8080/", "height": 204}
#Display Predictions On Training Data
learn.show_results(ds_type=DatasetType.Train,rows = 5)
# + colab_type="code" id="Ho9s8tIr1j26" outputId="883dea64-3738-4fa3-8ac5-578af8bfb27a" colab={"base_uri": "https://localhost:8080/", "height": 204}
#Display Predictions On Validation Data
learn.show_results(ds_type=DatasetType.Valid)
# + colab_type="code" id="POO2TIFc1j3J" outputId="7d2ad68b-0101-44ba-a372-2909b72b6e88" colab={"base_uri": "https://localhost:8080/", "height": 102}
#Getting The Training And Validation Errors
tr = learn.validate(learn.data.train_dl)
va = learn.validate(learn.data.valid_dl)
print("The Metrics used In Evaluating The Network:", str(learn.metrics))
print("\nThe calculated RMSE & R-Squared For The Training Set :", tr[1:])
print("\nThe calculated RMSE & R-Squared For The Validation Set :", va[1:])
# + [markdown] id="Tx9o36q0CLWs" colab_type="text"
# Summary:
#
# The Root Mean Squared Error is the standard deviation of the errors/residuals. It tells us the 'Goodness Of Fit' of a model. The lower the value of RMSE the better the model.
#
# The R-Squared metric also called the coefficient of determination is used to understand the variation in the dependent variable(y) and the independent variable(X).The closer the value of R-Squared is to one, the better the model.
#
# **The above output suggests that:**
#
# **The model/network was able to attain an RMSE of 1.4678 and an R_squared of 0.9726 while training and an RMSE of 3.1737 and an R_squared of 0.9107 while Validating on the validation set.**
#
#
#
# + id="YUKxTHXkVpPv" colab_type="code" outputId="fa04c351-ec24-4f87-c8b7-e328f2a51932" colab={"base_uri": "https://localhost:8080/", "height": 283}
#Plotting The losses for training and validation
learn.recorder.plot_losses()
# + [markdown] id="geTYEndBzt4F" colab_type="text"
# The above graph shows the change is loss during the course of training the network. At the beginning of the training we can see a high loss value. As the networks learned from the data, the loss started to drop until it could no longer improve during the course of training.
#
# The validation shows a relatively consistent and low loss values.
#
#
# **Note :**
#
# The validation losses are only calculated once per epoch, whereas training losses are calculated after
#
# + id="eFwkk6DJWYRE" colab_type="code" outputId="f23ceed7-798a-4ab5-802e-d081768a747a" colab={"base_uri": "https://localhost:8080/", "height": 283}
#Plotting Momentum & Learning Rate
learn.recorder.plot_lr(show_moms=True)
# + [markdown] id="6TA6_2R11Njc" colab_type="text"
# The above plots learning rate and momentum during the course of training.
#
#
# + id="YWPxEegNWlPS" colab_type="code" outputId="b2fca3df-d25c-49d8-8b18-6e963bf3d9d0" colab={"base_uri": "https://localhost:8080/", "height": 500}
#Plotting the metrics of evaluation
learn.recorder.plot_metrics()
# + [markdown] id="xz7HGNnb8ir6" colab_type="text"
# The decreasing RMSE and increasing R-Squared depicts the Goodness Of Fit.
#
# + [markdown] id="aveEvEXHxv55" colab_type="text"
# ### Exploring Validation Predictions
# + id="RLGU4fqRXmh0" colab_type="code" colab={}
val = train_data.tail(1203)
# + id="b94vi3UnZyJ9" colab_type="code" colab={}
#Converting the prediction to DataFrame for Comparing
val_preds = learn.get_preds(ds_type=DatasetType.Valid)[0]
val_preds = [i[0] for i in val_preds.tolist()]
val['Predicted'] = val_preds
# + id="aKgGxIpCa_Gg" colab_type="code" outputId="88c79fda-8075-4158-9b3f-2defc2f77ec7" colab={"base_uri": "https://localhost:8080/", "height": 204}
val.head()
# + [markdown] id="MxWc5nVF20ax" colab_type="text"
# #### Calculating RMLSE For Validation Predictions
# + [markdown] id="efhkDuVK6iMI" colab_type="text"
# Since the metric used in the hackathon for evaluating the predictions is RMSLE , we will calculate te same for the validation predictions to evaluate our model.
# + colab_type="code" id="5VxjcGMfIQDE" outputId="a0da833d-e08a-4f86-afa8-b5ac33536183" colab={"base_uri": "https://localhost:8080/", "height": 34}
import numpy as np
Y_true = val['Price']
pred = val['Predicted']
#RMSLE
error = np.square(np.log10(pred + 1) - np.log10(Y_true +1)).mean() ** 0.5
score = 1 - error
print("SCORE For Validation : ",score)
# + [markdown] id="iDw_LeRz3KJV" colab_type="text"
# #### A Simple Analysis On Predictions
# + id="WISX6CKIWzK-" colab_type="code" outputId="b5abf55b-16c8-43bb-ab6d-c708e382c764" colab={"base_uri": "https://localhost:8080/", "height": 241}
#Plotting The Average Price For A Given Car Brand, -- Actual vs Predicted
import matplotlib.pyplot as plt
plt.figure(figsize=(30, 3))
plt.plot(val.groupby(['Brand']).mean()['Price'], linewidth = 3, )
plt.plot(val.groupby(['Brand']).mean()['Predicted'],linewidth = 5, ls = '--')
plt.title('Average Price By Brands')
plt.xlabel('Brands')
plt.ylabel('Price In Lacs')
plt.legend()
plt.show()
# + [markdown] id="c_1NzLkAQ_ao" colab_type="text"
# The above graph shows comparison of the the average actual price by Brand and the predicted price.
# + id="r_1PdfhD3xQc" colab_type="code" outputId="cef2bc78-8cfc-4eb6-db41-85bdc4491358" colab={"base_uri": "https://localhost:8080/", "height": 34}
print("R-Squared For Validation Set : ", r2_score(learn.get_preds(ds_type=DatasetType.Valid)[0], learn.get_preds(ds_type=DatasetType.Valid)[1]))
# + id="HeeVpQ_mzF6t" colab_type="code" outputId="ea81b945-c738-4e2e-9211-a3cf3ea4c395" colab={"base_uri": "https://localhost:8080/", "height": 51}
print("\nRMSE For Validation Set : ",root_mean_squared_error(learn.get_preds(ds_type=DatasetType.Valid)[0], learn.get_preds(ds_type=DatasetType.Valid)[1]))
# + [markdown] id="7qFsgJtBWgG3" colab_type="text"
# ###Predicting For Test Data
# + [markdown] id="q11vuGb7Vkpp" colab_type="text"
# ####Predicting For A Single Row OF Test Set
# + id="hiyDn-uLa6id" colab_type="code" outputId="9b4a0b6c-74d2-446a-d076-8747d3717c43" colab={"base_uri": "https://localhost:8080/", "height": 255}
#Test set data for row 0
test_data.iloc[0]
# + id="8I6LCzrmbO0z" colab_type="code" outputId="8a99d4e6-07e4-4cf3-e82f-528e4c78fe51" colab={"base_uri": "https://localhost:8080/", "height": 34}
#Prediction in float for Test set data for row 0
float(learn.predict(test_data.iloc[0])[1])
# + [markdown] id="HhrV-irCopGk" colab_type="text"
# ####Predicting For Test Set
# + id="hIzD49jsZ8R4" colab_type="code" colab={}
test_predictions = learn.get_preds(ds_type=DatasetType.Test)[0]
# + id="b1DXjHPQ--EH" colab_type="code" colab={}
#Converting the tensor output to a list of predicted values
test_predictions = [i[0] for i in test_predictions.tolist()]
# + id="qMaeW6gI_jDH" colab_type="code" colab={}
#Converting the prediction to . a dataframe
test_predictions = pd.DataFrame(test_predictions, columns = ['Price'])
# + id="KFFvii6ognQn" colab_type="code" colab={}
#Writing the predictions to an excel file.
predictions.to_excel("Fast_ai_solution.xlsx", index = False)
# + [markdown] id="hPPigGmAos3r" colab_type="text"
# **Submit the above file [here](https://www.machinehack.com/course/predicting-the-costs-of-used-cars-hackathon-by-imarticus/leaderboard) to find out your score. Good Luck!**
#
|
A_HANDS-ON_GUIDE_TO_REGRESSION_WITH_FASTAI.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# load and summarize the dataset
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
# generate regression dataset
X, y = make_regression(n_samples=1000, n_features=100, n_informative=10, noise=0.1,
random_state=1)
# split into train and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=1)
# summarize
print('Train', X_train.shape, y_train.shape)
print('Test', X_test.shape, y_test.shape)
# example of correlation feature selection for numerical data
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import f_regression
from matplotlib import pyplot
# feature selection
def select_features(X_train, y_train, X_test):
# configure to select all features
fs = SelectKBest(score_func=f_regression, k='all')
# learn relationship from training data
fs.fit(X_train, y_train)
# transform train input data
X_train_fs = fs.transform(X_train)
# transform test input data
X_test_fs = fs.transform(X_test)
return X_train_fs, X_test_fs, fs
# load the dataset
X, y = make_regression(n_samples=1000, n_features=100, n_informative=10, noise=0.1,
random_state=1)
# split into train and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=1)
# feature selection
X_train_fs, X_test_fs, fs = select_features(X_train, y_train, X_test)
# what are scores for the features
for i in range(len(fs.scores_)):
print('Feature %d: %f' % (i, fs.scores_[i]))
# plot the scores
pyplot.bar([i for i in range(len(fs.scores_))], fs.scores_)
pyplot.show()
# example of mutual information feature selection for numerical input data
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import mutual_info_regression
from matplotlib import pyplot
# feature selection
def select_features(X_train, y_train, X_test):
# configure to select all features
fs = SelectKBest(score_func=mutual_info_regression, k='all')
# learn relationship from training data
fs.fit(X_train, y_train)
# transform train input data
X_train_fs = fs.transform(X_train)
# transform test input data
X_test_fs = fs.transform(X_test)
return X_train_fs, X_test_fs, fs
# load the dataset
X, y = make_regression(n_samples=1000, n_features=100, n_informative=10, noise=0.1,
random_state=1)
# split into train and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=1)
# feature selection
X_train_fs, X_test_fs, fs = select_features(X_train, y_train, X_test)
# what are scores for the features
for i in range(len(fs.scores_)):
print('Feature %d: %f' % (i, fs.scores_[i]))
# plot the scores
pyplot.bar([i for i in range(len(fs.scores_))], fs.scores_)
pyplot.show()
# evaluation of a model using all input features
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_absolute_error
# load the dataset
X, y = make_regression(n_samples=1000, n_features=100, n_informative=10, noise=0.1,
random_state=1)
# split into train and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=1)
# fit the model
model = LinearRegression()
model.fit(X_train, y_train)
# evaluate the model
yhat = model.predict(X_test)
# evaluate predictions
mae = mean_absolute_error(y_test, yhat)
print('MAE: %.3f' % mae)
# evaluation of a model using 10 features chosen with correlation
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import f_regression
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_absolute_error
# feature selection
def select_features(X_train, y_train, X_test):
# configure to select a subset of features
fs = SelectKBest(score_func=f_regression, k=10)
# learn relationship from training data
fs.fit(X_train, y_train)
# transform train input data
X_train_fs = fs.transform(X_train)
# transform test input data
X_test_fs = fs.transform(X_test)
return X_train_fs, X_test_fs, fs
# load the dataset
X, y = make_regression(n_samples=1000, n_features=100, n_informative=10, noise=0.1,
random_state=1)
# split into train and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=1)
# feature selection
X_train_fs, X_test_fs, fs = select_features(X_train, y_train, X_test)
# fit the model
model = LinearRegression()
model.fit(X_train_fs, y_train)
# evaluate the model
yhat = model.predict(X_test_fs)
# evaluate predictions
mae = mean_absolute_error(y_test, yhat)
print('MAE: %.3f' % mae)
# evaluation of a model using 88 features chosen with correlation
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import f_regression
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_absolute_error
# feature selection
def select_features(X_train, y_train, X_test):
# configure to select a subset of features
fs = SelectKBest(score_func=f_regression, k=88)
# learn relationship from training data
fs.fit(X_train, y_train)
# transform train input data
X_train_fs = fs.transform(X_train)
# transform test input data
X_test_fs = fs.transform(X_test)
return X_train_fs, X_test_fs, fs
# load the dataset
X, y = make_regression(n_samples=1000, n_features=100, n_informative=10, noise=0.1,
random_state=1)
# split into train and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=1)
# feature selection
X_train_fs, X_test_fs, fs = select_features(X_train, y_train, X_test)
# fit the model
model = LinearRegression()
model.fit(X_train_fs, y_train)
# evaluate the model
yhat = model.predict(X_test_fs)
# evaluate predictions
mae = mean_absolute_error(y_test, yhat)
print('MAE: %.3f' % mae)
# evaluation of a model using 88 features chosen with mutual information
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import mutual_info_regression
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_absolute_error
# feature selection
def select_features(X_train, y_train, X_test):
# configure to select a subset of features
fs = SelectKBest(score_func=mutual_info_regression, k=88)
# learn relationship from training data
fs.fit(X_train, y_train)
# transform train input data
X_train_fs = fs.transform(X_train)
# transform test input data
X_test_fs = fs.transform(X_test)
return X_train_fs, X_test_fs, fs
# load the dataset
X, y = make_regression(n_samples=1000, n_features=100, n_informative=10, noise=0.1,
random_state=1)
# split into train and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=1)
# feature selection
X_train_fs, X_test_fs, fs = select_features(X_train, y_train, X_test)
# fit the model
model = LinearRegression()
model.fit(X_train_fs, y_train)
# evaluate the model
yhat = model.predict(X_test_fs)
# evaluate predictions
mae = mean_absolute_error(y_test, yhat)
print('MAE: %.3f' % mae)
# compare different numbers of features selected using mutual information
from sklearn.datasets import make_regression
from sklearn.model_selection import RepeatedKFold
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import mutual_info_regression
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import Pipeline
from sklearn.model_selection import GridSearchCV
# define dataset
X, y = make_regression(n_samples=1000, n_features=100, n_informative=10, noise=0.1,
random_state=1)
# define the evaluation method
cv = RepeatedKFold(n_splits=10, n_repeats=3, random_state=1)
# define the pipeline to evaluate
model = LinearRegression()
fs = SelectKBest(score_func=mutual_info_regression)
pipeline = Pipeline(steps=[('sel',fs), ('lr', model)])
# define the grid
grid = dict()
grid['sel__k'] = [i for i in range(X.shape[1]-20, X.shape[1]+1)]
# define the grid search
search = GridSearchCV(pipeline, grid, scoring='neg_mean_absolute_error', n_jobs=-1, cv=cv)
# perform the search
results = search.fit(X, y)
# summarize best
print('Best MAE: %.3f' % results.best_score_)
print('Best Config: %s' % results.best_params_)
# summarize all
means = results.cv_results_['mean_test_score']
params = results.cv_results_['params']
for mean, param in zip(means, params):
print('>%.3f with: %r' % (mean, param))
# compare different numbers of features selected using mutual information
from numpy import mean
from numpy import std
from sklearn.datasets import make_regression
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedKFold
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import mutual_info_regression
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import Pipeline
from matplotlib import pyplot
# define dataset
X, y = make_regression(n_samples=1000, n_features=100, n_informative=10, noise=0.1,
random_state=1)
# define number of features to evaluate
num_features = [i for i in range(X.shape[1]-19, X.shape[1]+1)]
# enumerate each number of features
results = list()
for k in num_features:
# create pipeline
model = LinearRegression()
fs = SelectKBest(score_func=mutual_info_regression, k=k)
pipeline = Pipeline(steps=[('sel',fs), ('lr', model)])
# evaluate the model
cv = RepeatedKFold(n_splits=10, n_repeats=3, random_state=1)
scores = cross_val_score(pipeline, X, y, scoring='neg_mean_absolute_error', cv=cv,
n_jobs=-1)
results.append(scores)
# summarize the results
print('>%d %.3f (%.3f)' % (k, mean(scores), std(scores)))
# plot model performance for comparison
pyplot.boxplot(results, labels=num_features, showmeans=True)
pyplot.show()
|
Select Features for Numerical Output.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# Dated: 30-3-18
#
# CNN Tutorial with adam and using Data Augmentation
#
# Dataset-- MNIST
#
# In this tutorial, i am going to show simple CNN network working with data augmentation and matplot display for images
#
# Data Augmentation is done for the purpose of creating dataset(mainly images more variety)...
#
# It can helpful for creating a dataset with much more richer images
#
# The model is trained on small amt of data only....
# Installing Dependencies
import keras.backend as K
K._backend='tensorflow' if K.backend() else print("Requires no change in backend")
#Basic Necessary libraries
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# %matplotlib inline
np.random.seed(124) #for reproducibility purpose
# +
#Installing Main Libraries
from keras.datasets import mnist
from keras.models import Sequential
from keras.layers import Conv2D,MaxPooling2D,GlobalAveragePooling2D
from keras.layers import Dense,Dropout,Activation,Flatten
from keras.layers.normalization import BatchNormalization
from keras.layers.advanced_activations import LeakyReLU
from keras.optimizers import adam
from keras.utils import np_utils
from keras.preprocessing.image import ImageDataGenerator
# -
#Creating Training and Testing data
(trainX,trainY),(testX,testY)=mnist.load_data()
#Showing Mnist Image of 5 digit
plt.imshow(trainX[0],cmap='gray')
plt.xticks([])
plt.yticks([])
plt.title("Class: "+str(trainY[0]))
plt.show()
print(trainX[0].shape)
# +
#Preprocessing Input Data i.e X
trainX=trainX.reshape(trainX.shape[0],28,28,1)
testX=testX.reshape(testX.shape[0],28,28,1)
print(trainX.shape)
trainX=trainX.astype('float32')
testX=testX.astype('float32')
trainX/=255
testX/=255
print(trainX.shape,testX.shape,trainY.shape,testY.shape)
# -
#Preprocessing Output label i.e. Y
num_class=10
print(trainY.shape)
trainY=np_utils.to_categorical(trainY,num_class)
testY=np_utils.to_categorical(testY,num_class)
print(trainY.shape,testY.shape)
# ### Creating Convolution Architecture
# # 1.Convolution
# # 2.Pooling
# # 3.Dropout
# Repeat step 1,2,3 to add more convolution layers in network
#
# # 4.Fully Connected layer
# Repeat to add more feed forward layers
#
# # 5.Flatten
# # 6.Classify Sample
# Creating Architecture for CNN Model
# +
#Model Creation phase
model=Sequential()
model.add(Conv2D(32,(3,3),input_shape=(28,28,1)))
model.add(Activation('relu'))
BatchNormalization(axis=-1)
model.add(Conv2D(32,(3,3)))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2,2)))
BatchNormalization(axis=-1)
model.add(Conv2D(64,(3,3)))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2,2)))
model.add(Flatten())
#Creating Fully Connected Network
model.add(Dense(512))
model.add(Activation('relu'))
BatchNormalization(axis=-1)
model.add(Dense(256))
BatchNormalization(axis=-1)
model.add(Dropout(0.5))
model.add(Dense(10))
model.add(Activation('softmax'))
#compilation phase
#finding loss and backpropagating
model.compile(loss='categorical_crossentropy',optimizer="rmsprop",metrics=['accuracy'])
# -
model.summary()
# +
#Data Augmentation for creating rich datset
traingen = ImageDataGenerator(rotation_range=8, width_shift_range=0.08, shear_range=0.3,
height_shift_range=0.08, zoom_range=0.08) #for training data augmentation ....properties are defined
testgen=ImageDataGenerator() #for test data we don't need anytype of augmentation
# -
#defining Genrator training phase
train_generator=traingen.flow(trainX,trainY,batch_size=64)
test_generator=testgen.flow(testX,testY,batch_size=64)
# # Training Phase
# +
data=model.fit_generator(train_generator,steps_per_epoch=60000//200,
epochs=3,validation_data=test_generator,validation_steps=10000//200)
# -
#Prediciting Accuracy
score=model.evaluate(testX,testY)
print("Loss: {0} \t Accuracy: {1}%".format(round(score[0],5),round(score[1],3)*100))
|
CNN_MNIST-Part-1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Underactuated cartpole control with iLQR, MPPI
# This example shows model predictive control to swing up the underactuated cartpole.
#
# 
#
# ## Problem
#
# **Model.** The "cartpole" is a free pendulum on a linear cart. The input to the system is a force on the cart $f$.
#
# $$
# m l \ddot{p} \cos(\theta) + m l^2 \ddot{\theta} - m g l \sin(\theta) = 0 \\
# (m + m_c) \ddot{p} + m l \ddot{\theta} \cos(\theta) - m l \dot{\theta}^2 \sin(\theta) = f
# $$
# where $\theta = 0$ is the angle of the pendulum when completely upright, and $p$ is the position of the cart. The state of the system is $x = (p, \theta, \dot{p}, \dot{\theta})^\top$. Parameters are the mass of the pendulum at the tip $m = 0.15$ kg, length of the pendulum $l = 0.75$ m, acceleration due to gravity $g = 9.8$ m/s , and the mass of the cart $m_c=1$ kg.
#
# **Control.** The objective is to move the cart so that the pendulum will stand up vertically. This is a classic controls and RL problem and is a typical benchmark test for new algorithms. We use the quadratic cost function
#
# $$
# J = \sum_{i=1}^{N} x_i^\top Q x_i + \sum_{i=1}^{N-1} r u_i^2
# $$
#
# where $Q = \text{diag}(1.25, 6, 12, 0.25)$ is chosen to drive the system states 0, and the penalty $r = 0.01$ tradeoffs the input magnitude.
#
# **Comparison to MPPI.** The video above shows iLQR which works well for this problem. Examining MPPI (sampling-based control) in the video below, the algorithm seems to find a control that achieves the desired swing up behavior and temporarily stabilizes the system, however if the algorithm is left to run long enough, the system destabilizes and the controller is unable to maintain the upright posture. This is believed due to a deficiency in the sampling approach as the noise in the control is amplified to attempt to maintain stability.
#
# 
# ## Example
#
# To run the example, build and install the C++ and Python libraries from the main README instructions. Start the docker container.
# ```
# # Run the experiment
# # cd /libsia/bin
# ./example-cartpole --datafile /libsia/data/cartpole.csv --algorithm ilqr
#
# # Run the python script
# # cd /libsia/examples/cartpole
# python cartpole.py --help
# python cartpole.py --datafile /libsia/data/cartpole.csv
# ```
# +
# This example imports data generated by the executable
from cartpole import plot_cartpole_trajectory
# This is the same as running the python script
plot_cartpole_trajectory(datafile="/libsia/data/cartpole.csv",
animate=False,
trace=True,
video_name="cartpole-animated.mp4",
dpi=150,
fps=30,
clean_axes=True)
# -
# ## Learning from expert demonstration
#
# [1] <NAME> paper
# [2] P. Owan thesis
#
# Assume now we don't know the cartpole model. We need to learn a model from data. We use GMR
# $$
# \mathbb{E}[x_{k+1}] = f(x_k, u_k)
# $$
#
# State dimension is too high, compress it.
# $$
# z = \xi(x)
# $$
#
# Instead we do regression on the reduced space
# $$
# z_{k+1} = \hat{f}(z_k, u_k)
# $$
#
# Recover the state by plugging in to model
# $$
# x_{k+1} = \xi^{-1}(\hat{f}(\xi(x_k), u_k))
# $$
# +
import subprocess
num_trials = 20
datafiles = ["/libsia/data/cartpole-{}.csv".format(i) for i in range(num_trials)]
# Peform n trials with an expert policy
for datafile in datafiles:
print("Running case {}".format(datafile))
subprocess.call(["/libsia/bin/example-cartpole",
"--measurement_noise",
"1e-6",
"--process_noise",
"1e-6",
"--datafile",
datafile])
# +
import pandas as pd
import numpy as np
from sklearn.decomposition import PCA
# Import plotting helpers
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_theme(style="whitegrid")
# Time step at which the data was collected
dt = 0.02
# Load data and perform some analysis
df = pd.DataFrame()
for datafile in datafiles:
df = df.append(pd.read_csv(datafile))
t = df["t"]
x = df[["p", "a", "v", "w"]].values
u = df["f"].values
# Run PCA on the state
n = 2
pca = PCA(n_components=n)
z = pca.fit_transform(x)
pca_pct = np.sum(pca.explained_variance_ratio_)
print("PCA with n={0:d} encodes {1:.4f}% of data".format(n, pca_pct))
# Stack the inputs and ouputs into X
uk = np.reshape(u[:-1], (len(u[:-1]), 1))
zk = z[:-1, :]
zkp1 = z[1:, :]
X = np.hstack((zk, uk, zkp1))
# Run GMM
import pysia as sia
gmm = sia.GMM(X.T, K=3, regularization=1e-6)
# Extract the means for visualization
means = np.zeros((gmm.numClusters(), gmm.dimension()))
for i in range(gmm.numClusters()):
means[i,:] = gmm.gaussian(i).mean()
# Run GMR to condition z_kp1 on zk, uk
gmr = sia.GMR(gmm, input_indices=[0, 1, 2], output_indices=[3, 4])
# +
# Plot the probabilities
f, ax = plt.subplots(nrows=n, ncols=n+1, figsize=(15, 8))
sns.despine(f, left=True, bottom=True)
for i in range(n):
for j in range(n):
ax[i, j].plot(z[:-1, j], z[1:, i], ".k", ms=1, label="Data")
ax[i, j].plot(means[:, j], means[:, i+3], ".r", ms=15, label="GMM")
ax[i, j].set_ylabel("z{}_kp1".format(i))
ax[i, j].set_xlabel("z{}_k".format(j))
ax[i, j].legend()
ax[i, n].plot(u[:-1], z[1:, i], ".k", ms=1)
ax[i, n].plot(means[:, 2], means[:, i+3], ".r", ms=15)
ax[i, n].set_ylabel("z{}_kp1".format(i))
ax[i, n].set_xlabel("u_k".format(j))
# +
# Plot the vector field given inputs u
f, ax = plt.subplots(nrows=1, ncols=1, figsize=(12, 12))
sns.despine(f, left=True, bottom=True)
ax.quiver(X[:, 0],
X[:, 1],
(X[:, 3]-X[:, 0])/dt,
(X[:, 4]-X[:, 1])/dt,
color='b',
headwidth=1.5)
Y = np.zeros((len(X), 2))
for i in range(len(X)):
Y[i, :] = gmr.predict(X[i,:3]).mean()
ax.quiver(X[:, 0],
X[:, 1],
(Y[:, 0]-X[:, 0])/dt,
(Y[:, 1]-X[:, 1])/dt,
color='r',
headwidth=1.5);
|
examples/cartpole/cartpole.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd, numpy as np
import matplotlib.pyplot as plt
# %matplotlib inline
ro=['5765358043206','9812808043220','9576658043223','1699958043227','7225068043228','265208043229']
hu=['8073718043234','2087988043232','6247548043235']
p='C:/Users/csala/Onedrive - Lancaster University/Datarepo/szekelydata/klima/high_res/'
stations=[]
for i in ro:
stations.append(pd.read_csv(p+'raw/ro/'+i+'stn+.txt',delimiter= '+',skiprows=2,header=None))
print(i)
station=pd.concat(stations)
station=station.drop_duplicates()
station[2]=station[2].str.strip()
station[3]=station[3].str.strip()
# **!!! 16G memory required at least, 64G recommended**
dfs=[]
for i in ro:
df=pd.read_csv(p+'raw/ro/'+i+'dat.txt',delimiter= '\s+')
dfs.append(df)
print(i)
dfz=pd.concat(dfs)
dfs=None #free memory
df=None #free memory
dfz.head()
# +
#!!!! DO NOT DO THIS
#dfz=dfz.drop_duplicates()
# -
dfz['time']=pd.to_datetime(dfz['YR--MODAHRMN'],format='%Y%m%d%H%M')
dfz['year']=dfz['time'].dt.year
dfz['month']=dfz['time'].dt.month
dfz['day']=dfz['time'].dt.day
dfz['hour']=dfz['time'].dt.hour
#keep only months with at least 6 days to avoid anomalies (20%)
filt=dfz.groupby(['USAF','year','month'])[['day']].nunique()
filt2=filt[filt>5].dropna()
#keep only years with at least 3 months to avoid anomalies (20%)
filt3=filt2.reset_index().groupby(['USAF','year'])[['month']].nunique()
filt4=filt3[filt3>3].dropna()
filt4.head()
filt4.index.unique(0)
for i in filt4.index.unique(0):
d=df_avg2.loc[i].loc[filt4.loc[i].index.unique()]
dfz[i]=d
d.to_csv('data/'+str(i)+'.csv')
print(i)
# Load
import os
arr = os.listdir('data/')
for i in arr:
if i not in ['all.csv']:
dfz[i[:-4]]=pd.read_csv('data/'+i)
print(i)
stationc=station.set_index(0)[2]
for z in dfz:
dfz[z]=dfz[z].reset_index()
stationx={}
for z in dfz:
stationx[stationc.loc[int(z)]]={'id':z,'yrs':len(dfz[z]['year'].unique())}
dq=pd.DataFrame(stationx).T.reset_index().set_index('yrs').sort_index(ascending=False)
dq.head(5)
dds=[]
indicator='temp_avg'
for a in dq.head(500)['id'].values:
dw=dfz[a]
tmean=dw.groupby(['month','hour']).mean()[[indicator]]
tmean.columns=['temp_mean']
dw=dw.loc[1980:]
dw=dw.loc[:2010]
tmean80=dw.groupby(['month','hour']).mean()[[indicator]]
tmean80.columns=['temp_mean80']
dc=dfz[a].groupby(['year','month','hour']).mean()[[indicator]].join(tmean).join(tmean80)
dc['temp_delta']=dc[indicator]-dc['temp_mean']
dc['temp_delta80']=dc[indicator]-dc['temp_mean80']
dd=dc.groupby(['year']).mean()
dd=np.round(dd,1)
dd['varos']=stationc[int(a)]
dd['value']=1
dds.append(dd)
ddb=pd.concat(dds)
ddb.to_csv('stripes/geo.csv')
dgeo=ddb.reset_index().set_index('varos').join(station.set_index(2))
dgeo[dgeo[3]=='HUNGARY'].to_csv('stripes/geotest.csv')
dds=[]
indicator='temp_avg'
# clean_months=[1,4,7,10]
clean_months=[1,2,3,4,5,6,7,8,9,10,11,12]
# clean_hours=[0,6,12,18]
clean_hours=[0,3,6,12,15,18,21]
# clean_hours=[6]
clean_slice=[(i,j) for i in clean_months for j in clean_hours]
for a in dq['id'].values:
dw=dfz[a].groupby(['month','hour']).mean().loc[clean_slice]
if dw[indicator].count()==len(clean_hours)*len(clean_months):
dc=dfz[a].set_index(['month','hour']).loc[clean_slice].reset_index()
dx=dc.groupby(['year']).nunique()
full_data_years=dx[((dx['month']==len(clean_months))&(dx['hour']==len(clean_hours)))].index
tmean=dw.groupby(['month','hour']).mean()[[indicator]]
tmean.columns=['temp_mean']
dw=dfz[a].set_index(['month','hour']).loc[clean_slice].reset_index().set_index(['year']).loc[full_data_years].reset_index()
tmean_full_years=dw.groupby(['month','hour']).mean()[[indicator]]
tmean_full_years.columns=['temp_mean_full_years']
dc=dc.groupby(['year','month','hour']).mean()[[indicator]].loc[full_data_years].join(tmean).join(tmean_full_years)
dc['temp_delta']=dc[indicator]-dc['temp_mean']
dc['temp_delta_full_years']=dc[indicator]-dc['temp_mean_full_years']
if ((2018 in dw['year'].unique()) and (2010 in dw['year'].unique())):
tmean_last10=dw[dw['year']>2009].groupby(['month','hour']).mean()[[indicator]]
tmean_last10.columns=['temp_mean_last10']
dc=dc.join(tmean_last10)
dc['temp_delta_last10']=dc[indicator]-dc['temp_mean_last10']
dd=dc.groupby(['year']).mean()
dd=np.round(dd,1)
dd['varos']=stationc[int(a)]
dd['value']=1
dds.append(dd)
ddb=pd.concat(dds)
dgeo=ddb.reset_index().set_index('varos').join(station.set_index(2))
dgeo[dgeo[3]=='HUNGARY'].to_csv('stripes/hu.csv')
dgeo[dgeo[3]=='ROMANIA'].to_csv('stripes/ro.csv')
dgeo.to_csv('stripes/huro.csv')
dds=[]
indicator='temp_avg'
clean_months=[1,5,9]
# clean_months=[1,2,3,4,5,6,7,8,9,10,11,12]
# clean_hours=[0,6,12,18]
# clean_hours=[0,3,6,12,15,18,21]
clean_hours=[6]
clean_slice=[(i,j) for i in clean_months for j in clean_hours]
for a in dq['id'].values:
dw=dfz[a].groupby(['month','hour']).mean().loc[clean_slice]
if dw[indicator].count()==len(clean_hours)*len(clean_months):
dc=dfz[a].set_index(['month','hour']).loc[clean_slice].reset_index()
dx=dc.groupby(['year']).nunique()
full_data_years=dx[((dx['month']==len(clean_months))&(dx['hour']==len(clean_hours)))].index
tmean=dw.groupby(['month','hour']).mean()[[indicator]]
tmean.columns=['temp_mean']
dw=dfz[a].set_index(['month','hour']).loc[clean_slice].reset_index().set_index(['year']).loc[full_data_years].reset_index()
tmean_full_years=dw.groupby(['month','hour']).mean()[[indicator]]
tmean_full_years.columns=['temp_mean_full_years']
dc=dc.groupby(['year','month','hour']).mean()[[indicator]].loc[full_data_years].join(tmean).join(tmean_full_years)
dc['temp_delta']=dc[indicator]-dc['temp_mean']
dc['temp_delta_full_years']=dc[indicator]-dc['temp_mean_full_years']
if ((2018 in dw['year'].unique()) and (2010 in dw['year'].unique())):
tmean_last10=dw[dw['year']>2009].groupby(['month','hour']).mean()[[indicator]]
tmean_last10.columns=['temp_mean_last10']
dc=dc.join(tmean_last10)
dc['temp_delta_last10']=dc[indicator]-dc['temp_mean_last10']
dd=dc.groupby(['year']).mean()
dd=np.round(dd,1)
dd['varos']=stationc[int(a)]
dd['value']=1
dds.append(dd)
ddb=pd.concat(dds)
dgeo=ddb.reset_index().set_index('varos').join(station.set_index(2))
dgeo[dgeo[3]=='HUNGARY'].to_csv('stripes/hu_mini.csv')
dgeo[dgeo[3]=='ROMANIA'].to_csv('stripes/ro_mini.csv')
dgeo.to_csv('stripes/huro_mini.csv')
station[station[2]=='DEBRECEN']
namer={"AGARD":"Agárd",
"AUREL VLAICU":"Bukarest - Aurel Vlaicu",
"BACAU":"Bákó",
"BAJA":"Baja",
"BEKESCSABA":"Békéscsaba",
"BOBOC AIR BASE":"Boboc légi bázis",
"BOTOSANI":"Botoșani",
"BUDAPEST/PESTSZENTLORINC":"Budapest - Pestszentlőrinc",
"BUZAU":"Buzău",
"CALARASI":"Călărasi",
"CAMPIA TURZII":"Aranyosgyéres",
"CARANSEBES":"Káránszebes",
"CATALOI":"Tulcea - Cataloi",
"CEAHLAU TOACA":"Csalhó",
"CLUJ NAPOCA":"Kolozsvár",
"CONSTANTA":"Konstanca",
"DEBRECEN":"Debrecen",
"DEVA":"Déva",
"DROBETA TURNU SEVERIN":"Szörényvár",
"EGER":"Eger",
"FERIHEGY":"Budapest - Ferihegy",
"GALATI":"Galac",
"GYOR":"Győr",
"HENRI COANDA":"Bukarest - Henri Coandă",
"IASI":"Jászvásár",
"JOSVAFO":"Jósvafő",
"KECSKEMET":"Kecskemét",
"KEKESTETO":"Kékestető",
"MIERCUREA CIUC":"Csíkszereda",
"<NAME>":"Konstanca - <NAME>",
"MISKOLC":"Miskolc",
"MOSONMAGYAROVAR":"Mosonmagyaróvár",
"NAGYKANIZSA":"Nagykanizsa",
"NYIREGYHAZA":"Nyíregyháza",
"OCNA SUGATAG":"Aknasugatag",
"ORADEA":"Nagyvárad",
"PAKS":"Paks",
"PAPA":"Pápa",
"PECS SOUTH":"Pécs",
"POROSZLO":"Poroszló",
"<NAME>":"<NAME>",
"ROSIORII DE VEDE":"Roșiorii De Vede",
"SARMELLEK":"Balaton - Sármellék",
"SAT<NAME>":"Szatmár",
"SIBIU":"Nagyszeben",
"SIOFOK":"Siófok",
"SOPRON":"Sopron",
"STEFAN CEL MARE":"Suceava - Ștefan C<NAME>",
"SULINA":"Sulina",
"SZECSENY":"Szécsény",
"SZEGED (AUT)":"Szeged",
"SZENTGOTTHARD/FARKASFA":"Szentgotthárd",
"SZOLNOK":"Szolnok",
"SZOMBATHELY ARPT / VAS":"Szombathely",
"TAT":"Tát",
"TATA":"Tata",
"TAUTII MAGHERAUS":"Nagybánya - Miszmogyorós",
"TRAIAN VUIA":"Temesvár - Traian Vuia",
"VARFU OMU":"Bucsecs - Omu csúcs",
"VESZPREM/SZENTKIRALYSZABADJA":"Veszprém",
"VIDRASAU":"Marosvásárhely - Vidrátszeg",
"ZAHONY":"Záhony",
"ZALAEGERSZEG/ANDRASHIDA":"Zalaegerszeg"}
import json
open('namer.json','w').write(json.dumps(namer))
df=df.replace({'******':np.nan,'*****':np.nan,'****':np.nan,'***':np.nan,'**':np.nan,'*':np.nan})
df['time']=pd.to_datetime(df['YR--MODAHRMN'],format='%Y%m%d%H%M')
#df=df[['time','USAF','SPD','TEMP','PCP06','SD','MW','AW','W']]
df['TEMP']=(pd.to_numeric(df['TEMP'], errors='coerce')-32)*5/9
df['SPD']=pd.to_numeric(df['SPD'], errors='coerce')*1.61
df['PCP06']=pd.to_numeric(df['PCP06'], errors='coerce')*25.4
df['SD']=pd.to_numeric(df['SD'], errors='coerce')*25.4
dfs['time']=pd.to_datetime(df['YR--MODAHRMN'],format='%Y%m%d%H%M')
dfs['year']=dfs['time'].dt.year
dfs['month']=dfs['time'].dt.month
dfs['day']=dfs['time'].dt.day
dfs['hour']=dfs['time'].dt.hour
|
nepi/archive/1a_parser_high_res_climate_data.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .jl
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Julia 0.5.0
# language: julia
# name: julia-0.5
# ---
include("lin_int2.jl")
println(readstring(`cmd /c type lin_int2.jl`))
# +
#=
Solving the optimal growth problem via value function iteration.
@author : <NAME> <<EMAIL>>
@date : 2014-07-05
References
----------
Simple port of the file quantecon.models.optgrowth
http://quant-econ.net/jl/dp_intro.html
=#
#=
This type defines the primitives representing the growth model. The
default values are
f(k) = k**alpha, i.e, Cobb-Douglas production function
u(c) = ln(c), i.e, log utility
See the constructor below for details
=#
using Plots
using Optim
"""
Neoclassical growth model
##### Fields
- `f::Function` : Production function
- `bet::Real` : Discount factor in (0, 1)
- `u::Function` : Utility function
- `grid_max::Int` : Maximum for grid over savings values
- `grid_size::Int` : Number of points in grid for savings values
- `grid::LinSpace{Float64}` : The grid for savings values
"""
type GrowthModel
f::Function
bet::Float64
u::Function
grid_max::Int
grid_size::Int
grid::LinSpace{Float64}
end
default_f(k) = k^0.65
default_u(c) = log(c)
"""
Constructor of `GrowthModel`
##### Arguments
- `f::Function(k->k^0.65)` : Production function
- `bet::Real(0.95)` : Discount factor in (0, 1)
- `u::Function(log)` : Utility function
- `grid_max::Int(2)` : Maximum for grid over savings values
- `grid_size::Int(150)` : Number of points in grid for savings values
"""
function GrowthModel(f=default_f, bet=0.95, u=default_u, grid_max=2,
grid_size=150)
grid = linspace(1e-6, grid_max, grid_size)
return GrowthModel(f, bet, u, grid_max, grid_size, grid)
end
"""
Apply the Bellman operator for a given model and initial value.
##### Arguments
- `g::GrowthModel` : Instance of `GrowthModel`
- `w::Vector`: Current guess for the value function
- `out::Vector` : Storage for output.
- `;ret_policy::Bool(false)`: Toggles return of value or policy functions
##### Returns
None, `out` is updated in place. If `ret_policy == true` out is filled with the
policy function, otherwise the value function is stored in `out`.
"""
function bellman_operator!(g::GrowthModel, w::Vector, out::Vector;
ret_policy::Bool=false)
# Apply linear interpolation to w
Aw = lin_inter(g.grid, w)
for (i, k) in enumerate(g.grid)
objective(c) = - g.u(c) - g.bet * Aw(g.f(k) - c)
res = optimize(objective, 1e-6, g.f(k))
c_star = res.minimum
if ret_policy
# set the policy equal to the optimal c
out[i] = c_star
else
# set Tw[i] equal to max_c { u(c) + beta w(f(k_i) - c)}
out[i] = - objective(c_star)
end
end
return out
end
function bellman_operator(g::GrowthModel, w::Vector;
ret_policy::Bool=false)
out = similar(w)
bellman_operator!(g, w, out, ret_policy=ret_policy)
end
"""
Extract the greedy policy (policy function) of the model.
##### Arguments
- `g::GrowthModel` : Instance of `GrowthModel`
- `w::Vector`: Current guess for the value function
- `out::Vector` : Storage for output
##### Returns
None, `out` is updated in place to hold the policy function
"""
function get_greedy!(g::GrowthModel, w::Vector, out::Vector)
bellman_operator!(g, w, out, ret_policy=true)
end
get_greedy(g::GrowthModel, w::Vector) = bellman_operator(g, w, ret_policy=true)
gm = GrowthModel()
alpha = 0.65
bet = gm.bet
grid_max = gm.grid_max
grid_size = gm.grid_size
grid = gm.grid
ab = alpha * gm.bet
c1 = (log(1 - ab) + log(ab) * ab / (1 - ab)) / (1 - gm.bet)
c2 = alpha / (1 - ab)
v_star(k) = c1 .+ c2 .* log(k)
function main(n::Int=35)
w_init = 5 .* log(grid) .- 25 # An initial condition -- fairly arbitrary
w = copy(w_init)
ws = []
colors = []
for i=1:n
w = bellman_operator(gm, w)
push!(ws, w)
push!(colors, RGBA(0, 0, 0, i/n))
end
p = plot(gm.grid, w_init, color=:green, linewidth=2, alpha=0.6,
label="initial condition")
plot!(gm.grid, ws, color=colors', label="", linewidth=2)
plot!(gm.grid, v_star(gm.grid), color=:blue, linewidth=2, alpha=0.8,
label="true value function")
plot!(ylims=(-40, -20), xlims=(minimum(gm.grid), maximum(gm.grid)))
return p
end
# -
main()
|
A Simple Optimal Growth Model Interpolation2.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [default]
# language: python
# name: python3
# ---
import tensorflow as tf
import numpy as np
import pandas as pd
logit_list = [0.1, 0.5, 0.4]
label_list = [0]
logits = tf.Variable(np.array([logit_list]), dtype=tf.float32, name="logits")
labels = tf.Variable(np.array(label_list), dtype=tf.int32, name="labels")
result = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=labels, logits=logits, name='result')
init = tf.global_variables_initializer()
with tf.Session() as sess:
init.run()
ret = sess.run(result)
print(ret)
# +
# Next, I am trying to implement softmax cross entropy my self
# reference: https://deepnotes.io/softmax-crossentropy
# reference: https://ml-cheatsheet.readthedocs.io/en/latest/loss_functions.html#cross-entropy
# -
def softmax(logits):
exps = np.exp(logits)
return exps / np.sum(exps)
print(softmax(logit_list))
def cross_entropy(label, y_hat):
return -np.log(y_hat[label])
y_hat = np.array(softmax(logit_list))
print(cross_entropy(label_list[0], y_hat=y_hat))
# We can see my implementation matches the tensorflow results
|
HandsOnML/ch09/Play with cross entropy.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="R3En9MVqilRY"
# # Train on multiple GPUs
#
# In this notebook, we will use Nobrainer to train a model for brain extraction. Brain extraction is a common step in processing neuroimaging data. It is a voxel-wise, binary classification task, where each voxel is classified as brain or not brain. Incidentally, the name for the Nobrainer framework comes from creating models for brain extraction.
#
# In the following cells, we will:
#
# 1. Get sample T1-weighted MR scans as features and FreeSurfer segmentations as labels.
# - We will binarize the FreeSurfer to get a precise brainmask.
# 2. Convert the data to TFRecords format.
# 3. Create two Datasets of the features and labels.
# - One dataset will be for training and the other will be for evaluation.
# 4. Instantiate a 3D convolutional neural network.
# 5. Choose a loss function and metrics to use.
# 6. Train on part of the data across multiple GPUs.
# 7. Evaluate on the rest of the data.
#
# ## Google Colaboratory
#
# If you are using Colab, please switch your runtime to GPU. To do this, select `Runtime > Change runtime type` in the top menu. Then select GPU under `Hardware accelerator`. A GPU is not necessary to prepare the data, but a GPU is helpful for training a model, which we demonstrate at the end of this notebook. This will give you access to one GPU, but the code will still run properly. To actually train a model on multiple GPUs, you will have to use Cloud services, a high-performance computing cluster, or your own hardware.
# + id="cxESnCBdiwEW"
# !pip install --no-cache-dir nobrainer nilearn
# + id="GetIT8J5ilRb"
import nobrainer
# + [markdown] id="nOL3zIrfilRc"
# # Get sample features and labels
#
# We use 9 pairs of volumes for training and 1 pair of volumes for evaluation. Many more volumes would be required to train a model for any useful purpose.
# + id="3gngTmxLilRc"
csv_of_filepaths = nobrainer.utils.get_data()
filepaths = nobrainer.io.read_csv(csv_of_filepaths)
train_paths = filepaths[:9]
evaluate_paths = filepaths[9:]
# + id="PzZnQFawi3zZ"
import matplotlib.pyplot as plt
from nilearn import plotting
fig = plt.figure(figsize=(12, 6))
plotting.plot_roi(train_paths[0][1], bg_img=train_paths[0][0], alpha=0.4, vmin=0, vmax=1, figure=fig)
# + [markdown] id="ksd2O-irilRd"
# # Convert medical images to TFRecords
#
# Remember how many full volumes are in the TFRecords files. This will be necessary to know how many steps are in on training epoch. The default training method needs to know this number, because Datasets don't always know how many items they contain.
# + id="74U_9sjqilRd"
# Verify that all volumes have the same shape and that labels are integer-ish.
invalid = nobrainer.io.verify_features_labels(train_paths, num_parallel_calls=2)
assert not invalid
invalid = nobrainer.io.verify_features_labels(evaluate_paths)
assert not invalid
# + id="Yvlr0TgcilRd"
# !mkdir -p data
# + id="fiUZIjuVilRe"
# Convert training and evaluation data to TFRecords.
nobrainer.tfrecord.write(
features_labels=train_paths,
filename_template='data/data-train_shard-{shard:03d}.tfrec',
examples_per_shard=3)
nobrainer.tfrecord.write(
features_labels=evaluate_paths,
filename_template='data/data-evaluate_shard-{shard:03d}.tfrec',
examples_per_shard=1)
# + id="iHtGGm3KilRe"
# !ls data
# + [markdown] id="e2oKUM8BilRe"
# # Create Datasets
#
# The batch is split evenly across the available GPUs. For example, if you have 4 GPUs and a batch size of 8, each GPU will get a batch of 2.
# + id="sCdkPNBxilRf"
n_classes = 1
batch_size = 2
volume_shape = (256, 256, 256)
block_shape = (128, 128, 128)
n_epochs = None
augment = False
shuffle_buffer_size = 10
num_parallel_calls = 2
# + id="SqoUkgpmilRf"
dataset_train = nobrainer.dataset.get_dataset(
file_pattern='data/data-train_shard-*.tfrec',
n_classes=n_classes,
batch_size=batch_size,
volume_shape=volume_shape,
block_shape=block_shape,
n_epochs=n_epochs,
augment=augment,
shuffle_buffer_size=shuffle_buffer_size,
num_parallel_calls=num_parallel_calls,
)
dataset_evaluate = nobrainer.dataset.get_dataset(
file_pattern='data/data-evaluate_shard-*.tfrec',
n_classes=n_classes,
batch_size=batch_size,
volume_shape=volume_shape,
block_shape=block_shape,
n_epochs=1,
augment=False,
shuffle_buffer_size=None,
num_parallel_calls=1,
)
# + id="BZlKggChilRg"
dataset_train
# + id="PjF_jDTVilRg"
dataset_evaluate
# + id="ZeRc0YQ5ilRg"
# Get the steps for an epoch of training and an epoch of validation.
steps_per_epoch = nobrainer.dataset.get_steps_per_epoch(
n_volumes=len(train_paths),
volume_shape=volume_shape,
block_shape=block_shape,
batch_size=batch_size)
validation_steps = nobrainer.dataset.get_steps_per_epoch(
n_volumes=len(evaluate_paths),
volume_shape=volume_shape,
block_shape=block_shape,
batch_size=batch_size)
# + [markdown] id="i9aAVkBVilRg"
# # Instantiate and compile model within scope
# + id="chyWsFIdilRh"
import tensorflow as tf
# + id="k8yg94NQilRh"
strategy = tf.distribute.MirroredStrategy()
# + id="LekCIjc9ilRh"
optimizer = tf.keras.optimizers.Adam(learning_rate=1e-04)
with strategy.scope():
model = nobrainer.models.unet(
n_classes=n_classes,
input_shape=(*block_shape, 1),
batchnorm=True)
model.compile(
optimizer=optimizer,
loss=nobrainer.losses.jaccard,
metrics=[nobrainer.metrics.dice])
# + id="zALpc6SNilRh"
model.fit(
dataset_train,
epochs=5,
steps_per_epoch=steps_per_epoch,
validation_data=dataset_evaluate,
validation_steps=validation_steps)
# + [markdown] id="L4n8idapilRh"
# # Predict medical images without TFRecords
# + id="dO-yhzWmilRi"
from nobrainer.volume import standardize
import nibabel as nib
image_path = evaluate_paths[0][0]
out = nobrainer.prediction.predict_from_filepath(image_path,
model,
block_shape = block_shape,
batch_size = batch_size,
normalizer = standardize,
)
out.shape
# + id="FDpD7oT9jJ14"
fig = plt.figure(figsize=(12, 6))
plotting.plot_roi(out, bg_img=image_path, alpha=0.4, figure=fig)
# + id="SgrzFoBvj_Ze"
|
guide/train_on_multiple_gpus.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda env:tensorflow] *
# language: python
# name: conda-env-tensorflow-py
# ---
num_friends = [100.0,49,41,40,25,21,21,19,19,18,18,16,15,15,15,15,14,14,13,13,13,13,12,12,11,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,9,9,9,9,9,9,9,9,9,9,9,9,9,9,9,9,9,9,8,8,8,8,8,8,8,8,8,8,8,8,8,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1]
# +
from collections import Counter
import matplotlib.pyplot as plt
friend_counts = Counter(num_friends)
xs = range(101) # largest value is 100
ys = [friend_counts[x] for x in xs] # height is just # of friends
plt.bar(xs, ys)
plt.axis([0, 101, 0, 25])
plt.title("Histogram of Friend Counts")
plt.xlabel("# of friends")
plt.ylabel("# of people")
plt.show()
# +
num_points = len(num_friends) # 204
assert num_points == 204
largest_value = max(num_friends) # 100
smallest_value = min(num_friends) # 1
assert largest_value == 100
assert smallest_value == 1
sorted_values = sorted(num_friends)
smallest_value = sorted_values[0] # 1
second_smallest_value = sorted_values[1] # 1
second_largest_value = sorted_values[-2] # 49
assert smallest_value == 1
assert second_smallest_value == 1
assert second_largest_value == 49
# +
from typing import List
def mean(xs: List[float]) -> float:
return sum(xs) / len(xs)
mean(num_friends) # 7.333333
assert 7.3333 < mean(num_friends) < 7.3334
# +
# The underscores indicate that these are "private" functions, as they're
# intended to be called by our median function but not by other people
# using our statistics library.
def _median_odd(xs: List[float]) -> float:
"""If len(xs) is odd, the median is the middle element"""
return sorted(xs)[len(xs) // 2]
def _median_even(xs: List[float]) -> float:
"""If len(xs) is even, it's the average of the middle two elements"""
sorted_xs = sorted(xs)
hi_midpoint = len(xs) // 2 # e.g. length 4 => hi_midpoint 2
return (sorted_xs[hi_midpoint - 1] + sorted_xs[hi_midpoint]) / 2
def median(v: List[float]) -> float:
"""Finds the 'middle-most' value of v"""
return _median_even(v) if len(v) % 2 == 0 else _median_odd(v)
assert median([1, 10, 2, 9, 5]) == 5
assert median([1, 9, 2, 10]) == (2 + 9) / 2
assert median(num_friends) == 6
# +
def quantile(xs: List[float], p: float) -> float:
"""Returns the pth-percentile value in x"""
p_index = int(p * len(xs))
return sorted(xs)[p_index]
assert quantile(num_friends, 0.10) == 1
assert quantile(num_friends, 0.25) == 3
assert quantile(num_friends, 0.75) == 9
assert quantile(num_friends, 0.90) == 13
# +
def mode(x: List[float]) -> List[float]:
"""Returns a list, since there might be more than one mode"""
counts = Counter(x)
max_count = max(counts.values())
return [x_i for x_i, count in counts.items()
if count == max_count]
assert set(mode(num_friends)) == {1, 6}
# +
# "range" already means something in Python, so we'll use a different name
def data_range(xs: List[float]) -> float:
return max(xs) - min(xs)
assert data_range(num_friends) == 99
# +
#from scratch.linear_algebra import sum_of_squares
Vector = List[float]
def dot(v: Vector, w: Vector) -> float:
"""Computes v_1 * w_1 + ... + v_n * w_n"""
assert len(v) == len(w), "vectors must be same length"
return sum(v_i * w_i for v_i, w_i in zip(v, w))
def sum_of_squares(v: Vector) -> float:
"""Returns v_1 * v_1 + ... + v_n * v_n"""
return dot(v, v)
def de_mean(xs: List[float]) -> List[float]:
"""Translate xs by subtracting its mean (so the result has mean 0)"""
x_bar = mean(xs)
return [x - x_bar for x in xs]
def variance(xs: List[float]) -> float:
"""Almost the average squared deviation from the mean"""
assert len(xs) >= 2, "variance requires at least two elements"
n = len(xs)
deviations = de_mean(xs)
return sum_of_squares(deviations) / (n - 1)
assert 81.54 < variance(num_friends) < 81.55
# +
import math
def standard_deviation(xs: List[float]) -> float:
"""The standard deviation is the square root of the variance"""
return math.sqrt(variance(xs))
assert 9.02 < standard_deviation(num_friends) < 9.04
def interquartile_range(xs: List[float]) -> float:
"""Returns the difference between the 75%-ile and the 25%-ile"""
return quantile(xs, 0.75) - quantile(xs, 0.25)
assert interquartile_range(num_friends) == 6
|
scratch/chapter5.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import json
import pickle
from indra.literature.adeft_tools import universal_extract_text
from indra.databases.hgnc_client import get_hgnc_name, get_hgnc_id
from indra_db.util.content_scripts import get_text_content_from_pmids
from indra_db.util.content_scripts import get_stmts_with_agent_text_like
from indra_db.util.content_scripts import get_text_content_from_stmt_ids
from adeft.discover import AdeftMiner
from adeft.gui import ground_with_gui
from adeft.modeling.label import AdeftLabeler
from adeft.modeling.classify import AdeftClassifier
from adeft.disambiguate import AdeftDisambiguator
from adeft_indra.s3 import model_to_s3
from adeft_indra.ground import gilda_ground
# -
shortforms = ['PBT']
genes = []
families = {}
groundings = [f'HGNC:{get_hgnc_id(gene)}' for gene in genes]
for family, members in families.items():
genes.extend(members)
groundings.append(f'FPLX:{family}')
with open('../data/entrez_all_pmids.json', 'r') as f:
all_pmids = json.load(f)
entrez_texts = []
entrez_refs = set()
for gene, grounding in zip(genes, groundings):
try:
pmids = all_pmids[gene]
except KeyError:
continue
_, content = get_text_content_from_pmids(pmids)
entrez_texts.extend([(universal_extract_text(text), grounding)
for text in content.values() if text])
entrez_refs.update(content.keys())
miners = dict()
all_texts = set()
for shortform in shortforms:
stmts = get_stmts_with_agent_text_like(shortform)[shortform]
_, content = get_text_content_from_stmt_ids(stmts)
shortform_texts = [universal_extract_text(text, contains=shortforms)
for ref, text in content.items() if text and ref not in entrez_refs]
miners[shortform] = AdeftMiner(shortform)
miners[shortform].process_texts(shortform_texts)
all_texts |= set(shortform_texts)
# It's then necessary to check if Acromine produced the correct results. We must fix errors manually
top = miners['PBT'].top()
top
longforms0 = miners['PBT'].get_longforms()
list(enumerate(longforms0))
longforms0 = [(longform, score) for i, (longform, score) in enumerate(longforms0)
if i not in [2]]
list(enumerate(top))
longforms0.extend((longform, score) for i, (longform, score) in enumerate(top)
if i in [5, 8, 15, 32, 33, 34])
longforms = longforms0
longforms.sort(key=lambda x: -x[1])
longforms, scores = zip(*longforms0)
longforms
grounding_map = {}
names = {}
for longform in longforms:
grounding = gilda_ground(longform)
if grounding[0]:
grounding_map[longform] = f'{grounding[0]}:{grounding[1]}'
names[grounding_map[longform]] = grounding[2]
grounding_map
names
grounding_map, names, pos_labels = ground_with_gui(longforms, scores, grounding_map=grounding_map, names=names)
result = (grounding_map, names, pos_labels)
result
grounding_map, names, pos_labels = ({'papilla based thickness': 'ungrounded',
'payback times': 'ungrounded',
'perioperative blood transfusion': 'MESH:D001803',
'peripheral blood t': 'ungrounded',
'peripheral blood t cells': 'ungrounded',
'platinum based therapy': 'ungrounded',
'poly butylene terephthalate': 'ungrounded',
'polyamine blockade therapy': 'ungrounded',
'polyamine blocking therapy': 'ungrounded',
'polybutylene terephthalate': 'ungrounded',
'proton beam therapy': 'MESH:D061766'},
{'MESH:D001803': 'Blood Transfusion', 'MESH:D061766': 'Proton Therapy'},
['MESH:D001803', 'MESH:D061766'])
grounding_dict = {'PBT': grounding_map}
classifier = AdeftClassifier('PBT', pos_labels=pos_labels)
param_grid = {'C': [100.0], 'max_features': [10000]}
labeler = AdeftLabeler(grounding_dict)
corpus = labeler.build_from_texts(shortform_texts)
corpus.extend(entrez_texts)
texts, labels = zip(*corpus)
classifier.cv(texts, labels, param_grid, cv=5, n_jobs=8)
classifier.stats
disamb = AdeftDisambiguator(classifier, grounding_dict, names)
d = disamb.disambiguate(shortform_texts)
a = [text for pred, text in zip(d, shortform_texts)if pred[0] == 'HGNC:6342']
a[40]
disamb.dump('PBT', '../results')
from adeft.disambiguate import load_disambiguator, load_disambiguator_directly
disamb.classifier.training_set_digest
model_to_s3(disamb)
d.disambiguate(texts[0])
print(d.info())
a = load_disambiguator('AR')
a.disambiguate('Androgen')
logit = d.classifier.estimator.named_steps['logit']
logit.classes_
model_to_s3(disamb)
classifier.feature_importances()['FPLX:RAC']
d = load_disambiguator('ALK', '../results')
d.info()
print(d.info())
model_to_s3(d)
d = load_disambiguator('TAK', '../results')
print(d.info())
model_to_s3(d)
from adeft import available_shortforms
print(d.info())
d.classifier.feature_importances()
from adeft import __version__
__version__
from adeft.disambiguate import load_disambiguator_directly
d = load_disambiguator_directly('../results/TEK/')
print(d.info())
model_to_s3(d)
d.grounding_dict
# !python -m adeft.download --update
from adeft import available_shortforms
len(available_shortforms)
available_shortforms
'TEC' in available_shortforms
'TECs' in available_shortforms
# !python -m adeft.download --update
# !python -m adeft.download --update
|
notebooks/PBT_model.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# %matplotlib notebook
np.random.seed(12345)
# Create Random data
df = pd.DataFrame([np.random.normal(32000,200000,3650),
np.random.normal(43000,100000,3650),
np.random.normal(43500,140000,3650),
np.random.normal(48000,70000,3650)],
index=[1992,1993,1994,1995])
# Transpose data
df = df.T
# +
# Get mean and margin of error
# T-value of 95% of normal distribution
C = 1.96
# Mean and standard deviation
m = df.mean()
s = df.std()
# Square root of sample size
r_n = np.sqrt(df.shape[0])
# Margin of error
yerr = (C * (s/r_n))
# Add mean and yerr to dataframe
agg_df = pd.DataFrame({'Mean': m, 'yerr': yerr})
# -
def insert_colour(df, y_value):
# Insert colour column which gives colour for each mean according to y value
colour_map = {
10: '#00386D', # Dark blue
8: '#0073DF',
6: '#2394FF',
4: '#63B3FF',
2: '#B3DAFF',
0.0: '#D8D5D5',
-2: '#FFC2C2',
-4: '#FF7777',
-6: '#F91B1B',
-8: '#D50000',
-10: '#710000' # Dark red
}
# Get range
y_range = max(df['Mean']) - min(df['Mean'])
# Get distance of each mean value from y_value
distance = ((y_value - (df['Mean']))/y_range)
# Round to the nearest even number
distance = [int(round((x * 10)/2)*2) for x in distance]
# Replace values > 10 and < -10 to 10 and -10
distance = [10 if x > 10 else x for x in distance]
distance = [-10 if x < -10 else x for x in distance]
df['colour'] = [colour_map[x] for x in distance]
return df
# +
initial_y_value = 42000
plt.figure()
def plot_bargraph(df, y_value):
df = insert_colour(df, y_value)
bargraph = plt.bar(
df.index, df['Mean'], tick_label=df.index,
yerr=df['yerr'], capsize=10,
color=df['colour'], width=0.45
)
return bargraph
plot_bargraph(agg_df, initial_y_value)
plt.gca().set_title('Click on the graph to select y-value')
def onclick(event):
plt.cla()
y_value = event.ydata
plot_bargraph(agg_df, y_value)
plt.gca().set_title('y={:.0f}'.format(y_value))
# tell mpl_connect we want to pass a 'button_press_event' into onclick when the event is detected
plt.gcf().canvas.mpl_connect('button_press_event', onclick)
|
Course2 - Applied Plotting, Charting & Data Representation in Python/week3/.ipynb_checkpoints/Assignment 3 - Building a Custom Visualization-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Simple KubeFlow Pipeline
#
# Lightweight python components do not require you to build a new container image for every code change.
# They're intended to use for fast iteration in notebook environment.
#
# #### Building a lightweight python component
# To build a component just define a stand-alone python function and then call kfp.components.func_to_container_op(func) to convert it to a component that can be used in a pipeline.
#
# There are several requirements for the function:
# * The function should be stand-alone. It should not use any code declared outside of the function definition. Any imports should be added inside the main function. Any helper functions should also be defined inside the main function.
# * The function can only import packages that are available in the base image. If you need to import a package that's not available you can try to find a container image that already includes the required packages. (As a workaround you can use the module subprocess to run pip install for the required package.)
# * If the function operates on numbers, the parameters need to have type hints. Supported types are ```[int, float, bool]```. Everything else is passed as string.
# * To build a component with multiple output values, use the typing.NamedTuple type hint syntax: ```NamedTuple('MyFunctionOutputs', [('output_name_1', type), ('output_name_2', float)])```
# + tags=["parameters"]
# Install the KubeFlow Pipeline SDK
# !pip3 install https://storage.googleapis.com/ml-pipeline/release/0.1.16/kfp.tar.gz --upgrade
# -
# Simple function that just add two numbers:
#Define a Python function
def add_fn(a: float, b: float) -> float:
'''Calculates sum of two arguments'''
return a + b
# Convert the function to a pipeline operation
# +
import kfp.components as comp
add_op = comp.func_to_container_op(add_fn)
# -
# A bit more advanced function which demonstrates how to use imports, helper functions and produce multiple outputs.
from typing import NamedTuple
def div_fn(dividend: float, divisor:float, output_dir:str = './') -> NamedTuple('DivOutput', [('quotient', float), ('remainder', float)]):
'''Divides two numbers and calculate the quotient and remainder'''
#Imports inside a component function:
import numpy as np
#This function demonstrates how to use nested functions inside a component function:
def nested_div_helper(dividend, divisor):
return np.divmod(dividend, divisor)
(quotient, remainder) = nested_div_helper(dividend, divisor)
from tensorflow.python.lib.io import file_io
import json
# Exports two sample metrics:
metrics = {
'metrics': [{
'name': 'quotient',
'numberValue': float(quotient),
},{
'name': 'remainder',
'numberValue': float(remainder),
}]}
with file_io.FileIO(output_dir + 'mlpipeline-metrics.json', 'w') as f:
json.dump(metrics, f)
from collections import namedtuple
output = namedtuple('DivOutput', ['quotient', 'remainder'])
return output(quotient, remainder)
# Test running the python function directly
div_fn(100, 7)
# #### Convert the function to a pipeline operation
#
# You can specify an alternative base container image (the image needs to have Python 3.5+ installed).
div_op = comp.func_to_container_op(div_fn, base_image='tensorflow/tensorflow:1.11.0-py3')
# #### Define the pipeline
# Pipeline function has to be decorated with the `@dsl.pipeline` decorator
import kfp.dsl as dsl
@dsl.pipeline(
name='Calculation pipeline',
description='A toy pipeline that performs arithmetic calculations.'
)
def add_div_pipeline(
a='a',
b='7',
c='17',
):
#Passing pipeline parameter and a constant value as operation arguments
add_task = add_op(a, 4) #Returns a dsl.ContainerOp class instance.
#Passing a task output reference as operation arguments
#For an operation with a single return value, the output reference can be accessed using `task.output` or `task.outputs['output_name']` syntax
div_task = div_op(add_task.output, b, '/')
#For an operation with a multiple return values, the output references can be accessed using `task.outputs['output_name']` syntax
result_task = add_op(div_task.outputs['quotient'], c)
# #### Compile the pipeline
pipeline_func = add_div_pipeline
pipeline_filename = pipeline_func.__name__ + '.pipeline.tar.gz'
import kfp.compiler as compiler
compiler.Compiler().compile(pipeline_func, pipeline_filename)
# #### Submit the pipeline for execution
# +
#Specify pipeline argument values
arguments = {'a': '7', 'b': '8'}
#Get or create an experiment and submit a pipeline run
import kfp
client = kfp.Client()
experiment = client.create_experiment('simple_add_div_pipeline')
#Submit a pipeline run
run_name = pipeline_func.__name__ + ' run'
run_result = client.run_pipeline(experiment.id, run_name, pipeline_filename, arguments)
# -
|
kubeflow/notebooks/08_Simple_KubeFlow_ML_Pipeline.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# # Hospital Readmissions Data Analysis and Recommendations for Reduction
#
# ### Background
# In October 2012, the US government's Center for Medicare and Medicaid Services (CMS) began reducing Medicare payments for Inpatient Prospective Payment System hospitals with excess readmissions. Excess readmissions are measured by a ratio, by dividing a hospital’s number of “predicted” 30-day readmissions for heart attack, heart failure, and pneumonia by the number that would be “expected,” based on an average hospital with similar patients. A ratio greater than 1 indicates excess readmissions.
#
# ### Exercise Directions
#
# In this exercise, you will:
# + critique a preliminary analysis of readmissions data and recommendations (provided below) for reducing the readmissions rate
# + construct a statistically sound analysis and make recommendations of your own
#
# More instructions provided below. Include your work **in this notebook and submit to your Github account**.
#
# ### Resources
# + Data source: https://data.medicare.gov/Hospital-Compare/Hospital-Readmission-Reduction/9n3s-kdb3
# + More information: http://www.cms.gov/Medicare/medicare-fee-for-service-payment/acuteinpatientPPS/readmissions-reduction-program.html
# + Markdown syntax: http://nestacms.com/docs/creating-content/markdown-cheat-sheet
# ****
# +
# %matplotlib inline
import pandas as pd
from __future__ import division
import numpy as np
import matplotlib.pyplot as plt
import bokeh.plotting as bkp
from mpl_toolkits.axes_grid1 import make_axes_locatable
# -
# read in readmissions data provided
hospital_read_df = pd.read_csv('data/cms_hospital_readmissions.csv')
# ****
# ## Preliminary Analysis
# deal with missing and inconvenient portions of data
clean_hospital_read_df = hospital_read_df[hospital_read_df['Number of Discharges'] != 'Not Available']
clean_hospital_read_df.loc[:, 'Number of Discharges'] = clean_hospital_read_df['Number of Discharges'].astype(int)
clean_hospital_read_df = clean_hospital_read_df.sort_values('Number of Discharges')
# +
# generate a scatterplot for number of discharges vs. excess rate of readmissions
# lists work better with matplotlib scatterplot function
x = [a for a in clean_hospital_read_df['Number of Discharges'][81:-3]]
y = list(clean_hospital_read_df['Excess Readmission Ratio'][81:-3])
fig, ax = plt.subplots(figsize=(8,5))
ax.scatter(x, y,alpha=0.2)
ax.fill_between([0,350], 1.15, 2, facecolor='red', alpha = .15, interpolate=True)
ax.fill_between([800,2500], .5, .95, facecolor='green', alpha = .15, interpolate=True)
ax.set_xlim([0, max(x)])
ax.set_xlabel('Number of discharges', fontsize=12)
ax.set_ylabel('Excess rate of readmissions', fontsize=12)
ax.set_title('Scatterplot of number of discharges vs. excess rate of readmissions', fontsize=14)
ax.grid(True)
fig.tight_layout()
# -
# ****
#
# ## Preliminary Report
#
# Read the following results/report. While you are reading it, think about if the conclusions are correct, incorrect, misleading or unfounded. Think about what you would change or what additional analyses you would perform.
#
# **A. Initial observations based on the plot above**
# + Overall, rate of readmissions is trending down with increasing number of discharges
# + With lower number of discharges, there is a greater incidence of excess rate of readmissions (area shaded red)
# + With higher number of discharges, there is a greater incidence of lower rates of readmissions (area shaded green)
#
# **B. Statistics**
# + In hospitals/facilities with number of discharges < 100, mean excess readmission rate is 1.023 and 63% have excess readmission rate greater than 1
# + In hospitals/facilities with number of discharges > 1000, mean excess readmission rate is 0.978 and 44% have excess readmission rate greater than 1
#
# **C. Conclusions**
# + There is a significant correlation between hospital capacity (number of discharges) and readmission rates.
# + Smaller hospitals/facilities may be lacking necessary resources to ensure quality care and prevent complications that lead to readmissions.
#
# **D. Regulatory policy recommendations**
# + Hospitals/facilties with small capacity (< 300) should be required to demonstrate upgraded resource allocation for quality care to continue operation.
# + Directives and incentives should be provided for consolidation of hospitals and facilities to have a smaller number of them with higher capacity and number of discharges.
# +
# A. Do you agree with the above analysis and recommendations? Why or why not?
import seaborn as sns
relevant_columns = clean_hospital_read_df[['Excess Readmission Ratio', 'Number of Discharges']][81:-3]
sns.regplot(relevant_columns['Number of Discharges'], relevant_columns['Excess Readmission Ratio'])
# -
# ****
# <div class="span5 alert alert-info">
# ### Exercise
#
# Include your work on the following **in this notebook and submit to your Github account**.
#
# A. Do you agree with the above analysis and recommendations? Why or why not?
#
# B. Provide support for your arguments and your own recommendations with a statistically sound analysis:
#
# 1. Setup an appropriate hypothesis test.
# 2. Compute and report the observed significance value (or p-value).
# 3. Report statistical significance for $\alpha$ = .01.
# 4. Discuss statistical significance and practical significance. Do they differ here? How does this change your recommendation to the client?
# 5. Look at the scatterplot above.
# - What are the advantages and disadvantages of using this plot to convey information?
# - Construct another plot that conveys the same information in a more direct manner.
#
#
#
# You can compose in notebook cells using Markdown:
# + In the control panel at the top, choose Cell > Cell Type > Markdown
# + Markdown syntax: http://nestacms.com/docs/creating-content/markdown-cheat-sheet
# </div>
# ****
# - Overall, rate of readmissions is trending down with increasing number of discharges
# - Agree, according to regression trend line shown above
#
# - With lower number of discharges, there is a greater incidence of excess rate of readmissions (area shaded red)
# - Agree
#
# - With higher number of discharges, there is a greater incidence of lower rates of readmissions (area shaded green)
# - Agree
# +
rv =relevant_columns
print rv[rv['Number of Discharges'] < 100][['Excess Readmission Ratio']].mean()
print '\nPercent of subset with excess readmission rate > 1: ', len(rv[(rv['Number of Discharges'] < 100) & (rv['Excess Readmission Ratio'] > 1)]) / len(rv[relevant_columns['Number of Discharges'] < 100])
print '\n', rv[rv['Number of Discharges'] > 1000][['Excess Readmission Ratio']].mean()
print '\nPercent of subset with excess readmission rate > 1: ', len(rv[(rv['Number of Discharges'] > 1000) & (rv['Excess Readmission Ratio'] > 1)]) / len(rv[relevant_columns['Number of Discharges'] > 1000])
# -
# - In hospitals/facilities with number of discharges < 100, mean excess readmission rate is 1.023 and 63% have excess readmission rate greater than 1
# - Accurate
#
# - In hospitals/facilities with number of discharges > 1000, mean excess readmission rate is 0.978 and 44% have excess readmission rate greater than 1
# - Correction: mean excess readmission rate is 0.979, and 44.565% have excess readmission rate > 1
np.corrcoef(rv['Number of Discharges'], rv['Excess Readmission Ratio'])
# - There is a significant correlation between hospital capacity (number of discharges) and readmission rates.
# - The correlation coefficient shows a very, very weak correlation between the two variables. More evidence needed to establish a correlation.
# - Smaller hospitals/facilities may be lacking necessary resources to ensure quality care and prevent complications that lead to readmissions.
# - More evidence needed to asses the veracity of this statement.
|
Statistics_Exercises/sliderule_dsi_inferential_statistics_exercise_3.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .r
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: R
# language: R
# name: ir
# ---
library(Seurat)
library(ggplot2)
library(Matrix)
#SLE flare data read in
#can be accessed through https://www.ncbi.nlm.nih.gov/geo/query/acc.cgi?acc=GSE137029
mm<-readMM('./project/sle_flare_GSE137029/matrix.mtx.gz')
features=read.table('./project/sle_flare_GSE137029/features.tsv.gz',sep='\t')
bar<-read.table('./project/sle_flare_GSE137029/barcodes.tsv.gz',sep='\t')
rownames(mm)<-bar$V1
colnames(mm)<-features$V1
sle<-CreateSeuratObject(counts=t(mm),project='sle')
#HD Sample
##can be accessed through https://cells.ucsc.edu/?ds=multimodal-pbmc+sct data download page
##hd rds
##first time processing hd data please run following step for first hd data processing
##mat <- fread("exprMatrix.tsv.gz")
##meta <- read.table("meta.tsv", header=T, sep="\t", as.is=T, row.names=1)
##genes = mat[,1][[1]]
##genes = gsub(".+[|]", "", genes)
##mat = data.frame(mat[,-1], row.names=genes)
##hd <- CreateSeuratObject(counts = mat, project = "hd", meta.data=meta)
##hd@meta.data$orig.ident<-'hd'
##saveRDS(hd,ucsc_pbmc_hd.rds)
hd<-readRDS('./project/ucsc_pbmc_hd.rds')
####child sle used datasets
path<-'./project/GSE135779_SLE/cSLE/SLE_HEAVY/'
file<-dir(path)
file
# +
file.path<-lapply(file,function(x){
paste(path,x,sep='')
})
csle_heavy<-list()
for(i in 1:length(file.path)){
csle_heavy[[i]]<-Read10X(file.path[[i]])
csle_heavy[[i]]<-CreateSeuratObject(csle_heavy[[i]],project='csle_heavy')
csle_heavy[[i]]@meta.data$orig.ident<-'csle_heavy'
}
# -
csle_heavy_m<-csle_heavy[[1]]
for(i in 2:length(csle_heavy)){
csle_heavy_m<-merge(csle_heavy_m,csle_heavy[[i]])
}
sle<-merge(sle,csle_heavy_m)
data.list<-list(sle,hd)
data.list <- lapply(X = data.list, FUN = function(x) {
x <- NormalizeData(x, verbose = FALSE)
x <- FindVariableFeatures(x, verbose = FALSE)
})
features <- SelectIntegrationFeatures(object.list = data.list)
data.list <- lapply(X = data.list, FUN = function(x) {
x <- ScaleData(x, features = features, verbose = FALSE)
x <- RunPCA(x, features = features, verbose = FALSE)
})
anchors <- FindIntegrationAnchors(object.list = data.list, reference = c(1,2), reduction = "rpca",
dims = 1:50)
data.integrated <- IntegrateData(anchorset = anchors, dims = 1:50)
data.integrated <- ScaleData(data.integrated, verbose = FALSE)
data.integrated <- RunPCA(data.integrated, verbose = FALSE)
data.integrated <- RunUMAP(data.integrated, dims = 1:50)
data.integrated<-FindNeighbors(data.integrated,dims=1:50)
DefaultAssay(data.integrated)<-'integrated'
data.integrated<-FindClusters(data.integrated,res=0.2)
DimPlot(data.integrated,group.by=c('seurat_clusters','celltype.l1'),label=T,raster=F)
new.cluster.ids <- c("T", "Mono", "T", "T", "B", "NK",
"Mono", "Mono", "Mono",'DC','other','DC','other','T','other','T','other','DC','B','other')
names(new.cluster.ids) <- levels(data.integrated)
data.integrated <- RenameIdents(data.integrated, new.cluster.ids)
DimPlot(data.integrated, reduction = "umap", label = TRUE, pt.size = 0.5) + NoLegend()
saveRDS(data.integrated,'./project/sle_nature_communiation_and_immunnology_merge_include_hd.rds')
|
jupyter notebook/3.SLE_HD_cellchat_preprocessing.ipynb
|
# ---
# title: "Feedforward Neural Networks For Regression"
# author: "<NAME>"
# date: 2017-12-20T11:53:49-07:00
# description: "How to train a feed-forward neural network for regression in Python."
# type: technical_note
# draft: false
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Preliminaries
# +
# Load libraries
import numpy as np
from keras.preprocessing.text import Tokenizer
from keras import models
from keras import layers
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
from sklearn import preprocessing
# Set random seed
np.random.seed(0)
# -
# ## Generate Training Data
# +
# Generate features matrix and target vector
features, target = make_regression(n_samples = 10000,
n_features = 3,
n_informative = 3,
n_targets = 1,
noise = 0.0,
random_state = 0)
# Divide our data into training and test sets
train_features, test_features, train_target, test_target = train_test_split(features,
target,
test_size=0.33,
random_state=0)
# -
# ## Create Neural Network Architecture
# +
# Start neural network
network = models.Sequential()
# Add fully connected layer with a ReLU activation function
network.add(layers.Dense(units=32, activation='relu', input_shape=(train_features.shape[1],)))
# Add fully connected layer with a ReLU activation function
network.add(layers.Dense(units=32, activation='relu'))
# Add fully connected layer with no activation function
network.add(layers.Dense(units=1))
# -
# ## Compile Neural Network
#
# Because we are training a regression, we should use an appropriate loss function and evaluation metric, in our case the mean square error:
#
# $$\operatorname {MSE}={\frac {1}{n}}\sum\_{{i=1}}^{n}({\hat {y\_{i}}}-y\_{i})^{2}$$
#
# where $n$ is the number of observations, $y\_{i}$ is the true value of the target we are trying to predict, $y$, for observation $i$, and ${\hat {y\_{i}}}$ is the model's predicted value for $y\_{i}$.
# Compile neural network
network.compile(loss='mse', # Mean squared error
optimizer='RMSprop', # Optimization algorithm
metrics=['mse']) # Mean squared error
# ## Train Neural Network
# Train neural network
history = network.fit(train_features, # Features
train_target, # Target vector
epochs=10, # Number of epochs
verbose=0, # No output
batch_size=100, # Number of observations per batch
validation_data=(test_features, test_target)) # Data for evaluation
|
docs/deep_learning/keras/feedforward_neural_network_for_regression.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Indexes
#
# Today we're going to be talking about pandas' [`Index`es](http://pandas.pydata.org/pandas-docs/version/0.18.0/api.html#index).
# They're essential to pandas, but can be a difficult concept to grasp at first.
# I suspect this is partly because they're unlike what you'll find in SQL or R.
#
# `Index`es offer
#
# - a metadata container
# - easy label-based row selection and assignment
# - easy label-based alignment in operations
#
# One of my first tasks when analyzing a new dataset is to identify a unique identifier for each observation, and set that as the index. It could be a simple integer, or like in our first chapter, it could be several columns (`carrier`, `origin` `dest`, `tail_num` `date`).
#
# To demonstrate the benefits of proper `Index` use, we'll first fetch some weather data from sensors at a bunch of airports across the US.
# See [here](https://github.com/akrherz/iem/blob/master/scripts/asos/iem_scraper_example.py) for the example scraper I based this off of.
# Those uninterested in the details of fetching and prepping the data and [skip past it](#set-operations).
#
# At a high level, here's how we'll fetch the data: the sensors are broken up by "network" (states).
# We'll make one API call per state to get the list of airport IDs per network (using `get_ids` below).
# Once we have the IDs, we'll again make one call per state getting the actual observations (in `get_weather`).
# Feel free to skim the code below, I'll highlight the interesting bits.
#
# +
# %matplotlib inline
import os
import json
import glob
import datetime
from io import StringIO
import requests
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import prep
sns.set_style('ticks')
# States are broken into networks. The networks have a list of ids, each representing a station.
# We will take that list of ids and pass them as query parameters to the URL we built up ealier.
states = """AK AL AR AZ CA CO CT DE FL GA HI IA ID IL IN KS KY LA MA MD ME
MI MN MO MS MT NC ND NE NH NJ NM NV NY OH OK OR PA RI SC SD TN TX UT VA VT
WA WI WV WY""".split()
# IEM has Iowa AWOS sites in its own labeled network
networks = ['AWOS'] + ['{}_ASOS'.format(state) for state in states]
# -
def get_weather(stations, start=pd.Timestamp('2014-01-01'),
end=pd.Timestamp('2014-01-31')):
'''
Fetch weather data from MESONet between ``start`` and ``stop``.
'''
url = ("http://mesonet.agron.iastate.edu/cgi-bin/request/asos.py?"
"&data=tmpf&data=relh&data=sped&data=mslp&data=p01i&data=v"
"sby&data=gust_mph&data=skyc1&data=skyc2&data=skyc3"
"&tz=Etc/UTC&format=comma&latlon=no"
"&{start:year1=%Y&month1=%m&day1=%d}"
"&{end:year2=%Y&month2=%m&day2=%d}&{stations}")
stations = "&".join("station=%s" % s for s in stations)
weather = (pd.read_csv(url.format(start=start, end=end, stations=stations),
comment="#")
.rename(columns={"valid": "date"})
.rename(columns=str.strip)
.assign(date=lambda df: pd.to_datetime(df['date']))
.set_index(["station", "date"])
.sort_index())
float_cols = ['tmpf', 'relh', 'sped', 'mslp', 'p01i', 'vsby', "gust_mph"]
weather[float_cols] = weather[float_cols].apply(pd.to_numeric, errors="corce")
return weather
def get_ids(network):
url = "http://mesonet.agron.iastate.edu/geojson/network.php?network={}"
r = requests.get(url.format(network))
md = pd.io.json.json_normalize(r.json()['features'])
md['network'] = network
return md
# There isn't too much in `get_weather` worth mentioning, just grabbing some CSV files from various URLs.
# They put metadata in the "CSV"s at the top of the file as lines prefixed by a `#`.
# Pandas will ignore these with the `comment='#'` parameter.
#
# I do want to talk briefly about the gem of a method that is [`json_normalize`](http://pandas.pydata.org/pandas-docs/version/0.18.0/generated/pandas.io.json.json_normalize.html) .
# The weather API returns some slightly-nested data.
# +
url = "http://mesonet.agron.iastate.edu/geojson/network.php?network={}"
r = requests.get(url.format("AWOS"))
js = r.json()
js['features'][:2]
# -
# If we just pass that list off to the `DataFrame` constructor, we get this.
pd.DataFrame(js['features']).head()
# In general, DataFrames don't handle nested data that well.
# It's often better to normalize it somehow.
# In this case, we can "lift"
# the nested items (`geometry.coordinates`, `properties.sid`, and `properties.sname`)
# up to the top level.
pd.io.json.json_normalize(js['features'])
# Sure, it's not *that* difficult to write a quick for loop or list comprehension to extract those,
# but that gets tedious.
# If we were using the latitude and longitude data, we would want to split
# the `geometry.coordinates` column into two. But we aren't so we won't.
#
# Going back to the task, we get the airport IDs for every network (state)
# with `get_ids`. Then we pass those IDs into `get_weather` to fetch the
# actual weather data.
# +
import os
ids = pd.concat([get_ids(network) for network in networks], ignore_index=True)
gr = ids.groupby('network')
store = 'data/weather.h5'
if not os.path.exists(store):
os.makedirs("data/weather", exist_ok=True)
for k, v in gr:
weather = get_weather(v['id'])
weather.to_csv("data/weather/{}.csv".format(k))
weather = pd.concat([
pd.read_csv(f, parse_dates=['date'], index_col=['station', 'date'])
for f in glob.glob('data/weather/*.csv')
]).sort_index()
weather.to_hdf("data/weather.h5", "weather")
else:
weather = pd.read_hdf("data/weather.h5", "weather")
# -
weather.head()
# OK, that was a bit of work. Here's a plot to reward ourselves.
# +
airports = ['W43', 'AFO', '82V', 'DUB']
weather.sort_index(inplace=True)g = sns.FacetGrid(weather.loc[airports].reset_index(),
col='station', hue='station', col_wrap=2, size=4)
g.map(sns.regplot, 'sped', 'gust_mph')
# -
# ## Set Operations
#
# Indexes are set-like (technically *multi*sets, since you can have duplicates), so they support most python `set` operations. Since indexes are immutable you won't find any of the inplace `set` operations.
# One other difference is that since `Index`es are also array-like, you can't use some infix operators like `-` for `difference`. If you have a numeric index it is unclear whether you intend to perform math operations or set operations.
# You can use `&` for intersection, `|` for union, and `^` for symmetric difference though, since there's no ambiguity.
#
# For example, lets find the set of airports that we have both weather and flight information on. Since `weather` had a MultiIndex of `airport, datetime`, we'll use the `levels` attribute to get at the airport data, separate from the date data.
# +
# Bring in the flights data
flights = pd.read_hdf('data/flights.h5', 'flights')
weather_locs = weather.index.levels[0]
# The `categories` attribute of a Categorical is an Index
origin_locs = flights.origin.cat.categories
dest_locs = flights.dest.cat.categories
airports = weather_locs & origin_locs & dest_locs
airports
# +
print("Weather, no flights:\n\t", weather_locs.difference(origin_locs | dest_locs), end='\n\n')
print("Flights, no weather:\n\t", (origin_locs | dest_locs).difference(weather_locs), end='\n\n')
print("Dropped Stations:\n\t", (origin_locs | dest_locs) ^ weather_locs)
# -
# ## Flavors
#
# Pandas has many subclasses of the regular `Index`, each tailored to a specific kind of data.
# Most of the time these will be created for you automatically, so you don't have to worry about which one to choose.
#
# 1. [`Index`](http://pandas.pydata.org/pandas-docs/version/0.18.0/generated/pandas.Index.html#pandas.Index)
# 2. `Int64Index`
# 3. `RangeIndex`: Memory-saving special case of `Int64Index`
# 4. `FloatIndex`
# 5. `DatetimeIndex`: Datetime64[ns] precision data
# 6. `PeriodIndex`: Regularly-spaced, arbitrary precision datetime data.
# 7. `TimedeltaIndex`
# 8. `CategoricalIndex`
# 9. `MultiIndex`
#
# You will sometimes create a `DatetimeIndex` with [`pd.date_range`](http://pandas.pydata.org/pandas-docs/version/0.18.0/generated/pandas.date_range.html) ([`pd.period_range`](http://pandas.pydata.org/pandas-docs/version/0.18.0/generated/pandas.period_range.html) for `PeriodIndex`).
# And you'll sometimes make a `MultiIndex` directly too (I'll have an example of this in my post on performace).
#
# Some of these specialized index types are purely optimizations; others use information about the data to provide additional methods.
# And while you might occasionally work with indexes directly (like the set operations above), most of they time you'll be operating on a Series or DataFrame, which in turn makes use of its Index.
#
# ### Row Slicing
# We saw in part one that they're great for making *row* subsetting as easy as column subsetting.
weather.loc['DSM'].head()
# Without indexes we'd probably resort to boolean masks.
weather2 = weather.reset_index()
weather2[weather2['station'] == 'DSM'].head()
# Slightly less convenient, but still doable.
# ### Indexes for Easier Arithmetic, Analysis
# It's nice to have your metadata (labels on each observation) next to you actual values. But if you store them in an array, they'll get in the way of your operations.
# Say we wanted to translate the Fahrenheit temperature to Celsius.
# +
# With indecies
temp = weather['tmpf']
c = (temp - 32) * 5 / 9
c.to_frame()
# +
# without
temp2 = weather.reset_index()[['station', 'date', 'tmpf']]
temp2['tmpf'] = (temp2['tmpf'] - 32) * 5 / 9
temp2.head()
# -
# Again, not terrible, but not as good.
# And, what if you had wanted to keep Fahrenheit around as well, instead of overwriting it like we did?
# Then you'd need to make a copy of everything, including the `station` and `date` columns.
# We don't have that problem, since indexes are immutable and safely shared between DataFrames / Series.
temp.index is c.index
# ### Indexes for Alignment
#
# I've saved the best for last.
# Automatic alignment, or reindexing, is fundamental to pandas.
#
# All binary operations (add, multiply, etc.) between Series/DataFrames first *align* and then proceed.
#
# Let's suppose we have hourly observations on temperature and windspeed.
# And suppose some of the observations were invalid, and not reported (simulated below by sampling from the full dataset). We'll assume the missing windspeed observations were potentially different from the missing temperature observations.
# +
dsm = weather.loc['DSM']
hourly = dsm.resample('H').mean()
temp = hourly['tmpf'].sample(frac=.5, random_state=1).sort_index()
sped = hourly['sped'].sample(frac=.5, random_state=2).sort_index()
# -
temp.head().to_frame()
sped.head()
# Notice that the two indexes aren't identical.
#
# Suppose that the `windspeed : temperature` ratio is meaningful.
# When we go to compute that, pandas will automatically align the two by index label.
sped / temp
# This lets you focus on doing the operation, rather than manually aligning things, ensuring that the arrays are the same length and in the same order.
# By deault, missing values are inserted where the two don't align.
# You can use the method version of any binary operation to specify a `fill_value`
sped.div(temp, fill_value=1)
# And since I couldn't find anywhere else to put it, you can control the axis the operation is aligned along as well.
hourly.div(sped, axis='index')
# The non row-labeled version of this is messy.
# +
temp2 = temp.reset_index()
sped2 = sped.reset_index()
# Find rows where the operation is defined
common_dates = pd.Index(temp2.date) & sped2.date
pd.concat([
# concat to not lose date information
sped2.loc[sped2['date'].isin(common_dates), 'date'],
(sped2.loc[sped2.date.isin(common_dates), 'sped'] /
temp2.loc[temp2.date.isin(common_dates), 'tmpf'])],
axis=1).dropna(how='all')
# -
# And we have a bug in there. Can you spot it?
# I only grabbed the dates from `sped2` in the line `sped2.loc[sped2['date'].isin(common_dates), 'date']`.
# Really that should be `sped2.loc[sped2.date.isin(common_dates)] | temp2.loc[temp2.date.isin(common_dates)]`.
# But I think leaving the buggy version states my case even more strongly. The `temp / sped` version where pandas aligns everything is better.
# ## Merging
#
# There are two ways of merging DataFrames / Series in pandas.
#
# 1. Relational Database style with `pd.merge`
# 2. Array style with `pd.concat`
#
# Personally, I think in terms of the `concat` style.
# I learned pandas before I ever really used SQL, so it comes more naturally to me I suppose.
#
# ### Concat Version
pd.concat([temp, sped], axis=1).head()
# The `axis` parameter controls how the data should be stacked, `0` for vertically, `1` for horizontally.
# The `join` parameter controls the merge behavior on the shared axis, (the Index for `axis=1`). By default it's like a union of the two indexes, or an outer join.
pd.concat([temp, sped], axis=1, join='inner')
# ### Merge Version
#
# Since we're joining by index here the merge version is quite similar.
# We'll see an example later of a one-to-many join where the two differ.
pd.merge(temp.to_frame(), sped.to_frame(), left_index=True, right_index=True).head()
pd.merge(temp.to_frame(), sped.to_frame(), left_index=True, right_index=True,
how='outer').head()
# Like I said, I typically prefer `concat` to `merge`.
# The exception here is one-to-many type joins. Let's walk through one of those,
# where we join the flight data to the weather data.
# To focus just on the merge, we'll aggregate hour weather data to be daily, rather than trying to find the closest recorded weather observation to each departure (you could do that, but it's not the focus right now). We'll then join the one `(airport, date)` record to the many `(airport, date, flight)` records.
#
# Quick tangent, to get the weather data to daily frequency, we'll need to resample (more on that in the timeseries section). The resample essentially splits the recorded values into daily buckets and computes the aggregation function on each bucket. The only wrinkle is that we have to resample *by station*, so we'll use the `pd.TimeGrouper` helper.
# +
idx_cols = ['unique_carrier', 'origin', 'dest', 'tail_num', 'fl_num', 'fl_date']
data_cols = ['crs_dep_time', 'dep_delay', 'crs_arr_time', 'arr_delay',
'taxi_out', 'taxi_in', 'wheels_off', 'wheels_on', 'distance']
df = flights.set_index(idx_cols)[data_cols].sort_index()
# +
def mode(x):
'''
Arbitrarily break ties.
'''
return x.value_counts().index[0]
aggfuncs = {'tmpf': 'mean', 'relh': 'mean',
'sped': 'mean', 'mslp': 'mean',
'p01i': 'mean', 'vsby': 'mean',
'gust_mph': 'mean', 'skyc1': mode,
'skyc2': mode, 'skyc3': mode}
# TimeGrouper works on a DatetimeIndex, so we move `station` to the
# columns and then groupby it as well.
daily = (weather.reset_index(level="station")
.groupby([pd.TimeGrouper('1d'), "station"])
.agg(aggfuncs))
daily.head()
# -
# Now that we have daily flight and weather data, we can merge.
# We'll use the `on` keyword to indicate the columns we'll merge on (this is like a `USING (...)` SQL statement), we just have to make sure the names align.
# ### The merge version
# +
m = pd.merge(flights, daily.reset_index().rename(columns={'date': 'fl_date', 'station': 'origin'}),
on=['fl_date', 'origin']).set_index(idx_cols).sort_index()
m.head()
# -
# Since data-wrangling on its own is never the goal, let's do some quick analysis.
# Seaborn makes it easy to explore bivariate relationships.
m.sample(n=10000).pipe((sns.jointplot, 'data'), 'sped', 'dep_delay');
# Looking at the various [sky coverage states](https://en.wikipedia.org/wiki/METAR#Cloud_reporting):
#
#
m.groupby('skyc1').dep_delay.agg(['mean', 'count']).sort_values(by='mean')
import statsmodels.api as sm
# Statsmodels (via [patsy](http://patsy.readthedocs.org/) can automatically convert dummy data to dummy variables in a formula with the `C` function).
mod = sm.OLS.from_formula('dep_delay ~ C(skyc1) + distance + tmpf + relh + sped + mslp', data=m)
res = mod.fit()
res.summary()
fig, ax = plt.subplots()
ax.scatter(res.fittedvalues, res.resid, color='k', marker='.', alpha=.25)
ax.set(xlabel='Predicted', ylabel='Residual')
sns.despine()
# Those residuals should look like white noise.
# Looks like our linear model isn't flexible enough to model the delays,
# but I think that's enough for now.
#
# ---
#
# We'll talk more about indexes in the Tidy Data and Reshaping section.
# [Let me know](http://twitter.com/tomaugspurger) if you have any feedback.
# Thanks for reading!
|
modern_3_indexes.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # PyVIMS package playground
#
# This jupyter notebook allow you to play with the [VIMS data](https://vims.univ-nantes.fr/) without any prior installation.
# Press <kbd>shift</kbd> + <kbd>Enter</kbd> to run the different cells.
#
# __Note:__ This live demo will **not** be saved but you can download it in `File > Download as > notebook (.ipynb)`.
#
# For more information on the PyVIMS package, refer to this [notebook](pyvims.ipynb).
# +
# %matplotlib inline
from pyvims import VIMS
# -
cube = VIMS('1487096932_1')
cube
|
notebooks/playground.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# ---
bres_trend_micro,bres_trend_agg = [make_trend(bres_proc,sector_var=v) for v in ['sector','sector_aggregated']]
# +
fig,ax = plt.subplots()
plot_trend(bres_trend_agg,ax=ax)
ax.legend(bbox_to_anchor=(1,1))
# +
fig,ax = plt.subplots()
plot_trend(bres_trend_micro,ax=ax)
ax.legend(bbox_to_anchor=(1,1))
# +
fig,ax = plt.subplots()
plot_bar(bres_trend_micro,ax,norm=True)
ax.legend(bbox_to_anchor=(1,1))
# -
# ### b. Geographies
lad_bres_shares_09,lad_bres_shares_17 = [make_lorenz(bres_proc,y=year) for year in [2009,2017]]
# +
fig,ax = plt.subplots(figsize=(5,6),sharey=True)
plot_lorenz(lad_bres_shares_17,ax)
ax.legend(bbox_to_anchor=(1,1))
# -
plot__histo_lorenz(lad_bres_shares_09,lad_bres_shares_17)
# ### Some maps
plot_kwargs = {'scheme':'Fisher_Jenks','cmap':'viridis','edgecolor':'grey','linewidth':0,'legend':True}
# +
fig,ax = plt.subplots(figsize=(14,10),ncols=2)
year_comp(bres_proc,'sector_aggregated','journalism',ax=ax,**plot_kwargs)
plt.tight_layout()
# +
fig,ax = plt.subplots(figsize=(14,10),ncols=2)
sect_comp(bres_proc,'sector_aggregated',['other','journalism'],ax=ax,**plot_kwargs)
# +
fig,ax = plt.subplots(figsize=(21,10),ncols=3)
sect_comp(bres_proc,'sector',['publishing_newspapers','web_portals','computer_programming'],ax=ax,**plot_kwargs)
# +
fig,ax = plt.subplots(figsize=(14,10),ncols=2)
sect_comp(bres_proc,'sector',['tv_programming_broadcasting','radio_broadcasting'],ax=ax,**plot_kwargs)
# -
# +
fig,ax = plt.subplots(figsize=(12,7),nrows=2,sharex=True,gridspec_kw={'height_ratios':[3,1]})
sectors = ['artificial_intelligence','advertising','creative_content','news_high','public_news']
for n,s in enumerate(sectors):
(100*pd.crosstab(cb['year'],cb[s]>0.75,normalize=0)).loc[np.arange(2000,2019)][True].rolling(window=3).mean().dropna().plot(
ax=ax[0],color=colors[n],linewidth=3 if 'news' in s else 1)
ax[0].set_ylabel('% of all companies')
ax[0].legend(sectors,bbox_to_anchor=(1,1))
news = cb.loc[cb['news_high']==True]
(100*pd.crosstab(news['year'],news['public_news']>0.75,normalize=0)).loc[np.arange(2000,2019)][True].rolling(window=3).mean().dropna().plot(
ax=ax[1],color='blue',linewidth=3)
ax[1].set_ylabel('% of all \n news companies')
plt.tight_layout()
plt.savefig('../../reports/figures/research_slides/cb/activity_trends.pdf')
# -
100*pd.crosstab(cb['year'],cb['public_news']>0.75,normalize=0).loc[np.arange(2000,2019)][True][2018]
# #### Evolution of funding?
#
# We get the CB funding data and match it with companies
#
# That will allow us to get levels of funding and funders for various sources
# #### Analysis
# Next steps:
# * Create dummies for news, public interest news and AI and look at trends and actors
rel_sets = [set(cb.loc[cb[s]>0.75]['id']) for s in ['artificial_intelligence','advertising','creative_content','news_high','public_news']]
# +
cb_fr_df['ai'],cb_fr_df['advertising'],cb_fr_df['creative_content'],cb_fr_df['news'],cb_fr_df['pi_news'] = [
[x in one_set for x in cb_fr_df['company_id']] for one_set in rel_sets]
cb_fr_df['any_sector'] = 1
rel_sectors = ['ai','advertising',
'creative_content',
'news','pi_news','any_sector']
# +
ax = cb_fr_df.groupby('year')[rel_sectors[:-1]].sum().loc[np.arange(2000,2019)].rolling(window=3).mean().dropna().plot(color=colors)
ax.set_ylabel('Number of deals')
# -
# Totals raised
# +
fig,ax = plt.subplots(figsize=(12,7),nrows=2,sharex=True,gridspec_kw={'height_ratios':[3,1]})
total_raised = pd.concat([cb_fr_df.loc[cb_fr_df[s]==True].groupby('year')['raised_amount_usd'].sum() for s in rel_sectors],axis=1).fillna(0)/1e9
total_raised.columns = rel_sectors
total_raised.loc[np.arange(2000,2020),rel_sectors[:-1]].rolling(window=3).mean().dropna().plot(color=colors,ax=ax[0])
ax[0].set_ylabel('$ Billion')
news_funding= cb_fr_df.loc[cb_fr_df['news']==True]
(100*news_funding.groupby(['year','pi_news'])['raised_amount_usd'].sum().reset_index(drop=False).pivot(
index='year',columns='pi_news',values='raised_amount_usd').apply(lambda x: x/x.sum(),axis=1).loc[np.arange(2000,2019)].fillna(0).rolling(
window=3).mean()).dropna()[True].plot(color='blue',ax=ax[1],linewidth=3)
ax[1].set_ylabel('PI news as \n % of all news')
plt.tight_layout()
plt.savefig('../../reports/figures/research_slides/cb/funding_trends.pdf')
# -
|
notebooks/dev/scraps.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] pycharm={}
# # Classification with Delira and SciKit-Learn - A very short introduction
# *Author: <NAME>*
#
# *Date: 31.07.2019*
#
# This Example shows how to set up a basic classification model and experiment using SciKit-Learn.
#
# Let's first setup the essential hyperparameters. We will use `delira`'s `Parameters`-class for this:
# + pycharm={"is_executing": false}
logger = None
from delira.training import Parameters
import sklearn
params = Parameters(fixed_params={
"model": {},
"training": {
"batch_size": 64, # batchsize to use
"num_epochs": 10, # number of epochs to train
"optimizer_cls": None, # optimization algorithm to use
"optimizer_params": {}, # initialization parameters for this algorithm
"losses": {}, # the loss function
"lr_sched_cls": None, # the learning rate scheduling algorithm to use
"lr_sched_params": {}, # the corresponding initialization parameters
"metrics": {"mae": mean_absolute_error} # and some evaluation metrics
}
})
# + [markdown] pycharm={}
# Since we did not specify any metric, only the `CrossEntropyLoss` will be calculated for each batch. Since we have a classification task, this should be sufficient. We will train our network with a batchsize of 64 by using `Adam` as optimizer of choice.
#
# ## Logging and Visualization
# To get a visualization of our results, we should monitor them somehow. For logging we will use `Tensorboard`. Per default the logging directory will be the same as our experiment directory.
# + [markdown] pycharm={}
#
# ## Data Preparation
# ### Loading
# Next we will create some fake data. For this we use the `ClassificationFakeData`-Dataset, which is already implemented in `deliravision`. To avoid getting the exact same data from both datasets, we use a random offset.
# + pycharm={"is_executing": false}
from deliravision.data.fakedata import ClassificationFakeData
dataset_train = ClassificationFakeData(num_samples=10000,
img_size=(3, 32, 32),
num_classes=10)
dataset_val = ClassificationFakeData(num_samples=1000,
img_size=(3, 32, 32),
num_classes=10,
rng_offset=10001
)
# + [markdown] pycharm={}
# ### Augmentation
# For Data-Augmentation we will apply a few transformations:
# + pycharm={"is_executing": false}
from batchgenerators.transforms import RandomCropTransform, \
ContrastAugmentationTransform, Compose
from batchgenerators.transforms.spatial_transforms import ResizeTransform
from batchgenerators.transforms.sample_normalization_transforms import MeanStdNormalizationTransform
transforms = Compose([
RandomCropTransform(24), # Perform Random Crops of Size 24 x 24 pixels
ResizeTransform(32), # Resample these crops back to 32 x 32 pixels
ContrastAugmentationTransform(), # randomly adjust contrast
MeanStdNormalizationTransform(mean=[0.5], std=[0.5])])
# + [markdown] pycharm={}
# With these transformations we can now wrap our datasets into datamanagers:
# + pycharm={"is_executing": false}
from delira.data_loading import DataManager, SequentialSampler, RandomSampler
manager_train = DataManager(dataset_train, params.nested_get("batch_size"),
transforms=transforms,
sampler_cls=RandomSampler,
n_process_augmentation=4)
manager_val = DataManager(dataset_val, params.nested_get("batch_size"),
transforms=transforms,
sampler_cls=SequentialSampler,
n_process_augmentation=4)
# + [markdown] pycharm={}
# ## Model
#
# After we have done that, we can specify our model: We will use a very simple MultiLayer Perceptron here.
# In opposite to other backends, we don't need to provide a custom implementation of our model, but we can simply use it as-is. It will be automatically wrapped by `SklearnEstimator`, which can be subclassed for more advanced usage.
#
# ## Training
# Now that we have defined our network, we can finally specify our experiment and run it.
# + pycharm={"is_executing": true}
import warnings
warnings.simplefilter("ignore", UserWarning) # ignore UserWarnings raised by dependency code
warnings.simplefilter("ignore", FutureWarning) # ignore FutureWarnings raised by dependency code
from sklearn.neural_network import MLPClassifier
from delira.training import SklearnExperiment
if logger is not None:
logger.info("Init Experiment")
experiment = PyTorchExperiment(params, MLPClassifier,
name="ClassificationExample",
save_path="./tmp/delira_Experiments",
key_mapping={"X": "X"}
gpu_ids=[0])
experiment.save()
model = experiment.run(manager_train, manager_val)
# + [markdown] pycharm={}
# Congratulations, you have now trained your first Classification Model using `delira`, we will now predict a few samples from the testset to show, that the networks predictions are valid (for now, this is done manually, but we also have a `Predictor` class to automate stuff like this):
# + pycharm={}
import numpy as np
from tqdm.auto import tqdm # utility for progress bars
preds, labels = [], []
with torch.no_grad():
for i in tqdm(range(len(dataset_val))):
img = dataset_val[i]["data"] # get image from current batch
img_tensor = img.astype(np.float) # create a tensor from image, push it to device and add batch dimension
pred_tensor = model(img_tensor) # feed it through the network
pred = pred_tensor.argmax(1).item() # get index with maximum class confidence
label = np.asscalar(dataset_val[i]["label"]) # get label from batch
if i % 1000 == 0:
print("Prediction: %d \t label: %d" % (pred, label)) # print result
preds.append(pred)
labels.append(label)
# calculate accuracy
accuracy = (np.asarray(preds) == np.asarray(labels)).sum() / len(preds)
print("Accuracy: %.3f" % accuracy)
|
notebooks/classification_examples/sklearn.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# make high resolution animation from svg
import os
import glob
import cairosvg
import IPython
from PIL import Image
import numpy as np
def pure_pil_alpha_to_color_v2(image, color=(255, 255, 255)):
"""Alpha composite an RGBA Image with a specified color.
Simpler, faster version than the solutions above.
Source: http://stackoverflow.com/a/9459208/284318
Keyword Arguments:
image -- PIL RGBA Image object
color -- Tuple r, g, b (default 255, 255, 255)
"""
image.load() # needed for split()
background = Image.new('RGB', image.size, color)
background.paste(image, mask=image.split()[3]) # 3 is the alpha channel
return background
frames = []
imgs = glob.glob("canvas_record.*.svg")
imgs.sort()
for file in imgs:
print(file)
cairosvg.svg2png(url=file, write_to=file+".png", scale=4)
# make a gif
frames = []
imgs = glob.glob("canvas_record.*.svg.png")
for file in imgs:
new_frame = Image.open(file)
frames.append(pure_pil_alpha_to_color_v2(new_frame))
frames[0].save('hires.gif', save_all=True, append_images=frames[1:], optimize=True, duration=200, loop=0)
# +
#IPython.display.Image('hires.gif', format='png')
# -
|
examples/notebooks/HighResGIFfromSVG.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Creating a Filter, Edge Detection
# ### Import resources and display image
# +
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
import cv2
import numpy as np
# %matplotlib inline
# Read in the image
image = mpimg.imread('data/curved_lane.jpg')
plt.imshow(image)
# -
# ### Convert the image to grayscale
# +
# Convert to grayscale for filtering
gray = cv2.cvtColor(image, cv2.COLOR_RGB2GRAY)
plt.imshow(gray, cmap='gray')
# -
# ### TODO: Create a custom kernel
#
# Below, you've been given one common type of edge detection filter: a Sobel operator.
#
# The Sobel filter is very commonly used in edge detection and in finding patterns in intensity in an image. Applying a Sobel filter to an image is a way of **taking (an approximation) of the derivative of the image** in the x or y direction, separately. The operators look as follows.
#
# <img src="notebook_ims/sobel_ops.png" width=200 height=200>
#
# **It's up to you to create a Sobel x operator and apply it to the given image.**
#
# For a challenge, see if you can put the image through a series of filters: first one that blurs the image (takes an average of pixels), and then one that detects the edges.
# +
# Create a custom kernel
# 3x3 array for edge detection
sobel_y = np.array([[ -1, -2, -1],
[ 0, 0, 0],
[ 1, 2, 1]])
# Filter the image using filter2D, which has inputs: (grayscale image, bit-depth, kernel)
filtered_image = cv2.filter2D(gray, -1, sobel_y)
plt.imshow(filtered_image, cmap='gray')
# +
## TODO: Create and apply a Sobel x operator
sobel_x = np.array([[-1,0,1],[-2,0,2],[-1,0,1]])
filtered_image2 = cv2.filter2D(gray,-1,sobel_x)
plt.imshow(filtered_image2,cmap='gray')
# -
filtered_image_both = cv2.filter2D(filtered_image,-1,sobel_x)
plt.imshow(filtered_image_both,cmap='gray')
# ### Test out other filters!
#
# You're encouraged to create other kinds of filters and apply them to see what happens! As an **optional exercise**, try the following:
# * Create a filter with decimal value weights.
# * Create a 5x5 filter
# * Apply your filters to the other images in the `images` directory.
#
#
custom_filter = np.array([[-2,-2,-2,-2,-2],
[-1,-1,-1,-1,-1],
[0,0,0,0,0],
[1,1,1,1,1],
[2,2,2,2,2]])
custom_filtered_image = cv2.filter2D(gray,-1,custom_filter)
plt.imshow(custom_filtered_image, cmap='gray')
|
convolutional-neural-networks/conv-visualization/custom_filters.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
def shuffle(nums, n):
res = []
for i in range(n):
res.append(nums[i])
res.append(nums[n + i])
return res
print(shuffle([1,2], 1))
# -
|
Anjani/Leetcode/Array/Shuffle the Array.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import requests
from bs4 import BeautifulSoup
import csv
import re
import json
import sqlite3
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from time import sleep
import os
from collections import Counter
import pickle
import warnings
import time
warnings.filterwarnings("ignore")
from wordcloud import WordCloud
import matplotlib.pyplot as plt
import PIL
from PIL import Image, ImageFilter
from selenium import webdriver
from selenium.webdriver.common.action_chains import ActionChains
from selenium.webdriver.chrome.options import Options
import boto3
import botocore
# %matplotlib inline
# Use proxy and headers for safe web scraping
# os.environ['HTTPS_PROXY'] = 'http://172.16.31.10:8080'
# pd.options.mode.chained_assignment = None
headers = {
'user-agent': 'Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/'
'537.36 (KHTML, like Gecko) Chrome/75.0.3770.100 Safari/537.36'}
# -
countries_link = {'USA':'https://www.amazon.com',
'Australia':'https://www.amazon.com.au',
'UK':'https://www.amazon.co.uk',
'India':'https://www.amazon.in',
'Japan':'https://www.amazon.co.jp/',
'UAE':'https://amazon.ae'}
# ##### List of Products
# +
amazon_usa = {'health_and_beauty':{'hair_products':{'shampoo':'https://www.amazon.com/s?i=beauty-intl-ship&bbn=16225006011&rh=n%3A%2116225006011%2Cn%3A11057241%2Cn%3A17911764011%2Cn%3A11057651&dc&',
'conditioner':'https://www.amazon.com/s?i=beauty-intl-ship&bbn=16225006011&rh=n%3A%2116225006011%2Cn%3A11057241%2Cn%3A17911764011%2Cn%3A11057251&dc&',
'hair_scalp_treatment':'https://www.amazon.com/s?i=beauty-intl-ship&bbn=16225006011&rh=n%3A%2116225006011%2Cn%3A11057241%2Cn%3A11057431&dc&',
'treatment_oil':'https://www.amazon.com/s?i=beauty-intl-ship&bbn=16225006011&rh=n%3A%2116225006011%2Cn%3A11057241%2Cn%3A10666439011&dc&',
'hair_loss':'https://www.amazon.com/s?i=beauty-intl-ship&bbn=16225006011&rh=n%3A%2116225006011%2Cn%3A11057241%2Cn%3A10898755011&dc&'},
'skin_care':{'body':{'cleansers':'https://www.amazon.com/s?i=beauty-intl-ship&bbn=16225006011&rh=n%3A%2116225006011%2Cn%3A11060451%2Cn%3A11060521%2Cn%3A11056281&dc&',
'moisturizers':'https://www.amazon.com/s?i=beauty-intl-ship&bbn=16225006011&rh=n%3A%2116225006011%2Cn%3A11060451%2Cn%3A11060521%2Cn%3A11060661&dc&',
'treatments':'https://www.amazon.com/s?i=beauty-intl-ship&bbn=16225006011&rh=n%3A%2116225006011%2Cn%3A11060451%2Cn%3A11060521%2Cn%3A11056421&dc&'},
'eyes':{'creams':'https://www.amazon.com/s?i=beauty-intl-ship&bbn=16225006011&rh=n%3A%2116225006011%2Cn%3A11060451%2Cn%3A11061941%2Cn%3A7730090011&dc&',
'gels':'https://www.amazon.com/s?i=beauty-intl-ship&bbn=16225006011&rh=n%3A%2116225006011%2Cn%3A11060451%2Cn%3A11061941%2Cn%3A7730092011&dc&',
'serums':'https://www.amazon.com/s?i=beauty-intl-ship&bbn=16225006011&rh=n%3A%2116225006011%2Cn%3A11060451%2Cn%3A11061941%2Cn%3A7730098011&dc&'},
'face':{'f_cleansers':'https://www.amazon.com/s?i=beauty-intl-ship&bbn=16225006011&rh=n%3A%2116225006011%2Cn%3A11060451%2Cn%3A11060711%2Cn%3A11060901&dc&',
'f_moisturizers':'https://www.amazon.com/s?i=beauty-intl-ship&bbn=16225006011&rh=n%3A%2116225006011%2Cn%3A11060451%2Cn%3A11060711%2Cn%3A11060901&dc&',
'scrubs':'https://www.amazon.com/s?i=beauty-intl-ship&bbn=16225006011&rh=n%3A%2116225006011%2Cn%3A11060451%2Cn%3A11060711%2Cn%3A11061091&dc&',
'toners':'https://www.amazon.com/s?i=beauty-intl-ship&bbn=16225006011&rh=n%3A%2116225006011%2Cn%3A11060451%2Cn%3A11060711%2Cn%3A11061931&dc&',
'f_treatments':'https://www.amazon.com/s?i=beauty-intl-ship&bbn=16225006011&rh=n%3A%2116225006011%2Cn%3A11060451%2Cn%3A11060711%2Cn%3A11061931&dc&'},
'lipcare':'https://www.amazon.com/s?i=beauty-intl-ship&bbn=16225006011&rh=n%3A%2116225006011%2Cn%3A11060451%2Cn%3A3761351&dc&'}},
'food':{'tea':{'herbal':'https://www.amazon.com/s?k=tea&i=grocery&rh=n%3A16310101%2Cn%3A16310231%2Cn%3A16521305011%2Cn%3A16318401%2Cn%3A16318511&dc&',
'green':'https://www.amazon.com/s?k=tea&i=grocery&rh=n%3A16310101%2Cn%3A16310231%2Cn%3A16521305011%2Cn%3A16318401%2Cn%3A16318471&dc&',
'black':'https://www.amazon.com/s?k=tea&i=grocery&rh=n%3A16310101%2Cn%3A16310231%2Cn%3A16521305011%2Cn%3A16318401%2Cn%3A16318411&dc&',
'chai':'https://www.amazon.com/s?k=tea&i=grocery&rh=n%3A16310101%2Cn%3A16310231%2Cn%3A16521305011%2Cn%3A16318401%2Cn%3A348022011&dc&'},
'coffee':'https://www.amazon.com/s?k=tea&i=grocery&rh=n%3A16310101%2Cn%3A16310231%2Cn%3A16521305011%2Cn%3A16318031%2Cn%3A2251593011&dc&',
'dried_fruits':{'mixed':'https://www.amazon.com/s?k=dried+fruits&i=grocery&rh=n%3A16310101%2Cn%3A6506977011%2Cn%3A9865332011%2Cn%3A9865334011%2Cn%3A9865348011&dc&',
'mangoes':'https://www.amazon.com/s?k=dried+fruits&rh=n%3A16310101%2Cn%3A9865346011&dc&'},
'nuts':{'mixed':'https://www.amazon.com/s?k=nuts&rh=n%3A16310101%2Cn%3A16322931&dc&',
'peanuts':'https://www.amazon.com/s?k=nuts&i=grocery&rh=n%3A16310101%2Cn%3A18787303011%2Cn%3A16310221%2Cn%3A16322881%2Cn%3A16322941&dc&',
'cashews':'https://www.amazon.com/s?k=nuts&i=grocery&rh=n%3A16310101%2Cn%3A18787303011%2Cn%3A16310221%2Cn%3A16322881%2Cn%3A16322901&dc&'}},
'supplements':{'sports':{'pre_workout':'https://www.amazon.com/s?k=supplements&i=hpc&rh=n%3A3760901%2Cn%3A6973663011%2Cn%3A6973697011&dc&',
'protein':'https://www.amazon.com/s?k=supplements&i=hpc&rh=n%3A3760901%2Cn%3A6973663011%2Cn%3A6973704011&dc&',
'fat_burner':'https://www.amazon.com/s?k=supplements&i=hpc&rh=n%3A3760901%2Cn%3A6973663011%2Cn%3A6973679011&dc&',
'weight_gainer':'https://www.amazon.com/s?k=supplements&i=hpc&rh=n%3A3760901%2Cn%3A6973663011%2Cn%3A6973725011&dc&'},
'vitamins_dietary':{'supplements':'https://www.amazon.com/s?k=supplements&i=hpc&rh=n%3A3760901%2Cn%3A3764441%2Cn%3A6939426011&dc&',
'multivitamins':'https://www.amazon.com/s?k=supplements&i=hpc&rh=n%3A3760901%2Cn%3A3774861&dc&'}},
'wellness':{'ayurveda':'https://www.amazon.com/s?k=supplements&i=hpc&rh=n%3A3760901%2Cn%3A10079996011%2Cn%3A13052911%2Cn%3A13052941&dc&',
'essential_oil_set':'https://www.amazon.com/s?k=supplements&i=hpc&rh=n%3A3760901%2Cn%3A10079996011%2Cn%3A13052911%2Cn%3A18502613011&dc&',
'massage_oil':'https://www.amazon.com/s?k=supplements&i=hpc&rh=n%3A3760901%2Cn%3A10079996011%2Cn%3A14442631&dc&'},
'personal_accessories':{'bags':{'women':{'clutches':'https://www.amazon.com/s?k=bags&i=fashion-womens-handbags&bbn=15743631&rh=n%3A7141123011%2Cn%3A%217141124011%2Cn%3A7147440011%2Cn%3A15743631%2Cn%3A17037745011&dc&',
'crossbody':'https://www.amazon.com/s?k=bags&i=fashion-womens-handbags&bbn=15743631&rh=n%3A7141123011%2Cn%3A%217141124011%2Cn%3A7147440011%2Cn%3A15743631%2Cn%3A2475899011&dc&',
'fashion':'https://www.amazon.com/s?k=bags&i=fashion-womens-handbags&bbn=15743631&rh=n%3A7141123011%2Cn%3A%217141124011%2Cn%3A7147440011%2Cn%3A15743631%2Cn%3A16977745011&dc&',
'hobo':'https://www.amazon.com/s?k=bags&i=fashion-womens-handbags&bbn=15743631&rh=n%3A7141123011%2Cn%3A%217141124011%2Cn%3A7147440011%2Cn%3A15743631%2Cn%3A16977747011&dc&'}},
'jewelry':{'anklets':'https://www.amazon.com/s?i=fashion-womens-intl-ship&bbn=16225018011&rh=n%3A16225018011%2Cn%3A7192394011%2Cn%3A7454897011&dc&',
'bracelets':'https://www.amazon.com/s?i=fashion-womens-intl-ship&bbn=16225018011&rh=n%3A16225018011%2Cn%3A7192394011%2Cn%3A7454898011&dc&',
'earrings':'https://www.amazon.com/s?i=fashion-womens-intl-ship&bbn=16225018011&rh=n%3A16225018011%2Cn%3A7192394011%2Cn%3A7454917011&dc&',
'necklaces':'https://www.amazon.com/s?i=fashion-womens-intl-ship&bbn=16225018011&rh=n%3A16225018011%2Cn%3A7192394011%2Cn%3A7454917011&dc&',
'rings':'https://www.amazon.com/s?i=fashion-womens-intl-ship&bbn=16225018011&rh=n%3A16225018011%2Cn%3A7192394011%2Cn%3A7454939011&dc&'},
'artisan_fabrics':'https://www.amazon.com/s?k=fabrics&rh=n%3A2617941011%2Cn%3A12899121&dc&'}}
amazon_uk = {'health_and_beauty':{'hair_products':{'shampoo':'https://www.amazon.co.uk/b/ref=amb_link_5?ie=UTF8&node=74094031&pf_rd_m=A3P5ROKL5A1OLE&pf_rd_s=merchandised-search-leftnav&pf_rd_r=KF9SM53J2HXHP4EJD3AH&pf_rd_r=KF9SM53J2HXHP4EJD3AH&pf_rd_t=101&pf_rd_p=aaaa7182-fdd6-4b35-8f0b-993e78880b69&pf_rd_p=aaaa7182-fdd6-4b35-8f0b-993e78880b69&pf_rd_i=66469031',
'conditioner':'https://www.amazon.co.uk/b/ref=amb_link_6?ie=UTF8&node=2867976031&pf_rd_m=A3P5ROKL5A1OLE&pf_rd_s=merchandised-search-leftnav&pf_rd_r=KF9SM53J2HXHP4EJD3AH&pf_rd_r=KF9SM53J2HXHP4EJD3AH&pf_rd_t=101&pf_rd_p=aaaa7182-fdd6-4b35-8f0b-993e78880b69&pf_rd_p=aaaa7182-fdd6-4b35-8f0b-993e78880b69&pf_rd_i=66469031',
'hair_loss':'https://www.amazon.co.uk/b/ref=amb_link_11?ie=UTF8&node=2867979031&pf_rd_m=A3P5ROKL5A1OLE&pf_rd_s=merchandised-search-leftnav&pf_rd_r=KF9SM53J2HXHP4EJD3AH&pf_rd_r=KF9SM53J2HXHP4EJD3AH&pf_rd_t=101&pf_rd_p=aaaa7182-fdd6-4b35-8f0b-993e78880b69&pf_rd_p=aaaa7182-fdd6-4b35-8f0b-993e78880b69&pf_rd_i=66469031',
'hair_scalp_treatment':'https://www.amazon.co.uk/b/ref=amb_link_7?ie=UTF8&node=2867977031&pf_rd_m=A3P5ROKL5A1OLE&pf_rd_s=merchandised-search-leftnav&pf_rd_r=KF9SM53J2HXHP4EJD3AH&pf_rd_r=KF9SM53J2HXHP4EJD3AH&pf_rd_t=101&pf_rd_p=aaaa7182-fdd6-4b35-8f0b-993e78880b69&pf_rd_p=aaaa7182-fdd6-4b35-8f0b-993e78880b69&pf_rd_i=66469031',
'treatment_oil':'https://www.amazon.co.uk/hair-oil-argan/b/ref=amb_link_8?ie=UTF8&node=2867981031&pf_rd_m=A3P5ROKL5A1OLE&pf_rd_s=merchandised-search-leftnav&pf_rd_r=KF9SM53J2HXHP4EJD3AH&pf_rd_r=KF9SM53J2HXHP4EJD3AH&pf_rd_t=101&pf_rd_p=aaaa7182-fdd6-4b35-8f0b-993e78880b69&pf_rd_p=aaaa7182-fdd6-4b35-8f0b-993e78880b69&pf_rd_i=66469031'},
'skin_care':{'body':{'cleanser':'https://www.amazon.co.uk/s/ref=lp_344269031_nr_n_3?fst=as%3Aoff&rh=n%3A117332031%2Cn%3A%21117333031%2Cn%3A118464031%2Cn%3A344269031%2Cn%3A344282031&bbn=344269031&ie=UTF8&qid=1581612722&rnid=344269031',
'moisturizers':'https://www.amazon.co.uk/s/ref=lp_344269031_nr_n_1?fst=as%3Aoff&rh=n%3A117332031%2Cn%3A%21117333031%2Cn%3A118464031%2Cn%3A344269031%2Cn%3A2805272031&bbn=344269031&ie=UTF8&qid=1581612722&rnid=344269031'},
'eyes':{'creams':'https://www.amazon.co.uk/s/ref=lp_118465031_nr_n_0?fst=as%3Aoff&rh=n%3A117332031%2Cn%3A%21117333031%2Cn%3A118464031%2Cn%3A118465031%2Cn%3A344259031&bbn=118465031&ie=UTF8&qid=1581612984&rnid=118465031',
'gels':'https://www.amazon.co.uk/s/ref=lp_118465031_nr_n_1?fst=as%3Aoff&rh=n%3A117332031%2Cn%3A%21117333031%2Cn%3A118464031%2Cn%3A118465031%2Cn%3A344258031&bbn=118465031&ie=UTF8&qid=1581613044&rnid=118465031',
'serums':'https://www.amazon.co.uk/s/ref=lp_118465031_nr_n_3?fst=as%3Aoff&rh=n%3A117332031%2Cn%3A%21117333031%2Cn%3A118464031%2Cn%3A118465031%2Cn%3A344257031&bbn=118465031&ie=UTF8&qid=1581613044&rnid=118465031'},
'face':{'cleansers':'https://www.amazon.co.uk/s/ref=lp_118466031_nr_n_1?fst=as%3Aoff&rh=n%3A117332031%2Cn%3A%21117333031%2Cn%3A118464031%2Cn%3A118466031%2Cn%3A344265031&bbn=118466031&ie=UTF8&qid=1581613120&rnid=118466031',
'moisturizers':'https://www.amazon.co.uk/s/ref=lp_118466031_nr_n_3?fst=as%3Aoff&rh=n%3A117332031%2Cn%3A%21117333031%2Cn%3A118464031%2Cn%3A118466031%2Cn%3A2805291031&bbn=118466031&ie=UTF8&qid=1581613120&rnid=118466031',
'toners':'https://www.amazon.co.uk/s/ref=lp_118466031_nr_n_0?fst=as%3Aoff&rh=n%3A117332031%2Cn%3A%21117333031%2Cn%3A118464031%2Cn%3A118466031%2Cn%3A344267031&bbn=118466031&ie=UTF8&qid=1581613120&rnid=118466031',
'treatments':'https://www.amazon.co.uk/s?bbn=118466031&rh=n%3A117332031%2Cn%3A%21117333031%2Cn%3A118464031%2Cn%3A118466031%2Cn%3A18918424031&dc&fst=as%3Aoff&qid=1581613120&rnid=118466031&ref=lp_118466031_nr_n_7'},
'lipcare':'https://www.amazon.co.uk/s/ref=lp_118464031_nr_n_4?fst=as%3Aoff&rh=n%3A117332031%2Cn%3A%21117333031%2Cn%3A118464031%2Cn%3A118467031&bbn=118464031&ie=UTF8&qid=1581613357&rnid=118464031'}},
'food':{'tea':{'herbal':'https://www.amazon.co.uk/s?k=tea&i=grocery&rh=n%3A340834031%2Cn%3A358584031%2Cn%3A11711401%2Cn%3A406567031&dc&qid=1581613483&rnid=344155031&ref=sr_nr_n_1',
'green':'https://www.amazon.co.uk/s?k=tea&i=grocery&rh=n%3A340834031%2Cn%3A358584031%2Cn%3A11711401%2Cn%3A406566031&dc&qid=1581613483&rnid=344155031&ref=sr_nr_n_3',
'black':'https://www.amazon.co.uk/s?k=tea&i=grocery&rh=n%3A340834031%2Cn%3A358584031%2Cn%3A11711401%2Cn%3A406564031&dc&qid=1581613483&rnid=344155031&ref=sr_nr_n_2'},
'coffee':'https://www.amazon.co.uk/s?k=coffee&rh=n%3A340834031%2Cn%3A11711391&dc&qid=1581613715&rnid=1642204031&ref=sr_nr_n_2',
'dried_fruits':{'mixed':'https://www.amazon.co.uk/s?k=dried+fruits&rh=n%3A340834031%2Cn%3A9733163031&dc&qid=1581613770&rnid=1642204031&ref=sr_nr_n_2'},
'nuts':{'mixed':'https://www.amazon.co.uk/s?k=mixed&rh=n%3A359964031&ref=nb_sb_noss',
'peanuts':'https://www.amazon.co.uk/s?k=peanuts&rh=n%3A359964031&ref=nb_sb_noss',
'cashews':'https://www.amazon.co.uk/s?k=cashew&rh=n%3A359964031&ref=nb_sb_noss'}},
'supplements':{'sports':{'pre_workout':'https://www.amazon.co.uk/b/?node=5977685031&ref_=Oct_s9_apbd_odnav_hd_bw_b35Hc3L_1&pf_rd_r=C5MZHH5TH5F868B6FQWD&pf_rd_p=8086b6c9-ae16-5c3c-a879-030afa4ee08f&pf_rd_s=merchandised-search-11&pf_rd_t=BROWSE&pf_rd_i=2826478031',
'protein':'https://www.amazon.co.uk/b/?node=2826510031&ref_=Oct_s9_apbd_odnav_hd_bw_b35Hc3L_0&pf_rd_r=C5MZHH5TH5F868B6FQWD&pf_rd_p=8086b6c9-ae16-5c3c-a879-030afa4ee08f&pf_rd_s=merchandised-search-11&pf_rd_t=BROWSE&pf_rd_i=2826478031',
'fat_burner':'https://www.amazon.co.uk/b/?node=5977737031&ref_=Oct_s9_apbd_odnav_hd_bw_b35Hc3L_2&pf_rd_r=C5MZHH5TH5F868B6FQWD&pf_rd_p=8086b6c9-ae16-5c3c-a879-030afa4ee08f&pf_rd_s=merchandised-search-11&pf_rd_t=BROWSE&pf_rd_i=2826478031'},
'vitamins_dietary':{'supplements':'https://www.amazon.co.uk/b/?_encoding=UTF8&node=2826534031&bbn=65801031&ref_=Oct_s9_apbd_odnav_hd_bw_b35Hdc7_2&pf_rd_r=AY01DQVCB4SE7VVE7MTK&pf_rd_p=1ecdbf02-af23-502a-b7ab-9916ddd6690c&pf_rd_s=merchandised-search-11&pf_rd_t=BROWSE&pf_rd_i=2826484031',
'multivitamins':'https://www.amazon.co.uk/b/?_encoding=UTF8&node=2826506031&bbn=65801031&ref_=Oct_s9_apbd_odnav_hd_bw_b35Hdc7_1&pf_rd_r=AY01DQVCB4SE7VVE7MTK&pf_rd_p=1ecdbf02-af23-502a-b7ab-9916ddd6690c&pf_rd_s=merchandised-search-11&pf_rd_t=BROWSE&pf_rd_i=2826484031'}},
'wellness':{'massage_oil':'https://www.amazon.co.uk/b/?node=3360479031&ref_=Oct_s9_apbd_odnav_hd_bw_b50nmJ_4&pf_rd_r=GYVYF52HT2004EDTY67W&pf_rd_p=3f8e4361-c00b-588b-a07d-ff259bf98bbc&pf_rd_s=merchandised-search-11&pf_rd_t=BROWSE&pf_rd_i=74073031',
'ayurveda':'https://www.amazon.co.uk/s?k=ayurveda&rh=n%3A65801031%2Cn%3A2826449031&dc&qid=1581686978&rnid=1642204031&ref=sr_nr_n_22'},
'personal_accessories':{'bags':{'women':{'clutches':'https://www.amazon.co.uk/b/?node=1769563031&ref_=Oct_s9_apbd_odnav_hd_bw_b1vkt8h_3&pf_rd_r=VC8RX89R4V4JJ5TEBANF&pf_rd_p=cefca17f-8dac-5c80-848f-812aff1bfdd7&pf_rd_s=merchandised-search-11&pf_rd_t=BROWSE&pf_rd_i=1769559031',
'crossbody':'https://www.amazon.co.uk/b/?node=1769564031&ref_=Oct_s9_apbd_odnav_hd_bw_b1vkt8h_1&pf_rd_r=VC8RX89R4V4JJ5TEBANF&pf_rd_p=cefca17f-8dac-5c80-848f-812aff1bfdd7&pf_rd_s=merchandised-search-11&pf_rd_t=BROWSE&pf_rd_i=1769559031',
'fashion':'https://www.amazon.co.uk/b/?node=1769560031&ref_=Oct_s9_apbd_odnav_hd_bw_b1vkt8h_5&pf_rd_r=VC8RX89R4V4JJ5TEBANF&pf_rd_p=cefca17f-8dac-5c80-848f-812aff1bfdd7&pf_rd_s=merchandised-search-11&pf_rd_t=BROWSE&pf_rd_i=1769559031',
'hobo':'https://www.amazon.co.uk/b/?node=1769565031&ref_=Oct_s9_apbd_odnav_hd_bw_b1vkt8h_4&pf_rd_r=VC8RX89R4V4JJ5TEBANF&pf_rd_p=cefca17f-8dac-5c80-848f-812aff1bfdd7&pf_rd_s=merchandised-search-11&pf_rd_t=BROWSE&pf_rd_i=1769559031'}},
'jewelry':{'anklets':'https://www.amazon.co.uk/s/ref=lp_10382835031_nr_n_0?fst=as%3Aoff&rh=n%3A193716031%2Cn%3A%21193717031%2Cn%3A10382835031%2Cn%3A10382860031&bbn=10382835031&ie=UTF8&qid=1581687575&rnid=10382835031',
'bracelets':'https://www.amazon.co.uk/s/ref=lp_10382835031_nr_n_1?fst=as%3Aoff&rh=n%3A193716031%2Cn%3A%21193717031%2Cn%3A10382835031%2Cn%3A10382861031&bbn=10382835031&ie=UTF8&qid=1581687575&rnid=10382835031',
'earrings':'https://www.amazon.co.uk/s/ref=lp_10382835031_nr_n_4?fst=as%3Aoff&rh=n%3A193716031%2Cn%3A%21193717031%2Cn%3A10382835031%2Cn%3A10382865031&bbn=10382835031&ie=UTF8&qid=1581687575&rnid=10382835031',
'necklaces':'https://www.amazon.co.uk/s/ref=lp_10382835031_nr_n_7?fst=as%3Aoff&rh=n%3A193716031%2Cn%3A%21193717031%2Cn%3A10382835031%2Cn%3A10382868031&bbn=10382835031&ie=UTF8&qid=1581687575&rnid=10382835031',
'rings':'https://www.amazon.co.uk/s/ref=lp_10382835031_nr_n_10?fst=as%3Aoff&rh=n%3A193716031%2Cn%3A%21193717031%2Cn%3A10382835031%2Cn%3A10382871031&bbn=10382835031&ie=UTF8&qid=1581687575&rnid=10382835031'},
'artisan_fabrics':'https://www.amazon.co.uk/s?k=fabric&rh=n%3A11052681%2Cn%3A3063518031&dc&qid=1581687726&rnid=1642204031&ref=a9_sc_1'}}
amazon_india = {'health_and_beauty':{'hair_products':{'shampoo':'https://www.amazon.in/b/ref=s9_acss_bw_cg_btyH1_2a1_w?ie=UTF8&node=1374334031&pf_rd_m=A1K21FY43GMZF8&pf_rd_s=merchandised-search-5&pf_rd_r=JHDJ4QHM0APVS05NGF4G&pf_rd_t=101&pf_rd_p=41b9c06b-1514-47de-a1c6-f4f13fb55ffe&pf_rd_i=1374305031',
'conditioner':'https://www.amazon.in/b/ref=s9_acss_bw_cg_btyH1_2b1_w?ie=UTF8&node=1374306031&pf_rd_m=A1K21FY43GMZF8&pf_rd_s=merchandised-search-5&pf_rd_r=CBABMCW6C69JRBGZNWWP&pf_rd_t=101&pf_rd_p=41b9c06b-1514-47de-a1c6-f4f13fb55ffe&pf_rd_i=1374305031',
'treatment_oil':''},
'skin_care':[],
'wellness_product':[]},
'food':{'tea':[],
'coffee':[],
'dried_fruits':[],
'nuts':[],
'supplements':[]},
'personal_accessories':{'bags':[],
'jewelry':[],
'artisan_fabrics':[]}}
amazon_aus = {'health_and_beauty':{'hair_products':{'shampoo':'https://www.amazon.com.au/b/?_encoding=UTF8&node=5150253051&bbn=4851917051&ref_=Oct_s9_apbd_odnav_hd_bw_b5cXATz&pf_rd_r=6SEM7GFDN7CQ2W4KXM9M&pf_rd_p=9dd4b462-1094-5e36-890d-bb1b694c8b53&pf_rd_s=merchandised-search-12&pf_rd_t=BROWSE&pf_rd_i=5150070051',
'conditioner':'https://www.amazon.com.au/b/?_encoding=UTF8&node=5150226051&bbn=4851917051&ref_=Oct_s9_apbd_odnav_hd_bw_b5cXATz&pf_rd_r=6SEM7GFDN7CQ2W4KXM9M&pf_rd_p=9dd4b462-1094-5e36-890d-bb1b694c8b53&pf_rd_s=merchandised-search-12&pf_rd_t=BROWSE&pf_rd_i=5150070051'},
'skin_care':[],
'wellness_product':[]},
'food':{'tea':{'herbal':'',
'green':'https://www.amazon.com.au/s/ref=lp_5555388051_nr_n_3?fst=as%3Aoff&rh=n%3A5547635051%2Cn%3A%215547636051%2Cn%3A5555314051%2Cn%3A5555388051%2Cn%3A5555543051&bbn=5555388051&ie=UTF8&qid=1584282626&rnid=5555388051',
'black':'https://www.amazon.com.au/s/ref=lp_5555388051_nr_n_0?fst=as%3Aoff&rh=n%3A5547635051%2Cn%3A%215547636051%2Cn%3A5555314051%2Cn%3A5555388051%2Cn%3A5555541051&bbn=5555388051&ie=UTF8&qid=1584285938&rnid=5555388051',
'chai':''},
'coffee':'https://www.amazon.com.au/s/ref=lp_5555314051_nr_n_0?fst=as%3Aoff&rh=n%3A5547635051%2Cn%3A%215547636051%2Cn%3A5555314051%2Cn%3A5555382051&bbn=5555314051&ie=UTF8&qid=1584207291&rnid=5555314051',
'dried_fruits':{'mixed':'',
'mangoes':''},
'nuts':{'mixed':'https://www.amazon.com.au/s?k=mixed%20nuts&ref=nb_sb_noss&rh=n%3A5555474051&url=node%3D5555474051',
'peanuts':'https://www.amazon.com.au/s?k=peanuts&ref=nb_sb_noss&rh=n%3A5555474051&url=node%3D5555474051',
'cashews':'https://www.amazon.com.au/s?k=cashews&ref=nb_sb_noss&rh=n%3A5555474051&url=node%3D5555474051'}},
'supplements':{'sports':{'pre_workout':'https://www.amazon.com.au/b/?_encoding=UTF8&node=5148339051&bbn=4851917051&ref_=Oct_s9_apbd_odnav_hd_bw_b5cPRoZ_3&pf_rd_r=HN11C6S8SDVY38KJZYV3&pf_rd_p=1c658db3-169d-5f89-8673-898e1fd5ee1e&pf_rd_s=merchandised-search-10&pf_rd_t=BROWSE&pf_rd_i=5148230051',
'protein':'https://www.amazon.com.au/b/?_encoding=UTF8&node=5148365051&bbn=4851917051&ref_=Oct_s9_apbd_odnav_hd_bw_b5cPRoZ_0&pf_rd_r=6GVHZAP9J9WY7HGH888R&pf_rd_p=1c658db3-169d-5f89-8673-898e1fd5ee1e&pf_rd_s=merchandised-search-10&pf_rd_t=BROWSE&pf_rd_i=5148230051',
'fat_burner':'https://www.amazon.com.au/b/?_encoding=UTF8&node=5148760051&bbn=4851917051&ref_=Oct_s9_apbd_odnav_hd_bw_b5cPRoZ_4&pf_rd_r=6GVHZAP9J9WY7HGH888R&pf_rd_p=1c658db3-169d-5f89-8673-898e1fd5ee1e&pf_rd_s=merchandised-search-10&pf_rd_t=BROWSE&pf_rd_i=5148230051',
'weight_gainer':''},
'vitamins_dietary':{'supplements':'https://www.amazon.com.au/b/?_encoding=UTF8&node=5148358051&bbn=4851917051&ref_=Oct_s9_apbd_odnav_hd_bw_b5cPS4h_0&pf_rd_r=VGHE5D2HR7JYWNCAAVYT&pf_rd_p=214a2f58-0505-577e-aa86-fdd72d600a9a&pf_rd_s=merchandised-search-10&pf_rd_t=BROWSE&pf_rd_i=5148231051',
'multivitamins':'https://www.amazon.com.au/b/?_encoding=UTF8&node=5148351051&bbn=4851917051&ref_=Oct_s9_apbd_odnav_hd_bw_b5cPS4h_2&pf_rd_r=VGHE5D2HR7JYWNCAAVYT&pf_rd_p=214a2f58-0505-577e-aa86-fdd72d600a9a&pf_rd_s=merchandised-search-10&pf_rd_t=BROWSE&pf_rd_i=5148231051'}},
'wellness':{'ayurveda':'https://www.amazon.com.au/s?k=ayurveda&ref=nb_sb_noss&rh=n%3A5148210051&url=node%3D5148210051',
'essential_oil_set':'https://www.amazon.com.au/s?k=essential+oil&rh=n%3A5148210051&ref=nb_sb_noss',
'massage_oil':'https://www.amazon.com.au/s?k=massage%20oil&ref=nb_sb_noss&rh=n%3A5148210051&url=node%3D5148210051'},
'personal_accessories':{'bags':{'women':{'clutches':'https://www.amazon.com.au/b/?_encoding=UTF8&node=5131114051&bbn=4851856051&ref_=Oct_s9_apbd_odnav_hd_bw_b5bEF3L_2&pf_rd_r=YZ7JGTT62DKZB8C97D3H&pf_rd_p=bf3f7e2d-f60e-5998-994f-a490e47553c6&pf_rd_s=merchandised-search-10&pf_rd_t=BROWSE&pf_rd_i=5130783051',
'crossbody':'https://www.amazon.com.au/b/?_encoding=UTF8&node=5131115051&bbn=4851856051&ref_=Oct_s9_apbd_odnav_hd_bw_b5bEF3L_3&pf_rd_r=YZ7JGTT62DKZB8C97D3H&pf_rd_p=bf3f7e2d-f60e-5998-994f-a490e47553c6&pf_rd_s=merchandised-search-10&pf_rd_t=BROWSE&pf_rd_i=5130783051',
'fashion':'',
'hobo':''}},
'jewelry':{'anklets':'',
'bracelets':'',
'earrings':'',
'necklaces':'',
'rings':''},
'artisan_fabrics':''}}
amazon = {'USA':amazon_usa,
'UK':amazon_uk,
'India':amazon_india,
'Australia':amazon_aus}
# +
def hover(browser, xpath):
'''
This function makes an automated mouse hovering in the selenium webdriver
element based on its xpath.
PARAMETER
---------
browser: Selenium based webbrowser
xpath: str
xpath of the element in the webpage where hover operation has to be
performed.
'''
element_to_hover_over = browser.find_element_by_xpath(xpath)
hover = ActionChains(browser).move_to_element(element_to_hover_over)
hover.perform()
element_to_hover_over.click()
def browser(link):
'''This funtion opens a selenium based chromebrowser specifically tuned
to work for amazon product(singular item) webpages. Few functionality
includes translation of webpage, clicking the initial popups, and hovering
over product imagesso that the images can be scrape
PARAMETER
---------
link: str
Amazon Product item link
RETURN
------
driver: Selenium web browser with operated functions
'''
options = Options()
prefs = {
"translate_whitelists": {"ja":"en","de":'en'},
"translate":{"enabled":"true"}
}
# helium = r'C:\Users\Dell-pc\AppData\Local\Google\Chrome\User Data\Default\Extensions\njmehopjdpcckochcggncklnlmikcbnb\4.2.12_0'
# options.add_argument(helium)
options.add_experimental_option("prefs", prefs)
options.headless = True
driver = webdriver.Chrome(chrome_options=options)
driver.get(link)
try:
driver.find_element_by_xpath('//*[@id="nav-main"]/div[1]/div[2]/div/div[3]/span[1]/span/input').click()
except:
pass
try:
hover(driver,'//*[@id="altImages"]/ul/li[3]')
except:
pass
try:
driver.find_element_by_xpath('//*[@id="a-popover-6"]/div/header/button/i').click()
except:
pass
try:
hover(driver,'//*[@id="altImages"]/ul/li[4]')
except:
pass
try:
driver.find_element_by_xpath('//*[@id="a-popover-6"]/div/header/button/i').click()
except:
pass
try:
hover(driver,'//*[@id="altImages"]/ul/li[5]')
except:
pass
try:
driver.find_element_by_xpath('//*[@id="a-popover-6"]/div/header/button/i').click()
except:
pass
try:
hover(driver,'//*[@id="altImages"]/ul/li[6]')
except:
pass
try:
driver.find_element_by_xpath('//*[@id="a-popover-6"]/div/header/button/i').click()
except:
pass
try:
hover(driver,'//*[@id="altImages"]/ul/li[7]')
except:
pass
try:
driver.find_element_by_xpath('//*[@id="a-popover-6"]/div/header/button/i').click()
except:
pass
try:
hover(driver,'//*[@id="altImages"]/ul/li[8]')
except:
pass
try:
driver.find_element_by_xpath('//*[@id="a-popover-6"]/div/header/button/i').click()
except:
pass
try:
hover(driver,'//*[@id="altImages"]/ul/li[9]')
except:
pass
try:
driver.find_element_by_xpath('//*[@id="a-popover-6"]/div/header/button/i').click()
except:
pass
return driver
def scroll_temp(driver):
'''
Automated Scroller in Selenium Webbrowser
PARAMETER
---------
driver: Selenium Webbrowser
'''
pre_scroll_height = driver.execute_script('return document.body.scrollHeight;')
run_time, max_run_time = 0, 2
while True:
iteration_start = time.time()
# Scroll webpage, the 100 allows for a more 'aggressive' scroll
driver.execute_script('window.scrollTo(0,0.6*document.body.scrollHeight);')
post_scroll_height = driver.execute_script('return document.body.scrollHeight;')
scrolled = post_scroll_height != pre_scroll_height
timed_out = run_time >= max_run_time
if scrolled:
run_time = 0
pre_scroll_height = post_scroll_height
elif not scrolled and not timed_out:
run_time += time.time() - iteration_start
elif not scrolled and timed_out:
break
# def scroll(driver):
# scroll_temp(driver)
# from selenium.common.exceptions import NoSuchElementException
# try:
# element = driver.find_element_by_xpath('//*[@id="reviewsMedley"]/div/div[1]')
# except NoSuchElementException:
# try:
# element = driver.find_element_by_xpath('//*[@id="reviewsMedley"]')
# except NoSuchElementException:
# element = driver.find_element_by_xpath('//*[@id="detail-bullets_feature_div"]')
# actions = ActionChains(driver)
# actions.move_to_element(element).perform()
def scroll(driver):
scroll_temp(driver)
from selenium.common.exceptions import NoSuchElementException
try:
try:
element = driver.find_element_by_xpath('//*[@id="reviewsMedley"]/div/div[1]')
except NoSuchElementException:
try:
element = driver.find_element_by_xpath('//*[@id="reviewsMedley"]')
except NoSuchElementException:
element = driver.find_element_by_xpath('//*[@id="detail-bullets_feature_div"]')
actions = ActionChains(driver)
actions.move_to_element(element).perform()
except NoSuchElementException:
pass
# -
def browser_link(product_link,country):
'''Returns all the web link of the products based on the first
page of the product category. It captures product link of all the pages for
that specific product.
PARAMETER
---------
link: str
The initial web link of the product page. This is generally the
first page of the all the items for that specfic product
RETURN
------
links: list
It is a list of strings which contains all the links of the items
for the specific product
'''
driver = browser(product_link)
soup = BeautifulSoup(driver.page_source, 'lxml')
try:
pages_soup = soup.findAll("ul",{"class":"a-pagination"})
pages = int(pages_soup[0].findAll("li",{'class':'a-disabled'})[1].text)
except:
pass
try:
pages_soup = soup.findAll("div",{"id":"pagn"})
pages = int(pages_soup[0].findAll("span",{'class':'pagnDisabled'})[0].text)
except:
try:
pages_soup = soup.findAll("div",{"id":"pagn"})
pages = int(pages_soup[0].findAll("span",{'class':'pagnDisabled'})[1].text)
except:
pass
print(pages)
links = []
for page in range(1,pages+1):
print(page)
link_page = product_link + '&page=' + str(page)
driver_temp = browser(link_page)
time.sleep(2)
soup_temp = BeautifulSoup(driver_temp.page_source, 'lxml')
try:
search = soup_temp.findAll("div",{"id":"mainResults"})
temp_search = search[1].findAll("a",{'class':'a-link-normal s-access-detail-page s-color-twister-title-link a-text-normal'})
for i in range(len(temp_search)):
if country == 'Australia':
link = temp_search[i].get('href')
else:
link = countries_link[country] + temp_search[i].get('href')
links.append(link)
print(len(links))
except:
try:
search = soup_temp.findAll("div",{"class":"s-result-list s-search-results sg-row"})
temp_search = search[1].findAll("h2")
if len(temp_search) < 2:
for i in range(len(search[0].findAll("h2"))):
temp = search[0].findAll("h2")[i]
for j in range(len(temp.findAll('a'))):
link = countries_link[country]+temp.findAll('a')[j].get('href')
links.append(link)
print(len(links))
else:
for i in range(len(search[1].findAll("h2"))):
temp = search[1].findAll("h2")[i]
for j in range(len(temp.findAll('a'))):
link = countries_link[country]+temp.findAll('a')[j].get('href')
links.append(link)
print(len(links))
except:
pass
try:
search = soup_temp.findAll("div",{"id":"mainResults"})
temp_search = search[0].findAll("a",{'class':'a-link-normal s-access-detail-page s-color-twister-title-link a-text-normal'})
for i in range(len(temp_search)):
if country == 'Australia':
link = temp_search[i].get('href')
else:
link = countries_link[country] + temp_search[i].get('href')
links.append(link)
print(len(links))
except:
try:
search = soup_temp.findAll("div",{"class":"s-result-list s-search-results sg-row"})
temp_search = search[1].findAll("h2")
if len(temp_search) < 2:
for i in range(len(search[0].findAll("h2"))):
temp = search[0].findAll("h2")[i]
for j in range(len(temp.findAll('a'))):
link = countries_link[country]+temp.findAll('a')[j].get('href')
links.append(link)
print(len(links))
else:
for i in range(len(search[1].findAll("h2"))):
temp = search[1].findAll("h2")[i]
for j in range(len(temp.findAll('a'))):
link = countries_link[country]+temp.findAll('a')[j].get('href')
links.append(link)
print(len(links))
except:
print('Not Scrapable')
return links
# +
def indexes(amazon_links,link_list):
amazon_dict = amazon_links
if len(link_list) == 5:
return amazon_dict[link_list[0]][link_list[1]][link_list[2]][link_list[3]][link_list[4]]
elif len(link_list) == 4:
return amazon_dict[link_list[0]][link_list[1]][link_list[2]][link_list[3]]
elif len(link_list) == 3:
return amazon_dict[link_list[0]][link_list[1]][link_list[2]]
elif len(link_list) == 2:
return amazon_dict[link_list[0]][link_list[1]]
elif len(link_list) == 1:
return amazon_dict[link_list[0]]
else:
return print("Invalid Product")
def products_links(country, **kwargs):
amazon_links = amazon[country]
directory_temp = []
for key, value in kwargs.items():
directory_temp.append(value)
directory = '/'.join(directory_temp)
print(directory)
product_link = indexes(amazon_links,directory_temp)
main_links = browser_link(product_link,country=country)
return main_links,directory
# -
# ### Product Scraper Function
# +
def delete_images(filename):
import os
file_path = '/home/jishu/Amazon_AU/'
os.remove(file_path + filename)
def upload_s3(filename,key):
key_id = '<KEY>'
access_key = '<KEY>'
bucket_name = 'amazon-data-ecfullfill'
s3 = boto3.client('s3',aws_access_key_id=key_id,
aws_secret_access_key=access_key)
try:
s3.upload_file(filename,bucket_name,key)
except FileNotFoundError:
pass
def product_info(link,directory,country):
'''Get all the product information of an Amazon Product'''
#Opening Selenium Webdrive with Amazon product
driver = browser(link)
time.sleep(4)
scroll(driver)
time.sleep(2)
#Initializing BeautifulSoup operation in selenium browser
selenium_soup = BeautifulSoup(driver.page_source, 'lxml')
time.sleep(2)
#Product Title
try:
product_title = driver.find_element_by_xpath('//*[@id="productTitle"]').text
except:
product_title = 'Not Scrapable'
print(product_title)
#Ratings - Star
try:
rating_star = float(selenium_soup.findAll('span',{'class':'a-icon-alt'})[0].text.split()[0])
except:
rating_star = 'Not Scrapable'
print(rating_star)
#Rating - Overall
try:
overall_rating = int(selenium_soup.findAll('span',{'id':'acrCustomerReviewText'})[0].text.split()[0].replace(',',''))
except:
overall_rating = 'Not Scrapable'
print(overall_rating)
#Company
try:
company = selenium_soup.findAll('a',{'id':'bylineInfo'})[0].text
except:
company = 'Not Scrapable'
print(country)
#Price
try:
if country=='UAE':
denomination = selenium_soup.findAll('span',{'id':'priceblock_ourprice'})[0].text[:3]
price = float(selenium_soup.findAll('span',{'id':'priceblock_ourprice'})[0].text[3:])
else:
denomination = selenium_soup.findAll('span',{'id':'priceblock_ourprice'})[0].text[0]
price = float(selenium_soup.findAll('span',{'id':'priceblock_ourprice'})[0].text[1:])
except:
try:
if country=='UAE':
try:
price = float(selenium_soup.findAll('span',{'id':'priceblock_ourprice'})[0].text[3:].replace(',',''))
except:
price = float(selenium_soup.findAll('span',{'id':'priceblock_dealprice'})[0].text[3:].replace(',',''))
else:
try:
price = float(selenium_soup.findAll('span',{'id':'priceblock_ourprice'})[0].text[3:].replace(',',''))
except:
price = float(selenium_soup.findAll('span',{'id':'priceblock_dealprice'})[0].text[3:].replace(',',''))
except:
denomination = 'Not Scrapable'
price = 'Not Scrapable'
print(denomination,price)
#Product Highlights
try:
temp_ph = selenium_soup.findAll('ul',{'class':'a-unordered-list a-vertical a-spacing-none'})[0].findAll('li')
counter_ph = len(temp_ph)
product_highlights = []
for i in range(counter_ph):
raw = temp_ph[i].text
clean = raw.strip()
product_highlights.append(clean)
product_highlights = '<CPT14>'.join(product_highlights)
except:
try:
temp_ph = selenium_soup.findAll('div',{'id':'rich-product-description'})[0].findAll('p')
counter_ph = len(temp_ph)
product_highlights = []
for i in range(counter_ph):
raw = temp_ph[i].text
clean = raw.strip()
product_highlights.append(clean)
product_highlights = '<CPT14>'.join(product_highlights)
except:
product_highlights = 'Not Available'
print(product_highlights)
#Product Details/Dimensions:
#USA
try:
temp_pd = selenium_soup.findAll('div',{'class':'content'})[0].findAll('ul')[0].findAll('li')
counter_pd = len(temp_pd)
for i in range(counter_pd):
try:
if re.findall('ASIN',temp_pd[i].text)[0]:
try:
asin = temp_pd[i].text.split(' ')[1]
except:
pass
except IndexError:
pass
try:
if re.findall('Product Dimensions|Product Dimension|Product dimensions',temp_pd[i].text)[0]:
pd_temp = temp_pd[i].text.strip().split('\n')[2].strip().split(';')
try:
product_length = float(pd_temp[0].split('x')[0])
except IndexError:
pass
try:
product_width = float(pd_temp[0].split('x')[1])
except IndexError:
pass
try:
product_height = float(pd_temp[0].split('x')[2].split(' ')[1])
except IndexError:
pass
try:
pd_unit = pd_temp[0].split('x')[2].split(' ')[2]
except IndexError:
pass
try:
product_weight = float(pd_temp[1].split(' ')[1])
except IndexError:
pass
try:
weight_unit = pd_temp[1].split(' ')[2]
except IndexError:
pass
except:
pass
try:
if re.findall('Shipping Weight|Shipping weight|shipping weight',temp_pd[i].text)[0]:
sweight_temp = temp_pd[i].text.split(':')[1].strip().split(' ')
shipping_weight = float(sweight_temp[0])
shipping_weight_unit = sweight_temp[1]
except IndexError:
pass
try:
if re.findall('Amazon Best Sellers Rank|Amazon Bestsellers Rank',temp_pd[i].text)[0]:
x = temp_pd[i].text.replace('\n','').split(' ')
indexes = []
for j,k in enumerate(x):
if re.findall('#',k):
indexes.append(j)
try:
best_seller_cat = int(temp_pd[i].text.strip().replace('\n','').split(' ')[3].replace(',',''))
best_seller_prod = int(x[indexes[0]].split('#')[1].split('in')[0])
except:
try:
best_seller_cat = x[indexes[0]].split('#')[1]
except:
pass
try:
best_seller_prod = x[indexes[1]].split('#')[1].split('in')[0]
except:
pass
except IndexError:
pass
print(asin)
except:
pass
try:
temp_pd = selenium_soup.findAll('div',{'class':'content'})[1].findAll('ul')[0].findAll('li')
counter_pd = len(temp_pd)
for i in range(counter_pd):
try:
if re.findall('ASIN',temp_pd[i].text)[0]:
try:
asin = temp_pd[i].text.split(' ')[1]
except:
pass
except IndexError:
pass
try:
if re.findall('Product Dimensions|Product Dimension|Product dimensions',temp_pd[i].text)[0]:
pd_temp = temp_pd[i].text.strip().split('\n')[2].strip().split(';')
try:
product_length = float(pd_temp[0].split('x')[0])
except IndexError:
pass
try:
product_width = float(pd_temp[0].split('x')[1])
except IndexError:
pass
try:
product_height = float(pd_temp[0].split('x')[2].split(' ')[1])
except IndexError:
pass
try:
pd_unit = pd_temp[0].split('x')[2].split(' ')[2]
except IndexError:
pass
try:
product_weight = float(pd_temp[1].split(' ')[1])
except IndexError:
pass
try:
weight_unit = pd_temp[1].split(' ')[2]
except IndexError:
pass
except:
pass
try:
if re.findall('Shipping Weight|Shipping weight|shipping weight',temp_pd[i].text)[0]:
sweight_temp = temp_pd[i].text.split(':')[1].strip().split(' ')
shipping_weight = float(sweight_temp[0])
shipping_weight_unit = sweight_temp[1]
except IndexError:
pass
try:
if re.findall('Amazon Best Sellers Rank|Amazon Bestsellers Rank',temp_pd[i].text)[0]:
x = temp_pd[i].text.replace('\n','').split(' ')
indexes = []
for j,k in enumerate(x):
if re.findall('#',k):
indexes.append(j)
try:
best_seller_cat = int(temp_pd[i].text.strip().replace('\n','').split(' ')[3].replace(',',''))
best_seller_prod = int(x[indexes[0]].split('#')[1].split('in')[0])
except:
try:
best_seller_cat = x[indexes[0]].split('#')[1]
except:
pass
try:
best_seller_prod = x[indexes[1]].split('#')[1].split('in')[0]
except:
pass
except IndexError:
pass
print(asin)
except:
pass
#India
try:
temp_pd = selenium_soup.findAll('div',{'class':'content'})[0].findAll('ul')[0].findAll('li')
counter_pd = len(temp_pd)
for i in range(counter_pd):
try:
if re.findall('ASIN',temp_pd[i].text)[0]:
asin = temp_pd[i].text.split(' ')[1]
except:
pass
try:
if re.findall('Product Dimensions|Product Dimension|Product dimensions',temp_pd[i].text)[0]:
pd_temp = temp_pd[i].text.strip().split('\n')[2].strip().split(' ')
try:
product_length = float(pd_temp[0])
except:
pass
try:
product_width = float(pd_temp[2])
except:
pass
try:
product_height = float(pd_temp[4])
except:
pass
try:
pd_unit = pd_temp[5]
except:
pass
try:
product_weight = float(pd_temp[1].split(' ')[1])
except:
pass
try:
weight_unit = pd_temp[1].split(' ')[2]
except:
pass
print(asin)
except IndexError:
pass
try:
if re.findall('Shipping Weight|Shipping weight|shipping weight',temp_pd[i].text)[0]:
sweight_temp = temp_pd[i].text.split(':')[1].strip().split(' ')
shipping_weight = float(sweight_temp[0])
shipping_weight_unit = sweight_temp[1]
except IndexError:
pass
try:
if re.findall('Item Weight|Product Weight|Item weight|Product weight|Boxed-product Weight',temp_pd[i].text)[0]:
pd_weight_temp = temp_pd[i].text.replace('\n','').strip().split(' ')[1].strip()
product_weight = float(pd_weight_temp.split(' ')[0])
weight_unit = pd_weight_temp.split(' ')[1]
except IndexError:
pass
try:
if re.findall('Amazon Best Sellers Rank|Amazon Bestsellers Rank',temp_pd[i].text)[0]:
x = temp_pd[i].text.strip().replace('\n','').split(' ')
indexes = []
for j,k in enumerate(x):
if re.findall('#',k):
indexes.append(j)
try:
best_seller_cat = int(temp_pd[i].text.strip().replace('\n','').split(' ')[3].replace(',',''))
best_seller_prod = int(x[indexes[0]].split('#')[1].split('in')[0])
except:
try:
best_seller_cat = x[indexes[0]].split('#')[1]
except:
pass
try:
best_seller_prod = x[indexes[1]].split('#')[1].split('in')[0]
except:
pass
except IndexError:
pass
print(asin)
except:
pass
try:
try:
asin = list(selenium_soup.findAll('div',{'class':'pdTab'})[1].findAll('tr')[0].findAll('td')[1])[0]
except:
pass
try:
dimensions = list(selenium_soup.findAll('div',{'class':'pdTab'})[0].findAll('tr')[0].findAll('td')[1])[0]
except:
pass
try:
weight_temp = list(selenium_soup.findAll('div',{'class':'pdTab'})[1].findAll('tr')[1].findAll('td')[1])[0]
except:
pass
try:
best_seller_cat = float(list(selenium_soup.findAll('div',{'class':'pdTab'})[1].findAll('tr')[5].findAll('td')[1])[0].split('\n')[-1].split(' ')[0].replace(',',''))
except:
pass
try:
best_seller_prod = int(list(list(list(list(selenium_soup.findAll('div',{'class':'pdTab'})[1].findAll('tr')[5].findAll('td')[1])[5])[1])[1])[0].replace('#',''))
except:
pass
try:
product_length = float(dimensions.split('x')[0])
except:
pass
try:
product_width = float(dimensions.split('x')[1])
except:
pass
try:
product_height = float(dimensions.split('x')[2].split(' ')[1])
except:
pass
try:
product_weight = weight_temp.split(' ')[0]
except:
pass
try:
weight_unit = weight_temp.split(' ')[1]
except:
pass
try:
pd_unit = dimensions.split(' ')[-1]
except:
pass
print(asin)
except:
try:
for j in [0,1]:
temp_pd = selenium_soup.findAll('table',{'class':'a-keyvalue prodDetTable'})[j].findAll('tr')
for i in range(len(temp_pd)):
if re.findall('ASIN',temp_pd[i].text):
asin = temp_pd[i].text.strip().split('\n')[3].strip()
if re.findall('Item Model Number|Item model number',temp_pd[i].text):
bait = temp_pd[i].text.strip().split('\n')[3].strip()
if re.findall('Best Sellers Rank|Amazon Best Sellers Rank|Amazon Bestsellers Rank',temp_pd[i].text):
x = temp_pd[i].text.strip().replace('\n','').split(' ')
indexes = []
for j,k in enumerate(x):
if re.findall('#',k):
indexes.append(j)
best_seller_cat = int(x[indexes[0]].split('#')[1])
best_seller_prod = int(x[indexes[1]].split('#')[1].split('in')[0])
if re.findall('Product Dimensions|Product dimension|Product Dimension',temp_pd[i].text):
dimensions = temp_pd[i].text.strip().split('\n')[3].strip().split('x')
product_length = float(dimensions[0].strip())
product_width = float(dimensions[1].strip())
product_height = float(dimensions[2].strip().split(' ')[0])
pd_unit = dimensions[2].strip().split(' ')[1]
if re.findall('Item Weight|Product Weight|Item weight|Boxed-product Weight',temp_pd[i].text):
weight_temp = temp_pd[i].text.strip().split('\n')[3].strip()
product_weight = float(weight_temp.split(' ')[0])
weight_unit = weight_temp.split(' ')[1]
if re.findall('Shipping Weight|Shipping weight|shipping weight',temp_pd[i].text):
sweight_temp = temp_pd[i].text.replace('\n','').strip().split(' ')[1].lstrip().split(' ')
shipping_weight = float(sweight_temp[0])
shipping_weight_unit = sweight_temp[1]
print(asin,bait)
except:
try:
temp_pd = selenium_soup.findAll('div',{'id':'prodDetails'})[0].findAll('tr')
for i in range(len(temp_pd)):
if re.findall('ASIN',temp_pd[i].text):
asin = temp_pd[i].text.strip().split('\n')[3].strip()
if re.findall('Best Sellers Rank|Amazon Best Sellers Rank|Amazon Bestsellers Rank',temp_pd[i].text):
x = temp_pd[i].text.strip().replace('\n','').split(' ')
indexes = []
for j,k in enumerate(x):
if re.findall('#',k):
indexes.append(j)
best_seller_cat = int(x[indexes[0]].split('#')[1])
best_seller_prod = int(x[indexes[1]].split('#')[1].split('in')[0])
if re.findall('Product Dimensions|Product dimension|Product Dimension',temp_pd[i].text):
dimensions = temp_pd[i].text.strip().split('\n')[3].strip().split('x')
product_length = float(dimensions[0].strip())
product_width = float(dimensions[1].strip())
product_height = float(dimensions[2].strip().split(' ')[0])
pd_unit = dimensions[2].strip().split(' ')[1]
if re.findall('Item Weight|Product Weight|Item weight|Boxed-product Weight',temp_pd[i].text):
weight_temp = temp_pd[i].text.strip().split('\n')[3].strip()
product_weight = float(weight_temp.split(' ')[0])
weight_unit = weight_temp.split(' ')[1]
if re.findall('Shipping Weight|Shipping weight|shipping weight',temp_pd[i].text):
sweight_temp = temp_pd[i].text.replace('\n','').strip().split(' ')[1].lstrip().split(' ')
shipping_weight = float(sweight_temp[0])
shipping_weight_unit = sweight_temp[1]
except:
try:
temp_pd = selenium_soup.findAll('div',{'id':'detail_bullets_id'})[0].findAll('tr')[0].findAll('li')
for i in range(len(temp_pd)):
if re.findall('ASIN',temp_pd[i].text):
asin = temp_pd[i].text.strip().split(':')[1].strip()
if re.findall('Best Sellers Rank|Amazon Best Sellers Rank|Amazon Bestsellers Rank',temp_pd[i].text):
x = temp_pd[i].text.strip().replace('\n','').split(' ')
indexes = []
for j,k in enumerate(x):
if re.findall('#',k):
indexes.append(j)
best_seller_cat = int(x[indexes[0]].split('#')[1])
best_seller_prod = int(x[indexes[1]].split('#')[1].split('in')[0])
if re.findall('Product Dimensions|Product dimension|Product Dimension',temp_pd[i].text):
dimensions = temp_pd[i].text.strip().split('\n')[2].strip().split('x')
product_length = float(dimensions[0].strip())
product_width = float(dimensions[1].strip())
product_height = float(dimensions[2].strip().split(' ')[0])
pd_unit = dimensions[2].strip().split(' ')[1]
if re.findall('Item Weight|Product Weight|Item weight|Boxed-product Weight',temp_pd[i].text):
weight_temp = temp_pd[i].text.strip().split('\n')[2].strip()
product_weight = float(weight_temp.split(' ')[0])
weight_unit = weight_temp.split(' ')[1]
if re.findall('Shipping Weight|Shipping weight|shipping weight',temp_pd[i].text):
sweight_temp = temp_pd[i].text.replace('\n','').strip().split(' ')[1].lstrip().split(' ')
shipping_weight = float(sweight_temp[0])
shipping_weight_unit = sweight_temp[1]
except:
pass
try:
print(asin)
except NameError:
asin = 'Not Scrapable'
try:
print(best_seller_cat)
except NameError:
best_seller_cat = 'Not Scrapable'
try:
print(best_seller_prod)
except NameError:
best_seller_prod = 'Not Scrapable'
try:
print(product_length)
except NameError:
product_length = 'Not Scrapable'
try:
print(product_width)
except NameError:
product_width = 'Not Scrapable'
try:
print(product_height)
except NameError:
product_height = 'Not Scrapable'
try:
print(product_weight)
except NameError:
product_weight = 'Not Scrapable'
try:
print(weight_unit)
except NameError:
weight_unit = 'Not Scrapable'
try:
print(pd_unit)
except NameError:
pd_unit = 'Not Scrapable'
try:
print(shipping_weight_unit)
except NameError:
shipping_weight_unit = 'Not Scrapable'
try:
print(shipping_weight)
except NameError:
shipping_weight = 'Not Scrapable'
print(product_length,product_width,product_height,product_weight,asin,pd_unit,
best_seller_cat,best_seller_prod,weight_unit,shipping_weight,shipping_weight_unit)
#Customer Review Ratings - Overall
time.sleep(0.5)
try:
temp_crr = selenium_soup.findAll('table',{'id':'histogramTable'})[1].findAll('a')
crr_main = {}
crr_temp = []
counter_crr = len(temp_crr)
for i in range(counter_crr):
crr_temp.append(temp_crr[i]['title'])
crr_temp = list(set(crr_temp))
for j in range(len(crr_temp)):
crr_temp[j] = crr_temp[j].split(' ')
stopwords = ['stars','represent','of','rating','reviews','have']
for word in list(crr_temp[j]):
if word in stopwords:
crr_temp[j].remove(word)
print(crr_temp[j])
try:
if re.findall(r'%',crr_temp[j][1])[0]:
crr_main.update({int(crr_temp[j][0]): int(crr_temp[j][1].replace('%',''))})
except:
crr_main.update({int(crr_temp[j][1]): int(crr_temp[j][0].replace('%',''))})
except:
try:
temp_crr = selenium_soup.findAll('table',{'id':'histogramTable'})[1].findAll('span',{'class':'a-offscreen'})
crr_main = {}
counter_crr = len(temp_crr)
star = counter_crr
for i in range(counter_crr):
crr_main.update({star:int(temp_crr[i].text.strip().split('/n')[0].split(' ')[0].replace('%',''))})
star -= 1
except:
pass
try:
crr_5 = crr_main[5]
except:
crr_5 = 0
try:
crr_4 = crr_main[4]
except:
crr_4 = 0
try:
crr_3 = crr_main[3]
except:
crr_3 = 0
try:
crr_2 = crr_main[2]
except:
crr_2 = 0
try:
crr_1 = crr_main[1]
except:
crr_1 = 0
#Customer Review Ratings - By Feature
time.sleep(1)
try:
driver.find_element_by_xpath('//*[@id="cr-summarization-attributes-list"]/div[4]/a/span').click()
temp_fr = driver.find_element_by_xpath('//*[@id="cr-summarization-attributes-list"]').text
temp_fr = temp_fr.split('\n')
crr_feature_title = []
crr_feature_rating = []
for i in [0,2,4]:
crr_feature_title.append(temp_fr[i])
for j in [1,3,5]:
crr_feature_rating.append(temp_fr[j])
crr_feature = dict(zip(crr_feature_title,crr_feature_rating))
except:
try:
temp_fr = driver.find_element_by_xpath('//*[@id="cr-summarization-attributes-list"]').text
temp_fr = temp_fr.split('\n')
crr_feature_title = []
crr_feature_rating = []
for i in [0,2,4]:
crr_feature_title.append(temp_fr[i])
for j in [1,3,5]:
crr_feature_rating.append(temp_fr[j])
crr_feature = dict(zip(crr_feature_title,crr_feature_rating))
except:
crr_feature = 'Not Defined'
try:
crr_feature_key = list(crr_feature.keys())
except:
pass
try:
crr_fr_1 = crr_feature[crr_feature_key[0]]
except:
crr_fr_1 = 0
try:
crr_fr_2 = crr_feature[crr_feature_key[1]]
except:
crr_fr_2 = 0
try:
crr_fr_3 = crr_feature[crr_feature_key[2]]
except:
crr_fr_3 = 0
#Tags:
time.sleep(1)
try:
temp_tags = selenium_soup.findAll('div',{'class':'cr-lighthouse-terms'})[0]
counter_tags = len(temp_tags)
print('Counter Tags:',counter_tags)
tags = []
for i in range(counter_tags):
tags.append(temp_tags.findAll('span')[i].text.strip())
print(tags[i])
except:
tags = ['None']
try:
for feature in crr_feature_key:
tags.append(feature)
except:
pass
tags = list(set(tags))
tags = '<CPT14>'.join(tags)
print(tags)
#Images
images = []
for i in [0,3,4,5,6,7,8,9]:
try:
images.append(selenium_soup.findAll('div',{'class':'imgTagWrapper'})[i].find('img')['src'])
except:
pass
import urllib.request
for i in range(len(images)):
if asin =='Not Scrapable':
product_image = "{}_{}.jpg".format(product_title,i)
product_image = product_image.replace('/','')
urllib.request.urlretrieve(images[i],product_image)
upload_s3("{}_{}.jpg".format(product_title,i),
directory+"/images/" + product_image)
delete_images(product_image)
else:
product_image = "{}_{}.jpg".format(asin,i)
product_image = product_image.replace('/','')
urllib.request.urlretrieve(images[i],product_image)
upload_s3("{}_{}.jpg".format(asin,i),
directory+"/images/" + product_image)
delete_images(product_image)
return [product_title,rating_star,overall_rating,company,price,
product_highlights,product_length,product_width,product_height,
product_weight,asin,pd_unit,best_seller_cat,best_seller_prod,
weight_unit,shipping_weight,shipping_weight_unit,crr_5,crr_4,
crr_3,crr_2,crr_1,crr_fr_1,crr_fr_2,crr_fr_3,tags,directory]
# -
# ### Data Wrangling
def database(product_data,**kwargs):
try:
try:
link = kwargs['link']
except KeyError:
print('Error in Link')
try:
country = kwargs['country']
except KeyError:
print("Enter Country Name")
try:
cat1 = kwargs['cat1']
except KeyError:
pass
try:
cat2 = kwargs['cat2']
except KeyError:
pass
try:
cat3 = kwargs['cat3']
except KeyError:
pass
try:
cat4 = kwargs['cat4']
except KeyError:
pass
try:
product = kwargs['product']
except KeyError:
print("Enter Product Name")
metadata = [link,country,cat1,cat2,cat3,cat4,product]
except NameError:
try:
cat4 = None
metadata = [link,country,cat1,cat2,cat3,cat4,product]
except NameError:
try:
cat4 = None
cat3 = None
metadata = [link,country,cat1,cat2,cat3,cat4,product]
except NameError:
cat4 = None
cat3 = None
cat2 = None
metadata = [link,country,cat1,cat2,cat3,cat4,product]
conn = sqlite3.connect('{}.db'.format(product))
headers = ['link','country','cat1','cat2','cat3','cat4','product','product_title',
'rating_star','overall_rating','company','price',
'product_highlights','product_length','product_width','product_height',
'product_weight','asin','pd_unit','best_seller_cat','best_seller_prod',
'weight_unit','shipping_weight','shipping_weight_unit','crr_5','crr_4',
'crr_3','crr_2','crr_1','crr_fr_1','crr_fr_2','crr_fr_3','tags','images_link']
product_data.append(metadata)
product_data = product_data[-1] + product_data[:len(product_data)-1]
temp = pd.DataFrame(data= [product_data],columns=headers)
temp.to_sql('Product',conn,if_exists='append')
upload_s3(product+'.db',directory+'/'+product+'.db')
conn.close()
def checkpoint(link_list,directory,product):
BUCKET_NAME = 'amazon-data-ecfullfill'
key_id = '<KEY>'
access_key = '<KEY>'
KEY = '{}/{}.db'.format(directory,product)
s3 = boto3.resource('s3',aws_access_key_id=key_id,
aws_secret_access_key=access_key)
try:
s3.Bucket(BUCKET_NAME).download_file(KEY, 'test.db')
except botocore.exceptions.ClientError as e:
if e.response['Error']['Code'] == "404":
print("The object does not exist.")
else:
raise
conn = sqlite3.connect('test.db')
try:
df = pd.read_sql('''SELECT * FROM Product''', conn)
product_link = df['link'].unique()
new_list = []
for i in link_list:
if i in product_link:
pass
else:
new_list.append(i)
except:
new_list = link_list
return new_list
# ### Execution
#Initializing the product per Jupyter Notebook
country = 'Australia'
cat1 = 'wellness'
# cat2='None'
# cat3='None'
# cat4 = 'None'
product='massage_oil'
links,directory = products_links(country=country,category=cat1,product=product)
test_1 = {'links':links,'directory':directory}
import pickle
with open('au_wellness_massage_oil.pkl', 'wb') as f:
pickle.dump(test_1, f)
with open('au_wellness_massage_oil.pkl', 'rb') as f:
file = pickle.load(f)
links = file['links']
directory = 'Amazon_AU/wellness/massage_oil'
#replace links with new_links if interruption
for link in new_links:
data = product_info(link=link,directory=directory,country=country)
conn = sqlite3.connect('{}.db'.format(product))
database(product_data=data,link=link,country=country,
cat1=cat1,cat2=cat2,product=product)
# Run if there is an interruption
new_links = checkpoint(links,directory,product)
len(new_links)
len(links)
# #### Testing the datasets in S3
# +
BUCKET_NAME = 'amazon-data-ecfullfill' # replace with your bucket name
key_id = '<KEY>'
access_key = '<KEY>'
KEY = 'Amazon_USA/health_and_beauty/hair_products/shampoo/shampoo.db' # replace with your object key
s3 = boto3.resource('s3',aws_access_key_id=key_id,
aws_secret_access_key=access_key)
try:
s3.Bucket(BUCKET_NAME).download_file(KEY, 'test.db')
except botocore.exceptions.ClientError as e:
if e.response['Error']['Code'] == "404":
print("The object does not exist.")
else:
raise
# -
conn = sqlite3.connect('shampoo.db')
df_USA = pd.read_sql("SELECT * FROM Product",conn)
df_USA.iloc[:,:15]
df_USA.iloc[:,15:]
len(link_db)
# +
# def upload_s3(filename,key):
# key_id = '<KEY>'
# access_key = '<KEY>'
# bucket_name = 'amazon-data-ecfullfill'
# s3 = boto3.client('s3',aws_access_key_id=key_id,
# aws_secret_access_key=access_key)
# # s3.put_object(Bucket=bucket_name, Key='Amazon/health_and_beauty/hair_product/shampoo')
# s3.upload_file(filename,bucket_name,key)
|
Data Warehouse/Amazon Australia/.ipynb_checkpoints/Amazon_AU - Wellness - Massage oil --s-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import plotly
print(plotly.__version__) # version >1.9.4 required
plotly.offline.init_notebook_mode() # run at the start of every notebook
|
APIS/algo/Untitled1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ### Name: <NAME>
# ### Email: <EMAIL>
# ### Importing necessary libraries
import pandas as pd
import numpy as np
import os
import datetime
import seaborn as sns
import pylab
import warnings
warnings.filterwarnings('ignore')
# %matplotlib inline
import matplotlib.pyplot as plt
from scipy.stats import ttest_ind,probplot,mannwhitneyu,levene
from sklearn.metrics import confusion_matrix,roc_auc_score,classification_report
# +
# Defining required functions
def readCsv(workdir, filePath):
"""
Description: Function to read csv files.
Input: Filepath
Output: Dataframe with csv data
"""
raw_data_path = os.path.join(workdir, filePath)
data = pd.read_csv(raw_data_path)
return data
def getWeekNumber(dataframe):
"""
Description: Function to get week number from date.
Input: dataframe with date column
Output: Dataframe with week number column
"""
dataframe['Week_Number'] = dataframe['date'].dt.week
return dataframe
def meanOrderValue(dataframe, gender):
"""
Description: Function to get mean value of column.
Input: data and gender(0 or 1)
Output: value of mean
"""
return dataframe[dataframe['gender']==gender].value.mean()
# -
workdir = os.getcwd()
data = readCsv(workdir, 'screening_exercise_orders_v201810.csv')
# understanding data
data.info()
# Transforming date column to datetime
data['date'] = pd.to_datetime(data['date'], format= "%Y-%m-%d %H:%M:%S")
# ### Data analysis and arranging data in following format:
# 1. Customer_id
# 2. gender
# 3. Most_recent_order_date
# 4. order_count (number of orders placed by this customer)
#
# Sorting the dataframe by customer_id in ascending order and displaying the first 10 records.
dataInFormat = data.groupby('customer_id') \
.agg({'gender':np.max,'date': np.max,'value': np.size}) \
.rename(columns={'date':'most_recent_order_date','value':'order_count'}) \
.reset_index()
dataInFormat.head(10)
# ### Counting of number of orders per week
dataWithWeekNumber = getWeekNumber(data)
dataToPlot = dataWithWeekNumber.groupby('Week_Number').agg({'value': np.size}).reset_index()
dataToPlot.head()
plt.plot(dataToPlot['Week_Number'] , dataToPlot['value'])
plt.title('Distribution of orders per week')
plt.xlabel('Number of weeks')
plt.ylabel('Number of orders')
plt.show()
# **OBSERVATION:**
#
# The above plot is week number Vs order count for the year 2017.
# 1. Week 20 was the most successful week in terms for order count
# 2. The lowest order count was in week 43 which is in the month of October and increases in the week of 47 which is the Black Friday week of the month.
# #### Computing the mean order value for gender 0 and gender 1. Statistical inference on whether it is significant or not.
#
# Assuming significance level 5% throughout to interpret the test results
print('Mean of gender 0 is: {0}'.format(meanOrderValue(data,0)))
print('Mean of gender 1 is: {0}'.format(meanOrderValue(data,1)))
gender_0 = data[data["gender"]==0].value.values
gender_1 = data[data["gender"]==1].value.values
print('Total number of rows for gender 0 is {0}'.format(len(gender_0)))
print('Total number of rows for gender 1 is {0}'.format(len(gender_1)))
print('Variance of gender 0 is {0}'.format(np.var(gender_0)))
print('Variance of gender 1 is {0}'.format(np.var(gender_1)))
# Now let's look at the data distribution for both the genders.
sns.distplot(gender_0)
# As observed data is right skewed and not normally distributed
sns.distplot(gender_1)
# As observed data is right skewed and not normally distributed
# **OBSERVATION:**
#
# The above plots show that data is skewed towards the right. This is due to the fact that there are outliers in the data. Let us perform some analysis for the same.
# ### Outlier analysis
b0 = plt.boxplot(gender_0)
b1 = plt.boxplot(gender_1)
# **OBSERVATION:**
#
# Certain outliers are causing data distribution to be right skewed in both the cases as seen in above plots, hence let us remove the outliers and look at the distribution again.
def outlier_treatment(datacolumn):
sorted(datacolumn)
Q1,Q3 = np.percentile(datacolumn , [25,75])
IQR = Q3 - Q1
lower_range = Q1 - (1.5 * IQR)
upper_range = Q3 + (1.5 * IQR)
return lower_range,upper_range
lowerbound_g0,upperbound_g0 = outlier_treatment(data[data["gender"]==0].value)
lowerbound_g1,upperbound_g1 = outlier_treatment(data[data["gender"]==1].value)
# removing outliers
gender_0 = list(filter(lambda x: x!=0 and x<upperbound_g0,gender_0))
gender_1 = list(filter(lambda x: x!=0 and x<upperbound_g1,gender_1))
# ### Graphs after removing outliers
sns.distplot(gender_0)
sns.distplot(gender_1)
# **OBSERVATION:**
#
# By observing above graphs after removing outliers, it looks like data is some what normally distributed but still not 100% normal. There are a lot of similar values because of which data still remains skewed. Hence, let us test if data is well normally distributed.
# ### Normality test using QQ-plot
probplot(gender_0,plot=pylab)
pylab.show()
probplot(gender_1,plot=pylab)
pylab.show()
# **Observation:**
#
# Above observation proves that data is not normally distributed. We can apply transformations to make the distribution normal, lets transform to data to check if it will be useful or not.
# adding 1 and applying log transformation to the data
g0 = list(map(lambda x: x+1,gender_0))
sns.distplot(np.log(g0))
# It seems current data can't be transformed to normal distribution by logarithmic transformation.
#
# Hence, I am considering our initial data distribution which seems almost normal and applying welch's t-test and student's t-test
# ### Test to assess equality of variances
# Testing non-normal distribution for equal variances.
levene(gender_0,gender_1)
# By referencing the p-value we can conclude that it is lower than significance level which is highly significant and hence, we reject null hypothesis and both gender 0 and gender 1 samples have unequal variances.
# ## Student's t-test
# +
# Assumption: assuming gender_0 and gender_1 dataframe data distribution is normal.
t,p = ttest_ind(gender_0,gender_1,equal_var=True)
print('Value of t-statistic is: {0} and p-value is {1}'.format(t,p))
# -
# ## Welch's t-test
t,p = ttest_ind(gender_0,gender_1,equal_var=False)
print('Value of t-statistic is: {0} and p-value is {1}'.format(t,p))
# Observed p-value is 0.05937 and 0.5934 slightly higher than significance level 0.05 (5%), meaning it is not significant enough to reject the null hypothesis and conclude that there is not much significant difference between the two means of two groups.
# ## Mann-Whitney U test
u,p = mannwhitneyu(gender_0,gender_1,alternative='two-sided')
print('p-value is {0}'.format(p))
# Here, the p-value is much higher than significance level which means that we cannot reject null hypothesis and hence means are equal. This observation is inline with the observation from welch's t-test and student's t-test.
# #### Assuming a single gender prediction was made for each customer, let us generate a confusion matrix for predicted gender and understand what does this confusion matrix tell about the quality of the predictions.
# Finding the confusion matrix for the given columns i.e. gender and predicted_gender
cf = confusion_matrix(data['gender'],data['predicted_gender'])
sns.heatmap(cf,annot=True,fmt="d")
print(classification_report(data['gender'],data['predicted_gender']))
# 1. Precision is the ratio of tp/(tp+fp) where tp is number of true positives and fp is number of false positives.
# 2. Recall is the ratio of tp/(tp+fn) where tp is number of true positives and fn is number of false negative.
# 3. The F1 score can be interpreted as a weighted average of the precision and recall, where an F1 score reaches its best value at 1 and worst score at 0
#
# F1 = 2 * (precision * recall) / (precision + recall)
roc_auc_score(data['gender'],data['predicted_gender'])
# Since it is a binary classification (predicted gender = 0 or 1), a random guess has 50% chance of getting a correct answer. Here, we get an AUC score of 0.63 and precision of 0.70 for gender 0 and 0.61 for gender 1 which isn't a very good score for binary classifier and hence we can conclude that model isn't a good classifier.
# #### ------------------------------------------------------------------THANK YOU---------------------------------------------------------------------------------
|
Statistical Analysis on Customer Data.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
#
import simplejson as json
json_string = '{"pname":"Dino","unmae":"Magri"}'
arq_json = json.loads(json_string)
# + active=""
#
# -
arq_json['pname']
json_lista = ['foo', {'bar':('baz', None, 0.1)}]
from time import sleep, time
time()
print("esperando sleep")
sleep(5)
print("apareceu depois de 5s")
|
Python/2016-08-01/Untitled.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3.10.4 ('openai')
# language: python
# name: python3
# ---
# +
# miniconda3/ openai
import openai
import pandas as pd
# +
# response = openai.Engine("ada").search(
# search_model="ada",
# query="discrete stat distribution",
# max_rerank=3,
# file="file-NdM8EkdPCKFmEcL9ksaKR27K",
# return_metadata=True
# )
# response
# -
for document in response['data']:
print('Title: {}\n{}\n'.format(document['metadata']['title'], document['text']))
import json
hi = json.load(open("one_search_response.json"))
hi
openai.api_key = None #YOUR API KEY HERE
openai.Engine.list()
# glob all md files in current directory into list of files
from pathlib import Path
# current working directory
# Path()
notion_export_path = Path.cwd() / r'Notion-exports'
mdfiles = list(notion_export_path.glob("**/*.md"))
print("found files:", len(mdfiles))
# # limits
# https://beta.openai.com/docs/api-reference/searches
#
# 200 docs max per upload
# docs cant be too long...
# The maximum document length (in tokens) is 2034 minus the number of tokens in the query.
#
#
#
# The similarity score is a positive score that usually ranges from 0 to 300 (but can sometimes go higher), where a score above 200 usually means the document is semantically similar to the query.
# +
# CLEAN NOTION NOTION DATABASE EXPORT (from right click, export as csv)
data = []
for filepath in mdfiles:
file = open(filepath, 'r')
text = ""
date_created = ""
date_modified = ""
for idx, line in enumerate(file.readlines()):
if idx == 0:
line = line.strip("# ")
title = line
# keep title in body
# continue
while line.startswith(' '):
line = line[1:]
if line.startswith('Date Created:'):
line = line[14:] # remove first 14 chars.
date_created = line
continue
if line.startswith('Date Modified:'):
line = line[15:] # remove first 15 chars for "Date Modified: "
date_modified = line
continue
if line.startswith('[http'):
# Keeps links that have an alias!! Yay. Should remove link http part... and clean formatting
# todo, keep just the [] part and not the () part in "[text](link)"
continue
if not line.startswith('!') and len(line) >= 3:
text = text + str(line)
# DANGER: limit each doc size!
# also, only 200 doc limit. RN I have 135 docs.
text = text[0:2500]
data.append([title,date_created,date_modified, text])
# print(text)
# break
df = pd.DataFrame(data=data)
df.columns = ["title","date_created","date_modified", "text"]
# save dataframe df as csv file
df.to_csv("firsttry_all_base_notes.csv", index=False)
df
# -
# pandas load csv to dataframe
notes = pd.read_csv("curiosity_notes_clean.csv")#,header=None)
notes
# +
# openai.File.create(file=open("myfile.jsonl"), purpose="search")
# +
# {"text": "text of file"}
# filename = 'alltext.jsonl'
# for line in notes.text:
# print(line)
# out =
# out = f"\{\"text\"\}:\"{line}\""
# break
# +
# find total words
notes = pd.read_csv("firsttry_all_base_notes.csv")#,header=None)
alltext = notes.text.sum()
res = len(alltext.split())
res
# 16_613 words for curiosity notes database
# 224_924 words for all base directory notes (counting space-delimited words)
# -
# ## Write Jsonl for OpenAI
# +
# Encode csv into jsonl format for Openai File upload
notes = pd.read_csv("firsttry_all_base_notes.csv")#,header=None)
# create metatdata formated for Openai
notes['metadata'] = notes.apply(lambda row: {'date_created':row['date_created'], 'date_modified':row['date_modified'], 'title': row['title']}, axis=1)
notes.drop(["date_created", "date_modified", "title"], axis=1, inplace=True)
# notes.to_json(orient='records', lines=True)
# notes['merged']
# export to file
notes.to_json("allBaseNots_withMetadata.jsonl", orient='records', lines=True)
# -
# ## Run search
# +
openai.File.create(file=open("allBaseNots_withMetadata.jsonl"), purpose="search")
# <File file id=file-YvfHj7utJala3er24T0ZqeLb at 0x15eccf3d0> JSON: {
# "bytes": 137010,
# "created_at": 1649388503,
# "filename": "curiosityNotes.jsonl",
# "id": "file-YvfHj7utJala3er24T0ZqeLb",
# "object": "file",
# "purpose": "search",
# "status": "uploaded",
# "status_details": null
# }
# file-YvfHj7utJala3er24T0ZqeLb # before metadata
# file-8wiFt4uSxNPRpaEwsCG0s6qD # after including metadata
# file-NdM8EkdPCKFmEcL9ksaKR27K allBaseNots_withMetadata.jsonl
# -
response = openai.Engine("ada").search(
search_model="ada",
query="discrete stat distribution",
max_rerank=7,
file="file-NdM8EkdPCKFmEcL9ksaKR27K",
return_metadata=True
)
openai.Engine("ada").search(
search_model="ada",
query="quantum",
max_rerank=5,
file="file-YvfHj7utJala3er24T0ZqeLb"
)
openai.Engine("ada").search(
search_model="ada",
query="distributed computing",
max_rerank=5,
file="file-YvfHj7utJala3er24T0ZqeLb"
)
openai.Engine("ada").search(
search_model="ada",
query="advanced computing",
max_rerank=5,
file="file-YvfHj7utJala3er24T0ZqeLb"
)
openai.Engine("ada").search(
search_model="ada",
query="excellent researcher",
max_rerank=5,
file="file-YvfHj7utJala3er24T0ZqeLb"
)
# +
## GOOD ONE!!
openai.Engine("ada").search(
search_model="ada",
query="good learning material",
max_rerank=6,
file="file-YvfHj7utJala3er24T0ZqeLb"
)
# -
openai.Engine("ada").search(
search_model="ada",
query="good learning material",
max_rerank=6,
file="file-YvfHj7utJala3er24T0ZqeLb"
)
openai.Engine("ada").search(
search_model="davinci",
query="good learning material",
max_rerank=6,
file="file-YvfHj7utJala3er24T0ZqeLb"
)
import os
# import openai
# openai.api_key = os.getenv("OPENAI_API_KEY")
openai.Completion.create(
engine="text-davinci-002",
prompt="A winning solution",
max_tokens=40,
temperature=1.5, # higher = more creative. Deafult: 1.
top_p=0.3, #lower = limiting
)
df
|
notion_preprocess_and_embed.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Tutorial: optimal binning with binary target - large scale
# Continuing with the previous tutorial, version 0.4.0 introduced four new ``monotonic_trend`` options: "auto_heuristic", "auto_asc_desc", "peak_heuristic" and "valley_heuristic". These new heuristic options are devised to produce a remarkable speedup for large size instances, at the expense of not guaranteeing optimal solutions (although the optimal solution is found in the majority of cases).
# Let's start by loading the training data.
import pandas as pd
df = pd.read_csv("data/kaggle/HomeCreditDefaultRisk/application_train.csv", engine='c')
# We choose the same variable to discretize and the binary target.
variable = "REGION_POPULATION_RELATIVE"
x = df[variable].values
y = df.TARGET.values
from optbinning import OptimalBinning
# We use the same options to generate a granular binning, and fit the optimal binning with ``monotonic_trend="auto"``.
optb = OptimalBinning(name=variable, dtype="numerical", solver="cp",
monotonic_trend="auto", max_n_prebins=100,
min_prebin_size=0.001, time_limit=200)
optb.fit(x, y)
optb.status
optb.information(print_level=1)
binning_table = optb.binning_table
binning_table.build()
binning_table.analysis()
binning_table.plot(metric="event_rate")
# This is a large combinatorial problem, and it took roughly 140 seconds... but we can try the ``monotonic_trend="auto_heuristic"`` to accelerate the solution process
optb_auto = OptimalBinning(name=variable, dtype="numerical", solver="cp",
monotonic_trend="auto_heuristic", max_n_prebins=100,
min_prebin_size=0.001, time_limit=200)
optb_auto.fit(x, y)
optb_auto.status
optb_auto.information(print_level=1)
binning_table = optb_auto.binning_table
binning_table.build()
binning_table.analysis()
binning_table.plot(metric="event_rate")
# For this example, we found the optimal solution with an overall **19x** speedup, where optimization time is reduced by **99%!!**
|
doc/source/tutorials/tutorial_binary_large_scale.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# # Chapter 2: Multi-armed Bandits Solutions
# ## 1. Exercise 2.1
# In ε-greedy action selection, for the case of two actions and $\epsilon=0.5$, what is the probability that the greedy action is selected?
#
# ### Solution
# - Greedy Action is $a$, Non-greedy Action is $b$
# - $p(b)=0.5 * \epsilon = 0.25$
# - $p(a)=1-p(b)=0.75$
# ## 2. Exercise 2.2: Bandit example
# Consider a *k-armed* bandit problem with $k = 4$ actions, denoted $1, 2, 3$, and $4$. Consider applying to this problem a bandit algorithm using ε-greedy action selection, sample-average action-value estimates, and initial estimates of $Q_1(a) = 0$, for all $a$. Suppose the initial sequence of actions and rewards is $A_1 = 1, R_1 =1,A_2 =2,R_2 =1,A_3 =2,R_3 =2,A_4 =2,R_4 =2,A_5 =3,R_5 =0$. On some of these time steps the $\epsilon$ case may have occurred, causing an action to be selected at random. On which time steps did this definitely occur? On which time steps could this possibly have occurred?
#
# ### Solution
# - $\epsilon$ case is definitely occurred when $a \neq \arg\max\limits_aQ_t(a)$, other for possibly have occorred
# - Definitely occurred: $t\in\{2, 5\}$
# - Possibly occurred: $t\in\{1, 3, 4\}$
# ## 3. Exercise 2.3
# In the comparison shown in Figure 2.2, which method will perform best in the long run in terms of cumulative reward and probability of selecting the best action? How much better will it be? Express your answer quantitatively.
#
# 
#
# ### Solution
#
# ## 4. Exercise 2.4
# If the step-size parameters, $\alpha_n$, are not constant, then the estimate $Q_n$ is a weighted average of previously received rewards with a weighting different from that given by (2.6). What is the weighting on each prior reward for the general case, analogous to (2.6), in terms of the sequence of step-size parameters?
#
# $$Q_{n+1}=(1-\alpha)^nQ_1+\sum_{i=1}^n \alpha(1-\alpha)^{n-i}R_i ~~~, (2.6)$$
#
# ### Solution
# $$
# \begin{aligned}
# Q_{n+1} &= Q_n + \alpha_n\big[R_n-Q_n\big]
# \\ &= \alpha_nR_n + (1-\alpha_n)Q_n
# \\ &= \alpha_nR_n + (1-\alpha_n)\big[\alpha_{n-1}R_{n-1} + (1-\alpha_{n-1})Q_{n-1}\big]
# \\ &= \alpha_nR_n + (1-\alpha_n)\alpha_{n-1}R_{n-1} + (1-\alpha_n)(1-\alpha_{n-1})Q_{n-1}
# \\ &= \alpha_nR_n + (1-\alpha_n)\alpha_{n-1}R_{n-1} + (1-\alpha_n)(1-\alpha_{n-1})Q_{n-1} + ... + R_1\alpha_1\prod_{i=2}^n(1-\alpha_i) + Q_1\prod_{i=1}^n(1-\alpha_i)
# \\ &= Q_1\prod_{i=1}^n(1-\alpha_i) + \sum_{i=1}^nR_i\alpha_i\prod_{j=i+1}^n(1-\alpha_j)
# \end{aligned}
# $$
# ## 5. Exercise 2.5 (programming)
# Design and conduct an experiment to demonstrate the difficulties that sample-average methods have for nonstationary problems. Use a modified version of the 10-armed testbed in which all the $q_∗(a)$ start out equal and then take independent random walks (say by adding a normally distributed increment with mean zero and standard deviation $0.01$ to all the $q_∗(a)$ on each step). Prepare plots like Figure 2.2 for an action-value method using sample averages, incrementally computed, and another action-value method using a constant step-size parameter, $α = 0.1$. Use $ε = 0.1$ and longer runs, say of $10,000$ steps.
#
# ### Code
# +
# %matplotlib inline
from __future__ import print_function
import matplotlib.pyplot as plt
import numpy as np
class Bandit:
def __init__(self, kArm=10, randWalkStdDeviation=0.01, epsilon=0.1, alpha=0.1):
self.kArm = kArm
self.randWalkStdDeviation = randWalkStdDeviation
self.epsilon = epsilon
self.alpha = alpha
self.qTrue = np.zeros(self.kArm)
self.qEst = np.zeros(self.kArm)
self.actCnt = np.zeros(self.kArm)
def getOptimalAction(self):
return np.argmax(self.qTrue)
def selectAction(self):
# random walks for all qTrue
for k in range(0, self.kArm):
self.qTrue[k] += self.randWalkStdDeviation * np.random.randn()
# select an action
action = 0
if np.random.binomial(1, self.epsilon) == 1:
action = np.random.choice(self.kArm)
else:
action = np.argmax(self.qEst)
# get reward
reward = np.random.randn() + self.qTrue[action]
# estimate Q
stepSize = self.alpha
if stepSize == 0:
self.actCnt[action] += 1
stepSize = 1.0 / self.actCnt[action]
self.qEst[action] += stepSize * (reward - self.qEst[action])
return action, reward
def run(nBandits=2000, time=10000, epsilon=0.1, alphas=[]):
optimalActions = [np.zeros(time, dtype='float') for _ in range(0, len(alphas))]
averageRewards = [np.zeros(time, dtype='float') for _ in range(0, len(alphas))]
for idx, alpha in enumerate(alphas):
totalOptimalAction = 0
totalReward = 0
for _ in range(0, nBandits):
bandit = Bandit(epsilon=epsilon, alpha=alpha)
for t in range(0, time):
action, reward = bandit.selectAction()
averageRewards[idx][t] += reward
if action == bandit.getOptimalAction():
optimalActions[idx][t] += 1
# get average
optimalActions[idx] /= nBandits
averageRewards[idx] /= nBandits
return optimalActions, averageRewards
alphas = [0, 0.1]
results = run(alphas=alphas)
for idx, result in enumerate(results):
plt.figure(figsize=(8,4),dpi=100)
for alpha, data in zip(alphas, result):
plt.plot(data, label='alpha = '+str(alpha))
plt.xlabel('Steps')
plt.ylabel('% optimal action' if idx == 0 else 'average reward')
plt.legend()
plt.show()
# -
# ## 6. Exercise 2.6: Mysterious Spikes
# The results shown in Figure 2.3 should be quite reliable because they are averages over $2,000$ individual, randomly chosen 10-armed bandit tasks. Why, then, are there oscillations and spikes in the early part of the curve for the optimistic method? In other words, what might make this method perform particularly better or worse, on average, on particular early steps?
#
# ### Solution
# Explore until $Q_1$, so optimal action may not be selected usually.
# ## 7. Exercise 2.7: Unbiased Constant-Step-Size Trick
# In most of this chapter we have used sample averages to estimate action values because sample averages do not produce the initial bias that constant step sizes do (see the analysis leading to (2.6)). However, sample averages are not a completely satisfactory solution because they may perform poorly on nonstationary problems. Is it possible to avoid the bias of constant step sizes while retaining their advantages on nonstationary problems? One way is to use a step size of
# $$\beta_n = \dfrac{\alpha}{\overline o_n}~~~ (2.8)$$
# to process the nth reward for a particular action, where $α > 0$ is a conventional constant
# step size, and o ̄n is a trace of one that starts at $0$:
# $$\overline o_n=\overline o_{n-1}+\alpha(1-\overline o_{n-1}), \text{for } n\geq 0, \text{with } \overline o_0=0 ~~~(2.9)$$
# Carry out an analysis like that in (2.6) to show that $Q_n$ is an exponential recency-weighted average *without initial bias*.
#
# ### Solution
# With step-size $\beta_n$, we have:
# $$Q_{n+1} = Q_1\prod_{i=1}^n(1-\beta_i) + \sum_{i=1}^nR_i\beta_i\prod_{j=i+1}^n(1-\beta_j)$$
#
# Let check the $\prod_{i=1}^n(1-\beta_i)$ term. Replace, $\beta_i$ by $\frac{\alpha}{\overline o_i}$:
# $$
# \begin{aligned}
# \prod_{i=1}^n(1-\beta_i) &= \prod_{i=1}^n\Big(1-\frac{\alpha}{\overline o_i}\Big)
# \\ &= \prod_{i=1}^n\frac{\overline o_i-\alpha}{\overline o_i}
# \\ &= \prod_{i=1}^n\frac{(1-\alpha)\overline o_{i-1}}{\overline o_i}
# \\ &= \frac{(1-\alpha)\overline o_0}{\overline o_1}\prod_{i=2}^n\frac{(1-\alpha)\overline o_{i-1}}{\overline o_i}
# \end{aligned}
# $$
#
# Because of $\overline o_0=0$, so:
# $$\prod_{i=1}^n(1-\beta_i) = 0$$
#
# In other word, $Q_n$ is an exponential recency-weighted average without initial bias $Q_1$.
# ### 8. Exercise 2.8: UCB Spikes
# In Figure 2.4 the UCB algorithm shows a distinct spike in performance on the 11th step. Why is this? Note that for your answer to be fully satisfactory it must explain both why the reward increases on the 11th step and why it decreases on the subsequent steps. Hint: if $c = 1$, then the spike is less prominent.
#
# ### Solution
# ## 9. Exercise 2.9
# Show that in the case of two actions, the soft-max distribution is the same as that given by the logistic, or sigmoid, function often used in statistics and artificial neural networks.
#
# ### Solution
# - 2 action's preferences: $H_1, H_2$
# - Probability of $H_1$:
# $$
# \begin{aligned}
# p(H_1) &= \dfrac{e^{H_1}}{e^{H_1}+e^{H_2}}
# \\ &= \dfrac{1}{1+e^{H_2-H_1}}
# \\ &= \dfrac{1}{1+e^{H}}
# \end{aligned}
# $$
# - Probability of $H_2$:
# $$
# \begin{aligned}
# p(H_2) &= \dfrac{e^{H_2}}{e^{H_1}+e^{H_2}}
# \\ &= \dfrac{e^{H_2-H_1}}{1+e^{H_2-H_1}}
# \\ &= \dfrac{e^{H}}{1+e^{H}}
# \end{aligned}
# $$
# - That is `sigmoid` form
# ## 10. Exercise 2.10
# Suppose you face a 2-armed bandit task whose true action values change randomly from time step to time step. Specifically, suppose that, for any time step, the true values of actions 1 and 2 are respectively 0.1 and 0.2 with probability 0.5 (case A), and 0.9 and 0.8 with probability 0.5 (case B). If you are not able to tell which case you face at any step, what is the best expectation of success you can achieve and how should you behave to achieve it? Now suppose that on each step you are told whether you are facing case A or case B (although you still don’t know the true action values). This is an associative search task. What is the best expectation of success you can achieve in this task, and how should you behave to achieve it?
#
# ### Solution
#
# ## 11. Exercise 2.11 (programming)
# Make a figure analogous to Figure 2.6 for the nonstationary case outlined in Exercise 2.5. Include the constant-step-size ε-greedy algorithm with $\alpha=0.1$. Use runs of $200,000$ steps and, as a performance measure for each algorithm and parameter setting, use the average reward over the last $100,000$ steps.
#
# ### Code
|
chap2-solutions.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="ElXOa7R7g37i" colab_type="text"
# # Tutorial Part 5: Putting Multitask Learning to Work
#
# This notebook walks through the creation of multitask models on MUV [1]. The goal is to demonstrate that multitask methods outperform singletask methods on MUV.
#
# ## Colab
#
# This tutorial and the rest in this sequence are designed to be done in Google colab. If you'd like to open this notebook in colab, you can use the following link.
#
# [](https://colab.research.google.com/github/deepchem/deepchem/blob/master/examples/tutorials/05_Putting_Multitask_Learning_to_Work.ipynb)
#
#
# ## Setup
#
# To run DeepChem within Colab, you'll need to run the following cell of installation commands. This will take about 5 minutes to run to completion and install your environment.
# + id="Fc_4bSWJg37l" colab_type="code" outputId="d6d577c7-aa9e-4db1-8bb2-6269f2817012" colab={"base_uri": "https://localhost:8080/", "height": 462}
# %tensorflow_version 1.x
# !curl -Lo deepchem_installer.py https://raw.githubusercontent.com/deepchem/deepchem/master/scripts/colab_install.py
import deepchem_installer
# %time deepchem_installer.install(version='2.3.0')
# + [markdown] id="9Ow2nQtZg37p" colab_type="text"
# The MUV dataset is a challenging benchmark in molecular design that consists of 17 different "targets" where there are only a few "active" compounds per target. The goal of working with this dataset is to make a machine learnign model which achieves high accuracy on held-out compounds at predicting activity. To get started, let's download the MUV dataset for us to play with.
# + id="FGi-ZEfSg37q" colab_type="code" outputId="1ac2c36b-66b0-4c57-bf4b-114a7425b85e" colab={"base_uri": "https://localhost:8080/", "height": 85}
import os
import deepchem as dc
current_dir = os.path.dirname(os.path.realpath("__file__"))
dataset_file = "medium_muv.csv.gz"
full_dataset_file = "muv.csv.gz"
# We use a small version of MUV to make online rendering of notebooks easy. Replace with full_dataset_file
# In order to run the full version of this notebook
dc.utils.download_url("https://s3-us-west-1.amazonaws.com/deepchem.io/datasets/%s" % dataset_file,
current_dir)
dataset = dc.utils.save.load_from_disk(dataset_file)
print("Columns of dataset: %s" % str(dataset.columns.values))
print("Number of examples in dataset: %s" % str(dataset.shape[0]))
# + [markdown] id="c9t912ODg37u" colab_type="text"
# Now, let's visualize some compounds from our dataset
# + id="KobfUjlWg37v" colab_type="code" outputId="01025d0f-3fb1-485e-bb93-82f2b3e062f9" colab={"base_uri": "https://localhost:8080/", "height": 1000}
from rdkit import Chem
from rdkit.Chem import Draw
from itertools import islice
from IPython.display import Image, display, HTML
def display_images(filenames):
"""Helper to pretty-print images."""
for filename in filenames:
display(Image(filename))
def mols_to_pngs(mols, basename="test"):
"""Helper to write RDKit mols to png files."""
filenames = []
for i, mol in enumerate(mols):
filename = "MUV_%s%d.png" % (basename, i)
Draw.MolToFile(mol, filename)
filenames.append(filename)
return filenames
num_to_display = 12
molecules = []
for _, data in islice(dataset.iterrows(), num_to_display):
molecules.append(Chem.MolFromSmiles(data["smiles"]))
display_images(mols_to_pngs(molecules))
# + [markdown] id="kDUrLw8Mg37y" colab_type="text"
# There are 17 datasets total in MUV as we mentioned previously. We're going to train a multitask model that attempts to build a joint model to predict activity across all 17 datasets simultaneously. There's some evidence [2] that multitask training creates more robust models.
#
# As fair warning, from my experience, this effect can be quite fragile. Nonetheless, it's a tool worth trying given how easy DeepChem makes it to build these models. To get started towards building our actual model, let's first featurize our data.
# + id="eqEQiNDpg37z" colab_type="code" outputId="e1b919ac-1bb3-4224-ff91-65d2e3d16f3b" colab={"base_uri": "https://localhost:8080/", "height": 357}
MUV_tasks = ['MUV-692', 'MUV-689', 'MUV-846', 'MUV-859', 'MUV-644',
'MUV-548', 'MUV-852', 'MUV-600', 'MUV-810', 'MUV-712',
'MUV-737', 'MUV-858', 'MUV-713', 'MUV-733', 'MUV-652',
'MUV-466', 'MUV-832']
featurizer = dc.feat.CircularFingerprint(size=1024)
loader = dc.data.CSVLoader(
tasks=MUV_tasks, smiles_field="smiles",
featurizer=featurizer)
dataset = loader.featurize(dataset_file)
# + [markdown] id="QQfINH2Ag371" colab_type="text"
# We'll now want to split our dataset into training, validation, and test sets. We're going to do a simple random split using `dc.splits.RandomSplitter`. It's worth noting that this will provide overestimates of real generalizability! For better real world estimates of prospective performance, you'll want to use a harder splitter.
# + id="-f03zjeIg372" colab_type="code" outputId="5472a51a-42e9-43bc-e73e-d947ae3c6a33" colab={"base_uri": "https://localhost:8080/", "height": 136}
splitter = dc.splits.RandomSplitter(dataset_file)
train_dataset, valid_dataset, test_dataset = splitter.train_valid_test_split(
dataset)
#NOTE THE RENAMING:
valid_dataset, test_dataset = test_dataset, valid_dataset
# + [markdown] id="6nRCpb08g375" colab_type="text"
# Let's now get started building some models! We'll do some simple hyperparameter searching to build a robust model.
# + id="BvfbTbsEg376" colab_type="code" outputId="9f96de90-ad90-4492-cced-0f5e74dcacb6" colab={"base_uri": "https://localhost:8080/", "height": 853}
import numpy as np
import numpy.random
params_dict = {"activation": ["relu"],
"momentum": [.9],
"batch_size": [50],
"init": ["glorot_uniform"],
"data_shape": [train_dataset.get_data_shape()],
"learning_rate": [1e-3],
"decay": [1e-6],
"nb_epoch": [1],
"nesterov": [False],
"dropouts": [(.5,)],
"nb_layers": [1],
"batchnorm": [False],
"layer_sizes": [(1000,)],
"weight_init_stddevs": [(.1,)],
"bias_init_consts": [(1.,)],
"penalty": [0.],
}
n_features = train_dataset.get_data_shape()[0]
def model_builder(model_params, model_dir):
model = dc.models.MultitaskClassifier(
len(MUV_tasks), n_features, **model_params)
return model
metric = dc.metrics.Metric(dc.metrics.roc_auc_score, np.mean)
optimizer = dc.hyper.HyperparamOpt(model_builder)
best_dnn, best_hyperparams, all_results = optimizer.hyperparam_search(
params_dict, train_dataset, valid_dataset, [], metric)
# + [markdown] id="QhZAgZ9gg379" colab_type="text"
# # Congratulations! Time to join the Community!
#
# Congratulations on completing this tutorial notebook! If you enjoyed working through the tutorial, and want to continue working with DeepChem, we encourage you to finish the rest of the tutorials in this series. You can also help the DeepChem community in the following ways:
#
# ## Star DeepChem on [GitHub](https://github.com/deepchem/deepchem)
# This helps build awareness of the DeepChem project and the tools for open source drug discovery that we're trying to build.
#
# ## Join the DeepChem Gitter
# The DeepChem [Gitter](https://gitter.im/deepchem/Lobby) hosts a number of scientists, developers, and enthusiasts interested in deep learning for the life sciences. Join the conversation!
#
# # Bibliography
#
# [1] https://pubs.acs.org/doi/10.1021/ci8002649
#
# [2] https://pubs.acs.org/doi/abs/10.1021/acs.jcim.7b00146
|
examples/tutorials/05_Putting_Multitask_Learning_to_Work.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Assignment 5
# - toc: true
# - badges: true
# - comments: true
# - categories: [jupyter]
# Train a deep learning model to classify beetles, cockroaches and dragonflies using [images](https://www.dropbox.com/s/fn73sj2e6c9rhf6/insects.zip?dl=0)
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim
import torchvision
import torchvision.transforms as transforms
import torch.optim as optim
import matplotlib.pyplot as plt
import numpy as np
import shap
# First load the images from the website. The size of the images are different so first we need to resize the images to the same size. We set the batch size = 100
train_root = 'insects/train/'
test_root = 'insects/test/'
transform = transforms.Compose(
[transforms.Resize([256, 256]),
transforms.ToTensor(),
transforms.Normalize((0.5,), (0.5,)),])
train_dataset = torchvision.datasets.ImageFolder(train_root, transform = transform)
test_dataset = torchvision.datasets.ImageFolder(test_root, transform = transform)
train_loader = torch.utils.data.DataLoader(train_dataset, batch_size=100, shuffle=True, num_workers = 0)
test_loader = torch.utils.data.DataLoader(test_dataset, batch_size=100, shuffle=False, num_workers = 0)
# Considering that it is an image classcification problem, Convolutional Neural Network is usually used to train the model. A typical CNN model looks like below:
#
# 
#
# Source: https://towardsdatascience.com/a-comprehensive-guide-to-convolutional-neural-networks-the-eli5-way-3bd2b1164a53
# The Convolutional neural network usually has several components:
# #### Define the Convolutional layer:
#
# ```torch.nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, bias=True)```
#
# The convolution operation is shown as below:
# 
#
# Source: https://anhreynolds.com/blogs/cnn.html
#
# *in_channels*: depends on whether the image is black and white(in_channels = 1) or colored(in_channels = 3)
#
# *kernal_size*: the dimension of the kernal used in the convolution operation.In the example, the kernal size is (3,3)
#
# *stride*: Stride of the convolution
#
# 
#
# In this case, the stride is 2.
#
# *padding*: Padding added to all four sides of the input
#
# 
# In this case, the padding is 1.
#
# Source: https://deepai.org/machine-learning-glossary-and-terms/padding
# #### Define the Activation function:
#
# There are many types of activation function, most famous ones are *sigmoid* function, *relu* function, *tanh* function:
# - sigmoid:
# $f(x)= \frac{1}{1+e^{-x}}$
#
# 
#
# - Relu:
# $f(x) = max(0, x)$
# 
#
# - Tanh:
# $f(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}$
# 
#
# #### Define the Dropout layer:
#
# Dropout is often used to avoid overfitting. It simply sets a propotional nodes to 0. Commonly chosen rate is 0.5.
#
# #### Define the Pooling layer:
# Common pooling methods are max pooling.
# 
#
# Source: https://medium.com/@duanenielsen/deep-learning-cage-match-max-pooling-vs-convolutions-e42581387cb9
# #### Define the fully connected layer:
# ```torch.nn.Linear(in_features, out_features, bias=True, device=None, dtype=None)```
class CNN_Model(nn.Module):
def __init__(self):
super(CNN_Model, self).__init__()
self.layer_1 = nn.Sequential(
nn.Conv2d(in_channels=3, out_channels=32, kernel_size=3, padding=1),
nn.ReLU(),
nn.MaxPool2d(kernel_size=4, stride=4)
)
self.layer_2 = nn.Sequential(
nn.Conv2d(in_channels=32, out_channels= 64, kernel_size=3,padding = 1),
nn.ReLU(),
nn.MaxPool2d(kernel_size=4,stride=4)
)
self.fc1 = nn.Linear(in_features=64*16*16, out_features=500)
self.fc2 = nn.Linear(in_features=500, out_features=120)
self.fc3 = nn.Linear(in_features=120, out_features=3)
def forward(self, x):
out = self.layer_1(x)
out = self.layer_2(out)
out = out.view(out.size(0),-1)
out = self.fc1(out)
out = self.fc2(out)
out = self.fc3(out)
return out
print(model)
def train(model, train_loader, criterion, optimizer, epoch):
train_loss = 0
model.train()
for batch_idx, (image, label) in enumerate(train_loader):
optimizer.zero_grad()
output = model(image)
loss = criterion(output, label)
loss.backward()
optimizer.step()
train_loss += loss.item()
if batch_idx % (len(train_loader)//2) == 0:
print('Train({})[{:.0f}%]: Loss: {:.4f}'.format(
epoch, 100. * batch_idx / len(train_loader), train_loss/(batch_idx+1)))
def test(model, test_loader, criterion, epoch):
model.eval()
test_loss = 0
correct = 0
with torch.no_grad():
for image, label in test_loader:
#image, label = image.to(device), label.to(device)
output = model(image)
test_loss += criterion(output, label).item() # sum up batch loss
pred = output.argmax(dim=1, keepdim=True) # get the index of the max log-probability
correct += pred.eq(label.view_as(pred)).sum().item()
test_loss = (test_loss*100)/len(test_loader.dataset)
print('Test({}): Loss: {:.4f}, Accuracy: {:.4f}%'.format(
epoch, test_loss, 100. * correct / len(test_loader.dataset)))
# #### Optimizer:
# Adam algorithm is an improvement on stochastic gradient descent, the detailed algorithm is shown below:
#
# 
# #### Criterion:
# Cross-entropy is a commonly used loss function for classification problem
#
# $L = \sum\limits_{k = 1}^M y_k \log(p_k)$,$y_k$ is the true label and $p_k$ is the probability for that label
model = CNN_Model()
optimizer = torch.optim.Adam(model.parameters(),lr=0.001)
criterion = torch.nn.CrossEntropyLoss()
epochs = 5
for epoch in range(1, epochs + 1):
train(model, train_loader, criterion, optimizer, epoch)
test(model, test_loader, criterion, epoch)
batch = next(iter(test_loader))
images, _ = batch
# +
background = images[:9]
test_images = images[9:11]
e = shap.GradientExplainer(model, background)
shap_values = e.shap_values(test_images)
shap_numpy = [np.swapaxes(np.swapaxes(s, 1, -1), 1, 2) for s in shap_values]
test_numpy = np.swapaxes(np.swapaxes(test_images.cpu().numpy(), 1, -1), 1, 2)
shap.image_plot(shap_numpy, -test_numpy)
# -
# Based on the above shap plot, anything that is colored in red enhance the model confidence while the blue decreases the model confidence.
|
_notebooks/2021-11-13-Assignment5-Yili Lin.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import sklearn as sk
from sklearn import linear_model
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
from sklearn.preprocessing import MinMaxScaler
# -
# Набор данных взят с https://www.kaggle.com/aungpyaeap/fish-market
# Параметры нескольких популярных промысловых рыб
# length 1 = Body height
# length 2 = Total Length
# length 3 = Diagonal Length
fish_data = pd.read_csv("datasets/Fish.csv", delimiter=',')
print(fish_data)
# Выделим две переменных
x_label = 'Length1'
y_label = 'Weight'
data = fish_data[[x_label, y_label]]
print(data)
# Определим размер валидационной и тестовой выборок
val_test_size = round(0.2*len(data))
print(val_test_size)
# Генерируем уникальный seed
my_code = "Маргарян"
seed_limit = 2 ** 32
my_seed = int.from_bytes(my_code.encode(), "little") % seed_limit
# Создадим обучающую, валидационную и тестовую выборки
random_state = my_seed
train_val, test = train_test_split(data, test_size=val_test_size, random_state=random_state)
train, val = train_test_split(train_val, test_size=val_test_size, random_state=random_state)
print(len(train), len(val), len(test))
# +
# Преобразуем данные к ожидаемому библиотекой skleran формату
train_x = np.array(train[x_label]).reshape(-1,1)
train_y = np.array(train[y_label]).reshape(-1,1)
val_x = np.array(val[x_label]).reshape(-1,1)
val_y = np.array(val[y_label]).reshape(-1,1)
test_x = np.array(test[x_label]).reshape(-1,1)
test_y = np.array(test[y_label]).reshape(-1,1)
# -
# Нарисуем график
plt.plot(train_x, train_y, 'o')
plt.show()
# Создадим модель линейной регрессии и обучим ее на обучающей выборке.
model1 = linear_model.LinearRegression()
model1.fit(train_x, train_y)
# +
# Результат обучения: значения a и b: y = ax+b
print(model1.coef_, model1.intercept_)
a = model1.coef_[0]
b = model1.intercept_
print(a, b)
# +
# Добавим полученную линию на график
x = np.linspace(min(train_x), max(train_x), 100)
y = a * x + b
plt.plot(train_x, train_y, 'o')
plt.plot(x, y)
plt.show()
# -
# Проверим результат на валидационной выборке
val_predicted = model1.predict(val_x)
mse1 = mean_squared_error(val_y, val_predicted)
print(mse1)
# +
# Результат не очень хорош для интерпретации, попробуем сначала нормировать значения
scaler_x = MinMaxScaler()
scaler_x.fit(train_x)
scaled_train_x = scaler_x.transform(train_x)
scaler_y = MinMaxScaler()
scaler_y.fit(train_y)
scaled_train_y = scaler_y.transform(train_y)
plt.plot(scaled_train_x, scaled_train_y, 'o')
plt.show()
# +
# Строим модель и выводим результаты для нормированных данных
model2 = linear_model.LinearRegression()
model2.fit(scaled_train_x, scaled_train_y)
a = model2.coef_[0]
b = model2.intercept_
x = np.linspace(min(scaled_train_x), max(scaled_train_x), 100)
y = a * x + b
plt.plot(scaled_train_x, scaled_train_y, 'o')
plt.plot(x, y)
plt.show()
# +
# Проверим результат на валидационной выборке
scaled_val_x = scaler_x.transform(val_x)
scaled_val_y = scaler_y.transform(val_y)
val_predicted = model2.predict(scaled_val_x)
mse2 = mean_squared_error(scaled_val_y, val_predicted)
print(mse2)
# +
# Построим модель линейной регресси с L1-регуляризацией и выведем результаты для нормированных данных.
model3 = linear_model.Lasso(alpha=0.01)
model3.fit(scaled_train_x, scaled_train_y)
a = model3.coef_[0]
b = model3.intercept_
x = np.linspace(min(scaled_train_x), max(scaled_train_x), 100)
y = a * x + b
plt.plot(scaled_train_x, scaled_train_y, 'o')
plt.plot(x, y)
plt.show()
# +
# Проверим результат на валидационной выборке
scaled_val_x = scaler_x.transform(val_x)
scaled_val_y = scaler_y.transform(val_y)
val_predicted = model3.predict(scaled_val_x)
mse3 = mean_squared_error(scaled_val_y, val_predicted)
print(mse3)
# Можете поэкспериментировать со значением параметра alpha, чтобы уменьшить ошибку
# +
# Построим модель линейной регресси с L2-регуляризацией и выведем результаты для нормированных данных
model4 = linear_model.Ridge(alpha=0.01)
model4.fit(scaled_train_x, scaled_train_y)
a = model4.coef_[0]
b = model4.intercept_
x = np.linspace(min(scaled_train_x), max(scaled_train_x), 100)
y = a * x + b
plt.plot(scaled_train_x, scaled_train_y, 'o')
plt.plot(x, y)
plt.show()
# +
# Проверим результат на валидационной выборке
scaled_val_x = scaler_x.transform(val_x)
scaled_val_y = scaler_y.transform(val_y)
val_predicted = model4.predict(scaled_val_x)
mse4 = mean_squared_error(scaled_val_y, val_predicted)
print(mse4)
# Можете поэкспериментировать со значением параметра alpha, чтобы уменьшить ошибку
# +
# Построим модель линейной регресси с ElasticNet-регуляризацией и выведем результаты для нормированных данных
model5 = linear_model.ElasticNet(alpha=0.01, l1_ratio = 0.01)
model5.fit(scaled_train_x, scaled_train_y)
a = model5.coef_[0]
b = model5.intercept_
x = np.linspace(min(scaled_train_x), max(scaled_train_x), 100)
y = a * x + b
plt.plot(scaled_train_x, scaled_train_y, 'o')
plt.plot(x, y)
plt.show()
# +
# Проверим результат на валидационной выборке
scaled_val_x = scaler_x.transform(val_x)
scaled_val_y = scaler_y.transform(val_y)
val_predicted = model5.predict(scaled_val_x)
mse5 = mean_squared_error(scaled_val_y, val_predicted)
print(mse5)
# Можете поэкспериментировать со значениями параметров alpha и l1_ratio, чтобы уменьшить ошибку
# -
# Выведем ошибки для моделей на нормированных данных
print(mse2, mse3, mse4, mse5)
# +
# Минимальное значение достигается для второй модели, получим итоговую величину ошибки на тестовой выборке
scaled_test_x = scaler_x.transform(test_x)
scaled_test_y = scaler_y.transform(test_y)
test_predicted = model2.predict(scaled_test_x)
mse_test = mean_squared_error(scaled_test_y, test_predicted)
print(mse_test)
# +
# Повторите выделение данных, нормирование, и анализ 4 моделей
# (обычная линейная регрессия, L1-регуляризация, L2-регуляризация, ElasticNet-регуляризация)
# для x = Length2 и y = Width.
# -
x_label = 'Length2'
y_label = 'Weight'
data = fish_data[[x_label, y_label]]
print(data)
# Определим размер валидационной и тестовой выборок
val_test_size = round(0.2*len(data))
print(val_test_size)
# Создадим обучающую, валидационную и тестовую выборки
random_state = my_seed
train_val, test = train_test_split(data, test_size=val_test_size, random_state=random_state)
train, val = train_test_split(train_val, test_size=val_test_size, random_state=random_state)
print(len(train), len(val), len(test))
# +
# Преобразуем данные к ожидаемому библиотекой skleran формату
train_x = np.array(train[x_label]).reshape(-1,1)
train_y = np.array(train[y_label]).reshape(-1,1)
val_x = np.array(val[x_label]).reshape(-1,1)
val_y = np.array(val[y_label]).reshape(-1,1)
test_x = np.array(test[x_label]).reshape(-1,1)
test_y = np.array(test[y_label]).reshape(-1,1)
# -
# Нарисуем график
plt.plot(train_x, train_y, 'o')
plt.show()
# Создадим модель линейной регрессии и обучим ее на обучающей выборке.
model1 = linear_model.LinearRegression().fit(train_x, train_y)
# +
# Результат обучения: значения a и b: y = ax+b
print(model1.coef_, model1.intercept_)
a = model1.coef_[0]
b = model1.intercept_
print(a, b)
# +
# Добавим полученную линию на график
x = np.linspace(min(train_x), max(train_x), 100)
y = a * x + b
plt.plot(train_x, train_y, 'o')
plt.plot(x, y)
plt.show()
# -
# Проверим результат на валидационной выборке
val_predicted = model1.predict(val_x)
mse1 = mean_squared_error(val_y, val_predicted)
print(mse1)
# +
# Результат не очень хорош для интерпретации, попробуем сначала нормировать значения
scaler_x = MinMaxScaler().fit(train_x)
scaled_train_x = scaler_x.transform(train_x)
scaler_y = MinMaxScaler().fit(train_y)
scaled_train_y = scaler_y.transform(train_y)
plt.plot(scaled_train_x, scaled_train_y, 'o')
plt.show()
# +
# Строим модель и выводим результаты для нормированных данных
model2 = linear_model.LinearRegression().fit(scaled_train_x, scaled_train_y)
a = model2.coef_[0]
b = model2.intercept_
x = np.linspace(min(scaled_train_x), max(scaled_train_x), 100)
y = a * x + b
plt.plot(scaled_train_x, scaled_train_y, 'o')
plt.plot(x, y)
plt.show()
# +
# Проверим результат на валидационной выборке
scaled_val_x = scaler_x.transform(val_x)
scaled_val_y = scaler_y.transform(val_y)
val_predicted = model2.predict(scaled_val_x)
mse2 = mean_squared_error(scaled_val_y, val_predicted)
print(mse2)
# +
# Построим модель линейной регресси с L1-регуляризацией и выведем результаты для нормированных данных.
model3 = linear_model.Lasso(alpha=0.01).fit(scaled_train_x, scaled_train_y)
a = model3.coef_[0]
b = model3.intercept_
x = np.linspace(min(scaled_train_x), max(scaled_train_x), 100)
y = a * x + b
plt.plot(scaled_train_x, scaled_train_y, 'o')
plt.plot(x, y)
plt.show()
# +
# Проверим результат на валидационной выборке
scaled_val_x = scaler_x.transform(val_x)
scaled_val_y = scaler_y.transform(val_y)
val_predicted = model3.predict(scaled_val_x)
mse3 = mean_squared_error(scaled_val_y, val_predicted)
print(mse3)
# Можете поэкспериментировать со значением параметра alpha, чтобы уменьшить ошибку
# +
# Построим модель линейной регресси с L2-регуляризацией и выведем результаты для нормированных данных
model4 = linear_model.Ridge(alpha=0.01).fit(scaled_train_x, scaled_train_y)
a = model4.coef_[0]
b = model4.intercept_
x = np.linspace(min(scaled_train_x), max(scaled_train_x), 100)
y = a * x + b
plt.plot(scaled_train_x, scaled_train_y, 'o')
plt.plot(x, y)
plt.show()
# +
# Проверим результат на валидационной выборке
scaled_val_x = scaler_x.transform(val_x)
scaled_val_y = scaler_y.transform(val_y)
val_predicted = model4.predict(scaled_val_x)
mse4 = mean_squared_error(scaled_val_y, val_predicted)
print(mse4)
# Можете поэкспериментировать со значением параметра alpha, чтобы уменьшить ошибку
# +
# Построим модель линейной регресси с ElasticNet-регуляризацией и выведем результаты для нормированных данных
model5 = linear_model.ElasticNet(alpha=0.01, l1_ratio = 0.01)
model5.fit(scaled_train_x, scaled_train_y)
a = model5.coef_[0]
b = model5.intercept_
x = np.linspace(min(scaled_train_x), max(scaled_train_x), 100)
y = a * x + b
plt.plot(scaled_train_x, scaled_train_y, 'o')
plt.plot(x, y)
plt.show()
# +
# Проверим результат на валидационной выборке
scaled_val_x = scaler_x.transform(val_x)
scaled_val_y = scaler_y.transform(val_y)
val_predicted = model5.predict(scaled_val_x)
mse5 = mean_squared_error(scaled_val_y, val_predicted)
print(mse5)
# Можете поэкспериментировать со значениями параметров alpha и l1_ratio, чтобы уменьшить ошибку
# -
# Выведем ошибки для моделей на нормированных данных
print(mse2, mse3, mse4, mse5)
# +
# Минимальное значение достигается для второй модели, получим итоговую величину ошибки на тестовой выборке
scaled_test_x = scaler_x.transform(test_x)
scaled_test_y = scaler_y.transform(test_y)
test_predicted = model2.predict(scaled_test_x)
mse_test = mean_squared_error(scaled_test_y, test_predicted)
print(mse_test)
|
2020 Осенний семестр/Практическое задание 5/Маргарян - практика 5.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Building Simple Neural Networks
#
# In this section you will:
#
# * Import the MNIST dataset from Keras.
# * Format the data so it can be used by a Sequential model with Dense layers.
# * Split the dataset into training and test sections data.
# * Build a simple neural network using Keras Sequential model and Dense layers.
# * Train that model.
# * Evaluate the performance of that model.
#
# While we are accomplishing these tasks, we will also stop to discuss important concepts:
#
# * Splitting data into test and training sets.
# * Training rounds, batch size, and epochs.
# * Validation data vs test data.
# * Examining results.
#
# ## Importing and Formatting the Data
#
# Keras has several built-in datasets that are already well formatted and properly cleaned. These datasets are an invaluable learning resource. Collecting and processing datasets is a serious undertaking, and deep learning tactics perform poorly without large high quality datasets. We will be leveraging the [Keras built in datasets](https://keras.io/datasets/) extensively, and you may wish to explore them further on your own.
#
# In this exercise, we will be focused on the MNIST dataset, which is a set of 70,000 images of handwritten digits each labeled with the value of the written digit. Additionally, the images have been split into training and test sets.
# +
# For drawing the MNIST digits as well as plots to help us evaluate performance we
# will make extensive use of matplotlib
from matplotlib import pyplot as plt
# All of the Keras datasets are in keras.datasets
from keras.datasets import mnist
# Keras has already split the data into training and test data
(training_images, training_labels), (test_images, test_labels) = mnist.load_data()
# Training images is a list of 60,000 2D lists.
# Each 2D list is 28 by 28—the size of the MNIST pixel data.
# Each item in the 2D array is an integer from 0 to 255 representing its grayscale
# intensity where 0 means white, 255 means black.
print(len(training_images), training_images[0].shape)
# training_labels are a value between 0 and 9 indicating which digit is represented.
# The first item in the training data is a 5
print(len(training_labels), training_labels[0])
# -
# Lets visualize the first 100 images from the dataset
for i in range(100):
ax = plt.subplot(10, 10, i+1)
ax.axis('off')
plt.imshow(training_images[i], cmap='Greys')
# ## Problems With This Data
#
# There are (at least) two problems with this data as it is currently formatted, what do you think they are?
# 1. The input data is formatted as a 2D array, but our deep neural network needs to data as a 1D vector.
# * This is because of how deep neural networks are constructed, it is simply not possible to send anything but a vector as input.
# * These vectors can be/represent anything, but from the computer's perspective they must be a 1D vector.
# 2. Our labels are numbers, but we're not performing regression. We need to use a 1-hot vector encoding for our labels.
# * This is important because if we use the number values we would be training our network to think of these values as continuous.
# * If the digit is supposed to be a 2, guessing 1 and guessing 9 are both equally wrong.
# * Training the network with numbers would imply that a prediction of 1 would be "less wrong" than a prediction of 9, when in fact both are equally wrong.
# ### Fixing the data format
#
# Luckily, this is a common problem and we can use two methods to fix the data: `numpy.reshape` and `keras.utils.to_categorical`. This is nessesary because of how deep neural networks process data, there is no way to send 2D data to a `Sequential` model made of `Dense` layers.
# +
from keras.utils import to_categorical
# Preparing the dataset
# Setup train and test splits
(training_images, training_labels), (test_images, test_labels) = mnist.load_data()
# 28 x 28 = 784, because that's the dimensions of the MNIST data.
image_size = 784
# Reshaping the training_images and test_images to lists of vectors with length 784
# instead of lists of 2D arrays. Same for the test_images
training_data = training_images.reshape(training_images.shape[0], image_size)
test_data = test_images.reshape(test_images.shape[0], image_size)
# [
# [1,2,3]
# [4,5,6]
# ]
# => [1,2,3,4,5,6]
# Just showing the changes...
print("training data: ", training_images.shape, " ==> ", training_data.shape)
print("test data: ", test_images.shape, " ==> ", test_data.shape)
# +
# Create 1-hot encoded vectors using to_categorical
num_classes = 10 # Because it's how many digits we have (0-9)
# to_categorical takes a list of integers (our labels) and makes them into 1-hot vectors
training_labels = to_categorical(training_labels, num_classes)
test_labels = to_categorical(test_labels, num_classes)
# -
# Recall that before this transformation, training_labels[0] was the value 5. Look now:
print(training_labels[2])
# ## Building a Deep Neural Network
#
# Now that we've prepared our data, it's time to build a simple neural network. To start we'll make a deep network with 3 layers—the input layer, a single hidden layer, and the output layer. In a deep neural network all the layers are 1 dimensional. The input layer has to be the shape of our input data, meaning it must have 784 nodes. Similarly, the output layer must match our labels, meaning it must have 10 nodes. We can choose the number of nodes in our hidden layer, I've chosen 32 arbitrarally.
# +
from keras.models import Sequential
from keras.layers import Dense
# Sequential models are a series of layers applied linearly.
model = Sequential()
# The first layer must specify it's input_shape.
# This is how the first two layers are added, the input layer and the hidden layer.
model.add(Dense(units=32, activation='sigmoid', input_shape=(image_size,)))
# This is how the output layer gets added, the 'softmax' activation function ensures
# that the sum of the values in the output nodes is 1. Softmax is very
# common in classification networks.
model.add(Dense(units=num_classes, activation='softmax'))
# This function provides useful text data for our network
model.summary()
# -
# ## Compiling and Training a Model
#
# Our model must be compiled and trained before it can make useful predictions. Models are trainined with the training data and training labels. During this process Keras will use an optimizer, loss function, metrics of our chosing to repeatedly make predictions and recieve corrections. The loss function is used to train the model, the metrics are only used for human evaluation of the model during and after training.
#
# Training happens in a series of epochs which are divided into a series of rounds. Each round the network will recieve `batch_size` samples from the training data, make predictions, and recieve one correction based on the errors in those predictions. In a single epoch, the model will look at every item in the training set __exactly once__, which means individual data points are sampled from the training data without replacement during each round of each epoch.
#
# During training, the training data itself will be broken into two parts according to the `validation_split` parameter. The proportion that you specify will be left out of the training process, and used to evaluate the accuracy of the model. This is done to preserve the test data, while still having a set of data left out in order to test against — and hopefully prevent — overfitting. At the end of each epoch, predictions will be made for all the items in the validation set, but those predictions won't adjust the weights in the model. Instead, if the accuracy of the predictions in the validation set stops improving then training will stop early, even if accuracy in the training set is improving.
# +
# sgd stands for stochastic gradient descent.
# categorical_crossentropy is a common loss function used for categorical classification.
# accuracy is the percent of predictions that were correct.
model.compile(optimizer="sgd", loss='categorical_crossentropy', metrics=['accuracy'])
# The network will make predictions for 128 flattened images per correction.
# It will make a prediction on each item in the training set 5 times (5 epochs)
# And 10% of the data will be used as validation data.
history = model.fit(training_data, training_labels, batch_size=128, epochs=5, verbose=True, validation_split=.1)
# -
# ## Evaluating Our Model
#
# Now that we've trained our model, we want to evaluate its performance. We're using the "test data" here although in a serious experiment, we would likely not have done nearly enough work to warrent the application of the test data. Instead, we would rely on the validation metrics as a proxy for our test results until we had models that we believe would perform well.
#
# Once we evaluate our model on the test data, any subsequent changes we make would be based on what we learned from the test data. Meaning, we would have functionally incorporated information from the test set into our training procedure which could bias and even invalidate the results of our research. In a non-research setting the real test might be more like putting this feature into production.
#
# Nevertheless, it is always wise to create a test set that is not used as an evaluative measure until the very end of an experimental lifecycle. That is, once you have a model that you believe __should__ generalize well to unseen data you should test it on the test data to test that hypothosis. If your model performs poorly on the test data, you'll have to reevaluate your model, training data, and procedure.
# +
loss, accuracy = model.evaluate(test_data, test_labels, verbose=True)
plt.plot(history.history['acc'])
plt.plot(history.history['val_acc'])
plt.title('model accuracy')
plt.ylabel('accuracy')
plt.xlabel('epoch')
plt.legend(['training', 'validation'], loc='best')
plt.show()
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['training', 'validation'], loc='best')
plt.show()
print(f'Test loss: {loss:.3}')
print(f'Test accuracy: {accuracy:.3}')
# -
# ## How Did Our Network Do?
#
# * Why do we only have one value for test loss and test accuracy, but a chart over time for training and validation loss and accuracy?
# * Our model was more accurate on the validation data than it was on the training data.
# * Is this okay? Why or why not?
# * What if our model had been more accurate on the training data than the validation data?
# * Did our model get better during each epoch?
# * If not: why might that be the case?
# * If so: should we always expect this, where each epoch strictly improves training/validation accuracy/loss?
# ### Answers:
#
#
# * Why do we only have one value for test loss and test accuracy, but a chart over time for training and validation loss and accuracy?
# * __Because we only evaluate the test data once at the very end, but we evaluate training and validation scores once per epoch.__
# * Our model was more accurate on the validation data than it was on the training data.
# * Is this okay? Why or why not?
# * __Yes, this is okay, and even good. When our validation scores are better than our training scores, it's a sign that we are probably not overfitting__
# * What if our model had been more accurate on the training data than the validation data?
# * __This would concern us, because it would suggest we are probably overfitting.__
# * Did our model get better during each epoch?
# * If not: why might that be the case?
# * __Optimizers rely on the gradient to update our weights, but the 'function' we are optimizing (our neural network) is not a ground truth. A single batch, and even a complete epoch, may very well result in an adjustment that hurts overall performance.__
# * If so: should we always expect this, where each epoch strictly improves training/validation accuracy/loss?
# * __Not at all, see the above answer.__
# ## Look at Specific Results
#
# Often, it can be illuminating to view specific results, both when the model is correct and when the model is wrong. Lets look at the images and our model's predictions for the first 16 samples in the test set.
# +
from numpy import argmax
# Predicting once, then we can use these repeatedly in the next cell without recomputing the predictions.
predictions = model.predict(test_data)
# For pagination & style in second cell
page = 0
fontdict = {'color': 'black'}
# +
# Repeatedly running this cell will page through the predictions
for i in range(16):
ax = plt.subplot(4, 4, i+1)
ax.axis('off')
plt.imshow(test_images[i + page], cmap='Greys')
prediction = argmax(predictions[i + page])
true_value = argmax(test_labels[i + page])
fontdict['color'] = 'black' if prediction == true_value else 'red'
plt.title("{}, {}".format(prediction, true_value), fontdict=fontdict)
page += 16
plt.tight_layout()
plt.show()
# + [markdown] heading_collapsed=true
# ## Will A Different Network Perform Better?
#
# Given what you know so far, use Keras to build and train another sequential model that you think will perform __better__ than the network we just built and trained. Then evaluate that model and compare its performance to our model. Remember to look at accuracy and loss for training and validation data over time, as well as test accuracy and loss.
# + hidden=true
# Your code here...
# -
# ## Bonus questions: Go Further
#
# Here are some questions to help you further explore the concepts in this lab.
#
# * Does the original model, or your model, fail more often on a particular digit?
# * Write some code that charts the accuracy of our model's predictions on the test data by digit.
# * Is there a clear pattern? If so, speculate about why that could be...
# * Training for longer typically improves performance, up to a point.
# * For a simple model, try training it for 20 epochs, and 50 epochs.
# * Look at the charts of accuracy and loss over time, have you reached diminishing returns after 20 epochs? after 50?
# * More complex networks require more training time, but can outperform simpler networks.
# * Build a more complex model, with at least 3 hidden layers.
# * Like before, train it for 5, 20, and 50 epochs.
# * Evaluate the performance of the model against the simple model, and compare the total amount of time it took to train.
# * Was the extra complexity worth the additional training time?
# * Do you think your complex model would get even better with more time?
# * A little perspective on this last point: Some models train for [__weeks to months__](https://openai.com/blog/ai-and-compute/).
|
01-intro-to-deep-learning/02-building-simple-neural-networks.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
from utils import *
import tensorflow as tf
from sklearn.cross_validation import train_test_split
import time
trainset = sklearn.datasets.load_files(container_path = 'data', encoding = 'UTF-8')
trainset.data, trainset.target = separate_dataset(trainset,1.0)
print (trainset.target_names)
print (len(trainset.data))
print (len(trainset.target))
ONEHOT = np.zeros((len(trainset.data),len(trainset.target_names)))
ONEHOT[np.arange(len(trainset.data)),trainset.target] = 1.0
train_X, test_X, train_Y, test_Y, train_onehot, test_onehot = train_test_split(trainset.data,
trainset.target,
ONEHOT, test_size = 0.2)
concat = ' '.join(trainset.data).split()
vocabulary_size = len(list(set(concat)))
data, count, dictionary, rev_dictionary = build_dataset(concat, vocabulary_size)
print('vocab from size: %d'%(vocabulary_size))
print('Most common words', count[4:10])
print('Sample data', data[:10], [rev_dictionary[i] for i in data[:10]])
GO = dictionary['GO']
PAD = dictionary['PAD']
EOS = dictionary['EOS']
UNK = dictionary['UNK']
class Model:
def __init__(self, size_layer, num_layers, embedded_size,
dict_size, dimension_output, learning_rate):
def cells(reuse=False):
return tf.nn.rnn_cell.GRUCell(size_layer,reuse=reuse)
self.X = tf.placeholder(tf.int32, [None, None])
self.Y = tf.placeholder(tf.float32, [None, dimension_output])
encoder_embeddings = tf.Variable(tf.random_uniform([dict_size, embedded_size], -1, 1))
encoder_embedded = tf.nn.embedding_lookup(encoder_embeddings, self.X)
rnn_cells = tf.nn.rnn_cell.MultiRNNCell([cells() for _ in range(num_layers)])
outputs, _ = tf.nn.dynamic_rnn(rnn_cells, encoder_embedded, dtype = tf.float32)
W = tf.get_variable('w',shape=(size_layer, dimension_output),initializer=tf.orthogonal_initializer())
b = tf.get_variable('b',shape=(dimension_output),initializer=tf.zeros_initializer())
self.logits = tf.matmul(outputs[:, -1], W) + b
self.cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits = self.logits, labels = self.Y))
self.optimizer = tf.train.AdamOptimizer(learning_rate = learning_rate).minimize(self.cost)
correct_pred = tf.equal(tf.argmax(self.logits, 1), tf.argmax(self.Y, 1))
self.accuracy = tf.reduce_mean(tf.cast(correct_pred, tf.float32))
size_layer = 128
num_layers = 2
embedded_size = 128
dimension_output = len(trainset.target_names)
learning_rate = 1e-3
maxlen = 50
batch_size = 128
tf.reset_default_graph()
sess = tf.InteractiveSession()
model = Model(size_layer,num_layers,embedded_size,vocabulary_size+4,dimension_output,learning_rate)
sess.run(tf.global_variables_initializer())
EARLY_STOPPING, CURRENT_CHECKPOINT, CURRENT_ACC, EPOCH = 5, 0, 0, 0
while True:
lasttime = time.time()
if CURRENT_CHECKPOINT == EARLY_STOPPING:
print('break epoch:%d\n'%(EPOCH))
break
train_acc, train_loss, test_acc, test_loss = 0, 0, 0, 0
for i in range(0, (len(train_X) // batch_size) * batch_size, batch_size):
batch_x = str_idx(train_X[i:i+batch_size],dictionary,maxlen)
acc, loss, _ = sess.run([model.accuracy, model.cost, model.optimizer],
feed_dict = {model.X : batch_x, model.Y : train_onehot[i:i+batch_size]})
train_loss += loss
train_acc += acc
for i in range(0, (len(test_X) // batch_size) * batch_size, batch_size):
batch_x = str_idx(test_X[i:i+batch_size],dictionary,maxlen)
acc, loss = sess.run([model.accuracy, model.cost],
feed_dict = {model.X : batch_x, model.Y : test_onehot[i:i+batch_size]})
test_loss += loss
test_acc += acc
train_loss /= (len(train_X) // batch_size)
train_acc /= (len(train_X) // batch_size)
test_loss /= (len(test_X) // batch_size)
test_acc /= (len(test_X) // batch_size)
if test_acc > CURRENT_ACC:
print('epoch: %d, pass acc: %f, current acc: %f'%(EPOCH,CURRENT_ACC, test_acc))
CURRENT_ACC = test_acc
CURRENT_CHECKPOINT = 0
else:
CURRENT_CHECKPOINT += 1
print('time taken:', time.time()-lasttime)
print('epoch: %d, training loss: %f, training acc: %f, valid loss: %f, valid acc: %f\n'%(EPOCH,train_loss,
train_acc,test_loss,
test_acc))
EPOCH += 1
logits = sess.run(model.logits, feed_dict={model.X:str_idx(test_X,dictionary,maxlen)})
print(metrics.classification_report(test_Y, np.argmax(logits,1), target_names = trainset.target_names))
|
text-classification/13.gru-rnn.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Creating datetimes by hand
# Often you create datetime objects based on outside data. Sometimes though, you want to create a datetime object from scratch.
#
# You're going to create a few different datetime objects from scratch to get the hang of that process. These come from the bikeshare data set that you'll use throughout the rest of the chapter.
# +
# Import datetime
from datetime import datetime
# Create a datetime object
dt = datetime(2017, 10, 1, 15, 26, 26)
# Print the results in ISO 8601 format
print(dt.isoformat())
# +
# Import datetime
from datetime import datetime
# Create a datetime object
dt = datetime(2017, 12, 31, 15, 19, 13)
# Print the results in ISO 8601 format
print(dt.isoformat())
# +
# Import datetime
from datetime import datetime
# Create a datetime object
dt = datetime(2017, 12, 31, 15, 19, 13)
# Replace the year with 1917
dt_old = dt.replace(year=1917)
# Print the results in ISO 8601 format
print(dt_old)
# -
# # Counting events before and after noon
# In this chapter, you will be working with a list of all bike trips for one Capital Bikeshare bike, W20529, from October 1, 2017 to December 31, 2017. This list has been loaded as onebike_datetimes.
#
# Each element of the list is a dictionary with two entries: start is a datetime object corresponding to the start of a trip (when a bike is removed from the dock) and end is a datetime object corresponding to the end of a trip (when a bike is put back into a dock).
#
# You can use this data set to understand better how this bike was used. Did more trips start before noon or after noon?
# +
import pandas as pd
captial_onebike = pd.read_csv('../datasets/capital-onebike.csv')
fmt = "%Y-%m-%d %H:%M:%S"
onebike_datetime_strings = list(zip(captial_onebike['Start date'], captial_onebike['End date']))
onebike_datetimes = []
# Loop over all trips
for (start, end) in onebike_datetime_strings:
trip = {'start': datetime.strptime(start, fmt),
'end': datetime.strptime(end, fmt)}
# Append the trip
onebike_datetimes.append(trip)
# Create dictionary to hold results
trip_counts = {'AM': 0, 'PM': 0}
# Loop over all trips
for trip in onebike_datetimes:
# Check to see if the trip starts before noon
if trip['start'].hour < 12:
# Increment the counter for before noon
trip_counts['AM'] += 1
else:
# Increment the counter for after noon
trip_counts['PM'] += 1
print(trip_counts)
# -
# # Turning strings into datetimes
# When you download data from the Internet, dates and times usually come to you as strings. Often the first step is to turn those strings into datetime objects.
#
# In this exercise, you will practice this transformation.
#
# | Reference | |
# |-----------|----|
# |%Y|4 digit year (0000-9999)|
# |%m|2 digit month (1-12)|
# |%d|2 digit day (1-31)|
# |%H|2 digit hour (0-23)|
# |%M|2 digit minute (0-59)|
# |%S|2 digit second (0-59)
#
# +
# Import the datetime class
from datetime import datetime
# Starting string, in YYYY-MM-DD HH:MM:SS format
s = '2017-02-03 00:00:01'
# Write a format string to parse s
fmt = '%Y-%m-%d %H:%M:%S'
# Create a datetime object d
d = datetime.strptime(s, fmt)
# Print d
print(d)
# +
# Import the datetime class
from datetime import datetime
# Starting string, in YYYY-MM-DD format
s = '2030-10-15'
# Write a format string to parse s
fmt = '%Y-%m-%d'
# Create a datetime object d
d = datetime.strptime(s, fmt)
# Print d
print(d)
# +
# Import the datetime class
from datetime import datetime
# Starting string, in MM/DD/YYYY HH:MM:SS format
s = '12/15/1986 08:00:00'
# Write a format string to parse s
fmt = '%m/%d/%Y %H:%M:%S'
# Create a datetime object d
d = datetime.strptime(s, fmt)
# Print d
print(d)
# -
# # Parsing pairs of strings as datetimes
# Up until now, you've been working with a pre-processed list of datetimes for W20529's trips. For this exercise, you're going to go one step back in the data cleaning pipeline and work with the strings that the data started as.
#
# Explore onebike_datetime_strings in the IPython shell to determine the correct format. datetime has already been loaded for you.
#
# | Reference | |
# |-----------|----|
# |%Y|4 digit year (0000-9999)|
# |%m|2 digit month (1-12)|
# |%d|2 digit day (1-31)|
# |%H|2 digit hour (0-23)|
# |%M|2 digit minute (0-59)|
# |%S|2 digit second (0-59)
# +
import pandas as pd
captial_onebike = pd.read_csv('../datasets/capital-onebike.csv')
captial_onebike
# +
# Write down the format string
fmt = "%Y-%m-%d %H:%M:%S"
# Initialize a list for holding the pairs of datetime objects
onebike_datetimes = []
onebike_datetime_strings = list(zip(captial_onebike['Start date'], captial_onebike['End date']))
# Loop over all trips
for (start, end) in onebike_datetime_strings:
trip = {'start': datetime.strptime(start, fmt),
'end': datetime.strptime(end, fmt)}
# Append the trip
onebike_datetimes.append(trip)
onebike_datetimes
# -
# # Recreating ISO format with strftime()
# In the last chapter, you used strftime() to create strings from date objects. Now that you know about datetime objects, let's practice doing something similar.
#
# Re-create the .isoformat() method, using .strftime(), and print the first trip start in our data set.
# +
# Import datetime
from datetime import datetime
# Pull out the start of the first trip
first_start = onebike_datetimes[0]['start']
# Format to feed to strftime()
fmt = "%Y-%m-%dT%H:%M:%S"
# Print out date with .isoformat(), then with .strftime() to compare
print(first_start.isoformat())
print(first_start.strftime(fmt))
# -
# # Unix timestamps
# Datetimes are sometimes stored as Unix timestamps: the number of seconds since January 1, 1970. This is especially common with computer infrastructure, like the log files that websites keep when they get visitors.
# +
# Import datetime
from datetime import datetime
# Starting timestamps
timestamps = [1514665153, 1514664543]
# Datetime objects
dts = []
# Loop
for ts in timestamps:
dts.append(datetime.fromtimestamp(ts))
# Print results
print(dts)
# -
# # Turning pairs of datetimes into durations
# When working with timestamps, we often want to know how much time has elapsed between events. Thankfully, we can use datetime arithmetic to ask Python to do the heavy lifting for us so we don't need to worry about day, month, or year boundaries. Let's calculate the number of seconds that the bike was out of the dock for each trip.
#
# Continuing our work from a previous coding exercise, the bike trip data has been loaded as the list onebike_datetimes. Each element of the list consists of two datetime objects, corresponding to the start and end of a trip, respectively.
# +
# Initialize a list for all the trip durations
onebike_durations = []
for trip in onebike_datetimes:
# Create a timedelta object corresponding to the length of the trip
trip_duration = trip['end'] - trip['start']
# Get the total elapsed seconds in trip_duration
trip_length_seconds = trip_duration.total_seconds()
# Append the results to our list
onebike_durations.append(trip_length_seconds)
onebike_durations
# -
# # Average trip time
# W20529 took 291 trips in our data set. How long were the trips on average? We can use the built-in Python functions sum() and len() to make this calculation.
#
# Based on your last coding exercise, the data has been loaded as onebike_durations. Each entry is a number of seconds that the bike was out of the dock.
# +
# What was the total duration of all trips?
total_elapsed_time = sum(onebike_durations)
# What was the total number of trips?
number_of_trips = len(onebike_durations)
# Divide the total duration by the number of trips
print(total_elapsed_time / number_of_trips)
# -
# # The long and the short of why time is hard
# Out of 291 trips taken by W20529, how long was the longest? How short was the shortest? Does anything look fishy?
#
# As before, data has been loaded as onebike_durations.
# +
# Calculate shortest and longest trips
shortest_trip = min(onebike_durations)
longest_trip = max(onebike_durations)
# Print out the results
print("The shortest trip was " + str(shortest_trip) + " seconds")
print("The longest trip was " + str(longest_trip) + " seconds")
|
working-with-dates-and-times-in-python/2. Combining Dates and Times/notebook_section_2.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
#Here we will Improve model performance
# # Importing the libraries
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
# # Importing the dataset
dataset = pd.read_csv('E:\Edu\Data Science and ML\Machinelearningaz\Datasets\Part 10 - Model Selection & Boosting\Section 48 - Model Selection//Social_Network_Ads.csv')
X = dataset.iloc[:, [2, 3]].values
y = dataset.iloc[:, 4].values
# # Splitting the dataset into the Training set and Test set
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.25, random_state = 0)
# # Feature Scaling
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)
# # Fitting Kernel SVM to the Training set
# +
from sklearn.svm import SVC
#before grid search
#classifier = SVC(kernel = 'rbf', random_state = 0)
#after grid search
classifier = SVC(C=1,kernel = 'rbf',gamma=0.7, random_state = 0)
classifier.fit(X_train, y_train)
# -
# # Predicting the Test set results
y_pred = classifier.predict(X_test)
# # Making the Confusion Matrix
from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_test, y_pred)
cm
# # Applying k-Fold Cross Validation
from sklearn.model_selection import cross_val_score
accuracies = cross_val_score(estimator = classifier, X = X_train, y = y_train, cv = 10)
print(accuracies.mean())
print(accuracies.std())
#low bias low variance
# # Applying Grid Search to find the best model and the best parameters
from sklearn.model_selection import GridSearchCV
parameters = [{'C': [1, 10, 100, 1000], 'kernel': ['linear']},
{'C': [1, 10, 100, 1000], 'kernel': ['rbf'], 'gamma': [0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9]}]
grid_search = GridSearchCV(estimator = classifier,
param_grid = parameters,
scoring = 'accuracy',
cv = 10,
n_jobs = -1)
grid_search = grid_search.fit(X_train, y_train)
best_accuracy = grid_search.best_score_
best_parameters = grid_search.best_params_
print(best_accuracy)
print(best_parameters)
# # Visualising the Training set results
from matplotlib.colors import ListedColormap
X_set, y_set = X_train, y_train
X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 1, stop = X_set[:, 0].max() + 1, step = 0.01),
np.arange(start = X_set[:, 1].min() - 1, stop = X_set[:, 1].max() + 1, step = 0.01))
plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape),
alpha = 0.75, cmap = ListedColormap(('red', 'green')))
plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)):
plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1],
c = ListedColormap(('red', 'green'))(i), label = j)
plt.title('Kernel SVM (Training set)')
plt.xlabel('Age')
plt.ylabel('Estimated Salary')
plt.legend()
plt.show()
# # Visualising the Test set results
from matplotlib.colors import ListedColormap
X_set, y_set = X_test, y_test
X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 1, stop = X_set[:, 0].max() + 1, step = 0.01),
np.arange(start = X_set[:, 1].min() - 1, stop = X_set[:, 1].max() + 1, step = 0.01))
plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape),
alpha = 0.75, cmap = ListedColormap(('red', 'green')))
plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)):
plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1],
c = ListedColormap(('red', 'green'))(i), label = j)
plt.title('Kernel SVM (Test set)')
plt.xlabel('Age')
plt.ylabel('Estimated Salary')
plt.legend()
plt.show()
|
7 Model Selection Boosting/Model Selection/ Grid Search .ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/yusufdalva/TensorFlow_Practice/blob/callbacks-1/fundamentals/callbacks.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="Ca18EVXA8xOo" colab_type="text"
# ### Callbacks example using MNIST dataset with Tensorflow
# This notebook demonstrates the usage of callbacks in training. A simple CNN is constructed. This code is written by modeling the assignment in https://colab.research.google.com/github/lmoroney/dlaicourse/blob/master/Course%201%20-%20Part%204%20-%20Lesson%202%20-%20Notebook.ipynb#scrollTo=BLMdl9aP8nQ0.
#
# The only intention is practice.
# + [markdown] id="hROc7Fwu9YL0" colab_type="text"
# ### Importing and checking Tensorflow version
# Import statement for tensorflow and version check.
# + id="74cV4KPZ9pCv" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="c41c1d05-d7b8-4b6f-c8d1-0215fa637aa3"
import tensorflow as tf
print("TensorFlow version: ", tf.__version__)
# + [markdown] id="m28-8h1_90vW" colab_type="text"
# ## Importing MNIST dataset
# This notebook uses MNIST dataset for demonstration purposes. The following part shows the import and preprocessing for the dataset
# + id="0M1f8aBz9vIW" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 153} outputId="7b307cdc-0739-415a-8108-0ac094f3e6c3"
mnist_dataset = tf.keras.datasets.fashion_mnist
(train_samples, train_labels), (test_samples, test_labels) = mnist_dataset.load_data()
# + [markdown] id="hm3hDYUv-b6F" colab_type="text"
# Data format of the dataset is shown below:
# + id="Tz3LWjiJ-XLg" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 85} outputId="70081aff-ae31-40c1-ac2b-5e0ca05344ca"
import numpy as np
import matplotlib.pyplot as plt
print("Training samples dimensions: ", train_samples.shape)
print("Training labels dimensions: ", train_labels.shape)
print("Test samples dimensions: ", test_samples.shape)
print("Test labels dimensions: ", test_labels.shape)
# + id="F93ZKWtR_P9i" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 68} outputId="32acb544-f3a7-45e7-ddc6-2a61c7eaf06f"
print("Data sample dimensions: ", train_samples.shape[1:])
assert train_samples.shape[1:] == test_samples.shape[1:] # Assertion to prove the equality of dimensions in test samples and training samples
print("Training sample count: ", train_samples.shape[0])
print("Test sample count: ", test_samples.shape[0])
# + [markdown] id="KFJ0FewIABLL" colab_type="text"
# ### Data Sample
# To show the task, one random data sample from training set is selected with its corresponding label
# + id="Gpd12LPF_7iD" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 299} outputId="3b3fb7c0-4915-423a-bb4f-5344996ce77f"
import random
random.seed(1) # For consistency in different runs
random_idx = int(random.random() * train_samples.shape[0]) # Corresponds to the index of a training example
data_sample, data_label = train_samples[random_idx], train_labels[random_idx]
print('Label of the data sample: ', data_label)
plt.imshow(data_sample, cmap = 'gray')
# + [markdown] id="2J6o6QCVB-bK" colab_type="text"
# ### Data Normalization
# To reduce the variance in both test and training set, normalization applied (Min-max feature scaling) The normalization formula is as follows:</br></br>
# $\large{X' = \frac{X - X_{min}}{X_{max}}}$</br></br>
# Note that minimum pixel value is 0 and maximum pixel value is 255 here
# + id="-PFPI0ExEAH6" colab_type="code" colab={}
train_samples = train_samples / 255.0
test_samples = test_samples / 255.0
# + [markdown] id="5PdRthz5EjEe" colab_type="text"
# #Model
# In the model here, there are no convolutional layers included as it is just an entry level example. The neural network model here will consist of 2 fully connected layers, which one has 256 neurons and the other has 128 neurons as an example. For the classification, as this is a multi-class classification problem, **softmax** activation has been used for 10 neurons (10 = # of classes)
# + id="c-d0WaWAEe7K" colab_type="code" colab={}
X_in = tf.keras.layers.Input(shape = train_samples.shape[1:]) # Input layer
X = tf.keras.layers.Flatten()(X_in)
X = tf.keras.layers.Dense(units = 256, activation = 'relu')(X)
X = tf.keras.layers.Dense(units = 128, activation = 'relu')(X)
out = tf.keras.layers.Dense(units = 10, activation = 'softmax')(X) # Output layer
model = tf.keras.Model(inputs = X_in, outputs = out)
# + [markdown] id="5uNJyUaaIVjE" colab_type="text"
# ## Compile the model
# After constructing the model, the desired metrics to observe during training (**metrics**), the loss function for training (**loss**) and the optimization algorithm is needed to be specified (**optimizer**). The following metrics has been selected:
# - **Optimizer: Adam Optimizer**, to make use of moving average and momentum
# - **Loss: Sparse Categorical Crossentropy**, the task is multiclass classification and the labels are not in the form of one-hot vector </br>(eg. for label 2, one-hot vector representation is: $\begin{bmatrix}0&0&1&0&...&0&0\end{bmatrix}$)
# - **Metrics: Accuracy**, to keep track of training accuracy
# + id="x4STHBvuIT4T" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 697} outputId="4f71fe76-f42f-45c9-cb02-f2f648eafe0e"
epoch_count = 20
model.compile(optimizer = 'adam',
loss = 'sparse_categorical_crossentropy',
metrics = ['accuracy'])
# Training the model with training samples and labels -- training for 20 epochs
history = model.fit(x = train_samples, y = train_labels, epochs = epoch_count)
# + id="ViT4yHT0U-Ch" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 350} outputId="6f84f6e2-c5fc-4f6a-850d-b29458163f98"
# Visualizing the changes in training loss and training accuracy values
fig, ax = plt.subplots(1,2, figsize = (15,5))
ax[0].plot(range(1,epoch_count + 1), history.history['loss'])
ax[0].set_xlabel('epochs')
ax[0].set_ylabel('Training Loss')
ax[0].set_title('Change in Training Loss')
ax[1].plot(range(1,epoch_count + 1), history.history['accuracy'])
ax[1].set_xlabel('epochs')
ax[1].set_ylabel('Training_accuracy')
ax[1].set_title('Change in Training Accuracy')
fig.show()
# + [markdown] id="jrboyeOeLUb2" colab_type="text"
# ## Evaluating the model
# Now with the test data, the model will be evaluated with prediction accuracy.
#
# + id="oFGiKlnVLJWW" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 68} outputId="10d445c8-2a51-4877-c2c8-9bc8e711754a"
eval = model.evaluate(test_samples, test_labels)
print('Testing loss: ', eval[0])
print('Testing accuracy: ', eval[1])
# + [markdown] id="LFozyjFzX-HI" colab_type="text"
# ## Adding a Callback
# To have more control in training, a callback is defined while fitting the model. In this notebook, the callback function described does two things. They are:
# - At the end of each epoch, prints a summary of the epoch.
# - Stops training if loss is less than 0.15
# + id="3L8Lalc9LnYK" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 867} outputId="946c192e-3f3f-4e07-f078-e59cb7e60c54"
class controlCallbakck(tf.keras.callbacks.Callback):
def on_epoch_end(self, epoch, logs = {}):
print("\nFor epoch " + str(epoch) + ", loss is " + str(logs.get('loss')) + " and accuracy is " + str(logs.get('accuracy')))
if logs.get('loss') < 0.15:
print("Loss too low, stopping training...")
self.model.stop_training = True
callback = controlCallbakck()
X_in = tf.keras.layers.Input(shape = train_samples.shape[1:]) # Input layer
X = tf.keras.layers.Flatten()(X_in)
X = tf.keras.layers.Dense(units = 256, activation = 'relu')(X)
X = tf.keras.layers.Dense(units = 128, activation = 'relu')(X)
out = tf.keras.layers.Dense(units = 10, activation = 'softmax')(X) # Output layer
model = tf.keras.Model(inputs = X_in, outputs = out)
epoch_count = 30
model.compile(optimizer = 'adam',
loss = 'sparse_categorical_crossentropy',
metrics = ['accuracy'])
model.fit(x = train_samples, y = train_labels, epochs = epoch_count, callbacks = [callback], verbose = 0)
# + [markdown] id="fyEXT_upc2CH" colab_type="text"
# ### Evaluating the model in terms of accuracy
# In the following, the model which the training is interrupted early due to the loss is evaluated in terms of accuracy.
# + id="dEFaBNXddLsM" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 68} outputId="6c6f3736-d27e-4b65-d21e-4f9528e2f995"
eval = model.evaluate(test_samples, test_labels)
print('Testing loss: ', eval[0])
print('Testing accuracy: ', eval[1])
|
Tensorflow_fundamentals/callbacks.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <img src="images/MCG.png" style="width: 100px">
#
#
# # Gaussian Bayesian Networks (GBNs)
#
# ## Generate $x_1$ $x_2$ and $Y$ from a Multivariate Gaussian Distribution with a Mean and a Variance.
#
# What if the inputs to the linear regression were correlated? This often happens in linear dynamical systems. Linear Gaussian Models are useful for modeling probabilistic PCA, factor analysis and linear dynamical systems. Linear Dynamical Systems have variety of uses such as tracking of moving objects. This is an area where Signal Processing methods have a high overlap with Machine Learning methods. When the problem is treated as a state-space problem with added stochasticity, then the future samples depend on the past. The latent parameters, $\beta_i$ where $i \in [1,...,k]$ provide a linear combination of the univariate gaussian distributions as shown in the figure.
#
# <img src="images/gbn.png", style="width: 400px">
#
# The observed variable, $y_{jx}$ can be described as a sample that is drawn from the conditional distribution:
#
# $$\mathcal{N}(y_{jx} | \sum_{i=1}^k \beta_i^T x_i + \beta_0; \sigma^2)$$
#
# The latent parameters $\beta_is$ and $\sigma^2$ need to be determined.
# +
#### import numpy as np
# %matplotlib inline
import pandas as pd
import seaborn as sns
import numpy as np
from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D
from scipy.stats import multivariate_normal
from matplotlib import pyplot
# Obtain the X and Y which are jointly gaussian from the distribution
mu_x = np.array([7, 13])
sigma_x = np.array([[4 , 3],
[3 , 6]])
# Variables
states = ['X1', 'X2']
all_states = ['X1', 'X2', 'P_X']
sym_coefs = ['b1_coef', 'b2_coef']
# Generate samples from the distribution
X_Norm = multivariate_normal(mean=mu_x, cov=sigma_x)
X_samples = X_Norm.rvs(size=10000)
X_df = pd.DataFrame(X_samples, columns=states)
# Generate
X_df['P_X'] = X_df.apply(X_Norm.pdf, axis=1)
X_df.head()
g = sns.jointplot(X_df['X1'], X_df['X2'], kind="kde", height=10, space=0)
# -
# ## Linear Gaussian Models - The Process
#
# The linear gaussian model in supervised learning scheme is nothing but a linear regression where inputs are drawn from a jointly gaussian distribution.
#
# Determining the Latent Parameters via Maximum Likelihood Estimation (MLE)
#
# The samples drawn from the conditional linear gaussian distributions are observed as:
#
# $$ p(Y|X) = \cfrac{1}{\sqrt(2\pi\sigma_c^2} \times exp(\cfrac{(\sum_{i=1}^k \beta_i^T x_i + \beta_0 - x[m])^2}{2\sigma^2})$$
#
# Taking log,
#
# $$ log(p(Y|X)) = (\sum_{i=1}^k[-\cfrac{1}{2}log(2\pi\sigma^2) - \cfrac{1}{2\sigma^2}( \beta_i^T x_i + \beta_0 - x[m])^2)]$$
#
# Differentiating w.r.t $\beta_i$, we can get k+1 linear equations as shown below:
#
#
# ### The Condtional Distribution p(Y|X)
#
# <img src="images/lgm.png" style="width: 700px">
#
# The betas can easily be estimated by inverting the coefficient matrix and multiplying it to the right-hand side.
# +
beta_vec = np.array([.7, .3])
beta_0 = 2
sigma_c = 4
def genYX(x):
'''
Generates samples distributed according to Gaussian Normal Distributions.
Args:
x (row): Dataframe row
Returns:
(float): Sample distributed as Gaussian
'''
x = [x['X1'], x['X2']]
var_mean = np.dot(beta_vec.transpose(), x) + beta_0
Yx_sample = np.random.normal(var_mean, sigma_c, 1)
return Yx_sample[0]
X_df['(Y|X)'] = X_df.apply(genYX, axis=1)
X_df.head()
sns.distplot(X_df['(Y|X)'])
# -
# # Determine parameters $\beta_0, \beta_1, \beta_2$ using Maximum Likelihood Estimation (MLE)
#
# +
x_len = len(states)
def exp_value(xi, xj):
'''
Computes sum of product of two columns of a dataframe.
Args:
xi (column): Column of a dataframe
xj (columns): Column of a dataframe
Returns:
(float): Sum of product of two columns
'''
prod_xixj = xi*xj
return np.sum(prod_xixj)
sum_X = X_df.sum()
X = [sum_X['(Y|X)']]
print(sum_X)
print(X)
coef_matrix = pd.DataFrame(columns=sym_coefs)
# First we compute just the coefficients of beta_1 to beta_N.
# Later we compute beta_0 and append it.
for i in range(0, x_len):
X.append(exp_value(X_df['(Y|X)'], X_df[states[i]]))
for j in range(0, x_len):
coef_matrix.loc[i, sym_coefs[j]] = exp_value(X_df[states[i]], X_df[states[j]])
coef_matrix.insert(0, 'b0_coef', sum_X.values[0:x_len])
row_1 = np.append([len(X_df)], sum_X.values[0:x_len])
coef_matrix.loc[-1] = row_1
coef_matrix.index = coef_matrix.index + 1 # shifting index
coef_matrix.sort_index(inplace=True)
# Compute beta values
# https://cedar.buffalo.edu/~srihari/CSE574/Chap8/Ch8-PGM-GaussianBNs/8.5%20GaussianBNs.pdf
beta_coef_matrix = np.matrix(coef_matrix.values, dtype='float')
coef_inv = np.linalg.inv(beta_coef_matrix)
beta_est = np.array(np.matmul(coef_inv, np.transpose(X)))
beta_est = beta_est[0]
print(beta_est)
# -
# This retrieves the beta parameters. Feel free to use the notebook/images for commerical/non-commercial purpose as long as you have the logos in place.
#
# ## Estimating Variance
#
# $$\sigma^2 = cov[y;y] - \sum_i \sum_j \beta_i \beta_j Cov_D[X_i;X_j]$$
# +
# First we compute just the coefficients of beta_1 to beta_N.
# Later we compute beta_0 and append it.
sigma_est = 0
M = len(X_df)
for i in range(0, x_len):
for j in range(0, x_len):
sigma_est += beta_est[i+1]*beta_est[j+1]*(exp_value(X_df[states[i]], X_df[states[j]])/M - np.mean(X_df[states[i]])*np.mean(X_df[states[j]]))
# Estimate Variance
sigma_est = np.sqrt(exp_value(X_df['(Y|X)'], X_df['(Y|X)'])/M - np.mean(X_df['(Y|X)'])*np.mean(X_df['(Y|X)']) - sigma_est)
print(sigma_est)
# -
#
# For any questions feel free to contact hkashyap [at] icloud.com. Thanks to <NAME> for the diagrams(diagram.ai), <NAME> and <NAME> for proof reading the math.
|
Gaussian Bayesian Networks (GBNs).ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# ## Accuracy as a function taxon evenness & % atom 13C
#
# ### Variable parameters:
#
# * Partition communities into 'dominant' and 'rare' subsets
# * __dominant/rare cutoff: 1% relative abundance?__
# * Assess sensitivity & specificity for each subset
# * __Note:__
# * Much less time to perform if using data from past simulation run datasets
#
# ### Analysis:
#
# * Sup Figures:
# * Same as above simulation runs, but split into 'dominant' vs 'rare'
# # User variables
workDir = '/home/nick/notebook/SIPSim/dev/bac_genome1210/'
sourceDir = os.path.join(workDir, 'atomIncorp_evenness')
buildDir = os.path.join(workDir, 'atomIncorp_evenness_abund')
R_dir = '/home/nick/notebook/SIPSim/lib/R/'
# # Init
import glob
from os.path import abspath
import nestly
from IPython.display import Image, display
# %load_ext rpy2.ipython
# + language="R"
# library(ggplot2)
# library(dplyr)
# library(tidyr)
# library(gridExtra)
# -
if not os.path.isdir(buildDir):
os.makedirs(buildDir)
# # Nestly
# +
# building tree structure
nest = nestly.Nest()
## varying params
#-- full run --#
#nest.add('percIncorp', [0, 25, 50, 100])
#nest.add('percTaxa', [1, 5, 10, 25, 50])
#nest.add('rep', range(1,21))
#-- full run --#
nest.add('abund_dist_p', ['mean:10,sigma:1','mean:10,sigma:2','mean:10,sigma:3'])
nest.add('percIncorp', [0,5,10,15,20,30,40,50,75,100])
nest.add('rep', range(1,21))
## set params
nest.add('percTaxa', [10], create_dir=False)
nest.add('np', [6], create_dir=False)
nest.add('abs', ['1e9'], create_dir=False)
nest.add('subsample_mean', [30000], create_dir=False)
nest.add('subsample_scale', [5000], create_dir=False)
nest.add('BD_min', [1.71], create_dir=False)
nest.add('BD_max', [1.75], create_dir=False)
nest.add('padj', [0.1], create_dir=False)
nest.add('log2', [0.25], create_dir=False)
nest.add('topTaxaToPlot', [100], create_dir=False)
## input/output files
nest.add('buildDir', [buildDir], create_dir=False)
nest.add('sourceDir', [sourceDir], create_dir=False)
nest.add('frag_file', ['ampFrags_kde_dif'], create_dir=False)
nest.add('comm_file', ['comm.txt'], create_dir=False)
nest.add('R_dir', [R_dir], create_dir=False)
# building directory tree
nest.build(buildDir)
# -
bashFile = os.path.join(buildDir, 'SIPSimRun.sh')
# +
# %%writefile $bashFile
# #!/bin/bash
export PATH={R_dir}:$PATH
# copying DESeq files
# cp {sourceDir}/{abund_dist_p}/{percIncorp}/{rep}/{comm_file} .
# cp {sourceDir}/{abund_dist_p}/{percIncorp}/{rep}/OTU_n2_abs{abs}_sub-norm_DESeq2 .
# cp {sourceDir}/{abund_dist_p}/{percIncorp}/{rep}/{frag_file}_incorp_BD-shift.txt .
## DESeq2
DESeq2_rare-dominant.r \
OTU_n2_abs{abs}_sub-norm_DESeq2 \
{comm_file} \
-o OTU_n2_abs{abs}_sub-norm_DESeq2
## Confusion matrix
### dominant
DESeq2_confuseMtx.r \
{frag_file}_incorp_BD-shift.txt \
OTU_n2_abs{abs}_sub-norm_DESeq2_dom \
--padj {padj} \
-o DESeq2-cMtx_dom
### rare
DESeq2_confuseMtx.r \
{frag_file}_incorp_BD-shift.txt \
OTU_n2_abs{abs}_sub-norm_DESeq2_rare \
--padj {padj} \
-o DESeq2-cMtx_rare
# -
# !chmod 775 $bashFile
# !cd $workDir; \
# nestrun -j 20 --template-file $bashFile -d atomIncorp_evenness_abund --log-file log.txt
# ### Adding DESeq results table of 'NA' if file is not present
# +
p = os.path.join(workDir, 'atomIncorp_evenness_abund', 'mean*/*/*', 'DESeq2-cMtx_rare_byClass.csv')
rareFiles = glob.glob(p)
p = os.path.join(workDir, 'atomIncorp_evenness_abund', 'mean*/*/*', 'DESeq2-cMtx_dom_byClass.csv')
domFiles = glob.glob(p)
print len(rareFiles)
print len(domFiles)
# +
byClass_tmp = [
['Sensitivity','NA','NA',0,0],
['Specificity','NA','NA',0,0],
['Pos Pred Value','NA','NA',0,0],
['Neg Pred Value','NA','NA',0,0],
['Prevalence','NA','NA',0,0],
['Detection Rate','NA','NA',0,0],
['Detection Prevalence','NA','NA',0,0],
['Balanced Accuracy','NA','NA',0,0]
]
byClass_tmp = pd.DataFrame(byClass_tmp, columns=['','byClass','abund_dist_p','percIncorp','rep'])
# +
# finding files not present
rareFiles = set([x.rstrip('_rare_byClass.csv') for x in rareFiles])
domFiles = set([x.rstrip('_dom_byClass.csv') for x in domFiles])
# in rare but not in dominant list
missingFiles = list(rareFiles - domFiles)
cols = ['abund_dist_p','percIncorp','rep']
for f in missingFiles:
df_tmp = byClass_tmp.copy()
x = f.split('/')
df_tmp.loc[:,cols] = x[-4:-1]
outFile = '_'.join([f, 'dom_byClass.csv'])
df_tmp.to_csv(outFile)
# -
# ## aggregating confusion matrix data
# +
## byClass
### dominant
# !cd $workDir; \
# nestagg delim \
# -d atomIncorp_evenness_abund \
# -k abund_dist_p,percIncorp,rep \
# -o ./atomIncorp_evenness_abund/DESeq2-cMtx_dom_byClass.csv \
# DESeq2-cMtx_dom_byClass.csv
### rare
# !cd $workDir; \
# nestagg delim \
# -d atomIncorp_evenness_abund \
# -k abund_dist_p,percIncorp,rep \
# -o ./atomIncorp_evenness_abund/DESeq2-cMtx_rare_byClass.csv \
# DESeq2-cMtx_rare_byClass.csv
# -
# # Plotting accuracy
# ## Dominant taxa
# + magic_args="-i workDir" language="R"
# setwd(workDir)
#
# byClass = read.csv('./atomIncorp_evenness_abund/DESeq2-cMtx_dom_byClass.csv')
# byClass %>% head
# + magic_args="-w 700" language="R"
# to.keep = c('Sensitivity', 'Specificity', 'Balanced Accuracy')
#
# byClass.f = byClass %>%
# filter(X %in% to.keep) %>%
# mutate(percIncorp = as.character(percIncorp))
#
# byClass.f$percIncorp = factor(byClass.f$percIncorp, levels=sort(unique(as.numeric(byClass.f$percIncorp))))
#
# ggplot(byClass.f, aes(percIncorp, byClass, fill=abund_dist_p)) +
# geom_boxplot() +
# labs(y='Value', x='Atom percent 13C') +
# facet_grid(X ~ .) +
# theme(
# text = element_text(size=16)
# )
# -
# ## Rare taxa
# + magic_args="-i workDir" language="R"
# setwd(workDir)
#
# byClass = read.csv('./atomIncorp_evenness_abund/DESeq2-cMtx_rare_byClass.csv')
# byClass %>% head
# + magic_args="-w 700" language="R"
# to.keep = c('Sensitivity', 'Specificity', 'Balanced Accuracy')
#
# byClass.f = byClass %>%
# filter(X %in% to.keep) %>%
# mutate(percIncorp = as.character(percIncorp))
#
# byClass.f$percIncorp = factor(byClass.f$percIncorp, levels=sort(unique(as.numeric(byClass.f$percIncorp))))
#
# ggplot(byClass.f, aes(percIncorp, byClass, fill=abund_dist_p)) +
# geom_boxplot() +
# labs(y='Value', x='Atom percent 13C') +
# facet_grid(X ~ .) +
# theme(
# text = element_text(size=16)
# )
# -
# # Sample size of dominants and rares
#
# * Method:
# * Get number of taxa from dominant/rare-parsed DESeq2 object files
# + magic_args="-i workDir" language="R"
# setwd(workDir)
#
# dom.files = grep('DESeq2_dom$', list.files('./atomIncorp_evenness_abund/', recursive=TRUE), value=TRUE)
# rare.files = grep('DESeq2_rare$', list.files('./atomIncorp_evenness_abund/', recursive=TRUE), value=TRUE)
#
# read_taxa = function(file.name, dir='atomIncorp_evenness_abund'){
# f = paste(c(dir, file.name), collapse='/')
# deseq.res = readRDS(f)
# n.taxa = length(unique(rownames(deseq.res)))
# return(n.taxa)
# }
#
# dom.taxa = list()
# for(f in dom.files){
# dom.taxa[[f]] = read_taxa(f)
# }
#
# rare.taxa = list()
# for(f in rare.files){
# rare.taxa[[f]] = read_taxa(f)
# }
#
# + language="R"
# tbl.dom = as.data.frame(do.call(rbind, dom.taxa))
# tbl.dom$abund = 'Dominant'
# tbl.rare = as.data.frame(do.call(rbind, rare.taxa))
# tbl.rare$abund = 'Rare'
#
# tbl.dom.rare = rbind(tbl.dom, tbl.rare)
# colnames(tbl.dom.rare)[1] = 'N.taxa'
# tbl.dom.rare$file = rownames(tbl.dom.rare)
# tbl.dom.rare = tbl.dom.rare %>%
# separate(file, c('abund_dist_p','percIncorp','rep','file'), sep='/')
# tbl.dom.rare %>% head
# + magic_args="-w 700 -h 400" language="R"
#
# tbl.dom.rare$percIncorp = factor(tbl.dom.rare$percIncorp, levels=sort(unique(as.numeric(tbl.dom.rare$percIncorp))))
# #tbl.dom.rare$abund_dist_p = factor(tbl.dom.rare$abund_dist_p, levels=sort(unique(as.numeric(tbl.dom.rare$abund_dist_p))))
#
# ggplot(tbl.dom.rare, aes(percIncorp, N.taxa, fill=abund_dist_p)) +
# geom_boxplot(position='dodge') +
# labs(y='Number of taxa', x='Atom percent 13C') +
# facet_grid(abund ~ ., scales='free_y') +
# theme(
# text = element_text(size=16)
# )
# -
# # Plotting sensitivity ~ taxon_abundance
#
# * Method:
# * table join: DESeq res file & BD-shift
# * join on taxon
# * use cutoffs to select which taxa 'incorporated'
# * padj < 0.1
# * compare DESeq result to true result
# * TP,FP,TN,FN
#
# * Figure:
# * axes: taxon ~ abundance (pointrange: replicates)
# * ordered by abundance
# * color by classification (TP,FP,TN,FN)
# * facet: percIncorp ~ percTaxa
# + magic_args="-s \"$R_dir\"" language="bash"
#
# find atomIncorp_evenness_abund/ -name "*DESeq2" | \
# perl -pe 's/(.+\/).+/\1/' | \
# xargs -P 30 -I % bash -c \
# "$1DESeq2_addInfo.r %OTU_n2_abs1e9_sub-norm_DESeq2 %comm.txt %ampFrags_kde_dif_incorp_BD-shift.txt > %OTU_n2_abs1e9_sub-norm_DESeq2_info"
#
# + magic_args="-i workDir" language="R"
# setwd(workDir)
#
# deseq.files = grep('_DESeq2_info$', list.files('./atomIncorp_evenness_abund/', recursive=TRUE), value=TRUE)
#
#
# tbl.l = list()
# for(f in deseq.files){
# f = paste(c('./atomIncorp_evenness_abund/', f), collapse='/')
# tbl.l[[f]] = readRDS(f) %>% mutate(file = f)
# }
#
# tbl = do.call(rbind, tbl.l)
# rownames(tbl) = seq(1,nrow(tbl))
#
# tbl %>% head
# + language="R"
# tbl.e = tbl %>%
# mutate(file = gsub('.+//','', file)) %>%
# separate(file, c('abund_dist_p','percIncorp','rep','file'), sep='/') #%>%
# #unite(percIncorp_percTaxa, percIncorp, percTaxa, sep='_', remove=FALSE)
# tbl.e %>% head
# + language="R"
# BD.shift.cut = 0.05
# padj.cut = 0.1
#
#
# clsfy = function(guess,known){
# if(is.na(guess) | is.na(known)){
# return(NA)
# }
# if(guess == TRUE){
# if(guess == known){
# return('TP')
# } else {
# return('FP')
# }
# } else
# if(guess == FALSE){
# if(guess == known){
# return('TN')
# } else {
# return('FN')
# }
# } else {
# stop('Error: true or false needed')
# }
# }
#
# tbl.e = tbl.e %>%
# mutate(true_incorp = BD_shift > BD.shift.cut,
# DESeq_incorp = padj < padj.cut,
# cls = mapply(clsfy, DESeq_incorp, true_incorp))
#
# tbl.e %>% head
# + language="R"
# tbl.e$taxon = reorder(tbl.e$taxon, dense_rank(tbl.e$mean_rel_abund_perc))
# tbl.e$percIncorp = factor(tbl.e$percIncorp, levels=sort(unique(as.numeric(tbl.e$percIncorp))))
# #tbl.e$percTaxa = factor(tbl.e$percTaxa, levels=sort(unique(as.numeric(tbl.e$percTaxa))))
# + magic_args="-w 1000" language="R"
#
# ggplot(tbl.e, aes(taxon, mean_rel_abund_perc, color=cls)) +
# geom_point(alpha=0.5) +
# facet_grid(abund_dist_p ~ percIncorp) +
# theme(
# text = element_text(size=16),
# axis.text.x = element_blank()
# )
# + language="R"
#
# clsfy = function(guess,known){
# if(is.na(guess) | is.na(known)){
# return(NA)
# }
# if(guess == TRUE){
# if(guess == known){
# return(1)
# } else {
# return(NA)
# }
# } else
# if(guess == FALSE){
# if(guess == known){
# return(NA)
# } else {
# return(0)
# }
# } else {
# stop('Error: true or false needed')
# }
# }
#
# tbl.s.c = tbl.e %>%
# mutate(TP_FN = mapply(clsfy, DESeq_incorp, true_incorp)) %>%
# filter(! is.na(TP_FN)) %>%
# group_by(percIncorp, abund_dist_p) %>%
# summarize(cor.pearson = cor(mean_rel_abund_perc, TP_FN))
#
# tbl.s.c %>% head
# + magic_args="-w 700 -h 350" language="R"
# ggplot(tbl.s.c, aes(percIncorp, cor.pearson, fill=abund_dist_p)) +
# geom_bar(stat='identity', position='dodge', width=0.5) +
# labs(x='Atom percent 13C', y='r_pb', title='Point-biserial correlation coefficients') +
# theme(
# text = element_text(size=16)
# )
# -
# __Notes:__
#
#
# ***
# # SANDBOX
# + magic_args="-i workDir" language="R"
# setwd(workDir)
#
# x.deseq = './validation/OTU_n2_abs1e10_sub20000_DESeq2'
# deseq.res = readRDS(x.deseq)
# deseq.res = as.data.frame(deseq.res)
# deseq.res$taxon = rownames(deseq.res)
# deseq.res %>% head
# + magic_args="-i workDir" language="R"
# setwd(workDir)
#
# x.comm = 'validation/comm.txt'
# comm = read.delim(x.comm, sep='\t')
# comm.s = comm %>%
# group_by(taxon_name) %>%
# summarize(mean_rel_abund_perc = mean(rel_abund_perc)) %>%
# mutate(rank = dense_rank(mean_rel_abund_perc))
# comm.s %>% head
# + magic_args="-i workDir" language="R"
# setwd(workDir)
#
# x.BD = 'validation/ampFrags_kde_dif_incorp_BD-shift.txt'
# BD.shift = read.delim(x.BD, sep='\t')
# BD.shift = BD.shift %>%
# filter(lib2 == 2)
# BD.shift %>% head
# + language="R"
#
# tbl.j = inner_join(deseq.res, BD.shift, c('taxon' = 'taxon'))
# tbl.j = inner_join(tbl.j, comm.s, c('taxon' = 'taxon_name'))
# tbl.j %>% head
# + language="R"
# BD.shift.cut = 0.05
# padj.cut = 0.1
#
#
# clsfy = function(guess,known){
# if(guess == TRUE){
# if(guess == known){
# return('TP')
# } else {
# return('FP')
# }
# } else
# if(guess == FALSE){
# if(guess == known){
# return('TN')
# } else {
# return('FN')
# }
# } else {
# stop('Error: true or false needed')
# }
# }
#
# tbl.j = tbl.j %>%
# mutate(true_incorp = BD_shift > BD.shift.cut,
# DESeq_incorp = padj < padj.cut,
# cls = mapply(clsfy, DESeq_incorp, true_incorp))
#
# tbl.j %>% head
# + magic_args="-w 900" language="R"
#
# tbl.j$taxon = reorder(tbl.j$taxon, tbl.j$mean_rel_abund_perc)
#
# ggplot(tbl.j, aes(taxon, mean_rel_abund_perc, color=cls)) +
# geom_point()
# -
# ***
# + magic_args="-i workDir" language="R"
# setwd(workDir)
#
# deseq.res = readRDS('./validation/OTU_n2_abs1e10_sub20000_DESeq2')
# + language="R"
#
# comm = read.delim('./validation/comm.txt', sep='\t')
# comm.s = comm %>%
# group_by(taxon_name) %>%
# summarize(mean_rel_abund_perc = mean(rel_abund_perc))
# comm.s %>% head
# + language="R"
# tmp = deseq.res %>%
# as.data.frame()
# tmp$taxon_name = rownames(tmp)
#
# tmp = inner_join(tmp, comm.s, c('taxon_name' = 'taxon_name'))
# tmp = tmp %>%
# mutate(dom_rare = mean_rel_abund_perc > 1)
#
# tmp %>% head
# + language="R"
# tmp %>% filter(dom_rare == FALSE) %>% nrow %>% print
# tmp %>% filter(dom_rare == TRUE) %>% nrow %>% print
# -
|
ipynb/bac_genome/n1210/.ipynb_checkpoints/atomIncorp_evenness_abund-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# +
import requests
import MySQLdb
import datetime
import time
import pandas as pd
import xml.etree.ElementTree as ET
from ConfigParser import ConfigParser
#get xml from url and turn into tree
url = 'https://tfl.gov.uk/tfl/syndication/feeds/cycle-hire/livecyclehireupdates.xml'
r = requests.get(url)
r = r.text
root = ET.fromstring(r)
#get time from xml root
timestamp = float(root.attrib['lastUpdate'])
timestamp = time.strftime("%Y-%m-%d %H:%M:%S", time.gmtime(timestamp / 1000.0))
#parse data from tree
list = []
for child in root:
list.append([item.text for item in child])
#convert to dataframe and give columns names
g = pd.DataFrame(list)
g.columns = ['station_id', 'name', 'terminalName', 'lat', 'long', 'installed', 'locked', 'install_date', 'removal_date', 'temporary', 'nb_bikes', 'nb_empty_docks', 'nb_docks']
# -
output = g[['station_id', 'name', 'terminalName', 'lat', 'long', 'installed', 'locked', 'install_date', 'removal_date', 'temporary', 'nb_docks']]
output['install_date'] = pd.to_datetime(pd.to_numeric(output.install_date, errors='ignore') * 1000000)
output['removal_date'] = pd.to_datetime(pd.to_numeric(output.removal_date, errors='ignore') * 1000000)
output.to_csv('stations.csv', sep = ',', index = False)
output.head()
|
boris_stations.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# %load_ext autoreload
# %autoreload 2
# +
from __future__ import print_function
import numpy as np
from astropy.io import fits
# -
np.random.seed(42)
# +
generator = rotate_angle_generator()
def image_augementation_generator(zoom_factor):
def _rotate_angle_generator():
while True:
angle = np.random.randint(0, 360)
yield angle
def _zoom_generator():
while True:
zoom = np.round(zoom_factor * (np.random.random() - 0.5), 3) + 1.0
yield zoom
def _boolean_generator():
while True:
prob = np.random.random()
yield prob >= 0.5
rotate_angle_generator = _rotate_angle_generator()
zoom_generator = _zoom_generator()
horiztonal_flip_generator = _boolean_generator()
vertical_flip_generator = _boolean_generator()
while True:
rotate_angle = next(rotate_angle_generator)
zoom = next(zoom_generator)
horiztonal_flip = next(horiztonal_flip_generator)
vertical_flip = next(vertical_flip_generator)
yield rotate_angle, zoom, horiztonal_flip, vertical_flip
for idx, value in enumerate(image_augementation_generator(0.1)):
print(value)
if idx == 20:
break
# -
np.random.random()
# %ls -l
fits_file = fits.open('obj-1237658491746254860.fits.bz2')
# +
from astropy.wcs import WCS
WCS(fits_file[0].header)
# -
def plot_images(imgs, size):
num_rows = int(np.ceil(size/3.0))
figsize_y = 5 * num_rows
fig = plt.figure(figsize=(20,figsize_y))
for idx in range(0, size):
img = imgs[idx]
# make scale between 0 and 1.0 plotting
img_min = img.min()
img_max = img.max()
img = (img - img_min) / (img_max - img_min)
fig.add_subplot(num_rows, 3, idx + 1)
plt.imshow(img, cmap=plt.get_cmap('gray'), interpolation='bicubic')
plt.show()
# +
from PIL import Image
def flip_horizontal(data):
return np.flip(data, 2)
def flip_vertical(data):
return np.flip(data, 1)
def rotate(data, deg):
for idx in range(data.shape[0]):
img = Image.fromarray(data[idx])
img = img.rotate(deg, resample=Image.BICUBIC, expand=True)
if (idx == 0):
out = np.empty((3,) + img.size)
out[idx] = np.array(img)
return out
def resize(data, factor):
new_size = int(np.round(factor * data.shape[1]))
out = np.empty((3, new_size, new_size))
for idx in range(data.shape[0]):
img = Image.fromarray(data[idx])
img = img.resize((new_size, new_size), resample=Image.BICUBIC)
out[idx] = np.array(img)
return out
def crop(data, crop_size=42):
curr_size = data.shape[1]
out = np.empty((3, 42, 42))
top = int((curr_size - crop_size)/2)
bttm = top + crop_size
for idx in range(3):
out[idx] = data[idx, top:bttm, top:bttm]
return out
img_data = fits_file[0].data
outputs = np.empty((9, 3, 42, 42))
outputs[0] = sgd.scale_rgb(crop(img_data), sigma=1/6)
generator = image_augementation_generator(0.5)
for idx in range(1,9):
angle, zoom, flip_h, flip_v = next(generator)
print(f'Rotate: {angle}, Zoom: {zoom}, Flip Horizon.: {flip_h}, Flip Vertical: {flip_v}')
data = rotate(img_data, angle)
data = resize(data, zoom)
if flip_h:
data = flip_horizontal(data)
if flip_v:
data = flip_vertical(data)
data = crop(data)
outputs[idx] = sgd.scale_rgb(data, sigma=1/6)
plot_images(np.moveaxis(outputs, 1, -1), 9)
# +
import sdss_gz_data as sgd
import matplotlib.pyplot as plt
#Image.fromarray(np.moveaxis(sgd.scale_rgb(img_data), 0, -1))
plt.imshow(np.moveaxis(sgd.scale_rgb(crop(img_data)), 0, -1), interpolation='bicubic')
# -
plt.imshow(np.moveaxis(sgd.scale_rgb(crop(rotated_image)), 0, -1), interpolation='bicubic')
plt.imshow(np.moveaxis(sgd.scale_rgb(crop(resized)), 0, -1), interpolation='bicubic')
from astropy.io import fits
fits_file = fits.open('data/obj-1237650369407221944.fits.bz2')
data = fits_file[0].data
data.shape
nans = np.isnan(data)
data[nans] = 0
np.min(data)
data[nans] = np.min(data)
data
|
notebooks/Simple Data Generator.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] colab_type="text" id="Tce3stUlHN0L"
# ##### Copyright 2019 The TensorFlow Authors.
#
# + cellView="form" colab={} colab_type="code" id="tuOe1ymfHZPu"
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
# + [markdown] colab_type="text" id="MfBg1C5NB3X0"
# # Distributed training in TensorFlow
# + [markdown] colab_type="text" id="r6P32iYYV27b"
# <table class="tfo-notebook-buttons" align="left">
# <td>
# <a target="_blank" href="https://colab.research.google.com/github/tensorflow/docs/blob/master/site/en/r1/tutorials/distribute/keras.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
# </td>
# <td>
# <a target="_blank" href="https://github.com/tensorflow/docs/blob/master/site/en/r1/tutorials/distribute/keras.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on GitHub</a>
# </td>
# </table>
# + [markdown] colab_type="text" id="xHxb-dlhMIzW"
# ## Overview
#
# The `tf.distribute.Strategy` API provides an abstraction for distributing your training
# across multiple processing units. The goal is to allow users to enable distributed training using existing models and training code, with minimal changes.
#
# This tutorial uses the `tf.distribute.MirroredStrategy`, which
# does in-graph replication with synchronous training on many GPUs on one machine.
# Essentially, it copies all of the model's variables to each processor.
# Then, it uses [all-reduce](http://mpitutorial.com/tutorials/mpi-reduce-and-allreduce/) to combine the gradients from all processors and applies the combined value to all copies of the model.
#
# `MirroredStategy` is one of several distribution strategy available in TensorFlow core. You can read about more strategies at [distribution strategy guide](../../guide/distribute_strategy.ipynb).
#
# + [markdown] colab_type="text" id="MUXex9ctTuDB"
# ### Keras API
#
# This example uses the `tf.keras` API to build the model and training loop. For custom training loops, see [this tutorial](training_loops.ipynb).
# + [markdown] colab_type="text" id="Dney9v7BsJij"
# ## Import Dependencies
# + colab={} colab_type="code" id="r8S3ublR7Ay8"
from __future__ import absolute_import, division, print_function, unicode_literals
# + colab={} colab_type="code" id="74rHkS_DB3X2"
# Import TensorFlow
try:
# # %tensorflow_version only exists in Colab.
# %tensorflow_version 2.x
except Exception:
pass
import tensorflow.compat.v1 as tf
import tensorflow_datasets as tfds
import os
# + [markdown] colab_type="text" id="hXhefksNKk2I"
# ## Download the dataset
# + [markdown] colab_type="text" id="OtnnUwvmB3X5"
# Download the MNIST dataset and load it from [TensorFlow Datasets](https://www.tensorflow.org/datasets). This returns a dataset in `tf.data` format.
# + [markdown] colab_type="text" id="lHAPqG8MtS8M"
# Setting `with_info` to `True` includes the metadata for the entire dataset, which is being saved here to `ds_info`.
# Among other things, this metadata object includes the number of train and test examples.
#
# + colab={} colab_type="code" id="iXMJ3G9NB3X6"
datasets, ds_info = tfds.load(name='mnist', with_info=True, as_supervised=True)
mnist_train, mnist_test = datasets['train'], datasets['test']
# + [markdown] colab_type="text" id="GrjVhv-eKuHD"
# ## Define Distribution Strategy
# + [markdown] colab_type="text" id="TlH8vx6BB3X9"
# Create a `MirroredStrategy` object. This will handle distribution, and provides a context manager (`tf.distribute.MirroredStrategy.scope`) to build your model inside.
# + colab={} colab_type="code" id="4j0tdf4YB3X9"
strategy = tf.distribute.MirroredStrategy()
# + colab={} colab_type="code" id="cY3KA_h2iVfN"
print ('Number of devices: {}'.format(strategy.num_replicas_in_sync))
# + [markdown] colab_type="text" id="lNbPv0yAleW8"
# ## Setup Input pipeline
# + [markdown] colab_type="text" id="psozqcuptXhK"
# If a model is trained on multiple GPUs, the batch size should be increased accordingly so as to make effective use of the extra computing power. Moreover, the learning rate should be tuned accordingly.
# + colab={} colab_type="code" id="p1xWxKcnhar9"
# You can also do ds_info.splits.total_num_examples to get the total
# number of examples in the dataset.
num_train_examples = ds_info.splits['train'].num_examples
num_test_examples = ds_info.splits['test'].num_examples
BUFFER_SIZE = 10000
BATCH_SIZE_PER_REPLICA = 64
BATCH_SIZE = BATCH_SIZE_PER_REPLICA * strategy.num_replicas_in_sync
# + [markdown] colab_type="text" id="0Wm5rsL2KoDF"
# Pixel values, which are 0-255, [have to be normalized to the 0-1 range](https://en.wikipedia.org/wiki/Feature_scaling). Define this scale in a function.
# + colab={} colab_type="code" id="Eo9a46ZeJCkm"
def scale(image, label):
image = tf.cast(image, tf.float32)
image /= 255
return image, label
# + [markdown] colab_type="text" id="WZCa5RLc5A91"
# Apply this function to the training and test data, shuffle the training data, and [batch it for training](https://www.tensorflow.org/api_docs/python/tf/data/Dataset#batch).
#
# + colab={} colab_type="code" id="gRZu2maChwdT"
train_dataset = mnist_train.map(scale).shuffle(BUFFER_SIZE).batch(BATCH_SIZE)
eval_dataset = mnist_test.map(scale).batch(BATCH_SIZE)
# + [markdown] colab_type="text" id="4xsComp8Kz5H"
# ## Create the model
# + [markdown] colab_type="text" id="1BnQYQTpB3YA"
# Create and compile the Keras model in the context of `strategy.scope`.
# + colab={} colab_type="code" id="IexhL_vIB3YA"
with strategy.scope():
model = tf.keras.Sequential([
tf.keras.layers.Conv2D(32, 3, activation='relu', input_shape=(28, 28, 1)),
tf.keras.layers.MaxPooling2D(),
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(64, activation='relu'),
tf.keras.layers.Dense(10, activation='softmax')
])
model.compile(loss='sparse_categorical_crossentropy',
optimizer=tf.keras.optimizers.Adam(),
metrics=['accuracy'])
# + [markdown] colab_type="text" id="8i6OU5W9Vy2u"
# ## Define the callbacks.
#
# + [markdown] colab_type="text" id="YOXO5nvvK3US"
# The callbacks used here are:
#
# * *Tensorboard*: This callback writes a log for Tensorboard which allows you to visualize the graphs.
# * *Model Checkpoint*: This callback saves the model after every epoch.
# * *Learning Rate Scheduler*: Using this callback, you can schedule the learning rate to change after every epoch/batch.
#
# For illustrative purposes, add a print callback to display the *learning rate* in the notebook.
# + colab={} colab_type="code" id="A9bwLCcXzSgy"
# Define the checkpoint directory to store the checkpoints
checkpoint_dir = './training_checkpoints'
# Name of the checkpoint files
checkpoint_prefix = os.path.join(checkpoint_dir, "ckpt_{epoch}")
# + colab={} colab_type="code" id="wpU-BEdzJDbK"
# Function for decaying the learning rate.
# You can define any decay function you need.
def decay(epoch):
if epoch < 3:
return 1e-3
elif epoch >= 3 and epoch < 7:
return 1e-4
else:
return 1e-5
# + colab={} colab_type="code" id="jKhiMgXtKq2w"
# Callback for printing the LR at the end of each epoch.
class PrintLR(tf.keras.callbacks.Callback):
def on_epoch_end(self, epoch, logs=None):
print ('\nLearning rate for epoch {} is {}'.format(
epoch + 1, tf.keras.backend.get_value(model.optimizer.lr)))
# + colab={} colab_type="code" id="YVqAbR6YyNQh"
callbacks = [
tf.keras.callbacks.TensorBoard(log_dir='./logs'),
tf.keras.callbacks.ModelCheckpoint(filepath=checkpoint_prefix,
save_weights_only=True),
tf.keras.callbacks.LearningRateScheduler(decay),
PrintLR()
]
# + [markdown] colab_type="text" id="70HXgDQmK46q"
# ## Train and evaluate
# + [markdown] colab_type="text" id="6EophnOAB3YD"
# Now, train the model in the usual way, calling `fit` on the model and passing in the dataset created at the beginning of the tutorial. This step is the same whether you are distributing the training or not.
#
# + colab={} colab_type="code" id="7MVw_6CqB3YD"
model.fit(train_dataset, epochs=10, callbacks=callbacks)
# + [markdown] colab_type="text" id="NUcWAUUupIvG"
# As you can see below, the checkpoints are getting saved.
# + colab={} colab_type="code" id="JQ4zeSTxKEhB"
# check the checkpoint directory
# !ls {checkpoint_dir}
# + [markdown] colab_type="text" id="qor53h7FpMke"
# To see how the model perform, load the latest checkpoint and call `evaluate` on the test data.
#
# Call `evaluate` as before using appropriate datasets.
# + colab={} colab_type="code" id="JtEwxiTgpQoP"
model.load_weights(tf.train.latest_checkpoint(checkpoint_dir))
eval_loss, eval_acc = model.evaluate(eval_dataset)
print ('Eval loss: {}, Eval Accuracy: {}'.format(eval_loss, eval_acc))
# + [markdown] colab_type="text" id="IIeF2RWfYu4N"
# To see the output, you can download and view the TensorBoard logs at the terminal.
#
# ```
# $ tensorboard --logdir=path/to/log-directory
# ```
# + colab={} colab_type="code" id="LnyscOkvKKBR"
# !ls -sh ./logs
# + [markdown] colab_type="text" id="kBLlogrDvMgg"
# ## Export to SavedModel
# + [markdown] colab_type="text" id="Xa87y_A0vRma"
# If you want to export the graph and the variables, SavedModel is the best way of doing this. The model can be loaded back with or without the scope. Moreover, SavedModel is platform agnostic.
# + colab={} colab_type="code" id="h8Q4MKOLwG7K"
path = 'saved_model/'
# + colab={} colab_type="code" id="4HvcDmVsvQoa"
tf.keras.experimental.export_saved_model(model, path)
# + [markdown] colab_type="text" id="vKJT4w5JwVPI"
# Load the model without `strategy.scope`.
# + colab={} colab_type="code" id="T_gT0RbRvQ3o"
unreplicated_model = tf.keras.experimental.load_from_saved_model(path)
unreplicated_model.compile(
loss='sparse_categorical_crossentropy',
optimizer=tf.keras.optimizers.Adam(),
metrics=['accuracy'])
eval_loss, eval_acc = unreplicated_model.evaluate(eval_dataset)
print ('Eval loss: {}, Eval Accuracy: {}'.format(eval_loss, eval_acc))
# + [markdown] colab_type="text" id="8uNqWRdDMl5S"
# ## What's next?
#
# Read the [distribution strategy guide](../../guide/distribute_strategy_tf1.ipynb).
#
# Note: `tf.distribute.Strategy` is actively under development and we will be adding more examples and tutorials in the near future. Please give it a try. We welcome your feedback via [issues on GitHub](https://github.com/tensorflow/tensorflow/issues/new).
|
site/en/r1/tutorials/distribute/keras.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Time series exploration
#
# Exploring the extent to which time series data is available and plotting based on time stamps
#
# ---
# Import all relevant modules:
# +
import os
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
pd.options.mode.chained_assignment = None
plt.style.use('ggplot')
# +
data_dir = "../Data"
country_file = 'case_time_series.csv'
states_file = 'states.csv'
cities_file = 'city_counts_post11.csv'
districts_file = 'districts.csv'
country_path = os.path.join(data_dir, country_file)
districts_path = os.path.join(data_dir, districts_file)
states_path = os.path.join(data_dir, states_file)
cities_path = os.path.join(data_dir, cities_file)
#Read all as data frames
df_country = pd.read_csv(country_path)
df_districts = pd.read_csv(districts_path)
df_states = pd.read_csv(states_path)
df_cities = pd.read_csv(cities_path)
# -
# ## Task 1
#
# List out all cities that we have to consider
#casefold helps with case-insensitive searching
cities = [ i.casefold() for i in df_cities['City']]
print(cities)
# ## Task 2
# See if these cities fall in the same district categories
# +
#Find unique districts in districts.csv file
unique_districts = []
for i in df_districts['District']:
if not i in unique_districts:
unique_districts.append(i)
#See how many of these districts match our cities
cities_to_plot = []
for i in unique_districts:
if i.casefold() in cities:
#Do not use casefold
#when appending as we
#will use this element
#to search in our dataframe
cities_to_plot.append(i)
print(cities_to_plot)
# -
#Default arguments added for testing
def plot_city(df_districts, start_date = '2021-4-10', end_date = '2021-5-30', city_name='Delhi'):
df_filtered = df_districts[df_districts['District'] == city_name]
df_filtered['Date'] = pd.to_datetime(df_filtered['Date'], format='%Y-%m-%d')
mask = (df_filtered['Date'] >= start_date) & (df_filtered['Date'] <= end_date)
df_filtered = df_filtered.loc[mask]
change_in_cases = [0]
count = 0
for i in df_filtered['Confirmed']:
if count == 0:
prev = int(i)
else:
change_in_cases.append(int(i) - prev)
prev = int(i)
count += 1
#matplotlib plotting:
#first convert to numpy
cases_np = np.array(change_in_cases)
plt.scatter(df_filtered['Date'],cases_np)
plt.show()
# +
#Edit dates and city here:
#dates in yyyy-
start_date = '2021-4-10'
end_date = '2021-5-30'
#change city. Ristrict to ones posted above
city_name='Delhi'
plot_city(df_districts, start_date, end_date, city_name)
|
notebooks/Time series.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [default]
# language: python
# name: python3
# ---
import keras
keras.__version__
# # 5.1 - Introduction to convnets
#
# This notebook contains the code sample found in Chapter 5, Section 1 of [Deep Learning with Python](https://www.manning.com/books/deep-learning-with-python?a_aid=keras&a_bid=76564dff). Note that the original text features far more content, in particular further explanations and figures: in this notebook, you will only find source code and related comments.
#
# ----
#
# First, let's take a practical look at a very simple convnet example. We will use our convnet to classify MNIST digits, a task that you've already been
# through in Chapter 2, using a densely-connected network (our test accuracy then was 97.8%). Even though our convnet will be very basic, its
# accuracy will still blow out of the water that of the densely-connected model from Chapter 2.
#
# The 6 lines of code below show you what a basic convnet looks like. It's a stack of `Conv2D` and `MaxPooling2D` layers. We'll see in a
# minute what they do concretely.
# Importantly, a convnet takes as input tensors of shape `(image_height, image_width, image_channels)` (not including the batch dimension).
# In our case, we will configure our convnet to process inputs of size `(28, 28, 1)`, which is the format of MNIST images. We do this via
# passing the argument `input_shape=(28, 28, 1)` to our first layer.
# +
from keras import layers
from keras import models
model = models.Sequential()
model.add(layers.Conv2D(32, (3, 3), activation='relu', input_shape=(28, 28, 1)))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(64, (3, 3), activation='relu'))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(64, (3, 3), activation='relu'))
# -
# Let's display the architecture of our convnet so far:
model.summary()
# You can see above that the output of every `Conv2D` and `MaxPooling2D` layer is a 3D tensor of shape `(height, width, channels)`. The width
# and height dimensions tend to shrink as we go deeper in the network. The number of channels is controlled by the first argument passed to
# the `Conv2D` layers (e.g. 32 or 64).
#
# The next step would be to feed our last output tensor (of shape `(3, 3, 64)`) into a densely-connected classifier network like those you are
# already familiar with: a stack of `Dense` layers. These classifiers process vectors, which are 1D, whereas our current output is a 3D tensor.
# So first, we will have to flatten our 3D outputs to 1D, and then add a few `Dense` layers on top:
model.add(layers.Flatten())
model.add(layers.Dense(64, activation='relu'))
model.add(layers.Dense(10, activation='softmax'))
# We are going to do 10-way classification, so we use a final layer with 10 outputs and a softmax activation. Now here's what our network
# looks like:
model.summary()
# As you can see, our `(3, 3, 64)` outputs were flattened into vectors of shape `(576,)`, before going through two `Dense` layers.
#
# Now, let's train our convnet on the MNIST digits. We will reuse a lot of the code we have already covered in the MNIST example from Chapter
# 2.
# +
from keras.datasets import mnist
from keras.utils import to_categorical
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()
train_images = train_images.reshape((60000, 28, 28, 1))
train_images = train_images.astype('float32') / 255
test_images = test_images.reshape((10000, 28, 28, 1))
test_images = test_images.astype('float32') / 255
train_labels = to_categorical(train_labels)
test_labels = to_categorical(test_labels)
# -
model.compile(optimizer='rmsprop',
loss='categorical_crossentropy',
metrics=['accuracy'])
model.fit(train_images, train_labels, epochs=5, batch_size=64)
# Let's evaluate the model on the test data:
test_loss, test_acc = model.evaluate(test_images, test_labels)
test_acc
# While our densely-connected network from Chapter 2 had a test accuracy of 97.8%, our basic convnet has a test accuracy of 99.3%: we
# decreased our error rate by 68% (relative). Not bad!
|
Keras/deep-learning-Keras/.ipynb_checkpoints/5.1-introduction-to-convnets-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3.6 - AzureML
# language: python
# name: python3-azureml
# ---
# ## Creating an AzureML Environment for Stan
# First, we'll create a Docker container by way of an AzureML Environment.
#
# For this, I've written a [Dockerfile](../Dockerfile) that downloads and installs Stan. This is based on the IntelMPI image published by the Azure ML team. (You can find the Dockerfile for that image [here](https://github.com/Azure/AzureML-Containers/blob/master/base/cpu/intelmpi2018.3-ubuntu16.04/Dockerfile).)
# +
from azureml.core import Workspace, Environment
ws = Workspace.from_config()
# -
# For this example, we've built the Dockerfile and pushed it to the Azure Container Registry that was created with AML. It is possible to pass the Dockerfile text as a parameter to the Environment, but as of January 27th, 2020 this is not supported in ML Pipelines.
#
#
# ```python
# # Read our Dockerfile into a Python string object.
# with open('../Dockerfile', 'r') as file_obj:
# docker_file = file_obj.read()
# ```
#
# ```python
# env.docker.base_image = None
# env.docker.base_dockerfile = docker_file
# ```
# +
# Instatiate an Environment object from AML. We've named it 'stan-intelmpi'
env = Environment('stan-intelmpi')
# Next, set the Docker settings for the environment - first setting Docker to enabled, then setting the
# base_dockerfile property to the Docker string we published before.
# Note - we set the base_image property to None - as base_image and base_dockerfile are mutually exclusive
env.docker.enabled = True
env.docker.base_image = "amldemocr.azurecr.io/cmdstan:intelmpi2018.3-ubuntu16.04-stan2.21"
env.docker.base_dockerfile = None
# Next, set the Python settings. This will set the pip or conda packages that need to be installed in the container.
env.python.conda_dependencies.set_python_version('3.7.6')
env.python.conda_dependencies.add_pip_package('azureml-defaults')
env.python.conda_dependencies.add_pip_package('cmdstanpy==0.8.0')
env.python.conda_dependencies.add_pip_package('mpi4py==3.0.3')
env.python.conda_dependencies.add_pip_package('azureml-dataprep[fuse,pandas]')
# Finally, register the environment.
env = env.register(ws)
# +
# This is NOT required, but you can prebuild the Docker container by running the env.build step.
# If you choose not to do this, the container will be build the first time you submit the model for building
env_build = env.build(ws)
env_build.wait_for_completion(show_output=True)
# -
|
notebooks/00 - Environment.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + id="bJ1ROiQxJ-vY"
# !pip install git+https://github.com/tensorflow/examples.git
# + id="lhSsUx9Nyb3t"
import tensorflow as tf
# + id="YfIk2es3hJEd"
import tensorflow_datasets as tfds
from tensorflow_examples.models.pix2pix import pix2pix
import os
import time
import matplotlib.pyplot as plt
from IPython.display import clear_output
AUTOTUNE = tf.data.AUTOTUNE
# + id="iuGVPOo7Cce0"
dataset, metadata = tfds.load('cycle_gan/horse2zebra',
with_info=True, as_supervised=True)
train_horses, train_zebras = dataset['trainA'], dataset['trainB']
test_horses, test_zebras = dataset['testA'], dataset['testB']
# + id="2CbTEt448b4R"
BUFFER_SIZE = 1000
BATCH_SIZE = 1
IMG_WIDTH = 256
IMG_HEIGHT = 256
# + id="Yn3IwqhiIszt"
def random_crop(image):
cropped_image = tf.image.random_crop(
image, size=[IMG_HEIGHT, IMG_WIDTH, 3])
return cropped_image
# + id="muhR2cgbLKWW"
# normalizing the images to [-1, 1]
def normalize(image):
image = tf.cast(image, tf.float32)
image = (image / 127.5) - 1
return image
# + id="fVQOjcPVLrUc"
def random_jitter(image):
# resizing to 286 x 286 x 3
image = tf.image.resize(image, [286, 286],
method=tf.image.ResizeMethod.NEAREST_NEIGHBOR)
# randomly cropping to 256 x 256 x 3
image = random_crop(image)
# random mirroring
image = tf.image.random_flip_left_right(image)
return image
# + id="tyaP4hLJ8b4W"
def preprocess_image_train(image, label):
image = random_jitter(image)
image = normalize(image)
return image
# + id="VB3Z6D_zKSru"
def preprocess_image_test(image, label):
image = normalize(image)
return image
# + id="RsajGXxd5JkZ"
train_horses = train_horses.cache().map(
preprocess_image_train, num_parallel_calls=AUTOTUNE).shuffle(
BUFFER_SIZE).batch(BATCH_SIZE)
train_zebras = train_zebras.cache().map(
preprocess_image_train, num_parallel_calls=AUTOTUNE).shuffle(
BUFFER_SIZE).batch(BATCH_SIZE)
test_horses = test_horses.map(
preprocess_image_test, num_parallel_calls=AUTOTUNE).cache().shuffle(
BUFFER_SIZE).batch(BATCH_SIZE)
test_zebras = test_zebras.map(
preprocess_image_test, num_parallel_calls=AUTOTUNE).cache().shuffle(
BUFFER_SIZE).batch(BATCH_SIZE)
# + id="e3MhJ3zVLPan"
sample_horse = next(iter(train_horses))
sample_zebra = next(iter(train_zebras))
# + id="4pOYjMk_KfIB"
plt.subplot(121)
plt.title('Horse')
plt.imshow(sample_horse[0] * 0.5 + 0.5)
plt.subplot(122)
plt.title('Horse with random jitter')
plt.imshow(random_jitter(sample_horse[0]) * 0.5 + 0.5)
# + id="0KJyB9ENLb2y"
plt.subplot(121)
plt.title('Zebra')
plt.imshow(sample_zebra[0] * 0.5 + 0.5)
plt.subplot(122)
plt.title('Zebra with random jitter')
plt.imshow(random_jitter(sample_zebra[0]) * 0.5 + 0.5)
# + id="8ju9Wyw87MRW"
OUTPUT_CHANNELS = 3
generator_g = pix2pix.unet_generator(OUTPUT_CHANNELS, norm_type='instancenorm')
generator_f = pix2pix.unet_generator(OUTPUT_CHANNELS, norm_type='instancenorm')
discriminator_x = pix2pix.discriminator(norm_type='instancenorm', target=False)
discriminator_y = pix2pix.discriminator(norm_type='instancenorm', target=False)
# + id="wDaGZ3WpZUyw"
to_zebra = generator_g(sample_horse)
to_horse = generator_f(sample_zebra)
plt.figure(figsize=(8, 8))
contrast = 8
imgs = [sample_horse, to_zebra, sample_zebra, to_horse]
title = ['Horse', 'To Zebra', 'Zebra', 'To Horse']
for i in range(len(imgs)):
plt.subplot(2, 2, i+1)
plt.title(title[i])
if i % 2 == 0:
plt.imshow(imgs[i][0] * 0.5 + 0.5)
else:
plt.imshow(imgs[i][0] * 0.5 * contrast + 0.5)
plt.show()
# + id="O5MhJmxyZiy9"
plt.figure(figsize=(8, 8))
plt.subplot(121)
plt.title('Is a real zebra?')
plt.imshow(discriminator_y(sample_zebra)[0, ..., -1], cmap='RdBu_r')
plt.subplot(122)
plt.title('Is a real horse?')
plt.imshow(discriminator_x(sample_horse)[0, ..., -1], cmap='RdBu_r')
plt.show()
# + [markdown] id="0FMYgY_mPfTi"
# ## Loss functions
# + id="cyhxTuvJyIHV"
LAMBDA = 10
# + id="Q1Xbz5OaLj5C"
loss_obj = tf.keras.losses.BinaryCrossentropy(from_logits=True)
# + id="wkMNfBWlT-PV"
def discriminator_loss(real, generated):
real_loss = loss_obj(tf.ones_like(real), real)
generated_loss = loss_obj(tf.zeros_like(generated), generated)
total_disc_loss = real_loss + generated_loss
return total_disc_loss * 0.5
# + id="90BIcCKcDMxz"
def generator_loss(generated):
return loss_obj(tf.ones_like(generated), generated)
# + id="NMpVGj_sW6Vo"
def calc_cycle_loss(real_image, cycled_image):
loss1 = tf.reduce_mean(tf.abs(real_image - cycled_image))
return LAMBDA * loss1
# + id="05ywEH680Aud"
def identity_loss(real_image, same_image):
loss = tf.reduce_mean(tf.abs(real_image - same_image))
return LAMBDA * 0.5 * loss
# + [markdown] id="G-vjRM7IffTT"
# Initialize the optimizers for all the generators and the discriminators.
# + id="iWCn_PVdEJZ7"
generator_g_optimizer = tf.keras.optimizers.Adam(2e-4, beta_1=0.5)
generator_f_optimizer = tf.keras.optimizers.Adam(2e-4, beta_1=0.5)
discriminator_x_optimizer = tf.keras.optimizers.Adam(2e-4, beta_1=0.5)
discriminator_y_optimizer = tf.keras.optimizers.Adam(2e-4, beta_1=0.5)
# + [markdown] id="aKUZnDiqQrAh"
# ## Checkpoints
# + id="WJnftd5sQsv6"
checkpoint_path = "./checkpoints/train"
ckpt = tf.train.Checkpoint(generator_g=generator_g,
generator_f=generator_f,
discriminator_x=discriminator_x,
discriminator_y=discriminator_y,
generator_g_optimizer=generator_g_optimizer,
generator_f_optimizer=generator_f_optimizer,
discriminator_x_optimizer=discriminator_x_optimizer,
discriminator_y_optimizer=discriminator_y_optimizer)
ckpt_manager = tf.train.CheckpointManager(ckpt, checkpoint_path, max_to_keep=5)
# if a checkpoint exists, restore the latest checkpoint.
if ckpt_manager.latest_checkpoint:
ckpt.restore(ckpt_manager.latest_checkpoint)
print ('Latest checkpoint restored!!')
# + [markdown] id="Rw1fkAczTQYh"
# ## Training
#
# Note: This example model is trained for fewer epochs (40) than the paper (200) to keep training time reasonable for this tutorial. Predictions may be less accurate.
# + id="NS2GWywBbAWo"
EPOCHS = 40
# + id="RmdVsmvhPxyy"
def generate_images(model, test_input):
prediction = model(test_input)
plt.figure(figsize=(12, 12))
display_list = [test_input[0], prediction[0]]
title = ['Input Image', 'Predicted Image']
for i in range(2):
plt.subplot(1, 2, i+1)
plt.title(title[i])
# getting the pixel values between [0, 1] to plot it.
plt.imshow(display_list[i] * 0.5 + 0.5)
plt.axis('off')
plt.show()
# + id="KBKUV2sKXDbY"
@tf.function
def train_step(real_x, real_y):
# persistent is set to True because the tape is used more than
# once to calculate the gradients.
with tf.GradientTape(persistent=True) as tape:
# Generator G translates X -> Y
# Generator F translates Y -> X.
fake_y = generator_g(real_x, training=True)
cycled_x = generator_f(fake_y, training=True)
fake_x = generator_f(real_y, training=True)
cycled_y = generator_g(fake_x, training=True)
# same_x and same_y are used for identity loss.
same_x = generator_f(real_x, training=True)
same_y = generator_g(real_y, training=True)
disc_real_x = discriminator_x(real_x, training=True)
disc_real_y = discriminator_y(real_y, training=True)
disc_fake_x = discriminator_x(fake_x, training=True)
disc_fake_y = discriminator_y(fake_y, training=True)
# calculate the loss
gen_g_loss = generator_loss(disc_fake_y)
gen_f_loss = generator_loss(disc_fake_x)
total_cycle_loss = calc_cycle_loss(real_x, cycled_x) + calc_cycle_loss(real_y, cycled_y)
# Total generator loss = adversarial loss + cycle loss
total_gen_g_loss = gen_g_loss + total_cycle_loss + identity_loss(real_y, same_y)
total_gen_f_loss = gen_f_loss + total_cycle_loss + identity_loss(real_x, same_x)
disc_x_loss = discriminator_loss(disc_real_x, disc_fake_x)
disc_y_loss = discriminator_loss(disc_real_y, disc_fake_y)
# Calculate the gradients for generator and discriminator
generator_g_gradients = tape.gradient(total_gen_g_loss,
generator_g.trainable_variables)
generator_f_gradients = tape.gradient(total_gen_f_loss,
generator_f.trainable_variables)
discriminator_x_gradients = tape.gradient(disc_x_loss,
discriminator_x.trainable_variables)
discriminator_y_gradients = tape.gradient(disc_y_loss,
discriminator_y.trainable_variables)
# Apply the gradients to the optimizer
generator_g_optimizer.apply_gradients(zip(generator_g_gradients,
generator_g.trainable_variables))
generator_f_optimizer.apply_gradients(zip(generator_f_gradients,
generator_f.trainable_variables))
discriminator_x_optimizer.apply_gradients(zip(discriminator_x_gradients,
discriminator_x.trainable_variables))
discriminator_y_optimizer.apply_gradients(zip(discriminator_y_gradients,
discriminator_y.trainable_variables))
# + id="2M7LmLtGEMQJ"
for epoch in range(EPOCHS):
start = time.time()
n = 0
for image_x, image_y in tf.data.Dataset.zip((train_horses, train_zebras)):
train_step(image_x, image_y)
if n % 10 == 0:
print ('.', end='')
n += 1
clear_output(wait=True)
# Using a consistent image (sample_horse) so that the progress of the model
# is clearly visible.
generate_images(generator_g, sample_horse)
if (epoch + 1) % 5 == 0:
ckpt_save_path = ckpt_manager.save()
print ('Saving checkpoint for epoch {} at {}'.format(epoch+1,
ckpt_save_path))
print ('Time taken for epoch {} is {} sec\n'.format(epoch + 1,
time.time()-start))
# + [markdown] id="1RGysMU_BZhx"
# ## Generate using test dataset
# + id="KUgSnmy2nqSP"
# Run the trained model on the test dataset
for inp in test_horses.take(5):
generate_images(generator_g, inp)
|
SIP_Project/cyclegan.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # FishboneMoncriefID: An Einstein Toolkit Initial Data Thorn for Fishbone-Moncrief initial data
#
# ## Author: <NAME>
# ### Formatting improvements courtesy <NAME>
#
# <font color ='red'> **While this compiles, it has not been validated against the old version of the code.**</font>
#
# ### NRPy+ Source Code for this module: [FishboneMoncriefID/FishboneMoncriefID.py](../edit/FishboneMoncriefID/FishboneMoncriefID.py) [\[tutorial\]](Tutorial-FishboneMoncriefID.ipynb) Constructs SymPy expressions for plane-wave initial data
#
# ## Introduction:
# In this part of the tutorial, we will construct an Einstein Toolkit (ETK) thorn (module) that will set up Fishbone-Moncrief initial data. In the [Tutorial-FishboneMoncriefID](Tutorial-FishboneMoncriefID.ipynb) tutorial module, we used NRPy+ to contruct the SymPy expressions for plane-wave initial data.
#
# We will construct this thorn in two steps.
#
# 1. Call on NRPy+ to convert the SymPy expressions for the initial data into one C-code kernel.
# 1. Write the C code and linkages to the Einstein Toolkit infrastructure (i.e., the .ccl files) to complete this Einstein Toolkit module.
# <a id='toc'></a>
#
# # Table of Contents
# $$\label{toc}$$
#
# This module is organized as follows
#
# 1. [Step 1](#initializenrpy): Call on NRPy+ to convert the SymPy expression for the Fishbone-Moncrief initial data into a C-code kernel
# 1. [Step 2](#einstein): Interfacing with the Einstein Toolkit
# 1. [Step 2.a](#einstein_c): Constructing the Einstein Toolkit C-code calling functions that include the C code kernels
# 1. [Step 2.b](#einstein_ccl): CCL files - Define how this module interacts and interfaces with the larger Einstein Toolkit infrastructure
# 1. [Step 2.c](#einstein_list): Add the C code to the Einstein Toolkit compilation list
# 1. [Step 3](#latex_pdf_output): Output this module to $\LaTeX$-formatted PDF
# <a id='initializenrpy'></a>
#
# # Step 1: Call on NRPy+ to convert the SymPy expression for the Fishbone-Moncrief initial data into a C-code kernel \[Back to [top](#toc)\]
# $$\label{initializenrpy}$$
#
# After importing the core modules, we will set $\text{GridFuncMemAccess}$ to $\text{ETK}$. SymPy expressions for plane wave initial data are written inside [FishboneMoncriefID/FishboneMoncriefID.py](../edit/FishboneMoncriefID/FishboneMoncriefID.py), and we simply import them for use here.
# +
# Step 1: Call on NRPy+ to convert the SymPy expression for the
# Fishbone-Moncrief initial data into a C-code kernel
# Step 1a: Import needed NRPy+ core modules:
import NRPy_param_funcs as par
import indexedexp as ixp
import grid as gri
import finite_difference as fin
from outputC import *
import loop
# Step 1b: This is an Einstein Toolkit (ETK) thorn. Here we
# tell NRPy+ that gridfunction memory access will
# therefore be in the "ETK" style.
par.set_parval_from_str("grid::GridFuncMemAccess","ETK")
par.set_parval_from_str("grid::DIM", 3)
DIM = par.parval_from_str("grid::DIM")
# Step 1c: Call the FishboneMoncriefID() function from within the
# FishboneMoncriefID/FishboneMoncriefID.py module.
import FishboneMoncriefID.FishboneMoncriefID as fmid
# Step 1d: Within the ETK, the 3D gridfunctions x, y, and z store the
# Cartesian grid coordinates. Setting the gri.xx[] arrays
# to point to these gridfunctions forces NRPy+ to treat
# the Cartesian coordinate gridfunctions properly --
# reading them from memory as needed.
xcoord,ycoord,zcoord = gri.register_gridfunctions("AUX",["xcoord","ycoord","zcoord"])
gri.xx[0] = xcoord
gri.xx[1] = ycoord
gri.xx[2] = zcoord
# Step 1e: Set up the Fishbone-Moncrief initial data. This sets all the ID gridfunctions.
fmid.FishboneMoncriefID()
Valencia3velocityU = ixp.register_gridfunctions_for_single_rank1("EVOL","Valencia3velocityU")
# -={ Spacetime quantities: Generate C code from expressions and output to file }=-
KerrSchild_to_print = [\
lhrh(lhs=gri.gfaccess("out_gfs","alpha"),rhs=fmid.IDalpha),\
lhrh(lhs=gri.gfaccess("out_gfs","betaU0"),rhs=fmid.IDbetaU[0]),\
lhrh(lhs=gri.gfaccess("out_gfs","betaU1"),rhs=fmid.IDbetaU[1]),\
lhrh(lhs=gri.gfaccess("out_gfs","betaU2"),rhs=fmid.IDbetaU[2]),\
lhrh(lhs=gri.gfaccess("out_gfs","gammaDD00"),rhs=fmid.IDgammaDD[0][0]),\
lhrh(lhs=gri.gfaccess("out_gfs","gammaDD01"),rhs=fmid.IDgammaDD[0][1]),\
lhrh(lhs=gri.gfaccess("out_gfs","gammaDD02"),rhs=fmid.IDgammaDD[0][2]),\
lhrh(lhs=gri.gfaccess("out_gfs","gammaDD11"),rhs=fmid.IDgammaDD[1][1]),\
lhrh(lhs=gri.gfaccess("out_gfs","gammaDD12"),rhs=fmid.IDgammaDD[1][2]),\
lhrh(lhs=gri.gfaccess("out_gfs","gammaDD22"),rhs=fmid.IDgammaDD[2][2]),\
lhrh(lhs=gri.gfaccess("out_gfs","KDD00"),rhs=fmid.IDKDD[0][0]),\
lhrh(lhs=gri.gfaccess("out_gfs","KDD01"),rhs=fmid.IDKDD[0][1]),\
lhrh(lhs=gri.gfaccess("out_gfs","KDD02"),rhs=fmid.IDKDD[0][2]),\
lhrh(lhs=gri.gfaccess("out_gfs","KDD11"),rhs=fmid.IDKDD[1][1]),\
lhrh(lhs=gri.gfaccess("out_gfs","KDD12"),rhs=fmid.IDKDD[1][2]),\
lhrh(lhs=gri.gfaccess("out_gfs","KDD22"),rhs=fmid.IDKDD[2][2]),\
]
# Force outCverbose=False for this module to avoid gigantic C files
# filled with the non-CSE expressions for the Weyl scalars.
KerrSchild_CcodeKernel = fin.FD_outputC("returnstring",KerrSchild_to_print,params="outCverbose=False")
# -={ GRMHD quantities: Generate C code from expressions and output to file }=-
FMdisk_GRHD_rho_initial_to_print = [lhrh(lhs=gri.gfaccess("out_gfs","rho_initial"),rhs=fmid.rho_initial)]
FMdisk_GRHD_rho_initial_CcodeKernel = fin.FD_outputC("returnstring",FMdisk_GRHD_rho_initial_to_print)
FMdisk_GRHD_velocities_to_print = [\
lhrh(lhs=gri.gfaccess("out_gfs","Valencia3velocityU0"),rhs=fmid.IDValencia3velocityU[0]),\
lhrh(lhs=gri.gfaccess("out_gfs","Valencia3velocityU1"),rhs=fmid.IDValencia3velocityU[1]),\
lhrh(lhs=gri.gfaccess("out_gfs","Valencia3velocityU2"),rhs=fmid.IDValencia3velocityU[2]),\
]
FMdisk_GRHD_velocities_CcodeKernel = fin.FD_outputC("returnstring",FMdisk_GRHD_velocities_to_print)
#KerrSchild_looped = loop.loop(["i2","i1","i0"],["0","0","0"],["cctk_lsh[2]","cctk_lsh[1]","cctk_lsh[0]"],\
# ["1","1","1"],["#pragma omp parallel for","",""],"",\
# KerrSchild_CcodeKernel.replace("time","cctk_time"))
#FMdisk_GRHD_velocities_looped = loop.loop(["i2","i1","i0"],["0","0","0"],["cctk_lsh[2]","cctk_lsh[1]","cctk_lsh[0]"],\
# ["1","1","1"],["#pragma omp parallel for","",""],"",\
# FMdisk_GRHD_velocities_CcodeKernel.replace("time","cctk_time"))
#FMdisk_GRHD_rho_initial_looped = loop.loop(["i2","i1","i0"],["0","0","0"],["cctk_lsh[2]","cctk_lsh[1]","cctk_lsh[0]"],\
# ["1","1","1"],["#pragma omp parallel for","",""],"",\
# FMdisk_GRHD_rho_initial_CcodeKernel.replace("time","cctk_time"))
# Step 1f: Create directories for the thorn if they don't exist.
# !mkdir FishboneMoncriefID 2>/dev/null # 2>/dev/null: Don't throw an error if the directory already exists.
# !mkdir FishboneMoncriefID/src 2>/dev/null # 2>/dev/null: Don't throw an error if the directory already exists.
# Step 1g: Write the C code kernel to file.
with open("FishboneMoncriefID/src/KerrSchild.h", "w") as file:
file.write(str(KerrSchild_CcodeKernel.replace("time","cctk_time")))
with open("FishboneMoncriefID/src/FMdisk_GRHD_velocities.h", "w") as file:
file.write(str(FMdisk_GRHD_velocities_CcodeKernel.replace("time","cctk_time")))
with open("FishboneMoncriefID/src/FMdisk_GRHD_rho_initial.h", "w") as file:
file.write(str(FMdisk_GRHD_rho_initial_CcodeKernel.replace("time","cctk_time")))
hm1string = outputC(fmid.hm1,"hm1",filename="returnstring")
with open("FishboneMoncriefID/src/FMdisk_GRHD_hm1.h", "w") as file:
file.write(str(hm1string))
# -
# <a id='einstein'></a>
#
# # Step 2: Interfacing with the Einstein Toolkit \[Back to [top](#toc)\]
# $$\label{einstein}$$
#
# <a id='einstein_c'></a>
#
# ## Step 2.a: Constructing the Einstein Toolkit C-code calling functions that include the C code kernels \[Back to [top](#toc)\]
# $$\label{einstein_c}$$
#
# We will write another C file with the functions we need here.
# +
# %%writefile FishboneMoncriefID/src/InitialData.c
#include <math.h>
#include <stdio.h>
#include <stdbool.h>
#include <stdlib.h> // For drand48()
#include "cctk.h"
#include "cctk_Parameters.h"
#include "cctk_Arguments.h"
// Alias for "vel" vector gridfunction:
#define velx (&vel[0*cctk_lsh[0]*cctk_lsh[1]*cctk_lsh[2]])
#define vely (&vel[1*cctk_lsh[0]*cctk_lsh[1]*cctk_lsh[2]])
#define velz (&vel[2*cctk_lsh[0]*cctk_lsh[1]*cctk_lsh[2]])
void FishboneMoncrief_KerrSchild(const cGH* restrict const cctkGH,const CCTK_INT *cctk_lsh,
const CCTK_INT i0,const CCTK_INT i1,const CCTK_INT i2,
const CCTK_REAL *xcoordGF,const CCTK_REAL *ycoordGF,const CCTK_REAL *zcoordGF,
CCTK_REAL *alphaGF,CCTK_REAL *betaU0GF,CCTK_REAL *betaU1GF,CCTK_REAL *betaU2GF,
CCTK_REAL *gammaDD00GF,CCTK_REAL *gammaDD01GF,CCTK_REAL *gammaDD02GF,CCTK_REAL *gammaDD11GF,CCTK_REAL *gammaDD12GF,CCTK_REAL *gammaDD22GF,
CCTK_REAL *KDD00GF,CCTK_REAL *KDD01GF,CCTK_REAL *KDD02GF,CCTK_REAL *KDD11GF,CCTK_REAL *KDD12GF,CCTK_REAL *KDD22GF)
{
DECLARE_CCTK_PARAMETERS
#include "KerrSchild.h"
}
void FishboneMoncrief_FMdisk_GRHD_velocities(const cGH* restrict const cctkGH,const CCTK_INT *cctk_lsh,
const CCTK_INT i0,const CCTK_INT i1,const CCTK_INT i2,
const CCTK_REAL *xcoordGF,const CCTK_REAL *ycoordGF,const CCTK_REAL *zcoordGF,
CCTK_REAL *Valencia3velocityU0GF, CCTK_REAL *Valencia3velocityU1GF, CCTK_REAL *Valencia3velocityU2GF)
{
DECLARE_CCTK_PARAMETERS
#include "FMdisk_GRHD_velocities.h"
}
void FishboneMoncrief_ET_GRHD_initial(CCTK_ARGUMENTS) {
DECLARE_CCTK_ARGUMENTS;
DECLARE_CCTK_PARAMETERS;
printf("Fishbone-Moncrief Disk Initial data.\n");
printf("Using input parameters of\n a = %e,\n M = %e,\nr_in = %e,\nr_at_max_density = %e\nkappa = %e\ngamma = %e\n",a,M,r_in,r_at_max_density,kappa,gamma);
// First compute maximum density
CCTK_REAL rho_max;
{
CCTK_REAL hm1;
CCTK_REAL xcoord = r_at_max_density;
CCTK_REAL ycoord = 0.0;
CCTK_REAL zcoord = 0.0;
{
#include "FMdisk_GRHD_hm1.h"
}
rho_max = pow( hm1 * (gamma-1.0) / (kappa*gamma), 1.0/(gamma-1.0) );
}
#pragma omp parallel for
for(CCTK_INT k=0;k<cctk_lsh[2];k++) for(CCTK_INT j=0;j<cctk_lsh[1];j++) for(CCTK_INT i=0;i<cctk_lsh[0];i++) {
CCTK_INT idx = CCTK_GFINDEX3D(cctkGH,i,j,k);
CCTK_REAL xcoord = x[idx];
CCTK_REAL ycoord = y[idx];
CCTK_REAL zcoord = z[idx];
CCTK_REAL rr = r[idx];
FishboneMoncrief_KerrSchild(cctkGH,cctk_lsh,
i,j,k,
x,y,z,
alp,betax,betay,betaz,
gxx,gxy,gxz,gyy,gyz,gzz,
kxx,kxy,kxz,kyy,kyz,kzz);
CCTK_REAL hm1;
bool set_to_atmosphere=false;
if(rr > r_in) {
{
#include "FMdisk_GRHD_hm1.h"
}
if(hm1 > 0) {
rho[idx] = pow( hm1 * (gamma-1.0) / (kappa*gamma), 1.0/(gamma-1.0) ) / rho_max;
press[idx] = kappa*pow(rho[idx], gamma);
// P = (\Gamma - 1) rho epsilon
eps[idx] = press[idx] / (rho[idx] * (gamma - 1.0));
FishboneMoncrief_FMdisk_GRHD_velocities(cctkGH,cctk_lsh,
i,j,k,
x,y,z,
velx,vely,velz);
} else {
set_to_atmosphere=true;
}
} else {
set_to_atmosphere=true;
}
// Outside the disk? Set to atmosphere all hydrodynamic variables!
if(set_to_atmosphere) {
// Choose an atmosphere such that
// rho = 1e-5 * r^(-3/2), and
// P = k rho^gamma
// Add 1e-100 or 1e-300 to rr or rho to avoid divisions by zero.
rho[idx] = 1e-5 * pow(rr + 1e-100,-3.0/2.0);
press[idx] = kappa*pow(rho[idx], gamma);
eps[idx] = press[idx] / ((rho[idx] + 1e-300) * (gamma - 1.0));
w_lorentz[idx] = 1.0;
velx[idx] = 0.0;
vely[idx] = 0.0;
velz[idx] = 0.0;
}
}
CCTK_INT final_idx = CCTK_GFINDEX3D(cctkGH,cctk_lsh[0]-1,cctk_lsh[1]-1,cctk_lsh[2]-1);
printf("===== OUTPUTS =====\n");
printf("betai: %e %e %e \ngij: %e %e %e %e %e %e \nKij: %e %e %e %e %e %e\nalp: %e\n\n",betax[final_idx],betay[final_idx],betaz[final_idx],gxx[final_idx],gxy[final_idx],gxz[final_idx],gyy[final_idx],gyz[final_idx],gzz[final_idx],kxx[final_idx],kxy[final_idx],kxz[final_idx],kyy[final_idx],kyz[final_idx],kzz[final_idx],alp[final_idx]);
printf("rho: %.15e\nPressure: %.15e\nvx: %.15e\nvy: %.15e\nvz: %.15e\n",rho[final_idx],press[final_idx],velx[final_idx],vely[final_idx],velz[final_idx]);
}
void FishboneMoncrief_ET_GRHD_initial__perturb_pressure(CCTK_ARGUMENTS) {
DECLARE_CCTK_ARGUMENTS;
DECLARE_CCTK_PARAMETERS;
#pragma omp parallel for
for(CCTK_INT k=0;k<cctk_lsh[2];k++) for(CCTK_INT j=0;j<cctk_lsh[1];j++) for(CCTK_INT i=0;i<cctk_lsh[0];i++) {
CCTK_INT idx = CCTK_GFINDEX3D(cctkGH,i,j,k);
CCTK_REAL random_number_between_min_and_max = random_min + (random_max - random_min)*drand48();
press[idx] = press[idx]*(1.0 + random_number_between_min_and_max);
// Add 1e-300 to rho to avoid division by zero when density is zero.
eps[idx] = press[idx] / ((rho[idx] + 1e-300) * (gamma - 1.0));
}
}
# -
# <a id='einstein_ccl'></a>
#
# ## Step 2.b: CCL files - Define how this module interacts and interfaces with the larger Einstein Toolkit infrastructure \[Back to [top](#toc)\]
# $$\label{einstein_ccl}$$
#
# Writing a module ("thorn") within the Einstein Toolkit requires that three "ccl" files be constructed, all in the root directory of the thorn:
#
# 1. $\text{interface.ccl}$: defines the gridfunction groups needed, and provides keywords denoting what this thorn provides and what it should inherit from other thorns. Specifically, this file governs the interaction between this thorn and others; more information can be found in the [official Einstein Toolkit documentation](http://cactuscode.org/documentation/referencemanual/ReferenceManualch8.html#x12-260000C2.2).
# With "implements", we give our thorn its unique name. By "inheriting" other thorns, we tell the Toolkit that we will rely on variables that exist and are declared "public" within those functions.
# %%writefile FishboneMoncriefID/interface.ccl
implements: FishboneMoncriefID
inherits: admbase grid hydrobase
# 2. $\text{param.ccl}$: specifies free parameters within the thorn, enabling them to be set at runtime. It is required to provide allowed ranges and default values for each parameter. More information on this file's syntax can be found in the [official Einstein Toolkit documentation](http://cactuscode.org/documentation/referencemanual/ReferenceManualch8.html#x12-265000C2.3).
# +
# %%writefile FishboneMoncriefID/param.ccl
shares: grid
shares: ADMBase
USES CCTK_INT lapse_timelevels
USES CCTK_INT shift_timelevels
USES CCTK_INT metric_timelevels
USES KEYWORD metric_type
EXTENDS KEYWORD initial_data
{
"FishboneMoncriefID" :: "Initial data from FishboneMoncriefID solution"
}
EXTENDS KEYWORD initial_lapse
{
"FishboneMoncriefID" :: "Initial lapse from FishboneMoncriefID solution"
}
EXTENDS KEYWORD initial_shift
{
"FishboneMoncriefID" :: "Initial shift from FishboneMoncriefID solution"
}
EXTENDS KEYWORD initial_dtlapse
{
"FishboneMoncriefID" :: "Initial dtlapse from FishboneMoncriefID solution"
}
EXTENDS KEYWORD initial_dtshift
{
"FishboneMoncriefID" :: "Initial dtshift from FishboneMoncriefID solution"
}
shares: HydroBase
EXTENDS KEYWORD initial_hydro
{
"FishboneMoncriefID" :: "Initial GRHD data from FishboneMoncriefID solution"
}
#["r_in","r_at_max_density","a","M"] A_b, kappa, gamma
restricted:
CCTK_REAL r_in "Fixes the inner edge of the disk"
{
0.0:* :: "Must be positive"
} 6.0
restricted:
CCTK_REAL r_at_max_density "Radius at maximum disk density. Needs to be > r_in"
{
0.0:* :: "Must be positive"
} 12.0
restricted:
CCTK_REAL a "The spin parameter of the black hole"
{
-1.0:1.0 :: "Positive values, up to 1. Negative disallowed, as certain roots are chosen in the hydro fields setup. Check those before enabling negative spins!"
} 0.9375
restricted:
CCTK_REAL M "Kerr-Schild BH mass. Probably should always set M=1."
{
0.0:* :: "Must be positive"
} 1.0
restricted:
CCTK_REAL A_b "Scaling factor for the vector potential"
{
*:* :: ""
} 1.0
restricted:
CCTK_REAL kappa "Equation of state: P = kappa * rho^gamma"
{
0.0:* :: "Positive values"
} 1.0e-3
restricted:
CCTK_REAL gamma "Equation of state: P = kappa * rho^gamma"
{
0.0:* :: "Positive values"
} 1.3333333333333333333333333333
##################################
# PRESSURE PERTURBATION PARAMETERS
private:
CCTK_REAL random_min "Floor value of random perturbation to initial pressure, where perturbed pressure = pressure*(1.0 + (random_min + (random_max-random_min)*RAND[0,1)))"
{
*:* :: "Any value"
} -0.02
private:
CCTK_REAL random_max "Ceiling value of random perturbation to initial pressure, where perturbed pressure = pressure*(1.0 + (random_min + (random_max-random_min)*RAND[0,1)))"
{
*:* :: "Any value"
} 0.02
# -
# 3. $\text{schedule.ccl}$: allocates storage for gridfunctions, defines how the thorn's functions should be scheduled in a broader simulation, and specifies the regions of memory written to or read from gridfunctions. $\text{schedule.ccl}$'s official documentation may be found [here](http://cactuscode.org/documentation/referencemanual/ReferenceManualch8.html#x12-268000C2.4).
#
# We specify here the standardized ETK "scheduling bins" in which we want each of our thorn's functions to run.
# +
# %%writefile FishboneMoncriefID/schedule.ccl
STORAGE: ADMBase::metric[metric_timelevels], ADMBase::curv[metric_timelevels], ADMBase::lapse[lapse_timelevels], ADMBase::shift[shift_timelevels]
schedule FishboneMoncrief_ET_GRHD_initial IN HydroBase_Initial
{
LANG: C
READS: grid::x(Everywhere)
READS: grid::y(Everywhere)
READS: grid::y(Everywhere)
WRITES: admbase::alp(Everywhere)
WRITES: admbase::betax(Everywhere)
WRITES: admbase::betay(Everywhere)
WRITES: admbase::betaz(Everywhere)
WRITES: admbase::kxx(Everywhere)
WRITES: admbase::kxy(Everywhere)
WRITES: admbase::kxz(Everywhere)
WRITES: admbase::kyy(Everywhere)
WRITES: admbase::kyz(Everywhere)
WRITES: admbase::kzz(Everywhere)
WRITES: admbase::gxx(Everywhere)
WRITES: admbase::gxy(Everywhere)
WRITES: admbase::gxz(Everywhere)
WRITES: admbase::gyy(Everywhere)
WRITES: admbase::gyz(Everywhere)
WRITES: admbase::gzz(Everywhere)
WRITES: hydrobase::velx(Everywhere)
WRITES: hydrobase::vely(Everywhere)
WRITES: hydrobase::velz(Everywhere)
WRITES: hydrobase::rho(Everywhere)
WRITES: hydrobase::eps(Everywhere)
WRITES: hydrobase::press(Everywhere)
} "Set up general relativistic hydrodynamic (GRHD) fields for Fishbone-Moncrief disk"
schedule FishboneMoncrief_ET_GRHD_initial__perturb_pressure IN CCTK_INITIAL AFTER Seed_Magnetic_Fields BEFORE IllinoisGRMHD_ID_Converter
{
LANG: C
} "Add random perturbation to initial pressure, after seed magnetic fields have been set up (in case we'd like the seed magnetic fields to depend on the pristine pressures)"
# -
# <a id='einstein_list'></a>
#
# ## Step 2.c: Add the C code to the Einstein Toolkit compilation list \[Back to [top](#toc)\]
# $$\label{einstein_list}$$
#
# We will also need $\text{make.code.defn}$, which indicates the list of files that need to be compiled. This thorn only has the one C file to compile.
# %%writefile FishboneMoncriefID/src/make.code.defn
SRCS = InitialData.c
# <a id='latex_pdf_output'></a>
#
# # Step 3: Output this module to $\LaTeX$-formatted PDF file \[Back to [top](#toc)\]
# $$\label{latex_pdf_output}$$
#
# The following code cell converts this Jupyter notebook into a proper, clickable $\LaTeX$-formatted PDF file. After the cell is successfully run, the generated PDF may be found in the root NRPy+ tutorial directory, with filename
# [Tutorial-ETK_thorn-FishboneMoncriefID.pdf](Tutorial-ETK_thorn-FishboneMoncriefID.pdf) (Note that clicking on this link may not work; you may need to open the PDF file through another means.)
# !jupyter nbconvert --to latex --template latex_nrpy_style.tplx Tutorial-ETK_thorn-FishboneMoncriefID.ipynb
# !pdflatex -interaction=batchmode Tutorial-ETK_thorn-FishboneMoncriefID.tex
# !pdflatex -interaction=batchmode Tutorial-ETK_thorn-FishboneMoncriefID.tex
# !pdflatex -interaction=batchmode Tutorial-ETK_thorn-FishboneMoncriefID.tex
# !rm -f Tut*.out Tut*.aux Tut*.log
|
Tutorial-ETK_thorn-FishboneMoncriefID.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda env:miniconda-ctsm]
# language: python
# name: conda-env-miniconda-ctsm-py
# ---
# # Notebook overview on data preprocessing, analysis and plotting in Vanderkelen et al. 2022 GMD
# ## 1. Preprocessing
# ### 1.1 Irrigation topology derivation
#
# - [irrigtopo_snake.ipynb](/analysis/irrigtopo_casestudy_snake/irrigtopo_snake.ipynb): Snake case study: derivation and plotting
# - [determine_irrigtopo_global.ipynb](/preprocessing/determine_irrigtopo_global.ipynb): derivation of global irrigation topology
#
# + [markdown] jp-MarkdownHeadingCollapsed=true tags=[]
# ### 1.2 CTSM simulations
#
# - [setup_IHistClm50Sp_360x720cru_CTL.sh](preprocessing/setup_IHistClm50Sp_360x720cru_CTL.sh): script to set up CTSM simulation
# - [nl_clm_CTL.sh](preprocessing/nl_clm_CTL.sh): namelist file used in CTSM simulation
# + [markdown] tags=[]
# ### 1.2 MizuRoute simulations
# in order of usage
# -
# - [pp_clm_for_mizuroute.ipynb](preprocessing/pp_clm_for_mizuroute.ipynb): notebook processing CTSM output for MizuRoute including: (i) preparing irrigation water demands for irrigation topology (ii) merging and preparing runoff, evaporation and precip for mizuRoute input
# - [prepare_ntopo_HDMA_D03.ipynb](/preprocessing/prepare_ntopo_HDMA_D03.ipynb): prepare parameter topology for natural lake simulation with mizuRoute
# - [prepare_ntopo_nolake.ipynb](/preprocessing/prepare_ntopo_nolake.ipynb): prepare parameter topology for no lake simulation with mizuRoute
# - [pp_calc_inflowseasonality_natlake.ipynb](preprocessing/pp_calc_inflowseasonality_natlake.ipynb): notebook calculating inflow seasonality based on mizuRoute simulations with natural lakes, (necessary as parameters for Hanasaki implementation)
# - [apply_irrigtopo_global.ipynb](/preprocessing/apply_irrigtopo_global.ipynb): application of global irrigation topology on observed seasonal irrigation demands
# - [prepare_ntopo_HDMA_H06.ipynb](/preprocessing/prepare_ntopo_HDMA_H06.ipynb): prepare parameter topology for Hanasaki simulation with mizuRoute
#
# ## 2. Analysis and plotting
# + [markdown] tags=[]
# ### 2.1 Local mizuRoute simulations
#
# - [local_Hanasaki_resobs_plotting.ipynb](analysis/local_Hanasaki_resobs_plotting.ipynb): Analysis with local mizuRoute simulations
# + [markdown] tags=[]
# ### 2.2 Global mizuRoute simulations
# #### 2.2.1 Evaluation using reservoir observations
#
# - [global_mizuRoute_Hanasaki_resobs.ipynb](analysis/global_mizuRoute_Hanasaki_resobs.ipynb): processing and plotting of global mizuRoute simulations compared to reservoir observations
# - [global_steyaert_evaluation_mizuRoute_Hanasaki.ipynb](analysis/global_steyaert_evaluation_mizuRoute_Hanasaki.ipynb): evaluation with observations from the ResOpsUS dataset of Steyaert et al., 2022
# + [markdown] tags=[]
# #### 2.2.2 Runoff evaluation
#
# - [pp_clm_evaluate_runoff_paperplot.ipynb](analysis/pp_clm_evaluate_runoff_paperplot.ipynb): evaluation of CTSM runoff with GRUN (maps)
# + [markdown] tags=[]
# #### 2.2.3 Global evaluation with GSIM stream indices
#
# - [pp_gsim_processing_paper.ipynb](analysis/pp_gsim_processing_paper.ipynb): processing script loading obs and calculating metrics (saving as dict)
# - [pp_gsim_plotting.ipynb](analysis/pp_gsim_processing_paper.ipynb): plotting script loading saved dict and producing maps
# -
#
#
|
main.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/HarvinderSinghDiwan/Heart-Disease-Prediction/blob/master/HeartDIseasePrediction.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + colab={"base_uri": "https://localhost:8080/"} id="TyDbLlWXTY71" outputId="8a83f0a9-b8fd-4ac5-faa3-3ca51821f6d4"
# !wget https://github.com/kb22/Heart-Disease-Prediction/blob/master/dataset.csv
# + id="8Ui-jQ_8UDBO"
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib import rcParams
from matplotlib.cm import rainbow
# %matplotlib inline
import warnings
warnings.filterwarnings('ignore')
# + id="TsiSGEY2UXlj"
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
# + id="33uvRKi3UcgU"
from sklearn.neighbors import KNeighborsClassifier
from sklearn.svm import SVC
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier
# + id="7Eee6MevUi0Q"
dataset = pd.read_csv("/content/data.csv")
# + colab={"base_uri": "https://localhost:8080/"} id="UhtjsUf5UmY8" outputId="d03b1d96-8312-4d27-f641-b74af6e72f28"
dataset.info()
# + colab={"base_uri": "https://localhost:8080/", "height": 302} id="ZyC4tF0XVR88" outputId="0491b3fb-cf35-428c-9c46-34702201d724"
dataset.describe()
# + colab={"base_uri": "https://localhost:8080/", "height": 723} id="C5hdwHBDZzAZ" outputId="cbf45938-8164-422e-baa1-fe08cbfa601b"
rcParams['figure.figsize'] = 20,12
plt.matshow(dataset.corr())
plt.yticks(np.arange(dataset.shape[1]), dataset.columns)
plt.xticks(np.arange(dataset.shape[1]), dataset.columns)
plt.colorbar()
# + colab={"base_uri": "https://localhost:8080/", "height": 912} id="tGhvSKUEZ2vf" outputId="cfde32b3-7dae-4400-c717-6e942a760a30"
dataset.hist()
# + colab={"base_uri": "https://localhost:8080/", "height": 422} id="s_zLRPVUaXIu" outputId="a277b755-0808-48b9-a355-c851a1faa42c"
rcParams['figure.figsize'] = 8,6
plt.bar(dataset['target'].unique(), dataset['target'].value_counts(), color = ['red', 'green'])
plt.xticks([0, 1])
plt.xlabel('Target Classes')
plt.ylabel('Count')
plt.title('Count of each Target Class')
# + id="3m8Ey6Hla1Wu"
dataset = pd.get_dummies(dataset, columns = ['sex', 'cp', 'fbs', 'restecg', 'exang', 'slope', 'ca', 'thal'])
# + id="0uPndxqhnHGk"
standardScaler = StandardScaler()
columns_to_scale = ['age', 'trestbps', 'chol', 'thalach', 'oldpeak']
dataset[columns_to_scale] = standardScaler.fit_transform(dataset[columns_to_scale])
# + id="mvV6X7OpnRq8"
y = dataset['target']
X = dataset.drop(['target'], axis = 1)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size =0.33, random_state = 0)
# + id="rvnbpC8DnU8u"
knn_scores = []
for k in range(1,21):
knn_classifier = KNeighborsClassifier(n_neighbors = k)
knn_classifier.fit(X_train, y_train)
knn_scores.append(knn_classifier.score(X_test, y_test))
# + colab={"base_uri": "https://localhost:8080/", "height": 313} id="FBaznvHJnYfC" outputId="dc5059f9-4bfa-470d-b56e-56237fe034bb"
plt.plot([k for k in range(1, 21)], knn_scores, color = 'red')
for i in range(1,21):
plt.text(i, knn_scores[i-1], (i, knn_scores[i-1]))
plt.xticks([i for i in range(1, 21)])
plt.xlabel('Number of Neighbors (K)')
plt.ylabel('Scores')
plt.title('K Neighbors Classifier scores for different K values')
# + colab={"base_uri": "https://localhost:8080/"} id="MJxOjEjwnbtO" outputId="b5ec2bbf-b2e6-4f11-cfcf-c33b2d524fe0"
print("The score for K Neighbors Classifier is {}% with {} nieghbors.".format(knn_scores[7]*100, 8))
# + id="bvf-wif0nhXy"
svc_scores = []
kernels = ['linear', 'poly', 'rbf', 'sigmoid']
for i in range(len(kernels)):
svc_classifier = SVC(kernel = kernels[i])
svc_classifier.fit(X_train, y_train)
svc_scores.append(svc_classifier.score(X_test, y_test))
# + colab={"base_uri": "https://localhost:8080/", "height": 313} id="6dw16FjUnkgD" outputId="80b6d9f5-428a-4a5a-ac4b-bd5a6c3497ef"
colors = rainbow(np.linspace(0, 1, len(kernels)))
plt.bar(kernels, svc_scores, color = colors)
for i in range(len(kernels)):
plt.text(i, svc_scores[i], svc_scores[i])
plt.xlabel('Kernels')
plt.ylabel('Scores')
plt.title('Support Vector Classifier scores for different kernels')
# + colab={"base_uri": "https://localhost:8080/"} id="rK2ep4FPnoxa" outputId="3d1d35cd-246d-4d4d-cd76-1c1b13f51cfb"
print("The score for Support Vector Classifier is {}% with {} kernel.".format(svc_scores[0]*100, 'linear'))
# + id="ii6p7zvenvpW"
dt_scores = []
for i in range(1, len(X.columns) + 1):
dt_classifier = DecisionTreeClassifier(max_features = i, random_state = 0)
dt_classifier.fit(X_train, y_train)
dt_scores.append(dt_classifier.score(X_test, y_test))
# + colab={"base_uri": "https://localhost:8080/", "height": 313} id="cYM65FZAnyMu" outputId="69ee28ed-9561-479b-fe39-568de0a2f713"
plt.plot([i for i in range(1, len(X.columns) + 1)], dt_scores, color = 'green')
for i in range(1, len(X.columns) + 1):
plt.text(i, dt_scores[i-1], (i, dt_scores[i-1]))
plt.xticks([i for i in range(1, len(X.columns) + 1)])
plt.xlabel('Max features')
plt.ylabel('Scores')
plt.title('Decision Tree Classifier scores for different number of maximum features')
# + colab={"base_uri": "https://localhost:8080/"} id="couI3MqTn0ba" outputId="a46aa973-c27b-4989-a040-ee1b48da0ddc"
print("The score for Decision Tree Classifier is {}% with {} maximum features.".format(dt_scores[17]*100, [2,4,18]))
# + id="BzLsdBfxn4fR"
rf_scores = []
estimators = [10, 100, 200, 500, 1000]
for i in estimators:
rf_classifier = RandomForestClassifier(n_estimators = i, random_state = 0)
rf_classifier.fit(X_train, y_train)
rf_scores.append(rf_classifier.score(X_test, y_test))
# + colab={"base_uri": "https://localhost:8080/", "height": 313} id="4nY9I0rLn8Ey" outputId="9575824c-35f5-4aa7-b42c-5d5352a5edef"
colors = rainbow(np.linspace(0, 1, len(estimators)))
plt.bar([i for i in range(len(estimators))], rf_scores, color = colors, width = 0.8)
for i in range(len(estimators)):
plt.text(i, rf_scores[i], rf_scores[i])
plt.xticks(ticks = [i for i in range(len(estimators))], labels = [str(estimator) for estimator in estimators])
plt.xlabel('Number of estimators')
plt.ylabel('Scores')
plt.title('Random Forest Classifier scores for different number of estimators')
# + colab={"base_uri": "https://localhost:8080/"} id="qXv3wwp4oBXB" outputId="882383b6-2739-4a15-dd4e-ddaa79bfd07d"
print("The score for Random Forest Classifier is {}% with {} estimators.".format(rf_scores[1]*100, [100, 500]))
# + id="oXZNs_42oD46"
# + id="cF9im7booHXu"
|
HeartDIseasePrediction.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import torch
import math
from time import time
import torch.distributions as tdis
import matplotlib.pyplot as plt
from torch import nn
from torch import optim
from torch.utils.data import TensorDataset, RandomSampler, BatchSampler, DataLoader
# +
dim = 20
d = 0.9
cov1 = torch.eye(int(dim / 2))
cov2 = cov1 * d
covt = torch.cat([cov1, cov2], 1)
covb = torch.cat([cov2, cov1], 1)
cov = torch.cat([covt, covb], 0)
m = tdis.MultivariateNormal(torch.zeros(dim), cov)
b = m.sample([4000])
x = b[:, :dim//2]
y = b[:, dim//2:]
tmi = -math.log(1 - d**2) * dim / 2
print("dimension =",dim, "Rho =",d)
print("Theoretical MI =", tmi)
|
Data Generation.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Decoupling Logic and Execution
#
# In the last section, we used Fugue's transform function to port pandas code to Spark. Decoupling logic and execution is one of the primary motivations of Fugue. When transitioning a project from pandas to Spark, the majority of the code normally has has to be re-written. This is because using either pandas or Spark makes code highly coupled with that framework. This leads to a couple of problems:
#
# 1. Users have to learn an entirely new framework to work with distributed compute problems
# 2. Logic written for a *small data* project does not become reusable for a *big data* project
# 3. Testing becomes a heavyweight process for distributed compute, especially Spark
# 4. Along with number 3, iterations for distributed compute problems become slower and more expensive
#
# Fugue believes that code should minimize dependency on frameworks as much as possible. This provides flexibility and portability. **By decoupling logic and execution, we can focus on our logic in a scale-agnostic way, and then choose which engine to use when the time arises.**
# ## Differences between Pandas and Spark
#
# To illustrate the first two main points above, we'll use a simple example. For the data below, we are interested in getting the first three digits of the `phone` column and populating a new column called `location` by using a dictionary that maps the values. We start by preparing the sample data and defining the mapping.
# +
import pandas as pd
_area_code_map = {"217": "Champaign, IL", "407": "Orlando, FL", "510": "Fremont, CA"}
data = pd.DataFrame({"phone": ["(217)-123-4567", "(217)-234-5678", "(407)-123-4567",
"(407)-234-5678", "(510)-123-4567"]})
data.head()
# -
# First, we'll perform the operation in pandas. It's very simple because of the `.map()` method in pandas
# +
def map_phone_to_location(df: pd.DataFrame) -> pd.DataFrame:
df["location"] = df["phone"].str.slice(1,4).map(_area_code_map)
return df
map_phone_to_location(data.copy())
# -
# Next we'll perform the same operation in Spark and see how different the syntax is.
# Setting up Spark session
from pyspark.sql import SparkSession, DataFrame
spark = SparkSession.builder.getOrCreate()
# +
from pyspark.sql.functions import create_map, col, lit, substring
from itertools import chain
df = spark.createDataFrame(data) # converting the previous Pandas DataFrame
mapping_expr = create_map([lit(x) for x in chain(*_area_code_map.items())])
def map_phone_to_location(df: DataFrame) -> DataFrame:
_df = df.withColumn("location", mapping_expr[substring(col("phone"),2,3)])
return _df
map_phone_to_location(df).show()
# -
# Looking at the two code examples, we had to reimplement the exact same functionality with completely different syntax. This isn't a cherry-picked example. Data practitioners will often have to write two implementations of the same logic, one for each framework, especially as the logic gets more specific.
#
# This is where Fugue comes in. Users can use the abstraction layer to only write one implementation of the function. This can then be applied to pandas, Spark, and Dask. All we need to do is apply a `transformer` decorator to the pandas implementation of the function. The decorator takes in a string that specifies the output schema. The `transform` function does the same thing to the function that is passed in.
# +
from fugue import transformer
@transformer("*, location:str")
def map_phone_to_location(df: pd.DataFrame) -> pd.DataFrame:
df["location"] = df["phone"].str.slice(1,4).map(_area_code_map)
return df
# -
# By wrapping the function with the decorator, we can then use it inside a `FugueWorkflow`. The `FugueWorkflow` constructs a directed-acyclic graph (DAG) where the inputs and outputs are DataFrames. More details will follow in the next sections but the important thing for now is to show how it's used. The code block below is still running in Pandas.
# +
from fugue import FugueWorkflow
with FugueWorkflow() as dag:
df = dag.df(data.copy()) # Still the original Pandas DataFrame
df = df.transform(map_phone_to_location)
df.show()
# -
# In order to bring it to Spark, all we need to do is pass the `SparkExecutionEngine` into `FugueWorkflow`, similar to how we used the `transform` function to Spark in the last section. Now all the code underneath the `with` statement will run on Spark. We did not make any modifications to `map_phone_to_location` in order to bring it to Spark. By wrapping the function with a `transformer`, it became agnostic to the ExecutionEngine it was operating on. We can use the same function in Spark or Dask without making modifications.
# +
from fugue_spark import SparkExecutionEngine
with FugueWorkflow(SparkExecutionEngine) as dag:
df = dag.df(data.copy()) # Still the original Pandas DataFrame
df = df.transform(map_phone_to_location)
df.show()
# -
# ## `transform` versus `FugueWorkflow`
#
# We have seen the two approaches to bring Python and pandas code to Spark with Fugue. The `transform` function introduced in the first section allows users to leave a function in pandas or Python, and then port it to Spark and Dask. Meanwhile, `FugueWorkflow` does the same for full workflows as opposed to one function.
#
# For example, if we had five different functions to call `transform` on and bring to Spark, we would need to specify the `SparkExecutionEngine` five times. The `FugueWorkflow` allows us to make the entire computation run on either pandas, Spark, or Dask. Both are similar in principle, in that they leave the original functions decoupled to the execution environment.
# ## Independence from Frameworks
#
# We earlier said that the abstraction layer Fugue provides makes code independent of any framework. To show this is true, we can actually rewrite the `map_phone_to_location` function in native Python and still apply it on the pandas and Spark engines.
#
# Below is the implementation in native Python. Similar to earlier, we are running this on Spark by passing in the `SparkExecutionEngine`. A function written in native Python can be ported to pandas, Spark, and Dask.
# +
from typing import List, Dict, Any
# schema: *, location:str
def map_phone_to_location(df: List[Dict[str,Any]]) -> List[Dict[str,Any]]:
for row in df:
row["location"] = _area_code_map[row["phone"][1:4]]
return df
with FugueWorkflow(SparkExecutionEngine) as dag:
df = dag.df(data.copy()) # Still the original Pandas DataFrame
df = df.transform(map_phone_to_location)
df.show()
# -
# Notice the `@transformer` decorator was removed from `map_phone_to_location`. Instead, it was replaced with a comment that specified the schema. Fugue reads in this comment as the **schema hint**. Now, this function is truly independent of any framework and written in native Python. **It is even independent from Fugue itself.** Fugue only appears when we reach the execution part of the code. The logic, however, is not coupled with any framework. The type annotations in the `map_phone_to_location` caused the DataFrame to be converted as it was used by the function. If users want to offboard from Fugue, they can use their function with Pandas `apply` or Spark user-defined functions (UDFs).
#
# Is the native Python implementation or Pandas implementation of `map_phone_to_location` better? Is the native Spark implementation better?
#
# The main concern of Fugue is clear readable code. **Users can write code in whatever expresses their logic the best**. The compute efficiency lost by using Fugue is unlikely to be significant, especially in comparison to the developer efficiency gained through more rapid iterations and easier maintenance. In fact, Fugue is designed in a way that often sees speed ups compared to inexperienced users working with native Spark code. Fugue handles a lot of the tricks necessary to use Spark effectively.
#
# Fugue also future-proofs the code. If one day Spark and Dask are replaced by a more efficient framework, a new ExecutionEngine can be added to Fugue to support that new framework.
# ## Testability and Maintainability
#
# Fugue code becomes easily testable because the function contains logic that is portable across all pandas, Spark, and Dask. All we have to do is run some values through the defined function. We can test code without the need to spin up compute resources (such as Spark or Dask clusters). This hardware often takes time to spin up just for a simple test, making it painful to run unit tests on Spark. Now, we can test quickly with native Python or pandas, and then execute on Spark when needed. Developers that use Fugue benefit from more rapid iterations in their data projects.
# Remember the input was List[Dict[str,Any]]
map_phone_to_location([{'phone': '(407)-234-5678'},
{'phone': '(407)-234-5679'}])
# Even if the output here is a `List[Dict[str,Any]]`, Fugue takes care of converting it back to a DataFrame.
# ## Fugue as a Mindset
#
# Fugue is a framework, but more importantly, it is a mindset.
#
# 1. Fugue believes that the framework should adapt to the user, not the other way around
# 2. Fugue lets users code express logic in a scale-agnostic way, with the tools they prefer
# 3. Fugue values readability and maintainability of code over deep framework-specific optimizations
#
# Using distributed computing is currently harder than it needs to be. However, these systems often follow similar patterns, which have been abstracted to create a framework that lets users focus on defining their logic. We cover these concepts in the rest of tutorials. If you're new to distributed computing, Fugue is the perfect place to get started.
#
# ## [Optional] Comparison to Modin and Koalas
#
# Fugue gets compared a lot of Modin and Koalas. Modin is a pandas interface for execution on Dask, and Koalas is a pandas interface for execution on Spark. Fugue, Modin, and Koalas have similar goals in making an easier distributed computing experience. The main difference is that Modin and Koalas use pandas as the grammar for distributed compute. Fugue, on the other hand, uses native Python and SQL as the grammar for distributed compute (though pandas is also supported).
#
# The clearest example of pandas not being compatible with Spark is the acceptance of mixed-typed columns. A single column can have numeric and string values. Spark on the other hand, is strongly typed and enforces the schema. More than that, pandas is strongly reliant on the index for operations. As users transition to Spark, the index mindset does not hold as well. Order is not always guaranteed in a distributed system, there is an overhead to maintain a global index and moreover it is often not necessary.
|
tutorials/beginner/decoupling_logic_and_execution.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] deletable=true editable=true
# # Solving problems by Searching
#
# This notebook serves as supporting material for topics covered in **Chapter 3 - Solving Problems by Searching** and **Chapter 4 - Beyond Classical Search** from the book *Artificial Intelligence: A Modern Approach.* This notebook uses implementations from [search.py](https://github.com/aimacode/aima-python/blob/master/search.py) module. Let's start by importing everything from search module.
# + deletable=true editable=true
from search import *
# Needed to hide warnings in the matplotlib sections
import warnings
warnings.filterwarnings("ignore")
# + [markdown] deletable=true editable=true
# ## Review
#
# Here, we learn about problem solving. Building goal-based agents that can plan ahead to solve problems, in particular, navigation problem/route finding problem. First, we will start the problem solving by precisely defining **problems** and their **solutions**. We will look at several general-purpose search algorithms. Broadly, search algorithms are classified into two types:
#
# * **Uninformed search algorithms**: Search algorithms which explore the search space without having any information about the problem other than its definition.
# * Examples:
# 1. Breadth First Search
# 2. Depth First Search
# 3. Depth Limited Search
# 4. Iterative Deepening Search
#
#
# * **Informed search algorithms**: These type of algorithms leverage any information (heuristics, path cost) on the problem to search through the search space to find the solution efficiently.
# * Examples:
# 1. Best First Search
# 2. Uniform Cost Search
# 3. A\* Search
# 4. Recursive Best First Search
#
# *Don't miss the visualisations of these algorithms solving the route-finding problem defined on Romania map at the end of this notebook.*
# + [markdown] deletable=true editable=true
# ## Problem
#
# Let's see how we define a Problem. Run the next cell to see how abstract class `Problem` is defined in the search module.
# + deletable=true editable=true
# %psource Problem
# + [markdown] deletable=true editable=true
# The `Problem` class has six methods.
#
# * `__init__(self, initial, goal)` : This is what is called a `constructor` and is the first method called when you create an instance of the class. `initial` specifies the initial state of our search problem. It represents the start state from where our agent begins its task of exploration to find the goal state(s) which is given in the `goal` parameter.
#
#
# * `actions(self, state)` : This method returns all the possible actions agent can execute in the given state `state`.
#
#
# * `result(self, state, action)` : This returns the resulting state if action `action` is taken in the state `state`. This `Problem` class only deals with deterministic outcomes. So we know for sure what every action in a state would result to.
#
#
# * `goal_test(self, state)` : Given a graph state, it checks if it is a terminal state. If the state is indeed a goal state, value of `True` is returned. Else, of course, `False` is returned.
#
#
# * `path_cost(self, c, state1, action, state2)` : Return the cost of the path that arrives at `state2` as a result of taking `action` from `state1`, assuming total cost of `c` to get up to `state1`.
#
#
# * `value(self, state)` : This acts as a bit of extra information in problems where we try to optimise a value when we cannot do a goal test.
# + [markdown] deletable=true editable=true
# We will use the abstract class `Problem` to define our real **problem** named `GraphProblem`. You can see how we define `GraphProblem` by running the next cell.
# + deletable=true editable=true
# %psource GraphProblem
# + [markdown] deletable=true editable=true
# Now it's time to define our problem. We will define it by passing `initial`, `goal`, `graph` to `GraphProblem`. So, our problem is to find the goal state starting from the given initial state on the provided graph. Have a look at our romania_map, which is an Undirected Graph containing a dict of nodes as keys and neighbours as values.
# + deletable=true editable=true
romania_map = UndirectedGraph(dict(
Arad=dict(Zerind=75, Sibiu=140, Timisoara=118),
Bucharest=dict(Urziceni=85, Pitesti=101, Giurgiu=90, Fagaras=211),
Craiova=dict(Drobeta=120, Rimnicu=146, Pitesti=138),
Drobeta=dict(Mehadia=75),
Eforie=dict(Hirsova=86),
Fagaras=dict(Sibiu=99),
Hirsova=dict(Urziceni=98),
Iasi=dict(Vaslui=92, Neamt=87),
Lugoj=dict(Timisoara=111, Mehadia=70),
Oradea=dict(Zerind=71, Sibiu=151),
Pitesti=dict(Rimnicu=97),
Rimnicu=dict(Sibiu=80),
Urziceni=dict(Vaslui=142)))
romania_map.locations = dict(
Arad=(91, 492), Bucharest=(400, 327), Craiova=(253, 288),
Drobeta=(165, 299), Eforie=(562, 293), Fagaras=(305, 449),
Giurgiu=(375, 270), Hirsova=(534, 350), Iasi=(473, 506),
Lugoj=(165, 379), Mehadia=(168, 339), Neamt=(406, 537),
Oradea=(131, 571), Pitesti=(320, 368), Rimnicu=(233, 410),
Sibiu=(207, 457), Timisoara=(94, 410), Urziceni=(456, 350),
Vaslui=(509, 444), Zerind=(108, 531))
# + [markdown] deletable=true editable=true
# It is pretty straightforward to understand this `romania_map`. The first node **Arad** has three neighbours named **Zerind**, **Sibiu**, **Timisoara**. Each of these nodes are 75, 140, 118 units apart from **Arad** respectively. And the same goes with other nodes.
#
# And `romania_map.locations` contains the positions of each of the nodes. We will use the straight line distance (which is different from the one provided in `romania_map`) between two cities in algorithms like A\*-search and Recursive Best First Search.
#
# **Define a problem:**
# Hmm... say we want to start exploring from **Arad** and try to find **Bucharest** in our romania_map. So, this is how we do it.
# + deletable=true editable=true
romania_problem = GraphProblem('Arad', 'Bucharest', romania_map)
# + [markdown] deletable=true editable=true
# # Romania map visualisation
#
# Let's have a visualisation of Romania map [Figure 3.2] from the book and see how different searching algorithms perform / how frontier expands in each search algorithm for a simple problem named `romania_problem`.
# + [markdown] deletable=true editable=true
# Have a look at `romania_locations`. It is a dictionary defined in search module. We will use these location values to draw the romania graph using **networkx**.
# + deletable=true editable=true
romania_locations = romania_map.locations
print(romania_locations)
# + [markdown] deletable=true editable=true
# Let's start the visualisations by importing necessary modules. We use networkx and matplotlib to show the map in the notebook and we use ipywidgets to interact with the map to see how the searching algorithm works.
# + deletable=true editable=true
# %matplotlib inline
import networkx as nx
import matplotlib.pyplot as plt
from matplotlib import lines
from ipywidgets import interact
import ipywidgets as widgets
from IPython.display import display
import time
# + [markdown] deletable=true editable=true
# Let's get started by initializing an empty graph. We will add nodes, place the nodes in their location as shown in the book, add edges to the graph.
# + deletable=true editable=true
# initialise a graph
G = nx.Graph()
# use this while labeling nodes in the map
node_labels = dict()
# use this to modify colors of nodes while exploring the graph.
# This is the only dict we send to `show_map(node_colors)` while drawing the map
node_colors = dict()
for n, p in romania_locations.items():
# add nodes from romania_locations
G.add_node(n)
# add nodes to node_labels
node_labels[n] = n
# node_colors to color nodes while exploring romania map
node_colors[n] = "white"
# we'll save the initial node colors to a dict to use later
initial_node_colors = dict(node_colors)
# positions for node labels
node_label_pos = { k:[v[0],v[1]-10] for k,v in romania_locations.items() }
# use this while labeling edges
edge_labels = dict()
# add edges between cities in romania map - UndirectedGraph defined in search.py
for node in romania_map.nodes():
connections = romania_map.get(node)
for connection in connections.keys():
distance = connections[connection]
# add edges to the graph
G.add_edge(node, connection)
# add distances to edge_labels
edge_labels[(node, connection)] = distance
# + deletable=true editable=true
# initialise a graph
G = nx.Graph()
# use this while labeling nodes in the map
node_labels = dict()
# use this to modify colors of nodes while exploring the graph.
# This is the only dict we send to `show_map(node_colors)` while drawing the map
node_colors = dict()
for n, p in romania_locations.items():
# add nodes from romania_locations
G.add_node(n)
# add nodes to node_labels
node_labels[n] = n
# node_colors to color nodes while exploring romania map
node_colors[n] = "white"
# we'll save the initial node colors to a dict to use later
initial_node_colors = dict(node_colors)
# positions for node labels
node_label_pos = { k:[v[0],v[1]-10] for k,v in romania_locations.items() }
# use this while labeling edges
edge_labels = dict()
# add edges between cities in romania map - UndirectedGraph defined in search.py
for node in romania_map.nodes():
connections = romania_map.get(node)
for connection in connections.keys():
distance = connections[connection]
# add edges to the graph
G.add_edge(node, connection)
# add distances to edge_labels
edge_labels[(node, connection)] = distance
# + [markdown] deletable=true editable=true
# We have completed building our graph based on romania_map and its locations. It's time to display it here in the notebook. This function `show_map(node_colors)` helps us do that. We will be calling this function later on to display the map at each and every interval step while searching, using variety of algorithms from the book.
# + deletable=true editable=true
def show_map(node_colors):
# set the size of the plot
plt.figure(figsize=(18,13))
# draw the graph (both nodes and edges) with locations from romania_locations
nx.draw(G, pos = romania_locations, node_color = [node_colors[node] for node in G.nodes()])
# draw labels for nodes
node_label_handles = nx.draw_networkx_labels(G, pos = node_label_pos, labels = node_labels, font_size = 14)
# add a white bounding box behind the node labels
[label.set_bbox(dict(facecolor='white', edgecolor='none')) for label in node_label_handles.values()]
# add edge lables to the graph
nx.draw_networkx_edge_labels(G, pos = romania_locations, edge_labels=edge_labels, font_size = 14)
# add a legend
white_circle = lines.Line2D([], [], color="white", marker='o', markersize=15, markerfacecolor="white")
orange_circle = lines.Line2D([], [], color="orange", marker='o', markersize=15, markerfacecolor="orange")
red_circle = lines.Line2D([], [], color="red", marker='o', markersize=15, markerfacecolor="red")
gray_circle = lines.Line2D([], [], color="gray", marker='o', markersize=15, markerfacecolor="gray")
green_circle = lines.Line2D([], [], color="green", marker='o', markersize=15, markerfacecolor="green")
plt.legend((white_circle, orange_circle, red_circle, gray_circle, green_circle),
('Un-explored', 'Frontier', 'Currently Exploring', 'Explored', 'Final Solution'),
numpoints=1,prop={'size':16}, loc=(.8,.75))
# show the plot. No need to use in notebooks. nx.draw will show the graph itself.
plt.show()
# + [markdown] deletable=true editable=true
# We can simply call the function with node_colors dictionary object to display it.
# + deletable=true editable=true
show_map(node_colors)
# + [markdown] deletable=true editable=true
# Voila! You see, the romania map as shown in the Figure[3.2] in the book. Now, see how different searching algorithms perform with our problem statements.
# + [markdown] deletable=true editable=true
# ## Searching algorithms visualisations
#
# In this section, we have visualisations of the following searching algorithms:
#
# 1. Breadth First Tree Search - Implemented
# 2. Depth First Tree Search
# 3. Depth First Graph Search
# 4. Breadth First Search - Implemented
# 5. Best First Graph Search
# 6. Uniform Cost Search - Implemented
# 7. Depth Limited Search
# 8. Iterative Deepening Search
# 9. A\*-Search - Implemented
# 10. Recursive Best First Search
#
# We add the colors to the nodes to have a nice visualisation when displaying. So, these are the different colors we are using in these visuals:
# * Un-explored nodes - <font color='black'>white</font>
# * Frontier nodes - <font color='orange'>orange</font>
# * Currently exploring node - <font color='red'>red</font>
# * Already explored nodes - <font color='gray'>gray</font>
#
# Now, we will define some helper methods to display interactive buttons and sliders when visualising search algorithms.
# + deletable=true editable=true
def final_path_colors(problem, solution):
"returns a node_colors dict of the final path provided the problem and solution"
# get initial node colors
final_colors = dict(initial_node_colors)
# color all the nodes in solution and starting node to green
final_colors[problem.initial] = "green"
for node in solution:
final_colors[node] = "green"
return final_colors
def display_visual(user_input, algorithm=None, problem=None):
if user_input == False:
def slider_callback(iteration):
# don't show graph for the first time running the cell calling this function
try:
show_map(all_node_colors[iteration])
except:
pass
def visualize_callback(Visualize):
if Visualize is True:
button.value = False
global all_node_colors
iterations, all_node_colors, node = algorithm(problem)
solution = node.solution()
all_node_colors.append(final_path_colors(problem, solution))
slider.max = len(all_node_colors) - 1
for i in range(slider.max + 1):
slider.value = i
#time.sleep(.5)
slider = widgets.IntSlider(min=0, max=1, step=1, value=0)
slider_visual = widgets.interactive(slider_callback, iteration = slider)
display(slider_visual)
button = widgets.ToggleButton(value = False)
button_visual = widgets.interactive(visualize_callback, Visualize = button)
display(button_visual)
if user_input == True:
node_colors = dict(initial_node_colors)
if algorithm == None:
algorithms = {"Breadth First Tree Search": breadth_first_tree_search,
"Breadth First Search": breadth_first_search,
"Uniform Cost Search": uniform_cost_search,
"A-star Search": astar_search}
algo_dropdown = widgets.Dropdown(description = "Search algorithm: ",
options = sorted(list(algorithms.keys())),
value = "Breadth First Tree Search")
display(algo_dropdown)
def slider_callback(iteration):
# don't show graph for the first time running the cell calling this function
try:
show_map(all_node_colors[iteration])
except:
pass
def visualize_callback(Visualize):
if Visualize is True:
button.value = False
problem = GraphProblem(start_dropdown.value, end_dropdown.value, romania_map)
global all_node_colors
if algorithm == None:
user_algorithm = algorithms[algo_dropdown.value]
# print(user_algorithm)
# print(problem)
iterations, all_node_colors, node = user_algorithm(problem)
solution = node.solution()
all_node_colors.append(final_path_colors(problem, solution))
slider.max = len(all_node_colors) - 1
for i in range(slider.max + 1):
slider.value = i
# time.sleep(.5)
start_dropdown = widgets.Dropdown(description = "Start city: ",
options = sorted(list(node_colors.keys())), value = "Arad")
display(start_dropdown)
end_dropdown = widgets.Dropdown(description = "Goal city: ",
options = sorted(list(node_colors.keys())), value = "Fagaras")
display(end_dropdown)
button = widgets.ToggleButton(value = False)
button_visual = widgets.interactive(visualize_callback, Visualize = button)
display(button_visual)
slider = widgets.IntSlider(min=0, max=1, step=1, value=0)
slider_visual = widgets.interactive(slider_callback, iteration = slider)
display(slider_visual)
# + [markdown] deletable=true editable=true
#
# ## Breadth first tree search
#
# We have a working implementation in search module. But as we want to interact with the graph while it is searching, we need to modify the implementation. Here's the modified breadth first tree search.
#
#
# + deletable=true editable=true
def tree_search(problem, frontier):
"""Search through the successors of a problem to find a goal.
The argument frontier should be an empty queue.
Don't worry about repeated paths to a state. [Figure 3.7]"""
# we use these two variables at the time of visualisations
iterations = 0
all_node_colors = []
node_colors = dict(initial_node_colors)
#Adding first node to the queue
frontier.append(Node(problem.initial))
node_colors[Node(problem.initial).state] = "orange"
iterations += 1
all_node_colors.append(dict(node_colors))
while frontier:
#Popping first node of queue
node = frontier.pop()
# modify the currently searching node to red
node_colors[node.state] = "red"
iterations += 1
all_node_colors.append(dict(node_colors))
if problem.goal_test(node.state):
# modify goal node to green after reaching the goal
node_colors[node.state] = "green"
iterations += 1
all_node_colors.append(dict(node_colors))
return(iterations, all_node_colors, node)
frontier.extend(node.expand(problem))
for n in node.expand(problem):
node_colors[n.state] = "orange"
iterations += 1
all_node_colors.append(dict(node_colors))
# modify the color of explored nodes to gray
node_colors[node.state] = "gray"
iterations += 1
all_node_colors.append(dict(node_colors))
return None
def breadth_first_tree_search(problem):
"Search the shallowest nodes in the search tree first."
iterations, all_node_colors, node = tree_search(problem, FIFOQueue())
return(iterations, all_node_colors, node)
# + [markdown] deletable=true editable=true
# Now, we use ipywidgets to display a slider, a button and our romania map. By sliding the slider we can have a look at all the intermediate steps of a particular search algorithm. By pressing the button **Visualize**, you can see all the steps without interacting with the slider. These two helper functions are the callback functions which are called when we interact with the slider and the button.
#
#
# + deletable=true editable=true
all_node_colors = []
romania_problem = GraphProblem('Arad', 'Fagaras', romania_map)
display_visual(user_input = False, algorithm = breadth_first_tree_search, problem = romania_problem)
# + [markdown] deletable=true editable=true
# ## Breadth first search
#
# Let's change all the node_colors to starting position and define a different problem statement.
# + deletable=true editable=true
def breadth_first_search(problem):
"[Figure 3.11]"
# we use these two variables at the time of visualisations
iterations = 0
all_node_colors = []
node_colors = dict(initial_node_colors)
node = Node(problem.initial)
node_colors[node.state] = "red"
iterations += 1
all_node_colors.append(dict(node_colors))
if problem.goal_test(node.state):
node_colors[node.state] = "green"
iterations += 1
all_node_colors.append(dict(node_colors))
return(iterations, all_node_colors, node)
frontier = FIFOQueue()
frontier.append(node)
# modify the color of frontier nodes to blue
node_colors[node.state] = "orange"
iterations += 1
all_node_colors.append(dict(node_colors))
explored = set()
while frontier:
node = frontier.pop()
node_colors[node.state] = "red"
iterations += 1
all_node_colors.append(dict(node_colors))
explored.add(node.state)
for child in node.expand(problem):
if child.state not in explored and child not in frontier:
if problem.goal_test(child.state):
node_colors[child.state] = "green"
iterations += 1
all_node_colors.append(dict(node_colors))
return(iterations, all_node_colors, child)
frontier.append(child)
node_colors[child.state] = "orange"
iterations += 1
all_node_colors.append(dict(node_colors))
node_colors[node.state] = "gray"
iterations += 1
all_node_colors.append(dict(node_colors))
return None
# + deletable=true editable=true
all_node_colors = []
romania_problem = GraphProblem('Arad', 'Bucharest', romania_map)
display_visual(user_input = False, algorithm = breadth_first_search, problem = romania_problem)
# + [markdown] deletable=true editable=true
# ## Uniform cost search
#
# Let's change all the node_colors to starting position and define a different problem statement.
# + deletable=true editable=true
def best_first_graph_search(problem, f):
"""Search the nodes with the lowest f scores first.
You specify the function f(node) that you want to minimize; for example,
if f is a heuristic estimate to the goal, then we have greedy best
first search; if f is node.depth then we have breadth-first search.
There is a subtlety: the line "f = memoize(f, 'f')" means that the f
values will be cached on the nodes as they are computed. So after doing
a best first search you can examine the f values of the path returned."""
# we use these two variables at the time of visualisations
iterations = 0
all_node_colors = []
node_colors = dict(initial_node_colors)
f = memoize(f, 'f')
node = Node(problem.initial)
node_colors[node.state] = "red"
iterations += 1
all_node_colors.append(dict(node_colors))
if problem.goal_test(node.state):
node_colors[node.state] = "green"
iterations += 1
all_node_colors.append(dict(node_colors))
return(iterations, all_node_colors, node)
frontier = PriorityQueue(min, f)
frontier.append(node)
node_colors[node.state] = "orange"
iterations += 1
all_node_colors.append(dict(node_colors))
explored = set()
while frontier:
node = frontier.pop()
node_colors[node.state] = "red"
iterations += 1
all_node_colors.append(dict(node_colors))
if problem.goal_test(node.state):
node_colors[node.state] = "green"
iterations += 1
all_node_colors.append(dict(node_colors))
return(iterations, all_node_colors, node)
explored.add(node.state)
for child in node.expand(problem):
if child.state not in explored and child not in frontier:
frontier.append(child)
node_colors[child.state] = "orange"
iterations += 1
all_node_colors.append(dict(node_colors))
elif child in frontier:
incumbent = frontier[child]
if f(child) < f(incumbent):
del frontier[incumbent]
frontier.append(child)
node_colors[child.state] = "orange"
iterations += 1
all_node_colors.append(dict(node_colors))
node_colors[node.state] = "gray"
iterations += 1
all_node_colors.append(dict(node_colors))
return None
def uniform_cost_search(problem):
"[Figure 3.14]"
iterations, all_node_colors, node = best_first_graph_search(problem, lambda node: node.path_cost)
return(iterations, all_node_colors, node)
# + [markdown] deletable=true editable=true
# ## A* search
#
# Let's change all the node_colors to starting position and define a different problem statement.
# + deletable=true editable=true
all_node_colors = []
romania_problem = GraphProblem('Arad', 'Bucharest', romania_map)
display_visual(user_input = False, algorithm = uniform_cost_search, problem = romania_problem)
# + deletable=true editable=true
def best_first_graph_search(problem, f):
"""Search the nodes with the lowest f scores first.
You specify the function f(node) that you want to minimize; for example,
if f is a heuristic estimate to the goal, then we have greedy best
first search; if f is node.depth then we have breadth-first search.
There is a subtlety: the line "f = memoize(f, 'f')" means that the f
values will be cached on the nodes as they are computed. So after doing
a best first search you can examine the f values of the path returned."""
# we use these two variables at the time of visualisations
iterations = 0
all_node_colors = []
node_colors = dict(initial_node_colors)
f = memoize(f, 'f')
node = Node(problem.initial)
node_colors[node.state] = "red"
iterations += 1
all_node_colors.append(dict(node_colors))
if problem.goal_test(node.state):
node_colors[node.state] = "green"
iterations += 1
all_node_colors.append(dict(node_colors))
return(iterations, all_node_colors, node)
frontier = PriorityQueue(min, f)
frontier.append(node)
node_colors[node.state] = "orange"
iterations += 1
all_node_colors.append(dict(node_colors))
explored = set()
while frontier:
node = frontier.pop()
node_colors[node.state] = "red"
iterations += 1
all_node_colors.append(dict(node_colors))
if problem.goal_test(node.state):
node_colors[node.state] = "green"
iterations += 1
all_node_colors.append(dict(node_colors))
return(iterations, all_node_colors, node)
explored.add(node.state)
for child in node.expand(problem):
if child.state not in explored and child not in frontier:
frontier.append(child)
node_colors[child.state] = "orange"
iterations += 1
all_node_colors.append(dict(node_colors))
elif child in frontier:
incumbent = frontier[child]
if f(child) < f(incumbent):
del frontier[incumbent]
frontier.append(child)
node_colors[child.state] = "orange"
iterations += 1
all_node_colors.append(dict(node_colors))
node_colors[node.state] = "gray"
iterations += 1
all_node_colors.append(dict(node_colors))
return None
def astar_search(problem, h=None):
"""A* search is best-first graph search with f(n) = g(n)+h(n).
You need to specify the h function when you call astar_search, or
else in your Problem subclass."""
h = memoize(h or problem.h, 'h')
iterations, all_node_colors, node = best_first_graph_search(problem, lambda n: n.path_cost + h(n))
return(iterations, all_node_colors, node)
# + deletable=true editable=true
all_node_colors = []
romania_problem = GraphProblem('Arad', 'Bucharest', romania_map)
display_visual(user_input = False, algorithm = astar_search, problem = romania_problem)
# + deletable=true editable=true
all_node_colors = []
# display_visual(user_input = True, algorithm = breadth_first_tree_search)
display_visual(user_input = True)
# + [markdown] deletable=true editable=true
# ## Genetic Algorithm
#
# Genetic algorithms (or GA) are inspired by natural evolution and are particularly useful in optimization and search problems with large state spaces.
#
# Given a problem, algorithms in the domain make use of a *population* of solutions (also called *states*), where each solution/state represents a feasible solution. At each iteration (often called *generation*), the population gets updated using methods inspired by biology and evolution, like *crossover*, *mutation* and *selection*.
# + [markdown] deletable=true editable=true
# ### Overview
#
# A genetic algorithm works in the following way:
#
# 1) Initialize random population.
#
# 2) Calculate population fitness.
#
# 3) Select individuals for mating.
#
# 4) Mate selected individuals to produce new population.
#
# * Random chance to mutate individuals.
#
# 5) Repeat from step 2) until an individual is fit enough or the maximum number of iterations was reached.
# + [markdown] deletable=true editable=true
# ### Glossary
#
# Before we continue, we will lay the basic terminology of the algorithm.
#
# * Individual/State: A string of chars (called *genes*) that represent possible solutions.
#
# * Population: The list of all the individuals/states.
#
# * Gene pool: The alphabet of possible values for an individual's genes.
#
# * Generation/Iteration: The number of times the population will be updated.
#
# * Fitness: An individual's score, calculated by a function specific to the problem.
# + [markdown] deletable=true editable=true
# ### Crossover
#
# Two individuals/states can "mate" and produce one child. This offspring bears characteristics from both of its parents. There are many ways we can implement this crossover. Here we will take a look at the most common ones. Most other methods are variations of those below.
#
# * Point Crossover: The crossover occurs around one (or more) point. The parents get "split" at the chosen point or points and then get merged. In the example below we see two parents get split and merged at the 3rd digit, producing the following offspring after the crossover.
#
# 
#
# * Uniform Crossover: This type of crossover chooses randomly the genes to get merged. Here the genes 1, 2 and 5 where chosen from the first parent, so the genes 3, 4 will be added by the second parent.
#
# 
# + [markdown] deletable=true editable=true
# ### Mutation
#
# When an offspring is produced, there is a chance it will mutate, having one (or more, depending on the implementation) of its genes altered.
#
# For example, let's say the new individual to undergo mutation is "abcde". Randomly we pick to change its third gene to 'z'. The individual now becomes "ab<font color='red'>z</font>de" and is added to the population.
# + [markdown] deletable=true editable=true
# ### Selection
#
# At each iteration, the fittest individuals are picked randomly to mate and produce offsprings. We measure an individual's fitness with a *fitness function*. That function depends on the given problem and it is used to score an individual. Usually the higher the better.
#
# The selection process is this:
#
# 1) Individuals are scored by the fitness function.
#
# 2) Individuals are picked randomly, according to their score (higher score means higher chance to get picked). Usually the formula to calculate the chance to pick an individual is the following (for population *P* and individual *i*):
#
# $$ chance(i) = \dfrac{fitness(i)}{\sum\limits_{k \, in \, P}{fitness(k)}} $$
# + [markdown] deletable=true editable=true
# ### Implementation
#
# Below we look over the implementation of the algorithm in the `search` module.
#
# First the implementation of the main core of the algorithm:
# + deletable=true editable=true
# %psource genetic_algorithm
# + [markdown] deletable=true editable=true
# The algorithm takes the following input:
#
# * `population`: The initial population.
#
# * `fitness_fn`: The problem's fitness function.
#
# * `gene_pool`: The gene pool of the states/individuals. Genes need to be chars. By default '0' and '1'.
#
# * `f_thres`: The fitness threshold. If an individual reaches that score, iteration stops. By default 'None', which means the algorithm will try and find the optimal solution.
#
# * `ngen`: The number of iterations/generations.
#
# * `pmut`: The probability of mutation.
#
# The algorithm gives as output the state with the largest score.
# + [markdown] deletable=true editable=true
# For each generation, the algorithm updates the population. First it calculates the fitnesses of the individuals, then it selects the most fit ones and finally crosses them over to produce offsprings. There is a chance that the offspring will be mutated, given by `pmut`. If at the end of the generation an individual meets the fitness threshold, the algorithm halts and returns that individual.
#
# The function of mating is accomplished by the method `reproduce`:
# + deletable=true editable=true
def reproduce(x, y):
n = len(x)
c = random.randrange(0, n)
return x[:c] + y[c:]
# + [markdown] deletable=true editable=true
# The method picks at random a point and merges the parents (`x` and `y`) around it.
#
# The mutation is done in the method `mutate`:
# + deletable=true editable=true
def mutate(x, gene_pool):
n = len(x)
g = len(gene_pool)
c = random.randrange(0, n)
r = random.randrange(0, g)
new_gene = gene_pool[r]
return x[:c] + new_gene + x[c+1:]
# + [markdown] deletable=true editable=true
# We pick a gene in `x` to mutate and a gene from the gene pool to replace it with.
#
# To help initializing the population we have the helper function `init_population`":
# + deletable=true editable=true
def init_population(pop_number, gene_pool, state_length):
g = len(gene_pool)
population = []
for i in range(pop_number):
new_individual = ''.join([gene_pool[random.randrange(0, g)]
for j in range(state_length)])
population.append(new_individual)
return population
# + [markdown] deletable=true editable=true
# The function takes as input the number of individuals in the population, the gene pool and the length of each individual/state. It creates individuals with random genes and returns the population when done.
# + [markdown] deletable=true editable=true
# ### Usage
#
# Below we give two example usages for the genetic algorithm, for a graph coloring problem and the 8 queens problem.
#
# #### Graph Coloring
#
# First we will take on the simpler problem of coloring a small graph with two colors. Before we do anything, let's imagine how a solution might look. First, we have only two colors, so we can represent them with a binary notation: 0 for one color and 1 for the other. These make up our gene pool. What of the individual solutions though? For that, we will look at our problem. We stated we have a graph. A graph has nodes and edges, and we want to color the nodes. Naturally, we want to store each node's color. If we have four nodes, we can store their colors in a string of genes, one for each node. A possible solution will then look like this: "1100". In the general case, we will represent each solution with a string of 1s and 0s, with length the number of nodes.
#
# Next we need to come up with a fitness function that appropriately scores individuals. Again, we will look at the problem definition at hand. We want to color a graph. For a solution to be optimal, no edge should connect two nodes of the same color. How can we use this information to score a solution? A naive (and ineffective) approach would be to count the different colors in the string. So "1111" has a score of 1 and "1100" has a score of 2. Why that fitness function is not ideal though? Why, we forgot the information about the edges! The edges are pivotal to the problem and the above function only deals with node colors. We didn't use all the information at hand and ended up with an ineffective answer. How, then, can we use that information to our advantage?
#
# We said that the optimal solution will have all the edges connecting nodes of different color. So, to score a solution we can count how many edges are valid (aka connecting nodes of different color). That is a great fitness function!
#
# Let's jump into solving this problem using the `genetic_algorithm` function.
# + [markdown] deletable=true editable=true
# First we need to represent the graph. Since we mostly need information about edges, we will just store the edges. We will denote edges with capital letters and nodes with integers:
# + deletable=true editable=true
edges = {
'A': [0, 1],
'B': [0, 3],
'C': [1, 2],
'D': [2, 3]
}
# + [markdown] deletable=true editable=true
# Edge 'A' connects nodes 0 and 1, edge 'B' connects nodes 0 and 3 etc.
#
# We already said our gene pool is 0 and 1, so we can jump right into initializing our population. Since we have only four nodes, `state_length` should be 4. For the number of individuals, we will try 8. We can increase this number if we need higher accuracy, but be careful! Larger populations need more computating power and take longer. You need to strike that sweet balance between accuracy and cost (the ultimate dilemma of the programmer!).
# + deletable=true editable=true
population = init_population(8, ['0', '1'], 4)
print(population)
# + [markdown] deletable=true editable=true
# We created and printed the population. You can see that the genes in the individuals are random and there are 8 individuals each with 4 genes.
#
# Next we need to write our fitness function. We previously said we want the function to count how many edges are valid. So, given a coloring/individual `c`, we will do just that:
# + deletable=true editable=true
def fitness(c):
return sum(c[n1] != c[n2] for (n1, n2) in edges.values())
# + [markdown] deletable=true editable=true
# Great! Now we will run the genetic algorithm and see what solution it gives.
# + deletable=true editable=true
solution = genetic_algorithm(population, fitness)
print(solution)
# + [markdown] deletable=true editable=true
# The algorithm converged to a solution. Let's check its score:
# + deletable=true editable=true
print(fitness(solution))
# + [markdown] deletable=true editable=true
# The solution has a score of 4. Which means it is optimal, since we have exactly 4 edges in our graph, meaning all are valid!
#
# *NOTE: Because the algorithm is non-deterministic, there is a chance a different solution is given. It might even be wrong, if we are very unlucky!*
# + [markdown] deletable=true editable=true
# #### Eight Queens
#
# Let's take a look at a more complicated problem.
#
# In the *Eight Queens* problem, we are tasked with placing eight queens on an 8x8 chessboard without any queen threatening the others (aka queens should not be in the same row, column or diagonal). In its general form the problem is defined as placing *N* queens in an NxN chessboard without any conflicts.
#
# First we need to think about the representation of each solution. We can go the naive route of representing the whole chessboard with the queens' placements on it. That is definitely one way to go about it, but for the purpose of this tutorial we will do something different. We have eight queens, so we will have a gene for each of them. The gene pool will be numbers from 0 to 7, for the different columns. The *position* of the gene in the state will denote the row the particular queen is placed in.
#
# For example, we can have the state "03304577". Here the first gene with a value of 0 means "the queen at row 0 is placed at column 0", for the second gene "the queen at row 1 is placed at column 3" and so forth.
#
# We now need to think about the fitness function. On the graph coloring problem we counted the valid edges. The same thought process can be applied here. Instead of edges though, we have positioning between queens. If two queens are not threatening each other, we say they are at a "non-attacking" positioning. We can, therefore, count how many such positionings are there.
#
# Let's dive right in and initialize our population:
# + deletable=true editable=true
population = init_population(100, [str(i) for i in range(8)], 8)
print(population[:5])
# + [markdown] deletable=true editable=true
# We have a population of 100 and each individual has 8 genes. The gene pool is the integers from 0 to 7, in string form. Above you can see the first five individuals.
#
# Next we need to write our fitness function. Remember, queens threaten each other if they are at the same row, column or diagonal.
#
# Since positionings are mutual, we must take care not to count them twice. Therefore for each queen, we will only check for conflicts for the queens after her.
#
# A gene's value in an individual `q` denotes the queen's column, and the position of the gene denotes its row. We can check if the aforementioned values between two genes are the same. We also need to check for diagonals. A queen *a* is in the diagonal of another queen, *b*, if the difference of the rows between them is equal to either their difference in columns (for the diagonal on the right of *a*) or equal to the negative difference of their columns (for the left diagonal of *a*). Below is given the fitness function.
# + deletable=true editable=true
def fitness(q):
non_attacking = 0
for row1 in range(len(q)):
for row2 in range(row1+1, len(q)):
col1 = int(q[row1])
col2 = int(q[row2])
row_diff = row1 - row2
col_diff = col1 - col2
if col1 != col2 and row_diff != col_diff and row_diff != -col_diff:
non_attacking += 1
return non_attacking
# + [markdown] deletable=true editable=true
# Note that the best score achievable is 28. That is because for each queen we only check for the queens after her. For the first queen we check 7 other queens, for the second queen 6 others and so on. In short, the number of checks we make is the sum 7+6+5+...+1. Which is equal to 7\*(7+1)/2 = 28.
#
# Because it is very hard and will take long to find a perfect solution, we will set the fitness threshold at 25. If we find an individual with a score greater or equal to that, we will halt. Let's see how the genetic algorithm will fare.
# + deletable=true editable=true
solution = genetic_algorithm(population, fitness, f_thres=25)
print(solution)
print(fitness(solution))
# + [markdown] deletable=true editable=true
# Above you can see the solution and its fitness score, which should be no less than 25.
# + [markdown] deletable=true editable=true
# With that this tutorial on the genetic algorithm comes to an end. Hope you found this guide helpful!
|
search.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Linear Models for Classification
# # Exercise
# Load and preprocess the adult data as before.
# include dummy encoding and scaling
# Learn a logistic regression model and visualize the coefficients.
# Then grid-search the regularization parameter C.
# Compare the coefficients of the best model with the coefficients of a model with more regularization.
import pandas as pd
pd.read_csv("data/adult.csv", index_col=0)
# +
# # %load solutions/adult_classification.py
|
notebooks/04 - Linear Models for Classification.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Programming Exercise 4: Neural Networks Learning
#
# ## Introduction
#
# In this exercise, you will implement the backpropagation algorithm for neural networks and apply it to the task of hand-written digit recognition. Before starting on the programming exercise, we strongly recommend watching the video lectures and completing the review questions for the associated topics.
#
#
# All the information you need for solving this assignment is in this notebook, and all the code you will be implementing will take place within this notebook. The assignment can be promptly submitted to the coursera grader directly from this notebook (code and instructions are included below).
#
# Before we begin with the exercises, we need to import all libraries required for this programming exercise. Throughout the course, we will be using [`numpy`](http://www.numpy.org/) for all arrays and matrix operations, [`matplotlib`](https://matplotlib.org/) for plotting, and [`scipy`](https://docs.scipy.org/doc/scipy/reference/) for scientific and numerical computation functions and tools. You can find instructions on how to install required libraries in the README file in the [github repository](https://github.com/dibgerge/ml-coursera-python-assignments).
# +
# used for manipulating directory paths
import os
# Scientific and vector computation for python
import numpy as np
# Plotting library
from matplotlib import pyplot
# Optimization module in scipy
from scipy import optimize
# will be used to load MATLAB mat datafile format
from scipy.io import loadmat
# library written for this exercise providing additional functions for assignment submission, and others
import utils
# define the submission/grader object for this exercise
grader = utils.Grader()
# tells matplotlib to embed plots within the notebook
# %matplotlib inline
# -
# ## Submission and Grading
#
#
# After completing each part of the assignment, be sure to submit your solutions to the grader. The following is a breakdown of how each part of this exercise is scored.
#
#
# | Section | Part | Submission function | Points
# | :- |:- | :- | :-:
# | 1 | [Feedforward and Cost Function](#section1) | [`nnCostFunction`](#nnCostFunction) | 30
# | 2 | [Regularized Cost Function](#section2) | [`nnCostFunction`](#nnCostFunction) | 15
# | 3 | [Sigmoid Gradient](#section3) | [`sigmoidGradient`](#sigmoidGradient) | 5
# | 4 | [Neural Net Gradient Function (Backpropagation)](#section4) | [`nnCostFunction`](#nnCostFunction) | 40
# | 5 | [Regularized Gradient](#section5) | [`nnCostFunction`](#nnCostFunction) |10
# | | Total Points | | 100
#
#
# You are allowed to submit your solutions multiple times, and we will take only the highest score into consideration.
#
# <div class="alert alert-block alert-warning">
# At the end of each section in this notebook, we have a cell which contains code for submitting the solutions thus far to the grader. Execute the cell to see your score up to the current section. For all your work to be submitted properly, you must execute those cells at least once.
# </div>
# ## Neural Networks
#
# In the previous exercise, you implemented feedforward propagation for neural networks and used it to predict handwritten digits with the weights we provided. In this exercise, you will implement the backpropagation algorithm to learn the parameters for the neural network.
#
# We start the exercise by first loading the dataset.
# +
# training data stored in arrays X, y
data = loadmat(os.path.join('Data', 'ex4data1.mat'))
X, y = data['X'], data['y'].ravel()
# set the zero digit to 0, rather than its mapped 10 in this dataset
# This is an artifact due to the fact that this dataset was used in
# MATLAB where there is no index 0
y[y == 10] = 0
# Number of training examples
m = y.size
# -
# ### 1.1 Visualizing the data
#
# You will begin by visualizing a subset of the training set, using the function `displayData`, which is the same function we used in Exercise 3. It is provided in the `utils.py` file for this assignment as well. The dataset is also the same one you used in the previous exercise.
#
# There are 5000 training examples in `ex4data1.mat`, where each training example is a 20 pixel by 20 pixel grayscale image of the digit. Each pixel is represented by a floating point number indicating the grayscale intensity at that location. The 20 by 20 grid of pixels is “unrolled” into a 400-dimensional vector. Each
# of these training examples becomes a single row in our data matrix $X$. This gives us a 5000 by 400 matrix $X$ where every row is a training example for a handwritten digit image.
#
# $$ X = \begin{bmatrix} - \left(x^{(1)} \right)^T - \\
# - \left(x^{(2)} \right)^T - \\
# \vdots \\
# - \left(x^{(m)} \right)^T - \\
# \end{bmatrix}
# $$
#
# The second part of the training set is a 5000-dimensional vector `y` that contains labels for the training set.
# The following cell randomly selects 100 images from the dataset and plots them.
# +
# Randomly select 100 data points to display
rand_indices = np.random.choice(m, 100, replace=False)
sel = X[rand_indices, :]
utils.displayData(sel)
# -
# ### 1.2 Model representation
#
# Our neural network is shown in the following figure.
#
# 
#
# It has 3 layers - an input layer, a hidden layer and an output layer. Recall that our inputs are pixel values
# of digit images. Since the images are of size $20 \times 20$, this gives us 400 input layer units (not counting the extra bias unit which always outputs +1). The training data was loaded into the variables `X` and `y` above.
#
# You have been provided with a set of network parameters ($\Theta^{(1)}, \Theta^{(2)}$) already trained by us. These are stored in `ex4weights.mat` and will be loaded in the next cell of this notebook into `Theta1` and `Theta2`. The parameters have dimensions that are sized for a neural network with 25 units in the second layer and 10 output units (corresponding to the 10 digit classes).
# +
# Setup the parameters you will use for this exercise
input_layer_size = 400 # 20x20 Input Images of Digits
hidden_layer_size = 25 # 25 hidden units
num_labels = 10 # 10 labels, from 0 to 9
# Load the weights into variables Theta1 and Theta2
weights = loadmat(os.path.join('Data', 'ex4weights.mat'))
# Theta1 has size 25 x 401
# Theta2 has size 10 x 26
Theta1, Theta2 = weights['Theta1'], weights['Theta2']
# swap first and last columns of Theta2, due to legacy from MATLAB indexing,
# since the weight file ex3weights.mat was saved based on MATLAB indexing
Theta2 = np.roll(Theta2, 1, axis=0)
# Unroll parameters
nn_params = np.concatenate([Theta1.ravel(), Theta2.ravel()])
# -
# <a id="section1"></a>
# ### 1.3 Feedforward and cost function
#
# Now you will implement the cost function and gradient for the neural network. First, complete the code for the function `nnCostFunction` in the next cell to return the cost.
#
# Recall that the cost function for the neural network (without regularization) is:
#
# $$ J(\theta) = \frac{1}{m} \sum_{i=1}^{m}\sum_{k=1}^{K} \left[ - y_k^{(i)} \log \left( \left( h_\theta \left( x^{(i)} \right) \right)_k \right) - \left( 1 - y_k^{(i)} \right) \log \left( 1 - \left( h_\theta \left( x^{(i)} \right) \right)_k \right) \right]$$
#
# where $h_\theta \left( x^{(i)} \right)$ is computed as shown in the neural network figure above, and K = 10 is the total number of possible labels. Note that $h_\theta(x^{(i)})_k = a_k^{(3)}$ is the activation (output
# value) of the $k^{th}$ output unit. Also, recall that whereas the original labels (in the variable y) were 0, 1, ..., 9, for the purpose of training a neural network, we need to encode the labels as vectors containing only values 0 or 1, so that
#
# $$ y =
# \begin{bmatrix} 1 \\ 0 \\ 0 \\\vdots \\ 0 \end{bmatrix}, \quad
# \begin{bmatrix} 0 \\ 1 \\ 0 \\ \vdots \\ 0 \end{bmatrix}, \quad \cdots \quad \text{or} \qquad
# \begin{bmatrix} 0 \\ 0 \\ 0 \\ \vdots \\ 1 \end{bmatrix}.
# $$
#
# For example, if $x^{(i)}$ is an image of the digit 5, then the corresponding $y^{(i)}$ (that you should use with the cost function) should be a 10-dimensional vector with $y_5 = 1$, and the other elements equal to 0.
#
# You should implement the feedforward computation that computes $h_\theta(x^{(i)})$ for every example $i$ and sum the cost over all examples. **Your code should also work for a dataset of any size, with any number of labels** (you can assume that there are always at least $K \ge 3$ labels).
#
# <div class="alert alert-box alert-warning">
# **Implementation Note:** The matrix $X$ contains the examples in rows (i.e., X[i,:] is the i-th training example $x^{(i)}$, expressed as a $n \times 1$ vector.) When you complete the code in `nnCostFunction`, you will need to add the column of 1’s to the X matrix. The parameters for each unit in the neural network is represented in Theta1 and Theta2 as one row. Specifically, the first row of Theta1 corresponds to the first hidden unit in the second layer. You can use a for-loop over the examples to compute the cost.
# </div>
# <a id="nnCostFunction"></a>
# +
def nnCostFunction(nn_params,
input_layer_size,
hidden_layer_size,
num_labels,
X, y, lambda_=0.0):
"""
Implements the neural network cost function and gradient for a two layer neural
network which performs classification.
Parameters
----------
nn_params : array_like
The parameters for the neural network which are "unrolled" into
a vector. This needs to be converted back into the weight matrices Theta1
and Theta2.
input_layer_size : int
Number of features for the input layer.
hidden_layer_size : int
Number of hidden units in the second layer.
num_labels : int
Total number of labels, or equivalently number of units in output layer.
X : array_like
Input dataset. A matrix of shape (m x input_layer_size).
y : array_like
Dataset labels. A vector of shape (m,).
lambda_ : float, optional
Regularization parameter.
Returns
-------
J : float
The computed value for the cost function at the current weight values.
grad : array_like
An "unrolled" vector of the partial derivatives of the concatenatation of
neural network weights Theta1 and Theta2.
Instructions
------------
You should complete the code by working through the following parts.
- Part 1: Feedforward the neural network and return the cost in the
variable J. After implementing Part 1, you can verify that your
cost function computation is correct by verifying the cost
computed in the following cell.
- Part 2: Implement the backpropagation algorithm to compute the gradients
Theta1_grad and Theta2_grad. You should return the partial derivatives of
the cost function with respect to Theta1 and Theta2 in Theta1_grad and
Theta2_grad, respectively. After implementing Part 2, you can check
that your implementation is correct by running checkNNGradients provided
in the utils.py module.
Note: The vector y passed into the function is a vector of labels
containing values from 0..K-1. You need to map this vector into a
binary vector of 1's and 0's to be used with the neural network
cost function.
Hint: We recommend implementing backpropagation using a for-loop
over the training examples if you are implementing it for the
first time.
- Part 3: Implement regularization with the cost function and gradients.
Hint: You can implement this around the code for
backpropagation. That is, you can compute the gradients for
the regularization separately and then add them to Theta1_grad
and Theta2_grad from Part 2.
Note
----
We have provided an implementation for the sigmoid function in the file
`utils.py` accompanying this assignment.
"""
# Reshape nn_params back into the parameters Theta1 and Theta2, the weight matrices
# for our 2 layer neural network
Theta1 = np.reshape(nn_params[:hidden_layer_size * (input_layer_size + 1)],
(hidden_layer_size, (input_layer_size + 1)))
Theta2 = np.reshape(nn_params[(hidden_layer_size * (input_layer_size + 1)):],
(num_labels, (hidden_layer_size + 1)))
# Setup some useful variables
m = y.size
# You need to return the following variables correctly
J = 0
Theta1_grad = np.zeros(Theta1.shape)
Theta2_grad = np.zeros(Theta2.shape)
# ====================== YOUR CODE HERE ======================
# print('input_layer_size', input_layer_size)
# print('hidden_layer_size', hidden_layer_size)
# print('num_labels', num_labels)
# Add ones to the X data matrix
X = np.concatenate([np.ones((m, 1)), X], axis=1)
# Encoding y
# > recall that whereas the original labels (in the variable y) were 0, 1, ..., 9,
# > for the purpose of training a neural network, we need to encode the labels as
# > vectors containing only values 0 or 1
y_encoded = np.zeros((y.size, num_labels)) # y_encoded will be of size m x k
y_encoded[np.arange(y.size), y] = 1
Z2 = Theta1 @ X.T
A2 = utils.sigmoid(Z2).T
A2 = np.concatenate([np.ones((A2.shape[0], 1)), A2], axis=1) # add bias term to A2 (hidden layer units)
Z3 = Theta2 @ A2.T
A3 = utils.sigmoid(Z3).T # hypothesis
hyp = A3
for i in range(m):
J += (y_encoded[i] @ np.log(hyp[i]) + (1 - y_encoded[i]) @ np.log(1 - hyp[i]))
regularization = (lambda_ / (2 * m)) * (np.sum(Theta1[:,1:] ** 2) + np.sum(Theta2[:,1:] ** 2))
J = - (1 / m) * J + regularization
for t in range(m):
a1 = X[t]
z2 = Theta1 @ a1
a2 = utils.sigmoid(z2)
a2 = np.concatenate([[1], a2])
z3 = Theta2 @ a2
a3 = utils.sigmoid(z3) # hypothesis
delta_3 = a3 - y_encoded[t]
delta_2 = (Theta2.T @ delta_3) * (a2 * (1 - a2))
delta_2 = delta_2[1:]
Theta2_grad = Theta2_grad + delta_3.reshape(-1, 1) @ a2.reshape(-1, 1).T
Theta1_grad = Theta1_grad + delta_2.reshape(-1, 1) @ a1.reshape(-1, 1).T
Theta2_regularization = (lambda_ / m) * Theta2[:, 1:]
Theta2_regularization = np.hstack((np.zeros((Theta2.shape[0], 1)), Theta2_regularization))
Theta1_regularization = (lambda_ / m) * Theta1[:, 1:]
Theta1_regularization = np.hstack((np.zeros((Theta1.shape[0], 1)), Theta1_regularization))
Theta2_grad = (1 / m) * Theta2_grad + Theta2_regularization
Theta1_grad = (1 / m) * Theta1_grad + Theta1_regularization
# ================================================================
# Unroll gradients
# grad = np.concatenate([Theta1_grad.ravel(order=order), Theta2_grad.ravel(order=order)])
grad = np.concatenate([Theta1_grad.ravel(), Theta2_grad.ravel()])
return J, grad
# -
# <div class="alert alert-box alert-warning">
# Use the following links to go back to the different parts of this exercise that require to modify the function `nnCostFunction`.<br>
#
# Back to:
# - [Feedforward and cost function](#section1)
# - [Regularized cost](#section2)
# - [Neural Network Gradient (Backpropagation)](#section4)
# - [Regularized Gradient](#section5)
# </div>
# Once you are done, call your `nnCostFunction` using the loaded set of parameters for `Theta1` and `Theta2`. You should see that the cost is about 0.287629.
lambda_ = 0
J, _ = nnCostFunction(nn_params, input_layer_size, hidden_layer_size,
num_labels, X, y, lambda_)
print('Cost at parameters (loaded from ex4weights): %.6f ' % J)
print('The cost should be about : 0.287629.')
# *You should now submit your solutions.*
grader = utils.Grader()
grader[1] = nnCostFunction
grader.grade()
# <a id="section2"></a>
# ### 1.4 Regularized cost function
#
# The cost function for neural networks with regularization is given by:
#
#
# $$ J(\theta) = \frac{1}{m} \sum_{i=1}^{m}\sum_{k=1}^{K} \left[ - y_k^{(i)} \log \left( \left( h_\theta \left( x^{(i)} \right) \right)_k \right) - \left( 1 - y_k^{(i)} \right) \log \left( 1 - \left( h_\theta \left( x^{(i)} \right) \right)_k \right) \right] + \frac{\lambda}{2 m} \left[ \sum_{j=1}^{25} \sum_{k=1}^{400} \left( \Theta_{j,k}^{(1)} \right)^2 + \sum_{j=1}^{10} \sum_{k=1}^{25} \left( \Theta_{j,k}^{(2)} \right)^2 \right] $$
#
# You can assume that the neural network will only have 3 layers - an input layer, a hidden layer and an output layer. However, your code should work for any number of input units, hidden units and outputs units. While we
# have explicitly listed the indices above for $\Theta^{(1)}$ and $\Theta^{(2)}$ for clarity, do note that your code should in general work with $\Theta^{(1)}$ and $\Theta^{(2)}$ of any size. Note that you should not be regularizing the terms that correspond to the bias. For the matrices `Theta1` and `Theta2`, this corresponds to the first column of each matrix. You should now add regularization to your cost function. Notice that you can first compute the unregularized cost function $J$ using your existing `nnCostFunction` and then later add the cost for the regularization terms.
#
# [Click here to go back to `nnCostFunction` for editing.](#nnCostFunction)
# Once you are done, the next cell will call your `nnCostFunction` using the loaded set of parameters for `Theta1` and `Theta2`, and $\lambda = 1$. You should see that the cost is about 0.383770.
# +
# Weight regularization parameter (we set this to 1 here).
lambda_ = 1
J, _ = nnCostFunction(nn_params, input_layer_size, hidden_layer_size,
num_labels, X, y, lambda_)
print('Cost at parameters (loaded from ex4weights): %.6f' % J)
print('This value should be about : 0.383770.')
# -
# *You should now submit your solutions.*
grader[2] = nnCostFunction
grader.grade()
# ## 2 Backpropagation
#
# In this part of the exercise, you will implement the backpropagation algorithm to compute the gradient for the neural network cost function. You will need to update the function `nnCostFunction` so that it returns an appropriate value for `grad`. Once you have computed the gradient, you will be able to train the neural network by minimizing the cost function $J(\theta)$ using an advanced optimizer such as `scipy`'s `optimize.minimize`.
# You will first implement the backpropagation algorithm to compute the gradients for the parameters for the (unregularized) neural network. After you have verified that your gradient computation for the unregularized case is correct, you will implement the gradient for the regularized neural network.
# <a id="section3"></a>
# ### 2.1 Sigmoid Gradient
#
# To help you get started with this part of the exercise, you will first implement
# the sigmoid gradient function. The gradient for the sigmoid function can be
# computed as
#
# $$ g'(z) = \frac{d}{dz} g(z) = g(z)\left(1-g(z)\right) $$
#
# where
#
# $$ \text{sigmoid}(z) = g(z) = \frac{1}{1 + e^{-z}} $$
#
# Now complete the implementation of `sigmoidGradient` in the next cell.
# <a id="sigmoidGradient"></a>
def sigmoidGradient(z):
"""
Computes the gradient of the sigmoid function evaluated at z.
This should work regardless if z is a matrix or a vector.
In particular, if z is a vector or matrix, you should return
the gradient for each element.
Parameters
----------
z : array_like
A vector or matrix as input to the sigmoid function.
Returns
--------
g : array_like
Gradient of the sigmoid function. Has the same shape as z.
Instructions
------------
Compute the gradient of the sigmoid function evaluated at
each value of z (z can be a matrix, vector or scalar).
Note
----
We have provided an implementation of the sigmoid function
in `utils.py` file accompanying this assignment.
"""
g = np.zeros(z.shape)
# ====================== YOUR CODE HERE ======================
g = utils.sigmoid(z) * (1 - utils.sigmoid(z))
# =============================================================
return g
# When you are done, the following cell call `sigmoidGradient` on a given vector `z`. Try testing a few values by calling `sigmoidGradient(z)`. For large values (both positive and negative) of z, the gradient should be close to 0. When $z = 0$, the gradient should be exactly 0.25. Your code should also work with vectors and matrices. For a matrix, your function should perform the sigmoid gradient function on every element.
z = np.array([-1, -0.5, 0, 0.5, 1])
g = sigmoidGradient(z)
print('Sigmoid gradient evaluated at [-1 -0.5 0 0.5 1]:\n ')
print(g)
# *You should now submit your solutions.*
grader[3] = sigmoidGradient
grader.grade()
# ## 2.2 Random Initialization
#
# When training neural networks, it is important to randomly initialize the parameters for symmetry breaking. One effective strategy for random initialization is to randomly select values for $\Theta^{(l)}$ uniformly in the range $[-\epsilon_{init}, \epsilon_{init}]$. You should use $\epsilon_{init} = 0.12$. This range of values ensures that the parameters are kept small and makes the learning more efficient.
#
# <div class="alert alert-box alert-warning">
# One effective strategy for choosing $\epsilon_{init}$ is to base it on the number of units in the network. A good choice of $\epsilon_{init}$ is $\epsilon_{init} = \frac{\sqrt{6}}{\sqrt{L_{in} + L_{out}}}$ where $L_{in} = s_l$ and $L_{out} = s_{l+1}$ are the number of units in the layers adjacent to $\Theta^{l}$.
# </div>
#
# Your job is to complete the function `randInitializeWeights` to initialize the weights for $\Theta$. Modify the function by filling in the following code:
#
# ```python
# # Randomly initialize the weights to small values
# W = np.random.rand(L_out, 1 + L_in) * 2 * epsilon_init - epsilon_init
# ```
# Note that we give the function an argument for $\epsilon$ with default value `epsilon_init = 0.12`.
def randInitializeWeights(L_in, L_out, epsilon_init=0.12):
"""
Randomly initialize the weights of a layer in a neural network.
Parameters
----------
L_in : int
Number of incomming connections.
L_out : int
Number of outgoing connections.
epsilon_init : float, optional
Range of values which the weight can take from a uniform
distribution.
Returns
-------
W : array_like
The weight initialiatized to random values. Note that W should
be set to a matrix of size(L_out, 1 + L_in) as
the first column of W handles the "bias" terms.
Instructions
------------
Initialize W randomly so that we break the symmetry while training
the neural network. Note that the first column of W corresponds
to the parameters for the bias unit.
"""
# You need to return the following variables correctly
W = np.zeros((L_out, 1 + L_in))
# ====================== YOUR CODE HERE ======================
# Randomly initialize the weights to small values
W = np.random.rand(L_out, 1 + L_in) * 2 * epsilon_init - epsilon_init
# ============================================================
return W
# *You do not need to submit any code for this part of the exercise.*
#
# Execute the following cell to initialize the weights for the 2 layers in the neural network using the `randInitializeWeights` function.
# +
print('Initializing Neural Network Parameters ...')
initial_Theta1 = randInitializeWeights(input_layer_size, hidden_layer_size)
initial_Theta2 = randInitializeWeights(hidden_layer_size, num_labels)
# Unroll parameters
initial_nn_params = np.concatenate([initial_Theta1.ravel(), initial_Theta2.ravel()], axis=0)
# -
# <a id="section4"></a>
# ### 2.4 Backpropagation
#
# 
#
# Now, you will implement the backpropagation algorithm. Recall that the intuition behind the backpropagation algorithm is as follows. Given a training example $(x^{(t)}, y^{(t)})$, we will first run a “forward pass” to compute all the activations throughout the network, including the output value of the hypothesis $h_\theta(x)$. Then, for each node $j$ in layer $l$, we would like to compute an “error term” $\delta_j^{(l)}$ that measures how much that node was “responsible” for any errors in our output.
#
# For an output node, we can directly measure the difference between the network’s activation and the true target value, and use that to define $\delta_j^{(3)}$ (since layer 3 is the output layer). For the hidden units, you will compute $\delta_j^{(l)}$ based on a weighted average of the error terms of the nodes in layer $(l+1)$. In detail, here is the backpropagation algorithm (also depicted in the figure above). You should implement steps 1 to 4 in a loop that processes one example at a time. Concretely, you should implement a for-loop `for t in range(m)` and place steps 1-4 below inside the for-loop, with the $t^{th}$ iteration performing the calculation on the $t^{th}$ training example $(x^{(t)}, y^{(t)})$. Step 5 will divide the accumulated gradients by $m$ to obtain the gradients for the neural network cost function.
#
# 1. Set the input layer’s values $(a^{(1)})$ to the $t^{th }$training example $x^{(t)}$. Perform a feedforward pass, computing the activations $(z^{(2)}, a^{(2)}, z^{(3)}, a^{(3)})$ for layers 2 and 3. Note that you need to add a `+1` term to ensure that the vectors of activations for layers $a^{(1)}$ and $a^{(2)}$ also include the bias unit. In `numpy`, if a 1 is a column matrix, adding one corresponds to `a_1 = np.concatenate([np.ones((m, 1)), a_1], axis=1)`.
#
# 1. For each output unit $k$ in layer 3 (the output layer), set
# $$\delta_k^{(3)} = \left(a_k^{(3)} - y_k \right)$$
# where $y_k \in \{0, 1\}$ indicates whether the current training example belongs to class $k$ $(y_k = 1)$, or if it belongs to a different class $(y_k = 0)$. You may find logical arrays helpful for this task (explained in the previous programming exercise).
#
# 1. For the hidden layer $l = 2$, set
# $$ \delta^{(2)} = \left( \Theta^{(2)} \right)^T \delta^{(3)} * g'\left(z^{(2)} \right)$$
# Note that the symbol $*$ performs element wise multiplication in `numpy`.
#
# 1. Accumulate the gradient from this example using the following formula. Note that you should skip or remove $\delta_0^{(2)}$. In `numpy`, removing $\delta_0^{(2)}$ corresponds to `delta_2 = delta_2[1:]`.
# $$ \Delta^{(l)} = \Delta^{(l)} + \delta^{(l+1)} (a^{(l)})^{(T)} $$
#
# 1. Obtain the (unregularized) gradient for the neural network cost function by dividing the accumulated gradients by $\frac{1}{m}$:
# $$ \frac{\partial}{\partial \Theta_{ij}^{(l)}} J(\Theta) = D_{ij}^{(l)} = \frac{1}{m} \Delta_{ij}^{(l)}$$
#
# <div class="alert alert-box alert-warning">
# **Python/Numpy tip**: You should implement the backpropagation algorithm only after you have successfully completed the feedforward and cost functions. While implementing the backpropagation alogrithm, it is often useful to use the `shape` function to print out the shapes of the variables you are working with if you run into dimension mismatch errors.
# </div>
#
# [Click here to go back and update the function `nnCostFunction` with the backpropagation algorithm](#nnCostFunction).
#
#
# **Note:** If the iterative solution provided above is proving to be difficult to implement, try implementing the vectorized approach which is easier to implement in the opinion of the moderators of this course. You can find the tutorial for the vectorized approach [here](https://www.coursera.org/learn/machine-learning/discussions/all/threads/a8Kce_WxEeS16yIACyoj1Q).
# After you have implemented the backpropagation algorithm, we will proceed to run gradient checking on your implementation. The gradient check will allow you to increase your confidence that your code is
# computing the gradients correctly.
#
# ### 2.4 Gradient checking
#
# In your neural network, you are minimizing the cost function $J(\Theta)$. To perform gradient checking on your parameters, you can imagine “unrolling” the parameters $\Theta^{(1)}$, $\Theta^{(2)}$ into a long vector $\theta$. By doing so, you can think of the cost function being $J(\Theta)$ instead and use the following gradient checking procedure.
#
# Suppose you have a function $f_i(\theta)$ that purportedly computes $\frac{\partial}{\partial \theta_i} J(\theta)$; you’d like to check if $f_i$ is outputting correct derivative values.
#
# $$
# \text{Let } \theta^{(i+)} = \theta + \begin{bmatrix} 0 \\ 0 \\ \vdots \\ \epsilon \\ \vdots \\ 0 \end{bmatrix}
# \quad \text{and} \quad \theta^{(i-)} = \theta - \begin{bmatrix} 0 \\ 0 \\ \vdots \\ \epsilon \\ \vdots \\ 0 \end{bmatrix}
# $$
#
# So, $\theta^{(i+)}$ is the same as $\theta$, except its $i^{th}$ element has been incremented by $\epsilon$. Similarly, $\theta^{(i−)}$ is the corresponding vector with the $i^{th}$ element decreased by $\epsilon$. You can now numerically verify $f_i(\theta)$’s correctness by checking, for each $i$, that:
#
# $$ f_i\left( \theta \right) \approx \frac{J\left( \theta^{(i+)}\right) - J\left( \theta^{(i-)} \right)}{2\epsilon} $$
#
# The degree to which these two values should approximate each other will depend on the details of $J$. But assuming $\epsilon = 10^{-4}$, you’ll usually find that the left- and right-hand sides of the above will agree to at least 4 significant digits (and often many more).
#
# We have implemented the function to compute the numerical gradient for you in `computeNumericalGradient` (within the file `utils.py`). While you are not required to modify the file, we highly encourage you to take a look at the code to understand how it works.
#
# In the next cell we will run the provided function `checkNNGradients` which will create a small neural network and dataset that will be used for checking your gradients. If your backpropagation implementation is correct,
# you should see a relative difference that is less than 1e-9.
#
# <div class="alert alert-box alert-success">
# **Practical Tip**: When performing gradient checking, it is much more efficient to use a small neural network with a relatively small number of input units and hidden units, thus having a relatively small number
# of parameters. Each dimension of $\theta$ requires two evaluations of the cost function and this can be expensive. In the function `checkNNGradients`, our code creates a small random model and dataset which is used with `computeNumericalGradient` for gradient checking. Furthermore, after you are confident that your gradient computations are correct, you should turn off gradient checking before running your learning algorithm.
# </div>
#
# <div class="alert alert-box alert-success">
# <b>Practical Tip:</b> Gradient checking works for any function where you are computing the cost and the gradient. Concretely, you can use the same `computeNumericalGradient` function to check if your gradient implementations for the other exercises are correct too (e.g., logistic regression’s cost function).
# </div>
utils.checkNNGradients(nnCostFunction)
# *Once your cost function passes the gradient check for the (unregularized) neural network cost function, you should submit the neural network gradient function (backpropagation).*
grader[4] = nnCostFunction
grader.grade()
# <a id="section5"></a>
# ### 2.5 Regularized Neural Network
#
# After you have successfully implemented the backpropagation algorithm, you will add regularization to the gradient. To account for regularization, it turns out that you can add this as an additional term *after* computing the gradients using backpropagation.
#
# Specifically, after you have computed $\Delta_{ij}^{(l)}$ using backpropagation, you should add regularization using
#
# $$ \begin{align}
# & \frac{\partial}{\partial \Theta_{ij}^{(l)}} J(\Theta) = D_{ij}^{(l)} = \frac{1}{m} \Delta_{ij}^{(l)} & \qquad \text{for } j = 0 \\
# & \frac{\partial}{\partial \Theta_{ij}^{(l)}} J(\Theta) = D_{ij}^{(l)} = \frac{1}{m} \Delta_{ij}^{(l)} + \frac{\lambda}{m} \Theta_{ij}^{(l)} & \qquad \text{for } j \ge 1
# \end{align}
# $$
#
# Note that you should *not* be regularizing the first column of $\Theta^{(l)}$ which is used for the bias term. Furthermore, in the parameters $\Theta_{ij}^{(l)}$, $i$ is indexed starting from 1, and $j$ is indexed starting from 0. Thus,
#
# $$
# \Theta^{(l)} = \begin{bmatrix}
# \Theta_{1,0}^{(i)} & \Theta_{1,1}^{(l)} & \cdots \\
# \Theta_{2,0}^{(i)} & \Theta_{2,1}^{(l)} & \cdots \\
# \vdots & ~ & \ddots
# \end{bmatrix}
# $$
#
# [Now modify your code that computes grad in `nnCostFunction` to account for regularization.](#nnCostFunction)
#
# After you are done, the following cell runs gradient checking on your implementation. If your code is correct, you should expect to see a relative difference that is less than 1e-9.
# +
# Check gradients by running checkNNGradients
lambda_ = 3
utils.checkNNGradients(nnCostFunction, lambda_)
# Also output the costFunction debugging values
debug_J, _ = nnCostFunction(nn_params, input_layer_size,
hidden_layer_size, num_labels, X, y, lambda_)
print('\n\nCost at (fixed) debugging parameters (w/ lambda = %f): %f ' % (lambda_, debug_J))
print('(for lambda = 3, this value should be about 0.576051)')
# -
grader[5] = nnCostFunction
grader.grade()
# ### 2.6 Learning parameters using `scipy.optimize.minimize`
#
# After you have successfully implemented the neural network cost function
# and gradient computation, the next step we will use `scipy`'s minimization to learn a good set parameters.
# +
# After you have completed the assignment, change the maxiter to a larger
# value to see how more training helps.
options= {'maxiter': 500}
# You should also try different values of lambda
lambda_ = 1
# Create "short hand" for the cost function to be minimized
costFunction = lambda p: nnCostFunction(p, input_layer_size,
hidden_layer_size,
num_labels, X, y, lambda_)
# Now, costFunction is a function that takes in only one argument
# (the neural network parameters)
res = optimize.minimize(costFunction,
initial_nn_params,
jac=True,
method='TNC',
options=options)
# get the solution of the optimization
nn_params = res.x
# Obtain Theta1 and Theta2 back from nn_params
Theta1 = np.reshape(nn_params[:hidden_layer_size * (input_layer_size + 1)],
(hidden_layer_size, (input_layer_size + 1)))
Theta2 = np.reshape(nn_params[(hidden_layer_size * (input_layer_size + 1)):],
(num_labels, (hidden_layer_size + 1)))
# -
# After the training completes, we will proceed to report the training accuracy of your classifier by computing the percentage of examples it got correct. If your implementation is correct, you should see a reported
# training accuracy of about 95.3% (this may vary by about 1% due to the random initialization). It is possible to get higher training accuracies by training the neural network for more iterations. We encourage you to try
# training the neural network for more iterations (e.g., set `maxiter` to 400) and also vary the regularization parameter $\lambda$. With the right learning settings, it is possible to get the neural network to perfectly fit the training set.
pred = utils.predict(Theta1, Theta2, X)
print('Training Set Accuracy: %f' % (np.mean(pred == y) * 100))
# ## 3 Visualizing the Hidden Layer
#
# One way to understand what your neural network is learning is to visualize what the representations captured by the hidden units. Informally, given a particular hidden unit, one way to visualize what it computes is to find an input $x$ that will cause it to activate (that is, to have an activation value
# ($a_i^{(l)}$) close to 1). For the neural network you trained, notice that the $i^{th}$ row of $\Theta^{(1)}$ is a 401-dimensional vector that represents the parameter for the $i^{th}$ hidden unit. If we discard the bias term, we get a 400 dimensional vector that represents the weights from each input pixel to the hidden unit.
#
# Thus, one way to visualize the “representation” captured by the hidden unit is to reshape this 400 dimensional vector into a 20 × 20 image and display it (It turns out that this is equivalent to finding the input that gives the highest activation for the hidden unit, given a “norm” constraint on the input (i.e., $||x||_2 \le 1$)).
#
# The next cell does this by using the `displayData` function and it will show you an image with 25 units,
# each corresponding to one hidden unit in the network. In your trained network, you should find that the hidden units corresponds roughly to detectors that look for strokes and other patterns in the input.
utils.displayData(Theta1[:, 1:])
# ### 3.1 Optional (ungraded) exercise
#
# In this part of the exercise, you will get to try out different learning settings for the neural network to see how the performance of the neural network varies with the regularization parameter $\lambda$ and number of training steps (the `maxiter` option when using `scipy.optimize.minimize`). Neural networks are very powerful models that can form highly complex decision boundaries. Without regularization, it is possible for a neural network to “overfit” a training set so that it obtains close to 100% accuracy on the training set but does not as well on new examples that it has not seen before. You can set the regularization $\lambda$ to a smaller value and the `maxiter` parameter to a higher number of iterations to see this for youself.
|
jupyter-notebooks/ml-coursera-python-assignments/Exercise4/exercise4.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import sys
sys.path.append('../')
# %load_ext autoreload
# %autoreload 1
# %aimport log_plotter
from log_plotter import get_accuracies
import matplotlib.ticker as mtick
import matplotlib
matplotlib.rcParams['pdf.fonttype'] = 3
matplotlib.rcParams['ps.fonttype'] = 3
import matplotlib.pyplot as plt
plt.rcParams.update({'font.size': 16})
import numpy as np
def format_accuracies(unf_accuracies, tag='Tacc'):
reformed_accuracies = {}
for accuracy in unf_accuracies:
for method in accuracy[tag][0]:
# sample data ((0.0, 76.3499984741211), 'NUQ')
acc = method[0][1]
err = method[0][0]
method_name = method[1]
if method_name not in list(reformed_accuracies):
reformed_accuracies[method_name] = [acc]
else:
reformed_accuracies[method_name].append(acc)
return reformed_accuracies
x = np.arange(0, 10, 0.1)
colors = [
(0.00784313725490196, 0.24313725490196078, 1.0),
(1.0, 0.48627450980392156, 0.0),
(0.9098039215686274, 0.0, 0.043137254901960784),
(0.5450980392156862, 0.16862745098039217, 0.8862745098039215),
(0.6235294117647059, 0.2823529411764706, 0.0)]
for color in colors:
plt.plot(x, color=color)
plt.show()
# +
def plot_accuracies(accuracies, xaxis, filename, xtitle, ytitle, xscale=True):
colors = [
(0.00784313725490196, 0.24313725490196078, 1.0),
(1.0, 0.48627450980392156, 0.0),
(0.9098039215686274, 0.0, 0.043137254901960784),
(0.5450980392156862, 0.16862745098039217, 0.8862745098039215),
(0.6235294117647059, 0.2823529411764706, 0.0)]
colors2 = [(0.00392156862745098, 0.45098039215686275, 0.6980392156862745),
(0.8705882352941177, 0.5607843137254902, 0.0196078431372549),
(0.00784313725490196, 0.6196078431372549, 0.45098039215686275),
(0.8352941176470589, 0.3686274509803922, 0.0),
(0.8, 0.47058823529411764, 0.7372549019607844),
(0.792156862745098, 0.5686274509803921, 0.3803921568627451)]
colors3 = [(0.7561707035755478, 0.21038062283737025, 0.22352941176470587),
(0.940715109573241, 0.6099192618223759, 0.4812764321414839),
(0.9856978085351787, 0.8889657823913879, 0.8320645905420992),
(0.8605151864667436, 0.9174163783160324, 0.9487120338331411),
(0.530026912725875, 0.7456362937331797, 0.8560553633217994),
(0.1843137254901961, 0.47266435986159167, 0.7116493656286044)]
dark =[(0.0, 0.10980392156862745, 0.4980392156862745),
(0.6941176470588235, 0.25098039215686274, 0.050980392156862744),
(0.07058823529411765, 0.44313725490196076, 0.10980392156862745),
(0.5490196078431373, 0.03137254901960784, 0.0),
(0.34901960784313724, 0.11764705882352941, 0.44313725490196076),
(0.34901960784313724, 0.1843137254901961, 0.050980392156862744)]
color = [[0.00784314, 0.24313725, 1.],
[1., 0.48627451, 0.],
[0.10196078, 0.78823529, 0.21960784],
[0.90980392, 0., 0.04313725],
[0.54509804, 0.16862745, 0.88627451]]
#style = ['-', '--', ':', '-.']
styles = ['-']
orders = [ 'ALQ', 'AMQ', 'ALQ-N', 'AMQ-N','Qinf', 'TRN', 'NUQ,p=0.5', 'SignSGD', 'SignSGDInf']
import collections
# markers =
colors = color
# styles = ['-', '--', ':', '-.']
markers = ['o', 'X', 'p', '*', 'd', 'v']
index = 0
accuracies = collections.OrderedDict(sorted(accuracies.items()))
print(accuracies)
for method, vals in accuracies.items():
style = styles[0]
index_2 = orders.index(method)
color = colors[(index_2) % len(colors)]
marker = markers[(index_2) % len(markers)]
vals = np.array(vals)
indexes = vals != 0
plt.plot(np.array(xaxis)[indexes], vals[indexes], label=method, color=color, linestyle=style, marker=marker, markersize=10+index_2, markevery=2+index_2%3)
index += 1
ax = plt.gca()
if xscale:
ax.set_xscale('log')
ax.xaxis.set_major_formatter(mtick.ScalarFormatter())
ax.ticklabel_format(axis="x", style="sci", scilimits=(0,0))
ax.set_xlabel(xtitle)
plt.grid(linewidth=1)
ax.set_ylabel(ytitle + ' (%)')
handles, labels = plt.gca().get_legend_handles_labels()
# plt.title(ytitle + ' vs ' + xtitle)
norders = []
for order in orders:
if order in labels:
norders.append(order)
order = []
for label in labels:
order.append(norders.index(label))
nlabels = np.arange(len(labels)).tolist()
nhandles = np.arange(len(handles)).tolist()
for idx, label, handle in zip(order, labels, handles):
nlabels[idx] = label
nhandles[idx] = handle
print(nlabels)
dirn = 'figs_acc/'
plt.savefig(dirn + filename, dpi=100, bbox_inches='tight')
plt.legend(nhandles, nlabels, bbox_to_anchor=(1.01, 1.0))
plt.savefig(dirn+'lo-'+filename, dpi=100, bbox_inches='tight')
plt.legend(nhandles, nlabels)
plt.savefig(dirn+'li-'+filename, dpi=100, bbox_inches='tight')
# -
def trim_name(name, accuracies, pad=None):
new_accuracies = [0]*pad
for method, vals in accuracies.items():
new_accuracies += vals
return {
name: new_accuracies
}
# +
lg_tags = ['estim_sgd', 'nuq_method', 'nuq_mul']
logdir = '/h/iman/Code/nuqsgd/runs'
tag = 'Vacc'
ytitle = 'Validation Accuracy'
lg_replace = [('p2_', 'P='), ('estim_sgd', 'SGD'), ('nuq_mul_', 'p='), ('ngpu_', 'GPU='), ('nuq_method', ''), ('_q', 'Q'), ('nuq_inv_', 'Inv'), ('nuq_sym_', 'Sym'), ('_amq_nb', 'AMQ'), ('_amq', 'AMQ-N'), ('_alq_nb', 'ALQ'), ('_trn', 'TRN'), ('_alq', 'ALQ-N'), ('_qinf', 'Qinf'), ('kfac', 'K-FAC'), ('SGD,K-FAC', 'K-FAC'), ('estim_ntk', 'NTK'), ('adamw', 'AdamW'), ('adam', 'Adam'), ('lr_', 'LR='), ('LR=0.001', 'LR=1e-3'), ('LR=0.0001', 'LR=1e-4'), ('LR=0.0005', 'LR=5e-4'), ('LR=0.0002', 'LR=2e-4'), ('batch_size_', 'bs='), ('optim_start_', 'Start='), ('damping_', '$\epsilon=$'), ('_l2q', 'L2Q'), ('_none', 'SuperSGD'), ('nuq_layer_1', 'w/o layers'), ('nuq_layer_0', 'w/ layers'),('_nuq', 'NUQ')]
bucket_sizes = ['32', '64', '128', '256', '512', '1024', '2048', '4096', '8192', '16384', '32768']
accuracies_bs = []
for bucket_size in bucket_sizes:
patterns = ['.*runs_cifar10_full/bs_.*nuq_bucket_size_' + bucket_size + '.*,(?!(.*nuq_sym.*|.*nuq_inv))']
accuracies_bs.append(get_accuracies(patterns, lg_replace, lg_tags, logdir, tag))
accuracies_sgi = []
lg_tags = ['sa2']
lg_replace = [('sa2_', 'SignSGDInf')]
bucket_sizes = ['2048', '4096', '8192', '16384', '32768']
for bucket_size in bucket_sizes:
patterns = ['.*runs_cifar10_full/sa2_.*nuq_bucket_size_' + bucket_size + '.*,(?!(.*nuq_sym.*|.*nuq_inv))']
accuracies_sgi.append(get_accuracies(patterns, lg_replace, lg_tags, logdir, tag))
accuracies_sg = []
lg_tags = ['sa3']
lg_replace = [('sa3_', 'SignSGD')]
for bucket_size in bucket_sizes:
patterns = ['.*runs_cifar10_full/sa3_.*nuq_bucket_size_' + bucket_size + '.*,(?!(.*nuq_sym.*|.*nuq_inv))']
accuracies_sg.append(get_accuracies(patterns, lg_replace, lg_tags, logdir, tag))
# -
accuracies_bs
reformed_accuracies_sgi = format_accuracies(accuracies_sgi, tag)
reformed_accuracies_sg = format_accuracies(accuracies_sg, tag)
trimmed_accuracies_sgi = trim_name('SignSGDInf', reformed_accuracies_sgi, pad=6)
trimmed_accuracies_sg = trim_name('SignSGD', reformed_accuracies_sg, pad=6)
reformed_accuracies_bs = format_accuracies(accuracies_bs, tag)
reformed_accuracies_bs['SignSGD'] = trimmed_accuracies_sg['SignSGD']
reformed_accuracies_bs['SignSGDInf'] = trimmed_accuracies_sgi['SignSGDInf']
bucket_sizes = ['32', '64', '128', '256', '512', '1024', '2048', '4096', '8192', '16384', '32768']
bucket_sizes = list(map(int, bucket_sizes))
plot_accuracies(reformed_accuracies_bs, bucket_sizes, 'bucket-size-t.pdf', xtitle='Bucket Size', ytitle=ytitle)
# +
accuracies_bits = []
bits = ['2']
for bit in bits:
patterns = ['.*runs_cifar10_full/bi3_.*nuq_bits_' + bit + ',.*,(?!(.*nuq_sym.*|.*nuq_inv))']
accuracies_bits.append(get_accuracies(patterns, lg_replace, lg_tags, logdir))
bits = [ '3', '4', '5']
for bit in bits:
patterns = ['.*runs_cifar10_full/bi2_.*nuq_bits_' + bit + ',.*,(?!(.*nuq_sym.*|.*nuq_inv))']
accuracies_bits.append(get_accuracies(patterns, lg_replace, lg_tags, logdir))
bits = ['6']
for bit in bits:
patterns = ['.*runs_cifar10_full/bi4_.*nuq_bits_' + bit + ',.*,(?!(.*nuq_sym.*|.*nuq_inv))']
accuracies_bits.append(get_accuracies(patterns, lg_replace, lg_tags, logdir))
bits = [ '7']
for bit in bits:
patterns = ['.*runs_cifar10_full/bi2_.*nuq_bits_' + bit + ',.*,(?!(.*nuq_sym.*|.*nuq_inv))']
accuracies_bits.append(get_accuracies(patterns, lg_replace, lg_tags, logdir))
# -
accuracies_bits
bits = ['2', '3', '4', '5', '6', '7']
reformed_accuracies_bits = format_accuracies(accuracies_bits, tag)
bits = list(map(int, bits))
plot_accuracies(reformed_accuracies_bits, bits, 'bits-t.pdf', '# bits', xscale=False, ytitle=ytitle)
|
notebooks/figs_acc.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <center>
# <img src="../../img/ods_stickers.jpg">
# ## Открытый курс по машинному обучению
# </center>
# Автор материала: программист-исследователь Mail.ru Group, старший преподаватель Факультета Компьютерных Наук ВШЭ Юрий Кашницкий. Материал распространяется на условиях лицензии [Creative Commons CC BY-NC-SA 4.0](https://creativecommons.org/licenses/by-nc-sa/4.0/). Можно использовать в любых целях (редактировать, поправлять и брать за основу), кроме коммерческих, но с обязательным упоминанием автора материала.
# # Тема 7. Обучение без учителя: PCA и кластеризация
# ## <center>Бонус. Метод главных компонент. Игрушечный пример
# +
import numpy as np
# %matplotlib inline
from matplotlib import pyplot as plt
# -
# **Пусть дана выборка X.**
X = np.array([[1.0, 3.0], [3.0, 5.0], [5.0, 1.0], [7.0, 4.0], [4.0, 7.0]])
plt.scatter(X[:, 0], X[:, 1]);
# **Как выбрать направление, в проекции на которое дисперсия координат точек максимальна? Синия прямая или зеленая? А может, красная?**
plt.scatter(X[:, 0], X[:, 1])
plt.plot(np.linspace(1, 8, 10), np.linspace(1, 8, 10))
plt.plot(np.linspace(1, 8, 10), np.linspace(2, 4, 10))
plt.plot(np.linspace(1, 8, 10), np.linspace(5, 2, 10));
# **Стандартизуем матрицу X. Вычитаем средние по столбцам (4 и 4) и делим на стандартные отклонения по столбцам (2 и 2). Кстати, пришлось писать код, чтоб подобрать координаты так, чтоб все средние и отклонения были целыми :)**
from sklearn.preprocessing import StandardScaler
X_scaled = StandardScaler().fit_transform(X)
X_scaled
plt.scatter(X_scaled[:, 0], X_scaled[:, 1])
plt.plot([-2, 2], [0, 0], c="black")
plt.plot([0, 0], [-2, 2], c="black")
plt.xlim(-2, 2)
plt.ylim(-2, 2);
# **Назовем новые координаты (стоблцы матрицы X_scaled) $x_1$ и $x_2$. Задача: найти такую линейную комбинацию $z = \alpha x_1 + \beta x_2$, что дисперсия $z$ максимальна. При этом должно выполняться $\alpha^2 + \beta^2 = 1.$**
# **Заметим что $$\Large D[z] = E[(z - E[z])^2] = E[z^2] = \frac{1}{n} \sum_i^n z_i^2,$$ поскольку $E[z] = \alpha E[x_1] + \beta E[x_2] = 0$ (новые координаты центрированы).**
#
# **Тогда задача формализуется так:**
# $$\Large \begin{cases} \max_{\alpha, \beta} \sum_i^n (\alpha x_{1_i} + \beta x_{2_i})^2 \\ \alpha^2 + \beta^2 = 1\end{cases}$$
# У нас $2z = [-3\alpha -\beta,\ -\alpha +\beta,\ \alpha -3\beta,\ 3\alpha,\ 3\beta]^T$ (Для задачи максимизации неважно, что мы умножили на 2, зато так удобней).
#
# Распишем в нашем случае: $ \sum_i^n (\alpha x_{1_i} + \beta x_{2_i})^2 = (-3\alpha -\beta)^2 + ( -\alpha +\beta)^2 +( \alpha -3\beta)^2 +( 3\alpha)^2 +( 3\beta)^2 = 20\alpha^2 - 2\alpha\beta + 20\beta^2$ = <font color='green'>\\ поскольку $\alpha^2 + \beta^2 = 1$ \\ </font> = $20 - 2\alpha\beta$. Осталось только минимизировать $\alpha\beta$. Можно это делать методом Лагранжа, но в данном случае можно проще
#
# $$\Large \begin{cases} \min_{\alpha, \beta} \alpha\beta \\ \alpha^2 + \beta^2 = 1\end{cases}$$
#
# $\Large \alpha\beta = \beta^2(\frac{\alpha}{\beta})$ = <font color='green'>\\ замена t = $\frac{\alpha}{\beta}, \alpha^2 + \beta^2 = 1$ \\ </font> = $\Large \frac{t}{1+t^2}$. Ищем минимум функции одной переменной, находим, что $t^* = -1$.
#
# Значит, $$\Large \begin{cases} \alpha^* = -\beta^*\\ (\alpha^*)^2 + (\beta^*)^2 = 1\end{cases} \Rightarrow \alpha^* =
# \frac{1}{\sqrt{2}}, \beta^* = - \frac{1}{\sqrt{2}}$$
# Итак, $$\Large z = \frac{1}{\sqrt{2}} x_1 - \frac{1}{\sqrt{2}}x_2$$ То есть ось $z$ повернута на 45 градусов относительно $x_1$ и $x_2$ и "направлена на юго-восток".
plt.scatter(X_scaled[:, 0], X_scaled[:, 1])
plt.plot([-2, 2], [0, 0], c="black")
plt.plot([0, 0], [-2, 2], c="black")
plt.plot([-2, 2], [2, -2], c="red");
# **Новые координаты точек по оси z:**
X_scaled.dot(np.array([1.0 / np.sqrt(2), -1.0 / np.sqrt(2)]))
# ## Сингулярное разложение матрицы X
# Представление будет таким: $X = U\Sigma V^T$.
#
# - Матрица $U$ составлена из собственных векторов матрицы $XX^T$. Это левые сингулярные векторы матрицы $X$;
# - Матрица $V$ составлена из собственных векторов матрицы $X^TX$. Это правые сингулярные векторы матрицы $X$;
# - Матрица $\Sigma$ - диагональная (вне главной диагонали нули), и на диагонали стоят корни из собственных значений матрицы $X^TX$ (или $XX^T$). Это сингулярные числа матрицы $X$.
# $XX^T$ выглядит так:
X_scaled.dot(X_scaled.T)
# $X^TX$ выглядит так:
X_scaled.T.dot(X_scaled)
# Собственные вектора $XX^T$ (левые сингулярные):
np.linalg.eig(X_scaled.dot(X_scaled.T))[1]
# Собственные вектора $X^TX$ (правые сингулярные). Эти вектора задают представление главных компонент через исходные координаты (то есть они задают поворот).
np.linalg.eig(X_scaled.T.dot(X_scaled))[1]
# Видно, что главные компоненты: $$\Large z_1 = \frac{1}{\sqrt{2}} x_1 - \frac{1}{\sqrt{2}}x_2,\ z_2 = \frac{1}{\sqrt{2}} x_1 + \frac{1}{\sqrt{2}}x_2$$
# Собственные значения $X^TX$ (сингулярные числа):
np.linalg.eig(X_scaled.T.dot(X_scaled))[0]
np.linalg.eig(X_scaled.dot(X_scaled.T))[0]
# +
from scipy.linalg import svd
U, Sigma, VT = svd(X_scaled)
# -
# Действительно. На диагонали матрицы $\Sigma$ стоят корни из собственных значений $X^TX$ ($\sqrt{5.25} \approx 2.29, \sqrt{4.75} \approx 2.18$):
Sigma
# Вектора матрицы $VT$ (правые сингулярные векторы для исходной матрицы) задают поворот. То есть первая главная компонента "смотрит на юго-восток", вторая - на юго-запад.
VT
# Представление данных в проекции на 2 главные компоненты $Z = XV$:
X_scaled.dot(VT.T)
plt.scatter(X_scaled[:, 0], X_scaled[:, 1])
plt.plot([-2, 2], [0, 0], c="black")
plt.plot([0, 0], [-2, 2], c="black")
plt.plot([-2, 2], [2, -2], c="red")
plt.plot([-2, 2], [-2, 2], c="red");
# Здесь SVD SciPy "направил" ось z1 вправо и вниз, а ось z2 - влево и вниз. Можно проверить, что представление получилось правильным.
|
jupyter_russian/topic07_unsupervised/topic7_bonus_PCA_toy_example.ipynb
|