question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
sliding-window-median
|
Easy to understand O(nlogk) Java solution using TreeMap
|
easy-to-understand-onlogk-java-solution-gqgcc
|
TreeMap is used to implement an ordered MultiSet.\n\nIn this problem, I use two Ordered MultiSets as Heaps. One heap maintains the lowest 1/2 of the elements, a
|
brendon4565
|
NORMAL
|
2017-01-10T10:58:28.099000+00:00
|
2018-08-25T21:31:54.273252+00:00
| 18,145 | false |
TreeMap is used to implement an ordered MultiSet.\n\nIn this problem, I use two Ordered MultiSets as Heaps. One heap maintains the lowest 1/2 of the elements, and the other heap maintains the higher 1/2 of elements.\n \nThis implementation is faster than the usual implementation that uses 2 PriorityQueues, because unlike PriorityQueue, TreeMap can remove arbitrary element in logarithmic time.\n```\npublic class Solution {\n public double[] medianSlidingWindow(int[] nums, int k) {\n double[] res = new double[nums.length-k+1];\n TreeMap<Integer, Integer> minHeap = new TreeMap<Integer, Integer>();\n TreeMap<Integer, Integer> maxHeap = new TreeMap<Integer, Integer>(Collections.reverseOrder());\n \n int minHeapCap = k/2; //smaller heap when k is odd.\n int maxHeapCap = k - minHeapCap; \n \n for(int i=0; i< k; i++){\n maxHeap.put(nums[i], maxHeap.getOrDefault(nums[i], 0) + 1);\n }\n int[] minHeapSize = new int[]{0};\n int[] maxHeapSize = new int[]{k};\n for(int i=0; i< minHeapCap; i++){\n move1Over(maxHeap, minHeap, maxHeapSize, minHeapSize);\n }\n \n res[0] = getMedian(maxHeap, minHeap, maxHeapSize, minHeapSize);\n int resIdx = 1;\n \n for(int i=0; i< nums.length-k; i++){\n int addee = nums[i+k];\n if(addee <= maxHeap.keySet().iterator().next()){\n add(addee, maxHeap, maxHeapSize);\n } else {\n add(addee, minHeap, minHeapSize);\n }\n \n int removee = nums[i];\n if(removee <= maxHeap.keySet().iterator().next()){\n remove(removee, maxHeap, maxHeapSize);\n } else {\n remove(removee, minHeap, minHeapSize);\n }\n\n //rebalance\n if(minHeapSize[0] > minHeapCap){\n move1Over(minHeap, maxHeap, minHeapSize, maxHeapSize);\n } else if(minHeapSize[0] < minHeapCap){\n move1Over(maxHeap, minHeap, maxHeapSize, minHeapSize);\n }\n \n res[resIdx] = getMedian(maxHeap, minHeap, maxHeapSize, minHeapSize);\n resIdx++;\n }\n return res;\n }\n\n public double getMedian(TreeMap<Integer, Integer> bigHeap, TreeMap<Integer, Integer> smallHeap, int[] bigHeapSize, int[] smallHeapSize){\n return bigHeapSize[0] > smallHeapSize[0] ? (double) bigHeap.keySet().iterator().next() : ((double) bigHeap.keySet().iterator().next() + (double) smallHeap.keySet().iterator().next()) / 2.0;\n }\n \n //move the top element of heap1 to heap2\n public void move1Over(TreeMap<Integer, Integer> heap1, TreeMap<Integer, Integer> heap2, int[] heap1Size, int[] heap2Size){\n int peek = heap1.keySet().iterator().next();\n add(peek, heap2, heap2Size);\n remove(peek, heap1, heap1Size);\n }\n \n public void add(int val, TreeMap<Integer, Integer> heap, int[] heapSize){\n heap.put(val, heap.getOrDefault(val,0) + 1);\n heapSize[0]++;\n }\n \n public void remove(int val, TreeMap<Integer, Integer> heap, int[] heapSize){\n if(heap.put(val, heap.get(val) - 1) == 1) heap.remove(val);\n heapSize[0]--;\n }\n}\n```
| 51 | 3 |
[]
| 11 |
sliding-window-median
|
Python SortedArray (beats 100%) and 2-Heap(beats 90%) solution
|
python-sortedarray-beats-100-and-2-heapb-ixw1
|
\n### Array based solution: \n- the window is an array maintained in sorted order\n- the mid of the array is used to calculate the median\n- every iteration, t
|
bharanidharan
|
NORMAL
|
2017-07-27T05:05:16.647000+00:00
|
2018-10-26T04:05:02.096555+00:00
| 9,232 | false |
\n### Array based solution: \n- the window is an array maintained in sorted order\n- the mid of the array is used to calculate the median\n- every iteration, the incoming number is added in sorted order in the array using insert - `O(log K)` ?\n- every iteration, the outgoing number is removed from the array using bisect `O(log K)` ?\n\n`O(N logK)` beats 100%\n```\n# 132 ms\nclass SolutionSortedArrayFast(object):\n def medianSlidingWindow(self, nums, k):\n win, rv = nums[:k], []\n win.sort()\n odd = k%2\n for i,n in enumerate(nums[k:],k):\n rv.append((win[k/2]+win[k/2-1])/2. if not odd else win[(k-1)/2]*1.)\n win.pop(bisect(win, nums[i-k])-1) # <<< bisect is faster than .remove()\n insort(win, nums[i])\n rv.append((win[k/2]+win[k/2-1])/2. if not odd else win[(k-1)/2]*1.)\n return rv\n```\n\n### 2-heap (min, max) based solution: \n- uses 2 heaps left-(max)heap `lh` and right-(min)heap `rh`. The key idea is the maintain the size invariance of the heaps as we add and remove elements. The top of both the heaps can be used to calculate the median.\n- We use `lazy-deletion` from the heap \n- using the first `k` elements construct a min heap `lh`. Then pop `k-k/2` and add it to the `rh`. Now the heap sized are set at `k/2` and `k-k/2`\n- Iterate over rest of the numbers and add it to the appropriate heap and maintain heap size invariance by moving the top number from one heap to another as needed.\n\n`O(N logK)` beats 90%\n\n```\n# avg:180ms\nclass SolutionHeap(object):\n def medianSlidingWindow(self, nums, k):\n lh,rh,rv = [],[],[]\n # create the initial left and right heap\n for i,n in enumerate(nums[:k]): heappush(lh, (-n,i))\n for i in range(k-k/2):\n heappush(rh, (-lh[0][0], lh[0][1]))\n heappop(lh)\n for i,n in enumerate(nums[k:]):\n rv.append(rh[0][0]/1. if k%2 else (rh[0][0] - lh[0][0])/2.)\n if n >= rh[0][0]:\n heappush(rh,(n,i+k)) # rh +1\n if nums[i] <= rh[0][0]: # lh-1, unbalanced\n heappush(lh, (-rh[0][0], rh[0][1]))\n heappop(rh)\n # else: pass # rh-1, balanced\n else:\n heappush(lh,(-n,i+k)) # rh +1\n if nums[i] >= rh[0][0]: # rh-1, unbalanced\n heappush(rh, (-lh[0][0], lh[0][1]))\n heappop(lh)\n # else: pass # lh-1, balanced\n while(lh and lh[0][1] <= i): heappop(lh) # lazy-deletion\n while(rh and rh[0][1] <= i): heappop(rh) # lazy-deletion\n rv.append(rh[0][0]/1. if k%2 else (rh[0][0] - lh[0][0])/2.)\n return rv\n```
| 48 | 4 |
[]
| 12 |
sliding-window-median
|
C++ 95 ms single multiset O(n * log n)
|
c-95-ms-single-multiset-on-log-n-by-votr-046r
|
The reason to use two heaps is to have O(1) lookup for the median. It's is O(n) if we use multiset, but what if we reuse the median pointer when we can?\nThe so
|
votrubac
|
NORMAL
|
2017-01-09T06:23:09.141000+00:00
|
2017-01-09T06:23:09.141000+00:00
| 9,630 | false |
The reason to use two heaps is to have O(1) lookup for the median. It's is O(n) if we use multiset, but what if we reuse the median pointer when we can?\nThe solution below still has the O(n^2) worst case run-time, and the average case run-time is O(n * log n). We can achieve O(n * log n) in the worst case if we make sure that the multiset comparator is stable. \n```\nvector<double> medianSlidingWindow(vector<int>& nums, int k)\n{\n int size = nums.size(), median_pos = k - k / 2 - 1;\n vector<double> res(size - k + 1);\n multiset<int> s(nums.begin(), nums.begin() + k);\n auto it = next(s.begin(), median_pos);\n\n for (auto i = k; i <= size; ++i)\n {\n res[i - k] = ((double)*it + (k % 2 != 0 ? *it : *next(it))) / 2;\n if (i < size)\n {\n // magic numbers (instead of enum) for brevity. INT_MAX means to retrace the iterator from the beginning.\n int repos_it = INT_MAX; \n if (k > 2)\n {\n // if inserted or removed item equals to the current median, we need to retrace.\n // we do not know which exact element will be removed/inserted, and we cannot compare multiset iterators.\n // otherwise, we can keep or increment/decrement the current median iterator.\n if ((nums[i - k] < *it && nums[i] < *it) || (nums[i - k] > *it && nums[i] > *it)) repos_it = 0;\n else if (nums[i - k] < *it && nums[i] > *it) repos_it = 1; // advance forward.\n else if (nums[i - k] > *it && nums[i] < *it) repos_it = -1; // advance backward.\n }\n s.insert(nums[i]);\n s.erase(s.find(nums[i - k]));\n\n if (repos_it == INT_MAX) it = next(s.begin(), median_pos);\n else if (repos_it == 1) ++it;\n else if (repos_it == -1) --it;\n }\n }\n return res;\n}\n```
| 40 | 0 |
[]
| 6 |
sliding-window-median
|
Easiest solution using only vector | C++
|
easiest-solution-using-only-vector-c-by-dv0xw
|
\nclass Solution {\npublic:\n vector<double> medianSlidingWindow(vector<int>& nums, int k) {\n \n vector<double> res;\n vector<long long
|
user7392a
|
NORMAL
|
2020-09-28T10:02:54.867129+00:00
|
2020-09-28T10:10:26.305434+00:00
| 4,556 | false |
```\nclass Solution {\npublic:\n vector<double> medianSlidingWindow(vector<int>& nums, int k) {\n \n vector<double> res;\n vector<long long> med;\n \n for(int i= 0; i<k; i++)\n med.insert(lower_bound(med.begin(),med.end(),nums[i]),nums[i]);\n if(k%2==0)\n res.push_back((double)(med[k/2]+med[k/2-1])/2 );\n else\n res.push_back((double)med[k/2]);\n \n \n for(int i=k; i<nums.size(); i++)\n {\n med.erase(lower_bound(med.begin(),med.end(),nums[i-k]));\n med.insert(lower_bound(med.begin(),med.end(),nums[i]),nums[i]);\n if(k%2==0)\n res.push_back((double)(med[k/2]+med[k/2-1])/2 );\n else\n res.push_back((double)med[k/2]);\n }\n return res;\n }\n};\n```
| 38 | 0 |
['C', 'C++']
| 6 |
sliding-window-median
|
Java | TC: O(N*logK) | SC: (K) | Optimized sliding window using TreeSet
|
java-tc-onlogk-sc-k-optimized-sliding-wi-5zia
|
In following solution we are using TreeSet. Here, the remove operation in Java is most optimized\njava\n/**\n * Using TreeSet. (Here time complexity is most opt
|
NarutoBaryonMode
|
NORMAL
|
2021-10-07T07:19:41.311240+00:00
|
2021-10-07T07:52:52.440158+00:00
| 6,063 | false |
**In following solution we are using TreeSet. Here, the remove operation in Java is most optimized**\n```java\n/**\n * Using TreeSet. (Here time complexity is most optimized)\n *\n * Very similar to https://leetcode.com/problems/find-median-from-data-stream/\n *\n * Time Complexity: O((N-K)*log K + N*log K) = O(N * log K)\n * Add Elements = O(N*Log K)\n * Remove Elements = O((N-K)*log K) ==> TreeSet.remove() in JAVA is O(log K)\n *\n * Space Complexity: O(K)\n *\n * N = Length of nums array. K = Input k.\n */\nclass Solution {\n public double[] medianSlidingWindow(int[] nums, int k) {\n if (nums == null || k <= 0) {\n throw new IllegalArgumentException("Input is invalid");\n }\n\n int len = nums.length;\n double[] result = new double[len - k + 1];\n if (k == 1) {\n for (int i = 0; i < len; i++) {\n result[i] = (double) nums[i];\n }\n return result;\n // return Arrays.stream(nums).asDoubleStream().toArray();\n }\n\n Comparator<Integer> comparator = (a, b) -> (nums[a] != nums[b] ? Integer.compare(nums[a], nums[b]) : Integer.compare(a, b));\n TreeSet<Integer> smallNums = new TreeSet<>(comparator.reversed());\n TreeSet<Integer> largeNums = new TreeSet<>(comparator);\n\n for (int i = 0; i < len; i++) {\n if (i >= k) {\n removeElement(smallNums, largeNums, nums, i - k);\n }\n addElement(smallNums, largeNums, i);\n if (i >= k - 1) {\n result[i - (k - 1)] = getMedian(smallNums, largeNums, nums);\n }\n }\n\n return result;\n }\n\n private void addElement(TreeSet<Integer> smallNums, TreeSet<Integer> largeNums, int idx) {\n smallNums.add(idx);\n largeNums.add(smallNums.pollFirst());\n if (smallNums.size() < largeNums.size()) {\n smallNums.add(largeNums.pollFirst());\n }\n }\n\n private void removeElement(TreeSet<Integer> smallNums, TreeSet<Integer> largeNums, int[] nums, int idx) {\n if (largeNums.contains(idx)) {\n largeNums.remove(idx);\n if (smallNums.size() == largeNums.size() + 2) {\n largeNums.add(smallNums.pollFirst());\n }\n } else {\n smallNums.remove(idx);\n if (smallNums.size() < largeNums.size()) {\n smallNums.add(largeNums.pollFirst());\n }\n }\n }\n\n private double getMedian(TreeSet<Integer> smallNums, TreeSet<Integer> largeNums, int[] nums) {\n if (smallNums.size() == largeNums.size()) {\n return ((double) nums[smallNums.first()] + nums[largeNums.first()]) / 2;\n }\n return nums[smallNums.first()];\n }\n}\n```\n\n----\n**In following solution we are using Priority Queue (heap). Here, the remove operation in Java is not optimized**\n\n```java\n/**\n * Using Priority Queue. (Here time complexity is not optimized)\n *\n * Very similar to https://leetcode.com/problems/find-median-from-data-stream/\n *\n * Time Complexity: O((N-K)*K + N*log K).\n * Add Elements = O(N*Log K)\n * Remove Elements = O((N-K)*K) ==> PQ.remove() in JAVA is O(K)\n *\n * Space Complexity: O(K)\n *\n * N = Length of nums array. K = Input k.\n */\nclass Solution {\n public double[] medianSlidingWindow(int[] nums, int k) {\n if (nums == null || k <= 0) {\n throw new IllegalArgumentException("Input is invalid");\n }\n\n int len = nums.length;\n double[] result = new double[len - k + 1];\n if (k == 1) {\n for (int i = 0; i < len; i++) {\n result[i] = (double) nums[i];\n }\n return result;\n // return Arrays.stream(nums).asDoubleStream().toArray();\n }\n\n // MaxHeap\n PriorityQueue<Integer> smallNums = new PriorityQueue<>(Collections.reverseOrder());\n // Min Heap\n PriorityQueue<Integer> largeNums = new PriorityQueue<>();\n\n for (int i = 0; i < len; i++) {\n if (i >= k) {\n removeElement(smallNums, largeNums, nums[i - k]);\n }\n addElement(smallNums, largeNums, nums[i]);\n if (i >= k - 1) {\n result[i - (k - 1)] = getMedian(smallNums, largeNums);\n }\n }\n\n return result;\n }\n\n private void addElement(PriorityQueue<Integer> smallNums, PriorityQueue<Integer> largeNums, int n) {\n smallNums.offer(n);\n largeNums.offer(smallNums.poll());\n if (smallNums.size() < largeNums.size()) {\n smallNums.offer(largeNums.poll());\n }\n }\n\n private void removeElement(PriorityQueue<Integer> smallNums, PriorityQueue<Integer> largeNums, int n) {\n if (n >= largeNums.peek()) {\n largeNums.remove(n);\n if (smallNums.size() == largeNums.size() + 2) {\n largeNums.offer(smallNums.poll());\n }\n } else {\n smallNums.remove(n);\n if (smallNums.size() < largeNums.size()) {\n smallNums.offer(largeNums.poll());\n }\n }\n }\n\n private double getMedian(PriorityQueue<Integer> smallNums, PriorityQueue<Integer> largeNums) {\n if (smallNums.size() == largeNums.size()) {\n return ((double) smallNums.peek() + largeNums.peek()) / 2.0;\n }\n return smallNums.peek();\n }\n}\n```\n\n\n---\n\nSolutions to other Sliding Window questions on LeetCode:\n- [76. Minimum Window Substring](https://leetcode.com/problems/minimum-window-substring/discuss/1496754/Java-or-TC:-O(S+T)-or-SC:-O(T)-or-Space-optimized-Sliding-Window-using-Two-Pointers)\n- [340. Longest Substring with At Most K Distinct Characters](https://leetcode.com/problems/longest-substring-with-at-most-k-distinct-characters/discuss/1496838/Java-or-TC:-O(N)-or-SC:-O(K)-or-One-Pass-Sliding-Window-using-LinkedHashMap)\n- [159. Longest Substring with At Most Two Distinct Characters](https://leetcode.com/problems/longest-substring-with-at-most-two-distinct-characters/discuss/1496840/Java-or-TC:-O(N)-or-SC:-O(1)-or-One-Pass-Sliding-Window-using-LinkedHashMap)\n- [438. Find All Anagrams in a String](https://leetcode.com/problems/find-all-anagrams-in-a-string/discuss/1500039/Java-or-TC:-O(S+P)-or-SC:-O(1)-or-Sliding-window-solution)\n- [3. Longest Substring Without Repeating Characters](https://leetcode.com/problems/longest-substring-without-repeating-characters/discuss/1500874/Java-or-TC:-O(N)-or-SC:-O(1)-or-Sliding-Window-using-HashMap-and-Two-Pointers)\n- [209. Minimum Size Subarray Sum](https://leetcode.com/problems/minimum-size-subarray-sum/discuss/1500877/Java-or-Both-O(N)-and-O(N-logN)-solutions-with-O(1)-space-or-Sliding-Window-and-Binary-Search-solutions)\n- [219. Contains Duplicate II](https://leetcode.com/problems/contains-duplicate-ii/discuss/1500887/Java-or-TC:-O(N)-or-SC:-O(min(N-K))-or-Sliding-Window-using-HashSet)\n- [220. Contains Duplicate III](https://leetcode.com/problems/contains-duplicate-iii/discuss/1500895/Java-or-TC:-O(N)-or-SC:-O(min(NK))-or-Sliding-Window-using-Buckets)\n- [567. Permutation in String](https://leetcode.com/problems/permutation-in-string/discuss/1500902/Java-or-TC:-O(S2)-or-SC:-O(1)-or-Constant-space-Sliding-Window-solution)\n- [239. Sliding Window Maximum](https://leetcode.com/problems/sliding-window-maximum/discuss/1506048/Java-or-TC:-O(N)-or-SC:-O(K)-or-Using-Deque-as-Sliding-Window)\n- [487. Max Consecutive Ones II](https://leetcode.com/problems/max-consecutive-ones-ii/discuss/1508045/Java-or-TC:-O(N)-or-SC:-O(1)-or-Four-solutions-with-Follow-up-handled)\n- [1004. Max Consecutive Ones III](https://leetcode.com/problems/max-consecutive-ones-iii/discuss/1508044/Java-or-TC:-O(N)-or-SC:-O(1)-or-One-Pass-Optimized-Sliding-Window)
| 36 | 0 |
['Array', 'Tree', 'Sliding Window', 'Heap (Priority Queue)', 'Ordered Set', 'Java']
| 7 |
sliding-window-median
|
Easy to understand Java solution using 2 Priority Queues
|
easy-to-understand-java-solution-using-2-1cu4
|
\nclass Solution {\n \n public double[] medianSlidingWindow(int[] nums, int k) {\n MeanQueue queue = new MeanQueue();\n double[] result = ne
|
pradeepneo
|
NORMAL
|
2018-08-10T18:40:24.192389+00:00
|
2018-08-27T06:45:04.795962+00:00
| 2,930 | false |
```\nclass Solution {\n \n public double[] medianSlidingWindow(int[] nums, int k) {\n MeanQueue queue = new MeanQueue();\n double[] result = new double[nums.length - k + 1];\n int index = 0;\n \n for(int i = 0; i < nums.length; i++){\n queue.offer(nums[i]);\n if(queue.size() == k){\n result[index++] = queue.getMedian();\n queue.remove(nums[i+1 - k]);\n }\n }\n\n return result;\n }\n \n class MeanQueue{\n PriorityQueue<Integer> max = new PriorityQueue<Integer>(Collections.reverseOrder()); //max is a Max-heap stores smaller half of nums\n PriorityQueue<Integer> min = new PriorityQueue<Integer>(); // min is a Min-heap stores larger half of nums\n \n // Adds a number into the data structure\n void offer(int num){\n max.offer(num); // Add number\n min.offer(max.poll()); // Balancing step\n \n if(max.size() < min.size()){ // maintain size property\n max.offer(min.poll());\n }\n }\n \n double getMedian(){\n return max.size() > min.size() ? max.peek() : ((long)max.peek() + min.peek()) * 0.5;\n }\n \n int size(){\n return max.size() + min.size();\n }\n \n boolean remove(int x){\n return max.remove(x) || min.remove(x);\n }\n \n }\n}\n```
| 29 | 2 |
[]
| 3 |
sliding-window-median
|
[C++] SIMPLE code using Multiset, Shorter, Replicable for Interviews
|
c-simple-code-using-multiset-shorter-rep-pee5
|
The idea can be borrowed from https://leetcode.com/problems/find-median-from-data-stream/ i.e. using a max-heap and min-heap for the left and right halves of th
|
penrosecat
|
NORMAL
|
2021-07-26T22:40:11.024769+00:00
|
2021-07-26T22:40:11.024812+00:00
| 1,852 | false |
The idea can be borrowed from https://leetcode.com/problems/find-median-from-data-stream/ i.e. using a max-heap and min-heap for the left and right halves of the window elements. \n\nHowever, we also want efficient insertion and deletion from the heaps, so instead of priority queue we can use set in C++ to store sorted values with O(logn) insert/find/delete. Now, if we can insert and balance the heaps as in the solution to the linked problem, the only thing that is different is to add a deletion of the old element before adding the new element from the window. \n\nTo make the code easier to read, I convert insert, balance and median finding into separate functions. Since elements can be repeated, multiset can be used, and because this question has edge cases using INT_MAX, double is used instead of int to avoid overflow. \n\n```\n void insert(multiset<double,greater<double>> &left, multiset<double> &right, int num)\n {\n if(left.empty() || num < *left.begin())\n {\n left.insert(num);\n }\n else\n {\n right.insert(num);\n }\n }\n \n void balance(multiset<double,greater<double>> &left, multiset<double> &right)\n {\n if(left.size() + 1 < right.size())\n {\n left.insert(*right.begin());\n right.erase(right.begin());\n }\n else if(right.size() + 1 < left.size())\n {\n right.insert(*left.begin());\n left.erase(left.begin());\n }\n }\n \n void add_median(multiset<double,greater<double>> &left, multiset<double> &right, vector<double> &median)\n {\n if(right.size() == left.size())\n {\n median.push_back((*left.begin() + *right.begin())/2.0);\n }\n else if(right.size() > left.size())\n {\n median.push_back(*right.begin());\n }\n else\n {\n median.push_back(*left.begin());\n }\n \n }\n \n vector<double> medianSlidingWindow(vector<int>& nums, int k) {\n multiset<double> right;\n multiset<double,greater<double>> left;\n \n vector<double> median;\n \n for(int i = 0; i<k; i++)\n {\n insert(left,right,nums[i]);\n balance(left,right);\n }\n \n add_median(left,right,median);\n\n for(int i = k; i<nums.size(); i++)\n {\n auto lcheck = left.find(nums[i-k]);\n auto rcheck = right.find(nums[i-k]);\n \n if(lcheck != left.end())\n {\n left.erase(lcheck);\n }\n else\n {\n right.erase(rcheck);\n }\n \n balance(left,right);\n insert(left,right,nums[i]);\n balance(left,right);\n add_median(left,right,median);\n \n }\n \n return median;\n }\n```\n\nSince all the operations are O(logk) where k is the window size, and we have to do the same for n elements, the time complexity is O(nlogk).
| 28 | 0 |
['C']
| 6 |
sliding-window-median
|
Java + Easy to understand + 2 Heaps
|
java-easy-to-understand-2-heaps-by-learn-hs29
|
Inutition\nIf we can maintain 2 Heaps - maxHeap and minHeap, where maxHeap stores the smaller half values and minHeap stores the larger half values, so that any
|
learn4Fun
|
NORMAL
|
2021-02-17T05:45:29.556808+00:00
|
2021-02-17T05:52:14.329127+00:00
| 3,636 | false |
#### Inutition\nIf we can maintain 2 Heaps - `maxHeap` and `minHeap`, where `maxHeap` stores the smaller half values and `minHeap` stores the larger half values, so that any point of time the top most element of the 2 heaps will provide the median.\n\n#### Code\n```\nclass Solution {\n private PriorityQueue<Integer> minHeap = new PriorityQueue<>();\n private PriorityQueue<Integer> maxHeap = new PriorityQueue<>(Collections.reverseOrder());\n \n public double[] medianSlidingWindow(int[] nums, int k) {\n \n double[] median = new double[nums.length - k + 1];\n for(int i=0; i < nums.length; i++){\n add(nums[i]);\n\t\t\t// When the index reaches size of k, we can find the median and remove the first element in the window\n if (i + 1 >= k) {\n median[i-k+1] = findMedian();\n remove(nums[i-k+1]);\n }\n }\n return median;\n }\n \n\t// For odd number of elements, top most element in maxHeap is the median of the current window, \n\t// else mean of maxHeap top & minHeap top represents the median\n private double findMedian(){\n return maxHeap.size() > minHeap.size() ? maxHeap.peek() : minHeap.peek() / 2.0 + maxHeap.peek() / 2.0;\n }\n\n\t// This method adds the next element in the sliding window in the appropriate heap and rebalances the heaps\n private void add(int num){\n if (maxHeap.size() == 0 || maxHeap.peek() >= num) \n maxHeap.add(num);\n else minHeap.add(num);\n rebalanceHeaps();\n }\n\n\t// This method removes the first element in the sliding window from the appropriate heap and rebalances the heaps\n private void remove(int num){\n if (num > maxHeap.peek())\n minHeap.remove(num);\n else maxHeap.remove(num);\n rebalanceHeaps();\n } \n \n\t// This method keeps the height of the 2 heaps same\n private void rebalanceHeaps(){\n if (maxHeap.size() == minHeap.size())\n return;\n if (maxHeap.size() > minHeap.size() + 1)\n minHeap.add(maxHeap.poll());\n else if (maxHeap.size() < minHeap.size())\n maxHeap.add(minHeap.poll()); \n }\n}\n```
| 23 | 1 |
['Sliding Window', 'Java']
| 6 |
sliding-window-median
|
Java clean and easily readable solution with a helper class
|
java-clean-and-easily-readable-solution-3e5p8
|
\n public double[] medianSlidingWindow(int[] nums, int k) {\n MedianQueue window = new MedianQueue();\n double[] median = new double[nums.lengt
|
yuxiangmusic
|
NORMAL
|
2017-01-11T05:30:09.214000+00:00
|
2017-01-11T05:30:09.214000+00:00
| 3,755 | false |
```\n public double[] medianSlidingWindow(int[] nums, int k) {\n MedianQueue window = new MedianQueue();\n double[] median = new double[nums.length - k + 1]; \n for (int i = 0; i < nums.length; i++) {\n window.add(nums[i]);\n if (i >= k) window.remove(nums[i - k]);\n if (i >= k - 1) median[i - k + 1] = window.median();\n } \n return median;\n } \n\n static class MedianQueue {\n Queue<Long> maxHeap = new PriorityQueue<>(Collections.reverseOrder()), minHeap = new PriorityQueue<>();\n\n public void add(long n) {\n maxHeap.add(n);\n minHeap.add(maxHeap.poll());\n } \n\n public double median() {\n while (maxHeap.size() - minHeap.size() >= 2) minHeap.offer(maxHeap.poll());\n while (minHeap.size() - maxHeap.size() >= 1) maxHeap.offer(minHeap.poll());\n return maxHeap.size() == minHeap.size() ? (maxHeap.peek() + minHeap.peek()) / 2.0 : maxHeap.peek();\n } \n\n public boolean remove(long n) {\n return maxHeap.remove(n) || minHeap.remove(n);\n }\n }\n```
| 23 | 1 |
[]
| 4 |
sliding-window-median
|
Simple C++ || Two Heap || Explained || Comments
|
simple-c-two-heap-explained-comments-by-y1w0a
|
```\nclass Solution {\npublic:\n vector medianSlidingWindow(vector& nums, int k) {\n vector medians;\n int n = nums.size();\n unordered_
|
mohit_motwani
|
NORMAL
|
2022-05-18T15:52:05.831818+00:00
|
2022-05-18T15:52:05.831862+00:00
| 4,633 | false |
```\nclass Solution {\npublic:\n vector<double> medianSlidingWindow(vector<int>& nums, int k) {\n vector<double> medians;\n int n = nums.size();\n unordered_map<int,int> mp; // for late deletion\n priority_queue<int> maxh; // max heap for lower half\n priority_queue<int, vector<int>, greater<int>> minh; // min heap for upper half\n \n for(int i=0;i<k;i++) {\n maxh.push(nums[i]);\n }\n for(int i=0;i<(k/2);i++) {\n minh.push(maxh.top());\n maxh.pop();\n }\n // always try to main the middle element on the top of maxh heap\n // if we have even elements in both the heaps, median is avg of top of both heaps\n for(int i=k;i<n;i++) {\n if(k&1) { // if k is odd, we will have median on the top of maxheap\n medians.push_back(maxh.top()*1.0);\n }\n else {\n medians.push_back(((double)maxh.top()+(double)minh.top())/2);\n }\n int p=nums[i-k], q=nums[i]; // \n // we need to remove p and add q;\n // we will delete p when it will come on the top\n // to keep track we will maintain map\n int balance = 0; // keep heaps in balance, for correct ans\n // we decrese balance when remove elements from maxh, so basically if balance<0 it means maxheap has lesser elemets the minheap\n // removing p or adding p to map to delete it later\n if(p<=maxh.top()) { // p is in maxheap\n balance--;\n if(p==maxh.top())\n maxh.pop();\n else\n mp[p]++;\n }\n else { // p is min heap\n balance++;\n if(p == minh.top())\n minh.pop();\n else\n mp[p]++;\n }\n \n // inserting q to the right heap\n if(!maxh.empty() and q<=maxh.top()) { // pushing q to maxheap\n maxh.push(q);\n balance++;\n }\n else { // pushing q to minheap\n minh.push(q);\n balance--;\n }\n \n // balancing both the heaps\n if(balance<0) {\n maxh.push(minh.top());\n minh.pop();\n }\n else if(balance>0) {\n minh.push(maxh.top());\n maxh.pop();\n }\n \n // removing top elements if they exist in our map(late deletion)\n while(!maxh.empty() and mp[maxh.top()]) {\n mp[maxh.top()]--;\n maxh.pop();\n }\n while(!minh.empty() and mp[minh.top()]) {\n mp[minh.top()]--;\n minh.pop();\n }\n }\n if(k&1) {\n medians.push_back(maxh.top()*1.0);\n }\n else {\n medians.push_back(((double)maxh.top()+(double)minh.top())/2.0);\n }\n return medians;\n }\n};
| 21 | 0 |
['C', 'Heap (Priority Queue)', 'C++']
| 4 |
sliding-window-median
|
Two Heaps, Lazy removals, Python3
|
two-heaps-lazy-removals-python3-by-solai-v5rb
|
Intuition\nWant to use somehow changed version of MedianFinder from problem 295.\n\n# Approach\nThe class maintains a balance variable, which indicates the size
|
solairerove
|
NORMAL
|
2023-11-10T06:21:21.530046+00:00
|
2023-11-10T06:21:21.530079+00:00
| 2,865 | false |
# Intuition\nWant to use somehow changed version of MedianFinder from problem 295.\n\n# Approach\nThe class maintains a balance variable, which indicates the size difference between the two heaps. A negative balance\nindicates that the `small` heap has more elements, while a positive balance indicates that the `large` heap has more.\n\n\n# Complexity\n- Time complexity:\n$$O(n * log(k))$$\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```\nclass MedianFinder:\n def __init__(self):\n self.small, self.large = [], []\n self.lazy = collections.defaultdict(int)\n self.balance = 0\n \n def add(self, num):\n if not self.small or num <= -self.small[0]:\n heapq.heappush(self.small, -num)\n self.balance -= 1\n else:\n heapq.heappush(self.large, num)\n self.balance += 1\n \n self.rebalance()\n \n def remove(self, num):\n self.lazy[num] += 1\n if num <= -self.small[0]:\n self.balance += 1\n else:\n self.balance -= 1\n \n self.rebalance()\n self.lazy_remove()\n \n def find_median(self):\n if self.balance == 0:\n return (-self.small[0] + self.large[0]) / 2\n elif self.balance < 0:\n return -self.small[0]\n else:\n return self.large[0]\n\n def rebalance(self):\n while self.balance < 0:\n heapq.heappush(self.large, -heapq.heappop(self.small))\n self.balance += 2\n \n while self.balance > 0:\n heapq.heappush(self.small, -heapq.heappop(self.large))\n self.balance -= 2\n \n def lazy_remove(self):\n while self.small and self.lazy[-self.small[0]] > 0:\n self.lazy[-self.small[0]] -= 1\n heapq.heappop(self.small)\n \n while self.large and self.lazy[self.large[0]] > 0:\n self.lazy[self.large[0]] -= 1\n heapq.heappop(self.large)\n\n\nclass Solution:\n def medianSlidingWindow(self, nums: List[int], k: int) -> List[float]:\n res = []\n median_finder = MedianFinder()\n for i, num in enumerate(nums):\n median_finder.add(num)\n\n if i >= k:\n median_finder.remove(nums[i - k])\n \n if i >= k - 1:\n res.append(median_finder.find_median())\n \n return res\n```
| 20 | 0 |
['Heap (Priority Queue)', 'Python3']
| 1 |
sliding-window-median
|
Short and Clear O(nlogk) Java Solutions
|
short-and-clear-onlogk-java-solutions-by-s36w
|
Use 2 priorityQueues:\n3 steps: remove out-of-bound element, add new element and keep small.peek()<=big.peek(), and get median. \nTime: O(nk). The drawback is r
|
lceveryday
|
NORMAL
|
2017-02-17T01:33:37.003000+00:00
|
2017-02-17T01:33:37.003000+00:00
| 2,299 | false |
**Use 2 priorityQueues:**\n3 steps: remove out-of-bound element, add new element and keep small.peek()<=big.peek(), and get median. \nTime: O(nk). The drawback is remove function of priorityQueue takes O(k) time. \n```\npublic class Solution {\n public double[] medianSlidingWindow(int[] nums, int k) {\n double[] res = new double[nums.length - k + 1];\n int idx = 0;\n boolean useBoth = k % 2 == 0;\n PriorityQueue<Integer> small = new PriorityQueue<>((a, b)->{return (int)((double)b-a);});\n PriorityQueue<Integer> big = new PriorityQueue<>();\n for(int i = 0; i<nums.length; i++){\n if(small.size() + big.size()==k){\n Integer toRemove = new Integer(nums[i-k]);\n if(toRemove <= small.peek()) small.remove(toRemove);\n else big.remove(toRemove);\n }\n //always keep small.size() == big.size() or small.size() == big.size()+1\n if(small.size()<=big.size()) small.add(nums[i]);\n else big.add(nums[i]);\n if(big.size()>0){\n while(small.peek()>big.peek()){\n big.add(small.poll());\n small.add(big.poll());\n }\n }\n if(small.size() + big.size()==k){\n if(useBoth) res[idx++] = ((double)small.peek() + big.peek())/2.0;\n else res[idx++] = (double)small.peek();\n }\n }\n return res;\n }\n}\n```\n\nTo overcome priorityQueue's remove O(k) problem and make our solution O(nlogk), we can replace head/priorityQueue to BST, which is treemap, as below. This would be complicated to write, because we need to deal with duplicated elements and update counts, but the logic is entirely the same as the above solution. \nTime: O(nlogk).\n\n```\npublic class Solution {\n public double[] medianSlidingWindow(int[] nums, int k) {\n double[] res = new double[nums.length - k + 1];\n int idx = 0;\n boolean useBoth = k % 2 == 0;\n TreeMap<Integer, Integer> small = new TreeMap<>((a, b)->{return (int)((double)b-a);});\n int smallSize = 0; \n TreeMap<Integer, Integer> big = new TreeMap<>();\n int bigSize = 0;\n for(int i = 0; i<nums.length; i++){\n if(smallSize + bigSize == k){\n if(nums[i-k] <= small.firstKey()){\n remove(small, nums[i-k]);\n smallSize--;\n }else{\n remove(big, nums[i-k]);\n bigSize--;\n }\n }\n\n if(smallSize<=bigSize){\n add(small, nums[i]);\n smallSize++;\n }else{\n add(big, nums[i]);\n bigSize++;\n }\n if(bigSize>0){\n while(small.firstKey()>big.firstKey()){\n add(big, remove(small, small.firstKey()));\n add(small, remove(big, big.firstKey()));\n }\n }\n \n if(smallSize + bigSize==k){\n if(useBoth) res[idx++] = ((double)small.firstKey() + big.firstKey())/2.0;\n else res[idx++] = (double)small.firstKey();\n }\n }\n return res;\n }\n \n private int remove(TreeMap<Integer, Integer> map, int i){\n map.put(i, map.get(i)-1);\n if(map.get(i)==0) map.remove(i);\n return i; \n }\n \n private void add(TreeMap<Integer, Integer> map, int i){\n if(!map.containsKey(i)) map.put(i, 1);\n else map.put(i, map.get(i)+1);\n }\n}\n```
| 18 | 0 |
[]
| 4 |
sliding-window-median
|
Python3 O(nlogk) heap with intuitive lazy deletion - Sliding Window Median
|
python3-onlogk-heap-with-intuitive-lazy-gfu18
|
\nimport heapq\n\nclass Heap:\n def __init__(self, indices: List[int], nums: List[int], max=False) -> None:\n self.max = max\n self.heap = [[-n
|
r0bertz
|
NORMAL
|
2020-05-08T08:56:25.209509+00:00
|
2020-05-08T09:05:58.231745+00:00
| 4,901 | false |
```\nimport heapq\n\nclass Heap:\n def __init__(self, indices: List[int], nums: List[int], max=False) -> None:\n self.max = max\n self.heap = [[-nums[i], i] if self.max else [nums[i],i] for i in indices]\n self.indices = set(indices)\n heapq.heapify(self.heap)\n \n def __len__(self) -> int:\n return len(self.indices)\n \n def remove(self, index: int) -> None:\n if index in self.indices:\n self.indices.remove(index)\n \n def pop(self) -> List[int]:\n while self.heap and self.heap[0][1] not in self.indices:\n heapq.heappop(self.heap)\n item = heapq.heappop(self.heap)\n self.indices.remove(item[1])\n return [-item[0], item[1]] if self.max else item\n \n def push(self, item: List[int]) -> None:\n self.indices.add(item[1])\n heapq.heappush(self.heap, [-item[0], item[1]] if self.max else item)\n \n def peek(self) -> int:\n while self.heap and self.heap[0][1] not in self.indices:\n heapq.heappop(self.heap)\n v, _ = self.heap[0]\n return -v if self.max else v\n \n\nclass Solution:\n def medianSlidingWindow(self, nums: List[int], k: int) -> List[float]:\n indices = sorted(range(k), key=lambda x:nums[x])\n minheap = Heap(indices[(k+1)//2:], nums)\n maxheap = Heap(indices[:(k+1)//2], nums, max=True)\n median = ((lambda: maxheap.peek()) if k % 2 else \n\t\t (lambda: (minheap.peek() + maxheap.peek()) / 2))\n ans = []\n ans.append(median())\n for i in range(k, len(nums)):\n v = nums[i]\n minheap.remove(i-k)\n maxheap.remove(i-k)\n maxheap.push([v, i])\n minheap.push(maxheap.pop())\n if len(minheap) > len(maxheap):\n maxheap.push(minheap.pop())\n ans.append(median())\n return ans\n```
| 17 | 2 |
['Heap (Priority Queue)', 'Python', 'Python3']
| 4 |
sliding-window-median
|
Easy to understand C++ Solution with multiset
|
easy-to-understand-c-solution-with-multi-oge0
|
\nmultiset <double> m;\n \n double findMedian(double remove, double add) {\n m.insert(add);\n m.erase(m.find(remove));\n int n = m.si
|
narendrant7
|
NORMAL
|
2019-07-25T05:34:13.939153+00:00
|
2019-07-25T05:34:13.939196+00:00
| 2,350 | false |
```\nmultiset <double> m;\n \n double findMedian(double remove, double add) {\n m.insert(add);\n m.erase(m.find(remove));\n int n = m.size();\n double a = *next(m.begin(), n/2 - 1);\n double b = *next(m.begin(), n/2);\n return n & 1? b : (a + b) * 0.5;\n }\n \n vector<double> medianSlidingWindow(vector<int>& nums, int k) {\n vector <double> ans;\n if(nums.size() < k)\n return ans;\n for(int i=0; i<k; i++) {\n m.insert(nums[i]);\n }\n ans.push_back(findMedian(0, 0));\n for(int i=k; i<nums.size(); i++) {\n ans.push_back(findMedian(nums[i-k], nums[i]));\n }\n return ans;\n }\n```
| 16 | 2 |
['C', 'C++']
| 3 |
sliding-window-median
|
Two heaps + sliding window approach; O( n * k ) runtime O(k) space
|
two-heaps-sliding-window-approach-o-n-k-he1lh
|
\n"""\n# BCR\nRuntime: O(n)\nSpacetime: O(1)\n\n# Brute force soultion\nCreate z subsets of nums, where z is len(nums) / k\nSort z\ncalcuate median\nRuntime: O(
|
agconti
|
NORMAL
|
2019-10-23T23:36:00.810486+00:00
|
2019-10-23T23:36:00.810539+00:00
| 4,186 | false |
```\n"""\n# BCR\nRuntime: O(n)\nSpacetime: O(1)\n\n# Brute force soultion\nCreate z subsets of nums, where z is len(nums) / k\nSort z\ncalcuate median\nRuntime: O(n * k * log k) -- calling merge sort on each subset in z\nSpacetime: O(z), -- where z is len(nums) / k\n\n# Two heap apporach\ncreate a max heap and min heap to effecintly model the middle of the array so its easy to calculat the median.\nuse a sliding window of size k, to iterate through nums and populate the heaps\ncalcuate the median when heaps equal size k \nslide the window, remove the value that is no longer included, add the new value\nrepeat\n\nRuntime: O( n * k )\nSpacetime: O(k)\n\n"""\nimport heapq\nfrom heapq import * \n\nclass Solution:\n \n @staticmethod\n def calculate_median(max_heap: List[int], min_heap: List[int]) -> float:\n if len(max_heap) == len(min_heap):\n return (-max_heap[0] + min_heap[0]) / 2.0\n return min_heap[0]\n \n @staticmethod\n def add_to_heaps(max_heap: List[int], min_heap: List[int], num) -> None:\n heappush(max_heap, -heappushpop(min_heap, num))\n \n if len(max_heap) > len(min_heap):\n heappush(min_heap, -heappop(max_heap))\n \n @staticmethod\n def remove_from_heap(heap: List[int], num) -> None:\n index = heap.index(num)\n # delete in O(1)\n # replace the value we want to remove with the last value\n heap[index] = heap[-1]\n del heap[-1]\n \n # Restore heap property thoughout the tree\n if index < len(heap):\n heapq._siftup(heap, index)\n heapq._siftdown(heap, 0, index)\n \n def remove_from_heaps(self, max_heap: List[int], min_heap: List[int], num) -> None:\n if min_heap[0] <= num:\n self.remove_from_heap(min_heap, num)\n return\n self.remove_from_heap(max_heap, -num)\n \n def medianSlidingWindow(self, nums: List[int], k: int) -> List[float]:\n max_heap: List[int] = []\n min_heap: List[int] = []\n result: List[int] = []\n size_of_k = k - 1\n\n for i in range(size_of_k):\n self.add_to_heaps(max_heap, min_heap, nums[i])\n \n for i in range(size_of_k, len(nums)):\n self.add_to_heaps(max_heap, min_heap, nums[i])\n median = self.calculate_median(max_heap, min_heap)\n result.append(median)\n self.remove_from_heaps(max_heap, min_heap, nums[i - size_of_k ])\n \n return result\n```
| 14 | 0 |
['Heap (Priority Queue)', 'Python', 'Python3']
| 3 |
sliding-window-median
|
C++ two multiset solution
|
c-two-multiset-solution-by-hanafubuki-86nv
|
Similar idea as 295. Find Median from Data Stream\nKeep a max heap and a min heap\nBut in this case, we need to keep on removing elements out of the window\nSo
|
hanafubuki
|
NORMAL
|
2017-01-08T23:40:37.820000+00:00
|
2018-10-16T23:16:43.970321+00:00
| 1,293 | false |
Similar idea as 295. Find Median from Data Stream\nKeep a max heap and a min heap\nBut in this case, we need to keep on removing elements out of the window\nSo use multiset insead of heap\nT = O(n*log(k)), S = O(k)\n\n```\nclass Solution {\npublic:\n vector<double> medianSlidingWindow(vector<int>& nums, int k) {\n vector<double> res;\n multiset<int> u, l;\n int n = nums.size();\n for (int i = 0; i < n; ++i) {\n \n // Insert new number\n if (u.empty() or nums[i] >= *u.begin())\n u.insert(nums[i]);\n else l.insert(nums[i]);\n \n // Remove number out of the window\n if (i >= k) {\n if (nums[i-k] >= *u.begin())\n u.erase(u.find(nums[i-k]));\n else l.erase(l.find(nums[i-k]));\n }\n \n // Balance the size of two sets\n while (u.size() < l.size()) {\n u.insert(*l.rbegin());\n l.erase(--l.end());\n }\n while (u.size() > l.size() + 1) {\n l.insert(*u.begin());\n u.erase(u.begin());\n }\n \n // Push back median\n if (i >= k-1) {\n if (k & 1) res.push_back(*u.begin());\n else res.push_back(((double)*u.begin() + *l.rbegin()) / 2);\n }\n }\n return res;\n }\n};
| 14 | 0 |
[]
| 0 |
sliding-window-median
|
JAVA Time 100% space 100% Using Binary Search, Explained
|
java-time-100-space-100-using-binary-sea-w1xp
|
\nclass Solution {\n public double[] medianSlidingWindow(int[] nums, int k) {\n int len = nums.length, p = 0;\n double[] sol = new double[len -
|
adarshv19
|
NORMAL
|
2021-06-10T16:55:38.934062+00:00
|
2021-06-13T00:21:32.114404+00:00
| 1,883 | false |
```\nclass Solution {\n public double[] medianSlidingWindow(int[] nums, int k) {\n int len = nums.length, p = 0;\n double[] sol = new double[len - k + 1];\n boolean flag = (k % 2 == 0);\n List<Integer> list = new ArrayList<>();\n \n //Insert first k-1 elements into the Arraylist \n for (int j = 0; j < k - 1; j++) list.add(nums[j]);\n \n //sort the initial list with k-1 elements, later on we will just add and remove elements from this sorted list\n Collections.sort(list);\n \n for (int i = k - 1; i < len; i++) {\n //Binary search if the element is already present in the list \n //below function returns index if the element is present else it returns the -(expected position +1) , yeah thats the negative sign\n int expectedindex = Collections.binarySearch(list, nums[i]);\n\n if (expectedindex > -1) {\n list.add(expectedindex + 1, nums[i]); // add just next to it\n } \n else {\n list.add(Math.abs(expectedindex + 1), nums[i]); // add it in its expected position\n }\n\n //Insert into the sol list the median according to the value of k \n if (flag) {\n sol[i - k + 1] = list.get((k / 2) - 1) / 2.0 + list.get((k / 2)) / 2.0;\n } else {\n sol[i - k + 1] = list.get((k / 2));\n }\n\n // when the window slides by one element, we just find its positon in the sorted list and delete it \n int index = Collections.binarySearch(list, nums[p]);\n list.remove(index);\n p++;\n }\n\n return sol;\n }\n}\n```\n We are adding the element that slides in at the expected position into the sorted list and removing the element that slides out from the window using binary search.\n \n Please **Upvote** if you found it useful.
| 11 | 0 |
['Binary Tree', 'Java']
| 4 |
sliding-window-median
|
Evolve from brute force to optimal
|
evolve-from-brute-force-to-optimal-by-yu-uiyd
|
The idea is similar to 239. Sliding Window Maximum.\n1. Array O(nk) Store the window in a sorted list.\n\n\tpublic double[] medianSlidingWindow(int[] nums, int
|
yu6
|
NORMAL
|
2017-02-06T00:31:50.504000+00:00
|
2020-12-07T01:04:27.978888+00:00
| 1,903 | false |
The idea is similar to [239. Sliding Window Maximum](https://leetcode.com/problems/sliding-window-maximum/discuss/887170/Evolve-from-brute-force-to-optimal).\n1. Array O(nk) Store the window in a sorted list.\n```\n\tpublic double[] medianSlidingWindow(int[] nums, int k) {\n int n=nums.length;\n double[] median=new double[n-k+1];\n List<Integer> window = new ArrayList<>();\n for(int i=0;i<n;i++) {\n int j = Collections.binarySearch(window,nums[i]);\n if(j<0)\n j=-j-1;\n window.add(j,nums[i]);\n if(i>=k) {\n window.remove(new Integer(nums[i-k]));\n }\n if(i>=k-1) {\n median[i-k+1]=((long)window.get(k/2)+window.get((k-1)/2))/2.0;\n }\n }\n return median;\n }\n```\n2. Heap O(nk). Another simple idea is to reuse [295. Find Median from Data Stream](https://leetcode.com/problems/find-median-from-data-stream/discuss/957550/Evolve-from-brute-force). Add is O(logk), findMedian is O(1), remove is O(k) for priorty queue. Same as 295, we want the invariance that heap sizes are be equal or the left heap is larger by 1 to simplify the logic to findMedian. This can be achieved by remove old number before adding new number. After removing, left size could be smaller by one or larger by two in the worst case. Then we add to the smaller heap to satisfy the invariance. \n```\n\tpublic double[] medianSlidingWindow(int[] nums, int k) {\n int n=nums.length;\n double[] median=new double[n-k+1];\n PriorityQueue<Integer> small=new PriorityQueue<>((a,b)->b.compareTo(a)), large=new PriorityQueue<>();\n for(int i=0;i<n;i++) {\n if(i>=k) {\n if(!small.remove(nums[i-k])) {\n large.remove(nums[i-k]); \n }\n }\n addNum(nums[i],small, large);\n if(i>=k-1)\n median[i-k+1] = findMedian(small, large);\n }\n return median;\n }\n private void addNum(int num, Queue<Integer> small, Queue<Integer> large) {\n if(small.size()>large.size()) {\n small.add(num);\n large.add(small.poll());\n } else {\n large.add(num);\n small.add(large.poll()); \n }\n }\n private double findMedian(Queue<Integer> small, Queue<Integer> large) {\n if(small.size()>large.size()) {\n return small.peek(); \n } else {\n return ((long)small.peek()+large.peek())/2.0;\n }\n }\n```\n3. Binary search tree O(nlogk). BST can remove in log(k). Use two bst to store the smaller half and the larger half of the current window. The challenge is how to store duplicate in BST. An easy approach is to store array index in BST and overload the comparator so that it is sorted by value.\n* java\n```\n\tpublic double[] medianSlidingWindow(int[] nums, int k) {\n int n=nums.length;\n double[] median=new double[n-k+1];\n Comparator<Integer> comp = (i,j)->nums[i]==nums[j]?i-j:nums[i] - nums[j];\n TreeSet<Integer> small=new TreeSet<>(comp), large=new TreeSet<>(comp);\n for(int i=0;i<n;i++) {\n if(i>=k) {\n if(!small.remove(i-k)) {\n large.remove(i-k); \n }\n }\n addNum(i, small, large);\n if(i>=k-1)\n median[i-k+1] = findMedian(nums, small, large);\n }\n return median;\n }\n private void addNum(int i, TreeSet<Integer> small, TreeSet<Integer> large) {\n if(small.size() > large.size()) {\n small.add(i);\n large.add(small.pollLast()); \n } else {\n large.add(i);\n small.add(large.pollFirst()); \n } \n }\n private double findMedian(int[] nums, TreeSet<Integer> small, TreeSet<Integer> large) {\n if(small.size() > large.size()) {\n return nums[small.last()]; \n } else {\n return ((long)nums[small.last()]+nums[large.first()])/2.0;\n }\n }\n```\nAfter each add or erase, the two bst are balanced so that their sizes differ by at most 1. This makes it easier to partition the number and compute the median.\n* c++\n```\nclass Solution {\npublic:\n vector<double> medianSlidingWindow(vector<int>& nums, int k) {\n int n = nums.size();\n vector<double> med(n-k+1);\n for(int i=0;i<n;i++) {\n if(i>k-1) {\n auto it = sm.find(nums[i-k]);\n if(it!=sm.end()) sm.erase(it);\n else lg.erase(lg.find(nums[i-k]));\n balance();\n }\n if(sm.empty()||nums[i]<=*sm.rbegin()) sm.insert(nums[i]);\n else lg.insert(nums[i]);\n balance();\n if(i>=k-1) med[i-k+1] = sm.size()>lg.size() ? *sm.rbegin() : \n lg.size()>sm.size() ? *lg.begin() : ((long)*sm.rbegin()+*lg.begin())/2.0;\n }\n return med;\n }\nprivate:\n void balance() {\n if(sm.size()>lg.size()+1) {\n lg.insert(*sm.rbegin());\n sm.erase(--sm.end());\n }\n if(lg.size()>sm.size()+1) {\n sm.insert(*lg.begin());\n lg.erase(lg.begin());\n }\n }\n multiset<int> sm,lg;\n};\n```\n4. O(nlogk) , we can just use one bst and keep track of the middle element. The great idea is from [@StefanPochmann](https://discuss.leetcode.com/topic/74963/o-n-log-k-c-using-multiset-and-updating-middle-iterator). The idea is to keep the middle pointer points to index k/2 after insertion and erasure. \n```\n vector<double> medianSlidingWindow(vector<int>& nums, int k) {\n int n = nums.size();\n vector<double> med(n-k+1);\n multiset<double> window(nums.begin(),nums.begin()+k);\n auto m = next(window.begin(),k/2);\n for(int i=k;;i++) {\n med[i-k] = ((double)*m+*next(m,k%2-1))/2;\n if(i==n) return med;\n window.insert(nums[i]);\n if(nums[i]<*m) m--;\n if(nums[i-k]<=*m) m++;\n window.erase(window.lower_bound(nums[i-k]));\n }\n }\n```
| 11 | 3 |
['C', 'Java']
| 1 |
sliding-window-median
|
✅Beginner Friendly (C++/Java/Python) Solution With Detailed Explanation✅
|
beginner-friendly-cjavapython-solution-w-4yit
|
Intuition\nThe medianSlidingWindow function maintains a sorted window of elements using vector operations and calculates medians as the window slides through th
|
suyogshete04
|
NORMAL
|
2024-01-25T04:09:18.026173+00:00
|
2024-01-25T04:09:18.026196+00:00
| 3,220 | false |
# Intuition\nThe `medianSlidingWindow` function maintains a sorted window of elements using vector operations and calculates medians as the window slides through the input array. It utilizes efficient insertions and deletions with `lower_bound` and updates the result vector with calculated medians. The final result vector contains medians for each sliding window.\n\n# Approach\n\n1. **Initialization**: The function starts by initializing the result vector `res`, indices `i` and `j` to manage the sliding window, and a temporary vector `temp` with the first `k-1` elements of the input vector `nums`. This temporary vector is sorted to represent the initial sliding window.\n\n2. **Sliding Window**: The main loop runs while the end index `j` is within the range of the input vector `nums`. In each iteration:\n - The current element (`nums[j]`) is inserted into the sorted window `temp` at the correct position using `lower_bound`.\n - The median of the current window is calculated based on the size of the window `k`.\n - If `k` is odd, the median is the middle element; otherwise, it is the average of the middle two elements.\n - The median is then pushed into the result vector `res`.\n\n3. **Updating Window**: After calculating the median, the oldest element in the window (`nums[i]`) is removed using `erase` and `lower_bound`.\n - The indices `i` and `j` are incremented to slide the window to the next position.\n\n4. **Final Result**: The function returns the result vector `res` containing the medians for each sliding window.\n\n\n# Complexity\n**Time Complexity:**\n\nThe time complexity of the `medianSlidingWindow` function is primarily dominated by the operations inside the main loop. Let \\( n \\) be the length of the input array `nums`.\n\n1. Sorting the initial window (`temp`): \\( O(k \\log k) \\) - Sorting a window of size \\( k-1 \\).\n2. Main Loop: \\( O(n \\log k) \\) - Iterating through the array and performing insertion and deletion operations on the sorted window.\n\nTherefore, the overall time complexity is \\( O(n \\log k) \\).\n\n**Space Complexity:**\n\nThe space complexity is determined by the space used to store the temporary window (`temp`) and the result vector (`res`).\n\n1. Temporary Window (`temp`): \\( O(k) \\) - The size of the sorted window.\n2. Result Vector (`res`): \\( O(n) \\) - In the worst case, the result vector contains one median for each window.\n\nTherefore, the overall space complexity is \\( O(k + n) \\).\n\n# Code\n```C++ []\nclass Solution {\npublic:\n vector<double> medianSlidingWindow(vector<int>& nums, int k) {\n vector<double> res;\n int n = nums.size();\n int i = 0;\n int j = k - 1;\n vector<int> temp = {nums.begin(), nums.begin() + k - 1};\n sort(temp.begin(), temp.end());\n while (j < n) {\n temp.insert(lower_bound(temp.begin(), temp.end(), nums[j]),\n nums[j]);\n\n if (k & 1) {\n double median = (double)temp[k / 2];\n res.push_back(median);\n } else {\n int idx = k / 2;\n double median1 = (double)temp[idx];\n double median2 = (double)temp[idx - 1];\n res.push_back((median1 + median2) / 2);\n }\n\n temp.erase(lower_bound(temp.begin(), temp.end(), nums[i]));\n i++;\n j++;\n }\n\n return res;\n }\n};\n```\n```Java []\nimport java.util.ArrayList;\nimport java.util.Collections;\nimport java.util.List;\n\npublic class Solution {\n public double[] medianSlidingWindow(int[] nums, int k) {\n List<Double> resList = new ArrayList<>();\n int n = nums.length;\n int i = 0;\n int j = k - 1;\n List<Integer> temp = new ArrayList<>();\n for (int x = 0; x < k - 1; x++) {\n temp.add(nums[x]);\n }\n Collections.sort(temp);\n while (j < n) {\n int num = nums[j];\n int insertIdx = Collections.binarySearch(temp, num);\n if (insertIdx < 0) {\n insertIdx = -insertIdx - 1;\n }\n temp.add(insertIdx, num);\n\n if (k % 2 == 1) {\n double median = (double) temp.get(k / 2);\n resList.add(median);\n } else {\n int idx = k / 2;\n double median1 = (double) temp.get(idx);\n double median2 = (double) temp.get(idx - 1);\n resList.add((median1 + median2) / 2);\n }\n\n int removeIdx = Collections.binarySearch(temp, nums[i]);\n if (removeIdx < 0) {\n removeIdx = -removeIdx - 1;\n }\n temp.remove(removeIdx);\n\n i++;\n j++;\n }\n\n double[] resArray = new double[resList.size()];\n for (int x = 0; x < resList.size(); x++) {\n resArray[x] = resList.get(x);\n }\n\n return resArray;\n }\n}\n```\n```Python []\nfrom sortedcontainers import SortedList\n\nclass Solution:\n def medianSlidingWindow(self, nums: List[int], k: int) -> List[float]:\n res = []\n window = SortedList(nums[:k])\n\n for i in range(k, len(nums)):\n if k % 2 == 1:\n median = window[k // 2]\n else:\n median = (window[k // 2] + window[k // 2 - 1]) / 2\n\n res.append(float(median))\n\n window.discard(nums[i - k])\n window.add(nums[i])\n\n # Process the last window\n if k % 2 == 1:\n median = window[k // 2]\n else:\n median = (window[k // 2] + window[k // 2 - 1]) / 2\n\n res.append(float(median))\n\n return res\n\n```
| 10 | 0 |
['Sliding Window', 'C++', 'Java', 'Python3']
| 2 |
sliding-window-median
|
C++ Solution using Two Heaps | Using Multi Set
|
c-solution-using-two-heaps-using-multi-s-p5kt
|
\nclass Solution {\n private:\n multiset<double>MinH, MaxH;\n vector<double> ans;\n \n public: \n void balance()\n {\n if(MaxH.siz
|
chirags_30
|
NORMAL
|
2021-08-14T09:44:00.616441+00:00
|
2021-08-14T09:44:00.616492+00:00
| 1,265 | false |
```\nclass Solution {\n private:\n multiset<double>MinH, MaxH;\n vector<double> ans;\n \n public: \n void balance()\n {\n if(MaxH.size() > MinH.size() + 1)\n {\n MinH.insert(*MaxH.rbegin());\n MaxH.erase(MaxH.find(*MaxH.rbegin()));\n }\n else if(MaxH.size() + 1 < MinH.size())\n {\n MaxH.insert(*MinH.begin());\n MinH.erase(MinH.find(*MinH.begin()));\n }\n }\n \n void addNum(double n)\n {\n \n if(MaxH.size()==0)\n MaxH.insert(n);\n else\n {\n if(n < *MaxH.rbegin())\n MaxH.insert(n);\n else\n MinH.insert(n);\n \n balance();\n } \n }\n \n void addAns()\n {\n if(MaxH.size() == MinH.size())\n ans.push_back((*MaxH.rbegin() + *MinH.begin())/2);\n else\n {\n if(MaxH.size() > MinH.size())\n ans.push_back(*MaxH.rbegin());\n else\n ans.push_back(*MinH.begin());\n }\n }\n \n void slideWindow(double n)\n {\n if(MaxH.size() and MaxH.find(n) != MaxH.end())\n MaxH.erase(MaxH.find(n));\n else\n MinH.erase(MinH.find(n));\n \n balance();\n }\n \n vector<double> medianSlidingWindow(vector<int>& nums, int k) {\n \n for(int i=0; i<nums.size(); i++)\n {\n addNum(nums[i]*1.0);\n if(i + 1 >= k)\n {\n addAns();\n slideWindow(nums[i-k+1]*1.0);\n }\n }\n return ans;\n }\n};\n```
| 10 | 0 |
['C', 'Heap (Priority Queue)']
| 1 |
sliding-window-median
|
C# SortedSet O(n*log(k))
|
c-sortedset-onlogk-by-1988hz-scgs
|
Referencing https://leetcode.com/problems/sliding-window-median/discuss/96346/Java-using-two-Tree-Sets-O(n-logk)\n\nThe idea is to reduct the time complexity in
|
1988hz
|
NORMAL
|
2021-01-31T14:12:24.993173+00:00
|
2021-01-31T14:13:58.474098+00:00
| 443 | false |
Referencing https://leetcode.com/problems/sliding-window-median/discuss/96346/Java-using-two-Tree-Sets-O(n-logk)\n\nThe idea is to reduct the time complexity in the inner loop. C# has a few built in data structures\n* List/SortedList - The search is always O(log(k)), but insert and delete are O(k). So the total complexicty becomes O(n * k)\n* Sorted Set - It\'s basically a advanced heap. The search, insert, delete all are O(log(k)). (A standard heap delete take O(k) as well).\nBut the problem is it can\'t take duplicates. So we can use different Comparer to handle this.\n\n```\npublic class Solution{\n void BalanceHeap(SortedSet<int> left, SortedSet<int> right){\n if(Math.Abs(left.Count - right.Count) <= 1)\n return;\n else if(left.Count > right.Count){ \n var max = left.Max;\n left.Remove(max);\n right.Add(max); \n }\n else{\n var min = right.Min;\n right.Remove(min);\n left.Add(min); \n }\n }\n \n double GetMedian(SortedSet<int> left, SortedSet<int> right, int[] nums, bool isOdd){\n if(isOdd)\n return left.Count > right.Count ? nums[left.Max] : nums[right.Min];\n else\n return nums[left.Max] * 0.5 + nums[right.Min] * 0.5;\n }\n \n public double[] MedianSlidingWindow(int[] nums, int k) {\n var comparer = Comparer<int>.Create((x, y)=> nums[x] != nums[y] ? (nums[x] > nums[y] ? 1 : -1) : (x-y));\n var leftHeap = new SortedSet<int>(comparer);\n var rightHeap = new SortedSet<int>(comparer);\n var isOdd = k % 2 == 1; \n var res = new double[nums.Length - k + 1];\n \n for(var i = 0; i< nums.Length; i ++){\n var val = nums[i];\n if(leftHeap.Count > 0 && nums[leftHeap.Max] >= val){\n leftHeap.Add(i); \n }else if(rightHeap.Count > 0 && nums[rightHeap.Min] < val){\n rightHeap.Add(i); \n }else{\n leftHeap.Add(i);\n }\n \n BalanceHeap(leftHeap, rightHeap); \n if(i >= k -1){\n res[i - k + 1] = GetMedian(leftHeap, rightHeap, nums, isOdd);\n \n if(!leftHeap.Remove(i-k + 1))\n rightHeap.Remove(i-k + 1); \n }\n }\n return res;\n }\n}\n```
| 10 | 0 |
[]
| 3 |
sliding-window-median
|
C++ Sliding Window Solution Using MultiSet (Solution Updated After Recently Added TestCase)
|
c-sliding-window-solution-using-multiset-9rwp
|
\nclass Solution {\npublic:\n vector<double> medianSlidingWindow(vector<int>& nums, int k) {\n vector<double> ans;\n multiset<double> window(be
|
_limitlesspragma
|
NORMAL
|
2022-09-09T16:54:15.581269+00:00
|
2023-05-11T13:07:14.234269+00:00
| 1,476 | false |
```\nclass Solution {\npublic:\n vector<double> medianSlidingWindow(vector<int>& nums, int k) {\n vector<double> ans;\n multiset<double> window(begin(nums), begin(nums) + k);\n auto it = next(begin(window), (k - 1) / 2); //take the iterator to mid position\n \n for(int i=k; ;++i){\n const double median = ((k & 1) ? *it : (*it + *next(it)) / 2.);\n ans.emplace_back(median);\n \n if(i == nums.size()) break;\n \n window.insert(nums[i]);\n \n if(nums[i] < *it) // If the inserted number is smaller than mid, obviously the iterator must have moved one position ahead..... which means we should take it one step backwards\n --it;\n if(nums[i - k] <= *it) // If the number inserted k steps before is smaller than or equal to the mid, the iterator must have moved one position backwards, because of which we should move it forward by one.\n ++it;\n \n window.erase(window.lower_bound(nums[i - k]));\n }\n return ans;\n }\n};\n```
| 9 | 0 |
['C++']
| 1 |
sliding-window-median
|
The Most Optimal T-O(NlogK), S-O(K) using 2 Heaps C++ Commented Solution
|
the-most-optimal-t-onlogk-s-ok-using-2-h-lk0e
|
\nclass Solution {\npublic:\n\t// Custom structures for max & min heaps\n struct maxstruct{\n bool operator()(pair<double,double>& a, pair<double,doub
|
ankurharitosh
|
NORMAL
|
2020-08-07T10:28:27.980291+00:00
|
2020-12-31T16:04:37.584108+00:00
| 1,995 | false |
```\nclass Solution {\npublic:\n\t// Custom structures for max & min heaps\n struct maxstruct{\n bool operator()(pair<double,double>& a, pair<double,double>& b){\n return a.second<b.second;\n } \n };\n struct minstruct{\n bool operator()(pair<double,double>& a, pair<double,double>& b){\n return a.second>b.second;\n } \n };\n vector<double> medianSlidingWindow(vector<int>& nums, int k) {\n int n=nums.size();\n vector<double> result;\n\t\t\n\t\t//max_heap for left half and min_heap for right half\n priority_queue<pair<double,double>, vector<pair<double,double>>, maxstruct> max_heap;\n priority_queue<pair<double,double>, vector<pair<double,double>>, minstruct> min_heap;\n \n\t\t//Initialize both Heaps\n for(int i=0; i<k; i++)\n max_heap.push({i, nums[i]});\n \n while(max_heap.size()>min_heap.size()+1){\n min_heap.push(max_heap.top());\n max_heap.pop();\n }\n \n for(int i=k; i<n; i++){\n\t\t\n\t\t\t// Store median into result for previous window\n if(k%2==0){\n double ans=max_heap.top().second + min_heap.top().second;\n ans/=2;\n result.push_back(ans);\n }\n else\n result.push_back(max_heap.top().second);\n \n\t\t\t// Main Part\n double outgoing=nums[i-k], incoming=nums[i], balance=0;\n // Balance for outgoing element\n if(outgoing<max_heap.top().second || (outgoing==max_heap.top().second && max_heap.top().first<=i-k) || (!min_heap.empty() && outgoing<min_heap.top().second))\n balance--;\n else\n balance++;\n \n\t\t\t// Balance for incoming element\n if(incoming<max_heap.top().second || (incoming==max_heap.top().second && max_heap.top().first>i-k) ||(!min_heap.empty() && incoming<min_heap.top().second)){\n balance++;\n max_heap.push({i, incoming});\n }\n else{\n balance--;\n min_heap.push({i, incoming});\n }\n \n\t\t\t// Check Balance\n if(!min_heap.empty() && balance<0){\n max_heap.push(min_heap.top());\n min_heap.pop();\n balance++;\n }\n else if(!max_heap.empty() && balance>0){\n min_heap.push(max_heap.top());\n max_heap.pop();\n balance--;\n }\n \n\t\t\t// Lazy Removal when out of window range element at the top\n while(!min_heap.empty() && min_heap.top().first<=i-k)\n min_heap.pop();\n \n while(!max_heap.empty() && max_heap.top().first<=i-k)\n max_heap.pop();\n }\n \n\t\t\t// Store median into result for last window\n if(k%2==0){\n double ans=max_heap.top().second + min_heap.top().second;\n ans/=2;\n result.push_back(ans);\n }\n else\n result.push_back(max_heap.top().second);\n \n return result;\n }\n};\n```\nI appreciate your upvote !!
| 9 | 1 |
['C', 'Heap (Priority Queue)', 'C++']
| 3 |
sliding-window-median
|
Javascript solution beats 98.81%
|
javascript-solution-beats-9881-by-darynk-rhcn
|
The idea is pretty simple. You need to keep the sorted array, adding and deleting numbers one by one. For this purpose, you can use binary insertion and binary
|
darynkaypbaev
|
NORMAL
|
2020-02-25T22:00:55.012606+00:00
|
2020-02-25T22:00:55.012654+00:00
| 1,942 | false |
The idea is pretty simple. You need to keep the sorted array, adding and deleting numbers one by one. For this purpose, you can use binary insertion and binary deletion.\n\n\tconst medianSlidingWindow = (nums, k) => {\n\t\tconst arr = []\n\t\tconst output = []\n\t\tconst isEven = k % 2 === 0\n\t\tconst m = k >> 1\n\n\t\tfor (let i = 0; i < nums.length; i++) {\n\t\t\tbinaryInsertion(arr, nums[i])\n\n\t\t\tif (arr.length > k) {\n\t\t\t\tbinaryDeletion(arr, nums[i - k])\n\t\t\t}\n\n\t\t\tif (arr.length === k) {\n\t\t\t\toutput.push(isEven ? (arr[m - 1] + arr[m]) / 2 : arr[m])\n\t\t\t}\n\t\t}\n\n\t\treturn output\n\t}\n\n\tconst binaryInsertion = (arr, target) => {\n\t\tlet left = 0\n\t\tlet right = arr.length\n\n\t\twhile (left < right) {\n\t\t\tconst mid = (left + right) >> 1\n\n\t\t\tif (target > arr[mid]) {\n\t\t\t\tleft = mid + 1\n\t\t\t} else {\n\t\t\t\tright = mid\n\t\t\t}\n\t\t}\n\n\t\tarr.splice(left, 0, target)\n\t}\n\n\tconst binaryDeletion = (arr, target) => {\n\t\tlet left = 0\n\t\tlet right = arr.length\n\n\t\twhile (left < right) {\n\t\t\tconst mid = (left + right) >> 1\n\n\t\t\tif (target === arr[mid]) {\n\t\t\t\tarr.splice(mid, 1)\n\t\t\t\tbreak\n\t\t\t} else if (target > arr[mid]) {\n\t\t\t\tleft = mid + 1\n\t\t\t} else {\n\t\t\t\tright = mid\n\t\t\t}\n\t\t}\n\t}
| 9 | 0 |
['Binary Search', 'JavaScript']
| 3 |
sliding-window-median
|
Easy to understand with explanation - Python Two heaps - O(N * K) and O(K)
|
easy-to-understand-with-explanation-pyth-tf5n
|
Explanation:\nSimilar to finding median from a stream with the following changes:\n- We need to keep track of a sliding window of "k" numbers.\n- This means, in
|
mpatel_21
|
NORMAL
|
2021-01-04T20:03:55.646872+00:00
|
2021-01-04T20:23:51.558073+00:00
| 1,786 | false |
# Explanation:\nSimilar to finding median from a stream with the following changes:\n- We need to keep track of a sliding window of "k" numbers.\n- This means, in each iteration, when we insert a new number in the heaps, we need to remove one number from the heaps which is going out of the sliding window.\n - After the removal, we need to re-balance the heaps in the same way that we did while inserting.\n\n# Time complexity: O(N * K)\nWhere N is the total number of elements in the input array and K is the size of the sliding window!\n- Inserting/removing numbers from heaps of Size K: O(log K)\n- Removing the element going out of the sliding window from the heap takes: O(K)\n\n# Space complexity: O(K) \n- We will be storing all the numbers within the sliding window.\n\n\n# Code:\n```\nclass SlidingWindowMedian:\n def __init__(self):\n self.max_heap = [] # max heap to store smaller numbers, get largest of small numbers\n self.min_heap = [] # min heap to store larger numbers, get smallest of large numbers\n\n def find_median_in_sliding_window(self, nums, k):\n\t\tresult = [0.0 for _ in range(len(nums) - k + 1)] # avoid getting index out of bound error later on if initialized as empty\n\n for i in range(0, len(nums)):\n\t\t\t# negative sign for max heap since python has min heap by default, so negative sign is to simulate the proposed max heap!\n\t\t\t# basically remember: \n\t\t\t# - Add negative sign before the number when adding to max heap!\n\t\t\t# - Put back the negative sign while popping the number!\n\t\t\t# - Keep the sign in while comparing the top element of max heap to any number!\n if not self.max_heap or nums[i] <= -self.max_heap[0]:\n heappush(self.max_heap, -nums[i])\n else:\n heappush(self.min_heap, nums[i])\n\n # re-balance heaps after inserting every number in the heaps\n self.rebalance_heaps()\n\n # if we have at least "k" elements in the sliding window\n if i - k + 1 >= 0:\n # add the median to the resulting array\n if len(self.max_heap) == len(self.min_heap):\n # we got even number of elements, take avg of the top of the element from both heaps\n result[i-k+1] = (self.min_heap[0] + (- self.max_heap[0])) / 2.0\n else:\n # get the top element from the max heap\n result[i-k+1] = -self.max_heap[0] / 1.0\n\n # remove the element going out of the window, from the heap\n element_to_remove = nums[i-k+1]\n if element_to_remove <= -self.max_heap[0]:\n self.remove_element_from_heap(self.max_heap, -element_to_remove)\n else:\n self.remove_element_from_heap(self.min_heap, element_to_remove)\n\n # re-balance the heaps after element removal\n self.rebalance_heaps()\n\n return result\n\n @staticmethod\n def remove_element_from_heap(heap, element):\n # find the index of the element to remove from the heap\n index = heap.index(element)\n # move this indexed element to the end of the heap to remove it\n heap[index] = heap[-1] # this basically overrides the element at index to that of last element\n # now remove the last element, thereby removing the indexed element (because of previous step)\n del heap[-1]\n\n # adjust only one element instead of using heapify (heapify takes O(K), this takes O(Log K))\n if index < len(heap):\n heapify(heap)\n # TODO, understand this better\n # heapq._siftup(heap, index)\n # heapq._siftdown(heap, 0, index)\n\n def rebalance_heaps(self):\n # either both the heaps will have equal number of elements or max-heap will have\n # one more element than the min-heap\n if len(self.max_heap) > len(self.min_heap) + 1:\n heappush(self.min_heap, -heappop(self.max_heap))\n elif len(self.max_heap) < len(self.min_heap):\n heappush(self.max_heap, -heappop(self.min_heap))\n\n```
| 8 | 0 |
['Python', 'Python3']
| 3 |
sliding-window-median
|
Python 2 Heap Solution O(N*K)
|
python-2-heap-solution-onk-by-satwik95-yk6z
|
Use a deque to slide through and 2 heaps to compute the median of the stream of data. Tc = O(N*K), K because of heapify in remove(). \nFinding median of a strea
|
satwik95
|
NORMAL
|
2020-07-30T21:18:09.537793+00:00
|
2020-08-21T03:48:20.305688+00:00
| 1,595 | false |
Use a deque to slide through and 2 heaps to compute the median of the stream of data. Tc = O(N*K), K because of heapify in remove(). \nFinding median of a stream: https://leetcode.com/problems/find-median-from-data-stream/discuss/74062/Short-simple-JavaC%2B%2BPython-O(log-n)-%2B-O(1)\n```\nfrom heapq import *\nfrom collections import deque\nclass MedianFinder:\n\n def __init__(self):\n """\n initialize your data structure here.\n """\n self.small = [] # max heap\n self.large = [] # min heap\n\n def addNum(self, num: int) -> None:\n heappush(self.small, -heappushpop(self.large, num))\n if len(self.large)<len(self.small):\n heappush(self.large, -heappop(self.small))\n\n def findMedian(self) -> float:\n if len(self.large)>len(self.small): return self.large[0]\n else: return (self.large[0]-self.small[0])/2\n \n def remove(self, heap, element):\n ind = heap.index(element) \n heap[ind] = heap[-1]\n del heap[-1]\n heapify(heap)\n \nclass Solution:\n \n def medianSlidingWindow(self, nums: List[int], k: int) -> List[float]:\n start = 0\n obj= MedianFinder()\n window = deque()\n res = []\n for i in range(len(nums)):\n window.append(nums[i])\n obj.addNum(nums[i])\n if len(window)==k:\n res.append(obj.findMedian())\n x = window.popleft()\n if obj.small and x<=-obj.small[0]: obj.remove(obj.small, -x)\n else: obj.remove(obj.large, x)\n return res\n```
| 8 | 0 |
['Heap (Priority Queue)', 'Python3']
| 5 |
sliding-window-median
|
Python Hash Heap Implementation
|
python-hash-heap-implementation-by-hanke-6y05
|
Apparently, we need a data structure which supports both Insert and Remove operation in O(log K) time and supports getMin operation in O(1) or O(log K) time.\n\
|
hankerzheng
|
NORMAL
|
2017-01-19T21:37:16.231000+00:00
|
2017-01-19T21:37:16.231000+00:00
| 4,399 | false |
Apparently, we need a data structure which supports both `Insert` and `Remove` operation in `O(log K)` time and supports `getMin` operation in `O(1)` or `O(log K)` time.\n\nThe Data Structure we could choose may be Balanced BST or Hash Heap. But there is no such implemented data structure in Python. Here is my implementation of Hash Heap in Python. Then, with this data structure, this problem could be easily solved just as [LeetCode 295 Find Median from Data Stream](https://leetcode.com/problems/find-median-from-data-stream/). \n\n[The Chinese version on my blog](http://hankerzheng.com/blog/Python-Hash-Heap)\n\n```python\n# This is the Python implementation of Hash Heap based on the list implementation \n# of binary heap. The difference between Hash Heap and Binary Heap is that Hash\n# Heap supports the `heapRemove` operation in O(log n) time and can check whether\n# certain element is in the Hash Heap or not in O(1) time.\n# \n# Basic automatic tests are given in `pushpopTest()` and `removeTest()`.\n# Note: It may takes about 10 seconds to run both test functions.\n\n# import random module for test use.\nimport random\n\nclass HeapNode(object):\n """\n The node in the HashHeap to deal with duplicates.\n Each node store the value of each element and the number of duplicates\n with the same value.\n """\n def __init__(self, val, cnt):\n self.val = val\n self.cnt = cnt\n\n def __cmp__(self, other):\n return self.val - other.val\n\n def __str__(self):\n return "[%s, %d]" % (self.val, self.cnt)\n __repr__ = __str__\n\nclass HashHeap(object):\n """\n This HashHeap is the same as the list implementation of binary heap, but with\n a hashMap to map the value of one elemnt to its index in the list.\n """\n def __init__(self, arr):\n """\n `_cap` - the number of elements in the HashHeap\n `_maxIdx` - the max index of the binary heap\n `_data` - the list implementation of the binary heap\n `_hashMap` - mapping the element to its index in the binary heap\n """\n elemCnt = self._preProcess(arr)\n self._cap = len(arr)\n self._maxIdx = len(elemCnt) - 1\n self._data = [HeapNode(key, value) for key, value in elemCnt.items()]\n self._hashMap = {node.val: idx for idx, node in enumerate(self._data)}\n self._heapify()\n\n def _preProcess(self, arr):\n """\n Convert the input array into a dict object.\n The key to the dict is the value of the element.\n The value of the dict is the occurence of each element.\n """\n elemCnt = {}\n for elem in arr:\n elemCnt[elem] = elemCnt.get(elem, 0) + 1\n return elemCnt\n\n def _swap(self, idx1, idx2):\n """\n Swap the 2 elements in the heap.\n Also, change the index stored in `self._hashMap`\n """\n elem1, elem2 = self._data[idx1], self._data[idx2]\n self._hashMap[elem1.val] = idx2\n self._hashMap[elem2.val] = idx1\n self._data[idx1], self._data[idx2] = elem2, elem1\n\n def _heapify(self):\n idx = self._maxIdx\n while idx > 0:\n parentIdx = (idx - 1) / 2\n if self._data[parentIdx] > self._data[idx]:\n self._swap(parentIdx, idx)\n self._siftDown(idx)\n idx -= 1\n\n def _siftDown(self, idx):\n def heapValid(idx):\n left, right = idx * 2 + 1, idx * 2 + 2\n if left > self._maxIdx:\n return True\n if right > self._maxIdx:\n return self._data[idx] <= self._data[left]\n return self._data[idx] <= self._data[left] and self._data[idx] <= self._data[right]\n def smallerChild(idx):\n left, right = idx * 2 + 1, idx * 2 + 2\n if left > self._maxIdx:\n return None\n if right > self._maxIdx:\n return left\n return left if self._data[left] < self._data[right] else right\n\n current = idx\n while not heapValid(current):\n child = smallerChild(current)\n self._swap(current, child)\n current = child\n\n def _siftUp(self, idx):\n current = idx\n parent = (current - 1) / 2\n while current > 0 and self._data[parent] > self._data[current]:\n self._swap(parent, current)\n current = parent\n parent = (current - 1) / 2\n\n def _removeLastNode(self):\n rmNode = self._data.pop(-1)\n self._cap -= 1\n self._maxIdx -= 1\n self._hashMap.pop(rmNode.val)\n\n def _removeByIdx(self, idx):\n thisNode = self._data[idx]\n retVal = thisNode.val\n if thisNode.cnt > 1:\n thisNode.cnt -= 1\n self._cap -= 1\n elif idx == self._maxIdx:\n # the node itself is the last node\n self._removeLastNode()\n else:\n self._swap(idx, self._maxIdx)\n self._removeLastNode()\n pidx = (idx - 1) / 2\n # check to see we should sift up or sift down\n if pidx >= 0 and self._data[pidx] > self._data[idx]:\n self._siftUp(idx)\n else:\n self._siftDown(idx)\n return retVal\n\n @property\n def length(self):\n """\n Return the number of elements in the Hash Heap\n """\n return self._cap\n\n def heapPeep(self):\n """\n Return the MIN element in the Hash Heap\n """\n if not self._data:\n return float("inf")\n return self._data[0].val\n\n def heapPop(self):\n """\n Remove the MIN element from the Hash Heap and return its value\n """\n return self._removeByIdx(0)\n\n def heapPush(self, elem):\n """\n Push a new element into the Hash Heap\n """\n self._cap += 1\n if elem not in self._hashMap:\n self._maxIdx += 1\n self._data.append(HeapNode(elem, 1))\n self._hashMap[elem] = self._maxIdx\n self._siftUp(self._maxIdx)\n else:\n idx = self._hashMap[elem]\n self._data[idx].cnt += 1\n \n def heapRemove(self, elem):\n """\n Remove a existing element from the Hash Heap\n If the element to be removed is not in the Hash Heap, raise an error.\n """\n if elem not in self._hashMap:\n raise ValueError("Element to be removed is not in HashHeap!!!")\n idx = self._hashMap[elem]\n self._removeByIdx(idx)\n\n def __contains__(self, value):\n return value in self._hashMap\n\n def __str__(self):\n return "%s" % [elem.val for elem in self._data]\n __repr__ = __str__\n\n\ndef pushpopTest():\n """\n Randomly generate a list, and push each element into the heap.\n Test HeapPush by comparing the first element in the heap with the \n smallest element in the List.\n Test HeapPop by comparing the popped element from the heap with the\n sorted list one by one. \n """\n for _ in xrange(100):\n thisHeap = HashHeap([0])\n testList = [0]\n for i in xrange(1000):\n thisRandom = random.randrange(-100, 100000)\n thisHeap.heapPush(thisRandom)\n testList.append(thisRandom)\n assert min(testList) == thisHeap.heapPeep()\n assert len(testList) == thisHeap.length\n assert len(thisHeap._hashMap) == thisHeap._maxIdx + 1\n testList.sort()\n assert len(testList) == thisHeap.length\n for idx, num in enumerate(testList):\n assert num == thisHeap.heapPop()\n assert len(testList) - 1 - idx == thisHeap.length\n assert len(thisHeap._hashMap) == thisHeap._maxIdx + 1\n\ndef removeTest():\n """\n Randomly generate a list, and push each element into the heap.\n Test HeapRemove by randomly delete one element from the heap by the probability\n of 0.2, and then check whether the first element in the heap is the same as the\n smallest element in the list.\n """\n for _ in xrange(100):\n thisHeap = HashHeap([0])\n testList = [0]\n for i in xrange(1000):\n thisRandom = random.randrange(-100, 100000)\n thisHeap.heapPush(thisRandom)\n if random.random() < 0.2:\n thisHeap.heapRemove(thisRandom)\n else:\n testList.append(thisRandom)\n assert min(testList) == thisHeap.heapPeep()\n assert len(testList) == thisHeap.length\n assert len(thisHeap._hashMap) == thisHeap._maxIdx + 1\n testList.sort()\n assert len(testList) == thisHeap.length\n for idx, num in enumerate(testList):\n assert num == thisHeap.heapPop()\n assert len(testList) - 1 - idx == thisHeap.length\n assert len(thisHeap._hashMap) == thisHeap._maxIdx + 1\n\n\nif __name__ == '__main__':\n pushpopTest()\n removeTest()\n```
| 8 | 1 |
[]
| 4 |
sliding-window-median
|
C++ Solution O(n*k)
|
c-solution-onk-by-kevin36-3o9g
|
The idea is to maintain a BST of the window and just search for the k/2 largest element and k/2 smallest element then the average of these two is the median of
|
kevin36
|
NORMAL
|
2017-01-08T05:15:32.283000+00:00
|
2017-01-08T05:15:32.283000+00:00
| 2,320 | false |
The idea is to maintain a BST of the window and just search for the k/2 largest element and k/2 smallest element then the average of these two is the median of the window.\n\n Now if the STL's multiset BST maintained how many element were in each subtree finding each median would take O(log k) time but since it doesn't it takes O(k) time to find each median.\n\n```class Solution {\npublic:\n vector<double> medianSlidingWindow(vector<int>& nums, int k) {\n multiset<int> mp;\n vector<double> med;\n \n for(int i=0; i<k-1; ++i) mp.insert(nums[i]);\n \n for(int i=k-1; i< nums.size(); ++i){\n mp.insert(nums[i]); // Add the next number\n \n auto itb = mp.begin(); advance(itb, (k-1)/2); //Find the lower median\n auto ite = mp.end(); advance(ite, -(k+1)/2); //Find the upper median\n \n double avg = ((long)(*itb) + (*ite)) / 2.0;\n med.push_back(avg);\n \n mp.erase(mp.find(nums[i-k+1])); //Remove the oldest element\n }\n \n return med;\n }\n};
| 7 | 2 |
[]
| 1 |
sliding-window-median
|
Java, Two Heaps and HashMap for lazy removes
|
java-two-heaps-and-hashmap-for-lazy-remo-bim2
|
Intuition\nThe main tricky point in this problem is to remove an elememnt from PriorityQueue. Regular method remove(i) takes O(n) and such solution fails by LTE
|
Vladislav-Sidorovich
|
NORMAL
|
2023-07-29T16:40:43.985614+00:00
|
2023-07-29T16:41:25.995408+00:00
| 1,123 | false |
# Intuition\nThe main tricky point in this problem is to remove an elememnt from `PriorityQueue`. Regular method `remove(i)` takes `O(n)` and such solution fails by LTE.\nAll the rest is similart to https://leetcode.com/problems/find-median-from-data-stream/ \n\n# Approach\nLet\'s keep removed items in `HashMap` and remove them only from the top of `PriorityQueue`. It will cost us + `O(n)` memory, but reduce remove to regual `poll` method with `O(logn)` time complexity.\nThe next point is to keep heap balanced:\n1. if need to remove number from `mins`, so the top of this queue should be replaced by smallest number from `maxes`.\n2. if need to remove number from `maxes`, od vice versa\n\nAlso we need to balance queue after adding new number.\n\nIt\'s a little tricky, visualization on paper will help you understand it better. It took me several hours to correctly write the code with this logic.\n\n# Code\n```\nclass Solution {\n \n public double[] medianSlidingWindow(int[] nums, int k) {\n double[] res = new double[nums.length - k + 1];\n Map<Integer, Integer> removed = new HashMap<>();\n\n PriorityQueue<Integer> mins = new PriorityQueue<>((a, b) -> Integer.compare(b, a));\n PriorityQueue<Integer> maxs = new PriorityQueue<>((a, b) -> Integer.compare(a, b));\n for (int i=0; i<k; i++) {\n maxs.add(nums[i]);\n mins.add(maxs.poll());\n if (mins.size() - maxs.size() > 1) {\n maxs.add(mins.poll());\n }\n }\n\n for (int i=k; i<=nums.length; i++) {\n res[i-k] = mediane(mins, maxs, k);\n\n if (i < nums.length) {\n int balance = nums[i-k] <= mins.peek() ? -1 : 1;\n markRemove(nums[i-k], removed);\n\n if (nums[i] <= mins.peek()) {\n mins.add(nums[i]);\n balance++;\n } else {\n maxs.add(nums[i]);\n balance--;\n }\n \n if (balance < 0) {\n mins.add(maxs.poll());\n }\n if (balance > 0) {\n maxs.add(mins.poll());\n }\n\n tryRemove(mins, removed);\n tryRemove(maxs, removed);\n }\n }\n\n return res;\n }\n\n private void tryRemove(PriorityQueue<Integer> queue, Map<Integer, Integer> removed) {\n while (!queue.isEmpty() && removed.getOrDefault(queue.peek(), 0) > 0) {\n int a = queue.poll();\n removed.put(a, removed.get(a) - 1);\n }\n }\n\n private void markRemove(int a, Map<Integer, Integer> removed) {\n removed.put(a, removed.getOrDefault(a, 0) + 1);\n }\n\n private double mediane(PriorityQueue<Integer> mins, PriorityQueue<Integer> maxs, int k) {\n if (k % 2 == 0) {\n double val = mins.peek() * 0.5 + maxs.peek() * 0.5;\n return val; \n } else {\n return mins.peek();\n }\n }\n}\n```
| 6 | 0 |
['Hash Table', 'Sliding Window', 'Heap (Priority Queue)', 'Java']
| 1 |
sliding-window-median
|
[Java] Optimal Sliding Window using two PriorityQueues
|
java-optimal-sliding-window-using-two-pr-pac0
|
\nclass Solution {\n public double[] medianSlidingWindow(int[] nums, int k) {\n \n double[] result = new double[nums.length - k + 1];\n
|
nagato19
|
NORMAL
|
2022-08-22T15:09:48.093598+00:00
|
2022-08-22T15:09:48.093630+00:00
| 2,014 | false |
```\nclass Solution {\n public double[] medianSlidingWindow(int[] nums, int k) {\n \n double[] result = new double[nums.length - k + 1];\n int p = 0;\n PriorityQueue<Integer> max = new PriorityQueue<>(Collections.reverseOrder());\n PriorityQueue<Integer> min = new PriorityQueue<>();\n \n int i=0, j=0;\n while(j < nums.length) {\n \n if(max.size() <= min.size()) {\n min.add(nums[j]);\n max.add(min.poll());\n }\n else {\n max.add(nums[j]);\n min.add(max.poll());\n }\n if(j-i+1 < k) j++;\n \n else if(j-i+1 == k) {\n if(max.size() == min.size())\n result[p++] = (double) ((long)max.peek() + (long)min.peek()) / 2.0;\n else\n result[p++] = (double)max.peek();\n \n if(!max.remove(nums[i])) min.remove(nums[i]);\n i++; j++;\n }\n }\n \n return result;\n }\n}\n```
| 6 | 0 |
['Sliding Window', 'Heap (Priority Queue)', 'Java']
| 1 |
sliding-window-median
|
Java max + min heaps cleaned up version
|
java-max-min-heaps-cleaned-up-version-by-fm5k
|
\tPriorityQueue max = new PriorityQueue<>(Collections.reverseOrder());\n PriorityQueue min = new PriorityQueue<>();\n\n public double[] medianSlidingWindo
|
didado
|
NORMAL
|
2021-01-24T02:49:38.641453+00:00
|
2021-01-24T02:50:29.361035+00:00
| 447 | false |
\tPriorityQueue<Integer> max = new PriorityQueue<>(Collections.reverseOrder());\n PriorityQueue<Integer> min = new PriorityQueue<>();\n\n public double[] medianSlidingWindow(int[] nums, int k) {\n double[] res = new double[nums.length - k + 1];\n\n for (int i = 0; i < nums.length; i++) {\n add(nums[i]);\n\n if (i >= k - 1) {\n res[i - k + 1] = getMedian();\n remove(nums[i - k + 1]);\n }\n }\n\n return res;\n }\n\n private void add(int n) {\n max.add(n);\n min.add(max.poll());\n\n if (min.size() > max.size())\n max.add(min.poll());\n }\n\n private void remove(int n) {\n if (max.peek() >= n) \n max.remove(n);\n else \n min.remove(n);\n\n if (min.size() > max.size())\n max.add(min.poll());\n if (max.size() > min.size())\n min.add(max.poll());\n }\n\n private double getMedian() {\n if (min.size() == max.size()) \n return ((double) min.peek() + (double) max.peek()) / 2;\n else\n return (double) max.peek();\n }
| 6 | 0 |
['Java']
| 1 |
sliding-window-median
|
Using ArrayList in Java, faster than 99% of the codes
|
using-arraylist-in-java-faster-than-99-o-p7k4
|
\npublic double[] medianSlidingWindow(int[] nums, int k) {\n double[] res=new double[nums.length-k+1];\n List<Integer> list = new ArrayList<Intege
|
hitesh_bhalotia
|
NORMAL
|
2020-07-28T12:03:00.426619+00:00
|
2020-07-28T12:04:26.621612+00:00
| 732 | false |
```\npublic double[] medianSlidingWindow(int[] nums, int k) {\n double[] res=new double[nums.length-k+1];\n List<Integer> list = new ArrayList<Integer>();\n for(int i=0;i<k;i++){ // used to get the first window only\n list.add(nums[i]);\n }\n Collections.sort(list);\n res[0] = (k%2==0) ? ((double)list.get(k/2-1) + (double)list.get(k/2))/2 : list.get(k/2);\n\t\t\n\t\t// if there are more than one window \n for(int i=0;i<nums.length-k;i++){\n int left=nums[i]; // number to be removed from the window\n int right=nums[i+k]; // number to be added to the window\n int index=Collections.binarySearch(list,right);\n if(index>=0) // if already present insert at the already existing position\n\t\t\t\tlist.add(index,right);\n else\n\t\t\t\tlist.add(-index-1,right);\n\t\t\t/* if element is not present binarySearch returns\n\t\t\t-(index)-1 which is the index at which it should be inserted to\n\t\t\tbe in the correct order.*/ \n index=Collections.binarySearch(list,left);\n list.remove(index);\n res[i+1]=(k%2==0)?((double)list.get(k/2-1)+(double)list.get(k/2))/2:list.get(k/2);\n }\n return res;\n}\n```
| 6 | 0 |
['Array', 'Binary Tree', 'Java']
| 1 |
sliding-window-median
|
JavaScript solution | Binary search [81%, 100%]
|
javascript-solution-binary-search-81-100-froe
|
Idea behind this solution is to use binary search to insert right number and remove left number when moving the sliding window to the right.\n\nRuntime: 108 ms,
|
i-love-typescript
|
NORMAL
|
2020-04-25T23:14:37.815840+00:00
|
2020-04-26T15:12:05.539278+00:00
| 964 | false |
Idea behind this solution is to use binary search to insert right number and remove left number when moving the sliding window to the right.\n\nRuntime: 108 ms, faster than 81.03% of JavaScript online submissions for Sliding Window Median.\nMemory Usage: 40 MB, less than 100.00% of JavaScript online submissions for Sliding Window Median.\n\n```\nfunction binarySearch(arr, target, l, r) {\n while (l < r) {\n const mid = Math.floor((l + r) / 2);\n if (arr[mid] < target) l = mid + 1;\n else if (arr[mid] > target) r = mid;\n else return mid;\n }\n if (l === r) return arr[l] >= target ? l : l + 1;\n}\n\n\nfunction medianSlidingWindow(nums, k) {\n let l = 0, r = k - 1, ret = [];\n // Create and sort window\n const window = nums.slice(l, k);\n window.sort((a, b) => a - b);\n while (r < nums.length) {\n // Calculate median and add it to the return array\n const median = k % 2 === 0\n ? (window[Math.floor(k / 2) - 1] + window[Math.floor(k / 2)]) / 2\n : window[Math.floor(k / 2)];\n ret.push(median);\n \n // Remove char from the left\n let char = nums[l++];\n let index = binarySearch(window, char, 0, window.length - 1);\n window.splice(index, 1);\n\n // Add char from the right\n char = nums[++r];\n index = binarySearch(window, char, 0, window.length - 1);\n window.splice(index, 0, char);\n }\n return ret;\n}\n```\n
| 6 | 0 |
['JavaScript']
| 0 |
sliding-window-median
|
Python SortedList solution
|
python-sortedlist-solution-by-drfirestre-rhg6
|
Just to remind we have quite a standard sortedcontainers library to deal with such problems very easily in O(n log k) in contrast to practically fast but arguab
|
drfirestream
|
NORMAL
|
2020-01-09T09:38:50.218704+00:00
|
2020-01-09T09:38:50.218750+00:00
| 1,170 | false |
Just to remind we have quite a standard sortedcontainers library to deal with such problems very easily in O(n log k) in contrast to practically fast but arguable from algorithmic point of view O(n k) solution that uses insort from bisect library\n\n```\nfrom sortedcontainers import SortedList\nclass Solution:\n def medianSlidingWindow(self, nums: List[int], k: int) -> List[float]:\n if len(nums) == 0:\n return []\n ar = SortedList(nums[:k])\n is_odd = k % 2 == 0\n medians = [(ar[k//2 - 1] + ar[k//2]) / 2.0 if is_odd else ar[k//2]]\n for i in range(len(nums) - k):\n ar.discard(nums[i])\n ar.add(nums[i + k])\n medians.append((ar[k//2 - 1] + ar[k//2]) / 2.0 if is_odd else ar[k//2])\n return medians\n```
| 6 | 0 |
['Python', 'Python3']
| 2 |
sliding-window-median
|
Python O(NlogN) using heap
|
python-onlogn-using-heap-by-danny7226-ydwo
|
python heap solution with run time O(NlogN)\n\n\n def medianSlidingWindow(self, nums, k):\n low, high = [], [] # heap\n for i in range(k):\n
|
danny7226
|
NORMAL
|
2019-07-12T08:32:44.828545+00:00
|
2019-07-12T08:33:25.284733+00:00
| 1,809 | false |
python heap solution with run time O(NlogN)\n\n```\n def medianSlidingWindow(self, nums, k):\n low, high = [], [] # heap\n for i in range(k):\n heapq.heappush(high, (nums[i], i)) # high is a min-heap\n for _ in range(k>>1):\n self.convert(high, low)\n ans = [high[0][0]*1. if k&1 else (high[0][0]-low[0][0])/2.]\n for i in range(len(nums[k:])):\n if nums[i+k] >= high[0][0]:\n heapq.heappush(high, (nums[i+k], i+k))\n if nums[i] <= high[0][0]: # keep the number of elements between two heap always in balance\n self.convert(high, low)\n else:\n heapq.heappush(low, (-nums[i+k], i+k))\n if nums[i] >= high[0][0]:\n self.convert(low, high)\n while low and low[0][1] <= i: heapq.heappop(low)\n while high and high[0][1] <= i: heapq.heappop(high)\n ans.append(high[0][0]*1. if k&1 else (high[0][0]-low[0][0])/2.)\n return ans\n \n \n def convert(self, heap1, heap2): # convert min-heap1 to max-heap2\n element, index = heapq.heappop(heap1)\n heapq.heappush(heap2, (-element, index))\n```
| 6 | 0 |
['Heap (Priority Queue)', 'Python']
| 4 |
sliding-window-median
|
Simple Solution with Diagrams in Video - JavaScript, C++, Java, Python
|
simple-solution-with-diagrams-in-video-j-vriw
|
Video\nPlease upvote here so others save time too!\n\nLike the video on YouTube if you found it useful\n\nClick here to subscribe on YouTube:\nhttps://www.youtu
|
danieloi
|
NORMAL
|
2024-11-26T14:19:20.558032+00:00
|
2024-11-26T14:19:20.558074+00:00
| 1,897 | false |
# Video\nPlease upvote here so others save time too!\n\nLike the video on YouTube if you found it useful\n\nClick here to subscribe on YouTube:\nhttps://www.youtube.com/@mayowadan?sub_confirmation=1\n\nThanks!\n\nhttps://youtu.be/QL6eAE_WopE?si=RKW9MF_rI_EuMdGD\n\n```Javascript []\n/**\n * @param {number[]} nums\n * @param {number} k\n * @return {number[]}\n */\nvar medianSlidingWindow = function (nums, k) {\n // To store the medians\n let medians = [];\n\n // To keep track of the numbers that need to be removed from the heaps\n let outgoingNum = {};\n\n // Max heap\n let smallList = new MinHeap();\n\n // Min heap\n let largeList = new MinHeap();\n\n // Initialize the max heap by multiplying each element by -1\n for (let i = 0; i < k; i++)\n smallList.offer(-1 * nums[i]);\n\n // Transfer the top 50% of the numbers from max heap to min heap\n // while restoring the sign of each number\n for (let i = 0; i < Math.floor(k / 2); i++)\n largeList.offer(-1 * smallList.poll());\n\n // Variable to keep the heaps balanced\n let balance = 0;\n\n let i = k;\n while (true) {\n // If the window size is odd\n if ((k & 1) === 1)\n medians.push(parseFloat(smallList.peek() * -1));\n else\n medians.push((parseFloat(smallList.peek() * -1) + parseFloat(largeList.peek())) * 0.5);\n\n // Break the loop if all elements have been processed\n if (i >= nums.length)\n break;\n\n // Outgoing number\n const outNum = nums[i - k];\n\n // Incoming number\n const inNum = nums[i];\n i += 1;\n\n // If the outgoing number is from max heap\n if (outNum <= smallList.peek() * -1)\n balance -= 1;\n else\n balance += 1;\n\n // Add/Update the outgoing number in the hash map\n if (outNum in outgoingNum)\n outgoingNum[outNum] = outgoingNum[outNum] + 1;\n else\n outgoingNum[outNum] = 1;\n\n // If the incoming number is less than the top of the max heap, add it in that heap\n // Otherwise, add it in the min heap\n if (smallList.size() > 0 && inNum <= smallList.peek() * -1) {\n balance += 1;\n smallList.offer(inNum * -1);\n } else {\n balance -= 1;\n largeList.offer(inNum);\n }\n\n // Re-balance the heaps\n if (balance < 0)\n smallList.offer(-1 * largeList.poll());\n else if (balance > 0)\n largeList.offer(-1 * smallList.poll());\n\n // Since the heaps have been balanced, we reset the balance variable to 0. \n // This ensures that the two heaps contain the correct elements for the calculations to be performed on the elements in the next window.\n balance = 0;\n\n // Remove invalid numbers present in the hash map from top of max heap\n while (smallList.peek() * -1 in outgoingNum && outgoingNum[smallList.peek() * -1] > 0)\n outgoingNum[smallList.peek() * -1] = outgoingNum[smallList.poll() * -1] - 1;\n\n // Remove invalid numbers present in the hash map from top of min heap\n while (largeList.size() > 0 && largeList.peek() in outgoingNum && outgoingNum[largeList.peek()] > 0)\n outgoingNum[largeList.peek()] = outgoingNum[largeList.poll()] - 1;\n }\n return medians;\n};\n\nclass MinHeap {\n constructor(data = new Array()) {\n this.data = data;\n this.compareVal = (a, b) => a - b;\n this.heapify();\n }\n\n heapify() {\n if (this.size() < 2) {\n return;\n }\n for (let i = 1; i < this.size(); i++) {\n this.percolateUp(i);\n }\n }\n\n peek() {\n if (this.size() === 0) {\n return null;\n }\n return this.data[0];\n }\n\n offer(value) {\n this.data.push(value);\n this.percolateUp(this.size() - 1);\n }\n\n poll() {\n if (this.size() === 0) {\n return null;\n }\n const result = this.data[0];\n const last = this.data.pop();\n if (this.size() !== 0) {\n this.data[0] = last;\n this.percolateDown(0);\n }\n return result;\n }\n\n percolateUp(index) {\n while (index > 0) {\n const parentIndex = (index - 1) >> 1;\n if (this.compareVal(this.data[index], this.data[parentIndex]) < 0) {\n this.swap(index, parentIndex);\n index = parentIndex;\n } else {\n break;\n }\n }\n }\n\n percolateDown(index) {\n const lastIndex = this.size() - 1;\n while (true) {\n const leftIndex = index * 2 + 1;\n const rightIndex = index * 2 + 2;\n let findIndex = index;\n\n if (\n leftIndex <= lastIndex &&\n this.compareVal(this.data[leftIndex], this.data[findIndex]) < 0\n ) {\n findIndex = leftIndex;\n }\n\n if (\n rightIndex <= lastIndex &&\n this.compareVal(this.data[rightIndex], this.data[findIndex]) < 0\n ) {\n findIndex = rightIndex;\n }\n\n if (index !== findIndex) {\n this.swap(index, findIndex);\n index = findIndex;\n } else {\n break;\n }\n }\n }\n\n swap(index1, index2) {\n [this.data[index1], this.data[index2]] = [\n this.data[index2],\n this.data[index1],\n ];\n }\n\n size() {\n return this.data.length;\n }\n}\n```\n```Python []\nclass Solution:\n def medianSlidingWindow(self, nums: List[int], k: int) -> List[float]:\n # To store the medians\n medians = []\n\n # To keep track of the numbers that need to be removed from the heaps\n outgoing_num = {}\n\n # Max heap\n small_list = []\n\n # Min heap\n large_list = []\n\n # Initialize the max heap by multiplying each element by -1\n for i in range(k):\n heappush(small_list, -nums[i])\n\n # Transfer the top 50% of the numbers from max heap to min heap\n # while restoring the sign of each number\n for i in range(k // 2):\n element = heappop(small_list)\n heappush(large_list, -element)\n\n # Variable to keep the heaps balanced\n balance = 0\n\n i = k\n while True:\n # If the window size is odd\n if k % 2 == 1:\n medians.append(float(-small_list[0]))\n else:\n medians.append((-small_list[0] + large_list[0]) * 0.5)\n\n # Break the loop if all elements have been processed\n if i >= len(nums):\n break\n\n # Outgoing number\n out_num = nums[i - k]\n\n # Incoming number\n in_num = nums[i]\n i += 1\n\n # If the outgoing number is from max heap\n if out_num <= -small_list[0]:\n balance -= 1\n else:\n balance += 1\n\n # Add/Update the outgoing number in the hash map\n outgoing_num[out_num] = outgoing_num.get(out_num, 0) + 1\n\n # If the incoming number is less than the top of the max heap, add it in that heap\n # Otherwise, add it in the min heap\n if in_num <= -small_list[0]:\n balance += 1\n heappush(small_list, -in_num)\n else:\n balance -= 1\n heappush(large_list, in_num)\n\n # Re-balance the heaps\n if balance < 0:\n heappush(small_list, -heappop(large_list))\n elif balance > 0:\n heappush(large_list, -heappop(small_list))\n\n # Since the heaps have been balanced, we reset the balance variable to 0.\n balance = 0\n\n # Remove invalid numbers present in the hash map from top of max heap\n while (\n small_list\n and -small_list[0] in outgoing_num\n and outgoing_num[-small_list[0]] > 0\n ):\n outgoing_num[-small_list[0]] -= 1\n heappop(small_list)\n\n # Remove invalid numbers present in the hash map from top of min heap\n while (\n large_list\n and large_list[0] in outgoing_num\n and outgoing_num[large_list[0]] > 0\n ):\n outgoing_num[large_list[0]] -= 1\n heappop(large_list)\n\n return medians\n\n```\n```Java []\nclass Solution {\n public double[] medianSlidingWindow(int[] nums, int k) {\n double[] medians = new double[nums.length - k + 1];\n Map<Integer, Integer> outgoingNum = new HashMap<>();\n PriorityQueue<Integer> smallList = new PriorityQueue<>(Collections.reverseOrder());\n PriorityQueue<Integer> largeList = new PriorityQueue<>();\n\n for (int i = 0; i < k; i++) {\n smallList.offer(nums[i]);\n }\n\n for (int i = 0; i < k / 2; i++) {\n largeList.offer(smallList.poll());\n }\n\n int balance = 0;\n int index = 0;\n\n for (int i = k;; i++) {\n if (k % 2 == 1) {\n medians[index] = smallList.peek();\n } else {\n medians[index] = ((double) smallList.peek() + largeList.peek()) / 2.0;\n }\n\n if (i >= nums.length)\n break;\n\n int outNum = nums[i - k];\n int inNum = nums[i];\n index++;\n\n balance += (outNum <= smallList.peek()) ? -1 : 1;\n\n outgoingNum.put(outNum, outgoingNum.getOrDefault(outNum, 0) + 1);\n\n if (inNum <= smallList.peek()) {\n balance++;\n smallList.offer(inNum);\n } else {\n balance--;\n largeList.offer(inNum);\n }\n\n if (balance < 0) {\n smallList.offer(largeList.poll());\n } else if (balance > 0) {\n largeList.offer(smallList.poll());\n }\n\n balance = 0;\n\n while (outgoingNum.getOrDefault(smallList.peek(), 0) > 0) {\n outgoingNum.put(smallList.peek(), outgoingNum.get(smallList.peek()) - 1);\n smallList.poll();\n }\n\n while (!largeList.isEmpty() && outgoingNum.getOrDefault(largeList.peek(), 0) > 0) {\n outgoingNum.put(largeList.peek(), outgoingNum.get(largeList.peek()) - 1);\n largeList.poll();\n }\n }\n\n return medians;\n }\n}\n\n```\n```C++ []\nclass Solution {\npublic:\n vector<double> medianSlidingWindow(vector<int>& nums, int k) {\n vector<double> medians;\n unordered_map<int, int> outgoingNum;\n priority_queue<int> smallList;\n priority_queue<int, vector<int>, greater<int>> largeList;\n\n for (int i = 0; i < k; i++) {\n smallList.push(nums[i]);\n }\n\n for (int i = 0; k && i < k / 2; i++) {\n largeList.push(smallList.top());\n smallList.pop();\n }\n\n int balance = 0;\n int i = k;\n\n while (true) {\n if (k % 2 == 1) {\n medians.push_back(smallList.top());\n } else {\n medians.push_back(\n ((long long)smallList.top() + (long long)largeList.top()) *\n 0.5);\n }\n\n if (i >= nums.size()) {\n break;\n }\n\n int outNum = nums[i - k];\n int inNum = nums[i];\n i++;\n\n if (outNum <= smallList.top()) {\n balance -= 1;\n } else {\n balance += 1;\n }\n\n outgoingNum[outNum]++;\n\n if (!smallList.empty() && inNum <= smallList.top()) {\n balance += 1;\n smallList.push(inNum);\n } else {\n balance -= 1;\n largeList.push(inNum);\n }\n\n if (balance < 0) {\n smallList.push(largeList.top());\n largeList.pop();\n } else if (balance > 0) {\n largeList.push(smallList.top());\n smallList.pop();\n }\n\n balance = 0;\n\n while (!smallList.empty() && outgoingNum[smallList.top()]) {\n outgoingNum[smallList.top()]--;\n smallList.pop();\n }\n\n while (!largeList.empty() && outgoingNum[largeList.top()]) {\n outgoingNum[largeList.top()]--;\n largeList.pop();\n }\n }\n\n return medians;\n }\n};\n\n```\n
| 5 | 0 |
['Python', 'C++', 'Java', 'Python3', 'JavaScript']
| 0 |
sliding-window-median
|
Python | Easy | Heap | Sliding Window Median
|
python-easy-heap-sliding-window-median-b-xzdk
|
\nsee the Successfully Accepted Submission\nPython\nfrom sortedcontainers import SortedList # Import the SortedList class from the sortedcontainers module\n\nc
|
Khosiyat
|
NORMAL
|
2023-10-12T14:24:05.784403+00:00
|
2023-10-12T14:24:05.784428+00:00
| 643 | false |
\n[see the Successfully Accepted Submission](https://leetcode.com/submissions/detail/1069477256/)\n```Python\nfrom sortedcontainers import SortedList # Import the SortedList class from the sortedcontainers module\n\nclass Solution:\n def medianSlidingWindow(self, nums, k):\n window = SortedList(nums[:k]) # Create a SortedList containing the first \'k\' elements of \'nums\'\n mid = window[k // 2] # Calculate the initial median value based on the SortedList\n medians = [] # Initialize an empty list to store medians\n\n for i in range(k, len(nums)): # Iterate through \'nums\' starting from the \'k\'-th element\n medians.append((window[k // 2] + window[(k - 1) // 2]) / 2.0) # Calculate and append the median to \'medians\' list\n\n window.add(nums[i]) # Add the next element to the sliding window\n if nums[i - k] <= mid: # Check if the element to be removed is less than or equal to the previous median\n mid -= 1 # Decrement the \'mid\' value if necessary (to maintain the median in the SortedList)\n window.remove(nums[i - k]) # Remove the element that is no longer in the sliding window\n\n medians.append((window[k // 2] + window[(k - 1) // 2]) / 2.0) # Calculate and append the last median\n\n return medians # Return the list of medians for each sliding window\n\n```\n\n\n
| 5 | 0 |
['Heap (Priority Queue)', 'Python']
| 1 |
sliding-window-median
|
[Python3] SortedList
|
python3-sortedlist-by-ye15-7c98
|
\n\nfrom sortedcontainers import SortedList\n\nclass Solution:\n def medianSlidingWindow(self, nums: List[int], k: int) -> List[float]:\n ans = []\n
|
ye15
|
NORMAL
|
2021-06-18T00:41:04.556518+00:00
|
2021-06-18T00:41:04.556549+00:00
| 286 | false |
\n```\nfrom sortedcontainers import SortedList\n\nclass Solution:\n def medianSlidingWindow(self, nums: List[int], k: int) -> List[float]:\n ans = []\n sl = SortedList()\n for i, x in enumerate(nums): \n sl.add(x)\n if i >= k: sl.remove(nums[i-k])\n if i+1 >= k: \n val = sl[k//2]\n if not k&1: val = (sl[(k-1)//2] + val)/2\n ans.append(val)\n return ans \n```
| 5 | 1 |
['Python3']
| 2 |
sliding-window-median
|
JAVA || Clean & Concise & Optimal Code || Binary Search or Two Heaps Data Structure
|
java-clean-concise-optimal-code-binary-s-dv0t
|
Solution 1: Binary Search Algorithm\n\n\nclass Solution {\n \n public void addElement (List<Integer> list, int num) {\n \n int index = Colle
|
anii_agrawal
|
NORMAL
|
2021-05-04T19:31:50.619839+00:00
|
2021-05-04T19:31:50.619881+00:00
| 910 | false |
# Solution 1: Binary Search Algorithm\n\n```\nclass Solution {\n \n public void addElement (List<Integer> list, int num) {\n \n int index = Collections.binarySearch (list, num);\n index = index < 0 ? Math.abs (index) - 1 : index;\n list.add (index, num);\n }\n \n public void removeElement (List<Integer> list, int num) {\n \n int index = Collections.binarySearch (list, num);\n list.remove (index);\n }\n \n public double findMedian (List<Integer> list, int k) {\n \n return k % 2 == 0 ? ((double) list.get (k / 2 - 1) + list.get (k / 2)) / 2 : list.get (k / 2);\n }\n \n public double[] medianSlidingWindow(int[] nums, int k) {\n \n double[] medianArray = new double[nums.length - k + 1];\n List<Integer> list = new ArrayList<> ();\n \n for (int i = 0, j = 0; i < nums.length; i++) {\n addElement (list, nums[i]);\n \n if (i >= k - 1) {\n medianArray[j++] = findMedian (list, k);\n removeElement (list, nums[i - k + 1]);\n }\n }\n \n return medianArray;\n }\n}\n\nTime Complexity: O(N * log K)\nSpace Complexity: O(K)\n```\n\n# Solution 2: Min & Max Heap (2 Priority Queues)\n\n```\nclass Solution {\n \n PriorityQueue<Integer> minHeap;\n PriorityQueue<Integer> maxHeap;\n \n public void balanceHeaps () {\n \n if (maxHeap.size () > minHeap.size ()) {\n minHeap.offer (maxHeap.poll ());\n }\n }\n \n public void removeElement (int num) {\n \n if (num > maxHeap.peek ()) {\n minHeap.remove (num);\n }\n else {\n maxHeap.remove (num);\n }\n \n balanceHeaps ();\n }\n \n public double findMedian (int k) {\n \n return k % 2 == 0 ? ((double) minHeap.peek () + maxHeap.peek ()) / 2 : minHeap.peek ();\n }\n \n public double[] medianSlidingWindow(int[] nums, int k) {\n \n double[] medianArray = new double[nums.length - k + 1];\n minHeap = new PriorityQueue<> ();\n maxHeap = new PriorityQueue<> ((a, b) -> Integer.compare (b, a));\n \n if (k == 1) {\n for (int i = 0; i < nums.length; i++) {\n medianArray[i] = nums[i];\n }\n \n return medianArray;\n }\n \n for (int i = 0, j = 0; i < nums.length; i++) {\n minHeap.offer (nums[i]);\n maxHeap.offer (minHeap.poll ());\n balanceHeaps ();\n \n if (i >= k - 1) {\n medianArray[j++] = findMedian (k);\n removeElement (nums[i - k + 1]);\n }\n }\n \n return medianArray;\n }\n}\n\nTime Complexity: O(N * K)\nSapce Complexity: O(K) \n```\n\nPlease help to **UPVOTE** if this post is useful for you.\nIf you have any questions, feel free to comment below.\n\n**LOVE CODING :)\nHAPPY CODING :)\nHAPPY LEARNING :)**
| 5 | 1 |
['Heap (Priority Queue)', 'Binary Tree', 'Java']
| 2 |
sliding-window-median
|
My concise version with two TreeSet (JAVA)
|
my-concise-version-with-two-treeset-java-jj74
|
This quesiton is very similar to LC295 Find Median from Data Stream. We use two PriorityQueue in that question. However, the remove(Object) is O(n) for Priority
|
deepli
|
NORMAL
|
2020-08-13T05:56:59.760252+00:00
|
2020-08-13T05:57:29.271948+00:00
| 171 | false |
This quesiton is very similar to LC295 Find Median from Data Stream. We use two PriorityQueue in that question. However, the remove(Object) is O(n) for PriorityQueue. We want O(logn), so we use TreeSet. To handle the duplicate case, we store the index instead of the array value in the TreeSet.\n```\npublic double[] medianSlidingWindow(int[] nums, int k) {\n double[] result = new double[nums.length - k + 1];\n int start = 0;\n \n TreeSet<Integer> lo = new TreeSet<>((a, b) -> (nums[a] != nums[b] ? Integer.compare(nums[a], nums[b]) : a - b));\n TreeSet<Integer> hi = new TreeSet<>((a, b) -> (nums[a] != nums[b] ? Integer.compare(nums[a], nums[b]) : a - b));\n \n for (int i = 0; i < nums.length; i++) {\n lo.add(i);\n hi.add(lo.pollLast());\n if(hi.size()>lo.size()) lo.add(hi.pollFirst());\n if (lo.size() + hi.size() == k) {\n result[start]=lo.size()==hi.size()? nums[lo.last()]/2.0+ nums[hi.first()]/2.0: nums[lo.last()]/1.0;\n if (!lo.remove(start)) hi.remove(start);\n start++;\n }\n }\n return result;\n }\n
| 5 | 0 |
[]
| 1 |
sliding-window-median
|
[Rust] Just write a avl tree library
|
rust-just-write-a-avl-tree-library-by-ye-0ock
|
since rust doesn\'t have multiset like C++, I created it myself. The code is long, but works :) and beats 100% time and memory.\n\n\n#![allow(dead_code)]\n\n#[d
|
yeetcoder4736
|
NORMAL
|
2020-07-15T17:17:09.038251+00:00
|
2020-07-15T17:17:09.038311+00:00
| 321 | false |
since rust doesn\'t have multiset like C++, I created it myself. The code is long, but works :) and beats 100% time and memory.\n\n```\n#![allow(dead_code)]\n\n#[derive(Debug)]\nstruct MultiSetNode<T> {\n /// The value being stored.\n value: T,\n /// The number of times this value is stored.\n count: usize,\n\n /// The left and right subtrees.\n left: Option<Box<MultiSetNode<T>>>,\n right: Option<Box<MultiSetNode<T>>>,\n\n /// The size of this subtree.\n size: usize,\n /// The height of this subtree.\n height: usize,\n}\n\n#[derive(Clone, Copy, Debug)]\nenum Rotation {\n Clockwise,\n Anticlockwise,\n}\n\n#[derive(Clone, Copy, Debug)]\nenum Child {\n Left,\n Right,\n}\n\nimpl Child {\n pub fn opposite(&self) -> Child {\n match self {\n Child::Left => Child::Right,\n Child::Right => Child::Left,\n }\n }\n}\n\nimpl<T> MultiSetNode<T>\nwhere\n T: std::cmp::PartialOrd + std::fmt::Debug,\n{\n pub fn new(value: T) -> MultiSetNode<T> {\n MultiSetNode {\n value,\n count: 1,\n left: None,\n right: None,\n size: 1,\n height: 1,\n }\n }\n\n fn get_child(&mut self, child: Child) -> &mut Option<Box<MultiSetNode<T>>> {\n match child {\n Child::Left => &mut self.left,\n Child::Right => &mut self.right,\n }\n }\n\n fn swap_values(x: &mut MultiSetNode<T>, y: &mut MultiSetNode<T>) {\n std::mem::swap(&mut x.value, &mut y.value);\n std::mem::swap(&mut x.count, &mut y.count);\n }\n\n // Rotates the subtree by `rotation`.\n // If `rotation` is Rotation::Anticlockwise, then the tree after rotation becomes:\n // A C\n // B C ==> A G\n // F G B F\n //\n // If `rotation` is Rotation::Clockwise, then the tree after rotation becomes:\n // A B\n // B C ==> D A\n // D E E C\n fn rotate(&mut self, rotation: Rotation) {\n // If anti-clockwise, the procedure is exactly the same, except left and right children are swapped.\n let (l_child, r_child) = match rotation {\n Rotation::Clockwise => (Child::Left, Child::Right),\n Rotation::Anticlockwise => (Child::Right, Child::Left),\n };\n\n // 1) Detach the left subtree from root.\n // A(self)\n // B C\n // D E\n let mut detached_left_opt = None;\n std::mem::swap(self.get_child(l_child), &mut detached_left_opt);\n let mut detached_left = match detached_left_opt {\n None => return, // If no left subtree, return early.\n Some(detached_left) => detached_left,\n };\n\n // 2) Swap the children of `detached_left`.\n // A(self)\n // B C\n // E D\n std::mem::swap(&mut detached_left.left, &mut detached_left.right);\n\n // 3) Swap the values and counts of root (`self`) and `detached_left`.\n // B(self)\n // A C\n // E D\n MultiSetNode::swap_values(self, &mut detached_left);\n\n // 4) Swap the right children of the root and `detached_left`.\n // B(self)\n // A D\n // E C\n std::mem::swap(self.get_child(r_child), detached_left.get_child(r_child));\n\n // 5) Swap the children of root.\n // B(self)\n // A D\n // E C\n std::mem::swap(&mut self.left, &mut self.right);\n\n // 6) Set root\'s right child to `detached_left`.\n // B(self)\n // D A\n // E C\n *self.get_child(r_child) = Some(detached_left);\n }\n\n fn child_heights(&self) -> (usize, usize) {\n (\n self.left.as_ref().map(|node| node.height).unwrap_or(0),\n self.right.as_ref().map(|node| node.height).unwrap_or(0),\n )\n }\n\n pub fn balance(&mut self) {\n let (l_height, r_height) = self.child_heights();\n\n if l_height > r_height + 1 {\n // Safe unwrap as `l_height` >= 1.\n let left = self.left.as_mut().unwrap();\n let (ll_height, lr_height) = left.child_heights();\n // Make sure left-left subtree is at least as tall as left-right subtree.\n if ll_height < lr_height {\n left.rotate(Rotation::Anticlockwise);\n }\n self.rotate(Rotation::Clockwise);\n } else if r_height > l_height + 1 {\n // Safe unwrap as `r_height` >= 1.\n let right = self.right.as_mut().unwrap();\n let (rl_height, rr_height) = right.child_heights();\n // Make sure right-right subtree is at least as tall as right-left subtree.\n if rr_height < rl_height {\n right.rotate(Rotation::Clockwise);\n }\n self.rotate(Rotation::Anticlockwise);\n }\n\n // Re-calculate meta info after rotations.\n if let Some(left) = &mut self.left {\n left.update_meta();\n }\n if let Some(right) = &mut self.right {\n right.update_meta();\n }\n self.update_meta();\n }\n\n fn update_meta(&mut self) {\n // Size is `self.count` + left size + right size.\n self.size = self.count\n + self.left.as_ref().map(|node| node.size).unwrap_or(0)\n + self.right.as_ref().map(|node| node.size).unwrap_or(0);\n\n // Height is 1 + max(left height, right height).\n let (l_height, r_height) = self.child_heights();\n self.height = 1 + std::cmp::max(l_height, r_height);\n }\n\n fn fix(&mut self) {\n self.update_meta();\n self.balance();\n }\n\n fn insert(opt_node: &mut Option<Box<MultiSetNode<T>>>, value: T) {\n let node = match opt_node {\n None => {\n *opt_node = Some(Box::new(MultiSetNode::new(value)));\n return;\n }\n Some(node) => node,\n };\n\n if value < node.value {\n MultiSetNode::insert(&mut node.left, value)\n } else if value > node.value {\n MultiSetNode::insert(&mut node.right, value)\n } else {\n node.count += 1;\n }\n\n node.fix();\n }\n\n fn remove_node(opt_node: &mut Option<Box<MultiSetNode<T>>>) {\n let node = match opt_node {\n None => return,\n Some(node) => node,\n };\n\n let child = match (node.left.as_mut(), node.right.as_mut()) {\n (Some(_), Some(right)) => {\n if let Some(_) = right.left.as_mut() {\n let mut parent = right;\n while parent.left.as_mut().unwrap().left.as_mut().is_some() {\n parent = parent.left.as_mut().unwrap();\n }\n let to_swap = parent.left.as_mut().unwrap();\n std::mem::swap(&mut node.value, &mut to_swap.value);\n std::mem::swap(&mut node.count, &mut to_swap.count);\n\n let mut to_swap_right = None;\n std::mem::swap(&mut to_swap_right, &mut to_swap.right);\n parent.left = to_swap_right;\n\n fn fix_left<T>(x_opt: &mut Option<Box<MultiSetNode<T>>>)\n where\n T: std::cmp::PartialOrd + std::fmt::Debug,\n {\n if let Some(x) = x_opt {\n fix_left(&mut x.left);\n x.fix();\n }\n }\n fix_left(&mut node.right);\n\n node.fix();\n return;\n } else {\n Child::Right\n }\n }\n (None, None) | (None, Some(_)) => Child::Right,\n (Some(_), None) => Child::Left,\n };\n\n let mut detached_child = None;\n std::mem::swap(node.get_child(child), &mut detached_child);\n\n let otherchild = child.opposite();\n let mut detached_otherchild = None;\n std::mem::swap(node.get_child(otherchild), &mut detached_otherchild);\n\n if let Some(detached_child_node) = detached_child.as_mut() {\n *detached_child_node.get_child(otherchild) = detached_otherchild;\n detached_child_node.fix();\n }\n\n *opt_node = detached_child;\n }\n\n fn remove(opt_node: &mut Option<Box<MultiSetNode<T>>>, value: T) {\n let node = match opt_node {\n None => return,\n Some(node) => node,\n };\n\n if value < node.value {\n MultiSetNode::remove(&mut node.left, value)\n } else if value > node.value {\n MultiSetNode::remove(&mut node.right, value)\n } else {\n node.count -= 1;\n if node.count == 0 {\n return MultiSetNode::remove_node(opt_node);\n }\n };\n\n node.fix();\n }\n\n /// Returns the count of the given key.\n pub fn get(opt_node: &Option<Box<MultiSetNode<T>>>, value: T) -> usize {\n let node = match &opt_node {\n None => return 0,\n Some(node) => node,\n };\n\n if value < node.value {\n MultiSetNode::get(&node.left, value)\n } else if value > node.value {\n MultiSetNode::get(&node.right, value)\n } else {\n node.count\n }\n }\n\n pub fn len(&self) -> usize {\n self.size\n }\n\n fn fmt_with_indents(\n opt_node: &Option<Box<MultiSetNode<T>>>,\n f: &mut std::fmt::Formatter<\'_>,\n level: usize,\n child: Option<Child>,\n ) -> std::fmt::Result {\n if let Some(node) = opt_node {\n let indent = (0..level).map(|_| " ").collect::<String>();\n\n let _ = write!(\n f,\n "{}child={:?},val={:?},size={},count={},height={}\\n",\n indent, child, node.value, node.size, node.count, node.height\n );\n let _ = MultiSetNode::fmt_with_indents(&node.left, f, level + 1, Some(Child::Left));\n MultiSetNode::fmt_with_indents(&node.right, f, level + 1, Some(Child::Right))\n } else {\n write!(f, "",)\n }\n }\n\n pub fn nth_node<\'a>(\n opt_node: &\'a mut Option<Box<MultiSetNode<T>>>,\n n: usize,\n ) -> Option<&\'a mut Box<MultiSetNode<T>>> {\n let node = match opt_node {\n None => return None,\n Some(node) => node,\n };\n\n let left_size = node.left.as_ref().map(|node| node.size).unwrap_or(0);\n if n < left_size {\n MultiSetNode::nth_node(&mut node.left, n)\n } else if n < left_size + node.count {\n Some(node)\n } else {\n MultiSetNode::nth_node(&mut node.right, n - left_size - node.count)\n }\n }\n\n pub fn nth_item(&self, n: usize) -> &T {\n let left_size = self.left.as_ref().map(|node| node.size).unwrap_or(0);\n if n < left_size {\n MultiSetNode::nth_item(self.left.as_ref().unwrap(), n)\n } else if n < left_size + self.count {\n &self.value\n } else {\n MultiSetNode::nth_item(self.right.as_ref().unwrap(), n - left_size - self.count)\n }\n }\n}\n\n#[derive(Debug)]\npub struct MultiSet<T> {\n root: Option<Box<MultiSetNode<T>>>,\n}\n\nimpl<T> MultiSet<T>\nwhere\n T: std::cmp::PartialOrd + std::fmt::Debug,\n{\n pub fn new() -> MultiSet<T> {\n MultiSet { root: None }\n }\n\n pub fn len(&self) -> usize {\n match &self.root {\n None => 0,\n Some(node) => node.len(),\n }\n }\n\n /// Inserts `value`. Duplicates are allowed.\n pub fn insert(&mut self, value: T) {\n MultiSetNode::insert(&mut self.root, value);\n }\n\n /// Returns true if `value` was successfully removed.\n pub fn remove(&mut self, value: T) {\n MultiSetNode::remove(&mut self.root, value);\n }\n\n pub fn get(&self, value: T) -> usize {\n MultiSetNode::get(&self.root, value)\n }\n\n /// Gets the nth item in the MultiSet where n in `[0, len())`. Panics if `n` not in this range.\n pub fn nth_item(&self, n: usize) -> &T {\n if n >= self.len() {\n panic!("Item out of bounds!");\n }\n\n MultiSetNode::nth_item(self.root.as_ref().unwrap(), n)\n }\n}\n\nimpl<T> std::fmt::Display for MultiSet<T>\nwhere\n T: std::cmp::PartialOrd + std::fmt::Debug,\n{\n fn fmt(&self, f: &mut std::fmt::Formatter<\'_>) -> std::fmt::Result {\n MultiSetNode::fmt_with_indents(&self.root, f, 0, None)\n }\n}\n\n#[cfg(test)]\nmod test {\n use super::*;\n use std::collections::HashMap;\n\n // Checks constraints and returns (size and height).\n fn check<T>(\n opt_node: &Option<Box<MultiSetNode<T>>>,\n min_val_opt: Option<&T>,\n max_val_opt: Option<&T>,\n ) -> (usize, usize)\n where\n T: std::cmp::PartialOrd + std::fmt::Debug,\n {\n let node = match opt_node {\n None => return (0, 0),\n Some(node) => node,\n };\n if let Some(min_val) = min_val_opt {\n assert!(min_val < &node.value);\n }\n if let Some(max_val) = max_val_opt {\n assert!(&node.value < max_val);\n }\n\n let (l_size, l_height) = check(&node.left, min_val_opt, Some(&node.value));\n let (r_size, r_height) = check(&node.right, Some(&node.value), max_val_opt);\n assert_eq!(node.size, node.count + l_size + r_size);\n assert_eq!(node.height, 1 + std::cmp::max(l_height, r_height));\n // Max height difference between left and right subtrees is 1.\n assert!((l_height as i64 - r_height as i64).abs() <= 1);\n\n (node.size, node.height)\n }\n\n fn insert_<T>(m: &mut MultiSet<T>, value: T)\n where\n T: std::cmp::PartialOrd + std::fmt::Debug,\n {\n let old_len = m.len();\n m.insert(value);\n assert_eq!(m.len(), old_len + 1);\n check(&m.root, None, None);\n }\n\n fn remove_<T>(m: &mut MultiSet<T>, value: T)\n where\n T: std::cmp::PartialOrd + std::fmt::Debug + Copy + std::fmt::Display,\n {\n let old_len = m.len();\n m.remove(value);\n assert_eq!(m.len(), old_len - 1);\n check(&m.root, None, None);\n }\n\n #[test]\n fn test_multiset_remove_some_some() {\n let mut m = MultiSet::new();\n insert_(&mut m, 11);\n insert_(&mut m, 10);\n insert_(&mut m, 8);\n insert_(&mut m, 9);\n insert_(&mut m, 7);\n insert_(&mut m, 6);\n remove_(&mut m, 11);\n\n remove_(&mut m, 8);\n }\n\n #[test]\n fn test_multiset_insert() {\n let mut m = MultiSet::new();\n insert_(&mut m, 10);\n insert_(&mut m, 10);\n insert_(&mut m, 10);\n assert_eq!(m.get(10), 3);\n\n insert_(&mut m, 11);\n assert_eq!(m.get(11), 1);\n\n insert_(&mut m, 12);\n insert_(&mut m, 13);\n insert_(&mut m, 14);\n insert_(&mut m, 15);\n insert_(&mut m, 16);\n assert_eq!(m.get(16), 1);\n assert_eq!(m.len(), 9);\n }\n\n #[test]\n fn test_multiset_remove() {\n let mut m = MultiSet::new();\n let items = vec![11, 99, 7, 8, 12, 10, 10];\n for item in &items {\n insert_(&mut m, *item);\n }\n assert_eq!(m.len(), items.len());\n\n remove_(&mut m, 10);\n assert_eq!(m.get(10), 1);\n assert_eq!(m.len(), items.len() - 1);\n remove_(&mut m, 10);\n assert_eq!(m.get(10), 0);\n assert_eq!(m.len(), items.len() - 2);\n\n assert_eq!(m.get(11), 1);\n assert_eq!(m.get(12), 1);\n }\n\n #[test]\n fn test_multiset_sequential() {\n let mut m = MultiSet::new();\n let mut items = vec![];\n for i in 1..100 {\n for j in 1..i + 1 {\n items.push((i * j + 2 * j + 12) % 25);\n }\n }\n let mut d = HashMap::new();\n for (i, item) in items.iter().enumerate() {\n *d.entry(*item).or_insert(0) += 1;\n insert_(&mut m, *item);\n assert_eq!(m.len(), i + 1);\n\n assert_eq!(m.get(*item), d[item]);\n }\n\n let num_removes = items.len() / 2;\n for i in 0..num_removes {\n let removed_item = items.remove(i);\n remove_(&mut m, removed_item);\n *d.get_mut(&removed_item).unwrap() -= 1;\n\n assert_eq!(m.get(removed_item), d[&removed_item]);\n }\n\n items.sort();\n for (i, item) in items.iter().enumerate() {\n assert_eq!(m.get(*item), d[item]);\n assert_eq!(m.nth_item(i), item);\n }\n }\n}\n\n\npub fn median_sliding_window(nums: Vec<i32>, k: i32) -> Vec<f64> {\n assert!(k > 0);\n let k = std::cmp::min(k as usize, nums.len());\n\n fn get_median(m: &MultiSet<i32>) -> f64 {\n let first_item = *m.nth_item((m.len() - 1) / 2) as f64;\n if m.len() % 2 != 0 {\n return first_item;\n }\n\n let second_item = *m.nth_item(m.len() / 2) as f64;\n (first_item + second_item) / 2.0\n }\n\n let mut map = MultiSet::new();\n let mut medians = vec![];\n\n for num in nums[0..k].iter() {\n map.insert(*num);\n }\n medians.push(get_median(&map));\n\n for (num_remove, num_add) in nums.iter().zip(nums[k..].iter()) {\n map.remove(*num_remove);\n map.insert(*num_add);\n medians.push(get_median(&map));\n }\n\n medians\n}\n\n\n\nimpl Solution {\n pub fn median_sliding_window(nums: Vec<i32>, k: i32) -> Vec<f64> {\n median_sliding_window(nums, k)\n }\n}\n```
| 5 | 0 |
['Rust']
| 1 |
sliding-window-median
|
Swift 100/100 using binary search
|
swift-100100-using-binary-search-by-mode-qthj
|
\nclass Solution {\n \n func getMedian(_ arr: inout [Int]) -> Double {\n if arr.count % 2 != 0 {\n return Double(arr[arr.count / 2])\n
|
moderator1
|
NORMAL
|
2020-03-08T12:28:03.342383+00:00
|
2020-03-08T12:28:03.342420+00:00
| 264 | false |
```\nclass Solution {\n \n func getMedian(_ arr: inout [Int]) -> Double {\n if arr.count % 2 != 0 {\n return Double(arr[arr.count / 2])\n } else {\n return Double((Double(arr[arr.count/2]) + Double(arr[arr.count/2 - 1])) / 2.0)\n }\n }\n \n\t\n func binaryRemove(_ num: Int, arr: inout [Int]) {\n var left = 0\n var right = arr.count - 1\n while left <= right {\n let mid = left + (right - left) / 2\n if num > arr[mid] {\n left = mid + 1\n } else if num < arr[mid] {\n right = mid - 1\n } else {\n left = mid\n break\n }\n }\n \n\t\t// O(n)\n arr.remove(at: left)\n }\n \n\n func binaryInsert(_ num: Int, arr: inout [Int]) {\n var left = 0\n var right = arr.count - 1\n while left <= right {\n let mid = left + (right - left) / 2\n if num > arr[mid] {\n left = mid + 1\n } else if num < arr[mid] {\n right = mid - 1\n } else {\n left = mid\n break\n }\n }\n\t\t\n\t\t// O(n)\n arr.insert(num, at: left)\n }\n \n func medianSlidingWindow(_ nums: [Int], _ k: Int) -> [Double] {\n guard nums.count > 0 else { return [] }\n var medians = [Double]()\n var slidingWindow = [Int]()\n \n for i in 0..<nums.count {\n if i < k {\n binaryInsert(nums[i], arr: &slidingWindow)\n } else {\n medians.append(getMedian(&slidingWindow))\n binaryRemove(nums[i-k], arr: &slidingWindow)\n binaryInsert(nums[i], arr: &slidingWindow)\n\n }\n }\n medians.append(getMedian(&slidingWindow))\n return medians\n }\n}\n```
| 5 | 0 |
[]
| 1 |
sliding-window-median
|
C# SortedList
|
c-sortedlist-by-user638-m14p
|
C# SortedList\n\npublic class Solution\n{\n public double[] MedianSlidingWindow(int[] nums, int k)\n {\n var res = new List<double>();\n var
|
user638
|
NORMAL
|
2020-02-11T06:54:05.744341+00:00
|
2020-02-11T06:54:05.744388+00:00
| 437 | false |
C# SortedList\n```\npublic class Solution\n{\n public double[] MedianSlidingWindow(int[] nums, int k)\n {\n var res = new List<double>();\n var sl = new SortedList<long, int>();\n for (var i = 0; i < nums.Length; i++)\n {\n sl.Add(GetId(i, nums), nums[i]);\n if (sl.Count > k)\n {\n sl.Remove(GetId(i - k, nums));\n }\n if (sl.Count == k)\n {\n if (k % 2 == 0) res.Add((sl[sl.Keys[k / 2 - 1]] / 2.0 + sl[sl.Keys[k / 2]] / 2.0));\n else res.Add(sl[sl.Keys[k / 2]]);\n }\n }\n\n return res.ToArray();\n }\n\n public long GetId(int i, int[] nums)\n {\n return Convert.ToInt64(nums[i]) * nums.Length + i;\n }\n}\n```
| 5 | 0 |
[]
| 2 |
sliding-window-median
|
JavaScript 2 Heaps & Binary Search [2 approaches]
|
javascript-2-heaps-binary-search-2-appro-6xjt
|
2 Heaps\nSlower than below but better at scale\njavascript\n/**\n * @param {number[]} nums\n * @param {number} k\n * @return {number[]}\n */\nvar medianSlidingW
|
stevenkinouye
|
NORMAL
|
2020-01-13T04:18:42.100601+00:00
|
2020-01-15T03:49:40.713773+00:00
| 1,239 | false |
# 2 Heaps\nSlower than below but better at scale\n```javascript\n/**\n * @param {number[]} nums\n * @param {number} k\n * @return {number[]}\n */\nvar medianSlidingWindow = function(nums, k) {\n const window = new Window();\n for (let i = 0; i < k - 1; i++) window.add(nums[i]);\n let res = [];\n for (let i = k - 1; i < nums.length; i++) {\n window.add(nums[i]);\n res.push(window.median());\n window.remove(nums[i - k + 1]);\n }\n return res;\n};\n\nclass Window {\n constructor() {\n this.minHeap = new Heap((a,b) => a < b);\n this.maxHeap = new Heap((a,b) => a > b);\n }\n\n add(value) {\n this.heap(value).add(value);\n this.balance();\n }\n\n remove(value) {\n this.heap(value).remove(value);\n this.balance();\n }\n\n median() {\n if (this.minHeap.size() === this.maxHeap.size()) {\n return (this.minHeap.peak() + this.maxHeap.peak()) / 2;\n }\n return this.minHeap.peak();\n }\n\n heap(value) {\n return BigInt(value) < this.median() ? this.maxHeap : this.minHeap\n }\n\n balance() {\n const diff = this.maxHeap.size() - this.minHeap.size()\n if (diff > 0) this.minHeap.add(this.maxHeap.pop());\n else if (diff < -1) this.maxHeap.add(this.minHeap.pop());\n }\n}\n\nclass Heap {\n constructor(fn) {\n this.store = [];\n this.fn = fn;\n }\n\n peak() {\n return this.store[0] || 0;\n }\n\n size() {\n return this.store.length;\n }\n\n isEmpty() {\n return this.store.length === 0;\n }\n\n add(value) {\n this.store.push(value);\n this.heapifyUp(this.store.length - 1);\n }\n\n remove(value) {\n const idx = this.store.indexOf(value);\n if (idx === this.store.length - 1) return this.store.pop();\n this.store[idx] = this.store.pop()\n this.heapifyDown(this.heapifyUp(idx));\n }\n\n pop() {\n if (this.store.length < 2) return this.store.pop();\n const result = this.store[0];\n this.store[0] = this.store.pop();\n this.heapifyDown(0);\n return result;\n }\n\n heapifyDown(parent) {\n const childs = [1,2].map((n) => parent * 2 + n).filter((n) => n < this.store.length);\n let child = childs[0];\n if (childs[1] && this.fn(this.store[childs[1]], this.store[child])) {\n child = childs[1];\n }\n if (child && this.fn(this.store[child], this.store[parent])) {\n const temp = this.store[child];\n this.store[child] = this.store[parent];\n this.store[parent] = temp;\n return this.heapifyDown(child);\n }\n return parent;\n }\n\n heapifyUp(child) {\n const parent = Math.floor((child - 1) / 2);\n if (child && this.fn(this.store[child], this.store[parent])) {\n const temp = this.store[child];\n this.store[child] = this.store[parent];\n this.store[parent] = temp;\n return this.heapifyUp(parent);\n }\n return child;\n }\n}\n```\n# Indexed Heap Implementation for logn removal\n```javascript\nclass Heap {\n constructor(fn) {\n this.store = [];\n this.fn = fn;\n this.idxs = {};\n }\n\n peak() {\n return this.store[0] || 0;\n }\n\n size() {\n return this.store.length;\n }\n\n isEmpty() {\n return this.store.length === 0;\n }\n\n add(value) {\n this.store.push(value);\n const idx = this.store.length - 1;\n if (!this.idxs[value]) this.idxs[value] = new Set([idx]);\n else this.idxs[value].add(idx)\n this.heapifyUp(idx);\n }\n\n remove(value) {\n let idx;\n for (let i of this.idxs[value]) {\n idx = i;\n break;\n }\n this.idxs[value].delete(idx);\n if (idx === this.store.length - 1) return this.store.pop();\n this.store[idx] = this.store.pop()\n this.idxs[this.store[idx]].delete(this.store.length);\n this.idxs[this.store[idx]].add(idx);\n this.heapifyDown(this.heapifyUp(idx));\n }\n\n pop() {\n const value = this.store[0];\n this.idxs[value].delete(0);\n if (this.store.length < 2) return this.store.pop();\n this.store[0] = this.store.pop();\n this.idxs[this.store[0]].delete(this.store.length);\n this.idxs[this.store[0]].add(0);\n this.heapifyDown(0);\n return value;\n }\n\n heapifyDown(parent) {\n const childs = [1,2].map((n) => parent * 2 + n).filter((n) => n < this.store.length);\n let child = childs[0];\n if (childs[1] && this.fn(this.store[childs[1]], this.store[child])) {\n child = childs[1];\n }\n if (child && this.fn(this.store[child], this.store[parent])) {\n const childVal = this.store[child];\n const parentVal = this.store[parent];\n this.store[child] = parentVal;\n this.store[parent] = childVal;\n this.idxs[childVal].delete(child);\n this.idxs[childVal].add(parent);\n this.idxs[parentVal].delete(parent);\n this.idxs[parentVal].add(child);\n return this.heapifyDown(child);\n }\n return parent;\n }\n\n heapifyUp(child) {\n const parent = Math.floor((child - 1) / 2);\n if (child && this.fn(this.store[child], this.store[parent])) {\n const childVal = this.store[child];\n const parentVal = this.store[parent];\n this.store[child] = parentVal;\n this.store[parent] = childVal;\n this.idxs[childVal].delete(child);\n this.idxs[childVal].add(parent);\n this.idxs[parentVal].delete(parent);\n this.idxs[parentVal].add(child);\n return this.heapifyUp(parent);\n }\n return child;\n }\n}\n```\n\n# Binary Search Deletion (fastest on LC but not at scale)\n```javascript\nclass Window {\n constructor() {\n this.store = [];\n }\n \n add(value) {\n let idx = this.indexOf(value);\n if (value > this.store[idx]) idx++;\n this.store.splice(idx, 0, value);\n }\n \n remove(value) {\n const idx = this.indexOf(value);\n this.store.splice(idx, 1);\n }\n \n median() {\n const mid = Math.floor((this.store.length / 2));\n const median = this.store[mid];\n return this.store.length % 2 ? median : (median + this.store[mid - 1]) / 2;\n }\n \n indexOf(value) {\n let lo = 0;\n let hi = this.store.length - 1;\n while (lo < hi) {\n const mid = Math.floor((lo + hi) / 2);\n if (this.store[mid] < value) {\n lo = mid + 1;\n } else {\n hi = mid;\n }\n }\n return lo\n }\n}\n\n/**\n * @param {number[]} nums\n * @param {number} k\n * @return {number[]}\n */\nvar medianSlidingWindow = function(nums, k) {\n const window = new Window();\n for (let i = 0; i < k - 1; i++) {\n window.add(nums[i]);\n }\n const result = [];\n for (let i = k - 1; i < nums.length; i++) {\n window.add(nums[i]); \n result.push(window.median());\n window.remove(nums[i - k + 1]);\n }\n return result;\n};\n```
| 5 | 0 |
['Binary Search', 'Heap (Priority Queue)', 'JavaScript']
| 7 |
sliding-window-median
|
Java solution using 2 heap simplify.
|
java-solution-using-2-heap-simplify-by-k-p96j
|
\nclass Solution {\n PriorityQueue<Integer> maxHeap; // 1st part\n PriorityQueue<Integer> minHeap; // 2nd part\n \n public Solution() {\n //
|
kode_4_living
|
NORMAL
|
2020-01-03T05:30:36.616957+00:00
|
2020-01-03T05:34:31.132237+00:00
| 682 | false |
```\nclass Solution {\n PriorityQueue<Integer> maxHeap; // 1st part\n PriorityQueue<Integer> minHeap; // 2nd part\n \n public Solution() {\n // use Collections.reverseOrder() as comparator as this will work when input number as max integer, can\'t use (a,b)->b-a\n maxHeap = new PriorityQueue<>(Collections.reverseOrder()); \n minHeap = new PriorityQueue<>();\n }\n \n void addNum(int n) {\n if(maxHeap.size()==0 || n <= maxHeap.peek()) {\n maxHeap.offer(n); \n } else {\n minHeap.offer(n);\n }\n \n rebalance();\n }\n \n void remove(int num) {\n if(num <= maxHeap.peek()) maxHeap.remove(num);\n else minHeap.remove(num);\n rebalance();\n }\n \n void rebalance() {\n if(minHeap.size() > maxHeap.size()) maxHeap.offer(minHeap.poll());\n // max heap can has one extra node than min heap, as we will use for returning the median when total input size is odd number\n else if(maxHeap.size() > minHeap.size() + 1) minHeap.offer(maxHeap.poll());\n }\n \n double findMedian() {\n if(maxHeap.size() == minHeap.size()) return maxHeap.peek()/2.0 + minHeap.peek() /2.0;\n else return maxHeap.peek();\n }\n \n public double[] medianSlidingWindow(int[] nums, int k) {\n int start = 0;\n double[] result = new double[nums.length - k + 1 ];\n \n for(int end=0; end < nums.length; end++) {\n addNum(nums[end]);\n if(end + 1 >= k) {// shrink the window & calculate the median\n result[start] = findMedian();\n remove(nums[start]); // remove the start number as we move forward the next window size\n start++; // move start window ahead\n }\n }\n \n \n return result;\n }\n}\n```
| 5 | 0 |
['Heap (Priority Queue)', 'Java']
| 1 |
sliding-window-median
|
Easy to understand Python solution O(nk)
|
easy-to-understand-python-solution-onk-b-sdqj
|
\n\nclass Solution(object):\n def medianSlidingWindow(self, nums, k):\n """\n :type nums: List[int]\n :type k: int\n :rtype: List
|
hkhushk3
|
NORMAL
|
2017-10-03T06:13:38.543000+00:00
|
2018-08-09T19:53:44.276377+00:00
| 968 | false |
\n```\nclass Solution(object):\n def medianSlidingWindow(self, nums, k):\n """\n :type nums: List[int]\n :type k: int\n :rtype: List[float]\n """\n medians = []\n sortedwindow = sorted(nums[ : k])\n medians.append((sortedwindow[k/2] + sortedwindow[k/2 - (k%2 ==0)])/2.)\n \n for i in range(len(nums) - k):\n \n sortedwindow.remove(nums[i])\n bisect.insort(sortedwindow, nums[k+i])\n medians.append((sortedwindow[k/2] + sortedwindow[k/2 - (k%2 ==0)])/2.)\n \n return medians\n```
| 5 | 0 |
[]
| 0 |
sliding-window-median
|
Utilize to heaps to find median, and hashmap for counts when updating window
|
utilize-to-heaps-to-find-median-and-hash-r866
|
Intuition\n Describe your first thoughts on how to solve this problem. \nThis problem is similar to the "Find Median from data stream" problem, but the main dif
|
yqd5143
|
NORMAL
|
2024-10-22T21:41:56.572826+00:00
|
2024-10-22T21:41:56.572842+00:00
| 496 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThis problem is similar to the "Find Median from data stream" problem, but the main difference is that we are looking to find the median for all possible window of an arbitrary size k <= n which is the size of our nums list. \n\nTo find the median we are going to have 2 heaps (min and max) this is done, so we can have constant lookup to the middle values of the window. The logic is that max_heap will store the values from the left side of the window, and the min_heap will store values from the right handside. We are going to allow the max_heap to have at most one more value than the min_heap. This is done in the event k is an odd number, so we have a constant time lookup for the median. If it is even we can still compute in constant time, but we have to alos lookup the top of our min_heap. Once the heaps are populate we add our first median to our return array ret, and store the median in a variable for later.\n\nWe now utilize a for loop from k to n, and update the window each time prior to computing the median. First thing we do is check our value prev which is the value leaving the window that is why we utilize i-k for indexing. We increment our heap_count[prev] as we are goign to use this when updating the heaps. The variable balance is used to show which heap the value is leaving from, and based on our constraint earlier our max_heap must have at most 1 more value than our min_heap for this solution to work. In the case the prev <= median theat means we set balance to -1 as prev will be in the left half of the window, so our max_heap is going to decrease, and it will be 1 to show the exact opposite. \n\nWe now add our current nums[i] value to one of the heaps, and this is dependent on our a whether it is less than or equal to the median. In the case it is we push the value to our max_heap, and increment our balance variable as we added a value to our max_heap. We do the exact opposite if it is greater than the median. \n\nWe now check to see if balance <0 in this case we take a value from the min_heap and push it to the max_heap, and do the exact opposite if balance >0. \n\nWe know utilize to while loops to remove the top each queue if their respective heap_count[foo]>0 and their heap is not empty. We use this conditon because as long as the top of the queue is valid then the computation will still be the same. The loop is simple we decrement our hashmap value and remove the top of the heap in constant time until it is satisfactory. We then compute the median, append it to our ret array and continue.\n\n\n\n# Code\n```python3 []\nimport heapq\nimport collections\nclass Solution:\n def medianSlidingWindow(self, nums: List[int], k: int) -> List[float]:\n ret = []\n min_heap,max_heap = [],[]\n heap_count = collections.defaultdict(int)\n for i in range(k):\n heapq.heappush(max_heap,-nums[i])\n heapq.heappush(min_heap,-heapq.heappop(max_heap))\n if len(min_heap) >len(max_heap):\n heapq.heappush(max_heap,-heapq.heappop(min_heap))\n ###################################################\n if k%2 ==1:\n ret.append(-max_heap[0])\n else:\n ret.append((-max_heap[0]+min_heap[0])/2)\n median = ret[-1]\n n = len(nums)\n for i in range(k,n):\n prev = nums[i-k]\n heap_count[prev] +=1\n balance = -1 if prev <=median else 1\n if nums[i] <= median:\n balance +=1\n heapq.heappush(max_heap,-nums[i])\n else:\n balance -=1\n heapq.heappush(min_heap,nums[i])\n ##########################\n if balance <0:\n heapq.heappush(max_heap,-heapq.heappop(min_heap))\n elif balance >0:\n heapq.heappush(min_heap,-heapq.heappop(max_heap))\n \n while(max_heap and heap_count[-max_heap[0]]>0):\n heap_count[-max_heap[0]]-=1\n heapq.heappop(max_heap)\n while(min_heap and heap_count[min_heap[0]]>0):\n heap_count[min_heap[0]]-=1\n heapq.heappop(min_heap)\n #########################\n if k%2 ==1:\n ret.append(-max_heap[0])\n else:\n ret.append((-max_heap[0]+min_heap[0])/2)\n median = ret[-1]\n return ret\n```
| 4 | 0 |
['Hash Table', 'Sliding Window', 'Heap (Priority Queue)', 'Python3']
| 0 |
sliding-window-median
|
simple and easy solution using PBDS 😍❤️🔥
|
simple-and-easy-solution-using-pbds-by-s-4vsh
|
if it\'s help, please up \u2B06 vote! \u2764\uFE0F\n\n# Code\n\n#include<ext/pb_ds/assoc_container.hpp>\n#include<ext/pb_ds/tree_policy.hpp>\nusing namespace __
|
shishirRsiam
|
NORMAL
|
2024-05-25T13:26:20.914625+00:00
|
2024-05-25T13:26:20.914655+00:00
| 1,078 | false |
# if it\'s help, please up \u2B06 vote! \u2764\uFE0F\n\n# Code\n```\n#include<ext/pb_ds/assoc_container.hpp>\n#include<ext/pb_ds/tree_policy.hpp>\nusing namespace __gnu_pbds;\n\ntemplate <typename T> using pbds = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;\n\nclass Solution {\npublic:\n vector<double> medianSlidingWindow(vector<int>& nums, int k) \n {\n int pos = k / 2, poss = pos;\n if(k%2==0) poss--;\n\n vector<double> ans;\n pbds<pair<int,int>>pbds;\n int i = 0, j = 0, n = nums.size();\n while(j<n)\n {\n pbds.insert({nums[j], j});\n if(j-i+1 == k)\n {\n auto it = pbds.find_by_order(pos);\n auto itt = pbds.find_by_order(poss);\n\n double val = (double(it->first) + double(itt->first)) / 2;\n ans.push_back(val);\n pbds.erase({nums[i], i});\n i++;\n }\n j++;\n }\n return ans;\n }\n};\n```
| 4 | 0 |
['Array', 'Hash Table', 'Sliding Window', 'C++']
| 3 |
sliding-window-median
|
Multiset and advance() - O(nlog(k))
|
multiset-and-advance-onlogk-by-ritvic-ag-cqwy
|
Code\n\nclass Solution {\npublic:\n vector<double> medianSlidingWindow(vector<int>& nums, int k) {\n multiset<long> s; // create a multiset to store the e
|
ritvic-agg
|
NORMAL
|
2022-12-31T07:22:22.709330+00:00
|
2023-01-03T14:25:53.321312+00:00
| 1,294 | false |
# Code\n```\nclass Solution {\npublic:\n vector<double> medianSlidingWindow(vector<int>& nums, int k) {\n multiset<long> s; // create a multiset to store the elements of the window\n vector<double> v; // create a vector to store the median values\n // insert the first k-1 elements into the multiset\n for(int i=0;i<k-1;i++)\n s.insert(nums[i]);\n \n // initialize the variable for the index of the element to be inserted\n int j=k-1;\n \n // loop through the rest of the elements\n while(j<nums.size()) {\n s.insert(nums[j]); // insert the current element into the multiset\n auto it=s.begin(); // initialize an iterator to the beginning of the multiset\n long long x; // variable to store the value of the median if k is even\n \n // if k is even, advance the iterator to the (k/2)-1th element and store it in x\n if(k/2>=1) {\n advance(it,k/2-1);\n x=*it;\n advance(it,1); // advance the iterator one more time to point to the median\n }\n // if k is odd, the median is the value pointed to by the iterator\n if(k%2!=0)\n v.push_back(double(*it)/double(1));\n // if k is even, the median is the average of the values pointed to by the iterator and x\n else\n v.push_back(double(*it+x)/double(2));\n \n s.erase(s.lower_bound(nums[j-k+1])); // remove the element at the beginning of the window from the multiset\n j++; // increment the index of the element to be inserted\n }\n return v; // return the vector of median values\n }\n};\n```
| 4 | 0 |
['C++']
| 3 |
sliding-window-median
|
Using multiset beats 90% C++
|
using-multiset-beats-90-c-by-idvjojo123-9z59
|
\nclass Solution {\npublic:\n int b;\n double picaro;\n multiset<long long > halfmin,halfmax;\n vector<double> ans;\n void huy(int v)\n {\n
|
idvjojo123
|
NORMAL
|
2022-12-29T15:21:40.539936+00:00
|
2022-12-29T15:21:40.539965+00:00
| 1,090 | false |
```\nclass Solution {\npublic:\n int b;\n double picaro;\n multiset<long long > halfmin,halfmax;\n vector<double> ans;\n void huy(int v)\n {\n b=0;\n if(halfmin.size()==halfmax.size())\n {\n b=1;\n if(v>*halfmax.begin()) halfmax.insert(v);\n else halfmin.insert(v);\n }\n if(halfmin.size()>halfmax.size()&&b==0)\n {\n if(v>=*halfmin.rbegin()) halfmax.insert(v);\n if(v<*halfmin.rbegin())\n {\n int huy=*halfmin.rbegin();\n halfmin.erase(halfmin.find(huy));\n halfmax.insert(huy);\n halfmin.insert(v);\n }\n }\n if(halfmin.size()<halfmax.size()&&b==0)\n {\n if(v<=*halfmax.begin()) halfmin.insert(v);\n if(v>*halfmax.begin())\n {\n int huy=*halfmax.begin();\n halfmax.erase(halfmax.find(huy));\n halfmin.insert(huy);\n halfmax.insert(v);\n }\n }\n }\n vector<double> medianSlidingWindow(vector<int>& nums, int k) {\n if(nums.size()==1){ ans.push_back(nums[0]); return ans; }\n if(k==1)\n {\n for(int i=0;i<=nums.size()-1;i++) ans.push_back(nums[i]);\n return ans;\n }\n if(k==2)\n {\n for(int i=1;i<=nums.size()-1;i++) \n {\n long long g=long(nums[i])+long(nums[i-1]);\n ans.push_back(double(g)/2);\n }\n return ans;\n }\n for(int i=0;i<=nums.size()-1;i++)\n {\n if(i<=k-1)\n {\n if(i==0) halfmin.insert(nums[i]);\n if(i==1) \n {\n halfmax.insert(nums[i]);\n if(*halfmax.begin()<*halfmin.rbegin())\n halfmax.swap(halfmin);\n // cout << *halfmax.begin() << " " << *halfmin.rbegin();\n }\n if(i>1)\n {\n huy(nums[i]);\n }\n if(i==k-1)\n {\n if(k%2==0)\n {\n picaro=double(double(*halfmin.rbegin())+double(*halfmax.begin()))/2;\n ans.push_back(picaro); \n }\n if(k%2==1)\n {\n if(halfmin.size()>halfmax.size())\n ans.push_back(*halfmin.rbegin());\n if(halfmin.size()<halfmax.size())\n ans.push_back(*halfmax.begin());\n // cout << halfmin.size() << " " << halfmax.size();\n }\n }\n }\n else\n {\n if(halfmin.count(nums[i-k])==0&&halfmax.count(nums[i-k])!=0)\n halfmax.erase(halfmax.find(nums[i-k]));\n if(halfmin.count(nums[i-k])!=0)\n halfmin.erase(halfmin.find(nums[i-k]));\n huy(nums[i]);\n if(k%2==0)\n {\n picaro=double(double(*halfmin.rbegin())+double(*halfmax.begin()))/2;\n ans.push_back(picaro); \n }\n if(k%2==1)\n {\n if(halfmin.size()>halfmax.size())\n ans.push_back(*halfmin.rbegin());\n if(halfmin.size()<halfmax.size())\n ans.push_back(*halfmax.begin());\n }\n }\n /* if(i!=0)\n {\n cout << *halfmin.begin() << " " << *halfmin.rbegin() << endl;\n cout << *halfmax.begin() << " " << *halfmax.rbegin() << endl;\n cout << endl;\n }\n */ \n }\n return ans;\n }\n };\n\t```
| 4 | 0 |
['C']
| 0 |
sliding-window-median
|
[C++] 2 solutions: Binary Search | Height Balanced Tree + Pointer movement [Detailed Explanation]
|
c-2-solutions-binary-search-height-balan-bnef
|
\n/*\n https://leetcode.com/problems/sliding-window-median/\n \n 1. SOLUTION 1: Binary Search\n \n The core idea is we maintain a sorted window o
|
cryptx_
|
NORMAL
|
2022-07-25T10:31:52.388178+00:00
|
2022-07-25T10:31:52.388249+00:00
| 675 | false |
```\n/*\n https://leetcode.com/problems/sliding-window-median/\n \n 1. SOLUTION 1: Binary Search\n \n The core idea is we maintain a sorted window of elements. Initially we make the 1st window and sort all its elements.\n Then from there onwards any insertion or deletion is done by first finding the appropriate position where the element \n exists/shoudl exist. This search is done using binary search.\n \n TC: O(klogk (Sorting) + (n - k) * (k + logk)), Binary search in window takes O(logk), but since it is array, insert or delete can take O(k)\n SC: O(k)\n \n 2. SOLUTION 2: Height Balanced Tree\n \n Core idea is to use a height balanced tree to save all the elements of window. Since it is a height balanced tree, insertion and deletion takes\n logk. Now we directly want to reach the k/2 th element, then it takes O(k/2). So we need to optimize the mid point fetch.\n \n Initially when the 1st window is built, we find the middle element with O(k/2). Then from there onwards we always adjust the middle position\n by +1 or -1. Since only one element is either added or deleted at a time, so we can move the median left or right based on the situation.\n Eg: [1,2,3,4,5,6,7], median = 4\n \n if we add one element say 9\n [1,2,3,4,5,6,7,9], then check (9 < median): this means 1 extra element on right, don\'t move and wait to see what happens on deletion\n \n Similarly, now if 2 is deleted, we can just check (2 <= median(4)): this means there will be one less element on left.\n So move median to right by 1. If say an element on right like 7 was deleted, we would have not moved and hence the mid ptr would be \n at its correct position.\n \n \n (1st window insertion) + remaining_windows * (delete element + add element + get middle)\n TC: O(klogk + (n-k) * (logk + logk + 1)) \n ~O(klogk + (n-k)*logk) ~O(nlogk)\n SC: O(k)\n*/\nclass Solution {\npublic:\n ///////////////////// SOLUTION 1: Binary Search\n vector<double> binarySearchSol(vector<int>& nums, int k) {\n vector<double> medians;\n vector<int> window;\n // K is over the size of array\n if(k > nums.size())\n return medians;\n \n int i = 0;\n // add the elements of 1st window\n while(i < k) {\n window.emplace_back(nums[i]);\n ++i;\n }\n \n // sort the window\n sort(window.begin(), window.end());\n // get the median of 1st window\n double median = k % 2 ? window[k / 2] : (double) ((double)window[k/2 - 1] + window[k/2]) / 2;\n medians.emplace_back(median);\n \n for(; i < nums.size(); i++) {\n // search the position of 1st element of the last window using binary search\n auto it = lower_bound(window.begin(), window.end(), nums[i - k]);\n window.erase(it);\n // find the position to insert the new element for the current window\n it = lower_bound(window.begin(), window.end(), nums[i]);\n window.insert(it, nums[i]);\n // Since the window is sorted, we can directly compute the median\n double median = k % 2 ? window[k / 2] : (double) ((double)window[k/2 - 1] + window[k/2]) / 2;\n medians.emplace_back(median);\n }\n return medians;\n }\n \n //////////////////////////// SOLUTION 2: Height Balanced Tree\n vector<double> treeSol(vector<int>& nums, int k) {\n multiset<int> elements;\n vector<double> medians;\n \n int i = 0;\n // process the 1st window\n while(i < k) {\n elements.insert(nums[i]);\n ++i;\n }\n \n // median of 1st window\n auto mid = next(elements.begin(), k / 2);\n double median = k % 2 ? *mid : ((double)*mid + *prev(mid)) / 2;\n medians.emplace_back(median);\n \n for(; i < nums.size(); i++) {\n // insert last element of current window\n elements.insert(nums[i]);\n // If the number lies on the left, left side will have 1 more element.\n // So shift left by 1 pos\n if(nums[i] < *mid)\n --mid;\n \n // remove 1st element of last window\n auto delete_pos = elements.find(nums[i - k]);\n // If the element to be deleted in [first : mid], then right will have extra element\n // so move the mid to right by 1\n // NOTE: We insert the new element and then delete previous element because, if the window has just one element\n // then deleting first will make mid point to invalid position. But inserting first will ensure that there is an \n // element to point to\n if(nums[i-k] <= *mid)\n ++mid;\n elements.erase(delete_pos);\n \n double median = k % 2 ? *mid : ((double)*mid + *prev(mid)) / 2;\n medians.emplace_back(median);\n }\n \n return medians;\n }\n \n vector<double> medianSlidingWindow(vector<int>& nums, int k) {\n // return binarySearchSol(nums, k);\n return treeSol(nums, k);\n }\n};\n```
| 4 | 0 |
['Binary Search', 'Tree', 'C', 'C++']
| 0 |
sliding-window-median
|
Java Solution using 2 Priority Queues | Median Priority Queue | Easy to Understand
|
java-solution-using-2-priority-queues-me-o83s
|
Please upvote, if you find it useful :)\n\n\nclass Solution {\n \n public PriorityQueue<Integer> left = new PriorityQueue<>(Collections.reverseOrder());\n
|
kxbro
|
NORMAL
|
2022-06-08T14:38:48.516371+00:00
|
2022-06-08T14:43:37.984212+00:00
| 1,394 | false |
Please upvote, if you find it useful :)\n\n```\nclass Solution {\n \n public PriorityQueue<Integer> left = new PriorityQueue<>(Collections.reverseOrder());\n public PriorityQueue<Integer> right = new PriorityQueue<>();\n \n public double[] medianSlidingWindow(int[] nums, int k) {\n for(int i=0; i<k; i++) {\n addNum(nums[i]);\n }\n \n double[] ans = new double[nums.length - k + 1];\n int j = 0;\n ans[j] = findMedian();\n for(int i=k; i<nums.length; i++) {\n remove(nums[j]);\n addNum(nums[i]);\n j += 1;\n ans[j] = findMedian();\n }\n \n return ans;\n }\n\n public void addNum(int num) {\n if(right.peek() == null) {\n left.add(num);\n } else if(num > right.peek()){\n right.add(num);\n } else {\n left.add(num);\n }\n \n if(Math.abs(left.size() - right.size()) > 1) {\n if(left.size() > right.size()) {\n right.add(left.remove());\n } else {\n left.add(right.remove());\n }\n }\n }\n \n public void remove(int num) {\n if(right.size() > 0 && num >= right.peek()) {\n right.remove(num);\n } else {\n left.remove(num);\n }\n \n if(Math.abs(left.size() - right.size()) > 1) {\n if(left.size() > right.size()) {\n right.add(left.remove());\n } else {\n left.add(right.remove());\n }\n }\n }\n \n public double findMedian() {\n if(left.size() > right.size()) {\n return (double)left.peek();\n } else if(right.size() > left.size()) {\n return (double)right.peek();\n } else {\n return (left.peek() / 2.0) + (right.peek() / 2.0);\n }\n }\n}\n```
| 4 | 0 |
['Java']
| 3 |
sliding-window-median
|
C++ || Simplest Code to Understand || Explained || Priority Queue
|
c-simplest-code-to-understand-explained-hy9do
|
Please do upvote if you liked my code ;)\n\n\nclass Solution {\npublic:\n multiset<double> minH;\n multiset<double, greater<double>> maxH;\n \n void
|
markrash4
|
NORMAL
|
2022-05-15T18:50:19.159319+00:00
|
2022-05-15T18:50:19.159360+00:00
| 433 | false |
**Please do upvote if you liked my code ;)**\n\n```\nclass Solution {\npublic:\n multiset<double> minH;\n multiset<double, greater<double>> maxH;\n \n void balanceHeaps()\n {\n if(maxH.size() > minH.size())\n {\n minH.insert(*maxH.begin()); \n maxH.erase(maxH.begin());\n }\n }\n \n double getMedian(int k)\n {\n if(k%2 == 0)\n return (*minH.begin() + *maxH.begin())*0.5;\n else return *minH.begin();\n }\n \n vector<double> medianSlidingWindow(vector<int>& nums, int k) \n {\n vector<double> ans;\n \n for(int i=0; i<nums.size(); i++)\n {\n if(i >= k) // Only delete element from one of the heaps\n {\n if(minH.find(nums[i-k]) != minH.end()) minH.erase(minH.find(nums[i-k]));\n else maxH.erase(maxH.find(nums[i-k]));\n }\n \n // The idea here is very simple: First we insert the current element in the min heap\n // The we insert the top of min heap to max heap\n // Then we balance the heaps i.e. move element from max to min heap if max heap has\n // greater size\n minH.insert(nums[i]);\n maxH.insert(*minH.begin());\n minH.erase(minH.begin());\n \n balanceHeaps(); \n \n if(i >= k-1) ans.push_back(getMedian(k)); \n }\n \n return ans;\n }\n};\n```
| 4 | 0 |
['C', 'Heap (Priority Queue)', 'C++']
| 0 |
sliding-window-median
|
Multiset Solution | Simple & Short | Easy to Understand
|
multiset-solution-simple-short-easy-to-u-me71
|
Idea?\n Maintain two multisets for each k size subarray.\n First multiset will store the first (k+1)/2 integers while second multiset will store k/2 elements.\n
|
sunny_38
|
NORMAL
|
2022-03-10T13:28:21.534311+00:00
|
2022-03-10T13:28:41.123445+00:00
| 142 | false |
**Idea?**\n* Maintain **two multisets** for each k size subarray.\n* First multiset will store the first **(k+1)/2** integers while second multiset will store **k/2** elements.\n* Note that first multiset stores element in non-increasing order while second multiset will store the elements in non-decreasing order.\n* When *size of subarray is odd*, return the topmost element of first multiset.\n* When *size of subarray is even*, return the **average value** of the top elements of first and second multiset.\n* Note that at each step(while inserting and deleting elements), we need to **balance the sets** when the sizees of the sets aren\'t the desired sizes.\n\n```\nclass Solution {\npublic:\n \n // Time Complexity:- O(NlogK)\n // Space Complexity:- O(K)\n \n #define ll long long\n \n multiset<ll> right;\n multiset<ll,greater<ll>> left;\n \n double GetMedian(){\n int n = left.size() + right.size();\n if(n&1){\n return (double)*left.begin();\n }\n return ((double)(*left.begin()+*right.begin()))/2.0;\n }\n \n void BalanceSets(){\n while((int)right.size()>(int)left.size()){\n left.insert(*right.begin());\n right.erase(right.begin());\n }\n while((int)left.size()-(int)right.size()>1){\n right.insert(*left.begin());\n left.erase(left.begin());\n }\n }\n \n vector<double> medianSlidingWindow(vector<int>& nums, int k) {\n int n = nums.size();\n \n // odd length array, size(left) - size(right) == 1\n // even length array, size(left) == size(right)\n \n // insert all the elements [0,k-1];\n for(int i=0;i<k;i++){\n if(left.empty()){\n left.insert(nums[i]);\n }\n else if(right.empty()){\n if(nums[i]<*left.begin()){\n right.insert(*left.begin());\n left.erase(left.begin());\n \n left.insert(nums[i]);\n }\n else{\n right.insert(nums[i]);\n }\n }\n else{\n if(nums[i]<=*left.begin()){\n left.insert(nums[i]);\n }\n else{\n right.insert(nums[i]);\n }\n }\n \n BalanceSets(); \n }\n \n vector<double> ans = {GetMedian()};\n \n for(int i=k;i<n;i++){\n // insert nums[i]\n if(nums[i]<=*left.begin()){\n left.insert(nums[i]);\n }\n else{\n right.insert(nums[i]);\n }\n \n // delete the nums[i-k]\n if(left.count(nums[i-k])){\n left.erase(left.find(nums[i-k]));\n }\n else{\n right.erase(right.find(nums[i-k]));\n }\n \n // balance the sets\n BalanceSets();\n \n ans.push_back(GetMedian()); \n }\n return ans;\n }\n};\n```\n\n**Don\'t Forget to Upvote!**
| 4 | 0 |
[]
| 0 |
sliding-window-median
|
C++ | 2 heaps | O(nlogn)
|
c-2-heaps-onlogn-by-tanyarajhans7-2gg3
|
\nclass Solution {\npublic:\n vector<double> ans;\n unordered_map<int, int> m; //to store the elements to be discarded\n priority_queue<int> maxh; //ma
|
tanyarajhans7
|
NORMAL
|
2022-03-07T07:59:35.005331+00:00
|
2022-03-07T07:59:35.005363+00:00
| 674 | false |
```\nclass Solution {\npublic:\n vector<double> ans;\n unordered_map<int, int> m; //to store the elements to be discarded\n priority_queue<int> maxh; //max heap for lower half \n priority_queue<int, vector<int>, greater<int>> minh; //min heap for upper half \n \n vector<double> medianSlidingWindow(vector<int>& nums, int k) {\n int n=nums.size();\n for(int i=0;i<k;i++){\n maxh.push(nums[i]);\n }\n for(int i=k/2;i>0;i--){\n minh.push(maxh.top());\n maxh.pop();\n }\n for(int i=k;i<n;i++){\n if(k%2==0){\n ans.push_back(((double)maxh.top()+(double)minh.top())/2.0);\n }\n else{\n ans.push_back(maxh.top()*1.0);\n }\n int p=nums[i-k];\n int q=nums[i];\n int balance=0;\n \n // discarding p if it\'s at the top, otherwise storing it in map\n if(p<=maxh.top()){\n balance--;\n if(p==maxh.top()){\n maxh.pop();\n }\n else{\n m[p]++;\n }\n }\n else{\n balance++;\n if(p==minh.top()){\n minh.pop();\n }\n else{\n m[p]++;\n }\n }\n \n // balancing, if needed\n \n if(!maxh.empty() && q<=maxh.top()){\n balance++;\n maxh.push(q);\n }\n else{\n balance--;\n minh.push(q);\n }\n \n if(balance<0){\n maxh.push(minh.top());\n minh.pop();\n }\n else if(balance>0){\n minh.push(maxh.top());\n maxh.pop();\n }\n \n // popping off the top if it\'s present in the map\n \n while(!maxh.empty() && m[maxh.top()]){\n m[maxh.top()]--;\n maxh.pop();\n }\n \n while(!minh.empty() && m[minh.top()]){\n m[minh.top()]--;\n minh.pop();\n }\n }\n if(k%2==0){\n ans.push_back(((double)maxh.top()+(double)minh.top())/2.0);\n }\n else{\n ans.push_back(maxh.top()*1.0);\n }\n return ans;\n }\n};\n```
| 4 | 1 |
['Heap (Priority Queue)']
| 1 |
sliding-window-median
|
Python simple solution using SortedList
|
python-simple-solution-using-sortedlist-2qvdh
|
Adding and removing from sortedList is O(logk) operation. \n\nSo time complexity is O(n* logk) and Space is O(k) for sortedList \n\nfrom sortedcontainers import
|
ikna
|
NORMAL
|
2021-11-08T07:06:16.713073+00:00
|
2021-11-08T07:06:28.666736+00:00
| 424 | false |
Adding and removing from sortedList is O(logk) operation. \n\nSo time complexity is O(n* logk) and Space is O(k) for sortedList \n```\nfrom sortedcontainers import SortedList\nclass Solution:\n def medianSlidingWindow(self, nums: List[int], k: int) -> List[float]:\n res = []\n sl = SortedList()\n for i in range(len(nums)):\n \n sl.add(nums[i])\n \n if i < k-1:\n continue\n \n if k % 2:\n res.append(sl[k//2]*1.0)\n else:\n res.append((sl[(k//2)-1] + sl[k//2]) / 2.0)\n \n sl.remove(nums[i-k+1])\n \n return res\n```
| 4 | 0 |
['Python']
| 1 |
sliding-window-median
|
Short Python solution, O(n log k)
|
short-python-solution-on-log-k-by-404akh-g0fw
|
\nfrom sortedcontainers import SortedList\n\nclass Solution:\n def medianSlidingWindow(self, nums, k):\n sl = SortedList(nums[:k - 1])\n wd = [
|
404akhan
|
NORMAL
|
2021-09-22T12:02:28.344123+00:00
|
2021-09-22T12:02:28.344218+00:00
| 492 | false |
```\nfrom sortedcontainers import SortedList\n\nclass Solution:\n def medianSlidingWindow(self, nums, k):\n sl = SortedList(nums[:k - 1])\n wd = []\n\n for i in range(k - 1, len(nums)):\n sl.add(nums[i])\n wd.append((sl[(k - 1) // 2] + sl[k // 2]) / 2)\n sl.remove(nums[i - k + 1])\n return wd\n```\nInitialize sorted list with first `k - 1` elements of `nums`. When sliding the window add a new element and remove old one in `O(log k)`. Record medians with tricky formula that works for both odd and even length windows.
| 4 | 0 |
[]
| 1 |
sliding-window-median
|
C++ | Simple Approach | Sorted Vector - O(N*K) | Beats 99.52% on memory use
|
c-simple-approach-sorted-vector-onk-beat-ay9r
|
We define a custom class sorted_vector with only 3 operations\n1. add element by value\n2. remove element by value\n3. get median\n\nWe only keep K elements of
|
pratham1002
|
NORMAL
|
2021-08-02T10:51:44.827042+00:00
|
2021-08-13T20:06:18.158160+00:00
| 853 | false |
We define a custom class `sorted_vector` with only 3 operations\n1. add element by value\n2. remove element by value\n3. get median\n\nWe only keep K elements of the sliding window in the `sorted_vector` .\n\nTrust me, this is the simplest approach to this question.\n\nFor those of you who aren\'t familiar with `std::lower_bound`, it simply binary searches the first `element >= val` and returns an `iterator` to it.\n\n```cpp\nclass sorted_vector {\nprivate:\n vector<int> arr;\n int k;\npublic:\n sorted_vector(int k) {\n this->k = k;\n arr = vector<int>();\n }\n \n void add(int val) {\n auto lb = lower_bound(arr.begin(), arr.end(), val);\n arr.insert(lb, val);\n }\n \n void remove(int val) {\n auto lb = lower_bound(arr.begin(), arr.end(), val);\n arr.erase(lb);\n }\n \n double median() {\n if (k%2 == 0) {\n return ((double) arr[k/2] + arr[k/2-1])/2;\n }\n else\n return arr[k/2];\n }\n};\n\nclass Solution {\npublic:\n vector<double> medianSlidingWindow(vector<int>& nums, int k) {\n int n = nums.size();\n int i = 0;\n \n vector<double> ans(n-k+1);\n \n sorted_vector arr(k);\n \n\t\t// simply push the first k-1 elements\n while (i < k-1) {\n arr.add(nums[i]);\n i++;\n }\n \n\t\t// in each iteration, push one element, get median, pop out the last one.\n while (i < n) {\n arr.add(nums[i]);\n ans[i-k+1] = arr.median();\n arr.remove(nums[i-k+1]);\n i++;\n }\n \n return ans;\n }\n};\n```
| 4 | 0 |
['Array', 'Sorting', 'C++']
| 3 |
sliding-window-median
|
c++ solution (two multiset)
|
c-solution-two-multiset-by-dilipsuthar60-78ax
|
\nclass Solution {\npublic:\n multiset<int,greater<int>>left;\n multiset<int>right;\n void balance()\n {\n if(left.size()-right.size()==2)\
|
dilipsuthar17
|
NORMAL
|
2021-06-25T08:20:40.302323+00:00
|
2021-06-25T08:20:40.302359+00:00
| 412 | false |
```\nclass Solution {\npublic:\n multiset<int,greater<int>>left;\n multiset<int>right;\n void balance()\n {\n if(left.size()-right.size()==2)\n {\n int val=*left.begin();\n left.erase(left.begin());\n right.insert(val);\n }\n else if(right.size()-left.size()==2)\n {\n int val=*right.begin();\n right.erase(right.begin());\n left.insert(val);\n }\n }\n void remove(int x)\n {\n if(left.find(x)!=left.end())\n {\n left.erase(left.find(x));\n }\n else if(right.find(x)!=right.end())\n {\n right.erase(right.find(x));\n }\n balance();\n }\n void add(int num)\n {\n if(right.size()>0&&num>*right.begin())\n {\n right.insert(num);\n }\n else\n {\n left.insert(num);\n }\n balance();\n }\n double med()\n {\n long long val1=*left.begin();\n long long val2=*right.begin();\n if(left.size()==right.size())\n {\n return (double)(val1+val2)/2.0;\n }\n else if(left.size()>right.size())\n {\n return (double)(*left.begin());\n }\n else\n {\n return (double)(*right.begin());\n }\n }\n vector<double> medianSlidingWindow(vector<int>& nums, int k) \n {\n vector<double>v;\n for(int i=0;i<k;i++)\n {\n add(nums[i]);\n }\n v.push_back(med());\n for(int i=k;i<nums.size();i++)\n {\n remove(nums[i-k]);\n add(nums[i]);\n v.push_back(med());\n }\n return v;\n }\n};\n```
| 4 | 0 |
['C', 'C++']
| 0 |
sliding-window-median
|
O(nlogk) c++ using ordered multiset (policy based data structure)
|
onlogk-c-using-ordered-multiset-policy-b-limo
|
\n#include <ext/pb_ds/assoc_container.hpp> \nusing namespace __gnu_pbds; \ntypedef tree<int, null_type, \n less_equal<int>, rb_tree_tag, \n
|
devanshuraj226
|
NORMAL
|
2020-12-23T14:18:40.575984+00:00
|
2020-12-23T14:18:40.576025+00:00
| 1,350 | false |
```\n#include <ext/pb_ds/assoc_container.hpp> \nusing namespace __gnu_pbds; \ntypedef tree<int, null_type, \n less_equal<int>, rb_tree_tag, \n tree_order_statistics_node_update> \n ordered_set; \nclass Solution {\npublic:\n vector<double> medianSlidingWindow(vector<int>& arr, int k) {\n int n=arr.size();\n vector<double>res;\n ordered_set os;\n for(int i=0;i<k;i++){\n os.insert(arr[i]);\n }\n if(k&1)\n {\n int ans=*os.find_by_order(k/2);\n res.push_back((double)(ans));\n \n for(int i=0;i<n-k;i++){\n os.erase(os.find_by_order(os.order_of_key(arr[i])));\n os.insert(arr[i+k]);\n ans=*os.find_by_order(k/2);\n res.push_back((double)(ans));\n }\n }\n else\n {\n double l=*os.find_by_order(k/2-1);\n double r=*os.find_by_order(k/2);\n double ans=(l+r)/2.0;\n res.push_back(ans);\n for(int i=0;i<n-k;i++){\n os.erase(os.find_by_order(os.order_of_key(arr[i])));\n os.insert(arr[i+k]);\n l=*os.find_by_order(k/2-1);\n r=*os.find_by_order(k/2);\n ans=(l+r)/2.0;\n res.push_back(ans);\n }\n }\n return res;\n }\n};\n```\n
| 4 | 0 |
[]
| 0 |
sliding-window-median
|
[C++] using multiset beats 98%
|
c-using-multiset-beats-98-by-suhailakhta-vlsn
|
c++\n#define ll long long\nclass Solution {\npublic:\n vector<double> medianSlidingWindow(vector<int>& a, int k) {\n int n=a.size();\n multiset
|
suhailakhtar039
|
NORMAL
|
2020-09-28T18:41:14.582312+00:00
|
2020-09-28T18:41:14.582356+00:00
| 734 | false |
```c++\n#define ll long long\nclass Solution {\npublic:\n vector<double> medianSlidingWindow(vector<int>& a, int k) {\n int n=a.size();\n multiset<ll> m;\n for(ll i=0;i<k;i++)m.insert(a[i]);\n auto it=m.begin();\n for(ll i=0;i<k/2;i++)\n it++;\n ll med=*it;\n vector<double> ans;\n for(ll i=k;i<n;i++){\n auto ij=it;\n ij--;\n if(k%2==0)\n ans.push_back((*ij+*it)/2.0);\n else\n ans.push_back(*it);\n m.insert(a[i]);\n if(a[i]<*it)\n it--;\n if(a[i-k]<=*it)\n it++;\n m.erase(m.lower_bound(a[i-k]));\n }\n auto ij=it;\n ij--;\n if(k%2==0)\n ans.push_back((*ij+*it)/2.0);\n else\n ans.push_back(*it);\n return ans;\n }\n};\n```
| 4 | 1 |
['C', 'C++']
| 0 |
sliding-window-median
|
python on * k two heap solution
|
python-on-k-two-heap-solution-by-yingziq-nhes
|
this idea is from https://leetcode.com/problems/sliding-window-median/discuss/412047/Two-heaps-%2B-sliding-window-approach-O(-n-*-k-)-runtime-O(k)-space\nthanks
|
yingziqing123
|
NORMAL
|
2020-04-15T23:27:18.562096+00:00
|
2020-04-15T23:27:18.562130+00:00
| 661 | false |
this idea is from https://leetcode.com/problems/sliding-window-median/discuss/412047/Two-heaps-%2B-sliding-window-approach-O(-n-*-k-)-runtime-O(k)-space\nthanks @agconti\n```\nfrom heapq import * \nimport heapq\n\nclass Solution:\n def medianSlidingWindow(self, nums, k: int) :\n \'\'\'\n the concept/idea is that, you need to get access to the median every time you add a new element in to the heap\n also you need to remember to remove the passed one from the heap as well\n \'\'\'\n self.maxheap,self.minheap,result = [],[],[]\n if not nums or len(nums) < k:\n return []\n for i in range(k-1):\n self.add_element(nums[i])\n for i in range(k-1,len(nums)):\n self.add_element(nums[i])\n tmpmedian = self.get_median()\n result.append(tmpmedian)\n self.delete_element(nums[i-k+1])\n return result\n \n def get_median(self):\n if len(self.maxheap) == len(self.minheap):\n return (-self.maxheap[0] + self.minheap[0])/2\n else:\n return self.minheap[0]\n \n def add_element(self,nums):\n heappush(self.maxheap,-heappushpop(self.minheap,nums))\n if len(self.maxheap) > len(self.minheap):\n heappush(self.minheap,-heappop(self.maxheap))\n \n def delete_element_in_heap(self, heap, num) -> None:\n index = heap.index(num)\n # delete in O(1)\n # replace the value we want to remove with the last value\n heap[index] = heap[-1]\n del heap[-1]\n \n # Restore heap property thoughout the tree\n if index < len(heap):\n heapq._siftup(heap, index)\n heapq._siftdown(heap, 0, index)\n \n def delete_element(self,nums):\n if nums >= self.minheap[0]:\n self.delete_element_in_heap(self.minheap,nums)\n return\n self.delete_element_in_heap(self.maxheap,-nums)\n```
| 4 | 0 |
['Python3']
| 0 |
sliding-window-median
|
too long java code, AVL tree. 99% speed and 80% memory. Balanced and Unbalanced BSTs.
|
too-long-java-code-avl-tree-99-speed-and-gbr7
|
Hi, I tried to solve with AVL tree in java. Really good thing would be to use MultiSet but since java doesn\'t have it one built in, I tried to write own. Code
|
rostau3
|
NORMAL
|
2019-05-17T21:33:54.219408+00:00
|
2019-05-17T21:48:37.403277+00:00
| 305 | false |
Hi, I tried to solve with AVL tree in java. Really good thing would be to use MultiSet but since java doesn\'t have it one built in, I tried to write own. Code became long.\nTime complexity: O(n log(k))\nSpace coplexity: O(n) \n where n is size of array and k is the size of window.\n\n```\nclass Solution {\n public double[] medianSlidingWindow(int[] nums, int k) {\n if (nums == null || nums.length == 0)\n return new double[0];\n \n Node root = null;\n for (int i = 0; i < k; i++) {\n root = insert(root, nums[i]);\n }\n \n double[] r = new double[nums.length - k + 1];\n boolean even = k % 2 == 0;\n int j = 0;\n for (int i = k; i <= nums.length; i++) {\n double sum = 0.0;\n if (even)\n sum = (findSmallest(root, k/2).val + findSmallest(root, k/2 + 1).val) / 2.0;\n else\n sum = findSmallest(root, k/2 + 1).val;\n r[j++] = sum;\n if (i < nums.length) {\n root = insert(root, nums[i]);\n root = delete(root, nums[i - k]);\n }\n }\n \n return r;\n }\n \n private Node findSmallest(Node root, int k) {\n int s = countWith(root.left) + 1;\n if (s == k)\n return root;\n if (s > k) {\n return findSmallest(root.left, k);\n }\n return findSmallest(root.right, k - s);\n } \n \n private Node delete(Node root, long val) {\n if (root == null)\n return null;\n else if (val > root.val) \n root.right = delete(root.right, val);\n else if (val < root.val)\n root.left = delete(root.left, val);\n else {\n if (root.left == null)\n root = root.right;\n else if (root.right == null)\n root = root.left;\n else {\n Node t = findMin(root.right);\n root.val = t.val;\n root.right = delete(root.right, t.val);\n }\n }\n \n return updateNode(root);\n }\n \n private Node findMin(Node root) {\n if (root.left != null)\n return findMin(root.left);\n return root;\n }\n\n private Node insert(Node root, long val)\n {\n if (root == null)\n {\n return new Node(val);\n }\n if (val >= root.val)\n {\n root.right = insert(root.right, val);\n }\n else\n {\n root.left = insert(root.left, val);\n }\n \n return updateNode(root);\n }\n \n private Node updateNode(Node root) {\n int b = balance(root); \t\t\n if (b == 2 && balance(root.left) < 0)\n {\n root.left = leftRotate(root.left);\n root = rightRotate(root);\n }\n else if (b == -2 && balance(root.right) > 0)\n {\n root.right = rightRotate(root.right);\n root = leftRotate(root);\n }\n else if (b == 2)\n {\n root = rightRotate(root);\n }\n else if (b == -2)\n {\n root = leftRotate(root);\n }\n update(root);\n return root;\n }\n\n private Node leftRotate(Node n)\n {\n Node r = n.right;\n n.right = r.left;\n r.left = n;\n update(n);\n update(r);\n return r;\n }\n\n private Node rightRotate(Node n)\n {\n Node l = n.left;\n n.left = l.right;\n l.right = n;\n update(n);\n update(l);\n return l;\n }\n\n private int balance(Node n)\n {\n if (n==null)return 0;\n return height(n.left) - height(n.right);\n }\n\n private void update(Node n)\n {\n if (n==null)return;\n n.height = Math.max(height(n.left), height(n.right)) + 1;\n n.count = n.left != null ? n.left.count + 1 : 0;\n n.count += n.right != null ? n.right.count + 1 : 0;\n }\n\n private int height(Node n)\n {\n return n != null ? n.height : 0;\n }\n\n private int countWith(Node n)\n {\n return n != null ? n.count + 1 : 0;\n }\n\n static class Node\n {\n Node left;\n Node right;\n long val;\n int count;\n int height;\n\n Node(long val)\n {\n this.val = val;\n }\n }\n}\n\n\n\n```\n\n\n**For randomized input unbalanced BST** could be applied too, but worst case time complexity will be **O(n * k)**. The validating test cases for the submissions actually is giving random input, not targetting to hit the solution for unbalanced BST, so the following unbalanced bst aproach is also beats 99.8% by time. However wost case should not be forgetten.\n\n```\nclass Solution {\n public double[] medianSlidingWindow(int[] nums, int k) {\n if (nums == null || nums.length == 0)\n return new double[0];\n \n Node root = null;\n for (int i = 0; i < k; i++) {\n root = insert(root, nums[i]);\n }\n \n double[] r = new double[nums.length - k + 1];\n boolean even = k % 2 == 0;\n int j = 0;\n for (int i = k; i <= nums.length; i++) {\n double sum = 0.0;\n if (even)\n sum = (findSmallest(root, k/2).val + findSmallest(root, k/2 + 1).val) / 2.0;\n else\n sum = findSmallest(root, k/2 + 1).val;\n r[j++] = sum;\n if (i < nums.length) {\n root = insert(root, nums[i]);\n root = delete(root, nums[i - k]);\n }\n }\n \n return r;\n } \n \n private Node delete(Node root, long val) {\n if (root == null)\n return null;\n \n root.count--;\n if (val > root.val)\n root.right = delete(root.right, val);\n else if (val < root.val)\n root.left = delete(root.left, val);\n else {\n if (root.left == null && root.right == null)\n return null;\n else if (root.left == null || root.right == null) {\n return root.left == null ? root.right : root.left;\n } else {\n Node t = findMin(root.right); \n root.val = t.val;\n root.right = delete(root.right, t.val);\n }\n }\n return root;\n }\n \n private Node insert(Node root, long val)\n {\n if (root == null)\n return new Node(val);\n \n root.count++;\n if (val >= root.val) \n root.right = insert(root.right, val);\n else\n root.left = insert(root.left, val);\n \n return root;\n } \n \n private Node findSmallest(Node root, int k) {\n int s = countWith(root.left) + 1;\n if (s == k)\n return root;\n if (s > k) {\n return findSmallest(root.left, k);\n }\n return findSmallest(root.right, k - s);\n }\n \n private Node findMin(Node root) {\n if (root.left != null)\n return findMin(root.left);\n return root;\n } \n\n private int countWith(Node n)\n {\n return n != null ? n.count + 1 : 0;\n }\n\n static class Node\n {\n Node left;\n Node right;\n long val;\n int count;\n\n Node(long val)\n {\n this.val = val;\n }\n }\n}\n```
| 4 | 0 |
[]
| 0 |
sliding-window-median
|
O(nlogk) Python solution using Binary Search Tree
|
onlogk-python-solution-using-binary-sear-ched
|
My solution is to store the K elements in the current window in a BST. The BST node has other two attributes: dup store the number of duplicates, left_count sto
|
hx364
|
NORMAL
|
2017-01-16T03:34:56.623000+00:00
|
2017-01-16T03:34:56.623000+00:00
| 563 | false |
My solution is to store the K elements in the current window in a BST. The BST node has other two attributes: ```dup``` store the number of duplicates, ```left_count``` store the number of elements in the current node's left tree.\n\nThree methods of the BST class are implemented. ```insert``` inserts a new value to the tree, ```delete``` delete a value from the tree, ```find_kth``` find the kith smallest value in the tree. Each time the window moves, we deleted the old value, insert the new one, and using ```find_kth``` to find the median. All the above three methods are ```O(logk)```, so the time complexity is ```O(Nlogk)```\n\n\n```\nclass TreeNode(object):\n def __init__(self, val):\n self.val = val\n self.dup = 1\n self.left_count = 0\n self.left = None\n self.right = None\n \n def __repr__(self):\n return "val: %r dup: %r small: %r" %(self.val, self.dup, self.left_count)\n \n\nclass BST(object):\n def __init__(self):\n self.root = None\n self.count = 0\n \n def insert(self, num):\n #Insert number num into the BST\n self.count+=1\n \n if self.root==None:\n self.root = TreeNode(num)\n return\n \n prev, cur = None, self.root\n while cur is not None:\n prev = cur\n if cur.val == num:\n cur.dup+=1\n return\n elif cur.val < num:\n cur = cur.right\n else:\n #update the left_count\n cur.left_count+=1\n cur = cur.left\n if prev.val > num:\n prev.left = TreeNode(num)\n elif prev.val < num:\n prev.right = TreeNode(num)\n return\n \n def delete(self, num):\n #Delete number num from the BST, here it's guaranteed to find the number num\n self.count-=1\n \n prev, cur = None, self.root\n prev = TreeNode(-1000000)\n prev.right = self.root\n right_dir = True\n while True:\n if cur.val == num:\n break\n elif cur.val > num:\n cur.left_count-=1\n prev, cur = cur, cur.left\n right_dir = False\n else: #cur.val < num\n prev, cur = cur, cur.right\n right_dir = True\n \n #Find the node to delete, next step to delete the node\n if cur.dup>1:\n cur.dup-=1\n return\n \n #have to delete a node\n #node have no children\n if cur.left is None and cur.right is None:\n if cur==self.root: self.root=None\n elif right_dir: prev.right = None\n else: prev.left = None\n return\n #node have one childeren\n if cur.left is None:\n if cur == self.root: self.root = cur.right\n elif right_dir: prev.right = cur.right\n else: prev.left = cur.right\n return\n if cur.right is None:\n if cur == self.root: self.root = cur.left\n elif right_dir: prev.right = cur.left\n else: prev.left = cur.left\n return\n \n #node have two children\n next_prev, next_cur = cur, cur.right\n while next_cur.left is not None:\n next_prev, next_cur = next_cur, next_cur.left\n \n if next_cur == cur.right:\n cur.val = next_cur.val\n cur.dup = next_cur.dup\n cur.right = next_cur.right\n return\n \n elif next_cur != cur.right:\n next_prev.left = next_cur.right\n cur.val = next_cur.val\n cur.dup = next_cur.dup\n dup_to_del = cur.dup\n # next_prev.left = None\n p = cur.right\n while p is not None and p.val>=next_prev.val:\n p.left_count -= dup_to_del\n p = p.left\n return\n \n def find_median(self):\n k = (self.count+1)/2\n if self.count%2==1:\n return self.find_kth(k)+0.0\n else:\n return (0.+self.find_kth(k)+self.find_kth(k+1))/2\n \n def find_kth(self, k):\n #find the kth smallest element in the tree\n return self.find_kth_help(k, self.root)\n \n def find_kth_help(self, k, node):\n if node.left_count < k <= node.left_count+node.dup:\n return node.val\n if k <= node.left_count:\n return self.find_kth_help(k, node.left)\n else:\n return self.find_kth_help(k-node.left_count-node.dup, node.right)\n\n\nclass Solution(object):\n def medianSlidingWindow(self, nums, k):\n """\n :type nums: List[int]\n :type k: int\n :rtype: List[float]\n """\n if k==0:\n return []\n if k==1:\n return [i+0. for i in nums]\n \n tree = BST()\n for i in range(k):\n tree.insert(nums[i])\n \n result = []\n for i in range(k, len(nums)):\n result.append(tree.find_median())\n tree.delete(nums[i-k])\n tree.insert(nums[i])\n result.append(tree.find_median())\n # print result\n return result\n```
| 4 | 0 |
[]
| 0 |
sliding-window-median
|
C# BinarySearch solution
|
c-binarysearch-solution-by-liberwang-v8hu
|
\npublic double[] MedianSlidingWindow(int[] nums, int k) {\n List<double> llist = new List<double>();\n\n if (nums != null && nums.Length > 0 && k > 0) {\
|
liberwang
|
NORMAL
|
2017-01-18T20:48:23.207000+00:00
|
2017-01-18T20:48:23.207000+00:00
| 553 | false |
```\npublic double[] MedianSlidingWindow(int[] nums, int k) {\n List<double> llist = new List<double>();\n\n if (nums != null && nums.Length > 0 && k > 0) {\n int liPos1 = (k >> 1);\n int liPos2 = liPos1 + (k & 1) - 1;\n\n List<double> llistSlid = new List<double>();\n \n for( int i = 0; i < nums.Length; ++i ) {\n if (i >= k ) {\n llistSlid.Remove(nums[i - k ]);\n }\n\n int liIndex = llistSlid.BinarySearch(nums[i]);\n if (liIndex < 0) {\n liIndex = ~liIndex;\n }\n llistSlid.Insert(liIndex, nums[i]);\n\n if ( i >= k - 1 )\n llist.Add(liPos1 == liPos2 ? llistSlid[liPos1] : ((llistSlid[liPos1] + llistSlid[liPos2]) / 2));\n }\n }\n\n return llist.ToArray<double>();\n}\n```
| 4 | 0 |
[]
| 2 |
sliding-window-median
|
Sliding Window Median Using Balanced Multisets
|
sliding-window-median-using-balanced-mul-dhdm
|
IntuitionThe problem requires computing the median of every sliding window of size k in an array. Since the median is the middle element in a sorted window, an
|
sirravirathore
|
NORMAL
|
2025-03-30T19:46:38.290929+00:00
|
2025-03-30T19:46:38.290929+00:00
| 371 | false |
# Intuition
The problem requires computing the median of every sliding window of size `k` in an array. Since the median is the middle element in a sorted window, an efficient way to maintain a dynamically changing sorted window is needed.
# Approach
1. **Use two multisets** (`left` and `right`) to maintain a balanced window:
- `left` stores the smaller half (including the median if `k` is odd).
- `right` stores the larger half.
2. **Maintain balance** between both sets:
- Insert numbers into `left` or `right` while ensuring `left` has at most one more element than `right`.
- If necessary, move elements between sets to maintain order.
3. **Compute the median**:
- If `k` is odd, the median is the maximum of `left`.
- If `k` is even, the median is the average of the max of `left` and the min of `right`.
4. **Slide the window**:
- Remove the outgoing element from the appropriate set.
- Rebalance if necessary.
# Complexity
- **Time Complexity**:
$$O(n \log k)$$ – Each insertion and deletion in a multiset takes $$O(\log k)$$, and we perform this operation `n` times.
- **Space Complexity**:
$$O(k)$$ – We maintain two multisets of size `k`.
# Code
```cpp []
class Solution {
public:
vector<double> medianSlidingWindow(vector<int>& nums, int k) {
int n=nums.size();
multiset<double>left,right;
vector<double>res;
int i=0,j=0;
while(j<n){
if(left.empty() || left.size()<=right.size()){
left.insert(nums[j]);
}else{
right.insert(nums[j]);
}
if(!right.empty() && *left.rbegin()>*right.begin()){
double temp1=*left.rbegin();
double temp2=*right.begin();
left.erase(left.find(temp1));
right.erase(right.find(temp2));
right.insert(temp1);
left.insert(temp2);
}
if(j-i+1==k){
if(left.size()==right.size()){
double x = *left.rbegin() + *right.begin();
res.push_back((double)x/(2*1.0));
}else
res.push_back((double)*left.rbegin());
if(left.find(nums[i])!=left.end()){
left.erase(left.find(nums[i]));
}else{
right.erase(right.find(nums[i]));
}
i++;
}
j++;
}
return res;
}
};
```
| 3 | 0 |
['Array', 'Sliding Window', 'Ordered Set', 'C++']
| 0 |
sliding-window-median
|
easy readable few lines of code with clear explanation using in line comment ACCEPTED!!!!!!!
|
easy-readable-few-lines-of-code-with-cle-jjky
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
ResilientWarrior
|
NORMAL
|
2023-10-20T20:14:57.486452+00:00
|
2023-10-20T20:14:57.486493+00:00
| 301 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom bisect import bisect_left, insort\n#Purpose of bisect_left \n#The main purpose of bisect_left is to find the insertion point of a\n# target element in a sorted list, maintaining the sorted order, \n#or return the leftmost index where the target would be inserted if it wasn\'t found.\n\n#Purpose of insort\n#The main purpose of insort is to insert an element into a sorted list \n#while keeping the list sorted.\n\nclass Solution:\n def medianSlidingWindow(self, nums: List[int], k: int) -> List[float]:\n window = sorted(nums[:k])\n output = []\n output.append(self.getMedian(window,k))\n\n for i in range(1,len(nums)-k+1):\n # remove the leftmost element from our window, by finding its pos in nums, since window is sorted. \n window.pop(bisect_left(window,nums[i-1])) \n # insert a new element by expanding 0ne position to right and insert it to its respective, position in the window maintaining the sorted order.\n insort(window,nums[i+k-1])\n # append the median your output\n output.append(self.getMedian(window,k))\n \n return output\n \n def getMedian(self,window,k):\n # any odd number & 1 evaluates to 1 and any even number & 1 evaluates to 0 \n # in most programming languages 0 means False and 1 means True , \n if k & 1: \n return window[k//2]\n return (window[k//2] + window[k//2 - 1])/2 # return sum of the two middle values divided by 2 if k is even \n \n\n # I hope everything is clear !!!\n```
| 3 | 0 |
['Array', 'Sliding Window', 'Python', 'C++', 'Java', 'Python3']
| 0 |
sliding-window-median
|
ordered_multimap, Policy Based Data Structure in C++
|
ordered_multimap-policy-based-data-struc-6g3w
|
Intuition\nUsing policy based data strucuture, ordered_multimap\n\n# Code\n\n#include <bits/stdc++.h>\n\n#include <ext/pb_ds/assoc_container.hpp>\n#include <ext
|
theroyakash
|
NORMAL
|
2023-10-02T17:23:33.631477+00:00
|
2023-10-02T17:23:33.631500+00:00
| 794 | false |
# Intuition\nUsing policy based data strucuture, `ordered_multimap`\n\n# Code\n```\n#include <bits/stdc++.h>\n\n#include <ext/pb_ds/assoc_container.hpp>\n#include <ext/pb_ds/tree_policy.hpp>\n\nusing namespace __gnu_pbds;\n\ntypedef tree<pair<double, int>, null_type, less<pair<double, int>>, rb_tree_tag, tree_order_statistics_node_update> ordered_multiset;\n\nvector<double> solve(int n, int k, vector<int>& a) {\n vector<double> answer;\n ordered_multiset omst;\n queue<pair<double, int>> q;\n \n for (int i = 0; i < n; i++) {\n if (q.size() == k) {\n if (k & 1) {\n double a = (*omst.find_by_order(k / 2)).first;\n answer.push_back(a);\n } else {\n double b = ((double)(*omst.find_by_order(k / 2 - 1)).first + (double)(*omst.find_by_order(k / 2)).first) / 2.0;\n answer.push_back(b);\n }\n \n double r = q.front().first;\n q.pop();\n \n omst.erase(omst.find_by_order(omst.order_of_key({r, -1})));\n }\n \n omst.insert({a[i], i});\n q.push({a[i], i});\n }\n \n // last window\n if (k & 1) {\n double a = (*omst.find_by_order(k / 2)).first;\n answer.push_back(a);\n } else {\n double b = ((*omst.find_by_order(k / 2 - 1)).first + (*omst.find_by_order(k / 2)).first) / 2.0;\n answer.push_back(b);\n }\n\n return answer;\n}\n\nclass Solution {\npublic:\n vector<double> medianSlidingWindow(vector<int>& nums, int k) {\n int n = nums.size();\n return solve(n, k, nums);\n }\n};\n```
| 3 | 0 |
['Ordered Map', 'C++']
| 0 |
sliding-window-median
|
C++ code with explanation
|
c-code-with-explanation-by-vi_05-ypkw
|
Complexity\n- Time complexity: O(nlogn)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(n)\n Add your space complexity here, e.g. O(n) \n\n
|
Vi_05
|
NORMAL
|
2023-06-06T08:52:08.880031+00:00
|
2023-06-06T08:52:08.880068+00:00
| 1,097 | false |
# Complexity\n- Time complexity: O(nlogn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n vector<double> medianSlidingWindow(vector<int>& nums, int k) {\n //vector to store median \n vector<double> median;\n //map to delete the elements that are to be removed from sliding window \n unordered_map<int,int> mp;\n //to store the element in heap in descending order\n priority_queue<int> maxHeap;\n //to store the element in heap in ascending order\n priority_queue<int, vector<int>, greater<int>> minHeap;\n\n //first insert the element upto the size of window in maxHeap\n for(int i=0;i<k;i++)\n {\n maxHeap.push(nums[i]);\n }\n\n //Now to balance the size of maxHeap and minHeap, insert half elements in minHeap\n for(int i=0; i<k/2; i++)\n {\n minHeap.push(maxHeap.top());\n maxHeap.pop();\n }\n\n //for rest of the elements\n for(int i=k; i<nums.size(); i++)\n {\n\n if(k%2 != 0) //if k is odd\n median.push_back(maxHeap.top()*1.0);\n else // if k is even\n median.push_back((maxHeap.top()*1.0 + minHeap.top()*1.0)/2);\n\n //to remove previous element from sliding window and inserting new element and checking the balance of maxHeap and minHeap\n int p = nums[i-k], q = nums[i], balance = 0;\n\n //if p is present in maxHeap\n if(p <= maxHeap.top())\n {\n balance--;\n if(p == maxHeap.top())\n {\n maxHeap.pop();\n }\n else\n {\n mp[p]++;\n }\n }\n else //if p is present in minHeap\n {\n balance++;\n if(p == minHeap.top())\n {\n minHeap.pop();\n }\n else\n {\n mp[p]++;\n }\n }\n\n //to insert q in maxHeap when q is smaller than top of the maxHeap\n if(!maxHeap.empty() && q<=maxHeap.top())\n {\n maxHeap.push(q);\n balance++;\n }\n else //if q is greater the top of maxHeap then insert it into minHeap\n {\n minHeap.push(q);\n balance--;\n }\n \n //if balance > 0\n if(balance > 0)\n {\n minHeap.push(maxHeap.top());\n maxHeap.pop();\n } //if balance < 0\n else if(balance < 0)\n {\n maxHeap.push(minHeap.top());\n minHeap.pop();\n }\n\n //to delete last element present in heap and for that map is used\n while(!maxHeap.empty() && mp[maxHeap.top()])\n {\n mp[maxHeap.top()]--;\n maxHeap.pop();\n }\n while(!minHeap.empty() && mp[minHeap.top()])\n {\n mp[minHeap.top()]--;\n minHeap.pop();\n }\n }\n if(k%2 != 0)\n median.push_back(maxHeap.top()*1.0);\n else \n median.push_back((maxHeap.top()*1.0 + minHeap.top()*1.0)/2);\n return median;\n }\n};\n```
| 3 | 0 |
['Sliding Window', 'Heap (Priority Queue)', 'C++']
| 0 |
sliding-window-median
|
Sliding Window Median (C#)
|
sliding-window-median-c-by-framebymahmud-kf4l
|
Intuition:\nThe problem asks for the median of each sliding window of size k in an input array. One approach to solving this problem is to maintain a sorted lis
|
framebymahmud
|
NORMAL
|
2023-05-12T11:13:22.860325+00:00
|
2023-05-12T11:13:22.860361+00:00
| 351 | false |
Intuition:\nThe problem asks for the median of each sliding window of size k in an input array. One approach to solving this problem is to maintain a sorted list of the elements in the current window, and compute the median from this list. To slide the window, we remove the leftmost element and insert the rightmost element in its correct position in the list.\n\nApproach:\nThe approach used in the code is as follows:\n\n1. Initialize an empty list with the first k elements of the input array, sorted in increasing order.\n2. Compute the median of the first window and store it in the result array.\n3. Slide the window one element at a time, removing the leftmost element and inserting the rightmost element in the list in its correct position.\n4. Compute the median of the current window and store it in the result array.\n\nComplexity:\nThe time and space complexity of the sliding window median algorithm depend on the size of the input array and the size of the sliding window. Let n be the length of the input array and k be the size of the sliding window.\n\nTime complexity: The time complexity of the algorithm is O(n log k), where the dominant factor is the time it takes to maintain the sorted list of size k. The insertion and removal of elements in the list take O(log k) time, and we do this n-k+1 times for each window, resulting in a total time complexity of O((n-k+1) log k).\n\nSpace complexity: The space complexity of the algorithm is O(k), which is the size of the sorted list we maintain. We also need O(n-k+1) space to store the result array, resulting in a total space complexity of O(n-k+1 + k) = O(n).\n\n# Code\n```\npublic class Solution {\n public double[] MedianSlidingWindow(int[] nums, int k) {\n int n = nums.Length;\n double[] res = new double[n - k + 1];\n List<int> list = new List<int>(nums.Take(k).OrderBy(x => x));\n res[0] = k % 2 == 0 ?\n ((double)list[k / 2 - 1] + (double)list[k / 2]) / 2 :\n (double)list[k / 2];\n for (int i = 1; i <= n - k; i++) {\n int left = nums[i - 1];\n int right = nums[i + k - 1];\n list.Remove(left);\n int j = list.BinarySearch(right);\n if (j < 0) j = ~j;\n list.Insert(j, right);\n res[i] = k % 2 == 0 ?\n ((double)list[k / 2 - 1] + (double)list[k / 2]) / 2 :\n (double)list[k / 2];\n }\n return res;\n }\n}\n\n```
| 3 | 0 |
['C#']
| 4 |
sliding-window-median
|
480: Solution with step by step explanation
|
480-solution-with-step-by-step-explanati-vemk
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n1. Check if the list is empty or the window size is greater than the list
|
Marlen09
|
NORMAL
|
2023-03-10T18:17:34.513444+00:00
|
2023-03-10T18:17:34.513478+00:00
| 2,282 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Check if the list is empty or the window size is greater than the list length. If either of these conditions is true, return an empty list.\n\n2. Create a helper function to calculate the median of a given subarray. If the length of the subarray is odd, return the middle element. If the length of the subarray is even, return the mean of the two middle elements.\n\n3. Create a deque to store the current window.\n\n4. Create an empty list to store the medians.\n\n5. Iterate over each element in the list. For each element:\na. Add the element to the deque.\nb. If the deque has reached the size of the window, calculate the median of the current window using the helper function and append it to the list of medians.\nc. Remove the leftmost element from the deque to maintain the window size.\n\n6. Return the list of medians.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def medianSlidingWindow(self, nums: List[int], k: int) -> List[float]:\n n = len(nums)\n # edge case: empty list or window size greater than list length\n if n == 0 or k > n:\n return []\n \n # helper function to get median of a subarray\n def get_median(arr):\n n = len(arr)\n # if length is odd, return middle element\n if n % 2 == 1:\n return arr[n // 2]\n # if length is even, return mean of middle elements\n return (arr[n // 2] + arr[n // 2 - 1]) / 2\n \n # initialize deque to store current window\n window = collections.deque()\n # initialize result list to store medians\n res = []\n \n # iterate over each element in nums\n for i, x in enumerate(nums):\n # add element to window\n window.append(x)\n # if window size is reached, get median and append to res\n if len(window) == k:\n res.append(get_median(sorted(window)))\n # remove leftmost element from window\n window.popleft()\n \n return res\n```
| 3 | 0 |
['Array', 'Hash Table', 'Sliding Window', 'Python', 'Python3']
| 3 |
sliding-window-median
|
Easy understandable implementation in c++ (ordered_set).
|
easy-understandable-implementation-in-c-0vwgi
|
Intuition\n Describe your first thoughts on how to solve this problem. \nJust think about the advance data structure ordered set .\n\n# Approach\n Describe your
|
ups1610
|
NORMAL
|
2022-11-28T15:11:07.752666+00:00
|
2022-11-28T15:11:07.752714+00:00
| 1,367 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nJust think about the advance data structure ordered set .\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nStore each k window elements in ordered set \nfind the median \nstore each k window median in an array\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(nlogn)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(N)\n\n# Code\n```\n#include <ext/pb_ds/assoc_container.hpp>\n#include <ext/pb_ds/tree_policy.hpp>\nusing namespace __gnu_pbds;\n#define ordered_set tree<pair<long double,long double>, null_type,less<pair<long double,long double>>, rb_tree_tag,tree_order_statistics_node_update>\nclass Solution {\npublic:\n vector<double> medianSlidingWindow(vector<int>& nums, int k) {\n ordered_set s;\n vector<double>ans;\n int n=nums.size();\n for(int i=0;i<k;i++)\n {\n s.insert({nums[i],i});\n }\n long double val=0.0;\n if(k%2!=0)\n {\n val=(s.find_by_order((k-1)/2)->first)/1.0;\n ans.push_back(val);\n }\n if(k%2==0)\n {\n val=((s.find_by_order((k-1)/2)->first)/1.0 + (s.find_by_order(k/2)->first)/1.0)/2.0;\n ans.push_back(val);\n }\n \n int j=0;\n for(int i=k;i<n;i++)\n {\n s.erase({nums[j],j});\n s.insert({nums[i],i});\n if(k%2==0){\n val=double(double(s.find_by_order((k-1)/2)->first) + double(s.find_by_order(k/2)->first))/2.0;\n }\n else{\n val=(s.find_by_order((k-1)/2)->first)/1.0;\n }\n ans.push_back(val);\n j++;\n }\n return ans;\n }\n\n};\n```
| 3 | 0 |
['C++']
| 1 |
sliding-window-median
|
✅Python short and very easy to understand
|
python-short-and-very-easy-to-understand-hv5a
|
```\ndef medianSlidingWindow(self, nums: List[int], k: int) -> List[float]:\n res = []\n for i in range(len(nums)-k+1):\n temp = sorted
|
SteveDes
|
NORMAL
|
2022-08-03T23:23:08.655766+00:00
|
2022-08-03T23:23:08.655794+00:00
| 580 | false |
```\ndef medianSlidingWindow(self, nums: List[int], k: int) -> List[float]:\n res = []\n for i in range(len(nums)-k+1):\n temp = sorted(nums[i:i+k])\n \n if k % 2 != 0:\n res.append(temp[k//2])\n else:\n avg = (temp[k//2] + temp[k//2-1])/2\n res.append(avg)\n return res
| 3 | 0 |
['Python']
| 0 |
sliding-window-median
|
Simple C++ Code || 2 multiset
|
simple-c-code-2-multiset-by-prosenjitkun-8x1y
|
Reference was taken from youtube channel.\n# If you like the implementation then Please help me by increasing my reputation. By clicking the up arrow on the lef
|
_pros_
|
NORMAL
|
2022-06-16T03:26:48.829049+00:00
|
2022-06-16T03:26:48.829087+00:00
| 145 | false |
# Reference was taken from youtube channel.\n# **If you like the implementation then Please help me by increasing my reputation. By clicking the up arrow on the left of my image.**\n\n```\nclass Solution {\npublic:\n vector<double> medianSlidingWindow(vector<int>& nums, int k) {\n multiset<double> asc;\n multiset<double, greater<double>> des;\n int n = nums.size();\n vector<double> ans;\n for(int i = 0; i < n; i++)\n {\n if(i >= k)\n {\n auto ita = asc.find(nums[i-k]);\n if(ita == asc.end())\n {\n auto itd = des.find(nums[i-k]);\n des.erase(itd);\n }\n else\n {\n asc.erase(ita);\n }\n }\n asc.insert(nums[i]);\n des.insert(*asc.begin());\n asc.erase(asc.begin());\n if(des.size() > asc.size())\n {\n asc.insert(*des.begin());\n des.erase(des.begin());\n }\n if(i >= k-1)\n {\n double medn;\n if(k%2 == 0)\n {\n medn = (*asc.begin() + *des.begin())/2;\n ans.push_back(medn); \n }\n else\n {\n medn = *asc.begin();\n ans.push_back(medn);\n }\n } \n }\n return ans;\n }\n};\n```
| 3 | 0 |
[]
| 0 |
sliding-window-median
|
Python - Easy to understand using 2 heap
|
python-easy-to-understand-using-2-heap-b-0xhn
|
\nimport heapq\n\nclass Solution:\n def getMedian(self, maxHeap: List[int], minHeap: List[int]) -> float:\n # minHeap stores larger half and maxHeap s
|
abrarjahin
|
NORMAL
|
2022-05-24T11:19:44.248335+00:00
|
2022-05-24T11:19:44.248372+00:00
| 1,644 | false |
```\nimport heapq\n\nclass Solution:\n def getMedian(self, maxHeap: List[int], minHeap: List[int]) -> float:\n # minHeap stores larger half and maxHeap stores small half elements\n # So data is like -> [maxHeap] + [minHeap]\n # if total no of element is odd, then maxHeap contains more elements than minHeap\n if len(maxHeap)==0: return 0\n elif len(maxHeap)!=len(minHeap): return -maxHeap[0]\n else: return (-maxHeap[0]+minHeap[0])/2\n\n def adjustHeapSize(self, maxHeap: List[int], minHeap: List[int]) -> None:\n while len(maxHeap)<len(minHeap) or len(maxHeap)>len(minHeap)+1:\n if len(maxHeap)>len(minHeap)+1:\n removedMaxHeapItem = -heapq.heappop(maxHeap)\n heapq.heappush(minHeap, removedMaxHeapItem)\n else:\n removedMaxHeapItem = heapq.heappop(minHeap)\n heapq.heappush(maxHeap, -removedMaxHeapItem)\n\n def addElement(self, maxHeap: List[int], minHeap: List[int], num: int, k: int) -> None:\n median = self.getMedian(maxHeap, minHeap)\n if num<=median: #Insert to maxHeap\n heapq.heappush(maxHeap, -num)\n else:\n heapq.heappush(minHeap, num)\n #print(num, maxHeap, minHeap, \'Before add adjust\')\n self.adjustHeapSize(maxHeap, minHeap)\n\n def removeElement(self, maxHeap: List[int], minHeap: List[int], num: int) -> None:\n median = self.getMedian(maxHeap, minHeap)\n #print(num, "Remove", maxHeap, minHeap, median)\n if num<=median: #Insert to maxHeap\n maxHeap.remove(-num)\n heapq.heapify(maxHeap)\n else:\n minHeap.remove(num)\n heapq.heapify(minHeap)\n #print(num, maxHeap, minHeap, \'Before remove adjust\')\n self.adjustHeapSize(maxHeap, minHeap)\n\n def medianSlidingWindow(self, nums: List[int], k: int) -> List[float]:\n maxHeap, minHeap, output = [], [], []\n for i in range(len(nums)):\n self.addElement(maxHeap, minHeap, nums[i], k)\n #print(maxHeap, minHeap, \'Added\', nums[i])\n if i>=k-1:\n output.append(self.getMedian(maxHeap, minHeap))\n #print(nums, i, i-k+1)\n self.removeElement(maxHeap, minHeap, nums[i-k+1])\n #print(maxHeap, minHeap, \'Removed\', nums[i-k+1])\n return output\n```
| 3 | 0 |
['Heap (Priority Queue)', 'Python', 'Python3']
| 1 |
sliding-window-median
|
O(n log k) | C++ | Straight Forward | Using two sets as heaps
|
on-log-k-c-straight-forward-using-two-se-chpz
|
The question is similar to find median in a stream https://leetcode.com/problems/find-median-from-data-stream/.\nI\'d suggest you to go through the above proble
|
onemol
|
NORMAL
|
2022-03-12T10:56:34.816708+00:00
|
2022-03-12T10:56:34.816733+00:00
| 187 | false |
The question is similar to find median in a stream https://leetcode.com/problems/find-median-from-data-stream/.\nI\'d suggest you to go through the above problem before proceeding with this one\n\nThere are two things to keep in mind: \n1. Create balanced heaps for current window. \n2. Discard elements that are out of current window.\n\nUnfortunately, priority_queue in C++ doesn\'t allow effecient O(log n) deletion, so we will use sets as heaps.\nwe can get max element of max heap using *(maxh.rbegin()) and min element of min heap using *(minh.begin())\n\nIn order to handle duplicates, we can use a pair of {number, index} instead of just number, this has an added advantage because pairs are by default evaluated by first value in C++, so there is no need to write a custom comparator like in a lot of other answers.\n\nCode: \n```\nclass Solution {\npublic:\n vector<double> medianSlidingWindow(vector<int>& nums, int k) {\n set<pair<int, int>> maxh; // get max element using *(maxh.rbegin());\n set<pair<int, int>> minh; // get min element using *(minh.begin());\n \n for(int i = 0; i < k; i++) {\n maxh.insert({nums[i], i}); // a {number, index} pair will always be unique (for handling duplicates)\n }\n \n for(int i = 0; i < k/2; i++) {\n minh.insert(*maxh.rbegin());\n maxh.erase(*maxh.rbegin());\n }\n \n vector<double> res;\n \n int n = nums.size();\n \n for(int i = k; i < n; i++) {\n if(k % 2 == 0) {\n res.push_back(((double)(maxh.rbegin())->first + (double)(minh.begin())->first) / 2.0);\n } else {\n res.push_back((double) (maxh.rbegin())->first);\n }\n \n // delete the element that is out of window, deletion in O(log k)\n \n if(maxh.find({nums[i-k], i-k}) != maxh.end()) {\n maxh.erase({nums[i-k], i-k});\n }\n \n if(minh.find({nums[i-k], i-k}) != minh.end()) {\n minh.erase({nums[i-k], i-k});\n }\n \n // insert new element\n \n if(maxh.size() == 0 || nums[i] <= (maxh.rbegin())->first) {\n maxh.insert({nums[i], i});\n } else {\n minh.insert({nums[i], i});\n }\n \n // balance the sets/heaps\n \n if(minh.size() > maxh.size()) {\n pair<int, int> x = *(minh.begin());\n minh.erase(x);\n maxh.insert(x);\n }\n \n // maxh can have at max one more element than minh\n \n if(maxh.size() > minh.size()+1) {\n pair<int, int> x = *(maxh.rbegin());\n maxh.erase(x);\n minh.insert(x);\n }\n }\n \n if(k % 2 == 0) {\n res.push_back(((double)(maxh.rbegin())->first + (double)(minh.begin())->first) / 2.0);\n } else {\n res.push_back((double) (maxh.rbegin())->first);\n }\n \n return res;\n }\n};\n\n```
| 3 | 0 |
['Heap (Priority Queue)', 'Ordered Set']
| 2 |
sliding-window-median
|
C# solution PriorityQueue || Similar solution for leet code 295 and leet code 480
|
c-solution-priorityqueue-similar-solutio-6kjy
|
Lets first understand the solution of problem #295 - Median of data streams\n\n1. Partition streaming numbers into 2 halves\n2. maxHeap - for all smaller number
|
adparoha
|
NORMAL
|
2022-02-13T00:02:11.592954+00:00
|
2022-02-13T00:04:09.673779+00:00
| 186 | false |
Lets first understand the solution of problem #295 - Median of data streams\n\n1. Partition streaming numbers into 2 halves\n2. maxHeap - for all smaller numbers\n3. minHeap - for all larger numbers\n4. Balance heap - whenever difference of both heap size > 1\n5. Find Median - for odd numbers - maxHeap peek is median, for even numbers - average of minHeap peek and maxHeap peek\n6. For problem #480, we need one extra step, maintain one sliding window of size k, when window size is reached remove left most element from heap\n\nLC 295\n\n```\n public class MedianFinder\n {\n private readonly PriorityQueue<int, int> _minHeap;\n private readonly PriorityQueue<int, int> _maxHeap;\n\n public MedianFinder()\n {\n _minHeap = new PriorityQueue<int, int>();\n _maxHeap = new PriorityQueue<int, int>(Comparer<int>.Create((a, b) => b.CompareTo(a)));\n }\n\n public void AddNum(int num)\n {\n if (_maxHeap.Count == 0 || _maxHeap.Peek() >= num)\n _maxHeap.Enqueue(num, num);\n else\n _minHeap.Enqueue(num, num);\n Balance();\n }\n\n public double FindMedian()\n {\n return _maxHeap.Count > _minHeap.Count ?\n _maxHeap.Peek() :\n _minHeap.Peek() / 2.0 + _maxHeap.Peek() / 2.0;\n }\n\n private void Balance()\n {\n if (_maxHeap.Count == _minHeap.Count)\n return;\n if (_maxHeap.Count > _minHeap.Count + 1)\n {\n int maxHeapPeek = _maxHeap.Dequeue();\n _minHeap.Enqueue(maxHeapPeek, maxHeapPeek);\n }\n else if (_maxHeap.Count < _minHeap.Count)\n {\n int minHeapPeek = _minHeap.Dequeue();\n _maxHeap.Enqueue(minHeapPeek, minHeapPeek);\n }\n }\n }\n```\n\nLC 480\n\n```\npublic class Solution {\n \n private PriorityQueue<int, int> _minHeap = new PriorityQueue<int, int>();//all bigger numbers\n private PriorityQueue<int, int> _maxHeap = new PriorityQueue<int, int>(Comparer<int>.Create((a, b) => b.CompareTo(a)));//all smaller numbers\n \n public double[] MedianSlidingWindow(int[] nums, int k) {\n double[] medians = new double[nums.Length - k + 1];\n for(int left = 0, right = 0; right < nums.Length; right++){\n AddNum(nums[right]);\n if(right - left + 1 == k){\n medians[right - k + 1] = FindMedian();\n Remove(nums[left]);\n left++;\n }\n }\n return medians;\n }\n \n public void AddNum(int num)\n {\n if(_maxHeap.Count == 0 || _maxHeap.Peek() >= num)\n _maxHeap.Enqueue(num, num);\n else\n _minHeap.Enqueue(num, num);\n Balance();\n }\n \n private void Balance(){\n if(_maxHeap.Count == _minHeap.Count)\n return;\n if(_maxHeap.Count > _minHeap.Count + 1)\n {\n int maxHeapPeek = _maxHeap.Dequeue();\n _minHeap.Enqueue(maxHeapPeek, maxHeapPeek);\n }\n else if(_maxHeap.Count < _minHeap.Count)\n {\n int minHeapPeek = _minHeap.Dequeue();\n _maxHeap.Enqueue(minHeapPeek, minHeapPeek);\n }\n }\n\n public double FindMedian()\n {\n return _maxHeap.Count > _minHeap.Count ?\n _maxHeap.Peek() :\n _minHeap.Peek() / 2.0 + _maxHeap.Peek() / 2.0;\n }\n \n public void Remove(int num){\n if(num > _maxHeap.Peek())\n Remove(_minHeap, num);\n else\n Remove(_maxHeap, num);\n Balance(); \n }\n \n public void Remove(PriorityQueue<int, int> heap, int num){\n List<int> buffer = new List<int>();\n while(heap.Count > 0 && heap.Peek() != num)\n buffer.Add(heap.Dequeue());\n heap.Dequeue();\n buffer.ForEach(n => heap.Enqueue(n, n));\n }\n}\n```
| 3 | 0 |
['Heap (Priority Queue)']
| 0 |
sliding-window-median
|
JAVA simple solution using min-heap and max-heap
|
java-simple-solution-using-min-heap-and-2p2pf
|
Slide through each of the window of size K and calculate median of each window.\nTime Complexity : O(nlogn)\nSpace Complexity: O(n)\n\n\nclass Solution {\n \
|
mitesh_pv
|
NORMAL
|
2022-01-15T06:41:13.861821+00:00
|
2022-01-15T06:47:03.999891+00:00
| 937 | false |
Slide through each of the window of size K and calculate median of each window.\nTime Complexity : **O(nlogn)**\nSpace Complexity: **O(n)**\n\n```\nclass Solution {\n \n PriorityQueue<Integer> maxHeap = new PriorityQueue<>(Collections.reverseOrder());\n PriorityQueue<Integer> minHeap = new PriorityQueue<>();\n \n \n private void removeFromHeap(int n) {\n if(n<=maxHeap.peek()) {\n if(maxHeap.size() > minHeap.size()) {\n maxHeap.remove(n);\n }else {\n maxHeap.remove(n);\n maxHeap.add(minHeap.poll());\n }\n }else {\n if(maxHeap.size() > minHeap.size()) {\n minHeap.remove(n);\n minHeap.add(maxHeap.poll());\n }else {\n minHeap.remove(n);\n }\n }\n }\n \n private void insertToHeap(int num) {\n if(maxHeap.isEmpty()) {\n maxHeap.add(num);\n }else {\n if(maxHeap.size() > minHeap.size()) {\n if(maxHeap.peek() < num) {\n minHeap.add(num);\n }else {\n minHeap.add(maxHeap.poll());\n maxHeap.add(num);\n }\n }else {\n if(maxHeap.peek() <= num) {\n minHeap.add(num);\n maxHeap.add(minHeap.poll());\n }else {\n maxHeap.add(num);\n }\n }\n }\n }\n \n private double median() {\n if(maxHeap.size()>minHeap.size()) {\n return maxHeap.peek();\n }\n long sum = (long)maxHeap.peek() + (long)minHeap.peek();\n return (double)((sum)/2.0);\n }\n \n public double[] medianSlidingWindow(int[] nums, int k) {\n int n = nums.length - k + 1;\n double[] res = new double[n];\n \n for(int i=0; i<=nums.length; ++i) {\n if(i>=k) {\n res[i-k] = median();\n removeFromHeap(nums[i-k]);\n }\n \n if(i<nums.length) {\n insertToHeap(nums[i]);\n }\n }\n \n return res;\n }\n}\n```
| 3 | 0 |
['Heap (Priority Queue)', 'Java']
| 1 |
sliding-window-median
|
C++ solution using GNU-PBDS
|
c-solution-using-gnu-pbds-by-mihir_devil-03dh
|
\n#include <ext/pb_ds/assoc_container.hpp>\n#include <ext/pb_ds/tree_policy.hpp>\nusing namespace __gnu_pbds;\n#define ordered_set tree<pair<int,int>,null_type,
|
mihir_devil
|
NORMAL
|
2021-07-05T23:00:58.520442+00:00
|
2021-07-05T23:00:58.520474+00:00
| 303 | false |
```\n#include <ext/pb_ds/assoc_container.hpp>\n#include <ext/pb_ds/tree_policy.hpp>\nusing namespace __gnu_pbds;\n#define ordered_set tree<pair<int,int>,null_type,less<pair<int,int>>,rb_tree_tag,tree_order_statistics_node_update>\nclass Solution {\npublic:\n vector<double> medianSlidingWindow(vector<int>& a, int k) {\n ordered_set os;\n int i,j,n=a.size();\n for(int i=0;i<k;i++){\n os.insert({a[i],i});\n }\n vector<double> v;\n k--;\n int t1=k/2,t2=k+1;\n t2/=2;\n k++;\n for(int i=k;i<=n;i++){\n long long int o=os.find_by_order(t1)->first;\n long long int t=os.find_by_order(t2)->first;\n if(k%2)\n v.push_back(o);\n else{\n o+=t;\n v.push_back(o/2.0);\n }\n os.erase({a[i-k],i-k});\n if(i<n)\n os.insert({a[i],i});\n }\n return v;\n }\n};\n```
| 3 | 0 |
[]
| 0 |
sliding-window-median
|
Multiset C++ Solution
|
multiset-c-solution-by-voquocthang99-2kr5
|
```\nclass Solution {\npublic:\n void Balance(multiset & left, multiset & right) {\n int n = left.size();\n int m = right.size();\n if (
|
voquocthang99
|
NORMAL
|
2021-05-10T07:06:23.714986+00:00
|
2021-05-10T07:06:23.715049+00:00
| 381 | false |
```\nclass Solution {\npublic:\n void Balance(multiset<int> & left, multiset<int> & right) {\n int n = left.size();\n int m = right.size();\n if (n == m || n+1 == m) return;\n if (n > m) {\n auto it = left.end();\n it--;\n right.emplace(*it);\n left.erase(it);\n } \n else {\n left.emplace(* right.begin());\n right.erase(right.begin());\n }\n }\n vector<double> medianSlidingWindow(vector<int>& nums, int k) {\n vector<double> ans;\n multiset<int> left;\n multiset<int> right;\n \n for(int i = 0; i < nums.size(); i++) {\n if (!right.empty() && nums[i] < * right.begin()) left.insert(nums[i]);\n else right.insert(nums[i]);\n Balance(left, right);\n if (i >= k) {\n auto it = left.find(nums[i-k]);\n if (it != left.end()) left.erase(it);\n else it = right.find(nums[i-k]), right.erase(it);\n Balance(left, right);\n }\n if (i >= k-1) { \n double res = 0;\n auto it = right.begin();\n if (k % 2 == 0) { \n auto it_ = left.end();\n it_--;\n res = (double)( (long long) *it + *it_ ) / 2;\n }\n else res = *it;\n ans.push_back(res);\n }\n }\n return ans;\n }\n};
| 3 | 0 |
[]
| 3 |
sliding-window-median
|
Java Solution - TreeSet - O(n*logk)
|
java-solution-treeset-onlogk-by-mycafeba-0fne
|
\nclass Solution {\n public double[] medianSlidingWindow(int[] nums, int k) {\n Comparator<Integer> comparator = (a, b) -> nums[a] != nums[b] ? Intege
|
mycafebabe
|
NORMAL
|
2021-05-07T06:15:02.257694+00:00
|
2021-05-07T06:15:02.257736+00:00
| 239 | false |
```\nclass Solution {\n public double[] medianSlidingWindow(int[] nums, int k) {\n Comparator<Integer> comparator = (a, b) -> nums[a] != nums[b] ? Integer.compare(nums[a], nums[b]) : a - b;\n TreeSet<Integer> left = new TreeSet<>(comparator);\n TreeSet<Integer> right = new TreeSet<>(comparator);\n List<Double> list = new ArrayList<>();\n for (int i = 0; i < k; i++) {\n right.add(i);\n }\n for (int i = 0; i < k / 2; i++) {\n left.add(right.pollFirst());\n }\n putMedian(nums, list, left, right);\n for (int i = 0, j = k; j < nums.length; i++, j++) {\n insert(nums, left, right, j);\n remove(nums, left, right, i);\n rebalance(left, right);\n putMedian(nums, list, left, right);\n }\n double[] ans = new double[list.size()];\n for (int i = 0; i < list.size(); i++) {\n ans[i] = list.get(i);\n }\n return ans;\n }\n \n private void rebalance(TreeSet<Integer> left, TreeSet<Integer> right) {\n if (left.size() + 2 == right.size()) {\n left.add(right.pollFirst());\n } else if (left.size() == right.size() + 1) {\n right.add(left.pollLast());\n }\n }\n \n private void insert(int[] nums, TreeSet<Integer> left, TreeSet<Integer> right, int i) {\n if (left.size() != right.size()) {\n right.add(i);\n left.add(right.pollFirst());\n } else {\n left.add(i);\n right.add(left.pollLast());\n }\n }\n \n private void remove(int[] nums, TreeSet<Integer> left, TreeSet<Integer> right, int i) {\n if (!left.remove(i)) {\n right.remove(i);\n }\n }\n \n private void putMedian(int[] nums, List<Double> list, TreeSet<Integer> left, TreeSet<Integer> right) {\n if (left.size() != right.size()) {\n list.add(nums[right.first()] * 1.0);\n } else {\n long sum = (long)nums[left.last()] + (long)nums[right.first()];\n list.add((sum) / 2.0);\n }\n }\n}\n```
| 3 | 1 |
[]
| 0 |
sliding-window-median
|
TypeScript O(nk + klogk) solution. No heap
|
typescript-onk-klogk-solution-no-heap-by-f9lf
|
You can\'t write a heap data structure during the interview if you use JS/TS\nSort the first window using O(klogk). Then use O(k) to keep the window sorted when
|
pike96
|
NORMAL
|
2021-04-27T05:50:35.623695+00:00
|
2021-04-27T05:50:35.623742+00:00
| 167 | false |
You can\'t write a heap data structure during the interview if you use JS/TS\nSort the first window using O(klogk). Then use O(k) to keep the window sorted when adding & removing elements\n\nIt\'s actually O(nk + klogk)\n\n```\nfunction medianSlidingWindow(nums: number[], k: number): number[] {\n const medians: number[] = [];\n \n let window: number[];\n \n for (let i: number = 0; i + k <= nums.length; i++) {\n // Do the sorting only for the 1st window\n if (i === 0) {\n window = nums.slice(0, k);\n window.sort((a: number, b: number) => a - b);\n medians.push(getMedianFromWin(window, k));\n }\n else {\n // Add & Remove meanwhile keep it sorted\n // 0 1 2\n // 1 2 3\n // remove: i - 1 add: i + k - 1\n window.splice(window.indexOf(nums[i - 1]), 1);\n const toAdd: number = nums[i + k - 1];\n let j: number = 0;\n for (; j < window.length; j++) {\n if (window[j] >= toAdd) {\n break;\n }\n }\n window.splice(j, 0, toAdd);\n medians.push(getMedianFromWin(window, k));\n }\n }\n \n return medians;\n};\n\nfunction getMedianFromWin(win: number[], k: number): number {\n if (k & 1) {\n return win[k >> 1];\n }\n else {\n return (win[(k >> 1) - 1] + win[k >> 1]) / 2;\n }\n}\n```
| 3 | 0 |
['TypeScript']
| 0 |
sliding-window-median
|
Python bisect solution, easy to understand, faster than 99.83%
|
python-bisect-solution-easy-to-understan-hnhf
|
\nimport bisect\n\nclass Solution:\n\tdef median(self, nums: List[int]) -> float:\n\t\tmid = len(nums) // 2\n\t\tif len(nums) % 2:\n\t\t\treturn nums[mid]\n\t\t
|
tumepjlah
|
NORMAL
|
2021-02-12T08:44:45.133501+00:00
|
2021-02-14T09:26:34.924905+00:00
| 715 | false |
```\nimport bisect\n\nclass Solution:\n\tdef median(self, nums: List[int]) -> float:\n\t\tmid = len(nums) // 2\n\t\tif len(nums) % 2:\n\t\t\treturn nums[mid]\n\t\treturn (nums[mid-1] + nums[mid])/2\n \n\tdef medianSlidingWindow(self, nums: List[int], k: int) -> List[float]:\n\t\tif not nums:\n\t\t\treturn []\n\n\t\tans = []\n\t\tprev_idx = 0\n\t\twin = sorted(nums[:(k-1)])\n\t\tfor n in nums[(k-1):]:\n\t\t\tbisect.insort(win, n)\n\t\t\tans.append(self.median(win))\n\t\t\tdel win[bisect.bisect_left(win, nums[prev_idx])]\n\t\t\tprev_idx += 1\n\t\treturn ans\n```\n
| 3 | 0 |
['Python', 'Python3']
| 2 |
sliding-window-median
|
Sliding Window Easy to understand cpp solution
|
sliding-window-easy-to-understand-cpp-so-k124
|
\nclass Solution {\npublic:\n int getIndex(vector<int>& window,int element){ //binary search\n int first = 0;\n int last = window.size()-1;\n
|
hd_16
|
NORMAL
|
2020-10-02T12:59:51.555030+00:00
|
2020-10-02T12:59:51.555062+00:00
| 198 | false |
```\nclass Solution {\npublic:\n int getIndex(vector<int>& window,int element){ //binary search\n int first = 0;\n int last = window.size()-1;\n while(first<=last){\n int mid = (first+last)/2;\n if(window[mid] == element)\n return mid;\n if(window[mid] > element)\n {\n last = mid - 1;\n }\n else\n {\n first = mid + 1;\n }\n }\n return first; //if not found return position where element needs to be inserted\n }\n void eraseAndAdd(vector<int>& slidingWindow,int deleteElement,int addElement){\n int size = slidingWindow.size();\n int deleteIndex = getIndex(slidingWindow,deleteElement);\n slidingWindow.erase(slidingWindow.begin()+deleteIndex);\n int addIndex = getIndex(slidingWindow,addElement);\n slidingWindow.insert(slidingWindow.begin()+addIndex,addElement);\n // cout<<" delete index "<<deleteElement<<" is "<<deleteIndex<<" insert index "<<addElement<<" is"<<addIndex<<endl; \n }\n vector<double> medianSlidingWindow(vector<int>& nums, int k) {\n vector<int> slidingWindow;\n vector<double> result;\n for(int i = 0;i<k;i++)\n {\n slidingWindow.push_back(nums[i]); //initial window creation\n }\n sort(slidingWindow.begin(),slidingWindow.end()); //sorting initial window\n bool even=false;\n if(k%2 == 1){\n result.push_back(slidingWindow[(k/2)]);\n }\n else{\n result.push_back(slidingWindow[(k/2)]/2.0 + slidingWindow[(k/2)-1]/2.0);\n even=true;\n }\n int size = nums.size();\n for(int i = 1;i<size-k+1;i++){\n eraseAndAdd(slidingWindow,nums[i-1],nums[i+k-1]); //adding next element to window & deleting element before start of window\n if(even)\n {\n result.push_back(slidingWindow[(k/2)]/2.0 + slidingWindow[(k/2)-1]/2.0);\n }\n else\n {\n result.push_back(slidingWindow[(k/2)]);\n } \n }\n return result;\n }\n};\n```
| 3 | 0 |
[]
| 0 |
sliding-window-median
|
C++ using multiset
|
c-using-multiset-by-degalasivasairam-ni8l
|
//next(it,n) returns the iterator at the next address of the given n from it\n\n vector<double> medianSlidingWindow(vector<int>& nums, int k) {\n vector<doub
|
DegalaSivaSaiRam
|
NORMAL
|
2020-06-10T16:56:16.037077+00:00
|
2020-06-10T16:56:16.037122+00:00
| 366 | false |
//next(it,n) returns the iterator at the next address of the given n from it\n```\n vector<double> medianSlidingWindow(vector<int>& nums, int k) {\n vector<double> ans;\n if (k == 0) return ans;\n multiset<int>s(nums.begin(), nums.begin() + k);\n auto mid = next(s.begin(), (k - 1) / 2);\n if(k%2!=0)\n {\n ans.push_back(*(mid)/1.0);\n }\n else\n {\n ans.push_back(((*mid)/1.0 + *next(mid, (k + 1) % 2)) / 2.0);\n }\n for (int i = k; i < nums.size(); ++i) \n { \n s.erase(s.lower_bound(nums[i - k])); \n s.insert(nums[i]);\n mid = next(s.begin(), (k - 1) / 2);\n if(k%2!=0)\n {\n ans.push_back(*(mid)/1.0);\n }\n else\n {\n ans.push_back(((*mid)/1.0 + *next(mid, (k + 1) % 2)) / 2.0);\n }\n }\n return ans;\n }\n\t```
| 3 | 0 |
[]
| 1 |
sliding-window-median
|
Simple Javascript solution with sliding window
|
simple-javascript-solution-with-sliding-radyj
|
\nvar medianSlidingWindow = function(nums, k) {\n if (!nums.length) {\n return [];\n }\n\n // find the median of the first window\n const fir
|
bozilhan
|
NORMAL
|
2020-03-01T15:38:11.208671+00:00
|
2020-03-01T15:38:11.208719+00:00
| 861 | false |
```\nvar medianSlidingWindow = function(nums, k) {\n if (!nums.length) {\n return [];\n }\n\n // find the median of the first window\n const firstSlided = nums.slice(0, k);\n\n let medians = [findMedian(firstSlided)];\n\n for (let i = k; i < nums.length; i++) {\n const slidedArr = nums.slice(i - k + 1, i + 1);\n medians.push(findMedian(slidedArr));\n }\n\n return medians;\n};\n\nconst findMedian = (arr) => {\n // get copy of the original array\n const a = arr.slice();\n\n // should be SORTED\n a.sort((a, b) => a - b);\n\n const n = a.length;\n\n const middle = a[Math.floor(n / 2)];\n\n // ODD LENGTH\n if ((n & 1) !== 0) {\n return middle;\n } else {\n // EVEN LENGTH\n return (Math.floor(a[Math.floor((n - 1) / 2)] + middle) / 2);\n }\n};\n```
| 3 | 0 |
[]
| 1 |
sliding-window-median
|
Short and Simple Java Solution
|
short-and-simple-java-solution-by-zlareb-6age
|
\nclass Solution {\n public double[] medianSlidingWindow(int[] nums, int k) {\n double[] res=new double[nums.length-k+1];\n if(nums==null || nu
|
zlareb1
|
NORMAL
|
2019-08-08T16:39:00.809261+00:00
|
2019-08-08T16:39:00.809294+00:00
| 284 | false |
```\nclass Solution {\n public double[] medianSlidingWindow(int[] nums, int k) {\n double[] res=new double[nums.length-k+1];\n if(nums==null || nums.length==0 || k<=0) return res;\n PriorityQueue<Integer> left=new PriorityQueue<>(Collections.reverseOrder());\n PriorityQueue<Integer> right=new PriorityQueue<>();\n for(int i=0;i<nums.length;i++){\n if(left.size()<=right.size()){\n right.add(nums[i]);\n left.add(right.remove());\n }\n else{\n left.add(nums[i]);\n right.add(left.remove());\n }\n if(left.size()+right.size()==k){\n double median;\n if(left.size()==right.size()) median=(double)((long)left.peek()+(long)right.peek())/2;\n else median=(double)left.peek();\n int start=i-k+1;\n res[start]=median;\n if(!left.remove(nums[start]))\n right.remove(nums[start]);\n }\n }\n return res;\n }\n}\n```
| 3 | 0 |
[]
| 1 |
sliding-window-median
|
Design and implement the interface of Hash Heap in Java
|
design-and-implement-the-interface-of-ha-m4od
|
\nclass Solution {\n\n public double[] medianSlidingWindow(int[] nums, int k) {\n \n // maxHeap maitians the half small part\n // maitai
|
wirybeaver
|
NORMAL
|
2019-03-20T22:04:06.183363+00:00
|
2019-03-20T22:04:06.183406+00:00
| 2,643 | false |
```\nclass Solution {\n\n public double[] medianSlidingWindow(int[] nums, int k) {\n \n // maxHeap maitians the half small part\n // maitain the propetry (*): maxHeap.size() - minHeap.size() = 0 or 1 \n if(nums.length==0 || k<=0){\n return new double[nums.length];\n }\n int mincap = k/2, maxcap = k-k/2, n = nums.length;\n HashHeap<Integer> maxHeap = new HashHeap<>(Collections.reverseOrder());\n HashHeap<Integer> minHeap = new HashHeap<>();\n for(int i=0; i<k; i++){\n maxHeap.offer(nums[i]);\n }\n for(int i=0; i<mincap; i++){\n minHeap.offer(maxHeap.poll());\n }\n double[] ans = new double[n-k+1];\n ans[0] = getMedian(maxHeap, minHeap, k);\n for(int i=k; i<n; i++){\n \n // remove: maxHeap.size()-minHeap.size() falls in the range [-1, 0];\n if(maxHeap.contains(nums[i-k])){\n maxHeap.remove(nums[i-k]);\n }\n else{\n minHeap.remove(nums[i-k]);\n }\n \n // always add new element into the maxHeap.\n maxHeap.offer(nums[i]);\n \n // Claim: maxHeap.size()-minHeap.size() falls in the range [0, 3]\n // rebalance only if maxHeap.size90 - minHeap.size() = 2 or 3 in order to maintain the property *.\n if(maxHeap.size()-minHeap.size()>1){\n minHeap.offer(maxHeap.poll());\n }\n \n if(minHeap.size()>0 && maxHeap.peek()>minHeap.peek()){\n int tmp1 = maxHeap.poll();\n int tmp2 = minHeap.poll();\n maxHeap.offer(tmp2);\n minHeap.offer(tmp1);\n }\n \n ans[i-k+1] = getMedian(maxHeap, minHeap, k);\n }\n \n return ans;\n }\n \n private double getMedian(HashHeap<Integer> maxHeap, HashHeap<Integer> minHeap, int k){\n double left = maxHeap.peek();\n if((k&1)==1){\n return left;\n }\n return (left + minHeap.peek())/2;\n }\n \n private class HashHeap<T>{\n \n // all method take logarithmic time\n TreeMap<T, Integer> mp;\n int size;\n HashHeap(){\n mp = new TreeMap<>();\n }\n HashHeap(Comparator<T> comparator){\n mp = new TreeMap<>(comparator);\n }\n \n int size(){\n return size;\n }\n\n T peek(){\n if(size==0){\n return null;\n }\n\n return mp.firstEntry().getKey();\n }\n\n T poll(){\n if(size==0){\n return null;\n }\n size--;\n Map.Entry<T, Integer> top= mp.firstEntry();\n if(top.getValue()==1){\n mp.remove(top.getKey());\n }\n else{\n mp.put(top.getKey(), top.getValue()-1);\n }\n return top.getKey();\n }\n\n void offer(T item){\n size++;\n mp.put(item, mp.getOrDefault(item, 0)+1);\n }\n\n boolean contains(T item){\n return mp.containsKey(item);\n }\n\n boolean remove(T item){\n Integer freq = mp.get(item);\n if(freq==null){\n return false;\n }\n size--;\n int f = freq;\n if(f==1){\n mp.remove(item);\n }\n else{\n mp.put(item, f-1);\n }\n return true;\n }\n }\n \n \n}\n```
| 3 | 0 |
[]
| 3 |
alternating-groups-ii
|
✔️ Sliding Window | Python | C++ | Java | JS | C# | Go | Swift | Rust
|
sliding-window-python-by-otabek_kholmirz-7pg5
|
IntuitionThe problem requires finding alternating groups of length k. A key observation is that we can extend the array to simulate a cyclic sequence, ensuring
|
otabek_kholmirzaev
|
NORMAL
|
2025-03-09T00:30:37.552522+00:00
|
2025-03-09T02:25:13.151386+00:00
| 27,130 | false |
# Intuition
The problem requires finding alternating groups of length `k`. A key observation is that we can extend the array to simulate a cyclic sequence, ensuring we check all possible groups without worrying about wrapping around.
# Approach
1. Extend the array
- We append the first `(k-1)` elements to the end of the array. This simulates a cyclic sequence, allowing us to check alternating groups that might wrap around.
2. Sliding Window Technique:
- Maintain two pointers: `left` and `right`, where `right` iterates over the array.
- If two consecutive elements are the same, reset `left` = `right`, breaking the alternating sequence.
- Whenever the window size reaches at least `k`, count it as a valid alternating group.
# Complexity
- Time complexity: O(n + k)
- Space complexity: O(k)
# Code
```python3 []
class Solution:
def numberOfAlternatingGroups(self, colors: List[int], k: int) -> int:
colors.extend(colors[:(k-1)])
count = 0
left = 0
for right in range(len(colors)):
if right > 0 and colors[right] == colors[right - 1]:
left = right
if right - left + 1 >= k:
count += 1
return count
```
```cpp []
class Solution {
public:
int numberOfAlternatingGroups(vector<int>& colors, int k) {
colors.insert(colors.end(), colors.begin(), colors.begin() + (k - 1));
int count = 0;
int left = 0;
for (int right = 0; right < colors.size(); ++right) {
if (right > 0 && colors[right] == colors[right - 1]) {
left = right;
}
if (right - left + 1 >= k) {
count++;
}
}
return count;
}
};
```
```java []
class Solution {
public int numberOfAlternatingGroups(int[] colors, int k) {
int n = colors.length;
int[] temp = new int[n + k - 1];
System.arraycopy(colors, 0, temp, 0, n);
System.arraycopy(colors, 0, temp, n, k - 1);
int count = 0;
int left = 0;
for (int right = 0; right < temp.length; right++) {
if (right > 0 && temp[right] == temp[right - 1]) {
left = right;
}
if (right - left + 1 >= k) {
count++;
}
}
return count;
}
}
```
```javascript []
var numberOfAlternatingGroups = function(colors, k) {
colors.push(...colors.slice(0, k - 1));
let count = 0;
let left = 0;
for (let right = 0; right < colors.length; right++) {
if (right > 0 && colors[right] === colors[right - 1]) {
left = right;
}
if (right - left + 1 >= k) {
count++;
}
}
return count;
};
```
```csharp []
public class Solution {
public int NumberOfAlternatingGroups(int[] colors, int k) {
var temp = new List<int>(colors);
temp.AddRange(colors[..(k - 1)]);
int count = 0;
int left = 0;
for (int right = 0; right < temp.Count; right++) {
if (right > 0 && temp[right] == temp[right - 1]) {
left = right;
}
if (right - left + 1 >= k) {
count++;
}
}
return count;
}
}
```
```go []
func numberOfAlternatingGroups(colors []int, k int) int {
colors = append(colors, colors[:k-1]...)
count := 0
left := 0
for right := 0; right < len(colors); right++ {
if right > 0 && colors[right] == colors[right-1] {
left = right
}
if right-left+1 >= k {
count++
}
}
return count
}
```
```swift []
class Solution {
func numberOfAlternatingGroups(_ colors: [Int], _ k: Int) -> Int {
var colors = colors + colors.prefix(k - 1)
var count = 0
var left = 0
for right in 0..<colors.count {
if right > 0 && colors[right] == colors[right - 1] {
left = right
}
if right - left + 1 >= k {
count += 1
}
}
return count
}
}
```
```rust []
impl Solution {
pub fn number_of_alternating_groups(colors: Vec<i32>, k: i32) -> i32 {
let mut temp = colors.clone();
temp.extend_from_slice(&colors[..(k as usize - 1)]);
let mut count = 0;
let mut left = 0;
for right in 0..temp.len() {
if right > 0 && temp[right] == temp[right - 1] {
left = right;
}
if right - left + 1 >= k as usize {
count += 1;
}
}
count
}
}
```
---
# Bonus (without using extra space)
```python3 []
class Solution:
def numberOfAlternatingGroups(self, colors: List[int], k: int) -> int:
n = len(colors)
count = 0
left = 0
for right in range(n + k - 1):
if right > 0 and colors[right % n] == colors[(right - 1) % n]:
left = right
if right - left + 1 >= k:
count += 1
return count
```
```cpp []
class Solution {
public:
int numberOfAlternatingGroups(vector<int>& colors, int k) {
int n = colors.size();
int count = 0;
int left = 0;
for (int right = 0; right < n + k - 1; ++right) {
if (right > 0 && colors[right % n] == colors[(right - 1) % n]) {
left = right;
}
if (right - left + 1 >= k) {
count++;
}
}
return count;
}
};
```
```java []
class Solution {
public int numberOfAlternatingGroups(int[] colors, int k) {
int n = colors.length;
int count = 0;
int left = 0;
for (int right = 0; right < n + k - 1; right++) {
if (right > 0 && colors[right % n] == colors[(right - 1) % n]) {
left = right;
}
if (right - left + 1 >= k) {
count++;
}
}
return count;
}
}
```
---

| 164 | 3 |
['Swift', 'Sliding Window', 'Python', 'C++', 'Java', 'Go', 'Python3', 'Rust', 'JavaScript', 'C#']
| 10 |
alternating-groups-ii
|
Solution By Dare2Solve | Detailed Explanation | Clean Code
|
solution-by-dare2solve-detailed-explanat-bpvk
|
Explanation []\nauthorslog.vercel.app/blog/CB5AJHUJFs\n\n\n# Code\n\ncpp []\nclass Solution {\npublic:\n int numberOfAlternatingGroups(vector<int>& colors, i
|
Dare2Solve
|
NORMAL
|
2024-07-06T16:04:36.436116+00:00
|
2024-07-06T16:07:47.725876+00:00
| 4,837 | false |
```Explanation []\nauthorslog.vercel.app/blog/CB5AJHUJFs\n```\n\n# Code\n\n```cpp []\nclass Solution {\npublic:\n int numberOfAlternatingGroups(vector<int>& colors, int k) {\n for (int i = 0; i < k - 1; ++i) colors.push_back(colors[i]);\n int res = 0;\n int cnt = 1;\n for (int i = 1; i < colors.size(); ++i) {\n if (colors[i] != colors[i - 1]) ++cnt;\n else cnt = 1;\n if (cnt >= k) ++res;\n }\n return res;\n }\n};\n```\n\n```python []\nclass Solution:\n def numberOfAlternatingGroups(self, colors: List[int], k: int) -> int:\n n = len(colors)\n colors += colors[:k - 1]\n res = 0\n cnt = 1\n for i in range(1, len(colors)):\n if colors[i] != colors[i - 1]:\n cnt += 1\n else:\n cnt = 1\n if cnt >= k:\n res += 1\n return res\n```\n\n```java []\nclass Solution {\n public int numberOfAlternatingGroups(int[] colors, int k) {\n int n = colors.length;\n int[] extendedColors = new int[n + k - 1];\n System.arraycopy(colors, 0, extendedColors, 0, n);\n System.arraycopy(colors, 0, extendedColors, n, k - 1);\n int res = 0;\n int cnt = 1;\n for (int i = 1; i < extendedColors.length; ++i) {\n if (extendedColors[i] != extendedColors[i - 1]) ++cnt;\n else cnt = 1;\n if (cnt >= k) ++res;\n } \n return res;\n }\n}\n```\n\n```javascript []\n/**\n * @param {number[]} colors\n * @param {number} k\n * @return {number}\n */\nvar numberOfAlternatingGroups = function (colors, k) {\n for (var i = 0; i < k - 1; ++i) colors.push(colors[i]);\n var res = 0;\n var cnt = 1;\n for (var i = 1; i < colors.length; ++i) {\n if (colors[i] !== colors[i - 1]) ++cnt;\n else cnt = 1;\n if (cnt >= k) ++res;\n }\n return res;\n};\n```
| 58 | 5 |
['Python', 'C++', 'Java', 'Python3', 'JavaScript']
| 20 |
alternating-groups-ii
|
n + k - 2
|
n-k-2-by-votrubac-msly
|
We count alternating elements for i up to n + k - 2. \n\nIf two neighbours have the same color, we reset the count to 1.\n\nWhen the count reaches or exceeds k,
|
votrubac
|
NORMAL
|
2024-07-06T16:01:26.668469+00:00
|
2024-07-06T16:56:54.586888+00:00
| 2,220 | false |
We count alternating elements for `i` up to `n + k - 2`. \n\nIf two neighbours have the same color, we reset the count to 1.\n\nWhen the count reaches or exceeds `k`, we found an alternating group.\n\n**C++**\n```cpp\nint numberOfAlternatingGroups(vector<int>& colors, int k) {\n int n = colors.size(), res = 0, cnt = 1;\n for (int i = 0; i < n + k - 2; ++i) {\n cnt = colors[i % n] != colors[(i + 1) % n] ? cnt + 1 : 1; \n res += cnt >= k; \n }\n return res;\n}\n```
| 43 | 6 |
[]
| 6 |
alternating-groups-ii
|
1 pass||36ms Beats 100%
|
1-pass39ms-beats-100-by-anwendeng-72uk
|
IntuitionAgain sliding window
1 pass can solve it.
C++, Python & C are made.Approach
let n=|color|, sz=n+k-1
Initialize ans=0, alt=1, prev=color[0] where ans is
|
anwendeng
|
NORMAL
|
2025-03-09T00:20:24.107416+00:00
|
2025-03-09T04:06:10.104715+00:00
| 3,784 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
Again sliding window
1 pass can solve it.
C++, Python & C are made.
# Approach
<!-- Describe your approach to solving the problem. -->
1. let `n=|color|, sz=n+k-1`
2. Initialize `ans=0, alt=1, prev=color[0]` where `ans` is the answer to return
3. Use a loop from i=1 to sz-1 do the following
```
// if adjacent ones are equal reset alt to 1, otherwise increase by 1
alt=(prev==colors[i%n])?1:alt+1;
ans+=(alt>=k); //when alt>=k increase ans by 1
prev=colors[i%n]; // update prev
```
4. return `ans`
5. Python code is done in the similar way
6. C code is made 67ms beats 100%
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
$O(n+k)$
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
$O(1)$
# Code||C++ 36ms Beats 100%|C 67ms beats 100%
```cpp []
class Solution {
public:
static int numberOfAlternatingGroups(vector<int>& colors, int k) {
const int n=colors.size(), sz=n+k-1;
int ans=0, alt=1, prev=colors[0];
for(int i=1; i<sz; i++){
alt=(prev==colors[i%n])?1:alt+1;
ans+=(alt>=k);
prev=colors[i%n];
}
return ans;
}
};
auto init = []() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
return 'c';
}();
```
```Python []
class Solution:
def numberOfAlternatingGroups(self, colors: List[int], k: int) -> int:
n=len(colors)
sz=n+k-1
ans, alt, prev=0, 1, colors[0]
for i in range(1, sz):
i0=i%n
alt=1 if prev==colors[i0] else alt+1
ans+=(alt>=k)
prev=colors[i0]
return ans
```
```C []
#pragma GCC optimize("O3, unroll-loops")
int numberOfAlternatingGroups(int* colors, int n, int k) {
const int sz=n+k-1;
int ans=0, alt=1, prev=colors[0];
for(int i=1; i<sz; i++){
const int i0=i>=n?i-n:i;
alt=(prev==colors[i0])?1:alt+1;
ans+=(alt>=k);
prev=colors[i0];
}
return ans;
}
```
| 31 | 0 |
['C', 'Sliding Window', 'C++', 'Python3']
| 5 |
alternating-groups-ii
|
✅ Sliding Window - Cyclic Comparison 🔥| Visualization ✨| Math | Python | Java | C++ | C ✨
|
sliding-window-cyclic-comparison-visuali-ux6m
|
Approach
Complexity
Time complexity: O(n+k)
Space complexity: O(1)
Code
|
Raw_Ice
|
NORMAL
|
2025-03-09T02:15:07.784344+00:00
|
2025-03-09T02:26:02.177822+00:00
| 6,034 | false |
# Approach


# Complexity
- Time complexity: $$O(n+k)$$
- Space complexity: $$O(1)$$
# Code
```Python []
class Solution:
def numberOfAlternatingGroups(self, colors, k):
w = 1
ans = 0
n = len(colors)
for i in range(1, n+k-2 + 1):
if colors[i % n] != colors[(i - 1 + n) % n]:
w += 1
else:
w = 1
if w >= k:
ans += 1
return ans
```
```cpp []
class Solution {
public:
int numberOfAlternatingGroups(vector<int>& colors, int k) {
int maxLen = 1, ans = 0, n = colors.size();
for(int i=1; i<=n+k-2; i++){
if (colors[i%n]!= colors[(i-1+n)%n]){
maxLen++;
}else{
maxLen = 1;
}
if (maxLen >= k) ans++;
}
return ans;
}
};
```
```Java []
class Solution {
public int numberOfAlternatingGroups(int[] colors, int k) {
int w = 1, ans = 0, n = colors.length;
for (int i = 1; i <= n+k-2; i++) {
if (colors[i % n] != colors[(i - 1 + n) % n]) {
w++;
} else {
w = 1;
}
if (w >= k) {
ans++;
}
}
return ans;
}
}
```
```c []
#include <stdio.h>
int numberOfAlternatingGroups(int* colors, int colorsSize, int k) {
int w = 1, ans = 0, n = colorsSize;
for (int i = 1; i <= n+k-2; i++) {
if (colors[i % n] != colors[(i - 1 + n) % n]) {
w++;
} else {
w = 1;
}
if (w >= k) {
ans++;
}
}
return ans;
}
```

| 24 | 0 |
['Array', 'Math', 'Dynamic Programming', 'C', 'Counting', 'Python', 'C++', 'Java', 'Python3']
| 5 |
alternating-groups-ii
|
EASY O(N) || Sliding Window
|
easy-on-sliding-window-by-mohit_kukreja-fib3
|
Intuition\nUse simple sliding window technique.\n\nCount bad pairs in a window. \nWhen the window size reaches k check if there is any bad pair or not. \nNow sh
|
Mohit_kukreja
|
NORMAL
|
2024-07-06T16:12:19.187573+00:00
|
2024-07-07T05:43:44.748342+00:00
| 2,105 | false |
# Intuition\nUse simple **sliding window** technique.\n\n*Count bad pairs* in a window. \nWhen the window size reaches k check if there is any bad pair or not. \nNow shift the window and remember to adjust the bad pairs.\n\n# Complexity\n- Time complexity: O(n) Just a simple traversal\n\n- Space complexity: O(1)\n\n# Code\n```\nclass Solution {\npublic:\n int numberOfAlternatingGroups(vector<int>& s, int k) {\n int size = s.size();\n int start = 0, end = 1;\n int bad = 0; // count the trouble causing pairs in the window\n int res = 0;\n\n // why start < size ? every element can act \n // as the start of the window.\n while(start < size){\n if(s[end % size] == s[(end - 1) % size]) bad++;\n if(end - start + 1 == k){\n if(bad == 0) res++;\n start++;\n\n // Subtract the effect of removed pair on bad count\n if(s[start % size] == s[(start - 1) % size]) bad--; \n }\n end++;\n }\n return res;\n\n // Please do UPVOTE :)\n }\n};\n```
| 24 | 4 |
['Sliding Window', 'C++']
| 5 |
alternating-groups-ii
|
🔥BEATS 💯 % 🎯 |✨SUPER EASY BEGINNERS 👏| JAVA | C | C++ | PYTHON| JAVASCRIPT | DART
|
beats-super-easy-beginners-java-c-c-pyth-t7i0
|
IntuitionThe problem requires us to determine the number of valid alternating groups of size k in a circular array. A valid alternating group means that no two
|
CodeWithSparsh
|
NORMAL
|
2025-03-09T06:45:42.742940+00:00
|
2025-03-09T07:11:57.842520+00:00
| 2,156 | false |
-----
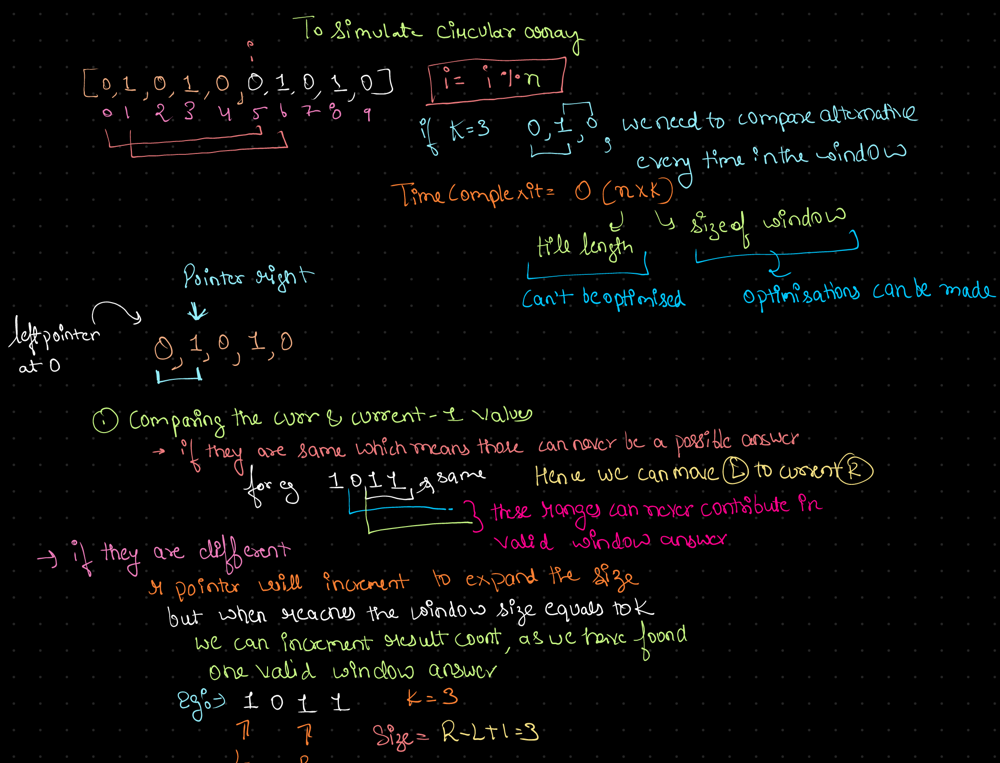
------
## **Intuition**
The problem requires us to determine the number of valid alternating groups of size `k` in a circular array. A valid alternating group means that no two adjacent elements in the group should be the same.
Since the array is circular, we can extend our sliding window approach beyond the last index by considering modular arithmetic to wrap around.
## **Approach**
1. **Sliding Window Technique**:
- Maintain a left (`left`) and right (`right`) pointer to form a window.
- If adjacent elements have the same color, update the `left` pointer.
- Whenever the window size reaches `k`, increment the `count`.
2. **Circular Handling**:
- Use `% n` to handle circular behavior.
- Expand the window up to `n + k - 1` to ensure all possible valid windows are considered.
---
## **Complexity Analysis**
- **Time Complexity:** \(O(n)\) — We iterate through the array once.
- **Space Complexity:** \(O(1)\) — Only a few variables are used.
---
```dart []
class Solution {
int numberOfAlternatingGroups(List<int> colors, int k) {
int n = colors.length;
int count = 0;
int left = 0;
for (int right = 1; right < n + k - 1; right++) {
if (colors[right % n] == colors[(right - 1) % n]) {
left = right;
}
if (right - left + 1 >= k) count++;
}
return count;
}
}
```
```python []
class Solution:
def numberOfAlternatingGroups(self, colors: list[int], k: int) -> int:
n = len(colors)
count = 0
left = 0
for right in range(1, n + k - 1):
if colors[right % n] == colors[(right - 1) % n]:
left = right
if right - left + 1 >= k:
count += 1
return count
```
```java []
class Solution {
public int numberOfAlternatingGroups(int[] colors, int k) {
int n = colors.length;
int count = 0;
int left = 0;
for (int right = 1; right < n + k - 1; right++) {
if (colors[right % n] == colors[(right - 1) % n]) {
left = right;
}
if (right - left + 1 >= k) {
count++;
}
}
return count;
}
}
```
```cpp []
class Solution {
public:
int numberOfAlternatingGroups(vector<int>& colors, int k) {
int n = colors.size();
int count = 0;
int left = 0;
for (int right = 1; right < n + k - 1; right++) {
if (colors[right % n] == colors[(right - 1) % n]) {
left = right;
}
if (right - left + 1 >= k) {
count++;
}
}
return count;
}
};
```
```javascript []
var numberOfAlternatingGroups = function(colors, k) {
let n = colors.length;
let count = 0;
let left = 0;
for (let right = 1; right < n + k - 1; right++) {
if (colors[right % n] === colors[(right - 1) % n]) {
left = right;
}
if (right - left + 1 >= k) {
count++;
}
}
return count;
};
```
---
## **Summary**
| Language | Time Complexity | Space Complexity |
|-----------|---------------|----------------|
| **Dart** | \(O(n)\) | \(O(1)\) |
| **Python** | \(O(n)\) | \(O(1)\) |
| **Java** | \(O(n)\) | \(O(1)\) |
| **C++** | \(O(n)\) | \(O(1)\) |
| **JavaScript** | \(O(n)\) | \(O(1)\) |
This approach efficiently counts valid alternating groups using **sliding window** and **circular array handling**. 🚀
-----
 {:style='width:250px'}
| 21 | 0 |
['Array', 'C', 'Sliding Window', 'Python', 'C++', 'Java', 'Python3', 'JavaScript', 'Dart', 'Python ML']
| 2 |
alternating-groups-ii
|
Iterate with alternate check
|
iterate-with-alternate-check-by-kreakemp-mfgv
|
\n\n# Approach 1: (two pass)\n- Simply count the alternate contiguous items length\n- As soon as the count more equal to k, increase ans by one as we found one
|
kreakEmp
|
NORMAL
|
2024-07-06T16:01:36.342732+00:00
|
2024-07-06T16:21:41.330453+00:00
| 2,825 | false |
\n\n# Approach 1: (two pass)\n- Simply count the alternate contiguous items length\n- As soon as the count more equal to k, increase ans by one as we found one group\n- Once we reach end, continue counting from begin again up to k-1 items due to circular nature.\n\n\n```\nint numberOfAlternatingGroups(vector<int>& colors, int k) {\n int last = colors[0], ans = 0, count = 1; \n for(int i = 1; i < colors.size(); ++i){\n count = (colors[i] != last)? count + 1: 1;\n if(count >= k) ans++;\n last = colors[i];\n }\n for(int i = 0; i < k-1; ++i){ // circulate one more time upto k-1 \n count = (colors[i] != last)? count + 1: 1;\n if(count >= k) ans++;\n last = colors[i];\n }\n return ans;\n}\n```\n\n----\n\n# Approach 2: ( single pass)\n\n```\nint numberOfAlternatingGroups(vector<int>& colors, int k) {\n int ans = 0, count = 1, n = colors.size(); \n for(int i = 1; i < n + k-1; ++i){\n count = ( colors[i % n] != colors[(n + i - 1)%n] )? count + 1: 1;\n if(count >= k) ans++;\n }\n return ans;\n}\n```\n\n----\n\n<b> Here is an article of my recent interview experience - A Journey to FAANG Company, I recomand you to go through this to know which all resources I have used & how I cracked interview at Amazon:\nhttps://leetcode.com/discuss/interview-experience/3171859/Journey-to-a-FAANG-Company-Amazon-or-SDE2-(L5)-or-Bangalore-or-Oct-2022-Accepted\n\n---
| 17 | 5 |
['C++']
| 6 |
alternating-groups-ii
|
[Java/Python 3] Sliding window 1 pass O(n) codes w/ brief explanation and analysis.
|
javapython-3-sliding-window-1-pass-on-co-2c0r
|
Note: Sliding window lower boundary lo is exclusive, and upper boundary hi is inclusive. That is, (lo, hi] is the sliding window range.
Append first k - 1 items
|
rock
|
NORMAL
|
2024-07-06T16:04:18.175482+00:00
|
2025-03-09T11:35:24.610121+00:00
| 1,579 | false |
**Note:** Sliding window lower boundary `lo` is exclusive, and upper boundary `hi` is inclusive. That is, `(lo, hi]` is the sliding window range.
1. Append first `k - 1` items to the end of the input `colors` so that we will NOT omit those groups including first and last items;
2. Traverse the modified array in 1, and compare current item and the previous one, if they are different, keep counting to get the size of the sliding window; otherwise reset the left boundary of the sliding window, `lo`, to previous index, `hi - 1`;
3. If current sliding window size is of size at least `k`, count it into result.
```java
public int numberOfAlternatingGroups(int[] colors, int k) {
int cnt = 0;
for (int n = colors.length, lo = -1, hi = 1; hi < n + k - 1; ++hi) {
if (colors[hi % n] == colors[(hi - 1) % n]) {
lo = hi - 1;
}else if (hi - lo >= k) {
++cnt;
}
}
return cnt;
}
```
```python 3
def numberOfAlternatingGroups(self, colors: List[int], k: int) -> int:
colors = colors + colors[: k - 1]
cnt, lo = 0, -1
for hi, (x, y) in enumerate(pairwise(colors), 1):
if x == y:
lo = hi - 1
elif hi - lo >= k:
cnt += 1
return cnt
```
The above python 3 code is space `O(n)`.
```python 3
def numberOfAlternatingGroups(self, colors: List[int], k: int) -> int:
cnt, lo, n = 0, -1, len(colors)
for hi in range(1, n + k - 1):
if colors[hi % n] == colors[(hi - 1) % n]:
lo = hi - 1
elif hi - lo >= k:
cnt += 1
return cnt
```
**Analysis:**
Visit each item at most `3` times, therefore
Time: `O(n)`, space: `O(1)`, where `n = colors.length`.
**Q & A**
*Q1:* Why do you reset lower bound `lo` to previous index `hi - 1`, not current index `hi`?
*A1:* Whenever current item equal to previous one, that is, `nums[hi] == nums[hi - 1]`, we need to exclude the previous item, of which the index is `hi - 1`. We should NOT exclude current item `nums[hi]`, which could be in the next valid group.
| 15 | 0 |
['Sliding Window', 'Java', 'Python3']
| 6 |
alternating-groups-ii
|
Python 3 || 7 lines, iterate and count || T/S: 97% / 98%
|
python-3-8-lines-iterate-and-count-ts-97-1gdp
|
Here's the plan:
We extend colors by the initial k - 1 elements of 'colors` in order to eschew all the modular arithmetic.
We iterate through colors by pairs, c
|
Spaulding_
|
NORMAL
|
2024-07-06T19:05:01.425827+00:00
|
2025-03-09T03:07:04.399122+00:00
| 165 | false |
Here's the plan:
1. We extend `colors` by the initial *k* - 1 elements of 'colors` in order to eschew all the modular arithmetic.
2. We iterate through `colors` by pairs, checking whether the colors are equal.
3. If equal, we know the current subarray is not alternating. We end the current subarray by incrementing `ans` by the count of alternating sequences (if any) and resetting the count to 0.
4. We increment the count by 1.
5. Finally we return `ans`, incremented by the count of the current alternating subarray if necessary.
```
class Solution:
def numberOfAlternatingGroups(self, colors: List[int],
k: int, ans = 0, cnt = 1) -> int:
colors.extend(colors[0: k - 1]) # <-- 1)
for color1, color2 in pairwise(colors): # <-- 2)
if color1 == color2: # <-- 3)
ans+= max(0, cnt - k + 1) #
cnt = 0 #
cnt+= 1 # <-- 4)
return ans + max(0, cnt - k + 1) # <-- 5)
```
[https://leetcode.com/problems/alternating-groups-ii/submissions/1326680290/](https://leetcode.com/problems/alternating-groups-ii/submissions/1326680290/)
I could be wrong, but I think that time complexity is *O*(*N*) and space complexity is *O*(*N*), in which *N* ~ `len(colors)`.
| 12 | 0 |
['Python', 'Python3']
| 1 |
alternating-groups-ii
|
Beats 100% ✅ || Short code with Detailed explanation 🔥 || Very Easy to understand for beginners 💯
|
beats-100-short-code-with-detailed-expla-40l1
|
Intuition\nTo solve this problem, we need to count the number of alternating groups of length \uD835\uDC58 in a circular array of tiles. An alternating group is
|
soukarja
|
NORMAL
|
2024-07-06T16:01:23.087498+00:00
|
2024-07-06T16:01:23.087533+00:00
| 1,234 | false |
# Intuition\nTo solve this problem, we need to count the number of alternating groups of length `\uD835\uDC58` in a circular array of tiles. An alternating group is a sequence of tiles where each tile has a different color than its adjacent tiles. Since the array is circular, the last tile is considered adjacent to the first tile.\n\n---\n\n# Approach\n1. ### Initialization:\n\n - Initialize `l` to 1 to keep track of the length of the current alternating sequence.\n - Initialize `r` to 0 to count the number of alternating groups.\n - Initialize `a` to the color of the last tile in the array to handle the circular nature.\n \n2. ### Linear Traversal:\n\n - Traverse the array from the second tile to the last tile.\n - For each tile, check if it has a different color than the previous tile.\n - If it does, increment the length l of the current alternating sequence.\n - If l reaches k, increment the count r of alternating groups.\n - If the current tile has the same color as the previous tile, reset l to 1.\n \n3. ### Circular Check:\n\n - Traverse the first `\uD835\uDC58 \u2212 1` tiles to handle the circular nature.\n - For each tile, check if it has a different color than the last tile.\n - If it does, increment the length l of the current alternating sequence.\n - If l reaches k, increment the count r of alternating groups.\n - If the current tile has the same color as the last tile, reset l to 1.\n - Return the count r of alternating groups.\n\n---\n\n# Complexity\n- Time complexity:\nThe algorithm performs a single traversal of the array and a partial traversal up to `k\u22121`tiles.\nHence, the time complexity is `O(n)`, where `n` is the length of the array.\n\n- Space complexity:\nThe space complexity is `O(1)` because we only use a fixed amount of extra space for the variables `l`, `r`, and `a`.\n\n---\n\n# Code\n``` C++ []\nclass Solution {\npublic:\n int numberOfAlternatingGroups(vector<int>& c, int k) {\n int l = 1, r = 0, a = c[c.size() - 1]; // Initialize l, r and a.\n for(int i = 1; i < c.size(); ++i) // Traverse the array from the second tile.\n if(c[i] != c[i - 1] and ++l >= k) ++r; // If current tile is different from previous and length reaches k, increment r.\n else if (c[i] == c[i - 1]) l = 1; // If current tile is same as previous, reset length to 1.\n for(int i = 0 ; i < k - 1; ++i) // Traverse the first k-1 tiles to handle circular nature.\n if(c[i] != a){ if(++l >= k) ++r; a = c[i]; } // If current tile is different from last, check length and increment r if needed.\n else l = 1; // If current tile is same as last, reset length to 1.\n return r; // Return the count of alternating groups.\n}\n};\n```\n\n``` Python []\nclass Solution:\n def numberOfAlternatingGroups(self, colors: List[int], k: int) -> int:\n l = 1\n r = 0\n a = colors[-1] # Last element to handle the circular nature\n n = len(colors)\n \n # Traverse the array from the second element\n for i in range(1, n):\n if colors[i] != colors[i - 1]:\n l += 1\n if l >= k:\n r += 1\n else:\n l = 1\n \n # Traverse the first k-1 elements to handle circular nature\n for i in range(k - 1):\n if colors[i] != a:\n l += 1\n if l >= k:\n r += 1\n a = colors[i]\n else:\n l = 1\n \n return r\n```\n\n``` Java []\nint l = 1;\n int r = 0;\n int n = colors.length;\n int a = colors[n - 1]; // Last element to handle the circular nature\n\n // Traverse the array from the second element\n for (int i = 1; i < n; ++i) {\n if (colors[i] != colors[i - 1]) {\n l++;\n if (l >= k) {\n r++;\n }\n } else {\n l = 1;\n }\n }\n\n // Traverse the first k-1 elements to handle circular nature\n for (int i = 0; i < k - 1; ++i) {\n if (colors[i] != a) {\n l++;\n if (l >= k) {\n r++;\n }\n a = colors[i];\n } else {\n l = 1;\n }\n }\n\n return r;\n```\n\n---\n
| 11 | 0 |
['C++', 'Java', 'Python3']
| 5 |
alternating-groups-ii
|
JAVA (5ms) Simplest Solution
|
java-5ms-simplest-solution-by-devansh_ya-x5tr
|
IntuitionWe need to find alternating groups of length k in a circular array. Instead of checking every possible group from scratch, we can efficiently track the
|
Devansh_Yadav_11
|
NORMAL
|
2025-03-09T07:05:05.694945+00:00
|
2025-03-09T07:05:05.694945+00:00
| 569 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
We need to find alternating groups of length k in a circular array. Instead of checking every possible group from scratch, we can efficiently track the length of alternating sequences as we traverse the array.
# Approach
<!-- Describe your approach to solving the problem. -->
- Use a sliding window to track the length of alternating sequences.
- If two adjacent elements are different, increase the valid sequence length.
- If we reach k, count the group but continue sliding forward.
- If two adjacent elements are the same, reset the sequence.
- Use modulo indexing (% n) to handle circular behavior.
# Complexity
- Time complexity: O(n) – Each element is processed once.
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(1) – Only a few variables are used.
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int numberOfAlternatingGroups(int[] colors, int k) {
int n = colors.length;
int count = 0;
int validSize = 1;
for (int i = 1; i < n + k - 1; i++)
{
if (colors[i % n] != colors[(i - 1) % n])
{
validSize++;
if (validSize >= k)
{
count++;
}
}
else
{
validSize = 1;
}
}
return count;
}
}
```
| 7 | 0 |
['Java']
| 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.