question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
divide-intervals-into-minimum-number-of-groups | Line sweep-> sort -> radix sort||153ms beats 100% | line-sweep-sort-radix-sort153ms-beats-10-16i2 | Intuition\n Describe your first thoughts on how to solve this problem. \nThis question can be solved with line sweep; it takes $O(n\uFF0B\max(right)+1)$ time wh | anwendeng | NORMAL | 2024-10-12T03:05:52.932896+00:00 | 2024-10-12T06:54:49.203955+00:00 | 2,179 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThis question can be solved with line sweep; it takes $O(n\uFF0B\\max(right)+1)$ time where right<=1e6.\n\nUsing sort it can be reduced to $O(n\\log n)$ time. If other sorting method is applied, the time complexity can be furthermore reduced.\n\nUsing radix sort, its elapsed time is only 153ms.\n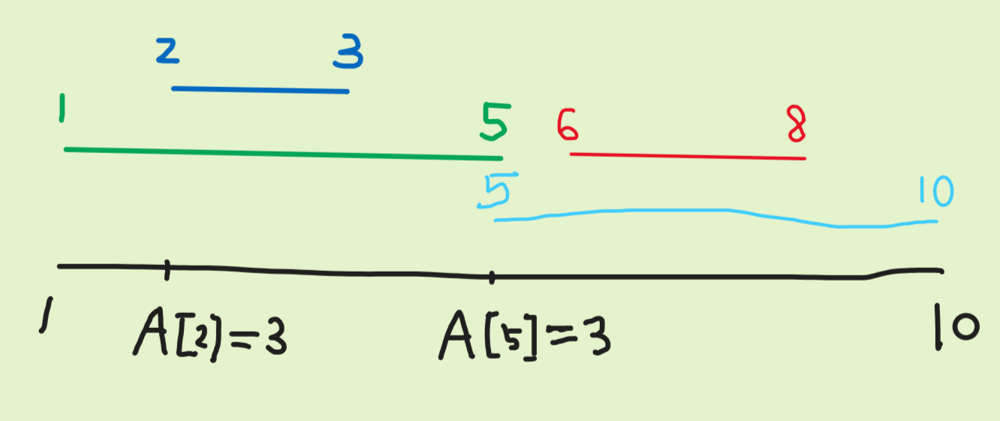\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. The very basic idea is to use line sweep; it might be the slowest one, but easy to understand.\n2. Every interval has 2 ends, left & right, set x=left, y=right+1, followed the idea from line sweep, when encountering x or y, increase by 1 or decrease by 1. It needs only to sort the info on intervals.\n3. Using std::sort is fast when the sorting object is vector over ints, the info on interval can be easily packed into a int.\n4. Radix sort is of course applicable for this, A linear solution $O(n)$ is doable.\n5. The `radix_sort` function needs 128 bucket for sorting; it needs to perform 3 rounds to complete the task.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n $$O(n+\\max(right)+1) \\to O(n\\log n)\\to O(n)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nline sweep: $$O(1e6+2)$$\nsort:$$O(n)$$\nradix sort: $O(128+n)$\n# Code using sort||171ms beats 100%\n```cpp []\nclass Solution {\npublic:\n static int minGroups(vector<vector<int>>& intervals) {\n const int n=intervals.size();\n vector<int> P;\n P.reserve(n*2);\n for(auto& I: intervals){\n int x=I[0], y=I[1]+1;\n P.push_back((x<<1)+1);\n P.push_back(y<<1);\n }\n sort(P.begin(), P.end());\n int cnt=0, x=0;\n for(int z: P){\n x+=(z&1)?1:-1;\n cnt=max(cnt, x);\n }\n \n return cnt; \n }\n};\n\n\n\nauto init = []() {\n ios::sync_with_stdio(false);\n cin.tie(nullptr);\n cout.tie(nullptr);\n return \'c\';\n}();\n```\n# C++ using line sweep||195ms Beats 99.10%\n```\nclass Solution {\npublic:\n int minGroups(vector<vector<int>>& intervals) {\n const unsigned N=1e6+2;\n int A[N]={0}, ans=0;\n for (auto& int2: intervals){\n int x=int2[0], y=int2[1]+1;\n A[x]++, A[y]--;\n }\n for (int i=1; i<N; i++){\n A[i]+=A[i-1];\n ans=max(ans, A[i]);\n }\n return ans;\n }\n};\n\n```\n# Using radix sort||153ms beats 100%\n```\nvector<int> bucket[128]; \nvoid radix_sort(vector<int>& nums) {\n // 1st round\n for (int& x : nums) {\n bucket[x & 127].push_back(x);\n }\n int i = 0;\n for (auto& B : bucket) {\n for (auto v : B)\n nums[i++] = v;\n B.clear();\n }\n // 2nd round\n for (int& x : nums)\n bucket[(x >> 7) & 127].push_back(x);\n i = 0;\n for (auto& B : bucket) {\n for (auto v : B)\n nums[i++] = v;\n B.clear();\n }\n // 3rd round\n for (int& x : nums)\n bucket[x >> 14].push_back(x);\n i = 0;\n for (auto& B : bucket) {\n for (auto v : B) \n nums[i++] = v ;\n B.clear();\n }\n}\nclass Solution {\npublic:\n static int minGroups(vector<vector<int>>& intervals) {\n const int n=intervals.size();\n vector<int> P;\n P.reserve(n*2);\n for(auto& I: intervals){\n int x=I[0], y=I[1]+1;\n P.push_back((x<<1)+1);\n P.push_back(y<<1);\n }\n radix_sort(P);\n int cnt=0, x=0;\n for(int z: P){\n x+=(z&1)?1:-1;\n cnt=max(cnt, x);\n }\n \n return cnt; \n }\n};\n\nauto init = []() {\n ios::sync_with_stdio(false);\n cin.tie(nullptr);\n cout.tie(nullptr);\n return \'c\';\n}();\n``` | 18 | 0 | ['Array', 'Line Sweep', 'Sorting', 'C++'] | 6 |
divide-intervals-into-minimum-number-of-groups | [C++] Similar to minimum plateforms required problem | c-similar-to-minimum-plateforms-required-oznu | \nclass Solution {\npublic:\n bool static comp(vector<int> &a,vector<int> &b) {\n return a[1]<b[1];\n }\n int minGroups(vector<vector<int>>& int | Ayush479 | NORMAL | 2022-09-11T05:23:45.555631+00:00 | 2022-09-11T05:23:45.555681+00:00 | 1,128 | false | ```\nclass Solution {\npublic:\n bool static comp(vector<int> &a,vector<int> &b) {\n return a[1]<b[1];\n }\n int minGroups(vector<vector<int>>& intervals) {\n // Your code here\n vector<int>arr,dep;\n int n=intervals.size();\n for(auto x:intervals){\n arr.push_back(x[0]);\n dep.push_back(x[1]);\n }\n sort(arr.begin(),arr.end());\n sort(dep.begin(),dep.end());\n int i = 1, count = 1;\n int j = 0, ans = 1;\n while (i < n && j < n)\n {\n if (arr[i] <= dep[j]) // one more platform needed\n {\n count++;\n i++;\n }\n else // one platform can be reduced\n {\n count--;\n j++;\n }\n ans = max(ans, count);\n }\n return ans;\n }\n};\n\n// if you liked the solution then please upvote it so that it can reach to more people \n// If you have any doubt or want to discuss any thing related to solution please leave a comment, so that all of the viewers can discuss it\n``` | 15 | 0 | ['C', 'Sorting'] | 2 |
divide-intervals-into-minimum-number-of-groups | C++ || Priority Queue | c-priority-queue-by-kirtipurohit025-ivc0 | \nclass Solution {\npublic:\n int minGroups(vector<vector<int>>& intervals) {\n priority_queue<int, vector<int>, greater<int>> pq;\n \n | kirtipurohit025 | NORMAL | 2022-09-11T04:09:31.216637+00:00 | 2022-09-11T04:09:31.216674+00:00 | 1,218 | false | ```\nclass Solution {\npublic:\n int minGroups(vector<vector<int>>& intervals) {\n priority_queue<int, vector<int>, greater<int>> pq;\n \n sort(intervals.begin(), intervals.end()); \n int ans=0;\n for (auto inter: intervals) {\n int start= inter[0], end= inter[1]; \n if (pq.size() < 1 or pq.top() > start) \n ans++; \n else pq.pop(); \n pq.push(end+1);\n }\n return ans;\n \n \n }\n};\n``` | 15 | 1 | ['C'] | 4 |
divide-intervals-into-minimum-number-of-groups | Simplest way || Prefix Sum || O(n) | simplest-way-prefix-sum-on-by-priyanshuh-4a51 | \nint minGroups(vector<vector<int>>& nums) {\n int n = INT_MIN;\n for(int i=0;i<nums.size();i++)\n n = max(n, nums[i][1]);\n \n | priyanshuHere27 | NORMAL | 2022-09-11T04:02:13.594059+00:00 | 2022-09-11T04:02:13.594115+00:00 | 2,391 | false | ```\nint minGroups(vector<vector<int>>& nums) {\n int n = INT_MIN;\n for(int i=0;i<nums.size();i++)\n n = max(n, nums[i][1]);\n \n vector<int> v(n+2, 0);\n for(int i=0;i<nums.size();i++)\n {\n v[nums[i][0]]++;\n v[nums[i][1]+1]--;\n }\n //prefix sum for count of elements present in different range\n for(int i=1;i<v.size();i++)\n v[i] = v[i] + v[i-1];\n \n int cn = 0;\n for(int i=0;i<v.size();i++)\n cn = max(cn, v[i]);\n \n return cn;\n }\n``` | 15 | 0 | ['C', 'Prefix Sum', 'C++'] | 9 |
divide-intervals-into-minimum-number-of-groups | Python | Sweep Line Pattern | python-sweep-line-pattern-by-khosiyat-8hjc | see the Successfully Accepted Submission\n\n# Code\npython3 []\nclass Solution:\n def minGroups(self, intervals: List[List[int]]) -> int:\n events = [ | Khosiyat | NORMAL | 2024-10-12T02:28:47.830223+00:00 | 2024-10-12T02:28:47.830246+00:00 | 1,034 | false | [see the Successfully Accepted Submission](https://leetcode.com/problems/divide-intervals-into-minimum-number-of-groups/submissions/1419533602/?envType=daily-question&envId=2024-10-12)\n\n# Code\n```python3 []\nclass Solution:\n def minGroups(self, intervals: List[List[int]]) -> int:\n events = []\n \n # Create start and end events for each interval\n for interval in intervals:\n left, right = interval\n events.append((left, 1)) # Start of an interval\n events.append((right + 1, -1)) # End of an interval (right + 1 to handle inclusive overlap)\n \n # Sort events by time; in case of tie, end events (-1) should come before start events (1)\n events.sort()\n \n max_groups = 0\n current_groups = 0\n \n # Sweep through the events\n for _, event in events:\n current_groups += event # Add 1 for start, subtract 1 for end\n max_groups = max(max_groups, current_groups)\n \n return max_groups\n\n```\n\n## Approach:\n\n### Understanding the overlap:\nTwo intervals overlap if there is at least one common point between them. Specifically, two intervals `[a, b]` and `[c, d]` overlap if `a <= d` and `b >= c`. Therefore, for each group of intervals, no two intervals should overlap.\n\n### Key observation:\nThe number of groups we need is determined by how many intervals are overlapping at any point in time. If several intervals overlap, we need at least that many groups to place them in.\n\n### Event-based solution:\n\nWe can treat this problem as a timeline of events. Each interval generates two events:\n- A **start event** at `lefti` when the interval starts.\n- An **end event** at `righti + 1` when the interval ends (we use `righti + 1` to mark the point just after the interval ends, to correctly handle the inclusive nature).\n\nThe number of overlapping intervals at any point in time is the difference between the number of start events and end events at that point.\n\n### Algorithm:\n\n1. For each interval, record its start and end events.\n2. Sort all events by the time they occur. For events that happen at the same time, process the end events before the start events (to avoid counting an interval that ends and starts at the same point as overlapping).\n3. Sweep through the events, keeping track of the maximum number of overlapping intervals at any point.\n\n### Time Complexity:\n\n- Sorting the events will take \\(O(n \\log n)\\), where \\(n\\) is the number of intervals.\n- The sweep through the events is \\(O(n)\\), so the total complexity is \\(O(n \\log n)\\).\n\n\n | 13 | 0 | ['Python3'] | 2 |
divide-intervals-into-minimum-number-of-groups | Python3 || 5 lines, dict, accumulate || T/S: 62% / 21% | python3-5-lines-dict-accumulate-ts-62-21-7uzn | \n\nclass Solution:\n def minGroups(self, intervals: List[List[int]]) -> int:\n\n d = defaultdict(int)\n\n for start, end in intervals:\n | Spaulding_ | NORMAL | 2022-09-15T21:06:56.395301+00:00 | 2024-06-14T18:06:53.751150+00:00 | 402 | false | \n```\nclass Solution:\n def minGroups(self, intervals: List[List[int]]) -> int:\n\n d = defaultdict(int)\n\n for start, end in intervals:\n d[start]+= 1\n d[end+1]-= 1\n\n return max(accumulate([d[n] for n in sorted(d)]))\n```\t\t\n[https://leetcode.com/problems/divide-intervals-into-minimum-number-of-groups/submissions/1288380428/](https://leetcode.com/problems/divide-intervals-into-minimum-number-of-groups/submissions/1288380428/)\n\nI could be wrong, but I think that time complexity is *O*(*N* log *N*) and space complexity is *O*(*N*), in which *N* ~ `len(intervals)`. | 12 | 1 | ['Python', 'Python3'] | 1 |
divide-intervals-into-minimum-number-of-groups | 🔥 [LeetCode The Hard Way] 🔥 Explained Line By Line | leetcode-the-hard-way-explained-line-by-uj7mx | Please check out LeetCode The Hard Way for more solution explanations and tutorials. \nI\'ll explain my solution line by line daily and you can find the full li | __wkw__ | NORMAL | 2022-09-12T04:50:55.289156+00:00 | 2022-09-12T04:50:55.289199+00:00 | 753 | false | Please check out [LeetCode The Hard Way](https://wingkwong.github.io/leetcode-the-hard-way/) for more solution explanations and tutorials. \nI\'ll explain my solution line by line daily and you can find the full list in my [Discord](https://discord.gg/Nqm4jJcyBf).\nIf you like it, please give a star, watch my [Github Repository](https://github.com/wingkwong/leetcode-the-hard-way) and upvote this post.\n\n**C++**\n\n```cpp\nclass Solution {\npublic:\n // it\'s almost same as 253. Meeting Rooms II ...\n // the idea is to use line sweep to find out the number of overlapped intervals\n // if it is overlapped, that means you need to create a new group\n // e.g. if 2 intervals are overlapped, you need 2 groups ...\n // e.g. if 3 intervals are overlapped, you need 3 groups ...\n int minGroups(vector<vector<int>>& intervals) {\n int ans = 0, cnt = 0;\n // use map for internally sorting\n map<int, int> m;\n // standard line sweep\n // - increase the count of starting point by 1\n // - decrease the count of ending point by 1\n // - take prefix sum and do something\n for (auto& x: intervals) {\n // in - increase by 1\n m[x[0]]++;\n // out - decrease by 1\n m[x[1] + 1]--;\n }\n // so now what we have is\n // intervals 1 2 3 4 5 6 7 8 9 10\n // + 2 1 0 0 1 1 0 0 0 0 \n // - 0 0 1 0 1 0 0 1 0 2\n // m 2 1 -1 0 0 1 0 -1 0 -2\n for (auto& x: m) {\n // here we calculate the prefix sum\n cnt += x.second;\n // and record the maximum overlapping intervals\n ans = max(ans, cnt);\n }\n return ans;\n }\n};\n\n``` | 11 | 0 | ['C', 'Prefix Sum', 'C++'] | 4 |
divide-intervals-into-minimum-number-of-groups | ✅✅Faster || Easy To Understand || C++ Code | faster-easy-to-understand-c-code-by-__kr-6xh8 | Using Sorting && Min. Heap\n\n Time Complexity :- O(NlogN)\n\n Space Complexity :- O(N)\n\n\nclass Solution {\npublic:\n int minGroups(vector<vector<int>>& a | __KR_SHANU_IITG | NORMAL | 2022-09-11T05:24:41.725965+00:00 | 2022-09-11T05:24:41.725994+00:00 | 820 | false | * ***Using Sorting && Min. Heap***\n\n* ***Time Complexity :- O(NlogN)***\n\n* ***Space Complexity :- O(N)***\n\n```\nclass Solution {\npublic:\n int minGroups(vector<vector<int>>& arr) {\n \n int n = arr.size();\n \n // sort the array on the basis of start in increasing order\n \n sort(arr.begin(), arr.end());\n \n // declare a min heap, which will store the ending value of every group till ith index\n \n priority_queue<int, vector<int>, greater<int>> pq;\n \n pq.push(arr[0][1]);\n \n // now iterate over array and make possible groups\n \n for(int i = 1; i < n; i++)\n {\n // start value is greater than end value, then we can include the curr interval in this group\n \n if(arr[i][0] > pq.top())\n {\n pq.pop();\n }\n \n // push the end value in the pq\n \n pq.push(arr[i][1]);\n }\n \n return pq.size();\n }\n};\n``` | 9 | 1 | ['C', 'Sorting', 'Heap (Priority Queue)', 'C++'] | 1 |
divide-intervals-into-minimum-number-of-groups | python/java heap | pythonjava-heap-by-akaghosting-tfjs | \tclass Solution:\n\t\tdef minGroups(self, intervals: List[List[int]]) -> int:\n\t\t\tintervals.sort()\n\t\t\tminHeap = []\n\t\t\tfor left, right in intervals:\ | akaghosting | NORMAL | 2022-09-11T04:01:11.833490+00:00 | 2022-09-11T04:01:11.833527+00:00 | 544 | false | \tclass Solution:\n\t\tdef minGroups(self, intervals: List[List[int]]) -> int:\n\t\t\tintervals.sort()\n\t\t\tminHeap = []\n\t\t\tfor left, right in intervals:\n\t\t\t\tif minHeap and left > minHeap[0]:\n\t\t\t\t\theapq.heappop(minHeap)\n\t\t\t\theapq.heappush(minHeap, right)\n\t\t\treturn len(minHeap)\n\n\n\tclass Solution {\n\t\tpublic int minGroups(int[][] intervals) {\n\t\t\tArrays.sort(intervals, (a, b) -> a[0] == b[0] ? a[1] - b[1] : a[0] - b[0]);\n\t\t\tQueue<Integer> minHeap = new PriorityQueue<>();\n\t\t\tfor (int[] interval: intervals) {\n\t\t\t\tint left = interval[0];\n\t\t\t\tint right = interval[1];\n\t\t\t\tif (!minHeap.isEmpty() && left > minHeap.peek()) {\n\t\t\t\t\tminHeap.poll();\n\t\t\t\t}\n\t\t\t\tminHeap.offer(right);\n\t\t\t}\n\t\t\treturn minHeap.size();\n\t\t}\n\t} | 9 | 1 | [] | 0 |
divide-intervals-into-minimum-number-of-groups | C++ Line Sweep | c-line-sweep-by-abhay5349singh-ckae | Connect with me on LinkedIn: https://www.linkedin.com/in/abhay5349singh/\n\nIntuition\n1. By sweep[l]++ & sweep[r+1]--, we are acknowledging the presence of a p | abhay5349singh | NORMAL | 2022-09-11T04:30:39.327051+00:00 | 2023-07-14T03:49:47.798828+00:00 | 1,260 | false | **Connect with me on LinkedIn**: https://www.linkedin.com/in/abhay5349singh/\n\n**Intuition**\n1. By sweep[l]++ & sweep[r+1]--, we are acknowledging the presence of a particular interval b/w [l,r].\n 2. by taking the cumulative sum over this sweep array gives a count of overlapping intervals present at any certain point.\n3. taking the max value out of sweep array gives \'max possible overlaps\' & hence we need to create these many groups so that we can keep these overlapping intervals in separate groups\n\n**Other Line Sweep Questions**\nSome Line Sweep problems on my github: https://github.com/AbhaySingh5349/Leet-Code-Questions/tree/main/Line-Sweep\n\n**Reference Video** \n For better insights : https://www.youtube.com/watch?v=lFBpH_Mt_LI&t=1s\n\n```\nclass Solution {\npublic:\n\n int minGroups(vector<vector<int>>& intervals) {\n vector<int> sweep(1e7+1,0);\n int val=0;\n for(int i=0;i<intervals.size();i++){\n int l=intervals[i][0], r=intervals[i][1];\n sweep[l]++, sweep[r+1]--;\n val=max(val,r);\n }\n \n int grps=1;\n for(int i=1;i<val+1;i++){\n sweep[i] += sweep[i-1];\n grps = max(grps,sweep[i]); // keeping track of maximum number of groups present at any instant\n }\n return grps;\n }\n};\n```\n\n**Do Upvote If It Helps** | 8 | 0 | ['C++'] | 5 |
divide-intervals-into-minimum-number-of-groups | Simplest way || Min Heap || Java Solution | simplest-way-min-heap-java-solution-by-p-wqg5 | \n\n\n\n\nclass Solution {\n public int minGroups(int[][] intervals) {\n \n PriorityQueuepq=new PriorityQueue<>();\n \n Arrays.so | Prabhat_17 | NORMAL | 2022-09-11T08:32:56.127875+00:00 | 2022-09-11T08:32:56.127899+00:00 | 722 | false | \n\n\n\n\nclass Solution {\n public int minGroups(int[][] intervals) {\n \n PriorityQueue<Integer>pq=new PriorityQueue<>();\n \n Arrays.sort(intervals,(a,b)->(a[0]==b[0])?a[1]-b[1]:a[0]-b[0]);\n \n for(int[] arr:intervals){\n if(pq.size()>0 && pq.peek()<arr[0]){\n pq.remove();\n }\n \n pq.add(arr[1]);\n }\n \n return pq.size();\n }\n} | 7 | 0 | ['Heap (Priority Queue)', 'Java'] | 2 |
divide-intervals-into-minimum-number-of-groups | C++ || Easy without Priority Queue✅✅ | c-easy-without-priority-queue-by-arunk_l-b984 | Intuition\nThe problem can be solved by considering the number of overlapping intervals at any given point. By treating the start and end of intervals as separa | arunk_leetcode | NORMAL | 2024-10-12T04:47:47.602944+00:00 | 2024-10-12T04:47:47.602978+00:00 | 1,419 | false | # Intuition\nThe problem can be solved by considering the number of overlapping intervals at any given point. By treating the start and end of intervals as separate events, we can track the number of intervals active at any point in time. The maximum number of intervals active simultaneously is the answer.\n\n# Approach\n1. For each interval, we store two events: one for when the interval starts and one for when it ends.\n2. Sort these events. If two events happen at the same time, the ending of an interval is processed before the start of a new interval.\n3. Traverse through the sorted events, keeping track of the current number of active intervals. Update the maximum number of active intervals seen so far.\n4. Return this maximum value, which represents the minimum number of groups required.\n\n# Complexity\n- Time complexity: \n Sorting the list of events takes $$O(n \\log n)$$ where $$n$$ is the number of intervals, and iterating through the list takes $$O(n)$$. Thus, the overall time complexity is $$O(n \\log n)$$.\n \n- Space complexity: \n We store two events for each interval, so the space complexity is $$O(n)$$.\n\n# Code\n```\nclass Solution {\npublic:\n int minGroups(vector<vector<int>>& intervals) {\n vector<pair<int, int>> vp;\n for(int i=0; i<intervals.size(); i++){\n vp.push_back({intervals[i][0], 1}); // start of interval\n vp.push_back({intervals[i][1] + 1, -1}); // end of interval (+1 to handle overlapping)\n }\n sort(vp.begin(), vp.end());\n \n int maxi = 1;\n int cnt = 0;\n \n for(auto it: vp){\n int type = it.second;\n cnt += type;\n maxi = max(maxi, cnt);\n }\n \n return maxi;\n }\n};\n\n```\n | 6 | 0 | ['Sorting', 'C++'] | 2 |
divide-intervals-into-minimum-number-of-groups | Intuitive Binary Search Approach ( With Comments ) | intuitive-binary-search-approach-with-co-ebv7 | \n // Please Upvote , if you find this logic intuitive :)\n \n int minGroups(vector>& v) {\n int n = v.size(); // Initialising the Size of given | tHe_lAZy_1 | NORMAL | 2022-09-11T07:13:07.917981+00:00 | 2022-09-11T08:37:05.433631+00:00 | 805 | false | \n // Please Upvote , if you find this logic intuitive :)\n \n int minGroups(vector<vector<int>>& v) {\n int n = v.size(); // Initialising the Size of given matrix\n \n vector<pair<int,int>>p; // Initialising a vector of pair \n \n /*\n Initialising a multiset of pair (It is important in our approach) {One can even use map}\n */\n multiset<pair<int,int>>ms; \n \n // Pushing values in the container\n for(int i = 0;i<v.size();i++)\n {\n p.push_back({v[i][0] , v[i][1]});\n ms.insert({v[i][0] , v[i][1]});\n }\n \n /* We need to sort it ...\n Reason :-\n We will be going greedy in our approach.\n */\n \n sort(p.begin(),p.end());\n \n // initialising the count which will account for all possible groups\n int cnt = 0;\n \n \n //\n for(int i = 0;i<n;i++)\n {\n /*\n Logic here is that , if we don\'t have the interval p[i] in our multiset,\n We can imply that it already is a part of some group\n */\n if(ms.find(p[i]) == ms.end()) continue;\n \n /*\n If it is present in our multiset, that means it will create its own group\n */\n cnt++;\n /*\n Initialised pair x for convenience.\n */\n pair<int,int>x = p[i]; \n \n /*\n One can Erase p[i] for covenience, but its not important as we will not be \n needing it again in our approach.\n */\n ms.erase(ms.find(p[i]));\n \n /*\n Here is the Binary Search Part :)\n \n We will be using Binary Search Greedily that is ,if we have [1,2] as our pair\n\t\t\t\t the next pair we will be searching would be lower bound of [3,3] or upper bound of[2,2].\n\t\t\t\t \n\t\t\t\t As in the given contraints of the problem left(i) <= right(i) , we can get Idea for the pair \n\t\t\t\t we need to search next using this constraint.\n We will greedily look for it , until we cannot search any further\n */\n while(ms.lower_bound({x.second + 1,x.second+1}) != ms.end())\n {\n auto it = ms.lower_bound({x.second + 1,x.second+1});\n \n /*\n Updating the value of the pair , with which we want to search next and \n will repeat that process.\n \n Here deletion is important, as we might encounter it again while traversing\n our main array , if we don\'t delete it , it will contradict our logic of it \n already being present in one of the groups\n */\n x = {it->first , it->second};\n ms.erase(it);\n }\n\n }\n return cnt;\n \n // Voila , You reach to your answer :)\n } | 6 | 0 | ['Binary Search', 'Greedy', 'C', 'Sorting', 'Binary Tree', 'C++'] | 2 |
divide-intervals-into-minimum-number-of-groups | ✅ One Line Solution | one-line-solution-by-mikposp-q5x9 | (Disclaimer: this is not an example to follow in a real project - it is written for fun and training mostly)\n\n# Code #1.1 - One Line\nTime complexity: O(n*log | MikPosp | NORMAL | 2024-10-12T19:37:52.750819+00:00 | 2024-10-12T19:37:52.750834+00:00 | 211 | false | (Disclaimer: this is not an example to follow in a real project - it is written for fun and training mostly)\n\n# Code #1.1 - One Line\nTime complexity: $$O(n*log(n))$$. Space complexity: $$O(n)$$.\n```python3\nclass Solution:\n def minGroups(self, a: List[List[int]]) -> int:\n return len((q:=[],[(q and q[0]<s and heappop(q),heappush(q,e)) for s,e in sorted(a)])[0])\n```\n\n# Code #1.2 - Unwrapped\n```python3\nclass Solution:\n def minGroups(self, a: List[List[int]]) -> int:\n q = []\n for s,e in sorted(a):\n if q and q[0] < s:\n heappop(q)\n\n heappush(q, e)\n\n return len(q)\n```\n\n(Disclaimer 2: code above is just a product of fantasy packed into one line, it is not claimed to be \'true\' oneliners - please, remind about drawbacks only if you know how to make it better) | 5 | 1 | ['Array', 'Sorting', 'Heap (Priority Queue)', 'Python', 'Python3'] | 3 |
divide-intervals-into-minimum-number-of-groups | 💡Easy Solution | O (n log n) | C++ 175ms Beats 99.77% | Minimum Number of Groups | 🧠 | easy-solution-o-n-log-n-c-175ms-beats-99-kvsb | \n\n#\n---\n> # Intuition \nTo solve this problem, we need to group the intervals such that no two intervals in the same group intersect. By sorting the interv | user4612MW | NORMAL | 2024-10-12T04:36:40.456737+00:00 | 2024-10-12T04:41:07.907957+00:00 | 305 | false | \n\n#\n---\n> # Intuition \nTo solve this problem, we need to group the intervals such that no two intervals in the same group intersect. By sorting the intervals\' start and end times and using a greedy approach, we can track how many intervals are active at any given time and determine the minimum number of groups required.\n\n> # Approach \nWe treat each interval as two events: an arrival (interval start) and a departure (interval end + 1). By sorting these events, we can iterate over them to track the number of currently active intervals. The maximum number of overlapping intervals at any point is the answer. The use of a priority queue or sorting makes sure efficiency in this approach.\n\n> # Complexity \n- **Time Complexity** $$O(n log n)$$, where n is the number of intervals due to sorting. \n- **Space Complexity** $$O(n)$$, for storing the events and additional space for tracking groups.\n\n---\n> # Code\n```cpp []\nclass Solution {\npublic:\n int minGroups(vector<vector<int>>& iv) {\n vector<pair<int, int>> ev;\n for (auto& i : iv) ev.emplace_back(i[0], 1), ev.emplace_back(i[1] + 1, -1);\n sort(ev.begin(), ev.end());\n int grp{0}, cur{0};\n for (auto& e : ev) cur += e.second, grp = max(grp, cur);\n return grp;\n }\n};\nauto io_opt = [] { ios::sync_with_stdio(false); cin.tie(nullptr); return 0; }();\n```\n\n---\n> **CPP**\n> \n\n\n---\n | 5 | 0 | ['C++'] | 3 |
divide-intervals-into-minimum-number-of-groups | Easy Solution | easy-solution-by-viratkohli-ojob | Complexity\n- Time complexity:O(n*log(n))\n Add your time complexity here, e.g. O(n) \n\n- Space complexity:O(n)\n Add your space complexity here, e.g. O(n) \n\ | viratkohli_ | NORMAL | 2024-10-12T02:51:13.779799+00:00 | 2024-10-12T02:51:13.779832+00:00 | 310 | false | # Complexity\n- Time complexity:O(n*log(n))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int minGroups(vector<vector<int>>& intervals) {\n priority_queue<int, vector<int>, greater<>> minHeap;\n ranges::sort(intervals);\n\n for(vector<int>& interval:intervals){\n if(!minHeap.empty() && interval[0]>minHeap.top()){\n minHeap.pop();\n }\n minHeap.push(interval[1]);\n }\n \n return minHeap.size();\n }\n};\n``` | 5 | 0 | ['Array', 'Sorting', 'Heap (Priority Queue)', 'C++'] | 1 |
divide-intervals-into-minimum-number-of-groups | I'm a Beginner/Newbie just like you! | im-a-beginnernewbie-just-like-you-by-sat-8btd | Intuition\n- Try meeting rooms 3 before this problem. (ofc thats much harder than this, but if u dont get that one also-once try it for better understanding of | satwika-55 | NORMAL | 2024-10-12T02:17:08.959774+00:00 | 2024-10-12T02:18:48.078415+00:00 | 274 | false | # Intuition\n- Try meeting rooms 3 before this problem. (ofc thats much harder than this, but if u dont get that one also-once try it for better understanding of this question)\n\n# Code\n```python3 []\nclass Solution:\n def minGroups(self, intervals: List[List[int]]) -> int:\n # afterall, who can give you more priority than heaps :)\n\n pq = [] # insertion format -> end time, group number\n\n count = 0\n intervals.sort()\n\n for start,end in intervals:\n if pq and pq[0][0] < start:\n# we can insert off our current interval in some existing group\n time,num = heappop(pq)\n heappush(pq,(end,num))\n else:\n# else, we create a new group for out current interval\n heappush(pq,(end,count))\n count += 1\n#count represents the number of grops we created\n return count\n\n \n```\n\n# ALL THE BEST\n- keep rocking dont give up guys!\n- no begging for upvotes :) | 5 | 2 | ['Python3'] | 1 |
divide-intervals-into-minimum-number-of-groups | EASY SOLUTION USING SET FOR BEGINNERS!!! | easy-solution-using-set-for-beginners-by-vq8x | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | aero_coder | NORMAL | 2024-10-12T00:33:08.778370+00:00 | 2024-10-12T00:59:34.212338+00:00 | 779 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int minGroups(vector<vector<int>>& intervals) {\n ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);\n int ans = 0;\n multiset<pair<int, int>> st; // Use multiset instead of set because the intervals are not unique\n for (auto it : intervals)\n {\n st.insert(make_pair(it[0], it[1])); \n }\n while (!st.empty()) {\n auto it = *st.begin();\n st.erase(st.begin());\n int cur = it.second;\n while (true) {\n auto mx = st.upper_bound(make_pair(cur, INT_MAX)); // works in log(n) time\n if (mx == st.end()) break;\n cur = mx->second;\n st.erase(mx);\n }\n ans++;\n }\n return ans;\n }\n};\n\n\n``` | 5 | 0 | ['C++'] | 2 |
divide-intervals-into-minimum-number-of-groups | Solution similar to 253. Meeting Rooms II (similar problems listed) | solution-similar-to-253-meeting-rooms-ii-wuov | Please see and vote for my solutions for similar problems.\n253. Meeting Rooms II\n2406. Divide Intervals Into Minimum Number of Groups\n2402. Meeting Rooms III | otoc | NORMAL | 2022-09-19T00:43:22.264903+00:00 | 2022-09-19T14:50:38.694782+00:00 | 909 | false | Please see and vote for my solutions for similar problems.\n[253. Meeting Rooms II](https://leetcode.com/problems/meeting-rooms-ii/discuss/322622/Simple-Python-solutions)\n[2406. Divide Intervals Into Minimum Number of Groups](https://leetcode.com/problems/divide-intervals-into-minimum-number-of-groups/discuss/2594874/Solutions-similar-to-253.-Meeting-Rooms-II-(similar-problems-listed))\n[2402. Meeting Rooms III](https://leetcode.com/problems/meeting-rooms-iii/discuss/2597443/Python-Heap-Solution-similar-problems-listed)\n[731. My Calendar II](https://leetcode.com/problems/my-calendar-ii/discuss/323479/Simple-C%2B%2B-Solution-using-built-in-map-(Same-as-253.-Meeting-Rooms-II))\n[732. My Calendar III](https://leetcode.com/problems/my-calendar-iii/discuss/302492/Simple-C%2B%2B-Solution-using-built-in-map-(Same-as-253.-Meeting-Rooms-II))\n[1094. Car Pooling](https://leetcode.com/problems/car-pooling/discuss/319088/Simple-Python-solution)\n[1109. Corporate Flight Bookings](https://leetcode.com/problems/corporate-flight-bookings/discuss/328949/Simple-Python-solution)\n[218. The Skyline Problem](https://leetcode.com/problems/the-skyline-problem/discuss/325070/SImple-Python-solutions)\n\n\nIf we map [left_i, right_i+1] to [start_i, end_i], it\'s exactly the problem as 252. Meeting Rooms II.\n\nSolution 1: sort all time points\ntime: O(n log n), space: O(n)\n```\n def minGroups(self, intervals: List[List[int]]) -> int:\n lst = []\n for start, end in intervals:\n lst.append((start, 1))\n lst.append((end + 1, -1))\n lst.sort()\n res, curr_groups = 0, 0\n for t, n in lst:\n curr_groups += n\n res = max(res, curr_groups)\n return res\n```\n\nSolution 2: heap solution\ntime: O(n log n), space: O(n)\n```\n def minGroups(self, intervals: List[List[int]]) -> int:\n intervals.sort(key = lambda x: x[0])\n res = 0\n heap, heap_size = [], 0\n for interval in intervals:\n while heap and heap[0] <= interval[0]:\n heapq.heappop(heap)\n heap_size -= 1\n heapq.heappush(heap, interval[1] + 1)\n heap_size += 1\n res = max(res, heap_size)\n return res\n```\n\n\n\n\n | 5 | 0 | [] | 0 |
divide-intervals-into-minimum-number-of-groups | ✅Something New || Something Different || Using Fenwick Tree || (◍•ᴗ•◍) | something-new-something-different-using-itp5u | Approach\n Describe your approach to solving the problem. \nOne of the key observations in this question is that the minimum number of groups needed to divide t | Arcturus_22 | NORMAL | 2024-10-12T05:27:47.635350+00:00 | 2024-10-12T08:07:31.898760+00:00 | 271 | false | # Approach\n<!-- Describe your approach to solving the problem. -->\nOne of the key observations in this question is that the minimum number of groups needed to divide the intervals corresponds to the maximum number of intervals that a number lies in, or in other words, the maximum number of overlapping intervals at any given time.\n\nWhat we are doing here is **Range Updates** and **Point Queries**. For every interval, we update the BIT (Binary Indexed Tree) array, implying that all the numbers in the range are counted once in this range.\n\nIn the last for loop, we are finding the number (index of the BIT array) having the maximum sum, meaning number of interval the number lies in.\n# Complexity\n- Time complexity: O(nlogn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\nvector<int> bit;\nint N;\n int sum(int id){\n int ans = 0;\n while(id > 0){\n ans += bit[id];\n id = (id - (id & -id));\n }\n return ans;\n }\n void update(int id, int x){\n\n while(id <= N){\n bit[id] += x;\n id = (id + (id & -id));\n }\n }\n void updateRange(int l, int r){\n update(l,1);\n update(r+1,-1);\n }\n int minGroups(vector<vector<int>>& a) {\n \n for(int i=0;i<a.size();i++){\n N = max(N, a[i][1]);\n }\n bit = vector<int> (N+2,0);\n\n for(int i=0;i<a.size();i++){\n updateRange(a[i][0],a[i][1]);\n }\n\n int ans = 0;\n for(int i =1;i<bit.size();i++){\n ans = max(ans, sum(i));\n }\n\n return ans;\n }\n};\n```\n```java []\nclass Solution {\n\n int[] bit;\n int N;\n\n int sum(int id){\n int ans = 0;\n while(id > 0){\n ans += bit[id];\n id = (id - (id & -id));\n }\n return ans;\n }\n void update(int id, int x){\n\n while(id <= N){\n bit[id] += x;\n id = (id + (id & -id));\n }\n }\n void updateRange(int l, int r){\n update(l,1);\n update(r+1,-1);\n }\n\n public int minGroups(int[][] a) {\n \n for(int i=0;i<a.length;i++){\n N = Math.max(N, a[i][1]);\n }\n bit = new int[N+2];\n\n for(int i=0;i<a.length;i++){\n updateRange(a[i][0],a[i][1]);\n }\n\n int ans = 0;\n for(int i =1;i<bit.length;i++){\n ans = Math.max(ans, sum(i));\n }\n\n return ans;\n }\n}\n```\n\n\n\nThe runtime will be very high for the above codes as the size of N is also large but it can be reduced using Coordinate Compression. Below is the code for the same.\n\n```cpp []\nclass Solution {\npublic:\n vector<int> bit;\n int N;\n \n int sum(int id) {\n int ans = 0;\n while (id > 0) {\n ans += bit[id];\n id = (id - (id & -id));\n }\n return ans;\n }\n \n void update(int id, int x) {\n while (id <= N) {\n bit[id] += x;\n id = (id + (id & -id));\n }\n }\n \n void updateRange(int l, int r) {\n update(l, 1);\n update(r + 1, -1);\n }\n \n int minGroups(vector<vector<int>>& a) {\n // Coordinate compression\n vector<int> coords;\n for (auto &interval : a) {\n coords.push_back(interval[0]);\n coords.push_back(interval[1]);\n }\n sort(coords.begin(), coords.end());\n coords.erase(unique(coords.begin(), coords.end()), coords.end());\n \n // Assigning the new coordinates in the intervals\n for (auto &interval : a) {\n interval[0] = lower_bound(coords.begin(), coords.end(), interval[0]) - coords.begin() + 1;\n interval[1] = lower_bound(coords.begin(), coords.end(), interval[1]) - coords.begin() + 1;\n }\n \n // Size of BITarray\n N = coords.size();\n bit = vector<int>(N + 2, 0); // Adjusted size after compression\n \n // BIT Update for each interval with adjusted coordinate values, reducing size of BIT array\n for (int i = 0; i < a.size(); i++) {\n updateRange(a[i][0], a[i][1]);\n }\n \n // For maximum overlap, number lying in most intervals\n int ans = 0;\n for (int i = 1; i <= N; i++) {\n ans = max(ans, sum(i));\n }\n \n return ans;\n }\n};\n```\n\nDo **Upvote** the post if it was helpful in any way and you liked it!\nComment down for any doubts or suggestions.\n\nSigning off,\nArcturus_22\n\n\n\n | 4 | 0 | ['Binary Indexed Tree', 'C++', 'Java'] | 2 |
divide-intervals-into-minimum-number-of-groups | 2Ways || StepWise ||JAVA C++ PYTHON. | 2ways-stepwise-java-c-python-by-abhishek-lq6b | BOISS JUST UPVOTE , I WORK SO HARD WRITNG THIS OUT AND YOU SHAMELESS PEOPLE SONT EVEN LIKE THE POST . PLS UPVOTE IT.\n# METHOD 1.)\n\n### Steps:\n\n1. Sort the | Abhishekkant135 | NORMAL | 2024-10-12T04:58:09.111092+00:00 | 2024-10-12T08:03:12.841630+00:00 | 563 | false | # BOISS JUST UPVOTE , I WORK SO HARD WRITNG THIS OUT AND YOU SHAMELESS PEOPLE SONT EVEN LIKE THE POST . PLS UPVOTE IT.\n# METHOD 1.)\n\n### Steps:\n\n1. Sort the intervals by their start time.\n2. Use a priority queue to track the end times of the intervals.\n3. For each interval, check if the current interval can be grouped with an existing interval (by comparing its start with the smallest end time).\n4. If it can, update the end time in the priority queue; if not, add it as a new group.\n\n### Code :\n\n```java []\nclass Solution {\n public int minGroups(int[][] intervals) {\n // Sort intervals by their start times\n Arrays.sort(intervals, (a, b) -> a[0] - b[0]);\n \n // Min-heap (priority queue) to track end times of the current groups\n PriorityQueue<Integer> pq = new PriorityQueue<>();\n \n for (int[] interval : intervals) {\n // If the current interval\'s start is greater than or equal to the smallest end time\n if (!pq.isEmpty() && pq.peek() < interval[0]) {\n pq.poll(); // Remove the interval with the smallest end time\n }\n \n // Add the current interval\'s end time to the heap\n pq.offer(interval[1]);\n }\n \n // The size of the heap is the number of groups required\n return pq.size();\n }\n}\n```\n```C++ []\n\n\nclass Solution {\npublic:\n int minGroups(std::vector<std::vector<int>>& intervals) {\n // Sort intervals by their start time\n std::sort(intervals.begin(), intervals.end(), [](const std::vector<int>& a, const std::vector<int>& b) {\n return a[0] < b[0];\n });\n\n // Min-heap to track end times of the current groups\n std::priority_queue<int, std::vector<int>, std::greater<int>> pq;\n\n for (const auto& interval : intervals) {\n // If the current interval\'s start is greater than or equal to the smallest end time\n if (!pq.empty() && pq.top() < interval[0]) {\n pq.pop(); // Remove the interval with the smallest end time\n }\n \n // Add the current interval\'s end time to the heap\n pq.push(interval[1]);\n }\n\n // The size of the heap is the number of groups required\n return pq.size();\n }\n};\n\n```\n```python []\nimport heapq\nfrom typing import List\n\nclass Solution:\n def minGroups(self, intervals: List[List[int]]) -> int:\n # Sort intervals by their start time\n intervals.sort(key=lambda x: x[0])\n \n # Min-heap to track the end times of active intervals\n heap = []\n \n for start, end in intervals:\n # If the current interval\'s start time is greater than or equal to\n # the earliest end time, remove that interval from the heap\n if heap and heap[0] < start:\n heapq.heappop(heap)\n \n # Add the current interval\'s end time to the heap\n heapq.heappush(heap, end)\n \n # The size of the heap represents the number of groups needed\n return len(heap)\n```\n\n\n\n\n### Time Complexity:\n- **Sorting the intervals**: `O(n log n)` where `n` is the number of intervals.\n- **Heap operations**: For each interval, we perform a `poll` and an `offer`, both of which take `O(log k)`, where `k` is the number of groups (in the worst case, `k = n`).\n - Overall, the time complexity is `O(n log n)` due to sorting and heap operations.\n\n\n# METHOD 2\n\n\n### Steps:\n\n1. For each interval, record two events:\n - A start event at `start` (add `1`).\n - An end event at `end + 1` (subtract `1`), because the end of an interval at time `t` does not overlap with a new interval starting at time `t`.\n\n2. Sort the events based on the time. If two events have the same time, process the end events first.\n\n3. Traverse through the sorted events and track the maximum number of overlapping intervals.\n\n### Code Implementation:\n\n```java []\n\nclass Solution {\n public int minGroups(int[][] intervals) {\n // List to store events (time, type), where type is +1 for start and -1 for end\n List<int[]> events = new ArrayList<>();\n \n // Convert intervals to events\n for (int[] interval : intervals) {\n events.add(new int[]{interval[0], 1}); // Start event\n events.add(new int[]{interval[1] + 1, -1}); // End event (non-overlapping)\n }\n \n // Sort events by time, and in case of a tie, sort by type (-1 should come before +1)\n Collections.sort(events, (a, b) -> a[0] == b[0] ? a[1] - b[1] : a[0] - b[0]);\n \n int currentGroups = 0;\n int maxGroups = 0;\n \n // Traverse through events and calculate the number of groups\n for (int[] event : events) {\n currentGroups += event[1]; // Add or subtract based on event type\n maxGroups = Math.max(maxGroups, currentGroups); // Update maxGroups\n }\n \n return maxGroups;\n }\n}\n```\n```C++ []\n\n\nclass Solution {\npublic:\n int minGroups(std::vector<std::vector<int>>& intervals) {\n std::vector<std::pair<int, int>> events;\n\n // Convert intervals to events\n for (const auto& interval : intervals) {\n events.push_back({interval[0], 1}); // Start of an interval (+1)\n events.push_back({interval[1] + 1, -1}); // End of an interval (-1)\n }\n\n // Sort events by time, and by type (-1 before +1 when times are equal)\n std::sort(events.begin(), events.end(), [](const std::pair<int, int>& a, const std::pair<int, int>& b) {\n return a.first == b.first ? a.second < b.second : a.first < b.first;\n });\n\n int currentGroups = 0;\n int maxGroups = 0;\n\n // Traverse through the events and compute the maximum overlapping intervals\n for (const auto& event : events) {\n currentGroups += event.second; // Add 1 for start, subtract 1 for end\n maxGroups = std::max(maxGroups, currentGroups);\n }\n\n return maxGroups;\n }\n};\n\n```\n```python []\n\nclass Solution:\n def minGroups(self, intervals: List[List[int]]) -> int:\n events = []\n \n # Convert intervals into events\n for start, end in intervals:\n events.append((start, 1)) # Start of an interval (+1)\n events.append((end + 1, -1)) # End of an interval (-1)\n \n # Sort events: first by time, then by type (-1 before +1 for the same time)\n events.sort(key=lambda x: (x[0], x[1]))\n\n current_groups = 0\n max_groups = 0\n \n # Traverse through the events to calculate the maximum number of groups\n for _, event_type in events:\n current_groups += event_type # Add for start, subtract for end\n max_groups = max(max_groups, current_groups)\n \n return max_groups\n```\n\n\n\n | 4 | 0 | ['Two Pointers', 'Sorting', 'Heap (Priority Queue)', 'Python', 'C++', 'Java'] | 2 |
divide-intervals-into-minimum-number-of-groups | let's step by step Understand Intuition, with added YouTube link | lets-step-by-step-understand-intuition-w-8wbi | YouTube link https://youtu.be/RpL05RSTUF0\n# Intuition and Approach\nas we have intervals array then if we traverse through intervals array ==> if we maintain a | vinod_aka_veenu | NORMAL | 2024-10-12T03:46:05.588510+00:00 | 2024-10-12T06:57:32.617314+00:00 | 977 | false | # YouTube link https://youtu.be/RpL05RSTUF0\n# Intuition and Approach\nas we have intervals array then if we traverse through intervals array ==> if we maintain a Ordered Map we can keep on increasing count at **start** value in MAP by 1 AND **decrease** the count at **(end + 1)** by 1.\n\n**you might have question, why (end+1) ?? prove the intention behind this whole idea?**\n\nwell so lets take an example intervals[] = {[4, 5], [3, 4], [1, 7]}\n\n\n**now an simple observation is at startTime an interval is being added and at endTime its getting finished** ===> so in an ordered map we would increase count at startTime and decrease it by 1 at endTime+1.\nmap would look like below:-\n**key val**\n1 -> 1 \n8 -> -1 (endTime+1 is the key)\n2 -> 1\n5 -> -1 **(4+1 as endTime+1)**\n3 ->1\n5 -> -2 **4 +1 occured again at last interval in sorted array**\n\nif keep on traversing in an Ordered Map it will give us value in increasing order of keys so sum would look like below :- \n\nat key 1 ==> 1\nat key 2 ==> 1+1 = 2\nat key 3 ==> 1+1+1 = **3**\nat key 5 ==> 1+1+1-2 = 1\nat key 8 ==> 1+1+1-2-1 = 0\n\nso 3 was the highest sum ===> means **3 of the intervals** had intersection ===> **3 different group** were **required max** ==> answer.\n\n**BUT BUT still some curious guy would ask me why end+1?? why not only end as its doesn\'t seem to create a problem**\n\nwell so let say**we have intervals = [[3, 3]]** ==> 1 group would be formed, agree?\n\nbut when we will store the values in Map ==> increae val at start ==> 3 - 1 , then for end ===> decrease ==> 3 - 0 ===> now when we would traverse in Map , we will find only 0 ===> but **actually we need 1 **group===> to handle such cases lets store end+1 as key for decrease operation.\n\n**BUT bros might still ask ordered Map takes O(n log n), can\'t we do it better??**\n\nwe so if you guys know the concept of Counting sort, when ranges are not very huge we can create an array of the size (MaxEndTime in the Interval + 2) ===> **+ 2 because we start from 0, and storing end value at end+1 index so 2 extra place needed**\n\nnow we would traverse throw interval and **keep on increasing the index startTime in the new array by 1 and decreasing by 1 at index end+1**\n\nand then would keep on doing sum from left to right starting from **minStart** index in couting array and find the max sum value ever occured as our answer.\n\n**now time complexity is O(n)**\n\n**still have doubt? no problem would release a youtube video soon**\n\n\n\n\n\n\n\n\n\n# Code\n```java []\nclass Solution {\n public int minGroups(int[][] intervals) {\n int minStart = Integer.MAX_VALUE;\n int maxEnd = Integer.MIN_VALUE;\n for(int d[] : intervals)\n {\n minStart = Math.min(minStart, d[0]);\n maxEnd = Math.max(maxEnd, d[1]);\n } \n\n int arr[] = new int[maxEnd+2];\n int ans = 0; \n\n for(int d[] : intervals)\n {\n arr[d[0]]++;\n arr[d[1]+1]--; \n } \n \n int curr = 0; \n for(int i=0; i<arr.length; i++)\n {\n curr += arr[i] ; \n ans = Math.max(ans, curr);\n }\n\n return ans;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int minGroups(std::vector<std::vector<int>>& intervals) {\n int minStart = INT_MAX;\n int maxEnd = INT_MIN;\n \n for (const auto& d : intervals) {\n minStart = std::min(minStart, d[0]);\n maxEnd = std::max(maxEnd, d[1]);\n }\n\n std::vector<int> arr(maxEnd + 2, 0);\n int ans = 0;\n for (const auto& d : intervals) {\n arr[d[0]]++;\n arr[d[1] + 1]--;\n }\n int curr = 0;\n for (int i = 0; i < arr.size(); i++) {\n curr += arr[i];\n ans = std::max(ans, curr);\n }\n\n return ans;\n }\n};\n\n```\n\n\n | 4 | 0 | ['Array', 'Math', 'Ordered Map', 'Counting Sort', 'C++', 'Java'] | 1 |
divide-intervals-into-minimum-number-of-groups | Faster || Efficient Approach || C++ || Divide intervals into minimum number of groups | faster-efficient-approach-c-divide-inter-jip5 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Shuklajii109 | NORMAL | 2024-10-12T03:24:06.262011+00:00 | 2024-10-12T03:24:06.262030+00:00 | 333 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int minGroups(vector<vector<int>>& intervals) {\n \n int n = intervals.size();\n int res[10000001] = {0};\n\n for(int i=0; i<n; i++)\n {\n res[intervals[i][0]]++;\n res[intervals[i][1]+1]--;\n }\n\n int maxi = -1;\n\n for(int i=1; i<10000001; i++)\n {\n res[i] += res[i-1];\n maxi = max(maxi, res[i]);\n }\n\n return maxi;\n }\n};\n``` | 4 | 0 | ['Array', 'Two Pointers', 'Greedy', 'Sorting', 'Heap (Priority Queue)', 'Prefix Sum', 'C++'] | 1 |
divide-intervals-into-minimum-number-of-groups | 37ms nlogn Beats 100% - two sorted vecs for start and end of interval. Count up and down and track. | 37ms-nlogn-beats-100-two-sorted-vecs-for-pngd | Intuition\nThe question is really saying "what\'s the max intersections at one time", and that\'s something we can find with a counter and a max. Keep track of | jkoudys | NORMAL | 2024-10-12T02:15:06.003603+00:00 | 2024-10-12T12:45:12.867680+00:00 | 221 | false | # Intuition\nThe question is really saying "what\'s the max intersections at one time", and that\'s something we can find with a counter and a max. Keep track of how many ranges are active.\n\n# Approach\nWe do two sorts. One against a Vec of the interval start positions, and one against the end. Then we keep checking to see if the next smallest index is a start or an end. If it\'s a start, we increment the total ongoing intervals and check if this is the maximum total intersections. If the next index is an end, we decrement it (no need to check for max here).\nWe can just exit once all the starts are done, as there\'s no reason to keep looking at ends once we\'ve found it.\n\n# Complexity\n- Time complexity:\n$$O(n log n)$$\nTwo sorts followed by a simple iteration.\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```rust []\nimpl Solution {\n pub fn min_groups(intervals: Vec<Vec<i32>>) -> i32 {\n // Step 1: Collect starts and ends into two vectors\n let mut starts: Vec<i32> = Vec::with_capacity(intervals.len());\n let mut ends: Vec<i32> = Vec::with_capacity(intervals.len());\n\n for interval in &intervals {\n starts.push(interval[0]);\n ends.push(interval[1]);\n }\n\n // Step 2: Sort the starts and ends\n starts.sort_unstable();\n ends.sort_unstable();\n\n let mut total = 0;\n let mut max_total = 0;\n let mut start_idx = 0;\n let mut end_idx = 0;\n\n // Step 3: Traverse through sorted starts and ends\n while start_idx < intervals.len() {\n if starts[start_idx] <= ends[end_idx] {\n // Process the next start\n total += 1;\n start_idx += 1;\n max_total = max_total.max(total);\n } else {\n // Process the next end\n total -= 1;\n end_idx += 1;\n }\n }\n\n max_total\n }\n}\n\n```\n\n```typescript []\n// 260ms - beats 100% on memory and runtime for typescript.\nfunction minGroups(intervals: number[][]): number {\n const [starts, ends] = intervals.reduce(\n (a, inter) => {\n a[0].push(inter[0]);\n a[1].push(inter[1]);\n return a;\n }, [[], []]);\n starts.sort((a, b) => a - b);\n ends.sort((a, b) => a - b);\n let total = 0;\n let maxTotal = 0;\n let si = 0;\n let ei = 0;\n while (si < intervals.length) {\n if (starts[si] <= ends[ei]) {\n total += 1;\n si += 1;\n maxTotal = Math.max(maxTotal, total);\n } else {\n total -= 1;\n ei += 1;\n }\n }\n return maxTotal;\n};\n```\n\n```php []\n// 446ms, beats 100% cpu and mem\nclass Solution {\n\n /**\n * @param Integer[][] $intervals\n * @return Integer\n */\n function minGroups($intervals) {\n $intervalsSize = count($intervals);\n\n // Step 1: Collect starts and ends into two arrays\n $starts = [];\n $ends = [];\n\n foreach ($intervals as $interval) {\n $starts[] = $interval[0];\n $ends[] = $interval[1];\n }\n\n // Step 2: Sort the starts and ends\n sort($starts);\n sort($ends);\n\n $total = 0;\n $maxTotal = 0;\n $startIdx = 0;\n $endIdx = 0;\n\n // Step 3: Traverse through sorted starts and ends\n while ($startIdx < $intervalsSize) {\n if ($starts[$startIdx] <= $ends[$endIdx]) {\n // Process the next start\n $total++;\n $startIdx++;\n $maxTotal = max($maxTotal, $total);\n } else {\n // Process the next end\n $total--;\n $endIdx++;\n }\n }\n\n return $maxTotal;\n }\n}\n``` | 4 | 0 | ['Array', 'PHP', 'Sorting', 'TypeScript', 'Rust'] | 2 |
divide-intervals-into-minimum-number-of-groups | C#| Line Sweep Algo | c-line-sweep-algo-by-krishnamhn009-1m57 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\nLine sweep algorithm\n Describe your approach to solving the problem. \n\ | krishnamhn009 | NORMAL | 2024-05-04T19:17:06.869810+00:00 | 2024-05-04T19:17:06.869857+00:00 | 115 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nLine sweep algorithm\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n- O(n+k)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\npublic class Solution {\n public int MinGroups(int[][] intervals) {\n int max = 0;//getting max range \n foreach (var inter in intervals){\n max = Math.Max(max, inter[1]);\n }\n\n int[] line =new int[max+2];\n foreach (var inter in intervals){\n line[inter[0]]++;\n line[inter[1] + 1]--;\n }\n int maxOverlap = 0;\n int currOverlap = 0;\n for (int i = 0; i < line.Length; i++){\n currOverlap += line[i];\n maxOverlap = Math.Max(maxOverlap, currOverlap);\n }\n\n return maxOverlap;\n }\n}\n``` | 4 | 0 | ['C#'] | 1 |
divide-intervals-into-minimum-number-of-groups | [Python 3] Line Sweep - Difference Array | python-3-line-sweep-difference-array-by-8w6q6 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | dolong2110 | NORMAL | 2023-05-06T17:55:35.626389+00:00 | 2023-05-06T17:55:35.626487+00:00 | 308 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minGroups(self, intervals: List[List[int]]) -> int:\n d = collections.defaultdict(int)\n for l, r in intervals:\n d[l] += 1\n d[r + 1] -= 1\n overlaps = res = 0\n for _, v in sorted(d.items()):\n overlaps += v\n res = max(res, overlaps)\n return res\n``` | 4 | 0 | ['Array', 'Prefix Sum', 'Python3'] | 1 |
divide-intervals-into-minimum-number-of-groups | Line Sweep Method | O(n) Solution | line-sweep-method-on-solution-by-dsharma-ence | ```\n//\t\tLine sweep methods is used when all the queries are done and we have to find\n//\t\tsome answer after that.\n\t\t\n//\t\tAssign Line array with all 0 | dsharma007 | NORMAL | 2022-09-30T20:33:19.544278+00:00 | 2022-09-30T20:38:11.909016+00:00 | 291 | false | ```\n//\t\tLine sweep methods is used when all the queries are done and we have to find\n//\t\tsome answer after that.\n\t\t\n//\t\tAssign Line array with all 0\'s.\n//\t\tLine sweep method for range(low, right) to add k works as follows:-\n//\t\t\t-> assign line[low] = k and assign line[right + 1] = -k;\n//\t\t\t-> Now after adding the following we can see that \n//\t\t\t\t* prefix Sum from [0, low) = 0;\n//\t\t\t\t* prefix Sum from [low, right] = k;\n//\t\t\t\t* prefix Sum from [right + 1, end] = 0, again \n//\t\t\t\t\tbecause +k from low and -k from right + 1 makes 0;\n\t\t\n\t\t\n//\t\texample: {{5,10},{6,8},{1,5},{2,3},{1,10}}; interval[0] = start, interval[1] = end;\n\t\t\n//\t\tLine array of max time + 1;\n\t\t\n//\t\t0 1 2 3 4 5 6 7 8 9 10 11 \n//\t\t0 0 0 0 0 0 0 0 0 0 0 0\n\t\t\n//\t\tFor interval [6 - 8] add Line[6] = 1 and Line[8 + 1] = -1;\n//\t\t0 1 2 3 4 5 6 7 8 9 10 11 \n//\t\t0 0 0 0 0 1 1 0 0 -1 0 -1\n\t\t\n//\t\tFor interval [1 - 5] add Line[1] = 1 and Line[5 + 1] = -1;\n//\t\t0 1 2 3 4 5 6 7 8 9 10 11 \n//\t\t0 1 0 0 0 1 1 0 0 -1 0 -1\n//\t\t\t\t\t -1\n\t\t\n//\t\tFor interval [2 - 3] add Line[2] = 1 and Line[3 + 1] = -1;\n//\t\t0 1 2 3 4 5 6 7 8 9 10 11 \n//\t\t0 1 1 0 -1 0 1 0 0 -1 0 -1\n\t\t\n//\t\tFor interval [1 - 10] add Line[1] = 1 and Line[10 + 1] = -1;\n//\t\t0 1 2 3 4 5 6 7 8 9 10 11 \n//\t\t0 2 1 0 -1 0 1 0 0 -1 0 -2\n\t\t\n\t\t\n//\t\tFinally Line -> 0 2 1 0 -1 0 1 0 0 -1 0 -2\n//\t\tLine prefix Sum -> 0 2 3 3 2 2 3 3 3 2 2 0\n\t\t\n//\t\tFrom this Line prefix Sum we can deduce that these many intervals coincide at every \n//\t\ttime point. The max from these is our answer;\n\t\t\n//\t\tLine prefix Sum -> 0 2 3 3 2 2 3 3 3 2 2 0\n\t\t\n//\t\t | | | | |\n//\t\t | | | | | | | | | |\n//\t\t_ | | | | | | | | | | _ This the merge interval graph;\n//\t\t\n//\t\t0 1 2 3 4 5 6 7 8 9 10 11\n\npublic static int minGroups(int[][] intervals) {\t\t\n\t\t\n\t\tint line[] = new int[1000002];\n\n\t\tfor (int[] time : intervals) {\n\t\t\tline[time[0]]++;\n\t\t\tline[time[1] + 1]--;\n\t\t}\n\n\t\tint max = line[0];\n\n\t\tfor (int i = 1; i < line.length; i++) {\n\t\t\tline[i] += line[i - 1];\n\n\t\t\tmax = Math.max(max, line[i]);\n\t\t}\n\n\t\treturn max;\n\n\t} | 4 | 0 | ['Java'] | 1 |
divide-intervals-into-minimum-number-of-groups | C++ || All methods summarised | c-all-methods-summarised-by-dash28-1ly5 | Method 1 (Optimised Brute Force)\n\nI am sure this was one of the questions you would want to avoid if you haven\'t solved questions on Line-sweep or interval m | Dash28 | NORMAL | 2022-09-11T06:58:51.401458+00:00 | 2022-09-11T10:21:55.990617+00:00 | 237 | false | Method 1 (Optimised Brute Force)\n\nI am sure this was one of the questions you would want to avoid if you haven\'t solved questions on Line-sweep or interval merging before. So I was trying to come up with a simple approach that a person might take up without any prior knowledge on how to go about merging intervals through some intelligent idea. \nThe following code is not the fastest or the most optmised version in it\'s current form, but it works correctly in elminating intervals having any sort of intersection among them. Also, complexity wise, it is O(NlogN) - please do share a more optimised version in the comments.\nYou start with any interval - say [start_0, end_0] -> the intervals that can be put into the same group as this would either have a start time of greater than *end_0* or an end time before *start_0*. How would I be able to detect such intervals efficiently? Using a set - if you can store the occurences of all start and end elements, you can simply just keep eliminating elements that could be put together in a group. So every time, I first find an interval with a given start and end, I next find all starts of intervals which are after end (you can do it easily with upper_bound function in c++). For every interval I find, I will erase the corresponding start and end values from my sets. Since you know a particular start value can be common to intervals, you need to either maintain a multiset, or make these two start values unique -> use a set of pairs with first element of the pair as the value itself, and the second one as it\'s index in the interval array. Similarly, I delete all intervals that end before the start time of the original interval we started with. Note that this is just a sanity check, you might not find such intervals at all if you sort the intervals array in the beginning. \nThe answer will be the number of times we have to do this operation.\nPlease go through the code below, I have used a set of pairs to handle duplicate start and end times. An idea using multisets works well too. Let me know in case you have any doubts. \n\n```\nclass Solution {\npublic:\n int minGroups(vector<vector<int>>& intervals) {\n sort(intervals.begin(), intervals.end());\n set<pair<int,int>> starts;\n set<pair<int,int>> ends;\n \n for(int i = 0;i < intervals.size();i++)\n {\n starts.insert({intervals[i][0], i});\n ends.insert({intervals[i][1], i});\n }\n int count = 0;\n \n while(starts.size())\n {\n auto b = starts.begin();\n int s = b->first;\n int ind = b->second;\n int e = intervals[ind][1];\n starts.erase({s,ind});\n ends.erase({e, ind});\n count++;\n int olds = s;\n \n auto it = starts.upper_bound({e,INT_MAX});\n while(it != starts.end())\n {\n s = it->first;\n ind = it->second;\n e =intervals[ind][1];\n starts.erase({s,ind});\n ends.erase({e, ind});\n olds = min(s, olds);\n it = starts.upper_bound({e,INT_MAX});\n \n }\n \n it = ends.begin();\n auto it2 = ends.lower_bound({olds, INT_MIN});\n while( it != ends.end() && it->first < olds)\n {\n e = it->first;\n ind = it->second;\n s =intervals[ind][0];\n starts.erase({s, ind});\n ends.erase({e, ind});\n it++;\n olds= min(olds, s);\n it2 = ends.lower_bound({olds, INT_MIN});\n \n }\n }\n \n return count;\n \n }\n};\n```\n\nMethod 2 - Inspired by @votrubac - MIN HEAP\n\nSuppose you have representative intervals of every group - These will be the ones having the largest end values. How would you know the group a particular interval should be added to ? You find the group whose representative element\'s end value is lesser than the start value of this particular interval - that means these won\'t intersect. If for all the given groups there is no such relation, you make a new group with this particular element as the representative. \nUse a priority queue to track all the end values, this can give you the end values of all representative elements, pop when you find a start value greater than the lowest end value in priority queue. Keep pushing the new end value. \nThe answer is the size of this queue after you process the whole array.\n```\nclass Solution {\npublic:\n int minGroups(vector<vector<int>>& intervals) {\n sort(intervals.begin(), intervals.end());\n \n priority_queue<int, vector<int>, greater<int>> pq;\n for(auto i : intervals)\n {\n if(!pq.empty() && pq.top() < i[0])\n {\n pq.pop();\n }\n pq.push(i[1]);\n }\n \n return pq.size();\n }\n};\n```\n\nMethod 3 - inspired by @lee215 (maximum intersecting intervals)\n\nYou can also view the statement in this way - if two intervals intersect they must be in different groups. What\'s the maximum number of groups we need - we need to find the maximum intersecting group of intervals (where each interval intersects with the other one). We are going to need atleast these many groups. To track the intersection of intervals, denote the start of an interval with +1 and end with -1, and put it in a vector. If the total sum I have encountered yet is 1, I am inside this interval (after start, before end, one interval case) else I am outside this interval. The maximum value of the ongoing sum after sorting the new vector would give us the maximum intersecting group -> this is our answer. \n\n```\nclass Solution {\npublic:\n int minGroups(vector<vector<int>>& intervals) {\n sort(intervals.begin(), intervals.end());\n \n vector<vector<int>> track;\n for(auto i : intervals)\n {\n track.push_back(vector<int>{i[0], 1});\n track.push_back(vector<int>{i[1]+1, -1});\n }\n \n sort(track.begin(), track.end());\n int res = 0;\n int cur = 0;\n for(int i = 0;i < track.size(); i++)\n {\n cur += track[i][1];\n res = max(res, cur);\n }\n return res;\n }\n};\n```\n\nHope it helps! Let me know in case of any doubts. | 4 | 0 | ['C'] | 2 |
divide-intervals-into-minimum-number-of-groups | sorting approach with two pointers | sorting-approach-with-two-pointers-by-ka-i1m5 | Intuition\nEarliest interval comes first. when an intervals comes, it will be checked for an empty group based on minimum end time of any interval already exist | kanna-naveen | NORMAL | 2024-10-12T14:09:51.096132+00:00 | 2024-10-12T14:09:51.096157+00:00 | 24 | false | # Intuition\nEarliest interval comes first. when an intervals comes, it will be checked for an empty group based on minimum end time of any interval already existed in any group. empty group indicates that already existed minimum end time is smaller than current start time.\n\n# Complexity\n- Time complexity:\nstoring start and endtimes separately -> N\ntwo sortings -> 2NlogN\nwhile lopp -> N\nTotal Time complexity = N+2NlogN+N = 2N+2NlogN = O(NlogN)\n\n- Space complexity:\ntwo arrays -> 2N\ntotal space complexity = 2N = O(N)\n\n# Code\n```java []\nclass Solution {\n public int minGroups(int[][] intervals) {\n// storing the start times and end times separately\n int[] startTimes=new int[intervals.length];\n int[] endTimes=new int[intervals.length];\n for(int i=0;i<intervals.length;i++){\n startTimes[i]=intervals[i][0];\n endTimes[i]=intervals[i][1];\n }\n// sortig the start and end times in ascending order to ensure that earliest times are processed first\n Arrays.sort(startTimes);\n Arrays.sort(endTimes);\n// one group is mandatry for first start time\n int minGroups=1;\n int i=1;\n//starting from 2nd start time\n int j=0;\n// j pointer keeps the track of minimum end Time\n while(i<intervals.length){\n//if new start time is less than or equal to minimum end time, it is indicating the two intervals are overlapping. So new group is required\n if(startTimes[i]<=endTimes[j]){\n minGroups++;\n }\n else{\n j++;\n }\n i++;\n }\n return minGroups;\n }\n}\n``` | 3 | 0 | ['Two Pointers', 'Sorting', 'Java'] | 0 |
divide-intervals-into-minimum-number-of-groups | Go solution with the explanation | go-solution-with-the-explanation-by-alek-x8jy | Intuition\n\nThe key challenge here is determining how many overlapping intervals we can have at any given time. If two intervals overlap, they must be in separ | alekseiapa | NORMAL | 2024-10-12T07:35:48.210375+00:00 | 2024-10-12T07:35:48.210399+00:00 | 68 | false | # Intuition\n\nThe key challenge here is determining how many overlapping intervals we can have at any given time. If two intervals overlap, they must be in separate groups. We can visualize this problem similarly to the "meeting rooms" problem, where overlapping meetings need separate rooms.\n\nTo solve this efficiently, we need to:\n1. Sort the intervals based on their start times.\n2. Keep track of the ending times of the current groups (or active intervals) to see if a new interval can fit into an existing group or if it needs a new group.\n\nA **min-heap** (priority queue) can help manage the ending times of intervals in a way that allows us to easily check if an interval can reuse an existing group.\n\n---\n\n# Approach\n\n1. **Sort the intervals**:\n - First, we sort the intervals based on their start times. This allows us to process them in chronological order.\n\n2. **Use a Min-Heap**:\n - We use a **min-heap** to keep track of the earliest ending intervals. The idea is that the interval with the smallest end time is the best candidate for reuse by a new interval that starts after it.\n\n3. **Processing intervals**:\n - For each interval, check if its start time is greater than or equal to the smallest end time in the heap. If it is, we can reuse that group (remove the top of the heap). Otherwise, we need to create a new group (push the interval\u2019s end time onto the heap).\n\n4. **Heap size**:\n - The size of the heap at the end of the process will represent the number of groups required, as each group corresponds to one currently active interval at a given time.\n\n\n# Code\n```golang []\n// MinHeap is a priority queue to keep track of the minimum end times\ntype MinHeap []int\n\nfunc (h MinHeap) Len() int { return len(h) }\nfunc (h MinHeap) Less(i, j int) bool { return h[i] < h[j] }\nfunc (h MinHeap) Swap(i, j int) { h[i], h[j] = h[j], h[i] }\n\nfunc (h *MinHeap) Push(x interface{}) {\n\t*h = append(*h, x.(int))\n}\n\nfunc (h *MinHeap) Pop() interface{} {\n\told := *h\n\tn := len(old)\n\tx := old[n-1]\n\t*h = old[:n-1]\n\treturn x\n}\n\nfunc minGroups(intervals [][]int) int {\n\t// Step 1: Sort intervals by the start time\n\tsort.Slice(intervals, func(i, j int) bool {\n\t\treturn intervals[i][0] < intervals[j][0]\n\t})\n\n\t// Step 2: Use a min-heap to keep track of the minimum end times\n\th := &MinHeap{}\n\theap.Init(h)\n\n\tfor _, interval := range intervals {\n\t\tstart, end := interval[0], interval[1]\n\n\t\t// Step 3: If the current interval starts after the earliest ending interval,\n\t\t// we can reuse the group, so pop the top of the heap\n\t\tif h.Len() > 0 && (*h)[0] < start {\n\t\t\theap.Pop(h)\n\t\t}\n\n\t\t// Step 4: Push the current interval\'s end time onto the heap\n\t\theap.Push(h, end)\n\t}\n\n\t// The number of groups needed is the size of the heap\n\treturn h.Len()\n}\n\n``` | 3 | 0 | ['Go'] | 0 |
divide-intervals-into-minimum-number-of-groups | C++ Solution || Easy to Understand || Without heap | c-solution-easy-to-understand-without-he-lh6f | Intuition\nThe problem asks for the minimum number of groups required such that no intervals within a group overlap. To solve this, we can think of treating eac | Rohit_Raj01 | NORMAL | 2024-10-12T05:55:55.795041+00:00 | 2024-10-12T05:55:55.795075+00:00 | 276 | false | # Intuition\nThe problem asks for the minimum number of groups required such that no intervals within a group overlap. To solve this, we can think of treating each interval as two events: a `start` event and an `end` event. By processing these events in order, we can keep track of the number of overlapping intervals at any point in time, and the`maximum overlap` at any point will give us the minimum number of groups required.\n\n# Approach\n1. **Transform intervals into events**:\n - For each interval `[start, end]`, consider two events:\n - A start event at time `start`, where the number of overlapping intervals increases by 1.\n - An end event at time `end + 1`, where the number of overlapping intervals decreases by 1 (we add 1 to ensure that an interval ending at time t does not overlap with another starting at the same time).\n2. **Sort events**:\n - We then sort all these events in ascending order. The idea is to process all events in chronological order, applying the necessary updates to the count of overlapping intervals.\n3. **Process the event**s:\n - As we process each event, we maintain a running count of how many intervals are currently active (overlapping at the current time). The highest value this count reaches is the answer, as it represents the maximum number of intervals that overlap at any point in time, which directly translates to the minimum number of groups required.\n\n# Complexity\n- Time complexity: $$O(nlogn)$$\n\n- Space complexity: $$O(n)$$\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int minGroups(vector<vector<int>>& intervals) {\n vector<pair<int, int>> events;\n \n for (auto& interval : intervals) {\n events.push_back({interval[0], 1}); \n events.push_back({interval[1] + 1, -1}); \n }\n \n sort(events.begin(), events.end());\n \n int maxGroups = 0, currentGroups = 0;\n \n for (auto& event : events) {\n currentGroups += event.second;\n maxGroups = max(maxGroups, currentGroups);\n }\n \n return maxGroups;\n }\n};\n\n```\n\n> ***It\u2019s not about how many challenges overlap, it\u2019s about how you manage them. Focus, organize, and the solution follows.***\n\n\n | 3 | 0 | ['Array', 'Greedy', 'Sorting', 'C++'] | 1 |
divide-intervals-into-minimum-number-of-groups | Beats 99.77% | 2 solutions | Priority Queue & Sorting | beats-9977-2-solutions-priority-queue-so-l68e | \n# Intuition\n- For both versions of the solution, the problem can be understood as finding the minimum number of groups required to hold non-overlapping inter | B_I_T | NORMAL | 2024-10-12T05:30:30.409649+00:00 | 2024-10-12T05:30:30.409685+00:00 | 678 | false | \n# Intuition\n- For both versions of the solution, the problem can be understood as finding the minimum number of groups required to hold non-overlapping intervals.\n1. Version 1 (Heap-based approach):\n\n - We use a min-heap (or priority queue) to track the end times of intervals.\n - The basic idea is that if a new interval starts after the earliest ending interval, we can reuse that group. Otherwise, we need to create a new group (push to the heap).\n2. Version 2 (Event counting approach):\n\n - We treat each interval as two events: start and end.\n - For every interval, when we encounter a start, we increase the count of active groups, and when an interval ends, we decrease the count.\n - The goal is to find the maximum number of active intervals at any point in time, which gives us the minimum number of groups needed.\n---\n# Approach (Version 1 - Heap-based)\n1. Sort intervals by start time: We first sort the intervals based on their start time.\n2. Min-heap for end times: Use a min-heap to keep track of the end times of active intervals.\n3. Greedy Group Assignment: For each interval:\n - If the current interval starts after the earliest ending interval (the top of the heap), we can reuse that group and pop the top.\n - Otherwise, we need to assign a new group (push to the heap).\n4. Result: The size of the heap at the end represents the minimum number of groups required.\n# Time Complexity (Version 1)\n - Sorting the intervals takes O(n log n), where n is the number of intervals.\n - For each interval, heap operations (push and pop) take O(log n). So the total time complexity is O(n log n).\n# Space Complexity (Version 1)\n - We use a heap, which stores at most n elements, so the space complexity is O(n).\n# Code\n```cpp []\nclass Solution {\npublic:\n int minGroups(vector<vector<int>>& intervals) {\n sort(intervals.begin(),intervals.end());\n priority_queue<int,vector<int>,greater<int>> pq;\n for(const auto & interval : intervals){\n if(!pq.empty() && pq.top() < interval[0]){\n pq.pop();\n }\n pq.push(interval[1]);\n }\n return pq.size();\n }\n};\n```\n```Java []\nclass Solution {\n public int minGroups(int[][] intervals) {\n Arrays.sort(intervals, (a, b) -> Integer.compare(a[0], b[0]));\n PriorityQueue<Integer> pq = new PriorityQueue<>();\n \n for (int[] interval : intervals) {\n if (!pq.isEmpty() && pq.peek() < interval[0]) {\n pq.poll();\n }\n pq.offer(interval[1]);\n }\n \n return pq.size();\n }\n}\n\n```\n```Python3 []\n\nclass Solution:\n def minGroups(self, intervals: List[List[int]]) -> int:\n events = []\n \n for start, end in intervals:\n events.append((start, 1))\n events.append((end + 1, -1))\n \n events.sort()\n \n res = curr = 0\n for _, delta in events:\n curr += delta\n res = max(res, curr)\n \n return res\n```\n```Javascript []\nvar minGroups = function(intervals) {\n intervals.sort((a, b) => a[0] - b[0]);\n let pq = new MinPriorityQueue();\n \n for (let [start, end] of intervals) {\n if (!pq.isEmpty() && pq.front().element < start) {\n pq.dequeue();\n }\n pq.enqueue(end);\n }\n \n return pq.size();\n};\n\n```\n# Approach (Version 2 - Event-based)\n1. Transform intervals to events:\n - For each interval, create two events:\n - One for the start of the interval (+1 event).\n - One for the end of the interval (-1 event, adjusted to be exclusive by adding 1 to the end time).\n2. Sort events: Sort the events based on the time.\n3. Simulate event processing:\n - Traverse through the events, updating the number of active intervals (groups).\n - Track the maximum number of active intervals, which will give the minimum number of groups required.\n# Time Complexity (Version 2)\n- Creating the event list takes O(n).\n- Sorting the events takes O(n log n).\n- Traversing the events takes O(n).\n- Therefore, the total time complexity is O(n log n).\n# Space Complexity (Version 2)\n- We use an auxiliary list of events, which takes O(2n) space. So, the space complexity is O(n).\n# Code\n```cpp []\nclass Solution {\npublic:\n int minGroups(vector<vector<int>>& intervals) {\n vector<pair<int,int>> vec;\n for(const auto & interval : intervals){\n vec.push_back({interval[0],1});\n vec.push_back({interval[1]+1,-1});\n }\n sort(vec.begin(),vec.end());\n int res = 0,maxi = 0;\n for(const auto & [i,j] : vec){\n maxi += j;\n res = max(res,maxi);\n }\n return res;\n }\n};\n```\n```Java []\n\nclass Solution {\n public int minGroups(int[][] intervals) {\n List<int[]> events = new ArrayList<>();\n \n // Create events for start and end times\n for (int[] interval : intervals) {\n events.add(new int[] {interval[0], 1}); // start event\n events.add(new int[] {interval[1] + 1, -1}); // end event (add 1 to make end exclusive)\n }\n \n // Sort by time, and for same time, process end (-1) before start (+1)\n events.sort((a, b) -> {\n if (a[0] != b[0]) return Integer.compare(a[0], b[0]);\n return Integer.compare(a[1], b[1]); // prioritize end events (-1) over start events (+1)\n });\n \n int res = 0, curr = 0;\n // Process events and track maximum concurrent intervals\n for (int[] event : events) {\n curr += event[1]; // add or subtract based on event type (+1 for start, -1 for end)\n res = Math.max(res, curr);\n }\n \n return res;\n }\n}\n\n\n```\n```Python3 []\nclass Solution:\n def minGroups(self, intervals: List[List[int]]) -> int:\n events = []\n \n for start, end in intervals:\n events.append((start, 1))\n events.append((end + 1, -1))\n \n events.sort()\n \n res = curr = 0\n for _, delta in events:\n curr += delta\n res = max(res, curr)\n \n return res\n\n```\n```Javascript []\nvar minGroups = function(intervals) {\n let events = [];\n \n // Create events for start and end times\n for (let [start, end] of intervals) {\n events.push([start, 1]); // Start event (increment)\n events.push([end + 1, -1]); // End event (decrement)\n }\n \n // Sort events by time, with end events (-1) prioritized if same time\n events.sort((a, b) => {\n if (a[0] !== b[0]) {\n return a[0] - b[0]; // Sort by time\n } else {\n return a[1] - b[1]; // Prioritize end event (-1) over start event (+1)\n }\n });\n \n let res = 0, curr = 0;\n // Process the events\n for (let [, delta] of events) {\n curr += delta; // Update current number of overlapping intervals\n res = Math.max(res, curr); // Track the maximum overlap\n }\n \n return res;\n};\n\n\n```\n\n | 3 | 0 | ['Array', 'Greedy', 'Sorting', 'Heap (Priority Queue)', 'C++', 'Java', 'Python3', 'JavaScript'] | 2 |
divide-intervals-into-minimum-number-of-groups | Python | Line Sweep | 89% T 40% S | python-line-sweep-89-t-40-s-by-patrikk-kw68 | Intuition\n\n\nAn alternative approach to this problem is simply "returning the max number of overlapping intervals". \n\nThis can easily be accomplished using | Patrikk_ | NORMAL | 2024-10-12T00:40:18.174934+00:00 | 2024-10-12T00:40:18.174965+00:00 | 181 | false | **Intuition**\n\n\nAn alternative approach to this problem is simply "returning the max number of overlapping intervals". \n\nThis can easily be accomplished using the line-sweep algorithm where we increment the start of our interval by ```1``` and decrement the ```end + 1``` interval by ```1```. We decrement the ```end + 1``` value because our range is inclusive.\n\nWe can then sort the keys in our ```intervalMap``` and iterate over all the ranges with a ```runner``` variable, storing the maximum value.\n\n\n\n**Complexity**\n\n\nTime Complexity: O(n log n)\nSpace Complexity: O(n)\n\n```python\nfrom collections import defaultdict\nclass Solution:\n def minGroups(self, intervals: List[List[int]]) -> int:\n \n intervalMap = defaultdict(int)\n runner, output = 0, 0\n \n # populate interval map\n for start, end in intervals:\n intervalMap[start] += 1\n intervalMap[end+1] -= 1 # inclusive range\n \n # line-sweep interval map\n for key in sorted(intervalMap.keys()):\n runner += intervalMap[key]\n output = max(output, runner)\n \n return output\n\n```\n\n**Without Sorting**\n\nA possible optimization is not sorting - we can store the min/max of our ranges while populating our ```intervalMap``` and just loop over those. This might result in extraneous calculations depending on the possible size of the interval values themselves.\n\n**Complexity**\n\nO(n + m) where m is the range of all possible values within our interval\nO(n)\n\n```python\nfrom collections import defaultdict\nclass Solution:\n def minGroups(self, intervals: List[List[int]]) -> int:\n \n intervalMap = defaultdict(int)\n runner, output = 0, 0\n minRange, maxRange = float(\'inf\'), float(\'-inf\')\n \n # populate interval map\n for start, end in intervals:\n \n minRange = min(minRange, start)\n maxRange = max(maxRange, end)\n \n intervalMap[start] += 1\n intervalMap[end+1] -= 1 # inclusive range\n \n # line-sweep interval map\n for key in range(minRange, maxRange + 1):\n runner += intervalMap[key]\n output = max(output, runner)\n \n return output | 3 | 0 | ['Sorting', 'Python', 'Python3'] | 1 |
divide-intervals-into-minimum-number-of-groups | C++ || turn into events for opening and closing the intervals | c-turn-into-events-for-opening-and-closi-5hqy | Solution 1: turn into discrete events for the left and right end of the interval and sweep\n\ncpp\n static int minGroups(const vector<vector<int>>& intervals | heder | NORMAL | 2022-09-11T16:26:55.370538+00:00 | 2022-09-11T16:26:55.370580+00:00 | 146 | false | ### Solution 1: turn into discrete events for the left and right end of the interval and sweep\n\n```cpp\n static int minGroups(const vector<vector<int>>& intervals) {\n vector<int> events;\n events.reserve(size(intervals) * 2);\n for (const vector<int>& interval : intervals) {\n const int left = interval[0] << 1;\n // The closing event are after the opening events of the\n // intervals. With that we get the overlap we want.\n const int right = (interval[1] << 1) | 1;\n events.push_back(left);\n events.push_back(right);\n }\n sort(begin(events), end(events));\n int overlaps = 0;\n int max_overlaps = 0;\n for (const int event : events) {\n overlaps += (event & 1) ? -1 : 1;\n max_overlaps = max(max_overlaps, overlaps);\n }\n return max_overlaps;\n }\n```\n\n**Complexity Analysis**\n * Time Complexity: O(n log n). The sorting is the dominate part.\n * Space Complexity: O(n). We need twice the memory for the events.\n\n_As always: Feedback, comments, and questions are welcome. Please upvote if you like this post._\n | 3 | 0 | ['C'] | 1 |
divide-intervals-into-minimum-number-of-groups | Simple Java Solution || EAsy to understand || O(n) solution | simple-java-solution-easy-to-understand-9c50p | \nclass Solution {\n public int minGroups(int[][] intervals) {\n int m = 0; \n for(int i[] : intervals){\n m = Math.max(m,i[0]);\n | Himanshu_Goyal_517 | NORMAL | 2022-09-11T04:40:03.826395+00:00 | 2022-09-11T04:40:03.826437+00:00 | 308 | false | ```\nclass Solution {\n public int minGroups(int[][] intervals) {\n int m = 0; \n for(int i[] : intervals){\n m = Math.max(m,i[0]);\n m = Math.max(m,i[1]);\n }\n long arr[] = new long[m+2];\n for(int a[] : intervals){\n arr[a[0]] += 1;\n arr[a[1]+1] -= 1;\n }\n long max = 0l;\n for(int i = 1; i <= m +1; i++){\n arr[i] += arr[i-1];\n max = Math.max(max,arr[i]);\n \n }\n return (int)max;\n }\n}\n``` | 3 | 0 | ['Prefix Sum', 'Java'] | 2 |
divide-intervals-into-minimum-number-of-groups | c++ solution line sweep | c-solution-line-sweep-by-dilipsuthar60-p2bx | \nclass Solution {\npublic:\n int minGroups(vector<vector<int>>& nums) {\n map<int,int>mp;\n for(auto it:nums)\n {\n mp[it[0] | dilipsuthar17 | NORMAL | 2022-09-11T04:03:15.565770+00:00 | 2022-09-11T04:03:15.565807+00:00 | 231 | false | ```\nclass Solution {\npublic:\n int minGroups(vector<vector<int>>& nums) {\n map<int,int>mp;\n for(auto it:nums)\n {\n mp[it[0]]++;\n mp[it[1]+1]--;\n }\n int sum=0;\n for(auto &[a,b]:mp)\n {\n sum+=b;\n b=sum;\n }\n int ans=0;\n for(auto &[a,b]:mp)\n {\n ans=max(ans,b);\n }\n return ans;\n }\n};\n``` | 3 | 0 | ['C', 'C++'] | 1 |
divide-intervals-into-minimum-number-of-groups | [Python3] Sort + Heap | python3-sort-heap-by-helnokaly-f7xx | \nclass Solution:\n def minGroups(self, intervals: List[List[int]]) -> int:\n intervals.sort()\n pq = []\n for interval in intervals:\n | helnokaly | NORMAL | 2022-09-11T04:01:18.846754+00:00 | 2022-09-11T04:18:53.353805+00:00 | 553 | false | ```\nclass Solution:\n def minGroups(self, intervals: List[List[int]]) -> int:\n intervals.sort()\n pq = []\n for interval in intervals:\n if not pq or interval[0] <= pq[0]:\n heapq.heappush(pq, interval[1])\n else:\n\t\t\t\theapq.heappop(pq)\n\t\t\t\theapq.heappush(pq, interval[1])\n return len(pq)\n``` | 3 | 0 | ['Sorting', 'Heap (Priority Queue)', 'Python3'] | 0 |
divide-intervals-into-minimum-number-of-groups | [Python3/Rust] Max DP Overlap | python3rust-max-dp-overlap-by-agrpractic-71t6 | Weekly Contest 310 Submission\n\nDisclaimer \nMy contest submission was written in Python3. I attempted submissions after the contest and noticed that this solu | AgrPractice | NORMAL | 2022-09-11T04:00:26.678102+00:00 | 2023-01-16T19:05:53.422291+00:00 | 632 | false | **Weekly Contest 310 Submission**\n\n**Disclaimer** \nMy contest submission was written in ```Python3```. I attempted submissions after the contest and noticed that this solution will TLE on average (as noted by ```xavier-xia-99``` it seems to be an approximate 10% acceptance chance in ```Python3```). Following the contest I wrote the same solution in ```Rust``` which does not TLE as of writing.\n\n**Intuition**\nIf we add a new interval to the input array that does not overlap with any other interval we can always group it with an existing group (no effect on the answer, unless added to an empty array). Furthermore, if an additional interval is added and does not overlap the current largest group it can be added to another group (resulting in the answer remaining the same). The problem becomes: **At what frequency does the most common subinterval occur?**\n\n**Max DP Overlap**\n1. Find the maximum ending value in all intervals (```max_val```).\n2. Create a ```dp``` array of size ```max_val``` that represents the occurrence of each number in the intervals from 1 to ```max_val```.\n3. Linearly compute the occurrences through a prefix sum.\n4. Return the maximum occurrence.\n\n**Python3 (will TLE on average)**\n```Python3 []\nclass Solution:\n def minGroups(self, I: List[List[int]]) -> int:\n max_val = max([v for _, v in I])\n dp = [0]*(max_val + 2)\n \n #Define intervals\n for u, v in I:\n dp[u] += 1\n dp[v + 1] -= 1\n \n #Compute prefix sum to get frequency\n for idx in range(1, len(dp)):\n dp[idx] += dp[idx - 1]\n \n #Return maximum overlap\n return max(dp)\n```\n**Rust (passes)**\n```Rust []\nimpl Solution {\n pub fn min_groups(I: Vec<Vec<i32>>) -> i32 {\n let mut max_val = 0;\n let mut res = 0;\n \n for idx in 0..I.len() {\n max_val = max_val.max(I[idx][1]);\n }\n \n let mut dp = vec![0; (max_val) as usize + 2];\n \n //Define intervals\n for idx in 0..I.len() {\n dp[I[idx][0] as usize] += 1;\n dp[I[idx][1] as usize + 1] -= 1;\n }\n \n //Compute prefix sum to get frequency\n for idx in 1..dp.len() {\n dp[idx] += dp[idx - 1];\n res = res.max(dp[idx]);\n }\n \n //Return maximum overlap\n res\n }\n}\n``` | 3 | 0 | ['Prefix Sum', 'Python3', 'Rust'] | 3 |
divide-intervals-into-minimum-number-of-groups | sort & priority_queue(simple & easy) | sort-priority_queuesimple-easy-by-kamoji-jghn | Intuition\nWe need to divide the intervals into groups such that no two intervals in the same group overlap. The idea is to keep track of how many groups are ne | kamojishashank00 | NORMAL | 2024-10-19T19:17:33.531929+00:00 | 2024-10-19T19:17:33.531960+00:00 | 6 | false | # Intuition\nWe need to divide the intervals into groups such that no two intervals in the same group overlap. The idea is to keep track of how many groups are needed at a time, using a priority queue (min-heap) to maintain the minimum end times of the groups that are being formed.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nSort intervals: \nFirst, we sort the intervals by their start time. This helps us process intervals in increasing order of their start times, ensuring that we are placing the earliest available intervals into groups.\n\nUse a min-heap: \nA min-heap (priority queue) is used to store the end times of the intervals in the current groups. The top of the heap (smallest element) represents the earliest end time among all the ongoing intervals in the groups.\n\nProcessing intervals:\nFor each interval, check if the current interval\'s start time is greater than the smallest end time in the heap (pq.top()). If it is, this means that the current interval can be placed in an existing group, so we remove the top of the heap and add the new end time to the heap.\nIf the interval cannot fit into an existing group (i.e., it overlaps with the earliest ending interval), we need to create a new group, so we simply add the interval\'s end time to the heap and increment the group count.\nReturn the number of groups: The size of the heap at the end will give the minimum number of groups needed since each element in the heap represents the end time of an interval in a separate group.\n# Complexity\n- Time complexity: \nO(nlogn)\n\n- Space complexity:\nO(n) \n\n# Code\n```cpp []\nclass Solution {\npublic:\n int minGroups(vector<vector<int>>& intervals) {\n std::priority_queue<int,vector<int>,greater<int>>pq;\n std::sort(intervals.begin(),intervals.end());\n pq.push(intervals[0][1]);\n int count=1;\n for(int i=1;i<intervals.size();i++){\n if(intervals[i][0]>pq.top()){\n pq.pop(); pq.push(intervals[i][1]);\n }\n else{\n pq.push(intervals[i][1]); count++;\n }\n }\n return count;\n }\n};\n``` | 2 | 0 | ['Heap (Priority Queue)', 'C++'] | 0 |
divide-intervals-into-minimum-number-of-groups | Most Simple Approach || Fast 100% Beats || Using a Min-Heap | most-simple-approach-fast-100-beats-usin-js8v | Code\npython3 []\nclass Solution:\n def minGroups(self, intervals: List[List[int]]) -> int:\n intervals.sort(key=lambda x: x[0])\n ok = []\n\n | anand_shukla1312 | NORMAL | 2024-10-12T15:07:37.015964+00:00 | 2024-10-12T15:07:37.016004+00:00 | 56 | false | # Code\n```python3 []\nclass Solution:\n def minGroups(self, intervals: List[List[int]]) -> int:\n intervals.sort(key=lambda x: x[0])\n ok = []\n\n for i,j in intervals:\n if ok and ok[0] < i:\n heappop(ok)\n heappush(ok,j)\n \n a = len(ok)\n return a\n\n``` | 2 | 0 | ['Python3'] | 1 |
divide-intervals-into-minimum-number-of-groups | simplest code using 2 pointers | simplest-code-using-2-pointers-by-yourst-g07h | Intuition\nUse 2 pointers\n\n# Complexity\n- Time complexity:\nO(nlogn)\n\n- Space complexity:\nO(n)\n\n# Code\npython3 []\nclass Solution:\n def minGroups(s | Yourstruly_priyanshu | NORMAL | 2024-10-12T13:29:46.069909+00:00 | 2024-10-12T13:29:46.069948+00:00 | 9 | false | # Intuition\nUse 2 pointers\n\n# Complexity\n- Time complexity:\nO(nlogn)\n\n- Space complexity:\nO(n)\n\n# Code\n```python3 []\nclass Solution:\n def minGroups(self, intervals: List[List[int]]) -> int:\n s = sorted(i[0] for i in intervals)\n end = sorted(i[1] for i in intervals)\n e, g = 0, 0\n for s in s:\n if s > end[e]:\n e += 1\n else:\n g += 1\n return g\n``` | 2 | 0 | ['Two Pointers', 'Python3'] | 0 |
divide-intervals-into-minimum-number-of-groups | 🔥BEATS 💯 % 🎯 |✨SUPER EASY BEGINNERS 👏 | beats-super-easy-beginners-by-codewithsp-ggdt | \n\n# Intuition\nThe problem asks to find the minimum number of groups that can accommodate overlapping intervals. This can be thought of as an interval schedul | CodeWithSparsh | NORMAL | 2024-10-12T11:11:01.930416+00:00 | 2024-10-12T11:11:01.930449+00:00 | 19 | false | \n\n# Intuition\nThe problem asks to find the minimum number of groups that can accommodate overlapping intervals. This can be thought of as an interval scheduling problem where we need to track how many intervals overlap at any given point in time. Each overlapping interval would require its own group.\n\n# Approach\n1. **Event-based approach**:\n - Convert each interval into two events: a start event and an end event.\n - For the start of an interval, it indicates an interval is beginning, and for the end of an interval, it indicates an interval is ending.\n \n2. **Processing events**:\n - We process all events in chronological order. For overlapping intervals, the number of ongoing intervals at a particular time would increase.\n - To maintain the correct sequence of events, we sort the events by their time, and in case of a tie (same time), we prioritize the end event.\n \n3. **Track the maximum number of active intervals**:\n - As we iterate through the sorted events, we track how many intervals are active at any point. The maximum number of active intervals at any given time is the number of groups we need.\n\n# Complexity\n- **Time Complexity**: \n - Creating the events list takes \\(O(n)\\), where `n` is the number of intervals.\n - Sorting the events takes \\(O(n \\log n)\\) due to sorting.\n - Processing the events takes \\(O(n)\\).\n - Overall time complexity is \\(O(n \\log n)\\).\n \n- **Space Complexity**: \n - We use an additional list to store the events, which takes \\(O(n)\\) space.\n\n```dart []\nclass Solution {\n int minGroups(List<List<int>> intervals) {\n List<List<int>> events = [];\n\n // Create events for the start and end of each interval\n for (var interval in intervals) {\n int start = interval[0];\n int end = interval[1];\n events.add([start, 1]); // 1 indicates an interval is starting\n events.add([end + 1, -1]); // -1 indicates an interval is ending\n }\n\n // Sort events: first by time, and in case of a tie, by type of event\n events.sort((a, b) {\n if (a[0] == b[0]) {\n return a[1].compareTo(b[1]);\n }\n return a[0].compareTo(b[0]);\n });\n\n int maxGroups = 0;\n int activeIntervals = 0;\n\n // Process all events\n for (var event in events) {\n activeIntervals += event[1]; // Add or subtract based on event type\n maxGroups = maxGroups < activeIntervals ? activeIntervals : maxGroups;\n }\n\n return maxGroups;\n }\n}\n```\n\n\n```python []\nclass Solution:\n def minGroups(self, intervals: List[List[int]]) -> int:\n events = []\n \n # Create events for the start and end of each interval\n for interval in intervals:\n start, end = interval\n events.append((start, 1)) # 1 indicates an interval is starting\n events.append((end + 1, -1)) # -1 indicates an interval is ending\n \n # Sort events by time, and in case of tie, by type of event\n events.sort(key=lambda x: (x[0], x[1]))\n\n max_groups = 0\n active_intervals = 0\n\n # Process all events\n for event in events:\n active_intervals += event[1]\n max_groups = max(max_groups, active_intervals)\n\n return max_groups\n```\n\n```java []\nimport java.util.*;\n\nclass Solution {\n public int minGroups(int[][] intervals) {\n List<int[]> events = new ArrayList<>();\n \n // Create events for the start and end of each interval\n for (int[] interval : intervals) {\n events.add(new int[]{interval[0], 1}); // 1 indicates interval is starting\n events.add(new int[]{interval[1] + 1, -1}); // -1 indicates interval is ending\n }\n \n // Sort events: first by time, and in case of tie, by type of event\n Collections.sort(events, (a, b) -> {\n if (a[0] == b[0]) return Integer.compare(a[1], b[1]);\n return Integer.compare(a[0], b[0]);\n });\n\n int maxGroups = 0;\n int activeIntervals = 0;\n\n // Process all events\n for (int[] event : events) {\n activeIntervals += event[1];\n maxGroups = Math.max(maxGroups, activeIntervals);\n }\n\n return maxGroups;\n }\n}\n```\n```javascript []\nvar minGroups = function(intervals) {\n let events = [];\n\n // Create events for the start and end of each interval\n for (let [start, end] of intervals) {\n events.push([start, 1]); // 1 indicates interval is starting\n events.push([end + 1, -1]); // -1 indicates interval is ending\n }\n\n // Sort events: first by time, and in case of tie, by type of event\n events.sort((a, b) => {\n if (a[0] === b[0]) return a[1] - b[1];\n return a[0] - b[0];\n });\n\n let maxGroups = 0;\n let activeIntervals = 0;\n\n // Process all events\n for (let [time, type] of events) {\n activeIntervals += type;\n maxGroups = Math.max(maxGroups, activeIntervals);\n }\n\n return maxGroups;\n};\n```\n```cpp []\nclass Solution {\npublic:\n int minGroups(vector<vector<int>>& intervals) {\n vector<pair<int, int>> events;\n \n // Create events for the start and end of each interval\n for (auto& interval : intervals) {\n events.push_back({interval[0], 1}); // 1 indicates interval is starting\n events.push_back({interval[1] + 1, -1}); // -1 indicates interval is ending\n }\n\n // Sort events: first by time, and in case of tie, by type of event\n sort(events.begin(), events.end(), [](pair<int, int>& a, pair<int, int>& b) {\n if (a.first == b.first) return a.second < b.second;\n return a.first < b.first;\n });\n\n int maxGroups = 0;\n int activeIntervals = 0;\n\n // Process all events\n for (auto& event : events) {\n activeIntervals += event.second;\n maxGroups = max(maxGroups, activeIntervals);\n }\n\n return maxGroups;\n }\n};\n```\n\n {:style=\'width:250px\'}\n | 2 | 0 | ['C++', 'Python3', 'JavaScript', 'Dart'] | 0 |
divide-intervals-into-minimum-number-of-groups | Original Solution🔥🔥|| Using maps and greedy✍️✍️ || C++ | original-solution-using-maps-and-greedy-5ooeg | Intuition\n Describe your first thoughts on how to solve this problem. \nThe first thought to solving this question is to find out the maximum number of interva | Johnnys_Zero | NORMAL | 2024-10-12T10:25:57.062923+00:00 | 2024-10-12T10:25:57.062968+00:00 | 3 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe first thought to solving this question is to find out the maximum number of intervals that intersect at a certain point, which will be the minimum number of groups required.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nTo find this maximum intersection point of intervals, we first iterate through the intervals vector and keep note of 3 things using a set and 2 maps, all the time values that appear in the vector (so we can iterate through this set later on, rather than having to iterate from 1 to 1e6 to get our answer) and the maps keep track of number of intervals beginning and ending at certain times.\n```C++ []\nfor(int i=0;i<n;i++){\n total.insert(intervals[i][0]);\n total.insert(intervals[i][1]);\n m1[intervals[i][0]]++;\n m2[intervals[i][1]]++;\n}\n```\n\n\n\nNow we iterate through the set and keep a track of active intervals at all points of time, while also keeping a track of the maximum value of active yet, which will be our answer at the end.\n```C++ []\nfor(int x: total){\n if(m1[x]>0){\n active+=m1[x];\n }\n ans = max(active,ans);\n if(m2[x]>0){\n active-=m2[x];\n }\n}\n```\n\n# Complexity\n- Time complexity: O(NLogN)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int minGroups(vector<vector<int>>& intervals) {\n int n = intervals.size();\n map <int,int> m1,m2;\n set<int>total; //Set holds any time value that appears in intervals\n for(int i=0;i<n;i++){\n total.insert(intervals[i][0]);\n total.insert(intervals[i][1]);\n m1[intervals[i][0]]++; //m1 holds the number of intervals that start at a certain time\n m2[intervals[i][1]]++; //m2 holds the number of intervals that end at a certain time\n }\n int active = 0;//active will store the number of active intervals at any certain point\n int ans = 0;//ans will hold the max value of active\n for(int x: total){\n if(m1[x]>0){\n active+=m1[x];//addings new intervals to active\n }\n ans = max(active,ans);\n if(m2[x]>0){\n active-=m2[x];//removing intervals that have ended\n }\n }\n return ans;\n }\n};\n``` | 2 | 0 | ['Greedy', 'Sorting', 'C++'] | 0 |
divide-intervals-into-minimum-number-of-groups | ✅ Simple Java Solution | simple-java-solution-by-harsh__005-x42y | CODE\n\n### Solution 1:\nJava []\npublic int minGroups(int[][] intervals) {\n\tArrays.sort(intervals, (a,b)->{\n\t\tif(a[0] == b[0]) return a[1]-b[1];\n\t\tretu | Harsh__005 | NORMAL | 2024-10-12T09:15:46.464349+00:00 | 2024-10-12T09:26:42.738793+00:00 | 83 | false | ## **CODE**\n\n### Solution 1:\n```Java []\npublic int minGroups(int[][] intervals) {\n\tArrays.sort(intervals, (a,b)->{\n\t\tif(a[0] == b[0]) return a[1]-b[1];\n\t\treturn a[0]-b[0];\n\t});\n\n\tint n = intervals.length, max = 0, size = 0;\n\tTreeMap<Integer, Integer> map = new TreeMap<>();\n\tfor(int[] inv: intervals) {\n\t\tif(map.floorKey(inv[0]-1) != null) {\n\t\t\tint key = map.floorKey(inv[0]-1);\n\t\t\tint value = map.get(key);\n\t\t\tif(value == 1) map.remove(key);\n\t\t\telse map.put(key, value-1);\n\t\t} else {\n\t\t\tmax++;\n\t\t}\n\t\tmap.put(inv[1], map.getOrDefault(inv[1], 0) + 1);\n\t}\n\treturn max;\n}\n```\n---\n\n### Solution 2:\n```Java []\npublic int minGroups(int[][] intervals) {\n\tTreeMap<Integer, Integer> map = new TreeMap<>();\n\tfor(int[] inv: intervals) {\n\t\tmap.put(inv[0], map.getOrDefault(inv[0], 0) + 1);\n\t\tmap.put(inv[1]+1, map.getOrDefault(inv[1]+1, 0) - 1);\n\t}\n\n\tint ct=0, max = 0;\n\tfor(int key : map.keySet()) {\n\t\tct += map.get(key);\n\t\tmax = Math.max(max, ct);\n\t}\n\treturn max;\n}\n``` | 2 | 0 | ['Heap (Priority Queue)', 'Java'] | 1 |
divide-intervals-into-minimum-number-of-groups | O(NLogN) solution || Priority Queue || Very easy to understand | onlogn-solution-priority-queue-very-easy-8jk2 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n1. Sort the array based | anonymous_now | NORMAL | 2024-10-12T05:45:39.053645+00:00 | 2024-10-12T05:45:39.053668+00:00 | 97 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Sort the array based on left value\n2. We can add a interval in a group if and only if its left value is greater than group max value (max right value)\n3. So we need to find smallest (right) value from any group which is less than current interval left value\n4. Use Min-heap to get this value in O(1) time , add every interval right value in min-heap\n5. if min-heap top has a value less than this interval left value then it means we can add it in pre existing group which ends at min-heap peek value\n6. If min-heap top dont have a value less than this interval left then create a new group by inc grp var\n5. Add the current interval right value in min-heap\n6. return grp at last \n\n# Complexity\n- Time complexity: O(NLogN)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```kotlin []\nclass Solution {\n fun minGroups(intervals: Array<IntArray>): Int {\n intervals.sortWith(compareBy{it[0]})\n val pq = PriorityQueue<Int>()\n var grp = 1\n pq.add(intervals[0][1])\n for(i in 1..intervals.size-1){\n if(pq.peek() < intervals[i][0]){\n pq.poll()\n } else {\n grp++\n }\n pq.add(intervals[i][1])\n }\n return grp \n }\n}\n// [[1, 5], [3, 8], [10, 15], [1, 5], [3, 8]]\n//(1,5),(10,25)\n//(3,8)\n//(1,5)\n// (3,8)\n``` | 2 | 0 | ['Sorting', 'Heap (Priority Queue)', 'Kotlin'] | 1 |
divide-intervals-into-minimum-number-of-groups | Detailed step by step easy explanation || Sweepline || Index Compression || Clean Code || C++ | detailed-step-by-step-easy-explanation-s-ijdg | Approach\n Describe your approach to solving the problem. \nWe consider a sorted array containing t_minimum to t_maximum. \nFor example, consider [5, 10], [6, 8 | shayonp | NORMAL | 2024-10-12T05:27:02.866906+00:00 | 2024-10-12T05:27:02.866938+00:00 | 15 | false | # Approach\n<!-- Describe your approach to solving the problem. -->\nWe consider a sorted array containing t_minimum to t_maximum. \nFor example, consider [5, 10], [6, 8], [1, 5] [2, 3] and [1, 10]. We have to update the array, [1, 2, 3, 4, 5, 6, 7, 8, 9, 10],according to each of the intervals.\n\nSo, originally we have.\n\nNow we process the intervals one by one.\n[5, 10]\n\n[6, 8]\n\n[1, 5]\n\n[2, 3]\n\n[1, 10]\n\nAs we can see the maximum number of intervals at any point is 3, so the answer is 3. In general the answer is the maximum element of the array.\nThere are two main problems here, t_max - t_min can go upto 1e9 exceeding the memory constraints and the updates if done individuallt and pointwise will exceed the time constrants.\nTo address the latter, we will use a sweep-line algorithm.[[https://leetcode.com/discuss/study-guide/2166045/line-sweep-algorithms]()]\nFor the former, we observe that every index that is not present in the original array, i.e, the indices which are not the ends of an interval can be discarded without changing the answer. Therefore we can use index compression to reduce the size of the array to permissible limits.\nEg-> [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] becomes [1, 2, 3, 5, 6, 8, 10].\nThis can be achieved using a hashmap. \n\n# Code\n```cpp []\nclass Solution {\npublic:\n int minGroups(vector<vector<int>>& intervals) {\n set<int> st;\n for(auto &interval: intervals) {\n st.insert(interval[0]);\n st.insert(interval[1]);\n }\n\n vector<int> timestamps;\n for(int val: st) {\n timestamps.push_back(val);\n }\n\n unordered_map<int, int> compressed_indices;\n for(int i = 0; i < timestamps.size(); i++) {\n compressed_indices[timestamps[i]] = i + 1;\n }\n int n = timestamps.size();\n vector<int> sweep_line(n + 2, 0);\n\n for(auto &interval: intervals) {\n sweep_line[compressed_indices[interval[0]]]++;\n sweep_line[compressed_indices[interval[1]] + 1]--;\n }\n \n int minimumGroups = 0;\n for(int i = 1; i <= n; i++) {\n sweep_line[i] = sweep_line[i - 1] + sweep_line[i];\n minimumGroups = max(minimumGroups, sweep_line[i]);\n }\n return minimumGroups;\n }\n};\n``` | 2 | 0 | ['C++'] | 1 |
divide-intervals-into-minimum-number-of-groups | Easy C++ Solution Set Lower Bound | easy-c-solution-set-lower-bound-by-sahil-yfxj | Approach\nFind a end time in set which is just previous to current start time.\n\n# Complexity\n- Time complexity:O(NLogN)\n\n- Space complexity:O(N)\n\n# Code\ | Sahil_0902 | NORMAL | 2024-10-12T04:56:17.648679+00:00 | 2024-10-12T04:56:17.648716+00:00 | 71 | false | # Approach\nFind a end time in set which is just previous to current start time.\n\n# Complexity\n- Time complexity:O(NLogN)\n\n- Space complexity:O(N)\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int minGroups(vector<vector<int>>& intervals) {\n \n sort(begin(intervals),end(intervals));\n multiset<int>s;\n\n for(auto x:intervals){\n int st=x[0],en=x[1];\n auto it=s.lower_bound(st);\n if(it!=s.begin()) s.erase(--it);\n s.insert(en);\n }\n return s.size();\n }\n};\n``` | 2 | 0 | ['Array', 'Greedy', 'Sorting', 'C++'] | 1 |
divide-intervals-into-minimum-number-of-groups | Best way to solve in java do not forget to UPVOTE | best-way-to-solve-in-java-do-not-forget-08qnn | Intuition\nWe need to group intervals such that no intervals in the same group overlap. By sorting the intervals based on their start and end times, we can trac | rnt07s | NORMAL | 2024-10-12T04:14:59.495973+00:00 | 2024-10-12T04:14:59.496007+00:00 | 99 | false | # Intuition\nWe need to group intervals such that no intervals in the same group overlap. By sorting the intervals based on their start and end times, we can track how many intervals overlap at any given point. If a new interval starts after an earlier one has ended, we can assign it to the same group. Otherwise, we need to create a new group.\n\n# Approach\nSort start and end times: Sorting helps track when intervals start and end.\n\nTwo pointers:\n\nstart_ptr iterates through start times.\nend_ptr tracks the earliest end time. If the current interval starts after the earliest end, reuse a group by incrementing end_ptr; otherwise, create a new group.\nResult: The number of active groups after processing all intervals is the minimum number of groups required.\n\n# Complexity\n- Time complexity:\nTime complexity:\nO(NLogN)\n\nSpace complexity:\nO(N)\n\n# Code\n```java []\nclass Solution {\n public int minGroups(int[][] intervals) {\n int n = intervals.length;\n int[] start_times = new int[n];\n int[] end_times = new int[n];\n\n // Extract start and end times\n for (int i = 0; i < n; i++) {\n start_times[i] = intervals[i][0];\n end_times[i] = intervals[i][1];\n }\n\n // Sort start and end times\n Arrays.sort(start_times);\n Arrays.sort(end_times);\n\n int end_ptr = 0, group_count = 0;\n\n // Traverse through the start times\n for (int start : start_times) {\n if (start > end_times[end_ptr]) {\n end_ptr++;\n } else {\n group_count++;\n }\n }\n\n return group_count;\n }\n}\n``` | 2 | 0 | ['Java'] | 0 |
divide-intervals-into-minimum-number-of-groups | Java Clean Frequency Count Solution | java-clean-frequency-count-solution-by-s-9g1w | Complexity\n- Time complexity:O(n)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity:O(1_000_002)\n Add your space complexity here, e.g. O(n) \n | Shree_Govind_Jee | NORMAL | 2024-10-12T03:44:39.415817+00:00 | 2024-10-12T03:44:39.415849+00:00 | 277 | false | # Complexity\n- Time complexity:$$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(1_000_002)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int minGroups(int[][] intervals) {\n int[] cnt = new int[1_000_002];\n for(var i:intervals){\n cnt[i[0]]++;\n cnt[i[1]+1]--;\n }\n\n\n int maxi=0, temp=0;\n for(int c:cnt){\n temp += c;\n maxi = Math.max(maxi, temp);\n }\n return maxi;\n }\n}\n``` | 2 | 0 | ['Array', 'Two Pointers', 'Greedy', 'Sorting', 'Heap (Priority Queue)', 'Prefix Sum', 'Java'] | 1 |
divide-intervals-into-minimum-number-of-groups | Swift | Event Line | swift-event-line-by-pagafan7as-5kzc | Code\nswift []\nclass Solution {\n // Defines an "event" as the entering or exiting of an interval.\n // It helps to think of those as time intervals.\n | pagafan7as | NORMAL | 2024-10-12T03:38:58.978939+00:00 | 2024-10-12T21:28:01.734009+00:00 | 36 | false | # Code\n```swift []\nclass Solution {\n // Defines an "event" as the entering or exiting of an interval.\n // It helps to think of those as time intervals.\n struct Event: Comparable {\n enum EventType { case enter, exit }\n\n let time: Int\n let type: EventType\n\n static func <(lhs: Event, rhs: Event) -> Bool {\n lhs.time < rhs.time || lhs.time == rhs.time && lhs.type == .enter\n }\n }\n\n func minGroups(_ intervals: [[Int]]) -> Int {\n // Create the list of all events.\n var events = [Event]()\n for interval in intervals {\n events.append(Event(time: interval[0], type: .enter))\n events.append(Event(time: interval[1], type: .exit))\n }\n\n events.sort()\n\n // Count the maximum number of overlapping intervals.\n var res = 0\n var overlapCount = 0\n for event in events {\n switch event.type {\n case .enter: overlapCount += 1\n case .exit: overlapCount -= 1\n }\n res = max(res, overlapCount)\n }\n return res\n }\n}\n``` | 2 | 0 | ['Swift'] | 0 |
divide-intervals-into-minimum-number-of-groups | Easy Approach || O(n log(n)) || Python || C++ || Greedy | easy-approach-on-logn-python-c-greedy-by-4rmj | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | shra_1906 | NORMAL | 2024-10-12T03:06:41.399462+00:00 | 2024-10-12T09:55:33.426987+00:00 | 365 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(nlogn)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n\n\n# Code\n\n```python []\nevents = []\n \n # Convert intervals into start and end events\n for interval in intervals:\n events.append((interval[0], 1)) # start event\n events.append((interval[1] + 1, -1)) # end event (right + 1 to handle inclusive intervals)\n \n # Sort the events: first by time, then by type (start before end)\n events.sort()\n \n maxGroups = 0\n activeGroups = 0\n \n # Process all events\n for event in events:\n activeGroups += event[1] # +1 for start, -1 for end\n maxGroups = max(maxGroups, activeGroups) # Track the max number of active groups\n \n return maxGroups\n```\n\n\n```cpp []\nclass Solution {\npublic:\n int minGroups(vector<vector<int>>& intervals) {\n vector<pair<int, int>> ans;\n \n \n for (const auto& interval : intervals) {\n ans.push_back({interval[0], 1}); \n ans.push_back({interval[1] + 1, -1}); \n }\n \n \n sort(ans.begin(), ans.end());\n \n int ma = 0;\n int a = 0;\n \n \n for (const auto& i : ans) {\n a += i.second; \n ma = max(ma, a); \n }\n \n return ma;\n }\n};\n``` | 2 | 0 | ['Greedy', 'Sorting', 'Python', 'C++'] | 2 |
divide-intervals-into-minimum-number-of-groups | Easy to understand ✅✅✅| nlog(n) time complexity💯🫡 | cpp👑🎯 | easy-to-understand-nlogn-time-complexity-54on | \n\n\n# Code\ncpp []\nclass Solution {\npublic:\n int minGroups(vector<vector<int>>& intervals) {\n vector<pair<int, int>> events;\n for (auto& | ritik6g | NORMAL | 2024-10-12T00:05:09.883852+00:00 | 2024-10-12T00:05:09.883873+00:00 | 222 | false | \n\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int minGroups(vector<vector<int>>& intervals) {\n vector<pair<int, int>> events;\n for (auto& interval : intervals) {\n events.push_back({interval[0], 1});\n events.push_back({interval[1] + 1, -1});\n }\n\n sort(events.begin(), events.end());\n int max_groups = 0, curr_groups = 0;\n\n for (auto& event : events) {\n curr_groups += event.second;\n max_groups = max(max_groups, curr_groups);\n }\n\n return max_groups;\n }\n};\n\n\n``` | 2 | 0 | ['C++'] | 1 |
divide-intervals-into-minimum-number-of-groups | [Java] ✅99% ✅ LINE SWEEP ✅ CLEAN CODE ✅ CLEAR EXPLANATIONS | java-99-line-sweep-clean-code-clear-expl-vwa9 | Approach\n1. Use two arrays: start[1_000_001] and stop[1_000_001]\n2. For each interval, mark beginning and end on start[begin_interval]++ and stop[end_interval | StefanelStan | NORMAL | 2024-01-27T18:29:16.696042+00:00 | 2024-01-27T18:29:16.696065+00:00 | 109 | false | # Approach\n1. Use two arrays: start[1_000_001] and stop[1_000_001]\n2. For each interval, mark beginning and end on start[begin_interval]++ and stop[end_interval]++ \n3. Traverse start & stop and keep track of how many active intervals you have\n - increment activeIntervals by start[i]\n - set maxActiveIntervals(maxActiveIntervals, activeIntervals)\n - decrement activeIntervals by end[i].\n4. EG: intervals [1,100],[2,4],[4,5],[6,7]\n - reach 1, increment activeIntervals and set maxActive (active = 1, maxActive =1)\n - reach 2, increment again (active =2, maxActive = 2)\n - reach 4, increment again (active = 3, maxActive = 3), but also decrement by 1, as end[4] == 1 so active = 2, maxActive =3\n - reach 5, decrement active by 1 (because end[5] = 1); active = 1, maxActive =3\n - reach 6, increment active by 1 (active = 2, maxActive = 3)\n - .. 7: decrement by 1: active =1, maxActive = 3\n - .. 100: decrement by 1: active =0.\n5. Return maxActiveIntervals\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int minGroups(int[][] intervals) {\n int[] start = new int[1_000_001];\n int[] stop = new int[1_000_001];\n int left = Integer.MAX_VALUE, right = 0;\n for (int[] interval : intervals) {\n right = Math.max(right, interval[0]);\n left = Math.min(left, interval[0]);\n start[interval[0]]++;\n stop[interval[1]]++;\n }\n int activeIntervals = 0, maxActiveIntervals = 0;\n for (int i = left; i <= right; i++) {\n activeIntervals += start[i];\n maxActiveIntervals = Math.max(maxActiveIntervals, activeIntervals);\n activeIntervals -= stop[i];\n }\n return maxActiveIntervals;\n }\n}\n``` | 2 | 0 | ['Line Sweep', 'Java'] | 0 |
divide-intervals-into-minimum-number-of-groups | JAVA solution | java-solution-by-21arka2002-suo2 | \n# Code\n\nclass Solution {\n public int minGroups(int[][] intervals) {\n Arrays.sort(intervals,(a,b)->\n {\n if(a[0]==b[0])return | 21Arka2002 | NORMAL | 2023-04-03T08:09:01.208883+00:00 | 2023-04-03T08:09:01.208911+00:00 | 442 | false | \n# Code\n```\nclass Solution {\n public int minGroups(int[][] intervals) {\n Arrays.sort(intervals,(a,b)->\n {\n if(a[0]==b[0])return a[1]-b[1];\n else return a[0]-b[0];\n });\n PriorityQueue<Integer>pq=new PriorityQueue<>();\n for(int i=0;i<intervals.length;i++)\n {\n if(pq.size()>0 && pq.peek()<intervals[i][0])pq.remove();\n pq.add(intervals[i][1]);\n }\n return pq.size();\n }\n}\n``` | 2 | 0 | ['Array', 'Greedy', 'Sorting', 'Heap (Priority Queue)', 'Java'] | 1 |
divide-intervals-into-minimum-number-of-groups | Line Sweep | Map | C++ | line-sweep-map-c-by-tusharbhart-cr9h | \nclass Solution {\npublic:\n int minGroups(vector<vector<int>>& intervals) {\n map<int, int> m;\n for(auto i : intervals) {\n m[i[0 | TusharBhart | NORMAL | 2023-02-28T14:16:39.805753+00:00 | 2023-02-28T14:16:39.805800+00:00 | 102 | false | ```\nclass Solution {\npublic:\n int minGroups(vector<vector<int>>& intervals) {\n map<int, int> m;\n for(auto i : intervals) {\n m[i[0]]++;\n m[i[1] + 1]--;\n }\n int ans = 0, s = 0;\n for(auto i : m) {\n s += i.second;\n ans = max(ans, s);\n }\n return ans;\n }\n};\n``` | 2 | 0 | ['Ordered Map', 'Line Sweep', 'C++'] | 1 |
divide-intervals-into-minimum-number-of-groups | Java solution nlogn | java-solution-nlogn-by-skyhuangxy-jk08 | build a timeline, order by time with start point at fromt. Then, count how many intervals are opend. If there are 3 open intervals, it means there are three ove | skyhuangxy | NORMAL | 2022-11-22T07:07:57.706377+00:00 | 2022-11-22T07:09:41.821772+00:00 | 398 | false | build a timeline, order by time with start point at fromt. Then, count how many intervals are opend. If there are 3 open intervals, it means there are three overlap parts which allow the sequence to split into three groups. \n\nSame intuition as Meeting Room II.\n\n# Complexity\n- Time complexity: nlogn\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: n\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int minGroups(int[][] intervals) {\n int n = intervals.length;\n List<int[]> timeline = new ArrayList<>();\n for (int[] each : intervals) {\n timeline.add(new int[]{each[0], 1});\n timeline.add(new int[]{each[1], -1});\n }\n Collections.sort(timeline, (arr1, arr2) -> arr1[0] == arr2[0] ? arr2[1] - arr1[1] : arr1[0] - arr2[0]);\n\n int res = 0;\n int openinterval = 0;\n for (int[] timepoint : timeline) {\n openinterval += timepoint[1];\n res = Math.max(res, openinterval);\n }\n return res;\n }\n}\n\n\n``` | 2 | 0 | ['Java'] | 1 |
divide-intervals-into-minimum-number-of-groups | C++ Min Heap soln | c-min-heap-soln-by-sting285-kpsn | \nclass Solution {\npublic:\n int minGroups(vector<vector<int>>& intervals) {\n sort(intervals.begin(), intervals.end());\n priority_queue<int, | Sting285 | NORMAL | 2022-11-01T16:54:15.093090+00:00 | 2022-11-01T16:54:15.093131+00:00 | 806 | false | ```\nclass Solution {\npublic:\n int minGroups(vector<vector<int>>& intervals) {\n sort(intervals.begin(), intervals.end());\n priority_queue<int, vector<int>, greater<int>>pq;\n int res = 0;\n \n for(int i=0;i<intervals.size();i++){\n if(pq.size() == 0){\n pq.push(intervals[i][1]);\n ++res;\n }\n else{\n if(pq.top() >= intervals[i][0]){\n ++res;\n pq.push(intervals[i][1]);\n }\n else{\n pq.pop();\n pq.push(intervals[i][1]);\n }\n }\n }\n \n return res;\n }\n};\n``` | 2 | 0 | ['C', 'Sorting', 'Heap (Priority Queue)', 'C++'] | 2 |
divide-intervals-into-minimum-number-of-groups | C++ || Hashmap || start++ || end-- || Short & Clean Code | c-hashmap-start-end-short-clean-code-by-c16ew | <~ Upvote if this post is helpful\n\nApproach :\nSo the answer for the problem is maximum number of intervals that overlap, as we need to put them in separate g | Harsh_0903 | NORMAL | 2022-10-09T10:03:18.746424+00:00 | 2022-10-09T10:03:18.746465+00:00 | 206 | false | <~ **Upvote** if this post is helpful\n\nApproach :\nSo the answer for the problem is maximum number of intervals that overlap, as we need to put them in separate groups. Now, in our approach we are using a ordered map \n* incrementing the count of start of any interval , which represents a new interval is started\n* and decrementing the (end+1) of every interval that represents that a previous interval has ended here.\n* After doing above 2 steps we again traverse the map, and add freq. of each element in a temporary variable(sum in my case) which is representing that at the current instant this many number of intervals are overlapping. Along with this we are also taking into account the maximum overlapping that has taken place in ans variable.\n\n```\nclass Solution {\npublic:\n int minGroups(vector<vector<int>>& intervals) {\n map<int,int> m;\n for(auto it : intervals){\n m[it[0]]++;\n m[it[1]+1]--;\n }\n int ans = 0;\n int sum = 0;\n for(auto it : m){\n sum += it.second;\n ans = max(ans,sum);\n }\n return ans;\n }\n};\n```\n\nThankyou !!\n**Upvote** is encouraging ; ) | 2 | 1 | [] | 0 |
divide-intervals-into-minimum-number-of-groups | ✅ [Rust] 55ms, fastest solution (100%) with BinaryHeap (with detailed comments) | rust-55ms-fastest-solution-100-with-bina-2ca9 | This solution employs BinaryHeap for the quick access to the minimal of groups\' end times. It demonstrated 55 ms runtime (100.00%) and used 8.9 MB memory (100. | stanislav-iablokov | NORMAL | 2022-09-11T18:37:43.794582+00:00 | 2022-10-23T12:57:56.846042+00:00 | 74 | false | This [solution](https://leetcode.com/submissions/detail/797349032/) employs BinaryHeap for the quick access to the minimal of groups\' end times. It demonstrated **55 ms runtime (100.00%)** and used **8.9 MB memory (100.00%)**. Detailed comments are provided.\n\n**IF YOU LIKE THIS SOLUTION, PLEASE UPVOTE.**\n```\nuse std::collections::BinaryHeap;\nuse std::cmp::Reverse;\n\nimpl Solution \n{\n pub fn min_groups(mut intervals: Vec<Vec<i32>>) -> i32 \n {\n // [1] initialize storage for last elements in each group\n let mut groups_last: BinaryHeap<Reverse<i32>> = BinaryHeap::with_capacity(intervals.len());\n\n // [2] sorting of intervals allows us to check the intersection of each interval \n // with only the last interval in each group\n intervals.sort_unstable_by_key(|interval| interval[0]);\n \n // [3] iterate over sorted intervals\n intervals.into_iter().for_each(|interval|\n {\n // [4] searching for a group to attach new \'interval\', \n // i.e., taking a group with \'end\' < \'start of interval\';\n // it is sufficient to check the group with the minimal \'end\' value,\n // thus, we use BinaryHeap for quick (log-complexity) access\n if let Some(Reverse(end)) = groups_last.peek()\n {\n // [5] if there is such a group, prepare to update it...\n if *end < interval[0] { groups_last.pop(); }\n }\n // [6] either update an existing group or add a new one\n groups_last.push(Reverse(interval[1]));\n }\n );\n\n return groups_last.len() as i32;\n }\n}\n\n``` | 2 | 0 | ['Rust'] | 1 |
divide-intervals-into-minimum-number-of-groups | C++ | Line Sweep | Related Problems | c-line-sweep-related-problems-by-kiranpa-m9qp | Use Line Sweep\n- Return the maximum element in the entire range.\ncpp\nclass Solution {\npublic:\n int minGroups(vector<vector<int>>& intervals) {\n\n | kiranpalsingh1806 | NORMAL | 2022-09-11T10:31:22.610278+00:00 | 2022-09-11T10:31:22.610326+00:00 | 253 | false | - Use Line Sweep\n- Return the maximum element in the entire range.\n```cpp\nclass Solution {\npublic:\n int minGroups(vector<vector<int>>& intervals) {\n\n int line[1000005] = {};\n int maxEle = -1;\n\n for(auto &e : intervals) {\n int start = e[0], end = e[1];\n line[start] += 1;\n line[end + 1] -= 1;\n }\n\n for(int i = 1; i < 1000001; i++) {\n line[i] += line[i - 1];\n maxEle = max(maxEle, line[i]);\n }\n\n return maxEle;\n }\n};\n```\n\n**Line Sweep**\n1. [1854. Maximum Population Year](https://leetcode.com/problems/maximum-population-year/)\n2. [1943. Describe The Painting](https://leetcode.com/problems/describe-the-painting/)\n3. [2381. Shifting Letters II](https://leetcode.com/problems/shifting-letters-ii/)\n4. [218. The Skyline Problem](https://leetcode.com/problems/the-skyline-problem/)\n5. [732. My Calendar III](https://leetcode.com/problems/my-calendar-iii/)\n6. [2251. Number of Flowers in Full Bloom](https://leetcode.com/problems/number-of-flowers-in-full-bloom/)\n7. [1851. Minimum Interval To Include Each Query](https://leetcode.com/problems/minimum-interval-to-include-each-query/) | 2 | 0 | ['C', 'C++'] | 1 |
divide-intervals-into-minimum-number-of-groups | C++| Prefix-Sum | c-prefix-sum-by-kumarabhi98-sl3a | Hint: find the Max no.s of interval overlapping at any point\n\nclass Solution {\npublic:\n int minGroups(vector<vector<int>>& nums) {\n map<int,int> | kumarabhi98 | NORMAL | 2022-09-11T10:11:45.368706+00:00 | 2022-09-11T10:11:45.368747+00:00 | 120 | false | `Hint: find the Max no.s of interval overlapping at any point`\n```\nclass Solution {\npublic:\n int minGroups(vector<vector<int>>& nums) {\n map<int,int> mp;\n for(int i = 0; i<nums.size();++i){\n mp[nums[i][0]]++; mp[nums[i][1]+1]--;\n }\n int re = 0, sum = 0;\n for(auto&[i,val]:mp){\n sum+=val;\n re = max(re,sum);\n }\n return re;\n }\n};\n``` | 2 | 0 | ['C'] | 2 |
divide-intervals-into-minimum-number-of-groups | C++ || Multiset || Easy Solution | c-multiset-easy-solution-by-manavmajithi-n199 | \nclass Solution {\npublic:\n int minGroups(vector<vector<int>>& arr) {\n multiset<int> m;\n int n = arr.size();\n sort(arr.begin(),arr. | manavmajithia6 | NORMAL | 2022-09-11T06:21:30.276918+00:00 | 2022-09-11T06:21:30.276954+00:00 | 61 | false | ```\nclass Solution {\npublic:\n int minGroups(vector<vector<int>>& arr) {\n multiset<int> m;\n int n = arr.size();\n sort(arr.begin(),arr.end());\n m.insert(arr[0][1]);\n for(int i = 1;i < n;i++){\n auto it = m.lower_bound(arr[i][0]); // checking if any end range has value less than current starting range\n if(it != m.begin()){\n it--;\n m.erase(m.find(*it));\n m.insert(arr[i][1]); // Inserting all the end ranges\n }\n else{\n m.insert(arr[i][1]);\n }\n }\n return m.size();\n }\n};\n``` | 2 | 0 | ['C', 'C++'] | 1 |
divide-intervals-into-minimum-number-of-groups | Sorting and Min Heap Solution | sorting-and-min-heap-solution-by-travanj-s9qi | cpp\nclass Solution {\npublic:\n int minGroups(vector<vector<int>> &intervals) {\n sort(intervals.begin(), intervals.end());\n priority_queue<i | travanj05 | NORMAL | 2022-09-11T06:02:08.353592+00:00 | 2022-09-11T06:02:08.353632+00:00 | 54 | false | ```cpp\nclass Solution {\npublic:\n int minGroups(vector<vector<int>> &intervals) {\n sort(intervals.begin(), intervals.end());\n priority_queue<int, vector<int>, greater<int>> pq; // Min Heap\n int res = 0;\n for (const vector<int> &interval : intervals) {\n int start = interval[0], end = interval[1];\n if (pq.empty() || pq.top() > start) res++;\n else pq.pop();\n pq.push(end + 1);\n }\n return res;\n }\n};\n```\n\nPlease do **upvote** and **share**. | 2 | 0 | ['Sorting', 'Heap (Priority Queue)'] | 1 |
divide-intervals-into-minimum-number-of-groups | javascript sweep line 1007ms + greedy with PQ 541ms two solutions | javascript-sweep-line-1007ms-greedy-with-7d6w | Solution 1: sweep line + 1 -1\n\nconst minGroups = (a) => sweepLineIntervals(a)\n\nconst sweepLineIntervals = (a) => {\n let d = [], h = 0, res = 0;\n fo | henrychen222 | NORMAL | 2022-09-11T04:37:48.305155+00:00 | 2022-09-11T07:02:54.954178+00:00 | 214 | false | Solution 1: sweep line + 1 -1\n```\nconst minGroups = (a) => sweepLineIntervals(a)\n\nconst sweepLineIntervals = (a) => {\n let d = [], h = 0, res = 0;\n for (const [l, r] of a) {\n d.push([l, 1]);\n d.push([r + 1, -1]);\n }\n d.sort((x, y) => {\n if (x[0] != y[0]) return x[0] - y[0];\n return x[1] - y[1];\n });\n for (const [, mark] of d) {\n h += mark; // sweeping, find L add, R minus\n res = Math.max(res, h);\n }\n return res;\n};\n```\nsimilar problem:\nhttps://leetcode.com/problems/my-calendar-iii/\nhttps://atcoder.jp/contests/abc257/tasks/abc257_c\nhttps://leetcode.com/problems/number-of-flowers-in-full-bloom/\n\nmy solution:\nhttps://leetcode.com/problems/my-calendar-iii/discuss/1295136/javascript-treemap-1164ms\nhttps://atcoder.jp/contests/abc257/submissions/32752658\nhttps://leetcode.com/problems/number-of-flowers-in-full-bloom/discuss/1977865/javascript-rearrange-intervals-626ms\n\n************************************************************************************************\nSolution 2: greedy + PQ\n```\nconst minGroups = (a) => {\n a.sort((x, y) => x[0] - y[0]);\n let pq = new MinPriorityQueue();\n for (const [l, r] of a) {\n if (pq.size() && pq.front().element < l) pq.dequeue(); // if exist a group, this group max R < current L, then current can be add to this group\n pq.enqueue(r);\n }\n return pq.size();\n};\n``` | 2 | 0 | ['Sorting', 'Heap (Priority Queue)', 'JavaScript'] | 1 |
divide-intervals-into-minimum-number-of-groups | [JavaScript] similar to LC253 meeting rooms - sort start and end time | javascript-similar-to-lc253-meeting-room-lay5 | https://leetcode.com/problems/meeting-rooms-ii/\n\n\nvar minGroups = function(intervals) {\n const starts = intervals.map((el) => el[0]).sort((a, b) => a - | jialihan | NORMAL | 2022-09-11T04:30:39.566282+00:00 | 2022-09-11T04:30:39.566316+00:00 | 124 | false | https://leetcode.com/problems/meeting-rooms-ii/\n\n```\nvar minGroups = function(intervals) {\n const starts = intervals.map((el) => el[0]).sort((a, b) => a - b);\n const ends = intervals.map((el) => el[1]).sort((a, b) => a - b);\n let room = 0;\n let endIdx = 0;\n for (i = 0; i < starts.length; i++) {\n if (starts[i] <= ends[endIdx]) {\n room++;\n } else {\n endIdx++;\n }\n }\n return room;\n};\n``` | 2 | 0 | ['JavaScript'] | 1 |
divide-intervals-into-minimum-number-of-groups | Rust | BinaryHeap | With Comments | rust-binaryheap-with-comments-by-wallice-qc8x | This is my unrevised submission for the 2022-09-11 Weekly Contest 310. Sort the intervals by ascending starting time (using time here because it\'s easier to co | wallicent | NORMAL | 2022-09-11T04:19:30.416647+00:00 | 2022-09-11T04:19:30.416681+00:00 | 68 | false | This is my unrevised submission for the 2022-09-11 Weekly Contest 310. Sort the intervals by ascending starting time (using time here because it\'s easier to conceptualize maybe) followed by ascending end time. We keep a min heap / priority queue with ending times, so that we can know the soonest end time available. For each new interval, we pick the soonest end time that is less that the new interval start time, if possible. If possible, we add the interval to this group, pushing the new end time to the min heap. If not available, we need to form a new group. The number of groups is the final size of the heap.\n\nComment: This one tripped me up a bit first, and having to use Reverse is a bit of a hassle. But really happy with the outcome.\n\n```\nuse std::{collections::BinaryHeap, cmp::Reverse};\n\nimpl Solution {\n pub fn min_groups(intervals: Vec<Vec<i32>>) -> i32 {\n let mut end_times = BinaryHeap::<Reverse<i32>>::new();\n let mut intervals = intervals.into_iter().map(|a| (a[0], a[1])).collect::<Vec<_>>();\n intervals.sort_unstable();\n for (start_time, end_time) in intervals {\n if let Some(Reverse(soonest)) = end_times.peek().copied() {\n if soonest < start_time {\n end_times.pop();\n }\n }\n end_times.push(Reverse(end_time));\n }\n end_times.len() as _\n }\n}\n``` | 2 | 0 | ['Rust'] | 0 |
divide-intervals-into-minimum-number-of-groups | Line sweep | python | O(10^6) | Similar to shifting letters ii | line-sweep-python-o106-similar-to-shifti-dacp | similar problem: https://leetcode.com/problems/shifting-letters-ii/\t\n\n\t\tn = 1000001\n prefix = [0]*(n+1)\n for i,j in a: \n prefix | NaveenprasanthSA | NORMAL | 2022-09-11T04:13:26.897759+00:00 | 2022-09-11T04:14:36.540588+00:00 | 254 | false | similar problem: https://leetcode.com/problems/shifting-letters-ii/\t\n\n\t\tn = 1000001\n prefix = [0]*(n+1)\n for i,j in a: \n prefix[i]+=1 \n prefix[j+1]-=1 \n cursum = 0\n res = 0\n for i in prefix:\n cursum+=i\n res = max(res,cursum)\n return res\n\t\t\n\t\t | 2 | 0 | ['Python'] | 3 |
divide-intervals-into-minimum-number-of-groups | C# || Priority Queue | c-priority-queue-by-cdev-e528 | Method 1: Priority Queue\n\n public int MinGroups(int[][] intervals) \n {\n Array.Sort(intervals, (a, b) => a[0].CompareTo(b[0]));\n Priorit | CDev | NORMAL | 2022-09-11T04:07:36.729423+00:00 | 2022-09-11T21:34:12.368742+00:00 | 45 | false | **Method 1: Priority Queue**\n```\n public int MinGroups(int[][] intervals) \n {\n Array.Sort(intervals, (a, b) => a[0].CompareTo(b[0]));\n PriorityQueue<int, int> pq = new PriorityQueue<int, int>();\n int max = 0;\n foreach (int[] interval in intervals)\n {\n while (pq.Count > 0 && pq.Peek() < interval[0])\n pq.Dequeue();\n pq.Enqueue(interval[1], interval[1]);\n max = Math.Max(max, pq.Count);\n }\n return max;\n }\n```\n**Method 2: Array**\n```\n public int MinGroups(int[][] intervals)\n {\n int n = intervals.Max(i => i[1]);\n int[] change = new int[n + 2];\n foreach (int[] interval in intervals)\n {\n change[interval[0]]++;\n change[interval[1] + 1]--;\n }\n int max = 0;\n int curr = 0;\n for (int i = 0; i <= n; i++)\n {\n curr += change[i];\n max = Math.Max(max, curr);\n }\n return max;\n }\n``` | 2 | 0 | [] | 1 |
divide-intervals-into-minimum-number-of-groups | Simplest Way | without set and priority queue | Easy Understanding | CPP | simplest-way-without-set-and-priority-qu-9x0w | Same as Minimum Platforms Required Problem\n \n\nint minGroups(vector<vector<int>>& intervals)\n {\n vector<int> a;\n vector<int> b;\n \ | rajat0206 | NORMAL | 2022-09-11T04:06:24.992089+00:00 | 2022-09-11T04:12:01.413960+00:00 | 111 | false | Same as Minimum Platforms Required Problem\n \n```\nint minGroups(vector<vector<int>>& intervals)\n {\n vector<int> a;\n vector<int> b;\n \n for(auto &ele : intervals)\n {\n a.push_back(ele[0]);\n b.push_back(ele[1]);\n }\n \n sort(a.begin(), a.end());\n sort(b.begin(), b.end());\n \n\t\t//Two Pointers for traversing\n int i = 1;\n int j = 0;\n\t\t\n int maxi = 1;\n\t\tint cnt = 1; \n while(i < a.size() && j < b.size())\n {\n if(a[i] < b[j])\n {\n cnt++;\n i++;\n \n maxi = max(maxi, cnt);\n }\n else\n {\n cnt--;\n j++;\n }\n }\n \n return maxi;\n }\n``` | 2 | 1 | ['C', 'Sorting', 'C++'] | 0 |
divide-intervals-into-minimum-number-of-groups | [Python] Heap Solution | python-heap-solution-by-coldgingerale-wz6d | \nclass Solution:\n def minGroups(self, intervals: List[List[int]]) -> int:\n intervals.sort()\n groups = []\n \n for interval in | coldgingerale | NORMAL | 2022-09-11T04:03:40.037252+00:00 | 2022-09-11T04:07:55.057108+00:00 | 107 | false | ```\nclass Solution:\n def minGroups(self, intervals: List[List[int]]) -> int:\n intervals.sort()\n groups = []\n \n for interval in intervals:\n start, end = interval\n if groups and groups[0] < start:\n heappop(groups)\n heappush(groups, end)\n \n return len(groups)\n``` | 2 | 1 | [] | 2 |
divide-intervals-into-minimum-number-of-groups | JAVA Priority Queue | java-priority-queue-by-pgthebigshot-jkyv | Here if(max>=a[0]&&pq.peek()>=a[0]) checking if the total max i.e max of all right interval is greater then a[0] or not and the min value of all right interval | pgthebigshot | NORMAL | 2022-09-11T04:01:53.162516+00:00 | 2022-09-11T04:01:53.162554+00:00 | 258 | false | Here if(max>=a[0]&&pq.peek()>=a[0]) checking if the total max i.e max of all right interval is greater then a[0] or not and the min value of all right interval is greater then a[0] or not if both condition gets true then we are adding a group\n\n````\nclass Solution {\n public int minGroups(int[][] intervals) {\n \n int ans=0, max=0;\n \n Arrays.sort(intervals, (a,b)->((a[0]==b[0])?(a[1]-b[1]):(a[0]-b[0]))); // sorting accending order\n \n PriorityQueue<Integer> pq=new PriorityQueue();\n \n pq.add(1000001);\n \n for(int[] a: intervals)\n {\n if(max>=a[0]&&pq.peek()>=a[0]) // checking if the total max i.e max of all right interval is greater then a[0] or not and the min value of all right interval is greater then a[0] or not if both condition gets true then we are adding a group\n ans++;\n else \n {\n pq.poll(); // removing min value as we are adding a interval which will change the min value\n max=a[1]; // updating max value\n }\n pq.add(a[1]);\n }\n return ans+1; // adding 1 as atleast a group already exits.\n }\n}\n```` | 2 | 0 | ['Heap (Priority Queue)'] | 2 |
divide-intervals-into-minimum-number-of-groups | Similar as "253. Meeting Rooms II" ✅ ✅ Python | similar-as-253-meeting-rooms-ii-python-b-lnqv | \n # similar as "253. Meeting Rooms II", the only difference is the definition of "intersect"\n def minGroups(self, intervals):\n """\n :typ | ufoaixam | NORMAL | 2022-09-11T04:01:09.062154+00:00 | 2022-09-11T04:39:57.023263+00:00 | 368 | false | ```\n # similar as "253. Meeting Rooms II", the only difference is the definition of "intersect"\n def minGroups(self, intervals):\n """\n :type intervals: List[List[int]]\n :rtype: int\n """\n arr = []\n for s, e in intervals:\n arr.append((s, \'s\'))\n arr.append((e, \'e\'))\n \n # sort it and let "start" appear earlier than "end"\n arr.sort(key = lambda x: (x[0], -ord(x[1]))) \n \n cnt = 0\n maxV = 0\n for v, t in arr:\n if t == \'s\':\n cnt += 1\n else:\n cnt -= 1\n maxV = max(maxV, cnt)\n return maxV\n``` | 2 | 0 | ['Sorting', 'Python'] | 1 |
divide-intervals-into-minimum-number-of-groups | Minimum Number of Groups to Cover All Intervals | minimum-number-of-groups-to-cover-all-in-let0 | ✅ IntuitionThe problem is essentially about grouping overlapping intervals. If intervals overlap, they must be placed in separate groups. We need to determine t | vishwajeetwalekar037 | NORMAL | 2025-04-09T19:21:49.231956+00:00 | 2025-04-09T19:21:49.231956+00:00 | 3 | false |
### ✅ Intuition
The problem is essentially about grouping overlapping intervals. If intervals overlap, they must be placed in separate groups. We need to determine the **minimum number of such groups** required so that no intervals in the same group overlap.
---
### 🔍 Approach
1. **Separate Start and End Times**:
- Create two arrays: one for all start times and one for end times of the intervals.
2. **Sort Both Arrays**:
- This helps us simulate the timeline, allowing us to compare the next interval's start time with the earliest ending interval.
3. **Two Pointer Technique**:
- Use one pointer (`end_ptr`) to track the current end time.
- For each start time:
- If the current start time is greater than the current end time, the interval can reuse an existing group (move the `end_ptr` forward).
- Otherwise, we need a new group (increment `group_count`).
4. **Return `group_count`**:
- This keeps track of how many overlapping intervals we currently have, which is the minimum number of groups needed.
---
### ⏱️ Complexity
- **Time complexity:**
$$O(n \log n)$$
Sorting both start and end arrays takes \(O(n \log n)\), and the traversal is \(O(n)\).
- **Space complexity:**
$$O(n)$$
For the `start_times` and `end_times` arrays, each of size \(n\).
---
### ✅ Code
```java
class Solution {
public int minGroups(int[][] intervals) {
int n = intervals.length;
int[] start_times = new int[n];
int[] end_times = new int[n];
// Extract start and end times
for (int i = 0; i < n; i++) {
start_times[i] = intervals[i][0];
end_times[i] = intervals[i][1];
}
// Sort start and end times
Arrays.sort(start_times);
Arrays.sort(end_times);
int end_ptr = 0, group_count = 0;
// Traverse through the start times
for (int start : start_times) {
if (start > end_times[end_ptr]) {
end_ptr++;
} else {
group_count++;
}
}
return group_count;
}
}
```
### ❌ Code With TLE
```java
class Solution {
public int minGroups(int[][] intervals) {
Arrays.sort(intervals, (a, b) -> Integer.compare(a[0], b[0]));
int count = 0;
boolean[] visited = new boolean[intervals.length];
for (int i = 0; i < intervals.length; i++) {
if (!visited[i]) {
visited[i] = true;
int currentEnd = intervals[i][1]; // Track end of current group
for (int j = i + 1; j < intervals.length; j++) {
if (!visited[j] && currentEnd < intervals[j][0]) {
visited[j] = true;
currentEnd = intervals[j][1]; // Update end to new group member
}
}
count++; // One group formed
}
}
return count;
}
}
``` | 1 | 0 | ['Array', 'Two Pointers', 'Greedy', 'Sorting', 'Heap (Priority Queue)', 'Prefix Sum', 'Java'] | 0 |
divide-intervals-into-minimum-number-of-groups | C# | c-by-adchoudhary-meu1 | Code | adchoudhary | NORMAL | 2025-03-04T05:07:48.369504+00:00 | 2025-03-04T05:07:48.369504+00:00 | 5 | false | # Code
```csharp []
public class Solution {
public int MinGroups(int[][] intervals) {
int max = 0;//getting max range
foreach (var inter in intervals)
{
max = Math.Max(max, inter[1]);
}
int[] line = new int[max + 2];
foreach (var inter in intervals)
{
line[inter[0]]++;
line[inter[1] + 1]--;
}
int maxOverlap = 0;
int currOverlap = 0;
for (int i = 0; i < line.Length; i++)
{
currOverlap += line[i];
maxOverlap = Math.Max(maxOverlap, currOverlap);
}
return maxOverlap;
}
}
``` | 1 | 0 | ['C#'] | 0 |
divide-intervals-into-minimum-number-of-groups | Java | java-by-siyadhri-rnso | \n\n# Code\njava []\nclass Solution {\n public int minGroups(int[][] intervals) {\n int n = intervals.length;\n int[] start_times = new int[n]; | siyadhri | NORMAL | 2024-10-19T13:24:46.947336+00:00 | 2024-10-19T13:24:46.947373+00:00 | 2 | false | \n\n# Code\n```java []\nclass Solution {\n public int minGroups(int[][] intervals) {\n int n = intervals.length;\n int[] start_times = new int[n];\n int[] end_times = new int[n];\n\n // Extract start and end times\n for (int i = 0; i < n; i++) {\n start_times[i] = intervals[i][0];\n end_times[i] = intervals[i][1];\n }\n\n // Sort start and end times\n Arrays.sort(start_times);\n Arrays.sort(end_times);\n\n int end_ptr = 0, group_count = 0;\n\n // Traverse through the start times\n for (int start : start_times) {\n if (start > end_times[end_ptr]) {\n end_ptr++;\n } else {\n group_count++;\n }\n }\n\n return group_count;\n }\n}\n``` | 1 | 0 | ['Java'] | 0 |
divide-intervals-into-minimum-number-of-groups | Divide Intervals to Minimum Groups: Efficient Priority Queue Algo | divide-intervals-to-minimum-groups-effic-yz9c | Intuition\nThe idea is to use a priority queue to efficiently track the end times of the intervals and manage the groupings.\n Describe your first thoughts on h | madhusudanrathi99 | NORMAL | 2024-10-12T18:50:53.988849+00:00 | 2024-10-12T18:51:14.388197+00:00 | 15 | false | # Intuition\nThe idea is to use a priority queue to efficiently track the end times of the intervals and manage the groupings.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. **Sort the intervals**: First, we sort the `intervals` by their `left`. This allows us to process the `intervals` in the order they appear.\n2. **Use a priority queue**: Maintain a priority queue that stores the `right` of the `intervals`.\n3. **Process each interval**: For each interval, we check the earliest `right` in the priority queue. If this `right` is less than the `left` of the current interval, it means this interval can be added to an existing group. Otherwise, we need to create a new group for this interval.\n4. **Update the priority queue**: After processing the interval, update the priority queue to include the current interval\'s `right`.\n5. **Track the maximum number of groups**: Keep track of the maximum size of the priority queue, which represents the number of groups needed.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(n \\log n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```csharp []\npublic class Solution {\n public int MinGroups(int[][] intervals) {\n Array.Sort(intervals, Comparer<int[]>.Create((a, b) => a[0] - b[0]));\n int n = intervals.Length;\n int ans = 0;\n PriorityQueue<int, int> pque = new();\n for(int i = 0; i < n; i++) {\n int left = intervals[i][0];\n int right = intervals[i][1];\n while(pque.Count > 0 && pque.Peek() < left) {\n pque.Dequeue();\n }\n pque.Enqueue(right, right);\n ans = Math.Max(ans, pque.Count);\n }\n return ans;\n }\n}\n``` | 1 | 0 | ['Array', 'Two Pointers', 'Greedy', 'Sorting', 'Heap (Priority Queue)', 'Prefix Sum', 'C#'] | 1 |
divide-intervals-into-minimum-number-of-groups | C++ Solution | (O(n log n)) | c-solution-on-log-n-by-22bce041-xy79 | Intuition\nThe core idea is to track when intervals start and end. For each interval, we treat the start and end as events and sort them. By processing these ev | 22BCE041 | NORMAL | 2024-10-12T18:29:48.177577+00:00 | 2024-10-13T04:13:17.253804+00:00 | 3 | false | # Intuition\nThe core idea is to track when intervals start and end. For each interval, we treat the start and end as events and sort them. By processing these events in order, we can maintain a count of how many intervals are currently overlapping. The maximum number of overlapping intervals at any given point will give us the minimum number of groups required.\n\n# Approach\n1. **Convert Intervals to Events**: \n - For each interval `[start, end]`, create two events:\n - A "start" event at `start` (represented as `+1`).\n - An "end" event at `end + 1` (represented as `-1` to indicate the interval has finished at `end`).\n - We push these events into a list, and for each interval `[start, end]`, we add two corresponding events. \n\n2. **Sort the Events**: \n - We then sort all the events by time. In case two events happen at the same time, we process the "start" event (`+1`) before the "end" event (`-1`) to ensure accurate overlap counting.\n\n3. **Count Active Intervals**:\n - We process each event sequentially, updating the number of active intervals by adding or subtracting 1 depending on whether it is a start or end event.\n - The maximum number of active intervals during the process will give the minimum number of groups required.\n\n# Complexity\n- Time complexity: \n - Sorting the events takes \\(O(n log n)\\), where \\(n\\) is the number of intervals.\n - Processing the events takes \\(O(n)\\).\n - Thus, the total time complexity is \\(O(n log n)\\).\n\n- Space complexity: \n - We need \\(O(2n)\\) space to store the events (two events per interval).\n - Thus, the space complexity is \\(O(n)\\).\n\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int minGroups(vector<vector<int>>& intervals) {\n vector<pair<int, int>> events;\n \n for (auto& interval : intervals) {\n events.push_back({interval[0], 1});\n events.push_back({interval[1] + 1, -1}); \n //We need to sort the events based on the time,\n //and in case of ties, \n //we prioritize the \'start\' events (+1) before \'end\' events (-1).\n }\n \n sort(events.begin(), events.end());\n \n int maxgrps = 0;\n int curgroups = 0;\n \n for (auto& event : events) {\n curgroups += event.second;\n maxgrps = max(maxgrps, curgroups);\n }\n \n return maxgrps;\n }\n};\n\n```\n\n# Example\n\n```\nIntervals = [[5,10],[6,8],[1,5],[2,3],[1,10]]\n```\nAfter processing all intervals:\n```\nevents = [\n {5, 1}, {11, -1}, // from interval [5, 10]\n {6, 1}, {9, -1}, // from interval [6, 8]\n {1, 1}, {6, -1}, // from interval [1, 5]\n {2, 1}, {4, -1}, // from interval [2, 3]\n {1, 1}, {11, -1} // from interval [1, 10]\n]\n```\n\nSort the events:\n```\nevents = [\n {1, 1}, {1, 1}, // two intervals start at time 1\n {2, 1}, // one interval starts at time 2\n {4, -1}, // one interval ends after time 3 (interval [2, 3])\n {5, 1}, // one interval starts at time 5\n {6, -1}, {6, 1}, // one ends at time 5, and another starts at time 6\n {9, -1}, // one interval ends after time 8 (interval [6, 8])\n {11, -1}, {11, -1} // two intervals end after time 10\n]\n\n```\n\n### Process the events:\n\n- We iterate through the sorted events, keeping track of how many intervals are currently active (currentGroups), and find the maximum number of overlapping intervals (maxGroups).\n\nHere\'s how it works at each event:\n\n- At time 1, two intervals start (currentGroups = 2).\n- At time 2, one more interval starts (currentGroups = 3).\n- At time 4, one interval ends (currentGroups = 2).\n- At time 5, one interval starts (currentGroups = 3).\n- At time 6, one interval ends, and another starts (currentGroups = 3 remains unchanged).\n- At time 9, one interval ends (currentGroups = 2).\n- At time 11, two intervals end (currentGroups = 0).\n\n*The maximum value of currentGroups during this process is **3**.*\n\n | 1 | 0 | ['Sorting', 'C++'] | 0 |
divide-intervals-into-minimum-number-of-groups | Compact Solution Using Priority Queue and Sorting | TypeScript | compact-solution-using-priority-queue-an-clit | Intuition\nCompact solution using a priority queue and sorting.\n\n# Approach\nWe first sort the interval by start time. We then initialize a priority queue, wh | BurtTheAlert | NORMAL | 2024-10-12T18:22:09.211542+00:00 | 2024-10-12T18:22:09.211571+00:00 | 16 | false | # Intuition\nCompact solution using a priority queue and sorting.\n\n# Approach\nWe first sort the interval by start time. We then initialize a priority queue, which is to represent our interval groups. Each group is represented in the queue simply by its last end time, and the priority of the queue is this end time, such that the smallest end time has the highest priority.\n\nThis allows us to solve the problem using a greedy approach: By assigning the intervals in order, we always try to assign them to the group with smallest end time. If the interval cannot be assigned to that group, then it cannot be assigned to any other group either as they have larger end times. In this case, we create a new group and assign the new interval there.\n\nFinally, the number of elements in our priority queue is the number of interval groups needed, so we simply return that number.\n\n# Complexity\n- Time complexity:\n$$O(n \\log n)$$\n- Space complexity:\n$$O(n)$$ in the worst case\n\n# Code\n```typescript []\nfunction minGroups(intervals: number[][]): number {\n intervals.sort((a, b) => a[0] - b[0]);\n const groups = new MinPriorityQueue();\n\n for (const int of intervals) {\n if (!groups.isEmpty() && groups.front().element < int[0]) groups.dequeue();\n groups.enqueue(int[1]);\n }\n\n return groups.size();\n}\n``` | 1 | 0 | ['Sorting', 'Heap (Priority Queue)', 'TypeScript', 'JavaScript'] | 0 |
divide-intervals-into-minimum-number-of-groups | (python) simple solution using heap - same as seat problems | python-simple-solution-using-heap-same-a-kgvw | Intuition\nThis problem is similar with Unoccupied chair problems.\n# Approach\n1.\tSort the intervals by their start times.\n2.\tUse a min-heap to track the en | saais8217 | NORMAL | 2024-10-12T17:51:11.676813+00:00 | 2024-10-12T17:51:11.676831+00:00 | 6 | false | # Intuition\nThis problem is similar with Unoccupied chair problems.\n# Approach\n1.\tSort the intervals by their start times.\n2.\tUse a min-heap to track the end times of current intervals in different groups.\n3.\tFor each interval, check if it can fit into an existing group (i.e., if its start time is after the earliest end time). If so, reuse the group by popping the heap.\n4.\tPush the current interval\u2019s end time into the heap and return the heap size as the result.\n\n# Code\n```python3 []\nclass Solution:\n def minGroups(self, intervals: List[List[int]]) -> int:\n seats = []\n sorted_intervals = sorted(intervals)\n for x, y in sorted_intervals :\n if seats and seats[0] < x : \n heappop(seats)\n heappush(seats, y)\n return len(seats)\n``` | 1 | 0 | ['Python3'] | 0 |
divide-intervals-into-minimum-number-of-groups | Java Solution | java-solution-by-aarshpriyam-z94i | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | aarshpriyam | NORMAL | 2024-10-12T17:01:15.558814+00:00 | 2024-10-12T17:01:15.558837+00:00 | 38 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int minGroups(int[][] intervals) {\n int min = Integer.MAX_VALUE;\n int max = Integer.MIN_VALUE;\n int n = intervals.length;\n\n // Find the global min and max of interval ranges\n for (int i = 0; i < n; i++) {\n min = Math.min(min, intervals[i][0]);\n max = Math.max(max, intervals[i][1]);\n }\n\n int[] eventCount = new int[max + 2]; // +2 to handle boundaries safely\n\n // Populate eventCount with starts and ends of intervals\n for (int i = 0; i < n; i++) {\n eventCount[intervals[i][0]]++; // Interval starts\n eventCount[intervals[i][1] + 1]--; // Interval ends\n }\n\n int maxOverlaps = 0;\n int sum = 0;\n\n // Calculate max overlap using the eventCount array\n for (int i = min; i <= max; i++) {\n sum += eventCount[i]; // Track the running sum\n maxOverlaps = Math.max(maxOverlaps, sum); // Keep track of max overlap\n }\n\n return maxOverlaps;\n }\n}\n\n``` | 1 | 0 | ['Java'] | 1 |
divide-intervals-into-minimum-number-of-groups | Easy way to divide intervals into minimum number of groups. | easy-way-to-divide-intervals-into-minimu-hekw | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Narendra_Sai | NORMAL | 2024-10-12T16:11:59.565473+00:00 | 2024-10-12T16:11:59.565497+00:00 | 2 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int minGroups(int[][] intervals) {\n Arrays.sort(intervals, (a,b)->a[0]-b[0]);\n PriorityQueue<Integer> pq=new PriorityQueue<>();\n for(int[] interval:intervals){\n int start=interval[0],end=interval[1];\n if(!pq.isEmpty() && pq.peek()<start){\n pq.poll();\n }\n pq.add(end);\n }\n return pq.size();\n }\n}\n``` | 1 | 0 | ['Java'] | 0 |
divide-intervals-into-minimum-number-of-groups | Partial Sum || C++ | partial-sum-c-by-yousseffcai-3d7s | Code\ncpp []\nclass Solution {\npublic:\n int minGroups(vector<vector<int>>& intervals) {\n vector<int> partial(1e6 + 2);\n for (auto x : inter | yousseffcai | NORMAL | 2024-10-12T15:21:32.253007+00:00 | 2024-10-12T15:21:32.253061+00:00 | 3 | false | # Code\n```cpp []\nclass Solution {\npublic:\n int minGroups(vector<vector<int>>& intervals) {\n vector<int> partial(1e6 + 2);\n for (auto x : intervals) {\n partial[x[0]]++;\n partial[x[1] + 1]--;\n }\n int ans = 0;\n for (int i = 1; i <= 1e6; i++) {\n partial[i] += partial[i - 1];\n ans = max(ans, partial[i]);\n }\n return ans;\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
divide-intervals-into-minimum-number-of-groups | Optimal solution | optimal-solution-by-hdsedighi-e667 | Intuition\n Describe your first thoughts on how to solve this problem. \nThe problem asks us to group intervals such that no two intervals in the same group ove | hdsedighi | NORMAL | 2024-10-12T14:38:36.991200+00:00 | 2024-10-12T14:38:36.991226+00:00 | 19 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem asks us to group intervals such that no two intervals in the same group overlap. The key idea is to realize that the number of groups required depends on the maximum number of overlapping intervals at any point in time. If multiple intervals overlap, they need to be placed in separate groups. To track these overlaps, we can treat the interval endpoints as events and count how many intervals are active (overlapping) at any given time.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. **Event-based approach**: \n - For each interval, treat the start as a `+1` event and the end as a `-1` event. The number of overlapping intervals at any time is the sum of these events.\n - Specifically, we add a start event for the beginning of each interval and an end event for one unit past the end of the interval to ensure the boundary condition (e.g., [1,5] and [5,8] intersect at 5).\n \n2. **Sorting events**: \n - Sort the events by time. In case of a tie (i.e., two events happen at the same time), prioritize the end event (`-1`) over the start event (`+1`) to avoid falsely counting two intervals as overlapping when they only share a boundary.\n\n3. **Counting the maximum overlap**: \n - Traverse through the sorted events and maintain a running count of active intervals. Track the maximum number of simultaneous active intervals, as this will represent the minimum number of groups required.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n - Sorting the events takes \\(O(n \\log n)\\), where \\(n\\) is the number of intervals.\n - Traversing the sorted list of events takes \\(O(n)\\).\n - Therefore, the overall time complexity is \\(O(n \\log n)\\).\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n - We use an additional list to store the events, which has \\(2n\\) elements since each interval contributes two events (start and end). Thus, the space complexity is \\(O(n)\\).\n\n\n# Code\n```csharp []\nusing System;\nusing System.Collections.Generic;\n\npublic class Solution\n{\n public int MinGroups(int[][] intervals)\n {\n // List to hold both start and end points as events\n List<(int time, int type)> events = new List<(int time, int type)>();\n\n // Fill the events list with start and end points\n foreach (var interval in intervals)\n {\n events.Add((interval[0], 1)); // Start of interval (marked as +1)\n events.Add((interval[1] + 1, -1)); // End of interval (marked as -1)\n }\n\n // Sort events based on time; if two events have the same time, prioritize the \'end\' (-1) event\n events.Sort((a, b) =>\n {\n if (a.time == b.time)\n return a.type.CompareTo(b.type); // Sort by type if times are equal\n return a.time.CompareTo(b.time); // Otherwise, sort by time\n });\n\n int maxGroups = 0;\n int currentGroups = 0;\n\n // Traverse through the events to find the maximum overlap\n foreach (var ev in events)\n {\n currentGroups += ev.type; // Add 1 for a start, subtract 1 for an end\n maxGroups = Math.Max(maxGroups, currentGroups); // Track the maximum number of overlaps\n }\n\n return maxGroups; // The maximum number of overlaps is the minimum number of groups needed\n }\n}\n\n``` | 1 | 0 | ['Array', 'Two Pointers', 'Greedy', 'Sorting', 'Heap (Priority Queue)', 'Prefix Sum', 'C#'] | 1 |
divide-intervals-into-minimum-number-of-groups | JS solution O(n log n) | js-solution-on-log-n-by-22xiao-d8s6 | Intuition\n Describe your first thoughts on how to solve this problem. \nThis problem essentially boils down to finding the maximum overlap between intervals, s | 22xiao | NORMAL | 2024-10-12T13:42:09.557534+00:00 | 2024-10-12T13:42:09.557574+00:00 | 62 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThis problem essentially boils down to finding the **maximum overlap** between intervals, since the number of groups required equals the maximum number of intervals that overlap at any point in time.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n\n - Each interval can be split into two events: a **start event** and an **end event**.\n - We create a list of events for all intervals, where each start is treated as an event that increases the number of ongoing intervals, and each end decreases it.\n - Sort these events primarily by time. In case of a tie (i.e., when start and end events happen at the same time), prioritize **start events** to ensure intervals that start first are added before counting new overlapping intervals.\n - After sorting the events, traverse them while keeping a running count of how many intervals are currently active. The maximum count observed at any point during this traversal will be the number of groups required.\n\n# Complexity\n\n- **Time Complexity**: `O(n log n)`, where `n` is the number of intervals. This is because sorting the events dominates the time complexity.\n- **Space Complexity**: `O(n)`, as we store the start and end events for each interval.\n\n# Code\n```javascript []\n/**\n * @param {number[][]} intervals\n * @return {number}\n */\nvar minGroups = function(intervals) {\n let events = []\n\n // Split each interval into two events: start (+1) and end (-1)\n for (let [left, right] of intervals) {\n events.push([left, 1])\n events.push([right, -1])\n }\n\n // Sort events by time, with start (+1) coming before end (-1) when times are equal\n events.sort((a, b) => a[0] == b[0] ? b[1] - a[1] : a[0] - b[0])\n\n let cur = 0, max = 0\n // Traverse sorted events to calculate the maximum number of overlapping intervals\n for (let [time, type] of events) {\n if (type == 1) {\n cur++\n } else {\n cur--\n }\n max = Math.max(max, cur)\n }\n return max\n};\n``` | 1 | 0 | ['JavaScript'] | 1 |
divide-intervals-into-minimum-number-of-groups | Easy solution without priority_queue | easy-solution-without-priority_queue-by-3gwpl | Intuition\n Describe your first thoughts on how to solve this problem. \n\nwe need to find the maximum number of overlaping groups at a give time(or value);\nti | harsh_sharawat | NORMAL | 2024-10-12T13:25:30.344243+00:00 | 2024-10-12T13:25:30.344281+00:00 | 19 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\nwe need to find the maximum number of overlaping groups at a give time(or value);\ntime ranges from 1 to 1e6;\n\n# Approach\n<h2>solution without priority_queue </h2>\n<!-- Describe your approach to solving the problem. -->\ncreate a hash for time range and intialize with 0 :\n -- for each interval increament all the time in that interval by one \n-- -- to increament all the time in current interval just increment the start time and decrement the (end_time+1) and later take the prefix sum of time array\n\n-- find the max value from the prefix sum of of time array\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(1e6)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1e6)\n\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int minGroups(vector<vector<int>>& arr) {\n vector<long long > hash(1e6+2,0);\n for(auto it: arr){\n hash[ it[0] ] ++;\n hash[ it[1]+1 ] --;\n }\n for(int i=1;i<1e6+2;i++) hash[i]+=hash[i-1];\n long long maxi=0;\n for(auto it: hash) maxi=max(maxi,it);\n return maxi;\n \n }\n};\n``` | 1 | 0 | ['Hash Table', 'Prefix Sum', 'C++'] | 2 |
divide-intervals-into-minimum-number-of-groups | C# Solution for Divide Intervals Into Minimum Number of Groups Problem | c-solution-for-divide-intervals-into-min-y0zo | Intuition\n Describe your first thoughts on how to solve this problem. \nThe idea behind this approach is to use a min-heap (priority queue) to track the end ti | Aman_Raj_Sinha | NORMAL | 2024-10-12T13:17:05.709554+00:00 | 2024-10-12T13:17:05.709578+00:00 | 79 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe idea behind this approach is to use a min-heap (priority queue) to track the end times of the ongoing intervals. As we process the intervals in order of their start times, we check if the current interval can reuse a group by checking if its start time is after the earliest ending interval. If it can, we remove the interval that has ended, thus freeing a group. If it can\u2019t, we add the new interval\u2019s end time to the heap, indicating that a new group is needed.\n\nThe min-heap helps us efficiently manage the intervals by always keeping track of the earliest ending interval, allowing us to decide when a group is available for reuse.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1.\tSort by Start Time:\n\t\u2022\tSort the intervals based on their start times. This ensures that we process the intervals sequentially, from the earliest to the latest.\n2.\tPriority Queue (Min-Heap):\n\t\u2022\tUse a priority queue (min-heap) to store the end times of the intervals currently in progress (i.e., active intervals).\n\t\u2022\tFor each new interval, if its start time is greater than or equal to the earliest end time in the heap, it means the earliest interval has finished, and we can reuse its group by removing the end time from the heap.\n\t\u2022\tOtherwise, we need a new group, so we add the interval\u2019s end time to the heap.\n3.\tGroup Management:\n\t\u2022\tThe size of the heap at the end represents the minimum number of groups required, because it indicates the maximum number of overlapping intervals at any point in time.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n1.\tSorting: Sorting the intervals by their start time takes O(n log n), where n is the number of intervals.\n2.\tHeap Operations: Each insertion and deletion from the heap takes O(log k), where k is the number of groups (at most n). Since we are processing each interval once, we may perform O(n) heap operations.\n\nTherefore, the total time complexity is:\n\n\u2022\tO(n log n) for sorting.\n\u2022\tO(n log n) for heap operations (insertion and removal).\n\nThus, the overall time complexity is O(n log n).\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n1.\tSorting: Sorting requires no additional space apart from storing the intervals, so this is O(n).\n2.\tMin-Heap: In the worst case, all intervals might overlap, requiring the heap to store up to n intervals at the same time. Therefore, the space complexity for the heap is O(n).\n\nThus, the overall space complexity is O(n).\n\n# Code\n```csharp []\npublic class Solution {\n public int MinGroups(int[][] intervals) {\n Array.Sort(intervals, (a, b) => a[0].CompareTo(b[0]));\n\n PriorityQueue<int, int> minHeap = new PriorityQueue<int, int>();\n\n foreach (var interval in intervals) {\n int start = interval[0];\n int end = interval[1];\n\n if (minHeap.Count > 0 && minHeap.Peek() < start) {\n minHeap.Dequeue(); \n }\n\n minHeap.Enqueue(end, end);\n }\n\n return minHeap.Count;\n }\n}\n``` | 1 | 0 | ['C#'] | 1 |
divide-intervals-into-minimum-number-of-groups | Priority Queue 4 line easy solution | priority-queue-4-line-easy-solution-by-k-08mi | Intuition\nGreedy\n\n# Approach\nSort the array.\nStore the second ele of each interval\n\n# Complexity\n- Time complexity:\nO(nlogn)\n\n- Space complexity:\nO( | kanishka1 | NORMAL | 2024-10-12T13:13:06.594822+00:00 | 2024-10-12T13:13:06.594854+00:00 | 12 | false | # Intuition\nGreedy\n\n# Approach\nSort the array.\nStore the second ele of each interval\n\n# Complexity\n- Time complexity:\nO(nlogn)\n\n- Space complexity:\nO(n)\n\n# Code\n```java []\nclass Solution {\n public int minGroups(int[][] inte) {\n PriorityQueue<Integer> pq=new PriorityQueue<>();\n Arrays.sort(inte,(a,b)->Integer.compare(a[0],b[0]));\n for(int[] i: inte){\n if(pq.size()>0 && (pq.peek() < i[0])){\n pq.remove();\n } \n pq.add(i[1]);\n }\n return pq.size();\n }\n}\n``` | 1 | 0 | ['Java'] | 1 |
divide-intervals-into-minimum-number-of-groups | Java Solution for Divide Intervals Into Minimum Number of Groups Problem | java-solution-for-divide-intervals-into-nc1i0 | Intuition\n Describe your first thoughts on how to solve this problem. \nThe problem asks us to group intervals such that no two intervals in the same group ove | Aman_Raj_Sinha | NORMAL | 2024-10-12T13:12:42.407566+00:00 | 2024-10-12T13:12:42.407588+00:00 | 23 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem asks us to group intervals such that no two intervals in the same group overlap. The intuition here is to treat intervals as events: each interval has a start and an end. By sorting these events and processing them in order, we can track how many intervals are \u201Cactive\u201D at any given time. The maximum number of overlapping intervals at any point will tell us the minimum number of groups needed.\n\nFor example, if 3 intervals overlap at one point, we will need at least 3 groups to separate them.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1.\tEvent Creation:\n\t\u2022\tFor each interval [lefti, righti], treat the starting point lefti as an event where an interval begins (denoted as +1), and the ending point righti + 1 as an event where the interval ends (denoted as -1).\n2.\tSorting:\n\t\u2022\tSort all the events. If two events occur at the same time, prioritize ending events (-1) over starting events (+1). This ensures that when an interval ends and another starts at the same point, we do not count them as overlapping.\n3.\tTracking Active Intervals:\n\t\u2022\tTraverse the sorted events while maintaining a count of the currently active intervals. Increment the count when an interval starts and decrement it when an interval ends.\n4.\tMaximum Overlap:\n\t\u2022\tAs you process events, keep track of the maximum number of active intervals at any point. This gives the minimum number of groups required, as each active interval represents an overlap that needs a separate group.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\u2022\tEvent Creation: Creating start and end events for each interval takes O(n), where n is the number of intervals.\n\u2022\tSorting: Sorting the 2n events takes O(n log n).\n\u2022\tEvent Traversal: Processing all events takes O(n).\n\nThus, the overall time complexity is O(n log n), dominated by the sorting step.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\u2022\tWe create a list of events, which contains two events (start and end) for each interval. Therefore, the space complexity is O(n) for storing the events.\n\u2022\tNo additional significant space is used beyond the event list and a few variables for tracking the count.\n\nThus, the space complexity is O(n).\n\n# Code\n```java []\nclass Solution {\n public int minGroups(int[][] intervals) {\n List<int[]> events = new ArrayList<>();\n \n for (int[] interval : intervals) {\n events.add(new int[]{interval[0], 1}); \n events.add(new int[]{interval[1] + 1, -1}); \n }\n \n Collections.sort(events, (a, b) -> (a[0] == b[0]) ? a[1] - b[1] : a[0] - b[0]);\n \n int maxGroups = 0;\n int currentGroups = 0;\n\n for (int[] event : events) {\n currentGroups += event[1]; \n maxGroups = Math.max(maxGroups, currentGroups); \n }\n \n return maxGroups;\n }\n}\n``` | 1 | 0 | ['Java'] | 1 |
divide-intervals-into-minimum-number-of-groups | c++ unique approach | c-unique-approach-by-shreyasurbhisinha-gjg0 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | shreyasurbhisinha | NORMAL | 2024-10-12T13:00:24.703831+00:00 | 2024-10-12T13:00:24.703869+00:00 | 27 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int minGroups(vector<vector<int>>& intervals) {\n int n=intervals.size();\n int cnt=0;\n vector<int> start,end;\n int endptr=0;\n for(auto it:intervals){\n start.push_back(it[0]);\n end.push_back(it[1]);\n }\n sort(start.begin(),start.end());\n sort(end.begin(),end.end());\n for(auto a:start){\n if(a>end[endptr]){\n endptr++;\n }\n else{\n cnt++;\n }\n }\n return cnt;\n\n \n \n }\n};\n``` | 1 | 0 | ['C++'] | 1 |
sliding-window-median | Java using two Tree Sets - O(n logk) | java-using-two-tree-sets-on-logk-by-kido-d02p | Inspired by this solution. to the problem: 295. Find Median from Data Stream\n\nHowever instead of using two priority queue's we use two Tree Sets as we want O( | kidoptimo | NORMAL | 2017-02-13T07:04:26.896000+00:00 | 2018-10-17T22:34:06.671364+00:00 | 38,942 | false | Inspired by this [solution](https://discuss.leetcode.com/topic/27521/short-simple-java-c-python-o-log-n-o-1). to the problem: [295. Find Median from Data Stream](https://leetcode.com/problems/find-median-from-data-stream/)\n\nHowever instead of using two priority queue's we use two ```Tree Sets``` as we want ```O(logk)``` for ```remove(element)```. Priority Queue would have been ```O(k)``` for ```remove(element)``` giving us an overall time complexity of ```O(nk)``` instead of ```O(nlogk)```.\n\nHowever there is an issue when it comes to duplicate values so to get around this we store the ```index``` into ```nums``` in our ```Tree Set```. To break ties in our Tree Set comparator we compare the index.\n\n```\npublic double[] medianSlidingWindow(int[] nums, int k) {\n Comparator<Integer> comparator = (a, b) -> nums[a] != nums[b] ? Integer.compare(nums[a], nums[b]) : a - b;\n TreeSet<Integer> left = new TreeSet<>(comparator.reversed());\n TreeSet<Integer> right = new TreeSet<>(comparator);\n \n Supplier<Double> median = (k % 2 == 0) ?\n () -> ((double) nums[left.first()] + nums[right.first()]) / 2 :\n () -> (double) nums[right.first()];\n \n // balance lefts size and rights size (if not equal then right will be larger by one)\n Runnable balance = () -> { while (left.size() > right.size()) right.add(left.pollFirst()); };\n \n double[] result = new double[nums.length - k + 1];\n \n for (int i = 0; i < k; i++) left.add(i);\n balance.run(); result[0] = median.get();\n \n for (int i = k, r = 1; i < nums.length; i++, r++) {\n // remove tail of window from either left or right\n if(!left.remove(i - k)) right.remove(i - k);\n\n // add next num, this will always increase left size\n right.add(i); left.add(right.pollFirst());\n \n // rebalance left and right, then get median from them\n balance.run(); result[r] = median.get();\n }\n \n return result;\n}\n``` | 329 | 14 | [] | 55 |
sliding-window-median | O(n log k) C++ using multiset and updating middle-iterator | on-log-k-c-using-multiset-and-updating-m-2bhh | Keep the window elements in a multiset and keep an iterator pointing to the middle value (to "index" k/2, to be precise). Thanks to @votrubac's solution and com | stefanpochmann | NORMAL | 2017-01-11T01:58:51.459000+00:00 | 2018-09-17T22:10:43.660085+00:00 | 52,541 | false | Keep the window elements in a multiset and keep an iterator pointing to the middle value (to "index" k/2, to be precise). Thanks to [@votrubac's solution and comments](https://discuss.leetcode.com/topic/74739/c-95-ms-single-multiset-o-n-log-n).\n\n vector<double> medianSlidingWindow(vector<int>& nums, int k) {\n multiset<int> window(nums.begin(), nums.begin() + k);\n auto mid = next(window.begin(), k / 2);\n vector<double> medians;\n for (int i=k; ; i++) {\n \n // Push the current median.\n medians.push_back((double(*mid) + *prev(mid, 1 - k%2)) / 2);\n \n // If all done, return.\n if (i == nums.size())\n return medians;\n \n // Insert nums[i].\n window.insert(nums[i]);\n if (nums[i] < *mid)\n mid--;\n \n // Erase nums[i-k].\n if (nums[i-k] <= *mid)\n mid++;\n window.erase(window.lower_bound(nums[i-k]));\n }\n } | 286 | 2 | [] | 51 |
sliding-window-median | Never create max heap in java like this... | never-create-max-heap-in-java-like-this-wu5ak | I spent 2 hours debugging my code because I couldn't pass the last test case:\n\n[-2147483648,-2147483648,2147483647,-2147483648,1,3,-2147483648,-100,8,17,22,-2 | loushengbo | NORMAL | 2017-08-16T11:30:16.378000+00:00 | 2017-08-16T11:30:16.378000+00:00 | 10,338 | false | I spent 2 hours debugging my code because I couldn't pass the last test case:\n```\n[-2147483648,-2147483648,2147483647,-2147483648,1,3,-2147483648,-100,8,17,22,-2147483648,-2147483648,2147483647,2147483647,2147483647,2147483647,-2147483648,2147483647,-2147483648]\n6\n```\nFinally, I found out why:\n\nI created my max heap like this:\n```\nPriorityQueue<Integer> max = new PriorityQueue<Integer>(1, new Comparator<Integer>(){\n @Override\n public int compare(Integer x, Integer y){\n return y-x;\n }\n});\n```\nseems pretty standard right? I always create max heap like this in java\n\nIt works correctly most of the time, however, consider this case: ```x = 1, y=-2147483648```, now ```y-x``` will cause overflow, ```y-x=2147483647``` which is the wrong result. \n\nDamn, I'm stupid.. ( \u02c9 \u2313 \u02c9 \u0e51)\ufeff\ufeff\n\nFor those who creates max heap like this, please don't do it again, create max heap correctly as follows:\n```\nPriorityQueue<Integer> max = new PriorityQueue<>(1, Collections.reverseOrder());\n```\nor like this:\n```\nPriorityQueue<Integer> max = new PriorityQueue<Integer>(1, new Comparator<Integer>(){\n @Override\n public int compare(Integer x, Integer y){\n return y.compareTo(x);\n }\n});\n```\nPlease vote this if you made the same mistake as I did. | 253 | 4 | [] | 18 |
sliding-window-median | Python Small & Large Heaps | python-small-large-heaps-by-wangqiuc-rcrw | To calculate the median, we can maintain divide array into subarray equally: small and large. All elements in small are no larger than any element in large. So | wangqiuc | NORMAL | 2019-03-26T23:22:50.191770+00:00 | 2019-11-02T23:46:13.477067+00:00 | 24,395 | false | To calculate the median, we can maintain divide array into subarray equally: **small** and **large**. All elements in **small** are no larger than any element in **large**. So median would be (largest in **small** + smallest in **large**) / 2 if **small**\'s size = **large**\'s size. If large\'s size = small\'s size + 1, median is smallest in **large**.\n\nThus, we can use heap here to maintain **small**(max heap) and **large**(min heap) so we can fetch smallest and largest element in logarithmic time.\n\nWe can also maintain "**large**\'s size - **small**\'s size <= 1" and "smallest in **large** >= largest in **small**" by heap\'s property: once **large**\'s size - **small**\'s size > 1, we pop one element from large and add it to small. And vice versa when **small**\'s size > **large**\'s size.\n\nBesides, since its a sliding window median, we need to keep track of window ends. So we will also push element\'s index to the heap. So each element takes a form of (val, index). Since Python\'s heapq is a min heap, so we convert small to a max heap by pushing (-val, index).\n\nIntially for first k elements, we push them all into **small** and then pop k/2 element from **small** and add them to **large**. \nThen we can intialize our answer array as ```[large[0][0] if k & 1 else (large[0][0]-small[0][0])/2]``` as we discussed above.\n\nThen for rest iterations, each time we add a new element **x** whose index is **i+k**, and remove an old element **nums[i]** which is out of window scope. Then we calculate our median in current window as the same way before.\nIf right end\'s **x** is no smaller than **large[0]**, then it belongs to **large** heap. If left end\'s **nums[i]** is no larger than **large[0]**, then it belongs to **small** heap. So we will add one to **large** while remove one from **small** and heaps\' sizes will be unbalanced. So we will move **large[0]** to **small** to rebalance two heaps.\nVice versa when we have to add one to **small** while remove one from **large**.\n\nBut we don\'t have to hurry and remove element in each iteration. As long as **nums[i]** is neither **small[0]** nor **large[0]**, it has no effect to median calculation. So we wait later and use a while loop to remove those out-of-window **small[0]** or **large[0]** at one time. This also make whole logic clearer.\n```\ndef medianSlidingWindow(nums, k):\n\tsmall, large = [], []\n\tfor i, x in enumerate(nums[:k]): \n\t\theapq.heappush(small, (-x,i))\n\tfor _ in range(k-(k>>1)): \n\t\tmove(small, large)\n\tans = [get_med(small, large, k)]\n\tfor i, x in enumerate(nums[k:]):\n\t\tif x >= large[0][0]:\n\t\t\theapq.heappush(large, (x, i+k))\n\t\t\tif nums[i] <= large[0][0]: \n\t\t\t\tmove(large, small)\n\t\telse:\n\t\t\theapq.heappush(small, (-x, i+k))\n\t\t\tif nums[i] >= large[0][0]: \n\t\t\t\tmove(small, large)\n\t\twhile small and small[0][1] <= i: \n\t\t\theapq.heappop(small)\n\t\twhile large and large[0][1] <= i: \n\t\t\theapq.heappop(large)\n\t\tans.append(get_med(small, large, k))\n\treturn ans\n\ndef move(h1, h2):\n\tx, i = heapq.heappop(h1)\n\theapq.heappush(h2, (-x, i))\n\t\ndef get_med(h1, h2, k):\n\treturn h2[0][0] * 1. if k & 1 else (h2[0][0]-h1[0][0]) / 2.\n```\nSince we are using k-size heap here, the time complexity is O(nlogk) and space complexity is O(logk). | 230 | 5 | [] | 28 |
sliding-window-median | Solution | solution-by-deleted_user-ojse | C++ []\nclass Solution {\npublic:\n vector<double> medianSlidingWindow(vector<int>& nums, int k) {\n vector<double> medians;\n unordere | deleted_user | NORMAL | 2023-01-05T19:30:47.085127+00:00 | 2023-03-07T08:37:35.478122+00:00 | 17,180 | false | ```C++ []\nclass Solution {\npublic:\n vector<double> medianSlidingWindow(vector<int>& nums, int k) {\n vector<double> medians;\n unordered_map<int, int> hashTable;\n priority_queue<int> lo;\n priority_queue<int, vector<int>, greater<int>> hi;\n\n int i = 0;\n\n while(i < k){\n lo.push(nums[i++]);\n }\n for(int j = 0; j < k / 2; ++j){\n hi.push(lo.top());\n lo.pop();\n }\n\n while(true){\n medians.push_back(k & 1 ? lo.top() : ((double)lo.top() + (double)hi.top()) * 0.5);\n\n if(i >= nums.size()) break;\n\n int outNum = nums[i - k];\n int inNum = nums[i++];\n int balance = 0;\n\n balance += outNum <= lo.top() ? -1 : 1;\n hashTable[outNum]++;\n\n if(!lo.empty() && inNum <= lo.top()){\n balance++;\n lo.push(inNum);\n }\n else{\n balance--;\n hi.push(inNum);\n }\n\n if(balance < 0){\n lo.push(hi.top());\n hi.pop();\n balance++;\n }\n if(balance > 0){\n hi.push(lo.top());\n lo.pop();\n balance--;\n }\n\n while(hashTable[lo.top()]){\n hashTable[lo.top()]--;\n lo.pop();\n }\n\n while(!hi.empty() && hashTable[hi.top()]){\n hashTable[hi.top()]--;\n hi.pop();\n }\n }\n return medians;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def medianSlidingWindow(self, nums: List[int], k: int) -> List[float]:\n if k == 1:\n return nums\n if k == 2:\n return [(p + q) / 2 for p,q in pairwise(nums)]\n kodd = k % 2\n ref = sorted(nums[:k])\n hl = [-x for x in ref[:k//2]]\n hl.reverse()\n hr = ref[k//2:]\n if kodd:\n out = [hr[0]]\n else:\n out = [(hr[0] - hl[0]) / 2]\n hrd = []\n hld = []\n def cleanr():\n while hrd and hrd[0] == hr[0]:\n heappop(hrd)\n heappop(hr)\n def cleanl():\n while hld and hld[0] == hl[0]:\n heappop(hld)\n heappop(hl)\n for idx,x in enumerate(nums[k:]):\n y = nums[idx]\n mid = hr[0]\n if y >= mid:\n if x < mid:\n x = -heappushpop(hl, -x)\n cleanl()\n heappush(hr, x)\n heappush(hrd, y)\n cleanr()\n else:\n if x >= mid:\n x = heappushpop(hr, x)\n cleanr()\n heappush(hl, -x)\n heappush(hld, -y)\n cleanl()\n if kodd:\n out.append(hr[0])\n else:\n out.append((hr[0] - hl[0]) / 2)\n return out\n```\n\n```Java []\nclass Solution {\n public double[] medianSlidingWindow(int[] nums, int k) {\n if (nums == null || nums.length == 0)\n return new double[0];\n \n Node root = null;\n for (int i = 0; i < k; i++) {\n root = insert(root, nums[i]);\n }\n \n double[] r = new double[nums.length - k + 1];\n boolean even = k % 2 == 0;\n int j = 0;\n for (int i = k; i <= nums.length; i++) {\n double sum = 0.0;\n if (even)\n sum = (findSmallest(root, k/2).val + findSmallest(root, k/2 + 1).val) / 2.0;\n else\n sum = findSmallest(root, k/2 + 1).val;\n r[j++] = sum;\n if (i < nums.length) {\n root = insert(root, nums[i]);\n root = delete(root, nums[i - k]);\n }\n }\n \n return r;\n }\n \n private Node findSmallest(Node root, int k) {\n int s = countWith(root.left) + 1;\n if (s == k)\n return root;\n if (s > k) {\n return findSmallest(root.left, k);\n }\n return findSmallest(root.right, k - s);\n } \n \n private Node delete(Node root, long val) {\n if (root == null)\n return null;\n else if (val > root.val) \n root.right = delete(root.right, val);\n else if (val < root.val)\n root.left = delete(root.left, val);\n else {\n if (root.left == null)\n root = root.right;\n else if (root.right == null)\n root = root.left;\n else {\n Node t = findMin(root.right);\n root.val = t.val;\n root.right = delete(root.right, t.val);\n }\n }\n \n return updateNode(root);\n }\n \n private Node findMin(Node root) {\n if (root.left != null)\n return findMin(root.left);\n return root;\n }\n\n private Node insert(Node root, long val)\n {\n if (root == null)\n {\n return new Node(val);\n }\n if (val >= root.val)\n {\n root.right = insert(root.right, val);\n }\n else\n {\n root.left = insert(root.left, val);\n }\n \n return updateNode(root);\n }\n \n private Node updateNode(Node root) {\n int b = balance(root); \t\t\n if (b == 2 && balance(root.left) < 0)\n {\n root.left = leftRotate(root.left);\n root = rightRotate(root);\n }\n else if (b == -2 && balance(root.right) > 0)\n {\n root.right = rightRotate(root.right);\n root = leftRotate(root);\n }\n else if (b == 2)\n {\n root = rightRotate(root);\n }\n else if (b == -2)\n {\n root = leftRotate(root);\n }\n update(root);\n return root;\n }\n\n private Node leftRotate(Node n)\n {\n Node r = n.right;\n n.right = r.left;\n r.left = n;\n update(n);\n update(r);\n return r;\n }\n\n private Node rightRotate(Node n)\n {\n Node l = n.left;\n n.left = l.right;\n l.right = n;\n update(n);\n update(l);\n return l;\n }\n\n private int balance(Node n)\n {\n if (n==null)return 0;\n return height(n.left) - height(n.right);\n }\n\n private void update(Node n)\n {\n if (n==null)return;\n n.height = Math.max(height(n.left), height(n.right)) + 1;\n n.count = n.left != null ? n.left.count + 1 : 0;\n n.count += n.right != null ? n.right.count + 1 : 0;\n }\n\n private int height(Node n)\n {\n return n != null ? n.height : 0;\n }\n\n private int countWith(Node n)\n {\n return n != null ? n.count + 1 : 0;\n }\n\n static class Node\n {\n Node left;\n Node right;\n long val;\n int count;\n int height;\n\n Node(long val)\n {\n this.val = val;\n }\n }\n}\n```\n | 215 | 3 | ['C++', 'Java', 'Python3'] | 6 |
sliding-window-median | Java solution using two PriorityQueues | java-solution-using-two-priorityqueues-b-it87 | Almost the same idea of Find Median from Data Stream https://leetcode.com/problems/find-median-from-data-stream/\n1. Use two Heaps to store numbers. maxHeap for | shawngao | NORMAL | 2017-01-09T03:58:50.751000+00:00 | 2018-10-19T22:51:28.799438+00:00 | 43,252 | false | Almost the same idea of ```Find Median from Data Stream``` https://leetcode.com/problems/find-median-from-data-stream/\n1. Use two ```Heaps``` to store numbers. ```maxHeap``` for numbers smaller than current median, ```minHeap``` for numbers bigger than and ```equal``` to current median. A small trick I used is always make size of ```minHeap``` equal (when there are ```even``` numbers) or 1 element more (when there are ```odd``` numbers) than the size of ```maxHeap```. Then it will become very easy to calculate current median.\n2. Keep adding number from the right side of the sliding window and remove number from left side of the sliding window. And keep adding current median to the result.\n```\npublic class Solution {\n PriorityQueue<Integer> minHeap = new PriorityQueue<Integer>();\n PriorityQueue<Integer> maxHeap = new PriorityQueue<Integer>(\n new Comparator<Integer>() {\n public int compare(Integer i1, Integer i2) {\n return i2.compareTo(i1);\n }\n }\n );\n\t\n public double[] medianSlidingWindow(int[] nums, int k) {\n int n = nums.length - k + 1;\n\tif (n <= 0) return new double[0];\n double[] result = new double[n];\n \n for (int i = 0; i <= nums.length; i++) {\n if (i >= k) {\n \tresult[i - k] = getMedian();\n \tremove(nums[i - k]);\n }\n if (i < nums.length) {\n \tadd(nums[i]);\n }\n }\n \n return result;\n }\n \n private void add(int num) {\n\tif (num < getMedian()) {\n\t maxHeap.add(num);\n\t}\n\telse {\n\t minHeap.add(num);\n\t}\n\tif (maxHeap.size() > minHeap.size()) {\n minHeap.add(maxHeap.poll());\n\t}\n if (minHeap.size() - maxHeap.size() > 1) {\n maxHeap.add(minHeap.poll());\n }\n }\n\t\n private void remove(int num) {\n\tif (num < getMedian()) {\n\t maxHeap.remove(num);\n\t}\n\telse {\n\t minHeap.remove(num);\n\t}\n\tif (maxHeap.size() > minHeap.size()) {\n minHeap.add(maxHeap.poll());\n\t}\n if (minHeap.size() - maxHeap.size() > 1) {\n maxHeap.add(minHeap.poll());\n }\n }\n\t\n private double getMedian() {\n\tif (maxHeap.isEmpty() && minHeap.isEmpty()) return 0;\n\t \n\tif (maxHeap.size() == minHeap.size()) {\n\t return ((double)maxHeap.peek() + (double)minHeap.peek()) / 2.0;\n\t}\n\telse {\n return (double)minHeap.peek();\n\t}\n }\n}\n``` | 141 | 10 | [] | 32 |
sliding-window-median | Python clean solution (easy to understand) | python-clean-solution-easy-to-understand-3g0t | I was confused by the official solution and many of the top posts. This problem shouldn\'t be that hard! I ended up using the same template as in Question 295 a | ziweigu | NORMAL | 2019-09-30T19:30:59.756493+00:00 | 2019-09-30T19:35:18.998710+00:00 | 10,242 | false | I was confused by the official solution and many of the top posts. This problem shouldn\'t be that hard! I ended up using the same template as in Question 295 and passed all tests on my first attempt. The key is using two heaps (just like 295) and keeping track of just two things - the element to include and the element to remove. Below is my Python solution:\n```\nimport heapq\nfrom collections import defaultdict\nclass Solution:\n def medianSlidingWindow(self, nums: List[int], k: int) -> List[float]:\n if not nums or not k:\n return []\n lo = [] # max heap\n hi = [] # min heap\n for i in range(k):\n if len(lo) == len(hi):\n heapq.heappush(hi, -heapq.heappushpop(lo, -nums[i]))\n else:\n heapq.heappush(lo, -heapq.heappushpop(hi, nums[i]))\n ans = [float(hi[0])] if k & 1 else [(hi[0] - lo[0]) / 2.0]\n to_remove = defaultdict(int)\n for i in range(k, len(nums)): # right bound of window\n heapq.heappush(lo, -heapq.heappushpop(hi, nums[i])) # always push to lo\n out_num = nums[i-k]\n if out_num > -lo[0]:\n heapq.heappush(hi, -heapq.heappop(lo))\n to_remove[out_num] += 1\n while lo and to_remove[-lo[0]]:\n to_remove[-lo[0]] -= 1\n heapq.heappop(lo)\n while to_remove[hi[0]]:\n to_remove[hi[0]] -= 1\n heapq.heappop(hi)\n if k % 2:\n ans.append(float(hi[0]))\n else:\n ans.append((hi[0] - lo[0]) / 2.0)\n return ans\n```\nA few important things to clarify:\n1. Two heaps (lo and hi). The size of hi, as measured by the number of **valid** elements it contains, is either equal to that of lo or one greater than that of lo, depending on the value of k. (This is an invariant we enforce when we add and remove elements from lo and hi). It\'s worth noting that by "valid" I mean elements **within the current window**. \n2. Lazy removal. I used a defaultdict to_remove to keep track of elements to be removed and their occurrances, and remove them if and only if they are at the top of either heaps. \n3. How to add and remove. The logic is extremely straightforward. When adding a new element, we always add to lo. If the element to be removed is in lo as well, great! We don\'t need to do anything because the heap sizes do not change. However, if the element to be removed happen to be in hi, we then pop an element from lo and add it to hi. **Important: that element we pop is guaranteed be a valid element(!!) because otherwise it should have been removed during the previous iteration.**\n4. Some may be worried that removing elements makes heaps imbalanced. That never happens! No matter how many elements are removed at the end of an iteration, they are invalid elements! The heap lo can contain all the invalid elements and much greater in size than hi, but still in perfect balance with hi. As long as lo and hi each contains half (or (half, half+1) when k is odd) of the **elements in the current window**, we say that they are balanced. | 126 | 1 | [] | 15 |
sliding-window-median | O(n*log(n)) Time C++ Solution Using Two Heaps and a Hash Table | onlogn-time-c-solution-using-two-heaps-a-m0ek | There are a few solutions using BST with worst case time complexity O(nk), but we know k can be become large. I wanted to come up with a solution that is guaran | ipt | NORMAL | 2017-01-08T22:14:29.003000+00:00 | 2018-09-04T18:04:48.031716+00:00 | 15,981 | false | There are a few solutions using BST with worst case time complexity O(n*k), but we know k can be become large. I wanted to come up with a solution that is guaranteed to run in O(n\\*log(n)) time. This is in my opinion the best solution so far.\n\nThe idea is inspired by solutions to [Find Median from Data Stream](https://leetcode.com/problems/find-median-from-data-stream/): use two heaps to store numbers in the sliding window. However there is the issue of numbers moving out of the window, and it turns out that a hash table that records these numbers will just work (and is surprisingly neat). The recorded numbers will only be deleted when they come to the top of the heaps.\n```\nclass Solution {\npublic:\n vector<double> medianSlidingWindow(vector<int>& nums, int k) {\n vector<double> medians;\n unordered_map<int, int> hash; // count numbers to be deleted\n priority_queue<int, vector<int>> bheap; // heap on the bottom\n priority_queue<int, vector<int>, greater<int>> theap; // heap on the top\n \n int i = 0;\n \n // Initialize the heaps\n while (i < k) { bheap.push(nums[i++]); }\n for (int count = k/2; count > 0; --count) {\n theap.push(bheap.top()); bheap.pop();\n }\n \n while (true) {\n // Get median\n if (k % 2) medians.push_back(bheap.top());\n else medians.push_back( ((double)bheap.top() + theap.top()) / 2 );\n \n if (i == nums.size()) break;\n int m = nums[i-k], n = nums[i++], balance = 0;\n \n // What happens to the number m that is moving out of the window\n if (m <= bheap.top()) { --balance; if (m == bheap.top()) bheap.pop(); else ++hash[m]; }\n else { ++balance; if (m == theap.top()) theap.pop(); else ++hash[m]; }\n \n // Insert the new number n that enters the window\n if (!bheap.empty() && n <= bheap.top()) { ++balance; bheap.push(n); }\n else { --balance; theap.push(n); }\n \n // Rebalance the bottom and top heaps\n if (balance < 0) { bheap.push(theap.top()); theap.pop(); }\n else if (balance > 0) { theap.push(bheap.top()); bheap.pop(); }\n \n // Remove numbers that should be discarded at the top of the two heaps\n while (!bheap.empty() && hash[bheap.top()]) { --hash[bheap.top()]; bheap.pop(); }\n while (!theap.empty() && hash[theap.top()]) { --hash[theap.top()]; theap.pop(); }\n }\n \n return medians;\n }\n};\n```\nSince both heaps will never have a size greater than n, the time complexity is O(n*log(n)) in the worst case. | 84 | 0 | [] | 14 |
sliding-window-median | Easy Python O(nk) | easy-python-onk-by-stefanpochmann-yjph | Just keep the window as a sorted list.\n\n def medianSlidingWindow(self, nums, k):\n window = sorted(nums[:k])\n medians = []\n for a, b | stefanpochmann | NORMAL | 2017-01-08T11:24:23.726000+00:00 | 2018-09-22T05:54:45.299505+00:00 | 16,700 | false | Just keep the window as a sorted list.\n\n def medianSlidingWindow(self, nums, k):\n window = sorted(nums[:k])\n medians = []\n for a, b in zip(nums, nums[k:] + [0]):\n medians.append((window[k/2] + window[~(k/2)]) / 2.)\n window.remove(a)\n bisect.insort(window, b)\n return medians | 83 | 2 | [] | 16 |
sliding-window-median | Python real O(nlogk) solution - easy to understand | python-real-onlogk-solution-easy-to-unde-ybyj | Solution 1: O(nk)\nMaitain a sorted window. We can use binary search for remove and insert. \nBecause insert takes O(k), the overall time complexity is O(nk).\ | happy_little_pig | NORMAL | 2020-08-22T22:51:35.815802+00:00 | 2023-11-24T00:53:23.587096+00:00 | 7,858 | false | **Solution 1: `O(nk)`**\nMaitain a sorted window. We can use binary search for remove and insert. \nBecause insert takes `O(k)`, the overall time complexity is `O(nk)`.\n\n**Solution 2: `O(nk)`**\nSimilar with LC 295, we need to maintain two heaps in the window, leftHq and rightHq. \nTo slide one step is actually to do two things: \n- Step 1: add a number, which is exactly the same as that in LC 295, which is `O(logk)`\n- Step 2: remove the number that is outside the window; there is not a remove method in heapq, so it takes ```\nO(k)\n```. So overall the heapq solution will take `O(nk)`.\n\n**Solution 3: O(nlogk)**\nUse a SortedList structure, which was implemented using self-balanced tree. \nSortedList enables `O(logk)` add and `O(logk)` remove. So the total time complexity is `O(nlogk)`.\n\n```\nfrom sortedcontainers import SortedList\n\nclass Solution:\n def medianSlidingWindow(self, nums: List[int], k: int) -> List[float]:\n lst = SortedList() # maintain a sorted list\n \n res = []\n for i in range(len(nums)):\n lst.add(nums[i]) # O(logk)\n if len(lst) > k:\n lst.remove(nums[i-k]) # if we use heapq here, it will take O(k), but for sortedList, it takes O(logk)\n if len(lst) == k:\n median = lst[k//2] if k%2 == 1 else (lst[k//2-1] + lst[k//2]) / 2\n res.append(median)\n\n return res\n``` | 71 | 0 | ['Python', 'Python3'] | 14 |
sliding-window-median | ✅ Easiest Python O(n log k) Two Heaps (Lazy Removal), 96.23% | easiest-python-on-log-k-two-heaps-lazy-r-dj61 | How to understand this solution:\n1) After we build our window, the length of window will ALWAYS be the same (now we will keep the length of valid elements in m | AntonBelski | NORMAL | 2022-04-13T10:08:47.422508+00:00 | 2022-06-29T16:03:58.527334+00:00 | 8,018 | false | How to understand this solution:\n1) After we build our window, the length of window will ALWAYS be the same (now we will keep the length of valid elements in max_heap and min_heap the same too)\n2) Based on this, when we slide our window, the balance variable can be equal to 0, 2 or -2. It will NEVER be -1 or 1.\nExamples:\n0 -> when we remove an element from max_heap and then add a new one back to max_heap (or the same for min_heap)\n-2 -> when we remove an element from max_heap and then add a new one to min_heap (max_heap will have two less elements)\n2 -> when we remove an element from min_heap and then add a new one to max_heap (min_heap will have two less elements)\n3) Based on this - it is enough for us to move 1 element from one heap to another when the balance variable is equal to 2 or -2\n\nIf some points are not clear - Approach 2 in leetcode solutions should help. Best Regards!\n```\nclass Solution:\n # TC - O((n - k)*log(k))\n # SC - O(k)\n\t# 121 ms, faster than 96.23%\n\n def find_median(self, max_heap, min_heap, heap_size):\n if heap_size % 2 == 1:\n return -max_heap[0]\n else:\n return (-max_heap[0] + min_heap[0]) / 2\n\n def medianSlidingWindow(self, nums: List[int], k: int) -> List[float]:\n max_heap = []\n min_heap = []\n heap_dict = defaultdict(int)\n result = []\n \n for i in range(k):\n heappush(max_heap, -nums[i])\n heappush(min_heap, -heappop(max_heap))\n if len(min_heap) > len(max_heap):\n heappush(max_heap, -heappop(min_heap))\n \n median = self.find_median(max_heap, min_heap, k)\n result.append(median)\n \n for i in range(k, len(nums)):\n prev_num = nums[i - k]\n heap_dict[prev_num] += 1\n\n balance = -1 if prev_num <= median else 1\n \n if nums[i] <= median:\n balance += 1\n heappush(max_heap, -nums[i])\n else:\n balance -= 1\n heappush(min_heap, nums[i])\n \n if balance < 0:\n heappush(max_heap, -heappop(min_heap))\n elif balance > 0:\n heappush(min_heap, -heappop(max_heap))\n\n while max_heap and heap_dict[-max_heap[0]] > 0:\n heap_dict[-max_heap[0]] -= 1\n heappop(max_heap)\n \n while min_heap and heap_dict[min_heap[0]] > 0:\n heap_dict[min_heap[0]] -= 1\n heappop(min_heap)\n\n median = self.find_median(max_heap, min_heap, k)\n result.append(median)\n \n return result\n``` | 59 | 0 | ['Heap (Priority Queue)', 'Python', 'Python3'] | 11 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.