Perplexity of fixed-length models¶
Perplexity (PPL) is one of the most common metrics for evaluating language models. Before diving in, we should note that the metric applies specifically to classical language models (sometimes called autoregressive or causal language models) and is not well defined for masked language models like BERT (see summary of the models).
Perplexity is defined as the exponentiated average negative log-likelihood of a sequence. If we have a tokenized sequence \(X = (x_0, x_1, \dots, x_t)\), then the perplexity of \(X\) is,
where \(\log p_\theta (x_i|x_{<i})\) is the log-likelihood of the ith token conditioned on the preceding tokens \(x_{<i}\) according to our model. Intuitively, it can be thought of as an evaluation of the model’s ability to predict uniformly among the set of specified tokens in a corpus. Importantly, this means that the tokenization procedure has a direct impact on a model’s perplexity which should always be taken into consideration when comparing different models.
This is also equivalent to the exponentiation of the cross-entropy between the data and model predictions. For more intuition about perplexity and its relationship to Bits Per Character (BPC) and data compression, check out this fantastic blog post on The Gradient.
Calculating PPL with fixed-length models¶
If we weren’t limited by a model’s context size, we would evaluate the model’s perplexity by autoregressively factorizing a sequence and conditioning on the entire preceding subsequence at each step, as shown below.
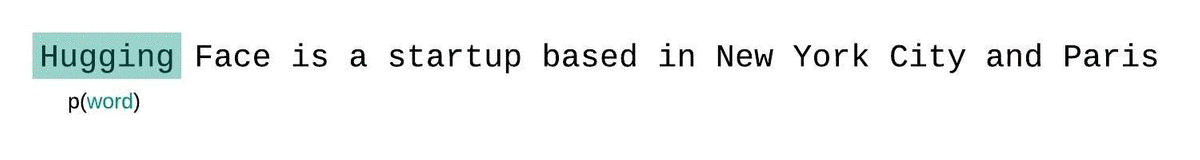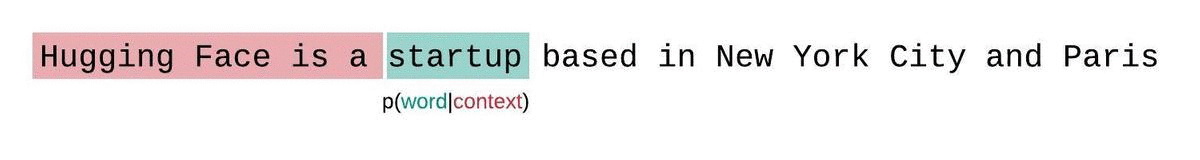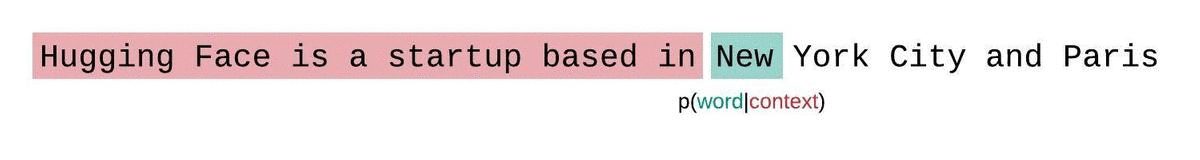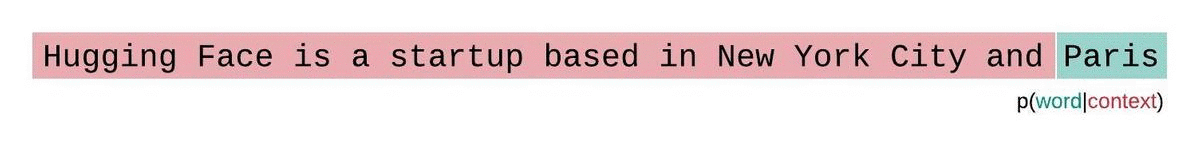
When working with approximate models, however, we typically have a constraint on the number of tokens the model can process. The largest version of GPT-2, for example, has a fixed length of 1024 tokens, so we cannot calculate \(p_\theta(x_t|x_{<t})\) directly when \(t\) is greater than 1024.
Instead, the sequence is typically broken into subsequences equal to the model’s maximum input size. If a model’s max input size is \(k\), we then approximate the likelihood of a token \(x_t\) by conditioning only on the \(k-1\) tokens that precede it rather than the entire context. When evaluating the model’s perplexity of a sequence, a tempting but suboptimal approach is to break the sequence into disjoint chunks and add up the decomposed log-likelihoods of each segment independently.
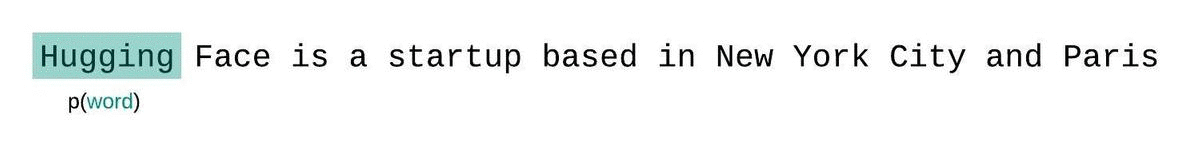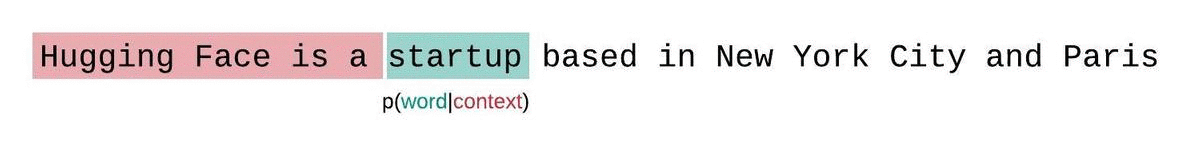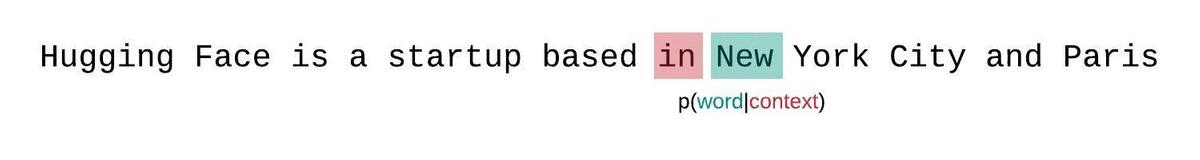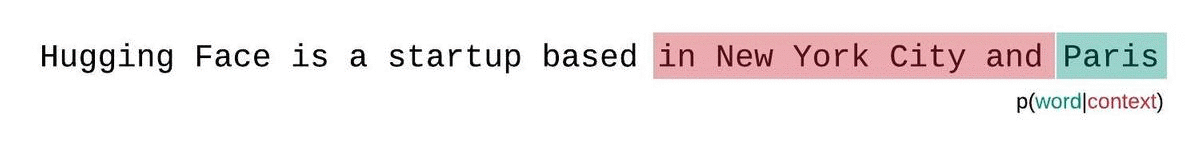
This is quick to compute since the perplexity of each segment can be computed in one forward pass, but serves as a poor approximation of the fully-factorized perplexity and will typically yield a higher (worse) PPL because the model will have less context at most of the prediction steps.
Instead, the PPL of fixed-length models should be evaluated with a sliding-window strategy. This involves repeatedly sliding the context window so that the model has more context when making each prediction.

This is a closer approximation to the true decomposition of the sequence probability and will typically yield a more favorable score. The downside is that it requires a separate forward pass for each token in the corpus. A good practical compromise is to employ a strided sliding window, moving the context by larger strides rather than sliding by 1 token a time. This allows computation to proceed much faster while still giving the model a large context to make predictions at each step.
Example: Calculating perplexity with GPT-2 in 🤗 Transformers¶
Let’s demonstrate this process with GPT-2.
from transformers import GPT2LMHeadModel, GPT2TokenizerFast
device = 'cuda'
model_id = 'gpt2-large'
model = GPT2LMHeadModel.from_pretrained(model_id).to(device)
tokenizer = GPT2TokenizerFast.from_pretrained(model_id)
We’ll load in the WikiText-2 dataset and evaluate the perplexity using a few different sliding-window strategies. Since this dataset is small and we’re just doing one forward pass over the set, we can just load and encode the entire dataset in memory.
from datasets import load_dataset
test = load_dataset('wikitext', 'wikitext-2-raw-v1', split='test')
encodings = tokenizer('\n\n'.join(test['text']), return_tensors='pt')
With 🤗 Transformers, we can simply pass the input_ids as the labels to our model, and the average negative
log-likelihood for each token is returned as the loss. With our sliding window approach, however, there is overlap in
the tokens we pass to the model at each iteration. We don’t want the log-likelihood for the tokens we’re just treating
as context to be included in our loss, so we can set these targets to -100 so that they are ignored. The following
is an example of how we could do this with a stride of 512. This means that the model will have at least 512 tokens
for context when calculating the conditional likelihood of any one token (provided there are 512 preceding tokens
available to condition on).
import torch
from tqdm import tqdm
max_length = model.config.n_positions
stride = 512
nlls = []
for i in tqdm(range(0, encodings.input_ids.size(1), stride)):
begin_loc = max(i + stride - max_length, 0)
end_loc = min(i + stride, encodings.input_ids.size(1))
trg_len = end_loc - i # may be different from stride on last loop
input_ids = encodings.input_ids[:,begin_loc:end_loc].to(device)
target_ids = input_ids.clone()
target_ids[:,:-trg_len] = -100
with torch.no_grad():
outputs = model(input_ids, labels=target_ids)
neg_log_likelihood = outputs[0] * trg_len
nlls.append(neg_log_likelihood)
ppl = torch.exp(torch.stack(nlls).sum() / end_loc)
Running this with the stride length equal to the max input length is equivalent to the suboptimal, non-sliding-window strategy we discussed above. The smaller the stride, the more context the model will have in making each prediction, and the better the reported perplexity will typically be.
When we run the above with stride = 1024, i.e. no overlap, the resulting PPL is 19.64, which is about the same
as the 19.93 reported in the GPT-2 paper. By using stride = 512 and thereby employing our striding window
strategy, this jumps down to 16.53. This is not only a more favorable score, but is calculated in a way that is
closer to the true autoregressive decomposition of a sequence likelihood.