question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
goat-latin | Ruby O(n) using map 😤😤😤😤😤😤😤 | ruby-on-using-map-by-deter-abcu | Split the given string by spaces so you have an array of each string, and then map through the array and perform the requested actions on each string. Join at t | deter | NORMAL | 2018-08-23T21:05:45.894327+00:00 | 2018-10-25T14:13:42.403653+00:00 | 184 | false | Split the given string by spaces so you have an array of each string, and then map through the array and perform the requested actions on each string. Join at the end and seperate by spaces to create the final string\n```\n# @param {String} s\n# @return {String}\n\ndef to_goat_latin(s)\n\n vowels = {"a" => true, "e" => true, "i" => true, "o" => true, "u" => true}\n splut = s.split()\n splut.map.with_index do |x, i|\n unless vowels[x[0].downcase]\n first_char = x.slice!(0)\n x << first_char\n end\n x << "ma"\n x << "a" * (i+1)\n end\n splut.join(" ")\n \nend\n```\n\nmap is a godsend \uD83D\uDE24\uD83D\uDE24\uD83D\uDE24\uD83D\uDE24\uD83D\uDE24\uD83D\uDE24\uD83D\uDE24 | 2 | 0 | [] | 0 |
goat-latin | Java 16ms solution | java-16ms-solution-by-yxzrandom-v88j | \nclass Solution {\n public String toGoatLatin(String S) {\n if (S == null || S.length() == 0) {\n return "";\n }\n String[] | yxzrandom | NORMAL | 2018-06-10T07:39:31.010574+00:00 | 2018-10-25T14:13:48.237489+00:00 | 295 | false | ```\nclass Solution {\n public String toGoatLatin(String S) {\n if (S == null || S.length() == 0) {\n return "";\n }\n String[] str = S.split(" ");\n String source = "aeiouAEIOU";\n StringBuilder res = new StringBuilder();\n for (int i = 0; i < str.length; i++) {\n StringBuilder sb = new StringBuilder();\n if (source.contains(str[i].substring(0, 1))) {\n sb.append(str[i]);\n } else {\n sb.append(str[i].substring(1));\n sb.append(str[i].charAt(0));\n }\n sb.append("ma" + genA(i + 1));\n res.append(sb);\n res.append(" ");\n }\n return res.toString().trim();\n }\n \n public String genA(int num) {\n StringBuilder sb = new StringBuilder();\n while (num > 0) {\n sb.append("a");\n num--;\n }\n return sb.toString();\n }\n}\n``` | 2 | 0 | [] | 0 |
goat-latin | JavaScript solution | javascript-solution-by-jessieyang-9al9 | \nvar toGoatLatin = function(S) {\n\n const vowel = [\'a\', \'e\', \'i\', \'o\', \'u\'];\n let arr = S.split(\' \');\n\t\t\t\t\n for (let i | jessieyang | NORMAL | 2018-05-21T06:28:36.582545+00:00 | 2018-05-21T06:28:36.582545+00:00 | 238 | false | ```\nvar toGoatLatin = function(S) {\n\n const vowel = [\'a\', \'e\', \'i\', \'o\', \'u\'];\n let arr = S.split(\' \');\n\t\t\t\t\n for (let i = 0; i < arr.length; i++) {\n let word = arr[i];\n if (vowel.indexOf(word[0].toLowerCase()) > -1) {\n word += \'ma\';\n } else {\n word += word[0];\n word = word.slice(1) + \'ma\';\n }\n for (let j = 0; j <= i; j++) {\n word += \'a\';\n }\n arr[i] = word;\n }\n\t\t\t\t\n return arr.join(\' \');\n\t\t\t\t\n };\n``` | 2 | 0 | [] | 0 |
goat-latin | Java: 27ms Clean | java-27ms-clean-by-solodjavadev91-n7se | \nclass Solution {\n public String toGoatLatin(String S) {\n String[] sp = S.split("\\\\s+");\n StringBuilder r = new StringBuilder();\n | solodjavadev91 | NORMAL | 2018-05-17T07:32:39.724059+00:00 | 2018-10-25T14:14:01.477888+00:00 | 181 | false | ```\nclass Solution {\n public String toGoatLatin(String S) {\n String[] sp = S.split("\\\\s+");\n StringBuilder r = new StringBuilder();\n int i = 1;\n for(String s : sp){\n r.append(iBuild(s,i));\n r.append(" ");\n i++;\n }\n r.setLength(r.length() -1);\n return r.toString();\n }\n \n public String iBuild(String S,int i){\n char[] c = S.toCharArray();\n StringBuilder r = new StringBuilder();\n \n switch(c[0]){\n case \'a\':\n case \'A\':\n case \'e\':\n case \'E\':\n case \'i\':\n case \'I\':\n case \'o\':\n case \'O\':\n case \'U\':\n case \'u\':\n {\n r.append(String.valueOf(c));\n r.append("ma");\n r.append(new String(new char[i]).replace("\\0","a"));\n return r.toString();\n }\n }\n \n r.append(String.valueOf(c));\n r.append(c[0]);\n r.append("ma");\n r.append(new String(new char[i]).replace("\\0","a"));\n String temp = r.toString();\n return temp.substring(1,temp.length());\n \n }\n}\n``` | 2 | 0 | [] | 0 |
goat-latin | [ Javascript / Python3 / C++ ] solutions | javascript-python3-c-solutions-by-clayto-7pwy | Javascript\n\nlet toGoatLatin = (words, isVowel = c => 0 <= \'aeiou\'.indexOf(c.toLowerCase())) =>\n words.split(\' \')\n .map(s => isVowel(s[0]) ? s | claytonjwong | NORMAL | 2018-05-02T03:56:50.034715+00:00 | 2020-08-19T23:54:21.899886+00:00 | 244 | false | *Javascript*\n```\nlet toGoatLatin = (words, isVowel = c => 0 <= \'aeiou\'.indexOf(c.toLowerCase())) =>\n words.split(\' \')\n .map(s => isVowel(s[0]) ? s : s.substring(1, s.length) + s[0])\n .map((s, i) => s + \'ma\' + \'a\'.repeat(i + 1)).join(\' \');\n```\n\n*Python3*\n```\nclass Solution:\n def toGoatLatin(self, words: str, vowels = set([ \'a\',\'e\',\'i\',\'o\',\'u\' ])) -> str:\n isVowel = lambda s: s[0].lower() in vowels\n return \' \'.join(s + \'ma\' + \'a\' * (i + 1) for i, s in enumerate([s if isVowel(s) else s[1:] + s[0] for s in split(\' \', words)]))\n```\n\n*C++*\n```\nclass Solution {\npublic:\n string toGoatLatin(string words, string s = {}, int i = 0, string vowels = "aeiouAEIUO", ostringstream os = ostringstream()) {\n istringstream is{ words };\n while (is >> s) {\n if (vowels.find(s[0]) == string::npos)\n s = s.substr(1) + s[0];\n os << s << "ma", fill_n(ostream_iterator<char>(os), ++i, \'a\'), os << (0 < is.tellg() ? " " : "");\n }\n return os.str();\n }\n};\n``` | 2 | 0 | [] | 1 |
goat-latin | Java O(n) Solution | java-on-solution-by-vjsfbay-zmc3 | \nString[] strArr = S.split(" ");\n StringBuilder strBld = new StringBuilder();\n\n Set<Character> vowel = new HashSet<>();\n for (char c : | vjsfbay | NORMAL | 2018-04-30T01:07:39.113335+00:00 | 2018-10-25T14:14:49.815967+00:00 | 551 | false | ```\nString[] strArr = S.split(" ");\n StringBuilder strBld = new StringBuilder();\n\n Set<Character> vowel = new HashSet<>();\n for (char c : "aeiouAEIOU".toCharArray()) vowel.add(c);\n StringBuilder aCounter = new StringBuilder();\n aCounter.append("a");\n\n for (int i = 0; i < strArr.length; i++) {\n if (vowel.contains(strArr[i].toLowerCase().charAt(0))) {\n strBld.append(strArr[i] + "ma");\n } else {\n strBld.append(strArr[i].substring(1, strArr[i].length()) + strArr[i].charAt(0) + "ma");\n }\n strBld.append(aCounter + " ");\n aCounter.append("a");\n }\n return strBld.toString().substring(0, strBld.length() - 1);\n``` | 2 | 0 | [] | 1 |
goat-latin | Java: If you think like me.. | java-if-you-think-like-me-by-coder11-ekfz | \nclass Solution {\n public String toGoatLatin(String S) {\n if(S==null || S.length()==0) return S;\n Set<Character> vowels = new HashSet<Chara | coder11 | NORMAL | 2018-04-29T22:40:31.760042+00:00 | 2018-10-25T14:14:18.151536+00:00 | 195 | false | ```\nclass Solution {\n public String toGoatLatin(String S) {\n if(S==null || S.length()==0) return S;\n Set<Character> vowels = new HashSet<Character>(Arrays.asList(\'a\',\'e\',\'i\',\'o\',\'u\',\'A\',\'E\',\'I\',\'O\',\'U\'));\n \n StringBuilder prev_a=new StringBuilder(),res=new StringBuilder();\n String ma="ma";\n \n String[] arr=S.split("\\\\s+");\n for(String st:arr)\n {\n char first=st.charAt(0);\n StringBuilder sb=new StringBuilder();\n prev_a.append("a");\n //Comparing if the first char is a vowel or not\n if(vowels.contains(first))\n {\n sb.append(st).append(ma).append(prev_a);\n }\n else\n {\n sb.append(st).append(first).append(ma).append(prev_a);\n sb.deleteCharAt(0);\n }\n res.append(sb.toString()).append(" ");\n }\n return res.toString().trim();\n }\n}\n``` | 2 | 0 | [] | 0 |
goat-latin | Simulation | simulation-by-khaled-alomari-hm86 | Complexity
Time complexity:
O(n2)
Space complexity:
O(n2)
Code | khaled-alomari | NORMAL | 2025-03-06T17:34:03.866608+00:00 | 2025-03-06T17:40:45.290963+00:00 | 45 | false | # Complexity
- Time complexity:
$$O(n^2)$$
- Space complexity:
$$O(n^2)$$
# Code
```typescript []
function toGoatLatin(sentence: string) {
const vowels = new Set(['a', 'e', 'i', 'o', 'u', 'A', 'E', 'I', 'O', 'U']);
return sentence.split(' ').map((w, i) => {
const conso = !vowels.has(w[0]);
return w.substring(+conso) + w[0].repeat(+conso) + 'ma' + 'a'.repeat(i + 1);
}).join(' ');
}
```
```javascript []
function toGoatLatin(sentence) {
const vowels = new Set(['a', 'e', 'i', 'o', 'u', 'A', 'E', 'I', 'O', 'U']);
return sentence.split(' ').map((w, i) => {
const conso = !vowels.has(w[0]);
return w.substring(+conso) + w[0].repeat(+conso) + 'ma' + 'a'.repeat(i + 1);
}).join(' ');
}
``` | 1 | 0 | ['Array', 'Hash Table', 'String', 'String Matching', 'Simulation', 'Iterator', 'TypeScript', 'JavaScript'] | 0 |
goat-latin | Easy answer in 1 loop | easy-answer-in-1-loop-by-saksham_gupta-his7 | Complexity
Time complexity: O(n)
Space complexity: O(n)
Code | Saksham_Gupta_ | NORMAL | 2025-01-30T17:41:53.268029+00:00 | 2025-01-30T17:41:53.268029+00:00 | 256 | false |
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity: ***O(n)***
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: ***O(n)***
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public String toGoatLatin(String sentence) {
String[] words = sentence.split(" ");
StringBuilder res = new StringBuilder();
String vowels = "aeiouAEIOU";
for(int i=0; i<words.length; i++){
String word = words[i];
if(vowels.indexOf(word.charAt(0)) != -1){
word += "ma";
}
else{
word = word.substring(1) + word.charAt(0) + "ma";
}
word += "a".repeat(i+1);
// Now add to res
res.append(word).append(" ");
}
return res.toString().trim();
}
}
``` | 1 | 0 | ['String', 'Java'] | 0 |
goat-latin | Do As it Says | Simple | Readable | Linear O(N) | do-as-it-says-simple-readable-linear-on-wv56e | CodeComplexity
Time complexity: O(N)
Space complexity: O(N) | Apakg | NORMAL | 2024-12-24T08:58:01.813918+00:00 | 2024-12-24T08:58:01.813918+00:00 | 185 | false | # Code
```java []
class Solution {
Set<String> set = Set.of("a", "e", "i", "o", "u", "A", "E", "I", "O", "U");
public String toGoatLatin(String sentence) {
String[] words = sentence.split("\\s");
StringBuilder stack = new StringBuilder();
int wordsProcessed = 0;
for(String word: words){
++wordsProcessed;
if(set.contains(String.valueOf(word.charAt(0)))){
String newWord = word + "ma" + requestA(wordsProcessed);
stack.append(newWord);
}
else { // if not a vowel.
char firstNonVowel = word.charAt(0);
String newWordConso = word.substring(1, word.length()).concat(String.valueOf(firstNonVowel)) + "ma" + requestA(wordsProcessed);
stack.append(newWordConso);
}
stack.append(" ");
}
return stack.toString().trim();
}
public String requestA(int count){
int wordsCnt = count;
if(wordsCnt == 1) return "a";
return "a".repeat(count);
}
}
```
# Complexity
- Time complexity: O(N)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(N)
<!-- Add your space complexity here, e.g. $$O(n)$$ --> | 1 | 0 | ['String', 'Stack', 'Ordered Set', 'Java'] | 0 |
goat-latin | Brute Force approach | brute-force-approach-by-anshsavadatti-8m4f | Intuition\n Describe your first thoughts on how to solve this problem. \nAfter looking at the problem, came to a conclusing that basic STL operations, especiall | anshsavadatti | NORMAL | 2024-09-24T13:32:25.592689+00:00 | 2024-09-24T13:32:25.592725+00:00 | 252 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nAfter looking at the problem, came to a conclusing that basic STL operations, especially of strings can solve the problem.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nBrute Force, using Standard Templete Library.\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(n)\n\n# Code\n```cpp []\nclass Solution {\nprivate:\n string addma(string &s){\n s += "ma";\n return s;\n }\n string adda(string &s, int n){\n for(int i =0; i < n; i++){\n s.push_back(\'a\');\n }\n return s;\n }\n bool checkVowel(char ch){\n return ch == \'a\' || ch == \'e\' || ch == \'i\' || ch == \'o\' || ch == \'u\' || ch == \'A\' || ch == \'E\' || ch == \'I\' || ch == \'O\' || ch == \'U\';\n }\n void breakString(string ss, vector<string>& s){\n string temp = "";\n for(auto it : ss){\n if(it == \' \'){\n s.push_back(temp);\n temp = "";\n }else{\n temp.push_back(it);\n }\n }\n if(!temp.empty()) s.push_back(temp);\n return;\n }\n\npublic:\n string toGoatLatin(string sentence) {\n string ans = "";\n vector<string> strings;\n breakString(sentence, strings);\n\n for(int i = 0; i < strings.size(); i++){\n string word = strings[i];\n if(checkVowel(word[0])){\n ans += word;\n }else{\n char ch = word[0];\n word = word.substr(1);\n ans += word;\n ans.push_back(ch);\n }\n addma(ans);\n adda(ans, i + 1);\n ans.push_back(\' \');\n }\n if(ans[ans.size() - 1] == \' \'){\n ans.pop_back();\n }\n return ans;\n }\n};\n``` | 1 | 0 | ['Array', 'String', 'C++'] | 0 |
goat-latin | ho gya !!! :D | ho-gya-d-by-yesyesem-tcir | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | yesyesem | NORMAL | 2024-09-24T13:04:34.072515+00:00 | 2024-09-24T13:04:34.072544+00:00 | 119 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n string toGoatLatin(string sentence) {\n\n vector<string>vec;\n int n=sentence.length();\n string s;\n\n for(int i=0;i<n;i++)\n {\n if(sentence[i]==\' \')\n {\n if(!s.empty())\n { \n vec.push_back(s);\n s.clear();\n }\n }\n if(sentence[i]!=\' \')\n s.push_back(sentence[i]);\n }\n\n vec.push_back(s);\n string ans="";\n for(int i=0;i<vec.size();i++)\n {\n if(vec[i][0]==\'a\'||vec[i][0]==\'e\'||vec[i][0]==\'i\'||vec[i][0]==\'o\'||vec[i][0]==\'u\'||vec[i][0]==\'A\'||vec[i][0]==\'E\'||vec[i][0]==\'I\'||vec[i][0]==\'O\'||vec[i][0]==\'U\')\n {\n vec[i].push_back(\'m\');\n vec[i].push_back(\'a\');\n }\n else\n {\n char ch=vec[i][0];\n vec[i].erase(0,1);\n vec[i].push_back(ch);\n vec[i].push_back(\'m\');\n vec[i].push_back(\'a\');\n\n }\n\n for(int k=0;k<i+1;k++)\n {\n vec[i].push_back(\'a\');\n }\n\n ans+=vec[i];\n ans+=\' \';\n \n\n\n }\n ans.pop_back();\n\n \n return ans;\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
goat-latin | [Java] Easy solution | java-easy-solution-by-ytchouar-84x1 | java\nimport java.util.StringJoiner;\n\nclass Solution {\n public String toGoatLatin(final String sentence) {\n final String[] words = sentence.split( | YTchouar | NORMAL | 2024-05-28T19:08:39.906199+00:00 | 2024-05-28T19:08:39.906216+00:00 | 683 | false | ```java\nimport java.util.StringJoiner;\n\nclass Solution {\n public String toGoatLatin(final String sentence) {\n final String[] words = sentence.split("\\\\s+");\n final StringJoiner sj = new StringJoiner(" ");\n\n int n = 1;\n\n for(final String word : words) {\n final char first = word.charAt(0), firstLower = Character.toLowerCase(first);\n final StringBuilder sb = new StringBuilder();\n\n if(firstLower == \'a\' || firstLower == \'e\' || firstLower == \'i\' || firstLower == \'o\' || firstLower == \'u\') {\n sb.append(word);\n } else {\n sb.append(word.substring(1));\n sb.append(first);\n }\n\n sb.append("ma");\n\n for(int i = 0; i < n; ++i)\n sb.append(\'a\');\n\n sj.add(sb.toString());\n\n n++;\n }\n\n return sj.toString();\n }\n}\n``` | 1 | 0 | ['Java'] | 0 |
goat-latin | Python solution without split() | python-solution-without-split-by-trisham-j3w0 | Key Terms\n- prev: Initialize to space. Each time prev = space, you\'ve reached the start of a new word.\n- As: Initialize to one, meaning one \'a\' will be add | trishamorris | NORMAL | 2024-05-12T00:57:29.940130+00:00 | 2024-05-12T00:57:29.940154+00:00 | 229 | false | # Key Terms\n- prev: Initialize to space. Each time prev = space, you\'ve reached the start of a new word.\n- As: Initialize to one, meaning one \'a\' will be added to the end of the first word. Increment As for each word encountered. Multiply \'a\' by As each time you are adding a\'s to the end of a word\n- append: If append equals some character, we are working with a consonant. Add append to the end of the consonant before adding \'ma\'.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def toGoatLatin(self, sentence: str) -> str:\n prev = \' \'\n As = 1 # a\'s to add\n vowels = {\'a\':0, \'e\':0, \'i\':0, \'o\':0, \'u\':0, \'A\':0, \'E\':0, \'I\':0, \'O\':0, \'U\':0}\n append = \'\'\n\n ch = 0\n while ch < len(sentence) - 1:\n if sentence[ch] != \' \' and prev == \' \': # reached the start of a word\n if sentence[ch] not in vowels: # consonant\n append = sentence[ch]\n before = sentence[:ch]\n after = sentence[ch+1:] # remove first letter\n sentence = before + after\n\n if sentence[ch] == \' \' and prev != \' \': # end of a word and not end of string\n if append != \'\': # consonant\n insert = append + \'ma\' + \'a\'*As\n else:\n insert = \'ma\' + \'a\'*As\n\n before = sentence[:ch] \n after = sentence[ch:]\n sentence = before + insert + after\n \n if append != \'\':\n ch = ch+3+1*As # increment ch to the end of the word\n append = \'\'\n else:\n ch = ch+2+1*As \n As += 1\n \n elif sentence[ch] == \' \' and append != \'\': # one word consonant\n before = sentence[:ch]\n insert = append + \'ma\' + \'a\'*As\n append = \'\'\n after = sentence[ch:]\n sentence = before + insert + after\n ch = ch+3+1*As\n As += 1\n\n prev = sentence[ch] # increment\n ch += 1\n\n # last word of string\n if append != \'\': # consonant\n insert = append + \'ma\' + \'a\'*As\n else:\n insert = \'ma\' + \'a\'*As\n\n sentence = sentence + insert\n\n return sentence\n\n```\nLeave any questions in the chat and I\'ll try to answer them shortly :3 | 1 | 0 | ['Python3'] | 1 |
goat-latin | Kotlin || O(N) Time and Space | kotlin-on-time-and-space-by-girl_coder_s-cs03 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | girl_coder_s | NORMAL | 2024-04-03T18:01:06.307265+00:00 | 2024-04-03T18:01:06.307298+00:00 | 112 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n fun toGoatLatin(str: String): String {\n val words = str.split(" ")\n val result = StringBuilder()\n for ((index, word) in words.withIndex()) {\n val processedWord = processWords(word, index + 1)\n result.append(processedWord).append(\' \')\n }\n result.deleteCharAt(result.length - 1) // Remove trailing space\n return result.toString()\n }\n\n private fun isFirstCharVowel(char: Char): Boolean {\n return char in "aeiouAEIOU"\n }\n\n private fun getAppndStr(idx: Int): String {\n return "a".repeat(idx)\n }\n\n private fun processWords(word: String, idx: Int): String {\n val firstChar = word[0]\n val appndStr = getAppndStr(idx)\n return if (isFirstCharVowel(firstChar)) {\n word + "ma" + appndStr\n } else {\n word.substring(1) + firstChar + "ma" + appndStr\n }\n }\n}\n\n``` | 1 | 0 | ['Kotlin'] | 0 |
goat-latin | Easy Beginner Level Java Code | easy-beginner-level-java-code-by-saurabh-zq11 | Complexity\n- Time complexity:\nO(n*n)\n- Space complexity:\nO(n)\n# Code\n\nclass Solution {\n public String toGoatLatin(String sentence) {\n HashSet | Saurabh_Mishra06 | NORMAL | 2024-01-18T14:15:39.006619+00:00 | 2024-01-18T14:15:39.006650+00:00 | 483 | false | # Complexity\n- Time complexity:\nO(n*n)\n- Space complexity:\nO(n)\n# Code\n```\nclass Solution {\n public String toGoatLatin(String sentence) {\n HashSet<Character> vowels = new HashSet();\n for(char c : "aeiouAEIOU".toCharArray()){\n vowels.add(c);\n }\n\n String result = "";\n int index = 1;\n for(String word : sentence.split("\\\\s")){\n if(index > 1){\n result += " ";\n }\n\n char letter = word.charAt(0);\n if(vowels.contains(letter)){\n result += word + "ma";\n }else {\n result += word.substring(1) + letter + "ma";\n }\n\n for(int j=0; j<index; j++){\n result += "a";\n }\n\n index += 1;\n }\n\n return result;\n }\n}\n``` | 1 | 0 | ['Java'] | 0 |
goat-latin | Easy C++ Solution || Basic Approach & 3 line code | easy-c-solution-basic-approach-3-line-co-csfg | \n\n\n\n# Code\n\nclass Solution {\npublic:\n string toGoatLatin(string sentence) {\n string ans="";\n vector<string>p;\n string pp="";\ | tiwariswapnil100 | NORMAL | 2024-01-10T16:31:42.430823+00:00 | 2024-01-10T16:31:42.430872+00:00 | 187 | false | \n\n\n\n# Code\n```\nclass Solution {\npublic:\n string toGoatLatin(string sentence) {\n string ans="";\n vector<string>p;\n string pp="";\n for(auto x:sentence){\n if(x==\' \'){\n p.push_back(pp);\n pp="";\n }\n else{\n pp=pp+x;\n }\n }\n p.push_back(pp);\n \n int t=p.size();\n int k=1;\n for(auto x:p){\n string y="";\n char ch=x[0];\n if (ch == \'a\' || ch == \'e\' || ch == \'i\' || \n ch == \'o\' || ch == \'u\' || ch == \'A\' || \n ch== \'E\' || ch == \'I\' || ch == \'O\' || ch == \'U\') {\n y=x;\n y+="ma";\n }\n else{\n for(int i=1;i<x.size();i++){\n y+=x[i];\n }\n y+=x[0];\n y+="ma";\n\n }\n for(int i=0;i<k;i++){\n y+=\'a\';\n }\n k++;\n if(k<=t)\n y+=" ";\n ans+=y;\n\n\n\n }\n return ans;\n \n }\n};\n```\n# 3 LIne code \n```\n string toGoatLatin(string S) {\n unordered_set<char> vowel({\'a\', \'e\', \'i\', \'o\', \'u\', \'A\', \'E\', \'I\', \'O\', \'U\'});\n istringstream iss(S);\n string res, w;\n int i = 0, j;\n while (iss >> w) {\n res += \' \' + (vowel.count(w[0]) == 1 ? w : w.substr(1) + w[0]) + "ma";\n for (j = 0, ++i; j < i; ++j) res += "a";\n }\n return res.substr(1);\n }\n```\n\n\n | 1 | 0 | ['C++'] | 1 |
goat-latin | JAVA ~> Goat Latin :) | java-goat-latin-by-01aas-wvxi | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | agent_001 | NORMAL | 2023-12-03T16:48:21.094875+00:00 | 2023-12-03T16:48:21.094909+00:00 | 7 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public String toGoatLatin(String sentence) {\n \n String []data = sentence.split(" ");\n StringBuilder sb = new StringBuilder();\n for(int a =0 ; a < data.length ; a++){\n if(data[a].startsWith("a") || data[a].startsWith("e") || data[a].startsWith("i") || data[a].startsWith("o") || data[a].startsWith("u") || data[a].startsWith("A") || data[a].startsWith("E") || data[a].startsWith("I") || data[a].startsWith("O") || data[a].startsWith("U") ){\n sb.append(data[a]);\n sb.append("ma");\n }\n else{\n char first = data[a].charAt(0);\n data[a] =data[a].substring(1, data[a].length());\n sb.append(data[a]);\n sb.append(first);\n sb.append("ma");\n }\n\n int temp = a + 1;\n while(temp>0){\n \n sb.append("a");\n\n temp--;\n }\n sb.append(" ");\n\n }\n sb.deleteCharAt(sb.length()-1);\n\nreturn sb.toString();\n }\n}\n``` | 1 | 0 | ['Java'] | 0 |
goat-latin | C++ simple solution || beats 100% [0ms]💯 | c-simple-solution-beats-100-0ms-by-shrey-qing | Code\n\nclass Solution {\npublic:\n string toGoatLatin(string sentence) {\n string result = "", word = "", vowels = "aeiouAEIOU";\n int index = | shreya4dhingra | NORMAL | 2023-11-10T07:11:21.491648+00:00 | 2023-11-10T07:11:21.491674+00:00 | 33 | false | # Code\n```\nclass Solution {\npublic:\n string toGoatLatin(string sentence) {\n string result = "", word = "", vowels = "aeiouAEIOU";\n int index = 1;\n for(int i=0; i<sentence.size(); i++) {\n if(sentence[i] == \' \') {\n if(vowels.find(word[0]) == string::npos)\n word = word.substr(1) + word[0];\n result += word + "ma" + string(index++,\'a\') + " ";\n word = "";\n }\n else\n word += sentence[i];\n }\n if(vowels.find(word[0]) == string::npos)\n word = word.substr(1) + word[0];\n result += word + "ma" + string(index++,\'a\');\n return result;\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
goat-latin | BEATS 100%😎 || JAVA VERY EASY SOLUTION 🔥🔥🔥 | beats-100-java-very-easy-solution-by-sum-gkw3 | \n\n# Code\n\nclass Solution {\n public String toGoatLatin(String sentence) {\n String[] s=sentence.split(" ");\n StringBuilder sb=new StringBu | sumo25 | NORMAL | 2023-09-01T18:52:37.092933+00:00 | 2023-09-01T18:52:37.092957+00:00 | 7 | false | \n\n# Code\n```\nclass Solution {\n public String toGoatLatin(String sentence) {\n String[] s=sentence.split(" ");\n StringBuilder sb=new StringBuilder();\n for(int i=0;i<s.length;i++){\n String str=s[i];\n if(str.charAt(0)==\'a\'|| str.charAt(0)==\'e\' || str.charAt(0)==\'i\' || str.charAt(0)==\'o\' || str.charAt(0)==\'u\' || str.charAt(0)==\'A\' || str.charAt(0)==\'E\' || str.charAt(0)==\'I\' || str.charAt(0)==\'O\' || str.charAt(0)==\'U\'){\n sb.append(str);\n sb.append("ma");\n for(int j=0;j<=i;j++){\n sb.append(\'a\');\n }\n sb.append(\' \');\n }\n else{\n char ch=str.charAt(0);\n String strr=str.substring(1,str.length());\n sb.append(strr);\n sb.append(ch);\n sb.append("ma");\n for(int j=0;j<=i;j++){\n sb.append(\'a\');\n }\n sb.append(\' \');\n }\n }\n return sb.toString().trim();\n }\n}\n``` | 1 | 0 | ['Java'] | 0 |
goat-latin | Easy java solution using simpler concepts | easy-java-solution-using-simpler-concept-fde2 | \n\n# Code\n\nclass Solution {\n public String toGoatLatin(String sentence) {\n sentence.toLowerCase();\n String[] words=sentence.split(" ",0); | Palakpreet | NORMAL | 2023-05-07T07:48:16.174565+00:00 | 2023-05-07T07:48:16.174606+00:00 | 636 | false | \n\n# Code\n```\nclass Solution {\n public String toGoatLatin(String sentence) {\n sentence.toLowerCase();\n String[] words=sentence.split(" ",0);\n int i=1;\n String ans="";\n for(String word:words){\n \n char p1=word.charAt(0);\n char p=word.toLowerCase().charAt(0);\n String k="";\n if(p==\'a\'||p==\'i\'||p==\'o\'||p==\'e\'||p==\'u\'){\n k+=word+"ma";\n }\n else{\n k+=word.substring(1,word.length());\n k+=p1;\n k+="ma";\n }\n for(int m=0;m<i;m++){\n k+=\'a\';\n }\n ans+=k;\n if(i!=words.length)ans+=" ";\n i++;\n }\n return ans;\n }\n}\n``` | 1 | 0 | ['Java'] | 0 |
goat-latin | Goat Latin 100% runtime beats | goat-latin-100-runtime-beats-by-swakshan-da30 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Swakshan | NORMAL | 2023-04-05T17:56:10.289709+00:00 | 2023-04-05T17:56:10.289751+00:00 | 199 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n string toGoatLatin(string sentence) {\n string h;\n vector<string> ans;\n for(int i = 0; i<sentence.length(); i++ ) {\n if(sentence[i]!=\' \'){\n h+=sentence[i];\n }\n else{\n ans.push_back(h);\n h = "";\n }\n }\n if(h.length()>0)\n ans.push_back(h);\n string j;\n string ma = "ma";\n string aAlpha = "a";\n for(int i = 0; i<ans.size(); i++ ) {\n string k = ans[i];\n if(k[0]==\'a\'||k[0]==\'e\'||k[0]==\'i\'||k[0]==\'o\'||k[0]==\'u\'||k[0]==\'A\'||k[0]==\'E\'||k[0]==\'I\'||k[0]==\'O\'||k[0]==\'U\') {\n j+=k;\n j+=ma;\n }\n if(k[0]!=\'a\'&&k[0]!=\'e\'&&k[0]!=\'i\'&&k[0]!=\'o\'&&k[0]!=\'u\'&&k[0]!=\'A\'&&k[0]!=\'E\'&&k[0]!=\'I\'&&k[0]!=\'O\'&&k[0]!=\'U\') {\n int start = 1;\n while(start<k.length()) {\n j+=k[start++];\n }\n j+=k[0];\n j+=ma;\n }\n int d = i+1;\n while(d>0) {\n j+=aAlpha;\n d--;\n }\n j+=" ";\n }\n string yop;\n for(int i = 0; i<j.length()-1; i++ ) {\n yop.push_back(j[i]);\n }\n return yop;\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
goat-latin | Best [C++] Solution || Beats 100% | best-c-solution-beats-100-by-yashgagrani-hwg9 | Code\n\nclass Solution {\npublic:\n bool isValid(string &ans){\n if(ans[0]==\'a\' || ans[0]==\'e\' || ans[0]==\'i\' || ans[0]==\'o\' || ans[0]==\'u\' | YashGagrani- | NORMAL | 2023-02-16T14:21:11.172419+00:00 | 2023-02-16T14:21:11.172466+00:00 | 1,221 | false | # Code\n```\nclass Solution {\npublic:\n bool isValid(string &ans){\n if(ans[0]==\'a\' || ans[0]==\'e\' || ans[0]==\'i\' || ans[0]==\'o\' || ans[0]==\'u\' || ans[0]==\'A\' || ans[0]==\'E\' || ans[0]==\'I\' || ans[0]==\'O\' || ans[0]==\'U\') return true;\n return false;\n }\n string toGoatLatin(string sentence) {\n string val;\n vector<string>ans;\n for(int i=0; i<sentence.length(); i++){\n string temp;\n while(i<sentence.length() && sentence[i]!=\' \'){\n temp+=sentence[i];\n i++;\n }\n ans.push_back(temp);\n }\n string a1 = "a";\n for(int i=0; i<ans.size(); i++){\n if(isValid(ans[i])){\n val+=ans[i];\n val+="ma";\n val+=a1;\n a1+=\'a\';\n }else{\n char a = ans[i][0];\n val+=ans[i].substr(1,ans[i].length()-1);\n val+=a;\n val+="ma";\n val+=a1;\n a1+=\'a\';\n }\n if(i==ans.size()-1){\n return val;\n }else{\n val+=\' \';\n }\n }\n return val;\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
goat-latin | C++ find | c-find-by-neillee1210-iyeo | Intuition\n Describe your first thoughts on how to solve this problem. \nlinear search \n# Approach\n Describe your approach to solving the problem. \nSearch a | NeilLee1210 | NORMAL | 2023-01-15T15:33:24.895630+00:00 | 2023-01-15T15:34:32.635291+00:00 | 38 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nlinear search \n# Approach\n<!-- Describe your approach to solving the problem. -->\nSearch a word in sentense\n\nConvert to goat latin\n\nCombine it to new sentense\n\nNext search\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\nprivate:\n using Word = struct {\n string &sentence;\n string::size_type idx;\n string::size_type pos;\n string::size_type len;\n };\n\n bool IsVowel(Word &word)\n {\n string check;\n check.push_back(tolower(word.sentence[word.pos]));\n string::size_type pos = check.find_first_of("aeiou");\n return (pos != string::npos);\n }\n \n string ToLatinVowel(Word &word)\n {\n return (word.sentence.substr(word.pos, word.len) + "ma");\n }\n \n string ToLatinConsonant(Word &word)\n {\n string latinWord = word.sentence.substr(word.pos+1, word.len-1);\n latinWord.push_back(word.sentence[word.pos]);\n latinWord += "ma";\n return latinWord;\n }\n\n void AddLatinA(string &latinWord, string::size_type number)\n {\n latinWord += string(number,\'a\');\n }\npublic:\n string toGoatLatin(string sentence)\n {\n string latinStce;\n Word sentenceWord = {\n .sentence = sentence,\n // default one word in sentence\n .idx = 0,\n .pos = 0,\n .len = sentence.size()\n };\n\n // Word sentenceWord = { 0, 0, sentence.size() };\n string::size_type pos = 0;\n while (pos != string::npos) {\n string latinWord;\n ++sentenceWord.idx;\n // Find a word\n pos = sentence.find(" ", sentenceWord.pos);\n if ( pos != string::npos) {\n sentenceWord.len = pos - sentenceWord.pos;\n } else {\n sentenceWord.len = sentence.size() - sentenceWord.pos;\n }\n // Convert\n if (IsVowel(sentenceWord)) {\n latinWord = ToLatinVowel(sentenceWord);\n } else {\n latinWord = ToLatinConsonant(sentenceWord);\n }\n AddLatinA(latinWord, sentenceWord.idx);\n latinStce += latinWord + " ";\n // Next word search start\n sentenceWord.pos = pos + 1;\n }\n latinStce.pop_back();\n return latinStce;\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
goat-latin | [Accepted] Swift | accepted-swift-by-vasilisiniak-lqsv | \nclass Solution {\n func toGoatLatin(_ sentence: String) -> String {\n sentence\n .components(separatedBy: " ")\n .enumerated() | vasilisiniak | NORMAL | 2022-12-27T09:35:03.751167+00:00 | 2022-12-27T09:35:03.751198+00:00 | 269 | false | ```\nclass Solution {\n func toGoatLatin(_ sentence: String) -> String {\n sentence\n .components(separatedBy: " ")\n .enumerated()\n .map { i, w -> String in\n if "aeiou".contains(w.first!.lowercased()) {\n return "\\(w)ma\\(String(repeating: "a", count: i + 1))"\n }\n else {\n return "\\(w.dropFirst())\\(w.first!)ma\\(String(repeating: "a", count: i + 1))"\n }\n }\n .joined(separator: " ")\n }\n}\n``` | 1 | 0 | ['Swift'] | 1 |
goat-latin | JavaScript | JS | Easy To Understand | Simple Solution | javascript-js-easy-to-understand-simple-yhvm5 | \n\n/**\n * @param {string} sentence\n * @return {string}\n */\nvar toGoatLatin = function(sentence) {\n const vowelSet = new Set([\'a\', \'e\', \'i\', \'o\' | seungwoo321 | NORMAL | 2022-12-11T13:23:39.655454+00:00 | 2022-12-11T13:23:39.655495+00:00 | 424 | false | \n```\n/**\n * @param {string} sentence\n * @return {string}\n */\nvar toGoatLatin = function(sentence) {\n const vowelSet = new Set([\'a\', \'e\', \'i\', \'o\', \'u\', \'A\', \'E\', \'I\', \'O\', \'U\']);\n return sentence.split(\' \').map((str, i) => {\n return (\n vowelSet.has(str[0]) ?\n str + \'ma\' :\n str.substring(1) + str[0] + \'ma\'\n ) + \'a\'.repeat(i + 1);\n }).join(\' \');\n};\n``` | 1 | 0 | ['JavaScript'] | 0 |
goat-latin | c# faster than 100% 69ms | c-faster-than-100-69ms-by-wenhuan-zlgu | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | wenhuan | NORMAL | 2022-12-05T03:17:15.395364+00:00 | 2022-12-05T03:20:37.013767+00:00 | 503 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\npublic class Solution {\n public string ToGoatLatin(string sentence) {\n StringBuilder strBuilder = new StringBuilder(), postfix = new StringBuilder();\n var arr = sentence.Split(" ");\n for(int i = 0; i< arr.Length; i ++)\n {\n var word = arr[i];\n postfix.Append("a");\n if(!StartsWithVowel(word[0]))\n {\n arr[i] = word.Substring(1) + word[0];\n }\n strBuilder.Append(arr[i]);\n strBuilder.Append("ma");\n strBuilder.Append(postfix);\n strBuilder.Append(" ");\n } \n return strBuilder.ToString().Trim();\n }\n\n public bool StartsWithVowel(char firstLetter)\n {\n return firstLetter == \'A\' || firstLetter == \'E\' || firstLetter == \'I\' || firstLetter == \'O\' \n || firstLetter == \'U\' || firstLetter == \'a\' || firstLetter == \'e\' || firstLetter == \'i\'\n || firstLetter == \'o\' || firstLetter == \'u\';\n\n }\n}\n``` | 1 | 0 | ['C#'] | 0 |
goat-latin | JS easy solution with O(n) | js-easy-solution-with-on-by-kunkka1996-ru0n | \nconst vowel = {\n "a": "a",\n "e": "e",\n "i": "i",\n "o": "o",\n "u": "u",\n "A": "A",\n "E": "E",\n "I": "I",\n "O": "O",\n "U | kunkka1996 | NORMAL | 2022-09-10T04:32:29.860323+00:00 | 2022-09-10T04:32:29.860356+00:00 | 754 | false | ```\nconst vowel = {\n "a": "a",\n "e": "e",\n "i": "i",\n "o": "o",\n "u": "u",\n "A": "A",\n "E": "E",\n "I": "I",\n "O": "O",\n "U": "U",\n}\n\nvar toGoatLatin = function(sentence) {\n let output = \'\';\n sentence = sentence.split(\' \');\n\n for (let i = 0; i < sentence.length; i++) {\n let word = sentence[i];\n \n if (vowel[word[0]]) {\n word += "ma";\n } else {\n word = word.substr(1, word.length) + word[0] + "ma";\n }\n \n for (let j = 0; j <= i; j++) {\n word += "a";\n }\n \n output += word + (i !== sentence.length - 1 ? \' \' : \'\');\n }\n \n return output;\n};\n``` | 1 | 0 | ['JavaScript'] | 1 |
goat-latin | Java easy to understand solution & super optimized solution | java-easy-to-understand-solution-super-o-4fgs | \nimport java.util.*;\nclass Solution {\n public String toGoatLatin(String sentence) {\n StringTokenizer st=new StringTokenizer(sentence," ");\n | mdmehedihassan | NORMAL | 2022-08-18T11:15:40.052841+00:00 | 2022-08-18T11:18:35.562186+00:00 | 347 | false | ```\nimport java.util.*;\nclass Solution {\n public String toGoatLatin(String sentence) {\n StringTokenizer st=new StringTokenizer(sentence," ");\n StringBuilder sb=new StringBuilder();\n String a="a";\n while(st.hasMoreTokens()){\n String word=st.nextToken();\n if(!isVowel(word.charAt(0))){\n if(word.length()>1){\n word=word.substring(1,word.length())+word.charAt(0);\n }\n }\n sb.append(word+"ma"+a+" ");\n a+="a";\n }\n return sb.toString().trim();\n \n }\n private boolean isVowel(char c){\n if(c==\'a\'||c==\'e\'||c==\'i\'||c==\'o\'||\n c==\'u\'||c==\'A\'||c==\'E\'||c==\'I\'||c==\'O\'||c==\'U\'){\n return true;\n }\n return false;\n }\n}\n``` | 1 | 0 | ['Java'] | 1 |
goat-latin | 📌Easy & Fast Java☕ Solution using StringBuilder | easy-fast-java-solution-using-stringbuil-mo8y | ```\nclass Solution {\n public String toGoatLatin(String sentence) {\n String s[] = sentence.split(" ");\n StringBuilder sb = new StringBuilder | saurabh_173 | NORMAL | 2022-07-25T14:34:21.258682+00:00 | 2022-07-25T14:34:21.258737+00:00 | 179 | false | ```\nclass Solution {\n public String toGoatLatin(String sentence) {\n String s[] = sentence.split(" ");\n StringBuilder sb = new StringBuilder();\n int i=1;\n for(String sen:s)\n {\n if(check(sen.charAt(0)))\n sb.append(sen);\n else\n sb.append(sen.substring(1)+sen.charAt(0));\n sb.append("ma");\n for(int j=0;j<i;j++)\n sb.append("a");\n sb.append(" ");\n i++;\n }\n return sb.toString().trim();\n }\n public boolean check(char c)\n {\n if("aeiouAEIOU".contains(c+""))\n return true;\n return false;\n }\n} | 1 | 0 | ['String', 'Java'] | 0 |
most-profitable-path-in-a-tree | ✔✔✔ 2 DFS || 1 DFS || Simple Approach || C++ | 2-dfs-1-dfs-simple-approach-c-by-brehamp-mcmp | Main Idea \nAlice can travel to any leaf from 0 but there is only one path for Bob. So we will find the path Bob will follow and update the contribution of each | brehampie | NORMAL | 2022-11-12T16:00:57.947739+00:00 | 2022-11-13T03:39:52.022383+00:00 | 10,114 | false | <h5>Main Idea</h5>\nAlice can travel to any leaf from 0 but there is only one path for Bob. So we will find the path Bob will follow and update the contribution of each node in the path first.\n\nWith the first dfs we will find the time to travel to each node <b>\'u\'</b> from 0 and previous node of <b>\'u\'</b> in the path.\nNow we can follow the path from Bob\'s node to 0 using the previous node we found earlier. In each node \'u\' we will check if Alice will reach it first or Bob will. If Bob reaches it faster than Alice, we will make amount[u] = 0 and if both of them reaches at the same time we make amount[u] =amount[u]/2.\n\nFinally we will run our second dfs to find the cumulative sum of amount in the path to each leaf and return the maximum.\n<h5>Sample Code</h5>\n\n```\nclass Solution {\npublic:\n vector<vector<int>>adj;\n vector<int>par,dis;\n\t//Find the parent and distance from node 0\n void dfs(int u,int p = 0,int d = 0){\n dis[u] = d;\n par[u] = p;\n for(int v:adj[u]){\n if(v==p)continue;\n dfs(v,u,d+1);\n }\n }\n\t// Find total sum to each node\n int dfs2(int u,vector<int>&amount,int p= 0){\n int ret = amount[u];\n int mxc = -INT_MAX;\n for(int v:adj[u]){\n if(v!=p){\n mxc= max(mxc,dfs2(v,amount,u));\n }\n }\n\t\t//if the node is leaf we just return its amount\n if(mxc==-INT_MAX)return ret;\n else return ret+mxc;\n }\n int mostProfitablePath(vector<vector<int>>& edges, int bob, vector<int>& amount) {\n int n = amount.size();\n adj.resize(n,vector<int>());\n for(auto&e:edges){\n adj[e[0]].push_back(e[1]);\n adj[e[1]].push_back(e[0]);\n }\n par.resize(n);\n dis.resize(n);\n dfs(0);\n int cur = bob;\n int bob_dis = 0;\n\t\t//update the path of from Bob to 0\n while(cur!=0){\n if(dis[cur]>bob_dis){\n amount[cur] = 0;\n }else if(dis[cur]==bob_dis){\n amount[cur]/=2;\n }\n cur = par[cur];\n bob_dis++;\n }\n return dfs2(0,amount);\n }\n \n};\n```\n<h5>Single DFS </h5>\nThe idea was taken from <a href="https://leetcode.com/problems/most-profitable-path-in-a-tree/discuss/2807411/Python-One-DFS">this</a> solution.\n\nThe first dfs we ran earlier is only used to calculate the path and depth. We can merge this first dfs with the second one by taking additional vector that stores the distance from Bob\'s node.Then we can update the amount array and calculate path some at the same time. \n\nSample Code\n```\nclass Solution {\npublic:\n vector<vector<int>>adj;\n vector<int>disFromBob;\n int bobNode;\n int dfs(int u,int par,int depth,vector<int>&amount){\n int ret = 0;\n if(u==bobNode) disFromBob[u] = 0;\n else disFromBob[u] = amount.size();\n int maxChild = -INT_MAX;\n for(int v:adj[u]){\n if(v==par)continue;\n maxChild = max(maxChild,dfs(v,u,depth+1,amount));\n disFromBob[u] = min(disFromBob[u],disFromBob[v]+1);\n }\n if(disFromBob[u]>depth)ret+=amount[u];\n else if(disFromBob[u]==depth)ret+=amount[u]/2;\n if(maxChild==-INT_MAX) return ret;\n else return ret+maxChild;\n }\n int mostProfitablePath(vector<vector<int>>& edges, int bob, vector<int>& amount) {\n int n = amount.size();\n bobNode = bob;\n adj.resize(n,vector<int>());\n for(auto&e:edges){\n adj[e[0]].push_back(e[1]);\n adj[e[1]].push_back(e[0]);\n }\n disFromBob.resize(n);\n return dfs(0,0,0,amount);\n }\n \n};\n``` | 124 | 5 | ['Depth-First Search', 'C'] | 16 |
most-profitable-path-in-a-tree | C++ || Simple DFS and BFS || Detailed explanation | c-simple-dfs-and-bfs-detailed-explanatio-62iy | \nclass Solution {\npublic:\n bool DFS(int src, int time, unordered_map<int,int> &path, vector<bool> &visited, vector<vector<int>> &graph){\n path[src | _Potter_ | NORMAL | 2022-11-12T16:04:29.985790+00:00 | 2022-11-12T18:05:16.833920+00:00 | 5,755 | false | ```\nclass Solution {\npublic:\n bool DFS(int src, int time, unordered_map<int,int> &path, vector<bool> &visited, vector<vector<int>> &graph){\n path[src] = time;\n visited[src] = true;\n if(src == 0){\n return true;\n }\n for(auto adj: graph[src]){\n if(!visited[adj]){\n if(DFS(adj, time+1, path, visited, graph)){\n return true;\n }\n }\n } \n path.erase(src);\n return false;\n }\n \n int mostProfitablePath(vector<vector<int>>& edges, int bob, vector<int>& amount) {\n int n = edges.size()+1;\n vector<vector<int>> graph(n);\n for(auto it: edges){\n graph[it[0]].push_back(it[1]);\n graph[it[1]].push_back(it[0]);\n }\n \n // Find the path taken by bob to reach zero along with the time at which bob visited that node\n unordered_map<int,int> path;\n vector<bool> visited(n, false);\n DFS(bob, 0, path, visited, graph);\n \n // Push {src, time, income}\n queue<vector<int>> q;\n q.push({0, 0, 0});\n visited.assign(n, false);\n \n int ans = INT_MIN;\n while(!q.empty()){\n int src = q.front()[0], time = q.front()[1], income = q.front()[2];\n q.pop();\n visited[src] = true;\n \n // If bob didn\'t visit this node\n if(path.find(src) == path.end()){\n income += amount[src];\n }\n else{\n // Alice visits it first\n if(time < path[src]){\n income += amount[src];\n }\n // Both visit at the same time\n else if(time == path[src]){\n income += (amount[src]/2);\n }\n }\n \n // Updating when it is leaf\n if(graph[src].size() == 1 && src != 0){\n ans = max(ans, income);\n }\n\t\t\t// Exploring adjacent vertices\n for(auto adj: graph[src]){\n if(!visited[adj]){\n q.push({adj, time+1, income});\n }\n }\n }\n \n return ans;\n }\n};\n```\n```\ncout << "Upvote the solution if you like it !!" << endl;\n``` | 77 | 9 | ['C', 'C++'] | 8 |
most-profitable-path-in-a-tree | 🚀Beats 100% | Most Profitable Path in a Tree | DFS Solution 🌳 | beats-100-most-profitable-path-in-a-tree-3ohk | Youtube🚀Beats 100% | Most Profitable Path in a Tree | DFS Solution 🌳🔼 Please Upvote🔼 Please Upvote🔼 Please Upvote🔼 Please Upvote💡If this helped, don’t forget to | rahulvijayan2291 | NORMAL | 2025-02-24T05:26:19.852052+00:00 | 2025-02-24T05:26:19.852052+00:00 | 15,820 | false | # Youtube
https://youtu.be/2DioKI5nSjA
# 🚀 **Beats 100% | Most Profitable Path in a Tree | DFS Solution 🌳**
---
# **🔼 Please Upvote**
# **🔼 Please Upvote**
# **🔼 Please Upvote**
# **🔼 Please Upvote**
💡 **If this helped, don’t forget to upvote! 🚀🔥**
---
## **💡 Problem Breakdown**
We are given a **tree (undirected graph without cycles)** where each node has a **monetary value**.
- Alice starts from **node `0`** and explores any path.
- Bob starts from **node `bob`** and moves **towards node `0`**.
- If Alice and Bob **meet at the same time**, Alice gets **half the amount** of that node.
- The goal is to **maximize Alice’s total collected amount**.
### **Example:**
#### **Input:**
```plaintext
edges = [[0,1],[1,2],[1,3],[3,4],[3,5]]
bob = 4
amount = [5,10,20,25,15,30]
```
#### **Output:**
```plaintext
Alice’s max profit = 45
```
---
## **🚀 Approach Overview**
### 🔹 **Key Observations:**
1. The **graph is a tree** (a connected acyclic graph).
2. Bob **always moves towards node `0`**.
3. Alice **chooses any path** to maximize profit.
4. If Alice and Bob meet at a node, she gets **only half** of the amount.
### 🔹 **Strategy:**
1. **Build an adjacency list** from `edges`.
2. **Find Bob’s path** from `bob` to `0` to track timestamps.
3. **Use DFS for Alice**:
- If Alice reaches before Bob → take the full amount.
- If Alice and Bob meet at the same time → take half the amount.
- Explore all possible paths and return the **maximum profit**.
---
## **⏳ Complexity Analysis**
- **Time Complexity:** `O(N)` → Each node is visited once.
- **Space Complexity:** `O(N)` → Graph storage and recursion stack.
---
## **📝 Code Implementation**
### **🔵 Java Solution**
```java
class Solution {
public int mostProfitablePath(int[][] edges, int bob, int[] amount) {
ArrayList<Integer>[] graph = new ArrayList[amount.length];
for (int i = 0; i < graph.length; i++) graph[i] = new ArrayList<>();
for (int[] edge : edges) {
graph[edge[0]].add(edge[1]);
graph[edge[1]].add(edge[0]);
}
int[] bobPath = new int[amount.length];
Arrays.fill(bobPath, -1);
ArrayList<Integer> path = new ArrayList<>();
fillBobPath(bob, -1, path, graph);
for (int i = 0; i < path.size(); i++) {
bobPath[path.get(i)] = i;
}
return getAliceMaxScore(0, -1, 0, bobPath, graph, 0, amount);
}
private boolean fillBobPath(int node, int parentNode, ArrayList<Integer> path, ArrayList<Integer>[] graph) {
if (node == 0) return true;
for (int neighborNode : graph[node]) {
if (neighborNode != parentNode) {
path.add(node);
if (fillBobPath(neighborNode, node, path, graph)) return true;
path.remove(path.size() - 1);
}
}
return false;
}
private int getAliceMaxScore(int node, int parentNode, int currScore, int[] bobPath, ArrayList<Integer>[] graph, int timestamp, int[] amount) {
if (bobPath[node] == -1 || bobPath[node] > timestamp) {
currScore += amount[node];
} else if (bobPath[node] == timestamp) {
currScore += amount[node] / 2;
}
if (graph[node].size() == 1 && node != 0) return currScore;
int maxScore = Integer.MIN_VALUE;
for (int neighborNode : graph[node]) {
if (neighborNode != parentNode) {
maxScore = Math.max(maxScore, getAliceMaxScore(neighborNode, node, currScore, bobPath, graph, timestamp + 1, amount));
}
}
return maxScore;
}
}
```
---
### **🟢 C++ Solution**
```cpp
class Solution {
public:
int mostProfitablePath(vector<vector<int>>& edges, int bob, vector<int>& amount) {
int n = amount.size();
vector<vector<int>> graph(n);
for (auto& edge : edges) {
graph[edge[0]].push_back(edge[1]);
graph[edge[1]].push_back(edge[0]);
}
vector<int> bobPath(n, -1);
vector<int> path;
function<bool(int, int)> fillBobPath = [&](int node, int parent) {
if (node == 0) return true;
for (int neighbor : graph[node]) {
if (neighbor != parent) {
path.push_back(node);
if (fillBobPath(neighbor, node)) return true;
path.pop_back();
}
}
return false;
};
fillBobPath(bob, -1);
for (int i = 0; i < path.size(); i++) {
bobPath[path[i]] = i;
}
function<int(int, int, int, int)> getAliceMaxScore = [&](int node, int parent, int currScore, int timestamp) {
if (bobPath[node] == -1 || bobPath[node] > timestamp) {
currScore += amount[node];
} else if (bobPath[node] == timestamp) {
currScore += amount[node] / 2;
}
if (graph[node].size() == 1 && node != 0) return currScore;
int maxScore = INT_MIN;
for (int neighbor : graph[node]) {
if (neighbor != parent) {
maxScore = max(maxScore, getAliceMaxScore(neighbor, node, currScore, timestamp + 1));
}
}
return maxScore;
};
return getAliceMaxScore(0, -1, 0, 0);
}
};
```
---
### **🟣 Python3 Solution**
```python
class Solution:
def mostProfitablePath(self, edges: List[List[int]], bob: int, amount: List[int]) -> int:
graph = {i: [] for i in range(len(amount))}
for u, v in edges:
graph[u].append(v)
graph[v].append(u)
bobPath = [-1] * len(amount)
path = []
def fillBobPath(node, parent):
if node == 0:
return True
for neighbor in graph[node]:
if neighbor != parent:
path.append(node)
if fillBobPath(neighbor, node):
return True
path.pop()
fillBobPath(bob, -1)
for i, node in enumerate(path):
bobPath[node] = i
def getAliceMaxScore(node, parent, currScore, timestamp):
if bobPath[node] == -1 or bobPath[node] > timestamp:
currScore += amount[node]
elif bobPath[node] == timestamp:
currScore += amount[node] // 2
return currScore if len(graph[node]) == 1 and node != 0 else max(getAliceMaxScore(neighbor, node, currScore, timestamp + 1) for neighbor in graph[node] if neighbor != parent)
return getAliceMaxScore(0, -1, 0, 0)
```
---
# **🔼 Please Upvote**
# **🔼 Please Upvote**
# **🔼 Please Upvote**
# **🔼 Please Upvote**
💡 **If this helped, don’t forget to upvote! 🚀🔥**
🔥 **Challenge:** Try different tree structures and analyze Alice's best path! 🚀🔥 | 76 | 1 | ['Array', 'Tree', 'Depth-First Search', 'Breadth-First Search', 'Graph', 'C++', 'Java', 'Python3'] | 3 |
most-profitable-path-in-a-tree | [Python] One DFS | python-one-dfs-by-lee215-cxkm | Explanation\nd0 is the distance from node 0 to node i\ndb is the distance from node i to node bob.\nIf node i is not ancestor of bob, we define db >= n.\n\nSo i | lee215 | NORMAL | 2022-11-12T16:40:49.519000+00:00 | 2022-11-12T16:40:49.519036+00:00 | 5,600 | false | # **Explanation**\n`d0` is the distance from node `0` to node `i`\n`db` is the distance from node `i` to node `bob`.\nIf node `i` is not ancestor of `bob`, we define `db >= n`.\n\nSo in the dfs, we first pick out the biggest sum of sub path.\nIf the node has no child, then the biggest sum is `0`.\nnow we compare `d0` and `db`.\nIf `d0 == db`, this node is in the middle point between node 0 and node bob.\nIf `d0 < db`, Bob will arrive this node first, so no score.\n\nFinally we return the score `res` and the incremented distance `db + 1`.\n<br>\n\n# **Complexity**\nTime `O(n)`\nSpace `O(n)`\n<br>\n\n\n**Python**\n```py\n def mostProfitablePath(self, edges: List[List[int]], bob: int, amount: List[int]) -> int:\n n = len(edges) + 1\n G = [[] for i in range(n)]\n for i,j in edges:\n G[i].append(j)\n G[j].append(i)\n seen = [0] * n\n\n def dfs(i, d0):\n seen[i] = 1\n res = -inf\n db = 0 if i == bob else n\n for j in G[i]:\n if seen[j]: continue\n cur, kk = dfs(j, d0 + 1)\n res = max(res, cur)\n db = min(db, kk)\n if res == -inf: res = 0\n if d0 == db: res += amount[i] // 2\n if d0 < db: res += amount[i]\n return res, db + 1\n\n return dfs(0, 0)[0]\n```\n | 67 | 3 | [] | 7 |
most-profitable-path-in-a-tree | Was this actually tough for Leetcode Medium? | was-this-actually-tough-for-leetcode-med-f5co | i felt this question was bit tougher for a typical Leetcode C. Using BFS+DFS+Time Synchroniazation in just one problem is bit of overkill for Leetcode C.\n\nMy | harem_jutsu | NORMAL | 2022-11-12T16:22:39.132006+00:00 | 2022-11-12T16:22:39.132047+00:00 | 3,577 | false | i felt this question was bit tougher for a typical Leetcode C. Using BFS+DFS+Time Synchroniazation in just one problem is bit of overkill for Leetcode C.\n\nMy opinion only. You can have different take on this. | 41 | 10 | [] | 14 |
most-profitable-path-in-a-tree | twice DFS ||C++ 43ms beats 100% Py3 | twice-dfs-c-51ms-beats-9971-by-anwendeng-5rmw | IntuitionUse DFS to solve, but twice.
1st one finds the parent
2nd one computes the max leaf sumC++ & Python are done.
Approach
Declare global arraysadj, parent | anwendeng | NORMAL | 2025-02-24T01:19:39.079518+00:00 | 2025-02-24T13:33:38.601536+00:00 | 7,562 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
Use DFS to solve, but twice.
1. 1st one finds the parent
2. 2nd one computes the max leaf sum
C++ & Python are done.
# Approach
<!-- Describe your approach to solving the problem. -->
0. Declare global arrays `adj, parent & Bob` with size `1e5`
1. Define `dfs` to find the parent
2. define `dfs_sum` to compute the max leaf sum
3. In `mostProfitablePath` build the adjacent list
4. call `dfs(0, -1)`
5. Use a loop to compute the Bob reaching time for each node toward root & store them in the array `Bob[]`
6. return `dfs_sum(0, 0, -1, amount)`
7. Python code is made in the similar way
8. C++ is using some extra optimization to beat 100%.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
$$O(n)$$
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
$$O(n)$$
# Code||C++ with some optimization 43ms beats 100%
```cpp []
vector<int> adj[100000];
int parent[100000], Bob[100000];
class Solution {
public:
static void dfs(int i, int p) {
parent[i]=p;
for (int j : adj[i]) {
if (j==p) continue;
dfs(j, i);
}
}
static int dfs_sum(int i, int dist, int prev, vector<int>& amount) {
int alice=0;
if (dist < Bob[i]) alice=amount[i]; // Alice gets full amount
else if (dist == Bob[i]) alice= amount[i]/2; // Split with Bob
bool isLeaf=1;// set isLeaf flag
int maxLeafSum=INT_MIN;
[[unroll]]
for (int j : adj[i]) {
if (j==prev) continue;
isLeaf=0;// has child=> no leaf
maxLeafSum = max(maxLeafSum, dfs_sum(j, dist+1, i, amount));
}
return alice+(isLeaf?0:maxLeafSum);
}
static int mostProfitablePath(vector<vector<int>>& edges, int bob, vector<int>& amount) {
const int n=edges.size()+1;
[[unroll]]
for (int i=0; i < n; i++) adj[i].clear();
[[unroll]]
for (auto& e : edges) {
int u=e[0], v=e[1];
adj[u].push_back(v);
adj[v].push_back(u);
}
dfs(0, -1);
// Compute Bob's reach time
fill(Bob, Bob+n, INT_MAX);
[[unroll]]
for (int x=bob, move=0; x != -1; x=parent[x]) {
Bob[x]=move++;
}
return dfs_sum(0, 0, -1, amount);
}
};
auto init = []() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
return 'c';
}();
```
```Python []
class Solution:
def mostProfitablePath(self, edges: List[List[int]], bob: int, amount: List[int]) -> int:
n=len(edges)+1
adj=[[] for _ in range(n)]
parent=[-1]*n
Bob=[float('inf')]*n
for u, v in edges:
adj[u].append(v)
adj[v].append(u)
# Step 1: Build parent information using DFS
def dfs(i, p):
parent[i] = p
for j in adj[i]:
if j == p: continue
dfs(j, i)
dfs(0, -1) # Start with -1 as the parent of root
# Step 2: Compute Bob's arrival times
x=bob
move=0
while x!=-1:
Bob[x]=move
move+=1
x=parent[x]
# Step 3: DFS to compute Alice's best profit path
def dfs_sum(i, dist, prev):
alice=0
if dist < Bob[i]:
alice=amount[i] # Alice takes full amount
elif dist==Bob[i]:
alice=amount[i]//2 # Both reach at the same time
isLeaf=True
maxLeafSum=-float('inf')
for j in adj[i]:
if j == prev: continue
isLeaf=False
maxLeafSum = max(maxLeafSum, dfs_sum(j, dist+1, i))
return alice if isLeaf else alice + maxLeafSum
return dfs_sum(0, 0, -1)
``` | 29 | 0 | ['Depth-First Search', 'C++', 'Python3'] | 5 |
most-profitable-path-in-a-tree | 🔥SIMPLE 💯 % 🎯 |✨SUPER EASY BEGINNERS 👏| JAVA | C | C++ | PYTHON| JAVASCRIPT | DART | simple-super-easy-beginners-java-c-c-pyt-y581 | IntuitionThe problem requires us to find the maximum profit Alice can collect while moving along a tree structure. Alice starts from the root, and Bob starts fr | CodeWithSparsh | NORMAL | 2025-02-24T08:46:04.555215+00:00 | 2025-02-24T08:50:45.547943+00:00 | 3,316 | false |

---
# Intuition
The problem requires us to find the maximum profit Alice can collect while moving along a tree structure. Alice starts from the root, and Bob starts from a specific node, both moving towards the leaves. The profit from each node depends on who reaches it first or if they reach at the same time.
We need to track Bob’s path to adjust Alice’s profit calculations. The goal is to use DFS to explore all paths and determine the maximum possible profit Alice can collect.
---
# Approach
1. **Graph Representation**:
- Convert the `edges` list into an adjacency list representation for easy traversal.
2. **Bob's Path Calculation**:
- Use DFS to find Bob’s path from his starting position to the root (node 0).
- Store the depth (timestamp) at which Bob reaches each node.
3. **Alice's Profit Calculation**:
- Use DFS to explore all possible paths Alice can take.
- Modify the profit at each node based on Alice’s and Bob’s arrival times:
- If Alice reaches before Bob → Take full amount.
- If Bob reaches before Alice → Take no amount.
- If both arrive at the same time → Take half the amount.
- Track the maximum profit Alice can collect using DFS.
---
# Complexity
- **Time Complexity**:
- Constructing the graph takes **\(O(n)\)**.
- Finding Bob’s path takes **\(O(n)\)**.
- DFS traversal for Alice takes **\(O(n)\)**.
- Overall complexity: **\(O(n)\)**.
- **Space Complexity**:
- Adjacency list storage: **\(O(n)\)**.
- Bob’s path storage: **\(O(n)\)**.
- Recursive DFS calls (stack memory): **\(O(n)\)**.
- Overall complexity: **\(O(n)\)**.
---
```dart []
import 'dart:collection';
class Solution {
int mostProfitablePath(List<List<int>> edges, int bob, List<int> amount) {
int n = amount.length;
List<List<int>> graph = List.generate(n, (_) => []);
for (var edge in edges) {
graph[edge[0]].add(edge[1]);
graph[edge[1]].add(edge[0]);
}
List<int> bobPath = List.filled(n, -1);
List<int> path = [];
_fillBobPath(bob, -1, path, graph);
for (int i = 0; i < path.length; i++) {
bobPath[path[i]] = i;
}
return _getAliceMaxScore(0, -1, 0, bobPath, graph, 0, amount);
}
bool _fillBobPath(int node, int parent, List<int> path, List<List<int>> graph) {
if (node == 0) return true;
for (int neighbor in graph[node]) {
if (neighbor != parent) {
path.add(node);
if (_fillBobPath(neighbor, node, path, graph)) return true;
path.removeLast();
}
}
return false;
}
int _getAliceMaxScore(int node, int parent, int currScore, List<int> bobPath,
List<List<int>> graph, int timestamp, List<int> amount) {
if (bobPath[node] == -1 || bobPath[node] > timestamp) {
currScore += amount[node];
} else if (bobPath[node] == timestamp) {
currScore += (amount[node] ~/ 2);
}
if (graph[node].length == 1 && node != 0) return currScore;
int maxScore = -999999;
for (int neighbor in graph[node]) {
if (neighbor != parent) {
maxScore = maxScore > _getAliceMaxScore(neighbor, node, currScore, bobPath, graph, timestamp + 1, amount)
? maxScore
: _getAliceMaxScore(neighbor, node, currScore, bobPath, graph, timestamp + 1, amount);
}
}
return maxScore;
}
}
```
```python []
from collections import defaultdict
class Solution:
def mostProfitablePath(self, edges, bob, amount):
graph = defaultdict(list)
for u, v in edges:
graph[u].append(v)
graph[v].append(u)
bob_path = [-1] * len(amount)
path = []
self.fill_bob_path(bob, -1, path, graph)
for i, node in enumerate(path):
bob_path[node] = i
return self.get_alice_max_score(0, -1, 0, bob_path, graph, 0, amount)
def fill_bob_path(self, node, parent, path, graph):
if node == 0:
return True
for neighbor in graph[node]:
if neighbor != parent:
path.append(node)
if self.fill_bob_path(neighbor, node, path, graph):
return True
path.pop()
return False
def get_alice_max_score(self, node, parent, curr_score, bob_path, graph, timestamp, amount):
if bob_path[node] == -1 or bob_path[node] > timestamp:
curr_score += amount[node]
elif bob_path[node] == timestamp:
curr_score += amount[node] // 2
if len(graph[node]) == 1 and node != 0:
return curr_score
max_score = float('-inf')
for neighbor in graph[node]:
if neighbor != parent:
max_score = max(max_score, self.get_alice_max_score(neighbor, node, curr_score, bob_path, graph, timestamp + 1, amount))
return max_score
```
```cpp []
#include <vector>
#include <unordered_map>
using namespace std;
class Solution {
public:
int mostProfitablePath(vector<vector<int>>& edges, int bob, vector<int>& amount) {
int n = amount.size();
vector<vector<int>> graph(n);
for (auto& edge : edges) {
graph[edge[0]].push_back(edge[1]);
graph[edge[1]].push_back(edge[0]);
}
vector<int> bobPath(n, -1);
vector<int> path;
fillBobPath(bob, -1, path, graph);
for (int i = 0; i < path.size(); i++) {
bobPath[path[i]] = i;
}
return getAliceMaxScore(0, -1, 0, bobPath, graph, 0, amount);
}
private:
bool fillBobPath(int node, int parent, vector<int>& path, vector<vector<int>>& graph) {
if (node == 0) return true;
for (int neighbor : graph[node]) {
if (neighbor != parent) {
path.push_back(node);
if (fillBobPath(neighbor, node, path, graph)) return true;
path.pop_back();
}
}
return false;
}
int getAliceMaxScore(int node, int parent, int currScore, vector<int>& bobPath, vector<vector<int>>& graph, int timestamp, vector<int>& amount) {
if (bobPath[node] == -1 || bobPath[node] > timestamp) {
currScore += amount[node];
} else if (bobPath[node] == timestamp) {
currScore += amount[node] / 2;
}
if (graph[node].size() == 1 && node != 0) return currScore;
int maxScore = INT_MIN;
for (int neighbor : graph[node]) {
if (neighbor != parent) {
maxScore = max(maxScore, getAliceMaxScore(neighbor, node, currScore, bobPath, graph, timestamp + 1, amount));
}
}
return maxScore;
}
};
```
``` java []
class Solution {
public int mostProfitablePath(int[][] edges, int bob, int[] amount) {
ArrayList<Integer>[] graph = new ArrayList[amount.length];
for (int i = 0; i < graph.length; i++) graph[i] = new ArrayList<>();
for (int[] edge : edges) {
graph[edge[0]].add(edge[1]);
graph[edge[1]].add(edge[0]);
}
int[] bobPath = new int[amount.length];
Arrays.fill(bobPath, -1);
ArrayList<Integer> path = new ArrayList<>();
fillBobPath(bob, -1, path, graph);
for (int i = 0; i < path.size(); i++) {
bobPath[path.get(i)] = i;
}
return getAliceMaxScore(0, -1, 0, bobPath, graph, 0, amount);
}
private boolean fillBobPath(int node, int parentNode, ArrayList<Integer> path, ArrayList<Integer>[] graph) {
if (node == 0) return true;
for (int neighborNode : graph[node]) {
if (neighborNode != parentNode) {
path.add(node);
if (fillBobPath(neighborNode, node, path, graph)) return true;
path.remove(path.size() - 1);
}
}
return false;
}
private int getAliceMaxScore(int node, int parentNode, int currScore, int[] bobPath, ArrayList<Integer>[] graph, int timestamp, int[] amount) {
if (bobPath[node] == -1 || bobPath[node] > timestamp) {
currScore += amount[node];
} else if (bobPath[node] == timestamp) {
currScore += amount[node] / 2;
}
if (graph[node].size() == 1 && node != 0) return currScore;
int maxScore = Integer.MIN_VALUE;
for (int neighborNode : graph[node]) {
if (neighborNode != parentNode) {
maxScore = Math.max(maxScore, getAliceMaxScore(neighborNode, node, currScore, bobPath, graph, timestamp + 1, amount));
}
}
return maxScore;
}
}
```
``` javascript []
class Solution {
mostProfitablePath(edges, bob, amount) {
const graph = new Map();
for (const [u, v] of edges) {
if (!graph.has(u)) graph.set(u, []);
if (!graph.has(v)) graph.set(v, []);
graph.get(u).push(v);
graph.get(v).push(u);
}
let bobPath = new Array(amount.length).fill(-1);
let path = [];
this.fillBobPath(bob, -1, path, graph);
for (let i = 0; i < path.length; i++) {
bobPath[path[i]] = i;
}
return this.getAliceMaxScore(0, -1, 0, bobPath, graph, 0, amount);
}
fillBobPath(node, parent, path, graph) {
if (node === 0) return true;
for (const neighbor of graph.get(node) || []) {
if (neighbor !== parent) {
path.push(node);
if (this.fillBobPath(neighbor, node, path, graph)) return true;
path.pop();
}
}
return false;
}
getAliceMaxScore(node, parent, currScore, bobPath, graph, timestamp, amount) {
if (bobPath[node] === -1 || bobPath[node] > timestamp) {
currScore += amount[node];
} else if (bobPath[node] === timestamp) {
currScore += Math.floor(amount[node] / 2);
}
if ((graph.get(node) || []).length === 1 && node !== 0) return currScore;
let maxScore = -Infinity;
for (const neighbor of graph.get(node) || []) {
if (neighbor !== parent) {
maxScore = Math.max(
maxScore,
this.getAliceMaxScore(neighbor, node, currScore, bobPath, graph, timestamp + 1, amount)
);
}
}
return maxScore;
}
}
```
---
 {:style='width:250px'}
| 22 | 0 | ['Array', 'Tree', 'Depth-First Search', 'Graph', 'C', 'Python', 'C++', 'Java', 'Python3', 'JavaScript'] | 2 |
most-profitable-path-in-a-tree | ✅ [Python] finally a concise DFS solution with clean code (explained) | python-finally-a-concise-dfs-solution-wi-9a5x | \u2705 IF YOU LIKE THIS SOLUTION, PLEASE UPVOTE.\n*\nThis solution employs a Depth First Search approach to find both Bob\'s path to 0 and Alice\'s most profita | stanislav-iablokov | NORMAL | 2022-11-12T21:18:32.859664+00:00 | 2022-11-12T21:37:41.693478+00:00 | 1,554 | false | **\u2705 IF YOU LIKE THIS SOLUTION, PLEASE UPVOTE.**\n****\nThis solution employs a Depth First Search approach to find both Bob\'s path to `0` and Alice\'s most profitable path. Time complexity is linear: **O(N)**. Space complexity is linear: **O(N)**.\n\n**Python.**\n```\nfrom numpy import sign\n\nclass Solution:\n def mostProfitablePath(self, edges: List[List[int]], bob: int, amt: List[int]) -> int:\n\n graph = defaultdict(set) # transform the edge matrix\n for x, y in edges: # into the adjacency map\n graph[x].add(y)\n graph[y].add(x)\n \n def income(a, t): # this function returns Alice\'s\n if a not in time : return amt[a] # profit depending on whether Bob\n else : return (sign(time[a]-t)+1)*amt[a]//2 # has visited node \'a\' or not\n \n def bob_dfs(b, p, move): # this function finds Bob\'s path to 0\n move[b] = p\n if b == 0: # the 0\'th node was found, thus, we\n path = [] # backtrace to the initial Bob\'s node\n while b != -1: # that was marked with parent -1\n path.append(b) \n b = move[b]\n return path[::-1]\n \n gen = (bob_dfs(n, b, move) for n in graph[b] if n != move[b])\n res = list(filter(lambda path: path != None, gen)) or [None]\n return res[0]\n \n def alice_dfs(a, p, t): # this one-liner performs DFS\n return max([alice_dfs(n,a,t+1) # to calculate Alice\'s maximal\n for n in graph[a] # profit along all paths\n if n != p] or [0]) + income(a,t)\n \n path = bob_dfs(bob, -1, [bob] * len(amt)) # [1] obtain Bob\'s path to the 0\'th node\n time = {b : t for t,b in enumerate(path)} # [2] map time for each node Bob has visited\n return alice_dfs(0, -1, 0) # [3] get Alice\'s maximal profit\n``` | 18 | 0 | [] | 3 |
most-profitable-path-in-a-tree | DP on Trees, Easy Readable Code with Explanation | dp-on-trees-easy-readable-code-with-expl-hc4k | ```\nIdea -> 1. The first thing to notice is we have a specfic only path from Bob to 0 root. \n We\'ll do a dfs to find that path and mark the verti | akshattuknait123 | NORMAL | 2022-11-12T16:06:58.085617+00:00 | 2022-11-13T15:15:22.508138+00:00 | 2,706 | false | ```\nIdea -> 1. The first thing to notice is we have a specfic only path from Bob to 0 root. \n We\'ll do a dfs to find that path and mark the vertices on those path at how much distance they\'re at.\n\t 2. Now, we\'ll traverse the whole tree from 0, we can do a dfs search with taking distance as a reference too.\n\t 3. If this current X vertice was visited by Bob, we\'ll simply check if the Distance of X from 0 is < or = or > the distance from Bob. If less we\'ll take A[x] as whole. If More we\'ll take 0 and if equal A[x]/2;\n\t 4. Now, the remain question left is to take the best path we can choose from the given children.\n \n\n vector<int>adj[200001];\n int vis[200001],dis[200001];\n int par[200001];\n int dp[200001];\n void dfs(int x,int p)\n {\n par[x]=p;\n for(int k:adj[x])\n {\n if(k!=p)\n {\n dfs(k,x);\n }\n }\n }\n int solve(int x,int d,vector<int>&a,int p)\n {\n int ok=0;\n int ans=-1e9;\n if(dis[x]!=-1)\n {\n if(dis[x]<d)\n {\n ok=0;\n }else if(dis[x]==d)\n {\n ok=a[x]/2;\n }else\n {\n ok=a[x];\n }\n }else\n {\n ok=a[x];\n }\n\n int cur=-1e9;\n int check=0;\n for(int j:adj[x])\n {\n if(j!=p)\n {\n check=1;\n solve(j,d+1,a,x);\n cur=max(cur,dp[j]);\n }\n }\n if(!check)\n {\n cur=0;\n }\n\n ok=ok+cur;\n cout<<ok<<" "<<x<<endl;\n ans=ok;\n return dp[x]=ans;\n \n }\n \n int mostProfitablePath(vector<vector<int>>& e, int bob, vector<int>& a) {\n for(vector<int>x:e)\n {\n int a1=x[0]; int b=x[1];\n adj[a1].push_back(b);\n adj[b].push_back(a1);\n }\n memset(dis,-1,sizeof(dis));\n memset(dp,-1,sizeof(dp));\n dfs(0,-1);\n vector<int>path;\n int ok= bob;\n while(ok!=0)\n {\n path.push_back(ok);\n ok=par[ok];\n }\n path.push_back(0);\n dis[bob]=0;\n for(int i=1;i<path.size();i++)\n {\n dis[path[i]]=i;\n }\n int ans= solve(0,0,a,-1);\n \n return ans;\n }\n | 18 | 8 | ['Dynamic Programming', 'Depth-First Search'] | 3 |
most-profitable-path-in-a-tree | Java || DFS ( Find Path ) + DFS ( get maxSum ) || Explained | java-dfs-find-path-dfs-get-maxsum-explai-apmo | find path bob -> ... -> alice\n2. modify the amount of node in the path by rule :\n\nleft half nodes to 0 (bob reaches first), if exact middle node exist, make | cooper-- | NORMAL | 2022-11-12T16:03:54.721472+00:00 | 2022-11-12T16:11:46.256256+00:00 | 2,201 | false | 1. find path `bob -> ... -> alice`\n2. modify the `amount` of `node` in the path by rule :\n```\nleft half nodes to 0 (bob reaches first), if exact middle node exist, make it half (reaching same time)\n```\n3. backtrack traverse tree to get max path Sum\n\n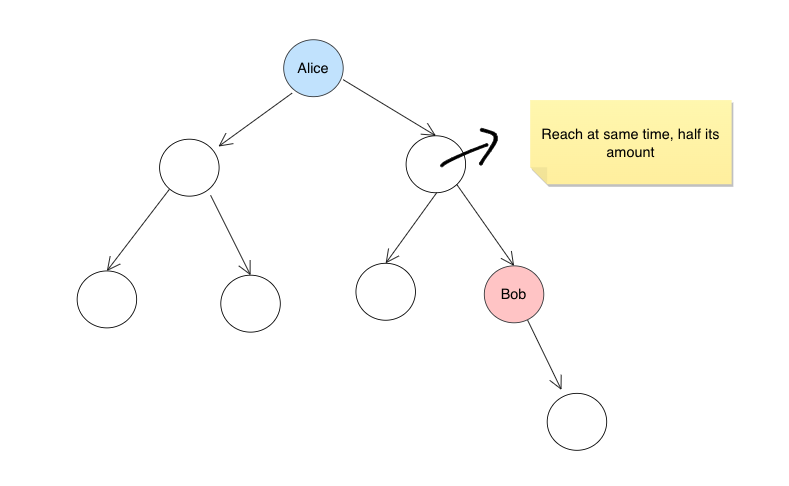\n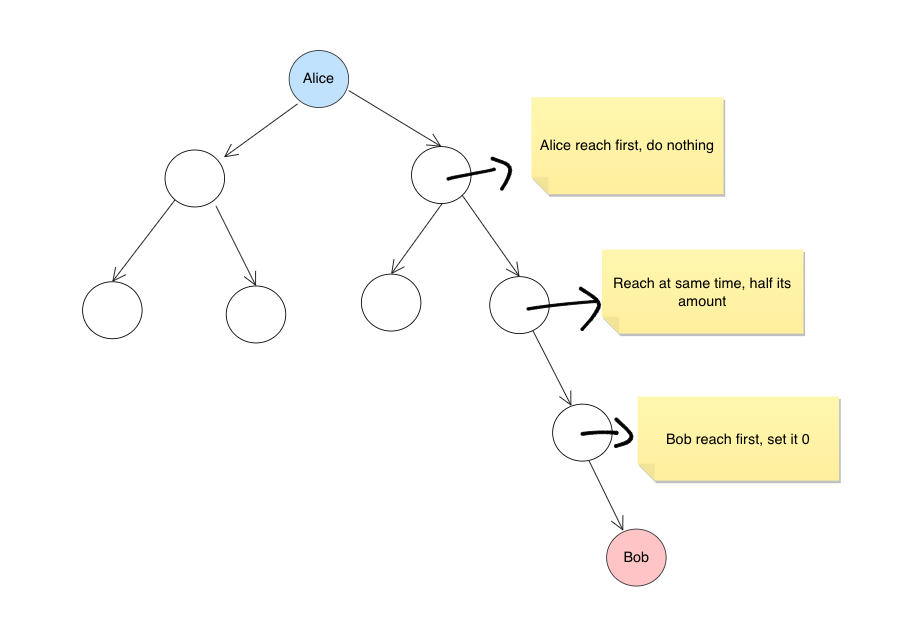\n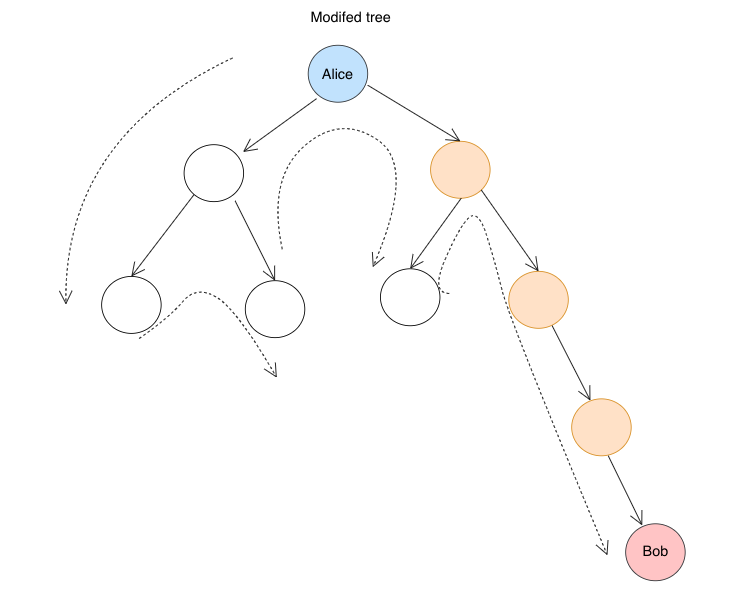\n\n```java\nclass Solution {\n\n List<Integer> b2a = new ArrayList<>();\n int maxSum = Integer.MIN_VALUE;\n \n public int mostProfitablePath(int[][] edges, int bob, int[] amount) {\n int n = amount.length;\n\n Map<Integer, Set<Integer>> graph = new HashMap<>();\n \n for (int i = 0; i < n; i++) graph.put(i, new HashSet<>());\n \n for (int[] edge : edges) {\n int u = edge[0];\n int v = edge[1];\n graph.get(v).add(u);\n graph.get(u).add(v);\n }\n \n // 1. find path\n dfs(bob, 0, graph, new ArrayList<Integer>(){{add(bob); }}, new HashSet<Integer>(){{add(bob); }});\n\n // 2. modify tree\n for (int i = 0; i < b2a.size() / 2; i++) {\n amount[b2a.get(i)] = 0;\n }\n if (b2a.size() % 2 != 0) {\n int m = b2a.get(b2a.size() / 2);\n amount[m] /= 2;\n }\n \n // 3. get result\n Set<Integer> visited = new HashSet<>();\n visited.add(0);\n maxPathSum(0, graph, amount, visited, amount[0]);\n return maxSum;\n }\n \n private boolean dfs(int root, int target, Map<Integer, Set<Integer>> graph, List<Integer> currPath, Set<Integer> visited) {\n if (root == target) {\n b2a = new ArrayList<>(currPath);\n return true;\n }\n \n for (int neighbor : graph.get(root)) {\n if (visited.contains(neighbor)) continue;\n visited.add(neighbor);\n currPath.add(neighbor);\n \n if (dfs(neighbor, target, graph, currPath, visited)) return true;\n \n currPath.remove(currPath.size() - 1);\n visited.remove(neighbor);\n }\n return false;\n }\n \n private void maxPathSum(int root, Map<Integer, Set<Integer>> graph, int[] amount, Set<Integer> visited, int currSum) {\n int cnt = 0;\n for (int child : graph.get(root)) {\n if (visited.contains(child)) continue;\n \n visited.add(child);\n maxPathSum(child, graph, amount, visited, currSum + amount[child]);\n visited.remove(child);\n cnt++;\n \n }\n // leafNode\n if (cnt == 0) maxSum = Math.max(maxSum, currSum);\n return;\n }\n \n /*\n\n}\n``` | 14 | 0 | ['Java'] | 2 |
most-profitable-path-in-a-tree | 🚀 Java: faster than 100%: resolve Bob then optimize Alice | java-faster-than-100-resolve-bob-then-op-8lti | Intuition: We can compute Bob\'s path up to the root (0), and resolve what happens at each gate right away. Up to, but not including, the halfway point, Bob ta | mattihito | NORMAL | 2022-11-13T00:52:41.714143+00:00 | 2022-12-29T07:05:38.464321+00:00 | 1,726 | false | **Intuition**: We can compute Bob\'s path up to the root (0), and resolve what happens at each gate right away. Up to, but not including, the halfway point, Bob takes or pays the entire reward/fee at each gate. So we set `amount[i]` to 0 for each such node. If Bob\'s path has an even number of steps (an odd number of nodes included on the path, including his starting node (`bob`) and `0`, his ending point), then at the middle point, Bob takes or pays half of the reward/fee at that gate. So we set `amount[i] /= 2` at that specific node (if it exists). By doing this, we can then focus entirely on optimizing Alice\'s path. We are not doing things out of order so much as we are precomputing Bob\'s effects on Alice\'s net income should their paths overlap.\n\n**Traps to avoid**: As Bob nagivates towards zero, we have to track where he came from. We\'re in an undirected graph, but really, it\'s a tree. The directions matter (towards 0, away from 0). But we can handle this by simply not allowing either Alice or Bob to return to the node they came from. Additionally, we need to remember that both players resolve their starting position (pay or collect at their starting node) before moving to their next gate, and their starting positions may be the same point (i.e. `bob` could be `0`). And, we need to avoid off-by-one errors when computing Bob\'s path and whether there\'s a middle point where he might meet Alice at the same time.\n\n**Optimizations**: We\'ll find Bob\'s path to `0` by starting at `0` and exploring until we reach Bob\'s starting point `bob`. We\'ll use a node object with a parent reference (and length count) to be able to track backwards when we find Bob\'s starting point. This functions like a linked list of steps of Bob\'s path from `bob` to `0`, but we find it in reverse.\n\n**Syntax Stuff**: I don\'t like unparameterized uses of parameterized types. But you can\'t instantiate a `new ArrayList<Integer>[]`. (I don\'t like `new ArrayList[]` because of the unchecked warning/etc.) So I extend `ArrayList<Integer>` with a class called `IntList`. I find reading `IntList[]` nicer than reading `List<Integer>[]` anyway. It\'s a personal preference, but that\'s the primary reason that class is there. The static array factory method on it is just a nice way to initialize an `IntList[]` of size `n` with non-null elements and do it outside of the main solution method. But it\'s not necessary to do it that way. I just find it cleaner. If you don\'t like it, you can make your adjacency list array (or list of lists) however you like! Also, I isolate the resolution of Bob\'s path on nodes that Alice may encounter (modifying the amounts array) within a separate inline block `{...}`. It\'s totally unnecessary, I just like the way it reads. And finally, I use an int array of size one (`max`) to track the maximum. I have an aversion to having solutions that have state (I do not like having fields on the Solution class). By wrapping the max in an array, we can modify its value, and still pass it by reference as we search. Not having it as a field means our solution remains thread-safe, etc. It just feels like a good habit. (We could also use some other wrapper like AtomicInteger or write a class specifically for this, but `int[1]` is pretty convenient as it is.)\n\n**Java Code**: O(n) time for exploring every node to compute Alice\'s optimal path, and O(n) space for adjacency lists (graph). Runtime as of November 12, 2022: 104ms / faster than 100%.\n\n```\nclass Solution {\n\n public int mostProfitablePath(int[][] edges, int bob, int[] amount) {\n final int n = amount.length;\n\t\t// Build adjacency lists (graph):\n final IntList[] graph = IntList.arrayOfSize(n);\n for (int[] edge : edges) {\n graph[edge[0]].add(edge[1]);\n graph[edge[1]].add(edge[0]);\n }\n\t\t// Find Bob\'s path to 0 by searching depth-first from 0 to Bob\'s starting location:\n final Node root = new Node(0);\n final Node bobNode = findBob(root, bob, graph, null);\n final int bobLength = bobNode.length;\n\t\t// Resolve Bob\'s impact on amounts as a result of his path.\n {\n Node node = bobNode;\n\t\t\t// Handle nodes before the halfway point (if any).\n while (node.length > (bobLength >> 1)) {\n amount[node.index] = 0;\n node = node.parent;\n }\n\t\t\t// If there is a halfway point, take or pay half of the amount at that node.\n\t\t\t// Is bobLength (number of steps, not nodes) even? If so there\'s a halfway point.\n\t\t\t// And, because of the way we\'ve iterated, if it exists, it is `node`, because we\n\t\t\t// have stopped zeroing out amounts just short of that midway point.\n if ((bobLength & 1) == 0) {\n amount[node.index] /= 2;\n }\n }\n\t\t// Now, optimize Alice\'s path with a depth-first search and return her max income.\n int[] max = new int[] { Integer.MIN_VALUE };\n optimizeAlice(0, -1, graph, amount, amount[0], max);\n return max[0];\n }\n\n private Node findBob(Node node, int bob, IntList[] graph, Node parent) {\n if (node.index == bob) {\n return node;\n }\n for (int n : graph[node.index]) {\n\t\t\t// Search neighbors except the neighbor we just came from.\n if (parent == null || parent.index != n) {\n final Node bobNode = findBob(new Node(n, node), bob, graph, node);\n if (bobNode != null) {\n return bobNode;\n }\n }\n }\n return null;\n }\n\n private void optimizeAlice(int i, int lastI, IntList[] graph, int[] amount, int income, int[] max) {\n\t\t// Track number of children (neighbors not equal to lastI) so we know when we are at a leaf.\n int children = 0;\n for (int n : graph[i]) {\n\t\t\t// Search neighbors except the neighbor we just came from.\n if (n != lastI) {\n children++;\n optimizeAlice(n, i, graph, amount, income + amount[n], max);\n }\n }\n if (children == 0) {\n // We are at a leaf - check if income is a new maximum.\n if (income > max[0]) {\n max[0] = income;\n }\n }\n }\n\n static class IntList extends ArrayList<Integer> {\n\n static IntList[] arrayOfSize(int n) {\n final IntList[] out = new IntList[n];\n for (int i = 0; i < n; ++i) {\n out[i] = new IntList();\n }\n return out;\n }\n }\n\n static class Node {\n int length;\n int index;\n Node parent;\n\n Node(int index) {\n this.index = index;\n this.length = 0;\n }\n\n Node(int index, Node parent) {\n this(index);\n this.parent = parent;\n this.length = 1 + parent.length;\n }\n }\n\t\n}\n```\n\n**Standard Plea**: If you found this useful, or interesting, or at least not a waste of time, I\'d **appreciate your upvote so others can find this** (if you think it would be worth them reading, too). If not, **I\'d appreciate any constructive criticism you are willing to offer** so I can write better solutions in the future.\n\nThanks for reading, and happy coding!\n | 10 | 0 | ['Depth-First Search', 'Java'] | 0 |
most-profitable-path-in-a-tree | 4ms C++ beats 100%, thank you again Adjacency Sum | 4ms-c-beats-100-thank-you-again-adjacenc-pzl0 | The general structure of the solution is probably explained in the editorial and all the other solutions, so I'll make it brief. First, we need to find the path | yjian012 | NORMAL | 2025-02-24T06:22:15.199780+00:00 | 2025-02-24T16:48:32.580069+00:00 | 889 | false | The general structure of the solution is probably explained in the editorial and all the other solutions, so I'll make it brief. First, we need to find the path from Alice to Bob. Then, we must find the nodes on the path that's closer to Bob than to Alice and change their `amount` to zero. If there's one right in the middle, its `amount` is halved.
Finally, we need to find the maximum sum of `amount` on any path that is from Alice to any leaf.
The first part can be done with a simple BFS or DFS, and the second part is typically solved with DFS.
But, since this is another tree problem, I decided to give my Adjacency Sum algorithm another go, and see how that performs.
If you don't know what "Adjacency Sum" is, it's a super efficient tree traversing algorithm that I invented. [I explained it on my blog](https://hyper-meta.blogspot.com/2024/12/traversing-tree-with-adjacecncy-sums.html). I've used it on 3 other problems before, all of them gave great result: [2872. Maximum Number of K-Divisible Components
](https://leetcode.com/problems/maximum-number-of-k-divisible-components/solutions/6169967/c-beats-100-the-most-efficient-algorithm-ndm7/), [3203. Find Minimum Diameter After Merging Two Trees
](https://leetcode.com/problems/find-minimum-diameter-after-merging-two-trees/solutions/6179612/19ms-c-beats-100-by-yjian012-kxv7/), and [684. Redundant Connection
](https://leetcode.com/problems/redundant-connection/solutions/6342370/0ms-c-on-no-dynamic-allocation-adjacency-7mja/).
For this problem, here is the main function:
```cpp
struct pa{int s,d;} adjs[100000],adjs1[100000];
int pending[100000];
int sz;
int mostProfitablePath(const vector<vector<int>>& edges,int bob,vector<int>& amount) {
//prepare the Adjacency Sum
sz=edges.size()+1;
memset(adjs,0,sz*sizeof(adjs[0]));
for(const auto &v:edges){
adjs[v[0]].s^=v[1];
adjs[v[0]].d++;
adjs[v[1]].s^=v[0];
adjs[v[1]].d++;
}
//create a copy of the Adjacency Sum and do the first part
memcpy(adjs1,adjs,sz*sizeof(adjs[0]));
clearBob(bob,amount);
//do the second part
for(int i=0;i<sz;++i) pending[i]=INT_MIN;
getMoney(amount);
return amount[0]+pending[0];
}
```
Now, let's think about the first part with Adjacency Sum algorithm. Notice that "Path" is not defined in this algorithm if there are nodes with degree >2 on the path connecting the source and target. So, first we have to remove all the other branches from the tree until we are left with a chain from the source to the target.
Thus, the first part, `clearBob()`, goes like this:
Start from each leaf, keep going along the chain. If we are at Alice or Bob, stop and go to the next leaf. If we reach a branching node, remove this branch. Eventually we're left with a chain from Alice to Bob.
Next, we simply move along that chain until Alice and Bob meet. The nodes that Bob visits will have its `amount` changed to 0. And if they meet in the middle, its `amount` is halved.
```cpp
void clearBob(int b,vector<int>& amount){
int nxta,nxtb;
//Adjacency Sum algorithm
for(int i=0;i<sz;++i) if(adjs1[i].d==1){
int pre=0,cur=i;
while(1){
int nxt=adjs1[cur].s^pre;
if(cur==0){nxta=nxt;break;}//exit at Alice
else if(cur==b){nxtb=nxt;break;}//exit at Bob
if(adjs1[nxt].d>2){//branch removed
adjs1[nxt].d--;
adjs1[nxt].s^=cur;
break;
}
pre=cur;
cur=nxt;
}
}
//now the only thing left is a path from Alice to Bob
int a=0,prea=0,preb=0;
while(1){
amount[b]=0;
if(nxta==b) return;//passes each other
if(nxta==nxtb){amount[nxtb]>>=1;return;}//meet in the middle
prea=a,a=nxta,nxta=adjs1[a].s^prea;
preb=b,b=nxtb,nxtb=adjs1[b].s^preb;
}
}
```
Notice that with either BFS or DFS, we can stop right away once we found the target, but with Adjacency Sum, we must process the entire tree. Also, we will destroy the Adjacency Sum in the process. So we must make a copy of the Adjacency Sum beforehand. This makes me wonder if it can actually outperform any BFS or DFS algorithm.
The second part is more suitable for the Adjacency Sum algorithm. First, we create the `pending` array, because if we reach a branching point, we need to store the sum of the current branch somewhere. We start from each leaf, update its `pending` value if the current sum is greater, and keep moving forward until we reach Alice or a branching point. Eventually, the tree is reduced to a single node, Alice, and the `pending` value of Alice will be the maximum sum from her to any leaf (excluding her own `amount`). The result is just `pending[Alice]+amount[Alice]`.
```cpp
void getMoney(vector<int>& amount){
//Adjacency Sum algorithm
for(int i=1;i<sz;++i) if(adjs[i].d==1){
int pre=0,cur=i;
while(1){
int nxt=adjs[cur].s^pre;
pending[nxt]=max(pending[nxt],amount[cur]);
if(nxt==0) break;//exit at Alice
if(adjs[nxt].d>2){//branch removed
adjs[nxt].s^=cur;
adjs[nxt].d--;
break;
}
//reusing "amount" for sum to save space
amount[nxt]+=pending[nxt];
pre=cur;
cur=nxt;
}
}
}
```
I submitted the program, and -
[4ms submission](https://leetcode.com/problems/most-profitable-path-in-a-tree/submissions/1553461393/), while the old record of runtime is 48ms. The memory usage is around 116mb while the old record is 133mb, also a huge improvement.
It significantly outperforms all BFS or DFS based solutions again.
Time O(N) Space O(N)
Please add a link to my solution if you use the algorithm anywhere else or translate it into another language, thank you!
# Full Code
```cpp []
//@yjian012 https://hyper-meta.blogspot.com/
//https://leetcode.com/problems/most-profitable-path-in-a-tree/solutions/6461478/4ms-c-beats-100-thank-you-again-adjacenc-pzl0/
#pragma GCC optimize("O3","unroll-loops")
#pragma GCC target("avx,mmx,sse2,sse3,sse4")
auto _=[]()noexcept{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);return 0;}();
struct pa{int s,d;} adjs[100000],adjs1[100000];
int pending[100000];
class Solution {
int sz;
void clearBob(int b,vector<int>& amount){
int nxta,nxtb;
for(int i=0;i<sz;++i) if(adjs1[i].d==1){
int pre=0,cur=i;
while(1){
int nxt=adjs1[cur].s^pre;
if(cur==0){nxta=nxt;break;}
else if(cur==b){nxtb=nxt;break;}
if(adjs1[nxt].d>2){
adjs1[nxt].d--;
adjs1[nxt].s^=cur;
break;
}
pre=cur;
cur=nxt;
}
}
int a=0,prea=0,preb=0;
while(1){
amount[b]=0;
if(nxta==b) return;
if(nxta==nxtb){amount[nxtb]>>=1;return;}
prea=a,a=nxta,nxta=adjs1[a].s^prea;
preb=b,b=nxtb,nxtb=adjs1[b].s^preb;
}
}
void getMoney(vector<int>& amount){
for(int i=1;i<sz;++i) if(adjs[i].d==1){
int pre=0,cur=i;
while(1){
int nxt=adjs[cur].s^pre;
pending[nxt]=max(pending[nxt],amount[cur]);
if(nxt==0) break;
if(adjs[nxt].d>2){
adjs[nxt].s^=cur;
adjs[nxt].d--;
break;
}
amount[nxt]+=pending[nxt];
pre=cur;
cur=nxt;
}
}
}
public:
int mostProfitablePath(const vector<vector<int>>& edges,int bob,vector<int>& amount) {
sz=edges.size()+1;
memset(adjs,0,sz*sizeof(adjs[0]));
for(const auto &v:edges){
adjs[v[0]].s^=v[1];
adjs[v[0]].d++;
adjs[v[1]].s^=v[0];
adjs[v[1]].d++;
}
memcpy(adjs1,adjs,sz*sizeof(adjs[0]));
clearBob(bob,amount);
for(int i=0;i<sz;++i) pending[i]=INT_MIN;
getMoney(amount);
return amount[0]+pending[0];
}
};
```
---
# An Update:
So I thought, is it possible to do it in one pass? That way, I don't have to make a copy of the Adjacency Sum.
Turns out, of course it's possible! But it's a little more complicated.
Here is the full code for one pass:
```
//@yjian012 https://hyper-meta.blogspot.com/
//https://leetcode.com/problems/most-profitable-path-in-a-tree/solutions/6461478/4ms-c-beats-100-thank-you-again-adjacenc-pzl0/
#pragma GCC optimize("O3","unroll-loops")
#pragma GCC target("avx,mmx,sse2,sse3,sse4")
auto _=[]()noexcept{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);return 0;}();
struct pa{int s,d;} adjs[100000];
int pending[100000];
class Solution {
public:
int mostProfitablePath(const vector<vector<int>>& edges,int bob,vector<int>& amount) {
int sz=edges.size()+1;
memset(adjs,0,sz*sizeof(adjs[0]));
for(const auto &v:edges){
adjs[v[0]].s^=v[1];
adjs[v[0]].d++;
adjs[v[1]].s^=v[0];
adjs[v[1]].d++;
}
memset(pending,-128,sz*sizeof(pending[0]));
if(adjs[bob].d==1) pending[bob]=0;
int preb=0,cnt=0;
for(int i=1;i<sz;++i) if(adjs[i].d==1){
int pre=0,cur=i;
while(1){
if(cur==bob){preb=pre;break;}
cnt++;
int nxt=adjs[cur].s^pre;
pending[nxt]=max(pending[nxt],amount[cur]);
if(nxt==0) break;
if(adjs[nxt].d>2){
adjs[nxt].s^=cur;
adjs[nxt].d--;
break;
}
amount[nxt]+=pending[nxt];
pre=cur;
cur=nxt;
}
}
int dp1=sz-cnt,m=dp1/2;//dp1=distance+1
for(int i=0;i<m;++i){
int nxtb=adjs[bob].s^preb;
pending[nxtb]=max(pending[nxtb],pending[bob]);
preb=bob,bob=nxtb;
}
if(dp1&1){
int nxtb=adjs[bob].s^preb;
pending[nxtb]=max(pending[nxtb],(amount[bob]>>1)+pending[bob]);
preb=bob,bob=nxtb;
}
for(int i=0;i<m-1;++i){
int nxtb=adjs[bob].s^preb;
pending[nxtb]=max(pending[nxtb],amount[bob]+pending[bob]);
preb=bob,bob=nxtb;
}
return amount[0]+pending[0];
}
};
```
Again, we process the other branches first, leaving only the path from Alice to Bob. But this time, we also update their values. We also keep track of how many nodes are processed.
Next, since we know the number of nodes left, we know the distance. We move Bob through these nodes, while updating the maximum money they can provide. For the first half, we don't include the `amount` of the nodes, since Bob will take them. If there's a middle point, we include half of it. For the next half, we include the full `amount`.
The number of steps are `(d+1)/2`,`1 if d is even, else 0`,`(d-1)/2`, as the following examples show:
```text
Alice Bob
o - o - o - o - o - o : d=5, 3 steps left (no amount), 2 steps left (full amount)
Alice Bob
o - o - o - o - o : d=4, 2 steps left (no amount), 1 step left (half amount), 1 step left (full amount)
``` | 9 | 0 | ['C++'] | 2 |
most-profitable-path-in-a-tree | C++ Solution || Detailed Explanation | c-solution-detailed-explanation-by-rohit-62mg | IntuitionThe problem requires traversing the tree efficiently while considering the movement constraints imposed by Bob. Since it's a tree, we can use DFS and B | Rohit_Raj01 | NORMAL | 2025-02-24T00:40:46.947577+00:00 | 2025-02-24T00:40:46.947577+00:00 | 3,001 | false | # Intuition
The problem requires traversing the tree efficiently while considering the movement constraints imposed by Bob. Since it's a tree, we can use DFS and BFS to construct a proper traversal strategy.
# Approach
1. **Tree Construction**: Convert the given `edges` list into an adjacency list representation.
2. **Tree Traversal using BFS**: Convert the adjacency list into a directed tree where every node points to its children.
3. **Tracking Bob’s Path**: Store Bob's path and timestamps to track the nodes he visits.
4. **Depth-First Search (DFS) for Maximum Profit**:
- Traverse the tree recursively using DFS.
- Adjust node profits based on Bob’s presence.
- Accumulate maximum profit along the path.
# Complexity
- **Time Complexity**: $$O(N)$$, since we traverse the tree multiple times but never revisit nodes unnecessarily.
- **Space Complexity**: $$O(N)$$, due to storage of the adjacency list, parent tracking, and recursive DFS stack.
# Code Implementation
```cpp
class Solution {
public:
int dfs(vector<vector<int>>&adj, int node, int t, map<int,int>&visited, vector<int>&amount) {
int currVal = amount[node];
if (visited.count(node)) {
if (visited[node] < t) currVal = 0;
else if (visited[node] == t) currVal /= 2;
}
if (adj[node].size() == 0) return currVal;
int res = INT_MIN;
for (auto nbr : adj[node]) {
res = max(res, dfs(adj, nbr, t+1, visited, amount));
}
return currVal + res;
}
int mostProfitablePath(vector<vector<int>>& edges, int bob, vector<int>& amount) {
int n = edges.size() + 1;
vector<vector<int>> adj(n, vector<int>());
vector<vector<int>> tree(n, vector<int>());
vector<int> parent(n, 0);
for (int i = 0; i < n-1; i++) {
adj[edges[i][0]].push_back(edges[i][1]);
adj[edges[i][1]].push_back(edges[i][0]);
}
vector<int> added(n, 0);
queue<int> q;
q.push(0);
added[0] = 1;
while (!q.empty()) {
int node = q.front();
q.pop();
for (auto nbr : adj[node]) {
if (!added[nbr]) {
added[nbr]++;
tree[node].push_back(nbr);
q.push(nbr);
}
}
}
for (int i = 0; i < n; i++) {
for (auto child : tree[i]) {
parent[child] = i;
}
}
map<int, int> visited;
int t = 0;
int node = bob;
while (node != 0) {
visited[node] = t++;
node = parent[node];
}
return dfs(tree, 0, 0, visited, amount);
}
};
```
# Explanation
- We first construct an adjacency list from `edges`.
- Using BFS, we convert this adjacency list into a directed tree.
- We determine Bob's path and track the times when he visits each node.
- Using DFS, we traverse the tree to calculate the maximum profit considering Bob's impact on the nodes.
# Edge Cases Considered
- Tree with a single node.
- Bob's movement affecting the profit calculation.
- Large inputs where efficiency matters.

| 9 | 0 | ['Array', 'Tree', 'Breadth-First Search', 'Graph', 'C++'] | 2 |
most-profitable-path-in-a-tree | 🌟 Beats 93.59% 🌟 | ✔️ Easiest Solution & Beginner Friendly ✔️ | 🔥 DFS + Backtracking 🔥 | beats-9359-easiest-solution-beginner-fri-l02d | IntuitionThe problem involves a tree structure whereAlicemoves towards aleafnode whileBobmoves towards theroot. The key idea is to determine Bob’spathand adjust | ntrcxst | NORMAL | 2025-02-24T03:17:39.565537+00:00 | 2025-02-24T03:17:39.565537+00:00 | 1,850 | false | ---
---
# Intuition
The problem involves a tree structure where **Alice** moves towards a **leaf** node while **Bob** moves towards the **root**. The key idea is to determine Bob’s `path` and adjust Alice’s **earnings** accordingly. We use **Depth First Search (DFS)** to calculate Alice’s maximum net `profit` while considering Bob’s **impact**. If Alice and Bob reach a `node` at the **same time**, the `reward/cost` is split. If Bob arrives **earlier**, Alice gets nothing from that `node`. The challenge is to find the most **profitable** `path` for Alice while factoring in Bob’s **influence**.
# Approach
`Step 1` **Build the Tree**
- Use an `adjacencyList` to store the tree representation from the given **edges array**.
`Step 2` **Track Bob’s Path to Root**
- Use DFS to store the time at which Bob reaches each node in an array `bobTime[]`.
`Step 3` **DFS for Alice’s Maximum Profit**
- Perform **DFS** from `node 0` to explore all `paths` Alice can take.
- For each `node`, adjust Alice’s **income based on Bob’s arrival time**
- If Bob arrives later, Alice takes the **full amount**.
- If Bob arrives at the same time, Alice **takes half**.
- If Bob arrives earlier, Alice **gets zero**.
`Step 4` **Choose the Most Profitable Path**
- Continue DFS, tracking the `maxProfit` Alice can obtain from a **leaf node**.
- If a node is a `leaf`, return the `netIncome`.
# Complexity
- Time complexity : $$O(n)$$
- Space complexity : $$O(n)$$
# Code
```Java []
class Solution
{
public int mostProfitablePath(int[][] edges, int bob, int[] amount)
{
int n = amount.length;
List<Integer>[] tree = new ArrayList[n];
for (int i = 0; i < n; i++) tree[i] = new ArrayList<>();
// Step 1: Build the adjacency list representation of the tree
for (int[] e : edges)
{
tree[e[0]].add(e[1]);
tree[e[1]].add(e[0]);
}
int[] bobTime = new int[n];
Arrays.fill(bobTime, -1);
// Step 2: Track Bob’s path and record when he reaches each node
findBobPath(bob, 0, tree, bobTime, 0);
// Step 3: Use DFS for Alice to find the most profitable path
return dfs(0, -1, tree, amount, 0, bobTime);
}
private boolean findBobPath(int node, int time, List<Integer>[] tree, int[] bobTime, int bob)
{
bobTime[node] = time;
if (node == 0) return true;
for (int neighbor : tree[node])
{
if (bobTime[neighbor] == -1 && findBobPath(neighbor, time + 1, tree, bobTime, bob))
{
return true;
}
}
bobTime[node] = -1;
return false;
}
private int dfs(int node, int parent, List<Integer>[] tree, int[] amount, int time, int[] bobTime)
{
int income = amount[node];
// Step 4: Adjust Alice’s income based on Bob’s arrival time
if (bobTime[node] != -1)
{
if (bobTime[node] > time)
{
}
else if (bobTime[node] == time)
{
income /= 2;
}
else
{
income = 0;
}
}
int maxProfit = Integer.MIN_VALUE;
boolean isLeaf = true;
for (int neighbor : tree[node])
{
if (neighbor != parent)
{
isLeaf = false;
maxProfit = Math.max(maxProfit, dfs(neighbor, node, tree, amount, time + 1, bobTime));
}
}
// Step 5: If leaf node, return income, else return maxProfit + income
return income + (isLeaf ? 0 : maxProfit);
}
}
```
``` C++ []
class Solution
{
public:
int mostProfitablePath(vector<vector<int>>& edges, int bob, vector<int>& amount)
{
int n = amount.size();
vector<vector<int>> tree(n);
for (auto& e : edges)
{
tree[e[0]].push_back(e[1]);
tree[e[1]].push_back(e[0]);
}
vector<int> bobTime(n, -1);
// Step 1: Track Bob’s path using DFS
findBobPath(bob, 0, tree, bobTime, 0);
// Step 2: DFS for Alice's maximum profit
return dfs(0, -1, tree, amount, 0, bobTime);
}
private:
bool findBobPath(int node, int time, vector<vector<int>>& tree, vector<int>& bobTime, int bob)
{
bobTime[node] = time;
if (node == 0)
{
return true;
}
for (int neighbor : tree[node])
{
if (bobTime[neighbor] == -1 && findBobPath(neighbor, time + 1, tree, bobTime, bob))
{
return true;
}
}
bobTime[node] = -1;
return false;
}
int dfs(int node, int parent, vector<vector<int>>& tree, vector<int>& amount, int time, vector<int>& bobTime)
{
int income = amount[node];
// Step 3: Adjust Alice's profit based on Bob's arrival time
if (bobTime[node] != -1)
{
if (bobTime[node] > time)
{
// Alice arrives first, full reward
}
else if (bobTime[node] == time)
{
// Both reach at the same time, split amount
income /= 2;
}
else
{
// Bob arrives earlier, Alice gets nothing
income = 0;
}
}
int maxProfit = INT_MIN;
bool isLeaf = true;
for (int neighbor : tree[node])
{
if (neighbor != parent)
{
isLeaf = false;
maxProfit = max(maxProfit, dfs(neighbor, node, tree, amount, time + 1, bobTime));
}
}
// Step 4: If leaf node, return income, else return maxProfit + income
return income + (isLeaf ? 0 : maxProfit);
}
};
```
| 8 | 0 | ['Array', 'Greedy', 'Tree', 'Depth-First Search', 'Breadth-First Search', 'Graph', 'Recursion', 'Shortest Path', 'C++', 'Java'] | 1 |
most-profitable-path-in-a-tree | One Pass | one-pass-by-votrubac-wli6 | We traverse the tree, tracking the max profit and the current distance dist to node 0.\n\nIf we step on node bob, it means that open = dist + 1 nodes (this one | votrubac | NORMAL | 2022-11-15T08:17:24.044086+00:00 | 2022-11-15T08:36:58.344819+00:00 | 1,242 | false | We traverse the tree, tracking the max profit and the current distance `dist` to node `0`.\n\nIf we step on node `bob`, it means that `open = dist + 1` nodes (this one and previous) are opened.\n\nWe return `{res, open - 2}` to track the maximum `res` and the number of opened nodes.\n\n**C++**\n```cpp\npair<int, int> dfs(int i, int prev, int dist, int bob, vector<vector<int>> &al, vector<int>& amount) {\n int res = INT_MIN, open = i == bob ? dist + 1 : 0;\n for (auto j : al[i])\n if (j != prev) {\n auto res_j = dfs(j, i, dist + 1, bob, al, amount);\n res = max(res, res_j.first);\n open = max(open, res_j.second);\n }\n if (open)\n amount[i] = open == 1 ? amount[i] / 2 : 0;\n return {(res == INT_MIN ? 0 : res) + amount[i], open - 2 };\n}\nint mostProfitablePath(vector<vector<int>>& edges, int bob, vector<int>& amount) {\n vector<vector<int>> al(amount.size());\n for (auto &e : edges) {\n al[e[0]].push_back(e[1]);\n al[e[1]].push_back(e[0]);\n }\n return dfs(0, -1, 0, bob, al, amount).first;\n}\n``` | 8 | 1 | ['C'] | 1 |
most-profitable-path-in-a-tree | Preprocess then DFS || Java | preprocess-then-dfs-java-by-abdulazizms-yzaj | \n# Approach\nWe first find the unique path that Bob traversed as well as the distance from Bob\'s initial position to any node along the path.\nThen, a DFS sta | abdulazizms | NORMAL | 2022-11-12T16:10:12.368788+00:00 | 2022-11-12T16:14:04.187830+00:00 | 1,182 | false | \n# Approach\nWe first find the unique path that Bob traversed as well as the distance from Bob\'s initial position to any node along the path.\nThen, a DFS starting from the root to find the max income Alice can get. \n\n# Code\n```\nclass Solution {\n static int [] par;\n static int result; \n static int mostProfitablePath(int[][] edges, int bob, int[] amount) {\n par = new int [amount.length];\n List<List<Integer>> adj = new ArrayList<>();\n result = (int)(-1e9);\n for(int i = 0; i < amount.length; i++) adj.add(new ArrayList<>());\n for(int []edge: edges){\n adj.get(edge[0]).add(edge[1]);\n adj.get(edge[1]).add(edge[0]);\n }\n setPar(0, adj, -1, par);\n Map<Integer, Integer> bobDist = new HashMap<>();\n int cur = bob, cnt = 0;\n while(cur != par[cur]){\n bobDist.put(cur, cnt++);\n cur = par[cur];\n }\n getResult(0, adj, bobDist, 0, amount, -1, amount[0]);\n return result;\n }\n\n static void getResult(int node, List<List<Integer>> adj, Map<Integer, Integer> bobDist,\n int dist, int[] amount, int p, int income) {\n int ans = amount[node];\n boolean flag = true;\n for(int child : adj.get(node)){\n if(child != p){\n if(bobDist.containsKey(child) && dist+1 == bobDist.get(child))\n getResult(child, adj, bobDist, dist+1, amount, node, amount[child]/2 + income);\n else if(bobDist.get(child) == null || dist + 1 < bobDist.get(child))\n getResult(child, adj, bobDist, dist+1, amount, node, amount[child] + income);\n else getResult(child, adj, bobDist, dist+1, amount, node, income);\n flag = false;\n }\n }\n if(flag){\n //leaf node.\n result = Math.max(result, income);\n }\n }\n\n static void setPar(int cur, List<List<Integer>> adj, int p, int [] par){\n for(int child : adj.get(cur)){\n if(child != p){\n par[child] = cur;\n setPar(child, adj, cur, par);\n }\n }\n }\n}\n``` | 7 | 0 | ['Java'] | 1 |
most-profitable-path-in-a-tree | ✅ Easy Explanation | Tree | DFS | Java | C++ | Python Detailed Video Explanation 🔥 | easy-explanation-tree-dfs-java-c-python-59if2 | IntuitionThe problem involves navigating a tree where Alice and Bob move along different paths. Bob starts from a given node and follows the shortest path to th | sahilpcs | NORMAL | 2025-02-24T03:18:55.134049+00:00 | 2025-02-24T03:18:55.134049+00:00 | 1,851 | false | # Intuition
The problem involves navigating a tree where Alice and Bob move along different paths. Bob starts from a given node and follows the shortest path to the root (node 0). Alice starts from the root and explores all paths to maximize her profit while considering Bob's journey.
# Approach
1. Construct an adjacency list to represent the tree.
2. Use DFS to determine Bob's path and the time at which he reaches each node.
3. Use another DFS traversal for Alice to explore all paths while computing the income based on Bob's arrival time at each node.
4. Track the maximum profit encountered on any leaf-to-root path.
# Complexity
- Time complexity:
- Constructing the adjacency list takes $$O(n)$$.
- DFS traversals for Bob and Alice take $$O(n)$$ each.
- Overall complexity is $$O(n)$$.
- Space complexity:
- Adjacency list storage takes $$O(n)$$.
- Recursive DFS calls take $$O(n)$$ in the worst case.
- HashMap for Bob's path takes $$O(n)$$.
- Overall space complexity is $$O(n)$$.
# Code
```java []
class Solution {
ArrayList<Integer>[] adj; // Adjacency list representation of the graph
Map<Integer, Integer> bobPath; // Stores the path of Bob with time taken to reach each node
int max = Integer.MIN_VALUE; // Stores the maximum profit Alice can collect
int[] amount; // Stores the profit associated with each node
boolean[] visited; // Tracks visited nodes to prevent cycles
public int mostProfitablePath(int[][] edges, int bob, int[] amount) {
// Prepare adjacency list
int n = amount.length;
bobPath = new HashMap<Integer, Integer>();
this.amount = amount;
adj = new ArrayList[n];
for(int i = 0; i < n; i++)
adj[i] = new ArrayList<Integer>();
visited = new boolean[n];
// Build the adjacency list from edges
for(int[] edge: edges){
int u = edge[0];
int v = edge[1];
adj[u].add(v);
adj[v].add(u);
}
// Find Bob's path to node 0
bobPath(bob, 0); // Starting node of Bob, time initialized to 0
// Find Alice's maximum profit path
Arrays.fill(visited, false); // Reset visited array
alice(0, 0, 0); // Start Alice from node 0
return max; // Return the maximum profit Alice can achieve
}
private boolean bobPath(int node, int time) {
visited[node] = true;
bobPath.put(node, time); // Store the time Bob reaches this node
if(node == 0) { // If Bob reaches node 0, return true
return true;
}
// Traverse neighbors to find a path to node 0
for(int nei : adj[node]) {
if(!visited[nei] && bobPath(nei, time + 1)) {
return true;
}
}
// Undo the path if not leading to node 0
bobPath.remove(node);
return false;
}
// DFS to calculate maximum income for Alice
private void alice(int node, int time, int income) {
visited[node] = true;
// If Alice reaches first, collect full amount
if(!bobPath.containsKey(node) || time < bobPath.get(node)) {
income += amount[node];
}
// If both reach at the same time, collect half the amount
else if(time == bobPath.get(node)) {
income += amount[node] / 2;
}
// If leaf node (not root), update max profit
if(adj[node].size() == 1 && node != 0) {
max = Math.max(max, income);
}
// Recur for all unvisited neighbors
for(int nei : adj[node]) {
if(!visited[nei]) {
alice(nei, time + 1, income);
}
}
}
}
```
```cpp []
class Solution {
public:
vector<vector<int>> adj;
unordered_map<int, int> bobPath;
int maxProfit = INT_MIN;
vector<int> amount;
vector<bool> visited;
int mostProfitablePath(vector<vector<int>>& edges, int bob, vector<int>& amount) {
int n = amount.size();
this->amount = amount;
adj.resize(n);
visited.resize(n, false);
for (auto& edge : edges) {
adj[edge[0]].push_back(edge[1]);
adj[edge[1]].push_back(edge[0]);
}
findBobPath(bob, 0);
fill(visited.begin(), visited.end(), false);
findAlicePath(0, 0, 0);
return maxProfit;
}
bool findBobPath(int node, int time) {
visited[node] = true;
bobPath[node] = time;
if (node == 0) return true;
for (int nei : adj[node]) {
if (!visited[nei] && findBobPath(nei, time + 1)) {
return true;
}
}
bobPath.erase(node);
return false;
}
void findAlicePath(int node, int time, int income) {
visited[node] = true;
if (!bobPath.count(node) || time < bobPath[node])
income += amount[node];
else if (time == bobPath[node])
income += amount[node] / 2;
if (adj[node].size() == 1 && node != 0)
maxProfit = max(maxProfit, income);
for (int nei : adj[node]) {
if (!visited[nei]) {
findAlicePath(nei, time + 1, income);
}
}
}
};
```
```python []
from collections import defaultdict
class Solution:
def mostProfitablePath(self, edges: List[List[int]], bob: int, amount: List[int]) -> int:
adj = defaultdict(list)
for u, v in edges:
adj[u].append(v)
adj[v].append(u)
bobPath = {}
visited = set()
def findBobPath(node, time):
visited.add(node)
bobPath[node] = time
if node == 0:
return True
for nei in adj[node]:
if nei not in visited and findBobPath(nei, time + 1):
return True
bobPath.pop(node)
return False
findBobPath(bob, 0)
visited.clear()
maxProfit = float('-inf')
def findAlicePath(node, time, income):
nonlocal maxProfit
visited.add(node)
if node not in bobPath or time < bobPath[node]:
income += amount[node]
elif time == bobPath[node]:
income += amount[node] // 2
if len(adj[node]) == 1 and node != 0:
maxProfit = max(maxProfit, income)
for nei in adj[node]:
if nei not in visited:
findAlicePath(nei, time + 1, income)
findAlicePath(0, 0, 0)
return maxProfit
```
https://youtu.be/ngTRBEr7z2g
| 6 | 0 | ['Array', 'Tree', 'Depth-First Search', 'Graph', 'Python', 'C++', 'Java', 'Python3'] | 1 |
most-profitable-path-in-a-tree | DFS Solution | dfs-solution-by-richyrich2004-aa2s | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | RichyRich2004 | NORMAL | 2025-02-24T01:15:50.407226+00:00 | 2025-02-24T01:15:50.407226+00:00 | 1,095 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def mostProfitablePath(self, edges: List[List[int]], bob: int, amount: List[int]) -> int:
# build adjacency list
graph = defaultdict(list)
for edge in edges:
graph[edge[0]].append(edge[1])
graph[edge[1]].append(edge[0])
visited = set()
def dfs(curr):
if curr == 0:
return [curr]
visited.add(curr)
l = []
for e in graph[curr]:
if e not in visited:
l = dfs(e)
if l:
return [curr] + l
# first move bob, and track visited times
bob_path = dfs(bob)
bob_visited_times = {}
for i, v in enumerate(bob_path):
bob_visited_times[v] = i
visited = set()
def dfs_alice(curr, visit_time):
max_amount = float('-inf')
visited.add(curr)
for e in graph[curr]:
if e not in visited:
max_amount = max(max_amount, dfs_alice(e, visit_time + 1))
vertex_income = amount[curr]
if curr in bob_visited_times and bob_visited_times[curr] < visit_time:
vertex_income = 0
elif curr in bob_visited_times and bob_visited_times[curr] == visit_time:
vertex_income = amount[curr] // 2
if max_amount == float('-inf'):
return vertex_income
return max_amount + vertex_income
# then move alice. if alice gets to a vertex (explored by bob) with lower visited time, then alice takes the amount
return dfs_alice(0, 0)
``` | 6 | 0 | ['Python3'] | 0 |
most-profitable-path-in-a-tree | 🔥 Recursive DFS-based O(N) DP || 23ms in Rust & ~30ms in Go | recursive-dfs-based-on-dp-23ms-in-rust-3-4qzq | 🚀 IntuitionInstead of performing multiple passes (BFS + DP), we solve the problem in one recursive DFS traversal.
Alice moves towards a leaf while maximizing he | rutsh | NORMAL | 2025-02-24T11:55:53.998659+00:00 | 2025-02-24T13:45:01.572000+00:00 | 308 | false | # 🚀 Intuition
Instead of performing multiple passes (__BFS + DP__), we solve the problem in __one recursive DFS traversal__.
- Alice moves towards a leaf while maximizing her profit.
- Bob moves towards the root, reducing profits at shared nodes.
- We compute both Alice’s max profit & Bob’s distance in a single DFS, efficiently handling all cases.
# 🔍 Approach
1. __Build the tree__: using an adjacency list.
2. __Use a recursive DFS__ (`dp_rec`) to compute:
- `alice_profit[node]`: Max profit Alice can collect from this subtree.
- `bob_distance[node]`: Distance of Bob from this node.
3. __Base case__: If node is a leaf (except root)
- Return `amount[node]` or `0` (if it's bob node)
4. __Recursive case:__
- Traverse child nodes.
- Track Bob's shortest distance.
- Pick the best Alice's profit path.
- Adjust profit based on Bob's presence (`0`, `amount[node]`, or `amount[node] / 2`).
5. __Return the maximum profit__ Alice can achieve.
# Complexity
- __🕒 Time Complexity__: $O(N)$
- _Tree traversal_: We visit each node once ($O(N)$).
- __📦 Space Complexity__: $O(N)$
- _Tree storage_: $O(N)$ (<ins>adjacency list</ins>).
- _Recursion stack_: Worst case $O(N)$ (<ins>skewed tree</ins>).
- No «**extra DP arrays**» used!
# Code
```rust []
use std::cmp::Ordering::{Less, Equal, Greater};
struct ProblemContext<'a> {
bob: usize,
amount: &'a [i32],
tree: &'a [Vec<usize>],
}
impl Solution {
pub fn most_profitable_path(edges: Vec<Vec<i32>>, bob: i32, amount: Vec<i32>) -> i32 {
let n = amount.len();
let mut tree = vec![vec![]; n];
// Construct adjacency list
for edge in &edges {
let (u, v) = (edge[0] as usize, edge[1] as usize);
tree[u].push(v);
tree[v].push(u);
}
let ctx = ProblemContext {
bob: bob as usize,
amount: &amount,
tree: &tree,
};
// Start DFS from the root (0), parent set as usize::MAX (invalid parent)
let (alice_profit, _) = Self::dp_rec(0, usize::MAX, 0, &ctx);
alice_profit
}
// Recursive DFS to compute Alice's max profit and Bob's distance from `node`
fn dp_rec(node: usize, parent: usize, current_depth: usize, ctx: &ProblemContext) -> (i32, usize) {
let bob_init_depth = if node == ctx.bob { 0 } else { ctx.tree.len() };
// If `node` is a leaf (not the root), handle Alice's profit correctly
if ctx.tree[node].len() == 1 && current_depth != 0 {
let alice_profit = if node == ctx.bob { 0 } else { ctx.amount[node] };
return (alice_profit, bob_init_depth);
}
// Explore child nodes recursively and find:
// - Maximum profit Alice can collect (`alice_profit`)
// - Minimum distance Bob needs to reach this node (`bob_distance`)
let (alice_profit, bob_distance) = ctx.tree[node]
.iter()
.filter(|&&neighbor| neighbor != parent) // Avoid backtracking to parent
.map(|&neighbor| Self::dp_rec(neighbor, node, current_depth + 1, ctx))
.fold((i32::MIN, bob_init_depth), |(a_profit, b_dist), (a, b)| {
(a_profit.max(a), b_dist.min(b + 1))
});
// Adjust Alice's profit based on when Bob arrives at this node
let adjusted_profit = match current_depth.cmp(&bob_distance) {
Less => alice_profit + ctx.amount[node], // Alice arrives first → full amount
Equal => alice_profit + ctx.amount[node] / 2, // Alice & Bob arrive together → split amount
Greater => alice_profit, // Bob arrives first → Alice gets nothing
};
(adjusted_profit, bob_distance)
}
}
```
``` golang []
type ProblemContext struct {
Amount []int
Bob int
Tree [][]int
}
func mostProfitablePath(edges [][]int, bob int, amount []int) int {
n := len(edges) + 1
tree := make([][]int, n)
// Construct adjacency list
for _, e := range edges {
tree[e[0]] = append(tree[e[0]], e[1])
tree[e[1]] = append(tree[e[1]], e[0])
}
ctx := &ProblemContext{Amount: amount, Bob: bob, Tree: tree}
aliceProfit, _ := dpRec(0, -1, 0, ctx)
return aliceProfit
}
// dpRec computes Alice's max profit and Bob's distance from `node`
func dpRec(node int, parent int, currentDepth int, ctx *ProblemContext) (aliceProfit int, bobDistance int) {
// Case: Leaf node (not root)
if len(ctx.Tree[node]) == 1 && currentDepth != 0 {
if node != ctx.Bob {
aliceProfit = ctx.Amount[node]
bobDistance = len(ctx.Tree) // Effectively ∞
}
return
}
bobDistance = len(ctx.Tree) // Set as ∞ initially
aliceProfit = math.MinInt
if node == ctx.Bob {
bobDistance = 0
}
// Traverse child nodes
for _, neighbor := range ctx.Tree[node] {
if neighbor != parent {
nProfit, nBobDistance := dpRec(neighbor, node, currentDepth+1, ctx)
bobDistance = min(bobDistance, nBobDistance+1)
aliceProfit = max(aliceProfit, nProfit)
}
}
// Adjust Alice's profit based on Bob's position
if currentDepth < bobDistance {
aliceProfit += ctx.Amount[node] // Alice takes full amount
} else if currentDepth == bobDistance {
aliceProfit += ctx.Amount[node] / 2 // Alice splits with Bob
}
return
}
``` | 5 | 0 | ['Dynamic Programming', 'Tree', 'Recursion', 'Go', 'Rust'] | 0 |
most-profitable-path-in-a-tree | 🔴💎 Solution! | solution-by-quantummaniac609-pkmt | IntuitionLooking at this problem, I realized we need to track two simultaneous paths: Alice's path from root to any leaf, and Bob's path from his starting posit | quantummaniac609 | NORMAL | 2025-02-24T05:43:34.091802+00:00 | 2025-02-24T05:43:34.091802+00:00 | 88 | false | # Intuition
Looking at this problem, I realized we need to track two simultaneous paths: Alice's path from root to any leaf, and Bob's path from his starting position to root. The key insight is that we can first determine Bob's path and timing, then use this information while exploring Alice's possible paths to find the maximum income.
# Approach
The solution breaks down into three main steps:
1. Build an adjacency list representation of the tree:
- Convert edges array into a graph where each node points to its neighbors
- This makes traversal easier
2. Find Bob's path to root:
- Use DFS with backtracking to find the exact path
- Store timing information (when Bob reaches each node)
- Only keep nodes that are actually in the path to root
```ruby
bob_path = {node => time} # When Bob reaches each node
```
3. Find Alice's maximum possible income:
- Use DFS to explore all possible paths to leaf nodes
- At each node, calculate income based on timing:
* Full amount if Bob never reaches node
* Half amount if they arrive simultaneously
* Full amount if Alice arrives first
* Zero if Bob arrives first
- Track visited nodes to avoid cycles
- Update maximum income when reaching leaf nodes
For example:
```
edges = [[0,2],[2,3]], bob = 3, amount = [-2,4,2]
1. Bob's path: 3->2->0 with times {3:0, 2:1, 0:2}
2. Alice's path: 0->2->3
- At 0: -2 (full amount, Bob arrives later)
- At 2: 2 (half amount, shared)
- At 3: 0 (no amount, Bob was there first)
```
# Complexity
- Time complexity: O(N)
- Building graph: O(N)
- Finding Bob's path: O(N)
- Finding Alice's maximum income: O(N)
- Each node is visited at most once in each DFS
- Space complexity: O(N)
- Adjacency list: O(N)
- Bob's path hash: O(N)
- Recursion stack: O(N)
- Visited array: O(N)
# Code
```ruby []
# @param {Integer[][]} edges
# @param {Integer} bob
# @param {Integer[]} amount
# @return {Integer}
def most_profitable_path(edges, bob, amount)
n = amount.length
# Build adjacency list
graph = Array.new(n) { [] }
edges.each do |a, b|
graph[a] << b
graph[b] << a
end
# Find Bob's path to root (0)
bob_path = {}
@found_bob_path = false
def find_bob_path(node, parent, target, time, path, graph)
if node == target
path[node] = time
@found_bob_path = true
return true
end
graph[node].each do |next_node|
next if next_node == parent
path[node] = time
if find_bob_path(next_node, node, target, time + 1, path, graph)
return true
end
end
path.delete(node) unless @found_bob_path
false
end
find_bob_path(bob, -1, 0, 0, bob_path, graph)
# Find Alice's maximum income
@max_income = -Float::INFINITY
def find_max_income(node, parent, time, income, bob_path, amount, graph, visited)
visited[node] = true
curr_amount = amount[node]
# Calculate gate amount based on Alice and Bob's positions
if !bob_path.key?(node)
# Bob never reaches this node
curr_amount = amount[node]
elsif time == bob_path[node]
# Alice and Bob reach simultaneously
curr_amount = amount[node] / 2
elsif time < bob_path[node]
# Alice reaches before Bob
curr_amount = amount[node]
else
# Bob reaches before Alice
curr_amount = 0
end
income += curr_amount
# If leaf node, update max_income
is_leaf = true
graph[node].each do |next_node|
next if next_node == parent || visited[next_node]
is_leaf = false
find_max_income(next_node, node, time + 1, income, bob_path, amount, graph, visited)
end
@max_income = [@max_income, income].max if is_leaf
visited[node] = false
end
visited = Array.new(n, false)
find_max_income(0, -1, 0, 0, bob_path, amount, graph, visited)
@max_income
end
``` | 5 | 0 | ['Ruby'] | 0 |
most-profitable-path-in-a-tree | Simple DFS Traversal | simple-dfs-traversal-by-mj30-umkw | //Mayank Jain\n\nThe idea is to construct parent vector firstly and setting parent value for each of the nodes. This will be helpful for Bob while traversing in | MJ30 | NORMAL | 2022-11-16T08:59:59.617953+00:00 | 2022-11-16T08:59:59.617991+00:00 | 584 | false | //Mayank Jain\n\nThe idea is to construct parent vector firstly and setting parent value for each of the nodes. This will be helpful for Bob while traversing in upwards direction towards source node 0. \n\n-> We will do a DFS graph traversal for both Alice (starting node as 0) & Bob (starting node as bob) and will mark visiting nodes as true during traversal.\n-> If Alice and Bob are on the same nodes, then Alice can take half of the contribution in total sum value else if Alice visits a node already been visited by Bob, then nothing will be added in total sum.\n-> We will have to check for all the leaf nodes optimally as to maximize total sum value stored in ans variable in the end.\n\n```\n//Mayank Jain\n\nclass Solution {\npublic:\n vector<int> parent; \n vector<vector<int>> graph;\n vector<bool> vis;\n int ans = INT_MIN; //value that has to be maximized before returning\n\t\n void solve(int src,int par){ //setting parent of each node\n parent[src] = par;\n for(auto itr:graph[src]){\n if(itr!=parent[src]) solve(itr,src);\n }\n }\n\t\n void solve2(int src,int end,vector<int>&amt,int sum){\n int sum2 = sum;\n if(vis[src]==false){ //visiting node for the first time\n vis[src] = true;\n if(src==end){ //If Alice and Bob are on the same nod\n sum2+= amt[src]/2;\n }\n else sum2+= amt[src];\n }\n for(auto itr:graph[src]){\n if(itr!=parent[src]){ //Alice has to move down towards the leaf node\n int res = -1;\n if(end!=-1){\n res = parent[end]; //Bob has to move upwards towards src node 0\n\t\t\t\t\t//Note that there is always only one unique path for Bob\n vis[end] = true; //marking node where Bob stands as true\n }\n solve2(itr,res,amt,sum2); \n if(end!=-1) vis[end] = false;\n }\n }\n if(graph[src].size()<=1 && parent[src]!=-1) ans = max(ans,sum2); //Leaf node case where ans value needs to be checked and maximized\n vis[src] = false;\n }\n\t\n int mostProfitablePath(vector<vector<int>>& edges, int bob, vector<int>& amount) {\n parent.resize(100001,-1); \n graph.resize(edges.size()+1);\n for(int i=0;i<edges.size();i++){ //constructing graph from edges vector\n graph[edges[i][0]].push_back(edges[i][1]);\n graph[edges[i][1]].push_back(edges[i][0]);\n }\n solve(0,-1); //function to set parent of each node \n\t\t//Note that parent of src node 0 is set to -1\n\t\t\n vis.resize(100001,false); //boolean vector vis to keep track of all visited nodes\n solve2(0,bob,amount,0);\n return ans;\n }\n};\n``` | 5 | 0 | ['Backtracking', 'Depth-First Search', 'Recursion'] | 0 |
most-profitable-path-in-a-tree | Double DFS || Level checking || Easy to understand || C++ | double-dfs-level-checking-easy-to-unders-br2p | \n\n# Code\n\nclass Solution {\n vector<int>g[100005];\n int level_bob[100005];\n bool vis[100005];\n \n int pa[100005];\n \n long long max | BlueSharK_14 | NORMAL | 2022-11-12T16:05:19.214761+00:00 | 2022-11-12T16:46:00.767034+00:00 | 1,161 | false | \n\n# Code\n```\nclass Solution {\n vector<int>g[100005];\n int level_bob[100005];\n bool vis[100005];\n \n int pa[100005];\n \n long long max_amount=-1e9;\n vector<int>Amount;\npublic:\n int mostProfitablePath(vector<vector<int>>& edges, int bob, vector<int>& amount) {\n Amount = amount;\n for(auto v: edges){\n g[v[0]].push_back(v[1]);\n g[v[1]].push_back(v[0]);\n }\n \n for(int i=0; i<edges.size()+1; i++) level_bob[i]=1e9;\n memset(vis, false , sizeof(vis));\n level_bob[bob]=0;\n dfs_bob(bob, -1);\n \n \n /// Path from 0 to bob\'s node and mark these node using map\n map<int, bool>mpp;\n int node=0;\n while(pa[node]!=-1){\n mpp[node]=true;\n node =pa[node];\n }\n mpp[bob]=true;\n \n for(int i=0; i<edges.size()+1; i++)\n {\n if(!mpp[i]){ /// if this node isn\'t in the bob\'s path then set level to MAX_INT\n level_bob[i]=1e9;\n }\n }\n \n \n \n memset(vis, false, sizeof(vis)); /// clear vis array\n int level=0;\n long long sum_amount=0;\n dfs_alice(0, level, sum_amount);\n \n return (int)max_amount;\n }\n \n void dfs_bob(int u, int p)\n {\n vis[u]=true;\n pa[u]=p; /// parent set\n for(auto v: g[u]){\n if(!vis[v]){\n level_bob[v]=level_bob[u]+1; /// level update\n dfs_bob(v, u);\n }\n }\n }\n \n void dfs_alice(int u, int level, long long sum_amount)\n {\n vis[u]=true;\n if(level<level_bob[u]) sum_amount+=Amount[u]; /// if alice\'s current level is lower then it means that bob didn\'t reach this node before alice thats why add the Amount\n else if(level==level_bob[u]) sum_amount+=(Amount[u]/2); /// if alice\'s current level is equal to bob that means they are in that node at the same time thats why they will share amount so half goes to alice\n \n if( u!=0 && g[u].size()==1){ /// if this node is leaf node not the 0 node\n max_amount=max(max_amount, sum_amount); /// max_amount update\n }\n for(auto v: g[u]){\n if(!vis[v]){\n dfs_alice(v, level+1, sum_amount);\n }\n }\n }\n \n};\n``` | 5 | 0 | ['C++'] | 0 |
most-profitable-path-in-a-tree | C++ 🚀 | 2 DFS 🥳 | Intuition and Approach 🌟 | c-intuition-and-approach-by-jatin1510-hhdf | IntuitionIn this problem, Alice wants to maximize her earnings by moving from the root (node0) to a leaf node, while Bob moves toward the root (0). The difficul | jatin1510 | NORMAL | 2025-02-24T14:14:28.258508+00:00 | 2025-02-24T14:21:08.950094+00:00 | 378 | false | # Intuition
In this problem, Alice wants to maximize her earnings by moving from the root (node `0`) to a leaf node, while Bob moves toward the root (`0`). The difficulty arises because:
- If Bob reaches a node before Alice, the reward is completely lost.
- If Alice and Bob reach the node at the same time, they split the cost or reward equally.
- If Alice reaches the node first, she gets the full reward.
Since Bob’s path is predetermined, we can track which nodes he visits and adjust Alice’s profit calculations accordingly. The key insight is to identify:
1. Nodes Bob reaches first: No profit for Alice.
2. Nodes Alice and Bob reach simultaneously: Alice receives only half the reward.
3. Nodes Alice reaches first: Alice gets the full reward.
By computing the best path Alice can take while considering Bob’s influence, we determine the maximum profit Alice can achieve.
---
# Approach
### Step 1: Construct the Tree
- Convert the `edges` list into an adjacency list representation for easy traversal.
### Step 2: Track Bob’s Path to the Root
- Perform a parent tracking DFS to find each node’s parent.
- Backtrack (Not actual) from Bob’s starting node to the root and store his path.
### Step 3: Mark Nodes Affected by Bob
- Identify the "midpoint node" where Alice and Bob arrive at the same time.
- Mark nodes where Bob arrives first so Alice gets no profit.
- Mark nodes where Alice and Bob arrive together, and ensure Alice gets half the reward there.
### Step 4: Use DFS to Compute Alice’s Maximum Profit
- Perform Depth-First Search (DFS) from node `0`:
- Keep track of Alice’s accumulated earnings.
- If a node is already influenced by Bob, adjust Alice’s earnings accordingly.
- Stop when a leaf node is reached.
- Track the maximum profit possible among all leaf nodes.
### Step 5: Return the Best Possible Profit
- After DFS traversal, return the maximum profit Alice can earn by choosing the best leaf node.
# Code
```cpp []
class Solution {
int midNode = -1;
public:
void findParent(int node, int par, vector<int> adj[], unordered_map<int, int> &mp) {
mp[node] = par;
for (auto i : adj[node]) {
if (i != par) {
findParent(i, node, adj, mp);
}
}
}
void dfs(int node, int par, int sum, vector<int> adj[], vector<int> &amount, vector<int> &dist, vector<int> &leaf, vector<bool> &zeroNodes) {
bool isLeaf = true;
dist[node] = sum;
for (auto i : adj[node]) {
if (i != par) {
isLeaf = false;
if (i == midNode) {
dfs(i, node, sum + (amount[i] / 2), adj, amount, dist, leaf, zeroNodes);
} else if (zeroNodes[i]) {
dfs(i, node, sum, adj, amount, dist, leaf, zeroNodes);
} else {
dfs(i, node, sum + amount[i], adj, amount, dist, leaf, zeroNodes);
}
}
}
leaf[node] = isLeaf;
}
int mostProfitablePath(vector<vector<int>> &edges, int bob, vector<int> &amount) {
int n = edges.size() + 1;
vector<int> adj[n];
for (auto e : edges) {
adj[e[0]].push_back(e[1]);
adj[e[1]].push_back(e[0]);
}
unordered_map<int, int> parent;
findParent(0, -1, adj, parent);
vector<int> bobNodes;
do {
bobNodes.push_back(bob);
bob = parent[bob];
} while (bob != -1);
if (bobNodes.size() % 2 == 1) {
midNode = bobNodes[bobNodes.size() / 2];
}
vector<bool> zeroNodes(n, 0);
for (int i = 0; i < bobNodes.size(); i++) {
if (i < bobNodes.size() / 2) {
zeroNodes[bobNodes[i]] = 1;
}
}
vector<int> dist(n, INT_MIN), leaf(n);
dfs(0, -1, amount[0], adj, amount, dist, leaf, zeroNodes);
int ans = INT_MIN;
for (int i = 0; i < n; i++) {
if (leaf[i]) {
ans = max(ans, dist[i]);
}
}
return ans;
}
};
```
# Time Complexity
- Tree Construction: `O(n)`
- Finding Bob’s Path: `O(n)`
- DFS for Alice’s Path: `O(n)`
- Overall Complexity: `O(n)`
---
# Space Complexity
- Adjacency List: `O(n)`
- Bob’s Path Tracking: `O(n)`
- DFS Helper Structures (`dist`, `leaf`, `zeroNodes`): `O(n)`
- Overall Complexity: `O(n)`
| 4 | 0 | ['Tree', 'Depth-First Search', 'Graph', 'C++'] | 0 |
most-profitable-path-in-a-tree | Only 1 DFS call C++ solution. | only-1-dfs-call-c-solution-by-saraldwive-6j2g | IntuitionWe are given an undirected tree with 𝑛 nodes labeled from 0 to 𝑛−1, rooted at node 0. The tree is represented by the edges list, where each entry [𝑎𝑖,𝑏 | SaralDwivedi21 | NORMAL | 2025-02-24T12:26:40.214196+00:00 | 2025-02-24T12:26:40.214196+00:00 | 239 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
We are given an undirected tree with 𝑛 nodes labeled from 0 to 𝑛−1, rooted at node 0. The tree is represented by the edges list, where each entry [𝑎𝑖,𝑏𝑖] represents an edge between nodes 𝑎𝑖 and 𝑏𝑖.
At each node 𝑖,there is a gate that can either:
--Reward money (if amount[i] is positive).
--Require payment to open (if amount[i] is negative).
Gameplay Rules:
--Alice starts at node 0 and moves towards a leaf node.
--Bob starts at node bob and moves towards node 0.
--At every second, both Alice and Bob move to an adjacent node in their respective directions.
Gate Interaction:
--If only Alice arrives at a node, she gains or loses the full amount[i].
--If only Bob arrives at a node, he does nothing (but can prevent Alice from gaining a reward).
--If both arrive at the same time, they split the amount[i] equally.
Goal:
Find the maximum net income Alice can obtain if she moves towards the best possible leaf node
# Approach
<!-- Describe your approach to solving the problem. -->
Step 1: Constructing the Tree
```
unordered_map<int,list<int>> adj;
for(int i=0;i<edges.size();i++)
{
int u=edges[i][0],v=edges[i][1];
adj[u].push_back(v);
adj[v].push_back(u);
}
```
This code constructs an adjacency list from the given edges input.
Since it is a tree, every node has a unique path to every other node.
Step 2: Finding Bob's Path and Modifying amount
```
stack<int> s;
if(node == bob)
{
int size = s.size();
for(int i = 0; i < size / 2; i++)
{
amount[s.top()] = 0;
s.pop();
}
if(size % 2 == 1)
{
amount[s.top()] /= 2;
}
while(s.size() < size)
{
s.push(0);
}
}
```
When profit(node) is called, we track Bob's path using a stack s.
If we reach Bob’s starting position (bob):
--Nodes in the first half of Bob's path are completely nullified (Alice gets nothing from these nodes).
--If the path length is odd, the middle node's amount is halved (Bob and Alice share the amount).
Step 3: DFS to Maximize Alice's Profit
```
int profit(int node)
{
s.push(node);
vis[node] = true;
int ans = INT_MIN;
for(int nbr : g[node])
{
if(!vis[nbr])
{
ans = max(ans, profit(nbr));
}
}
if(ans == INT_MIN) ans = 0; // If no valid paths, set profit to 0.
s.pop();
return ans + amount[node]; // Return max profit including current node.
}
```
DFS traversal explores all possible paths from Alice’s perspective.
We keep track of visited nodes (vis[node]).
If node is a leaf node, it gets base profit 0 (since Alice stops there).
If not, the maximum profit of any child is added to the current node’s amount.
# Complexity
- Time complexity: O(n)
# Code
```cpp []
class graph
{
public:
unordered_map<int,list<int>> g;
int bob;
vector<int> amount;
unordered_map<int,bool> vis;
stack<int> s;
graph(unordered_map<int,list<int>>& adj,int bb,vector<int>& amt)
{
this->g=adj;
this->bob=bb;
this->amount=amt;
}
int profit(int node)
{
s.push(node);
vis[node]=true;
if(node==bob)
{
int size=s.size();
for(int i=0;i<size/2;i++)
{
amount[s.top()]=0;
s.pop();
}
if(size%2==1)
{
amount[s.top()]/=2;
}
while(s.size()<size)
{
s.push(0);
}
}
int ans=INT_MIN;
for(int nbr:g[node])
{
if(!vis[nbr])
{
ans=max(ans,profit(nbr));
}
}
if(ans==INT_MIN) ans=0;
s.pop();
return ans+amount[node];
}
};
class Solution {
public:
int mostProfitablePath(vector<vector<int>>& edges, int bob, vector<int>& amount) {
unordered_map<int,list<int>> adj;
for(int i=0;i<edges.size();i++)
{
int u=edges[i][0],v=edges[i][1];
adj[u].push_back(v);
adj[v].push_back(u);
}
graph ob(adj,bob,amount);
return ob.profit(0);
}
};
``` | 4 | 0 | ['C++'] | 1 |
most-profitable-path-in-a-tree | DFS || Hard Solution || Best Solution || Beats 20% Users|| | dfs-hard-solution-best-solution-beats-20-xqgb | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | Heisenberg_wc | NORMAL | 2025-02-24T05:52:13.175991+00:00 | 2025-02-24T05:52:13.175991+00:00 | 369 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
bool dfs(int node,unordered_map<int,list<int>>&adj,unordered_map<int,bool>&vis,vector<int>&time, int timer){
vis[node]=true;
time[node]=timer;
if(node==0) return true;
for(auto i:adj[node]){
if(!vis[i]){
if(dfs(i,adj,vis,time,timer+1)){return true;}
}
}
time[node]=-1;
return false;
}
long long adfs(int node , int time,unordered_map<int,bool>&v,unordered_map<int,list<int>>&adj,vector<int>&timeBob,vector<int>&amount){
if(adj[node].size() == 1 && node != 0) {
if(timeBob[node]==time) return amount[node]/2;
else if(timeBob[node]<time && timeBob[node]!=-1) return 0;
else return amount[node];
}
long long ans=INT_MIN;
v[node]=true;
//long long
for(auto i:adj[node]){
if(!v[i]){
if(timeBob[node]==time){ans=max(ans,(amount[node]/2)+adfs(i,time+1,v,adj,timeBob,amount));}
else if(timeBob[node]<time && timeBob[node]!=-1){ans=max(ans,0+adfs(i,time+1,v,adj,timeBob,amount));}
else{ans=max(ans,(amount[node])+adfs(i,time+1,v,adj,timeBob,amount));}
}
}
return ans;
}
int mostProfitablePath(vector<vector<int>>& edges, int bob, vector<int>& amount) {
int n=edges.size()+1;
unordered_map<int,list<int>>adj;
for(auto i:edges){
adj[i[0]].push_back(i[1]);
adj[i[1]].push_back(i[0]);
}
vector<int>time(n+1,-1);
int timer=0;
time[bob]=timer;
unordered_map<int,bool>vis;
vis[bob]=true;
for(auto i:adj[bob]){
if(dfs(i,adj,vis,time,timer+1)){break;}
}
for(auto i:time) cout<<i<<" ";
unordered_map<int,bool>v;
int t=0;
long long ans=INT_MIN;
cout<<ans<<" "<<endl;
ans=max(ans,adfs(0,t,v,adj,time,amount));
return ans;
}
};
``` | 4 | 0 | ['C++'] | 0 |
most-profitable-path-in-a-tree | 🤯10 Lines C++ Concise Code 🚀 | 10-lines-c-concise-code-by-sapilol-u9ui | C++ | LeadingTheAbyss | NORMAL | 2025-02-24T05:06:14.558875+00:00 | 2025-02-24T05:09:54.958258+00:00 | 385 | false | # C++
```cpp
int mostProfitablePath(vector<vector<int>>& e, int b, vector<int>& a) {
int n = a.size(), ans = -1e9; vector<vector<int>> g(n);
for(auto&e:e) g[e[0]].push_back(e[1]),g[e[1]].push_back(e[0]);
vector<int> p(n,-1) , nums(n,1e9);
function<void(int,int)> f=[&](int u,int par){ p[u] = par; for(int v:g[u]) if(v != par) f(v,u);}; f(0,-1);
for(int t = 0,x = b; x != -1; x = p[x]) nums[x] = t++;
function<void(int,int,int,int)> dfs=[&](int u,int par,int t,int s){
int res = s + (t < nums[u] ? a[u] : (t == nums[u] ? a[u]/2 : 0));
if(u && g[u].size() == 1) ans = max(ans,res);
for(int v:g[u]) if(v != par) dfs(v,u,t+1,res);
};
dfs(0,-1,0,0);
return ans;
}
``` | 4 | 0 | ['Depth-First Search', 'Graph', 'C++'] | 0 |
most-profitable-path-in-a-tree | Single DFS, simple approach with Video | single-dfs-simple-approach-with-video-by-jn6i | YouTube solutionIntuition and approachwe can solve it in single DFS pass with below intuition1)lets keep track the distance of every node from bobwhy ?? how??be | vinod_aka_veenu | NORMAL | 2025-02-24T03:26:14.935375+00:00 | 2025-02-24T03:26:14.935375+00:00 | 1,127 | false | # YouTube solution https://youtu.be/eflbh5qS_68?si=BYHfj_XBktuvhw2K
# Intuition and approach
we can solve it in single DFS pass with below intuition
1)lets keep track the distance of every node from bob
**why ?? how??** because we need to keep track when Alic would reach at some node what would the reaching time is it **before** Bob, **after** of **simaltanously** with bob.
2) now from ALICE we will start at time = 0. we started at node 0, we will also keep track of parent of src because tree are undirected and from adjacency list we can not pick parent because we already came from parent till this node.
3) now recursivley we would keep updating the distFromBob for all nodes, if src is same as bob then disancd from bob would be 0. also we will keep on chaking below 2 conditions
if **alice time to reach < distance from Bob of src**
==> alice reached already at the node
income += amount[src]
if they reach simaltanouly
**alice time to reach == distance from Bob of src**
income += amount[src]/2
our blow util method would called and it would finally return the max amount achieved by Alice
# Code
```java []
class Solution {
List<List<Integer>>adj;
int[] distFromBob;
int n;
public int mostProfitablePath(int[][] edges, int bob, int[] amount) {
adj = new ArrayList<>();
n = amount.length;
distFromBob = new int[n];
for(int i=0; i<n; i++)
adj.add(new ArrayList());
for(int [] d : edges)
{
adj.get(d[0]).add(d[1]);
adj.get(d[1]).add(d[0]);
}
return util(0, 0, 0, bob, amount);
}
public int util(int src, int parent, int time, int bob, int amount[])
{
int maxIncome = 0;
int maxChild = Integer.MIN_VALUE;
if(src==bob)
distFromBob[src] = 0;
else
distFromBob[src] = n;
for(int node : adj.get(src))
{
if(node!=parent)
{
maxChild = Math.max(maxChild, util(node, src, time+1, bob, amount));
distFromBob[src] = Math.min(distFromBob[src], distFromBob[node]+1);
}
}
if(distFromBob[src]>time)
maxIncome += amount[src];
else if(distFromBob[src]==time)
maxIncome += amount[src]/2;
return maxChild == Integer.MIN_VALUE ? maxIncome : maxIncome + maxChild;
}
}
``` | 4 | 0 | ['Java'] | 1 |
most-profitable-path-in-a-tree | C++ Solution Using BFS and DFS | c-solution-using-bfs-and-dfs-by-dellwynt-u0st | \n# Approach\n Describe your approach to solving the problem. \n\nWhat is given to us is an undirected tree rooted at node 0. Now, bob moves from a given node t | dellwyntennison | NORMAL | 2023-07-06T12:07:33.685244+00:00 | 2023-07-06T12:07:33.685261+00:00 | 465 | false | \n# Approach\n<!-- Describe your approach to solving the problem. -->\n\nWhat is given to us is an undirected tree rooted at node `0`. Now, bob moves from a given node to the root `0`. In a tree, there is always only one path between any two nodes. Therefore, we can identify which nodes Bob passes through and also the times at which he does so. To do this, we root the tree at `0` and convert it into a directed tree. Doing this helps us identify the parent of each node (Each node in a tree has exactly one parent.) We use an array `parents` to keep track of each nodes parent and then we move backwards from bobs node to node `0` moving from child to parent. A map is used to keep track of the time each node in the path was visited. \nNext we run DFS from the root node to find the maximum path to a leaf node while keeping track of the time at which we visit each node. If the current time is greater than the time at which bob had visited that node, then the amount at the node is `0`. If the current time is equal to the time at which bob had visited that node, then the amount at the node is divided by two. If Bob had not visited that node at all, then the amount remains the same.\n\n\n\n# Code\n```\nclass Solution {\npublic:\n int dfs(vector<vector<int>>&adj,int node,int t,map<int,int>&visited,vector<int>&amount){\n int currVal=amount[node];\n if(visited.count(node)){\n if(visited[node]<t) currVal=0;\n else if(visited[node]==t) currVal/=2;\n }\n if(adj[node].size()==0) return currVal;\n int res=INT_MIN;\n for(auto nbr:adj[node]){\n res=max(res,dfs(adj,nbr,t+1,visited,amount));\n }\n return currVal+res;\n }\n int mostProfitablePath(vector<vector<int>>& edges, int bob, vector<int>& amount) {\n int n=edges.size()+1;\n vector<vector<int>>adj(n,vector<int>());\n vector<vector<int>>tree(n,vector<int>());\n\n vector<int>parent(n,0);\n for(int i=0;i<n-1;i++){\n adj[edges[i][0]].push_back(edges[i][1]);\n adj[edges[i][1]].push_back(edges[i][0]);\n } \n vector<int>added(n,0);\n queue<int>q;\n q.push(0);\n added[0]=1;\n while(!q.empty()){\n int node=q.front();\n q.pop();\n for(auto nbr:adj[node]){\n if(!added[nbr]) {\n added[nbr]++;\n tree[node].push_back(nbr);\n q.push(nbr);\n }\n }\n }\n for(int i=0;i<n;i++){\n for(auto child:tree[i]){\n parent[child]=i;\n }\n }\n map<int,int>visited;\n int t=0;\n int node=bob;\n while(node!=0){\n visited[node]=t++;\n node=parent[node];\n }\n return dfs(tree,0,0,visited,amount);\n\n }\n};\n``` | 4 | 0 | ['Tree', 'Depth-First Search', 'Breadth-First Search', 'C++'] | 1 |
most-profitable-path-in-a-tree | [Python3] Easiest | DFS + BFS | O(N) | | python3-easiest-dfs-bfs-on-by-shriyansna-hbkt | Intuition\nSince this is a tree we know that there is only 1 path between any 2 given nodes. With this knowledge we now know that bob only has one path so we ca | shriyansnaik | NORMAL | 2023-01-06T07:37:43.263946+00:00 | 2023-01-06T07:37:43.263990+00:00 | 500 | false | # Intuition\nSince this is a tree we know that there is only 1 path between any 2 given nodes. With this knowledge we now know that bob only has one path so we can actually record at what step bob reaches a given gate. Then we can traverse as Alice and take the amount accordingly.\n\n# Approach\n1. Do a DFS and record at what step bob reaches a gate in his path.\n2. Do a BFS and for each gate, find how much amount alice will get/give based on the number of steps she has taken.\n - If bob has not visited the gate or if bob has not visited the gate **yet**, then Alice will get/give the entire amount.\n - If bob and Alice have both taken same number of steps, then we split the amount.\n - And if bob has visited the gate before Alice could, then the amount Alice will get/give is 0.\n3. When we reach a leaf gate (The gate where Alice starts which is 0 is also a leaf, so make sure you add a condition to check that gate should not be equal to 0) update the max_income.\n\n# Complexity\n- Time complexity:\n$$O(N)+O(N)$$ *for dfs and bfs*\n\n- Space complexity:\n$$O(N)+O(N)$$ *for adj list and queue*\n\n# Code\n```\nclass Solution:\n def mostProfitablePath(self, edges: List[List[int]], bob: int, amount: List[int]) -> int:\n bobPath,adj = {},defaultdict(list)\n for u,v in edges:\n adj[u].append(v)\n adj[v].append(u)\n\n def bobTraverse(gate,parent,step):\n bobPath[gate] = step\n if gate==0: return True\n for nei in adj[gate]:\n if nei==parent: continue\n if bobTraverse(nei,gate,step+1): return True\n \n del bobPath[gate]\n return False\n \n bobTraverse(bob,-1,0)\n \n max_net_income,queue = float("-inf"),deque()\n queue.append((0,-1,0,0))\n while queue:\n gate,parent,cur_net_income,step = queue.popleft()\n cur_net_income += self.getGateAmount(bobPath,gate,step,amount)\n if len(adj[gate])==1 and gate!=0:\n max_net_income = max(max_net_income,cur_net_income)\n \n for nei in adj[gate]:\n if nei==parent: continue\n queue.append((nei,gate,cur_net_income,step+1))\n \n return max_net_income\n\n def getGateAmount(self,bobPath,gate,step,amount):\n if gate not in bobPath: return amount[gate]\n if bobPath[gate]>step: return amount[gate]\n if bobPath[gate]==step: return amount[gate]//2\n return 0\n \n``` | 4 | 0 | ['Python3'] | 0 |
most-profitable-path-in-a-tree | Java | 2 solutions | DFS | BFS | java-2-solutions-dfs-bfs-by-conchwu-aq4b | 2. one DFS\n\n\t//2. one DFS\n //Runtime: 82 ms, faster than 100.00% of Java online submissions for Most Profitable Path in a Tree.\n //Memory Usage: 185. | conchwu | NORMAL | 2022-11-12T18:36:37.212943+00:00 | 2022-11-12T18:36:45.066232+00:00 | 985 | false | # 2. one DFS\n```\n\t//2. one DFS\n //Runtime: 82 ms, faster than 100.00% of Java online submissions for Most Profitable Path in a Tree.\n //Memory Usage: 185.1 MB, less than 25.00% of Java online submissions for Most Profitable Path in a Tree.\n public int mostProfitablePath(int[][] edges, int bob, int[] amount) {\n //Time: O(E); Space: O(N + E)\n //build graph\n List<Integer>[] graph = new ArrayList[amount.length];\n for (int i = 0; i < amount.length; i++) graph[i] = new ArrayList<>();\n for (int[] edge: edges) {\n graph[edge[0]].add(edge[1]);\n graph[edge[1]].add(edge[0]);\n }\n return helper_dfs(graph, 0, bob, amount, new boolean[amount.length], 1)[0];\n }\n\n //Time: O(N); Space: O(N)\n private int[] helper_dfs(List<Integer>[] graph, int node, int bob, int[] amount, boolean[] seen, int height) {\n int res = Integer.MIN_VALUE;\n seen[node] = true;\n\n int bobPathLen = node == bob ? 1 : 0;\n\n for (int nextNode : graph[node]) {\n if (seen[nextNode] == true) continue;\n int[] tmp = helper_dfs(graph, nextNode, bob, amount, seen, height + 1);\n if (tmp[1] > 0) bobPathLen = tmp[1] + 1;\n res = Math.max(res, tmp[0]);\n }\n\n if (bobPathLen > 0 && bobPathLen <= height){\n if (bobPathLen == height) amount[node] = amount[node] / 2;\n else amount[node] = 0;\n }\n\n return new int[]{res == Integer.MIN_VALUE ? amount[node] : amount[node] + res, bobPathLen};\n }\n\n```\n# 1. BFS + DFS\n```\n //1. BFS + DFS\n //Runtime: 85 ms, faster than 100.00% of Java online submissions for Most Profitable Path in a Tree.\n //Memory Usage: 144 MB, less than 50.00% of Java online submissions for Most Profitable Path in a Tree.\n //Time: O(E + N); Space: O(E + N)\n public int mostProfitablePath_1(int[][] edges, int bob, int[] amount) {\n //Time: O(E); Space: O(N + E)\n //build graph\n List<Integer>[] graph = new ArrayList[amount.length];\n for (int i = 0; i < amount.length; i++) graph[i] = new ArrayList<>();\n for (int[] edge: edges) {\n graph[edge[0]].add(edge[1]);\n graph[edge[1]].add(edge[0]);\n }\n //update amount\n helper_bfs(graph, bob, amount);\n return helper_dfs(graph, 0, amount, new boolean[amount.length]);\n }\n\n //Time: O(N); Space: O(N)\n private void helper_bfs(List<Integer>[] graph, int bob, int[] amount) {\n int[] preList = new int[amount.length];\n boolean[] seen = new boolean[amount.length];\n seen[bob] = true;\n\n //Time: O(N); Space: O(N)\n Queue<Integer> queue = new ArrayDeque<>();\n queue.add(bob);\n while (!queue.isEmpty()) {\n int currNode = queue.poll();\n for (int nextNode : graph[currNode]) {\n if (seen[nextNode] == true) continue;\n preList[nextNode] = currNode;\n if (nextNode == 0) break;\n\n queue.add(nextNode);\n seen[nextNode] = true;\n }\n }\n\n List<Integer> list = new ArrayList<>();\n list.add(0);\n int p = 0;\n while (p != bob) {\n p = preList[p]; list.add(p);\n }\n\n int resListSize = list.size();\n for (int i = 0; i < resListSize / 2; i++) amount[list.get(list.size() - 1 - i)] = 0;\n\n if (resListSize % 2 != 0) {\n int midIdx = resListSize / 2;\n amount[list.get(midIdx)] = amount[list.get(midIdx)] / 2;\n }\n }\n\n //Time: O(N); Space: O(N)\n private int helper_dfs(List<Integer>[] graph, int node, int[] amount, boolean[] seen) {\n int res = Integer.MIN_VALUE;\n seen[node] = true;\n for (int nextNode : graph[node]) {\n if (seen[nextNode] == true) continue;\n res = Math.max(res, helper_dfs(graph, nextNode, amount, seen));\n }\n return res == Integer.MIN_VALUE ? amount[node] : amount[node] + res;\n }\n``` | 4 | 0 | ['Depth-First Search', 'Breadth-First Search', 'Java'] | 1 |
most-profitable-path-in-a-tree | Video Explanation (zero to building the solution itself with inutitions) | video-explanation-zero-to-building-the-s-uwdk | https://www.youtube.com/watch?v=QBb8zUX2KlY\n\nClick here if the preview doesn\'t work | codingmohan | NORMAL | 2022-11-12T17:37:48.889308+00:00 | 2022-11-12T17:37:48.889355+00:00 | 459 | false | https://www.youtube.com/watch?v=QBb8zUX2KlY\n\n[Click here if the preview doesn\'t work](https://www.youtube.com/watch?v=QBb8zUX2KlY) | 4 | 0 | ['C++'] | 1 |
most-profitable-path-in-a-tree | ✅✅✅ Java visit one level at the time O(N) | java-visit-one-level-at-the-time-on-by-r-66d6 | We first build the tree from the root so that each node has its children and parent set\n Then we start from root, and then we visit each level at the time. \n | ricola | NORMAL | 2022-11-12T17:06:27.403507+00:00 | 2022-11-13T10:35:57.218351+00:00 | 738 | false | * We first build the tree from the root so that each node has its children and parent set\n* Then we start from root, and then we visit each level at the time. \n* While Alice goes down one level, Bob goes up one level. If Bob is at the same node, we split the amount. Once Bob visits a node, we set its amount to 0\n* For each node we visit, we store the income to arrive there. We keep the max income of all leaf nodes\n\nWe don\'t need to keep any distance since we are processing the two in parallel.\n\n```\nclass Solution {\n\n public int mostProfitablePath(int[][] edges, int bob, int[] amounts) {\n Node[] nodes = buildTree(edges, amounts);\n\n List<Node> level = new ArrayList<>();\n\n Node bobNode = nodes[bob];\n\n int max = Integer.MIN_VALUE;\n\n level.add(nodes[0]);\n\n while(!level.isEmpty()){\n List<Node> nextLevel = new ArrayList<>();\n for (Node node : level) {\n int amount = bobNode == node ? node.amount/2 : node.amount;\n node.income = (node.parent == null ? 0 : node.parent.income) + amount;\n\n // leaf\n if(node.children.isEmpty()) max = Math.max(node.income, max);\n\n nextLevel.addAll(node.children);\n }\n\n // bob has visited this node, so the gate is open now\n bobNode.amount = 0;\n if(bobNode.parent != null) bobNode = bobNode.parent;\n\n level = nextLevel;\n }\n\n return max;\n\n }\n\n private Node[] buildTree(int[][] edges, int[] amounts) {\n int n = amounts.length;\n\n // for O(1) lookup\n Map<Integer, Set<Integer>> neighbors = new HashMap<>();\n for (int[] edge : edges) {\n neighbors.computeIfAbsent(edge[0], _k -> new HashSet<>()).add(edge[1]);\n neighbors.computeIfAbsent(edge[1], _k -> new HashSet<>()).add(edge[0]);\n }\n\n\n Node[] nodes = new Node[n];\n for (int i = 0; i < n; i++) {\n nodes[i] = new Node(amounts[i]);\n }\n\n List<Integer> level = new ArrayList<>();\n\n level.add(0);\n\n // build tree level by level\n while(!level.isEmpty()){\n List<Integer> nextLevel = new ArrayList<>();\n for (int i : level) {\n Node node = nodes[i];\n for (int u : neighbors.get(i)) {\n Node other = nodes[u];\n node.children.add(other);\n other.parent = node;\n\n // we already added this edge and its inverse (the parent), so we remove its inverse from the map\n neighbors.get(u).remove(i);\n\n nextLevel.add(u);\n }\n }\n level = nextLevel;\n }\n\n return nodes;\n }\n\n private class Node{\n int amount;\n List<Node> children = new ArrayList<>();\n Node parent;\n int income;\n\n public Node(int amount) {\n this.amount = amount;\n }\n }\n}\n``` | 4 | 0 | [] | 0 |
most-profitable-path-in-a-tree | py soltion :( | py-soltion-by-noam971-dbxz | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | noam971 | NORMAL | 2025-02-24T14:24:24.601594+00:00 | 2025-02-24T14:24:24.601594+00:00 | 119 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def mostProfitablePath(self, edges: List[List[int]], bob: int, amount: List[int]) -> int:
adj = defaultdict(list)
for u, v in edges:
adj[u].append(v)
adj[v].append(u)
mp, ans = {}, float('-inf')
# Find the path from Bob to node 0 and store distances in mp
def path_to_zero(node, steps, visited):
visited[node] = True
if node == 0:
mp[node] = steps
return True
for neighbor in adj[node]:
if not visited[neighbor]:
if path_to_zero(neighbor, steps + 1, visited):
mp[neighbor] = steps
return True
return False
# DFS for Alice to find max profit
def dfs(node, steps, total, visited):
nonlocal ans
visited[node] = True
if len(adj[node]) == 1 and node != 0: # Leaf node
ans = max(ans, total)
return
for neighbor in adj[node]:
if not visited[neighbor]:
add_val = 0
if neighbor in mp: # Bob's path
if mp[neighbor] == steps + 1:
add_val = amount[neighbor] // 2
elif mp[neighbor] > steps + 1:
add_val = amount[neighbor]
else:
add_val = amount[neighbor]
dfs(neighbor, steps + 1, total + add_val, visited)
visited_bob = [False] * len(amount)
path_to_zero(bob, 1, visited_bob)
mp[bob] = 0
visited_alice = [False] * len(amount)
dfs(0, 0, amount[0], visited_alice)
return ans
``` | 3 | 0 | ['Python3'] | 1 |
most-profitable-path-in-a-tree | 🚀 Most Profitable Path in a Tree | Optimized BFS Approach ✨ | most-profitable-path-in-a-tree-optimized-i7zb | IntuitionThe problem involves traversing a tree (represented as an undirected graph) to find the most profitable path for a player, while considering the moveme | Ajay_Prabhu | NORMAL | 2025-02-24T14:11:09.770344+00:00 | 2025-02-24T14:11:09.770344+00:00 | 134 | false | ### Intuition
The problem involves traversing a tree (represented as an undirected graph) to find the most profitable path for a player, while considering the movement of another player (Bob) who is trying to reach the root (node 0). The goal is to maximize the player's score by collecting points from nodes, while Bob's movement affects the points available at each node.
### Approach
1. **Graph Construction**: Build an adjacency list to represent the tree structure.
2. **Bob's Path Calculation**: Use BFS to determine the path Bob takes from his starting position to the root (node 0). Store the time Bob takes to reach each node.
3. **Player's Path Calculation**: Use BFS to traverse the tree from the root (node 0). At each node, calculate the score based on whether Bob has already visited the node, is visiting it at the same time, or hasn't visited it yet.
4. **Score Calculation**: Adjust the player's score based on Bob's path and the amount available at each node.
5. **Max Profit Calculation**: Track the maximum profit the player can achieve by exploring all possible paths to leaf nodes.
### Complexity
- **Time Complexity**:
- Building the graph: `O(n)`, where n is the number of edges.
- Finding Bob's path: `O(n)`, using BFS.
- Finding the player's path: `O(n)`, using BFS.
- Overall: `O(n)`.
- **Space Complexity**:
- Storing the graph: `O(n)`.
- Storing Bob's path and player's traversal: `O(n)`.
- Overall: `O(n)`.
### Code
```java
class Solution {
public static int mostProfitablePath(int[][] edges, int bob, int[] amount) {
// Step 1: Build the graph
List<List<Integer>> adj = buildGraph(edges);
// Step 2: Find Bob's path and the time he takes to reach each node
Map<Integer, Integer> bobPathWithCoordinates = findBobPath(adj, bob);
// Step 3: Find the maximum profit path for the player
return findMaxProfitPath(adj, bobPathWithCoordinates, amount);
}
// Helper function to find the maximum profit path for the player
public static int findMaxProfitPath(List<List<Integer>> adj, Map<Integer, Integer> bobPathWithCoordinates, int[] amount) {
Queue<int[]> q = new ArrayDeque<>(); // {node, time, currentPoints}
Set<Integer> vis = new HashSet<>();
q.add(new int[] { 0, 0, 0 }); // Start from node 0 with time 0 and 0 points
vis.add(0);
int maxPoints = Integer.MIN_VALUE; // Track the maximum points
// BFS traversal
while (!q.isEmpty()) {
int[] data = q.remove();
int node = data[0], time = data[1], curPoints = data[2];
// Calculate the score for the current node
curPoints += getScore(bobPathWithCoordinates, node, time, amount);
// If it's a leaf node (other than the root), update maxPoints
if (node != 0 && adj.get(node).size() == 1) {
maxPoints = Math.max(maxPoints, curPoints);
}
// Explore neighbors
for (int neighbour : adj.get(node)) {
if (!vis.contains(neighbour)) {
vis.add(neighbour);
q.add(new int[] { neighbour, time + 1, curPoints });
}
}
}
return maxPoints;
}
// Helper function to calculate the score for a node
public static int getScore(Map<Integer, Integer> bobPathWithCoordinates, int node, int time, int[] amount) {
if (!bobPathWithCoordinates.containsKey(node)) {
// Bob hasn't visited this node, so the player gets the full amount
return amount[node];
}
int bobTime = bobPathWithCoordinates.get(node);
if (bobTime > time) {
// Bob hasn't reached this node yet, so the player gets the full amount
return amount[node];
} else if (bobTime == time) {
// Bob and the player reach the node at the same time, so the player gets half the amount
return amount[node] / 2;
}
// Bob has already visited the node, so the player gets nothing
return 0;
}
// Helper function to build the graph
public static List<List<Integer>> buildGraph(int[][] edges) {
List<List<Integer>> adj = new ArrayList<>();
int n = edges.length + 1; // Number of nodes is edges.length + 1
for (int i = 0; i < n; i++) {
adj.add(new ArrayList<>());
}
// Add edges to the adjacency list
for (int[] edge : edges) {
int u = edge[0], v = edge[1];
adj.get(u).add(v);
adj.get(v).add(u);
}
return adj;
}
// Helper function to find Bob's path and the time he takes to reach each node
public static Map<Integer, Integer> findBobPath(List<List<Integer>> adj, int bobStart) {
Map<Integer, Integer> bobTimeCoordinates = new HashMap<>(); // {node: time}
Queue<int[]> q = new ArrayDeque<>(); // {node, time}
Set<Integer> vis = new HashSet<>();
Map<Integer, Integer> parentMap = new HashMap<>(); // {node: parent}
q.add(new int[] { bobStart, 0 }); // Start from Bob's position with time 0
vis.add(bobStart);
parentMap.put(bobStart, null);
// BFS to find Bob's path
while (!q.isEmpty()) {
int[] data = q.remove();
int node = data[0], time = data[1];
bobTimeCoordinates.put(node, time);
// If Bob reaches the root, stop
if (node == 0) {
break;
}
// Explore neighbors
for (int neighbour : adj.get(node)) {
if (!vis.contains(neighbour)) {
vis.add(neighbour);
parentMap.put(neighbour, node);
q.add(new int[] { neighbour, time + 1 });
}
}
}
// Build the path map from Bob's position to the root
return buildPathMap(parentMap, bobTimeCoordinates);
}
// Helper function to build the path map from Bob's position to the root
public static Map<Integer, Integer> buildPathMap(Map<Integer, Integer> parentMap, Map<Integer, Integer> timeMap) {
LinkedList<Integer> path = new LinkedList<>();
Integer current = 0;
while (current != null) {
path.addFirst(current); // Add nodes in reverse order (from root to Bob's position)
current = parentMap.get(current);
}
// Create a map of {node: time} for Bob's path
Map<Integer, Integer> resMap = new LinkedHashMap<>();
for (Integer node : path) {
resMap.put(node, timeMap.get(node));
}
return resMap;
}
}
```
If this was helpful, please upvote! 👍
| 3 | 0 | ['Array', 'Tree', 'Breadth-First Search', 'Graph', 'Java'] | 0 |
most-profitable-path-in-a-tree | Fast C and Python3 solutions | fast-c-and-python3-solutions-by-lequan-76sy | ApproachConstruct the graph. Coerce graph in to tree. Compute bob's path.Modify amount with respect to bob's path. Traverse the treeand compute the maximum scor | lequan | NORMAL | 2025-02-24T05:16:36.166223+00:00 | 2025-02-24T05:16:36.166223+00:00 | 149 | false | # Approach
<!-- Describe your approach to solving the problem. -->
Construct the graph. Coerce graph in to tree. Compute bob's path.
Modify amount with respect to bob's path. Traverse the tree
and compute the maximum score.
# Complexity
- Time complexity: $$O(n)$$. All traversals are bounded by the number of nodes.
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: $$O(n)$$. The sizes of all data structures are bound by the number of nodes, of to a constant.
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def mostProfitablePath(self, edges: List[List[int]], bob: int, amount: List[int]) -> int:
# compute graph
g = {}
for u, v in edges:
if u not in g: g[u] = [v]
else: g[u].append(v)
if v not in g: g[v] = [u]
else: g[v].append(u)
parent = [0] * len(amount)
stack = [0]
while stack:
u = stack.pop()
for v in g[u]:
stack.append(v)
g[v].remove(u)
parent[v] = u
path = [bob]
while parent[bob] != bob:
path.append(parent[bob])
bob = parent[bob]
d = len(path)
for i in range(d // 2): amount[path[i]] = 0
if d % 2: amount[path[d // 2]] >>= 1
stack.append(0)
ans = -float('inf')
while stack:
u = stack.pop()
if g[u]:
for v in g[u]:
stack.append(v)
amount[v] += amount[u]
elif ans < amount[u]:
ans = amount[u]
return ans
```
```c []
struct node {
int val;
struct node *next;
};
void add_neighbor(struct node **g, int u, int v) {
struct node *n = malloc(sizeof(struct node));
struct node *head = g[u];
g[u] = n;
n->val = v;
n->next = head;
}
int mostProfitablePath(int** edges, int edgesSize, int* edgesColSize, int bob, int* amount, int amountSize) {
// form the graph.
struct node **g = calloc(amountSize, sizeof(void *));
int u, v;
for (int i = 0; i < edgesSize; i++) {
u = edges[i][0];
v = edges[i][1];
add_neighbor(g, u, v); // THIS IS THE BOTTLENECK
add_neighbor(g, v, u);
}
int *parents = calloc(amountSize, sizeof(int));
int *stack = calloc(amountSize, sizeof(int));
int j = 0;
struct node *curr;
while (j >= 0) {
u = stack[j--];
curr = g[u];
while (curr) {
v = curr->val;
if (v != parents[u]) {
// remove_neighbor(g, v, u); // remove u fron g[v]
stack[++j] = v;
parents[v] = u;
}
curr = curr->next;
}
}
// get path length to bob
int pathlen = 1, *path = calloc(amountSize, sizeof(int));
path[0] = bob;
while (parents[bob] != bob) {
path[pathlen++] = parents[bob];
bob = parents[bob];
}
// for (j=0; j<pathlen; j++) {
// printf("path[%d] = %d\n", j, path[j]);
// }
// modify amounts
j = 0;
while (pathlen > 0) {
if (pathlen == 1) {
amount[path[j]] >>= 1; // since amounts are even
} else {
amount[path[j]] = 0;
}
// printf("amount[%d] = %d\n", j, amount[j]);
j++; pathlen -= 2;
}
// propogate ans
j = 0; stack[0] = 0;
bool leaf, first = 1;
int ans = 0;
while (j >= 0) {
u = stack[j--];
leaf = 1;
curr = g[u];
while (curr) {
v = curr->val;
if (v != parents[u]) {
stack[++j] = v;
amount[v] += amount[u];
leaf = 0;
}
curr = curr->next;
}
if (leaf) {
if (first) {
first = 0;
ans = amount[u];
} else if (ans < amount[u]) {
ans = amount[u];
}
}
}
free(stack);
free(parents);
free(path);
// destroy g
return ans;
}
``` | 3 | 0 | ['C', 'Python3'] | 0 |
most-profitable-path-in-a-tree | Python | Two DFS | O(n), O(n) | Beats 99% | python-two-dfs-on-on-beats-99-by-2pillow-1yix | CodeComplexity
Time complexity: O(n). find_bob_path() and find_alice_path() visit each node once, time is n + n, simplifies to n.
Space complexity: O(n). Max | 2pillows | NORMAL | 2025-02-24T01:55:51.718810+00:00 | 2025-02-24T06:35:08.884766+00:00 | 518 | false | # Code
```python3 []
class Solution:
def mostProfitablePath(self, edges: List[List[int]], bob: int, amount: List[int]) -> int:
n = len(amount)
graph = [[] for _ in range(n)] # make graph with connected nodes for each node
for u, v in edges:
graph[u].append(v)
graph[v].append(u)
bob_time = [n] * n # [node] = time, time that bob reached node in path
def find_bob_path(node, prev, time):
if node == 0:
bob_time[node] = time # 0 is last in path
return True
for nxt in graph[node]:
if nxt != prev and find_bob_path(nxt, node, time + 1): # avoid loops and check connected nodes
bob_time[node] = time # path lead to 0, set time for current node
return True
return False # path didn't lead to 0
find_bob_path(bob, -1, 0) # set values for bob_time
max_income = float('-inf')
def find_alice_path(node, prev, time, income):
if time < bob_time[node]:
income += amount[node] # alice reached gate node first
elif time == bob_time[node]:
income += amount[node] // 2 # alice and bob arrived at same time
if node != 0 and len(graph[node]) == 1: # check if at leaf, node != 0 to pass starting node
nonlocal max_income
max_income = max(max_income, income) # set new max income
return # arrived at leaf, path over
for nxt in graph[node]: # exlpore connected nodes
if nxt != prev: # avoid looping
find_alice_path(nxt, node, time + 1, income)
find_alice_path(0, -1, 0, 0) # find alice's max income
return max_income
```
# Complexity
- Time complexity: $$O(n)$$. find_bob_path() and find_alice_path() visit each node once, time is n + n, simplifies to n.
- Space complexity: $$O(n)$$. Maximum recursion depth is all n nodes. graph has length of n nodes and 2 * (n - 1) total edges since each edge has 2 nodes. Space is n + 2 * (n - 1), simplifies to n.
# Performance
| 3 | 0 | ['Depth-First Search', 'Python3'] | 2 |
most-profitable-path-in-a-tree | Kotlin || DFS | kotlin-dfs-by-nazmulcuet11-1z03 | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | nazmulcuet11 | NORMAL | 2025-02-24T01:10:46.582267+00:00 | 2025-02-24T01:10:46.582267+00:00 | 58 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```kotlin []
class Solution {
private var n = 0
private var tree = Array(0) { mutableListOf<Int>() }
private var parent = intArrayOf()
private var amount = intArrayOf()
private var bobNodeToTime = intArrayOf()
private fun buildTree(edges: Array<IntArray>) {
for (e in edges) {
tree[e[0]].add(e[1])
tree[e[1]].add(e[0])
}
}
private fun populateParent(n: Int, p: Int) {
parent[n] = p
for (c in tree[n]) {
if (c != p) {
populateParent(c, n)
}
}
}
private fun moveBob(n: Int, t: Int) {
if (n == -1) {
return
}
bobNodeToTime[n] = t
moveBob(parent[n], t + 1)
}
private fun moveAlice(n: Int, t: Int): Int {
var profitFromNode = 0
if (bobNodeToTime[n] == -1 || bobNodeToTime[n] > t) {
profitFromNode += amount[n]
} else if (bobNodeToTime[n] == t) {
profitFromNode += amount[n] / 2
}
var maxProfitFromChild = Int.MIN_VALUE
for (c in tree[n]) {
if (c != parent[n]) {
maxProfitFromChild = max(
maxProfitFromChild,
moveAlice(c, t + 1)
)
}
}
if (maxProfitFromChild == Int.MIN_VALUE) {
return profitFromNode
}
return profitFromNode + maxProfitFromChild
}
fun mostProfitablePath(
edges: Array<IntArray>,
bob: Int,
amount: IntArray
): Int {
this.n = amount.size
this.amount = amount
this.tree = Array(n) { mutableListOf<Int>() }
buildTree(edges)
this.parent = IntArray(n) { -1 }
populateParent(0, -1)
this.bobNodeToTime = IntArray(n) { -1 }
moveBob(bob, 0)
return moveAlice(0, 0)
}
}
``` | 3 | 0 | ['Depth-First Search', 'Kotlin'] | 0 |
most-profitable-path-in-a-tree | ✅ Most Profitable Path in a Tree | JS🔥 | beats 99%🚀 | 🚀highly optimised & easy to understand ✅ | most-profitable-path-in-a-tree-js-beats-vi68g | Intuition
Here's an optimized JavaScript solution for the problem along with a detailed explanation of the approach
This solution efficiently finds the most pro | Naveen_sachan | NORMAL | 2025-02-24T00:46:03.475641+00:00 | 2025-02-24T00:46:03.475641+00:00 | 533 | false | # Intuition
- Here's an optimized JavaScript solution for the problem along with a detailed explanation of the approach
- This solution efficiently finds the most profitable path while handling simultaneous arrivals of Alice and Bob correctly
# Approach
> **Graph Construction:**
- We first construct an adjacency list representation of the tree using the given edges.
> **Bob's Path Calculation:**
- We perform a DFS from bob to store the time at which Bob reaches each node (bobTime array).
> **Alice’s DFS Traversal:**
- We use another DFS from node 0 to track Alice’s traversal.
- Alice collects the full reward if she reaches a node before Bob.
- If Alice and Bob reach at the same time, Alice takes half the amount.
- If Bob reaches first, Alice gets nothing.
- We track the max income possible when Alice reaches a leaf node.
# Complexity
> **Time complexity:**
- O(N) (since we perform DFS twice, once for Bob and once for Alice)
> **Space complexity:**
- O(N) (for adjacency list and time tracking arrays)
# Code
```javascript []
/**
* @param {number[][]} edges
* @param {number} bob
* @param {number[]} amount
* @return {number}
*/
var mostProfitablePath = function (edges, bob, amount) {
const n = amount.length;
const graph = Array.from({ length: n }, () => []);
// Step 1: Construct adjacency list for the tree
for (const [u, v] of edges) {
graph[u].push(v);
graph[v].push(u);
}
// Step 2: Find the exact path of Bob from `bob` to `0`
let bobTime = Array(n).fill(Infinity);
let bobPath = new Map();
function findBobPath(node, parent, depth) {
bobPath.set(node, depth);
if (node === 0) return true;
for (const neighbor of graph[node]) {
if (neighbor !== parent && findBobPath(neighbor, node, depth + 1)) {
return true;
}
}
bobPath.delete(node);
return false;
}
findBobPath(bob, -1, 0);
// Mark Bob's reach time from his path
bobTime = Array(n).fill(Infinity);
let time = 0;
for (const [node, t] of bobPath.entries()) {
bobTime[node] = t;
}
let maxIncome = -Infinity;
// Step 3: DFS for Alice to find the most profitable path
function dfsAlice(node, parent, currTime, income) {
// Case 1: Alice reaches first -> Full reward
if (currTime < bobTime[node]) {
income += amount[node];
}
// Case 2: Both reach at the same time -> Half reward
else if (currTime === bobTime[node]) {
income += amount[node] / 2;
}
// Case 3: Bob reaches first -> No reward
let isLeaf = true;
for (const neighbor of graph[node]) {
if (neighbor !== parent) {
isLeaf = false;
dfsAlice(neighbor, node, currTime + 1, income);
}
}
// If it's a leaf, update maxIncome
if (isLeaf) {
maxIncome = Math.max(maxIncome, income);
}
}
dfsAlice(0, -1, 0, 0);
return maxIncome;
};
```

| 3 | 0 | ['JavaScript'] | 1 |
most-profitable-path-in-a-tree | ☑️✅Easy JAVA Solution || DFS Solution Explained Step by Step✅☑️ | easy-java-solution-dfs-solution-explaine-rqij | Intuition\nWe will first traverse bob towards 0 and storing the time at which he visited the node and then we will traverse alice towards leaf node.\n Describe | vritant-goyal | NORMAL | 2024-02-26T18:12:24.597785+00:00 | 2024-02-27T16:22:29.289613+00:00 | 418 | false | # Intuition\nWe will first traverse bob towards 0 and storing the time at which he visited the node and then we will traverse alice towards leaf node.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nExplained Step by Step in Code.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:$$O(V+ElogV)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n# Code\n```\nclass pair{\n boolean val;\n int time;\n pair(){\n val=false;\n }\n pair(boolean a,int b){\n val=a;\n time=b;\n }\n}\nclass Solution {\n public int mostProfitablePath(int[][] edges, int bob, int[] amount) {\n ArrayList<ArrayList<Integer>>adj=new ArrayList<>(); // creating adjacency list\n\n int n=amount.length; // number of nodes in graph\n for(int i=0;i<n;i++){\n adj.add(new ArrayList<>());\n }\n for(int i=0;i<edges.length;i++){\n int st=edges[i][0];\n int dst=edges[i][1];\n adj.get(st).add(dst); // adding edge in both the nodes\n adj.get(dst).add(st);\n }\n\n pair[]vis=new pair[n]; // this pair will help the alice to check if bob has visited this node or not and at what time he visited it.\n\n boolean[]visitedBob=new boolean[n];// visited array for bob\n\n boolean[]visitedAlice=new boolean[n]; // visited for alice\n for(int i=0;i<n;i++){\n vis[i]=new pair(); //initializing pair array\n }\n\n dfsbob(adj,vis,0,bob,visitedBob); // dfs traversal call for bob\n return dfsalice(adj,vis,0,visitedAlice,0,amount); // dfs traversal for alice\n }\n public int dfsbob(ArrayList<ArrayList<Integer>>adj,pair[]vis,int time,int st,boolean[]visited){\n visited[st]=true; // marking the node to visited\n if(st==0)return 0; // base case,if bob comes to node 0\n for(int it:adj.get(st)){ // traversing adjacent nodes\n\n if(!visited[it]){ // we should not visit the \n int vri=dfsbob(adj,vis,time+1,it,visited); // giving call to adjacent node\n if(vri==0){ // if the above traversal returns 0,we will mark this node and time in pair class for alice future use\n vis[st]=new pair(true,time);\n return 0;\n }\n }\n }\n return -1; // returning -1 as we have not found the node 0\n }\n public int dfsalice(ArrayList<ArrayList<Integer>>adj,pair[]vis,int time,boolean[]visited,int st,int[]amount){\n visited[st]=true; // marking node as visited\n int cost=0;\n\n if(vis[st].val==false){ // if the node is not visited by bob,alice has to pay full price\n cost=amount[st];\n }else{\n int bobtime=vis[st].time; // time at which bob visited this node\n\n if(time>bobtime){ // if bob visited the node before alice it means gate was already open,alice has to pay no price\n cost=0;\n }else if(time==bobtime){ // if they visited the node at same time,they will pay half the price\n cost=amount[st]/2;\n }else{\n cost=amount[st]; // in this case,bob visited the node but after alice,so alice has to pay full price\n }\n }\n int ans=(int)(-1e9);\n for(int it:adj.get(st)){ // traversing adjacent nodes\n if(!visited[it]){ \n ans=Math.max(ans,dfsalice(adj,vis,time+1,visited,it,amount)); \n }\n }\n if(ans==(int)(-1e9))return cost;\n return cost+ans; // returning the maximum cost\n }\n}\n``` | 3 | 0 | ['Depth-First Search', 'Graph', 'Java'] | 0 |
most-profitable-path-in-a-tree | Simple Two traversal DFS C++ Solution | simple-two-traversal-dfs-c-solution-by-d-lh53 | Intuition\n Describe your first thoughts on how to solve this problem. \n# Just two traversals one for Bob and other for Alice\n# Approach\n Describe your appro | dhairyarajbabbar | NORMAL | 2023-08-14T18:01:15.797618+00:00 | 2023-08-14T18:01:15.797649+00:00 | 376 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n# **Just two traversals one for Bob and other for Alice**\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- I first traversed to find the node from where Bob is starting and then marked the half path node vals as 0 and if some node is in between then making its val as half of the previous val as if Alice is also going through the same path he and Bob will encounter them in this particular node;\n\n- For finding that weather i will be on the upper half or the lower half i used count which is the current distance from the node 0;\n\n- Now from the node 0 I found the max node to leaf pathsum I can obtain;\n\n- And then simply returned this pathsum;\n\n# Complexity\n- Time complexity: O(n) where n is the number of nodes in the tree\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n) for making the map\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n unordered_map<int, vector<int>> map;\n unordered_map<int, int> vis;\n int findbob(int bob, vector<int>& val, int ind=0, int count=1){\n if(ind==bob) {\n if(count==1) val[ind]/=2;\n else val[ind]=0;\n return count;\n }\n vis[ind]=1;\n for(auto &it: map[ind]){\n if(!vis.count(it)){\n int temp=findbob(bob, val, it, count+1);\n if(temp!=-1){\n if(temp%2){\n if(count>(temp+1)/2) val[ind]=0;\n if(count==(temp+1)/2) val[ind]/=2;\n }\n else{\n if(count>temp/2) val[ind]=0;\n }\n return temp;\n }\n }\n }\n return -1;\n }\n int bestpath(vector<int>& val, int ind=0){\n int ans=-1e9;\n vis[ind]++;\n for(auto &it:map[ind]){\n if(!vis.count(it)){\n ans=max(ans, bestpath(val, it));\n }\n }\n if(ans==-1e9) ans=0;\n return ans+val[ind];\n }\n int mostProfitablePath(vector<vector<int>>& edges, int bob, vector<int>& amount) {\n for(int i=0;i<edges.size();i++){\n map[edges[i][0]].push_back(edges[i][1]);\n map[edges[i][1]].push_back(edges[i][0]);\n }\n findbob(bob, amount);\n vis.clear();\n int ans=bestpath(amount);\n return ans;\n }\n};\n\n``` | 3 | 0 | ['Tree', 'Depth-First Search', 'C++'] | 0 |
most-profitable-path-in-a-tree | C++|| Easiest Solution || Detailed Solution Fully Explained || DFS + BFS || Graph | c-easiest-solution-detailed-solution-ful-15j8 | Intuition\n1.First store the time take by bob to reach the node 0 and the nodes in the path mark their time when will bob reach at them while reaching 0\n2.Now | yeah_boi123 | NORMAL | 2023-05-24T03:47:11.022370+00:00 | 2023-05-24T03:47:11.022400+00:00 | 143 | false | # Intuition\n1.First store the time take by bob to reach the node 0 and the nodes in the path mark their time when will bob reach at them while reaching 0\n2.Now come to alice start his traversal and check who has first reached at that node alice or bob if alice reached then add the amount to alice if both at same time then divide it and if alice reach later than bob then add 0 or you can ignore that case\n3.Third and most important update the ans only when you reach the leaf node \n\n# Approach\n1.for the first step i did a dfs only special thing here was for storing time i used the map so that i can easily remove those nodes which are not the part of my path \n2.now for second step simple bfs works just do as asked in the that\n3. how to know it is leaf node see it does not have any child so you can say that in the adjacency list of leaf only one node will be there and hence adj[leaf].size()==0 thats it \n\n# Complexity\n- Time complexity:\nO(V+E) as it is simple dfs and bfs where v is no of vertices and e is no of edges\n\n- Space complexity:\nO(V+E) for the adjcency list and O(V) for map and vis so overall it will be O(V+E)\n\n# Code\n```\nclass Solution {\npublic:\n bool dfs(int node,int t,vector<int> &vis,unordered_map<int,int> &path,vector<int> adj[]){\n vis[node]=1;\n path[node]=t;\n if(node==0){\n return true;\n }\n for(auto child:adj[node]){\n if(!vis[child]){\n if(dfs(child,t+1,vis,path,adj)){\n return true;\n }\n }\n }\n path.erase(node);\n return false;\n }\n\n\n int mostProfitablePath(vector<vector<int>>& edges, int bob, vector<int>& amount) {\n int n=amount.size();\n vector<int> adj[n];\n for(auto it:edges){\n int x=it[0];\n int y=it[1];\n adj[x].push_back(y);\n adj[y].push_back(x);\n }\n vector<int> vis(n,0);\n unordered_map<int,int> path;\n dfs(bob,0,vis,path,adj);\n\n queue<vector<int>> q;\n q.push({0,0,0}); // node time tot \n vis.assign(n,0);\n\n int ans=INT_MIN;\n while(!q.empty()){\n vector<int> v=q.front();\n int node=v[0];\n int time=v[1];\n int tot=v[2];\n q.pop();\n vis[node]=1;\n\n if(path.find(node)==path.end()){\n tot+=amount[node];\n }\n else{\n\n if(time<path[node]){\n tot+=amount[node];\n }\n else if(time==path[node]){\n tot+=(amount[node]/2);\n }\n }\n\n if(adj[node].size()==1 && node!=0){\n ans=max(ans,tot);\n }\n\n for(auto child:adj[node]){\n if(!vis[child]){\n q.push({child,time+1,tot});\n }\n }\n }\n return ans;\n }\n};\n``` | 3 | 0 | ['Depth-First Search', 'Breadth-First Search', 'Recursion', 'C++'] | 0 |
most-profitable-path-in-a-tree | Easy, Intuitive JS Solution | 1 BFS & 1 DFS | Backtracking | easy-intuitive-js-solution-1-bfs-1-dfs-b-5f7b | Easy intuitive JS solution using backtracking\n First determine Bob\'s path to Root\n Do a short BFS and then constrcut the path using prev array\n* Once you ha | loid_forger | NORMAL | 2022-11-15T05:16:12.783330+00:00 | 2022-11-15T05:16:12.783379+00:00 | 1,126 | false | ### Easy intuitive JS solution using backtracking\n* First determine Bob\'s path to Root\n* Do a short BFS and then constrcut the path using prev array\n* Once you have Bob\'s step outlined we can just use backtracking to seek out all the paths and find the one with max profits\n```\n/**\n * @param {number[][]} edges\n * @param {number} bob\n * @param {number[]} amount\n * @return {number}\n */\nvar mostProfitablePath = function(edges, bob, amount) {\n // Construct graph\n const graph = Array(edges.length + 1).fill(0).map(ele => []);\n edges.forEach(([node1, node2]) => {\n graph[node1].push(node2);\n graph[node2].push(node1);\n \n });\n // Get Bob path to Root node\n let queue = [bob];\n const prev = Array(graph.length).fill(null);\n let visited = initVisited(graph.length);\n while(queue.length){\n const popped = queue.shift();\n for(const neighbor of graph[popped]){\n if(!visited[neighbor]){\n visited[neighbor] = true;\n prev[neighbor] = popped;\n queue.push(neighbor);\n }\n }\n if(visited[0])\n break;\n }\n // construct bob\'s path to root\n const bobPath = [0];\n let dest = 0;\n while(dest !== bob){\n bobPath.push(prev[dest]);\n dest = prev[dest]\n }\n bobPath.reverse();\n const maxIncome = [Number.MIN_SAFE_INTEGER];\n visited = initVisited(graph.length);\n finalDfs(graph, 0, 0, 0, amount, visited, bobPath, maxIncome);\n return maxIncome[0];\n};\n\nfunction finalDfs(graph, node, step, currIncome, amount, visited, bobPath, maxIncome){\n // terminate if leaf node\n if(node !== 0 && graph[node].length === 1){\n maxIncome[0] = Math.max(maxIncome[0], currIncome + amount[node]);\n // console.log({node, max: maxIncome[0]})\n return;\n }\n if(!visited[node]){\n visited[node] = true;\n const storeAliceNodeAmount = amount[node];\n const storeBobNodeAmount = step < bobPath.length ? amount[bobPath[step]] : null;\n if(bobPath[step] === node){\n amount[node] = amount[node] / 2;\n }\n currIncome += amount[node];\n amount[node] = 0;\n if(step < bobPath.length)\n amount[bobPath[step]] = 0;\n for(const neighbor of graph[node]){\n if(!visited[neighbor]){\n finalDfs(graph, neighbor, step + 1, currIncome, amount, visited, bobPath, maxIncome);\n }\n }\n // Backtrack\n if(bobPath[step] === node){\n currIncome -= storeAliceNodeAmount / 2\n }else{\n currIncome -= storeAliceNodeAmount;\n }\n if(step < bobPath.length)\n amount[bobPath[step]] = storeBobNodeAmount;\n amount[node] = storeAliceNodeAmount;\n }\n \n}\n\nfunction initVisited(len){\n return Array(len).fill(false);\n}\n```\nIt is not the fastest solution out there but one that is easy to think through and come up with the solution in an interview.\n`Runtime: 693 ms, faster than 51.72% of JavaScript online submissions for Most Profitable Path in a Tree.` | 3 | 0 | ['Backtracking', 'Depth-First Search', 'Breadth-First Search', 'JavaScript'] | 0 |
most-profitable-path-in-a-tree | Python 3, DFS Backtracking with Explanation | python-3-dfs-backtracking-with-explanati-etpf | Since the undirected tree has n nodes and n-1 edges, there is only one path from bob to root 0. The path from bob to root 0 as well as the time Bob reaches each | cuongmng | NORMAL | 2022-11-13T15:04:24.205387+00:00 | 2022-11-13T15:04:24.205447+00:00 | 546 | false | Since the undirected tree has $$n$$ nodes and $$n-1$$ edges, there is only one path from bob to root $$0$$. The path from bob to root 0 as well as the time Bob reaches each node on the path is used to compute the reward (price) Alice gets at each node. \n\nWe will first use a DFS backtracking to determine Bob\'s path. The second backtracking is then implemented to compute the incomes Alice has when she travels to each leaf node.\n\nInline explanation is provided in the code. The code looks long but the two backtracking functions are quite similar, so the code is actually easy to understand.\n\nTime complexity: $$O(n)$$.\n\n# Python\n```\nclass Solution:\n def mostProfitablePath(self, edges: List[List[int]], bob: int, amount: List[int]) -> int:\n n = len(amount) # number of nodes\n graph = [set() for _ in range(n)] # adjacency list presentation of the tree\n for i,j in edges:\n graph[i].add(j)\n graph[j].add(i)\n bobpath = dict() # use hashmap to record nodes on the path from bob to root 0 \n # as well as time: node = key, time = value\n self.stop = False # True when Bob reaches root 0, this helps stop the DFS\n visited = [False]*n # True if node is visited, initialized as False for all nodes\n def backtrackbob(node,time): # the first backtracking, with time at each node\n bobpath[node] = time # add node:time to the hashmap\n visited[node] = True # mark node as visited\n if node==0: # root 0 is reached\n self.stop = True # this helps stop the DFS\n return None\n count = 0 # this helps determine if a node is leaf node\n for nei in graph[node]: \n if not visited[nei]:\n count += 1\n break\n if count==0: # node is leaf node if all neighbors are already visited\n del bobpath[node] # delete leaf node from hashmap before retreating from leaf node\n return None\n for nei in graph[node]: # explore unvisited neighbors of node\n if self.stop: return None # if root 0 is already reached, stop the DFS\n if not visited[nei]:\n backtrackbob(nei,time+1)\n if not self.stop: # if root 0 is reached, keep node in the hashmap when backtracking\n del bobpath[node] # otherwise, delete node before retreating\n return None\n\n backtrackbob(bob,0) # execute the first backtracking, time at bob is initialized = 0\n\n self.ans = float(-inf) # answer of the problem\n self.income = 0 # income of Alice when travelling to leaf nodes, initialized = 0\n visited = [False]*n # True if node is visited, initialized as False for all nodes\n def backtrackalice(node,time): # second backtracking, with time at each node\n visited[node] = True\n if node in bobpath: # if the node Alice visits is on Bob\'s path, there are 3 cases\n if time == bobpath[node]: # Alice and Bob reach the node at the same time\n reward = amount[node]//2\n elif time<bobpath[node]: # Alice reachs node before Bob\n reward = amount[node]\n else: # Alice reachs node after Bob\n reward = 0\n else: # if the node Alice visits is not on Bob\'s path\n reward = amount[node]\n self.income += reward # add the reward (price) at this node to the income\n count = 0 # this helps determine if a node is leaf node\n for nei in graph[node]:\n if not visited[nei]:\n count += 1\n break\n if count==0: # node is leaf node if all neighbors are already visited\n self.ans = max(self.ans,self.income) # update the answer\n self.income -= reward # remove the reward (price) at leaf node before backtracking\n return None\n for nei in graph[node]: # explore unvisited neighbors of node\n if not visited[nei]:\n backtrackalice(nei,time+1)\n self.income -= reward # remove the reward (price) at this node before retreating\n return None\n\n backtrackalice(0,0) # execute the second backtracking, time at root 0 is initialized = 0\n\n return self.ans\n``` | 3 | 0 | ['Backtracking', 'Depth-First Search', 'Python3'] | 0 |
most-profitable-path-in-a-tree | Asked in Intuit Coding Round Recently. See my solution | asked-in-intuit-coding-round-recently-se-yx0f | One month ago, I gave Intuit coding round for FTE. This exact problem had come in it. Wasn\'t able to solve it then. Amazed to see it appear on Leetcode contest | aknov711 | NORMAL | 2022-11-13T05:57:00.992495+00:00 | 2022-11-13T05:58:31.120774+00:00 | 653 | false | One month ago, I gave Intuit coding round for FTE. This exact problem had come in it. Wasn\'t able to solve it then. Amazed to see it appear on Leetcode contest. xD! \n```\nclass Solution {\nvoid dfs(int s,int par,vector<int> adj[],int p[]){\n p[s]=par;\n for(auto e:adj[s]){\n if(e==par)\n continue;\n dfs(e,s,adj,p);\n }\n}\n \n void dfs1(int s,int p,vector<int>adj[],vector<int> &amount,int &ans){\n if(p!=-1)\n amount[s]+=amount[p];\n int cnt=0;\n for(auto e:adj[s]){\n if(e==p)\n continue;\n ++cnt;\n dfs1(e,s,adj,amount,ans);\n }\n \n if(cnt==0)\n ans=max(ans,amount[s]);\n }\n \n \n public:\n int mostProfitablePath(vector<vector<int>>& edges, int bob, vector<int>& amount) {\n int n=amount.size();\n vector<int>adj[n+1];\n \n for(auto e:edges){\n int u=e[0];\n int v=e[1];\n // --u;\n // --v;\n adj[u].push_back(v);\n adj[v].push_back(u);\n }\n \n \n int p[n];\n memset(p,-1,sizeof(p));\n \n dfs(0,-1,adj,p);\n \n vector<int>path;\n // bob--;\n int cur=bob;\n \n while(cur!=-1){\n path.push_back(cur);\n cur=p[cur];\n }\n \n for(int i=0;i<path.size()/2;i++){\n amount[path[i]]=0;\n }\n \n // cout<<path.size()<<endl;\n \n if(path.size()%2){\n int x=(path.size())/2;\n \n amount[path[x]]/=2;\n }\n \n int ans=INT_MIN;\n \n for(int i=0;i<amount.size();i++)\n cout<<amount[i]<<endl;\n \n dfs1(0,-1,adj,amount,ans);\n \n return ans;\n }\n};\n``` | 3 | 0 | [] | 0 |
most-profitable-path-in-a-tree | easy short efficient clean code | easy-short-efficient-clean-code-by-maver-e6hs | There exists exactly 1 path for Bob to reach 0. FIXED!\nAny Alice path from 0 to a leaf will have some of its prefix common with Bob\'s path. ( 0, a, b, ...)\nS | maverick09 | NORMAL | 2022-11-12T16:03:29.909642+00:00 | 2022-11-12T16:15:46.086432+00:00 | 564 | false | There exists exactly 1 path for Bob to reach 0. FIXED!\nAny Alice path from 0 to a leaf will have some of its prefix common with Bob\'s path. ( 0, a, b, ...)\nSince the graph is undirected, therefore apart from this prefix, there cannot be any nod common between Bob\'s path and Alice\'s this path.\nSo all that remains is to precompute timestamps for all nodes in Bob\'s path, and then do a dfs for Alice.\n```\nclass Solution {\ntypedef long long ll;\n#define vi(x) vector<x>\npublic:\nvi(vi(ll))g; // graph\nll n;\nvi(ll)tsb; // timeStampsBob\nbool bdfs(ll nd, ll ts, ll par){ // dfs for Bob\n tsb[nd]=ts;\n if(nd==0){\n return 1;\n }\n for(ll child:g[nd]){\n if(child!=par && bdfs(child, ts+1, nd)){\n return 1;\n }\n }\n tsb[nd]=-1;\n return 0;\n}\nll adfs(ll par, ll nd, ll ts, const vi(int)&cost){ // dfs for Alice\n ll ans=LLONG_MIN;\n for(ll child:g[nd]){\n if(child!=par){\n ans=max(ans, adfs(nd, child, ts+1, cost));\n }\n }\n if(ans==LLONG_MIN){\n ans=0;\n }\n if(tsb[nd]==-1 || tsb[nd]>ts){\n ans+=cost[nd];\n } // bob either never visited or visited later. Alice will have to unlock.\n else if(tsb[nd]==ts){\n ans+=cost[nd]/2; \n } // both arrived at same point, thus equally distribute\n\t/*else{\n\t\tbob arrived earlier, nothing for alice to gain/lose at this node;\n\t}*/\n return ans;\n}\n int mostProfitablePath(vector<vector<int>>&e, int bob, vector<int>&v) {\n n=v.size(), g.resize(n), tsb.assign(n, -1);\n for(const auto&edge:e){\n g[edge[0]].pb(edge[1]), g[edge[1]].pb(edge[0]);\n }\n bdfs(bob, 0, -1);\n return adfs(-1, 0, 0, v);\n }\n};\n``` | 3 | 0 | ['Greedy', 'Depth-First Search'] | 0 |
most-profitable-path-in-a-tree | Simple DFS clearly Expained | simple-dfs-clearly-expained-by-aadithya1-jk2v | ApproachUse DFS. Try to visit children first and get the maximum value we can get children to root nodes and add root value and return back to parent.
When you | aadithya18 | NORMAL | 2025-02-24T19:17:09.882754+00:00 | 2025-02-24T19:17:09.882754+00:00 | 49 | false | # Approach
<!-- Describe your first thoughts on how to solve this problem. -->
Use DFS. Try to visit children first and get the maximum value we can get children to root nodes and add root value and return back to parent.
When you see Bob node in between, Remember on which level we encountered bob node. Check the current node will be visited by bob 1st or Alice first.
For, this all the nodes that belongs to first half from alice to bob are alice nodes and rest are bob nodes. If there are odd number of nodes in between, we encounter the parellel situation. CHeck for these 2 coditions and add the amount accordingly.
# Code
```cpp []
class Solution {
public:
pair<int, int> fun(unordered_map<int, vector<int>> &graph, int &bob, vector<int>& amount, int node, int level, vector<bool> &vis){
int inc = INT_MIN, blevel = -1;
vis[node] = 0;
for(int i: graph[node]){
if(vis[i]){
auto pair = fun(graph, bob, amount, i, level+1, vis);
inc = max(pair.first, inc);
if(pair.second != -1) blevel = pair.second;
}
}
if(bob == node) { blevel = level;}
if(level * 2 == blevel) {
amount[node]/=2;
}
else if(blevel!=-1 and (level * 2 > blevel)) amount[node] = 0;
if(inc == INT_MIN) inc = 0;
// cout<<node<<" -> "<<inc + amount[node]<<"\n";
return make_pair(inc + amount[node], blevel);
}
int mostProfitablePath(vector<vector<int>>& edges, int bob, vector<int>& amount) {
unordered_map<int, vector<int>> graph;
for(auto v: edges){
graph[v[0]].push_back(v[1]);
graph[v[1]].push_back(v[0]);
}
vector<bool> vis(amount.size(), 1);
auto res = fun(graph, bob, amount, 0, 0, vis);
return res.first;
}
};
``` | 2 | 0 | ['Array', 'Tree', 'Depth-First Search', 'Graph', 'C++'] | 0 |
most-profitable-path-in-a-tree | C# Solution for Most Profitable Path In a Tree Problem | c-solution-for-most-profitable-path-in-a-brvm | IntuitionThe problem requires Alice to maximize her net income while moving towards a leaf in a tree, while Bob moves towards the root. Since Bob can affect Ali | Aman_Raj_Sinha | NORMAL | 2025-02-24T19:03:45.929020+00:00 | 2025-02-24T19:03:45.929020+00:00 | 68 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
The problem requires Alice to maximize her net income while moving towards a leaf in a tree, while Bob moves towards the root. Since Bob can affect Alice’s profit by reaching a node before or at the same time as her, we must carefully track both their paths.
Key insights:
• If Alice reaches a node first, she takes the full reward or pays the full cost.
• If Bob reaches a node first, the gate is already open, so Alice gets no profit.
• If they reach a node simultaneously, they share the reward or cost equally.
• Alice should move towards the most profitable leaf node to maximize her income.
# Approach
<!-- Describe your approach to solving the problem. -->
1. Build the Tree using an Adjacency List
• Convert the given edge list into an adjacency list for efficient traversal.
2. Find Bob’s Path to Root using DFS
• Track Bob’s distance to each node from his starting position.
• Helps determine whether Bob reaches a node before, after, or at the same time as Alice.
3. Perform DFS for Alice to Find the Most Profitable Path
• Start at node 0 (root).
• Calculate Alice’s profit at each node based on Bob’s arrival:
• Alice arrives first → Take full amount.
• Bob arrives first → Take nothing.
• Both arrive together → Take half the amount.
• Recursive DFS to explore all possible paths and find the maximum profit.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
1. Building the adjacency list → O(n)
2. Finding Bob’s path → O(n) (DFS traversal)
3. Finding Alice’s maximum profit → O(n) (DFS traversal)
4. Total Complexity: O(n) + O(n) = O(n)
This is efficient and optimal for large constraints (n ≤ 10⁵).
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
1. Adjacency list storage → O(n)
2. Bob’s distance array → O(n)
3. Recursive stack space (for DFS) → O(n) in the worst case (if the tree is skewed).
4. Total Space: O(n) + O(n) + O(n) = O(n)
This ensures a memory-efficient solution.
# Code
```csharp []
public class Solution {
public int MostProfitablePath(int[][] edges, int bob, int[] amount) {
int n = amount.Length;
List<int>[] tree = new List<int>[n];
for (int i = 0; i < n; i++) {
tree[i] = new List<int>();
}
foreach (var edge in edges) {
tree[edge[0]].Add(edge[1]);
tree[edge[1]].Add(edge[0]);
}
int[] bobDist = new int[n];
Array.Fill(bobDist, -1);
FindBobPath(bob, -1, 0, tree, bobDist);
return DfsAlice(0, -1, 0, 0, tree, bobDist, amount);
}
private bool FindBobPath(int node, int parent, int depth, List<int>[] tree, int[] bobDist) {
bobDist[node] = depth;
if (node == 0) return true;
foreach (int neighbor in tree[node]) {
if (neighbor == parent) continue;
if (FindBobPath(neighbor, node, depth + 1, tree, bobDist)) {
return true;
}
}
bobDist[node] = -1;
return false;
}
private int DfsAlice(int node, int parent, int depth, int currentProfit, List<int>[] tree, int[] bobDist, int[] amount) {
if (bobDist[node] == -1 || depth < bobDist[node]) {
currentProfit += amount[node];
} else if (depth == bobDist[node]) {
currentProfit += amount[node] / 2;
}
if (tree[node].Count == 1 && node != 0) {
return currentProfit;
}
int maxProfit = int.MinValue;
foreach (int neighbor in tree[node]) {
if (neighbor == parent) continue;
maxProfit = Math.Max(maxProfit, DfsAlice(neighbor, node, depth + 1, currentProfit, tree, bobDist, amount));
}
return maxProfit;
}
}
``` | 2 | 0 | ['C#'] | 0 |
most-profitable-path-in-a-tree | Alice and Bob || C++ || BFS/DFS. | alice-and-bob-c-bfsdfs-by-rishiinsane-zmob | IntuitionSince alice's val needs to be maximised based on the path that bob chooses hence we try and find a path to node 0 for bob first and store the timestamp | RishiINSANE | NORMAL | 2025-02-24T17:37:23.256787+00:00 | 2025-02-24T17:37:23.256787+00:00 | 70 | false | # Intuition
Since alice's val needs to be maximised based on the path that bob chooses hence we try and find a path to node 0 for bob first and store the timestamps accordingly.
Then we move alice from node 0 to a leaf node other than 0 such that the val collected by him is maximum based on the path of bob.
Alice gains full value when he chooses a path other than the bob's path or when he arrives on that node before bob does else if they arrive at the same time they share the val.
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
O(n)
- Space complexity:
O(n)
# Code
```cpp []
class Solution {
public:
int mostProfitablePath(vector<vector<int>>& edges, int bob,
vector<int>& amount) {
int n = amount.size(), ans = INT_MIN;
unordered_map<int, int> pathTime;
vector<vector<int>> adj(n);
vector<bool> vis(n, false);
//make the graph
for (auto it : edges) {
int u = it[0], v = it[1];
adj[u].push_back(v);
adj[v].push_back(u);
}
//move bob to node 0
dfs(bob, 0, pathTime, vis, adj);
vis.assign(n, false);
//move alice
queue<pair<int, pair<int, int>>> q;
q.push({0, {0, 0}});
vis[0] = true;
while (!q.empty()) {
auto it = q.front();
q.pop();
int node = it.first;
int time = it.second.first;
int val = it.second.second;
//gains full value
if (pathTime.find(node) == pathTime.end() || time < pathTime[node])
val += amount[node];
//gains half value
else if (time == pathTime[node])
val += (amount[node] / 2);
//arrives at a leaf node other than 0
if (adj[node].size() == 1 && node)
ans = max(ans, val);
//moves across all possible paths
for (auto it : adj[node]) {
if (!vis[it]) {
vis[it] = true;
q.push({it, {time + 1, val}});
}
}
}
return ans;
}
bool dfs(int node, int time, unordered_map<int, int>& pathTime,
vector<bool>& vis, vector<vector<int>>& adj) {
pathTime[node] = time;
vis[node] = true;
if (!node)
return true;
for (int it : adj[node]) {
if (!vis[it]) {
if (dfs(it, time + 1, pathTime, vis, adj))
return true;
}
}
//remove because couldn't reach node 0 hence backtracks
pathTime.erase(node);
return false;
}
};
``` | 2 | 0 | ['C++'] | 0 |
most-profitable-path-in-a-tree | Functional JavaScript 1-liner recursion 100% | functional-javascript-1-liner-recursion-usfgp | IntuitionBuild graph as adjacency list.Traverse graph starting from root 0 node, keeping track of current depth.Return maximum profit from each subtree.On the w | Serhii_Hrynko | NORMAL | 2025-02-24T16:45:56.238461+00:00 | 2025-02-24T16:46:39.990990+00:00 | 53 | false | # Intuition
Build graph as adjacency list.
Traverse graph starting from root 0 node, keeping track of current depth.
Return maximum profit from each subtree.
On the way back to root, move Bob to parent node and keep track of number of steps taken by Bob.
Once Bob took as many steps as Alice, ignore Bob.
```
mostProfitablePath = (
edges,
bob,
amount,
graph = edges.reduce((g, [a, b]) => (g[a].push(b), g[b].push(a), g), amount.map(() => [])),
k = 0,
$ = (a, l, p, o = graph[a]) => o.reduce(
(m, b) => b == p ? m : Math.max(m, $(+b, l+1, a)),
!a || o.length > 1 ? -Infinity : 0
) + amount[a] * (bob !== a || (bob = p, k++ > l) || (k > l) / 2)
) => $(0, 0)
```
Time/space: $$O(n)$$
| 2 | 0 | ['JavaScript'] | 0 |
most-profitable-path-in-a-tree | dfs_alice + dfs_bob :) | dfs_alice-dsf_bob-by-tavvfikk-i0ea | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | tavvfikk | NORMAL | 2025-02-24T16:24:24.631114+00:00 | 2025-02-24T16:31:52.257516+00:00 | 48 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
vector<vector<int>> graph;
vector<int> bob_steps;
int ans = INT_MIN;
bool dfs_bob(int u, int p, int steps) {
bob_steps[u] = steps;
if (u == 0)
return true;
for (int v : graph[u]) {
if (v == p)
continue;
if (dfs_bob(v, u, steps + 1))
return true;
}
bob_steps[u] = INT_MAX;
return false;
}
void dfs_alice(int u, int p, int steps, int income, vector<int>& amount) {
int cost = amount[u];
if (bob_steps[u] < steps)
cost = 0;
else if (bob_steps[u] == steps)
cost /= 2;
income += cost;
bool is_leaf = true;
for (int v : graph[u]) {
if (v == p)
continue;
is_leaf = false;
dfs_alice(v, u, steps + 1, income, amount);
}
if (is_leaf)
ans = max(ans, income);
}
int mostProfitablePath(vector<vector<int>>& edges, int bob, vector<int>& amount) {
int n = amount.size();
graph = vector<vector<int>>(n);
bob_steps = vector<int>(n, INT_MAX);
for (const auto& edge : edges) {
graph[edge[0]].push_back(edge[1]);
graph[edge[1]].push_back(edge[0]);
}
dfs_bob(bob, -1, 0);
dfs_alice(0, -1, 0, 0, amount);
return ans;
}
};
``` | 2 | 0 | ['Depth-First Search', 'C++'] | 0 |
most-profitable-path-in-a-tree | ✅✅ Using DFS || Simple Traversal ||Easy Solution | using-dfs-simple-traversal-easy-solution-wg6d | IntuitionAlice and Bob start at different nodes in a tree, and we need to determine the maximum income Alice can collect while considering Bob's path. Bob moves | Karan_Aggarwal | NORMAL | 2025-02-24T15:57:37.724192+00:00 | 2025-02-24T15:57:37.724192+00:00 | 12 | false | # Intuition
Alice and Bob start at different nodes in a tree, and we need to determine the maximum income Alice can collect while considering Bob's path. Bob moves optimally toward node 0, and Alice can collect full, half, or no amount from each node based on whether Bob reached it first, at the same time, or later.
# Approach
1. **Graph Construction**:
- Build an adjacency list from the given edges.
2. **Bob’s DFS**:
- Perform DFS from Bob's starting node to track his arrival time at each node.
- Store this in `bobMap` (node → arrival time).
3. **Alice’s DFS**:
- Start DFS from node 0 and track the collected income.
- If Alice reaches a node before Bob, collect the full amount.
- If Alice and Bob arrive at the same time, collect half.
- If Bob arrives earlier, collect nothing.
- Track the maximum income Alice can earn when reaching a leaf node.
# Complexity Analysis
- **Time Complexity**:
- **Graph Construction**: \(O(n)\)
- **DFS for Bob**: \(O(n)\)
- **DFS for Alice**: \(O(n)\)
- **Total**: \(O(n)\), where \(n\) is the number of nodes.
- **Space Complexity**:
- **Adjacency List**: \(O(n)\)
- **Visited Arrays & Maps**: \(O(n)\)
- **Recursive Call Stack**: \(O(n)\) (in the worst case)
- **Total**: \(O(n)\)
# Code
```cpp []
class Solution {
public:
unordered_map<int,vector<int>>adj;
unordered_map<int,int>bobMap;
int aliceIncome;
bool dfsBob(vector<bool>&visited,int currNode,int t){
visited[currNode]=true;
bobMap[currNode]=t;
if(currNode==0) return true;
for(auto &ngbr:adj[currNode]){
if(!visited[ngbr]){
if(dfsBob(visited,ngbr,t+1)==true) return true;
}
}
bobMap.erase(currNode);
return false;
}
void dfsAlice(vector<bool>&visited,int currNode,int t,int income,vector<int>&amount){
visited[currNode]=true;
if(bobMap.find(currNode)==bobMap.end() || bobMap[currNode]>t){
income+=amount[currNode];
} else if(t==bobMap[currNode]){
income+=(amount[currNode]/2);
}
if(adj[currNode].size()==1 && currNode!=0){
aliceIncome=max(aliceIncome,income);
}
for(int &ngbr:adj[currNode]){
if(!visited[ngbr]){
dfsAlice(visited,ngbr,t+1,income,amount);
}
}
}
int mostProfitablePath(vector<vector<int>>& edges, int bob, vector<int>& amount) {
int n=amount.size();
for(auto &edge:edges){
adj[edge[0]].push_back(edge[1]);
adj[edge[1]].push_back(edge[0]);
}
// Bob DFS
int bobTime=0;
vector<bool>visited(n,false);
dfsBob(visited,bob,bobTime);
// Alice DFS
int income=0;
aliceIncome=INT_MIN;
visited.assign(0,false);
dfsAlice(visited,0,0,income,amount);
return aliceIncome;
}
};
```
# Have a Good Day 😊 UpVote? | 2 | 0 | ['Array', 'Tree', 'Depth-First Search', 'Graph', 'C++'] | 0 |
most-profitable-path-in-a-tree | Optimal DFS Strategy: Maximizing Alice’s Profit While Tracking Bob’s Path in a Tree | optimal-dfs-strategy-maximizing-alices-p-g6tk | 🔼 Please Upvote🔼 Please Upvote🔼 Please Upvote🔼 Please Upvote💡If this helped, don’t forget to upvote! 🚀🔥IntuitionAlice and Bob move through the tree, collecting | alperensumeroglu | NORMAL | 2025-02-24T14:40:21.274066+00:00 | 2025-02-24T14:40:21.274066+00:00 | 10 | false | **🔼 Please Upvote
🔼 Please Upvote
🔼 Please Upvote
🔼 Please Upvote**
**💡If this helped, don’t forget to upvote! 🚀🔥**
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
Alice and Bob move through the tree, collecting amounts from nodes. The challenge is to determine the most profitable path Alice can take, considering that Bob might reach some nodes earlier and take part of the amount.
# Approach
<!-- Describe your approach to solving the problem. -->
1. Convert the given edges into an undirected adjacency list.
2. Find Bob's path to the root and store his arrival time at each node.
3. Use depth-first search (DFS) to track Alice’s movement while maximizing her collected amount.
4. If Bob arrives first, he takes the full amount; if they arrive at the same time, they split the amount.
5. The goal is to find the leaf node where Alice can collect the highest possible amount.
# Complexity
• Time complexity: $$O(n)$$, as we traverse all nodes once.
• Space complexity: $$O(n)$$, due to adjacency list storage and recursion depth in DFS.
**🔼 Please Upvote
🔼 Please Upvote
🔼 Please Upvote
🔼 Please Upvote**
**💡If this helped, don’t forget to upvote! 🚀🔥**
# Code
```python3 []
class Solution:
def mostProfitablePath(self, edges, bob, amount):
# Step 1: Construct adjacency list for an undirected tree
adjacency_list = {}
for u, v in edges:
if u not in adjacency_list:
adjacency_list[u] = []
if v not in adjacency_list:
adjacency_list[v] = []
adjacency_list[u].append(v)
adjacency_list[v].append(u)
# Step 2: Find Bob's path to the root (node 0)
bob_path = {}
visited = set()
def track_bob_path(node, time):
""" Recursive function to track Bob's path to node 0 """
visited.add(node)
bob_path[node] = time
if node == 0:
return True
for neighbor in adjacency_list[node]:
if neighbor not in visited and track_bob_path(neighbor, time + 1):
return True
bob_path.pop(node)
return False
track_bob_path(bob, 0)
# Step 3: Perform DFS to determine the maximum profit for Alice
visited.clear()
max_profit = float('-inf')
def explore_alice_path(node, time, income):
""" DFS function to track Alice's path and compute the maximum profit """
nonlocal max_profit
visited.add(node)
# Alice collects amount if Bob hasn't reached the node yet
if node not in bob_path or time < bob_path[node]:
income += amount[node]
elif time == bob_path[node]:
income += amount[node] // 2 # Bob and Alice split the amount
# If the node is a leaf and not the root, check for maximum profit
if len(adjacency_list[node]) == 1 and node != 0:
max_profit = max(max_profit, income)
# Continue DFS exploration
for neighbor in adjacency_list[node]:
if neighbor not in visited:
explore_alice_path(neighbor, time + 1, income)
explore_alice_path(0, 0, 0)
return max_profit
``` | 0 | 0 | ['Python3'] | 0 |
most-profitable-path-in-a-tree | Step by Step Explained C++ Solution | TC - 0(N) | SC - 0(N) | DFS | Easy | step-by-step-explained-c-solution-tc-0n-wscil | Complexity
Time complexity:O(N)
Space complexity:O(N)
Code | ujjwal141 | NORMAL | 2025-02-24T14:15:41.413189+00:00 | 2025-02-24T14:18:40.876498+00:00 | 87 | false | # Complexity
- Time complexity:
O(N)
- Space complexity:
O(N)
# Code
```cpp []
class Solution {
public:
// TC - O(N) & SC - O(N)
int ans = INT_MIN; // contain answer
unordered_map<int, int> mp; // node -> distance
bool pathTileZero(int bob, int cnt, unordered_map<int, vector<int>> &adjList,
vector<int> &visitedB){
visitedB[bob] = 1;
if(bob == 0){
mp[bob] = cnt;
return 1;
}
for(auto pa:adjList[bob]){
if(!visitedB[pa]){
bool flag = pathTileZero(pa, cnt+1, adjList, visitedB);
if(flag){
mp[pa] = cnt;
return 1;
}
}
}
return 0;
}
void solve( int alice, int cnt, int sum, unordered_map<int, vector<int>> &adjList,
vector<int> &visitedA, vector<int>& amount){
visitedA[alice] = 1;
cnt++;
if(adjList[alice].size() == 1 && alice != 0){
ans = max(ans, sum);
return;
}
for(auto pa:adjList[alice]){
if(!visitedA[pa]){
int addedVal = 0;
// if Node come in the path of bob to 0 then we have 3 case
// case 1 : mp[pa] > cnt i.e. bob not visited yet.
// case 2 : mp[pa] < cnt i.e. bob already visited so add 0.
// case 3 : mp[pa] == cnt i.e. bob and alice visited together
if(mp.find(pa) != mp.end()){
if(mp[pa] == cnt)
addedVal = amount[pa] / 2;
if(mp[pa] > cnt)
addedVal = amount[pa];
}
else // node not occur in bob to 0 path.
addedVal = amount[pa];
solve(pa, cnt, sum + addedVal, adjList, visitedA, amount);
}
}
}
int mostProfitablePath(vector<vector<int>>& edges, int bob, vector<int>& amount) {
int size = edges.size() + 1; // no. of node
unordered_map<int, vector<int>> adjList;
for(int i=0 ;i<edges.size() ;i++){
int u = edges[i][0];
int v = edges[i][1];
adjList[u].push_back(v);
adjList[v].push_back(u);
}
vector<int> visitedA(size, 0), visitedB(size, 0);
pathTileZero(bob, 1, adjList, visitedB); // Find the path from bob to 0 and insert into map as node -> no. of step need to reach at particular node
mp[bob] = 0;
solve(0, 0, amount[0], adjList, visitedA, amount);
return ans;
}
};
``` | 2 | 0 | ['Tree', 'Depth-First Search', 'Graph', 'C++'] | 0 |
most-profitable-path-in-a-tree | Single DFS solution with explanation | 199~227ms (75~100) | 111.14~117.5 (25~50) | single-dfs-solution-with-explanation-199-zyna | IntuitionWe can rethink the problem by breaking it down into two subproblems:
Bob moves from his starting node along the unique path toward the root node. The t | whats2000 | NORMAL | 2025-02-24T10:12:29.659992+00:00 | 2025-02-24T10:12:29.659992+00:00 | 154 | false | # Intuition
We can rethink the problem by breaking it down into two subproblems:
- Bob moves from his starting node along the unique path toward the root node. The time Bob reaches each node can be understood as the shortest distance from Bob's starting node to that node.
- Alice starts from the root node and traverses along different paths to the leaves. At each node, she calculates the profit based on the node's Bob arrival time and her own step count (i.e., current DFS depth). She only considers the path with the highest profit, as Alice will only choose one path.
Although we could perform separate Depth First Searches to calculate Bob's arrival time and Alice's maximum profit, this would lead to redundant calculations.
We can merge these two processes with the following approach:
- As we perform DFS from the root, we recursively return Bob's shortest distance information from child nodes and use it to update the current node's Bob arrival time (`bobDist[node] = min(bobDist[node], bobDist[child] + 1)`).
- During recursion, we can compute Alice's profit at each node based on the current DFS depth (Alice's arrival time) and Bob's arrival time. This eliminates redundant calculations.
By traversing the entire tree once, we can determine Alice's maximum profit.
---
# Approach
## Step 1: Initialize Storage and Variables
We first construct an Adjacency List to store the tree structure and initialize Bob's distances to a large value.
```typescript
const n = amount.length;
const adj: number[][] = Array.from({ length: n }, () => []);
const bobDist: number[] = new Array(n).fill(n);
```
## Step 2: Construct the Adjacency List
Convert the `edges` array into an adjacency list for easier traversal in the next steps.
```typescript
for (const [u, v] of edges) {
adj[u].push(v);
adj[v].push(u);
}
```
## Step 3: Recursively Compute Bob's Arrival Time
Perform DFS to compute Bob's arrival time:
- If the node is Bob's starting point, set its arrival time to 0.
- Traverse all child nodes and update Bob's arrival time.
- Once Bob's arrival time is determined, calculate Alice's profit at the node.
- Finally, if it is a leaf node, return the node's profit; otherwise, add the highest child profit to the current node's profit.
```typescript
function dfs(node: number, parent: number, depth: number): number {
// If this node is Bob's starting point, set the arrival time to 0.
if (node === bob) {
bobDist[node] = 0;
}
let bestChildProfit = -Infinity;
let profitHere = 0;
// Traverse all child nodes.
for (let child of adj[node]) {
if (child === parent) continue;
const childProfit = dfs(child, node, depth + 1);
bestChildProfit = childProfit > bestChildProfit ? childProfit : bestChildProfit;
// Update Bob's arrival time.
bobDist[node] = Math.min(bobDist[node], bobDist[child] + 1);
}
// Update the current node's profit:
if (depth < bobDist[node]) {
// If Alice (depth) arrives earlier than Bob (bobDist[node]), she can take the full profit.
profitHere += amount[node];
} else if (depth === bobDist[node]) {
// If Alice and Bob arrive at the same time, she takes half the profit.
profitHere += (amount[node] >> 1); // Equivalent to Math.floor(amount[node] / 2)
}
// If there is no child contributing profit (i.e., leaf node), return profitHere.
// Otherwise, add the maximum child profit.
return bestChildProfit === -Infinity ? profitHere : profitHere + bestChildProfit;
}
```
---
# Complexity
- **Time Complexity:**
- Constructing the Adjacency List requires iterating through all edges, which is $$O(n)$$.
- The Depth First Search visits each node only once, leading to a time complexity of $$O(n)$$.
- The overall time complexity is **$$O(n)$$**.
- **Space Complexity:**
- The Adjacency List requires **$$O(n)$$** space.
- The array storing Bob's arrival times also requires **$$O(n)$$** space.
- Other variables require **$$O(1)$$** space.
- The total space complexity is **$$O(n)$$**.
---
# Code
```typescript []
/**
* @param {number[][]} edges
* @param {number} bob
* @param {number[]} amount
* @return {number}
*/
function mostProfitablePath(edges: number[][], bob: number, amount: number[]): number {
const n = amount.length;
const adj: number[][] = Array.from({ length: n }, () => []);
// Use n as the initial “infinite” distance.
const bobDist: number[] = new Array(n).fill(n);
// Build the undirected tree.
for (const [u, v] of edges) {
adj[u].push(v);
adj[v].push(u);
}
/**
* Single DFS that computes both Bob's arrival time (stored in bobDist) and
* the maximum profit Alice can achieve from the current node.
* @param node {number} - current node
* @param parent {number} - parent node
* @param depth {number} - depth of the current node
*/
function dfs(node: number, parent: number, depth: number): number {
// If this node is Bob's starting point, set its distance to 0.
if (node === bob) {
bobDist[node] = 0;
}
let bestChildProfit = -Infinity;
let profitHere = 0;
// Visit children.
for (let child of adj[node]) {
if (child === parent) continue;
const childProfit = dfs(child, node, depth + 1);
bestChildProfit = childProfit > bestChildProfit ? childProfit : bestChildProfit;
// Update Bob's distance for the current node.
bobDist[node] = Math.min(bobDist[node], bobDist[child] + 1);
}
// Update profit at the current node depending on arrival times:
// If Alice (depth) is earlier than Bob (bobDist[node]), she takes the full amount.
// If she arrives exactly when Bob does, she gets half.
if (depth < bobDist[node]) {
profitHere += amount[node];
} else if (depth === bobDist[node]) {
profitHere += (amount[node] >> 1); // equivalent to Math.floor(amount[node]/2)
}
// If no child contributed profit (i.e. it's a leaf), return profitHere.
// Otherwise, add the best profit from one of the children.
return bestChildProfit === -Infinity ? profitHere : profitHere + bestChildProfit;
}
return dfs(0, -1, 0);
}
```
```javascript []
/**
* @param {number[][]} edges
* @param {number} bob
* @param {number[]} amount
* @return {number}
*/
function mostProfitablePath(edges, bob, amount) {
const n = amount.length;
const adj = Array.from({ length: n }, () => []);
// Use n as the initial “infinite” distance.
const bobDist = new Array(n).fill(n);
// Build the undirected tree.
for (const [u, v] of edges) {
adj[u].push(v);
adj[v].push(u);
}
// Single DFS that computes both Bob's arrival time (stored in bobDist) and
// the maximum profit Alice can achieve from the current node.
function dfs(node, parent, depth) {
// If this node is Bob's starting point, set its distance to 0.
if (node === bob) {
bobDist[node] = 0;
}
let bestChildProfit = -Infinity;
let profitHere = 0;
// Visit children.
for (let child of adj[node]) {
if (child === parent) continue;
const childProfit = dfs(child, node, depth + 1);
bestChildProfit = childProfit > bestChildProfit ? childProfit : bestChildProfit;
// Update Bob's distance for the current node.
bobDist[node] = Math.min(bobDist[node], bobDist[child] + 1);
}
// Update profit at the current node depending on arrival times:
// If Alice (depth) is earlier than Bob (bobDist[node]), she takes the full amount.
// If she arrives exactly when Bob does, she gets half.
if (depth < bobDist[node]) {
profitHere += amount[node];
} else if (depth === bobDist[node]) {
profitHere += (amount[node] >> 1); // equivalent to Math.floor(amount[node]/2)
}
// If no child contributed profit (i.e. it's a leaf), return profitHere.
// Otherwise, add the best profit from one of the children.
return bestChildProfit === -Infinity ? profitHere : profitHere + bestChildProfit;
}
return dfs(0, -1, 0);
}
```
---
# Result
| 2 | 0 | ['Array', 'Tree', 'Depth-First Search', 'Graph', 'Simulation', 'TypeScript', 'JavaScript'] | 0 |
most-profitable-path-in-a-tree | Breadth First Search Approach | breadth-first-search-approach-by-biniyam-6opd | ApproachFirst find bob's path, then iterate through the graph for both alice and bob while tracking which node bob visited before alice reached there. Also don' | biniyamnegasa17 | NORMAL | 2025-02-24T06:25:35.582454+00:00 | 2025-02-24T06:25:35.582454+00:00 | 108 | false | # Approach
<!-- Describe your approach to solving the problem. -->
First find bob's path, then iterate through the graph for both alice and bob while tracking which node bob visited before alice reached there. Also don't forget to track alice's score, then update the maximum value alice has, when you are at a leaf node.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
O(N)
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
O(N)
# Code
```python3 []
class Solution:
def mostProfitablePath(self, edges: List[List[int]], bob: int, amount: List[int]) -> int:
n = len(edges) + 1
graph = [[] for _ in range(n)]
for a, b in edges:
graph[a].append(b)
graph[b].append(a)
bob_path = {bob: -1}
q = deque([bob])
visited = set([bob])
while q:
node = q.popleft()
if node == 0:
break
for child in graph[node]:
if child not in visited:
bob_path[child] = node
visited.add(child)
q.append(child)
real_bob_path = []
curr = 0
while curr != -1:
real_bob_path.append(curr)
curr = bob_path[curr]
q = deque([[0, 0]])
visited = set()
yegara = set()
mx = float('-inf')
while q:
m = len(q)
comp = real_bob_path.pop() if real_bob_path else -1
for _ in range(m):
node, alice = q.popleft()
visited.add(node)
if node not in yegara:
if node == comp:
temp = amount[node]//2
alice += temp
else:
alice += amount[node]
yegara.add(node)
is_leaf = 1
for child in graph[node]:
if child not in visited:
is_leaf = 0
q.append([child, alice])
if is_leaf:
mx = max(mx, alice)
if comp != -1:
yegara.add(comp)
return mx
``` | 2 | 0 | ['Python3'] | 1 |
most-profitable-path-in-a-tree | Simple Easy Solution | Cpp | DFS + BFS | simple-easy-solution-cpp-dfs-bfs-by-its_-5vs3 | IntuitionFor Bob there will be only one way to reach the root node. So find the bob path and mark the distance/time for reaching each node. Then do the bfs for | its_navneet | NORMAL | 2025-02-24T06:23:31.540923+00:00 | 2025-02-24T06:23:31.540923+00:00 | 326 | false | # Intuition
For Bob there will be only one way to reach the root node. So find the bob path and mark the distance/time for reaching each node. Then do the bfs for Alice and get all possible sum to reach the child node.
# Complexity
- Time complexity:
$$O(n)$$
# Code
```cpp []
class Solution {
void dfs(int node, auto &gr, int bob, auto &curr,vector<int>&path,int par = -1){
curr.push_back(node);
if(node == bob){
path = curr ;
return ;
}
for(int x:gr[node]){
if(x != par){
dfs(x,gr,bob,curr,path,node);
}
}
curr.pop_back();
}
public:
int mostProfitablePath(vector<vector<int>>& edges, int bob, vector<int>& amount) {
int ans = -1e9 ;
int n = edges.size()+1;
vector<vector<int>>gr(n);
for(auto x:edges){
gr[x[0]].push_back(x[1]);
gr[x[1]].push_back(x[0]);
}
vector<int>curr,path;
dfs(0,gr,bob,curr,path) ;
reverse(path.begin(),path.end());
vector<int>dis(n,n+1) ;
for(int i=0;i<path.size();i++){
dis[path[i]] = i ;
}
queue<vector<int>>q;
vector<int>vis(n,0);
q.push({amount[0],0,0}); // amount, dis ,node
while(!q.empty()){
auto p = q.front();
q.pop();
int currSum = p[0];
int d = p[1];
int node = p[2];
vis[node] =1 ;
int child = 0;
for(int x:gr[node]){
if(!vis[x]){
child++;
int temp= ((d+1) < dis[x] ? amount[x] : ((d+1) > dis[x] ? 0: amount[x]/2));
q.push({currSum+temp,d+1,x});
}
}
if(child == 0){
ans = max(ans,currSum);
}
}
return ans ;
}
};
``` | 2 | 0 | ['C++'] | 0 |
most-profitable-path-in-a-tree | [C++] Two DFS | c-two-dfs-by-bora_marian-75am | The key observation for this problem is that both Alice and Bob are moving in a tree. There is one single way for Bob to move from parent to parent till node 0. | bora_marian | NORMAL | 2025-02-24T05:49:43.938839+00:00 | 2025-02-24T05:49:43.938839+00:00 | 148 | false | The key observation for this problem is that both Alice and Bob are moving in a tree. There is one single way for Bob to move from parent to parent till node 0. For Alice we can calculate the way to all nodes using DFS and the amount she can reach the node.
Steps:
- calculate bob path and add the number of steps necessary to reach that node.
- use Dfs to calculate the sum of the nodes from 0 to the current. If the node belongs to Bob's path also we compare to see if they reach simultaneously or Bob arrived first, or Alice arrived first
# Code
```cpp []
class Solution {
public:
unordered_map<int, int> bobPath;
unordered_map<int, int> profit;
vector<int> amount;
int mostProfitablePath(vector<vector<int>>& edges, int bob, vector<int>& amn) {
int n = edges.size() + 1;
amount = amn;
vector<int> parent;
parent.reserve(n);
vector<int> visit(n, 0);
vector<vector<int>>g(n);
for (auto &edge : edges) {
g[edge[0]].push_back(edge[1]);
g[edge[1]].push_back(edge[0]);
}
parent[0] = -1;
dfs(g, 0, visit, parent);
int bobstep = 0;
while (bob >= 0) {
bobPath[bob] = bobstep;
bob = parent[bob];
bobstep++;
}
for (int i = 0; i < n; i++) {
visit[i] = 0;
}
dfs_profit(g, 0, visit, 0, 0);
int result = INT_MIN;
for (auto pr : profit) {
if (pr.first != 0 && g[pr.first].size() == 1)
result = max(result, pr.second);
}
return result;
}
void dfs_profit(vector<vector<int>> &g, int node, vector<int>& visit, int lvl, int prf) {
if (bobPath.find(node) != bobPath.end()) {
if (bobPath[node] < lvl) {
profit[node] = prf;
} else if (bobPath[node] == lvl) {
profit[node] = prf + amount[node] / 2;
} else {
profit[node] = prf + amount[node];
}
} else {
profit[node] = prf + amount[node];
}
visit[node] = 1;
for (auto adjNode: g[node]) {
if (visit[adjNode] == 0) {
dfs_profit(g, adjNode, visit, lvl + 1, profit[node]);
}
}
}
void dfs(vector<vector<int>> &g, int node, vector<int>& visit, vector<int>& parent) {
visit[node] = 1;
for (int adjNode: g[node]) {
if (visit[adjNode] == 0) {
parent[adjNode] = node;
dfs(g, adjNode, visit, parent);
}
}
}
};
``` | 2 | 0 | ['C++'] | 0 |
most-profitable-path-in-a-tree | Easy code | Must try | Beats 80% | easy-code-must-try-beats-80-by-notaditya-zoj1 | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | NotAditya09 | NORMAL | 2025-02-24T05:36:50.632701+00:00 | 2025-02-24T05:36:50.632701+00:00 | 386 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int mostProfitablePath(int[][] edges, int bob, int[] amount) {
final int n = amount.length;
List<Integer>[] tree = new List[n];
int[] parent = new int[n];
int[] aliceDist = new int[n];
Arrays.fill(aliceDist, -1);
for (int i = 0; i < n; ++i)
tree[i] = new ArrayList<>();
for (int[] edge : edges) {
final int u = edge[0];
final int v = edge[1];
tree[u].add(v);
tree[v].add(u);
}
dfs(tree, 0, -1, 0, parent, aliceDist);
// Modify the amount along the path from node Bob to node 0.
// For each node,
// 1. If Bob reaches earlier than Alice does, change the amount to 0.
// 2. If Bob and Alice reach simultaneously, devide the amount by 2.
for (int u = bob, bobDist = 0; u != 0; u = parent[u], ++bobDist)
if (bobDist < aliceDist[u])
amount[u] = 0;
else if (bobDist == aliceDist[u])
amount[u] /= 2;
return getMoney(tree, 0, -1, amount);
}
// Fills `parent` and `dist`.
private void dfs(List<Integer>[] tree, int u, int prev, int d, int[] parent, int[] dist) {
parent[u] = prev;
dist[u] = d;
for (final int v : tree[u]) {
if (dist[v] == -1)
dfs(tree, v, u, d + 1, parent, dist);
}
}
private int getMoney(List<Integer>[] tree, int u, int prev, int[] amount) {
// a leaf node
if (tree[u].size() == 1 && tree[u].get(0) == prev)
return amount[u];
int maxPath = Integer.MIN_VALUE;
for (final int v : tree[u])
if (v != prev)
maxPath = Math.max(maxPath, getMoney(tree, v, u, amount));
return amount[u] + maxPath;
}
}
``` | 2 | 0 | ['Java'] | 0 |
most-profitable-path-in-a-tree | EASY TO UNDERSTAND | JAVA | Explained With Comments !!! | easy-to-understand-java-explained-with-c-a6rr | Code | Siddharth_Bahuguna | NORMAL | 2025-02-24T03:34:48.996132+00:00 | 2025-02-24T03:34:48.996132+00:00 | 307 | false |
# Code
```java []
class Solution {
public int mostProfitablePath(int[][] edges, int bob, int[] amount) {
int n = amount.length;
tree = new ArrayList<>();
bobPath = new HashMap<>();
visited = new boolean[n];
for (int i = 0; i < n; i++) {
tree.add(new ArrayList<>());
}
// Form tree with edges
for (int[] edge : edges) {
tree.get(edge[0]).add(edge[1]);
tree.get(edge[1]).add(edge[0]);
}
// Find the path taken by Bob to reach node 0 and the times it takes to get there
findBobPath(bob, 0);
// Find Alice's optimal path
Arrays.fill(visited, false);
findAlicePath(0, 0, 0, amount);
return maxIncome;
}
private Map<Integer, Integer> bobPath;
private boolean[] visited;
private List<List<Integer>> tree;
private int maxIncome = Integer.MIN_VALUE;
// Depth First Search to find Bob's path
private boolean findBobPath(int sourceNode, int time) {
// Mark and set time node is reached
bobPath.put(sourceNode, time);
visited[sourceNode] = true;
// Destination for Bob is found
if (sourceNode == 0) {
return true;
}
// Traverse through unvisited nodes
for (int adjacentNode : tree.get(sourceNode)) {
if (!visited[adjacentNode] && findBobPath(adjacentNode, time + 1)) {
return true;
}
}
// If node 0 isn't reached, remove current node from path
bobPath.remove(sourceNode);
return false;
}
// Depth First Search to find Alice's optimal path
private void findAlicePath(
int sourceNode,
int time,
int income,
int[] amount
) {
// Mark node as explored
visited[sourceNode] = true;
// Alice reaches the node first
if (
!bobPath.containsKey(sourceNode) || time < bobPath.get(sourceNode)
) {
income += amount[sourceNode];
}
// Alice and Bob reach the node at the same time
else if (time == bobPath.get(sourceNode)) {
income += amount[sourceNode] / 2;
}
// Update max value if current node is a new leaf
if (tree.get(sourceNode).size() == 1 && sourceNode != 0) {
maxIncome = Math.max(maxIncome, income);
}
// Traverse through unvisited nodes
for (int adjacentNode : tree.get(sourceNode)) {
if (!visited[adjacentNode]) {
findAlicePath(adjacentNode, time + 1, income, amount);
}
}
}
}
``` | 2 | 0 | ['Java'] | 0 |
most-profitable-path-in-a-tree | Easy To Understand C++ Solution || (Using DFS) ✅✅ | easy-to-understand-c-solution-using-dfs-4gewm | Code\n\nclass Solution {\npublic:\n int dfs(vector<int> *adj,vector<int> &values,vector<int> &vis,vector<int> &dis,int node,int time){\n vis[node]=1;\ | Abhi242 | NORMAL | 2024-02-26T19:25:48.476662+00:00 | 2024-02-26T19:25:48.476690+00:00 | 197 | false | # Code\n```\nclass Solution {\npublic:\n int dfs(vector<int> *adj,vector<int> &values,vector<int> &vis,vector<int> &dis,int node,int time){\n vis[node]=1;\n int ans=-1e8;\n int cost=0;\n if(dis[node]>time){\n cost=values[node];\n }else if(dis[node]==time){\n cost=values[node]/2;\n }else if(dis[node]<time){\n cost=0;\n }\n for(auto a:adj[node]){\n if(vis[a]) continue;\n ans=max(ans,cost + dfs(adj,values,vis,dis,a,time+1));\n }\n if(ans==-1e8){\n return cost;\n }\n return ans;\n }\n int helper(vector<int>*adj,vector<int> &dis,int bob,int time){\n if(bob==0){\n return 0;\n }\n for(auto a:adj[bob]){\n if(dis[a]==1e8){\n dis[a]=time;\n if(helper(adj,dis,a,time+1)==0){\n return 0;\n };\n dis[a]=INT_MAX;\n }\n }\n return 1;\n }\n int mostProfitablePath(vector<vector<int>>& edges, int bob, vector<int>& amount) {\n int n=edges.size()+1;\n vector<int> adj[n];\n for(int i=0;i<n-1;i++){\n adj[edges[i][0]].push_back(edges[i][1]);\n adj[edges[i][1]].push_back(edges[i][0]);\n }\n vector<int> dis(n,1e8);\n dis[bob]=0;\n vector<int> vis(n,0);\n helper(adj,dis,bob,1);\n return dfs(adj,amount,vis,dis,0,0);\n }\n};\n``` | 2 | 0 | ['Tree', 'Depth-First Search', 'C++'] | 0 |
most-profitable-path-in-a-tree | DFS+BFS || C++ ✔✔ | dfsbfs-c-by-deepak_5910-khye | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Deepak_5910 | NORMAL | 2023-10-19T20:03:58.084053+00:00 | 2023-10-19T20:03:58.084075+00:00 | 264 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> path;\n void dfs(vector<vector<int>> &adj,vector<int> &v,vector<int> &vis,int src)\n {\n vis[src] = 1;\n v.push_back(src);\n if(src==0)\n {\n path = v;\n return ;\n } \n for(auto x : adj[src])\n {\n if(vis[x]==0)\n {\n dfs(adj,v,vis,x);\n }\n }\n v.pop_back();\n vis[src] = 0;\n }\n int mostProfitablePath(vector<vector<int>>& e, int b, vector<int>& cost) {\n int n = e.size()+1,ans = INT_MIN;\n vector<vector<int>> adj(n+1);\n\n for(int i = 0;i<e.size();i++)\n {\n adj[e[i][0]].push_back(e[i][1]);\n adj[e[i][1]].push_back(e[i][0]);\n }\n vector<int> vis(n+1,0),v;\n dfs(adj,v,vis,b); \n\n int num = 0; \n\n int m = path.size();\n for(int i = 0;i<m/2;i++) cost[path[i]] = 0; \n if(m%2) cost[path[m/2]]/=2;\n \n \n queue<pair<int,int>> q;\n q.push({0,cost[0]});\n vis = vector<int>(n+1,0);\n\n while(!q.empty())\n {\n int node = q.front().first;\n int val = q.front().second; q.pop();\n\n if(adj[node].size()==1 && node!=0)\n {\n int tmp = num+val;\n ans = max(ans,tmp);\n continue;\n }\n for(auto x : adj[node])\n {\n if(vis[x]==0)\n {\n vis[x] = 1;\n q.push({x,val+cost[x]});\n }\n }\n }\n return ans;\n }\n};\n``` | 2 | 0 | ['Depth-First Search', 'Breadth-First Search', 'C++'] | 1 |
most-profitable-path-in-a-tree | DFS + BFS || easy beginner friendly solution | dfs-bfs-easy-beginner-friendly-solution-aywq7 | we will find the path for bob from his current position to root with time stamp and as it\'s given that it\'s tree so their will be single path so it makes ever | demon_code | NORMAL | 2023-08-17T01:47:29.205392+00:00 | 2023-08-17T01:47:29.205423+00:00 | 279 | false | we will find the path for bob from his current position to root with time stamp and as it\'s given that it\'s tree so their will be single path so it makes everything stright forward.\nwe will use map <node -> time> to store info for easy access later\n\nnow once we are done with bob then come to alice \nwe are gpoing to use queue <{node, amount, time}> \n\nwe will run level order traversal from root till leaves and at each current node we will check is this node is already visited /not visited or simultineously visited accordingly we will add amount \nand also we will keep checking that the curr node is leaf node or not iff yess then take maxima with answer \nand keep moving till the queue is empty\n\n```\nUPVOTE IF U LIKE :)\n```\n\n\n\n```\n\nclass Solution {\npublic:\n \n vector<vector<int>> g;\n unordered_map<int,int> m;\n bool dfs(int s,int t)\n {\n m[s]=t;\n if(s==0) return true;\n \n for(auto i: g[s])\n {\n if(m.find(i)==m.end())\n {\n if(dfs(i,t+1)) return true;\n }\n }\n \n m.erase(s);// unmark bcz we didn\'t reach destination\n return false;\n \n \n }\n \n \n int mostProfitablePath(vector<vector<int>>& edges, int bob, vector<int>&pr) \n {\n int n=edges.size()+1;\n \n g.resize(n);\n \n for(auto i: edges)\n {\n g[i[0]].push_back(i[1]);\n g[i[1]].push_back(i[0]);\n }\n \n m.clear(); // conatins all path info with time after dfs\n dfs(bob,0);\n \n // for(auto i: m) cout<<i.first<<" "<<i.second<<endl;\n using vt=vector<int>;\n \n queue<vt> q;\n q.push({0,0,0}); //use level order to get all path from root to leaves,cdtion of leaves in undired grph is it has one connection only\n \n vector<int> v(n,0);\n v[0]=1;\n int ans=INT_MIN;\n while(!q.empty())\n {\n vt tem=q.front();\n q.pop();\n int t=tem[2];\n int p=tem[1];\n int curr=tem[0];\n v[curr]=1;\n if(m.find(curr)==m.end())// didn\'t visited this\n {\n p+=pr[curr];\n }else if(m[curr]>t)// didn\'t arrived yet\n {\n p+=pr[curr];\n }else if(m[curr]==t) p+=pr[curr]/2;// arrived at same time\n \n if(g[curr].size()==1 && curr!=0) // curr!=0 bcz root is not a child but seems like when tree is 0->1->2->3 but it\'s not\n ans= max(ans, p);\n \n for(auto i: g[curr])\n {\n if(v[i]==0)\n {\n q.push({i,p,t+1});\n }\n }\n }\n \n \n return ans;\n \n \n \n \n }\n};\n\n\n\n``` | 2 | 0 | ['Depth-First Search', 'Breadth-First Search', 'C'] | 0 |
most-profitable-path-in-a-tree | Simple DFS Solution, bets 97% runtime | simple-dfs-solution-bets-97-runtime-by-v-bphg | Intuition\n1) Calculate the distance of nodes in the path of bob from his initial position. \n2) Make dfs call from 0 to get the maximum value.\n3) Make sure to | vivek_sangwan | NORMAL | 2023-04-05T15:36:41.908756+00:00 | 2023-04-05T15:36:41.908784+00:00 | 146 | false | # Intuition\n1) Calculate the distance of nodes in the path of bob from his initial position. \n2) Make dfs call from 0 to get the maximum value.\n3) Make sure to check for overflow and root node codition\n\nUpvote if you like the solution.\n\n# Code\n```\nclass Solution {\n public int mostProfitablePath(int[][] edges, int bob, int[] amount) {\n int n = amount.length;\n List<Integer>[] g = new ArrayList[n];\n for(int i=0;i<n;i++) g[i] = new ArrayList<>();\n for(int[] edge:edges){\n g[edge[0]].add(edge[1]);\n g[edge[1]].add(edge[0]);\n }\n int count = 0;\n int[] visited = new int[n];\n moveToZero(bob,-1,1,visited,g);\n return (int)dfs(0,-1,1,visited,g,amount);\n }\n\n private boolean moveToZero(int src,int prnt,int level,int[] visited,List<Integer>[] g){\n if(src==0){\n visited[src] = level;\n return true;\n }\n visited[src] = level;\n for(int ngb:g[src]){\n if(ngb!=prnt){\n if(moveToZero(ngb,src,level+1,visited,g)) return true;\n }\n }\n // If current node is not in the path of bob to 0. Make sure to make it 0 again.\n visited[src] = 0;\n return false;\n }\n\n private long dfs(int src,int prnt,int level,int[] visited,List<Integer>[] g,int[] amount){\n long cost = 0;\n\n // Check if current node is already been visited or not.\n if(visited[src]==0) cost += amount[src];\n else if(visited[src]>level) cost += amount[src];\n else if(visited[src]==level) cost += (amount[src]/2);\n\n // Maximum minimum value possible\n long current = -100_00_00_00_0;\n for(int ngb:g[src]){\n if(ngb!=prnt){\n current = Math.max(dfs(ngb,src,level+1,visited,g,amount),current);\n }\n }\n // Checks for root node condition \n if(current==(-100_00_00_00_0)) return cost;\n return cost+current;\n }\n}\n``` | 2 | 0 | ['Tree', 'Depth-First Search', 'Java'] | 1 |
most-profitable-path-in-a-tree | C++ Easy/Medium , Explained with diagram | c-easymedium-explained-with-diagram-by-n-sq8x | Intuition\nThere is always a uniue path between two nodes in a tree.\nSo we need to see the path between Alice and Bob , this will be the only path that will be | neembu_mirch | NORMAL | 2023-01-02T06:31:37.662429+00:00 | 2023-01-02T06:31:37.662476+00:00 | 339 | false | # Intuition\nThere is always a uniue path between two nodes in a tree.\nSo we need to see the path between Alice and Bob , this will be the only path that will be affected by movement of both Alice and Bob , rest paths depend only on Alice.\n\n# Approach\nFind the path between Alice and Bob , if this path contain odd number of nodes , reduce the amount of mid node to be half. Rest node after the mid will be 0 for Alice. Now run a simple dfs from root to check for the max valued path.\n\n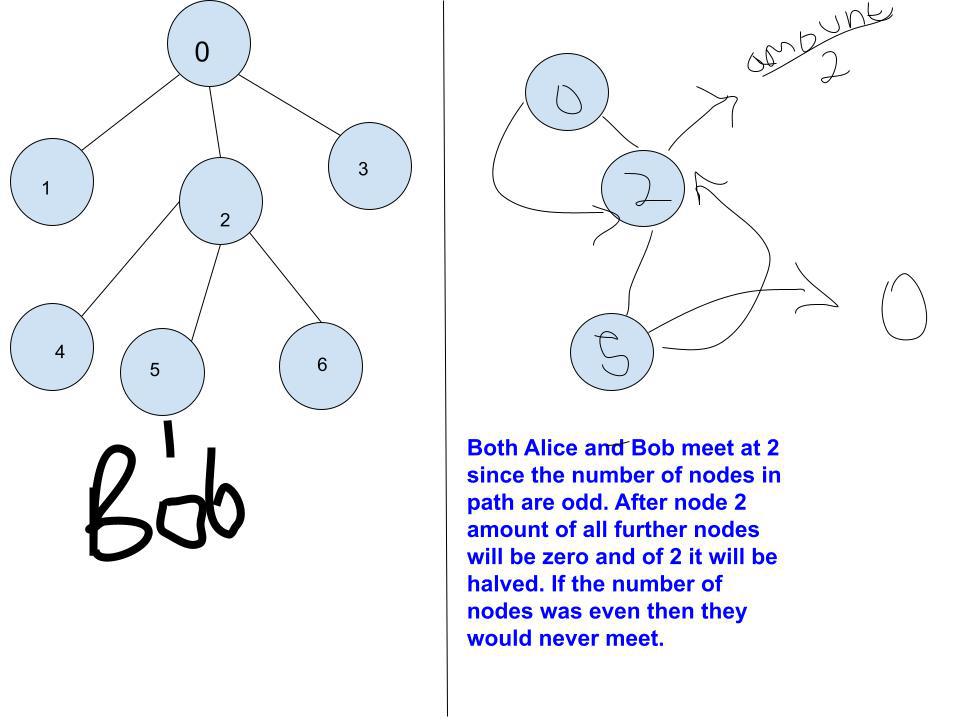\n\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> adj[100007];\n bool vis[100007];\n int ans;\n int cur;\n//dfs to find path between alice and bob\n void dfs(int x, int bob,vector<int> &v,vector<int> &path){\n v.push_back(x);\n \n if(!vis[x]&&x==bob){\n path = v;\n return;\n }\n vis[x]=1;\n for(auto y:adj[x]){\n if(!vis[y]){\n dfs(y,bob,v,path);\n }\n }\n v.pop_back();\n \n }\n\n// dfs to find the max valued path\n void dfs_max(int x, vector<int>& a){\n vis[x]=1;\n cur += a[x];\n for(auto y:adj[x]){\n if(!vis[y]){\n dfs_max(y,a);\n }\n }\n if(x&&adj[x].size()==1) // if x is a leaf node update answer\n ans = max(ans,cur);\n cur-=a[x];\n }\n\n int mostProfitablePath(vector<vector<int>>& edges, int bob, vector<int>& amount) {\n int n = amount.size();\n for(int i =0;i<n;i++) vis[i]=0;\n for(auto x: edges){\n adj[x[0]].push_back(x[1]);\n adj[x[1]].push_back(x[0]);\n }\n vector<int> v;\n vector<int>path;\n dfs(0,bob,v,path);\n int ps = path.size();\n int st;\n if(ps&1){\n amount[path[ps/2]]/=2;\n st = ps/2+1;\n }else{\n st = ps/2;\n }\n for(auto x: path) cout<<x<<" ";\n for(int i =st;i<ps;i++){\n amount[path[i]]=0;\n }\n for(int i =0;i<n;i++) vis[i] = 0;\n ans = INT_MIN;\n cur =0;\n dfs_max(0, amount);\n return ans;\n }\n};\n``` | 2 | 0 | ['C++'] | 0 |
most-profitable-path-in-a-tree | Tracking Bob | tracking-bob-by-ayushy_78-kgjv | Intuition\nAs Bob is moving toward the root so it\'s definite that there is only one path for Bob. \nWhile Alice a varity of options dfs of the tree.\nWe find t | SelfHelp | NORMAL | 2022-11-21T18:26:16.709099+00:00 | 2022-11-21T18:26:16.709141+00:00 | 248 | false | # Intuition\nAs Bob is moving toward the root so it\'s definite that there is only one path for Bob. \nWhile Alice a varity of options dfs of the tree.\nWe find that Path for Bob then we do dfs for Alice to find the maximum profitable path.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nFirst Creating a bireacted graph to prepresnt the tree.\nThen use Backtraking to find the path to the root for `bob`.\nThen use Depth-First Search to find the Most profitable path use the path followed by Bob to know any open or shared paths.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: *`O(n)`*\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: *`O(n)`*\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n#define has(s, k) (s.find(k) != s.end())\n\nclass Solution {\npublic:\n void findRoot(vector<vector<int>>& graph, vector<bool>& visited, int i, vector<int>& res, vector<int>& path) {\n path.push_back(i);\n \n if(i == 0) {\n res = path;\n path.pop_back();\n return;\n }\n visited[i] = true;\n \n for(int v: graph[i])\n if(!visited[v])\n findRoot(graph, visited, v, res, path);\n \n visited[i] = false;\n path.pop_back();\n }\n \n void dfsLeaf(vector<vector<int>>& graph, vector<bool>& visited, int u, int step, int profit, int& res, unordered_map<int, int>& bobp, vector<int>& amount) {\n bool isLeaf = true;\n visited[u] = true;\n \n if(has(bobp, u)) {\n int s = bobp[u];\n if(s == step)\n profit += amount[u] / 2;\n else if(s > step)\n profit += amount[u];\n }\n else\n profit += amount[u];\n \n for(int v: graph[u]) {\n if(!visited[v]) {\n dfsLeaf(graph, visited, v, step + 1, profit, res, bobp, amount);\n isLeaf = false;\n }\n }\n \n visited[u] = false;\n \n if(isLeaf)\n res = max(res, profit);\n }\n \n int mostProfitablePath(vector<vector<int>>& edges, int bob, vector<int>& amount) {\n int n = amount.size();\n vector<vector<int>> graph(n + 1);\n for(vector<int>& edge: edges) {\n graph[edge[0]].push_back(edge[1]);\n graph[edge[1]].push_back(edge[0]);\n }\n vector<bool> visited(n, false);\n vector<int> bp, a;\n findRoot(graph, visited, bob, bp, a);\n unordered_map<int, int> bobp;\n for(int i = bp.size() - 1; i >= 0; i--)\n bobp[bp[i]] = i;\n int res = INT_MIN;\n dfsLeaf(graph, visited, 0, 0, 0, res, bobp, amount);\n return res;\n }\n};\n``` | 2 | 0 | ['Hash Table', 'Backtracking', 'Tree', 'Depth-First Search', 'C++'] | 1 |
most-profitable-path-in-a-tree | Python 3 beats 100% | python-3-beats-100-by-mmmichelle27-buqs | \tclass Solution:\n def mostProfitablePath(self, edges: List[List[int]], bob: int, amount: List[int]) -> int:\n adj = defaultdict(list)\n \n | Mmmichelle27 | NORMAL | 2022-11-13T18:29:03.524866+00:00 | 2022-11-13T18:29:03.524901+00:00 | 237 | false | \tclass Solution:\n def mostProfitablePath(self, edges: List[List[int]], bob: int, amount: List[int]) -> int:\n adj = defaultdict(list)\n \n for a, b in edges:\n adj[a].append(b)\n adj[b].append(a)\n \n # Update the tree based on Bob\n bRoute = []\n visited = {bob}\n def findRoot(cur):\n nonlocal bRoute\n nonlocal visited\n \n if cur == 0:\n bRoute.append(cur)\n return True\n \n for nei in adj[cur]:\n if nei not in visited:\n visited.add(nei)\n if findRoot(nei):\n bRoute.append(cur)\n return True\n \n return False\n \n findRoot(bob)\n pathIds = bRoute[::-1]\n pathLen = len(bRoute)\n \n for i in range((pathLen+1)//2):\n if i == (pathLen+1)//2-1 and pathLen%2 == 1:\n amount[pathIds[i]] //= 2\n else:\n amount[pathIds[i]] = 0\n \n # Use bfs to find the maximum amount that A can get\n ans = float(\'-inf\')\n visited = {0}\n que = deque([(0, amount[0])])\n while que:\n cur, cum = que.popleft()\n isLeaf = True\n for nei in adj[cur]:\n if nei not in visited:\n visited.add(nei)\n que.append((nei, cum+amount[nei]))\n isLeaf = False\n \n if isLeaf:\n ans = max(ans, cum)\n \n return ans | 2 | 0 | [] | 1 |
most-profitable-path-in-a-tree | DFS [Fully Explained with Comments] | dfs-fully-explained-with-comments-by-ms9-422x | Approach:\nNOTE: Alice can Move only Down , Bob only Above as per Ques\n1. Move Bob first from node B to node 0 , updating amount to 0(if Bob travels before Ali | MSJi | NORMAL | 2022-11-12T21:51:10.180346+00:00 | 2022-11-12T21:51:10.180381+00:00 | 314 | false | **Approach:**\nNOTE: Alice can Move only Down , Bob only Above as per Ques\n1. Move Bob first from node B to node 0 , updating amount to 0(if Bob travels before Alice , as the gate is OPEN for Alice) **or** amount/2 (if both reach simultaneously)\n2. Find Max path sum from node 0 to leaf Node (**answer may or may NOT include Bob path**) \n```\n void dfs1(int node,int par,int disF0,vector<int>& distance,vector<int>& parent,vector<vector<int>>& adjM){\n \n distance[node] = disF0;\n parent[node] = par;\n \n for(auto v:adjM[node]){\n if(v == par){\n // node calling recursion on parent\n continue;\n }\n dfs1(v,node,disF0 +1,distance,parent,adjM);\n }\n }\n \n int dfs2(int node,int par,vector<vector<int>>& adjM,vector<int>& amount){\n \n int ans = INT_MIN;\n for(auto v:adjM[node]){\n //Find Max from either Left or Right\n if(v != par){\n ans = max(ans,dfs2(v,node,adjM,amount));\n }\n }\n \n if(ans == INT_MIN){\n return amount[node];\n }\n return ans + amount[node];\n }\n \n int mostProfitablePath(vector<vector<int>>& edges, int bob, vector<int>& amount) {\n int n = amount.size(); // Number Of Nodes\n vector<int> parent(n,-1); // Needed to Move Bob from node B to node 0\n vector<int> distance(n,0); // Needed to decide whether Alice moves first or Bob to current Node\n vector<vector<int>> adjM(n);\n \n for(int i=0;i<edges.size();i++){\n int u = edges[i][0]; \n int v = edges[i][1];\n adjM[u].push_back(v);\n //Undirected Given in ques\n adjM[v].push_back(u);\n\n }\n \n //Fill parent and distance , to help in Bob traversal , starting from node 0\n dfs1(0,-1,0,distance,parent,adjM);\n \n //Travel from Bob to 0\n int cur = bob ,curDisOfBob = 0;\n while(cur != 0){\n //Note: distance[cur] here denotes How away Alice in right now from Bob\n if(curDisOfBob < distance[cur]){\n //Bob already traversed , so gate open for ALice\n amount[cur] = 0;\n }\n else if(curDisOfBob == distance[cur]){\n //Both reaches simultaneously , divide equally (price(-) or reward(+))\n amount[cur] = amount[cur]/2;\n }\n\n\n cur = parent[cur];\n curDisOfBob++;\n }\n \n \n //Maximum sum from node 0 till leaf Node\n \n return dfs2(0,-1,adjM,amount);\n \n }\n```\n**TC:**\nO[n] \n\n**SC:**\nO[n] | 2 | 0 | ['Depth-First Search', 'C'] | 1 |
most-profitable-path-in-a-tree | Python | DFS approach | python-dfs-approach-by-divyanshugairola-qgo7 | Intuition\n Describe your first thoughts on how to solve this problem. \nAlice can reach to Bob from one path only as no. of edges is n - 1 and it is given that | divyanshugairola | NORMAL | 2022-11-12T16:20:21.759594+00:00 | 2022-11-12T16:20:21.759620+00:00 | 565 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nAlice can reach to Bob from one path only as no. of edges is n - 1 and it is given that it is a tree.\n\n**First DFS**\nWe will first run a dfs to find the bob and in post order while returning from that path update the amount that will be bob\'s contribution.\n\n**Second DFS**\nThen run a second dfs to calculate the max income.\n\n# Approach\nRun two dfs \n- 1st to remove the bob\'s contribution \n- 2nd to calculate the max income which alice can get.\n\n# Complexity\n- Time complexity:\nO(N)\n\n- Space complexity:\nO(N)\n\n# Code\n```\nimport math\nfrom collections import deque, defaultdict\nimport sys\nsys.setrecursionlimit(10**5) \nclass Solution:\n def mostProfitablePath(self, edges: List[List[int]], bob: int, amount: List[int]) -> int:\n graph = defaultdict(set)\n for u, v in edges:\n graph[u].add(v)\n graph[v].add(u)\n visited = set()\n self.lvl = 0\n self.sum = 0\n self.max = -math.inf\n def remove_bob_income(src, bob, lvl):\n if src == bob:\n self.lvl = lvl\n amount[bob] = 0\n return True\n visited.add(src)\n for child in graph[src]:\n if child not in visited:\n ans = remove_bob_income(child, bob, lvl + 1)\n if ans:\n if self.lvl & 1 and lvl == (self.lvl + 1)//2:\n amount[src] //= 2\n elif lvl > (self.lvl // 2):\n amount[src] = 0\n else:\n self.sum += amount[src] \n return True\n return False\n \n visited.remove(src)\n \n def dfs(src, income, visited):\n if len(graph[src]) == 1 and src != 0:\n self.max = max(self.max, income)\n return\n visited.add(src)\n for child in graph[src]:\n if child not in visited:\n dfs(child, income + amount[child], visited)\n visited.remove(src)\n \n remove_bob_income(0, bob, 1)\n dfs(0, amount[0], set())\n return self.max\n \n \n \n``` | 2 | 0 | ['Tree', 'Depth-First Search', 'Python', 'Python3'] | 0 |
most-profitable-path-in-a-tree | C++ || DFS + BFS || TIME 100% faster O(n), SPACE 100% smaller O(n) | c-dfs-bfs-time-100-faster-on-space-100-s-llvq | First step: Do DFS to find the Bob path (only one possible path) to reach node 0, and save the path in Vpath_B \nSecond step: Do BFS on Alice, while at each st | tangerrine2112 | NORMAL | 2022-11-12T16:19:01.166354+00:00 | 2022-11-12T16:19:01.166417+00:00 | 934 | false | First step: Do DFS to find the Bob path (only one possible path) to reach node 0, and save the path in Vpath_B \nSecond step: Do BFS on Alice, while at each step of BFS move Bob a node further by deleting one node from Vpath_B\n\n```\nclass Solution {\nprivate:\n vector<vector<int>> Adj;\n vector<int> visited;\n vector<int> Vpath_B;\n //DFS for Bob\n int find_path_B(int n){\n if(n == 0){Vpath_B.push_back(n); return 1;}\n \n if(visited[n] == 1){return 0;}\n visited[n] = 1;\n \n for(auto &v: Adj[n]){\n int flag = find_path_B(v);\n if(flag != 1){continue;}\n \n Vpath_B.push_back(n);\n return 1;\n }\n \n return 0;\n }\npublic:\n int mostProfitablePath(vector<vector<int>>& edges, int bob, vector<int>& amount) {\n \n int len_n = amount.size();\n Adj.resize(len_n, vector<int>());\n for(auto &E:edges){\n int u = E[0], v = E[1];\n Adj[u].push_back(v);\n Adj[v].push_back(u);\n }\n \n //DFS of bob\n visited.resize(len_n, 0);\n find_path_B(bob);\n \n// vector<int> Vp2 = Vpath_B;\n// for(int i = 0; i < Vp2.size(); i++){\n// cout << Vp2[i] << " ";\n// }\n// cout << endl << endl;\n \n amount[bob] = 0;\n Vpath_B.pop_back();\n \n \n using pii = pair<int,int>;\n int val = amount[0];\n queue<pii> Q({{0,val}});\n int Max = INT_MIN;\n \n vector<int> visited2(len_n, 0);\n visited2[0] = 1;\n //BFS for Alice, while maintaing Bob location on its path\n while(!Q.empty()){\n int len_Q = Q.size();\n\t\t\t\n\t\t\t//maintaing Bob\'s position\n int n_bob = -1;\n if(!Vpath_B.empty()){\n n_bob = Vpath_B.back();\n Vpath_B.pop_back();\n }\n\n\t\t\t//Alice\'s next move\n while(len_Q--){\n int u = Q.front().first;\n int val = Q.front().second;\n Q.pop();\n \n \n if(Adj[u].size() == 1 && u != 0){ //leaf\n Max = max(Max, val);\n continue;\n }\n \n for(int &v: Adj[u]){\n if(visited2[v] == 1){continue;}\n visited2[v] = 1; \n \n if(v != n_bob){\n Q.push({v, val+ amount[v]});\n continue;\n }\n \n Q.push({v, val+amount[v]/2});\n }\n }\n \n\t\t\t//rewards and costs taken away by Bob\n if(n_bob != -1){amount[n_bob] = 0;}\n }\n \n return Max;\n \n }\n};\n``` | 2 | 0 | [] | 0 |
most-profitable-path-in-a-tree | DFS + BT | dfs-bt-by-claytonjwong-htcm | Perform DFS + BT (depth-first-search with back-tracking)\n\n1. Find Bob\'s path to node 0 via DFS + BT\n2. Then DFS + BT all possibilities for Alice\'s path in | claytonjwong | NORMAL | 2022-11-12T16:00:26.419730+00:00 | 2022-11-13T16:03:19.683011+00:00 | 1,885 | false | Perform DFS + BT (depth-first-search with back-tracking)\n\n1. Find Bob\'s path to node `0` via DFS + BT\n2. Then DFS + BT all possibilities for Alice\'s path in parallel with each `i`<sup>th</sup> node of Bob\'s path\n\nThere\'s 3 possibilities for `cost` we can `take` which is accumulated onto what we `have`:\n\n1. if Alice and Bob are on the same node, we `take` half the `cost`\n2. if Bob hasn\'t seen Alice\'s node, we `take` the full `cost`\n3. otherwise we `take` nothing\n\nUpon reaching a leaf node in the set of `leaves`, we consider the maximum of what we `have` as the `best` answer.\n\n* Note: if node `0` is one of the `leaves` we remove it, since it is not a `leaf` node candidate\n\n---\n\n**\u2B50\uFE0F Back-Tracking (BT) example:**\n\n"BT" is back-tracking, ie. during our DFS traversal we `go()` visit adjacent nodes, if we arrive at a node which is a "`fork` in the road" we explore each unique path\'s state by back-tracking to the node where the path forked as the recursive stack unwinds. The recusive stack unwinds as the base cases (leaf nodes) are reached, ie. as we `return` from the recursive invocations of `go()`. So before we `return`, we "unset" what was "set" in reverse to revert back to each previous state.\n\n**\uD83D\uDE80 What does it mean to recursively `go()` perform a Depth-First-Search (DFS) traversal?**\n\nLet each edge\'s nodes be denoted as (`u`, `v`) pairs, ie. `u` --> `v`, then "`here`" is node `u` and "`there`" is node `v`.\n\u2022 See [\uD83C\uDFA8 The ART of Dynamic Programming](https://leetcode.com/discuss/general-discussion/712010/The-ART-of-Dynamic-Programming-An-Intuitive-Approach%3A-from-Apprentice-to-Master) for more details and a picture, ie. "`here`" is relative to "`there`"\n\n\n\nAn example of BT can be observed in the `find_bob_path` function (see comments below):\n\n```\n def find_bob_path(path = [bob], seen = set([bob])):\n nonlocal bob_path\n u = path[-1]\n if not u:\n bob_path = path[:]\n if len(bob_path):\n return\n for v in adj[u]:\n if v not in seen:\n path.append(v); seen.add(v) # \uD83D\uDC49 forward-tracking (ie. "set" state here)\n find_bob_path(path, seen) # \uD83D\uDE80 recursively perform DFS traversal\n path.pop(); seen.remove(v) # \uD83D\uDC48 back-tracking (ie. "unset" state here)\n```\n\n---\n\n*Python3*\n```\nclass Solution:\n def mostProfitablePath(self, E: List[List[int]], bob: int, cost: List[int]) -> int:\n N = len(cost)\n adj = defaultdict(list)\n for u, v in E:\n adj[u].append(v)\n adj[v].append(u)\n leaves = set()\n for u in range(N):\n if len(adj[u]) == 1:\n leaves.add(u)\n if 0 in leaves:\n leaves.remove(0)\n bob_path = []\n def find_bob_path(path = [bob], seen = set([bob])):\n nonlocal bob_path\n u = path[-1]\n if not u:\n bob_path = path[:]\n if len(bob_path):\n return\n for v in adj[u]:\n if v not in seen:\n path.append(v); seen.add(v)\n find_bob_path(path, seen)\n path.pop(); seen.remove(v)\n find_bob_path()\n best = float(\'-inf\')\n def go(u = 0, i = 0, have = 0, seen_a = set([0]), seen_b = set([])):\n nonlocal best\n if i < len(bob_path):\n seen_b.add(bob_path[i])\n take = cost[u] // 2 if i < len(bob_path) and u == bob_path[i] else cost[u] if u not in seen_b else 0\n have += take\n if u in leaves:\n best = max(best, have)\n for v in adj[u]:\n if v not in seen_a:\n seen_a.add(v)\n go(v, i + 1, have, seen_a, seen_b)\n seen_a.remove(v)\n if i < len(bob_path):\n seen_b.remove(bob_path[i])\n go()\n return best\n```\n | 2 | 0 | [] | 4 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.