Datasets:
kaysss
/
leetcode-problem-solutions

Dataset card Data Studio Files Community
question_slug
stringlengths
3
77
title
stringlengths
1
183
slug
stringlengths
12
45
summary
stringlengths
1
160
⌀
author
stringlengths
2
30
certification
stringclasses
2 values
created_at
stringdate
2013-10-25 17:32:12
2025-04-12 09:38:24
updated_at
stringdate
2013-10-25 17:32:12
2025-04-12 09:38:24
hit_count
int64
0
10.6M
has_video
bool
2 classes
content
stringlengths
4
576k
upvotes
int64
0
11.5k
downvotes
int64
0
358
tags
stringlengths
2
193
comments
int64
0
2.56k
contain-virus
Efficient JS solution (Beat 100% both time and memory)
efficient-js-solution-beat-100-both-time-g46j
\n\n# Intuition\nFirst BFS, then BFS, and BFS right after that. Finally, BFS.\n*Edit: I forgot that we also need BFS.\n\n# Complexity\n- Time complexity: O((mn)
CuteTN
NORMAL
2023-09-24T11:28:35.855727+00:00
2023-09-24T11:28:35.855758+00:00
27
false
![image.png](https://assets.leetcode.com/users/images/493ed78a-e2d2-42ae-af85-71868c93ddda_1695554753.422481.png)\n\n# Intuition\nFirst BFS, then BFS, and BFS right after that. Finally, BFS.\n*Edit: I forgot that we also need BFS.\n\n# Complexity\n- Time complexity: $$O((mn)^2)$$\n- Space complexity: $$O(mn)$$\n\n# Code\n```js\n/**\n * @template TItem\n */\nclass CircularQueue {\n /**\n * @param {number} capacity\n */\n constructor(capacity) {\n /**\n * @private\n * @type {number}\n */\n this._capacity = capacity;\n /**\n * @private\n * @type {number}\n */\n this._size = 0;\n /**\n * @private\n * @type {number}\n */\n this._bottom = 0;\n\n /**\n * @private\n * @type {TItem[]}\n */\n this._data = Array(capacity).fill(undefined);\n }\n\n /**\n * @private\n * @param {number} index\n * @returns {number}\n */\n _getCircularIndex(index) {\n const result = index % this._capacity;\n if (result < 0) result += this._capacity;\n return result;\n }\n\n get capacity() {\n return this._capacity;\n }\n\n get size() {\n return this._size;\n }\n\n get nextItem() {\n return this._size ? this._data[this._bottom] : undefined;\n }\n\n get lastItem() {\n return this._size\n ? this._data[this._getCircularIndex(this._bottom + this._size - 1)]\n : undefined;\n }\n\n /**\n * @param {...TItem} items\n */\n enqueue(...items) {\n if (this._size + items.length > this._capacity)\n throw new Error("Queue capacity exceeded.");\n\n let queueIndex = (this._bottom + this._size) % this._capacity;\n this._size += items.length;\n for (let i = 0; i < items.length; i++) {\n this._data[queueIndex] = items[i];\n queueIndex = (queueIndex + 1) % this._capacity;\n }\n }\n\n /**\n * @returns {TItem | undefined}\n */\n dequeue() {\n if (!this._size) return undefined;\n\n const result = this._data[this._bottom];\n this._bottom = (this._bottom + 1) % this._capacity;\n this._size--;\n\n return result;\n }\n\n clear() {\n this._size = 0;\n }\n}\n\nconst qr = new CircularQueue(2500);\nconst qc = new CircularQueue(2500);\n\nconst threats = [];\nconst fences = [];\nfunction initLabel(x) {\n while (x >= threats.length) {\n threats.push(0);\n fences.push(0);\n }\n threats[x] = 0;\n fences[x] = 0;\n}\n\nconst DIR_R = [0, 0, 1, -1];\nconst DIR_C = [1, -1, 0, 0];\n\n/**\n * guideline:\n * &7\n * 0: uninfected and not (yet) threaten\n * 1: infected but unvisited\n * 2: infected and visited\n * 3: uninfected and threaten\n * 4: locked up\n * >>3\n * label\n */\n\n/**\n * @param {number[][]} isInfected\n * @return {number}\n */\nvar containVirus = function (isInfected) {\n let n = isInfected[0].length;\n let m = isInfected.length;\n let label = 0;\n let res = 0;\n\n function bfs(ir, ic, label) {\n qr.enqueue(ir);\n qc.enqueue(ic);\n let labelState = (label << 3) | 2;\n isInfected[ir][ic] = labelState;\n initLabel(label);\n\n while (qr.size) {\n let r = qr.dequeue();\n let c = qc.dequeue();\n\n for (let i = 0; i < 4; i++) {\n let rr = r + DIR_R[i];\n let cc = c + DIR_C[i];\n let state = isInfected[rr]?.[cc];\n if (state == undefined) continue;\n\n switch (state & 7) {\n case 0: {\n isInfected[rr][cc] = (label << 3) | 3;\n fences[label]++;\n threats[label]++;\n break;\n }\n case 1: {\n qr.enqueue(rr);\n qc.enqueue(cc);\n isInfected[rr][cc] = labelState;\n break;\n }\n case 3: {\n fences[label]++;\n if ((state >> 3) != label) {\n threats[label]++;\n isInfected[rr][cc] = (label << 3) | 3;\n }\n break;\n }\n }\n }\n }\n }\n\n function isStillThreaten(r, c, lockedLabel) {\n for (let i = 0; i < 4; i++) {\n let rr = r + DIR_R[i];\n let cc = c + DIR_C[i];\n let state = isInfected[rr]?.[cc];\n if ((state & 7) == 2 && (state >> 3) != lockedLabel) return true;\n }\n }\n\n while (true) {\n label = 0;\n let lockedLabel = 0;\n\n for (let r = 0; r < m; r++) {\n for (let c = 0; c < n; c++) {\n if (isInfected[r][c] == 1) {\n bfs(r, c, label);\n if (threats[label] > threats[lockedLabel]) lockedLabel = label;\n label++;\n }\n }\n }\n\n if (!label) return res;\n\n res += fences[lockedLabel];\n\n for (let r = 0; r < m; r++) {\n for (let c = 0; c < n; c++) {\n if ((isInfected[r][c] & 7) == 3) {\n if (isStillThreaten(r, c, lockedLabel)) isInfected[r][c] = 1;\n else isInfected[r][c] = 0;\n }\n }\n }\n\n for (let r = 0; r < m; r++) {\n for (let c = 0; c < n; c++) {\n let state = isInfected[r][c];\n if ((state & 7) == 2) {\n if ((state >> 3) == lockedLabel) isInfected[r][c] = 4;\n else isInfected[r][c] = 1;\n }\n }\n }\n }\n};\n```
0
0
['Breadth-First Search', 'Queue', 'JavaScript']
0
contain-virus
ONLY GOD KNOWS
only-god-knows-by-hrtoimukra-h05h
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
hrtoimukra
NORMAL
2023-09-01T06:50:16.980176+00:00
2023-09-01T06:50:16.980197+00:00
61
false
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n\n int bfs(int r,int c,vector<vector<int>>& isInfected,vector<vector<bool>>& vis,vector<vector<bool>>& cont){\n int count=0;\n int row=isInfected.size();\n int col=isInfected[0].size(); \n\n queue<pair<int,int>> q;\n q.push({r,c}); \n vis[r][c]=true;\n\n int dx[4]={0,-1,0,1};\n int dy[4]={1,0,-1,0};\n\n vector<vector<bool>> seen(row,vector<bool>(col,false)); \n\n while(!q.empty()){\n\n int u=q.front().first;\n int v=q.front().second;\n q.pop();\n\n for(int k=0;k<4;++k){\n int nr=u+dx[k];\n int nc=v+dy[k];\n\n if(0<=nr && nr<row && 0<=nc && nc<col && !vis[nr][nc] && !cont[nr][nc]){\n if(isInfected[nr][nc]){\n vis[nr][nc]=true;\n q.push({nr,nc}); \n }\n else if(!isInfected[nr][nc]){\n if(!seen[nr][nc]){\n seen[nr][nc]=true;\n count++; \n } \n } \n } \n } \n }\n\n return count; \n } \n\n int quarantine(int r,int c,vector<vector<int>>& isInfected,vector<vector<bool>>& cont){\n \n int row=isInfected.size();\n int col=isInfected[0].size();\n\n int dx[4]={0,-1,0,1};\n int dy[4]={1,0,-1,0};\n\n int walls=0;\n\n queue<pair<int,int>> q;\n\n vector<vector<bool>> vis(row,vector<bool>(col,false));\n\n vis[r][c]=true; \n cont[r][c]=true;\n q.push({r,c});\n \n while(!q.empty()){\n\n int u=q.front().first;\n int v=q.front().second; \n q.pop();\n\n for(int k=0;k<4;++k){\n int nr=u+dx[k];\n int nc=v+dy[k];\n\n if(0<=nr && nr<row && 0<=nc && nc<col){\n if(!vis[nr][nc] && isInfected[nr][nc] && !cont[nr][nc]){\n vis[nr][nc]=true;\n cont[nr][nc]=true;\n q.push({nr,nc}); \n } \n else if(!isInfected[nr][nc])\n walls++;\n } \n }\n }\n //std::cout<<"Returning"<<std::endl;\n return walls; \n } \n\n void spread(int r,int c,vector<vector<int>>& isInfected,vector<vector<bool>>& seen,vector<vector<bool>>& mark,vector<vector<bool>>& cont){\n \n int row=isInfected.size();\n int col=isInfected[0].size();\n \n int dx[4]={0,-1,0,1};\n int dy[4]={1,0,-1,0};\n\n queue<pair<int,int>> q;\n\n q.push({r,c});\n seen[r][c]=true;\n\n while(!q.empty()){\n\n int u=q.front().first;\n int v=q.front().second;\n\n q.pop();\n\n for(int k=0;k<4;++k){\n\n int nr=u+dx[k];\n int nc=v+dy[k];\n\n if(0<=nr && nr<row && 0<=nc && nc<col){\n if(!seen[nr][nc] && isInfected[nr][nc] && !cont[nr][nc] && !mark[nr][nc]){\n seen[nr][nc]=true;\n q.push({nr,nc});\n } \n else if(!isInfected[nr][nc]){\n isInfected[nr][nc]=1;\n mark[nr][nc]=true; \n } \n } \n } \n } \n\n std::cout<<"No control here"<<std::endl; \n } \n\n int containVirus(vector<vector<int>>& isInfected) {\n int row=isInfected.size();\n int col=isInfected[0].size();\n\n int walls=0;\n vector<vector<bool>> cont(row,vector<bool>(col,false));\n\n while(true){\n\n vector<vector<bool>> vis(row,vector<bool>(col,false));\n \n int maxm=0;\n int maxr;\n int maxc;\n\n for(int i=0;i<row;++i){\n for(int j=0;j<col;++j){\n if(isInfected[i][j] && !vis[i][j] && !cont[i][j]){\n int infect=bfs(i,j,isInfected,vis,cont);\n\n //std::cout<<"Infected="<<infect<<std::endl;\n \n if(maxm<infect){\n maxm=infect;\n maxr=i;\n maxc=j; \n } \n } \n } \n }\n\n std::cout<<"First Iteration completed"<<std::endl;\n\n std::cout<<"Maximum Infected="<<maxm<<std::endl;\n if(maxm==0)\n break;\n\n walls+=quarantine(maxr,maxc,isInfected,cont);\n\n std::cout<<"Walls required="<<walls<<std::endl;\n \n vector<vector<bool>> seen(row,vector<bool>(col,false));\n vector<vector<bool>> mark(row,vector<bool>(col,false));\n\n for(int i=0;i<row;++i){\n for(int j=0;j<col;++j){\n if(isInfected[i][j] && !seen[i][j] && !cont[i][j] && !mark[i][j])\n spread(i,j,isInfected,seen,mark,cont); \n } \n } \n\n std::cout<<"Spread Done"<<std::endl; \n }\n return walls;\n }\n};\n```
0
0
['C++']
0
contain-virus
Easiest Solution
easiest-solution-by-kunal7216-0gsu
\n\n# Code\njava []\nclass Solution {\n \n private static final int[][] DIR = new int[][]{\n {1, 0}, {-1, 0}, {0, 1}, {0, -1}\n };\n \n pu
Kunal7216
NORMAL
2023-08-28T14:50:39.970699+00:00
2023-08-28T14:50:39.970729+00:00
142
false
\n\n# Code\n``` java []\nclass Solution {\n \n private static final int[][] DIR = new int[][]{\n {1, 0}, {-1, 0}, {0, 1}, {0, -1}\n };\n \n public int containVirus(int[][] isInfected) {\n int m = isInfected.length, n = isInfected[0].length;\n int ans = 0;\n \n while( true ) {\n // infected regions, sorted desc according to the number of nearby \n // uninfected nodes\n PriorityQueue<Region> pq = new PriorityQueue<Region>();\n // already visited cells\n boolean[][] visited = new boolean[m][n];\n \n // find regions\n for(int i=0; i<m; i++) {\n for(int j=0; j<n; j++) {\n \n // if current cell is infected, and it\'s not visited\n if( isInfected[i][j] != 1 || visited[i][j] ) \n continue;\n \n // we found a new region, dfs to find all the infected\n // and uninfected cells in the current region\n Region reg = new Region();\n dfs(i, j, reg, isInfected, visited, new boolean[m][n], m, n);\n \n // if there are some uninfected nodes in this region, \n // we can contain it, so add it to priority queue\n if( reg.uninfected.size() != 0)\n pq.offer(reg);\n }\n }\n \n // if there are no regions to contain, break\n if( pq.isEmpty() )\n break;\n\n // Contain region with most uninfected nodes\n Region containReg = pq.poll();\n ans += containReg.wallsRequired;\n \n // use (2) to mark a cell as contained\n for(int[] cell : containReg.infected)\n isInfected[cell[0]][cell[1]] = 2;\n \n // Spread infection to uninfected nodes in other regions\n while( !pq.isEmpty() ) {\n Region spreadReg = pq.poll();\n \n for(int[] cell : spreadReg.uninfected)\n isInfected[cell[0]][cell[1]] = 1;\n }\n }\n return ans;\n }\n \n private void dfs(int i, int j, Region reg, int[][] grid, boolean[][] visited, boolean[][] uninfectedVis, int m, int n) {\n visited[i][j] = true;\n reg.addInfected(i, j);\n \n for(int[] dir : DIR) {\n int di = i + dir[0];\n int dj = j + dir[1];\n \n // continue, if out of bounds OR contained OR already visited\n if( di < 0 || dj < 0 || di == m || dj == n || grid[di][dj] == 2 || visited[di][dj] )\n continue;\n \n // if neighbour node is not infected\n if( grid[di][dj] == 0 ) {\n // a wall will require to stop the spread from cell (i,j) to (di, dj)\n reg.wallsRequired++;\n \n // if this uninfected node is not already visited for current region\n if( !uninfectedVis[di][dj] ) {\n uninfectedVis[di][dj] = true;\n reg.addUninfected(di, dj);\n }\n } else \n dfs(di, dj, reg, grid, visited, uninfectedVis, m, n);\n }\n }\n}\nclass Region implements Comparable<Region> {\n public List<int[]> infected;\n public List<int[]> uninfected;\n public int wallsRequired;\n \n public Region() {\n infected = new ArrayList();\n uninfected = new ArrayList();\n }\n \n public void addInfected(int row, int col) {\n infected.add(new int[]{ row, col });\n }\n \n public void addUninfected(int row, int col) {\n uninfected.add(new int[]{ row, col });\n }\n \n @Override\n public int compareTo(Region r2) {\n return Integer.compare(r2.uninfected.size(), uninfected.size());\n }\n}\n```\n```c++ []\nclass Solution {\npublic:\n int dx[4]={-1,0,1,0},dy[4]={0,1,0,-1};\n int walls=0;\n \n bool isValid(int i,int j,int m,int n,vector<vector<int>> &vis)\n {\n return (i>=0 && i<m && j>=0 && j<n && !vis[i][j]); \n }\n \n int find(int i,int j,int m,int n,vector<vector<int>>& a)\n {\n int c=0;\n \n queue<pair<int,int>> q;\n vector<vector<int>> vis(m,vector<int>(n,0));\n \n a[i][j]=2;\n q.push({i,j});\n \n while(!q.empty())\n {\n i=q.front().first;\n j=q.front().second;\n q.pop();\n \n for(int k=0;k<4;k++)\n {\n if(isValid(i+dx[k],j+dy[k],m,n,vis))\n {\n if(a[i+dx[k]][j+dy[k]]==0)\n c++;\n else if(a[i+dx[k]][j+dy[k]]==1)\n {\n a[i+dx[k]][j+dy[k]]=2;\n q.push({i+dx[k],j+dy[k]});\n }\n \n vis[i+dx[k]][j+dy[k]]=1;\n \n }\n }\n }\n \n return c;\n }\n \n void putwalls(pair<int,int> &change,int m,int n,vector<vector<int>>& a)\n {\n int i,j;\n i=change.first;\n j=change.second;\n \n queue<pair<int,int>> q;\n vector<vector<int>> vis(m,vector<int>(n,0));\n \n q.push({i,j});\n \n while(!q.empty())\n {\n i=q.front().first;\n j=q.front().second;\n a[i][j]=-1;\n q.pop();\n \n \n for(int k=0;k<4;k++)\n {\n if(isValid(i+dx[k],j+dy[k],m,n,vis))\n {\n if(a[i+dx[k]][j+dy[k]]==2)\n {\n q.push({i+dx[k],j+dy[k]});\n a[i+dx[k]][j+dy[k]]=-1;\n vis[i+dx[k]][j+dy[k]]=1; \n } \n else if(a[i+dx[k]][j+dy[k]]==0)\n walls++;\n }\n }\n }\n }\n \n void spread(int m,int n,vector<vector<int>>& a)\n {\n int i,j;\n queue<pair<int,int>> q;\n vector<vector<int>> vis(m,vector<int>(n,0));\n \n for(i=0;i<m;i++)\n {\n for(j=0;j<n;j++)\n {\n if(a[i][j]==2)\n {\n a[i][j]=1;\n q.push({i,j});\n\n }\n }\n }\n \n while(!q.empty())\n {\n i=q.front().first;\n j=q.front().second;\n q.pop();\n \n for(int k=0;k<4;k++)\n {\n if(isValid(i+dx[k],j+dy[k],m,n,vis) && a[i+dx[k]][j+dy[k]]==0)\n {\n a[i+dx[k]][j+dy[k]]=1;\n vis[i+dx[k]][j+dy[k]]=1; \n }\n }\n }\n }\n \n int containVirus(vector<vector<int>>& a) {\n int m=a.size(),n=a[0].size();\n int i,j;\n \n int infected=INT_MIN;\n pair<int,int> change;\n \n while(infected!=0)\n {\n infected=0;\n for(i=0;i<m;i++)\n {\n for(j=0;j<n;j++)\n {\n if(a[i][j]==1)\n {\n int x=find(i,j,m,n,a);\n if(x>infected)\n {\n change={i,j};\n infected=x;\n }\n }\n }\n }\n \n if(infected!=0)\n {\n putwalls(change,m,n,a);\n spread(m,n,a);\n }\n }\n \n return walls;\n }\n};\n```\n```python3 []\nclass Solution:\n def containVirus(self, isInfected: List[List[int]]) -> int:\n \'\'\'\n isInfected[r][c]:\n 0 : Uninfected\n 1 : Infected\n 2 : Infected & restricted\n \'\'\'\n m = len(isInfected)\n n = len(isInfected[0])\n\n borders = 0\n threatened = 0\n def dfs(r, c, id):\n nonlocal borders, threatened\n if r < 0 or r>=m or c < 0 or c>=n:\n return\n\n if isInfected[r][c] == 1:\n if visited[r][c] == 0:\n visited[r][c] = 1\n dfs(r-1, c, id)\n dfs(r+1, c, id)\n dfs(r, c-1, id)\n dfs(r, c+1, id)\n else:\n pass\n elif isInfected[r][c] == 0:\n if visited[r][c] == id:\n borders += 1\n else:\n borders += 1\n threatened += 1\n visited[r][c] = id\n \n def flood(r, c, find, repl):\n if r < 0 or r>=m or c < 0 or c>=n or isInfected[r][c] != find:\n return\n isInfected[r][c] = repl\n flood(r-1, c, find, repl)\n flood(r+1, c, find, repl)\n flood(r, c-1, find, repl)\n flood(r, c+1, find, repl)\n \n def expand(r, c, id):\n if r < 0 or r>=m or c < 0 or c>=n or visited[r][c] == 1:\n return\n visited[r][c] = 1\n if isInfected[r][c] == 0:\n isInfected[r][c] = 1\n elif isInfected[r][c] == 1:\n expand(r+1, c, id)\n expand(r-1, c, id)\n expand(r, c-1, id)\n expand(r, c+1, id) \n\n total_walls = 0\n\n while True:\n # Day ---------------------------------------------------\n max_th = 0\n max_th_loc = (None, None)\n max_th_border = 0\n id = 3\n visited = [[0] * n for _ in range(m)]\n\n for r in range(m):\n for c in range(n):\n if isInfected[r][c]==1 and visited[r][c] == 0:\n \n borders = 0\n threatened = 0\n dfs(r, c, id)\n id += 1\n if threatened > max_th:\n max_th = threatened\n max_th_loc = r, c\n max_th_border = borders\n \n if max_th == 0:\n break\n total_walls += max_th_border\n # Restrict bordered region by making them dormant\n flood(*max_th_loc, 1, 2)\n\n # Night -------------------------------------------------\n\n visited = [[0] * n for _ in range(m)]\n for r in range(m):\n for c in range(n):\n if isInfected[r][c]==1 and visited[r][c] == 0:\n expand(r, c, id)\n id += 1\n\n return total_walls\n\n\n\n\n\n```
0
0
['C++', 'Java', 'Python3']
0
contain-virus
C++ faster than 92%
c-faster-than-92-by-ialight-cxqk
First get the new infection count for every region without spreading the infection. Also save the infected area cells for spreading the infection later. To coun
ialight
NORMAL
2023-08-06T16:28:00.184064+00:00
2023-08-06T16:28:00.184089+00:00
20
false
First get the new infection count for every region without spreading the infection. Also save the infected area cells for spreading the infection later. To count the possibly infected cells for every region, I am using different area/region code for visited matrix to not skip the non-infected cells. \n\nAfter that get the wall count for maximum infected area and spread infection from other areas.\n\n```\nclass Solution {\n int dir[4][2] = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};\n \n int getInfectionCount(vector<vector<int>>& grid, vector<vector<int>>& isVis, vector<pair<int, int>>& areaCells, int areaCode, int i, int j) {\n if (i < 0 or j < 0 or i >= grid.size() or j >= grid[0].size() or isVis[i][j] == areaCode or grid[i][j] == 2) {\n return 0;\n }\n\n isVis[i][j] = areaCode;\n if (grid[i][j] == 0) {\n return 1;\n }\n \n areaCells.push_back({i, j});\n \n int infectedCellsCount = 0;\n for (int d = 0; d < 4; d++) {\n infectedCellsCount += getInfectionCount(grid, isVis, areaCells, areaCode, i + dir[d][0], j + dir[d][1]);\n }\n \n return infectedCellsCount;\n }\n \n int infectAndGetWallCount(vector<vector<int>>& grid, vector<pair<int, int>>& areaCells, bool infect) {\n int wallCount = 0;\n \n for (auto[i, j] : areaCells) {\n if (!infect) {\n grid[i][j] = 2;\n }\n for (int d = 0; d < 4; d++) {\n int ii = i + dir[d][0];\n int jj = j + dir[d][1];\n \n if (ii < 0 or jj < 0 or ii >= grid.size() or jj >= grid[0].size()) continue;\n \n if (grid[ii][jj] == 0) {\n if (infect) {\n grid[ii][jj] = 1;\n }\n else {\n wallCount++;\n }\n }\n }\n }\n \n return wallCount;\n }\n \npublic:\n int containVirus(vector<vector<int>>& isInfected) {\n int m = isInfected.size(), n = isInfected[0].size(), totalWalls = 0;\n \n while (true) {\n int maxInfectionCount = 0, maxArea = -1;\n vector<vector<pair<int, int>>> areas;\n vector<vector<int>> isVis(m, vector<int>(n, 0));\n int areaCode = 1;\n\n for (int i = 0; i < m; i++) { \n for (int j = 0; j < n; j++) {\n if (isInfected[i][j] == 1 and isVis[i][j] == 0) {\n vector<pair<int, int>> areaCells;\n int infectionCount = getInfectionCount(isInfected, isVis, areaCells, areaCode, i, j);\n areaCode++;\n \n if (infectionCount > maxInfectionCount) {\n maxInfectionCount = infectionCount;\n maxArea = areas.size();\n }\n areas.push_back(areaCells);\n }\n }\n }\n \n if (maxArea == -1) break;\n \n totalWalls += infectAndGetWallCount(isInfected, areas[maxArea], false);\n for (int i = 0; i < areas.size(); i++) {\n if (i == maxArea) continue;\n infectAndGetWallCount(isInfected, areas[i], true);\n }\n }\n \n return totalWalls;\n }\n};\n```
0
0
['Depth-First Search']
0
contain-virus
C++ Solution which is easy to understand
c-solution-which-is-easy-to-understand-b-mexm
Intuition\n The objective is to identify the region that affects the maximum number of blocks and construct walls around it. This process is repeated until th
next_big_thing
NORMAL
2023-07-22T19:59:30.632428+00:00
2023-07-22T20:03:11.395600+00:00
93
false
# Intuition\n The objective is to identify the region that affects the maximum number of blocks and construct walls around it. This process is repeated until there are no remaining open regions\n\n# Approach\n\n1. find region which impacts maximum blocks\n2. contruct walls around it and deidentify the region and add walls to the ans.\n3. spread contamination to 1 neighbour blocks for each region present with virus\n4. repat step 1 until there is no region left\n\n\n\n\n\n# Code\n```\nclass Solution {\npublic:\n int containVirus(vector<vector<int>>& inf) {\n\n \n int m = inf.size();\n int n = inf[0].size();\n int ans = FindWalls(m,n,inf); \n return ans; \n\n }\n\n int FindWalls(int m , int n , vector<vector<int>>& inf)\n {\n \n int ans = 0;\n int maxima = 0 ;\n int start_x = 0;\n int start_y = 0;\n \n while(true)\n {\n maxima = 0;\n int local_ans = 0;\n vector<vector<int>> v(m,vector<int>(n,0));\n for(int i = 0 ; i< m;i++)\n {\n for(int j = 0 ;j<n;j++)\n {\n \n \n if(inf[i][j]==1&&v[i][j]==0)\n {\n initialize(v,m,n,inf);\n local_ans = blocks(i,j,v,inf,m,n);\n if(local_ans>maxima)\n {\n start_x = i;\n start_y = j;\n }\n maxima = max(maxima,local_ans);\n }\n\n }\n\n }\n\n if(maxima == 0)\n return ans;\n \n for(int i = 0 ;i<m;i++)\n for(int j =0 ; j<n;j++)\n v[i][j]=0;\n ans+=blockToSpread(start_x,start_y,v,inf,m,n);\n vector<vector<int>> G(m,vector<int>(n,0));\n Dismantle(start_x,start_y,inf,G,m,n);\n ContaminateMarking(inf,m,n); \n Contaminate(inf,m,n); \n }\n }\n\n \nvoid initialize(vector<vector<int>>& v, int m , int n,vector<vector<int>>& inf)\n {\n for(int i = 0 ;i<m;i++)\n {\n for(int j = 0 ; j<n;j++)\n {\n if(inf[i][j]==0)\n v[i][j]=0;\n }\n }\n }\n\n int blocks(int x, int y,vector<vector<int>>& v, vector<vector<int>>& inf , int m , int n)\n {\n if(x<0||x>=m||y<0||y>=n)\n return 0 ;\n \n \n\n if(v[x][y]==1)\n return 0;\n\n v[x][y] = 1;\n \n if(inf[x][y]==0)\n return 1;\n if(inf[x][y]==-1)\n return 0; \n\n\n int sum = 0 ;\n if(inf[x][y]==1)\n {\n sum+=blocks(x+1,y,v,inf,m,n);\n sum+=blocks(x-1,y,v,inf,m,n);\n sum+=blocks(x,y-1,v,inf,m,n);\n sum+=blocks(x,y+1,v,inf,m,n);\n }\n return sum;\n\n\n }\n\n int blockToSpread(int x, int y,vector<vector<int>>& v, vector<vector<int>>& inf , int m , int n)\n {\n if(x<0||x>=m||y<0||y>=n)\n return 0 ;\n \n if(inf[x][y]==0)\n {\n return 1;\n }\n\n if(v[x][y]==1)\n return 0;\n\n v[x][y] = 1;\n \n int sum = 0 ;\n if(inf[x][y]==1)\n {\n sum+=blockToSpread(x+1,y,v,inf,m,n);\n sum+=blockToSpread(x-1,y,v,inf,m,n);\n sum+=blockToSpread(x,y-1,v,inf,m,n);\n sum+=blockToSpread(x,y+1,v,inf,m,n);\n }\n return sum;\n\n\n }\n\n\n void Dismantle(int x, int y, vector<vector<int>>& inf , vector<vector<int>>& G , int m, int n)\n {\n if(x<0||x>=m||y<0||y>=n)\n return;\n\n if(G[x][y]==1)\n return;\n\n G[x][y]=1;\n\n if(inf[x][y]==1)\n {\n inf[x][y]=-1;\n Dismantle(x+1,y,inf,G,m,n);\n Dismantle(x-1,y,inf,G,m,n);\n Dismantle(x,y+1,inf,G,m,n);\n Dismantle(x,y-1,inf,G,m,n);\n\n }\n else\n {\n return;\n }\n \n }\n\n void ContaminateMarking(vector<vector<int>>& inf , int m , int n)\n {\n \n\n for(int i = 0 ;i<m;i++)\n {\n for(int j = 0 ; j<n;j++)\n {\n if(inf[i][j]==1)\n {\n ContaminateBlockMarking(i+1,j,inf,m,n);\n ContaminateBlockMarking(i-1,j,inf,m,n);\n ContaminateBlockMarking(i,j+1,inf,m,n);\n ContaminateBlockMarking(i,j-1,inf,m,n);\n }\n }\n }\n \n \n return;\n\n }\n\n void ContaminateBlockMarking(int x , int y , vector<vector<int>>& inf, int m ,int n )\n {\n if(x<0||x>=m||y<0||y>=n)\n return;\n \n if(inf[x][y] == 0)\n inf[x][y] = -2;\n\n return;\n\n }\n\n void Contaminate(vector<vector<int>>& inf , int m , int n)\n {\n for(int i = 0 ;i<m;i++)\n {\n for(int j = 0 ; j<n;j++)\n {\n if(inf[i][j]==-2)\n inf[i][j]= 1;\n }\n }\n return;\n }\n\n};\n```
0
0
['Greedy', 'Depth-First Search', 'C++']
0
contain-virus
Detailed and clear solution
detailed-and-clear-solution-by-mdakram28-db9m
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
mdakram28
NORMAL
2023-04-14T00:24:48.793514+00:00
2023-04-14T00:24:48.793546+00:00
104
false
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def containVirus(self, isInfected: List[List[int]]) -> int:\n \'\'\'\n isInfected[r][c]:\n 0 : Uninfected\n 1 : Infected\n 2 : Infected & restricted\n \'\'\'\n m = len(isInfected)\n n = len(isInfected[0])\n\n borders = 0\n threatened = 0\n def dfs(r, c, id):\n nonlocal borders, threatened\n if r < 0 or r>=m or c < 0 or c>=n:\n return\n\n if isInfected[r][c] == 1:\n if visited[r][c] == 0:\n visited[r][c] = 1\n dfs(r-1, c, id)\n dfs(r+1, c, id)\n dfs(r, c-1, id)\n dfs(r, c+1, id)\n else:\n pass\n elif isInfected[r][c] == 0:\n if visited[r][c] == id:\n borders += 1\n else:\n borders += 1\n threatened += 1\n visited[r][c] = id\n \n def flood(r, c, find, repl):\n if r < 0 or r>=m or c < 0 or c>=n or isInfected[r][c] != find:\n return\n isInfected[r][c] = repl\n flood(r-1, c, find, repl)\n flood(r+1, c, find, repl)\n flood(r, c-1, find, repl)\n flood(r, c+1, find, repl)\n \n def expand(r, c, id):\n if r < 0 or r>=m or c < 0 or c>=n or visited[r][c] == 1:\n return\n visited[r][c] = 1\n if isInfected[r][c] == 0:\n isInfected[r][c] = 1\n elif isInfected[r][c] == 1:\n expand(r+1, c, id)\n expand(r-1, c, id)\n expand(r, c-1, id)\n expand(r, c+1, id) \n\n total_walls = 0\n\n while True:\n # Day ---------------------------------------------------\n max_th = 0\n max_th_loc = (None, None)\n max_th_border = 0\n id = 3\n visited = [[0] * n for _ in range(m)]\n\n for r in range(m):\n for c in range(n):\n if isInfected[r][c]==1 and visited[r][c] == 0:\n \n borders = 0\n threatened = 0\n dfs(r, c, id)\n id += 1\n if threatened > max_th:\n max_th = threatened\n max_th_loc = r, c\n max_th_border = borders\n \n if max_th == 0:\n break\n total_walls += max_th_border\n # Restrict bordered region by making them dormant\n flood(*max_th_loc, 1, 2)\n\n # Night -------------------------------------------------\n\n visited = [[0] * n for _ in range(m)]\n for r in range(m):\n for c in range(n):\n if isInfected[r][c]==1 and visited[r][c] == 0:\n expand(r, c, id)\n id += 1\n\n return total_walls\n\n\n\n\n\n\n```
0
0
['Python3']
0
contain-virus
Simple Explained Solution
simple-explained-solution-by-darian-cata-yuic
\n\nclass Solution {\npublic:\n int m, n;\n int ans = 0;\n \n // -1 means disinfected\n int color = 2;\n \n // for perimeter calculation we
darian-catalin-cucer
NORMAL
2023-02-12T10:28:55.872303+00:00
2023-02-12T10:28:55.872348+00:00
237
false
\n```\nclass Solution {\npublic:\n int m, n;\n int ans = 0;\n \n // -1 means disinfected\n int color = 2;\n \n // for perimeter calculation we cannot go to cells marked -1 but we can goto all other cells\n int perimeter = 0;\n \n // we can go to cells marked as 0 only\n // this will store the area being threatened\n int areat = 0;\n \n int containVirus(vector<vector<int>>& a) {\n m = a.size();\n n = a[0].size();\n\n while(1){\n int restrictX, restrictY;\n int big = -1;\n for(int i = 0 ; i < m ; i++){\n for(int j = 0 ; j < n ; j++){\n if(a[i][j] == color-1){\n \n //capture this region and color it with color\n dfs(a, i, j);\n areat = 0;\n set<pair<int, int>> visited;\n calculateAreat(a, i, j, visited);\n //calculateAreat marks the region with -2 so we will restore\n restore(a, i, j);\n if(big < areat){\n big = areat;\n restrictX = i;\n restrictY = j;\n }\n }\n }\n }\n \n if(big != -1){\n perimeter = 0;\n calculatePerimeter(a, restrictX, restrictY);\n ans += perimeter;\n int temp = color;\n color = -1;\n // disinfect this region by marking as -1\n restore(a, restrictX, restrictY);\n \n color = temp+1;\n for(int i = 0 ; i < m ; i++){\n for(int j = 0 ; j < n ; j++){\n if(a[i][j] == color-1){\n expand(a, i, j, a[i][j]);\n // expand marks the region as -2 so we restore it to color\n restore(a, i, j);\n }\n }\n }\n color++;\n }\n else{\n break;\n }\n }\n \n return ans;\n }\n \n void expand(vector<vector<int>>& a, int x, int y, int currcolor){\n if(x < 0 || y < 0 || x >= m || y >= n){\n return;\n }\n \n if(a[x][y] == 0){\n a[x][y] = -2;\n return;\n }\n \n if(a[x][y] == -2 || a[x][y] == -1 || a[x][y] != currcolor){\n return;\n }\n \n a[x][y] = -2;\n expand(a, x+1, y, currcolor);\n expand(a, x, y+1, currcolor);\n expand(a, x, y-1, currcolor);\n expand(a, x-1, y, currcolor);\n }\n \n void dfs(vector<vector<int>>& a, int x, int y){\n if(x < 0 || y < 0 || x >= m || y >= n || a[x][y] == 0 || a[x][y] == -1){\n return;\n }\n \n if(a[x][y] == color){\n return;\n }\n \n a[x][y] = color;\n dfs(a, x+1, y);\n dfs(a, x, y+1);\n dfs(a, x, y-1);\n dfs(a, x-1, y);\n }\n \n void restore(vector<vector<int>>& a, int x, int y){\n if(x < 0 || y < 0 || x >= m || y >= n || a[x][y] == 0 || a[x][y] != -2){\n return;\n }\n \n a[x][y] = color;\n restore(a, x+1, y);\n restore(a, x, y+1);\n restore(a, x, y-1);\n restore(a, x-1, y);\n }\n \n // -2 is under processing\n void calculatePerimeter(vector<vector<int>>& a, int x, int y){\n if(x < 0 || y < 0 || x >= m || y >= n || a[x][y] == -1 || a[x][y] == -2){\n return;\n }\n \n if(a[x][y] == 0){\n perimeter++;\n return;\n }\n \n a[x][y] = -2;\n calculatePerimeter(a, x+1, y);\n calculatePerimeter(a, x, y+1);\n calculatePerimeter(a, x, y-1);\n calculatePerimeter(a, x-1, y);\n }\n \n // -2 is under processing\n void calculateAreat(vector<vector<int>>& a, int x, int y, set<pair<int, int>> &visited){\n if(x < 0 || y < 0 || x >= m || y >= n || a[x][y] == -2 \n || a[x][y] == -1 || visited.count({x,y})){\n return;\n }\n \n if(a[x][y] == 0){\n visited.insert({x,y});\n areat++;\n return;\n }\n \n a[x][y] = -2;\n calculateAreat(a, x+1, y, visited);\n calculateAreat(a, x, y+1, visited);\n calculateAreat(a, x, y-1, visited);\n calculateAreat(a, x-1, y, visited);\n }\n \n void print(vector<vector<int>> &a){\n for(int i = 0 ; i < m ; i++){\n for(int j = 0 ; j < n ; j++){\n cout<<a[i][j]<<"\\t";\n }\n cout<<endl;\n }\n cout<<endl;\n }\n};\n```
0
0
['C++', 'Scala', 'Ruby', 'Kotlin', 'JavaScript']
0
contain-virus
[Golang] DFS easy to understand
golang-dfs-easy-to-understand-by-user044-b833
go\nfunc containVirus(isInfected [][]int) int {\n m, n := len(isInfected), len(isInfected[0])\n var res int\n for {\n // Let\'s do a depth first search an
user0440H
NORMAL
2023-01-10T12:57:23.268070+00:00
2023-01-10T12:57:23.268115+00:00
110
false
```go\nfunc containVirus(isInfected [][]int) int {\n m, n := len(isInfected), len(isInfected[0])\n var res int\n for {\n // Let\'s do a depth first search and find the region that spread the most cells\n // (i.e) needs more walls to be built\n visited := make([][]bool, m)\n for i := 0; i < m; i++ {\n visited[i] = make([]bool, n)\n }\n // We want to focus on the region that can affect the most unaffected neighbors\n // The unaffected neighbors and the walls needed is different because an unaffected neighbor\n // can be infected by multiple neighbors and hence will need multiple walls.\n var wallsNeeded [][4]int // <x, y, uninfectedNeighbors, walls>\n for i := 0; i < m; i++ {\n for j := 0; j < n; j++ {\n if isInfected[i][j] == 1 && !visited[i][j] {\n visited[i][j] = true\n uninfectedNeighbors := make(map[[2]int]bool)\n count := countWalls(isInfected, visited, i, j, uninfectedNeighbors)\n wallsNeeded = append(wallsNeeded, [4]int{i, j, len(uninfectedNeighbors), count})\n }\n }\n }\n if len(wallsNeeded) == 0 {\n break\n }\n // Let\'s sort wallsNeeded in descending order on the number of walls\n sort.Slice(wallsNeeded, func(i, j int) bool {\n return wallsNeeded[i][2] > wallsNeeded[j][2]\n })\n res += wallsNeeded[0][3]\n buildWall(isInfected, wallsNeeded[0][0], wallsNeeded[0][1])\n spread(isInfected)\n }\n return res\n}\n\nvar directions = [4][2]int{{0, -1}, {-1, 0}, {1, 0}, {0, 1}}\n\nfunc countWalls(isInfected [][]int, visited [][]bool, row, col int, uninfectedNeighbors map[[2]int]bool) int {\n m, n := len(isInfected), len(isInfected[0])\n var walls int\n for _, dir := range directions {\n x, y := row + dir[0], col + dir[1]\n if x >= 0 && x < m && y >= 0 && y < n && !visited[x][y] {\n if isInfected[x][y] == 0 {\n uninfectedNeighbors[[2]int{x, y}] = true\n walls++\n } else if isInfected[x][y] == 1 {\n visited[x][y] = true\n walls += countWalls(isInfected, visited, x, y, uninfectedNeighbors)\n }\n }\n }\n return walls\n}\n\n// buildWall builds the wall around the given region (specified by a single cell)\n// It uses DFS and marks the cells with -1 which means the region is contained\nfunc buildWall(isInfected [][]int, row, col int) {\n m, n := len(isInfected), len(isInfected[0])\n isInfected[row][col] = -1\n for _, dir := range directions {\n x, y := row+dir[0], col+dir[1]\n if x >= 0 && x < m && y >= 0 && y < n && isInfected[x][y] == 1 {\n buildWall(isInfected, x, y)\n }\n }\n}\n\n// spread spreads the virus from the infected positions to their neighbor cells\nfunc spread(isInfected [][]int) {\n m, n := len(isInfected), len(isInfected[0])\n for i := 0; i < m; i++ {\n for j := 0; j < n; j++ {\n if isInfected[i][j] == 1 {\n for _, dir := range directions {\n x, y := i+dir[0], j+dir[1]\n if x >= 0 && x < m && y >= 0 && y < n && isInfected[x][y] == 0 {\n // newly infected cells with special character since we don\'t want the neighbor\n // of this cell to be infected\n isInfected[x][y] = 2 \n }\n }\n }\n }\n }\n // Remove the special marking\n for i := 0; i < m; i++ {\n for j := 0; j < n; j++ {\n if isInfected[i][j] == 2 {\n isInfected[i][j] = 1\n }\n }\n }\n}\n```
0
0
['Go']
0
contain-virus
Python Short and Easy to Understand Solution
python-short-and-easy-to-understand-solu-2vyd
\n\nclass Solution:\n def containVirus(self, isInfected: List[List[int]]) -> int:\n walls_needed = 0\n\n # identify infected and uninfected cel
kensverse
NORMAL
2022-12-27T14:36:52.045026+00:00
2022-12-27T14:36:52.045057+00:00
300
false
\n```\nclass Solution:\n def containVirus(self, isInfected: List[List[int]]) -> int:\n walls_needed = 0\n\n # identify infected and uninfected cells\n infected = [(i, j) for i in range(len(isInfected)) for j in range(len(isInfected[0])) if isInfected[i][j] == 1]\n uninfected = [(i, j) for i in range(len(isInfected)) for j in range(len(isInfected[0])) if isInfected[i][j] != 1]\n\n # group infected cells\n def grp_infected(infected):\n grp = []\n while infected:\n cur = [infected.pop()]\n cur_grp = [cur[0]]\n while cur:\n cur_dot = cur.pop()\n south = (cur_dot[0] - 1, cur_dot[1]); north = (cur_dot[0] + 1, cur_dot[1])\n west = (cur_dot[0], cur_dot[1] - 1); east = (cur_dot[0], cur_dot[1] + 1)\n for i in [south, north, west, east]:\n if i in infected:\n cur_grp.append(i)\n cur.append(i)\n infected.remove(i)\n grp.append(cur_grp)\n return grp\n grp = grp_infected(infected)\n\n # identify next-to-be infected cells and select the correct group to quarantine\n while grp and uninfected:\n next_grp = []\n for i in grp:\n next_grp_temp = []\n for cur_dot in i:\n south = (cur_dot[0] - 1, cur_dot[1]); north = (cur_dot[0] + 1, cur_dot[1])\n west = (cur_dot[0], cur_dot[1] - 1); east = (cur_dot[0], cur_dot[1] + 1)\n for k in [south, north, west, east]:\n if k in uninfected:\n next_grp_temp.append(k)\n next_grp.append(next_grp_temp)\n\n max_infected = [len(set(i)) for i in next_grp]\n idx = max_infected.index(max(max_infected))\n walls_needed += len(next_grp[idx])\n\n del next_grp[idx]\n del grp[idx]\n grp = [i + j for i, j in zip(next_grp, grp)]\n next_grp = list(set(j for i in next_grp for j in i))\n for i in next_grp:\n uninfected.remove(i)\n grp = grp_infected(list(set(j for i in grp for j in i)))\n return walls_needed\n```
0
0
['Python3']
0
contain-virus
[Python] DFS and simulation. explained
python-dfs-and-simulation-explained-by-w-p5he
(1) DFS to find all the infected regions\n (2) Pick the region that will infect the largetest number of cells in the next day, and build a wall around it\n (3)
wangw1025
NORMAL
2022-12-21T23:58:34.557894+00:00
2022-12-22T00:00:44.359008+00:00
208
false
* (1) DFS to find all the infected regions\n* (2) Pick the region that will infect the largetest number of cells in the next day, and build a wall around it\n* (3) Update the infected regions\nthe cells that are in the wall is updated with "controlled" state (i.e., value 2)\nthe cells that is on the boundary of uncontrolled regions are updated with "infected" state (i.e., value 1)\n* (4) Go back to step (1) until all the regions are controlled or all the cells are infected.\n\n```\nimport heapq\n\nclass Solution:\n def containVirus(self, isInfected: List[List[int]]) -> int:\n self.n_row = len(isInfected)\n self.n_col = len(isInfected[0])\n self.ifstat = isInfected\n \n self.visited = []\n for _ in range(self.n_row):\n self.visited.append([False for _ in range(self.n_col)])\n self.directions = {(0, 1), (1, 0), (0, -1), (-1, 0)}\n self.infect_region = []\n self.infect_boundary_wall_cnt = [] # a list of the number of walls required to control a region\n self.infect_boundary_mheap = [] \n \n\t\t# step 1: find all the regions that are infected, including the number of walls required to "control" this region\n visited = copy.deepcopy(self.visited)\n region_idx = 0\n for i in range(self.n_row):\n for j in range(self.n_col):\n if self.ifstat[i][j] == 1 and (not visited[i][j]):\n tr, tb, tbc = list(), set(), [0]\n self.dfsFindVirus(i, j, tr, tb, tbc, visited)\n self.infect_region.append(tr)\n self.infect_boundary_wall_cnt.append(tbc[0])\n heapq.heappush(self.infect_boundary_mheap, (-(len(tb)), region_idx, list(tb)))\n region_idx += 1\n \n # step 2, simulation the progress of virus infection\n ans = 0\n while self.infect_boundary_mheap:\n # pick the region that can infect largest region next day, and build a wall for it\n _, ridx, _ = heapq.heappop(self.infect_boundary_mheap)\n for i, j in self.infect_region[ridx]:\n self.ifstat[i][j] = 2\n ans += self.infect_boundary_wall_cnt[ridx]\n\t\t\t\n # update the cells will be infected next day\n while self.infect_boundary_mheap:\n _, _, b_list = heapq.heappop(self.infect_boundary_mheap)\n for i, j in b_list:\n self.ifstat[i][j] = 1\n # check the map and find the new region and boundary\n visited = copy.deepcopy(self.visited)\n region_idx = 0\n t_ir = []\n t_ibc = []\n self.infect_boundary_wall_cnt.clear()\n while self.infect_region:\n start = self.infect_region.pop()\n i, j = start[0]\n if self.ifstat[i][j] == 1 and (not visited[i][j]):\n tr, tb, tbc = list(), set(), [0]\n self.dfsFindVirus(i, j, tr, tb, tbc, visited)\n t_ir.append(tr)\n t_ibc.append(tbc[0])\n heapq.heappush(self.infect_boundary_mheap, (-(len(tb)), region_idx, list(tb)))\n region_idx += 1\n self.infect_boundary_wall_cnt = t_ibc\n self.infect_region = t_ir\n return ans\n \n \n def dfsFindVirus(self, i, j, region, boundary, bcnt, visited):\n if visited[i][j] or self.ifstat[i][j] == 2:\n return\n \n if self.ifstat[i][j] == 0:\n # this is a boundary\n boundary.add((i, j))\n bcnt[0] += 1\n return\n \n visited[i][j] = True\n region.append((i, j))\n \n for nidx in self.directions:\n ni = i + nidx[0]\n nj = j + nidx[1]\n \n if ni >= 0 and ni < self.n_row and nj >= 0 and nj < self.n_col and (not visited[ni][nj]):\n self.dfsFindVirus(ni, nj, region, boundary, bcnt, visited)\n\n \n```
0
0
['Depth-First Search', 'Python3']
0
contain-virus
Python Object Oriented Solution - Easy to understand
python-object-oriented-solution-easy-to-9f506
Intuition\n Describe your first thoughts on how to solve this problem. \nThis is Python version:\nFor explanation please refer CPP Version\nCredit goes to: rai0
hidden_hive
NORMAL
2022-12-20T07:11:43.939538+00:00
2022-12-20T15:18:42.332416+00:00
245
false
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThis is Python version:\nFor explanation please refer [CPP Version](https://leetcode.com/problems/contain-virus/solutions/847507/cpp-dfs-solution-explained/)\nCredit goes to: [rai02](https://leetcode.com/rai02/)\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nDFS with Creating Cluster objects(for walls,tobeContaminated cells)\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(M*N)^^2\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(M*N)\n# Code\n```\nfrom heapq import heapify,heappush,heappop\nclass Cluster:\n def __init__(self):\n self.contaminated = set()\n self.toBeContaminated = set()\n self.wallCnt = 0\n # sorting based on # of toBeContaminated in reverse order\n def __lt__(self,nxt):\n return len(self.toBeContaminated) > len(nxt.toBeContaminated)\n\nclass Solution:\n\n def containVirus(self, isInfected: List[List[int]]) -> int:\n rows = len(isInfected)\n cols = len(isInfected[0])\n ans = 0\n \n def dfs(i,j,cluster):\n dirs = [(1,0),(-1,0),(0,1),(0,-1)]\n for r,c in dirs:\n nr = i + r\n nc = j + c\n if 0<=nr<rows and 0<=nc<cols:\n if isInfected[nr][nc]==1 and (nr,nc) not in visited:\n cluster.contaminated.add((nr,nc))\n visited.add((nr,nc))\n dfs(nr,nc,cluster)\n elif isInfected[nr][nc]==0:\n # note: we dont add to visited here as two virus cells can attack common normal cell\n cluster.wallCnt += 1\n cluster.toBeContaminated.add((nr,nc))\n\n\n while True:\n visited = set()\n hh = []\n for i in range(rows):\n for j in range(cols):\n if isInfected[i][j]==1 and (i,j) not in visited:\n cluster = Cluster()\n cluster.contaminated.add((i,j))\n visited.add((i,j))\n dfs(i,j,cluster)\n hh.append(cluster)\n if not hh:\n break\n heapify(hh)\n # this will return cluster with max toBeContaminated cells\n cluster = heappop(hh)\n # stopping the virus by building walls\n for i,j in cluster.contaminated:\n isInfected[i][j] = -1\n ans += cluster.wallCnt\n\n while hh:\n cluster = hh.pop()\n for i,j in cluster.toBeContaminated:\n isInfected[i][j] = 1\n\n return ans\n\n\n\n\n\n\n\n\n```
0
0
['Depth-First Search', 'Python3']
0
contain-virus
Just a runnable solution
just-a-runnable-solution-by-ssrlive-47g0
Code\n\nstruct MySolution {\n infected: Vec<Vec<i32>>,\n n: usize,\n m: usize,\n c: i32,\n mx: usize,\n w: i32,\n r: i32,\n ans: i32,\n
ssrlive
NORMAL
2022-12-14T09:31:56.215579+00:00
2022-12-14T09:31:56.215626+00:00
47
false
# Code\n```\nstruct MySolution {\n infected: Vec<Vec<i32>>,\n n: usize,\n m: usize,\n c: i32,\n mx: usize,\n w: i32,\n r: i32,\n ans: i32,\n itr: i32,\n s: std::collections::HashSet<usize>,\n}\n\nimpl MySolution {\n fn new() -> Self {\n MySolution {\n infected: vec![vec![]],\n n: 0,\n m: 0,\n c: 2,\n mx: 0,\n w: 0,\n r: 0,\n ans: 0,\n itr: 0,\n s: std::collections::HashSet::new(),\n }\n }\n\n fn dfs(&mut self, i: i32, j: i32) -> i32 {\n if i < 0 || j < 0 {\n return 0;\n }\n let (i, j) = (i as usize, j as usize);\n if i >= self.n || j >= self.m || self.infected[i][j] != 1 {\n return 0;\n }\n let mut ans = 0;\n if i + 1 < self.n && self.infected[i + 1][j] == 0 {\n self.s.insert((i + 1) * self.m + j);\n ans += 1;\n }\n if i >= 1 && self.infected[i - 1][j] == 0 {\n self.s.insert((i - 1) * self.m + j);\n ans += 1;\n }\n if j + 1 < self.m && self.infected[i][j + 1] == 0 {\n self.s.insert(i * self.m + (j + 1));\n ans += 1;\n }\n if j >= 1 && self.infected[i][j - 1] == 0 {\n self.s.insert(i * self.m + (j - 1));\n ans += 1;\n }\n self.infected[i][j] = self.c;\n ans += self.dfs(i as i32 + 1, j as i32);\n ans += self.dfs(i as i32 - 1, j as i32);\n ans += self.dfs(i as i32, j as i32 + 1);\n ans += self.dfs(i as i32, j as i32 - 1);\n ans\n }\n\n fn contain_virus(&mut self, infected: Vec<Vec<i32>>) -> i32 {\n self.infected = infected;\n self.n = self.infected.len();\n self.m = self.infected[0].len();\n self.ans = 0;\n loop {\n self.c = 2;\n self.mx = 0;\n for i in 0..self.n {\n for j in 0..self.m {\n if self.infected[i][j] == 1 {\n self.s.clear();\n let walls = self.dfs(i as i32, j as i32);\n if self.mx < self.s.len() {\n self.mx = self.s.len();\n self.w = walls;\n self.r = self.c;\n }\n self.c += 1;\n }\n }\n }\n if self.mx == 0 {\n break;\n }\n self.ans += self.w;\n for i in 0..self.n {\n for j in 0..self.m {\n if self.infected[i][j] == self.r {\n self.infected[i][j] = 1e9 as i32;\n } else if self.infected[i][j] > 1 && self.infected[i][j] != 1e9 as i32 {\n self.infected[i][j] = 1;\n if i + 1 < self.n && self.infected[i + 1][j] == 0 {\n self.infected[i + 1][j] = 1;\n }\n if i >= 1 && self.infected[i - 1][j] == 0 {\n self.infected[i - 1][j] = 1;\n }\n if j + 1 < self.m && self.infected[i][j + 1] == 0 {\n self.infected[i][j + 1] = 1;\n }\n if j >= 1 && self.infected[i][j - 1] == 0 {\n self.infected[i][j - 1] = 1;\n }\n }\n }\n }\n }\n self.ans\n }\n}\n\nimpl Solution {\n pub fn contain_virus(is_infected: Vec<Vec<i32>>) -> i32 {\n let mut my_solution = MySolution::new();\n my_solution.contain_virus(is_infected)\n }\n}\n```
0
0
['Rust']
0
contain-virus
Simulation approach utilizing Union-Find to keep track of regions and BFS to expand a virus region.
simulation-approach-utilizing-union-find-6r9r
Intuition\nWe will perform an actual simulation of the virus infection.\n\n# Approach\nThe logical approach isn\'t a complicated one, rather it\'s even presente
lynnlu
NORMAL
2022-12-02T04:01:10.756232+00:00
2022-12-02T04:01:10.756258+00:00
157
false
# Intuition\nWe will perform an actual simulation of the virus infection.\n\n# Approach\nThe logical approach isn\'t a complicated one, rather it\'s even presented in the problem statement:\n- Keep track of the virus regions\n- For each virus region, find the cells threatened by that region.\n - all these cells will either be used to help build a border or they will be used to allow the virus to expand into them.\n- For the region which threatens the most unaffected cells, border it.\n- For all the other regions, expand into the threatened cells.\n- If any regions touch, they become one region.\n\nThe difficulty comes when deciding how to best represent the data, and it seems that UnionFind fits the bill decently (especially good at handling regions coming into contact). (but even so, it requires decent amount of coding).\n\n# Complexity\n- Time complexity:\n - Union-find operations require O(1) amortized time.\n - for each simulation day, we swipe once over the matrix with a BFS per region, total cumulating under O(m*n)\n - initial number of regions can be O(m*n), but, without doing too much crazy math, it seems that the more regions there are, the faster they would connect, reducing fast the number of iterations.\n - upper bound time complexity O(m^2*n^2), but in practice should be lower\n\n- Space complexity:\nO(m*n) since we\'re keeping track of the grid, the union-find forest, and the cumulated regional BFSes do not go over the size of the matrix.\n\n# Code\n```\nimport scala.collection._\nimport VirusQuarantine._\n\nobject Solution {\n def containVirus(isInfected: Array[Array[Int]]): Int = {\n val positions = (for {\n r <- isInfected.indices\n c <- isInfected(r).indices\n } yield {\n Position(r, c)\n })\n new VirusQuarantine(isInfected, positions).quarantine()\n }\n}\n\nobject VirusQuarantine {\n case class Position(r: Int, c: Int)\n\n case class ThreatenedCells(virusCellThreat: Position, uninfectedCells: Seq[Position])\n\n implicit class PositionOps(p: Position) {\n def +(q: Position): Position = Position(p.r + q.r, p.c + q.c)\n }\n\n val Directions = Seq(Position(1, 0), Position(-1, 0), Position(0, 1), Position(0, -1))\n}\n\nclass VirusQuarantine(grid: Array[Array[Int]], positions: Seq[Position]) extends UnionFind[Position](positions) {\n private val rows = grid.size\n private val cols = grid(0).size\n\n // init the union-find forest.\n for {\n r <- 0 until rows\n c <- 0 until cols\n p = Position(r, c)\n if p.isInfected()\n } {\n if (c < cols - 1 && grid(r)(c + 1) == 1)\n union(p)(Position(r, c + 1))\n if (r < rows - 1 && grid(r + 1)(c) == 1)\n union(p)(Position(r + 1, c))\n }\n\n def quarantine(): Int = {\n var wallsCount = 0\n\n val containedRegionsRoots = mutable.Set[Position]()\n\n while (true) {\n val uncontainedRegionsRoots = roots().filter(_.isInfected).toSet.diff(containedRegionsRoots)\n \n if (uncontainedRegionsRoots.isEmpty) return wallsCount\n\n val threatenedCellsByRegion = uncontainedRegionsRoots.map(findThreatenedCells)\n val maxCellCountThreatenedByOneRegion = threatenedCellsByRegion.map(_.uninfectedCells.size).max\n\n val threatenedCellsToBorder = threatenedCellsByRegion.find(_.uninfectedCells.size == maxCellCountThreatenedByOneRegion).get\n \n val remainingUncontainedRegions = threatenedCellsByRegion - threatenedCellsToBorder\n \n wallsCount += border(threatenedCellsToBorder)\n containedRegionsRoots += find(threatenedCellsToBorder.virusCellThreat)\n \n remainingUncontainedRegions.map(_.uninfectedCells.map(_.infect))\n }\n\n throw new IllegalStateException("unreachable statement")\n }\n\n private implicit class GridPositionOps(p: Position) {\n def isWithinBounds(): Boolean = \n 0 <= p.r && p.r < rows && 0 <= p.c && p.c < cols\n\n def isInfected(): Boolean = grid(p.r)(p.c) == 1\n\n def infect(): Unit = {\n grid(p.r)(p.c) = 1\n getReachableNeighbors(p)\n .filter(_.isInfected)\n .foreach(union(p))\n }\n }\n\n private def findThreatenedCells(infectedPosition: Position): ThreatenedCells = {\n val root = find(infectedPosition)\n val q = mutable.Queue[Position](root)\n val vis = mutable.Set[Position](root)\n\n val uninfectedCells = mutable.Set[Position]()\n\n while (q.nonEmpty) {\n val currPosition = q.dequeue()\n\n val (virusNeighbors, uninfectedNeighbors) = \n getReachableNeighbors(currPosition)\n .filterNot(vis.contains)\n .partition(_.isInfected)\n\n q ++= virusNeighbors\n vis ++= virusNeighbors\n\n uninfectedCells ++= uninfectedNeighbors\n }\n\n ThreatenedCells(infectedPosition, uninfectedCells.toSeq)\n }\n\n private def border(threatenedCells: ThreatenedCells): Int =\n threatenedCells.uninfectedCells.map { uninfectedCell =>\n getReachableNeighbors(uninfectedCell).collect { \n case neigh if find(neigh) == find(threatenedCells.virusCellThreat) => addBorder(neigh, uninfectedCell)\n }.size\n }.sum\n\n private def getReachableNeighbors(p: Position): Seq[Position] = \n Directions\n .map(_ + p)\n .filter(_.isWithinBounds)\n .filterNot(isBorderPresent(p))\n\n private val borders = mutable.Set[(Position, Position)]()\n \n def addBorder(a: Position, b: Position): Unit = borders ++= Set((a, b), (b, a))\n\n def isBorderPresent(a: Position)(b: Position): Boolean = borders.contains((a, b))\n}\n\n\nclass UnionFind[T](collection: Iterable[T]) {\n\n private val parent: mutable.Map[T, T] = collection.map(item => item -> item).to(mutable.Map)\n\n def roots(): Set[T] = parent.keys.map(find).toSet\n\n def union(a: T)(b: T): T = {\n val aAncestor = find(a)\n val bAncestor = find(b)\n if (aAncestor != bAncestor) {\n parent(aAncestor) = bAncestor\n }\n bAncestor\n }\n\n def find(a: T): T = {\n val aParent = parent(a)\n if (parent(a) != a) {\n parent(a) = find(parent(a))\n }\n parent(a)\n }\n}\n\n\n\n```
0
0
['Breadth-First Search', 'Union Find', 'Scala']
0
contain-virus
Contain Virus O(n*m*max(n,m)) || DFS || Leetcode Hard
contain-virus-onmmaxnm-dfs-leetcode-hard-1740
Intuition\n Describe your first thoughts on how to solve this problem. \nBasically I am trying to traverse First ifected cell then dfs after that spreading the
kgstrivers
NORMAL
2022-11-18T22:37:21.169682+00:00
2022-11-18T22:40:40.901191+00:00
241
false
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nBasically I am trying to traverse First ifected cell then dfs after that spreading the infected case by adjacent untill I get the optimal answer,So that\'s why while(true) every time I chck that infected cell then dfs and it will repaeting\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nBasically using through DFS when the infected cell is found then it will return wall number it will comparison through the set. after that when one traversal iscompleted and it addded 1 as adjacent after checking that will not violate the rules of matrix overflow\n\n# Complexity\n- Time complexity: O(n*m*max(m,n))\nn =isinfectedd.size()\nm = isinfectedd[0].size()\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n\n- Space complexity: O(n*m)\nwhere \nn =isinfectedd.size()\nm = isinfectedd[0].size()\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n# Code\n```\nclass Solution {\npublic:\n int n,m,r,mx;\n int col;\n int ans;\n unordered_set<int> st;\n int wall;\n vector<vector<int>> isInfected;\n\n int dfs(int i,int j)\n {\n if(i<0 || j<0 || i>=n || j>=m || isInfected[i][j]!=1)\n {\n return 0;\n }\n\n int ans = 0;\n\n if(i-1>=0 && isInfected[i-1][j] == 0)\n {\n st.insert((i-1)*m + j);\n ans++;\n }\n if(i+1<n && isInfected[i+1][j] == 0)\n {\n st.insert((i+1)*m + j);\n ans++;\n }\n\n if(j-1>=0 && isInfected[i][j-1] == 0)\n {\n st.insert(i*m + (j-1));\n ans++;\n }\n\n if(j+1<m && isInfected[i][j+1] == 0)\n {\n st.insert(i*m + (j+1));\n ans++;\n }\n\n\n isInfected[i][j] = col;\n\n ans+=dfs(i+1,j);\n ans+=dfs(i-1,j);\n ans+=dfs(i,j-1);\n ans+=dfs(i,j+1);\n\n\n return ans;\n\n\n }\n int containVirus(vector<vector<int>>& isInfectedd) {\n\n\n n = isInfectedd.size();\n m = isInfectedd[0].size();\n\n isInfected = isInfectedd;\n ans = 0;\n\n \n while(true)\n {\n mx = 0;\n col = 2;\n for(int i=0;i<n;i++)\n {\n for(int j=0;j<m;j++)\n {\n if(isInfected[i][j] == 1)\n {\n st.clear();\n int w = dfs(i,j);\n if(mx<st.size())\n {\n mx = st.size();\n wall = w;\n r = col;\n }\n col++;\n }\n \n }\n }\n\n if(mx == 0)\n {\n break;\n }\n ans+=wall;\n\n\n for(int i=0;i<n;i++)\n {\n for(int j=0;j<m;j++)\n {\n if(isInfected[i][j] == r)\n {\n isInfected[i][j] = 1e9;\n }\n else if(isInfected[i][j] > 1 and isInfected[i][j] != 1e9)\n {\n isInfected[i][j] = 1;\n if(i-1>=0 and !isInfected[i-1][j])\n {\n isInfected[i-1][j] = 1;\n }\n if(i+1<n and !isInfected[i+1][j])\n {\n isInfected[i+1][j] = 1;\n }\n if(j-1>=0 and !isInfected[i][j-1])\n {\n isInfected[i][j-1] = 1;\n }\n if(j+1<m and !isInfected[i][j+1])\n {\n isInfected[i][j+1] = 1;\n }\n }\n }\n }\n }\n\n\n return ans;\n\n \n }\n};\n```
0
0
['Graph', 'Matrix', 'C++']
0
contain-virus
C++ dfs
c-dfs-by-tushrrrocks-fy2p
\n\nclass Solution {\npublic:\n vector<vector<int> > g;\n int n, m, c, mx, w, r, ans, itr;\n unordered_set<int> s;\n \n int dfs(int i, int j){\n
tushrrrocks
NORMAL
2022-11-18T19:55:58.472995+00:00
2022-11-18T19:55:58.473035+00:00
139
false
```\n\nclass Solution {\npublic:\n vector<vector<int> > g;\n int n, m, c, mx, w, r, ans, itr;\n unordered_set<int> s;\n \n int dfs(int i, int j){\n if(i<0 || i>=n || j<0 || j>=m || g[i][j]!=1)\n return 0;\n int ans=0;\n if(i+1<n && g[i+1][j]==0){\n s.insert((i+1)*m+j);\n ans++;\n }\n if(i-1>=0 && g[i-1][j]==0){\n s.insert((i-1)*m+j);\n ans++;\n }\n if(j+1<m && g[i][j+1]==0){\n s.insert(i*m+(j+1));\n ans++;\n }\n if(j-1>=0 && g[i][j-1]==0){\n s.insert(i*m+(j-1));\n ans++;\n }\n g[i][j]=c;\n ans+=dfs(i+1, j);\n ans+=dfs(i-1, j);\n ans+=dfs(i, j+1);\n ans+=dfs(i, j-1);\n return ans; // total number of walls needed to block this connected component\n }\n \n int containVirus(vector<vector<int>>& grid) {\n g=grid, n=g.size(), m=g[0].size(), ans=0;\n while(true){\n c=2, mx=0;\n for(int i=0; i<n; i++){\n for(int j=0; j<m; j++){\n if(g[i][j]==1){\n s.clear();\n int walls=dfs(i, j);\n if(mx<s.size()){\n mx=s.size();\n w=walls;\n r=c;\n }\n c++;\n }\n }\n }\n if(mx==0)\n break;\n ans+=w;\n for(int i=0; i<n; i++){\n for(int j=0; j<m; j++){\n if(g[i][j]==r)\n g[i][j]=1e9;\n else if(g[i][j]>1 && g[i][j]!=1e9){\n g[i][j]=1;\n if(i+1<n && !g[i+1][j]) g[i+1][j]=1;\n if(i-1>=0 && !g[i-1][j]) g[i-1][j]=1;\n if(j+1<m && !g[i][j+1]) g[i][j+1]=1;\n if(j-1>=0 && !g[i][j-1]) g[i][j-1]=1;\n }\n }\n }\n }\n return ans;\n }\n};\n\n```
0
0
['Depth-First Search', 'Graph', 'C', 'Matrix']
0
symmetric-tree
🔥Easy Solutions in Java 📝, Python 🐍, and C++ 🖥️🧐Look at once 💻
easy-solutions-in-java-python-and-c-look-zypw
Intuition\n Describe your first thoughts on how to solve this problem. \n To check if a binary tree is symmetric, we need to compare its left subtree and right
Vikas-Pathak-123
NORMAL
2023-03-13T00:22:59.481572+00:00
2023-03-13T00:22:59.481609+00:00
91,994
false
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n To check if a binary tree is symmetric, we need to compare its left subtree and right subtree. To do this, we can traverse the tree recursively and compare the left and right subtrees at each level. If they are symmetric, we continue the traversal. Otherwise, we can immediately return false.\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe can define a recursive helper function that takes two nodes as input, one from the left subtree and one from the right subtree. The helper function returns true if both nodes are null, or if their values are equal and their subtrees are symmetric.\n\n\n# Complexity\n- Time complexity:The time complexity of the algorithm is $$O(n)$$, where n is the number of nodes in the binary tree. We need to visit each node once to check if the tree is symmetric.\n- Space complexity:\nThe space complexity of the algorithm is $$O(h)$$, where h is the height of the binary tree. In the worst case, the tree can be completely unbalanced, and the recursion stack can go as deep as the height of the tree.\n\n\n![image.png](https://assets.leetcode.com/users/images/b427e686-2e5d-469a-8e7a-db5140022a6b_1677715904.0948765.png)\n\n\n# Please Upvote\uD83D\uDC4D\uD83D\uDC4D\n```\nThanks for visiting my solution.\uD83D\uDE0A Keep Learning\nPlease give my solution an upvote! \uD83D\uDC4D\nIt\'s a simple way to show your appreciation and\nkeep me motivated. Thank you! \uD83D\uDE0A\n```\n# Code\n``` Java []\nclass Solution {\n public boolean isSymmetric(TreeNode root) {\n if (root == null) {\n return true;\n }\n return isMirror(root.left, root.right);\n }\n \n private boolean isMirror(TreeNode node1, TreeNode node2) {\n if (node1 == null && node2 == null) {\n return true;\n }\n if (node1 == null || node2 == null) {\n return false;\n }\n return node1.val == node2.val && isMirror(node1.left, node2.right) && isMirror(node1.right, node2.left);\n }\n}\n\n```\n```Python []\nclass Solution(object):\n def isMirror(self, left, right):\n if not left and not right:\n return True\n if not left or not right:\n return False\n return left.val == right.val and self.isMirror(left.left, right.right) and self.isMirror(left.right, right.left)\n \n def isSymmetric(self, root):\n if not root:\n return True\n return self.isMirror(root.left, root.right)\n\n```\n```C++ []\nclass Solution {\npublic:\n bool isMirror(TreeNode* left, TreeNode* right) {\n if (!left && !right) return true;\n if (!left || !right) return false;\n return (left->val == right->val) && isMirror(left->left, right->right) && isMirror(left->right, right->left);\n}\n\nbool isSymmetric(TreeNode* root) {\n if (!root) return true;\n return isMirror(root->left, root->right);\n}\n\n};\n\n\n```\n# Please Comment\uD83D\uDC4D\uD83D\uDC4D\n```\nThanks for visiting my solution comment below if you like it.\uD83D\uDE0A\n```
848
5
['Depth-First Search', 'Binary Tree', 'Python', 'C++', 'Java']
31
symmetric-tree
Recursive and non-recursive solutions in Java
recursive-and-non-recursive-solutions-in-95ma
Recursive--400ms:\n\n public boolean isSymmetric(TreeNode root) {\n return root==null || isSymmetricHelp(root.left, root.right);\n }\n \n pri
lvlolitte
NORMAL
2014-12-12T08:03:34+00:00
2018-10-20T15:12:41.559022+00:00
183,004
false
Recursive--400ms:\n\n public boolean isSymmetric(TreeNode root) {\n return root==null || isSymmetricHelp(root.left, root.right);\n }\n \n private boolean isSymmetricHelp(TreeNode left, TreeNode right){\n if(left==null || right==null)\n return left==right;\n if(left.val!=right.val)\n return false;\n return isSymmetricHelp(left.left, right.right) && isSymmetricHelp(left.right, right.left);\n }\n\nNon-recursive(use Stack)--460ms:\n\n public boolean isSymmetric(TreeNode root) {\n if(root==null) return true;\n \n Stack<TreeNode> stack = new Stack<TreeNode>();\n TreeNode left, right;\n if(root.left!=null){\n if(root.right==null) return false;\n stack.push(root.left);\n stack.push(root.right);\n }\n else if(root.right!=null){\n return false;\n }\n \n while(!stack.empty()){\n if(stack.size()%2!=0) return false;\n right = stack.pop();\n left = stack.pop();\n if(right.val!=left.val) return false;\n \n if(left.left!=null){\n if(right.right==null) return false;\n stack.push(left.left);\n stack.push(right.right);\n }\n else if(right.right!=null){\n return false;\n }\n \n if(left.right!=null){\n if(right.left==null) return false;\n stack.push(left.right);\n stack.push(right.left);\n }\n else if(right.left!=null){\n return false;\n }\n }\n \n return true;\n }
770
8
['Stack', 'Recursion', 'Java']
102
symmetric-tree
Recursively and iteratively solution in Python
recursively-and-iteratively-solution-in-noyi3
Basically, this question is recursively. Or we can say, the tree structure is recursively, so the recursively solution maybe easy to write:\n\nTC: O(b) SC: O(lo
wizcabbit
NORMAL
2014-11-02T08:35:29+00:00
2018-10-22T04:12:23.448576+00:00
75,870
false
Basically, this question is recursively. Or we can say, the tree structure is recursively, so the recursively solution maybe easy to write:\n\nTC: O(b) SC: O(log n)\n\n class Solution:\n def isSymmetric(self, root):\n if root is None:\n return True\n else:\n return self.isMirror(root.left, root.right)\n\n def isMirror(self, left, right):\n if left is None and right is None:\n return True\n if left is None or right is None:\n return False\n\n if left.val == right.val:\n outPair = self.isMirror(left.left, right.right)\n inPiar = self.isMirror(left.right, right.left)\n return outPair and inPiar\n else:\n return False\n\nThe essence of recursively is Stack, so we can use our own stack to rewrite it into iteratively:\n\n class Solution2:\n def isSymmetric(self, root):\n if root is None:\n return True\n\n stack = [[root.left, root.right]]\n\n while len(stack) > 0:\n pair = stack.pop(0)\n left = pair[0]\n right = pair[1]\n\n if left is None and right is None:\n continue\n if left is None or right is None:\n return False\n if left.val == right.val:\n stack.insert(0, [left.left, right.right])\n\n stack.insert(0, [left.right, right.left])\n else:\n return False\n return True
344
4
[]
44
symmetric-tree
1ms recursive Java Solution, easy to understand
1ms-recursive-java-solution-easy-to-unde-68nj
public boolean isSymmetric(TreeNode root) {\n if(root==null) return true;\n return isMirror(root.left,root.right);\n }\n public boolean isM
yangneu2015
NORMAL
2015-11-01T18:20:28+00:00
2018-10-17T21:13:16.046628+00:00
41,060
false
public boolean isSymmetric(TreeNode root) {\n if(root==null) return true;\n return isMirror(root.left,root.right);\n }\n public boolean isMirror(TreeNode p, TreeNode q) {\n if(p==null && q==null) return true;\n if(p==null || q==null) return false;\n return (p.val==q.val) && isMirror(p.left,q.right) && isMirror(p.right,q.left);\n }
270
3
[]
31
symmetric-tree
My C++ Accepted code in 16ms with iteration solution
my-c-accepted-code-in-16ms-with-iteratio-o7ad
/**\n * Definition for binary tree\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeN
jayfonlin
NORMAL
2014-10-23T06:13:59+00:00
2018-09-04T23:38:33.406717+00:00
51,207
false
/**\n * Definition for binary tree\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode(int x) : val(x), left(NULL), right(NULL) {}\n * };\n */\n class Solution {\n public:\n bool isSymmetric(TreeNode *root) {\n TreeNode *left, *right;\n if (!root)\n return true;\n \n queue<TreeNode*> q1, q2;\n q1.push(root->left);\n q2.push(root->right);\n while (!q1.empty() && !q2.empty()){\n left = q1.front();\n q1.pop();\n right = q2.front();\n q2.pop();\n if (NULL == left && NULL == right)\n continue;\n if (NULL == left || NULL == right)\n return false;\n if (left->val != right->val)\n return false;\n q1.push(left->left);\n q1.push(left->right);\n q2.push(right->right);\n q2.push(right->left);\n }\n return true;\n }\n };
237
3
[]
25
symmetric-tree
15 lines of c++ solution / 8 ms
15-lines-of-c-solution-8-ms-by-pankit-zwwm
bool isSymmetric(TreeNode *root) {\n if (!root) return true;\n return helper(root->left, root->right);\n }\n \n bool
pankit
NORMAL
2015-03-01T18:00:27+00:00
2015-03-01T18:00:27+00:00
28,323
false
bool isSymmetric(TreeNode *root) {\n if (!root) return true;\n return helper(root->left, root->right);\n }\n \n bool helper(TreeNode* p, TreeNode* q) {\n if (!p && !q) {\n return true;\n } else if (!p || !q) {\n return false;\n }\n \n if (p->val != q->val) {\n return false;\n }\n \n return helper(p->left,q->right) && helper(p->right, q->left); \n }
210
1
['Recursion']
26
symmetric-tree
C++ easy solution with comments 0ms 100% faster
c-easy-solution-with-comments-0ms-100-fa-iwd9
\nclass Solution {\npublic:\n bool isSymmetric(TreeNode* root) {\n \n if(root==NULL) return true; //Tree is empty\n \n return isS
Akshatkamboj37
NORMAL
2021-02-14T05:07:51.033207+00:00
2021-11-09T08:27:59.834373+00:00
20,572
false
```\nclass Solution {\npublic:\n bool isSymmetric(TreeNode* root) {\n \n if(root==NULL) return true; //Tree is empty\n \n return isSymmetricTest(root->left,root->right);\n }\n \n bool isSymmetricTest(TreeNode* p , TreeNode* q){\n if(p == NULL && q == NULL) //left & right node is NULL \n return true; \n \n else if(p == NULL || q == NULL) //one of them is Not NULL\n return false; \n \n else if(p->val!=q->val) \n return false;\n \n return isSymmetricTest(p->left,q->right) && isSymmetricTest(p->right,q->left); //comparing left subtree\'s left child with right subtree\'s right child --AND-- comparing left subtree\'s right child with right subtree\'s left child\n }\n};\n```
208
1
['C', 'C++']
21
symmetric-tree
【Video】Going to left side and right side at the same time
video-going-to-left-side-and-right-side-vxt9k
Intuition\nGoing to left side and right side at the same time\n\n# Solution Video\n\nhttps://youtu.be/ywAZyIjRmoo\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget
niits
NORMAL
2024-12-02T14:19:12.798940+00:00
2024-12-02T14:19:31.974377+00:00
17,602
false
# Intuition\nGoing to left side and right side at the same time\n\n# Solution Video\n\nhttps://youtu.be/ywAZyIjRmoo\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 11,448\nThank you for your support!\n\n---\n\n# Approach\n\nWe are going to left side and right side at the same time.\n\nWe have two base cases.\n\n---\n\n\u25FD\uFE0F Base Cases\n\nIf both sides are null at the same time, return `True` because we reach the end of a tree.\n\nIf one of sides is null, return `False` because it\'s not symmetric.\n\n---\n\n##### How we move to left side and right side?\n\nLook at the tree below. This is a `True` case.\n\n```\n 1\n / \\\n 2 2\n \\ / \n 3 3\n```\n\nEvery time we have to compare two nodes from both sides.\n\n---\n\n\u2B50\uFE0F Points\n\nIf we go left on the left side, we should go right on the right side.(= node `2` case).\n\nIf we go right on the left side, we should go left on the right side.(= node `3` case).\n\n---\n\n**Because `True` case of the tree is like mirror from center line.**\n```\n 1\n /|\\\n 2 | 2\n \\|/ \n 3|3\n```\n\nEasy!\uD83D\uDE04\nLet\'s see solution codes!\n\n---\n\nhttps://youtu.be/bU_dXCOWHls\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(h)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n```python []\nclass Solution:\n def isSymmetric(self, root: Optional[TreeNode]) -> bool:\n \n def is_mirror(n1, n2): # n1:left, n2:right\n if not n1 and not n2:\n return True\n \n if not n1 or not n2:\n return False\n \n return n1.val == n2.val and is_mirror(n1.left, n2.right) and is_mirror(n1.right, n2.left)\n \n return is_mirror(root.left, root.right)\n```\n```javascript []\nvar isSymmetric = function(root) {\n const isMirror = (n1, n2) => {\n if (!n1 && !n2) {\n return true;\n }\n \n if (!n1 || !n2) {\n return false;\n }\n \n return n1.val === n2.val && isMirror(n1.left, n2.right) && isMirror(n1.right, n2.left);\n };\n \n return isMirror(root.left, root.right);\n};\n```\n```java []\nclass Solution {\n public boolean isSymmetric(TreeNode root) {\n return isMirror(root.left, root.right);\n }\n \n private boolean isMirror(TreeNode n1, TreeNode n2) {\n if (n1 == null && n2 == null) {\n return true;\n }\n \n if (n1 == null || n2 == null) {\n return false;\n }\n \n return n1.val == n2.val && isMirror(n1.left, n2.right) && isMirror(n1.right, n2.left);\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n bool isSymmetric(TreeNode* root) {\n return isMirror(root->left, root->right);\n }\n\nprivate:\n bool isMirror(TreeNode* n1, TreeNode* n2) {\n if (n1 == nullptr && n2 == nullptr) {\n return true;\n }\n \n if (n1 == nullptr || n2 == nullptr) {\n return false;\n }\n \n return n1->val == n2->val && isMirror(n1->left, n2->right) && isMirror(n1->right, n2->left);\n }\n};\n```\n\n# Step by Step Algorithm\n\n##### 1. **Helper Function `is_mirror` Definition**\n```python\ndef is_mirror(n1, n2): # n1:left, n2:right\n```\n- **Explanation**: `is_mirror` is a nested helper function that checks if two subtrees (`n1` and `n2`) are mirror images of each other. This function will be called recursively to compare corresponding nodes in the left and right subtrees of the tree.\n\n##### 2. **Base Case: Both Nodes Are `None`**\n```python\nif not n1 and not n2:\n return True\n```\n- **Explanation**: If both `n1` and `n2` are `None`, it means that both corresponding nodes in the left and right subtrees are absent. Since an empty subtree is symmetric to another empty subtree, this part of the code returns `True`.\n\n##### 3. **Base Case: One Node Is `None` and the Other Is Not**\n```python\nif not n1 or not n2:\n return False\n```\n- **Explanation**: If one of the nodes (`n1` or `n2`) is `None` while the other is not, it means that the structure of the two subtrees is different, and therefore they cannot be mirror images of each other. This part of the code returns `False`.\n\n##### 4. **Recursive Case: Compare Values and Subtrees**\n```python\nreturn n1.val == n2.val and is_mirror(n1.left, n2.right) and is_mirror(n1.right, n2.left)\n```\n- **Explanation**: This line checks three conditions:\n 1. The values of `n1` and `n2` should be the same (`n1.val == n2.val`).\n 2. The left subtree of `n1` should be a mirror image of the right subtree of `n2` (`is_mirror(n1.left, n2.right)`).\n 3. The right subtree of `n1` should be a mirror image of the left subtree of `n2` (`is_mirror(n1.right, n2.left)`).\n \n If all three conditions are `True`, the function returns `True`, indicating that the subtrees rooted at `n1` and `n2` are mirror images of each other.\n\n##### 5. **Initial Call to `is_mirror`**\n```python\nreturn is_mirror(root.left, root.right)\n```\n- **Explanation**: The `isSymmetric` method calls the `is_mirror` function with the left and right children of the root node (`root.left` and `root.right`). This initiates the recursive process of checking whether the left and right subtrees of the root are mirror images of each other.\n\n##### 6. **Return the Result**\n- **Explanation**: The final result of the `is_mirror` function call determines whether the tree is symmetric. If the left and right subtrees of the root are mirror images, the function returns `True`; otherwise, it returns `False`.\n\n---\n\nThank you for reading my post. Please upvote it and don\'t forget to subscribe to my channel!\n\n### \u2B50\uFE0F Subscribe URL\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n### \u2B50\uFE0F Twitter\nhttps://twitter.com/CodingNinjaAZ\n\n### \u2B50\uFE0F Related Video\n\n#100 Same Tree\n\nhttps://youtu.be/tRFQ7p0ucUw\n
168
0
['Tree', 'Depth-First Search', 'Binary Tree', 'C++', 'Java', 'Python3', 'JavaScript']
1
symmetric-tree
Easiest Beginner Friendly Sol with Diagram || DFS || O(n) time and O(h) space
easiest-beginner-friendly-sol-with-diagr-45ql
For Iterative approach please find below link :\nhttps://leetcode.com/problems/symmetric-tree/solutions/3290155/day-72-with-diagram-iterative-and-recursive-easi
singhabhinash
NORMAL
2023-01-24T13:27:11.851093+00:00
2023-04-01T10:52:43.234100+00:00
18,766
false
**For Iterative approach please find below link :**\nhttps://leetcode.com/problems/symmetric-tree/solutions/3290155/day-72-with-diagram-iterative-and-recursive-easiest-beginner-friendly-sol/\n# Intuition\nWe need to validate only 3 conditions including base condition and recursively call to the function:\n- If both "leftRoot" and "rightRoot" are null, return true\n- If only one of "leftRoot" or "rightRoot" is null, return false\n- If "leftRoot" and "rightRoot" are not null and their values are not equal, return false\n- If "leftRoot" and "rightRoot" are not null and their values are equal, recursively call "isTreeSymmetric" on the left child of "leftRoot" and the right child of "rightRoot", and the right child of "leftRoot" and the left child of "rightRoot"\n\n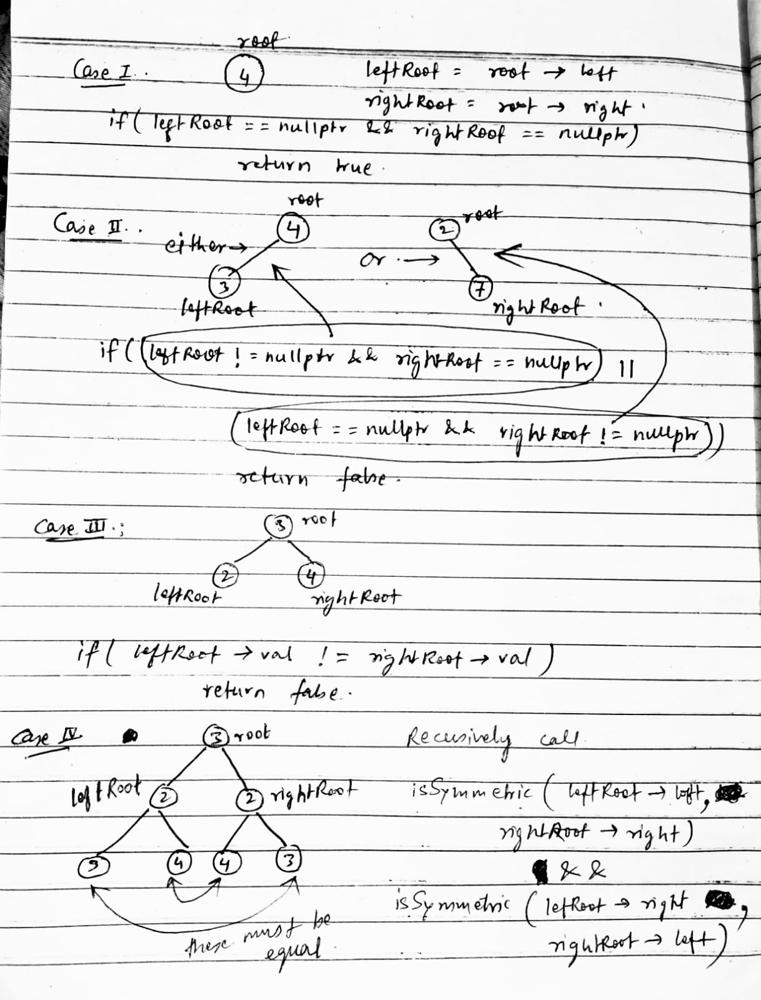![WhatsApp Image 2023-01-24 at 6.54.24 PM.jpeg](https://assets.leetcode.com/users/images/3ce67a24-c51f-4cff-a5ac-58425726b650_1674566690.8242106.jpeg)\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Define a function "isTreeSymmetric" that takes in two TreeNode pointers as inputs, "leftRoot" and "rightRoot"\n2. If both "leftRoot" and "rightRoot" are null, return true\n3. If only one of "leftRoot" or "rightRoot" is null, return false\n4. If "leftRoot" and "rightRoot" are not null and their values are not equal, return false\n5. If "leftRoot" and "rightRoot" are not null and their values are equal, recursively call "isTreeSymmetric" on the left child of "leftRoot" and the right child of "rightRoot", and the right child of "leftRoot" and the left child of "rightRoot"\n6. Return true if both recursive calls return true, else return false\n7. Define a function "isSymmetric" that takes in a TreeNode pointer "root" as input\n8. Call "isTreeSymmetric" on the left child of "root" and the right child of "root" and return the result\n<!-- Describe your approach to solving the problem. -->\n\n# Code\n```C++ []\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n bool isTreeSymmetric(TreeNode* leftRoot, TreeNode* rightRoot){\n if(leftRoot == nullptr && rightRoot == nullptr)\n return true;\n if((leftRoot == nullptr && rightRoot != nullptr) || (leftRoot != nullptr && rightRoot == nullptr))\n return false;\n if(leftRoot -> val != rightRoot -> val)\n return false;\n return isTreeSymmetric(leftRoot -> left, rightRoot -> right) && isTreeSymmetric(leftRoot -> right, rightRoot -> left);\n }\n bool isSymmetric(TreeNode* root) {\n return isTreeSymmetric(root -> left, root -> right);\n }\n};\n```\n```Java []\nclass Solution {\n public boolean isTreeSymmetric(TreeNode leftRoot, TreeNode rightRoot){\n if(leftRoot == null && rightRoot == null)\n return true;\n if((leftRoot == null && rightRoot != null) || (leftRoot != null && rightRoot == null))\n return false;\n if(leftRoot.val != rightRoot.val)\n return false;\n return isTreeSymmetric(leftRoot.left, rightRoot.right) && isTreeSymmetric(leftRoot.right, rightRoot.left);\n }\n public boolean isSymmetric(TreeNode root) {\n return isTreeSymmetric(root.left, root.right);\n }\n}\n\n```\n```Python []\nclass Solution:\n def isTreeSymmetric(self, leftRoot, rightRoot):\n if leftRoot is None and rightRoot is None:\n return True\n if (leftRoot is None and rightRoot is not None) or (leftRoot is not None and rightRoot is None):\n return False\n if leftRoot.val != rightRoot.val:\n return False\n return self.isTreeSymmetric(leftRoot.left, rightRoot.right) and self.isTreeSymmetric(leftRoot.right, rightRoot.left)\n def isSymmetric(self, root):\n return self.isTreeSymmetric(root.left, root.right)\n\n```\n\n# Complexity\n- Time complexity: **O(n)**, where n is the total number of nodes in the binary tree. This is because the solution visits each node once and compares its values with the corresponding symmetric node, thus the function isTreeSymmetric() is called on each node at most once. The time complexity of the isTreeSymmetric() function is O(n/2) because it only visits half of the nodes (in the best case when the tree is symmetric) and in the worst case it visits all nodes in the tree (when the tree is not symmetric).\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: **O(h)**, where h is the height of the binary tree. This is because the recursive calls made by the solution consume memory on the call stack equal to the height of the tree. In the worst case when the binary tree is linear, the height of the tree is equal to n, thus the space complexity becomes O(n). However, in the best case when the binary tree is perfectly balanced, the height of the tree is log(n), thus the space complexity becomes O(log(n)).\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->
150
0
['Depth-First Search', 'Binary Tree', 'Python', 'C++', 'Java']
7
symmetric-tree
6line AC python
6line-ac-python-by-so_kid-n030
\n\n\n def isSymmetric(self, root):\n def isSym(L,R):\n if not L and not R: return True\n if L and R and L.val =
so_kid
NORMAL
2015-02-05T11:08:19+00:00
2018-10-02T22:13:09.092019+00:00
25,735
false
\n\n\n def isSymmetric(self, root):\n def isSym(L,R):\n if not L and not R: return True\n if L and R and L.val == R.val: \n return isSym(L.left, R.right) and isSym(L.right, R.left)\n return False\n return isSym(root, root)
149
2
['Python']
13
symmetric-tree
Easy || 0 ms 100% (Fully Explained)(Java, C++, Python, JS, Python3)
easy-0-ms-100-fully-explainedjava-c-pyth-kk8m
Java Solution:\nRuntime: 0 ms, faster than 100.00% of Java online submissions for Symmetric Tree.\n\nclass Solution {\n public boolean isSymmetric(TreeNode r
PratikSen07
NORMAL
2022-08-14T09:26:26.634288+00:00
2022-08-14T09:30:00.630963+00:00
29,406
false
# **Java Solution:**\nRuntime: 0 ms, faster than 100.00% of Java online submissions for Symmetric Tree.\n```\nclass Solution {\n public boolean isSymmetric(TreeNode root) {\n // Soecial case...\n if (root == null)\n\t\t return true;\n // call the function recursively...\n\t return isSymmetric(root.left, root.right);\n }\n // After division the tree will be divided in two parts...\n // The root of the left part is rootleft & the root of the right part is rootright...\n public boolean isSymmetric(TreeNode rootleft, TreeNode rootright) {\n // If root of the left part & the root of the right part is same, return true...\n\t if (rootleft == null && rootright == null) {\n\t\t return true;\n\t }\n // If root of any part is null, then the binary tree is not symmetric. So return false...\n else if (rootright == null || rootleft == null) {\n\t\t return false;\n\t }\n // If the value of the root of the left part is not equal to the value of the root of the right part...\n if (rootleft.val != rootright.val)\n\t\t return false;\n // In case of not symmetric...\n if (!isSymmetric(rootleft.left, rootright.right))\n\t\t return false;\n\t if (!isSymmetric(rootleft.right, rootright.left))\n\t\t return false;\n // Otherwise, return true...\n return true;\n }\n}\n```\n\n# **C++ Solution:**\n```\nclass Solution {\npublic:\n bool isSymmetric(TreeNode* root) {\n // Special case...\n if(root == nullptr) return true;\n // Return the function recursively...\n return isSymmetric(root->left,root->right);\n }\n // A tree is called symmetric if the left subtree must be a mirror reflection of the right subtree...\n bool isSymmetric(TreeNode* leftroot,TreeNode* rightroot){\n // If both root nodes are null pointers, return true...\n if(!leftroot && !rightroot) return true;\n // If exactly one of them is a null node, return false...\n if(!leftroot || !rightroot) return false;\n // If root nodes haven\'t same value, return false...\n if(leftroot->val != rightroot->val) return false;\n // Return true if the values of root nodes are same and left as well as right subtrees are symmetric...\n return isSymmetric(leftroot->left, rightroot->right) && isSymmetric(leftroot->right, rightroot->left);\n }\n};\n```\n\n# **Python Solution:**\n```\nclass Solution(object):\n def isSymmetric(self, root):\n # Special case...\n if not root:\n return true;\n # Return the function recursively...\n return self.isSame(root.left, root.right)\n # A tree is called symmetric if the left subtree must be a mirror reflection of the right subtree...\n def isSame(self, leftroot, rightroot):\n # If both root nodes are null pointers, return true...\n if leftroot == None and rightroot == None:\n return True\n # If exactly one of them is a null node, return false...\n if leftroot == None or rightroot == None:\n return False\n # If root nodes haven\'t same value, return false...\n if leftroot.val != rightroot.val:\n return False\n # Return true if the values of root nodes are same and left as well as right subtrees are symmetric...\n return self.isSame(leftroot.left, rightroot.right) and self.isSame(leftroot.right, rightroot.left)\n```\n \n# **JavaScript Solution:**\nRuntime: 66 ms, faster than 97.80% of JavaScript online submissions for Symmetric Tree.\n```\nvar isSymmetric = function(root) {\n // Special case...\n if (!root)\n return true;\n // Return the function recursively...\n return isSame(root.left, root.right);\n};\n// A tree is called symmetric if the left subtree must be a mirror reflection of the right subtree...\nvar isSame = function (leftroot, rightroot) {\n // If both root nodes are null pointers, return true...\n // If exactly one of them is a null node, return false...\n // If root nodes haven\'t same value, return false...\n if ((!leftroot && rightroot) || (leftroot && !rightroot) || (leftroot && rightroot && leftroot.val !== rightroot.val))\n return false;\n // Return true if the values of root nodes are same and left as well as right subtrees are symmetric...\n if (leftroot && rightroot)\n return isSame(leftroot.left, rightroot.right) && isSame(leftroot.right, rightroot.left);\n return true;\n};\n```\n\n# **Python3 Solution:**\n```\nclass Solution:\n def isSymmetric(self, root: Optional[TreeNode]) -> bool:\n # Special case...\n if not root:\n return true;\n # Return the function recursively...\n return self.isSame(root.left, root.right)\n # A tree is called symmetric if the left subtree must be a mirror reflection of the right subtree...\n def isSame(self, leftroot, rightroot):\n # If both root nodes are null pointers, return true...\n if leftroot == None and rightroot == None:\n return True\n # If exactly one of them is a null node, return false...\n if leftroot == None or rightroot == None:\n return False\n # If root nodes haven\'t same value, return false...\n if leftroot.val != rightroot.val:\n return False\n # Return true if the values of root nodes are same and left as well as right subtrees are symmetric...\n return self.isSame(leftroot.left, rightroot.right) and self.isSame(leftroot.right, rightroot.left)\n```\n**I am working hard for you guys...\nPlease upvote if you find any help with this code...**
148
0
['Recursion', 'C', 'Python', 'Java', 'Python3', 'JavaScript']
9
symmetric-tree
Python short recursive and iterative solutions
python-short-recursive-and-iterative-sol-9vb5
\n def isSymmetric(self, root):\n if not root:\n return True\n return self.dfs(root.left, root.right)\n \n def dfs(self, l
oldcodingfarmer
NORMAL
2015-08-13T08:20:18+00:00
2020-09-06T14:32:07.843624+00:00
17,948
false
\n def isSymmetric(self, root):\n if not root:\n return True\n return self.dfs(root.left, root.right)\n \n def dfs(self, l, r):\n if l and r:\n return l.val == r.val and self.dfs(l.left, r.right) and self.dfs(l.right, r.left)\n return l == r\n\t\t\n\tdef isSymmetric(self, root):\n if not root:\n return True\n stack = [(root.left, root.right)]\n while stack:\n l, r = stack.pop()\n if not l and not r:\n continue\n if not l or not r or (l.val != r.val):\n return False\n stack.append((l.left, r.right))\n stack.append((l.right, r.left))\n return True
136
1
['Recursion', 'Python']
11
symmetric-tree
Short and clean java iterative solution
short-and-clean-java-iterative-solution-m0h8k
public boolean isSymmetric(TreeNode root) {\n Queue<TreeNode> q = new LinkedList<TreeNode>();\n if(root == null) return true;\n
moorelee10
NORMAL
2015-06-23T18:22:46+00:00
2018-10-26T22:30:21.017303+00:00
14,670
false
public boolean isSymmetric(TreeNode root) {\n Queue<TreeNode> q = new LinkedList<TreeNode>();\n if(root == null) return true;\n q.add(root.left);\n q.add(root.right);\n while(q.size() > 1){\n TreeNode left = q.poll(),\n right = q.poll();\n if(left== null&& right == null) continue;\n if(left == null ^ right == null) return false;\n if(left.val != right.val) return false;\n q.add(left.left);\n q.add(right.right);\n q.add(left.right);\n q.add(right.left); \n }\n return true;\n }
126
0
[]
17
symmetric-tree
JavaScript recursive and iterative solutions
javascript-recursive-and-iterative-solut-ir5x
The idea is to check whether the tree's left and right subtrees are mirroring each other, we can use preorder traversal:\n\nvar isSymmetric = function(root) {\n
jeantimex
NORMAL
2017-10-12T21:42:50.222000+00:00
2018-09-15T07:22:47.524840+00:00
6,102
false
The idea is to check whether the tree's left and right subtrees are mirroring each other, we can use preorder traversal:\n```\nvar isSymmetric = function(root) {\n if (!root) { // Sanity check\n return true;\n }\n\n // Check if tree s & t are mirroring each other\n function isMirror(s, t) {\n if (!s && !t) {\n return true; // Both nodes are null, ok\n }\n if (!s || !t || s.val !== t.val) {\n return false; // Found a mismatch\n }\n // Compare the left subtree of `s` with the right subtree of `t`\n // and the right subtree of `s` with the left subtree of `t`\n return isMirror(s.left, t.right) && isMirror(s.right, t.left);\n }\n\n return isMirror(root.left, root.right);\n};\n```\nAs it's preorder DFS, time complexity is `O(n)`, and space complexity is `O(1)` if we ignore the recursion stack which is the height of the tree.\n\nThe question asks us to implement the solution iteratively, and it's easy to convert the above preorder to make it traverse iteratively using stack:\n```\nfunction isMirror(p, q) {\n // Create two stacks\n var s1 = [p], s2 = [q];\n\n // Perform preorder traversal\n while (s1.length > 0 || s2.length > 0) {\n var n1 = s1.pop(), n2 = s2.pop();\n\n // Two null nodes, let's continue\n if (!n1 && !n2) continue;\n\n // Return false as long as there is a mismatch\n if (!n1 || !n2 || n1.val !== n2.val) return false;\n\n // Scan tree s from left to right\n // and scan tree t from right to left\n s1.push(n1.left); s1.push(n1.right);\n s2.push(n2.right); s2.push(n2.left);\n }\n\n return true;\n}\n```\nTime complexity is still `O(n)`, and space complexity is the height of the tree.\n\nAnother solution is to use BFS, we just need to traverse both subtrees in level order, one from left to right, and the other is right to left, let's modify the above `isMirror` function to the following:\n```\nfunction isMirror(s, t) {\n var q1 = [s], q2 = [t];\n\n // Perform breadth-first search\n while (q1.length > 0 || q2.length > 0) {\n // Dequeue\n var n1 = q1.shift(), n2 = q2.shift();\n\n // Two null nodes, let's continue\n if (!n1 && !n2) continue;\n\n // Return false as long as there is a mismatch\n if (!n1 || !n2 || n1.val !== n2.val) return false;\n\n // Scan tree s from left to right\n // and scan tree t from right to left\n q1.push(n1.left); q1.push(n1.right);\n q2.push(n2.right); q2.push(n2.left);\n }\n\n return true;\n}\n```\nTime complexity is `O(n)` and space complexity is the width of the tree.
116
1
[]
11
symmetric-tree
Image Explanation🏆 - [Recursive & Non-Recursive] - Complete Intuition
image-explanation-recursive-non-recursiv-fzzy
Video Solution\nhttps://youtu.be/41j4iR4Gx9s\n\n# Approach & Intuition\n\n\n\n\n\n\n\n\n\n\n\n\n# Recursive Code\n\nclass Solution {\npublic:\n bool isSymmet
aryan_0077
NORMAL
2023-03-13T01:12:03.110553+00:00
2023-03-13T02:14:23.682467+00:00
11,628
false
# Video Solution\nhttps://youtu.be/41j4iR4Gx9s\n\n# Approach & Intuition\n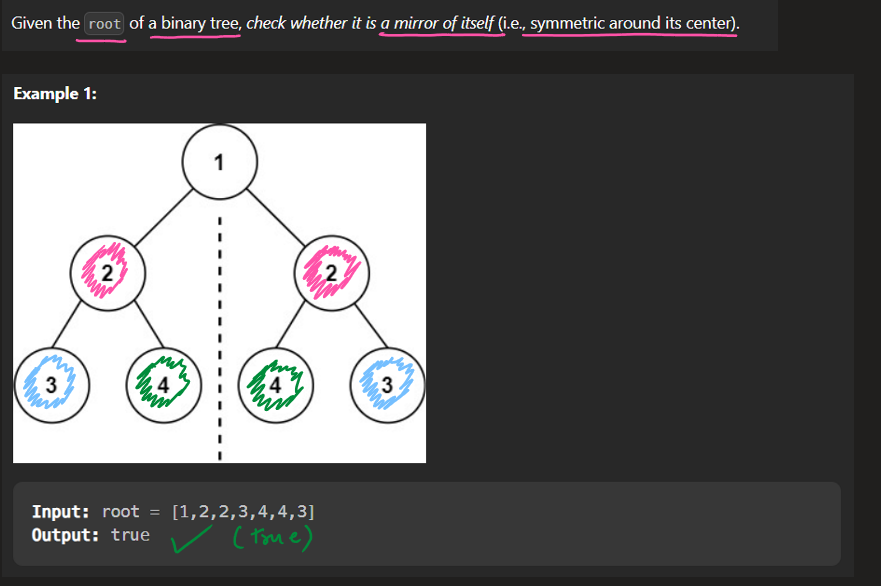![image.png](https://assets.leetcode.com/users/images/a0ec0746-4ddd-4dec-adbd-d540f823e889_1678669824.4317465.png)\n![image.png](https://assets.leetcode.com/users/images/a7825991-e7bf-44b1-ba38-c68853372580_1678669848.2439427.png)\n![image.png](https://assets.leetcode.com/users/images/7065f13f-bb82-4066-983e-cba9fc6239ab_1678669858.1537697.png)\n![image.png](https://assets.leetcode.com/users/images/c86dff88-7545-47af-a3ee-214e784692ff_1678669864.8307462.png)\n![image.png](https://assets.leetcode.com/users/images/8f319a20-de8c-496c-9b8b-a0594c51114e_1678669872.3450804.png)\n![image.png](https://assets.leetcode.com/users/images/a1a5be50-9390-4d6a-9019-08f2eb5dae6f_1678669881.0141463.png)\n![image.png](https://assets.leetcode.com/users/images/401aedaf-4111-4649-81c8-16282f60662a_1678669890.8298717.png)\n![image.png](https://assets.leetcode.com/users/images/a2194d4e-58e3-45ec-9f0b-79968f851827_1678669898.3149576.png)\n![image.png](https://assets.leetcode.com/users/images/01d99578-7858-415f-9e4f-931f458bf59c_1678669906.1509514.png)\n![image.png](https://assets.leetcode.com/users/images/da50d440-dc6b-4c47-a46e-b4a5376151b3_1678669914.0028672.png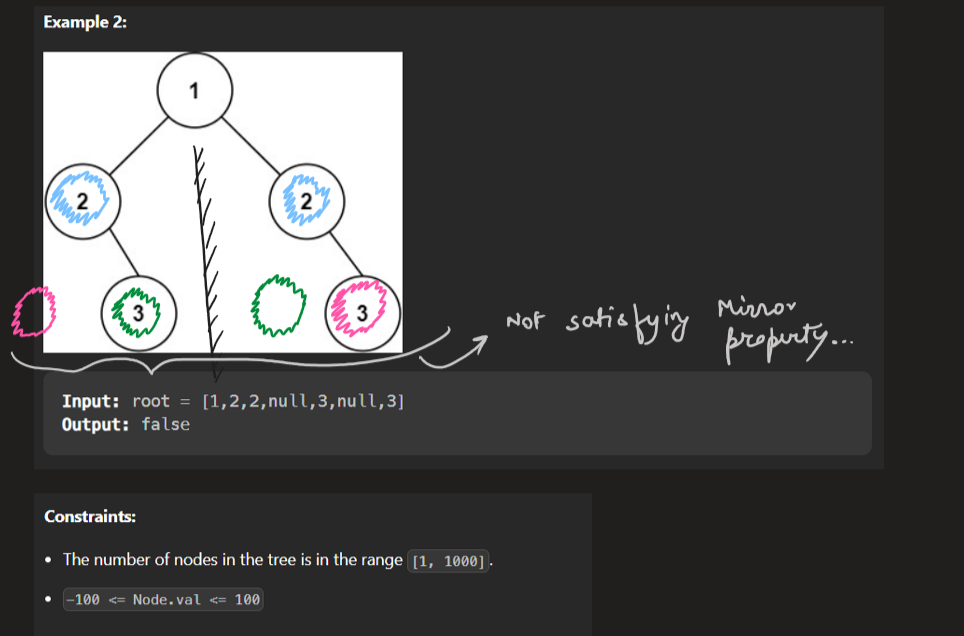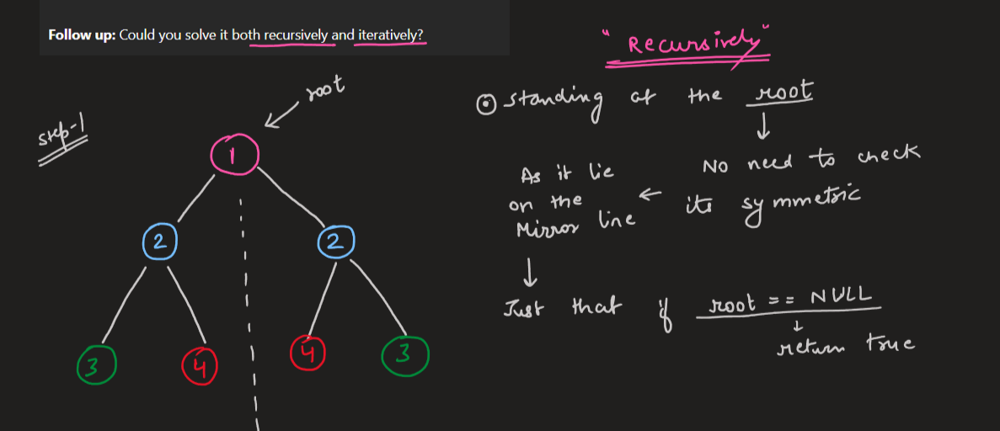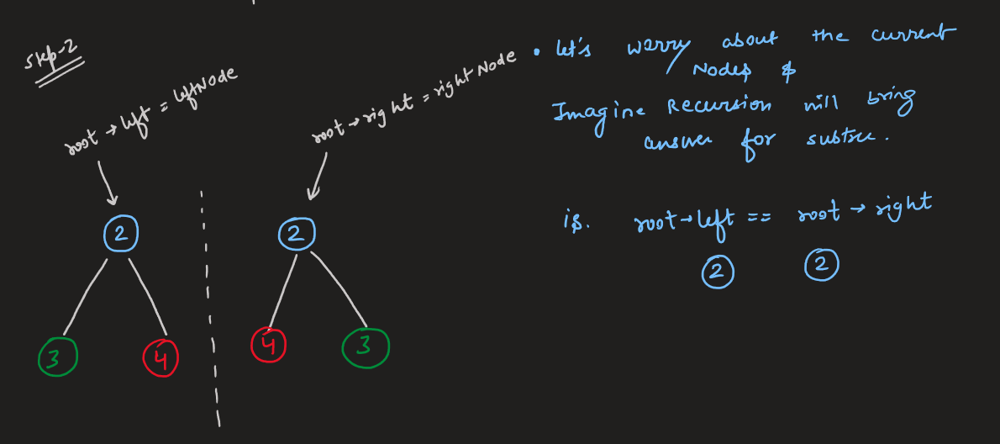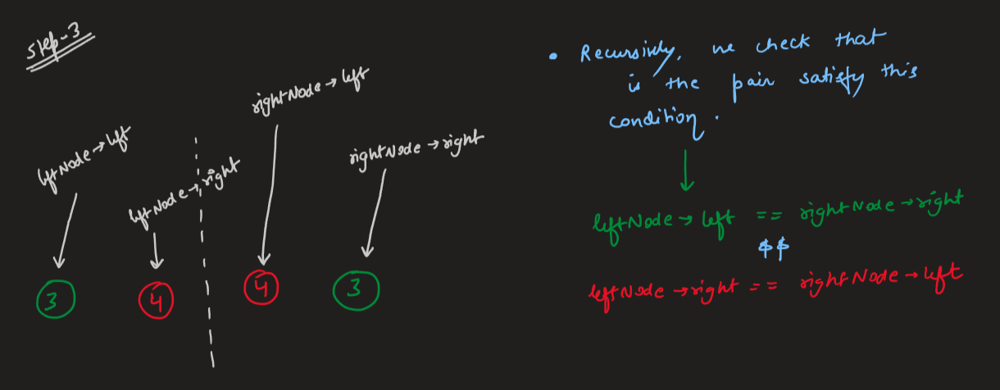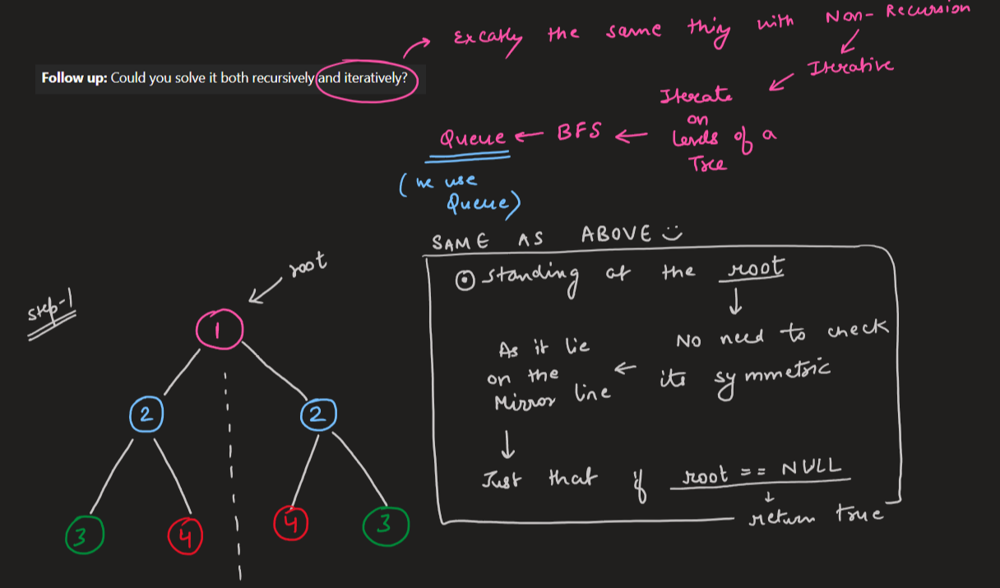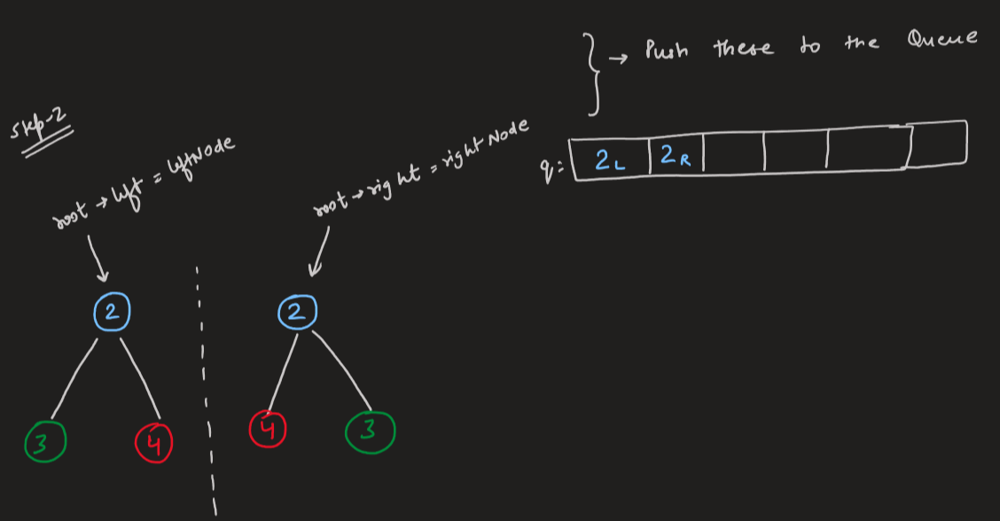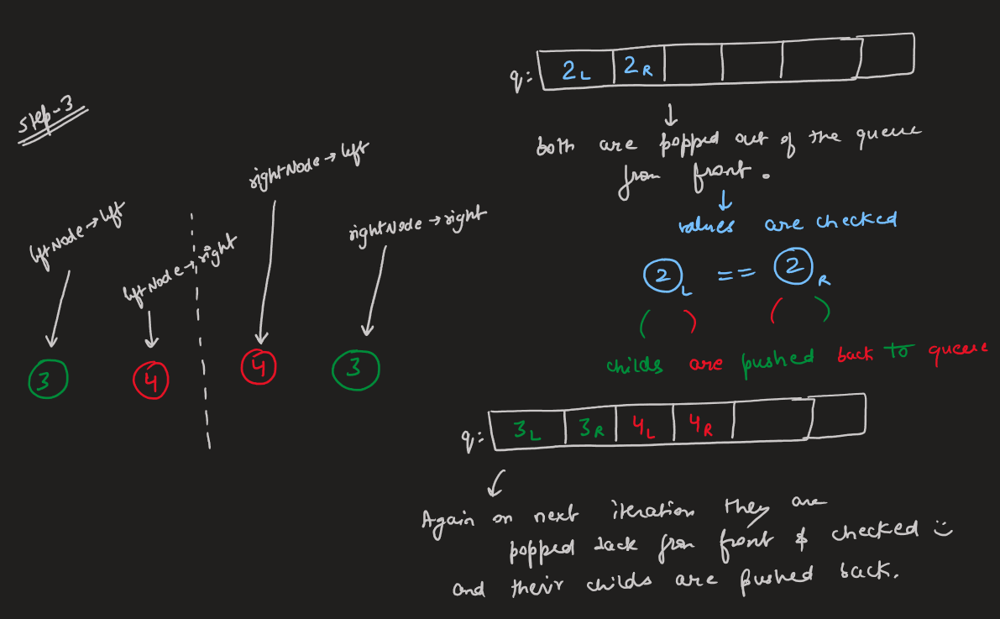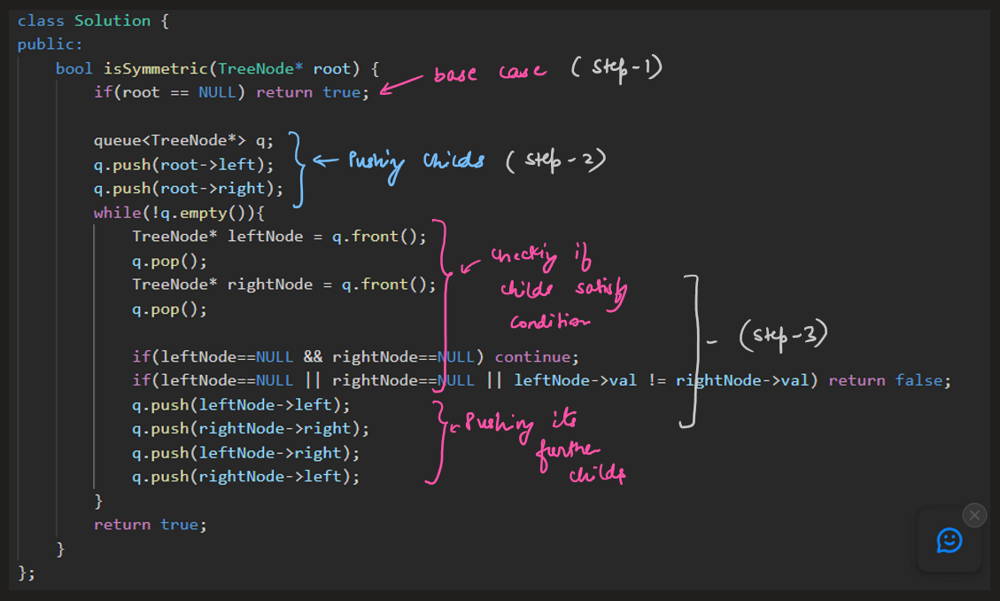)\n\n\n# Recursive Code\n```\nclass Solution {\npublic:\n bool isSymmetricHelper(TreeNode* leftNode, TreeNode* rightNode){\n if(leftNode==NULL && rightNode==NULL) return true;\n if(leftNode==NULL || rightNode==NULL || leftNode->val != rightNode->val) return false;\n \n return isSymmetricHelper(leftNode->left, rightNode->right) && isSymmetricHelper(leftNode->right, rightNode->left);\n }\n\n bool isSymmetric(TreeNode* root) {\n if(root == NULL) return true;\n return isSymmetricHelper(root->left, root->right);\n }\n};\n```\n\n# Non-Recursive Code\n```\nclass Solution {\npublic:\n bool isSymmetric(TreeNode* root) {\n if(root == NULL) return true;\n\n queue<TreeNode*> q;\n q.push(root->left);\n q.push(root->right);\n while(!q.empty()){\n TreeNode* leftNode = q.front();\n q.pop();\n TreeNode* rightNode = q.front();\n q.pop();\n\n if(leftNode==NULL && rightNode==NULL) continue;\n if(leftNode==NULL || rightNode==NULL || leftNode->val != rightNode->val) return false;\n q.push(leftNode->left);\n q.push(rightNode->right);\n q.push(leftNode->right);\n q.push(rightNode->left);\n }\n return true;\n }\n};\n```
87
1
['C++']
7
symmetric-tree
[isMirror] DFS (Recursion, One/Two Stacks) + BFS (Queue) Solution in Java
ismirror-dfs-recursion-onetwo-stacks-bfs-i4ld
Reference: LeetCode EPI 9.2\nDifficulty: Easy\n\n## Problem\n\n> Given a binary tree, check whether it is a mirror of itself (ie, symmetric around its center).\
junhaowanggg
NORMAL
2019-11-19T18:28:34.146230+00:00
2019-11-19T18:28:34.146276+00:00
5,117
false
Reference: [LeetCode](https://leetcode.com/problems/symmetric-tree/) <span class="gray">EPI 9.2</span>\nDifficulty: <span class="green">Easy</span>\n\n## Problem\n\n> Given a binary tree, check whether it is a mirror of itself (ie, symmetric around its center).\n\n**Example:** \n\n`[1,2,2,3,4,4,3]` is symmetric:\n\n```java\n 1\n / \\\n 2 2\n / \\ / \\\n3 4 4 3\n```\n\nBut the following `[1,2,2,null,3,null,3]` is not:\n\n```java\n 1\n / \\\n 2 2\n \\ \\\n 3 3\n```\n\n**Follow up:** Bonus points if you could solve it both `recursively` and `iteratively`.\n\n\n\n\n## Analysis\n\n**Idea:** A tree is symmetric if it is a `mirror reflection` of itself.\n\n**Note:** Distinguish the concept of `symmetric` (one tree) and `mirror reflection` (two trees).\n\n```java\n 1\n / \\\n 2 2 t1 & t2\n / \\ / \\\n3 4 4 3\n| | | |\n---|-|-----> isMirror(t1.left, t2.right)\n | | \n --------> isMirror(t1.right, t2.left)\n```\n\nThe question is when are two trees a mirror reflection of each other? **Three conditions:**\n\n- Their two roots have the same value.\n- The right subtree `t1.right` of each tree `t1` is a mirror reflection of the left subtree `t2.left` of the other tree `t2`.\n- The left subtree `t1.left` of each tree `t1` is a mirror reflection of the right subtree `t2.right` of the other tree `t2`.\n\n**Bad Idea (the wrong direction):**\n\nA tree is symmetric if its left subtree is symmetric and its right subtree is symmetric. Consider this case:\n\n```java\n 1\n / \\\n 2 2\n / \\ / \\\n3 4 4 3\n```\n\nTwo subtrees of root are not symmetric, but the root is symmetric.\n\n\nFrom EPI, swapping any subtrees of a tree and comparing with the original is also workable.\n\n\n\n### Recursion\n\nCome up with the recursive structure.\n\n```java\npublic boolean isSymmetric(TreeNode root) {\n return isMirror(root, root);\n}\n\nprivate boolean isMirror(TreeNode t1, TreeNode t2) {\n // base case\n if (t1 == null && t2 == null) return true;\n if (t1 == null || t2 == null) return false;\n // check values\n if (t1.val != t2.val) return false;\n // check left subtree and right subtree\n return isMirror(t1.right, t2.left) && isMirror(t1.left, t2.right);\n}\n```\n\n**Improvement:**\n\nActually, there is not too much improvement since it is bounded by a constant `2`.\n\n```java\npublic boolean isSymmetric(TreeNode root) {\n if (root == null) { // required\n return true;\n }\n return isMirror(root.left, root.right); // so t1 and t2 are different trees\n}\n```\n\n**Time:** `O(N)` because we traverse the entire input tree once (`\\sim 2N`).\n**Space:** `O(h)`\n\n\n\n\n### Iteration (One/Two Stacks)\n\nUse two stacks to simulate the recursive method.\n\n**Note:** Null check => Value check\n\n```java\npublic boolean isSymmetric(TreeNode root) {\n if (root == null) { // need checking because we use root\'s value\n return true;\n }\n Stack<TreeNode> lStack = new Stack<>();\n Stack<TreeNode> rStack = new Stack<>();\n // Preorder-like traversal\n lStack.push(root.left); rStack.push(root.right);\n \n while (lStack.size() > 0 && rStack.size() > 0) {\n TreeNode t1 = lStack.pop();\n TreeNode t2 = rStack.pop();\n // null check\n if (t1 == null && t2 == null) continue;\n if (t1 == null || t2 == null) return false;\n // value check\n if (t1.val != t2.val) return false;\n // push children\n lStack.push(t1.right); lStack.push(t1.left); // could be null\n rStack.push(t2.left); rStack.push(t2.right);\n }\n // One of the stack might be empty\n return lStack.size() == 0 && rStack.size() == 0;\n}\n```\n\nOr just use one stack:\n\n- Be careful of the ordering of pushing.\n\n```java\npublic boolean isSymmetric(TreeNode root) {\n if (root == null) {\n return true;\n }\n if (root.left == null && root.right == null) return true;\n if (root.left == null || root.right == null) return false;\n // children are not null\n Stack<TreeNode> stack = new Stack<>();\n stack.push(root.left);\n stack.push(root.right);\n \n while (stack.size() > 0) {\n TreeNode t1 = stack.pop();\n TreeNode t2 = stack.pop();\n // null check\n if (t1 == null && t2 == null) continue;\n if (t1 == null || t2 == null) return false;\n // value check\n if (t1.val != t2.val) return false;\n // push children\n stack.push(t1.right); stack.push(t2.left); // could be null\n stack.push(t1.left); stack.push(t2.right);\n }\n \n return true;\n}\n```\n\n\n**Time:** `O(N)`\n**Space:** `O(h)`\n\n\n\n\n### Iteration (BFS)\n\nCompare nodes at each layer.\n- Each two consecutive nodes in the queue should be equal.\n- Each time, two nodes are extracted and their values are compared.\n- Then their right and left children of the two nodes are enqueued in opposite order.\n\n```java\n 1\n / \\\n 2 2 queue: 2 2 (t1)\n / \\ / \\\n3 4 4 3 queue: 4 4 3 3\n t2.r t1.l\n```\n\n```java\npublic boolean isSymmetric(TreeNode root) {\n if (root == null) {\n return true;\n }\n Queue<TreeNode> queue = new LinkedList<>();\n queue.offer(root.left);\n queue.offer(root.right);\n\n while (queue.size() > 0) {\n TreeNode t1 = queue.poll();\n TreeNode t2 = queue.poll();\n // check\n if (t1 == null && t2 == null) continue;\n if (t1 == null || t2 == null) return false;\n if (t1.val != t2.val) return false;\n // offer children\n queue.offer(t1.left);\n queue.offer(t2.right);\n\n queue.offer(t1.right);\n queue.offer(t2.left);\n }\n return true;\n}\n```\n\n\n**Time:** `O(N)`\n**Space:** `O(w)` where `w` is the maximum number nodes in a level of the tree.\n\n
84
0
['Breadth-First Search', 'Recursion', 'Iterator', 'Java']
5
symmetric-tree
Recursive and iterative (DFS and BFS) in C++. Easy to understand.
recursive-and-iterative-dfs-and-bfs-in-c-teg7
Iterative in BFS:\n\n bool isSymmetric(TreeNode root) {\n if(!root) return true;\n queue q;\n q.push(make_pair(root->left, root->right))
1grc1t86
NORMAL
2016-02-24T08:00:36+00:00
2016-02-24T08:00:36+00:00
9,170
false
**Iterative in BFS**:\n\n bool isSymmetric(TreeNode* root) {\n if(!root) return true;\n queue<nodepair> q;\n q.push(make_pair(root->left, root->right));\n while(!q.empty()){\n nodepair p = q.front();\n q.pop();\n if(!p.first && !p.second) continue;\n if(!p.first || !p.second) return false;\n if(p.first->val != p.second->val) return false;\n q.push(make_pair(p.first->left, p.second->right));\n q.push(make_pair(p.first->right, p.second->left));\n }\n return true;\n }\n\n**Iterative in DFS**:\n\n bool isSymmetric(TreeNode* root) {\n if(!root) return true;\n stack<TreeNode*> sl, sr;\n sl.push(root);\n sr.push(root);\n TreeNode * lp = root->left, *rp = root->right;\n while(lp || ! sl.empty() || rp || !sl.empty()){\n if((!lp && rp) || (lp && !rp)) return false;\n if(lp && rp){\n if(lp->val != rp->val) return false;\n sl.push(lp);\n sr.push(rp);\n lp = lp->left;\n rp = rp->right;\n }else{\n lp = sl.top()->right;\n rp = sr.top()->left;\n sl.pop();\n sr.pop();\n }\n }\n return true;\n }\n\n**Recursive**:\n\n bool isSymmetric(TreeNode* root) {\n if(!root) return true;\n return helper(root->left, root->right);\n }\n bool helper(TreeNode* left, TreeNode* right){\n if(!left && !right) return true;\n if(!left || !right) return false;\n return (left->val == right->val) && helper(left->left, right->right) && helper(left->right, right->left);\n }
63
0
['Depth-First Search', 'Breadth-First Search', 'C++']
9
symmetric-tree
✅✅C++ || Easy Solution || 💯💯Recursive Approach || Heavily Commented
c-easy-solution-recursive-approach-heavi-33qg
\u2705\u2705C++ || Easy Solution || \uD83D\uDCAF\uD83D\uDCAFRecursive Approach || Heavily Commented\n# Please Upvote as it really motivates me\n\n\nclass Soluti
Conquistador17
NORMAL
2023-03-13T02:17:48.190057+00:00
2023-03-13T02:17:48.190087+00:00
6,331
false
## **\u2705\u2705C++ || Easy Solution || \uD83D\uDCAF\uD83D\uDCAFRecursive Approach || Heavily Commented**\n# **Please Upvote as it really motivates me**\n\n```\nclass Solution {\npublic:\n bool isEqual(TreeNode*r1,TreeNode*r2){\n //if we have both root to nullptr then we will return true\n //else we will be returning false\n \n if(!r1||!r2)\n return r1==r2;\n //if not null then we will check for the r1 and r2 values\n if(r1->val==r2->val){\n //we will check for the r1 left and r2 right because they will be on opposite sides\n return isEqual(r1->left,r2->right)&&isEqual(r1->right,r2->left);\n }\n //if r1 val not equal to r2 val then return false\n return false;\n }\n bool isSymmetric(TreeNode* root) {\n //The Approach is simple i.e. we will have to check if \n //1. the right and left is equal \n return isEqual(root->left,root->right);\n }\n};\n```\n\n![image](https://assets.leetcode.com/users/images/7f423b57-81a2-46ce-9ab2-72ad38f668f7_1675480558.466273.png)\n
55
0
['Recursion', 'C', 'C++']
3
symmetric-tree
C++ | Recursive | Well Commented
c-recursive-well-commented-by-abhi_vee-a14o
\nclass Solution {\npublic:\n bool solve(TreeNode * r1, TreeNode * r2)\n { \n if(r1 == NULL && r2 == NULL)\n return true; \n\t\t\n
abhi_vee
NORMAL
2021-08-12T07:32:58.738468+00:00
2022-04-03T10:18:00.454469+00:00
3,628
false
```\nclass Solution {\npublic:\n bool solve(TreeNode * r1, TreeNode * r2)\n { \n if(r1 == NULL && r2 == NULL)\n return true; \n\t\t\n else if(r1 == NULL || r2 == NULL || r1->val != r2->val)\n return false; \n \n return solve(r1->left, r2->right) && solve(r1->right, r2->left);\n }\n \n bool isSymmetric(TreeNode* root) \n {\n return solve(root->left, root->right); \n }\n};\n```\n\nExplanation :\n\n```\nclass Solution {\npublic:\n bool solve(TreeNode * r1, TreeNode * r2)\n {\n // See the tree diagram are r1 and r2 null ? No, so this line dont execute\n if(r1 == NULL && r2 == NULL)\n return true; \n\t\t\n // Is any one of r1 or r2 null ? Or are these values different ? No. Both values are\n // same so this else if wont execute either\n else if(r1 == NULL || r2 == NULL || r1->val != r2->val)\n return false; \n \n // Now comes the main part, we are calling 2 seperate function calls \n return solve(r1->left, r2->right) && solve(r1->right, r2->left);\n // First solve() before && will execute\n // r1->left is 3 and r2->right = 3\n // Both values are same , they will by pass both if and else if statement\n // Now again r1->left is null and r2->right is null\n // So they will return true from first if condtion\n // Now the scene is : we have executed first solve() before && and it has\n // returned us True so expression becomes \' return true && solve() \'\n // Now solve after && will execute \n // Similarly it will check for 4 and 4 , it will by pass if else statements\n // next time both will become null, so will return true\n // Thus 2nd solve() at the end will also hold true\n // and we know \'true && true\' is true\n // so true will be returned to caller, and thus tree is mirror of itself.\n // Similarly you can check for any testcase, flow of execution will remain same.\n \n }\n \n bool isSymmetric(TreeNode* root) \n {\n // Imagine a tree: 1\n // 2 2\n // 3 4 4 3\n // We are standing on root that is 1, function begins\n // and now r1 and r2 points to 2 and 2 respectively. \n return solve(root->left, root->right); \n }\n};\n```
47
0
['Recursion', 'C', 'C++']
3
symmetric-tree
Python iterative way using a queue
python-iterative-way-using-a-queue-by-sh-es7p
Each iteration, it checks whether two nodes are symmetric and then push (node1.left, node2.right), (node1.right, node2.left) to the end of queue.\n\n class S
shawny
NORMAL
2015-02-26T10:56:43+00:00
2018-09-21T19:38:42.277582+00:00
7,608
false
Each iteration, it checks whether two nodes are symmetric and then push (node1.left, node2.right), (node1.right, node2.left) to the end of queue.\n\n class Solution:\n # @param root, a tree node\n # @return a boolean\n def isSymmetric(self, root):\n if not root:\n return True\n\n dq = collections.deque([(root.left,root.right),])\n while dq:\n node1, node2 = dq.popleft()\n if not node1 and not node2:\n continue\n if not node1 or not node2:\n return False\n if node1.val != node2.val:\n return False\n # node1.left and node2.right are symmetric nodes in structure\n # node1.right and node2.left are symmetric nodes in structure\n dq.append((node1.left,node2.right))\n dq.append((node1.right,node2.left))\n return True
43
0
['Python']
4
symmetric-tree
[Javascript] 95% speed, 100% memory - w/ comments
javascript-95-speed-100-memory-w-comment-m5lm
\nvar isSymmetric = function(root) {\n if (root == null) return true;\n \n return symmetryChecker(root.left, root.right);\n};\n\nfunction symmetryCheck
user9682w
NORMAL
2020-01-31T02:31:42.074272+00:00
2020-02-02T15:45:35.248408+00:00
4,832
false
```\nvar isSymmetric = function(root) {\n if (root == null) return true;\n \n return symmetryChecker(root.left, root.right);\n};\n\nfunction symmetryChecker(left, right) {\n if (left == null && right == null) return true; // If both sub trees are empty\n if (left == null || right == null) return false; // If only one of the sub trees are empty\n if (left.val !== right.val) return false; // If the values dont match up\n \n\t// Check both subtrees but travelled in a mirrored/symmetric fashion\n\t// (one goes left, other goes right) and make sure they\'re both symmetric\n return symmetryChecker(left.left, right.right) &&\n symmetryChecker(left.right, right.left);\n}\n```
41
0
['JavaScript']
2
symmetric-tree
[ Python ] ✅✅ Simple Python Solution Using Recursion 🥳✌👍
python-simple-python-solution-using-recu-gfp2
If You like the Solution, Don\'t Forget To UpVote Me, Please UpVote! \uD83D\uDD3C\uD83D\uDE4F\n# Runtime: 41 ms, faster than 29.46% of Python3 online submission
ashok_kumar_meghvanshi
NORMAL
2022-02-28T03:41:43.569372+00:00
2023-03-13T08:25:01.682540+00:00
3,879
false
# If You like the Solution, Don\'t Forget To UpVote Me, Please UpVote! \uD83D\uDD3C\uD83D\uDE4F\n# Runtime: 41 ms, faster than 29.46% of Python3 online submissions for Symmetric Tree.\n# Memory Usage: 13.8 MB, less than 99.68% of Python3 online submissions for Symmetric Tree.\n\tclass Solution:\n\t\tdef isSymmetric(self, root: Optional[TreeNode]) -> bool:\n\n\t\t\tdef check_mirror_image(root1, root2):\n\n\t\t\t\tif root1 == None and root2 == None:\n\t\t\t\t\treturn True\n\n\t\t\t\tif root1 != None and root2 == None or root1 == None and root2 != None:\n\t\t\t\t\treturn False\n\n\t\t\t\tif root1.val == root2.val:\n\t\t\t\t\treturn check_mirror_image(root1.left, root2.right) and check_mirror_image(root1.right, root2.left)\n\n\t\t\treturn check_mirror_image(root, root)\n\t\t\t\n# Thank You So Much \uD83E\uDD73\u270C\uD83D\uDC4D\n
36
0
['Recursion', 'Python', 'Python3']
5
symmetric-tree
Slim Java solution
slim-java-solution-by-alexthegreat-ecsc
The idea is:\n1. level traversal.\n2. push nodes onto stack, every 2 consecutive is a pair, and should either be both null or have equal value.\nrepeat until st
alexthegreat
NORMAL
2014-12-30T02:42:24+00:00
2014-12-30T02:42:24+00:00
5,408
false
The idea is:\n1. level traversal.\n2. push nodes onto stack, every 2 consecutive is a pair, and should either be both null or have equal value.\nrepeat until stack is empty.\n\n public boolean isSymmetric(TreeNode root) {\n if (root == null)\n return true;\n Stack<TreeNode> stack = new Stack<TreeNode>();\n stack.push(root.left);\n stack.push(root.right);\n while (!stack.isEmpty()) {\n TreeNode node1 = stack.pop();\n TreeNode node2 = stack.pop();\n if (node1 == null && node2 == null)\n continue;\n if (node1 == null || node2 == null)\n return false;\n if (node1.val != node2.val)\n return false;\n stack.push(node1.left);\n stack.push(node2.right);\n stack.push(node1.right);\n stack.push(node2.left);\n }\n return true;\n }
33
0
[]
6
symmetric-tree
Another passed Java solution
another-passed-java-solution-by-jeantime-cndg
public class Solution {\n public boolean isSymmetric(TreeNode root) {\n if (root == null) \n return true;\n \n
jeantimex
NORMAL
2015-06-28T17:40:22+00:00
2015-06-28T17:40:22+00:00
3,097
false
public class Solution {\n public boolean isSymmetric(TreeNode root) {\n if (root == null) \n return true;\n \n return isSymmetric(root.left, root.right);\n }\n \n boolean isSymmetric(TreeNode left, TreeNode right) {\n if (left == null && right == null) \n return true;\n\n if (left == null || right == null) \n return false;\n\n if (left.val != right.val) \n return false;\n\n return isSymmetric(left.left, right.right) && isSymmetric(left.right, right.left);\n }\n }
28
0
['Java']
2
symmetric-tree
python, best and explained O(n) recursion
python-best-and-explained-on-recursion-b-vpk7
python\nclass Solution:\n def isSymmetric(self, root: TreeNode) -> bool:\n if not root:\n return True\n \n def isMirror(tree1
serdarkuyuk
NORMAL
2020-11-18T05:26:46.325291+00:00
2020-11-18T05:26:46.325334+00:00
3,728
false
```python\nclass Solution:\n def isSymmetric(self, root: TreeNode) -> bool:\n if not root:\n return True\n \n def isMirror(tree1, tree2):\n if not tree1 or not tree2: # if one of them is null\n return tree2 == tree1 # compare them\n if tree1.val != tree2.val: # if above not executed, means they are both number\n return False # if they are both different return false\n # if they are similar go and look further\n return isMirror(tree1.left, tree2.right) and isMirror(tree1.right, tree2.left)\n \n return isMirror(root.left, root.right)\n```
27
1
['Recursion', 'Python', 'Python3']
2
symmetric-tree
[Python 3] DFS iterative solution using stack. Easy to understand.
python-3-dfs-iterative-solution-using-st-byz1
\nclass Solution:\n def isSymmetric(self, root):\n stack = []\n if root: stack.append([root.left, root.right])\n\n while(len(stack) > 0)
abstractart
NORMAL
2020-07-21T21:02:14.618256+00:00
2020-08-21T07:57:08.760565+00:00
2,101
false
```\nclass Solution:\n def isSymmetric(self, root):\n stack = []\n if root: stack.append([root.left, root.right])\n\n while(len(stack) > 0):\n left, right = stack.pop()\n \n if left and right:\n if left.val != right.val: return False\n stack.append([left.left, right.right])\n stack.append([right.left, left.right])\n \n elif left or right: return False\n \n return True\n```
27
0
['Python', 'Python3']
5
symmetric-tree
Share my recursive C++ solution,easy to understand
share-my-recursive-c-solutioneasy-to-und-eimm
class Solution {\n public:\n bool isSymmetric(TreeNode* root) {\n if (root == NULL)\n return true;\n \n
vdvvdd
NORMAL
2016-01-10T06:38:25+00:00
2016-01-10T06:38:25+00:00
2,188
false
class Solution {\n public:\n bool isSymmetric(TreeNode* root) {\n if (root == NULL)\n return true;\n \n return checkSymmetric(root->left, root->right);\n }\n //check the two nodes in symmetric position\n bool checkSymmetric(TreeNode *leftSymmetricNode, TreeNode *rightSymmetricNode)\n {\n if (leftSymmetricNode == NULL && rightSymmetricNode == NULL)\n return true;\n if (leftSymmetricNode == NULL || rightSymmetricNode == NULL)\n return false;\n if (leftSymmetricNode->val == rightSymmetricNode->val)\n return checkSymmetric(leftSymmetricNode->left, rightSymmetricNode->right) && checkSymmetric(leftSymmetricNode->right, rightSymmetricNode->left);\n return false;\n }\n };
27
1
['C++']
3
symmetric-tree
✅🚀 TS Easy Solution || Recursive
ts-easy-solution-recursive-by-viniciuste-gigw
Let me know in comments if you have any doubts. I will be happy to answer.\nPlease upvote if you found the solution useful.\n\n\nconst isSymmetric = (root: Tree
viniciusteixeiradias
NORMAL
2022-11-02T22:50:20.104722+00:00
2022-11-02T22:50:39.978319+00:00
2,565
false
Let me know in comments if you have any doubts. I will be happy to answer.\nPlease upvote if you found the solution useful.\n\n```\nconst isSymmetric = (root: TreeNode | null): boolean => {\n return isMirror(root, root);\n};\n \nconst isMirror = (t1: TreeNode | null, t2: TreeNode | null): boolean => {\n if (t1 === null && t2 === null) return true;\n if (t1 === null || t2 === null) return false;\n \n return (t1.val === t2.val) && isMirror(t1.left, t2.right) && isMirror(t1.right, t2.left);\n}\n```
26
0
['TypeScript', 'JavaScript']
3
symmetric-tree
Easy and simple using one queue iterative in java
easy-and-simple-using-one-queue-iterativ-8lln
public class Solution {\n public boolean isSymmetric(TreeNode root) {\n if(root == null) return true;\n Queue<TreeNode> queue = new
chen2
NORMAL
2015-11-21T05:42:31+00:00
2018-08-30T03:03:54.649078+00:00
2,519
false
public class Solution {\n public boolean isSymmetric(TreeNode root) {\n if(root == null) return true;\n Queue<TreeNode> queue = new LinkedList<TreeNode>();\n queue.offer(root.left);\n queue.offer(root.right);\n while(!queue.isEmpty()){\n TreeNode left = queue.poll();\n TreeNode right = queue.poll();\n if(left == null && right == null) continue;\n if(left == null || right == null) return false;\n if(left.val != right.val) return false;\n queue.offer(left.left);\n queue.offer(right.right);\n queue.offer(left.right);\n queue.offer(right.left);\n \n }\n return true;\n \n }\n }
26
0
[]
5
symmetric-tree
✅ [PHP][JavaScript] Recursive & Iterative Solutions
phpjavascript-recursive-iterative-soluti-j1h9
1. Recursive Solution\nThis solution uses recursion to check if a binary tree is symmetric. The recursive helper function isMirror() checks if the two nodes of
akunopaka
NORMAL
2023-03-13T18:25:04.624745+00:00
2023-03-13T18:28:49.286169+00:00
1,849
false
### 1. Recursive Solution\nThis solution uses recursion to check if a binary tree is symmetric. The recursive helper function isMirror() checks if the two nodes of the binary tree are mirror images of each other, by comparing their values, and then recursively checking if their left and right nodes are mirror images of each other. If the values are equal and the subtrees are mirrors, then the function returns true. Otherwise, it returns false.\n\nThe *time complexity* of this solution is O(n) as all nodes in the binary tree must be visited in order to determine if the tree is symmetric. \nThe *space complexity* is also O(n) as the recursive stack may contain up to n elements.\n\n\n```javascript []\nvar isSymmetric = function (root) {\n if (root == null) return true;\n return isMirror(root.left, root.right);\n\n function isMirror(leftNode, rightNode) {\n if (leftNode == null && rightNode == null) return true;\n if (leftNode == null || rightNode == null) return false;\n return leftNode.val === rightNode.val &&\n isMirror(leftNode.left, rightNode.right) &&\n isMirror(leftNode.right, rightNode.left);\n }\n};\n```\n```PHP []\nclass Solution\n{\n /**\n * @param TreeNode $root\n * @return Boolean\n */\n function isSymmetric(TreeNode $root): bool {\n if ($root === null) {\n return true;\n }\n return $this->isNodesMirror($root->left, $root->right);\n }\n\n function isNodesMirror(?TreeNode $leftNode, ?TreeNode $rightNode): bool {\n if ($leftNode === null && $rightNode === null) {\n return true;\n }\n if ($leftNode === null || $rightNode === null) {\n return false;\n }\n return $leftNode->val === $rightNode->val &&\n $this->isNodesMirror($leftNode->left, $rightNode->right) &&\n $this->isNodesMirror($leftNode->right, $rightNode->left);\n }\n}\n```\n\n\n### 2. Iterative Solution\nThis solution uses a Breadth-First Search approach to traverse the tree. A queue is used to store left and right nodes of the tree at each level. If the left node and right node are both null then the loop continues. If either one is null or the values of the nodes do not match then false is returned. If the values match then the left and right children of each node are pushed to the queue for comparison. If the loop completes without returning false then true is returned.\n*Time complexity*: O(n) as the algorithm visits each node once.\n*Space complexity*: O(n) as the queue stores all nodes at each level.\n\n```javascript []\nvar isSymmetric = function (root) {\n if (root == null) return true;\n let queue = [root.left, root.right];\n while (queue.length > 0) {\n let leftNode = queue.shift();\n let rightNode = queue.shift();\n if (leftNode == null && rightNode == null) continue;\n if (leftNode == null ||\n rightNode == null ||\n leftNode.val !== rightNode.val) {\n return false;\n }\n queue.push(leftNode.left, rightNode.right);\n queue.push(leftNode.right, rightNode.left);\n }\n return true;\n}\n```\n```PHP []\nclass Solution\n{\n /**\n * @param TreeNode $root\n * @return Boolean\n */\n function isSymmetric(?TreeNode $root): bool {\n if ($root === null) {\n return true;\n }\n $queue = [[$root->left, $root->right]];\n\n while ($queue) {\n $newQueue = [];\n foreach ($queue as [$leftNode, $rightNode]) {\n if ($leftNode === null && $rightNode === null) {\n continue;\n }\n if ($leftNode->val !== $rightNode->val ||\n $leftNode === null ||\n $rightNode === null) {\n return false;\n }\n $newQueue[] = [$leftNode->left, $rightNode->right];\n $newQueue[] = [$leftNode->right, $rightNode->left];\n }\n $queue = $newQueue;\n }\n return true;\n }\n}\n```\n\n\n\n### If my work was useful for you, please upvote\n\uD83D\uDC4D\uD83D\uDC4D\uD83D\uDC4D
25
0
['PHP', 'JavaScript']
3
symmetric-tree
Easy to understand Python
easy-to-understand-python-by-cglotr-0kag
Recursive\n\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, x):\n# self.val = x\n# self.left = None\n#
cglotr
NORMAL
2019-06-14T14:35:06.863731+00:00
2019-06-14T14:44:14.846920+00:00
2,814
false
Recursive\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, x):\n# self.val = x\n# self.left = None\n# self.right = None\n\nclass Solution:\n def isSymmetric(self, root: TreeNode) -> bool:\n if not root:\n return True\n return self.check(root.left, root.right)\n \n def check(self, left, right):\n if left is None and right is None:\n return True\n if left is None or right is None:\n return False\n if left.val != right.val:\n return False\n a = self.check(left.left, right.right)\n b = self.check(left.right, right.left)\n return a and b\n```\nIterative\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, x):\n# self.val = x\n# self.left = None\n# self.right = None\n\nclass Solution:\n def isSymmetric(self, root: TreeNode) -> bool:\n if not root:\n return True\n stack = collections.deque([(root.left, root.right)])\n while stack:\n l, r = stack.pop()\n if l is None and r is None:\n continue\n if l is None or r is None:\n return False\n if l.val != r.val:\n return False\n stack.append((l.left, r.right))\n stack.append((l.right, r.left))\n return True\n```
25
0
['Stack', 'Depth-First Search', 'Recursion', 'Iterator', 'Python']
2
symmetric-tree
Elegant Swift solution by conforming to Equatable
elegant-swift-solution-by-conforming-to-c38ae
\nclass Solution {\n func isSymmetric(_ root: TreeNode?) -> Bool {\n\t\troot?.left == root?.right\n\t}\n}\n\nextension TreeNode: Equatable {\n public stat
hak0suka
NORMAL
2020-10-04T15:50:05.264510+00:00
2020-11-10T11:04:58.170827+00:00
808
false
```\nclass Solution {\n func isSymmetric(_ root: TreeNode?) -> Bool {\n\t\troot?.left == root?.right\n\t}\n}\n\nextension TreeNode: Equatable {\n public static func ==(lhs: TreeNode, rhs: TreeNode) -> Bool {\n lhs.val == rhs.val && lhs.left == rhs.right && lhs.right == rhs.left\n }\n}\n```
24
0
['Swift']
4
symmetric-tree
Python solution
python-solution-by-zitaowang-6asi
Recursive:\n\nclass Solution(object):\n def isSymmetric(self, root):\n """\n :type root: TreeNode\n :rtype: bool\n """\n d
zitaowang
NORMAL
2018-08-17T01:46:04.211018+00:00
2018-08-17T01:46:04.211063+00:00
2,332
false
Recursive:\n```\nclass Solution(object):\n def isSymmetric(self, root):\n """\n :type root: TreeNode\n :rtype: bool\n """\n def isSym(root1, root2):\n if root1 == None and root2 == None:\n return True\n elif root1 == None and root2 != None:\n return False\n elif root1 != None and root2 == None:\n return False\n else:\n if root1.val != root2.val:\n return False\n else:\n return isSym(root1.left, root2.right) and isSym(root1.right,root2.left)\n return root == None or isSym(root.left,root.right)\n```\nIterative (DFS):\n```\nclass Solution(object):\n def isSymmetric(self, root):\n """\n :type root: TreeNode\n :rtype: bool\n """\n if root == None:\n return True\n stack = [root,root]\n while stack:\n r1 = stack.pop()\n r2 = stack.pop()\n if r1 == None and r2 == None:\n continue\n if r1 == None or r2 == None:\n return False\n if r1.val != r2.val:\n return False\n stack.append(r1.left)\n stack.append(r2.right)\n stack.append(r1.right)\n stack.append(r2.left)\n return True\n```\nIterative (BFS):\n```\nclass Solution(object):\n def isSymmetric(self, root):\n """\n :type root: TreeNode\n :rtype: bool\n """\n if root == None:\n return True\n queue = collections.deque([root, root])\n while queue:\n r1 = queue.pop()\n r2 = queue.pop()\n if r1 == None and r2 == None:\n continue\n if r1 == None or r2 == None:\n return False\n if r1.val != r2.val:\n return False\n queue.append(r1.left)\n queue.append(r2.right)\n queue.append(r1.right)\n queue.append(r2.left)\n return True\n```
23
0
[]
3
symmetric-tree
Explained with images 💻. Easy to understand. 📝
explained-with-images-easy-to-understand-3yih
Approach\nStarting from the root, we have to check that the left and right subtrees of the tree are mirrors of each other. The tree containing a single element
Kunal_Tajne
NORMAL
2024-08-18T15:44:47.805736+00:00
2024-08-18T15:50:31.619994+00:00
2,148
false
# Approach\nStarting from the root, we have to check that the left and right subtrees of the tree are mirrors of each other. The tree containing a single element root is always symmetric; we will return TRUE in this case. Otherwise, we will use the following algorithm:\n\n- We take a queue with root\'s right and left nodes.\n- Iterate a loop till the queue is not empty.\n- In each iteration, we dequeue two elements from the queue and store them in two variables, left and right.\n- If both left and right are NULL, it means that the node doesn\u2019t have any child. So, we move to the next interaction.\n- If any from left and right is NULL, it means that either the left child or right child of the node doesn\u2019t exist, which leads us to the conclusion that the tree is not symmetric; we return FALSE.\n- If the values of left and right are different, it also means that the tree is not symmetric; we return FALSE.\n- Then, we append the left node of left, the right node of right, the left node of right, and the right node of left in the queue in the same order, and we move to the next interaction.\n- After completing all interactions, if the algorithm is not returned from any step, this indicates that the tree is symmetric, so we return TRUE.\n\n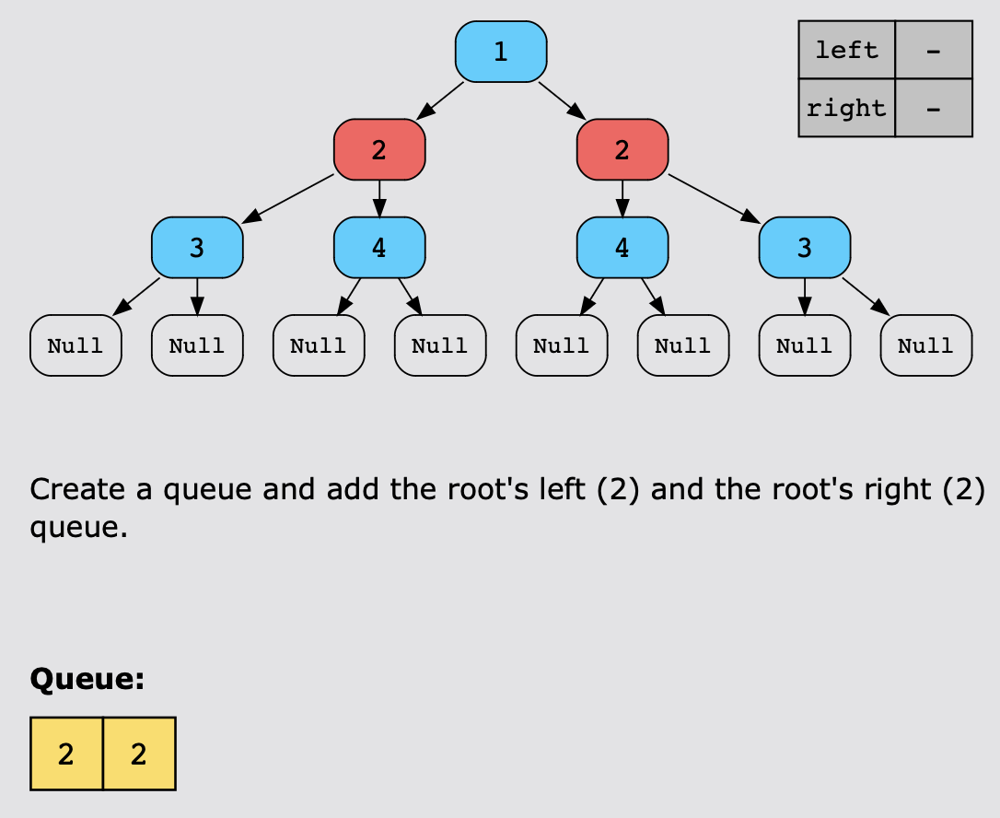![Screenshot 2024-08-18 at 11.34.29\u202FAM.png](https://assets.leetcode.com/users/images/9d515f90-bd16-4f38-a238-91262a6caf9d_1723995703.9023194.png)\n![Screenshot 2024-08-18 at 11.34.32\u202FAM.png](https://assets.leetcode.com/users/images/97bb8ded-5ea9-4120-9d25-83c601f9dd37_1723995711.2255645.png)\n![Screenshot 2024-08-18 at 11.34.35\u202FAM.png](https://assets.leetcode.com/users/images/58b910b2-f07e-455c-aafe-f734250e80b0_1723995717.696814.png)\n![Screenshot 2024-08-18 at 11.34.37\u202FAM.png](https://assets.leetcode.com/users/images/6aa17afb-5665-49ee-9726-e2a2436ca2b5_1723995729.528055.png)\n![Screenshot 2024-08-18 at 11.34.40\u202FAM.png](https://assets.leetcode.com/users/images/656ad6fd-c72c-4684-82f5-fa7a94191e1c_1723995762.855101.png)\n![Screenshot 2024-08-18 at 11.34.42\u202FAM.png](https://assets.leetcode.com/users/images/168276ed-17e3-4e2e-8a6b-1057b8420cd7_1723995772.0533068.png)\n![Screenshot 2024-08-18 at 11.34.44\u202FAM.png](https://assets.leetcode.com/users/images/8d33e3ad-4de3-493d-822c-0dc74f480f0a_1723995780.7840984.png)\n![Screenshot 2024-08-18 at 11.34.46\u202FAM.png](https://assets.leetcode.com/users/images/aaa8cc64-2707-4811-9766-01dd49048312_1723995801.8745077.png)\n![Screenshot 2024-08-18 at 11.34.48\u202FAM.png](https://assets.leetcode.com/users/images/ab2a1b43-89aa-42f3-ada0-e232090d45c2_1723995810.7984197.png)\n![Screenshot 2024-08-18 at 11.34.50\u202FAM.png](https://assets.leetcode.com/users/images/a8a4a832-9651-4bd0-9592-02a592fde8d8_1723995820.3829515.png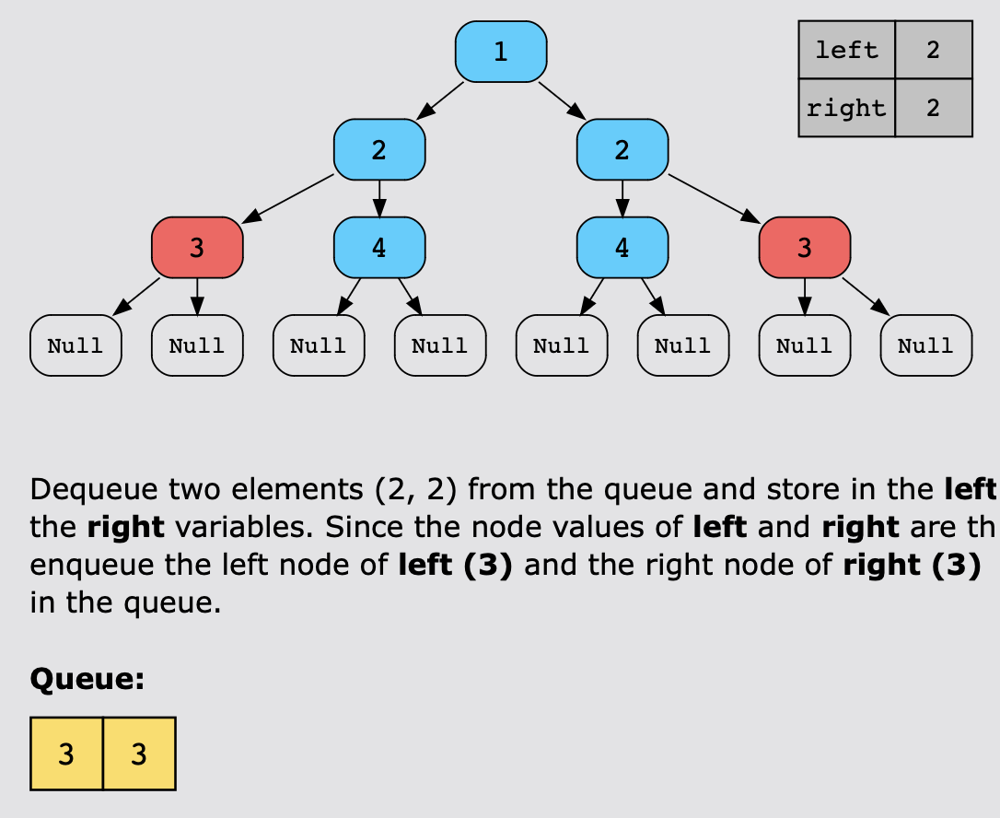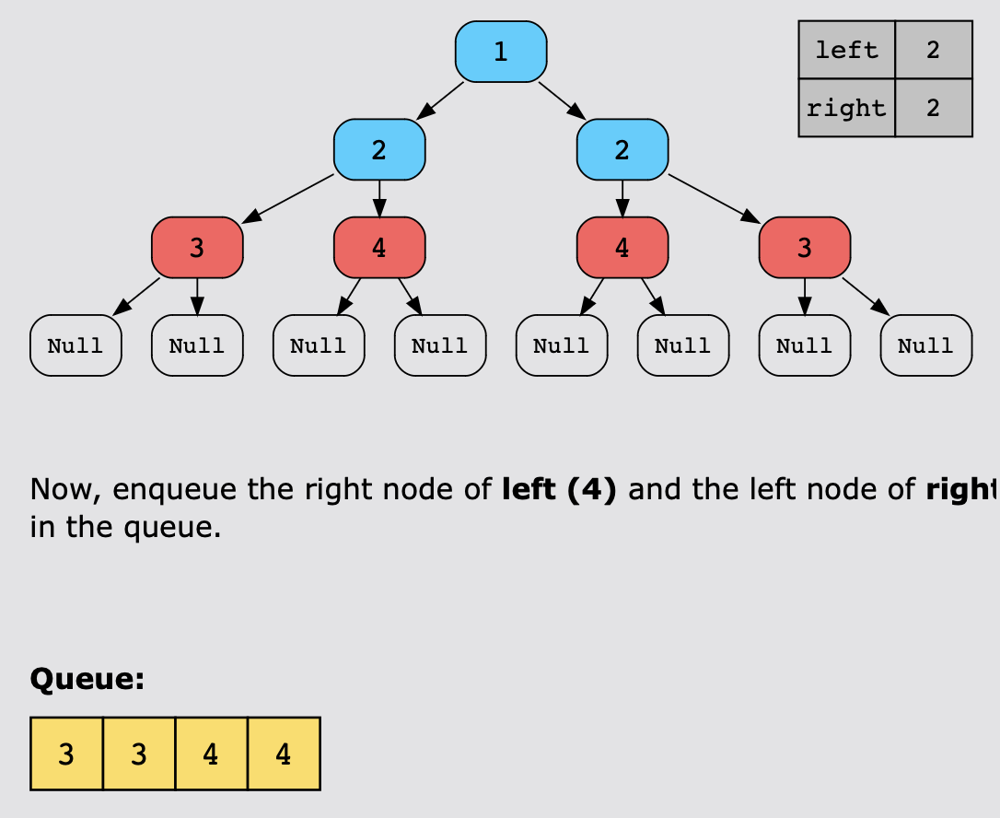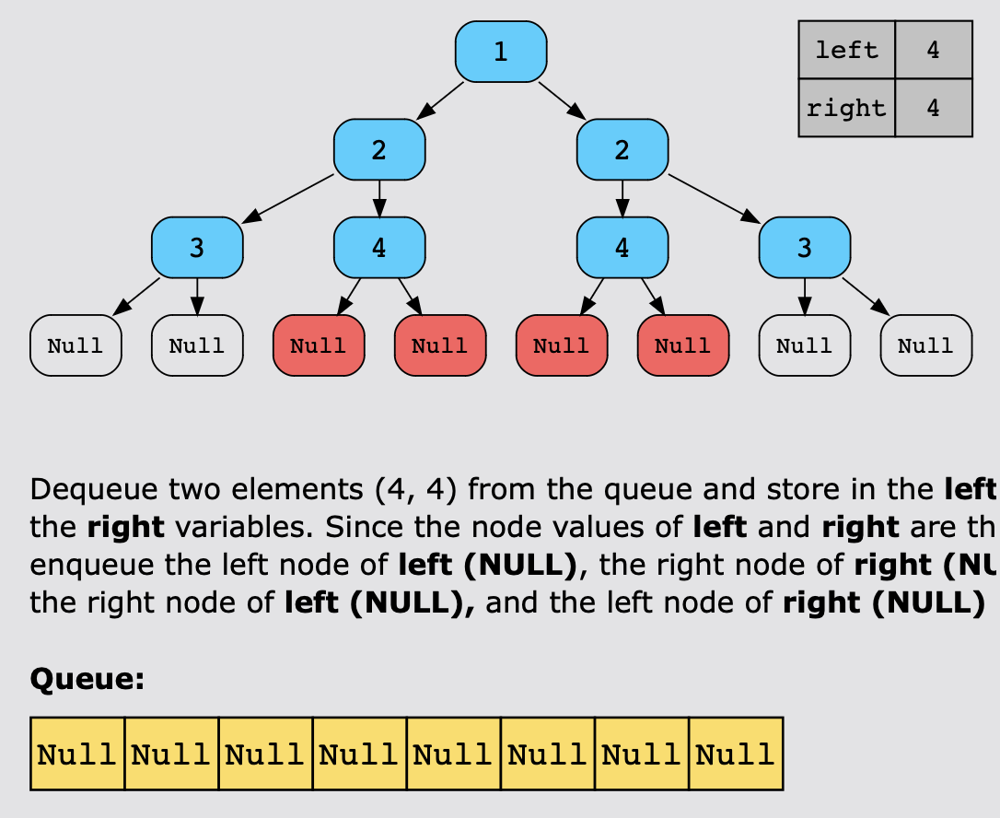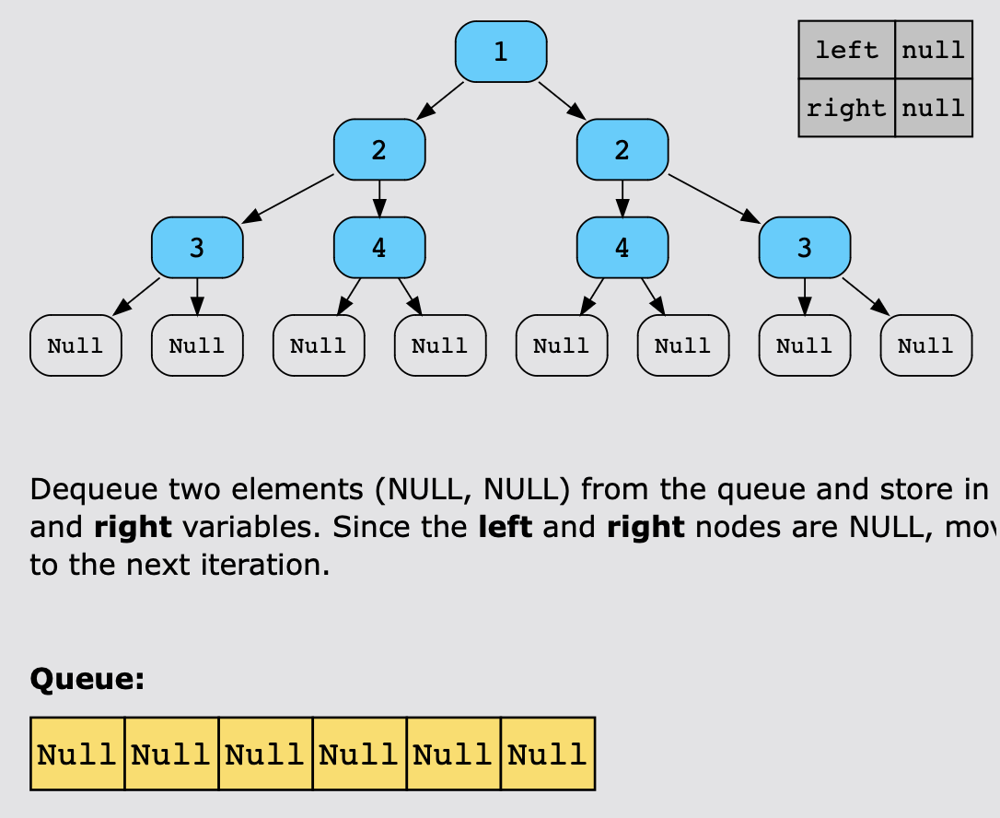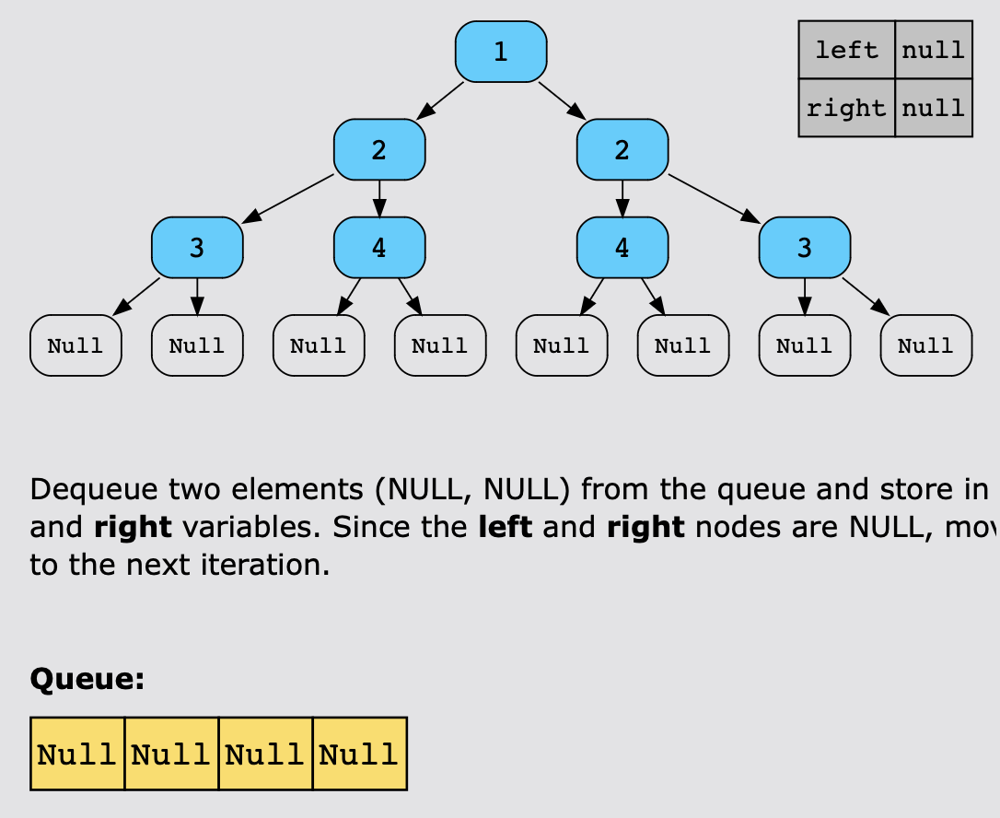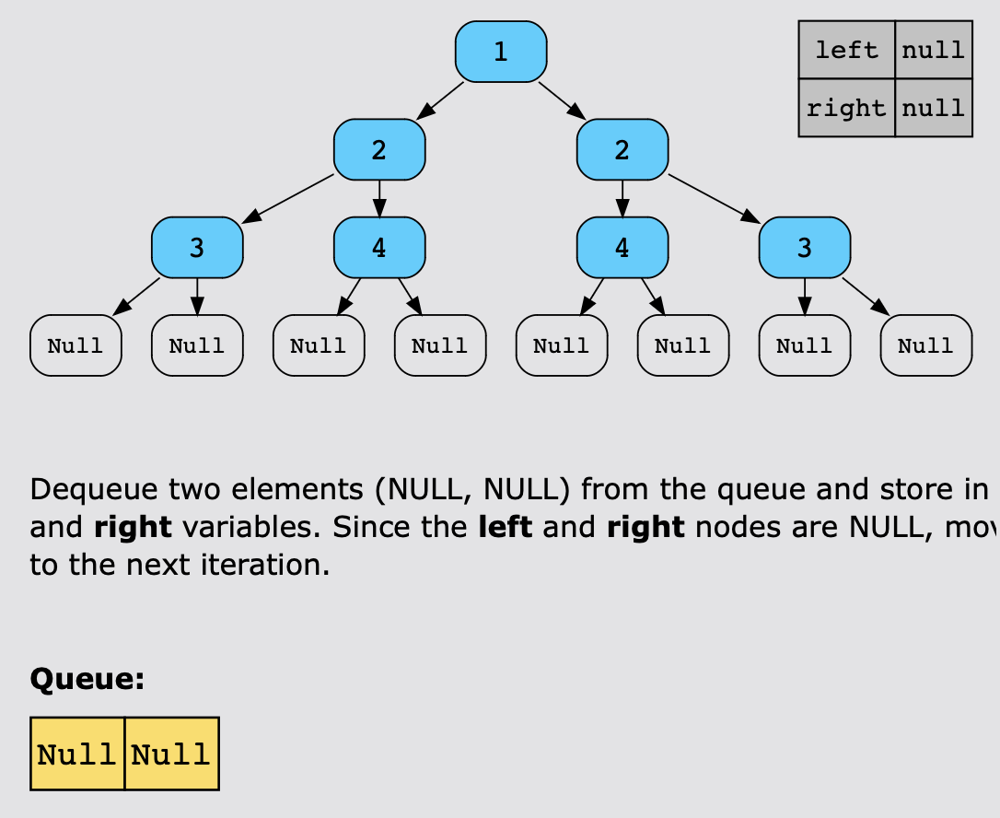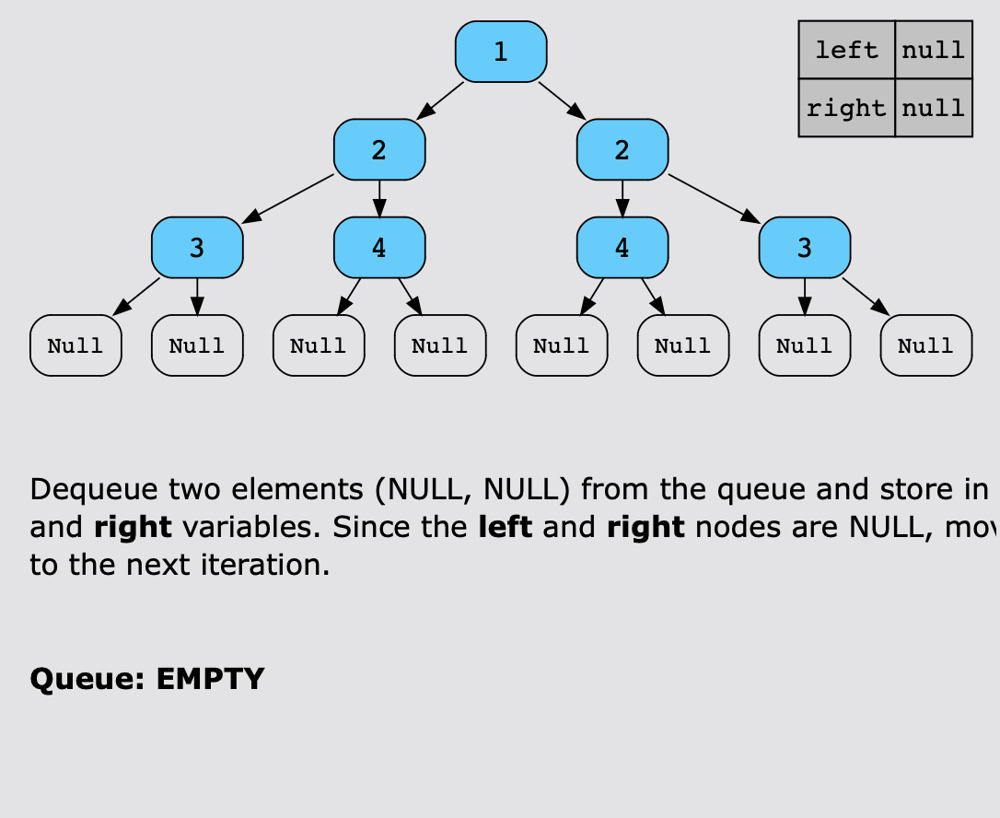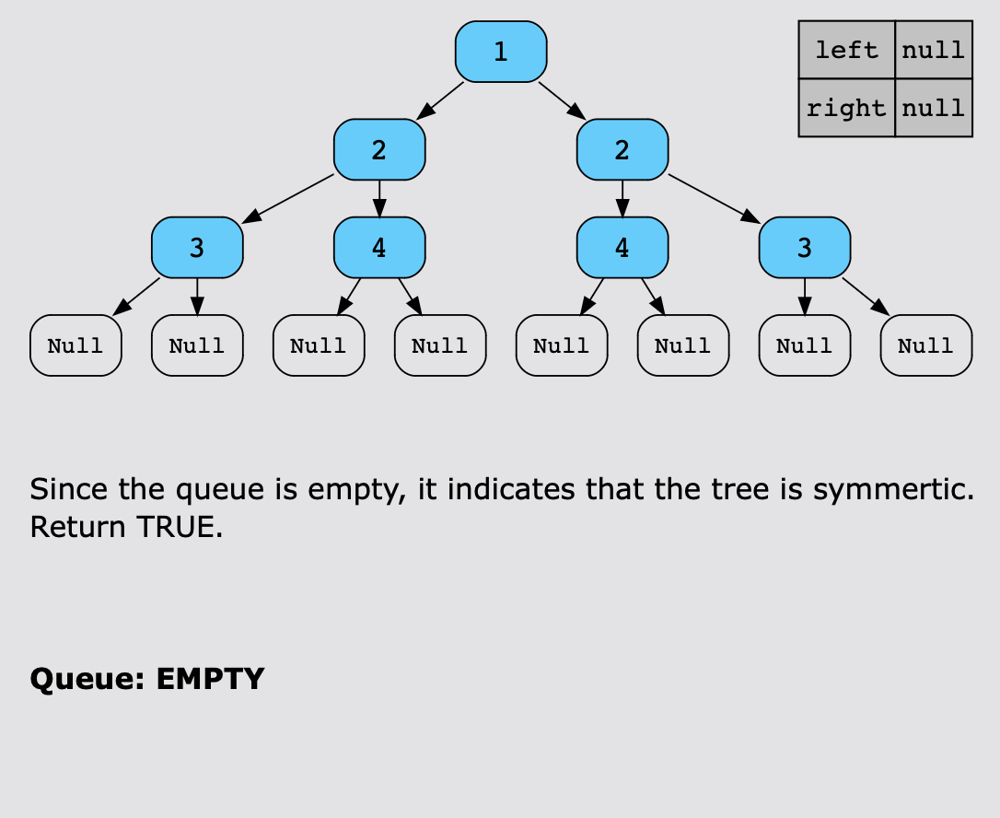)\n\n\n# Complexity\nTime complexity: The time complexity of this solution is $$O(n)$$, where n n is the total number of nodes in the tree. This is because we traverse the entire tree once.\n\nSpace complexity: Additional space is required to store a maximum of n elements in the queue, where n is the total number of nodes in the tree. So, the space complexity of this solution is $$O(n)$$ .\n\n\n# Code\n```\n\nclass Solution {\n public boolean isSymmetric(TreeNode root) {\n\n // Create a queue to help compare nodes in pairs\n Queue<TreeNode> queueOfNodes = new LinkedList<>();\n\n // Add the left and right children of the root to the queue\n queueOfNodes.add(root.left);\n queueOfNodes.add(root.right);\n\n // Continue processing as long as there are nodes in the queue\n while (!queueOfNodes.isEmpty()) {\n\n // Get the next pair of nodes from the queue\n TreeNode left = queueOfNodes.poll();\n TreeNode right = queueOfNodes.poll();\n\n // If both nodes are null, continue to the next pair (they are symmetric at this level)\n if (left == null && right == null) \n continue;\n\n // If one node is null and the other is not, the tree is not symmetric\n if (left == null || right == null)\n return false;\n\n // If the values of the two nodes are different, the tree is not symmetric\n if (left.val != right.val)\n return false;\n\n // Add the next level of nodes to the queue\n // Check the outer pair: left\'s left with right\'s right\n queueOfNodes.add(left.left);\n queueOfNodes.add(right.right);\n\n // Check the inner pair: left\'s right with right\'s left\n queueOfNodes.add(left.right);\n queueOfNodes.add(right.left);\n }\n\n // If all pairs are symmetric, return true\n return true;\n }\n}\n\n\n```\n\nPlease Upvote if found helpful :)\n\n
22
0
['Tree', 'Breadth-First Search', 'Binary Tree', 'C++', 'Java']
2
symmetric-tree
✅ 🔥 0 ms Runtime Beats 100% User🔥|| Code Idea ✅ || Algorithm & Solving Step ✅ ||
0-ms-runtime-beats-100-user-code-idea-al-s33p
\n\n\u2705 IF YOU LIKE THIS SOLUTION, PLEASE UPVOTE AT THE END \u2705 :\n\n\n### Key Idea :\nA binary tree is symmetric if:\n1. Its left and right subtrees hav
Letssoumen
NORMAL
2024-11-28T03:09:23.360619+00:00
2024-11-28T03:09:23.360660+00:00
3,365
false
![Screenshot 2024-11-28 at 8.25.14\u202FAM.png](https://assets.leetcode.com/users/images/2bcc33e0-e4e8-4bd8-831e-6f556e7eee44_1732763144.7556474.png)\n\n\u2705 IF YOU LIKE THIS SOLUTION, PLEASE UPVOTE AT THE END \u2705 :\n\n\n### **Key Idea** :\nA binary tree is symmetric if:\n1. Its left and right subtrees have the same structure.\n2. The values in the left and right subtrees mirror each other.\n\n---\n\n### **Approach** :\n\nWe can solve this using **recursion** or **iteration**:\n1. **Recursive Approach**:\n - Compare the left and right subtrees of the root.\n - For two subtrees to be mirrors:\n - Their root values must be equal.\n - The left subtree of one must be a mirror of the right subtree of the other, and vice versa.\n - Recursively check this condition for all nodes.\n\n2. **Iterative Approach**:\n - Use a queue to perform a level-order traversal, checking symmetry at each level.\n - Push pairs of nodes to the queue for comparison.\n\n---\n\n### **Algorithm** :\n\n#### Recursive\n1. If the root is `null`, the tree is symmetric.\n2. Define a helper function that:\n - Compares the values of two nodes.\n - Recursively checks the left subtree of the first node with the right subtree of the second, and vice versa.\n3. Return `true` if all checks pass.\n\n#### Iterative :\n1. Use a queue to store node pairs for comparison.\n2. While the queue is not empty:\n - Remove a pair from the queue.\n - Check if both nodes are `null`. If yes, continue.\n - If only one is `null`, return `false`.\n - Check if their values are equal.\n - Add their children to the queue in a mirrored order (left-right for one node and right-left for the other).\n\n---\n\n### **Complexity Analysis** :\n- **Time Complexity**: O(n), where n is the number of nodes in the tree. Each node is visited once.\n- **Space Complexity**:\n - Recursive: O(h), where h is the height of the tree (call stack).\n - Iterative: O(n), for the queue in the worst case.\n\n---\n\n### **Code Implementation**\n\n#### **C++**\n```cpp\nclass Solution {\npublic:\n bool isSymmetric(TreeNode* root) {\n if (!root) return true;\n return isMirror(root->left, root->right);\n }\n\n bool isMirror(TreeNode* t1, TreeNode* t2) {\n if (!t1 && !t2) return true;\n if (!t1 || !t2) return false;\n return (t1->val == t2->val) &&\n isMirror(t1->left, t2->right) &&\n isMirror(t1->right, t2->left);\n }\n};\n```\n\n**Iterative Approach** :\n```cpp\nclass Solution {\npublic:\n bool isSymmetric(TreeNode* root) {\n if (!root) return true;\n queue<TreeNode*> q;\n q.push(root->left);\n q.push(root->right);\n while (!q.empty()) {\n TreeNode* t1 = q.front(); q.pop();\n TreeNode* t2 = q.front(); q.pop();\n if (!t1 && !t2) continue;\n if (!t1 || !t2 || t1->val != t2->val) return false;\n q.push(t1->left);\n q.push(t2->right);\n q.push(t1->right);\n q.push(t2->left);\n }\n return true;\n }\n};\n```\n\n---\n\n#### **Java** :\n```java\nclass Solution {\n public boolean isSymmetric(TreeNode root) {\n if (root == null) return true;\n return isMirror(root.left, root.right);\n }\n\n private boolean isMirror(TreeNode t1, TreeNode t2) {\n if (t1 == null && t2 == null) return true;\n if (t1 == null || t2 == null) return false;\n return (t1.val == t2.val) &&\n isMirror(t1.left, t2.right) &&\n isMirror(t1.right, t2.left);\n }\n}\n```\n\n**Iterative Approach** :\n```java\nclass Solution {\n public boolean isSymmetric(TreeNode root) {\n if (root == null) return true;\n Queue<TreeNode> queue = new LinkedList<>();\n queue.add(root.left);\n queue.add(root.right);\n while (!queue.isEmpty()) {\n TreeNode t1 = queue.poll();\n TreeNode t2 = queue.poll();\n if (t1 == null && t2 == null) continue;\n if (t1 == null || t2 == null || t1.val != t2.val) return false;\n queue.add(t1.left);\n queue.add(t2.right);\n queue.add(t1.right);\n queue.add(t2.left);\n }\n return true;\n }\n}\n```\n\n---\n\n#### **Python 3** :\n```python\nclass Solution:\n def isSymmetric(self, root: Optional[TreeNode]) -> bool:\n if not root:\n return True\n return self.isMirror(root.left, root.right)\n\n def isMirror(self, t1: Optional[TreeNode], t2: Optional[TreeNode]) -> bool:\n if not t1 and not t2:\n return True\n if not t1 or not t2:\n return False\n return (t1.val == t2.val and\n self.isMirror(t1.left, t2.right) and\n self.isMirror(t1.right, t2.left))\n```\n\n**Iterative Approach**\n```python\nfrom collections import deque\n\nclass Solution:\n def isSymmetric(self, root: Optional[TreeNode]) -> bool:\n if not root:\n return True\n queue = deque([root.left, root.right])\n while queue:\n t1 = queue.popleft()\n t2 = queue.popleft()\n if not t1 and not t2:\n continue\n if not t1 or not t2 or t1.val != t2.val:\n return False\n queue.append(t1.left)\n queue.append(t2.right)\n queue.append(t1.right)\n queue.append(t2.left)\n return True\n```\n\n---\n\n### **Example Walkthrough** :\n\n#### Example 1:\n- **Input**: `[1, 2, 2, 3, 4, 4, 3]`\n- **Execution**:\n - Compare `2` and `2`: Equal.\n - Compare `3` and `3`: Equal.\n - Compare `4` and `4`: Equal.\n- **Output**: `true`.\n\n#### Example 2:\n- **Input**: `[1, 2, 2, null, 3, null, 3]`\n- **Execution**:\n - Compare `2` and `2`: Equal.\n - Compare `null` and `3`: Not equal.\n- **Output**: `false`.\n\n---\n\n### **Edge Cases** :\n1. **Empty Tree**: `root = null` \u2192 Symmetric (`true`).\n2. **Single Node**: `root = [1]` \u2192 Symmetric (`true`).\n3. **Unbalanced Tree**: `root = [1, 2, 2, 3, null, null, 3]` \u2192 Not symmetric (`false`).\n\n![image.png](https://assets.leetcode.com/users/images/a3e89fc7-bde6-4538-a83e-f08130ec2cdd_1732763353.596884.png)\n
20
0
['Tree', 'Depth-First Search', 'C++', 'Java', 'Python3']
1
symmetric-tree
JAVA | BFS and DFS ✅
java-bfs-and-dfs-by-sourin_bruh-gs6d
Please Upvote \uD83D\uDE07\n---\n##### 1. DFS approach:\n\nclass Solution {\n public boolean isSymmetric(TreeNode root) {\n return help(root.left, roo
sourin_bruh
NORMAL
2022-10-27T18:17:35.190824+00:00
2023-03-13T08:59:19.550370+00:00
2,336
false
# Please Upvote \uD83D\uDE07\n---\n##### 1. DFS approach:\n```\nclass Solution {\n public boolean isSymmetric(TreeNode root) {\n return help(root.left, root.right);\n }\n\n private boolean help(TreeNode left, TreeNode right) {\n if (left == null || right == null) {\n return left == right;\n }\n if (left.val != right.val) {\n return false;\n }\n boolean check1 = help(left.left, right.right);\n boolean check2 = help(left.right, right.left);\n return check1 && check2;\n }\n}\n\n// TC: O(n), SC: O(n)\n```\n---\n##### 2. BFS approach:\n```\nclass Solution {\n public boolean isSymmetric(TreeNode root) {\n Queue<TreeNode> q = new LinkedList<>();\n q.offer(root);\n\n while (!q.isEmpty()) {\n int n = q.size();\n List<Integer> list = new ArrayList<>();\n\n for (int i = 0; i < n; i++) {\n TreeNode curr = q.poll();\n\n if (curr == null) list.add(null);\n else {\n list.add(curr.val);\n q.offer(curr.left);\n q.offer(curr.right);\n }\n }\n\n if (!checkSymmetry(list)) return false;\n }\n\n return true;\n }\n\n public boolean checkSymmetry(List<Integer> list) {\n int l = 0, r = list.size() - 1;\n\n while (l < r) {\n if (list.get(l++) != list.get(r--)) {\n return false;\n }\n }\n\n return true;\n }\n}\n\n// TC: O(n), SC: O(n)\n```
18
0
['Tree', 'Depth-First Search', 'Breadth-First Search', 'Binary Tree', 'Java']
2
symmetric-tree
JAVA ||Easy Recursive solution || Easiest Approach || Runtime: 0 ms
java-easy-recursive-solution-easiest-app-xsgx
\nclass Solution {\n public boolean isSymmetric(TreeNode root) {\n return root == null || isMirror(root.left, root.right);\n }\n boolean isMirror
duke05
NORMAL
2022-10-11T07:52:08.023926+00:00
2022-10-11T07:52:08.023958+00:00
2,440
false
```\nclass Solution {\n public boolean isSymmetric(TreeNode root) {\n return root == null || isMirror(root.left, root.right);\n }\n boolean isMirror(TreeNode node1, TreeNode node2) {\n if (node1 == null && node2 == null) return true;\n \n if (node1 == null || node2 == null) return false;\n \n if (node1.val != node2.val) return false;\n return isMirror(node1.left, node2.right) && isMirror(node1.right, node2.left);\n }\n}\n\n```\n![image](https://assets.leetcode.com/users/images/0ad972be-ccb4-4c1f-92f1-2ec39d38b178_1665474715.5691338.png)\n
18
0
['Depth-First Search', 'Binary Tree', 'Java']
2
symmetric-tree
Python Solution with EASY Explanation
python-solution-with-easy-explanation-by-fhab
Please Upvote if it helps ! \n\n---\n\n- # Intuition\n Describe your first thoughts on how to solve this problem. \n\nTo check whether a tree is mirror symmetri
namanpuri
NORMAL
2023-03-13T05:50:58.177826+00:00
2023-03-13T05:50:58.177866+00:00
3,118
false
> # *Please Upvote if it helps !* \n\n---\n\n- # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\nTo check whether a tree is mirror symmetric or not, we need to compare the left and right subtrees of each node. If they are mirror images of each other, then the tree is mirror symmetric.\n\n- # Approach\n<!-- Describe your approach to solving the problem. -->\n\nIn this code, we first check if the root of the tree is None, in which case we return True because an empty tree is mirror symmetric.\n\nThen, we define a helper function called `isMirror` which takes two nodes as input and checks whether they are mirror images of each other. If both nodes are None, we return True. If one of them is None, we return False because a node cannot be a mirror image of None. \n\nOtherwise, we check if the values of the nodes are equal and then recursively check whether the left subtree of the first node is a mirror image of the right subtree of the second node, and whether the right subtree of the first node is a mirror image of the left subtree of the second node.\n\nFinally, we call the `isMirror` function with the left and right subtrees of the root node and return the result. If the tree is mirror symmetric, the function will return True, otherwise it will return False.\n\n- # Code\n\nHere is the `Python` code to check whether a tree is mirror symmetric or not:\n\n```\n\nclass Solution:\n def isSymmetric(self, root: TreeNode) -> bool:\n def isMirror(t1, t2):\n if not t1 and not t2:\n return True\n if not t1 or not t2:\n return False\n return t1.val == t2.val and isMirror(t1.right, t2.left) and isMirror(t1.left, t2.right)\n \n return isMirror(root, root)\n```\n
17
0
['Python3']
3
symmetric-tree
Python | DFS | BFS
python-dfs-bfs-by-kevinjm17-l2le
DFS Solution\n\nclass Solution:\n def isSymmetric(self, root: Optional[TreeNode]) -> bool:\n if not root:\n return True\n \n
kevinjm17
NORMAL
2022-09-28T19:56:43.325680+00:00
2022-09-28T19:57:52.762364+00:00
1,930
false
**DFS Solution**\n```\nclass Solution:\n def isSymmetric(self, root: Optional[TreeNode]) -> bool:\n if not root:\n return True\n \n def dfs(l, r):\n if not l and not r:\n return True\n \n if not l or not r:\n return False\n \n if l.val == r.val:\n return dfs(l.left, r.right) and dfs(l.right, r.left)\n \n return False\n \n return dfs(root.left, root.right)\n```\n\n**BFS Solution**\n```\nclass Solution:\n def isSymmetric(self, root: Optional[TreeNode]) -> bool:\n if not root:\n return True\n \n q = deque()\n q.append((root.left, root.right))\n while q:\n for _ in range(len(q)):\n left, right = q.popleft()\n if not left and not right:\n continue\n \n elif not left or not right:\n return False\n \n else:\n if left.val != right.val:\n return False\n \n q.append((left.left, right.right))\n q.append((left.right, right.left))\n \n return True\n```\n**Please upvote if you find this helpful**
17
0
['Depth-First Search', 'Breadth-First Search', 'Python']
0
symmetric-tree
2 lines Java solution use 1ms
2-lines-java-solution-use-1ms-by-zbl-tqr6
\n\n public class Solution {\n public boolean isSymmetric(TreeNode root) {\n return isMirror(root,root);\n }\n \n public b
zbl
NORMAL
2016-04-26T09:10:59+00:00
2016-04-26T09:10:59+00:00
1,909
false
\n\n public class Solution {\n public boolean isSymmetric(TreeNode root) {\n return isMirror(root,root);\n }\n \n public boolean isMirror(TreeNode a,TreeNode b){\n return a==null||b==null?a==b:a.val==b.val&&isMirror(a.left,b.right)&&isMirror(a.right,b.left);\n }\n }
17
0
[]
2
symmetric-tree
Beautiful Recursive and Iterative Solutions
beautiful-recursive-and-iterative-soluti-d1sp
Very simple ideas. Notice how both look similar to each other.\n\n /\n * Definition for binary tree\n * struct TreeNode {\n * int val;\n
1337beef
NORMAL
2014-09-18T15:03:54+00:00
2014-09-18T15:03:54+00:00
6,663
false
Very simple ideas. Notice how both look similar to each other.\n\n /**\n * Definition for binary tree\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode(int x) : val(x), left(NULL), right(NULL) {}\n * };\n */\n #include<queue>\n using namespace std;\n typedef pair<TreeNode*,TreeNode*> nodepair;\n class Solution {\n public:\n bool isSymmetricRecursive(TreeNode*a,TreeNode*b){\n if(a){\n return b && a->val==b->val && \n isSymmetricRecursive(a->left,b->right) &&\n isSymmetricRecursive(a->right,b->left);\n }\n return !b;\n }\n bool isSymmetricRecursive(TreeNode*root){\n return !root || isSymmetricRecursive(root->left,root->right);\n }\n bool isSymmetric(TreeNode *root) {\n // Level-order BFS.\n queue<nodepair> q;\n if(root)\n q.push(make_pair(root->left,root->right));\n while(q.size()){\n nodepair p=q.front(); q.pop();\n if(p.first){\n if(!p.second)return false;\n if(p.first->val != p.second->val) return false;\n // the order of children pushed to q is the key to the solution.\n q.push(make_pair(p.first->left,p.second->right));\n q.push(make_pair(p.first->right,p.second->left));\n }\n else if(p.second) return false;\n }\n return true;\n }\n };
16
3
[]
10
symmetric-tree
java || easiest solution
java-easiest-solution-by-ashutosh_369-29lq
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
Ashutosh_369
NORMAL
2023-03-13T02:17:37.231464+00:00
2023-03-13T02:17:37.231507+00:00
2,334
false
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * Definition for a binary tree node.\n * public class TreeNode {\n * int val;\n * TreeNode left;\n * TreeNode right;\n * TreeNode() {}\n * TreeNode(int val) { this.val = val; }\n * TreeNode(int val, TreeNode left, TreeNode right) {\n * this.val = val;\n * this.left = left;\n * this.right = right;\n * }\n * }\n */\n\nclass Solution {\n static boolean mir( TreeNode t1 , TreeNode t2 )\n {\n if( t1==null && t2== null ) return true;\n else if( t1==null || t2==null ) return false;\n\n return ( t1.val==t2.val ) && mir( t1.right , t2.left ) && mir( t1.left , t2.right );\n }\n public boolean isSymmetric(TreeNode root) \n {\n return mir( root , root );\n \n }\n}\n```
15
0
['Java']
0
symmetric-tree
Day 72 || With Diagram || Iterative and Recursive || Easiest Beginner Friendly Sol
day-72-with-diagram-iterative-and-recurs-7tss
NOTE - PLEASE READ INTUITION AND APPROACH FIRST THEN SEE THE CODE. YOU WILL DEFINITELY UNDERSTAND THE CODE LINE BY LINE AFTER SEEING THE APPROACH.\n\n# Intuitio
singhabhinash
NORMAL
2023-03-13T00:50:21.879829+00:00
2023-03-13T05:14:40.613943+00:00
1,479
false
**NOTE - PLEASE READ INTUITION AND APPROACH FIRST THEN SEE THE CODE. YOU WILL DEFINITELY UNDERSTAND THE CODE LINE BY LINE AFTER SEEING THE APPROACH.**\n\n# Intuition of this Problem:\nWe need to validate only 3 conditions including base condition and recursively call to the function:\n- If both "leftRoot" and "rightRoot" are null, return true\n- If only one of "leftRoot" or "rightRoot" is null, return false\n- If "leftRoot" and "rightRoot" are not null and their values are not equal, return false\n- If "leftRoot" and "rightRoot" are not null and their values are equal, recursively call "isTreeSymmetric" on the left child of "leftRoot" and the right child of "rightRoot", and the right child of "leftRoot" and the left child of "rightRoot"\n\n![WhatsApp Image 2023-01-24 at 6.54.24 PM.jpeg](https://assets.leetcode.com/users/images/3ce67a24-c51f-4cff-a5ac-58425726b650_1674566690.8242106.jpeg)\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach for this Problem:\n1. Define a function "isTreeSymmetric" that takes in two TreeNode pointers as inputs, "leftRoot" and "rightRoot"\n2. If both "leftRoot" and "rightRoot" are null, return true\n3. If only one of "leftRoot" or "rightRoot" is null, return false\n4. If "leftRoot" and "rightRoot" are not null and their values are not equal, return false\n5. If "leftRoot" and "rightRoot" are not null and their values are equal, recursively call "isTreeSymmetric" on the left child of "leftRoot" and the right child of "rightRoot", and the right child of "leftRoot" and the left child of "rightRoot"\n6. Return true if both recursive calls return true, else return false\n7. Define a function "isSymmetric" that takes in a TreeNode pointer "root" as input\n8. Call "isTreeSymmetric" on the left child of "root" and the right child of "root" and return the result\n<!-- Describe your approach to solving the problem. -->\n\n# Humble Request:\n- If my solution is helpful to you then please **UPVOTE** my solution, your **UPVOTE** motivates me to post such kind of solution.\n- Please let me know in comments if there is need to do any improvement in my approach, code....anything.\n- **Let\'s connect on** https://www.linkedin.com/in/abhinash-singh-1b851b188\n\n![57jfh9.jpg](https://assets.leetcode.com/users/images/c2826b72-fb1c-464c-9f95-d9e578abcaf3_1674104075.4732099.jpeg)\n\n# Code:\n```C++ []\n//Iterative approach\n// TC - O(n), where n is the number of nodes in the binary tree. This is because the code visits each node in the binary tree once, and the while loop iterates over all nodes in the worst-case scenario.\n// SC - O(n), where n is the number of nodes in the binary tree. This is because the code uses a queue to store nodes in a level-by-level manner, and in the worst-case scenario, the queue will contain all the nodes of the binary tree. Therefore, the space required by the queue will be proportional to the number of nodes in the tree, leading to O(n) space complexity.\nclass Solution {\npublic:\n bool isSymmetric(TreeNode* root) {\n if (root == nullptr)\n return true;\n queue<TreeNode*> q;\n q.push(root -> left);\n q.push(root -> right);\n while (!q.empty()) {\n TreeNode *leftRoot = q.front();\n q.pop();\n TreeNode *rightRoot = q.front();\n q.pop();\n if (leftRoot == nullptr && rightRoot == nullptr)\n continue;\n if ((leftRoot == nullptr && rightRoot != nullptr) || (leftRoot != nullptr && rightRoot == nullptr))\n return false;\n if (leftRoot -> val != rightRoot -> val)\n return false;\n q.push(leftRoot -> left);\n q.push(rightRoot -> right);\n q.push(leftRoot -> right);\n q.push(rightRoot -> left);\n }\n return true;\n }\n};\n```\n```C++ []\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n bool isTreeSymmetric(TreeNode* leftRoot, TreeNode* rightRoot){\n if(leftRoot == nullptr && rightRoot == nullptr)\n return true;\n if((leftRoot == nullptr && rightRoot != nullptr) || (leftRoot != nullptr && rightRoot == nullptr))\n return false;\n if(leftRoot -> val != rightRoot -> val)\n return false;\n return isTreeSymmetric(leftRoot -> left, rightRoot -> right) && isTreeSymmetric(leftRoot -> right, rightRoot -> left);\n }\n bool isSymmetric(TreeNode* root) {\n return isTreeSymmetric(root -> left, root -> right);\n }\n};\n```\n```Java []\nclass Solution {\n public boolean isTreeSymmetric(TreeNode leftRoot, TreeNode rightRoot){\n if(leftRoot == null && rightRoot == null)\n return true;\n if((leftRoot == null && rightRoot != null) || (leftRoot != null && rightRoot == null))\n return false;\n if(leftRoot.val != rightRoot.val)\n return false;\n return isTreeSymmetric(leftRoot.left, rightRoot.right) && isTreeSymmetric(leftRoot.right, rightRoot.left);\n }\n public boolean isSymmetric(TreeNode root) {\n return isTreeSymmetric(root.left, root.right);\n }\n}\n```\n```Python []\nclass Solution:\n def isTreeSymmetric(self, leftRoot, rightRoot):\n if leftRoot is None and rightRoot is None:\n return True\n if (leftRoot is None and rightRoot is not None) or (leftRoot is not None and rightRoot is None):\n return False\n if leftRoot.val != rightRoot.val:\n return False\n return self.isTreeSymmetric(leftRoot.left, rightRoot.right) and self.isTreeSymmetric(leftRoot.right, rightRoot.left)\n def isSymmetric(self, root):\n return self.isTreeSymmetric(root.left, root.right)\n```\n\n# Time Complexity and Space Complexity:\n- Time complexity: **O(n)**, where n is the total number of nodes in the binary tree. This is because the solution visits each node once and compares its values with the corresponding symmetric node, thus the function isTreeSymmetric() is called on each node at most once. The time complexity of the isTreeSymmetric() function is O(n/2) because it only visits half of the nodes (in the best case when the tree is symmetric) and in the worst case it visits all nodes in the tree (when the tree is not symmetric).\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: **O(h)**, where h is the height of the binary tree. This is because the recursive calls made by the solution consume memory on the call stack equal to the height of the tree. In the worst case when the binary tree is linear, the height of the tree is equal to n, thus the space complexity becomes O(n). However, in the best case when the binary tree is perfectly balanced, the height of the tree is log(n), thus the space complexity becomes O(log(n)).\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->
15
5
['Depth-First Search', 'Binary Tree', 'C++', 'Java', 'Python3']
1
symmetric-tree
C++ short simple recursive code
c-short-simple-recursive-code-by-jeetaks-n2zz
\n# Approach\n Describe your approach to solving the problem. \nRecurively check for the subtrees. Return false if they aren\'t equal.\n\n# Code\n\nclass Soluti
Jeetaksh
NORMAL
2023-01-15T07:52:48.191088+00:00
2023-01-15T07:52:48.191119+00:00
2,377
false
\n# Approach\n<!-- Describe your approach to solving the problem. -->\nRecurively check for the subtrees. Return false if they aren\'t equal.\n\n# Code\n```\nclass Solution {\npublic:\n\n bool isSame(TreeNode* t1, TreeNode* t2){\n if(!t1 && !t2){return true;}\n if(t1 && !t2){return false;}\n if(t2 && !t1){return false;}\n if(t1->val==t2->val){return isSame(t1->left,t2->right) && isSame(t1->right,t2->left);}\n return false;\n }\n\n bool isSymmetric(TreeNode* root) {\n return isSame(root->left,root->right); \n }\n};\n```\n**Please upvote if it helped. Happy Coding!**
15
0
['C++']
0
symmetric-tree
✔️ 100% Fastest Swift Solution, time: O(n), space: O(n).
100-fastest-swift-solution-time-on-space-r0w7
\n/**\n * Definition for a binary tree node.\n * public class TreeNode {\n * public var val: Int\n * public var left: TreeNode?\n * public var right
sergeyleschev
NORMAL
2022-04-08T13:41:27.305857+00:00
2022-04-08T13:41:27.305903+00:00
1,299
false
```\n/**\n * Definition for a binary tree node.\n * public class TreeNode {\n * public var val: Int\n * public var left: TreeNode?\n * public var right: TreeNode?\n * public init() { self.val = 0; self.left = nil; self.right = nil; }\n * public init(_ val: Int) { self.val = val; self.left = nil; self.right = nil; }\n * public init(_ val: Int, _ left: TreeNode?, _ right: TreeNode?) {\n * self.val = val\n * self.left = left\n * self.right = right\n * }\n * }\n */\nclass Solution {\n // - Complexity:\n // - time: O(n), where n is the number of nodes.\n // - space: O(n), where n is the number of nodes.\n \n func isSymmetric(_ root: TreeNode?) -> Bool {\n isMirror(root, root)\n }\n \n \n private func isMirror(_ left: TreeNode?, _ right: TreeNode?) -> Bool {\n if left == nil, right == nil { return true }\n \n guard left?.val == right?.val else { return false }\n \n return isMirror(left?.left, right?.right) && isMirror(left?.right, right?.left)\n }\n\n}\n```\n\nLet me know in comments if you have any doubts. I will be happy to answer.\n\nPlease upvote if you found the solution useful.
15
0
['Swift']
0
symmetric-tree
100% faster 0ms runtime short C++ solution
100-faster-0ms-runtime-short-c-solution-36njz
\n\n\n bool isMirror(TreeNode* root1,TreeNode *root2){\n if(root1==NULL && root2==NULL)\n return true;\n if(root1 && root2 && root1-
reetisharma
NORMAL
2021-03-21T15:54:08.295678+00:00
2021-03-21T15:54:08.295722+00:00
1,328
false
```\n\n\n bool isMirror(TreeNode* root1,TreeNode *root2){\n if(root1==NULL && root2==NULL)\n return true;\n if(root1 && root2 && root1->val == root2->val)\n return isMirror(root1->left,root2->right) && isMirror(root1->right,root2->left);\n \n return false;\n }\n bool isSymmetric(TreeNode* root) {\n return isMirror(root,root);\n }\n\n```
15
1
['Recursion', 'C']
1
symmetric-tree
c++ solution recursive and iterative
c-solution-recursive-and-iterative-by-fi-5l9o
Note\nThe answer is true when root is nullptr.\n\nclass Solution\n{\npublic:\n\t// recursive : 12 ms 16.7 MB\n\tbool isSymmetric(TreeNode* root) {\n\t\treturn !
fifamvp
NORMAL
2020-11-22T08:49:20.436906+00:00
2020-11-22T08:49:20.436948+00:00
1,302
false
**Note**\nThe answer is true when root is nullptr.\n```\nclass Solution\n{\npublic:\n\t// recursive : 12 ms 16.7 MB\n\tbool isSymmetric(TreeNode* root) {\n\t\treturn !root || isEquivalent(root->left, root->right);\n\t}\n\n\tbool isEquivalent(TreeNode* leftNode, TreeNode* rightNode)\n\t{\n\t\tif (!leftNode && rightNode || leftNode && !rightNode) return false;\n\n\t\treturn !leftNode || leftNode->val == rightNode->val && isEquivalent(leftNode->left, rightNode->right) && isEquivalent(leftNode->right, rightNode->left);\n\t}\n\n\t// iterative : 4 ms\t16.9 MB\n\tbool isSymmetric3(TreeNode* root) {\n\t\tif (!root) return true;\n\t\tqueue<TreeNode*> pending({ root->left, root->right });\n\n\t\twhile (!pending.empty())\n\t\t{\n\t\t\tTreeNode* l = pending.front();\n\t\t\tpending.pop();\n\t\t\tTreeNode* r = pending.front();\n\t\t\tpending.pop();\n\n\t\t\tif (!l && r || l && !r) return false;\n\t\t\tif (l)\n\t\t\t{\n\t\t\t\tif (l->val != r->val) return false;\n\t\t\t\tpending.push(l->left);\n\t\t\t\tpending.push(r->right);\n\t\t\t\tpending.push(l->right);\n\t\t\t\tpending.push(r->left);\n\t\t\t}\n\t\t}\n\n\t\treturn true;\n\t}\n};\n```
15
0
['Recursion', 'C', 'Iterator']
1
symmetric-tree
Clean iterative solution in C++
clean-iterative-solution-in-c-by-bei-zi-aosvz
/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n *
bei-zi-jun
NORMAL
2015-05-26T18:03:51+00:00
2015-05-26T18:03:51+00:00
2,232
false
/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode(int x) : val(x), left(NULL), right(NULL) {}\n * };\n */\n class Solution {\n public:\n bool isSymmetric(TreeNode* root) {\n if(!root) return true;\n stack<TreeNode*> sk;\n sk.push(root->left);\n sk.push(root->right);\n \n TreeNode* pA, *pB;\n while(!sk.empty()) {\n pA = sk.top();\n sk.pop();\n pB = sk.top();\n sk.pop();\n \n if(!pA && !pB) continue;\n if(!pA || !pB) return false;\n if(pA->val != pB->val) return false;\n \n sk.push(pA->left);\n sk.push(pB->right);\n sk.push(pA->right);\n sk.push(pB->left);\n }\n \n return true;\n }\n };
15
2
[]
1
symmetric-tree
4ms Simple C++ code
4ms-simple-c-code-by-davidyw-a9av
class Solution {\n public:\n bool isSymmetric(TreeNode* root) {\n if (!root){\n return true;\n }\n else{\n
davidyw
NORMAL
2015-09-27T22:12:04+00:00
2015-09-27T22:12:04+00:00
2,199
false
class Solution {\n public:\n bool isSymmetric(TreeNode* root) {\n if (!root){\n return true;\n }\n else{\n return isSame(root->left, root->right);\n }\n }\n private: // hide functions in the private helps to improve running time\n bool isSame (TreeNode* n1, TreeNode* n2){\n if (!n1 || !n2){\n return n1 == n2;\n }\n else{\n return (n1->val == n2->val && isSame(n1->left, n2->right) && isSame(n1->right, n2->left));\n }\n }\n };
15
0
['Recursion', 'C++']
3
symmetric-tree
*Java* iterative & recursive solutions
java-iterative-recursive-solutions-by-el-mnj7
Recursive#\n public boolean isSymmetric(TreeNode root) {\n \tif(root==null) return true;\n \treturn isSymmetric(root.left, root.right);\n }\n pri
elementnotfoundexception
NORMAL
2016-01-23T06:37:03+00:00
2016-01-23T06:37:03+00:00
2,460
false
#Recursive#\n public boolean isSymmetric(TreeNode root) {\n \tif(root==null) return true;\n \treturn isSymmetric(root.left, root.right);\n }\n private boolean isSymmetric(TreeNode root1, TreeNode root2) {\n \tif(root1==null && root2==null) return true;\n \tif(root1==null || root2==null) return false;\n \tif(root1.val!=root2.val) return false;\n \treturn isSymmetric(root1.left, root2.right) && isSymmetric(root1.right, root2.left);\n }\n#Iterative#\n public boolean isSymmetric(TreeNode root) {\n \tif(root==null) return true;\n \tQueue<TreeNode> q1=new LinkedList<>(), q2=new LinkedList<>();\n \tq1.add(root.left); \n \tq2.add(root.right);\n \twhile(!q1.isEmpty() && !q2.isEmpty()) {\n \t\tint size1=q1.size(), size2=q2.size();\n \t\tif(size1!=size2) return false;\n \t\tfor(int i=0; i<size1; i++) {\n \t\t\tTreeNode current1=q1.remove(), current2=q2.remove();\n \t\t\tif(current1==null && current2==null) continue;\n \t\t\tif(current1==null || current2==null) return false; \n \t\t\tif(current1.val!=current2.val) return false;\n \t\t\tq1.add(current1.left);\n \t\t\tq1.add(current1.right);\n \t\t\tq2.add(current2.right);\n \t\t\tq2.add(current2.left);\n \t\t}\n \t}\n \treturn q1.isEmpty() && q2.isEmpty();\n }
15
0
['Java']
1
symmetric-tree
✅ C++ solution | Easy to understand | O(N)
c-solution-easy-to-understand-on-by-kosa-v0jt
Complexity\n- Time complexity: O(1)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(1)\n Add your space complexity here, e.g. O(n) \n\n# Co
kosant
NORMAL
2023-05-13T06:34:27.763208+00:00
2023-05-13T06:34:27.763247+00:00
2,209
false
# Complexity\n- Time complexity: O(1)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n bool isEqual(TreeNode* left, TreeNode* right) {\n if (!left && !right)\n return true;\n \n if (!left || !right || left->val != right->val)\n return false;\n \n return isEqual(left->left, right->right) && isEqual(left->right, right->left);\n }\n bool isSymmetric(TreeNode* root) {\n return isEqual(root->left, root->right);\n }\n};\n```
14
0
['Tree', 'C', 'Binary Tree', 'C++']
1
symmetric-tree
0 ms100% Iteration && Recursion
0-ms100-iteration-recursion-by-shikuan-7vb0
Iteration\n\ngolang\nfunc isSymmetric(root *TreeNode) bool {\n if root == nil {\n\t\treturn true\n\t}\n\tvar stack []*TreeNode\n\tstack = append(stack, root.
shikuan
NORMAL
2022-11-09T15:12:08.136681+00:00
2022-11-09T15:12:08.136724+00:00
1,772
false
#### Iteration\n\n```golang\nfunc isSymmetric(root *TreeNode) bool {\n if root == nil {\n\t\treturn true\n\t}\n\tvar stack []*TreeNode\n\tstack = append(stack, root.Left, root.Right)\n\tfor len(stack) > 0 {\n\t\tl, r := stack[0], stack[1]\n\t\tstack = stack[2:]\n\t\tif l == nil && r == nil {\n\t\t\tcontinue\n\t\t} else if (l == nil && r != nil) || l != nil && r == nil {\n\t\t\treturn false\n\t\t} else if l.Val != r.Val {\n\t\t\treturn false\n\t\t}\n\t\tstack = append(stack, l.Left, r.Right, l.Right, r.Left)\n\t}\n\treturn true\n}\n```\n\n#### Recursion\n\n```golang\nfunc isSymmetric(root *TreeNode) bool {\n\tif root == nil {\n\t\treturn true\n\t}\n\treturn helper(root.Left, root.Right)\n}\n\nfunc helper(left *TreeNode, right *TreeNode) bool {\n\tif left == nil || right == nil {\n\t\treturn left == right\n\t}\n\tif left.Val != right.Val {\n\t\treturn false\n\t}\n\treturn helper(left.Left, right.Right) && helper(left.Right, right.Left)\n}\n```
14
0
['Go']
2
symmetric-tree
Facebook, Amazon Interview, 100ms Easy to understand, Very clean code, TC: O(N), SC: O(N)
facebook-amazon-interview-100ms-easy-to-1vugd
\nclass Solution {\npublic:\n bool isSymmetric(TreeNode* root) {\n \n if(root==NULL) return true; //To check if tree is empty or not\n \
DarshanAgarwal95
NORMAL
2022-05-30T03:26:52.315163+00:00
2022-05-30T03:27:29.330714+00:00
637
false
```\nclass Solution {\npublic:\n bool isSymmetric(TreeNode* root) {\n \n if(root==NULL) return true; //To check if tree is empty or not\n \n return isSymmetricTest(root->left,root->right);\n }\n bool isSymmetricTest(TreeNode* p , TreeNode* q){\n if(p == NULL && q == NULL) // left & right node are NULL \n return true; \n \n else if(p == NULL || q == NULL) // one of them is Not NULL\n return false; \n \n else if(p->val!=q->val) \n return false;\n \n return isSymmetricTest(p->left,q->right) && isSymmetricTest(p->right,q->left);\n }\n};\n```\n\n# If you understand this solution, then please please upvote!!!
14
0
['Depth-First Search', 'C', 'Binary Tree']
0
symmetric-tree
Py3 Sol: in just few lines, 24ms, beats 97.63%
py3-sol-in-just-few-lines-24ms-beats-976-ceob
\ndef isSymmetricBst(node1, node2):\n if node1==None and node2==None:\n return True\n elif node1==None or node2==None:\n return False\n e
ycverma005
NORMAL
2020-03-10T07:47:55.812098+00:00
2020-03-10T07:53:54.629140+00:00
2,901
false
```\ndef isSymmetricBst(node1, node2):\n if node1==None and node2==None:\n return True\n elif node1==None or node2==None:\n return False\n else:\n return node1.val==node2.val and isSymmetricBst(node1.left,node2.right) and isSymmetricBst(node1.right, node2.left)\n \nclass Solution:\n def isSymmetric(self, root: TreeNode) -> bool:\n if not root:\n return True\n# since we need to check whether left is mirror to right, vice versa\n return isSymmetricBst(root.left, root.right)\n```
14
0
['Python', 'Python3']
4
symmetric-tree
☕Java Solution | 🚀0ms Runtime - beats 100%🔥| Easy to Understand😇
java-solution-0ms-runtime-beats-100-easy-420a
Intuition\n Describe your first thoughts on how to solve this problem. \nBy seeing the problem my first intuition was to use BFS to solve the problem,by taking
5p7Ro0t
NORMAL
2023-02-25T07:05:28.582803+00:00
2023-02-25T08:02:32.255267+00:00
1,906
false
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nBy seeing the problem my first intuition was to use BFS to solve the problem,by taking a queue but as i approached the problem i understand that using DFS is more optimal and less complex to solve this problem.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThere are two parts of the tree - the left one and the right one.\n**Some Observations :**\n- The `leftnode` of left subtree is equal to the `rightnode` of right subtree.\n- Similarly the `rightnode` of left subtree is equal to the `leftnode` of right subtree.\n\nSo we can apply these recursively to check if the nodes are equal or not.\nIf the tree is symmetric then the algorithm reaches the leaf nodes where each node is null, then we return `true`.\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * Definition for a binary tree node.\n * public class TreeNode {\n * int val;\n * TreeNode left;\n * TreeNode right;\n * TreeNode() {}\n * TreeNode(int val) { this.val = val; }\n * TreeNode(int val, TreeNode left, TreeNode right) {\n * this.val = val;\n * this.left = left;\n * this.right = right;\n * }\n * }\n */\nclass Solution {\n public boolean isSymmetric(TreeNode root) {\n if(root == null){\n return true;\n }\n return checkSymmetric(root.left,root.right);\n }\n public boolean checkSymmetric(TreeNode leftNode,TreeNode rightNode){\n if(leftNode == null && rightNode == null){\n return true;\n }\n if(leftNode == null ^ rightNode == null){\n return false;\n }\n if(leftNode.val != rightNode.val){\n return false;\n }\n return checkSymmetric(leftNode.left,rightNode.right) && checkSymmetric(leftNode.right,rightNode.left);\n\n }\n}\n```\nIf any doubt or suggestions, Please do comment :)\n\nPLEASE DO UPVOTE GUYS!!! :)\n\nThank You!!!
13
0
['Tree', 'Depth-First Search', 'Recursion', 'Java']
3
symmetric-tree
[Python] Simple BFS Iterative Approach with Explaination
python-simple-bfs-iterative-approach-wit-7jf1
Think in pairs would really help. \nTo check if a tree is symmetric, we need a BFS on 2 sides of symmetry: left and right. If left and right value match, we sho
judyzzy
NORMAL
2020-05-21T01:22:33.406659+00:00
2020-05-21T01:22:33.406781+00:00
851
false
Think in pairs would really help. \nTo check if a tree is symmetric, we need a BFS on 2 sides of symmetry: left and right. If left and right value match, we should proceed. \nThe key is to add the children of left and right in the proper order: outter match, then inner match. Because we are queuing in pairs, the children of inner pairs will match with the inner grandchildren, and so are the outter pairs. \n```\nclass Solution(object):\n def isSymmetric(self, root):\n """\n :type root: TreeNode\n :rtype: bool\n """\n \n if not root:\n return True\n \n queue = [root.left, root.right]\n \n while len(queue) > 0:\n # pop 2 from queue\n left = queue.pop(0)\n right = queue.pop(0)\n \n # Evalate the pair\n if not left and not right:\n continue\n elif left and right and left.val == right.val:\n pass\n else:\n return False\n \n # Enqueue children\n queue.append(left.left)\n queue.append(right.right)\n queue.append(left.right)\n queue.append(right.left)\n \n return True\n```
13
0
['Breadth-First Search', 'Python']
0
symmetric-tree
Symmetric Tree Solution in C++
symmetric-tree-solution-in-c-by-the_kuna-wfqd
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
The_Kunal_Singh
NORMAL
2023-08-19T14:23:36.401177+00:00
2023-08-19T14:23:36.401200+00:00
1,190
false
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n# Code\n```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n bool check(TreeNode* root1, TreeNode* root2)\n {\n if(root1==NULL && root2==NULL)\n return true;\n if(root1==NULL || root2==NULL)\n return false;\n if(root1->val==root2->val)\n return check(root1->left, root2->right) && check(root1->right, root2->left);\n return false;\n }\n bool isSymmetric(TreeNode* root) {\n return check(root->left, root->right);\n }\n};\n```\n![upvote new.jpg](https://assets.leetcode.com/users/images/21243a90-9cb4-4904-acec-45e72bc6ede1_1692455011.561149.jpeg)\n
12
0
['C++']
1
symmetric-tree
Java
java-by-niyazjava-xvaj
If you like it pls upvote\n\n\n\n public boolean isSymmetric(TreeNode root) {\n if (root == null) return true;\n Stack<TreeNode> stack = new Stack<>();\n sta
NiyazJava
NORMAL
2022-11-15T14:33:45.719927+00:00
2022-11-20T01:35:39.158837+00:00
925
false
If you like it pls upvote\n\n```\n\n public boolean isSymmetric(TreeNode root) {\n if (root == null) return true;\n Stack<TreeNode> stack = new Stack<>();\n stack.push(root.left);\n stack.push(root.right);\n\n while (!stack.isEmpty()) {\n TreeNode n1 = stack.pop();\n TreeNode n2 = stack.pop();\n\n if (n1 == null && n2 == null) continue;\n if (n1 == null || n2 == null || n1.val != n2.val) return false;\n\n stack.push(n1.left);\n stack.push(n2.right);\n stack.push(n1.right);\n stack.push(n2.left);\n }\n\n return true;\n }\n\n\n```
12
0
['Java']
1
symmetric-tree
Recursively and iteratively (level order traversal) in Python
recursively-and-iteratively-level-order-2nxkz
Solution 1. recursively solution\n\n\ndef isSymmetric(self, root):\n\tdef treeMatch(root1, root2):\n\t\tif not root1 and not root2:\n\t\t\treturn True\n\t\tif (
imssssshan
NORMAL
2022-01-28T08:34:18.526970+00:00
2022-01-28T08:34:18.527016+00:00
555
false
**Solution 1. recursively solution**\n\n```\ndef isSymmetric(self, root):\n\tdef treeMatch(root1, root2):\n\t\tif not root1 and not root2:\n\t\t\treturn True\n\t\tif (root1 and not root2) or (root2 and not root1):\n\t\t\treturn False\n\t\tif root1.val != root2.val:\n\t\t\treturn False\n\t\treturn treeMatch(root1.left, root2.right) and treeMatch(root1.right, root2.left)\n\treturn treeMatch(root.left, root.right)\n```\n\n**Solution 2. iteratively solution, using level order traversal**\n```\ndef isSymmetric(self, root):\n\n\tdef levelSymetric(nums):\n\t\treturn nums[:] == nums[::-1]\n\n\ttree = [root]\n\twhile tree:\n\t\tlevel = []\n\t\tfor _ in range(len(tree)):\n\t\t\ttmp = tree.pop(0)\n\t\t\tif not tmp:\n\t\t\t\tlevel.append(None)\n\t\t\telse:\n\t\t\t\tlevel.append(tmp.val)\n\t\t\t\ttree.append(tmp.left)\n\t\t\t\ttree.append(tmp.right)\n\t\tif not levelSymetric(level):\n\t\t\treturn False\n\treturn True\n```
12
0
['Binary Tree', 'Iterator', 'Python']
1
symmetric-tree
Swift: Symmetric Tree (+ Test Cases)
swift-symmetric-tree-test-cases-by-asahi-ww0a
swift\nclass Solution {\n func isSymmetric(_ root: TreeNode?) -> Bool {\n return check(root, root)\n }\n private final func check(_ l: TreeNode?
AsahiOcean
NORMAL
2021-07-08T05:48:42.017815+00:00
2021-07-08T05:48:42.017861+00:00
1,107
false
```swift\nclass Solution {\n func isSymmetric(_ root: TreeNode?) -> Bool {\n return check(root, root)\n }\n private final func check(_ l: TreeNode?, _ r: TreeNode?) -> Bool {\n if [l,r].allSatisfy({$0 == nil}) { return true }\n if l == nil || r == nil { return false }\n let n = (l?.left, r?.right)\n return l?.val == r?.val && check(n.0,n.1) && check(n.1,n.0)\n }\n}\n```\n\n```swift\nimport XCTest\n\n// Executed 2 tests, with 0 failures (0 unexpected) in 0.065 (0.067) seconds\n\nclass Tests: XCTestCase {\n private let s = Solution()\n func test1() {\n let res = s.isSymmetric(.init([1,2,2,3,4,4,3]))\n XCTAssertEqual(res, true)\n }\n func test2() {\n let res = s.isSymmetric(.init([1,2,2,nil,3,nil,3]))\n XCTAssertEqual(res, false)\n }\n}\n\nTests.defaultTestSuite.run()\n```\n\n```swift\npublic class TreeNode {\n public var val: Int\n public var left: TreeNode?\n public var right: TreeNode?\n public init() { self.val = 0; self.left = nil; self.right = nil; }\n public init(_ val: Int) { self.val = val; self.left = nil; self.right = nil; }\n public init(_ val: Int, _ left: TreeNode?, _ right: TreeNode?) {\n self.val = val\n self.left = left\n self.right = right\n }\n public init?(_ array: [Int?]) {\n var values = array\n guard !values.isEmpty, let head = values.removeFirst() else { return nil }\n \n val = head; left = nil; right = nil\n \n var queue = [self]\n while !queue.isEmpty {\n let node = queue.removeFirst()\n if !values.isEmpty, let val = values.removeFirst() {\n node.left = TreeNode(val)\n queue.append(node.left!)\n }\n if !values.isEmpty, let val = values.removeFirst() {\n node.right = TreeNode(val)\n queue.append(node.right!)\n }\n }\n }\n}\n```
12
0
['Swift']
0
symmetric-tree
Javascript, Iterative, commented
javascript-iterative-commented-by-melgab-4i1w
\n/**\nTime Complexity: O(n)\nSpace Complexity: O(n)\n*/\nvar isSymmetric = function(root) {\n// if there is no root that means it is a symettric tree\n
melgabal
NORMAL
2020-06-30T04:18:02.662073+00:00
2020-06-30T04:18:02.662101+00:00
1,504
false
```\n/**\nTime Complexity: O(n)\nSpace Complexity: O(n)\n*/\nvar isSymmetric = function(root) {\n// if there is no root that means it is a symettric tree\n if(!root) return true\n// Start 2 queue one for the left banch and one for the right branch\n let q1 = [root.left], q2 = [root.right]\n// traverse through both branches, until they are both exhausted at the same time\n while (q1.length > 0 && q2.length > 0){\n// get current left and compare it to the right of each branch (this is how a mirror works)\n let node1 = q1.shift()\n let node2 = q2.shift()\n// if both are null at the same time, just move on\n if(!node1 && !node2) continue\n// if the current level is not symmetric (1 of them is null or they are not equal) return false\n if(!node1 || !node2 || node1.val !== node2.val) return false\n// to mentain comparing left to right (this is the tricky part, you have to push left and right & reverse for each branch)\n q1.push(node1.left)\n q2.push(node2.right)\n q1.push(node1.right)\n q2.push(node2.left)\n }\n// If both are exhausted at the same time and they are symmeteric return true\n return true\n \n};\n```
12
0
['Breadth-First Search', 'JavaScript']
2
symmetric-tree
Concise Recursive Java Solution
concise-recursive-java-solution-by-siyan-ydey
This method is my best recursive try. Use two TreeNode as parameters.\n\nIf you are willing to help, \n\nPlease go to https://oj.leetcode.com/discuss/24968/is-m
siyang3
NORMAL
2015-02-10T18:42:35+00:00
2015-02-10T18:42:35+00:00
1,039
false
This method is my best recursive try. Use two TreeNode as parameters.\n\nIf you are willing to help, \n\nPlease go to https://oj.leetcode.com/discuss/24968/is-my-method-a-recursive-one-java-solution\nto see my another recursive solution and give some comment on that recursive method.\n \n\n public class Solution {\n public boolean isSymmetric(TreeNode root) {\n if(root==null){return true;}\n return isSymmetric(root.left, root.right);\n }\n \n private boolean isSymmetric(TreeNode a, TreeNode b){\n if(a==null&&b==null){return true;}\n if(a==null||b==null){return false;}\n if(a.val!=b.val){return false;}\n return isSymmetric(a.left,b.right)&&isSymmetric(a.right,b.left);\n }\n }
12
0
['Recursion', 'Java']
1
symmetric-tree
0 ms C solution [DoneRecusively] :)
0-ms-c-solution-donerecusively-by-sai-vjoq
\n\nbool isSymmetricRecursively(struct TreeNode Lnode ,struct TreeNode Rnode ){\n \n if(Lnode==NULL && Rnode==NULL)\n return true;\n \n i
sai
NORMAL
2015-05-30T16:16:31+00:00
2015-05-30T16:16:31+00:00
1,497
false
\n\nbool isSymmetricRecursively(struct TreeNode* Lnode ,struct TreeNode* Rnode ){\n \n if(Lnode==NULL && Rnode==NULL)\n return true;\n \n if(Lnode==NULL || Rnode==NULL)\n return false ;\n \n \n return ((Lnode->val==Rnode->val) &&\n isSymmetricRecursively(Lnode->left,Rnode->right) \n && isSymmetricRecursively(Lnode->right,Rnode->left )) ;\n \n} \n\nbool isSymmetric(struct TreeNode* root) {\n \n if(root==NULL)\n return true;\n \n return isSymmetricRecursively(root->left ,root->right); \n}
12
1
[]
1
symmetric-tree
Java Solution #1ms 4 lines code #Recursive Easy To Understand
java-solution-1ms-4-lines-code-recursive-2kh9
\tpublic static boolean isSymmetric(TreeNode root) {\n\t\treturn isSymmetric(root,root);\n\t}\n\t\n\tpublic static boolean isSymmetric(TreeNode p, TreeNode q){\
therealfakebatman
NORMAL
2016-03-16T21:11:30+00:00
2016-03-16T21:11:30+00:00
1,286
false
\tpublic static boolean isSymmetric(TreeNode root) {\n\t\treturn isSymmetric(root,root);\n\t}\n\t\n\tpublic static boolean isSymmetric(TreeNode p, TreeNode q){\n\t\tif(p==null && q==null) return true;\n\t\tif(p==null || q==null) return false;\n\t\t\n\t\treturn p.val ==q.val&&isSymmetric(p.left,q.right)&&isSymmetric(p.right,q.left);\n\t}
12
0
[]
2
symmetric-tree
[ ITERATIVE (BFS) ] 0 ms beats 100% cpp submissions.
iterative-bfs-0-ms-beats-100-cpp-submiss-rp37
Intuition\nChecking Tree\'s symmetry comparing values of same level nodes in left and right subtrees.\n\n# Approach\nPerform Breadth-first search using queue da
ScorpioDagger
NORMAL
2023-03-13T15:59:20.257848+00:00
2023-07-24T08:11:53.155791+00:00
1,467
false
# Intuition\nChecking Tree\'s symmetry comparing values of same level nodes in left and right subtrees.\n\n# Approach\nPerform **Breadth-first search** using queue data structure to do a level order traversal of the tree comparing values of corresponding level nodes in left and right subtrees thus know whether symmetric or not. Pushing two copies of each node into the queue so the comparison of nodes that are non-direct children of each other is feasible. For instance, nodes seperated by null values.\n\n# Complexity\n- Time complexity:\nWorst case : O(N) where N is the number of nodes in the tree.\n\n- Space complexity:\nO(W) where W is the maximum width of the tree.\n# Code\n```\nclass Solution {\npublic:\n bool isSymmetric(TreeNode* root) {\n if(!root) return 1;\n queue<TreeNode*> q;\n q.push(root), q.push(root);\n while(!q.empty()) {\n TreeNode* n(q.front());\n q.pop();\n TreeNode* n2(q.front());\n q.pop();\n if(n==nullptr and n2==nullptr) continue;\n if(n==nullptr or n2==nullptr or n->val!=n2->val) return 0;\n q.push(n->left), q.push(n2->right), q.push(n->right), q.push(n2->left);\n }\n return 1;\n }\n};\n```
11
0
['Breadth-First Search', 'Binary Tree', 'C++']
0
symmetric-tree
0ms | JAVA | 10 Lines | Recursive | EXPLAINING FULL | FEW LINES | EASY TO UNDERSTAND
0ms-java-10-lines-recursive-explaining-f-e63z
So the solution is a little simple, \nthe first step is how to build the algorithm if two tree is the same (The link about that excercise https://leetcode.com/
Jkize
NORMAL
2022-07-14T20:49:41.189907+00:00
2022-07-14T20:50:51.163179+00:00
477
false
So the solution is a little simple, \nthe first step is how to build the algorithm if two tree is the same (The link about that excercise https://leetcode.com/problems/same-tree/) \n\nThis is the code to compare if two **tree is the same** (https://leetcode.com/problems/same-tree/discuss/32687/Five-line-Java-solution-with-recursion)\n\n```\npublic boolean isSameTree(TreeNode p, TreeNode q) {\n if(p == null && q == null) return true;\n if(p == null || q == null) return false;\n if(p.val == q.val)\n return isSameTree(p.left, q.left) && isSameTree(p.right, q.right);\n return false;\n}\n```\n\nSo, When we developed the excersice before so we only have a little change for do this excercise. The change is the method isSameTree, how the root in the middle have a mirror so in the part of isSameTree we only do a reverse so we compare left with right and right with left. \n\nAnd the call with the root \n\n```\nclass Solution {\n public boolean isSymmetric(TreeNode root) { \n return isSameTree(root.right, root.left);\n }\n \n public boolean isSameTree(TreeNode p, TreeNode q) {\n if(p == null && q == null) return true;\n if(p == null || q == null) return false;\n if(p.val == q.val)\n return isSameTree(p.left, q.right) && isSameTree(p.right, q.left);\n return false;\n }\n}\n```
11
0
['Recursion', 'Java']
1
symmetric-tree
[C++] 100% Runtime Iterative Solution
c-100-runtime-iterative-solution-by-huna-xsej
\nbool isSymmetric(TreeNode* root) {\n if(!root) return true;\n queue<TreeNode*> queue;\n queue.push(root->left);\n queue.push(root-
hunarbatra
NORMAL
2021-12-14T09:07:47.660790+00:00
2021-12-14T09:07:47.660819+00:00
847
false
```\nbool isSymmetric(TreeNode* root) {\n if(!root) return true;\n queue<TreeNode*> queue;\n queue.push(root->left);\n queue.push(root->right);\n while(!queue.empty()) {\n TreeNode *left = queue.front(); queue.pop();\n TreeNode *right = queue.front(); queue.pop();\n if(!left && !right) continue;\n if(!left || !right) return false;\n if(left->val != right->val) return false;\n queue.push(left->left);\n queue.push(right->right);\n queue.push(left->right);\n queue.push(right->left);\n }\n return true;\n }\n```
11
0
['C', 'Iterator', 'C++']
1
symmetric-tree
Javascript - queue in 10 lines
javascript-queue-in-10-lines-by-nemtsv-rnbu
\nvar isSymmetric = function(root) {\n const q = [root, root];\n while (q.length) {\n const [l, r] = [q.shift(), q.shift()];\n if (!l && !r) continue;\n
nemtsv
NORMAL
2019-12-09T17:47:07.234610+00:00
2019-12-11T00:56:03.647048+00:00
1,618
false
```\nvar isSymmetric = function(root) {\n const q = [root, root];\n while (q.length) {\n const [l, r] = [q.shift(), q.shift()];\n if (!l && !r) continue;\n if (!!l !== !!r || l.val !== r.val) return false;\n q.push(l.left, r.right, l.right, r.left);\n }\n \n return true;\n};\n\n```
11
0
['Queue', 'JavaScript']
0
symmetric-tree
javascript
javascript-by-yinchuhui88-c7ks
\nvar isSymmetric = function(root) {\n if(!root) \n return true;\n return dfs(root.left, root.right);\n \n function dfs(leftNode, rightNode)
yinchuhui88
NORMAL
2018-10-16T03:48:38.521980+00:00
2018-10-16T03:48:38.522027+00:00
2,217
false
```\nvar isSymmetric = function(root) {\n if(!root) \n return true;\n return dfs(root.left, root.right);\n \n function dfs(leftNode, rightNode) {\n if (!leftNode && !rightNode) {\n return true;\n }\n if(leftNode && !rightNode || !leftNode && rightNode || leftNode.val !== rightNode.val) {\n return false;\n }\n return dfs(leftNode.right, rightNode.left) && dfs(leftNode.left, rightNode.right);\n }\n};\n```
11
1
[]
1
symmetric-tree
Clean Java solution
clean-java-solution-by-jopiko123-7ijt
public class Solution {\n public boolean isSymmetric(TreeNode root) {\n return isSymmetric(root, root);\n }\n \n boolean
jopiko123
NORMAL
2015-12-29T16:19:07+00:00
2015-12-29T16:19:07+00:00
1,445
false
public class Solution {\n public boolean isSymmetric(TreeNode root) {\n return isSymmetric(root, root);\n }\n \n boolean isSymmetric(TreeNode n1, TreeNode n2) {\n if(n1 == null && n2 == null) return true;\n if(n1 == null || n2 == null) return false;\n if(n1.val != n2.val) return false;\n return isSymmetric(n1.left, n2.right) && isSymmetric(n2.right, n1.left);\n }\n }
11
0
['Java']
0
symmetric-tree
JAVA EASY SOLUTION BEATS 100%| 0MS
java-easy-solution-beats-100-0ms-by-saad-9j1l
IntuitionTo check if a tree is symmetric, think of folding it down the middle. If the left side is a mirror image of the right side, then the tree is symmetric.
saadiyamalan23
NORMAL
2025-01-17T19:15:36.236034+00:00
2025-01-18T09:43:25.007950+00:00
1,620
false
# Intuition <!-- Describe your first thoughts on how to solve this problem. --> To check if a tree is symmetric, think of folding it down the middle. If the left side is a mirror image of the right side, then the tree is symmetric. For every node on the left, there should be a matching node on the right with the same value, and their children should also be flipped and symmetric. If at any point the nodes or their children don't match, the tree is not symmetric. # Approach <!-- Describe your approach to solving the problem. --> Handles base cases: -Returns true if both nodes are null. -Returns false if only one node is null. -Checks the current node values (p.val == q.val). -Recursively compares the left and right children for symmetry: -Left subtree of p vs. right subtree of q. -Right subtree of p vs. left subtree of q. # Complexity - Time complexity: <!-- Add your time complexity here, e.g. $$O(n)$$ --> O(n) - Space complexity: <!-- Add your space complexity here, e.g. $$O(n)$$ --> # Code ```java [] /** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode() {} * TreeNode(int val) { this.val = val; } * TreeNode(int val, TreeNode left, TreeNode right) { * this.val = val; * this.left = left; * this.right = right; * } * } */ class Solution { public boolean check(TreeNode p,TreeNode q){ if(p==null && q==null) return true; if(p==null || q==null) return false; return (p.val==q.val && check(p.left,q.right) && check(p.right,q.left)); } public boolean isSymmetric(TreeNode root) { if(root==null) return true; return check(root.left,root.right); } } ```
10
0
['Tree', 'Depth-First Search', 'Breadth-First Search', 'Recursion', 'Binary Tree', 'Java']
5
symmetric-tree
C++ recursive solution|Easy Observation|Day 13-SUCCESSFULL|#LEETCODEDAILY
c-recursive-solutioneasy-observationday-l4yk4
Intuition\n Describe your first thoughts on how to solve this problem. \nOn observing we clearly see we have to perform repetitive task for two roots which are
pawas48ram
NORMAL
2023-03-13T04:46:52.976474+00:00
2023-03-13T04:52:16.633309+00:00
1,273
false
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nOn observing we clearly see we have to perform repetitive task for two roots which are mainly the left and right part we want to compare \nSo we can divide our bigger problem into smaller problem of taking the whole tree and only compare the left and right part of the root which hints us towards recursion.\n\n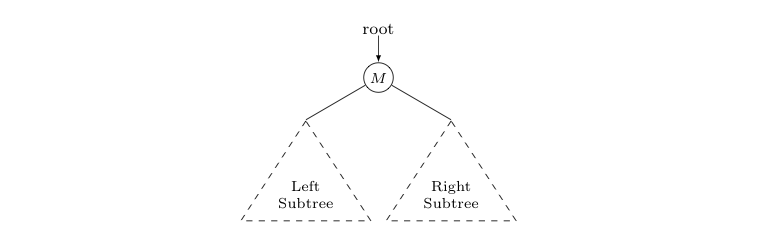![subtrees.png](https://assets.leetcode.com/users/images/a72ac51c-afe5-4eee-982b-a88e3050788e_1678681623.2849514.png)\n\n \n\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe can observe that a binary tree is symmetric if the following conditions are met:\n\n- The value of the left subtree\'s root node is equal to the value of the right subtree\'s root node.\n- The left subtree\'s left child is identical to the right subtree\'s right child.\n- The left subtree\'s right child is identical to the right subtree\'s left child.\n- Both the left and right subtrees are either empty (NULL) or non-empty.\nIt is important to note that if only one of the left and right subtrees is non-empty, we cannot compare further as the identical part of the subtree is missing. Therefore, both subtrees must be either empty or non-empty in a symmetric binary tree.\n\n# Complexity\n- ## Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n**O(n)**, where n is the total number of nodes in the binary tree. The time complexity of the symmetric() function is **O(n/2) because it only visits half of the nodes (in the best case when the tree is symmetric)** and in the worst case it **visits all nodes in the tree (when the tree is not symmetric) in this case it is 0(N)**.\n\n\n- ## Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n**O(h)**, where h is the height of the binary tree. This is because the recursive calls made by the solution consume memory on the call stack equal to the height of the tree. In the worst case when the binary tree is linear, **the height of the tree is equal to n, thus the space complexity becomes O(n)**. However, in the best case when the binary tree is **perfectly balanced, the height of the tree is log(n), thus the space complexity becomes O(log(n))**.\n\nFeel free to share any improvements that can be done to the code \n# If u wish to connect with me [LinkedIn](https://www.linkedin.com/in/pawas-goyal/)\n\n\n# Code\n```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n bool symmetric(TreeNode *lst,TreeNode *rst){\n if(lst==NULL && rst==NULL)return true;\n if(lst==NULL || rst==NULL)return false;\n if(lst->val!=rst->val)return false;\n return symmetric(lst->left,rst->right)&&symmetric(lst->right,rst->left);\n \n }\n bool isSymmetric(TreeNode* root) {\n if(!root || root->right==NULL && root->left==NULL)return true;\n return symmetric(root->left,root->right);\n \n }\n};\n```\n![06351dc5-1e55-461d-acf2-60c9048c4726_1675165944.4721575.webp](https://assets.leetcode.com/users/images/6c305529-29d2-4a58-b09d-ee292769d403_1678682609.1504712.webp)\n\n# UPVOTE IF U LIKE THE SOLUTION\n\n
10
0
['C++']
2
symmetric-tree
✅✅Easy-Understand ||✅✅ recursion || ✅✅C++
easy-understand-recursion-c-by-arpit507-2ht0
\npublic:\n bool is_same(TreeNode *root1, TreeNode *root2){\n if(!root1 && !root2) return true;\n if((!root1 && root2) || (root1 && !root2)) re
Arpit507
NORMAL
2022-10-11T19:09:02.172363+00:00
2022-10-22T06:34:05.926268+00:00
901
false
```\npublic:\n bool is_same(TreeNode *root1, TreeNode *root2){\n if(!root1 && !root2) return true;\n if((!root1 && root2) || (root1 && !root2)) return false;\n \n if(root1->val == root2->val) return is_same(root1->left , root2->right) && is_same(root1->right , root2->left);\n else return false;\n }\n \n bool isSymmetric(TreeNode* root) {\n return is_same(root->left, root->right);\n }\n};\n/* If you like it please upvote */\n```\nIf you like it please upvote
10
0
['Recursion', 'C']
0
symmetric-tree
C++ || 4 MS || EASY TO UNDERSTAND
c-4-ms-easy-to-understand-by-bhuvisha020-02w4
\tclass Solution {\n\tpublic:\n\t\tbool isSymmetric(TreeNode root) {\n\t\t\treturn (root==NULL || isSymmetricHelp(root->left,root->right));\n\t\t}\n\t\tbool isS
bhuvisha0208
NORMAL
2022-02-16T03:54:53.376613+00:00
2022-02-16T03:55:51.081498+00:00
598
false
\tclass Solution {\n\tpublic:\n\t\tbool isSymmetric(TreeNode* root) {\n\t\t\treturn (root==NULL || isSymmetricHelp(root->left,root->right));\n\t\t}\n\t\tbool isSymmetricHelp(TreeNode*left,TreeNode*right){\n\t\t\tif(left==NULL || right==NULL)\n\t\t\t\treturn left==right;\n\t\t\tif(left->val != right->val)\n\t\t\t\treturn false;\n\t\t\treturn isSymmetricHelp(left->left,right->right) && isSymmetricHelp(left->right,right->left);\n\t\t}\n\t};\n\t\n\tTC : O(N)\n\n\tfeel free to ask your doubts :)\n\tand pls upvote if it was helpful :)
10
0
['Recursion', 'C']
0
symmetric-tree
C# recursive 76ms, faster than 100%
c-recursive-76ms-faster-than-100-by-pawe-y6b7
Runtime: 76 ms, faster than 100.00% of C# online submissions for Symmetric Tree.\nMemory Usage: 25.7 MB, less than 50.29% of C# online submissions for Symmetric
pawel753
NORMAL
2020-10-31T10:45:55.078706+00:00
2020-10-31T10:45:55.078738+00:00
1,746
false
Runtime: 76 ms, faster than 100.00% of C# online submissions for Symmetric Tree.\nMemory Usage: 25.7 MB, less than 50.29% of C# online submissions for Symmetric Tree.\n```\npublic class Solution {\n public bool IsSymmetric(TreeNode root) => CheckSymetry(root?.left, root?.right);\n \n private bool CheckSymetry(TreeNode left, TreeNode right)\n {\n if(left == null || right == null)\n return left?.val == right?.val;\n if(left.val != right.val)\n return false;\n\n return CheckSymetry(left.left, right.right) && CheckSymetry(left.right, right.left);\n }\n}\n```
10
1
['C#']
1
symmetric-tree
In C
in-c-by-lettty17-9k5t
\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * struct TreeNode *left;\n * struct TreeNode *right;\n * };\n */\n
lettty17
NORMAL
2020-05-11T01:25:09.406215+00:00
2020-05-11T01:25:09.406252+00:00
1,444
false
```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * struct TreeNode *left;\n * struct TreeNode *right;\n * };\n */\n\nbool parallel_traverse(struct TreeNode* a, struct TreeNode* b)\n{\n if (a == NULL && b == NULL)\n return true;\n \n if (a == NULL || b == NULL)\n return false;\n\n if (a->val != b->val)\n return false;\n \n return parallel_traverse(a->left, b->right) && parallel_traverse(a->right, b->left);\n}\n\nbool isSymmetric(struct TreeNode* root)\n{\n if (root == NULL)\n return true;\n return parallel_traverse(root->left, root->right);\n}\n```
10
0
['C']
1
symmetric-tree
Tree versions in Java: recursion, optimized tail recursion and pre-order iteration
tree-versions-in-java-recursion-optimize-5zvg
The most simple version is normal recursion:\n\n public class Solution {\n \tpublic boolean isSymmetric(TreeNode root) {\n \t\treturn this.isMirror(roo
vision57
NORMAL
2015-01-30T13:59:09+00:00
2015-01-30T13:59:09+00:00
1,466
false
The most simple version is normal recursion:\n\n public class Solution {\n \tpublic boolean isSymmetric(TreeNode root) {\n \t\treturn this.isMirror(root, root);\n \t}\n \n \tprivate boolean isMirror(TreeNode t0, TreeNode t1) {\n\t\tif (t0 == null || t1 == null) {\n\t\t\treturn t0 == t1;\n\t\t}\n\t\treturn t0.val == t1.val\n\t\t\t\t&& this.isMirror(t0.left, t1.right)\n\t\t\t\t&& this.isMirror(t0.right, t1.left);\n \t}\n }\n\nAnd the last recursive call in method isMirror() above can be optimized to loop, this will reduce the actual recursive calls:\n\n public class Solution {\n \tpublic boolean isSymmetric(TreeNode root) {\n \t\treturn this.isMirror(root, root);\n \t}\n \n \tprivate boolean isMirror(TreeNode t0, TreeNode t1) {\n \t\twhile (t0 != null && t1 != null) {\n \t\t\tif (t0.val != t1.val || !this.isMirror(t0.left, t1.right)) {\n \t\t\t\treturn false;\n \t\t\t}\n \t\t\tt0 = t0.right;\n \t\t\tt1 = t1.left;\n \t\t}\n \t\treturn t0 == t1;\n \t}\n }\nThere are two kinds of iteration at least. The BFS-like iteration, which is based on queue, has a space complexity of O(n). And the DFS-like iteration, which is based on stack, has a better space complexity of O(log n).\n\nHere is the DFS-like pre-order iteration:\n\n public class Solution {\n \tpublic boolean isSymmetric(TreeNode root) {\n \t\tDeque<TreeNode[]> stack = new LinkedList<>();\n \t\tstack.push(new TreeNode[]{root, root});\n \t\twhile (!stack.isEmpty()) {\n \t\t\tTreeNode[] pair = stack.pop();\n \t\t\tTreeNode t0 = pair[0], t1 = pair[1];\n \t\t\tif (t0 == null && t1 == null) {\n \t\t\t\tcontinue;\n \t\t\t}\n \t\t\tif (t0 == null || t1 == null || t0.val != t1.val) {\n \t\t\t\treturn false;\n \t\t\t}\n \t\t\tstack.push(new TreeNode[]{t0.left, t1.right});\n \t\t\tstack.push(new TreeNode[]{t0.right, t1.left});\n \t\t}\n \t\treturn true;\n \t}\n }
10
0
[]
3
symmetric-tree
A simple python recursive solution - O(n) 60ms
a-simple-python-recursive-solution-on-60-iagy
# Definition for a binary tree node.\n # class TreeNode:\n # def __init__(self, x):\n # self.val = x\n # self.left = None\n #
google
NORMAL
2015-05-24T20:16:05+00:00
2015-05-24T20:16:05+00:00
2,098
false
# Definition for a binary tree node.\n # class TreeNode:\n # def __init__(self, x):\n # self.val = x\n # self.left = None\n # self.right = None\n \n class Solution:\n # @param {TreeNode} root\n # @return {boolean}\n def isSymmetric(self, root):\n if not root:\n return True\n \n return self.isSymmetricTree(root.left, root.right)\n \n def isSymmetricTree(self, node1, node2):\n if node1 and node2:\n return node1.val == node2.val and self.isSymmetricTree(node1.left, node2.right) and self.isSymmetricTree(node1.right, node2.left)\n else:\n return node1 == node2
10
0
['Python']
4
symmetric-tree
Recursive and non-recursive solutions in Python
recursive-and-non-recursive-solutions-in-vfb6
Recursive solution (68ms):\n\n class Solution(object):\n def isSymmetric(self, root):\n if not root:\n return True\n
hweicdl
NORMAL
2015-11-18T12:07:02+00:00
2018-09-21T19:35:15.781517+00:00
1,053
false
Recursive solution (68ms):\n\n class Solution(object):\n def isSymmetric(self, root):\n if not root:\n return True\n return self.equals(root.left, root.right)\n \n def equals(self, node1, node2):\n if not node1 and not node2:\n return True\n elif node1 and node2 and node1.val == node2.val:\n return self.equals(node1.left, node2.right) and self.equals(node1.right, node2.left)\n else:\n return False\n\nNon-Recursive solution (52ms):\n\n class Solution(object):\n def isSymmetric(self, root):\n if not root:\n return True\n stack = []\n stack.append((root.left, root.right))\n \n while stack:\n left, right = stack.pop()\n if not left and not right:\n continue\n elif left and right and left.val == right.val:\n stack.append((left.left, right.right))\n stack.append((left.right, right.left))\n else:\n return False\n \n return True
10
0
['Recursion']
2
symmetric-tree
My AC Code ,is there a better method ?
my-ac-code-is-there-a-better-method-by-l-rsz5
public boolean checkSymmetric(TreeNode lsubTree,TreeNode rsubTree){\n if(lsubTree==null&&rsubTree==null) return true;\n else if(lsubTree!=null&&r
lzklee
NORMAL
2014-03-03T08:05:05+00:00
2014-03-03T08:05:05+00:00
2,080
false
public boolean checkSymmetric(TreeNode lsubTree,TreeNode rsubTree){\n if(lsubTree==null&&rsubTree==null) return true;\n else if(lsubTree!=null&&rsubTree==null) return false;\n else if(lsubTree==null&&rsubTree!=null) return false;\n else if(lsubTree.val!=rsubTree.val) return false;\n boolean lt=checkSymmetric(lsubTree.left,rsubTree.right);\n boolean rt=checkSymmetric(lsubTree.right,rsubTree.left);\n return lt&&rt;\n }\n public boolean isSymmetric(TreeNode root) {\n if(root==null) return true;\n return checkSymmetric(root.left,root.right);\n }
10
0
[]
2
symmetric-tree
101. Symmetric Tree | JS
101-symmetric-tree-js-by-ahmedaboelfadle-ijio
Intuition\n Describe your first thoughts on how to solve this problem. \n- At first i was thinking to solve it with iterative approach, but it would be costly t
AhmedAboElfadle
NORMAL
2022-12-19T09:35:53.834061+00:00
2022-12-19T09:47:57.172378+00:00
1,864
false
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n- At first i was thinking to solve it with iterative approach, but it would be costly to use a queue for this, so i thought to use the recursive approach.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- We use recursive approach to solve this problem, the tree would be symmetric if it\'s foldable you know, so we should start by checking first if the root is null so we have a symmetric tree.\n\n- A tree would only be foldable - symmetric - if the left sub-tree leftNode is equivalent to the right sub-tree rightNode and left sub-tree rightNode is equivalent to right sub-tree leftNode.\n- so we build isMirror function that takes two nodes the left sub-tree parent and the right sub-tree parent and start the comparison as mentioned above in the second point.\n- If there is any failure for any tested condition the function will be terminated and return false so we don\'t have to check any more, that\'s because we are processing the tree level by level, so that\'s why we will be using o(h) where is h is the height of the tree at worst case.\n# Complexity\n- Time complexity: O(n) where is n is the nodes number because we check every single node.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(h) where is h is the tree height.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * Definition for a binary tree node.\n * function TreeNode(val, left, right) {\n * this.val = (val===undefined ? 0 : val)\n * this.left = (left===undefined ? null : left)\n * this.right = (right===undefined ? null : right)\n * }\n */\n/**\n * @param {TreeNode} root\n * @return {boolean}\n */\nvar isSymmetric = function(root) {\n if(root == null) return true;\n return isMirror(root.left, root.right);\n}; \n\nconst isMirror = (leftNode, rightNode) => {\n if(leftNode == null && rightNode == null) return true;\n if(leftNode == null || rightNode == null) return false;\n if(leftNode.val !== rightNode.val) return false;\n \n return isMirror(leftNode.left, rightNode.right) && isMirror(leftNode.right, rightNode.left);\n}\n\n\n\n\n\n\n```
9
0
['Tree', 'Recursion', 'Binary Tree', 'JavaScript']
1
symmetric-tree
C++ 7ms shortest solution
c-7ms-shortest-solution-by-nilesh_5-ao85
This question is just an another part of checking two same trees.we treat both left and right subtrees as different. Here we will need to compare left value of
Nilesh_5
NORMAL
2022-08-18T16:42:51.548005+00:00
2022-08-18T16:42:51.548035+00:00
622
false
This question is just an another part of checking two same trees.we treat both left and right subtrees as different. Here we will need to compare left value of one tree with right value of another tree.\n```\nclass Solution {\nprivate:\n bool isSameTree(TreeNode *p, TreeNode *q) {\n if (p == NULL || q == NULL) return (p == q);\n return (p->val == q->val && isSameTree(p->left, q->right) && isSameTree(p->right, q->left));\n }\npublic:\n bool isSymmetric(TreeNode* root) {\n return isSameTree(root->left,root->right);\n }\n};\n```\n**-->UPVOTE IF FOUND USEFUL OR LEARNED ANYTHING!!!**
9
0
['Recursion', 'C', 'C++']
0
symmetric-tree
Clean and Easy Recursive and Iterative solutions
clean-and-easy-recursive-and-iterative-s-ncba
Recursive\n\n\nvar isSymmetric = function(root) {\n \n const helper = (node1, node2) => {\n if(node1 === null && node2 === null)\n retur
dollysingh
NORMAL
2022-05-09T18:00:41.920508+00:00
2022-05-09T18:00:41.920534+00:00
882
false
**Recursive**\n\n```\nvar isSymmetric = function(root) {\n \n const helper = (node1, node2) => {\n if(node1 === null && node2 === null)\n return true;\n \n if(node1 === null || node2 === null)\n return false;\n \n if(node1.val === node2.val) {\n return helper(node1.left, node2.right) && helper(node1.right, node2.left);\n } else {\n return false;\n }\n }\n \n return helper(root.left, root.right);\n};\n```\n\n**Iterative**\n\n```\nvar isSymmetric = function(root) {\n \n const arr = [];\n \n arr.push([root.left, root.right]);\n \n while(arr.length) {\n let [node1, node2] = arr.pop();\n \n if(node1 === null && node2 === null)\n continue;\n \n if(node1 === null || node2 === null)\n return false;\n \n if(node1.val === node2.val) {\n arr.push([node1.left, node2.right]);\n arr.push([node1.right, node2.left]);\n } else {\n return false;\n }\n }\n \n return true;\n};\n```
9
0
['Recursion', 'Iterator', 'JavaScript']
1
symmetric-tree
python | iterative | recursive
python-iterative-recursive-by-fatemebesh-la26
recursive\n\n\tclass Solution:\n\t\tdef isSymmetric(self, root):\n\t\t\tif not root:\n\t\t\t\treturn False\n\t\t\tdef helper(l, r):\n\t\t\t\tif not l and not r:
fatemebesharat766
NORMAL
2021-12-12T17:24:26.728505+00:00
2021-12-12T17:48:02.518608+00:00
699
false
recursive\n\n\tclass Solution:\n\t\tdef isSymmetric(self, root):\n\t\t\tif not root:\n\t\t\t\treturn False\n\t\t\tdef helper(l, r):\n\t\t\t\tif not l and not r:\n\t\t\t\t\treturn True\n\t\t\t\tif l and r and l.val == r.val:\n\t\t\t\t\treturn helper(l.left, r.right) and helper(l.right, r.left)\n\n\t\t\treturn helper(root, root)\n\t\t\t\niterative\n\n\tclass Solution:\n\t\tdef isSymmetric(self, root):\n\t\t\tqueue = [(root, root)]\n\t\t\twhile queue:\n\t\t\t\tl, r = queue.pop(0)\n\t\t\t\tif l is None and r is None:\n\t\t\t\t\tcontinue\n\n\t\t\t\tif l is None or r is None:\n\t\t\t\t\treturn False\n\t\t\t\tif l.val == r.val:\n\t\t\t\t\tqueue.append((l.left, r.right))\n\t\t\t\t\tqueue.append((l.right, r.left))\n\t\t\t\telse:\n\t\t\t\t\treturn False\n\t\t\treturn True
9
1
['Recursion', 'Iterator', 'Python', 'Python3']
1
symmetric-tree
Python 3 simple recursion, faster than 97% and less memory than 100%
python-3-simple-recursion-faster-than-97-49qd
\n\n\nclass Solution:\n def isSymmetric(self, root: TreeNode) -> bool:\n \n if not root:\n return True\n \n left=root.
claret
NORMAL
2020-01-14T01:40:47.351117+00:00
2020-01-14T01:40:47.351167+00:00
1,730
false
\n\n```\nclass Solution:\n def isSymmetric(self, root: TreeNode) -> bool:\n \n if not root:\n return True\n \n left=root.left\n right=root.right\n \n if not left and not right:\n return True\n \n def check(t1, t2):\n if not t1 and not t2:\n return True\n if t1 and not t2:\n return False\n if not t1 and t2:\n return False\n if t1.val!=t2.val:\n return False\n return check(t1.left, t2.right) and check(t1.right, t2.left)\n \n return check(left, right)\n \n```
9
0
['Python', 'Python3']
5