questionid
stringlengths 36
36
| RA_number
int64 0
23
| RA_choice
int64 0
10
| RA_none
int64 0
9
| modulename
int64 0
24
| module
int64 0
6
| level
int64 0
3
| setnumber
int64 0
17
| questionnumber
int64 0
32
| masterContent
stringlengths 2
447k
⌀ | partContent
stringlengths 9
447k
| partposition
int64 1
11
| skill
float64 0
1
| roundedDuration
int64 0
4
| tutorial
stringlengths 2
4.74k
⌀ | workedsolution
stringlengths 2
20.4k
⌀ | total_text
stringlengths 47
447k
⌀ | text_len
int64 1
1.95k
| latex_len
int64 0
115
| latex_len_solution
int64 0
95
| latex_len_tutorial
int64 0
95
| text_len_solution
int64 0
2.89k
| text_len_tutorial
int64 0
83
| text_len_parts
int64 1
1.87k
| latex_len_parts
int64 0
108
| embeddings
int64 0
8
| questionContent
stringlengths 15
5.94k
| question_sentence_len
int64 0
47
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
001f060c-6b7e-4705-a37d-f740a61334a2 | 4 | 0 | 0 | 2 | 1 | 2 | 3 | 4 | Water (density $\rho _{H_{2}O}=1000\,$kg/m$^3$) flows up the slanted pipe, which is at an angle of $\theta=30^\circ\,$to the horizontal, as shown below.
  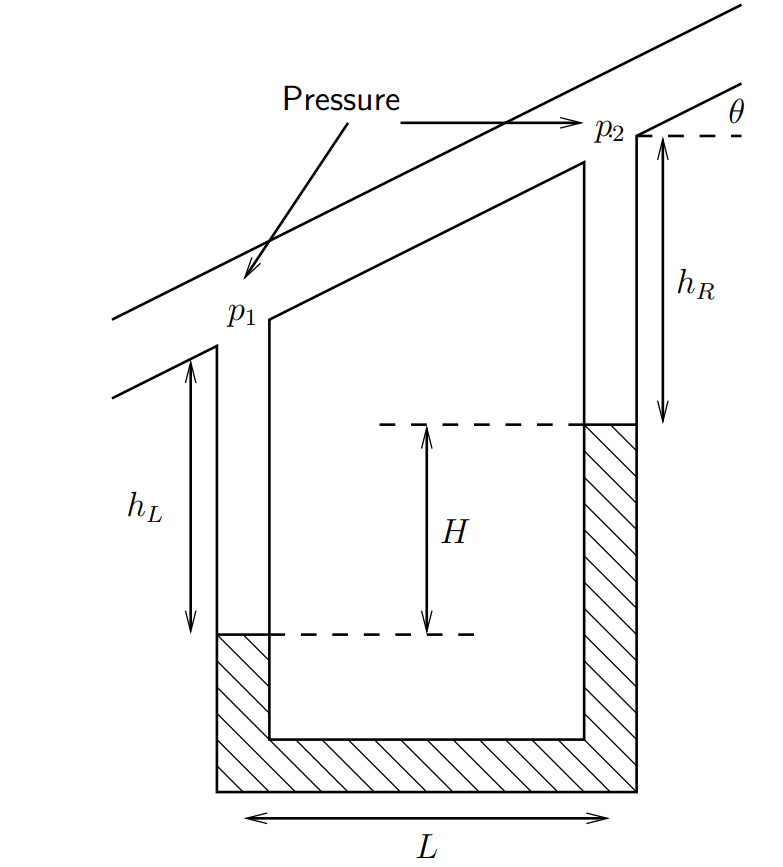
The bottom of the loop is filled with mercury (density $\rho_{Hg}=13,600\,$kg/m$^3$), which acts as a manometer, and you may assume is not flowing. The loop has width $L=5\,$cm, and in this question you should assume that $g=10\,$m/s$^2$.
(Based on P2.35 in White) 
| What would be the pressure drop $p_1 - p_2\,$if the fluid were stationary?
\nIf the height difference $H=0.1\,$cm, what is the pressure difference $p_1-p_2\,$ in the pipe? You may use the fact that from geometry we have $H+h_r-h_L=L\tan(\theta)$.
\nWhat is the difference between the values in parts 5b and 5a? Why is this extra pressure needed?
\nIf the fluid were not flowing, what would the height difference $H\,$ be?
| 4 | 0.666667 | 3 | The pressure difference would be given by $p_1-p_2=\rho gz$. Find $z$ (length of the opposite part of the triangle) by creating a triangle using $L$ and the angle $\theta$ given in the question. Substitute this and all values given back in to get a final numerical answer.
\nWe cannot simply calculate the hydrostatic pressure difference between the two points. This is because the water is flowing, meaning that the pressure is not hydrostatic. Let us define the pressure at the water--mercury interface in the left-hand arm as $p_L$, and the height of the column of water above that point as $h_L$, and let us define the column of water in the right-hand arm as $h_R$.
From the geometry, we have
$H+h_R-h_L=L\tan\theta.$
From hydrostatic balance (i.e. using the general pressure equation $p=p_0 -\rho gz$ and finding $p_0$ and substituting in) find $p_1$ and $p_2$.
***
We get $p_1=p_L-\rho_{H_2O}gh_L$ and $p_2=p_L-\rho_{Hg}gH-\rho_{H_2O}gh_R.$ Now take $p_2$ away form $p_1$ to find the pressure difference. 
***
We get $p_1-p_2=\rho_{Hg}gH+\rho_{H_2O}gh_R-\rho_{H_2O}gh_L$. Simplify to get an expression which factors out $h_R$ and $h_L$. Use the equation form the geometry to replace $h_R - h_L$
***
Substitute in values from the question to get your final numeric answer
\n\nTo understand this, suppose that the depths of mercury are $d_L$ and $d_R$ in the left-hand and right-hand columns of the manometer, respectively. Consider travelling from the bottom of the U-bend through the left-hand tube and along the slanted pipe to the point where $p_2$ is measured. We go through a depth $d_L$ of mercury and $h_{TOT}-d_L$ of water, where $h_{TOT}$ is the total height.
***
Compare that with travelling up the right-hand tube to the same point, in which case we go through a depth $d_R$ and $h_{\sf TOT}-d_R$ of mercury and water, respectively.
***
The total pressure change on the left path equals $\rho_{Hg}gd_L+\rho_{H_2O}g(h_{TOT}-d_L)$, whilst the pressure change on the right path equals $\rho_{Hg}gd_R+\rho_{H_2O}g(h_{TOT}-d_R)$. These two pressure changes must be equal, and the only way this can happen is if $d_L=d_R$. Hence $H=0$.
| The pressure difference between the two points would be given by the hydrostatic formula: $p_1-p_2=\rho gL\tan\theta=1,000\times10\times0.05\tan30^\circ=290$Pa.
\nWe cannot simply calculate the hydrostatic pressure difference between the two points. This is because the water is flowing, meaning that the pressure is not hydrostatic. Let us define the pressure at the water--mercury interface in the left-hand arm as $p_L$, and the height of the column of water above that point as $h_L$, and let us define the column of water in the right-hand arm as $h_R$.
From the geometry, we have
$H+h_R-h_L=L\tan\theta.$
Using hydrostatic balance in the left column, we have
$p_1=p_L-\rho_{H_2O}gh_L.$
The hydrostatic balance in the right-hand column gives
$p_2=p_L-\rho_{Hg}gH-\rho_{H_2O}gh_R.$
Hence
$p_1-p_2=\rho_{Hg}gH+\rho_{H_2O}gh_R-\rho_{H_2O}gh_L$
$=\rho_{Hg}gH+\rho_{H_2O}g(h_R-h_L)$
$=\rho_{Hg}gH+\rho_{H_2O}g(L\tan\theta-H)$
$=13,600\times10\times0.001+1000\times10\times(0.05\tan30^\circ-0.001)$
$=136+279=410$ Pa (2 s.f.).
\n\nIn this case the pressure is hydrostatic, which means that $H=0$.
To understand this, suppose that the depths of mercury are $d_L$ and $d_R$ in the left-hand and right-hand columns of the manometer, respectively. Consider travelling from the bottom of the U-bend through the left-hand tube and along the slanted pipe to the point where $p_2$ is measured. We go through a depth $d_L$ of mercury and $h_{TOT}-d_L$ of water, where $h_{TOT}$ is the total height. Compare that with travelling up the right-hand tube to the same point, in which case we go through a depth \$d\_R\$ and $h_{\sf TOT}-d_R$ of mercury and water, respectively. The total pressure change on the left path equals $\rho_{Hg}gd_L+\rho_{H_2O}g(h_{TOT}-d_L)$, whilst the pressure change on the right path equals $\rho_{Hg}gd_R+\rho_{H_2O}g(h_{TOT}-d_R)$. These two pressure changes must be equal, and the only way this can happen is if $d_L=d_R$. Hence $H=0$.
| Water (density $\rho _{H_{2}O}=1000\,$kg/m$^3$) flows up the slanted pipe, which is at an angle of $\theta=30^\circ\,$to the horizontal, as shown below.
  
The bottom of the loop is filled with mercury (density $\rho_{Hg}=13,600\,$kg/m$^3$), which acts as a manometer, and you may assume is not flowing. The loop has width $L=5\,$cm, and in this question you should assume that $g=10\,$m/s$^2$.
(Based on P2.35 in White) 
What would be the pressure drop $p_1 - p_2\,$if the fluid were stationary?
\nIf the height difference $H=0.1\,$cm, what is the pressure difference $p_1-p_2\,$ in the pipe? You may use the fact that from geometry we have $H+h_r-h_L=L\tan(\theta)$.
\nWhat is the difference between the values in parts 5b and 5a? Why is this extra pressure needed?
\nIf the fluid were not flowing, what would the height difference $H\,$ be?
| 145 | 13 | 25 | 25 | 270 | 32 | 70 | 5 | 1 | The bottom of the loop is filled with mercury density $\rho_{Hg}=13,600\,$kg/m$^3$, which acts as a manometer, and you may assume is not flowing. The loop has width $L=5\,$cm, and in this question you should assume that $g=10\,$m/s$^2$. Based on P2.35 in White What would be the pressure drop $p_1 - p_2\,$if the fluid were stationary? If the height difference $H=0.1\,$cm, what is the pressure difference $^3$0 in the pipe? You may use the fact that from geometry we have $^3$1. What is the difference between the values in parts 5b and 5a? Why is this extra pressure needed? If the fluid were not flowing, what would the height difference $^3$2 be? | 8 |
008875c9-9c5b-4f18-b79c-e21c3ed8e14f | 4 | 4 | 0 | 19 | 6 | 1 | 5 | 2 | **(L8)**: Use Gaussian elimination to solve the system of equations below (**Note**: these are the same equations as Q1, so you know the type of solution to expect).
***
You are asked to input the nature of the intersection of the planes. If the planes intersect at a point, input the point of intersection. If not, look at the '*Final Answer*' to check if your equation of intersection is correct.
| $$
\begin{aligned}
x+y+z&=6\, ,\\
2x+y-z&=3\, ,\\
x+y&=4\, .
\end{aligned}
$$
\n$$
\begin{aligned}
x+y+z&=6\, ,\\
2x+y-z&=3\, ,\\
4x+3y+z&=1\, .
\end{aligned}
$$
\n$$
\begin{aligned}
x+y+z&=6\, ,\\
2x+y-z&=3\, ,\\
2x+2y+2z&=12\, .
\end{aligned}
$$
\n$$
\begin{aligned}
-x+2y-2z&=1, \\
4x-y+6z&=2\, ,\\
2x+3y+2z&=4\, ,\\
\end{aligned}
$$
| 4 | 0.666667 | 3 | Before starting Gaussian Elimination, ensure you have answered *Question 1* to identify the type of solution that you will expect.
***
Set-up the augmented matrix (**section 2.8**)...
***
... Attempt to manipulate the matrix into triangular form, e.g. :
$$
\left( \begin{array}{ccc|r} a & b & c & \ d\\ 0 & e & f & g\\ 0 & 0 & h & i \end{array} \right)
$$
There are three cases that can occur (**section 2.9**, **2.10**, **2.11**)...
***
1. $h=0$ and $i=0$ (i.e., R3 is a row of zeros). In this case, you will be able to derive a line/plane of intersection. 
2. $h=0$ and $i\ne0$. This is an inconsistency, and so there are no solutions. 
3. $h\ne0$. In this case, you can solve for a point of intersection $(x,y,z)$. 
(see more information on case 1 and 3 below)...
***
... In *case 1*, to derive the line/plane equation, take the equations out of augmented matrix form, and set one variable equal to $\lambda$. Then, solve for $\lambda$. 
***
In *case 3*, manipulate the matrix into the form:
$$
\left( \begin{array}{ccc|r} 1 & 0 & 0 & \ a\\ 0 & 1 & 0 & b\\ 0 & 0 & 1 & c \end{array} \right)
$$
Now $x=a,y=b,z=c$. 
\nBefore starting Gaussian Elimination, it may help you to answer *Question 1* to identify the type of solution that you will expect.
***
Set-up the augmented matrix (**section 2.8**)...
***
... Attempt to manipulate the matrix into triangular form, e.g. :
$$
\left( \begin{array}{ccc|r} a & b & c & \ d\\ 0 & e & f & g\\ 0 & 0 & h & i \end{array} \right)
$$
There are three cases that can occur (**section 2.9**, **2.10**, **2.11**)...
***
1. $h=0$ and $i=0$ (i.e., R3 is a row of zeros). In this case, you will be able to derive a line/plane of intersection. 
2. $h=0$ and $i\ne0$. This is an inconsistency, and so there are no solutions. 
3. $h\ne0$. In this case, you can solve for a point of intersection $(x,y,z)$. 
(see more information on case 1 and 3 below)...
***
... In *case 1*, to derive the line/plane equation, take the equations out of augmented matrix form, and set one variable equal to $\lambda$. Then, solve for $\lambda$. 
***
In *case 3*, manipulate the matrix into the form:
$$
\left( \begin{array}{ccc|r} 1 & 0 & 0 & \ a\\ 0 & 1 & 0 & b\\ 0 & 0 & 1 & c \end{array} \right)
$$
Now $x=a,y=b,z=c$. 
\nBefore starting Gaussian Elimination, it may help you to answer *Question 1* to identify the type of solution that you will expect.
***
Set-up the augmented matrix (**section 2.8**)...
***
... Attempt to manipulate the matrix into triangular form, e.g. :
$$
\left( \begin{array}{ccc|r} a & b & c & \ d\\ 0 & e & f & g\\ 0 & 0 & h & i \end{array} \right)
$$
There are three cases that can occur (**section 2.9**, **2.10**, **2.11**)...
***
1. $h=0$ and $i=0$ (i.e., R3 is a row of zeros). In this case, you will be able to derive a line/plane of intersection. 
2. $h=0$ and $i\ne0$. This is an inconsistency, and so there are no solutions. 
3. $h\ne0$. In this case, you can solve for a point of intersection $(x,y,z)$. 
(see more information on case 1 and 3 below)...
***
... In *case 1*, to derive the line/plane equation, take the equations out of augmented matrix form, and set one variable equal to $\lambda$. Then, solve for $\lambda$. 
***
In *case 3*, manipulate the matrix into the form:
$$
\left( \begin{array}{ccc|r} 1 & 0 & 0 & \ a\\ 0 & 1 & 0 & b\\ 0 & 0 & 1 & c \end{array} \right)
$$
Now $x=a,y=b,z=c$. 
\nBefore starting Gaussian Elimination, it may help you to answer *Question 1* to identify the type of solution that you will expect.
***
Set-up the augmented matrix (**section 2.8**)...
***
... Attempt to manipulate the matrix into triangular form, e.g. :
$$
\left( \begin{array}{ccc|r} a & b & c & \ d\\ 0 & e & f & g\\ 0 & 0 & h & i \end{array} \right)
$$
There are three cases that can occur (**section 2.9**, **2.10**, **2.11**)...
***
1. $h=0$ and $i=0$ (i.e., R3 is a row of zeros). In this case, you will be able to derive a line/plane of intersection. 
2. $h=0$ and $i\ne0$. This is an inconsistency, and so there are no solutions. 
3. $h\ne0$. In this case, you can solve for a point of intersection $(x,y,z)$. 
(see more information on case 1 and 3 below)...
***
... In *case 1*, to derive the line/plane equation, take the equations out of augmented matrix form, and set one variable equal to $\lambda$. Then, solve for $\lambda$. 
***
In *case 3*, manipulate the matrix into the form:
$$
\left( \begin{array}{ccc|r} 1 & 0 & 0 & \ a\\ 0 & 1 & 0 & b\\ 0 & 0 & 1 & c \end{array} \right)
$$
Now $x=a,y=b,z=c$. 
| Refer to **section 2.8** for Gaussian elimination rules. In question 1 (a), we found that this system of equations intersects at a point. Therefore, we will attempt to re-arrange the augmented matrix into the form:
$$
\left( \begin{array}{ccc|r} 1 & 0 & 0 & \ a\\ 0 & 1 & 0 & b\\ 0 & 0 & 1 & c \end{array} \right)
$$
Setting up the augmented matrix:
***
$$
\left( \begin{array}{ccc|r} 1 & 1 & 1 & \ 6\\ 2 & 1 & -1 & 3\\ 1 & 1 & 0 & 4 \end{array} \right)
$$
***
* R2-2R1
* R3-R1
***
$$
\rightarrow\left( \begin{array}{ccc|r} 1 & 1 & 1 & \ 6\\ 0 & -1 & -3 & -9\\ 0 & 0 & -1 & -2 \end{array} \right)
$$
***
* \-R2, -R3
***
$$
\rightarrow \left(\begin{array}{ccc|r} 1 & 1 & 1 & \ 6\\ 0 & 1 & 3 & 9\\ 0 & 0 & 1 & 2 \end{array} \right)
$$
***
* R1-R3
* R2-3R3
***
$$
\rightarrow \left(\begin{array}{ccc|r} 1 & 1 & 0 & \ 4\\ 0 & 1 & 0 & 3\\ 0 & 0 & 1 & 2 \end{array} \right)
$$
***
* R1-R2
***
$$
\rightarrow \left(\begin{array}{ccc|r} 1 & 0 & 0 & \ 1\\ 0 & 1 & 0 & 3\\ 0 & 0 & 1 & 2 \end{array} \right)
$$
***
Hence the point of intersection is $x=1,y=3,z=2\rightarrow(1,3,2)$
\nRefer to **section 2.8** for Gaussian elimination rules. In question 1 (b), we found that this system of equations has **no solutions**. This can be verified using Gaussian elimination.
Setting up the augmented matrix:
***
$$
\left(\begin{array}{ c c c | c }
1 & 1 & 1 & 6\\
2 & 1 & -1 & 3\\
4 & 3 & 1 & 1
\end{array}\right)
$$
***
* R2-2R1
* R3-4R1
***
$$
\rightarrow\left(\begin{array}{ c c c | c }
1 & 1 & 1 & 6\\
0 & -1 & -3 & -9\\
0 & -1 & -3 & -23
\end{array}\right)
$$
***
* R3-R2, -R2:
***
$$
\left(\begin{array}{ c c c | c }
1 & 1 & 1 & 6\\
0 & 1 & 3 & 9\\
0 & 0 & 0 & -14
\end{array}\right)
$$
***
The bottom row is inconsistent, because $0\ne14$. Hence we have no solutions, as expected. 
\nRefer to **section 2.8** for Gaussian elimination rules. In question 1 (b), we found that this system of equations has an infinity of solutions. The goal is to find the equation of the line/plane along which these planes intersect. Setting up the augmented matrix:
***
$$
\left( \begin{array}{ccc|r} 1 & 1 & 1 & 6\\ 2 & 1 & -1 & 3\\ 2 & 2 & 2 & 12 \end{array} \right)
$$
***
* R3-2R1 (notice that R3=2R1). 
* R2-2R1
***
$$
\rightarrow \left(\begin{array}{ccc|r} 1 & 1 & 1 & 6\\ 0 & -1 & -3 & -9\\ 0 & 0 & 0 & 0 \end{array} \right)
$$
The third line is consistent, as it implies that $0=0$. Simplifying R1 and R2:
***
* R1+R2
* \-R2
***
$$
\rightarrow \left(\begin{array}{ccc|r}1 & 0 & -2 & -3\\ 0 & 1 & 3 & 9\\ 0 & 0 & 0 & 0 \end{array} \right)
$$
***
Now, exiting the augmented matrix:
***
$$
\begin{aligned}
&x-2z=-3\\
&y+3z=9
\end{aligned}
$$
Setting $z=\lambda$:
***
$$
\begin{align*}
\begin{array}{r l}
x & =-3 + 2\lambda\, ,\\
y &= 9-3\lambda ,\\
z &= \lambda\, .
\end{array} \Bigg\} \qquad
\begin{pmatrix} x \\ y \\ z \end{pmatrix} =
\begin{pmatrix} -3 \\ 9 \\ 0 \end{pmatrix} +
\lambda \begin{pmatrix} 2 \\ -3 \\ \ 1 \end{pmatrix}
\end{align*}
$$
This is the vector equation of a line; or, in Cartesian form:
***
$$
\lambda = \dfrac{x+3}{2} = \dfrac{9-y}{3} = z
$$
\nRefer to **section 2.8** for Gaussian elimination rules. In question 1 (b), we found that this system of equations has an infinity of solutions. The goal is to find the equation of the line/plane along which these planes intersect. Setting up the augmented matrix:
***
$$
\left( \begin{array}{ccc|r} -1 & 2 & -2 & 1\\ 4 & -1 & 6 & 2\\ 2 & 3 & 2 & 4 \end{array} \right)
$$
***
* R2+4R1
* R3+2R1
***
$$
\rightarrow \left( \begin{array}{ccc|r} -1 & 2 & -2 & 1\\ 0 & 7 & -2 & 6\\ 0 & 7 & -2 & 6 \end{array} \right)
$$
***
* R1-R2
* R3-R2
***
$$
\rightarrow\left( \begin{array}{ccc|r} -1 & -5 & 0 & -5\\ 0 & 7 & -2 & 6\\ 0 & 0 & 0 & 0 \end{array} \right)\rightarrow\left( \begin{array}{ccc|r} 1 & 5 & 0 & 5\\ 0 & 7 & -2 & 6\\ 0 & 0 & 0 & 0 \end{array} \right)
$$
In the final stage, we took -R1. The third line is consistent, as it implies that $0=0$. 
***
Exiting the augmented matrix:
***
$$
\begin{aligned}
&x+5y=5\\
&7y-2z=6
\end{aligned}
$$
Setting $y=\lambda$:
***
$$
\begin{align*}
\begin{array}{r l}
x & = 5 - 5 \lambda\, ,\\
y &= \lambda ,\\
z &= -3 + \tfrac{7}{2} \lambda\,
\end{array} \Bigg\} \qquad
\begin{pmatrix} x \\ y \\ z \end{pmatrix} =
\begin{pmatrix} 5 \\ 9 \\ -3 \end{pmatrix} +
\lambda \begin{pmatrix} -5 \\ 1 \\ \ \tfrac{7}{2} \end{pmatrix}
\end{align*}
$$
This is the vector equation of a line; or, in Cartesian form:
***
$$
\lambda = \dfrac{5-x}{5} = y = \dfrac{2z+6}{7}
$$
| **(L8)**: Use Gaussian elimination to solve the system of equations below (**Note**: these are the same equations as Q1, so you know the type of solution to expect).
***
You are asked to input the nature of the intersection of the planes. If the planes intersect at a point, input the point of intersection. If not, look at the '*Final Answer*' to check if your equation of intersection is correct.
$$
\begin{aligned}
x+y+z&=6\, ,\\
2x+y-z&=3\, ,\\
x+y&=4\, .
\end{aligned}
$$
\n$$
\begin{aligned}
x+y+z&=6\, ,\\
2x+y-z&=3\, ,\\
4x+3y+z&=1\, .
\end{aligned}
$$
\n$$
\begin{aligned}
x+y+z&=6\, ,\\
2x+y-z&=3\, ,\\
2x+2y+2z&=12\, .
\end{aligned}
$$
\n$$
\begin{aligned}
-x+2y-2z&=1, \\
4x-y+6z&=2\, ,\\
2x+3y+2z&=4\, ,\\
\end{aligned}
$$
| 77 | 4 | 27 | 27 | 350 | 44 | 7 | 4 | 0 | L8: Use Gaussian elimination to solve the system of equations below Note: these are the same equations as Q1, so you know the type of solution to expect. \end{aligned} $ $ \begin{aligned} x+y+z&=6\, ,\\ 2x+y-z&=3\, ,\\ 4x+3y+z&=1\, . \end{aligned} $ $ \begin{aligned} x+y+z&=6\, ,\\ 2x+y-z&=3\, ,\\ 2x+2y+2z&=12\, . \end{aligned} $ $ \begin{aligned} -x+2y-2z&=1, \\ 4x-y+6z&=2\, ,\\ 2x+3y+2z&=4\, ,\\ \end{aligned} $ | 4 |
012cc4b4-bb47-4ac4-a702-370084cef4cd | 1 | 2 | 0 | 13 | 4 | 2 | 5 | 2 | An experimental vehicle is fitted with a gyroscope to counteract completely the tendency of the vehicle to tip when rounding a bend.
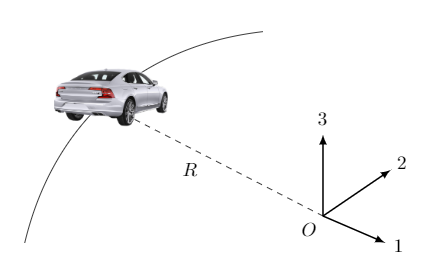
The gyroscope rotor is mounted on a horizontal shaft fixed across the vehicle frame, parallel with the rear axle and has a mass moment of inertia $I = 3000~\mathrm{kgm^2}$ about its spin axis. The vehicle has a total mass $m = 1200~\mathrm{kg}$ and its centre of mass is at a height $h = 0.8~\mathrm{m}$ above the road surface. The mass of the wheels may be ignored. The situation is modelled as follows:
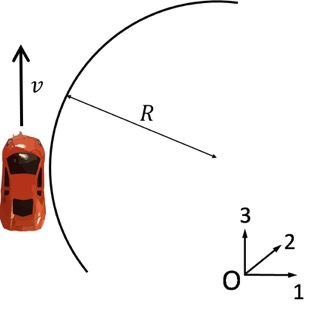
In the diagram, the coordinate system is at the centre of the car's circular motion. The car's velocity is in the direction labelled 2, direction 1 is perpendicular to the car's velocity and directed away from the car's position, whilst 3 is the upward normal to the road surface.
| Find the angular velocity $\Omega$ that the gyroscope rotor should spin at if the car is travelling with velocity $v = 15~\mathrm{m/s}$.
\nIn which direction should the gyroscope spin?
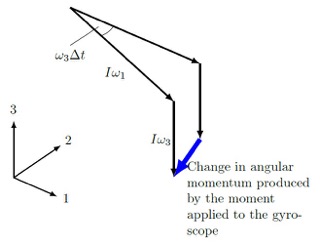
\nObserve the two diagrams below:
### **Diagram A**
### **Diagram B**
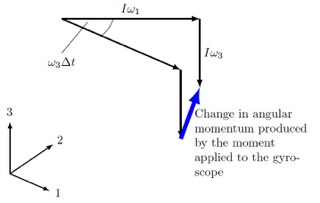
Which diagram shows the correct change in angular momentum caused by the gyroscope?
| 3 | 0.666667 | 4 | Draw the car rounding a bend and introduce a suitable system for your vector conventions. The question may seem complicated but the solution is fairly straight forward.
***
Relate the car speed $v$ and the radius of the bend to its angular momentum around the centre of the bend.
***
You’ll then need to think of an expression describing the moment imposed on the car through the wheels due to the centripetal force taking into account $h$, the height of the centre of mass of the car off the ground – this is the moment you need to counteract with the gyro!
***
Combining these two expressions and Equation 5.1 from your notes will give you an expression of the required angular velocity of the gyro, taking the angular velocity of precession as the angular velocity of the whole car around the bend.
\nThe direction of spin required can be deducted using your vector diagram of the change in angular momentum once again, making use of the right hand rule one last time.
\nSee worked solutions in part a
| 
***
Centripetal moment applied to the car:
$$
M=\cfrac{{mv}^2h}{R}~~\mathrm{(Equation~1)}
$$
***
Where:
$$
v=\omega_3R~~\mathrm{(Equation~2)}
$$
***
Substituting Equation 2 into Equation 1:
$$
M=mv\omega_3h~~\mathrm{(Equation~3)}
$$
***
Moment applied to the gyroscope:
$$
M=I\omega_3\omega_1~~\mathrm{(Equation~4)}
$$
***
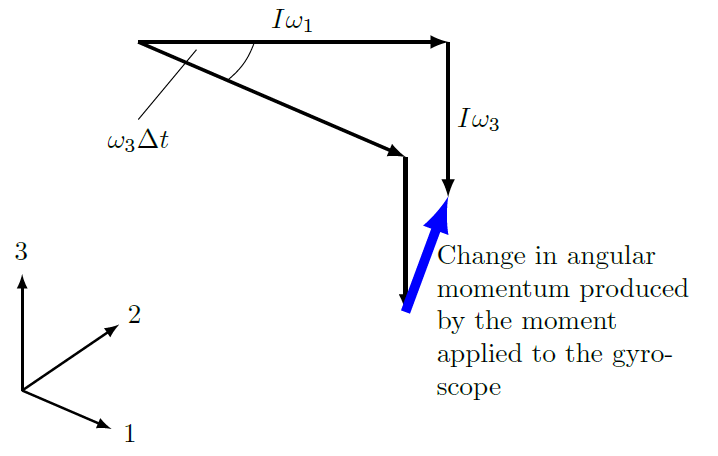
If the gyroscope spins in the opposite direction to the wheels, the gyroscope vector diagram is shown below:
***
Equating the moments from Equations 3 and 4:
$$
M=mv\omega_3h=I\omega_3\omega_1
$$
***
Hence the angular velocity of the rotor is:
$$
\omega_1=\cfrac{mvh}{I}
$$
***
Substituting the values of the parameters gives:
$$
\omega_1=\cfrac{1200\times15\times0.8}{3000}
$$
$$
\omega_1=4.8~\mathrm{rad/s}
$$
(In a direction opposite to the road wheels)
\n\n | An experimental vehicle is fitted with a gyroscope to counteract completely the tendency of the vehicle to tip when rounding a bend.

The gyroscope rotor is mounted on a horizontal shaft fixed across the vehicle frame, parallel with the rear axle and has a mass moment of inertia $I = 3000~\mathrm{kgm^2}$ about its spin axis. The vehicle has a total mass $m = 1200~\mathrm{kg}$ and its centre of mass is at a height $h = 0.8~\mathrm{m}$ above the road surface. The mass of the wheels may be ignored. The situation is modelled as follows:
In the diagram, the coordinate system is at the centre of the car's circular motion. The car's velocity is in the direction labelled 2, direction 1 is perpendicular to the car's velocity and directed away from the car's position, whilst 3 is the upward normal to the road surface.
Find the angular velocity $\Omega$ that the gyroscope rotor should spin at if the car is travelling with velocity $v = 15~\mathrm{m/s}$.
\nIn which direction should the gyroscope spin?
\nObserve the two diagrams below:
### **Diagram A**

### **Diagram B**

Which diagram shows the correct change in angular momentum caused by the gyroscope?
| 190 | 5 | 8 | 8 | 86 | 2 | 53 | 2 | 3 | The situation is modelled as follows: In the diagram, the coordinate system is at the centre of the car's circular motion. Find the angular velocity $\Omega$ that the gyroscope rotor should spin at if the car is travelling with velocity $v = 15~\mathrm{m/s}$. In which direction should the gyroscope spin? Observe the two diagrams below: ### Diagram A ### Diagram B Which diagram shows the correct change in angular momentum caused by the gyroscope? | 4 |
01e1b7d0-d39c-4cdf-8200-05e95de00232 | 4 | 0 | 0 | 6 | 4 | 1 | 2 | 1 | As part of another design project, you are tasked with verifying whether a certain engine is suitable for driving the wheels of a lawn mower. You need to check that the engine will have a suitable cylinder capacity to generate the required 3kW of power at its minimum operating speed.

| First, given that the lawnmower is rated for speeds between 1 and 5 m/s, you need to determine the range of the engine rpm if the lawn mower wheels are 0.4m in diameter and the following drive transmission is used: (you may assume no change in rotational speed other than from the drive transmission below)
| Stage | First Transmission Component | Second Transmission Component |
| :---- | :--------------------------- | :---------------------------- |
| 1 | 14 tooth sprocket | 24 tooth sprocket |
| 2 | 30mm diameter pulley | 70mm diameter pulley |
| 3 | 10 tooth gear | 26 tooth gear |
\nThe engine you need to confirm the performance of is shown below:
Given that the temperature and pressure at stages 1, 2, 3 and 4 are as shown in the table below, determine the specific net work of the engine.
| Stage | Temperature (K) | Pressure (bar) |
| :---- | :-------------- | :------------- |
| 1 | 298 | 1.013 |
| 2 | | |
| 3 | | |
| 4 | | |
\nDetermine the minimum required cylinder capacity to ensure a minimum of 3kW is supplied at all engine speeds.
| 3 | 0.666667 | 3 | \n\nRefer to your thermodynamics problem sheets.
| \nThe first step to this question is to use the picture of the engine to determine what type of engine it is. This engine is clearly a petrol engine as you can see a spark plug in the picture.
  
***
Next, you need to use the SFEE to complete calculations for each process.
\n | As part of another design project, you are tasked with verifying whether a certain engine is suitable for driving the wheels of a lawn mower. You need to check that the engine will have a suitable cylinder capacity to generate the required 3kW of power at its minimum operating speed.

First, given that the lawnmower is rated for speeds between 1 and 5 m/s, you need to determine the range of the engine rpm if the lawn mower wheels are 0.4m in diameter and the following drive transmission is used: (you may assume no change in rotational speed other than from the drive transmission below)
| Stage | First Transmission Component | Second Transmission Component |
| :---- | :--------------------------- | :---------------------------- |
| 1 | 14 tooth sprocket | 24 tooth sprocket |
| 2 | 30mm diameter pulley | 70mm diameter pulley |
| 3 | 10 tooth gear | 26 tooth gear |
\nThe engine you need to confirm the performance of is shown below:
Given that the temperature and pressure at stages 1, 2, 3 and 4 are as shown in the table below, determine the specific net work of the engine.
| Stage | Temperature (K) | Pressure (bar) |
| :---- | :-------------- | :------------- |
| 1 | 298 | 1.013 |
| 2 | | |
| 3 | | |
| 4 | | |
\nDetermine the minimum required cylinder capacity to ensure a minimum of 3kW is supplied at all engine speeds.
| 253 | 0 | 0 | 0 | 56 | 0 | 202 | 0 | 1 | As part of another design project, you are tasked with verifying whether a certain engine is suitable for driving the wheels of a lawn mower. First, given that the lawnmower is rated for speeds between 1 and 5 m/s, you need to determine the range of the engine rpm if the lawn mower wheels are 0.4m in diameter and the following drive transmission is used: you may assume no change in rotational speed other than from the drive transmission below table Determine the minimum required cylinder capacity to ensure a minimum of 3kW is supplied at all engine speeds. | 2 |
02c18d44-dd40-467d-b0e5-1ad57dc32713 | 0 | 0 | 2 | 24 | 6 | 1 | 0 | 14 | In ordinary derivatives a function $y(x)$ implicitly defines $x=x(y)$ and their derivatives obey:
$$
\frac{dx}{dy} = \frac{1}{\left(\dfrac{dy}{dx}\right)}
$$
(check e.g. for $y=x^2$). In higher dimensions a similar relation holds, but it is important to keep track of which variable is being kept constant. The correct relation is
$$
\left( \frac{\partial y}{\partial x}\right)_{z} = \frac{1}{ \left(\dfrac{\partial x}{\partial y}\right)_{z}}
$$
but e.g.
$$
\left( \frac{\partial y}{\partial x}\right)_{z} \neq \frac{1}{ \left(\dfrac{\partial x}{\partial y}\right)_{r}}
$$
The reciprocal rule only holds if the same variable is being kept constant on both sides of the equation.
|  Confirm the above for $z=x^2-y^2$, $r=\sqrt{x^2+y^2}$ by calculating $\left(\frac{\partial y}{\partial x}\right)_{z}$, $\left(\frac{\partial x}{\partial y}\right)_{z}$, $\left(\frac{\partial y}{\partial x}\right)_{r}$, $\left(\frac{\partial x}{\partial y}\right)_{r}$. 
\nFor $z=x^2-y^2$ confirm the cyclic rule for partial derivatives
$$
\left( \frac{\partial y}{\partial x}\right)_{z}\left( \frac{\partial x}{\partial z}\right)_{y}\left( \frac{\partial z}{\partial y}\right)_{x} = -1
$$
| 2 | 0.666667 | 2 | Start by finding the partial derivatives holding $z$ constant...
***
Re-arrange $z=z(x,y)$ into the form $y=y(x,z)$. Then, find $\partial y/\partial x$ holding $z$ constant. Repeat for $x=x(y,z)$. Does the reciprocal rule hold?
***
Repeat the above process but instead holding $r$ constant. Again, does the reciprocal rule hold?
***
Does the reciprocal rule hold for partial derivatives where different variables are held constant?
\nYou have already found $(\partial y/\partial x)_z$ in part (a). Express this in terms of $x$ and $y$.
***
Re-arrange for $x=x(y,z)$ and find $(\partial x/\partial z)_y$. Can you express this in terms of $x$ and $y$? Repeat for $z=z(x,y)$. 
***
Multiply the results together. Do they equal $-1$?
| Starting with the two partial derivatives where we hold $z$ constant:
***
$$
y(x,z) = (x^2-z)^{1/2}
$$
***
Using the chain rule and holding $z$ constant:
$$
\left(\dfrac{\partial y}{\partial x}\right)_z = \frac{x}{(x^2-z)^{1/2}} = \frac{x}{y}
$$
***
$$
x(y,z)=(y^2+z)^{1/2}
$$
***
$$
\therefore\left(\dfrac{\partial x}{\partial y}\right)_z = \frac{y}{(y^2+z)^{1/2}} = \frac{y}{x}
$$
This verifies that:
$$
\left( \frac{\partial y}{\partial x}\right)_{z} = \frac{1}{ \left(\dfrac{\partial x}{\partial y}\right)_{z}}
$$
Now, for $r$:
***
$$
y(x,r) = (r^2-x^2)^{1/2}
$$
***
Using the chain rule and holding $r$ constant:
$$
\left(\dfrac{\partial y}{\partial x}\right)_r = -\frac{x}{(r^2-x^2)^{1/2}}=-\frac{x}{y}
$$
***
$$
x(y,r)=(r^2-y^2)^{1/2}
$$
***
$$
\therefore\left(\frac{\partial x}{\partial y}\right)_r = -\frac{y}{(r^2-y^2)^{1/2}} = -\frac{y}{x}
$$
This verifies that:
$$
\left( \frac{\partial y}{\partial x}\right)_{z} = \frac{1}{ \left(\dfrac{\partial x}{\partial y}\right)_{z}}
$$
This also verifies that:
$$
\left( \frac{\partial y}{\partial x}\right)_{z} \neq \frac{1}{ \left(\dfrac{\partial x}{\partial y}\right)_{r}}
$$
\nFrom part (a), 
$$
\left(\dfrac{\partial y}{\partial x}\right)_z = \frac{2x}{(x^2-z)^{1/2}} = \frac{x}{y}
$$
Now, to find the other partial derivatives: re-arranging for $x=x(y,z)$,
***
$$
x=(y^2+z)^{1/2}
$$
Partially differentiating with respect to $z$ and holding $y$ constant:
***
$$
\left(\frac{\partial x}{\partial z}\right)_y = \frac{1}{2(y^2+z)^{1/2}} = \frac{1}{2x}
$$
***
Finally, partially differentiating $z=z(x,y)$ with respect to $y$ and holding $x$ constant:
***
$$
\left(\frac{\partial z}{\partial y}\right)_x = -2y
$$
Multiplying each partial derivative together:
***
$$
\left( \frac{\partial y}{\partial x}\right)_{z}\left( \frac{\partial x}{\partial z}\right)_{y}\left( \frac{\partial z}{\partial y}\right)_{x} = \frac{x}{y}\frac{1}{2x}(-2y)= -1
$$
| In ordinary derivatives a function $y(x)$ implicitly defines $x=x(y)$ and their derivatives obey:
$$
\frac{dx}{dy} = \frac{1}{\left(\dfrac{dy}{dx}\right)}
$$
(check e.g. for $y=x^2$). In higher dimensions a similar relation holds, but it is important to keep track of which variable is being kept constant. The correct relation is
$$
\left( \frac{\partial y}{\partial x}\right)_{z} = \frac{1}{ \left(\dfrac{\partial x}{\partial y}\right)_{z}}
$$
but e.g.
$$
\left( \frac{\partial y}{\partial x}\right)_{z} \neq \frac{1}{ \left(\dfrac{\partial x}{\partial y}\right)_{r}}
$$
The reciprocal rule only holds if the same variable is being kept constant on both sides of the equation.
 Confirm the above for $z=x^2-y^2$, $r=\sqrt{x^2+y^2}$ by calculating $\left(\frac{\partial y}{\partial x}\right)_{z}$, $\left(\frac{\partial x}{\partial y}\right)_{z}$, $\left(\frac{\partial y}{\partial x}\right)_{r}$, $\left(\frac{\partial x}{\partial y}\right)_{r}$. 
\nFor $z=x^2-y^2$ confirm the cyclic rule for partial derivatives
$$
\left( \frac{\partial y}{\partial x}\right)_{z}\left( \frac{\partial x}{\partial z}\right)_{y}\left( \frac{\partial z}{\partial y}\right)_{x} = -1
$$
| 94 | 14 | 26 | 26 | 111 | 16 | 27 | 8 | 0 | Confirm the above for $z=x^2-y^2$, $r=\sqrt{x^2+y^2}$ by calculating $\left(\frac{\partial y}{\partial x}\right)_{z}$, $\left(\frac{\partial x}{\partial y}\right)_{z}$, $x=x(y)$0, $x=x(y)$1. | 1 |
0315f302-37e4-420c-89aa-1674824e3cf5 | 4 | 0 | 0 | 15 | 5 | 0 | 3 | 2 | The acid dissociation constant, $K_{a}$ , is a measure of the strength of an acid ($\mathrm{HA}$), and is defined as the equilibrium constant for the reaction:
$$
\text{HA} \rightleftharpoons \text{H}^{+}+\text{A}^{-}
$$
It has a value of:
$$
K_{a}=\frac{[H^+][A^-]}{[HA]}
$$
To create a buffer solution, we can mix together solutions of a weak acid and its conjugate base (usually supplied using a salt of the weak acid). To calculate the ratio of acid to base needed for a buffer of a particular $pH$, we use the Henderson-Hasselbalch equation, which you are now going to derive.
| Rearrange the first equation to give an expression for $[H^+]$ in terms of $K_a$, $[A^-]$ and $[HA]$
\nTake the base-10 logarithm of this equation, and simplify it, so the right hand side contains one term in $K_{a}$ and a second in $[HA]$ and $[A^-]$ . Enter $\log_{10}(x)$ as 'log10(x)'.
\nUsing the definitions of $pH$ and $pK_a$ shown below, write a equation that gives $pH$ in terms of $pK_a$ and the ratio of **acid to base**, $\frac{[HA]}{[A^{-}]}$.
$$
pK_{a}=-\log_{10}K_{a}
$$
$$
pH=-\log_{10}[H^+]
$$
\nUsing your knowledge of how logs work, give an equation for the $pH$ in terms of $pK_a$ and the ratio of **base to acid**, $\frac{[A^-]}{[HA]}$.
This *is* the Henderson-Hasselbalch equation.
| 4 | 1 | 2 | \n\n\n | $$
[H^+]=\frac{K_{a} \cdot [HA]}{[A^{-}]}
$$
\n$$
\log_{10}[H^+]=\log_{10}(\frac{K_a[HA]}{[A^-]})=\log_{10} K_a+\log_{10}(\frac{[HA]}{[A^{-}]})
$$
\nFrom the previous part:
$$
\log_{10} [H^+]=\log_{10}(\frac{K_a[HA]}{[A^-]})=\log_{10} K_a+\log_{10}(\frac{[HA]}{[A^{-}]})
$$
Multiply through by $-1$:
$$
-\log_{10} [H^+]=-\log_{10}K_a-\log_{10}(\frac{[HA]}{[A^-]})
$$
Identify the two terms as $pH$ and $pK_a$:
$$
pH=pK_a-\log_{10}(\fracpH=pK_a-\log_{10}(\frac{[HA]}{[A^-]}){[HA]}{[A^-]})
$$
\nFrom the previous part:
$$
pH=pK_a-\log_{10}(\frac{[HA]}{[A^-]})
$$
Using the identity $\log(\frac{x}{y})=-\log(\frac{y}{x})$
$$
pH=pK_a+\log_{10}\frac{[A^-]}{[HA]}
$$
| The acid dissociation constant, $K_{a}$ , is a measure of the strength of an acid ($\mathrm{HA}$), and is defined as the equilibrium constant for the reaction:
$$
\text{HA} \rightleftharpoons \text{H}^{+}+\text{A}^{-}
$$
It has a value of:
$$
K_{a}=\frac{[H^+][A^-]}{[HA]}
$$
To create a buffer solution, we can mix together solutions of a weak acid and its conjugate base (usually supplied using a salt of the weak acid). To calculate the ratio of acid to base needed for a buffer of a particular $pH$, we use the Henderson-Hasselbalch equation, which you are now going to derive.
Rearrange the first equation to give an expression for $[H^+]$ in terms of $K_a$, $[A^-]$ and $[HA]$
\nTake the base-10 logarithm of this equation, and simplify it, so the right hand side contains one term in $K_{a}$ and a second in $[HA]$ and $[A^-]$ . Enter $\log_{10}(x)$ as 'log10(x)'.
\nUsing the definitions of $pH$ and $pK_a$ shown below, write a equation that gives $pH$ in terms of $pK_a$ and the ratio of **acid to base**, $\frac{[HA]}{[A^{-}]}$.
$$
pK_{a}=-\log_{10}K_{a}
$$
$$
pH=-\log_{10}[H^+]
$$
\nUsing your knowledge of how logs work, give an equation for the $pH$ in terms of $pK_a$ and the ratio of **base to acid**, $\frac{[A^-]}{[HA]}$.
This *is* the Henderson-Hasselbalch equation.
| 202 | 23 | 11 | 11 | 34 | 0 | 111 | 18 | 0 | The acid dissociation constant, $K_{a}$ , is a measure of the strength of an acid $\mathrm{HA}$, and is defined as the equilibrium constant for the reaction: $ \text{HA} \rightleftharpoons \text{H}^{+}+\text{A}^{-} $ It has a value of: $ K_{a}=\frac{[H^+][A^-]}{[HA]} $ To create a buffer solution, we can mix together solutions of a weak acid and its conjugate base usually supplied using a salt of the weak acid. To calculate the ratio of acid to base needed for a buffer of a particular $pH$, we use the Henderson-Hasselbalch equation, which you are now going to derive. Rearrange the first equation to give an expression for $[H^+]$ in terms of $K_a$, $[A^-]$ and $[HA]$ Take the base-10 logarithm of this equation, and simplify it, so the right hand side contains one term in $K_{a}$ and a second in $[HA]$ and $[A^-]$ . Enter $\mathrm{HA}$2 as 'log10x'. Using the definitions of $pH$ and $\mathrm{HA}$4 shown below, write a equation that gives $pH$ in terms of $\mathrm{HA}$4 and the ratio of acid to base, $\mathrm{HA}$7. $\mathrm{HA}$8 $\mathrm{HA}$9 Using your knowledge of how logs work, give an equation for the $pH$ in terms of $\mathrm{HA}$4 and the ratio of base to acid, $ \text{HA} \rightleftharpoons \text{H}^{+}+\text{A}^{-} $2. | 6 |
03568619-d5de-4cc4-bbca-ed5fca655d1a | 0 | 0 | 2 | 4 | 3 | 3 | 1 | 11 | An engine was left running in a large unventilated garage, resulting in a steady-state concentration of carbon monoxide, $C_{0}=24\ \mathrm{mg/m^{3}}$. At $t=0$ the engine is turned off and a large garage door is opened. Under the assumption that buoyancy effects are negligible and that the release can be regarded one-dimensional, plot the concentration profile after one minute under the different conditions that follow.
| Assuming that there is only molecular diffusion: $D = 0.202\ \mathrm{cm^{2}/s}$.
\nAssuming the flow is turbulent: $D = 10^4\ \mathrm{cm^{2}/s}$.
| 2 | 1 | 3 | \n | Given that the vertical and lateral extent of the garage door is large, the release may be treated as being one-dimensional. We also assume that the garage has infinite length and has an opening at $x=0$, which means that the initial condition of the concentration is given by
$$
C(x,t=0)=
\begin{cases}
C_{0}&\ \ \mathrm{if}\ x\leq 0\\
0&\ \ \mathrm{if}\ x> 0,
\end{cases}
$$
and we can use the solution derived in the previous question,
$$
C(x, t) = \dfrac{C_0}{2}\mathrm{erfc}\left(\dfrac{x}{\sqrt{2} \sigma}\right).
$$
***
This solution is shown in the figure below. It should be noted that the error function is not available on the calculators you have available during the exam, so you will not be expected to evaluate this expression numerically under those conditions. Evaluation here should be done with MATLAB.
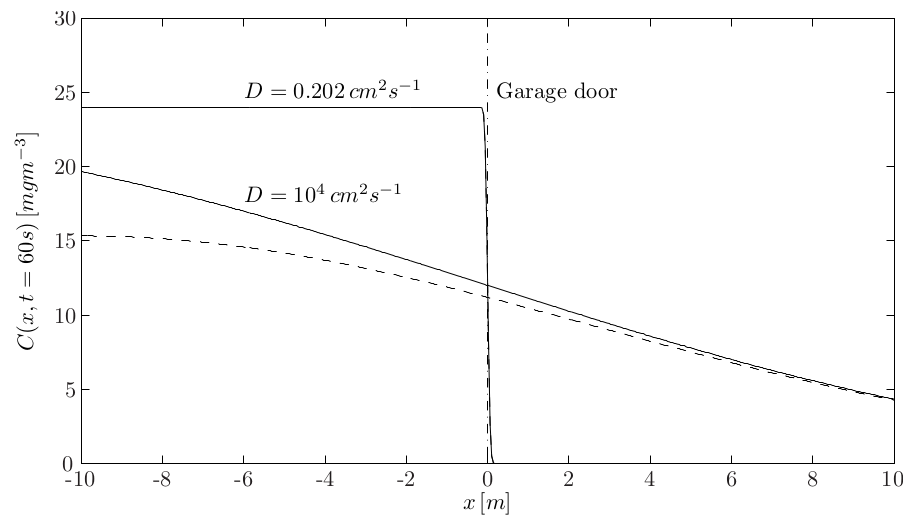
*Concentration $C\ \mathrm{[mg/m^3]}$ at $t = 60\ \mathrm{s}$ as a function of $x$; infinite garage length ($\text{---}$) and finite $(L=10\ \mathrm{m})$ garage length ($-\,-\,-$).*
\nGiven that the vertical and lateral extent of the garage door is large, the release may be treated as being one-dimensional. We also assume that the garage has infinite length and has an opening at $x=0$, which means that the initial condition of the concentration is given by
$$
C(x,t=0)=
\begin{cases}
C_{0}&\ \ \mathrm{if}\ x\leq 0\\
0&\ \ \mathrm{if}\ x> 0,
\end{cases}
$$
and we can use the solution derived in the previous question
$$
C(x, t) = \dfrac{C_0}{2}\mathrm{erfc}\left(\dfrac{x}{\sqrt{2} \sigma}\right).
$$
***
This solution is shown in the figure below. It should be noted that the error function is not available on the calculators you have available during the exam, so you will not be expected to evaluate this expression numerically under those conditions. Evaluation here should be done with MATLAB.

*Concentration $C\ \mathrm{[mg/m^3]}$ at $t = 60\ \mathrm{s}$ as a function of $x$; infinite garage length ($\text{---}$) and finite $(L=10\ \mathrm{m})$ garage length ($-\,-\,-$).*
| An engine was left running in a large unventilated garage, resulting in a steady-state concentration of carbon monoxide, $C_{0}=24\ \mathrm{mg/m^{3}}$. At $t=0$ the engine is turned off and a large garage door is opened. Under the assumption that buoyancy effects are negligible and that the release can be regarded one-dimensional, plot the concentration profile after one minute under the different conditions that follow.

Assuming that there is only molecular diffusion: $D = 0.202\ \mathrm{cm^{2}/s}$.
\nAssuming the flow is turbulent: $D = 10^4\ \mathrm{cm^{2}/s}$.
| 80 | 4 | 3 | 3 | 151 | 0 | 16 | 2 | 1 | Under the assumption that buoyancy effects are negligible and that the release can be regarded one-dimensional, plot the concentration profile after one minute under the different conditions that follow. Assuming that there is only molecular diffusion: $D = 0.202\ \mathrm{cm^{2}/s}$. Assuming the flow is turbulent: $D = 10^4\ \mathrm{cm^{2}/s}$. | 3 |
037b6b33-24e8-4efa-a376-2e2d9e5261a7 | 0 | 0 | 1 | 9 | 4 | 2 | 4 | 0 | The most readily available resistor values are the ‘E12 series’: $1, 1.2, 1.5, 1.8, 2.2, 2.7, 3.3, 3.9, 4.7, 5.6, 6.8, 8.2$ and $10~\Omega$ and factors of $10$ larger or smaller (e.g. $180~ \Omega$, $18 ~\mathrm{k}\Omega$, etc.).
| Design a non-inverting amplifier with a gain of $263$, using fixed E12 resistors. A deviation of $\pm 1\%$ of the nominal gain is acceptable. Remember that resistors can be connected in parallel.
| 1 | 0.333333 | 1 | null | A non-inverting op-amp stage appears as follows:
  
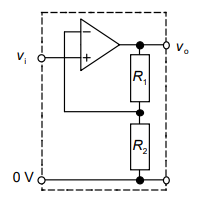
***
For a non-inverting op-amp, the gain can be calculated as follows:
  
$A_\mathrm{v} = \frac{R_1+R_2}{R_2}$
***
This question requires a bit of trial and error. However, this can be done methodically:
***
Choose one resistor value and plug it into the above equation, along with the gain to calculate $R_2$.
***
If $R_2$ is not equal to any of the E12 resistor values, check if there is a series or parallel combination of resistors that would lead to this value.
***
Note that if there is a resistor combination that gives a gain within $1%$ of the nominal value, it is still acceptable.
| The most readily available resistor values are the ‘E12 series’: $1, 1.2, 1.5, 1.8, 2.2, 2.7, 3.3, 3.9, 4.7, 5.6, 6.8, 8.2$ and $10~\Omega$ and factors of $10$ larger or smaller (e.g. $180~ \Omega$, $18 ~\mathrm{k}\Omega$, etc.).
Design a non-inverting amplifier with a gain of $263$, using fixed E12 resistors. A deviation of $\pm 1\%$ of the nominal gain is acceptable. Remember that resistors can be connected in parallel.
| 58 | 7 | 4 | 4 | 112 | 0 | 32 | 2 | 0 | $180~ \Omega$, $18 ~\mathrm{k}\Omega$, etc.. Design a non-inverting amplifier with a gain of $263$, using fixed E12 resistors. Remember that resistors can be connected in parallel. | 2 |
03baff5d-e329-4336-8cd5-a97e93fc94a9 | 2 | 0 | 0 | 11 | 4 | 2 | 5 | 1 | At the inlet to a compressor stage, the absolute flow velocity is measured to be $250 ~\mathrm{m/s}$ at an angle of $17^{\circ}$ to the axis. 
| If the blade speed is $350 ~\mathrm{m/s}$, calculate the velocity and flow angle relative to the rotor blades.
| 1 | 0.333333 | 2 | null | Draw a velocity triangle, for which:
***
$C_2 = 250~\mathrm{m/s}$
  
$\alpha = 17^{\circ}$
  
$U = 350~\mathrm{m/s}$
***
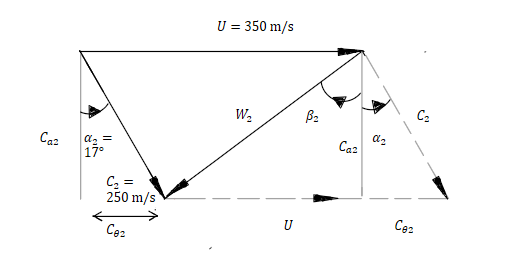
where the triangle with the dotted lines is in the same orientation as the one in the notes.
***
To find the relative velocity, $W_2$, add up the absolute and blade velocity vectors nose-to-tail:
***
$\bar{W}_2 = \bar{C}_2-\bar{U}$
***
The axial and tangential components of the absolute and blade velocities need to be calculated:
***
Absolute velocity:
***
Axial: 
  
$C_\mathrm{a2} = 250\mathrm{cos}(17)$
  
$U_\mathrm{a} =0$
***
Tangential:
  
$C_{\theta2} = 250\mathrm{sin}(17)$
  
$U_\theta = U = 350~\mathrm{m/s}$
***
Adding up the axial and tangential components and taking the magnitude:
  
$W_2 = \sqrt{(250\mathrm{cos}(17)-0)^2 + (250\mathrm{sin}(17)-350)^2} = 365.8~\mathrm{m/s}$ 
***
Calculate $\beta_2$:
  
$\beta_2 = \mathrm{cos}^{-1}(\frac{C_\mathrm{a2}}{W_2})$
***
Substituting in numbers:
  
$\beta_2 = \mathrm{cos}^{-1}(\frac{250\mathrm{cos}(17)}{365.8}) = -49.2^{\circ}$
  
Note that the angle is negative as it is measured anticlockwise from the axis $C_\mathrm{a}$.
| At the inlet to a compressor stage, the absolute flow velocity is measured to be $250 ~\mathrm{m/s}$ at an angle of $17^{\circ}$ to the axis. 
If the blade speed is $350 ~\mathrm{m/s}$, calculate the velocity and flow angle relative to the rotor blades.
| 42 | 3 | 14 | 14 | 126 | 0 | 18 | 1 | 0 | If the blade speed is $350 ~\mathrm{m/s}$, calculate the velocity and flow angle relative to the rotor blades. | 1 |
0592be77-e032-469d-bfca-4d9408f3632b | 1 | 1 | 0 | 9 | 4 | 2 | 6 | 32 | The speed of a D.C. motor is governed by a proportional control system with unity feedback. The shaft of the motor is subject to an external torque causing a maximum speed reduction of $50~\mathrm{rad/s}$. What is the value of $K_\mathrm{P}$ needed to sustain the speed within $1\%$ of the desired value $100~\mathrm{rad/s}$?
  
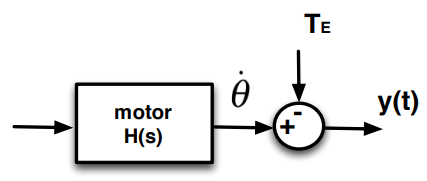
| The parameters of the D.C. motor are:
  
$K_\mathrm{e} = 5~\mathrm{V/krpm}$
$K_\mathrm{t} = 4~\mathrm{Ncm/A}$
$R_\mathrm{a} = 2~\Omega$
$J = 0.1~\mathrm{Ncm/krpm}$
$K_\mathrm{f} = 0$ (No frictional losses)
| 1 | 1 | 3 | null | From the lecture notes Section 3.5.3 (see inside for full derivation), the gain and time constant of a D.C. motor are as follows:
  
$K = \frac{K_\mathrm{t}}{K_\mathrm{f}R_\mathrm{a}+K_\mathrm{e}K_\mathrm{t}}$
  
$\tau = \frac{JR_\mathrm{a}}{K_\mathrm{f}R_\mathrm{a}+K_\mathrm{e}K_\mathrm{t}}$
***
The motor transfer constant is of the form:
  
$H(s) = \frac{K}{1+\tau s}$
***
Substituting in $K$ and $\tau$:
  
$H(s) = \dfrac{\frac{K_\mathrm{t}}{K_\mathrm{f}R_\mathrm{a}+K_\mathrm{e}K_\mathrm{t}}}{1+\frac{JR_\mathrm{a}}{K_\mathrm{f}R_\mathrm{a}+K_\mathrm{e}K_\mathrm{t}}s}$
***
Tidying up:
  
$H(s) = \frac{K_\mathrm{t}}{K_\mathrm{f}R_\mathrm{a}+K_\mathrm{e}K_\mathrm{t} +JR_\mathrm{a}s}$
***
Substituting in parameter values (remembering to convert units):
  
$H(s) = \frac{0.04}{(0.005\times \frac{60}{2\pi}\times 0.04)+(0.000001\times \frac{60}{2\pi}\times 2)s}$
***
Simplifying to canonical form:
  
$H(s) = \dfrac{0.04}{\frac{0.006}{\pi}+\frac{0.00006}{\pi}s}$
  
$H(s) = \dfrac{\frac{20}{3}\pi}{1+0.01s}$
***
It can now be helpful to draw a full diagram of the system:
  
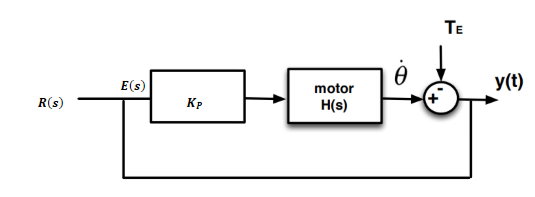
***
Find an expression for $Y(s)$ by converting $y(t)$ and the speed reduction caused by the torque, $\dot{\theta}$, to the Laplace domain:
  
$Y(s) = E(s)K_\mathrm{P}H(s)-\Theta(s)$
  
where $E(s) = R(s)-Y(s)$.
***
Hence:
  
$Y(s) = R(s)K_\mathrm{P}H(s)-Y(s)K_\mathrm{P}H(s)-\Theta(s)$
***
The total steady-state error is caused by both the closed-loop steady-state error and the disturbance error. Hence, both the closed-loop transfer function and the disturbance transfer function need to be calculated.
***
Calculate the closed-loop transfer function by setting $\Theta(s)$ to $0$:
  
$G(s) = \frac{Y(s)}{R(s)} = \frac{K_\mathrm{P}H(s)}{1+K_\mathrm{P}H(s)}$
***
Substituting in $H(s)$:
  
$G(s) = \dfrac{\frac{\frac{20\pi K_\mathrm{P}}{3}}{1+0.01s}}{1+\frac{\frac{20\pi K_\mathrm{P}}{3}}{1+0.01s}}$
***
Tidying up:
  
$G(s) = \frac{20\pi K_\mathrm{P}}{3+0.03s+20\pi K_\mathrm{P}}$
***
Find the closed-loop steady state value:
  
$y_\mathrm{ss} = \lim\limits_{s\rightarrow 0}sG(s)R(s)$
  
$y_\mathrm{ss} = \lim\limits_{s\rightarrow 0} s\cdot \frac{20\pi K_\mathrm{P}}{3+0.03s+20\pi K_\mathrm{P}}\cdot\frac{100}{s}$
***
Simplifying:
  
$y_\mathrm{ss} = \frac{2000\pi K_\mathrm{P}}{3+20\pi K_\mathrm{P}}$
***
Find the closed-loop steady-state error:
  
$e_\mathrm{ss} = r_\mathrm{ss}-y_\mathrm{ss}$
  
$e_\mathrm{ss} = 100-\frac{2000\pi K_\mathrm{P}}{3+20\pi K_\mathrm{P}}$
***
Simplifying:
  
$e_\mathrm{ss} = \frac{300}{3+20\pi K_\mathrm{P}}$
***
Now find an expression for the disturbance transfer function by setting $R(s)$ to $0$:
  
$S(s) = \frac{Y(s)}{\Theta(s)} = \frac{-1}{1+K_\mathrm{P}H(s)}$
***
Substitute in the expression for $H(s)$:
  
$S(s) = \dfrac{-1}{1+\frac{\frac{20}{3}\pi K_\mathrm{P}}{1+0.01s}}$
***
Simplifying:
  
$S(s) = \frac{-3-0.03s}{3+0.03s +20\pi K_\mathrm{P}}$
***
The disturbance steady-state value can be found as follows:
  
$y_\mathrm{Ds} = \lim\limits_{s\rightarrow 0}sS(s)\Theta(s)$
  
$y_\mathrm{Ds} = \lim\limits_{s\rightarrow 0} s\cdot \frac{-3-0.03s}{3+0.03s +20\pi K_\mathrm{P}}\cdot \frac{50}{s}$
***
Simplifying:
  
$y_\mathrm{Ds} = \frac{-150}{3+20\pi K_\mathrm{P}}$
***
Find the disturbance steady-state error:
  
$e_\mathrm{Ds} = 0-y_\mathrm{Ds}$
  
$e_\mathrm{Ds} = \frac{150}{3+20\pi K_\mathrm{P}}$
***
Find the total steady-state error:
  
$e_\mathrm{ts} = e_\mathrm{ss}+e_\mathrm{Ds}$
  
$e_\mathrm{ts} = \frac{300}{3+20\pi K_\mathrm{P}}+\frac{150}{3+20\pi K_\mathrm{P}}= \frac{450}{3+20\pi K_\mathrm{P}}$
***
The total error must not exceed $1\%$:
  
$1>\frac{450}{3+20\pi K_\mathrm{P}}$
***
Solving for $K_\mathrm{P}$:
  
$K_\mathrm{P} > 7.1$
  
  
| The speed of a D.C. motor is governed by a proportional control system with unity feedback. The shaft of the motor is subject to an external torque causing a maximum speed reduction of $50~\mathrm{rad/s}$. What is the value of $K_\mathrm{P}$ needed to sustain the speed within $1\%$ of the desired value $100~\mathrm{rad/s}$?
  

The parameters of the D.C. motor are:
  
$K_\mathrm{e} = 5~\mathrm{V/krpm}$
$K_\mathrm{t} = 4~\mathrm{Ncm/A}$
$R_\mathrm{a} = 2~\Omega$
$J = 0.1~\mathrm{Ncm/krpm}$
$K_\mathrm{f} = 0$ (No frictional losses)
| 72 | 9 | 45 | 45 | 298 | 0 | 16 | 5 | 1 | What is the value of $K_\mathrm{P}$ needed to sustain the speed within $1\%$ of the desired value $100~\mathrm{rad/s}$? | 1 |
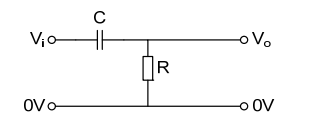
05b6833a-94f9-46a4-8e93-018225fb5cd0 | 0 | 0 | 1 | 9 | 4 | 2 | 5 | 0 | Using complex impedances develop the gain and phase shift relationships between the input and output voltages of the passive high-pass filter below and draw a Bode diagram of the filter.
| 
| 1 | 0.666667 | 2 | null | Use the potential divider equation to describe the relationship between input and output voltages:
***
$V_\mathrm{o} = \frac{Z_\mathrm{R}}{Z_\mathrm{R}+Z_\mathrm{C}}V_\mathrm{i}$
  
where $Z_\mathrm{R}$ and $Z_\mathrm{C}$ are the impedances of the resistor and capacitor respectively.
***
From the notes: 
***
$Z_\mathrm{C} = \frac{1}{j\omega C}$
***
$Z_\mathrm{R} = R$ 
***
Substituting the impedances into the potential divider equation:
***
$V_\mathrm{o} = \dfrac{R}{R+\frac{1}{j\omega C}}V_\mathrm{i}$
***
The ratio of the input and output voltages is:
  
$H = \dfrac{V_\mathrm{o}}{V_\mathrm{i}} =\dfrac{R}{R+\frac{1}{j\omega C}}$ 
***
Multiplying by $\frac{j\omega C}{j\omega C}$:
  
$H= \frac{j\omega RC}{j\omega RC + 1}$
***
Taking the magnitude to find the gain:
  
$|H| = \frac{\omega RC}{\sqrt{(\omega RC)^2+1}}$
***
Calculate the phase shift:
  
$\phi = \phi_\mathrm{o}-\phi_\mathrm{i}$
***
$\phi_\mathrm{o} = \tan^{-1}(\frac{\omega RC}{0})= 90^{\circ}$
  
$\phi_\mathrm{i} = \tan^{-1}(\frac{\omega RC}{1}) = \tan^{-1}(\omega RC)$
***
Hence:
  
$\phi = 90^{\circ} - \tan^{-1}(\omega RC)$
***
Bode diagram:
  
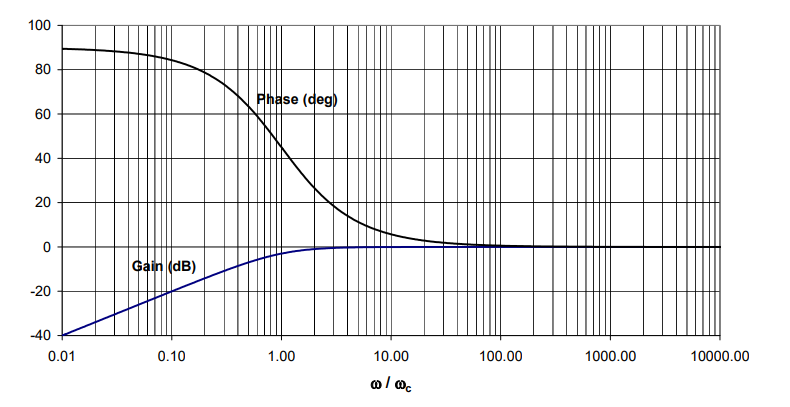  
| Using complex impedances develop the gain and phase shift relationships between the input and output voltages of the passive high-pass filter below and draw a Bode diagram of the filter.

| 31 | 0 | 14 | 14 | 101 | 0 | 1 | 0 | 1 | Using complex impedances develop the gain and phase shift relationships between the input and output voltages of the passive high-pass filter below and draw a Bode diagram of the filter. | 1 |
05dac5a1-05ac-4a85-a191-0221ff134294 | 2 | 0 | 0 | 11 | 4 | 2 | 3 | 5 | A room contains air at $20^{\circ}\mathrm{C}$ and $0.98$ bar with a relative humidity of $85\%$. Determine:
| The partial pressure of the dry-air component.
\nThe specific humidity of the air.
| 2 | 0.333333 | 1 | \n | From the definition of relative humidity:
  
$\phi = \frac{P_\mathrm{v}}{P_\mathrm{sat}(T)}$
***
The saturation pressure, $P_\mathrm{sat}$, at $20^{\circ}\mathrm{C}$, can be found from Data and Formula book (Table E19):
  
$P_\mathrm{sat}(20^{\circ}) = 0.02339$ bar
***
Substituting this value back into the equation for relative humidity:
  
$P_\mathrm{v} = 0.85\times 0.2339 = 0.01988$ bar
***
The total pressure is the sum of the partial pressures of air and vapour. Therefore:
  
$P_\mathrm{a} = P_\mathrm{tot} - P_\mathrm{v}$
***
Substituting in numbers:
  
$P_\mathrm{a} = 0.98-0.01988 = 0.9601$ bar $ = 96.01~\mathrm{kPa} $
\nUsing the equation for specific humidity:
  
$\omega = 0.622\frac{P_\mathrm{v}}{P_\mathrm{a}}$
***
Since both of the partial pressures have been calculated in part (a), they can be substituted in to the above equation:
  
$\omega = 0.622\times\frac{0.01988}{0.9601} = 0.0129$
| A room contains air at $20^{\circ}\mathrm{C}$ and $0.98$ bar with a relative humidity of $85\%$. Determine:
The partial pressure of the dry-air component.
\nThe specific humidity of the air.
| 30 | 3 | 10 | 10 | 102 | 0 | 13 | 0 | 0 | Determine: The partial pressure of the dry-air component. | 1 |
061a2ba6-c482-4891-be40-1a18f21b89bf | 6 | 0 | 0 | 15 | 5 | 0 | 1 | 0 | The Michaelis-Menten equation describes enzyme kinetics.
$$
v=\frac{v_{max}[S]}{K_{M}+[S]}
$$
* $v$ Velocity of enzyme-catalysed reaction ($\mathrm{mmol \cdot s^{-1}}$)
* $v_{max}$ Maximum rate of the reaction ($\mathrm{mmol \cdot s^{-1}}$)
* $K_{M}$ Michaelis constant ($\mathrm{mM}$)
* $[S]$ Concentration of substrate ($\mathrm{mM}$)
| Sketch the graph of this equation: $v$ is the $y$-variable, $[S]$ is the $x$-variable. What is the horizontal limit in terms of its variables?
\nNext, we will prove an important property of the Michalis-Menten equation. Find the value of $v$ when $[S]$=$K_{M}$.
\nThis graph is not very user-friendly as far as extracting $v_{max}$ and $K_{M}$ from a graph is concerned. The Lineweaver-Burk equation is the reciprocal transformation of the Michaelis-Menten equation, which allows us to linearise this equation and easily estimate values for $v_{max}$ and $K_{M}$.
Convert the Michaelis-Menten equation into the Lineweaver-Burk equation by taking reciprocal of both sides, so that the $X$-variable becomes $\frac{1}{[S]}$ and the $Y$-variable becomes $\frac{1}{v}$. What is the $Y$-intercept of this transform?
\nWhat is the gradient of this transform?
\nFinally when plotting this equation we need to consider the units for each axis.
What are the units for the X-axis? (To write a power, use '\*\*', *i.e. *write $x^{-1}$ as 'x\*\*-1')
\nFinally when plotting this equation we need to consider the units for each axis.
What are the units for the Y-axis? (Treat the unit symbols as algebra: use a '\*' to represent a multiplication, *i.e.* write $\mathrm{kg\,m\,s^{-2}}$ as 'kg\*m\*s\*\*-2' or 'kg\*m/s\*\*2'.)
| 6 | 1 | 2 | \n\n\n\n\n | As $[S] \to \infty$ adding the finite value $K_M$ to $[S]$ becomes less and less significant compared to the size of $[S]$ alone. Therefore, $v =\frac{v_{max} [S]}{K_M + [S]} \to \frac{v_{max} [S]}{[S]}=v_{max}$. The horizontal asymptote is therefore at $v=v_{max}$.
  
\nWhen $[S] = K_M$ , then $v =\frac{v_{max} [S]}{[S] + [S]}= \frac{v_{max} [S]}{2[S]}=\frac{v_{max}}{2}$
\n$$
v =\frac{v_{max} [S]}{K_M + [S]}
$$
Take reciprocals:
$$
\frac{1}{v} = \frac{1}{\frac{v_{max} [S]}{K_M + [S]}} = \frac{K_M + [S]}{v_{max} [S]}
$$
Separate sum in numerator:
$$
\frac{1}{v} = \frac{K_M}{v_{max} [S]} + \frac{[S]}{v_{max} [S]}
$$
Cancel terms in $[S]$:
$$
\frac{1}{v} = \frac{K_M \times 1}{v_{max} [S]} + \frac{1}{v_{max}}
$$
Force into $Y=mX+c$ form:
$$
\frac{1}{v} = \frac{K_M}{v_{max}} \times \frac{1}{[S]} + \frac{1}{v_{max}}
$$
The $Y$-intercept is $\frac{1}{v_{max}}$
\nSee previous section for worked solution.
The gradient is $\frac{K_M}{v_{max}}$
\nThe units of the transformed $x$-axis are those of $1/[S]$ , *i.e.* $\mathrm{mM}^{−1}$ (or $\mathrm{L \cdot mmol^{−1}}$),
\nThe units of the transformed $Y$-axis are those of $1/v$*, i.e.* $\mathrm{s \cdot mmol^{−1}}$.
| The Michaelis-Menten equation describes enzyme kinetics.
$$
v=\frac{v_{max}[S]}{K_{M}+[S]}
$$
* $v$ Velocity of enzyme-catalysed reaction ($\mathrm{mmol \cdot s^{-1}}$)
* $v_{max}$ Maximum rate of the reaction ($\mathrm{mmol \cdot s^{-1}}$)
* $K_{M}$ Michaelis constant ($\mathrm{mM}$)
* $[S]$ Concentration of substrate ($\mathrm{mM}$)
Sketch the graph of this equation: $v$ is the $y$-variable, $[S]$ is the $x$-variable. What is the horizontal limit in terms of its variables?
\nNext, we will prove an important property of the Michalis-Menten equation. Find the value of $v$ when $[S]$=$K_{M}$.
\nThis graph is not very user-friendly as far as extracting $v_{max}$ and $K_{M}$ from a graph is concerned. The Lineweaver-Burk equation is the reciprocal transformation of the Michaelis-Menten equation, which allows us to linearise this equation and easily estimate values for $v_{max}$ and $K_{M}$.
Convert the Michaelis-Menten equation into the Lineweaver-Burk equation by taking reciprocal of both sides, so that the $X$-variable becomes $\frac{1}{[S]}$ and the $Y$-variable becomes $\frac{1}{v}$. What is the $Y$-intercept of this transform?
\nWhat is the gradient of this transform?
\nFinally when plotting this equation we need to consider the units for each axis.
What are the units for the X-axis? (To write a power, use '\*\*', *i.e. *write $x^{-1}$ as 'x\*\*-1')
\nFinally when plotting this equation we need to consider the units for each axis.
What are the units for the Y-axis? (Treat the unit symbols as algebra: use a '\*' to represent a multiplication, *i.e.* write $\mathrm{kg\,m\,s^{-2}}$ as 'kg\*m\*s\*\*-2' or 'kg\*m/s\*\*2'.)
| 253 | 27 | 0 | 0 | 158 | 0 | 209 | 18 | 0 | The Michaelis-Menten equation describes enzyme kinetics. What is the horizontal limit in terms of its variables? Find the value of $v$ when $[S]$=$K_{M}$. Convert the Michaelis-Menten equation into the Lineweaver-Burk equation by taking reciprocal of both sides, so that the $\mathrm{mmol \cdot s^{-1}}$0-variable becomes $\mathrm{mmol \cdot s^{-1}}$1 and the $\mathrm{mmol \cdot s^{-1}}$2-variable becomes $\mathrm{mmol \cdot s^{-1}}$3. What is the $\mathrm{mmol \cdot s^{-1}}$2-intercept of this transform? What is the gradient of this transform? Finally when plotting this equation we need to consider the units for each axis. What are the units for the X-axis? To write a power, use '', i.e. write $\mathrm{mmol \cdot s^{-1}}$5 as 'x-1' Finally when plotting this equation we need to consider the units for each axis. What are the units for the Y-axis? Treat the unit symbols as algebra: use a '' to represent a multiplication, i.e. write $\mathrm{mmol \cdot s^{-1}}$6 as 'kgms-2' or 'kgm/s2'. | 13 |
06696572-f255-45b9-bafa-cabbe184e559 | 2 | 1 | 0 | 4 | 3 | 3 | 5 | 0 | A wide freshwater stream has a smooth granular bed with a bed slope of $S = 0.002$, a uniform flow depth of $h =2.0\ \mathrm{m}$ and a median grain size of $d_{50} =2\ \mathrm{mm}$.
You may wish to use [the Shields diagram](https://bb.imperial.ac.uk/webapps/blackboard/execute/content/file?cmd=view\&content_id=_2543151_1\&course_id=_30255_1).
| Compute the bed shear stress, $\tau_0$ $\mathrm{[N/m^2]}$.
\nWhat is the critical bed shear stress, $\tau_{cr}\ \mathrm{[N/m^2]}$, for this channel?
\nIs the channel bed stable in terms of initiation of motion for this flow?
| 3 | 0.333333 | 1 | \n\n | The bed sear stress is computed as: $\tau_0 = \rho g h S = 39.240\ \mathrm{N/m^2}$.
\nThe shear velocity $u_*$ is obtained from
$$
u_* = \sqrt{\dfrac{\tau_0}{\rho}} = \sqrt{\dfrac{39.2}{1000}} = 0.198\ \mathrm{m/s}.
$$
The shear Reynolds number is
$$
\mathrm{Re}_* = \dfrac{u_* d_{50}}{\nu} = \dfrac{0.198\cdot 2 \times 10^{-3}}{10^{-6}} = 396.18.
$$
Using the Shields diagram we can obtain a value for $\theta_{cr}$ for $\mathrm{Re}_* = 396.18$. It is important to remember that the diagram is in semilogarithmic axes. The critical Shields parameter in this case is: $\theta_{cr} \approx 0.058$.
Therefore the critical bed shear stress is
$$
\tau_{cr} = \theta_{cr}\cdot \rho \cdot g (s-1) \cdot d_{50} = 1.88\ \mathrm{N/m^2},
$$
where $s=\rho_s/\rho_w = 2.65$ is the relative sediment density.
\nTo determine whether there will be initiation of motion, the bed shear stress is compared to the critical bed shear stress. Since $\tau_0>\tau_{cr}$, the channel bed is not stable.
| A wide freshwater stream has a smooth granular bed with a bed slope of $S = 0.002$, a uniform flow depth of $h =2.0\ \mathrm{m}$ and a median grain size of $d_{50} =2\ \mathrm{mm}$.
You may wish to use [the Shields diagram](https://bb.imperial.ac.uk/webapps/blackboard/execute/content/file?cmd=view\&content_id=_2543151_1\&course_id=_30255_1).
Compute the bed shear stress, $\tau_0$ $\mathrm{[N/m^2]}$.
\nWhat is the critical bed shear stress, $\tau_{cr}\ \mathrm{[N/m^2]}$, for this channel?
\nIs the channel bed stable in terms of initiation of motion for this flow?
| 70 | 6 | 10 | 10 | 104 | 0 | 34 | 3 | 0 | You may wish to use . Compute the bed shear stress, $\tau_0$ $\mathrm{[N/m^2]}$. What is the critical bed shear stress, $\tau_{cr}\ \mathrm{[N/m^2]}$, for this channel? Is the channel bed stable in terms of initiation of motion for this flow? | 4 |
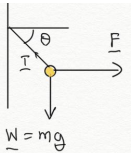
071be152-c0bf-4be1-8a82-3514e08b18ea | 1 | 0 | 0 | 19 | 6 | 1 | 0 | 4 | null | (L2) A weight of mass 10 kg is attached to a wall with a string, and is pulled horizontally with a force $\vec{F}$ so that it is in equilibrium, as in the diagram. Find the magnitude of the force $F$ required for the string to make an angle of $\theta=60^\circ$ to the *normal* to the wall.
| 1 | 0.333333 | 0 | * One approach is to equate vertical and horizontal forces, then solve each equation separately, but actually there is no need to do this; there is a shorter way.
***
* A shorter approach is to draw a triangle, and use trigonometric to solve directly for $F$.
| Redrawing the forces, since the mass is in equilibrium $ \vec{F}+\vec{T}+\vec{W}=0 $.
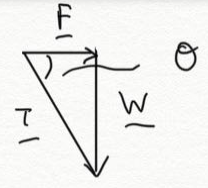
***
From the triangle, we see that $\tan \theta = \dfrac{W}{F} \quad \rightarrow \quad F = mg / \tan\theta$.
***
For $\theta=60^\circ,$ $F = (10\times9.81)/\tan{60^\circ} = 56.6{N}$.
,
, Horizontal Components:
$$
F=T\cos{\theta}\tag{1}
$$
Vertical Components:
$$
T\sin{\theta}= mg \tag{2}
$$
***
Re-arranging eq. (2) for $T$:
$$
T = mg/\sin{\theta}
$$
***
Inserting this result into eq. (1):
$$
F = \frac{mg}{\sin\theta}\cos\theta = \frac{mg}{\tan\theta} = \frac{10\times9.81}{\tan{60^\circ}}=56.6\text{N}
$$
| null | 1 | 0 | 9 | 9 | 50 | 1 | 56 | 3 | 0 | (L2) A weight of mass 10 kg is attached to a wall with a string, and is pulled horizontally with a force $\vec{F}$ so that it is in equilibrium, as in the diagram. Find the magnitude of the force $F$ required for the string to make an angle of $\theta=60^\circ$ to the *normal* to the wall.

| 0 |
07558792-2199-462d-8f3e-bf701a870259 | 1 | 0 | 0 | 18 | 6 | 1 | 1 | 1 | In Lecture 4 we derived the velocity addition formula for a particle moving with speed $u$ along the $x$ axis, in a frame moving at velocity $v$ in the $x$ direction. If the particle velocity is not just directed along the $x$ axis, then the velocity transformation formula needs to be written as $u_x^\prime = \frac{u_x - v}{1- vu_x/c^2}.$
   
Use the same method as in the lecture to work out the transformation rule for one of the perpendicular velocity components, e.g. $u_y$. | In Lecture 4 we derived the velocity addition formula for a particle moving with speed $u$ along the $x$ axis, in a frame moving at velocity $v$ in the $x$ direction. If the particle velocity is not just directed along the $x$ axis, then the velocity transformation formula needs to be written as $u_x^\prime = \frac{u_x - v}{1- vu_x/c^2}.$
   
Use the same method as in the lecture to work out the transformation rule for one of the perpendicular velocity components, e.g. $u_y$. | 1 | 0.333333 | 2 | How can you write $u'_y$ in terms of $y'$ and $t'$?
***
   
What do you know about the relative direction of $y'$ and $v$? How des this knowledge let us easily relate $y$ and $y'$?
***
   
As $y'$ is perpendicular to $v$, there will be no length contraction in this direction so $y=y'$. Thus, the only coordinate where we need to consider the Lorentz transformation is the time coordinate. The formula for this is given in question 2.1.
***
   
You can use the Lorentz formula to write $t'$ in terms of $x$ and $t$. Remeber that $u'_y = y'/t'$ and $u_x = x/t$.  | We know that $y=u_y t$ and $y^\prime = u_y^\prime t^\prime$. We also know $y^\prime = y$ as the frame only moves in the $x$ direction. 
***
The Lorentz transformation for $t$ only involves the $x$ coordinate for which $x=u_xt$, so this gives
***
   
$$
ct^\prime = \gamma (ct - \beta x) = \gamma \left(ct- \frac{v}{c} u_x t\right)
= \gamma ct \left(1 - \frac{v u_x}{c^2}\right)
$$
***
Hence, the $y$ velocity in the moving frame is
$$
u_y^\prime=\frac{y^\prime}{t^\prime}
=\frac{u_y t}{t^\prime} = \frac{u_y t}{\gamma t(1 - v u_x/c^2)}
=\frac{u_y}{\gamma(1-vu_x/c^2)}
$$
A similar expression holds for $u_z^\prime$. | In Lecture 4 we derived the velocity addition formula for a particle moving with speed $u$ along the $x$ axis, in a frame moving at velocity $v$ in the $x$ direction. If the particle velocity is not just directed along the $x$ axis, then the velocity transformation formula needs to be written as $u_x^\prime = \frac{u_x - v}{1- vu_x/c^2}.$
   
Use the same method as in the lecture to work out the transformation rule for one of the perpendicular velocity components, e.g. $u_y$. | 80 | 7 | 11 | 11 | 60 | 15 | 80 | 7 | 0 | In Lecture 4 we derived the velocity addition formula for a particle moving with speed $u$ along the $x$ axis, in a frame moving at velocity $v$ in the $x$ direction. If the particle velocity is not just directed along the $x$ axis, then the velocity transformation formula needs to be written as $u_x^\prime = \frac{u_x - v}{1- vu_x/c^2}.$ Use the same method as in the lecture to work out the transformation rule for one of the perpendicular velocity components, e.g. | 2 |
09429e36-172e-4f9c-8e4d-206d50606944 | 7 | 0 | 0 | 19 | 6 | 1 | 8 | 1 | **(L14)**: The matrices below represent rotations in $\mathbb{R}^3$ about the $x$-axis ($\text{R}_1$) and about the $y$-axis ($\text{R}_2$), each by 90$^\circ$ in the counter-clockwise direction:
$$
\text{R}_1=
\left(\begin{array}{ccr}
1&\hskip12pt 0&\hskip3pt 0\\
0&\hskip12pt 0&\hskip3pt -1\\
0&\hskip12pt 1&\hskip3pt 0
\end{array}\right)\, ,\qquad
\text{R}_2=
\left(\begin{array}{rcc}
0&\hskip12pt 0&\hskip12pt 1\\
0&\hskip12pt 1&\hskip12pt 0\\
-1&\hskip12pt 0&\hskip12pt 0
\end{array}\right)\, .
$$
| Find the real eigenvalues of $\text{R}_1$ and $\text{R}_2$ (denoted $\lambda_1$, $\lambda_2$ respectively). Determine the normalised eigenvectors corresponding to the eigenvalues.
\nFind the products ${\mathbf{\text{R}}}_1{\mathbf{\text{R}}}_2$ and ${\mathbf{\text{R}}}_2{\mathbf{\text{R}}}_1$ and show they do not commute.
\nDetermine the rotation axes of ${\mathbf{\text{R}}}_1{\mathbf{\text{R}}}_2$ and ${\mathbf{\text{R}}}_2{\mathbf{\text{R}}}_1$ (represent these as normalised eigenvectors $\mathbf{{u}_{12}},\mathbf{{u}_{21}}$), and comment on your results in light of the result in part (b).
| 3 | 0.666667 | 3 | Set up and solve the characteristic equations $p(\lambda)=\det{(\text{R} - \lambda\mathbb{I}_3)}$ for each rotation matrix (see **section 3.19**). 
***
After finding the eigenvalue, in each case solve $(\text{R}- \lambda \mathbb{I}_3)\mathbf{\underline{x}}=0$ for the eigenvector $\mathbf{\underline{x}}=(x,y,z)$...
***
... You may find solutions with no dependency on $x,y$ or $z$. This means that your choice of $x,y$ or $z$ is arbitrary (thus choose $x,y$ or $z$ that give a normalised vector).
\nSee matrix multiplication, **section 3.3**.
\nTake $\text{R}_1\text{R}_2$ and $\text{R}_2\text{R}_1$ from part (b), and calculate their normalised eigenvectors as in part (a). This tells you the rotation axes because rotation axes are invariant under rotations. 
***
Are the eigenvectors you found equivalent? This will verify if $\text{R}_1\text{R}_2$ and $\text{R}_2\text{R}_1$ commute.
| Solving the characteristic equation for $\text{R}_1$ (see section **3.19**). 
***
$$
\det(\text{R}_1-\lambda\mathbb{I}_3)=
\left|\begin{array}{crr}
1-\lambda&0&\hskip3pt 0\\
0&-\lambda&\hskip3pt -1\\
0&1&\hskip3pt -\lambda
\end{array}\right|=\lambda^2(1-\lambda)+(1-\lambda)=(1-\lambda)(\lambda^2+1)=0,
$$
which yields one real eigenvalue $\lambda_1=1$. The corresponding eigenvector $\mathbf{\underline{x}}=(x,y,z)$ is found from solving 
$(\text{R}_1 - \lambda \mathbb{I}_3)\mathbf{\underline{x}}=0$:
***
$$
\begin{aligned}
\left(\begin{array}{crr}
0&\hskip3pt 0&\hskip3pt 0\\
0&\hskip3pt -1&\hskip3pt -1\\
0&\hskip3pt 1&\hskip3pt -1
\end{array}\right)
\left(
\begin{array}{c}
x\\
y\\
z
\end{array}
\right)=
\left(
\begin{array}{r}
0\hskip12pt\\
-y-z\\
y-z
\end{array}
\right)=\left(
\begin{array}{c}
0\\
0\\
0
\end{array}
\right),
\end{aligned}
$$
***
which shows $y=z=0$. However, our choice of $x$ is arbitrary here (it is unaffected by the matrix operation), so we may take as our normalised eigenvector $ \mathbf{\hat{u}}_1=\left(\begin{array}{c}1\\0\\0\end{array}\right) $, which is the $x$-axis (as we expect for a rotation about the $x$-axis).
***
Similarly, for $\text{R}_2$, the eigenvalues are determined from:
***
$$
\det({\mathbf{\text{R}}}_2-\lambda\mathbb{I})=\left|\begin{array}{rcr}-\lambda&\hskip8pt \hskip3pt 0&\hskip3pt 1\\0&\hskip8pt 1-\lambda&\hskip3pt 0\\-1&\hskip8pt 0&\hskip3pt -\lambda\end{array}\right|=\lambda^2(1-\lambda)+(1-\lambda)=(1-\lambda)(\lambda^2+1)=0\,
$$
which yields the real eigenvalue $\lambda_2=1$. The corresponding eigenvector is,
***
$$
\begin{align*}
\left(\begin{array}{crr}
0&\hskip3pt 0&\hskip3pt 0\\
0&\hskip3pt -1&\hskip3pt -1\\
0&\hskip3pt 1&\hskip3pt -1
\end{array}\right)
\left(
\begin{array}{c}
x\\
y\\
z
\end{array}
\right)=
\left(
\begin{array}{r}
0\hskip12pt\\
-y-z\\
y-z
\end{array}
\right)=\left(
\begin{array}{c}
0\\
0\\
0
\end{array}
\right),
\end{align*}
$$
which shows that $x=z=0$, but $y$ is arbitrary, so we may take as our normalised eigenvector $ \mathbf{\hat{u}}_2=\left(\begin{array}{c} 0\\ 1\\ 0\end{array}\right), $ which is the $y$-axis (as we expect for a rotation about the $y$-axis).
\n$$
{\mathbf{\text{R}}}_1{\mathbf{\text{R}}}_2 =\left(\begin{array}{ccr}1&\hskip12pt 0&\hskip3pt 0\\0&\hskip12pt 0&\hskip3pt -1\\0&\hskip12pt 1&\hskip3pt 0\end{array}\right)\left(\begin{array}{rcc}0&\hskip12pt 0&\hskip12pt 1\\0&\hskip12pt 1&\hskip12pt 0\\-1&\hskip12pt 0&\hskip12pt 0\end{array}\right)=\left(\begin{array}{ccc}0&\hskip12pt 0&\hskip12pt 1\\1&\hskip12pt 0&\hskip12pt 0\\0&\hskip12pt 1&\hskip12pt 0\end{array}\right),
$$
***
$$
{\mathbf{\text{R}}}_2{\mathbf{\text{R}}}_1 =\left(\begin{array}{rcc}0&\hskip12pt 0&\hskip12pt 1\\0&\hskip12pt 1&\hskip12pt 0\\-1&\hskip12pt 0&\hskip12pt 0\end{array}\right)\left(\begin{array}{ccr}1&\hskip12pt 0&\hskip3pt 0\\0&\hskip12pt 0&\hskip3pt -1\\0&\hskip12pt 1&\hskip3pt 0\end{array}\right)=\left(\begin{array}{rcr}0&\hskip12pt 1&\hskip3pt 0\\0&\hskip12pt 0&\hskip3pt -1\\-1&\hskip12pt 0&\hskip3pt 0\end{array}\right),
$$
which shows that ${\mathbf{\text{R}}}_1{\mathbf{\text{R}}}_2\ne{\mathbf{\text{R}}}_2{\mathbf{\textsf{R}}}_1$.
\nThe eigenvalues of ${\mathbf{\text{R}}}_1{\mathbf{\text{R}}}_2$ are calculated as:
***
$$
\begin{aligned}
\det({\mathbf{\text{R}}}_1{\mathbf{\text{R}}}_2-\lambda\mathbb{I})=\left|\begin{array}{rrr}
-\lambda&\hskip3pt 0&\hskip3pt 1\\
1&\hskip3pt -\lambda&\hskip3pt 0\\
0&\hskip3pt 1&\hskip3pt -\lambda
\end{array}\right|=-\lambda^3+1=0\, ,
\end{aligned}
$$
so the real eigenvalue is $\lambda=1$, with a corresponding eigenvector,
***
$$
\begin{aligned}
\left(\begin{array}{rrr}
-1&\hskip3pt 0&\hskip3pt 1\\
1&\hskip3pt -1&\hskip3pt 0\\
0&\hskip3pt 1&\hskip3pt -1
\end{array}\right)\left(
\begin{array}{c}
x\\
y\\
z
\end{array}
\right)=
\left(
\begin{array}{r}
-x+z\\
x-y \\
y-z
\end{array}
\right)=\left(
\begin{array}{c}
0\\
0\\
0
\end{array}
\right),
\end{aligned}
$$
***
We have that $x=y=z$. Thus, we may take as our eigenvector $ \mathbf{\hat{u}}_{12}=\dfrac{1}{\sqrt{3}}\left(\begin{array}{c}1\\1\\1\end{array}\right). $
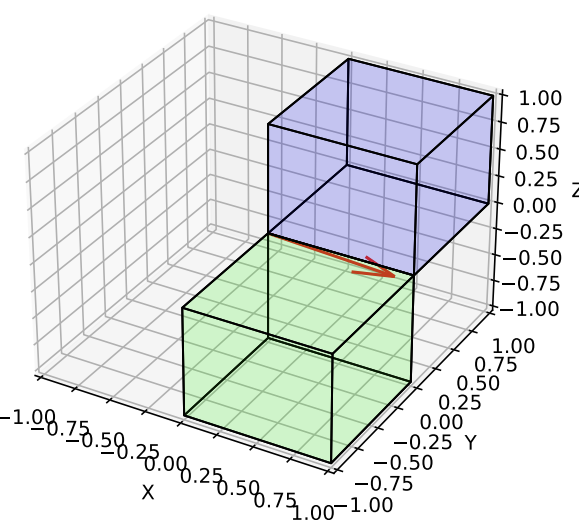  
The invariant vector is actually in the $(+x)(+y)(-z)$ quadrant, though it might not look like that in the figure.
Carrying out the same process for $\text{R}_2\text{R}_1$:
***
$$
\det({\mathbf{\text{R}}}_2{\mathbf{\text{R}}}_1-\lambda\mathbb{I})=\left|\begin{array}{rrr}-\lambda&\hskip3pt 1&\hskip3pt 0\\0&\hskip3pt -\lambda&\hskip3pt -1\\-1&\hskip3pt 0&\hskip3pt -\lambda\end{array}\right|=-\lambda^3+1=0.
$$
***
So the real eigenvalue is again: $\lambda=1$. The corresponding eigenvector is given by,
$$
\begin{aligned}
\left(\begin{array}{rrr}
-1&\hskip3pt 1&\hskip3pt 0\\
0&\hskip3pt -1&\hskip3pt -1\\
-1&\hskip3pt 0&\hskip3pt -1
\end{array}\right)\left(
\begin{array}{c}
x\\
y\\
z
\end{array}
\right)=
\left(
\begin{array}{r}
-x+y\\
-y-z\\
-x-z
\end{array}
\right)=\left(
\begin{array}{c}
0\\
0\\
0
\end{array}
\right)\, ,
\end{aligned}
$$
which implies that $x=y=-z$.
Thus, we may take $ \mathbf{\hat{u}}_{21}=\dfrac{1}{\sqrt{3}}\left(\begin{array}{r}1\\1\\-1\end{array}\right) $,
(it might look like it hasn’t moved but the cube has rotated around the eigenvector - hence the slightly different colouring) which again shows the multiplication of ${\mathbf{\text{R}}}_1$ and ${\mathbf{\text{R}}}_2$ does not commute; the different products result in quite different operations.
| **(L14)**: The matrices below represent rotations in $\mathbb{R}^3$ about the $x$-axis ($\text{R}_1$) and about the $y$-axis ($\text{R}_2$), each by 90$^\circ$ in the counter-clockwise direction:
$$
\text{R}_1=
\left(\begin{array}{ccr}
1&\hskip12pt 0&\hskip3pt 0\\
0&\hskip12pt 0&\hskip3pt -1\\
0&\hskip12pt 1&\hskip3pt 0
\end{array}\right)\, ,\qquad
\text{R}_2=
\left(\begin{array}{rcc}
0&\hskip12pt 0&\hskip12pt 1\\
0&\hskip12pt 1&\hskip12pt 0\\
-1&\hskip12pt 0&\hskip12pt 0
\end{array}\right)\, .
$$
Find the real eigenvalues of $\text{R}_1$ and $\text{R}_2$ (denoted $\lambda_1$, $\lambda_2$ respectively). Determine the normalised eigenvectors corresponding to the eigenvalues.
\nFind the products ${\mathbf{\text{R}}}_1{\mathbf{\text{R}}}_2$ and ${\mathbf{\text{R}}}_2{\mathbf{\text{R}}}_1$ and show they do not commute.
\nDetermine the rotation axes of ${\mathbf{\text{R}}}_1{\mathbf{\text{R}}}_2$ and ${\mathbf{\text{R}}}_2{\mathbf{\text{R}}}_1$ (represent these as normalised eigenvectors $\mathbf{{u}_{12}},\mathbf{{u}_{21}}$), and comment on your results in light of the result in part (b).
| 93 | 16 | 38 | 38 | 278 | 13 | 61 | 9 | 0 | $ Find the real eigenvalues of $\text{R}_1$ and $\text{R}_2$ denoted $\lambda_1$, $x$0 respectively. Determine the normalised eigenvectors corresponding to the eigenvalues. Find the products $x$1 and $x$2 and show they do not commute. Determine the rotation axes of $x$1 and $x$2 represent these as normalised eigenvectors $x$5, and comment on your results in light of the result in part b. | 4 |
0b9fe9b9-efd5-40d5-a797-1efe86da2328 | 1 | 0 | 4 | 14 | 4 | 2 | 8 | 1 | Using three-dimensional Cartesian coordinates write all the components of: | $$
\vec{\mathcal{T}}^{\left(\hat{n}\right)}=\underline{\underline{{\sigma}}}^T\hat{n}
$$
\n$$
\vec{\mathcal{T}}^{\left(\hat{\mathrm{e}}_y\right)}=\underline{\underline{\sigma}}^T\hat{\mathrm{e}}_y
$$
\n$$
\mathrm{div}\left(\vec{\mathcal{T}}^{\left(\hat{\mathrm{e}}_y\right)}\right)
$$\n$$
\overrightarrow{\mathrm{div}}\left(\underline{\underline{\sigma}}\right)
$$
\n$$
-\frac{1}{\rho}\overrightarrow{\mathrm{grad}}\left(p\right)+\frac{1}{\rho}\overrightarrow{\mathrm{div}}\left(\underline{\underline{\tau}}\right)
$$
| 5 | 0.5 | 2 | \n\n\n\n | \n\n\n\n | Using three-dimensional Cartesian coordinates write all the components of:$$
\vec{\mathcal{T}}^{\left(\hat{n}\right)}=\underline{\underline{{\sigma}}}^T\hat{n}
$$
\n$$
\vec{\mathcal{T}}^{\left(\hat{\mathrm{e}}_y\right)}=\underline{\underline{\sigma}}^T\hat{\mathrm{e}}_y
$$
\n$$
\mathrm{div}\left(\vec{\mathcal{T}}^{\left(\hat{\mathrm{e}}_y\right)}\right)
$$\n$$
\overrightarrow{\mathrm{div}}\left(\underline{\underline{\sigma}}\right)
$$
\n$$
-\frac{1}{\rho}\overrightarrow{\mathrm{grad}}\left(p\right)+\frac{1}{\rho}\overrightarrow{\mathrm{div}}\left(\underline{\underline{\tau}}\right)
$$
| 18 | 5 | 0 | 0 | 1 | 0 | 9 | 5 | 0 | Using three-dimensional Cartesian coordinates write all the components of:$ \vec{\mathcal{T}}^{\left(\hat{n}\right)}=\underline{\underline{{\sigma}}}^T\hat{n} $ $ \vec{\mathcal{T}}^{\left(\hat{\mathrm{e}}_y\right)}=\underline{\underline{\sigma}}^T\hat{\mathrm{e}}_y $ $ \mathrm{div}\left(\vec{\mathcal{T}}^{\left(\hat{\mathrm{e}}_y\right)}\right) $ $ \overrightarrow{\mathrm{div}}\left(\underline{\underline{\sigma}}\right) $ $ -\frac{1}{\rho}\overrightarrow{\mathrm{grad}}\left(p\right)+\frac{1}{\rho}\overrightarrow{\mathrm{div}}\left(\underline{\underline{\tau}}\right) $ | 1 |
0ba3880d-0abb-480d-a028-280c196df8ca | 1 | 0 | 0 | 17 | 6 | 1 | 2 | 2 | A woman of mass 60 kg stands at one end of a 10 m plank of mass 20 kg, which itself lies on a (frictionless) frozen lake. She walks to the other end of the plank. By using the principle of conservation of momentum, work out how far she has travelled relative to the lake.
\[Those of you who already know about the centre of mass may see an easier way to do this problem, but it is good practice to try it using conservation of momentum only. See *Problem Sheet 4, Question 3* for the centre of mass approach.]
| Distance $x_\text{w}$ travelled by woman relative to lake:
| 1 | 0.666667 | 1 | Call the mass of the woman $m_{\text{w}}$ and her velocity $v_{\text{w}}$. The mass and velocity of the plank are $m_{\text{p}}$ and $v_{\text{p}}$.
***
What is the initial momentum of the system? 
***
Use conservation of momentum to express this in terms of $m_{\text{w}}$, $v_{\text{w}}$, $m_{\text{p}}$, and $v_{\text{p}}$. This should give you an equation for $v_\text{w}$ as a function of the other variables...
***
... Can you express this equation in terms of displacements, $x_\text{w}$ and $x_{\text{p}}$, rather than velocities? ...
***
... You can do this by integration or state the relationship logically.
***
You now know how far the plank moves in one direction if the woman moves in the other direction. Use this to find the distance the woman travels relative to the lake if she walks the entire $10\text{m}$ length of the plank.
| Call the mass of the woman $m_{\text{w}}$ and her velocity $v_{\text{w}}$. The mass and velocity of the plank are $m_{\text{p}}$ and $v_{\text{p}}$. Since no externally applied horizontal forces are acting on the system consisting of the woman and the plank, its total momentum, which starts off equal to zero, must remain equal to zero:
***
$$
m_{\text{w}} v_{\text{w}} + m_{\text{p}} v_{\text{p}} = 0 \quad
\text{at all times.}
\implies v_{\text{p}} = - \frac{m_{\text{w}}}{m_{\text{p}}} v_{\text{w}} = - 3
v_{\text{w}},
$$
where $m_{\text{w}}/m_{\text{p}} = 60$kg$/20$kg $= 3$. 
***
Since the velocities of the woman and plank are always proportional, so are their displacements:
$$
x_{\text{p}} = - 3 x_{\text{w}} .
$$
If you want a more mathematical derivation of the step from $v_{\text{p}} = - 3 v_{\text{w}}$ to $x_{\text{p}} = - 3 x_{\text{w}}$, you can do it using integration:
$$
\begin{aligned}
&v_{\text{p}}(t) = - 3 v_{\text{w}}(t) \\
\Rightarrow \qquad
&\frac{dx_{\text{p}}(t)}{dt} = - 3 \frac{dx_{\text{w}}(t)}{dt} \\
\end{aligned}
$$
$\ldots$
***
$$
\begin{aligned}
\Rightarrow \qquad
&\int_{t'=0}^{t} \frac{dx_{\text{p}}(t')}{dt'} dt' =
- 3 \int_{t'=0}^{t} \frac{dx_{\text{w}}(t')}{dt'} dt' \\
\Rightarrow \qquad
&\left [ x_{\text{p}}(t') \right ]_{0}^{t} = - 3 \left [
x_{\text{w}}(t') \right ]_{0}^{t} \\
\Rightarrow \qquad
& x_{\text{p}}(t) = - 3 x_{\text{w}}(t).
\end{aligned}
$$
It is not necessary to assume that the woman walks at a constant speed.
***
These displacements are measured relative to the frozen lake. For every 1 m the woman moves to the right, the plank moves 3 m to the left, and the woman progresses 4 m along the plank. 
***
By the time she reaches the far end of the 10 m long plank, she has moved 2.5 m to the right and the plank has moved 7.5 m to the left. The woman has travelled 2.5 m relative to the lake.
| A woman of mass 60 kg stands at one end of a 10 m plank of mass 20 kg, which itself lies on a (frictionless) frozen lake. She walks to the other end of the plank. By using the principle of conservation of momentum, work out how far she has travelled relative to the lake.
\[Those of you who already know about the centre of mass may see an easier way to do this problem, but it is good practice to try it using conservation of momentum only. See *Problem Sheet 4, Question 3* for the centre of mass approach.]
Distance $x_\text{w}$ travelled by woman relative to lake:
| 105 | 1 | 14 | 14 | 194 | 12 | 8 | 1 | 0 | By using the principle of conservation of momentum, work out how far she has travelled relative to the lake. Those of you who already know about the centre of mass may see an easier way to do this problem, but it is good practice to try it using conservation of momentum only. See Problem Sheet 4, Question 3 for the centre of mass approach. | 3 |
0ba7ab1f-f9af-439a-b379-e4b2a1fb959f | 1 | 0 | 0 | 9 | 4 | 2 | 6 | 11 | Find the value of the capacitor $C$ needed in the circuit below to ensure a step response faster than $2~\mathrm{ms}$. The resistor values are $R_1 = 1~\mathrm{k\Omega}$ and $R_2 = 4~\mathrm{k\Omega}$.
| 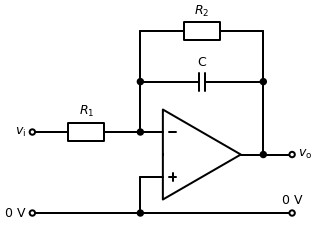
| 1 | 0.666667 | 1 | null | The circuit shown is an active low-pass filter, for which the transfer function can be written as follows:
  
$|H| = \frac{R_2}{R_1}\frac{1}{\sqrt{1+(\omega R_2C)^2}}$
***
This can be re-written in complex form:
  
$|H| = \frac{R_2}{R_1}\frac{1}{1+j\omega R_2C}$
***
Setting $s = j\omega$:
  
$|H| = \frac{R_2}{R_1}\frac{1}{1+R_2Cs}$
***
Hence:
  
$K = \frac{R_2}{R_1}$
  
$\tau = R_2C$
***
To ensure a step response faster than $2~\mathrm{ms}$:
  
$0.002> R_2C$
***
Substituting in the value of $R_2$ and rearranging to find $C$:
  
$C < 0.5~\mu\mathrm{F}$
  
| Find the value of the capacitor $C$ needed in the circuit below to ensure a step response faster than $2~\mathrm{ms}$. The resistor values are $R_1 = 1~\mathrm{k\Omega}$ and $R_2 = 4~\mathrm{k\Omega}$.

| 30 | 4 | 11 | 11 | 70 | 0 | 1 | 0 | 1 | Find the value of the capacitor $C$ needed in the circuit below to ensure a step response faster than $2~\mathrm{ms}$. | 1 |
0bed6097-529a-4f4e-8d35-2734a1d1c0c4 | 1 | 2 | 0 | 17 | 6 | 1 | 0 | 6 | Using a torsion balance, Roll, Krotkov and Dicke [Ann. Phys. **26**(3), 442 (1963)] established the equality of gravitational and inertial mass, $m_G$ and $m_I$, to an accuracy of 3 parts in $10^{11}$.
| Suppose that $m^{\text{Cu}}_{G}/m^{\text{Cu}}_{I} = 1$ but $m^{\text{Pb}}_{G}/m^{\text{Pb}}_{I} = 1 + 3 \times 10^{-11}$. If copper and lead balls were dropped together from the top of the Tower of Pisa, which would hit the ground first?
\nGiven that the tower is 60 m high, what is the separation of the two balls when the first hits the ground? Ignore all forces other than gravity.
\nWould the separation change if you moved the Tower of Pisa to the Moon, where $g$ is approximately six times smaller than on Earth? If so, by what factor would it change?
| 3 | 0.666667 | 3 | The gravitational force uses the gravitational mass $m_G$, whereas N2 uses inertial mass $m_I$. 
***
The gravitational force is equal to the N2 force. Hence solve for the 'inertial' acceleration $a$ of N2.
***
This should tell you which ball accelerates faster, and therefore which ball hits the ground first. 
\nUsing SUVAT equations entirely algebraically at first...
***
... What is the time taken for the lead ball to hit the ground? ...
***
... What distance does the copper ball travel in this time? 
***
... Hence, what is the height $\Delta s$ of the copper ball above the ground?
***
Your expression should contain the relative acceleration of the two particles $a_{\text{Cu}}/{a_{\text{Pb}}}= [1 + (3 \times 10^{-11})]^{-1}$...
***
Since $3\times 10^{-11}$ is exceedingly small, your calculator will not process it when added with $1$. Therefore, perform a binomial expansion to find $a_{\text{Cu}}/{a_{\text{Pb}}}$ analytically.
***
Hence find $\Delta s$.
\nIn your analysis from part (b), did $g$ affect the final answer?
| The acceleration $a$ of a falling object with inertial mass $m_I$ and gravitational mass $m_G$ is given by
***
$$
F = m_G g = m_I a \qquad \Rightarrow \qquad
a = \frac{m_G g}{m_I}.
$$
***
The value of $m_G/m_I$ is larger for lead, so $a_{\text{Pb}} > a_{\text{Cu}}$ and the lead ball hits the ground first.
\nThe lead ball is dropped from the top of the tower of height $h = 60,$m at time $t=0,$s and falls with constant acceleration $a_{\text{Pb}}$ until it hits the ground at time:
***
$$
t_{\text{Pb}} = \sqrt{\frac{2h}{a_{\text{Pb}}}} .
$$
At this exact time, the Cu ball has dropped a distance:
***
$$
s_{\text{Cu}} = \frac{1}{2} a_{\text{Cu}} t_{\text{Pb}}^2 =
\frac{a_{\text{Cu}} h}{a_{\text{Pb}}}.
$$
***
The distance it still has to go (which is the separation of the two balls when the first hits the ground) is:
***
$$
\Delta s = h - s_{\text{Cu}} = \left ( 1 -
\frac{a_{\text{Cu}}}{a_{\text{Pb}}} \right ) h.
$$
***
We are told that $m_G / m_I = 1$ for Cu and $1 + 3 \times 10^{-11}$ for Pb, so
$$
\frac{a_{\text{Cu}}}{a_{\text{Pb}}} = \frac{1}{1 + (3 \times
10^{-11})} = [1 + (3 \times 10^{-11})]^{-1} .
$$
***
Using the binomial (or Taylor) expansion to express this number (the reason why you shouldn't just use a calculator/Python is explained at the end): 
***
$$
\begin{aligned}
(1 + x)^{-1}
&= 1 + (-1)x + \frac{(-1)(-2)}{2!}x^2 + \frac{(-1)(-2)(-3)}{3!} x^3
+ \ldots \\
&= 1 - x + x^2 - x^3 + \ldots ,
\end{aligned}
$$
***
with $x = 3 \times 10^{-11}$ gives
$$
\begin{aligned}
\frac{a_{\text{Cu}}}{a_{\text{Pb}}}
&= 1 - (3\times 10^{-11}) + (3 \times
10^{-11})^2 - (3 \times 10^{-11})^3 + \ldots \\
&\approx 1 - (3 \times 10^{-11}).
\end{aligned}
$$
The approximation in the last line is *very* good because $3
\times 10^{-11}$ is such a small number. Hence:
***
$$
\Delta s \approx 3 \times 10^{-11} h = 1.8 \times 10^{-9}\, \text{m}
= 1.8\,\text{nm}.
$$
***
You might wonder why we used a power expansion? Why not just work out the value of $60 \left ( 1 - \frac{1}{1 + 3 \times 10^{-11}} \right )$ using a calculator or the Python interpreter? That method works fine in this example, but if the $3 \times 10^{-11}$ is replaced by $3 \times 10^{-20}$, Python says the result is exactly zero (try it and see). The problem is that $1/(1 + 3\times 10^{-20}) = 1 - 3\times 10^{-20} + \ldots$ is so close to 1 that computers and calculators, which only keep a finite number of significant figures (around 14 in the case of Python), cannot tell the difference. When working with numbers of very different magnitudes, it is safer to expand in powers of the small number *before* using a computer or calculator.
\n The value of $g$ cancels out of the analysis above so the separation on the Moon would be the same as on Earth.
| Using a torsion balance, Roll, Krotkov and Dicke [Ann. Phys. **26**(3), 442 (1963)] established the equality of gravitational and inertial mass, $m_G$ and $m_I$, to an accuracy of 3 parts in $10^{11}$.
Suppose that $m^{\text{Cu}}_{G}/m^{\text{Cu}}_{I} = 1$ but $m^{\text{Pb}}_{G}/m^{\text{Pb}}_{I} = 1 + 3 \times 10^{-11}$. If copper and lead balls were dropped together from the top of the Tower of Pisa, which would hit the ground first?
\nGiven that the tower is 60 m high, what is the separation of the two balls when the first hits the ground? Ignore all forces other than gravity.
\nWould the separation change if you moved the Tower of Pisa to the Moon, where $g$ is approximately six times smaller than on Earth? If so, by what factor would it change?
| 119 | 6 | 25 | 25 | 312 | 10 | 87 | 3 | 0 | Using a torsion balance, Roll, Krotkov and Dicke Ann. Suppose that $m^{\text{Cu}}_{G}/m^{\text{Cu}}_{I} = 1$ but $m^{\text{Pb}}_{G}/m^{\text{Pb}}_{I} = 1 + 3 \times 10^{-11}$. If copper and lead balls were dropped together from the top of the Tower of Pisa, which would hit the ground first? Given that the tower is 60 m high, what is the separation of the two balls when the first hits the ground? Ignore all forces other than gravity. Would the separation change if you moved the Tower of Pisa to the Moon, where $g$ is approximately six times smaller than on Earth? If so, by what factor would it change? | 7 |
0bf0e821-13b2-4de7-9c7c-2c2cf4b5c13b | 6 | 0 | 0 | 8 | 4 | 2 | 5 | 0 | A steel pipe with $0.125 \text{ m}$ internal diameter, wall thickness $10 \text{ mm}$, is subjected to an internal pressure of $11.0\text{ MPa}$. Use the notation: $K=\frac{r_\text{o}}{r_\text{i}}$ ratio of outer radius to inner radius, $P=$ internal pressure, and external pressure $=0$.
| What are the maximum hoop, radial and shear stresses, if the axial stress is zero **when treated as a thin cylinder**.
\nWhat are the maximum hoop, radial and shear stresses, if the axial stress is zero **when treated as a thick cylinder**. 
   
Show that the maximum hoop stress is given by: $\sigma_\theta=P\frac{K^2+1}{K^2-1}$.
| 2 | 0.333333 | 3 | \n | When using the thin-walled assumption and equations from ME1-SAN:
   
$$
\sigma_\theta=\frac{Pr}{t}=\frac{11\times0.0625}{0.01}=\boxed{68.75\text{ MPa}}
$$
   
***
For thin-walled assumption, because $r>>t$, the radial stress is negligible:
   
$$
\sigma_r=\boxed{0 \text{ MPa}}
$$
   
***
And the maximum shear stress (using the Tresca failure criterion):
   
$$
\hat{\tau}=\frac{\sigma_\theta-\sigma_r}{2}=\boxed{34.38\text{ MPa}}
$$
\nUsing the following equations from the Data & Formulae Booklet for thick-walled analysis:
   
$$
\begin{align}
\sigma_r=A-\frac{B}{r^2}~~~~~~~~~~~~~~~~\sigma_\theta=A+\frac{B}{r^2}
\end{align}
$$
   
***
For an internally pressurised cylinder, the following boundary conditions are applied:
   
$$
\begin{align}
\sigma_r=-&P \text{ at }r=r_i \\
\sigma_r=0&\text{ at }r=r_o
\end {align}
$$
   
***
So:
   
$$
\begin{align}
A-\frac{B}{r_\text{i}^2}=P~~~~~~~~~~~~A-\frac{B}{r_\text{o}^2}=0
\end{align}
$$
   
***
Solving the equations simultaneously for $A$ and $B$:
   
$$
\begin{align}
A=\frac{P}{\frac{r_\text{o}^2}{r_\text{i}^2}-1}~~~~~~~~~~~~~~B=\frac{Pr_\text{o}^2}{\frac{r_\text{o}^2}{r_\text{i}^2}-1}
\end{align}
$$
   
***
Then substituting $K=\frac{r_\text{o}^2}{r_\text{i}^2}$:
   
$$
\begin{align}
A=\frac{P}{K^2-1}~~~~~~~~~~~~~~B=\frac{Pr_\text{o}^2}{K^2-1}
\end{align}
$$
   
***
Substituting $A$ and $B$ back into $(1)$:
   
$$
\begin{align}
\sigma_r=\frac{P}{K^2-1}(1-\frac{r_\text{o}^2}{r^2})\\
~~~~~~~~~~~~~~~~\nonumber\\
\sigma_\theta=\frac{P}{K^2-1}(1+\frac{r_\text{o}^2}{r^2})\\
\end{align}
$$
   
***
As such, $\sigma_\theta$ can be expressed as equation $(9)$ when $r=r_\text{i}$ and substituting $K$.
   
$$
\begin{align}
\sigma_\theta=P\frac{K^2+1}{K^2-1}
\end{align}
$$
   
***
For an internally pressurised cylinder, the max hoop, radial, and hence shear stresses are at the bore $(r=r_\text{i})$.
   
***
Using equation $(8)$ to find hoop stress:
   
$$
\begin{align}
\sigma_\theta&=\frac{P}{K^2-1}(1+\frac{r_\text{o}^2}{r_\text{i}^2}) \\
\nonumber &=\frac{11\times10^6}{(\frac{0.0725}{0.0625})^2-1}(1+\frac{0.0725^2}{0.0625^2})\\
\nonumber &=\boxed{74.66\text{ MPa}}
\end{align}
$$
   
***
Simplifying and using equation $(8)$ to find radial stress:
   
$$
\begin{align}
\sigma_r&=-P =\boxed{-11.0 \text{ MPa}}
\end{align}
$$
   
***
Finally, the maximum shear stress using the Tresca failure criteria can be calculated as:
   
$$
\hat{\tau}=\frac{\sigma_\theta-\sigma_r}{2}=\boxed{42.83\text{ MPa}}
$$
| A steel pipe with $0.125 \text{ m}$ internal diameter, wall thickness $10 \text{ mm}$, is subjected to an internal pressure of $11.0\text{ MPa}$. Use the notation: $K=\frac{r_\text{o}}{r_\text{i}}$ ratio of outer radius to inner radius, $P=$ internal pressure, and external pressure $=0$.
What are the maximum hoop, radial and shear stresses, if the axial stress is zero **when treated as a thin cylinder**.
\nWhat are the maximum hoop, radial and shear stresses, if the axial stress is zero **when treated as a thick cylinder**. 
   
Show that the maximum hoop stress is given by: $\sigma_\theta=P\frac{K^2+1}{K^2-1}$.
| 94 | 7 | 27 | 27 | 215 | 0 | 55 | 1 | 0 | Use the notation: $K=\frac{r_\text{o}}{r_\text{i}}$ ratio of outer radius to inner radius, $P=$ internal pressure, and external pressure $=0$. What are the maximum hoop, radial and shear stresses, if the axial stress is zero when treated as a thin cylinder. What are the maximum hoop, radial and shear stresses, if the axial stress is zero when treated as a thick cylinder. Show that the maximum hoop stress is given by: $\sigma_\theta=P\frac{K^2+1}{K^2-1}$. | 4 |
0c44ba33-2e71-4e4f-9ea3-d60b94200685 | 1 | 1 | 0 | 17 | 6 | 1 | 4 | 4 | Any object moving in a circle is continuously being accelerated towards the centre with centripetal acceleration is given by the formula
$$
a_{\text{centripetal}} = -\omega^2 r = -\frac{v_{\phi}^2}{r},
$$
where $\omega = v_{\phi}/r$ is the angular velocity and $v_{\phi}$ is the speed of the mass around the circumference of the circle.
  
The video linked from the image below shows an Imperial College physics student doing a simple experiment with a pendulum.
[https://www.youtube.com/watch?v=19TKQ7\_lAHA](https://www.youtube.com/watch?v=19TKQ7_lAHA "https://www.youtube.com/watch?v=19TKQ7_lAHA")  
Analyse the experiment mathematically, assuming for simplicity that the string has been replaced by a light but stiff rod so that the starting angle can range from $0$ to $\pi$ radians. Using energy conservation and the concept of centripetal acceleration, find a formula for the minimum angle of release required for a smaller mass $m$ to lift a larger mass $M$. What is the smallest mass $m$ capable of lifting $M$? Does the length of the rod matter?
| Any object moving in a circle is continuously being accelerated towards the centre with centripetal acceleration is given by the formula
$$
a_{\text{centripetal}} = -\omega^2 r = -\frac{v_{\phi}^2}{r},
$$
where $\omega = v_{\phi}/r$ is the angular velocity and $v_{\phi}$ is the speed of the mass around the circumference of the circle.
  
The video linked from the image below shows an Imperial College physics student doing a simple experiment with a pendulum.
[https://www.youtube.com/watch?v=19TKQ7\_lAHA](https://www.youtube.com/watch?v=19TKQ7_lAHA "https://www.youtube.com/watch?v=19TKQ7_lAHA")  
Analyse the experiment mathematically, assuming for simplicity that the string has been replaced by a light but stiff rod so that the starting angle can range from $0$ to $\pi$ radians. Using energy conservation and the concept of centripetal acceleration, find a formula for the minimum angle of release required for a smaller mass $m$ to lift a larger mass $M$. What is the smallest mass $m$ capable of lifting $M$? Does the length of the rod matter?
| 1 | 0.666667 | 4 | How can you use Conservation of Energy to get an expression for the velocity of the mass as a function of $\theta$ after it is released from rest at a starting angle of $\theta_0$? At what value of $\theta$ is the speed of the mass greatest?
***
What force is responsible for lifting the larger mass? Can you write an expression for this force in terms of the angle $\theta$? It may help to resolve the forces on the smaller mass along the direction parallel to the stiff rod. 
***
What condition must the tension satisfy in order for the larger mass to be lifted? Can you use this condition to create an inequality involving $\theta$, $m$ and $M$? If we want to find the smallest mass, $m$, capable of lifting $M$, from which angle must we release $m$?
***
Does your inequality involve the length of the rod? Why does it matter that we use a stiff rod, rather than a string?
| As it swings down to the bottom, the mass $m$ loses gravitational potential energy $mgl(1 - \cos\theta)$. By energy conservation, this must be equal to its kinetic energy $K$ at the bottom of the swing:
$$
K = mgl(1 - \cos\theta).
$$
Since $K = \frac{1}{2}mv^2$, the speed $v_{\phi}$ of the mass at the bottom of the swing is
$$
v_{\phi} = \sqrt{\frac{2K}{m}} = \sqrt{2gl(1 - \cos\theta)}.
$$
***
The mass is not accelerating horizontally when it reaches the bottom of the swing (because there are no horizontal forces acting there) but it still has a centripetal acceleration,
$$
a_{\text{centripetal}} = \frac{v_{\phi}^2}{l} = 2g(1 - \cos\theta),
$$
vertically upwards. The forces acting on the mass are the tension $T$ upwards and the force of gravity $mg$ downwards. Applying Newton's Second Law vertically,
$$
m a_{\text{centripetal}} = T - mg ,
$$
tells us the tension
$$
T = mg + m a_{\text{centripetal}} = m(g + 2g(1 - \cos\theta))
= 3mg - 2mg\cos\theta.
$$
If $\theta = 0$ (the pendulum is just hanging there, stationary and vertical), then $\cos\theta = 1$ and the formula for the tension becomes $T = mg$, which seems sensible. As $\theta$ increases from $0$ to $\pi$, $\cos\theta$ decreases and $T$ rises, which also seems right.
***
For the smaller mass to lift the larger mass, $T$ must be greater than $Mg$, so
$$
\begin{aligned}
&& 3mg - 2mg\cos\theta &> Mg &&\\
\Rightarrow && 2mg\cos\theta &< 3mg - Mg &&\\
\Rightarrow && \theta &> \cos^{-1}\left ( \frac{3m - M}{2m} \right
). &&
\end{aligned}
$$
  
The maximum possible value of $T$ occurs when the release angle $\theta
= \pi$, so that $\cos\theta = -1$. This gives
$$
T_{\text{max}} = 5mg.
$$
If allowed to swing the full 180$^\circ$, a pendulum of mass $m$ would just about be able to lift a mass $5m$. Equivalently, a pendulum with a bob of mass $m$ is capable of lifting a larger mass $M$ as long as $m >
M/5$.
***
The length of the rod does not matter. Although doubling the length doubles the KE (and thus the value of $v_{\phi}^2$) at the bottom of the swing, the maximum centripetal acceleration $v_{\phi}^2/l$ is unaffected.
  
\[If the pendulum had a string instead of a stiff light rod, the string would not remain taut if the bob was released at any angle $\theta > \pi/2$, complicating the analysis. If released from angle $\pi/2$, the swinging mass $m$ would just about be able to lift a mass $M = 3m$.]
| Any object moving in a circle is continuously being accelerated towards the centre with centripetal acceleration is given by the formula
$$
a_{\text{centripetal}} = -\omega^2 r = -\frac{v_{\phi}^2}{r},
$$
where $\omega = v_{\phi}/r$ is the angular velocity and $v_{\phi}$ is the speed of the mass around the circumference of the circle.
  
The video linked from the image below shows an Imperial College physics student doing a simple experiment with a pendulum.
[https://www.youtube.com/watch?v=19TKQ7\_lAHA](https://www.youtube.com/watch?v=19TKQ7_lAHA "https://www.youtube.com/watch?v=19TKQ7_lAHA")  
Analyse the experiment mathematically, assuming for simplicity that the string has been replaced by a light but stiff rod so that the starting angle can range from $0$ to $\pi$ radians. Using energy conservation and the concept of centripetal acceleration, find a formula for the minimum angle of release required for a smaller mass $m$ to lift a larger mass $M$. What is the smallest mass $m$ capable of lifting $M$? Does the length of the rod matter?
| 145 | 9 | 38 | 38 | 354 | 10 | 145 | 9 | 1 | Any object moving in a circle is continuously being accelerated towards the centre with centripetal acceleration is given by the formula $ a_{\text{centripetal}} = -\omega^2 r = -\frac{v_{\phi}^2}{r}, $ where $\omega = v_{\phi}/r$ is the angular velocity and $v_{\phi}$ is the speed of the mass around the circumference of the circle. Analyse the experiment mathematically, assuming for simplicity that the string has been replaced by a light but stiff rod so that the starting angle can range from $0$ to $\pi$ radians. Using energy conservation and the concept of centripetal acceleration, find a formula for the minimum angle of release required for a smaller mass $m$ to lift a larger mass $M$. What is the smallest mass $m$ capable of lifting $M$? Does the length of the rod matter? | 5 |
0c714910-48e8-4c59-bed0-de230105e923 | 3 | 0 | 0 | 15 | 5 | 0 | 0 | 1 | The amount of oxygen and blood pumped by the mammalian heart can be modelled by the following:
$$
V_{O_{2}}=Q(C_{a}-C_{v})
$$
$$
Q=f\cdot S
$$
* $V_{O_{2}}$ Volume of oxygen consumed $(\mathrm{ml\cdot min^{-1}})$
* $Q$ Cardiac output ($\mathrm{mL \cdot min^{-1}}$)
* $C_{a}$ Oxygen content in arterial blood ($\mathrm{mL \, O_{2} \cdot mL \, blood^{-1}}$)
* $C_{v}$ Oxygen content in venous blood ($\mathrm{mL \, O_{2} \cdot mL \, blood^{-1}}$)
* $f$ Heartbeat frequency ($\mathrm{min^{-1}}$)
* $S$ Stroke volume ($\mathrm{mL}$)
By rearranging these equations, we can work out a value for the stroke volume, $S$, of the heart, which is more difficult to measure directly than the other variables.
| Rearrange the second equation, $Q = f S$ so that we could work out stroke volume when cardiac output and heartbeat frequency are known.
\nRearrange the equations so we can calculate stroke volume if we know the difference in oxygen content between arterial and venous blood, as well as the volume of oxygen consumed and the heartbeat frequency? (*i.e.* combine the two equations and solve for $S$).
\nIf the difference in oxygen content between arterial and venous blood is $0.1\,\mathrm{mL \, O_{2} \cdot mL \, blood^{-1}}$, the heartbeat frequency is $1\,\mathrm{s^{-1}}$ and the oxygen consumption rate is $420\,\mathrm{mL\cdot min^{-1}}$, what is the stroke volume of the heart?
| 3 | 1 | 1 | \n\n | $$
Q=S\cdot f
$$
Divide through by $f$
$$
\frac{Q}{f}=\frac{S f}{f}
$$
Cancel $f$ in fraction on RHS:
$$
\frac{Q}{f}=S
$$
Swap LHS and RHS
$$
S=\frac{Q}{f}
$$
\n$$
S=\frac{Q}{f}
$$
And
$$
V_{O_{2}}=Q(C_{a}-C_{v})
$$
Rearrange second for $Q$:
$$
Q=\frac{V_{O_{2}}}{(C_{a}-C_{v})}
$$
Substitute in this value for $Q$ to the first equation:
$$
S=\frac{Q}{f}=\frac{\frac{V_{O_{2}}}{(C_{a}-C_{v})}}{f}
$$
Combine the two denominators:
$$
S=\frac{V_{O_{2}}}{f(C_a-C_v)}
$$
\n$$
S=\frac{420\,\mathrm{mL\,min^{-1}}}{1\,\mathrm{s^{-1}} \times 60\,\mathrm{s\,min^{-1}}\times0.1}=70\,\mathrm{mL}
$$
| The amount of oxygen and blood pumped by the mammalian heart can be modelled by the following:
$$
V_{O_{2}}=Q(C_{a}-C_{v})
$$
$$
Q=f\cdot S
$$
* $V_{O_{2}}$ Volume of oxygen consumed $(\mathrm{ml\cdot min^{-1}})$
* $Q$ Cardiac output ($\mathrm{mL \cdot min^{-1}}$)
* $C_{a}$ Oxygen content in arterial blood ($\mathrm{mL \, O_{2} \cdot mL \, blood^{-1}}$)
* $C_{v}$ Oxygen content in venous blood ($\mathrm{mL \, O_{2} \cdot mL \, blood^{-1}}$)
* $f$ Heartbeat frequency ($\mathrm{min^{-1}}$)
* $S$ Stroke volume ($\mathrm{mL}$)
By rearranging these equations, we can work out a value for the stroke volume, $S$, of the heart, which is more difficult to measure directly than the other variables.
Rearrange the second equation, $Q = f S$ so that we could work out stroke volume when cardiac output and heartbeat frequency are known.
\nRearrange the equations so we can calculate stroke volume if we know the difference in oxygen content between arterial and venous blood, as well as the volume of oxygen consumed and the heartbeat frequency? (*i.e.* combine the two equations and solve for $S$).
\nIf the difference in oxygen content between arterial and venous blood is $0.1\,\mathrm{mL \, O_{2} \cdot mL \, blood^{-1}}$, the heartbeat frequency is $1\,\mathrm{s^{-1}}$ and the oxygen consumption rate is $420\,\mathrm{mL\cdot min^{-1}}$, what is the stroke volume of the heart?
| 197 | 20 | 14 | 14 | 46 | 0 | 100 | 5 | 0 | The amount of oxygen and blood pumped by the mammalian heart can be modelled by the following: $ V_{O_{2}}=Q(C_{a}-C_{v}) $ $ Q=f\cdot S $ $V_{O_{2}}$ Volume of oxygen consumed $(\mathrm{ml\cdot min^{-1}})$ $Q$ Cardiac output $\mathrm{mL \cdot min^{-1}}$ $C_{a}$ Oxygen content in arterial blood $\mathrm{mL \, O_{2} \cdot mL \, blood^{-1}}$ $C_{v}$ Oxygen content in venous blood $\mathrm{mL \, O_{2} \cdot mL \, blood^{-1}}$ $ Q=f\cdot S $0 Heartbeat frequency $ Q=f\cdot S $1 $ Q=f\cdot S $2 Stroke volume $ Q=f\cdot S $3 By rearranging these equations, we can work out a value for the stroke volume, $ Q=f\cdot S $2, of the heart, which is more difficult to measure directly than the other variables. Rearrange the second equation, $ Q=f\cdot S $5 so that we could work out stroke volume when cardiac output and heartbeat frequency are known. Rearrange the equations so we can calculate stroke volume if we know the difference in oxygen content between arterial and venous blood, as well as the volume of oxygen consumed and the heartbeat frequency? combine the two equations and solve for $ Q=f\cdot S $2. If the difference in oxygen content between arterial and venous blood is $ Q=f\cdot S $7, the heartbeat frequency is $ Q=f\cdot S $8 and the oxygen consumption rate is $ Q=f\cdot S $9, what is the stroke volume of the heart? | 5 |
0c82de4f-4a34-49dd-9d48-1605e94b1af5 | 1 | 1 | 0 | 2 | 1 | 2 | 2 | 4 | Manometers are instruments used to measure pressure based on columns of liquid. The figure below shows a u-bend manometer, usually used to measure small pressures.
| What is the relationship between the pressures $p_1\,$and $p_2$?
\nWhat is the pressure at $p_2\,$and hence at $p_1$?. You can assume that the fluid in the manometer is water with density $\rho=1000\,$kg/m$^3\,$and $h=10\,$cm.
| 2 | 0.333333 | 1 | \n$\frac{\delta p}{\delta z}=-\rho g$. Solve this to find an expression for $p$.
***
By integration we get $p=-\rho gz +p_0$. To find the value of the constant $p_0$ we can set $z=0$ at the top of the pipe, where the pressure is atmospheric pressure, $p_a$. 
Substitute $p_o$ into the equation for $p$ that you found to get a general equation for pressure.
***
You should find that $p_0=p_a$ and that $P=-\rho gz +p_a$. At point 2 the $z$ co-ordinate is $-h$ (note we are measuring the height h downwards from the top of the pipe so it is in a negative direction),
Using this and the general equation for pressure, find an equation for $p_2$
***
You should find that $p_2=-\rho g(-h) +p_a$. Taking $p_a= 101$ kPa and $g=9.81$ m/s$^2$ find $p_2$.
Use this and the relationship between $p_1$ and $p_2$ from the previous part to find the value for $p_1$.
***
Convert the value of $p_1$ to a gauge pressure.
| \n$\frac{\delta p}{\delta z}=-\rho g$ so integrating we get $P=-\rho gz +P_0$
To find the value of the constant $P_0$ we can set $z=0$ at the top of the pipe, where the pressure is atmospheric pressure, $p_a$. Then we substitute these values for pressure and $z$ into the general equation $P=-\rho gz +P_0=p_a=0+P_0$ and so $P_0$ must equal $p_a$. The general equation for pressure can then be written $P=-\rho gz +p_a$
At point 2 the $z$ co-ordinate is $-h$ (note we are measuring the height h downwards from the top of the pipe so it is in a negative direction).$p_2=-\rho g(-h) +p_a$.
Taking $p_a= 101$ kPa and $g=9.81$ m/s$^2$ then $p_2=-1000*9.81*(-0.1)+101 000 = 101.981$ kPa = $p_1$
In this case it is probably more appropriate to give the answer as a gauge pressure (i.e. relative to atmospheric pressure) $p_1=981$ Pa
| Manometers are instruments used to measure pressure based on columns of liquid. The figure below shows a u-bend manometer, usually used to measure small pressures.

What is the relationship between the pressures $p_1\,$and $p_2$?
\nWhat is the pressure at $p_2\,$and hence at $p_1$?. You can assume that the fluid in the manometer is water with density $\rho=1000\,$kg/m$^3\,$and $h=10\,$cm.
| 67 | 7 | 19 | 19 | 130 | 22 | 41 | 7 | 1 | Manometers are instruments used to measure pressure based on columns of liquid. The figure below shows a u-bend manometer, usually used to measure small pressures. What is the relationship between the pressures $p_1\,$and $p_2$? What is the pressure at $p_2\,$and hence at $p_1$?. You can assume that the fluid in the manometer is water with density $\rho=1000\,$kg/m$^3\,$and $h=10\,$cm. | 5 |
0cb8c336-3d09-4f2e-bd02-ee344c226af7 | 0 | 0 | 1 | 16 | 6 | 1 | 7 | 8 | In search of an Arts Council grant, the artist Damien Worst wishes to paint the **inside** surface of the musical funnel obtained by rotating the curve $y = {1\over x}$ for $(1\leq x\leq \infty)$ about the $x$-axis. His 'friend' Banxy has told him that he will surely need an infinite amount of paint - and he senses that this might be expensive...
His partner Andromeda observes that the volume inside the funnel is finite so all he has to do is to pour in the correct volume of paint and pour away any surplus. 
He thinks she might be joking. Can you help Damien to resolve this apparent paradox?!
| In search of an Arts Council grant, the artist Damien Worst wishes to paint the **inside** surface of the musical funnel obtained by rotating the curve $y = {1\over x}$ for $(1\leq x\leq \infty)$ about the $x$-axis. His 'friend' Banxy has told him that he will surely need an infinite amount of paint - and he senses that this might be expensive...
His partner Andromeda observes that the volume inside the funnel is finite so all he has to do is to pour in the correct volume of paint and pour away any surplus. 
He thinks she might be joking. Can you help Damien to resolve this apparent paradox?!
| 1 | 1 | 2 | If you were painting a wall, how would you go about calculating the volume of paint that you would need to buy?
***
What conclusion can you draw from this? Consider when a finite/infinite amount of paint would be required based on the required thickness of the paint.
***
You can show that the volume would be finite using the formula for volumes of revolution about the $x$ axis.
***
Now you can find an expression for the surface area of the funnel, and compare this to the integral of ${1\over x}$ with the same limits to show that the surface area would be infinite.
| You can show that the volume would be finite using the formula for volumes of revolution about the $x$ axis.
***
The volume,
$$
\begin{aligned}
V = \pi \int_1^\infty {1\over x^2}\mathrm{d}x = \pi
\end{aligned}
$$
is finite.
***
Now you can find an expression for the surface area of the funnel, and compare this to the integral of ${1\over x}$ with the same limits to show that the surface area would be infinite.
***
The (inside) surface area of the musical funnel is
$$
\begin{aligned}
S = 2\pi \int_1^\infty {1\over x}\left(1+{1\over x^4}\right)^{1\over2} \mathrm{d}x > 2\pi\int_1^\infty {1\over x}\mathrm{d} x \to \infty
\end{aligned}
$$
so the surface area is infinite.
***
What conclusion can you draw from this? Consider when a finite/infinite amount of paint would be required based on the requiredd thickness of the paint.
***
So if the paint is required to have a certain thickness $d>0$, then an infinite amount *would* be required (This cannot be achieved using the 'fill and pour' method), but of course, the funnel gets narrower than any such finite $d$!. 
But if there are no limitations on thickness, then a finite amount of paint can be used to cover the funnel.
\[This result is essentially about Torricelli's Funnel / Gabrielle's Horn]
| In search of an Arts Council grant, the artist Damien Worst wishes to paint the **inside** surface of the musical funnel obtained by rotating the curve $y = {1\over x}$ for $(1\leq x\leq \infty)$ about the $x$-axis. His 'friend' Banxy has told him that he will surely need an infinite amount of paint - and he senses that this might be expensive...
His partner Andromeda observes that the volume inside the funnel is finite so all he has to do is to pour in the correct volume of paint and pour away any surplus. 
He thinks she might be joking. Can you help Damien to resolve this apparent paradox?!
| 105 | 3 | 6 | 6 | 179 | 2 | 105 | 3 | 0 | Can you help Damien to resolve this apparent paradox? | 1 |
0ce1cf22-a410-4a4f-8800-780ed360edeb | 0 | 0 | 2 | 14 | 4 | 2 | 16 | 4 | Consider a turbulent and incompressible flow. | Apply Reynolds decomposition to the velocity field and time-average the continuity equation to show that:
$$
\frac{\partial \bar{u}}{\partial x}+\frac{\partial \bar{v}}{\partial y}+\frac{\partial \bar{w}}{\partial z} = 0.
$$\nShow that the velocity fluctuations also satisfy the continuity equation, that is:
$$
\frac{\partial u^\prime}{\partial x} + \frac{\partial v^\prime}{\partial y} + \frac{\partial w^\prime}{\partial z} = 0.
$$ | 2 | 0.5 | 2 | \n | \n | Consider a turbulent and incompressible flow.Apply Reynolds decomposition to the velocity field and time-average the continuity equation to show that:
$$
\frac{\partial \bar{u}}{\partial x}+\frac{\partial \bar{v}}{\partial y}+\frac{\partial \bar{w}}{\partial z} = 0.
$$\nShow that the velocity fluctuations also satisfy the continuity equation, that is:
$$
\frac{\partial u^\prime}{\partial x} + \frac{\partial v^\prime}{\partial y} + \frac{\partial w^\prime}{\partial z} = 0.
$$ | 34 | 2 | 0 | 0 | 1 | 0 | 29 | 2 | 0 | Consider a turbulent and incompressible flow.Apply Reynolds decomposition to the velocity field and time-average the continuity equation to show that: $ \frac{\partial \bar{u}}{\partial x}+\frac{\partial \bar{v}}{\partial y}+\frac{\partial \bar{w}}{\partial z} = 0. | 1 |
0d2632f2-1c09-48e8-b0ec-13b3bf89315c | 1 | 0 | 0 | 15 | 5 | 0 | 6 | 4 | An ecologist is using a clinometer to estimate the height (and therefore the biomass) of a tree. A clinometer is a tube attached to a protractor with a weighted string (see the diagram below), which can be used to measure angles between the ground and a distant point. The ecologist stands exactly $10 \, \mathrm{m}$ from the base of the tree on level ground and sights the top of the tree through the tube of the clinometer. The clinometer is held exactly $1 \, \mathrm{m}$ above the ground. The angle made by the weight and the tube of the clinometer is $42 ^\circ$. 
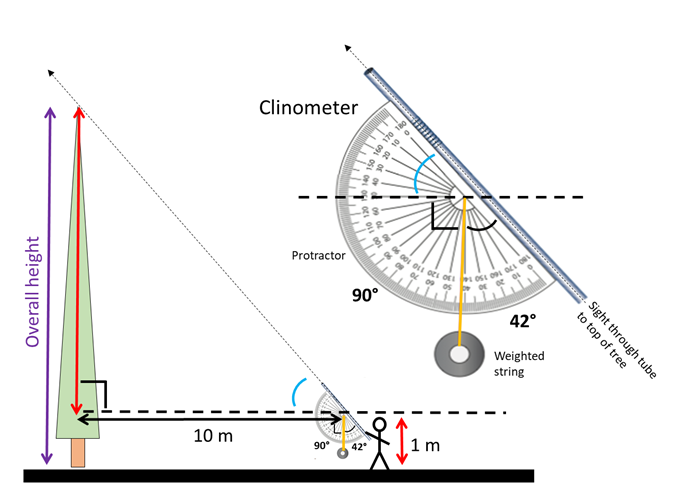
| What is the *overall* height of the tree to the closest metre?
| 1 | 1 | 1 | null | $$
1\,\mathrm{m} + 10\,\mathrm{m} \times \tan(90\degree -42\degree) = 12.1\,\mathrm{m}
$$
| An ecologist is using a clinometer to estimate the height (and therefore the biomass) of a tree. A clinometer is a tube attached to a protractor with a weighted string (see the diagram below), which can be used to measure angles between the ground and a distant point. The ecologist stands exactly $10 \, \mathrm{m}$ from the base of the tree on level ground and sights the top of the tree through the tube of the clinometer. The clinometer is held exactly $1 \, \mathrm{m}$ above the ground. The angle made by the weight and the tube of the clinometer is $42 ^\circ$. 

What is the *overall* height of the tree to the closest metre?
| 110 | 3 | 1 | 1 | 1 | 0 | 10 | 0 | 1 | An ecologist is using a clinometer to estimate the height and therefore the biomass of a tree. A clinometer is a tube attached to a protractor with a weighted string see the diagram below, which can be used to measure angles between the ground and a distant point. What is the overall height of the tree to the closest metre? | 3 |
0d36ee3e-25fd-49a8-9452-894589501cb0 | 0 | 4 | 0 | 19 | 6 | 1 | 5 | 0 | **(L7/8)**: For each of the following sets of simultaneous equations, determine if there is:
1. A unique solution
2. No solutions
3. An infinity of solutions
| $$
\begin{aligned}
x+y+z&=6\, ,\\
2x+y-z&=3\, ,\\
x+y&=4\, .
\end{aligned}
$$
\n$$
\begin{aligned}
x+y+z&=6\, ,\\
2x+y-z&=3\, ,\\
4x+3y+z&=1\, .
\end{aligned}
$$
\n$$
\begin{aligned}
x+y+z&=6\, ,\\
2x+y-z&=3\, ,\\
2x+2y+2z&=12\, .
\end{aligned}
$$
\n$$
\begin{aligned}
-x+2y-2z&=1, \\
4x-y+6z&=2\, ,\\
2x+3y+2z&=4\, ,\\
\end{aligned}
$$
| 4 | 0.333333 | 3 | Refer to **section 2.7**: what are the Cramer's Rule conditions for unique solutions, no solutions or an infinity of solutions? **Note:** In some cases, you *may* be able to deduce the type of solution by inspecting the simultaneous equations: are the planes independent?
***
Start by evaluating $\Delta$ (to speed this up, use determinant properties from **section 2.2**)...
***
... If $\Delta=0$, you must now check for unique solutions, or an infinity of solutions. 
***
Evaluate one of $\Delta_{1,2 ~\text{or} ~3}$. If you find that any are non-zero, this indicates no solutions.
***
For an infinity of solutions, each of $\Delta_{1,2~\text{and}~3}$ must be zero.
\nRefer to **section 2.7**: what are the Cramer's Rule conditions for unique solutions, no solutions or an infinity of solutions? **Note:** In some cases, you *may* be able to deduce the type of solution by inspecting the simultaneous equations: are the planes independent?
***
Start by evaluating $\Delta$ (to speed this up, use determinant properties from **section 2.2**)...
***
... If $\Delta=0$, you must now check for unique solutions, or an infinity of solutions. 
***
Evaluate one of $\Delta_{1,2 ~\text{or} ~3}$. If you find that any are non-zero, this indicates no solutions.
***
For an infinity of solutions, each of $\Delta_{1,2~\text{and}~3}$ must be zero.
\nRefer to **section 2.7**: what are the Cramer's Rule conditions for unique solutions, no solutions or an infinity of solutions? **Note:** In some cases, you *may* be able to deduce the type of solution by inspecting the simultaneous equations: are the planes independent?
***
Start by evaluating $\Delta$ (to speed this up, use determinant properties from **section 2.2**)...
***
... If $\Delta=0$, you must now check for unique solutions, or an infinity of solutions. 
***
Evaluate one of $\Delta_{1,2 ~\text{or} ~3}$. If you find that any are non-zero, this indicates no solutions.
***
For an infinity of solutions, each of $\Delta_{1,2~\text{and}~3}$ must be zero.
\nRefer to **section 2.7**: what are the Cramer's Rule conditions for unique solutions, no solutions or an infinity of solutions? **Note:** In some cases, you *may* be able to deduce the type of solution by inspecting the simultaneous equations: are the planes independent?
***
Start by evaluating $\Delta$ (to speed this up, use determinant properties from **section 2.2**)...
***
... If $\Delta=0$, you must now check for unique solutions, or an infinity of solutions. 
***
Evaluate one of $\Delta_{1,2 ~\text{or} ~3}$. If you find that any are non-zero, this indicates no solutions.
***
For an infinity of solutions, each of $\Delta_{1,2~\text{and}~3}$ must be zero.
| (**Section 2.8**): We start by evaluating $\Delta$. If $\Delta\ne0$, there are unique solutions. If $\Delta=0$, we check for the other two cases:
* For no solutions, *one of* $\Delta_{1,2~\text{or}~3}$ is non-zero. 
* For an infinity of solutions, *all of* $\Delta_{1,2~\text{and}~3}$ must be zero. 
***
Evaluating $\Delta$, using determinant properties to simplify the evaluation:
***
$$
\Delta \ =
\begin{vmatrix} \ 1 &\ 1 &\ 1\\ 2 & 1 & -1\\ 1 & 1 & 0 \end{vmatrix} =
-\begin{vmatrix} \ 1 & 1 & 0\\ 2 & 1 & -1\\ 1 & 1 & 1 \end{vmatrix} =
-\begin{vmatrix} \ 1 & 0 & 0\\ 2 & -1 & -1\\ 1 & 0 & 1 \end{vmatrix} \
$$
* First, swapped R1 and R3.
* Then, subtracted C1 from C2. 
Reducing this to a 2$\times$2 determinant:
***
$$
=\
-\begin{vmatrix} -1 & -1\\ 0 & 1 \end{vmatrix} = 1
$$
$\Delta\ne0\implies$**Unique solutions**. 
\n(**Section 2.8**): We start by evaluating $\Delta$. If $\Delta\ne0$, there are unique solutions. If $\Delta=0$, we check for the other two cases:
* For no solutions, *one of* $\Delta_{1,2~\text{or}~3}$ is non-zero. 
* For an infinity of solutions, *all of* $\Delta_{1,2~\text{and}~3}$ must be zero. 
***
Evaluating $\Delta$, using determinant properties to simplify the evaluation:
***
$$
\Delta \ =
\begin{vmatrix} \ 1 &\ 1 &\ 1\\ 2 & 1 & -1\\ 4 & 3 & 1 \end{vmatrix} =
\begin{vmatrix} 1 & 0 & 0\\ 2 & -1 & -3\\ 4 & -1 & -3 \end{vmatrix} =\ \begin{vmatrix} \ 1 & 3 \\ \ 1 & 3 \end{vmatrix} =0\
$$
* Subtracted C1 from C2 and C3.
***
$\Delta=0\implies$No unique solutions. Now we must check for no solutions or an infinity of solutions. We start by choosing any of $\Delta_{1,2,~\text{or}~3}$ to evaluate, e.g. $\Delta_3$:
***
$$
\Delta _{3} \ =\begin{vmatrix} \ 1 &\ 1 &\ 6\\ 2 & 1 & 3\\ 4 & 3 & 1 \end{vmatrix} = \begin{vmatrix} 1 & 0 & 0\\ 2 & -1 & -9\\ 4 & -1 & -23 \end{vmatrix} =\
\begin{vmatrix} 1 & 9\\ 1 & 23 \end{vmatrix} =14
$$
* Subtracted C1 from C2, and 6$\times$C1 from C3. 
We have found a single determinant that in non-zero, so there are **no solutions** to this system of equations.
\n(**Section 2.8**): We start by evaluating $\Delta$. If $\Delta\ne0$, there are unique solutions. If $\Delta=0$, we check for the other two cases:
* For no solutions, *one of* $\Delta_{1,2~\text{or}~3}$ is non-zero. 
* For an infinity of solutions, *all of* $\Delta_{1,2~\text{and}~3}$ must be zero.
**Note:** In this question, it is possible to see the type of solution by inspecting the equations: are the planes linearly independent? (the methodology behind this is discussed at the end)
***
Evaluating $\Delta$, using determinant properties to simplify the evaluation:
***
$$
\Delta \ =
\begin{vmatrix}\ 1 &\ 1 & 1\\ 2 & 1 & -1\\ 2 & 2 & 2 \end{vmatrix} =
\begin{vmatrix}\ 1 &\ 0 & 0\\ 2 & 1 & -1\\ 2 & 0 & 0 \end{vmatrix} =0
$$
* We notice that R3 is simply 2$\times$R1, and so we could multiply R3 so that R1=R3. If two determinant row/columns are equivalent, the determinant evaluates to 0. 
***
$\Delta=0\implies$No unique solutions. Now we must check for no solutions or an infinity of solutions. We start by choosing any of $\Delta_{1,2,~\text{or}~3}$ to evaluate.
***
$$
\Delta _{1} \ =
\begin{vmatrix} 6 & 1 & 1\\ 3 & 1 & -1\\ 12 & 2 & 2 \end{vmatrix} = 0 ,
\qquad
\Delta _{2} \ =
\begin{vmatrix}\ 1 &\ 1 & 1\\ 2 & 1 & -1\\ 2 & 2 & 2 \end{vmatrix} = 0,
\qquad
\Delta _{3} \ =
\begin{vmatrix}\ 1 &\ 1 & 1\\ 2 & 1 & -1\\ 2 & 2 & 2 \end{vmatrix} = 0
$$
* In each case, R3 is a multiple of R1, so as before, they immediately evaluate to 0. 
***
Since each of $\Delta_{1,2 ~ \text{and} ~ 3}$ is zero, there are an **infinity** **of solutions**. Indeed, we could have spotted initially that the bottom equation is multiple of top, so there are only two independent equations for three unknowns $ \rightarrow $ not enough to have a unique solution. Hence there will just be an intersection between the two independent planes.
\n(**Section 2.8**): We start by evaluating $\Delta$. If $\Delta\ne0$, there are unique solutions. If $\Delta=0$, we check for the other two cases:
* For no solutions, *one of* $\Delta_{1,2~\text{or}~3}$ is non-zero. 
* For an infinity of solutions, *all of* $\Delta_{1,2~\text{and}~3}$ must be zero. 
***
Evaluating $\Delta$, using determinant properties to simplify the evaluation:
***
$$
\Delta \ =\begin{vmatrix} -1 & 2 & -2\\ 4 & -1 & 6\\ 2 & 3 & 2 \end{vmatrix} =
\begin{vmatrix} -1 & 0 & 0\\ 4 & 7 & -2\\ 2 & 7 & -2 \end{vmatrix} \ =\
\begin{vmatrix} 7 & -2\\ 7 & -2 \end{vmatrix} =0
$$
* Added 2$\times$C1 to C2, and subtracted 2$\times$C1 from C3. 
***
$\Delta=0\implies$No unique solutions. Now we must check for no solutions or an infinity of solutions. We start by choosing any of $\Delta_{1,2,~\text{or}~3}$ to evaluate.
***
$$
\begin{aligned}
&
\Delta _{1} \ =
\begin{vmatrix} 1 & 2 & -2\\ 2 & -1 & 6\\ 4 & 3 & 2 \end{vmatrix} =
\begin{vmatrix} 1 & 0 & 0\\ 2 & -5 & 10\\ 4 & -5 & 10 \end{vmatrix} = 0,\\
\end{aligned}
$$
* Subtracted 2$\times$C1 from C2, and added 2$\times$C1 to C3.
* Observe that the resulting 2$\times$2 determinant has equal rows/columns, and so evaluates to 0.
***
$$
\begin{aligned}
&
\Delta _{2} \ =
\begin{vmatrix} -1 & 1 & -2\\ 4 & 2 & 6\\ 2 & 4 & 2 \end{vmatrix} =
\begin{vmatrix} -1 & 0 & 0\\ 4 & 6 & -2\\ 2 & 6 & -2 \end{vmatrix} =
0\\
\end{aligned}
$$
* Added C1 to C2, and subtracted 2$\times$C1 from C3.
* Observe that the resulting 2$\times$2 determinant has equal rows/columns, and so evaluates to 0.
***
$$
\begin{aligned}
&
\Delta _{3} \ =\begin{vmatrix} -1 & 2 & 1\\ 4 & -1 & 2\\ 2 & 3 & 4 \end{vmatrix} =
\begin{vmatrix} -1 & 0 & 0\\ 4 & 7 & 6\\ 2 & 7 & 6 \end{vmatrix} \ =\
\begin{vmatrix} 7 & 6\\ 7 & 6 \end{vmatrix} =0
\end{aligned}
$$
* Added 2$\times$C1 to C2, and added C1 to C3.
* Observe that the resulting 2$\times$2 determinant has equal rows/columns, and so evaluates to 0.
***
Since each of $\Delta_{1,2 ~ \text{and} ~ 3}$ is zero, there are an **infinity** **of solutions**. This was not so obvious from the simultaneous equations. 
| **(L7/8)**: For each of the following sets of simultaneous equations, determine if there is:
1. A unique solution
2. No solutions
3. An infinity of solutions
$$
\begin{aligned}
x+y+z&=6\, ,\\
2x+y-z&=3\, ,\\
x+y&=4\, .
\end{aligned}
$$
\n$$
\begin{aligned}
x+y+z&=6\, ,\\
2x+y-z&=3\, ,\\
4x+3y+z&=1\, .
\end{aligned}
$$
\n$$
\begin{aligned}
x+y+z&=6\, ,\\
2x+y-z&=3\, ,\\
2x+2y+2z&=12\, .
\end{aligned}
$$
\n$$
\begin{aligned}
-x+2y-2z&=1, \\
4x-y+6z&=2\, ,\\
2x+3y+2z&=4\, ,\\
\end{aligned}
$$
| 33 | 4 | 57 | 57 | 650 | 16 | 7 | 4 | 0 | L7/8: For each of the following sets of simultaneous equations, determine if there is: 1. \end{aligned} $ $ \begin{aligned} x+y+z&=6\, ,\\ 2x+y-z&=3\, ,\\ 4x+3y+z&=1\, . \end{aligned} $ $ \begin{aligned} x+y+z&=6\, ,\\ 2x+y-z&=3\, ,\\ 2x+2y+2z&=12\, . \end{aligned} $ $ \begin{aligned} -x+2y-2z&=1, \\ 4x-y+6z&=2\, ,\\ 2x+3y+2z&=4\, ,\\ \end{aligned} $ | 4 |
0d4b9dc3-b242-493c-982a-e08fefe374f5 | 0 | 0 | 1 | 11 | 4 | 2 | 6 | 4 | Consider a counterflow heat exchanger in which the fluids on the hot and cold sides have inlet temperatures $T_\mathrm{hi}$ and $T_\mathrm{ci}$ respectively, while the temperature of the environment is $T_0$. The fluids can be taken to be the same gas on each side, assumed to behave as a perfect gas with constant-pressure specific heat $c_\mathrm{p}$. The mass flow rate $\dot{m}$ is the same on each side, so that the temperature difference $\Delta T$ between the hot and cold sides is constant throughout the heat exchanger. Heat loss from the heat exchanger casing and frictional pressure drops can be neglected. Show that the exergy destruction $\dot{B}_\mathrm{destroyed}$ or irreversibility $\dot{I}$ can be expressed in dimensionless form by:
| $\frac{\dot{B}_\mathrm{destroyed}}{\dot{m}c_\mathrm{p}T_0} = \frac{\dot{I}}{\dot{m}c_\mathrm{p}T_0} = \mathrm{ln}(1+K_1\Delta T + K_2(\Delta T)^2)$
  
where
  
$K_1 = \frac{T_\mathrm{hi}- T_\mathrm{ci}}{T_\mathrm{hi}T_\mathrm{ci}}$
  
and 
  
$K_2 = -\frac{1}{T_\mathrm{hi}T_\mathrm{ci}}$
| 1 | 1 | 2 | null | It can be helpful to draw a diagram of the heat exchanger:
***
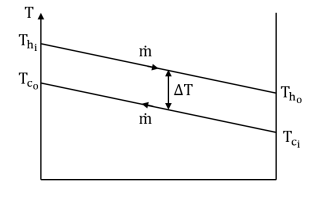
***
$\dot{B}_\mathrm{destroyed} = \dot{I} = T_0\dot{S}_\mathrm{gen}$
***
where $\dot{S}_\mathrm{gen} = \dot{S_2}-\dot{S_1}$
***
For a perfect gas:
  
$\dot{S_2}-\dot{S_1} = \dot{m}[c_\mathrm{p} \mathrm{ln}(\frac{T_2}{T_1})+R\mathrm{ln}(\frac{P_2}{P_1})]$
***
Since there is no pressure drop, $P_2 = P_1$ and the above expression simplifies to:
***
$\dot{S_2}-\dot{S_1} = \dot{m}c_\mathrm{p} \mathrm{ln}(\frac{T_2}{T_1})$
***
For both streams together:
  
$\dot{S_2}-\dot{S_1} = \dot{m}c_\mathrm{p}[\mathrm{ln}(\frac{T_\mathrm{h_o}}{T_\mathrm{h_i}}) + \mathrm{ln}(\frac{T_\mathrm{c_o}}{T_\mathrm{c_i}})]$
***
$\dot{S_2}-\dot{S_1} = \dot{m}c_\mathrm{p}\mathrm{ln}(\frac{T_\mathrm{h_o}T_\mathrm{c_o}}{T_\mathrm{h_i}T_\mathrm{c_i}})$
***
$T_\mathrm{h_o} = T_\mathrm{c_i} + \Delta T$
   
$T_\mathrm{c_o} = T_\mathrm{h_i} - \Delta T$
***
Hence:
  
$\dot{S_2}-\dot{S_1} = \dot{m}c_\mathrm{p}\mathrm{ln}(\frac{(T_\mathrm{c_i} + \Delta T)(T_\mathrm{h_i} - \Delta T)}{T_\mathrm{h_i}T_\mathrm{c_i}})$
***
Expanding the numerator:
  
$\dot{S_2}-\dot{S_1} = \dot{m}c_\mathrm{p}\mathrm{ln}(\frac{T_\mathrm{c_i}T_\mathrm{h_i} + \Delta T(T_\mathrm{h_i} -T_\mathrm{c_i}) - (\Delta T)^2}{T_\mathrm{h_i}T_\mathrm{c_i}})$
***
Simplifiying:
  
$\dot{S_2}-\dot{S_1} = \dot{m}c_\mathrm{p}\mathrm{ln}(1 + K_1\Delta T + K_2 (\Delta T)^2)$
***
Therefore:
  
$\dot{B}_\mathrm{destroyed} = \dot{I} = T_0\dot{m}c_\mathrm{p}\mathrm{ln}(1 + K_1\Delta T + K_2 (\Delta T)^2)$
***
Dividing by $\dot{m}c_\mathrm{p}T_0$:
  
$\frac{\dot{B}_\mathrm{destroyed}}{\dot{m}c_\mathrm{p}T_0} = \frac{\dot{I}}{\dot{m}c_\mathrm{p}T_0} = \mathrm{ln}(1+K_1\Delta T + K_2(\Delta T)^2)$
| Consider a counterflow heat exchanger in which the fluids on the hot and cold sides have inlet temperatures $T_\mathrm{hi}$ and $T_\mathrm{ci}$ respectively, while the temperature of the environment is $T_0$. The fluids can be taken to be the same gas on each side, assumed to behave as a perfect gas with constant-pressure specific heat $c_\mathrm{p}$. The mass flow rate $\dot{m}$ is the same on each side, so that the temperature difference $\Delta T$ between the hot and cold sides is constant throughout the heat exchanger. Heat loss from the heat exchanger casing and frictional pressure drops can be neglected. Show that the exergy destruction $\dot{B}_\mathrm{destroyed}$ or irreversibility $\dot{I}$ can be expressed in dimensionless form by:
$\frac{\dot{B}_\mathrm{destroyed}}{\dot{m}c_\mathrm{p}T_0} = \frac{\dot{I}}{\dot{m}c_\mathrm{p}T_0} = \mathrm{ln}(1+K_1\Delta T + K_2(\Delta T)^2)$
  
where
  
$K_1 = \frac{T_\mathrm{hi}- T_\mathrm{ci}}{T_\mathrm{hi}T_\mathrm{ci}}$
  
and 
  
$K_2 = -\frac{1}{T_\mathrm{hi}T_\mathrm{ci}}$
| 125 | 11 | 15 | 15 | 81 | 0 | 9 | 3 | 0 | Consider a counterflow heat exchanger in which the fluids on the hot and cold sides have inlet temperatures $T_\mathrm{hi}$ and $T_\mathrm{ci}$ respectively, while the temperature of the environment is $T_0$. The fluids can be taken to be the same gas on each side, assumed to behave as a perfect gas with constant-pressure specific heat $c_\mathrm{p}$. Show that the exergy destruction $\dot{B}_\mathrm{destroyed}$ or irreversibility $\dot{I}$ can be expressed in dimensionless form by: $\frac{\dot{B}_\mathrm{destroyed}}{\dot{m}c_\mathrm{p}T_0} = \frac{\dot{I}}{\dot{m}c_\mathrm{p}T_0} = \mathrm{ln}(1+K_1\Delta T + K_2(\Delta T)^2)$ where $K_1 = \frac{T_\mathrm{hi}- T_\mathrm{ci}}{T_\mathrm{hi}T_\mathrm{ci}}$ and $T_\mathrm{ci}$0 | 3 |
0d81759e-b284-40f7-854b-fce603b34a62 | 1 | 0 | 0 | 13 | 4 | 2 | 4 | 0 | A wheel is rolling along a horizontal path towards a step which lies across its path.
The wheel, of radius $r = 0.5~\mathrm{m}$ and radius of gyration $k = 0.4~\mathrm{m}$ about its centre, rolls with angular velocity $\omega=2~\mathrm{rad/s}$ along a horizontal path towards a step of height $h = 0.2~ \mathrm{m}$ ($ < r $).
| Find the angular velocity $\dot{\theta}_2$ of the wheel at the instant when it leaves the path and starts to mount the step. Assume no slip and no rebound from the step.
*(Take rotation in the clockwise direction to be positive)*
| 1 | 0.666667 | 3 | Let’s take angular momentum about a fixed point to make our lives easier and apply the conservation of momentum principle. What would be a suitable point? 
***
The top tip of the step serves this purpose very well in this case for example. 
Remember that the total angular momentum about a point is the sum of the angular momentum of the moving body around its own centre of gravity and the moment produced by its linear momentum about the chosen point –in this case it would be the angular momentum of the wheel around its centre and the moment of its linear momentum about the tip of the step (momentum times the perpendicular distance).
***
After impact, the wheel spins about itself as well as the step (consider the tangential velocity here), so the angular momentum equation about the step tip will have two respective expressions. The conservation of momentum method will help you find an expression for the angular velocity after impact. You’ll find it easier to first write your expressions of angular momentum in terms of linear velocities, the mass of the wheel and the mass moment of inertia about its centre of gravity.
***
After rearranging to find an expression for the angular velocity after impact, substitute in the variables given to you in the questions as the required answer is only in terms of the variables provided (i.e. the angular velocity before impact, the radius of the wheel $r$, the radius of gyration of the wheel $k$ about its centre and the height of the step $h$).
| Free body diagram and kinematic diagram:
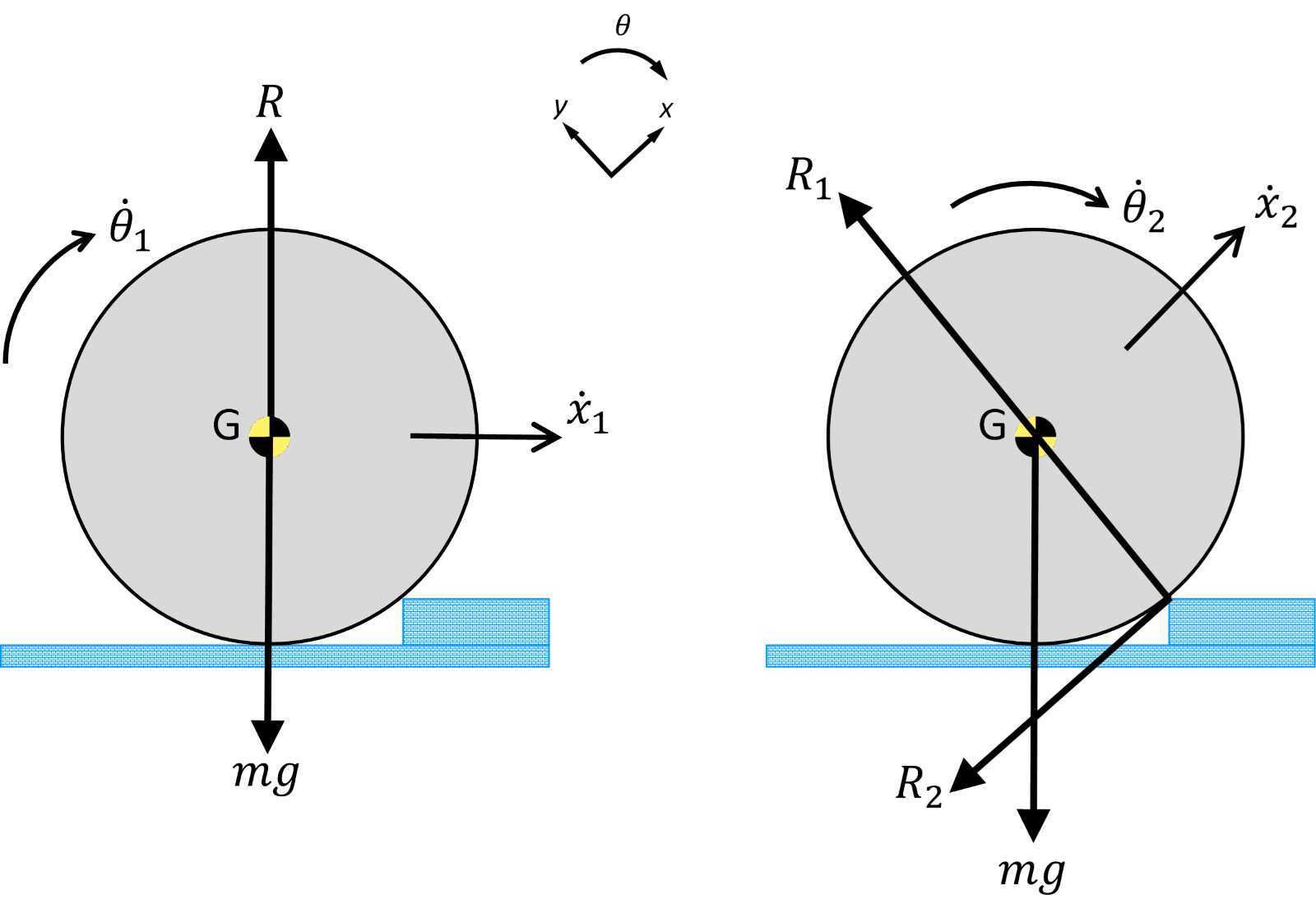
***
Starting with the equation for angular momentum about a general point:
$$
\begin{aligned}
H_O=I_G\dot{\theta}+m{\dot{x}}_G\left(y_G-y_O\right)-m{\dot{y}}_G\left(x_G-x_O\right)
\end{aligned}
$$
***
Consider the angular momentum at point O before the impact:
$$
\begin{aligned}
H_{O,1}=I_G{\dot{\theta}}_1+m{\dot{x}}_1\left(r-h\right)~~\mathrm{(Equation~1)}
\end{aligned}
$$
***
Consider the angular momentum at point O after the impact:
$$
\begin{aligned}
H_{O,2}=I_G{\dot{\theta}}_2+m{\dot{x}}_2r~~\mathrm{(Equation~2)}
\end{aligned}
$$
***
Applying conservation of momentum by combining Equations 1 and 2:
$$
\begin{aligned}
I_G{\dot{\theta}}_1+m{\dot{x}}_1\left(r-h\right)=I_G{\dot{\theta}}_2+m{\dot{x}}_2r~~\mathrm{(Equation~3)}
\end{aligned}
$$
***
But there is no slip so:
$$
\begin{aligned}
\dot{x}=r\dot{\theta}
\end{aligned}
$$
***
And the moment of inertia is given by:
$$
\begin{aligned}
I_G=mk^2
\end{aligned}
$$
***
Equation 3 can therefore be rewritten as:
$$
\begin{aligned}
\left(mk^2\right){\dot{\theta}}_1+m\left(r{\dot{\theta}}_1\right)\left(r-h\right)={\left(mk^2\right)\dot{\theta}}_2+m\left(r{\dot{\theta}}_2\right)r
\end{aligned}
$$
***
Rearranging for ${\dot{\theta}}_2$:
$$
\begin{aligned}
{\dot{\theta}}_2={\dot{\theta}}_1\frac{\left(k^2+r\left(r-h\right)\right)}{\left(r^2+k^2\right)}
\end{aligned}
$$
***
Substituting the values of the parameters gives:
$$
\begin{aligned}
{\dot{\theta}}_2=2\times\frac{\left({0.4}^2+0.5\times\left(0.5-0.2\right)\right)}{\left({0.5}^2+{0.4}^2\right)}
\end{aligned}
$$
$$
{\dot{\theta}}_2=1.51~\mathrm{rad/s}
$$
| A wheel is rolling along a horizontal path towards a step which lies across its path.

The wheel, of radius $r = 0.5~\mathrm{m}$ and radius of gyration $k = 0.4~\mathrm{m}$ about its centre, rolls with angular velocity $\omega=2~\mathrm{rad/s}$ along a horizontal path towards a step of height $h = 0.2~ \mathrm{m}$ ($ < r $).
Find the angular velocity $\dot{\theta}_2$ of the wheel at the instant when it leaves the path and starts to mount the step. Assume no slip and no rebound from the step.
*(Take rotation in the clockwise direction to be positive)*
| 88 | 6 | 11 | 11 | 99 | 3 | 40 | 1 | 1 | Find the angular velocity $\dot{\theta}_2$ of the wheel at the instant when it leaves the path and starts to mount the step. Assume no slip and no rebound from the step. Take rotation in the clockwise direction to be positive | 3 |
0da53862-6330-4f62-a563-840b35c837dd | 2 | 0 | 0 | 14 | 4 | 2 | 4 | 3 | Tests on a model propeller in a wind tunnel at sea level (air density $\rho = 1.2\,\mathrm{kg/m}^3$) gave the following results for the thrust at a number of forward velocities.
  
$$
\begin{array} {c|ccccc} \mathrm{U (m/s)}&\mathrm{0}&\mathrm{10}&\mathrm{15}&\mathrm{20}&\mathrm{30}\\ \hline \mathrm{Thrust (N)}&\mathrm{300}&\mathrm{278}&\mathrm{245}&\mathrm{211}&\mathrm{100} \end{array}
$$
  
The propeller diameter was $0.8,\mathrm{m}$ and it was spun at $2000,\mathrm{rpm}$.
| Using dimensional analysis find the non-dimensional parameters which govern this observed behavior.\nUsing experimental data given in the table, find the thrust generated by a geometrically similar propeller of diameter $3\,\mathrm{m}$, spinning at $1500\,\mathrm{rpm}$ at a forward velocity of $45\,\mathrm{m/s}$, while operating at an altitude where the density is half that at sea level. You may interpolate from tabulated values. | 2 | 0.5 | 2 | \n | \n | Tests on a model propeller in a wind tunnel at sea level (air density $\rho = 1.2\,\mathrm{kg/m}^3$) gave the following results for the thrust at a number of forward velocities.
  
$$
\begin{array} {c|ccccc} \mathrm{U (m/s)}&\mathrm{0}&\mathrm{10}&\mathrm{15}&\mathrm{20}&\mathrm{30}\\ \hline \mathrm{Thrust (N)}&\mathrm{300}&\mathrm{278}&\mathrm{245}&\mathrm{211}&\mathrm{100} \end{array}
$$
  
The propeller diameter was $0.8,\mathrm{m}$ and it was spun at $2000,\mathrm{rpm}$.
Using dimensional analysis find the non-dimensional parameters which govern this observed behavior.\nUsing experimental data given in the table, find the thrust generated by a geometrically similar propeller of diameter $3\,\mathrm{m}$, spinning at $1500\,\mathrm{rpm}$ at a forward velocity of $45\,\mathrm{m/s}$, while operating at an altitude where the density is half that at sea level. You may interpolate from tabulated values. | 105 | 7 | 0 | 0 | 1 | 0 | 61 | 3 | 0 | Tests on a model propeller in a wind tunnel at sea level air density $\rho = 1.2\,\mathrm{kg/m}^3$ gave the following results for the thrust at a number of forward velocities. Using dimensional analysis find the non-dimensional parameters which govern this observed behavior. Using experimental data given in the table, find the thrust generated by a geometrically similar propeller of diameter $3\,\mathrm{m}$, spinning at $1500\,\mathrm{rpm}$ at a forward velocity of $45\,\mathrm{m/s}$, while operating at an altitude where the density is half that at sea level. | 3 |
0df0dd8e-3185-427a-9f46-f4e28cddca81 | 1 | 0 | 0 | 10 | 4 | 2 | 8 | 2 | The creep rupture properties of Nimonic 105 are shown in the figure below. Using this figure, estimate the maximum operating temperature of a gas turbine blade made out of this material which is to withstand a stress of $150\text{ MPa}$ for a duration of $10,000$ hours. 
   
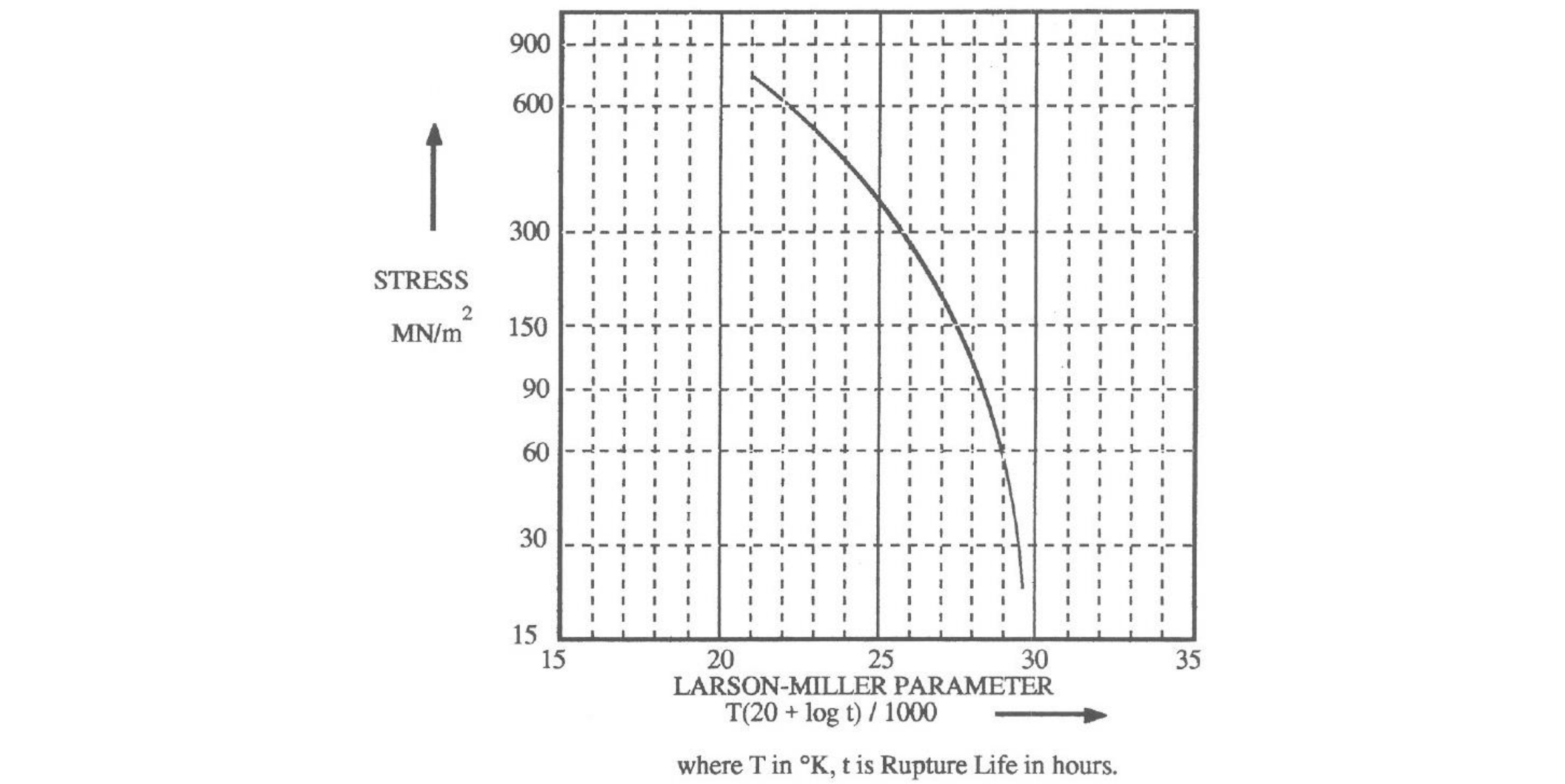
$$
\footnotesize
\text{Figure Q4.3: Graph of Larson-Miller Parameter vs. Stress}
$$
| What would be the new design life if the engine rate $40^\circ\text{C}$ hotter?
| 1 | 0.666667 | 2 | null | Using the following equation for the Larson-Miller Parameter:
   
$$
P_{LM}=T(\log t_r+C)
$$
   
Where $T$ is the temperature, $t_r$ is the time to rupture, and $C=T(20+\log t)$.
   
***
Using values read from the graph at $150\text{ MPa}$:
   
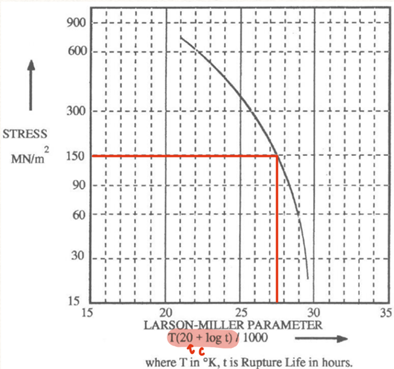
$$
\footnotesize
\text{Figure Q4.3.1: Annotated Larson-Miller Parameter vs. Stress graph.}
$$
   
***
And then substituting numbers into the earlier equation:
   
$$
27.5\times10^3=T(\log10,000+20)\\
~\\
T=1146\text{ K}=873\degree\text{C}
$$
   
***
Increasing $T$ by $40\degree \text{C}$ and then substituting back into the equation to find a new value for $t_r$.
   
$$
T=913\degree\text{C}=1186\text{ K}
$$
   
$$
27.5\times10^3=1186(\log t_r+20)\\ ~\\
t_r=1538\text{ hours}\approx\boxed{1500\text{ hours}}
$$
| The creep rupture properties of Nimonic 105 are shown in the figure below. Using this figure, estimate the maximum operating temperature of a gas turbine blade made out of this material which is to withstand a stress of $150\text{ MPa}$ for a duration of $10,000$ hours. 
   

$$
\footnotesize
\text{Figure Q4.3: Graph of Larson-Miller Parameter vs. Stress}
$$
What would be the new design life if the engine rate $40^\circ\text{C}$ hotter?
| 62 | 4 | 12 | 12 | 85 | 0 | 13 | 1 | 1 | Using this figure, estimate the maximum operating temperature of a gas turbine blade made out of this material which is to withstand a stress of $150\text{ MPa}$ for a duration of $10,000$ hours. Stress} $ What would be the new design life if the engine rate $40^\circ\text{C}$ hotter? | 2 |
0ea1717d-dcaa-4eec-a76f-2f7a350b1878 | 0 | 1 | 0 | 2 | 1 | 2 | 0 | 13 | Select all of the features that describe a turbulent flow.
| Select all of the features that describe a turbulent flow.
| 1 | 0.333333 | 0 | null | null | Select all of the features that describe a turbulent flow.
| 10 | 0 | 0 | 0 | 0 | 0 | 10 | 0 | 0 | Select all of the features that describe a turbulent flow. | 1 |
0f457acf-716d-416e-924b-091158ac4995 | 3 | 0 | 0 | 19 | 6 | 1 | 9 | 4 | A particle starts at position $\vec{r}_{0}=(0, 1, 0)$ with a velocity $\vec{v} = (2, 1, 3)$. It collides with a wall whose position is given by the equation $x+y+z = 4$. (You may assume throughout this question that all physical quantities are given in dimensionless units, and there are no external forces acting on the particle.)
| Give an expression for the trajectory of the particle before the collision. 
\nFind the position at which the particle strikes the wall. 
\nFind the velocity of the particle after the collision with the wall, assuming the collision is elastic.
| 3 | 0.666667 | 2 | $\vec{r}(t) = \vec{r}_0 + \vec{v}t$
\nYour goal is to find the intersection of the linear trajectory of the particle and the plane.
***
Express your trajectory equation from part (a) as $x=x(t),y=y(t),z=z(t)$. 
***
Insert these results into the equation of the plane and solve for the time of intersection.
***
Using this time, can you find the *point* of intersection?
\nDraw a diagram of the plane, and the incoming and outgoing trajectories. Add to your diagram the velocity components perpendicular and parallel to the plane.
***
Split the velocity *before* the collision into components parallel and perpendicular to the plane...
***
... The perpendicular component is the one parallel to the *normal* of the plane. 
***
Find this by computing the projection of $\vec{v}$ onto $\mathbf{\hat{n}}$.
***
After this, can you compute the parallel velocity component to the plane?
***
After the collision, which of the velocity components change, and how? Hence calculate the new velocity.
| $$
\vec{r}(t) = \vec{r}_0 + \vec{v}t=\begin{pmatrix}0\\1\\0\end{pmatrix}+\begin{pmatrix}2\\1\\3\end{pmatrix}t=\begin{pmatrix}2t\\1+1t\\3t\end{pmatrix}
$$
\nFrom part (a): $x=2 t, \quad y=1+t, \quad z=3 t$. Inserting this into the plane equation:
***
$$
\begin{array}{l l }
\text{in} \qquad x+y+z=4, \quad
& \Rightarrow 2 t+(1+t)+3 t=4 \\
&\Rightarrow \quad 6 t=3 \\
&\Rightarrow \quad t=1 / 2 \\
\end{array}
$$
***
Inserting this time into the trajectory of the particle yields the point of collision:
***
$$
\begin{array}{l}
\quad & \vec{r}_{\text {coll }}=\left(\begin{array}{l}
0 \\
1 \\
0
\end{array}\right)+\dfrac{1}{2}\left(\begin{array}{l}
2 \\
1 \\
3
\end{array}\right)=\left(\begin{array}{c}
1\\ 3 / 2 \\ 3 / 2
\end{array}\right)
\end{array}
$$
\n
***
We start by expressing the velocity before the collision in terms of components *perpendicular* to the wall, and parallel to the wall.
***
The perpendicular component of the velocity is parallel to the normal vector $\mathbf{\underline{n}}=(1,1,1)$ of the plane. 
***
Hence, to find this component, we find the projection of $\vec{v}$ onto the normalised normal vector, using the dot product:
***
$$
\vec{n}=\left(\begin{array}{l}
1 \\ 1 \\ 1
\end{array}\right) \qquad \rightarrow \qquad \mathbf{\hat{n}}=\frac{1}{\sqrt{3}}\left(\begin{array}{l}
1 \\ 1 \\ 1
\end{array}\right)
$$
***
$$
\begin{align*}
\vec{v}_{\perp} \ =\ \frac{1}{\sqrt{3}}\left\{\left(\begin{array}{l}
1 \\ 1 \\ 1
\end{array}\right) \cdot\left(\begin{array}{l}
2 \\ 3 \\ 1
\end{array}\right)\right\}\frac{1}{\sqrt{3}}\left(\begin{array}{l}
1 \\ 1 \\ 1
\end{array}\right)\ = \
\frac{1}{3}\{6\} \cdot\left(\begin{array}{l}
1 \\
1 \\
1
\end{array}\right) \
=\ \left(\begin{array}{l}
2 \\ 2 \\ 2
\end{array}\right)
\end{align*}
$$
***
The parallel component to the plane before collision is found by negating the perpendicular component from $\vec{v}$ (see diagram):
***
$$
\vec{v}_{||}=\left(\begin{array}{l}
2 \\ 1 \\ 3
\end{array}\right)-\left(\begin{array}{l}
2 \\ 2 \\ 2
\end{array}\right)=\left(\begin{array}{c}
0 \\ -1 \\ 1
\end{array}\right)
$$
***
After the collision, the parallel component is unchanged, but the perpendicular component reverses. Therefore, 
$$
\vec{v}_{\perp}{^{\prime}}=\left(\begin{array}{l}
-2 \\ -2 \\ -2
\end{array}\right)
$$
Thus, the velocity vector after collision is:
***
$$
\vec{v}_{\text {after}}= \vec{v}_{\perp}{^{\prime}} +\vec{v}_{||}=\left(\begin{array}{c}
-2 \\
-2 \\
-2
\end{array}\right)+\left(\begin{array}{c}
0 \\
-1 \\
1
\end{array}\right) =\left(\begin{array}{c}
-2 \\
-3 \\
-1
\end{array}\right)
$$
| A particle starts at position $\vec{r}_{0}=(0, 1, 0)$ with a velocity $\vec{v} = (2, 1, 3)$. It collides with a wall whose position is given by the equation $x+y+z = 4$. (You may assume throughout this question that all physical quantities are given in dimensionless units, and there are no external forces acting on the particle.)
Give an expression for the trajectory of the particle before the collision. 
\nFind the position at which the particle strikes the wall. 
\nFind the velocity of the particle after the collision with the wall, assuming the collision is elastic.
| 89 | 3 | 12 | 12 | 144 | 4 | 39 | 0 | 0 | It collides with a wall whose position is given by the equation $x+y+z = 4$. You may assume throughout this question that all physical quantities are given in dimensionless units, and there are no external forces acting on the particle. Give an expression for the trajectory of the particle before the collision. Find the position at which the particle strikes the wall. Find the velocity of the particle after the collision with the wall, assuming the collision is elastic. | 5 |
10703359-bbd8-4c73-b85e-57c27e140d16 | 3 | 0 | 0 | 15 | 5 | 0 | 3 | 1 | If a population of cells is exposed to radioactive UTP labelled with $^{32}\mathrm{P}$ (a radioactive isotope of phosphorus), the mRNA being formed at that moment will be labelled. As the mRNA is degraded, the amount of labelled mRNA decreases exponentially with time (we will assume no radioactive uracil is recycled):
$$
L=L_{0}\cdot e^{-\lambda \cdot t}
$$
$$
\lambda = \frac{\ln{2}}{H}
$$
* $L$ Mass of labelled mRNA
<!---->
* $L_{0}$ Mass of labelled mRNA at beginning of experiment
<!---->
* $H$ Half-life of the mRNA (time it takes for half the mRNA to degrade)
<!---->
* $\lambda$ Decay constant
| Rearrange the left-hand equation for $\lambda$
\nCalculate the half-lives of histone H3 and fructose-*bis*-phosphatase mRNAs from the data below. How much longer lived is FBP mRNA than H3 mRNA?
| mRNA | Mass of labelled mRNA at $t=0 \,\mathrm{min}$ ($\mathrm{\mu g \cdot L^{-1}}$) | Mass of labelled mRNA at $t=180 \mathrm{min}$ ($\mathrm{\mu g \cdot L^{-1}}$) |
| :--------- | :---------------------------------------------------------------------------- | :---------------------------------------------------------------------------- |
| FBP | 1.00 | 0.812 |
| Histone H3 | 20.0 | 0.313 |
\nAfter messing about with all this radioactivity, you need to dispose of the radioactive waste. Given that the waste has an activity of $3360 \, \mathrm{Bq}$ (the Becquerel is the SI unit of radioactivity), and that $^{32}\mathrm{P}$ has a half-life of $14.28 \mathrm{days}$, how long would you need to wait until the activity has decayed to just $10 \, \mathrm{Bq}$?
| 3 | 1 | 1 | \n\n | $\lambda=\frac{-\ln{\frac{L}{L_0}}}{t}=\frac{\ln{L_0}-\ln{L}}{t}$
There are lots of other ways of writing this!
\nHalf-lives are $10$ and $0.5$
$10/0.5= 20$
| mRNA | Calculation | $H$ |
| :--------- | :---------------------------------------------------------------- | :---- |
| FBP | $H=\frac{\ln{2}}{\left(\frac{\ln{1}-\ln{0.812}}{180}\right)}=600$ | $10$ |
| Histone H3 | $H=\frac{\ln{2}}{\left(\frac{\ln{20}-\ln{0.313}}{180}\right)}=30$ | $0.5$ |
\n$$
P=P_0e^{-\left(\frac{\ln{2}}{H}\right)t}\
\newline
t=-\frac{\ln{\left(\frac{P}{P_0}\right)}}{\left(\frac{\ln{2}}{H}\right)}=-\frac{\ln{\left(\frac{10}{3360}\right)}}{\left(\frac{\ln{2}}{14.28}\right)}=120\,\mathrm{d}
$$
| If a population of cells is exposed to radioactive UTP labelled with $^{32}\mathrm{P}$ (a radioactive isotope of phosphorus), the mRNA being formed at that moment will be labelled. As the mRNA is degraded, the amount of labelled mRNA decreases exponentially with time (we will assume no radioactive uracil is recycled):
$$
L=L_{0}\cdot e^{-\lambda \cdot t}
$$
$$
\lambda = \frac{\ln{2}}{H}
$$
* $L$ Mass of labelled mRNA
<!---->
* $L_{0}$ Mass of labelled mRNA at beginning of experiment
<!---->
* $H$ Half-life of the mRNA (time it takes for half the mRNA to degrade)
<!---->
* $\lambda$ Decay constant
Rearrange the left-hand equation for $\lambda$
\nCalculate the half-lives of histone H3 and fructose-*bis*-phosphatase mRNAs from the data below. How much longer lived is FBP mRNA than H3 mRNA?
| mRNA | Mass of labelled mRNA at $t=0 \,\mathrm{min}$ ($\mathrm{\mu g \cdot L^{-1}}$) | Mass of labelled mRNA at $t=180 \mathrm{min}$ ($\mathrm{\mu g \cdot L^{-1}}$) |
| :--------- | :---------------------------------------------------------------------------- | :---------------------------------------------------------------------------- |
| FBP | 1.00 | 0.812 |
| Histone H3 | 20.0 | 0.313 |
\nAfter messing about with all this radioactivity, you need to dispose of the radioactive waste. Given that the waste has an activity of $3360 \, \mathrm{Bq}$ (the Becquerel is the SI unit of radioactivity), and that $^{32}\mathrm{P}$ has a half-life of $14.28 \mathrm{days}$, how long would you need to wait until the activity has decayed to just $10 \, \mathrm{Bq}$?
| 225 | 16 | 10 | 10 | 47 | 0 | 131 | 9 | 3 | As the mRNA is degraded, the amount of labelled mRNA decreases exponentially with time we will assume no radioactive uracil is recycled: $ L=L_{0}\cdot e^{-\lambda \cdot t} $ $ \lambda = \frac{\ln{2}}{H} $ $L$ Mass of labelled mRNA embedded $L_{0}$ Mass of labelled mRNA at beginning of experiment embedded $H$ Half-life of the mRNA time it takes for half the mRNA to degrade embedded $\lambda$ Decay constant Rearrange the left-hand equation for $\lambda$ Calculate the half-lives of histone H3 and fructose-bis-phosphatase mRNAs from the data below. How much longer lived is FBP mRNA than H3 mRNA? Given that the waste has an activity of $3360 \, \mathrm{Bq}$ the Becquerel is the SI unit of radioactivity, and that $^{32}\mathrm{P}$ has a half-life of $ L=L_{0}\cdot e^{-\lambda \cdot t} $0, how long would you need to wait until the activity has decayed to just $ L=L_{0}\cdot e^{-\lambda \cdot t} $1? | 3 |
10cb0c12-9685-4f7f-9bc4-fe7f3022a872 | 3 | 0 | 0 | 8 | 4 | 2 | 3 | 2 | Two strain gauges are fitted at $\pm45^{\circ}$ to the axis of a $75\text{ mm}$ diameter steel shaft. The shaft is rotating, and in addition to transmitting power, it is subjected to an unknown bending moment and a direct thrust. The readings of the gauges are recorded, and it is found that the maxima or minima values for each gauge occur at $180^{\circ}$ intervals of shaft rotation and are $-0.00060$ and $+0.00030$ for the two gauges at one instant, and $-0.00050$ and $+0.00040$ for the same gauges $180^{\circ}$ of rotation later. Assume that all the forces and moments are steady, i.e. they do not vary during each rotation of the shaft.
| Calculate the transmitted torque.
\nCalculate the applied bending moment.
\nCalculate the end thrust.
| 3 | 1 | 4 | \n\n | First draw a diagram of the problem:
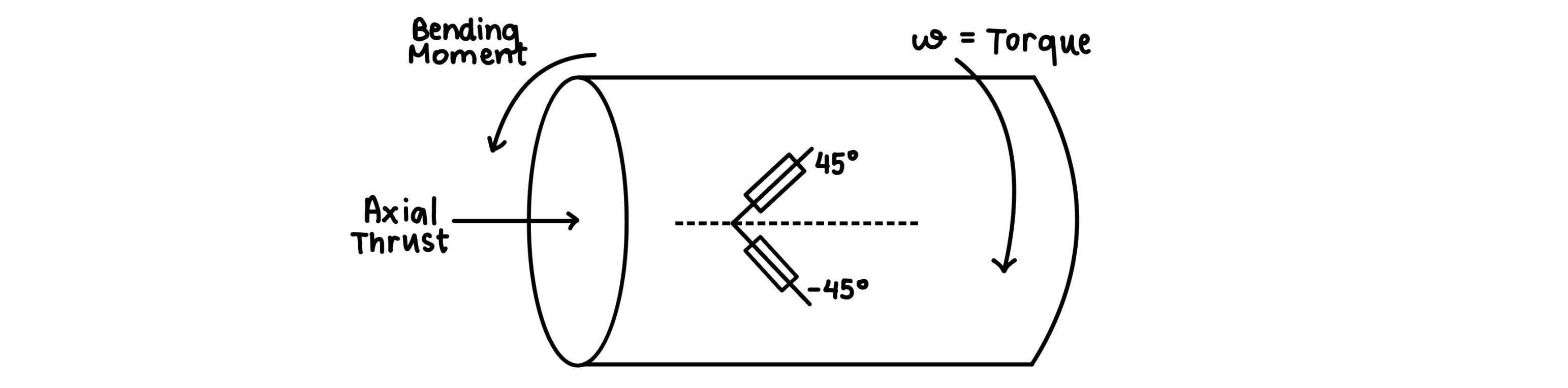  
The strain gauges readings pre rotation:
   
$$
e_{45}=-0.00060 \hspace{30pt} e_{-45}=+0.00030
$$
   
The strain gauge readings post rotation:
   
$$
e_{45}=-0.00050 \hspace{30pt} e_{-45}=+0.00040
$$
   
***
To calculate the transmitted torque, $\gamma_{\theta z}$ needs to be found.
   
***
Looking at both of the strain gauges and using equation 1 (note that the strain gauge values prior to rotation are used as it's best to find the shear stress that results from the torque alone.)
   
$$
\begin{align}
e_\text{n}=\frac{e_\theta+e_z}{2}+\frac{e_\theta-e_z}{2}\cos2\theta+\frac{\gamma_{\theta z}}{2}\sin2\theta
\end{align}
$$
   
***
@ $45\degree$:
$$
\begin{align*}
e_\text{45}&=\frac{e_\theta+e_z}{2}+\cancel{\frac{e_\theta-e_z}{2}\cos90}+\frac{\gamma_{\theta z}}{2}\cancel{\sin90}\\
\hspace{10pt}
\end{align*} \\
$$
$$
\begin{align}
-0.0006=\frac{e_\theta+e_z}{2}+\frac{\gamma_{\theta z}}{2}
\end{align}
$$
   
***
@ $-45\degree$:
$$
\begin{align*}
e_\text{45}&=\frac{e_\theta+e_z}{2}+\cancel{\frac{e_\theta-e_z}{2}\cos(-90)}+\frac{\gamma_{\theta z}}{2}\cancel{\sin(-90)}\\
\hspace{10pt}\\
\end{align*}
$$
$$
\begin{align}
0.0003&=\frac{e_\theta+e_z}{2}-\frac{\gamma_{\theta z}}{2}
\end{align}
$$
   
***
Using equation $(2)$ and $(3)$:
$$
\cancel{\frac{e_\theta+e_z}{2}}+\frac{\gamma_{\theta z}}{2}+0.0006=\cancel{\frac{e_\theta+e_z}{2}}-\frac{\gamma_{\theta z}}{2}-0.0003 \\
\hspace{10pt} \\
\gamma_{\theta z}=-0.0009
$$
   
***
To now find the transmitted torque, using equations from ME1-SAN:
   
$$
\tau=\frac{Tr}{J} \hspace{50pt} G=\frac{\tau}{\gamma}
$$
   
***
Combining the two equations, then solving for torque ($T$):
  
$$
\frac{Tr}{J}=G\gamma\\
\hspace{10pt} \\
\begin{aligned}
T&=\frac{G\gamma J}{r}\\
&=\left( \frac{79.6\times10^9\times-0.0009\times\frac{\pi}{32}(75\times10^{-3})^4}{(75\times10^{-3})}\right)\\
&=\boxed{-5.934\text{ kN}}
\end{aligned}
$$
   
Note that it is also possible to have the torque be positive as it depends on the chosen coordinate system.
\nTo find the bending moment, the following relationship needs to be used:
   
$$
\begin{align}
\sigma_{z, \text{ BM}}=\frac{My}{I} \hspace{30pt}\rightarrow \hspace{30pt}M=\frac{\sigma_{z, \text{ BM}}I}{y}
\end{align}
$$
   
***
First calculate the second moment of area ($I$) and the neutral axis ($y$). $\sigma_{z, \text{ BM}}$ is unknown.
   
$$
\begin{align}
I=\frac{\pi r^4}{4}=\frac{\pi(\frac{75}{2}\times10^{-3})^4}{4}=1.553\times10^{-6}\text{ m}^4
\end{align}
$$
   
$$
\begin{align}
y=r=0.0375 \text{ m}
\end{align}
$$
 
***
Looking at the strain in the normal direction as derived from part (a) for strain gauges that are $\pm\hspace{2pt}45\degree$
   
$$
\begin{align}
(\text{for strain gauge at }45\degree)\text{ }e_\text{n}&=\frac{e_z+e_\theta}{2}+\frac{\gamma_{\theta z}}{2}\\
(\text{for strain gauge at }-45\degree)\text{ }e_\text{n}&=\frac{e_z+e_\theta}{2}-\frac{\gamma_{\theta z}}{2}
\end{align}
$$
   
***
Then find the strain in the axial direction, making sure to include the axial strain as a result of the axial force applied to the shaft and the bending moment.
   
$$
\begin{align}
e_z=e_{AF}+e_{z,\text{ BM}}
\end{align}
$$
   
And find the hoop strain using the definition of Poisson's ratio:
   
$$
\begin{align}
\nu=-\frac{e_\theta}{e_z} \hspace{20pt} \rightarrow \hspace{20pt} e_\theta=-\nu e_z
\end{align}
$$
   
***
Substituting $e_\theta$ and $e_z$ into the equation for $e_\text{n}$:
   
$$
\begin{align}
e_\text{n}=\frac{(e_{AF}+e_{z,\text{BM}})-\nu(e_{AF}+e_{z,\text{BM}})}{2}\pm\frac{\gamma_{\theta z}}{2}
\end{align}
$$
   
***
First looking at the strain gauges prior to rotation:
   
$$
\begin{align}
-0.0006=\frac{1}{2}[(e_{AF}+e_{z,\text{BM}})(1-\nu)+\gamma_{\theta z}] \\
+0.0003=\frac{1}{2}[(e_{AF}+e_{z,\text{BM}})(1-\nu)-\gamma_{\theta z}]
\end{align}
$$
   
***
Subtract equation $(9)$ and equation $(10)$:
   
$$
\begin{align}
-0.0003=(e_{AF}+e_{z,\text{BM}})(1-\nu)
\end{align}
$$
   
***
Then substitute the values of the strain gauges post rotation, note the negative sign to accommodate the $180\degree$ rotation. 
   
$$
\begin{align}
-0.0005=\frac{1}{2}[(e_{AF}-e_{z,\text{BM}})(1-\nu)+\gamma_{\theta z}] \\
+0.0004=\frac{1}{2}[(e_{AF}-e_{z,\text{BM}})(1-\nu)-\gamma_{\theta z}]
\end{align}
$$
   
***
Subtract equation $(12)$ and $(13)$:
   
$$
\begin{align}
-0.0001=(e_{AF}-e_{z,\text{BM}})(1-\nu)
\end{align}
$$
   
***
Then add equations $(11)$ and $(14)$:
   
$$
\begin{align}
-0.0004=2(e_{AF})(1-\nu)
\end{align}
$$
   
***
Rearrange and solve for , using $\nu=0.3$:$e_{AF}$
$$
e_{AF}=-0.0002857
$$
   
***
Substitute $e_{AF}$ into equation $(11)$ to find $e_{z,\text{ BM}}$:
   
$$
\begin{align}
-0.0003&=(-0.002857+e_{z,\text{ BM}})(1-0.3)\\
e_{z,\text{ BM}}&=-0.0001429
\end{align}
$$
   
***
By definition, Young's Modulus is:
   
$$
\begin{align}
E=\frac{\sigma_{z,\text{ BM}}}{e_{z,\text{ BM}}} \hspace{30pt} \rightarrow \hspace{30pt} \sigma_{z,\text{ BM}}=E\times e_{z,\text{ BM}}
\end{align}
$$
   
As such, this can then be used to find the bending moment.
   
***
Going back to equation $(1)$ and substituting the values from $(2), (3),$ and $(17)$ to solve for the bending moment (where $E=207 \text{ GPa}$).
$$
M=\frac{E\times e_{z,\text{ BM}}\times I}{y}=\boxed{-1.225 \text{ kNm}}
$$
\nTo find the axial thrust, use the axial strain ($e_{AF}$) calculated in (b):
   
$$
F_{AF}=\sigma_{AF}\times{A}
$$
***
   
$$
\sigma_{AF}=-0.0002857\times207\times10^9=-59.14\text{ MPa} \\
\hspace{10pt}\\
F_{AF}=\frac{-59.14\times10^6}{\pi (37.5\times10^{-3})^2}=\boxed{-2.613\text{ kPa}}
$$
   
Note the negative sign as the shaft is in compression.
| Two strain gauges are fitted at $\pm45^{\circ}$ to the axis of a $75\text{ mm}$ diameter steel shaft. The shaft is rotating, and in addition to transmitting power, it is subjected to an unknown bending moment and a direct thrust. The readings of the gauges are recorded, and it is found that the maxima or minima values for each gauge occur at $180^{\circ}$ intervals of shaft rotation and are $-0.00060$ and $+0.00030$ for the two gauges at one instant, and $-0.00050$ and $+0.00040$ for the same gauges $180^{\circ}$ of rotation later. Assume that all the forces and moments are steady, i.e. they do not vary during each rotation of the shaft.
Calculate the transmitted torque.
\nCalculate the applied bending moment.
\nCalculate the end thrust.
| 122 | 8 | 58 | 58 | 491 | 0 | 13 | 0 | 0 | The readings of the gauges are recorded, and it is found that the maxima or minima values for each gauge occur at $180^{\circ}$ intervals of shaft rotation and are $-0.00060$ and $+0.00030$ for the two gauges at one instant, and $-0.00050$ and $+0.00040$ for the same gauges $180^{\circ}$ of rotation later. Assume that all the forces and moments are steady, i.e. Calculate the transmitted torque. Calculate the applied bending moment. Calculate the end thrust. | 5 |
117dcbfd-a250-41f3-8eeb-4be2993a67c3 | 0 | 1 | 0 | 15 | 5 | 0 | 1 | 1 | The binding of calcium ions to the signalling protein calmodulin can be modelled by the equation:
$$
\theta=\frac{C^{n}}{K_{d}+C^n}
$$
Where:
* $\theta$ is the fraction of calmodulin molecules bound to calcium 
* $C$ is the concentration of calcium
* $n$ is a constant, greater than zero
* $K_{d}$ is the apparent dissociation constant for the calmodulin/calcium complex; also a number greater than zero
| Consider a plot of $\theta$ ($Y$-axis) against $C$ ($X$-axis).
Which one of the following is true?
| 1 | 1 | 0 | null | As $C$ becomes very large compared to $K_d$, $θ$ tends to $C^{n} / ( C^{n} ) = 1 $
| The binding of calcium ions to the signalling protein calmodulin can be modelled by the equation:
$$
\theta=\frac{C^{n}}{K_{d}+C^n}
$$
Where:
* $\theta$ is the fraction of calmodulin molecules bound to calcium 
* $C$ is the concentration of calcium
* $n$ is a constant, greater than zero
* $K_{d}$ is the apparent dissociation constant for the calmodulin/calcium complex; also a number greater than zero
Consider a plot of $\theta$ ($Y$-axis) against $C$ ($X$-axis).
Which one of the following is true?
| 81 | 9 | 4 | 4 | 13 | 0 | 20 | 4 | 0 | Which one of the following is true? | 1 |
11b0aaf1-ec0d-4b38-b8fb-084e6ce20788 | 5 | 0 | 0 | 19 | 6 | 1 | 1 | 7 | **(L3)**: A solar panel of unit area ($A = 1\text{m}^2$) is placed on the equator on the equinox (i.e. a day of 12 hours of sunlight with the sun passing directly overhead).
| Given that the normal to the solar panel is along the $x$-axis and the sun moves in the $xy$ plane, give an expression for the unit vector $\hat{\mathbf{k}}$ along the direction of the sunlight when it makes an angle $\theta$ to the normal.
\nGive an expression for the angle $\theta$ as a function of the hour $t$ assuming the sun starts at dawn pointing along the $y$-axis. Hence find the *flux* of solar energy falling on the solar panel as a function of the hour since sunrise given that at midday (i.e., sun directly overhead) the sun provides an intensity of $I = 1.0 kW\ m^{-2}$.  
\nIntegrate the total energy falling on the solar panel per day, and compare to the amount that could be received if the panel was tilted during the day so as to always be normal to the flow of solar radiation.
\nRecalculate the energy falling on the panel if it is now placed flat on the ground at a location with latitude $\phi^{\circ}$. (**Hint:** Find the new normal vector of the solar panel.) Hence, find the maximum solar energy (with no solar panel tilting) that can be obtained in London ($\phi = 51.5^\circ$) as compared to the equator.
| 4 | 1 | 4 | Draw the $xy$ plane including:
* The normal to the solar panel.
* The direction of the sunlight vector, at angle $\theta$ to the -axis.
***
Can you now deduce the unit vector $\hat{\mathbf{k}}$? ...
***
... The sunlight vector points *towards* the origin.
\nThink how the power incident on the solar panel would change throughout the daytime (i.e. $0\le h \le 12$):
* When would the power be 0? 
* When would the power be a maximum?
***
You can either deduce the answer logically, or take a more mathematical approach. 
In both approaches, you will need to use the result from **section 1.11** that the flux ($P$ in this case) is the product of the *normal* intensity component and area. 
***
For the mathematical approach, start by considering how to express $P$ in terms of a dot product...
***
... We are concerned with the projection of the sunlight vector onto the solar panel normal as a function of $\theta$...
***
... Then, you need to use your expression for $\theta$ as a function of hour $h$.
\nSince the result from part (b) is a function of hour $h$, you must also convert the intensity $I_\odot$ to be in terms of hour...
***
... Consider how many seconds are in one hour. 
***
Integrate the power with respect to hour $h$. The reason you are doing this is because:
$$
dE = P dt \implies E = \int{P\,dt}
$$
***
For the second part, consider that the power as a function of $h$ would be *constant* if the solar panel normal was tilted in the direction of the sun.
\nThe below diagram may help you to find the new normal vector:

***
Proceed as you did in part (b) to find $P$...
***
... This should tell you the factor by which $P$ is reduced at latitude $\phi$. Hence multiply your result from part (c) by this factor. 
| *North Pole is up*. $\mathbf{\hat{n}}$ is the normal to the solar panel, which is $(1,0,0)$.
***
From the diagram, we see $\hat{\mathbf{k}} = (-\cos\theta, -\sin\theta, 0)$.
\nAt $h=6$, the flux would be $P=AI_\odot = I_\odot$, since $A=1$. 
***
Looking at the figure in the part (a) solutions, we see that the sunlight at a general hour $h$ would be based on the projection of $\mathbf{\hat{k}}$ onto the normal vector. 
***
Utilising that the flux is the dot product of the area and the intensity (power per unit area): $P = \vec{A}\cdot\vec{I_\odot}$, we have:
***
$$
{P} = \left| I_{\odot}\hat{\mathbf{k}}\cdot (- A\hat{\mathbf{n}})\right| = I_{\odot} \cos\theta
$$
Now we express $\theta$ as a function of hour $h$:
***
$$
\theta = \dfrac{\pi}{2} - \pi\dfrac{h}{12}
$$
Substituting into $P$ and applying a trigonometric identity for simplification, we have:
***
$$
P = I_{\odot} \cos\left(\dfrac{\pi}{2} - \dfrac{h\pi}{12} \right) = I_{\odot} \sin\left(\dfrac{h \pi}{12} \right)
$$
where we applied the identity $\cos(\frac{\pi}{2}-x) = \sin{x}$.

\nTo begin integration, we need to convert $I_\odot$ to be in terms of the unit of hour, $h$. Currently, it is in seconds. 
***
The 'energy incident per hour' is given by: $I_{h\odot} = 3600 I_{\odot}$. Then, to find the energy, we integrate the power with respect to time. This is because:
$$
dE = P dt \implies E = \int{P\,dt}
$$
***
$$
\begin{aligned}
E_{eq} & = \int_{0}^{12} I_{h\odot} \sin\left(\pi\dfrac{h}{12} \right) \, dh
\end{aligned}
$$
***
$$
\begin{aligned}
E_{\text{eq}}&= \frac{12\times3600I_{\odot}}{\pi} \left[-\cos\left( \pi\dfrac{h}{12} \right) \right]_{0}^{12} = \frac{2\times12\times3600I_{\odot}}{\pi} \\
& = 27.5\text{MJ}
\end{aligned}
$$
***
If the sunlight fell orthogonally all day, the incident power would be constant, and so: $\displaystyle E_\text{max} = I_{h\odot}\times 12 = I_{\odot}\times 12 \times 3600 = 43.2\text{MJ}$.
So, by not moving the panel you receive only $\dfrac{2}{\pi} = 63.7\%$ of the sunlight.
\nWhen the solar panel was at the equator ($\phi = 0$) latitude, $\mathbf{\hat{n}}=(1,0,0)$. But, at a latitude $\phi$ the normal vector points in the below direction:

***
$$
\hat{\mathbf{n}} = (\cos\phi, 0, \sin\phi)
$$
Proceeding as before:
***
$$
{P} = \left| I_{\odot}\mathbf{\vec{k}}\cdot (-A\mathbf{\vec{n}})\right| = I_{\odot} \cos\theta \cos\phi
$$
So incident sunlight is reduced by $\cos\phi$. Therefore, in London, 
***
$$
E = E_{eq} \cos(51.5^\circ) = 17.1\text{MJ}
$$
| **(L3)**: A solar panel of unit area ($A = 1\text{m}^2$) is placed on the equator on the equinox (i.e. a day of 12 hours of sunlight with the sun passing directly overhead).
Given that the normal to the solar panel is along the $x$-axis and the sun moves in the $xy$ plane, give an expression for the unit vector $\hat{\mathbf{k}}$ along the direction of the sunlight when it makes an angle $\theta$ to the normal.
\nGive an expression for the angle $\theta$ as a function of the hour $t$ assuming the sun starts at dawn pointing along the $y$-axis. Hence find the *flux* of solar energy falling on the solar panel as a function of the hour since sunrise given that at midday (i.e., sun directly overhead) the sun provides an intensity of $I = 1.0 kW\ m^{-2}$.  
\nIntegrate the total energy falling on the solar panel per day, and compare to the amount that could be received if the panel was tilted during the day so as to always be normal to the flow of solar radiation.
\nRecalculate the energy falling on the panel if it is now placed flat on the ground at a location with latitude $\phi^{\circ}$. (**Hint:** Find the new normal vector of the solar panel.) Hence, find the maximum solar energy (with no solar panel tilting) that can be obtained in London ($\phi = 51.5^\circ$) as compared to the equator.
| 236 | 11 | 21 | 21 | 230 | 17 | 204 | 10 | 0 | Given that the normal to the solar panel is along the $x$-axis and the sun moves in the $xy$ plane, give an expression for the unit vector $\hat{\mathbf{k}}$ along the direction of the sunlight when it makes an angle $\theta$ to the normal. Give an expression for the angle $\theta$ as a function of the hour $t$ assuming the sun starts at dawn pointing along the $y$-axis. Hence find the flux of solar energy falling on the solar panel as a function of the hour since sunrise given that at midday i.e., sun directly overhead the sun provides an intensity of $I = 1.0 kW\ m^{-2}$. Integrate the total energy falling on the solar panel per day, and compare to the amount that could be received if the panel was tilted during the day so as to always be normal to the flow of solar radiation. Recalculate the energy falling on the panel if it is now placed flat on the ground at a location with latitude $\phi^{\circ}$. Hint: Find the new normal vector of the solar panel. Hence, find the maximum solar energy with no solar panel tilting that can be obtained in London $x$0 as compared to the equator. | 7 |
11dff774-e524-47dd-bfa9-b66c2bd3dcc9 | 0 | 4 | 0 | 11 | 4 | 2 | 0 | 6 | Entropy change, in general, is defined by the two relationships
  
$\Delta S = \int(\frac{\delta Q}{T})_{\mathrm{rev}}$
  
and
  
$\Delta S_{\mathrm{irrev}} > \Delta S_{\mathrm{rev}}$
| Does the entropy of a system remain constant during reversible and irreversible adiabatic processes?
\nWhat happens to the entropy when heat is transferred from the system to the environment?
| 2 | 0.333333 | 0 | \n | Entropy change can be calculated as
  
$\Delta S = \int(\frac{\delta Q}{T})_{\mathrm{rev}}$
***
For a reversible, adiabatic process, $\delta Q_{\mathrm{rev}}= 0$.
***
Therefore:
  
$\Delta S_{\mathrm{rev}} = 0$
***
For an irreversible, adiabatic process, $\delta Q_{\mathrm{irrev}}= 0$, but we do not know $\delta Q_{\mathrm{rev}}$.
***
From the second relationship, $\Delta S_{\mathrm{irrev}} > \Delta S_{\mathrm{rev}}$
***
Therefore:
  
$ \Delta S_{\mathrm{irrev}} > 0 $
\nSince the heat is transferred from the system to the environment, $\delta Q$ is negative.
***
Therefore, given the relation $\Delta S = \int(\frac{\delta Q}{T})_{\mathrm{rev}}$, it follows that $\Delta S$ is also negative for a reversible process.
***
For an irreversible process: $\Delta S_{\mathrm{irrev}} > \Delta S_{\mathrm{rev}}$
***
Therefore, depending on the magnitude of the irreversibility, $\Delta S$ could be positive, negative or constant.
| Entropy change, in general, is defined by the two relationships
  
$\Delta S = \int(\frac{\delta Q}{T})_{\mathrm{rev}}$
  
and
  
$\Delta S_{\mathrm{irrev}} > \Delta S_{\mathrm{rev}}$
Does the entropy of a system remain constant during reversible and irreversible adiabatic processes?
\nWhat happens to the entropy when heat is transferred from the system to the environment?
| 45 | 2 | 12 | 12 | 99 | 0 | 29 | 0 | 0 | Entropy change, in general, is defined by the two relationships $\Delta S = \int(\frac{\delta Q}{T})_{\mathrm{rev}}$ and $\Delta S_{\mathrm{irrev}} > \Delta S_{\mathrm{rev}}$ Does the entropy of a system remain constant during reversible and irreversible adiabatic processes? What happens to the entropy when heat is transferred from the system to the environment? | 2 |
1222244a-4ad8-4452-9ade-2959a563ef7e | 1 | 0 | 0 | 11 | 4 | 2 | 7 | 11 | Gaseous fuel must be provided for combustion in gas turbines. In a gasifier, solid carbon and steam (as oxidant) form gaseous carbon monoxide and hydrogen. This mixture is known as "water gas" and is used as fuel for turbines. The steam supplied to the gasifier at $1$ atm is dry-saturated and the carbon is at $25^{\circ}\mathrm{C}$. For simplicity, assume that steam is an ideal gas. The product mixture is at a temperature of $300^{\circ}\mathrm{C}$ and contains no excess steam or carbon (i.e. complete reaction). The entry and exit velocities are negligible. Heat transfer occurs between the reaction mixture and the surroundings. 
| Determine the magnitude and the direction of the heat transfer per kilogram of carbon burnt.
| 1 | 1 | 2 | null | Write the balanced equation for the reaction:
***
$\mathrm{C}+\mathrm{H_2O} \rightarrow \mathrm{CO}+\mathrm{H_2}$
***
The equation is already balanced.
***
Apply the SFEE, bearing in mind that there is no work transfer and that kinetic and potential energy changes can be neglected:
  
$\frac{\dot{Q}}{\dot{n}_\mathrm{C}} = \sum\limits_\mathrm{products} \dot{n}_\mathrm{i}\bar{h}_\mathrm{i} - \sum\limits_\mathrm{reactants} \dot{n}_\mathrm{i}\bar{h}_\mathrm{i}$
***
where $\bar{h}_\mathrm{i} = \bar{h}_\mathrm{f}^0 + (\bar{h}_\mathrm{@300^{\circ}C}-\bar{h}_\mathrm{@25^{\circ}C})$ for all species apart from water vapour.
***
***
The water is saturated at $1$ bar. Therefore, $T_\mathrm{H_2O}= 100^{\circ}\mathrm{C}$:
  
$\bar{h}_\mathrm{H_2O} = \bar{h}_\mathrm{f}^0 + (\bar{h}_\mathrm{@100^{\circ}C}-\bar{h}_\mathrm{@25^{\circ}C})$
***
The enthalpies of formation for all species can be found in Table E6 whereas the sensible enthalpies can be found in Table E7. 
***
Substituting in numbers:
  
$\frac{\dot{Q}}{\dot{n}_\mathrm{C}} = [-110530+(8155-0)]+[0+(8005-0)]-[0+0]-[-241820+(2513-0)] =144937~\mathrm{kJ/kg}$
***
Per $\mathrm{kg}$ of carbon:
  
$\frac{\dot{Q}}{\dot{m}_\mathrm{C}} = \frac{144937}{12} = +12073~\mathrm{kJ/kg}$
***
The direction of the heat transfer is positive, indicating that the reaction is endothermic.
| Gaseous fuel must be provided for combustion in gas turbines. In a gasifier, solid carbon and steam (as oxidant) form gaseous carbon monoxide and hydrogen. This mixture is known as "water gas" and is used as fuel for turbines. The steam supplied to the gasifier at $1$ atm is dry-saturated and the carbon is at $25^{\circ}\mathrm{C}$. For simplicity, assume that steam is an ideal gas. The product mixture is at a temperature of $300^{\circ}\mathrm{C}$ and contains no excess steam or carbon (i.e. complete reaction). The entry and exit velocities are negligible. Heat transfer occurs between the reaction mixture and the surroundings. 
Determine the magnitude and the direction of the heat transfer per kilogram of carbon burnt.
| 117 | 3 | 9 | 9 | 116 | 0 | 15 | 0 | 0 | This mixture is known as "water gas" and is used as fuel for turbines. For simplicity, assume that steam is an ideal gas. Determine the magnitude and the direction of the heat transfer per kilogram of carbon burnt. | 3 |
12a5ea53-b0fa-4108-895a-62af8577bc67 | 0 | 0 | 1 | 19 | 6 | 1 | 2 | 7 | **(L5)**: A particle of mass $m$ with position vector $\vec{r}$ relative to origin $O$ experiences a force $\vec{F}$, producing a torque $\vec{\tau}=\vec{r}\times\vec{F}$. The angular momentum of the particle around $O$ is given by $\vec{L}=\vec{r}\times m\vec{v}$, where $\vec{v}$ is the velocity of the particle. Show that the rate of change of angular momentum $d\vec{L}/dt$ is equal to the applied torque.
| **(L5)**: A particle of mass $m$ with position vector $\vec{r}$ relative to origin $O$ experiences a force $\vec{F}$, producing a torque $\vec{\tau}=\vec{r}\times\vec{F}$. The angular momentum of the particle around $O$ is given by $\vec{L}=\vec{r}\times m\vec{v}$, where $\vec{v}$ is the velocity of the particle. Show that the rate of change of angular momentum $d\vec{L}/dt$ is equal to the applied torque.
| 1 | 0.666667 | 0 | To begin, it may help you to look at **section 1.19** and **1.20** to see how cross products are applied to physics scenarios. 
***
To find $d\vec{L}/dt$, refer to **section 1.18**... 
***
... The method is very similar to the product rule for differentiation. 
***
Recall that $\vec{v} = d\vec{r}/dt$ and $\vec{a}= d\vec{v}/dt$...
***
... One of your terms will vanish because the cross product of a vector with itself is 0. 
| We have $\vec{L} = \vec{r}\times(m\vec{v})$. To differentiate this with respect to time, we apply the rule for differentiating vector cross products (**section 1.18**): 
***
$$
\displaystyle \rightarrow \qquad \frac{d\vec{L}}{d t} = \frac{d}{dt} \left( \vec{r}\times(m\vec{v}) \right) = m\left( \frac{d \vec{r}}{dt}\times\vec{v} \right) + m\left( \vec{r}\times\frac{d\vec{v}}{dt} \right)
$$
We factored out $m$, and differentiated $\vec{r}\times\vec{v}$ similar to the product rule. 
***
In the first expression, $d\vec{r}/dt = \vec{v}$; and so $\vec{v}\times\vec{v}=0$:
$$
\frac{d\vec{L}}{dt} = m\left(\vec{r}\times \frac{d\vec{v}}{dt}\right)
$$
***
... Then, factoring $m$ back into the second term, we have by Newton's Second Law that $\vec{F} = m \frac{d\vec{v}}{dt}$. Therefore:
***
$$
\displaystyle \rightarrow \qquad \frac{d\vec{L}}{d t} = \left( \vec{r}\times \vec{F} \right) = \vec{\tau}
$$
As required.
| **(L5)**: A particle of mass $m$ with position vector $\vec{r}$ relative to origin $O$ experiences a force $\vec{F}$, producing a torque $\vec{\tau}=\vec{r}\times\vec{F}$. The angular momentum of the particle around $O$ is given by $\vec{L}=\vec{r}\times m\vec{v}$, where $\vec{v}$ is the velocity of the particle. Show that the rate of change of angular momentum $d\vec{L}/dt$ is equal to the applied torque.
| 61 | 9 | 10 | 10 | 73 | 3 | 61 | 9 | 0 | The angular momentum of the particle around $O$ is given by $\vec{L}=\vec{r}\times m\vec{v}$, where $\vec{v}$ is the velocity of the particle. Show that the rate of change of angular momentum $d\vec{L}/dt$ is equal to the applied torque. | 2 |
12ff524b-68b8-40aa-9d3f-2a68d3fc82aa | 5 | 0 | 1 | 8 | 4 | 2 | 3 | 5 | A mild steel beam of rectangular cross-section, $12.5 \text{ mm}$ wide, $100\text{ mm}$ deep, carries loads which cause a bending moment $M$ and a shear force $F$ at a section $\text{YY}$ along its length. An electric resistance strain gauge rosette, placed at the section as shown below indicates the following strains:
   

$$
\text{along xx}=3.5\times10^{-4} \\
\text{along aa}=-0.75\times10^{-4}\\
\text{along bb}=4.25\times10^{-4}
$$

| Use Mohr's strain circle to determine the magnitude and direction of the principal strains at the site of the rosette.
\nUse an analytical method to confirm the answers found in (a).
\nCalculate the bending moment acting at this cross-section.
\nCalculate the shear force acting across this section, assuming that it is uniform across the whole cross-section.
| 4 | 0.666667 | 4 | \n\n\n | When drawing a Mohr's strain circle, first an $x$-axis is drawn and the three different strain gauges are drawn out:
   
  
***
Then overlay an extended strain gauge rosette configuration on the intermediate strain line ($e_x$ in this case) so it intersects with the $e_a$ and $e_b$ lines.
   
  
***
The three points where these intersect will form three points on the strain circle. 
   
  
***
The perpendicular bisectors of the lines between strain gauges intersect at the center of the circle.
  \
  
***
Mohr's circle can now be drawn.
   
  
***
And the value of the principal strains can also be found.
  
***
The principal angle can also be found (noting that all angles are doubled in Mohr's circle.)
  
***
Therefore, the following values are found from the Mohr's circle:
   
$$
e_1=\boxed{0.00048}~~~~~e_2=\boxed{-0.00013}~~~~~\theta_p=\boxed{27.5\degree}
$$
\nUsing equation $1$ to find the strain measured by each of the strain gauges:
   
$$
\begin{align}
e_n=\frac{1}{2}(e_x+e_y)+\frac{1}{2}(e_x-e_y)\cos2\theta+\frac{\gamma_{xy}}{2}\sin2\theta \\
\end{align}
$$
   
***
Looking at the strain gauges within the rosette:
At $0\degree$, $e_y$ cancels out so the bar only experiences $e_x$.
   
$$
\begin{align}
e_0=\frac{e_x+e_y}{2}+\frac{e_x-e_y}{2}=0.00035~~~~\rightarrow~~~~e_x=0.00035
\end{align}
$$
   
***
Additionally, $\pm45\degree$ can also be considered:
   
$$
\begin{align}
e_{45}=\frac{e_x+e_y}{2}+\frac{\gamma_{xy}}{2}=0.000425\\
e_{-45}=\frac{e_x+e_y}{2}-\frac{\gamma_{xy}}{2}=-0.000075
\end{align}
$$
   
***
Adding equations $(3)+(4)$:
   
$$
\begin{align}
e_x+e_y=0.00035\\
\end{align}
$$
   
And since $e_x=0.00035$, $e_y=0$.  
   
***
Subtracting equations $(4)-(3)$:
   
$$
\begin{align}
\gamma_{xy}=0.0005
\end{align}
$$
   
***
The principal strains can now be calculated using equation $(7)$, and substituting in $(5)$, $(6)$:
   
$$
\begin{align}
e_{1,2}=\frac{(e_x+e_y)}{2}\pm\frac{1}{2}\sqrt{(e_x-e_y)^2+\gamma_{xy}^2}
\end{align}
$$
   
***
As such, the principal strains are:
   
$$
e_1=\boxed{0.0004802}~~~~e_2=\boxed{-0.0001306}
$$
   
***
The principal angle can also be found as such:
   
$$
\tan2\theta=\frac{\gamma_{xy}}{e_x-e_y}~~~~\rightarrow~~~~\theta_p=\boxed{27.5\degree}
$$
\nTo find the bending moment, the axial stress needs to be calculated first, this can be done using Hooke's Law in the $x$ and $y$ directions:
   
$$
\begin{align}
e_x&=\frac{1}{E}(\sigma_x-\nu\sigma_y)\\
e_y&=\frac{1}{E}(\sigma_y-\nu\sigma_x)=0
\end{align}
$$
   
***
Looking at equation $(2)$ and rearranging:
   
$$
\begin{align}
\sigma_y=\nu\sigma_x
\end{align}
$$
   
***
Rearranging equation $(1)$ and substituting in $(3)$:
   
$$
\begin{align}
\nu\sigma_x=\frac{\sigma_x-Ee_x}{\nu}\\
\sigma_x=\frac{Ee_x}{1-\nu^2}
\end{align}
$$
   
***
Substituting values into equation $(5)$, noting that $E=207\text{ GPa and } \nu=0.3$ for steel.
   
$$
\begin{align}
\sigma_x=\frac{(207\times10^ 9)(3.5\times10^{-4})}{1-(0.3)^2}=79.62 \text{ MPa}
\end{align}
$$
   
***
Additionally, since the applied axial stress ($\sigma_x$) is at $y=19\text{ mm}$ from the neutral axis, therefore, at the top and bottom surfaces:
   
$$
\sigma_{BM}=\frac{\text{length}}{\text{distance from neutral axis}}(\sigma_x)=\frac{50}{19}\times79.61=209.5\text{ MPa}
$$
   
***
Using the following relationship, the bending moment can be found.
   
$$
M=\frac{\sigma_{\text{BM}}I}{y}=\frac{(209.5\times10^9)(\frac{0.0125\times0.1^3}{12})}{0.05}=\boxed{4.394\text{ kN}}
$$
\nTo find the shear force:
   
$$
\begin{align*}
\text{SF}&=\tau_{xy}\times A \\
\end{align*}
$$
   
***
Substituting $\tau=G\gamma$ and then solving:
   
$$
\begin{align*}
\text{SF}&=G\gamma_{xy}\times A\\
&=79.6\times10^9\times 0.0005\times0.0125\times0.1
=\boxed{49.75\text{ kN}}
\end{align*}
$$
| A mild steel beam of rectangular cross-section, $12.5 \text{ mm}$ wide, $100\text{ mm}$ deep, carries loads which cause a bending moment $M$ and a shear force $F$ at a section $\text{YY}$ along its length. An electric resistance strain gauge rosette, placed at the section as shown below indicates the following strains:
   

$$
\text{along xx}=3.5\times10^{-4} \\
\text{along aa}=-0.75\times10^{-4}\\
\text{along bb}=4.25\times10^{-4}
$$

Use Mohr's strain circle to determine the magnitude and direction of the principal strains at the site of the rosette.
\nUse an analytical method to confirm the answers found in (a).
\nCalculate the bending moment acting at this cross-section.
\nCalculate the shear force acting across this section, assuming that it is uniform across the whole cross-section.
| 109 | 6 | 43 | 43 | 427 | 0 | 56 | 0 | 1 | An electric resistance strain gauge rosette, placed at the section as shown below indicates the following strains: $ \text{along xx}=3.5\times10^{-4} \\ \text{along aa}=-0.75\times10^{-4}\\ \text{along bb}=4.25\times10^{-4} $ Use Mohr's strain circle to determine the magnitude and direction of the principal strains at the site of the rosette. Use an analytical method to confirm the answers found in a. Calculate the bending moment acting at this cross-section. Calculate the shear force acting across this section, assuming that it is uniform across the whole cross-section. | 4 |
1306d7c8-8825-4ea0-9ba6-1c1ae1c1034b | 1 | 0 | 0 | 2 | 1 | 2 | 7 | 0 | (Based on P4.9, White) An incompressible flow has a velocity field of the form 
${\bf u}=4xy^2 {\bf i}+f(y){\bf j}-zy^2{\bf k}$
What is $f(y)$?
| (Based on P4.9, White) An incompressible flow has a velocity field of the form 
${\bf u}=4xy^2 {\bf i}+f(y){\bf j}-zy^2{\bf k}$
What is $f(y)$?
| 1 | 0.333333 | 0 | The continuity equation for incompressible flow is
$ \nabla\cdot{\bf u}=0 $
Expand this by getting the divergence of $\bf{u}$.
***
Rearrange the equation you have to isolate the $f$ term on one side. Integrate to get an expression for $f$.
| The continuity equation for incompressible flow is
$\nabla\cdot{\bf u}=0 \quad\Rightarrow\quad 4y^2+\frac{df}{dy}-y^2=0 \quad\Rightarrow\quad f=c-y^3$ where $c$ is constant.
| (Based on P4.9, White) An incompressible flow has a velocity field of the form 
${\bf u}=4xy^2 {\bf i}+f(y){\bf j}-zy^2{\bf k}$
What is $f(y)$?
| 19 | 2 | 2 | 2 | 12 | 4 | 19 | 2 | 0 | Based on P4.9, White An incompressible flow has a velocity field of the form ${\bf u}=4xy^2 {\bf i}+f(y){\bf j}-zy^2{\bf k}$ What is $f(y)$? | 1 |
134244e5-2124-4b14-b8fb-1b682a5aa9e3 | 2 | 0 | 0 | 16 | 6 | 1 | 2 | 4 | Integrate
| $$
\displaystyle {x^4 \over x^2 + 1}
$$
\n$$
\displaystyle {1\over x\ln x}
$$
| 2 | 0.666667 | 2 | To simplify the integrand, you want to get $\displaystyle {x^4 \over x^2 + 1}$, which is in the form $\displaystyle \frac{\mathrm{4th\,degree}}{\mathrm{quadratic}}$, into the form $\displaystyle \mathrm{quadratic} + {\mathrm{linear}\over \mathrm{quadratic}}$ , as you know how to evaluate integrals in this form.
***
There are a few methods to do this, for example, long division, or inspection. Use whichever method you prefer to change it into this form.
Then you can evaluate the integral as normal.
\nTry the substitution $u=\ln x$ 
***
With this substitution, $x=e^u$ and $\displaystyle {\mathrm{d}x\over \mathrm{d}u} = e^u$.
Can you evaluate the integral now?
***
Substitute $u=\ln x$ at the end, to get it into a function of $x$ not $u$.
| To simplify the integrand, you want to get $\displaystyle {x^4 \over x^2 + 1}$, which is in the form $\displaystyle \frac{\mathrm{4th\,degree}}{\mathrm{quadratic}}$, into the form $\displaystyle \mathrm{quadratic} + {\mathrm{linear}\over \mathrm{quadratic}}$ , as you know how to evaluate integrals in this form.
There are a few methods to do this, for example, long division, or inspection. Use whichever method you prefer to change it into this form.
***
Using inspection,
$$
\begin{aligned} {x^4 \over x^2 + 1} = \frac{x^2(x^2+1)-1(x^2+1)}{x^2+1} = x^2-1 + {1\over x^2+1} \end{aligned}
$$
or,
$$
\begin{aligned} {x^4 \over x^2 + 1} = {x^4-1 \over x^2+1} + {1\over x^2+1} = \frac{(x^2-1)(x^2+1)}{x^2+1}+{1\over x^2+1} = x^2-1 + \frac{1}{x^2+1} \end{aligned}
$$
Now can you evaluate the integral?
***
$$
\begin{aligned}
\int {x^4 \over x^2+1} \mathrm{d}x
&= \int x^2-1+\frac{1}{x^2+1} \mathrm{d}x \\
&= {1\over3}x^3-x+\tan^{-1}x + c
\end{aligned}
$$
\nTry the substitution $u=\ln x$ 
***
With this substitution, $x=e^u$ and $\displaystyle {\mathrm{d}x\over\mathrm{d}u}= e^u$.
Can you evaluate the integral now?
***
$$
\begin{aligned}
\int\frac{1}{x\ln x}\,\mathrm{d}x
&= \int\frac{1}{e^uu}\frac{\mathrm{d}x}{\mathrm{d}u} \,\mathrm{d}u
\\
&= \int {1\over u} \,\mathrm{d}u
\\
&= \ln u +c
\end{aligned}
$$
***
Substituting $u=\ln x$,
$$
= \ln(\ln x) + c
$$
where $c$ is an integration constant.
Note: take care with $x$ domain. e.g. $0<x<1$ gives $\ln x<0$ and $\ln(\ln x)$ is not real.
| Integrate
$$
\displaystyle {x^4 \over x^2 + 1}
$$
\n$$
\displaystyle {1\over x\ln x}
$$
| 4 | 2 | 17 | 17 | 118 | 9 | 3 | 2 | 0 | Integrate $ \displaystyle {x^4 \over x^2 + 1} $ $ \displaystyle {1\over x\ln x} $ | 1 |
13ef2460-a035-442a-82fa-5666c31e06fa | 4 | 0 | 0 | 11 | 4 | 2 | 7 | 9 | Consider combustion of oil and wood in air.
| Calculate the air requirements and the atmospheric nitrogen in the products if air is used for stoichiometric combustion of $100~\mathrm{kg}$ of oil.
\n Calculate the stoichiometric air requirements and excess air in the products if $100~\mathrm{kg}$ of wood is burnt with $30\%$ excess air.
| 2 | 1 | 2 | \n | Since the nitrogen in the air mixture does not react, the mass of the $\mathrm{O_2}$ in the reactant air mixture and the mass of the $\mathrm{CO_2}$ and $\mathrm{H_2O}$ in the products will be the same as in Q9a:
  
Mass $\mathrm{O_2} = 337.1~\mathrm{kg}$
  
Mass $\mathrm{CO_2} = 318.3~\mathrm{kg}$
  
Mass $\mathrm{H_2O} = 118.8~\mathrm{kg}$
***
Calculate the total mass of nitrogen in the air:
  
$337.1\times \frac{76.8}{23.2} = 1115.9~\mathrm{kg}$
***
Calculate the total mass of air:
  
$1115.9+337.1 = 1453~\mathrm{kg}$
\nAs in part (a), the nitrogen does not react. Therefore, the mass of $\mathrm{O_2}$ in the reactant air and the mass of the $\mathrm{CO_2}$ and $\mathrm{H_2O}$ in the products will be the same as in Q9b for stoichiometric combustion:
  
Mass $\mathrm{O_2} = 116.7~\mathrm{kg}$
  
Mass $\mathrm{CO_2} = 155.8~\mathrm{kg}$
  
Mass $\mathrm{H_2O} = 60.9~\mathrm{kg}$
***
Calculate the total mass of nitrogen in the products for stoichiometric combustion:
  
$116.7\times\frac{76.8}{23.2} = 386.3~\mathrm{kg}$
***
Calculate the total mass of air required for stoichiometric combustion:
  
$386.3+116.7 = 503~\mathrm{kg}$
***
***
Calculate the excess air in products:
  
$503\times 0.3 = 150.9~\mathrm{kg}$
| Consider combustion of oil and wood in air.
Calculate the air requirements and the atmospheric nitrogen in the products if air is used for stoichiometric combustion of $100~\mathrm{kg}$ of oil.
\n Calculate the stoichiometric air requirements and excess air in the products if $100~\mathrm{kg}$ of wood is burnt with $30\%$ excess air.
| 51 | 3 | 17 | 17 | 154 | 0 | 43 | 3 | 0 | Consider combustion of oil and wood in air. Calculate the air requirements and the atmospheric nitrogen in the products if air is used for stoichiometric combustion of $100~\mathrm{kg}$ of oil. Calculate the stoichiometric air requirements and excess air in the products if $100~\mathrm{kg}$ of wood is burnt with $30\%$ excess air. | 3 |
13f4f722-af7c-4bfe-b4ee-b4018b2cf9b2 | 1 | 0 | 0 | 11 | 4 | 2 | 5 | 4 | Steam enters a turbine at $600^{\circ}\mathrm{C}$ and $20$ bar, and leaves at $0.1$ bar (all total conditions). 
| If the turbine total-to-total isentropic efficiency is $92\%$, what is the specific work output?
| 1 | 0.333333 | 2 | null | Apply the SFEE, bearing in mind that there is no heat transfer and kinetic and potential energy changes can be neglected:
  
$-\frac{\dot{W}}{\dot{m}} = h_{03} - h_{01}$
***
The enthalpies can be found using the steam tables.
***
At state $1$, the vapour is superheated. From Table E26 at $600^{\circ}\mathrm{C}$, $20$ bar:
  
$h_{01} = 3690.7~\mathrm{K}$
***
For the case of an isentropic process, $ s_{03\mathrm{s}} = s_{01} = 7.704~\mathrm{kJ/kgK} $ (from Table E26).
***
The dryness fraction $ x_{03\mathrm{s}} $ can be calculated using values of $s_\mathrm{f}$ and $s_\mathrm{g}$ at $0.1$ bar (Table E20):
  
$x_{03\mathrm{s}} = \frac{s_{03\mathrm{s}} - s_\mathrm{f}}{s_\mathrm{g} - s_\mathrm{f}}$
***
Substituting in numbers:
  
$x_{03\mathrm{s}} - \frac{7.704-0.6492}{8.149-0.6492} = 0.94$
***
Now the enthalpy, $h_{03\mathrm{s}}$, can be calculated using the values of $h_\mathrm{f}$ and $h_\mathrm{g}$ at $0.1$ bar (Table E20):
  
$h_{03\mathrm{s}} =191.81 + 0.94(2392.1) = 2440.4~\mathrm{kJ/kg}$
***
$h_{03}$ can be calculated using the equation for isentropic efficiency for a turbine:
  
$\eta_{tt} = \frac{h_{01} - h_{03}}{h_{01} - h_{03\mathrm{s}}}$
***
Substituting in numbers and rearranging for $h_{03}$:
  
$h_{03} = 3690.7 - 0.92(3690.7 - 2440.4) = 2540.4~\mathrm{kJ/kg}$
***
Substituting this back into the original SFEE equation:
  
$\frac{\dot{W}}{\dot{m}} = -(2540.4-3690.7) = 1150~\mathrm{kJ/kg}$
| Steam enters a turbine at $600^{\circ}\mathrm{C}$ and $20$ bar, and leaves at $0.1$ bar (all total conditions). 
If the turbine total-to-total isentropic efficiency is $92\%$, what is the specific work output?
| 32 | 4 | 22 | 22 | 152 | 0 | 15 | 1 | 0 | If the turbine total-to-total isentropic efficiency is $92\%$, what is the specific work output? | 1 |
148040a4-9421-4696-b8b9-7d976a131fde | 1 | 0 | 0 | 16 | 6 | 1 | 7 | 5 |  Show that the function 
$$
u(x, y) = x^4 + 4x^2y^2 - 2x^2 + 2y^2 -1
$$
has three stationary points - two local minima and one saddle point.
|  Show that the function 
$$
u(x, y) = x^4 + 4x^2y^2 - 2x^2 + 2y^2 -1
$$
has three stationary points - two local minima and one saddle point.
| 1 | 0.666667 | 2 | From section 5.5 of the notes, stationary points of a function $u(x,y)$ are where
$$
\begin{aligned}
{\partial u\over\partial x} = 0 = {\partial u\over\partial y}
\end{aligned}
$$
By finding these partial derivatives and applying this condition, find the three stationary points of $u$.
***
You can determine their nature using
$$
\displaystyle
E_0 = \left[(u_{xy})^2 - (u_{xx})(u_{xy}) \right]_{x_0, y_0}
= \left[\left({\partial^2u\over \partial x\partial y}\right)^2 - \left({\partial^2u\over\partial x^2}\right)\left({\partial^2u\over\partial y^2}\right)\right]_{x_0, y_0}
$$
where $(x_0, y_0)$ is the position of the stationary point.
If $E_0>0$ it is a saddle point.
If $E_0<0$ then if $\displaystyle \left({\partial^2u\over\partial x^2}\right)_{x_0, y_0} < 0$ it is a local maximum or if $ \displaystyle \left({\partial^2u\over\partial x^2}\right)_{x_0, y_0} > 0 $ it is a local minimum.
If $E_0 = 0$ then you need to look at higher derivatives.
Now, can you determine their nature of each of the stationary points?
| From section 5.5 of the notes, stationary points of a function $u(x,y)$ are where
$$
\begin{aligned}
{\partial u\over\partial x} = 0 = {\partial u\over\partial y}
\end{aligned}
$$
By finding these partial derivatives and applying this condition, find the three stationary points of $u$.
***
$$
\begin{aligned}
{\partial u\over\partial x} &= 4x^3+8xy^2-4x =x(x^2+2y^2-1) &= 0 \quad(1) \\
{\partial u\over\partial y} &= 8x^2y+4y =y(2x^2+1)&=0 \quad(2)
\end{aligned}
$$
Can you find the stationary points now?
***
Giving $y=0$ and $x^2=-{1\over2}$, where the second one is invalid as it has no real roots. 
By substituting in $y=0$ to $(1)$,
$$
\begin{aligned}
x(x^2-1)&=0 \\
x&=0,\pm 1
\end{aligned}
$$
Giving the three stationary points,
$$
(0,0), (-1,0), (1,0)
$$
Now can you try to determine their nature? \[4.7 in lectures]
***
You can determine their nature using
$$
\displaystyle
E_0 = \left[(u_{xy})^2 - (u_{xx})(u_{xy}) \right]_{x_0, y_0}
= \left[\left({\partial^2u\over \partial x\partial y}\right)^2 - \left({\partial^2u\over\partial x^2}\right)\left({\partial^2u\over\partial y^2}\right)\right]_{x_0, y_0}
$$
where $(x_0, y_0)$ is the position of the stationary point.
If $E_0>0$ it is a saddle point.
If $E_0<0$ then if $\displaystyle \left({\partial^2u\over\partial x^2}\right)_{x_0, y_0} < 0$ it is a local maximum or if $ \displaystyle \left({\partial^2u\over\partial x^2}\right)_{x_0, y_0} > 0 $ it is a local minimum.
If $E_0 = 0$ then you need to look at higher derivatives.
Now, can you determine their nature of each of the stationary points?
***
$$
\begin{aligned}
{\partial^2u\over\partial x^2} &= 12x^2+8y^2-4 \\
{\partial^2u\over\partial y^2} &= 8x^2+4 \\
{\partial^2u\over \partial x\partial y} = {\partial^2u\over \partial y\partial x} &= 16xy
\end{aligned}
$$
For $(-1,0)$,
$$
\begin{aligned}
{\partial^2u\over\partial x^2} &= 8 >0\\
{\partial^2u\over\partial y^2} &=12 \\
{\partial^2u\over \partial x\partial y}&= 0 \\
E_0 &= -96 < 0
\end{aligned}
$$
So it is a local minimum.
Have a go at finding the nature of the other points using this method.
***
For $(0,0)$,
$$
\begin{aligned}
{\partial^2u\over\partial x^2} &= -4 \\
{\partial^2u\over\partial y^2} &=4 \\
{\partial^2u\over \partial x\partial y}&= 0 \\
E_0 &= 16 > 0
\end{aligned}
$$
So it is a saddle point.
For $(1,0)$,
$$
\begin{aligned}
{\partial^2u\over\partial x^2} &= 8 >0\\
{\partial^2u\over\partial y^2} &=12 \\
{\partial^2u\over \partial x\partial y}&= 0 \\
E_0 &= -96 < 0
\end{aligned}
$$
So it is a local minimum.
$(0,0) \rightarrow$ Saddle point
$(1,0) \rightarrow$ Local minimum
$(-1,0) \rightarrow$ Local minimum

|  Show that the function 
$$
u(x, y) = x^4 + 4x^2y^2 - 2x^2 + 2y^2 -1
$$
has three stationary points - two local minima and one saddle point.
| 17 | 1 | 10 | 10 | 82 | 7 | 17 | 1 | 0 |  Show that the function 
$$
u(x, y) = x^4 + 4x^2y^2 - 2x^2 + 2y^2 -1
$$
has three stationary points - two local minima and one saddle point.
| 0 |
148e2545-9224-4659-8e6e-732dd07642ca | 9 | 0 | 0 | 9 | 4 | 2 | 0 | 0 | Calculate the resistor nominal value and upper and lower limits for each of the following parameters:
| The resistor parameters are given in the table below:
| *a* | *b* | *c* | *tol* |
| :------- | :------- | :---- | :-------- |
| *Yellow* | *Orange* | *Red* | *Nothing* |

\nThe resistor parameters are given in the table below:
| *a* | *b* | *c* | *tol* |
| :------- | :------ | :------- | :----- |
| *Yellow* | *Black* | *Orange* | *Gold* |

\nThe resistor parameters are given in the table below:
| *a* | *b* | *c* | *tol* |
| :------ | :----- | :---- | :------- |
| *Green* | *Blue* | *Red* | *Silver* |

| 3 | 0.333333 | 2 | \n\n | $R = ab \times 10^c$
***
$R = 43 \times 10^2 = 4300~\Omega$
***
No tolerance specification - $\pm 20\%$
***
Therefore:
$R_{\mathrm{min}} = 4300 - (20\%\times 4300) = 3400~\Omega$
$R_{\mathrm{max}} = 4300 + (20\% \times 4300) = 5160~\Omega$
\n$R = ab \times 10^c$
***
$R = 40 \times 10^3 = 40000~\Omega$
***
Gold tolerance - $\pm5 \%$
***
Therefore:
$R_{\mathrm{min}} = 40000 - (5 \% \times 40000) = 38000~\Omega$
$R_{\mathrm{max}} = 40000 + (5 \% \times 40000) = 42000~\Omega$
\n$R = ab \times 10^c$
***
$R = 56\times 10^2 = 5600~\Omega$ 
***
Silver tolerance - $\pm 10\%$
***
Therefore:
$R_{\mathrm{min}} = 5600 - (10\% \times 5600) = 5040~\Omega$
$R_{\mathrm{max}} = 5600 + (10\% \times 5600) = 6160~\Omega$
| Calculate the resistor nominal value and upper and lower limits for each of the following parameters:
The resistor parameters are given in the table below:
| *a* | *b* | *c* | *tol* |
| :------- | :------- | :---- | :-------- |
| *Yellow* | *Orange* | *Red* | *Nothing* |

\nThe resistor parameters are given in the table below:
| *a* | *b* | *c* | *tol* |
| :------- | :------ | :------- | :----- |
| *Yellow* | *Black* | *Orange* | *Gold* |

\nThe resistor parameters are given in the table below:
| *a* | *b* | *c* | *tol* |
| :------ | :----- | :---- | :------- |
| *Green* | *Blue* | *Red* | *Silver* |

| 127 | 0 | 15 | 15 | 40 | 0 | 111 | 0 | 3 | Calculate the resistor nominal value and upper and lower limits for each of the following parameters: The resistor parameters are given in the table below: table | 1 |
14cdfbb9-4bfd-4237-92d4-1349478acf69 | 0 | 4 | 0 | 19 | 6 | 1 | 2 | 0 | **(L4):** Find whether $\vec{p}\times\vec{q}$ points into or out of the page for the following pairs of vectors:
| 
\n
\n
\n
| 4 | 0.333333 | 0 | 
\n
\n
\n
***
What happens to the cross-product if the two vectors are (anti-)parallel?
| \n\n\n | **(L4):** Find whether $\vec{p}\times\vec{q}$ points into or out of the page for the following pairs of vectors:

\n
\n
\n
| 21 | 1 | 0 | 0 | 1 | 0 | 4 | 0 | 1 | L4: Find whether $\vec{p}\times\vec{q}$ points into or out of the page for the following pairs of vectors: | 1 |
15068760-4517-48f5-8e66-40e108676d7c | 0 | 0 | 1 | 20 | 6 | 1 | 1 | 2 | null | Explain why the magnitudes of $\cos{z}$ and $\sin{z}$ are unbounded (i.e., can go to infinity).
| 1 | 0.333333 | 1 | Use the hyperbolic/trigonometric formula for $\cos{z}$ in terms of $x$ and $y$ (refer to **section 2.6** of the notes).
***
Find the magnitude of cos z using this formula. 
***
Can you use trigonometric/hyperbolic identities to simplify your expression?
***
Does this simplified formula prove that $\cos{z}$ is unbounded? 
***
Do the same for $\sin{z}$. 
| Consider first the complex cosine function:
$$
\begin{equation*}
\cos z=\cos x\cosh y-i\,\sin x\sinh y\, .
\end{equation*}
$$
***
Find the magnitude of this function and simplify as follows:
$$
\begin{align*}
|\cos z|
&=\bigl(\cos^2x\cosh^2y+\sin^2x\sinh^2y\bigr)^{1/2}\\
\end{align*}
$$
***
Simplify this by making use of trigonometric and hyperbolic identities:
$$
\begin{align*}
|\cos z|
&=\bigl[\cos^2x\cosh^2y+(1-\cos^2x)\sinh^2y\bigr]^{1/2}\\
&=\bigl[\cos^2x(\cosh^2y-\sinh^2y)+\sinh^2y\bigr]^{1/2}\\
&=\bigl(\cos^2x+\sinh^2y\bigr)^{1/2}\, .
\end{align*}
$$
***
Since:
$$
\begin{equation*}
\sinh y={e^{y}-e^{-y}\over2}\, ,
\end{equation*}
$$
***
We see that:
$$
\begin{equation*}
\lim_{y\to\infty}|\cos z|\to{\textstyle{1\over2}}e^y\to\infty\, .
\end{equation*}
$$
***
You can use an analogous argument to show that the complex sine function is also unbounded.
| null | 1 | 0 | 5 | 5 | 56 | 5 | 15 | 2 | 0 | Explain why the magnitudes of $\cos{z}$ and $\sin{z}$ are unbounded (i.e., can go to infinity).
| 0 |
150d356e-54d3-4aa5-9b2b-94fa0a483d7b | 1 | 0 | 1 | 14 | 4 | 2 | 6 | 0 | Suppose that you were lucky enough to take the following picture of a Super Hornet flying slightly above the speed of sound at sea level. The weather conditions are just perfect so that a Mach cone is made visible thanks to a condensation phenomenon.
 | You are tasked with estimating the aircraft speed, based on the picture. List all the necessary assumptions.\nEstimate the aircraft speed. | 2 | 0.333333 | 1 | \n | \n | Suppose that you were lucky enough to take the following picture of a Super Hornet flying slightly above the speed of sound at sea level. The weather conditions are just perfect so that a Mach cone is made visible thanks to a condensation phenomenon.
You are tasked with estimating the aircraft speed, based on the picture. List all the necessary assumptions.\nEstimate the aircraft speed. | 64 | 0 | 0 | 0 | 1 | 0 | 20 | 0 | 0 | Suppose that you were lucky enough to take the following picture of a Super Hornet flying slightly above the speed of sound at sea level. List all the necessary assumptions. Estimate the aircraft speed. | 3 |
15defe31-8d74-4dee-9128-f837439584e2 | 2 | 0 | 1 | 8 | 4 | 2 | 1 | 0 | At a central point in a boiler rivet, the material of the rivet is undergoing a shear stress of $77 \text{ MPa}$ while resisting movement between the boiler plates and a tensile stress of $62 \text{ MPa}$ due to the extension of the rivet.
   

| Draw an element of material at the point of interest, and indicate the stresses acting on its faces.
\nFind the magnitude of the tensile stresses acting at a point on the two planes making an angle of $80^{\circ}$ to the axis of the rivet. *(Hint: Noting direction of rivet axis on element, draw the planes to create triangular elements and $\sigma_A > \sigma_B$*).
| 2 | 0.333333 | 2 | \n | \nFirst construct the triangular element based on Plane A:

$$
\footnotesize
\text{Figure 2: Triangular element along plane A.}
$$
   
***
Using the assumption that the element has a thickness of 1 unit, force equilibrium only needs to be applied along the direction of the red line as seen in Figure 1 from solution Q2.1(a).
   
Apply trigonometry:
$$
\begin{align}
OB =AB\sin(80)\\
OA=AB\cos(80)
\end{align}
$$
   
***
Then apply equilibrium equations to find the tensile stress. Keep in mind that terms associated with $77\text{ MPa}$ are for shear stress (blue lines), whilst the terms with $62 \text{ MPa}$ are for axial stress (black line).
   
$$
\begin{equation}
\sigma_A=(62\times OB\sin80)+(77\times OB\cos80)+(77\times OA\sin80)
\end{equation}
$$
   
***
Using equations $(1)$ and \$(2, the equation above becomes:
   
$$
\begin{align*}
\sigma_A&=62\sin^280+77\sin80\cos80+77\sin80\cos80 \\
&=62\sin^280+154\sin80\cos80 \\
&=\boxed{86.46 \text{ MPa}}
\end{align*}
$$
   
***
The same process is applied to the triangular element based on Plane B:

$$
\footnotesize
\text{Figure 2: Triangular element along plane B.}
$$
   
***
Application of the trigonometry:
   
$$
\begin{align}
AO=AB\sin80 \\
BO=AB\cos80
\end{align}
$$
   
***
Apply equilibrium equations, noting that the shear force now acts towards $\sigma$ instead of away such as in A. Meaning there needs to be a change of signs for the shear stresses.
  
$$
\begin{align}
\sigma_B=(62\times AO\sin80)-(77\times AO\cos80)-(77\times BO\sin80)
\end{align}
$$
   
***
Substituting 4, 5 into 6 results in:
   
$$
\sigma_B=\boxed{33.80 \text{ MPa}}
$$
  
| At a central point in a boiler rivet, the material of the rivet is undergoing a shear stress of $77 \text{ MPa}$ while resisting movement between the boiler plates and a tensile stress of $62 \text{ MPa}$ due to the extension of the rivet.
   

Draw an element of material at the point of interest, and indicate the stresses acting on its faces.
\nFind the magnitude of the tensile stresses acting at a point on the two planes making an angle of $80^{\circ}$ to the axis of the rivet. *(Hint: Noting direction of rivet axis on element, draw the planes to create triangular elements and $\sigma_A > \sigma_B$*).
| 105 | 4 | 16 | 16 | 133 | 0 | 62 | 2 | 1 | Draw an element of material at the point of interest, and indicate the stresses acting on its faces. Find the magnitude of the tensile stresses acting at a point on the two planes making an angle of $80^{\circ}$ to the axis of the rivet. Hint: Noting direction of rivet axis on element, draw the planes to create triangular elements and $\sigma_A > \sigma_B$. | 3 |
1649c34b-d403-4a71-bf49-440b32a8ffd7 | 2 | 0 | 0 | 11 | 4 | 2 | 5 | 3 | Air enters a compressor at $1$ bar, $22^{\circ}\mathrm{C}$ and is compressed to $10$ bar (all total conditions). The isentropic total-to-total efficiency is $0.75$. Calculate:
| The temperature of the air leaving the compressor.
\nThe specific work transfer to the air.
| 2 | 0.333333 | 2 | \n | Calculate the temperature for an isentropic compression:
  
$\frac{T_{04\mathrm{s}}}{T_{02}} = (\frac{P_{04}}{P_{02}})^{\frac{\gamma - 1}{\gamma}}$
***
Substituting in numbers and rearranging for $T_{04\mathrm{s}}$:
  
$T_{04\mathrm{s}} = (22+273.15)(\frac{10}{1})^{\frac{1.4-1}{1.4}} = 569.8~\mathrm{K}$
***
Using the isentropic total-to-total efficiency equation:
  
$\eta_{\mathrm{tt}} = \frac{h_{04s} - h_{02}}{h_{04} - h_{02}}$
  
For an ideal gas:
  
$\eta_{\mathrm{tt}} = \frac{T_{04s} - T_{02}}{T_{04} - T_{02}}$
***
Substituting in numbers and rearranging for $T_{04}$:
  
$T_{04} = \frac{569.8-(22+273.15)}{0.75} + (22+273.15) = 661.35~\mathrm{K}$
\nApplying the SFEE and bearing in mind that there is no heat transfer and that kinetic and potential energy stores can be neglected:
  
$-\frac{\dot{W}}{\dot{m}} = h_{04}- h_{02}$ 
***
For an ideal gas:
  
$-\frac{\dot{W}}{\dot{m}} = c_\mathrm{p}(T_{04}- T_{02})$
***
Substituting in numbers:
  
$\frac{\dot{W}}{\dot{m}} = -1.01(661.35-(22+273.15)) = -370~\mathrm{kJ/kg}$
| Air enters a compressor at $1$ bar, $22^{\circ}\mathrm{C}$ and is compressed to $10$ bar (all total conditions). The isentropic total-to-total efficiency is $0.75$. Calculate:
The temperature of the air leaving the compressor.
\nThe specific work transfer to the air.
| 40 | 4 | 10 | 10 | 86 | 0 | 15 | 0 | 0 | The temperature of the air leaving the compressor.
\nThe specific work transfer to the air.
| 0 |
16eb7876-b1be-42cc-8deb-e26ead614877 | 1 | 0 | 0 | 15 | 5 | 0 | 2 | 1 | When double-stranded DNA is heated, the two strands separate (‘melt’). The temperature ($T_{m}$) in degrees Celsius at which this melting occurs depends on the composition of bases in the DNA, because C and G are held together by more hydrogen bonds than A and T.
If we call the percentage of bases that are guanine or cytosine $P_{G+C}$, then $T_{m}$ can be modelled approximately by the equation below. 
$$
P_{G+C}=2.5T_{m}-175
$$
| What is the melting temperature of a sample of DNA that is $21\%$ adenine?
| 1 | 1 | 1 | null | If the DNA is $21\%$ A, it is also $21\%$ T, and therefore $58\%$ G+C ($29\%$ each), so $T_m=\frac{P_{G+C}+175}{2.5}=\frac{58+175}{2.5}= 93\,\degree\mathrm{C}$
| When double-stranded DNA is heated, the two strands separate (‘melt’). The temperature ($T_{m}$) in degrees Celsius at which this melting occurs depends on the composition of bases in the DNA, because C and G are held together by more hydrogen bonds than A and T.
If we call the percentage of bases that are guanine or cytosine $P_{G+C}$, then $T_{m}$ can be modelled approximately by the equation below. 
$$
P_{G+C}=2.5T_{m}-175
$$
What is the melting temperature of a sample of DNA that is $21\%$ adenine?
| 86 | 5 | 5 | 5 | 20 | 0 | 14 | 1 | 0 | When double-stranded DNA is heated, the two strands separate ‘melt’. $ P_{G+C}=2.5T_{m}-175 $ What is the melting temperature of a sample of DNA that is $21\%$ adenine? | 2 |
1782eae8-f4c0-4a16-a3d7-5906736d742c | 1 | 2 | 1 | 17 | 6 | 1 | 3 | 8 | In the chemical reaction $\text{NO} + \text{O}_3 \rightarrow
\text{NO}_2 + \text{O}_2$, there is an intermediate step where the $\text{NO}$ and $\text{O}_3$ molecules combine to form an activated complex $[\text{NO--O}_3]^{\ast}$. The diagram below shows an empirical potential energy curve representing the three different stages of the reaction.
  
Although the $x$ axis corresponds to an unspecified reaction coordinate, the diagram can be interpreted as any other potential function. The peak of the potential curve is 9.6 kJ$\cdot$ mol$^{-1}$ above the combined potential energy of the $\text{NO} + \text{O}_3$ reactants; this is the "activation energy" required for the reaction to take place. One mole consists of Avogadro’s number, $6.022 \times
10^{23}$, of $[\text{NO--O}_3]^{\ast}$ complexes. The mass of a nitrogen atom is 14 atomic mass units and the mass of an oxygen atom is 16 atomic mass units (where one atomic mass unit is $m_u \approx 1.66 \times 10^{-27}$). 
  
An $\text{NO}$ molecule travelling in the $x$ direction at speed $u_{\text{NO}} = -550\,\text{m}\cdot\text{s}^{-1}$ and an $\text{O}_3$ molecule travelling at $u_{\text{O}_3} = +550\,\text{m}\cdot\text{s}^{-1}$ collide. After the collision, the molecules temporarily coalesce to form an $[\text{NO--O}_3]^{\ast}$ complex.
| Find the velocity of the $[\text{NO--O}_3]^{\ast}$ complex after the collision.
\nShow that the collision is inelastic. What has happened to the kinetic energy lost in the collision?
\nWill this collision lead to the formation of $\text{NO}_2$? Explain your answer.
\nTwo oxygen atoms collide in isolation. Could the collision result in the formation of an $\text{O}_2$ molecule in the right circumstances?
| 4 | 0.666667 | 3 | Find the total mass of the $\text{NO}$ and $\text{O}_3$ molecules, and hence also the $[\text{NO--O}_3]^{\ast}$ complex. 
***
Use conservation of momentum to find the velocity of the complex.
\nThe overall kinetic energy of a system decreases in an inelastic collision.
***
Therefore, show that the kinetic energy of the collision is lower after the collision than before. 
***
What forms is energy transferred to in a chemical reaction? ...
***
... How is the complex held together?
\nThe collision will only form the products if the internal energy of the complex exceeds the activation barrier.
***
Some of the energy of the complex was stored as kinetic energy. The rest of the energy is internal energy (i.e., energy in the bond, rotation etc.). 
***
Hence find $ \Delta K $ in the reaction (go back to part (b))
***
Compare this to the activation energy. You will have to convert one of the energies so that the units are equivalent. 
\nSet the potential energy of the interaction to zero when the two oxygen atoms are far apart. 
***
For the entire system, what is the initial (i.e., when the oxygen atoms are far apart):
*  sign of the energy (consider that the atoms have kinetic energy),
* value of the momentum?
Both of these are conserved.
***
When the atoms become closer together, they are accelerated due to the strong force...
***
... This causes the potential energy of the system to decrease (i.e., become negative).
***
Draw a potential function (similar to *Problem Sheet 2, Question* *3* but without the Coulomb barrier) to describe the situation. Draw a line showing the total energy of the system. 
***
Is the viable region of the potential function such that the atoms will settle into an equilibrium, or is the arrangement instead unstable?
| The total momentum before the collision that forms the complex is
***
$$
p_{\text{tot}} = m_{\text{NO}} u_{\text{NO}} + m_{\text{O}_3}
u_{\text{O}_3} = (14 + 16)m_u u_{\text{NO}} + (3\times 16)m_u u_{\text{O}_3},
$$
where $m_u \approx 1.66 \times 10^{-27}$kg is the atomic mass unit. Setting the value of $u_{\text{NO}}$ to $-550$m$\cdot$ s$^{-1}$ and $u_{\text{O}_3} = +550$m$\cdot$s$^{-1}$ gives:
$$
p_{\text{tot}} \approx 1.64 \times 10^{-23}\,\text{kg}\cdot\text{m}\cdot\text{s}^{-1}.
$$
***
The total momentum is conserved during the collision in which the two molecules bind to form the \[NO–O$_3$]$^{\ast}$ complex, so:
$$
p_{\text{[NO--O$_3$]}^{\ast}} \approx 1.64 \times
10^{-23}\,\text{kg}\cdot\text{m}\cdot\text{s}^{-1}
$$
and the velocity of the complex is:
***
$$
v_{\text{[NO--O$_3$]}^{\ast}} \approx \frac{1.64 \times
10^{-23}}{[(14 + 16) + (3 \times 16)] m_u} \approx
127\,\text{m}\cdot\text{s}^{-1}.
$$
\nThe total kinetic energy before the collision is
***
$$
K = \frac{1}{2} m_{\text{NO}}v_{\text{NO}}^2 + \frac{1}{2}
m_{{\text{O}}_3} v_{{\text{O}}_3}^2
= \frac{1}{2} [ (14 + 16) + (3 \times 16) ] m_u (550)^2
\approx 1.96\times 10^{-20}\,\text{J}.
$$
The total kinetic energy after the collision is
***
$$
K' = \frac{1}{2} m_{\text{[NO--O$_3$]}^{\ast}} \,
v_{\text{[NO--O$_{3}$]}^{\ast}}^2 \\
= \frac{1}{2} (78 m_u) (127)^2 \\
\approx 1.04 \times 10^{-21}\,\text{J}.
$$
The total KE has reduced so the collision was inelastic.
***
The KE lost has gone into the internal energy of the activated complex, which has higher chemical energy than the two molecules of which it is formed (it is only metastable) plus internal vibrational and rotational energy.
\nThe collision will only form the products if the internal energy of the complex exceeds the activation barrier. The internal energy is:
***
$$
E^{\text{internal}}_{[\text{NO--O}_3]^{\ast}} = K - K' \approx
1.96 \times 10^{-20} - 1.04 \times 10^{-21}
\approx 1.85 \times 10^{-20}\,\text{J}.
$$
***
An activation barrier of $9.6\text{kJ}\cdot\text{mol}^{-1}$ translates into
***
$$
\frac{9.6 \times 10^3}{6.022 \times 10^{23}} \approx 1.59 \times
10^{-20} \, \text{J per complex}.
$$
This is less than the internal energy provided by the collision, so the NO$_2$ and O$_2$ products will be formed (some of the time, at least).
\nSet the potential energy of interaction to zero when the two oxygen atoms are far apart. Since the atoms are approaching each other, they already have some kinetic energy even before the attractive part of the interaction starts accelerating them towards each other. This means that their total energy $E$ is greater than zero. If we choose to work in the centre-of-mass frame, the total momentum is zero and the two oxygen atoms approach each other with equal and opposite momentum.
***
Momentum and total energy are conserved, so the O$_2$ molecule must have zero total momentum but positive total energy $E$. If the molecule is to form, the kinetic energy of the molecules arriving at their equilibrium spacing (the difference between $E$ and the minimum value of $U(r)$) must be transferred into internal vibrational, rotational and electronic degrees freedom of the O$_2$ molecule. A negative potential energy must exist between the particles during acceleration (such that the kinetic energy can increase).
***
Since the total energy of the molecule is greater than zero, it is large enough to provide the two O atoms with enough kinetic energy to unbind and escape to infinity. Unless some other nearby atom or molecule takes away the excess energy before it is too late, the highly-excited oxygen molecule will soon break up.
***
  
The figure above illustrates the situation. It shows the potential energy $U(r)$ of the two O atoms as a function of their separation $r$. The total energy $E$, indicated by the dashed red line, is greater than zero. The total kinetic energy at separation $r$, indicated by the green arrow, is $E -
U(r)$. Because $E > 0$, the two escaping atoms will keep moving away from each other even as $r \rightarrow \infty$, i.e., the viable region exists for $r\to \infty$. 
| In the chemical reaction $\text{NO} + \text{O}_3 \rightarrow
\text{NO}_2 + \text{O}_2$, there is an intermediate step where the $\text{NO}$ and $\text{O}_3$ molecules combine to form an activated complex $[\text{NO--O}_3]^{\ast}$. The diagram below shows an empirical potential energy curve representing the three different stages of the reaction.
  
Although the $x$ axis corresponds to an unspecified reaction coordinate, the diagram can be interpreted as any other potential function. The peak of the potential curve is 9.6 kJ$\cdot$ mol$^{-1}$ above the combined potential energy of the $\text{NO} + \text{O}_3$ reactants; this is the "activation energy" required for the reaction to take place. One mole consists of Avogadro’s number, $6.022 \times
10^{23}$, of $[\text{NO--O}_3]^{\ast}$ complexes. The mass of a nitrogen atom is 14 atomic mass units and the mass of an oxygen atom is 16 atomic mass units (where one atomic mass unit is $m_u \approx 1.66 \times 10^{-27}$). 
  
An $\text{NO}$ molecule travelling in the $x$ direction at speed $u_{\text{NO}} = -550\,\text{m}\cdot\text{s}^{-1}$ and an $\text{O}_3$ molecule travelling at $u_{\text{O}_3} = +550\,\text{m}\cdot\text{s}^{-1}$ collide. After the collision, the molecules temporarily coalesce to form an $[\text{NO--O}_3]^{\ast}$ complex.
Find the velocity of the $[\text{NO--O}_3]^{\ast}$ complex after the collision.
\nShow that the collision is inelastic. What has happened to the kinetic energy lost in the collision?
\nWill this collision lead to the formation of $\text{NO}_2$? Explain your answer.
\nTwo oxygen atoms collide in isolation. Could the collision result in the formation of an $\text{O}_2$ molecule in the right circumstances?
| 249 | 3 | 18 | 18 | 141 | 4 | 61 | 3 | 0 | An $\text{NO}$ molecule travelling in the $x$\text{NO}$2u_{text{NO}} = -550,text{m}cdottext{s}^{-1}$ and an $\text{O}_3$ molecule travelling at $u_{text{O}_3} = +550,text{m}cdottext{s}^{-1}$\text{NO}$5text{NO--O}_3^{ast}$\text{NO}$6text{NO--O}_3^{ast}$\text{NO}$7text{NO}_2$\text{NO}$8text{O}_2$ molecule in the right circumstances? | 1 |
1791621e-fcec-45c6-8e95-497341743143 | 2 | 0 | 0 | 16 | 6 | 1 | 0 | 5 | Find the third derivative of
$$
x^3\cos(5x+ 1)
$$
| ...directly
\n...using the Leibniz formula (lectures).
| 2 | 0.333333 | 2 | To find the derivative directly, find $\displaystyle \frac{\mathrm{d}y}{\mathrm{d}x}$, from there $\displaystyle {\mathrm{d}^2y \over \mathrm{d}x^2}$, and from there $\displaystyle {\mathrm{d}^3y \over \mathrm{d}x^3}$.
Now you can have a go at finding these.
***
You can use the product rule to calculate $\displaystyle \frac{\mathrm{d}y}{\mathrm{d}x}$
***
You can use the product rule again to calculate $\displaystyle \frac{\mathrm{d}^2y}{\mathrm{d}x^2}$
***
You can use the product rule again to calculate $\displaystyle \frac{\mathrm{d}^3y}{\mathrm{d}x^3}$
\nThe Leibniz formula is in section 2.2 of the notes. Consider $f(x) = x^3$ and $g(x) = \cos(5x+1)$
For $n=3$, what is the formula?
***
$$
\displaystyle \frac{\mathrm{d}^3y}{\mathrm{d}x^3} = \frac{\mathrm{d}^3f}{\mathrm{d}x^3}g + 3{\mathrm{d}^2f\over \mathrm{d}x^2}{dg \over dx} + 3{\mathrm{d}f\over \mathrm{d}x}{\mathrm{d}^2g\over \mathrm{d}x^2} + f{\mathrm{d}^3g\over \mathrm{d}x^3}
$$
is the Leibniz formula for $n=3$. (where 1,3,3,1 are the third row of binomial coefficients) 
Try calculating these derivatives, and then substitute them back into Leibniz formula.
| To find the derivative directly, find $\displaystyle \frac{\mathrm{d}y}{\mathrm{d}x}$, from there $\displaystyle {\mathrm{d}^2y \over \mathrm{d}x^2}$, and from there $\displaystyle {\mathrm{d}^3y \over \mathrm{d}x^3}$.
Now you can have a go at finding these.
***
You can use the product rule to calculate $\displaystyle \frac{\mathrm{d}y}{\mathrm{d}x}$
***
$$
\displaystyle \frac{\mathrm{d}y}{\mathrm{d}x} = 3x^2\cos(5x+1) - 5x^3\sin(5x+1)
$$
***
You can use the product rule again to calculate $\displaystyle \frac{\mathrm{d}^2y}{\mathrm{d}x^2}$
***
$$
\begin{aligned}
\frac{\mathrm{d}^2y}{\mathrm{d}x^2} &= 6x\cos(5x+1) - 15x^2\sin(5x+1) - 15x^2\sin(5x+1) - 25x^3\cos(5x+1)
\\
&= 6x\cos(5x+1) -30x^2\sin(5x+1) - 25x^3\cos(5x+1)
\end{aligned}
$$
***
You can use the product rule again to calculate $\displaystyle \frac{\mathrm{d}^3y}{\mathrm{d}x^3}$
***
$$
\begin{aligned}
\frac{\mathrm{d}^3y}{\mathrm{d}x^3} &= 6\cos(5x+1) - 30x\sin(5x+1) -60x\sin(5x+1) - 150x^2\cos(5x+1) - 75x^2\cos(5x+1) + 125x^3\sin(5x+1)
\\
&=6\cos(5x+1)- 90x\sin(5x+1) - 225x^2\cos(5x+1) + 125x^3\sin(5x+1)
\end{aligned}
$$
\nLeibniz formula is in section 2.2 of the notes. Consider $f(x) = x^3$ and $g(x) = \cos(5x+1)$
For $n=3$, what is the formula?
***
$$
\displaystyle \frac{\mathrm{d}^3y}{\mathrm{d}x^3} = \frac{\mathrm{d}^3f}{\mathrm{d}x^3}g + 3{\mathrm{d}^2f\over \mathrm{d}x^2}{\mathrm{d}g \over \mathrm{d}x} + 3{\mathrm{d}f\over \mathrm{d}x}{\mathrm{d}^2g\over \mathrm{d}x^2} + f{\mathrm{d}^3g\over \mathrm{d}x^3}
$$
is the Leibniz formula for $n=3$. (where 1,3,3,1 are the third row of binomial coefficients)
Try calculating these derivatives, and then substitute them back into Leibniz formula.
***
$$
\displaystyle {\mathrm{d}f\over \mathrm{d}x} = 3x^2, \quad {\mathrm{d}^2f\over \mathrm{d}x^2} = 6x, \quad
{\mathrm{d}^3f\over \mathrm{d}x^3} = 6
$$
$$
\displaystyle {\mathrm{d}g\over \mathrm{d}x} = -5\sin(5x+1), \,\,\, {\mathrm{d}^2g\over \mathrm{d}x^2}=-25\cos(5x+1), \,\,\, {\mathrm{d}^3g\over \mathrm{d}x^3}=125\sin(5x+1)
$$
Now can you put these into the formula? Is it what you expect?
***
$$
\begin{aligned}
\frac{\mathrm{d}^3}{\mathrm{d}x^3}\Big[x^3\cos(5x+1)\Big] &= 6\cos(5x+1) + 3(6x)(-5\sin(5x+1)) + 3(3x^2)(-25\cos(5x+1)) + x^3(125\sin(5x+1))
\\
\frac{\mathrm{d}^3}{\mathrm{d}x^3}\Big[x^3\cos(5x+1)\Big] &= 6\cos(5x+1) - 90x\sin(5x+1) - 225x^2\cos(5x+1) + 125x^3\sin(5x+1)
\end{aligned}
$$
which agrees with part(a) as expected. (Which one was quicker/easier?!)
| Find the third derivative of
$$
x^3\cos(5x+ 1)
$$
...directly
\n...using the Leibniz formula (lectures).
| 12 | 1 | 17 | 17 | 142 | 11 | 6 | 0 | 0 | Find the third derivative of $ x^3\cos(5x+ 1) $ ...directly ...using the Leibniz formula lectures. | 1 |
17c2d6dd-27f7-4911-a94d-2db22124026e | 1 | 0 | 0 | 24 | 6 | 1 | 4 | 3 | **\[Boas 6.11.3]** Use Stokes' Theorem to evaluate:
$$
\iint_S (\nabla\times\vec{V})\cdot{d\vec{S}}
$$
where $\vec{V} = x^2\mathbf{\hat{i}} + z^2\mathbf{\hat{j}} -y^2\mathbf{\hat{k}}$ and $S$ is the part of the surface $z=4-x^2-y^2$ above the $x-y$ plane.
| **\[Boas 6.11.3]** Use Stokes' Theorem to evaluate:
$$
\iint_S (\nabla\times\vec{V})\cdot{d\vec{S}}
$$
where $\vec{V} = x^2\mathbf{\hat{i}} + z^2\mathbf{\hat{j}} -y^2\mathbf{\hat{k}}$ and $S$ is the part of the surface $z=4-x^2-y^2$ above the $x-y$ plane.
| 1 | 0.333333 | 1 | Start by sketching the surface $z=4-x^2-y^2$. To do this, consider the equation of the surface at a fixed $z$ (e.g., $z=0,4$). What happens as $z$ increases?
***
There are two ways to apply Stokes' Theorem to this problem:
1. Reduce the surface integral to a line integral by direct application of Stokes' theorem.
2. Simplify the surface using a principle of Stokes' theorem.
***
**(Method 1)** Stokes' Theorem states:
$$
\iint_{S}(\nabla\times\vec{V})\cdot d\vec{S}=\oint_{C,\text{ccw}}{\vec{V}\cdot d\vec{r}}
$$
where the RHS is the line integral evaluated anti-clockwise around the loop $C$ that encloses the opening of the surface.
***
**(Method 1)** What is the equation of $C$? 
***
**(Method 1)** It may help to perform a substitution into a different coordinate system to evaluate the line integral.
***
**(Method 2)** Stokes' Theorem dictates that it does not matter which open surface is considered as long as the opening remains the same. 
***
**(Method 2)** Can you think of any surface 'attached' to the opening that will be easier to evaluate the surface integral over? 
***
**(Method 2)** Hence evaluate the curl, and integrate the curl over this surface.
| Stokes' Theorem states:
$$
\iint_{S}(\nabla\times\vec{V})\cdot d\vec{S}=\oint_{C,\text{ccw}}{\vec{V}\cdot d\vec{r}}
$$
where the RHS is the line integral evaluated anti-clockwise around the loop $C$ that encloses the opening of the surface. This is a circle of radius $2$ in the $(x,y)$ plane. 
***
Setting $z=0$ and $dz=0$, 
***
$$
\vec{V}\cdot d\vec{r} = x^2dx
$$
***
Since we are integrating around a circle, it is favourable to use polar coordinates. 
***
$$
x=\rho\cos\phi = 2\cos\phi \implies \frac{dx}{d\phi} = -2\sin\phi
$$
***
$$
\vec{V}\cdot d\vec{r} = -8\cos^2\phi \sin\phi
$$
***
Integrating anti-clockwise over the limits $0\le\phi\le 2\pi$:
***
$$
\oint_C{\vec{V}\cdot d\vec{r}} = -8\int_{\phi=0}^{2\pi}\cos^2\phi\sin\phi
$$
***
$$
\begin{aligned}
&=-8\left[\frac{\cos^3\phi}{3}\right]_{0}^{2\pi} \\
& = -8\left[\frac{1}{3}-\frac{1}{3}\right]=0
\end{aligned}
$$
, $z=4-x^2-y^2$ is a paraboloid. 
* When $z=0$, $x^2+y^2=4$. This is a circle of radius $2$ in the $xy$ plane.
*  When $z=4$, $(x,y)=(0,0)$. 

, Another method is to recognise that Stokes' Theorem dictates that it does not matter which open surface is considered as long as the opening remains the same. 
***
Therefore, we can 'collapse' the paraboloid surface into the disk enclosed by $C$, radius $2$, in the $xy$ plane, for which:
$$
d\vec{S}=dx\,dy\,\mathbf{\hat{k}}
$$
***
So, taking just the $\mathbf{\hat{k}}$ component of curl,
***
$$
\nabla\times\vec{V}_{\,|\mathbf{\hat{k}}} = \frac{\partial V_y}{\partial x}-\frac{\partial V_x}{\partial y} = \frac{\partial z^2}{\partial x} - \frac{\partial x^2}{\partial y} = 0
$$
Therefore,
$$
\iint_{S}(\nabla\times\vec{V})\cdot d\vec{S}=0
$$
| **\[Boas 6.11.3]** Use Stokes' Theorem to evaluate:
$$
\iint_S (\nabla\times\vec{V})\cdot{d\vec{S}}
$$
where $\vec{V} = x^2\mathbf{\hat{i}} + z^2\mathbf{\hat{j}} -y^2\mathbf{\hat{k}}$ and $S$ is the part of the surface $z=4-x^2-y^2$ above the $x-y$ plane.
| 23 | 5 | 11 | 11 | 163 | 7 | 23 | 5 | 0 | **\[Boas 6.11.3]** Use Stokes' Theorem to evaluate:
$$
\iint_S (\nabla\times\vec{V})\cdot{d\vec{S}}
$$
where $\vec{V} = x^2\mathbf{\hat{i}} + z^2\mathbf{\hat{j}} -y^2\mathbf{\hat{k}}$ and $S$ is the part of the surface $z=4-x^2-y^2$ above the $x-y$ plane.
| 0 |
184e6da2-45c4-4ea3-b27e-2354a37e2d22 | 4 | 0 | 2 | 20 | 6 | 1 | 2 | 6 | Consider two systems labelled $A$ and $B$ which are weakly coupled according to the ODEs
$$
\begin{aligned}
\frac{dx_A}{dt} &= \phantom{\varepsilon} x_A + \varepsilon x_B\\
\frac{dx_B}{dt} &= \varepsilon x_A + \phantom{\varepsilon} x_B \ ,
\end{aligned}
$$
where $\varepsilon \ll 1$.
| Show that if we define two new variables,
$$
\begin{aligned}
x_1 &= x_A + x_B \nonumber \\
x_2 &= x_A - x_B \nonumber
\end{aligned}
$$
then the ODE expressed in terms of $x_1$ and $x_2$ are not coupled.
\nSolve the two separate ODEs in $x_1$ and $x_2$ and use this to find the general solutions for $x_A$ and $x_B$.
Use $C_1$ as the constant of integration for $x_1$ and $C_2$ as the constant of integration for $x_2$. 
\nIf $x_A=x_B=1$ at $t=0$, show that the solutions are of the form:
$$
x_A = x_B = e^{(1+\varepsilon)t}
$$
 Discuss if this makes sense in terms of the limit $\varepsilon \to 0$.
\nCompare the solution for $x_A$ (with $x_A=x_B=1$ at $t=0$) to the one with no coupling $(\varepsilon=0)$ (maybe form the ratio between the two) and discuss why it can be very difficult to measure if a system has a small coupling.
| 4 | 0.666667 | 3 | See sections **3.1** and **5.1.2** to understand the term *coupled differential equation*.
***
Start by differentiating $x_1$ and $x_2$ with respect to $t$.
***
Insert the expressions for $dx_A/dt$ and $dx_B/dt$ into your equations.
***
Now express the equations in terms of $x_1$ and $x_2$...
***
... Does this demonstrate that the equations are coupled (i.e., are variables shared between the equations)?
\nStart with the $dx_1/dt$ and $dx_2/dt$ from part (a).
***
Solve these differential equations for $x_1$ and $x_2$...
***
... Use separation of variables and remember the constant of integration.
***
Use the definitions of $x_1$ and $x_2$ to express $x_A$ and $x_B$.
\nInsert the boundary conditions to find $C_1$ and $C_2$.
***
After inserting $C_1$ and $C_2$ into your equations, let $\varepsilon\rightarrow0$. What happens to the equations?
\nFind the ratio between the solution to part (c), and the solution to part (b) if $\varepsilon$ is set equal to $0$. 
***
If a system has low coupling, what happens to $\varepsilon$? 
***
How does this influence the ratio you found? 
***
Does this make it difficult to distinguish between coupled and uncoupled systems on a small time scale?
| Starting with the definitions of $x_1$ and $x_2$ and differentiating with respect to $t$:
***
$$
\begin{aligned}
\frac{dx_1}{dt} &= \frac{dx_A}{dt} + \frac{dx_B}{dt} \\
\frac{dx_2}{dt} &= \frac{dx_A}{dt} - \frac{dx_B}{dt}
\end{aligned}
$$
***
Next, we insert $dx_A/dt$ and $dx_B/dt$ into equations (1) and (2):
***
$$
\begin{aligned}
\frac{dx_1}{dt} &= x_A + x_B + \varepsilon(x_A + x_B)\\
\frac{dx_2}{dt} &= x_A - x_B - \varepsilon(x_A - x_B)
\end{aligned}
$$
***
Then replace these expressions with $x_1$ and $x_2$:
***
$$
\begin{aligned}
\frac{dx_1}{dt} &= (1+\varepsilon)x_1 \nonumber \\
\frac{dx_2}{dt} &= (1-\varepsilon)x_2
\end{aligned}
$$
***
and we see that these are two *independent* ODEs: $x_1$ does not occur in $dx_2/dt$ and $x_2$ does not occur in $dx_1/dt$; the equations are not linked (or *coupled*) in any way.
\nSeparation of variables can be used to solve these ODEs. For example, for $dx_1/dt$:
***
$$
\int{\frac{1}{x_1}\hspace{1pt} dx_1} = (1+\varepsilon)\int{dt}
$$
***
$$
\ln{x_1} = (1+\varepsilon)t +C_1
$$
***
$$
\begin{align*}
&x_1=e^{(1+\varepsilon)t + C_1}\\
&=C_1e^{(1+\varepsilon)t}
\end{align*}
$$
**Note:** We separated $e^{C_1}$ from the exponential, and let $C_1 = e^{C_1}$ (this is acceptable because $e^{C_1}$ is a constant).
***
Performing the same process for to solve $dx_2/dt$, we have the solutions:
***
$$
\begin{align}
x_1 &= C_1 e^{(1+\varepsilon)t} \nonumber \\
x_2 &= C_2 e^{(1-\varepsilon)t} \ , \nonumber
\end{align}
$$
***
Given $x_1 = x_A + x_B$ and $x_2 = x_A - x_B$, we can solve simultaneously for $x_A$ and $x_B$:
***
$$
x_A = \frac{x_1 + x_2}{2} \\
x_B = \frac{x_1 - x_2}{2}
$$
Inserting $x_1$ and $x_2$ and redefining the arbitrary constants ($C_1/2\rightarrow C_1$ and $C_2/2\rightarrow C_2$):
***
$$
\begin{align}
x_A &= C_1 e^{(1+\varepsilon)t} + C_2 e^{(1-\varepsilon)t} \nonumber \\
x_B &= C_1 e^{(1+\varepsilon)t} - C_2 e^{(1-\varepsilon)t} \ . \nonumber
\end{align}
$$\nInserting the boundary conditions and solving for $C_1$ and $C_2$ gives
***
$C_1=1$ and $C_2=0$. Thus the solutions are:
***
$$
\begin{align}
x_A &= e^{(1+\varepsilon)t} \nonumber \\
x_B &= e^{(1+\varepsilon)t} \ . \nonumber
\end{align}
$$
***
In the limit of $\varepsilon \to 0$ the original ODEs turn uncoupled with solutions:
***
$$
\begin{align}
x_A &= e^{t} \nonumber \\
x_B &= e^{t} \ , \nonumber
\end{align}
$$
 which is exactly what happens in the limit of the previous solutions. This seems very reasonable.
\nFrom part (c), we have that:
$$
\begin{align}
x_{A,1} &= e^{(1+\varepsilon)t} \nonumber \\
\end{align}
$$
***
 Returning to part (b) for the general solution:
$$
x_A = C_1 e^{(1+\varepsilon)t} + C_2 e^{(1-\varepsilon)t}
$$
and setting $\varepsilon=0$, we have:
***
$$
x_A = e^t (C_1+C_2)
$$
With $C_1=1$ and $C_2=0$, 
***
$$
x_{A,2} = e^t
$$
***
The ratio between the two solutions is:
$$
\frac{x_{A,1}}{x_{A,2}} = \frac{e^{(1+\varepsilon)t}}{e^t}=e^{\epsilon t}
$$
***
The ratio between the coupled and the uncoupled solution only differs by the factor $\exp(\varepsilon t)$. If $\varepsilon$ is very small, it will take a long time for the coupled system to have any noticeable difference from the uncoupled one. Over such long time periods, the calibration of the measurement system may drift and it might not be possible at all to find the effect.
| Consider two systems labelled $A$ and $B$ which are weakly coupled according to the ODEs
$$
\begin{aligned}
\frac{dx_A}{dt} &= \phantom{\varepsilon} x_A + \varepsilon x_B\\
\frac{dx_B}{dt} &= \varepsilon x_A + \phantom{\varepsilon} x_B \ ,
\end{aligned}
$$
where $\varepsilon \ll 1$.
Show that if we define two new variables,
$$
\begin{aligned}
x_1 &= x_A + x_B \nonumber \\
x_2 &= x_A - x_B \nonumber
\end{aligned}
$$
then the ODE expressed in terms of $x_1$ and $x_2$ are not coupled.
\nSolve the two separate ODEs in $x_1$ and $x_2$ and use this to find the general solutions for $x_A$ and $x_B$.
Use $C_1$ as the constant of integration for $x_1$ and $C_2$ as the constant of integration for $x_2$. 
\nIf $x_A=x_B=1$ at $t=0$, show that the solutions are of the form:
$$
x_A = x_B = e^{(1+\varepsilon)t}
$$
 Discuss if this makes sense in terms of the limit $\varepsilon \to 0$.
\nCompare the solution for $x_A$ (with $x_A=x_B=1$ at $t=0$) to the one with no coupling $(\varepsilon=0)$ (maybe form the ratio between the two) and discuss why it can be very difficult to measure if a system has a small coupling.
| 149 | 23 | 50 | 50 | 325 | 23 | 130 | 19 | 0 | Consider two systems labelled $A$ and $B$ which are weakly coupled according to the ODEs $ \begin{aligned} \frac{dx_A}{dt} &= \phantom{\varepsilon} x_A + \varepsilon x_B\\ \frac{dx_B}{dt} &= \varepsilon x_A + \phantom{\varepsilon} x_B \ , \end{aligned} $ where $\varepsilon \ll 1$. Show that if we define two new variables, $ \begin{aligned} x_1 &= x_A + x_B onumber \\ x_2 &= x_A - x_B onumber \end{aligned} $ then the ODE expressed in terms of $x_1$ and $x_2$ are not coupled. Solve the two separate ODEs in $x_1$ and $x_2$ and use this to find the general solutions for $x_A$ and $B$0. Use $B$1 as the constant of integration for $x_1$ and $B$3 as the constant of integration for $x_2$. Compare the solution for $x_A$ with $B$5 at $B$6 to the one with no coupling $ \begin{aligned} \frac{dx_A}{dt} &= \phantom{\varepsilon} x_A + \varepsilon x_B\\ \frac{dx_B}{dt} &= \varepsilon x_A + \phantom{\varepsilon} x_B \ , \end{aligned} $2 maybe form the ratio between the two and discuss why it can be very difficult to measure if a system has a small coupling. | 5 |
18cc9219-397a-486a-9c41-ca1e76ce2007 | 2 | 0 | 0 | 16 | 6 | 1 | 4 | 2 | Consider the elliptical lamina bounded by the curve $\displaystyle {{x^2}\over{ a^2}} + {{y^2}\over{b^2}} = 1$.
(lamina = thin sheet)
| Find the area the ellipse encloses.
\n Assuming the lamina to be of uniform density, find the position of the centre of mass of the part that lies in the first quadrant ($x\geq 0, y\geq 0)$.
| 2 | 0.666667 | 2 | To find the area under a curve specified in Cartesian coordinates, you can rearrange to the form $y=...$ and then use regular integration.
What limits should you use? You could try sketching the curve.
***
You should have an equation for $y$ containing a $\pm$. How should you deal with this?
Is there a way to deal with this to make the integral more straightforward? 
***
**Method 1: Symmetry**
By considering symmetry, what do you notice about the ellipse?
You can integrate over just a section of the ellipse, and then consider the symmetry of the curve to find the total area, which will make the integral easier to evaluate. What limits could you use?
 
**Method 2: Integrate over the whole ellipse**
Considering the sketch you can see that the ellipse is made up of the 2 curves described by $y$. 
$$
\begin{aligned}
A
&= \int_{-a}^a b\left(1-{x^2\over a^2}\right)^{1\over2} \mathrm{d}x + \int_{a}^{-a} -b\left(1-{x^2\over a^2}\right)^{1\over2} \mathrm{d}x
\end{aligned}
$$
Can you see how to simplify this into one integral?
***
**Method 1: Symmetry**
Try using just the region in the first quadrant. You can see that the total area will be 4 times larger than this, due to symmetry.
Can you find the appropriate limits now and evaluate the integral?

**Method 2: Integrate over the whole ellipse**
Use the property $ \displaystyle - \int_{a}^{-a} \mathrm{d}x= + \int^a_{-a} \mathrm{d}x $ to simplify it into one integral.
***
**Method 1: Symmetry**
From the sketch, you can see the limits in the first quadrant only are $0<x<a$. Also note that $y$ is positive in the first quadrant.
***
Can you use a substitution to evaluate the integral now?
***
Try using the trigonometric substitution $x=a\sin\theta$ to evaluate the integral.
Are you able to find $A$ now?
\nWhat is the equation for the coordinates $(\bar{x}, \bar{y})$ of the centre of mass? This is covered in section 3.6 of the lectures.
***
$$
\begin{aligned}
\bar{x}= \frac{\mathrm{First\,moment\,of\,mass}}{\mathrm{Total\,mass}}
\\
\bar{y}= \frac{\mathrm{First\,moment\,of\,mass}}{\mathrm{Total\,mass}}
\end{aligned}
$$
The lamina is of uniform density, which you can denote as the mass per unit **area**, $\sigma$.
Now can you find the centre of mass? First, what is the total mass in the 1st quadrant?

***
The mass in the first quadrant is the $\mathrm{area} \times \mathrm{density}$, so you need the area of the first quadrant.
After that, try calculating the first moment of mass in $x$ and $y$. 
***
First, write down the moments of mass in summation form.
You can work the first moment in mass in $x$ out by thinking of the total moment of lots of small masses about the line $x=0$ (or recall from lectures)
How can you write these in integral form?
***
Now try substituting in for $y$ the equation of the ellipse. Remember to add appropriate limits.
***
As you are looking at the first quadrant, by considering a sketch of the equation, you can see that this is in the range $0\leq x \leq a$. The vertical range is $0\leq y \leq b$, so you use the positive value of $\displaystyle y = \pm b(1-{x^2 \over a^2})^{1\over2}$.
Can you find the integrals now?
***
Using the equations above for $\bar{x}$ and $\bar{y}$ to find the center of mass coordinates.
| By considering symmetry, what do you notice about the ellipse?
You can integrate over just a section of the ellipse, and then consider the symmetry of the curve to find the total area, which will make the integral easier to evaluate. What limits could you use?
***
Try using just the region in the first quadrant. You can see that the total area will be 4 times larger than this, due to symmetry.
Can you find the appropriate limits now and evaluate the integral?

***
From the sketch, you can see the limits in the first quadrant only are $0<x<a$.
$$
\displaystyle
A_1 = \int_0^a y \,\mathrm{d}x
$$
Rearranging for $y$,
$$
\begin{aligned}
y &= \pm b \left( 1-{x^2\over a^2} \right)^{1\over2}
\end{aligned}
$$
Which of the two equations for $y$ should you use for the region in the first quadrant? Can you find the integral now?
***
$y$ is positive in the first quadrant, so you can use $\displaystyle y = b \left( 1-{x^2\over a^2} \right)^{1\over2}$.
$$
\displaystyle
A_1 = \int_0^a b \left( 1-{x^2\over a^2} \right)^{1\over2} \mathrm{d}x
$$
 Can you calculate the integral now?
***
To simplify this, try a trigonometric substitution.
***
Try the substitution $x=a\sin\theta$
***
When $x=a, \theta = {\pi\over2}$ and when $x=0, \theta=0$  
$\displaystyle{dx \over d\theta} = a\cos\theta$
Substituting these in,
$$
\begin{aligned}
A_1
&= \int_0^{\pi\over2} b\left(1-{(a\sin\theta)^2\over a^2}\right)^{1\over2} {dx\over d\theta}\mathrm{d}\theta
\\
&= \int_0^{\pi\over2} b\left(1-\sin^2\theta\right)^{1\over2} a\cos\theta \,\mathrm{d}\theta
\\
&= ab\int_0^{\pi\over2} \cos^2\theta \,\mathrm{d}\theta
\\
&= {ab\over2}\int_0^{\pi\over2} 1+\cos2\theta \,\mathrm{d}\theta
\end{aligned}
$$
where $\cos2\theta = 2\cos^2\theta - 1$ was used.
$$
\begin{aligned}
A_1 &= {ab\over2}\left[\theta + {1\over2}\sin(2\theta)\right]_0^{\pi\over2}
\\
&= {\pi ab\over4}
\end{aligned}
$$
Can you find the total area of the ellipse now?
***
$$
\displaystyle A_T = 4\times {\pi ab\over4} = \pi ab
$$
, From the sketch, you can see the limits are $-a<x<a$.
$$
\begin{aligned}
A &= \int_{-a}^a y \,\mathrm{d}x
\end{aligned}
$$
Rearranging for $y$,
$$
\begin{aligned}
y &= \pm b \left( 1-{x^2\over a^2} \right)^{1\over2}
\end{aligned}
$$
How can you deal with the $\pm$ sign?
***
Considering the sketch you can see that the ellipse is made up of the 2 curves described by $y$. 
$$
\begin{aligned}
A
&= \int_{-a}^a b\left(1-{x^2\over a^2}\right)^{1\over2} \mathrm{d}x + \int_{a}^{-a} -b\left(1-{x^2\over a^2}\right)^{1\over2} \mathrm{d}x
\end{aligned}
$$
Can you see how to simplify this into one integral?
***
Use the property $ \displaystyle - \int_{a}^{-a} \mathrm{d}x= + \int^a_{-a} \mathrm{d}x $,
***
$$
\begin{aligned}
A
&= \int_{-a}^a b\left(1-{x^2\over a^2}\right)^{1\over2} \mathrm{d}x + \int_{-a}^a b\left(1-{x^2\over a^2}\right)^{1\over2} \mathrm{d}x
\end{aligned}
$$
And, as expected because the area under the curve is symmetrical above and below the $x$ axis, the two terms are equal, so
$$
\begin{aligned}
A
&= \int_{-a}^a 2b\left(1-{x^2\over a^2}\right)^{1\over2} \mathrm{d}x
\end{aligned}
$$
To simplify this, try a trigonometric substitution.
***
Try $x=a\sin\theta$
***
When $x=a, \theta = {\pi\over2}$ and when $x=-a, \theta=-{\pi\over2}$  
$\displaystyle{dx \over d\theta} = a\cos\theta$
Substituting these in,
$$
\begin{aligned}
A
&= \int_{-{\pi\over2}}^{\pi\over2} 2b\left(1-{(a\sin\theta)^2\over a^2}\right)^{1\over2} {dx\over d\theta}\mathrm{d}\theta
\\
&= \int_{-{\pi\over2}}^{\pi\over2} 2b\left(1-\sin^2\theta\right)^{1\over2} a\cos\theta \,\mathrm{d}\theta
\\
&= 2ab\int_{-{\pi\over2}}^{\pi\over2} \cos^2\theta \,\mathrm{d}\theta
\\
&= ab\int_{-{\pi\over2}}^{\pi\over2} 1+\cos2\theta \,\mathrm{d}\theta
\end{aligned}
$$
where $\cos2\theta = 2\cos^2\theta - 1$ was used.
$$
\begin{aligned}
A &= ab\left[\theta + {1\over2}\sin(2\theta)\right]_{-{\pi\over2}}^{\pi\over2}
\\
&= \pi ab
\end{aligned}
$$
, To find the area under a curve specified in Cartesian coordinates, you can rearrange it to the form $y=\ldots$ and then use regular integration.
What limits should you use? You could try sketching the curve.
***
Can you find the area under the curve now?
\nWhat is the equation for the coordinates $(\bar{x}, \bar{y})$ of the centre of mass? This is covered in section 3.6 of the lectures.
***
$$
\begin{aligned}
\bar{x}= \frac{\mathrm{First\,moment\,of\,mass}}{\mathrm{Total\,mass}}
\\
\bar{y}= \frac{\mathrm{First\,moment\,of\,mass}}{\mathrm{Total\,mass}}
\end{aligned}
$$
The lamina is of uniform density, which you can denote as the mass per unit **area**, $\sigma$.
Now you can begin to find the centre of mass. First, what is the total mass in the 1st quadrant?

***
The area in the first quadrant is a quarter of the total area, and so is $\displaystyle {\pi ab \over 4}$. Therefore the mass in the first quadrant is the $\mathrm{area} \times \mathrm{density}$, 
$$
\displaystyle M = {\sigma \pi ab \over4}.
$$
Now try calculating the first moment of mass in $x$ and $y$. 
***
First, write down the moment in summation form.
You can work this out by thinking of the total moment of lots of small masses about the line $x=0$ that the first moment in mass in $x$ can be written (as in lectures)
$$
\begin{aligned}
M\bar{x}=\sum_{i=1}^Nm_ix_i
\end{aligned}
$$
Similarly, from the total moment of lots of small masses about the line $y=0$, the first moment in mass in $y$ is
$$
\begin{aligned}
M\bar{y}=\sum_{j=1}^Nm_jy_j
\end{aligned}
$$
What are they in integral form?
***
This is clearer if you note that in the summation form we could have recognised that the masses *$m_i$* and $m_j$ are small and so written them as $\delta m_i$ and $\delta m_j$
$$
\begin{aligned}
M\bar{x}=\sum_{i=1}^Nx_i\delta m_i \, \, and \, \, M\bar{y}=\sum_{j=1}^Ny_j\delta m_j
\end{aligned}
$$
***
Taking the infinitesimal-element limit, $\sum \delta m \rightarrow \int dm$
$$
\begin{aligned}
\mathrm{First\,moment\,of\,mass\,in\,} x = M\bar{x}
&= \int x \,\mathrm{d} m \\
&= \int x\sigma y \,\mathrm{d}x \\
\\
\mathrm{First\,moment\,of\,mass\,in\,} y = M\bar{y}
&= \int {y\over2} \,\mathrm{d} m \\
&= \int {y\over2}\sigma y \,\mathrm{d}x \\
&= \int {\sigma\over2} y^2 \mathrm{d}x
\end{aligned}
$$
Now try substituting in for $y$ with the equation of the ellipse. Remember to add appropriate limits.
***
As you are looking at the first quadrant, by considering a sketch of the equation, you can see that this is in the range $0\leq x \leq a$. The vertical range is $0\leq y \leq b$, so you use the positive value of $\displaystyle y = \pm b\left(1-{x^2 \over a^2}\right)^{1\over2}$.
Can you find the integrals now?
***
$$
\begin{aligned}
\mathrm{First\,moment\,of\,mass\,in\,} x
&= \int_0^a \sigma x b \left( 1-{x^2 \over a^2} \right)^{1\over2} \, \mathrm{d}x
\\
&= \left[ -{\sigma b a^2 \over 3} \left(1-{x^2\over a^2} \right)^{3\over2} \right]^a_0
\\
&= {\sigma b a^2 \over 3}
\\
\mathrm{First\,moment\,of\,mass\,in\,} y
&= \int_0^a {\sigma\over2} b^2 \left(1-{x^2\over a^2} \right) \,\mathrm{d}x
\\
&= \left[{\sigma b^2 \over 2} \left(x-{x^3\over 3a^2} \right) \right]^a_0
\\
&= {\sigma ab^2\over3}
\end{aligned}
$$
Now you can find the centre of mass coordinates!
***
Using the equations above for $\bar{x}$ and $\bar{y}$,
$$
\begin{aligned}
\bar{x} &= \frac{\sigma ba^2\over3}{\sigma \pi ab \over 4}= {4a \over 3\pi}
\\
\bar{y} &= \frac{\sigma ab^2 \over 3}{\sigma\pi ab \over4} = {4b\over3\pi}
\\
\mathrm{Centre\,of\,mass} &= \left({4a\over3\pi}, {4b\over3\pi}\right)
\end{aligned}
$$
| Consider the elliptical lamina bounded by the curve $\displaystyle {{x^2}\over{ a^2}} + {{y^2}\over{b^2}} = 1$.
(lamina = thin sheet)
Find the area the ellipse encloses.
\n Assuming the lamina to be of uniform density, find the position of the centre of mass of the part that lies in the first quadrant ($x\geq 0, y\geq 0)$.
| 48 | 2 | 14 | 14 | 687 | 24 | 34 | 1 | 0 | Consider the elliptical lamina bounded by the curve $\displaystyle {{x^2}\over{ a^2}} + {{y^2}\over{b^2}} = 1$. lamina = thin sheet Find the area the ellipse encloses. Assuming the lamina to be of uniform density, find the position of the centre of mass of the part that lies in the first quadrant $x\geq 0, y\geq 0)$. | 3 |
19205aba-f145-48b6-aa1e-c5c321c4bfa3 | 1 | 0 | 3 | 21 | 6 | 1 | 0 | 8 | Consider the interval $[-1,1]$ and develop a series of polynomials of successively higher order that form an orthonormal set. Let $p_n(x)$ denote a polynomial of order $n$. 
| Let $p_0(x)=\sqrt{\frac{1}{2}}$ . Show that $p_1(x)= \sqrt{\frac{3}{2}}x$ is normalised and is orthogonal to $p_0(x)$.
\nFind a second order polynomial $p_2(x)$ which is orthogonal to both $p_0$ and $p_1$, and is normalised.
\nDescribe a method to find $p_n$ satisfying the criteria for an orthonormal set given that all $p_m$ with $m<n$ are already known.
\nSearch around online and try to figure out what this series of polynomials is called (remembering that the sign of each polynomium is not well defined).
| 4 | 1 | 3 | To show that $p_1(x)$ is normalised, show that the inner product $ \braket{p_1 | p_1} $ (see **section 2.3** of the notes) is 1.
***
To show that $p_0(x)$ and $p_1(x)$ are orthogonal, show that their inner product $ \braket{p_0 | p_1} $ is 0. 
\nExpress $p_2(x)$ as a general second-order polynomial (you may use your own symbols).
***
Set-up three inner products equations from the given conditions. 
***
Use the three equations to solve for the three unknown constants of $p_2$. 
\nGo back to part (b), where you found a $p_2$ that was:
* Orthogonal with $p_0$ and $p_1$
* Normalised
How many equations were required to solve for $p_2$?
***
Now, how would you generalise to a $p_n$?
\n | To show that $p_1(x)$ is normalised, we must show that the inner product $ \braket{p_1 | p_1} $ (see **section 2.3** of the notes) is 1 in the interval $[-1,1]$.
***
$$
\begin{aligned}
\braket{p_1 | p_1}
&= \int_{-1}^1{\sqrt{\frac{3}{2}}x\sqrt{\frac{3}{2}}x dx} \\
&= \int_{-1}^1{\frac{3}{2}x^2 dx} \\
&= \left[\frac{x^3}{2}\right]_{-1}^1 \\
&= 1
\end{aligned}
$$
***
For $p_1$ being orthogonal to $p_0$, we have that $ \braket{p_0 | p_1} $ must be 0. 
***
$$
\begin{aligned}
\braket{p_0 | p_1}
&= \int_{-1}^1{\sqrt{\frac{1}{2}}\sqrt{\frac{3}{2}}x dx} \\
&= \left[\sqrt{\frac{3}{4}}x^2\right]_{-1}^1 \\
&= 0 \; .
\end{aligned}
$$
\nLet $p_2$ be of the form:
$$
p_2(x) = \alpha + \beta x + \gamma x^2
$$
and now solve for $\alpha$, $\beta$ and $\gamma$ by setting up three equations in terms of $p_0,p_1,p_2$ using the given conditions: 
***
$$
\begin{align}
\braket{p_0 | p_2} &= 0 \\
\braket{p_1 | p_2} &= 0 \\
\braket{p_2 | p_2} &= 1 \; .
\end{align}
$$
By evaluating the inner product integrals (simple integration of polynomials), we obtain the three results:
***
$\beta=0$, $\alpha^2=\frac{5}{8}$ and $\gamma=-3\alpha$. The sign of $ \alpha $ is arbitrary (you can pick the $z$ axis in a cartesian coordinate system to form either a right-handed or left-handed system by changing its direction but in both cases it is orthogonal to the $x$ and $y$ axis). 
***
So, there are two possible solutions for $p_2(x)$. If we pick $\alpha$ to be positive:
$$
p_2(x) = \sqrt{\frac{5}{8}}(1-3x^2) \; .
$$
\nIn part (b), we found that $3$ equations (one for normalisation, and two for orthogonality with $p_0,p_1$) were required to find $p_2(x)$. Now, we generalise this to $p_n$. 
***
The method is to write down a general form of an $n^\text{th}$ order polynomial and then write down the $n+1$ equations that express orthogonality and normalisation.
\nThe polynomials developed like this are called Legendre polynomials and are in particular relevant for finding solutions to electrostatic problems. In the same way that a periodic function can be expanded in terms of a Fourier series, a function on the interval $[-1,1]$ can be expanded in terms of Legendre polynomials.
| Consider the interval $[-1,1]$ and develop a series of polynomials of successively higher order that form an orthonormal set. Let $p_n(x)$ denote a polynomial of order $n$. 
Let $p_0(x)=\sqrt{\frac{1}{2}}$ . Show that $p_1(x)= \sqrt{\frac{3}{2}}x$ is normalised and is orthogonal to $p_0(x)$.
\nFind a second order polynomial $p_2(x)$ which is orthogonal to both $p_0$ and $p_1$, and is normalised.
\nDescribe a method to find $p_n$ satisfying the criteria for an orthonormal set given that all $p_m$ with $m<n$ are already known.
\nSearch around online and try to figure out what this series of polynomials is called (remembering that the sign of each polynomium is not well defined).
| 108 | 12 | 32 | 32 | 268 | 12 | 80 | 9 | 0 | Consider the interval $[-1,1]$ and develop a series of polynomials of successively higher order that form an orthonormal set. Let $p_n(x)$ denote a polynomial of order $n$. Let $p_0(x)=\sqrt{\frac{1}{2}}$ . Show that $p_1(x)= \sqrt{\frac{3}{2}}x$ is normalised and is orthogonal to $p_0(x)$. Find a second order polynomial $p_2(x)$ which is orthogonal to both $p_0$ and $p_1$, and is normalised. Describe a method to find $p_n$ satisfying the criteria for an orthonormal set given that all $p_n(x)$0 with $p_n(x)$1 are already known. Search around online and try to figure out what this series of polynomials is called remembering that the sign of each polynomium is not well defined. | 7 |
1929083d-ee49-47da-8f1a-7a423af519bd | 0 | 0 | 8 | 14 | 4 | 2 | 16 | 3 | Let $f$ and $g$ be two spatio-temporal functions (i.e. they both depend on $x$, $y$, $z$ and $t$). We assume that $f$ and $g$ are *bounded*, meaning that there exists a strictly positive real constant $M$ such that $|f|\leq M$ and $|g|\leq M$ for any point in space and time. Let $\lambda$ be a real constant. The time-average operator (denoted by the *overbar*) is given by:
$$
\\ \bar{f}(x,y,z) \equiv \frac{1}{T}\int_{t_0}^{t_0+T}{f(x,y,z,t)\,\mathrm{d}t},\\
$$
where $t_0$ is a prescribed instant in time (the same applies to $g$). The assumption that $f$ is bounded ensures that the integral is finite (for example, functions of the type $1/(t-t_0)$ would not be satisfying this constraint).
*prime* or *dash* (i.e. $^{\prime}$) represents the fluctuating component of the function, that is:
$$
f = \bar{f} + f^\prime
$$
Show that: | $$
\bar{\bar{f}} = \bar{f}
$$\n$$
\overline{f + \lambda g} = \bar{f} + \lambda \bar{g}
$$\n$$
\overline{f^\prime} = 0
$$\n$$
\overline{f^\prime \bar{g}} = \overline{g^\prime \bar{f}} = 0
$$\n$$
\overline{fg} = \bar{f}\bar{g} + \overline{f^\prime g^\prime}
$$\n$$
\overline{\partial f/\partial x} = \partial\bar{f}/\partial x
$$\n$$
\overline{f^\prime g^\prime} = \overline{g^\prime f^\prime}
$$\n$\overline{\partial f/\partial t} = 0$ if $T \to +\infty$ *Hint: you need to use the assumption that $f$ is bounded.* | 8 | 0.5 | 3 | \n\n\n\n\n\n\n | \n\n\n\n\n\n\n | Let $f$ and $g$ be two spatio-temporal functions (i.e. they both depend on $x$, $y$, $z$ and $t$). We assume that $f$ and $g$ are *bounded*, meaning that there exists a strictly positive real constant $M$ such that $|f|\leq M$ and $|g|\leq M$ for any point in space and time. Let $\lambda$ be a real constant. The time-average operator (denoted by the *overbar*) is given by:
$$
\\ \bar{f}(x,y,z) \equiv \frac{1}{T}\int_{t_0}^{t_0+T}{f(x,y,z,t)\,\mathrm{d}t},\\
$$
where $t_0$ is a prescribed instant in time (the same applies to $g$). The assumption that $f$ is bounded ensures that the integral is finite (for example, functions of the type $1/(t-t_0)$ would not be satisfying this constraint).
*prime* or *dash* (i.e. $^{\prime}$) represents the fluctuating component of the function, that is:
$$
f = \bar{f} + f^\prime
$$
Show that:$$
\bar{\bar{f}} = \bar{f}
$$\n$$
\overline{f + \lambda g} = \bar{f} + \lambda \bar{g}
$$\n$$
\overline{f^\prime} = 0
$$\n$$
\overline{f^\prime \bar{g}} = \overline{g^\prime \bar{f}} = 0
$$\n$$
\overline{fg} = \bar{f}\bar{g} + \overline{f^\prime g^\prime}
$$\n$$
\overline{\partial f/\partial x} = \partial\bar{f}/\partial x
$$\n$$
\overline{f^\prime g^\prime} = \overline{g^\prime f^\prime}
$$\n$\overline{\partial f/\partial t} = 0$ if $T \to +\infty$ *Hint: you need to use the assumption that $f$ is bounded.* | 153 | 29 | 0 | 0 | 1 | 0 | 28 | 10 | 0 | Let $f$ and $g$ be two spatio-temporal functions i.e. We assume that $f$ and $g$ are bounded, meaning that there exists a strictly positive real constant $M$ such that $[table]\leq M$ for any point in space and time. Let $g$0 be a real constant. The time-average operator denoted by the overbar is given by: $g$1 where $g$2 is a prescribed instant in time the same applies to $g$. $g$6 represents the fluctuating component of the function, that is: $g$7 Show that:$g$8 $g$9 $x$0 $x$1 $x$2 $x$3 $x$4 $x$5 if $x$6 Hint: you need to use the assumption that $f$ is bounded. | 5 |
1a604759-45f4-43de-907c-3426ec48d8d8 | 1 | 0 | 0 | 24 | 6 | 1 | 3 | 7 | Evaluate the surface integral $\oiint_{S}{\vec{B}\cdot d\vec{S}}$ where $\vec{B}=r\mathbf{\hat{r}}$ in spherical polar coordinates and $S$ is a sphere of radius $2$ centred at the origin. Apply the divergence theorem to this integral and show that $\iiint_{V}{(\nabla\cdot\vec{B})dV}$gives the same answer.
| Evaluate the surface integral $\oiint_{S}{\vec{B}\cdot d\vec{S}}$ where $\vec{B}=r\mathbf{\hat{r}}$ in spherical polar coordinates and $S$ is a sphere of radius $2$ centred at the origin. Apply the divergence theorem to this integral and show that $\iiint_{V}{(\nabla\cdot\vec{B})dV}$gives the same answer.
| 1 | 0.333333 | 2 | (**Surface Integral**) You can use the result derived in lectures that $d\vec{S}$ for a sphere of radius $a$ is given by $a^2\sin\theta d\theta d\phi\mathbf{\hat{r}}$. 
***
(**Surface Integral**) Hence find $\vec{B}\cdot d\vec{S}$. Evaluate this over the limits of $\theta$ and $\phi$ for the sphere. 
***
(**Divergence**) The divergence in spherical coordinates (ignoring $\mathbf{\hat{\theta}}$ and $\mathbf{\hat{\phi}}$ components as these do not exist) is:
$$
(\nabla\cdot\vec{B})_r =\frac{1}{r^2}\frac{\partial}{\partial r}(r^2B_r)
$$
***
(**Divergence**) After finding the divergence, can you see how to compute the divergence over the sphere$ \iiint_{V}{(\nabla\cdot\vec{B})dV} $ without explicitly evaluating the triple integral?
***
(**Divergence**) Another way is to write $dV$ in spherical coordinates, remembering the Jacobian term, and perform a triple integral over the limits of the sphere. 
***
The surface integral and divergence integral should be the same according to the divergence theorem.
| On a sphere of radius $a=2$: 
$$
d\vec{S} = a^2\sin\theta\,d\theta\,d\phi \,\mathbf{\hat{r}} = 4\sin\theta\,d\theta\,d\phi\,\mathbf{\hat{r}}
$$
This result was derived in lectures (you may wish to prove it to yourself by the cross product). 
***
On the surface of the sphere, $\vec{B} = r\mathbf{\hat{r}} = 2\mathbf{\hat{r}}$. Evaluating $\vec{B}\cdot d\vec{S}$:
***
$$
\vec{B}\cdot d\vec{S} =8\sin\theta\,d\theta\,d\phi
$$
The limits of the sphere are:
***
$$
\begin{aligned}
\theta: 0\to\pi\\
\phi: 0\to2\pi
\end{aligned}
$$
Integrating over the sphere:
***
$$
\iint_{S}\vec{B}\cdot d\vec{S} = 8\int_{\phi=0}^{2\pi}\int_{0}^{\pi}{\sin\theta\,d\theta\,d\phi}
$$
***
$$
= 16\pi[-\cos\theta]_0^\pi=32\pi
$$
, The divergence of the vector field $\vec{B}$ is given by:
$$
(\nabla\cdot\vec{B})_r =\frac{1}{r^2}\frac{\partial}{\partial r}(r^2B_r)
$$
(the $\theta$ and $\phi$ components evaluate to $0$). 
***
$$
\nabla\cdot\vec{B} = \frac{1}{r^2}\frac{\partial}{\partial r}(r^3) = 3
$$
Integrating over the volume of the sphere:
***
$$
\iiint_V{(\nabla\cdot\vec{B})dV}=3\iiint_V{dV} = 3\left(\frac{4}{3}\pi r^3\right) = 32\pi
$$
Here, rather than explicitly evaluating the integral, we applied the formula for the volume of a sphere. 
***
Alternately, in spherical coordinates, the Jacobian is $ r^2\sin\theta $ (do not insert the radius $a=2$ of the sphere here because we are evaluating over the entire volume of the sphere). So,
$$
dV = r^2\sin\theta \,dr\,d\theta\,d\phi
$$
This can be integrated over the limits of the sphere:
$$
\begin{aligned}
&r: 0\to 2\\
&\theta: 0\to \pi\\
&\phi: 0\to 2\pi
\end{aligned}
$$
,
| Evaluate the surface integral $\oiint_{S}{\vec{B}\cdot d\vec{S}}$ where $\vec{B}=r\mathbf{\hat{r}}$ in spherical polar coordinates and $S$ is a sphere of radius $2$ centred at the origin. Apply the divergence theorem to this integral and show that $\iiint_{V}{(\nabla\cdot\vec{B})dV}$gives the same answer.
| 38 | 5 | 19 | 19 | 149 | 11 | 38 | 5 | 0 | Evaluate the surface integral $\oiint_{S}{\vec{B}\cdot d\vec{S}}$ where $\vec{B}=r\mathbf{\hat{r}}$ in spherical polar coordinates and $S$ is a sphere of radius $2$ centred at the origin. Apply the divergence theorem to this integral and show that $\iiint_{V}{( abla\cdot\vec{B})dV}$gives the same answer. | 2 |
1b6227b3-1883-4c7a-a50b-e03bb8de05db | 0 | 2 | 0 | 16 | 6 | 1 | 7 | 0 | Use the ratio test to determine whether each of these two series is convergent
| $$
\begin{aligned}
\sum_{n=0}^\infty {1\over (n + 1)!}
\end{aligned}
$$
\n$$
\begin{aligned}
\sum_{n=0}^\infty {(3 - 4i)^n \over n!}
\end{aligned}
$$
| 2 | 0.333333 | 1 | For the ratio test of a sum $\displaystyle \sum _{n = 0}^\infty u_n$, find
$$
\begin{aligned} L = \lim_{n\to\infty} \left| {u_{n+1}\over u_n}\right|
\end{aligned}
$$
Do you remember how the convergence/divergence of the series depends on $L$?
***
If $L<1$, it is convergent. If $L>1$, it is divergent. If $L=1$ need to use a different test.
Can you find out if it is convergent now?
***
Use this information to carry out the ratio test, by letting $\displaystyle u_n = {1\over (n+1)!}$
\nFor the ratio test of a sum $\displaystyle \sum _{n = 0}^\infty u_n$, find
$$
\begin{aligned} L = \lim_{n\to\infty} \left| {u_{n+1}\over u_n}\right|
\end{aligned}
$$
Do you remember how the convergence/divergence of the series depends on $L$?
***
If $L<1$, it is convergent. If $L>1$, it is divergent. If $L=1$ need to use a different test.
Can you see if it is convergent now?
***
Use this information to carry out the ratio test, by letting $\displaystyle u_n = {(3 - 4i)^n \over n!}$
***
The absolute value of a complex number, $z=x+iy$, is $|z| = \sqrt{x^2+y^2}$. Can you find $L$ now?
| For the ratio test of a sum $\displaystyle \sum _{n = 0}^\infty u_n$, find
$$
\begin{aligned} L = \lim_{n\to\infty} \left| {u_{n+1}\over u_n}\right|
\end{aligned}
$$
Do you remember how the convergence/divergence of the series depends on $L$?
***
If $L<1$, it is convergent. If $L>1$, it is divergent. If $L=1$ you need to use a different test.
Can you find out if it is convergent now?
***
Use this information to carry out the ratio test, by letting $\displaystyle u_n = {1\over (n+1)!}$
***
$$
\begin{aligned}
L &= \lim_{n\to\infty} \left| {u_{n+1}\over u_n}\right| \\
&= \lim_{n\to\infty}\left| {{1\over(n+2)!}\over {1\over(n+1)!}}\right| \\
&= \lim_{n\to\infty} \left| {(n+1)! \over (n+2)!} \right|
\\
&= \lim_{n\to\infty} \left| {(n+1)n(n-1)... \over (n+2)(n+1)n(n-1)...} \right|
\\
&= \lim_{n\to\infty}\left| {1 \over n+2} \right|
\\
&= 0
\end{aligned}
$$
$L<1$ so this sum is convergent.
\nFor the ratio test of a sum $\displaystyle \sum _{n = 0}^\infty u_n$, find
$$
\begin{aligned} L = \lim_{n\to\infty} \left| {u_{n+1}\over u_n}\right|
\end{aligned}
$$
Do you remember how the convergence/divergence of the series depends on $L$?
***
If $L<1$, it is convergent. If $L>1$, it is divergent. If $L=1$ need to use a different test.
Can you see if it is convergent now?
***
Use this information to carry out the ratio test, by letting $\displaystyle u_n = {(3 - 4i)^n \over n!}$
***
$$
\begin{aligned}
L &= \lim_{n\to\infty} \left| {u_{n+1}\over u_n}\right| \\
&= \lim_{n\to\infty} \left| {{(3-4i)^{n+1}\over (n+1)!}\over{(3 - 4i)^n \over n!} }\right|
\\
&= \lim_{n\to\infty} \left| {(3-4i)^{n+1}\over(3 - 4i)^n}{n! \over (n+1)! }\right|
\\
&= \lim_{n\to\infty} \left| (3-4i){n(n-1)(n-2)... \over (n+1)n(n-1)(n-2)... }\right|
\end{aligned}
$$
How can you find the absolute value of the complex number?
***
The absolute value of a complex number, $z=x+iy$, is $|z| = \sqrt{x^2+y^2}$. Can you find $L$ now?
***
$$
\begin{aligned}
L
&= \lim_{n\to\infty} {|3-4i|\over n+1}
\\
&= \lim_{n\to\infty} {5\over n+1}
\\
&= 0
\end{aligned}
$$
So it is convergent.
| Use the ratio test to determine whether each of these two series is convergent
$$
\begin{aligned}
\sum_{n=0}^\infty {1\over (n + 1)!}
\end{aligned}
$$
\n$$
\begin{aligned}
\sum_{n=0}^\infty {(3 - 4i)^n \over n!}
\end{aligned}
$$
| 17 | 2 | 13 | 13 | 135 | 13 | 3 | 2 | 0 | Use the ratio test to determine whether each of these two series is convergent $ \begin{aligned} \sum_{n=0}^\infty {1\over (n + 1)!} \end{aligned} $ $ \begin{aligned} \sum_{n=0}^\infty {(3 - 4i)^n \over n!} \end{aligned} $ | 3 |
1c0e2dba-6dfb-4939-a870-6a263d24cb65 | 2 | 0 | 0 | 11 | 4 | 2 | 6 | 2 | Gas enters the turbine of a gas turbine engine at $1500 ~\mathrm{K}$, with a mass flow rate of $500 ~\mathrm{kg/s}$, and expands adiabatically through a pressure ratio of $20$. The turbine isentropic efficiency is $0.90$. The ambient temperature is $288 ~\mathrm{K}$. The gas can be treated as perfect, with $c_\mathrm{p}= 1.16 ~\mathrm{kJ/kgK}$ and $\gamma = \frac{4}{3}$. Regarding all properties as stagnation (total) values and the efficiency as the total-to-total value: 
| Calculate the change in the exergy flow rate of the gas stream.
\n Compare the value obtained in part (a) with the turbine power in units of $\mathrm{MW}$.
| 2 | 0.666667 | 2 | \n | Assuming kinetic and potential energy changes can be neglected:
  
$\Delta \dot{B}_\mathrm{flowing\space fluid} = \dot{m}[(h_2-h_1) -T_0(s_2-s_1)]$
***
For a perfect gas:
  
$s_2 -s_1 = c_\mathrm{p} \mathrm{ln}(\frac{T_{02}}{T_{01}}) − R \mathrm{ln}( \frac{P_{02}}{P_{01}} )$
***
$\frac{P_{01}}{P_{02}}$ is the pressure ratio. Therefore:
  
$\frac{P_{02}}{P_{01}} = \frac{1}{20}$
***
$T_{01}$ is given in the question. 
***
To calculate $T_{02}$, first calculate the value at state $2$ for an isentropic process, $T_{02s}$ and then use the isentropic efficiency equation.
***
For an isentropic process:
  
${T_{02s}} = {T_{01}}(\frac{P_{02}}{P_{01}})^{(\frac{\gamma-1}{\gamma})}$
***
Substituting in numbers:
  
$T_\mathrm{02s} = 1500(\frac{1}{20})^{(\frac{\frac{4}{3} -1}{\frac{4}{3}})} = 709.3~\mathrm{K}$ 
***
Now use the isentropic efficiency equation for a perfect gas to calculate $T_{02}$:
  
$\eta = \frac{T_{01} - T_{02}}{T_{01} - T_{02s}}$
***
Substituting numbers and rearranging:
  
$T_{02} = 1500-0.9(1500-709.3) = 788.4~\mathrm{K}$
***
Calculate $R$:
  
$R = c_\mathrm{p} - c_\mathrm{v} = c_\mathrm{p} - \frac{c_\mathrm{p}}{\gamma}$
***
Substituting in numbers:
  
$R = 1.16-\frac{1.16}{\frac{4}{3}} = 0.29$
***
Hence:
  
$s_2 - s_1 = 1.16\mathrm{ln}(\frac{788.4}{1500})-0.29\mathrm{ln}(\frac{1}{20}) = 0.123~\mathrm{kJ/kgK}$
***
$h_2 - h_1 = c_\mathrm{p}(T_{02} - T_{01}) = 1.16(788.4-1500) = -825.5~\mathrm{kJ/kg}$
***
Therefore:
  
$\Delta \dot{B}_\mathrm{flowing\space fluid} = 500[-825.5 -288(0.123)] = -430~\mathrm{MW}$
***
Drop in exergy flow rate $ = -\Delta \dot{B}_\mathrm{flowing\space fluid} = 430~\mathrm{MW} $
\nUse the SFEE, bearing in mind that the process is adiabatic and kinetic and potential energy changes can be neglected:
  
$-\dot{W} = \dot{m}(h_2 - h_1)$
***
For a perfect gas:
  
$-\dot{W} = \dot{m}c_\mathrm{p}(T_{02} - T_{01})$
***
Substituting in numbers and rearranging:
  
$\dot{W} =500\times 1.16(1500-788.4) = 413~\mathrm{MW}$
***
This is lower than the magnitude of the change in exergy flow rate as calculated in part (a) due to irreversibility in the system.
| Gas enters the turbine of a gas turbine engine at $1500 ~\mathrm{K}$, with a mass flow rate of $500 ~\mathrm{kg/s}$, and expands adiabatically through a pressure ratio of $20$. The turbine isentropic efficiency is $0.90$. The ambient temperature is $288 ~\mathrm{K}$. The gas can be treated as perfect, with $c_\mathrm{p}= 1.16 ~\mathrm{kJ/kgK}$ and $\gamma = \frac{4}{3}$. Regarding all properties as stagnation (total) values and the efficiency as the total-to-total value: 
Calculate the change in the exergy flow rate of the gas stream.
\n Compare the value obtained in part (a) with the turbine power in units of $\mathrm{MW}$.
| 97 | 8 | 23 | 23 | 187 | 0 | 28 | 1 | 0 | Regarding all properties as stagnation total values and the efficiency as the total-to-total value: Calculate the change in the exergy flow rate of the gas stream. Compare the value obtained in part a with the turbine power in units of $\mathrm{MW}$. | 2 |
1c0fb18f-35b0-4e37-a35b-4ef651e69dc3 | 0 | 0 | 3 | 14 | 4 | 2 | 13 | 3 | Referring to data from the wind tunnel in Figure 14.6, measured velocity profiles, $u(y)$, are given at different locations, $x$.
To complete this question you will need to use that data. You can begin by reading from the graph but later will need the raw data and instructions are provided.
Figure 14.6 is replicated below as a reminder.

| Based on reading the graph, estimate (roughly!) the boundary layer thickness, $\delta_{99}$, for the ten profiles. Comment on the ratio $\delta(x)/x$ where $x$ is the distance along the wall. Add you own data from the Wind Tunnel and check if it agrees.\nDerive a method to estimate the average value, $V$, for a given velocity profile. $V$ is the transverse component of the velocity (perpendicular to the flat plate) at the edge of the boundary layer. You need to use a control volume analysis to answer this question. Hint: we only require an average over the control volume.\nImplement the solution in part (b) for the velocity profiles from the Wind Tunnel. This requires 'numerical integration', for example in MATLAB use `trapz` or in Python \`numpy.trapz. Plot values of $V/U$ and compare them to $\delta/x$. Is Equation (13.5) a reasonable approximation?
\
To answer this question you need data from the wind tunnel. Optionally you can use the following [>>data files<<](https://problem-set-app.s3.eu-west-2.amazonaws.com/media/t14/Q14_data_files.zip). \
 \
Guide to the data files:
* A \`starter' script is provided to read in the data and it indicates which lines to code your solutions for $U,V/U,\delta_{99}$. This makes it very convenient to complete the question yourself.
* A \`solution' script is also provided but you are advised not to look! Both scripts are provided in both MATLAB and Python.
| 3 | 1 | 4 | \n\n | \n\n | Referring to data from the wind tunnel in Figure 14.6, measured velocity profiles, $u(y)$, are given at different locations, $x$.
To complete this question you will need to use that data. You can begin by reading from the graph but later will need the raw data and instructions are provided.
Figure 14.6 is replicated below as a reminder.

Based on reading the graph, estimate (roughly!) the boundary layer thickness, $\delta_{99}$, for the ten profiles. Comment on the ratio $\delta(x)/x$ where $x$ is the distance along the wall. Add you own data from the Wind Tunnel and check if it agrees.\nDerive a method to estimate the average value, $V$, for a given velocity profile. $V$ is the transverse component of the velocity (perpendicular to the flat plate) at the edge of the boundary layer. You need to use a control volume analysis to answer this question. Hint: we only require an average over the control volume.\nImplement the solution in part (b) for the velocity profiles from the Wind Tunnel. This requires 'numerical integration', for example in MATLAB use `trapz` or in Python \`numpy.trapz. Plot values of $V/U$ and compare them to $\delta/x$. Is Equation (13.5) a reasonable approximation?
\
To answer this question you need data from the wind tunnel. Optionally you can use the following [>>data files<<](https://problem-set-app.s3.eu-west-2.amazonaws.com/media/t14/Q14_data_files.zip). \
 \
Guide to the data files:
* A \`starter' script is provided to read in the data and it indicates which lines to code your solutions for $U,V/U,\delta_{99}$. This makes it very convenient to complete the question yourself.
* A \`solution' script is also provided but you are advised not to look! Both scripts are provided in both MATLAB and Python.
| 285 | 10 | 0 | 0 | 1 | 0 | 224 | 8 | 1 | Referring to data from the wind tunnel in Figure 14.6, measured velocity profiles, $u(y)$, are given at different locations, $x$. To complete this question you will need to use that data. Based on reading the graph, estimate roughly! Add you own data from the Wind Tunnel and check if it agrees. Derive a method to estimate the average value, $V$, for a given velocity profile. You need to use a control volume analysis to answer this question. Is Equation 13.5 a reasonable approximation? Optionally you can use the following . Guide to the data files: A `starter' script is provided to read in the data and it indicates which lines to code your solutions for $U,V/U,\delta_{99}$. | 9 |
1c7a7f6c-55d0-445b-9aef-f251ced69b63 | 2 | 2 | 0 | 13 | 4 | 2 | 5 | 1 | A hand-held rotary sanding machine is shown in the diagram below.

It has a sanding disc which rotates at $2400~\mathrm{rev/min}$ in the direction shown. The sanding disc, which may be considered to be a uniform disc of mass $m = 0.3~\mathrm{kg}$, has a diameter $D = 0.28~\mathrm{m}$. The inertia of the rotating parts other than the disc may be neglected.
Determine the magnitude and direction of the couple which a person holding the sander must apply in order to rotate the sander about:
| The fixed x-axis at $0.5~\mathrm{rad/s}$ in the direction shown.
\nThe fixed z axis at $1.0~\mathrm{rad/s}$ in the direction shown.
| 2 | 0.666667 | 3 | Start off by calculating your values of the mass moment of inertia and the angular velocity of the uniform disk in rad/s (or any other units you may feel comfortable with!).
***
Refer to Equation 5.1 in your notes to calculate the magnitude of the moment required, keeping in mind that in this case the angular velocity the user is trying to apply to the disk is equivalent to the angular velocity of precession.
***
Draw the vector diagrams of the angular momentums using the right hand rule and the change in angular momentum of the rotor to graphically determine the direction of the required moment relative to the desired directions shown in the question.
\nSee tutorial in part a
| The gyroscopic moment about $x$ is given by:
$$
M_x=I{\dot{\theta}}_y{\dot{\theta}}_z
$$
***
Where the angular velocity of the sanding disc is given by:
$$
{\dot{\theta}}_y=2400\left(\cfrac{2\pi}{60}\right)
$$
$$
{\dot{\theta}}_y=251.3~\mathrm{rad/s}
$$
***
And the moment of inertia of the sanding disc is:
$$
I=\cfrac{mr^2}{2}
$$
$$
I=\cfrac{0.3\times{\left(\cfrac{0.28}{2}\right)}^2}{2}
$$
$$
I=0.00294~\mathrm{kgm^2}
$$
***
Substituting the values of the parameters gives:
$$
M_x = 0.00294 \times 251.3 \times 1.0
$$
$$
M_x=0.739~\mathrm{Nm}
$$
\nThe gyroscopic moment about $z$ is given by:
$$
M_z=I{\dot{\theta}}_y{\dot{\theta}}_x
$$
***
Substituting the values of the parameters gives:
$$
M_z = 0.00294 \times 251.3 \times 0.5
$$
$$
M_z=0.369~\mathrm{Nm}
$$
| A hand-held rotary sanding machine is shown in the diagram below.

It has a sanding disc which rotates at $2400~\mathrm{rev/min}$ in the direction shown. The sanding disc, which may be considered to be a uniform disc of mass $m = 0.3~\mathrm{kg}$, has a diameter $D = 0.28~\mathrm{m}$. The inertia of the rotating parts other than the disc may be neglected.
Determine the magnitude and direction of the couple which a person holding the sander must apply in order to rotate the sander about:
The fixed x-axis at $0.5~\mathrm{rad/s}$ in the direction shown.
\nThe fixed z axis at $1.0~\mathrm{rad/s}$ in the direction shown.
| 98 | 5 | 13 | 13 | 67 | 0 | 19 | 2 | 1 | Determine the magnitude and direction of the couple which a person holding the sander must apply in order to rotate the sander about: The fixed x-axis at $0.5~\mathrm{rad/s}$ in the direction shown. | 1 |
1c8bdc12-43a5-4b6a-a13a-1129f7e73552 | 2 | 0 | 2 | 14 | 4 | 2 | 10 | 2 | A viscous oil flows steadily down an inclined plate under the action of gravity, forming a film of constant thickness $h$. This is shown in the image, below, where a Cartesian frame of reference with $y$-axis normal to the plate has been defined. The flow is uniform along the plate (i.e. along $x$ and $z$ coordinates as shown in the image) and the ambient pressure $p_a$ is uniform and constant. The air above the oil is at rest and considered to be inviscid. The oil is a Newtonian fluid with constant and uniform density and viscosity. Using the Cartesian frame of reference shown:
 | If $\vec{u}=\left[u~~v~~w\right]^T$, show that $v=0$.\nShow that the shear stress $\tau_w$ acting on the wall is equal to $\tau_w=\rho g h \mathrm{sin}(\alpha)$.\nExplain why $u$ is a function of $y$ only and find an expression for $u(y)$.\nShow that the pressure, $p$, is a function of $y$ only and compute $p(y)$. | 4 | 1 | 4 | \n\n\n | \n\n\n | A viscous oil flows steadily down an inclined plate under the action of gravity, forming a film of constant thickness $h$. This is shown in the image, below, where a Cartesian frame of reference with $y$-axis normal to the plate has been defined. The flow is uniform along the plate (i.e. along $x$ and $z$ coordinates as shown in the image) and the ambient pressure $p_a$ is uniform and constant. The air above the oil is at rest and considered to be inviscid. The oil is a Newtonian fluid with constant and uniform density and viscosity. Using the Cartesian frame of reference shown:
If $\vec{u}=\left[u~~v~~w\right]^T$, show that $v=0$.\nShow that the shear stress $\tau_w$ acting on the wall is equal to $\tau_w=\rho g h \mathrm{sin}(\alpha)$.\nExplain why $u$ is a function of $y$ only and find an expression for $u(y)$.\nShow that the pressure, $p$, is a function of $y$ only and compute $p(y)$. | 156 | 15 | 0 | 0 | 1 | 0 | 51 | 10 | 0 | Using the Cartesian frame of reference shown: If $\vec{u}=\left[u~~v~~w\right]^T$, show that $v=0$. Show that the shear stress $\tau_w$ acting on the wall is equal to $\tau_w=\rho g h \mathrm{sin}(\alpha)$. Explain why $u$ is a function of $y$ only and find an expression for $y$1. Show that the pressure, $y$2, is a function of $y$ only and compute $y$4. | 4 |
1c94b03d-b0dd-4fce-b753-ca96a7c4d8c8 | 2 | 0 | 0 | 0 | 0 | 2 | 5 | 4 | The flow downstream of the shock wave in the figure below is turned through a Prandtl-Meyer expansion at C, until it has returned to its original flow direction.

| Determine the Mach number downstream of the expansion.
\nDetermine the pressure downstream of the expansion, if upstream the pressure is atmospheric. 
| 2 | 0.666667 | 2 | Knowing that across a left running expansion fan, $ \nu + \theta = \mathrm{constant} $, find $ \nu_{3} $ and use this quantity to find $ M_{3} $. 
***
Use tables to find the values of $ \beta_{1} $ and $ M_{2} $ after the oblique shock. Use tables again to find $ \nu_{2} $. 
\nKnowing that expansion fans are isentropic, express the ratio $ \frac{p_{3}}{p_{2}} $ as a function of ratios that can be obtained through tables. 
| Across an oblique shock, with $ \theta = 20^{\circ} $ and $ M_{1} = 2.2 $, from the tables we can get $ \beta_{1} = 48.025^{\circ} $ and the Mach number behind the shock is $M_{2} = 1.401$. 

***
To calculate the change in flow properties across the expansion, we need to go Prandtl-Meyer function before the expansion. From the 1D incompressible tables, for $M_{2} = 1.401$, 
 
 $ \nu_2 = 9.00^{\circ} $. 

***
Across an expansion fan, as this is a left running case, $ \nu + \theta = \mathrm{constant} $. Therefore:
  
$ \nu_{2} + \theta_{2} = \nu_{3} + \theta_{3} $
  
$ 9.0 + 20 = \nu_{3} + 0 $ 
  
So $ \nu_{3} = 29.00^{\circ} $
 
With this value of $\nu$, we can go to the tables to find the corresponding Mach number, which is $ M_{3} = 2.10 $:

\nExpansion fans are isentropic, so $\frac{p_{3}}{p_{2}} = \frac{p_{3}}{p_{03}} \cdot \frac{p_{02}}{p_{2}}$
   
From tables, with $ M_{1} = 2.2 $ and *$ \theta = 20^{\circ} $:*

***
$ M_{2} = 1.404 $, so from the 1D compressible tables below we can obtain the insetropic pressure ratio:
 
 $\frac{p_{02}}{p_{2}} =3.1823$. 

***
From part a), $ M_{3} = 2.10 $, so from the 1D compressible tables again, we can get the isentropic pressure ratio behind the expansion:
 $\frac{p_{03}}{p_{3}} = 9.1447$:

***
We can now calculate the pressure ratio across the expansion fan:
$\frac{p_{3}}{p_{2}} = \frac{3.1823}{9.1447} = 0.348$ 
  
And the pressure behind the expansion fan:
 
$p_{3} = \frac{p_{3}}{p_{2}} \cdot \frac{p_{2}}{p_{1}} \cdot p_{1} = 0.348 \cdot 2.956 \cdot 1 = 1.029 \ \mathrm{atm}$
| The flow downstream of the shock wave in the figure below is turned through a Prandtl-Meyer expansion at C, until it has returned to its original flow direction.

Determine the Mach number downstream of the expansion.
\nDetermine the pressure downstream of the expansion, if upstream the pressure is atmospheric. 
| 50 | 0 | 21 | 21 | 197 | 7 | 21 | 0 | 1 | Determine the Mach number downstream of the expansion. Determine the pressure downstream of the expansion, if upstream the pressure is atmospheric. | 2 |
1ca8908d-a1f1-44a0-8603-f5c8b6d3c43b | 10 | 0 | 0 | 8 | 4 | 2 | 0 | 4 | A $ 3 \text{ m} $ long horizontal beam of rectangular cross section, depth $ 200 \text{ mm} $ and thickness $ 50 \text{ mm} $ is built in at one end. The other end may be supported by one of the following methods (see parts (a)-(e)).
   
The beam is subjected to a load of $ 10 \text{ kN} $ acting vertically downwards $ 2 \text{ m} $ from the built in end.
   
For each of the cases, determine the *deflection of the beam* at the point of application of the load and find the *maximum stress* in the beam after the load has been applied. Assume the beam material has a relatively low density and a Modulus of Elasticity of $200 \text{ GPa}$.
| There is no support (i.e. the end is free.)
\nThe end just rests on a rigid roller, which is mounted on a rigid foundation.
\nSame as (b) but the roller is raised by $5 \text{ mm}$.
\nSame as (b) but the roller is lowered by $5 \text{ mm}$.
\nSame as (b) but the foundation has a vertical stiffness of $1 \text{ MNm}$
| 5 | 0.666667 | 4 | \n\n\n\n | Here, the worked solution for the general equation is included. The general equation will then be directly referenced in parts (b)-(e).
   
***
First draw a diagram of the system:
  
***
Second moment of area of beam:
   
$$
I = \frac{bd^3}{12}=\frac{0.05\times0.2^3}{12}=33.33\times10^{-6} \text{ m}^4
$$
   
$$
EI = (200\times10^9)(33.33\times10^{-6})=6.667\text{ MNm}^2
$$
   
***
Find the bending moment of the beam:
   
$$
EI \frac{d^2\nu}{dx^2} =M=P\langle2-x\rangle-R\langle3-x\rangle
$$
   
***
To find the deflection, integrate the above expression twice and apply boundary conditions.
   
$$
EI\frac{d\nu}{dx}=-\frac{P}{2}\langle2-x\rangle^2+\frac{R}{2}\langle3-x\rangle^2+A
$$
   
***
Apply the boundary condition for a built-in end, at $x=0, \frac{d\nu}{dx}=0$.
  
$$
0=-\frac{P}{2}\cdot 4+\frac{R}{2}\cdot 9 + A \hspace{20pt} \rightarrow \hspace{20pt} A = \frac{P}{2}\cdot 4-\frac{R}{2}\cdot9
$$
   
***
Substitute in $A$, rearrange and integrate again to find an expression for deflection.
   
$$
EI\frac{d\nu}{dx}=\frac{P}{2}[4-\langle2-x\rangle^2]-\frac{R}{2}[9-\langle3-x\rangle^2]
$$
   
$$
EI\nu = \frac{P}{2}[4x+\frac{\langle2-x\rangle^3}{3}]-\frac{R}{2}[9x-\frac{\langle3-x\rangle^3}{3}]+B
$$
   
***
Apply the boundary condition, also for the built in end, at $x=0, \nu=0$.
   
$$
0=-\frac{P}{2}\cdot \frac{8}{3}-\frac{R}{2}\cdot9+B \hspace{20pt} \rightarrow \hspace{20pt} B=\frac{R}{2}\cdot9-\frac{P}{2}\cdot\frac{8}{3}
$$
   
***
Therefore the full general solution would be:
   
$$
EI\nu = \frac{P}{2}[4x+\frac{\langle2-x\rangle^3}{3}-\frac{8}{3}]-\frac{R}{2}[9x+\frac{\langle3-x\rangle^3}{3}-9]
$$
   
***
Bending moment must be $0$ at $x=3$, so maximum bending moment will be at $x=0$ or $x=2$.
   
After substituting into the general equation, the maximum bending moment is $BM_{max}=2P-3R \text{ or } BM_{max}=-R$
   
***
For system (a), since the beam is a cantilever, $R=0$, and the maximum bending stress is $x=0$.
   
$$
\text{BM}_{max}=2(10,000)-3(0)=20 \text{ kNm}
$$
  
Use the following relation to find maximum stress.
   
$$
\sigma=\frac{My}{I}=\frac{M\cdot d}{I\cdot2}
$$
   
***
Maximum stress:
   
$$
\sigma_{max}=\frac{20\times10^3\times0.1}{33.33}=\boxed{60.01 \text{ MPa}}
$$
   
***
Deflection at point of application of load (i.e. $x=2$):
   
$$
(6.667\times10^6)\nu_{(x=2)} = \frac{10,000}{2}[4(2)+\frac{\langle2-2\rangle^3}{3}-\frac{8}{3}]-\frac{0}{2}[9(2)+\frac{\langle3-2\rangle^3}{3}-9] \\
\hspace{10pt} \\
(6.667\times10^6)\nu_{(x=2)}=\frac{10,000}{2}\langle8-\frac{8}{3}\rangle\\
\hspace{10pt} \\
\nu =\boxed{4.00 \text{ mm}}
$$
\nThe boundary condition means that $\nu=0$ at $x=3$, the reaction force $R$ is unknown.
  
Substitute into general equation:
$$
EI\nu = \frac{P}{2}[4x+\frac{\langle2-x\rangle^3}{3}-\frac{8}{3}]-\frac{R}{2}[9x+\frac{\langle3-x\rangle^3}{3}-9]
$$
   
$$
EI\nu_{(x=3)}\rightarrow 0=\frac{10,000}{2}[12-\frac{8}{3}]-\frac{R}{2}[27-9] \\
\hspace{10pt} \\
R = 5.185 \text{ kN}
$$
   
***
Deflection at $x=2$:
   
$$
EI\nu = \frac{P}{2}[4x+\frac{\langle2-x\rangle^3}{3}-\frac{8}{3}]-\frac{R}{2}[9x+\frac{\langle3-x\rangle^3}{3}-9]
$$
  
$$
(6.667\times10^6)\nu_{(x=2)} = \frac{10,000}{2}(8-\frac{8}{3})-\frac{5185}{2}(18+\frac{1}{3}-9)
$$
  
$$
\nu_{(x=2)}=\boxed{0.37 \text{ mm}}
$$
   
***
To find maximum stress, the maximum bending moment needs to be found (using equations found in part (a)).
  
$$
\begin{align*}
\text{At } x=0, M&=(10,000\times2)-(5185\times 3) = 4.445 \text{ kNM} \\
\text{At } x=2, M&= -5.185\text{ kNM}
\end{align*}
$$
  
Therefore, maximum BM is at $x=2$, and maximum bending stress can be found.
  
$$
\sigma_{max}=\frac{Md}{2I}=\frac{5.185\times10^3\times 0.2}{2\times33.33\times10^{-6}}=\boxed{15.56 \text{ MPa}}
$$
\nThe boundary condition implies that, $\nu=-5\text{ mm}$ at $x=3$, reactive force ($R$) is unknown.
   
Substituting into the general solution:
   
$$
EI\nu = \frac{P}{2}[4x+\frac{\langle2-x\rangle^3}{3}-\frac{8}{3}]-\frac{R}{2}[9x+\frac{\langle3-x\rangle^3}{3}-9]
$$
  
$$
(6.667\times10^6)(-5\times10^{-3})=5000[12-\frac{8}{3}]-9R
$$
  
$$
R=8.889 \text{ kN}
$$
   
***
Deflection at $x=2$:
   
$$
EI\nu = \frac{P}{2}[4x+\frac{\langle2-x\rangle^3}{3}-\frac{8}{3}]-\frac{R}{2}[9x+\frac{\langle3-x\rangle^3}{3}-9]
$$
   
$$
(6.667\times10^6)\nu_{(x=2)}=\frac{10,000}{2}(8-\frac{8}{3})-\frac{8889}{2}(18+\frac{1}{3}-9)
$$
   
$$
\nu_{(x=2)}=\boxed{-2.22\text{ mm}}
$$
   
***
To find maximum stress, the maximum bending moment needs to be found (using equations found in part (a)).
   
$$
\begin{align*}
\text{At } x=0, M&=(10,000\times2)-(5185\times 3) = -6.667\text{ kNM} \\
\text{At } x=2, M&= -8.889\text{ kNM}
\end{align*}
$$
   
Therefore, maximum BM is at $x=2$, and maximum bending stress can be found.
   
$$
\sigma_{max}=\frac{Md}{2I}=\frac{8.889\times10^3\times 0.2}{2\times33.33\times10^{-6}}=\boxed{26.67 \text{ MPa}}
$$
\nThe boundary condition implies that, $\nu=5\text{ mm}$ at $x=3$, reactive force ($R$) is unknown.
   
Substituting into the general solution:
   
$$
EI\nu = \frac{P}{2}[4x+\frac{\langle2-x\rangle^3}{3}-\frac{8}{3}]-\frac{R}{2}[9x+\frac{\langle3-x\rangle^3}{3}-9]
$$
  
$$
(6.667\times10^6)(5\times10^{-3})=5000[12-\frac{8}{3}]-9R
$$
  
$$
R=1.481 \text{ kN}
$$
   
***
Deflection at $x=2$:
   
$$
EI\nu = \frac{P}{2}[4x+\frac{\langle2-x\rangle^3}{3}-\frac{8}{3}]-\frac{R}{2}[9x+\frac{\langle3-x\rangle^3}{3}-9]
$$
   
$$
(6.667\times10^6)\nu_{(x=2)}=\frac{10,000}{2}(8-\frac{8}{3})-\frac{1481}{2}(18+\frac{1}{3}-9)
$$
   
$$
\nu_{(x=2)}=\boxed{2.96\text{ mm}}
$$
   
***
To find maximum stress, the maximum bending moment needs to be found (using equations found in part (a)).
   
$$
\begin{align*}
\text{At } x=0, M&=(10,000\times2)-(5185\times 3) = 15.557\text{ kNM} \\
\text{At } x=2, M&= 4.443\text{ kNM}
\end{align*}
$$
   
Therefore, maximum BM is at $x=0$, and maximum bending stress can be found.
   
$$
\sigma_{max}=\frac{Md}{2I}=\frac{15.557\times10^3\times 0.2}{2\times33.33\times10^{-6}}=\boxed{46.68 \text{ MPa}}
$$
\nLet mounting stiffness $=k$, deflection at $x=3$, $\nu_{(x=3)}=\frac{R}{k}$, reactive force ($R$) is unknown.
   
Substituting into the general solution:
   
$$
EI\nu = \frac{P}{2}[4x+\frac{\langle2-x\rangle^3}{3}-\frac{8}{3}]-\frac{R}{2}[9x+\frac{\langle3-x\rangle^3}{3}-9]
$$
  
$$
(6.667\times10^6)(\frac{R}{1\times10^6})=5000[12-\frac{8}{3}]-9R
$$
  
$$
R=2.979 \text{ kN}
$$
   
***
Deflection at $x=2$:
   
$$
EI\nu = \frac{P}{2}[4x+\frac{\langle2-x\rangle^3}{3}-\frac{8}{3}]-\frac{R}{2}[9x+\frac{\langle3-x\rangle^3}{3}-9]
$$
   
$$
(6.667\times10^6)\nu_{(x=2)}=\frac{10,000}{2}(8-\frac{8}{3})-\frac{2979}{2}(18+\frac{1}{3}-9)
$$
   
$$
\nu_{(x=2)}=\boxed{1.91\text{ mm}}
$$
   
***
To find maximum stress, the maximum bending moment needs to be found (using equations found in part (a)).
   
$$
\begin{align*}
\text{At } x=0, M&=(10,000\times2)-(2979\times 3) = 11.063\text{ kNM} \\
\text{At } x=2, M&= 2.979\text{ kNM}
\end{align*}
$$
   
Therefore, maximum BM is at $x=0$, and maximum bending stress can be found.
   
$$
\sigma_{max}=\frac{Md}{2I}=\frac{11.063\times10^3\times 0.2}{2\times33.33\times10^{-6}}=\boxed{4 \text{ MPa}}
$$
| A $ 3 \text{ m} $ long horizontal beam of rectangular cross section, depth $ 200 \text{ mm} $ and thickness $ 50 \text{ mm} $ is built in at one end. The other end may be supported by one of the following methods (see parts (a)-(e)).
   
The beam is subjected to a load of $ 10 \text{ kN} $ acting vertically downwards $ 2 \text{ m} $ from the built in end.
   
For each of the cases, determine the *deflection of the beam* at the point of application of the load and find the *maximum stress* in the beam after the load has been applied. Assume the beam material has a relatively low density and a Modulus of Elasticity of $200 \text{ GPa}$.
There is no support (i.e. the end is free.)
\nThe end just rests on a rigid roller, which is mounted on a rigid foundation.
\nSame as (b) but the roller is raised by $5 \text{ mm}$.
\nSame as (b) but the roller is lowered by $5 \text{ mm}$.
\nSame as (b) but the foundation has a vertical stiffness of $1 \text{ MNm}$
| 165 | 9 | 76 | 76 | 593 | 0 | 58 | 3 | 0 | The other end may be supported by one of the following methods see parts a-e. For each of the cases, determine the deflection of the beam at the point of application of the load and find the maximum stress in the beam after the load has been applied. Assume the beam material has a relatively low density and a Modulus of Elasticity of $200 \text{ GPa}$. | 3 |
1d3e94e1-f697-45ed-a04c-b3e62ab9d8fa | 0 | 5 | 0 | 24 | 6 | 1 | 0 | 3 | Determine which of the following are exact differentials:
| $$
(3x+2)y\,dx + x(x+1)\, dy
$$
\n$$
y\tan x\,dx + x\tan y\,dy
$$
\n$$
y^2(\ln x + 1)\,dx + 2xy\ln x\,dy
$$
\n$$
y^2(\ln x + 1)\,dy + 2xy\ln x\,dx
$$
\n$$
\left[ x/(x^2 + y^2)\right]\,dy - \left[ y/(x^2 + y^2 )\right]\,dx
$$
| 5 | 0.333333 | 2 | The differential of a function $\Omega$ in Cartesian form is:
$$
d\Omega = \frac{\partial \Omega}{\partial x}dx + \frac{\partial \Omega}{\partial y}dy
$$
The differentials given in the question are of the form:
$$
A(x,y)dx+ B(x,y)dy
$$
If:
$$
\frac{\partial A}{\partial y} = \frac{\partial B}{\partial x}
$$
We can conclude that $A = \partial \Omega / \partial x$ and $B = \partial \Omega / \partial y$. This is due to Clairaut's theorem (verified in *Question 3*). Hence, we can conclude that the differential links back to the original function $\Omega$, which is the condition for an exact differential. 
***
Therefore, in the differential, partially differentiate $A(x,y)$ with respect to $y$ and $B(x,y)$ with respect to $x$. 
***
If the partial derivatives are equivalent, the differential is exact. 
\nThe differential of a function $\Omega$ in Cartesian form is:
$$
d\Omega = \frac{\partial \Omega}{\partial x}dx + \frac{\partial \Omega}{\partial y}dy
$$
The differentials given in the question are of the form:
$$
A(x,y)dx+ B(x,y)dy
$$
If:
$$
\frac{\partial A}{\partial y} = \frac{\partial B}{\partial x}
$$
We can conclude that $A = \partial \Omega / \partial x$ and $B = \partial \Omega / \partial y$. This is due to Clairaut's theorem (verified in *Question 3*). Hence, we can conclude that the differential links back to the original function $\Omega$, which is the condition for an exact differential. 
***
Therefore, in the differential, partially differentiate $A(x,y)$ with respect to $y$ and $B(x,y)$ with respect to $x$. 
***
If the partial derivatives are equivalent, the differential is exact. 
\nThe differential of a function $\Omega$ in Cartesian form is:
$$
d\Omega = \frac{\partial \Omega}{\partial x}dx + \frac{\partial \Omega}{\partial y}dy
$$
The differentials given in the question are of the form:
$$
A(x,y)dx+ B(x,y)dy
$$
If:
$$
\frac{\partial A}{\partial y} = \frac{\partial B}{\partial x}
$$
We can conclude that $A = \partial \Omega / \partial x$ and $B = \partial \Omega / \partial y$. This is due to Clairaut's theorem (verified in *Question 3*). Hence, we can conclude that the differential links back to the original function $\Omega$, which is the condition for an exact differential. 
***
Therefore, in the differential, partially differentiate $A(x,y)$ with respect to $y$ and $B(x,y)$ with respect to $x$. 
***
If the partial derivatives are equivalent, the differential is exact. 
\nThe differential of a function $\Omega$ in Cartesian form is:
$$
d\Omega = \frac{\partial \Omega}{\partial x}dx + \frac{\partial \Omega}{\partial y}dy
$$
The differentials given in the question are of the form:
$$
A(x,y)dx+ B(x,y)dy
$$
If:
$$
\frac{\partial A}{\partial y} = \frac{\partial B}{\partial x}
$$
We can conclude that $A = \partial \Omega / \partial x$ and $B = \partial \Omega / \partial y$. This is due to Clairaut's theorem (verified in *Question 3*). Hence, we can conclude that the differential links back to the original function $\Omega$, which is the condition for an exact differential. 
***
Therefore, in the differential, partially differentiate $A(x,y)$ with respect to $y$ and $B(x,y)$ with respect to $x$. 
***
If the partial derivatives are equivalent, the differential is exact. 
\nThe differential of a function $\Omega$ in Cartesian form is:
$$
d\Omega = \frac{\partial \Omega}{\partial x}dx + \frac{\partial \Omega}{\partial y}dy
$$
The differentials given in the question are of the form:
$$
A(x,y)dx+ B(x,y)dy
$$
If:
$$
\frac{\partial A}{\partial y} = \frac{\partial B}{\partial x}
$$
We can conclude that $A = \partial \Omega / \partial x$ and $B = \partial \Omega / \partial y$. This is due to Clairaut's theorem (verified in *Question 3*). Hence, we can conclude that the differential links back to the original function $\Omega$, which is the condition for an exact differential. 
***
Therefore, in the differential, partially differentiate $A(x,y)$ with respect to $y$ and $B(x,y)$ with respect to $x$. 
***
If the partial derivatives are equivalent, the differential is exact. 
| See $\color{green}\textsf{Structured Tutorial}$ or the lecture notes for an explanation of exact differentials. 
***
Let $A(x,y) = (3x+2)y$ and $B(x,y) = x(x+1)$.
***
Differentiating $A$ with respect to $y$:
***
$$
\frac{\partial A}{\partial y} = 3x+2
$$
and $B$ with respect to $x$:
***
$$
\frac{\partial B}{\partial x} = 2x+1
$$
***
Since:
$$
\frac{\partial A}{\partial y}\ne\frac{\partial B}{\partial x}
$$
This is *not* an exact differential. 
\nSee $\color{green}\textsf{Structured Tutorial}$ or the lecture notes for an explanation of exact differentials. 
***
Let $A(x,y) = y\tan{x}$ and $B(x,y) = x\tan{y}$.
***
Differentiating $A$ with respect to $y$:
***
$$
\frac{\partial A}{\partial y} = \tan{x}
$$
and $B$ with respect to $x$:
***
$$
\frac{\partial B}{\partial x} = \tan{y}
$$
***
Since:
$$
\frac{\partial A}{\partial y}\ne\frac{\partial B}{\partial x}
$$
This is *not* an exact differential. 
\nSee $\color{green}\textsf{Structured Tutorial}$ or the lecture notes for an explanation of exact differentials. 
***
Let $A(x,y) = y^2(\ln{x}+1)$ and $B(x,y) = 2xy \ln{x}$.
***
Differentiating $A$ with respect to $y$:
***
$$
\frac{\partial A}{\partial y} = 2y(\ln{x}+1)
$$
and $B$ with respect to $x$ using the product rule:
***
$$
\frac{\partial B}{\partial x} = 2y\ln{x} + \frac{2xy}{x} = 2y(\ln{x}+1)
$$
***
Since:
$$
\frac{\partial A}{\partial y}=\frac{\partial B}{\partial x}
$$
This *is* an exact differential.
\nSee $\color{green}\textsf{Structured Tutorial}$ or the lecture notes for an explanation of exact differentials. Notice the opposite order of the differential terms to part (c). 
***
Let $A(x,y) = 2xy\ln{x}$ and $B(x,y) = y^2 (\ln{x}+1)$.
***
Differentiating $A$ with respect to $y$:
***
$$
\frac{\partial A}{\partial y} = 2x\ln{x}
$$
and $B$ with respect to $x$:
***
$$
\frac{\partial B}{\partial x} = \frac{y^2}{x}
$$
***
Since:
$$
\frac{\partial A}{\partial y}\ne\frac{\partial B}{\partial x}
$$
This is *not* an exact differential. 
\nSee $\color{green}\textsf{Structured Tutorial}$ or the lecture notes for an explanation of exact differentials. 
***
Let $A(x,y) = -y/(x^2+y^2)$ and $B(x,y) = x/(x^2+y^2)$.
***
Differentiating $A$ with respect to $y$ using the quotient rule:
***
$$
\frac{\partial A}{\partial y} = \frac{-(x^2+y^2)+2y^2}{(x^2+y^2)^2} = \frac{y^2-x^2}{(x^2+y^2)^2}
$$
and $B$ with respect to $x$ using the quotient rule:
***
$$
\frac{\partial B}{\partial x} = \frac{(x^2+y^2)-2x^2}{(x^2+y^2)^2} = \frac{y^2-x^2}{(x^2+y^2)^2}
$$
***
Since:
$$
\frac{\partial A}{\partial y}=\frac{\partial B}{\partial x}
$$
This *is* an exact differential.
| Determine which of the following are exact differentials:
$$
(3x+2)y\,dx + x(x+1)\, dy
$$
\n$$
y\tan x\,dx + x\tan y\,dy
$$
\n$$
y^2(\ln x + 1)\,dx + 2xy\ln x\,dy
$$
\n$$
y^2(\ln x + 1)\,dy + 2xy\ln x\,dx
$$
\n$$
\left[ x/(x^2 + y^2)\right]\,dy - \left[ y/(x^2 + y^2 )\right]\,dx
$$
| 17 | 5 | 50 | 50 | 248 | 55 | 9 | 5 | 0 | Determine which of the following are exact differentials: $ (3x+2)y\,dx + x(x+1)\, dy $ $ y\tan x\,dx + x\tan y\,dy $ $ y^2(\ln x + 1)\,dx + 2xy\ln x\,dy $ $ y^2(\ln x + 1)\,dy + 2xy\ln x\,dx $ $ \left[ x/(x^2 + y^2)\right]\,dy - \left[ y/(x^2 + y^2 )\right]\,dx $ | 1 |
1da7744a-6a6b-44ca-ace2-0dafe58f0c8c | 2 | 0 | 0 | 9 | 4 | 2 | 6 | 26 | 
$$
H(s) = \frac{4}{s+1}
$$
  
For the closed-loop system shown above, apply a PI controller to achieve a damping of $0.5$ and a natural frequency of $2~\mathrm{rad/s}$.
| 
$$
H(s) = \frac{4}{s+1}
$$
  
For the closed-loop system shown above, apply a PI controller to achieve a damping of $0.5$ and a natural frequency of $2~\mathrm{rad/s}$.
| 1 | 0.666667 | 2 | null | By converting $u(t)$ and $y(t)$ to the Laplace domain, find an expression for $Y(s)$:
  
$Y(s) = E(s)K(s)H(s)$
  
where $E(s) = U(s)-Y(s)$.
***
Hence:
  
$Y(s) = U(s)K(s)H(s)-Y(s)K(s)H(s)$
***
Find an expression for the transfer function:
  
$G(s) = \frac{Y(s)}{U(s)} = \frac{K(s)H(s)}{1+K(s)H(s)}$
***
For a PI controller:
  
$K(s) = K_\mathrm{P}+\frac{K_\mathrm{I}}{s}$
***
Substituting in the expressions for $K(s)$ and $H(s)$:
  
$G(s) = \dfrac{\frac{4K_\mathrm{P}+\frac{4K_\mathrm{I}}{s}}{s+1}}{1+\frac{4K_\mathrm{P}+\frac{4K_\mathrm{I}}{s}}{s+1}}$
***
Tidying up:
  
$G(s) = \frac{4K_\mathrm{P}s + 4K_\mathrm{I}}{s^2+s+4K_\mathrm{P}s + 4K_\mathrm{I}}$
***
In canonical form, a general second order system is as follows:
  
$G(s) = \dfrac{K_\mathrm{G}}{\frac{1}{\omega_\mathrm{G_n}^2}s^2+\frac{2\zeta_\mathrm{G}}{\omega_\mathrm{G_n}}s+1}$
***
Converting the expression for $G(s)$ into canonical form:
  
$G(s) = \dfrac{\frac{4K_\mathrm{P}s+4K_\mathrm{I}}{4K_\mathrm{I}}}{\frac{1}{4K_\mathrm{I}}s^2+\frac{1+4K_\mathrm{P}}{4K_\mathrm{I}}s+1}$
***
Equate the $s^2$ coefficents:
  
$\frac{1}{\omega_\mathrm{G_n}^2} = \frac{1}{4K_\mathrm{I}}$
***
By substituting in the value of $\omega_\mathrm{G_n}$ and rearranging, $K_\mathrm{I}$ can be calculated:
  
$K_\mathrm{I} = \frac{2^2}{4} = 1$
***
Equate the $s$ coefficients:
  
$\frac{2\zeta_\mathrm{G}}{\omega_\mathrm{G_n}} = \frac{1+4K_\mathrm{P}}{4K_\mathrm{I}}$
***
Substituting in the values of $\zeta_\mathrm{G}$, $\omega_\mathrm{G_n}$ and $K_\mathrm{I}$ and rearranging for $K_\mathrm{P}$:
  
$K_\mathrm{P} = \dfrac{\frac{2\times0.5\times 4\times1}{2}-1}{4}=0.25$
  
  
| 
$$
H(s) = \frac{4}{s+1}
$$
  
For the closed-loop system shown above, apply a PI controller to achieve a damping of $0.5$ and a natural frequency of $2~\mathrm{rad/s}$.
| 26 | 3 | 27 | 27 | 134 | 0 | 26 | 3 | 1 | $ H(s) = \frac{4}{s+1} $ For the closed-loop system shown above, apply a PI controller to achieve a damping of $0.5$ and a natural frequency of $2~\mathrm{rad/s}$. | 1 |
1e43fcca-b71a-43ba-9b27-a149926cdc75 | 0 | 0 | 2 | 19 | 6 | 1 | 2 | 6 | **(L5)**: A curve is defined by the parametric equation,
$$
{\bf\vec{r}} = (x,y,z) = (\cos t, \sin t, t)
$$
| Describe the curve
\nFind the derivative and the second derivative of the curve with respect to $t$. Show that the first and second derivatives are always perpendicular to one another. Describe how the vector describing the first derivative varies with $t$.
| 2 | 0.666667 | 1 | What does the curve look like in the x-y plane?
***
Continuing in the x-y plane, what is the angle made by ${\bf{\vec{r}}}$ to the x axis? How can you relate this angle to $t$? Thus, what is the shape traced out by the curve in the x-y pane as a function of $t$?
***
Remember that z also changes linearly with $t$ - what shape do you get by combining this with the shape described in the x-y plane?
\nDifferentiate this position vector twice to find its first and second derivatives (**section 1.17**).
***
What operation can you use to check these vectors are perpendicular to one another (hint: think about the previous problem set)?
***
What is the angle between the vector describing the first derivative and the z axis? 
***
As this angle is constant (i.e., independent of t), what shape is the vector sweeping out as it rotates around the z axis?
| In the $xy$ plane $|{\bf \vec{r}_{⊥}}| = \sqrt{\cos ^2 t +\sin ^2 t} = 1$ and $\tan θ = \sin t/\cos t → θ = t$. Hence the curve traces out a circle with angle varying linearly with $t$. 
***
  
However z also increases linearly with t, so this curve is a helix
\nThe position vector ${\bf\vec{r}}$ to a point on the helix is given by:
$$
{\bf\vec{r}} = (\cos t, \sin t, t)
$$
***
To find the first and second derivatives, we differentiate this result twice (**section 1.17**): 
$$
\frac{d\vec{{\bf r}} }{d\theta}= (-\sin t, \cos t, 1)
\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \frac{d^2\vec{{\bf r}} }{d\theta^2}= (-\cos t, \sin t, 0)
$$
***
Then 
$$
\frac{d^2\vec{{\bf r}} }{d\theta^2}\cdot \frac{d\vec{{\bf r}} }{d\theta} = -\cos t\sin t \ + \sin t\cos t = 0
$$
NB: the curve and its tangent vector are only normal to one another if the vector is of constant amplitude (as $\frac{d\vec{{\bf r}} }{d\theta}$ 
***
We note that $|\frac{d{\bf\vec{r}}_{\bot}}{dt}|$ = $\sqrt{\sin ^2 t + \cos ^2 t}$ = $1$, so the angle made by this normal to the z-axis is 
$$
\phi = \tan^{-1}(|\frac{d{\bf\vec{r}}_{\bot}}{dt}|/a_z) = \tan ^{-1}(1/1) = 45^{\circ}
$$
The vector makes a constant angle to the z-axis as it rotates around this axis and thus describes a cone. 
| **(L5)**: A curve is defined by the parametric equation,
$$
{\bf\vec{r}} = (x,y,z) = (\cos t, \sin t, t)
$$
Describe the curve
\nFind the derivative and the second derivative of the curve with respect to $t$. Show that the first and second derivatives are always perpendicular to one another. Describe how the vector describing the first derivative varies with $t$.
| 53 | 3 | 13 | 13 | 135 | 4 | 43 | 2 | 0 | L5: A curve is defined by the parametric equation, $ {\bf\vec{r}} = (x,y,z) = (\cos t, \sin t, t) $ Describe the curve Find the derivative and the second derivative of the curve with respect to $t$. Show that the first and second derivatives are always perpendicular to one another. Describe how the vector describing the first derivative varies with $t$. | 3 |
1ea69f1c-ae9b-438f-8dc4-b7a7077b9c66 | 1 | 1 | 0 | 15 | 5 | 0 | 0 | 2 | Photosynthesis relies on electrons in chlorophyll molecules absorbing photons of light energy. This energy promotes electrons from a low-energy ground state to a high-energy excited state. For the chlorophyll-a dimer in the reaction centre of photosystem I (PS-I), the difference in energy between the ground and excited states is about 171 $\mathrm{kJ \cdot mol^{-1}}$.
| By rearranging the equation below, calculate the wavelength of maximum absorbance of PS-I in nanometres $(1 \,\mathrm{nm} = 10^{-9} \, \mathrm{m})$.
$$
E=\frac{N_{a}\, \cdot \, h \, \cdot \, c}{\lambda}
$$
* $E$ Difference in energy between ground and excited states ($171 \, \mathrm{ kJ \cdot mol^{-1}}$)
* $N_{A}$ Avogadro constant ($6.022 \times 10^{23}\,\mathrm{mol}^{-1}$)
* $h$ Planck constant ($6.626\times10^{-34}\,\mathrm{J \cdot s}$)
* $c$ Speed of light ($3\times10^{8} \, \mathrm{m \cdot s^{-1}}$)
* $\lambda$ Wavelength of light ($\mathrm{m}$)
\nChloroplasts possess a second photosystem (PS-II) absorbing at a different wavelength. Would this absorb photons of higher or lower wavelength than PS-I, given that the energy difference for its reaction centre is about $176 \, \mathrm{kJ \cdot mol^{-1}}$?
| 2 | 1 | 0 | \n | $$
\lambda=\frac{N_Ahc}{E} = \frac{ 6.022 \times 10^{23}\,\mathrm{mol}^{-1} \times 6.626\times10^{-34}\,\mathrm{J \cdot s} \times 3\times10^{8} \, \mathrm{m \cdot s^{-1}}}{171000 \, \mathrm{ J \cdot mol^{-1}}} = 7.00 \times 10^{-7} \,\mathrm{m} = 700 \times 10^{-9} \,\mathrm{m} = \ 700\ \mathrm{nm}
$$
\nLower ($680 \mathrm{nm}$ in fact): $E$ and $\lambda$ are inversely proportional to one another, so a higher energy gap implies a shorter wavelength.
| Photosynthesis relies on electrons in chlorophyll molecules absorbing photons of light energy. This energy promotes electrons from a low-energy ground state to a high-energy excited state. For the chlorophyll-a dimer in the reaction centre of photosystem I (PS-I), the difference in energy between the ground and excited states is about 171 $\mathrm{kJ \cdot mol^{-1}}$.
By rearranging the equation below, calculate the wavelength of maximum absorbance of PS-I in nanometres $(1 \,\mathrm{nm} = 10^{-9} \, \mathrm{m})$.
$$
E=\frac{N_{a}\, \cdot \, h \, \cdot \, c}{\lambda}
$$
* $E$ Difference in energy between ground and excited states ($171 \, \mathrm{ kJ \cdot mol^{-1}}$)
* $N_{A}$ Avogadro constant ($6.022 \times 10^{23}\,\mathrm{mol}^{-1}$)
* $h$ Planck constant ($6.626\times10^{-34}\,\mathrm{J \cdot s}$)
* $c$ Speed of light ($3\times10^{8} \, \mathrm{m \cdot s^{-1}}$)
* $\lambda$ Wavelength of light ($\mathrm{m}$)
\nChloroplasts possess a second photosystem (PS-II) absorbing at a different wavelength. Would this absorb photons of higher or lower wavelength than PS-I, given that the energy difference for its reaction centre is about $176 \, \mathrm{kJ \cdot mol^{-1}}$?
| 155 | 14 | 4 | 4 | 25 | 0 | 102 | 13 | 0 | By rearranging the equation below, calculate the wavelength of maximum absorbance of PS-I in nanometres $(1 \,\mathrm{nm} = 10^{-9} \, \mathrm{m})$. Would this absorb photons of higher or lower wavelength than PS-I, given that the energy difference for its reaction centre is about $(1 \,\mathrm{nm} = 10^{-9} \, \mathrm{m})$3? | 2 |
1f35e909-d901-43a0-840f-cebe806dd2ec | 2 | 0 | 0 | 11 | 4 | 2 | 6 | 3 | Carbon dioxide, which can be treated as a perfect gas, flows steadily at a rate of $10 ~\mathrm{kg/s}$ through a heat exchanger where it is cooled at constant pressure (i.e. with negligible friction) from $600 ~\mathrm{K}$ to $400 ~\mathrm{K}$. The ambient temperature of the environment surrounding the heat exchanger is $T_0 = 300 ~\mathrm{K}$. Find the change in exergy flow rate in units of $\mathrm{kW}$ by two different methods: 
| Via the flow stream exergy change: 
$\hspace{5 cm}\Delta\dot{B}_\mathrm{flowing \space fluid} = \dot{m}(\Delta h - T_0\Delta s)$  
\nVia the differential version of the expression for thermal exergy (or work potential of heat transferred), $\mathrm{d}\dot{B}_\mathrm{heat} =(1-\frac{T_0}{T})\mathrm{d}\dot{Q}$ . 
  
Please note that $\mathrm{d}\dot{B}_\mathrm{heat}$ and $\mathrm{d}\dot{Q}$ are not exact differentials. We know this is true for heat transfer rate $\mathrm{d}\dot{Q}$ but why is the rate of exergy transfer by heat, $\mathrm{d}\dot{B}_\mathrm{heat}$, not an exact differential?
| 2 | 0.666667 | 2 | \n | For a perfect gas:
  
$\Delta h = c_\mathrm{p}\Delta T$
***
and:
  
$\Delta s = c_\mathrm{p} \mathrm{ln} ( \frac{T_2}{ T_1} ) − R \mathrm{ln} ( \frac{P_2}{ P_1} )$
***
Hence:
  
$\Delta \dot{B}_\mathrm{flowing\space fluid} = \dot{m}(c_\mathrm{p}\Delta T - T_0(c_\mathrm{p} \mathrm{ln} ( \frac{T_2}{ T_1} ) − R \mathrm{ln} ( \frac{P_2}{ P_1} )))$
***
Substituting in numbers:
  
$ \Delta \dot{B}_\mathrm{flowing\space fluid} = 10(0.84(400-600) - 300(0.84\mathrm{ln}(\frac{400}{600}) - 0.189\mathrm{ln}(1))) =-658~\mathrm{kW} $
\n$\mathrm{d}\dot{B}_\mathrm{heat} = (1-\frac{T_0}{T})\mathrm{d}\dot{Q}$
***
 Since $\mathrm{d}\dot{B}_\mathrm{heat}$ is a function of $\mathrm{d}\dot{Q}$ and $\mathrm{d}\dot{Q}$ is not an exact differential, it follows that $\mathrm{d}\dot{B}_\mathrm{heat}$ is also not an exact differential (the reason that $\mathrm{d}\dot{Q}$ is not an exact differential is that it is path dependent- the amount of heat transfer depends on how the process was performed). 
***
$\mathrm{d}\dot{Q} = \dot{m}c_\mathrm{p}\mathrm{d}T$
***
Hence:
  
$\mathrm{d}\dot{B}_\mathrm{heat} = (1-\frac{T_0}{T})\dot{m}c_\mathrm{p}\mathrm{d}T$
***
Integrate:
  
$B_2 - B_1 = \dot{m}c_\mathrm{p}[(T_2-T_1) -T_0\mathrm{ln}(\frac{T_2}{T_1})]$
***
Substituting in numbers:
  
$B_2 - B_1 = (10\times 0.84)[(400-600)-300\mathrm{ln}(\frac{400}{600})] = -658 ~\mathrm{kW}$
| Carbon dioxide, which can be treated as a perfect gas, flows steadily at a rate of $10 ~\mathrm{kg/s}$ through a heat exchanger where it is cooled at constant pressure (i.e. with negligible friction) from $600 ~\mathrm{K}$ to $400 ~\mathrm{K}$. The ambient temperature of the environment surrounding the heat exchanger is $T_0 = 300 ~\mathrm{K}$. Find the change in exergy flow rate in units of $\mathrm{kW}$ by two different methods: 
Via the flow stream exergy change: 
$\hspace{5 cm}\Delta\dot{B}_\mathrm{flowing \space fluid} = \dot{m}(\Delta h - T_0\Delta s)$  
\nVia the differential version of the expression for thermal exergy (or work potential of heat transferred), $\mathrm{d}\dot{B}_\mathrm{heat} =(1-\frac{T_0}{T})\mathrm{d}\dot{Q}$ . 
  
Please note that $\mathrm{d}\dot{B}_\mathrm{heat}$ and $\mathrm{d}\dot{Q}$ are not exact differentials. We know this is true for heat transfer rate $\mathrm{d}\dot{Q}$ but why is the rate of exergy transfer by heat, $\mathrm{d}\dot{B}_\mathrm{heat}$, not an exact differential?
| 128 | 11 | 14 | 14 | 90 | 0 | 63 | 6 | 0 | Find the change in exergy flow rate in units of $\mathrm{kW}$ by two different methods: Via the flow stream exergy change: $\hspace{5 cm}\Delta\dot{B}_\mathrm{flowing \space fluid} = \dot{m}(\Delta h - T_0\Delta s)$ Via the differential version of the expression for thermal exergy or work potential of heat transferred, $\mathrm{d}\dot{B}_\mathrm{heat} =(1-\frac{T_0}{T})\mathrm{d}\dot{Q}$ . We know this is true for heat transfer rate $\mathrm{d}\dot{Q}$ but why is the rate of exergy transfer by heat, $\mathrm{d}\dot{B}_\mathrm{heat}$, not an exact differential? | 2 |
1f39acd9-b66a-4a21-9401-613381437d73 | 0 | 0 | 1 | 17 | 6 | 1 | 3 | 9 | Show that the velocity $v(t)$ of a rocket starting from rest and accelerating against the Earth’s gravity is given by
$$
v(t) = u\ln \left ( \frac{M_0}{M(t)} \right ) - gt.
$$
The exhaust speed is $u$, the initial mass is $M_0$, and the mass after time $t$ is $M(t)$. Neglect the dependence of $g$ on height.
| Show that the velocity $v(t)$ of a rocket starting from rest and accelerating against the Earth’s gravity is given by
$$
v(t) = u\ln \left ( \frac{M_0}{M(t)} \right ) - gt.
$$
The exhaust speed is $u$, the initial mass is $M_0$, and the mass after time $t$ is $M(t)$. Neglect the dependence of $g$ on height.
| 1 | 1 | 2 | After ejecting fuel of mass $dM$, the rocket's speed increases from $v$ to $v+dv$...
***
... Hence write down the change in momentum of the rocket in a time $dt$ (see the lectures if you are unsure about this).
***
A change of momentum is an impulse. What is the impulse produced by gravity on this system in the time $dt$?
***
Hence equate your expression for the change of momentum to the gravitational impulse.
***
Next, you need to integrate this equation (i.e., integrate $dv$, $dM$ and $dt$). What are the limits of the integrals? **Note:** use a dummy variable in the integrand to avoid confusion with the limits.
***
Perform each integral over their limits. You should be able to re-arrange the resulting expression into the $v(t)$ in the question.
| 
***
The diagram below shows that the change in momentum of the rocket+fuel in time $dt$ can be found as follows:
$$
\begin{aligned}
\text{change in momentum}
&= \text{(momentum at time $t + dt$)} - \text{(momentum at time $t$)} \\
&=\big( (M + dM)(v + dv) + (-dM)(v-u) \big) - \big( Mv \big)\\
&= M dv + u dM . \qquad \text{(ignoring second-order terms)}
\end{aligned}
$$
***
Since the only external force acting on the system is gravity, this must be equal to the gravitational impulse $-Mg\hspace{1.5pt}dt$ (which is negative because gravity acts against the rocket’s acceleration):
***
$$
\begin{aligned}
&M dv + u dM = -Mg \, dt \\
\Rightarrow \qquad
&dv = -u\frac{dM}{M} - g \, dt \\
\end{aligned}
$$
***
Integrating this result over the limits of the system (using dummy variables in the integrand):
***
$$
\begin{aligned}
\Rightarrow \qquad
&\int_{0}^{v(t)} dv' = -u \int_{M_0}^{M(t)} \frac{dM'}{M'} -
g\int_0^{t} dt' \\
\end{aligned}
$$
***
$$
\begin{aligned}
&\left [ v' \right ]_0^{v(t)} = -u \left [ \ln M' \right
]_{M_0}^{M(t)} - g \left [ t' \right ]_0^{t} \\
\Rightarrow \qquad
&v(t) = -u \left \{ \ln(M(t)) - \ln(M_0) \right \} - gt \\
\Rightarrow \qquad
&v(t) = u\ln\left ( \frac{M_0}{M(t)} \right ) - gt,
\end{aligned}
$$
as required.
| Show that the velocity $v(t)$ of a rocket starting from rest and accelerating against the Earth’s gravity is given by
$$
v(t) = u\ln \left ( \frac{M_0}{M(t)} \right ) - gt.
$$
The exhaust speed is $u$, the initial mass is $M_0$, and the mass after time $t$ is $M(t)$. Neglect the dependence of $g$ on height.
| 49 | 7 | 6 | 6 | 78 | 9 | 49 | 7 | 0 | Show that the velocity $v(t)$ of a rocket starting from rest and accelerating against the Earth’s gravity is given by $ v(t) = u\ln \left ( \frac{M_0}{M(t)} \right ) - gt. Neglect the dependence of $g$ on height. | 2 |
1f3a8567-d040-4746-92b2-98b2caf040bf | 3 | 0 | 1 | 10 | 4 | 2 | 8 | 0 | The following data apply to extruded and cold rolled Nimonic 80A at $750^\circ \text{C}$. 
   
* Elastic (Young’s) Modulus $= 140 \times 10^3 \text{ MN/m}^2$ 
* $0.2\%$ Proof Stress $= 450\text{ MN/m}^2$
* Elongation to fracture = $25\%$ (short term tensile test)
* Mean Coefficient of Thermal Expansion ($20~–~750^\circ \text{C}$ range) $= 15.8 \times 10^{-6}$
  
The stress to cause a creep strain in 3000 hours is:
| Stress ($\text{MPa}$) | 110 | 130 | 160 |
| :-------------------- | :-- | :-- | :-- |
| Creep Strain $(\%)$ | 0.1 | 0.2 | 0.5 |
| Neglecting primary creep, calculate the secondary (steady state) creep strain rate at each stress level.
\nEstimate the coefficient $n$ in a power law representation between stress and strain rate.
\nWhat would be the total change in length of a bar of $50\text{ mm}$ initial length at $20^\circ\text{C}$, which is held at a stress of $150\text{ MPa}$ when immediately on heating to $750^\circ \text{C}$ and loading (i.e. thermal expansion).
\nWhat would be the total change in length of a bar of $50\text{ mm}$ initial length at $20^\circ\text{C}$, which is held at a stress of $150\text{ MPa}$ after remaining at $150\text{ MPa}$ for $3000$ hours.
| 4 | 1 | 3 | \n\n\n | Secondary creep strain is the **slope** of the **linear** region of the creep strain vs. time curve (see figure below.)
   

$$
\footnotesize
\text{Figure Q4.1.1: General form of a creep strain against time curve indicating primary,}\\
\text{secondary, and tertiary creep regions and the secondary creep rate.}
$$
   
***
Find the secondary creep rate (i.e. the slope of the secondary region) making sure that strain rate is as a decimal and time is left in hours.
   
$$
\dot{\epsilon}^c_s=\frac{\text{strain rate}}{\text{time}}
$$
   
***
Using the values for stress at $100\text{ MPa}$ to show example calculations:
   
$$
\dot{\epsilon}^c_s=\frac{0.1\times10^{-2}}{3000}=\boxed{3.33\times10^{-7}}
$$
   
***
Therefore, the secondary creep rate can be calculated as such for each of the different stress levels ($ 100\text{ MPa}, $ $130\text{ MPa}$ and $160\text{ MPa}$), when the specimen is left for $3000$ hours. 
| Stress ($\text{MPa}$) | $110$ | $130$ | $160$ |
| :-------------------- | :------------------ | :------------------ | :------------------ |
| Creep Strain ($\%$) | $0.1$ | $0.2$ | $0.5$ |
| Strain Rate | $3.33\times10^{-7}$ | $6.67\times10^{-7}$ | $1.67\times10^{-6}$ |
\n\nThe immediate heating of the bar from $20\degree\text{C}$ to $750\degree\text{C}$ will result in **thermal expansion**.
   
***
Using Hooke's Law for uniaxial stresses, making sure to include the elastic and the thermal strain:
   
$$
\epsilon=\frac{\Delta L}{l}=\frac{\sigma_x}{E}+\alpha\Delta T
$$
   
***
$$
\begin{align*}
\Delta L&=\left( \frac{\sigma_x}{E}+\alpha\Delta T\right)l\\
&=\left(\frac{150\times10^6}{140\times10^9}+15.8\times10^{-6}\times(750-20)\right)(50)\\
&=\boxed{0.63\text{ mm}}
\end{align*}
$$
\nMaking sure to include the elastic strain, initial thermal expansion and creep, the following equation is used to calculate strain:
   
$$
\epsilon=\frac{\Delta L}{l}=\left(\frac{\sigma_x}{E}+\alpha\Delta T+A\sigma^n\right)
$$
   
***
Substituting in numbers, using the values calculated from part (b).
   
$$
\begin{align*}
\Delta L&=\left(\frac{\sigma_x}{E}+\alpha\Delta T+A\sigma^nt\right)l\\
&=\left(\frac{150\times10^6}{140\times10^9}+(15.8\times10^{-6})(750-20)+ (4.1\times10^{-16})(150)^{4.4}(3000)\right)(50)\\
&=\boxed{0.82\text{ mm}}
\end{align*}
$$
$$
$$
| The following data apply to extruded and cold rolled Nimonic 80A at $750^\circ \text{C}$. 
   
* Elastic (Young’s) Modulus $= 140 \times 10^3 \text{ MN/m}^2$ 
* $0.2\%$ Proof Stress $= 450\text{ MN/m}^2$
* Elongation to fracture = $25\%$ (short term tensile test)
* Mean Coefficient of Thermal Expansion ($20~–~750^\circ \text{C}$ range) $= 15.8 \times 10^{-6}$
  
The stress to cause a creep strain in 3000 hours is:
| Stress ($\text{MPa}$) | 110 | 130 | 160 |
| :-------------------- | :-- | :-- | :-- |
| Creep Strain $(\%)$ | 0.1 | 0.2 | 0.5 |
Neglecting primary creep, calculate the secondary (steady state) creep strain rate at each stress level.
\nEstimate the coefficient $n$ in a power law representation between stress and strain rate.
\nWhat would be the total change in length of a bar of $50\text{ mm}$ initial length at $20^\circ\text{C}$, which is held at a stress of $150\text{ MPa}$ when immediately on heating to $750^\circ \text{C}$ and loading (i.e. thermal expansion).
\nWhat would be the total change in length of a bar of $50\text{ mm}$ initial length at $20^\circ\text{C}$, which is held at a stress of $150\text{ MPa}$ after remaining at $150\text{ MPa}$ for $3000$ hours.
| 190 | 19 | 26 | 26 | 233 | 0 | 99 | 10 | 0 | The following data apply to extruded and cold rolled Nimonic 80A at $750^\circ \text{C}$. Elastic Young’s Modulus $= 140 \times 10^3 \text{ MN/m}^2$ $0.2\%$ Proof Stress $= 450\text{ MN/m}^2$ Elongation to fracture = $25\%$ short term tensile test Mean Coefficient of Thermal Expansion $20~–~750^\circ \text{C}$ range $= 15.8 \times 10^{-6}$ The stress to cause a creep strain in 3000 hours is: table Neglecting primary creep, calculate the secondary steady state creep strain rate at each stress level. Estimate the coefficient $n$ in a power law representation between stress and strain rate. What would be the total change in length of a bar of $50\text{ mm}$ initial length at $20^\circ\text{C}$, which is held at a stress of $= 140 \times 10^3 \text{ MN/m}^2$0 when immediately on heating to $750^\circ \text{C}$ and loading i.e. What would be the total change in length of a bar of $50\text{ mm}$ initial length at $20^\circ\text{C}$, which is held at a stress of $= 140 \times 10^3 \text{ MN/m}^2$0 after remaining at $= 140 \times 10^3 \text{ MN/m}^2$0 for $= 140 \times 10^3 \text{ MN/m}^2$6 hours. | 5 |
1f7df9e2-c4c9-49fa-851b-5dbb51dea7b2 | 3 | 0 | 0 | 13 | 4 | 2 | 3 | 0 | The figure below shows a record turntable.

The electric drive of a record turntable develops a constant torque of $0.13~\mathrm{Nm}$ and takes $2$ seconds to accelerate to the turntable to its operating speed of $33.3~\mathrm{rpm}$. At this speed, a $300~\mathrm{mm}$ diameter vinyl record weighing $3~\mathrm{N}$ is dropped onto a turntable, slipping for a short period of time.\
  
*(Optional: See the video below for an explanation of how a record turntable works)*
[https://www.youtube.com/watch?v=3cyphJLljAM](https://www.youtube.com/watch?v=3cyphJLljAM "https://www.youtube.com/watch?v=3cyphJLljAM")
| What is the immediate reduction in the speed of the turntable?
\nHow long does it take before the correct speed is regained?
\nHow much energy is dissipated in friction as the record slips on the turntable?
| 3 | 0.666667 | 4 | This problem is analogous to linear momentum, where the record landing on the table can be taken as the impact event.
***
The moment of inertia of the turntable can be worked out using the information given about the electric drive torque and the time taken to reach the operating rotational speed (think of the rotational equivalent of $F = ma$). The moment of inertia of the record can be calculated as usual.
***
Remember to convert the rotational speed from $\mathrm{rpm}$ to a more suitable form! Also remember that the question is looking for the change in speed, not the speed directly after impact.
\nThe constant torque and the new combined moment of inertia can be used to find the new angular acceleration after impact.
***
As you already know the reduction in speed, the time to reach operating speed can be simply determined. Again, don’t get confused by your units of angular velocity!
\nExamine the kinetic energy before and after the record is dropped onto the table. Is there a difference? Where did the energy go?
| Kinetic diagram:

***
The turntable and vinyl rotate about the same axis, so apply conservation of momentum:
$$
I_{G,\text{table}}~\dot\theta_{\text{table}} = I_{G,\text{table}}~\dot\theta_{\text{vinyl}} + I_{G,\text{vinyl}}~\dot\theta_{\text{vinyl}}~~\mathrm{(Equation~1)}
$$
***
The moment of inertia of the vinyl is:
$$
I_{G,\text{vinyl}} = \cfrac{m_{\text{vinyl}} \times r^2_{\text{vinyl}}}{2}~~\mathrm{(Equation~2)}
$$
***
The moment of inertia of the turntable is not given, but the torque of the turntable $M_{\text{table}}$ is related by:
$$
M_{\text{table}} = I_{G,\text{table}}~\ddot\theta_{\text{table}}~~\mathrm{(Equation~3)}
$$
***
Where the angular velocity of the turntable is related by:
$$
\dot\theta_{\text{table}} = \ddot\theta_{\text{table}} \times t~~\mathrm{(Equation~4)}
$$
***
Hence by combining Equations 3 and 4, the moment of inertia of the turntable is:
$$
I_{G,\text{table}} = \cfrac{M_{\text{table}}}{(\cfrac{\dot\theta_{\text{table}}}{t})}~~\mathrm{(Equation~5)}
$$
***
Rearranging Equation 1 for $\dot\theta_{\text{vinyl}}$:
$$
\dot\theta_{\text{vinyl}} = \cfrac{\dot\theta_{\text{table}}}{(1 + \cfrac{I_{G,\text{vinyl}}}{I_{G,\text{table}}})}~~\mathrm{(Equation~6)}
$$
***
Substituting the expressions moment of inertia of the turntable (Equation 5) and of the vinyl (Equation 2) into Equation 6:
$$
\dot\theta_{\text{vinyl}} = \cfrac{\dot\theta_{\text{table}}}
{\left(1 + \cfrac{\left(\cfrac{m_{\text{vinyl}} \times r^2_{\text{vinyl}}}{2}\right)}
{\left(\cfrac{M_{\text{table}}}
{\left(\cfrac{\dot\theta_{\text{table}}}{t}\right)}\right)}\right)}
$$
***
Substituting the values of the parameters gives:
$$
\dot\theta_{\text{vinyl}} = \cfrac{33.3}{\left( 1 + \cfrac{\left( \cfrac{0.30581 \times 0.15^2}{2} \right)}{\left( \cfrac{0.13}{\cfrac{\left( 33.3 \times 2\pi/60 \right)}{2}} \right)} \right)}
$$
$$
\dot\theta_{\text{vinyl}} = 31.832126~\mathrm{rpm}
$$
***
Hence the reduction in speed of the turntable is:
$$
\Delta\dot\theta = 33.3 - 31.832126
$$
$$
\Delta\dot\theta = 1.47~\mathrm{rpm}
$$
\nThe turntable and vinyl move together with the same torque and combined moment of inertia:
$$
I_{G,\text{total}} = I_{G,\text{table}} + I_{G,\text{vinyl}}
$$
***
The system is accelerating due to the moment applied by the turntable:
$$
M_{\text{table}} = I_{G,\text{total}}\ddot\theta
$$
***
The acceleration is constant as the speed increases to its original angular velocity, so the time is:
$$
t = \cfrac{\Delta\dot\theta}{\ddot\theta}
$$
***
Which can then be simplified to:
$$
t = \cfrac{\Delta\theta}{\left( \cfrac{M_{\text{table}}}{I_{G,\text{total}}} \right)}
$$
***
Substituting the values of the parameters gives:
$$
t = \cfrac{1.47 \times (2\pi/60)}{\left( \cfrac{0.13}{\left( \cfrac{\left( \cfrac{3}{g} \right)\left( \cfrac{0.3}{2} \right)^2}{2} \right) + \left( \cfrac{0.13}{\cfrac{(33.3 \times 2\pi/60)}{2}} \right)} \right)}
$$
$$
t = \cfrac{(0.00344+0.074559) \times \left(\cfrac{1.47 \times 2 \times \pi}{60}\right)}{0.13}
$$
$$
\text{Time} = t = 0.0923~\mathrm{s}
$$
\nThere is no change in spring energy or gravitational potential energy, only rotational kinetic energy:
$$
KE_{\text{before impact}} = \cfrac{1}{2}~I_{G,\text{table}}\dot\theta_{\text{table}}^2
$$
$$
KE_{\text{after impact}} = \cfrac{1}{2}~\left( I_{G,\text{table}} + I_{G,\text{vinyl}} \right)\dot\theta_{\text{vinyl}}^2
$$
***
Therefore the energy dissipated is:
$$
\text{Energy loss} = \left[ \cfrac{1}{2}~I_{G,\text{table}}\dot\theta_{\text{table}}^2 \right] - \left[ \cfrac{1}{2}~\left( I_{G,\text{table}} + I_{G,\text{vinyl}} \right)\dot\theta_{\text{vinyl}}^2 \right]
$$
***
Substituting in the values of the parameters:
$$
\text{Energy loss} = \left[ \cfrac{1}{2}~I_{G,\text{table}}\dot\theta_{\text{table}}^2 \right] - \left[ \cfrac{1}{2}~\left( I_{G,\text{table}} + I_{G,\text{vinyl}} \right)\dot\theta_{\text{vinyl}}^2 \right] Needs~finishing
$$
$$
\text{Energy loss} = 0.020~\mathrm{J}
$$
| The figure below shows a record turntable.

The electric drive of a record turntable develops a constant torque of $0.13~\mathrm{Nm}$ and takes $2$ seconds to accelerate to the turntable to its operating speed of $33.3~\mathrm{rpm}$. At this speed, a $300~\mathrm{mm}$ diameter vinyl record weighing $3~\mathrm{N}$ is dropped onto a turntable, slipping for a short period of time.\
  
*(Optional: See the video below for an explanation of how a record turntable works)*
[https://www.youtube.com/watch?v=3cyphJLljAM](https://www.youtube.com/watch?v=3cyphJLljAM "https://www.youtube.com/watch?v=3cyphJLljAM")
What is the immediate reduction in the speed of the turntable?
\nHow long does it take before the correct speed is regained?
\nHow much energy is dissipated in friction as the record slips on the turntable?
| 111 | 5 | 25 | 25 | 234 | 2 | 36 | 0 | 2 | Optional: See the video below for an explanation of how a record turntable works What is the immediate reduction in the speed of the turntable? How long does it take before the correct speed is regained? How much energy is dissipated in friction as the record slips on the turntable? | 3 |
207213eb-f3c2-4640-90d5-e428a440c347 | 5 | 0 | 0 | 17 | 6 | 1 | 0 | 10 | Imperial College, in trying to maximise revenue from its new White City campus, decides to build a roller coaster using new, frictionless technology developed in the Mechanical Engineering department. 

A carriage is lifted from the ground at A to the top of the hill at B using a chain system, then released from B at a very low initial speed. It accelerates down to the ground at C, rises to D, and descends to E, which is at the same height as A. The carriage then returns to the starting point A along a flat track (not shown on diagram), where it is stopped for the passengers to alight. The tracks near points C and D are arcs of circles of radius 10 m. Assume for simplicity that $g = 10\text{m}\cdot\text{s}^{-2}$.
| Write down an expression (as algebra) for the speed of the carriage when it has dropped a height $h$ from point B.
\nThe acceleration of an object moving around a circle of radius $r$ at speed $v$ is $a = v^2/r$. In order to maximise excitement, passengers should feel three times their normal weight at point C. How far below point B should point C be placed?
\nAt point D the passengers should be weightless. How far below point B should point D be placed?
\nA carriage weighs 1500 kg including the passengers. How much work is done in lifting it from point A to point B?
\nThe College is aiming to operate one carriage every 5 minutes for twelve hours a day. What is its average power consumption over 24 hours?
| 5 | 0.333333 | 2 | Use conservation of energy.
\nAt point $C$, a person has a reaction force acting upwards and weight acting downwards...
***
... The reaction should be $3g$. What is the resulting centripetal acceleration $a$?
***
Hence use the result from part (a) to find the required height the rollercoaster must drop to achieve this speed.
\nReferring to the $\color{green} \textsf{Structured Tutorial}$ in part (b), the reaction force should now be zero. What $a$ is required to achieve this?
***
The result from part (a) still applies to a gain in height. Use this to solve for the drop between $B$ and $D$.  
***
In terms of energy conservation, you only need to consider the height difference between $B$ and $D$; you can exclude the drop/rise around point $C$. 
\nConsider conservation of energy.
\nHow many roller coaster rides are operated during the twelve hours of operation each day?
***
How much energy would this take? Hence find the average power.
| The potential energy lost is the kinetic energy gained, so $\frac{1}{2}mv^2 = mgh$ and $v = \sqrt{2gh}$.
\nFor passengers to feel three times their normal weight at C, a passenger of mass $m$ should experience a reaction force of $3mg$ instead of the usual $mg$ when in equilibrium. This means that their centripetal force should be $2mg$ ($\text{Reaction - Weight} = 3mg - mg = 2mg$). 
***
When we look at rotating frames at the end of the course you will see another way of looking at this: the passengers are in a rotating frame of reference which is noninertial; in rotating frames, Newton's laws are effectively modified and 'fictitious' forces appear. From the passengers' point of view, since they remain at rest in their frame they believe they experience an additional (fictitious) outward \`centrifugal' force such that the total force on them is zero, i.e. the fictitious force equal and opposite to the net force which provides the centripetal force in the inertial lab frame. This means they believe they are experiencing a force $3mg$ downwards and a force $3mg$ upwards.
The centripetal acceleration is therefore:
***
$$
\frac{v^2}{r} = 2g \quad \Rightarrow \quad
v = \sqrt{2gr} .
$$
***
Using the result from part (a), $\sqrt{2gh} = \sqrt{2gr}$, so $h = r = 10$m.
\nFor the passengers to feel weightless at D, they should feel no upward force from the track. This means that the net downward force is the weight alone must provide the centripetal force required:
***
$$
\frac{v^2}{r} = g \quad \Rightarrow \quad v = \sqrt{gr}.
$$
***
The speed of the carriage at D is still given by the result of (a), with $h$ now the height difference between B and D. 
***
Solving $\sqrt{gr} = \sqrt{2gh}$, the point D should be 5 m below the point B.
\nSince the carriage is moving so slowly when it reaches B, the work done is almost entirely expended in increasing its potential energy:
***
$$
\text{Work done} = mgh = 1500 \times 10 \times 10\,\text{J}
= 1.5 \times 10^5\,\text{J} = 150\,\text{kJ}.
$$
\nIf the College runs one carriage every 5 minutes for 12 hours, 144 carriages must be raised from A to B every day.
***
The total energy required to do this is $144 \times 150$kJ. The average power over the 24 hours of one day is then:
***
$$
\text{Average power} = \frac{144 \times 1.5 \times 10^{5}}{24
\times 60 \times 60} = 250\,\text{J}\cdot\text{s}^{-1} = 250\,\text{W}.
$$
| Imperial College, in trying to maximise revenue from its new White City campus, decides to build a roller coaster using new, frictionless technology developed in the Mechanical Engineering department. 

A carriage is lifted from the ground at A to the top of the hill at B using a chain system, then released from B at a very low initial speed. It accelerates down to the ground at C, rises to D, and descends to E, which is at the same height as A. The carriage then returns to the starting point A along a flat track (not shown on diagram), where it is stopped for the passengers to alight. The tracks near points C and D are arcs of circles of radius 10 m. Assume for simplicity that $g = 10\text{m}\cdot\text{s}^{-2}$.
Write down an expression (as algebra) for the speed of the carriage when it has dropped a height $h$ from point B.
\nThe acceleration of an object moving around a circle of radius $r$ at speed $v$ is $a = v^2/r$. In order to maximise excitement, passengers should feel three times their normal weight at point C. How far below point B should point C be placed?
\nAt point D the passengers should be weightless. How far below point B should point D be placed?
\nA carriage weighs 1500 kg including the passengers. How much work is done in lifting it from point A to point B?
\nThe College is aiming to operate one carriage every 5 minutes for twelve hours a day. What is its average power consumption over 24 hours?
| 260 | 5 | 18 | 18 | 341 | 10 | 130 | 4 | 1 | Imperial College, in trying to maximise revenue from its new White City campus, decides to build a roller coaster using new, frictionless technology developed in the Mechanical Engineering department. A carriage is lifted from the ground at A to the top of the hill at B using a chain system, then released from B at a very low initial speed. Write down an expression as algebra for the speed of the carriage when it has dropped a height $h$ from point B. In order to maximise excitement, passengers should feel three times their normal weight at point C. How far below point B should point C be placed? How far below point B should point D be placed? How much work is done in lifting it from point A to point B? What is its average power consumption over 24 hours? | 7 |
20a9b607-cd0f-4682-a66a-3c7e9d75e8b1 | 4 | 0 | 0 | 9 | 4 | 2 | 6 | 6 | What are the gain and the time constant of the following first order systems:
| $H(s) = \frac{4}{s+2}$
\n$H(s) = \frac{8}{4s+2}$
 
| 2 | 0.333333 | 0 | \n | Convert the expression for $H(s)$ to canonical form:
  
$H(s) = \frac{K}{1+\tau s} = \frac{2}{1+0.5s}$
***
Hence:
  
Gain: $K = 2$
  
Time constant: $\tau = 0.5$
\nConvert the expression for $H(s)$ to canonical form:
  
$H(s) = \frac{K}{1+\tau s} = \frac{4}{1+2s}$
***
Hence:
  
Gain: $K = 4$
  
Time constant: $\tau = 2$
| What are the gain and the time constant of the following first order systems:
$H(s) = \frac{4}{s+2}$
\n$H(s) = \frac{8}{4s+2}$
 
| 18 | 2 | 8 | 8 | 38 | 0 | 4 | 2 | 0 | What are the gain and the time constant of the following first order systems: $H(s) = \frac{4}{s+2}$ $H(s) = \frac{8}{4s+2}$ | 1 |
2187fc1b-a767-4956-a1de-b540b049a89a | 6 | 0 | 1 | 11 | 4 | 2 | 4 | 6 | A vapour-compression cycle using R134a has the following conditions: 
  
Evaporator pressure: $\hspace{2cm}$ $1.5$ bar 
Compressor inlet state: $\hspace{1.6cm}$ Superheated
Compressor inlet temperature: $\hspace{0.0cm}$ $-10^{\circ}\mathrm{C}$ 
Condenser pressure: $\hspace{1.96 cm}$ $10.0$ bar 
Expansion valve inlet state: $\hspace{1cm}$ Subcooled
Expansion valve inlet temperature: $\hspace{0 cm}$ $25^{\circ}\mathrm{C}$
  
Assuming that the cycle is "ideal" except for the extended processes in the evaporator and condenser: 
| Plot the cycle on the $P-h$ chart (found on Blackboard).
\nUsing enthalpies read from the $P - h$ chart, except at the expansion valve inlet where the usual approximation for subcooled liquid properties should be used, calculate the heat transfer in the evaporator, per $\mathrm{kg}$ of R134a. 
\nCalculate the work transfer in the compressor, per $\mathrm{kg}$ of R134a.
\nCalculate the heat transfer in the condenser, per $\mathrm{kg}$ of R134a.
\nCalculate the $COP$ in a refrigeration application.
\nCalculate the $COP$ in a heat pump application.
\nIf this cycle is used for an electrically-driven heat pump which replaces direct electric heating in a building, estimate the resulting annual reduction in $\mathrm{CO}_2$ emissions from power stations, with the following assumptions: 
  
Annual average heat requirement of building: $20 ~\mathrm{kW}$
   
Average $\mathrm{CO}_2$ emission from power stations: 
* Coal-fired: $800 ~\mathrm{g/kWh}$ 
* Gas-fired: $400 ~\mathrm{g/kWh}$ 
* Nuclear: $0$ 
Annual electricity generation from all power stations on network: $1/3$ each from coal-fired, gas-fired and nuclear plant.
| 7 | 0.666667 | 3 | \n\n\n\n\n\n | \nThe heat transfer in the evaporator is represented by process $4-1$. Applying the SFEE and bearing in mind that there is no shaft work and kinetic and potential energy changes can be neglected:
  
$\frac{\dot{Q}_{41}}{\dot{m}} = h_1 - h_4$
***
Process $3-4$ is isenthalpic so $h_4 = h_3$. 
***
At state $3$, the refrigerant is subcooled. Using the approximation for subcooled liquid properties to find $h_3$ :
  
$h_3 = h_4\approx h_\mathrm{f}$ at $25^{\circ}\mathrm{C}$
***
From Table E10:
  
$h_3 = h_4 \approx h_\mathrm{f} \approx 135~\mathrm{kJ/kg}$
***
From the $P-h$ diagram:
  
$h_1 = 295~\mathrm{kJ/kg}$
***
Substituting the enthalpy values back into the SFEE:
  
$\frac{\dot{Q}_{41}}{\dot{m}} = 295-135 = 160~\mathrm{kJ/kg}$
\nThe work transfer in the compressor is represented by process $1-2$.
***
Apply the SFEE to process $1-2$, bearing in mind that there is no heat transfer and that kinetic and potential energies can be neglected:
  
$-\frac{\dot{W}_{12}}{\dot{m}} = h_2-h_1$
***
From the $P-h$ diagram:
  
$h_2 = 335~\mathrm{kJ/kg}$
  
$h_1 = 295~\mathrm{kJ/kg}$
***
Therefore:
  
$\frac{\dot{W}_{12}}{\dot{m}} = -(335-295) = -40~\mathrm{kJ/kg}$
   
$|\frac{\dot{W}_{12}}{\dot{m}}| = 40~\mathrm{kJ/kg}$
\nHeat transfer in the condenser is represented by process $2-3$.
***
Apply the SFEE to process $2-3$, bearing in mind that there is no shaft work and that kinetic and potential energy changes can be neglected:
  
$\frac{\dot{Q}_{23}}{\dot{m}} = h_3-h_2$
***
From the $P-h$ diagram, $h_2 = 335~\mathrm{kJ/kg}$
***
From part (b), $h_3 = 135~\mathrm{kJ/kg}$
***
Therefore:
  
$\frac{\dot{Q}_{23}}{\dot{m}} = 135-335 = -200~\mathrm{kJ/kg}$
  
$|\frac{\dot{Q}_{23}}{\dot{m}}| = 200~\mathrm{kJ/kg}$
\nFor a refrigerator:
  
$COP_\mathrm{R} = \frac{\dot{Q}_{41}}{|\dot{W}_{12}|}$
***
Substituting the values for $\dot{Q}_{41}$ and $|\dot{W}_{12}|$ found in parts (b) and (c):
  
$COP_\mathrm{R} = \frac{160}{40} = 4$
\nFor a heat pump:
  
$COP_\mathrm{HP} = \frac{\dot{Q}_{23}}{|\dot{W}_{12}|}$
***
Using the values for $\dot{Q}_{23}$ and $|\dot{W}_{12}|$ found in parts (d) and (c):
  
$COP_\mathrm{HP} = \frac{200}{40} = 5$
\nCalculate the heat power in $\mathrm{kWh}$:
  
${20}\times{365\times 24} = 175200~\mathrm{kWh}$ per annum.
***
Calculate the number of $\mathrm{kWh}$ produced by each type of power station:
  
$\frac{1}{3} \times 175200 = 58400~\mathrm{kWh}$
***
Mass of $\mathrm{CO}_2$ from coal-fired plants:
  
$58400\times800 =46.72 ~\mathrm{tonnes}$
***
Mass of $\mathrm{CO}_2$ from gas-fired plants:
  
$58400\times400 = 23.36~\mathrm{tonnes}$
***
Total mass of $\mathrm{CO}_2$:
  
$46.72 + 23.36 = 70.08~\mathrm{tonnes}$
***
Since the heat pump has a $COP$ of $5$ (from part (f)):
***
The mass of $\mathrm{CO}_2$ produced by the heat pump is:
  
$\frac{70.08}{5} = 14.02~\mathrm{tonnes}$
***
Therefore, the reduction in $\mathrm{CO}_2$ emissions is:
  
$70.08-14.02 = 56.06~\mathrm{tonnes}$
| A vapour-compression cycle using R134a has the following conditions: 
  
Evaporator pressure: $\hspace{2cm}$ $1.5$ bar 
Compressor inlet state: $\hspace{1.6cm}$ Superheated
Compressor inlet temperature: $\hspace{0.0cm}$ $-10^{\circ}\mathrm{C}$ 
Condenser pressure: $\hspace{1.96 cm}$ $10.0$ bar 
Expansion valve inlet state: $\hspace{1cm}$ Subcooled
Expansion valve inlet temperature: $\hspace{0 cm}$ $25^{\circ}\mathrm{C}$
  
Assuming that the cycle is "ideal" except for the extended processes in the evaporator and condenser: 
Plot the cycle on the $P-h$ chart (found on Blackboard).
\nUsing enthalpies read from the $P - h$ chart, except at the expansion valve inlet where the usual approximation for subcooled liquid properties should be used, calculate the heat transfer in the evaporator, per $\mathrm{kg}$ of R134a. 
\nCalculate the work transfer in the compressor, per $\mathrm{kg}$ of R134a.
\nCalculate the heat transfer in the condenser, per $\mathrm{kg}$ of R134a.
\nCalculate the $COP$ in a refrigeration application.
\nCalculate the $COP$ in a heat pump application.
\nIf this cycle is used for an electrically-driven heat pump which replaces direct electric heating in a building, estimate the resulting annual reduction in $\mathrm{CO}_2$ emissions from power stations, with the following assumptions: 
  
Annual average heat requirement of building: $20 ~\mathrm{kW}$
   
Average $\mathrm{CO}_2$ emission from power stations: 
* Coal-fired: $800 ~\mathrm{g/kWh}$ 
* Gas-fired: $400 ~\mathrm{g/kWh}$ 
* Nuclear: $0$ 
Annual electricity generation from all power stations on network: $1/3$ each from coal-fired, gas-fired and nuclear plant.
| 220 | 24 | 52 | 52 | 336 | 0 | 160 | 14 | 0 | A vapour-compression cycle using R134a has the following conditions: Evaporator pressure: $\hspace{2cm}$ $1.5$ bar Compressor inlet state: $\hspace{1.6cm}$ Superheated Compressor inlet temperature: $\hspace{0.0cm}$ $-10^{\circ}\mathrm{C}$ Condenser pressure: $\hspace{1.96 cm}$ $10.0$ bar Expansion valve inlet state: $\hspace{1cm}$ Subcooled Expansion valve inlet temperature: $\hspace{0 cm}$ $25^{\circ}\mathrm{C}$ Assuming that the cycle is "ideal" except for the extended processes in the evaporator and condenser: Plot the cycle on the $1.5$0 chart found on Blackboard. Using enthalpies read from the $1.5$1 chart, except at the expansion valve inlet where the usual approximation for subcooled liquid properties should be used, calculate the heat transfer in the evaporator, per $1.5$2 of R134a. Calculate the work transfer in the compressor, per $1.5$2 of R134a. Calculate the heat transfer in the condenser, per $1.5$2 of R134a. Calculate the $1.5$5 in a refrigeration application. Calculate the $1.5$5 in a heat pump application. If this cycle is used for an electrically-driven heat pump which replaces direct electric heating in a building, estimate the resulting annual reduction in $1.5$7 emissions from power stations, with the following assumptions: Annual average heat requirement of building: $1.5$8 Average $1.5$7 emission from power stations: Coal-fired: $\hspace{1.6cm}$0 Gas-fired: $\hspace{1.6cm}$1 Nuclear: $\hspace{1.6cm}$2 Annual electricity generation from all power stations on network: $\hspace{1.6cm}$3 each from coal-fired, gas-fired and nuclear plant. | 7 |
219c6815-48ed-4752-b235-de33874ef529 | 0 | 1 | 7 | 14 | 4 | 2 | 16 | 2 | A fast response probe with sampling frequency equal to $5$ kHz has been placed at a given location (fixed in space) in the wake formed by an air flow ($\nu_{air}=1.8\times 10^{-5}$ $\mathrm{m^2/s}$) around a square bluff body with characteristic size $L=0.1$ m. The time history of the three components of velocity has been recorded for $2$ minutes. Post-process of the data shows that the mean velocity at that location is equal to zero and the RMS value of the velocity fluctuations is equal to $7$ $\mathrm{m/s}$ for all the velocity components. Time averages were calculated using all the data recorded.
| Compute the turbulence kinetic energy, $k$, of the flow at that location\nEstimate the velocity scale of the large eddies, $U_\mathrm{t}$.\nFind an estimate of the large-eddies time scale, $T_\mathrm{t}$.\nConsidering the flow to be statistically stationary, discuss whether the averaging period is sufficient to have converged statistics.
\nDetermine the order of magnitude of the rate of dissipation of turbulence kinetic energy.\nWhat is the size of the smallest scales in the turbulent flow?\nDiscuss if the sampling frequency is sufficient to capture the Kolmogorov scales.\nWould your answer of parts (d) and (g) change if the time averaged velocity was different from zero?
| 8 | 0.5 | 3 | \n\n\n\n\n\n\n | \n\n\n\n\n\n\n | A fast response probe with sampling frequency equal to $5$ kHz has been placed at a given location (fixed in space) in the wake formed by an air flow ($\nu_{air}=1.8\times 10^{-5}$ $\mathrm{m^2/s}$) around a square bluff body with characteristic size $L=0.1$ m. The time history of the three components of velocity has been recorded for $2$ minutes. Post-process of the data shows that the mean velocity at that location is equal to zero and the RMS value of the velocity fluctuations is equal to $7$ $\mathrm{m/s}$ for all the velocity components. Time averages were calculated using all the data recorded.
Compute the turbulence kinetic energy, $k$, of the flow at that location\nEstimate the velocity scale of the large eddies, $U_\mathrm{t}$.\nFind an estimate of the large-eddies time scale, $T_\mathrm{t}$.\nConsidering the flow to be statistically stationary, discuss whether the averaging period is sufficient to have converged statistics.
\nDetermine the order of magnitude of the rate of dissipation of turbulence kinetic energy.\nWhat is the size of the smallest scales in the turbulent flow?\nDiscuss if the sampling frequency is sufficient to capture the Kolmogorov scales.\nWould your answer of parts (d) and (g) change if the time averaged velocity was different from zero?
| 202 | 10 | 0 | 0 | 1 | 0 | 101 | 3 | 0 | A fast response probe with sampling frequency equal to $5$ kHz has been placed at a given location fixed in space in the wake formed by an air flow $ u_{air}=1.8\times 10^{-5}$ $\mathrm{m^2/s}$ around a square bluff body with characteristic size $L=0.1$ m. The time history of the three components of velocity has been recorded for $2$ minutes. Time averages were calculated using all the data recorded. Compute the turbulence kinetic energy, $k$, of the flow at that location Estimate the velocity scale of the large eddies, $U_\mathrm{t}$. Find an estimate of the large-eddies time scale, $T_\mathrm{t}$. Considering the flow to be statistically stationary, discuss whether the averaging period is sufficient to have converged statistics. Determine the order of magnitude of the rate of dissipation of turbulence kinetic energy. What is the size of the smallest scales in the turbulent flow? Discuss if the sampling frequency is sufficient to capture the Kolmogorov scales. Would your answer of parts d and g change if the time averaged velocity was different from zero? | 9 |
21bfda15-b80c-451e-9f5d-f3e4d3a1ca77 | 2 | 0 | 1 | 21 | 6 | 1 | 1 | 4 | (*Challenge*): The sine function can be approximated on the interval $[0,\pi]$ by a second-order polynomial, $p_2(x)$, that satisfies
$$
p_2(0) = 0, \qquad p_2(\pi/2) = 1, \qquad p_2(\pi)=0 \; .
$$
For the interval $[-\pi,0]$ the function is just defined as the *odd continuation* of the positive interval.
| Find the second-order polynomial that satisfies the criteria above.
\nFind the trigonometric Fourier series for $p_2(x)$ defined on the interval $[-\pi,\pi]$. 
\nBy plotting, compare this approximation of the sine function to the one obtained from a Taylor series expansion around $x=0$ and around $x=\pi/2$. Is the behaviour any different? If yes, why?
| 3 | 0.666667 | 4 | Write the polynomial in the general form $p_2(x) = Ax^2 + Bx + C$.
***
Set up 3 equations using the given conditions, and use them to solve for $A,B,C$.
\nSketch the function (**remember** that for the interval $[-\pi,0]$ the function is just defined as the odd continuation of the positive interval). 
***
Is $f(x)$ even or odd around $x=0$? Hence use arguments about the product of even/odd functions, and the integral of even/odd functions, to evaluate if $a_n$ or $b_n$ of the Fourier series are 0. 
***
Reduce the interval of the remaining integral(s) to $[0,\pi]$ by considering the symmetry of the function.
***
After this, you may be able to further simplify the calculation of the coefficients by determining if odd or even $n$ terms are 0...
***
... To do this, evaluate the parity (even/oddness) of the function about the half-interval $x=\pi/2$.
***
Finally, evaluate your remaining integral(s)...
***
... Use integration by parts to evaluate the integral(s).
\nThe formula for the Taylor series expansion about $x_0$ is:
$$
f(x) = \sum_{n=0}^{\infty}\frac{f^{n}(x_0)}{n!}(x-x_0)^n
$$
(see the **Functions** course for more details on evaluating the Taylor series). Carry out this expansion for $\sin(x)$ around $x=0$ and $x=\pi/2$. 
***
Sketch the three approximations (i.e., the two Taylor expansions, and the Fourier series). You may choose to use graphing software such as Desmos, or write a Python script using `matplotlib.pyplot`. 
***
Which expansions fit $\sin(x)$ the best over the largest range?
| Let
$$
p_2(x) = A x^2 + B x + C \; ,
$$
***
Then, we write down the three equations and solve for $A$, $B$ and $C$ using the given conditions: 
$$
\begin{align}
&p_2(0) = C = 0\\
&p_2(\pi/2) = A\left(\frac{\pi^2}{4}\right) + B\left(\frac{\pi}{2}\right) =1\\
&p_2(\pi) = A\pi^2+B\pi=0
\end{align}
$$
Solving equations (2) and (3) simultaneously yields:
***
$$
A = -\frac{4}{\pi^2} \qquad B = \frac{4}{\pi} \qquad C=0 \; ,
$$
and thus
$$
p_2(x) = \frac{4}{\pi}\left(x - \frac{x^2}{\pi} \right)
$$
\nFirst, we sketch the function found in part (a) in the interval $[0,\pi]$. Then, we extend this to $[-\pi,\pi]$, utilising the fact that for the interval $[-\pi,0]$ the function is defined as the *odd continuation* of the positive interval:
***
***
The function is odd about $x=0$, so $f(x)\cos(nx)$ is odd. This means that $a_n=0$ for all $n$. $b_n$ is non-zero.
***
Since $f(x)\sin(nx)$ is even, we can write:
$$
b_n = \frac{1}{\pi}\int^{\pi}_{-\pi}{f(x)\sin(nx)\,\text{d}x} = \frac{2}{\pi}\int^{\pi}_{0}{f(x)\sin(nx)\,\text{d}x}
$$
***
Around $x=\pi/2$: 
* $f(x)$ is even
* $\sin(nx)$ is even for odd $n$, and odd for even $n$. 
Hence, $b_n$ evaluates to $0$ for even $n$. 
***
Now, we only have to evaluate the integral for the $b_n$ terms where $n$ is odd.
$$
\begin{aligned}
b_n
&= \frac{2}{\pi}\int_0^\pi p_2(x) \sin nx \,\text{d}x \\
&= \frac{8}{\pi^2}\int_0^\pi
\left(
x - \frac{x^2}{\pi}
\right)\sin nx \,\text{d}x \\
\end{aligned}
$$
Each term in the integral can be evaluated by parts twice. This leaves us with: 
***
$$
\begin{aligned}
b_n
&= \frac{8}{\pi^2}\frac{1}{\pi n^3}
\left(
2 - 2\cos n\pi - n\pi\sin n\pi
\right) \\
&= \frac{32}{\pi^3n^3}
\end{aligned}
$$
We invoked that $\cos(n\pi)=(-1)^n=-1$ for odd $n$. 
***
$$
f(x) = \sum_{n=1,3,5,...}^{\infty}\frac{32}{\pi^3 n^3}\sin(nx)
$$
\nThe formula for the Taylor series expansion about $x_0$ is:
$$
f(x) = \sum_{n=0}^{\infty}\frac{f^{n}(x_0)}{n!}(x-x_0)^n
$$
(see the **Functions** course for more details on evaluating the Taylor series).
***
The Taylor series expansion around $x=0$ of $\sin(x)$ is:
***
$$
\begin{aligned}
T_0(x) &= x - \frac{1}{6}x^3 + \ldots \\
\end{aligned}
$$
***
while around $x=\pi/2$ it is:
$$
T_{\pi/2}(x) = \frac{1}{2}(x-\pi/2)^2 + \ldots
$$
***
The three different approximations are compared to $\sin x$ below. 

***
While the Taylor expansions are designed to provide the best possible fit close to the expansion point, they fail miserably elsewhere. Above, we see that $T_0(x)$ works well around $x=0$, and $T_1(x)$ works well around $x=\pi/2$; but the accuracy of the expansions fail as $x$ increases/decreases. The Fourier series, on the other hand, works effectively for all $x$. 
| (*Challenge*): The sine function can be approximated on the interval $[0,\pi]$ by a second-order polynomial, $p_2(x)$, that satisfies
$$
p_2(0) = 0, \qquad p_2(\pi/2) = 1, \qquad p_2(\pi)=0 \; .
$$
For the interval $[-\pi,0]$ the function is just defined as the *odd continuation* of the positive interval.
Find the second-order polynomial that satisfies the criteria above.
\nFind the trigonometric Fourier series for $p_2(x)$ defined on the interval $[-\pi,\pi]$. 
\nBy plotting, compare this approximation of the sine function to the one obtained from a Taylor series expansion around $x=0$ and around $x=\pi/2$. Is the behaviour any different? If yes, why?
| 91 | 8 | 7 | 7 | 118 | 16 | 54 | 4 | 0 | Find the second-order polynomial that satisfies the criteria above. Find the trigonometric Fourier series for $p_2(x)$ defined on the interval $[-\pi,\pi]$. By plotting, compare this approximation of the sine function to the one obtained from a Taylor series expansion around $x=0$ and around $x=\pi/2$. Is the behaviour any different? If yes, why? | 5 |
229aa45a-b762-4ed2-8497-9da06715bfb8 | 2 | 0 | 0 | 8 | 4 | 2 | 3 | 0 | A shaft, $25\text{ mm}$ diameter, $1500\text{ mm}$ long, is fitted with a strain gauge, the axis of which is inclined at $45^{\circ}$ to the axis of the shaft. When calibrated with the shaft in pure torsion, the gauge records a strain of $0.0008$. In service, there is an end load which causes the shaft to extend $2.3\text{ mm}$ in length and to contract $0.012\text{ mm}$ in diameter. (Assume that the strain gauge only responds to the component of tensile or compressive strain along its axis.)
| What would the strain gauge record in service if subjected to the same torque as before? 
\nWhat is the Poisson's ratio of the shaft material? 
| 2 | 0.666667 | 3 | \n | See the drawing of the strain gauge as it would look on the shaft:

***
Using the data book, the strain in torsion can be calculated, **prior to the load being applied.**
   
$$
e_n=\frac{1}{2}(e_z+e_\theta)+\frac{1}{2}(e_z-e_\theta)\cos(2\theta)+\frac{1}{2}\gamma_{\theta z}\sin(2\theta)
$$
   
***
Since in calibration, the shaft only undergoes torsion, $e_\theta=e_z=0$ and therefore the equation above simplifies to:
   
$$
e_n=\cancel{\frac{1}{2}(e_z+e_\theta)}+\cancel{\frac{1}{2}(e_z-e_\theta)\cos(2\theta)}+\frac{1}{2}\gamma_{\theta z}\sin(2\theta) \\
\hspace{10pt} \\
\gamma_{\theta z}=\frac{2e_n}{\sin(2\theta)}=0.0016
$$
   
***
Now, considering the case where **the load has been applied.** First the axial and hoop stress need to be calculated:
   
$$
e_z=\frac{\Delta L}{L}=\frac{2.3}{1500}=0.001533 \hspace{30pt} e_\theta=-\frac{0.012}{25}=0.00048
$$
   
***
Then returning to the original equation for strain, using the constant value of $\gamma_{\theta z}$ obtained in pure torsion, a new strain reading ($e'_n$) can be obtained:
   
$$
e'_n=\frac{1}{2}(0.001533-0.00048)+0+\frac{1}{2}(0.0016)=\boxed{0.001327}
$$
\nPoisson's ratio is found as:
   
$$
\nu=-\frac{e_\theta}{e_z}=\frac{0.00048}{0.001533}=\boxed{0.3131}
$$
| A shaft, $25\text{ mm}$ diameter, $1500\text{ mm}$ long, is fitted with a strain gauge, the axis of which is inclined at $45^{\circ}$ to the axis of the shaft. When calibrated with the shaft in pure torsion, the gauge records a strain of $0.0008$. In service, there is an end load which causes the shaft to extend $2.3\text{ mm}$ in length and to contract $0.012\text{ mm}$ in diameter. (Assume that the strain gauge only responds to the component of tensile or compressive strain along its axis.)
What would the strain gauge record in service if subjected to the same torque as before? 
\nWhat is the Poisson's ratio of the shaft material? 
| 107 | 6 | 8 | 8 | 126 | 0 | 25 | 0 | 0 | When calibrated with the shaft in pure torsion, the gauge records a strain of $0.0008$. Assume that the strain gauge only responds to the component of tensile or compressive strain along its axis. What would the strain gauge record in service if subjected to the same torque as before? What is the Poisson's ratio of the shaft material? | 4 |
22b6b30c-24b4-4094-affd-b44b8e139021 | 1 | 0 | 0 | 19 | 6 | 1 | 1 | 5 | **(L3)** A greengrocer sells the fruits $\text{(banana, apple, orange, kumquat)}$ at a price $\vec{p} = (40, 55, 50, 12)$ (in pence). On a certain day he sells $\vec{N} = (32, 14, 20, 40)$ of each respectively. Calculate $\vec{p}\cdot\vec{N}$ and give an interpretation of this quantity.
| **(L3)** A greengrocer sells the fruits $\text{(banana, apple, orange, kumquat)}$ at a price $\vec{p} = (40, 55, 50, 12)$ (in pence). On a certain day he sells $\vec{N} = (32, 14, 20, 40)$ of each respectively. Calculate $\vec{p}\cdot\vec{N}$ and give an interpretation of this quantity.
| 1 | 0.333333 | 0 | See **section 1.9** for how to evaluate a dot product. 
***
Writing out the full dot product algebraically may help you understand the physical interpretation of this quantity. 
| $$
\qquad \vec{p}\cdot\vec{N} = \begin{pmatrix}
40\\55\\50\\12
\end{pmatrix} \cdot \begin{pmatrix}
32\\14\\20\\40
\end{pmatrix}
$$
***
$$
=1280+770+1000+480 = \pounds 35.30
$$
The dot product is the sum of money the greengrocer made.
| **(L3)** A greengrocer sells the fruits $\text{(banana, apple, orange, kumquat)}$ at a price $\vec{p} = (40, 55, 50, 12)$ (in pence). On a certain day he sells $\vec{N} = (32, 14, 20, 40)$ of each respectively. Calculate $\vec{p}\cdot\vec{N}$ and give an interpretation of this quantity.
| 32 | 4 | 2 | 2 | 14 | 0 | 32 | 4 | 0 | Calculate $\vec{p}\cdot\vec{N}$ and give an interpretation of this quantity. | 1 |
231198e3-e44c-4104-9748-51c0d8906a1b | 0 | 0 | 1 | 17 | 6 | 1 | 2 | 4 | In lectures we showed that the change in momentum of an object is equal to the impulse applied:
$$
mv(t_f) - mv(t_i) = \int_{t_i}^{t_f} F(t) \, dt .
$$
Derive the three-dimensional vector equivalent:
$$
m\boldsymbol{\vec{v}}(t_f) - m\boldsymbol{\vec{v}}(t_i) = \int_{t_i}^{t_f} \boldsymbol{\vec{F}}(t) \, dt .
$$
  
| In lectures we showed that the change in momentum of an object is equal to the impulse applied:
$$
mv(t_f) - mv(t_i) = \int_{t_i}^{t_f} F(t) \, dt .
$$
Derive the three-dimensional vector equivalent:
$$
m\boldsymbol{\vec{v}}(t_f) - m\boldsymbol{\vec{v}}(t_i) = \int_{t_i}^{t_f} \boldsymbol{\vec{F}}(t) \, dt .
$$
  
| 1 | 0.333333 | 1 | Since you already know how to differentiate a vector with respect to $t$, you can integrate one too. An integral such as $\int \boldsymbol{\vec{F}}(t) , dt$ is really three integrals, one for each component:
 $\int \boldsymbol{\vec{F}}(t) , dt = \left ( \int F_x(t) , dt, \int F_y(t) , dt, \int F_z(t) , dt \right )$.
***
Start with Newton's second law in vector form.
Integrate both sides from time $t_i$ to $t_f$. 
***
Integrate both sides from time $t_i$ to $t_f$. 
| Since you already know how to differentiate a vector with respect to $t$, you can integrate one too. An integral such as $\int \boldsymbol{\vec{F}}(t) , dt$ is really three integrals, one for each component:
 $\int \boldsymbol{\vec{F}}(t) , dt = \left ( \int F_x(t) , dt, \int F_y(t) , dt, \int F_z(t) , dt \right )$.
***
All you have to do is write out the steps from the lecture notes, replacing scalars by vectors:
***
$$
\begin{aligned}
&
&
m \frac{d\boldsymbol{\vec{v}}}{dt}
&= \boldsymbol{\vec{F}}(t) \\
\end{aligned}
$$
***
Integrating from time $t_i$ to $t_f$:
***
$$
\begin{aligned}
&\Rightarrow\qquad
&
m\int_{t_i}^{t_f} \frac{d\boldsymbol{\vec{v}}(t)}{dt} dt
&= \int_{t_i}^{t_f} \boldsymbol{\vec{F}}(t) dt \\
\end{aligned}
$$
***
$$
\begin{aligned}
&\Rightarrow
&
m[\boldsymbol{\vec{v}}(t)]_{t_i}^{t_f}
&= \int_{t_i}^{t_f} \boldsymbol{\vec{F}}(t) dt \\
&\Rightarrow
&
m\boldsymbol{\vec{v}}(t_f) - m\boldsymbol{\vec{v}}(t_i)
&= \int_{t_i}^{t_f} \boldsymbol{\vec{F}}(t) dt .
\end{aligned}
$$
***
If you are unsure about this, you can deal with each component separately. For the $x$ component, you get:
$$
\begin{aligned}
&
&
m \frac{dv_x}{dt}
&= F_x(t) \\
&\Rightarrow\qquad
&
m\int_{t_i}^{t_f} \frac{dv_x(t)}{dt} dt
&= \int_{t_i}^{t_f} F_x(t) dt \\
&\Rightarrow
&
m[v_x(t)]_{t_i}^{t_f}
&= \int_{t_i}^{t_f} F_x(t) dt \\
&\Rightarrow
&
mv_{x}(t_f) - mv_{x}(t_i)
&= \int_{t_i}^{t_f} F_x(t) dt .
\end{aligned}
$$
The equivalent equations for the $y$ and $z$ components are derived in the same way.
| In lectures we showed that the change in momentum of an object is equal to the impulse applied:
$$
mv(t_f) - mv(t_i) = \int_{t_i}^{t_f} F(t) \, dt .
$$
Derive the three-dimensional vector equivalent:
$$
m\boldsymbol{\vec{v}}(t_f) - m\boldsymbol{\vec{v}}(t_i) = \int_{t_i}^{t_f} \boldsymbol{\vec{F}}(t) \, dt .
$$
  
| 26 | 2 | 12 | 12 | 104 | 7 | 26 | 2 | 0 | In lectures we showed that the change in momentum of an object is equal to the impulse applied: $ mv(t_f) - mv(t_i) = \int_{t_i}^{t_f} F(t) \, dt . $ Derive the three-dimensional vector equivalent: $ m\boldsymbol{\vec{v}}(t_f) - m\boldsymbol{\vec{v}}(t_i) = \int_{t_i}^{t_f} \boldsymbol{\vec{F}}(t) \, dt . | 2 |
237c59c3-85aa-4c7d-b311-3f23d5397b37 | 3 | 0 | 0 | 11 | 4 | 2 | 2 | 4 | This question relates to combined cycle plants and combined heat and power plants.
| A gas turbine (GT) with an efficiency of $36\%$ is used in a conventional gas-steam combined cycle. The energy lost in the exhaust duct from the heat recovery steam generator (HRSG), as a result of the exhaust gas being above ambient temperature, is $15\%$ of the energy supplied in the gas turbine fuel. Other losses from the GT and HRSG can be ignored. If the steam cycle efficiency is $34\%$, what is the overall efficiency of the combined cycle?
\nAn industrial site requires equal amounts of energy in the form of electricity and heat. It currently takes electricity from a network where the power stations have an average electricity generation efficiency of $40\%$, and produces heat from onsite boilers with an efficiency (i.e. heat output / energy in fuel burned) of $86\%$. These energy supplies are to be replaced by an on-site combined heat and power (CHP) plant where the prime mover has an efficiency (for electricity) of $38\%$ and a heat-to-power ratio of $1$ (matching the site requirements). What will be: 
  
(i) the energy utilisation factor of the CHP plant?
  
(ii) the percentage saving in fuel energy (considering fuel consumed on site and in power stations)?
| 2 | 0.666667 | 2 | \n | It can be helpful to draw what is happening as a diagram:
***
  

\n(i) The CHP produces one unit of power and one unit of heat. Since the prime mover efficiency is $38\%$, the total number of units available is:
  
$\frac{1}{0.38} = 2.63$
***
Therefore, the energy utilisation factor is:
  
$\frac{1+1}{2.63} = 76\%$
***
(ii) For the original plant, the units of power available:
  
$\frac{1}{0.4} = 2.5$
***
The units of heat available:
  
$\frac{1}{0.86} = 1.16$
***
Total units available:
  
$2.5+1.16 = 3.66$
***
Energy utilisation factor:
  
$\frac{1+1}{3.66} = 54.6\%$
***
Percentage saving:
  
$\frac{3.66-2.63}{3.66} = 28.1\%$
| This question relates to combined cycle plants and combined heat and power plants.
A gas turbine (GT) with an efficiency of $36\%$ is used in a conventional gas-steam combined cycle. The energy lost in the exhaust duct from the heat recovery steam generator (HRSG), as a result of the exhaust gas being above ambient temperature, is $15\%$ of the energy supplied in the gas turbine fuel. Other losses from the GT and HRSG can be ignored. If the steam cycle efficiency is $34\%$, what is the overall efficiency of the combined cycle?
\nAn industrial site requires equal amounts of energy in the form of electricity and heat. It currently takes electricity from a network where the power stations have an average electricity generation efficiency of $40\%$, and produces heat from onsite boilers with an efficiency (i.e. heat output / energy in fuel burned) of $86\%$. These energy supplies are to be replaced by an on-site combined heat and power (CHP) plant where the prime mover has an efficiency (for electricity) of $38\%$ and a heat-to-power ratio of $1$ (matching the site requirements). What will be: 
  
(i) the energy utilisation factor of the CHP plant?
  
(ii) the percentage saving in fuel energy (considering fuel consumed on site and in power stations)?
| 215 | 7 | 8 | 8 | 92 | 0 | 202 | 7 | 0 | A gas turbine GT with an efficiency of $36\%$ is used in a conventional gas-steam combined cycle. If the steam cycle efficiency is $34\%$, what is the overall efficiency of the combined cycle? What will be: i the energy utilisation factor of the CHP plant? ii the percentage saving in fuel energy considering fuel consumed on site and in power stations? | 4 |
23d553e2-62ee-43d2-b402-6b798bbb4f6e | 2 | 0 | 2 | 11 | 4 | 2 | 2 | 6 | In a steam power plant, the boiler produces $40 ~\mathrm{kg/s}$ of steam in the saturated vapour state at a pressure of $20$ bar. In order to run the turbine at less than full load, the boiler exit steam is throttled to a pressure of $10$ bar before entering the turbine, by means of a well-insulated, partly-closed valve. The turbine has an isentropic efficiency of $0.80$ and there is a heat loss of $100~ \mathrm{kW}$ from its casing to the atmosphere. At the turbine exhaust, the steam pressure is $0.1$ bar and the mean velocity is $350~ \mathrm{m/s}$. Kinetic energies everywhere else are negligible.
| Sketch the processes in the valve and turbine on an enthalpy - entropy ($h - s$) diagram, including the relevant isobars. (Assume that the steam is wet at the turbine exhaust).
\nShow that the dryness fraction of the steam at the turbine exhaust is $0.856$.
\nCalculate the shaft power produced.
\nCalculate the required flow cross-sectional area at the turbine exhaust.
| 4 | 1 | 3 | \n\n\n | On an $h-s$ diagram, the bell shape is slightly skewed.
Throttling is an isenthalpic process (see Q3), so process $1-2$ is a straight horizontal line.
Process $2-3$, had it been isentropic, would have been represented by a straight vertical line. However, since the isentropic efficiency is not $1$, entropy increases and therefore a straight diagonal line (leading to the right) is drawn instead.
\nAt state $1$, the steam is saturated vapour at $20$ bar. Therefore, looking at Table E21:
  
$h_1 = h_\mathrm{g} = 2798.4\mathrm{~kJ/kg}$
***
Since process $1-2$ is isenthalpic, $h_2 = h_1$. Therefore, the entropy at state $2$ can be found from the superheated steam tables at $10$ bar (Table E26).
***
However, since the exact value of $h$ does not appear in the table, it is necessary to interpolate:
  
$s_2 = \frac{2798.4-2777.4}{2828.3-2777.4}\times(6.695-6.586) + 6.586 = 6.631~\mathrm{kJ/kgK}$
***
State $2-3$ is not isentropic, but the isentropic efficiency is known. Therefore, the value of $h$ for the theoretical isentropic process ($h_{3\mathrm{s}}$) can be found, after which the equation for isentropic efficiency for a turbine can be used to find $h_3$.(*See note at the bottom)*
***
 First find the isentropic dryness fraction using values of $s_\mathrm{f}$ and $s_\mathrm{g}$ at $0.1$ bar (Table E20):
  
$x_{3\mathrm{s}} = \frac{6.631-0.6492}{8.149-0.6492} = 0.798~\mathrm{kJ/kgK}$
***
Now $h_{3\mathrm{s}}$ can be calculated using values of $h_\mathrm{f}$ and $h_\mathrm{g}$ at 0.1 bar (Table E20 again):
  
$h_{3\mathrm{s}} = 191.81+0.798(2392.1) = 2100.7~\mathrm{kJ/kg}$
***
The equation for isentropic efficiency can now be used to calculate $h_3$:
  
$\eta_\mathrm{s, turbine} = \frac{h_3-h_2}{h_{3\mathrm{s}}-h_2}$
***
Substituting in numbers and rearranging: 
  
$h_3 = 0.8(2100.7-2798.4)+2798.4 = 2240.24~\mathrm{kJ/kg}$
***
Now the dryness fraction, $x_3$ can be calculated using the values found from Table E20 for $h_\mathrm{f}$ and $h_\mathrm{g}$:
  
$x_3 = \frac{2240.24-191.81}{2392.1} = 0.856$
***
NOTE: Strictly speaking, isentropic efficiency should only be allowed for adiabatic processes. However, engineering practice is not so pedantic when $| \dot{Q}|<<|\Delta h|$ as it is in this case.
\nShaft power $= \dot{W}_\mathrm{net} = \dot{W}_{23}$
***
This can be found by applying the SFEE to process $2-3$, bearing in mind that potential energy changes can be neglected. Note that in this case, there is a change in kinetic energy.
***
Therefore:
  
$\dot{W}_{23} =\dot{Q}_{23} -\dot{m}[(h_3-h_2) + (\frac{c_3^2}{2}-\frac{c_2^2}{2})]$
***
The values for $\dot{m}$ and $c_3$ are given in the question, and $c_2$ is stated to be negligible. $h_3$ and $h_2$ were calculated in part (b). Therefore, substituting in numbers:
  
$\dot{W}_\mathrm{net} = -100-40[(2240.24-2798.4)+(\frac{350^2}{2\times 1000})] = 19.8~\mathrm{MW}$
\nThe required flow cross sectional area will depend on the flow rate and fluid velocity. 
***
Therefore, the following equation can be used:
  
$\dot{m} = \rho cA$
***
The flow rate and fluid velocity are known quantities. The density can be found by calculating the specific volume at state $3$ and taking the reciprocal.
***
At state $3$, the pressure is $0.1$ bar and the dryness fraction is $0.856$. Using Table E20 to find the values of $v_\mathrm{f}$ and $v_\mathrm{g}$:
  
$v_3 = 0.001010+0.856(14.67-0.001010) = 12.56~\mathrm{m^3/kg}$
***
Therefore:
  
$\rho = \frac{1}{12.56} = 0.0796~\mathrm{kg/m^3}$
***
Therefore:
  
$A = \frac{\dot{m}}{\rho c} = \frac{40}{0.0796\times 350} = 1.44~\mathrm{m^2}$
| In a steam power plant, the boiler produces $40 ~\mathrm{kg/s}$ of steam in the saturated vapour state at a pressure of $20$ bar. In order to run the turbine at less than full load, the boiler exit steam is throttled to a pressure of $10$ bar before entering the turbine, by means of a well-insulated, partly-closed valve. The turbine has an isentropic efficiency of $0.80$ and there is a heat loss of $100~ \mathrm{kW}$ from its casing to the atmosphere. At the turbine exhaust, the steam pressure is $0.1$ bar and the mean velocity is $350~ \mathrm{m/s}$. Kinetic energies everywhere else are negligible.
Sketch the processes in the valve and turbine on an enthalpy - entropy ($h - s$) diagram, including the relevant isobars. (Assume that the steam is wet at the turbine exhaust).
\nShow that the dryness fraction of the steam at the turbine exhaust is $0.856$.
\nCalculate the shaft power produced.
\nCalculate the required flow cross-sectional area at the turbine exhaust.
| 162 | 9 | 52 | 52 | 462 | 0 | 61 | 2 | 0 | Sketch the processes in the valve and turbine on an enthalpy - entropy $h - s$ diagram, including the relevant isobars. Assume that the steam is wet at the turbine exhaust. Show that the dryness fraction of the steam at the turbine exhaust is $0.856$. Calculate the shaft power produced. Calculate the required flow cross-sectional area at the turbine exhaust. | 5 |
24124ac6-4477-4d13-b8cc-1a192c099fec | 0 | 0 | 2 | 14 | 4 | 2 | 10 | 1 | Write the Laplacian, $\overrightarrow{\mathrm{Lap}}(\vec{u})$, of the velocity vector | in a Cartesian frame of reference (consider $\vec{u}=\left[u~~v~~w \right]^T$).\nin a cylindrical frame of reference (consider $\vec{u}=\left[u_r~~u_\theta~~u_z \right]^T$). | 2 | 0.5 | 2 | \n | \n | Write the Laplacian, $\overrightarrow{\mathrm{Lap}}(\vec{u})$, of the velocity vectorin a Cartesian frame of reference (consider $\vec{u}=\left[u~~v~~w \right]^T$).\nin a cylindrical frame of reference (consider $\vec{u}=\left[u_r~~u_\theta~~u_z \right]^T$). | 25 | 3 | 0 | 0 | 1 | 0 | 17 | 2 | 0 | Write the Laplacian, $\overrightarrow{\mathrm{Lap}}(\vec{u})$, of the velocity vectorin a Cartesian frame of reference consider $\vec{u}=\left[u~~v~~w \right]^T$. | 1 |
248240cb-dee7-445a-b5fc-83649bff2f7b | 0 | 0 | 1 | 17 | 6 | 1 | 3 | 6 | In one-dimensional inelastic collisions, the coefficient of restitution $e$ is defined by the equation
$$
v_2 - v_1 = -e (u_2 - u_1),
$$
where $v_1$ and $v_2$ are the final velocities of the two bodies and $u_1$ and $u_2$ are their initial velocities. Use this equation, plus momentum conservation, to derive the following expressions for the final velocities of the two bodies (of masses $m_1$ and $m_2$) in the case when the second body is initially at rest ($u_2 = 0$):
$$
\begin{aligned}
v_1 &= \frac{(m_1 - e m_2) u_1}{m_1 + m_2}, &
v_2 &= \frac{(1 + e)m_1 u_1}{m_1 + m_2}.
\end{aligned}
$$
| In one-dimensional inelastic collisions, the coefficient of restitution $e$ is defined by the equation
$$
v_2 - v_1 = -e (u_2 - u_1),
$$
where $v_1$ and $v_2$ are the final velocities of the two bodies and $u_1$ and $u_2$ are their initial velocities. Use this equation, plus momentum conservation, to derive the following expressions for the final velocities of the two bodies (of masses $m_1$ and $m_2$) in the case when the second body is initially at rest ($u_2 = 0$):
$$
\begin{aligned}
v_1 &= \frac{(m_1 - e m_2) u_1}{m_1 + m_2}, &
v_2 &= \frac{(1 + e)m_1 u_1}{m_1 + m_2}.
\end{aligned}
$$
| 1 | 0.333333 | 1 | Write down momentum conservation alongside the equation given in the question (remembering that $u_2=0$)
***
You now have a pair of simultaneous equations that you must solve for $v_1$ and $v_2$ in terms of $u_1$.
***
There are many ways to approach this, but one approach is to multiply $v_2 - v_1 = eu_1$ by $m_1$ and add it to the momentum conservation equation. Can you find $v_1$ and $v_2$ from here?
| Start by writing down the definition of the coefficient of restitution and the law of conservation of momentum in the case when $u_2 = 0$:
***
$$
\begin{align}
v_2 - v_1 &= eu_1 ,\\
m_1 v_1 + m_2 v_2 &= m_1 u_1 .
\end{align}
$$
***
Our job is to solve for $v_1$ and $v_2$ as functions of $u_1$. One way is to multiply equation (1) by $m_1$,
$$
m_1 v_2 - m_1 v_1 = e m_1 u_1,
$$
and add it to equation (2) to obtain:
***
$$
m_2 v_2 + m_1 v_2 = m_1 u_1 + e m_1 u_1 ,
$$
which rearranges to give $v_2$ equal to:
***
$$
v_2 = \frac{(1 + e)m_1 u_1}{m_1 + m_2}.
$$
Plugging this back into equation (1) and re-arranging for $v_1$ yields:
***
$$
v_1 = v_2 - eu_1 = \frac{(1+e)m_1 u_1}{m_1 + m_2} - \frac{e(m_1 +
m_2)u_1}{m_1 + m_2} = \frac{(m_1 - e m_2)u_1}{m_1 + m_2}.
$$
| In one-dimensional inelastic collisions, the coefficient of restitution $e$ is defined by the equation
$$
v_2 - v_1 = -e (u_2 - u_1),
$$
where $v_1$ and $v_2$ are the final velocities of the two bodies and $u_1$ and $u_2$ are their initial velocities. Use this equation, plus momentum conservation, to derive the following expressions for the final velocities of the two bodies (of masses $m_1$ and $m_2$) in the case when the second body is initially at rest ($u_2 = 0$):
$$
\begin{aligned}
v_1 &= \frac{(m_1 - e m_2) u_1}{m_1 + m_2}, &
v_2 &= \frac{(1 + e)m_1 u_1}{m_1 + m_2}.
\end{aligned}
$$
| 75 | 10 | 12 | 12 | 84 | 8 | 75 | 10 | 0 | Use this equation, plus momentum conservation, to derive the following expressions for the final velocities of the two bodies of masses $m_1$ and $m_2$ in the case when the second body is initially at rest $u_2 = 0$: $ \begin{aligned} v_1 &= \frac{(m_1 - e m_2) u_1}{m_1 + m_2}, & v_2 &= \frac{(1 + e)m_1 u_1}{m_1 + m_2}. \end{aligned} $ | 2 |
24a58bb8-afbf-45b5-8a21-baf48f42769c | 2 | 2 | 1 | 14 | 4 | 2 | 1 | 1 | Consider a simple straining flow in Cartesian coordinates, $\left(x,y\right)$, given by
$$
\vec{u}=\begin{bmatrix}1+\alpha x\\-\alpha y\end{bmatrix},
$$
where $\alpha$ is a constant real number.
| Plot the velocity field (by hand or computer).\nIn the channel flow pictured below, with water entering from the left, in which region (labelled A to F) is the flow field approximately the same as the 'straining flow' field described above?

\nSimplify the expression for velocity, $\vec{u}$, on $y=0$.\nDerive an expression for the acceleration, $\mathrm{D} \vec{u}/\mathrm{D} t$, on $y=0$. | 4 | 0.5 | 2 | \n\n\n | \n\n\n | Consider a simple straining flow in Cartesian coordinates, $\left(x,y\right)$, given by
$$
\vec{u}=\begin{bmatrix}1+\alpha x\\-\alpha y\end{bmatrix},
$$
where $\alpha$ is a constant real number.
Plot the velocity field (by hand or computer).\nIn the channel flow pictured below, with water entering from the left, in which region (labelled A to F) is the flow field approximately the same as the 'straining flow' field described above?

\nSimplify the expression for velocity, $\vec{u}$, on $y=0$.\nDerive an expression for the acceleration, $\mathrm{D} \vec{u}/\mathrm{D} t$, on $y=0$. | 81 | 7 | 0 | 0 | 1 | 0 | 61 | 4 | 1 | Consider a simple straining flow in Cartesian coordinates, $\left(x,y\right)$, given by $ \vec{u}=\begin{bmatrix}1+\alpha x\\-\alpha y\end{bmatrix}, $ where $\alpha$ is a constant real number. Plot the velocity field by hand or computer. In the channel flow pictured below, with water entering from the left, in which region labelled A to F is the flow field approximately the same as the 'straining flow' field described above? Simplify the expression for velocity, $\vec{u}$, on $y=0$. Derive an expression for the acceleration, $\mathrm{D} \vec{u}/\mathrm{D} t$, on $y=0$. | 5 |
24e6c3bc-efcf-4212-98a2-42c23b645666 | 2 | 0 | 0 | 16 | 6 | 1 | 0 | 7 | At some time $(t = - T)$ in the morning, it starts snowing at a constant heavy rate and continues to do so. A snow plough starts at noon $(t = 0)$ and moves along a road removing snow at a constant rate. The velocity $\displaystyle {\mathrm{d}x\over \mathrm{d}t}$ of the plough is given by
$$
\displaystyle {\mathrm{d}x\over \mathrm{d}t} = {K\over (t + T)}
$$
where $K$ is a constant. The plough travels 2 km in the first hour and 1 km in the second hour.
| At what time did it start snowing (i.e. find $T$)? 
Convert your answer to a decimal and type it in the answer box below
| 1 | 0.666667 | 2 | You can start by finding $x(t)$ from the equation of $\displaystyle {\mathrm{d}x\over \mathrm{d}t}$.
***
Now, look at the conditions given.
Find $x$ at the three conditions for $t$, and solve the simultaneous equations to find $T$.
***
Remember that $T$ is positive as it starts snowing before noon ($t=0$) at $t=-T$. So take the positive root of $T$.
| (This is not *too* unreasonable a model in that snow is removed at a constant rate by *volume*. There is a drawback when the snow depth is very small..)
You can start by finding $x(t)$ from the equation of $\displaystyle {\mathrm{d}x\over \mathrm{d}t}$.
***
By integrating (and where $C$ is an arbitrary integration constant), 
$$
\begin{aligned}
{{\mathrm{d}x}\over {\mathrm{d}t}} &= {K\over (t + T)}
\\
x(t) &= K\ln(t+T) + C
\end{aligned}
$$
***
Now, look at the conditions given.
Find $x$ at the three conditions for $t$, and solve the simultaneous equations to find $T$.
***
At noon, $t=0$,
$$
x(0) = K\ln(T) + C = 0
$$
where we have set $x(0)=0$ as the snow plough has not moved yet.
In the first hour, $t=1$
$$
x(1) = K\ln(1+T) + C = 2
$$
as it moved 2km in the first hour.
In the second hour, $t=2$, 
$$
x(2) = K\ln(2+T)+C = 2+1=3
$$
Now can you solve these simultaneous equations to find $T$?
***
There are a few ways to solve these simultaneous equations, you can use this way, but there are other methods that should give the same result:
$$
\begin{aligned}
\frac{x(2)-x(1)}{x(1)-x(0)} = {1\over2} &= \frac{\ln(2+T)-\ln(1+T)}{\ln(1+T)-\ln(T)}
\end{aligned}
$$
Can you finish rearranging to find $T$?
***
$$
\begin{aligned}
2\ln(2+T)-2\ln(1+T) &= \ln(1+T) - \ln(T)
\\
\ln\left(\frac{2+T}{1+T} \right)^2 &= \ln\left({1+T\over T}\right)
\\
T(2+T)^2 &= (1+T)^3
\\
T^2 + T - 1 &=0
\\
T & = -{1\over2}\pm{1\over2}\sqrt{5}
\end{aligned}
$$
***
Remember that $T$ is positive as it starts snowing before noon ($t=0$) at $t=-T$.
***
So we take the positive root $\displaystyle T={1\over2}(\sqrt{5}-1) = 0.618...$ hours.
Hence, it started to snow at $11:22$am, almost $11:23$am. 
($t=0$ was noon, 12:00, and 0.618.. of an hour is just over 37minutes, so the clock has not quite ticked over to $11:23$am.)
***
In passing, we note that the solution does coincidentally involve the golden ratio, $\tau$, which is defined such that $\tau -1 - \frac{1}{\tau}$
Solving this quadratic for $\tau$, we get 
$$
\begin{aligned}
\tau^2 - \tau &= 1\\\Rightarrow \tau _{roots} &= \frac{1 \pm 5}{2} \\ &= \pm 1.618...
\end{aligned}
$$
The golden ratio famously appears in art, and can also be related to the Fibonacci Sequence (i.e, 1, 1, 2, 3, 5, 8, 13, 21...)
$$
\begin{aligned}
\\
\mathrm{Fibonacci\ defined\ via}: u_{n+2} &= u_{n} + u_{n+1}\\
\Rightarrow \lim_{n \to \infty} \frac{u_{n+1}}{u_n} &= \tau
\end{aligned}
$$
This is also only the first in a sequence of 'snow plow problems'. You may also wish to consider the following scenario (very hard): what if there was a second plow following from 1 pm, say and even a third plow following from 2 pm? 

You will need to consider the fact that the snow builds up from when the previous plow passes by. There will be a collision. When? Where? Snow starts?
| At some time $(t = - T)$ in the morning, it starts snowing at a constant heavy rate and continues to do so. A snow plough starts at noon $(t = 0)$ and moves along a road removing snow at a constant rate. The velocity $\displaystyle {\mathrm{d}x\over \mathrm{d}t}$ of the plough is given by
$$
\displaystyle {\mathrm{d}x\over \mathrm{d}t} = {K\over (t + T)}
$$
where $K$ is a constant. The plough travels 2 km in the first hour and 1 km in the second hour.
At what time did it start snowing (i.e. find $T$)? 
Convert your answer to a decimal and type it in the answer box below
| 94 | 6 | 31 | 31 | 361 | 9 | 25 | 1 | 0 | The velocity $\displaystyle {\mathrm{d}x\over \mathrm{d}t}$ of the plough is given by $ \displaystyle {\mathrm{d}x\over \mathrm{d}t} = {K\over (t + T)} $ where $K$ is a constant. find $T$? Convert your answer to a decimal and type it in the answer box below | 3 |
250bd94a-2c36-42bd-a8a7-ce0360fc1620 | 2 | 0 | 0 | 22 | 6 | 1 | 0 | 1 | Pendulum clocks tick every half period of the pendulum’s swing.
|  Calculate the length of the pendulum needed to make a clock that ticks once every second.
\nThis pendulum is given an initial angular displacement of 6$^{\circ}$. Neglecting any dissipation, calculate the maximum speed attained by the pendulum.
| 2 | 0.333333 | 2 | Recall that $\omega_0 = \sqrt{g/l}$
***
The period of oscillation is related to the angular frequency: $T=2\pi/\omega_0$
***
Rearrange for $l$ and put the numbers into the formula.
\nStart from the solution for the displacement as a function of time: $x=x_0\cos(\omega_0 t)$
***
$x_0$ is given by the initial condition. If the initial angle is $\theta_0$ then the initial displacement is $x_0= l \theta_0$
***
Take the time derivative to get the velocity as a function of time.
***
Work out its maximum value.
| For a pendulum, $\omega_0 = \sqrt{g/l}$. 
***
The period is $T=2\pi/\omega_0$. Rearranging gives $l$:
***
 $l = T^2 g/(4\pi^2)$. 
***
To tick once per second, we need a period of $T=2$ s, so...
***
$l=99.4$ cm.
\nThe linear displacement is $x = x_0 \cos(\omega_0 t)$.
***
The initial displacement is $x_0 = l\theta_0$ where $\theta_0$ is the initial angle.
***
The velocity is $v=\dot{x}=-l\theta_0 \omega_0 \sin(\omega_0 t)$.
***
This has a maximum value $v_{\rm max} = l\theta_0 \omega_0$. 
***
Putting in the numbers, we get $v_{\rm max} = 0.327$ m/s.
| Pendulum clocks tick every half period of the pendulum’s swing.
 Calculate the length of the pendulum needed to make a clock that ticks once every second.
\nThis pendulum is given an initial angular displacement of 6$^{\circ}$. Neglecting any dissipation, calculate the maximum speed attained by the pendulum.
| 49 | 1 | 12 | 12 | 77 | 7 | 39 | 1 | 0 | Calculate the length of the pendulum needed to make a clock that ticks once every second. This pendulum is given an initial angular displacement of 6$^{\circ}$. Neglecting any dissipation, calculate the maximum speed attained by the pendulum. | 3 |
25481b22-b855-4627-8ea9-8788f6ed2f34 | 3 | 0 | 0 | 16 | 6 | 1 | 0 | 1 | Find $\displaystyle {\mathrm{d}y\over \mathrm{d}x}$ for each of these relationships:
| $$
y^3 = x^3 - xy
$$
\n$$
xe^{y} = \cos(xy)
$$
\n$$
y =\sec^{-1}(x)
$$
| 3 | 0.333333 | 0 | As this cannot simply be put into the form $y=f(x)$, use implicit differentiation. For implicit differentiation, take the derivative with respect to $x$ on both sides of the equation.
***
Take derivative $\displaystyle \frac{\mathrm{d}}{\mathrm{d}x}$ on both sides:
$$
\displaystyle {\mathrm{d}\over \mathrm{d}x}(y^3) = {\mathrm{d} \over \mathrm{d}x}(x^3 - xy)
$$
***
For $\displaystyle \frac{\mathrm{d}}{\mathrm{d}x}(y^3)$, remember that $\displaystyle \frac{\mathrm{d}}{\mathrm{d}x} f(y(x)) = \frac{\mathrm{d}f}{\mathrm{d}y} \cdot \frac{\mathrm{d}y}{\mathrm{d}x}$ using the chain rule (and consider $f(y) = y^3$).
For $\displaystyle \frac{\mathrm{d}}{dx}(xy)$ remember the product rule.
Now can you find the derivatives, and rearrange the expression to find $\displaystyle {\mathrm{d}y\over \mathrm{d}x}$?
\nAs this cannot simply be put into the form $y=f(x)$, use implicit differentiation. For implicit differentiation, take the derivative with respect to $x$, $\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}$, on both sides of the equation.
$$
\displaystyle{\frac{\mathrm{d}}{\mathrm{d}x}}(xe^{y} )= {\frac{\mathrm{d}}{\mathrm{d}x}}(\cos(xy))
$$
***
Use the product rule and the chain rule to evaluate the LHS and RHS
***
Let's first consider the LHS: 
Find $ \displaystyle\frac{\mathrm{d}}{\mathrm{d}x}(xe^y) $ using the product rule. Then use the chain rule, $\displaystyle\frac{\mathrm{d}}{\mathrm{d}x} f(y(x)) = \frac{\mathrm{d}f}{\mathrm{d}x} \cdot \frac{\mathrm{d}y}{\mathrm{d}x}$
Can you evaluate the LHS now?
***
Now consider the RHS:
$$
\displaystyle {\mathrm{d}\over \mathrm{d}x}(\cos(xy))
$$
As you have a function $\cos$ of another function $xy$, use the chain rule. To see this, you can use the substitution $u=xy$ so that you have
$$
\displaystyle {\mathrm{d}\over\mathrm{d}x}(\cos(u))
$$
Now can you rearrange the expression to find $\displaystyle {\frac{\mathrm{d}y}{\mathrm{d}x}}$?
\nFirst, get this into a form easier to handle.
$$
x=\sec(y)
$$
***
Using implicit differentiation, take the derivative with respect to $x$ on both sides.
***
Use $\displaystyle \frac{\mathrm{d}y}{\mathrm{d}y} (\sec(y))=\sec(y)\tan(y)$. Can you differentiate both sides now?
***
After rearranging to find $\displaystyle {\frac{\mathrm{d}y}{\mathrm{d}x}}$, get this into a function of $x$. 
***
Get the RHS in terms only of $\sec(y)$; try using a trigonometric identity involving $\tan y$ and $\sec y$.
***
Use the identity $1+\tan^2(x) = \sec^2(y)$
| As this cannot simply be put into the form $y=f(x)$, use implicit differentiation. For implicit differentiation, take the derivative with respect to $x$ on both sides of the equation.
***
Take derivative $\displaystyle \frac{\mathrm{d}}{\mathrm{d}x}$ on both sides:
$$
\displaystyle {\mathrm{d}\over \mathrm{d}x}(y^3) = {\mathrm{d} \over \mathrm{d}x}(x^3 - xy)
$$
***
For $\displaystyle \frac{\mathrm{d}}{\mathrm{d}x}(y^3)$, remember that $\displaystyle \frac{\mathrm{d}}{\mathrm{d}x} f(y(x)) = \frac{\mathrm{d}f}{\mathrm{d}y} \cdot \frac{\mathrm{d}y}{\mathrm{d}x}$ using the chain rule (and consider $f(y) = y^3$).
For $\displaystyle \frac{\mathrm{d}}{\mathrm{d}x}(xy)$ remember the product rule.
Now can you find the derivatives, and rearrange the expression to find $\displaystyle {\mathrm{d}y\over \mathrm{d}x}$?
***
$$
\displaystyle 3y^2\frac{\mathrm{d}y}{\mathrm{d}x} = 3x^2 - \left(y + x\frac{\mathrm{d}y}{\mathrm{d}x}\right)
$$
Rearrange to find $\displaystyle \frac{\mathrm{d}y}{\mathrm{d}x}$.
$$
\begin{aligned}
(3y^2+x)\frac{\mathrm{d}y}{\mathrm{d}x} &= 3x^2-y \\
\frac{\mathrm{d}y}{dx} &=\frac{3x^2-y}{3y^2+x}
\end{aligned}
$$
\nAs this cannot simply be put into the form $y=f(x)$, use implicit differentiation. For implicit differentiation, take the derivative with respect to $x$, $\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}$, on both sides of the equation.
$$
\displaystyle{\frac{\mathrm{d}}{\mathrm{d}x}}(xe^{y} )= {\frac{\mathrm{d}}{\mathrm{d}x}}(\cos(xy))
$$
***
Let's first consider the LHS: $\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}(xe^y) = \frac{\mathrm{d}}{\mathrm{d}x} e^y + x\frac{\mathrm{d}}{\mathrm{d}x}(e^y)$ using the product rule.
Then using the chain rule, let $f(y) = e^y$ and $\displaystyle\frac{\mathrm{d}}{\mathrm{d}x} f(y(x)) = \frac{\mathrm{d}f}{\mathrm{d}x} \cdot \frac{\mathrm{d}y}{\mathrm{d}x}$
Can you evaluate the LHS now?
***
$$
\begin{aligned}
e^y + xe^y\frac{\mathrm{d}y}{\mathrm{d}x}
\end{aligned}
$$
***
Now consider the RHS:
$$
\displaystyle {\mathrm{d}\over \mathrm{d}x}(\cos(xy))
$$
As you have a function $\cos$ of another function $xy$, use the chain rule. Use the substitution $u=xy$, so that you have
$$
\displaystyle {\mathrm{d}\over\mathrm{d}x}(\cos(u))
$$
***
Using the chain rule, let $f(u)=\cos(u)$ and $u=xy$, so that $\displaystyle \frac{\mathrm{d}f}{\mathrm{d}x} = \frac{\mathrm{d}f}{\mathrm{d}u} \cdot \frac{\mathrm{d}u}{\mathrm{d}x}$
***
Then, 
$$
\displaystyle \frac{\mathrm{d}}{\mathrm{d}x}(\cos(xy)) = -\sin(xy)\left(y + x\frac{\mathrm{d}y}{\mathrm{d}x}\right)
$$
Now rearrange,
***
$$
\begin{aligned}
e^y + xe^y\frac{\mathrm{d}y}{\mathrm{d}x} &= -\sin(xy)\left(y + x\frac{\mathrm{d}y}{\mathrm{d}x}\right)
\\ \frac{\mathrm{d}y}{\mathrm{d}x} &= -\frac{y\sin(xy) + e^y}{xe^y+x\sin(xy)}
\end{aligned}
$$
\nFirst, get this into a form easier to handle.
$$
x=\sec(y)
$$
***
Using implicit differentiation, take the derivative with respect to $x$ on both sides.
***
 $\displaystyle \frac{\mathrm{d}}{\mathrm{d}y} (\sec(y))=\sec(y)\tan(y)$. Can you differentiate both sides now?
***
$$
\displaystyle 1 = \sec(y)\tan(y)\frac{\mathrm{d}y}{\mathrm{d}x}
$$
Rearrange:
$$
\displaystyle \frac{\mathrm{d}y}{\mathrm{d}x} = \frac{1}{\sec(y)\tan(y)}
$$
Now, get this into a function of $x$. 
***
To get the RHS in terms only of $\sec(y)$, try using a trigonometric identity involving $\tan y$ and $\sec y$.
***
Use the identity $1+\tan^2(y) = \sec^2(y)$... Did you find the expression?
***
$$
\displaystyle \frac{\mathrm{d}y}{\mathrm{d}x} = \frac{1}{x \sqrt{x^2-1}}
$$
You might have written the answer as
$$
\displaystyle \frac{\mathrm{d}y}{\mathrm{d}x} = \frac{1}{|x| \sqrt{x^2-1}}
$$
Which answer is really the correct one? Hint: sketch $x(y)$ and consider the range of the function
| Find $\displaystyle {\mathrm{d}y\over \mathrm{d}x}$ for each of these relationships:
$$
y^3 = x^3 - xy
$$
\n$$
xe^{y} = \cos(xy)
$$
\n$$
y =\sec^{-1}(x)
$$
| 12 | 4 | 43 | 43 | 300 | 30 | 5 | 3 | 0 | Find $\displaystyle {\mathrm{d}y\over \mathrm{d}x}$ for each of these relationships: $ y^3 = x^3 - xy $ $ xe^{y} = \cos(xy) $ $ y =\sec^{-1}(x) $ | 1 |
256d9e06-c6aa-40e0-8b63-d39e54c73ffd | 3 | 1 | 0 | 4 | 3 | 3 | 2 | 3 | An explosion on a ship $5\ \mathrm{km}$ away from the coast releases a quantity $M$ of contaminant. The wind velocity is $U$ towards the shoreline. The contaminant diffuses at a rate of $D$. The release occurs at the water surface, which is modelled as a perfect reflector.
Here, the wind velocity is chosen along the $x$ axis; $z$ denotes the vertical direction.

| Give the equation for the three-dimensional time-evolution of contaminant concentration.
\nState the value of the maximum concentration $C_{\max}$ at time $t=10\ \mathrm{s}$. Repeat this calculation for every $10\ \mathrm{s}$ until $100\ \mathrm{s}$. From these values, sketch the maximum concentration and its location as a function of time. Take $M = 10\ \mathrm{kg}$, $U = 5\ \mathrm{m/s}$, $x = 5000\ \mathrm{m}$, and $D = 0.2\ \mathrm{m^2/s}$.
\nCalculate the maximum concentration $C_{\max}$ at $t=1000\ \mathrm{s}$, at the coastline directly in the path of the contaminant. Repeat this calculation for other time values. With these values, sketch the time evolution of concentration at the coastline directly in the path of contaminant.
\nDo you expect the profile of the concentration to be symmetric around the maximum concentration in all directions? Explain why.
| 4 | 0.666667 | 2 | \n\n\n | Diffusion occurs in the vertical $z$ direction, horizontal $x$ direction (towards the shoreline) and span-wise $y$ direction. Advection only occurs in the $x$ direction. Therefore, the equation governing the concentration distribution is given by
$$
\dfrac{\partial C}{\partial t} + U\dfrac{\partial C}{\partial x} = D \Bigg\lbrace{\dfrac{\partial^2 C}{\partial x^2} + \dfrac{\partial^2 C}{\partial y^2} + \dfrac{\partial^2 C}{\partial z^2} \Bigg\rbrace}.
$$
***
As the sea surface is modelled a perfect reflector, we require the concentration gradient at this location $(z = 0)$ to be zero so that there is no mass flux across it. In other words, there is no diffusion vertically downwards. To incorporate this into our solution, we introduce an image source of strength $M$ which is coincident with the actual source, i.e. at $z = 0$, such that the two sources diffuse at identical rates (if the distance to a reflector is $h$ from the actual source, an image source is placed at $2h$ from the actual source on the other side of the reflector, which is at $z=0$ in this case). This leads to a source strength at $z = 0$ of $2M$
$$
C(x,y,z,t)=C_{D}(X, y, z, t) = \dfrac{2M}{(2\pi)^{3/2} \sigma^3}e^{\dfrac{-(X^2 + y^2 + z^2)}{2\sigma^2}},
$$
where $X=x-Ut$ is a translated coordinate, moving with the fluid at velocity $U$, $\sigma=\sqrt{2Dt}$, and $C_{D}$ is a solution to the diffusion equation.
\nThe maximum concentration occurs at $(x = x_{\max} = Ut, y = 0, z = 0)$ and, hence, is given by
$$
C_{\max} = \dfrac{2M}{(2\pi)^{3/2} \sigma^3}.
$$
***
Taking $M = 10\ \mathrm{kg}$, $U = 5\ \mathrm{m/s}$, $x = 5000\ \mathrm{m}$, and $D = 0.2\ \mathrm{m^2/s}$, and the above above equation, the following table can be produced for $C_{\max}$.
| $t\ \mathrm{[s]}$ | $C_{\max} \mathrm{[kg/m^{3}]}$ |
| :---------------- | :----------------------------- |
| 10 | 0.159 |
| 20 | 0.056 |
| 30 | 0.031 |
| 40 | 0.020 |
| 50 | 0.014 |
| 60 | 0.011 |
| 70 | 0.009 |
| 80 | 0.007 |
| 90 | 0.006 |
| 100 | 0.005 |
The figures below show the plots of the maximum concentration $C_{\max}$ and the location $x_{\max} = Ut$ at which this occurs as a function of time.

*Maximum concentration *$C_{\max}\ \mathrm{[kg/m^3]}$* as a function of time $t$.*

*Location *$x_{\max}$* at which *$C_{\max}$* occurs a function of time $t$.*
\nWe examine the contaminant concentration at the coastline directly in line with the source, i.e. $x = 5000\ \mathrm{m}$, $y = z = 0$. Taking $M = 10\ \mathrm{kg}$, $U = 5\ \mathrm{m/s}$, $x = 5000\ \mathrm{m}$, and $D = 0.2\ \mathrm{m^2/s}$, the table below calculates $C$ from $C(x, y, z, t) = \dfrac{2M}{(2\pi)^{3/2} \sigma^3}e^{\dfrac{-((x - Ut)^2 + y^2 + z^2)}{2\sigma^2}}$ as a function of time $t$, where $C$ is in $\mathrm{mg/m^3}$.
***
| $t\ \mathrm{[s]}$ | $C\ \mathrm{[mg/m^3]}$ |
| :---------------- | :--------------------- |
| 990 | 0.007 |
| 995 | 0.073 |
| 1000 | 0.159 |
| 1005 | 0.073 |
| 1010 | 0.007 |
Thus, the figure below is an accurate plot of $C$ versus $t$ at $x=5000\ \mathrm{m}$.

*Concentration at the shoreline $(x = 5\ \mathrm{km})$ as a function of time $t$.*
\n | An explosion on a ship $5\ \mathrm{km}$ away from the coast releases a quantity $M$ of contaminant. The wind velocity is $U$ towards the shoreline. The contaminant diffuses at a rate of $D$. The release occurs at the water surface, which is modelled as a perfect reflector.
Here, the wind velocity is chosen along the $x$ axis; $z$ denotes the vertical direction.

Give the equation for the three-dimensional time-evolution of contaminant concentration.
\nState the value of the maximum concentration $C_{\max}$ at time $t=10\ \mathrm{s}$. Repeat this calculation for every $10\ \mathrm{s}$ until $100\ \mathrm{s}$. From these values, sketch the maximum concentration and its location as a function of time. Take $M = 10\ \mathrm{kg}$, $U = 5\ \mathrm{m/s}$, $x = 5000\ \mathrm{m}$, and $D = 0.2\ \mathrm{m^2/s}$.
\nCalculate the maximum concentration $C_{\max}$ at $t=1000\ \mathrm{s}$, at the coastline directly in the path of the contaminant. Repeat this calculation for other time values. With these values, sketch the time evolution of concentration at the coastline directly in the path of contaminant.
\nDo you expect the profile of the concentration to be symmetric around the maximum concentration in all directions? Explain why.
| 182 | 16 | 39 | 39 | 314 | 0 | 119 | 10 | 1 | Give the equation for the three-dimensional time-evolution of contaminant concentration. Repeat this calculation for every $10\ \mathrm{s}$ until $100\ \mathrm{s}$. From these values, sketch the maximum concentration and its location as a function of time. Take $M$0, $M$1, $M$2, and $M$3. Calculate the maximum concentration $C_{\max}$ at $M$5, at the coastline directly in the path of the contaminant. Repeat this calculation for other time values. With these values, sketch the time evolution of concentration at the coastline directly in the path of contaminant. Do you expect the profile of the concentration to be symmetric around the maximum concentration in all directions? Explain why. | 9 |
25a0a40c-6c6f-4ff3-8520-ec42cb4636f8 | 3 | 0 | 0 | 4 | 3 | 3 | 4 | 1 | Consider a river stream with the specific flow rate $q=Uh=1.60\ \mathrm{m^2/s}$, and a water depth of $h=2.0\ \mathrm{m}$. The sediment size at the river bed is described by $d_{50}=0.85\ \mathrm{mm}$.
| Compute the roughness scale, $z_0$.
\nCompute the coefficient of friction, $C_f$.
\nCompute the bed shear stress, $\tau_0$.
| 3 | 0.333333 | 2 | \n\n | The roughness scale is given by
$$
z_0 = \begin{cases}
\dfrac{\nu}{9u_*} \qquad & \text{for smooth turbulent flow, } \mathrm{Re_{k}} = \dfrac{u_* k_s}{\nu} < 10 \\
\dfrac{k_s}{30} \qquad &\text{for rough turbulent flow } \mathrm{Re_k} = \dfrac{u_* k_s}{\nu} >10
\end{cases}
$$
***
We start assuming rough turbulent flow and that
$$
z_0 = \dfrac{k_s}{30} = \dfrac{2.5 \cdot 0.85 \times 10^{-3} }{30} = 7.083 \cdot 10^{-5}\ \mathrm{m}
$$
***
The shear velocity is computed as
$$
u_* = \sqrt{\dfrac{\tau_0}{\rho}} = \sqrt{C_f}U,
$$
where U is the depth averaged velocity.
***
We can obtain $C_f$, assuming initially that the flow is rough turbulent as being
$$
C_f = \left[ \dfrac{1}{\kappa} \left( \ln \left( \dfrac{h}{z_0} \right) -1 \right) \right]^{-2}
= \left[ \dfrac{1}{0.41} \left( \ln \left( \dfrac{2}{7.083 \times 10^{-5}} \right) -1 \right) \right]^{-2}
= 0.001965,
$$
and the shear velocity as being
$$
u_* = \sqrt{C_f} U = \sqrt{C_f}\dfrac{q}{h} = \sqrt{0.001965} \dfrac{1.60\ \mathrm{m^2/s}}{2\ \mathrm{m}} = 0.03547\ \mathrm{m/s}.
$$
***
We can check now if the flow is rough or smooth turbulent with the roughness Reynolds number
$$
\mathrm{Re_k} = \dfrac{k_s u_*}{\nu} = \dfrac{2.5 \cdot 0.85 \cdot 10^{-3} \cdot 0.03547}{10^{-6}} = 75.36,
$$
which is much larger than 10 and the flow is indeed rough turbulent.
***
The roughness scale is then $z_0 = 7.083 \times 10^{−5}\ \mathrm{m}$.
\nThe coefficient of friction $C_f$ has already been computed as: $C_f = 1.965 \times 10^{-3}$.
(*from Part (a), as below*)
***
The roughness scale is given by
$$
z_0 = \begin{cases}
\dfrac{\nu}{9u_*} \qquad & \text{for smooth turbulent flow, } \mathrm{Re_{k}} = \dfrac{u_* k_s}{\nu} < 10 \\
\dfrac{k_s}{30} \qquad &\text{for rough turbulent flow } \mathrm{Re_k} = \dfrac{u_* k_s}{\nu} >10
\end{cases}
$$
***
We start assuming rough turbulent flow and so
$$
z_0 = \dfrac{k_s}{30} = \dfrac{2.5 \cdot 0.85 \times 10^{-3} }{30} = 7.083 \cdot 10^{-5}\ \mathrm{m}
$$
***
We can obtain $C_f$, assuming initially that the flow is rough turbulent, as being
$$
C_f = \left[ \dfrac{1}{\kappa} \left( \ln \left( \dfrac{h}{z_0} \right) -1 \right) \right]^{-2}
= \left[ \dfrac{1}{0.41} \left( \ln \left( \dfrac{2}{7.083 \times 10^{-5}} \right) -1 \right) \right]^{-2}
= 0.001965.
$$
\nThe bed shear stress is
$$
\tau_0 = \rho u_*^2 = 1000\ \mathrm{kg/m^3} \cdot (0.03547\ \mathrm{m/s})^2 = 1.258\ \mathrm{kg/ms^2}
$$
| Consider a river stream with the specific flow rate $q=Uh=1.60\ \mathrm{m^2/s}$, and a water depth of $h=2.0\ \mathrm{m}$. The sediment size at the river bed is described by $d_{50}=0.85\ \mathrm{mm}$.
Compute the roughness scale, $z_0$.
\nCompute the coefficient of friction, $C_f$.
\nCompute the bed shear stress, $\tau_0$.
| 50 | 6 | 13 | 13 | 190 | 0 | 20 | 3 | 0 | Consider a river stream with the specific flow rate $q=Uh=1.60\ \mathrm{m^2/s}$, and a water depth of $h=2.0\ \mathrm{m}$. The sediment size at the river bed is described by $d_{50}=0.85\ \mathrm{mm}$. Compute the roughness scale, $z_0$. Compute the coefficient of friction, $C_f$. Compute the bed shear stress, $\tau_0$. | 5 |
25c603f5-111c-4cca-b597-0999c8615452 | 3 | 0 | 0 | 10 | 4 | 2 | 8 | 3 | A steel is used in a steam turbine pipe which operates at $550^\circ\text{C}$. The creep rupture properties of the steel at this temperature are given by:
   
$$
t_r=1\times10^{22}~\sigma^{-6}
$$
   
Where $t_r$ is the rupture life in hours and $\sigma$ is the applied stress in $\text{MPa}$. The pipe maybe assumed thin and axial stresses neglected. Given that the pipe has an inner diameter of $300\text{ mm}$ and wall thickness $10\text{ mm}$.
| Assuming it operates continuously at a fixed pressure and temperature, calculate the maximum pressure that can be applied to the pipe for rupture to be avoided in 20 years.
\nThe pressure in the pipe can fluctuate, such that in a given week it can spend the following times at the following pressures at a constant temperate of $550^\circ\text{C}$.
   
$$
\footnotesize
\text{Table Q4.4: Pressure within a pipe and duration.}
$$
| $t$ (hours) | 100 | 30 | 38 |
| :----------------- | :-- | :- | :- |
| $P$ ($\text{MPa}$) | 50 | 45 | 48 |
   
Using the life fraction rule, calculate the creep damage fraction accumulated in a week. Therefore, assuming that the pressure fluctuations are the same each week, calculate the expected creep rupture time of the pipe.
| 2 | 0.666667 | 2 | \n | Starting from the equation provided in the question:
   
$$
t_r=1\times10^{22}\sigma^{-6}
$$
   
***
Converting 20 years into hours to find $t_r$, then solve to find $\sigma$.
   
$$
20\times365\times24=1\times10^{22}\times\sigma^{-6} \\
\sigma=620.5\text{ MPa}
$$
   
***
Then solve for the pressure in the pipe.
   
$$
\begin{align*}
\sigma&=\frac{PR_i}{t}\\
620.5\times10^6&=\frac{P(0.15)}{0.01}\\
~\\
P&=\boxed{41.37\text{ MPa}}
\end{align*}
$$
\nTo first calculate the creep damage fraction ($D_c$), the following equation is to be used:
   
$$
D_c=\sum_{
\begin{subarray}{l}
\sigma,t
\end{subarray}}
\frac{t(\sigma,T)}{t_r(\sigma,T)}
$$
   
***
The creep damage fraction depends on the stress the pipe experiences ($\sigma$) and not the pressure ($P$). First calculate the stress using the following equation for thin walled vessels.
   
$$
\sigma=\frac{PR_i}{t}
$$
   
$$
\footnotesize\text{Table Q4.4.1: Pressure within pipe, duration, and stress experienced by pipe.}
$$
| $t$ (hours) | 100 | 30 | 38 |
| :--------------------- | :-- | :-- | :-- |
| $P ~(\text{MPa})$ | 50 | 45 | 48 |
| $\sigma ~(\text{MPa})$ | 750 | 675 | 720 |
   
***
Using the values in table Q4.4.1 and using the equation for $t_r$ from the question.
   
$$
\begin{align*}
D_c&=\frac{100}{1\times10^{22}\times750^{-6}}+\frac{30}{1\times10^{22}\times675^{-6}}+\frac{38}{1\times10^{22}\times720^{-6}}\\
&=\boxed{2.59\times10^{-3}}
\end{align*}
$$
   
***
To then calculate the expected rupture time of the pipe, it should be known that rupture occurs at $D_c=1$.
   
***
Therefore, the following equation can be used:
   
$$
\begin{align*}
t_r&=\frac{1}{D_c}\\
&=\frac{1}{2.593\times10^{-3}}\\
&=385.7 \text{ weeks}\\
&=\boxed{7.4\text{ years}}
\end{align*}
$$
| A steel is used in a steam turbine pipe which operates at $550^\circ\text{C}$. The creep rupture properties of the steel at this temperature are given by:
   
$$
t_r=1\times10^{22}~\sigma^{-6}
$$
   
Where $t_r$ is the rupture life in hours and $\sigma$ is the applied stress in $\text{MPa}$. The pipe maybe assumed thin and axial stresses neglected. Given that the pipe has an inner diameter of $300\text{ mm}$ and wall thickness $10\text{ mm}$.
Assuming it operates continuously at a fixed pressure and temperature, calculate the maximum pressure that can be applied to the pipe for rupture to be avoided in 20 years.
\nThe pressure in the pipe can fluctuate, such that in a given week it can spend the following times at the following pressures at a constant temperate of $550^\circ\text{C}$.
   
$$
\footnotesize
\text{Table Q4.4: Pressure within a pipe and duration.}
$$
| $t$ (hours) | 100 | 30 | 38 |
| :----------------- | :-- | :- | :- |
| $P$ ($\text{MPa}$) | 50 | 45 | 48 |
   
Using the life fraction rule, calculate the creep damage fraction accumulated in a week. Therefore, assuming that the pressure fluctuations are the same each week, calculate the expected creep rupture time of the pipe.
| 202 | 12 | 18 | 18 | 202 | 0 | 129 | 5 | 0 | A steel is used in a steam turbine pipe which operates at $550^\circ\text{C}$. The creep rupture properties of the steel at this temperature are given by: $ t_r=1\times10^{22}~\sigma^{-6} $ Where $t_r$ is the rupture life in hours and $\sigma$ is the applied stress in $\text{MPa}$. The pipe maybe assumed thin and axial stresses neglected. Given that the pipe has an inner diameter of $300\text{ mm}$ and wall thickness $10\text{ mm}$. Assuming it operates continuously at a fixed pressure and temperature, calculate the maximum pressure that can be applied to the pipe for rupture to be avoided in 20 years. The pressure in the pipe can fluctuate, such that in a given week it can spend the following times at the following pressures at a constant temperate of $550^\circ\text{C}$. $ table Using the life fraction rule, calculate the creep damage fraction accumulated in a week. Therefore, assuming that the pressure fluctuations are the same each week, calculate the expected creep rupture time of the pipe. | 8 |
25cb003f-1f41-4d72-b4d6-39c351727767 | 2 | 0 | 0 | 8 | 4 | 2 | 6 | 6 | A bench top is supported by four tubular steel legs $0.9 \text{ m}$ long, with cross-section $25\text{ mm}$ outer diameter and $2\text{ mm}$ wall thickness. The legs are attached rigidly to the underside of the bench top, which is free-standing.
| At what load will the legs buckle, assuming that they are equally-loaded? Draw the buckling mode you expect.
\nIn order to make it more stable, the legs are attached rigidly to the floor. What buckling mode do you now expect, and what failure load?
| 2 | 0.666667 | 2 | \n | The expected buckling mode:
   
  
***
The Euler equivalent length is $2L$ as only one end is built-in. 
   
***
Therefore, the critical pressure for buckling per table leg is:
   
$$
\begin{align}
P_c=\frac{\pi^2EI}{(2L)^2}=\frac{\pi^2EI}{4L^2}
\end{align}
$$
   
***
The second moment of area for a circular cross section:
   
$$
\begin{align}
I&=\frac{\pi}{64}(d_\text{o}^4-d_\text{i}^4)\\
&=\frac{\pi}{64}(0.025^4-0.021^4) \nonumber\\
&=9.628\times10^{-9}\text{ m}^4 \nonumber
\end{align}
$$
   
***
Substituting values into equation $(1)$, where $E=207\text{ GPa}$ for steel:
   
$$
\begin{align*}
P_c=\frac{\pi^2(207\times10^9\times9.628\times10^{-9})}{4\times0.9^2}=6.07\text{ kN}
\end{align*}
$$
   
***
Therefore, the critical buckling pressure for all 4 table legs would be:
   
$$
4\times6.07=\boxed{24.28\text{ kN}}
$$
\nIf the legs are built into the floor, the expected buckling load would be as follows:
  
***
The Euler equivalent length for two built in ends is $L$ which is the distance between the two points of inflection.
   
***
Therefore, the critical buckling pressure per leg can be found using the equation below:\
   
$$
P_c=\frac{\pi^2EI}{L^2}
$$
   
***
The equation above is 4 times larger than the previous case $\left(P_c=\frac{\pi^2EI}{4L^2}\right)$.
   
***
Therefore, the bench will buckle at:
   
$$
4\times24.28=\boxed{97.12\text{ kN}}
$$
| A bench top is supported by four tubular steel legs $0.9 \text{ m}$ long, with cross-section $25\text{ mm}$ outer diameter and $2\text{ mm}$ wall thickness. The legs are attached rigidly to the underside of the bench top, which is free-standing.
At what load will the legs buckle, assuming that they are equally-loaded? Draw the buckling mode you expect.
\nIn order to make it more stable, the legs are attached rigidly to the floor. What buckling mode do you now expect, and what failure load?
| 80 | 3 | 11 | 11 | 175 | 0 | 44 | 0 | 0 | At what load will the legs buckle, assuming that they are equally-loaded? Draw the buckling mode you expect. What buckling mode do you now expect, and what failure load? | 3 |
26051694-deb0-4ec5-83a7-ef927c293740 | 1 | 0 | 0 | 24 | 6 | 1 | 2 | 5 | *\[Riley 11.3(c)]* $\vec{F}$ is a vector field $xy^2\mathbf{\hat{i}} + 2\mathbf{\hat{j}} + x\mathbf{\hat{k}}$ and $L$ is a path parameterised by $x=ct$, $y=c/t$, $z=d$ for the range $1\leq t \leq 2$. Evaluate $\int_{L}{\vec{F}\cdot d\vec{r}}$.
| *\[Riley 11.3(c)]* $\vec{F}$ is a vector field $xy^2\mathbf{\hat{i}} + 2\mathbf{\hat{j}} + x\mathbf{\hat{k}}$ and $L$ is a path parameterised by $x=ct$, $y=c/t$, $z=d$ for the range $1\leq t \leq 2$. Evaluate $\int_{L}{\vec{F}\cdot d\vec{r}}$.
| 1 | 0.333333 | 1 | $$
\int_L{\vec{F}\cdot d\vec{r}} = \int_L{F_x\,dx + F_y\,dy+\,F_z\,dz}
$$
***
Express the integral as a function of $t$...
***
... For this, you will also have to change the differentials, e.g., 
$$
dx = \frac{dx}{dt}dt
$$
***
Then, evaluate the integral over the limits $1\le t \le 2$. 
| $$
\int_L{\vec{F}\cdot d\vec{r}} = \int_L{F_x\,dx + F_y\,dy+\,F_z\,dz}
$$
Changing the differentials $dx$, $dy$, $dz$ to be a function of $t$: 
***
$$
\begin{aligned}
dx & = c\,dt\\
dy & = -\frac{c}{t^2}\,dt\\
dz & = 0
\end{aligned}
$$
Then, making $F_x$ and $F_y$ a function of $t$ ($F_z\,dz$ evaluates to zero), and inserting the limits $1\le t \le 2$:
***
$$
\int_L{\vec{F}\cdot d\vec{r}} = \int_{t=1}^{2}{(ct)\left(\frac{c^2}{t^2}\right)c\,dt - 2\left(\frac{c}{t^2}\right)dt} = \int_{t=1}^{2}{(c^4t^{-1}-2ct^{-2})dt}
$$
***
$$
\begin{aligned}
& = [c^4\ln{t} + 2c t^{-1}]_{1}^{2} = c^4\ln{2}-c
\end{aligned}
$$
| *\[Riley 11.3(c)]* $\vec{F}$ is a vector field $xy^2\mathbf{\hat{i}} + 2\mathbf{\hat{j}} + x\mathbf{\hat{k}}$ and $L$ is a path parameterised by $x=ct$, $y=c/t$, $z=d$ for the range $1\leq t \leq 2$. Evaluate $\int_{L}{\vec{F}\cdot d\vec{r}}$.
| 28 | 8 | 13 | 13 | 42 | 4 | 28 | 8 | 0 | Evaluate $\int_{L}{\vec{F}\cdot d\vec{r}}$. | 1 |
260779c5-4d24-4399-b48b-d5dc0fa34397 | 2 | 0 | 0 | 11 | 4 | 2 | 7 | 7 | A Diesel engine uses $15 ~\mathrm{kg/h}$ of the oil fuel specified in Table 8.4 of the lecture notes to produce a work output of $100 ~\mathrm{kW}$. 
| What are the efficiencies of the engine based on GCV and NCV respectively?
| 1 | 0.333333 | 1 | null | From the table in the notes:
 

***
The GCV $= 45600~\mathrm{kJ/kg}$
  
The NCV $= 42720~\mathrm{kJ/kg}$
***
Calculate $\frac{\dot{W}}{\dot{m}}$, making sure to convert the mass flow rate to $\mathrm{kg/s}$ :
  
$\frac{\dot{W}}{\dot{m}} = \frac{100}{(\frac{15}{3600})} = 24000~\mathrm{kJ/kg}$
***
Efficiency based on GCV:
  
$\frac{24000}{45600} = 52.6\%$
***
Efficiency based on NCV:
  
$\frac{24000}{42720} = 56.2\%$
| A Diesel engine uses $15 ~\mathrm{kg/h}$ of the oil fuel specified in Table 8.4 of the lecture notes to produce a work output of $100 ~\mathrm{kW}$. 
What are the efficiencies of the engine based on GCV and NCV respectively?
| 38 | 2 | 7 | 7 | 47 | 0 | 13 | 0 | 0 | A Diesel engine uses $15 ~\mathrm{kg/h}$ of the oil fuel specified in Table 8.4 of the lecture notes to produce a work output of $100 ~\mathrm{kW}$. What are the efficiencies of the engine based on GCV and NCV respectively? | 2 |