# Perplexity of fixed-length models
[[open-in-colab]]
パープレキシティ(PPL)は言語モデルの評価に最も一般的な指標の1つです。深入りする前に、この指標は特に古典的な言語モデル(時にはオートレグレッシブまたは因果言語モデルとも呼ばれる)に適用され、BERTなどのマスクされた言語モデルには適していないことに注意すべきです(モデルの概要を参照してください[モデルの概要](model_summary))。
パープレキシティは、シーケンスの指数平均負の対数尤度として定義されます。トークン化されたシーケンス \\(X = (x_0, x_1, \dots, x_t)\\) がある場合、\\(X\\) のパープレキシティは次のように表されます。
$$\text{PPL}(X) = \exp \left\{ {-\frac{1}{t}\sum_i^t \log p_\theta (x_i|x_{
しかし、通常、近似モデルを使用する場合、モデルが処理できるトークン数に制約があります。例えば、最大の[GPT-2](model_doc/gpt2)のバージョンは1024トークンの固定長を持っているため、1024よりも大きい \\(t\\) に対して \\(p_\theta(x_t|x_{
これは各セグメントのパープレキシティが1回のフォワードパスで計算できるため、計算が迅速ですが、通常、モデルはほとんどの予測ステップでコンテキストが少ないため、完全に因子分解されたパープレキシティの悪い近似となり、通常、より高い(悪い)PPLを返します。
代わりに、固定長モデルのPPLはスライディングウィンドウ戦略を用いて評価するべきです。これには、モデルが各予測ステップでより多くのコンテキストを持つように、コンテキストウィンドウを繰り返しスライドさせるという方法が含まれます。
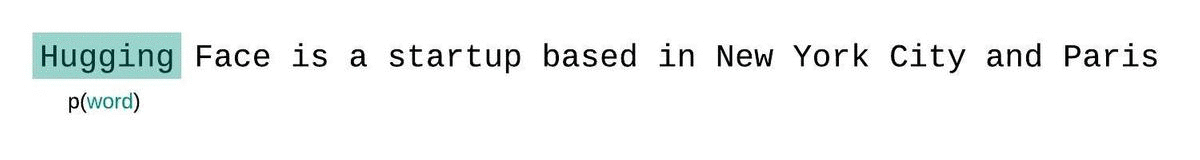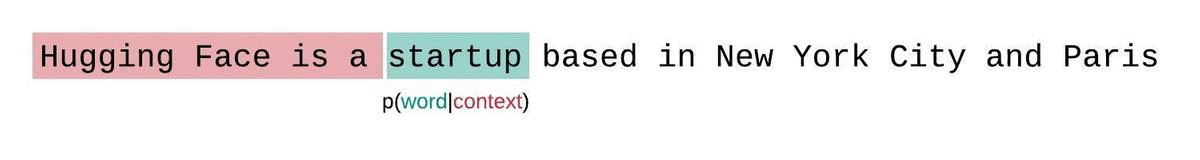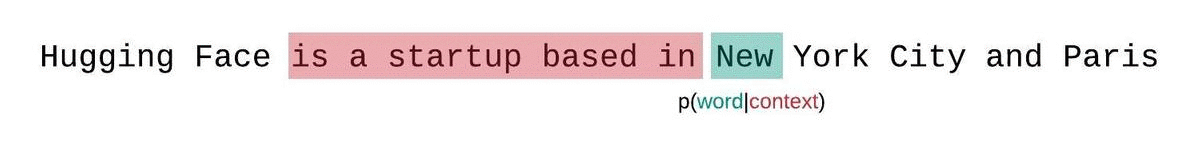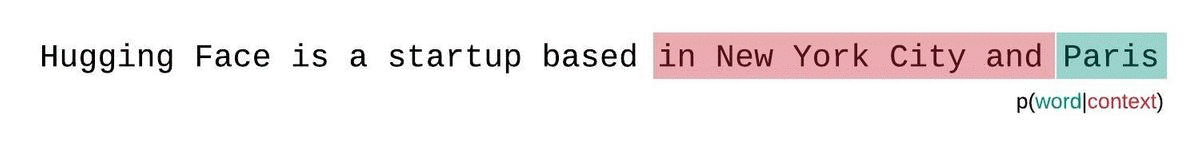 これはシーケンスの確率のより正確な分解に近いものであり、通常はより有利なスコアを生成します。欠点は、コーパス内の各トークンに対して別個の前方パスが必要です。実用的な妥協案は、1トークンずつスライドする代わりに、より大きなストライドでコンテキストを移動するストライド型のスライディングウィンドウを使用することです。これにより、計算がはるかに高速に進行できる一方で、モデルには各ステップで予測を行うための大きなコンテキストが提供されます。
## Example: Calculating perplexity with GPT-2 in 🤗 Transformers
GPT-2を使用してこのプロセスをデモンストレーションしてみましょう。
```python
from transformers import GPT2LMHeadModel, GPT2TokenizerFast
device = "cuda"
model_id = "openai-community/gpt2-large"
model = GPT2LMHeadModel.from_pretrained(model_id).to(device)
tokenizer = GPT2TokenizerFast.from_pretrained(model_id)
```
WikiText-2データセットを読み込み、異なるスライディングウィンドウ戦略を使用してパープレキシティを評価します。このデータセットは小規模で、セット全体に対して単一のフォワードパスを実行するだけなので、データセット全体をメモリに読み込んでエンコードするだけで十分です。
```python
from datasets import load_dataset
test = load_dataset("wikitext", "wikitext-2-raw-v1", split="test")
encodings = tokenizer("\n\n".join(test["text"]), return_tensors="pt")
```
🤗 Transformersを使用すると、単純に`input_ids`をモデルの`labels`として渡すことで、各トークンの平均負の対数尤度が損失として返されます。しかし、スライディングウィンドウのアプローチでは、各イテレーションでモデルに渡すトークンにオーバーラップがあります。私たちは、コンテキストとして扱っているトークンの対数尤度を損失に含めたくありません。そのため、これらの対象を `-100` に設定して無視されるようにします。以下は、ストライドを `512` とした場合の例です。これにより、モデルは任意のトークンの条件付けの尤度を計算する際に、少なくともコンテキストとして 512 トークンを持つことになります(512 個の前のトークンが利用可能である場合)。
```python
import torch
from tqdm import tqdm
max_length = model.config.n_positions
stride = 512
seq_len = encodings.input_ids.size(1)
nlls = []
prev_end_loc = 0
for begin_loc in tqdm(range(0, seq_len, stride)):
end_loc = min(begin_loc + max_length, seq_len)
trg_len = end_loc - prev_end_loc # may be different from stride on last loop
input_ids = encodings.input_ids[:, begin_loc:end_loc].to(device)
target_ids = input_ids.clone()
target_ids[:, :-trg_len] = -100
with torch.no_grad():
outputs = model(input_ids, labels=target_ids)
# loss is calculated using CrossEntropyLoss which averages over valid labels
# N.B. the model only calculates loss over trg_len - 1 labels, because it internally shifts the labels
# to the left by 1.
neg_log_likelihood = outputs.loss
nlls.append(neg_log_likelihood)
prev_end_loc = end_loc
if end_loc == seq_len:
break
ppl = torch.exp(torch.stack(nlls).mean())
```
ストライド長が最大入力長と同じ場合、上述の最適でないスライディングウィンドウ戦略と同等です。ストライドが小さいほど、モデルは各予測を行う際により多くのコンテキストを持つため、通常、報告される困難度(perplexity)が向上します。
上記のコードを `stride = 1024` で実行すると、オーバーラップがない状態で、結果の困難度(perplexity)は `19.44` になります。これは GPT-2 の論文に報告された `19.93` とほぼ同等です。一方、`stride = 512` を使用し、このようにストライディングウィンドウ戦略を採用すると、困難度(perplexity)が `16.45` に向上します。これはより好意的なスコアだけでなく、シーケンスの尤度の真の自己回帰分解により近い方法で計算されています。
これはシーケンスの確率のより正確な分解に近いものであり、通常はより有利なスコアを生成します。欠点は、コーパス内の各トークンに対して別個の前方パスが必要です。実用的な妥協案は、1トークンずつスライドする代わりに、より大きなストライドでコンテキストを移動するストライド型のスライディングウィンドウを使用することです。これにより、計算がはるかに高速に進行できる一方で、モデルには各ステップで予測を行うための大きなコンテキストが提供されます。
## Example: Calculating perplexity with GPT-2 in 🤗 Transformers
GPT-2を使用してこのプロセスをデモンストレーションしてみましょう。
```python
from transformers import GPT2LMHeadModel, GPT2TokenizerFast
device = "cuda"
model_id = "openai-community/gpt2-large"
model = GPT2LMHeadModel.from_pretrained(model_id).to(device)
tokenizer = GPT2TokenizerFast.from_pretrained(model_id)
```
WikiText-2データセットを読み込み、異なるスライディングウィンドウ戦略を使用してパープレキシティを評価します。このデータセットは小規模で、セット全体に対して単一のフォワードパスを実行するだけなので、データセット全体をメモリに読み込んでエンコードするだけで十分です。
```python
from datasets import load_dataset
test = load_dataset("wikitext", "wikitext-2-raw-v1", split="test")
encodings = tokenizer("\n\n".join(test["text"]), return_tensors="pt")
```
🤗 Transformersを使用すると、単純に`input_ids`をモデルの`labels`として渡すことで、各トークンの平均負の対数尤度が損失として返されます。しかし、スライディングウィンドウのアプローチでは、各イテレーションでモデルに渡すトークンにオーバーラップがあります。私たちは、コンテキストとして扱っているトークンの対数尤度を損失に含めたくありません。そのため、これらの対象を `-100` に設定して無視されるようにします。以下は、ストライドを `512` とした場合の例です。これにより、モデルは任意のトークンの条件付けの尤度を計算する際に、少なくともコンテキストとして 512 トークンを持つことになります(512 個の前のトークンが利用可能である場合)。
```python
import torch
from tqdm import tqdm
max_length = model.config.n_positions
stride = 512
seq_len = encodings.input_ids.size(1)
nlls = []
prev_end_loc = 0
for begin_loc in tqdm(range(0, seq_len, stride)):
end_loc = min(begin_loc + max_length, seq_len)
trg_len = end_loc - prev_end_loc # may be different from stride on last loop
input_ids = encodings.input_ids[:, begin_loc:end_loc].to(device)
target_ids = input_ids.clone()
target_ids[:, :-trg_len] = -100
with torch.no_grad():
outputs = model(input_ids, labels=target_ids)
# loss is calculated using CrossEntropyLoss which averages over valid labels
# N.B. the model only calculates loss over trg_len - 1 labels, because it internally shifts the labels
# to the left by 1.
neg_log_likelihood = outputs.loss
nlls.append(neg_log_likelihood)
prev_end_loc = end_loc
if end_loc == seq_len:
break
ppl = torch.exp(torch.stack(nlls).mean())
```
ストライド長が最大入力長と同じ場合、上述の最適でないスライディングウィンドウ戦略と同等です。ストライドが小さいほど、モデルは各予測を行う際により多くのコンテキストを持つため、通常、報告される困難度(perplexity)が向上します。
上記のコードを `stride = 1024` で実行すると、オーバーラップがない状態で、結果の困難度(perplexity)は `19.44` になります。これは GPT-2 の論文に報告された `19.93` とほぼ同等です。一方、`stride = 512` を使用し、このようにストライディングウィンドウ戦略を採用すると、困難度(perplexity)が `16.45` に向上します。これはより好意的なスコアだけでなく、シーケンスの尤度の真の自己回帰分解により近い方法で計算されています。
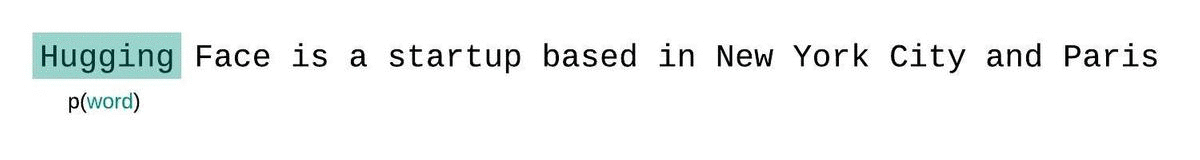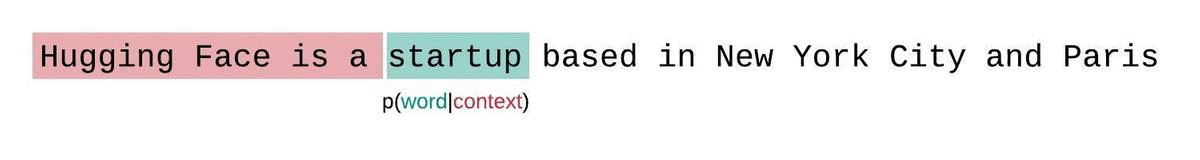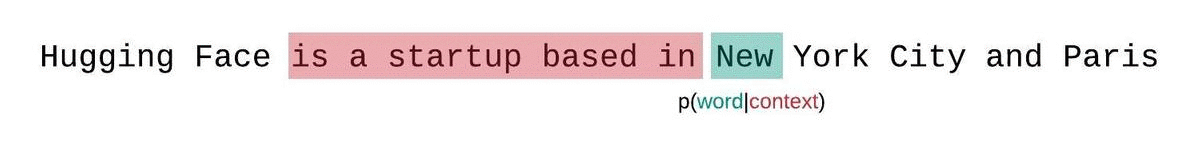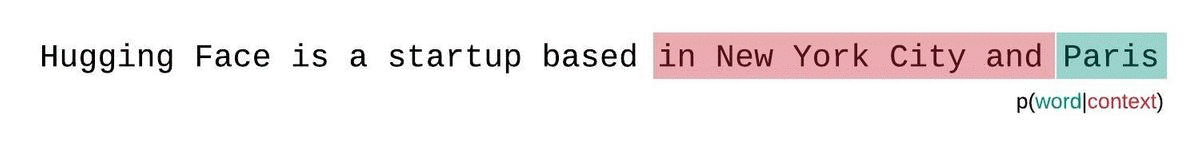 これはシーケンスの確率のより正確な分解に近いものであり、通常はより有利なスコアを生成します。欠点は、コーパス内の各トークンに対して別個の前方パスが必要です。実用的な妥協案は、1トークンずつスライドする代わりに、より大きなストライドでコンテキストを移動するストライド型のスライディングウィンドウを使用することです。これにより、計算がはるかに高速に進行できる一方で、モデルには各ステップで予測を行うための大きなコンテキストが提供されます。
## Example: Calculating perplexity with GPT-2 in 🤗 Transformers
GPT-2を使用してこのプロセスをデモンストレーションしてみましょう。
```python
from transformers import GPT2LMHeadModel, GPT2TokenizerFast
device = "cuda"
model_id = "openai-community/gpt2-large"
model = GPT2LMHeadModel.from_pretrained(model_id).to(device)
tokenizer = GPT2TokenizerFast.from_pretrained(model_id)
```
WikiText-2データセットを読み込み、異なるスライディングウィンドウ戦略を使用してパープレキシティを評価します。このデータセットは小規模で、セット全体に対して単一のフォワードパスを実行するだけなので、データセット全体をメモリに読み込んでエンコードするだけで十分です。
```python
from datasets import load_dataset
test = load_dataset("wikitext", "wikitext-2-raw-v1", split="test")
encodings = tokenizer("\n\n".join(test["text"]), return_tensors="pt")
```
🤗 Transformersを使用すると、単純に`input_ids`をモデルの`labels`として渡すことで、各トークンの平均負の対数尤度が損失として返されます。しかし、スライディングウィンドウのアプローチでは、各イテレーションでモデルに渡すトークンにオーバーラップがあります。私たちは、コンテキストとして扱っているトークンの対数尤度を損失に含めたくありません。そのため、これらの対象を `-100` に設定して無視されるようにします。以下は、ストライドを `512` とした場合の例です。これにより、モデルは任意のトークンの条件付けの尤度を計算する際に、少なくともコンテキストとして 512 トークンを持つことになります(512 個の前のトークンが利用可能である場合)。
```python
import torch
from tqdm import tqdm
max_length = model.config.n_positions
stride = 512
seq_len = encodings.input_ids.size(1)
nlls = []
prev_end_loc = 0
for begin_loc in tqdm(range(0, seq_len, stride)):
end_loc = min(begin_loc + max_length, seq_len)
trg_len = end_loc - prev_end_loc # may be different from stride on last loop
input_ids = encodings.input_ids[:, begin_loc:end_loc].to(device)
target_ids = input_ids.clone()
target_ids[:, :-trg_len] = -100
with torch.no_grad():
outputs = model(input_ids, labels=target_ids)
# loss is calculated using CrossEntropyLoss which averages over valid labels
# N.B. the model only calculates loss over trg_len - 1 labels, because it internally shifts the labels
# to the left by 1.
neg_log_likelihood = outputs.loss
nlls.append(neg_log_likelihood)
prev_end_loc = end_loc
if end_loc == seq_len:
break
ppl = torch.exp(torch.stack(nlls).mean())
```
ストライド長が最大入力長と同じ場合、上述の最適でないスライディングウィンドウ戦略と同等です。ストライドが小さいほど、モデルは各予測を行う際により多くのコンテキストを持つため、通常、報告される困難度(perplexity)が向上します。
上記のコードを `stride = 1024` で実行すると、オーバーラップがない状態で、結果の困難度(perplexity)は `19.44` になります。これは GPT-2 の論文に報告された `19.93` とほぼ同等です。一方、`stride = 512` を使用し、このようにストライディングウィンドウ戦略を採用すると、困難度(perplexity)が `16.45` に向上します。これはより好意的なスコアだけでなく、シーケンスの尤度の真の自己回帰分解により近い方法で計算されています。
これはシーケンスの確率のより正確な分解に近いものであり、通常はより有利なスコアを生成します。欠点は、コーパス内の各トークンに対して別個の前方パスが必要です。実用的な妥協案は、1トークンずつスライドする代わりに、より大きなストライドでコンテキストを移動するストライド型のスライディングウィンドウを使用することです。これにより、計算がはるかに高速に進行できる一方で、モデルには各ステップで予測を行うための大きなコンテキストが提供されます。
## Example: Calculating perplexity with GPT-2 in 🤗 Transformers
GPT-2を使用してこのプロセスをデモンストレーションしてみましょう。
```python
from transformers import GPT2LMHeadModel, GPT2TokenizerFast
device = "cuda"
model_id = "openai-community/gpt2-large"
model = GPT2LMHeadModel.from_pretrained(model_id).to(device)
tokenizer = GPT2TokenizerFast.from_pretrained(model_id)
```
WikiText-2データセットを読み込み、異なるスライディングウィンドウ戦略を使用してパープレキシティを評価します。このデータセットは小規模で、セット全体に対して単一のフォワードパスを実行するだけなので、データセット全体をメモリに読み込んでエンコードするだけで十分です。
```python
from datasets import load_dataset
test = load_dataset("wikitext", "wikitext-2-raw-v1", split="test")
encodings = tokenizer("\n\n".join(test["text"]), return_tensors="pt")
```
🤗 Transformersを使用すると、単純に`input_ids`をモデルの`labels`として渡すことで、各トークンの平均負の対数尤度が損失として返されます。しかし、スライディングウィンドウのアプローチでは、各イテレーションでモデルに渡すトークンにオーバーラップがあります。私たちは、コンテキストとして扱っているトークンの対数尤度を損失に含めたくありません。そのため、これらの対象を `-100` に設定して無視されるようにします。以下は、ストライドを `512` とした場合の例です。これにより、モデルは任意のトークンの条件付けの尤度を計算する際に、少なくともコンテキストとして 512 トークンを持つことになります(512 個の前のトークンが利用可能である場合)。
```python
import torch
from tqdm import tqdm
max_length = model.config.n_positions
stride = 512
seq_len = encodings.input_ids.size(1)
nlls = []
prev_end_loc = 0
for begin_loc in tqdm(range(0, seq_len, stride)):
end_loc = min(begin_loc + max_length, seq_len)
trg_len = end_loc - prev_end_loc # may be different from stride on last loop
input_ids = encodings.input_ids[:, begin_loc:end_loc].to(device)
target_ids = input_ids.clone()
target_ids[:, :-trg_len] = -100
with torch.no_grad():
outputs = model(input_ids, labels=target_ids)
# loss is calculated using CrossEntropyLoss which averages over valid labels
# N.B. the model only calculates loss over trg_len - 1 labels, because it internally shifts the labels
# to the left by 1.
neg_log_likelihood = outputs.loss
nlls.append(neg_log_likelihood)
prev_end_loc = end_loc
if end_loc == seq_len:
break
ppl = torch.exp(torch.stack(nlls).mean())
```
ストライド長が最大入力長と同じ場合、上述の最適でないスライディングウィンドウ戦略と同等です。ストライドが小さいほど、モデルは各予測を行う際により多くのコンテキストを持つため、通常、報告される困難度(perplexity)が向上します。
上記のコードを `stride = 1024` で実行すると、オーバーラップがない状態で、結果の困難度(perplexity)は `19.44` になります。これは GPT-2 の論文に報告された `19.93` とほぼ同等です。一方、`stride = 512` を使用し、このようにストライディングウィンドウ戦略を採用すると、困難度(perplexity)が `16.45` に向上します。これはより好意的なスコアだけでなく、シーケンスの尤度の真の自己回帰分解により近い方法で計算されています。