

Nvdiffrast is a PyTorch/TensorFlow library that provides high-performance primitive operations for rasterization-based differentiable rendering. It is a lower-level library compared to previous ones such as redner, SoftRas, or PyTorch3D — nvdiffrast has no built-in camera models, lighting/material models, etc. Instead, the provided operations encapsulate only the most graphics-centric steps in the modern hardware graphics pipeline: rasterization, interpolation, texturing, and antialiasing. All of these operations (and their gradients) are GPU-accelerated, either via CUDA or via the hardware graphics pipeline.
This documentation is intended to serve as a user's guide to nvdiffrast. For detailed discussion on the design principles, implementation details, and benchmarks, please see our paper:Modular Primitives for High-Performance Differentiable Rendering
Samuli Laine, Janne Hellsten, Tero Karras, Yeongho Seol, Jaakko Lehtinen, Timo Aila
ACM Transactions on Graphics 39(6) (proc. SIGGRAPH Asia 2020)
Paper: http://arxiv.org/abs/2011.03277
GitHub: https://github.com/NVlabs/nvdiffrast





Requirements:
To download nvdiffrast, either download the repository at https://github.com/NVlabs/nvdiffrast as a .zip file, or clone the repository using git:
We recommend running nvdiffrast on Docker. To build a Docker image with nvdiffrast and PyTorch 1.6 installed, run:
To try out some of the provided code examples, run:
Alternatively, if you have all the dependencies taken care of (consult the included Dockerfile for reference), you can install nvdiffrast in your local Python site-packages by running
at the root of the repository. You can also just add the repository root directory to your PYTHONPATH.
On Windows, nvdiffrast requires an external compiler for compiling the CUDA kernels. The development was done using Microsoft Visual Studio 2017 Professional Edition, and this version works with both PyTorch and TensorFlow versions of nvdiffrast. VS 2019 Professional Edition has also been confirmed to work with the PyTorch version of nvdiffrast. Other VS editions besides Professional Edition, including the Community Edition, should work but have not been tested.
If the compiler binary (cl.exe) cannot be found in PATH, nvdiffrast will search for it heuristically. If this fails you may need to add it manually via
"C:\Program Files (x86)\Microsoft Visual Studio\...\...\VC\Auxiliary\Build\vcvars64.bat"where the exact path depends on the version and edition of VS you have installed.
To install nvdiffrast in your local site-packages, run:
# Ninja is required run-time to build PyTorch extensions
pip install ninja
# Run at the root of the repository to install nvdiffrast
pip install .Instead of pip install . you can also just add the repository root directory to your PYTHONPATH.
Nvdiffrast offers four differentiable rendering primitives: rasterization, interpolation, texturing, and antialiasing. The operation of the primitives is described here in a platform-agnostic way. Platform-specific documentation can be found in the API reference section.
In this section we ignore the minibatch axis for clarity and assume a minibatch size of one. However, all operations support minibatches as detailed later.
The rasterization operation takes as inputs a tensor of vertex positions and a tensor of vertex index triplets that specify the triangles. Vertex positions are specified in NDC (Normalized Device Coordinate) space, i.e., after modelview and projection transformations. Performing these transformations is left as the user's responsibility. In NDC, the view frustum is a cube in homogeneous coordinates where x/w, y/w, z/w are all between -1 and +1.
The output of the rasterization operation is a 4-channel float32 image with tuple (u, v, z/w, triangle_id) in each pixel. Values u and v are the barycentric coordinates within a triangle: the first vertex in the vertex index triplet obtains (u, v) = (1, 0), the second vertex (u, v) = (0, 1) and the third vertex (u, v) = (0, 0). NDC-space depth value z/w is used later by the antialiasing operation to infer occlusion relations between triangles, and it does not propagate gradients to the vertex position input. Field triangle_id is the triangle index, offset by one. Pixels where no triangle was rasterized will receive a zero in all channels.
Rasterization is point-sampled, i.e., the geometry is not smoothed, blurred, or made partially transparent in any way, in contrast to some previous differentiable rasterizers. The contents of a pixel always represent a single surface point that is on the closest surface visible along the ray through the pixel center.
Point-sampled coverage does not produce vertex position gradients related to occlusion and visibility effects. This is because the motion of vertices does not change the coverage in a continuous way — a triangle is either rasterized into a pixel or not. In nvdiffrast, the occlusion/visibility related gradients are generated in the antialiasing operation that typically occurs towards the end of the rendering pipeline.

[..., 0:2] = barycentrics (u, v)

[..., 3] = triangle_id
The images above illustrate the output of the rasterizer. The left image shows the contents of channels 0 and 1, i.e., the barycentric coordinates, rendered as red and green, respectively. The right image shows channel 3, i.e., the triangle ID, using a random color per triangle. Spot model was created and released into public domain by Keenan Crane.
Depending on the shading and lighting models, a mesh typically specifies a number of attributes at its vertices. These can include, e.g., texture coordinates, vertex normals, reflection vectors, and material parameters. The purpose of the interpolation operation is to transfer these attributes specified at vertices to image space. In the hardware graphics pipeline, this happens automatically between vertex and pixel shaders. The interpolation operation in nvdiffrast supports an arbitrary number of attributes.
Concretely, the interpolation operation takes as inputs the buffer produced by the rasterizer and a buffer specifying the vertex attributes. The output is an image-size buffer with as many channels as there are attributes. Pixels where no triangle was rendered will contain all zeros in the output.

Above is an example of interpolated texture coordinates visualized in red and green channels. This image was created using the output of the rasterizer from the previous step, and an attribute buffer containing the texture coordinates.
Texture sampling is a fundamental operation in hardware graphics pipelines, and the same is true in nvdiffrast. The basic principle is simple: given a per-pixel texture coordinate vector, fetch a value from a texture and place it in the output. In nvdiffrast, the textures may have an arbitrary number of channels, which is useful in case you want to learn, say, an abstract field that acts as an input to a neural network further down the pipeline.
When sampling a texture, it is typically desirable to use some form of filtering. Most previous differentiable rasterizers support at most bilinear filtering, where sampling at a texture coordinate between texel centers will interpolate the value linearly from the four nearest texels. While this works fine when viewing the texture up close, it yields badly aliased results when the texture is viewed from a distance. To avoid this, the texture needs to be prefiltered prior to sampling it, removing the frequencies that are too high compared to how densely it is being sampled.
Nvdiffrast supports prefiltered texture sampling based on mipmapping. The required mipmap levels can be generated internally in the texturing operation, so that the user only needs to specify the highest-resolution (base level) texture. Currently the highest-quality filtering mode is isotropic trilinear filtering. The lack of anisotropic filtering means that a texture viewed at a steep angle will not alias in any direction, but it may appear blurry across the non-squished
direction.
In addition to standard 2D textures, the texture sampling operation also supports cube maps. Cube maps are addressed using 3D texture coordinates, and the transitions between cube map faces are properly filtered so there will be no visible seams. Cube maps support trilinear filtering similar to 2D textures. There is no explicit support for 1D textures but they can be simulated efficiently with 1×n textures. All the filtering, mipmapping etc. work with such textures just as they would with true 1D textures. For now there is no support for 3D volume textures.



The middle image above shows the result of texture sampling using the interpolated texture coordinates from the previous step. Why is the background pink? The texture coordinates (s, t) read as zero at those pixels, but that is a perfectly valid point to sample the texture. It happens that Spot's texture (left) has pink color at its (0, 0) corner, and therefore all pixels in the background obtain that color as a result of the texture sampling operation. On the right, we have replaced the color of the empty
pixels with a white color. Here's one way to do this in PyTorch:
where rast_out is the output of the rasterization operation. We simply test if the triangle_id field, i.e., channel 3 of the rasterizer output, is greater than zero, indicating that a triangle was rendered in that pixel. If so, we take the color from the textured image, and otherwise we take constant 1.0.
The last of the four primitive operations in nvdiffrast is antialiasing. Based on the geometry input (vertex positions and triangles), it will smooth out discontinuties at silhouette edges in a given image. The smoothing is based on a local approximation of coverage — an approximate integral over a pixel is calculated based on the exact location of relevant edges and the point-sampled colors at pixel centers.
In this context, a silhouette is any edge that connects to just one triangle, or connects two triangles so that one folds behind the other. Specifically, this includes both silhouettes against the background and silhouettes against another surface, unlike some previous methods (DIB-R) that only support the former kind.
It is worth discussing why we might want to go through this trouble to improve the image a tiny bit. If we're attempting to, say, match a real-world photograph, a slightly smoother edge probably won't match the captured image much better than a jagged one. However, that is not the point of the antialiasing operation — the real goal is to obtain gradients w.r.t. vertex positions related to occlusion, visibility, and coverage.
Remember that everything up to this point in the rendering pipeline is point-sampled. In particular, the coverage, i.e., which triangle is rasterized to which pixel, changes discontinuously in the rasterization operation.
This is the reason why previous differentiable rasterizers apply nonstandard image synthesis model with blur and transparency: Something has to make coverage continuous w.r.t. vertex positions if we wish to optimize vertex positions, camera position, etc., based on an image-space loss. In nvdiffrast, we do everything point-sampled so that we know that every pixel corresponds to a single, well-defined surface point. This lets us perform arbitrary shading computations without worrying about things like accidentally blurring texture coordinates across silhouettes, or having attributes mysteriously tend towards background color when getting close to the edge of the object. Only towards the end of the pipeline, the antialiasing operation ensures that the motion of vertex positions results in continuous change on silhouettes.
The antialiasing operation supports any number of channels in the image to be antialiased. Thus, if your rendering pipeline produces an abstract representation that is fed to a neural network for further processing, that is not a problem.



The left image above shows the result image from the last step, after performing antialiasing. The effect is quite small — some boundary pixels become less jagged, as shown in the closeups.
Notably, not all boundary pixels are antialiased as revealed by the left-side image below. This is because the accuracy of the antialiasing operation in nvdiffrast depends on the rendered size of triangles: Because we store knowledge of just one surface point per pixel, antialiasing is possible only when the triangle that contains the actual geometric silhouette edge is visible in the image. The example image is rendered in very low resolution and the triangles are tiny compared to pixels. Thus, triangles get easily lost between the pixels.
This results in incomplete-looking antialiasing, and the gradients provided by antialiasing become noisier when edge triangles are missed. Therefore it is advisable to render images in resolutions where the triangles are large enough to show up in the image at least most of the time.


The left image above shows which pixels were modified by the antialiasing operation in this example. On the right, we performed the rendering in 4×4 higher resolution and downsampled the final images back to the original size. This yields more accurate position gradients related to the silhouettes, so if you suspect your position gradients are too noisy, you may want to try simply increasing the resolution in which rasterization and antialiasing is done.
For purposes of shape optimization, the sparse-looking situation on the left would probably be perfectly fine. The gradients are still going to point in the right direction even if they are somewhat sparse, and you will need to use some sort of shape regularization anyway, which will greatly increase tolerance to noisy shape gradients.
Rendering images is easy with nvdiffrast, but there are a few practical things that you will need to take into account. The topics in this section explain the operation and usage of nvdiffrast in more detail, and hopefully help you avoid any potential misunderstandings and pitfalls.
Nvdiffrast follows OpenGL's coordinate systems and other conventions. This is partially because we use OpenGL to accelerate the rasterization operation, but mostly so that there is a single standard to follow.
As a word of advice, it is best to stay on top of coordinate systems and orientations used in your program. When something appears to be the wrong way around, it is much better to identify and fix the root cause than to randomly flip coordinates, images, buffers, and matrices until the immediate problem goes away.
As mentioned earlier, all operations in nvdiffrast support the minibatch axis efficiently. Related to this, we support two ways for representing the geometry: range mode and instanced mode. If you want to render a different mesh in each minibatch index, you need to use the range mode. However, if you are rendering the same mesh, but with potentially different viewpoints, vertex positions, attributes, textures, etc., in each minibatch index, the instanced mode will be much more convenient.
In range mode, you specify triangle index triplets as a 2D tensor of shape [num_triangles, 3], and vertex positions as a 2D tensor of shape [num_vertices, 4]. In addition to these, the rasterization operation requires an additional 2D range tensor of shape [minibatch_size, 2] where each row specifies a start index and count into the triangle tensor. As a result, the rasterizer will render the triangles in the specified ranges into each minibatch index of the output tensor. If you have multiple meshes, you should place all of them into the vertex and triangle tensors, and then choose which mesh to rasterize into each minibatch index via the contents of the range tensor. The attribute tensor in interpolation operation is handled in the same way as positions, and it has to be of shape [num_vertices, num_attributes] in range mode.
In instanced mode, the topology of the mesh will be shared for each minibatch index. The triangle tensor is still a 2D tensor with shape [num_triangles, 3], but the vertex positions are specified using a 3D tensor of shape [minibatch_size, num_vertices, 4]. With a 3D vertex position tensor, the rasterizer will not require the range tensor input, but will take the minibatch size from the first dimension of the vertex position tensor. The same triangles are rendered to each minibatch index, but with vertex positions taken from the corresponding slice of the vertex position tensor. In this mode, the attribute tensor in interpolation has to be a 3D tensor similar to position tensor, i.e., of shape [minibatch_size, num_vertices, num_attributes]. However, you can provide an attribute tensor with minibatch size of 1, and it will be broadcast across the minibatch.
We skirted around a pretty fundamental question in the description of the texturing operation above. In order to determine the proper amount of prefiltering for sampling a texture, we need to know how densely it is being sampled. But how can we know the sampling density when each pixel knows of a just a single surface point?
The solution is to track the image-space derivatives of all things leading up to the texture sampling operation. These are not the same thing as the gradients used in the backward pass, even though they both involve differentiation! Consider the barycentrics (u, v) produced by the rasterization operation. They change by some amount when moving horizontally or vertically in the image plane. If we denote the image-space coordinates as (X, Y), the image-space derivatives of the barycentrics would be ∂u/∂X, ∂u/∂Y, ∂v/∂X, and ∂v/∂Y. We can organize these into a 2×2 Jacobian matrix that describes the local relationship between (u, v) and (X, Y). This matrix is generally different at every pixel. For the purpose of image-space derivatives, the units of X and Y are pixels. Hence, ∂u/∂X is the local approximation of how much u changes when moving a distance of one pixel in the horizontal direction, and so on.
Once we know how the barycentrics change w.r.t. pixel position, the interpolation operation can use this to determine how the attributes change w.r.t. pixel position. When attributes are used as texture coordinates, we can therefore tell how the texture sampling position (in texture space) changes when moving around within the pixel (up to a local, linear approximation, that is). This texture footprint tells us the scale on which the texture should be prefiltered. In more practical terms, it tells us which mipmap level(s) to use when sampling the texture.
In nvdiffrast, the rasterization operation can be configured to output the image-space derivatives of the barycentrics in an auxiliary 4-channel output tensor, ordered (∂u/∂X, ∂u/∂Y, ∂v/∂X, ∂v/∂Y) from channel 0 to 3. The interpolation operation can take this auxiliary tensor as input and compute image-space derivatives of any set of attributes being interpolated. Finally, the texture sampling operation can use the image-space derivatives of the texture coordinates to determine the amount of prefiltering.
There is nothing magic about these image-space derivatives. They are tensors like the, e.g., the texture coordinates themselves, they propagate gradients backwards, and so on. For example, if you want to artificially blur or sharpen the texture when sampling it, you can simply multiply the tensor carrying the image-space derivatives of the texture coordinates ∂{s, t}/∂{X, Y} by a scalar value before feeding it into the texture sampling operation. This scales the texture footprints and thus adjusts the amount of prefiltering. If your loss function prefers a different level of sharpness, this multiplier will receive a nonzero gradient. Update: Since version 0.2.1, the texture sampling operation also supports a separate mip level bias input that would be better suited for this particular task, but the gist is the same nonetheless.
One might wonder if it would have been easier to determine the texture footprints simply from the texture coordinates in adjacent pixels, and skip all this derivative rubbish? In easy cases the answer is yes, but silhouettes, occlusions, and discontinuous texture parameterizations would make this approach rather unreliable in practice. Computing the image-space derivatives analytically keeps everything point-like, local, and well-behaved.
It should be noted that computing gradients related to image-space derivatives is somewhat involved and requires additional computation. At the same time, they are often not crucial for the convergence of the training/optimization. Because of this, the primitive operations in nvdiffrast offer options to disable the calculation of these gradients. We're talking about things like ∂Loss/∂(∂{u, v}/∂{X, Y}) that may look second-order-ish, but they're not.
Prefiltered texture sampling modes require mipmaps, i.e., downsampled versions, of the texture. The texture sampling operation can construct these internally, or you can provide your own mipmap stack, but there are limits to texture dimensions that need to be considered.
When mipmaps are constructed internally, each mipmap level is constructed by averaging 2×2 pixel patches of the preceding level (or of the texture itself for the first mipmap level). The size of the buffer to be averaged therefore has to be divisible by 2 in both directions. There is one exception: side length of 1 is valid, and it will remain as 1 in the downsampling operation.
For example, a 32×32 texture will produce the following mipmap stack:
| 32×32 | → | 16×16 | → | 8×8 | → | 4×4 | → | 2×2 | → | 1×1 |
| Base texture | Mip level 1 | Mip level 2 | Mip level 3 | Mip level 4 | Mip level 5 |
And a 32×8 texture, with both sides powers of two but not equal, will result in:
| 32×8 | → | 16×4 | → | 8×2 | → | 4×1 | → | 2×1 | → | 1×1 |
| Base texture | Mip level 1 | Mip level 2 | Mip level 3 | Mip level 4 | Mip level 5 |
For texture sizes like this, everything will work automatically and mipmaps are constructed down to 1×1 pixel size. Therefore, if you wish to use prefiltered texture sampling, you should scale your textures to power-of-two dimensions that do not, however, need to be equal.
How about texture atlases? You may have an object whose texture is composed of multiple individual patches, or a collection of textured meshes with a unique texture for each. Say we have a texture atlas composed of five 32×32 sub-images, i.e., a total size of 160×32 pixels. Now we cannot compute mipmap levels all the way down to 1×1 size, because there is a 5×1 mipmap in the way that cannot be downsampled (because 5 is not even):
| 160×32 | → | 80×16 | → | 40×8 | → | 20×4 | → | 10×2 | → | 5×1 | → | Error! |
| Base texture | Mip level 1 | Mip level 2 | Mip level 3 | Mip level 4 | Mip level 5 |
Scaling the atlas to, say, 256×32 pixels would feel silly because the dimensions of the sub-images are perfectly fine, and downsampling the different sub-images together — which would happen after the 5×1 resolution — would not make sense anyway. For this reason, the texture sampling operation allows the user to specify the maximum number of mipmap levels to be constructed and used. In this case, setting max_mip_level=5 would stop at the 5×1 mipmap and prevent the error.
It is a deliberate design choice that nvdiffrast doesn't just stop automatically at a mipmap size it cannot downsample, but requires the user to specify a limit when the texture dimensions are not powers of two. The goal is to avoid bugs where prefiltered texture sampling mysteriously doesn't work due to an oddly sized texture. It would be confusing if a 256×256 texture gave beautifully prefiltered texture samples, a 255×255 texture suddenly had no prefiltering at all, and a 254×254 texture did just a bit of prefiltering (one level) but not more.
If you compute your own mipmaps, their sizes must follow the scheme described above. There is no need to specify mipmaps all the way to 1×1 resolution, but the stack can end at any point and it will work equivalently to an internally constructed mipmap stack with a max_mip_level limit. Importantly, the gradients of user-provided mipmaps are not propagated automatically to the base texture — naturally so, because nvdiffrast knows nothing about the relation between them. Instead, the tensors that specify the mip levels in a user-provided mipmap stack will receive gradients of their own.
Nvdiffrast supports computation on multiple GPUs in both PyTorch and TensorFlow. As is the convention in PyTorch, the operations are always executed on the device on which the input tensors reside. All GPU input tensors must reside on the same device, and the output tensors will unsurprisingly end up on that same device. In addition, the rasterization operation requires that its OpenGL context was created for the correct device. In TensorFlow, the OpenGL context is automatically created on the device of the rasterization operation when it is executed for the first time.
On Windows, nvdiffrast implements OpenGL device selection in a way that can be done only once per process — after one context is created, all future ones will end up on the same GPU. Hence you cannot expect to run the rasterization operation on multiple GPUs within the same process. Trying to do so will either cause a crash or incur a significant performance penalty. However, with PyTorch it is common to distribute computation across GPUs by launching a separate process for each GPU, so this is not a huge concern. Note that any OpenGL context created within the same process, even for something like a GUI window, will prevent changing the device later. Therefore, if you want to run the rasterization operation on other than the default GPU, be sure to create its OpenGL context before initializing any other OpenGL-powered libraries.
On Linux everything just works, and you can create rasterizer OpenGL contexts on multiple devices within the same process.
Sometimes there is a need to render scenes with partially transparent surfaces. In this case, it is not sufficient to find only the surfaces that are closest to the camera, as you may also need to know what lies behind them. For this purpose, nvdiffrast supports depth peeling that lets you extract multiple closest surfaces for each pixel.
With depth peeling, we start by rasterizing the closest surfaces as usual. We then perform a second rasterization pass with the same geometry, but this time we cull all previously rendered surface points at each pixel, effectively extracting the second-closest depth layer. This can be repeated as many times as desired, so that we can extract as many depth layers as we like. See the images below for example results of depth peeling with each depth layer shaded and antialiased.



The API for depth peeling is based on DepthPeeler object that acts as a context manager, and its rasterize_next_layer method. The first call to rasterize_next_layer is equivalent to calling the traditional rasterize function, and subsequent calls report further depth layers. The arguments for rasterization are specified when instantiating the DepthPeeler object. Concretely, your code might look something like this:
with nvdiffrast.torch.DepthPeeler(glctx, pos, tri, resolution) as peeler:
for i in range(num_layers):
rast, rast_db = peeler.rasterize_next_layer()
(process or store the results)There is no performance penalty compared to the basic rasterization op if you end up extracting only the first depth layer. In other words, the code above with num_layers=1 runs exactly as fast as calling rasterize once.
Depth peeling is only supported in the PyTorch version of nvdiffrast. For implementation reasons, depth peeling reserves the OpenGL context so that other rasterization operations cannot be performed while the peeling is ongoing, i.e., inside the with block. Hence you cannot start a nested depth peeling operation or call rasterize inside the with block, unless you use a different OpenGL context.
For the sake of completeness, let us note the following small caveat: Depth peeling relies on depth values to distinguish surface points from each other. Therefore, culling "previously rendered surface points" actually means culling all surface points at the same or closer depth as those rendered into the pixel in previous passes. This matters only if you have multiple layers of geometry at matching depths — if your geometry consists of, say, nothing but two exactly overlapping triangles, you will see one of them in the first pass but never see the other one in subsequent passes, as it's at the exact depth that is already considered done.
Nvdiffrast can be used from PyTorch and from TensorFlow 1.x; the latter may change to TensorFlow 2.x if there is demand. These frameworks operate somewhat differently and that is reflected in the respective APIs. Simplifying a bit, in TensorFlow 1.x you construct a persistent graph out of persistent nodes, and run many batches of data through it. In PyTorch, there is no persistent graph or nodes, but a new, ephemeral graph is constructed for each batch of data and destroyed immediately afterwards. Therefore, there is also no persistent state for the operations. There is the torch.nn.Module abstraction for festooning operations with persistent state, but we do not use it.
As a consequence, things that would be part of persistent state of an nvdiffrast operation in TensorFlow must be stored by the user in PyTorch, and supplied to the operations as needed. In practice, this is a very small difference and amounts to just a couple of lines of code in most cases.
As an example, consider the OpenGL context used by the rasterization operation. In order to use hardware-accelerated rendering, an OpenGL context must be created and switched into before issuing OpenGL commands internally. Creating the context is an expensive operation, so we don't want to create and destroy one at every call of the rasterization operation. In TensorFlow, the rasterization operation creates a context when it is executed for the first time, and stashes it away in its persistent state to be reused later. In PyTorch, the user has to create the context using a separate function call, and supply it as a parameter to the rasterization operation.
Similarly, if you have a constant texture and want to use prefiltered texture sampling modes, the mipmap stack only needs to be computed once. In TensorFlow, you can specify that the texture is constant, in which case the texture sampling operation only computes the mipmap stack on the first execution and stores it internally. In PyTorch, you can compute the mipmap stack once using a separate function call, and supply it to the texture sampling operation every time. If you don't do that, the operation will compute the mipmap stack internally and discard it afterwards. This is exactly what you want if your texture changes at every iteration, and it's not wrong even if the texture is constant, just a bit inefficient.
Finally, the same holds for a thing called the topology hash that the antialiasing operation uses for identifying potential silhouette edges. Its contents depend only on the triangle tensor, not the vertex positions, so if the topology is constant, this auxiliary structure needs to be constructed only once. As before, in TensorFlow this is handled internally, whereas in PyTorch a separate function is provided for off-line
construction.
First, please note that handling OpenGL contexts manually is a very small optimization. It almost certainly won't be relevant unless you've already profiled and optimized your code with gusto, and you're on a mission to extract every last bit of performance possible.
In TensorFlow, the only option is to let nvdiffrast handle the OpenGL context management internally. This is because TensorFlow utilizes multiple CPU threads under the hood, and the active OpenGL context is a thread-local resource.
PyTorch isn't as unpredictable, and stays in the same CPU thread by default (although things like torch.utils.data.DataLoader do invoke additional CPU threads). As such, nvdiffrast lets the user choose between handling OpenGL context switching in automatic or manual mode. The default is automatic mode where the rasterization operation always sets/releases the context at the beginning/end of each execution, like we do in TensorFlow. This ensures that the rasterizer will always use the context that you supply, and the context won't remain active so nobody else can mess with it.
In manual mode, the user assumes the responsibility of setting and releasing the OpenGL context. Most of the time, if you don't have any other libraries that would be using OpenGL, you can just set the context once after having created it and keep it set until the program exits. However, keep in mind that the active OpenGL context is a thread-local resource, so it needs to be set in the same CPU thread as it will be used, and it cannot be set simultaneously in multiple CPU threads.
Nvdiffrast comes with a set of samples that were crafted to support the research paper. Each sample is available in both PyTorch and TensorFlow versions. Details such as command-line parameters, logging format, etc., may not be identical between the versions, and generally the PyTorch versions should be considered definitive. The command-line examples below are for the PyTorch versions.
This is a minimal sample that renders a triangle and saves the resulting image into a file (tri.png) in the current directory. Running this should be the first step to verify that you have everything set up correctly. Rendering is done using the rasterization and interpolation operations, so getting the correct output image means that both OpenGL and CUDA are working as intended under the hood.
Example command line:
python triangle.py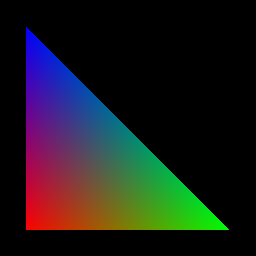
In this sample, we optimize the vertex positions and colors of a cube mesh, starting from a semi-randomly initialized state. The optimization is based on image-space loss in extremely low resolutions such as 4×4, 8×8, or 16×16 pixels. The goal of this sample is to examine the rate of geometrical convergence when the triangles are only a few pixels in size. It serves to illustrate that the antialiasing operation, despite being approximative, yields good enough position gradients even in 4×4 resolution to guide the optimization to the goal.
Example command line:
python cube.py --resolution 16 --display-interval 10

The image above shows a live view of the sample. Top row shows the low-resolution rendered image and reference image that the image-space loss is calculated from. Bottom row shows the current mesh (and colors) and reference mesh in high resolution so that convergence can be seen more easily visually.
In the pipeline diagram, green boxes indicate nvdiffrast operations, whereas blue boxes are other computation. Red boxes are the learned tensors and gray are non-learned tensors or other data.
The goal of this sample is to compare texture convergence with and without prefiltered texture sampling. The texture is learned based on image-space loss against high-quality reference renderings in random orientations and at random distances. When prefiltering is disabled, the texture is not learned properly because of spotty gradient updates caused by aliasing. This shows as a much worse PSNR for the texture, compared to learning with prefiltering enabled. See the paper for further discussion.
Example command lines:
python earth.py --display-interval 10
|
No prefiltering, bilinear interpolation. |
python earth.py --display-interval 10 --mip
|
Prefiltering enabled, trilinear interpolation. |


The interactive view shows the current texture mapped onto the mesh, with or without prefiltered texture sampling as specified via the command-line parameter. In this sample, no antialiasing is performed because we are not learning vertex positions and hence need no gradients related to them.
In this sample, a more complex shading model is used compared to the vertex colors or plain texture in the previous ones. Here, we learn a reflected environment map and parameters of a Phong BRDF model given a known mesh. The optimization is based on image-space loss against reference renderings in random orientations. The shading model of mirror reflection plus a Phong BRDF is not physically sensible, but it works as a reasonably simple strawman that would not be possible to implement with previous differentiable rasterizers that bundle rasterization, shading, lighting, and texturing together. The sample also illustrates the use of cube mapping for representing a learned texture in a spherical domain.
Example command line:
python envphong.py --display-interval 10
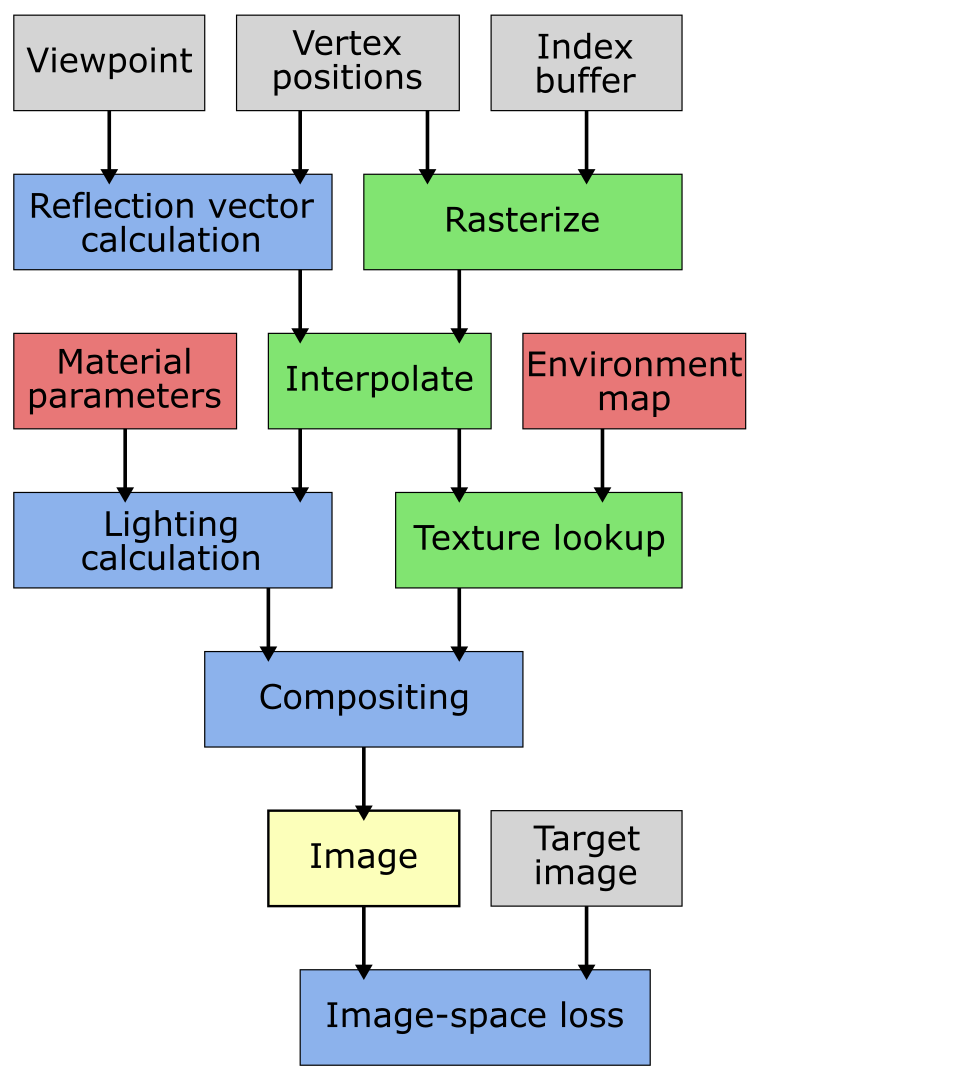
In the interactive view, we see the rendering with the current environment map and Phong BRDF parameters, both gradually improving during the optimization.
Pose fitting based on an image-space loss is a classical task in differentiable rendering. In this sample, we solve a pose optimization problem with a simple cube with differently colored sides. We detail the optimization method in the paper, but in brief, it combines gradient-free greedy optimization in an initialization phase and gradient-based optimization in a fine-tuning phase.
Example command line:
python pose.py --display-interval 10
The interactive view shows, from left to right: target pose, best found pose, and current pose. When viewed live, the two stages of optimization are clearly visible. In the first phase, the best pose updates intermittently when a better initialization is found. In the second phase, the solution converges smoothly to the target via gradient-based optimization.
nvdiffrast.torch.RasterizeGLContext(output_db=True, mode='automatic', device=None) ClassCreate a new OpenGL rasterizer context.
Creating an OpenGL context is a slow operation so you should reuse the same
context in all calls to rasterize() on the same CPU thread. The OpenGL context
is deleted when the object is destroyed.
| output_db | Compute and output image-space derivates of barycentrics. |
| mode | OpenGL context handling mode. Valid values are 'manual' and 'automatic'. |
| device | Cuda device on which the context is created. Type can be
torch.device, string (e.g., 'cuda:1'), or int. If not
specified, context will be created on currently active Cuda
device. |
| set_context() | Set (activate) OpenGL context in the current CPU thread. |
| release_context() | Release (deactivate) currently active OpenGL context. |
nvdiffrast.torch.rasterize(glctx, pos, tri, resolution, ranges=None, grad_db=True) FunctionRasterize triangles.
All input tensors must be contiguous and reside in GPU memory except for
the ranges tensor that, if specified, has to reside in CPU memory. The
output tensors will be contiguous and reside in GPU memory.
| glctx | OpenGL context of type RasterizeGLContext. |
| pos | Vertex position tensor with dtype torch.float32. To enable range
mode, this tensor should have a 2D shape [num_vertices, 4]. To enable
instanced mode, use a 3D shape [minibatch_size, num_vertices, 4]. |
| tri | Triangle tensor with shape [num_triangles, 3] and dtype torch.int32. |
| resolution | Output resolution as integer tuple (height, width). |
| ranges | In range mode, tensor with shape [minibatch_size, 2] and dtype
torch.int32, specifying start indices and counts into tri.
Ignored in instanced mode. |
| grad_db | Propagate gradients of image-space derivatives of barycentrics
into pos in backward pass. Ignored if OpenGL context was
not configured to output image-space derivatives. |
nvdiffrast.torch.DepthPeeler(...) ClassCreate a depth peeler object for rasterizing multiple depth layers.
Arguments are the same as in rasterize().
nvdiffrast.torch.DepthPeeler.rasterize_next_layer() MethodRasterize next depth layer.
Operation is equivalent to rasterize() except that previously reported
surface points are culled away.
rasterize().nvdiffrast.torch.interpolate(attr, rast, tri, rast_db=None, diff_attrs=None) FunctionInterpolate vertex attributes.
All input tensors must be contiguous and reside in GPU memory. The output tensors will be contiguous and reside in GPU memory.
| attr | Attribute tensor with dtype torch.float32.
Shape is [num_vertices, num_attributes] in range mode, or
[minibatch_size, num_vertices, num_attributes] in instanced mode.
Broadcasting is supported along the minibatch axis. |
| rast | Main output tensor from rasterize(). |
| tri | Triangle tensor with shape [num_triangles, 3] and dtype torch.int32. |
| rast_db | (Optional) Tensor containing image-space derivatives of barycentrics,
i.e., the second output tensor from rasterize(). Enables computing
image-space derivatives of attributes. |
| diff_attrs | (Optional) List of attribute indices for which image-space derivatives are to be computed. Special value 'all' is equivalent to list [0, 1, ..., num_attributes - 1]. |
rast_db and diff_attrs were specified, the second output tensor contains
the image-space derivatives of the selected attributes and has shape
[minibatch_size, height, width, 2 * len(diff_attrs)]. The derivatives of the
first selected attribute A will be on channels 0 and 1 as (dA/dX, dA/dY), etc.
Otherwise, the second output tensor will be an empty tensor with shape
[minibatch_size, height, width, 0].nvdiffrast.torch.texture(tex, uv, uv_da=None, mip_level_bias=None, mip=None, filter_mode='auto', boundary_mode='wrap', max_mip_level=None) FunctionPerform texture sampling.
All input tensors must be contiguous and reside in GPU memory. The output tensor will be contiguous and reside in GPU memory.
| tex | Texture tensor with dtype torch.float32. For 2D textures, must have shape
[minibatch_size, tex_height, tex_width, tex_channels]. For cube map textures,
must have shape [minibatch_size, 6, tex_height, tex_width, tex_channels] where
tex_width and tex_height are equal. Note that boundary_mode must also be set
to 'cube' to enable cube map mode. Broadcasting is supported along the minibatch axis. |
| uv | Tensor containing per-pixel texture coordinates. When sampling a 2D texture, must have shape [minibatch_size, height, width, 2]. When sampling a cube map texture, must have shape [minibatch_size, height, width, 3]. |
| uv_da | (Optional) Tensor containing image-space derivatives of texture coordinates.
Must have same shape as uv except for the last dimension that is to be twice
as long. |
| mip_level_bias | (Optional) Per-pixel bias for mip level selection. If uv_da is omitted,
determines mip level directly. Must have shape [minibatch_size, height, width]. |
| mip | (Optional) Preconstructed mipmap stack from a texture_construct_mip() call, or a list
of tensors specifying a custom mipmap stack. When specifying a custom mipmap stack,
the tensors in the list must follow the same format as tex except for width and
height that must follow the usual rules for mipmap sizes. The base level texture
is still supplied in tex and must not be included in the list. Gradients of a
custom mipmap stack are not automatically propagated to base texture but the mipmap
tensors will receive gradients of their own. If a mipmap stack is not specified
but the chosen filter mode requires it, the mipmap stack is constructed internally
and discarded afterwards. |
| filter_mode | Texture filtering mode to be used. Valid values are 'auto', 'nearest',
'linear', 'linear-mipmap-nearest', and 'linear-mipmap-linear'. Mode 'auto'
selects 'linear' if neither uv_da or mip_level_bias is specified, and
'linear-mipmap-linear' when at least one of them is specified, these being
the highest-quality modes possible depending on the availability of the
image-space derivatives of the texture coordinates or direct mip level information. |
| boundary_mode | Valid values are 'wrap', 'clamp', 'zero', and 'cube'. If tex defines a
cube map, this must be set to 'cube'. The default mode 'wrap' takes fractional
part of texture coordinates. Mode 'clamp' clamps texture coordinates to the
centers of the boundary texels. Mode 'zero' virtually extends the texture with
all-zero values in all directions. |
| max_mip_level | If specified, limits the number of mipmaps constructed and used in mipmap-based filter modes. |
nvdiffrast.torch.texture_construct_mip(tex, max_mip_level=None, cube_mode=False) FunctionConstruct a mipmap stack for a texture.
This function can be used for constructing a mipmap stack for a texture that is known to remain
constant. This avoids reconstructing it every time texture() is called.
| tex | Texture tensor with the same constraints as in texture(). |
| max_mip_level | If specified, limits the number of mipmaps constructed. |
| cube_mode | Must be set to True if tex specifies a cube map texture. |
texture()
in the mip argument.nvdiffrast.torch.antialias(color, rast, pos, tri, topology_hash=None, pos_gradient_boost=1.0) FunctionPerform antialiasing.
All input tensors must be contiguous and reside in GPU memory. The output tensor will be contiguous and reside in GPU memory.
| color | Input image to antialias with shape [minibatch_size, height, width, num_channels]. |
| rast | Main output tensor from rasterize(). |
| pos | Vertex position tensor used in the rasterization operation. |
| tri | Triangle tensor used in the rasterization operation. |
| topology_hash | (Optional) Preconstructed topology hash for the triangle tensor. If not specified, the topology hash is constructed internally and discarded afterwards. |
| pos_gradient_boost | (Optional) Multiplier for gradients propagated to pos. |
color input tensor.nvdiffrast.torch.antialias_construct_topology_hash(tri) FunctionConstruct a topology hash for a triangle tensor.
This function can be used for constructing a topology hash for a triangle tensor that is
known to remain constant. This avoids reconstructing it every time antialias() is called.
| tri | Triangle tensor with shape [num_triangles, 3]. Must be contiguous and reside in GPU memory. |
antialias() in the topology_hash argument.nvdiffrast.torch.get_log_level() FunctionGet current log level.
set_log_level() for possible values.nvdiffrast.torch.set_log_level(level) FunctionSet log level.
Log levels follow the convention on the C++ side of Torch: 0 = Info, 1 = Warning, 2 = Error, 3 = Fatal. The default log level is 1.
| level | New log level as integer. Internal nvdiffrast messages of this severity or higher will be printed, while messages of lower severity will be silent. |
Copyright © 2020, NVIDIA Corporation. All rights reserved.
This work is made available under the Nvidia Source Code License.
For business inquiries, please contact researchinquiries@nvidia.com
We do not currently accept outside contributions in the form of pull requests.
Environment map stored as part of samples/data/envphong.npz is derived from a Wave Engine sample material originally shared under MIT License. Mesh and texture stored as part of samples/data/earth.npz are derived from 3D Earth Photorealistic 2K model originally made available under TurboSquid 3D Model License.
@article{Laine2020diffrast,
title = {Modular Primitives for High-Performance Differentiable Rendering},
author = {Samuli Laine and Janne Hellsten and Tero Karras and Yeongho Seol and Jaakko Lehtinen and Timo Aila},
journal = {ACM Transactions on Graphics},
year = {2020},
volume = {39},
number = {6}
}We thank David Luebke, Simon Yuen, Jaewoo Seo, Tero Kuosmanen, Sanja Fidler, Wenzheng Chen, Jacob Munkberg, Jon Hasselgren, and Onni Kosomaa for discussions, test data, support with compute infrastructure, testing, reviewing, and suggestions for features and improvements.